1. Introduction
Since the first experiments by Klebanoff, Tidstrom & Sargent (Reference Klebanoff, Tidstrom and Sargent1962) and Kline et al. (Reference Kline, Reynolds, Schraub and Runstadler1967), the coherent structure of near-wall turbulence has been extensively investigated. In the vicinity of the wall, the flow is found to be highly organised and can be comprehended as a collection of recurrent patterns usually referred to as coherent structures or eddies, consisting of streamwise rolls/vortices and low- and high-speed streaks (Kline et al. Reference Kline, Reynolds, Schraub and Runstadler1967; Blackwelder & Eckelmann Reference Blackwelder and Eckelmann1979; Smith & Metzler Reference Smith and Metzler1983), that are involved in a quasi-periodic regeneration cycle (Robinson Reference Robinson1991; Panton Reference Panton2001; Adrian Reference Adrian2007). However, despite the large efforts devoted to the subject, questions still remain regarding the exact mechanisms by which turbulence self-sustains in wall-bounded turbulent shear flows and the dynamics in which these structures interact.
Townsend (Reference Townsend1976) hypothesised that the log region would be composed of self-similar energy-containing motions, the sizes of which are proportional to their distance from the wall. By a suitable superposition of these hypothetical motions, termed ‘attached eddies’, under the constraint of a constant Reynolds shear stress typical of the log layer, Townsend predicted that the wall-parallel velocity components of turbulence intensities in the log region would exhibit logarithmic wall-normal dependence. Traditionally, wall-attached eddies have been interpreted as statistical entities (Marusic et al. Reference Marusic, McKeon, Monkewitz, Nagib, Smits and Sreenivasan2010; Smits, McKeon & Marusic Reference Smits, McKeon and Marusic2011), but recent works suggest that they can also be identified as instantaneous features of the flow (Jiménez Reference Jiménez2018). The methodologies to identify instantaneous energy eddies are diverse and frequently complementary, ranging from the Fourier characterisation of the turbulent kinetic energy (Jiménez Reference Jiménez2013, Reference Jiménez2015) to adaptive mode decomposition (Hellström, Ganapathisubramani & Smits Reference Hellström, Ganapathisubramani and Smits2016; Agostini & Leschziner Reference Agostini and Leschziner2019; Cheng et al. Reference Cheng, Li, Lozano-Durán and Liu2019), and three-dimensional clustering techniques (Del Alamo & Jiménez Reference Del Alamo and Jiménez2006; Lozano-Durán, Flores & Jiménez Reference Lozano-Durán, Flores and Jiménez2012; Lozano-Durán & Jiménez Reference Lozano-Durán and Jiménez2014; Hwang & Sung Reference Hwang and Sung2018), to name a few.
In the buffer layer, important progress was made in the early 1990s using the ‘minimal flow unit’ approach, which revealed that buffer-layer streaks can self-sustain even when motions at larger scales are inhibited and that their existence, therefore, relies on an autonomous process (Jiménez & Moin Reference Jiménez and Moin1991). Hamilton, Kim & Waleffe (Reference Hamilton, Kim and Waleffe1995) utilised a similar approach for Couette flow, where either certain velocity modes were suppressed to remove streak formation or disturbances were added to allow streak breakdown. Jiménez & Pinelli (Reference Jiménez and Pinelli1999) further confirmed that this near-wall process is independent of the flow in the log and outer regions by showing the survival of the near-wall motions in the absence of outer turbulence. The consensus from these studies, along with many others that followed (e.g Waleffe Reference Waleffe1997; Schoppa & Hussain Reference Schoppa and Hussain2002; Farrell, Gayme & Ioannou Reference Farrell, Gayme and Ioannou2017), is that the streaks are significantly amplified by the quasi-streamwise vortices via the lift-up effect (Landahl Reference Landahl1975); the amplified streaks subsequently undergo a rapid streamwise meandering motion, reminiscent of streak instability or transient growth, which eventually results in the breakdown of the streaks and regeneration of new quasi-streamwise vortices (Swearingen & Blackwelder Reference Swearingen and Blackwelder1987; Waleffe Reference Waleffe1995; Kawahara et al. Reference Kawahara, Jiménez, Uhlmann and Pinelli2003). The cycle is restarted by the generation of new vortices from the perturbations created by the disrupted streaks through nonlinear interactions.
A similar but more disorganised scenario is hypothesised to occur for the larger wall-attached energy eddies within the log layer (Flores & Jiménez Reference Flores and Jiménez2010; Hwang & Cossu Reference Hwang and Cossu2011; Cossu & Hwang Reference Cossu and Hwang2017; Lozano-Durán, Bae & Encinar Reference Lozano-Durán, Bae and Encinar2020). The existence of a self-similar streak/roll structure in the log layer consistent with Townsend's attached-eddy model has been supported by the numerical studies by Del Alamo & Jiménez (Reference Del Alamo and Jiménez2006), Flores & Jiménez (Reference Flores and Jiménez2010), Hwang & Cossu (Reference Hwang and Cossu2011), Lozano-Durán et al. (Reference Lozano-Durán, Flores and Jiménez2012) and Lozano-Durán & Jiménez (Reference Lozano-Durán and Jiménez2014), among others. A growing body of evidence also indicates that the generation of the log-layer streaks has its origins in the linear lift-up effect (Kim & Lim Reference Kim and Lim2000; Del Alamo & Jiménez Reference Del Alamo and Jiménez2006; Pujals et al. Reference Pujals, García-Villalba, Cossu and Depardon2009; Hwang & Cossu Reference Hwang and Cossu2010; Moarref et al. Reference Moarref, Sharma, Tropp and McKeon2013; Alizard Reference Alizard2015) in conjunction with Orr's mechanism (Orr Reference Orr1907; Jiménez Reference Jiménez2012). Regarding roll formation, several works have speculated that rolls are the consequence of a sinuous secondary instability of the streaks that collapse through a rapid meander until breakdown (Andersson et al. Reference Andersson, Brandt, Bottaro and Henningson2001; Park, Hwang & Cossu Reference Park, Hwang and Cossu2011; Alizard Reference Alizard2015; Cassinelli, de Giovanetti & Hwang Reference Cassinelli, de Giovanetti and Hwang2017), while others advocate for transient growth (Schoppa & Hussain Reference Schoppa and Hussain2002) or parametric instability of the streamwise-averaged mean flow as the generating mechanism of the rolls (Farrell et al. Reference Farrell, Ioannou, Jiménez, Constantinou, Lozano-Durán and Nikolaidis2016).
The specific mechanism by which the coherent large-scale structures self-sustain can be further investigated by looking for the existence of invariant solutions of the Navier–Stokes equations (Waleffe Reference Waleffe1998, Reference Waleffe2001, Reference Waleffe2003). The nonlinear steady-state solutions and travelling wave solutions in plane Couette flow and the travelling wave solutions in plane Poiseuille flow, also known as exact coherent structures (ECS), are a combination of the three flow structures – streamwise vortices, streaks and waves – such that they maintain each other despite viscous decay. The idea was that these ECS act as an organising centre for the turbulence quasi-cycle. Kawahara & Kida (Reference Kawahara and Kida2001) detected periodic orbits resembling the time-dependent version of Waleffe's self-sustaining process (SSP) that shares the full regeneration cycle of the near-wall coherent structures in plane Couette turbulence. Further study was done in the large-scale motions (Cossu & Hwang Reference Cossu and Hwang2017) using over-damped large-eddy simulation to isolate the large-scale motions. However, while realistic turbulence does show similarity to ECS solutions, the actual dynamics of wall-bounded turbulence exhibits more complexity than the ones observed in ECS.
Several mechanisms for vortex regeneration have been proposed in the past, mostly focused on the buffer region (Jiménez & Moin Reference Jiménez and Moin1991; Hamilton et al. Reference Hamilton, Kim and Waleffe1995; Panton Reference Panton1997; Schoppa & Hussain Reference Schoppa and Hussain2002; Hwang & Bengana Reference Hwang and Bengana2016) due to the fundamentally nonlinear nature of the problem. Previous studies successfully identified the dominant wavenumbers involved in the nonlinear interaction (Hamilton et al. Reference Hamilton, Kim and Waleffe1995) and the structures involved in the regeneration mechanism based on instantaneous snapshots of turbulent flow (Jiménez & Moin Reference Jiménez and Moin1991; Hamilton et al. Reference Hamilton, Kim and Waleffe1995; Schoppa & Hussain Reference Schoppa and Hussain2002). However, additional insight is necessary to pinpoint the exact nonlinear interaction involved in the regeneration cycle, i.e. to understand the underlying flow composition that leads to the meaningful nonlinear interaction that produces the structures involved in the SSP, in realistic turbulent flows. A meaningful addition to the previous studies would be to find an orthonormal basis for the nonlinear term of the Navier–Stokes equations that isolates the most important nonlinear interaction leading to regeneration of streamwise vortices, which is the goal of the present study.
Various approaches rooted in the linearised equations have been utilised in the past to study turbulent flows, such as rapid distortion theory of Batchelor & Proudman (Reference Batchelor and Proudman1954) (see the reviews by Hunt & Carruthers (Reference Hunt and Carruthers1990) and Cambon & Scott (Reference Cambon and Scott1999) for more details), linear stability theory (Lin Reference Lin1944; Malkus Reference Malkus1956; Reynolds & Hussain Reference Reynolds and Hussain1972), optimal perturbation (Butler & Farrell Reference Butler and Farrell1993; Farrell & Ioannou Reference Farrell and Ioannou1993), input–output analysis (Jovanovic & Bamieh Reference Jovanovic and Bamieh2005) and resolvent analysis (McKeon & Sharma Reference McKeon and Sharma2010; McKeon Reference McKeon2017), among others. Early works focused their efforts on transition to turbulence, while more recent studies have been devoted to fully turbulent flows. Here we focus on the latter using resolvent analysis, as it has been successful at identifying the most energetic motions in actual turbulent flows by approximating the nonlinear forcing from the interaction of highly amplified coherent structures (McKeon & Sharma Reference McKeon and Sharma2010; McKeon Reference McKeon2017). Resolvent analysis identifies pairs of response (velocity) and forcing (nonlinear) modes and the corresponding amplification factor from the linearised Navier–Stokes operator while taking into account the non-normality of the linear Navier–Stokes equations. This results in a set of orthonormal bases for the velocity and nonlinear terms. A more detailed comparison of previous works on linearised Navier–Stokes equations with the resolvent analysis can be found in McKeon (Reference McKeon2017).
It has been shown that a rank-one approximation of the resolvent modes captures the characteristics of the most energetic modes of wall-bounded turbulent channels (Moarref et al. Reference Moarref, Sharma, Tropp and McKeon2013). We postulate that the principal (most amplified) forcing mode then must have the largest impact on the flow and, in particular, the regeneration cycle, and we show that the turbulence can be weakened by removing the nonlinear component corresponding to the principal forcing mode in both the buffer and the log layer. The orthonormality of the resolvent modes allows the removal of the spatio-temporal structure corresponding to the principal forcing mode by extracting the projection of forcing mode onto the nonlinear term. Furthermore, by identifying the most important contribution to the nonlinear term, conditional averaging can identify the underlying interaction that leads to the generation of this nonlinear term, making it possible to study the structures responsible for the nonlinear mechanism in the SSP. A preliminary version of this work can be found in Bae & McKeon (Reference Bae and McKeon2020).
The paper is organised as follows. We first introduce the method used to identify and remove resolvent forcing modes from the nonlinear term computed from the numerical simulations of low- and moderate-Reynolds-number minimal channel flow simulations, representing the buffer and log-layer dynamics, in § 2. We then present the resulting changes in the flow statistics once the resolvent forcing modes are projected out in § 3, where it is shown that the removal of the principal forcing modes can significantly reduce turbulence in both the buffer and log layers. The precursor velocity structures involved in the generation of the most amplified nonlinear term, and thus the structures involved in the nonlinear mechanisms of the SSP, are identified in § 4. Finally, our findings are summarised in § 5.
2. Methods
In the following, we consider a turbulent flow between two parallel walls. The streamwise, wall-normal and spanwise directions are denoted by ![]() $x$,
$x$, ![]() $y$ and
$y$ and ![]() $z$, respectively. The streamwise and spanwise directions are periodic. The flow velocities in the corresponding directions are given by
$z$, respectively. The streamwise and spanwise directions are periodic. The flow velocities in the corresponding directions are given by ![]() $\bar {U}$,
$\bar {U}$, ![]() $\bar {V}$ and
$\bar {V}$ and ![]() $\bar {W}$. We define two decompositions of the flow velocities,
$\bar {W}$. We define two decompositions of the flow velocities, ![]() $\bar {U} = U + u = \bar {u} + u'$, where
$\bar {U} = U + u = \bar {u} + u'$, where ![]() $U$ is the velocity averaged over the homogeneous directions and time, and
$U$ is the velocity averaged over the homogeneous directions and time, and ![]() $\bar {u}$ is the velocity averaged over the homogeneous directions only (analogously defined for
$\bar {u}$ is the velocity averaged over the homogeneous directions only (analogously defined for ![]() $\bar {V}$ and
$\bar {V}$ and ![]() $\bar {W}$). The flow is characterised by the friction Reynolds number
$\bar {W}$). The flow is characterised by the friction Reynolds number ![]() $Re_{\tau } = \delta u_{\tau }/\nu$, where
$Re_{\tau } = \delta u_{\tau }/\nu$, where ![]() $\delta$ is the channel half-height,
$\delta$ is the channel half-height, ![]() $u_{\tau }$ is the friction velocity and
$u_{\tau }$ is the friction velocity and ![]() $\nu$ is the kinematic viscosity.
$\nu$ is the kinematic viscosity.
2.1. Principal forcing modes
In order to identify the most amplified nonlinear component in the turbulent channel flow, we perform the resolvent analysis with the base mean flow being the mean velocity of a turbulent channel flow, ![]() $\boldsymbol {U}=(U,V,W)$. The incompressible Navier–Stokes equations can be Fourier-transformed in homogeneous directions and time, and reorganised as
$\boldsymbol {U}=(U,V,W)$. The incompressible Navier–Stokes equations can be Fourier-transformed in homogeneous directions and time, and reorganised as
for each ![]() $(k_x,k_z,\omega )\neq\, (0,0,0)$, where
$(k_x,k_z,\omega )\neq\, (0,0,0)$, where ![]() $(\,\tilde {\cdot }\,)$ is the Fourier transform in time and space,
$(\,\tilde {\cdot }\,)$ is the Fourier transform in time and space, ![]() $\tilde {\boldsymbol {u}}(k_x,k_z,\omega ) = [\tilde {u},\tilde {v},\tilde {w}]^{\textrm {T}}$,
$\tilde {\boldsymbol {u}}(k_x,k_z,\omega ) = [\tilde {u},\tilde {v},\tilde {w}]^{\textrm {T}}$, ![]() $\boldsymbol {U}= [U,V,W]^{\textrm {T}}$,
$\boldsymbol {U}= [U,V,W]^{\textrm {T}}$, ![]() $\tilde {\boldsymbol {f}}(k_x,k_z,\omega ) = [\,\tilde {f}_u,\tilde {f}_v,\tilde {f}_w]^{\textrm {T}}$ denotes the nonlinear advection terms and
$\tilde {\boldsymbol {f}}(k_x,k_z,\omega ) = [\,\tilde {f}_u,\tilde {f}_v,\tilde {f}_w]^{\textrm {T}}$ denotes the nonlinear advection terms and ![]() $\tilde {p}(k_x,k_z,\omega )$ is the pressure, all of which are functions of wall-normal distance
$\tilde {p}(k_x,k_z,\omega )$ is the pressure, all of which are functions of wall-normal distance ![]() $y$. The operators
$y$. The operators ![]() $\hat {\boldsymbol {\nabla }} = [\mathrm {i}k_x,\partial _y,\mathrm {i}k_z]^{\textrm {T}}$ and
$\hat {\boldsymbol {\nabla }} = [\mathrm {i}k_x,\partial _y,\mathrm {i}k_z]^{\textrm {T}}$ and ![]() $\hat {{\rm \Delta} } = \partial _{yy}-k_x^{2}-k_z^{2}$. Here, the triplet
$\hat {{\rm \Delta} } = \partial _{yy}-k_x^{2}-k_z^{2}$. Here, the triplet ![]() $(k_x,k_z,\omega )$ denotes the streamwise and spanwise wavenumbers and the temporal frequency, respectively. The length, velocity and time scales are non-dimensionalised using
$(k_x,k_z,\omega )$ denotes the streamwise and spanwise wavenumbers and the temporal frequency, respectively. The length, velocity and time scales are non-dimensionalised using ![]() $\delta$,
$\delta$, ![]() $u_{\tau }$ and
$u_{\tau }$ and ![]() $\delta /u_{\tau }$, respectively, and
$\delta /u_{\tau }$, respectively, and ![]() $k_x$,
$k_x$, ![]() $k_z$ and
$k_z$ and ![]() $\omega$ are non-dimensionalised using
$\omega$ are non-dimensionalised using ![]() $\delta ^{-1}$,
$\delta ^{-1}$, ![]() $\delta ^{-1}$ and
$\delta ^{-1}$ and ![]() $u_{\tau }/\delta$, respectively. Further, to facilitate the notation, we define
$u_{\tau }/\delta$, respectively. Further, to facilitate the notation, we define ![]() $k_x^{\circ } = 2{\rm \pi} \delta k_x/L_x$ and
$k_x^{\circ } = 2{\rm \pi} \delta k_x/L_x$ and ![]() $k_z^{\circ } = 2{\rm \pi} \delta k_z/L_z$ such that integer values of
$k_z^{\circ } = 2{\rm \pi} \delta k_z/L_z$ such that integer values of ![]() $k_x^{\circ }$ and
$k_x^{\circ }$ and ![]() $k_z^{\circ }$ indicate the number of wavelengths that fit in the streamwise and spanwise domain of size
$k_z^{\circ }$ indicate the number of wavelengths that fit in the streamwise and spanwise domain of size ![]() $(L_x,L_z)$, and, for any function
$(L_x,L_z)$, and, for any function ![]() $\zeta (k_x,k_z,\omega )$,
$\zeta (k_x,k_z,\omega )$, ![]() $\zeta ^{(a,b,c)} = \zeta (k_x^{\circ }=a,k_z^{\circ }=b,\omega =c)$.
$\zeta ^{(a,b,c)} = \zeta (k_x^{\circ }=a,k_z^{\circ }=b,\omega =c)$.
Equivalently, we can express the Navier–Stokes equations for ![]() $(k_x,k_z,\omega ) \neq\, (0,0,0)$ as
$(k_x,k_z,\omega ) \neq\, (0,0,0)$ as
 \begin{equation} \begin{bmatrix} \tilde{\boldsymbol{u}}(k_x,k_z,\omega)\\ \tilde{p}(k_x,k_z,\omega)\end{bmatrix} = \mathcal{H}(k_x,k_z,\omega) \begin{bmatrix} \tilde{\boldsymbol{f}}(k_x,k_z,\omega)\\ 0 \end{bmatrix}. \end{equation}
\begin{equation} \begin{bmatrix} \tilde{\boldsymbol{u}}(k_x,k_z,\omega)\\ \tilde{p}(k_x,k_z,\omega)\end{bmatrix} = \mathcal{H}(k_x,k_z,\omega) \begin{bmatrix} \tilde{\boldsymbol{f}}(k_x,k_z,\omega)\\ 0 \end{bmatrix}. \end{equation}
We refer to the linear operator ![]() $\mathcal {H}(k_x,k_z,\omega )$, which takes
$\mathcal {H}(k_x,k_z,\omega )$, which takes ![]() $\boldsymbol {U}$ as input, as the resolvent operator. The singular value decomposition of the resolvent operator returns an ordered basis pair
$\boldsymbol {U}$ as input, as the resolvent operator. The singular value decomposition of the resolvent operator returns an ordered basis pair ![]() $\{\tilde {\boldsymbol {\psi }}_j,\tilde {\boldsymbol {\phi }}_j\}$ along with the associated singular value
$\{\tilde {\boldsymbol {\psi }}_j,\tilde {\boldsymbol {\phi }}_j\}$ along with the associated singular value ![]() $\sigma _j$ (
$\sigma _j$ (![]() $\sigma _1 \ge \sigma _2 \ge \cdots \ge 0$), which can be used to express (2.2) as
$\sigma _1 \ge \sigma _2 \ge \cdots \ge 0$), which can be used to express (2.2) as
 \begin{equation} \begin{bmatrix} \tilde{\boldsymbol{u}}(k_x,k_z,\omega)\\ \tilde{p}(k_x,k_z,\omega)\end{bmatrix} = \sum_{j=1}^{\infty}\sigma_j(k_x,k_z,\omega) \tilde{\boldsymbol{\psi}}_j(k_x,k_z,\omega) \left\langle \tilde{\boldsymbol{\phi}}_j(k_x,k_z,\omega), \begin{bmatrix} \tilde{\boldsymbol{f}}(k_x,k_z,\omega)\\ 0 \end{bmatrix}\right\rangle, \end{equation}
\begin{equation} \begin{bmatrix} \tilde{\boldsymbol{u}}(k_x,k_z,\omega)\\ \tilde{p}(k_x,k_z,\omega)\end{bmatrix} = \sum_{j=1}^{\infty}\sigma_j(k_x,k_z,\omega) \tilde{\boldsymbol{\psi}}_j(k_x,k_z,\omega) \left\langle \tilde{\boldsymbol{\phi}}_j(k_x,k_z,\omega), \begin{bmatrix} \tilde{\boldsymbol{f}}(k_x,k_z,\omega)\\ 0 \end{bmatrix}\right\rangle, \end{equation}
where ![]() $\langle \cdot ,\cdot \rangle$ is the inner product corresponding to the kinetic energy norm, and the basis vectors
$\langle \cdot ,\cdot \rangle$ is the inner product corresponding to the kinetic energy norm, and the basis vectors ![]() $\tilde{\boldsymbol{\phi}}_i$ and
$\tilde{\boldsymbol{\phi}}_i$ and ![]() $\tilde{\boldsymbol{\psi}}_i$ vectors are unitary. We refer to
$\tilde{\boldsymbol{\psi}}_i$ vectors are unitary. We refer to ![]() $\tilde {\boldsymbol {\psi }}_j$ as the response modes and
$\tilde {\boldsymbol {\psi }}_j$ as the response modes and ![]() $\tilde {\boldsymbol {\phi }}_j$ as the forcing modes. The former identifies the most amplified coherent structures, which are considered to contain most of the energy. The latter are the basis for the nonlinear terms that create the response modes via the linear resolvent operator.
$\tilde {\boldsymbol {\phi }}_j$ as the forcing modes. The former identifies the most amplified coherent structures, which are considered to contain most of the energy. The latter are the basis for the nonlinear terms that create the response modes via the linear resolvent operator.
While the eddy viscosity formulation of the resolvent analysis, as in Morra et al. (Reference Morra, Semeraro, Henningson and Cossu2019), has been shown to improve the prediction of statistics for most energetic streamwise-constant streaks, a more recent study by Symon, Illingworth & Marusic (Reference Symon, Illingworth and Marusic2020) shows that eddy viscosity does not respect the conservative nature of the nonlinear energy transfer, which must sum to zero over all scales. Consequently, it is less effective for scales that receive energy from the nonlinear terms. Thus, for the purposes of this study, we find the original resolvent formulation without the additional eddy viscosity term more relevant.
Note that, due to the symmetry in the channel flow, the resolvent modes appear in pairs, and the modes corresponding to the two largest singular values, ![]() $\sigma _1$ and
$\sigma _1$ and ![]() $\sigma _2$, can be decomposed into two components that are symmetric about
$\sigma _2$, can be decomposed into two components that are symmetric about ![]() $y=1$. For the purpose of identifying modes that act primarily on the top or bottom of the channel, we define the principal mode as the linear combination of the two largest resolvent modes as follows. To find a principal forcing mode that acts mostly on the bottom half of the channel (
$y=1$. For the purpose of identifying modes that act primarily on the top or bottom of the channel, we define the principal mode as the linear combination of the two largest resolvent modes as follows. To find a principal forcing mode that acts mostly on the bottom half of the channel (![]() $0\le y\le 1$), we first define the symmetric and antisymmetric modes as a linear combination that is symmetric or antisymmetric, respectively, with respect to
$0\le y\le 1$), we first define the symmetric and antisymmetric modes as a linear combination that is symmetric or antisymmetric, respectively, with respect to ![]() $y=1$ and has positive real component when integrated from
$y=1$ and has positive real component when integrated from ![]() $y=0$ to
$y=0$ to ![]() $y=1$. We then focus on the principal forcing mode
$y=1$. We then focus on the principal forcing mode ![]() $\tilde {\boldsymbol {\phi }}_1 = [\tilde {\phi }_{1,u}, \tilde {\phi }_{1,v}, \tilde {\phi }_{1,w}, 0]^{\textrm {T}}$ computed by taking the sum of the symmetric and antisymmetric linear combination of the pair, such that the sum of the two will mostly affect flow in the bottom half (
$\tilde {\boldsymbol {\phi }}_1 = [\tilde {\phi }_{1,u}, \tilde {\phi }_{1,v}, \tilde {\phi }_{1,w}, 0]^{\textrm {T}}$ computed by taking the sum of the symmetric and antisymmetric linear combination of the pair, such that the sum of the two will mostly affect flow in the bottom half (![]() $0\le y \le 1$) of the channel. Consequently,
$0\le y \le 1$) of the channel. Consequently, ![]() $\tilde {\boldsymbol {\phi }}_2$ is the difference of the symmetric and antisymmetric linear combination of the pair corresponding to these two largest singular values such that the projection of the resolvent mode will mostly affect flow in the top half of the channel. All subsequent modes
$\tilde {\boldsymbol {\phi }}_2$ is the difference of the symmetric and antisymmetric linear combination of the pair corresponding to these two largest singular values such that the projection of the resolvent mode will mostly affect flow in the top half of the channel. All subsequent modes ![]() $\tilde {\boldsymbol {\phi }}_{3,4,\ldots }$ are defined analogously.
$\tilde {\boldsymbol {\phi }}_{3,4,\ldots }$ are defined analogously.
2.2. Numerical simulation
Two sets of numerical simulations are performed by solving the incompressible Navier–Stokes equations
using a computational domain tailored to isolate the most energetic eddies in either the buffer layer (Jiménez & Moin Reference Jiménez and Moin1991) or the log layer (Bae & Lozano-Durán Reference Bae and Lozano-Durán2019). This can be considered the simplest numerical set-up to study the SSP for wall-bounded energy-containing eddies of a given size.
In order to isolate the most energetic eddies in the buffer layer, defined as ![]() $5 < y^{+} < 30$, where the superscript
$5 < y^{+} < 30$, where the superscript ![]() $^{+}$ denotes viscous units, we perform a direct numerical simulation (DNS) of an incompressible turbulent channel flow at
$^{+}$ denotes viscous units, we perform a direct numerical simulation (DNS) of an incompressible turbulent channel flow at ![]() $Re_{\tau } \approx 186$. The simulations are performed by discretising the incompressible Navier–Stokes equations with a staggered, second-order-accurate, central finite-difference method in space (Orlandi Reference Orlandi2000), and an explicit third-order-accurate Runge–Kutta method for time advancement (Wray Reference Wray1990). The system of equations is solved via an operator splitting approach (Chorin Reference Chorin1968). Periodic boundary conditions are imposed in the streamwise and spanwise directions, and the no-slip condition is applied at the walls. The code has been validated in previous studies of turbulent channel flows (Bae et al. Reference Bae, Lozano-Durán, Bose and Moin2018, Reference Bae, Lozano-Durán, Bose and Moin2019). The streamwise, wall-normal and spanwise domain sizes are
$Re_{\tau } \approx 186$. The simulations are performed by discretising the incompressible Navier–Stokes equations with a staggered, second-order-accurate, central finite-difference method in space (Orlandi Reference Orlandi2000), and an explicit third-order-accurate Runge–Kutta method for time advancement (Wray Reference Wray1990). The system of equations is solved via an operator splitting approach (Chorin Reference Chorin1968). Periodic boundary conditions are imposed in the streamwise and spanwise directions, and the no-slip condition is applied at the walls. The code has been validated in previous studies of turbulent channel flows (Bae et al. Reference Bae, Lozano-Durán, Bose and Moin2018, Reference Bae, Lozano-Durán, Bose and Moin2019). The streamwise, wall-normal and spanwise domain sizes are ![]() $L_x^{+} \approx 340$,
$L_x^{+} \approx 340$, ![]() $L_y^{+}\approx 372$ and
$L_y^{+}\approx 372$ and ![]() $L_z^{+} \approx 170$, respectively. Jiménez & Moin (Reference Jiménez and Moin1991) showed that simulations in this domain constitute an elemental structural unit containing a single streamwise streak and a pair of staggered quasi-streamwise vortices, which reproduce reasonably well the statistics of the flow in larger domains. The grid spacings in the streamwise and spanwise directions are uniform, with
$L_z^{+} \approx 170$, respectively. Jiménez & Moin (Reference Jiménez and Moin1991) showed that simulations in this domain constitute an elemental structural unit containing a single streamwise streak and a pair of staggered quasi-streamwise vortices, which reproduce reasonably well the statistics of the flow in larger domains. The grid spacings in the streamwise and spanwise directions are uniform, with ![]() $\varDelta _x^{+}\approx 10.6$ and
$\varDelta _x^{+}\approx 10.6$ and ![]() $\varDelta _z^{+}\approx 5.3$; non-uniform meshes are used in the wall-normal direction, with the grid stretched towards the wall according to a hyperbolic tangent distribution with
$\varDelta _z^{+}\approx 5.3$; non-uniform meshes are used in the wall-normal direction, with the grid stretched towards the wall according to a hyperbolic tangent distribution with ![]() $\min (\varDelta _y^{+})\approx 0.17$ and
$\min (\varDelta _y^{+})\approx 0.17$ and ![]() $\max (\varDelta _y^{+})\approx 7.6$.
$\max (\varDelta _y^{+})\approx 7.6$.
In the case of the log layer, defined as ![]() $3 Re_{\tau }^{-1/2} < y < 0.15$ (Marusic et al. Reference Marusic, Monty, Hultmark and Smits2013), we perform a large-eddy simulation (LES) of an incompressible turbulent channel flow at
$3 Re_{\tau }^{-1/2} < y < 0.15$ (Marusic et al. Reference Marusic, Monty, Hultmark and Smits2013), we perform a large-eddy simulation (LES) of an incompressible turbulent channel flow at ![]() $Re_{\tau } \approx 2003$ with modified wall boundary conditions. The set-up of the simulations is similar to the buffer-layer case, but the no-slip boundary condition at the walls is replaced by a slip boundary condition of the form
$Re_{\tau } \approx 2003$ with modified wall boundary conditions. The set-up of the simulations is similar to the buffer-layer case, but the no-slip boundary condition at the walls is replaced by a slip boundary condition of the form
where ![]() $l_s = 0.05$ is the slip length. The choice to use LES with the slip boundary condition rather than DNS is deliberate in order to remove the presence of small-scale motions from the flow (Leonard Reference Leonard1975; Hwang & Bengana Reference Hwang and Bengana2016; Cossu & Hwang Reference Cossu and Hwang2017; Bae & Lozano-Durán Reference Bae and Lozano-Durán2019) and to suppress the formation of near-wall viscous layers and buffer-layer eddies (Lozano-Durán & Bae Reference Lozano-Durán and Bae2016, Reference Lozano-Durán and Bae2019a; Bae & Lozano-Durán Reference Bae and Lozano-Durán2019), as we are interested in energy-containing motions of the log layer. This modified channel flow is tailored to isolate the large-scale motions of the log layer. While the simulated log layer produces healthy turbulence only in a limited range of wall-normal locations, this allows a simplified approach to study the SSP of the isolated scales.
$l_s = 0.05$ is the slip length. The choice to use LES with the slip boundary condition rather than DNS is deliberate in order to remove the presence of small-scale motions from the flow (Leonard Reference Leonard1975; Hwang & Bengana Reference Hwang and Bengana2016; Cossu & Hwang Reference Cossu and Hwang2017; Bae & Lozano-Durán Reference Bae and Lozano-Durán2019) and to suppress the formation of near-wall viscous layers and buffer-layer eddies (Lozano-Durán & Bae Reference Lozano-Durán and Bae2016, Reference Lozano-Durán and Bae2019a; Bae & Lozano-Durán Reference Bae and Lozano-Durán2019), as we are interested in energy-containing motions of the log layer. This modified channel flow is tailored to isolate the large-scale motions of the log layer. While the simulated log layer produces healthy turbulence only in a limited range of wall-normal locations, this allows a simplified approach to study the SSP of the isolated scales.
The choice of the slip length is such that the adaptation length (Lozano-Durán & Bae Reference Lozano-Durán and Bae2019a), i.e. the vertical distance from the boundary above which the flow recovers to the nominal no-slip flow statistics, is below the lower bound of the log layer for this Reynolds number. The anisotropic minimum dissipation model (Rozema et al. Reference Rozema, Bae, Moin and Verstappen2015) is used as the subgrid-scale model for the LES. The streamwise, wall-normal and spanwise domain sizes of the simulation are ![]() $L_x \approx 1.57$,
$L_x \approx 1.57$, ![]() $L_y = 2$ and
$L_y = 2$ and ![]() $L_z\approx 0.79$, respectively. This domain size corresponds to a minimal box simulation for the log layer and is sufficient to isolate the relevant dynamical structures involved in the bursting process (Flores & Jiménez Reference Flores and Jiménez2010). Moreover, the choice of the domain size is such that the wall-normal distance below which flow exhibits healthy turbulence,
$L_z\approx 0.79$, respectively. This domain size corresponds to a minimal box simulation for the log layer and is sufficient to isolate the relevant dynamical structures involved in the bursting process (Flores & Jiménez Reference Flores and Jiménez2010). Moreover, the choice of the domain size is such that the wall-normal distance below which flow exhibits healthy turbulence, ![]() $l_d \approx L_z/3 \approx 0.25$ (Flores & Jiménez Reference Flores and Jiménez2010), is above the upper bound of the log layer. The domain is discretised using
$l_d \approx L_z/3 \approx 0.25$ (Flores & Jiménez Reference Flores and Jiménez2010), is above the upper bound of the log layer. The domain is discretised using ![]() $N_x = 256$ and
$N_x = 256$ and ![]() $N_z = 64$ points in the streamwise and spanwise directions, and
$N_z = 64$ points in the streamwise and spanwise directions, and ![]() $N_y = 101$ in the wall-normal direction. The grid spacings in the streamwise and spanwise directions are uniform with
$N_y = 101$ in the wall-normal direction. The grid spacings in the streamwise and spanwise directions are uniform with ![]() $\varDelta _x \approx 0.006$ and
$\varDelta _x \approx 0.006$ and ![]() $\varDelta _z \approx 0.012$ such that the grid captures 90 % of the turbulent kinetic energy at
$\varDelta _z \approx 0.012$ such that the grid captures 90 % of the turbulent kinetic energy at ![]() $y = 0.15$, which is necessary to accurately capture the coherent structures present in the flow (Lozano-Durán & Bae Reference Lozano-Durán and Bae2019b). Non-uniform meshes are used in the wall-normal direction, with the grid stretched towards the wall according to a hyperbolic tangent distribution with
$y = 0.15$, which is necessary to accurately capture the coherent structures present in the flow (Lozano-Durán & Bae Reference Lozano-Durán and Bae2019b). Non-uniform meshes are used in the wall-normal direction, with the grid stretched towards the wall according to a hyperbolic tangent distribution with ![]() $\min (\varDelta _y) \approx 0.003$ and
$\min (\varDelta _y) \approx 0.003$ and ![]() $\max (\varDelta _y) \approx 0.04$. Bae & Lozano-Durán (Reference Bae and Lozano-Durán2019) showed that simulations in this domain with the modified boundary conditions reproduce the statistics in the log layer of the flow in larger domains while suppressing the formation of the near-wall eddies. For details regarding this simulation, the reader is referred to Bae & Lozano-Durán (Reference Bae and Lozano-Durán2019).
$\max (\varDelta _y) \approx 0.04$. Bae & Lozano-Durán (Reference Bae and Lozano-Durán2019) showed that simulations in this domain with the modified boundary conditions reproduce the statistics in the log layer of the flow in larger domains while suppressing the formation of the near-wall eddies. For details regarding this simulation, the reader is referred to Bae & Lozano-Durán (Reference Bae and Lozano-Durán2019).
The flow is simulated for more than ![]() $100$ time units after transients for computation of the mean streamwise velocity profile in the undisturbed minimal channel, which we label
$100$ time units after transients for computation of the mean streamwise velocity profile in the undisturbed minimal channel, which we label ![]() $U^{F}$, shown in figure 1(a,b) for the two cases. The resolvent modes
$U^{F}$, shown in figure 1(a,b) for the two cases. The resolvent modes ![]() $\tilde {\boldsymbol {\phi }}_i$ and
$\tilde {\boldsymbol {\phi }}_i$ and ![]() $\tilde {\boldsymbol {\psi }}_i$ for the minimal buffer and log layer were then computed with the respective
$\tilde {\boldsymbol {\psi }}_i$ for the minimal buffer and log layer were then computed with the respective ![]() $U^{F}$, using the same staggered, second-order-accurate, central finite-difference method in the wall-normal direction and the corresponding wall boundary conditions. The Fourier discretisation in the computation of the resolvent modes in the streamwise and spanwise directions was updated to use the modified wavenumber corresponding to a staggered second-order finite-difference method. The mismatch of the mean velocity profile for the buffer-layer case away from the wall (
$U^{F}$, using the same staggered, second-order-accurate, central finite-difference method in the wall-normal direction and the corresponding wall boundary conditions. The Fourier discretisation in the computation of the resolvent modes in the streamwise and spanwise directions was updated to use the modified wavenumber corresponding to a staggered second-order finite-difference method. The mismatch of the mean velocity profile for the buffer-layer case away from the wall (![]() $y^{+}>30$) is expected due to the smaller box, which is designed to remove larger scales of motion and is in agreement with previous studies utilising minimal channels (Jiménez & Moin Reference Jiménez and Moin1991). In the log-layer case, the simulation is designed to remove both the viscous scales and subgrid scales as well as the larger outer-region scales, resulting in the mismatch in both the buffer and the outer region. The disruption of the viscous scale can be better observed from the lack of the inner peak in the streamwise turbulence intensity (figure 1d).
$y^{+}>30$) is expected due to the smaller box, which is designed to remove larger scales of motion and is in agreement with previous studies utilising minimal channels (Jiménez & Moin Reference Jiménez and Moin1991). In the log-layer case, the simulation is designed to remove both the viscous scales and subgrid scales as well as the larger outer-region scales, resulting in the mismatch in both the buffer and the outer region. The disruption of the viscous scale can be better observed from the lack of the inner peak in the streamwise turbulence intensity (figure 1d).

Figure 1. (a) Mean streamwise velocity profile, (c) turbulence intensities and (e) energy spectra at ![]() $y^{+} = 15$ of the buffer-layer minimal channel (black solid line) compared to the mean velocity profile of the channel flow for the domain size of
$y^{+} = 15$ of the buffer-layer minimal channel (black solid line) compared to the mean velocity profile of the channel flow for the domain size of ![]() $12{\rm \pi} \times 2\times 4{\rm \pi}$ (red dashed line) at
$12{\rm \pi} \times 2\times 4{\rm \pi}$ (red dashed line) at ![]() $Re_{\tau }\approx 186$ from Del Alamo & Jiménez (Reference Del Alamo and Jiménez2003). (b) Mean streamwise velocity profile, (d) turbulence intensities and (f) energy spectra at
$Re_{\tau }\approx 186$ from Del Alamo & Jiménez (Reference Del Alamo and Jiménez2003). (b) Mean streamwise velocity profile, (d) turbulence intensities and (f) energy spectra at ![]() $y = 0.15$ of the log-layer minimal channel (black solid line) compared to the mean velocity profile of the channel flow for the domain size of
$y = 0.15$ of the log-layer minimal channel (black solid line) compared to the mean velocity profile of the channel flow for the domain size of ![]() $8{\rm \pi} \times 2\times 3{\rm \pi}$ (red dashed line) at
$8{\rm \pi} \times 2\times 3{\rm \pi}$ (red dashed line) at ![]() $Re_{\tau }\approx 2003$ from Hoyas & Jiménez (Reference Hoyas and Jiménez2006). The mean streamwise velocity profile for the minimal channel in (b) is vertically shifted by 8.4 wall units such that the velocity at
$Re_{\tau }\approx 2003$ from Hoyas & Jiménez (Reference Hoyas and Jiménez2006). The mean streamwise velocity profile for the minimal channel in (b) is vertically shifted by 8.4 wall units such that the velocity at ![]() $y = 0.15$ coincides with the larger-domain case. Turbulence intensities are shown for streamwise (
$y = 0.15$ coincides with the larger-domain case. Turbulence intensities are shown for streamwise (![]() $\bigcirc$), wall-normal (
$\bigcirc$), wall-normal (![]() $\triangledown$) and spanwise (
$\triangledown$) and spanwise (![]() $\Box$) components. Dotted lines in (a–d) indicate lower and upper domains for buffer and log layer for corresponding cases. Dotted lines in (e,f) indicate the domain size of the minimal channel. Contour levels are 1 %, 5 % and 10 % for (e) and 10 %, 25 % and 40 % for (f) of the maximum value of the large-domain cases.
$\Box$) components. Dotted lines in (a–d) indicate lower and upper domains for buffer and log layer for corresponding cases. Dotted lines in (e,f) indicate the domain size of the minimal channel. Contour levels are 1 %, 5 % and 10 % for (e) and 10 %, 25 % and 40 % for (f) of the maximum value of the large-domain cases.
The new simulations are started from an initial condition from the channel flow described above that is modified such that ![]() $\bar {u} = U^{F}$. Then, an appropriate forcing at each time step is applied to (2.4a) to freeze the mean such that
$\bar {u} = U^{F}$. Then, an appropriate forcing at each time step is applied to (2.4a) to freeze the mean such that ![]() $\bar {u} = U^{F}$, or equivalently
$\bar {u} = U^{F}$, or equivalently ![]() $\partial \bar {u}/\partial t = 0$. This is done by setting the
$\partial \bar {u}/\partial t = 0$. This is done by setting the ![]() $(k_x,k_z)=(0,0)$ mode of the right-hand side of (2.4a) to zero at each time step. The mean velocity profile is frozen so that the most amplified resolvent modes remain constant throughout the simulation. It is also consistent with the aim of the study, which is to characterise the mechanisms that sustain the fluctuating velocities generated by the actual turbulent mean flow. Tuerke & Jiménez (Reference Tuerke and Jiménez2013) showed that turbulent channel flows with prescribed correct mean velocity profiles result in naturally occurring fluctuating velocities. An additional case without freezing the mean, i.e. not applying the additional forcing to set
$(k_x,k_z)=(0,0)$ mode of the right-hand side of (2.4a) to zero at each time step. The mean velocity profile is frozen so that the most amplified resolvent modes remain constant throughout the simulation. It is also consistent with the aim of the study, which is to characterise the mechanisms that sustain the fluctuating velocities generated by the actual turbulent mean flow. Tuerke & Jiménez (Reference Tuerke and Jiménez2013) showed that turbulent channel flows with prescribed correct mean velocity profiles result in naturally occurring fluctuating velocities. An additional case without freezing the mean, i.e. not applying the additional forcing to set ![]() $\partial \bar {u}/\partial t = 0$, is performed later in § 3.1 to study the effect of freezing the mean.
$\partial \bar {u}/\partial t = 0$, is performed later in § 3.1 to study the effect of freezing the mean.
The turbulence intensities and the energy spectra of the frozen-mean minimal-domain simulations are compared to the large-domain counterparts in figure 1(c–f). We see that, in the regions bounded by the vertical dotted lines in figure 1(c,d), which signify the lower and upper bounds of the buffer and log layer in the respective cases, the turbulence intensities follow the trend of its large-domain counterpart. The underprediction of the turbulence intensities in the log-layer simulation is due to the use of LES, where energy from the small- and largest-scale motions are not included. The two-dimensional premultiplied energy spectra at ![]() $y^{+}=15$ and
$y^{+}=15$ and ![]() $y = 0.15$, respectively, are shown in figure 1(e,f), and the results match well with the large-domain counterparts, with the exception of the missing large-scale motions, which extend beyond the respective domains, and the small-scale contributions in the log layer, which are modelled and not resolved in LES.
$y = 0.15$, respectively, are shown in figure 1(e,f), and the results match well with the large-domain counterparts, with the exception of the missing large-scale motions, which extend beyond the respective domains, and the small-scale contributions in the log layer, which are modelled and not resolved in LES.
In order to study the effect of the forcing modes on the flow, a separate simulation is advanced in time by removing the projection of the nonlinear term ![]() $\boldsymbol {f}' = -(\boldsymbol {u}'\boldsymbol {\cdot }\boldsymbol {\nabla })\boldsymbol {u}'$ onto the resolvent forcing mode
$\boldsymbol {f}' = -(\boldsymbol {u}'\boldsymbol {\cdot }\boldsymbol {\nabla })\boldsymbol {u}'$ onto the resolvent forcing mode ![]() $\tilde {\boldsymbol {\phi }}_1$ for the chosen
$\tilde {\boldsymbol {\phi }}_1$ for the chosen ![]() $(k_x,k_z,\omega )$ at each time step. Note that
$(k_x,k_z,\omega )$ at each time step. Note that ![]() $u' = u$ in the case when the mean is frozen in time. This is done by first taking the Fourier transform of the nonlinear term in the homogeneous directions and computing the projection
$u' = u$ in the case when the mean is frozen in time. This is done by first taking the Fourier transform of the nonlinear term in the homogeneous directions and computing the projection
 \begin{equation} \hat{\boldsymbol{g}}_1(k_x,k_z,\omega) = \left\langle \begin{bmatrix} \widehat{\boldsymbol{f}'}(k_x,k_z)\\ 0 \end{bmatrix},\tilde{\boldsymbol{\phi}}_1(k_x,k_z,\omega) \right\rangle \begin{bmatrix} \tilde{\boldsymbol{\phi}}_{1,u}(k_x,k_z,\omega)\\ \tilde{\boldsymbol{\phi}}_{1,v}(k_x,k_z,\omega)\\ \tilde{\boldsymbol{\phi}}_{1,w}(k_x,k_z,\omega) \end{bmatrix} \end{equation}
\begin{equation} \hat{\boldsymbol{g}}_1(k_x,k_z,\omega) = \left\langle \begin{bmatrix} \widehat{\boldsymbol{f}'}(k_x,k_z)\\ 0 \end{bmatrix},\tilde{\boldsymbol{\phi}}_1(k_x,k_z,\omega) \right\rangle \begin{bmatrix} \tilde{\boldsymbol{\phi}}_{1,u}(k_x,k_z,\omega)\\ \tilde{\boldsymbol{\phi}}_{1,v}(k_x,k_z,\omega)\\ \tilde{\boldsymbol{\phi}}_{1,w}(k_x,k_z,\omega) \end{bmatrix} \end{equation}
at each time step. The projection is then removed by subtracting the inverse Fourier-transformed ![]() $\hat {\boldsymbol {g}}_1$ from the right-hand side of (2.4a) and advancing in time. Symmetry of the Fourier modes is preserved by also removing
$\hat {\boldsymbol {g}}_1$ from the right-hand side of (2.4a) and advancing in time. Symmetry of the Fourier modes is preserved by also removing ![]() $\hat {\boldsymbol {g}}_1^{*\textrm {T}}$, the conjugate of
$\hat {\boldsymbol {g}}_1^{*\textrm {T}}$, the conjugate of ![]() $\hat {\boldsymbol {g}}_1$ (where superscript
$\hat {\boldsymbol {g}}_1$ (where superscript ![]() $^{*}$ denotes conjugate transpose and
$^{*}$ denotes conjugate transpose and ![]() $^\textrm {T}$ denotes transpose), from the nonlinear term
$^\textrm {T}$ denotes transpose), from the nonlinear term ![]() $\widehat {\boldsymbol {f}'}(-k_x,-k_z)$ at each time step. Projections onto
$\widehat {\boldsymbol {f}'}(-k_x,-k_z)$ at each time step. Projections onto ![]() $\tilde {\boldsymbol {\phi }}_i$ are analogously defined as
$\tilde {\boldsymbol {\phi }}_i$ are analogously defined as ![]() $\hat {\boldsymbol {g}}_i$.
$\hat {\boldsymbol {g}}_i$.
For the remainder of the paper, we denote the channel flow simulation with the mean fixed at each time step but no forcing mode removed as the ‘undamped’ case and the simulation with the forcing mode removed as the ‘damped’ case.
3. Effect of principal forcing modes on turbulence intensities
3.1. Buffer layer
As mentioned in the previous section, a choice of the target wavenumbers is required to identify the forcing modes that are removed at each time step. For this, we target the Fourier modes with the most energy content. Figure 2(a) shows the spectral energy content, ![]() $\hat {E}(k_x,k_z) = \tfrac {1}{2}(\hat {\boldsymbol {u}}^{*}\hat {\boldsymbol {u}})$, at
$\hat {E}(k_x,k_z) = \tfrac {1}{2}(\hat {\boldsymbol {u}}^{*}\hat {\boldsymbol {u}})$, at ![]() $y^{+}\approx 15$ for the buffer-layer case, as a function of streamwise and spanwise wavenumbers. There is a clear peak at
$y^{+}\approx 15$ for the buffer-layer case, as a function of streamwise and spanwise wavenumbers. There is a clear peak at ![]() $(k_x^{\circ },k_z^{\circ }) = (0,\pm 1)$. This is consistent with the fact that the domain size of the minimal channel is such that it isolates flow structures to be infinitely long in the streamwise direction and once-periodic in the spanwise direction. Thus, for our analysis, we choose the streamwise and spanwise wavenumbers
$(k_x^{\circ },k_z^{\circ }) = (0,\pm 1)$. This is consistent with the fact that the domain size of the minimal channel is such that it isolates flow structures to be infinitely long in the streamwise direction and once-periodic in the spanwise direction. Thus, for our analysis, we choose the streamwise and spanwise wavenumbers ![]() $(k_x^{\circ },k_z^{\circ }) = (0,1)$. This choice of streamwise and spanwise wavenumbers also coincides with the
$(k_x^{\circ },k_z^{\circ }) = (0,1)$. This choice of streamwise and spanwise wavenumbers also coincides with the ![]() $(k_x,k_z)$ with the largest
$(k_x,k_z)$ with the largest ![]() $\sigma _1$ over all values of
$\sigma _1$ over all values of ![]() $\omega$, which shows not only that this wavenumber pair holds the most energy, but also that it has the highest amplification within the resolvent framework. The temporal frequency is given as
$\omega$, which shows not only that this wavenumber pair holds the most energy, but also that it has the highest amplification within the resolvent framework. The temporal frequency is given as ![]() $\omega =0$, which corresponds to the highest
$\omega =0$, which corresponds to the highest ![]() $\sigma _1$ for
$\sigma _1$ for ![]() $(k_x^{\circ },k_z^{\circ }) = (0,1)$ (figure 2b). Note that the projection (2.6a,b) includes the contributions from various temporal frequencies apart from
$(k_x^{\circ },k_z^{\circ }) = (0,1)$ (figure 2b). Note that the projection (2.6a,b) includes the contributions from various temporal frequencies apart from ![]() $\omega = 0$ due to the fact that (2.6a,b) is time-dependent. However, it ascertains the removal of this particular forcing mode. Also, the singular value associated with
$\omega = 0$ due to the fact that (2.6a,b) is time-dependent. However, it ascertains the removal of this particular forcing mode. Also, the singular value associated with ![]() $\omega = 0$ is much larger than other temporal frequencies, making the removal of other frequency contents relatively less significant.
$\omega = 0$ is much larger than other temporal frequencies, making the removal of other frequency contents relatively less significant.

Figure 2. (a) Logarithm of spectral energy content, ![]() $\log (\hat {E})$, at
$\log (\hat {E})$, at ![]() $y^{+}\approx 15$ for the buffer-layer case. (b) Principal singular value
$y^{+}\approx 15$ for the buffer-layer case. (b) Principal singular value ![]() $\sigma _1$ as a function of
$\sigma _1$ as a function of ![]() $\omega$ for
$\omega$ for ![]() $(k_x^{\circ },k_z^{\circ }) = (0,1)$ for the buffer layer. (c,d) The
$(k_x^{\circ },k_z^{\circ }) = (0,1)$ for the buffer layer. (c,d) The ![]() $y$–
$y$–![]() $z$ plane of the principal (c) forcing mode
$z$ plane of the principal (c) forcing mode ![]() $\tilde {\boldsymbol {\phi }}_1$ and (d) response mode for
$\tilde {\boldsymbol {\phi }}_1$ and (d) response mode for ![]() $(k_x^{\circ },k_z^{\circ },\omega ) = (0,1,0)$ for the buffer-layer case. The streamwise component (colour) and the cross-flow component (arrows) are given, with the colour bar indicating magnitude for both components.
$(k_x^{\circ },k_z^{\circ },\omega ) = (0,1,0)$ for the buffer-layer case. The streamwise component (colour) and the cross-flow component (arrows) are given, with the colour bar indicating magnitude for both components.
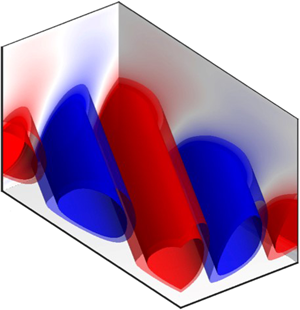
The principal forcing and response modes for this particular frequency–wavenumber triplet are given in figure 2(c,d). The forcing mode highlights a pair of streamwise rolls in the nonlinear term, i.e. the Reynolds stress contribution to the advection term, spanning the entire channel half-height. A much weaker streamwise streak in the nonlinear term whose magnitude (![]() $|\tilde {\boldsymbol {\phi }}_{1,u}|$) is approximately 5 % of that of the streamwise rolls,
$|\tilde {\boldsymbol {\phi }}_{1,u}|$) is approximately 5 % of that of the streamwise rolls, ![]() $(\tilde {\boldsymbol {\phi }}_{1,v}^{2}+\tilde {\boldsymbol {\phi }}_{1,w}^{2})^{1/2}$, is also present. The response modes exhibit streamwise streaks with alternating signs of the same magnitude (only the magnitude is shown in figure 2d) and weak cross-flow. The values above
$(\tilde {\boldsymbol {\phi }}_{1,v}^{2}+\tilde {\boldsymbol {\phi }}_{1,w}^{2})^{1/2}$, is also present. The response modes exhibit streamwise streaks with alternating signs of the same magnitude (only the magnitude is shown in figure 2d) and weak cross-flow. The values above ![]() $y = 1$ are negligible due to our definition of the principal mode. This shows that the streamwise rolls generated by the nonlinear term can be transformed through a linear process, i.e. the lift-up mechanism, to streamwise streaks, as expected from previous studies of the SSP. For the given
$y = 1$ are negligible due to our definition of the principal mode. This shows that the streamwise rolls generated by the nonlinear term can be transformed through a linear process, i.e. the lift-up mechanism, to streamwise streaks, as expected from previous studies of the SSP. For the given ![]() $(k_x,k_z,\omega )$, the principal forcing mode contains the largest energetic contribution under unit broadband forcing (approximately
$(k_x,k_z,\omega )$, the principal forcing mode contains the largest energetic contribution under unit broadband forcing (approximately ![]() $85\,\%$), defined as
$85\,\%$), defined as ![]() $(\sigma _i^{2}+\sigma _{i+1}^{2})/\sum _{k=1}^{\infty } \sigma _k^{2}$ for each
$(\sigma _i^{2}+\sigma _{i+1}^{2})/\sum _{k=1}^{\infty } \sigma _k^{2}$ for each ![]() $\widetilde {\boldsymbol {\phi }_i}$ for
$\widetilde {\boldsymbol {\phi }_i}$ for ![]() $i=1,3,5,\ldots$. The subsequent modes
$i=1,3,5,\ldots$. The subsequent modes ![]() $\widetilde {\boldsymbol {\phi }_3}$ and
$\widetilde {\boldsymbol {\phi }_3}$ and ![]() $\widetilde {\boldsymbol {\phi }_5}$ have an energetic contribution of approximately
$\widetilde {\boldsymbol {\phi }_5}$ have an energetic contribution of approximately ![]() $12\,\%$ and
$12\,\%$ and ![]() $2\,\%$, respectively (see figure 5a). The large separation in the singular values indicates that the principal forcing mode will be amplified by almost an order of magnitude more than the other forcing modes and thus will be integral in the SSP.
$2\,\%$, respectively (see figure 5a). The large separation in the singular values indicates that the principal forcing mode will be amplified by almost an order of magnitude more than the other forcing modes and thus will be integral in the SSP.
The effect of removing ![]() $\hat {\boldsymbol {g}}_1^{(0,1,0)}$ can be seen in figure 3(a) in the form of the turbulence kinetic energy (TKE) evolution in time. Although not shown, the dissipation rate as a function of time exhibits similar trends to that of the TKE. Figure 3(a) shows that removing
$\hat {\boldsymbol {g}}_1^{(0,1,0)}$ can be seen in figure 3(a) in the form of the turbulence kinetic energy (TKE) evolution in time. Although not shown, the dissipation rate as a function of time exhibits similar trends to that of the TKE. Figure 3(a) shows that removing ![]() $\hat {\boldsymbol {g}}_1^{(0,1,0)}$ reduces the TKE significantly. The steady-state root-mean-square (r.m.s.) velocity fluctuation profiles for this case are given in figure 3(b). As expected, the effect of removing the principal forcing term is observed only on the bottom half of the channel where the principal forcing term was isolated, with only minor changes in the statistics in the top half of the channel. At any instant in time of the undamped case, the contribution of
$\hat {\boldsymbol {g}}_1^{(0,1,0)}$ reduces the TKE significantly. The steady-state root-mean-square (r.m.s.) velocity fluctuation profiles for this case are given in figure 3(b). As expected, the effect of removing the principal forcing term is observed only on the bottom half of the channel where the principal forcing term was isolated, with only minor changes in the statistics in the top half of the channel. At any instant in time of the undamped case, the contribution of ![]() $\hat {\boldsymbol {g}}_1^{(0,1,0)}$ to the nonlinear advection term, defined as the average-in-time ratio of
$\hat {\boldsymbol {g}}_1^{(0,1,0)}$ to the nonlinear advection term, defined as the average-in-time ratio of ![]() $\int \hat {\boldsymbol {g}}_1^{(0,1,0)*}\hat {\boldsymbol {g}}_1^{(0,1,0)}\,\mathrm {d}y$ to
$\int \hat {\boldsymbol {g}}_1^{(0,1,0)*}\hat {\boldsymbol {g}}_1^{(0,1,0)}\,\mathrm {d}y$ to ![]() $\iiint \boldsymbol {f}'^{2}\,\mathrm {d}{\kern0.06em}x\,\mathrm {d}y\,\mathrm {d}z$, is less than
$\iiint \boldsymbol {f}'^{2}\,\mathrm {d}{\kern0.06em}x\,\mathrm {d}y\,\mathrm {d}z$, is less than ![]() $0.9\,\%$, and removing the same magnitude randomly from the advection term at each time step had no effect on the one-point statistics, which supports the importance of the spatial structure of the mode being projected out to the turbulent flow. Furthermore, if we remove
$0.9\,\%$, and removing the same magnitude randomly from the advection term at each time step had no effect on the one-point statistics, which supports the importance of the spatial structure of the mode being projected out to the turbulent flow. Furthermore, if we remove ![]() $\tfrac {1}{2}\hat {\boldsymbol {g}}_1^{(0,1,0)}$ at each time step rather than
$\tfrac {1}{2}\hat {\boldsymbol {g}}_1^{(0,1,0)}$ at each time step rather than ![]() $\hat {\boldsymbol {g}}_1^{(0,1,0)}$, the impact on the turbulence statistics is negligible compared to the undamped case, which further highlights the importance of the principal forcing term.
$\hat {\boldsymbol {g}}_1^{(0,1,0)}$, the impact on the turbulence statistics is negligible compared to the undamped case, which further highlights the importance of the principal forcing term.

Figure 3. (a) Temporal evolution of TKE at ![]() $y^{+}\approx 15$ for the damped buffer-layer case removing
$y^{+}\approx 15$ for the damped buffer-layer case removing ![]() $\hat {\boldsymbol {g}}_1^{(0,1,0)}$ (red) and the undamped buffer-layer minimal channel (black). (b) Streamwise (solid line), wall-normal (dashed line) and spanwise (dash-dotted line) r.m.s. velocity fluctuations for the damped case removing
$\hat {\boldsymbol {g}}_1^{(0,1,0)}$ (red) and the undamped buffer-layer minimal channel (black). (b) Streamwise (solid line), wall-normal (dashed line) and spanwise (dash-dotted line) r.m.s. velocity fluctuations for the damped case removing ![]() $\hat {\boldsymbol {g}}_1^{(0,1,0)}$ (red) and the undamped (black) buffer-layer minimal channel. (c,d) Same as (a,b), but removing
$\hat {\boldsymbol {g}}_1^{(0,1,0)}$ (red) and the undamped (black) buffer-layer minimal channel. (c,d) Same as (a,b), but removing ![]() $\hat {\boldsymbol {g}}_3^{(0,1,0)}$ (blue) or
$\hat {\boldsymbol {g}}_3^{(0,1,0)}$ (blue) or ![]() $\hat {\boldsymbol {g}}_5^{(0,1,0)}$ (green) at each time step instead of
$\hat {\boldsymbol {g}}_5^{(0,1,0)}$ (green) at each time step instead of ![]() $\hat {\boldsymbol {g}}_1^{(0,1,0)}$.
$\hat {\boldsymbol {g}}_1^{(0,1,0)}$.
In the case where the mean flow is not frozen but rather is allowed to evolve in time (figure 4a), the time evolution of TKE follows similar results as shown in figure 3(a) until ![]() $t\approx 12$, where it starts to increase again. This is due to the change in the mean velocity profile, as shown in figure 4(b). The initial reduction of turbulence intensities changes the dynamics of the flow such that the mean velocity profile approaches the laminar profile on the bottom half of the channel. The drastic change in the mean profile invalidates the relevance of the principal forcing mode obtained from the turbulent mean state,
$t\approx 12$, where it starts to increase again. This is due to the change in the mean velocity profile, as shown in figure 4(b). The initial reduction of turbulence intensities changes the dynamics of the flow such that the mean velocity profile approaches the laminar profile on the bottom half of the channel. The drastic change in the mean profile invalidates the relevance of the principal forcing mode obtained from the turbulent mean state, ![]() $U^{F}$, and causes the TKE to increase again. Even after the TKE becomes statistically stationary,
$U^{F}$, and causes the TKE to increase again. Even after the TKE becomes statistically stationary, ![]() $t>20$, the new equilibrium state after transients shown in figure 4(b) differs from the turbulence with mean profile
$t>20$, the new equilibrium state after transients shown in figure 4(b) differs from the turbulence with mean profile ![]() $U^{F}$.
$U^{F}$.

Figure 4. (a) Temporal evolution of TKE at ![]() $y^{+}\approx 15$ for the damped buffer-layer case removing
$y^{+}\approx 15$ for the damped buffer-layer case removing ![]() $\hat {\boldsymbol {g}}_1^{(0,1,0)}$ without fixing the mean (maroon) and the undamped buffer-layer minimal channel (black). (b) Mean streamwise velocity corresponding to
$\hat {\boldsymbol {g}}_1^{(0,1,0)}$ without fixing the mean (maroon) and the undamped buffer-layer minimal channel (black). (b) Mean streamwise velocity corresponding to ![]() $t = 12$ (maroon solid line) and averaged over
$t = 12$ (maroon solid line) and averaged over ![]() $20 < t < 100$ (maroon dotted line) for the case without fixing the mean and the fixed mean profile (black dashed line).
$20 < t < 100$ (maroon dotted line) for the case without fixing the mean and the fixed mean profile (black dashed line).
In order to study the effects of removing subsequent forcing modes, we repeat the previous frozen-mean experiment, but removing either ![]() $\hat {\boldsymbol {g}}_3^{(0,1,0)}$ or
$\hat {\boldsymbol {g}}_3^{(0,1,0)}$ or ![]() $\hat {\boldsymbol {g}}_5^{(0,1,0)}$, the secondary and tertiary forcing modes restricted primarily to the bottom half of the channel as defined in § 2.1, instead of
$\hat {\boldsymbol {g}}_5^{(0,1,0)}$, the secondary and tertiary forcing modes restricted primarily to the bottom half of the channel as defined in § 2.1, instead of ![]() $\hat {\boldsymbol {g}}_1^{(0,1,0)}$. We see that turbulence is sustained in both cases from figure 3(c), but the extreme peaks in TKE observed in the undamped case are not as prominent. We can also see in figure 3(d) that, while the effect of removing
$\hat {\boldsymbol {g}}_1^{(0,1,0)}$. We see that turbulence is sustained in both cases from figure 3(c), but the extreme peaks in TKE observed in the undamped case are not as prominent. We can also see in figure 3(d) that, while the effect of removing ![]() $\hat {\boldsymbol {g}}_3^{(0,1,0)}$ still has some impact on the steady-state turbulence intensities, especially around
$\hat {\boldsymbol {g}}_3^{(0,1,0)}$ still has some impact on the steady-state turbulence intensities, especially around ![]() $y^{+}\approx 15$, the net change in the statistics is much smaller than that of removing
$y^{+}\approx 15$, the net change in the statistics is much smaller than that of removing ![]() $\hat {\boldsymbol {g}}_1^{(0,1,0)}$. Removing
$\hat {\boldsymbol {g}}_1^{(0,1,0)}$. Removing ![]() $\hat {\boldsymbol {g}}_5^{(0,1,0)}$ has no impact on one-point statistics, and similar results are expected of subsequent forcing modes. Additionally, removing
$\hat {\boldsymbol {g}}_5^{(0,1,0)}$ has no impact on one-point statistics, and similar results are expected of subsequent forcing modes. Additionally, removing ![]() $\hat {\boldsymbol {g}}_3^{(0,1,0)}$ or
$\hat {\boldsymbol {g}}_3^{(0,1,0)}$ or ![]() $\hat {\boldsymbol {g}}_5^{(0,1,0)}$ in conjunction with
$\hat {\boldsymbol {g}}_5^{(0,1,0)}$ in conjunction with ![]() $\hat {\boldsymbol {g}}_1^{(0,1,0)}$ (not shown) resulted in similar statistics as removing only
$\hat {\boldsymbol {g}}_1^{(0,1,0)}$ (not shown) resulted in similar statistics as removing only ![]() $\hat {\boldsymbol {g}}_1^{(0,1,0)}$. At any instant in time, the average contribution of
$\hat {\boldsymbol {g}}_1^{(0,1,0)}$. At any instant in time, the average contribution of ![]() $\hat {\boldsymbol {g}}_3^{(0,1,0)}$ or
$\hat {\boldsymbol {g}}_3^{(0,1,0)}$ or ![]() $\hat {\boldsymbol {g}}_5^{(0,1,0)}$ in the undamped case is statistically similar to the contribution of
$\hat {\boldsymbol {g}}_5^{(0,1,0)}$ in the undamped case is statistically similar to the contribution of ![]() $\hat {\boldsymbol {g}}_1^{(0,1,0)}$ at
$\hat {\boldsymbol {g}}_1^{(0,1,0)}$ at ![]() $0.9\,\%$ of the total advection term, which shows the dominant impact of the principal forcing mode on the SSP.
$0.9\,\%$ of the total advection term, which shows the dominant impact of the principal forcing mode on the SSP.
Additionally, we also repeat the experiment, removing ![]() $\hat {\boldsymbol {g}}_1^{(0,2,0)}$, as
$\hat {\boldsymbol {g}}_1^{(0,2,0)}$, as ![]() $(k_x^{\circ },k_z^{\circ })=(0,2)$ contains a significant amount of energy in figure 2(a). However, compared to the triplet
$(k_x^{\circ },k_z^{\circ })=(0,2)$ contains a significant amount of energy in figure 2(a). However, compared to the triplet ![]() $(k_x^{\circ },k_z^{\circ },\omega )=(0,1,0)$, the amplification factor
$(k_x^{\circ },k_z^{\circ },\omega )=(0,1,0)$, the amplification factor ![]() $\sigma _1$ for
$\sigma _1$ for ![]() $(k_x^{\circ },k_z^{\circ },\omega )=(0,2,0)$ is an order of magnitude lower as seen in figure 5(a) and the principal mode has an energetic contribution of approximately 65 %, which is much lower than the 85 % for
$(k_x^{\circ },k_z^{\circ },\omega )=(0,2,0)$ is an order of magnitude lower as seen in figure 5(a) and the principal mode has an energetic contribution of approximately 65 %, which is much lower than the 85 % for ![]() $(k_x^{\circ },k_z^{\circ },\omega )=(0,1,0)$. The resulting time evolution of TKE shown in figure 5(b) is hence much less affected than removing
$(k_x^{\circ },k_z^{\circ },\omega )=(0,1,0)$. The resulting time evolution of TKE shown in figure 5(b) is hence much less affected than removing ![]() $\hat {\boldsymbol {g}}_1^{(0,1,0)}$, and removing
$\hat {\boldsymbol {g}}_1^{(0,1,0)}$, and removing ![]() $\hat {\boldsymbol {g}}_1^{(0,2,0)}$ in conjunction with
$\hat {\boldsymbol {g}}_1^{(0,2,0)}$ in conjunction with ![]() $\hat {\boldsymbol {g}}_1^{(0,1,0)}$ (not shown) resulted in marginal difference compared to removing only
$\hat {\boldsymbol {g}}_1^{(0,1,0)}$ (not shown) resulted in marginal difference compared to removing only ![]() $\hat {\boldsymbol {g}}_1^{(0,1,0)}$. Overall, the removal of the principal forcing mode corresponding to
$\hat {\boldsymbol {g}}_1^{(0,1,0)}$. Overall, the removal of the principal forcing mode corresponding to ![]() $(k_x^{\circ },k_z^{\circ },\omega )=(0,1,0)$ has the most impact on the flow, as expected.
$(k_x^{\circ },k_z^{\circ },\omega )=(0,1,0)$ has the most impact on the flow, as expected.

Figure 5. (a) Amplification factors ![]() $\sigma _i$ for
$\sigma _i$ for ![]() $(k_x^{\circ },k_z^{\circ },\omega )=(0,1,0)$ (black) and
$(k_x^{\circ },k_z^{\circ },\omega )=(0,1,0)$ (black) and ![]() $(k_x^{\circ },k_z^{\circ },\omega )=(0,2,0)$ (red) for the buffer-layer case. (b) Temporal evolution of TKE at
$(k_x^{\circ },k_z^{\circ },\omega )=(0,2,0)$ (red) for the buffer-layer case. (b) Temporal evolution of TKE at ![]() $y^{+}\approx 15$ for the damped buffer-layer case removing
$y^{+}\approx 15$ for the damped buffer-layer case removing ![]() $\hat {\boldsymbol {g}}_1^{(0,2,0)}$ (magenta) and the undamped buffer-layer minimal channel (black).
$\hat {\boldsymbol {g}}_1^{(0,2,0)}$ (magenta) and the undamped buffer-layer minimal channel (black).
3.2. Logarithmic layer
Using the same approach as in the buffer-layer case, we identify the target wavenumbers for the log-layer case. Figure 6(a) shows ![]() $\hat {E}(k_x,k_z) = \tfrac {1}{2}(\hat {\boldsymbol {u}}^{*}\hat {\boldsymbol {u}})$ at
$\hat {E}(k_x,k_z) = \tfrac {1}{2}(\hat {\boldsymbol {u}}^{*}\hat {\boldsymbol {u}})$ at ![]() $y \approx 0.15$ for the log-layer case, as a function of streamwise and spanwise wavenumbers. Again, there is a clear peak at
$y \approx 0.15$ for the log-layer case, as a function of streamwise and spanwise wavenumbers. Again, there is a clear peak at ![]() $(k_x^{\circ },k_z^{\circ }) = (0,\pm 1)$, which is consistent with the fact that the domain size of the minimal channel for the log layer is such that the most dominant flow structures are infinitely long in the streamwise direction and once-periodic in the spanwise direction. Thus, for our analysis, we again choose the streamwise and spanwise wavenumbers
$(k_x^{\circ },k_z^{\circ }) = (0,\pm 1)$, which is consistent with the fact that the domain size of the minimal channel for the log layer is such that the most dominant flow structures are infinitely long in the streamwise direction and once-periodic in the spanwise direction. Thus, for our analysis, we again choose the streamwise and spanwise wavenumbers ![]() $(k_x^{\circ },k_z^{\circ }) = (0,1)$. However, note that, unlike in the buffer-layer case, the spectral energy content of the log-layer case is distributed among various combinations of
$(k_x^{\circ },k_z^{\circ }) = (0,1)$. However, note that, unlike in the buffer-layer case, the spectral energy content of the log-layer case is distributed among various combinations of ![]() $k_x$ and
$k_x$ and ![]() $k_z$, in particular with large contributions from
$k_z$, in particular with large contributions from ![]() $(k_x^{\circ },k_z^{\circ })=({\pm }1,{\pm }1)$, indicating a more complex phenomenon in the SSP that cannot be isolated to one wavenumber, as seen in figure 6(a). However, similar to the analysis on
$(k_x^{\circ },k_z^{\circ })=({\pm }1,{\pm }1)$, indicating a more complex phenomenon in the SSP that cannot be isolated to one wavenumber, as seen in figure 6(a). However, similar to the analysis on ![]() $(k_x^{\circ },k_z^{\circ }) = (0,2)$ for the buffer-layer case, the largest singular values as well as the spectral gap for the non-fundamental wavenumbers are significantly lower than that of
$(k_x^{\circ },k_z^{\circ }) = (0,2)$ for the buffer-layer case, the largest singular values as well as the spectral gap for the non-fundamental wavenumbers are significantly lower than that of ![]() $(k_x^{\circ },k_z^{\circ })=(0,1)$, indicating that the effect of the principal resolvent modes for
$(k_x^{\circ },k_z^{\circ })=(0,1)$, indicating that the effect of the principal resolvent modes for ![]() $(k_x^{\circ },k_z^{\circ })\neq\, (0,1)$ are not as dominant as that of
$(k_x^{\circ },k_z^{\circ })\neq\, (0,1)$ are not as dominant as that of ![]() $(k_x^{\circ },k_z^{\circ })=(0,1)$. The temporal frequency identified by the highest
$(k_x^{\circ },k_z^{\circ })=(0,1)$. The temporal frequency identified by the highest ![]() $\sigma _1$ for
$\sigma _1$ for ![]() $(k_x^{\circ },k_z^{\circ }) = (0,1)$ (figure 6b) is
$(k_x^{\circ },k_z^{\circ }) = (0,1)$ (figure 6b) is ![]() $\omega = 0$, but the values of
$\omega = 0$, but the values of ![]() $\sigma _1$ do not decay as fast as in the buffer-layer case, indicating that more combinations of
$\sigma _1$ do not decay as fast as in the buffer-layer case, indicating that more combinations of ![]() $\omega$ may be involved compared to the buffer-layer case.
$\omega$ may be involved compared to the buffer-layer case.

Figure 6. (a) Logarithm of spectral energy content, ![]() $\log (\hat {E})$, at
$\log (\hat {E})$, at ![]() $y\approx 0.15$ for the log-layer case. (b) Principal singular value
$y\approx 0.15$ for the log-layer case. (b) Principal singular value ![]() $\sigma _1$ as a function of
$\sigma _1$ as a function of ![]() $\omega$ for
$\omega$ for ![]() $(k_x^{\circ },k_z^{\circ }) = (0,1)$ for the log-layer case. (c,d) The
$(k_x^{\circ },k_z^{\circ }) = (0,1)$ for the log-layer case. (c,d) The ![]() $y$–
$y$–![]() $z$ plane of the principal (c) forcing mode
$z$ plane of the principal (c) forcing mode ![]() $\tilde {\boldsymbol {\phi }}_1$ and (d) response mode for
$\tilde {\boldsymbol {\phi }}_1$ and (d) response mode for ![]() $(k_x^{\circ },k_z^{\circ },\omega ) = (0,1,0)$ for the log-layer case. The streamwise component (colour) and the cross-flow component (arrows) are given, with the colour bar indicating magnitude for both components.
$(k_x^{\circ },k_z^{\circ },\omega ) = (0,1,0)$ for the log-layer case. The streamwise component (colour) and the cross-flow component (arrows) are given, with the colour bar indicating magnitude for both components.
The principal forcing and response modes for this particular frequency–wavenumber triplet are given in figure 6(c,d). Despite the different Reynolds number and the wall boundary condition, the forcing and response modes of the log layer are similar to those of the buffer layer. The forcing mode highlights a pair of streamwise rolls spanning the entire channel half-height, and the response modes exhibit streamwise streaks with alternating signs of the same magnitude. For the given ![]() $(k_x,k_z,\omega )$, the principal forcing mode contains the largest energetic contribution under unit broadband forcing (approximately
$(k_x,k_z,\omega )$, the principal forcing mode contains the largest energetic contribution under unit broadband forcing (approximately ![]() $81\,\%$), similar to the buffer-layer case. The similarity in the identified principal resolvent modes indicates the similarity in the underlying mechanism for the SSP of the buffer and log layers, as has been hypothesised in the literature.
$81\,\%$), similar to the buffer-layer case. The similarity in the identified principal resolvent modes indicates the similarity in the underlying mechanism for the SSP of the buffer and log layers, as has been hypothesised in the literature.
The fact that the log-layer structure of the minimal flow unit spans the full boundary layer thickness can be further explained by the self-similar attached-eddy hypothesis (Townsend Reference Townsend1976; Perry & Chong Reference Perry and Chong1982; Meneveau & Marusic Reference Meneveau and Marusic2013; Agostini & Leschziner Reference Agostini and Leschziner2017; Marusic & Monty Reference Marusic and Monty2019). McKeon (Reference McKeon2019) has recently identified that an isolated resolvent mode with a given convection velocity constitutes only part of the full attached eddy, and a geometric progression of such modes needs to be considered for the fair comparison to the attached eddies. In particular, a single wall-normal location of the log layer will be affected by a series of wall-attached eddies whose footprint includes the given wall-normal height. From this viewpoint, the structures that impact the log layer would span the whole half-channel as observed in the current case.
The results of removing ![]() $\hat {\boldsymbol {g}}_1^{(0,1,0)}$ for the log layer are shown in figure 7. The TKE does not reduce as significantly as in the buffer-layer case, as seen in the time evolution of TKE in figure 7(a) and the time-averaged turbulence intensities in figure 7(b); however, we do see a significant reduction in the TKE. Similar to the buffer-layer case, the dissipation rate (not shown) follow the trends of the TKE. The relatively smaller effect of the principal forcing modes in the log layer is due to the complexity and the disorganisation of the log layer itself. Unlike the buffer layer, where only one scale is isolated by the minimal domain, the log layer still includes contributions from various scales that exist in the log layer (figure 6a), which makes it harder to affect the full system by removing only one scale. However, the significant reduction in TKE and turbulence intensities obtained by removing the principal forcing mode, which exhibit similar characteristics in both the buffer and log layer, shows that the mechanism in which turbulence self-sustains is similar in both regions. The results of removing secondary forcing modes and principal forcing modes for a different
$\hat {\boldsymbol {g}}_1^{(0,1,0)}$ for the log layer are shown in figure 7. The TKE does not reduce as significantly as in the buffer-layer case, as seen in the time evolution of TKE in figure 7(a) and the time-averaged turbulence intensities in figure 7(b); however, we do see a significant reduction in the TKE. Similar to the buffer-layer case, the dissipation rate (not shown) follow the trends of the TKE. The relatively smaller effect of the principal forcing modes in the log layer is due to the complexity and the disorganisation of the log layer itself. Unlike the buffer layer, where only one scale is isolated by the minimal domain, the log layer still includes contributions from various scales that exist in the log layer (figure 6a), which makes it harder to affect the full system by removing only one scale. However, the significant reduction in TKE and turbulence intensities obtained by removing the principal forcing mode, which exhibit similar characteristics in both the buffer and log layer, shows that the mechanism in which turbulence self-sustains is similar in both regions. The results of removing secondary forcing modes and principal forcing modes for a different ![]() $(k_x,k_z,\omega )$, while not reported here, show comparable trends as seen in the buffer layer, where the impact on the flow statistics is marginal compared to that of
$(k_x,k_z,\omega )$, while not reported here, show comparable trends as seen in the buffer layer, where the impact on the flow statistics is marginal compared to that of ![]() $\hat {\boldsymbol {g}}_1^{(0,1,0)}$.
$\hat {\boldsymbol {g}}_1^{(0,1,0)}$.

Figure 7. (a) Temporal evolution of TKE at ![]() $y\approx 0.15$ for the damped log-layer case removing
$y\approx 0.15$ for the damped log-layer case removing ![]() $\hat {\boldsymbol {g}}_1^{(0,1,0)}$ (red) and the undamped log-layer minimal channel (black). (b) Streamwise (solid line), wall-normal (dashed line) and spanwise (dash-dotted line) r.m.s. velocity fluctuations for the damped log-layer case removing
$\hat {\boldsymbol {g}}_1^{(0,1,0)}$ (red) and the undamped log-layer minimal channel (black). (b) Streamwise (solid line), wall-normal (dashed line) and spanwise (dash-dotted line) r.m.s. velocity fluctuations for the damped log-layer case removing ![]() $\hat {\boldsymbol {g}}_1^{(0,1,0)}$ (red) and the undamped (black) log-layer minimal channel.
$\hat {\boldsymbol {g}}_1^{(0,1,0)}$ (red) and the undamped (black) log-layer minimal channel.
4. Nonlinear interaction
As demonstrated in the previous section, the principal forcing mode ![]() $\tilde {\boldsymbol {\phi }}_1^{(0,1,0)}$ identifies the most amplified nonlinear interaction for the most energetic wavenumber and is integral in sustaining turbulence in the near-wall cycle for both the buffer and log layers. In order to study the nonlinear interactions that produce this term through dyadic interactions, we decompose the nonlinear term as a convolution sum in Fourier space,
$\tilde {\boldsymbol {\phi }}_1^{(0,1,0)}$ identifies the most amplified nonlinear interaction for the most energetic wavenumber and is integral in sustaining turbulence in the near-wall cycle for both the buffer and log layers. In order to study the nonlinear interactions that produce this term through dyadic interactions, we decompose the nonlinear term as a convolution sum in Fourier space,
 \begin{equation} \hat{\boldsymbol{f}}(k_x,k_z) = \sum_{k'_x,k'_z=-\infty}^{\infty} (\hat{\boldsymbol{u}}(k'_x,k'_z)\boldsymbol{\cdot}\hat{\boldsymbol{\nabla}}) \hat{\boldsymbol{u}}(k_x-k'_x,k_z-k'_z), \end{equation}
\begin{equation} \hat{\boldsymbol{f}}(k_x,k_z) = \sum_{k'_x,k'_z=-\infty}^{\infty} (\hat{\boldsymbol{u}}(k'_x,k'_z)\boldsymbol{\cdot}\hat{\boldsymbol{\nabla}}) \hat{\boldsymbol{u}}(k_x-k'_x,k_z-k'_z), \end{equation}
which is a function of ![]() $y$ and
$y$ and ![]() $t$. The contribution of each component of the convolution sum towards the projection of the principal forcing term onto
$t$. The contribution of each component of the convolution sum towards the projection of the principal forcing term onto ![]() $\tilde {\boldsymbol {\phi }}_1^{(0,1,0)}$ for any given flow field can be measured as
$\tilde {\boldsymbol {\phi }}_1^{(0,1,0)}$ for any given flow field can be measured as
 \begin{equation} \varPi(k'_x,k'_z;k_x,k_z,\omega) = \left\langle \begin{bmatrix} (\hat{\boldsymbol{u}}(k'_x,k'_z)\boldsymbol{\cdot}\hat{\boldsymbol{\nabla}}) \hat{\boldsymbol{u}}(k_x-k'_x,k_z-k'_z)\\ 0 \end{bmatrix},\tilde{\boldsymbol{\phi}}_1(k_x,k_z,\omega)\right\rangle. \end{equation}
\begin{equation} \varPi(k'_x,k'_z;k_x,k_z,\omega) = \left\langle \begin{bmatrix} (\hat{\boldsymbol{u}}(k'_x,k'_z)\boldsymbol{\cdot}\hat{\boldsymbol{\nabla}}) \hat{\boldsymbol{u}}(k_x-k'_x,k_z-k'_z)\\ 0 \end{bmatrix},\tilde{\boldsymbol{\phi}}_1(k_x,k_z,\omega)\right\rangle. \end{equation}
Note that integration over all ![]() $k'_x$ and
$k'_x$ and ![]() $k'_z$ of
$k'_z$ of ![]() $\varPi (k'_x,k'_z)^{(0,1,0)}$ gives the projection coefficient computed in (2.6a,b), where, by abuse of notation, we define
$\varPi (k'_x,k'_z)^{(0,1,0)}$ gives the projection coefficient computed in (2.6a,b), where, by abuse of notation, we define ![]() $\varPi (k'_x,k'_z)^{(a,b,c)}=\varPi (k'_x,k'_z;k_x^{\circ }=a,k_z^{\circ }=b,\omega =c)$ and
$\varPi (k'_x,k'_z)^{(a,b,c)}=\varPi (k'_x,k'_z;k_x^{\circ }=a,k_z^{\circ }=b,\omega =c)$ and ![]() $\varPi ^{(a,b;c,d,e)}=\varPi (k^{\prime \circ }_x=a,k^{\prime \circ }_z=b;k_x^{\circ }=c, k_z^{\circ }=d,$
$\varPi ^{(a,b;c,d,e)}=\varPi (k^{\prime \circ }_x=a,k^{\prime \circ }_z=b;k_x^{\circ }=c, k_z^{\circ }=d,$![]() $\omega =e)$. Also, due to incompressibility,
$\omega =e)$. Also, due to incompressibility, ![]() $\varPi$ is symmetric with respect to
$\varPi$ is symmetric with respect to ![]() $(k_x,k_z)$ for each flow field; that is,
$(k_x,k_z)$ for each flow field; that is, ![]() $\varPi (k'_x,k'_z;k_x,k_z,\omega ) = \varPi (k_x-k'_x,k_z-k'_z;k_x,k_z,\omega )$. The average spectral map of
$\varPi (k'_x,k'_z;k_x,k_z,\omega ) = \varPi (k_x-k'_x,k_z-k'_z;k_x,k_z,\omega )$. The average spectral map of ![]() $|\varPi (k'_x,k'_z)^{(0,1,0)}|$ normalised by the total contribution
$|\varPi (k'_x,k'_z)^{(0,1,0)}|$ normalised by the total contribution ![]() $|\sum _{k_x',k_z'}\varPi (k'_x,k'_z)^{(0,1,0)}|$ is computed from flow fields of the undamped minimal channel of the buffer and log layer and is depicted in figure 8. Both spectral maps show quantitatively similar features and identify two main sources of contribution from the wavenumber pair
$|\sum _{k_x',k_z'}\varPi (k'_x,k'_z)^{(0,1,0)}|$ is computed from flow fields of the undamped minimal channel of the buffer and log layer and is depicted in figure 8. Both spectral maps show quantitatively similar features and identify two main sources of contribution from the wavenumber pair ![]() $(k^{\prime \circ }_x,k^{\prime \circ }_z) = (1,0)$ and
$(k^{\prime \circ }_x,k^{\prime \circ }_z) = (1,0)$ and ![]() $((k_x-k'_x)^{\circ },(k_z-k'_z)^{\circ }) = (-1,1)$ and its mirror image in the
$((k_x-k'_x)^{\circ },(k_z-k'_z)^{\circ }) = (-1,1)$ and its mirror image in the ![]() $xy$-plane,
$xy$-plane, ![]() $(k^{\prime \circ }_x,k^{\prime \circ }_z) = (-1,1)$ and
$(k^{\prime \circ }_x,k^{\prime \circ }_z) = (-1,1)$ and ![]() $(-k^{\prime \circ }_x,1-k^{\prime \circ }_z) = (1,0)$, which account for approximately
$(-k^{\prime \circ }_x,1-k^{\prime \circ }_z) = (1,0)$, which account for approximately ![]() $40\,\%$ of the total contribution. This is consistent with the results from Hamilton et al. (Reference Hamilton, Kim and Waleffe1995), which used vorticity as a measure rather than the contribution towards resolvent forcing modes. While the contributions from other wavenumber pairs are not negligible, for the remainder of this paper, we focus on the two pairs of wavenumbers to identify the coherent structures responsible for the nonlinear forcing term and without loss of generality choose the pair
$40\,\%$ of the total contribution. This is consistent with the results from Hamilton et al. (Reference Hamilton, Kim and Waleffe1995), which used vorticity as a measure rather than the contribution towards resolvent forcing modes. While the contributions from other wavenumber pairs are not negligible, for the remainder of this paper, we focus on the two pairs of wavenumbers to identify the coherent structures responsible for the nonlinear forcing term and without loss of generality choose the pair ![]() $(k^{\prime \circ }_x,k^{\prime \circ }_z) = (1,0)$ and
$(k^{\prime \circ }_x,k^{\prime \circ }_z) = (1,0)$ and ![]() $((k_x-k'_x)^{\circ },(k_z-k'_z)^{\circ }) = (-1,1)$.
$((k_x-k'_x)^{\circ },(k_z-k'_z)^{\circ }) = (-1,1)$.

Figure 8. Average contribution of each convolution sum ![]() $|\varPi (k'_x=1,k'_z=0;k_x=0,k_z=1,\omega =0)|$ normalised by the total contribution
$|\varPi (k'_x=1,k'_z=0;k_x=0,k_z=1,\omega =0)|$ normalised by the total contribution ![]() $|\sum _{k'_x,k'_z}\varPi (k'_x,k'_z;k_x=0,k_z=1,\omega =0)|$ for the (a) buffer-layer case and (b) log-layer case.
$|\sum _{k'_x,k'_z}\varPi (k'_x,k'_z;k_x=0,k_z=1,\omega =0)|$ for the (a) buffer-layer case and (b) log-layer case.
To identify instantaneous flow configurations where the contribution towards ![]() $\tilde {\boldsymbol {\phi }}_1^{(0,1,0)}$ is strong or weak, we first observe values of
$\tilde {\boldsymbol {\phi }}_1^{(0,1,0)}$ is strong or weak, we first observe values of ![]() $\bar \varPi ^{(1,0;0,1,0)} = |\varPi ^{(1,0;0,1,0)}| / \langle \,\hat {\boldsymbol {f}}(k^{\prime \circ }_x=1,$
$\bar \varPi ^{(1,0;0,1,0)} = |\varPi ^{(1,0;0,1,0)}| / \langle \,\hat {\boldsymbol {f}}(k^{\prime \circ }_x=1,$ ![]() $k^{\prime \circ }_z=0), \hat {\boldsymbol {f}}(k^{\prime \circ }_x=1,k^{\prime \circ }_z=0)\rangle ^{1/2}$, which represents the normalised contribution to the principal forcing term with respect to the total energy of the nonlinear term in the
$k^{\prime \circ }_z=0), \hat {\boldsymbol {f}}(k^{\prime \circ }_x=1,k^{\prime \circ }_z=0)\rangle ^{1/2}$, which represents the normalised contribution to the principal forcing term with respect to the total energy of the nonlinear term in the ![]() $(k'_x,k'_z)$ mode, computed from flow fields of the undamped channel. We then determine the mean
$(k'_x,k'_z)$ mode, computed from flow fields of the undamped channel. We then determine the mean ![]() $\mu$ and standard deviation
$\mu$ and standard deviation ![]() $\varsigma$ of the distribution of
$\varsigma$ of the distribution of ![]() $\bar \varPi ^{(1,0;0,1,0)}$ over all time instants. The high-forcing-intensity events are defined as those with
$\bar \varPi ^{(1,0;0,1,0)}$ over all time instants. The high-forcing-intensity events are defined as those with ![]() $\bar \varPi ^{(1,0;0,1,0)} > \mu +2\varsigma$ and low forcing-intensity events as those with
$\bar \varPi ^{(1,0;0,1,0)} > \mu +2\varsigma$ and low forcing-intensity events as those with ![]() $\bar \varPi ^{(1,0;0,1,0)} < \mu -2\varsigma$. Both cases consist of approximately 5 % of the total events.
$\bar \varPi ^{(1,0;0,1,0)} < \mu -2\varsigma$. Both cases consist of approximately 5 % of the total events.

Figure 9. Average (a,d) ![]() $\mathcal {F}^{-1}(\hat {u})$, (b,e)
$\mathcal {F}^{-1}(\hat {u})$, (b,e) ![]() $\mathcal {F}^{-1}(\hat {v})$ and (c,f)
$\mathcal {F}^{-1}(\hat {v})$ and (c,f) ![]() $\mathcal {F}^{-1}(\hat {w})$ for
$\mathcal {F}^{-1}(\hat {w})$ for ![]() $(k^{\circ }_x,k^{\circ }_z)=(1,0)$ (a–c) and
$(k^{\circ }_x,k^{\circ }_z)=(1,0)$ (a–c) and ![]() $(-1,1)$ (d–f) conditioned to high-forcing-intensity events for the buffer-layer case. The isosurfaces are
$(-1,1)$ (d–f) conditioned to high-forcing-intensity events for the buffer-layer case. The isosurfaces are ![]() $0.41$ (solid red),
$0.41$ (solid red), ![]() $0.26$ (transparent red),
$0.26$ (transparent red), ![]() $-0.26$ (transparent blue) and
$-0.26$ (transparent blue) and ![]() $-0.41$ (solid blue).
$-0.41$ (solid blue).
The average ![]() $\mathcal {F}^{-1}(\hat {\boldsymbol {u}}(k^{\circ }_x=1,k^{\circ }_z=0))$ and
$\mathcal {F}^{-1}(\hat {\boldsymbol {u}}(k^{\circ }_x=1,k^{\circ }_z=0))$ and ![]() $\mathcal {F}^{-1}(\hat {\boldsymbol {u}}(k^{\circ }_x=-1,k^{\circ }_z=1))$ conditioned to high-forcing-intensity events for the buffer layer are shown in figure 9, where
$\mathcal {F}^{-1}(\hat {\boldsymbol {u}}(k^{\circ }_x=-1,k^{\circ }_z=1))$ conditioned to high-forcing-intensity events for the buffer layer are shown in figure 9, where ![]() $\mathcal {F}^{-1}$ is the inverse Fourier transform. The modes are phase-shifted before averaging such that they are phase-aligned for the streamwise velocity component at
$\mathcal {F}^{-1}$ is the inverse Fourier transform. The modes are phase-shifted before averaging such that they are phase-aligned for the streamwise velocity component at ![]() $y^{+}\approx 40$ in an effort to centre the underlying structures at a fixed location. The coherent structures identified by the
$y^{+}\approx 40$ in an effort to centre the underlying structures at a fixed location. The coherent structures identified by the ![]() $(k_x^{\circ },k_z^{\circ }) = (1,0)$ mode (figure 9a–c) are in the form of a pair of spanwise rolls that is being sheared in the spanwise direction by
$(k_x^{\circ },k_z^{\circ }) = (1,0)$ mode (figure 9a–c) are in the form of a pair of spanwise rolls that is being sheared in the spanwise direction by ![]() $w$. That is, the relative phase of the velocity components depicts the vertically displaced pairs of positive and negative streamwise velocity components located between the horizontally displaced pairs of positive and negative wall-normal velocity, forming a structure in the shape of a spanwise roll, which then are affected by the alternating sign of the
$w$. That is, the relative phase of the velocity components depicts the vertically displaced pairs of positive and negative streamwise velocity components located between the horizontally displaced pairs of positive and negative wall-normal velocity, forming a structure in the shape of a spanwise roll, which then are affected by the alternating sign of the ![]() $w$ components. The
$w$ components. The ![]() $(k_x^{\circ }, k_z^{\circ }) = (-1, 1)$ mode (figure 9d–f) shows oblique streaks, which are the components of meandering streaks, with high-speed streaks moving towards the wall and low-speed streaks moving away from the wall, corresponding to sweeps and ejections. Furthermore, the spatial autocorrelation coefficients of the streamwise, wall-normal and spanwise velocity fluctuations, denoted
$(k_x^{\circ }, k_z^{\circ }) = (-1, 1)$ mode (figure 9d–f) shows oblique streaks, which are the components of meandering streaks, with high-speed streaks moving towards the wall and low-speed streaks moving away from the wall, corresponding to sweeps and ejections. Furthermore, the spatial autocorrelation coefficients of the streamwise, wall-normal and spanwise velocity fluctuations, denoted ![]() $C_{uu}$,
$C_{uu}$, ![]() $C_{vv}$ and
$C_{vv}$ and ![]() $C_{ww}$, respectively, are computed, where
$C_{ww}$, respectively, are computed, where
is the correlation conditioned to high-forcing-intensity events at ![]() $y'^{+}\approx 40$ for the buffer layer and
$y'^{+}\approx 40$ for the buffer layer and ![]() $y' \approx 0.2$ for the log layer. Here,
$y' \approx 0.2$ for the log layer. Here, ![]() $q\in \{u,v,w\}$ and
$q\in \{u,v,w\}$ and ![]() $\mathbb {E}[\,\cdot \,]$ is the expectation, or alternatively the average quantity over homogeneous spatial directions and instants. The correlations for both cases, shown in figure 10, reveal structures very similar to those highlighted by the time-averaged
$\mathbb {E}[\,\cdot \,]$ is the expectation, or alternatively the average quantity over homogeneous spatial directions and instants. The correlations for both cases, shown in figure 10, reveal structures very similar to those highlighted by the time-averaged ![]() $\mathcal {F}^{-1}(\hat {\boldsymbol {u}}(k^{\circ }_x=1,k^{\circ }_z=0))$ and
$\mathcal {F}^{-1}(\hat {\boldsymbol {u}}(k^{\circ }_x=1,k^{\circ }_z=0))$ and ![]() $\mathcal {F}^{-1}(\hat {\boldsymbol {u}}(k^{\circ }_x=-1,k^{\circ }_z=1))$ and resemble spanwise-sheared spanwise rolls (
$\mathcal {F}^{-1}(\hat {\boldsymbol {u}}(k^{\circ }_x=-1,k^{\circ }_z=1))$ and resemble spanwise-sheared spanwise rolls (![]() $C_{vv}$ and
$C_{vv}$ and ![]() $C_{ww}$) with oblique streaks (
$C_{ww}$) with oblique streaks (![]() $C_{uu}$), which are shared for both the buffer and log layer. This indicates that not only the linear mechanism but also the nonlinear mechanism driving the SSP are similar in both regions with similar structures forming the precursor events leading to strong intensities of the principal resolvent forcing term.
$C_{uu}$), which are shared for both the buffer and log layer. This indicates that not only the linear mechanism but also the nonlinear mechanism driving the SSP are similar in both regions with similar structures forming the precursor events leading to strong intensities of the principal resolvent forcing term.

Figure 10. Correlations (a,d) ![]() $C_{uu}$, (b,e)
$C_{uu}$, (b,e) ![]() $C_{vv}$ and (c,f)
$C_{vv}$ and (c,f) ![]() $C_{ww}$ conditioned to high-forcing-intensity events for the buffer layer (a–c) and log layer (d–f). The isosurfaces are
$C_{ww}$ conditioned to high-forcing-intensity events for the buffer layer (a–c) and log layer (d–f). The isosurfaces are ![]() $0.1$ (red) and
$0.1$ (red) and ![]() $-0.04$ (blue).
$-0.04$ (blue).
On the contrary, although not shown, average ![]() $\mathcal {F}^{-1}(\hat {\boldsymbol {u}}(k^{\circ }_x=1,k^{\circ }_z=0))$ and
$\mathcal {F}^{-1}(\hat {\boldsymbol {u}}(k^{\circ }_x=1,k^{\circ }_z=0))$ and ![]() $\mathcal {F}^{-1}(\hat {\boldsymbol {u}}(k^{\circ }_x=-1,k^{\circ }_z=1))$ conditioned to low-forcing-intensity events are less coherent for these wave parameters. This can be observed from the conditional correlation of the buffer-layer case in figure 11(a–c), where the streamwise and wall-normal velocities only show structures resembling straight streaks corresponding to wavenumbers
$\mathcal {F}^{-1}(\hat {\boldsymbol {u}}(k^{\circ }_x=-1,k^{\circ }_z=1))$ conditioned to low-forcing-intensity events are less coherent for these wave parameters. This can be observed from the conditional correlation of the buffer-layer case in figure 11(a–c), where the streamwise and wall-normal velocities only show structures resembling straight streaks corresponding to wavenumbers ![]() $(k^{\circ }_x,k^{\circ }_z) = (0,2)$ and no structures resembling oblique streaks or spanwise rolls. Considering the fact that the total kinetic energy distributions for the strong and weak events are similar, these results show that the precursor to the nonlinear interaction that generates the principal forcing mode has more defined coherent structures in the form of spanwise rolls and oblique streaks, which interact to produce the principal forcing mode, which then plays an important role in the SSP of near-wall turbulence. Identifying these precursor events will allow development of new control mechanisms that aim to reduce the production of the resolvent forcing modes essential in sustaining turbulence.
$(k^{\circ }_x,k^{\circ }_z) = (0,2)$ and no structures resembling oblique streaks or spanwise rolls. Considering the fact that the total kinetic energy distributions for the strong and weak events are similar, these results show that the precursor to the nonlinear interaction that generates the principal forcing mode has more defined coherent structures in the form of spanwise rolls and oblique streaks, which interact to produce the principal forcing mode, which then plays an important role in the SSP of near-wall turbulence. Identifying these precursor events will allow development of new control mechanisms that aim to reduce the production of the resolvent forcing modes essential in sustaining turbulence.

Figure 11. Correlations (a,d) ![]() $C_{uu}$, (b,e)
$C_{uu}$, (b,e) ![]() $C_{vv}$ and (c,f)
$C_{vv}$ and (c,f) ![]() $C_{ww}$ conditioned to low-forcing-intensity events for the buffer layer (a–c) and log layer (d–f). The isosurfaces are
$C_{ww}$ conditioned to low-forcing-intensity events for the buffer layer (a–c) and log layer (d–f). The isosurfaces are ![]() $0.1$ (red) and
$0.1$ (red) and ![]() $-0.04$ (blue).
$-0.04$ (blue).
Unlike the buffer-layer case, the streamwise correlation conditioned to low-forcing-intensity events shown in figure 11(d–f) is not as different from the high-forcing-intensity events for the log-layer case. The wall-normal correlation still shows clear positive and negative correlation pairs in the streamwise direction when conditioned to low-forcing-intensity events, and the spanwise correlations are less pronounced in the spanwise direction. The similarity in the streamwise component, although less pronounced in the low-forcing-intensity events, shows that, even if the principal forcing mode is removed, the flow will still self-sustain structures necessary for regenerating streamwise vortices, which is corroborated in § 3.2. However, the most significant difference in the correlations conditioned to strong- and weak-forcing-intensity events are the wall-normal components that partly form the spanwise rolls. These spanwise rolls are observed in cases of drag increase in active and passive control (García-Mayoral & Jiménez Reference García-Mayoral and Jiménez2011, Reference García-Mayoral and Jiménez2012; Toedtli, Yu & McKeon Reference Toedtli, Yu and McKeon2019), which is consistent with our observation that these are precursor events to generation of the principal resolvent forcing term that is crucial in generating and self-sustaining turbulence.
5. Conclusions
We have studied the SSP of wall-bounded turbulence in the buffer and log layers with special emphasis on the nonlinear mechanisms involved in vortex regeneration. For this purpose, we have utilised resolvent analysis to identify the most amplified nonlinear term in the incompressible Navier–Stokes equations and studied the effect of this term on numerical simulations of turbulent channel flow tailored to study isolated structures in the buffer and log layer.
Simulations of the minimal channel for the buffer and log layer with a fixed mean streamwise velocity profile were performed to isolate the structures at a prescribed scale. The most amplified nonlinear term corresponding to the most energetic wavenumber was then computed from the resolvent analysis using the mean velocity profile of the minimal channel simulations. The identified mode was removed from the nonlinear term of the corresponding simulation for a minimal channel simulation with a fixed mean velocity profile at each time step. This is made possible by the orthonormality of the resolvent modes, which provides an orthonormal basis for the nonlinear term to be projected onto. We have shown that the removal of the principal forcing mode leads to a reduction of turbulence in the flow. We also applied the removal method for subsequent forcing modes as well as non-fundamental wavenumbers instead and observed only a marginal decrease in the turbulence intensities, which reinstates the principal forcing mode for the fundamental wavenumber as the most amplified, and thus the most important, component of the nonlinear term. The diminished effect on the log layer is attributed to the multi-scale nature of high-Reynolds-number turbulence due to the more complicated interaction between various scales.
Finally, we identified the coherent structures that, through the nonlinear interaction, form the principal forcing mode. The identified structures are in the form of spanwise-sheared spanwise rolls and oblique streaks for both the buffer and log layer. The interaction of the two components highlighted here regenerates streamwise vortices, which through the lift-up mechanism amplifies streamwise streaks. These streamwise streaks break down, spawning new generations of meandering streaks and spanwise rolls, completing the SSP. The similarities in the structures identified for the buffer and log layer highlight the similarity of the nonlinear process in the SSP of the two cases.
This new technique allows the analysis of nonlinear mechanisms by combining resolvent analysis with numerical simulations of fully nonlinear Navier–Stokes equations in a realistic turbulent flow. The results show that the nonlinear mechanism of the buffer and log layer are driven by similar structures and that, without these structures present in the flow, turbulence intensity is significantly reduced. The findings corroborate previous studies on nonlinear interaction of the SSP and allow the characterisation of the underlying quadratic interactions in the SSP in the buffer and log layer of wall-bounded turbulence using resolvent analysis. The study also supports the hypothesis that the SSP in the buffer and log layer are similar by showing the similarities in the form of the principal forcing mode as well as the structures of the flow correlations conditioned to high-forcing-intensity events that lead to the generation of the principal forcing mode.
Acknowledgements
This work was funded in part by the Coturb programme of the European Research Council (ERC-2014.AdG-669505) during the 2017 Coturb Turbulence Summer Workshop at the Universidad Politécnica de Madrid. B.J.M. is grateful for the support of ONR under N00014-17-1-3022. A.L.-D. acknowledges the support of NASA under NNX15AU93A and of ONR under N00014-17-1-2310. The authors thank Professor J. Jiménez, Dr Y. Kwon and Dr A. Guseva for their insightful comments.
Declaration of interests
The authors report no conflict of interest.