In the 19th century, a series of statistical congresses underlaid demographic studies, including twin research. Levi (Reference Levi1854) gave a detailed presentation of the suggestions concerning the annual registry of populations proposed in 1853 at the Brussels congress. According to Brown (Reference Brown1872), at the congress held in 1872 in St. Petersburg, the principal discussion was related to the movements of the population and the mode in which they should be registered. Later, Westergaard (Reference Westergaard1932) devoted an entire chapter to the presentation of the statistical congresses of the 19th century.
Hellin's (Reference Hellin1895) paper can be considered a milestone in the history of twin research, and one can divide the research into studies before and after Hellin. Spengler (Reference Spengler1848) presented birth data, including data concerning multiple births for Mecklenburg-Schwerin for the period 1777–1847. Veit (Reference Veit1855) published a data set from Prussia (1826–1849), but in these studies there were no discussions concerning the relation between the number of twin and triplet maternities. Bertillion (1898) considered multiple maternity data from different countries in Europe. He foreboded Hellin's law because he presented the number of twin maternities in relation to one triplet maternity. In 1877, Neefe published his classical work (Neefe, Reference Neefe1877). He focused on the importance of the standardization of the demographic registers in different countries and used the new possibilities that the improved birth registers offered. Although other contemporaneous studies were published, our view is that the history of twin research starts from his publication because he analyzed a long series of problems connected to twinning. These have been shown to be central in later studies. It is important to note that Neefe did not anticipate Hellin's law.
Strassmann (Reference Strassmann1889) analyzed data published by Veit (Reference Veit1855) concerning single and higher maternities. Strassmann noted that there is one twin maternity per 89 and one triplet maternity per (89)2 total maternities. Drejer (Reference Drejer1895) was apparently not aware of Hellin (Reference Hellin1895), but referred to Strassmann (Reference Strassmann1889) and stated that Strassmann had noted the relation between the rates of twin and triplet maternities (Fellman & Eriksson, Reference Fellman and Eriksson2009).
Hellin (Reference Hellin1895) observed an empirical relationship between the rates of twins and triplets. He stated that among human beings there is on average one twin maternity per 89 singleton maternities, one triplet maternity per (89)2 singleton maternities, and in general, within the range of the possibility, one x-tuplet maternity per (89)χ-1 singleton maternities. Strassmann related the number of multiple maternities to the number of all maternities, while Hellin related the number of multiple maternities to the number of single maternities. However, both used the same relation: 1:89.
Different studies of the seasonality of multiple maternities have been presented. James (Reference James1980) compared the seasonality of twin and triplet maternities. Bonnelykke et al. (Reference Bonnelykke, Søgaard and Nielsen1987) constructed seasonal models for twin maternities and included both temporal and seasonal components in the models. They included the temporal component because the twinning rate (TWR) showed strong temporal variations. In addition, they made use of the fact that the gestation for twin maternities is on average shorter than for singleton maternities. Elster and Bleyl (Reference Elster and Bleyl1991) studied the seasonality of triplet maternities. They published 1,050 triplet maternities for the period 1985–1988. These triplet data were compared with the natality statistics for the United States during the overlapping 4-year period in 1983–1986. Statistics for the exact comparison period were not published when Elster and Bleyl performed their study, so the closest complete overlapping 4-year period (1983–1986) was used instead of the exact one. Elster and Bleyl ignored the difference between the two periods and gave arguments for this. Furthermore, they did not present twinning data.
Methods and Materials
A problem that aggravates the discussion of Hellin's law is that the law is a mathematical rule concerning the theoretical rates, but all checks of the law are based on empirically obtained rates, and no exact proof to support the law can be obtained. In fact, one can only check whether observed inconsistencies are too large to be explained as random errors. In other studies, we have evaluated the association between the TWR, the triplet rate (TRR), and the Hellin-transformed triplet rate (HRR) when the data are grouped according to time (Fellman, Reference Fellman2017b).
In this study, we split the data according to season. When the seasonality is studied, one must distinguish between two alternative problems: (a) the general significant heterogeneity — for example, tested by the χ2 test given below; or (b) the application of specific seasonal models discussed later.
Seasonality Tests
Eriksson and Fellman (Reference Eriksson and Fellman2000) stressed that if one intends to identify the seasonality of multiple maternities, one must consider the seasonality of the corresponding rates. Doing this, the seasonality of the total maternities is eliminated.
Fellman (Reference Fellman2017a) tested the seasonality of births by χ2 tests. Let N
i be the observed number of births in month number i and let ki
be the length of the month in days. Furthermore, let
![]() $N = \sum\limits_{i = 1}^{12} {{N_i}} $
be the total number of births and let
$N = \sum\limits_{i = 1}^{12} {{N_i}} $
be the total number of births and let
![]() $k = \sum\limits_{i = 1}^{12} {{k_i}} $
be the length of the year. The expected number of births per day for the whole year is
$k = \sum\limits_{i = 1}^{12} {{k_i}} $
be the length of the year. The expected number of births per day for the whole year is
![]() $\frac{N}{k}$
and in month number i it is
$\frac{N}{k}$
and in month number i it is
![]() ${\hat{N}_i} = {k_i}\frac{N}{k}$
. The χ
2 test is
${\hat{N}_i} = {k_i}\frac{N}{k}$
. The χ
2 test is
 $$\begin{equation}
{\chi ^2} = \sum\limits_{i = 1}^{12} {\frac{{{{({N_i} - {{\hat{N}}_i})}^2}}}{{{{\hat{N}}_i}}}}
\end{equation}$$
$$\begin{equation}
{\chi ^2} = \sum\limits_{i = 1}^{12} {\frac{{{{({N_i} - {{\hat{N}}_i})}^2}}}{{{{\hat{N}}_i}}}}
\end{equation}$$
with 11 degrees of freedom.
For twin and other multiple maternities, we must modify the test. For instance, for twin sets, let ni
be the number of twin maternities in month number I, and let N be the total number of twin maternities. The total TWR is
![]() $r = \frac{n}{N}$
. The observed TWR for month i is
$r = \frac{n}{N}$
. The observed TWR for month i is
![]() ${r_i} = \frac{{{n_i}}}{{{N_i}}}$
. The expected number of twin maternities in month number i is
${r_i} = \frac{{{n_i}}}{{{N_i}}}$
. The expected number of twin maternities in month number i is
![]() ${\hat{n}_i} = r{N_i}$
. Hence, the χ
2 test for the twin data is
${\hat{n}_i} = r{N_i}$
. Hence, the χ
2 test for the twin data is
 $$\begin{equation}
{\chi ^2} = \sum\limits_{i = 1}^{12} {\frac{{{{({n_i} - {{\hat{n}}_i})}^2}}}{{{{\hat{n}}_i}}}} ,
\end{equation}$$
$$\begin{equation}
{\chi ^2} = \sum\limits_{i = 1}^{12} {\frac{{{{({n_i} - {{\hat{n}}_i})}^2}}}{{{{\hat{n}}_i}}}} ,
\end{equation}$$
with 11 degrees of freedom. A similar formula holds for higher multiple maternities and especially in this study for TRR. The critical values for χ 2 tests with 11 degrees of freedom are χ 2 = 19.68 for p < .05, χ 2 = 24.73 for p < .01, and χ 2 = 31.26 for p < .001.
Seasonality Models
If one intends to obtain a seasonal model, the simplest model could be the sinusoidal one:
 $$\begin{eqnarray}
R({t_i}) &=& K + R\sin ({t_i} + \alpha ) + {\varepsilon _i} \nonumber\\
&=& K + A\cos ({t_i}) + B\sin ({t_i}) + {\varepsilon _i},
\end{eqnarray}$$
$$\begin{eqnarray}
R({t_i}) &=& K + R\sin ({t_i} + \alpha ) + {\varepsilon _i} \nonumber\\
&=& K + A\cos ({t_i}) + B\sin ({t_i}) + {\varepsilon _i},
\end{eqnarray}$$
where A = R sin α, B = R cos α, and the error terms ε i are assumed to be independent and homoscedastic. However, it will be seen in many situations that although there are marked seasonal variations, the simple sine curve does not fit the data. For example, this is the case when the data show more than one marked peak. Data showing one peak and one trough may also differ markedly from the sine curve. The trough or the peak may be too long or the time between them may not be 6 months.
If one intends to obtain an improved seasonal model, it could be the trigonometric regression model (Fellman & Eriksson, Reference Fellman and Eriksson2002):
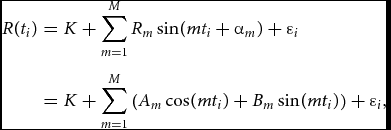 $$\begin{eqnarray}
R({t_i}) &=& K + \sum\limits_{m = 1}^M {{R_m}\sin (m{t_i} + {\alpha _m})} + {\varepsilon _i}\nonumber\\
&=& K + \sum\limits_{m = 1}^M {\left( {{A_m}\cos (m{t_i}) + {B_m}\sin (m{t_i})} \right)} + {\varepsilon _i},\hphantom{00}
\end{eqnarray}$$
$$\begin{eqnarray}
R({t_i}) &=& K + \sum\limits_{m = 1}^M {{R_m}\sin (m{t_i} + {\alpha _m})} + {\varepsilon _i}\nonumber\\
&=& K + \sum\limits_{m = 1}^M {\left( {{A_m}\cos (m{t_i}) + {B_m}\sin (m{t_i})} \right)} + {\varepsilon _i},\hphantom{00}
\end{eqnarray}$$
where M is the number of pairs of trigonometric terms, Am = Rm sin αm and Bm = Rm cos αm (m = 1, . . ., M). The error terms ε i are assumed to be independent and homoscedastic. With monthly data, one has to introduce the restriction M ≤ 5.
The parameters Am
and Bm
(m = 1, . . ., M) and K are estimated by ordinary least squares for the monthly data and the initial parameters αm
and the amplitudes
![]() ${R_m} = \sqrt {A_m^2 + B_m^2} $
(m = 1, . . ., M) can be estimated by the equations:
${R_m} = \sqrt {A_m^2 + B_m^2} $
(m = 1, . . ., M) can be estimated by the equations:
The angle αm
and the amplitudes Rm
have to be estimated from formulae (5) and (6) irrespective of the significance of the parameter estimates. Therefore, Fellman and Eriksson (Reference Fellman and Eriksson2002) recommended full pairs of trigonometric terms. The argument for this is that
![]() ${\hat{R}_m}$
may differ significantly from zero, but the angle αm
may be such that
${\hat{R}_m}$
may differ significantly from zero, but the angle αm
may be such that
![]() ${\hat{A}_m}$
or
${\hat{A}_m}$
or
![]() ${\hat{B}_m}$
is close to zero and consequently non-significant. From this, it follows that the tests of parameter significance should be applied to α
m
and
${\hat{B}_m}$
is close to zero and consequently non-significant. From this, it follows that the tests of parameter significance should be applied to α
m
and
![]() ${\hat{R}_m}$
(m = 1, . . ., M), but not to
${\hat{R}_m}$
(m = 1, . . ., M), but not to
![]() ${\hat{A}_m}$
or
${\hat{A}_m}$
or
![]() ${\hat{B}_m}$
.
${\hat{B}_m}$
.
Fellman and Eriksson (Reference Fellman and Eriksson2002) assumed that the model is optimal when the adjusted coefficient of determination,
![]() ${\bar{R}^2}$
, attains its maximum. If
${\bar{R}^2}$
, attains its maximum. If
![]() ${\bar{R}^2}$
increased monotonically with increasing M, they chose M = 4. In doing so, they left three degrees of freedom for the testing. The multiple trigonometric regression models and the corresponding tests of the estimates are discussed in detail in Fellman and Eriksson (Reference Fellman and Eriksson2000) and in some of the references given in that article.
${\bar{R}^2}$
increased monotonically with increasing M, they chose M = 4. In doing so, they left three degrees of freedom for the testing. The multiple trigonometric regression models and the corresponding tests of the estimates are discussed in detail in Fellman and Eriksson (Reference Fellman and Eriksson2000) and in some of the references given in that article.
In this study, we perform an alternative attempt, that is, we pursue optimal seasonal models before we compare the obtained models for the different rates, and therefore, we concentrate on the individual parameters {Am } and {Bm }. Hence, we include in the models all significant parameters and ignore the insignificant ones.
The triplet sets are very rare and consequently suitable data containing sufficiently large sets for statistical analyses of monthly triplet births are difficult to obtain. James (Reference James1980) had the opportunity to perform his studies based on data from England and Wales (1952–1975). He compared the seasonality of opposite-sex twin sets, monozygotic twin sets, and triplet sets. His findings are presented in the Discussion section. In this study, we base our analyses on James’ data and our central topic is to compare the seasonality of TWR, TRR, and HRR.
Elster and Bleyl (Reference Elster and Bleyl1991) published data about 1,050 triplet maternities for the period 1985–1988. These triplet data were compared with the natality statistics for the United States during the overlapping 4-year period in 1983–1986. They ignored the difference between the two periods and gave arguments for this. In our analyses, we accept the data and rules proposed by Elster and Bleyl.
Results
Seasonal Heterogeneity
We start with the tests of the seasonality. For James’ data, we obtain χ 2 = 30632.24 for the total births, χ 2 = 53.17 for TWR, and χ 2 = 16.31 for TRR. Hence, for the total number of births and the TWR the test values are significant (p < .001), but for the TRR it is non-significant (p > .05). Although the TRR shows marked variations, the data set is too small for significance.
The available data in Elster and Bleyl yield only approximate triplet rates. We accept the assumptions of Elster and Bleyl and approximate the TRR by assuming that the data are constant during the whole period in 1983–1988. For the Elster and Bleyl data, we obtain χ 2 = 19472.94 for the total births and χ 2 = 7.94 for TRR. Hence, for the total number of births the test value is significant (p < .001), but for the TRR, showing marked variations, it is non-significant (p > .05) because the triplet data set is too small.
To compare the seasonality in more detail, we standardized the total number of births, TWR, TRR, and HRR into monthly indices having means of 100 (Eriksson & Fellman Reference Eriksson and Fellman1999, Reference Eriksson and Fellman2000; Fellman & Eriksson, Reference Fellman and Eriksson1999). Statistical comparisons using standard deviations (SDs) are applicable when indices are studied. If one tests seasonal variations in the indices, one obtains the SDs 4.590 for total births, 10.067 for TRR, 5.062 for HRR, and 1.802 for TWR. The analyses of James’ data that reveal obvious discrepancies between TWR and HRR are obvious. If one tests seasonal variations in the indices for the Elster and Bleyl data, one obtains 3.78 for total births, 9.16 for TRR, and 4.508 for HRR. When we combine these findings, our conclusion is that all rates show seasonality. Furthermore, the results indicate the strongest seasonality in TRR, strong seasonality in the births and HRR, and only slight seasonality in TWR.
Trigonometric Regression Models
When we perform the proposed regression analyses, we obtain regression models for births, TWR, TRR, and HRR based on James’ data for England and Wales. The goodness of fit is strongest for the birth data, medium for TWR and TRR and slight for HRR (Table 1). For the U.S. data given by Elster and Bleyl, we consider births, TRR, and HRR. Twinning data were not available in the U.S. data. The best fit is observed for births, but slight goodness of fit is observed for TRR and HRR (Table 1).
TABLE 1 Trigonometric Regression Models Including the Adjusted Coefficients of Determination,
![]() ${\bar{R}^2}$
as Goodness of Fit Measure
${\bar{R}^2}$
as Goodness of Fit Measure

In Figure 1, we present the seasonality of TWR, TRR, and HRR based on James’ data for England and Wales (1952–1975). One observes that the seasonal fluctuations are strongest for TRR, and for TWR and HRR the seasonality is of similar strength. The discrepancies between the seasonality pattern of TWR, TRR, and HRR are obvious.
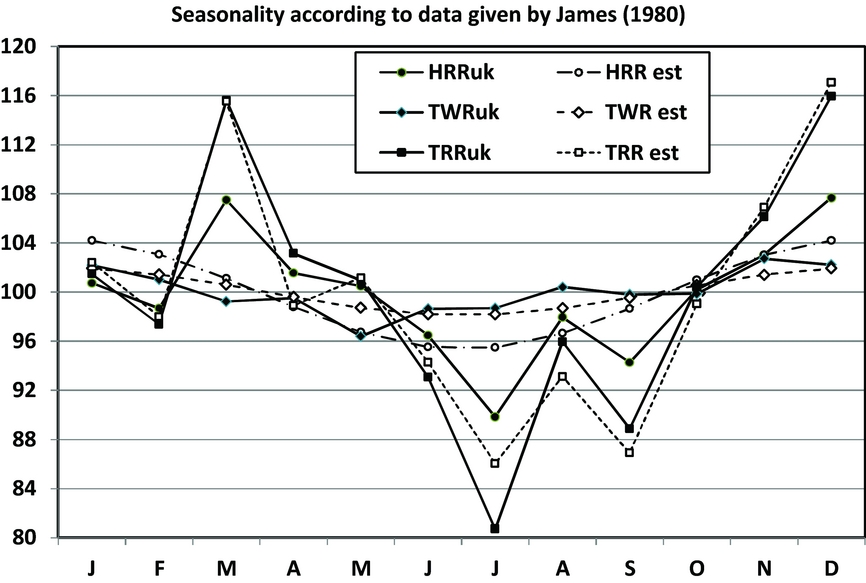
FIGURE 1 Comparison of the seasonality of twinning rate (TWR), triplet rate (TRR), and Hellin-transformed TRR (HRR) based on James’ data for England and Wales (1952–1975). The analysis is based on transformed indices with means of 100. The obtained regression models are given in Table 1, and the seasonal variations are discussed in the text.
In Figure 2, we present the seasonality of births, TRR, and HRR based on U.S. data (1983–1988). The births display the best goodness of fit (Table 1). One observes that the seasonal fluctuations are strongest for TRR. For births and HRR, the seasonality is of similar strength. The discrepancies between the seasonality pattern of births, TRR, and HRR are obvious.
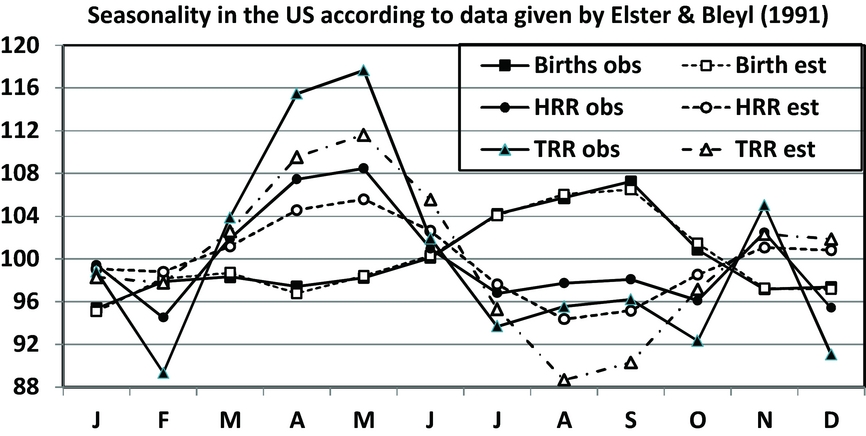
FIGURE 2 Comparison of the seasonality of total births (Births), TRR, and HRR for the United States (1983–1988). The analysis is based on the Elster and Bleyl data transformed to indices with means of 100. The obtained regression models are given in Table 1, and the seasonal variations are discussed in the text.
Discussion
It is commonly agreed that the main argument for Hellin's law is that the probabilities of additional ovulations and the fissions of fertilized eggs can be explained by stochastic models (see, e.g., Allen & Firschein, Reference Allen and Firschein1957; Fellman & Eriksson, Reference Fellman and Eriksson2009; Jenkins, Reference Jenkins1927; Reference Jenkins1929; Jenkins & Gwin, Reference Jenkins and Gwin1940; Zeleny, Reference Zeleny1921). Hence, in large data sets the averages could be stable and formulated by a mathematical relation (Hellin's law).
Zeleny (Reference Zeleny1921) discussed in a short note Hellin's law. He stated that from the statistical relations it would appear that triplets are produced by the coincidence of two independent processes occurring with equal frequencies. One of these processes by itself gives rise to twin pairs. This relation would apply to any mode of origin of multiple births or to different combinations of these provided that each followed the rule. In fact, Zeleny considered the Strassmann version that the rates are related to the total number of maternities. He also referred to the Veit (Reference Veit1855) data and found startlingly good agreement with the law. Zeleny's analyses yielded him the honor that some authors later renamed as the Hellin–Zeleny law. In addition, the arguments for the discrepancies are that after the fertilizations there is a long process influenced by disturbing factors. For example, Jenkins (Reference Jenkins1927) and Komai and Fukuoka (Reference Komai and Fukuoka1936) assumed that differential mortality of twins and triplets in utero could be a disturbing factor. Consequently, the final result shows only a weak resemblance with the outcome of a stochastic process. This seems to be one main cause of the discrepancies between Hellin's law and the empirical findings. Among other issues the proposed model may be too simple.
Already, Jenkins (Reference Jenkins1927) noted that Hellin's law can be assumed only for maternal age-specific disaggregated data and that the discrepancy between Hellin's law and the observed aggregated data demands the use of the formula:
Fellman and Eriksson (Reference Fellman and Eriksson1993) gave a mathematical proof that Hellin's law cannot hold exactly. If one aggregates heterogeneous data, the fluctuations are smoothed out, but the relation between the TWR and the TRR is not linear, and consequently, the aggregated and disaggregated data cannot simultaneously satisfy Hellin's law. In fact, Jenkins’ arguments coincide mathematically with the integral proposed by Fellman and Eriksson (Reference Fellman and Eriksson1993). However, Jenkins did not explain the disagreement between Hellin's law for aggregated and disaggregated data.
James (Reference James1980) observed that the TRR had a stronger seasonality than the TWR s (both the opposite-sex TWR and the monozygotic TWR). He found that there was good evidence that the incidence of opposite-sex twin births was seasonal. Triplet births seemed to show a seasonal variation at the same location and with double the amplitude. He stated that this seasonal variation of polyzygotic maternities was due to seasonal variation in the rates of multiple ovulations. Of importance is James’ remark that the monozygotic rate (MZR) and the dizygotic rate (DZR) are not observed rates, but estimated ones. Hence, the variance formulae given for observed rates are incorrect for these estimated rates. Following a different route, Fellman (Reference Fellman2013) later found similar results and presented exact alternative formulae for the SDs of the MZR and DZR. Elster and Bleyl (Reference Elster and Bleyl1991) noted seasonality in the number of triplet births and that its pattern differed markedly from the seasonality of the births of the entire U.S. population (cf. Figure 2).
The history of the studies of Hellin's law shows a long series of attempts to reduce the discrepancies between the observed data and Hellin's law. Some studies based on MZR and DZR give improved results, but cannot eliminate the obtained discrepancies in the data (Allen, Reference Allen1960; Bulmer, Reference Bulmer1970; Fellman & Eriksson, Reference Fellman and Eriksson2004). In conclusion, one can note that every ‘improved’ model has the same weakness as Hellin's law. The models are mathematically exact, but the analyses are based on empirical data. Hence, the question remains of whether the improvements are general or specific to the data considered.
Acknowledgments
We are grateful to the personnel at The National Library of Health Sciences at the University of Helsinki (Terkko) for providing us ― my late friend and colleague Aldur W. Eriksson and myself ― with copies of old publications concerning twin studies in the 19th century, which are otherwise difficult to obtain.





