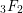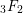AN ALGEBRO-GEOMETRIC STUDY OF SPECIAL VALUES OF HYPERGEOMETRIC FUNCTIONS $_{3}F_{2}$

Abstract

For a certain class of hypergeometric functions $_{3}F_{2}$ with rational parameters, we give a sufficient condition for the special value at $1$ to be expressed in terms of logarithms of algebraic numbers. We give two proofs, both of which are algebro-geometric and related to higher regulators.

1 Introduction

Special values of hypergeometric functions $_{p}F_{q}$ are sometimes expressed as an elementary function of their parameters. For example, we have the Euler–Gauss formula

$$\begin{eqnarray}_{2}F_{1}{a,b\atop c};1=\frac{B(c,c-a-b)}{B(c-a,c-b)}.\end{eqnarray}$$

Here, $B(a,b)=\int _{0}^{1}t^{a-1}(1-t)^{b-1}\,dt$ is the beta function. In this paper, we study the special values of $_{3}F_{2}$ -functions

(1.1) $$\begin{eqnarray}B(a,b)\cdot _{3}F_{2}\left(\begin{array}{@{}c@{}}a,b,q\\ a+b,q+1\end{array};1\right)\end{eqnarray}$$

for nonintegral rational numbers $a,b,q$ . There is a very classical formula of Watson [11] (see also [5, page 98, Example 9])

$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle 2B(a,b)\cdot _{3}F_{2}\left(\begin{array}{@{}c@{}}a,b,\frac{a+b-1}{2}\\ a+b,\frac{a+b+1}{2}\end{array};1\right)\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad =\unicode[STIX]{x1D713}\left(\frac{a+1}{2}\right)+\unicode[STIX]{x1D713}\left(\frac{b+1}{2}\right)-\unicode[STIX]{x1D713}\left(\frac{a}{2}\right)-\unicode[STIX]{x1D713}\left(\frac{b}{2}\right),\nonumber\end{eqnarray}$$

where $\unicode[STIX]{x1D713}(x)=\unicode[STIX]{x1D6E4}^{\prime }(x)/\unicode[STIX]{x1D6E4}(x)$ is the digamma function. In view of Gauss’ formula on the values of $\unicode[STIX]{x1D713}(x)$ at rational numbers (see [7, 1.7.3, page 18–19]), Watson’s formula implies that, when $q=(a+b-1)/2$ , the value (1.1) is a $\overline{\mathbb{Q}}$ -linear combination of finitely many $\log \unicode[STIX]{x1D6FC}$ with $\unicode[STIX]{x1D6FC}\in \mathbb{Q}(\unicode[STIX]{x1D707}_{\infty })$ .

On the other hand, the recent works [3, 4] by the first and second authors show that the value (1.1) appears as Beilinson’s regulator on the motivic cohomology of “hypergeometric fibrations” (see Theorem 3.1), which is an algebro-geometric invariant related conjecturally with special values of $L$ -functions. Under a certain geometric assumption concerning the Hodge type, the regulator is written in terms of logarithms. Hence one obtains a sufficient condition for (1.1) to be written in terms of the logarithms of algebraic numbers, which is the main result of this paper Theorem 2.1. After the works mentioned above, the third author pointed out that the theorem can also be deduced from the study of Fermat surfaces. In this paper, we explain both methods, as each one has its advantage and would be useful for future studies.

The class of $(a,b,q)$ we consider is wider than Watson’s formula (see Section 5). For example, one shows

$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle 2\unicode[STIX]{x1D70B}\cdot _{3}F_{2}\left(\begin{array}{@{}c@{}}\frac{1}{6},\frac{5}{6},\frac{1}{4}\\ 1,\frac{5}{4}\end{array};1\right)\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad =\frac{12^{3/4}}{2}\cdot \log \left(\frac{3^{5/4}-3^{3/4}+\sqrt{2}}{3^{5/4}-3^{3/4}-\sqrt{2}}\right)-12^{3/4}\cdot \text{Cos}^{-1}\left(\frac{3^{5/4}+3^{3/4}}{2\sqrt{5+3\sqrt{3}}}\right).\nonumber\end{eqnarray}$$

Here appear, contrary to Watson’s formula, the logarithms of noncyclotomic numbers. See also the examples (5.1).

This paper is organized as follows. The main theorem is stated in Section 2. We give two proofs of the main theorem in Sections 3 and 4. The first proof, due to the first and second authors, uses the regulator of hypergeometric fibrations. The second one, due to the third author, uses the regulator of Fermat surfaces. In Section 5, open questions are discussed.

Notations

Throughout this paper, $\unicode[STIX]{x1D6E4}(s)$ and $B(s,t)$ denote the gamma and beta functions, respectively. The hypergeometric function $_{3}F_{2}$ is defined by

$$\begin{eqnarray}_{3}F_{2}{a,b,c\atop d,e};x=\mathop{\sum }_{n=0}^{\infty }\frac{(a)_{n}(b)_{n}(c)_{n}}{(d)_{n}(e)_{n}n!}x^{n},\quad (a)_{n}=\mathop{\prod }_{i=0}^{n-1}(a+i).\end{eqnarray}$$

It converges as $x\rightarrow 1^{-}$ if and only if $d+e-a-b-c>0$ . We write

$$\begin{eqnarray}\unicode[STIX]{x1D6E4}{a_{1},\ldots ,a_{m}\atop b_{1},\ldots ,b_{n}}=\frac{\mathop{\prod }_{i=1}^{m}\unicode[STIX]{x1D6E4}(a_{i})}{\mathop{\prod }_{j=1}^{n}\unicode[STIX]{x1D6E4}(b_{j})}.\end{eqnarray}$$

For a positive integer $N$ , $\unicode[STIX]{x1D707}_{N}\subset \overline{\mathbb{Q}}^{\times }$ denotes the group of $N$ th roots of unity.

2 Main theorem

For $x\in \mathbb{Q}$ , $\{x\}:=x-\lfloor x\rfloor$ denotes the fractional part. The map $\{-\}:\mathbb{Q}\rightarrow [0,1)$ factors through $\mathbb{Q}/\mathbb{Z}$ , which we denote by the same notation. Let $\hat{\mathbb{Z}}=\mathop{\varprojlim }\nolimits_{N}\mathbb{Z}/N\mathbb{Z}$ be the profinite completion and $\hat{\mathbb{Z}}^{\times }=\mathop{\varprojlim }\nolimits_{N}(\mathbb{Z}/N\mathbb{Z})^{\times }$ the group of units. The ring $\hat{\mathbb{Z}}$ acts naturally on the additive group $\mathbb{Q}/\mathbb{Z}$ , and induces an isomorphism $\hat{\mathbb{Z}}^{\times }\cong \text{Aut}(\mathbb{Q}/\mathbb{Z})$ .

Our main theorem is the following.

Theorem 2.1. Let $a,b,q\in \mathbb{Q}$ such that $a,b,q,q-a,q-b,q-a-b\not \in \mathbb{Z}$ . Assume that

(2.1) $$\begin{eqnarray}\{sq\}+\{s(q-a-b)\}=\{s(q-a)\}+\{s(q-b)\},\quad s\in \hat{\mathbb{Z}}^{\times }.\end{eqnarray}$$

Then we have

(2.2) $$\begin{eqnarray}B(a,b)\cdot _{3}F_{2}\left(\begin{array}{@{}c@{}}a,b,q\\ a+b,q+1\end{array};1\right)\in \overline{\mathbb{Q}}+\overline{\mathbb{Q}}\log \overline{\mathbb{Q}}^{\times }.\end{eqnarray}$$

Here, $\overline{\mathbb{Q}}+\overline{\mathbb{Q}}\log \overline{\mathbb{Q}}^{\times }$ denotes the $\overline{\mathbb{Q}}$ -linear subspace of $\mathbb{C}$ spanned by $1$ , $2\unicode[STIX]{x1D70B}i$ and $\log \unicode[STIX]{x1D6FC}$ for all $\unicode[STIX]{x1D6FC}\in \overline{\mathbb{Q}}^{\times }$ .

We note that the action of $\hat{\mathbb{Z}}$ on the subgroup $\frac{1}{N}\mathbb{Z}/\mathbb{Z}$ factors through the finite quotient $(\mathbb{Z}/N\mathbb{Z})^{\times }$ . Therefore, taking $N$ so that $a,b,q\in \frac{1}{N}\mathbb{Z}$ , the assumption (2.1) is verified by taking as $s$ the integers $1,2,\ldots ,N-1$ prime to $N$ . When $q=(a+b)/2$ , the assumption is satisfied since $\{x\}+\{1-x\}=1$ for any $x\in \mathbb{R}\setminus \mathbb{Z}$ . Since (2.1) is also written as

$$\begin{eqnarray}\{sq\}+\{s(q-a-b)\}+\{s(a-q)\}+\{s(b-q)\}=2,\quad s\in \hat{\mathbb{Z}}^{\times },\end{eqnarray}$$

the condition is symmetric in $\{q,q-a-b,a-q,b-q\}$ . As well as the assumption, the conclusion of the theorem depends only on the classes of $a$ , $b$ , $q$ mod $\mathbb{Z}$ . This is because of the functional equation of the beta function, for example, $(a+b)B(a+1,b)=aB(a,b)$ , and the contiguous relations among $_{3}F_{2}$ -functions (see [4, Section 7.3]). The latter is the reason why we need to consider the values in $\overline{\mathbb{Q}}+\overline{\mathbb{Q}}\log \overline{\mathbb{Q}}^{\times }$ , not only in $\overline{\mathbb{Q}}\log \overline{\mathbb{Q}}^{\times }$ .

By using Thomae’s formula (see [5, Chapter III, 3.2(1)]) repeatedly, we obtain other expressions of (1.1) as follows:

$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle B(a,b)\cdot _{3}F_{2}\left(\begin{array}{@{}c@{}}a,b,q\\ a+b,q+1\end{array};1\right)\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad =\frac{q}{ab}\cdot _{3}F_{2}\left(\begin{array}{@{}c@{}}1,1,a+b-q\\ a+1,b+1\end{array};1\right)\quad (q>0)\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad =\frac{1}{a}\cdot _{3}F_{2}{a,q+1-b,1\atop a+1,q+1};1\quad (b>0)\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad =\frac{1}{b}\cdot _{3}F_{2}{b,q+1-a,1\atop b+1,q+1};1\quad (a>0)\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad =\frac{B(a,b)}{aB(a,q+1-a)}\cdot _{3}F_{2}{a,a,a+b-q\atop a+1,a+b};1\quad (q+1-a>0)\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad =\frac{B(a,b)}{bB(b,q+1-b)}\cdot _{3}F_{2}{b,b,a+b-q\atop b+1,a+b};1\quad (q+1-b>0)\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad =\frac{B(a,b)}{qB(a+b-q,q)}\cdot _{3}F_{2}{q+1-a,q+1-b,q\atop q+1,q+1};1\quad (a+b-q>0),\nonumber\end{eqnarray}$$

where the positivity condition in each line is needed for the convergence.

3 First proof: hypergeometric fibrations

We derive Theorem 2.1 from the regulator formula in [4] for what we call hypergeometric fibrations. In Sections 3.1 and 3.2, we recall necessary materials from [4].

3.1 Hypergeometric fibrations

Let $X$ be a smooth projective variety over $\overline{\mathbb{Q}}$ and $f:X\rightarrow \mathbb{P}^{1}$ be a surjective morphism. Let $t$ be the coordinate of $\mathbb{A}^{1}\subset \mathbb{P}^{1}$ , $X_{t}$ be the general fiber of $f$ , and $H^{\ast }(X_{t},\mathbb{Q})$ denote the Betti cohomology of $X_{t}(\mathbb{C})$ . Let $R_{0}$ be a semisimple finite-dimensional $\mathbb{Q}$ -algebra and $e_{0}:R_{0}\rightarrow E_{0}$ be a projection onto a number field. We say that $f$ is a hypergeometric fibration with respect to $e_{0}$ if the following conditions are satisfied:

1. (a) $f$ is smooth over $\mathbb{P}^{1}\setminus \{0,1,\infty \}$ .

2. (b) After restricting to a nonempty Zariski open subset of $\mathbb{P}^{1}$ , there is a ring homomorphism $R_{0}\rightarrow \text{End}(R^{1}f_{\ast }\mathbb{Q})$ , such that

   $$\begin{eqnarray}\dim _{E_{0}}e_{0}H^{1}(X_{t},\mathbb{Q})=2,\end{eqnarray}$$
   where we put $e_{0}M=E_{0}\otimes _{R_{0},e_{0}}M$ for an $R_{0}$ -module $M$ .

3. (c) The local monodromy $T_{1}$ at $t=1$ on $e_{0}H^{1}(X_{t},\mathbb{Q})$ is unipotent, and

   $$\begin{eqnarray}\text{rank}(\log T_{1})=[E_{0}:\mathbb{Q}].\end{eqnarray}$$

For each embedding $\unicode[STIX]{x1D712}:E_{0}{\hookrightarrow}\overline{\mathbb{Q}}$ , let $(R^{1}f_{\ast }\overline{\mathbb{Q}})^{\unicode[STIX]{x1D712}}$ denote the $\unicode[STIX]{x1D712}$ -part which is by definition the subspace on which $g\in E_{0}$ acts as multiplication by $\unicode[STIX]{x1D712}(g)$ . Let $T_{p}$ be the local monodromy at $t=p\in \{0,\infty \}$ on the rank-two $\overline{\mathbb{Q}}$ -local system $(R^{1}f_{\ast }\overline{\mathbb{Q}})^{\unicode[STIX]{x1D712}}$ . Then the eigenvalues of $T_{0}$ (resp. $T_{\infty }$ ) are written as $e^{2\unicode[STIX]{x1D70B}i\unicode[STIX]{x1D6FC}_{1}^{\unicode[STIX]{x1D712}}}$ , $e^{2\unicode[STIX]{x1D70B}i\unicode[STIX]{x1D6FC}_{2}^{\unicode[STIX]{x1D712}}}$ (resp. $e^{2\unicode[STIX]{x1D70B}i\unicode[STIX]{x1D6FD}_{1}^{\unicode[STIX]{x1D712}}}$ , $e^{2\unicode[STIX]{x1D70B}i\unicode[STIX]{x1D6FD}_{2}^{\unicode[STIX]{x1D712}}}$ ), where $\unicode[STIX]{x1D6FC}_{i}^{\unicode[STIX]{x1D712}},\unicode[STIX]{x1D6FD}_{i}^{\unicode[STIX]{x1D712}}\in \mathbb{Q}$ .

3.2 Regulator formula

Now, take a positive integer $l$ , and let $\unicode[STIX]{x1D70B}:\mathbb{P}^{1}\rightarrow \mathbb{P}^{1}$ be the map given by $\unicode[STIX]{x1D70B}(t)=t^{l}$ . We consider the variation of Hodge–de Rham structures

$$\begin{eqnarray}\mathscr{M}^{(l)}:=\unicode[STIX]{x1D70B}_{\ast }\mathbb{Q}\otimes R^{1}f_{\ast }\mathbb{Q},\end{eqnarray}$$

and the cohomology groups

$$\begin{eqnarray}H^{(l)}:=H^{1}(\mathbb{P}^{1},j_{\ast }\mathscr{M}^{(l)}),\qquad M^{(l)}:=H^{1}(\mathbb{P}^{1}\setminus \{0,1,\infty \},\mathscr{M}^{(l)}),\end{eqnarray}$$

where $j:\mathbb{P}^{1}\setminus \{0,1,\infty \}{\hookrightarrow}\mathbb{P}^{1}$ is the immersion. Then, there is an exact sequence of mixed Hodge–de Rham structures (see [4, Section 4.2])

(3.1) $$\begin{eqnarray}0\longrightarrow H^{(l)}\longrightarrow M^{(l)}\longrightarrow C^{(l)}\longrightarrow 0,\end{eqnarray}$$

where

$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle C^{(l)}:=\bigoplus _{p=0,1,\infty }C_{p}^{(l)},\nonumber\\ \displaystyle & & \displaystyle \displaystyle C_{p}^{(l)}:=(R^{1}j_{\ast }\mathscr{M}^{(l)})_{p}\cong \text{Coker}[T_{p}-1:\mathscr{M}_{p}^{(l)}\rightarrow \mathscr{M}_{p}^{(l)}].\nonumber\end{eqnarray}$$

We recall that a Hodge–de Rham structure is a quadruple $H=(H_{B},H_{\text{dR}},F^{\bullet },\unicode[STIX]{x1D704})$ of finite-dimensional vector spaces over $\overline{\mathbb{Q}}$ , a descending filtration of $H_{\text{dR}}$ , and a comparison isomorphism $H_{B,\mathbb{C}}\overset{\cong }{\rightarrow }H_{\text{dR},\mathbb{C}}$ satisfying standard properties (see [4, Section 2.1]).

Since $\text{Aut}(\unicode[STIX]{x1D70B})=\unicode[STIX]{x1D707}_{l}$ , the group ring $R:=R_{0}[\unicode[STIX]{x1D707}_{l}]$ acts on the exact sequence (3.1). Let $e:R\rightarrow E$ be a projection onto a number field $E$ which extends $e_{0}:R_{0}\rightarrow E_{0}$ . For each embedding $\unicode[STIX]{x1D712}:E{\hookrightarrow}\overline{\mathbb{Q}}$ , define $k^{\unicode[STIX]{x1D712}}\in \mathbb{Z}/l\mathbb{Z}$ by $\unicode[STIX]{x1D712}(\unicode[STIX]{x1D701})=\unicode[STIX]{x1D701}^{k^{\unicode[STIX]{x1D712}}}$ for $\unicode[STIX]{x1D701}\in \unicode[STIX]{x1D707}_{l}$ , and put $\unicode[STIX]{x1D705}^{\unicode[STIX]{x1D712}}=k^{\unicode[STIX]{x1D712}}/l\in \mathbb{Q}/\mathbb{Z}$ . We write the restriction of $\unicode[STIX]{x1D712}$ to $E_{0}$ by the same letter and then $\unicode[STIX]{x1D6FC}_{i}^{\unicode[STIX]{x1D712}}$ , $\unicode[STIX]{x1D6FD}_{i}^{\unicode[STIX]{x1D712}}\in \mathbb{Q}/\mathbb{Z}$ are defined as above.

Now we suppose:

(3.2) $$\begin{eqnarray}\unicode[STIX]{x1D705}^{\unicode[STIX]{x1D712}}+\unicode[STIX]{x1D6FC}_{1}^{\unicode[STIX]{x1D712}},\qquad \unicode[STIX]{x1D705}^{\unicode[STIX]{x1D712}}+\unicode[STIX]{x1D6FC}_{2}^{\unicode[STIX]{x1D712}},\qquad \unicode[STIX]{x1D705}^{\unicode[STIX]{x1D712}}-\unicode[STIX]{x1D6FD}_{1}^{\unicode[STIX]{x1D712}},\qquad \unicode[STIX]{x1D705}^{\unicode[STIX]{x1D712}}-\unicode[STIX]{x1D6FD}_{2}^{\unicode[STIX]{x1D712}}~\not \in \mathbb{Z}.\end{eqnarray}$$

Then, it is not hard to show that $eC^{(l)}=eC_{1}^{(l)}$ , $\dim _{E}eC^{(l)}=\dim _{E}eH^{(l)}=1$ , and that $eC^{(l)}$ (resp. $eH^{(l)}$ ) is a pure Hodge structure of type $(2,2)$ (resp. of weight $2$ ) (see [4, Section 4.3]). By an identification $eC^{(l)}=E(-2)$ , we obtain from (3.1) an exact sequence

$$\begin{eqnarray}0\longrightarrow eH^{(l)}(2)\longrightarrow eM(2)\longrightarrow E\longrightarrow 0.\end{eqnarray}$$

Throughout the remaining of this section, write for brevity $H=eH^{(l)}$ . We have the connecting homomorphism

$$\begin{eqnarray}\unicode[STIX]{x1D70C}:E\longrightarrow \text{Ext}^{1}(\mathbb{Q},H(2))\end{eqnarray}$$

to the Yoneda extension group of mixed Hodge–de Rham structures. Denote by $H^{\unicode[STIX]{x1D712}}=(H_{B}^{\unicode[STIX]{x1D712}},H_{\text{dR}}^{\unicode[STIX]{x1D712}},F^{\bullet },\unicode[STIX]{x1D704})$ the $\unicode[STIX]{x1D712}$ -part of $H$ , that is, the subspace on which each $\unicode[STIX]{x1D70E}\in G$ acts as multiplication by $\unicode[STIX]{x1D712}(\unicode[STIX]{x1D70E})$ . The period $\text{Per}(H^{\unicode[STIX]{x1D712}})\in \mathbb{C}^{\times }/\overline{\mathbb{Q}}^{\times }$ in the sense of Deligne [6] is defined by $\unicode[STIX]{x1D704}(H_{\text{dR}}^{\unicode[STIX]{x1D712}})=\text{Per}(H^{\unicode[STIX]{x1D712}})H_{B}^{\unicode[STIX]{x1D712}}$ . Choose a $\overline{\mathbb{Q}}$ -basis $\unicode[STIX]{x1D702}$ of $(eH_{\text{dR}}^{(l)})^{\unicode[STIX]{x1D712}}$ , and let $i_{\unicode[STIX]{x1D702}}$ be the composition of the following maps:

$$\begin{eqnarray}\displaystyle \text{Ext}^{1}(\mathbb{Q},H(2)) & \overset{\cong }{\longrightarrow } & \displaystyle H_{\text{dR},\mathbb{C}}/\left(F^{2}H_{\text{dR}}+\unicode[STIX]{x1D704}(H_{B}(2))\right)\nonumber\\ \displaystyle & \longrightarrow & \displaystyle H_{\text{dR},\mathbb{C}}^{\unicode[STIX]{x1D712}}/\left(F^{2}H_{\text{dR}}^{\unicode[STIX]{x1D712}}+\unicode[STIX]{x1D704}(H_{B}^{\unicode[STIX]{x1D712}}(2))\right)\nonumber\\ \displaystyle & \overset{\cong }{\longrightarrow } & \displaystyle \mathbb{C}/\left(\overline{\mathbb{Q}}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D712}}+\overline{\mathbb{Q}}\text{Per}(H^{\overline{\unicode[STIX]{x1D712}}})\right),\nonumber\end{eqnarray}$$

where we put $\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D712}}=0$ or $1$ depending on whether $F^{2}H_{\text{dR}}^{\unicode[STIX]{x1D712}}=0$ or not, and $\overline{\unicode[STIX]{x1D712}}$ is the complex conjugate of $\unicode[STIX]{x1D712}$ . Here, the first map is the Carlson isomorphism, the second map is the projection to the $\unicode[STIX]{x1D712}$ -part, and the last isomorphism sends $\unicode[STIX]{x1D702}$ to $1$ . Note that $\text{Per}(H^{\unicode[STIX]{x1D712}})\cdot \text{Per}(H^{\overline{\unicode[STIX]{x1D712}}})\in (2\unicode[STIX]{x1D70B}i)^{2}\overline{\mathbb{Q}}$ . Put $\unicode[STIX]{x1D70C}^{\unicode[STIX]{x1D712}}=i_{\unicode[STIX]{x1D702}}\circ \unicode[STIX]{x1D70C}$ .

Now, our regulator formula is the following.

Theorem 3.1. [4, Theorem 4.7]

Let the notation and assumption be as above. Then there exist $c_{1},c_{2}\in \overline{\mathbb{Q}}$ , $c_{2}\neq 0$ , such that

(3.3) $$\begin{eqnarray}\unicode[STIX]{x1D70C}^{\overline{\unicode[STIX]{x1D712}}}(1)=c_{1}+c_{2}B(\unicode[STIX]{x1D6FC}_{1}^{\unicode[STIX]{x1D712}}+\unicode[STIX]{x1D6FD}_{1}^{\unicode[STIX]{x1D712}},\unicode[STIX]{x1D6FC}_{1}^{\unicode[STIX]{x1D712}}+\unicode[STIX]{x1D6FD}_{2}^{\unicode[STIX]{x1D712}})~_{3}F_{2}\left(\begin{array}{@{}c@{}}\unicode[STIX]{x1D6FC}_{1}^{\unicode[STIX]{x1D712}}+\unicode[STIX]{x1D6FD}_{1}^{\unicode[STIX]{x1D712}},\unicode[STIX]{x1D6FC}_{1}^{\unicode[STIX]{x1D712}}+\unicode[STIX]{x1D6FD}_{2}^{\unicode[STIX]{x1D712}},\unicode[STIX]{x1D705}^{\unicode[STIX]{x1D712}}+\unicode[STIX]{x1D6FC}_{1}^{\unicode[STIX]{x1D712}}\\ 2\unicode[STIX]{x1D6FC}_{1}^{\unicode[STIX]{x1D712}}+\unicode[STIX]{x1D6FD}_{1}^{\unicode[STIX]{x1D712}}+\unicode[STIX]{x1D6FD}_{2}^{\unicode[STIX]{x1D712}},\unicode[STIX]{x1D705}^{\unicode[STIX]{x1D712}}+\unicode[STIX]{x1D6FC}_{1}^{\unicode[STIX]{x1D712}}+1\end{array};1\right)\end{eqnarray}$$

in $\mathbb{C}/(\overline{\mathbb{Q}}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D712}}+\overline{\mathbb{Q}}\text{Per}(H^{\unicode[STIX]{x1D712}}))$ .

The period formula [4, Theorem 4.5] (see also [3, Theorem 5.4]) reads

$$\begin{eqnarray}\text{Per}(H^{\unicode[STIX]{x1D712}}){\sim}_{\overline{\mathbb{Q}}^{\times }}2\unicode[STIX]{x1D70B}i\cdot \unicode[STIX]{x1D6E4}{\unicode[STIX]{x1D705}^{\unicode[STIX]{x1D712}}+\unicode[STIX]{x1D6FC}_{1}^{\unicode[STIX]{x1D712}},\unicode[STIX]{x1D705}^{\unicode[STIX]{x1D712}}+\unicode[STIX]{x1D6FC}_{2}^{\unicode[STIX]{x1D712}}\atop \unicode[STIX]{x1D705}^{\unicode[STIX]{x1D712}}-\unicode[STIX]{x1D6FD}_{1}^{\unicode[STIX]{x1D712}},\unicode[STIX]{x1D705}^{\unicode[STIX]{x1D712}}-\unicode[STIX]{x1D6FD}_{2}^{\unicode[STIX]{x1D712}}}.\end{eqnarray}$$

Note that the second term of the right-hand side of (3.3) is written as $cB(a,b)\cdot _{3}F_{2}\!{a,b,q\atop a+b,q+1};1\!$ by letting

$$\begin{eqnarray}a=\unicode[STIX]{x1D6FC}_{1}^{\unicode[STIX]{x1D712}}+\unicode[STIX]{x1D6FD}_{1}^{\unicode[STIX]{x1D712}},\qquad b=\unicode[STIX]{x1D6FC}_{1}^{\unicode[STIX]{x1D712}}+\unicode[STIX]{x1D6FD}_{2}^{\unicode[STIX]{x1D712}},\qquad q=\unicode[STIX]{x1D705}^{\unicode[STIX]{x1D712}}+\unicode[STIX]{x1D6FC}_{1}^{\unicode[STIX]{x1D712}}.\end{eqnarray}$$

Then, since $\unicode[STIX]{x1D6FC}_{1}^{\unicode[STIX]{x1D712}}+\unicode[STIX]{x1D6FC}_{2}^{\unicode[STIX]{x1D712}}+\unicode[STIX]{x1D6FD}_{1}^{\unicode[STIX]{x1D712}}+\unicode[STIX]{x1D6FD}_{2}^{\unicode[STIX]{x1D712}}\in \mathbb{Z}$ , we have

$$\begin{eqnarray}\unicode[STIX]{x1D6E4}{\unicode[STIX]{x1D705}^{\unicode[STIX]{x1D712}}+\unicode[STIX]{x1D6FC}_{1}^{\unicode[STIX]{x1D712}},\unicode[STIX]{x1D705}^{\unicode[STIX]{x1D712}}+\unicode[STIX]{x1D6FC}_{2}^{\unicode[STIX]{x1D712}}\atop \unicode[STIX]{x1D705}^{\unicode[STIX]{x1D712}}-\unicode[STIX]{x1D6FD}_{1}^{\unicode[STIX]{x1D712}},\unicode[STIX]{x1D705}^{\unicode[STIX]{x1D712}}-\unicode[STIX]{x1D6FD}_{2}^{\unicode[STIX]{x1D712}}}{\sim}_{\mathbb{Q}^{\times }}\unicode[STIX]{x1D6E4}{q,q-a-b\atop q-a,q-b}.\end{eqnarray}$$

By Koblitz–Ogus [6, page 344, Theorem], the condition (2.1) implies that

$$\begin{eqnarray}\unicode[STIX]{x1D6E4}{sq,s(q-a-b)\atop s(q-a),s(q-b)}\in \overline{\mathbb{Q}}^{\times }\end{eqnarray}$$

for any $s\in \hat{\mathbb{Z}}^{\times }$ , hence $\text{Per}(H^{\unicode[STIX]{x1D712}})\in \overline{\mathbb{Q}}(2\unicode[STIX]{x1D70B}i)$ for any $\unicode[STIX]{x1D712}$ .

3.3 Algebraic cycles

The connecting homomorphism $\unicode[STIX]{x1D70C}^{\unicode[STIX]{x1D712}}$ is related with Beilinson’s regulator map from the motivic cohomology group. Consider the diagram

where $X_{l}:=X\times _{\mathbb{P}^{1},f}\mathbb{P}^{1}$ and $i$ is the desingularization. Put $D^{(l)}:=$ $(\unicode[STIX]{x1D70B}\circ f^{(l)})^{-1}(1)$ , a union of $l$ copies of the fiber $f^{-1}(1)$ . There are canonical isomorphisms

$$\begin{eqnarray}\displaystyle C_{1}^{(l)} & \cong & \displaystyle H_{1}(D^{(l)},\mathbb{Q})(-2),\nonumber\\ \displaystyle H^{(l)} & \cong & \displaystyle \text{Ker}[H^{2}(X^{(l)},\mathbb{Q})/N_{\text{fib}}^{1}(X^{(l)})\rightarrow H^{2}(X_{t}^{(l)},\mathbb{Q})],\nonumber\end{eqnarray}$$

where $N_{\text{fib}}^{1}(X^{(l)})\subset$ denotes the classes of fibral divisors for $f^{(l)}$ . Then we have a commutative diagram [4, Proposition 4.8]

where the vertical maps are the regulators, with $\text{reg}_{D^{(l)}}$ being surjective, and the lower horizontal map is the connecting homomorphism induced by (3.1).

Proposition 3.2. Suppose that $H=eH^{(l)}$ is a Hodge structure of type $(1,1)$ . Then we have $\text{Im}(\unicode[STIX]{x1D70C}^{\unicode[STIX]{x1D712}})\subset \overline{\mathbb{Q}}\log \overline{\mathbb{Q}}^{\times }/\overline{\mathbb{Q}}\cdot 2\unicode[STIX]{x1D70B}i$ for any embedding $\unicode[STIX]{x1D712}:E{\hookrightarrow}\overline{\mathbb{Q}}$ .

Proof. Recall that the target of $\unicode[STIX]{x1D70C}^{\unicode[STIX]{x1D712}}$ is $\mathbb{C}/\overline{\mathbb{Q}}\cdot 2\unicode[STIX]{x1D70B}i$ by the assumption and the remark after Theorem 3.1. Since $\text{reg}_{D^{(l)}}$ is surjective, it suffices to consider the image of $H_{\mathscr{M},D^{(l)}}^{3}(X^{(l)},\mathbb{Q}(2))$ under $\unicode[STIX]{x1D70C}^{\unicode[STIX]{x1D712}}$ .

Let $N^{r}(X^{(l)})\subset H^{2r}(X^{(l)},\mathbb{Q})$ be the subspace generated by algebraic cycles of codimension $r$ . Note that it is generated by cycles defined over $\overline{\mathbb{Q}}$ . By the assumption and Lefschetz’s theorem (i.e., the Hodge conjecture for $H^{2}$ ), we have $eH^{(l)}\subset N^{1}(X^{(l)})$ . The intersection pairing $N^{1}(X^{(l)})\otimes N^{\dim X-1}(X^{(l)})\rightarrow \mathbb{Q}$ is nondegenerate by the nondegeneracy of the pairing on the Néron–Severi group. This implies that there is a smooth projective curve $C$ (not necessarily connected) and a morphism $C\rightarrow X^{(l)}$ such that the image of $C$ intersects properly with $D^{(l)}$ , the pull-back $H^{2}(X^{(l)})\rightarrow H^{2}(C)$ annihilates $N_{\text{fib}}^{1}(X^{(l)})$ , and the composition

$$\begin{eqnarray}H\rightarrow H^{2}(X^{(l)})/N_{\text{fib}}^{1}(X^{(l)},\mathbb{Q})\rightarrow H^{2}(C,\mathbb{Q})\end{eqnarray}$$

is injective. Then we have a commutative diagram

where the composite of the lower horizontal maps is injective.

Since $H^{2}(C,\mathbb{Q}(2))\cong \bigoplus _{C^{(0)}}\mathbb{Q}(1)$ , where $C^{(0)}$ denotes the set of connected components of $C$ , the map $\text{reg}_{D^{(l)}\cap C}$ is canonically identified with the logarithm map

$$\begin{eqnarray}\bigoplus _{D^{(l)}\cap C}\mathbb{Q}\otimes _{\mathbb{Z}}\overline{\mathbb{Q}}^{\times }\longrightarrow \bigoplus _{C^{(0)}}\mathbb{C}/\mathbb{Q}\cdot 2\unicode[STIX]{x1D70B}i.\end{eqnarray}$$

Since $H\cong \mathbb{Q}(-1)^{\oplus [E:\mathbb{Q}]}$ , we have $\text{Ext}^{1}(\mathbb{Q},H(2))\cong (\mathbb{C}/\mathbb{Q}\cdot 2\unicode[STIX]{x1D70B}i)^{\oplus [E:\mathbb{Q}]}$ , and this injects to $\bigoplus _{C^{(0)}}\mathbb{C}/\mathbb{Q}\cdot 2\unicode[STIX]{x1D70B}i$ . Hence, taking the $\unicode[STIX]{x1D712}$ -part, the lemma follows.◻

Proposition 3.3. Let the notation and assumption be as in Theorem 3.1. Then $H=eH^{(l)}$ is a Hodge structure of type $(1,1)$ if and only if

(3.4) $$\begin{eqnarray}\left\{\unicode[STIX]{x1D705}^{\unicode[STIX]{x1D712}}+\unicode[STIX]{x1D6FC}_{1}^{\unicode[STIX]{x1D712}}\right\}+\left\{\unicode[STIX]{x1D705}^{\unicode[STIX]{x1D712}}+\unicode[STIX]{x1D6FC}_{2}^{\unicode[STIX]{x1D712}}\right\}=\left\{\unicode[STIX]{x1D705}^{\unicode[STIX]{x1D712}}-\unicode[STIX]{x1D6FD}_{1}^{\unicode[STIX]{x1D712}}\right\}+\left\{\unicode[STIX]{x1D705}^{\unicode[STIX]{x1D712}}-\unicode[STIX]{x1D6FD}_{2}^{\unicode[STIX]{x1D712}}\right\}\end{eqnarray}$$

for any $\unicode[STIX]{x1D712}$ .

Proof. The first assertion follows from an explicit formula [2] of the Hodge type of $H$ , which is proven using the Riemann–Roch–Hirzebruch theorem. For the hypergeometric fibration of Gauss type, which will be used below to prove Theorem 2.1, this is computed in [3, Theorem 5.4] (the situation in [3] is more restricted but the same argument works in general). ◻

3.4 Hypergeometric fibration of Gauss type

We finish the proof of Theorem 2.1. In view of Theorem 3.1, Propositions 3.2 and 3.3, it suffices to find a fibration $f$ such that

$$\begin{eqnarray}a\equiv \unicode[STIX]{x1D6FC}_{1}^{\unicode[STIX]{x1D712}}+\unicode[STIX]{x1D6FD}_{1}^{\unicode[STIX]{x1D712}},\qquad b\equiv \unicode[STIX]{x1D6FC}_{1}^{\unicode[STIX]{x1D712}}+\unicode[STIX]{x1D6FD}_{2}^{\unicode[STIX]{x1D712}},\qquad q\equiv \unicode[STIX]{x1D6FC}_{1}^{\unicode[STIX]{x1D712}}+\unicode[STIX]{x1D705}^{\unicode[STIX]{x1D712}}\hspace{0.6em}({\rm mod}\hspace{0.2em}\mathbb{Z})\end{eqnarray}$$

for some $\unicode[STIX]{x1D712}$ , and the condition (3.4) is satisfied for any $\unicode[STIX]{x1D712}$ . Note that the condition (2.1) implies (3.4) for any $\unicode[STIX]{x1D712}$ . The nonintegrality condition of Theorem 2.1 is equivalent to $\unicode[STIX]{x1D6FC}_{i}^{\unicode[STIX]{x1D712}}+\unicode[STIX]{x1D6FD}_{j}^{\unicode[STIX]{x1D712}}\not \in \mathbb{Z}$ ( $i,j\in \{1,2\}$ ) and (3.2).

We may and do suppose $0<a,b,q<1$ . Let $N$ be the smallest positive integer such that $A:=Na$ , $B:=Nb\in \mathbb{Z}$ . Consider the hypergeometric fibration of Gauss type

$$\begin{eqnarray}y^{N}=x^{A}(1-x)^{B}(1-tx)^{N-B}.\end{eqnarray}$$

This is a principal example of hypergeometric fibrations studied in detail in [3] and in [4, Section 3.2]. Let $\unicode[STIX]{x1D701}_{N}\in \unicode[STIX]{x1D707}_{N}$ be a primitive $N$ th root of unity. The group ring $R_{0}:=\mathbb{Q}[\unicode[STIX]{x1D707}_{N}]$ acts on $X$ by letting $\unicode[STIX]{x1D701}_{N}$ act by $y\mapsto \unicode[STIX]{x1D701}_{N}^{-1}y$ . Let $e_{0}:R_{0}\rightarrow E_{0}=\mathbb{Q}(\unicode[STIX]{x1D707}_{N})$ be the natural projection. For each embedding $\unicode[STIX]{x1D712}:E_{0}{\hookrightarrow}\mathbb{C}$ , such that $\unicode[STIX]{x1D712}(\unicode[STIX]{x1D701}_{N})=\unicode[STIX]{x1D701}_{N}^{s}$ , we have

$$\begin{eqnarray}\unicode[STIX]{x1D6FC}_{1}^{\unicode[STIX]{x1D712}}=0,\qquad \unicode[STIX]{x1D6FC}_{2}^{\unicode[STIX]{x1D712}}=\{1-\unicode[STIX]{x1D6FD}_{1}^{\unicode[STIX]{x1D712}}-\unicode[STIX]{x1D6FD}_{2}^{\unicode[STIX]{x1D712}}\},\qquad \unicode[STIX]{x1D6FD}_{1}^{\unicode[STIX]{x1D712}}=\left\{\frac{sA}{N}\right\},\qquad \unicode[STIX]{x1D6FD}_{2}^{\unicode[STIX]{x1D712}}=\left\{\frac{sB}{N}\right\}.\end{eqnarray}$$

Hence we have $a=\unicode[STIX]{x1D6FC}_{1}^{\unicode[STIX]{x1D712}}+\unicode[STIX]{x1D6FD}_{1}^{\unicode[STIX]{x1D712}}$ , $b=\unicode[STIX]{x1D6FC}_{1}^{\unicode[STIX]{x1D712}}+\unicode[STIX]{x1D6FD}_{2}^{\unicode[STIX]{x1D712}}$ for the trivial embedding $\unicode[STIX]{x1D712}$ (i.e., $s=1$ ). Let $l$ be the smallest positive integer such that $Q:=lq\in \mathbb{Z}$ and let $e:R=R_{0}[\unicode[STIX]{x1D707}_{l}]\rightarrow E=E_{0}(\unicode[STIX]{x1D707}_{l})$ be an extension of $e_{0}$ given by $\unicode[STIX]{x1D701}_{l}\mapsto \unicode[STIX]{x1D701}_{l}^{Q}$ . Then, for the trivial embedding $\unicode[STIX]{x1D712}$ of $E$ , we have $q=\unicode[STIX]{x1D705}^{\unicode[STIX]{x1D712}}$ . Hence this fibration has the desired property and Theorem 2.1 is proved.

4 Second proof: Fermat surfaces

We give the second proof of Theorem 2.1, by studying extensions of mixed Hodge–de Rham structures coming from Fermat surfaces. Throughout this section, we assume $a,b,q\in \mathbb{Q}$ and $a,b,q,q-a,q-b,q-a-b\not \in \mathbb{Z}$ .

4.1 Integral representation

Let us begin with the integral representation of $_{3}F_{2}$ -function (cf. [9]):

$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle B(\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FD}_{1}-\unicode[STIX]{x1D6FC}_{1})B(\unicode[STIX]{x1D6FC}_{2},\unicode[STIX]{x1D6FD}_{2}-\unicode[STIX]{x1D6FC}_{2})_{3}F_{2}\left(\begin{array}{@{}c@{}}\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2},\unicode[STIX]{x1D6FC}_{3}\\ \unicode[STIX]{x1D6FD}_{1},\unicode[STIX]{x1D6FD}_{2}\end{array};z\right)\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad =\int _{0}^{1}\!\int _{0}^{1}\!t_{1}^{\unicode[STIX]{x1D6FC}_{1}-1}t_{2}^{\unicode[STIX]{x1D6FC}_{2}-1}(1-t_{1})^{\unicode[STIX]{x1D6FD}_{1}-\unicode[STIX]{x1D6FC}_{1}-1}(1-t_{2})^{\unicode[STIX]{x1D6FD}_{2}-\unicode[STIX]{x1D6FC}_{2}-1}(1-zt_{1}t_{2})^{-\unicode[STIX]{x1D6FC}_{3}}\,dt_{1}\,dt_{2}.\nonumber\end{eqnarray}$$

Set $(\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2},\unicode[STIX]{x1D6FC}_{3},\unicode[STIX]{x1D6FD}_{1},\unicode[STIX]{x1D6FD}_{2})=(a,q,b,a+b,q+1)$ . By the change of variables $x=t_{1}$ , $y=(1-t_{1})/(1-zt_{1}t_{2})$ , we obtain

$$\begin{eqnarray}B(a,b)_{3}F_{2}\left(\begin{array}{@{}c@{}}a,q,b\\ a+b,q+1\end{array};z\right)=qz^{-q}\int _{E_{z}}x^{a-q-1}y^{b-q-1}(x+y-1)^{q-1}\,dx\,dy,\end{eqnarray}$$

where $E_{z}$ is the domain in the $xy$ -plane corresponding to $\{(t_{1},t_{2})\mid 0\leqslant t_{1},t_{2}\leqslant 1\}$ . Suppose that $a,b,q\in \frac{1}{N}\mathbb{Z}$ . We take new variables $u,v,w$ such that

$$\begin{eqnarray}u^{N}=x,\qquad v^{N}=y,\qquad w^{N}=u^{N}+v^{N}-1=x+y-1.\end{eqnarray}$$

Then we have

$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle B(a,b)_{3}F_{2}\left(\begin{array}{@{}c@{}}a,q,b\\ a+b,q+1\end{array};z\right)\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad =N^{2}qz^{-q}\int _{\unicode[STIX]{x1D6E5}_{z}}u^{N(a-q)-1}v^{N(b-q)-1}w^{Nq-N}\,du\,dv,\nonumber\end{eqnarray}$$

where $\unicode[STIX]{x1D6E5}_{z}$ is an arbitrary domain in the $uv$ -plane which corresponds to $E_{z}$ . Substitute $z=1$ and choose the domain as

(4.1) $$\begin{eqnarray}\unicode[STIX]{x1D6E5}=\unicode[STIX]{x1D6E5}_{1}:=\left\{(u,v)\in \mathbb{R}^{2}\mid 0\leqslant u,v\leqslant 1,~1\leqslant u^{N}+v^{N}\right\}.\end{eqnarray}$$

Then we obtain

(4.2) $$\begin{eqnarray}B(a,b)_{3}F_{2}\left(\begin{array}{@{}c@{}}a,q,b\\ a+b,q+1\end{array};1\right)=N^{2}q\int _{\unicode[STIX]{x1D6E5}}u^{N(a-q)-1}v^{N(b-q)-1}w^{Nq-N}\,du\,dv.\end{eqnarray}$$

We shall give a motivic interpretation of this integral.

4.2 Fermat surface

The differential form

$$\begin{eqnarray}\unicode[STIX]{x1D714}:=u^{N(a-q)-1}v^{N(b-q)-1}w^{Nq-N}\,du\,dv\end{eqnarray}$$

defines a de Rham cohomology class $\unicode[STIX]{x1D702}\in H_{\text{dR}}^{2}(S)$ of the Fermat surface over  $\overline{\mathbb{Q}}$

$$\begin{eqnarray}S:u^{N}+v^{N}-1=w^{N}.\end{eqnarray}$$

Let the group $G:=\unicode[STIX]{x1D707}_{N}^{3}$ act on $S$ by $\unicode[STIX]{x1D70E}(u,v,w)=(\unicode[STIX]{x1D701}_{1}u,\unicode[STIX]{x1D701}_{2}v,\unicode[STIX]{x1D701}_{3}w)$ for $\unicode[STIX]{x1D70E}=(\unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{2},\unicode[STIX]{x1D701}_{3})\in G$ . This time, we first fix a $\mathbb{Q}$ -algebra homomorphism

$$\begin{eqnarray}\unicode[STIX]{x1D712}:\mathbb{Q}[G]\rightarrow \overline{\mathbb{Q}},\qquad \unicode[STIX]{x1D712}(\unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{2},\unicode[STIX]{x1D701}_{3})=\unicode[STIX]{x1D701}_{1}^{N(a-q)}\unicode[STIX]{x1D701}_{2}^{N(b-q)}\unicode[STIX]{x1D701}_{3}^{Nq}.\end{eqnarray}$$

Let $E$ be the coimage of $\unicode[STIX]{x1D712}$ , and $e\in \mathbb{Q}[G]$ be the corresponding idempotent, that is, $e^{2}=e$ and $e\mathbb{Q}[G]\cong E$ . Let $D$ be the union of curves on $S$ defined by

$$\begin{eqnarray}(u^{N}-1)(v^{N}-1)w=0,\end{eqnarray}$$

which is stable under the $G$ -action.

Lemma 4.1. We have

$$\begin{eqnarray}\dim _{E}eH_{1}(D,\mathbb{Q})=1,\qquad \dim _{E}eH_{2}(D,\mathbb{Q})=0,\qquad \dim _{E}eH_{2}(S,\mathbb{Q})=1.\end{eqnarray}$$

Moreover, $eH_{1}(D,\mathbb{Q})$ is a Hodge–de Rham structure of type $(0,0)$ .

Proof. The former statement is an easy exercise. To see the latter, let $\unicode[STIX]{x1D70B}:\widetilde{D}\rightarrow D$ be the normalization, $\unicode[STIX]{x1D6F4}$ be the set of singular points of $D$ and put $\widetilde{\unicode[STIX]{x1D6F4}}=\unicode[STIX]{x1D70B}^{-1}(\unicode[STIX]{x1D6F4})$ . Then there is an exact sequence

$$\begin{eqnarray}H^{0}(\widetilde{D})\longrightarrow \mathbb{Q}_{\widetilde{\unicode[STIX]{x1D6F4}}}/\mathbb{Q}_{\unicode[STIX]{x1D6F4}}\longrightarrow H^{1}(D)\longrightarrow H^{1}(\widetilde{D})\longrightarrow 0,\end{eqnarray}$$

where $\mathbb{Q}_{\unicode[STIX]{x1D6F4}}:=\text{Maps}(\unicode[STIX]{x1D6F4},\mathbb{Q})$ . This remains exact after applying $e$ . Since $D$ is a union of rational curves and the Fermat curve of degree $N$ , and $(1,1,\unicode[STIX]{x1D701}_{3})$ acts trivially on the latter, we have $eH^{1}(\widetilde{D})=0$ by the assumption $q\not \in \mathbb{Z}$ . Hence the assertion follows.◻

Put $H=eH_{2}(S)$ , a Hodge–de Rham structure of type $(0,-2)$ , $(-1,-1)$ , $(-2,0)$ .

Proposition 4.2. The Hodge type of $H$ is $(-1,-1)$ if and only if

$$\begin{eqnarray}\{sq\}+\{s(q-a-b)\}=\{s(q-a)\}+\{s(q-b)\}\end{eqnarray}$$

holds for any $s\in \hat{\mathbb{Z}}^{\times }$ .

Proof. As is well-known, the cohomology $eH^{2}(S,\mathbb{Q})$ is generated by the classes of rational $2$ -forms

$$\begin{eqnarray}\unicode[STIX]{x1D702}_{s}:=u^{N\{s(a-q)\}-1}v^{N\{s(b-q)\}-1}w^{N\{sq\}-N}\,du\,dv,\quad s\in (\mathbb{Z}/N\mathbb{Z})^{\times },\end{eqnarray}$$

and $\unicode[STIX]{x1D702}_{s}$ belongs to the Hodge $(p_{s},2-p_{s})$ -component, where

$$\begin{eqnarray}p_{s}:=\{s(q-a)\}+\{s(q-b)\}+\{-sq\}-\{s(q-a-b)\}.\end{eqnarray}$$

Since $eH_{2}(S,\mathbb{Q})$ has the Hodge type $(-1,-1)$ if and only if $eH^{2}(S,\mathbb{Q})$ has the Hodge type $(1,1)$ , the assertion follows.◻

4.3 Extension of mixed Hodge–de Rham structures

By Lemma 4.1, we have an exact sequence

$$\begin{eqnarray}0\longrightarrow H\longrightarrow eH_{2}(S,D;\mathbb{Q})\overset{\unicode[STIX]{x2202}}{\longrightarrow }eH_{1}(D,\mathbb{Q})\longrightarrow 0\end{eqnarray}$$

of mixed Hodge–de Rham structures. As before, we have the connecting map

$$\begin{eqnarray}\unicode[STIX]{x1D70C}:eH_{1}^{B}(D,\mathbb{Q})\longrightarrow \text{Ext}^{1}(\mathbb{Q},H)\end{eqnarray}$$

to the Yoneda extension group of mixed Hodge–de Rham structures. Regarding $\unicode[STIX]{x1D702}\in H_{\text{dR}}^{2}(S)^{\unicode[STIX]{x1D712}}$ as an element of $H_{2}^{\text{dR}}(S)^{\unicode[STIX]{x1D712}}$ by the Poincaré duality, we obtain as before a map

$$\begin{eqnarray}i_{\unicode[STIX]{x1D702}}:\text{Ext}^{1}(\mathbb{Q},H)\longrightarrow \mathbb{C}/\left(\overline{\mathbb{Q}}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D712}}+\overline{\mathbb{Q}}\text{Per}(H^{\overline{\unicode[STIX]{x1D712}}})\right)\!,\end{eqnarray}$$

where we put $\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D712}}=0$ or $1$ depending on whether $F^{0}H_{\text{dR}}^{\unicode[STIX]{x1D712}}=0$ or not, and $\overline{\unicode[STIX]{x1D712}}$ is the complex conjugate of $\unicode[STIX]{x1D712}$ . One easily sees that the cycle $\unicode[STIX]{x1D6E5}$ given in (4.1) defines a homology cycle in $H_{2}^{B}(S,D;\mathbb{Z})$ . Let $\unicode[STIX]{x1D6FF}:=\unicode[STIX]{x2202}(e\unicode[STIX]{x1D6E5})\in eH_{1}^{B}(D,\mathbb{Q})$ be the boundary.

Proposition 4.3. Write $\unicode[STIX]{x1D70C}^{\unicode[STIX]{x1D712}}=i_{\unicode[STIX]{x1D702}}\circ \unicode[STIX]{x1D70C}$ . Then we have

$$\begin{eqnarray}\unicode[STIX]{x1D70C}^{\unicode[STIX]{x1D712}}(\unicode[STIX]{x1D6FF})=c+\frac{1}{N^{2}q}B(a,b)\cdot _{3}F_{2}\left(\begin{array}{@{}c@{}}a,b,q\\ a+b,q+1\end{array};1\right)\end{eqnarray}$$

for some $c\in \overline{\mathbb{Q}}$ in $\mathbb{C}/(\overline{\mathbb{Q}}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D712}}+\overline{\mathbb{Q}}\text{Per}(H^{\overline{\unicode[STIX]{x1D712}}}))$ .

Proof. Consider the exact sequence

$$\begin{eqnarray}0\longrightarrow eH_{\text{dR}}^{1}(D)\overset{h}{\longrightarrow }eH_{\text{dR}}^{2}(S,D)\longrightarrow eH_{\text{dR}}^{2}(S)\longrightarrow 0.\end{eqnarray}$$

Let $\widetilde{\unicode[STIX]{x1D702}}\in eH_{\text{dR}}^{2}(S,D)^{\unicode[STIX]{x1D712}}$ be the unique lifting of $\unicode[STIX]{x1D702}\in eH_{\text{dR}}^{2}(S)^{\unicode[STIX]{x1D712}}$ contained in $F^{1}$ .

Let

$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \langle \,,\rangle :eH_{2}^{B}(S,D;\mathbb{Q})\otimes eH_{\text{dR}}^{2}(S,D)\rightarrow \mathbb{C},\nonumber\\ \displaystyle & & \displaystyle \displaystyle \langle \,,\rangle :eH_{1}^{B}(D,\mathbb{Q})\otimes eH_{\text{dR}}^{1}(D)\rightarrow \mathbb{C}\nonumber\end{eqnarray}$$

be the natural pairings. By Lemma 4.1, the latter maps to $\overline{\mathbb{Q}}$ . As is easily seen from the definition, we have $\unicode[STIX]{x1D70C}^{\unicode[STIX]{x1D712}}(\unicode[STIX]{x1D6FF})=\langle e\unicode[STIX]{x1D6E5},\widetilde{\unicode[STIX]{x1D702}}\rangle =\langle \unicode[STIX]{x1D6E5},\widetilde{\unicode[STIX]{x1D702}}\rangle$ in $\mathbb{C}/(\overline{\mathbb{Q}}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D712}}+\overline{\mathbb{Q}}\text{Per}(H^{\overline{\unicode[STIX]{x1D712}}}))$ . For an arbitrary lifting $\widetilde{\unicode[STIX]{x1D702}}^{\prime }\in eH_{\text{dR}}^{2}(S,D)^{\unicode[STIX]{x1D712}}$ of $\unicode[STIX]{x1D702}$ , there exists $\unicode[STIX]{x1D709}\in eH_{\text{dR}}^{1}(D)$ such that $h(\unicode[STIX]{x1D709})=\widetilde{\unicode[STIX]{x1D702}}-\widetilde{\unicode[STIX]{x1D702}}^{\prime }$ . Then we have $c:=\langle \unicode[STIX]{x1D6E5},\widetilde{\unicode[STIX]{x1D702}}-\widetilde{\unicode[STIX]{x1D702}}^{\prime }\rangle =\langle \unicode[STIX]{x1D6FF},\unicode[STIX]{x1D709}\rangle \in \overline{\mathbb{Q}}$ . As $\widetilde{\unicode[STIX]{x1D702}}^{\prime }$ , we can choose the one represented by the Čech cocycle

$$\begin{eqnarray}(0,0,\unicode[STIX]{x1D714})\in \mathbb{C}_{\widetilde{\unicode[STIX]{x1D6F4}}}/\mathbb{C}_{\unicode[STIX]{x1D6F4}}\oplus \mathscr{A}^{1}(\widetilde{D})\oplus \mathscr{A}^{2}(S),\end{eqnarray}$$

where $\mathscr{A}^{q}(M)$ denotes the space of smooth differential $q$ -forms on $M$ with $\mathbb{C}$ -coefficients (see [3, Section A.1]). Then, by [3, Theorem A.3], we have $\langle \unicode[STIX]{x1D6E5},\widetilde{\unicode[STIX]{x1D702}}^{\prime }\rangle =\int _{\unicode[STIX]{x1D6E5}}\unicode[STIX]{x1D714}$ in $\mathbb{C}/(\overline{\mathbb{Q}}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D712}}+\overline{\mathbb{Q}}\text{Per}(H^{\overline{\unicode[STIX]{x1D712}}}))$ . Hence the proposition follows by (4.2).◻

Now, by applying a similar argument as in Proposition 3.2, Theorem 2.1 follows from Propositions 4.2 and 4.3.

5 Open problems

First, contrary to Wilson’s formula, our result does not generally give an explicit formula expressing the value of $_{3}F_{2}$ in terms of logarithms.

Problem 5.1. Give an explicit description of (2.2) in terms of logarithms.

In the study of Hodge cycles on Fermat surfaces, Shioda [8] gave a conjecture which determines those $(a,b,q)$ satisfying the condition (2.1), and it was proved by Aoki [1]. Up to permutations of $\{q,q-a-b,a-q,b-q\}$ , those are (modulo $\mathbb{Z}^{3}$ ):

$$\begin{eqnarray}(a,b,q)=\left\{\begin{array}{@{}l@{}}\left(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\displaystyle \frac{\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}}{2}\right),\quad \\ \left(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FC}+\frac{1}{2},2\unicode[STIX]{x1D6FC}\right),\quad \\ \left(2\unicode[STIX]{x1D6FC}+\frac{1}{3},2\unicode[STIX]{x1D6FC}+\frac{2}{3},3\unicode[STIX]{x1D6FC}\right),\quad \\ \left(3\unicode[STIX]{x1D6FC}+\frac{1}{4},3\unicode[STIX]{x1D6FC}+\frac{3}{4},4\unicode[STIX]{x1D6FC}\right),\quad \end{array}\right.\quad \unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}\in \mathbb{Q},\end{eqnarray}$$

except for a finite number of exceptional cases (see [10, Appendix] for the list). Expanding the method in Section 3, Yabu [12] computes several examples including:

(5.1) $$\begin{eqnarray}\begin{array}{@{}l@{}}\displaystyle 2\unicode[STIX]{x1D70B}\cdot _{3}F_{2}{\frac{1}{6},\frac{5}{6},\frac{1}{3}\atop 1,\frac{4}{3}};1=2^{1/3}\sqrt{3}\cdot \log \unicode[STIX]{x1D6FC}-2^{7/3}\cdot \text{Cot}^{-1}\,\unicode[STIX]{x1D6FD},\\ \displaystyle 3\unicode[STIX]{x1D70B}\cdot _{3}F_{2}{\frac{1}{6},\frac{5}{6},\frac{2}{3}\atop 1,\frac{5}{3}};1=2^{2/3}\sqrt{3}\cdot \log \unicode[STIX]{x1D6FC}+2^{5/3}\cdot \text{Cot}^{-1}\,\unicode[STIX]{x1D6FD},\end{array}\end{eqnarray}$$

with

$$\begin{eqnarray}\unicode[STIX]{x1D6FC}=\frac{(2^{2/3}-1)^{2}+(2^{2/3}+\sqrt{3})^{2}}{(2^{2/3}-1)^{2}+(2^{2/3}-\sqrt{3})^{2}},\qquad \unicode[STIX]{x1D6FD}=\frac{3+2^{1/3}+2^{2/3}\cdot 3}{3}.\end{eqnarray}$$

Recently, expanding the method in Section 4, the third author [10] solved the problem except for the exceptional cases.

Finally, as we have seen, (2.1) is a necessary and sufficient condition for that $eH^{(l)}$ in Section 3 or $eH$ in Section 4 is isomorphic to the Tate object $E\otimes \mathbb{Q}(-1)$ or $E\otimes \mathbb{Q}(1)$ , respectively. If this is not the case, there is no reason for and it seems rather weird that the regulator value (2.2) is expressed in terms of logarithms of algebraic numbers. Hence it would be fair to raise the following conjecture.

Conjecture 5.2. Under the same assumption as in Theorem 2.1, (2.1) is a necessary condition for (2.2).