Hostname: page-component-745bb68f8f-g4j75 Total loading time: 0 Render date: 2025-01-12T23:20:51.779Z Has data issue: false hasContentIssue false
  • English
  • Français

COLORING ISOSCELES TRIANGLES IN CHOICELESS SET THEORY

Part of: Set theory Graph theory

Published online by Cambridge University Press:  11 September 2023

YUXIN ZHOU
YUXIN ZHOU*
Affiliation:
HAVERFORD COLLEGE
*
E-mail: yuxinzhou@cs.haverford.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

It is consistent relative to an inaccessible cardinal that ZF+DC holds, and the hypergraph of isosceles triangles on 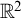$\mathbb {R}^2$ has countable chromatic number while the hypergraph of isosceles triangles on 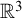$\mathbb {R}^3$ has uncountable chromatic number.

Keywords

choiceless set theorycountable coloringforcing

MSC classification

Primary: 03E25: Axiom of choice and related propositions 03E35: Consistency and independence results 05C15: Coloring of graphs and hypergraphs
Type
Article
Information
The Journal of Symbolic Logic , First View , pp. 1 - 30
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Blair, C. E., The Baire category theorem implies the principle of dependent choices . Bulletin de l’Académie Polonaise des Sciences, Série des Sciences Mathématiques, vol. 25 (1977), pp. 933–934.Google Scholar
Erdös, P. and Kakutani, S., On non-denumerable graphs . Bulletin of the American Mathematical Society, vol. 49 (1943), no. 6, pp. 457–461.CrossRefGoogle Scholar
Jech, T. J., Set Theory, Springer Monographs in Mathematics, vol. 14, Springer, Berlin, 2003.Google Scholar
Kunen, K., Partitioning Euclidean space . Mathematical Proceedings of the Cambridge Philosophical Society, vol. 102 (1987), pp. 379–383.CrossRefGoogle Scholar
Larson, P. B. and Zapletal, J., Geometric Set Theory, Mathematical Surveys and Monographs, vol. 248, American Mathematical Society, Providence, 2020.CrossRefGoogle Scholar
Marker, D., Model Theory: An Introduction, Graduate Texts in Mathematics, vol. 217, Springer, New York, 2006.Google Scholar
Oxley, J. G., Matroid Theory, vol. 3, Oxford University Press, New York, 2006.Google Scholar
Schmerl, J., Avoidable algebraic subsets of Euclidean space . Transactions of the American Mathematical Society, vol. 352 (2000), no. 6, pp. 2479–2489.CrossRefGoogle Scholar
Schmerl, J. H., Countable partitions of Euclidean space . Mathematical Proceedings of the Cambridge Philosophical Society, vol. 120 (1996), pp. 7–12.CrossRefGoogle Scholar
Solovay, R. M., A model of set-theory in which every set of reals is Lebesgue measurable . Annals of Mathematics, vol. 92 (1970), no. 1, pp. 1–56.CrossRefGoogle Scholar
Stern, J., On Lusin’s restricted continuum problem . Annals of Mathematics, vol. 120 (1984), no. 1, pp. 7–37.CrossRefGoogle Scholar
Zapletal, J., Coloring redundant algebraic hypergraphs, Preprint (2021), arXiv:2101.03437.Google Scholar
Zapletal, J., Coloring triangles and rectangles. Commentationes Mathematicae Universitatis Carolinae, vol. 64 (2023), no. 1, pp. 83–96.Google Scholar
Zapletal, J., Krull dimension in set theory. Annals of Pure and Applied Logic, vol. 174 (2023), no. 9, Paper No. 103299, 16 pp.CrossRefGoogle Scholar