Hostname: page-component-745bb68f8f-cphqk Total loading time: 0 Render date: 2025-01-13T13:18:51.306Z Has data issue: false hasContentIssue false
  • English
  • Français

A Berestycki–Lions type result for a class of degenerate elliptic problems involving the Grushin operator

Part of: Miscellaneous topics - Partial differential equations Partial differential equations Elliptic equations and systems

Published online by Cambridge University Press:  05 July 2022

Claudianor O. Alves  and
Angelo R. F. de Holanda
Claudianor O. Alves
Affiliation:
Universidade Federal de Campina Grande, Unidade Acadêmica de Matemática, 58429-970, Campina Grande, PB, Brazil (coalves@mat.ufcg.edu.br, angelo@mat.ufcg.edu.br)
Angelo R. F. de Holanda
Affiliation:
Universidade Federal de Campina Grande, Unidade Acadêmica de Matemática, 58429-970, Campina Grande, PB, Brazil (coalves@mat.ufcg.edu.br, angelo@mat.ufcg.edu.br)
Get access Rights & Permissions [Opens in a new window]

Abstract

In this work we study the existence of nontrivial solution for the following class of semilinear degenerate elliptic equations

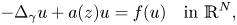
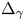\[ -\Delta_{\gamma} u + a(z)u = f(u) \quad \mbox{in}\ \mathbb{R}^{N}, \]
where $\Delta _{\gamma }$ is known as the Grushin operator, $z:=(x,y)\in \mathbb {R}^{m}\times \mathbb {R}^{k}$ 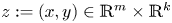and $m+k=N\geqslant 3$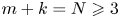, $f$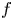 and $a$ 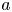are continuous function satisfying some technical conditions. In order to overcome some difficulties involving this type of operator, we have proved some compactness results that are crucial in the proof of our main results. For the case $a=1$, we have showed a Berestycki–Lions type result.

Keywords

Variational methodsdegenerate elliptic equationsP.D.E. on manifolds

MSC classification

Primary: 35A15: Variational methods
Secondary: 35J70: Degenerate elliptic equations 35R01: Partial differential equations on manifolds
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 153 , Issue 4 , August 2023 , pp. 1244 - 1271
Check for updates
Copyright
Copyright © The Author(s), 2022. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alves, C. O., Duarte, R. C. and Souto, M. A. S.. A Berestycki–Lions type result and applications. Rev. Mat. Iberoam. 35 (2019), 1859–1884.CrossRefGoogle Scholar
Alves, C. O., Montenegro, M. and Souto, M. A.. Existence of a ground state solution for a nonlinear scalar field equation with critical growth. Calc. Var. PDEs 43 (2012), 537–554.CrossRefGoogle Scholar
Alves, C. O., Figueiredo, G. M. and Siciliano, G.. Ground state solutions for fractional scalar filed equations under a general critical nonlinearity. Commun. Pure Appl. Anal. 18 (2019), 2199–2215.CrossRefGoogle Scholar
Alves, C. O. and Germano, G. F.. Existence and concentration phenomena for a class of indefinite variational problems with critical growth. Potential Anal. 52 (2020), 135–159.CrossRefGoogle Scholar
Anh, C. T. and My, B. K.. Existence of solutions to $\Delta _{\lambda }$-Laplace equations without the Ambrosetti–Rabinowitz condition. Complex Var. Elliptic Equ. 61 (2016), 137–150.CrossRefGoogle Scholar
Berestycki, H. and Lions, P. L.. Nonlinear scalar field equations, I existence of a ground state. Arch. Ration. Mech. Anal. 82 (1983), 313–345.CrossRefGoogle Scholar
Berestycki, H., Gallouet, T. and Kavian, O.. Equations de Champs scalaires euclidiens non linéaires dans le plan. C. R. Acad. Sci. Paris Ser. I Math. 297 (1984), 307–310.Google Scholar
Chang, X. and Wang, Z.-Q.. Ground state of scalar field equations involving a fractional Laplacian with general nonlinearity. Nonlinearity 26 (2013), 479–494.CrossRefGoogle Scholar
Bhakta, M. and Sandeep, K.. Poincaré–Sobolev equations in the hyperbolic space. Calc. Var. PDEs 44 (2012), 247–269.CrossRefGoogle Scholar
Birindelli, I. and Prajapat, J.. Nonlinear Liouville theorems in the Heisenberg group via the moving plane method. Commun. Partial Differ. Equ. 24 (1999), 1875–1890.Google Scholar
Brézis, H.. Functional analysis, Sobolev spaces and partial differential equations (2011), New York.Google Scholar
Coti Zelati, V. and Rabinowitz, P.. Homoclinic type solutions for a semilinear elliptic PDE on $\mathbb {R}^{N}$. Commun. Pure Appl. Math. 10 (1992), 1217–1269.Google Scholar
Chen, J., Tang, X. and Gao, Z.. Infinitely many solutions for semilinear $\Delta _{\lambda }$-Laplace equations with sign-changing potential and nonlinearity. Studia Sci. Math. Hungar. 54 (2017), 536–549.Google Scholar
Chung, N. T.. On a class of semilinear elliptic systems involving Grushin type operator. Commun. Korean Math. Soc. 29 (2014), 37–50.Google Scholar
D'Ambrosio, L.. Hardy inequalities related to Grushin operator. Proc. Am. Math. Soc. 132 (2003), 725–734.CrossRefGoogle Scholar
Duong, A. T. and Nguyen, N. T.. Liouville type theorems for elliptic equations involving Grushin operator and advection. Electron. J. Differ. Equ. 2017 (2017), 1–11.Google Scholar
Duong, A. T. and Phan, Q. H.. Liouville type theorem for nonlinear elliptic system involving Grushin operator. J. Math. Anal. Appl. 454 (2017), 785–801.Google Scholar
Franchi, B. and Lanconelli, E., Une métrique associée une classe d'opérateurs elliptiques dégénérés. Conference on linear partial and pseudodifferential operators (Torino, 1982), Rend. Sem. Mat. Univ. Politec. Torino 1983, Special Issue (1984), 105–114.Google Scholar
Franchi, B. and Lanconelli, E.. An embedding theorem for Sobolev spaces related to non-smooth vectors fields and Harnack inequality. Commun. Partial Differ. Equ. 9 (1984), 1237–1264.CrossRefGoogle Scholar
Grushin, V. V., On a class of hypoelliptic operators. 1970 Math. USSR Sb. 12 458.CrossRefGoogle Scholar
Grushin, V. V., On a class of hypoelliptic pseudodifferential operators degenerate on a submanifold. 1971 Math. USSR Sb. 13 155.Google Scholar
Hirata, J., Ikoma, N. and Tanaka, K.. Nonlinear scalar field equations in $\mathbb {R}^{N}$: mountain pass and symmetric mountain pass approaches. Topol. Methods Nonlinear Anal. 35 (2010), 253–276.Google Scholar
Jeanjean, L.. Existence of solutions with prescribed norm for semilinear elliptic equations. Nonlinear Anal. 28 (1997), 1633–1659.CrossRefGoogle Scholar
Kogoj, A. E. and Lanconelli, E.. On semilinear $\Delta _{\lambda }$-Laplace equation. Nonlinear Anal. 75 (2012), 4637–4649.CrossRefGoogle Scholar
Kogoj, A. E. and Lanconelli, E.. Linear and semilinear problems involving $\Delta _\lambda$-Laplacians. Electron. J. Differ. Equ. 25 (2018), 167–178.Google Scholar
Kogoj, A. E. and Sonner, S.. Attractors for a class of semi-linear degenerate parabolic equations. J. Evol. Equ. 13 (2013), 675–691.CrossRefGoogle Scholar
Kryszewski, W. and Szulkin, A.. Generalized linking theorem with an application to semilinear Schrödinger equation. Res. Rep. Math. Stockholm Univ. 7 (1996), 1–27.Google Scholar
Lions, P. L.. Symétrie et compacité dans les espaces de Sobolev. J. Funct. Anal. 49 (1982), 315–334.Google Scholar
Lions, P. L.. The concentration-compactness principle in the calculus ov variations. The locally compact case, part 2. Analles Inst. H. Poincaré Sect. C 1 (1984), 223–283.Google Scholar
Liu, M., Tang, Z. and Wang, C.. Infinitely many solutions for a critical Grushin-type problem via local Pohozaev identities. Ann. Mat. Pura Appl. 199 (2019), 1737–1762.CrossRefGoogle Scholar
Loiudice, A.. Asymptotic estimates and nonexistence results for critical problems with Hardy term involving Grushin-type operators. Ann. Mat. Pura Appl. 198 (2019), 1909–1930.CrossRefGoogle Scholar
Luyen, D. T. and Tri, N. M.. Existence and concentration phenomena for a class of indefinite variational problems with critical growth. Complex Var. Elliptic Equ. 64 (2019), 1050–1066.CrossRefGoogle Scholar
Monti, R.. Sobolev inequalities for weighted gradients. Commun. Partial Differ. Equ. 31 (2006), 1479–1504.CrossRefGoogle Scholar
Monti, R. and Morbidelli, D.. Kelvin transform for Grushin operators and critical semilinear equations. Duke Math. J. 131 (2006), 167–202.CrossRefGoogle Scholar
Palais, R. S.. The principle of symmetric criticality. Commun. Math. Phys. 69 (1979), 19–30.CrossRefGoogle Scholar
Rabinowitz, P. H.. On a class of nonlinear Schrödinger equations. Z. Angew Math. Phys. 43 (1992), 270–291.CrossRefGoogle Scholar
Rahal, B. and Hamdani, M. K.. Infinitely many solutions for $\Delta _{\alpha }$-Laplace equations with sign-changing potential. J. Fixed Point Theory Appl. 20 (2018), 137.CrossRefGoogle Scholar
Willem, M.. Minimax theorems. Progress in nonlinear differential equations and their applications, vol. 24 (Boston: BirkhIauser, 1996).CrossRefGoogle Scholar
Yu, X.. Liouville type theorem in the Heisenberg group with general nonlinearity. J. Differ. Equ. 254 (2013), 2173–2182.Google Scholar
Yu, X.. Liouville type theorem for nonlinear elliptic equation involving Grushin operators. Commun. Contemp. Math. 17 (2015), 1450050.CrossRefGoogle Scholar
Zhang, J. and Zou, W.. A Berestycki–Lions theorem revisited. Commun. Contemp. Math. 14 (2012), 12500331.CrossRefGoogle Scholar
Zhang, J. J., do Ó, J. M. and Squassina, M.. Fractional Schrödinger–Poisson systems with a general subcritical or critical nonlinearity. Adv. Nonlinear Stud. 16 (2016), 15–30.CrossRefGoogle Scholar