A Fast Gradual Fault Detection Method for Underwater Integrated Navigation Systems

Abstract

Gradual fault detection is always an important issue in integrated navigation systems, and the gradual fault is the most difficult fault to detect. To detect gradual faults in a timely and precise manner in integrated navigation systems, the statistical concepts of the normalised residual mean and the sum of absolute residuals are introduced according to the characteristics of gradual system failure in this paper. The applicability of the improved residual χ² detection method is discussed. Then, the gradual fault detection program based on the improved residual χ² detection method is designed with the criterion of normalised residual mean and the sum of absolute residual. The simulation results and vehicle tests show that: 1) The residual of the failed sub-system can be calculated accurately with the improved residual χ² detection method, which has strong applicability in gradual fault detection; 2) The gradual fault can be detected in a short time by using the normalised residual mean and the sum of absolute residual.

1. INTRODUCTION

Since there are many kinds of interference and disruption underwater, navigation devices may suffer various faults. If these faults are not detected and isolated quickly, the navigation information coupled with the faults will be introduced into the navigation system, affecting the whole system and reducing precision (Qin et al., 2012; Zhao et al., 2013). Therefore, the fault detection, isolation and system reconfiguration are key issues of a high quality underwater integrated navigation system (Zolghadri, 2012). However, the fault detection method for underwater integrated navigation requires development due to the high requirements of real time operations, the complex environment and a lack of navigation information (Zhao et al., 2013).

Early fault detection and diagnosis methods are mostly based on hardware redundancy (Qin et al., 2012). In these methods, the hardware configuration always exceeds the minimum necessary and a vote approach is used to detect the fault. Thus the navigation system can still work normally and supply accurate navigation information based on the rest of the sensors when one sensor fails. However, this may increase the volume, power consumption and cost of the navigation equipment. All of these run counter to the requirements of modern vehicles.

The analytical redundancy method was developed following the hardware redundancy method. It is based on mathematical models, which utilise the inherent relationship between the inputs and outputs of the diagnostic system. The advantage of the analytical redundancy method is that it can monitor the navigation sensors without increasing the number of sensors and changing the structure of the navigation equipment. However, the analytical redundancy method works normally and accurately based on an accurate model of the monitored object, which also needs prior statistical information of the measurement noise and the system process noise. Otherwise, it may result in a mistaken judgment (Jin and Zhang, 1997). The residual χ² detection method is one of the successful applications of the analytical redundancy method.

M-estimation (Maximum Likelihood Type Estimates) is a robust estimation method based on system models (Huber and Ronchetti, 2009). It can effectively monitor the outlier points in the measurement and adjust the gain matrix of the filter to reduce the influence of the outliers by monitoring the result (Zhang and Pang, 2005). In M-estimation, the curves of the objective function differ according to the objective function. However, they all reduce the weight when the residual becomes larger (Wang, 2013). M-estimation has been successfully used in PHINS (An Inertial Navigation Equipment Composed by Three Gyros and Three Accelerometers) produced by IxBlue, a French firm (IXBLUE, 2008). However, in the early stages, the M-estimation method can only be used in a linear system. Chang et al. (2012a; 2013) and Chang et al. (2012b) reconfigure the measurement by the Huber method and combine the M-estimation and the Unscented Kalman Filter (UKF). This method forms a robust non-linear Kalman filter. Although the M-estimation method does not need to increase the amount of sensors and has a low calculation burden, it is still based on an accurate system model and the change of the residual. Thus it can only detect a mutant fault accurately and fails in detecting the gradual fault.

With the development of computing technology in recent years, artificial intelligence, intelligent filtering and other methods have attracted experts' attention to improve fault detection. Genetic neural networks were applied to detect pre-treated sensor signals, which can efficiently diagnose the sensor fault (Qian and Wang, 2009). The Levenberg-Marquardt (LM) algorithm was applied to improve the standard Back Propagation (BP) neural networks algorithm, which optimises the training time and accuracy (Qian et al., 2009). An improved H∞ multi-fading tolerant filtering method is proposed in Chen and Yuan (2009), which solves the problem of orthogonal detection sensitivity mismatch due to the huge magnitude of differences between the observed values in the residual detection method. The advantages of artificial intelligence are instantaneity and robustness such that the system can still work properly even when system information is lost. So, it has a good performance in noise and is fault tolerant. Moreover, its performance is not limited to the restriction of an accurate mathematical model and other obstructions (Liu et al., 2009). However, all of these methods are based on prior information of the system fault characteristics and types. For the underwater integrated navigation system, these methods may fail because the system works in a complex environment and the performance of the faults are various. Artificial intelligence and intelligent filtering always involve a large amount of calculation. Furthermore, the dimensions of an underwater integrated navigation model are always high. This may lead to a great calculation burden on the navigation computer.

Given the high requirement of real-time performance, complex working environment and high dimension of the integrated navigation system, the χ² detection method, which belongs to the analytical redundancy category, which has less calculation and is sensitive to the change of the residual, is still widely used. Traditional χ² fault detection methods are divided into the state χ² detection method and the residual χ² detection method (Brumback and Srinath, 1987; Liu et al., 2009). When there is no update of measurement information in the recursive status process, the fault detection sensitivity of state χ² detection method is decreased. A method where two auxiliary filters are alternately used to correct the navigation system was proposed in Da (1994), which could overcome the disadvantage of the growing difference between the real states and the recursive states and also has a fault-detect capability. However, this method greatly increases the complexity of computation in a highly dynamic environment and decreases the sensitivity (Da and Lin, 1995; Qiu et al., 2005). The Residual χ² detection method that uses the system residual information to form the detection function can detect the faults in time with a small amount of calculation as well as high real-time feature, and it is also suitable for dynamic environments. However, it does not work well in gradual fault detection (Qian, 2004).

To resolve the problem analysed above, a fast gradual fault detection method is proposed in this paper. The details are as follows. According to the working properties of the assisted navigation devices and the structure feature of the underwater integrated navigation system 1) Normalised residual mean and the sum of absolute residual are introduced; 2) The applicability of the improved residual χ² detection method in gradual fault detection is discussed; 3) The gradual fault detection program with the criterion of normalised residual mean and the sum of absolute residual is designed.

To verify the effectiveness of the proposed method, simulation experiments and vehicle tests are done. These experiments results show that: 1) The residual of the failed sub-system can be calculated accurately with the improved residual χ² detection method and the improved residual χ² detection method has strong applicability in gradual fault detection; 2) The gradual fault can be detected in a short time according to the characteristics of the normalised residual mean and the sum of absolute residual.

The rest of this paper is organised as follows. The tolerant model of the underwater integrated navigation system and the principle of the residual χ² detect method is briefly described in Section 2. In Section 3, the applicability of the improved residual χ² detection method in gradual system fault detection is discussed and a method which is used to detect the gradual fault is designed by using the normalised residual mean and the sum of the absolute residual values. The reconfiguration of the integrated navigation system is also described simply. In Section 4, the gradual fault detection of the integrated navigation system are simulated and analysed. In Section 5, a land vehicle environment is used to simulate an underwater vehicle and experiments are conducted to test the gradual fault detection method introduced in this paper. Finally, the features of the gradual fault detection method proposed in this paper are summarised.

2. TOLERANT MODEL AND RESIDUAL Χ² DETECTION METHOD FOR INTEGRATED NAVIGATION SYSTEM

2.1. Fault detection program and information fusion model

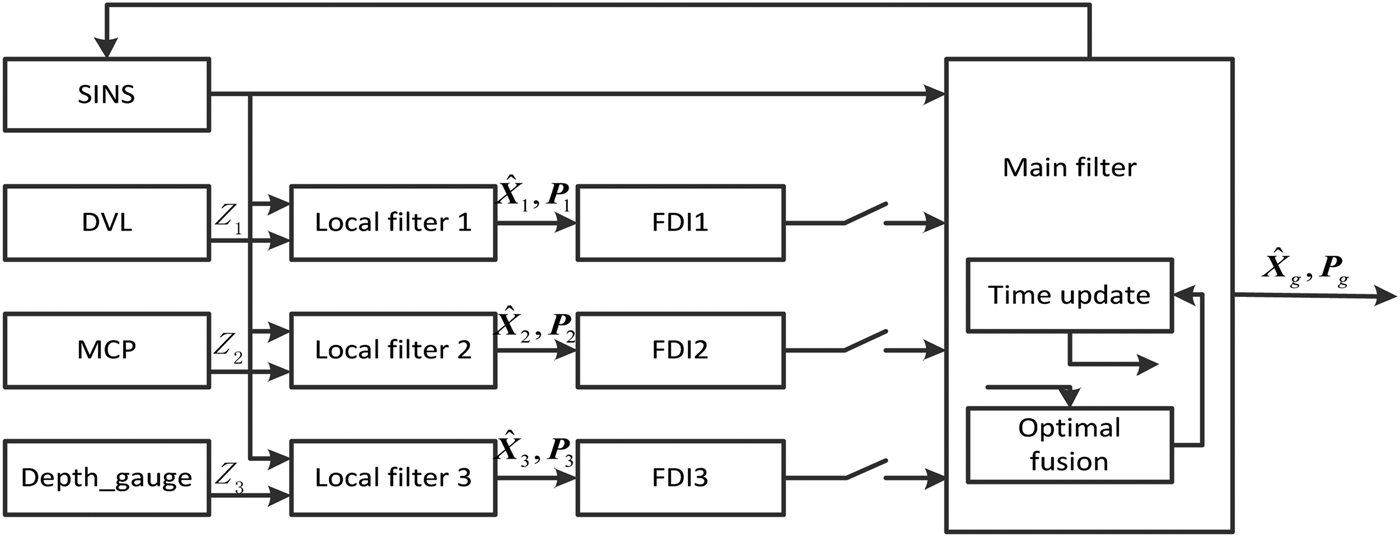
The integrated and information fusion model is shown in Figure 1. A Strapdown Inertial Navigation System (SINS) known as a common reference system is considered as a reliable system without fault in the navigation process. The assisted navigation devices are the Doppler Velocity Log (DVL), the Magnetic Compass (MCP) and the depth-gauge (Yang et al., 2006; Liu and Zhang, 2010; Zhang and Xu, 2012).

Figure 1. SINS/DVL/MCP/Depth-gauge integrated navigation system.

In the information fusion process, three separate fault detection and isolation (FDI) modules, FDI1, FDI2, FDI3, are used to detect the faults of the three subsystems. The subsystem will be isolated after the gradual fault detection time when the gradual fault occurs. The isolated subsystem will be restored and the information will be fused again when the fault is cleared.

2.2. Residual χ² detection method

In Figure 1, the discrete random linear model without controlling terms of the subsystem is described as

(1)$$\left\{ \matrix{{\hat{\bi X}}_{k/k - 1} = \phi _{k/k - 1} {\hat{\bi X}}_{k - 1} + {\bi W}_{k - 1} \hfill \cr \hskip-32pt{\bi Z}_k = {\bi H}_k {\hat X}_{k - 1} + {\bi V}_{k - 1}} \right.$$

where the subscript k denotes the k ^th time-step, ${\hat{\bi X}}$ is the state vector, Z represents the measurement vector, φ _k/k − 1 stands for the transition matrix of the dynamic model, H is the measurement model matrix, W ~ N(0,Q) is the process noise, and V ~ N(0,R) is the measurement noise. Q and R are the variance matrix of the process noise and the measurement noise, separately.

Kalman filters are widely used in integrated navigation systems. They are also fundamental in the residual χ² detection method. The basic Kalman filter equations of the random linear discrete system are as follows.

One step prediction of the state is

(2)$${\hat{\bi X}}_{k \comma k - 1} = \phi _{k \comma k - 1} {\hat{\bi X}}_{k - 1} $$

The state estimation is

(3)$${\hat{\bi X}}_k = {\hat{\bi X}}_{k \comma k - 1} + {\bi K}_k \left[ {{\bi Z}_k - {\bi H}_k {\hat{\bi X}}_{k \comma k - 1}} \right]$$

The gain matrix, K_k of the filter is

(4)$${\bi K}_k = {\bi P}_{k \comma k - 1} {\bi H}_k^T \left[ {{\bi H}_k {\bi P}_{k \comma k - 1} {\bi H}_k^T + {\bi R}_k} \right]^{ -1} $$

The error variance of the one step prediction, P_k,k−1, is

(5)$${\bi P}_{k \comma k - 1} = \phi _{k \comma k - 1} {\bi P}_{k - 1} \phi _{k \comma k - 1}^T + \tau _{k \comma k - 1} {\bi Q}_{k - 1} \tau _{k \comma k - 1}^T $$

The error variance of the state estimation is

(6)$${\bi P}_k = \left[ {{\bi I} - {\bi K}_k {\bi H}_k} \right]{\bi P}_{k \comma k - 1} \left[ {{\bi I} - {\bi K}_k {\bi H}_k} \right]^{ - 1} + {\bi K}_k {\bi R}_k {\bi K}_k^T $$

In a standard Kalman filter, the process noise and the measurement noise are assumed to satisfy the following assumptions

(7)$$\left\{ \matrix{E[{\bi W}_k ] = 0 \comma \,E[{\bi W}_k {\bi W}_j ^T ] = {\bi Q}_k \delta _{kj} \hfill \cr E[{\bi V}_k ] = 0\comma E[{\bi V}_k {\bi V}_j ^T ] = {\bi R}_k \delta _{kj} \hfill \cr E[{\bi W}_k {\bi V}_j ^T ] = 0 \hfill} \right.$$

The local filters in Figure 1 also comply with the above equations. Then, the residual of each local Kalman filter is

(8)$${\bi r}_k = {\bi Z}_k - {\bi H}_k {\hat{\bi X}}_{k/k - 1} $$

where, r_k is the residual of the local filter.

When no fault occurs, the residual of the local filter is part of the white noise. Such as

(9)$${\bi r}_k \sim N({\bi 0}\comma {\bi A}_k )$$

Equation (9) means r_k has zero mean and its variance is

(10)$${\bi A}_k = {\bi H}_k {\bi P}_{k/k - 1} {\bi H}_k^T + {\bi R}_k $$

If the auxiliary navigation equipment fails, the statistical characteristics of the measurement noise will change. Then, the residual r_k is no longer part of the white noise. Of course, the mean of the residual r_k is no longer equal to 0, which can be used to detect the occurrence of the mutant fault. The specific method is described as follows.

Firstly, a binary hypothesis to r_k is made as

H₀ denotes no fault where

$$E\{ {\bi r}_k \} = 0\comma \quad E\{{\bi r}_k {\bi r}_{k}^T\} = {\bi A}_k\comma $$

H₁ denotes the existence of fault where

$$E\left\{ {{\bi r}_k} \right\} = \mu\comma \quad E\left\{ {\left( {{\bi r}_k - \mu} \right)\left( {{\bi r}_k - \mu} \right)^T} \right\} = {\bi A}_k. $$

Then, the fault detection function is

(11)$$\gamma _k = {\bi r}_k^T {\bi A}_k^{ - 1} {\bi r}_k $$

where γ _k obeys the χ² distribution and its degree of freedom is m, i.e. γ _k ~ χ²(m), and m is the dimension of observations vector Z_k.

The fault detection criteria is

$$\left\{\matrix{if\, \gamma_k \gt T_D\comma \ some\,faults\,occur \hfill \cr if\,\gamma _k \lt T_D\comma \ no\,fault\,occurs \hfill} \right.$$

where the threshold T _D determines the performance of the fault detection method. According to the Neyman-Pearson criterion, when the false alarm rate is defined as P _f = α, the threshold T _D can be worked out through solving the equation P _f = P[γ _k > T _D / H ₀] = α. And the undetected rate is reduced to the lowest. Here P _f is

From Equations (8), (10) and (11), we can conclude that if the fault is serious enough, then the value of the fault detection function γ _k will be bigger than the threshold T _D. While the gradual fault information is always so faint that γ _k is far less than T _D, ${\hat{\bi X}}_{k \comma k - 1} $ will trace the gradual fault information which helps the γ _k remain smaller than T _D. Then, the residual χ² detection method is invalid in gradual fault detection. To avoid the tracking capability of ${\hat{\bi X}}_{k \comma k - 1} $ and the invalidity of the residual χ² detection method in gradual fault detection, two improvements are introduced and the gradual fault detection scheme is designed in the next section.

3. A FAST GRADUAL FAULT DETECTION

According to the above analysis, the traditional residual χ² detection method fails in detecting the gradual system fault. This section aims to explore this problem and introduces the applicability of the improved residual χ² detection method in gradual fault detection, the statistical characteristics of the gradual fault information and the gradual fault detection program with the criterion of normalised residual mean and the sum of absolute residual.

3.1. The applicability of the improved residual χ² detect method

The reasons why the traditional residual χ² detection method failed in gradual system fault detection should be analysed. As we know, one-step prediction of the state in a conditional Kalman filter is

(13)$${\hat{\bi X}}_{k/k - 1} = \phi _{k/k - 1} {\hat{\bi X}}_{k - 1} $$

where

(14)$$\eqalign{{\hat{\bi X}}_{k - 1} & = {\hat{\bi X}}_{k - 1/k - 2} + {\bi K}_{k - 1} [{\bi Z}_{k - 1} - {\bi H}_{k - 1} {\hat{\bi X}}_{k - 1/k - 2} ] \cr & = \phi _{k - 1/k - 2} {\hat{\bi X}}_{k - 2} + {\bi K}_{k - 1} [{\bi Z}_{k - 1} - {\bi H}_{k - 1} \phi _{k - 1/k - 2} {\hat{\bi X}}_{k - 2} ]\, \cr & = \,[{\bi I} - {\bi K}_{k - 1} {\bi H}_{k - 1} ]\phi _{k - 1/k - 2} {\hat{\bi X}}_{k - 2} + {\bi K}_{k - 1} {\bi Z}_{k - 1}} $$

Supposing that a continuous and stable fault occurs at the (k − 1)^th time-step, according to Equation (14), it can be seen that the observation vector Z_k − 1 is already corrupted by the fault information at this step. As a result, ${\hat{\bi X}}_{k - 1} $ contains the failure information. After going through one recursive step as per Equation (13), ${\hat{\bi X}}_{k/k - 1} $ contains the failure information, too. While in the low dynamic environment, there is no great difference between the observation vectors Z_k and Z_k − 1, due to the continuity and stability of the fault. If we still use ${\bi r}_k \, = \,{\bi Z}_k - {\bi H}_k {\hat{\bi X}}_{k/k - {\rm 1}} $ to calculate the residuals, the output of fault detect function γ _k will be less than the threshold, T _D. As a consequence, the fault detection system will mistakenly think the fault has disappeared. Then, the failed subsystem will be continuously combined with the other normal subsystem, and the fault information will pollute the whole integrated navigation system. According to the analysis above, it can be seen that the result of the fault detection function will be less than T _D because of the predicted value ${\hat{\bi X}}_{k/k - 1} $ which tracks the fault information of the failed subsystem by a Kalman filter when a continuous and stable mutant fault occurs. Then, the fault detection fails. The result of the fault detection function will not hop and exceed the threshold T _D until the fault disappears. Meanwhile, the fault detection system makes a misjudgement.

So, the first improvement in this paper is that we change the traditional residual equation into Equation (15).

(15)$${\bi r}_k = {\bi Z}_k - {\bi H}_k \phi _{k/k - 1} \left[ \matrix{{\hat{\bi X}}_{g\left( {k - 1} \right)} \hfill \cr {\hat{\bi X}}_{L\left( {k - 1} \right)} \hfill} \right]$$

where ${\hat{\bi X}}_{g(k - 1)} $ is the common state of each subsystem which is obtained directly by the main filter of the federated Kalman filter. ${\hat{\bi X}}_{L(k - 1)} $ denotes the special subsystem states that only belong to this subsystem in ${\hat{\bi X}}_{k - 1} $.

When a continuous and stable fault that is big enough to occur at the k ^th time-step occurs, γ _k hops and becomes bigger than T _D immediately. The failed subsystem is then isolated by the Fault Detection and Isolation (FDI) module. The fault information of the failed subsystem is stopped from being fused with the other normal subsystem at the (k−1)^th time-step. So, the predicted common state vector ${\hat{\bi X}} _g $ is not affected by the failure subsystem based on Figure 1, and ${\hat{\bi X}}_g $ will not trace the fault information. Then γ _k remains bigger than T _D until the fault disappears.

While a gradual fault always changes slowly in a short time and is much smaller than the system noise, a period of time to detect and isolate this fault is needed. As shown in Equation (14), before the gradual fault system is isolated, the residual contains the gradual failure information. When the fault is detected, it can stop the last step where interference of the gradual fault is generated. Comparing with Equation (8) it can be seen that the subsequent calculations of the residual by Equation (15) are not corrupted by the gradual fault because of using the predicted state of the main filter, ${\hat{\bi X}}_g $. In conclusion, the improved residual χ² detection method has a strong applicability in gradual fault detection.

3.2. The statistical characteristics of the gradual fault information

Since the change of the gradual fault is slow in the adjacent survey cycles and always much smaller than the system noise, there is no obvious difference between the observation vector Z_k − 1 and 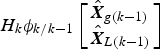$H_k \phi _{k/k - 1} \left[ \matrix{{\hat{\bi X}}_{g\left( {k - 1} \right)} \hfill \cr {\hat{\bi X}}_{L\left( {k - 1} \right)} \hfill} \right]$. The fault detection function γ _k is much lower than the threshold T _D. As a result, the gradual fault could not be detected and the failed subsystem could not be isolated by the improved residual χ² detection method. Some statistical characteristics can still be concluded from γ _k. Here, we introduce two statistical concepts, the residual mean and the sum of the absolute residual, basing on moving window technology to identify the gradual fault.

To simplify the analysis, a ramp fault is considered and a white noise is attached. The fault is

(16)$${\bi F} = {\bi K}t + {\bi white} - {\bi noise}$$

where F is the gradual fault, K is the changing trend of the gradual fault and it is very small, t is the duration time of the fault. white − noise denotes the white noise.

Supposing that a gradual fault occurs at the (k)^th time step, then Equation (15) becomes

(17)$${\bi r}_k = {\bi Z}_k + {\bi K} {\bf \cdot} 1{\bf\cdot} \Delta {\bi t} + {\bi white - noise} - {\bi H}_k \phi _{k/k - 1} \left[ \matrix{{\hat{\bi X}}_{g(k - 1)} \hfill \cr {\hat{\bi X}}_{L(k - 1)}} \right]$$

where, r_k is the residual with one step measurement error. Z_k is the supposed normal measurement, Δt is the cycle of the filter.

If there is no fault in the subsystem, the residual γ _k obtained by Equation (15) obeys the normal distribution, r _k ~ N(0,M). While the residual r_k obtained by Equation (17) no longer obeys the normal distribution and contains the information of ${\bi K}\cdot 1\cdot \Delta {\bi t} + {A}\cdot {\bi white - noise}$. Then Equation (3) changes into

(18)$${\hat{\bi X}}_k = {\hat{\bi X}}_{k \comma k - 1} + {\bi K}_k \left[ {{\bi Z}_k + {\bi K}{\bf\cdot} 1{\bf\cdot} \Delta {\bi t} + {\bi white - noise} - {\bi H}_k {\hat{\bi X}}_{k \comma k - 1}} \right]$$

where ${\hat{\bi X}}_k $ contains the fault information of the k ^th time-step, ${\bi K}{\bf\cdot} 1{\bf\cdot} \Delta {\bi t} + {\bi white - noise}$. Then the common states in ${\hat{\bi X}}_k $ are to be fused with the other normal subsystems and ${\hat{\bi X}}_g $ obtained from the main federated filter also contains the fault information ${\bi K}{\bf\cdot} 1{\bf\cdot} \Delta {\bi t} + {\bi white - noise}$ of the k ^th time-step. If the fault information remains the same as that in the k ^th time-step, then the residual obtained from the (k + 1)^th time-step will obey the normal distribution again. However, the fact is that the measurement changes in the next filter cycle because of the gradual fault and it is

(19)$${\bi Z}_{k + 1} = {\bi Z}_k + {\bi K}{\bf\cdot} 2{\bf\cdot} \Delta {\bi t} + {\bi white - noise}$$

Because of the outputs of the main filter of federal Kalman filter, ${\hat{\bi X}}_g $ only contains fault information ${\bi K}{\bf\cdot} 1{\bf\cdot} \Delta {\bi t} + {\bi white - noise}$ in the k ^th time-step, the residual r_k + 1 at this moment is

(20)$${\bi r}_{k + 1} = {\bi Z}_k + {\bi K}{\bf\cdot} 2{\bf\cdot} \Delta {\bi t} + {\bi white - noise} - {\bi H}_k \phi _{k/k - 1} \left[ \matrix{{\hat{\bi X}}_{g(k - 1)} \hfill \cr {\hat{\bi X}}_{L(k - 1)}} \right]$$

So, the residual r_k + 1 is mainly composed of ${\bi K}{\bf\cdot} 1{\bf\cdot} \Delta {\bi t} + {\bi white - noise}$. The residual ${\bi r}_{k + i} (i = 3\comma4 \cdots )$ in the following are the same as ${\bi r}_{k + 1} $.

According to the above analysis, the statistical characteristics in a moving window are proposed as follows.

Firstly, the length of the moving window and the fault detection time should be determined according to the application environment. If the length of the moving window is too short, the statistical features will be corrupted by the measurement noise or system noise. If the length of the gradual fault detection time is too long, more fault information will be fused in the integrated navigation system, the precision of the integrated navigation will also be reduced even if the gradual fault subsystem is isolated in the end. In the simulation environment, the length of the moving window is set at 20 and the fault detection time is set as 30 s.

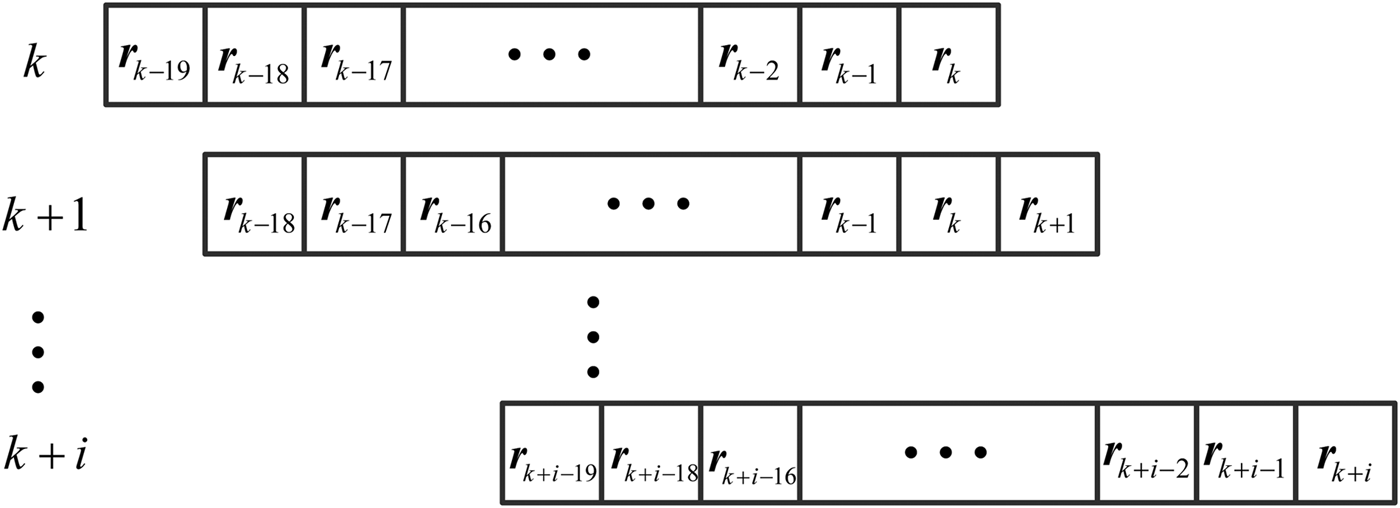
Then we calculate the residual mean and the sum of the absolute residual. The details of the moving window are shown in Figure 2.

Figure 2. Moving window.

At the k ^th time-step the residual mean of the moving window is

(21)$${\bar{\bi r}}_k = {{\left( {\sum\limits_{i = 1}^n {{\bi r}_{k - 20 + i}}} \right)} \bigg/ n}$$

where ${\bar{\bi r}}_k $ is the residual mean of the moving window and n is the length of the moving window.

The sum of the absolute residual is

(22)$$s\left\vert {{\bi r}_k} \right\vert = \sum\limits_{i = 1}^n {\left\vert {{\bi r}_{k - 20 + i}} \right\vert} $$

where, s|r_k| is the sum of the absolute residual.

As the fault information is only contained in the last element of the window, Equations (20) and (21) can be rewritten as

(23)$${{\bar{\bi r}}_k} = {{\left( \matrix{white - noise_{1} + white - noise_{2} + \cdots + \hfill \cr white - nois{e_{19}} + k{\bf \cdot} \Delta t + white - noise_{20} \hfill} \right)} \bigg/ {20}}$$

(24)$$\eqalign{s\left\vert {{{\bi r}_k}} \right\vert & = \left\vert {white - noise_{1}} \right\vert + \left\vert {white - noise_{2}} \right\vert \cr &\quad + \cdots + \left\vert {white - noise_{19}} \right\vert + \left\vert {k\Delta t + white - noise_{20}} \right\vert}$$

It is known that the white-noise obeys the normal distribution and kΔt is faint. Then, it can be concluded that ${{\bar{\bi r}}}_k$ almost equals to 0.

As the fault lasts and the window moves, the fault information becomes the main parts of the window. Then at the (k + i)^th (i ≥ 20) time-step, the residual mean and the sum of the absolute residual of the moving window is

(25)$${{{\bar{\bi r}}}_{k + i}} = {{\left( \matrix{k{\bf \cdot} \Delta t + white - noise_{1} + k{\bf \cdot} \Delta t + white - noise_{2} \hfill \cr + \cdots + k{\bf \cdot} \Delta t + white - noise_{20} \hfill} \right)} \bigg / {20}}$$

(26)$$\eqalign{s\left\vert {{{\bi r}_{k + i}}} \right\vert & = \left\vert {k{\bf \cdot} \Delta t + white - noise_{1}} \right\vert + \left\vert {k{\bf \cdot} \Delta t + white - noise_{2}} \right\vert \cr &\quad + \cdots + \left\vert {k{\bf \cdot} \Delta t + white - noise_{20}} \right\vert}$$

Then ${{\bar{\bi r}}}_{k + i} $ almost equals to $k{\bf \cdot} \Delta t$. By comparing Equations (26) and (24), we can conclude that when the gradual fault occurs, the sum of the absolute residual is bigger than the sum of the absolute residual when there is no fault.

According to the above statistical characteristics of the gradual fault, the gradual fault detection method is proposed in next section.

3.3. A scheme of gradual fault detection

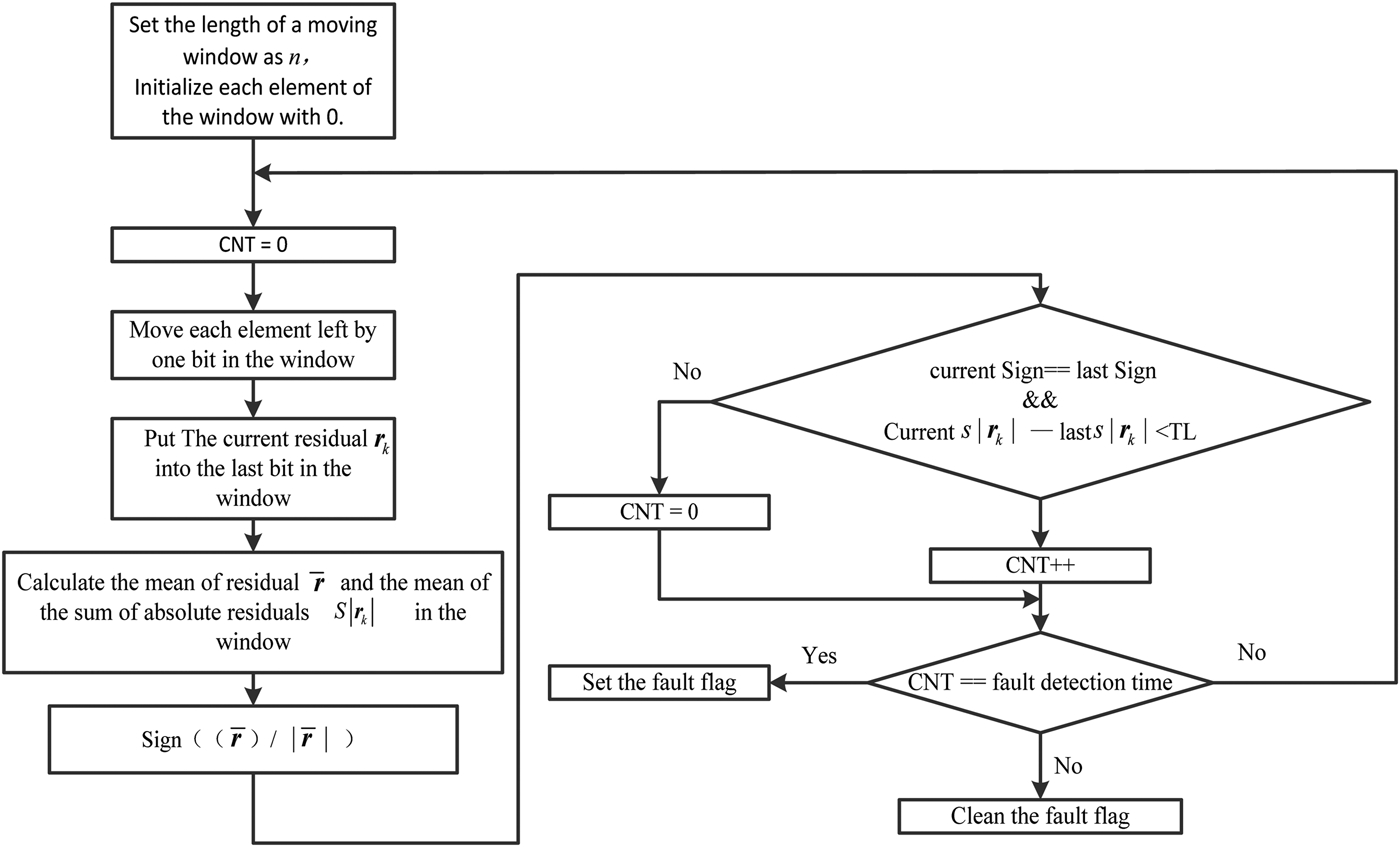
A diagram of our gradual fault detection method is shown in Figure 3, where the normalisation of ${\bar{\bi r}}_k $ is performed as

(27)$$sign({{\bar{\bi r}}}_k ) = {{{{\bar{\bi r}}}_k} / {\left\vert {{{\bar{\bi r}}}_k} \right\vert}}$$

where, $sign({{\bar{\bi r}}}_k )$ denotes the normalisation of ${\bar{\bi r}}_k $.

Figure 3. The gradual fault detection scheme.

Because of the features of gradual faults the mean of the residual could not have a great fluctuation during the adjacent periods. Meanwhile, the normalised residual means are equal in the adjacent periods. The sum of absolute residual is bigger than that when no fault occurs. There are rare differences between the sums of absolute residual in adjacent cycles, the absolute subtraction of them will be lower than the threshold T _L which is equal to 0·04 in this paper. According to our design, if there is no great difference between each mean of residuals and all normalised residual means are equal and the differences of residual mean in adjacent cycles are less than T _L in 30 consecutive updates, the gradual fault will be recognised, and the fault subsystem will be isolated immediately.

According to Figure 3, the gradual fault detection and system restored steps in this paper are as follows.

1. 1) Initialisation. The length of a statistical cycle is set to be 20 s, which means the length of moving window equals 20 and each element in the window is assigned a value of 0;

2. 2) Statistical calculations. Clean the counter (here we use CNT to denote the counter). Move each element left by one bit, calculate the current residual and put it into the last bit in the window at each update of the integrated navigation. Then, calculate the residual mean, the normalised residual mean and the sum of absolute residual of the window.

3. 3) Gradual fault detection. If in 30 consecutive updates, (30 s is the gradual fault detection time in this paper), there is no great difference between each mean of residual and all the normalised residual means are equal, the difference of sum of the absolute residual in adjacent cycles is lower than the threshold T _L (in this paper, T _L < 0·04), then, it is recognised that a gradual fault has occurred. Or, return to step 2.

4. 4) Isolation. If a gradual fault is recognised in step 3, isolate the faulty subsystem.

5. 5) System restoration. Take DVL as an example. When the fault disappears, there will be another hop in fault detection function. At this time, if the upward velocity is equal to the rate of the depth-gauge change, it means that the SINS/DVL system works properly again, and this subsystem should restored. This restoration time lasts 10 s in this paper.

6. 6) To avoid the misjudgement of the fault diagnosis system, which is caused by the oscillation of system in the restoring process of the aided navigation system, all the fault diagnosis systems stop working for 30 s right after the gradual fault is restored.

4. SIMULATION EXPERIMENT

4.1. Simulation conditions

The gyro constant drift is 0·04°/h with its random drift 0·04°${/\sqrt {\rm h}} $; the accelerometer constant bias is 50 μg (g = 9·8 m/s²) with its random bias 50 μg; the geographical position is 118° east longitude, 32° north latitude; and the carrier maintains its state to be uniform in a straight line with its east and north velocity components both constant at 0·5 m/s. To simplify the integrated navigation system model, the measurement errors of DVL, depth-gauge and MCP are set as white noise with amplitude of 0·02 m/s, 5 m and 0·2° respectively, and the information of all these aided navigation devices are updated at a frequency of 1 Hz. The integrated navigation system information fusion circle is set to be 1 s and the whole simulation time is 1000 s.

This paper takes DVL as an example to illustrate the working process of the gradual fault detection system. In the experiment, ramp function which is δV = (0·02*T)m/s and T as the gradual fault duration are attached to the output velocity of the DVL in the period of 200 s ~ 600 s, which simulates the gradual DVL fault.

To avoid navigation output fluctuation and a fault detection system misjudgement caused by filter instability during the start up of the integrated navigation system, in the first 10 s, outputs of the integrated navigation are only the SINS solution without feedback correction.

4.2. Simulation results and analysis

The monitoring result of the traditional residual χ² detection and M-estimation methods when the SINS/DVL subsystem meets a gradual fault are shown in Figures 4 and 5.

Figure 4. The detection function value of the traditional residual χ² detection system.

Figure 5. The residual of SINS/DVL by the M-estimation method.

In order to avoid the mistaken judgment of FDI result from the unstable outputs of the filter in the beginning, the fault detection function is not calculated until the integrated navigation system has worked for 50 seconds. So the start point 0 s in Figure 4 is the 50 s point to the integrated navigation system.

From Figure 4, it can be concluded that the value of the fault detection function which is used to detect the occurrence of the fault by traditional residual χ² detection method does not obviously change when the gradual fault occurs at 200 s. This leads the traditional residual χ² detection method to fail in detecting the gradual fault. When the gradual fault disappears at 600 s, the value of the fault detection function increases greatly which is bigger than the threshold T _D. Then the fault detection and isolation system mistakenly determines that the SINS/DVL subsystem meets a fault. Meanwhile, the fault detection and isolation system also isolates this subsystem which stops the SINS/DVL from being fused; this makes the accuracy of the integrated navigation system worse. From Figure 5 it can be concluded that the phenomenon of the residual in M-estimation is the same as that in Figure 4 by the traditional residual χ² detection method. Thus we can conclude that the traditional residual χ² detection method and the M-estimation both fail to detect the gradual fault.

To certify the effectiveness of the fault detection method proposed in this paper, three cases are discussed which are shown in Table 1.

Table 1. Three cases.

Figures 6 to 8 show the attitude errors, velocity errors and position errors of the integrated navigation system for the three cases. Figure 9 shows the mean values of system vertical velocity component residuals.

Figure 6. The integrated navigation system attitude errors curve when DVL fails with a gradual fault.

Figure 7. The integrated navigation system velocity errors curve when DVL fails with a gradual fault.

Figure 8. The integrated navigation system position errors curve when DVL fails with a gradual fault.

Figure 9. The mean of the upward velocity residual of SINS/DVL.

Figure 6(a) and 6(b) show that, when a gradual fault occurs in DVL without isolation, the horizontal attitude errors have constant values. While if the gradual fault of DVL is detected quickly and the subsystem SINS/DVL is isolated immediately, the horizontal attitude errors can be reduced to a certain extent. The horizontal constant attitude errors disappear when the gradual fault disappears and the subsystem SINS/DVL is then restored. The traditional residual χ² detection method fails to detect the gradual fault of the subsystem; it even results in an error of judgment when the gradual fault disappeared and mistakenly isolates the subsystem. From Figure 6 it also can be concluded that an accurate speed provided by DVL can effectively correct the horizontal attitudes of the integrated navigation.

From Figure 7 we can conclude that, in Cases 2 and 3, the integrated navigation system output velocity could track the gradual fault and velocity errors between the integrated navigation system and reference system and are equal to the fault information. In Case 1, the fault diagnosis system proposed in this paper can detect the SINS/DVL subsystem gradual fault in 30 s and isolate this failing subsystem quickly. Then the integrated navigation system with residual normal navigation devices continues to work properly, and the output navigation information is not polluted by the fault. When the gradual fault disappears, the velocity is integrated normally in Cases 1 and 3. However the integrated navigation velocity solution is still quickly divergent for the mistaken isolation in Case 2.

Comparing the results shown in Figure 8, it can be seen that a gradual fault could result in a great horizontal position error compared with the system without fault. However, if the gradual fault is detected quickly and isolated in time, the horizontal position error could be reduced to a great extent. The mistaken isolation in Case 2 can result in an intolerable error to the integrated navigation system.

In Figure 9(a) the mean of the upward velocity residual is identical to −0·02, the amplitude of which is equal to the change rate of the gradual fault. The normalised residual mean is identical to −1. In Figure 9(b) the gradual fault is detected at 233 s and the SINS/DVL subsystem is isolated immediately. The mean of the upward velocity residual begins to increase greatly.

5. TESTING IN A VEHICULAR ENVIRONMENT

The gradual fault detection method proposed was verified by car test to simulate the manoeuvre of an underwater vehicle. The prototype of a fibre optic gyroscope strapdown inertial navigation system was used in the experiment. The gyro constant drift is 0·006°/h, and its random drift is 0·005°$ /\sqrt {\rm h} $, the accelerometer constant bias is less than 50 μg. The reference navigation data came from the loose couple of PHINS developed by French firm IXBLUE and the FlexPark6 GNSS receiver developed by the NovAtel firm. The velocity vector projection in the carrier coordinate can be obtained by using the reference system's attitude matrix. White noise with amplitude of 0·02 m/s is attached to the obtained velocity to simulate a DVL output. Also, white noise is added to the heading information and height information of the reference system, with amplitude to be 0·2° and 5 m, so that it can simulate MCP and Depth-gauge output respectively. The navigation system information update frequency is 1 Hz, and the information fusion cycle of the integrated navigation system is 1 s. PHINS and the inertial measurement unit are fixed on the same mounting plate shown in Figure 10. Figure 11 shows the navigation experimental car with a red circle in Figure 11 to mark the GNSS receiver antenna.

Figure 10. Installation diagram.

Figure 11. Experimental car.

In the real environment, the gradual fault always changes slowly and is hard to detect. The interruption of the noise increases the difficulty of gradual fault detection. In this paper a ramp function (δV = (0·02*T)m/s, T is the gradual fault duration) is attached to the output velocity of the DVL in the period of 200 s ~ 500 s, which simulates the gradual faults of the DVL. The gradual fault detection time is set to 60 s.

The attitude errors, velocity errors and position errors of the integrated navigation systems under three conditions: fault-free, fault without isolation and fault with isolation, are shown in Figures 12 to 14. Figure 15 demonstrates the navigation trajectory from the experimental prototype. Figure 16 is the navigation trajectory from the reference systems and Figure 17 is the actual road map used for experiments.

Figure 12. The attitude error curves of the integrated navigation system.

Figure 13. The velocity error curves of the integrated navigation system.

Figure 14. The position error curves of the integrated navigation system.

Figure 15. Trace of integrated navigation system.

Figure 16. Reference trace route.

Figure 17. Real trace.

Figure 12 implies that the pitch error, roll error and heading error are nearly the same under the two conditions of fault-free and fault with isolation. Only a few hops whose values are less than 1° exist when the SINS/DVL subsystem is restored. Plenty of large fluctuations are apparent when a gradual fault exists and without isolation.

Figure 13 indicates that the output velocity of integrated navigation tracks the gradual fault from 200 s to 260 s. The fault detection method introduced in this paper can identify the gradual fault as long as the fault lasts for 60 s and isolates the failed subsystem, SINS/DVL subsystem, immediately. In the low dynamic environment, the velocities will not change very much. According to the previous 100 s results of the navigation system we have recorded, we take the mean of the first 30 s velocities as the current velocities. Then the velocities are mainly provided by SINS and show a certain tendency to diverge, but the divergent rate is much smaller than those under the condition that a fault occurs without isolation.

Figure 14 shows that under the conditions of fault-free, fault without isolation and fault with isolation, the attitude errors are 0·0016°, 0·0060°, 0·0014°, respectively. The longitude errors are 0·00091°, −0·0098°, −0·0063°, respectively. When DVL meets the gradual fault and the SINS/DVL subsystem is isolated successfully, the integrated navigation system output velocity errors increase accordingly, which results from the lack of DVL velocity correction. After the system is stable, the output latitude errors and longitude errors continue. The position errors still increase. Therefore, it can be concluded that the gradual fault detection method introduced in this paper can stop the interruption caused by the gradual fault, and the accurate DVL output velocity information can inhibit the position error effectively and efficiently. The statistical results of Figures 15 and 16 are summarised in Table 2.

Table 2. Statistical results of horizontal position errors relative to the reference system.

6. CONCLUSION

Owing to the fact that the residual χ² detection method fails to detect the gradual fault, the improved residual χ² detection method is only used to calculate the residual values in this paper. In the proposed method, the normalised residual and the sum of absolute residual are considered as the determinants of the gradual fault. If there is no great difference between each mean of residual, all the normalised residual mean values are equal, and the difference of adjacent periods is less than the threshold T _L in gradual fault detection time, a gradual fault is recognised and the faulty subsystem is isolated immediately. The simulation results and the vehicle tests show that the residual of the failed sub-system can be calculated accurately with the improved the residual χ² detection method and the improved residual χ² detection method has a strong applicability in gradual fault detection. Therefore, the gradual fault can be detected in a short time with the normalised residual mean and the sum of absolute residual. The gradual fault detection method proposed in this paper is effective in low dynamic environments.