Obesity, characterised by excessively accumulated body fat( Reference Deurenberg, Deurenberg-Yap and Guricci 1 ), is one of the well-established risk factors for many metabolic diseases, including type 2 diabetes (T2D)( Reference Pi-Sunyer 2 ). BMI has been widely used to define obesity in numerous epidemiological studies because of its simplicity and availability( Reference Wells and Fewtrell 3 ). Meanwhile, BMI does not discriminate between fat and lean tissue. Therefore, it may not be a very precise indicator of body fat percentage (BF%), which is associated with various metabolically abnormal phenotypes independent of BMI( Reference Shea, King and Yi 4 – Reference Oliveros, Somers and Sochor 6 ). In contrast, among individuals with well-developed musculature, BMI tends to overestimate the BF% levels( Reference Prentice and Jebb 7 ). Therefore, not only BMI but also BF% is important when screening susceptibilities of metabolic outcomes( Reference Gomez-Ambrosi, Silva and Galofre 8 ). To date, advanced technologies such as isotope dilution, MRI and dual-energy X-ray absorptiometry (DXA) have been employed to objectively measure BF%; however, their expensive, technologically complex and time-consuming natures( Reference Wells and Fewtrell 3 ) hinder their applications in epidemiological field studies, especially in underdeveloped countries and regions. Skinfold thickness is simpler and cheaper, but is still device-dependent and requires well-trained operators( Reference Ellis 9 ).
In recent years, numerous findings have suggested that equations incorporating age, sex, BMI and/or waist circumference (WC) could be alternatively used to predict BF%( Reference Lean, Han and Deurenberg 10 – Reference Gomez-Ambrosi, Silva and Catalan 13 ). Nevertheless, most of those equations were developed in Western populations, and ethnic differences in the relationship between simple anthropometric measurement and actual body adipose content have been suggested by many studies( Reference Jackson, Stanforth and Gagnon 11 , Reference Wang, Thornton and Russell 14 , Reference Deurenberg, Yap and van Staveren 15 ). Compared with Westerners, Asians are known to have higher body fat content at a given BMI or WC( Reference Lear, Humphries and Kohli 16 ), and also tend to accumulate more abdominal fat( Reference Lear, Humphries and Kohli 17 ). Even within Asian populations, BF% at the same adipose status may vary among Chinese, Thai and Indonesians( Reference Deurenberg, Yap and van Staveren 15 ), requiring the development of Chinese specific BF% equation(s). Given the relationship between adiposity and cardiometabolic outcomes, it is critical to evaluate whether equation-derived BF% performs well in the aforementioned associations( Reference Gomez-Ambrosi, Silva and Catalan 13 , Reference Steinberger, Jacobs and Raatz 18 ). However, as far as we know, the relationship between equation-derived BF% and metabolic deteriorations have only been examined in a few cross-sectional studies( Reference Gomez-Ambrosi, Silva and Catalan 13 , Reference Steinberger, Jacobs and Raatz 18 ), but not in any prospective cohort study.
Therefore, the aims of the present study were (1) to establish equations as alternatives of DXA to evaluate BF%, based on the anthropometric and demographic data from a population-based Chinese sample; (2) to validate the newly developed equations in another independent Chinese cohort sample for their accuracies and associations with 6-year changes of cardiometabolic risk factors and the risk of developing T2D, in comparison with BF% measured by DXA (BF%-DXA).
Methods
Study participants
The training sample was from the Gut Microbiota and Obesity (GMO) study, a population-based case–control study conducted among 1059 non-institutionalised Shanghai residents in China. The fieldwork was conducted in 2007–8, and a detailed study design has been described elsewhere( Reference Sun, Yu and Ye 19 ). Briefly, participants were recruited through advertisements, and the study population consists of both normal-weight (18 ≤ BMI < 24 kg/m2) and overweight/obese (BMI ≥ 24 kg/m2) individuals aged 35–54 years. People were included if they had been living in Shanghai for at least 10 years, but were excluded if they (1) were diagnosed with diabetes, cancer, CHD, stroke, severe kidney or liver diseases, infectious diseases, severe psychological disorders or physical disabilities; (2) used antibiotics for three consecutive days within 3 months before the study; (3) received gastrointestinal surgery within 1 year; or (4) were in pregnancy or lactation period. In the present study, a total of 960 individuals (352 men and 608 women) with complete data of DXA scan were included for the development of the equation.
Validation of our equations was conducted among subjects from the Nutrition and Health of Aging Population in China (NHAPC) study, a population-based prospective study conducted among community-living Chinese aged 50–70 years in Beijing and Shanghai, China. The study design and data collection at baseline and follow-up have been described elsewhere( Reference Ye, Yu and Li 20 , Reference Zong, Zhu and Sun 21 ). In brief, this study was initiated in 2005, and aimed to investigate the impacts of environmental and genetic factors and their interactions on age-related diseases. The eligible candidates were residents aged 50–70 years and who had been living in Beijing/Shanghai for at least 20 years. Those with any of the following conditions were excluded: (1) severe psychological disorders, physical disabilities, cancer, CVD, Alzheimer's disease, or dementia, within 6 months; or (2) currently diagnosed with communicable diseases. A 6-year follow-up survey was performed in 2011, and all participants were recruited by health workers from local Centers for Disease Control and Prevention and community clinics. Due to the fact that DXA scanner was available only in Shanghai, the DXA data were obtained from 1150 Shanghai participants at baseline, and were used to validate the equations. A total of 233 (20·3 %) participants were lost during the follow-up; eighty-three participants were diagnosed with diabetes at baseline; and another fifty-four participants did not provide fasting blood samples. After excluding these participants, 780 subjects were included in the analyses of prospective associations between BF% and cardiometabolic risk factors, and incident T2D. The present study was conducted according to the guidelines laid down in the Declaration of Helsinki, and all procedures involving human subjects/patients were approved by the Institutional Review Board of the Institute for Nutritional Sciences, Chinese Academy of Sciences. Written informed consent was obtained from all the participants.
Data collection
In both the GMO and the NHAPC studies, a face-to-face interview was conducted, and information of demographic variables (including ethnicity), health status and behaviours (including smoking, alcohol drinking and physical activity) were obtained using standardised questionnaires( Reference Sun, Yu and Ye 19 , Reference Ye, Yu and Li 20 ). Current alcohol drinking and/or smoking habits were grouped as ‘yes’ or ‘no’. Current smoking referred to daily smoking for >6 months and current alcohol drinking referred to people who consumed any alcohol. Physical activity was evaluated by using the International Physical Activity Questionnaire (short last 7-d format) and categorised as low, moderate or high ( < 77·5, 77·5–137·8 and ≥ 137·9) based on the metabolic equivalent-hours/week score( 22 ). The anthropometric and body fat measurements of the participants of the two studies were collected through the same standard protocols and devices. With participants wearing light clothes without shoes, body weight was measured to the nearest 0·1 kg, and height was measured to the nearest 0·1 cm. WC was measured at the mid-point between the lowest rib and the iliac crest to the nearest 0·1 cm, after inhalation and exhalation; while hip circumference was measured at the widest girth of the hip to the nearest 0·1 cm, using a plastic-coated fibreglass tape (Grafco 17-1340-2). Blood pressure was determined on the right arm, after a 5 min rest at minimum, using an electronic blood pressure monitor (Omron HEM-705CP); three measurements were performed, and the mean of the last two was applied in the analyses. Body fat data were measured with whole-body DXA scanner (Hologic QDR-4500), and BF% was calculated as total body fat mass divided by body weight. BMI was calculated as weight (in kg) divided by the squared height (in m). For the NHAPC study, overnight fasting blood samples were collected; plasma glucose, TAG, HDL-cholesterol, C-reactive protein (CRP) and uric acid (UA) levels were measured on an automatic analyser (Hitachi 7080) at baseline and at 6-year follow-up.
Definition of type 2 diabetes
T2D was defined as any of the following conditions: fasting glucose ≥ 7·0 mmol/l; previous diagnosis; use of anti-diabetic medications.
Statistical analysis
Stepwise linear regression was used to develop sex-specific BF% equations after forcing BMI (kg/m2) and WC (cm) into the model. The significance levels of entering the model and being removed were set as 0·10 and 0·05, respectively( Reference Kuk, Katzmarzyk and Nichaman 23 ). In addition to BMI and WC, the following candidate variables were also considered in the sex-specific equations: age; BMI square (kg2/m4); WC square (cm2); interaction terms between age and anthropometric variables. The general equation was developed based on the above candidate variables as well as sex and interaction between sex and anthropometric variables. The coefficient of determination (R 2) was used to evaluate the proportion of total variation of BF%-DXA explained by new equations. Correlations between two variables were computed by the Pearson correlation coefficient. Differences between any two correlations were evaluated by Wolfe's test( Reference Rosner 24 ). Bland–Altman analysis( Reference Bland and Altman 25 ) was performed to examine the agreement between BF% calculated using equations (BF%-C) and BF%-DXA. The difference was calculated by subtracting BF%-DXA from BF%-C, and the significance levels were tested by paired t test. The mean difference was also considered as an indicator of bias in the comparisons of our equations with others. A generalised linear model was conducted to evaluate the associations between BF% and 6-year changes in cardiometabolic risk factors, adjusted for baseline values of age, residence (urban and rural), a certain risk factor (glucose, TAG, HDL-cholesterol, blood pressure, CRP or UA), physical activity level (high, moderate or low), education attainment (0–6, 7–9 or ≥ 10 years), alcohol drinking (yes or no), smoking (yes or no), having cancer, CHD and stroke. To examine whether the associations with cardiometabolic markers were equivalent between BF% calculated using sex-specific equations (BF%-CSS) and BF%-DXA, the residuals of the indices and changes of cardiometabolic markers were derived by regressing these variables on the aforementioned covariates. The correlations between the residuals of a specific biomarker and the residuals of BF%-CSS and BF%-DXA were then calculated, respectively. Finally, Wolfe's test was used to compare the two correlation coefficients( Reference Rosner 24 ). When analysing the association with longitudinal change of CRP, thirty-eight subjects with CRP levels above 10 mg/l at baseline or at 6 years of follow-up were excluded. The area under the receiver operating characteristic curve was calculated to evaluate the associations of BF%-CSS or BF%-DXA with incident T2D and potential confounders included age, residence, levels of physical activity, education, alcohol drinking, smoking, presence of chronic diseases (cancer, CHD or stroke) and family history of diabetes. The data analysis for the present study was generated using SAS software, version 9.3 of the SAS system for Windows × 64 based systems. Copyright© 2002–2010 Institute, Inc., SAS and all other SAS Institute, Inc. product or service names are registered as trademarks or trademarks of SAS Institute, Inc. The significance level was set as P< 0·05 (two-sided).
Results
Characteristics of subjects
The characteristics of participants in the GMO study and the NHAPC study (baseline) are presented in Table 1. The BF%-DXA of the two samples were comparable for women, but not for men (GMO: 22·8 (sd 5·0) % v. NHAPC: 20·5 (sd 5·4) %, P< 0·05). Both samples represented a wide range of BMI (GMO: 18·0–41·6 kg/m2; NHAPC: 14·1–35·6 kg/m2) and BF%-DXA (GMO: 9·0–47·5 %; NHAPC: 7·9–45·5 %).
Table 1 Characteristics of participants in the training and validation samples (Mean values and standard deviations; number of participants and percentages)

GMO, Gut Microbiota and Obesity; NHAPC, Nutrition and Health of Aging Population in China; WC, waist circumference; BF%-DXA, body fat percentage measured by dual-energy X-ray absorptiometry.
* Comparisons were made for all variables between the two samples, and all of them were significant differences except for women's BF%-DXA.
Developed equations and their accuracies
Sex-specific and general equations were established in the training sample using stepwise selection in linear regression (Table 2). The R 2 and standard error of the estimate (SEE) were 66·5 and 2·91 % for men's equation, and 61·9 and 3·08 % for women's equation, respectively. The general equation had an R 2 of 81·1 % and a SEE of 3·02 %.
Table 2 The newly developed equations

SEE, standard error of the estimate; BF%, body fat percentage; WC, waist circumference.
* The R 2 and SEE were generated during the development of the equations, and the R 2 of general equation was 66·6 % for men and 61·8 % for women.
† Sex = 0 for men, and sex = 1 for women.
Validation analyses were performed for both sex-specific equations and the general equation. Herein, BF%-DXA was strongly correlated with BF%-CSS and BF% calculated using the general equation (BF%-CG; r 0·905 for both correlations), while correlations were relatively weaker between BF%-DXA and anthropometric indices, including BMI, WC, waist:hip ratio and body adiposity index (hip circumference/height1·5− 18, P for Wolfe's test < 0·05; Table 3). When analyses were performed separately by sex, the highest correlation coefficient between BF%-CSS or BF%-CG and BF%-DXA was maintained in women (P for Wolfe's test < 0·05), but not in men. The scatterplot of BF%-CSS against BF%-DXA showed that all dots were near the dashed line (intercept = 0; slope = 1), suggesting a similarity of the two measures (Fig. 1). Similar dot pattern was also observed in the scatterplot of BF%-CG against BF%-DXA (figure not shown). Overall, the result of Bland–Altman analysis indicated that the BF%-CSS had lower bias than BF%-CG (Table 4), although they had similar Bland–Altman plots (see online supplementary Fig. S1). The limit of agreement (mean difference) was 0·08 (2 sd 6·64) % for men's equation (P= 0·606) and 0·45 (2 sd 6·88) % for women's equation (P< 0·001). Moreover, the mean difference was smaller in individuals with BMI ≥ 24 kg/m2 or age ≥ 60 years than their counterparts (see online supplementary Table S1). In Bland–Altman analysis, our equations also showed lower biases (0·08–0·57 %) than four of the previous equations ( − 1·24–4·56 %) developed in other populations when age, sex and/or BMI were treated as independent variables (see online supplementary Table S2).
Table 3 Pearson's correlations between body fat indices and body fat percentage measured by dual-energy X-ray absorptiometry (BF%-DXA) in the validation sample*
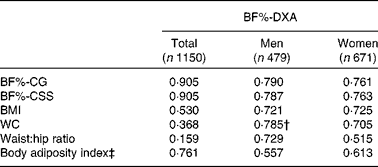
BF%-CG, body fat percentage calculated using the general equation; BF%-CSS, body fat percentage calculated using sex-specific equations; WC, waist circumference.
* Correlation coefficients were all significant, P< 0·001.
† Not significantly different from the correlation coefficient between BF%-DXA and BF%-CSS/BF%-CG in the same column using Wolfe's test.
‡ Body adiposity index, hip circumference/height1·5− 18.

Fig. 1 Agreement between body fat percentage (BF%) calculated using sex-specific equations (BF%-CSS) and BF% measured by dual-energy X-ray absorptiometry (BF%-DXA) in 1150 subjects of the NHAPC study. ![]() , Identical values of the two methods;
, Identical values of the two methods; ![]() , men;
, men; ![]() , women.
, women.
Table 4 Bland–Altman analysis of the equations in the validation sample

* Limit of agreement = mean difference – 2 sd to mean difference + 2 sd.
Associations of body fat percentage with changes in cardiometabolic profiles and incident type 2 diabetes
Among the 780 subjects without baseline diabetes in the NHAPC study, all the cardiometabolic risk factors including fasting plasma glucose, TAG, HDL-cholesterol, CRP and UA increased significantly over the 6-year follow-up, except for diastolic blood pressure in men and systolic blood pressure in women (see online supplementary Table S3). Sex-specific equations were further analysed for the associations with metabolic markers, given their better performance in Bland–Altman analysis. In the multivariate-adjusted model (adjusted for age, residence, physical activity level, education attainment, alcohol drinking, smoking, and having cancer, CHD or stroke), the BF%-CSS and BF%-DXA showed a comparable relationship with baseline levels of TAG, CRP and UA in both men and women (see online supplementary Table S4). Compared with BF%-DXA, the BF%-CSS was more strongly associated with glucose in men (P= 0·002), and was more strongly associated with HDL-cholesterol (P= 0·033), systolic blood pressure (P= 0·009) and diastolic blood pressure (P= 0·012) in women. Furthermore, BF%-CSS and BF%-DXA were largely comparable regarding the associations with 6-year change of those markers, except that the association between the BF%-CSS and 6-year change of systolic blood pressure was stronger in women (P= 0·028; Table 5). Among the 780 participants, 18·0 % of them developed T2D over the 6-year period. Area under the receiver operating characteristic curves were calculated to evaluate the associations of BF%-CSS or BF%-DXA with incident T2D. The area under the receiver operating characteristic curves were 0·62 (95 % CI 0·53, 0·71) for BF%-CSS and 0·59 (95 % CI 0·50, 0·68) for BF%-DXA in men (P for comparison = 0·327), and 0·66 (95 % CI 0·59, 0·72) for BF%-CSS and 0·64 (95 % CI 0·58, 0·70) for BF%-DXA in women (P for comparison = 0·159) (see online supplementary Fig. S2).
Table 5 β-Coefficients of body fat percentage (BF%) calculated using sex-specific equations (BF%-CSS) and BF% measured by dual-energy X-ray absorptiometry (BF%-DXA) from the multivariate linear regression on 6-year changes of metabolic risk factors* † (β-Coefficients and standard errors)

SBP, systolic blood pressure; DBP, diastolic blood pressure; CRP, C-reactive protein; UA, uric acid.
* n 293 for men and n 487 for women, except for CRP, n 282 for men and n 460 after excluding those with CRP levels above 10 mg/l, for UA, n 288 for men and n 483 for women because of missing data.
† Adjusted for baseline level of the risk factor, age, residence, education, alcohol drinking, smoking and physical activity, having CHD, stroke and cancer.
‡ Comparison between β coefficients for BF%-CSS and BF%-DXA.
Discussion
In the present study, we developed new equations to estimate BF% among 960 Chinese with a broad range of adiposity levels, and also conducted validation analyses in another independent Chinese cohort population. The validation analyses showed that BF%-CSS was in reasonable agreement with BF%-DXA. Meanwhile, BF%-CSS and BF%-DXA had comparable associations with changes in a series of cardiometabolic risk factors and incident T2D over 6 years. To our knowledge, this is thus by far the largest investigation that has developed BF% equations in Asian populations, and the findings from the present study also provided new information on the associations between equation-based BF% with changes in cardiometabolic risk factors and incident T2D over several years.
To clearly understand more detailed relationships between obese phenotypes and health status, not only BMI but also BF% needs to be evaluated in large-scale population studies. However, it is not cost-effective and time-efficient to apply standard devices such as MRI and DXA for BF% measurement for large epidemiological surveys. In such circumstance, equations based on anthropometry could be the simplest surrogate; however, it was proved to be highly ethnic-specific due to considerable variations in body composition and relationships between BF% and BMI or WC between different ethnic groups( Reference Jackson, Stanforth and Gagnon 11 , Reference Wang, Thornton and Russell 14 , Reference Deurenberg, Yap and van Staveren 15 ). As the largest developing country, China has experienced rapid urbanisation and changes in dietary and lifestyle choices in the past decades( Reference Hu, Liu and Willett 26 ). Accompanied with the changes, it is estimated that one-fifth of the world's overweight or obese people were Chinese( Reference Wu 27 ). Unfortunately, few studies have evaluated BF% and related health consequences using equation(s) generated from Chinese population so far. One skinfold-based BF% equation was reported by Kwok et al. ( Reference Kwok, Woo and Lau 28 ) based on the data of 613 Hong Kong residents aged 69–82 years. Apparently, skinfold measurement is more accessible than DXA or MRI method; however, its device-dependency and requiring skilful professionals are also not practical in dealing with large sample sizes. Moreover, the narrow age range in the subjects could limit the application of their equation to other Chinese populations. In contrast, the current BF% equation only included age, sex, BMI and WC as independent variables, all of which are routinely collected in epidemiological studies. Thus, our new, validated equations may facilitate the estimation of BF% in large-scale epidemiological studies, specifically among Chinese people.
Our validation analyses in 1150 subjects of the NHAPC study showed that BF%-CSS was highly correlated with BF%-DXA. Meanwhile, the bias in women's equation was smaller than some of the previous validation analyses of BMI or WC-derived equations from studies in Americans (White and Black), Spanish, Netherlander, Swedish and Japanese (mean differences − 1·0–2·9 %)( Reference Jackson, Stanforth and Gagnon 11 , Reference Gomez-Ambrosi, Silva and Catalan 13 , Reference Minematsu, Takamura and Goto 29 – Reference Larsson, Henning and Lindroos 31 ). Moreover, there was no significant bias in the equation for men. Those results suggested a satisfactory accuracy of our equations for the purposes of epidemiological assessment. In contrast, the R 2 of our sex-specific equations (66·5 % for men and 61·9 % for women) were lower than that of our general equation (81·1 %). This discrepancy may be partially interpreted by the fact that sex per se accounted for considerable BF% variances in the whole population, due to sex hormonal impact on body fat storage( Reference Geer and Shen 32 , Reference Barreira, Harrington and Staiano 33 ). The combined data set (7·9–45·5 %) and separated data sets (7·9–34·3 % in men; 14·2–45·5 % in women) had different ranges of dependent variable (BF%), which might also affect the magnitude of R 2 in linear regression( Reference Barrett 34 ). Therefore, a low R 2 may not necessarily indicate poor performance. The SEE could also provide information of estimated accuracy( Reference Hennig and Cooper 35 ). In fact, our sex-specific equations have similar SEE (approximately 3 %) compared with our general equation, as well as the equations developed by others( Reference Gomez-Ambrosi, Silva and Catalan 13 , Reference Deurenberg, Yap and van Staveren 15 , Reference Deurenberg, Weststrate and Seidell 30 ).
Previously, several studies have focused on the relationships between estimated BF% and cardiometabolic risk factors, and suggested the usefulness of BF% equation. For instance, Gomez-Ambrosi et al. ( Reference Gomez-Ambrosi, Silva and Catalan 13 ) reported that their equation-derived BF% exhibited better correlations with blood lipid profile, blood pressure or insulin resistance indices than using BMI or WC alone in 634 diabetic patients. However, that study did not compare estimated BF% with objectively measured BF% with regard to their associations with obesity-related risk factors; thus, it remains unclear whether the two approaches were interchangeable on those associations. In another cross-sectional study of 130 adolescents, Steinberger et al. ( Reference Steinberger, Jacobs and Raatz 18 ) found that BF% either estimated by Slaughter's equation or measured by DXA showed comparable correlations with cardiovascular risk factors including glucose utilisation, systolic blood pressure, HDL-cholesterol and insulin. However, no data were available regarding longitudinal associations between estimated BF% and changes of risk factors so far. In the present study, we further provided a novel evidence that baseline BF%-CSS and BF%-DXA have similar strength in terms of their associations with 6-year changes of diastolic blood pressure, TAG, HDL-cholesterol, glucose, inflammatory markers and UA, as well as with 6-year incident T2D.
Strengths of the present study included the following: (1) the new equations were developed from a large population-based sample with broad ranges of BMI and BF%, and the validation was conducted in an independent and large-scale cohort sample; (2) based on a prospective study design, we simultaneously documented associations with longitudinal changes of metabolic risk factors for both BF%-C and BF%-DXA for the first time. However, all the participants in our training sample and 99 % of participants in our validation sample are Chinese Hans. It remains to be confirmed whether our equations are applicable for other Chinese minority groups. Meanwhile, our validation sample only included Shanghai residents aged 50–70 years, and it is also to be confirmed in more future studies whether or to what extent our new equations could be generalised to nationwide Chinese or other Asian populations. Although DXA was frequently used as a reference method in BF% estimation( Reference Plank 36 ), its accuracy could be affected by the content of total body water( Reference Laskey 37 ). Since no data of total body water and body density were available, it was not possible to apply four-compartment model in present study.
In conclusion, anthropometry-based BF% equations were developed and validated for Chinese men and women. The new equations might serve as a useful tool in large-scale epidemiological surveys to estimate BF% among Chinese adults. More studies are needed to evaluate the application of our equations in different populations.
Supplementary material
To view supplementary material for this article, please visit http://dx.doi.org/10.1017/S0007114515000616
Acknowledgements
The authors thank Dr Jing Wang, Dr Hongyu Wu, Dr Wei Gan, Jingwen Zhu, He Zheng, Qianlu Jin and Yiqing Wang from the Institutes for Biological Sciences, Chinese Academy of Sciences and University of Chinese Academy of Sciences for their help in various stages of the present study.
The present study was supported by The Ministry of Science and Technology of China (2012CB524900), National Natural Science Foundation of China (81321062), the Knowledge Innovation Program of Shanghai Institutes for Biological Sciences, Chinese Academy of Sciences (2013KIP107) and the SA-SIBS Scholarship Program. These funding sources had no role in the study design, data collection, data analysis and the interpretation of the results.
The authors' contributions are as follows: X. Liu substantially contributed to the acquisition and analyses of the data, and drafted the manuscript; L. S., G. L., L. L., G. Z., X. Y. and H. L. contributed to data collection; Q. S. and B. R. substantially contributed to the conception of the study design, data analysis and revising of the manuscript; X. Lin made significant contributions to the study design, supervised data collection and interpretation, and revised the manuscript. All the authors involved in the writing of this article and approved the final content of the manuscript.
None of the authors has any conflict of interest to declare.









