1. Introduction
The interaction of colloids and electric fields is widely used for directed assembly and particle manipulation (Velev & Bhatt Reference Velev and Bhatt2006; Prieve, Sides & Wirth Reference Prieve, Sides and Wirth2010; van Blaaderen et al. Reference van Blaaderen, Dijkstra, van Roij, Imhof, Kamp, Kwaadgras, Vissers and Liu2013; Edwards & Bevan Reference Edwards and Bevan2014; Bharti & Velev Reference Bharti and Velev2015; Al Harraq, Choudhury & Bharti Reference Al Harraq, Choudhury and Bharti2022). In recent years, motile colloids energized by an applied electric field have become a popular model for self-propelled ‘active’ particles (Yan et al. Reference Yan, Han, Zhang, Xu, Luijten and Granick2016; Han, Shields & Velev Reference Han, Shields and Velev2018; Driscoll & Delmotte Reference Driscoll and Delmotte2019; Diwakar et al. Reference Diwakar, Kunti, Miloh, Yossifon and Velev2022; Boymelgreen et al. Reference Boymelgreen, Schiffbauer, Khusid and Yossifon2022). One propulsion mechanism exploits the induced-charge electrophoresis of colloids suspended in aqueous electrolyte solutions (Squires & Bazant Reference Squires and Bazant2004, Reference Squires and Bazant2006; Gangwal et al. Reference Gangwal, Cayre, Bazant and Velev2008; Nishiguchi & Sano Reference Nishiguchi and Sano2015; Ma et al. Reference Ma, Yang, Zhao and Wu2015). Another propulsion strategy is particle rolling on an electrode surface due to the Quincke rotation – a symmetry-breaking instability that gives rise to a torque on the particle in an applied uniform electric field (Bricard et al. Reference Bricard, Caussin, Desreumaux, Dauchot and Bartolo2013, Reference Bricard, Caussin, Das, Savoie, Chikkadi, Shitara, Chepizhko, Peruani, Saintillan and Bartolo2015; Snezhko Reference Snezhko2016; Karani, Pradillo & Vlahovska Reference Karani, Pradillo and Vlahovska2019; Pradillo, Karani & Vlahovska Reference Pradillo, Karani and Vlahovska2019; Zhang et al. Reference Zhang, Karani, Vlahovska and Snezhko2021a). The threshold for the Quincke rotation is very sensitive to the solvent conductivity and is accessible experimentally only in non-polar solvents, still at electric fields with magnitude of the order of 
${\textrm {MV}}\ {\textrm {m}}^{-1}$. At such strong electric fields, electric conduction may no longer be in the Ohmic regime due to fluid conductivity becoming dependent on electric field intensity (Onsager Reference Onsager1934; Castellanos Reference Castellanos1998). Field-enhanced conductivity arises from the electric field effect on the dissociation–recombination equilibrium between ion pairs and free ions (termed the Onsager effect). In a non-polar fluid, the electrolyte added to control conduction exists mostly in the form of neutral ion pairs (Prieve et al. Reference Prieve, Yezer, Khair, Sides and Schneider2017). The application of a strong electric field increases the rate of the ion pair dissociation, thereby increasing the number of charge carriers and accordingly the electrical conductivity (Castellanos Reference Castellanos1998). This effect is suggested to underlie the flow observed about colloids suspended in oil (Ryu et al. Reference Ryu, Park, Park and Kang2010), whose pattern resembles the induced-charge osmotic flow about an ideally polarizable particle in aqueous solutions, and the oscillatory motion of Quincke rollers (Zhang et al. Reference Zhang, Yuan, Dou, De La Cruz and Bishop2021b). Recent experiments have also reported that a charge-free, dielectric particle lifts off from the electrode (Pradillo et al. Reference Pradillo, Karani and Vlahovska2019) despite the attraction by the image dipole, which may involve electrohydrodynamic flow. Motivated by the potential impact of electrohydrodynamic flows on Quincke colloid ‘activity’ and collective dynamics, here we examine the possibility of a flow driven by conductivity gradients set by non-uniformities in the applied electric field. While the electric-field-driven flows about colloids near electrodes in aqueous electrolyte solutions have been subject to great interest (Ristenpart, Aksay & Saville Reference Ristenpart, Aksay and Saville2004, Reference Ristenpart, Aksay and Saville2007; Bazant et al. Reference Bazant, Kilic, Storey and Ajdari2009; Prieve et al. Reference Prieve, Sides and Wirth2010; Hashemi et al. Reference Hashemi, Bukosky, Rader, Ristenpart and Miller2018; Fernández-Mateo et al. Reference Fernández-Mateo, Calero, Morgan, García-Sánchez and Ramos2022; Khair Reference Khair2022; Katzmeier et al. Reference Katzmeier, Altaner, List, Gerland and Simmel2022), colloidal electrohydrodynamics in non-polar fluids is far less explored.
In this paper, we predict that an electrohydrodynamic flow driven by the Onsager effect arises about a spherical particle in an applied uniform electric field. We develop an asymptotic solution in the case of fluid conductivity varying linearly with the electric field intensity. We analyse the flow effect on the particle interaction with the electrode. The force on the particle due to the electrohydrodynamic flow is calculated using the Lorentz reciprocal theorem and found to be repulsive for insulating particles.
2. Problem formulation
Let us consider a non-polar liquid, e.g. hydrocarbon oil, containing an electrolyte, e.g. tetrabutylammonium bromide. In such solutions, the electrolyte exists mostly in the form of neutral ion pairs resulting in very low electric conductivity. (In contrast, in aqueous solutions ‘strong’ electrolytes are completely ionized.) The leaky dielectric model was developed to describe the flows is such weakly conducting fluids (Melcher & Taylor Reference Melcher and Taylor1969; Saville Reference Saville1997; Vlahovska Reference Vlahovska2019) adopting Ohm's law for the electric current, whose conservation at steady state results in
\begin{equation} \boldsymbol{\nabla}\boldsymbol{\cdot}(\sigma_m {\boldsymbol{E}})=0. \end{equation}
If the fluid conductivity is constant, then (2.1) implies that the bulk fluid is electroneutral. Charge accumulates only at interfaces separating media with different electric properties. A field-dependent conductivity 
$\sigma (E)$ due to field-enhanced electrolyte ionization (Onsager Reference Onsager1934) gives rise to space charge in a spatially inhomogeneous electric field as seen from the conservation of current (2.1) and Gauss’ law, 
$\varepsilon _m\,\boldsymbol {\nabla } \boldsymbol {\cdot } {\boldsymbol {E}} = \rho _f$:
\begin{equation} \rho_f ={-}\frac{\varepsilon_m}{\sigma_m}\,{\boldsymbol{E}} \boldsymbol{\cdot} \boldsymbol{\nabla}\sigma_m . \end{equation}The induced charge in the bulk would then drive flow, which in the creeping flow limit is described by the Stokes equation
\begin{equation} {-\boldsymbol{\nabla}}p + \mu\,\nabla^2 {\boldsymbol{u}} ={-}\rho_f {\boldsymbol{E}},\quad \boldsymbol{\nabla}\boldsymbol{\cdot} {\boldsymbol{u}} = 0, \end{equation}
where 
${\boldsymbol {u}}$ and 
$p$ are the fluid velocity and pressure, and 
$\mu$ is the fluid viscosity.
In this study, we ask the following questions. If a particle is introduced in a uniform electric field, would the resulting field inhomogeneities give rise to conductivity gradients and space-charge-driven flow? What is the correction due to the Onsager effect to the behaviour predicted by the leaky dielectric model, which is no flow about a solid particle?
2.1. The Onsager effect
If charge injection is negligible (Denat, Gosse & Gosse Reference Denat, Gosse and Gosse1982; Sainis, Merrill & Dufresne Reference Sainis, Merrill and Dufresne2008; Park et al. Reference Park, Ryu, Kim and Kang2009), then conduction is due to ions produced from the dissociation of the ion pairs (Castellanos Reference Castellanos1998; Prieve et al. Reference Prieve, Yezer, Khair, Sides and Schneider2017). In strong fields, the dissociation rate increases with field intensity (Onsager Reference Onsager1934). The activation energy for the ionization includes the Born self-energy of the two charged ions, the Coulomb energy of interaction between them, and the energy of separating the charged pair in the external electric field. The latter contribution leads to the fluid conductivity increasing as (Onsager Reference Onsager1934; Castellanos Reference Castellanos1998)
\begin{equation} \sigma_m= \sigma_0\,F(b)^{1/2}, \end{equation}
where 
$\sigma _0$ is the zero-field conductivity, and 
$F(b)$ is the Onsager function
\begin{equation} F(b)=\frac{{\textrm{I}}_1(2b)}{b},\quad b=\left(\frac{e^3 E}{4 {\rm \pi}\varepsilon_m (k_BT)^2}\right)^{1/2}. \end{equation}
Here, 
${\textrm {I}}_1$ is the modified Bessel function, 
$e$ is the electron charge, 
$k_BT$ is the thermal energy, 
$\varepsilon _m$ is the fluid permittivity, and 
$E$ is the field intensity. Equation (2.4) shows that conductivity is modified by the presence of an external electric field only if the field intensity is high, typically exceeding 
${\textrm {MV}}\ {\textrm {m}}^{-1}$. If 
$b\ll 1$, then 
$\sigma _m=\sigma _0$ is field-independent and the electrohydrodynamic flow is described by the leaky dielectric model (Melcher & Taylor Reference Melcher and Taylor1969).
2.2. Governing equations
We consider a spherical particle with radius 
$a$, permittivity 
$\varepsilon _p$ and field-independent conductivity 
$\sigma _p$ placed in a uniform electric field 
${\boldsymbol {E}}=E_0{\hat {\boldsymbol {e}}}_z$. The particle centre is located at a distance 
$d$ above a planar electrode at 
$z = 0$; see figure 1(a) for a sketch of the problem. We rescale all variables with particle radius 
$a$, applied electric field magnitude 
$E_0$, and the electrohydrodynamic time scale 
$t_{ehd} = \mu /(\varepsilon _m E_0^2)$. The dimensionless equations for the electric potential, fluid flow and charge conservation in the bulk are (Saville Reference Saville1997)
$$\begin{gather} \boldsymbol{\nabla}\boldsymbol{\cdot}(\tilde{\sigma}{\boldsymbol{E}})=0,\quad {\boldsymbol{E}}={-}\boldsymbol{\nabla}\varPhi, \end{gather}$$
$$\begin{gather}-\boldsymbol{\nabla} p + \nabla^2 {\boldsymbol{u}} ={-}{\boldsymbol{E}}\,\boldsymbol{\nabla}\boldsymbol{\cdot}{\boldsymbol{E}},\quad \boldsymbol{\nabla} \boldsymbol{\cdot} {\boldsymbol{u}} = 0, \end{gather}$$
where the Coulomb force on the fluid is obtained from the Maxwell stress tensor 
${\boldsymbol{\mathsf{T}}}={\boldsymbol {E}}{\boldsymbol {E}}-\frac {1}{2}E^2{\boldsymbol{\mathsf{I}}}$ as 
$\boldsymbol {\nabla }\boldsymbol {\cdot }{\boldsymbol{\mathsf{T}}}={\boldsymbol {E}}\,\boldsymbol {\nabla }\boldsymbol {\cdot }{\boldsymbol {E}}$, and 
$\tilde {\sigma }= \sigma /\sigma _0$ denotes the dimensionless conductivity. The dimensionless boundary conditions are summarized as
$$\begin{gather} \varPhi_m = \varPhi_p \quad(\mbox{continuous potential on the particle surface}~\mathcal{P}), \end{gather}$$
$$\begin{gather}\tilde{\sigma}_m {\boldsymbol{n}} \boldsymbol{\cdot} {\boldsymbol{E}}_m = \tilde{\sigma}_p {\boldsymbol{n}} \boldsymbol{\cdot} {\boldsymbol{E}}_p \quad(\mbox{continuous normal current on}~\mathcal{P}), \end{gather}$$
$$\begin{gather}\varPhi_m = 0 \quad(\mbox{grounded electrode on}~\mathcal{W}), \end{gather}$$
$$\begin{gather}{\boldsymbol{u}} = \boldsymbol{0} \quad(\mbox{no-slip}\,\, \mbox{on}~\mathcal{W}~\&~\mathcal{P}). \end{gather}$$
Another dimensionless parameter, the conductivity mismatch 
$\beta = (\tilde {\sigma }_p-1)/(\tilde {\sigma }_p+1)$, is used in this paper. The extreme cases of perfectly insulating (
$\sigma _p=0$) and perfectly conducting (
$\sigma _p\rightarrow \infty$) particles correspond to 
$\beta =-1$ and 
$\beta =1$, respectively. Far from the particle, the electric field is undisturbed and uniform, and the electrohydrodynamic flow vanishes.
Figure 1. (a) Sketch of the problem in cylindrical coordinates: a spherical particle of radius 
$a$ centred at 
$(r,z) = (0,d)$. (b) In bispherical coordinates, the particle surface is given by 
$\eta =\eta _0=\cosh ^{-1}(d/a)$, and the electrode surface is specified by 
$\eta =0$.
To solve the problem, we find it convenient to use bispherical coordinates 
$(\xi,\eta,\varphi )$ (see figure 1b), which are related to the cylindrical coordinates 
$(r,\varphi,z)$ as follows:
\begin{equation} r = \frac{c}{h}\sin\xi,\quad z = \frac{c}{h}\sinh\eta,\quad h \equiv \cosh\eta-\cos\xi, \end{equation}
where 
$c$ is a geometric constant related to the gap between the spherical particle and the electrode, 
$c = \sqrt {(2+\delta )\delta }$, with 
$\delta =(d-a)/a$. In bispherical coordinates, the particle surface and the electrode are iso-surfaces of the coordinate 
$\eta$:
\begin{equation} \mathcal{P}:~\eta = \eta_0 = \cosh^{{-}1}(1+\delta),\quad \mathcal{W}:~\eta = 0. \end{equation}3. Solution
In general, (2.5a,b)–(2.5a,b) can be solved only numerically. Analytical progress can be made by assuming small changes in the fluid conductivity with local field intensity. In this case, we develop an asymptotic analysis based on the linearization of (2.4) for 
$b\ll 1$:
\begin{equation} \sigma_m=\sigma_0(1+\gamma E), \quad \gamma=\frac{e^3}{16 {\rm \pi}\varepsilon_m (k_BT)^2}. \end{equation}
The dimensionless medium conductivity as a function of dimensionless electric field strength becomes 
$\tilde {\sigma }_m = 1 + \epsilon E$, where 
$\epsilon = \gamma E_0$ is a dimensionless parameter quantifying the magnitude of the conductivity change by the electric field. The small conductivity variation assumption implies 
$\epsilon \ll 1$. Estimating 
$\gamma$ shows that its order of magnitude is 
${\sim }10^{-6}\ {\textrm {m}}\ {\textrm {V}}^{-1}$, hence the linear approximation is valid for applied electric field less than 
$1\ {\textrm {MV}}\ {\textrm {m}}^{-1}$, which is typical for the experiments (Pradillo et al. Reference Pradillo, Karani and Vlahovska2019; Zhang et al. Reference Zhang, Yuan, Dou, De La Cruz and Bishop2021b). Having 
$\epsilon \ll 1$ allows for an analytical solution in terms of a regular perturbation series
$$\begin{gather} \varPhi = \varPhi^{{(0)}} + \epsilon \varPhi^{(1)}, \end{gather}$$
$$\begin{gather}{\boldsymbol{E}} ={-}\boldsymbol{\nabla} \varPhi = {\boldsymbol{E}}^{(0)} + \epsilon{\boldsymbol{E}}^{(1)}, \end{gather}$$
$$\begin{gather}p = \epsilon p^{(1)},\quad {\boldsymbol{u}} = \epsilon{\boldsymbol{u}}^{(1)}. \end{gather}$$
The leading-order problem (with superscripts 
$(0)$) corresponds to a spherical particle suspended in a charge-free fluid with constant, field-independent conductivity given by 
$\sigma _0$, which is exactly the leaky dielectric model. The solution predicts no flow about a solid particle, and attraction to a nearby electrode (Wang, Miksis & Vlahovska Reference Wang, Miksis and Vlahovska2022), with a force decaying in the far field as 
$1/d^4$, where 
$d$ is the distance between the colloid centre and the electrode. The solution is summarized in Appendix A.
3.1. The electrohydrodynamic flow
Here, we analyse the correction due to field-dependent conductivity to the leading-order solution obtained from the leaky dielectric model. Substituting the linearized relation (3.1a,b) and expansions (3.2)–(3.4a,b) into (2.5a,b)–(2.11), and collecting terms at 
$O(\epsilon )$, we find that the flow in the suspending fluid satisfies the equations
$$\begin{gather} \left. \begin{array}{c@{}} \displaystyle -\boldsymbol{\nabla} p^{(1)} + \nabla^2 {\boldsymbol{u}}^{(1)} ={-}{\boldsymbol{f}}, \\ \displaystyle \boldsymbol{\nabla}\boldsymbol{\cdot}{\boldsymbol{u}}^{(1)} = 0 \end{array} \right\} \quad \mbox{in}~\varOmega_m , \end{gather}$$
$$\begin{gather}{\boldsymbol{u}}^{(1)} = \boldsymbol{0} \quad \mbox{on}~\mathcal{W}~\&~\mathcal{P}, \end{gather}$$
where 
${\boldsymbol {f}}=(\boldsymbol {\nabla }\boldsymbol {\cdot }{\boldsymbol {E}}^{(1)}) {\boldsymbol {E}}^{(0)}$ is the Coulomb force on the fluid. Note that by (2.2), 
${\boldsymbol {f}}$ can be related directly to the leading-order (
$O(\epsilon )$) solution, 
$\boldsymbol {\nabla }\boldsymbol {\cdot }{\boldsymbol {E}}^{(1)} = - {\boldsymbol {E}}^{(0)} \boldsymbol {\cdot } \boldsymbol {\nabla }E^{(0)}$. We find the solution of (3.5)–(3.6) as a superposition of a particular solution 
$(p^{\boldsymbol {\textit {P}}},{\boldsymbol {u}}^{\boldsymbol {\textit {P}}})$ and a homogeneous solution 
$(p^{\boldsymbol {\textit {H}}},{\boldsymbol {u}}^{\boldsymbol {\textit {H}}})$:
\begin{equation} p^{(1)} = p^{\boldsymbol {\textit{P}}} + p^{\boldsymbol {\textit{H}}},\quad {\boldsymbol{u}}^{(1)} = {\boldsymbol{u}}^{\boldsymbol {\textit{P}}} + {\boldsymbol{u}}^{\boldsymbol {\textit{H}}}. \end{equation}
The particular solution solves the non-homogeneous Stokes equation in a particle-free space 
$\varOmega _p\cup \varOmega _m$, which is the upper half-space 
$z > 0$, with no-slip boundary condition on the electrode 
$\mathcal {W}$:
$$\begin{gather} \left. \begin{array}{c@{}} \displaystyle -\boldsymbol{\nabla} p^{\boldsymbol {\textit{P}}} + \nabla^2 {\boldsymbol{u}}^{\boldsymbol {\textit{P}}} ={-}\tilde{{\boldsymbol{f}}}, \\ \displaystyle \boldsymbol{\nabla}\boldsymbol{\cdot} {\boldsymbol{u}}^{\boldsymbol {\textit{P}}} = 0 \end{array} \right\} \quad \mbox{in}~\varOmega_p\cup\varOmega_m, \end{gather}$$
$$\begin{gather}{\boldsymbol{u}}^\boldsymbol{\textit{P}} = \boldsymbol{0} \quad\mbox{on}~\mathcal{W}. \end{gather}$$
Here, 
$\tilde {{\boldsymbol {f}}}$ is the extended force that is equal to the Coulomb force 
${\boldsymbol {f}}$ in the medium phase 
$\varOmega _m$, and zero in the particle phase 
$\varOmega _p$:
\begin{equation} \tilde{{\boldsymbol{f}}} = \begin{cases} {\boldsymbol{f}} & \mbox{in}~\varOmega_m, \\ \boldsymbol{0} & \mbox{in}~\varOmega_p. \end{cases} \end{equation}
To compensate for the non-zero velocity at the particle surface from the particular solution, the homogeneous solution is added, which solves the Stokes equations with velocity 
$-{\boldsymbol {u}}^{\boldsymbol {\textit {P}}}$ at the particle surface and no-slip condition on the electrode:
$$\begin{gather} \left.\begin{array}{c@{}} \displaystyle-\boldsymbol{\nabla} p^\boldsymbol{\textit{H}} + \nabla^2 {\boldsymbol{u}}^\boldsymbol{\textit{H}} = 0, \\ \displaystyle \boldsymbol{\nabla}\boldsymbol{\cdot} {\boldsymbol{u}}^\boldsymbol{\textit{H}} = 0 \end{array} \right\}\quad \mbox{in}~\varOmega_m, \end{gather}$$
$$\begin{gather}{\boldsymbol{u}}^\boldsymbol{\textit{H}} ={-}{\boldsymbol{u}}^\boldsymbol{\textit{P}} \quad\mbox{on}~\mathcal{P}, \end{gather}$$
$$\begin{gather}{\boldsymbol{u}}^\boldsymbol{\textit{H}} = 0 \quad \mbox{on}~\mathcal{W}. \end{gather}$$3.1.1. Particular solution
The particular solution solves the incompressible Stokes equation with extended force 
$\tilde {{\boldsymbol {f}}}$ in the upper half-space 
$z > 0$. In cylindrical coordinates 
$(r,\varphi,z)$, (3.8) and (3.9) read
$$\begin{gather} -\frac{\partial p^\boldsymbol{\textit{P}}}{\partial r} + \left(\mathscr{L}_{{-}1} + \frac{\partial^2}{\partial z^2}\right) u_r^\boldsymbol{\textit{P}} ={-}\tilde{f}_r, \end{gather}$$
$$\begin{gather}-\frac{\partial p^\boldsymbol{\textit{P}}}{\partial z} + \left(\mathscr{L}_0 + \frac{\partial^2}{\partial z^2}\right) u_z^\boldsymbol{\textit{P}} ={-}\tilde{f}_z, \end{gather}$$
$$\begin{gather}\frac{1}{r}\,\frac{\partial}{\partial r}\left(ru_r^\boldsymbol{\textit{P}}\right) + \frac{\partial u_z^\boldsymbol{\textit{P}}}{\partial z} = 0, \end{gather}$$
$$\begin{gather}u_r^\boldsymbol{\textit{P}}|_{z=0} = u_z^\boldsymbol{\textit{P}}|_{z=0}= 0, \end{gather}$$
where the operator 
$\mathscr {L}_{-n}$ is
\begin{equation} \mathscr{L}_{{-}n} = \frac{\partial^2}{\partial r^2} + \frac{1}{r}\,\frac{\partial}{\partial r} - \frac{n^2}{r^2}. \end{equation}The problem is solved by applying a Hankel–Fourier transform. The details of the calculation are in Appendix B. The obtained velocity components are
$$\begin{gather} u_r^\boldsymbol{\textit{P}}(r,z) ={-}\frac{2}{\rm \pi} \int_{0}^{\infty}\int_{0}^{\infty} \frac{\omega\,\hat{R}(k,\omega)}{(k^2+\omega^2)^2} \left[\cos(\omega z) - (1-kz)\,{\textrm{e}}^{{-}kz}\right] {\textrm{J}}_1(kr) \,{\textrm{d}}\omega \,{\textrm{d}}k, \end{gather}$$
$$\begin{gather}u_z^\boldsymbol{\textit{P}}(r,z) = \frac{2}{\rm \pi} \int_{0}^{\infty}\int_{0}^{\infty} \frac{k\,\hat{R}(k,\omega)}{(k^2+\omega^2)^2} \left[\sin(\omega z) - \omega z\,{\textrm{e}}^{{-}kz}\right] {\textrm{J}}_0(kr)\,{\textrm{d}}\omega \,{\textrm{d}}k, \end{gather}$$
where 
${\textrm {J}}_0$ and 
${\textrm {J}}_1$ are the Bessel functions of the first kind, and 
$\hat {R}(k,\omega )$ is the transform of the extended Coulomb force 
$\tilde {{\boldsymbol {f}}}$:
\begin{equation} \hat{R}(k,\omega) = \int_0^\infty \int_0^\infty \left(k^2\tilde{f}_z\,{\textrm{J}}_0(kr)\sin(\omega z) - k\omega \tilde{f}_r\,{\textrm{J}}_1(kr)\cos(\omega z) \right)r \,{\textrm{d}}r\,{\textrm{d}}z. \end{equation}3.1.2. Homogeneous solution
The homogeneous problem is found in bispherical coordinates using the general solution developed by Lee & Leal (Reference Lee and Leal1980). The detailed calculation is presented in Appendix C. The obtained velocity components in the cylindrical coordinate system, 
$u_r^\boldsymbol {\textit {H}}$ and 
$u_z^\boldsymbol {\textit {H}}$, are in the form
\begin{align} u_r^\boldsymbol{\textit{H}} &= \frac{\sin\xi}{2\sqrt{h}} \sum_{n=0}^{\infty} \left[A_n\sinh(\lambda_n\eta) + B_n\cosh(\lambda_n\eta)\right] P_n(\cos\xi) \nonumber\\ &\quad + \sqrt{h} \sum_{n=1}^{\infty} \left[E_n\sinh(\lambda_n\eta) + F_n\cosh(\lambda_n\eta)\right] P_n^1(\cos\xi), \end{align}
\begin{align} u_z^\boldsymbol{\textit{H}} &= \frac{\sinh\eta}{2\sqrt{h}} \sum_{n=0}^{\infty} \left[A_n\sinh(\lambda_n\eta) + B_n\cosh(\lambda_n\eta)\right] P_n(\cos\xi) \nonumber\\ &\quad + \sqrt{h} \sum_{n=0}^{\infty} \left[C_n\sinh(\lambda_n\eta) + D_n\cosh(\lambda_n\eta)\right] P_n(\cos\xi), \end{align}
where 
$\lambda _n = n+1/2$, 
$P_n$ are the Legendre polynomials, and 
$P_n^1$ are the associated Legendre polynomials. The procedure to obtain the coefficients 
$A_n$, 
$B_n$, 
$C_n$, 
$D_n$, 
$E_n$, 
$F_n$ is given in Appendix C.
3.2. Electrohydrodynamic force on the particle near the electrode
The electrohydrodynamic force on the particle is conveniently calculated using the Lorentz reciprocal theorem:
\begin{align} \oint_{\partial \varOmega_m} {\boldsymbol{u}}^{(1)} \boldsymbol{\cdot} ( \boldsymbol{{\boldsymbol{\sigma}}}' \boldsymbol{\cdot} {\boldsymbol{n}} ) \,{\textrm{d}}S - \int_{\varOmega_m} {\boldsymbol{u}}^{(1)} \boldsymbol{\cdot} (\boldsymbol{\nabla}\boldsymbol{\cdot}{\boldsymbol{\sigma}}') \,{\textrm{d}}V &= \oint_{\partial \varOmega_m} {\boldsymbol{u}}' \boldsymbol{\cdot} ( {\boldsymbol{\sigma}}^{(1)} \boldsymbol{\cdot} {\boldsymbol{n}} ) \,{\textrm{d}}S\nonumber\\ &\quad - \int_{\varOmega_m} {\boldsymbol{u}}' \boldsymbol{\cdot} (\boldsymbol{\nabla}\boldsymbol{\cdot}{\boldsymbol{\sigma}}^{(1)}) \,{\textrm{d}}V. \end{align}
The boundary of the medium phase is 
$\partial \varOmega _m = \mathcal {P} \cup \mathcal {W} \cup \mathcal {S}_\infty$, where 
$\mathcal {S}_\infty$ is a surface far from the particle. Due to the axial symmetry, the force has only a 
$z$-component. Note that in (3.24), the normal 
${\boldsymbol {n}}$ on the particle surface 
$\mathcal {P}$ points into the particle phase.
The velocity and stress fields 
${\boldsymbol {u}}'$ and 
${\boldsymbol {\sigma }}'$ are the solution to the problem for a translating sphere near a planar wall:
\begin{equation} \left.\begin{gathered} \left. \begin{array}{c@{}} \displaystyle -\boldsymbol{\nabla} p' + \nabla^2 {\boldsymbol{u}}' = 0, \\ \displaystyle \boldsymbol{\nabla}\boldsymbol{\cdot}{\boldsymbol{u}}' = 0 \end{array} \right\}\quad \mbox{in}~\varOmega_m, \\ {\boldsymbol{u}}' = \boldsymbol{0} \quad\mbox{on}~\mathcal{W}, \\ {\boldsymbol{u}}' = {\hat{\boldsymbol{e}}}_z \quad\mbox{on}~\mathcal{P}, \end{gathered}\right\} \end{equation}
where 
${\hat {\boldsymbol {e}}}_z$ is the unit vector in the 
$z$-direction. The equations are solved in bispherical coordinates; see Appendix C.
The particle has zero net charge. The leading-order electric field strength has the far-field behaviour 
$E^{(0)} = 1 + O(\rho ^{-3})$, where 
$\rho = \sqrt {r^2 + z^2}$. Consequently, we have 
$\|{\boldsymbol {f}}\| \sim O(\rho ^{-4})$ as 
$\rho \to \infty$. Therefore, in the far field, the velocity 
${\boldsymbol {u}}^{(1)}$ and stress 
${\boldsymbol {\sigma }}^{(1)}$ decay as 
$O(\rho ^{-2})$ and 
$O(\rho ^{-3})$, respectively. From Blake & Chwang (Reference Blake and Chwang1974), the velocity 
${\boldsymbol {u}}'$ and stress 
${\boldsymbol {\sigma }}'$ decay as 
$O(\rho ^{-3})$ and 
$O(\rho ^{-4})$. Consequently, integrals over the infinite surface 
$\mathcal {S}_\infty$ on both sides of the reciprocal identity (3.24) vanish:
\begin{equation} \int_{\mathcal{S}_\infty} {\boldsymbol{u}}^{(1)} \boldsymbol{\cdot} ({\boldsymbol{\sigma}}'\boldsymbol{\cdot}{\boldsymbol{n}}) \,{\textrm{d}}S = \int_{\mathcal{S}_\infty} {\boldsymbol{u}}' \boldsymbol{\cdot} ({\boldsymbol{\sigma}}^{(1)}\boldsymbol{\cdot}{\boldsymbol{n}}) \,{\textrm{d}}S = 0. \end{equation}
Thus the dimensionless electrohydrodynamic force on the particle, 
$C_f$, is calculated from a volume integral:
\begin{equation} C_f ={-}\int_{\mathcal{P}} {\hat{\boldsymbol{e}}}_z \boldsymbol{\cdot} ({\boldsymbol{\sigma}}^{(1)} \boldsymbol{\cdot} {\boldsymbol{n}}) \,{\textrm{d}}S = \int_{\varOmega_m} {\boldsymbol{u}}' \boldsymbol{\cdot} {\boldsymbol{f}} \,{\textrm{d}}V, \end{equation}
The dimensional form of the hydrodynamics force is 
$F = \gamma \varepsilon _m a^2\,|E_0^3|\,C_f$, where the absolute value indicates that the direction of the force is independent of the direction of the applied electric field.
The volume integral (3.27) is computed in bispherical coordinates, which conveniently map the medium phase 
$\varOmega _m$ onto a bounded rectangle region:
\begin{equation} C_f = 2{\rm \pi} c^3 \int_0^{\rm \pi} {\textrm{d}}\xi \int_0^{\eta_0} {\textrm{d}}\eta \,{\boldsymbol{u}}'\boldsymbol{\cdot} {\boldsymbol{f}}\, \frac{\sin\xi}{h^3}. \end{equation}
This double integral is evaluated numerically with Gauss quadratures. Using the volume integral to find the force coefficient has the following advantages. First, it does not require the solution of the tractions due to flow field 
${\boldsymbol {u}}^{(1)}$, which involves numerical evaluation of the integral transforms (3.19)–(3.21). Second, the velocity field 
${\boldsymbol {u}}'$ in the volume integral has an analytical solution in bispherical coordinates. The Coulomb force is evaluated by differentiating the leading-order electric field, which also has an analytical solution in bispherical coordinates.
4. Results and discussion
The leading-order electric field, the induced bulk charge, and the resulting 
$O(\epsilon )$ flow about conducting and insulating particles are shown in the unbounded domain in figures 2(a,c) and 3(a,c), and for a particle close to the electrode in figures 2(b,d) and 3(b,d). The unbounded problem with the particle centred at the origin is solved numerically in spherical coordinates with the Chebyshev collocation method (see Appendix D); it agrees with the bounded solution in the limit where the distance to the electrode is large. In all cases, the bulk charge is localized near the particle surface, where the electric field non-uniformities and resulting conductivity gradients are the largest. However, the charge distribution and fluid flow depend strongly on the particle conductivity.
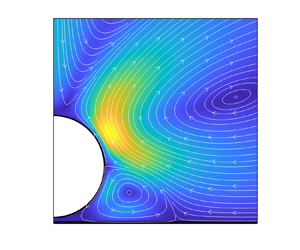
Figure 2. Electric field lines and flow streamlines about an insulating sphere (
$\beta = -1$): (a,c) in the unbounded domain, and (b,d) near the electrode 
$\delta = 0.1$. The colour map in the plots for the electric field shows the magnitude of the induced charge. The colour map in the plots for the flow shows the magnitude of the velocity field.
Figure 3. Electric field lines and flow streamlines about a conducting (
$\beta = 1$) particle: (a,c) in the unbounded domain, and (b,d) near the electrode 
$\delta = 0.5$. The colour map in the plots for the electric field shows the magnitude of the induced charge. The colour map in the plots for the flow shows the magnitude of the velocity field.
In the case of the insulating particle, the charge distribution resembles an octupole. The positive bulk charge above the equator and below the pole facing the electrode drives upward flows, while the negative charge drives flow in the opposite direction. The flows converge and lead to a total of five dividing streamlines (axisymmetric surfaces in 3D): fluid is drawn towards the particle at the equator and the poles, and pushed out in between. The bulk charges are mostly localized above and below the equator. Correspondingly, the velocity magnitude peaks near the equator.
In the case of a conducting particle, the bulk charge distribution presents a dipole pattern, i.e. opposite-sign charges localize near the poles. The flow is driven away from the poles, leading to inflow towards the equator.
The electrohydrodynamic flows about the conducting and insulating particles differ quantitatively and qualitatively. Quantitatively, the bulk charge density and velocity magnitude are greater for the conducting particle than for the insulating particle by an order of magnitude. Qualitatively, the recirculation and dividing streamlines near the two poles found in the insulating particle disappear for the conducting particle. Intriguingly, the flow pattern in the conducting particle case resembles the quadrupolar induced-charge electro-osmosis, but the direction is reversed.
The presence of a planar boundary (the electrode) does not significantly change the electrostatics or the hydrodynamics above the particle. The flow pattern in both insulating and conducting cases is similar to the unbounded results. However, the flows below the particle are geometrically frustrated, and vortices arise near the particle–wall gap. The vortices in both cases are in the anticlockwise direction.
The electrohydrodynamic force calculated from (3.27) is shown in figure 4. Figure 4(a) illustrates the effect of particle–electrode separation. The force magnitude decreases as the particle moves away from the electrode. Figure 4(b) shows that the force is also weakened as the difference in the conductivity between the two phases decreases. In general, the force is repulsive (positive). However, the force can be attractive (negative) when 
$\beta$ is close to 0 and 1. The change of sign can be seen from dips in figure 4(a) in the cases 
$\beta =-0.2$ and 
$1$. The electrostatic field and flow streamlines in these two attracting cases are shown in figure 5. In the first case, the particle is less conducting, and the charge distribution in figures 5(a,c) shows an octupole pattern. However, the bulk charge density peaks near the pole far from the electrode, and the corresponding downward flow is dominating, leading to the negative electrohydrodynamic force on the particle (attractive to the electrode). For a conducting particle, the charge distribution, and consequently the Coulomb force, in the thin gap is singularly large. The velocity magnitude in the gap is small. From the balance between the pressure gradient and the Coulomb force, 
$\boldsymbol {\nabla } p^{(1)} \sim {\boldsymbol {f}}$, we find that the pressure drop across the thin gap between the electrode and the particle surface is enormous. The low pressure in the gap region leads to the downward electrohydrodynamic force on the conducting particle. This effect disappears when the gap is large since large gaps allow the fluid to recirculate (see figures 3b,d) and reduce the singularity of the pressure. However, the high bulk charge density in the thin gap may indicate the violation of our assumption of the small change of conductivity. A more detailed analysis is required in this case.
Figure 4. (a) The absolute value of force coefficient 
$|C_f|$ as a function of the dimensionless separation from the electrode, 
$\delta$, for various conductivity mismatches 
$\beta$. (b). The force coefficient 
$C_f$ as a function of conductivity mismatch 
$\beta$ for various 
$\delta$.
Figure 5. Electric field lines and flow streamlines in the case of attractive electrohydrodynamic force: (a,c) 
$\delta = 0.1$, 
$\beta = -0.2$ (particle less conducting than the suspending fluid); (b,d) 
$\delta = 0.1$, 
$\beta = 1$ (perfectly conducting particle).
It is observed in figure 4(a) that the electrohydrodynamic force on the particle decays as 
$1/d^2$ when the particle is far from the electrode. The flow around a force-free and torque-free particle behaves like a stresslet in the far field. Accordingly, it is expected that the particle migration at large distances from the wall is driven by the flow due to image stresslet, which decays as the inverse square of the distance.
5. Conclusions
Nonlinear electrohydrodynamic flows driven by an electric field acting on its own induced space charge about colloidal particles in aqueous electrolyte solutions are well-documented and extensively studied topics. The prime example is the induced-charge electro-osmosis due to the electric field acting on charge accumulated near polarizable surfaces (Ristenpart et al. Reference Ristenpart, Aksay and Saville2004, Reference Ristenpart, Aksay and Saville2007; Squires & Bazant Reference Squires and Bazant2004)
Here, we show that nonlinear electrohydrodynamic flows can arise about particles suspended in non-polar, leaky dielectric fluids. The flows are driven by space charge generated by spatially varying conductivity due to the Onsager effect. For a spherical particle in an applied uniform electric field, the resulting flow pattern strongly depends on the particle conductivity. Intriguingly, for a conducting particle, the flow pattern is quadrupolar, resembling induced-charge electro-osmosis; however, the direction is reversed. The electrohydrodynamic flow gives rise to a force on the particle, which is in general repulsive. It decays more slowly with the distance to the electrode than the dielectrophoretic attractive force: quadratic versus fourth-power.
The leading-order problem in our analysis corresponds to the leaky dielectric model of Melcher & Taylor (Reference Melcher and Taylor1969). For a solid particle, there is no flow within the leaky dielectric model framework, hence the Onsager-effect flow becomes important. However, in the case of a drop, the leaky dielectric model flow due to the interfacial charge at the fluid/fluid interface would dominate over the Onsager-effect flow correction.
Our results have direct relevance to particle manipulation and assembly in non-polar fluids. The existence of a repulsive electrohydrodynamic force may explain the reported levitation above the electrode of colloids suspended in hexadecane (Pradillo et al. Reference Pradillo, Karani and Vlahovska2019). The electrohydrodynamic flows may also have strong effects on the collective dynamics of the Quincke rollers, a popular model of active matter systems (Bricard et al. Reference Bricard, Caussin, Desreumaux, Dauchot and Bartolo2013; Driscoll & Delmotte Reference Driscoll and Delmotte2019). The present analysis considers only a DC electric field. In AC fields, the large disparity in ions mobility may give rise to a steady component (Hashemi et al. Reference Hashemi, Bukosky, Rader, Ristenpart and Miller2018) and much richer electrohydrodynamic flows and colloidal dynamics.
Funding
This work was partially supported by NSF awards DMS-2108502 and CBET-2126498.
Declaration of interests
The authors report no conflict of interest.
Appendix A. Leading-order solution: electric field about a particle near an electrode
The leading-order problem is formulated below and solved in bispherical coordinates defined in (2.12a–c) (Wang et al. Reference Wang, Miksis and Vlahovska2022). (The more general case of a spherical particle between two electrodes is solved in Wang, Miksis & Vlahovska Reference Wang, Miksis and Vlahovska2023.) The governing equations are
$$\begin{gather} \nabla^2\varPhi^{(0)} = 0 \quad {\textrm{in}}~\varOmega_m\cup\varOmega_p, \end{gather}$$
$$\begin{gather}\varPhi_m^{(0)} = \varPhi_p^{(0)} \quad {\textrm{on}}~\mathcal{P}, \end{gather}$$
$$\begin{gather}{\hat{\boldsymbol{e}}}_\eta \boldsymbol{\cdot} {\boldsymbol{E}}_m^{(0)} = \tilde{\sigma}_p {\hat{\boldsymbol{e}}}_\eta \boldsymbol{\cdot} {\boldsymbol{E}}_p^{(0)} \quad {\textrm{on}}~\mathcal{P}, \end{gather}$$
$$\begin{gather}\varPhi_m^{(0)} \sim{-}z \quad {\textrm{as}}~\sqrt{r^2 + z^2} \to \infty, \end{gather}$$
where 
${\hat {\boldsymbol {e}}}_\eta$ is the unit vector in the 
$\eta$-direction and the inward normal on the particle surface. In bispherical coordinates, the electric potential is written as
\begin{equation} \left.\begin{gathered} \varPhi^{(0)}_p ={-}z + \sqrt{h} \sum_{n=0}^{\infty} \tilde{X}_n\,{\textrm{e}}^{-\lambda_n\eta}\,P_n(\cos\xi), \\ \varPhi^{(0)}_m ={-}z + 2 \sqrt{h} \sum_{n=0}^{\infty} X_n \sinh(\lambda_n\eta)\,P_n(\cos\xi), \end{gathered}\right\} \end{equation}
where 
$\lambda _n = n+1/2$, 
$\tilde {X}_n = X_n (\exp ({2\lambda _n\eta _0})-1)$, and 
$P_n$ are the Legendre polynomials. Coefficients 
$X_n$ are solved from the tridiagonal system
\begin{align} \mathcal{L}^e_{n,1} X_{n-1} + \mathcal{L}^e_{n,2} X_n + \mathcal{L}^e_{n,3} X_{n+1} = {\mathcal{R}}^e_n\quad (n \geqslant 0), \end{align}
where 
$\mathcal {L}^e_{n,1}$, 
$\mathcal {L}^e_{n,2}$, 
$\mathcal {L}^e_{n,3}$ and 
${\mathcal {R}}^e_n$ are
\begin{align} \left.\begin{gathered} \mathcal{L}^e_{n,1} = n\left( \exp({\lambda_{n-1}\eta_0}) - \beta \exp({-\lambda_{n-1}\eta_0}) \right), \\ \mathcal{L}^e_{n,2} = \left(\beta \sinh\eta_0-2\lambda_n\cosh\eta_0\right) \exp({\lambda_n\eta_0}) - \beta \left(\sinh\eta_0-2\lambda_n\cosh\eta_0\right) \exp({-\lambda_n\eta_0}), \\ \mathcal{L}^e_{n,3} = (n+1)\left( \exp({\lambda_{n+1}\eta_0}) - \beta \exp({-\lambda_{n+1}\eta_0}) \right), \\ {\mathcal{R}}^e_n = 2\sqrt{2}\beta \left[ 2\lambda_n \exp({-\lambda_n\eta_0}) - \cosh\eta_0 \left(n \exp({-\lambda_{n-1}\eta_0}) + (n+1) \exp({-\lambda_{n+1}\eta_0})\right) \right], \end{gathered}\right\} \end{align}
with 
$\beta$ the conductivity mismatch, 
$\beta = (\tilde {\sigma }_p-1)/(\tilde {\sigma }_p+1)$. The equation for 
$n=0$ in the system (A6) has only two terms with 
$X_0$ and 
$X_1$ since 
$\mathcal {L}^e_{0,1} = 0$. The cylindrical components of electric field strength, 
${\boldsymbol {E}}^{(0)} = -\boldsymbol {\nabla }\varPhi ^{(0)}$, are
\begin{align} \left.\begin{gathered} E_{p,r}^{(0)} ={-}\frac{\sqrt{h}}{2c} \sum_{n=1}^{\infty} \left( \tilde{X}_{n-1} - 2\tilde{X}_n + \tilde{X}_{n+1}\right) {\textrm{e}}^{-\lambda_n\eta}\,P_n^1(\cos\xi), \\ E_{p,z}^{(0)} = 1-\frac{\sqrt{h}}{2c} \sum_{n=0}^{\infty} \left[n\tilde{X}_{n-1} - (2n+1)\tilde{X}_n + (n+1)\tilde{X}_{n+1}\right] {\textrm{e}}^{-\lambda_n\eta}\,P_n(\cos\xi), \\ E_{m,r}^{(0)} ={-}\frac{\sqrt{h}}{c} \sum_{n=1}^{\infty} (X_{n-1} - 2X_n + X_{n+1}) \sinh(\lambda_n\eta)\, P_n^1(\cos\xi), \\ E_{m,z}^{(0)} = 1 + \frac{\sqrt{h}}{c} \sum_{n=0}^{\infty} [nX_{n-1} - (2n+1)X_n + (n+1)X_{n+1}] \cosh(\lambda_n\eta)\,P_n(\cos\xi). \end{gathered}\right\} \end{align}Appendix B. Particular solution in cylindrical coordinates
In this appendix, we solve (3.14)–(3.17) using integral transforms. The Hankel transform and its inverse are defined as
$$\begin{gather} G(k) = \mathscr{H}_n[g(r)] = \int_0^\infty r\,g(r)\,{\textrm{J}}_n(kr) \,{\textrm{d}}r, \end{gather}$$
$$\begin{gather}g(r) = \mathscr{H}^{{-}1}_n[G(k)] = \int_0^\infty k\,G(k)\,{\textrm{J}}_n(kr) \,{\textrm{d}}k, \end{gather}$$
where 
${\textrm {J}}_n$ is the Bessel function of the first kind. Hankel transforming the partial differential equations (3.14)–(3.16) to ordinary differential equations in 
$z$ gives
$$\begin{gather} kP + \left(\frac{{\textrm{d}}^2}{{\textrm{d}}z^2} - k^2 \right) V_r ={-}F_r, \end{gather}$$
$$\begin{gather}-\frac{{\textrm{d}}}{{\textrm{d}}z} P + \left(\frac{{\textrm{d}}^2}{{\textrm{d}}z^2} - k^2\right) V_z ={-}F_z, \end{gather}$$
$$\begin{gather}kV_r + \frac{{\textrm{d}}}{{\textrm{d}}z}V_z = 0. \end{gather}$$The Hankel transform variables are defined as
$$\begin{gather} P(z,k),V_z(z,k),F_z(z,k) = \mathscr{H}_0[p^\boldsymbol{\textit{P}}(r,z),v_z^\boldsymbol{\textit{P}}(r,z),\tilde{f}_z(r,z)], \end{gather}$$
$$\begin{gather}V_r(z,k),F_r(z,k) = \mathscr{H}_1[v_r^\boldsymbol{\textit{P}}(r,z),\tilde{f}_r(r,z)]. \end{gather}$$
Note that 
$F_r(z,k)$ and 
$F_z(z,k)$ are continuous even though the extended force 
$\tilde {{\boldsymbol {f}}}$ has a finite jump on the particle surface 
$\mathcal {P}$. These ordinary differential equations are simplified to a single equation in terms of 
$V_z$,
\begin{align} V''''_z - 2k^2 V''_z + k^4 V_z = R,\quad R = k^2 F_z + k F'_r, \end{align}
where the prime stands for the derivative with respect to 
$z$. From the no-slip boundary condition on the plane electrode, we find that the boundary conditions at 
$z = 0$ are 
$V_z|_{z=0} = V_r|_{z=0} = 0$, which is equivalent to 
$V_z|_{z=0} = V'_z|_{z=0} = 0$. The far-field boundary conditions are 
$V_z,V'_z \to 0$ as 
$z \to +\infty$.
We write the solution as the superposition of the particular solution 
$U(z,k)$ and the homogeneous solution 
$W(z,k)$, i.e. 
$V_z(z,k) = U(z,k)+W(z,k)$. The particular solution is solved from the following equation and boundary conditions:
\begin{align} U'''' - 2k^2 U'' + k^4 U = R,\quad U|_{z=0} = U''|_{z=0} = 0. \end{align}
The physical interpretation of the boundary condition 
$U''|_{z = 0} = 0$ is that the shear stress on the plane wall is zero. Inverse Hankel transforming the particular solution 
$U$ yields the flow driven by force 
$\tilde {{\boldsymbol {f}}}$ with zero shear stress and permeability on 
$\mathcal {W}$. We prescribe the second-order derivative to be zero so that 
$U$ could be constructed by Fourier sine transform:
$$\begin{gather} \hat{G}(\omega) = \mathscr{F}_s[G(z)] = \int_0^\infty G(z) \sin(\omega z) \,{\textrm{d}}z, \end{gather}$$
$$\begin{gather}G(z) = \mathscr{F}_s^{{-}1}[\hat{G}(\omega)] = \frac{2}{\rm \pi} \int_0^\infty \hat{G}(\omega) \sin(\omega z) \,{\textrm{d}}\omega. \end{gather}$$Fourier sine transforming (B8a,b) yields
\begin{align} \hat{U}(k,\omega) = \frac{\hat{R}(k,\omega)}{(\omega^2 + k^2)^2}, \end{align}
where 
$\hat {U}(k,\omega ) = \mathscr {F}_s[U(z,k)]$, and 
$\hat {R}(k,\omega )$ is given in (3.21). Inverse transforming 
$\hat {U}(k,\omega )$ gives
\begin{align} U(z,k) = \frac{2}{\rm \pi} \int_{0}^{\infty} \frac{\hat{R}(k,\omega)}{(\omega^2 + k^2)^2} \sin(\omega z)\,{\rm d}\omega. \end{align}
The homogeneous solution 
$W(z,k)$ is solved from the following equation and boundary conditions:
\begin{align} W'''' - 2k^2 W'' + k^4 W= 0,\quad W|_{z=0} = 0,\quad W'|_{z=0} ={-}U'|_{z=0}. \end{align}For convenience, we note
\begin{equation} U'|_{z=0} = U_0(k) = \frac{2}{\rm \pi} \int_{0}^{\infty} \frac{\hat{R}(k,\omega)}{(\omega^2+k^2)^2}\, \omega \,{\textrm{d}}\omega. \end{equation}
Solving the homogeneous equation and keeping terms that vanish as 
$z \to \infty$ and at 
$z=0$ gives
\begin{equation} W(z,k) ={-} U_0(k)\,z\,{\textrm{e}}^{{-}kz}. \end{equation}
Adding 
$U(z,k)$ and 
$W(z,k)$ gives the expression for 
$V_z(z,k)$:
\begin{equation} V_z(z,k) = \frac{2}{\rm \pi} \int_{0}^{\infty} \frac{\hat{R}(k,\omega)}{(\omega^2 + k^2)^2} \left[\sin(\omega z) - \omega z\,{\textrm{e}}^{{-}kz}\right] {\textrm{d}}\omega. \end{equation}
Substituting into (B5) gives the expression for 
$V_r(z,k)$:
\begin{equation} V_r(z,k) ={-}\frac{2}{k{\rm \pi}}\int_{0}^{\infty} \frac{\omega\,\hat{R}(k,\omega)}{(\omega^2+k^2)^2} \left[\cos(\omega z) - (1-kz)\,{\textrm{e}}^{{-}kz}\right] {\textrm{d}}\omega. \end{equation}
Inverse Hankel transforming 
$V_r(z,k)$ and 
$V_z(z,k)$ gives the solution (3.19) and (3.20).
Appendix C. Homogeneous solution in bispherical coordinates
In this appendix, we summarize the solution of the homogeneous Stokes equation
\begin{align} {-\boldsymbol{\nabla}}p + \nabla^2 {\boldsymbol{u}} = 0, \quad\boldsymbol{\nabla} \boldsymbol{\cdot} {\boldsymbol{u}} = 0, \end{align}
for arbitrary velocity distribution on the particle surface 
$\mathcal {P}$, and zero velocity on the electrode 
$\mathcal {W}$:
$$\begin{gather} u_r|_{\mathcal{W}} = u_z|_{\mathcal{W}} = 0, \end{gather}$$
$$\begin{gather}u_r|_{\mathcal{P}} = v_1,\quad u_z|_{\mathcal{P}} = v_2. \end{gather}$$
For a particle translating in the 
$z$-direction, 
$v_2=1$ and 
$v_1=0$. In bispherical coordinates, the asymmetric velocity field could be written as (Lee & Leal Reference Lee and Leal1980)
$$\begin{gather} p = p_0,\quad u_r = \frac{rp}{2} + u_0,\quad u_z = \frac{zp}{2} + w_0, \end{gather}$$
$$\begin{gather}p_0 = \frac{\sqrt{h}}{c} \sum_{n=0}^{\infty} [A_n\sinh(\lambda_n\eta) + B_n\cosh(\lambda_n\eta)]\,P_n(\cos\xi), \end{gather}$$
$$\begin{gather}u_0 = \sqrt{h} \sum_{n=1}^{\infty} [E_n\sinh(\lambda_n\eta) + F_n\cosh(\lambda_n\eta)]\,P_n^1(\cos\xi), \end{gather}$$
$$\begin{gather}w_0 = \sqrt{h}\sum_{n=0}^{\infty} [C_n\sinh(\lambda_n\eta) + D_n\cosh(\lambda_n\eta)]\,P_n(\cos\xi), \end{gather}$$
where 
$\lambda _n = n + 1/2$, 
$P_n$ are the Legendre polynomials, and 
$P_n^1$ are the associated Legendre polynomials. In the axisymmetric case, the incompressibility reads
\begin{equation} \frac{\partial u_r}{\partial r} + \frac{u_r}{r} + \frac{\partial u_z}{\partial z} = 0. \end{equation}
From the boundary condition 
$u_r|_{\mathcal {W}} = 0$, we obtain 
$D_n = 0$ (
$n\geqslant 0$). Substituting 
$u_r|_{\mathcal {W}} = 0$ into the incompressibility, we find
\begin{equation} \left. \frac{\partial u_z}{\partial z} \right|_{\mathcal{W}} = 0, \end{equation}which leads to
\begin{equation} p|_{\mathcal{W}} ={-}2 \left. \frac{\partial w_0}{\partial z}\right|_{\mathcal{W}}. \end{equation}
Substituting the expressions for 
$p$ and 
$w_0$ into the identity, we obtain
\begin{equation} B_n = nC_{n-1} - (2n+1)C_n + (n+1)C_{n+1}\quad (n\geqslant 0). \end{equation}
From the boundary condition 
$u_z|_{\mathcal {P}} = f_2$, we obtain the equation
\begin{align} &\frac{1}{2}\sinh\eta_0 \left[A_n\sinh(\lambda_n\eta_0) + B_n\cosh(\lambda_n\eta_0)\right] + C_n \cosh\eta_0 \sinh(\lambda_n\eta_0) \nonumber\\ &\quad- \frac{n}{2n-1} \sinh(\lambda_{n-1}\eta_0)\,C_{n-1} - \frac{n+1}{2n+3} \sinh(\lambda_{n+1}\eta_0)\,C_{n+1} = \alpha_n, \end{align}
where 
$\alpha _{n}$ comes from the expansion
\begin{align} \sqrt{\cosh\eta_0 -\cos\xi}\,v_2 = \sum_{n=0}^{\infty} \alpha_n\,P_n(\cos\xi). \end{align}
Expansion coefficients 
$\alpha _{n}$ are calculated using the orthogonality of Legendre polynomials:
\begin{align} \alpha_n = \lambda_n \int_0^{\rm \pi} \sqrt{\cosh\eta_0 - \cos\xi}\,v_2\,P_n(\cos\xi)\sin\xi \,{\textrm{d}}\xi\quad(n \geqslant 0). \end{align}
Substituting (C11) into (C12) allows us to write 
$A_n^0$ in terms of 
$C_n^0$:
\begin{align} A_n = \frac{2 \alpha_n}{\sinh\eta_0\sinh(\lambda_n\eta_0)} - 2 \kappa_n \left(\frac{n}{2n-1}\,C_{n-1} - C_n + \frac{n+1}{2n+3}\,C_{n+1}\right) \quad (n \geqslant 0), \end{align}
with coefficients 
$\kappa _n = \lambda _n\coth (\lambda _n\eta _0) - \coth \eta _0$. The boundary condition 
$u_r|_{\mathcal {W}} = 0$ leads to
\begin{align} u_0|_{\mathcal{W}} ={-}\frac{r}{2}\,p_0|_{\mathcal{W}} = r \left. \frac{\partial w_0}{\partial z}\right|_{\mathcal{W}}. \end{align}Substituting (C6) and (C7) into (C16), we find
\begin{align} F_n = \tfrac{1}{2} (C_{n+1} - C_{n-1})\quad (n\geqslant 1). \end{align}
Paralleling the two boundary conditions on 
$\mathcal {P}$ gives
\begin{align} -\frac{\sin\xi}{\sinh\eta_0}\,w_0|_{\mathcal{P}} + u_0|_{\mathcal{P}} = g,\quad g = v_1 - \frac{\sin\xi}{\sinh\eta_0}\, v_2. \end{align}Substituting (C6) and (C7) into (C18a), we obtain
\begin{align} &\frac{1}{2n-1}\sinh(\lambda_{n-1}\eta_0)\,C_{n-1} - \frac{1}{2n+3}\sinh(\lambda_{n+1}\eta_0)\,C_{n+1} \nonumber\\ &\quad + \sinh\eta_0\,[E_n\sinh(\lambda_n\eta_0) + F_n\cosh(\lambda_n\eta_0)] = \sinh\eta_0 \beta_n, \end{align}
where 
$\beta _n$ are coefficients in the expansion
\begin{align} \frac{g}{\sqrt{\cosh\eta_0 -\cos\xi}} = \sum_{n=1}^{\infty} \beta_n\,P_n^1(\cos\xi). \end{align}From the orthogonality of associated Legendre polynomials, we have
\begin{align} \beta_n = \frac{\lambda_n}{n(n+1)} \int_0^{\rm \pi} \frac{g}{\sqrt{\cosh\eta_0 - \cos\xi}}\,P_n^1(\cos\xi) \sin\xi \,{\textrm{d}}\xi \quad (n \geqslant 1). \end{align}
In the case 
$v_1 = 0$ and 
$v_2 = 1$ (translating spherical particle), the expansion coefficients 
$\alpha _n$ and 
$\beta _n$ are calculated analytically:
\begin{align} \left.\begin{gathered} \alpha_n = \sqrt{2}\,\textrm{e}^{-\lambda_n\eta_0} \left[\cosh\eta_0 - \frac{n\,{\textrm{e}}^{\eta_0}}{2n-1} - \frac{(n+1)\,{\textrm{e}}^{-\eta_0}}{2n+3}\right], \\ \beta_n = \frac{2\sqrt{2}}{\sinh\eta_0}\,{\textrm{e}}^{-\lambda_n\eta_0} \left[\cosh\eta_0 - \frac{(n-1)\,{\textrm{e}}^{\eta_0}}{2n-1} - \frac{(n+2)\,{\textrm{e}}^{-\eta_0}}{2n+3}\right]. \end{gathered}\right\} \end{align}
Substituting (C17) into (C19), we write coefficients 
$E_n$ in terms of 
$C_n$:
\begin{align} E_n = \frac{\beta_n}{\sinh(\lambda_n\eta_0)} + \kappa_n \left(\frac{1}{2n-1}\,C_{n-1} - \frac{1}{2n+3}\,C_{n+1}\right) \quad(n \geqslant 1). \end{align}From the incompressibility, we have the two equations
\begin{align} &-\tfrac{1}{2}nA_{n-1} + \tfrac{5}{2}A_n + \tfrac{1}{2}(n+1)A_{n+1} - (n-1)nE_{n-1} + 2n(n+1)E_n \nonumber\\ &\quad- (n+1)(n+2)E_{n+1} - nD_{n-1} + (2n+1)D_n - (n+1)D_{n+1} = 0, \end{align}
\begin{align} &-\tfrac{1}{2}nB_{n-1} + \tfrac{5}{2}B_n + \tfrac{1}{2}(n+1)B_{n+1} - (n-1)nF_{n-1} + 2n(n+1)F_n \nonumber\\ &\quad- (n+1)(n+2)F_{n+1} - nC_{n-1} + (2n+1)C_n - (n+1)C_{n+1} = 0. \end{align}
It is verified that (C25) is satisfied automatically using (C11) and (C17). Plugging (C15) and (C23) into (C24) yields a linear system for 
$C_n$:
\begin{equation} \mathcal{L}^h_{n,1} C_{n-1} + \mathcal{L}^h_{n,2} C_n + \mathcal{L}^h_{n,3} C_{n+1} = {\mathcal{R}}^h_n \quad(n \geqslant 0), \end{equation}
where 
$\mathcal {L}^h_{n,1}$, 
$\mathcal {L}^h_{n,2}$, 
$\mathcal {L}^h_{n,3}$ and 
${\mathcal {R}}^h_n$ are
\begin{align} \left.\begin{gathered}
\mathcal{L}^h_{n,1} ={-}n\kappa_{n-1} +
\frac{n(2n-3)}{2n-1}\,\kappa_n, \\ \mathcal{L}^h_{n,2} =
\frac{n(2n-1)}{2n+1}\,\kappa_{n-1} + 5\kappa_n -
\frac{(n+1)(2n+3)}{2n+1}\,\kappa_{n+1}, \\
\mathcal{L}^h_{n,3} ={-}\frac{(n+1)(2n+5)}{2n+3}\,\kappa_n
+ (n+1)\,\kappa_{n+1}, \\ {\mathcal{R}}^h_n =
\frac{n}{\sinh(\lambda_{n-1}\eta_0)}
\left[\frac{\alpha_{n-1}}{\sinh\eta_0} +
(n-1)\beta_{n-1}\right] - \frac{1}{\sinh(\lambda_n\eta_0)}
\left[\frac{5\alpha_n}{\sinh\eta_0} + 2n(n+1)\beta_n\right]
\\ - \frac{n+1}{\sinh(\lambda_{n+1}\eta_0)}
\left[\frac{\alpha_{n+1}}{\sinh\eta_0} -
(n+2)\beta_{n+1}\right]. \end{gathered}\right\}
\end{align}
The equation for 
$n = 0$ in the system (C26) has two terms involving 
$C_0$ and 
$C_1$ since 
$\mathcal {L}^h_{0,1} = 0$.
Appendix D. Flow and electric field in an unbounded domain
The unbounded problem is solved numerically in the spherical coordinates 
$(r,\theta,\varphi )$ originated at the centre of the particle. The electric potential solved from the leading-order electrostatics is
\begin{equation} \varPhi^0_p ={-}\frac{3}{\tilde{\sigma}_p+2}\,r\cos\theta,\quad\varPhi^0_m ={-}\left(r + \frac{\tilde{\sigma}_p-1}{\tilde{\sigma}_p+2}\,\frac{1}{r^2}\right)\cos\theta, \end{equation}
where 
$\tilde {\sigma }_p$ is the dimensionless particle conductivity, 
$\tilde {\sigma } = \sigma _p/\sigma _0$. The 
$O(\epsilon )$ electrohydrodynamic problem in spherical coordinates is
$$\begin{gather} \left( \frac{\partial^2}{\partial r^2} + \frac{2}{r}\,\frac{\partial}{\partial r} + \frac{\cot\theta}{r^2}\,\frac{\partial}{\partial\theta} + \frac{1}{r^2}\,\frac{\partial^2}{\partial\theta^2} - \frac{1}{r^2 \sin^2\theta}\right) \omega ={-}H, \end{gather}$$
$$\begin{gather}
\omega = \frac{1}{r}\left[\frac{\partial}{\partial r}(r u_\theta) -
\frac{\partial u_r}{\partial \theta}\right],
\end{gather}$$
$$\begin{gather}\frac{1}{r^2}\,\frac{\partial}{\partial r}(r^2 u_r) + \frac{1}{r\sin\theta}\,\frac{\partial}{\partial\theta}(\sin\theta u_\theta) = 0 , \end{gather}$$
where 
$u_r$ and 
$u_\theta$ are the velocity components, and 
$\omega$ is the vorticity. Equation (D2) is derived by taking the curl of the Stokes equation, and 
$H$ is the curl of the Coulomb force 
${\boldsymbol {f}}$:
\begin{equation} H = \frac{1}{r}\left[\frac{\partial}{\partial r}(rf_\theta) - \frac{\partial f_r}{\partial \theta}\right]. \end{equation}
Due to the symmetry, we can simplify the domain to be the quarter of the plane 
$r\in (r,+\infty )$ and 
$\theta \in (0,{\rm \pi} /2)$. The boundary conditions are
\begin{equation} \left.\begin{gathered}
u_\theta = \omega = 0,\quad\frac{\partial u_r}{\partial
\theta} = 0 \quad{\textrm{at}}~\theta = 0,{\rm \pi}/2, \\ u_r =
u_\theta = 0,\quad\omega = \frac{\partial u_\theta}{\partial r}\quad{\textrm{at}}~r = 1,\\ u_r \to
0,\quad u_\theta \to 0,\quad\omega \to 0\quad
{\textrm{as}}~r\to\infty. \end{gathered}\right\}
\end{equation}
The problem (D2)–(D4) is solved numerically with the Chebyshev collocation method (Trefethen Reference Trefethen2000). In a practical numerical implementation, (D2) and (D3) are combined to eliminate the vorticity 
$\omega$ and corresponding boundary conditions.
Open access
