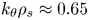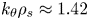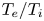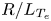1 Introduction
Radio frequency (RF) wave heating and current drive play a crucial role in achieving steady-state operation of a tokamak. It is generally found that the plasma transport level during the transition to high confinement mode (H-mode) via RF heating is much higher than the prediction by neoclassical transport theory. This anomalous transport primarily arises from the drift wave instabilities in plasmas (Diamond et al. Reference Diamond, Itoh, Itoh and Hahm2005). Among them, the ion temperature gradient (ITG) mode, trapped electron mode (TEM) and electron temperature gradient (ETG) mode are the most important candidates (Horton Reference Horton1999; Ryter et al. Reference Ryter, Angioni, Peeters, Leuterer, Fahrbach and Suttrop2005; Bonanomi et al. Reference Bonanomi, Mantica, Szepesi, Hawkes, Lerche, Migliano, Peeters, Sozzi, Tsalas and Van Eester2015). Although the ion turbulent transport driven by the ITG turbulence is well understood, understanding of the electron turbulent transport remains inadequate due to the complex kinetic mechanisms involved (Xiao et al. Reference Xiao, Holod, Zhang, Klasky and Lin2010). To achieve better performance for a tokamak operation scenario, several plasma heating and current drive methods are applied simultaneously in tokamaks, and positive synergistic effects of current drive are generally observed (Fidone et al. Reference Fidone, Giruzzi, Krivenski, Mazzucato and Ziebell1987; Dumont & Giruzzi Reference Dumont and Giruzzi2004; Giruzzi et al. Reference Giruzzi, Artaud, Dumont, Imbeaux, Bibet, Berger-By, Bouquey, Clary, Darbos, Ekedahl, Hoang, Lennholm, Maget, Magne, Ségui, Bruschi and Granucci2004). However, less work has been done on the turbulent transport during these combined heating processes, where a much steeper temperature profile is usually formed, which can affect the turbulence transport level in turn.
A complete understanding of the plasma turbulent transport is crucial in the operations of tokamaks. Gyrokinetic simulation offers valuable insights into turbulent transport driven by drift waves. Recent experiments at ASDEX Upgrade in H-mode have demonstrated through gyrokinetic simulations that the ITG mode contributes predominantly to ion heat transport, while also contributing partially to electron heat transport (Ryter et al. Reference Ryter, Angioni, Dunne, Fischer, Kurzan, Lebschy, McDermott, Suttrop, Tardini, Viezzer and Willensdorfer2019). In scenarios with high poloidal plasma beta $\beta _p$![]() and internal transport barriers (ITB) in EAST, the drift instabilities persist particularly for lower $q_{95}$
and internal transport barriers (ITB) in EAST, the drift instabilities persist particularly for lower $q_{95}$![]() values (<7.0). Various types of instabilities, including ITG, TEM and ETG, manifest their existence in different radial regions of tokamak plasmas (Ding et al. Reference Ding, Jian, Garofalo, Yan, Mcclenaghan, Guo and Grierson2019). Notably, advancements in electron modelling based on gyrokinetic theory have been developed, with integration into simulation codes such as GTC, GT3D and FULL (Lin et al. Reference Lin, Nishimura, Xiao, Holod, Zhang and Chen2007; Rewoldt, Lin & Idomura Reference Rewoldt, Lin and Idomura2007), allowing for a deeper investigation into the electron effects on turbulence.
values (<7.0). Various types of instabilities, including ITG, TEM and ETG, manifest their existence in different radial regions of tokamak plasmas (Ding et al. Reference Ding, Jian, Garofalo, Yan, Mcclenaghan, Guo and Grierson2019). Notably, advancements in electron modelling based on gyrokinetic theory have been developed, with integration into simulation codes such as GTC, GT3D and FULL (Lin et al. Reference Lin, Nishimura, Xiao, Holod, Zhang and Chen2007; Rewoldt, Lin & Idomura Reference Rewoldt, Lin and Idomura2007), allowing for a deeper investigation into the electron effects on turbulence.
In this work, the turbulence in the present EAST plasma under lower hybrid wave (LHW) and electron cyclotron wave (ECW) combined heating is studied numerically using the GTC code where the kinetic electrons are retained. The remaining sections of the paper are organized as follows. In § 2, the experimental performances associated with the combined heating are introduced for EAST tokamak plasmas. The simulation model and the related plasma parameter settings are described in § 3. In § 4, both the linear and nonlinear simulation results are presented. Parametric scans of the electron beta, the dimensionless ratio of $T_e/T_i$![]() and $R/L_{T_e}$
and $R/L_{T_e}$![]() , are carried out and their effects on the electrostatic drift wave instability are also shown. Turbulent transport and zonal flow physics are investigated for the combined heating cases. Finally, a discussion and conclusions are provided in § 5.
, are carried out and their effects on the electrostatic drift wave instability are also shown. Turbulent transport and zonal flow physics are investigated for the combined heating cases. Finally, a discussion and conclusions are provided in § 5.
2 Experimental set-up
EAST, a fully superconducting tokamak with a non-circular cross-section, has a major radius $R = 1.9$![]() m and a minor radius $a = 0.4$
m and a minor radius $a = 0.4$![]() m. Through continuous improvement in auxiliary heating systems, the 2022 campaign witnessed the attainment of H-mode plasmas sustained for a record of approximately 310 s. Notably, both ECW and LHW systems play crucial roles as the primary sources for electron heating and current drive, enabling EAST's long-pulse operations. Figure 1 illustrates a typical deuterium plasma discharge, as seen in EAST shot #98933, characterized by a toroidal magnetic field $B_T =2.4$
m. Through continuous improvement in auxiliary heating systems, the 2022 campaign witnessed the attainment of H-mode plasmas sustained for a record of approximately 310 s. Notably, both ECW and LHW systems play crucial roles as the primary sources for electron heating and current drive, enabling EAST's long-pulse operations. Figure 1 illustrates a typical deuterium plasma discharge, as seen in EAST shot #98933, characterized by a toroidal magnetic field $B_T =2.4$![]() T, a plasma current $I_p$
T, a plasma current $I_p$![]() of 518 kA, a line-averaged electron density of $n_e=1.7\times 10^{19}\ {\rm m}^{-3}$
of 518 kA, a line-averaged electron density of $n_e=1.7\times 10^{19}\ {\rm m}^{-3}$![]() and nearly zero loop voltage sustained throughout the discharge.
and nearly zero loop voltage sustained throughout the discharge.

Figure 1. Time traces of EAST discharge carried out with LHW and ECW. (a) Plasma current, (b) line-averaged electron density, (c) loop voltage and (d) heating powers of LHW and ECW.
During the discharge of EAST shot #98933, both LHW at 2.3 MW and 4.6 GHz, and ECW at 1.4 MW and 10 GHz were injected into the plasma starting from 1.7 s. However, the ECW power was temporarily shut down from 38 to 56 s. Another EAST shot #98958, exhibited similar discharge parameters to shot #98933, except that the ECW remained active throughout the entire discharge. In this study, shot #98933 at 50.3 s will be referred to as the LHW-only case and shot #98958 at 10.0 s will be referred to as the LHW+ECW case or the combined heating case. Figure 2 displays the radial profiles for electron temperature measured by Thomson scattering (TS) and of ion temperature measured by an X-ray crystal spectrometer (XCS). The data clearly indicate a decrease in peak electron temperature from 13 to 6.5 keV when the ECW system was deactivated. Magnetic equilibrium was determined using the EFIT equilibrium code, while electron density measurements were obtained via TS and reflectometry. The safety factor $q$![]() profile was derived by incorporating Faraday rotation measurements from a polarimeter and interferometer measurement as additional constraints in the EFIT code (Lao et al. Reference Lao, John, Stambaugh, Kellman and Pfeiffer1985; Wang et al. Reference Wang, Gao, Ling, Zhang, Zhang, Han, Liu, Liu, Liu and Ti2013; Qian et al. Reference Qian, Lao, Liu, Ding, Zeng, Luo, Ren, Huang, Huang, Brower, Hanada, Chen, Sun, Shen, Gong, Xiao and Wan2016).
profile was derived by incorporating Faraday rotation measurements from a polarimeter and interferometer measurement as additional constraints in the EFIT code (Lao et al. Reference Lao, John, Stambaugh, Kellman and Pfeiffer1985; Wang et al. Reference Wang, Gao, Ling, Zhang, Zhang, Han, Liu, Liu, Liu and Ti2013; Qian et al. Reference Qian, Lao, Liu, Ding, Zeng, Luo, Ren, Huang, Huang, Brower, Hanada, Chen, Sun, Shen, Gong, Xiao and Wan2016).

Figure 2. Electron and ion temperature radial profiles with ECW (EAST shot $\#98958$![]() ) and without ECW (EAST shot $\#98933$
) and without ECW (EAST shot $\#98933$![]() ).
).
3 Simulation model and set-up
The GTC code is a three-dimensional global gyrokinetic particle code that uses Boozer coordinates to handle realistic magnetic field geometry (Zhao & Xiao Reference Zhao and Xiao2018). Given that drift wave turbulence predominantly occurs on the ion gyro-radius scale, the GTC code employs gyrokinetics for ions and drift kinetics for electrons. The perturbation part of the ion distribution function $\delta {f}\approx f_{i}-f_{Mi}$![]() satisfies the following gyrokinetic equation (Hahm Reference Hahm1988; Lin et al. Reference Lin, Nishimura, Xiao, Holod, Zhang and Chen2007):
satisfies the following gyrokinetic equation (Hahm Reference Hahm1988; Lin et al. Reference Lin, Nishimura, Xiao, Holod, Zhang and Chen2007):

where $v_{\parallel }$![]() is the parallel velocity for the particle and $\mu =m{v}_{\perp }^{2}/2B$
is the parallel velocity for the particle and $\mu =m{v}_{\perp }^{2}/2B$![]() denotes its magnetic moment. In this equation, ${\boldsymbol {b}}^{* }=\boldsymbol {b}+ ({{m}_{i}c}/{({Z}_{i}eB})){v}_{\parallel }\boldsymbol {\nabla } \times \boldsymbol {b}$
denotes its magnetic moment. In this equation, ${\boldsymbol {b}}^{* }=\boldsymbol {b}+ ({{m}_{i}c}/{({Z}_{i}eB})){v}_{\parallel }\boldsymbol {\nabla } \times \boldsymbol {b}$![]() , ${\langle {v}_{E} \rangle }_{\varphi }=c\boldsymbol {b}\times \boldsymbol {\nabla } { \langle \phi \rangle }_{\varphi }/B$
, ${\langle {v}_{E} \rangle }_{\varphi }=c\boldsymbol {b}\times \boldsymbol {\nabla } { \langle \phi \rangle }_{\varphi }/B$![]() with ${\langle \phi \rangle }_{\varphi }=({1}/{2\pi })\int \phi ( \boldsymbol {x} )\delta ( \boldsymbol {x}-\boldsymbol {R}-\rho )\,{\rm d}\boldsymbol {x}\,{\rm d}\varphi$
with ${\langle \phi \rangle }_{\varphi }=({1}/{2\pi })\int \phi ( \boldsymbol {x} )\delta ( \boldsymbol {x}-\boldsymbol {R}-\rho )\,{\rm d}\boldsymbol {x}\,{\rm d}\varphi$![]() as the gyroaveraged electrostatic potential, $\boldsymbol {v}_d=\boldsymbol {v}_c+\boldsymbol {v}_g$
as the gyroaveraged electrostatic potential, $\boldsymbol {v}_d=\boldsymbol {v}_c+\boldsymbol {v}_g$![]() with ${\boldsymbol {v}}_{c}= ( {\boldsymbol {v}}_{\parallel }/{\varOmega }_{i} )\boldsymbol {\nabla } \times \boldsymbol {b}$
with ${\boldsymbol {v}}_{c}= ( {\boldsymbol {v}}_{\parallel }/{\varOmega }_{i} )\boldsymbol {\nabla } \times \boldsymbol {b}$![]() and ${\boldsymbol {v}}_{g}= ({\mu }/{{m}_{i}{\varOmega }_{i}} )\boldsymbol {b}\times \boldsymbol {\nabla } B$
and ${\boldsymbol {v}}_{g}= ({\mu }/{{m}_{i}{\varOmega }_{i}} )\boldsymbol {b}\times \boldsymbol {\nabla } B$![]() . The electron distribution function obeys ${f}_{e}\approx {f}_{Me}+ ( e\delta \phi /{T}_{e} ){f}_{Me}+\delta {g}_{e}$
. The electron distribution function obeys ${f}_{e}\approx {f}_{Me}+ ( e\delta \phi /{T}_{e} ){f}_{Me}+\delta {g}_{e}$![]() with $e\delta \phi /{T}_{e}\ll 1$
with $e\delta \phi /{T}_{e}\ll 1$![]() and satisfies the drift kinetic equation (Lin et al. Reference Lin, Nishimura, Xiao, Holod, Zhang and Chen2007):
and satisfies the drift kinetic equation (Lin et al. Reference Lin, Nishimura, Xiao, Holod, Zhang and Chen2007):

where $\delta {\boldsymbol {v}}_{E}= ( c\boldsymbol {b}\times \boldsymbol {\nabla } { \langle \delta \phi \rangle }_{\varphi } )/B$![]() . Following the electrostatic assumption, the gyrokinetic Poisson equation is used to calculate the electric potential $\phi$
. Following the electrostatic assumption, the gyrokinetic Poisson equation is used to calculate the electric potential $\phi$![]() :
:
with $\overline {{n}_{i1}}=\int \delta ( \boldsymbol {x-\boldsymbol {R-\rho }} )\delta {f}_{i}\,{\rm d}\boldsymbol {R}\,{\rm d}^{3}v$![]() and $\delta {n}_{e}^{(1)}=\int \delta ( \boldsymbol {x-\boldsymbol {R-\rho }} )\delta {g}_{e}\,{\rm d}\boldsymbol {R}\,{\rm d}^{3}v$
and $\delta {n}_{e}^{(1)}=\int \delta ( \boldsymbol {x-\boldsymbol {R-\rho }} )\delta {g}_{e}\,{\rm d}\boldsymbol {R}\,{\rm d}^{3}v$![]() . In the equation, $\tilde {\phi }$
. In the equation, $\tilde {\phi }$![]() is the second-order gyro-averaged potential as
is the second-order gyro-averaged potential as
Taking a flux surface average on both sides of (3.3), the zonal flow equation is can be obtained. Divide the perturbation potential into two parts, i.e. $\phi = \delta \phi + \langle \phi \rangle$![]() , where $\delta \phi$
, where $\delta \phi$![]() is the non-zonal flow part and $\langle \phi \rangle$
is the non-zonal flow part and $\langle \phi \rangle$![]() is the zonal flow part. The zonal flow part can be calculated by the following zonal flow equation:
is the zonal flow part. The zonal flow part can be calculated by the following zonal flow equation:
In the equation, $Z_i$![]() is the ion charged number, $n$
is the ion charged number, $n$![]() is the density and $\rho _i$
is the density and $\rho _i$![]() is the ion gyroradius. In the code, a nonlinear $\delta {f}$
is the ion gyroradius. In the code, a nonlinear $\delta {f}$![]() method is employed to simulate the complex nonlinear turbulence physics with relatively low particle noise (Dimits & Lee Reference Dimits and Lee1993; Lin, Tang & Lee Reference Lin, Tang and Lee1995) and the kinetic electron response is retained in the simulation.
method is employed to simulate the complex nonlinear turbulence physics with relatively low particle noise (Dimits & Lee Reference Dimits and Lee1993; Lin, Tang & Lee Reference Lin, Tang and Lee1995) and the kinetic electron response is retained in the simulation.
The electrostatic drift wave instabilities in tokamak plasmas are generally believed to be driven by plasma pressure gradients. The GTC code assumes a zero radial boundary condition for the global simulation. To eliminate the boundary effect, numerical flattening and smoothing are employed to reduce turbulence drive close to both boundaries (Xiao et al. Reference Xiao, Holod, Wang, Lin and Zhang2015).
Figure 3 displays the profiles of $q(r)$![]() , density gradient scale length ($R/L_{n}$
, density gradient scale length ($R/L_{n}$![]() ) and radial temperature gradient scale length ($R/L_{T\alpha }, \alpha = i, e$
) and radial temperature gradient scale length ($R/L_{T\alpha }, \alpha = i, e$![]() ) associated with the aforementioned shots. The data range from $r/a=0.1$
) associated with the aforementioned shots. The data range from $r/a=0.1$![]() to $r/a=0.4$
to $r/a=0.4$![]() for the LHW-only case and $r/a=0.28$
for the LHW-only case and $r/a=0.28$![]() to $r/a=0.57$
to $r/a=0.57$![]() for the LHW+ECW case correspond to the experimental profiles, while the remaining range is smoothed out artificially. Given the negligible change in the ion temperature profile during these discharges, a fixed ion temperature profile is adopted in this study. In figure 3, it is evident that the maximum $R/L_{T_e}$
for the LHW+ECW case correspond to the experimental profiles, while the remaining range is smoothed out artificially. Given the negligible change in the ion temperature profile during these discharges, a fixed ion temperature profile is adopted in this study. In figure 3, it is evident that the maximum $R/L_{T_e}$![]() significantly exceeds $R/L_{T_i}$
significantly exceeds $R/L_{T_i}$![]() and $R/L_{n}$
and $R/L_{n}$![]() along radial positions, where $L_{T}=-({\rm d}\ln T/{\rm d}r)^{-1}$
along radial positions, where $L_{T}=-({\rm d}\ln T/{\rm d}r)^{-1}$![]() and $L_{n}=-({\rm d}\ln n/{\rm d}r)^{-1}$
and $L_{n}=-({\rm d}\ln n/{\rm d}r)^{-1}$![]() . Table 1 lists several essential parameters at two radial diagnostic points used for the simulation, i.e. $r/a$
. Table 1 lists several essential parameters at two radial diagnostic points used for the simulation, i.e. $r/a$![]() = 0.40 and $r/a$
= 0.40 and $r/a$![]() = 0.22, where $\beta _{e}$
= 0.22, where $\beta _{e}$![]() denotes the electron plasma beta with $\beta _{e} = 8\pi n_{e}T_{e}/B^2$
denotes the electron plasma beta with $\beta _{e} = 8\pi n_{e}T_{e}/B^2$![]() and $s$
and $s$![]() represents the magnetic shear.
represents the magnetic shear.

Figure 3. (a) Radial profiles of $q(r)$![]() , gradient of plasma density and (b) gradient of plasma temperature.
, gradient of plasma density and (b) gradient of plasma temperature.
Table 1. Parameters of diagnostic points of two cases.

After conducting many numerical convergence tests, the radial grid number is set as $N_r = 100$![]() and poloidal grid number is set as $N_\theta = 1000$
and poloidal grid number is set as $N_\theta = 1000$![]() for the LHW-only case. For the LHW+ECW case, a radial grid number of 120 and a poloidal grid number of 800 have been chosen to ensure the convergence criterion is met. The time step $t_0=0.02 R_0/c_s$
for the LHW-only case. For the LHW+ECW case, a radial grid number of 120 and a poloidal grid number of 800 have been chosen to ensure the convergence criterion is met. The time step $t_0=0.02 R_0/c_s$![]() is deemed sufficient for our simulations, where the ion sound speed $c_s = \sqrt {T_e/m_i}$
is deemed sufficient for our simulations, where the ion sound speed $c_s = \sqrt {T_e/m_i}$![]() .
.
4 Simulation results
4.1 Linear simulation results
Preliminary simulation results indicate that the instability arises solely when kinetic electrons are taken into account. To enhance the numerical accuracy of the dispersion relation within the code, we implement a filtering method. This method involves selecting a specific toroidal mode $n$![]() at the diagnostic point, followed by selecting a set of poloidal modes $m$
at the diagnostic point, followed by selecting a set of poloidal modes $m$![]() based on the safety factor $q = m/n$
based on the safety factor $q = m/n$![]() . The dispersion relations are depicted in figure 4, where $k_\theta$
. The dispersion relations are depicted in figure 4, where $k_\theta$![]() represents the poloidal wave vector. To quantitatively compare the growth rate of the two cases, both $c_s$
represents the poloidal wave vector. To quantitatively compare the growth rate of the two cases, both $c_s$![]() and $\rho _s$
and $\rho _s$![]() are taken from the simulation results of the LHW-only case. As illustrated in the figure, the real frequency of the instability is intensified in the LHW-only case, along with an increase in $k_{\theta }\rho _{s}$
are taken from the simulation results of the LHW-only case. As illustrated in the figure, the real frequency of the instability is intensified in the LHW-only case, along with an increase in $k_{\theta }\rho _{s}$![]() . Additionally, all real frequencies are shown to be positive, implying the dominance of the collisionless trapped electron mode (CTEM), which propagates in the electron diamagnetic direction. Furthermore, the broadening of the growth rate spectrum in the LHW+ECW case suggests the possibility of more CTEMs with shorter wavelengths. On one hand, for the LHW-only case, the most unstable mode occurs at $k_{\theta }\rho _{s}\approx 0.65$
. Additionally, all real frequencies are shown to be positive, implying the dominance of the collisionless trapped electron mode (CTEM), which propagates in the electron diamagnetic direction. Furthermore, the broadening of the growth rate spectrum in the LHW+ECW case suggests the possibility of more CTEMs with shorter wavelengths. On one hand, for the LHW-only case, the most unstable mode occurs at $k_{\theta }\rho _{s}\approx 0.65$![]() with a growth rate of $1.19 c_s/R_0$
with a growth rate of $1.19 c_s/R_0$![]() , which may decrease to $1.12 c_s/R_0$
, which may decrease to $1.12 c_s/R_0$![]() at the same wavelength for the LHW+ECW case. On the other hand, in the LHW+ECW case, the most unstable mode appears at $k_{\theta }\rho _{s}\approx 1.42$
at the same wavelength for the LHW+ECW case. On the other hand, in the LHW+ECW case, the most unstable mode appears at $k_{\theta }\rho _{s}\approx 1.42$![]() with a growth rate of $1.33 c_s/R_0$
with a growth rate of $1.33 c_s/R_0$![]() .
.

Figure 4. Linear dispersion relations of electrostatic instability for shot #98933 (LHW-only) and #98958 (LHW+ECW). (a) Linear growth rate, (b) real frequency.
To investigate more about the linear dispersion physics as shown in figure 4, we conduct scans of several critical parameters, the results of which are presented in figure 5. Our analysis primarily focuses on the LHW-only case, specifically considering the most unstable mode $k_{\theta }\rho _{s}\approx 0.65$![]() . In figure 5, it is evident that the instability is amplified with increasing $R/L_{T_e}$
. In figure 5, it is evident that the instability is amplified with increasing $R/L_{T_e}$![]() , while an obvious decrease occurs with higher $\beta _e$
, while an obvious decrease occurs with higher $\beta _e$![]() and $T_{e}/T_{i}$
and $T_{e}/T_{i}$![]() . This observation suggests that the growth rate of the mode increases with increasing $R/L_{T_e}$
. This observation suggests that the growth rate of the mode increases with increasing $R/L_{T_e}$![]() , which accords with the physical description of CTEM. Since the electron temperature at the diagnostic point is fixed, so the ion diamagnetic velocity diminishes with increasing $T_{e}/T_{i}$
, which accords with the physical description of CTEM. Since the electron temperature at the diagnostic point is fixed, so the ion diamagnetic velocity diminishes with increasing $T_{e}/T_{i}$![]() . In our simulation, the electron temperature remains constant; hence, a relatively larger $\beta _e$
. In our simulation, the electron temperature remains constant; hence, a relatively larger $\beta _e$![]() corresponds to higher plasma density, elevating the trapped electron and ion density, and consequently increasing the growth rate. However, $\beta _e$
corresponds to higher plasma density, elevating the trapped electron and ion density, and consequently increasing the growth rate. However, $\beta _e$![]() values exceeding 0.6 % have resulted in a decrease in the growth rate, potentially due to the stabilizing effect of finite plasma pressure on drift wave instabilities (Dong, Chen & Zonca Reference Dong, Chen and Zonca1999). This implies that $R/L_{T_e}$
values exceeding 0.6 % have resulted in a decrease in the growth rate, potentially due to the stabilizing effect of finite plasma pressure on drift wave instabilities (Dong, Chen & Zonca Reference Dong, Chen and Zonca1999). This implies that $R/L_{T_e}$![]() serves as the primary factor influencing the discrepancy in growth rates of the most unstable modes.
serves as the primary factor influencing the discrepancy in growth rates of the most unstable modes.

Figure 5. Dependence of the linear growth rate for $k_{\theta }\rho _{s}=0.65$![]() on the following parameters: (a) $\beta _e$
on the following parameters: (a) $\beta _e$![]() ; (b) electron temperature gradient scale length $R/L_{T_e}$
; (b) electron temperature gradient scale length $R/L_{T_e}$![]() and (c) $T_e/T_i$
and (c) $T_e/T_i$![]() .
.
The two-dimensional poloidal mode structures for different $k_{\theta }\rho _{s}$![]() are plotted in figure 6 for the electrostatic potential at $t = 1800t_0$
are plotted in figure 6 for the electrostatic potential at $t = 1800t_0$![]() , corresponding to $k_{\theta }\rho _{s}\sim 0.65$
, corresponding to $k_{\theta }\rho _{s}\sim 0.65$![]() , $k_{\theta }\rho _{s}\sim 0.94$
, $k_{\theta }\rho _{s}\sim 0.94$![]() , $k_{\theta }\rho _{s}\sim 1.24$
, $k_{\theta }\rho _{s}\sim 1.24$![]() in the LHW-only case and $k_{\theta }\rho _{s}\sim 1.15$
in the LHW-only case and $k_{\theta }\rho _{s}\sim 1.15$![]() , $k_{\theta }\rho _{s}\sim 1.58$
, $k_{\theta }\rho _{s}\sim 1.58$![]() , $k_{\theta }\rho _{s}\sim 2.08$
, $k_{\theta }\rho _{s}\sim 2.08$![]() in the LHW+ECW case. A conventional ballooning mode structure, peaking at the outer mid-plane, is observed. Additionally, the width of the mode structure gradually narrows as $k_{\theta }\rho _{s}$
in the LHW+ECW case. A conventional ballooning mode structure, peaking at the outer mid-plane, is observed. Additionally, the width of the mode structure gradually narrows as $k_{\theta }\rho _{s}$![]() increases. These results align well with ballooning-mode theory, where the width of the mode structure is proportional to ${k}_{\theta }^{-2}$
increases. These results align well with ballooning-mode theory, where the width of the mode structure is proportional to ${k}_{\theta }^{-2}$![]() and the mode amplitude factor $A$
and the mode amplitude factor $A$![]() is proportional to ${n}^{-1/2}$
is proportional to ${n}^{-1/2}$![]() (Hahm, Wang & Madsen Reference Hahm, Wang and Madsen2009; Dickinson et al. Reference Dickinson, Roach, Skipp and Wilson2014).
(Hahm, Wang & Madsen Reference Hahm, Wang and Madsen2009; Dickinson et al. Reference Dickinson, Roach, Skipp and Wilson2014).

Figure 6. Poloidal structures of electrostatic potential (a–c) for the LHW-only case and (d–f) for the LHW+ECW case.
4.2 Nonlinear simulation results
Following the excitation of electrostatic instability, the zonal flow is triggered through nonlinear mode coupling among various high-n drift modes. Zonal flow typically serves as the primary saturation mechanism for ITG turbulence (Lin et al. Reference Lin, Hahm, Lee, Tang and White1998; Xiao et al. Reference Xiao, Holod, Zhang, Klasky and Lin2010). However, there remains a lack of definitive theory and consensus regarding the impact of zonal flow on TEM turbulence (Lang, Chen & Parker Reference Lang, Chen and Parker2007). Consequently, simulations are conducted with both artificially removed and self-consistently generated zonal flows to explore the zonal flow effect on the EAST plasma turbulence. Figure 7 illustrates time evolutions of turbulent heat diffusivity for both cases from the GTC simulation. The ion heat diffusivity $\chi _i$![]() can be calculated by the relationship ${q}_{j}={n}_{j}{\chi }_{j}\boldsymbol {\nabla } {T}_{j}$
can be calculated by the relationship ${q}_{j}={n}_{j}{\chi }_{j}\boldsymbol {\nabla } {T}_{j}$![]() . Heat flux $q_j$
. Heat flux $q_j$![]() is calculated in the simulation by ${q}_{j}= \int {\rm d}{v}^{3} ( {m}_{j}{v}^{2}/ 2-3{T}_{j}/2 )\delta {v}_{E}\delta {f}_{j}$
is calculated in the simulation by ${q}_{j}= \int {\rm d}{v}^{3} ( {m}_{j}{v}^{2}/ 2-3{T}_{j}/2 )\delta {v}_{E}\delta {f}_{j}$![]() , where $v_E$
, where $v_E$![]() represents the $E\times B$
represents the $E\times B$![]() drift induced by the turbulent fluctuations (Xie, Xiao & Lin Reference Xie, Xiao and Lin2017). It is evident from the figure that ion heat diffusivity significantly surpasses that of electrons in both cases during the nonlinear saturation phase of turbulence, which suggests the predominance of ion transport for this parameter setting. Interestingly, a similar phenomenon is also observed in EAST plasma during high $\beta _p$
drift induced by the turbulent fluctuations (Xie, Xiao & Lin Reference Xie, Xiao and Lin2017). It is evident from the figure that ion heat diffusivity significantly surpasses that of electrons in both cases during the nonlinear saturation phase of turbulence, which suggests the predominance of ion transport for this parameter setting. Interestingly, a similar phenomenon is also observed in EAST plasma during high $\beta _p$![]() discharge (Zheng et al. Reference Zheng, Zhang, Xue, Yu, Zhang, Huang, Xiao, Wu and Gong2022). Table 2 provides a quantitative comparison of particle heat diffusivities, revealing lower heat diffusivity when the zonal flow is preserved. For the LHW-only heating, ion heat diffusivity is reduced by 66 % by comparing cases with and without zonal flow, while for the LHW+ECW combined heating, it is reduced by 59 %. Moreover, the time-averaged ion heat diffusivity for the LHW+ECW case is approximately 52 % higher than that in the LHW-only case when the zonal flow is retained. This result indicates that the transport level of the LHW+ECW case exceeds that of the LHW-only case, attributed to the significantly higher growth rate of instability observed in the LHW+ECW case.
discharge (Zheng et al. Reference Zheng, Zhang, Xue, Yu, Zhang, Huang, Xiao, Wu and Gong2022). Table 2 provides a quantitative comparison of particle heat diffusivities, revealing lower heat diffusivity when the zonal flow is preserved. For the LHW-only heating, ion heat diffusivity is reduced by 66 % by comparing cases with and without zonal flow, while for the LHW+ECW combined heating, it is reduced by 59 %. Moreover, the time-averaged ion heat diffusivity for the LHW+ECW case is approximately 52 % higher than that in the LHW-only case when the zonal flow is retained. This result indicates that the transport level of the LHW+ECW case exceeds that of the LHW-only case, attributed to the significantly higher growth rate of instability observed in the LHW+ECW case.

Figure 7. Time evolutions of particles heat diffusivity $\chi _s$![]() (a,b) for the LHW-only case and (c,d) for the LHW+ECW case with zonal flow or removed in the nonlinear simulation.
(a,b) for the LHW-only case and (c,d) for the LHW+ECW case with zonal flow or removed in the nonlinear simulation.
Table 2. Time average ion and electron heat diffusivities in different cases with or without zonal flow.

Figure 8 illustrates the poloidal structures of turbulent electrostatic potential during the nonlinear saturation phases. It is evident from the figure that the electrostatic potentials in the outer mid-plane, where bad curvature occurs, are notably higher than those in the inner mid-plane, where good curvature occurs. Radial turbulent eddies with elongated structures are observed in figure 8(a,c). The intensity of turbulence transport decreases significantly as the radial elongated structures are destroyed in figure 8(b,d). This suggests that the shear effect of zonal flow contributes to the reduction of radial correlation length and thereby suppresses turbulent transport.

Figure 8. Poloidal mode structures of turbulence electrostatic potential (a,b) for the LHW-only case and (c,d) for the LHW+ECW case.
However, table 2 clearly shows that the time-averaged electron heat diffusivity is decreased by 57 % for the LHW+ECW combined heating case when the zonal flow is retained, which is 70 % for the LHW-only heating case. This finding suggests that the zonal flow does not exert the same regulation effect on electron heat transport for the two cases, which may be influenced by parameters such as $R/L_{T_e}$![]() and $T_e/T_i$
and $T_e/T_i$![]() in the CTEM turbulence (Lang, Parker & Chen Reference Lang, Parker and Chen2008). Conversely, a significant oscillation in ion heat diffusivity occurs in the LHW-only case during the turbulent saturation period when the zonal flow is retained. According to the theory of zonal flow dynamics, a low-frequency GAM during turbulent saturation stage typically manifests as an oscillation (Diamond et al. Reference Diamond, Itoh, Itoh and Hahm2005), suggesting the potential existence of a GAM in the simulation.
in the CTEM turbulence (Lang, Parker & Chen Reference Lang, Parker and Chen2008). Conversely, a significant oscillation in ion heat diffusivity occurs in the LHW-only case during the turbulent saturation period when the zonal flow is retained. According to the theory of zonal flow dynamics, a low-frequency GAM during turbulent saturation stage typically manifests as an oscillation (Diamond et al. Reference Diamond, Itoh, Itoh and Hahm2005), suggesting the potential existence of a GAM in the simulation.
The time history of the radial structure of the electric field $E_r$![]() associated with the zonal flow is shown in figure 9. Oscillations of $E_r$
associated with the zonal flow is shown in figure 9. Oscillations of $E_r$![]() are clearly observed in figure 9(a), indicating the presence of GAMs for the LHW-only heating case. Based on time evolution of GAM/ZF intensity at the reference radius in figure 10, the real frequency of the oscillation can be approximately calculated. In fact, we obtain $\omega _{\text {LHW-only}}^{\text {simulation}} = 1.25 c_s/R_0$
are clearly observed in figure 9(a), indicating the presence of GAMs for the LHW-only heating case. Based on time evolution of GAM/ZF intensity at the reference radius in figure 10, the real frequency of the oscillation can be approximately calculated. In fact, we obtain $\omega _{\text {LHW-only}}^{\text {simulation}} = 1.25 c_s/R_0$![]() , which is very close to theoretical prediction of tokamak magnetic configuration correction (Gao et al. Reference Gao, Itoh, Sanuki and Dong2006; Gao Reference Gao2010), i.e. $\omega _{\text {LHW-only}}^{\text {theory}} = 1.30 c_s/R_0$
, which is very close to theoretical prediction of tokamak magnetic configuration correction (Gao et al. Reference Gao, Itoh, Sanuki and Dong2006; Gao Reference Gao2010), i.e. $\omega _{\text {LHW-only}}^{\text {theory}} = 1.30 c_s/R_0$![]() . However, in the LHW+ECW case, the turbulent field does not excite GAM, which may be due to stronger GAM damping in the lower $q$
. However, in the LHW+ECW case, the turbulent field does not excite GAM, which may be due to stronger GAM damping in the lower $q$![]() region and the method that uses a uniform marker particle temperature in the simulation.
region and the method that uses a uniform marker particle temperature in the simulation.

Figure 9. Two-dimensional time and radial mode structure of zonal flow for electric field $E_r$![]() (a) in the LHW-only case and (b) in the LHW+ECW case.
(a) in the LHW-only case and (b) in the LHW+ECW case.

Figure 10. Time evolution of GAM/ZF intensity at the reference magnetic surface (a) in the LHW-only case and (b) in the LHW+ECW case.
5 Conclusion
The current EAST experiment, using combined heating from LHW and ECW, has demonstrated a notable effect on turbulent transport. In this study, gyrokinetic simulations employing the GTC code were conducted to investigate electrostatic drift wave instabilities and turbulence in EAST plasmas with the heating process of combining LHW and ECW. Our findings reveal that turbulent transport is locally heightened due to the steeper electron temperature gradient in the core plasma induced by LHW+ECW combined heating. Linear simulation results suggest that the CTEM is the dominant instability for both heating cases, with the most unstable modes occurring at $k_{\theta }\rho _{s}\approx 0.65$![]() and $k_{\theta }\rho _{s}\approx 1.42$
and $k_{\theta }\rho _{s}\approx 1.42$![]() for the LHW-only case and LHW+ECW case, respectively. Furthermore, a higher ratio of $T_e/T_i$
for the LHW-only case and LHW+ECW case, respectively. Furthermore, a higher ratio of $T_e/T_i$![]() is shown to positively reduce CTEM growth rate, while $R/L_{T_e}$
is shown to positively reduce CTEM growth rate, while $R/L_{T_e}$![]() serves as the primary factor responsible for high growth rates in both heating cases. As the poloidal wavelength decreases, the amplitude of the mode structure gradually decreases. Our nonlinear simulation results indicate significant suppression of ion heat transport when the zonal flow is retained, while the zonal flow expresses a stronger inhibition effect on electron heat transport in the LHW-only case. Moreover, the presence of GAM is identified in the simulations, which can play a significant regulatory role in turbulence dynamics.
serves as the primary factor responsible for high growth rates in both heating cases. As the poloidal wavelength decreases, the amplitude of the mode structure gradually decreases. Our nonlinear simulation results indicate significant suppression of ion heat transport when the zonal flow is retained, while the zonal flow expresses a stronger inhibition effect on electron heat transport in the LHW-only case. Moreover, the presence of GAM is identified in the simulations, which can play a significant regulatory role in turbulence dynamics.
Lastly, both heating scenarios feature relatively low ion temperatures. Experimentally, employing ion cyclotron resonance heating (ICRH) and neutral beam injection (NBI) can yield higher ion temperatures in principle. Consequently, the ion temperature gradient (ITG) mode may be excited, introducing an additional physics component into plasma turbulence. To comprehensively investigate instabilities under multi-wave combined heating and quantitatively compare simulations with experimental observations, more realistic gyrokinetic simulations are necessary, incorporating actual plasma profiles and equilibrium radial electric fields.
Acknowledgement
We thank Dr. Y.H. Huang and Y.F. Jin of the Institute of Plasma Physics, Chinese Academy of Sciences for providing experimental data.
Editor Hartmut Zohm thanks the referees for their advice in evaluating this article.
Funding
The work was supported by the National Natural Science Foundation of China under Grant No. 11775108.
Declaration of interests
The authors report no conflict of interest.