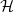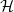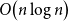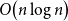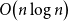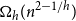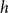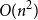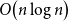1. Introduction
A graph
![]() $G$
is universal for a class
$G$
is universal for a class
![]() $\mathcal{H}$
of graphs if
$\mathcal{H}$
of graphs if
![]() $G$
contains every graph in
$G$
contains every graph in
![]() $\mathcal{H}$
as a subgraph. The study of universal graphs was initiated by Rado [Reference Rado30] in the 1960s. Obviously, the complete graph
$\mathcal{H}$
as a subgraph. The study of universal graphs was initiated by Rado [Reference Rado30] in the 1960s. Obviously, the complete graph
![]() $K_n$
is universal for any family
$K_n$
is universal for any family
![]() $\mathcal{H}$
of
$\mathcal{H}$
of
![]() $n$
-vertex graphs. Research focused on finding the minimum size (i.e. number of edges) of universal graphs for various families of sparse graphs on
$n$
-vertex graphs. Research focused on finding the minimum size (i.e. number of edges) of universal graphs for various families of sparse graphs on
![]() $n$
vertices. Babai, Chung, Erdős, Graham, and Spencer [Reference Babai, Chung, Erdős, Graham and Spencer5] proved that if
$n$
vertices. Babai, Chung, Erdős, Graham, and Spencer [Reference Babai, Chung, Erdős, Graham and Spencer5] proved that if
![]() $\mathcal{H}$
is the family of all graphs with
$\mathcal{H}$
is the family of all graphs with
![]() $m$
edges, then the size of a universal graph for
$m$
edges, then the size of a universal graph for
![]() $\mathcal{H}$
is in
$\mathcal{H}$
is in
![]() $\Omega \!\left(m^2/\log ^2 m\right)$
and
$\Omega \!\left(m^2/\log ^2 m\right)$
and
![]() $O\!\left(m^2\log \log m/ \log m\right)$
. Alon, Capalbo, Kohayakawa, Rödl, Rucinski, and Szemerédi [Reference Alon and Capalbo1, Reference Alon, Capalbo, Kohayakawa, Rödl, Rucinski and Szemerédi2] constructed a universal graph of optimal
$O\!\left(m^2\log \log m/ \log m\right)$
. Alon, Capalbo, Kohayakawa, Rödl, Rucinski, and Szemerédi [Reference Alon and Capalbo1, Reference Alon, Capalbo, Kohayakawa, Rödl, Rucinski and Szemerédi2] constructed a universal graph of optimal
![]() $\Theta (n^{2-2/k})$
size for
$\Theta (n^{2-2/k})$
size for
![]() $n$
-vertex graphs with maximum degree
$n$
-vertex graphs with maximum degree
![]() $k$
.
$k$
.
Significantly better bounds exist for minor-closed families. Esperet, Joret, and Morin [Reference Esperet, Joret and Morin23] proved recently that there exist a universal graph with
![]() $n\cdot 2^{O\left(\sqrt{\log n\cdot \log \log n}\right)}$
edges and vertices for
$n\cdot 2^{O\left(\sqrt{\log n\cdot \log \log n}\right)}$
edges and vertices for
![]() $n$
-vertex planar graphs, improving a longstanding previous record of
$n$
-vertex planar graphs, improving a longstanding previous record of
![]() $O\big(n^{3/2}\big)$
by Babai, Chung, Erdős, Graham, and Spencer [Reference Babai, Chung, Erdős, Graham and Spencer5]. For bounded-degree planar graphs, Capalbo [Reference Capalbo16] constructed universal graphs of linear size, improving an earlier bound by Bhatt, Chung, Leighton, and Rosenberg [Reference Bhatt, Chung, Leighton and Rosenberg9], which extends to other families with bounded bisection width. Böttcher, Pruessmann, Taraz, and Würfl [Reference Böttcher, Pruessmann, Taraz and Würfl13, Reference Böttcher, Schacht and Taraz14] proved that every
$O\big(n^{3/2}\big)$
by Babai, Chung, Erdős, Graham, and Spencer [Reference Babai, Chung, Erdős, Graham and Spencer5]. For bounded-degree planar graphs, Capalbo [Reference Capalbo16] constructed universal graphs of linear size, improving an earlier bound by Bhatt, Chung, Leighton, and Rosenberg [Reference Bhatt, Chung, Leighton and Rosenberg9], which extends to other families with bounded bisection width. Böttcher, Pruessmann, Taraz, and Würfl [Reference Böttcher, Pruessmann, Taraz and Würfl13, Reference Böttcher, Schacht and Taraz14] proved that every
![]() $n$
-vertex graph with minimum degree
$n$
-vertex graph with minimum degree
![]() $\Omega (n)$
is universal for
$\Omega (n)$
is universal for
![]() $n$
-vertex bounded-degree planar graphs. For
$n$
-vertex bounded-degree planar graphs. For
![]() $n$
-vertex trees, Chung and Graham [Reference Chung and Graham18, Reference Chung and Graham19] constructed an
$n$
-vertex trees, Chung and Graham [Reference Chung and Graham18, Reference Chung and Graham19] constructed an
![]() $n$
-vertex universal graph of size
$n$
-vertex universal graph of size
![]() $O(n\log n)$
, and showed that this bound is asymptotically optimal apart from constant factors.
$O(n\log n)$
, and showed that this bound is asymptotically optimal apart from constant factors.
Rado [Reference Rado30] introduced universality also for induced subgraphs. A graph
![]() $G$
is induced universal for a class
$G$
is induced universal for a class
![]() $\mathcal{H}$
of graphs if
$\mathcal{H}$
of graphs if
![]() $G$
contains every graph in
$G$
contains every graph in
![]() $\mathcal{H}$
as an induced subgraph. Alon and Nenadov [Reference Alon and Nenadov3] described a graph on
$\mathcal{H}$
as an induced subgraph. Alon and Nenadov [Reference Alon and Nenadov3] described a graph on
![]() $O(n^{\Delta/2})$
vertices that is induced universal for the class of
$O(n^{\Delta/2})$
vertices that is induced universal for the class of
![]() $n$
-vertex graphs of maximum degree
$n$
-vertex graphs of maximum degree
![]() $\Delta$
. Recently, Esperet, Joret, and Morin [Reference Esperet, Joret and Morin23] showed, improving earlier results by Bonamy, Gavoille, and Pilipczuk [Reference Bonamy, Gavoille and Pilipczuk11] and Dujmović, Esperet, Joret, Gavoille, Micek, and Morin [Reference Dujmović, Esperet, Gavoille, Joret, Micek and Morin22], that for every
$\Delta$
. Recently, Esperet, Joret, and Morin [Reference Esperet, Joret and Morin23] showed, improving earlier results by Bonamy, Gavoille, and Pilipczuk [Reference Bonamy, Gavoille and Pilipczuk11] and Dujmović, Esperet, Joret, Gavoille, Micek, and Morin [Reference Dujmović, Esperet, Gavoille, Joret, Micek and Morin22], that for every
![]() $n\in{\mathbb{N}}$
, there exists a graph
$n\in{\mathbb{N}}$
, there exists a graph
![]() $U_n$
with
$U_n$
with
![]() $n\cdot 2^{O\left(\sqrt{\log n\cdot \log \log n}\right)}$
edges and vertices that contains every
$n\cdot 2^{O\left(\sqrt{\log n\cdot \log \log n}\right)}$
edges and vertices that contains every
![]() $n$
-vertex planar graph as an induced subgraph.
$n$
-vertex planar graph as an induced subgraph.
In this paper, we extend the concept of universality to geometric graphs. A geometric graph is a graph together with a straight-line drawing in the plane in which the vertices are distinct points and the edges are straight-line segments not containing any vertex in their relative interiors. A geometric graph is convex if its vertices are in convex position (that is, they form the vertex set of a convex polygon in the plane).
A geometric graph is universal for a class
![]() $\mathcal H$
of planar graphs if it contains an embedding of every graph in
$\mathcal H$
of planar graphs if it contains an embedding of every graph in
![]() $\mathcal{H}$
. For an (abstract) graph
$\mathcal{H}$
. For an (abstract) graph
![]() $G_1$
and a geometric graph
$G_1$
and a geometric graph
![]() $G_2$
, an embedding of
$G_2$
, an embedding of
![]() $G_1$
into
$G_1$
into
![]() $G_2$
is an injective map
$G_2$
is an injective map
![]() $\varphi \,:\,V(G_1)\rightarrow V(G_2)$
such that (i) every edge
$\varphi \,:\,V(G_1)\rightarrow V(G_2)$
such that (i) every edge
![]() $uv\in E(G_1)$
is mapped to an edge
$uv\in E(G_1)$
is mapped to an edge
![]() $\varphi (u)\varphi (v)\in E(G_2)$
(that is,
$\varphi (u)\varphi (v)\in E(G_2)$
(that is,
![]() $\varphi$
is a graph homomorphism); and (ii) every pair of edges
$\varphi$
is a graph homomorphism); and (ii) every pair of edges
![]() $u_1v_1, u_2v_2\in E(G_1)$
is mapped to a pair of noncrossing line segments
$u_1v_1, u_2v_2\in E(G_1)$
is mapped to a pair of noncrossing line segments
![]() $\varphi (u_1)\varphi (v_1)$
and
$\varphi (u_1)\varphi (v_1)$
and
![]() $\varphi (u_2)\varphi (v_2)$
in the plane. When
$\varphi (u_2)\varphi (v_2)$
in the plane. When
![]() $\varphi \,:\,V(G_1)\rightarrow V(G_2)$
is bijective, we say that it is an embedding of
$\varphi \,:\,V(G_1)\rightarrow V(G_2)$
is bijective, we say that it is an embedding of
![]() $G_1$
onto
$G_1$
onto
![]() $G_2$
.
$G_2$
.
Previous research in the geometric setting was limited to finding the smallest complete geometric graph that is universal for the class of planar graphs on
![]() $n$
vertices. The intersection pattern of the edges in a geometric graph is determined by the location of its vertices; hence universal complete geometric graphs are commonly referred to as
$n$
vertices. The intersection pattern of the edges in a geometric graph is determined by the location of its vertices; hence universal complete geometric graphs are commonly referred to as
![]() $n$
-universal point sets. De Fraysseix, Pach, and Pollack [Reference de Fraysseix, Pach and Pollack20] proved that the
$n$
-universal point sets. De Fraysseix, Pach, and Pollack [Reference de Fraysseix, Pach and Pollack20] proved that the
![]() $2n\times n$
section of the integer lattice is an
$2n\times n$
section of the integer lattice is an
![]() $n$
-universal point set. Over the last 30 years, the upper bound on the size of an
$n$
-universal point set. Over the last 30 years, the upper bound on the size of an
![]() $n$
-universal point set has been improved from
$n$
-universal point set has been improved from
![]() $2n^2$
to
$2n^2$
to
![]() $n^2/4+O(n)$
[Reference Bannister, Cheng, Devanny and Eppstein6]; the current best lower bound is
$n^2/4+O(n)$
[Reference Bannister, Cheng, Devanny and Eppstein6]; the current best lower bound is
![]() $(1.293-o(1))n$
[Reference Scheucher, Schrezenmaier and Steiner31] (based on stacked triangulations, that is, maximal planar graphs of treewidth three; see also [Reference Cardinal, Hoffmann and Kusters17, Reference Kurowski28]). It is known that every set of
$(1.293-o(1))n$
[Reference Scheucher, Schrezenmaier and Steiner31] (based on stacked triangulations, that is, maximal planar graphs of treewidth three; see also [Reference Cardinal, Hoffmann and Kusters17, Reference Kurowski28]). It is known that every set of
![]() $n$
points in general position is universal for
$n$
points in general position is universal for
![]() $n$
-vertex outerplanar graphs [Reference Bose12, Reference Gritzmann, Mohar, Pach and Pollack26]. An
$n$
-vertex outerplanar graphs [Reference Bose12, Reference Gritzmann, Mohar, Pach and Pollack26]. An
![]() $O(n\log n)$
upper bound is known for 2-outerplanar and simply nested graphs [Reference Angelini, Bruckdorfer, Di Battista, Kaufmann, Mchedlidze, Roselli and Squarcella4], and an
$O(n\log n)$
upper bound is known for 2-outerplanar and simply nested graphs [Reference Angelini, Bruckdorfer, Di Battista, Kaufmann, Mchedlidze, Roselli and Squarcella4], and an
![]() $O(n^{3/2}\log n)$
upper bound for
$O(n^{3/2}\log n)$
upper bound for
![]() $n$
-vertex stacked triangulations [Reference Fulek and Tóth25].
$n$
-vertex stacked triangulations [Reference Fulek and Tóth25].
Our results. The results on universal point sets yield an upper bound of
![]() $O(n^4)$
for the size of a geometric graph that is universal for
$O(n^4)$
for the size of a geometric graph that is universal for
![]() $n$
-vertex planar graphs and
$n$
-vertex planar graphs and
![]() $O(n^2)$
for
$O(n^2)$
for
![]() $n$
-vertex outerplanar graphs, including trees. We improve the upper bound for
$n$
-vertex outerplanar graphs, including trees. We improve the upper bound for
![]() $n$
-vertex trees to an optimal
$n$
-vertex trees to an optimal
![]() $O(n\log n)$
, and show that the quadratic upper bound for outerplanar graphs is essentially tight for convex geometric graphs. More precisely, we prove the following results:
$O(n\log n)$
, and show that the quadratic upper bound for outerplanar graphs is essentially tight for convex geometric graphs. More precisely, we prove the following results:
-
• For every
 $n\in{\mathbb{N}}$
, there exists a geometric graph
$n\in{\mathbb{N}}$
, there exists a geometric graph
 $G$
with
$G$
with
 $n$
vertices and
$n$
vertices and
 $O(n\log n)$
edges that is universal for forests with
$O(n\log n)$
edges that is universal for forests with
 $n$
vertices (Theorem 1 in Section 2). The bound of
$n$
vertices (Theorem 1 in Section 2). The bound of
 $O(n\log n)$
edges is asymptotically optimal, apart from constant factors, even in the abstract setting, for caterpillars, and if the universal graph is allowed to have more than
$O(n\log n)$
edges is asymptotically optimal, apart from constant factors, even in the abstract setting, for caterpillars, and if the universal graph is allowed to have more than
 $n$
vertices [[Reference Chung and Graham18], Theorem 1]. The proof of universality is constructive and yields a polynomial-time algorithm that embeds any forest with
$n$
vertices [[Reference Chung and Graham18], Theorem 1]. The proof of universality is constructive and yields a polynomial-time algorithm that embeds any forest with
 $n$
vertices onto
$n$
vertices onto
 $G$
.
$G$
. -
• For every
 $h\in{\mathbb{N}}$
and
$h\in{\mathbb{N}}$
and
 $n\geq 3h^2$
, every
$n\geq 3h^2$
, every
 $n$
-vertex convex geometric graph that is universal for the family of
$n$
-vertex convex geometric graph that is universal for the family of
 $n$
-vertex cycles with
$n$
-vertex cycles with
 $h$
disjoint chords has
$h$
disjoint chords has
 $\Omega _h(n^{2-1/h})$
edges (Theorem 9 in Section 3); this almost matches the trivial
$\Omega _h(n^{2-1/h})$
edges (Theorem 9 in Section 3); this almost matches the trivial
 $O(n^2)$
upper bound, which hence cannot be improved by polynomial factors even for
$O(n^2)$
upper bound, which hence cannot be improved by polynomial factors even for
 $n$
-vertex outerplanar graphs of maximum degree three. For
$n$
-vertex outerplanar graphs of maximum degree three. For
 $n$
-vertex cycles with
$n$
-vertex cycles with
 $2$
disjoint chords, there exists an
$2$
disjoint chords, there exists an
 $n$
-vertex convex geometric graph with
$n$
-vertex convex geometric graph with
 $O\big(n^{3/2}\big)$
edges (Theorem 10 in Section 3), which matches the lower bound above.
$O\big(n^{3/2}\big)$
edges (Theorem 10 in Section 3), which matches the lower bound above. -
• For every
 $n\in{\mathbb{N}}$
, there exists a convex geometric graph
$n\in{\mathbb{N}}$
, there exists a convex geometric graph
 $G$
with
$G$
with
 $n$
vertices and
$n$
vertices and
 $O(n\log n)$
edges that is universal for
$O(n\log n)$
edges that is universal for
 $n$
-vertex caterpillars (Theorem 12 in Section 3).
$n$
-vertex caterpillars (Theorem 12 in Section 3).
2. Universal geometric graphs for forests
In this section, we prove the following theorem.
Theorem 1.
For every
![]() $n\in{\mathbb{N}}$
, there exists a geometric graph
$n\in{\mathbb{N}}$
, there exists a geometric graph
![]() $G$
with
$G$
with
![]() $n$
vertices and
$n$
vertices and
![]() $O(n\log n)$
edges that is universal for forests with
$O(n\log n)$
edges that is universal for forests with
![]() $n$
vertices.
$n$
vertices.

Figure 1. A schematic drawing of the universal graph for
![]() $n=15$
vertices (left) and a geometric drawing of the universal graph for
$n=15$
vertices (left) and a geometric drawing of the universal graph for
![]() $n=7$
vertices. The edges of the tree
$n=7$
vertices. The edges of the tree
![]() $B$
are shown black; the edges of the groups (E1), (E2), and (E3) are shown red, orange, and blue, respectively. Edges that belong to several of these groups are shown in the colour of the first group they belong to.
$B$
are shown black; the edges of the groups (E1), (E2), and (E3) are shown red, orange, and blue, respectively. Edges that belong to several of these groups are shown in the colour of the first group they belong to.
2.1. Construction
We adapt a construction due to Chung and Graham [Reference Chung and Graham19], originally designed for abstract graphs, to the geometric setting. For a given
![]() $n\in{\mathbb{N}}$
, they construct a graph
$n\in{\mathbb{N}}$
, they construct a graph
![]() $G$
with
$G$
with
![]() $n$
vertices and
$n$
vertices and
![]() $O(n\log n)$
edges such that
$O(n\log n)$
edges such that
![]() $G$
contains every forest on
$G$
contains every forest on
![]() $n$
vertices as a subgraph. Let us sketch this construction. For simplicity assume that
$n$
vertices as a subgraph. Let us sketch this construction. For simplicity assume that
![]() $n=2^h-1$
, for some integer
$n=2^h-1$
, for some integer
![]() $h\ge 2$
. Let
$h\ge 2$
. Let
![]() $B$
be a complete rooted ordered binary tree on
$B$
be a complete rooted ordered binary tree on
![]() $n$
vertices. A level is a set of vertices at the same distance from the root. The levels are labelled
$n$
vertices. A level is a set of vertices at the same distance from the root. The levels are labelled
![]() $1,\ldots,h$
, from the one containing the root to the one that contains the leaves of
$1,\ldots,h$
, from the one containing the root to the one that contains the leaves of
![]() $B$
. A pre-order traversal of
$B$
. A pre-order traversal of
![]() $B$
(which consists first of the root, then recursively of the vertices in its left subtree, and then recursively of the vertices in its right subtree) determines a total order on the vertices, and it also induces a total order on the vertices in each level of
$B$
(which consists first of the root, then recursively of the vertices in its left subtree, and then recursively of the vertices in its right subtree) determines a total order on the vertices, and it also induces a total order on the vertices in each level of
![]() $B$
. In each level, we call two consecutive elements in this order level-neighbours; in particular, any two siblings are level-neighbours. For a vertex
$B$
. In each level, we call two consecutive elements in this order level-neighbours; in particular, any two siblings are level-neighbours. For a vertex
![]() $v$
of
$v$
of
![]() $B$
, we denote by
$B$
, we denote by
![]() $B(v)$
the subtree of
$B(v)$
the subtree of
![]() $B$
rooted at
$B$
rooted at
![]() $v$
. The graph
$v$
. The graph
![]() $G$
contains
$G$
contains
![]() $B$
and three additional groups of edges defined as follows (see Figure 1 for an illustration).
$B$
and three additional groups of edges defined as follows (see Figure 1 for an illustration).
-
(E1) Every vertex
 $v$
is adjacent to all vertices in the subtree
$v$
is adjacent to all vertices in the subtree
 $B(v)$
;
$B(v)$
; -
(E2) for every vertex
 $v$
and every left or right level-neighbour
$v$
and every left or right level-neighbour
 $u$
of
$u$
of
 $v$
in
$v$
in
 $B$
, the vertex
$B$
, the vertex
 $v$
is adjacent to all vertices in the subtree
$v$
is adjacent to all vertices in the subtree
 $B(u)$
; and
$B(u)$
; and -
(E3) every vertex
 $v$
whose parent has a left level-neighbour
$v$
whose parent has a left level-neighbour
 $p$
is adjacent to all vertices in the subtree
$p$
is adjacent to all vertices in the subtree
 $B(p)$
.
$B(p)$
.
It is easily checked that
![]() $G$
has
$G$
has
![]() $O(n\log n)$
edges. Indeed, the binary tree
$O(n\log n)$
edges. Indeed, the binary tree
![]() $B$
has
$B$
has
![]() $2^{i-1}$
vertices on level
$2^{i-1}$
vertices on level
![]() $i$
, for
$i$
, for
![]() $i=1,\ldots,h$
. A vertex
$i=1,\ldots,h$
. A vertex
![]() $v$
on level
$v$
on level
![]() $i$
has
$i$
has
![]() $2^{h-i+1}-1$
descendants (including itself), and each of its level-neighbours have the same number of descendants. In addition, the left level-neighbour of the parent of
$2^{h-i+1}-1$
descendants (including itself), and each of its level-neighbours have the same number of descendants. In addition, the left level-neighbour of the parent of
![]() $v$
(if present) has
$v$
(if present) has
![]() $2\cdot (2^{h-i+1}-1)$
descendants (excluding itself). Altogether
$2\cdot (2^{h-i+1}-1)$
descendants (excluding itself). Altogether
![]() $v$
is adjacent to less than
$v$
is adjacent to less than
![]() $5\cdot 2^{h-i+1}$
vertices at the same or at lower levels of
$5\cdot 2^{h-i+1}$
vertices at the same or at lower levels of
![]() $B$
. Hence, the number of edges in
$B$
. Hence, the number of edges in
![]() $G$
is less than
$G$
is less than
 \begin{align*} 5\cdot \sum _{i=1}^h 2^{i-1} \cdot 2^{h-i+1} = 5\cdot 2^h \cdot h = 5(n+1)\cdot \log _2\! (n+1) \in O\!\left(n \log n\right). \end{align*}
\begin{align*} 5\cdot \sum _{i=1}^h 2^{i-1} \cdot 2^{h-i+1} = 5\cdot 2^h \cdot h = 5(n+1)\cdot \log _2\! (n+1) \in O\!\left(n \log n\right). \end{align*}
Chung and Graham [Reference Chung and Graham19] showed that
![]() $G$
is universal for forests, that is,
$G$
is universal for forests, that is,
![]() $G$
contains every forest on
$G$
contains every forest on
![]() $n$
vertices as a subgraph.Footnote
1
$n$
vertices as a subgraph.Footnote
1
Geometric representation
We next describe how to embed the vertices of
![]() $G$
into
$G$
into
![]() ${{\mathbb{R}}}^2$
; see Figure 2 (left) for an illustration. First, the
${{\mathbb{R}}}^2$
; see Figure 2 (left) for an illustration. First, the
![]() $x$
-coordinates of the vertices are assigned in the order determined by a pre-order traversal of
$x$
-coordinates of the vertices are assigned in the order determined by a pre-order traversal of
![]() $B$
. For simplicity, let us take these
$B$
. For simplicity, let us take these
![]() $x$
-coordinates to be
$x$
-coordinates to be
![]() $0,\ldots,n-1$
, so that the root of
$0,\ldots,n-1$
, so that the root of
![]() $B$
is placed on the
$B$
is placed on the
![]() $y$
-axis. The vertex of
$y$
-axis. The vertex of
![]() $G$
with
$G$
with
![]() $x$
-coordinate
$x$
-coordinate
![]() $i$
is denoted by
$i$
is denoted by
![]() $v_i$
.
$v_i$
.

Figure 2. Illustration for the assignment of
![]() $x$
- and
$x$
- and
![]() $y$
-coordinates to the vertices of
$y$
-coordinates to the vertices of
![]() $G$
, and for the definition of interval (left). Illustration for Observation 2(right).
$G$
, and for the definition of interval (left). Illustration for Observation 2(right).
The
![]() $y$
-coordinates of the vertices are determined by a BFS traversal of
$y$
-coordinates of the vertices are determined by a BFS traversal of
![]() $B$
starting from the root, in which at every vertex the right sibling is visited before the left sibling. Denote by
$B$
starting from the root, in which at every vertex the right sibling is visited before the left sibling. Denote by
![]() $\sigma$
the order of vertices of
$\sigma$
the order of vertices of
![]() $G$
in this traversal. If a vertex
$G$
in this traversal. If a vertex
![]() $u$
precedes a vertex
$u$
precedes a vertex
![]() $v$
in
$v$
in
![]() $\sigma$
, then
$\sigma$
, then
![]() $u$
gets a larger
$u$
gets a larger
![]() $y$
-coordinate than
$y$
-coordinate than
![]() $v$
. The gap between two consecutive
$v$
. The gap between two consecutive
![]() $y$
-coordinates is chosen so that every vertex is above all lines determined by any two vertices with smaller
$y$
-coordinates is chosen so that every vertex is above all lines determined by any two vertices with smaller
![]() $y$
-coordinates. This choice is feasible because no line through two vertices of
$y$
-coordinates. This choice is feasible because no line through two vertices of
![]() $G$
is vertical, due to the
$G$
is vertical, due to the
![]() $x$
-coordinate assignment. Thus, if the maximum difference between the
$x$
-coordinate assignment. Thus, if the maximum difference between the
![]() $y$
-coordinates of two vertices in a set
$y$
-coordinates of two vertices in a set
![]() $X\subseteq V(G)$
is some value
$X\subseteq V(G)$
is some value
![]() $Y$
, then any line through two vertices in
$Y$
, then any line through two vertices in
![]() $X$
has a slope whose absolute value is at most
$X$
has a slope whose absolute value is at most
![]() $Y$
. Hence, any point that is
$Y$
. Hence, any point that is
![]() $n\cdot Y$
units higher than every vertex in
$n\cdot Y$
units higher than every vertex in
![]() $X$
is above every line determined by two vertices in
$X$
is above every line determined by two vertices in
![]() $X$
.
$X$
.
Note that this choice of coordinates fixes the rotation system of the vertex set, which is the collection of circular sequences obtained as follows: For each vertex
![]() $v$
consider a ray
$v$
consider a ray
![]() $r_v$
emanating from
$r_v$
emanating from
![]() $v$
and record the sequence of other vertices as
$v$
and record the sequence of other vertices as
![]() $r_v$
encounters them while rotating counterclockwise around
$r_v$
encounters them while rotating counterclockwise around
![]() $v$
. The rotation system in turn determines for each pair of (straight-line) edges whether they cross [[Reference Kynčl29], Proposition 6].
$v$
. The rotation system in turn determines for each pair of (straight-line) edges whether they cross [[Reference Kynčl29], Proposition 6].
Our figures display the vertices of
![]() $B$
in the correct
$B$
in the correct
![]() $x$
- and
$x$
- and
![]() $y$
-order, but – with the exception of Figure 1 (right) – they are not to scale. The
$y$
-order, but – with the exception of Figure 1 (right) – they are not to scale. The
![]() $y$
-coordinates in our construction are rapidly increasing (similarly to constructions in [Reference Bukh, Matoušek and Nivasch15, Reference Fulek and Tóth25]). For this reason, in our figures we draw the edges in
$y$
-coordinates in our construction are rapidly increasing (similarly to constructions in [Reference Bukh, Matoušek and Nivasch15, Reference Fulek and Tóth25]). For this reason, in our figures we draw the edges in
![]() $B$
as straight-line segments and all other edges as Jordan arcs.
$B$
as straight-line segments and all other edges as Jordan arcs.
The choice of
![]() $y$
-coordinates of the vertices implies that, for any vertex
$y$
-coordinates of the vertices implies that, for any vertex
![]() $v$
, all vertices with larger
$v$
, all vertices with larger
![]() $y$
-coordinate than
$y$
-coordinate than
![]() $v$
see the vertices below
$v$
see the vertices below
![]() $v$
in the same circular order as
$v$
in the same circular order as
![]() $v$
. Furthermore, the vertices of
$v$
. Furthermore, the vertices of
![]() $G$
are in general position, that is, no three are collinear. In particular, we have the following property (see Figure 2 (right) for an example).
$G$
are in general position, that is, no three are collinear. In particular, we have the following property (see Figure 2 (right) for an example).
Observation 2.
If
![]() $ab, cd\in E(G)$
are such that (1)
$ab, cd\in E(G)$
are such that (1)
![]() $a$
has larger
$a$
has larger
![]() $y$
-coordinate than
$y$
-coordinate than
![]() $b$
,
$b$
,
![]() $c$
, and
$c$
, and
![]() $d$
, and (2)
$d$
, and (2)
![]() $b$
has smaller or larger
$b$
has smaller or larger
![]() $x$
-coordinate than both
$x$
-coordinate than both
![]() $c$
and
$c$
and
![]() $d$
, then
$d$
, then
![]() $ab$
and
$ab$
and
![]() $cd$
do not cross.
$cd$
do not cross.
Proof. By (2) we can assume, without loss of generality up to a switch of the labels of
![]() $c$
and
$c$
and
![]() $d$
, that
$d$
, that
![]() $d$
is below the line through
$d$
is below the line through
![]() $b$
and
$b$
and
![]() $c$
. By (1) and by construction,
$c$
. By (1) and by construction,
![]() $a$
is above the line through
$a$
is above the line through
![]() $b$
and
$b$
and
![]() $c$
, hence
$c$
, hence
![]() $ab$
and
$ab$
and
![]() $cd$
are separated by the line through
$cd$
are separated by the line through
![]() $b$
and
$b$
and
![]() $c$
and thus do not cross.
$c$
and thus do not cross.
2.2. Intervals and embeddings
For every interval
![]() $[i,j]\subseteq [0,n-1]$
we define
$[i,j]\subseteq [0,n-1]$
we define
![]() $G[i,j]$
to be the subgraph of
$G[i,j]$
to be the subgraph of
![]() $G$
induced by the vertices with
$G$
induced by the vertices with
![]() $x$
-coordinates in
$x$
-coordinates in
![]() $[i,j]$
. We call the graph
$[i,j]$
. We call the graph
![]() $G[i,j]$
an interval of
$G[i,j]$
an interval of
![]() $G$
. The length of an interval
$G$
. The length of an interval
![]() $G[i,j]$
of
$G[i,j]$
of
![]() $G$
is defined as
$G$
is defined as
![]() $|G[i,j]|=j-i+1$
, which is the number of vertices in
$|G[i,j]|=j-i+1$
, which is the number of vertices in
![]() $G[i,j]$
. If
$G[i,j]$
. If
![]() $I$
is an interval of integers, then we denote by
$I$
is an interval of integers, then we denote by
![]() $G(I)$
the corresponding interval of
$G(I)$
the corresponding interval of
![]() $G$
. For a subset
$G$
. For a subset
![]() $U\subseteq V(G)$
, we denote by
$U\subseteq V(G)$
, we denote by
![]() $G[U]$
the subgraph of
$G[U]$
the subgraph of
![]() $G$
induced by
$G$
induced by
![]() $U$
.
$U$
.
In Section 2.3, we present a recursive algorithm that can embed every tree on
![]() $h$
vertices onto every interval of length
$h$
vertices onto every interval of length
![]() $h$
of
$h$
of
![]() $G$
. In some cases, we embed the root of a tree at some vertex of the interval, and recurse on the subtrees. For this strategy, it is convenient to embed the root at the centre of a spanning star. The following lemma shows that every interval contains spanning stars.
$G$
. In some cases, we embed the root of a tree at some vertex of the interval, and recurse on the subtrees. For this strategy, it is convenient to embed the root at the centre of a spanning star. The following lemma shows that every interval contains spanning stars.
Lemma 3.
Every interval
![]() $G[i,j]$
of
$G[i,j]$
of
![]() $G$
on at least two vertices contains a noncrossing spanning star centred at the highest vertex
$G$
on at least two vertices contains a noncrossing spanning star centred at the highest vertex
![]() $v_k$
and a noncrossing spanning star centred at the second highest vertex
$v_k$
and a noncrossing spanning star centred at the second highest vertex
![]() $v_s$
of
$v_s$
of
![]() $G[i,j]$
.
$G[i,j]$
.
Proof. We first argue for the star centred at
![]() $v_k$
. By construction (pre-order traversal and increasing
$v_k$
. By construction (pre-order traversal and increasing
![]() $y$
-coordinates along each level from left to right), all vertices in
$y$
-coordinates along each level from left to right), all vertices in
![]() $G[k,j]$
belong to
$G[k,j]$
belong to
![]() $B(v_k)$
. By construction,
$B(v_k)$
. By construction,
![]() $G$
contains edges from
$G$
contains edges from
![]() $v_k$
to every vertex in
$v_k$
to every vertex in
![]() $B(v_k)$
; these edges are in
$B(v_k)$
; these edges are in
![]() $E(B)$
and in the edge group (E1). This completes the proof if
$E(B)$
and in the edge group (E1). This completes the proof if
![]() $k=i$
. Assume that
$k=i$
. Assume that
![]() $k\gt i$
. Then
$k\gt i$
. Then
![]() $v_k$
has a parent
$v_k$
has a parent
![]() $v_p$
; further, we have
$v_p$
; further, we have
![]() $p\lt i$
, because
$p\lt i$
, because
![]() $v_k$
is the highest vertex of
$v_k$
is the highest vertex of
![]() $G[i,j]$
and every vertex is higher than its descendants. Therefore,
$G[i,j]$
and every vertex is higher than its descendants. Therefore,
![]() $v_k$
has a left sibling
$v_k$
has a left sibling
![]() $v_\ell$
(which may or may not be in
$v_\ell$
(which may or may not be in
![]() $G[i,j]$
); all the vertices in
$G[i,j]$
); all the vertices in
![]() $G[i,k-1]$
are in
$G[i,k-1]$
are in
![]() $B(v_\ell )$
and hence are adjacent to
$B(v_\ell )$
and hence are adjacent to
![]() $v_k$
, via edges in the edge group (E2).
$v_k$
, via edges in the edge group (E2).
We now argue about the second highest vertex
![]() $v_s$
of
$v_s$
of
![]() $G[i,j]$
. We consider two cases.
$G[i,j]$
. We consider two cases.
If
![]() $k=j$
, then
$k=j$
, then
![]() $v_s$
is the highest vertex of
$v_s$
is the highest vertex of
![]() $G[i,j-1]$
. Therefore,
$G[i,j-1]$
. Therefore,
![]() $G[i,j-1]$
contains a spanning star centred at
$G[i,j-1]$
contains a spanning star centred at
![]() $v_s$
, as argued above if
$v_s$
, as argued above if
![]() $i\lt j-1$
; if
$i\lt j-1$
; if
![]() $i=j-1$
, then such a star trivially exists. The remaining edge between
$i=j-1$
, then such a star trivially exists. The remaining edge between
![]() $v_s$
and
$v_s$
and
![]() $v_k$
also exists, as it is part of the star centred at
$v_k$
also exists, as it is part of the star centred at
![]() $v_k$
.
$v_k$
.
Hence, we may assume that
![]() $k\lt j$
. We distinguish between two cases.
$k\lt j$
. We distinguish between two cases.
Assume first that
![]() $k+1\leq s\leq j$
. Note that
$k+1\leq s\leq j$
. Note that
![]() $v_s$
is a child of
$v_s$
is a child of
![]() $v_k$
: Namely, since no vertex in
$v_k$
: Namely, since no vertex in
![]() $G[i,j]$
is higher than
$G[i,j]$
is higher than
![]() $v_k$
, it follows that neither the right level-neighbour of
$v_k$
, it follows that neither the right level-neighbour of
![]() $v_k$
, if it exists, nor a vertex on a level higher than
$v_k$
, if it exists, nor a vertex on a level higher than
![]() $v_k$
are in
$v_k$
are in
![]() $G[i,j]$
, hence
$G[i,j]$
, hence
![]() $v_s$
is either the left or the right child of
$v_s$
is either the left or the right child of
![]() $v_k$
. We prove that
$v_k$
. We prove that
![]() $v_s$
is adjacent to all the vertices of
$v_s$
is adjacent to all the vertices of
![]() $G[i,k-1]$
, to
$G[i,k-1]$
, to
![]() $v_k$
, and to all the vertices of
$v_k$
, and to all the vertices of
![]() $G[k+1,j]$
. Concerning the vertices of
$G[k+1,j]$
. Concerning the vertices of
![]() $G[i,k-1]$
, we can assume that
$G[i,k-1]$
, we can assume that
![]() $k\gt i$
, as otherwise
$k\gt i$
, as otherwise
![]() $G[i,k-1]$
contains no vertex. Recall that
$G[i,k-1]$
contains no vertex. Recall that
![]() $k\gt i$
implies that
$k\gt i$
implies that
![]() $v_k$
has a left sibling
$v_k$
has a left sibling
![]() $v_\ell$
, which may or may not be in
$v_\ell$
, which may or may not be in
![]() $G[i,j]$
; regardless, all the vertices in
$G[i,j]$
; regardless, all the vertices in
![]() $G[i,k-1]$
are in
$G[i,k-1]$
are in
![]() $B(v_\ell )$
and are hence adjacent to
$B(v_\ell )$
and are hence adjacent to
![]() $v_s$
, via edges in the edge group (E3). Further, the edge between
$v_s$
, via edges in the edge group (E3). Further, the edge between
![]() $v_s$
and
$v_s$
and
![]() $v_k$
exists, as it is part of the star centred at
$v_k$
exists, as it is part of the star centred at
![]() $v_k$
. Finally, each vertex in
$v_k$
. Finally, each vertex in
![]() $G[k+1,j]$
is either in
$G[k+1,j]$
is either in
![]() $B(v_s)$
, hence it is adjacent to
$B(v_s)$
, hence it is adjacent to
![]() $v_s$
via an edge in
$v_s$
via an edge in
![]() $E(B)$
or in the edge group (E1), or in
$E(B)$
or in the edge group (E1), or in
![]() $B(v_q)$
, where
$B(v_q)$
, where
![]() $v_q$
is the child of
$v_q$
is the child of
![]() $v_k$
different from
$v_k$
different from
![]() $v_s$
, hence it is adjacent to
$v_s$
, hence it is adjacent to
![]() $v_s$
via an edge in the edge group (E2).
$v_s$
via an edge in the edge group (E2).
Assume next that
![]() $i\leq s\leq k-1$
. Then
$i\leq s\leq k-1$
. Then
![]() $v_s$
must be on a level higher than
$v_s$
must be on a level higher than
![]() $v_{k+1}$
, which is the left child of
$v_{k+1}$
, which is the left child of
![]() $v_k$
, and on a level lower than
$v_k$
, and on a level lower than
![]() $v_p$
, which is the parent of
$v_p$
, which is the parent of
![]() $v_k$
. Hence,
$v_k$
. Hence,
![]() $v_s$
is the left sibling of
$v_s$
is the left sibling of
![]() $v_k$
, which implies
$v_k$
, which implies
![]() $p=s-1$
and
$p=s-1$
and
![]() $s=i$
. Therefore,
$s=i$
. Therefore,
![]() $v_s$
is adjacent to all the vertices in
$v_s$
is adjacent to all the vertices in
![]() $G[i,k-1]$
via edges in
$G[i,k-1]$
via edges in
![]() $E(B)$
or in the edge group (E1) as well as to all the vertices of
$E(B)$
or in the edge group (E1) as well as to all the vertices of
![]() $G[k,j]$
, via edges in the edge group (E2); hence,
$G[k,j]$
, via edges in the edge group (E2); hence,
![]() $v_s$
is adjacent to all the vertices of
$v_s$
is adjacent to all the vertices of
![]() $G[i,j]$
.
$G[i,j]$
.
Finally, note that, as the vertices of
![]() $G$
are laid out in general position, every star in
$G$
are laid out in general position, every star in
![]() $G[i,j]$
is noncrossing.
$G[i,j]$
is noncrossing.
The recursive algorithm (Section 2.3) occasionally embeds a subtree of
![]() $T$
onto an induced subgraph of
$T$
onto an induced subgraph of
![]() $G$
that is ‘almost’ an interval, in the sense that it can be obtained from an interval of
$G$
that is ‘almost’ an interval, in the sense that it can be obtained from an interval of
![]() $G$
by deleting its highest vertex or by replacing its highest vertex with a vertex that does not belong to the interval. Lemmas 5 and 6 below provide the tools to construct such embeddings.
$G$
by deleting its highest vertex or by replacing its highest vertex with a vertex that does not belong to the interval. Lemmas 5 and 6 below provide the tools to construct such embeddings.
We first prove that the ‘structure’ of an interval without its highest vertex is similar to that of an interval; this is formalised by the following definition. Let
![]() $U$
and
$U$
and
![]() $W$
be two subsets of
$W$
be two subsets of
![]() $V(G)$
with
$V(G)$
with
![]() $h=|U|=|W|$
. Let
$h=|U|=|W|$
. Let
![]() $u_1,\dots,u_h$
and
$u_1,\dots,u_h$
and
![]() $w_1,\dots,w_h$
be the vertices of
$w_1,\dots,w_h$
be the vertices of
![]() $U$
and
$U$
and
![]() $W$
, respectively, ordered by increasing
$W$
, respectively, ordered by increasing
![]() $x$
-coordinates. We say that
$x$
-coordinates. We say that
![]() $G[U]$
and
$G[U]$
and
![]() $G[W]$
are crossing-isomorphic if the following conditions are satisfied:
$G[W]$
are crossing-isomorphic if the following conditions are satisfied:
-
(C1) For any two distinct integers
 $p,q\in \{1,\dots,h\}$
, the edge
$p,q\in \{1,\dots,h\}$
, the edge
 $u_pu_q$
is an edge of
$u_pu_q$
is an edge of
 $G[U]$
if and only if
$G[U]$
if and only if
 $w_pw_q$
is an edge of
$w_pw_q$
is an edge of
 $G[W]$
.
$G[W]$
. -
(C2) For any four distinct integers
 $p,q,r,s\in \{1,\dots,h\}$
such that both
$p,q,r,s\in \{1,\dots,h\}$
such that both
 $u_pu_q$
and
$u_pu_q$
and
 $u_ru_s$
are edges of
$u_ru_s$
are edges of
 $G[U]$
, the edges
$G[U]$
, the edges
 $u_pu_q$
and
$u_pu_q$
and
 $u_ru_s$
cross if and only if the edges
$u_ru_s$
cross if and only if the edges
 $w_pw_q$
and
$w_pw_q$
and
 $w_rw_s$
cross.
$w_rw_s$
cross. -
(C3) For any integer
 $i\in \{1,\dots,h\}$
,
$i\in \{1,\dots,h\}$
,
 $u_i$
is the highest vertex of
$u_i$
is the highest vertex of
 $G[U]$
if and only if
$G[U]$
if and only if
 $w_i$
is the highest vertex of
$w_i$
is the highest vertex of
 $G[W]$
.
$G[W]$
.
If
![]() $G[U]$
and
$G[U]$
and
![]() $G[W]$
are crossing-isomorphic, the graph isomorphism given by
$G[W]$
are crossing-isomorphic, the graph isomorphism given by
![]() $\lambda (u_i)=w_i$
, for all
$\lambda (u_i)=w_i$
, for all
![]() $i=1,\ldots, h$
, is a crossing-isomorphism. Clearly, the inverse of a crossing-isomorphism is also a crossing-isomorphism. We have the following.
$i=1,\ldots, h$
, is a crossing-isomorphism. Clearly, the inverse of a crossing-isomorphism is also a crossing-isomorphism. We have the following.
Lemma 4.
Let
![]() $v_k$
be the highest vertex in an interval
$v_k$
be the highest vertex in an interval
![]() $G[i,j]$
with
$G[i,j]$
with
![]() $i\lt j$
, and assume that
$i\lt j$
, and assume that
![]() $G[i,j]$
contains neither the right child of
$G[i,j]$
contains neither the right child of
![]() $v_k$
, nor the left child of the left sibling of
$v_k$
, nor the left child of the left sibling of
![]() $v_k$
(if it exists), nor any descendant of the left child of the left sibling of
$v_k$
(if it exists), nor any descendant of the left child of the left sibling of
![]() $v_k$
(if it exists). Then
$v_k$
(if it exists). Then
![]() $G[i,j]-v_k$
is crossing-isomorphic to some interval
$G[i,j]-v_k$
is crossing-isomorphic to some interval
![]() $G(I)$
of
$G(I)$
of
![]() $G$
. Moreover, the interval
$G$
. Moreover, the interval
![]() $G(I)$
can be computed in
$G(I)$
can be computed in
![]() $O(1)$
time.
$O(1)$
time.
Proof. If
![]() $k=i$
or
$k=i$
or
![]() $k=j$
, then
$k=j$
, then
![]() $G[i,j]-v_k$
is the interval
$G[i,j]-v_k$
is the interval
![]() $G[i+1,j]$
or
$G[i+1,j]$
or
![]() $G[i,j-1]$
, respectively, and the conclusion is immediate. So assume that
$G[i,j-1]$
, respectively, and the conclusion is immediate. So assume that
![]() $i\lt k\lt j$
and that the subtrees of
$i\lt k\lt j$
and that the subtrees of
![]() $B$
rooted at the children of
$B$
rooted at the children of
![]() $v_k$
have height
$v_k$
have height
![]() $\ell$
. Thus,
$\ell$
. Thus,
![]() $B(v_{k+1})$
has
$B(v_{k+1})$
has
![]() $D\,:\!=\,2^\ell -1$
vertices. Note that
$D\,:\!=\,2^\ell -1$
vertices. Note that
![]() $\ell \geq 1$
, that is,
$\ell \geq 1$
, that is,
![]() $v_k$
has children, as otherwise
$v_k$
has children, as otherwise
![]() $v_{k+1}$
would be either the right sibling of
$v_{k+1}$
would be either the right sibling of
![]() $v_k$
or a vertex at a higher level than
$v_k$
or a vertex at a higher level than
![]() $v_k$
, in both cases contradicting the assumption that
$v_k$
, in both cases contradicting the assumption that
![]() $v_k$
is the highest vertex in
$v_k$
is the highest vertex in
![]() $G[i,j]$
. Let
$G[i,j]$
. Let
![]() $I=[i-D,j-D-1]$
and note that
$I=[i-D,j-D-1]$
and note that
![]() $I$
can be computed in
$I$
can be computed in
![]() $O(1)$
time. We prove that
$O(1)$
time. We prove that
![]() $G[i,j]-v_k$
is crossing-isomorphic to
$G[i,j]-v_k$
is crossing-isomorphic to
![]() $G(I)$
. Let
$G(I)$
. Let
![]() $u_1,\dots,u_h$
be the vertices of
$u_1,\dots,u_h$
be the vertices of
![]() $G[i,j]-v_k$
, ordered by increasing
$G[i,j]-v_k$
, ordered by increasing
![]() $x$
-coordinates; further, let
$x$
-coordinates; further, let
![]() $w_1,\dots,w_h$
be the vertices of
$w_1,\dots,w_h$
be the vertices of
![]() $G(I)$
, ordered by increasing
$G(I)$
, ordered by increasing
![]() $x$
-coordinates. Refer to Figure 3.
$x$
-coordinates. Refer to Figure 3.
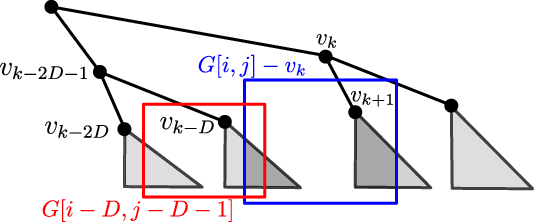
Figure 3. The interval
![]() $G[i,j]-v_k$
is crossing-isomorphic to the interval
$G[i,j]-v_k$
is crossing-isomorphic to the interval
![]() $G[i-D,j-D+1]$
.
$G[i-D,j-D+1]$
.
Since
![]() $v_k$
is the highest vertex in
$v_k$
is the highest vertex in
![]() $G[i,j]$
and
$G[i,j]$
and
![]() $i\lt k\lt j$
, it follows that
$i\lt k\lt j$
, it follows that
![]() $v_k$
is not the root of
$v_k$
is not the root of
![]() $B$
and
$B$
and
![]() $v_{k-1}$
is not the parent of
$v_{k-1}$
is not the parent of
![]() $v_k$
. Hence
$v_k$
. Hence
![]() $v_k$
is the right child of its parent and has a left sibling
$v_k$
is the right child of its parent and has a left sibling
![]() $v_{k-2D-1}$
; note that, since
$v_{k-2D-1}$
; note that, since
![]() $v_k$
has children, its left sibling
$v_k$
has children, its left sibling
![]() $v_{k-2D-1}$
also has children. Since by assumption
$v_{k-2D-1}$
also has children. Since by assumption
![]() $G[i,j]$
contains neither the left child of
$G[i,j]$
contains neither the left child of
![]() $v_{k-2D-1}$
nor any descendant of the left child of
$v_{k-2D-1}$
nor any descendant of the left child of
![]() $v_{k-2D-1}$
, it follows that
$v_{k-2D-1}$
, it follows that
![]() $G[i,k-1]$
is a subgraph of
$G[i,k-1]$
is a subgraph of
![]() $G$
induced by vertices in the right subtree of the left sibling of
$G$
induced by vertices in the right subtree of the left sibling of
![]() $v_k$
. Specifically,
$v_k$
. Specifically,
![]() $G[i,k-1]$
is induced by the last
$G[i,k-1]$
is induced by the last
![]() $k-i\leq D$
vertices (in a pre-order traversal) of the subtree
$k-i\leq D$
vertices (in a pre-order traversal) of the subtree
![]() $B(v_{k-D})$
of height
$B(v_{k-D})$
of height
![]() $\ell$
, rooted at the right child
$\ell$
, rooted at the right child
![]() $v_{k-D}$
of
$v_{k-D}$
of
![]() $v_{k-2D-1}$
. Further,
$v_{k-2D-1}$
. Further,
![]() $G[i-D,k-D-1]$
consists of the last
$G[i-D,k-D-1]$
consists of the last
![]() $k-i$
vertices (in a pre-order traversal) of the subtree
$k-i$
vertices (in a pre-order traversal) of the subtree
![]() $B(v_{k-2D})$
of height
$B(v_{k-2D})$
of height
![]() $\ell$
, rooted at the left child
$\ell$
, rooted at the left child
![]() $v_{k-2D}$
of
$v_{k-2D}$
of
![]() $v_{k-2D-1}$
. Hence,
$v_{k-2D-1}$
. Hence,
![]() $G[i,k-1]$
is crossing-isomorphic to
$G[i,k-1]$
is crossing-isomorphic to
![]() $G[i-D,k-D-1]$
.
$G[i-D,k-D-1]$
.
Since
![]() $v_{k+1}$
is the left child of
$v_{k+1}$
is the left child of
![]() $v_k$
and since the right child of
$v_k$
and since the right child of
![]() $v_k$
is not a vertex of
$v_k$
is not a vertex of
![]() $G[i,j]$
by assumption, it follows that
$G[i,j]$
by assumption, it follows that
![]() $G[k+1,j]$
is the subgraph of
$G[k+1,j]$
is the subgraph of
![]() $G$
induced by the first
$G$
induced by the first
![]() $j-k$
vertices (in a pre-order traversal) of the subtree
$j-k$
vertices (in a pre-order traversal) of the subtree
![]() $B(v_{k+1})$
of height
$B(v_{k+1})$
of height
![]() $\ell$
. Further,
$\ell$
. Further,
![]() $G[k-D,j-D-1]$
consists of the first
$G[k-D,j-D-1]$
consists of the first
![]() $j-k$
vertices (in a pre-order traversal) of the subtree
$j-k$
vertices (in a pre-order traversal) of the subtree
![]() $B(v_{k-D})$
of height
$B(v_{k-D})$
of height
![]() $\ell$
. Hence,
$\ell$
. Hence,
![]() $G[k+1,j]$
is crossing-isomorphic to
$G[k+1,j]$
is crossing-isomorphic to
![]() $G[k-D,j-D-1]$
.
$G[k-D,j-D-1]$
.
Condition (C1). In order to prove that Condition (C1) is satisfied (that is,
![]() $G[i,j]-v_k$
is isomorphic to
$G[i,j]-v_k$
is isomorphic to
![]() $G[I]$
), it remains to argue about the edges of
$G[I]$
), it remains to argue about the edges of
![]() $G[i,j]-v_k$
between
$G[i,j]-v_k$
between
![]() $G[i,k-1]$
and
$G[i,k-1]$
and
![]() $G[k+1,j]$
(that is, between
$G[k+1,j]$
(that is, between
![]() $\{u_1,\dots,u_{k-i}\}$
and
$\{u_1,\dots,u_{k-i}\}$
and
![]() $\{u_{k-i+1},\dots,u_h\}$
), and about the edges of
$\{u_{k-i+1},\dots,u_h\}$
), and about the edges of
![]() $G(I)$
between
$G(I)$
between
![]() $G[i-D,k-D-1]$
and
$G[i-D,k-D-1]$
and
![]() $G[k-D,j-D-1]$
(that is, between
$G[k-D,j-D-1]$
(that is, between
![]() $\{w_1,\dots,w_{k-i}\}$
and
$\{w_1,\dots,w_{k-i}\}$
and
![]() $\{w_{k-i+1},\dots,w_h\}$
). We claim that, for any pair of integers
$\{w_{k-i+1},\dots,w_h\}$
). We claim that, for any pair of integers
![]() $p\in [1,k-i]$
and
$p\in [1,k-i]$
and
![]() $q\in [k-i+1,h]$
,
$q\in [k-i+1,h]$
,
![]() $u_pu_q$
is an edge of
$u_pu_q$
is an edge of
![]() $G[i,j]-v_k$
if and only if
$G[i,j]-v_k$
if and only if
![]() $w_pw_q$
is an edge of
$w_pw_q$
is an edge of
![]() $G(I)$
.
$G(I)$
.
To prove the claim, recall that vertices
![]() $v_{k-2D}$
,
$v_{k-2D}$
,
![]() $v_{k-D}$
, and
$v_{k-D}$
, and
![]() $v_{k+1}$
are at height
$v_{k+1}$
are at height
![]() $\ell$
of
$\ell$
of
![]() $G$
, and the descendants of these vertices induce isomorphic subgraphs
$G$
, and the descendants of these vertices induce isomorphic subgraphs
![]() $G[k-2D,k-D-1]$
,
$G[k-2D,k-D-1]$
,
![]() $G[k-D,$
$G[k-D,$
![]() $k-1]$
, and
$k-1]$
, and
![]() $G[k+1,k+D]$
, respectively. Since
$G[k+1,k+D]$
, respectively. Since
![]() $u_p$
and
$u_p$
and
![]() $u_q$
(resp.,
$u_q$
(resp.,
![]() $w_p$
and
$w_p$
and
![]() $w_q$
) have different ancestors at height
$w_q$
) have different ancestors at height
![]() $\ell$
, they are not in an ancestor-descendant relationship, and so they cannot be connected by any edge in the edge group (E1). It remains to consider edges in the edge groups (E2) and (E3). In any case,
$\ell$
, they are not in an ancestor-descendant relationship, and so they cannot be connected by any edge in the edge group (E1). It remains to consider edges in the edge groups (E2) and (E3). In any case,
![]() $u_p$
and
$u_p$
and
![]() $w_p$
are on the same level, and similarly
$w_p$
are on the same level, and similarly
![]() $u_q$
and
$u_q$
and
![]() $w_q$
are on the same level.
$w_q$
are on the same level.
Note that the intervals
![]() $[k-2D,k-D-1]$
and
$[k-2D,k-D-1]$
and
![]() $[k-D,k-1]$
are consecutive, but there is a gap between
$[k-D,k-1]$
are consecutive, but there is a gap between
![]() $[k-D,k-1]$
and
$[k-D,k-1]$
and
![]() $[k+1,k+D]$
. This means that for any pair of integers
$[k+1,k+D]$
. This means that for any pair of integers
![]() $s\in [k-2D,k-D-1]$
and
$s\in [k-2D,k-D-1]$
and
![]() $t\in [k-D,k-1]$
, the vertices
$t\in [k-D,k-1]$
, the vertices
![]() $v_s$
and
$v_s$
and
![]() $v_t$
are level-neighbours if and only if the vertices
$v_t$
are level-neighbours if and only if the vertices
![]() $v_{s+D}$
and
$v_{s+D}$
and
![]() $v_{t+D+1}$
are level-neighbours (where
$v_{t+D+1}$
are level-neighbours (where
![]() $s+D\in [k-D,k-1]$
and
$s+D\in [k-D,k-1]$
and
![]() $t+D+1\in [k+1,k+D]$
). Consequently, for any
$t+D+1\in [k+1,k+D]$
). Consequently, for any
![]() $s\in [k-2D,k-D-1]$
and
$s\in [k-2D,k-D-1]$
and
![]() $t\in [k-D,k-1]$
,
$t\in [k-D,k-1]$
,
![]() $v_s v_t$
is in the edge group (E2) if and only if
$v_s v_t$
is in the edge group (E2) if and only if
![]() $v_{s+D}v_{t+D+1}$
is in the edge group (E2). It follows that
$v_{s+D}v_{t+D+1}$
is in the edge group (E2). It follows that
![]() $u_pu_q$
is in the edge group (E2) if and only if
$u_pu_q$
is in the edge group (E2) if and only if
![]() $w_pw_q$
is in the edge group (E2). The same argument establishes that
$w_pw_q$
is in the edge group (E2). The same argument establishes that
![]() $u_pu_q$
is in the edge group (E3) if and only if
$u_pu_q$
is in the edge group (E3) if and only if
![]() $w_pw_q$
is in the edge group (E3), assuming that the height of both
$w_pw_q$
is in the edge group (E3), assuming that the height of both
![]() $u_p$
and
$u_p$
and
![]() $u_q$
is at most
$u_q$
is at most
![]() $\ell -1$
. Only the vertices
$\ell -1$
. Only the vertices
![]() $v_{k-2D}$
,
$v_{k-2D}$
,
![]() $v_{k-D}$
, and
$v_{k-D}$
, and
![]() $v_{k+1}$
have height
$v_{k+1}$
have height
![]() $\ell$
in
$\ell$
in
![]() $G[k-2D,k-D-1]$
,
$G[k-2D,k-D-1]$
,
![]() $G[k-D,k-1]$
, and
$G[k-D,k-1]$
, and
![]() $G[k+1,k+D]$
. All edges incident to these vertices in
$G[k+1,k+D]$
. All edges incident to these vertices in
![]() $G(I)$
and
$G(I)$
and
![]() $G[i,j]-v_k$
are in the edge groups (E1) and (E2). (There are edges in the edge group (E3) between
$G[i,j]-v_k$
are in the edge groups (E1) and (E2). (There are edges in the edge group (E3) between
![]() $v_{k+1}$
and all vertices in
$v_{k+1}$
and all vertices in
![]() $G[k-2D,k-D]$
, but
$G[k-2D,k-D]$
, but
![]() $G[i,j]$
does not contain any vertex in
$G[i,j]$
does not contain any vertex in
![]() $G[k-2D,k-D]$
.)
$G[k-2D,k-D]$
.)
Condition (C2). Recall that
![]() $\sigma$
is the order of vertices in the BFS traversal of
$\sigma$
is the order of vertices in the BFS traversal of
![]() $B$
that determines their
$B$
that determines their
![]() $y$
-coordinates (that is, if a vertex
$y$
-coordinates (that is, if a vertex
![]() $u$
precedes another vertex
$u$
precedes another vertex
![]() $v$
in
$v$
in
![]() $\sigma$
, then
$\sigma$
, then
![]() $u$
gets a larger
$u$
gets a larger
![]() $y$
-coordinate than
$y$
-coordinate than
![]() $v$
.) We claim that
$v$
.) We claim that
![]() $\sigma$
determines the same permutation on the vertices
$\sigma$
determines the same permutation on the vertices
![]() $u_1,\dots,u_h$
of
$u_1,\dots,u_h$
of
![]() $G[i,j]-v_k$
and the vertices
$G[i,j]-v_k$
and the vertices
![]() $w_1,\dots,w_h$
of
$w_1,\dots,w_h$
of
![]() $G(I)$
, that is, a vertex
$G(I)$
, that is, a vertex
![]() $u_p$
precedes a vertex
$u_p$
precedes a vertex
![]() $u_q$
in
$u_q$
in
![]() $\sigma$
if and only if the vertex
$\sigma$
if and only if the vertex
![]() $w_p$
precedes the vertex
$w_p$
precedes the vertex
![]() $w_q$
in
$w_q$
in
![]() $\sigma$
. This property follows from the following facts:
$\sigma$
. This property follows from the following facts:
-
1. The vertices
 $u_1,\dots,u_{k-i}$
(resp.,
$u_1,\dots,u_{k-i}$
(resp.,
 $w_1,\dots,w_{k-i}$
) are the last
$w_1,\dots,w_{k-i}$
) are the last
 $k-i$
vertices in a pre-order traversal of the subtree
$k-i$
vertices in a pre-order traversal of the subtree
 $B(v_{k-D})$
(resp., of the subtree
$B(v_{k-D})$
(resp., of the subtree
 $B(v_{k-2D})$
) of
$B(v_{k-2D})$
) of
 $B$
of height
$B$
of height
 $\ell$
;
$\ell$
; -
2. the vertices
 $u_{k-i+1},\dots,u_h$
(resp.,
$u_{k-i+1},\dots,u_h$
(resp.,
 $w_{k-i+1},\dots,w_h$
) are the first
$w_{k-i+1},\dots,w_h$
) are the first
 $h-k+i$
vertices in a pre-order traversal of the subtree
$h-k+i$
vertices in a pre-order traversal of the subtree
 $B(v_{k+1})$
(resp., of the subtree
$B(v_{k+1})$
(resp., of the subtree
 $B(v_{k-D})$
) of
$B(v_{k-D})$
) of
 $B$
of height
$B$
of height
 $\ell$
; and
$\ell$
; and -
3. the vertices of
 $B(v_{k-D})$
(resp., of
$B(v_{k-D})$
(resp., of
 $B(v_{k-2D})$
) precede the vertices of
$B(v_{k-2D})$
) precede the vertices of
 $B(v_{k+1})$
(resp., of
$B(v_{k+1})$
(resp., of
 $B(v_{k-D})$
) in a pre-order traversal of
$B(v_{k-D})$
) in a pre-order traversal of
 $B$
.
$B$
.
Therefore, the rotation systems of
![]() $G[i,j]-v_k$
and
$G[i,j]-v_k$
and
![]() $G(I)$
are the same and so are the pairs of edges that cross.
$G(I)$
are the same and so are the pairs of edges that cross.
Condition (C3). Finally, note that
![]() $v_{k+1}$
is the highest vertex of
$v_{k+1}$
is the highest vertex of
![]() $G[i,j]-v_k$
and
$G[i,j]-v_k$
and
![]() $v_{k-D}$
is the highest vertex of
$v_{k-D}$
is the highest vertex of
![]() $G[i-D,j-D-1]$
. Since
$G[i-D,j-D-1]$
. Since
![]() $v_{k+1}=u_{k-i+1}$
and
$v_{k+1}=u_{k-i+1}$
and
![]() $v_{k-D}=w_{k-i+1}$
, Condition (C3) is also satisfied.
$v_{k-D}=w_{k-i+1}$
, Condition (C3) is also satisfied.
This concludes the proof that
![]() $G[i,j]-v_k$
and
$G[i,j]-v_k$
and
![]() $G(I)$
are crossing-isomorphic.
$G(I)$
are crossing-isomorphic.
We are now ready to present our tools for embedding trees onto ‘almost’ intervals. The first one deals with subgraphs of
![]() $G$
obtained by deleting the highest vertex from an interval.
$G$
obtained by deleting the highest vertex from an interval.
Lemma 5.
Let
![]() $G[i,j]$
be an interval of
$G[i,j]$
be an interval of
![]() $G$
with
$G$
with
![]() $h+1$
vertices and let
$h+1$
vertices and let
![]() $v_k$
be its highest vertex. Assume that there is a crossing-isomorphism
$v_k$
be its highest vertex. Assume that there is a crossing-isomorphism
![]() $\lambda$
from
$\lambda$
from
![]() $G[i,j]-v_k$
to some interval
$G[i,j]-v_k$
to some interval
![]() $G(I)$
of
$G(I)$
of
![]() $G$
with
$G$
with
![]() $h$
vertices. Further, assume that a tree
$h$
vertices. Further, assume that a tree
![]() $T$
with
$T$
with
![]() $h$
vertices admits an embedding
$h$
vertices admits an embedding
![]() $\varphi$
onto
$\varphi$
onto
![]() $G(I)$
. Then
$G(I)$
. Then
![]() $\varphi^{\prime}=\lambda ^{-1} \circ \varphi$
is an embedding of
$\varphi^{\prime}=\lambda ^{-1} \circ \varphi$
is an embedding of
![]() $T$
onto
$T$
onto
![]() $G[i,j]-v_k$
, and if
$G[i,j]-v_k$
, and if
![]() $a$
is the vertex of
$a$
is the vertex of
![]() $T$
such that
$T$
such that
![]() $\varphi (a)$
is the highest vertex of
$\varphi (a)$
is the highest vertex of
![]() $G(I)$
, then
$G(I)$
, then
![]() $\varphi^{\prime}(a)$
is the highest vertex of
$\varphi^{\prime}(a)$
is the highest vertex of
![]() $G[i,j]-v_k$
.
$G[i,j]-v_k$
.
Proof. Let
![]() $u_1,\dots,u_h$
and
$u_1,\dots,u_h$
and
![]() $w_1,\dots,w_h$
be the vertices of
$w_1,\dots,w_h$
be the vertices of
![]() $G(I)$
and
$G(I)$
and
![]() $G[i,j]-v_k$
, respectively, ordered by increasing
$G[i,j]-v_k$
, respectively, ordered by increasing
![]() $x$
-coordinates. Let
$x$
-coordinates. Let
![]() $a_1,\dots,a_h$
be the vertices of
$a_1,\dots,a_h$
be the vertices of
![]() $T$
ordered so that
$T$
ordered so that
![]() $\varphi (a_i)=u_i$
, for
$\varphi (a_i)=u_i$
, for
![]() $i=1,\dots,h$
. Note that
$i=1,\dots,h$
. Note that
![]() $\varphi^{\prime}=\lambda ^{-1} \circ \varphi$
yields
$\varphi^{\prime}=\lambda ^{-1} \circ \varphi$
yields
![]() $\varphi^{\prime}(a_i)=w_i$
for
$\varphi^{\prime}(a_i)=w_i$
for
![]() $i=1,\dots,h$
. We now prove that
$i=1,\dots,h$
. We now prove that
![]() $\varphi^{\prime}$
is an embedding of
$\varphi^{\prime}$
is an embedding of
![]() $T$
onto
$T$
onto
![]() $G[i,j]-v_k$
with the properties stated in the lemma.
$G[i,j]-v_k$
with the properties stated in the lemma.
First, for every
![]() $p,q\in \{1,\dots,h\}$
such that
$p,q\in \{1,\dots,h\}$
such that
![]() $a_pa_q$
is an edge in
$a_pa_q$
is an edge in
![]() $T$
, we have that
$T$
, we have that
![]() $\varphi^{\prime}(a_p)\varphi^{\prime}(a_q)=w_pw_q$
is an edge in
$\varphi^{\prime}(a_p)\varphi^{\prime}(a_q)=w_pw_q$
is an edge in
![]() $G[i,j]-v_k$
. In particular,
$G[i,j]-v_k$
. In particular,
![]() $\varphi (a_p)\varphi (a_q)=u_pu_q$
is an edge in
$\varphi (a_p)\varphi (a_q)=u_pu_q$
is an edge in
![]() $G(I)$
, given that
$G(I)$
, given that
![]() $\varphi$
is an embedding of
$\varphi$
is an embedding of
![]() $T$
onto
$T$
onto
![]() $G(I)$
. By Condition (C1) for
$G(I)$
. By Condition (C1) for
![]() $\lambda$
, the edge
$\lambda$
, the edge
![]() $w_pw_q$
is an edge of
$w_pw_q$
is an edge of
![]() $G[i,j]-v_k$
.
$G[i,j]-v_k$
.
Second, for every
![]() $p,q,r,s\in \{1,\dots,h\}$
such that
$p,q,r,s\in \{1,\dots,h\}$
such that
![]() $a_pa_q$
and
$a_pa_q$
and
![]() $a_ra_s$
are distinct edges of
$a_ra_s$
are distinct edges of
![]() $T$
, the edges
$T$
, the edges
![]() $\varphi^{\prime}(a_p)\varphi^{\prime}(a_q)=w_pw_q$
and
$\varphi^{\prime}(a_p)\varphi^{\prime}(a_q)=w_pw_q$
and
![]() $\varphi^{\prime}(a_r)\varphi^{\prime}(a_s)=w_rw_s$
do not cross each other. Namely,
$\varphi^{\prime}(a_r)\varphi^{\prime}(a_s)=w_rw_s$
do not cross each other. Namely,
![]() $\varphi (a_p)\varphi (a_q)=u_pu_q$
and
$\varphi (a_p)\varphi (a_q)=u_pu_q$
and
![]() $\varphi (a_r)\varphi (a_s)=u_ru_s$
do not cross each other, given that
$\varphi (a_r)\varphi (a_s)=u_ru_s$
do not cross each other, given that
![]() $\varphi$
is an embedding of
$\varphi$
is an embedding of
![]() $T$
onto
$T$
onto
![]() $G(I)$
. Then Condition (C2) for
$G(I)$
. Then Condition (C2) for
![]() $\lambda$
implies that
$\lambda$
implies that
![]() $w_pw_q$
and
$w_pw_q$
and
![]() $w_rw_s$
do not cross each other.
$w_rw_s$
do not cross each other.
Finally, let
![]() $a_t$
be the vertex of
$a_t$
be the vertex of
![]() $T$
such that
$T$
such that
![]() $\varphi (a_t)=u_t$
is the highest vertex of
$\varphi (a_t)=u_t$
is the highest vertex of
![]() $G(I)$
. Condition (C3) for
$G(I)$
. Condition (C3) for
![]() $\lambda$
implies that
$\lambda$
implies that
![]() $w_t$
is the highest vertex of
$w_t$
is the highest vertex of
![]() $G[i,j]-v_k$
. By construction,
$G[i,j]-v_k$
. By construction,
![]() $\varphi^{\prime}(a_t)=w_t$
. This concludes the proof of the lemma.
$\varphi^{\prime}(a_t)=w_t$
. This concludes the proof of the lemma.
The second tool deals with subgraphs of
![]() $G$
obtained by replacing the highest vertex of an interval with another ‘high’ vertex outside the interval; see Figure 4 for an illustration.
$G$
obtained by replacing the highest vertex of an interval with another ‘high’ vertex outside the interval; see Figure 4 for an illustration.

Figure 4. Illustration for the statement of Lemma 6.
Lemma 6.
Let
![]() $G[i,j]$
be an interval of
$G[i,j]$
be an interval of
![]() $G$
with
$G$
with
![]() $h$
vertices and let
$h$
vertices and let
![]() $v_k$
be its highest vertex. Let
$v_k$
be its highest vertex. Let
![]() $v_x$
be a vertex of
$v_x$
be a vertex of
![]() $G$
that is higher than all vertices in
$G$
that is higher than all vertices in
![]() $G[i,j]-v_k$
and that does not belong to
$G[i,j]-v_k$
and that does not belong to
![]() $G[i,j]$
. Assume that a tree
$G[i,j]$
. Assume that a tree
![]() $T$
with
$T$
with
![]() $h$
vertices admits an embedding
$h$
vertices admits an embedding
![]() $\varphi$
onto
$\varphi$
onto
![]() $G[i,j]$
. Let
$G[i,j]$
. Let
![]() $a$
be the vertex of
$a$
be the vertex of
![]() $T$
such that
$T$
such that
![]() $\varphi (a)=v_k$
; further, let
$\varphi (a)=v_k$
; further, let
![]() $\varphi^{\prime}(a)=v_x$
and
$\varphi^{\prime}(a)=v_x$
and
![]() $\varphi^{\prime}(b)=\varphi (b)$
for every vertex
$\varphi^{\prime}(b)=\varphi (b)$
for every vertex
![]() $b$
of
$b$
of
![]() $T$
other than
$T$
other than
![]() $a$
. Then
$a$
. Then
![]() $\varphi^{\prime}$
is an embedding of
$\varphi^{\prime}$
is an embedding of
![]() $T$
onto
$T$
onto
![]() $G[i,j]-v_k+v_x$
.
$G[i,j]-v_k+v_x$
.
Proof. By construction, we have
![]() $\varphi^{\prime}(b)=\varphi (b)$
for every vertex
$\varphi^{\prime}(b)=\varphi (b)$
for every vertex
![]() $b$
of
$b$
of
![]() $T$
other than
$T$
other than
![]() $a$
. Since
$a$
. Since
![]() $\varphi$
is an embedding of
$\varphi$
is an embedding of
![]() $T$
onto
$T$
onto
![]() $G[i,j]$
, we only need to prove that none of the edges incident to
$G[i,j]$
, we only need to prove that none of the edges incident to
![]() $a$
crosses any other edge of
$a$
crosses any other edge of
![]() $T$
in
$T$
in
![]() $\varphi^{\prime}(T)$
. Let
$\varphi^{\prime}(T)$
. Let
![]() $ab$
and
$ab$
and
![]() $cd$
be two edges of
$cd$
be two edges of
![]() $T$
, and let
$T$
, and let
![]() $v_p\,:\!=\,\varphi^{\prime}(b)$
,
$v_p\,:\!=\,\varphi^{\prime}(b)$
,
![]() $v_q\,:\!=\,\varphi^{\prime}(c)$
, and
$v_q\,:\!=\,\varphi^{\prime}(c)$
, and
![]() $v_r\,:\!=\,\varphi^{\prime}(d)$
, where
$v_r\,:\!=\,\varphi^{\prime}(d)$
, where
![]() $p,q,r\in [i,j]$
. We prove that
$p,q,r\in [i,j]$
. We prove that
![]() $v_xv_p$
and
$v_xv_p$
and
![]() $v_qv_r$
do not cross. We may assume, w.l.o.g., that
$v_qv_r$
do not cross. We may assume, w.l.o.g., that
![]() $q\lt r$
. Further, assume that
$q\lt r$
. Further, assume that
![]() $x\gt j$
, as the case in which
$x\gt j$
, as the case in which
![]() $x\lt i$
can be handled by a symmetric argument.
$x\lt i$
can be handled by a symmetric argument.
-
• If
 $r\lt p$
, then
$r\lt p$
, then
 $v_xv_p$
and
$v_xv_p$
and
 $v_qv_r$
do not cross as they use disjoint
$v_qv_r$
do not cross as they use disjoint
 $x$
-intervals.
$x$
-intervals. -
• If
 $p\lt q$
, then
$p\lt q$
, then
 $v_xv_p$
and
$v_xv_p$
and
 $v_qv_r$
do not cross by Observation 2.
$v_qv_r$
do not cross by Observation 2. -
• Finally, assume that
 $q\lt p\lt r$
. If
$q\lt p\lt r$
. If
 $v_p$
precedes both
$v_p$
precedes both
 $v_q$
and
$v_q$
and
 $v_r$
in the order
$v_r$
in the order
 $\sigma$
that determines the
$\sigma$
that determines the
 $y$
-coordinates of the vertices of
$y$
-coordinates of the vertices of
 $G$
, then the
$G$
, then the
 $y$
-coordinate of
$y$
-coordinate of
 $v_p$
is larger than that of
$v_p$
is larger than that of
 $v_q$
and
$v_q$
and
 $v_r$
, hence
$v_r$
, hence
 $v_xv_p$
and
$v_xv_p$
and
 $v_qv_r$
do not cross as they use disjoint
$v_qv_r$
do not cross as they use disjoint
 $y$
-intervals. Assume now that
$y$
-intervals. Assume now that
 $v_p$
succeeds
$v_p$
succeeds
 $v_q$
or
$v_q$
or
 $v_r$
(possibly both) in
$v_r$
(possibly both) in
 $\sigma$
. Suppose, for the sake of contradiction, that
$\sigma$
. Suppose, for the sake of contradiction, that
 $v_xv_p$
and
$v_xv_p$
and
 $v_qv_r$
cross. Then
$v_qv_r$
cross. Then
 $v_p$
lies below the line through
$v_p$
lies below the line through
 $v_q$
and
$v_q$
and
 $v_r$
. However, this implies that
$v_r$
. However, this implies that
 $v_kv_p$
and
$v_kv_p$
and
 $v_qv_r$
also cross, contradicting the assumption that
$v_qv_r$
also cross, contradicting the assumption that
 $\varphi$
is an embedding of
$\varphi$
is an embedding of
 $T$
onto
$T$
onto
 $G[i,j]$
.
$G[i,j]$
.
This concludes the proof of the lemma.
The following lemma is a variant of the (unique) lemma in [Reference Chung and Graham19]. It finds a subtree of a certain order in a rooted tree. For a vertex
![]() $v$
of a rooted tree
$v$
of a rooted tree
![]() $T$
, denote by
$T$
, denote by
![]() $T(v)$
the subtree of
$T(v)$
the subtree of
![]() $T$
rooted at
$T$
rooted at
![]() $v$
.
$v$
.
Lemma 7.
Given a rooted tree
![]() $T$
on
$T$
on
![]() $m\ge 2$
vertices and an integer
$m\ge 2$
vertices and an integer
![]() $s$
, with
$s$
, with
![]() $1\le s\le m$
, there is a vertex
$1\le s\le m$
, there is a vertex
![]() $c$
of
$c$
of
![]() $T$
such that
$T$
such that
![]() $|V(T(c))|\geq s$
but
$|V(T(c))|\geq s$
but
![]() $|V(T(d))|\leq s-1$
, for all children
$|V(T(d))|\leq s-1$
, for all children
![]() $d$
of
$d$
of
![]() $c$
. Such a vertex
$c$
. Such a vertex
![]() $c$
can be computed in
$c$
can be computed in
![]() $O(m)$
time.
$O(m)$
time.
Proof. We find vertex
![]() $c$
by the following walk on
$c$
by the following walk on
![]() $T$
starting from the root. Initially, let
$T$
starting from the root. Initially, let
![]() $c$
be the root of
$c$
be the root of
![]() $T$
. While
$T$
. While
![]() $c$
has a child
$c$
has a child
![]() $d$
such that
$d$
such that
![]() $|V(T(d))|\geq s$
, then set
$|V(T(d))|\geq s$
, then set
![]() $c\,:\!=\,d$
. At the end of the while loop,
$c\,:\!=\,d$
. At the end of the while loop,
![]() $|V(T(c))|\geq s$
but
$|V(T(c))|\geq s$
but
![]() $|V(T(d))|\leq s-1$
, for all children
$|V(T(d))|\leq s-1$
, for all children
![]() $d$
of
$d$
of
![]() $c$
. After precomputing the order of the subtree
$c$
. After precomputing the order of the subtree
![]() $T(v)$
for every vertex
$T(v)$
for every vertex
![]() $v$
of
$v$
of
![]() $T$
, the while loop runs in
$T$
, the while loop runs in
![]() $O(m)$
time.
$O(m)$
time.
2.3. Proof of Theorem 1
Given a tree
![]() $T$
on
$T$
on
![]() $h$
vertices and an interval
$h$
vertices and an interval
![]() $G[i,j]$
of length
$G[i,j]$
of length
![]() $h$
, we describe an algorithm that recursively constructs an embedding
$h$
, we describe an algorithm that recursively constructs an embedding
![]() $\varphi$
of
$\varphi$
of
![]() $T$
onto
$T$
onto
![]() $G[i,j]$
. For a subtree
$G[i,j]$
. For a subtree
![]() $T^{\prime}$
of
$T^{\prime}$
of
![]() $T$
, we denote by
$T$
, we denote by
![]() $\varphi (T^{\prime})$
the image of
$\varphi (T^{\prime})$
the image of
![]() $\varphi$
restricted to the vertices and edges of
$\varphi$
restricted to the vertices and edges of
![]() $T^{\prime}$
. A step of the algorithm explicitly embeds some vertices; the remaining vertices form subtrees that are recursively embedded onto pairwise disjoint subintervals of
$T^{\prime}$
. A step of the algorithm explicitly embeds some vertices; the remaining vertices form subtrees that are recursively embedded onto pairwise disjoint subintervals of
![]() $G[i,j]$
. In order to control the interaction between the recursively embedded subtrees and the edges connecting vertices of such subtrees to explicitly embedded vertices, we insist that in every subtree at most two vertices, called portals, are adjacent to external vertices (i.e. vertices that are not part of the subtree). We also ensure that whenever a subtree is embedded onto a subinterval, the external vertices that connect to the portals of that subtree are embedded above the whole subinterval.
$G[i,j]$
. In order to control the interaction between the recursively embedded subtrees and the edges connecting vertices of such subtrees to explicitly embedded vertices, we insist that in every subtree at most two vertices, called portals, are adjacent to external vertices (i.e. vertices that are not part of the subtree). We also ensure that whenever a subtree is embedded onto a subinterval, the external vertices that connect to the portals of that subtree are embedded above the whole subinterval.
For a point
![]() $p\in{{\mathbb{R}}}^2$
, we define two quarter-planes:
$p\in{{\mathbb{R}}}^2$
, we define two quarter-planes:
Observe that
![]() $Q^+(p)$
is set of points above and to the right of
$Q^+(p)$
is set of points above and to the right of
![]() $p$
, and similarly
$p$
, and similarly
![]() $Q^-(p)$
is the set of points above and to the left of
$Q^-(p)$
is the set of points above and to the left of
![]() $p$
. In Lemma 8 below, we require that these regions are empty of vertices and edges of the embedded graph, so that they can be used to add edges incident to
$p$
. In Lemma 8 below, we require that these regions are empty of vertices and edges of the embedded graph, so that they can be used to add edges incident to
![]() $p$
, when a portal is embedded onto it.
$p$
, when a portal is embedded onto it.

Figure 5. Illustration for Case 1.1: Tree
![]() $T$
(left) and its embedding onto
$T$
(left) and its embedding onto
![]() $G[i,j]$
(right).
$G[i,j]$
(right).
We inductively prove the following lemma, which immediately implies Theorem 1. Given an
![]() $n$
-vertex forest
$n$
-vertex forest
![]() $F$
, it suffices to define a tree
$F$
, it suffices to define a tree
![]() $T$
as an arbitrary
$T$
as an arbitrary
![]() $n$
-vertex tree that contains
$n$
-vertex tree that contains
![]() $F$
as a subgraph, to set
$F$
as a subgraph, to set
![]() $h=n$
and
$h=n$
and
![]() $G[i,j]=G[0,n-1]$
, and to choose a portal
$G[i,j]=G[0,n-1]$
, and to choose a portal
![]() $a$
in
$a$
in
![]() $T$
arbitrarily.
$T$
arbitrarily.
Lemma 8.
We are given a tree
![]() $T$
on
$T$
on
![]() $h$
vertices, an interval
$h$
vertices, an interval
![]() $G[i,j]$
of length
$G[i,j]$
of length
![]() $h$
, and
$h$
, and
-
1. either a single portal
 $a$
in
$a$
in
 $T$
or
$T$
or
-
2. two distinct portals
 $a$
and
$a$
and
 $b$
in
$b$
in
 $T$
.
$T$
.
Then there exists an embedding
![]() $\varphi$
of
$\varphi$
of
![]() $T$
onto
$T$
onto
![]() $G[i,j]$
with the following properties:
$G[i,j]$
with the following properties:
-
1. If only one portal
 $a$
is given, then
$a$
is given, then
-
(a)
 $\varphi (a)$
is the highest vertex in
$\varphi (a)$
is the highest vertex in
 $G[i,j]$
; and
$G[i,j]$
; and
-
(b) if
 $\deg _T(a)=1$
and
$\deg _T(a)=1$
and
 $a^{\prime}$
is the unique neighbour of
$a^{\prime}$
is the unique neighbour of
 $a$
in
$a$
in
 $T$
, then
$T$
, then
 $Q^-(\varphi (a^{\prime}))$
does not intersect any vertex or edge of the embedding
$Q^-(\varphi (a^{\prime}))$
does not intersect any vertex or edge of the embedding
 $\varphi (T(a^{\prime}))$
.
$\varphi (T(a^{\prime}))$
.
-
-
2. If two distinct portals
 $a$
and
$a$
and
 $b$
are given, then
$b$
are given, then
-
(a)
 $\varphi (a)$
is to the left of
$\varphi (a)$
is to the left of
 $\varphi (b)$
;
$\varphi (b)$
; -
(b)
 $Q^-(\varphi (a))$
does not intersect any edge or vertex of
$Q^-(\varphi (a))$
does not intersect any edge or vertex of
 $\varphi (T)$
; and
$\varphi (T)$
; and
-
(c)
 $Q^+(\varphi (b))$
does not intersect any edge or vertex of
$Q^+(\varphi (b))$
does not intersect any edge or vertex of
 $\varphi (T)$
.
$\varphi (T)$
.
-
Moreover, the embedding
![]() $\varphi$
can be found in
$\varphi$
can be found in
![]() $O(h^2)$
time.
$O(h^2)$
time.
Proof. We proceed by induction on the number of vertices of
![]() $T$
. In the base case,
$T$
. In the base case,
![]() $T$
has one vertex, which must be the portal
$T$
has one vertex, which must be the portal
![]() $a$
, and the map
$a$
, and the map
![]() $\varphi (a)=v_i$
maps
$\varphi (a)=v_i$
maps
![]() $a$
to the highest vertex of
$a$
to the highest vertex of
![]() $G[i,i]$
. For the induction step we assume that
$G[i,i]$
. For the induction step we assume that
![]() $h\geq 2$
and that the claim holds for all smaller trees.
$h\geq 2$
and that the claim holds for all smaller trees.
Case 1: There is only one portal
![]() $a$
. Let
$a$
. Let
![]() $v_k$
denote the highest vertex in
$v_k$
denote the highest vertex in
![]() $G[i,j]$
. We need to find an embedding of
$G[i,j]$
. We need to find an embedding of
![]() $T$
onto
$T$
onto
![]() $G[i,j]$
where
$G[i,j]$
where
![]() $\varphi (a)=v_k$
. Consider
$\varphi (a)=v_k$
. Consider
![]() $T$
to be rooted at
$T$
to be rooted at
![]() $a$
. We distinguish two cases depending on the degree of
$a$
. We distinguish two cases depending on the degree of
![]() $a$
in
$a$
in
![]() $T$
.
$T$
.
Case 1.1:
![]() $\deg _T(a)\geq 2$
. Assume that
$\deg _T(a)\geq 2$
. Assume that
![]() $a$
has
$a$
has
![]() $t$
children
$t$
children
![]() $a_1,\ldots,a_t$
. Refer to Figure 5. Partition the set of integers
$a_1,\ldots,a_t$
. Refer to Figure 5. Partition the set of integers
![]() $[i,j]\setminus \{k\}$
into
$[i,j]\setminus \{k\}$
into
![]() $t$
contiguous subsets
$t$
contiguous subsets
![]() $I_1,\ldots,I_t$
such that
$I_1,\ldots,I_t$
such that
![]() $|I_x|=|V(T(a_x))|$
, for
$|I_x|=|V(T(a_x))|$
, for
![]() $x=1,\ldots,t$
. Let
$x=1,\ldots,t$
. Let
![]() $q\in \{1,\dots,t\}$
be such that
$q\in \{1,\dots,t\}$
be such that
![]() $I_q$
contains
$I_q$
contains
![]() $k-1$
or
$k-1$
or
![]() $k+1$
, and so
$k+1$
, and so
![]() $I_q\cup \{k\}$
is an interval of integers.
$I_q\cup \{k\}$
is an interval of integers.
By induction, there is an embedding
![]() $\varphi _x$
of
$\varphi _x$
of
![]() $T(a_x)$
onto
$T(a_x)$
onto
![]() $G(I_x)$
such that
$G(I_x)$
such that
![]() $a_x$
is mapped to the highest vertex of
$a_x$
is mapped to the highest vertex of
![]() $G(I_x)$
, for all
$G(I_x)$
, for all
![]() $x\neq q$
. Similarly, there is an embedding
$x\neq q$
. Similarly, there is an embedding
![]() $\varphi _q$
of
$\varphi _q$
of
![]() $T-\bigcup _{x\neq q} T(a_x)$
onto
$T-\bigcup _{x\neq q} T(a_x)$
onto
![]() $G(I_q\cup \{k\})$
such that
$G(I_q\cup \{k\})$
such that
![]() $a$
is mapped to the highest vertex of
$a$
is mapped to the highest vertex of
![]() $G(I_q\cup \{k\})$
, which is
$G(I_q\cup \{k\})$
, which is
![]() $v_k$
. Note that these embeddings are pairwise noncrossing since they use pairwise disjoint intervals. Let
$v_k$
. Note that these embeddings are pairwise noncrossing since they use pairwise disjoint intervals. Let
![]() $\varphi \,:\,V(T)\rightarrow V(G[i,j])$
be the combination of these embeddings. Clearly, both Properties 1(a) and 1(b) (the latter vacuously) are satisfied by
$\varphi \,:\,V(T)\rightarrow V(G[i,j])$
be the combination of these embeddings. Clearly, both Properties 1(a) and 1(b) (the latter vacuously) are satisfied by
![]() $\varphi$
.
$\varphi$
.
The only edges of
![]() $T$
between distinct subtrees among
$T$
between distinct subtrees among
![]() $T(a_1),\dots,T(a_{q-1}),T(a_{q+1}),\dots,T(a_{t})$
, and
$T(a_1),\dots,T(a_{q-1}),T(a_{q+1}),\dots,T(a_{t})$
, and
![]() $T-\bigcup _{x\neq q} T(a_x)$
are of the form
$T-\bigcup _{x\neq q} T(a_x)$
are of the form
![]() $aa_x$
, for
$aa_x$
, for
![]() $x\neq q$
. The edges
$x\neq q$
. The edges
![]() $\varphi (a)\varphi (a_x)$
are in
$\varphi (a)\varphi (a_x)$
are in
![]() $G[i,j]$
and are pairwise noncrossing by Lemma 3. Moreover,
$G[i,j]$
and are pairwise noncrossing by Lemma 3. Moreover,
![]() $\varphi (a)\varphi (a_x)$
does not cross
$\varphi (a)\varphi (a_x)$
does not cross
![]() $\varphi (T(a_x))$
, as
$\varphi (T(a_x))$
, as
![]() $\varphi (a_x)$
is the highest vertex of
$\varphi (a_x)$
is the highest vertex of
![]() $\varphi (T(a_x))$
and
$\varphi (T(a_x))$
and
![]() $\varphi (a)$
is higher than
$\varphi (a)$
is higher than
![]() $\varphi (a_x)$
; further,
$\varphi (a_x)$
; further,
![]() $\varphi (a)\varphi (a_x)$
does not cross
$\varphi (a)\varphi (a_x)$
does not cross
![]() $\varphi (T(a_y))$
, where
$\varphi (T(a_y))$
, where
![]() $y\neq x$
, by Observation 2. Therefore,
$y\neq x$
, by Observation 2. Therefore,
![]() $\varphi$
is an embedding of
$\varphi$
is an embedding of
![]() $T$
onto
$T$
onto
![]() $G[i,j]$
, as required.
$G[i,j]$
, as required.
![]()
Case 1.2:
![]() $\deg _T(a)=1$
. Let
$\deg _T(a)=1$
. Let
![]() $a^{\prime}$
be the unique neighbour of
$a^{\prime}$
be the unique neighbour of
![]() $a$
in
$a$
in
![]() $T$
and let
$T$
and let
![]() $T^{\prime}=T(a^{\prime})$
. We need to construct an embedding
$T^{\prime}=T(a^{\prime})$
. We need to construct an embedding
![]() $\varphi$
of
$\varphi$
of
![]() $T$
onto
$T$
onto
![]() $G[i,j]$
such that
$G[i,j]$
such that
![]() $\varphi (a)=v_k$
and
$\varphi (a)=v_k$
and
![]() $\varphi (T^{\prime})=G[i,j]-v_k$
.
$\varphi (T^{\prime})=G[i,j]-v_k$
.
Case 1.2.1:
![]() $k=j$
. Set
$k=j$
. Set
![]() $\varphi (a)=v_k$
and recursively embed
$\varphi (a)=v_k$
and recursively embed
![]() $T^{\prime}$
onto
$T^{\prime}$
onto
![]() $G[i,k-1]$
with a single portal
$G[i,k-1]$
with a single portal
![]() $a^{\prime}$
, which is mapped to the highest vertex in
$a^{\prime}$
, which is mapped to the highest vertex in
![]() $G[i,k-1]$
(i.e. the second highest vertex in
$G[i,k-1]$
(i.e. the second highest vertex in
![]() $G[i,j]$
). Clearly, both Properties 1(a) and 1(b) are satisfied. Further,
$G[i,j]$
). Clearly, both Properties 1(a) and 1(b) are satisfied. Further,
![]() $\varphi$
is an embedding of
$\varphi$
is an embedding of
![]() $T$
onto
$T$
onto
![]() $G[i,j]$
, since
$G[i,j]$
, since
![]() $\varphi (a^{\prime})$
is the highest vertex of
$\varphi (a^{\prime})$
is the highest vertex of
![]() $\varphi (T^{\prime})$
and
$\varphi (T^{\prime})$
and
![]() $\varphi (a)$
is higher than
$\varphi (a)$
is higher than
![]() $\varphi (a^{\prime})$
, hence the edge
$\varphi (a^{\prime})$
, hence the edge
![]() $\varphi (a)\varphi (a^{\prime})$
, which exists by Lemma 3, does not cross
$\varphi (a)\varphi (a^{\prime})$
, which exists by Lemma 3, does not cross
![]() $\varphi (T^{\prime})$
.
$\varphi (T^{\prime})$
.
![]()
Case 1.2.2:
![]() $k=i$
. The discussion for this case is symmetric to the one for Case 1.2.1.
$k=i$
. The discussion for this case is symmetric to the one for Case 1.2.1.
![]()
Case 1.2.3:
![]() $i\lt k\lt j$
and the left sibling
$i\lt k\lt j$
and the left sibling
![]() $v_\ell$
of
$v_\ell$
of
![]() $v_k$
exists and is in
$v_k$
exists and is in
![]() $G[i,j]$
. It follows that
$G[i,j]$
. It follows that
![]() $\ell =i$
, as if
$\ell =i$
, as if
![]() $\ell \gt i$
, then
$\ell \gt i$
, then
![]() $v_{\ell -1}$
, which is the parent of
$v_{\ell -1}$
, which is the parent of
![]() $v_\ell$
and
$v_\ell$
and
![]() $v_k$
, would be a vertex in
$v_k$
, would be a vertex in
![]() $G[i,j]$
higher than
$G[i,j]$
higher than
![]() $v_k$
. By construction,
$v_k$
. By construction,
![]() $v_i$
is the second highest vertex in
$v_i$
is the second highest vertex in
![]() $G[i,j]$
. Recursively construct an embedding
$G[i,j]$
. Recursively construct an embedding
![]() $\psi$
of
$\psi$
of
![]() $T^{\prime}$
onto
$T^{\prime}$
onto
![]() $G[i+1,j]$
with a single portal
$G[i+1,j]$
with a single portal
![]() $a^{\prime}$
. By Property 1(a), we have
$a^{\prime}$
. By Property 1(a), we have
![]() $\psi (a^{\prime})=v_k$
. By Lemma 6, there exists an embedding
$\psi (a^{\prime})=v_k$
. By Lemma 6, there exists an embedding
![]() $\varphi$
of
$\varphi$
of
![]() $T^{\prime}$
onto
$T^{\prime}$
onto
![]() $G[i+1,j]-v_k+v_i=G[i,j]-v_k$
in which
$G[i+1,j]-v_k+v_i=G[i,j]-v_k$
in which
![]() $\varphi (a^{\prime})=v_i$
(hence
$\varphi (a^{\prime})=v_i$
(hence
![]() $\varphi$
satisfies Property 1(b)). Finally, set
$\varphi$
satisfies Property 1(b)). Finally, set
![]() $\varphi (a)=v_k$
(hence
$\varphi (a)=v_k$
(hence
![]() $\varphi$
satisfies Property 1(a)). As in Case 1.2.1, the edge
$\varphi$
satisfies Property 1(a)). As in Case 1.2.1, the edge
![]() $\varphi (a)\varphi (a^{\prime})=v_kv_i$
, which exists by Lemma 3, does not cross
$\varphi (a)\varphi (a^{\prime})=v_kv_i$
, which exists by Lemma 3, does not cross
![]() $\varphi (T^{\prime})$
, hence
$\varphi (T^{\prime})$
, hence
![]() $\varphi$
is an embedding of
$\varphi$
is an embedding of
![]() $T$
onto
$T$
onto
![]() $G[i,j]$
.
$G[i,j]$
.
![]()
Case 1.2.4:
![]() $i\lt k\lt j$
, the left sibling of
$i\lt k\lt j$
, the left sibling of
![]() $v_k$
does not exist or is not in
$v_k$
does not exist or is not in
![]() $G[i,j]$
, and the right child of
$G[i,j]$
, and the right child of
![]() $v_k$
is not in
$v_k$
is not in
![]() $G{[i,j]}$
. Refer to Figures 6–8. By construction, the left child of
$G{[i,j]}$
. Refer to Figures 6–8. By construction, the left child of
![]() $v_k$
is
$v_k$
is
![]() $v_{k+1}$
, which is in
$v_{k+1}$
, which is in
![]() $G[i,j]$
. Since the left sibling of
$G[i,j]$
. Since the left sibling of
![]() $v_k$
does not exist or is not in
$v_k$
does not exist or is not in
![]() $G[i,j]$
, and since the right child of
$G[i,j]$
, and since the right child of
![]() $v_k$
is not in
$v_k$
is not in
![]() $G[i,j]$
, it follows that
$G[i,j]$
, it follows that
![]() $v_{k+1}$
is the second highest vertex in
$v_{k+1}$
is the second highest vertex in
![]() $G[i,j]$
.
$G[i,j]$
.

Figure 6. Illustration for Case 1.2.4, if
![]() $c^{\prime}=a$
. Tree
$c^{\prime}=a$
. Tree
![]() $T$
(left) and its embedding onto
$T$
(left) and its embedding onto
![]() $G[i,j]$
(right).
$G[i,j]$
(right).

Figure 7. Illustration for Case 1.2.4, if
![]() $c^{\prime}=a^{\prime}$
. Tree
$c^{\prime}=a^{\prime}$
. Tree
![]() $T$
(left) and its embedding onto
$T$
(left) and its embedding onto
![]() $G[i,j]$
(right).
$G[i,j]$
(right).

Figure 8. Illustration for Case 1.2.4, if
![]() $c^{\prime}\neq a$
and
$c^{\prime}\neq a$
and
![]() $c^{\prime}\neq a^{\prime}$
. Tree
$c^{\prime}\neq a^{\prime}$
. Tree
![]() $T$
(left) and its embedding onto
$T$
(left) and its embedding onto
![]() $G[i,j]$
(right).
$G[i,j]$
(right).
Set
![]() $s=j-k+1$
, that is,
$s=j-k+1$
, that is,
![]() $s$
is the number of vertices in the interval
$s$
is the number of vertices in the interval
![]() $[k,j]$
. Note that
$[k,j]$
. Note that
![]() $s\lt h$
, given that
$s\lt h$
, given that
![]() $k\gt i$
. Lemma 7 then yields a vertex
$k\gt i$
. Lemma 7 then yields a vertex
![]() $c$
in
$c$
in
![]() $T^{\prime}$
such that
$T^{\prime}$
such that
![]() $|V(T^{\prime}(c))|\geq s$
but
$|V(T^{\prime}(c))|\geq s$
but
![]() $|V(T^{\prime}(d))|\leq s-1$
for all children
$|V(T^{\prime}(d))|\leq s-1$
for all children
![]() $d$
of
$d$
of
![]() $c$
, where
$c$
, where
![]() $c\neq a$
as
$c\neq a$
as
![]() $a\notin V(T^{\prime})$
.
$a\notin V(T^{\prime})$
.
Label the children of
![]() $c$
as
$c$
as
![]() $c_1,\ldots, c_t$
in an arbitrary order and let
$c_1,\ldots, c_t$
in an arbitrary order and let
![]() $\ell \in [1,t]$
be the smallest index such that
$\ell \in [1,t]$
be the smallest index such that
![]() $1+\sum _{x=1}^\ell |V(T(c_x))|\geq s$
. Since
$1+\sum _{x=1}^\ell |V(T(c_x))|\geq s$
. Since
![]() $|V(T(c_\ell ))|\leq s-1$
, we have
$|V(T(c_\ell ))|\leq s-1$
, we have
![]() $s\leq 1+\sum _{x=1}^\ell |V(T(c_x))|\leq 2s-2$
.
$s\leq 1+\sum _{x=1}^\ell |V(T(c_x))|\leq 2s-2$
.
Let
![]() $c^{\prime}$
be the parent of
$c^{\prime}$
be the parent of
![]() $c$
in
$c$
in
![]() $T$
. Note that it might be the case that
$T$
. Note that it might be the case that
![]() $c^{\prime}=a$
or
$c^{\prime}=a$
or
![]() $c^{\prime}= a^{\prime}$
. Let
$c^{\prime}= a^{\prime}$
. Let
![]() $H$
denote the subtree of
$H$
denote the subtree of
![]() $T$
induced by
$T$
induced by
![]() $c$
and the union of
$c$
and the union of
![]() $V(T(c_1)),\ldots, V(T(c_\ell ))$
, and let
$V(T(c_1)),\ldots, V(T(c_\ell ))$
, and let
![]() $m=|V(H)|$
. The above inequalities imply
$m=|V(H)|$
. The above inequalities imply
![]() $s\leq m\leq 2s-2$
. On the one hand,
$s\leq m\leq 2s-2$
. On the one hand,
![]() $j-k+1\leq m$
implies that the subinterval
$j-k+1\leq m$
implies that the subinterval
![]() $G[j-m,j]$
contains
$G[j-m,j]$
contains
![]() $v_k$
, and so
$v_k$
, and so
![]() $v_k$
is the highest vertex in
$v_k$
is the highest vertex in
![]() $G[j-m,j]$
. On the other hand, the interval
$G[j-m,j]$
. On the other hand, the interval
![]() $G[j-m,k-1]$
contains
$G[j-m,k-1]$
contains
![]() $k-1-j+m+1=m-s+1\leq s-1$
vertices, given that
$k-1-j+m+1=m-s+1\leq s-1$
vertices, given that
![]() $m\leq 2s-2$
; however, since the right child of
$m\leq 2s-2$
; however, since the right child of
![]() $v_k$
is not in
$v_k$
is not in
![]() $G{[i,j]}$
, we know that the order of a subtree of
$G{[i,j]}$
, we know that the order of a subtree of
![]() $B$
rooted at any vertex at the level below
$B$
rooted at any vertex at the level below
![]() $v_k$
is at least
$v_k$
is at least
![]() $s-1$
. It follows that
$s-1$
. It follows that
![]() $G[j-m,j]$
contains neither the left child of the left sibling of
$G[j-m,j]$
contains neither the left child of the left sibling of
![]() $v_k$
(if it exists) nor any descendants of the left child of the left sibling of
$v_k$
(if it exists) nor any descendants of the left child of the left sibling of
![]() $v_k$
(if it exists). By Lemma 4,
$v_k$
(if it exists). By Lemma 4,
![]() $G[j-m,j]-v_k$
is crossing-isomorphic to an interval
$G[j-m,j]-v_k$
is crossing-isomorphic to an interval
![]() $G(I)$
of size
$G(I)$
of size
![]() $m$
.
$m$
.
Recursively embed
![]() $H$
onto
$H$
onto
![]() $G(I)$
with one portal
$G(I)$
with one portal
![]() $c$
, which is mapped to the highest vertex of
$c$
, which is mapped to the highest vertex of
![]() $G(I)$
. By Lemma 5, there exists an embedding
$G(I)$
. By Lemma 5, there exists an embedding
![]() $\varphi$
of
$\varphi$
of
![]() $H$
onto
$H$
onto
![]() $G[j-m,j]-v_k$
such that
$G[j-m,j]-v_k$
such that
![]() $\varphi (c)=v_{k+1}$
. We complete
$\varphi (c)=v_{k+1}$
. We complete
![]() $\varphi$
into an embedding of
$\varphi$
into an embedding of
![]() $T$
onto
$T$
onto
![]() $G[i,j]$
as follows. Set
$G[i,j]$
as follows. Set
![]() $\varphi (a)=v_k$
(hence
$\varphi (a)=v_k$
(hence
![]() $\varphi$
satisfies Property 1(a)). If
$\varphi$
satisfies Property 1(a)). If
![]() $c$
has more than
$c$
has more than
![]() $\ell$
children, then embed the subtrees
$\ell$
children, then embed the subtrees
![]() $T(c_{\ell +1}),\ldots, T(c_t)$
on consecutive subintervals to the left of
$T(c_{\ell +1}),\ldots, T(c_t)$
on consecutive subintervals to the left of
![]() $G[j-m,j]$
, with single portals
$G[j-m,j]$
, with single portals
![]() $c_{\ell +1},\ldots, c_t$
, respectively. Finally, we distinguish three cases, based on whether
$c_{\ell +1},\ldots, c_t$
, respectively. Finally, we distinguish three cases, based on whether
![]() $c^{\prime}=a$
, or
$c^{\prime}=a$
, or
![]() $c^{\prime}=a^{\prime}$
, or
$c^{\prime}=a^{\prime}$
, or
![]() $c^{\prime}\notin \{a,a^{\prime}\}$
.
$c^{\prime}\notin \{a,a^{\prime}\}$
.
-
• If
 $c^{\prime}=a$
, as in Figure 6, then the embedding
$c^{\prime}=a$
, as in Figure 6, then the embedding
 $\varphi$
defined so far embeds the entire tree
$\varphi$
defined so far embeds the entire tree
 $T$
onto
$T$
onto
 $G[i,j]$
. Note that
$G[i,j]$
. Note that
 $\varphi$
satisfies Property 1(b), given that
$\varphi$
satisfies Property 1(b), given that
 $\varphi (a^{\prime})=\varphi (c)=v_{k+1}$
.
$\varphi (a^{\prime})=\varphi (c)=v_{k+1}$
. -
• If
 $c^{\prime}=a^{\prime}$
, as in Figure 7, then by induction, we can embed
$c^{\prime}=a^{\prime}$
, as in Figure 7, then by induction, we can embed
 $T^{\prime}-T(c)$
onto the remaining subinterval of
$T^{\prime}-T(c)$
onto the remaining subinterval of
 $G[i,j]$
with one portal
$G[i,j]$
with one portal
 $c^{\prime}=a^{\prime}$
(hence
$c^{\prime}=a^{\prime}$
(hence
 $\varphi$
satisfies Property 1(b), given that the embedding of
$\varphi$
satisfies Property 1(b), given that the embedding of
 $T^{\prime}-T(c)$
satisfies Property 1(a)).
$T^{\prime}-T(c)$
satisfies Property 1(a)). -
• If
 $c^{\prime}\neq a$
and
$c^{\prime}\neq a$
and
 $c^{\prime}\neq a^{\prime}$
, as in Figure 8, then by induction, we can embed
$c^{\prime}\neq a^{\prime}$
, as in Figure 8, then by induction, we can embed
 $T^{\prime}-T(c)$
onto the remaining subinterval of
$T^{\prime}-T(c)$
onto the remaining subinterval of
 $G[i,j]$
with two portals
$G[i,j]$
with two portals
 $a^{\prime}$
and
$a^{\prime}$
and
 $c^{\prime}$
(hence
$c^{\prime}$
(hence
 $\varphi$
satisfies Property 1(b), given that the embedding of
$\varphi$
satisfies Property 1(b), given that the embedding of
 $T^{\prime}-T(c)$
satisfies Property 2(b)).
$T^{\prime}-T(c)$
satisfies Property 2(b)).
The embeddings
![]() $\varphi (H),\varphi (T(c_{\ell +1})),\dots,\varphi (T(c_t)),\varphi (T^{\prime}-T(c))$
are pairwise noncrossing since they use pairwise disjoint intervals. Further, the edges
$\varphi (H),\varphi (T(c_{\ell +1})),\dots,\varphi (T(c_t)),\varphi (T^{\prime}-T(c))$
are pairwise noncrossing since they use pairwise disjoint intervals. Further, the edges
![]() $\varphi (c)\varphi (c_{\ell +1}),\dots,\varphi (c)\varphi (c_t)$
belong to
$\varphi (c)\varphi (c_{\ell +1}),\dots,\varphi (c)\varphi (c_t)$
belong to
![]() $G[i,j]$
and do not cross by Lemma 3, given that
$G[i,j]$
and do not cross by Lemma 3, given that
![]() $\varphi (c)=v_{k+1}$
is the second highest vertex of
$\varphi (c)=v_{k+1}$
is the second highest vertex of
![]() $G[i,j]$
; further, these edges do not cross
$G[i,j]$
; further, these edges do not cross
![]() $\varphi (H),\varphi (T(c_{\ell +1})),\dots,\varphi (T(c_t))$
by Observation 2 and do not cross
$\varphi (H),\varphi (T(c_{\ell +1})),\dots,\varphi (T(c_t))$
by Observation 2 and do not cross
![]() $\varphi (T^{\prime}-T(c))$
since they use intervals disjoint from the one used by
$\varphi (T^{\prime}-T(c))$
since they use intervals disjoint from the one used by
![]() $\varphi (T^{\prime}-T(c))$
. By analogous arguments, we can conclude that the edge
$\varphi (T^{\prime}-T(c))$
. By analogous arguments, we can conclude that the edge
![]() $\varphi (a)\varphi (a^{\prime})$
belongs to
$\varphi (a)\varphi (a^{\prime})$
belongs to
![]() $G[i,j]$
and does not cross
$G[i,j]$
and does not cross
![]() $\varphi (H),\varphi (T(c_{\ell +1})),\dots,\varphi (T(c_t)),\varphi (T^{\prime}-T(c))$
, and that the edge
$\varphi (H),\varphi (T(c_{\ell +1})),\dots,\varphi (T(c_t)),\varphi (T^{\prime}-T(c))$
, and that the edge
![]() $\varphi (c)\varphi (c^{\prime})$
belongs to
$\varphi (c)\varphi (c^{\prime})$
belongs to
![]() $G[i,j]$
and does not cross
$G[i,j]$
and does not cross
![]() $\varphi (H),\varphi (T(c_{\ell +1})),\dots,\varphi (T(c_t))$
. Further, the edge
$\varphi (H),\varphi (T(c_{\ell +1})),\dots,\varphi (T(c_t))$
. Further, the edge
![]() $\varphi (c)\varphi (c^{\prime})$
does not cross
$\varphi (c)\varphi (c^{\prime})$
does not cross
![]() $\varphi (T^{\prime}-T(c))$
; this comes from the fact that
$\varphi (T^{\prime}-T(c))$
; this comes from the fact that
![]() $\varphi (c^{\prime})$
is the highest vertex of
$\varphi (c^{\prime})$
is the highest vertex of
![]() $\varphi (T^{\prime}-T(c))$
if
$\varphi (T^{\prime}-T(c))$
if
![]() $c^{\prime}=a^{\prime}$
, and from the fact that
$c^{\prime}=a^{\prime}$
, and from the fact that
![]() $\varphi (T^{\prime}-T(c))$
satisfies Property 2(c) if
$\varphi (T^{\prime}-T(c))$
satisfies Property 2(c) if
![]() $c^{\prime}\neq a^{\prime}$
and
$c^{\prime}\neq a^{\prime}$
and
![]() $c^{\prime}\neq a$
(in fact,
$c^{\prime}\neq a$
(in fact,
![]() $\varphi (c)$
is in
$\varphi (c)$
is in
![]() $Q^+(\varphi (c^{\prime}))$
). It follows that
$Q^+(\varphi (c^{\prime}))$
). It follows that
![]() $\varphi$
is an embedding of
$\varphi$
is an embedding of
![]() $T$
onto
$T$
onto
![]() $G[i,j]$
.
$G[i,j]$
.
![]()
Case 1.2.5:
![]() $i\lt k\lt j$
, the left sibling of
$i\lt k\lt j$
, the left sibling of
![]() $v_k$
does not exist or is not in
$v_k$
does not exist or is not in
![]() $G[i,j]$
, and the right child
$G[i,j]$
, and the right child
![]() $v_r$
of
$v_r$
of
![]() $v_k$
is in
$v_k$
is in
![]() $G{[i,j]}$
. By assumption, we have
$G{[i,j]}$
. By assumption, we have
![]() $k+1\lt r\leq j$
; further, the second highest vertex in
$k+1\lt r\leq j$
; further, the second highest vertex in
![]() $G[i,j]$
is
$G[i,j]$
is
![]() $v_r$
.
$v_r$
.
Set
![]() $s=j-r+1$
, that is,
$s=j-r+1$
, that is,
![]() $s$
is the number of vertices in the interval
$s$
is the number of vertices in the interval
![]() $[r,j]$
. Note that
$[r,j]$
. Note that
![]() $s\lt h$
, given that
$s\lt h$
, given that
![]() $k\gt i$
(indeed,
$k\gt i$
(indeed,
![]() $s\leq h-3$
, since
$s\leq h-3$
, since
![]() $v_i$
,
$v_i$
,
![]() $v_k$
, and
$v_k$
, and
![]() $v_{k+1}$
do not belong to
$v_{k+1}$
do not belong to
![]() $G[r,j]$
). Lemma 7 then yields a vertex
$G[r,j]$
). Lemma 7 then yields a vertex
![]() $c$
in
$c$
in
![]() $T^{\prime}$
such that
$T^{\prime}$
such that
![]() $|V(T(c))|\geq s$
but
$|V(T(c))|\geq s$
but
![]() $|V(T(d))|\leq s-1$
for all children
$|V(T(d))|\leq s-1$
for all children
![]() $d$
of
$d$
of
![]() $c$
, where
$c$
, where
![]() $c\neq a$
as
$c\neq a$
as
![]() $a\notin V(T^{\prime})$
. Set
$a\notin V(T^{\prime})$
. Set
![]() $m=|V(T(c))|$
, and label the children of
$m=|V(T(c))|$
, and label the children of
![]() $c$
by
$c$
by
![]() $c_1,\ldots, c_t$
in an arbitrary order. Let
$c_1,\ldots, c_t$
in an arbitrary order. Let
![]() $c^{\prime}$
be the parent of
$c^{\prime}$
be the parent of
![]() $c$
and denote by
$c$
and denote by
![]() $T_c(c^{\prime})$
the subtree of
$T_c(c^{\prime})$
the subtree of
![]() $T$
induced by
$T$
induced by
![]() $c^{\prime}$
and
$c^{\prime}$
and
![]() $V(T(c))$
.
$V(T(c))$
.
Case 1.2.5.1:
![]() $m\leq j-k-1$
. Then the interval
$m\leq j-k-1$
. Then the interval
![]() $[j-m,j]$
contains
$[j-m,j]$
contains
![]() $r$
but does not contain
$r$
but does not contain
![]() $k$
, hence
$k$
, hence
![]() $v_r$
is the highest vertex in
$v_r$
is the highest vertex in
![]() $G[j-m,j]$
. Note that
$G[j-m,j]$
. Note that
![]() $m\leq j-k-1$
implies that
$m\leq j-k-1$
implies that
![]() $m\leq h-3$
, given that
$m\leq h-3$
, given that
![]() $k\geq i+1$
and that
$k\geq i+1$
and that
![]() $h=j-i+1$
. This implies that
$h=j-i+1$
. This implies that
![]() $c\neq a^{\prime}$
and
$c\neq a^{\prime}$
and
![]() $c^{\prime}\neq a$
, as otherwise
$c^{\prime}\neq a$
, as otherwise
![]() $m=|V(T(c))|=h-1$
. We construct an embedding
$m=|V(T(c))|=h-1$
. We construct an embedding
![]() $\varphi$
of
$\varphi$
of
![]() $T$
onto
$T$
onto
![]() $G[i,j]$
as follows. Refer to Figures 9 and 10. First, set
$G[i,j]$
as follows. Refer to Figures 9 and 10. First, set
![]() $\varphi (a)=v_k$
(hence
$\varphi (a)=v_k$
(hence
![]() $\varphi$
satisfies Property 1(a)).
$\varphi$
satisfies Property 1(a)).

Figure 9. Illustration for Case 1.2.5.1, if
![]() $c^{\prime}=a^{\prime}$
. Tree
$c^{\prime}=a^{\prime}$
. Tree
![]() $T$
(left) and its embedding onto
$T$
(left) and its embedding onto
![]() $G[i,j]$
(right).
$G[i,j]$
(right).

Figure 10. Illustration for Case 1.2.5.1, if
![]() $c^{\prime}\neq a^{\prime}$
. Tree
$c^{\prime}\neq a^{\prime}$
. Tree
![]() $T$
(left) and its embedding onto
$T$
(left) and its embedding onto
![]() $G[i,j]$
(right).
$G[i,j]$
(right).
By induction, there is an embedding
![]() $\psi _1$
of
$\psi _1$
of
![]() $T_c(c^{\prime})$
onto
$T_c(c^{\prime})$
onto
![]() $G[j-m,j]$
with a single portal
$G[j-m,j]$
with a single portal
![]() $c^{\prime}$
. By Property 1(a) of
$c^{\prime}$
. By Property 1(a) of
![]() $\psi _1$
, we have
$\psi _1$
, we have
![]() $\psi _1(c^{\prime})=v_r$
; further, by Property 1(b) of
$\psi _1(c^{\prime})=v_r$
; further, by Property 1(b) of
![]() $\psi _1$
, we have that
$\psi _1$
, we have that
![]() $Q^-(\psi _1(c))$
does not intersect any vertex or edge of
$Q^-(\psi _1(c))$
does not intersect any vertex or edge of
![]() $\psi _1(T(c))$
. Let
$\psi _1(T(c))$
. Let
![]() $\varphi (T(c))=\psi _1(T(c))$
. Note that this does not yet define the vertex of
$\varphi (T(c))=\psi _1(T(c))$
. Note that this does not yet define the vertex of
![]() $G[i,j]$
vertex
$G[i,j]$
vertex
![]() $c^{\prime}$
is embedded onto.
$c^{\prime}$
is embedded onto.
In order to complete the definition of
![]() $\varphi$
, we distinguish two cases, based on whether
$\varphi$
, we distinguish two cases, based on whether
![]() $c^{\prime}=a^{\prime}$
or
$c^{\prime}=a^{\prime}$
or
![]() $c^{\prime}\neq a^{\prime}$
. In the first case, shown in Figure 9, by induction, there is an embedding
$c^{\prime}\neq a^{\prime}$
. In the first case, shown in Figure 9, by induction, there is an embedding
![]() $\psi _2$
of
$\psi _2$
of
![]() $T^{\prime}-T(c)$
onto
$T^{\prime}-T(c)$
onto
![]() $G[i,j-m-1]$
with a single portal
$G[i,j-m-1]$
with a single portal
![]() $c^{\prime}=a^{\prime}$
. In the second case, shown in Figure 10, by induction, there is an embedding
$c^{\prime}=a^{\prime}$
. In the second case, shown in Figure 10, by induction, there is an embedding
![]() $\psi _2$
of
$\psi _2$
of
![]() $T^{\prime}-T(c)$
onto
$T^{\prime}-T(c)$
onto
![]() $G[i,j-m-1]$
with two portals
$G[i,j-m-1]$
with two portals
![]() $a^{\prime}$
and
$a^{\prime}$
and
![]() $c^{\prime}$
. In both cases, by Lemma 6, there is an embedding
$c^{\prime}$
. In both cases, by Lemma 6, there is an embedding
![]() $\varphi$
of
$\varphi$
of
![]() $T^{\prime}-T(c)$
onto
$T^{\prime}-T(c)$
onto
![]() $G[i,j-m-1]-v_k+v_r$
(this is part of the embedding
$G[i,j-m-1]-v_k+v_r$
(this is part of the embedding
![]() $\varphi$
of
$\varphi$
of
![]() $T$
onto
$T$
onto
![]() $G[i,j]$
), where the vertex of
$G[i,j]$
), where the vertex of
![]() $T$
that is mapped to
$T$
that is mapped to
![]() $v_k$
by
$v_k$
by
![]() $\psi _2$
is mapped to
$\psi _2$
is mapped to
![]() $v_r$
by
$v_r$
by
![]() $\varphi$
, and every other vertex of
$\varphi$
, and every other vertex of
![]() $T$
is mapped to the same vertex of
$T$
is mapped to the same vertex of
![]() $G[i,j]$
by
$G[i,j]$
by
![]() $\psi _2$
and by
$\psi _2$
and by
![]() $\varphi$
. If
$\varphi$
. If
![]() $\psi _2(a^{\prime})\neq v_k$
, then
$\psi _2(a^{\prime})\neq v_k$
, then
![]() $\varphi$
satisfies Property 1(b), given that
$\varphi$
satisfies Property 1(b), given that
![]() $\psi _2$
satisfies the same property (if
$\psi _2$
satisfies the same property (if
![]() $c^{\prime}=a^{\prime}$
) or given that
$c^{\prime}=a^{\prime}$
) or given that
![]() $\psi _2$
satisfies Property 2(b) (if
$\psi _2$
satisfies Property 2(b) (if
![]() $c^{\prime}\neq a^{\prime}$
). Further, if
$c^{\prime}\neq a^{\prime}$
). Further, if
![]() $\psi _2(a^{\prime})= v_k$
, then
$\psi _2(a^{\prime})= v_k$
, then
![]() $\varphi (a^{\prime})=v_r$
and the only vertex of
$\varphi (a^{\prime})=v_r$
and the only vertex of
![]() $G[i,j]$
in the interior of
$G[i,j]$
in the interior of
![]() $Q^-(\varphi (a^{\prime}))$
is
$Q^-(\varphi (a^{\prime}))$
is
![]() $\varphi (a)=v_k$
(hence
$\varphi (a)=v_k$
(hence
![]() $\varphi$
satisfies Property 1(b)). This completes the definition of
$\varphi$
satisfies Property 1(b)). This completes the definition of
![]() $\varphi$
.
$\varphi$
.
We argue that the edge
![]() $\varphi (c)\varphi (c^{\prime})$
is present in
$\varphi (c)\varphi (c^{\prime})$
is present in
![]() $G[i,j]$
. To simplify the notation, let
$G[i,j]$
. To simplify the notation, let
![]() $v_{p}=\varphi (c^{\prime})$
and
$v_{p}=\varphi (c^{\prime})$
and
![]() $v_q=\varphi (c)$
, and note that
$v_q=\varphi (c)$
, and note that
![]() $p\lt q$
or
$p\lt q$
or
![]() $p=r$
. We first discuss the case
$p=r$
. We first discuss the case
![]() $p=r$
. Notice that this case happens if
$p=r$
. Notice that this case happens if
![]() $\psi _2(c^{\prime})=v_k$
, which holds always true if
$\psi _2(c^{\prime})=v_k$
, which holds always true if
![]() $\psi _2$
embeds
$\psi _2$
embeds
![]() $T^{\prime}-T(c)$
onto
$T^{\prime}-T(c)$
onto
![]() $G[i,j-m-1]$
with a single portal
$G[i,j-m-1]$
with a single portal
![]() $c^{\prime}=a^{\prime}$
. Then the edge
$c^{\prime}=a^{\prime}$
. Then the edge
![]() $\varphi (c)\varphi (c^{\prime})$
is present in
$\varphi (c)\varphi (c^{\prime})$
is present in
![]() $G[i,j]$
, as
$G[i,j]$
, as
![]() $\psi _1(c^{\prime})=v_r$
and the edge
$\psi _1(c^{\prime})=v_r$
and the edge
![]() $cc^{\prime}$
belongs to
$cc^{\prime}$
belongs to
![]() $T_c(c^{\prime})$
. Assume next that
$T_c(c^{\prime})$
. Assume next that
![]() $p\lt q$
, which implies that
$p\lt q$
, which implies that
![]() $\psi _2$
embeds
$\psi _2$
embeds
![]() $T^{\prime}-T(c)$
onto
$T^{\prime}-T(c)$
onto
![]() $G[i,j-m-1]$
with two portals
$G[i,j-m-1]$
with two portals
![]() $a^{\prime}$
and
$a^{\prime}$
and
![]() $c^{\prime}$
. On the one hand, by Property 2(c) of
$c^{\prime}$
. On the one hand, by Property 2(c) of
![]() $\psi _2$
, we have that
$\psi _2$
, we have that
![]() $Q^+(\psi _2(c^{\prime}))$
does not contain any vertex or edge of
$Q^+(\psi _2(c^{\prime}))$
does not contain any vertex or edge of
![]() $\psi _2(T^{\prime}-T(c))$
, hence
$\psi _2(T^{\prime}-T(c))$
, hence
![]() $k\lt p$
, as otherwise
$k\lt p$
, as otherwise
![]() $v_k$
would be in
$v_k$
would be in
![]() $Q^+(\psi _2(c^{\prime}))$
. It follows that
$Q^+(\psi _2(c^{\prime}))$
. It follows that
![]() $v_p$
is the highest vertex in
$v_p$
is the highest vertex in
![]() $G[p,j-m-1]$
. On the other hand, by Property 1(b) of
$G[p,j-m-1]$
. On the other hand, by Property 1(b) of
![]() $\psi _1$
, we have that
$\psi _1$
, we have that
![]() $Q^-(\psi _1(c))$
does not contain any vertex or edge of
$Q^-(\psi _1(c))$
does not contain any vertex or edge of
![]() $\psi _1(T(c))$
. It follows that
$\psi _1(T(c))$
. It follows that
![]() $v_q$
is either the highest or the second highest vertex in
$v_q$
is either the highest or the second highest vertex in
![]() $G[j-m,q]$
(as
$G[j-m,q]$
(as
![]() $v_r$
might belong to such an interval). Overall, one of
$v_r$
might belong to such an interval). Overall, one of
![]() $v_p$
or
$v_p$
or
![]() $v_q$
is the highest or the second highest vertex in
$v_q$
is the highest or the second highest vertex in
![]() $G[p,q]$
. By Lemma 3,
$G[p,q]$
. By Lemma 3,
![]() $G[p,q]$
contains a star centred at
$G[p,q]$
contains a star centred at
![]() $v_p$
or
$v_p$
or
![]() $v_q$
, and so it contains the edge
$v_q$
, and so it contains the edge
![]() $v_p v_q=\varphi (c^{\prime})\varphi (c)$
, as required.
$v_p v_q=\varphi (c^{\prime})\varphi (c)$
, as required.
We now prove that
![]() $\varphi (T)$
is crossing-free. The embeddings
$\varphi (T)$
is crossing-free. The embeddings
![]() $\varphi (T(c))$
and
$\varphi (T(c))$
and
![]() $\varphi (T^{\prime}-T(c))$
are pairwise noncrossing, since they use disjoint intervals, with the exception of the edges of
$\varphi (T^{\prime}-T(c))$
are pairwise noncrossing, since they use disjoint intervals, with the exception of the edges of
![]() $\varphi (T^{\prime}-T(c))$
incident to
$\varphi (T^{\prime}-T(c))$
incident to
![]() $v_r$
, which however do not cross
$v_r$
, which however do not cross
![]() $\varphi (T(c))$
by Observation 2. It remains to deal with the edges
$\varphi (T(c))$
by Observation 2. It remains to deal with the edges
![]() $\varphi (c^{\prime})\varphi (c)$
and
$\varphi (c^{\prime})\varphi (c)$
and
![]() $\varphi (a)\varphi (a^{\prime})$
. Consider first the edge
$\varphi (a)\varphi (a^{\prime})$
. Consider first the edge
![]() $\varphi (c^{\prime})\varphi (c)$
.
$\varphi (c^{\prime})\varphi (c)$
.
-
• If
 $\varphi (c^{\prime})=v_r$
, then the edge
$\varphi (c^{\prime})=v_r$
, then the edge
 $\varphi (c^{\prime})\varphi (c)$
does not cross
$\varphi (c^{\prime})\varphi (c)$
does not cross
 $\varphi (T(c))$
as
$\varphi (T(c))$
as
 $\psi _1(c^{\prime})=v_r$
and
$\psi _1(c^{\prime})=v_r$
and
 $\psi _1$
defines an embedding of
$\psi _1$
defines an embedding of
 $T_c(c^{\prime})$
onto
$T_c(c^{\prime})$
onto
 $G[j-m,j]$
. The edge
$G[j-m,j]$
. The edge
 $\varphi (c^{\prime})\varphi (c)$
does not cross any edge of
$\varphi (c^{\prime})\varphi (c)$
does not cross any edge of
 $\varphi (T^{\prime}-T(c))$
incident to
$\varphi (T^{\prime}-T(c))$
incident to
 $v_r$
by Lemma 3, and it does not cross any edge of
$v_r$
by Lemma 3, and it does not cross any edge of
 $\varphi (T^{\prime}-T(c))$
not incident to
$\varphi (T^{\prime}-T(c))$
not incident to
 $v_r$
as they use disjoint intervals.
$v_r$
as they use disjoint intervals. -
• If
 $\varphi (c^{\prime})=v_p$
with
$\varphi (c^{\prime})=v_p$
with
 $p\neq r$
, then the edge
$p\neq r$
, then the edge
 $\varphi (c^{\prime})\varphi (c)$
does not cross
$\varphi (c^{\prime})\varphi (c)$
does not cross
 $\varphi (T(c))$
by Observation 2 and since
$\varphi (T(c))$
by Observation 2 and since
 $Q^-(\varphi (c))$
does not intersect
$Q^-(\varphi (c))$
does not intersect
 $\varphi (T(c))$
; it does not cross any edge of
$\varphi (T(c))$
; it does not cross any edge of
 $\varphi (T^{\prime}-T(c))$
not incident to
$\varphi (T^{\prime}-T(c))$
not incident to
 $v_r$
by Observation 2 and since
$v_r$
by Observation 2 and since
 $Q^+(\varphi (c^{\prime}))$
does not intersect
$Q^+(\varphi (c^{\prime}))$
does not intersect
 $\varphi (T^{\prime}-T(c))$
, except at
$\varphi (T^{\prime}-T(c))$
, except at
 $v_r$
and its incident edges; and we claim that it does not cross any edge of
$v_r$
and its incident edges; and we claim that it does not cross any edge of
 $\varphi (T^{\prime}-T(c))$
incident to
$\varphi (T^{\prime}-T(c))$
incident to
 $v_r$
, either. The latter can be proved as follows. Let again
$v_r$
, either. The latter can be proved as follows. Let again
 $\varphi (c)=v_q$
, and consider any edge
$\varphi (c)=v_q$
, and consider any edge
 $v_rv_s$
in
$v_rv_s$
in
 $\varphi (T^{\prime}-T(c))$
. Then we have
$\varphi (T^{\prime}-T(c))$
. Then we have
 $\max \{p,s\}\lt \min \{r,q\}$
. Since
$\max \{p,s\}\lt \min \{r,q\}$
. Since
 $v_r$
is higher than
$v_r$
is higher than
 $v_p$
,
$v_p$
,
 $v_q$
, and
$v_q$
, and
 $v_s$
, by Observation 2 the edges
$v_s$
, by Observation 2 the edges
 $v_pv_q$
and
$v_pv_q$
and
 $v_rv_s$
do not cross if
$v_rv_s$
do not cross if
 $s\lt p$
, hence we can assume that
$s\lt p$
, hence we can assume that
 $p\lt s$
. The last inequality implies that the edge
$p\lt s$
. The last inequality implies that the edge
 $v_kv_s$
of
$v_kv_s$
of
 $\psi _2(T^{\prime}-T(c))$
crosses
$\psi _2(T^{\prime}-T(c))$
crosses
 $Q^+(\varphi (c^{\prime}))$
, which however is not possible by Property 2(c) of
$Q^+(\varphi (c^{\prime}))$
, which however is not possible by Property 2(c) of
 $\psi _2(T^{\prime}-T(c))$
.
$\psi _2(T^{\prime}-T(c))$
.
Finally, the edge
![]() $\varphi (a)\varphi (a^{\prime})$
does not cross
$\varphi (a)\varphi (a^{\prime})$
does not cross
![]() $\varphi (T(c))$
, since they use disjoint intervals, and it does not cross
$\varphi (T(c))$
, since they use disjoint intervals, and it does not cross
![]() $\varphi (c^{\prime})\varphi (c)$
or any edge of
$\varphi (c^{\prime})\varphi (c)$
or any edge of
![]() $\varphi (T^{\prime}-T(c))$
, by Observation 2 and since
$\varphi (T^{\prime}-T(c))$
, by Observation 2 and since
![]() $Q^-(\varphi (a^{\prime}))$
does not intersect any edge or vertex of
$Q^-(\varphi (a^{\prime}))$
does not intersect any edge or vertex of
![]() $\varphi (T^{\prime}-T(c))$
, by Property 2(b) of
$\varphi (T^{\prime}-T(c))$
, by Property 2(b) of
![]() $\psi _2(T^{\prime}-T(c))$
.
$\psi _2(T^{\prime}-T(c))$
.
![]()
Case 1.2.5.2:
![]() $j-k-1\lt m$
. In this case, the interval
$j-k-1\lt m$
. In this case, the interval
![]() $[j-m,j]$
contains both
$[j-m,j]$
contains both
![]() $k$
and
$k$
and
![]() $r$
; further, we might have
$r$
; further, we might have
![]() $c^{\prime}=a^{\prime}$
or
$c^{\prime}=a^{\prime}$
or
![]() $c^{\prime}=a$
. Refer to Figure 11. Partition the set of integers
$c^{\prime}=a$
. Refer to Figure 11. Partition the set of integers
![]() $[j-m,j]\setminus \{k,r\}$
into
$[j-m,j]\setminus \{k,r\}$
into
![]() $t$
contiguous subsets
$t$
contiguous subsets
![]() $I_1,\ldots,I_t$
such that
$I_1,\ldots,I_t$
such that
![]() $|I_x|=|V(T(c_x))|$
, for
$|I_x|=|V(T(c_x))|$
, for
![]() $x=1,\ldots,t$
. Let
$x=1,\ldots,t$
. Let
![]() $q\in \{1,\dots,t\}$
be such that
$q\in \{1,\dots,t\}$
be such that
![]() $I_q$
contains
$I_q$
contains
![]() $r-1$
or
$r-1$
or
![]() $r+1$
. Note that the sets
$r+1$
. Note that the sets
![]() $I_1,\ldots,I_t$
are not necessarily intervals, since the set of integers
$I_1,\ldots,I_t$
are not necessarily intervals, since the set of integers
![]() $[j-m,j]\setminus \{k,r\}$
they partition is not an interval, either.
$[j-m,j]\setminus \{k,r\}$
they partition is not an interval, either.

Figure 11. Illustration for Case 1.2.5.2. Tree
![]() $T$
(left) and its embedding onto
$T$
(left) and its embedding onto
![]() $G[i,j]$
(right). In this example we have
$G[i,j]$
(right). In this example we have
![]() $p=1$
and
$p=1$
and
![]() $q=2$
.
$q=2$
.
Let
![]() $\mathcal{I}(c)$
be the collection of
$\mathcal{I}(c)$
be the collection of
![]() $t$
sets:
$t$
sets:
![]() $I_q\cup \{r\}$
and
$I_q\cup \{r\}$
and
![]() $I_x$
, for
$I_x$
, for
![]() $x\in [1,t]\setminus \{q\}$
. The sets in
$x\in [1,t]\setminus \{q\}$
. The sets in
![]() $\mathcal{I}(c)$
are contiguous subsets of
$\mathcal{I}(c)$
are contiguous subsets of
![]() $[j-m,j]\setminus \{k\}$
. Consequently, at least
$[j-m,j]\setminus \{k\}$
. Consequently, at least
![]() $t-1$
of them are intervals, and at most one of them, say
$t-1$
of them are intervals, and at most one of them, say
![]() $I_p$
, is an interval minus the element
$I_p$
, is an interval minus the element
![]() $k$
. Since
$k$
. Since
![]() $s=j-r+1$
and since all the vertices of
$s=j-r+1$
and since all the vertices of
![]() $G[r,j]$
belong to
$G[r,j]$
belong to
![]() $B(v_r)$
, as otherwise
$B(v_r)$
, as otherwise
![]() $v_k$
would not be the highest vertex in
$v_k$
would not be the highest vertex in
![]() $G[i,j]$
, it follows that the size of
$G[i,j]$
, it follows that the size of
![]() $B(v_r)$
is larger than or equal to
$B(v_r)$
is larger than or equal to
![]() $s$
. Consequently, also the size of the subtrees of
$s$
. Consequently, also the size of the subtrees of
![]() $B$
rooted at the left child of
$B$
rooted at the left child of
![]() $v_k$
and at the right child of the left level-neighbour of
$v_k$
and at the right child of the left level-neighbour of
![]() $v_k$
are larger than or equal to
$v_k$
are larger than or equal to
![]() $s$
. This, together with the fact that every tree
$s$
. This, together with the fact that every tree
![]() $T(c_i)$
has at most
$T(c_i)$
has at most
![]() $s-1$
vertices, implies that
$s-1$
vertices, implies that
![]() $G(I_p)$
contains neither the right child of
$G(I_p)$
contains neither the right child of
![]() $v_k$
, nor the left sibling of
$v_k$
, nor the left sibling of
![]() $v_k$
, nor any descendant of the left sibling of
$v_k$
, nor any descendant of the left sibling of
![]() $v_k$
. By Lemma 4, the graph
$v_k$
. By Lemma 4, the graph
![]() $G(I_p)$
is crossing-isomorphic to an interval. Therefore, by Lemma 5, we can embed
$G(I_p)$
is crossing-isomorphic to an interval. Therefore, by Lemma 5, we can embed
![]() $T(c_p)$
onto
$T(c_p)$
onto
![]() $G(I_p)$
. We also recursively embed
$G(I_p)$
. We also recursively embed
![]() $T(c_x)$
onto
$T(c_x)$
onto
![]() $G[I_x]$
for all
$G[I_x]$
for all
![]() $x\in [1,t]\setminus \{p,q\}$
and we recursively embed
$x\in [1,t]\setminus \{p,q\}$
and we recursively embed
![]() $T(c)-\bigcup _{x\neq q}T(c_x)$
, that is, the subtree of
$T(c)-\bigcup _{x\neq q}T(c_x)$
, that is, the subtree of
![]() $T$
induced by
$T$
induced by
![]() $c$
and by
$c$
and by
![]() $V(T(c_q))$
, onto
$V(T(c_q))$
, onto
![]() $G(I_q\cup \{r\})$
.
$G(I_q\cup \{r\})$
.
Embed
![]() $a$
at
$a$
at
![]() $v_k$
. If
$v_k$
. If
![]() $c^{\prime}=a$
(and
$c^{\prime}=a$
(and
![]() $c=a^{\prime}$
), then
$c=a^{\prime}$
), then
![]() $T^{\prime}$
coincides with
$T^{\prime}$
coincides with
![]() $T(c)$
and hence
$T(c)$
and hence
![]() $\varphi$
is the combination of the described embeddings. Otherwise,
$\varphi$
is the combination of the described embeddings. Otherwise,
![]() $\varphi$
also includes an embedding of
$\varphi$
also includes an embedding of
![]() $T^{\prime}-T(c)$
onto
$T^{\prime}-T(c)$
onto
![]() $G[i,j-m-1]$
. This embedding is constructed recursively with a single portal
$G[i,j-m-1]$
. This embedding is constructed recursively with a single portal
![]() $c^{\prime}$
(if
$c^{\prime}$
(if
![]() $c^{\prime}=a^{\prime}$
) or with two portals
$c^{\prime}=a^{\prime}$
) or with two portals
![]() $a^{\prime}$
and
$a^{\prime}$
and
![]() $c^{\prime}$
(if
$c^{\prime}$
(if
![]() $c^{\prime}\neq a^{\prime}$
). The proof that
$c^{\prime}\neq a^{\prime}$
). The proof that
![]() $\varphi$
is an embedding of
$\varphi$
is an embedding of
![]() $T$
onto
$T$
onto
![]() $G[i,j]$
satisfying Properties 1(a) and 1(b) is similar to the other cases. In particular,
$G[i,j]$
satisfying Properties 1(a) and 1(b) is similar to the other cases. In particular,
![]() $\varphi (c)=v_r$
is the second highest vertex of
$\varphi (c)=v_r$
is the second highest vertex of
![]() $G[i,j]$
, hence the edge
$G[i,j]$
, hence the edge
![]() $\varphi (c)\varphi (c^{\prime})$
exists by Lemma 3.
$\varphi (c)\varphi (c^{\prime})$
exists by Lemma 3.
![]()
Case 2: Two portals. We are given two portals
![]() $a$
and
$a$
and
![]() $b$
; refer to Figure 12. Let
$b$
; refer to Figure 12. Let
![]() $P=(a=c_1,\ldots,$
$P=(a=c_1,\ldots,$
![]() $c_t=b)$
be the path between
$c_t=b)$
be the path between
![]() $a$
and
$a$
and
![]() $b$
in
$b$
in
![]() $T$
, where
$T$
, where
![]() $t\geq 2$
. The deletion of the edges in
$t\geq 2$
. The deletion of the edges in
![]() $P$
splits
$P$
splits
![]() $T$
into
$T$
into
![]() $t$
trees rooted at
$t$
trees rooted at
![]() $c_1,\ldots,c_t$
. Partition
$c_1,\ldots,c_t$
. Partition
![]() $[i,j]$
into
$[i,j]$
into
![]() $t$
subintervals
$t$
subintervals
![]() $I_1,\ldots,I_t$
such that
$I_1,\ldots,I_t$
such that
![]() $|I_x|=|V(T(c_x))|$
, for
$|I_x|=|V(T(c_x))|$
, for
![]() $x=1,\ldots,t$
.
$x=1,\ldots,t$
.

Figure 12. Illustration for Case 2. Tree
![]() $T$
(left) and its embedding onto
$T$
(left) and its embedding onto
![]() $G[i,j]$
(right).
$G[i,j]$
(right).
For
![]() $x=1,\ldots,t$
, recursively construct an embedding
$x=1,\ldots,t$
, recursively construct an embedding
![]() $\varphi _x$
of
$\varphi _x$
of
![]() $T(c_x)$
onto
$T(c_x)$
onto
![]() $G(I_x)$
with one portal
$G(I_x)$
with one portal
![]() $c_x$
, in which
$c_x$
, in which
![]() $\varphi _x(c_x)$
is the highest vertex in
$\varphi _x(c_x)$
is the highest vertex in
![]() $G(I_x)$
. Let
$G(I_x)$
. Let
![]() $\varphi$
be the combination of these embeddings.
$\varphi$
be the combination of these embeddings.
For any distinct
![]() $x$
and
$x$
and
![]() $y$
in
$y$
in
![]() $\{1,\dots,t\}$
, we have that
$\{1,\dots,t\}$
, we have that
![]() $\varphi (T(c_x))$
and
$\varphi (T(c_x))$
and
![]() $\varphi (T(c_y))$
do not cross, since they use disjoint intervals. Only the edges in
$\varphi (T(c_y))$
do not cross, since they use disjoint intervals. Only the edges in
![]() $P$
connect vertices from distinct intervals. For
$P$
connect vertices from distinct intervals. For
![]() $x=1,\dots,t-1$
, let
$x=1,\dots,t-1$
, let
![]() $e_x$
be the edge
$e_x$
be the edge
![]() $\varphi (c_x)\varphi (c_{x+1})$
. Note that
$\varphi (c_x)\varphi (c_{x+1})$
. Note that
![]() $e_x$
is incident to the highest vertex in
$e_x$
is incident to the highest vertex in
![]() $G(I_x\cup I_{x+1})$
and hence belongs to
$G(I_x\cup I_{x+1})$
and hence belongs to
![]() $G(I_x\cup I_{x+1})$
by Lemma 3. Further,
$G(I_x\cup I_{x+1})$
by Lemma 3. Further,
![]() $e_x$
does not cross
$e_x$
does not cross
![]() $\varphi (T(c_y))$
, with
$\varphi (T(c_y))$
, with
![]() $y\lt x$
or
$y\lt x$
or
![]() $y\gt x+1$
, as the intervals spanned by
$y\gt x+1$
, as the intervals spanned by
![]() $e_x$
and
$e_x$
and
![]() $\varphi (T(c_y))$
are disjoint. Analogously,
$\varphi (T(c_y))$
are disjoint. Analogously,
![]() $e_x$
does not cross any edge
$e_x$
does not cross any edge
![]() $e_y$
, with
$e_y$
, with
![]() $y\neq x$
. Assume that
$y\neq x$
. Assume that
![]() $\varphi (c_{x+1})$
is higher than
$\varphi (c_{x+1})$
is higher than
![]() $\varphi (c_x)$
, the other case is symmetric. Then
$\varphi (c_x)$
, the other case is symmetric. Then
![]() $e_x$
does not cross
$e_x$
does not cross
![]() $\varphi (T(c_x))$
, as
$\varphi (T(c_x))$
, as
![]() $\varphi (c_x)$
is the highest vertex of
$\varphi (c_x)$
is the highest vertex of
![]() $\varphi (T(c_x))$
and
$\varphi (T(c_x))$
and
![]() $\varphi (c_{x+1})$
is higher than
$\varphi (c_{x+1})$
is higher than
![]() $\varphi (c_x)$
; finally,
$\varphi (c_x)$
; finally,
![]() $e_x$
does not cross
$e_x$
does not cross
![]() $\varphi (T(c_{x+1}))$
, by Observation 2. Therefore,
$\varphi (T(c_{x+1}))$
, by Observation 2. Therefore,
![]() $\varphi$
is an embedding of
$\varphi$
is an embedding of
![]() $T$
onto
$T$
onto
![]() $G[i,j]$
. It is easily checked that this embedding satisfies Properties 2(a), 2(b), and 2(c), as required.
$G[i,j]$
. It is easily checked that this embedding satisfies Properties 2(a), 2(b), and 2(c), as required.
Running time analysis. We conclude by inductively proving that the time complexity of the above described algorithm is at most
![]() $c \cdot h^2$
, for some suitably large constant
$c \cdot h^2$
, for some suitably large constant
![]() $c$
.
$c$
.
The statement is obviously true in the base case.
In Case 1 of the induction step, we recursively embed some vertex-disjoint subtrees of
![]() $T$
with a total of at most
$T$
with a total of at most
![]() $h-1$
vertices. By induction, this takes at most
$h-1$
vertices. By induction, this takes at most
![]() $\sum _{S} (c \cdot |V(S)|^2)\leq c \cdot (h-1)^2$
time, where the sum is over all subtrees
$\sum _{S} (c \cdot |V(S)|^2)\leq c \cdot (h-1)^2$
time, where the sum is over all subtrees
![]() $S$
of
$S$
of
![]() $T$
which are recursively embedded. Apart from these recursive embedding constructions, in Case 1 we explicitly embed in constant time (denoted as
$T$
which are recursively embedded. Apart from these recursive embedding constructions, in Case 1 we explicitly embed in constant time (denoted as
![]() $k_1$
) some vertices of
$k_1$
) some vertices of
![]() $T$
at vertices of
$T$
at vertices of
![]() $G[i,j]$
, we find in constant time (denoted as
$G[i,j]$
, we find in constant time (denoted as
![]() $k_2$
) a subtree with suitable order by means of Lemma 7, we modify in constant time (denoted as
$k_2$
) a subtree with suitable order by means of Lemma 7, we modify in constant time (denoted as
![]() $k_3$
) a recursively constructed embedding by means of Lemma 6, we modify in linear time (denoted as
$k_3$
) a recursively constructed embedding by means of Lemma 6, we modify in linear time (denoted as
![]() $k_4\cdot h$
) a recursively constructed embedding by means of Lemma 5, or we find in linear time (denoted as
$k_4\cdot h$
) a recursively constructed embedding by means of Lemma 5, or we find in linear time (denoted as
![]() $k_5\cdot h$
) some subintervals of
$k_5\cdot h$
) some subintervals of
![]() $G[i,j]$
of the proper size. Thus, it suffices to choose a sufficiently large constant
$G[i,j]$
of the proper size. Thus, it suffices to choose a sufficiently large constant
![]() $c$
so that
$c$
so that
![]() $({-}2c+k_4+k_5)\cdot h+(c+k_1+k_2+k_3)\lt 0$
, in order to verify that the time complexity of the algorithm is at most
$({-}2c+k_4+k_5)\cdot h+(c+k_1+k_2+k_3)\lt 0$
, in order to verify that the time complexity of the algorithm is at most
![]() $c \cdot h^2$
.
$c \cdot h^2$
.
In Case 2 of the induction step, we recursively embed some subtrees of
![]() $T$
with a total of
$T$
with a total of
![]() $h$
vertices and we find in linear time (denoted as
$h$
vertices and we find in linear time (denoted as
![]() $k\cdot h$
) some subintervals of
$k\cdot h$
) some subintervals of
![]() $G[i,j]$
of the proper size. By induction, this takes at most
$G[i,j]$
of the proper size. By induction, this takes at most
![]() $\sum _{S} (c \cdot |V(S)|^2) + k\cdot h$
time. Since in Case 2 there are at least two recursively embedded subtrees,
$\sum _{S} (c \cdot |V(S)|^2) + k\cdot h$
time. Since in Case 2 there are at least two recursively embedded subtrees,
![]() $\sum _{S} (c \cdot |V(S)|^2)$
is maximised when there is one subtree of order
$\sum _{S} (c \cdot |V(S)|^2)$
is maximised when there is one subtree of order
![]() $h-1$
and one subtree of order
$h-1$
and one subtree of order
![]() $1$
, which leads to
$1$
, which leads to
![]() $\sum _{S} (c \cdot |V(S)|^2) + k\cdot h\leq c \cdot (h-1)^2 +c + k\cdot h$
, which is smaller than
$\sum _{S} (c \cdot |V(S)|^2) + k\cdot h\leq c \cdot (h-1)^2 +c + k\cdot h$
, which is smaller than
![]() $c \cdot h^2$
time, as long as
$c \cdot h^2$
time, as long as
![]() $({-}2c+k)\cdot h+2c\lt 0$
, which is true for a sufficiently large
$({-}2c+k)\cdot h+2c\lt 0$
, which is true for a sufficiently large
![]() $c$
, given that
$c$
, given that
![]() $h\geq 2$
.
$h\geq 2$
.
3. Convex geometric graphs
Every graph embedded into a convex geometric graph is outerplanar. Clearly, a complete convex geometric graph on
![]() $n$
vertices has
$n$
vertices has
![]() $O(n^2)$
edges and is universal for
$O(n^2)$
edges and is universal for
![]() $n$
-vertex outerplanar graphs. In the next theorem we show that this trivial upper bound is almost tight. For
$n$
-vertex outerplanar graphs. In the next theorem we show that this trivial upper bound is almost tight. For
![]() $h\geq 0$
and
$h\geq 0$
and
![]() $n\geq 2h+2$
, let
$n\geq 2h+2$
, let
![]() $\mathcal{OP}_h(n)$
be the family of all outerplanar graphs on
$\mathcal{OP}_h(n)$
be the family of all outerplanar graphs on
![]() $n$
vertices that consist of a spanning cycle plus
$n$
vertices that consist of a spanning cycle plus
![]() $h$
pairwise vertex-disjoint chords. In the following, we write
$h$
pairwise vertex-disjoint chords. In the following, we write
![]() $f(n)\in \Omega _h(n)$
to represent
$f(n)\in \Omega _h(n)$
to represent
![]() $f(n)\geq c_h n$
, where
$f(n)\geq c_h n$
, where
![]() $c_h$
is a constant depending on
$c_h$
is a constant depending on
![]() $h$
only.
$h$
only.
Theorem 9.
For every positive integer
![]() $h$
and
$h$
and
![]() $n\geq 3h^2$
, every convex geometric graph on
$n\geq 3h^2$
, every convex geometric graph on
![]() $n$
vertices that is universal for
$n$
vertices that is universal for
![]() $\mathcal{OP}_h(n)$
has
$\mathcal{OP}_h(n)$
has
![]() $\Omega _h(n^{2-1/h})$
edges.
$\Omega _h(n^{2-1/h})$
edges.
Proof. The claim trivially holds for
![]() $h=1$
; we may assume
$h=1$
; we may assume
![]() $h\geq 2$
in the remainder of the proof. Let
$h\geq 2$
in the remainder of the proof. Let
![]() $C$
be a convex geometric graph on
$C$
be a convex geometric graph on
![]() $n$
vertices that is universal for
$n$
vertices that is universal for
![]() $\mathcal{OP}_h(n)$
, and denote by
$\mathcal{OP}_h(n)$
, and denote by
![]() $\partial C$
its outer (spanning) cycle. The length of a chord
$\partial C$
its outer (spanning) cycle. The length of a chord
![]() $uv$
of
$uv$
of
![]() $\partial C$
is the length of a shortest path between
$\partial C$
is the length of a shortest path between
![]() $u$
and
$u$
and
![]() $v$
along
$v$
along
![]() $\partial C$
. For
$\partial C$
. For
![]() $k\geq 2$
, denote by
$k\geq 2$
, denote by
![]() $E_k$
the set of length-
$E_k$
the set of length-
![]() $k$
chords in
$k$
chords in
![]() $C$
, and let
$C$
, and let
![]() $m\in \{2,\ldots, \lfloor n/(3h)\rfloor \}$
be an integer such that
$m\in \{2,\ldots, \lfloor n/(3h)\rfloor \}$
be an integer such that
![]() $|E_m|=\min \{|E_2|,\ldots,|E_{\lfloor n/(3h)\rfloor }|\}$
.
$|E_m|=\min \{|E_2|,\ldots,|E_{\lfloor n/(3h)\rfloor }|\}$
.
Let
![]() $\mathcal{L}$
be the set of vertex-labeled outerplanar graphs on
$\mathcal{L}$
be the set of vertex-labeled outerplanar graphs on
![]() $n$
vertices that consist of a spanning cycle
$n$
vertices that consist of a spanning cycle
![]() $(v_0,\ldots, v_{n-1})$
plus
$(v_0,\ldots, v_{n-1})$
plus
![]() $h$
pairwise vertex-disjoint chords of length
$h$
pairwise vertex-disjoint chords of length
![]() $m$
such that one chord is
$m$
such that one chord is
![]() $v_0v_m$
and all
$v_0v_m$
and all
![]() $h$
chords have both vertices on the path
$h$
chords have both vertices on the path
![]() $P=(v_0,\ldots, v_{\lfloor n/3\rfloor +hm-1})$
.
$P=(v_0,\ldots, v_{\lfloor n/3\rfloor +hm-1})$
.
Every graph
![]() $G\in \mathcal{L}$
has a unique spanning cycle
$G\in \mathcal{L}$
has a unique spanning cycle
![]() $H$
. If an edge
$H$
. If an edge
![]() $e$
of
$e$
of
![]() $H$
were embedded onto a chord of
$H$
were embedded onto a chord of
![]() $\partial C$
, then the path of
$\partial C$
, then the path of
![]() $H-e$
would cross
$H-e$
would cross
![]() $e$
, given that
$e$
, given that
![]() $C$
is a convex geometric graph. It follows that
$C$
is a convex geometric graph. It follows that
![]() $H$
is embedded onto
$H$
is embedded onto
![]() $\partial C$
. The four endpoints of any two chords of
$\partial C$
. The four endpoints of any two chords of
![]() $H$
are noninterleaving along
$H$
are noninterleaving along
![]() $H$
, otherwise
$H$
, otherwise
![]() $G$
would not be an outerplanar graph. Since they all have the same length, the
$G$
would not be an outerplanar graph. Since they all have the same length, the
![]() $h$
chords of
$h$
chords of
![]() $H$
have a well-defined cyclic order along
$H$
have a well-defined cyclic order along
![]() $H$
. A gap of
$H$
. A gap of
![]() $G$
is a path between two consecutive chords along
$G$
is a path between two consecutive chords along
![]() $H$
(in cyclic order). Note that
$H$
(in cyclic order). Note that
![]() $G$
has
$G$
has
![]() $h$
gaps.
$h$
gaps.
The length of the path
![]() $P$
is
$P$
is
![]() $\lfloor n/3\rfloor +hm-1\leq \lfloor n/3\rfloor +h\cdot \lfloor n/(3h)\rfloor -1\lt 2\lfloor n/3\rfloor$
. Consequently, the length of the gap between the last and the first chord of
$\lfloor n/3\rfloor +hm-1\leq \lfloor n/3\rfloor +h\cdot \lfloor n/(3h)\rfloor -1\lt 2\lfloor n/3\rfloor$
. Consequently, the length of the gap between the last and the first chord of
![]() $P$
is greater than
$P$
is greater than
![]() $n-2\lfloor n/3\rfloor =\lceil n/3\rceil$
. This is the longest gap, as the sum of the lengths of the remaining
$n-2\lfloor n/3\rfloor =\lceil n/3\rceil$
. This is the longest gap, as the sum of the lengths of the remaining
![]() $h-1$
gaps is at most
$h-1$
gaps is at most
![]() $\lfloor n/3\rfloor$
.
$\lfloor n/3\rfloor$
.
Let
![]() $\mathcal{U}$
denote the subset of unlabelled graphs in
$\mathcal{U}$
denote the subset of unlabelled graphs in
![]() $\mathcal{OP}_h(n)$
that correspond to some labelled graph in
$\mathcal{OP}_h(n)$
that correspond to some labelled graph in
![]() $\mathcal{L}$
. We give lower bounds for
$\mathcal{L}$
. We give lower bounds for
![]() $|\mathcal{L}|$
and
$|\mathcal{L}|$
and
![]() $|\mathcal{U}|$
. Each graph in
$|\mathcal{U}|$
. Each graph in
![]() $\mathcal{L}$
is determined by the
$\mathcal{L}$
is determined by the
![]() $h-1$
gaps between consecutive chords along
$h-1$
gaps between consecutive chords along
![]() $P$
. The sum of these distances is an integer between
$P$
. The sum of these distances is an integer between
![]() $h-1$
and
$h-1$
and
![]() $(\lfloor n/3\rfloor +hm-1)-hm \lt \lfloor n/3\rfloor$
. The number of compositions of
$(\lfloor n/3\rfloor +hm-1)-hm \lt \lfloor n/3\rfloor$
. The number of compositions of
![]() $\lfloor n/3\rfloor$
into
$\lfloor n/3\rfloor$
into
![]() $h$
positive integers (i.e.
$h$
positive integers (i.e.
![]() $h-1$
distances and a remainder) is
$h-1$
distances and a remainder) is
![]() $\binom{\lfloor n/3\rfloor }{h-1}\in \Theta _h\big(n^{h-1}\big)$
. Each unlabelled graph in
$\binom{\lfloor n/3\rfloor }{h-1}\in \Theta _h\big(n^{h-1}\big)$
. Each unlabelled graph in
![]() $\mathcal{U}$
corresponds to at most two labeled graphs in
$\mathcal{U}$
corresponds to at most two labeled graphs in
![]() $\mathcal{L}$
, since any graph automorphism setwise fixes the unique spanning cycle as well as the longest gap. Hence,
$\mathcal{L}$
, since any graph automorphism setwise fixes the unique spanning cycle as well as the longest gap. Hence,
![]() $|\mathcal{U}| \in \Theta (|\mathcal{L}|)\subseteq \Theta _h\big(n^{h-1}\big)$
.
$|\mathcal{U}| \in \Theta (|\mathcal{L}|)\subseteq \Theta _h\big(n^{h-1}\big)$
.
Since
![]() $C$
is universal for
$C$
is universal for
![]() $\mathcal{OP}_h(n)$
and
$\mathcal{OP}_h(n)$
and
![]() $\mathcal{U}\subset \mathcal{OP}_h(n)$
, every graph
$\mathcal{U}\subset \mathcal{OP}_h(n)$
, every graph
![]() $G$
in
$G$
in
![]() $\mathcal{U}$
embeds onto
$\mathcal{U}$
embeds onto
![]() $C$
. Since every embedding of
$C$
. Since every embedding of
![]() $G$
maps the spanning cycle of
$G$
maps the spanning cycle of
![]() $G$
onto the outer cycle
$G$
onto the outer cycle
![]() $\partial C$
and the
$\partial C$
and the
![]() $h$
chords of
$h$
chords of
![]() $G$
into a subset of
$G$
into a subset of
![]() $E_m$
, we have that
$E_m$
, we have that
![]() $C$
contains at most
$C$
contains at most
![]() $\binom{|E_m|}{h}\leq |E_m|^h$
graphs from
$\binom{|E_m|}{h}\leq |E_m|^h$
graphs from
![]() $\mathcal{U}$
. The combination of the lower and upper bounds for
$\mathcal{U}$
. The combination of the lower and upper bounds for
![]() $|\mathcal{U}|$
yields
$|\mathcal{U}|$
yields
![]() $|E_m|^h \in \Omega _h\big(n^{h-1}\big)$
, hence
$|E_m|^h \in \Omega _h\big(n^{h-1}\big)$
, hence
![]() $|E_m| \in \Omega _h\big(n^{1-1/h}\big)$
. Overall, the number of edges in
$|E_m| \in \Omega _h\big(n^{1-1/h}\big)$
. Overall, the number of edges in
![]() $C$
is at least
$C$
is at least
![]() $\sum _{i=1}^{\lfloor n/(3h)\rfloor } |E_i|\geq \lfloor n/(3h)\rfloor \cdot |E_m|\in \Omega _h\big(n^{2-1/h}\big)$
.
$\sum _{i=1}^{\lfloor n/(3h)\rfloor } |E_i|\geq \lfloor n/(3h)\rfloor \cdot |E_m|\in \Omega _h\big(n^{2-1/h}\big)$
.
For the case
![]() $h=2$
, the lower bound of Theorem 9 is the best possible, as shown in the following theorem.
$h=2$
, the lower bound of Theorem 9 is the best possible, as shown in the following theorem.
Theorem 10.
For every
![]() $n\in{\mathbb{N}}$
, there exists a convex geometric graph with
$n\in{\mathbb{N}}$
, there exists a convex geometric graph with
![]() $n$
vertices and
$n$
vertices and
![]() $O\big(n^{3/2}\big)$
edges that is universal for
$O\big(n^{3/2}\big)$
edges that is universal for
![]() $\mathcal{OP}_2(n)$
.
$\mathcal{OP}_2(n)$
.
Proof. We construct a convex geometric graph
![]() $C$
and then show that it is universal for
$C$
and then show that it is universal for
![]() $\mathcal{OP}_2(n)$
. The vertices
$\mathcal{OP}_2(n)$
. The vertices
![]() $v_0,\ldots,v_{n-1}$
of
$v_0,\ldots,v_{n-1}$
of
![]() $C$
form a regular convex
$C$
form a regular convex
![]() $n$
-gon, and the edges of this spanning cycle are in
$n$
-gon, and the edges of this spanning cycle are in
![]() $C$
. Denote
$C$
. Denote
and add (the edges of) a star centred at
![]() $v_s$
, for every
$v_s$
, for every
![]() $s\in S$
, to
$s\in S$
, to
![]() $C$
. Clearly,
$C$
. Clearly,
![]() $C$
contains
$C$
contains
![]() $O\big(n^{3/2}\big)$
edges. Moreover, for every
$O\big(n^{3/2}\big)$
edges. Moreover, for every
![]() $d\in \{1,\ldots,\lfloor n/2\rfloor \}$
there exist
$d\in \{1,\ldots,\lfloor n/2\rfloor \}$
there exist
![]() $a,b\in S$
so that
$a,b\in S$
so that
![]() $b-a=d$
. For any
$b-a=d$
. For any
![]() $G\in \mathcal{OP}_2(n)$
, let
$G\in \mathcal{OP}_2(n)$
, let
![]() $a,b\in S$
so that the distance along the outer cycle between the two closest vertices of the two chords of
$a,b\in S$
so that the distance along the outer cycle between the two closest vertices of the two chords of
![]() $G$
is
$G$
is
![]() $b-a$
. As
$b-a$
. As
![]() $C$
contains stars centred at both
$C$
contains stars centred at both
![]() $v_a$
and
$v_a$
and
![]() $v_b$
, the graph
$v_b$
, the graph
![]() $G$
embeds onto
$G$
embeds onto
![]() $C$
.
$C$
.
While we can prove a near-quadratic lower bound for the number of edges of an
![]() $n$
-vertex convex geometric graph that is universal for
$n$
-vertex convex geometric graph that is universal for
![]() $n$
-vertex outerplanar graphs, for
$n$
-vertex outerplanar graphs, for
![]() $n$
-vertex trees we only have an
$n$
-vertex trees we only have an
![]() $\Omega \!\left(n \log n\right)$
lower bound. This lower bound is valid even in the abstract setting and for caterpillars [[Reference Chung and Graham18], Theorem 1], where a caterpillar is a tree such that the removal of its leaves results in a path, called spine.
$\Omega \!\left(n \log n\right)$
lower bound. This lower bound is valid even in the abstract setting and for caterpillars [[Reference Chung and Graham18], Theorem 1], where a caterpillar is a tree such that the removal of its leaves results in a path, called spine.
We next prove that for caterpillars the above lower bound is tight. Namely, we construct a convex geometric graph
![]() $C$
with
$C$
with
![]() $n$
vertices and
$n$
vertices and
![]() $O\!\left(n \log n\right)$
edges that is universal for caterpillars with
$O\!\left(n \log n\right)$
edges that is universal for caterpillars with
![]() $n$
vertices. Our construction of
$n$
vertices. Our construction of
![]() $C$
relies on a simple recursive construction of integer sequences. Specifically, we define a sequence
$C$
relies on a simple recursive construction of integer sequences. Specifically, we define a sequence
![]() $\pi _n$
of
$\pi _n$
of
![]() $n$
integers. Let
$n$
integers. Let
![]() $\pi _1$
be a one-term sequence
$\pi _1$
be a one-term sequence
![]() $\pi _1=(1)$
. For every integer
$\pi _1=(1)$
. For every integer
![]() $m$
of the form
$m$
of the form
![]() $m=2^h-1$
, where
$m=2^h-1$
, where
![]() $h\geq 2$
, let
$h\geq 2$
, let
![]() $\pi _m = \pi _{(m-1)/2}(m)\pi _{(m-1)/2}$
. For example,
$\pi _m = \pi _{(m-1)/2}(m)\pi _{(m-1)/2}$
. For example,
![]() $\pi _{15}=(1,3,1,7,1,3,1,15,1,3,1,7,1,3,1)$
. Now for any
$\pi _{15}=(1,3,1,7,1,3,1,15,1,3,1,7,1,3,1)$
. Now for any
![]() $n\in{\mathbb{N}}$
, the sequence
$n\in{\mathbb{N}}$
, the sequence
![]() $\pi _n$
consists of the first
$\pi _n$
consists of the first
![]() $n$
integers in
$n$
integers in
![]() $\pi _m$
, where
$\pi _m$
, where
![]() $m\geq n$
and
$m\geq n$
and
![]() $m=2^h-1$
, for some integer
$m=2^h-1$
, for some integer
![]() $h\geq 1$
. For example,
$h\geq 1$
. For example,
![]() $\pi _{10}=(1,3,1,7,1,3,1,15,1,3)$
. For
$\pi _{10}=(1,3,1,7,1,3,1,15,1,3)$
. For
![]() $i=1,\dots,n$
, let
$i=1,\dots,n$
, let
![]() $\pi _n(i)$
be the
$\pi _n(i)$
be the
![]() $i$
th term of
$i$
th term of
![]() $\pi _n$
.
$\pi _n$
.
Property 11 ([Reference Frati, Patrignani and Roselli24]). For every
![]() $n\in{\mathbb{N}}$
,
$n\in{\mathbb{N}}$
,
![]() $\pi _n$
is a sequence of positive integers such that for every
$\pi _n$
is a sequence of positive integers such that for every
![]() $x$
with
$x$
with
![]() $1\leq x \leq n$
, the maximum of any
$1\leq x \leq n$
, the maximum of any
![]() $x$
consecutive elements in
$x$
consecutive elements in
![]() $\pi _n$
is at least
$\pi _n$
is at least
![]() $x$
.
$x$
.
The graph
![]() $C$
has vertices
$C$
has vertices
![]() $v_1,\dots,v_n$
, placed in clockwise order along a circle
$v_1,\dots,v_n$
, placed in clockwise order along a circle
![]() $c$
. Further, for
$c$
. Further, for
![]() $i=1,\dots,n$
, we have that
$i=1,\dots,n$
, we have that
![]() $C$
contains edges connecting
$C$
contains edges connecting
![]() $v_i$
to the
$v_i$
to the
![]() $\pi _n(i)$
vertices preceding
$\pi _n(i)$
vertices preceding
![]() $v_i$
and to the
$v_i$
and to the
![]() $\pi _n(i)$
vertices following
$\pi _n(i)$
vertices following
![]() $v_i$
along
$v_i$
along
![]() $c$
. We are now ready to prove the following.
$c$
. We are now ready to prove the following.
Theorem 12.
For every
![]() $n\in{\mathbb{N}}$
, there exists a convex geometric graph
$n\in{\mathbb{N}}$
, there exists a convex geometric graph
![]() $C$
with
$C$
with
![]() $n$
vertices and
$n$
vertices and
![]() $O(n\log n)$
edges that is universal for
$O(n\log n)$
edges that is universal for
![]() $n$
-vertex caterpillars.
$n$
-vertex caterpillars.
Proof. First, the number of edges of
![]() $C$
is at most twice the sum of the integers in
$C$
is at most twice the sum of the integers in
![]() $\pi _n$
; the latter is less than or equal to the sum of the integers in
$\pi _n$
; the latter is less than or equal to the sum of the integers in
![]() $\pi _m$
, where
$\pi _m$
, where
![]() $m\lt 2n$
and
$m\lt 2n$
and
![]() $m=2^h-1$
, for some integer
$m=2^h-1$
, for some integer
![]() $h\geq 1$
. Further,
$h\geq 1$
. Further,
![]() $\pi _m$
is easily shown to be equal to
$\pi _m$
is easily shown to be equal to
![]() $(h-1) \cdot 2^h +1\in O\!\left(n \log n\right)$
.
$(h-1) \cdot 2^h +1\in O\!\left(n \log n\right)$
.
Let
![]() $T$
be a caterpillar with
$T$
be a caterpillar with
![]() $n$
vertices and let
$n$
vertices and let
![]() $(u_1,u_2,\ldots,u_s)$
be the spine of
$(u_1,u_2,\ldots,u_s)$
be the spine of
![]() $T$
, for some
$T$
, for some
![]() $s\geq 1$
. For
$s\geq 1$
. For
![]() $i=1,\ldots,s$
, let
$i=1,\ldots,s$
, let
![]() $S_i$
be the star composed of
$S_i$
be the star composed of
![]() $u_i$
and its adjacent leaves; let
$u_i$
and its adjacent leaves; let
![]() $n_i$
be the number of vertices of
$n_i$
be the number of vertices of
![]() $S_i$
. Let
$S_i$
. Let
![]() $m_1=0$
and, for
$m_1=0$
and, for
![]() $i=2,\ldots,s$
, let
$i=2,\ldots,s$
, let
![]() $m_i=\sum _{j=1}^{i-1} n_j$
. For
$m_i=\sum _{j=1}^{i-1} n_j$
. For
![]() $i=1,\ldots,s$
, we embed
$i=1,\ldots,s$
, we embed
![]() $S_i$
onto the subgraph
$S_i$
onto the subgraph
![]() $C_i$
of
$C_i$
of
![]() $C$
induced by the vertices
$C$
induced by the vertices
![]() $v_{m_i+1},v_{m_i+2},\dots,v_{m_{i}+n_i}$
: This is done by embedding
$v_{m_i+1},v_{m_i+2},\dots,v_{m_{i}+n_i}$
: This is done by embedding
![]() $u_i$
at the vertex
$u_i$
at the vertex
![]() $v_{x_i}$
of
$v_{x_i}$
of
![]() $C_i$
whose degree (in
$C_i$
whose degree (in
![]() $C$
) is maximum, and by embedding the leaves of
$C$
) is maximum, and by embedding the leaves of
![]() $S_i$
at the remaining vertices of
$S_i$
at the remaining vertices of
![]() $C_i$
.
$C_i$
.
By Property 11, we have that
![]() $v_{x_i}$
is adjacent in
$v_{x_i}$
is adjacent in
![]() $C$
to the
$C$
to the
![]() $n_i$
vertices preceding it and the
$n_i$
vertices preceding it and the
![]() $n_i$
vertices following it along
$n_i$
vertices following it along
![]() $c$
(and possibly to more vertices). Hence,
$c$
(and possibly to more vertices). Hence,
![]() $v_{x_i}$
is adjacent to all other vertices of
$v_{x_i}$
is adjacent to all other vertices of
![]() $C_i$
, which proves that the above embedding of
$C_i$
, which proves that the above embedding of
![]() $S_i$
onto
$S_i$
onto
![]() $C_i$
is valid. We now prove that the edge
$C_i$
is valid. We now prove that the edge
![]() $v_{x_i}v_{x_{i+1}}$
belongs to
$v_{x_i}v_{x_{i+1}}$
belongs to
![]() $C$
for all
$C$
for all
![]() $i=1,\ldots,s-1$
. Again by Property 11, the vertex between
$i=1,\ldots,s-1$
. Again by Property 11, the vertex between
![]() $v_{x_i}$
and
$v_{x_i}$
and
![]() $v_{x_{i+1}}$
with the highest degree is adjacent to the
$v_{x_{i+1}}$
with the highest degree is adjacent to the
![]() $n_i+n_{i+1}$
vertices preceding and
$n_i+n_{i+1}$
vertices preceding and
![]() $n_i+n_{i+1}$
vertices following it along
$n_i+n_{i+1}$
vertices following it along
![]() $c$
(and possibly to more vertices). Hence, the vertex between
$c$
(and possibly to more vertices). Hence, the vertex between
![]() $v_{x_i}$
and
$v_{x_i}$
and
![]() $v_{x_{i+1}}$
with the highest degree is adjacent to all other vertices in
$v_{x_{i+1}}$
with the highest degree is adjacent to all other vertices in
![]() $\{v_{m_i+1},v_{m_i+2},\ldots,v_{m_{i+1}+n_{i+1}}\}$
, and in particular to the vertex between
$\{v_{m_i+1},v_{m_i+2},\ldots,v_{m_{i+1}+n_{i+1}}\}$
, and in particular to the vertex between
![]() $v_{x_i}$
and
$v_{x_i}$
and
![]() $v_{x_{i+1}}$
with the lowest degree. The proof is concluded by observing that the edges of the spine
$v_{x_{i+1}}$
with the lowest degree. The proof is concluded by observing that the edges of the spine
![]() $(u_1,u_2,\ldots,u_s)$
do not cross, since the vertices
$(u_1,u_2,\ldots,u_s)$
do not cross, since the vertices
![]() $u_1, u_2,\ldots, u_s$
appear in this clockwise order along
$u_1, u_2,\ldots, u_s$
appear in this clockwise order along
![]() $c$
.
$c$
.
4. Conclusions and open problems
In this paper we introduced and studied the problem of constructing geometric graphs with few vertices and edges that are universal for families of planar graphs. Our research raises several challenging problems.
Universal geometric graphs
First, what is the minimum number of edges in an
![]() $n$
-vertex convex geometric graph that is universal for
$n$
-vertex convex geometric graph that is universal for
![]() $n$
-vertex trees? We proved that the answer is in
$n$
-vertex trees? We proved that the answer is in
![]() $O\!\left(n \log n\right)$
if the convexity requirement is dropped, or if caterpillars, rather than trees, are considered, while the answer is close to
$O\!\left(n \log n\right)$
if the convexity requirement is dropped, or if caterpillars, rather than trees, are considered, while the answer is close to
![]() $\Omega (n^2)$
if outerplanar graphs, rather than trees, are considered.
$\Omega (n^2)$
if outerplanar graphs, rather than trees, are considered.
Second, what is the minimum number of edges in a geometric graph that is universal for all
![]() $n$
-vertex planar graphs? For abstract graphs, Babai, Chung, Erdős, Graham, and Spencer [Reference Babai, Chung, Erdős, Graham and Spencer5] constructed a universal graph with
$n$
-vertex planar graphs? For abstract graphs, Babai, Chung, Erdős, Graham, and Spencer [Reference Babai, Chung, Erdős, Graham and Spencer5] constructed a universal graph with
![]() $O\big(n^{3/2}\big)$
edges based on separators; and Esperet, Joret, and Morin [Reference Esperet, Joret and Morin23] improved the bound to
$O\big(n^{3/2}\big)$
edges based on separators; and Esperet, Joret, and Morin [Reference Esperet, Joret and Morin23] improved the bound to
![]() $n\cdot 2^{O\left(\sqrt{\log n\cdot \log \log n}\right)}$
using strong products of a path with a graph of treewidth at most eight. Can either of these methods be adapted to a geometric setting? The current best lower bound is
$n\cdot 2^{O\left(\sqrt{\log n\cdot \log \log n}\right)}$
using strong products of a path with a graph of treewidth at most eight. Can either of these methods be adapted to a geometric setting? The current best lower bound is
![]() $\Omega (n\log n)$
, the same as for trees [Reference Chung and Graham19], while the best upper bound is only
$\Omega (n\log n)$
, the same as for trees [Reference Chung and Graham19], while the best upper bound is only
![]() $O(n^4)$
.
$O(n^4)$
.
Third, for a constant
![]() $\Delta \in{\mathbb{N}}$
, what is the minimum number of edges in a geometric graph that is universal for all
$\Delta \in{\mathbb{N}}$
, what is the minimum number of edges in a geometric graph that is universal for all
![]() $n$
-vertex planar graphs of maximum degree
$n$
-vertex planar graphs of maximum degree
![]() $\Delta$
?
$\Delta$
?
Plane graphs
The notion of universality can be further extended to plane graphs, that is, planar graphs with given rotation systems. The rotation system of a graph embedded in the plane consists of the counterclockwise orders of the incident edges at all vertices. (A further generalisation to embedded graphs replaces the plane by an arbitrary orientable surface.) For a class
![]() $\mathcal H$
of plane graphs, a geometric graph is universal for
$\mathcal H$
of plane graphs, a geometric graph is universal for
![]() $\mathcal H$
if it contains an embedding of every graph in
$\mathcal H$
if it contains an embedding of every graph in
![]() $\mathcal{H}$
with the given rotation system. Our upper bounds do not extend to this setting. In particular, we do not know what is the minimum number of edges (i) in a geometric graph that is universal for all
$\mathcal{H}$
with the given rotation system. Our upper bounds do not extend to this setting. In particular, we do not know what is the minimum number of edges (i) in a geometric graph that is universal for all
![]() $n$
-vertex plane trees, and (ii) in a convex geometric graph that is universal for all
$n$
-vertex plane trees, and (ii) in a convex geometric graph that is universal for all
![]() $n$
-vertex plane caterpillars.
$n$
-vertex plane caterpillars.
Topological (multi-)graphs
Finally, the problems considered in this paper can be posed for topological (multi-)graphs, as well, in which edges are represented by Jordan arcs. Within this setting we observe a sub-quartic upper bound for the number of edges of a topological multigraph that is universal for all
![]() $n$
-vertex planar graphs.
$n$
-vertex planar graphs.
Theorem 13.
For every
![]() $n\in{\mathbb{N}}$
, there exists a topological multigraph with
$n\in{\mathbb{N}}$
, there exists a topological multigraph with
![]() $n$
vertices and
$n$
vertices and
![]() $O(n^3)$
edges that contains a planar drawing of every
$O(n^3)$
edges that contains a planar drawing of every
![]() $n$
-vertex planar graph.
$n$
-vertex planar graph.
Proof. Every planar graph admits a
![]() $2$
-page monotone topological book embedding [Reference Di Giacomo, Didimo, Liotta and Wismath21]. In such a drawing, every edge is either drawn on one page only, or it is drawn so that it crosses the spine exactly once. As there are
$2$
-page monotone topological book embedding [Reference Di Giacomo, Didimo, Liotta and Wismath21]. In such a drawing, every edge is either drawn on one page only, or it is drawn so that it crosses the spine exactly once. As there are
![]() $\binom{n}{2}$
possible pairs of endpoints, two choices for the page incident to the left endpoint, and less than
$\binom{n}{2}$
possible pairs of endpoints, two choices for the page incident to the left endpoint, and less than
![]() $n$
possible segments of the spine to cross, we have less than
$n$
possible segments of the spine to cross, we have less than
![]() $n^2(n-1)\in \Theta (n^3)$
edges to draw. A drawing that encompasses all those edges is universal for planar graphs on
$n^2(n-1)\in \Theta (n^3)$
edges to draw. A drawing that encompasses all those edges is universal for planar graphs on
![]() $n$
vertices.
$n$
vertices.
A planar graph is subhamiltonian if it is a subgraph of a Hamiltonian planar graph. In particular, planar graphs of degree at most four [Reference Bekos, Gronemann and Raftopoulou7], triconnected planar graphs of degree at most five [Reference Hoffmann and Klemz27], and planar graphs that do not contain a separating triangle [Reference Biedl, Kant and Kaufmann10, Reference Whitney32] are subhamiltonian.
Theorem 14.
For every
![]() $n\in{\mathbb{N}}$
, there exists a topological multigraph with
$n\in{\mathbb{N}}$
, there exists a topological multigraph with
![]() $n$
vertices and
$n$
vertices and
![]() $O(n^2)$
edges that contains a planar drawing of every
$O(n^2)$
edges that contains a planar drawing of every
![]() $n$
-vertex subhamiltonian planar graph.
$n$
-vertex subhamiltonian planar graph.
Proof. Every subhamiltonian planar graph admits a
![]() $2$
-page book embedding [Reference Bernhart and Kainen8]. On each page, draw the complete graph using
$2$
-page book embedding [Reference Bernhart and Kainen8]. On each page, draw the complete graph using
![]() $\binom{n}{2}$
circular arcs, and let
$\binom{n}{2}$
circular arcs, and let
![]() $D$
denote the union of these two drawings. Clearly,
$D$
denote the union of these two drawings. Clearly,
![]() $G$
contains
$G$
contains
![]() $n(n-1)=\Theta (n^2)$
edges and is universal for subhamiltonian planar graphs on
$n(n-1)=\Theta (n^2)$
edges and is universal for subhamiltonian planar graphs on
![]() $n$
vertices.
$n$
vertices.
Acknowledgements
This research was started at the 7th Annual Workshop on Geometry and Graphs held at Bellairs Research Institute in March 2019. Thanks to the other workshop participants for creating a productive working atmosphere.