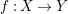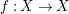AN INVERSE MAPPING THEOREM FOR BLOW-NASH MAPS ON SINGULAR SPACES

Abstract

A semialgebraic map $f:X\rightarrow Y$ between two real algebraic sets is called blow-Nash if it can be made Nash (i.e., semialgebraic and real analytic) by composing with finitely many blowings-up with nonsingular centers.

We prove that if a blow-Nash self-homeomorphism $f:X\rightarrow X$ satisfies a lower bound of the Jacobian determinant condition then $f^{-1}$ is also blow-Nash and satisfies the same condition.

The proof relies on motivic integration arguments and on the virtual Poincaré polynomial of McCrory–Parusiński and Fichou. In particular, we need to generalize Denef–Loeser change of variables key lemma to maps that are generically one-to-one and not merely birational.

1 Introduction

Blow-analytic maps were introduced in the early 1980s by Kuo in order to classify real singularities [26–28]. A map $f:X\rightarrow Y$ between real algebraic sets is called blow-analytic if there exists ${\it\sigma}:M\rightarrow X$ a finite sequence of blowings-up with nonsingular centers such that $f\circ {\it\sigma}$ is analytic. In the same vein a semialgebraic map between real algebraic sets is called blow-Nash if the composition with some finite sequence of blowings-up with nonsingular centers is Nash (i.e., semialgebraic and analytic). Arc-analytic maps were introduced by Kurdyka [29]. A map $f:X\rightarrow Y$ between two real algebraic sets is called arc-analytic if every real analytic arc on $X$ is mapped by $f$ to a real analytic arc on $Y$ . By a result of Bierstone and Milman [5] in response to a question of Kurdyka, if $f:X\rightarrow Y$ is semialgebraic (i.e., its graph is semialgebraic) and if $X$ is nonsingular then $f$ is arc-analytic if and only if it is blow-Nash. When $X$ is nonsingular, the set of points where such a map is analytic is dense [29, 5.2] and thus the Jacobian determinant of $f$ is defined everywhere except on a nowhere dense subset of $X$ .

The following Inverse Function theorem is known for $X$ nonsingular [13]: if the Jacobian determinant of a blow-Nash self-homeomorphism  $h:X\rightarrow X$ is locally bounded from below by a nonzero constant, on the set it is defined, then  $h^{-1}$ is blow-Nash and its Jacobian determinant is also locally bounded from below by a nonzero constant on the set it is defined.

In this paper, we generalize this theorem to singular algebraic sets.

We first introduce, in Section 2.3, the notion of generically arc-analytic maps which are maps $f:X\rightarrow Y$ between real algebraic sets such that there exists a nowhere dense subset $S$ of $X$ with the property that every arc on $X$ not entirely included in $S$ is mapped by $f$ to a real analytic arc on $Y$ . When $\operatorname{dim}\operatorname{Sing}(X)\geqslant 1$ , we see that this condition is strictly weaker than being arc-analytic, otherwise a continuous generically arc-analytic map is an arc-analytic map. Then we show that the semialgebraic generically arc-analytic maps are exactly the blow-Nash ones.

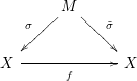
Given $f:X\rightarrow X$ a blow-Nash self-map on a real algebraic set $X$ , we have the following diagram

with ${\it\sigma}$ given by a sequence of blowings-up with nonsingular centers and $\tilde{{\it\sigma}}$ a Nash map.

We may now give an analogue of the lower bound of the Jacobian determinant condition: we say that $f$ satisfies the Jacobian hypothesis if the Jacobian ideal of ${\it\sigma}$ is included in the Jacobian ideal of $\tilde{{\it\sigma}}$ . This condition does not depend on the choice of ${\it\sigma}$ .

We are now able to state the main theorem of this paper: let $f:X\rightarrow X$ be a semialgebraic self-homeomorphism with $X$ an algebraic subset then $f$ is blow-Nash and satisfies the Jacobian hypothesis if and only if $f^{-1}$ satisfies the same conditions.

Heuristically, the main idea of the proof consists in comparing the “motivic volume” of the set of arcs on $X$ and the “motivic volume” of the set of arcs on $X$ coming from arcs on $M$ by $\tilde{{\it\sigma}}$ . This allows us to prove that we can uniquely lift by $\tilde{{\it\sigma}}$ an arc not entirely included in some nowhere dense subset of $X$ . Thereby, such an arc is mapped to an analytic arc by $f^{-1}$ . Thus $f^{-1}$ is generically arc-analytic and so blow-Nash.

Therefore, we first define the arc space on an algebraic subset $X$ of $\mathbb{R}^{N}$ as the set of germs of analytic arcs on $\mathbb{R}^{N}$ which lie in $X$ , that is, ${\it\gamma}:(\mathbb{R},0)\rightarrow X$ such that $\text{for all }f\in I(X),f({\it\gamma})=0$ . For $n\in \mathbb{N}$ , we define the space of $n$ -jets on $X$ as the set of $n$ -jets ${\it\gamma}$ on $\mathbb{R}^{N}$ such that $\text{for all }f\in I(X),f({\it\gamma}(t))\equiv 0\operatorname{mod}t^{n+1}$ . The Section 2.4 contains some general properties of these objects and some useful results for the proof of the main theorem.

The additive invariant used in order to apply motivic integration arguments is the virtual Poincaré polynomial which associates to a set of a certain class, denoted ${\mathcal{A}}{\mathcal{S}}$ , a polynomial with integer coefficients. We recall the main properties of the collection ${\mathcal{A}}{\mathcal{S}}$ in Section 2.1. The virtual Poincaré polynomial was constructed by McCrory and Parusiński [36] and Fichou [11]. The Section 2.2 contains the main properties of this invariant and motivates its use.

In order to compute the above-cited “motivic volumes”, we first prove a version of Denef–Loeser key lemma for the motivic change of variables formula which fulfills our requirements and with a weaker hypothesis: we do not assume the map to be birational but only generically one-to-one.

Based on these results, we may finally prove there exists a subset on $X$ such that every analytic arc on $X$ not entirely included in this subset may be uniquely lifted by $\tilde{{\it\sigma}}$ . This part relies on real analysis arguments and on the fact that an arc not entirely included in the center of a blowing-up may be lifted by this blowing-up.

2 Preliminaries

2.1 Constructible sets and maps

Arc-symmetric sets have been first defined and studied by Kurdyka in [29]. A subset of an analytic manifold $M$ is arc-symmetric if all analytic arcs on $M$ meet it at isolated points or are entirely included in it. Semialgebraic arc-symmetric sets are exactly the closed sets of a Noetherian topology ${\mathcal{A}}$ on $\mathbb{R}^{N}$ . We work with a slightly different framework defined by Parusiński in [41] and consider the collection of sets ${\mathcal{A}}{\mathcal{S}}$ defined as the Boolean algebra generated by semialgebraic arc-symmetric subsets of $\mathbb{P}_{\mathbb{R}}^{n}$ . The advantages of ${\mathcal{A}}{\mathcal{S}}$ over ${\mathcal{A}}$ are that we get a constructible category in the sense of [41] as explained below and a better control of the behavior at infinity. We refer the reader to [31] for a survey.

Definition 2.1. [41, 2.4]

Let ${\mathcal{C}}$ be a collection of semialgebraic sets. A map between two ${\mathcal{C}}$ -sets is a ${\mathcal{C}}$ -map if its graph is a ${\mathcal{C}}$ -set. We say that ${\mathcal{C}}$ is a constructible category if it satisfies the following axioms:

(A1)

${\mathcal{C}}$ contains the algebraic sets.

(A2)

${\mathcal{C}}$ is stable by Boolean operations $\cap$ , $\cup$ and $\setminus$ .

(A3)

1. (a) The inverse image of a ${\mathcal{C}}$ -set by a ${\mathcal{C}}$ -map is a ${\mathcal{C}}$ -set.

2. (b) The image of a ${\mathcal{C}}$ -set by an injective ${\mathcal{C}}$ -map is a ${\mathcal{C}}$ -set.

(A4)

Each locally compact $X\in {\mathcal{C}}$ is Euler in codimension 1, that is, there is a semialgebraic subset $Y\subset X$ with $\operatorname{dim}Y\leqslant \operatorname{dim}X-2$ such that $X\setminus Y$ is Euler ¹ .

Remark 2.2. A locally compact semialgebraic set $X$ is Euler in codimension $1$ if and only if it admits a fundamental class for the homology with coefficient in $\mathbb{Z}_{2}$ . For instance, this property is crucial in the construction of the virtual Poincaré polynomial in order to use the Poincaré duality.

Given a constructible category ${\mathcal{C}}$ , we have a notion of ${\mathcal{C}}$ -closure.

Theorem 2.3. [41, 2.5]

Let ${\mathcal{C}}$ be a constructible category and let $X\in {\mathcal{C}}$ be a locally closed set. Then for any subset $A\subset X$ there is a smallest closed subset of $X$ which belongs to ${\mathcal{C}}$ and contains $A$ . It is denoted by $\overline{A}^{\,{\mathcal{C}}}$ . Any other closed subset of $X$ that is in ${\mathcal{C}}$ and contains $A$ must contain $\overline{A}^{\,{\mathcal{C}}}$ .

Remark 2.4. [41, 2.7]

If $A$ is semialgebraic then $\operatorname{dim}\overline{A}^{\,{\mathcal{C}}}=\operatorname{dim}A$ . In particular, if $A\in {\mathcal{C}}$ then $\overline{A}^{\,{\mathcal{C}}}=A\cup \overline{\overline{A}\setminus A}^{\,{\mathcal{C}}}$ and hence $\operatorname{dim}\big(\overline{A}^{\,{\mathcal{C}}}\setminus A\big)<\operatorname{dim}A$ .

Definition 2.5. [41, Section 4.2]

A semialgebraic subset $A\subset \mathbb{P}_{\mathbb{R}}^{n}$ is an ${\mathcal{A}}{\mathcal{S}}$ -set if for every real analytic arc ${\it\gamma}:(-1,1)\rightarrow \mathbb{P}_{\mathbb{R}}^{n}$ such that ${\it\gamma}((-1,0))\subset A$ there exists ${\it\varepsilon}>0$ such that ${\it\gamma}((0,{\it\varepsilon}))\subset A$ .

Using the proof of [41, Theorem 2.5], we get the following proposition.

Proposition 2.6. There exists a unique Noetherian topology on $\mathbb{P}_{\mathbb{R}}^{n}$ whose closed sets are exactly the closed ${\mathcal{A}}{\mathcal{S}}$ -subsets.

Theorem 2.7. [41]

• ∙ The algebraically constructible sets form a constructible category denoted by ${\mathcal{A}}{\mathcal{C}}$ .

• ∙ ${\mathcal{A}}{\mathcal{S}}$ is a constructible category.

• ∙ Every constructible category contains ${\mathcal{A}}{\mathcal{C}}$ and is contained in ${\mathcal{A}}{\mathcal{S}}$ . This implies that each locally compact set in a constructible category is Euler.

• ∙ ${\mathcal{A}}{\mathcal{S}}$ is the only constructible category which contains the connected components of compact real algebraic sets.

In what follows, constructible subset stands for ${\mathcal{A}}{\mathcal{S}}$ -subset, constructible map stands for map with constructible graph and constructible isomorphism stands for ${\mathcal{A}}{\mathcal{S}}$ -homeomorphism.

In our proof of Lemma 4.5 we need the following result which is, in some sense, a replacement of Chevalley’s theorem for Zariski-constructible sets over an algebraically closed field.

Theorem 2.8. [41, 4.3]

Let $A$ be a semialgebraic subset of a real algebraic subset $X$ of $\mathbb{P}_{\mathbb{R}}^{n}$ . Then $A\in {\mathcal{A}}{\mathcal{S}}$ if and only if there exist a regular morphism of real algebraic varieties $f:Z\rightarrow X$ and $Z^{\prime }$ the union of some connected components of $Z$ such that

$$\begin{eqnarray}\displaystyle & x\in A\Leftrightarrow {\it\chi}\left(f^{-1}(x)\cap Z^{\prime }\right)\equiv 1\quad \text{mod}~2 & \displaystyle \nonumber\\ \displaystyle & x\notin A\Leftrightarrow {\it\chi}\left(f^{-1}(x)\cap Z^{\prime }\right)\equiv 0\quad \text{mod}~2 & \displaystyle \nonumber\end{eqnarray}$$

where ${\it\chi}$ is the Euler characteristic with compact support.

In particular the image of an ${\mathcal{A}}{\mathcal{S}}$ -subset by a regular map whose Euler characteristics with compact support of all the fibers are odd is an ${\mathcal{A}}{\mathcal{S}}$ -subset.

In this paper, we need to work with ${\mathcal{A}}{\mathcal{S}}$ -sets in order to use the virtual Poincaré polynomial discussed below.

In our settings, the Noetherianity of the ${\mathcal{A}}{\mathcal{S}}$ topology will also allow us to prove a version of Denef and Loeser key lemma for the motivic change of variables formula with a weaker hypothesis. Indeed, we will not assume that the map is birational but only Nash, proper and generically one-to-one.

2.2 The virtual Poincaré polynomial

McCrory and Parusiński proved in [36] there exists a unique additive invariant of real algebraic varieties which coincides with the Poincaré polynomial for (co)homology with $\mathbb{Z}_{2}$ coefficients for compact and nonsingular real algebraic varieties. Moreover, this invariant behaves well since its degree is exactly the dimension and the leading coefficient is positive. This virtual Poincaré polynomial has been generalized to ${\mathcal{A}}{\mathcal{S}}$ -subsets by Fichou in [11]. Furthermore Nash-equivalent ${\mathcal{A}}{\mathcal{S}}$ -subsets have the same virtual Poincaré polynomial. These proofs use the weak factorization theorem [1, 49] in a way similar of what has been done by Bittner in [7] to give a new description of the Grothendieck ring in terms of blowings-up.

Theorem 2.9. [11]

There is an additive invariant ${\it\beta}:{\mathcal{A}}{\mathcal{S}}\rightarrow \mathbb{Z}[u]$ , called the virtual Poincaré polynomial, which associates to an ${\mathcal{A}}{\mathcal{S}}$ -subset a polynomial with integer coefficients ${\it\beta}(X)=\sum {\it\beta}_{i}(X)u^{i}\in \mathbb{Z}[u]$ and satisfies the following properties:

• ∙ ${\it\beta}\left(\sqcup _{i=1}^{k}X_{i}\right)=\sum _{i=1}^{k}{\it\beta}(X_{i})$ .

• ∙ ${\it\beta}(X\times Y)={\it\beta}(X){\it\beta}(Y)$ .

• ∙ For $X\neq \varnothing$ , $\operatorname{deg}{\it\beta}(X)=\operatorname{dim}X$ and the leading coefficient of ${\it\beta}(X)$ is positive ² .

• ∙ If $X$ is nonsingular and compact then ${\it\beta}_{i}(X)=\operatorname{dim}H_{i}(X,\mathbb{Z}_{2})$ .

• ∙ If $X$ and $Y$ are Nash-equivalent then ${\it\beta}(X)={\it\beta}(Y)$ .

The virtual Poincaré polynomial is a more interesting additive invariant than the Euler characteristic with compact support since it stores more information, like the dimension. Notice that it is well known that if we forget the arc-symmetric hypothesis and work with all semialgebraic sets, the Euler characteristic with compact support is the only additive invariant [45].

2.3 Geometric settings

For the sake of convenience, we recall some basics of Nash geometry and arc-analytic maps before introducing generically arc-analytic maps.

A Nash function on an open semialgebraic subset of $\mathbb{R}^{N}$ is an analytic function which satisfies a nontrivial polynomial equation. This notion coincides with $C^{\infty }$ semialgebraic functions. We can therefore define the notion of Nash submanifold in an obvious way. This notion is powerful since we can use tools from both algebraic and analytic geometries, for example, we have a Nash implicit function theorem. For more details on Nash geometry, we refer the reader to [8] and [47].

Arc-analytic maps were first introduced by Kurdyka in relation with arc-symmetric sets in [29]. These are maps that send analytic arcs to analytic arcs by composition and hence it is suitable to work with arc-analytic maps between arc-symmetric sets. A semialgebraic map $f:M\rightarrow N$ is blow-Nash if there is a finite sequence of blowings-up with nonsingular centers ${\it\sigma}:\tilde{M}\rightarrow M$ such that $f\circ {\it\sigma}:\tilde{M}\rightarrow N$ is Nash. Let $M$ be an analytic manifold and $f:M\rightarrow \mathbb{R}$ a blow-analytic map, since we can lift an analytic arc by a blowing-up with nonsingular center of a nonsingular variety, $f$ is clearly arc-analytic. Kurdyka conjectured the converse with an additional semialgebraicity ³ hypothesis and Bierstone and Milman brought us the proof in [5]. Parusiński gave another proof in [40]. We refer the reader to [31] for a survey on arc-symmetric sets and arc-analytic maps.

Definition 2.10. Let $U$ be a semialgebraic open subset of $\mathbb{R}^{N}$ . Then an analytic function $f:U\rightarrow \mathbb{R}$ is said to be Nash if there are polynomials $a_{0},\ldots ,a_{d}$ with $a_{d}\neq 0$ such that

$$\begin{eqnarray}a_{d}(x)\left(f(x)\right)^{d}+\cdots +a_{0}(x)=0.\end{eqnarray}$$

Theorem 2.11. [8, Proposition 8.1.8]

Let $U$ be a semialgebraic open subset of $\mathbb{R}^{N}$ . Then $f:U\rightarrow \mathbb{R}$ is a Nash function if and only if $f$ is semialgebraic and of class $C^{\infty }$ .

Definition 2.12. A Nash submanifold of dimension $d$ is a semialgebraic subset $M$ of $\mathbb{R}^{p}$ such that every $x\in M$ admits a Nash chart $(V,{\it\varphi})$ , that is, there are $U$ an open semialgebraic neighborhood of $0\in \mathbb{R}^{p}$ , $V$ an open semialgebraic neighborhood of $x$ in $\mathbb{R}^{p}$ and ${\it\varphi}:U\rightarrow V$ a Nash-diffeomorphism satisfying ${\it\varphi}(0)=x$ and ${\it\varphi}((\mathbb{R}^{d}\times \{0\})\cap U)=M\cap V$ .

Remark 2.13. A nonsingular algebraic subset $M$ of $\mathbb{R}^{p}$ has a natural structure of Nash submanifold given by the Jacobian criterion and the Nash implicit function theorem.

Definition 2.14. [29]

Let $X$ and $Y$ be arc-symmetric subsets of two analytic manifolds. Then $f:X\rightarrow Y$ is arc-analytic if for all analytic arcs ${\it\gamma}:(-{\it\varepsilon},{\it\varepsilon})\rightarrow X$ the composition $f\circ {\it\gamma}:(-{\it\varepsilon},{\it\varepsilon})\rightarrow Y$ is again an analytic arc.

Theorem 2.15. [5]

Let $f$ be a semialgebraic map defined on a nonsingular algebraic subset. Then $f$ is arc-analytic if and only if $f$ is blow-Nash.

Remark 2.16. Let $f:X\rightarrow Y$ be a semialgebraic arc-analytic map between algebraic sets. Then $f$ is blow-Nash even if $X$ is singular. Indeed we may first use a resolution of singularities ${\it\rho}:U\rightarrow X$ given by a sequence of blowings-up with nonsingular centers [19] and apply Theorem 2.15 to $f\circ {\it\rho}:U\rightarrow Y$ .

Remark 2.17. If $M$ is a nonsingular algebraic set and ${\it\rho}:\tilde{M}\rightarrow M$ the blowing-up of $M$ with a nonsingular center, it is well known that we can lift an arc on $M$ by ${\it\rho}$ to an arc on $\tilde{M}$ . This result is obviously false for a singular algebraic set as shown in the following examples. However, if $X$ is a singular algebraic set and ${\it\rho}:\tilde{X}\rightarrow X$ the blowing-up of $X$ with a nonsingular center we can lift an arc on $X$ not entirely included in the center ⁴ and this lifting is unique.

Example 2.18. Consider the Whitney umbrella $X=V(x^{2}-zy^{2})$ and ${\it\rho}:\tilde{X}\rightarrow X$ the blowing-up along the singular locus $I(X_{\text{sing}})=(x,y)$ . Then we cannot lift by ${\it\rho}$ an arc included in the handle $\{x=0,y=0,z<0\}$ ( ${\it\rho}$ is not even surjective).

Example 2.19. This phenomenon still remains in the pure dimensional case. Let $X=V(x^{3}-zy^{3})$ . Then $X$ is of pure dimension $2$ and the blowing-up ${\it\rho}:\tilde{X}\rightarrow X$ along the singular locus $I(X_{\text{sing}})=(x,y)$ is surjective. However we cannot lift the (germ of) analytic arc ${\it\gamma}(t)=(0,0,t)$ to an analytic arc. In the $y$ -chart, $\tilde{X}=\{(X,Y,Z)\in \mathbb{R}^{3},X^{3}=Z\}$ and ${\it\rho}(X,Y,Z)=(XY,Y,Z)$ . Then the lifting of ${\it\gamma}$ should have the form $\tilde{{\it\gamma}}(t)=(t^{\frac{1}{3}},0,t)$ .

Remark 2.20. A continuous subanalytic map $f:U\rightarrow V$ is locally Hölder, that is, for each compact subset $K\subset U$ , there exist ${\it\alpha}>0$ and $C>0$ such that for all $x,y\in K$ , $\Vert f(x)-f(y)\Vert \leqslant C\Vert x-y\Vert ^{{\it\alpha}}$ . See for instance [17], it is a consequence of [20, Section 9, Inequality III]. See also [4, Corollary 6.7]. Or we can directly use Łojasiewicz inequality [4, Theorem 6.4] with $(x,y)\mapsto |f(x)-f(y)|$ and $(x,y)\mapsto |x-y|$ .

The following result will be useful.

Proposition 2.21. Let $f:X\rightarrow Y$ be a surjective proper subanalytic map (resp. proper semialgebraic map) and ${\it\gamma}:[0,{\it\varepsilon})\rightarrow Y$ a real analytic (resp. Nash) arc. Then there exist $m\in \mathbb{N}_{{>}0}$ and $\tilde{{\it\gamma}}:[0,{\it\delta})\rightarrow X$ analytic (resp. Nash) with ${\it\delta}^{m}\leqslant {\it\varepsilon}$ such that $f\circ \tilde{{\it\gamma}}(t)={\it\gamma}(t^{m})$ .

Proof. The proof is divided into two parts. First we use the properness of $f$ to lift ${\it\gamma}$ to an arc on $X$ and then we conclude thanks to Puiseux theorem.

Consider the following diagram

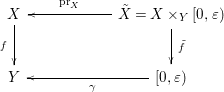
Let $X_{1}=\tilde{f}^{-1}((0,{\it\varepsilon}))$ . Since $f$ is proper, $\overline{X}_{1}\setminus X_{1}\subset \tilde{X}$ . Let $x_{0}\in \overline{X}_{1}\setminus X_{1}$ , then by the curve selection lemma ([8, Proposition 8.1.13] for the semialgebraic case) there exists ${\it\gamma}_{1}:[0,{\it\eta})\rightarrow \tilde{X}$ analytic (resp. Nash) such that ${\it\gamma}_{1}(0)=x_{0}$ and ${\it\gamma}_{1}((0,{\it\eta}))\subset X_{1}$ . We have the following diagram

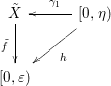
Then, $h(0)=0$ and $h((0,{\it\eta}))\subset (0,{\it\varepsilon})$ . Hence there exists ${\it\alpha}\in (0,{\it\eta})$ such that $h:[0,{\it\alpha})\rightarrow [0,{\it\beta})$ is a subanalytic (resp. semialgebraic) homeomorphism.

By Puiseux theorem ([8, Proposition 8.1.12] for the semialgebraic case; see also [42]), there exist $m\in \mathbb{N}_{{>}0}$ and ${\it\delta}\leqslant {\it\beta}^{\frac{1}{m}}$ such that $h^{-1}(t^{m})$ is analytic (resp. Nash) for $t\in [0,{\it\delta})$ .

Finally, $\tilde{{\it\gamma}}:[0,{\it\delta})\rightarrow X$ defined by $\tilde{{\it\gamma}}(t)=\text{pr}_{X}{\it\gamma}_{1}h^{-1}(t^{m})$ satisfies $f\circ \tilde{{\it\gamma}}(t)={\it\gamma}(t^{m})$ .◻

In the singular case we will work with a slightly different framework.

Definition 2.22. Let $X$ and $Y$ be two algebraic sets. A map $f:X\rightarrow Y$ is said to be generically arc-analytic in dimension  $d=\operatorname{dim}X$ if there exists an algebraic subset $S$ of $X$ with $\operatorname{dim}S<\operatorname{dim}X$ such that for all analytic arc ${\it\gamma}:(-{\it\varepsilon},{\it\varepsilon})\rightarrow X$ not entirely included ⁵ in $S$ , $f\circ {\it\gamma}:(-{\it\varepsilon},{\it\varepsilon})\rightarrow Y$ is analytic.

If $X$ is nonsingular, these maps are exactly the arc-analytic ones.

Lemma 2.23. Let $X$ be a nonsingular algebraic set of dimension ⁶ $d$ and $Y$ an algebraic set. Let $f:X\rightarrow Y$ be a continuous semialgebraic map. If $f$ is generically arc-analytic in dimension $d$ then $f$ is arc-analytic.

Proof. Let $S$ be as in Definition 2.22. By the Jacobian criterion and the Nash implicit function theorem we may assume that $S$ is locally a Nash subset of $\mathbb{R}^{d}$ . Taking the Zariski closure we may moreover assume that $S$ is an algebraic subset of $\mathbb{R}^{d}$ since it does not change the dimension. Let ${\it\gamma}:(-{\it\varepsilon},{\it\varepsilon})\rightarrow \mathbb{R}^{d}$ be an analytic arc entirely included in $S$ .

As in [30, Corollaire 2.7], by Puiseux theorem, we may assume that

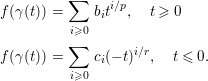$$\begin{eqnarray}\displaystyle f({\it\gamma}(t)) & = & \displaystyle \displaystyle \mathop{\sum }_{i\geqslant 0}b_{i}t^{i/p},\quad t\geqslant 0\nonumber\\ \displaystyle f({\it\gamma}(t)) & = & \displaystyle \displaystyle \mathop{\sum }_{i\geqslant 0}c_{i}(-t)^{i/r},\quad t\leqslant 0.\nonumber\end{eqnarray}$$

By [30, Corollaire 2.8 and Corollaire 2.9], two phenomena may prevent $f({\it\gamma}(t))$ from being analytic: either one of these expansions has a noninteger exponent or these expansions do not coincide.

To handle the first case, we assume that one of these expansions, for instance for $t\geqslant 0$ , has a noninteger exponent, that is,

$$\begin{eqnarray}f({\it\gamma}(t))=\mathop{\sum }_{i=0}^{m}b_{i}t^{i}+bt^{\frac{p}{q}}+\cdots \,,\quad b\neq 0,\;m<\frac{p}{q}<m+1,\;t\geqslant 0.\end{eqnarray}$$

It follows from Remark 2.20 there exists $N\in \mathbb{N}$ such that for every analytic arc ${\it\delta}$ we have $f({\it\gamma}(t)+t^{N}{\it\delta}(t))\equiv f({\it\gamma}(t))\operatorname{mod}t^{m+1}$ . We are going to prove that for ${\it\eta}\in \mathbb{R}^{d}$ generic, the arc $\tilde{{\it\gamma}}(t)={\it\gamma}(t)+t^{N}{\it\eta}$ is not entirely included in $S$ in order to get a contradiction since $f(\tilde{{\it\gamma}}(t))\equiv f({\it\gamma}(t))\operatorname{mod}t^{m+1}$ .

Let $t_{0}\in (-{\it\varepsilon},{\it\varepsilon})\setminus \{0\}$ . Since $\operatorname{dim}S<d$ , there is $\tilde{{\it\eta}}\in \mathbb{R}^{d}\setminus C_{{\it\gamma}(t_{0})}S$ where $C_{{\it\gamma}(t_{0})}S$ is the tangent cone of $S$ at ${\it\gamma}(t_{0})$ . Thus there exists $F\in I(S)$ with $F({\it\gamma}(t_{0})+x)=F_{{\it\mu}}(x)+\cdots +F_{{\it\mu}+r}(x)$ where $\operatorname{deg}F_{i}=i$ and such that $F_{{\it\mu}}(\tilde{{\it\eta}})\neq 0$ . Then $F\left({\it\gamma}(t_{0})+st_{0}^{N}\tilde{{\it\eta}}\right)=\left(st_{0}^{N}\right)^{{\it\mu}}F_{{\it\mu}}(\tilde{{\it\eta}})+\left(st_{0}^{N}\right)^{{\it\mu}+1}G(s,t)$ and hence for $s$ small enough the arc ${\it\gamma}(t)+t^{N}s\tilde{{\it\eta}}$ is not entirely included in $S$ .

Then we prove that the expansions coincide in a similar way. Assume that the expansions are different, that is,

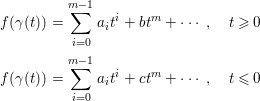$$\begin{eqnarray}\displaystyle f({\it\gamma}(t)) & = & \displaystyle \displaystyle \mathop{\sum }_{i=0}^{m-1}a_{i}t^{i}+bt^{m}+\cdots \,,\quad t\geqslant 0\nonumber\\ \displaystyle f({\it\gamma}(t)) & = & \displaystyle \displaystyle \mathop{\sum }_{i=0}^{m-1}a_{i}t^{i}+ct^{m}+\cdots \,,\quad t\leqslant 0\nonumber\end{eqnarray}$$

with $b\neq c$ . As in the previous case, we may construct an arc $\tilde{{\it\gamma}}$ not entirely included in $S$ such that $f{\it\gamma}(t)$ and $f\tilde{{\it\gamma}}(t)$ coincide up to order $m+1$ . That leads to a contradiction.◻

Remark 2.24. If $\operatorname{dim}\operatorname{Sing}(X)=0$ then a generically arc-analytic map $X\rightarrow Y$ is also arc-analytic since the analytic arcs contained in the singular locus are constant.

Remark 2.25. The previous proof fails when $X$ is not assumed to be nonsingular. Let $X=V(x^{3}-zy^{3})$ and $S=X_{\text{sing}}=O_{z}$ . Consider (germ of) analytic arc ${\it\gamma}(t)=(0,0,t)$ entirely included in $S$ . Given any $N\in \mathbb{N}$ we cannot find ${\it\eta}(t)$ such that $\tilde{{\it\gamma}}(t)={\it\gamma}(t)+t^{N}{\it\eta}(t)$ is not entirely included in $S$ . Indeed, if we inject the coordinates of $\tilde{{\it\gamma}}$ in the equation $x^{3}=zy^{3}$ we get a contradiction considering the orders of vanishing.

Remark 2.26. A continuous semialgebraic generically arc-analytic in dimension $d=\operatorname{dim}X$ map $f:X\rightarrow Y$ may not be arc-analytic if $\operatorname{dim}\operatorname{Sing}(X)\geqslant 1$ . Indeed, let $X=V(x^{3}-zy^{3})$ and $f:X\rightarrow \mathbb{R}$ be defined by $f(x,y,z)=\frac{x}{y}$ . Then $f(0,0,t)=t^{\frac{1}{3}}$ is not analytic.

In the nonsingular case, by Theorem 2.15, the blow-Nash maps are exactly the semialgebraic arc-analytic ones. With the following proposition, we notice that more generally the blow-Nash maps are exactly the semialgebraic generically arc-analytic ones.

Proposition 2.27. Let $X$ be an algebraic set of dimension $d$ . Let $f:X\rightarrow Y$ be a semialgebraic map which is continuous on $\overline{\operatorname{Reg}_{d}X}$ . Then $f$ is generically arc-analytic in dimension $d$ if and only if it is blow-Nash.

Proof. Assume that $f$ is generically arc-analytic. Let ${\it\rho}:U\rightarrow X$ be a resolution of singularities given by a sequence of blowings-up with nonsingular centers, then $f\circ {\it\rho}:U\rightarrow Y$ is semialgebraic and generically arc-analytic with $U$ nonsingular. Thus $f\circ {\it\rho}$ is arc-analytic by Lemma 2.23. By Theorem 2.15, there exists a sequence of blowings-up with nonsingular centers ${\it\eta}:M\rightarrow U$ such that $f\circ {\it\rho}\circ {\it\eta}$ is Nash. Finally $f\circ {\it\sigma}$ is Nash where ${\it\sigma}={\it\rho}\circ {\it\eta}:M\rightarrow X$ is a sequence of blowings-up with nonsingular centers.

Assume that $f$ is blow-Nash. Then there is ${\it\sigma}:M\rightarrow X$ a sequence of blowings-up with nonsingular centers such that $f\circ {\it\sigma}:M\rightarrow Y$ is Nash. Let ${\it\gamma}$ be an arc on $X$ not entirely included in the singular locus of $X$ and the center of ${\it\sigma}$ , then there is $\tilde{{\it\gamma}}$ an arc on $M$ such that ${\it\gamma}={\it\sigma}(\tilde{{\it\gamma}})$ . Thus $f({\it\gamma}(t))=f\circ {\it\sigma}(\tilde{{\it\gamma}}(t))$ is analytic.◻

2.4 Arcs and jets

Arc spaces and truncations of arcs were first introduced by Nash in 1964 [38] and their study has gained new momentum with the works of Kontsevich [24], Denef and Loeser [9] on motivic integration. We can notice that Kurdyka [29], Nobile [39], Lejeune-Jalabert [34], [15], Hickel [18] and others studied arc spaces and jet spaces before the advent of motivic integration. Most of these works concern the relationship between the singularities of a variety and its jet spaces.

In this section, we define the arc space and the jet spaces of a real algebraic set. We first work with the whole ambient Euclidean space and then use the equations of the algebraic set to define arcs and jets on it. Finally we will give and prove a collection of results concerning these objects.

The arc space on $\mathbb{R}^{N}$ is defined by

$$\begin{eqnarray}{\mathcal{L}}\left(\mathbb{R}^{N}\right)=\left\{{\it\gamma}:(\mathbb{R},0)\rightarrow \mathbb{R}^{N},{\it\gamma}\text{ analytic}\right\}\end{eqnarray}$$

and, for $n\in \mathbb{N}$ , the set of $n$ -jets on $\mathbb{R}^{N}$ is defined by

$$\begin{eqnarray}{\mathcal{L}}_{n}\left(\mathbb{R}^{N}\right)={\mathcal{L}}\left(\mathbb{R}^{N}\right)/{\sim}_{n}\end{eqnarray}$$

where ${\it\gamma}_{1}{\sim}_{n}{\it\gamma}_{2}$ if and only if ${\it\gamma}_{1}\equiv {\it\gamma}_{2}\operatorname{mod}t^{n+1}$ . Obviously, $L_{n}(\mathbb{R}^{N})\simeq (\mathbb{R}\{t\}/t^{n+1})^{N}$ . We also consider the truncation maps ${\it\pi}_{n}:{\mathcal{L}}(\mathbb{R}^{N})\rightarrow {\mathcal{L}}_{n}(\mathbb{R}^{N})$ and ${\it\pi}_{n}^{m}:{\mathcal{L}}_{m}(\mathbb{R}^{N})\rightarrow {\mathcal{L}}_{n}(\mathbb{R}^{N})$ , where $m>n$ . These maps are clearly surjective.

Next, assume that $X\subset \mathbb{R}^{N}$ is an algebraic subset. The set of analytic arcs on $X$ is

$$\begin{eqnarray}{\mathcal{L}}(X)=\left\{{\it\gamma}\in {\mathcal{L}}\left(\mathbb{R}^{N}\right),\forall f\in I(X),f({\it\gamma}(t))=0\right\}\end{eqnarray}$$

and, for $n\in \mathbb{N}$ , the set of $n$ -jets on $X$ is

$$\begin{eqnarray}{\mathcal{L}}_{n}(X)=\left\{{\it\gamma}\in {\mathcal{L}}_{n}\left(\mathbb{R}^{N}\right),\forall f\in I(X),f({\it\gamma}(t))\equiv 0\operatorname{mod}t^{n+1}\right\}.\end{eqnarray}$$

When $X$ is singular, we will see that the truncation maps may not be surjective.

Example 2.28. Let $X\subset \mathbb{R}^{N}$ be an algebraic subset, then ${\mathcal{L}}_{0}(X)\simeq X$ and ${\mathcal{L}}_{1}(X)\simeq T^{\text{Zar}}X=\sqcup T_{x}^{\text{Zar}}X$ . Indeed, we just apply Taylor expansion to $f(a+bt)$ where $f\in I(X)$ (or we may directly use that the Zariski tangent space at a point is given by the linear parts of the polynomials $f\in I(X)$ after a translation).

The following lemma is useful to find examples which are hypersurfaces since the constructions of arc space and jet spaces on an algebraic set are algebraic. See [8, Theorem 4.5.1] for a more general result with another proof. We may find similar results for nonprincipal ideals in [8, Proposition 3.3.16, Theorem 4.1.4]. See also [33, Section 6].

Lemma 2.29. Let $f\in \mathbb{R}[x_{1},\ldots ,x_{N}]$ be an irreducible polynomial which changes sign, then $I(V(f))=(f)$ .

Proof. The following proof comes from [33, Lemma 6.14]. After an affine change of coordinates, we may assume that $f(a,b_{1})<0<f(a,b_{2})$ with $a=(a_{1},\ldots ,a_{N-1})$ . Let $g\in I(V(f))$ and assume that $f\nmid g$ in $\mathbb{R}[x_{1},\ldots ,x_{N}]$ . In the PID (and hence UFD) $\mathbb{R}(x_{1},\ldots ,x_{N-1})[x_{N}]$ , $f$ is also irreducible and $f\nmid g$ too. In this PID, we may find ${\it\varphi}$ and ${\it\gamma}$ such that ${\it\varphi}f+{\it\gamma}g=1$ . Let ${\it\varphi}={\it\varphi}_{0}/h$ and ${\it\gamma}={\it\gamma}_{0}/h$ with $0\neq h\in \mathbb{R}[x_{1},\ldots ,x_{N-1}]$ and ${\it\varphi}_{0},{\it\gamma}_{0}\in \mathbb{R}[x_{1},\ldots ,x_{N-1}][x_{N}]$ . Then ${\it\varphi}_{0}f+{\it\gamma}_{0}g=h$ . Let $V$ be a neighborhood of $a$ in $\mathbb{R}^{N-1}$ such that $\text{for all }v\in V,f(v,b_{1})<0<f(v,b_{2})$ . By the IVT, for all $v\in V$ , there is $b_{1}\leqslant b_{v}\leqslant b_{2}$ such that $f(v,b_{v})=0$ , and so $g(v,b_{v})=0$ . Then $\text{for all }v\in V,h(v)=0$ and hence $h\equiv 0$ which is a contradiction.◻

Example 2.30. Let $X=V\left(y^{2}-x^{3}\right)$ . Since $y^{2}-x^{3}$ is irreducible and changes sign, we have $I(X)=\left(y^{2}-x^{3}\right)$ by Lemma 2.29. Hence we get,

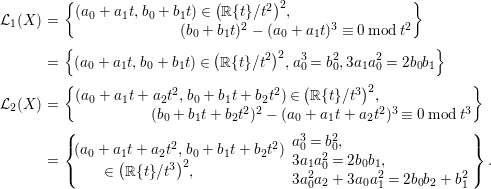$$\begin{eqnarray}\displaystyle {\mathcal{L}}_{1}(X) & = & \displaystyle \left\{\begin{array}{@{}l@{}}(a_{0}+a_{1}t,b_{0}+b_{1}t)\in \left(\mathbb{R}\{t\}/t^{2}\right)^{2}\!,\\ \hspace{75.60004pt}(b_{0}+b_{1}t)^{2}-(a_{0}+a_{1}t)^{3}\equiv 0\operatorname{mod}t^{2}\end{array}\right\}\nonumber\\ \displaystyle & = & \displaystyle \left\{(a_{0}+a_{1}t,b_{0}+b_{1}t)\in \left(\mathbb{R}\{t\}/t^{2}\right)^{2}\!,a_{0}^{3}=b_{0}^{2},3a_{1}a_{0}^{2}=2b_{0}b_{1}\right\}\nonumber\\ \displaystyle {\mathcal{L}}_{2}(X) & = & \displaystyle \left\{\begin{array}{@{}l@{}}(a_{0}+a_{1}t+a_{2}t^{2},b_{0}+b_{1}t+b_{2}t^{2})\in \left(\mathbb{R}\{t\}/t^{3}\right)^{2}\!,\\ \quad \quad \quad \quad \quad (b_{0}+b_{1}t+b_{2}t^{2})^{2}-(a_{0}+a_{1}t+a_{2}t^{2})^{3}\equiv 0\operatorname{mod}t^{3}\end{array}\right\}\nonumber\\ \displaystyle & = & \displaystyle \left\{\!\begin{array}{@{}l@{}}(a_{0}+a_{1}t+a_{2}t^{2},b_{0}+b_{1}t+b_{2}t^{2})\\ \qquad \in \left(\mathbb{R}\{t\}/t^{3}\right)^{2}\!,\end{array}\begin{array}{@{}l@{}}a_{0}^{3}=b_{0}^{2},\\ 3a_{1}a_{0}^{2}=2b_{0}b_{1},\\ 3a_{0}^{2}a_{2}+3a_{0}a_{1}^{2}=2b_{0}b_{2}+b_{1}^{2}\end{array}\!\right\}.\nonumber\end{eqnarray}$$

Then the preimage of $(0,t)\in {\mathcal{L}}_{1}(X)$ by ${\it\pi}_{1}^{2}$ is obviously empty.

We therefore take care not to confuse the set ${\mathcal{L}}_{n}(X)$ of $n$ -jets on $X$ and the set ${\it\pi}_{n}\left({\mathcal{L}}(X)\right)$ of $n$ -jets on $X$ which can be lifted to analytic arcs. Thanks to Hensel’s lemma and Artin approximation theorem [2], this phenomenon disappears in the nonsingular case.

Proposition 2.31. Let $X$ be an algebraic subset of $\mathbb{R}^{N}$ . The following are equivalent:

1. (i) For all $n$ , ${\it\pi}_{n}^{n+1}:L_{n+1}(X)\rightarrow {\mathcal{L}}_{n}(X)$ is surjective.

2. (ii) For all $n$ , ${\it\pi}_{n}:{\mathcal{L}}(X)\rightarrow {\mathcal{L}}_{n}(X)$ is surjective.

3. (iii) $X$ is nonsingular.

Proof. (iii) $\Rightarrow$ (ii) is obvious using Hensel’s lemma and Artin approximation theorem [2].

(ii) $\Rightarrow$ (i) is obvious since ${\it\pi}_{n}={\it\pi}_{n}^{n+1}\circ {\it\pi}_{n+1}$ .

(i) $\Rightarrow$ (iii): Assume that $0$ is a singular point of $X$ . We can find ${\it\gamma}={\it\alpha}t\in {\mathcal{L}}_{1}(X)$ which does not lie in the tangent cone of $X$ at $0$ , that is, such that $f({\it\alpha}t)\not \equiv 0\operatorname{mod}t^{m+1}$ for some $f\in I(X)$ of order $m$ . Such a $1$ -jet cannot be lifted to ${\mathcal{L}}_{m}(X)$ .◻

The set ${\mathcal{L}}_{n}(X)$ of $n$ -jets on $X\subset \mathbb{R}^{N}$ can be seen as a algebraic subset of $\mathbb{R}^{(n+1)N}$ . By a theorem of Greenberg [16], given an algebraic subset $X\subset \mathbb{R}^{N}$ , there exists $c\in \mathbb{N}_{{>}0}$ such that for all $n\in \mathbb{N}$ , ${\it\pi}_{n}({\mathcal{L}}(X))={\it\pi}_{n}^{cn}({\mathcal{L}}_{cn}(X))$ . Then if we work over $\mathbb{C}$ the sets ${\it\pi}_{n}({\mathcal{L}}(X))$ are Zariski-constructible by Chevalley theorem. See for instance [34] ⁷ , [15] or [9].

In our framework, the following example shows that the ${\it\pi}_{n}({\mathcal{L}}(X))$ may not even be ${\mathcal{A}}{\mathcal{S}}$ .

Example 2.32. Let $X=V(x^{2}-zy^{2})$ . Then for every $a\in \mathbb{R}$ , ${\it\gamma}_{a}(t)=(0,t^{2},at^{2})\in {\mathcal{L}}_{2}(X)$ . Let ${\it\eta}(t)=(bt^{3}+t^{4}{\it\eta}_{1}(t),t^{2}+t^{3}{\it\eta}_{2}(t),at^{2}+t^{3}{\it\eta}_{3}(t))\in {\mathcal{L}}(\mathbb{R}^{3})$ . Let $f(x,y,z)=x^{2}-zy^{2}$ , then $f({\it\eta}(t))=(b^{2}-a)t^{6}+t^{7}\tilde{{\it\eta}}(t)$ . So if $a<0$ , ${\it\gamma}_{a}(t)\notin {\it\pi}_{2}({\mathcal{L}}(X))$ . However if $a\geqslant 0$ , ${\it\gamma}_{a}(t)={\it\pi}_{2}(\sqrt{at}^{3},t^{2},at^{2})\in {\it\pi}_{2}({\mathcal{L}}(X))$ .

Proposition 2.33. Let $X\subset \mathbb{R}^{N}$ be an algebraic subset of dimension $d$ . Then:

1. (i) $\operatorname{dim}({\it\pi}_{n}({\mathcal{L}}(X)))=(n+1)d$ .

2. (ii) $\operatorname{dim}({\mathcal{L}}_{n}(X))\geqslant (n+1)d$ .

3. (iii) The fibers of $\tilde{{\it\pi}}_{n}^{m}={{\it\pi}_{n}^{m}}_{|{\it\pi}_{m}({\mathcal{L}}(X))}:{\it\pi}_{m}({\mathcal{L}}(X))\rightarrow {\it\pi}_{n}({\mathcal{L}}(X))$ are of dimension smaller than or equal to $(m-n)d$ where $m\geqslant n$ .

4. (iv) A fiber $({\it\pi}_{n}^{n+1})^{-1}({\it\gamma})$ of ${\it\pi}_{n}^{n+1}:{\mathcal{L}}_{n+1}(X)\rightarrow {\mathcal{L}}_{n}(X)$ is either empty or isomorphic to $T_{{\it\gamma}(0)}^{\text{Zar}}X$ .

If moreover we assume that $X$ is nonsingular, we get the following statement since ${\mathcal{L}}_{n}(X)={\it\pi}_{n}({\mathcal{L}}(X))$ ;

1. (v) $\operatorname{dim}({\mathcal{L}}_{n}(X))=(n+1)d$ .

Proof. We first notice that (i) is a direct consequence of (iii).

(ii) $({\it\pi}_{0}^{n})^{-1}(X\setminus X_{\text{sing}})$ is of dimension $(n+1)d$ since the fiber of ${\it\pi}_{0}^{n}$ over a nonsingular point is of dimension $nd$ .

(iii) We may assume that $m=n+1$ . Let ${\it\gamma}\in {\it\pi}_{n}({\mathcal{L}}(X))$ . We may assume that ${\it\gamma}\in (\mathbb{R}_{n}[t])^{N}$ . We consider the following diagram

with $p_{1}(x,t)={\it\gamma}(t)+t^{n+1}x$ and $p_{2}(x,t)=t$ . Let $\mathfrak{X}=\overline{p_{1}^{-1}(X)\cap \{t\neq 0\}}^{\,Zar}$ . For $c\neq 0$ , $\mathfrak{X}\cap p_{2}^{-1}(c)\simeq X$ and $\operatorname{dim}\mathfrak{X}\cap p_{2}^{-1}(c)=\operatorname{dim}\mathfrak{X}-1$ . Hence $\operatorname{dim}\mathfrak{X}\cap p_{2}^{-1}(0)\leqslant \operatorname{dim}\mathfrak{X}-1=\operatorname{dim}X$ .

We are looking for objects of the form ${\it\pi}_{n+1}({\it\gamma}(t)+t^{n+1}{\it\alpha}(t))$ with ${\it\gamma}(t)+t^{n+1}{\it\alpha}(t)\in {\mathcal{L}}(X)$ . Such an ${\it\alpha}$ is equivalent to a section of ${p_{2}}_{|\mathfrak{X}}$ , that is, $\begin{array}{@{}rcl@{}}\mathbb{R}\ & \rightarrow \ & \mathfrak{X}\\ ~\\ ~\\ t\ & \mapsto \ & ({\it\alpha}(t),t)\end{array}\!\!$ . Since we want an arc modulo $t^{n+2}$ , we are looking for the constant term of ${\it\alpha}$ , therefore $(\tilde{{\it\pi}}_{n}^{n+1})^{-1}({\it\gamma})\subset \mathfrak{X}\cap p_{2}^{-1}(0)$ .

(iv) Let ${\it\gamma}\in {\mathcal{L}}_{n}(X)$ . Let ${\it\eta}\in \mathbb{R}^{N}$ . Assume that $I(X)=(f_{1},\ldots ,f_{r})$ . By Taylor expansion we get

$$\begin{eqnarray}f_{i}({\it\gamma}+t^{n+1}{\it\eta})\equiv f_{i}({\it\gamma}(t))+t^{n+1}\left({\rm\nabla}_{{\it\gamma}(t)}f_{i}\right)({\it\eta})~\mod ~t^{n+2}\end{eqnarray}$$

Assume that $f_{i}({\it\gamma}(t))\equiv t^{n+1}{\it\alpha}_{i}\operatorname{mod}t^{n+2}$ . Since

$$\begin{eqnarray}t^{n+1}({\rm\nabla}_{{\it\gamma}(t)}f_{i})({\it\eta})\equiv t^{n+1}({\rm\nabla}_{{\it\gamma}(0)}f_{i})({\it\eta})\operatorname{mod}t^{n+2},\end{eqnarray}$$

we have

$$\begin{eqnarray}f_{i}({\it\gamma}+t^{n+1}{\it\eta})\equiv t^{n+1}\left({\it\alpha}_{i}+\left({\rm\nabla}_{{\it\gamma}(0)}f_{i}\right)({\it\eta})\right)~\mod ~t^{n+2}\end{eqnarray}$$

Hence, ${\it\gamma}(t)+t^{n+1}{\it\eta}$ is in the fiber $({\it\pi}_{n}^{n+1})^{-1}({\it\gamma})$ if and only if ${\it\alpha}_{i}+({\rm\nabla}_{{\it\gamma}(0)}f_{i})({\it\eta})=0,i=1,\ldots ,r$ .◻

An arc-analytic map $f:X\rightarrow Y$ induces a map $f_{\ast }:{\mathcal{L}}(X)\rightarrow {\mathcal{L}}(Y)$ . Moreover, if $f:X\rightarrow Y$ is analytic, then we also have maps at the level of $n$ -jets $f_{\ast n}:{\mathcal{L}}_{n}(X)\rightarrow {\mathcal{L}}_{n}(Y)$ such that the following diagram commutes

In particular, if $X$ is nonsingular, $\operatorname{Im}f_{\ast n}\subset {\it\pi}_{n}\left({\mathcal{L}}(Y)\right)$ since ${\it\pi}_{n}:{\mathcal{L}}(X)\rightarrow {\mathcal{L}}_{n}(X)$ is surjective.

For $M$ a nonsingular algebraic set and ${\it\sigma}:M\rightarrow X\subset \mathbb{R}^{N}$ analytic, we define $\operatorname{Jac}_{{\it\sigma}}(x)$ the Jacobian matrix of ${\it\sigma}$ at $x$ with respect to a coordinate system at $x$ in $M$ . For ${\it\gamma}$ an arc on $M$ with origin ${\it\gamma}(0)=x$ , we define the order of vanishing of ${\it\gamma}$ along $\operatorname{Jac}_{{\it\sigma}}$ by $\operatorname{ord}_{t}\operatorname{Jac}_{{\it\sigma}}({\it\gamma}(t))=\min \{\operatorname{ord}_{t}{\it\delta}({\it\gamma}(t)),\text{for all }{\it\delta}\text{ being a }m\text{-minor of }\operatorname{Jac}_{{\it\sigma}}\}$ where $m=\min (d,N)$ and ${\it\gamma}$ is expressed in the local coordinate system. This order of vanishing is independent of the choice of the coordinate system.

The critical locus of ${\it\sigma}$ is $C_{{\it\sigma}}=\{x\in M,{\it\delta}(x)=0,\text{for all }{\it\delta}\text{ being a }m-\text{minor of }\operatorname{Jac}_{{\it\sigma}}\}$ . If $E\subset M$ is locally described by an equation $f=0$ around $x$ and if ${\it\gamma}$ is an arc with origin ${\it\gamma}(0)=x$ then $\operatorname{ord}_{{\it\gamma}}E=\operatorname{ord}_{t}f({\it\gamma}(t))$ .

3 The main theorem

Lemma 3.1. Let $X$ be an algebraic subset of $\mathbb{R}^{N}$ and $f:X\rightarrow X$ a blow-Nash map. Let ${\it\sigma}:M\rightarrow X$ be a sequence of blowings-up with nonsingular centers such that $\tilde{{\it\sigma}}=f\circ {\it\sigma}:M\rightarrow X$ is Nash.

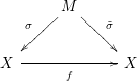
After adding more blowings-up, we may assume that the critical loci of ${\it\sigma}$ and $\tilde{{\it\sigma}}$ are simultaneously normal crossing and denote them by $\sum _{i\in I}{\it\nu}_{i}E_{i}$ and $\sum _{i\in I}\tilde{{\it\nu}}_{i}E_{i}$ .

Then the property

(1) $$\begin{eqnarray}\forall i\in I,\quad {\it\nu}_{i}\geqslant \tilde{{\it\nu}}_{i}\end{eqnarray}$$

does not depend on the choice of ${\it\sigma}$ .

Proof. Given ${\it\sigma}_{1}$ and ${\it\sigma}_{2}$ as in the statement and using Hironaka flattening theorem [21] (which works as it is in the real algebraic case), there exist ${\it\pi}_{1}$ and ${\it\pi}_{2}$ regular such that the following diagram commutes:

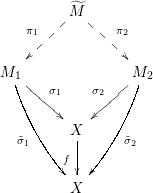
The relation 1 means exactly that the Jacobian ideal of ${\it\sigma}_{i}$ is included in the Jacobian ideal of $\tilde{{\it\sigma}}_{i}$ . By the chain rule, the relations at the level $M_{i}$ are preserved in $\widetilde{M}$ . Again by the chain rule and since the previous diagram commutes, the relations in $M_{1}$ and $M_{2}$ must coincide.◻

Definition 3.2. We say that a map $f:X\rightarrow X$ as in Lemma 3.1 verifying the relation (1) satisfies the Jacobian hypothesis.

Question 3.3. May we find a geometric interpretation of this hypothesis?

The following example is a direct consequence of the chain rule.

Example 3.4. Let $X$ be a nonsingular algebraic set and $f:X\rightarrow X$ a regular map satisfying $|\operatorname{det}\text{d}f|>c$ for a constant $c>0$ , then $f$ satisfies the Jacobian hypothesis.

Theorem 3.5. (Main theorem)

Let $X$ be an algebraic subset of $\mathbb{R}^{N}$ and $f:X\rightarrow X$ a semialgebraic homeomorphism (for the Euclidean topology). If $f$ is blow-Nash and satisfies the Jacobian hypothesis then $f^{-1}$ is blow-Nash and satisfies the Jacobian hypothesis too.

By Lemma 2.23 and Proposition 2.27, if $X$ is a nonsingular algebraic subset we get the following corollary.

Corollary 3.6. [13]

Let $X$ be a nonsingular algebraic subset and $f:X\rightarrow X$ a semialgebraic homeomorphism (for the Euclidean topology). If $f$ is arc-analytic and if there exists $c>0$ satisfying $|\operatorname{det}\text{d}f|>c$ then $f^{-1}$ is arc-analytic and there exists $\tilde{c}>0$ satisfying $|\operatorname{det}\text{d}f^{-1}|>\tilde{c}$ .

Remark 3.7. We recover [13, Theorem 1.1] using the last corollary and [13, Corollaries 2.2 and 2.3].

4 Proof of the main theorem

4.1 Change of variables

An algebraic version of the following lemma was already known in [10], [43] or [44, Section 2] with a proof in [48, 4.1]. The statement given below is more geometric and the proof is quite elementary.

Lemma 4.1. Let $X$ be a $d$ -dimensional algebraic subset of $\mathbb{R}^{N}$ . We consider the following ideal of $\mathbb{R}[x_{1},\ldots ,x_{N}]$

$$\begin{eqnarray}H=\mathop{\sum }_{f_{1},\ldots ,f_{N-d}\in I(X)}{\rm\Delta}(f_{1},\ldots ,f_{N-d})\left((f_{1},\ldots ,f_{N-d}):I(X)\right)\end{eqnarray}$$

where ${\rm\Delta}(f_{1},\ldots ,f_{N-d})$ is the ideal generated by the $(N-d)$ -minors of the matrix $\left(\frac{\partial f_{i}}{\partial x_{j}}\right)_{{i=1,\ldots ,N-d\atop j=1,\ldots ,N}}$ . Then $V(H)$ is the singular locus ⁸   $X_{\text{sing}}$ of $X$ .

Proof. Let $x\notin V(H)$ then there exist $f_{1},\ldots ,f_{N-d}\in I(X)$ , ${\it\delta}$ a $(N-d)$ -minor of $\left(\frac{\partial f_{i}}{\partial x_{j}}\right)_{{i=1,\ldots ,N-d\atop j=1,\ldots ,N}}$ and $h\in \mathbb{R}[x_{1},\ldots ,x_{N}]$ with $hI(X)\subset (f_{1},\ldots ,f_{N-d})$ and $h{\it\delta}(x)\neq 0$ . Since ${\it\delta}(x)\neq 0$ , $x$ is a nonsingular point of $V(f_{1},\ldots ,f_{N-d})$ . Furthermore we have $X=V(I(X))\subset V(f_{1},\ldots ,f_{N-d})\subset V(hI(X))$ and, since $h(x)\neq 0$ , in an open neighborhood $U$ of $x$ in $\mathbb{R}^{N}$ we have $V(hI(X))\cap U=X\cap U$ . Hence $V(f_{1},\ldots ,f_{N-d})\cap U=X\cap U$ . So $x$ is a nonsingular point of $X$ by [8, Proposition 3.3.10]. We proved that $X_{\text{sing}}\subset V(H)$ .

Now, assume that $x\in X\setminus X_{\text{sing}}$ . With the notation of [8, Section 3], the local ring ${\mathcal{R}}_{X,x}={\mathcal{R}}_{\mathbb{R}^{N},x}/I(X){\mathcal{R}}_{\mathbb{R}^{N},x}$ is regular, so we may find a regular system of parameters $(f_{1},\ldots ,f_{N})$ of ${\mathcal{R}}_{X,x}$ such that $I(X){\mathcal{R}}_{\mathbb{R}^{N},x}=(f_{1},\ldots ,f_{N-d}){\mathcal{R}}_{\mathbb{R}^{N},x}$ by [25, VI.1.8 and VI.1.10] ⁹ (see also [8, Proposition 3.3.7]). Moreover, we may assume that the $f_{1},\ldots ,f_{N-d}$ are polynomials. We may use the following classical argument. ${\it\theta}:\mathbb{R}[x_{1},\ldots ,x_{N}]\rightarrow \mathbb{R}^{N}$ defined by $f\mapsto f(x)$ induces an isomorphism ${\it\theta}^{\prime }:\mathfrak{m}_{x}/\mathfrak{m}_{x}^{2}\rightarrow \mathbb{R}^{N}$ . Then $\operatorname{rk}\left(\frac{\partial f_{i}}{\partial x_{j}}(x)\right)=\operatorname{dim}{\it\theta}((f_{1},\ldots ,f_{N-d}))$ which is, by ${\it\theta}^{\prime }$ , the dimension of $((f_{1},\ldots ,f_{N-d})+\mathfrak{m}_{x}^{2})/\mathfrak{m}_{x}^{2}$ as a subspace of $\mathfrak{m}_{x}/\mathfrak{m}_{x}^{2}$ . If we denote by $\mathfrak{m}$ the maximal ideal of ${\mathcal{R}}_{X,x}=\left(\mathbb{R}[x_{1},\ldots ,x_{N}]/(f_{1},\ldots ,f_{N-d})\right)_{\mathfrak{m}_{x}}$ , we have $\mathfrak{m}/\mathfrak{m}^{2}\simeq \mathfrak{m}_{x}/((f_{1},\ldots ,f_{N-d})+\mathfrak{m}_{x}^{2})$ . So we have $\operatorname{dim}\left(\mathfrak{m}/\mathfrak{m}^{2}\right)+\operatorname{rk}\left(\frac{\partial f_{i}}{\partial x_{j}}(x)\right)=N$ .

Furthermore, since ${\mathcal{R}}_{X,x}$ is a $d$ -dimensional regular local ring, $\operatorname{dim}\left(\mathfrak{m}/\mathfrak{m}^{2}\right)=d$ . Hence $\left(\frac{\partial f_{i}}{\partial x_{j}}(x)\right)_{{i=1,\ldots ,N-d\atop j=1,\ldots ,N}}$ is of rank $N-d$ and so there exists ${\it\delta}$ a $(N-d)$ -minor of $\left(\frac{\partial f_{i}}{\partial x_{j}}\right)_{{i=1,\ldots ,N-d\atop j=1,\ldots ,N}}$ such that ${\it\delta}(x)\neq 0$ . Assume that $I(X)=(g_{1},\ldots ,g_{r})$ in $\mathbb{R}[x_{1},\ldots ,x_{N}]$ . Then $g_{i}=\sum \frac{f_{j}}{q_{j}}$ with $q_{j}(x)\neq 0$ , so $g_{i}h_{i}\subset (f_{1},\ldots ,f_{N-d})$ with $h_{i}=\prod q_{j}$ . Then $h=\prod h_{i}$ satisfies $h(x)\neq 0$ and $hI(X)\subset (f_{1},\ldots ,f_{N-d})$ . So $x\notin V(H)$ . Hence $V(H)\subset X_{\text{sing}}\cup (\mathbb{R}^{N}\setminus X)$ .

To complete the proof, it remains to prove that $V(H)\subset X$ . Let $x\notin X$ . There exist $f_{1},\ldots ,f_{N-d}\in I(X)$ such that $f_{i}(x)\neq 0$ . We construct by induction $N-d$ polynomials of the form $g_{i}=a_{i}f_{i}$ with $g_{i}(x)\neq 0$ and $(\text{d}g_{1}\wedge \cdots \wedge \text{d}g_{N-d})_{x}\neq 0$ . Suppose that $g_{1},\ldots ,g_{j-1}$ are constructed, if $(\text{d}g_{1}\wedge \cdots \wedge \text{d}g_{j-1}\wedge \text{d}f_{j})_{x}\neq 0$ , we can take $a_{j}=1$ , so we may assume that $(\text{d}g_{1}\wedge \cdots \wedge \text{d}g_{j-1}\wedge \text{d}f_{j})_{x}=0$ . Then we just have to take some $a_{j}$ satisfying $(\text{d}g_{1}\wedge \cdots \wedge \text{d}g_{j-1}\wedge \text{d}a_{j})_{x}\neq 0$ and $a_{j}(x)\neq 0$ since $(\text{d}g_{1}\wedge \cdots \wedge \text{d}g_{j-1}\wedge \text{d}(a_{j}f_{j}))_{x}=f_{j}(x)(\text{d}g_{1}\wedge \cdots \wedge \text{d}g_{j-1}\wedge \text{d}a_{j})_{x}$ . Then we have $g_{1},\ldots ,g_{N-d}\in I(X)$ whose a $(N-d)$ -minor ${\it\delta}$ satisfies ${\it\delta}(x)\neq 0$ . Moreover we have $g_{i}(x)\neq 0$ and $g_{i}I\subset (g_{1},\ldots ,g_{N-d})$ . So $x\notin V(H)$ .◻

Definition 4.2. Let $X$ be an algebraic subset of $\mathbb{R}^{N}$ . For $e\in \mathbb{N}$ , we set

$$\begin{eqnarray}{\mathcal{L}}^{(e)}(X)=\left\{{\it\gamma}\in {\mathcal{L}}(X),\exists g\in H,g({\it\gamma}(t))\not \equiv 0\operatorname{mod}t^{e+1}\right\}\end{eqnarray}$$

where $H$ is defined in Lemma 4.1.

Remark 4.3. ${\mathcal{L}}(X)=\left(\bigcup _{e\in \mathbb{N}}{\mathcal{L}}^{(e)}(X)\right)\sqcup {\mathcal{L}}(X_{\text{sing}})$

Remark 4.4. In [9], Denef–Loeser set ${\mathcal{L}}^{(e)}(X)={\mathcal{L}}(X)\setminus {\it\pi}_{e}^{-1}({\mathcal{L}}_{e}(X_{\text{sing}}))$ and used the Nullstellensatz to get that $I(X_{\text{sing}})^{c}\subset H$ for some $c$ since $X_{\text{sing}}=V(H)$ . Since we cannot do that in our case, we defined differently ${\mathcal{L}}^{(e)}(X)$ .

The following lemma is an adaptation of Denef–Loeser key lemma [9, Lemma 3.4] to fulfill our settings. The aim of the above-mentioned lemma is to prove a generalization of Kontsevich’s birational transformation rule (change of variables) of [24] to handle singularities. We can find a first adaption to our settings in the nonsingular case in [23, Lemma 4.2].

Lemma 4.5. Let ${\it\sigma}:M\rightarrow X$ be a proper generically ¹⁰ one-to-one Nash map where $M$ is a nonsingular algebraic subset of $\mathbb{R}^{p}$ of dimension $d$ and $X$ an algebraic subset of $\mathbb{R}^{N}$ of dimension $d$ . For $e,e^{\prime }\in \mathbb{N}$ , we set

$$\begin{eqnarray}{\rm\Delta}_{e,e^{\prime }}=\left\{{\it\gamma}\in {\mathcal{L}}(M),\operatorname{ord}_{t}\left(\operatorname{Jac}_{{\it\sigma}}({\it\gamma}(t))\right)=e,{\it\sigma}_{\ast }({\it\gamma})\in {\mathcal{L}}^{(e^{\prime })}(X)\right\}.\end{eqnarray}$$

For $n\in \mathbb{N}$ , let ${\rm\Delta}_{e,e^{\prime },n}$ be the image of ${\rm\Delta}_{e,e^{\prime }}$ by ${\it\pi}_{n}$ . Let $e,e^{\prime },n\in \mathbb{N}$ with $n\geqslant \operatorname{max}(2e,e^{\prime })$ , then:

1. (i) Given ${\it\gamma}\in {\rm\Delta}_{e,e^{\prime }}$ and ${\it\delta}\in {\mathcal{L}}(X)$ with ${\it\sigma}_{\ast }({\it\gamma})\equiv {\it\delta}\operatorname{mod}t^{n+1}$ there exists a unique ${\it\eta}\in {\mathcal{L}}(M)$ such that ${\it\sigma}_{\ast }({\it\eta})={\it\delta}$ and ${\it\eta}\equiv {\it\gamma}\operatorname{mod}t^{n-e+1}$ .

2. (ii) Let ${\it\gamma},{\it\eta}\in {\mathcal{L}}(M)$ . If ${\it\gamma}\in {\rm\Delta}_{e,e^{\prime }}$ and ${\it\sigma}({\it\gamma})\equiv {\it\sigma}({\it\eta})\operatorname{mod}t^{n+1}$ then ${\it\gamma}\equiv {\it\eta}\operatorname{mod}t^{n-e+1}$ and ${\it\eta}\in {\rm\Delta}_{e,e^{\prime }}$ .

3. (iii) The set ${\rm\Delta}_{e,e^{\prime },n}$ is a union of fibers of ${\it\sigma}_{\ast n}$ .

4. (iv) ${\it\sigma}_{\ast n}({\rm\Delta}_{e,e^{\prime },n})$ is constructible and ${\it\sigma}_{\ast n|{\rm\Delta}_{e,e^{\prime },n}}:{\rm\Delta}_{e,e^{\prime },n}\rightarrow {\it\sigma}_{\ast n}({\rm\Delta}_{e,e^{\prime },n})$ is a piecewise trivial fibration ¹¹ with fiber $\mathbb{R}^{e}$ .

Remark 4.6. It is natural to use Taylor expansion to prove some approximation theorems concerning power series as we are going to do for 4.5 (i). For instance, we may find similar argument in [16], [3], or [10]. For 4.5 (i), we will follow the proof of [9, Lemma 3.4] with some differences to match our framework. Concerning 4.5 (iv), we cannot use anymore the section argument of [9] since ${\it\sigma}$ is not assumed to be birational.

Lemma 4.7. (Reduction to complete intersection)

Let $X$ be an algebraic subset of $\mathbb{R}^{N}$ of dimension $d$ . For each $e\in \mathbb{N}$ , ${\mathcal{L}}^{(e)}(X)$ is covered by a finite number of sets of the form

$$\begin{eqnarray}A_{h,{\it\delta}}=\left\{{\it\gamma}\in {\mathcal{L}}(\mathbb{R}^{N}),(h{\it\delta})({\it\gamma})\not \equiv 0\operatorname{mod}t^{e+1}\right\}\end{eqnarray}$$

with ${\it\delta}$ a $(N-d)$ -minor of the matrix $\left(\frac{\partial f_{i}}{\partial x_{j}}\right)_{{i=1,\ldots ,N-d\atop j=1,\ldots ,N}}$ and

$$\begin{eqnarray}h\in ((f_{1},\ldots ,f_{N-d}):I(X))\end{eqnarray}$$

for some $f_{1},\ldots ,f_{N-d}\in I(X)$ .

Moreover,

$$\begin{eqnarray}{\mathcal{L}}(X)\cap A_{h,{\it\delta}}=\left\{{\it\gamma}\in {\mathcal{L}}\left(\mathbb{R}^{N}\right),f_{1}({\it\gamma})=\cdots =f_{N-d}({\it\gamma})=0,h{\it\delta}({\it\gamma})\not \equiv 0\operatorname{mod}t^{e+1}\right\}.\end{eqnarray}$$

Remark 4.8. We may have different polynomials $f_{1},\ldots ,f_{N-d}$ for two different $A_{h,{\it\delta}}$ .

Proof. By Noetherianity, we may assume that $H=(h_{1}{\it\delta}_{1},\ldots ,h_{r}{\it\delta}_{r})$ with $h_{i},{\it\delta}_{i}$ as desired. Therefore, ${\mathcal{L}}^{(e)}(X)\subset \cup A_{h_{i},{\it\delta}_{i}}$ .

Finally,

$$\begin{eqnarray}\displaystyle {\mathcal{L}}(X)\cap A_{h,{\it\delta}} & = & \displaystyle \left\{{\it\gamma}\in {\mathcal{L}}\left(\mathbb{R}^{N}\right),\forall f\in I(X),f({\it\gamma})=0,h{\it\delta}({\it\gamma})\not \equiv 0\operatorname{mod}t^{e+1}\right\}\nonumber\\ \displaystyle & = & \displaystyle \left\{{\it\gamma}\in {\mathcal{L}}\left(\mathbb{R}^{N}\right),f_{1}({\it\gamma})=\cdots =f_{N-d}({\it\gamma})=0,h{\it\delta}({\it\gamma})\not \equiv 0\operatorname{mod}t^{e+1}\right\}.\nonumber\end{eqnarray}$$

Indeed, for the second equality, if $f\in I(X)$ then $hf\in (f_{1},\ldots ,f_{N-d})$ , hence if ${\it\gamma}$ vanishes the $f_{i}$ , then $hf({\it\gamma})=0$ , and so $f({\it\gamma})=0$ since $h({\it\gamma})\neq 0$ .◻

Proof of Lemma 4.5.

We first notice that 4.5 (iii) is a consequence of 4.5 (ii): $\text{for all }{\it\pi}_{n}({\it\gamma})\in {\rm\Delta}_{e,e^{\prime },n}$ we have

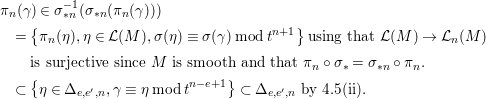$$\begin{eqnarray}\displaystyle & & \displaystyle {\it\pi}_{n}({\it\gamma})\in {\it\sigma}_{\ast n}^{-1}({\it\sigma}_{\ast n}({\it\pi}_{n}({\it\gamma})))\nonumber\\ \displaystyle & & \displaystyle \quad =\left\{{\it\pi}_{n}({\it\eta}),{\it\eta}\in {\mathcal{L}}(M),{\it\sigma}({\it\eta})\equiv {\it\sigma}({\it\gamma})\operatorname{mod}t^{n+1}\right\}\!\,\text{using that }{\mathcal{L}}(M)\rightarrow {\mathcal{L}}_{n}(M)\nonumber\\ \displaystyle & & \displaystyle \qquad \text{is surjective since }M\text{ is smooth and that }{\it\pi}_{n}\circ {\it\sigma}_{\ast }={\it\sigma}_{\ast n}\circ {\it\pi}_{n}.\nonumber\\ \displaystyle & & \displaystyle \quad \subset \left\{{\it\eta}\in {\rm\Delta}_{e,e^{\prime },n},{\it\gamma}\equiv {\it\eta}\operatorname{mod}t^{n-e+1}\right\}\subset {\rm\Delta}_{e,e^{\prime },n}\text{ by 4.5(ii)}.\nonumber\end{eqnarray}$$

Next 4.5 (ii) is a direct consequence of 4.5 (i). We apply 4.5 (i) to ${\it\gamma}$ with ${\it\delta}={\it\sigma}_{\ast }({\it\eta})$ , hence there exists a unique $\tilde{{\it\eta}}$ such that $\tilde{{\it\eta}}\equiv {\it\gamma}\operatorname{mod}t^{n-e+1}$ and ${\it\sigma}_{\ast }(\tilde{{\it\eta}})={\it\sigma}_{\ast }({\it\eta})$ . By the assumptions on ${\it\sigma}$ and the definition of ${\rm\Delta}_{e,e^{\prime }}$ , for ${\it\varphi}_{1}\in {\mathcal{L}}(M)$ and ${\it\varphi}_{2}\in {\rm\Delta}_{e,e^{\prime }}$ with ${\it\varphi}_{1}\neq {\it\varphi}_{2}$ we have ${\it\sigma}({\it\varphi}_{1})\neq {\it\sigma}({\it\varphi}_{2})$ . Hence ${\it\eta}=\tilde{{\it\eta}}$ and ${\it\eta}\equiv {\it\gamma}\operatorname{mod}t^{n-e+1}$ . Since ${\it\sigma}({\it\gamma})\equiv {\it\sigma}({\it\eta})\operatorname{mod}t^{n+1}$ and $n\geqslant e^{\prime }$ , ${\it\sigma}({\it\eta})\in {\mathcal{L}}^{(e^{\prime })}(X)$ . We may write ${\it\eta}(t)={\it\gamma}(t)+t^{n+1-e}u(t)$ and applying Taylor expansion to $\operatorname{Jac}_{{\it\sigma}}({\it\gamma}(t)+t^{n+1-e}u(t))$ we get that $\operatorname{Jac}_{{\it\sigma}}({\it\eta}(t))\equiv \operatorname{Jac}_{{\it\sigma}}({\it\gamma}(t))\operatorname{mod}t^{e+1}$ since $n+1-e\geqslant e+1$ . So ${\it\eta}\in {\rm\Delta}_{e,e^{\prime }}$ .

So we just have to prove 4.5 (i) and 4.5 (iv).

We begin to refine the cover of Lemma 4.7: for $e^{\prime \prime }\leqslant e^{\prime }$ , we set

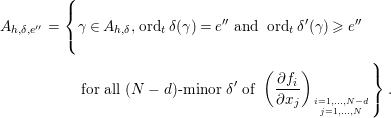$$\begin{eqnarray}\displaystyle A_{h,{\it\delta},e^{\prime \prime }} & = & \displaystyle \left\{{\it\gamma}\in A_{h,{\it\delta}},\operatorname{ord}_{t}{\it\delta}({\it\gamma})=e^{\prime \prime }\text{and }\operatorname{ord}_{t}{\it\delta}^{\prime }({\it\gamma})\geqslant e^{\prime \prime }\right.\nonumber\\ \displaystyle & & \displaystyle \quad \left.\text{for all }(N-d)\text{-minor }{\it\delta}^{\prime }\text{of }\left(\frac{\partial f_{i}}{\partial x_{j}}\right)_{{i=1,\ldots ,N-d\atop j=1,\ldots ,N}}\right\}.\nonumber\end{eqnarray}$$

Fix some $A=A_{h,{\it\delta},e^{\prime \prime }}$ , then it suffices to prove the lemma for ${\rm\Delta}_{e,e^{\prime }}\cap {\it\sigma}^{-1}(A)$ .

Up to renumbering the coordinates, we may also assume that ${\it\delta}$ is the determinant of the first $N-d$ columns of ${\rm\Delta}=\left(\frac{\partial f_{i}}{\partial x_{j}}\right)_{{i=1,\ldots ,N-d\atop j=1,\ldots ,N}}$ .

We choose a local coordinate system of $M$ at ${\it\gamma}(0)$ in order to define $\operatorname{Jac}_{{\it\sigma}}$ and express arcs of $M$ as elements of $\mathbb{R}\{t\}^{d}$ .

Now, a crucial observation is that the first $N-d$ rows of $\operatorname{Jac}_{{\it\sigma}}({\it\gamma})$ are $\mathbb{R}\{t\}$ -linear combinations of the last $d$ rows: the application

$$\begin{eqnarray}\begin{array}{@{}ccccc@{}}M & \longrightarrow & X & \longrightarrow & \mathbb{R}^{N-d}\\ y & \longmapsto & {\it\sigma}(y) & \longmapsto & \left(f_{i}({\it\sigma}(y))\right)_{i=1,\ldots ,N-d}\end{array}\end{eqnarray}$$

is identically zero, so its Jacobian matrix is identically zero too and thus ${\rm\Delta}({\it\sigma}({\it\gamma}))\operatorname{Jac}_{{\it\sigma}}({\it\gamma})=0$ . Let $P$ be the transpose of the comatrix of the submatrix of ${\rm\Delta}$ given by the first $N-d$ columns of ${\rm\Delta}$ , then $P{\rm\Delta}=({\it\delta}I_{N-d},W)$ . Moreover, we have $W({\it\sigma}({\it\gamma}))\equiv 0\operatorname{mod}t^{e^{\prime \prime }}$ . Indeed, if we denote ${\rm\Delta}_{1},\ldots ,{\rm\Delta}_{N-d}$ the $N-d$ first columns of ${\rm\Delta}$ and $W_{1},\ldots ,W_{d}$ the columns of $W$ , then $W_{j}({\it\sigma}({\it\gamma}))$ is solution of $({\rm\Delta}_{1}({\it\sigma}({\it\gamma})),\ldots ,{\rm\Delta}_{N-d}({\it\sigma}({\it\gamma})))X={\it\delta}({\it\sigma}({\it\gamma})){\rm\Delta}_{N-d+j}({\it\sigma}({\it\gamma}))$ since

$$\begin{eqnarray}\displaystyle {\it\delta}({\it\sigma}({\it\gamma})){\rm\Delta}({\it\sigma}({\it\gamma})) & = & \displaystyle \left({\rm\Delta}_{1}({\it\sigma}({\it\gamma})),\ldots ,{\rm\Delta}_{N-d}({\it\sigma}({\it\gamma}))\right)P({\it\sigma}({\it\gamma})){\rm\Delta}({\it\sigma}({\it\gamma}))\nonumber\\ \displaystyle & = & \displaystyle \left({\rm\Delta}_{1}({\it\sigma}({\it\gamma})),\ldots ,{\rm\Delta}_{N-d}({\it\sigma}({\it\gamma}))\right)\left({\it\delta}({\it\sigma}({\it\gamma}))I_{N-d},W({\it\sigma}({\it\gamma}))\right).\nonumber\end{eqnarray}$$

So, by Cramer’s rule,

$$\begin{eqnarray}\displaystyle \left(W_{j}({\it\sigma}({\it\gamma}))\right)_{i} & = & \displaystyle \operatorname{det}\left({\rm\Delta}_{1}({\it\sigma}({\it\gamma})),\ldots ,{\rm\Delta}_{i-1}({\it\sigma}({\it\gamma})),{\rm\Delta}_{N-d+j}({\it\sigma}({\it\gamma})),\right.\nonumber\\ \displaystyle & & \displaystyle \left.{\rm\Delta}_{i+1}({\it\sigma}({\it\gamma})),\ldots ,{\rm\Delta}_{N-d}({\it\sigma}({\it\gamma}))\right).\nonumber\end{eqnarray}$$

Finally, the congruence arises because the minor formed by the $N-d$ first columns is of minimal order by definition of $A$ .

Now the columns of $\operatorname{Jac}_{{\it\sigma}}({\it\gamma})$ are solutions of

(2) $$\begin{eqnarray}\left(t^{-e^{\prime \prime }}\cdot P({\it\sigma}({\it\gamma}))\cdot {\rm\Delta}({\it\sigma}({\it\gamma}))\right)X=0\end{eqnarray}$$

but since $t^{-e^{\prime \prime }}\cdot P({\it\sigma}({\it\gamma}))\cdot {\rm\Delta}({\it\sigma}({\it\gamma}))=(t^{-e^{\prime \prime }}{\it\delta}({\it\sigma}({\it\gamma}))I_{N-d},t^{-e^{\prime \prime }}W({\it\sigma}({\it\gamma})))$ we may express the first $N-d$ coordinates of each solution in terms of the last $d$ coordinates. This completes the proof of the observation.

For 4.5 (i), it suffices to prove that for all $v\in \mathbb{R}\{t\}^{N}$ satisfying ${\it\sigma}({\it\gamma})+t^{n+1}v\in {\mathcal{L}}(X)$ there exists a unique $u\in \mathbb{R}\{t\}^{d}$ such that

(3) $$\begin{eqnarray}{\it\sigma}({\it\gamma}+t^{n+1-e}u)={\it\sigma}({\it\gamma})+t^{n+1}v.\end{eqnarray}$$

By Taylor expansion, we have

(4) $$\begin{eqnarray}{\it\sigma}({\it\gamma}(t)+t^{n+1-e}u)={\it\sigma}({\it\gamma}(t))+t^{n+1-e}\operatorname{Jac}_{{\it\sigma}}({\it\gamma}(t))u+t^{2(n+1-e)}R({\it\gamma}(t),u)\end{eqnarray}$$

with $R({\it\gamma}(t),u)$ analytic in $t$ and $u$ . By (4), (3) is equivalent to

(5) $$\begin{eqnarray}t^{-e}\operatorname{Jac}_{{\it\sigma}}({\it\gamma}(t))u+t^{n+1-2e}R({\it\gamma}(t),u)=v\end{eqnarray}$$

with $n+1-2e\geqslant 1$ by hypothesis.

Since ${\it\sigma}({\it\gamma}(t))+t^{n+1}v\in {\mathcal{L}}(X)$ and using Taylor expansion, we get

$$\begin{eqnarray}0=f_{i}({\it\sigma}({\it\gamma}(t))+t^{n+1}v)=t^{n+1}{\rm\Delta}({\it\sigma}({\it\gamma}(t)))v+t^{2(n+1)}S({\it\gamma}(t),v)\end{eqnarray}$$

with $S({\it\gamma}(t),v)$ analytic in $t$ and $v$ . So $v$ is a solution of (2) and hence the first $N-d$ coefficients of $v$ are $\mathbb{R}\{t\}$ -linear combinations of the last $d$ coefficients with the same relations that for $\operatorname{Jac}_{{\it\sigma}}({\it\gamma})$ . This allows us to reduce (5) to

(6) $$\begin{eqnarray}\displaystyle t^{-e}\operatorname{Jac}_{p\circ {\it\sigma}}({\it\gamma}(t))u+t^{n+1-2e}p\left(R({\it\gamma}(t),u)\right)=p(v) & & \displaystyle\end{eqnarray}$$

where $p:\mathbb{R}^{N}\rightarrow \mathbb{R}^{d}$ is the projection on the last $d$ coordinates. The observation ensures that $\operatorname{ord}_{t}\operatorname{Jac}_{p\circ {\it\sigma}}({\it\gamma}(t))=\operatorname{ord}_{t}\operatorname{Jac}_{{\it\sigma}}({\it\gamma}(t))=e$ and thus (6) is equivalent to

(7) $$\begin{eqnarray}\displaystyle u=\left(t^{-e}\operatorname{Jac}_{p\circ {\it\sigma}}({\it\gamma}(t))\right)^{-1}p(v)-t^{n+1-2e}\left(t^{-e}\operatorname{Jac}_{p\circ {\it\sigma}}({\it\gamma}(t))\right)^{-1}p\left(R({\it\gamma}(t),u)\right). & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$

Applying the implicit function theorem to $u(t,v)$ ensures that given an analytic arc $v(t)$ there exists a solution $u_{v}(t)=u(t,v(t))$ . Using the same argument as in the proof of 4.5 (ii), the solution $u_{v}(t)$ is unique. This proves 4.5 (i).

Let us prove 4.5 (iv). Let ${\it\gamma}\in {\rm\Delta}_{e,e^{\prime }}\cap {\it\sigma}^{-1}(A)$ then

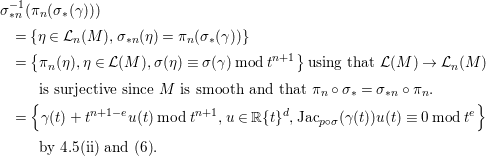$$\begin{eqnarray}\displaystyle & & \displaystyle {\it\sigma}_{\ast n}^{-1}({\it\pi}_{n}({\it\sigma}_{\ast }({\it\gamma})))\nonumber\\ \displaystyle & & \displaystyle \quad =\left\{{\it\eta}\in {\mathcal{L}}_{n}(M),{\it\sigma}_{\ast n}({\it\eta})={\it\pi}_{n}({\it\sigma}_{\ast }({\it\gamma}))\right\}\nonumber\\ \displaystyle & & \displaystyle \quad =\left\{{\it\pi}_{n}({\it\eta}),{\it\eta}\in {\mathcal{L}}(M),{\it\sigma}({\it\eta})\equiv {\it\sigma}({\it\gamma})\operatorname{mod}t^{n+1}\right\}\,\!\text{using that }{\mathcal{L}}(M)\rightarrow {\mathcal{L}}_{n}(M)\nonumber\\ \displaystyle & & \displaystyle \qquad \;\text{is surjective since }M\text{ is smooth and that }{\it\pi}_{n}\circ {\it\sigma}_{\ast }={\it\sigma}_{\ast n}\circ {\it\pi}_{n}.\nonumber\\ \displaystyle & & \displaystyle \quad =\left\{{\it\gamma}(t)+t^{n+1-e}u(t)\operatorname{mod}t^{n+1},u\in \mathbb{R}\{t\}^{d},\operatorname{Jac}_{p\circ {\it\sigma}}({\it\gamma}(t))u(t)\equiv 0\operatorname{mod}t^{e}\right\}\nonumber\\ \displaystyle & & \displaystyle \qquad \;\text{by 4.5(ii) and (6)}.\nonumber\end{eqnarray}$$

Thus, the fiber is an affine subspace of $\mathbb{R}^{de}$ . There are invertible matrices $A$ and $B$ with coordinates in $\mathbb{R}\{t\}$ such that $A\operatorname{Jac}_{p\circ {\it\sigma}}({\it\gamma}(t))B$ is diagonal with entries $t^{e_{1}},\ldots ,t^{e_{d}}$ such that $e=e_{1}+\cdots +e_{d}$ . Therefore the fiber is of dimension $e$ .

Since ${\it\sigma}$ is not assumed to be birational, we cannot use the section argument of [9, 3.4] or [23, 4.2], instead we use a topological Noetherianity argument to prove that ${\it\sigma}_{\ast n|{\rm\Delta}_{e,e^{\prime },n}}$ is a piecewise trivial fibration.

We may assume that $M$ is semialgebraically connected, then by Artin-Mazur theorem [8, 8.4.4], there exist $Y\subset \mathbb{R}^{p+q}$ a nonsingular irreducible algebraic set of dimension $\operatorname{dim}M$ , $M^{\prime }\subset Y$ an open semialgebraic subset of $Y$ , $s:M\rightarrow M^{\prime }$ a Nash-diffeomorphism and $g:Y\rightarrow \mathbb{R}^{N}$ a polynomial map such that the following diagram commutes

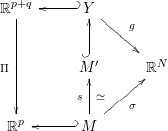
Thus, we have

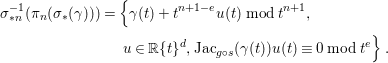$$\begin{eqnarray}\displaystyle & & \displaystyle {\it\sigma}_{\ast n}^{-1}({\it\pi}_{n}({\it\sigma}_{\ast }({\it\gamma})))=\left\{\vphantom{u\in \mathbb{R}\{t\}^{d},\operatorname{Jac}_{g\circ s}({\it\gamma}(t))u(t)\equiv 0\operatorname{mod}t^{e}}{\it\gamma}(t)+t^{n+1-e}u(t)\operatorname{mod}t^{n+1},\right.\nonumber\\ \displaystyle & & \displaystyle \qquad \qquad \qquad \qquad \left.u\in \mathbb{R}\{t\}^{d},\operatorname{Jac}_{g\circ s}({\it\gamma}(t))u(t)\equiv 0\operatorname{mod}t^{e}\right\}.\nonumber\end{eqnarray}$$

So ${\rm\Delta}_{e,e^{\prime },n}$ is constructible and we may assume that ${\it\sigma}_{\ast n}:{\rm\Delta}_{e,e^{\prime },n}\rightarrow {\it\sigma}_{\ast n}({\rm\Delta}_{e,e^{\prime },n})$ is polynomial up to working with arcs over $M^{\prime }$ via $s$ . The fibers (i.e., $\mathbb{R}^{e}$ ) have odd Euler characteristic with compact support, so by Theorem 2.8 the image ${\it\sigma}_{\ast n}({\rm\Delta}_{e,e^{\prime },n})$ is constructible.

Let $V=\{u_{0}+u_{1}t+\cdots +u_{n}t^{n},u_{i}\in \mathbb{R}^{d}\}$ and fix ${\rm\Lambda}_{0}:V\rightarrow V_{0}$ a linear projection on a subspace of dimension $e$ . The set ${\rm\Omega}_{0}=\{{\it\pi}_{n}({\it\gamma}(t))\in {\rm\Delta}_{e,e^{\prime },n},\operatorname{dim}{\rm\Lambda}_{0}({\it\sigma}_{\ast n}^{-1}({\it\pi}_{n}({\it\sigma}_{\ast }({\it\gamma}))))<e\}$ is closed, constructible and union of fibers of ${\it\sigma}_{\ast n}$ . Therefore $({\it\sigma}_{\ast n},{\rm\Lambda}_{0}):{\rm\Delta}_{e,e^{\prime },n}\setminus {\rm\Omega}_{0}\rightarrow {\it\sigma}_{\ast n}({\rm\Delta}_{e,e^{\prime },n}\setminus {\rm\Omega}_{0})\times V_{0}$ is a constructible isomorphism. We now repeat the argument to the closed constructible subset ${\it\sigma}_{\ast n}({\rm\Omega}_{0})$ and so on. Indeed, assume that ${\rm\Delta}_{e,e^{\prime },n}\supsetneq {\rm\Omega}_{0}\supsetneq {\rm\Omega}_{1}\supsetneq \cdots \supsetneq {\rm\Omega}_{i-1}$ are constructed as previously and that ${\rm\Omega}_{i-1}\neq \varnothing$ , then we may choose ${\rm\Lambda}_{i}$ such that ${\rm\Omega}_{i}\subsetneq {\rm\Omega}_{i-1}$ . So on the one hand the process continues until one ${\rm\Omega}_{i}$ is empty, on the other hand it must stop because of the Noetherianity of the ${\mathcal{A}}{\mathcal{S}}$ -topology. Therefore after a finite number of steps, one ${\rm\Omega}_{i}$ is necessarily empty.◻

4.2 Essence of the proof

By our hypothesis, there exists a sequence of blowings-up ${\it\sigma}:M\rightarrow X$ with nonsingular centers such that $\tilde{{\it\sigma}}=f\circ {\it\sigma}:M\rightarrow X$ is Nash.

After adding more blowings-up, we may assume that the critical loci of ${\it\sigma}$ and $\tilde{{\it\sigma}}$ are simultaneously normal crossing and denote them by $\sum {\it\nu}_{i}E_{i}$ and $\sum \tilde{{\it\nu}}_{i}E_{i}$ . Our hypothesis ensures that ${\it\nu}_{i}\geqslant \tilde{{\it\nu}}_{i}$ .

In the same way, we may ensure that the inverse images of $H$ (defined in Lemma 4.1) by ${\it\sigma}$ and $\tilde{{\it\sigma}}$ are also simultaneously normal crossing and denote them ${\it\sigma}^{-1}(H)=\sum _{i\in I}{\it\lambda}_{i}E_{i}$ (resp. $\tilde{{\it\sigma}}^{-1}(H)=\sum _{i\in I}\tilde{{\it\lambda}}_{i}E_{i}$ ).

We recall the usual notation ¹² . For $\mathbf{j}=(j_{i})_{i\in I}\in \mathbb{N}^{I}$ , we set $J=J(\mathbf{j})=\{i,j_{i}\neq 0\}\subset I$ , $E_{J}=\cap _{i\in J}E_{i}$ and $E_{J}^{\bullet }=E_{J}\setminus \cup _{i\in I\setminus J}E_{i}$ .

We also define: ${\mathcal{B}}_{\mathbf{j}}=\{{\it\gamma}\in {\mathcal{L}}(M),\text{for all }i\in J,\operatorname{ord}_{{\it\gamma}}E_{i}=j_{i},{\it\gamma}(0)\in E_{J}^{\bullet }\}$ and for all $n\in \mathbb{N}$ , ${\mathcal{B}}_{\mathbf{j},n}={\it\pi}_{n}({\mathcal{B}}_{\mathbf{j}})$ and $X_{\mathbf{j},n}({\it\sigma})={\it\pi}_{n}({\it\sigma}_{\ast }{\mathcal{B}}_{\mathbf{j}})={\it\sigma}_{\ast n}({\mathcal{B}}_{\mathbf{j},n})$ .

Lemma 4.9. We have ${\mathcal{B}}_{\mathbf{j}}\subset {\rm\Delta}_{e(\mathbf{j}),e^{\prime }(\mathbf{j})}({\it\sigma})$ where $e(\mathbf{j})=\sum _{i\in I}{\it\nu}_{i}j_{i}$ and $e^{\prime }(\mathbf{j})=\sum _{i\in I}{\it\lambda}_{i}j_{i}$ .

Proof. Let ${\it\gamma}\in {\mathcal{B}}_{\mathbf{j}}$ and choose a local coordinate system of $M$ at ${\it\gamma}(0)$ such that the critical locus of ${\it\sigma}$ is locally described by the equation $\prod _{i\in J}x_{i}^{{\it\nu}_{i}}=0$ and $E_{i}$ by the equation $x_{i}=0$ . Since $\operatorname{ord}_{{\it\gamma}}E_{i}=j_{i}$ , we have ${\it\gamma}_{i}(t)=c_{j_{i}}t^{j_{i}}+\cdots \,$ and $c_{j_{i}}\neq 0$ . Then $\prod _{i\in J}{\it\gamma}_{i}^{{\it\nu}_{i}}=ct^{e(\mathbf{j})}+\cdots \,$ with $c\neq 0$ .

So we have $\operatorname{ord}_{t}\left(\operatorname{Jac}_{{\it\sigma}}({\it\gamma}(t))\right)=e(\mathbf{j})$ .

In the same way, $\operatorname{ord}_{{\it\gamma}}{\it\sigma}^{-1}(H)=e^{\prime }(\mathbf{j})$ thus $\operatorname{ord}_{{\it\sigma}({\it\gamma})}(H)=e^{\prime }(\mathbf{j})$ .◻

Therefore we set $A_{n}({\it\sigma})=\left\{\mathbf{j},\sum _{i\in I}{\it\nu}_{i}j_{i}\leqslant \frac{n}{2},\sum _{i\in I}{\it\lambda}_{i}j_{i}\leqslant n\right\}$ . Indeed, for each $\mathbf{j}\in A_{n}({\it\sigma})$ , ${\mathcal{B}}_{\mathbf{j}}\subset {\rm\Delta}_{e(j),e^{\prime }(j)}({\it\sigma})$ and we may apply Lemma 4.5 at the level of $n$ -jets.

The argument of the following lemma is essentially the same as [13, Section 4.2].

Lemma 4.10. (A decomposition of jet spaces)

For all $\mathbf{j}\in A_{n}({\it\sigma})$ , the sets $X_{\mathbf{j},n}({\it\sigma})$ are constructible subsets of ${\mathcal{L}}_{n}(X)$ and $\operatorname{dim}X_{\mathbf{j},n}({\it\sigma})=d(n+1)-s_{\mathbf{j}}-\sum _{i\in I}{\it\nu}_{i}j_{i}$ where $s_{\mathbf{j}}=\sum _{i\in I}j_{i}$ . Moreover $\operatorname{Im}({\it\sigma}_{\ast n})=Z_{n}({\it\sigma})\sqcup \sqcup _{\mathbf{j}\in A_{n}({\it\sigma})}X_{\mathbf{j},n}({\it\sigma})$ and the set $Z_{n}({\it\sigma})$ satisfies $\operatorname{dim}Z_{n}({\it\sigma})<d(n+1)-\frac{n}{c}$ where $c=\operatorname{max}(2{\it\nu}_{\operatorname{max}},{\it\lambda}_{\operatorname{max}})$ .

Proof. Consider $\mathbf{j}$ such that $E_{J}^{\bullet }\neq \varnothing$ and $\text{for all }i\in I,0\leqslant j_{i}\leqslant n$ . The fiber of ${\mathcal{B}}_{\mathbf{j},n}\rightarrow E_{J}^{\bullet }$ is

$$\begin{eqnarray}\mathop{\prod }_{i\in J}(\mathbb{R}^{\ast }\times \mathbb{R}^{n-j_{i}})\times (\mathbb{R}^{n})^{d-|J|}\simeq (\mathbb{R}^{\ast })^{|J|}\times \mathbb{R}^{dn-s_{\mathbf{j}}}\end{eqnarray}$$

since truncating the coordinates of ${\it\gamma}\in {\mathcal{B}}_{\mathbf{j}}$ to degree $n$ produces $d-|J|$ polynomials of degree $n$ with fixed constant terms and for $i\in J$ a polynomial of the form $c_{j_{i}}t^{j_{i}}+c_{j_{i}+1}t^{j_{i}+1}+\cdots +c_{n}t^{n}$ with $c_{j_{i}}\in \mathbb{R}^{\ast }$ and other $c_{k}\in \mathbb{R}$ . We conclude that $\operatorname{dim}{\mathcal{B}}_{\mathbf{j},n}=d(n+1)-s_{\mathbf{j}}$ .

We first assume that $\mathbf{j}\in A_{n}({\it\sigma})$ . By Lemma 4.9, ${\mathcal{B}}_{\mathbf{j}}\subset {\rm\Delta}_{e(\mathbf{j}),e^{\prime }(\mathbf{j})}({\it\sigma})$ . Hence by 4.5 (iv), $X_{\mathbf{j},n}({\it\sigma})$ is constructible since it is the image of the constructible set ${\mathcal{B}}_{\mathbf{j},n}$ by the map ${\it\sigma}_{\ast n|{\rm\Delta}_{e(\mathbf{j}),e^{\prime }(\mathbf{j}),n}}$ with fibers of odd Euler characteristic with compact support. Let ${\it\gamma}_{1}\in {\mathcal{B}}_{\mathbf{j},n}$ and ${\it\gamma}_{2}\in {\rm\Delta}_{e(\mathbf{j}),e^{\prime }(\mathbf{j}),n}$ with ${\it\sigma}_{\ast n}({\it\gamma}_{1})={\it\sigma}_{\ast n}({\it\gamma}_{2})$ , then, by 4.5 (ii), ${\it\gamma}_{1}\equiv {\it\gamma}_{2}\operatorname{mod}t^{n-e(\mathbf{j})+1}$ with $n-e(\mathbf{j})\geqslant e(\mathbf{j})$ and hence ${\it\gamma}_{2}\in {\mathcal{B}}_{\mathbf{j},n}$ . Thus by 4.5 (iv) the map ${\mathcal{B}}_{\mathbf{j},n}\rightarrow X_{\mathbf{j},n}({\it\sigma})$ is a piecewise trivial fibration with fiber $\mathbb{R}^{e(\mathbf{j})}$ . So we have $\operatorname{dim}X_{\mathbf{j},n}({\it\sigma})=d(n+1)-s_{\mathbf{j}}-e(\mathbf{j})$ as claimed.

Otherwise $\mathbf{j}\notin A_{n}({\it\sigma})$ and then $\operatorname{dim}X_{\mathbf{j},n}\leqslant \operatorname{dim}{\mathcal{B}}_{\mathbf{j},n}=d(n+1)-s_{\mathbf{j}}<d(n+1)-\frac{n}{c}$ (since $\frac{n}{2}<e(\mathbf{j})\leqslant {\it\nu}_{\operatorname{max}}s_{\mathbf{j}}$ or $n<e^{\prime }(\mathbf{j})\leqslant {\it\lambda}_{\operatorname{max}}s_{\mathbf{j}}$ ).◻

Remark 4.11. The two previous lemmas work as they are if we replace ${\it\sigma}$ by $\tilde{{\it\sigma}}$ , ${\it\nu}_{i}$ by $\tilde{{\it\nu}}_{i}$ , ${\it\lambda}_{i}$ by $\tilde{{\it\lambda}}_{i}$ and $c$ by $\tilde{c}$ .

Remark 4.12. Remember that $\operatorname{Im}{\it\sigma}_{\ast n}\subset {\it\pi}_{n}({\mathcal{L}}(X))$ (resp. $\operatorname{Im}\tilde{{\it\sigma}}_{\ast n}\subset {\it\pi}_{n}({\mathcal{L}}(X))$ ). Moreover, since we may lift by ${\it\sigma}$ an arc not entirely included in the singular locus, ${\it\pi}_{n}({\mathcal{L}}(X))\setminus \operatorname{Im}{\it\sigma}_{\ast n}\subset {\it\pi}_{n}({\mathcal{L}}(X_{\text{sing}}))$ . The second part only works for ${\it\sigma}$ and does not stand for $\tilde{{\it\sigma}}$ .

In order to apply the virtual Poincaré polynomial, we are going to modify the objects of the partitions of Lemma 4.10.

Notation 4.13. We set

$$\begin{eqnarray}\displaystyle & \displaystyle \widetilde{{\it\pi}_{n}({\mathcal{L}}(X))}:=\overline{Z_{n}({\it\sigma})\sqcup ({\it\pi}_{n}({\mathcal{L}}(X))\setminus \operatorname{Im}{\it\sigma}_{\ast n})}^{\,{\mathcal{A}}S}\sqcup \mathop{\sqcup }_{\mathbf{j}\in A_{n}({\it\sigma})}X_{\mathbf{j},n}({\it\sigma}) & \displaystyle \nonumber\\ \displaystyle & \displaystyle \left(\text{resp. }\widetilde{\operatorname{Im}\tilde{{\it\sigma}}_{\ast n}}:=\overline{Z_{n}(\tilde{{\it\sigma}})}^{\,{\mathcal{A}}S}\sqcup \mathop{\sqcup }_{\mathbf{j}\in A_{n}(\tilde{{\it\sigma}})}X_{\mathbf{j},n}(\tilde{{\it\sigma}})\right) & \displaystyle \nonumber\end{eqnarray}$$

where the closure is taken in the complement of $\sqcup _{\mathbf{j}\in A_{n}({\it\sigma})}X_{\mathbf{j},n}({\it\sigma})(\text{resp. in }\widetilde{{\it\pi}_{n}({\mathcal{L}}(X))}\setminus \sqcup _{\mathbf{j}\in A_{n}(\tilde{{\it\sigma}})}X_{\mathbf{j},n}(\tilde{{\it\sigma}}))$ . Hence we still have the inclusion $\widetilde{\operatorname{Im}\tilde{{\it\sigma}}_{\ast n}}\subset \widetilde{{\it\pi}_{n}({\mathcal{L}}(X))}$ , the unions are still disjoint and the dimensions remain the same.

Lemma 4.14. For $\mathbf{j}\in A_{n}({\it\sigma})$ we have

$$\begin{eqnarray}{\it\beta}(X_{\mathbf{j},n}({\it\sigma}))={\it\beta}(E_{J}^{\bullet })(u-1)^{|J|}u^{nd-\sum ({\it\nu}_{i}+1)j_{i}}\end{eqnarray}$$

(resp. for $\mathbf{j}\in A_{n}(\tilde{{\it\sigma}})$ we have ${\it\beta}(X_{\mathbf{j},n}(\tilde{{\it\sigma}}))={\it\beta}(E_{J}^{\bullet })(u-1)^{|J|}u^{nd-\sum (\tilde{{\it\nu}}_{i}+1)j_{i}}$ ).

Proof. We have

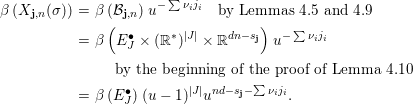$$\begin{eqnarray}\displaystyle {\it\beta}\left(X_{\mathbf{j},n}({\it\sigma})\right) & = & \displaystyle {\it\beta}\left({\mathcal{B}}_{\mathbf{j},n}\right)u^{-\sum {\it\nu}_{i}j_{i}}~~\text{ by Lemmas 4.5 and 4.9}\nonumber\\ \displaystyle & = & \displaystyle {\it\beta}\left(E_{J}^{\bullet }\times (\mathbb{R}^{\ast })^{|J|}\times \mathbb{R}^{dn-s_{\mathbf{j}}}\right)u^{-\sum {\it\nu}_{i}j_{i}}\nonumber\\ \displaystyle & & \displaystyle \quad \text{by the beginning of the proof of Lemma 4.10}\nonumber\\ \displaystyle & = & \displaystyle {\it\beta}\left(E_{J}^{\bullet }\right)(u-1)^{|J|}u^{nd-s_{\mathbf{j}}-\sum {\it\nu}_{i}j_{i}}.\nonumber\end{eqnarray}$$

The same argument works for $\tilde{{\it\sigma}}$ too.◻

Lemma 4.15. $\text{For all }i\in I,{\it\nu}_{i}=\tilde{{\it\nu}}_{i}$ .

Proof. Applying the virtual Poincaré polynomial to the partitions of Notation 4.13, we get

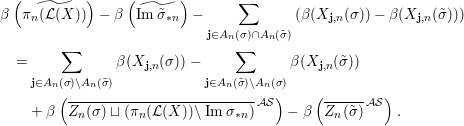$$\begin{eqnarray}\displaystyle & & \displaystyle {\it\beta}\left(\widetilde{{\it\pi}_{n}({\mathcal{L}}(X))}\right)-{\it\beta}\left(\widetilde{\operatorname{Im}\tilde{{\it\sigma}}_{\ast n}}\right)-\mathop{\sum }_{\mathbf{j}\in A_{n}({\it\sigma})\cap A_{n}(\tilde{{\it\sigma}})}\left({\it\beta}(X_{\mathbf{j},n}({\it\sigma}))-{\it\beta}(X_{\mathbf{j},n}(\tilde{{\it\sigma}}))\right)\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{\mathbf{j}\in A_{n}({\it\sigma})\setminus A_{n}(\tilde{{\it\sigma}})}{\it\beta}(X_{\mathbf{j},n}({\it\sigma}))-\mathop{\sum }_{\mathbf{j}\in A_{n}(\tilde{{\it\sigma}})\setminus A_{n}({\it\sigma})}{\it\beta}(X_{\mathbf{j},n}(\tilde{{\it\sigma}}))\nonumber\\ \displaystyle & & \displaystyle \qquad +\,{\it\beta}\left(\overline{Z_{n}({\it\sigma})\sqcup ({\it\pi}_{n}({\mathcal{L}}(X))\setminus \operatorname{Im}{\it\sigma}_{\ast n})}^{\,{\mathcal{A}}{\mathcal{S}}}\right)-{\it\beta}\left(\overline{Z_{n}(\tilde{{\it\sigma}})}^{\,{\mathcal{A}}{\mathcal{S}}}\right).\nonumber\end{eqnarray}$$

We set

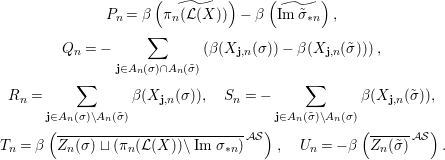$$\begin{eqnarray}\displaystyle & \displaystyle P_{n}={\it\beta}\left(\widetilde{{\it\pi}_{n}({\mathcal{L}}(X))}\right)-{\it\beta}\left(\widetilde{\operatorname{Im}\tilde{{\it\sigma}}_{\ast n}}\right), & \displaystyle \nonumber\\ \displaystyle & \displaystyle Q_{n}=-\mathop{\sum }_{\mathbf{j}\in A_{n}({\it\sigma})\cap A_{n}(\tilde{{\it\sigma}})}\left({\it\beta}(X_{\mathbf{j},n}({\it\sigma}))-{\it\beta}(X_{\mathbf{j},n}(\tilde{{\it\sigma}}))\right), & \displaystyle \nonumber\\ \displaystyle & \displaystyle R_{n}=\mathop{\sum }_{\mathbf{j}\in A_{n}({\it\sigma})\setminus A_{n}(\tilde{{\it\sigma}})}{\it\beta}(X_{\mathbf{j},n}({\it\sigma})),\quad \displaystyle S_{n}=-\mathop{\sum }_{\mathbf{j}\in A_{n}(\tilde{{\it\sigma}})\setminus A_{n}({\it\sigma})}{\it\beta}(X_{\mathbf{j},n}(\tilde{{\it\sigma}})), & \displaystyle \nonumber\\ \displaystyle & \displaystyle T_{n}={\it\beta}\left(\overline{Z_{n}({\it\sigma})\sqcup ({\it\pi}_{n}({\mathcal{L}}(X))\setminus \operatorname{Im}{\it\sigma}_{\ast n})}^{\,{\mathcal{A}}{\mathcal{S}}}\right),\quad \displaystyle U_{n}=-{\it\beta}\left(\overline{Z_{n}(\tilde{{\it\sigma}})}^{\,{\mathcal{A}}{\mathcal{S}}}\right). & \displaystyle \nonumber\end{eqnarray}$$

Assume there exists $i_{0}\in I$ such that ${\it\nu}_{i_{0}}>\tilde{{\it\nu}}_{i_{0}}$ .

Then for $n$ big enough,

$$\begin{eqnarray}K_{n}=\left\{s_{\mathbf{j}}+\mathop{\sum }_{i\in I}\tilde{{\it\nu}}_{i}j_{i},~\mathbf{j}\in A_{n}({\it\sigma})\cap A_{n}(\tilde{{\it\sigma}}),\mathop{\sum }_{i\in I}({\it\nu}_{i}-\tilde{{\it\nu}}_{i})j_{i}>0\right\}\end{eqnarray}$$

is not empty. The minimum $k_{n}=\min K_{n}$ stabilizes for $n$ greater than some rank $n_{0}$ . Let $k=k_{n_{0}}$ . Then, for $n\geqslant n_{0}$ , the degree of $Q_{n}$ is $\operatorname{max}\left\{d(n+1)-s_{\mathbf{j}}-\sum _{i\in I}\tilde{{\it\nu}}_{i}j_{i}\right\}=d(n+1)-k$ using the computation at the beginning of the proof of Lemma 4.10.

The leading coefficients of $P_{n}$ is positive since $P_{n}={\it\beta}\left(\widetilde{{\it\pi}_{n}({\mathcal{L}}(X))}\setminus \widetilde{\operatorname{Im}\tilde{{\it\sigma}}_{\ast n}}\right)$ . The leading coefficient of $Q_{n}$ is also positive. Hence the degree of the LHS is at least $d(n+1)-k$ .

Moreover, we have $\operatorname{deg}R_{n}<d(n+1)-\frac{n}{\tilde{c}}$ , $\operatorname{deg}S_{n}<d(n+1)-\frac{n}{c}$ , $\operatorname{deg}T_{n}<d(n+1)-\frac{n}{\operatorname{max}(c,1)}$ and $\operatorname{deg}U_{n}<d(n+1)-\frac{n}{\tilde{c}}$ . Indeed, for $T_{n}$ , ${\it\pi}_{n}({\mathcal{L}}(X))\setminus \!\operatorname{Im}{\it\sigma}_{\ast n}\subset {\it\pi}_{n}({\mathcal{L}}(X_{\text{sing}}))$ and $\operatorname{dim}\left({\it\pi}_{n}({\mathcal{L}}(X_{\text{sing}}))\right)\leqslant (n+1)(d-1)<d(n+1)-n$ by 2.33 (i). So the degree of the RHS is less than $d(n+1)-\frac{n}{\operatorname{max}(c,\tilde{c},1)}$ .

We get a contradiction for $n$ big enough.◻

Corollary 4.16. $Q_{n}=0$ .

Since $\tilde{{\it\sigma}}:M\rightarrow X$ is a proper Nash map generically one-to-one, there exists a closed semialgebraic subsets $S\subset X$ with $\operatorname{dim}S<d$ such that for every $p\in X\setminus S$ , $\tilde{{\it\sigma}}^{-1}(p)$ is a singleton.

Lemma 4.17. Every arc on $X$ not entirely included in $S\cup X_{\text{sing}}$ may be uniquely lifted by $\tilde{{\it\sigma}}$ .

Proof. Let ${\it\gamma}$ be an analytic arc on $X$ not entirely in $S$ and not entirely in the singular locus of $X$ .

Assume that ${\it\gamma}\notin \operatorname{Im}\tilde{{\it\sigma}}_{\ast }$ . Then, by Proposition 2.21, we have

$$\begin{eqnarray}\tilde{{\it\sigma}}^{-1}({\it\gamma}(t))=\mathop{\sum }_{i=0}^{m}b_{i}t^{i}+bt^{\frac{p}{q}}+\cdots \,,\quad b\neq 0,\;m<\frac{p}{q}<m+1,\;t\geqslant 0.\end{eqnarray}$$

Since $\tilde{{\it\sigma}}^{-1}$ is locally Hölder by Remark 2.20, there is $N\in \mathbb{N}$ such that for every analytic arc ${\it\eta}$ on $X$ with ${\it\gamma}\equiv {\it\eta}\operatorname{mod}t^{N}$ we have $\tilde{{\it\sigma}}^{-1}({\it\eta}(t))\equiv \tilde{{\it\sigma}}^{-1}({\it\gamma}(t))\operatorname{mod}t^{m+1}$ . Hence such an analytic arc ${\it\eta}$ is not in the image of $\tilde{{\it\sigma}}_{\ast }$ and for $n\geqslant N$ , ${\it\pi}_{n}({\it\eta})$ is not in the image of $\tilde{{\it\sigma}}_{\ast n}:{\mathcal{L}}_{n}(M)\rightarrow {\it\pi}_{n}({\mathcal{L}}(X))$ . Hence $({{\it\pi}_{N}^{n}}_{|{\it\pi}_{n}({\mathcal{L}}(X))})^{-1}({\it\pi}_{N}({\it\gamma}))\subset {\it\pi}_{n}({\mathcal{L}}(X))\setminus \operatorname{Im}(\tilde{{\it\sigma}}_{\ast n})$ .

The first step consists in computing the dimension of the fiber $({{\it\pi}_{N}^{n}}_{|{\it\pi}_{n}({\mathcal{L}}(X))})^{-1}({\it\pi}_{N}({\it\gamma}))$ where $n\geqslant N$ . For that, we will work with a resolution ${\it\rho}:\tilde{X}\rightarrow X$ (for instance ${\it\sigma}$ ) instead of $\tilde{{\it\sigma}}$ since every analytic arc on $X$ not entirely included in $X_{\text{sing}}$ may be lifted to $\tilde{X}$ by ${\it\rho}$ . Let ${\it\theta}$ be the unique analytic arc on $\tilde{X}$ such that ${\it\rho}({\it\theta})={\it\gamma}$ . Let $e=\operatorname{ord}_{t}(\operatorname{Jac}_{{\it\rho}}({\it\theta}(t)))$ and $e^{\prime }$ be such that ${\it\gamma}\in {\mathcal{L}}^{(e^{\prime })}(X)$ . We may assume that $N\geqslant \operatorname{max}(2e,e^{\prime })$ in order to apply Lemma 4.5 to ${\it\rho}$ for ${\it\gamma}$ .

We consider the following diagram

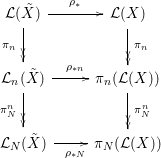
Since the fibers of ${{\it\rho}_{\ast n}}_{|{\rm\Delta}_{e,e^{\prime },n}}$ and ${{\it\rho}_{\ast N}}_{|{\rm\Delta}_{e,e^{\prime },N}}$ are of dimension $e$ , and since the fibers of ${\it\pi}_{N}^{n}:{\mathcal{L}}_{n}(\tilde{X})\rightarrow {\mathcal{L}}_{N}(\tilde{X})$ are of dimension $(n-N)d$ , we have $\operatorname{dim}\big(\big({{\it\pi}_{N}^{n}}_{|{\it\pi}_{n}({\mathcal{L}}(X))}\big)^{-1}({\it\pi}_{N}({\it\gamma}))\big)=(n-N)d$ .

Hence $\operatorname{dim}\left({\it\pi}_{n}({\mathcal{L}}(X))\setminus \operatorname{Im}(\tilde{{\it\sigma}}_{\ast n})\right)\geqslant (n-N)d$ . And so, with the notation of Lemma 4.15, we have

$$\begin{eqnarray}P_{n}+0=R_{n}+S_{n}+T_{n}+U_{n}\end{eqnarray}$$

with $\operatorname{deg}P_{n}\geqslant (n-N)d=(n+1)d-(N+1)d$ and $\operatorname{deg}(R_{n}+S_{n}+T_{n}+U_{n})<(n+1)d-\frac{n}{\operatorname{max}(c,\tilde{c},1)}$ .

We get a contradiction for $n$ big enough.◻

End of the proof of Theorem 3.5.

Let ${\it\gamma}$ be an analytic arc on $X$ not entirely included in $S\cup X_{\text{sing}}$ . By Lemma 4.17 and since ${\it\gamma}$ is not entirely included in $S\cup X_{\text{sing}}$ , $\tilde{{\it\sigma}}^{-1}({\it\gamma}(t))$ is well defined and analytic. Hence $f^{-1}({\it\gamma}(t))={\it\sigma}(\tilde{{\it\sigma}}^{-1}({\it\gamma}(t)))$ is real analytic. Finally $f^{-1}$ is generically arc-analytic in dimension $d=\operatorname{dim}X$ .

So $f^{-1}$ is blow-Nash by Proposition 2.27 and $\text{for all }i\in I,{\it\nu}_{i}=\tilde{{\it\nu}}_{i}$ by Lemma 4.15. Then, arguing as in Lemma 3.1, $f^{-1}$ satisfies the Jacobian hypothesis too.◻