1 Introduction and motivation
Not so many concepts in mathematics are defined recursively, but triviality is one of them: in the jargon of mathematicians, something is “trivial” when one understands it immediately or when one can prove it trivially. And a measure of success, when undertaking a mathematical journey, is the number of things that have become trivial by the end of this journey. Other measures of success include the ability to reuse the results and the methods that were acquired in the course of this journey, and the ability to explain these new methods, these new results, and these new trivialities, as per Boileau’s French alexandrines “what one understands well is told with clarity; and the words to say it arise easily” (1815).
Rota once singled out, among mathematicians, the “problem solvers” and the “theorizers” (1996). Problem solvers are after the goal, the more dazzling the better: the point of getting to a fountain is to drink, the sooner the better. Theorizers (or “theory builders” Gowers Reference Gowers2000) concur with the Little Prince about getting to the fountain; they see value in the means, the more enlightening the better: the point of getting to the fountain is not just to make a splash. Rota pointed out that most mathematicians are a mixture of theorizer and problem solver.
Computer scientists too oscillate between solving problems and developing tools to solve problems (or to develop other tools). As a result, our middle path is meandering. Take a statically typed programming language, for example. Do we care about why our program has a type? No of course, we are too busy forging ahead in the safety that evaluation cannot go wrong. But if the type inferencer rejects our program, oh, the pain: we are forced to understand the error message and therefore either or all of the type system, the type inferencer, and its implementation, when all we care about is for the type inferencer to accept our program so that we can forge ahead. In this context, the middle path is to know enough about the type system to understand the common error messages of the type inferencer, an extensible middle ground where we know enough theory to solve problems.
The situation is dual for proving a proposition in the Coq Proof Assistant Bertot & Castéran (Reference Bertot and Castéran2004): instead of using a type inferencer to infer a type for a given program, we need to infer a program (i.e, write a proof) for a given type (i.e, a proposition). The Coq Proof Assistant offers a fertile ground for problem solvers and for theorizers and has made it possible for students to prove more theorems in a few weeks or months than in their entire lifetime so far. On this fertile ground, new notions of triviality have emerged, such as the common succession of proof steps and proof strategies, and these mechanical steps and strategies have been automated. Today, the culture surrounding the Coq Proof Assistant is by and large that of advanced problem solvers: proving the goal justifies any automated means. For example, “Software Foundations” (2012) uses the simpl tactic early in the game. This approach is effective when the means are trivial, but triviality is an evolving concept: at the beginning, nothing is trivial. For another example, in his textbook (2013), Chlipala systematically uses the crush tactic upfront, consistently with the philosophy of having “short and automated proofs [as] the starting point.” The discourse then becomes less about the proofs and more about their automation, turning users into power-users.
For newcomers who simply want to become users, this current culture is challenging: for sure, using shortcuts without understanding what these automated simplification tactics cut short does enable one to prove many propositions. However, when one becomes stuck, it can be with no cognitive standing and no traction because these many proof trees now form a forest that is hiding the tree of knowledge, so to speak. For a less extreme but no less telling example, it also can be a sobering exercise to try to revisit textbook proofs that use a shortcut without using this shortcut.
All in all, the path taken by problem solvers is too steep for newcomers. What about the path a theorizer could take? This path would probably start with building a comfort zone with the basics, which includes understanding each proof step to build muscle memory in order to acquire a sense of how one mechanizes a proof in this proof assistant.
Over the last decade Danvy (Reference Danvy2011–2021), the author has been patiently designing such a path for newcomers Danvy (2019 b). Against this backdrop, the goal of the present tutorial is to describe how to mechanize equational reasoning about recursive programs. In the course of the 1970s, this equational reasoning was promoted by Burstall & Landin (Reference Burstall and Landin1969), Manna (Reference Manna1974) and Burstall and Darlington (Reference Burstall and Darlington1977), and since the 1980s, it is in common use to reason about functional programs (Bird & Wadler Reference Bird and Wadler1988; Thompson Reference Thompson1995; Thompson Reference Thompson2011), e.g, to manipulate them Jones et al. (Reference Jones, Gomard and Sestoft1993). At the heart of this mechanical reasoning lie fold–unfold steps to relate (a) calls to a structurally recursive function with arguments that correspond to one of its base cases or to one of its induction steps and (b) the corresponding case in its definition. It is the author’s thesis that these fold–unfold steps, once stated as fold–unfold lemmas, provide normal Coq users with an actionable understanding through a tractable middle path – the path of a theorizer – where they can distinguish between the trivial and the nontrivial and explain the whole process with clarity. The present tutorial is an overview of this middle path.
Roadmap: We start off with equational reasoning about the inductive specifications of programs (Section 2). Fold–unfold lemmas account for the clauses in the inductive specification of a program (Section 3), and they make it possible to reason about recursive programs (Section 4). In fact, they typically coincide with these clauses (Section 5), which we illustrate next with continuation-passing style, functionals that abstract structurally recursive computations (i.e, fold functions), mutual recursion, and with proving properties of recursive and co-recursive functions as well as the course-of-values induction principle (Section 6). We then turn to proving fold–unfold lemmas (Section 7), be it directly or using the functional-induction plugin or the Equations plugin, and to interfacing with preexisting recursive functions. Thus equipped, we describe how to reason not only about recursive equations but also about block-structured programs that use lexical scope (Section 8). We then put the present work into perspective (Section 9) before concluding (Section 10).
Prequisites and notations: An elementary knowledge of recursive programs, e.g, in OCaml, and no particular knowledge of the Coq Proof Assistant are expected from the reader. A deliberately reduced vocabulary of tactics is used here, each of them with one clear effect in the *goals* window (we are using Proof General), and all of them reviewed in appendix.
The term “fold–unfold” is due to Burstall and Darlington (Reference Burstall and Darlington1977) and is read “fold after unfold:”
-
The term “unfold” is used when a name is replaced by is denotation, and the Coq tactic unfold does exactly that. When the name denotes a function and occurs in a function call, this call is “unfolded” when this function is inlined: an instance of its body replaces the call where the actual parameters are substituted for its formal parameters. For example, if foo denotes fun x => if x then 1 else 0, then the call foo y is unfolded into if y then 1 else 0 using the tactic unfold foo. Some simplifications can take place during this inlining. For example, the call foo true is unfolded into 1 using the tactic unfold foo.
-
The term “fold” is used when a denotation is replaced by its name, and the Coq tactic fold does exactly that. When the name denotes a function and an expression is an instance of the body of this function, this instance is “folded” when this instance is replaced by a call to this function with suitable actual parameters. For example, if foo denotes fun x => if x then 1 else 0, then the expression if y then 1 else 0 is folded into foo y using the tactic fold (foo y), and the expression 1 is folded into foo true using the tactic fold (foo true).
As defined by Burstall et al., a fold–unfold step consists in (1) unfolding the call to a function and then (2) folding another call to this function in the resulting expression. Fold–unfold steps are most relevant for recursive functions because they make it possible to focus on what a recursive function does and disregard how it is implemented. So for example, if list_map denotes the recursive map function over lists, the two expressions list_map f (v :: vs) and f v :: list_map f vs are interderivable using one fold–unfold step.
Target audience and goal: This tutorial is written for people who are interested in reasoning about programs and who are curious about formulating this reasoning on a computer in a domain-specific language for writing proofs. The proofs and their pace are elementary to give the reader a chance to build a new knowledge on top of an existing knowledge instead of building yet another independent knowledge from scratch, kaleidoscopically. A not-uncommon side effect of this paced approach is a consolidation of this existing knowledge. And as in martial arts, the reader has then a chance to reach a mindful position where they can accelerate their moves safely, a side effect of having been patiently introduced to a logic of computing instead of having been made to start with its automation.
I want to give you
what I wish someone had given me
when I was your age.
– Samson Raphaelson (Reference Raphaelson1949)
2 Equational reasoning about specifications of programs
In the Coq Proof Assistant, equational reasoning is achieved using the rewrite tactic. This tactic, when applied to the Leibniz equality of two expressions, replaces one of these expressions by the other. Consider, for an elementary example, the mirroring function over binary trees in Gallina, the resident pure and total functional language in Coq:

The first declaration defines the polymorphic type of binary trees with payloads in the leaves. The second specifies the polymorphic mirror function inductively with two conjuncts, one for the leaves (base case) and one for the nodes (induction step).
To illustrate equational reasoning already, let us prove that at most one function satisfies this specification:

In words: any two functions mirror1 and mirror2 that satisfy the specification of the mirror function map the same input to the same output. The proof starts by naming assumptions and isolating the equality in the goal. Consistently with the policy that each tactic has one clearly identifiable effect in the *goals* window, we use an unfold step to replace the name specification_of_mirror by its denotation, i.e, a conjunction, before naming its two components:
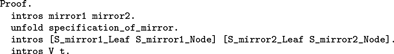
And indeed the *goals* buffer then contains named assumptions and the equality as a goal:

This equality is proved by structural induction. We first focus on the base case:
The *goals* buffer is the same as before, modulo the following changes:
-
the goal now reads mirror1 V (Leaf V v) = mirror2 V (Leaf V v), manifesting that we are in the base case where t is Leaf v; and
-
v : V stands instead of t : binary_tree V as the last assumption; v is the argument of the Leaf constructor.
Instantiating S_mirror1_Leaf and S_mirror2_Leaf with V and v provides two Leibniz equalities, one that matches the left-hand side of the goal and the other that matches the right-hand side of the goal. Based on these equalities, one can replace equals by equals in the goal using the rewrite tactic from left to right:
The goal then reads Leaf V v = Leaf V v, which can be proved using the reflexivity tactic since Leibniz equality is reflexive. The base case being established, one can next focus on the induction step:
The *goals* buffer now reads:

It is again the same as before, modulo the following changes:
-
the goal now reads mirror1 V (Node V t1 t2) = mirror2 V (Node V t1 t2), manifesting that we are in the induction step where t is Node V t1 t2; and
-
t1, t2 : binary_tree V stands instead of t : binary_tree V in the last assumption; t1 and t2 are the arguments of the Node constructor, and they stand along their associated induction hypotheses IHt1 and IHt2.
Instantiating S_mirror1_Node and S_mirror2_Node with V, t1, and t2 provides two Leibniz equalities, one that matches the left-hand side of the goal and the other that matches its right-hand side. Based on these equalities, one can replace equals by equals in the goal using the rewrite tactic:
The goal then reads Node V (mirror1 V t2) (mirror1 V t1) = Node V (mirror2 V t2) (mirror2 V t1). The induction hypotheses provide two Leibniz equalities which can be used to replace equals by equals in the goal:
The goal then reads Node V (mirror2 V t2) (mirror2 V t1) = Node V (mirror2 V t2) (mirror2 V t1), which again can be proved using the reflexivity tactic, which concludes the proof:
Likewise, one can prove equationally that a function satisfying the specification of mirror is involutory, i.e, that composing it with itself yields the identity function:

The proof is much as the one above, each step explicit and each of them with a simple explanation:

Both proofs feature equational reasoning, witness their extensive use of the rewrite tactic. The parts specific to the mirror function (S_mirror_Leaf, S_mirror_Node) are carried out based on its specification. Each time, a call to mirror on a leaf or on a node is replaced by the corresponding expression equated by the specification, which is called a “fold–unfold step” since Burstall and Darlington.
Would not it be nice if we could mechanically reason about programs – instead of about their specification – using fold–unfold steps?
For example, consider the following (obvious) implementation of the mirror function in direct style:

This implementation begs for the two following statements, one to the effect that it satisfies the specification and one to the effect that it is involutory. (The second is proved as a corollary of the first just below, but we would also like a direct proof.)

In words: applying the previous theorem to suitable arguments yields a quantified Leibniz equality that coincides with the statement of the theorem.
Besides rewrite, the Coq Proof Assistant offers two tactics to carry out fold–unfold steps: unfold that replaces a name by its denotation, and fold that replaces a denotation by an existing name. Using the unfold tactic over a recursive function exposes its internal representation and using the fold tactic is often chancy in this context, especially when the name is parameterized. Worse, this strategy does not scale as the programs to reason about become more complex.
The source of the problem is that the Coq users need to strategize every time they need to perform a fold–unfold step, i.e, every time a function is called.
Instead, we suggest that fold–unfold lemmas be stated once, when a recursive function is declared, and used when a function is called, as a predefined strategy.
3 Fold–unfold lemmas
Let us revisit the implementation of the mirror function:

By completeness, the mirror function can either be applied to a leaf or to a node, which elicits two fold–unfold lemmas:
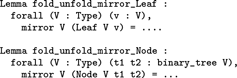
The first lemma aims to state the Leibniz equality associated to a call to the mirror function on a leaf and the second the Leibniz equality associated to a call to the mirror function on a node. Now what should one write instead of the ellipses? Answer – one should copy-paste the corresponding branch in the implementation:

4 Equational reasoning about recursive programs
Witness the following proof, the fold–unfold lemmas from Section 3 enable one to reason equationally as in the proofs in Section 2:
The proof starts by naming assumptions and isolating the equality in the goal:
And indeed the *goals* buffer then contains named assumptions and the equality as a goal. Compared to the *goals* buffer at the beginning of Section 2, only V and t are declared in the assumptions: the other assumptions (declaration of mirror and fold–unfold lemmas are now global:
The equality is proved by structural induction. We first focus on the base case:
The *goals* buffer is the same as before, modulo the following changes:
-
the goal now reads mirror V (mirror V (Leaf v)) = Leaf v, manifesting that we are in the base case where t is Leaf v; and
-
v : V stands instead of t : binary_tree V as the last assumption; v is the argument of the Leaf constructor.
Instantiating fold_unfold_mirror_Leaf with V and v provides a Leibniz equality that matches a subterm in the left-hand side of the goal. Based on this equality, one can replace equals by equals in the goal using the rewrite tactic:
The goal now coincides with this Leibniz equality, which makes it possible to complete the base case and to focus next on the induction step:
The *goals* buffer now reads:
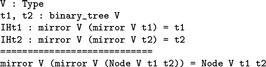
It is again the same as before, modulo the following changes:
-
the goal now reads mirror V (mirror V (Node V t1 t2)) = Node V t1 t2, manifesting that we are in the induction step where t is Node V t1 t2; and
-
t1, t2 : binary_tree V stands instead of t : binary_tree V in the last assumption; t1 and t2 are the arguments of the Node constructor, and they stand along their associated induction hypotheses IHt1 and IHt2.
One instantiation of fold_unfold_mirror_Node provides a Leibniz equality that matches a subterm in the left-hand side of the goal. Based on this equality, one can replace equals by equals in the goal using the rewrite tactic:
The goal then reads mirror V (Node V (mirror V t2) (mirror V t1)) = Node V t1 t2. Another instantiation of fold_unfold_ mirror_Node provides a Leibniz equality that matches its left-hand side. Based on this equality, one can replace equals by equals in the goal using the rewrite tactic:
The goal then reads Node V (mirror V (mirror V t1)) (mirror V (mirror V t2)) = Node V t1 t2. The induction hypotheses provide two Leibniz equalities which can be used to replace equals by equals in the goal:
The goal then reads Node V t1 t2 = Node V t1 t2, which is proved using the reflexivity tactic, which concludes the proof:
We find this formal proof remarkable because both in form and in content, it mechanizes an informal proof (Manna Reference Manna1974; Burge Reference Burge1975; Bird & Wadler Reference Bird and Wadler1988). Such a pen-and-paper proof is typically a series of equalities, each of them with a justification. Here, the successive goals enumerate these equalities, and each proof step propels the proof from goal to goal. This mechanization comforts the newcomers that their knowledge is not only actionable but also building up.
5 A closer look at the fold–unfold lemmas
Witness the following proof, the two fold–unfold lemmas above coincide with the two conjuncts in the specification of the mirror function, a consequence of the implementation being in direct style:

This coincidence exemplifies how fold–unfold lemmas provide the same expressive power to reason about recursive programs as the inductive specification of these recursive programs.
6 Applications
Fold–unfold lemmas scale seamlessly, e.g, to continuation-passing style (Section 6.1), fold functions (Section 6.2), and mutual recursion (Section 6.3), as well as to proving properties of recursive and co-recursive functions (Section 6.4) and to proving the course-of-values induction principle (Section 6.5).
6.1 Continuation-passing style
Consider the left-to-right continuation-passing implementation of the mirror function:

In words, the implementation is tail-recursive and uses a continuation that is initialized in the main function, mirror’. As a continuation-passing function, mirror’_cps is now polymorphic both with respect to the payloads in the leaves of the binary tree to mirror and with respect to a domain of answers and is also parameterized with a continuation that maps an intermediate result to an answer. In the base case, the computation continues by applying the current continuation to a new leaf. In the induction step, and given a current continuation, mirror’_cps tail-calls itself on the left subtree with a new continuation that, when applied, tail-calls mirror’_cps on the right subtree with another continuation that, when applied, sends a new node to the current continuation.
By completeness, the auxiliary function can either be applied to a leaf or to a node, which elicits two fold–unfold lemmas:

The first lemma aims to state the Leibniz equality associated to a call to the auxiliary function on a leaf, and the second the Leibniz equality associated to a call to the auxiliary function on a node. Now what should one write instead of the ellipses? Answer – one should copy-paste the corresponding branch in the implementation, just as in Section 3:

These fold–unfold lemmas enable one to prove the completeness of mirror’_cps equationally and its soundness relationally:

In words: if mirror maps a binary tree t to its mirror image t_m, then applying mirror’_cps to t and a continuation k leads to k being applied to t_m. The equivalence of mirror’ and mirror is a corollary:

Witness the accompanying.v file, the completeness lemma is proved by structural induction on t, using the fold–unfold lemmas in the base case and in the induction step. As for the soundness lemma, which admittedly is not needed here, it requires one to prove that continuations are injective if the initial continuation is also injective, which is the case here (see the accompanying.v file).
6.2 Functionals that abstract structurally recursive computations
Consider the following fold functionals over Peano numerals:

The first functional abstracts a tail-recursive computation over a natural number using an accumulator and the second an ordinary recursive computation over a natural number. And as it happens, these two functionals are equivalent Danvy (2019 a):
This theorem is proved by induction on n, using either of the following lemmas, which are also proved by induction on n, witness the accompanying.v file:

These three proofs all use the fold–unfold lemmas associated to the two functionals, making it possible for the user to focus on what to prove instead of also having to worry about how to proceed at every proof step:

Both Bird and Wadler’s duality theorems about lists (1988) and their ancestors Burge (Reference Burge1975) are formalized in a similar manner.
6.3 Mutual recursion
Consider the canonical implementation of the parity predicates:

This implementation gives rise to the following 4 fold–unfold lemmas, admitted for now:

These lemmas were mechanically stated by enumerating all the possible calls to evenp and oddp and by copy-pasting the corresponding branch in the implementation.
They enable one to prove the soundness and the completeness of the canonical implementation:

The theorem is proved by structural induction on n, using the fold–unfold lemmas in the base case and in the induction step. One can then verify, for example, that the converse cases are corollaries of soundness and completeness:

6.4 Proving properties of recursive and co-recursive functions
Witness the accompanying.v file, fold–unfold lemmas come handy to prove, e.g, that list concatenation is associative, which is a standard example. Ditto for for proving that the number of leaves in a binary tree equals its number of nodes, plus 1.
The idea readily transfers to streams:
Consider, for a playful example, a function that ostensibly concatenates one stream to another:

In order to prove that concatenating a given stream to another yields a stream that is bisimilar to the given stream, the following fold–unfold lemma provides a very useful stepping stone:
6.5 Proving the course-of-values induction principle
Given (1) a predicate P indexed by a natural number and (2) a natural number n, the following function computes P n /\… /\P 1 /\P 0:

Thus equipped, the course-of-values induction principle is stated as follows:

In the accompanying.v file, this induction principle is proved by mathematical induction using the fold–unfold lemmas associated to course_of_values.
7 Proving the fold–unfold lemmas
7.1 Using the unfold tactic and then the fold tactic
By their very name, fold–unfold lemmas are proved using the unfold tactic immediately followed by the fold tactic, which yields a Leibniz equality. So the proof of each fold–unfold lemma can be stated as an instance of the following one-liner:
In other words, the proof of both fold–unfold lemmas for the mirror function, for example, reads:
That being said, the reflexivity tactic itself uses fold and unfold as part of its normalization steps toward comparing normal forms, and therefore there is no need for these two tactics in the proof of fold–unfold lemmas, witness the following shorter proof script that does not even need the name of the function to unfold and to fold:
In other words, the proof of each fold–unfold lemma can read:
Equivalently, it can read:
Since the last two proofs look like magic, i.e, require explanations that use concepts that are more advanced than the concepts the students have been presented so far, the previous version (namely fold_unfold_tactic applied to the name of the function at hand) does the job better. At some point, a student may wonder why the proof assistant accepts the proof fold_unfold_tactic foo for a fold–unfold lemma about bar, at which point they are mature enough to be told about the unusual effectiveness of the reflexivity tactic in the Coq Proof Assistant (to say nothing of its efficiency Grégoire & Leroy (Reference Grégoire and Leroy2002)).
Further up the road, the limitation of the fold–unfold tactic will come to light, namely for functions whose recursion pattern depends on more than one argument. For example, consider List.nth, which has type forall V : Type, nat -> list V -> V -> V. Applying List.nth to an index i, a list vs, and a default value d yields d if i is “out of bounds” and otherwise the element at index i in vs. Accessing a given list at a given index can equivalently be defined by induction on the index or by induction on the list. Therefore, two pairs of fold–unfold lemmas arise.
-
The first pair is by cases on the given index:

-
The second pair is by cases on the given list:

One is even tempted to declare 4 fold–unfold lemmas to account for the 4 possibilities:

Each of these 4 lemmas is seamlessly proved using the fold–unfold tactic since the user has done the work of enumerating all cases in the statements of the lemmas. (Incidentally, stating these 4 lemmas could be used to define a function to access a given list at a given index, as done, e.g, in Isabelle Nipkow et al. (Reference Nipkow, Paulson and Wenzel2002).) Both Lemmas fold_unfold_nth_nil and fold_unfold_list_nth_cons are also seamlessly proved using the fold–unfold tactic. However, since List.nth is implemented by recursion on the list, the Coq Proof Assistant balks at proving the two previous lemmas like that. Instead, one needs to customize the following proof that explicitly distinguishes the two cases of a list:

And conversely, for a version of nth that is implemented by recursion on the index, the two first lemmas are seamlessly proved using the fold–unfold tactic, but for the two others, one needs to customize the following proof that explicitly distinguishes the two cases of an index:

In other words, to state fold–unfold lemmas for a recursive function, one either needs to know how this function is implemented or one needs to enumerate all possible configurations of its arguments by eta expanding them according to their type, as it were.
7.2 Using the functional-induction plugin
The functional-induction plugin (FunInd) provides a Function vernacular. This vernacular appeared in Coq v8.0 as part of this plugin, which was loaded by default. Since Coq v8.7, this plugin must be explicitly loaded with Require FunInd. When using Function instead of Fixpoint, an equation is generated – its “fixpoint equality,” to quote the section about Advanced Recursive Functions in the Coq Reference Manual:
This equation has direct relevance to fold–unfold lemmas.
For example, let us revisit the mirror function, declaring it with Function instead of with Fixpoint:

A by-product of this declaration is that from then on, mirror_alt_equation (i.e, the name of the function declared with Function, concatenated with _equation) has type

It is then immediate to declare the fold–unfold lemmas:

And indeed their type reads as follows:

These lemmas hold as instances of the equation.
So all in all, for recursive functions that are declared globally, i.e, for recursive equations, the Function vernacular provides fold–unfold lemmas for free. (And by that book it would be great to have a similar coFunction vernacular for co-recursive functions.)
7.3 The Equations plugin
Ostensibly Sozeau & Mangin (Reference Sozeau and Mangin2019), the Equations plugin “provides a syntax for defining programs by dependent pattern-matching and structural or well-founded recursion.” Concretely, and because to a person with a hammer, the world looks like a nail, this syntax is that of block-structured, scope-sensitive recursive functions which are then
![]() $\lambda$
lifted Johnsson (Reference Johnsson1985) into toplevel fold–unfold equations, a practical progress over the functional-induction plugin. Conceptually, and to the author’s eye, Sozeau and Mangin made the heretofore unidentified connection between functional elimination and
$\lambda$
lifted Johnsson (Reference Johnsson1985) into toplevel fold–unfold equations, a practical progress over the functional-induction plugin. Conceptually, and to the author’s eye, Sozeau and Mangin made the heretofore unidentified connection between functional elimination and
![]() $\lambda$
lifting in their Equations plugin. And so practically, the extra parameters in the resulting fold–unfold equations can also make sense, intuitively, in terms of
$\lambda$
lifting in their Equations plugin. And so practically, the extra parameters in the resulting fold–unfold equations can also make sense, intuitively, in terms of
![]() $\lambda$
lifting.
$\lambda$
lifting.
7.4 Interfacing with preexisting recursive functions
When using library functions, one cannot assume that they were declared with Function or with Equation, the vernacular provided by the Equations plugin. To reason about them uniformly, one can then state their associated fold–unfold lemmas at the outset, by enumerating the possible configurations of its arguments, as described in Section 7.1.
8 Reasoning about block-structured programs with lexical scope
There is more to functional programming than recursive equations, witness the implementations of nat_fold_left and nat_fold_right in Section 6.2 that use block structure (loop and visit are declared locally) and lexical scope (V, z, and s are global to loop and visit). It feels like pure luck that the fold–unfold tactic proves their fold–unfold lemmas.
Consider the following implementation for computing self-convolutions using the TABA (There and Back Again Danvy & Goldberg (Reference Danvy and Goldberg2005)) recursion pattern, where the list to convolve is traversed both through the calls to an auxiliary function visit and through the subsequent returns:

In words: during its successive recursive calls, visit traverses the given list, until it reaches the empty list, i.e, the base case. It then returns a pair holding the given list and an empty list of pairs. During the subsequent returns, the given list is traversed again and the convolution is constructed. The option type is only there to appease the type inferencer.
How does one proceed to prove, e.g, the soundness of this implementation?

In words: if applying convolve_thyself to a given list yields an optional result, then this optional result was constructed with Some and the argument of Some is a list of pairs that can be unzipped into the given list and its reverse, which is the definition of a symbolic self-convolution. This lemma establishes that convolve_thyself is total since it always returns a result constructed with Some, and that it is sound in that it does yield a self-convolution of the given list.
To prove this soundness, one option is (1) to
![]() $\lambda$
lift this implementation into two recursive equations and declare the new auxiliary function with Function, since it provides the two associated fold–unfold lemmas for free:
$\lambda$
lift this implementation into two recursive equations and declare the new auxiliary function with Function, since it provides the two associated fold–unfold lemmas for free:

and (2) to proceed with the following auxiliary lemma that characterizes both the control flow and the data flow of TABA:

The reader is referred to Section Section 2 of “Getting There and Back Again” Danvy (Reference Danvy2022) for more detail, but in essence, the third argument of visit_lifted, vs, is the given list and its second argument, vs_sfx, is the list traversed by the calls so far. So vs_sfx is a suffix of vs. In this lemma, this given list is also expressed as the concatenation of a prefix, ws_pfx, and a suffix, ws_sfx, which are such that the length of this prefix is the same as the length of the list traversed so far, vs_sfx. The lemma captures how the given list is traversed at call time and at return time: the lengths of vs_sfx and of ws_pfx are the number of remaining calls to traverse vs_sfx. By the very nature of structural recursion, this number is also the number of returns that yield Some (ws_sfx, ps). Therefore, the returns have traversed the current prefix of the given list, ws_pfx, and the returned list is its current suffix, ws_sfx. The lemma also captures that the returned list of pairs is a symbolic convolution of the list that remains to be traversed at call time, namely vs_sfx, and of the list that has been traversed at return time, namely ws_pfx. The control-flow aspect of the lemma expresses that ws_pfx has been traversed by the returns and that vs_sfx remains to be traversed by the calls. The data-flow aspect of the lemma expresses that the returned list of pairs is a symbolic convolution of these two lists. The lemma is proved by induction on vs_sfx, and the theorem follows as a corollary.
Is
![]() $\lambda$
lifting the only option? Can one only reason about
$\lambda$
lifting the only option? Can one only reason about
![]() $\lambda$
-lifted programs, i.e, recursive equations, with the Coq Proof Assistant? Well, no. One can reason about
$\lambda$
-lifted programs, i.e, recursive equations, with the Coq Proof Assistant? Well, no. One can reason about
![]() $\lambda$
-dropped programs Danvy & Schultz (Reference Danvy and Schultz2000), i.e, programs with block structure and lexical scope, with “
$\lambda$
-dropped programs Danvy & Schultz (Reference Danvy and Schultz2000), i.e, programs with block structure and lexical scope, with “
![]() $\lambda$
-dropped proofs,” i.e, proofs with block structure and local names. Here, the
$\lambda$
-dropped proofs,” i.e, proofs with block structure and local names. Here, the
![]() $\lambda$
-dropped proof starts by naming the recursive function as visit using the remember tactic. One then declares local lemmas using assert, starting with fold–unfold ones and continuing with an analogue of the one above, as illustrated in the accompanying.v file. The point here is that local recursive declarations, block structure, and lexical scope make sense for writing programs, and they make just as much sense for writing proofs, the Curry–Howard correspondence notwithstanding. And whereas the Function vernacular can only be used for recursive equations, the Equations plugin can be used for the worker/wrapper pattern.
$\lambda$
-dropped proof starts by naming the recursive function as visit using the remember tactic. One then declares local lemmas using assert, starting with fold–unfold ones and continuing with an analogue of the one above, as illustrated in the accompanying.v file. The point here is that local recursive declarations, block structure, and lexical scope make sense for writing programs, and they make just as much sense for writing proofs, the Curry–Howard correspondence notwithstanding. And whereas the Function vernacular can only be used for recursive equations, the Equations plugin can be used for the worker/wrapper pattern.
To drum this drum some more, what if one wants to make do without the intermediate option type in the auxiliary function to self-convolve a list? After all, this computation is a showcase for continuations:

In words: instead of returning an optional pair of values, visit is called with a continuation to which to send these two values. In the base case, the current continuation is sent the given list and an empty list of pairs. In the induction step, visit traverses the rest of the list tail-recursively with a new continuation. This new continuation, given a suffix of the given list and a list of pairs, will send the tail of this suffix and an extended list of pairs to the current continuation. The initial continuation is sent the empty list and the self-convolution: it discards one and returns the other.
Now for proving the soundness and the completeness of this continuation-based implementation, there is no need to massage it first (here: with
![]() $\lambda$
lifting) to make it fit any particular plugin, whether explicitly with the functional-induction plugin or implicitly with the Equations plugin. One can write a
$\lambda$
lifting) to make it fit any particular plugin, whether explicitly with the functional-induction plugin or implicitly with the Equations plugin. One can write a
![]() $\lambda$
-dropped proof similar to the one above. This is of course not a criticism of these plugins, on the contrary: once a beginner is then introduced to them, their reaction is less likely to be “Whatever. Will this be at the exam?” – it is more likely to be one of informed appreciation. Furthermore, no new concept is needed to write a
$\lambda$
-dropped proof similar to the one above. This is of course not a criticism of these plugins, on the contrary: once a beginner is then introduced to them, their reaction is less likely to be “Whatever. Will this be at the exam?” – it is more likely to be one of informed appreciation. Furthermore, no new concept is needed to write a
![]() $\lambda$
-dropped proof, which makes one feel secure in one’s knowledge, seeing that it is actionable as it is, a welcome relief to the perpetual (and doubt-inducing) need for new tools to solve new problems.
$\lambda$
-dropped proof, which makes one feel secure in one’s knowledge, seeing that it is actionable as it is, a welcome relief to the perpetual (and doubt-inducing) need for new tools to solve new problems.
Let us conclude this section with a simple proof of the simple fact that the lambda-lifted and the lambda-dropped versions of nat_fold_right are functionally equivalent (the accompanying.v file also contains a similar proof for nat_fold_left):

This proof is a routine mathematical induction that features both the global fold–unfold lemmas associated to nat_fold_right_lifted and the local fold–unfold lemmas associated to nat_fold_right_dropped:

The proof starts with the local declaration of visit as denoting the recursive function that is local to nat_fold_right_dropped in an assumption that is named D_visit:

Witness the *goals* buffer, this named assumption is in the scope of V, z, and s, just like visit in the definition of nat_fold_right_dropped:

We then state and prove two local fold–unfold lemmas for visit:

We are then in position to conduct a routine induction proof where the global and the local fold–unfold lemmas are used in synchrony (the local ones with fewer arguments):

The very facts that this induction proof is routine and that the fold–unfold lemmas are used in synchrony consolidate the newcomer’s grasp of block structure and lexical scope.
9 Reflections
The present work – harnessing the Coq Proof Assistant’s fold and the unfold tactics into fold–unfold lemmas to mechanize equational reasoning about functional programs – takes place in a wider context: other ways to reason equationally in Coq and other proof assistants. As other proof assistants have their own paradigms – and taking due note that the reviewers unanimously consider fold–unfold lemmas to be trivial in Agda, Isabelle, and Haskell – we only consider Coq. Pretty universally, all the other approaches the author is aware of use the simpl tactic, which performs simplifications that encompass fold–unfold steps. Very often, these simplifications save precious time, though at the cost of explainability: it is not always clear how some expressions were simplified and why some others were not. Also, simplifications can overshoot, which hides opportunities for shared lemmas. Take the following lemma, for example, which comes handy when reasoning about the parity predicates:
This lemma suffuses a problem solver with boredom (to quote Rota (Reference Rota1996)), but a theorizer is happy to see an undergraduate student displaying awareness and potential by stating a helper lemma twice : forall x : nat, x + x = 2 * x, and using it in tandem with plus_Sn_m and plus_n_Sm to prove about_twice:

At any rate, the simpl tactic is generally seen as a time saver for experienced users.
Debussy once retorted that of course, he knew the rules of the fugue, which is why he could break them. The situation appears to be similar here: shortcuts can be used fruitfully when one knows what they cut short. Unfortunately, using shortcuts, it is perfectly possible to learn the Coq Proof Assistant with very little understanding and then use it as one would play whack-a-mole. The proof of Lemma completeness_of_mirror’_cps in Section 6.1, for example, can proceed by first simplifying and then by mechanically writing the tactic that fits the current goal (and never mind the semiotics of H nor why one needs to conclude the proof by invoking reflexivity three times, Lewis–Carroll style):

This gaming strategy may work when one uses the Coq Proof Assistant in anger, but it is not sustainable because one learns nothing from what one does mindlessly: exercises and exams are not referentially transparent, nor are they an end in themselves – they are a means to acquire an actionable understanding.
Now what to do when a facetious undergraduate student swaps the joy of figuring things out for the glee of not figuring things out and getting away with it, because, hey, Coq accepted their proof? Rather than fighting this wave, we can surf on it and introduce Paul Erdös and his notion of a proof being from The Book. Since some proofs are from The Book, others are not. Extra credit can be given for proofs that are not from The Book if they come with an explanation or at least with an analysis, something students take seriously if 50% and 50% about the quality of one’s understanding being reflected by the clarity of one’s narrative (1815).
10 Summary and conclusion
Keep calm and write fold–unfold lemmas.
Fold–unfold lemmas complement the Coq Proof Assistant’s rewrite tactic to reason about recursive programs equationally. Their simplicity is deceiving. For beginners, not being able to state them is a tell-tale sign. For rookies, not being able to explain them is another tell-tale sign. Fold–unfold lemmas often feel beneath more advanced users, and it is impressive how often these more advanced users subsequently feel that their proof is above them. The reason for this feeling, however, is merely quantitative: fold–unfold lemmas offer expressive power to reason about calls to recursive functions, and it is more efficient to harness this expressive power at the outset, when declaring a recursive function locally or globally, than to re-invent the wheel each time a recursive function is called. As such, fold–unfold lemmas – be them stated implicitly using a plugin or stated explicitly by hand – provide a reliable foundation for reasoning about recursive programs using the Coq Proof Assistant.
Acknowledgments
The author is grateful to Julia Lawall for preliminary comments and for pointing to the functional-induction plugin in the Coq Proof Assistant and its undocumented feature. Thanks are also due to the anonymous reviewers for perceptive comments, which very much include pointing to the Equations plugin (Sozeau & Mangin Reference Sozeau and Mangin2019), and to Matthieu Sozeau for a subsequent email exchange in the fall of 2021. And of course pure and total thanks go to the Archimedean designers, developers, and maintainers of the Coq Proof Assistant and of Proof General for offering such a fulcrum to lift the world of computing. This research received no specific grant from any funding agency, commercial, or not-for-profit sectors.
Conflicts of interest
The author reports no conflict of interest.
Supplementary material
For supplementary material for this article, please visit https://doi.org/10.1017/S0956796822000107
Appendix
A Coq in no hurry
This appendix provides a minimalistic introduction to the Coq Proof Assistant, in the manner of Bertot (Reference Bertot2006). This proof assistant, like Agda, is based on the proposition-as-types paradigm, but unlike Agda, it has a separate tactics language. This tactics language has the imperative flavor of algebraic proofs in that the goal is incrementally modified until the completion of each proof. A proof follows the statement of a theorem/lemma/proposition/etc. Proofs are prefixed by Proof. and suffixed with Qed., unless, e.g, they are admitted.
A.1 Libraries
The Coq Proof Assistant comes with many libraries, e.g, the one for arithmetics over natural numbers, that have type nat and are represented as Peano numerals, with O and S as constructors. This library is imported as follows:
Given the name of a lemma in this library, the Check command tells us its type. For example, Arith features lemmas that correspond to the inductive definition of addition (base case and induction step) as well as its associativity:

Likewise, Arith features lemmas that correspond to the inductive definition of multiplication over the multiplier as well as its distribution over addition:

A.2 Applying lemmas
Lemmas that name universally quantified formulas are instantiated by applying their name to arguments:

Natural numbers are parsed into Peano numerals:
A.3 Definitions
To align the lemmas that correspond to the inductive definition of addition and multiplication with the corresponding fold–unfold lemmas, we can rename them:

As a functional language, Gallina makes it possible to declare functions. The square function, for example, is written fun (n : nat) => n * n and can be named using the traditional syntactic sugar of functional programs:
A.4 Structure of a proof
A proof is stated as a series of updates over the current goal, using tactics. Some of these tactics might create subgoals (e.g, for proofs by cases or proofs by induction). Then we focus on the current subgoal using itemization signs or using curly braces.
A.5 The tactics used in the present tutorial
To prove a universally quantified statement
![]() $\forall x. s$
, one typically picks an x and proceeds with s. This picking is achieved using the intro tactic. If the type of x is composite (e.g, a product or a sum), one uses the intros tactic with syntactic sugar to name the components.
$\forall x. s$
, one typically picks an x and proceeds with s. This picking is achieved using the intro tactic. If the type of x is composite (e.g, a product or a sum), one uses the intros tactic with syntactic sugar to name the components.
As described at the end of Section 1, the fold tactic replaces a name by its denotation and the unfold tactic replaces a denotation by its name.
As described at the beginning of Section 2, given an equality, the rewrite tactic replaces either side by the other.
Given an argument whose type is inductive, the induction tactic is used to conduct a structural induction proof at that type. So if this type is nat, this proof corresponds to mathematical induction since natural numbers are represented as Peano numerals.
The reflexivity tactic is used to prove the current goal when this goal is an equality with the same left-hand side and right-hand side.
Given an argument that coincides with the current goal, the exact tactic is used to prove this goal.
The assert and remember tactics are used to declare new assumptions.
Using a semicolon (;) instead of a period (.) between two proof steps conflates them into one. And if the first proof step creates subgoals, the second proof step takes place for each of these subgoals.
A.6 Three simple lemmas and their proof
We are now in position to mechanize algebraic proofs.
Proving that 1 is neutral on the left of multiplication is carried out with three successive fold–unfold steps:

Proving Lemma twice from Section 9 is carried out with one fold–unfold step and using Lemma mul_1_l:
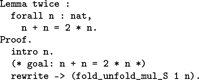
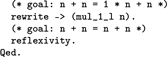
Likewise, and as illustrated in the accompanying.v file, proving the binary expansion at rank 2 is carried out from left to right by unfolding the left call to square, distributing multiplication over addition 3 times, reassociating addition twice, commuting a multiplication, applying Lemma twice, and folding two calls to square. (The accompanying.v file also contain a proof for binary expansion at rank 2 that is carried out from right to left.)
A.7 Addition is commutative
Since addition is defined recursively over its first argument, its commutativity is proved by nested induction, systematically using its fold–unfold lemmas. The outer induction is over the first argument on the left-hand side and the inner induction over the first argument on the right-hand side:







Discussions
No Discussions have been published for this article.