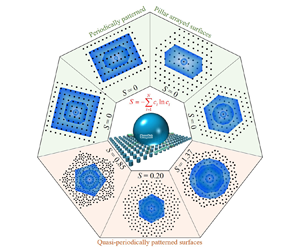
Impact Statement
A method for characterizing pillar-arrayed microstructured surfaces has been given. The concept of configurational entropy for pillar-arrayed microstructured surfaces has been introduced, and a detailed calculation has been provided. Subsequently, the values of configurational entropy for both periodically and quasiperiodically patterned pillar-arrayed surfaces have been calculated. The wetting morphology of liquid droplets on both periodically patterned pillar-arrayed surfaces and quasiperiodically patterned pillar-arrayed surfaces has been summarized. The influence of configurational entropy of surfaces on the wetting morphology and dynamics of liquid droplets in experiments has been discussed. The results may advance the control capability of complex wetting morphology, and are helpful in applications of microfluidics, self-cleaning materials, inkjet and 3D printing, etc.
1. Introduction
Liquid droplets spreading on solid surfaces are ubiquitous in both nature and practical applications, such as plant leaves, electrocapillary peeling (Reference Li, Huang and ZhaoLi, Huang & Zhao 2023a), dielectrophoresis (Reference Bercovici, Boyko, Gabay, Gat, Paratore and RamosBercovici et al. 2021), 3D printing (Reference Yuk, Lu, Lin, Qu, Xu, Luo and ZhaoYuk et al. 2020), energy/water harvesting (Reference Chen, Ran, Gan, Zhou, Zhang, Zhang, Zhang and JiangChen et al. 2018a; Reference Yu, Schimelman, Wang, Miller, Ma, You, Guan, Sun, Zhu and ChenYu et al. 2020; Reference Li, Wang, Deng, Yin, Li and GuoLi et al. 2023b), microfluidics (Reference Wang, Chen, Sun, Liu, Yin, Zhang, Xianyu, Shi, Hu and JiangWang et al. 2014a; Reference Yang, Wang, Liu, Chen, Zaworotko, Cheng, Ma and ZhangYang et al. 2021; Reference Li, Huang and ZhaoLi, Huang & Zhao 2022), ink-jet printing (Reference Wang, Wang, Li, Zhu, Wang, Zhang, Xie, Fuchs, Lei and ChiWang et al. 2014b; Reference Brockmann, Dörsam, Hussong, Roisman, Rothmann-Brumm and SauerBrockmann et al. 2024), self-cleaning (Reference Singh, Haverinen, Dhagat and JabbourSingh et al. 2010), etc. In these applications, the ability to control the morphology of the wetted area, that is, the morphology of the moving contact line, is of significant importance because the morphology is closely related to the fabrication process (Reference Yu, Zhang, Hu and LuoYu et al. 2021). Over the past few decades, researchers have devoted significant attention to this matter, yielding abundant results though experimentation, simulation and theoretical investigation. It has been found that the morphology of the wetted area of droplets is closely related to both the topology of rough surfaces and the liquid properties (Reference Cazabat and StuartCazabat & Stuart 1986, Reference Cazabat and Stuart1987; Reference Apel-Paz and MarmurApel-Paz & Marmur 1999; Reference Alberti and DesimoneAlberti & DeSimone 2005; Reference QuéréQuéré 2008; Reference Chamakos, Kavousanakis, Boudouvis and PapathanasiouChamakos et al. 2016; Reference ZhaoZhao 2016; Reference Wang, Huang, Yuan, Chen and YuWang et al. 2021). Surface chemical moderating techniques (Reference Jain and PitchumaniJain & Pitchumani 2017) and surface roughness preparation methods (Reference Raj, Enright, Zhu, Adera and WangRaj et al. 2012), particularly in the fabrication of surfaces with micropillars, are extensively employed (Reference Courbin, Denieul, Dressaire, Roper, Ajdari and StoneCourbin et al. 2007; Reference Jokinen, Leinikka and FranssilaJokinen, Leinikka & Franssila 2009; Reference Chu, Xiao and WangChu, Xiao & Wang 2010; Reference Lv, Yang, Hao, He and ZhengLv et al. 2010; Reference Xiao, Enright and WangXiao, Enright & Wang 2010; Reference Xiao and WangXiao & Wang 2011) to achieve the desired morphology of the wetted area of liquid droplets.
The method of fabricating roughness on solid surfaces is more stable than that of chemical moderating solid surfaces (Reference Duprat, Protiere, Beebe and StoneDuprat et al. 2012). Additionally, topology, roughness and geometry parameters can be designed in the method of fabricating microstructures on solid surfaces. As a result, the method of fabricating microstructures on solid surfaces gradually received more attention than that of chemical moderating solid surfaces (Reference Courbin, Denieul, Dressaire, Roper, Ajdari and StoneCourbin et al. 2007; Reference Lv, Yang, Hao, He and ZhengLv et al. 2010; Reference Xiao, Enright and WangXiao et al. 2010; Reference Kim, Moon, Lee, Lee, Chang and KimKim et al. 2011).
The characterization method of rough surfaces has been studied since the last century. In fact, solid surfaces in nature are usually rough. A common example is a rock's surface, on which the phenomenon of liquid droplet spreading has been pioneered by de Gennes (Reference Dufour, Brunet, Harnois, Boukherroub, Thomy and SenezDufour et al. 2012). Such a rough surface is called a fractal surface (Reference de Gennesde Gennes 1985), and the roughness of a fractal surface is ![]() ${(L/l)^{\xi - 2}}$, where L and l denote the largest and smallest sizes of the fractal surface, respectively. Besides the definition of surface roughness, fractal dimension (Reference PackhamPackham 2003) has also been proposed to characterize the disorder of rough surfaces. In the experiments, a rough surface can be prepared on a smooth glass surface by using different grades of abrasive powder and sand blasting (Reference MandelbrotMandelbrot 1918; Reference Cazabat and StuartCazabat & Stuart 1987). The characterization is usually the amplitude and the quadratic variation of the surface. However, the roughness of such a rough surface is random, and there is a lack of accurate characterization of the rough surface.
${(L/l)^{\xi - 2}}$, where L and l denote the largest and smallest sizes of the fractal surface, respectively. Besides the definition of surface roughness, fractal dimension (Reference PackhamPackham 2003) has also been proposed to characterize the disorder of rough surfaces. In the experiments, a rough surface can be prepared on a smooth glass surface by using different grades of abrasive powder and sand blasting (Reference MandelbrotMandelbrot 1918; Reference Cazabat and StuartCazabat & Stuart 1987). The characterization is usually the amplitude and the quadratic variation of the surface. However, the roughness of such a rough surface is random, and there is a lack of accurate characterization of the rough surface.
To model the pillar-arrayed microstructured surfaces, micropillars have been extensively used in recent decades. It is proved that the distribution parameters of micropillars on solid surfaces such as symmetry, density, roughness, height and the morphology of pillars, are all related to the morphology of the wetting area of liquid droplets on these surfaces (Reference Cazabat and StuartCazabat & Stuart 1986; Reference Courbin, Denieul, Dressaire, Roper, Ajdari and StoneCourbin et al. 2007). Liquid droplets of partial wetting on a smooth lyophilic surface may become complete wetting on a pillar-arrayed microstructured surface (Reference QuéréQuéré 2008; Reference ZhaoZhao 2012; Reference Chen, Yuan, Huang and ZhaoChen et al. 2016). For example, by fabricating a square array of micropillars on a solid surface, the droplets are more likely to spread into a square wetted area rather than circular ones (Reference ZhaoZhao 2014). By using soft-lithography techniques or/and reactive ion etching processes, the size of the micropillars can be controlled from several micrometres to tens of micrometres in experiments. Therefore, as the size of the micropillars decreases, the roughness of the micropillars increases dramatically. On the microstructured surface with small pillars, the morphology of the wetted area of a spreading droplet is strongly affected by the micropillars. The droplets can even spread into a bilayer structure (Reference Extrand, Moon, Hall and SchmidtExtrand et al. 2007). This means that the bottom of the droplet spreads within the pillars, forming a so-called fringe film, and the upper part of the droplet is above the pillars, which is called a bulk droplet. Liquid droplets with square projected fringe shape and circular projected bulk shape, octagonal projected fringe shape with circular projected bulk shapes, square projected fringe shape, octagonal projected fringe shape, circular fringe with circular projected bulk shapes, etc, have appeared on square arrayed micropillar surfaces (Reference Chen, Yuan, Huang and ZhaoChen et al. 2016). By changing the symmetry of the surface array to a rectangle, liquid droplets with a rectangular and stretched octagonal wetted area can be obtained (Reference Courbin, Denieul, Dressaire, Roper, Ajdari and StoneCourbin et al. 2007). In the same way, by changing the symmetry of the surface array to a hexagon, it is possible to obtain droplets with a hexagonal wetted area (Reference Raj, Adera, Enright and WangRaj et al. 2014). And droplets with a dodecagonal wetted area can be achieved on a pillar-arrayed surface with a hexagonal array (Reference Courbin, Bird, Reyssat and StoneCourbin et al. 2009). Among the above-mentioned studies, the symmetry of the various wetted areas of the droplets coincide with the symmetry of the pillar arrays on the microstructured surface. The wetted shapes of droplets on the square arrayed surface with four-fold symmetry, both square and octagon, are four-fold symmetric; the wetted shape of droplets on the rectangular arrayed surface with two-fold symmetry, including rectangular and stretched square, are two-fold symmetric; and similarly, the wetted shape of droplets on a hexagonal arrayed surface with six-fold symmetry, i.e. dodecagon and hexagon, are both six-fold symmetric.
Besides research on periodically patterned surfaces with two-, four- and six-fold symmetry (Reference Raj, Adera, Enright and WangRaj et al. 2014), it is noteworthy that quasiperiodically patterned surfaces have also been investigated (Reference Chen, Yuan and ZhaoChen, Yuan & Zhao 2018b). On such surfaces, the symmetry of the wetted area of droplets can decrease and restore spontaneously. For example, it is reported that on the surface with a five-fold quasiperiodically pattern, the symmetry of the wetted area of the droplets can be circular, five-fold, or ten-fold. And on six-fold quasiperiodically patterned surfaces, the symmetry of the wetted area of the droplets can be circular, six-fold or twelve-fold. This indicates a distinct difference between periodically patterned and quasiperiodically patterned surfaces. Nevertheless, there is currently a lack of characterization of pillar-arrayed micropatterned surfaces due to the inability of roughness, symmetry and the geometry parameters to differentiate between the two kinds of surfaces.
In this work, a calculating method of configurational entropy of the pillar-arrayed surfaces is given to characterize the degree of disorder of micropillars. The configurational entropy of commonly used pillar-arrayed micropatterned surfaces has been calculated and compared with the morphology transition of the wetted area of the droplets. It is found that the configurational entropy proposed in this study can describe the pillar-arrayed microstructured surface to some extent.
2. Problem
As mentioned in § 1, the characterization method for rough surfaces, particularly for pillar-arrayed microstructured surfaces includes surface roughness, the pillar density, aspect ratios and symmetry. The definition of surface roughness, ro, is described as the ratio of the actual area of solid surface, Sac, to the projected area of solid surface, Sp (Reference Chen, Yuan and ZhaoChen et al. 2018b),
According to this definition, the surface roughness is a constant on uniformly patterned pillar-arrayed surfaces, but a function of location on surfaces with non-uniform structures.
The definition of pillar density (Reference QuéréQuéré 2008), which is referred to as the density of defects or the surface area fraction of a solid surface (Reference Mchale, Newton and ShirtcliffeMcHale et al. 2009), is defined as the ratio of the projected area of the rough solid surface to the projected area of the total solid surface (Reference Yuan and ZhaoYuan & Zhao 2013),
Similar to surface roughness, ro, the pillar density of a solid surface or the surface area fraction of a solid surface is also a constant on uniformly patterned pillar-arrayed surfaces, but a function of location on surfaces with non-uniform structures.
The definition of aspect ratio is described as the ratio of height of a pillar, h, to the inner distance of pillars, l (Reference Mchale, Newton and ShirtcliffeMcHale et al. 2009),
as illustrated in figure 1(a). In some cases, the definition of aspect ratio is described as the ratio of height of a pillar, h, to the period of pillars, d (Reference Courbin, Denieul, Dressaire, Roper, Ajdari and StoneCourbin et al. 2007),
as illustrated in figure 1(b).

Figure 1. Illustration of aspect ratio of the pillars on surfaces. (a) The aspect ratio of Ai, which is the ratio of the height of a pillar h to the inner distance of pillars l (Reference Raj, Adera, Enright and WangRaj et al. 2014). (b) The aspect ratio of Ap, which is the ratio of the height of a pillar h to the period of pillars d (Reference Courbin, Denieul, Dressaire, Roper, Ajdari and StoneCourbin et al. 2007).
The symmetry of a pillar-arrayed microstructured surface could be identified by the topography of the array. While these methods of characterization have been proven effective in describing wetting, spreading morphology and dynamics in previous studies (Reference Yuan and ZhaoYuan & Zhao 2013; Reference Raj, Adera, Enright and WangRaj et al. 2014; Reference Yuan, Huang and ZhaoYuan, Huang & Zhao 2014), the shortage arises when the quasiperiodically patterned surfaces fabricated with micropillars are used to control the morphology of moving contact lines of liquid droplets. The roughness and pillar density of quasiperiodically patterned surfaces fabricated with micropillars exhibit variation in the short range with location, but remain constant in the long range (Reference StampfliStampfli 1986; Reference Kumar and RajKumar & Raj 2017) due to the characteristic of being disordered in the short range but ordered in the long range. Additionally, aspect ratios fail to adequately characterize quasiperiodically patterned surfaces fabricated with micropillars due to the disorder feature in the short range. Moreover, symmetry alone could not effectively characterize quasiperiodically patterned surfaces fabricated with micropillars, as certain types of quasiperiodically patterned surfaces exhibit the same symmetry as periodically patterned surfaces fabricated with micropillars arranged in an array. Thus, there is a need for a further characterization method of a pillar-arrayed surface.
3. Description
Firstly, the nearest-neighbour distance of pillars on a pillar-arrayed microstructured surface is defined. This approach simplifies each pillar to a dot, ignoring their size and shape, thus defining the nearest neighbour distance as the distance between one dot and its closest neighbour. Pillars on a microstructured surface arranged in a pillar array may exhibit variations in both the nearest neighbour distances and the number of nearest neighbour pillars. Considering pillars with identical nearest neighbour distances and numbers of nearest neighbour as one kind may result in multiple kinds of pillars on one surface. Then let i denote one kind of pillar, which has the same nearest neighbour distance and number of nearest neighbour pillars, ci denote the ratio of the number of i kinds of pillar to the number of all pillars on the surface and N denote the number of kinds of pillars. Thus, a formula can be derived as
 \begin{equation}\sum\limits_{i = 1}^N {{c_i}} = 1,\end{equation}
\begin{equation}\sum\limits_{i = 1}^N {{c_i}} = 1,\end{equation}which means the sum of ratios of all kinds of pillars is equal to 1.
Using i, ci and N, the configurational entropy, S, of a pillar-arrayed microstructured surface is given by
 \begin{equation}S = {-} \sum\limits_{i = 1}^N {{c_i}\ln {c_i}} .\end{equation}
\begin{equation}S = {-} \sum\limits_{i = 1}^N {{c_i}\ln {c_i}} .\end{equation}Here, the configurational entropy was given to characterize the geometry of a micro-pillar-arrayed surface.
4. Examples
We take figure 2 as an example to illustrate the kinds of pillars and the configurational entropy of pillar-arrayed microstructured surfaces. Note that in figure 2 the pillars, which are represented by two-dimensional dots, are arranged periodically.
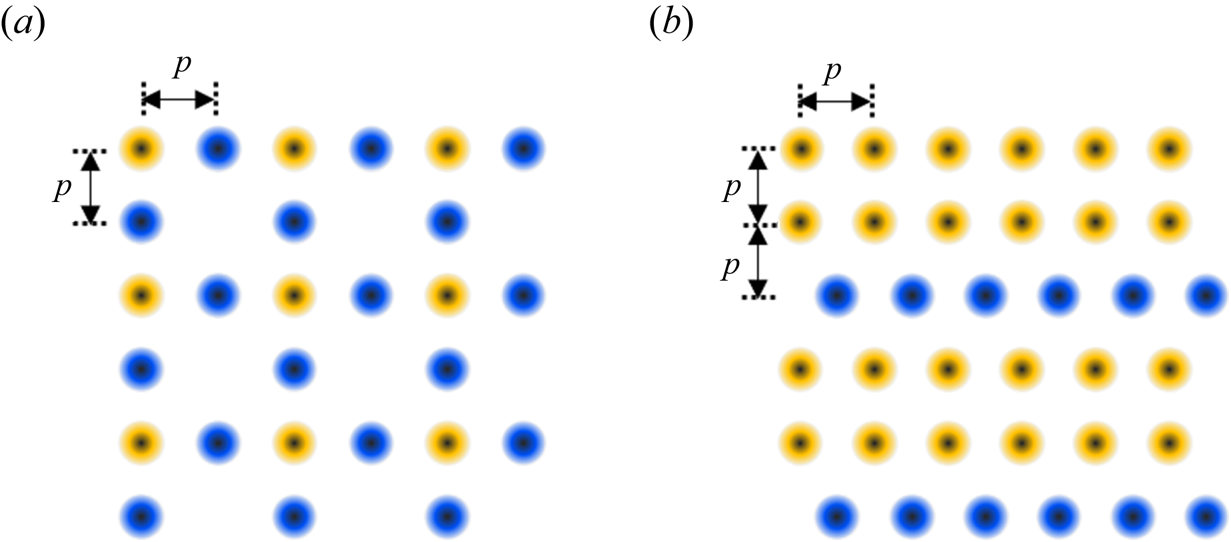
Figure 2. Illustration of configurational entropy on pillar-arrayed microstructured surfaces. Each dot denotes a pillar, each colour represents one kind of pillar on a surface and p denotes the distance between pillars. The pillars on surfaces are arranged periodically.
In figure 2(a), each yellow dot has four nearest neighbour dots with the nearest neighbour distance of p. Meanwhile, each blue dot has two nearest neighbour dots with the nearest neighbour distance of p. Consequently, the yellow dots are classified as one kind and the blue dots as another. Considering the periodically patterned surface, the ratio of yellow dots, denoted as c 1, is calculated to be 0.33, and the ratio of blue dots, denoted as c 2, is calculated to be 0.67. As a result, the configurational entropy of the surface in figure 2(a) is calculated to be 0.64.
In figure 2(b), each yellow dot has three nearest neighbour dots with the nearest neighbour distance of p. Meanwhile, each blue dot has two nearest neighbour dots with the nearest neighbour distance of p. Thus, the yellow dots are one kind and the blue ones another kind. Considering the periodical surface, the ratio of yellow dots c 1 is calculated to be 0.67, and the ratio of blue dots c 2 is calculated to be 0.33. As a result, the configurational entropy of the surface in figure 2(b) is calculated to be 0.64.
5. Results and discussion
To elucidate the relationship between the wetting morphology of liquid droplets and the pillar-arrayed microstructured surfaces, it is necessary to calculate the configurational entropy of pillar-arrayed microstructured surfaces. We first focus on the periodically patterned pillar-arrayed surfaces. Such surfaces, which are employed to manipulate the morphology of liquid droplets with complete wetting, are illustrated in figure 3(a). In figure 3(a), periodically patterned surfaces fabricated with square arrayed square pillars, square arrayed circular pillars, rectangular arrayed circular pillars, hexagonal arrayed circular pillars and stretched hexagonal arrayed circular pillars are illustrated. Using the method of calculating configurational entropy, it is found that the configurational entropy of each periodically patterned surface in figure 3(a) is zero, since the pillars on each periodically patterned surface have the same nearest neighbour distance and the number of nearest neighbour pillars.

Figure 3. (a) Illustrations of periodically patterned pillar-arrayed surfaces. (b) The wetting morphology of liquid droplets (blue polygons) on corresponding surfaces (the yellow dots denote micropillars) according to the experimental results in, e.g. Reference Courbin, Denieul, Dressaire, Roper, Ajdari and StoneCourbin et al. (2007), Reference Raj, Adera, Enright and WangRaj et al. (2014) and Reference Chen, Yuan, Huang and ZhaoChen et al. (2016).
The wetting morphology on periodically patterned pillar-arrayed surfaces, which may be inferred from the experimental findings such as those in Reference Courbin, Denieul, Dressaire, Roper, Ajdari and StoneCourbin et al. (2007), Reference Raj, Adera, Enright and WangRaj et al. (2014) and Reference Chen, Yuan, Huang and ZhaoChen et al. (2016), has been depicted in figure 3(b). Note that complete wetting liquid droplets on the surfaces are considered here. In addition to the initial circular projected wetted area of a liquid droplet, the possible symmetries of the wetted area can be four-fold, four-fold, two-fold, six-fold and two-fold from left to right, which are consistent with the symmetry of periodically patterned pillar-arrayed surface.
After discussion of periodically patterned pillar-arrayed surfaces, the quasiperiodically patterned pillar-arrayed surfaces are then discussed. Such quasiperiodically patterned pillar-arrayed surfaces, employed to manipulate the morphology of wetting liquid droplets are illustrated in figure 4(a–c), with pillars represented as colourful dots. In figure 4(a–c), quasiperiodically patterned surfaces fabricated with circular pillars of five-fold, six-fold and eight-fold symmetry, respectively, are depicted (Reference Chen, Yuan and ZhaoChen et al. 2018b). Each colour denotes one kind of pillar.
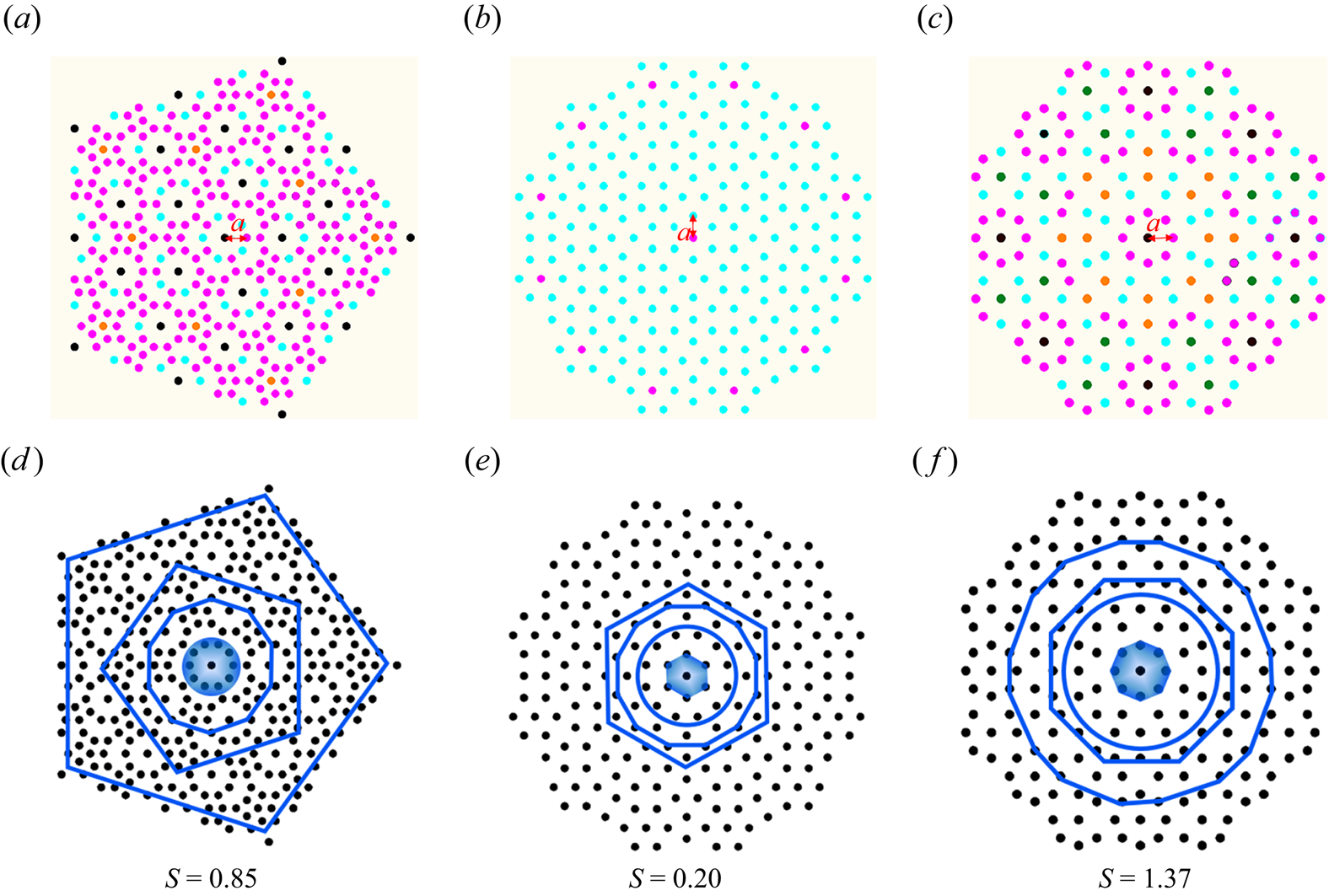
Figure 4. (a–c) Illustrations of quasiperiodically patterned pillar-arrayed surfaces: (a) five-fold; (b) six-fold; (c) eight-fold symmetry. The length of a in each illustration denotes the distance from the pillar at the symmetric centre to the nearest neighbour pillar. Colourful circular dots represent micropillars, and each colour in each illustration represent a special kind of pillar. (d–f) The wetting morphology of liquid droplets (blue polygons) on corresponding surfaces (the black dots denote micropillars) according to the experimental results in Reference Chen, Yuan and ZhaoChen et al. (2018b).
Seen from figure 4(a), each cyan dot has two nearest neighbour dots with the nearest neighbour distance of 0.62a (a denotes the distance from the pillar at symmetric centre to the nearest neighbour pillar), each magenta dot has three nearest neighbour dots with the nearest neighbour distance of 0.62a, each yellow dot has five nearest neighbour dots with the nearest neighbour distance of 0.62a, and each black dot has 10 nearest neighbour dots with the nearest neighbour distance of a. Considering the structural characteristics of the five-fold symmetric quasiperiodic surface described by Reference Chen, Yuan, Huang and ZhaoChen et al. (2016) (also refer to figure A(a) in the supplementary material available at https://doi.org/10.1017/flo.2024.10), the ratio of cyan dots c 1 is calculated to be 0.18, the ratio of magenta dots c 2 is calculated to be 0.71, the ratio of yellow dots c 3 is calculated to be 0.02 and the ratio of black dots c 4 is calculated to be 0.09. As a result, the configurational entropy of the five-fold symmetric quasiperiodical surface is calculated to be 0.85.
Seen from figure 4(b), each cyan dot has five nearest neighbour dots with the nearest neighbour distance equal to a, and each magenta dot has six nearest neighbour dots with the nearest neighbour distance of a. Considering the structural characteristics of the six-fold symmetric quasiperiodical surface (Reference PenrosePenrose 1979) (also see figure A(b) in the supplementary material), the ratio of cyan dots c 1 is calculated to be 0.95, and the ratio of magenta dots c 2 is calculated to be 0.05. As a result, the configurational entropy of the six-fold symmetric quasiperiodical surface in figure 4(b) is calculated to be 0.20.
Seen from figure 4(c), each the cyan dot has one nearest neighbour dot with the nearest neighbour distance of 0.77a, each magenta dot has two nearest neighbour dots with the nearest neighbour distance of 0.77a, each yellow dot has five nearest neighbour dots with the nearest neighbour distance of a, each green dot has six nearest neighbour dots with the nearest neighbour distance of a and each black dot has eight nearest neighbour dots with the nearest neighbour distance of a. Considering the structural feature of an eight-fold symmetric quasiperiodical surface (Reference StampfliStampfli 1986) (also see figure A(c) in the supplementary material), the ratio of cyan dots c 1 is calculated to be 0.24, the ratio of magenta dots c 2 is calculated to be 0.45, the ratio of yellow dots c 3 is calculated to be 0.15, the ratio of green dots c 4 is calculated to be 0.12 and the ratio of black dots c 5 is calculated to be 0.04. As a result, the configurational entropy of the surface in figure 4(c) is calculated to be 1.37. The calculated values of configurational entropy are summarized in table 1.
Table 1. The values of configurational entropy S of different kinds of pillar-arrayed surfaces.

The wetting morphology on quasiperiodically patterned pillar-arrayed surfaces (Reference BeenkerBeenker 1982), as observed in the experimental findings of Reference Chen, Yuan and ZhaoChen et al. (2018b), has been depicted in figure 4(d–f). On quasiperiodically patterned pillar-arrayed surfaces arranged with five-fold symmetry, as depicted in figure 4(d), the projected wetted area of a liquid droplet can exhibit circular, decagonal and pentagonal shapes, indicating that the symmetry of the projected wetted area can be axisymmetric, ten-fold and five-fold, respectively. On quasiperiodically patterned pillar-arrayed surfaces of six-fold symmetry, seen from figure 4(e), the projected wetted area of liquid droplet can be a hexagon, circle and dodecagon, which means that the symmetry of the projected wetted area can be six-fold, axisymmetric and twelve-fold. On quasiperiodically patterned pillar-arrayed surfaces of eight-fold symmetry, seen from figure 4(f), the projected wetted area of liquid droplet can be an octagon, circle and hexadecagon, which means that the symmetry of the projected wetted area can be eight-fold, and axisymmetric. Clearly, the wetting morphology on quasiperiodically patterned pillar-arrayed surfaces is more complex and diverse compared with that on periodically patterned pillar-arrayed surfaces.
The wetting morphology on both periodically and quasiperiodically patterned pillar-arrayed surfaces was clarified in figure 5(a). To quantify the relationship between pillar-arrayed surfaces and the complexity of the wetting morphology of liquid droplets, the configurational entropy, S, of pillar-arrayed surfaces and the number of the symmetries, Ns, of the projected wetted area of liquid droplets are shown in figure 5(b). From figure 5(b), one can find that once the configurational entropy is higher than 0, the number of symmetries of the projected wetted area of liquid droplets will be more than 1, indicating complex transition in the wetting process. Since the arrangement of pillars in the short range significantly influences the number of symmetries, as indicated in figure 4(d–f), the relationship between configurational entropy and the number of symmetries is nonlinear. However, the conclusion is clear that Ns > 1 if S > 0. This may imply that the configurational entropy proposed in this work can be used to characterize the pillar-arrayed microstructured surfaces roughly. Although there is a lack of high precision, configurational entropy may be an effective method for characterizing the pillar-arrayed microstructured surfaces in some ways.

Figure 5. (a) The wetting morphology on both periodically and quasiperiodically patterned pillar-arrayed surfaces. (b) The phase diagram of the relationship between the configurational entropy S of pillar-arrayed surfaces and the number of the symmetries Ns of projected wetted area of liquid droplets. The black square indicates S = 0. For the cases of S = 0, Ns = 1 and for the cases of S > 0, Ns > 1.
In order to further investigate the physics of surfaces with varying configurational entropy, the wetting dynamics is analysed. The wetting dynamics of a uniform and incompressible liquid can be described by the Navier–Stokes equations,
where ∇, v, t, p, ρ, ν and F denote the Hamiltonian operator, velocity, time, pressure, density, kinematic viscosity and volume force, respectively. Surface tension on the liquid–gas interface becomes significant when the droplet is sufficiently small. Consequently, the force on the liquid–gas surface under the isothermal assumption can be expressed as
where γ and n denote surface tension and unit normal vector on the liquid–gas interface.
Considering the roughness of the surface, the rate of change in the driving energy can be determined as
where γsg, γsl, θ and R are the solid–gas, solid–liquid interfacial tension, instant contact angle and average radius of the polygonal moving contact line. Using lubrication approximation, the scale becomes
Depending on the properties of the liquids and the roughness and configurational entropy of pillar-arrayed microstructured surfaces, the rate of change in the dissipation energy of the moving contact line may be determined as (Reference Yuan, Huang and ZhaoYuan et al. 2014; Reference Chen, Yuan, Huang and ZhaoChen et al. 2016, Reference Chen, Yuan and Zhao2018b)
Here, ζ denotes the coefficient of molecular friction. By comparing (5.6)–(5.8), it is evident that the dissipation energy scale of quasiperiodic surfaces with S > 0 differs significantly from that of periodic surfaces. This discrepancy can be attributed to the feature that the quasiperiodical surface with S > 0 is disorder in the short range but order in the long range. These theoretical predictions are validated through experiments by measuring the rate of increase in wetted area. Note that (5.8) is shown to be valid for quasiperiodic surfaces with moderate roughness and liquid viscosity. Further research may be carried to elucidate the geometric effects of the pillars on dissipation energy.
6. Conclusions
Firstly, a method for characterizing pillar-arrayed microstructured surfaces has been introduced. Configurational entropy of pillar-arrayed microstructured surfaces has been proposed and the detailed calculation has been put forward. Subsequently, the values of configurational entropy for both periodically patterned and quasiperiodically patterned pillar-arrayed surfaces have been calculated. Configurational entropy is zero for periodically patterned pillar-arrayed surfaces, whereas it is greater than zero for quasiperiodically patterned pillar-arrayed surfaces. The wetting morphology of liquid droplets on both periodically and quasiperiodically patterned pillar-arrayed surfaces has been summarized.
Finally, the influence of surface configurational entropy on the wetting morphology and dynamics of liquid droplets in experiments has been discussed. It is observed that the pillar-arrayed microstructured surfaces with configurational entropy greater than zero exhibit more complex wetting morphology of droplets compared to surfaces with zero configurational entropy. The configurational entropy proposed in this work may be helpful in understanding the mechanism of droplet wetting on microstructured surfaces and designing and characterizing microstructured surfaces.
Supplementary material
Supplementary material is available at https://doi.org/10.1017/flo.2024.10.
Declaration of interests
The authors declare no conflict of interest.
Funding statement
This work was jointly supported by the National Key R&D Program of China (grant nos 2022YFF0503500, 2022YFA1203200), the National Natural Science Foundation of China (grant nos. 12241205, 12032019, 12302349) and the Youth Innovation Promotion Association Chinese Academy of Sciences (grant no. 2020020).
Data availability statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.