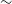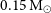1. Introduction
Planets in short-period orbits around white dwarfs (WDs) are predicted to be rare, as many are expected to be destroyed during post-main-sequence evolution or migrate to longer-period orbits (Nordhaus et al. Reference Nordhaus, Spiegel, Ibgui, Goodman and Burrows2010; Nordhaus & Spiegel Reference Nordhaus and Spiegel2013). However, the presence and characteristics of a planet in a short-period orbit around a WD can provide constraints on formation scenarios. First generation planets may migrate from large-period orbits via Kozai-Lidov cycles in hierarchical triple systems or near-coplanar scattering with other planets of similar mass (followed by tidal circularisation), or perhaps if they can survive a common envelope (CE) event (Lagos et al. Reference Lagos, Schreiber, Zorotovic, Gänsicke, Ronco and Hamers2021). Second generation planets have been suggested to form in the ejecta of the CE (Perets Reference Perets, Schuh, Drechsel and Heber2011; Kashi & Soker Reference Kashi and Soker2011; Völschow, Banerjee, & Hessman Reference Völschow, Banerjee and Hessman2014; Schleicher & Dreizler Reference Schleicher and Dreizler2014; Bear & Soker Reference Bear and Soker2014; Ledda, Danielski, & Turrini Reference Ledda, Danielski and Turrini2023). Other scenarios for second (or third) generation planet formation are discussed by Perets (Reference Perets, Schuh, Drechsel and Heber2011), Tutukov & Fedorova (Reference Tutukov and Fedorova2012), Perets & Kenyon (Reference Perets and Kenyon2013), and Hogg et al. (Reference Hogg, Wynn and Nixon2018). Formation of second generation giant planets around isolated WD debris discs is unlikely, as the surface densities are low, but the formation of low-mass planets may be possible (Bear & Soker Reference Bear and Soker2015; van Lieshout et al. Reference van Lieshout, Kral, Charnoz, Wyatt and Shannon2018).
Observational searches via various methods, such as eclipses, have revealed a few interesting WDs such as WD 1856+534, estimated to have mass
$M_\mathrm{wd}=0.518\pm0.055\,\mathrm{M_\odot}$
(Vanderburg et al. Reference Vanderburg2020),
$0.606\pm0.039$
(Alonso et al. Reference Alonso2021) or
$0.576\pm0.040\,\mathrm{M_\odot}$
(Xu et al. Reference Xu2021), and a detected planet, WD 1856+534 b, on a
$1.41\,\mathrm{d}$
orbit with mass
$1\,\mathrm{M_\mathrm{J}} \lesssim m_2 \lesssim 12\,\mathrm{M_\mathrm{J}}$
(Vanderburg et al. Reference Vanderburg2020; Xu et al. Reference Xu2021). Throughout this study, we scale our results to parameter values for this system.
WD 1856+534 b is difficult to explain using a single CE scenario (Vanderburg et al. Reference Vanderburg2020; Lagos et al. Reference Lagos, Schreiber, Zorotovic, Gänsicke, Ronco and Hamers2021; Chamandy et al. Reference Chamandy, Blackman, Nordhaus and Wilson2021, hereafter Reference Chamandy, Blackman, Nordhaus and WilsonC21; O’Connor et al. Reference O’Connor, Bildsten, Cantiello and Lai2023). In Reference Chamandy, Blackman, Nordhaus and WilsonC21, we proposed that WD 1856+534 b was instead dragged in from a wider orbit by a CE event involving a companion that tidally disrupts inside the envelope. In that scenario, a second CE event – the one with the observed planet – unbinds the remainder of the envelope. A somewhat different idea is that the planet was dragged in when the WD progenitor underwent a helium flash (Merlov, Bear, & Soker Reference Merlov, Bear and Soker2021). This work proposes a different scenario to explain such planets. As in Reference Chamandy, Blackman, Nordhaus and WilsonC21, a CE event takes place that leads to the tidal disruption of the companion. But in our new scenario, the observed planet forms in an accretion disc that results from the tidal disruption event. Notably, a somewhat similar scenario has been proposed to explain planets orbiting millisecond pulsars. In that scenario, a WD companion is disrupted, resulting in a disc around the neutron star out of which planets form. Accretion onto the neutron star causes it to spin up to millisecond periods (Stevens, Rees, & Podsiadlowski Reference Stevens, Rees and Podsiadlowski1992; van den Heuvel Reference van den Heuvel1992; Margalit & Metzger Reference Margalit and Metzger2017).
Other alternatives for explaining WD 1856+534 are migration due to the Zeipel–Lidov–Kozai effect driven by the distant binary M-dwarf companion system (Muñoz & Petrovich Reference Muñoz and Petrovich2020; O’Connor, Liu, & Lai Reference O’Connor, Liu and Lai2021; Stephan, Naoz, & Gaudi Reference Stephan, Naoz and Gaudi2021) and planet-planet scattering (Maldonado et al. Reference Maldonado, Villaver, Mustill, Chávez and Bertone2021; O’Connor, Teyssandier, & Lai Reference O’Connor, Teyssandier and Lai2022; Maldonado et al. Reference Maldonado, Villaver, Mustill and Chávez2022). While the latter scenario is plausible, searches for other planets in this system have so far come up empty (Kubiak et al. Reference Kubiak, Vanderburg, Becker, Gary, Rappaport, Xu and de Beurs2023).
Our proposed scenario begins with a CE event involving a
$\sim$
$1.5$
–
$2.5\,\mathrm{M_\odot}$
red giant branch (RGB) or asymptotic giant branch (AGB) star and a
$\sim0.15$
–
$1\,\mathrm{M_\odot}$
main sequence (MS) star. In such cases, the companion tidally disrupts to form an accretion disc that orbits the core of the WD progenitor. The formation and early evolution of such discs has been studied with hydrodynamic simulations, albeit with planetary or brown dwarf rather than stellar companions (Guidarelli et al. Reference Guidarelli, Nordhaus, Chamandy, Chen, Blackman, Frank, Carroll-Nellenback and Liu2019; Guidarelli et al. Reference Guidarelli, Nordhaus, Carroll-Nellenback, Chamanady, Frank and Blackman2022). Sufficient orbital energy can be liberated before, during, and after tidal disruption to eject the remainder of the CE, leaving a system consisting of a proto-WD core and an accretion disc of perhaps a few
$\times\,0.1\,\mathrm{M_\odot}$
in mass.
As the disc viscously spreads, it transitions from an advective, radiation pressure-dominated state with
$h\sim r$
(e.g. Nordhaus et al. Reference Nordhaus, Wellons, Spiegel, Metzger and Blackman2011) to a radiative cooling-dominated, gas pressure-dominated state with
$h\ll r$
(e.g. Shen & Matzner Reference Shen and Matzner2014), where h is the disc scale height at radius r. The disc then becomes gravitationally unstable near its outer radius and self-gravitating clumps of mass greater than the Jeans mass (of order
$1\,\mathrm{M_\mathrm{J}}$
) collapse to form puffed-up protoplanets that may be massive enough to clear a gap and avoid rapid inward (type I) migration down to their own tidal disruption separations (e.g. Boss Reference Boss1997; Boss Reference Boss1998; Zhu et al. Reference Zhu, Hartmann, Nelson and Gammie2012; Schleicher & Dreizler Reference Schleicher and Dreizler2014; Lichtenberg & Schleicher Reference Lichtenberg and Schleicher2015).
Table 1. List of stellar models with parameters, obtained by running single-star simulations with the 1D stellar evolution code MESA. C18 refers to Chamandy et al. (Reference Chamandy2018). Quantities are the stellar mass M, mass of its zero-age MS progenitor
$M_\mathrm{ZAMS}$
, mass of its core
$M_\mathrm{c}$
, radius R, the value of the dimensionless parameter
$\lambda$
appearing in equation (13) for the envelope binding energy
$E_\mathrm{bind}$
, which is listed in the final column, chosen so that the binding energy includes the gravitational potential energy and thermal energy. Models were evolved using MESA release 10108 with solar metallicity (
$Z=0.02$
) and with mass-loss parameters on the RGB and AGB of
$\eta_\mathrm{R}=0.7$
and
$\eta_\mathrm{B}=0.15$
, respectively, so as to match the initial-final mass relation of Cummings et al. (Reference Cummings, Kalirai, Tremblay, Ramirez-Ruiz and Choi2018), with the exception of the RGB(C18) model, which used MESA release 8845 with
$\eta_\mathrm{R}=1$
.
2. Constraining the proposed scenario
2.1 Progenitor
To obtain realistic examples of RGB and AGB progenitors, we employ Modules for Experiments in Stellar Astrophysics (MESA) (Paxton et al. Reference Paxton, Bildsten, Dotter, Herwig, Lesaffre and Timmes2011; Paxton et al. Reference Paxton2013; Paxton et al. Reference Paxton2015; Paxton et al. Reference Paxton2019). Table 1 summarises the progenitor models we consider. All models assume solar metallicity (
$Z=0.02$
). Models B-F are consistent with the observed initial-final mass relationships derived from cluster observations (Cummings et al. Reference Cummings, Kalirai, Tremblay, Ramirez-Ruiz and Choi2018; Hollands, Littlefair, & Parsons Reference Hollands, Littlefair and Parsons2023) and have been extensively used for CE studies (Wilson & Nordhaus Reference Wilson and Nordhaus2019; Wilson & Nordhaus Reference Wilson and Nordhaus2020; Wilson & Nordhaus Reference Wilson and Nordhaus2022; Kastner & Wilson Reference Kastner and Wilson2021). Model A has been used to model the initial stellar profile in a series of papers involving 3D simulations, starting with Chamandy et al. (Reference Chamandy2018), and uses the same parameter values as the other models except for a slightly different value of the Reimers mass loss parameter (
$\eta_\mathrm{R}=1$
instead of
$0.7$
).
Fig. 1 shows the stellar radius as a function of core mass for stellar models of various zero-age main sequence (ZAMS) masses and parameter values as in Models B-F. The core mass increases with time, so stars evolve from left to right. Observational mass estimates for WD 1856+534 are plotted as vertical lines for reference. That the observed WD mass coincides with the AGB phase suggests that the progenitor was on the AGB at the time of the CE event. However, as discussed below, the proto-WD core mass can increase by accreting the disrupted companion, so an RGB progenitor cannot immediately be ruled out.
Figure 1. Relationship between primary radius and core mass, for different values of
$M_\mathrm{ZAMS}$
. These results were obtained using MESA assuming solar metallicity (
$Z=0.02$
) and with Reimers and Blöcker scaling coefficients set to
$\eta_\mathrm{R}=0.7$
and
$\eta_\mathrm{B}=0.15$
, respectively, as motivated in Section 1. Constraints on
$M_\mathrm{ZAMS}$
for the system WD 1856+534 are highlighted in the plot. The lower limit of
$\approx1.4\,\mathrm{M_\odot}$
comes from the age upper limit of
$\sim10\,\mathrm{Gyr}$
(Vanderburg et al. Reference Vanderburg2020). Larger states most likely to undergo CE are boxed (RGB, AGB, TPAGB). For curves enclosed by the magenta (middle) rectangle, only those with
$M_\mathrm{ZAMS}\gtrsim2.0\,\mathrm{M_\odot}$
are likely because below this the maximum radius on the RGB is greater.
Given that the age of the WD 1856+534 system is
$\lesssim$
$10\,\mathrm{Gyr}$
and the cooling age of the WD is
$5.85\pm0.5\,\mathrm{Gyr}$
(Vanderburg et al. Reference Vanderburg2020), the WD progenitor spent
$\lesssim$
$4.6\,\mathrm{Gyr}$
on the MS, which implies a mass of
$M_\mathrm{ZAMS}\gtrsim1.4\,\mathrm{M_\odot}$
.Footnote a Furthermore, an AGB progenitor would likely have had
$M_\mathrm{ZAMS}\gtrsim2.0\,\mathrm{M_\odot}$
; otherwise, its RGB radius would have been larger, and it would have entered CE then. Given the steepness of the initial mass function above
$1\,\mathrm{M_\odot}$
(Salpeter Reference Salpeter1955; Hennebelle & Grudić Reference Hennebelle and Grudić2024), we choose examples with
$M_\mathrm{ZAMS}\le2.2\,\mathrm{M_\odot}$
(Table 1), but more massive progenitors are possible.
2.2 Disc formation and survival
A fraction of the disrupted companion forms an accretion disc around the AGB or RGB core, inside the remaining CE (Reyes-Ruiz & López Reference Reyes-Ruiz and López1999; Blackman, Frank, & Welch Reference Blackman, Frank and Welch2001; Nordhaus & Blackman Reference Nordhaus and Blackman2006; Nordhaus et al. Reference Nordhaus, Wellons, Spiegel, Metzger and Blackman2011; Nordhaus & Spiegel Reference Nordhaus and Spiegel2013; Guidarelli et al. Reference Guidarelli, Nordhaus, Chamandy, Chen, Blackman, Frank, Carroll-Nellenback and Liu2019; Guidarelli et al. Reference Guidarelli, Nordhaus, Carroll-Nellenback, Chamanady, Frank and Blackman2022). The hydrodynamic simulations performed by Guidarelli et al. (Reference Guidarelli, Nordhaus, Carroll-Nellenback, Chamanady, Frank and Blackman2022) involved 10–
$30\,\mathrm{M_\mathrm{J}}$
companions undergoing tidal disruption inside the envelope of an AGB star. About 60% of the mass of the disrupted companion formed a disc and the other 40% constituted an outwardly moving but gravitationally bound tidal tail that would eventually fall back. This is reminiscent of work by Shen & Matzner (Reference Shen and Matzner2014) on tidal disruption event discs around supermassive black holes. These authors find that a large fraction of the material from the disruption falls back and collides with itself, settling at a radius somewhat larger than the disruption radius. Guidarelli et al. (Reference Guidarelli, Nordhaus, Carroll-Nellenback, Chamanady, Frank and Blackman2022) find that the disc becomes quasi-Keplerian within a few dynamical times, with an aspect ratio
$0.05\lesssim h/r\lesssim0.2$
. Metzger et al. (Reference Metzger, Zenati, Chomiuk, Shen and Strader2021) model the tidal disruption of a star in a cataclysmic variable system and the disc that subsequently forms around the WD; the model explored in this work is in some ways similar to their model.
Guidarelli et al. (Reference Guidarelli, Nordhaus, Chamandy, Chen, Blackman, Frank, Carroll-Nellenback and Liu2019) simulated a disc surrounded by a hot AGB envelope and estimated that the disc is likely to be stable for at least 10 times the duration of the simulation, or 100 orbits at the outer radius of the disc. For a disc of outer radius equal to the minimum disruption separation
$\sim0.3$
$\,\mathrm{R_\odot}$
(Fig. 2a and Section 2.5), this corresponds to
$\sim3\,\mathrm{d}$
, whereas taking the disc outer radius to be the present orbital separation of WD 1856+534b of
$4.4$
$\,\mathrm{R_\odot}$
gives
$\sim0.4\,\mathrm{yr}$
. The actual disc survival time might be much longer, especially considering that the envelope would have expanded and spun up due to orbital energy and angular momentum transfer from the companion, reducing the destabilising effect of shear on the disc.
Figure 2. Panel (a): Orbital separation where stellar tidal disruption occurs
$a_\mathrm{d1}$
(solid lines), and where RLOF is initiated if the stellar companion has not already disrupted (dotted lines) for the giant star models of Table 0, as a function of the companion mass. The companion radius is shown as a dashed line (equation 11) and the difference between the observed WD mass according to Xu et al. (Reference Xu2021) and the core mass in the stellar model is shown in the legend. Panel (b): Maximum allowed value of the common envelope efficiency parameter
$\alpha_\mathrm{CE}$
as a function of the companion mass; above this value the companion unbinds the envelope before it can be disrupted (solid lines) or before RLOF is initiated (dotted lines). It is possible that the envelope could be ejected before disruption if RLOF leads to unstable mass transfer and inspiral down to
$a_\mathrm{d1}$
. Thus, for a given progenitor, the parameter space above the dotted line is excluded, and that below the dotted line but above the solid line is viable only if RLOF is initiated and ultimately leads to disruption. Panel (c): As the top panel, but now zoomed in to show the relevant parameter space for the planet, and with mass shown in units of
$\!\,\mathrm{M_\mathrm{J}}$
(
$1\,\mathrm{M_\mathrm{J}}\approx10^{-3}\,\mathrm{M_\odot}$
). The planet cannot be formed in the hatched region, which corresponds to separations less than its tidal disruption separation
$a_\mathrm{d2}$
.
If the envelope were to truncate the evolution of the disc and outlive it, this could provide challenges for the formation, survival, and emergence of the planet in its current orbit. However, we find that the envelope is likely removed before, during, or shortly after disc formation. In Appendix E, we discuss what processes may power envelope ejection, and estimate how long it takes. One possibility is that tidal disruption of the companion is preceded by a Roche lobe overflow (RLOF) phase that leads to unstable mass transfer and orbital tightening, and the transfer of orbital energy ejects the envelope prior to disruption. In this case, the disc of disrupted companion material would not be surrounded by a hot envelope, so would easily survive. Another possibility is that the envelope is removed by the release of energy during an early, possibly brief phase of advection-dominated accretion. We speculate that envelope unbinding might also be assisted by shocking during disc formation and nuclear reactions due to accretion onto the core.
If the envelope is not rapidly unbound by these processes, then it could be unbound by subsequent accretion at close to the Eddington rate, but this takes
$\sim$
$10^2$
yr. Whether the disc can survive for this long is not clear. In cases where early rapid removal of the envelope does not occur, survivability of the disc may be a bottleneck in our planet formation scenario that may help to explain why such planets are rare. In any case, after the envelope is ejected, ionising radiation from the hot central core photo-evaporates the disc in
$\sim$
10
$\,\mathrm{Myr}$
(Appendix A).
2.3 Minimum required companion and protoplanet masses
From the Toomre criterion (Toomre Reference Toomre1964), the disc is gravitationally unstable if
\begin{align} Q=\frac{h\Omega^2}{\pi G\Sigma} \lesssim1,\end{align}
where
\begin{align} \Omega=\left(\frac{GM_\mathrm{c}}{r^3}\right)^{1/2}\end{align}
is the angular rotation speed with
$M_\mathrm{c}$
the mass of the core of the giant star, and
$\Sigma$
is the gas surface density. We approximate the surface density as (e.g. Armitage & Rice Reference Armitage and Rice2005; Raymond & Morbidelli Reference Raymond, Morbidelli, Biazzo, Bozza, Mancini and Sozzetti2022)
\begin{align} \Sigma = \Sigma_\mathrm{out}\left(\frac{r}{r_\mathrm{out}}\right)^{-\beta},\end{align}
with
$1\lesssim\beta\lesssim3/2$
. A fraction f of the disrupted companion forms the disc, while the rest either accretes prior to disc formation or mixes with envelope material.
In Appendix B, we show that condition (1) leads to the following constraint on the disc mass:
\begin{align} fm_1\gtrsim0.12\,\mathrm{M_\odot}\frac{1}{2-\beta} \left(\frac{\theta}{0.1}\right) \left(\frac{M_\mathrm{c}}{0.576\,\mathrm{M_\odot}}\right) \left(\frac{r}{r_\mathrm{out}}\right)^{-(2-\beta)}.\end{align}
Since
$f\le1$
, gravitational instability requires
$m_1\gtrsim0.12\,\mathrm{M_\odot}$
, with
$m_1$
the mass of the disrupted companion. (Throughout, we use subscript ‘1’ to refer to the disrupted companion and subscript ‘2’ to refer to the extant companion, i.e. the planet.) For equation (2), we neglected the disc self-gravity, but it can be important if
$fm_1$
is comparable to
$M_\mathrm{c}$
.
The mass of the collapsing object must also exceed the Jeans mass (e.g. Binney & Tremaine Reference Binney and Tremaine2008),
\begin{align} M_\mathrm{Jeans} = \frac{\pi^{5/2}c_\mathrm{s}^3}{6G^{3/2}\rho^{1/2}},\end{align}
where
$c_\mathrm{s}$
is the sound speed. Substituting
$c_\mathrm{s}=h\Omega$
,
$\rho=\Sigma/2h$
,
$h=\theta r$
,
$\Omega$
from equation (2), and
$\Sigma$
from equations (3) and (B2), we obtain
\begin{align}\begin{split} M_\mathrm{Jeans} \approx \,& 2.7\,\mathrm{M_\mathrm{J}}\frac{1}{(2-\beta)^{1/2}} \bigg(\frac{M_\mathrm{c}}{0.576\,\mathrm{M_\odot}}\bigg)^{3/2} \bigg(\frac{fm_1}{0.3\,\mathrm{M_\odot}}\bigg)^{-1/2}\\ &\times\bigg(\frac{\theta}{0.1}\bigg)^{7/2} \bigg(\frac{r}{r_\mathrm{out}}\bigg)^{-1+\beta/2}.\end{split}\end{align}
If WD 1856+534 b formed this way, all of the material in the collapsing protoplanet was incorporated into the planet, and the planet retained the same mass up to the present time, then this would imply that
$m_2 \gtrsim M_\mathrm{Jeans}$
, but some protoplanetary mass could be lost due to inefficiencies or ablation in the formation process. Regardless, this result is consistent with the observational estimate,
$0.84\lesssim m_2/\,\mathrm{M_\mathrm{J}} \lesssim 11.7$
(Vanderburg et al. Reference Vanderburg2020; Xu et al. Reference Xu2021), as well as with the lower limit of
$2.4\,\mathrm{M_\mathrm{J}}$
found by Alonso et al. (Reference Alonso2021).
2.4 Timescale for planet formation
The protoplanet contracts on the free-fall timescale,
$t_\mathrm{ff}\lesssim1\,\mathrm{d}$
(see Appendix C). This can be compared with the viscous dissipation timescale
\begin{align} t_\mathrm{visc} = \frac{r^2}{\nu}\approx\frac{r^2}{\alpha_\mathrm{SS} c_\mathrm{s} h} \approx \frac{r^2}{\alpha_\mathrm{SS} h^2\Omega},\end{align}
where
$\alpha_\mathrm{SS}$
is the viscosity parameter (Shakura & Sunyaev Reference Shakura and Sunyaev1973). Making use of equation (2) we obtain
\begin{align} t_\mathrm{visc} \approx 6\,\mathrm{yr} \left(\frac{r}{4.4\,\mathrm{R_\odot}}\right)^{3/2}\!\! \left(\frac{\theta}{0.1}\right)^{-2}\!\! \left(\frac{M_\mathrm{wd}}{0.576\,\mathrm{M_\odot}}\right)^{-1/2}\!\! \left(\frac{\alpha_\mathrm{SS}}{0.01}\right)^{-1}\!\!,\end{align}
which easily exceeds
$t_\mathrm{ff}$
, facilitating giant gaseous protoplanet (GGPP) by direct collapse (Boss Reference Boss1998). Transformation of the GGPP into a full-fledged planet takes much longer and is mostly independent of the disc evolution other than possible migration.
2.5 Companion mass upper limit and the WD progenitor
The disrupted companion must have been massive enough for the disc to satisfy condition (4); but not so massive as to have avoided disruption by unbinding the envelope. The orbital separation at which tidal disruption occurs is given by (e.g. Nordhaus & Blackman Reference Nordhaus and Blackman2006)
\begin{align} a_\mathrm{d1}\approx\left(\frac{2M_\mathrm{c}}{m_1}\right)^{1/3}r_1,\end{align}
where
$M_\mathrm{c}$
is the mass of the core of the giant and
$r_1$
is the radius of the companion. Fig. 2a shows
$a_\mathrm{d1}$
as a function of
$m_1$
(solid lines). The colours represent stellar models listed in Table 1. Dotted lines show the orbital separation at which RLOF occurs (Eggleton Reference Eggleton1983),
\begin{align} a_\mathrm{RLOF} = \frac{0.6q^{2/3} + \ln(1+q^{1/3})}{0.49 q^{2/3}}r_1,\end{align}
where
$q=M_\mathrm{c}/m_1$
. If
$a_\mathrm{RLOF} \gt a_\mathrm{d1}$
, then the companion begins losing mass at around
$a_\mathrm{RLOF}$
. Assuming this mass transfer phase is unstable, the separation continues to decrease and the companion tidally disrupts at around
$a_\mathrm{d1}$
. If
$a_\mathrm{RLOF} \lt a_\mathrm{d1}$
, then tidal disruption happens directly, without any RLOF phase. To estimate the radius of the disrupted companion and that of the planet, we use the following approximation to the results of Chabrier et al. (Reference Chabrier, Baraffe, Leconte, Gallardo, Barman and Stempels2009):
\begin{align} \frac{r}{\!\,\mathrm{R_\odot}} = \begin{cases} 0.1 & \text{if } m/\!\,\mathrm{M_\odot}\le 0.077;\\ 0.1\left(\frac{m/\!\,\mathrm{M_\odot}}{0.077}\right)^{0.8} & \text{if } 0.077 \lt m/\!\,\mathrm{M_\odot}\le 0.4;\\ 0.1\left(\frac{0.4}{0.077}\right)^{0.8}\left(\frac{m/\!\,\mathrm{M_\odot}}{0.4}\right)^{1.075} & \text{if } m/\!\,\mathrm{M_\odot} \gt0.4. \end{cases}\end{align}
The value of
$r_1$
is shown as a black dashed line in Fig. 2a. It can be seen that
$r_1\unicode{x003E} a_\mathrm{d1}$
in some cases for large values of
$m_1$
, which means the model is not fully self-consistent for that small region of parameter space. This limitation of the model stems from its simplicity.Footnote b However, as such lack of precision in the modelling does not affect our final conclusions, we choose to keep the model as simple as possible.
The envelope remains bound if the liberated orbital energy
$\Delta E_\mathrm{orb}$
multiplied by the efficiency parameter
$\alpha_\mathrm{CE}$
is smaller than the envelope binding energy
$E_\mathrm{B}$
, that is,
\begin{align} \alpha_\mathrm{CE}\Delta E_\mathrm{orb} \unicode{x003C} E_\mathrm{B},\end{align}
where
\begin{align} E_\mathrm{B} = \frac{GM(M-M_\mathrm{c})}{\lambda R},\end{align}
M and R are the mass and radius of the WD progenitor, and
$\lambda$
is a parameter of order unity that depends on the stellar density and temperature profiles. To satisfy constraint (12) at the tidal disruption separation, we substitute
$\Delta E_\mathrm{orb} \approx GM_\mathrm{c} m_1/2a_\mathrm{d1}$
, where we have neglected the initial orbital energy. To satisfy the same constraint at the separation at which RLOF begins, we instead substitute
$\Delta E_\mathrm{orb} \approx GM_\mathrm{c} m_1/2a_\mathrm{RLOF}$
.
Fig. 2b shows the upper limit to
$\alpha_\mathrm{CE}$
below which the envelope is not completely unbound before the tidal disruption separation is reached (solid lines). The value of
$\alpha_\mathrm{CE}$
is not well constrained and likely varies from one system to another, but estimates for low-mass systems are typically between
$0.05$
and
$0.5$
(e.g. Iaconi & De Marco Reference Iaconi and De Marco2019; Wilson & Nordhaus Reference Wilson and Nordhaus2019; Scherbak & Fuller Reference Scherbak and Fuller2023). The same lines can be used to find the maximum value of
$m_1$
below which the envelope remains bound, for a given value of
$\alpha_\mathrm{CE}$
. However, RLOF inside the envelope may lead to runaway mass loss, orbital tightening, and tidal disruption, even if the envelope were ejected shortly after the onset of RLOF. The dotted lines again show upper limits on
$\alpha_\mathrm{CE}$
, but now requiring that the envelope remains bound until the onset of RLOF, which occurs at the separation
$a_\mathrm{RLOF}$
. For
$m_1\gtrsim0.1\,\mathrm{M_\odot}$
, we see from Fig. 2a that
$a_\mathrm{RLOF}\unicode{x003E} a_\mathrm{d1}$
, so RLOF could occur for
$m_1\gtrsim0.1\,\mathrm{M_\odot}$
.
Fig. 2b shows that the more distended models (RGB tip, shown in orange, and high/low mass thermally pulsing AGB (TPAGB), shown in violet/red) require
$m_1\lesssim0.08\,\mathrm{M_\odot}$
if
$\alpha_\mathrm{CE}=0.2$
, using the more conservative limit (solid lines). If
$\alpha_\mathrm{CE}=0.1$
, then the maximum value of
$m_1$
lies within the range
$(0.13,0.28)$
for these three models. Models with
$\alpha_\mathrm{CE}\ge0.2$
are ruled out because condition (4) is not satisfied: the orange, violet, and red lines all intersect
$\alpha_\mathrm{CE}$
at
$m_1\unicode{x003C}0.1\,\mathrm{M_\odot}$
. If
$0.1\unicode{x003C}\alpha_\mathrm{CE}\unicode{x003C}0.2$
, the allowed range of
$m_1$
is quite narrow. By constrast, the less distended RGB and AGB models accommodate a larger range of companion mass because the magnitude of the envelope binding energy is larger. Focussing, conservatively, on the solid rather than the dotted lines, the AGB model (Model D, green) admits companion masses up to
$\approx 1\,\mathrm{M_\odot}$
if
$\alpha_\mathrm{CE}=0.2$
, up to
$\approx0.3\,\mathrm{M_\odot}$
if
$\alpha_\mathrm{CE}=0.3$
, and up to
$\approx0.18\,\mathrm{M_\odot}$
if
$\alpha_\mathrm{CE}=0.4$
. The RGB(C18) model (Model A, brown) allows for slightly larger upper limits to the companion mass.
CE evolution culminating in tidal disruption of a companion massive enough to form a planet is thus more likely for less distended primary stars. Using the less conservative upper limit on
$\alpha_\mathrm{CE}$
corresponding to RLOF (dotted lines), the allowed ranges of
$\alpha_\mathrm{CE}$
and
$m_1$
are larger, but less distended progenitors are still favoured.
2.6 Implications of accretion for the WD mass
In the legend of Fig. 2, we show the approximate difference between
$M_\mathrm{wd}\approx0.576\,\mathrm{M_\odot}$
(Xu et al. Reference Xu2021) and the core mass of the primary (Table 1). This difference could be explained by accretion of material from the disrupted companion. For the RGB models,
$\sim$
$0.12$
–
$0.21\,\mathrm{M_\odot}$
must be accreted, whereas for the AGB/TPAGB models only
$\sim$
$0.01$
–
$0.06\,\mathrm{M_\odot}$
must be accreted. The AGB model (Model D, green) and RGB(C18) model (Model A, brown) can accommodate a larger range of disrupted companion masses than the other models (Section 2.5), but the AGB model requires less accretion of disrupted companion material onto the proto-WD core and may thus be more likely. In Appendix D, we estimate that
$\sim$
$10^{-3}$
–
$10^{-2}\,\mathrm{M_\odot}$
is accreted during a phase of advection-dominated accretion, but that another
$\sim$
$0.1\,\mathrm{M_\odot}$
may accrete in the next
$10^3$
–
$10^4\,\mathrm{yr}$
during an Eddington-limited phase.
2.7 Location of planet formation
The planet must form outside of its own tidal disruption separation
$a_\mathrm{d2}$
, plotted in Fig. 2c as a function of the planet mass
$m_2$
. For
$1\unicode{x003C} m_2/\!\,\mathrm{M_\mathrm{J}}\unicode{x003C}12$
, the range is
$0.5\lesssim a_\mathrm{d2}\lesssim 1.0\,\mathrm{R_\odot}$
, but
$a_\mathrm{d1} \unicode{x003C}0.5\,\mathrm{R_\odot}$
for
$m_1\lesssim0.4\,\mathrm{M_\odot}$
, and
$a_\mathrm{d1} \unicode{x003C}1\,\mathrm{R_\odot}$
for
$m_1\lesssim1.0\,\mathrm{M_\odot}$
, as shown in Fig. 2a, ignoring
$m_1\unicode{x003C}0.01\,\mathrm{M_\odot}$
, which is excluded by the lower limit (4). Thus, if the planet formed at
$a_\mathrm{d1}$
, this would imply a separate lower limit for
$m_1$
in the range
$0.5$
–
$1.0\,\mathrm{M_\odot}$
due to the minimum in the
$a_\mathrm{d1}$
vs. mass relation plotted in Fig. 2a. But could the planet instead form at a larger separation, or, for WD 1856+534 b, at its present location
$a_2\approx4.4\,\mathrm{R_\odot}$
?
For
$\theta=0.1$
, the disc can viscously spread out to to
$r_\mathrm{out}\sim a_2$
on the viscous timescale,
$\sim$
$6\,\mathrm{yr}$
(equation 8). But if the flow is advection-dominated then
$\theta\sim1$
, lowering the diffusion time by a factor of
$\sim$
100. At some point the disc transitions from the advection-dominated geometrically thick regime to the gas-pressure-dominated geometrically thin regime (e.g. Shen & Matzner Reference Shen and Matzner2014). Protoplanet formation can occur once Q drops below unity and Q is proportional to
$\theta$
and to a negative power of
$r/r_\mathrm{out}$
(equation B5). Thus, when the disc transitions,
$\theta$
and Q drop by an order of magnitude so this transition might trigger gravitational instability in the outer disc, leading to protoplanet formation at separations
$\unicode{x003E} a_\mathrm{d1}$
. Thus, WD 1856+534 b might have formed at or close to its present separation.
By the end of the simulations of Guidarelli et al. (Reference Guidarelli, Nordhaus, Carroll-Nellenback, Chamanady, Frank and Blackman2022), the expanding tidal tail formed during the disruption extends an order of magnitude larger than the tidal disruption separation
$a_\mathrm{d1}$
. This material may fall back and extend the disc (e.g. Shen & Matzner Reference Shen and Matzner2014). Mass transfer and disc formation may also begin in the RLOF phase, which begins at separations
$\unicode{x003E} a_\mathrm{d1}$
(Fig. 2a). Moreover, the companion likely inflates by accreting a quasi-hydrostatic atmosphere (Chamandy et al. Reference Chamandy2018), which would, in principle, cause it to overflow its Roche lobe at still larger separation. RLOF might also lead to mass transfer through the L2 point and circumbinary disc formation (e.g. MacLeod, Ostriker, & Stone Reference MacLeod, Ostriker and Stone2018). These processes could increase the outer radius of the disc, facilitating planet formation at separations
$\unicode{x003E} a_\mathrm{d1}$
.
2.8 Minimum mass to prevent type I migration
Once formed, the protoplanet can avoid destruction due to type I inward migration by opening a gap if (e.g. Papaloizou Reference Papaloizou2021)
\begin{align} m_2\gtrsim2\,\mathrm{M_\mathrm{J}}\left(\frac{M_\mathrm{wd}}{0.576\,\mathrm{M_\odot}}\right)\left(\frac{\theta}{0.1}\right)^3\end{align}
and
\begin{align} m_2\gtrsim2\,\mathrm{M_\mathrm{J}}\left(\frac{M_\mathrm{wd}}{0.576\,\mathrm{M_\odot}}\right)\left(\frac{\theta}{0.1}\right)^2\left(\frac{\alpha_\mathrm{SS}}{0.01}\right),\end{align}
which happen to be lower limits of similar magnitude to each other and to
$M_\mathrm{Jeans}$
(equation 6). Therefore, two separate lines of reasoning favour a planet mass
$\gtrsim 2\,\mathrm{M_\mathrm{J}}$
; this lower limit is thus a fairly robust prediction of our model.
3. Summary and conclusions
We have presented a second generation planet formation scenario that may explain the occurrence of giant planets in low-period orbits around WDs. In this scenario, planets form from gravitational instability of an accretion disc formed out of material from a low-mass star that was tidally disrupted due to CE interaction with the WD progenitor core. We showed that WD 1856+534 b may be explained by this scenario if: (i) the WD progenitor was a relatively compact AGB star with
$M\gtrsim2\,\mathrm{M_\odot}$
, (ii) the mass of the disrupted companion was in the range
$0.15\lesssim m_1/\!\,\mathrm{M_\odot}\lesssim 1\,\mathrm{M_\odot}$
, and (iii) the mass of the observed planet
$m_2\gtrsim2\,\mathrm{M_\mathrm{J}}$
. The latter can be considered as a prediction for WD 1856+534 b, and is similar to the lower limits obtained using transmission spectroscopy of
$2.4\,\mathrm{M_\mathrm{J}}$
(Alonso et al. Reference Alonso2021) and
$0.84\,\mathrm{M_\mathrm{J}}$
(Xu et al. Reference Xu2021), while remaining comfortably below the upper limit of
$\sim$
$12\,\mathrm{M_\mathrm{J}}$
, which is based on the non-detection of thermal emission (Vanderburg et al. Reference Vanderburg2020).
WD 1856+534 b might have formed at the orbital separation inferred from observations or might have migrated to it. Detailed models (e.g. Masset & Papaloizou Reference Masset and Papaloizou2003) show that the sense and timescale of type II migration can vary in time and can be sensitive to various parameters. The interplay between migration and evaporation by the hot WD core of the primary may account for the rarity of systems like WD1856+534 b, depending on where the planet forms before migration and how long it spends close enough to the WD core to be evaporated (Gänsicke et al. Reference Gänsicke, Schreiber, Toloza, Gentile Fusillo, Koester and Manser2019; Schreiber et al. Reference Schreiber, Gänsicke, Toloza, Hernandez and Lagos2019; Lagos et al. Reference Lagos, Schreiber, Zorotovic, Gänsicke, Ronco and Hamers2021; Gallo et al. Reference Gallo, Caldiroli, Spinelli, Biassoni, Haardt, Limbach, Becker and Adams2024). Future work is needed to address these issues.
Acknowledgements
We are grateful to the first referee for comments that helped to improve the presentation of this work, and to the second referee for various helpful comments. L.C. thanks R.I.T. for supporting his visit from 4 to 10 June, 2023.
Data availability statement
The codes used to produce the various figures are available upon request.
Funding statement
Financial support for this project was provided by the U. S. Department of Energy grants DE-SC0001063, DE-SC0020432 and DE-SC0020103, the U. S. National Science Foundation grants AST-1515648, AST-1813298, PHY-2020249, AST-2009713, and AST-2319326, and the Space Telescope Science Institute grant HST-AR-12832.01-A.
Competing interests
None.
Appendix A. Photo-evaporation timescale
The ionising luminosity is sensitive to the effective temperature. The hottest white dwarfs are observed to have
$T_\mathrm{eff}\sim10^5\,\mathrm{K}$
(Bédard, Bergeron, & Fontaine Reference Bédard, Bergeron and Fontaine2017). Theoretical models which track WD properties as a function of time predict that they are born with
$T_\mathrm{eff}\approx 0.9$
–
$1.1\times10^5\,\mathrm{K}$
and radius
$R_\mathrm{wd}\approx 0.022-0.027\,\mathrm{R_\odot}$
for
$M_\mathrm{wd}\sim0.55-0.60\,\mathrm{M_\odot}$
(Bédard et al. Reference Bédard, Bergeron, Brassard and Fontaine2020).Footnote c Or perhaps the exposed core would resemble a hot subdwarf B (sdB) star. Such stars are remnants of evolved stars often found in post-CE binary systems and have
$T_\mathrm{eff}\approx2-7\times10^4\,\mathrm{K}$
(Heber Reference Heber2016; Ge et al. Reference Ge2024).
For
$T_\mathrm{eff}=10^5\,\mathrm{K}$
, the Planck spectrum peaks at
$29\,\mathrm{nm}$
, in the extreme ultraviolet. Let us assume, conservatively, that all photons are ionising. The radiative flux impinging on the disc can then be equated with the wind power, with an efficiency factor
$\varepsilon$
,
\begin{align} 4\pi R_\mathrm{c}^2\sigma T_\mathrm{eff}^4 \frac{\theta}{\pi/2}\varepsilon \approx \frac{1}{2}\dot{M}_\mathrm{w}\frac{2GM_\mathrm{c}}{r},\end{align}
where
$\theta=h/r$
is the disc aspect ratio (assumed to be small), and we have used the escape speed from the central core for the wind speed. This gives a wind mass-loss rate of
\begin{align}\begin{split} \dot{M}_\mathrm{w} \approx 4&\times10^{-8} \,\mathrm{M_\odot\,yr^{-1}} \, \left(\frac{\varepsilon}{0.1}\right) \left(\frac{\theta}{0.1}\right) \left(\frac{R_\mathrm{c}}{0.025\,\mathrm{R_\odot}}\right)^2\\ &\times\left(\frac{T_\mathrm{eff}}{10^5\,\mathrm{K}}\right)^4 \left(\frac{r}{4.4\,\mathrm{R_\odot}}\right) \left(\frac{M_\mathrm{c}}{0.576\,\mathrm{M_\odot}}\right)^{-1},\end{split}\end{align}
where we have scaled r to the present orbital separation of WD 1856+534 b, assuming a circular orbit. If we instead adopt typical values for sdB stars, with
$R_\mathrm{c}$
about 5 times higher and
$T_\mathrm{eff}$
about 2 times lower than the above values, we obtain approximately the same numerical estimate for
$\dot{M}_\mathrm{w}$
.
Alternatively, we can try to apply detailed models from the literature which were designed for classical protoplanetary discs. We try the model of Alexander et al. (Reference Alexander, Clarke and Pringle2006) (see also Alexander et al. Reference Alexander, Pascucci, Andrews, Armitage, Cieza, Beuther, Klessen, Dullemond and Henning2014 and Kunitomo, Suzuki, & Inutsuka Reference Kunitomo, Suzuki and Inutsuka2020), which takes as input the number of ionising photons emanating from the star per unit time
$\Phi$
. We estimate
\begin{align} \Phi \approx \frac{4\pi R_\mathrm{c}^2\sigma T_\mathrm{eff}^4}{h\nu_\mathrm{max}},\end{align}
with
$\nu_\mathrm{max}$
given by Wien’s displacement law. Thus, we obtain
\begin{align} \Phi \approx 6\times10^{45}\,\mathrm{s}^{-1}\,\left(\frac{R_\mathrm{c}}{0.025\,\mathrm{R_\odot}}\right)^2 \left(\frac{T_\mathrm{eff}}{10^5\,\mathrm{K}}\right)^3.\end{align}
Then, using the Alexander et al. (Reference Alexander, Clarke and Pringle2006) model with
$CD=1$
,
$a=6$
, and
$\mu=1$
, and taking the outer disc radius to be much larger than the inner disc radius, we find
\begin{align}\begin{split} \dot{M}_\mathrm{w} \approx 6\times 10^{-9}\,\mathrm{M_\odot\,yr^{-1}}\, & \left(\frac{\theta}{0.1}\right)^{-1/2} \left(\frac{\Phi}{6\times 10^{45}\,\mathrm{s}^{-1}}\right)^{1/2}\\ &\times \left(\frac{r_\mathrm{in}}{4.4\,\mathrm{R_\odot}}\right)^{1/2},\end{split}\end{align}
where
$r_\mathrm{in}$
is the inner radius of the disc. Thus, this estimate gives a mass-loss rate that is of the same order of magnitude as that obtained in equation (A2). A disc of mass
$0.3\,\mathrm{M_\odot}$
would take
$\sim$
$10\,\mathrm{Myr}$
to evaporate, which is long compared to the timescales of other key processes, as discussed below.
Appendix B. Gravitational instability of the disc
The disc mass can be obtained by integrating equation (3), which gives
\begin{align} fm_1 = 2\pi\Sigma_\mathrm{out} r_\mathrm{out}^\beta\int_{r_\mathrm{in}}^{r_\mathrm{out}}r^{1-\beta}dr \approx \frac{2\pi\Sigma_\mathrm{out} r_\mathrm{out}^2}{2-\beta},\end{align}
where f is the fraction of the disrupted companion mass incorporated in the disc and we have assumed
$\beta\unicode{x003C}2$
and
$(r_\mathrm{in}/r_\mathrm{out})^{2-\beta}\ll1$
. Rearranging, we obtain
\begin{align} \Sigma_\mathrm{out}\approx\frac{(2-\beta)fm_1}{2\pi r_\mathrm{out}^2}.\end{align}
The volume density of the disc is given by
\begin{align} \rho = \frac{\Sigma}{2h} = \rho_\mathrm{out}\left(\frac{r}{r_\mathrm{out}}\right)^{-(\beta+1)},\end{align}
where
$\rho_\mathrm{out} = \Sigma_\mathrm{out}/(2\theta r_\mathrm{out})$
with
$\theta\equiv h/r$
the disc aspect ratio. Substituting expression (B2) for
$\Sigma_\mathrm{out}$
into this expression for
$\rho_\mathrm{out}$
and then substituting into equation (B3) gives
\begin{align} \rho\approx\frac{(2-\beta)fm_1}{4\pi r_\mathrm{out}^3\theta}\left(\frac{r}{r_\mathrm{out}}\right)^{-(\beta+1)}.\end{align}
A disc with
$\theta=0.1$
,
$fm_1=0.08\,\mathrm{M_\odot}$
, and
$r_\mathrm{out}=a_2\approx4.4\,\mathrm{R_\odot}$
has
$\rho(r_\mathrm{out})\approx 4\times10^{-3}(2-\beta)\,\mathrm{g\,cm^{-3}}$
. If
$r_\mathrm{out}=100\,\mathrm{R_\odot}$
, then
$\rho(4.4\,\mathrm{R_\odot})\approx2\times10^{-4}\,\mathrm{g\,cm^{-3}}$
if
$\beta=1$
or
$\approx5\times10^{-4}\,\mathrm{g\,cm^{-3}}$
if
$\beta=3/2$
. On the other hand, the density of the envelope of a ZAMS
$2\,\mathrm{M_\odot}$
AGB star is
$\rho_\mathrm{e}\approx10^{-4}\,\mathrm{ g\,cm^{-3}}$
at
$r=4.4\,\mathrm{R_\odot}$
. Thus, the disc is expected to have slightly higher density than the original envelope at the present orbital separation of WD 1856+534 b. However, at this stage, the envelope would have already experienced expansion and at least partial ejection, so
$\rho_\mathrm{e}$
would be significantly smaller than the above estimate and thus much smaller than the disc density.Footnote d
Combining equations (1), (2), (3), and (B2), we obtain
\begin{align} Q\approx \frac{2\theta}{2-\beta}\frac{M_\mathrm{c}}{fm_1}\left(\frac{r}{r_\mathrm{out}}\right)^{-(2-\beta)}.\end{align}
Thus, Q decreases with r and reaches a minimum at the disc outer radius
$r_\mathrm{out}$
. Now we can impose the condition for instability
$Q\lesssim1$
(constraint 1), which leads to constraint (4) on the mass of the disrupted companion.
Appendix C. Free-fall timescale for planet formation
The free-fall timescale is given by:
\begin{align} t_\mathrm{ff} = \left(\frac{3\pi}{32G\rho}\right)^{1/2}.\end{align}
Making use of equation (B4), we obtain
\begin{align}\begin{split} t_\mathrm{ff} \approx \frac{0.2\,\mathrm{d}}{(2-\beta)^{1/2}} & \left(\frac{\theta}{0.1}\right)^{1/2} \left(\frac{r_\mathrm{out}}{4.4\,\mathrm{R_\odot}}\right)^{3/2} \left(\frac{fm_1}{0.3\,\mathrm{M_\odot}}\right)^{-1/2}\\ &\times \left(\frac{r}{r_\mathrm{out}}\right)^{(\beta+1)/2},\end{split}\end{align}
which is somewhat smaller than the observed orbital period of
$1.41\,\mathrm{d}$
for WD 1856+534 b (Vanderburg et al. Reference Vanderburg2020).
Appendix D. Accretion onto the proto-WD
At early times, accretion of disc material onto the core of the primary may occur on the viscous timescale. Using equation (8) with
$r=a_\mathrm{d1}$
(equation 9), we find
\begin{align}\begin{split} \dot{M}_\mathrm{visc} & \approx \frac{fm_1}{t_\mathrm{visc}} \approx \frac{fm_1^{3/2}G^{1/2}\alpha_\mathrm{SS}\theta^2}{2^{1/2}r_1^{3/2}}\\ & \approx 91 \,\mathrm{M_\odot\,yr^{-1}} f \theta^2\! \left(\frac{\alpha_\mathrm{SS}}{0.01}\right)\!\! \left(\frac{m_1}{0.3\,\mathrm{M_\odot}}\right)^{3/2}\!\! \left(\frac{r_1}{0.4\,\mathrm{R_\odot}}\right)^{-3/2},\end{split}\end{align}
where
$\theta\sim1$
since the disc initially cannot cool efficiently. This accretion rate is several orders of magnitude higher than the Eddington rate of (Reference Chamandy, Blackman, Nordhaus and WilsonC21)
\begin{align} \dot{M}_\mathrm{Edd}\approx 2.7\times10^{-5}\,\mathrm{M_\odot\,yr^{-1}} \left(\frac{R_\mathrm{c}}{0.013\,\mathrm{R_\odot}}\right).\end{align}
At this stage, radiation is trapped and advected with the flow (e.g. Narayan & Yi Reference Narayan and Yi1995; Nordhaus et al. Reference Nordhaus, Wellons, Spiegel, Metzger and Blackman2011; Shen & Matzner Reference Shen and Matzner2014). Most of the mass may be directed into winds/jets (Blandford & Begelman Reference Blandford and Begelman1999; Armitage & Livio Reference Armitage and Livio2000; Hawley & Balbus Reference Hawley and Balbus2002; Ohsuga et al. Reference Ohsuga, Mori, Nakamoto and Mineshige2005), while a fraction accretes onto the central core.
This phase may be sustained by outflows or it may transition into an Eddington-limited phase if the accretion is quenched due to the buildup of gas pressure, which would happen on roughly a dynamical timescale,
\begin{align}\begin{split} \left.t_\mathrm{dyn}\sim\frac{1}{\Omega}\right|_{a_\mathrm{d1}} &\approx \left(\frac{2r_1^3}{Gm_1}\right)^{1/2}\\ &\approx 17\,\mathrm{min} \left(\frac{m_1}{0.3\,\mathrm{M_\odot}}\right)^{-1/2} \left(\frac{r_1}{0.4\,\mathrm{R_\odot}}\right)^{3/2},\end{split}\end{align}
where we made use of equations (2) and (9). The mass accreted during this time is
\begin{align} M_\mathrm{adv}& \approx \dot{M}_\mathrm{visc} t_\mathrm{dyn}\approx f\alpha_\mathrm{SS}\theta^2m_1 \nonumber \\ &\approx3\times10^{-3}\,\mathrm{M_\odot}\,f\theta^2 \left(\frac{\alpha_\mathrm{SS}}{0.01}\right)\left(\frac{m_1}{0.3\,\mathrm{M_\odot}}\right),\end{align}
Thus, during the advection-dominated phase, a few
$\!\,\mathrm{M_\mathrm{J}}$
of material would be deposited into an envelope around the WD (c.f. Nordhaus et al. Reference Nordhaus, Wellons, Spiegel, Metzger and Blackman2011). Subsequently, the WD may accrete a large fraction of the remaining disc material on the timescale
\begin{align} t_\mathrm{acc}\sim \frac{m_\mathrm{acc}}{\dot{M}_\mathrm{Edd}} \sim 4\times10^3\,\mathrm{yr} \left(\frac{m_\mathrm{acc}}{0.1\,\mathrm{M_\odot}}\right) \left(\frac{R_\mathrm{c}}{0.0126\,\mathrm{R_\odot}}\right)^{-1},\end{align}
where
$m_\mathrm{acc}$
is the mass of accreted material. Remaining disc material would gradually disperse on a timescale of perhaps
$\sim$
$10\,\mathrm{Myr}$
, as estimated in Appendix A.
Appendix E. Powering envelope ejection
The rate of energy release during this advection-dominated phase is roughly given by
\begin{align}\begin{split} L_\mathrm{adv}&\approx \,\frac{GM_\mathrm{c} \dot{M}_\mathrm{visc}}{2R_\mathrm{c}}\\ &\approx \, 2.5\times10^{44}\,\mathrm{erg \, s^{-1}} f \theta^2 \left(\frac{\alpha_\mathrm{SS}}{0.01}\right) \left(\frac{m_1}{0.3\,\mathrm{M_\odot}}\right)^{3/2}\\ &\quad\times \left(\frac{r_1}{0.4\,\mathrm{R_\odot}}\right)^{-3/2}\!\! \left(\frac{M_\mathrm{c}}{0.576\,\mathrm{M_\odot}}\right)\!\! \left(\frac{R_\mathrm{c}}{0.0126\,\mathrm{R_\odot}}\right)^{-1}\!,\end{split}\end{align}
where we have scaled
$R_\mathrm{c}$
to the measured WD radius
$R_\mathrm{wd}=0.01263\pm0.0050\,\mathrm{R_\odot}$
(Xu et al. Reference Xu2021). The energy liberated is estimated as
\begin{align}\begin{split} E_\mathrm{adv}\approx L_\mathrm{adv} t_\mathrm{dyn}\approx 3&\times10^{47}\,\mathrm{erg}\,f\theta^2 \left(\frac{\alpha_\mathrm{SS}}{0.01}\right) \left(\frac{m_1}{0.3\,\mathrm{M_\odot}}\right)\\ &\times \left(\frac{M_\mathrm{c}}{0.576\,\mathrm{M_\odot}}\right) \left(\frac{R_\mathrm{c}}{0.0126\,\mathrm{R_\odot}}\right)^{-1},\end{split}\end{align}
which is approximately the same as the initial binding energy of the envelope
$E_\mathrm{bind}$
(Table 1). If about 10% of the original binding energy remains at the time of tidal disruption, then the energy liberated is about an order of magnitude larger than the envelope binding energy. Thus, what remains of the envelope can be rapidly unbound if the energy transfer efficiency of the unbinding process is
$\gtrsim 0.1$
. Nuclear burning of accreted material may also assist envelope unbinding (Siess & Livio Reference Siess and Livio1999a; Siess & Livio Reference Siess and Livio1999b; Nordhaus et al. Reference Nordhaus, Wellons, Spiegel, Metzger and Blackman2011; Reference Chamandy, Blackman, Nordhaus and WilsonC21). The disc, on the other hand, is not as susceptible to unbinding both because its binding energy is larger –
$E_\mathrm{d}\sim GM_\mathrm{c} fm_1/a_\mathrm{d1}\sim10^{48}\,\mathrm{erg}$
– and because the released energy may be transported perpendicular to the disc.
If accretion proceeds at the Eddington rate thereafter (equation D5), then energy would be released at the rate
\begin{align} L_\mathrm{Edd} = 7.2\times10^{37}\,\mathrm{erg \, s^{-1}}\,\left(\frac{M_\mathrm{c}}{0.576\,\mathrm{M_\odot}}\right).\end{align}
If, as argued above,
$\sim3\times10^{47}\,\mathrm{erg}$
must be released to unbind the envelope (which already factors in the efficiency), we find that the envelope can be ejected in
$\sim$
$10^2\,\mathrm{yr}$
by Eddington-limited accretion alone.
Alternatively, the envelope might be removed before tidal disruption but after the onset of RLOF. In this case, once the envelope is ejected, further orbital tightening would need to be driven by a mechanism other than CE drag. Torques may arise at
$a\approx a_\mathrm{RLOF}$
that lead to orbital decay on timescales of a few hundred orbital periods (c.f. MacLeod et al. Reference MacLeod, Ostriker and Stone2018). Mass transfer is expected to be unstable for low-mass MS stars (e.g. Stevens et al. Reference Stevens, Rees and Podsiadlowski1992; Jones Reference Jones2020). Thus, even if the envelope is ejected at a separation
$a_\mathrm{d1} \lt a \lt a_\mathrm{RLOF}$
, orbital decay down to
$a_\mathrm{d1}$
is still likely to occur. To determine whether this scenario is plausible, we estimate the orbital energy released between
$a_\mathrm{RLOF}$
and
$a_\mathrm{d1}$
,
\begin{align} -\Delta E_\mathrm{orb} = \frac{GM_\mathrm{c} m_1}{2}\left(\frac{1}{a_\mathrm{d1}} - \frac{1}{a_\mathrm{RLOF}}\right).\end{align}
From Fig. 2a for
$m_1=0.3\,\mathrm{M_\odot}$
and the AGB model (Model D, green) with
$M_\mathrm{c}=0.52\,\mathrm{M_\odot}$
, we find
$a_\mathrm{RLOF}\approx0.72\,\mathrm{R_\odot}$
and
$a_\mathrm{d1}\approx0.44\,\mathrm{R_\odot}$
, which gives
$-\Delta E_\mathrm{orb}\approx 3\times10^{47}\,\mathrm{erg}$
for
$m_1=0.3\,\mathrm{M_\odot}$
, which is the same energy estimated to be released by accretion during the advection-dominated accretion phase (equation E2). As we have already argued, this amount of energy is probably sufficient to unbind the remaining envelope. The value of
$\Delta E_\mathrm{orb}$
is not sensitive to which of the models in Table 1 is adopted for the primary star.
Envelope removal may also be powered by shocking during accretion disc formation (e.g. Rees Reference Rees1988; Piran et al. Reference Piran, Svirski, Krolik, Cheng and Shiokawa2015; Bonnerot, Lu, & Hopkins Reference Bonnerot, Lu and Hopkins2021; Ryu et al. Reference Ryu, Krolik, Piran, Noble and Avara2023; Steinberg & Stone Reference Steinberg and Stone2024).
Open access
