1. Introduction
Anatole Katok (
![]() ), August 9, 1944–April 30, 2018, a cofounder of this journal, a leading dynamicist in the last 50 years, a fellow of the American Mathematical Society, and a member of the American Academy of Arts and Sciences, began his career in Moscow. After spending six years each at the University of Maryland and the California Institute of Technology, he worked at the Pennsylvania State University for almost three decades. He died in Danville, PA, from pneumonia and complications from an infection and now rests in the Spring Creek Presbyterian Cemetery in State College. Robert J. Zimmer of the University of Chicago called him ‘a whirlwind of mathematical activity’ who expanded the boundaries of his field and ‘brought new connections and engaged all around him with an infectious and buoyant enthusiasm for mathematics and its mysteries’ [Reference Weil297]. He ‘was an extraordinary man and a great mathematician, one of the giants in dynamical systems and ergodic theory’ [Gregory Margulis], ‘a singular indomitable force of will’ [Michael Boyle], and ‘one of the most inspired, and inspiring, mathematicians of a generation’ [Marcelo Viana], who
), August 9, 1944–April 30, 2018, a cofounder of this journal, a leading dynamicist in the last 50 years, a fellow of the American Mathematical Society, and a member of the American Academy of Arts and Sciences, began his career in Moscow. After spending six years each at the University of Maryland and the California Institute of Technology, he worked at the Pennsylvania State University for almost three decades. He died in Danville, PA, from pneumonia and complications from an infection and now rests in the Spring Creek Presbyterian Cemetery in State College. Robert J. Zimmer of the University of Chicago called him ‘a whirlwind of mathematical activity’ who expanded the boundaries of his field and ‘brought new connections and engaged all around him with an infectious and buoyant enthusiasm for mathematics and its mysteries’ [Reference Weil297]. He ‘was an extraordinary man and a great mathematician, one of the giants in dynamical systems and ergodic theory’ [Gregory Margulis], ‘a singular indomitable force of will’ [Michael Boyle], and ‘one of the most inspired, and inspiring, mathematicians of a generation’ [Marcelo Viana], who
worked tirelessly and effectively to push the field in the directions he thought important. He worked on all planes simultaneously, as a researcher, teacher, mentor, and administrator. He wrote textbooks and survey papers which are the main point of entry for generations of mathematicians; he initiated or was involved in the creation of at least three major journals, including this one; he mentored countless post-docs; he created a major center of dynamics at Penn StateFootnote †; he initiated the Brin prizes in dynamics; and the list goes on and on. Through these many actions he became one of the most influential dynamicists of our time. [Omri Sarig]
Indeed, from early in his career Katok stood out for his ability to be involved in essentially all areas of dynamical systems, as suggested even by his Annals papers alone [Reference Brin, Feldman and Katok44, Reference Damjanović and Katok72, Reference Einsiedler, Katok and Lindenstrauss83, Reference Hurder and Katok141, Reference Kalinin, Katok and Hertz149, Reference Katok163].
If I were to characterize Tolya in two sentences, the verse of XIX century Polish poet Adam Mickiewicz Footnote ‡ ‘This was a comet of the first magnitude and power’ and the verse of XX century Russian poet Nikolay Gumilyov ‘who plot on a tattered map with compass needles, their venturesome course’Footnote § seem to me best to describe him. [Jean-Marie Strelcyn]
But most of all I’ll miss his joy of life and his appreciation of many fine things in life; be these fine wines or food or cars or a good conversation or a story. He was a big personality, mathematically and in everyday life, a big presence in many ways, and now there is a void which will be felt for many years. [Viktor Ginzburg]
This article aims to give an impression of Katok’s life, personality, and mathematics, including through the eyes of numerous colleagues and friends. I am grateful to those I quoted hereFootnote † for permission to do so, and to them and many others for helpful comments and insights. Jean-Marie Strelcyn deserves particular thanks for repeated careful reading and heroic toil to perfect the references to Russian papers and their translationsFootnote ‡. The text is roughly but not strictly chronological; this serves to avoid the interruption of several narratives.
A briefer and illustrated memorial article appeared in the Notices of the American Mathematical Society [Reference Hasselblatt128], and a fuller scientific picture will emerge with the publication of the Collected Works of Anatole Katok by World Scientific Publishing Co.
2. Moscow
Anatole Katok, ‘Tolya’ to his friends and family, was born a mere 200 miles from where he last lived, in Washington, DC. His father Boris Lazarevich Katok (1901–1963), a metallurgical engineer, and his mother Dora Sorkin (1905–1998), a chemist, belonged to a Soviet delegation working with the American lend-lease program. Begun even before the attack on Pearl Harbor, this program aimed at defeating the axis powers by ‘lending’ food, oil, and materiel to a multitude of countries, principally the British Empire and the Soviet Union. The latter received some 11 billion US Dollars worth of support (out of over 50 billion total), and this was crucial for the Soviet military effort. Even much later, Katok recalled ancient US vehicles from this program as a significant part of the Soviet automobile landscape. Since his parents were not diplomats, Katok was a US citizen by birth, a material point in his later biography. And he relished to point out at times that he was therefore eligible to be elected president of the United States.
Katok’s father was a high-ranking official in the Soviet hierarchy, serving for several years on the council of the Ministry of Metallurgy after the war. Being among Stalin’s officials was stressful, and he died in his early sixties (apparently due to heart problems). He did not live with the family in his last several years, so Katok was raised principally by his mother. This was her second marriage, her first husband having been a victim of Stalin’s great purge in the late 1930s. From this earlier marriage, Katok had a half-brother 10 years his senior, Alexander (Sasha) Gruz, who, together with Dora, emigrated to the US in 1975. They first lived in Chicago then Baltimore, before moving to Rockville, MD, where she lived to the age of 93.
His mother recognized and cherished Katok’s talents early, and he was an acknowledged wunderkind. Among his favorite childhood books was the Great Soviet Encyclopedia (and he later recalled with amusement his puzzlement at how many names of prominent Nazis began with the same letter: Goebbels, Goering, Gitler, Gimmler, Gess, Geydrich…). He grew up with a focus on the intellectual at the expense of the practical and did not always take to technology naturally. In the initial years in Maryland, he did not care to even acquire a driver’s license—yet soon learned to drive cars with a manual transmission in the ancient beetle of E. Arthur ‘Robbie’ Robinson, his first US doctoral student. He loved cars (his coolest was probably the yellow early 1970s Mercedes-Benz convertible with hard and soft tops), and many colleagues have vivid recollections of a ride with him. In the late 1980s, there was also surprise when colleagues first got an email from him. Indeed, he was no Luddite: he embraced email and learned
![]() $\mathrm{\TeX}$
and
$\mathrm{\TeX}$
and
![]() $\mathrm{\LaTeX}$
. Over time, his index fingers would hammer out substantial texts. And he maintained a large and useful web pageFootnote † as well as a Google Scholar account.
$\mathrm{\LaTeX}$
. Over time, his index fingers would hammer out substantial texts. And he maintained a large and useful web pageFootnote † as well as a Google Scholar account.
2.1. Moscow State University
Katok attended Moscow schools 69 (first and eighth grades) and 637 (second to seventh)Footnote ‡, and in the 9th grade, he transferred to Moscow School N59, from where the likes of V. I. Arnold and V. P. Maslov had graduated. As a 14-year-old high-school student, he
had one good teacher who forced me to enter a Mathematics Olympiad. I was fortunate to earn a high honor. It was then I knew I wanted to be a mathematician.
He wished to enter the Lomonosov Moscow State University before his 10th and final grade. With the help of Aleksei Markushevich, the vice-minister of education of the RSFSR, he obtained permission to take the external examination for high schoolers after the 9th grade (at not quite 16 years old) and so never needed to graduate from high school. Yulij Ilyashenko recalls a newspaper headline ‘Markushevich was struck by the mathematical talent of the youth’. Katok having been an alumnus of ‘mathematical circles’ for high-school children (in his case, supervised by A. Egorov and N. Vasiliev), his next move was to affect his life well beyond his career. Upon entering the university in 1960, he immediately began teaching such a circle himself. Among his students was Svetlana RosenfeldFootnote §, almost three years his junior, also at Moscow School N59, and the daughter of Boris Abramovich Rosenfeld (1917–2008) and Lucy Lvovna DavidovaFootnote ¶ (1919–2020). Boris Rosenfeld was a geometer and
a historian of mathematics with a wide range of interests, from ancient Greece and the medieval Middle East up to 19th-century non-Euclidean geometry. He spoke English as well as German, later he studied French, Arabic and other oriental languages, becoming a savant in the best tradition of the Russian intelligentsia. [Reference Vogt295]
Anatole and Svetlana fell in love and married on June 5, 1965, soon after Svetlana turned 18; the flame of their love burned strongly for well over 50 years of marriage. Their daughter Elena Katok was born in Moscow and is now the Ashbel Smith Professor at the Naveen Jindal School of Management of the University of Texas at Dallas. Their son BorisFootnote † Katok, also born in Moscow, is a Senior Software Developer and the owner of Coconut Tree Software in Reno, Nevada. Daniela (Danya) Katok was born in Hollywood and is an acclaimed soprano in New York City.
Anatole continued to teach in mathematical circles, and it is worth describing the evolution of these as the context of his service as one of six assistants to Eugene Dynkin.
Due to a secondary education reform in the USSR, special magnet mathematical high schools were opened in the 1960s. In addition to outstanding high school teachers, mathematicians of different levels from upper division undergraduates to professors and academicians volunteered to teach in mathematical schools. Dynkin played an exceptional role in the early development of mathematical schools. In 1963 he founded the Evening Mathematical School (EMS) as an addition to the Moscow school #2; and next year, with help of the school principal V. F. Ovchinnikov, he organized a section (three groups, around 100 students total) for mathematically gifted children in grades 9–10 (1964–1966).
Dynkin was not the first well known mathematician who worked within the structure of mathematical schools, which was drastically different from the established and famous tradition of mathematical circles and olympiads. However, his approach had some unique features. Working in school #2 Dynkin showed himself as a talented organizer which is not typical for actively working mathematicians. Dynkin’s section in school #2 was well thought through and organized. Twice a week he lectured for the whole section. Each of his six immediate assistants was responsible for a group of 15–20 students. Each assistant had two upper division undergraduate students who helped them. The lessons in the groups were not similar to university studies. They were closer in style to a more intense version of a mathematical circle. This combination of a well organized lecture system and spontaneous but intense atmosphere of group studies was quite unique.
In spite of his preference for system and organization Dynkin encouraged a more spontaneous and ‘chaotic’ approach for his assistants. It was an unusual but remarkable harmony. [Reference Katok and Kuznetsov201]
In the 1960s, dynamical systems emerged as an independent mathematical discipline in its own right due to seminal developments in the 1950s and around 1960, such as the KAM theory (Kolmogorov, Arnold, Moser [Reference Arnold16, Reference Kolmogorov233, Reference Kolmogorov, Abraham and Marsden234, Reference Moser255]), entropy (Kolmogorov, Sinai [Reference Katok184, Reference Kolmogorov235, Reference Kolmogorov236, Reference Sinaĭ284, Reference Sinaĭ285]), and hyperbolicity (Smale, Anosov, Sinai [Reference Anosov4–Reference Anosov6, Reference Anosov11, Reference Anosov and Sinaĭ15, Reference Smale288])Footnote † Young mathematicians, such as Gurevich, Margulis, Oseledets, Ratner, Stepin, and Katok, found this rapidly developing theory exciting and attractive, and began to work in it. Katok started his third year under the supervision of Robert Minlos, but his enthusiasm waned by the end of the year. While Minlos was a distinguished mathematician and an inspiring teacher, the problems he assigned in his seminar required a lot of technical skill and did not captivate Katok. Much later, Katok voiced the opinion that Minlos was at his best ‘when he collaborated with others who were able to show him the way’Footnote ‡. For instance, although Minlos started to work on statistical physics earlier than Sinai, Katok believed that real progress began only when Sinai entered the field and gave direction to Minlos’ superb technical skills (to work on phase transitions in the Ising model [Reference Minlos and Sinaĭ253, Reference Minlos and Sinaĭ254]). Thus—and on the advice of Minlos—Katok started attending Sinai’s special course on ergodic theory (K-systems and related topics) in 1963, at the very time Sinai began to receive wide recognition [Reference Mešalkin and Sinaĭ251, Reference Rohlin and Sinaĭ276, Reference Sinaĭ286, Reference Sinaĭ287]. They started meeting and discussing mathematical problems, and Katok worked with Sinai for the last two and a half years at the university as well as in graduate schoolFootnote §. Leonid Bunimovich recalls:
In the department it was impossible not to notice Katok. He was tall, handsome, spoke loudly, and he immediately stole one of the most attractive girls.
2.2. Two approximations
Katok received his doctoral degree from Moscow State University in 1968, and his dissertation reflected the much-cited work with Stepin [Reference Katok153, Reference Katok152, Reference Katok and Stepin223, Reference Katok and Stepin224] (and Oseledets, see [Reference Dynkin80, p. 7] and the review of [Reference Katok152]), which Sinai had encouraged and supported. This concerns periodic approximations of probability-preserving transformations. A
![]() $\mu $
-preserving invertible transformation T of a probability space
$\mu $
-preserving invertible transformation T of a probability space
![]() $(X,\mu )$
is said to allow approximation by periodic transformations with speed
$(X,\mu )$
is said to allow approximation by periodic transformations with speed
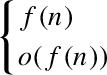 $\scriptsize \begin {cases}f(n)\\o(f(n))\end {cases}\!$
if there are finite partitions
$\scriptsize \begin {cases}f(n)\\o(f(n))\end {cases}\!$
if there are finite partitions
![]() $\xi _n=\{C_n^k\mid 1\le k\le q_n\}\to \mathcal {E}$
(the point partition) and
$\xi _n=\{C_n^k\mid 1\le k\le q_n\}\to \mathcal {E}$
(the point partition) and
![]() $q_n$
-periodic invertible
$q_n$
-periodic invertible
![]() $\mu $
-preserving transformations
$\mu $
-preserving transformations
![]() $S_n$
, such that
$S_n$
, such that
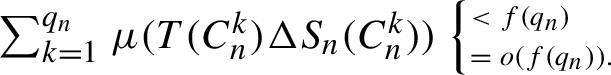 $\scriptsize \sum _{k=1}^{q_n}\mu (T(C_n^k)\Delta S_n(C_n^k))\begin {cases}<f(q_n)\\=o(f(q_n)).\end {cases}\!$
Depending on f, this has various dynamical consequences such as ergodicity, mixing, multiplicity of the spectrum, and entropy bounds. For instance, an ergodic T can be approximated with speed
$\scriptsize \sum _{k=1}^{q_n}\mu (T(C_n^k)\Delta S_n(C_n^k))\begin {cases}<f(q_n)\\=o(f(q_n)).\end {cases}\!$
Depending on f, this has various dynamical consequences such as ergodicity, mixing, multiplicity of the spectrum, and entropy bounds. For instance, an ergodic T can be approximated with speed
![]() $o(1/\ln n)$
if and only if its entropy
$o(1/\ln n)$
if and only if its entropy
![]() $h(T)$
is 0, and if T is ergodic, then
$h(T)$
is 0, and if T is ergodic, then
This has applications to interval-exchange transformations (which in turn are connected to geodesic flows on flat surfaces), square roots of transformations, and flows on
![]() $\mathbb T^2$
[Reference Katok152, Reference Katok and Stepin224].
$\mathbb T^2$
[Reference Katok152, Reference Katok and Stepin224].
The work helped solve some long-standing problems that went back to von Neumann and Kolmogorov, and it earned Katok and Stepin the prize of the Moscow Mathematical Society for young mathematiciansFootnote †. Katok presented it in a 15-minute communication at the 1966 International Congress of Mathematicians in Moscow. Yulij Ilyashenko recalls that
He continued his excited talk well beyond the allotted time until he was stopped by a question: ‘Is this a short communication or an invited talk?’
Also in 1966, Katok took a reading course on algebraic topology with Dmitri Anosov, which included pondering a specific, then unsolved, problem relating topology and dynamics: rationality of the
![]() $\zeta $
-function for Anosov diffeomorphisms [Reference Manning245]. Pontrjagin’s favorite student [Reference Katok187, p. 11], Anosov was a dynamicist at the Steklov Institute (or Mathematical Institute of the USSR Academy of Sciences), who played a central role in the creation of the modern theory of hyperbolic dynamical systems, and whose name has since been attached to important classes of such dynamical systems. Their interaction continued, and Katok recalled:
$\zeta $
-function for Anosov diffeomorphisms [Reference Manning245]. Pontrjagin’s favorite student [Reference Katok187, p. 11], Anosov was a dynamicist at the Steklov Institute (or Mathematical Institute of the USSR Academy of Sciences), who played a central role in the creation of the modern theory of hyperbolic dynamical systems, and whose name has since been attached to important classes of such dynamical systems. Their interaction continued, and Katok recalled:
If our interaction during the topology course gave me an impression of Anosov as a scholar, some time after that I had a superb opportunity to observe and appreciate his creativity… . In front of my eyes Anosov invented the core of what has become known as the ‘Anosov–Katok method’ for construction of dynamical systems with interesting, often exotic properties… . I am pretty sure this was during the second half of 1968. I very quickly added my essential and extensive contributions that greatly extended the power of the method and several weeks of discussions followed. Then I remember vividly having written a complete [50 page] draft of the paper just from my head in three successive evenings on Friday, Saturday and Sunday. [Reference Katok187, p. 3]
Much later, Katok told Ilyashenko that the ‘best way to overcome a depression is to sit and write a mathematical paper’. The Anosov–Katok ‘approximation by conjugation’ (‘AbC’) method [Reference Katok and Hasselblatt190, §12.6] or ‘method of fast periodic approximations’ [Reference Anosov and Katok13, Reference Anosov and Katok14] produces, just for starters, area-preserving ergodic diffeomorphisms of the disk. This itself is surprising, not least because elliptic islands around generic elliptic fixed points are an obstruction to ergodicity. Some experts called this work ‘the main event of the year in ergodic theory’, and the method has over the decades yielded ever more astonishing examples of dynamical systems [Reference Banerjee24–Reference Banerjee and Kunde26, Reference Benhenda31, Reference Bronšteĭn52, Reference Fathi and Herman87–Reference Fayad and Saprykina91, Reference Gunesch and Katok115, Reference Gunesch and Kunde116, Reference Katok153, Reference Katok156, Reference Katok157, Reference Kunde238–Reference Kunde241, Reference Melbourne and Windsor250, Reference Sadovskaya279, Reference Saprykina280]Footnote †. It is an ingenious tour de force in elliptic dynamics, and its framework owes to the Katok–Stepin theory of periodic approximations. Here is a brief outline of this singular idea (following [Reference Fayad and Katok88, Reference Katok187]). Consider a manifold with a non-trivial smooth
![]() $\mathbb R/\mathbb Z$
-action
$\mathbb R/\mathbb Z$
-action
![]() $\mathcal S=\{S_t\}_{t\in \mathbb R/\mathbb Z}$
and an invariant (averaged) Riemannian metric and volume
$\mathcal S=\{S_t\}_{t\in \mathbb R/\mathbb Z}$
and an invariant (averaged) Riemannian metric and volume
![]() $\nu $
. The desired exotic examples are obtained as
$\nu $
. The desired exotic examples are obtained as
![]() $f=\lim _{n\to \infty }f_n$
of
$f=\lim _{n\to \infty }f_n$
of
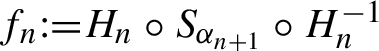 $f_n {:=}H_n\circ S_{\alpha _{n+1}}\circ H_n^{-1}$
with
$f_n {:=}H_n\circ S_{\alpha _{n+1}}\circ H_n^{-1}$
with
![]() $\alpha _n=({p_n}/{q_n})\in \mathbb Q$
and
$\alpha _n=({p_n}/{q_n})\in \mathbb Q$
and
![]() $H_n=h_1\circ \cdots \circ h_n$
, where the
$H_n=h_1\circ \cdots \circ h_n$
, where the
![]() $h_n$
are
$h_n$
are
![]() $\nu $
-preserving diffeomorphisms of M that commute with
$\nu $
-preserving diffeomorphisms of M that commute with
![]() $S_{\alpha _n}$
, which is achieved by defining
$S_{\alpha _n}$
, which is achieved by defining
![]() $h_n$
as a map between one fundamental domain of
$h_n$
as a map between one fundamental domain of
![]() $S_{1/q_n}$
and another one (or the same) and extending periodically to M. This is implemented by choosing
$S_{1/q_n}$
and another one (or the same) and extending periodically to M. This is implemented by choosing
![]() $h_n$
and then picking
$h_n$
and then picking
![]() $\alpha _{n+1}$
close enough to
$\alpha _{n+1}$
close enough to
![]() $\alpha _n$
(in particular with large enough denominator) to make this converge, such as
$\alpha _n$
(in particular with large enough denominator) to make this converge, such as
![]() $|\alpha _{n+1}-\alpha _n|\le 1/(2^nq_n\|H_n\|_{C^n})$
. Katok at times called this an ‘uncontrolled induction’. The ingenuity is that this way, one makes the
$|\alpha _{n+1}-\alpha _n|\le 1/(2^nq_n\|H_n\|_{C^n})$
. Katok at times called this an ‘uncontrolled induction’. The ingenuity is that this way, one makes the
![]() $f_n$
converge while the
$f_n$
converge while the
![]() $H_n$
diverge wildly, though with just enough control for the purpose at hand, which centers on spreading the orbits of the circle action around M. In a related solo paper [Reference Katok153], Katok showed that the Hamiltonian
$H_n$
diverge wildly, though with just enough control for the purpose at hand, which centers on spreading the orbits of the circle action around M. In a related solo paper [Reference Katok153], Katok showed that the Hamiltonian
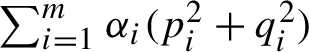 $\sum _{i=1}^m\alpha _i(p_i^2+q_i^2)$
with all
$\sum _{i=1}^m\alpha _i(p_i^2+q_i^2)$
with all
![]() $\alpha _i>0$
can be
$\alpha _i>0$
can be
![]() $C^r$
-perturbed (for any r) in such a way that on every energy level, the Hamiltonian flow is ergodic and has discrete spectrum. However,
$C^r$
-perturbed (for any r) in such a way that on every energy level, the Hamiltonian flow is ergodic and has discrete spectrum. However,
On the other hand, my own interests during the period were moving more and more toward hyperbolic dynamics and its variations, and [I] was greatly influenced, directly and indirectly, by Anosov and his workFootnote ‡. [Reference Katok187, p. 3]
It has been said that the Moscow ‘Dynamical community was somewhat divided between the followers of Sinai and those of Anosov’ [Reference Katok186, p. 19], and Katok once explained that
Their approaches were never completely reconciled. Anosov always looked at the subject as development of the classical theory of differential equations enriched by ideas and insights from topology, whereas for Sinai the sources of inspiration and insight were in the theory of probabilty and later more and more in mathematical physics.
Katok was drawn to Anosov’s mathematical personality. They shared (with much of the Moscow mathematics community) an interest in the aesthetic side of mathematics and liked to obtain elegant and internally beautiful results. This brings to mind a description by Katok’s Caltech colleague Richard Feynman of mathematicians (at Princeton) as ‘a happy bunch of boys who were developing things, and they were terrifically excited about it’ [Reference Feynman, Leighton and Hutchings99, p. 86]. Those who knew him could plainly see that Katok was having fun doing mathematics for its intrinsic appeal rather than working on problems dictated by extrinsic scientific necessity (see also page 41). Indeed,
I think the most impact he had on the life of a PhD student was the way he made them feel ‘pumped up’ and ‘ready to work’. After every interaction I had as a graduate student in his office or home, I felt excited. Excited about mathematics and the need to think more on the problem I am thinking about. Conversations were always respectful and encouraging. [Shilpak Banerjee]
2.3. History and politics
Katok’s time at Moscow University fell into the golden age of Moscow mathematics [Reference Zdravkovska and Duren303], and Katok at times explained that his choice of mathematics as a vocation was influenced by the relative freedom mathematicians enjoyed because their discipline was least affected and controlled by ideological impositions. He thought that otherwise he might have chosen to become a historian or a diplomat. To those who knew him, diplomacy seems a less natural fit, but even though he was never shy about his opinions,
in political discussions, he fully possessed the very important quality, in my view, of respectful disagreement, of engaged respectful discussion. I felt that with him any political topic could be discussed, and argued for or against, and no disagreement would have changed the feelings of esteem and respect. [Giovanni Forni]
Indeed, he had an inclination to statesmanship when it was for a good cause. The Katoks visited Kiev in 2014, and then again in June 2015 after the Russian attack on Ukraine. A planned conference had been canceled, then postponed, because participation had collapsed in the face of news coverage. He encouraged others to go, spoke at the conference, and made a point of staying longer to show support for Ukraine and Ukrainian mathematics. He understood that sometimes just being there goes a long way. Likewise,
Anatole was a real friend of Poland and of Polish mathematicians… . He spent quite a time in Poland in the last years. Mainly, organizing doctoral schools and conferences in Będlewo, which was really his passion. These schools, or rather minisemesters, were of enormous scientific success:
Dynamical Systems: Geometric structures and rigidity, Będlewo, July 7–26, 2008 Modern Dynamics and its Interaction with Analysis, Geometry, and Number Theory, minisemester (school and conference), Będlewo 27.06–24.07, 2011
If one looks at the names of participants/students, one can see easily how many of them became respected scientists! Anatole never forgot about some complements to mathematics: educational tourists visits, some physical activity—he himself liked long hikes. [Mariusz Lemańczyk]
Lest the reader wrongly suspect a central-European bias,
Tolya attended most of the special years on Dynamical Systems topics at Warwick over the past 40 yearsFootnote †. He liked to come for several weeks with his family and stay in one of the Mathematics Research Centre houses, which were a few yards away from the then Mathematics Institute. On these visits he liked to give a short course of lectures on a topic he was currently working on, and these were excellent for graduate students and people wanting to work in that topic. He loved these visits and all the interaction with other mathematicians. The place became more vibrant after he arrived. [Peter Walters]
History and politics remained a strong interest of his throughout his life, and stories abound about his prowess in that field. Among these are many about his command of the underlying facts. Adam Abrams recalls:
At the end of each semester, the dynamics group at Penn State would all go out to dinner together. Mathematics and current events were the most common topics of conversation, and at the 2014 dinner at Fuji and Jade there was a lengthy discussion comparing and contrasting various nations that used to be part of the Soviet Union. At one point someone claimed that Armenia currently had ‘a population of 3 million’ and Anatole countered that their population was not quite that large. ‘Not 3 million, I don’t think so, maybe 2.9 million at most’, he suggested. After a short debate over whether that discrepancy even mattered, some of us took out our phones to look up what the actual population was. The most recently recorded (2013) population of Armenia: 2.89 million.
Yakov Pesin recalls a party during which the challenge arose to name all US Presidents. Katok dismissed this as a trivial exercise and proceeded to name them all, add in all vice-presidents and throw in all Roman emperors in order without hesitation, with apologies for not knowing in every case the exact years of their reign. For Mariusz Lemańczyk [Reference Katok and Lemańczyk202], the first conversation
with him in this matter (many years ago) started with an ‘exam’ question, I was obliged to explain to him why an exceptionally good prosperity of the historical kingdom of Poland began in the second half of the XIVth century (the answer was that Black Death (the plague) did not touch the territory of Poland).
Vaughn Climenhaga remembers one of the conferences in Będlewo when there was a bus excursion, and
on the drive there, Tolya took it upon himself to take the microphone at the front of the bus and bring everybody up to speed on the relevant pieces of Polish history. The drive was not short, and neither was the history lesson.
Of course, as in mathematics, recall of the facts is helpful, but understanding how to work with them is a higher skill—which Katok possessed in both mathematics and history. Pesin (as do others) recalls a ca. 1970 special lecture given by the well-known topologist Mikhail Postnikov on a ‘new chronology’ in history. Nowadays, an internet search turns up the basic context quicklyFootnote † [Reference Diacu77]: this is a fringe theory to the effect (in short) that the dark ages never happened, that this is the reason for the paucity of pertinent documents, and that we are therefore by centuries closer to Roman times (say) than per the accepted chronology. This theory was developed by Nikolai Alexandrovich Morozov and had fallen into obscurity when Postnikov (and much later, Anatoly Fomenko) took it upon himself to bring mathematics to bear on this problem and ‘rescue’ the theory. Having been preceded by a lecture series at the History Institute of the Soviet Academy of Sciences, his lecture on this subject to this auditorium packed with mathematicians was compelling. A few in the audience had questions. Then Anatole Katok, a lowly junior mathematician and, as such, in the back of the auditorium, rose to say that he had no questions but wanted to make some comments and that this might take some time. He then dismantled in a perfectly professional manner Postnikov’s position on every single fact from the lecture. The audience, having just been persuaded by Postnikov, was now convinced of the contrary and looked at Postnikov for a reply. After a pause, Postnikov said ‘A week ago I gave the same presentation at a meeting of the Moscow Historical Society to professional historians. None of them presented such serious professional comments, and I have to think about them’. Next, the well-known historian Lev GumilyovFootnote † came to the podium and said that he had been invited to present his view, but that his ‘young colleague’ had already said everything he had to say. Katok had great respect for Gumilyov and was very proud of having been called his colleague.
A recent topical project of his was a paper about missed opportunities during the last four centuries for Russia to become (in a sense) a more Western country, whatever that may be, and Domokos Szász recalled that after 1990, Katok had the idea that Hungary should become a constitutional monarchy with Otto Habsburg as king. ‘In retrospect I am much sorry our country did not consider this alternative’.
2.4. Seminars
Regrettably, mathematics in the Soviet Union became less sheltered in the late 1960sFootnote ‡. The mathematics department at MSU saw increased antisemitism and general oppression against liberal thought, and almost no Jews were accepted as either undergraduate or graduate students, or faculty [Reference Brin and Pesin51, Reference Katok186, Reference Katok187]. So, upon his graduation, Katok was recognized as a prominent mathematician and definitely fit for a position either at the Moscow State University or at the Steklov Institute, but that was impossible by now. He instead assumed his first and only appointment in the Soviet Union, as Scientific Research Worker at the Central Economics–Mathematics Institute of the USSR Academy of Science (CEMI)Footnote §, a known ‘haven’ for some mathematicians because it employed those whom others did not. Eugene Dynkin is a case in point: ‘The powers that be did not like Dynkin’s independent thinking, and he had to leave the MSU in the spring of 1968. After a jobless period, he at last got a position of senior researcher in the department of mathematics of CEMI’ [Reference Katok and Kuznetsov201]. CEMI allowed these mathematicians to combine their work on mathematical problems in economics, if any, with research in pure mathematics:
CEMI went to the extreme liberalism of mandating only a token presence… . I had… virtually total professional and practical freedom, and my CEMI superiors made it clear that my mathematical work was appreciated and considered a legitimate professional output… . I was free to dedicate to mathematical research as much time and energy as I saw fit. I was also encouraged to teach both dynamical systems and mathematical economics at the Mech-Mat part-time. [Reference Katok186, p. 12f]
The liberal and progressive character of the CEMI culture and its leadership proved important for Katok’s career and that of others, and its location almost next door to the Steklov Institute was convenient for the collaboration with Anosov. Katok taught topics courses in dynamical systems and ergodic theory. (For Michael Brin and Yakov Pesin, these were the only coursework in dynamics [Reference Katok186]; of course, the Anosov–Katok seminar, which both attended from undergraduate days on, provided a deep and broad education at the cutting edge [Reference Katok186, p. 7f]. One should note that ‘undergraduate’ education in Moscow went for 5 years, of which the last 2 were what in the US would be considered graduate level, leaving students ready to pass US qualifiers in virtually any mathematical subject area.)
Katok had been attending the Sinai–Alekseev Footnote † seminar at Moscow State University regularly from 1963 and continued to do so through 1970 and then intermittently until 1977. In the fall of 1969, he and Anosov started another seminar at the Steklov Institute (which had to move to CEMI in 1975 [Reference Katok186, p. 8f]) with Katok as the driving force. While Katok was rather fortunate in his appointment, at that time, many mathematicians beginning their research careers took jobs in organizations wholly unrelated to mathematical research or the teaching of mathematics. These seminars were at the heart of Moscow mathematical culture and a vital connection to the research enterprise for those laboring in these day jobs outside of mathematics and who were otherwise utter outsiders with no standing at these institutions.Footnote ‡ The role of the seminars was twofold: in addition to talks about research by participants and guests, many talks were about works by other mathematicians, mostly foreigners, very often based on preprints, which were rare and precious. The seminars served as incubators of a staggering amount of mathematics, and here as well, Katok’s generosity in sharing ideas was important yet rarely reflected in the literature. For instance, it was his idea to consider the ‘stadium’ as a candidate for an ergodic non-dispersing billiard system [Reference Katok183, p. 239]. The seminars typically met weekly in the afternoon or evening, with well-defined start times and much less well-defined end times, though officially they were scheduled for some two hours duration. For two decades, the Sinai–Alekseev and Anosov–Katok seminars were the main engine that put Moscow at the forefront of developing the modern theory of dynamical systems. To illustrate the point, the core participants of the Steklov seminar were A. A. Blokhin, M. I. Brin, L. A. Bunimovich, E. I. Dinaburg, R. I. Grigorchuk, A. A. Gura, M. V. Jakobson, S. B. Katok, Y. I. Kifer, A. V. Kochergin, A. B. Krygin, G. A. Margulis, Y. B. Pesin, B. S. Pitskel, R. V. Plykin, E. A. Satayev, and (occasionally) T. V. Lokot, V. I. Oseledets, L. D. Pustylnikov, and A. M. Stepin. The long list does not imply that everyone attended all the time; ‘sometimes in the room were two professors and two students’ [Rostislav Grigorchuk].
Rostislav Grigorchuk retains a characteristic memory from his first research talk, which Anosov and Katok had invited him to give at their Steklov seminar in 1975, when he was still a 5th-year undergraduate at Moscow State University and had proved his first result (the now well-known cogrowth criterion of amenability of groups [Reference Grigorchuk112, Reference Grigorchuk113]). Grigorchuk
went to the blackboard and in few minutes formulated my result. After that Tolya ‘jumped’ to the blackboard and started to prove it. After 10 minutes of sharing with him the space near the blackboard I understood that I have to sit down and try to follow Tolya’s arguments. He had an interesting idea but after one hour and a half, as far as I remember, I managed to show that his argument does not work. Seems he agreed. My time had expired because of the end of the seminar.
Pre-empting the speaker or producing the speaker’s theorem or proof was not usually the point. Quite the contrary, as described by Giovanni Forni from being on the ‘receiving end’ of such treatment:
Giving a talk in front of Tolya was definitely very intimidating, as he regularly intervened and made comments. I remember clearly that during a talk I gave at [the] Banach Center in Poland in 1995, Tolya interrupted me several times and jumped to the board to explain the significance of the results. It was certainly difficult to conclude the talk, but I also felt that he was motivated by interest and appreciation of the work and he wanted to let everybody know his perspective on it. I felt very honored… . Let me add that my talk at Banach Center turned around the existence of ‘invariant distributions’ for a class of dynamical systems. I did not know then that Tolya had found invariant distributions earlier in other contextsFootnote †. However, he did not call attention to his own work, which I discovered only later… . His comments were always enlightening and I always tried to learn from them.
For many, these comments were most eagerly anticipated. As Amie Wilkinson put it:
Whenever I proved a new result, I immediately thought ‘what will Tolya think of this?’ and looked forward to telling him about it.
Aside from matters of taste, the interest in a piece of mathematics is also related to the context, and he
allowed himself to change his mind about things and tell you about it. Once I met Tolya in Paris, we were at a Conference at IHP. He asked me what I was working on, and I told him I had just generalized to dimension three a result by Bochi and Mañé [Reference Bochi38, Reference Mañé244], about the
![]() $C^1$
-generic dichotomy of Lyapunov exponents [Reference Hertz275] (this result was later obtained for any dimension by Avila, Crovisier and Wilkinson [Reference Avila, Crovisier and Wilkinson20]). I told him I knew he didn’t like
$C^1$
-generic dichotomy of Lyapunov exponents [Reference Hertz275] (this result was later obtained for any dimension by Avila, Crovisier and Wilkinson [Reference Avila, Crovisier and Wilkinson20]). I told him I knew he didn’t like
![]() $C^1$
-generic results, and he told me ‘You are right, but what you get is what you get’. Some years later (I think it was 2015) I was invited to talk in PSU colloquium, and I chose to talk about genericity of ergodicity in different topologies, including
$C^1$
-generic results, and he told me ‘You are right, but what you get is what you get’. Some years later (I think it was 2015) I was invited to talk in PSU colloquium, and I chose to talk about genericity of ergodicity in different topologies, including
![]() $C^1$
, and when the time of comments arrived, he told everybody that he hadn’t liked this type of results for years, but he recently had discovered that there are some tools in the area that are useful to get insights for deeper topics, so he had started to look at them with different eyes. And he told me he had enjoyed the talk. It is not at all common that a mathematician makes such a statement.
$C^1$
, and when the time of comments arrived, he told everybody that he hadn’t liked this type of results for years, but he recently had discovered that there are some tools in the area that are useful to get insights for deeper topics, so he had started to look at them with different eyes. And he told me he had enjoyed the talk. It is not at all common that a mathematician makes such a statement.
Tolya was known for making strong statements, but perhaps this aspect is less known: he was one of the very few mathematicians who was capable to publicly recognize that he had changed his mind. And even to apologize (in Toronto 2006 he stood up in a conference at the Fields institute and publicly apologized to Avila for some comment he had made). This made him very unique, certainly a very human and great mathematician. [Jana Rodriguez Hertz]
Indeed, whenever Katok went on the record, notably in his historical and biographical writing, he was quite scrupulous about being fair in his assessments. He told me about the difficulties he faced when writing about Anosov [Reference Katok187]: in his latter years Anosov himself wrote about the history of dynamics with an emphasis on the developments in his lifetime, and it was not easy for Katok to describe these fairly without marring this account by pointing to conspicuous shortcomings, which would have been at odds with the purpose of Katok’s article as well as a distraction from the appraisal of the valuable work Anosov himself had been involved in. Katok was appalled and struggled with this for some time until he seized upon the device to briefly discuss the distortions and omissions in these writings and to refer to Mathematical Reviews (specifically my review of [Reference Anosov10]) for a more detailed discussion of these problems.
Generally, Katok’s active seminar and conference participation is well remembered for the way in which it enriched the experience and value of a talk for both the audience and the speaker. He would comment on the meaning of a result, the context which makes it interesting, prior work on which it builds, and why it is important and interestingFootnote † —and sometimes at length:
Of all that I learned from Tolya, this appreciation for the importance of understanding the broad picture and for putting mathematical results in their proper context is one of the things that I value the most.
My enduring picture of the working seminar is… an image that represents multiple occasions: Tolya standing at the blackboard for one of any number of reasons—the speaker had not been able to make it today, or he had decided the topic needed some further introduction before the speaker started talking, or some other reason why an intervention was necessary—and then delivering, off the cuff without notes or preparation, some remarks ranging in length anywhere from 5 minutes to an hour or more, in which it was always quite clear that he knew exactly where he was coming from, where he was going, and how everything fit into the broader picture. [Vaughn Climenhaga]
Moreover, his presence in seminars strongly reflected both the best of the Moscow seminar culture as well as the way in which Katok himself discovered new mathematics, especially in collaboration:
His seminars were notorious for the speaker, but fantastic for graduate students. Usually they were two and a half to three and a half hours long, with a short quarter hour break in the middle for snacks and coffee. The speaker would be grilled from the beginning for examples to give an understanding of the material presented, and they would, by hook or by crook, become accustomed to the back and forth. This was a much welcome change of pace from the usual style of talk, where the speaker will cover the background material out of formality. This is not useful for audience members unfamiliar with all of the material leading up to the result. Prof. Katok made sure that the audience got something out of every talk, and most importantly understood the relevance of the speaker’s results. He enjoyed the back and forth, and felt, I think, that the truth of the material was made apparent through this struggle. In math you arrive at the truth after some wrangling, and for him, this was true in the spoken version as well as the written version. [David Hughes]
However, sometimes the speaker virtually disappeared:
I remember Tolya in Oberwolfach, at the bi-annual meeting Dynamische Systeme. In the 90’s Michel Herman was also a regular participant and there were frequent discussions, sometimes heated, between Tolya and Michel, often during someone else’s talk. I could not always grasp what they were saying, but it made those meetings among the most intellectually vibrant in my memory. Despite the uncomfortable moments for the speakers, there was much to learn from these exchanges. [Giovanni Forni]
Helmut Hofer, who now co-organizes these Oberwolfach meetings, describes these exchanges by telling the emblematic story of the ‘Katok diagonal argument’. Katok’s usual seat was in the front right (sitting in front was his general custom, and the doors being on the right in the main Oberwolfach meeting room makes this the natural side for late-comers). Michel Herman might sit in the very left-rear corner. It was not uncommon for one of Katok’s amendments to someone else’s talk to be countered by Herman from the opposite corner: ‘I can’t believe that I am hearing this! I have three counterexamples to that statement. No, I have infinitely many counterexamples to what you are saying…’, and so the argument across the diagonal of the room was on. This is well-remembered, of course, not only because it was entertaining, but because these interactions were illuminating for those present and emblematic of the creative spark of those meetings—which was in no small part due to Katok.
Likewise, I remember from the classes he taught those distinctive moments when he turned from the board to face the audience and explain what it all means. He did not prepare the technical points of his classes in advance, and the proofs were presented off the cuff, which meant that details could be missing or incorrect. But proofs serve to illuminate, and their ideas as well as the rich context he provided gave a unique picture of the subject.
In my Caltech days, Katok ran a seminar as well as a working seminar; in the latter one, students learned the communal practice of mathematics, and they would often be organized around a topic. I recall presenting the classification of higher-rank non-positively curved manifolds after Ballmann, Brin, Burns and Spatzier [Reference Ballmann21, Reference Ballmann, Brin and Spatzier23, Reference Ballmann, Brin and Eberlein22, Reference Burns and Spatzier58, Reference Burns and Spatzier59], and possibly learning more from the questions I was asked than the preparation I had undertaken. I also do not ever remember him taking notes in a seminar or any other context. In an interview, he confessed to this as a weakness, but to my mind it always reflected two major characteristics. Thanks to his prodigious memory, he did not need notes in the first place, and furthermore, his encyclopedic knowledge and vision of mathematics made every new thing an organic part of an interconnected landscape he consummately inhabited and in which he could locate each item at will.
He was always thinking of the big picture: Where is the field going and where does it come from? How does a particular result fit in the general scheme of things? How does it advance us towards understanding the main issues? And how did the main ideas develop historically?
He had an all-encompassing coherent overview of the field of dynamical systems and its position within the general mathematical world. He also had a view on the history of ideas of the field: what led to what and how. This big picture, which is described in detail in many of his historical surveys and books, was central to his activity as a mathematician both as a researcher and as an intellectual leader. It led him to judgements of which directions should be given emphasis, and sometimes also which ‘blue-prints’ to follow to develop them. [Omri Sarig]
2.5. Research in CEMI years
Returning to the post-doctoral decade in Moscow, it is striking how Katok’s work quickly spanned the breadth of dynamical systems—and more so than a literature search easily reveals. Beyond the multiple papers on periodic approximation, he produced a substantial body of work on what he called ‘monotone equivalence’ (often called Kakutani equivalence and based on a far-reaching generalization of the concept of time-change in flows; ergodic theorists such as Feldman, Ornstein, Rudolph and Weiss were also working on this at about the same time). Here is one application of this notion.
Monotone equivalence is a useful source of counterexamples in the isomorphism theory. For example, if one constructs a K-automorphism T which is monotone equivalent to a transformation with a nonstandard zero entropy factor, then T is not loosely Bernoulli and hence not Bernoulli. This observation was used in the earliest construction of a classical system which is K but not Bernoulli. [Reference Katok185, p. 561]
His student Evgueni A. (Zhenya) Satayev did ‘excellent thesis work on Kakutani equivalence theory that came earlier than a similar project by the giants of ergodic theory, D. Ornstein, D. Rudolph, and B. Weiss, and was only marginally weaker than theirs’ [Reference Katok187, p. 6], [Reference Sataev282]. A 1975 announcement [Reference Katok159] was followed by what was meant to be a complete presentation but by no means exhausted the subject at that time [Reference Katok161] because the editor-in-chief of Izvestija was I. M. Vinogradov, an inveterate antisemite whose approval was going to be required for a paper of the necessary length, but would not be forthcoming [Reference Katok187, p. 7ff]. The published paper consisted of half of the intended paper plus announcements of the intended contents of the second half—which could not be published as a separate paper because Katoks’ emigration was then drawing nearFootnote †. (Previously, Katok and Satayev had worked on the number of invariant measures for a flow on a surface [Reference Katok158, Reference Sataev281], and later, they applied the theory of monotone equivalence to flows on surfaces [Reference Katok and Sataev214].)
An oft-cited elliptic foray and a novel application of the Anosov–Katok method was the striking construction of ergodic perturbations of degenerate integrable Hamiltonian systems [Reference Katok157]: The famed and astonishing Kolmogorov–Arnold–Moser Theorem tells us that for small-enough perturbations of completely integrable dynamical systems, a set of almost full measure will retain the orderly dynamics of the original integrable system—provided that system is non-degenerate. This work established that without the non-degeneracy assumption, one can produce the very opposite of this conclusion with arbitrarily small perturbations. The iconic example is that if the geodesic flow of the standard round 2-sphere is perturbed by the addition of an ‘equatorial wind’, that is, a drift akin to a rotation, the resulting dynamics is a Finsler geodesic flow with two ergodic components, indeed, just two closed orbits (the equator run in both directions). These two works illustrate that several of the high points in Katok’s work are difficult specific constructions and mindboggling counterexamples. But he was always thinking of the big picture, including how a particular result fits in the general scheme of things. In these two cases, this fits into a big question on which he worked to a considerable extent during his career: ‘Is there such a thing as smooth ergodic theory?’ Abstract ergodic theory is a discipline dominated by examples and constructions, and he meant to keep in mind the origins of this field by looking for smooth realizations of these various examples and phenomena. Viktor Ginzburg points to the depth and prescience:
I still feel awe when I read some of his old papers. His 1973 paper on ergodic perturbations is a masterpiece. I read it some 30 years later and I could not believe how much he understood and anticipated back then. Likewise his 1980 IHES Publications paper on topological entropy [Reference Katok165].
Katok’s entry into what is now (thanks to Katok [Reference Katok183]; see page 48) called parabolic dynamics proved lastingly influential as well: it involved the creation of the (Katok–Zemlyakov) ‘unfolding’ method for the study of polygonal billiards [Reference Zemlyakov and Katok304, Reference Zemlyakov and Katok305]Footnote ‡. To study billiards (the free motion of a particle with ‘optical’—or ‘specular’—reflections in the boundary of a region) in polygons with a view to the presence of periodic or dense orbits, say, one can, instead of tracking reflections of the particle, ‘unfold’ each reflection by reflecting the polygon itself in the corresponding side, which for rational polygons may yield a flat surface whose study in turn illuminates the behavior of the original billiard system. While it sounds simple, this idea was foundational for important parts of parabolic dynamics; the paper is among Katok’s most cited ones, and it permanently put Zemlyakov’s name on the map, who published only one other research paperFootnote †.
Much later, during the the Program in Ergodic Theory and Dynamical Systems at MSRI in 1983–84, Katok influenced this field in an entirely different way.
One of the problem sessions at the MSRI workshop was dedicated to billiards. In particular, I gave a rather detailed presentation of the state of the problem of ergodicity for polygonal billiards. It was so lengthy that it annoyed Steve Kerckhoff who complained that other problems were not given an adequate hearing. However, it was exactly that discussion that introduced Kerckhoff to the problem and started a very fruitful collaboration between him, Howie Masur and John Smillie who were also among the participants of the MSRI program. It resulted in the complete solution of the problem for rational polygons in 1984. Masur’s talk on the joint work was the highlight of the Spring 1985 Caltech workshop which was centered around geodesic flows and billiards. I am very happy to have annoyed Steve Kerckhoff in such a productive way. [Reference Katok177]
The theory of hyperbolic dynamical systems made explosive progress in this period, and a significant part of it carries Anosov’s name [Reference Anosov4–Reference Anosov7, Reference Anosov and Sinaĭ15]. Katok naturally also joined this frontier of research, and his second publication (after [Reference Katok154]) in this area marks a strand of writing that was to permeate Katok’s career henceforth. His lectures from a 1971 summer school in Katsiveli on the Black Sea [Reference Katok, Mitropolskiĭ and Šarkovskiĭ155] appeared with others on hyperbolic dynamics [Reference Alexeyev, Katok, Kushnirenko, Mitropolskiĭ and Šarkovskiĭ1], and together, these became the main early Moscow text on differentiable dynamics. Katok’s lectures are a systematic presentation of hyperbolic dynamics based on both studying some of the Western work and on filling the Anosov blueprint [Reference Anosov8] for studying the topological dynamics of hyperbolic sets using shadowingFootnote ‡ (he did so again in the supplement to [Reference Nitecki258], which he had also translatedFootnote § and annotated, and the approach can also be found in [Reference Fisher and Hasselblatt102, Reference Hasselblatt127, Reference Yoccoz300]).Footnote ¶. It is notable that this was a much-needed and influential exposition but also cutting-edge mathematics, and that this summer school occurred a mere three years after Katok’s doctorate.
Searching the literature by authorship alone misses essential contributions of his, however. As the mentor of Brin and Pesin, Katok supported the development of the theories of both partially and non-uniformly hyperbolic dynamical systems [Reference Brin and Pesin51, Reference Katok186]. While in a (uniformly) hyperbolic dynamical system, each tangent space splits into complementary sub-bundles in which the action expands or contracts, respectively, a partially hyperbolic dynamical system includes a third sub-bundle, in which contraction and expansion are allowed but at lesser rates than in the former subspaces. Non-uniformly hyperbolic dynamical systems are just that: they possess expanding and contracting sub-bundles as well, but there is no uniform control of the contraction and expansion rates. While it is natural to expect that pushing the techniques from uniformly hyperbolic dynamics is the right strategy, the technical challenges are substantial.
Anosov was the adviser of record for Brin and Pesin—Katok could not serve as such because this would have combined a Jewish student with an adviser who was also Jewish and at an economics institute rather than a university. According to the accepted mode of operation in the Moscow community, Anosov did not propose a problem or provide much guidance, but he was an important listener, and his comments were important—as were his (and Katok’s) machinations and horse-trading to help Brin and Pesin to defend their dissertationsFootnote † [Reference Brin and Pesin51, Reference Katok186, Reference Katok187].
Katok had proposed to Brin and Pesin that they work out what happens if, in addition to the expanding and contracting sub-bundles, there is a sub-bundle with less contraction or expansion, and he gave them a pertinent paper by Sacksteder [Reference Sacksteder278], [Reference Katok186, p. 14]. From there, they proceeded to develop the theory of partially hyperbolic dynamical systems [Reference Brin and Pesin49, Reference Brin and Pesin50]. Katok and Anosov listened and commented, but did not get otherwise involved. When asked whether this work would be enough for dissertations, Anosov told them that they needed to say who proved what, as what they had would only be sufficient for non-Jewish candidates; Jews would need an additional paper. Brin proceeded to study frame flows as an application of partial hyperbolicity [Reference Brin41–Reference Brin43, Reference Brin and Gromov45, Reference Brin and Karcher46, Reference Brin and Pesin48], and as Pesin was casting about for a project, he went back to a book on differential equations ‘with non-zero exponents’ [Reference Bylov, Vinograd, Grobman and Nemyckiĭ61], which Anosov had given him along with the suggestion that it might be useful. Together with the motivation to extend ergodicity of geodesic flows of compact surfaces from metrics with negative curvature to those without focal points, this was the origin of his theory of non-uniform hyperbolicity [Reference Barreira and Pesin27, Reference Pesin263–Reference Pesin268], [Reference Katok186, p. 17].
His first approach assumed that while the contraction and expansion rates may vary discontinuously with the orbit, the attached constant would be uniform. He presented this to Anosov as an add-on to the Brin–Pesin theory, and Anosov saw right away that this could not be right, sending Pesin back to the drawing board. On the two-hour subway ride home, Pesin figured it out, wrote up a draft at home and called Anosov with the good news. Anosov did not buy it and said that he was not willing to listen to more nonsense, but as a last chance he gave Pesin five minutes to convince him. Eventually, Pesin presented this work in the seminar, and it became clear that this was both correct and important. Pesin then wrote the Uspehi paper [Reference Pesin265] (his third paper and second major one), and he recalls being lost in how to explain his theory of non-uniform hyperbolicity (that is, of systems with non-zero Lyapunov exponents) in the publication. Katok read drafts and discussed them generously, he helped the exposition and with putting this work in context—his vision and perspective were well ahead of Pesin’s at the time and crucial for this work. Yet, despite this deep involvement in the work, Katok refused to be named as a coauthor of what is now known as the Pesin theory. (Indeed, Katok and Pesin have no joint publication. Brin and Katok coauthored two papers, of which one [Reference Brin, Feldman and Katok44] builds on Brin’s dissertation work [Reference Brin41, Reference Brin42].)
This is why Brin and Pesin (and the Mathematics Genealogy Project) consider Katok their doctoral advisor even though he was not allowed to officially serve as such and Anosov’s involvement was deep and crucial as well [Reference Katok187]. Katok’s promotion of this work continued past its completion:
Of course, Pesin was not able to lecture about his work outside of the Soviet Union so the task fell on me when I found myself in 1978 first for six months in Western Europe and then in the United States. [Reference Katok186, p. 19]
Thus, within a decade from his doctorate, Katok was profoundly influential and internationally known not only in ergodic theory but in (what is now known as) elliptic, parabolic, and hyperbolic dynamics.
3. Metropolitan Moves
Domestically, the situation started less ideally for the Katoks. Together with their daughter Elena, they lived in a single room of some 220–240 ft
![]() ${}^2$
(20–22 m
${}^2$
(20–22 m
![]() ${}^2$
) in an apartment with two other families and a 4th room occupied until 1970 by Svetlana’s grandparentsFootnote †, quite a step down from Anatole Katok’s upbringing in a single-family apartment. Around that time, emigration became a realistic possibility, and some friends and colleagues started leavingFootnote ‡. The Katoks discussed the possibility but decided against it. Occasionally ‘cooperative apartments’, whose construction began in the 1960s, became available for purchase, and the family was eligible for an apartment of approximately 750–800 ft
${}^2$
) in an apartment with two other families and a 4th room occupied until 1970 by Svetlana’s grandparentsFootnote †, quite a step down from Anatole Katok’s upbringing in a single-family apartment. Around that time, emigration became a realistic possibility, and some friends and colleagues started leavingFootnote ‡. The Katoks discussed the possibility but decided against it. Occasionally ‘cooperative apartments’, whose construction began in the 1960s, became available for purchase, and the family was eligible for an apartment of approximately 750–800 ft
![]() ${}^2$
(70–75 m
${}^2$
(70–75 m
![]() ${}^2$
). These were difficult to get, but they found that a rather large and expensive one was available. However, there was no apparent way of producing the required down payment of 40%, which amounted to 18 months of their gross household income. They recall with gratitude that Anosov lent them the entire sum without interest and with an indefinite term of repayment [Reference Katok187, p. 14]. (Decades later, after a large expansion of their State College house, Katok told Ilyashenko ‘Now I reach in the US the same level of lodging that I had in the Soviet Union: it is at the top level among those of my colleagues’ and added that a university professor should be wealthy and not ashamed to show it in order to increase the prestige of the profession.)
${}^2$
). These were difficult to get, but they found that a rather large and expensive one was available. However, there was no apparent way of producing the required down payment of 40%, which amounted to 18 months of their gross household income. They recall with gratitude that Anosov lent them the entire sum without interest and with an indefinite term of repayment [Reference Katok187, p. 14]. (Decades later, after a large expansion of their State College house, Katok told Ilyashenko ‘Now I reach in the US the same level of lodging that I had in the Soviet Union: it is at the top level among those of my colleagues’ and added that a university professor should be wealthy and not ashamed to show it in order to increase the prestige of the profession.)
In 1972, the Banach Center in Warsaw was established by the Academies of Sciences of Bulgaria, Czechoslovakia, East Germany, Hungary, Poland, Romania, and the USSRFootnote †, with the aim to promote and stimulate international cooperation in mathematics, especially between the East and West. Anatole Katok’s first trip abroad was for a 1975 conference there. By then, the family’s tolerance for life in the Soviet Union was wearing thin, and they decided to leave the country. Katok returned to Warsaw in 1977 [Reference Katok162] for an international conference that provided a major encounter between ‘the East’ and ‘the West’. His participation (and that of M. Brin and M. Jakobson) was ostensibly on private invitations of the Polish colleagues, while Anosov, Stepin, and (Sinai’s wife) Elena B. Vul were the official delegation [Reference Katok187, p. 10]. This was the height of the period when Jewish scientists and mathematicians could leave the Soviet Union, and Katok made no secret of the plans to emigrate. Several people brought this to the attention of William Kirwan Footnote ‡, newly chair of the department of mathematics at the University of Maryland, suggesting that Katok was a rising star with the potential to become a superstar and that he would have many offers from prestigious universities. The department had great ambition to become one of the best mathematics departments in the country among public universities, and Kirwan recalls that
I had a fax of his vita that included his telephone number in Moscow. So one afternoon I said, what the heck, let me try and beat everyone to the punch and reach him in Moscow. So I placed a call. In those days, such a call had to go through an international operator, who told me she would try and reach the party but it would take about 30 minutes. Sure enough, 30 minutes or so later the phone rings and the operator puts me through to Tolya. He had no idea who I was. I explained that I was chair of UM’s Math Department, that I knew he was about to leave the Soviet Union and that I wanted to offer him a job, initially as a visitor but almost assuredly as an endowed professor once he got here and we could follow the process. Ironically, he didn’t know how much in demand he was. From his perspective, he had a wife and two children, they were leaving their home and he had no idea how he would be able to support them. So my offer sounded very good to him, especially at the salary I proposed. Believe it or not, he said ‘yes’ and the deal was done on that phone call. When he got to Maryland, my wife and I took the Katoks under our wing and helped them get settled. Tolya and I were very close. He played an critical role in building the quality of the department and in recruiting.
The family applied for emigration in July 1977, and this quickly became public knowledge (which caused the aforementioned publication issues with the work on monotone equivalence [Reference Katok187, p. 8f]).
That May, Giancarlo Benettin and Jean-Marie Strelcyn had submitted a study of the ‘stochastic transition’ in a one-parameter family of plane billiards called ‘generalized stadium’ or Benettin–Strelcyn billiard [Reference Dullin, Richter and Wittek81, Reference Hénon and Wisdom134] that interpolates between the Bunimovich stadium and the circle as follows: circle arcs surmount the sides of a square, matching tangent lines at the corners [Reference Benettin and Strelcyn30, p. 777]. The paper numerically estimated the Liouville entropy [Reference Benettin and Strelcyn30, Figure 14] using the Pesin entropy formula [Reference Pesin263], and Strelcyn asked Katok whether the entropy formula could be applied in this contextFootnote †. As Katok and Pesin thought how to extend the Pesin theory to systems with discontinuities, such as these billiards, their trips to the Anosov seminar provided opportunity for discussion. Part of the itinerary was a 30-minute bus ride, and one day, Pesin realized on this bus that the missing sufficient condition (beyond previously known assumptions on derivatives) was that the volume of a neighborhood of the discontinuity set be bounded by a power of the thickness of that neighborhood. Just then, the passengers were asked to produce their tickets, and the pair realized that in their mathematical excitement they had forgotten to buy any. The fine was some 10 times as much as the bus fare, and Katok declared that ‘this is the price of a new mathematical discovery’. Their levity over this appraisal caused some puzzlement among the other riders.
Because the impending departure of the Katoks made it infeasible to collaborate on writing this result up together, Katok and Pesin agreed that Katok would do so and publish it himself abroad. Katok wrote to Strelcyn that undoubtely the entropy formula can be applied to billiards but that the proof for this case had to be written [Reference Ledrappier and Strelcyn243]. Their resulting book has since been the standard reference on hyperbolic systems with singularities [Reference Katok, Strelcyn, Ledrappier and Przytycki225]Footnote ‡. Almost all the text was written by Strelcyn (and its generality owes to insights by Feliks Przytycki in an essential way [Reference Katok, Strelcyn, Ledrappier and Przytycki225, p. VIII])Footnote §. Katok had
suggested the general plan of the work and worked out the arguments and… the first draft of the theory… was presented by [Strelcyn] in December 1978 at the Seminar of Mathematical Physics at IHES [Institut des Hautes Études Scientifiques] (Bures-sur-Yvette, France). The material of this book represents a part of the ‘Thèse d’état’ of [Strelcyn], defended 30 April 1982 at University Paris VI. [Reference Katok, Strelcyn, Ledrappier and Przytycki225, p. VII]
For Jean-Marie Strelcyn, this was an important career moment, and he describes Katok as ‘an absolutely exceptional man who determined my life’, a sentiment I can echo myself.
On February 15, 1978, the Katoks emigrated from the Soviet Union. The usual route for this exodus was via Vienna to Rome, where one got the US immigration documents at the office of HIAS (a Jewish American non-profit organization founded as the Hebrew Immigrant Aid Society, which provides humanitarian aid and assistance to refugees)Footnote † In Vienna, they stayed with Karl Sigmund and his family. He and they long recalled their joy at discovering, during their wanderings around town, a restaurant that offered a unique winning combination of cleanliness and price—but when they reported their discovery, Sigmund asked suspiciously, whether the name of the restaurant was, by any chance, McDonald’s. It was, and this story remained a joke among them for years. In fact, this was the first McDonald’s in Vienna, and had just opened (in the magnificent Palais Wertheim on Schwarzenbergplatz). Twenty years later, we made a pilgrimage there together.
In Rome, the Katoks learned that since Anatole was born in the US, he was not eligible for refugee status and had to apply for a US passportFootnote ‡ instead—and that this might take well over a year! Since his appointment at Maryland was to start in August, this was a problem. Brit Kirwan came to the rescue and worked some connections in the State Department, which got Anatole his passport within 35 days! The others were now family of a US citizen and hence eligible for Green Cards. Just then, Anatole received an invitation from IHES in Bures-sur-Yvette near Paris, and the family decided to go to Paris and get the documents there. There was one hitch: other than Anatole, they were stateless because the Soviet authorities had taken away their passports and only given them ‘exit visas’. But they were able to obtain suitable travel documents in Rome; it helped that Ida ChagallFootnote § sent a private invitation to Svetlana. They traveled first to Milan (as guests of Strelcyn’s collaborator Luigi Galgani [Reference Benettin, Galgani and Strelcyn29, Reference Benettin and Strelcyn30]), then to Geneva, where they visited Anatole’s uncle (a cousin of Boris Lazarevich Katok, who worked for many years at the UN in Geneva) and his American wife.
We arrived in Paris by train and were greeted at the railway station by Jean-Marie Strelcyn and Michel Herman, who took us to the Residence Ormaille [at the IHES] where the refrigerator was full with food. I will never forget their hospitality.
There was an office of HIAS in Paris headed by a Hungarian Jew named Ivar Svartz, unlike the office in Rome, almost deserted. Our Green Cards were processed there in a couple of months, but most importantly, Tolya discovered a new and much more comfortable way of emigration for mathematicians from the USSR: through Paris HIAS in conjunction with an invitation to IHES. Several mathematicians followed this route: definitely Mityagin and Brin, but probably moreFootnote †. [Svetlana Katok]
At the IHES, Anatole Katok found himself, for the first time in his life, with an appointment as a mathematician at a mathematics institute, and with an office of his own. Here he obtained some of his best-known and most widely quoted results in the non-uniformly hyperbolic theory [Reference Katok163, Reference Katok165], [Reference Katok and Hasselblatt190, Supplement]. He always recalled with gratitude the warmth with which the community of dynamicists in these cities received and supported them.
From the IHES, he traveled to the June 1978 Oberwolfach Workshop on ergodic theory organized by Manfred Denker and Konrad Jacobs, where many Western ergodic theorists met him for the first time. Denker echoes Bunimovich in recalling his first impression of Katok as someone tall and loud who knows everything—and who thought that all good mathematics had already been done in Moscow, often saying something like ‘oh, that is known in Russia for a long time’.
3.1. Maryland
In August, the family was picked up at Dulles airport by Sasha Gruz and Dora Katok, who had moved to Rockville a little earlier. After staying with them for several days, the Katoks moved to a rental apartment in College Park and settled in. Svetlana was finally able to pursue her doctorate in mathematicsFootnote ‡ and Anatole, now 34, assumed his first professorship.
A few remarks on some of the works from that period. Several of these owe to the preceding time at the IHES, such as the book on hyperbolic dynamical systems with singularities [Reference Katok, Strelcyn, Ledrappier and Przytycki225]. Two Annals papers produced Bernoulli diffeomorphisms on any compact connected
![]() $C^\infty $
manifold, possibly with boundary, of dimension greater than 1. The first was written by Katok at the IHESFootnote † [Reference Katok163] and produces Bernoulli diffeomorphisms on surfaces, notably on a disk. This is profoundly astonishing: these are area-preserving diffeomorphisms which, up to a measurable change of ‘coordinates’, are isomorphic to a Bernoulli shift, that is, the probabilistic model of a fair coin toss (with possibly more than two sides). At the core lies the Pesin theory: when obtained from hyperbolicity in the right circumstances, ergodicity implies the Bernoulli property. The ideas are so natural that they cannot be omitted here. Katok starts with a linear hyperbolic automorphism of the 2-torus with four fixed points. He ‘slows it down’ at the fixed points so these become neutral instead of hyperbolic; the resulting Katok map is non-uniformly hyperbolic but topologically conjugate to the initial automorphism; it has stable and unstable foliations with smooth leaves and is Bernoulli by the Pesin theory. The slow-down is carried out with enough symmetry that the map factors through the branched double covering of the 2-sphere (which is smooth off the four fixed points). Puncturing at the branch point gives a like map on the disk (
$C^\infty $
manifold, possibly with boundary, of dimension greater than 1. The first was written by Katok at the IHESFootnote † [Reference Katok163] and produces Bernoulli diffeomorphisms on surfaces, notably on a disk. This is profoundly astonishing: these are area-preserving diffeomorphisms which, up to a measurable change of ‘coordinates’, are isomorphic to a Bernoulli shift, that is, the probabilistic model of a fair coin toss (with possibly more than two sides). At the core lies the Pesin theory: when obtained from hyperbolicity in the right circumstances, ergodicity implies the Bernoulli property. The ideas are so natural that they cannot be omitted here. Katok starts with a linear hyperbolic automorphism of the 2-torus with four fixed points. He ‘slows it down’ at the fixed points so these become neutral instead of hyperbolic; the resulting Katok map is non-uniformly hyperbolic but topologically conjugate to the initial automorphism; it has stable and unstable foliations with smooth leaves and is Bernoulli by the Pesin theory. The slow-down is carried out with enough symmetry that the map factors through the branched double covering of the 2-sphere (which is smooth off the four fixed points). Puncturing at the branch point gives a like map on the disk (
![]() $C^\infty $
tangent to the identity at the boundary), which in turn can be identified with the complement of the skeleton of the desired surface. Such Katok maps on the torus (usually with only one fixed point for simplicity and under the name ‘the Katok map’, or, more generally, almost Anosov maps, that is, maps that are hyperbolic except for finitely many neutral fixed points) have been of growing independent interest as a proving ground for the theory of non-uniformly hyperbolic dynamical systems because they lie at the very edge of uniform hyperbolicity and so are more tractable in many respects than other non-uniformly hyperbolic dynamical systems [Reference Alves and Leplaideur3, Reference Hu and Young135–Reference Hu, Pesin and Talitskaya139, Reference Pesin, Senti and Zhang262, Reference Veconi291, Reference Wang296, Reference Zhou306].
$C^\infty $
tangent to the identity at the boundary), which in turn can be identified with the complement of the skeleton of the desired surface. Such Katok maps on the torus (usually with only one fixed point for simplicity and under the name ‘the Katok map’, or, more generally, almost Anosov maps, that is, maps that are hyperbolic except for finitely many neutral fixed points) have been of growing independent interest as a proving ground for the theory of non-uniformly hyperbolic dynamical systems because they lie at the very edge of uniform hyperbolicity and so are more tractable in many respects than other non-uniformly hyperbolic dynamical systems [Reference Alves and Leplaideur3, Reference Hu and Young135–Reference Hu, Pesin and Talitskaya139, Reference Pesin, Senti and Zhang262, Reference Veconi291, Reference Wang296, Reference Zhou306].
This first result in turn provided two steps of four in the proof that the same can be done on any manifold: Feldman and Brin each developed a method for inserting this example into a higher-dimensional manifold (Brin’s method being showcased as being of independent interest), and a sophisticated result by Rudolph provided the isomorphism to a Bernoulli shift of the resulting diffeomorphism [Reference Brin, Feldman and Katok44]Footnote ‡.
Also partially written at the IHES, Katok’s most cited paper by far,
Lyapunov exponents, entropy, and periodic orbits for diffeomorphisms [Reference Katok165], produced several celebrated results by combining the shadowing approach of Anosov and Bowen (to whose memory the paper is dedicated—some two months older than Svetlana Katok, he had died just as the Katoks arrived in the US) with the Pesin theory to great effect [Reference Katok and Hasselblatt190, Supplement]. A core idea sounds deceptively simple: an orbit that is Lyapunov-regular in the sense of the Pesin set has enough hyperbolicity to implement the Anosov–Bowen approach. What makes the applications stand out is that they are so simple to state and effective, such as density of periodic points and lower bounds on their number as well as exhaustion of topological entropy by horseshoes. Corollary (4.2): A
![]() $C^{1+\alpha }$
diffeomorphism of a compact manifold with a non-atomic invariant Borel probability measure that has non-zero Lyapunov exponents has positive topological entropy. Bringing in periodic points and an important and entirely new definition of entropy (see [Reference Brin and Katok47] on local entropy, a topological version of the Shannon–McMillan–Breiman Theorem and Katok’s second-most cited paper, as well as [Reference Gurevich117, Reference Katok184, Reference Vershik294]) now produced effective lower bounds on their growth rate and, as Corollary (4.3), the most well-known result of the paper: A
$C^{1+\alpha }$
diffeomorphism of a compact manifold with a non-atomic invariant Borel probability measure that has non-zero Lyapunov exponents has positive topological entropy. Bringing in periodic points and an important and entirely new definition of entropy (see [Reference Brin and Katok47] on local entropy, a topological version of the Shannon–McMillan–Breiman Theorem and Katok’s second-most cited paper, as well as [Reference Gurevich117, Reference Katok184, Reference Vershik294]) now produced effective lower bounds on their growth rate and, as Corollary (4.3), the most well-known result of the paper: A
![]() $C^{1+\alpha }$
diffeomorphism of a compact surface with positive topological entropy contains a horseshoe [Reference Fayad and Zhang92]. He was more proud of this work than anything else and lectured on it in Brazil [Reference Katok168], the 1982 Rufus Bowen Memorial Lectures at BerkeleyFootnote †, as well as at the 1983 International Congress of Mathematicians in Warsaw [Reference Katok173]. Indeed, the latter address announced significant extensions to appear in a forthcoming publication on ‘Lyapunov exponents, entropy, hyperbolic sets, and
$C^{1+\alpha }$
diffeomorphism of a compact surface with positive topological entropy contains a horseshoe [Reference Fayad and Zhang92]. He was more proud of this work than anything else and lectured on it in Brazil [Reference Katok168], the 1982 Rufus Bowen Memorial Lectures at BerkeleyFootnote †, as well as at the 1983 International Congress of Mathematicians in Warsaw [Reference Katok173]. Indeed, the latter address announced significant extensions to appear in a forthcoming publication on ‘Lyapunov exponents, entropy, hyperbolic sets, and
![]() $\epsilon $
-orbits’. That publication did not materialize soon or in the intended form, but the subject remained on Katok’s mind. It appeared in a Caltech topics course during the academic year 1986–1987, which was attended by Leonardo Mendoza. The two of them embarked on the project of a proper self-contained account of this within one of non-uniformly hyperbolic dynamics. Due at least in part to Mendoza’s move to Venezuela and a subsequent career change, this project stalled, but not before Mendoza extracted from it in the early nineties a shorter text, which in part concentrated on the two-dimensional context. I remember that Katok showed this to me at the time and was at a bit of a loss as to what to do with this manuscript. It occurred to me that its size was comparable to that of the chapters of ‘Introduction to the Modern Theory of Dynamical Systems’, which was just nearing completion, and we soon decided to include it as a supplement. Its introduction explains what might have been:
$\epsilon $
-orbits’. That publication did not materialize soon or in the intended form, but the subject remained on Katok’s mind. It appeared in a Caltech topics course during the academic year 1986–1987, which was attended by Leonardo Mendoza. The two of them embarked on the project of a proper self-contained account of this within one of non-uniformly hyperbolic dynamics. Due at least in part to Mendoza’s move to Venezuela and a subsequent career change, this project stalled, but not before Mendoza extracted from it in the early nineties a shorter text, which in part concentrated on the two-dimensional context. I remember that Katok showed this to me at the time and was at a bit of a loss as to what to do with this manuscript. It occurred to me that its size was comparable to that of the chapters of ‘Introduction to the Modern Theory of Dynamical Systems’, which was just nearing completion, and we soon decided to include it as a supplement. Its introduction explains what might have been:
Remarkably, a considerable part of the theory can be developed without constructing the families of stable (contracting) and unstable (expanding) manifolds which are usually presented as the cornerstone of the subject. Instead it is sufficient to use their approximations, admissible manifolds…, which can be constructed in a straightforward fashion.
It is exactly this part of the nonuniformly hyperbolic theory that is treated in the present work. In order to make the presentation lighter, we for the most part restrict the argument to the case of invertible maps of a two-dimensional manifold. Some of the principal applications of the theory…deal with this case anyway.
This work can be viewed as a modest step toward the more ambitious goal of presenting the theory of nonuniformly hyperbolic dynamical systems in its up-to-date form from a unified point of view based on the technical devices of
![]() $\epsilon $
-reduction (see §S.2d), regular neighborhoods, and admissible manifolds. A core of that project is realized in our unpublished and unfinished notes ‘Smooth Ergodic Theory’ which were allowed a limited circulation. These notes contain all the material of the present work in the general case including a complete proof of the multiplicative ergodic theorem. Aside from that there is an extensive treatment of several classes of examples, a much more thorough discussion of regular neighborhoods including volume estimates, a proof of local ergodicity, and some material concerning families of stable and unstable manifolds. At the present moment it is hard to predict the future of this project. We hope, however, to come back to it, maybe within the context of an even broader exposition of smooth ergodic theory.
$\epsilon $
-reduction (see §S.2d), regular neighborhoods, and admissible manifolds. A core of that project is realized in our unpublished and unfinished notes ‘Smooth Ergodic Theory’ which were allowed a limited circulation. These notes contain all the material of the present work in the general case including a complete proof of the multiplicative ergodic theorem. Aside from that there is an extensive treatment of several classes of examples, a much more thorough discussion of regular neighborhoods including volume estimates, a proof of local ergodicity, and some material concerning families of stable and unstable manifolds. At the present moment it is hard to predict the future of this project. We hope, however, to come back to it, maybe within the context of an even broader exposition of smooth ergodic theory.
While no Katok–Mendoza book along these lines ever materialized, these notes, though themselves now apocryphal, became part of the canon nonetheless. They ‘served as the basis for the first draft of Chapters 1–5 and parts of Chapters 6–7’ [Reference Barreira and Pesin27, Foreword] (that is, close to half) of what is now the standard work on the subject. Katok also ‘fully participated in designing the content of the book in its present form’.
From about the time of the Katoks’ move to Maryland, Keith Burns recalls:
My first memory of Tolya is Anthony Manning telling me that I would be interested in things that Katok was doing. For some reason my initial reaction was negative. But pretty soon I was reading Tolya’s papers, in particular the paper about geodesic flows on surfaces, which existed as a short preprint for a good many years before it appeared in a much expanded form. The recollection is amusing in the light of my subsequent career. It goes to show that thesis supervisors usually know more than graduate students.
Here, Katok considered geodesic flows [Reference Katok169, Reference Katok175] and gave effective lower bounds on the growth of the number of closed geodesics on a surface, continuing on to what is now called entropy-rigidity for surfaces. If a Riemannian surface has negative Euler characteristic E and volume V, then
![]() $\sqrt {-2\pi E/V}$
lies between the topological entropy and the Liouville entropy of the geodesic flow, and when equality holds on either side (in particular, when both entropies coincide), the metric has constant curvature. With Ralf Spatzier, Katok went on to compute both entropies for locally symmetric spaces in arbitrary dimension and found that they agree in all cases. The resulting table is followed by the comment that
$\sqrt {-2\pi E/V}$
lies between the topological entropy and the Liouville entropy of the geodesic flow, and when equality holds on either side (in particular, when both entropies coincide), the metric has constant curvature. With Ralf Spatzier, Katok went on to compute both entropies for locally symmetric spaces in arbitrary dimension and found that they agree in all cases. The resulting table is followed by the comment that
It looks like a reasonable conjecture that those are the only cases of manifolds of negative curvature for which the Liouville measure has maximal entropy.
Before long, this understated aside became known as the Katok Entropy-Rigidity ConjectureFootnote †. As Spatzier tells it:
I don’t remember anything about how the conjecture was arrived at—except for wishful thinking or reasons of beauty and symmetry, and then the fact that it works for surfaces (which I had nothing to do with).
Then Tolya asked me to work on this entropy conjecture. Well, I did not make much headway. He teased me many years later off and on that I had not solved my thesis problem.
The conjecture is still open, and rigidity theory more broadly has been active ever since, thanks in no small part to Katok himself. He not only worked on this conjecture himself but put much effort into popularizing it by giving talks, organizing a series of conferences over two decades, and directing the interest of mathematicians towards this conjecture and related ones. Rigidity theory was becoming a veritable industry, and has been going strong since; among the high points with respect to this particular conjecture are an early paper by Flaminio that made progress but also showed up a material challenge [Reference Flaminio103] (hyperbolic manifolds do not maximize Liouville entropy, even locally), the result of Besson, Courtois, and Gallot that the topological entropy of the geodesic flow is minimized only for locally symmetric metrics [Reference Besson, Courtois and Gallot36, Reference Besson, Courtois and Gallot37], and the extensions of Katok’s result to contact and then volume-preserving Anosov 3-flows by Patrick Foulon [Reference Foulon105] and De Simoi, Leguil, Vinhage and Yang [Reference De Simoi, Leguil, Vinhage and Yang283]. Lyapunov-exponent rigidity [Reference Butler60] is closely related, and early on, this program and the rigidity conferencesFootnote † also developed strong interactions with the Zimmer program [Reference Fisher100, Reference Fisher101, Reference Katok177].
True to form, simultaneously with these papers on hyperbolic dynamics, Katok did notable work on both elliptic and parabolic dynamics as well as ergodic theory.
In elliptic dynamics, he worked on variational methods [Reference Bernstein and Katok35] and gave a new proof of Mather’s then-recent theorem about the existence for twist maps of quasiperiodic orbits of all frequencies in an interval [Reference Mather247], which went back to Birkhoff’s original methods. This produced further insights into these Mather sets [Reference Katok171]. (A yet different method had some two years prior to Mather led Aubry to like results [Reference Aubry and Le Daeron19]—with different motivation and terminology—and the invariant Cantor sets have come to be called Aubry–Mather sets.) Katok and Mather thought about a joint paper that would combine their different methods, but this only resulted in unpublished 1982 preprints (More about Birkhoff periodic orbits and Mather sets for twist maps and Continuation of the preprint ‘More about Birkhoff periodic orbits and Mather sets for twist maps’) by Katok. Some of that common perspective is discussed in a proceedings paper [Reference Katok172]; see also [Reference Mather249] and [Reference Katok and Hasselblatt190, Chs 9 and 12].
A study of interval-exchange transformations and polygonal billiards [Reference Katok164] established the absence of mixing: no interval-exchange transformation is mixing with respect to any invariant Borel measure. The same goes for special flows built on these under a function of bounded variation. Therefore, no flow of a rational polygonal billiard is mixing on any level set of the angle function.
Katok continued his quest to understand which phenomena from ergodic theory are realized in smooth dynamics [Reference Katok166]: there are diffeomorphisms with the Kolmogorov property which do not have the Bernoulli property. Even in a purely measure-theoretic context, it is not a simple exercise to find such an example.
The ability to travel internationally and invite visitors to Maryland from all over the world made a real difference in what Katok was now able to do; this can be seen in the acknowledgments in [Reference Katok169, pp. 343–344] and [Reference Katok, Strelcyn, Ledrappier and Przytycki225, p. VIII], as well as the very existence of [Reference Katok and Kifer196]Footnote †. Indeed, Katok loved traveling and collaborationFootnote ‡ and over time, held visiting appointments (of a month or more) at Cambridge University, ETH Zürich, Erwin Schrödinger International Institute for Mathematics and Physics (Vienna), Federal University (Mexico City), Hebrew University (Jerusalem), IHES (Bures-sur-Yvette), Instituto de Matemática Pura e Aplicada (Rio de Janeiro), Independent University of Moscow, Institut Mittag-Leffler (Stockholm), Japan Society for the Promotion of Science (Invitation Fellowship), Mathematical Sciences Research Institute (Berkeley), Mathematical Institute of the Polish Academy of Sciences (Warsaw), Mathematics Research Center of the University of Warwick, Chinese Academy of Sciences Morningside Center of Mathematics (Beijing), National University of Uruguay, Nicolaus Copernicus University (Toruń), SFB ‘Geometrie und Analysis’ (Göttingen), Stanford University, Stefan Banach Center (Polish Academy of Sciences, Warsaw), Tata Institute for Fundamental Research (Bombay), Tsing Hua University (Taiwan), Université de Grenoble I, University of Paris VI, VII, XIII, University of Rome, University of Rome II, Weizmann Institute of Science (Rehovot, Israel), and Yeshiva University.
In the US, Katok was also in a position to build a research group. At Maryland, he found Joseph Auslander, Kenneth Berg, Nelson Markley, Walter Neumann, Daniel Sweet, Scott Wolpert, and James Yorke, and during his time, the department was joined (among many others) by Michael Brin, Daniel Rudolph, and Marlies Gerber, a former student of Feldman’s, who came as an NSF postdoc [Reference Gerber and Katok109]:
I was fortunate to be his first postdoctoral student in the US (1979–81)… . I realized that in the near future he would be surrounded by many students and postdocs, but then he had a lot of time for mathematical discussions with me. We had many lunches together at a dining room in the Union. Svetlana would sit a few tables away with her thesis advisor, Don Zagier. One thing that never changed is that Tolya always made time for me when I needed to talk to him about mathematics or for career advice. ‘Too busy’ was not part of his vocabulary, even when he was obviously very busy running a conference or in the midst of a collaboration with someone else. He would come in early before the conference, or stay late in the afternoon, or find time during an excursion, whatever was needed.
Katok also immediately took on doctoral students, E. A. Robinson [Reference Arthur Robinson274] and Charles Toll Footnote ¶ being the first (plus, for a time, Chris Hall), as well as Ralf Spatzier (whose advisor of record was Caroline Series at the University of Warwick). Collectively, Changguang Dong, Alena Erchenko, David Hughes, and Daren Wei, who were Katok’s students in 2018, expressed some of their memories:
Professor Anatole Katok had many graduate students and very much enjoyed training the next generation of mathematicians. Even though he had serious health problems, Professor Katok continued to work with students including his four current graduate students.
Professor Anatole Katok was a wonderful advisor who cared about his students and was ready to spend a lot of time with them in ways ranging from holding weekly seminars for new graduate students interested in dynamics to accompanying his student on a hospital visit in case of serious health problems. The doors of his house were always open for his students either for mathematical discussions or getting together for a barbecue. Moreover, everybody knows about the famous working seminar in dynamics at Penn State which was organized by Professor Katok and was a great opportunity for his students to learn the field. During the seminar, he always freely interrupted the speaker either to ask a question or to make a comment with the purpose of clarifying the material for students and explaining the history of the topic at hand.
It seems that Professor Anatole Katok knew everything and was a ‘walking library’. If you look at the topics that his students work on, you will see how spread out these topics are in the large field of dynamical systems. Professor Katok’s vast knowledge and intuition in a variety of topics was astounding. Professor Katok taught his students to work independently, stand up for their ideas, and feel free to ask any questions, however naïve.
As case studies of supporting his students well past their doctorate, one can consider the biographies of Michael Brin and Yakov Pesin, and the ways in which Katok played an instrumental role in their lives [Reference Brin and Pesin51, Reference Katok186] while and after they got their doctorates (see page 19). When Brin and Pesin graduated from the university in 1970, they were not even recommended to the graduate program called ‘aspirantura’ because of the new political headwinds. Brin got a junior position at the economics research institute of Gosplan, considered a good job. He could have made a career there, including a PhD in economics. Unlike at CEMI, this was a real economics job, though, and Brin did not greatly enjoy it [Reference Katok186, p. 13]Footnote †. So he asked Katok a couple of years in, whether if he went into mathematics, there would a place and a job for him. Katok said yes—something one might consider almost foolhardy in the circumstances:
Sometimes my actions verged on irresponsibility… . In retrospect it is clear that my fortunate circumstances engendered a not fully justified optimism which influenced Brin and Pesin whose circumstances were quite a bit less favorable. A more objective hard-headed view would probably have discouraged them and terminated their mathematical careers… . While Brin and Pesin produced their work under difficult and unfortunate conditions, they at least were fortunate with its publication…having their outstanding work appear in a premier journal. [Reference Katok186, pp. 7, 13–15]
While this ‘saved’ Brin for mathematics, it did not provide a mathematics job in Moscow after the dissertation defense. In 1978, Katok arranged an official invitation for the Brins from fictitious relatives in Israel, which they received that summer, and which was required for permission to emigrate. They used this invitation to apply for permission to emigrate to Israel in September 1978, and Brin was fired within a month. He recalls eking out a living with odd jobs, such as translating works by Boris Rosenfeld into English, until they left for Vienna in June 1979, from where he took up an invitation to the IHES arranged by Katok. This helped the visibility of Brin’s work and resulted in a collaboration with Gromov Footnote † [Reference Brin and Gromov45]. Katok furthermore utilized the upcoming special year in Maryland to get Brin hired there on a visiting (later permanent) positionFootnote ‡. Indeed, when Katok
took up a position at the University of Maryland he obtained lots of grants for young mathematicians to spend years at Maryland, on leave from their universities, and they benefitted from his tuition and guidance. Several of them have become outstanding research mathematicians. [Peter Walters]
Brin had never before held an academic appointment or taught, and he remembers Katok’s mentoring in these new ventures.
Like many others, the Pesins were less fortunate and did not receive permission to emigrate before the doors slammed shut for a decade as the war in Afghanistan started in 1980—and Pesin was stuck in a job even less desirable than Brin’s (at the Industrial Institute of Optical and Physical Measurements; meanwhile, Natasha, Brin’s wife, was a senior editor in the division of mathematics at the ‘Education’ Publishing House). Joel Lebowitz invited Pesin to visit in 1988 (knowing full well that the Soviet authorities would typically deny travel permits for conferences ‘because there is not enough lead time’, he had made it an open invitation, and thanks to this and glasnost, Pesin was actually allowed to go). In what sounds like a trope from crime fiction, the IHES allowed guests one free call outside Paris, and Pesin used this to call Brin in Maryland—they had not talked for a decadeFootnote §. Pesin spoke of wanting to emigrate, and Brin said he should send a CV. Pesin sent whatever he thought that meant, and between them, Brin and Katok made it usable and sent it to Bob Zimmer, then chair of mathematics at the University of Chicago. When the Pesins had received permission to emigrate and started preparations, the University of Chicago called to say that Pesin had a (temporary) job there starting January 1, 1990, and asked when they were going to arrive. They had no idea but in the end made it there by January 23, finding a month’s salary waiting for them, and support from the Zimmers well beyond the call of duty. Along the way, Pesin had been invited to talk in Karl Sigmund’s seminar in Vienna (whom Brin or Katok had contacted), where he also met Josef Hofbauer and Mitchell Feigenbaum; Sigmund’s financial support made them ‘wealthy’ enough to even support some indigent emigrants in turn. Then Laura Tedeschini-Lalli called from Rome (at the instigation of Brin) with an offer of a two-month appointment—and it turned out that they spent three.
From Chicago, the Pesins visited the Katoks (and Caltech) in February—at the very time Katok was negotiating with Pennsylvania State University, and by early March there was an offer for Pesin of a permanent position at Penn State. Since several other institutions were thinking about making him an offer, he consulted with Brin, who told him to go to Penn State: ‘Tolya will be there, and he’ll organize everything, and you can just keep doing mathematics’. So it was, and now Pesin directs the Anatole Katok Center for Dynamical Systems and Geometry.
Academic appointments in the US offered entirely new outlets for Katok’s legendary organizational and collaborative energies. While he always maintained intense seminar activities, upon his arrival in the US, he immediately set about organizing special years such as 1979–1980 at Maryland [Reference Katok167, Reference Katok170], which contributed to cementing early on his reputation in the West as having boundless energy, and 1983–1984 at the Mathematical Sciences Research Institute (MSRI)Footnote †. Later he organized special semesters at the Banach Mathematical Center in Warsaw 1995 and at the Newton Institute in Cambridge 2000, as well as a well-remembered 3-week AMS Summer Institute on Smooth Ergodic Theory in Seattle 1999. (Several of these events produced substantial proceedings volumes.) He was able to travel extensively, and rare was the year in which he did not visit multiple continents.
3.2. Ergodic Theory and Dynamical Systems
Among the early trips were visits to Warwick in 1979 and 1980, and he and William Parry there noted that while dynamics as a research discipline had very much come into its own in the past decade, research publications by dynamicists in the West were scattered across a variety of journals unlike in the Soviet Union, where the important papers could be found among a few journals of record. They saw the need for a unifying voice in this vigorous emerging field, and
Tolya was one of the people who pushed for the founding of the journal Ergodic Theory and Dynamical Systems. In the late 1970s he and Bill Parry convinced David Tranah, the Cambridge University Press Mathematics Editor at the time, that it was important to start a journal specialising in these fields, and the first issue appeared in 1981 based at the University of Warwick with Klaus Schmidt and Peter Walters as managing editors and Tolya and Michel Herman as the other two executive editors. He was very enthusiastic about the project and was always looking for ways to make the journal more useful for graduate students and recent PhDs, such as having invited survey articles on certain topics. The journal is still going strong 37 years later. [Peter Walters]
The way Katok recalls it,
I believe that idea of starting a journal dedicated to the growing field of dynamical systems came independently to Bill Parry and to me; in my case the influence of those impressions in the late 1970s was essential.
Let me explain my motivation. I realized how different the publication scene in the free world was compared to the Soviet one. In the Soviet Union there were no more than half a dozen serious journals and the group of people who controlled publication in those through editorships, recommendations and refereeing, was quite small. During the Golden Age of the 1960s and 70s the overall quality of at least three or four leading journals was quite high, despite in-fighting of various cliques, discrimination of Jews and other attendant factors. And the field of dynamical systems was already…represented in those leading journals: Uspehi, Doklady, Izvestija, Sbornik and then-new Funkctionalnyj Analiz.
In the West the scene was much greater in volume and much more diffuse. Interesting papers in dynamics kept appearing in a variety of journals, both general and more specialized. It looked natural to try to create a journal dedicated mostly to the field that [had] progressed greatly in the previous decade or so.
My early exchanges with Bill Parry related to the subject took place during my visits to Warwick in 1979 and 1980. According to recollections of Peter Walters and others, several crucial developments took place at the London Mathematical Society Symposium on Ergodic Theory in Durham in the summer of 1980. That was quite a remarkable gathering that certainly influenced the scene in dynamics for a number of years to come. I presume (although I do not remember the specifics) that it was there that Michel Herman became involved in the discussions and was brought on board as one of the founding editors.
Projected enterprise took shape quickly and pretty painlessly…and…it transpired that Cambridge University Press on the initiative of the indomitable David Tranah was interested in setting up the journal and anchoring it at WarwickFootnote †.
Katok published far more papers in Ergodic Theory and Dynamical Systems than in any other journal, and he maintained his association throughout: Executive Editor 1981–1987, Editorial Board 1988–1993, Survey Editor 1994–2011, Editor 1997–2011, Editorial Board from 2011Footnote ‡.
A quarter-century on, he did it again and started the Journal of Modern Dynamics with a view to being a highly selective dynamics journal with a broad focus and a democratic editorial boardFootnote †. Giovanni Forni succeeded him as editor-in-chief:
He founded the journal with a different model in mind compared to most other journals. The editors are all on equal footing and recommend papers, or can challenge a recommendation by another editor. Tolya reminded editors to keep high standards and sometimes challenged recommendations of papers which he thought were not good enough for the journal. As far as I know, he was the only editor to do so. In this role he was clearly well served by his encyclopedic knowledge of the field, and while of course he had his personal preferences, he was definitely not dogmatic, and was always open to discussion, which he encouraged.
Tolya taught me a way of thinking about my own work and to put it in a broader perspective. By asking me to be part of several of his initiatives, he allowed me to contribute to mathematics and to our research community much beyond my own means. Although he was not my advisor or official mentor I consider him in many ways as my mathematical father.
3.3. California
Svetlana obtained her doctorate from the University of Maryland in 1983 (with Don Zagier [Reference Katok228–Reference Katok230]), whereupon the Katoks departed for a year in Berkeley, where Svetlana was a lecturer at UC, while Anatole was at MSRIFootnote ‡ as one of the organizers of a special year at MSRI; in 1990, he described its import as follows.
The year-long program during the second year of MSRI (still operating in its temporary quarters on campus) was the central event of the early eighties for several rapidly growing and changing fields… . It is fair to say that by the time of the MSRI program most of those theories had already achieved a measure of conceptual understanding of principal structural components involved and the stage was being prepared for two new developments which became the dominant themes of dynamics in the eighties, namely extensive use of new general methods and paradigms in the study of various more or less concrete classes of dynamical systems and much more extensive interaction than before between various branches of dynamics on one hand and between dynamics and other mathematical disciplines on the other. The MSRI program in Ergodic theory and Dynamical systems played a very large role in both stimulating and accelerating those trends where they had already been present and in initiating new onesFootnote §. [Reference Katok177]
Indeed, the first of the dozens of aforementioned rigidity conferences occurred as part of this special year. It
marked the beginning of the coherent development of a new synthetic field, which incorporates ideas and methods from Lie groups, symmetric spaces, theory of group representations, ergodic theory, smooth dynamical systems, and differential geometry. In particular, the workshop included four problem sessions, dedicated to different aspects of the emerging subject. Two of those sessions resulted in extended problem lists: one on manifolds with non-positive curvature and related geometric and dynamical topics prepared by Burns and myself with substantial contributions from Ballmann, Brin, Eberlein and Osserman and another on rigidity of group actions and cocycles prepared by Hurder. Those lists which were published in the Ergodic Theory and Dynamical Systems journal in 1985 contained not only problems but also motivations, background and in some cases even possible strategies for solution. Those lists turned out to be very influential in focusing research efforts by a number of mathematicians who previously worked in different areas. [Reference Katok177]
The need of the Katoks for two jobs in one region was no secret, and Barry Simon initiated an offer of a professorship for Anatole from Caltech, where they moved in 1984, with Svetlana having a 2-year adjunct position at UCLA (presumably engineered by W. A. J. Luxemburg, then chair at Caltech). For their first time, they did not live in a capital city.
Now 40, Anatole settled into this position, while over time, Svetlana held positions at more than half of the University of California campusesFootnote †. From this move onward, Katok maintained a continuous stream, if not torrent, of doctoral students, 44 in the course of 45 years (four in the Soviet Union, three in Maryland, seven at Caltech, the rest at Pennsylvania State University)Footnote ‡. For most of us, this afforded a communal experience not entirely unlike what the Moscow seminars must have been like, and this was not only due to the multiplicity of doctoral students at any one time but also Katok’s ability to further build a research group by hiring postdocs and faculty, inviting visitors, and drawing on interactions with related disciplines.
A few recollections from my early career may illustrate this. Having come to the University of Maryland as a physics student on a Fulbright scholarship, I happened to live literally around the corner from Laura Tedeschini-Lalli, then a student of Jim Yorke’s, who told me that ‘someone called Katok’ was going to give a course on classical mechanics in the Spring of 1983. That semester, I decided to become a mathematics doctoral student at Maryland, and in the year 1983–1984, took first-year courses plus dynamical systems from Michael Brin and ergodic theory from Dan Rudolph. In April of 1984, I got a letter from the other coast (email would only become widely available later). Katok wrote from MSRI (then at 2223 Fulton Street) that he was moving to Caltech and I was invited to join him there. He cautioned that this much smaller department might feel different from Maryland, because
there are no large groups working in particular areas. The number of seminars is smaller. The visitors program is very active. If you come, your contacts in the area of dynamical systems will be with me and with visitors… . There is also a chance that in 1985 one or two postdoctoral fellows working in the field will be hired… . I hope that when I come, more students will become interested in the area.
When I started there, Mark Muldoon [Reference Muldoon257], who had intended to be a student of Barry Simon’s, also began to work with Katok, and soon after, so did Renato Feres [Reference Feres93], who arrived in 1985 from São Paolo. Before long, the number of doctoral students in dynamics rose, and Caltech saw a steady stream of high-caliber seminar speakers and medium-term visitors from around the globe, such as Shmuel Friedland (Visiting Associate 1984), Jean Bourgain (Visiting Associate 1985–1986), Carlos Gutierrez (Visiting Associate 1985–1986), Gerhard Knieper (Bateman Instructor 1985–1987), Howard Weiss (Chaim Weizmann Research Fellow 1986–1989, NSFpostdoc 1989–1990), Hillel Furstenberg (Sherman Fairchild Distinguished Scholar 1986–1987), Jane Hawkins (Visiting Assistant Professor 1986–1987), Leonardo Mendoza-D’Paola (Visiting Associate 1986–1987), Livio Flaminio (Bateman Instructor 1987–1989), David Ruelle (Sherman Fairchild Distinguished Scholar 1987–1988), Endre Szemerédi (Sherman Fairchild Distinguished Scholar 1987–1988), Ursula Hamenstädt (Assistant Professor 1988–1990), Masahiko Kanai (Bateman Instructor 1988–1989), James Lewis (Bateman Instructor 1989–1990), Peter Sarnak (Sherman Fairchild Distinguished Scholar 1990), Mark Pollicott (Associate Professor 1990), among othersFootnote †, plus an active working seminar and almost annual courses on dynamics by Katok, never twice the same. This included some conferences organized at Caltech, of one of which I have a rather unusual memory. On one morning of the third rigidity conference (titled Dynamical Systems Workshop) in March 1988, I sauntered into the department just in time to hear the first talk, when Katok approached me and told me that the speaker had not shown up. ‘Can you talk about your result?’ he asked. I have since consistently had more than five minutes notice when invited to speak. But I had already given seminar talks about the same subject, and this was a first opportunity for me to present it publicly, as well as a good exercise towards developing a central life skill for an academic: to appear to be prepared. I was also given support for conference travel every year (Oberwolfach 1985, Warwick 1986, Maryland 1987, Durham (UK) 1988, Phoenix 1989, Boulder 1989, Oberwolfach 1989), and for several summers in Göttingen.
From the Caltech days, a few larger mathematics projects are worth singling out. With Knieper, Pollicott, and H. Weiss, Katok carefully studied the dependence of entropy on perturbations of Anosov flows [Reference Katok, Knieper, Pollicott and Weiss197–Reference Katok, Knieper and Weiss199], and with Hurder he deeply connected dynamics with foliation theory [Reference Hurder and Katok140–Reference Hurder and Katok142]. Their study of the Godbillon–Vey class became seminal in an initially unintended direction: it necessitated a more careful study of the (transverse) regularity of the invariant foliations of an Anosov 3-flow, which led to another rigidity conjecture: that an Anosov flow is smoothly conjugate to an algebraic one if these invariant foliations are transversely
![]() $C^2$
. In Japan, Kanai then almost immediately made a key construction (the Bott–Kanai connection) that enabled him to prove the first such result for geodesic flows on manifolds of dimension greater than two [Reference Kanai150]. He then came to Caltech as a Bateman Instructor.
$C^2$
. In Japan, Kanai then almost immediately made a key construction (the Bott–Kanai connection) that enabled him to prove the first such result for geodesic flows on manifolds of dimension greater than two [Reference Kanai150]. He then came to Caltech as a Bateman Instructor.
The [March] 1988 Caltech conference was particularly important for the development of the geometric rigidity program which crystallized at MSRI. Masahiko Kanai and Ursula Hamenstädt presented their landmark works on the rigidity of optimal pinching and on geodesic flows with smooth horosheric foliations respectively. Those presentations as well as discussions during the conference stimulated a number of young mathematicians including several students to get involved in the subject. Some of the fruits were apparent at the Colorado conference next year where in particular an extensive progress in the study of geodesic flows and Anosov system with smooth foliations was reported. This conference was remarkable by the number of very young invited speakers, five of them graduating PhDs (Feres, Grzegorczyk, Hasselblatt, Iozzi, Lewis) and about as many within three years of their dissertations. [Reference Katok177]
Katok and Feres began to build on Kanai’s insights and embarked on the chase of the comprehensive such result [Reference Feres94–Reference Feres and Katok96] (see also [Reference Flaminio and Katok104]). And a chase it was: they were aware that in Paris, Patrick Foulon and François Labourie, soon joined by Yves Benoist, were onto the same target. The Feres–Katok strategy was to buttress Kanai’s line of argument with ever more sophisticated dynamical refinements to progressively weaken the needed curvature-pinching hypothesis. Some of this work took place during a summer in Göttingen (with Manfred Denker as host), and I remember the exhilaration of progress as well as the competitive spiritFootnote †. In the end, Benoist, Foulon and Labourie got there first. While it was a consolation that the French team had gotten there using a ‘big hammer’, the open-dense orbit theorem of Gromov, they had also far exceeded the target by treating contact Anosov flows, that is, they obtained rigidity without assuming even the topological structure of a geodesic flow in the first place [Reference Benoist, Foulon and Labourie32–Reference Benoist and Labourie34]Footnote ‡.
The Anosov cocycle and smooth rigidity theory, as well as the later higher-rank rigidity program also motivated normal-forms theory as a through-line [Reference Delatte76, Reference Guysinsky120].
Only after the Caltech days did a project end that had languished as a 1988 preprint [Reference Katok179], in which Katok produced general criteria for ergodicity and the Bernoulli property for volume-preserving diffeormorphisms and flows by ‘prepending’ the Pesin theory with a suitably general version of Wojtkowski’s method of eventually strictly invariant cone families [Reference Wojtkowski299] and then appending the conclusions of the Pesin theory with a uniformity criterion for the cone families that ensures enough stretching of invariant manifolds to go beyond open ergodic components and achieve ergodicity and indeed the Bernoulli property. (These criteria imply, for instance, that every ergodic component with non-zero Lyapunov exponents of a contact flow is Bernoulli and that every compact 3-dimensional manifold has a smooth Riemannian metric whose geodesic flow is Bernoulli.) Keith Burns visited Katok at the IHES for a week in 1991 to get this preprint into publishable form:
Marlies Gerber and I… worked on the paper about product manifolds [Reference Burns and Gerber56]. In that paper the Bernoulli property was no longer just an interesting improvement on ergodicity. Instead it played an essential role in our inductive argument. We were both uncomfortable with the idea of a central part of the argument being based on a never-to-be-published preprint, so I offered to visit Tolya and do whatever was necessary to get it ready for publication. It worked. I stayed in Tolya’s house at IHES. He pretty much laid out what we needed to say. I worked on writing, and we got it done in a week.
Of course, the two had already collaborated in a somewhat similar way during the 1984 MSRI semester (with substantial contributions from Ballmann, Brin, Eberlein, and Osserman).
The two main things I did at MSRI were working on higher rank in nonpositive curvature with Ralf Spatzier [Reference Burns and Spatzier58, Reference Burns and Spatzier59] and writing the list of problems about manifolds with nonpositive curvature that appeared in Ergodic Theory and Dynamical Systems [Reference Burns and Katok57]. This grew out of a problem session held at a conference probably in May 1984. I was designated note taker and wrote furiously for about two to three hours during the session. The rough notes and written submissions from a number of people were worked into the final text. I did a good deal of the grunt work, but the list in the form in which it appeared was hugely influenced by Tolya’s taste and knowledge.
Ursula Hamenstädt (I think) and Tom Farrell (definitely) have told me that they were made aware of problems by that list. In the paper we explained why the space of negatively curved metrics on a surface is connected and asked if the same were true in higher dimensions. Farrell [Reference Farrell and Ontaneda86] showed that the answer is definitely no. In high enough dimensions there are uncountably components to the space. The paper did not conjecture that the space was connected, but I think that’s the answer we were hoping forFootnote †.
Billiards, by the way, continued to be Katok’s ‘playground’ [Reference Katok183] in a broad way. He studied polygonal billiards further, both alone [Reference Katok174] and with Eugene Gutkin, who was then at the University of Southern California [Reference Gutkin and Katok118], a collaboration that was to be followed up years later with remarkable joint work on convex billiards [Reference Gutkin and Katok119] that implemented some ‘reverse KAM theory’ as follows. KAM theory implies that a strictly convex billiard has (many) caustics near the boundary [Reference Lazutkin242], but Mather showed that there are no such invariant circles if the curvature of the boundary vanishes at any point [Reference Mather248]. This paper quantifies that result to show ‘that if the minimal curvature of the billiard table (appropriately normalized) is sufficiently small, then the convex caustics are located only near the boundary of the table. In particular, we estimate from below the area… which is free of convex caustics… . To interpret our results, let us consider the following ‘mental experiment’.… Suppose that… the minimal curvature of [the table] is gradually decreasing to zero, while the global shape of the table remains essentially unchanged. Then… the convex caustics are gradually pushed out to the boundary’. The paper contains corresponding results for outer billiards as wellFootnote †, and in this case they establish that if there is a point with small radius of curvature, then an annulus surrounds the table that is free of caustics (there will be plenty near the table and others near infinity); the largest such annulus is a Birkhoff region of instability bounded by ‘the last outer caustics of their kind’. This paper further produces interesting examples of caustics, notably, non-convex ones, a significantly more challenging subject.
4. The Center of Pennsylvania
‘Moscow, Vienna, Rome, Paris, Washington, Los Angeles—State College???’ was a refrain briefly heard among dynamicists in 1990. The previous metropolitan biography of the Katoks made their next move a little implausible.
Due to the scale of Caltech’s mathematics department, it was challenging to build and maintain a large research group, and Svetlana’s position at UC Santa Cruz was too far from home (well over 5 hours driving) for a family with a young child. Once again, the need of the Katoks for two jobs in one region was no secret. Santa Cruz made an offer to Anatole, and the University of Arizona extended offers to them both, but they did not accept either. Then Richard Herman Footnote ‡, the department chair at the Pennsylvania State University, engineered a quadruple offer for the Katoks, Pesin, and H. Weiss.
It was very much in Richard Herman’s style to hire several people in the same area and to create a new area of strength in the department. [Svetlana Katok]
Indeed, Herman was ambitious for the department to expand its base of excellence and was fortunate enough to garner the support of the best colleagues in the department and therefore of critical administrators. And:
The second part of my philosophy was ‘opportunistic’. I looked for special situations… Ȯf course I knew of [the Katoks] and heard about their physically disparate situation (from Howie Weiss, I believe who had interviewed). I also had deep connections to Maryland (where I was a graduate student and became a dean after Penn State). I spent some time talking to the President, Brit Kirwan, about the Katoks… . I felt that I could create a circumstance for Tolya and Sveta and proceeded to invite them both… . I believe I made them offers before they left and Tolya immediately raised the issue of Howie Weiss [and] the dean supported Howie’s appointment financially… . Needless to say, I was very pleased, and we closed the deal… the Katoks stayed and with Pesin (yes, Tolya brought him up) who came next, made Penn State one of ‘the’ places in dynamical systems. [Richard Herman]
Lest the conditions of the appointments were not sufficient to reel in the Katoks, the department undertook to vigorously ‘sell’ its location:
I did not know Tolya at that time, but checked with folks I did know and was immediately convinced that this would be a very good move for the Penn State mathematics department. So George Andrews, Richard, me and a couple of others worked hard to paint an attractive picture of State College as a place to live. [Jerry Bona]
While dynamicists initially had doubts about how long the Katoks would last at Penn State, they never left (but also spent nary a summer there). And they fully engaged from the start, helped by the simultaneous arrival of Pesin and H. Weiss. They went on to build the department into the most prominent center of dynamical systems in the country. Mathematically as well, one might call this a new period.
In addition to the aforementioned seminal rigidity work, Katok became engaged with the Zimmer program [Reference Fisher100, Reference Katok and Lewis203, Reference Katok, Lewis and Zimmer204, Reference Zimmer307], the core conjectures of which were just yielding at the end of his lifetime [Reference Brown53–Reference Brown, Fisher and Hurtado55, Reference Fisher101]. He heartily jumped in together with others. From Katok’s arrival at Pennsylvania State University, Viorel Niţică recalls:
I was among Tolya’s first PhD students at Penn State. I remember very well the first Dynamical Systems seminar that he organized there. The goal of the seminar was to carry us over the ‘super-mathematics’ of the day, Margulis–Zimmer superrigidity, as presented in Robert Zimmer’s famous book. The rigidity seminar ran during Tolya’s first two years at Penn State and then slowly morphed into a more general Dynamical Systems seminar. Rigidity still remained a cornerstone for years to come.
At our first meeting the room was packed with about 20 people, quite unusual for a topic of such depth. The topic required expertise in ergodic theory, functional analysis, Lie groups and algebras and their representations, unitary representations of groups, algebraic groups and algebraic geometry.
Tolya kept the participants together, and encouraged everyone to participate. It was his first year at Penn State and he worked very hard to bring people to rigidity theory and to build a research school. Nevertheless, in his quite frank manner he told us that not all the participants were going to write papers in this field. I think he was pleasantly surprised, years later, when he saw that most of the participants actually wrote papers in rigidity theory, and that many of them defended PhD theses under his supervision. Among the people in the room were Cheng-Bo Yue [Reference Yue302], Nantian Qian [Reference Qian272], Mirko Degli Esposti [Reference Degli-Esposti75], Alexey Kononenko [Reference Kononenko237], Sergey Ferleger [Reference Ferleger98], Viorel Niţică [Reference Nitica259], Andrew Török [Reference Török290], and other more senior mathematicians.
Indeed, several of these students were to work on lattice actions, and after the initial papers with Lewis [Reference Katok and Lewis203, Reference Katok, Lewis and Zimmer204], Katok himself returned to the subject in a collaboration with Federico Rodriguez Hertz [Reference Katok and Hertz211]. But his focus was on the program on rigidity of actions of higher-rank abelian groups, that is, to show that faithful actions of
![]() $\mathbb R^k$
or
$\mathbb R^k$
or
![]() $\mathbb Z^k$
are standard. Local rigidity is a like statement for actions close to the standard one [Reference Katok and Spatzier221, Corollary 5]. This is among Katok’s most impressive contribution to dynamics in terms of number of research papers, and he carried this out in large part with (former) students, such as Spatzier [Reference Katok and Spatzier217–Reference Katok and Spatzier222], Damjanović [Reference Damjanović68, Reference Damjanović and Katok9–Reference Damjanović and Katok74], Kalinin [Reference Kalinin143–Reference Kalinin, Katok and Hertz149], Niţică [Reference Katok and Niţică205–Reference Katok, Niţică and Török207, Reference Nitica259], Török [Reference Katok, Niţică and Török207, Reference Török290], Kononenko [Reference Katok and Kononenko200, Reference Kononenko237], and Guysinsky [Reference Guysinsky and Katok122, Reference Guysinsky120], as well as with Svetlana Katok [Reference Katok and Katok192, Reference Katok and Katok193, Reference Katok, Katok and Schmidt196] and Klaus Schmidt [Reference Katok, Katok and Schmidt195, Reference Katok and Schmidt215], and solo [Reference Katok180]. This latter paper is somewhat seminal for the measure rigidity of abelian actions. It also happens to have the distinction of representing his last solo research project—with this 1996 exception, his arrival at Pennsylvania State University marks a shift from a previous average of more than one solo research paper per year to research being exclusively done in collaborations. (The other single-author items after 1990 are three historical/biographical articles [Reference Katok184, Reference Katok186, Reference Katok187]Footnote † and the ‘playground’ survey [Reference Katok183], while [Reference Katok178, Reference Katok179] were originally Caltech preprints and the monograph on ergodic theory [Reference Katok181, Reference Katok182] was mostly written in 1982–1983—I remember seeing a camera-ready typewritten version in the early Caltech days).
$\mathbb Z^k$
are standard. Local rigidity is a like statement for actions close to the standard one [Reference Katok and Spatzier221, Corollary 5]. This is among Katok’s most impressive contribution to dynamics in terms of number of research papers, and he carried this out in large part with (former) students, such as Spatzier [Reference Katok and Spatzier217–Reference Katok and Spatzier222], Damjanović [Reference Damjanović68, Reference Damjanović and Katok9–Reference Damjanović and Katok74], Kalinin [Reference Kalinin143–Reference Kalinin, Katok and Hertz149], Niţică [Reference Katok and Niţică205–Reference Katok, Niţică and Török207, Reference Nitica259], Török [Reference Katok, Niţică and Török207, Reference Török290], Kononenko [Reference Katok and Kononenko200, Reference Kononenko237], and Guysinsky [Reference Guysinsky and Katok122, Reference Guysinsky120], as well as with Svetlana Katok [Reference Katok and Katok192, Reference Katok and Katok193, Reference Katok, Katok and Schmidt196] and Klaus Schmidt [Reference Katok, Katok and Schmidt195, Reference Katok and Schmidt215], and solo [Reference Katok180]. This latter paper is somewhat seminal for the measure rigidity of abelian actions. It also happens to have the distinction of representing his last solo research project—with this 1996 exception, his arrival at Pennsylvania State University marks a shift from a previous average of more than one solo research paper per year to research being exclusively done in collaborations. (The other single-author items after 1990 are three historical/biographical articles [Reference Katok184, Reference Katok186, Reference Katok187]Footnote † and the ‘playground’ survey [Reference Katok183], while [Reference Katok178, Reference Katok179] were originally Caltech preprints and the monograph on ergodic theory [Reference Katok181, Reference Katok182] was mostly written in 1982–1983—I remember seeing a camera-ready typewritten version in the early Caltech days).
He also hired and prolifically collaborated with Manfred Einsiedler Footnote ‡ [Reference Einsiedler and Katok81, Reference Einsiedler and Katok82] and Federico Rodriguez Hertz Footnote § [Reference Kalinin, Katok and Hertz147–Reference Kalinin, Katok and Hertz149, Reference Katok, Katok and Hertz194, Reference Katok and Hertz209–Reference Katok and Hertz213], mostly on rigidity questions.
As to the motivation for studying abelian actions,
higher-rank lattice actions certainly motivated his work, but to my understanding he thought of abelian actions as a more important (broader) subject. Moreover, he was interested in dynamics. He wanted to understand dynamics of a lot of different sources, from abstract ergodic theory to homogeneous dynamics, anything having to do with dynamics, and the study of abelian actions was one important place where all type of dynamics will show up and could be understood. The fact that this could later be applied to higher-rank semisimple group actions (e.g., the Zimmer program) or that it could be applied to number theory (e.g., the Littlewood Conjecture) was thought of as a great side effect that only enhanced the interest of the study of abelian action. So, abelian actions were studied for their intrinsic interest and not for their applications. [Federico Rodriguez Hertz]
The collaboration with Einsiedler acquired a new direction together with Lindenstrauss by addressing the Littlewood Conjecture [Reference Einsiedler, Katok and Lindenstrauss83, Reference Venkatesh292], which had been seen to be amenable to dynamical methods. Lindenstrauss went on to win a Fields medal. With Thouvenot, Katok studied slow entropy [Reference Katok and Thouvenot226], and in his latter years, the work with Alena Erchenko initiated a ‘flexibility’ program quite complementary to rigidity: to show that in many volume-preserving systems, the volume entropy can be quite far from the topological entropy [Reference Alsedà, Misiurewicz and Pérez2, Reference Barthelmé and Erchenko28, Reference Erchenko84, Reference Erchenko and Katok85] or, more generally, that dynamical invariants can take arbitrary values subject only to natural restrictions.
Mainly during the Penn State years, Katok also engaged in significant biographical and historical writing [Reference Anosov12, Reference Hasselblatt and Katok129, Reference Katok176, Reference Katok184, Reference Katok186, Reference Katok187, Reference Katok and Katok191]Footnote †. While he described this collectively as ‘a personal view’, these articles make him in particular an important chronicler of Moscow mathematics in the 1960s and 1970s, not only because of the richness and sharpness of his recollections but also because of the historical, political, and sociological perspectives he was able to bring to bear on the subject. Although the occasion for several of them engendered a primarily biographical focus [Reference Anosov12, Reference Hasselblatt and Katok129, Reference Katok176, Reference Katok186, Reference Katok187], those on Anosov [Reference Katok187] and on the Moscow seminars and the early careers of Brin and Pesin [Reference Katok186] (see also [Reference Brin and Pesin51]) give an unrivaled perspective of the Moscow dynamics community in this period and the national and global context in which it existed. These insights also informed the article the Katoks wrote on women in mathematics [Reference Katok and Katok191] whose focus was sociological. There were also numerous occasions that called for lectures of his on some history, and some otherwise unpublished writings related to these are available from his web page and will be included in his collected works.
4.1. Mentoring and collaboration
Throughout, Katok vigorously recruited students, and the vast majority of his doctoral students graduated from Pennsylvania State University. Andrey Gogolev [Reference Gogolyev111] is still amused by how their formal relationship began:
I set up an appointment with him at his Whitmore office…Footnote ‡. I was there early, sitting on some kind of bench by his office door. He was running late, it was raining. Finally, he showed up with a wet umbrella, looked at me, walked into his office and shut the door. I was fairly certain that he did recognize me and decided that he probably needed some time to deal with the umbrella etc. After about five minutes I knocked. He told me right away that he is actually writing me an email about me being late and then gave me a mini-lecture about the importance of punctuality.
David Hughes recalls how such a first conversation might then go.
When I first met Prof. Katok to discuss my thesis research he described what he expected and where he thought the research would go. As he described certain things that may be true, he mentioned one probable theorem with the caveat that ‘this is a theorem for the twenty-second century’. I do not think he was joking either, at least not totally. In this sense his attitude was both practical and romantic. Many mathematicians are good researchers, but have difficulty understanding and managing people, or sometimes vice versa. He was outstanding at both, provided people could handle his honesty.
This clearly lays out one way in which Katok’s approach diverged from the prevailing practice in Moscow that left students largely to their own devices when seeking a dissertation problem and an approach to it; he was always ready to suggest problems in which he thought a student might be interested, multiple ones if need be, and had a sense of what the outcome would be and what approaches might work. I believe he told me more than once that when a student was working a problem he had suggested, faith (and perseverance) were all that was going to be required. He was invariably generous with his time—I remember only one single occurrence when I came to his office unannounced and he did not immediately drop everything and spend as much time as needed. (And that one time he simply asked whether I could return an hour later instead.) On the other hand, he was also quite willing to give students their own space as described by Spatzier, who recalls that Katok
really had a knack in cultivating talent, and adjusting his mentoring to the student and their abilities. He pretty much left me alone for example. At some point though we had a conversation that it was time to write a thesis. I had the result in my first paper at that time, and then the plan was formed that I investigate geodesic flows in higher-rank symmetric spaces which became the second part of my thesis, and (with some changes) §5 of my paper with Ballmann and Brin [Reference Ballmann, Brin and Spatzier23]. On the other hand, I believe others had much closer supervision, at least back then in my time.
I also do remember one afternoon very clearly—after I realized a mistake in an early version of my first paper, a stupid linear algebra mistake. Tolya made time for a whole Sunday afternoon to discuss the problem. We did not find a fix, and that part of the work was just wrong. That he took all that time made a strong impression on me.
He was also really good about inviting us all to meals with visitors and being part of the community.
Katok also delighted in being surprised by new ideas. I recall him taking me from Caltech to a USC seminar in which Jean-Pierre Otal presented his proof of marked length-spectrum rigidity [Reference Otal260, Reference Otal261, Reference Wilkinson298]. I did not know that this was a breakthrough on an infamous problem and only registered that this involved an almost simpleminded central idea. But then I saw Katok listening—he was leaning forward, his eyes popping out and his mouth open. On the drive back, he expressed his amazement that none of the big guns working on this had seen this idea. ‘I am glad I wasn’t working on this, because I would be pretty upset now to have missed this idea’Footnote †.
Among Alena Erchenko’s early memories is that Katok told her at the beginning of the PhD program: ‘You will never know as much as I do. Therefore, the best route is to learn something that I do not know’. She and I think he liked when his students were able to prove something that he had thought should be different. In her work with him,
it seemed originally that there might be restrictions on pairs of entropies, but then we discovered a polyhedral model which allowed us to ‘trick topology’ and vary metric entropy without changing topological entropy much [Reference Barthelmé and Erchenko28, Reference Erchenko84, Reference Erchenko and Katok85].
Likewise, my dissertation result involved a geometric ‘threading’ mechanism [Reference Fisher and Hasselblatt102, §9.6] rather than one of a cohomological nature as in any previous work.
Another conversation with a memorable piece of advice occurred in the aforementioned home extension in State College, where he entertained Jana Rodriguez Hertz and Raúl Ures:
He had a huge library, he read about many topics, was extremely curious about many things. And he also enjoyed discussing about topics off Mathematics, especially History and Politics. While we were at the library, he told us something I will never forget: ‘If you want to succeed in Mathematics, then one possibility is to be Margulis. But if, like in my case, you are not Margulis, then you have to work like crazy. There is no other way’.
His care for his students went well-beyond attentiveness to their mathematical needs and development. Howard Weiss called Katok the most gregarious mathematician he has known, and the frequent social events hosted by the Katoks have been an important center of a community, serving a sometimes urgent need. As Renato Feres wrote to Svetlana:
Both Tolya and you are very important persons in my life. I owe so much to him professionally, intellectually, and personally. Beyond his role as PhD advisor, he stepped in to help me at key moments to steady my professional path, something for which I’ve always been very grateful. I’m also very fond of the memories of the many social events, dinners, parties at your house, the many interesting people I came to know through both of you. From the very beginning, as an international student with no family members in the US, the social and emotional support these events provided are perhaps much more important than you may estimate.
He supported his students individually beyond mathematics when he saw a need. He helped me move from one end of the Caltech campus to an upper-floor apartment on the other end, and when Cheng-Bo Yue was recovering from a violent assault, he made sure that we all took turns looking in on him. This did not only happen in the vigor of his 40s but to the end. Changguang Dong:
He is such a responsible, humble man, an extremely knowledgeable teacher, a helpful advisor, and further for me also like my grandfather. There is certainly a lot to say about him from my perspective, for example I think he did a lot for enrolling also my girlfriend in the PhD program, he spent a lot of time with me together answering stupid questions, he showed some worry about my postdoc search (I will never know how much he did for my postdoc offer). He did much but said little.
I would like to share my special experience to see a gastroenterologist with him. It was the Spring of 2015. In fact he knew I had the stomach problem for years, and at that time the problem became worse with a cough. He might think I have seen the doctor many times but still not become better, and also he knew the doctor very well (maybe he saw the doctor before!). So he chose to go with me. I still remember that he did not feel too good at that time (because he canceled some appointments), and the time of my appointment was exactly during the working seminar. I cannot imagine why he offered to help me with that, but I do know how much this meant to me. He is just several years younger than my grandfather, but I do truly think he acted not just like an advisor but also a grandfather full of care.
Indeed, it was among his last wishes, and Svetlana’s, that instead of sending flowers, well-wishers donate to a fund in support of extreme medical expenses for one of his prominent collaborators and former students.
As was the case when teaching mathematical circles or running the seminar in Moscow, Katok always went well beyond his students, postdocs, and colleagues as he supported young mathematicians. He was sure to include young mathematicians in the conferences he organized, his active participation drew them more deeply into the mathematics, and he supported many careers: as Svetlana Katok organized his files after his death, she realized that he had, over time, written letters of recommendation for virtually all dynamicists—for many of them on multiple occasions. Sometimes recommendations were not enough—Keith Burns is quite aware how his career might have gone rather differently had Katok been less active about engaging him:
I wrote my paper about ergodicity of geodesic flows in early 1982 and sent it to Katok as well as to Ergodic Theory and Dynamical Systems. I also enquired about a job at Maryland for the coming academic year. Katok understandably replied I was too late and everything was filled for the coming year (I knew nothing then about how or when to do things). But he also said that I must apply to the program at MSRI that he was organizing with Bob Zimmer in 1983/84Footnote †. I had no idea what he was talking about and forgot about it. I ended up at Southern Illinois for the 1982/83 academic year. At some time during that year I was considerably surprised to receive an invitation to the program. Somebody must have tracked down my whereabouts (perhaps Tolya asked Ralf Spatzier who might have known where I was). I remember somebody at SIU saying ‘somebody must love you’ when I mentioned the invitation. I also received an invitation to spend two years at the School of Research Studies at Australian National University (I suppose I must have applied there—I can’t remember). Anyway I chose the MSRI program. With hindsight it’s clear that… I made the right decision.
It is worth noting that Keith Burns was neither a student nor a postdoc of Katok’s. Indeed, generally Katok
had a deep and varied influence on my (and many others’) work. He was very generous in sharing his insights and ideas, and there were a lot of them. He was also generous with young people, aware of the fragile ego of some beginners, in a way which is rare among people of his stature. [François Ledrappier]
That it had taken until 1990 for the Katoks to have good jobs for both Anatole and Svetlana can only have helped attune them to the need for the needs and opportunities associated with such circumstances. Giovanni Forni well remembers how much Katok was invested in this:
Tolya was generous with his support in difficult personal circumstances, and possibly by personal experience, was sympathetic to that plight of academic couples, the ‘two-body problem’. In 2004–2005, my wife and I were separated, as she took up a job in New Orleans, where our first son was born, while I was at Northwestern in Chicago. Tolya worked to arrange for us to move to Penn State. We ended up moving to Toronto (the French Department there gave my wife a better offer), but in the uncertainty it was a great relief to have his support. It was not the first time that he supported our move to Penn State (the first was when I was on the job market in 2001), but I never felt that he was displeased or that he held my double ‘decline’ against me.
Boris Kalinin and Victoria Sadovskaya accepted a double offer to the department and are both tenured at Pennsylvania State University.
Even his mathematical engagement alone could work wonders. Andrey Kochergin, his first doctoral student, volunteers that after 20 fallow years, he again started producing (much-cited) mathematics, once Katok started traveling to Moscow in 1999, and he has remained productive sinceFootnote †. That first trip back engendered a newfound enthusiasm for MoscowFootnote ‡ so strong that he frequently returned and at some point thought aloud about buying an apartment there. However, by 2003, and some 10 visits later, the enchantment had worn off, and the trips ceased.
Ralf Spatzier shared some perspective on collaboration style:
He was often very clear explaining other people’s math—and we all learned a ton that way. But working with him was often difficult since he was not very clear expressing his own thoughts and ideas. Sometimes this could be frustrating especially when in the end it turned out that it could be expressed in a more standard way. Of course he had great insights. But he also spent an enormous amount of time and energy writing the papers… . I don’t know if this was true for all his collaborations or only some. In my case, we spent a lot of time in an office and just wrote together.
4.2. Books
Indeed, he was increasingly happy to let his collaborators take the lead in writing, just as Burns described (page 38). Yet, he wrote a lot. My large collaborations with Katok involved writing both separately and jointly. They mainly took place during the Penn State years. In my first year at Caltech, I had taken careful notes in his dynamical systems course, and I had polished them in the months after. They went untouched for years, but before leaving Caltech, after completion of my degree in 1989, I brought this up since we had previously considered writing a book on dynamics. It helped that Katok had taught dynamics courses virtually annually, and because of that earlier conversation had obtained class notes from some of those courses. I had in mind a book of some 100 pages, maybe in the Lecture Notes series, and this conversation did not greatly refine the plans, but we parted having decided to give it a go. It helped that I was departing for a tenure-track appointment rather than a postdoc. It probably helped even more that we had no idea what we were getting ourselves into.
A year later, I got married in Pasadena, and we newlyweds embarked on a 1-year honeymoon in Europe: I had deferred offers of visits at the IHES and the ETH in order to take up my Tufts appointment, and after two weeks of tourism in Ireland, we settled in for 5 months each outside Paris and in Zürich—poor as church mice, but quite happy. While I was pursuing research projects [Reference Hasselblatt123–Reference Hasselblatt126], the book project also got serious attention, and it acquired more bulk in the following year. Katok and I both long remembered the particularly harrowing project of writing up the proof of the Stable-Manifold Theorem. During the 1992 special year on Lie Groups and Ergodic Theory with Applications to Number Theory and Geometry Footnote †, we both spent two months at MSRI in Berkeley, and it was here that an unwieldy jumble of written material took shape as a book with gaps to be filled. This was a major turning point, and combined with the realization that we had something in the works quite distinctive from anything else, we had the motivation and momentum for the downhill stretch to the finish line and were done in 1994. It says a lot that our friendship survived 800 pages of writing (and, more so, rewriting). Appraisals of ‘Introduction to the Modern Theory of Dynamical Systems’ [Reference Katok and Hasselblatt190] can be found elsewhere, so I quote David Hughes, who was a doctoral student of Katok’s at the time of his death:
The book that he co-authored with Boris Hasselblatt, the ‘Bible’ of Dynamics, was my first introduction to him. The details are not brushed under definitions, but left in the proofs. This is unlike most mathematical textbooks, where a mountain of theory is first built, without much motivation. He would present some problem and then introduce more theory, so that as the theory became more complex one’s understanding of the problem deepened. The most valuable and fun part of his classes were always the problem sets. I think his style of presentation in the book was a deliberate choice. Reading it is like looking at a Swiss clock, where village scenes are played out mechanically on the hour. In this sense, the human character of the book reflected Prof. Katok’s own interest in how people work together. I think it was part of the same organizing philosophy.
During a July 10–31, 1996 visit of mine to Montevideo, which overlapped with a visit by the Katoks (who coincidentally arrived by the same flight), we started a follow-on book project ‘for undergraduates’ (no manifolds and no measure theory, so mostly example-driven) [Reference Hasselblatt and Katok132], which was half the size but was to take twice as long to write.
On the subject of Katok’s numerous books, one should mention two publications that aren’t quite books, but of comparable size. At over 130 pages, the current-research survey with Sinai and Stepin [Reference Katok, Sinaĭ and Stepin216] might have served its purpose as a stand-alone book, and indeed, as previously mentioned, effectively became the Moscow textbook on its subject—although the evolution of ergodic theory within the Moscow school from this point onward may not quite have been what the authors must have hoped at the time:
The announcement of Ornstein’s solution in 1969 came as a shock to Moscow. The ‘philosophy’ of Ornstein’s approach was not absorbed quickly, and the efforts shifted even more than before from ‘pure’ ergodic theory to interface with other disciplines, primarily smooth dynamics and statistical mechanics. Leadership in the development of pure ergodic theory passed to Ornstein, Hillel Furstenberg, and their ‘schools’. [Reference Katok185, p. 556]
‘Principal Structures’ [Reference Hasselblatt and Katok131] lays out for the ‘adult mathematician’ the structure of the theory of dynamical systems in 200 pages in order to provide a common background for the other chapters in the two Handbook volumes [Reference Hasselblatt and Katok130, Reference Hasselblatt and Katok133] of over 1200 pages each.
It may be worth calling attention to a perspective that came into being as we worked on this chapter. It took shape July 15–August 15, 1998, while we worked at the Erwin Schrödinger International Institute for Mathematics and Physics in Vienna (and made our anniversary pilgrimage to McDonald’s). We realized that ‘Introduction to the Modern Theory of Dynamical Systems’ [Reference Katok and Hasselblatt190] had not been as clear about differentiable dynamics as it might have been, by taking ‘low-dimensional phenomena’ as the catch-all for non-hyperbolic dynamics. In dynamics generally, the prevailing prominent paradigms of stable and random dynamics [Reference Moser256] were in the foreground, where ‘stable’ is elliptic dynamics, KAM theory, and related phenomena, while ‘random’ is hyperbolic dynamics, positive entropy, etc. Missing between these opposites is ‘intermediate’ dynamics with polynomial growth such as polygonal billiards, interval-exchange maps, and several parts of homogeneous dynamics. In this chapter, accordingly, we developed the framework of viewing smooth dynamics in terms of elliptic, parabolic, and hyperbolic dynamics. Maybe this has since been absorbed into the fabric of the discipline to such an extent as to sound commonplace, but it was clearly not in our consciousness in the early 1990s as we shaped the organization of ‘Introduction to the Modern Theory of Dynamical Systems’. Katok’s March 1999 Moscow lecture [Reference Katok183] was among the early public enunciations of this point of view.
The aforementioned book with Jean-Marie Strelcyn (and the collaboration of François Ledrappier [Reference Ledrappier and Strelcyn243] and Feliks Przytycki) on hyperbolic systems with singularities [Reference Katok, Strelcyn, Ledrappier and Przytycki225] is one of two monographs of his; the other, ‘Rigidity in higher rank abelian group actions. Volume I. Introduction and cocycle problem’ [Reference Katok and Niţică206] with Niţică, was meant to be followed by a second volume with applications: it introduces the subject with definitions, examples, and preliminaries from dynamics and analysis, then studies rigidity of cocycles. This is an enormous contribution to pull together much of the core of over two decades of research, and at this time, one can only imagine the companion volume. Based on notes with his student E. A. Robinson, ‘Combinatorial constructions in ergodic theory and dynamics.’ [Reference Katok182] was decades in coming [Reference Katok181, p. 108]:
The present work is an updated, revised and expanded version of the second of the four parts of our work ‘Constructions in Ergodic Theory’ originally intended to appear as a book form, which was mostly written in 1982–83, appended during the eighties and which has been circulated in the manuscript form… . An updated version of the first part which contains a definitive account of the general concept of periodic approximation as well as its applications to establishing genericity of various ergodic properties in a variety of categories is about to appear as [K1]. The third and fourth parts were left unfinished and their fate at the time of writing remains uncertain.
It lets the reader learn ‘from a master of the subject, presenting some of his tools’ [Klaus Schmidt]. The first part lays out the approximation and construction of ergodic transformations by periodic processes from the beginnings of Katok’s career and the second one lays out cohomological constructions, including invariant distributions of partially hyperbolic and parabolic systems, and ‘nice’ coboundaries with ‘complicated’ cobounding functions.
Katok was also seminally involved in the writing of the book on non-uniformly hyperbolic dynamics, though ultimately not as a coauthor [Reference Barreira and Pesin27, Preface].
Two more books are worth mentioning—in the context of a characteristic imprint on undergraduate mathematics education the Katoks made at Pennsylvania State University. George Andrews recalls:
We are also deeply indebted to him and Svetlana for the creation of the Mathematics Advanced Study Semesters program (or MASS). This occurred at a time when I was a freshly installed department head, and I was under great pressure to do something to improve mathematics education. Most of what was being suggested by upper levels of the administration horrified me. However, it was clear that we had to do something. To my great delight, Anatole and Svetlana came to the rescue by proposing the creation of MASS. This wonderful program is a major contribution to mathematics education and has provided a springboard to graduate education for many students from small colleges who otherwise would have been inadequately prepared for graduate education.
For over two decades, the program assembled undergraduate mathematics majors from all over the country for an intensive one-semester immersion of specially designed courses, seminars, and research-oriented projects. Its core principles and structure were inspired by what the Katoks recalled as the strengths of mathematics education in Moscow, but informed in equal part by having seen that system crush fragile egos of young students with great potential. Anatole Katok taught courses in the MASS program multiple times, and on two of the latter such occasions, Vaughn Climenhaga, then a graduate student, was the assistant for the course. Katok’s unique exposition and Climenhaga’s writing chops produced two lovely volumes [Reference Climenhaga and Katok63, Reference Katok and Climenhaga188] best introduced by Climenhaga’s recollections of assisting with these classes:
When I think of my mathematical interactions with Tolya, the thing that has always stood out the most for me is that I have never met anyone better at teaching me something I thought I already knew. I noticed this most prominently in the MASS courses for which I was his TA, where in both cases he took a topic that I thought I understood relatively well (geometry/topology of surfaces in the first course, and group theory with emphasis on geometric symmetry in the second), and told the story in a way that gave me a much better appreciation of the landscape in which the topic sits and the way in which the things hold together as a coherent whole.
4.3. Organization
At Pennsylvania State University, Katok was able to build lasting structures to support dynamical systems worldwide, and he did not take long to get started. Since October 18, 1990, the Penn State–University of Maryland Semi-annual Workshop in Dynamical Systems and Related Topics has been repeated at Pennsylvania State University every fall, with a companion meeting at the University of Maryland every Spring since 1992, the meetings being jointly sponsored by the two institutions and regularly supported by the National Science Foundation. Each time, numerous participants travel from one of these institutions to the other, and they are joined by participants from across the US and the globe. This has by now long been such an established institution that individual invitations are no longer needed; everyone knows to await the announcement of the next date, often during the previous meeting, and to then register. This alone puts Penn State on the mental map of every dynamicist in the world.
Out of this conference, faculty hiring, a visitor program, an ever larger footprint in the graduate program, and Katok’s energy and funds grew the Center for Dynamical Systems and Geometry at Penn State, which consists of a large group of faculty members, graduate students, postdocs, and associate members from other institutions. Its program includes a weekly Dynamical Systems Seminar, the Center for Dynamics and Geometry Colloquium, a Working Seminar on Dynamics and its Working Tools, a Dynamics Student Seminar, a special lecture series, graduate and undergraduate courses, and the Penn State–University of Maryland Semi-annual Workshop. It is this center which has been endowed and named in Katok’s honor.
One concern of Katok’s had long been that dynamical systems as a discipline is less visible than it should be. Much earlier, this had been among the motivations that led to the founding of Ergodic Theory and Dynamical Systems. Characteristically, he perceived that this particularly impacts young dynamicists at critical career stages. Together with Michael Brin, he chose to address this. In 2008, Brin endowed an international prize for outstanding work in the theory of dynamical systems and related areas, given for specific mathematical achievements that appear as a single or a series of publications in refereed journals, proceedings, or monographsFootnote †. The goal of the prize is to recognize mathematicians who have made substantial impact in the field at an early stage of their careers (no more than fourteen years from their PhD). The first Brin Prize was presented in 2008 at the Maryland session of the semi-annual workshop, which was dedicated to Brin’s 60th birthday. Until 2017, this prize was awarded every other year, and it became annual in 2018 (presented at Maryland in the Spring in even years, and at the Penn State meeting in odd years). Giovanni Forni gives us a glimpse behind the scenes:
In 2008 Michael Brin established the Brin Prize in Dynamical Systems with Tolya as chair of the selection committee. After becoming a committee member myself (in 2013) I realized with some surprise that in his role as a Chair he never had to cast his vote. According to the prize rules, which he himself presumably largely established, he was supposed to vote only to break ties. However, he led the committee in discussion until a consensus emerged, usually unanimous or overwhelming, and never had to cast a vote.
Since 2016, a further annual prize, now called the Michael Brin Dynamical Systems Prize for Young MathematiciansFootnote ‡, recognizes outstanding contributions to dynamical systems made by researchers within a few years of their PhD (within four years after the PhD at the beginning of the prize calendar year).
Together with the countless doctoral students and postdocs who cycled through the department in these three decades, plus faculty hired during his time, whether still at Penn State or not, Katok made Penn State a center of dynamics, and dynamics central to Penn State—with a broad perspective.
Throughout the 19th century there were mathematicians who were able to maintain a knowledge of mathematics that encompassed all or most of its fields, and in the early 20th century a select few, such as Hilbert, managed to come close to this ideal. These mathematicians were important to the enterprise of mathematics, but the rapid growth of the discipline made it impossible to sustain such breadth. Today the role of universally educated mathematicians is played by those very few who have a comprehensive view of a field and an understanding of the interaction of its parts as well as its connections to other areas of mathematics. Anatole Katok belongs to this select group, representing the theory of dynamical systems. [Reference Pesin, Brin, Hasselblatt, Brin, Hasselblatt and Pesin271]
Jerry Bona was the department chair at Pennsylvania State University during the first five years of the Katoks’ tenure there:
Tolya was an ideal faculty member. He did not bother me incessantly, but when he scheduled an appointment, he always had very interesting suggestions to offer… . The Penn State group in dynamical systems theory was already on the map by the time I left. I put this down mainly to Tolya’s persistence, skill and very good taste.
Another former department chair, Yuxi Zheng, noted that:
Truly, I feel fortunate to have been colleagues with him. His high achievements have brought Penn State a worldwide reputation, not just in dynamical systems. He introduced many outstanding colleagues to Penn State, who were otherwise not necessarily interested in Penn State. From my interaction with him in the past 17 years, I found that Anatole was always fair, logical, and passionate about mathematics and the building up of the mathematics department.
And George Andrews adds:
Anatole made immense contributions to Penn State mathematics. The rise of the reputation of our department owes much to his leadership both in his own research and teaching and in bringing outstanding mathematicians to our department.
5. Epilogue
Anatole Katok’s zest for life had many dimensions. He loved conversations about mathematics, history, and almost any other topic, the spark of which is eloquently described by Omri Sarig:
Tolya enjoyed testing and finessing his opinions by discussing them with other mathematicians, junior and senior. Often he would initiate such a discussion by making an intentionally provocative statement, which was often very funny, but was also of the kind that simply could be allowed to pass in silence. A lively discussion would then follow with an abundance of technical, meta-mathematical, and historical arguments thrown in into the air. I witnessed many such conversations, sometimes at a restaurant over wine, sometimes at his home, and sometimes at the end of a seminar or a lecture over coffee and cookies. Tolya’s sharp tongue, quick mind, fantastic memory and boundless sources of knowledge and energy meant that arguing with him was not for the faint of heart, but when an adversary was found who had the confidence to answer back, the result was a unique and exhilarating intellectual experience, and very fun to watch. Occasionally both sides changed their minds!
Zoë Brigley Thompson, a writer most known for feminist poetry (in fact, she wrote the Wikipedia entry on feminist poetry) gave another testimonial to Katok’s encyclopedic reputation:
He was a most remarkable man, and I must say that I was very fond of him. I loved our conversations about women from history like Elizabeth I and Catherine the Great. He was a mathematician, but also a renaissance man—I remember his wonderful book collection. He made great speeches, and I loved his pride when he watched his daughter Danya’s sublime singing. We often joked about me ghostwriting his autobiography for him—I wish I had, because no doubt there are many remarkable stories from a rich and remarkable life.
Katok enjoyed tooling around with the top of his convertible down on a Fall day, and he was not beyond the silly—we once elaborately measured that a Riedel wine goblet holds an entire liter of liquid, that is, well more than a whole bottle of wine. He loved good wine and good books—to each of these a substantial part of his house was dedicated. (First, his love for books, especially art books, created the problem of lacking space, then the expansion of the house created the problem of having to fill the much larger library.) Art was a shared love of Anatole and Svetlana, her family being replete with artists, including her granduncle Marc Chagall and their niece Alexandra Rozenman, whose art work was among the most prominently displayed in their home, its evocation of a kinship with Chagall fittingly floating above the living room. In their daughter Danya, the practice of the musical arts became incarnate. Ralf Spatzier remembers how big a part of his life family was:
I always thought that his relationship with Sveta was remarkable, close and supportive and very proud of each other. When I met him last, in February, he told me a little about his children. It sure became clear how much he loved them and how proud he was of them, through life’s ups and downs. It seemed he also really went out of his way on occasion to support them. I always had thought of him as a family man. But this was stronger, much to my liking.
Katok loved good food wherever he traveled, but also in State College (recalls Shilpak Banerjee: ‘He really liked the restaurant “Fuji and Jade” at State College where he would always order “aromatic beef”’), including at home, where the Katoks did not only entertain large numbers of conference participants as a matter of course, but also individual guests whom they always culinarily spoiled. Jana Rodriguez Hertz recalls this with particularly pertinent expertise:
We were once invited to his house, where we spent a wonderful night. He cooked steaks, and he really knew how to do it. And let me tell you that it is not easy to impress an Argentinian or Uruguayan at that.
While an inveterate urban traveler, Katok also enjoyed the great outdoors. Many of the older generation remember the obligatory vigorous conference hikes, such as the clambers up the San Gabriel mountains or the workshop Sundays in the hills of Pennsylvania. Alas, in 1988, this had to pause. Katok was diagnosed with Hodgkin’s lymphoma, for which the standard of care at the time prescribed rather aggressive treatment that exacted a heavy toll. Yet, Livio Flaminio recalls:
It was in the years of the post-doc at Caltech that I came to know the man Katok. How impressed I was by the energy with which he fought the illness! Anybody else would have taken a leave and rest. But Tolya came to every seminar and continued to work as usual, defying the heavy side-effects of the cure.
Indeed, the gallows’ humor in the research group had it that this crisis had reduced Katok’s energies to those of a mere mortal. Fortunately, he was before long pronounced fully cured, and we perceived no trace of it soon after, save for a lingering throat irritation from the radiation therapy that took years to taper off. Alas, his throat was not the only organ in the path of intense stray radiation—which may be related to events during the 1996 visits in Montevideo. There I met Jana Rodriguez Hertz, largely while watching over Danya Katok, and here is how she recalls the events there.
I first met Tolya in Montevideo, when I was a graduate student, at the International Conference on Dynamical Systems in 1995. It was the first important conference in mathematics in Uruguay, we all had worked a lot for it. I was impressed, because it was not frequent in Uruguay to have the opportunity to meet in person the mathematicians that produce the theorems you study. He liked very much the conference, and had fun in the banquet, which consisted in a big barbecue with drums, we all danced at the end with the drums, and he danced too. He really had fun. I think he liked Montevideo, since he came back [in 1996], with Svetlana and Danya. Danya was 12 at the time, if I remember correctly… . He and Svetlana rented our apartment, the apartment was right in front of the Engineering School, where the Math Department was. While he was in Montevideo, he had a health episode with his heart. We were very worried, and looked immediately for the best hospital we could get. I remember that he told me that while he was walking, he had a small pain in his chest, so instead of getting quiet and look for a doctor, he walked like 10 more kilometers and at the end he took a cold shower. Then the pain appeared again and it was more severe, it was only then that he called us to get a doctor. He had to get hospitalized.
While we were watching Danya, Svetlana was at the hospital, where he got excellent care—consonant with the earlier allusion to the fact that Uruguayans consume more meat per capita than any other country and are also known for their cardiologistsFootnote †. Katok had chosen a good location for this adventure, and he recovered well. However, of the three decades the cancer cure had bought him, only the first was to be care-free. Heart and lung problems recurred with increasing severity, including a grave episode in ParisFootnote ‡. Yet he persistently threw himself into life and mathematics. In Montevideo, we were beginning our second book project [Reference Hasselblatt and Katok132], and we would see it finished within a decade, while completing large other projects ‘on the side’ or thereafter [Reference Hasselblatt and Katok130, Reference Hasselblatt and Katok131, Reference Hasselblatt and Katok133] and starting yet others now left in limbo. Starting in 2005, we made plans for a book project Origins and Development of Modern Dynamics (up to around 1970) with both Katoks and myself as editors. All this during his extensive research productivity on higher-rank rigidity and many other topics, plus an unabated flow of expository writing, including books [Reference Climenhaga and Katok62, Reference Climenhaga and Katok63, Reference Feres and Katok97, Reference Hasselblatt and Katok131, Reference Hasselblatt and Katok132, Reference Katok183, Reference Katok and Climenhaga188, Reference Katok and Hasselblatt190, Reference Katok, Sinaĭ and Stepin216, Reference Katok and Thouvenot227] and historic/sociological works [Reference Anosov12, Reference Hasselblatt and Katok129, Reference Katok176, Reference Katok184, Reference Katok186, Reference Katok187, Reference Katok and Katok191]—plus the editing of journalsFootnote † and books [Reference Hasselblatt and Katok130, Reference Hasselblatt and Katok133, Reference Katok167, Reference Katok171, Reference Katok, de la Llave, Pesin and Weiss189, Reference Katok, Pesin and Hertz208].
In 2016, he took up a permanent visiting appointment at Yeshiva University, the alma mater of Hillel Furstenberg, with the charge to enhance the New York City dynamics seminar. With Patrick Hooper (CUNY) and Marian Gidea (Yeshiva) they aimed to make this seminar a center of activity in ‘Modern dynamics’ in the New York City area. He invited me to give the Yeshiva colloquium on the Washington Heights Campus and the New York City Dynamics seminar on the Midtown campus in early March 2016. Over those 3 Penn State decades, I lost count how often I had stayed in the house of the Katoks, and now for the first time, I got to stay in an apartment of the Katoks—they had bought a Manhattan apartment in 2015; this was motivated by their daughter Danya living nearby but also had the benefit of providing easy access to excellent medical careFootnote ‡. When I was there, he was not doing great but on the upswing. My next visit with them was again in State College, where in August 2016, we reworked a perennial book project into a different form that would make it more feasible in reasonable time—but he warned me that because he was doing well enough to work on such projects, he was going to have a few others on his front burner. The Swedish Research Council had appointed him to the Tage Erlander Guest Professorship 2018 in recognition of his excellent services to science, and he was scheduled to consummate it in the second half of that calendar year. His enthusiasm and engagement never stopped, but this was not to be, and these numerous projects are suspended. Alena Erchenko remembers:
T. Barthelmé and I were also able to prove that there exists a uniform lower bound on a systole for a family of negatively curved metrics conformally equivalent to a fixed hyperbolic metric with fixed total area on a fixed compact surface of negative Euler characteristic [Reference Barthelmé and Erchenko28]. Originally, Anatole seemed to think that there is no such uniform lower bound in the considered class. I was able to tell him that I know how to do that right before he went to the hospital, and he was intrigued by it.
Changguang Dong wrote:
The last chat between us was when he told me he will be away for a few weeks due to a health problem. That was mid-March. I did not think it was that serious at that moment, and it seemed to me he looked good. I do not believe it even now that it was the last time I saw him. It became my permanent regret that I never had any photo with him, and how I wish he could make it to my defense. I will miss him forever.
Less than three weeks before the end of his life, I submitted a finalized application to the Banach Center for a 75th birthday conference in Będlewo, and within a month after it, the Banach Center approved an August 11–16, 2019 memorial conference. The 29th Fall meeting of the Semi-annual Workshop in Dynamical Systems and Related Topics on October 4–7, 2018 was dedicated to the memory of Anatole Katok, by which time Michael Brin had endowed the Anatole Katok Chair in Mathematics (now held by Federico Rodriguez Hertz) and, together with Sergey Ferleger and Alexey Kononenko, the newly named Anatole Katok Center for Dynamical Systems and Geometry at Pennsylvania State University.
Katok’s passing signifies the end of an era in dynamical systems and the Russian mathematics tradition. He is greatly missed—working in dynamics with a true understanding of the field as a whole, contributing to all its major branches throughout his career, mentoring and inspiring multitudes of doctoral students and researchers, shaping so many research agendas, and organizing and enriching conferences and seminars. But his mentorship was empowering and prepared us well for carrying the torch. He created enough inspiration, momentum, infrastructure, and leadership talent that we can expect dynamical systems to do him proud in years to come.



