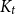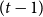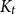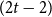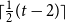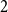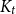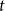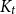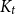1. Introduction
Given an integer
![]() $t \ge 1$
, a
$t \ge 1$
, a
![]() $K_t$
-model is a graph
$K_t$
-model is a graph
![]() $F$
consisting of
$F$
consisting of
![]() $t$
vertex-disjoint trees
$t$
vertex-disjoint trees
![]() $(T_s)_{s=1}^t$
, each two of them joined by exactly one additional edge. We say that a graph
$(T_s)_{s=1}^t$
, each two of them joined by exactly one additional edge. We say that a graph
![]() $G$
contains
$G$
contains
![]() $K_t$
as a minor, or that it contains a
$K_t$
as a minor, or that it contains a
![]() $K_t$
-minor, if
$K_t$
-minor, if
![]() $G$
contains a subgraph which is a
$G$
contains a subgraph which is a
![]() $K_t$
-model.
$K_t$
-model.
The work in this paper is motivated by the famous graph colouring conjecture of Hadwiger.
Conjecture 1.1. (Hadwiger’s conjecture, 1943, [Reference Hadwiger7]). For every integer
![]() $t \ge 2$
, if
$t \ge 2$
, if
![]() $G$
is a graph not containing a
$G$
is a graph not containing a
![]() $K_t$
-minor, then
$K_t$
-minor, then
![]() $G$
is properly
$G$
is properly
![]() $(t-1)$
-colourable.
$(t-1)$
-colourable.
A lot of work in graph theory has been inspired by and built around Hadwiger’s conjecture. A survey of results and open problems covering the state of the art up until roughly
![]() $3$
years ago was written by Seymour [Reference Seymour25]. Hadwiger’s conjecture has been proved for all values
$3$
years ago was written by Seymour [Reference Seymour25]. Hadwiger’s conjecture has been proved for all values
![]() $t \le 6$
(see Robertson, Seymour and Thomas [Reference Robertson, Seymour and Thomas24]). It remains open starting from
$t \le 6$
(see Robertson, Seymour and Thomas [Reference Robertson, Seymour and Thomas24]). It remains open starting from
![]() $t=7$
. For a long time, the best asymptotic upper bound on the chromatic number of graphs with no
$t=7$
. For a long time, the best asymptotic upper bound on the chromatic number of graphs with no
![]() $K_t$
-minor has remained
$K_t$
-minor has remained
![]() $O(t\sqrt{\log t})$
as established independently by Kostochka and Thomason [Reference Kostochka15, Reference Thomason27]. However, this bound was improved considerably recently, see [Reference Delcourt and Postle2, Reference Norin, Postle and Song18, Reference Norin and Postle19, Reference Postle21, Reference Postle22]. The current best bound of
$O(t\sqrt{\log t})$
as established independently by Kostochka and Thomason [Reference Kostochka15, Reference Thomason27]. However, this bound was improved considerably recently, see [Reference Delcourt and Postle2, Reference Norin, Postle and Song18, Reference Norin and Postle19, Reference Postle21, Reference Postle22]. The current best bound of
![]() $O(t\log \log t)$
was obtained roughly a year ago by Delcourt and Postle [Reference Delcourt and Postle2].
$O(t\log \log t)$
was obtained roughly a year ago by Delcourt and Postle [Reference Delcourt and Postle2].
A
![]() $K_t$
-model
$K_t$
-model
![]() $F$
is said to be odd if there exists a
$F$
is said to be odd if there exists a
![]() $2$
-colouring
$2$
-colouring
![]() $c$
of
$c$
of
![]() $V(F)$
such that the restriction of
$V(F)$
such that the restriction of
![]() $c$
to any single tree
$c$
to any single tree
![]() $T_s$
forms a proper colouring of that tree, while every edge joining two distinct trees is monochromatic with respect to
$T_s$
forms a proper colouring of that tree, while every edge joining two distinct trees is monochromatic with respect to
![]() $c$
, i.e., has the same colours at its endpoints. We say that a graph
$c$
, i.e., has the same colours at its endpoints. We say that a graph
![]() $G$
contains an odd
$G$
contains an odd
![]() $K_t$
-minor or that it contains
$K_t$
-minor or that it contains
![]() $K_t$
as an odd minor if
$K_t$
as an odd minor if
![]() $G$
has a subgraph which is an odd
$G$
has a subgraph which is an odd
![]() $K_t$
-model. Gerards and Seymour (see [Reference Jensen and Toft6], Section 6.5) proposed the following strengthening of Hadwiger’s conjecture, called Odd Hadwiger’s conjecture.
$K_t$
-model. Gerards and Seymour (see [Reference Jensen and Toft6], Section 6.5) proposed the following strengthening of Hadwiger’s conjecture, called Odd Hadwiger’s conjecture.
Conjecture 1.2. (Odd Hadwiger’s conjecture, 1995, [Reference Jensen and Toft6]). For every integer
![]() $t \ge 2$
, if
$t \ge 2$
, if
![]() $G$
is a graph not containing an odd
$G$
is a graph not containing an odd
![]() $K_t$
-minor, then
$K_t$
-minor, then
![]() $G$
is properly
$G$
is properly
![]() $(t-1)$
-colourable.
$(t-1)$
-colourable.
To see that this conjecture indeed considerably strengthens Hadwiger’s conjecture, consider for example
![]() $t=3$
. While Hadwiger’s conjecture in this case amounts to saying that forests (the
$t=3$
. While Hadwiger’s conjecture in this case amounts to saying that forests (the
![]() $K_3$
-minor-free graphs) are
$K_3$
-minor-free graphs) are
![]() $2$
-colourable, the Odd Hadwiger’s conjecture captures the more general statement that all graphs without odd cycles (the odd
$2$
-colourable, the Odd Hadwiger’s conjecture captures the more general statement that all graphs without odd cycles (the odd
![]() $K_3$
-minor-free graphs) are
$K_3$
-minor-free graphs) are
![]() $2$
-colourable. In general, every
$2$
-colourable. In general, every
![]() $K_t$
-minor-free graph is also odd
$K_t$
-minor-free graph is also odd
![]() $K_t$
-minor-free, but there are odd
$K_t$
-minor-free, but there are odd
![]() $K_3$
-minor-free (i.e., bipartite) graphs which contain arbitrarily large clique minors.
$K_3$
-minor-free (i.e., bipartite) graphs which contain arbitrarily large clique minors.
The above conjecture has been verified for
![]() $t \le 4$
by Catlin [Reference Catlin1], and a solution for the case
$t \le 4$
by Catlin [Reference Catlin1], and a solution for the case
![]() $t=5$
was announced by Guenin (cf. [Reference Seymour25]). For
$t=5$
was announced by Guenin (cf. [Reference Seymour25]). For
![]() $t \ge 6$
the conjecture remains wide open. As for Hadwiger’s conjecture, asymptotic upper bounds on the chromatic number of odd
$t \ge 6$
the conjecture remains wide open. As for Hadwiger’s conjecture, asymptotic upper bounds on the chromatic number of odd
![]() $K_t$
-minor-free graphs have been studied. An upper bound of
$K_t$
-minor-free graphs have been studied. An upper bound of
![]() $O(t\sqrt{\log t})$
was proved by Geelen, Gerards, Reed, Seymour and Vetta in [Reference Geelen, Gerards, Reed, Seymour and Vetta5] (see also [Reference Kawarabayashi11]). Recently this has been improved in [Reference Delcourt and Postle2, Reference Norin and Song20, Reference Postle23, Reference Steiner26], with the current best bound being
$O(t\sqrt{\log t})$
was proved by Geelen, Gerards, Reed, Seymour and Vetta in [Reference Geelen, Gerards, Reed, Seymour and Vetta5] (see also [Reference Kawarabayashi11]). Recently this has been improved in [Reference Delcourt and Postle2, Reference Norin and Song20, Reference Postle23, Reference Steiner26], with the current best bound being
![]() $O(t\log \log t)$
from [Reference Steiner26]. For more results around the Odd Hadwiger’s conjecture, we refer the interested reader to Section 7 of the survey [Reference Seymour25].
$O(t\log \log t)$
from [Reference Steiner26]. For more results around the Odd Hadwiger’s conjecture, we refer the interested reader to Section 7 of the survey [Reference Seymour25].
Given a (not necessarily proper) colouring
![]() $c:V(G)\rightarrow S$
of a graph
$c:V(G)\rightarrow S$
of a graph
![]() $G$
, a subset of vertices is called a monochromatic component, if it is a component of the induced subgraph
$G$
, a subset of vertices is called a monochromatic component, if it is a component of the induced subgraph
![]() $G[c^{-1}(s)]$
for some
$G[c^{-1}(s)]$
for some
![]() $s \in S$
. For instance, a colouring is proper iff all its monochromatic components have size
$s \in S$
. For instance, a colouring is proper iff all its monochromatic components have size
![]() $1$
.
$1$
.
The purpose of this paper is to prove the following relaxation of the Odd Hadwiger’s conjecture, in which we allow our colouring to be improper, but instead require a constant bound (depending only on
![]() $t$
) for the maximum size of its monochromatic components. In return, our colouring uses much fewer colours than the known results for proper colourings.
$t$
) for the maximum size of its monochromatic components. In return, our colouring uses much fewer colours than the known results for proper colourings.
Theorem 1.3.
Let
![]() $t \ge 3$
be an integer. Then every graph
$t \ge 3$
be an integer. Then every graph
![]() $G$
without an odd
$G$
without an odd
![]() $K_t$
-minor admits a (not necessarily proper) vertex colouring using
$K_t$
-minor admits a (not necessarily proper) vertex colouring using
![]() $2t-2$
colours such that all monochromatic components have size at most
$2t-2$
colours such that all monochromatic components have size at most
![]() $\lceil \frac{1}{2}(t-2) \rceil$
.
$\lceil \frac{1}{2}(t-2) \rceil$
.
Theorem 1.3 lines up with a wide set of results on so-called improper colourings of graphs with excluded minors. Instead of giving a long list of the individual results, let us just point to the comprehensive 70 page-survey on improper colourings written recently by Wood [Reference Wood29] as well as to Section 6 of Seymour’s survey [Reference Seymour25]. Two main variants of improper colourings have been studied: clustered and defective colourings. Given a graph
![]() $G$
and integers
$G$
and integers
![]() $k,c, d$
, we say that a
$k,c, d$
, we say that a
![]() $k$
-vertex colouring of
$k$
-vertex colouring of
![]() $G$
has clustering
$G$
has clustering
![]() $c$
if all monochromatic components have size at most
$c$
if all monochromatic components have size at most
![]() $c$
, and we say that it has defect
$c$
, and we say that it has defect
![]() $d$
if the maximum degree of all monochromatic components is bounded by
$d$
if the maximum degree of all monochromatic components is bounded by
![]() $d$
. Clearly, every
$d$
. Clearly, every
![]() $k$
-colouring with clustering
$k$
-colouring with clustering
![]() $c$
also has defect
$c$
also has defect
![]() $c-1$
. We may therefore rephrase Theorem 1.3 by saying that for
$c-1$
. We may therefore rephrase Theorem 1.3 by saying that for
![]() $t \ge 3$
, every odd
$t \ge 3$
, every odd
![]() $K_t$
-minor-free graph is
$K_t$
-minor-free graph is
![]() $2(t-1)$
-colourable with clustering
$2(t-1)$
-colourable with clustering
![]() $\lceil \frac{1}{2}(t-2) \rceil$
and defect
$\lceil \frac{1}{2}(t-2) \rceil$
and defect
![]() $\lceil \frac{1}{2}(t-4) \rceil$
. The number of colours in our result improves upon previous results for this problem by Kawarabayashi [Reference Kawarabayashi10], Kang and Oum [Reference Kang and Oum9] and Liu and Wood [Reference Liu and Wood17], summarized in Table 1 below. It is optimal up to a factor of
$\lceil \frac{1}{2}(t-4) \rceil$
. The number of colours in our result improves upon previous results for this problem by Kawarabayashi [Reference Kawarabayashi10], Kang and Oum [Reference Kang and Oum9] and Liu and Wood [Reference Liu and Wood17], summarized in Table 1 below. It is optimal up to a factor of
![]() $2$
, as it was shown in [Reference Edwards, Kang, Kim, Oum and Seymour4, Reference Kang and Oum9] that (odd)
$2$
, as it was shown in [Reference Edwards, Kang, Kim, Oum and Seymour4, Reference Kang and Oum9] that (odd)
![]() $K_t$
-minor-free graphs in general do not admit
$K_t$
-minor-free graphs in general do not admit
![]() $(t-2)$
-colourings with clustering bounded as a function of
$(t-2)$
-colourings with clustering bounded as a function of
![]() $t$
.
$t$
.
Table 1 Bounds for improper colourings of odd
![]() $K_t$
-minor-free graphs. The functions
$K_t$
-minor-free graphs. The functions
![]() $f_1(t),\ldots,f_4(t)$
are used to indicate that the bound guaranteed on the defect or clustering is only dependent on
$f_1(t),\ldots,f_4(t)$
are used to indicate that the bound guaranteed on the defect or clustering is only dependent on
![]() $t$
. These functions depend on bounds from the graph minor structure theorem of Robertson and Seymour
$t$
. These functions depend on bounds from the graph minor structure theorem of Robertson and Seymour

As an additional advantage, our result also improves the dependency of the size of the clustering on
![]() $t$
. Namely, the bounds on the clustering from [Reference Kang and Oum9, Reference Kawarabayashi10, Reference Liu and Wood17] were functions of
$t$
. Namely, the bounds on the clustering from [Reference Kang and Oum9, Reference Kawarabayashi10, Reference Liu and Wood17] were functions of
![]() $t$
depending on bounds for the graph minor structure theorem of Robertson and Seymour.
$t$
depending on bounds for the graph minor structure theorem of Robertson and Seymour.
Clustered and defective colourings of
![]() $K_t$
-minor-free graphs have also been extensively studied, see [Reference Edwards, Kang, Kim, Oum and Seymour4, Reference van den Heuvel and Wood8, Reference Kawarabayashi and Mohar12, Reference Liu and Oum16, Reference Liu and Wood17, Reference Wood28]. Here the state of the art bounds are as follows: For defective colouring it was shown by Edwards, Kang, Kim, Oum and Seymour [Reference Edwards, Kang, Kim, Oum and Seymour4] that
$K_t$
-minor-free graphs have also been extensively studied, see [Reference Edwards, Kang, Kim, Oum and Seymour4, Reference van den Heuvel and Wood8, Reference Kawarabayashi and Mohar12, Reference Liu and Oum16, Reference Liu and Wood17, Reference Wood28]. Here the state of the art bounds are as follows: For defective colouring it was shown by Edwards, Kang, Kim, Oum and Seymour [Reference Edwards, Kang, Kim, Oum and Seymour4] that
![]() $K_t$
-minor-free graphs can be
$K_t$
-minor-free graphs can be
![]() $(t-1)$
-coloured with bounded defects. Van den Heuvel and Wood [Reference van den Heuvel and Wood8] proved that the defect can be bounded by
$(t-1)$
-coloured with bounded defects. Van den Heuvel and Wood [Reference van den Heuvel and Wood8] proved that the defect can be bounded by
![]() $t-2$
. For clustered colouring, it has been proved that
$t-2$
. For clustered colouring, it has been proved that
![]() $K_t$
-minor-free graphs can be
$K_t$
-minor-free graphs can be
![]() $(t+1)$
-coloured with bounded clustering by Liu and Wood [Reference Liu and Wood17]. An optimal bound of
$(t+1)$
-coloured with bounded clustering by Liu and Wood [Reference Liu and Wood17]. An optimal bound of
![]() $t-1$
colours was announced in 2017 by Dvořák and Norin [Reference Dvořák and Norin3]. A weaker bound on the number of colours, however with an explicit bound on the clustering, was previously shown by van den Heuvel and Wood, namely that every
$t-1$
colours was announced in 2017 by Dvořák and Norin [Reference Dvořák and Norin3]. A weaker bound on the number of colours, however with an explicit bound on the clustering, was previously shown by van den Heuvel and Wood, namely that every
![]() $K_t$
-minor-free graph is
$K_t$
-minor-free graph is
![]() $(2t-2)$
-colourable with clustering
$(2t-2)$
-colourable with clustering
![]() $\lceil \frac{1}{2}(t-2) \rceil$
. Theorem 1.3 extends this result by van den Heuvel and Wood to odd
$\lceil \frac{1}{2}(t-2) \rceil$
. Theorem 1.3 extends this result by van den Heuvel and Wood to odd
![]() $K_t$
-minor-free graphs.
$K_t$
-minor-free graphs.
In the remainder of this paper, we give the proof of Theorem 1.3. Our proof follows closely a method introduced by van den Heuvel and Wood in [Reference van den Heuvel and Wood8] to first establish a decomposition of the considered graphs into nicely structured disjoint subgraphs, from which a clustered colouring can then easily be obtained. Our decomposition result (Theorem 2.3) is similar to a corresponding result for
![]() $K_t$
-minor-free graphs by van den Heuvel and Wood, but enhances it by some additional features, through which the extension from
$K_t$
-minor-free graphs by van den Heuvel and Wood, but enhances it by some additional features, through which the extension from
![]() $K_t$
-minor-free graphs to odd
$K_t$
-minor-free graphs to odd
![]() $K_t$
-minor-free graphs becomes possible.
$K_t$
-minor-free graphs becomes possible.
2. Proof of Theorem 1.3
We need the following lemma proved by van den Heuvel and Wood in [Reference van den Heuvel and Wood8].
Lemma 2.1. (cf. Lemma 8, item (4) in [Reference van den Heuvel and Wood8]). Let
![]() $G$
be a connected graph, and let
$G$
be a connected graph, and let
![]() $S \subseteq V(G)$
be such that
$S \subseteq V(G)$
be such that
![]() $|S|=k \ge 1$
. Let
$|S|=k \ge 1$
. Let
![]() $H \subseteq G$
be an induced connected subgraph with a minimum number of vertices such that
$H \subseteq G$
be an induced connected subgraph with a minimum number of vertices such that
![]() $S \subseteq V(H)$
.
$S \subseteq V(H)$
.
Then
![]() $H$
admits a partition of its vertex-set into two disjoint (possibly empty) subsets
$H$
admits a partition of its vertex-set into two disjoint (possibly empty) subsets
![]() $A$
and
$A$
and
![]() $B$
such that both
$B$
such that both
![]() $G[A]$
and
$G[A]$
and
![]() $G[B]$
have all their connected components of size at most
$G[B]$
have all their connected components of size at most
![]() $\lceil \frac{k}{2} \rceil$
.
$\lceil \frac{k}{2} \rceil$
.
The main idea of our proof is the following modified version of the above lemma, which will be useful for constructing odd minors. We use the following notation: Given a graph
![]() $H$
and a partition of its vertex-set into subsets
$H$
and a partition of its vertex-set into subsets
![]() $A$
and
$A$
and
![]() $B$
, we denote by
$B$
, we denote by
![]() $H[A,B]$
the spanning bipartite subgraph containing all the edges with one endpoint in
$H[A,B]$
the spanning bipartite subgraph containing all the edges with one endpoint in
![]() $A$
and one endpoint in
$A$
and one endpoint in
![]() $B$
.
$B$
.
Lemma 2.2.
Let
![]() $G$
be a connected graph, and let
$G$
be a connected graph, and let
![]() $S \subseteq V(G)$
be such that
$S \subseteq V(G)$
be such that
![]() $|S|=k \ge 1$
. Then there exists a connected induced subgraph
$|S|=k \ge 1$
. Then there exists a connected induced subgraph
![]() $H \subseteq G$
with
$H \subseteq G$
with
![]() $S \subseteq V(H)$
such that the following hold:
$S \subseteq V(H)$
such that the following hold:
-
1.
 $H$
admits a partition of its vertex-set into two disjoint subsets
$H$
admits a partition of its vertex-set into two disjoint subsets
 $A$
and
$A$
and
 $B$
such that both
$B$
such that both
 $G[A]$
and
$G[A]$
and
 $G[B]$
have maximum component-size at most
$G[B]$
have maximum component-size at most
 $\lceil \frac{k}{2} \rceil$
.
$\lceil \frac{k}{2} \rceil$
. -
2.
 $H[A,B]$
is connected.
$H[A,B]$
is connected.
-
3. For every vertex
 $v \in V(G)\setminus V(H)$
which is adjacent in
$v \in V(G)\setminus V(H)$
which is adjacent in
 $G$
to at least one vertex in
$G$
to at least one vertex in
 $V(H)$
, there exist vertices
$V(H)$
, there exist vertices
 $a \in A$
and
$a \in A$
and
 $b \in B$
such that
$b \in B$
such that
 $av, bv \in E(G)$
.
$av, bv \in E(G)$
.
Proof. By Lemma 2.1, there exists at least one connected induced subgraph
![]() $H_0$
of
$H_0$
of
![]() $G$
such that
$G$
such that
![]() $S \subseteq V(H_0)$
and a partition of
$S \subseteq V(H_0)$
and a partition of
![]() $V(H_0)$
into subsets
$V(H_0)$
into subsets
![]() $A_0, B_0$
such that both
$A_0, B_0$
such that both
![]() $G[A_0], G[B_0]$
have maximum component-size at most
$G[A_0], G[B_0]$
have maximum component-size at most
![]() $\lceil \frac{k}{2} \rceil$
.
$\lceil \frac{k}{2} \rceil$
.
Now, let
![]() $(H,A,B)$
be a triple consisting of a connected induced subgraph
$(H,A,B)$
be a triple consisting of a connected induced subgraph
![]() $H \subseteq G$
with
$H \subseteq G$
with
![]() $S \subseteq V(H)$
and a partition
$S \subseteq V(H)$
and a partition
![]() $V(H)=A \cup B$
of its vertex-set such that
$V(H)=A \cup B$
of its vertex-set such that
![]() $G[A]$
and
$G[A]$
and
![]() $G[B]$
have maximum component-size at most
$G[B]$
have maximum component-size at most
![]() $\lceil \frac{k}{2}\rceil$
, chosen such that the number of edges in
$\lceil \frac{k}{2}\rceil$
, chosen such that the number of edges in
![]() $H[A,B]$
is maximized among all possible choices of such triples.
$H[A,B]$
is maximized among all possible choices of such triples.
We now claim that
![]() $H$
with the partition
$H$
with the partition
![]() $A, B$
satisfies all three properties required by the lemma. Statement
$A, B$
satisfies all three properties required by the lemma. Statement
![]() $(1)$
follows directly by our choice of the triple. To verify
$(1)$
follows directly by our choice of the triple. To verify
![]() $(2)$
, suppose towards a contradiction that
$(2)$
, suppose towards a contradiction that
![]() $H[A,B]$
is disconnected. This would mean that there exists a partition of
$H[A,B]$
is disconnected. This would mean that there exists a partition of
![]() $V(H)$
into non-empty sets
$V(H)$
into non-empty sets
![]() $X, Y$
such that there are no edges between
$X, Y$
such that there are no edges between
![]() $X \cap A$
and
$X \cap A$
and
![]() $Y \cap B$
, and no edges between
$Y \cap B$
, and no edges between
![]() $X \cap B$
and
$X \cap B$
and
![]() $Y \cap A$
in
$Y \cap A$
in
![]() $H$
. Now define a new partition of
$H$
. Now define a new partition of
![]() $V(H)$
by
$V(H)$
by
![]() $A'\;:\!=\;(X \cap A) \cup (Y \cap B)$
, and
$A'\;:\!=\;(X \cap A) \cup (Y \cap B)$
, and
![]() $B'\;:\!=\;(X \cap B) \cup (Y \cap A)$
. It is easy to see that since no edges in
$B'\;:\!=\;(X \cap B) \cup (Y \cap A)$
. It is easy to see that since no edges in
![]() $G$
connect
$G$
connect
![]() $X \cap A$
and
$X \cap A$
and
![]() $Y \cap B$
or
$Y \cap B$
or
![]() $X \cap B$
and
$X \cap B$
and
![]() $Y \cap A$
, every component of
$Y \cap A$
, every component of
![]() $G[A']$
or
$G[A']$
or
![]() $G[B']$
is fully contained in either
$G[B']$
is fully contained in either
![]() $A$
or
$A$
or
![]() $B$
. Hence it is contained in a component of either
$B$
. Hence it is contained in a component of either
![]() $G[A]$
or
$G[A]$
or
![]() $G[B]$
, and hence has size at most
$G[B]$
, and hence has size at most
![]() $\lceil \frac{k}{2}\rceil$
. However, since
$\lceil \frac{k}{2}\rceil$
. However, since
![]() $H$
is connected, there exists at least one edge
$H$
is connected, there exists at least one edge
![]() $e \in E(H)$
with endpoints in
$e \in E(H)$
with endpoints in
![]() $X$
and
$X$
and
![]() $Y$
. This edge must then connect
$Y$
. This edge must then connect
![]() $X \cap A$
and
$X \cap A$
and
![]() $Y \cap A$
or
$Y \cap A$
or
![]() $X \cap B$
and
$X \cap B$
and
![]() $Y \cap B$
. In each case,
$Y \cap B$
. In each case,
![]() $e$
is contained in the bipartite subgraph of
$e$
is contained in the bipartite subgraph of
![]() $H$
spanned between
$H$
spanned between
![]() $A'$
and
$A'$
and
![]() $B'$
. Also, every edge of
$B'$
. Also, every edge of
![]() $H[A,B]$
has exactly one endpoint in
$H[A,B]$
has exactly one endpoint in
![]() $A'$
and in
$A'$
and in
![]() $B'$
. Hence,
$B'$
. Hence,
![]() $(H,A',B')$
is a triple satisfying all required properties which has strictly more edges between different sets in the partition than
$(H,A',B')$
is a triple satisfying all required properties which has strictly more edges between different sets in the partition than
![]() $(H,A,B)$
. This is a contradiction to our choice of
$(H,A,B)$
. This is a contradiction to our choice of
![]() $(H,A,B)$
, and proves
$(H,A,B)$
, and proves
![]() $(2)$
.
$(2)$
.
Finally, let us verify
![]() $(3)$
. Towards a contradiction, suppose that there exists a vertex
$(3)$
. Towards a contradiction, suppose that there exists a vertex
![]() $v \in V(G)\setminus V(H)$
such that
$v \in V(G)\setminus V(H)$
such that
![]() $v$
is adjacent in
$v$
is adjacent in
![]() $G$
to at least one vertex in
$G$
to at least one vertex in
![]() $V(H)$
, but it does not have neighbours both in
$V(H)$
, but it does not have neighbours both in
![]() $A$
and in
$A$
and in
![]() $B$
. Then, w.l.o.g. (renaming
$B$
. Then, w.l.o.g. (renaming
![]() $A$
and
$A$
and
![]() $B$
if necessary) we may assume that
$B$
if necessary) we may assume that
![]() $v$
has no neighbours in
$v$
has no neighbours in
![]() $A$
. Now, let
$A$
. Now, let
![]() $H'\;:\!=\;G[V(H) \cup \{v\}]$
and put
$H'\;:\!=\;G[V(H) \cup \{v\}]$
and put
![]() $A'\;:\!=\;A \cup \{v\}$
and
$A'\;:\!=\;A \cup \{v\}$
and
![]() $B'\;:\!=\;B$
. Then
$B'\;:\!=\;B$
. Then
![]() $H'$
is a connected induced subgraph of
$H'$
is a connected induced subgraph of
![]() $G$
with
$G$
with
![]() $S \subseteq V(H)\subseteq V(H')$
. Since
$S \subseteq V(H)\subseteq V(H')$
. Since
![]() $v$
has no neighbours in
$v$
has no neighbours in
![]() $A$
, every component in
$A$
, every component in
![]() $G[A']$
or
$G[A']$
or
![]() $G[B']$
is either a component of
$G[B']$
is either a component of
![]() $G[A]$
or
$G[A]$
or
![]() $G[B]$
and hence has size at most
$G[B]$
and hence has size at most
![]() $\lceil \frac{k}{2}\rceil$
, or is equal to
$\lceil \frac{k}{2}\rceil$
, or is equal to
![]() $\{v\}$
and has size
$\{v\}$
and has size
![]() $1 \le \lceil \frac{k}{2}\rceil$
.
$1 \le \lceil \frac{k}{2}\rceil$
.
Furthermore, the number of edges in
![]() $H'$
spanned between
$H'$
spanned between
![]() $A'$
and
$A'$
and
![]() $B'$
is strictly greater than the number of edges in
$B'$
is strictly greater than the number of edges in
![]() $H$
spanned between
$H$
spanned between
![]() $A$
and
$A$
and
![]() $B$
, since in addition to these edges we have the edges incident to
$B$
, since in addition to these edges we have the edges incident to
![]() $v$
in
$v$
in
![]() $H'$
. This again shows that
$H'$
. This again shows that
![]() $(H',A',B')$
is a triple satisfying all required properties with more edges between different sets in the partition than
$(H',A',B')$
is a triple satisfying all required properties with more edges between different sets in the partition than
![]() $(H,A,B)$
, contradicting our maximality assumption. This shows that also
$(H,A,B)$
, contradicting our maximality assumption. This shows that also
![]() $(3)$
is satisfied for
$(3)$
is satisfied for
![]() $(H,A,B)$
and concludes the proof of the lemma. □
$(H,A,B)$
and concludes the proof of the lemma. □
We next use the above lemma to prove the following decomposition result, which resembles a corresponding decomposition theorem proved by van den Heuvel and Wood in [Reference van den Heuvel and Wood8] for
![]() $K_t$
-minor-free graphs (compare Theorem 11 in [Reference van den Heuvel and Wood8]). It extends part of the latter result with some additional features that will allow us to relate to odd minor containment instead of ordinary minor containment when building the decomposition of our graph. Once the decomposition theorem (Theorem 2.3 below) is established, Theorem 1.3 will follow easily. In the following, given a graph
$K_t$
-minor-free graphs (compare Theorem 11 in [Reference van den Heuvel and Wood8]). It extends part of the latter result with some additional features that will allow us to relate to odd minor containment instead of ordinary minor containment when building the decomposition of our graph. Once the decomposition theorem (Theorem 2.3 below) is established, Theorem 1.3 will follow easily. In the following, given a graph
![]() $G$
and two vertex-disjoint subgraphs
$G$
and two vertex-disjoint subgraphs
![]() $H_1$
and
$H_1$
and
![]() $H_2$
of
$H_2$
of
![]() $G$
, we say that
$G$
, we say that
![]() $H_1$
and
$H_1$
and
![]() $H_2$
are adjacent (in
$H_2$
are adjacent (in
![]() $G$
) if there exist vertices
$G$
) if there exist vertices
![]() $x \in V(H_1), y \in V(H_2)$
such that
$x \in V(H_1), y \in V(H_2)$
such that
![]() $xy \in E(G)$
.
$xy \in E(G)$
.
Theorem 2.3.
Let
![]() $t \ge 3$
be an integer, and let
$t \ge 3$
be an integer, and let
![]() $G$
be a connected graph without an odd
$G$
be a connected graph without an odd
![]() $K_t$
-minor. Then there exists
$K_t$
-minor. Then there exists
![]() $\ell \in \mathbb{N}$
and a collection
$\ell \in \mathbb{N}$
and a collection
![]() $H_1\ldots,H_\ell$
of vertex-disjoint induced connected subgraphs of
$H_1\ldots,H_\ell$
of vertex-disjoint induced connected subgraphs of
![]() $G$
with
$G$
with
![]() $V(H_1) \cup \cdots \cup V(H_\ell )=V(G)$
such that all of the following properties are satisfied for every
$V(H_1) \cup \cdots \cup V(H_\ell )=V(G)$
such that all of the following properties are satisfied for every
![]() $i \in [\ell ]$
:
$i \in [\ell ]$
:
-
1.
 $H_i$
admits a partition of its vertex-set into two disjoint parts
$H_i$
admits a partition of its vertex-set into two disjoint parts
 $A_i$
and
$A_i$
and
 $B_i$
such that in each of
$B_i$
such that in each of
 $G[A_i]$
,
$G[A_i]$
,
 $G[B_i]$
, the maximum component-size is at most
$G[B_i]$
, the maximum component-size is at most
 $\lceil \frac{t-2}{2} \rceil$
.
$\lceil \frac{t-2}{2} \rceil$
. -
2.
 $H_i[A_i,B_i]$
is connected.
$H_i[A_i,B_i]$
is connected.
-
3. For every vertex
 $v \in V(G)\setminus (V(H_1) \cup \cdots \cup V(H_i))$
which is adjacent in
$v \in V(G)\setminus (V(H_1) \cup \cdots \cup V(H_i))$
which is adjacent in
 $G$
to at least one vertex in
$G$
to at least one vertex in
 $V(H_i)$
, there exist vertices
$V(H_i)$
, there exist vertices
 $a \in A_i, b \in B_i$
such that
$a \in A_i, b \in B_i$
such that
 $av, bv \in E(G)$
.
$av, bv \in E(G)$
. -
4. For every connected component
 $C$
of
$C$
of
 $G-(V(H_1) \cup \cdots \cup V(H_i))$
, at most
$G-(V(H_1) \cup \cdots \cup V(H_i))$
, at most
 $(t-2)$
among the subgraphs
$(t-2)$
among the subgraphs
 $H_1, \ldots, H_i$
are adjacent to
$H_1, \ldots, H_i$
are adjacent to
 $C$
, and these subgraphs are pairwise adjacent to each other.
$C$
, and these subgraphs are pairwise adjacent to each other.
Proof. We construct the induced connected subgraphs
![]() $H_1,\ldots,H_\ell$
iteratively, maintaining the properties
$H_1,\ldots,H_\ell$
iteratively, maintaining the properties
![]() $(1)-(4)$
for all already constructed subgraphs in the sequence during the process.
$(1)-(4)$
for all already constructed subgraphs in the sequence during the process.
Let
![]() $\mathcal{Z}$
denote the collection of all vertex-subsets
$\mathcal{Z}$
denote the collection of all vertex-subsets
![]() $Z \subseteq V(G)$
such that
$Z \subseteq V(G)$
such that
![]() $G[Z]$
is bipartite and connected (note that
$G[Z]$
is bipartite and connected (note that
![]() $\mathcal{Z} \neq \emptyset$
, since every singleton-set in
$\mathcal{Z} \neq \emptyset$
, since every singleton-set in
![]() $V(G)$
belongs to
$V(G)$
belongs to
![]() $\mathcal{Z}$
). Let now
$\mathcal{Z}$
). Let now
![]() $X \in \mathcal{Z}$
be an inclusion-wise maximal member of
$X \in \mathcal{Z}$
be an inclusion-wise maximal member of
![]() $\mathcal{Z}$
. Define
$\mathcal{Z}$
. Define
![]() $H_1\;:\!=\;G[X]$
. By choice of
$H_1\;:\!=\;G[X]$
. By choice of
![]() $X$
, the subgraph
$X$
, the subgraph
![]() $H_1$
of
$H_1$
of
![]() $G$
is induced, bipartite and connected. Let us further verify that the invariants
$G$
is induced, bipartite and connected. Let us further verify that the invariants
![]() $(1)-(4)$
are satisfied: To verify
$(1)-(4)$
are satisfied: To verify
![]() $(1)$
, we can simply let
$(1)$
, we can simply let
![]() $A_1, B_1$
be the colour classes of a bipartition of
$A_1, B_1$
be the colour classes of a bipartition of
![]() $H_1$
. Item
$H_1$
. Item
![]() $(2)$
is satisfied trivially, since
$(2)$
is satisfied trivially, since
![]() $H_1$
is connected and all edges of
$H_1$
is connected and all edges of
![]() $H_1$
join
$H_1$
join
![]() $A_1$
and
$A_1$
and
![]() $B_1$
. For item
$B_1$
. For item
![]() $(3)$
, consider any vertex
$(3)$
, consider any vertex
![]() $v \in V(G)\setminus X$
which has a neighbour in
$v \in V(G)\setminus X$
which has a neighbour in
![]() $X$
. We have
$X$
. We have
![]() $X \cup \{v\} \notin \mathcal{Z}$
by our choice of
$X \cup \{v\} \notin \mathcal{Z}$
by our choice of
![]() $X$
, and hence,
$X$
, and hence,
![]() $G[X \cup \{v\}]$
is non-bipartite. This means that
$G[X \cup \{v\}]$
is non-bipartite. This means that
![]() $v$
must have neighbours both in
$v$
must have neighbours both in
![]() $A_1$
and
$A_1$
and
![]() $B_1$
, for otherwise either
$B_1$
, for otherwise either
![]() $(A_1 \cup \{v\},B_1)$
or
$(A_1 \cup \{v\},B_1)$
or
![]() $(A_1,B_1\cup \{v\})$
would form a bipartition of
$(A_1,B_1\cup \{v\})$
would form a bipartition of
![]() $G[X \cup \{v\}]$
. Finally, this implies that there are neighbours
$G[X \cup \{v\}]$
. Finally, this implies that there are neighbours
![]() $a \in A_1, b \in B_1$
of
$a \in A_1, b \in B_1$
of
![]() $v$
, as required. Finally, item
$v$
, as required. Finally, item
![]() $(4)$
is trivially satisfied, since
$(4)$
is trivially satisfied, since
![]() $t-2 \ge 1$
.
$t-2 \ge 1$
.
Next, suppose that for some integer
![]() $i \ge 1$
we have already constructed disjoint induced connected subgraphs
$i \ge 1$
we have already constructed disjoint induced connected subgraphs
![]() $H_1,\ldots,H_i$
of
$H_1,\ldots,H_i$
of
![]() $G$
, each satisfying the invariants
$G$
, each satisfying the invariants
![]() $(1)-(4)$
, but such that
$(1)-(4)$
, but such that
![]() $V(H_1) \cup \cdots \cup V(H_i) \neq V(G)$
. Now, pick (arbitrarily) a connected component
$V(H_1) \cup \cdots \cup V(H_i) \neq V(G)$
. Now, pick (arbitrarily) a connected component
![]() $C$
of the graph
$C$
of the graph
![]() $G-(V(H_1) \cup \cdots \cup V(H_i))$
. Let
$G-(V(H_1) \cup \cdots \cup V(H_i))$
. Let
![]() $Q_1,\ldots,Q_k$
be the (ordered) sublist of
$Q_1,\ldots,Q_k$
be the (ordered) sublist of
![]() $H_1,\ldots,H_i$
, containing exactly those subgraphs which are adjacent to
$H_1,\ldots,H_i$
, containing exactly those subgraphs which are adjacent to
![]() $G[C]$
. Since
$G[C]$
. Since
![]() $G$
is connected, we have
$G$
is connected, we have
![]() $k \ge 1$
. By the invariant
$k \ge 1$
. By the invariant
![]() $(4)$
we furthermore know that
$(4)$
we furthermore know that
![]() $k \le t-2$
and that
$k \le t-2$
and that
![]() $Q_1, \ldots, Q_k$
are pairwise adjacent to each other. For every index
$Q_1, \ldots, Q_k$
are pairwise adjacent to each other. For every index
![]() $j \in [k]$
, by definition there exists a vertex
$j \in [k]$
, by definition there exists a vertex
![]() $v_j \in C$
such that
$v_j \in C$
such that
![]() $v_j$
has a neighbour in
$v_j$
has a neighbour in
![]() $Q_j$
. Let
$Q_j$
. Let
![]() $S\;:\!=\;\{v_1,\ldots,v_k\}$
. Now, apply Lemma 2.2 to the connected graph
$S\;:\!=\;\{v_1,\ldots,v_k\}$
. Now, apply Lemma 2.2 to the connected graph
![]() $G[C]$
and the set
$G[C]$
and the set
![]() $S$
. We conclude that there exists an induced and connected subgraph
$S$
. We conclude that there exists an induced and connected subgraph
![]() $H$
of
$H$
of
![]() $G$
such that
$G$
such that
![]() $S \subseteq V(H) \subseteq C$
, equipped with a partition of its vertex-sets into subsets
$S \subseteq V(H) \subseteq C$
, equipped with a partition of its vertex-sets into subsets
![]() $A$
and
$A$
and
![]() $B$
such that
$B$
such that
-
• all components of
 $G[A]$
and
$G[A]$
and
 $G[B]$
have size at most
$G[B]$
have size at most
 $\left \lceil \frac{|S|}{2} \right \rceil \le \lceil \frac{k}{2} \rceil \le \lceil \frac{t-2}{2} \rceil$
,
$\left \lceil \frac{|S|}{2} \right \rceil \le \lceil \frac{k}{2} \rceil \le \lceil \frac{t-2}{2} \rceil$
, -
•
 $H[A,B]$
is connected,
$H[A,B]$
is connected, -
• every vertex
 $v \in C\setminus V(H)$
which is adjacent to a vertex in
$v \in C\setminus V(H)$
which is adjacent to a vertex in
 $V(H)$
has neighbours both in
$V(H)$
has neighbours both in
 $A$
and in
$A$
and in
 $B$
.
$B$
.
We now finally define
![]() $H_{i+1}\;:\!=\;H$
and
$H_{i+1}\;:\!=\;H$
and
![]() $A_{i+1}\;:\!=\;A, B_{i+1}\;:\!=\;B$
, and claim that the extended sequence
$A_{i+1}\;:\!=\;A, B_{i+1}\;:\!=\;B$
, and claim that the extended sequence
![]() $H_1,\ldots, H_i, H_{i+1}$
still satisfies the invariants
$H_1,\ldots, H_i, H_{i+1}$
still satisfies the invariants
![]() $(1)-(4)$
. That the invariants
$(1)-(4)$
. That the invariants
![]() $(1)$
and
$(1)$
and
![]() $(2)$
remain valid is an immediate consequence of the first two properties of
$(2)$
remain valid is an immediate consequence of the first two properties of
![]() $H$
listed above. Let us now verify that invariants
$H$
listed above. Let us now verify that invariants
![]() $(3)$
and
$(3)$
and
![]() $(4)$
hold (and clearly, these need only be checked for the index
$(4)$
hold (and clearly, these need only be checked for the index
![]() $i+1$
, since the claim is satisfied for smaller indices by assumption).
$i+1$
, since the claim is satisfied for smaller indices by assumption).
For invariant
![]() $(3)$
, let a vertex
$(3)$
, let a vertex
![]() $v \in V(G) \setminus (V(H_1) \cup \cdots \cup V(H_i) \cup V(H_{i+1}))$
be given arbitrarily, and suppose that
$v \in V(G) \setminus (V(H_1) \cup \cdots \cup V(H_i) \cup V(H_{i+1}))$
be given arbitrarily, and suppose that
![]() $v$
has at least one neighbour in
$v$
has at least one neighbour in
![]() $H_{i+1}$
. Note that this implies that
$H_{i+1}$
. Note that this implies that
![]() $v \in C$
, since
$v \in C$
, since
![]() $C$
is a connected component of
$C$
is a connected component of
![]() $G-(V(H_1) \cup \cdots \cup V(H_i))$
and
$G-(V(H_1) \cup \cdots \cup V(H_i))$
and
![]() $V(H_{i+1})=V(H) \subseteq C$
. Therefore, by the third property of
$V(H_{i+1})=V(H) \subseteq C$
. Therefore, by the third property of
![]() $H$
listed above, we conclude that
$H$
listed above, we conclude that
![]() $v$
has neighbours both in
$v$
has neighbours both in
![]() $A_{i+1}=A$
and in
$A_{i+1}=A$
and in
![]() $B_{i+1}=B$
. This verifies that the invariant
$B_{i+1}=B$
. This verifies that the invariant
![]() $(3)$
remains satisfied.
$(3)$
remains satisfied.
Finally, let us consider invariant
![]() $(4)$
. For this purpose, let a connected component
$(4)$
. For this purpose, let a connected component
![]() $C'$
of the graph
$C'$
of the graph
![]() $G-(V(H_1) \cup \cdots \cup V(H_i) \cup V(H_{i+1}))$
be given to us arbitrarily. Let
$G-(V(H_1) \cup \cdots \cup V(H_i) \cup V(H_{i+1}))$
be given to us arbitrarily. Let
![]() $\mathcal{Q} \subseteq \{H_1,\ldots,H_i,H_{i+1}\}$
contain all the subgraphs adjacent to
$\mathcal{Q} \subseteq \{H_1,\ldots,H_i,H_{i+1}\}$
contain all the subgraphs adjacent to
![]() $G[C']$
in
$G[C']$
in
![]() $G$
. In order to verify invariant
$G$
. In order to verify invariant
![]() $(4)$
for
$(4)$
for
![]() $C'$
, we need to show that
$C'$
, we need to show that
![]() $|\mathcal{Q}|\le t-2$
and that the members of
$|\mathcal{Q}|\le t-2$
and that the members of
![]() $\mathcal{Q}$
are pairwise adjacent to each other.
$\mathcal{Q}$
are pairwise adjacent to each other.
Since
![]() $C$
is a connected component of
$C$
is a connected component of
![]() $G-(V(H_1) \cup \cdots \cup V(H_i))$
, we must either have
$G-(V(H_1) \cup \cdots \cup V(H_i))$
, we must either have
![]() $C' \cap C=\emptyset$
or
$C' \cap C=\emptyset$
or
![]() $C' \subseteq C$
, for otherwise
$C' \subseteq C$
, for otherwise
![]() $C \cup C'$
would induce a connected subgraph of
$C \cup C'$
would induce a connected subgraph of
![]() $G-(V(H_1) \cup \cdots \cup V(H_i))$
and strictly contain
$G-(V(H_1) \cup \cdots \cup V(H_i))$
and strictly contain
![]() $C$
, a contradiction. For the same reason, if
$C$
, a contradiction. For the same reason, if
![]() $C' \cap C = \emptyset$
then there is no edge in
$C' \cap C = \emptyset$
then there is no edge in
![]() $G$
connecting
$G$
connecting
![]() $C$
to
$C$
to
![]() $C'$
, and hence
$C'$
, and hence
![]() $C'$
in particular forms a connected component also of the graph
$C'$
in particular forms a connected component also of the graph
![]() $G-(V(H_1) \cup \cdots \cup V(H_i))$
, and
$G-(V(H_1) \cup \cdots \cup V(H_i))$
, and
![]() $H_{i+1} \notin \mathcal{Q}$
. Therefore, in the case
$H_{i+1} \notin \mathcal{Q}$
. Therefore, in the case
![]() $C' \cap C = \emptyset$
the facts that
$C' \cap C = \emptyset$
the facts that
![]() $|\mathcal{Q}|\le t-2$
and that the members of
$|\mathcal{Q}|\le t-2$
and that the members of
![]() $\mathcal{Q}$
are pairwise adjacent to each other follow from invariant
$\mathcal{Q}$
are pairwise adjacent to each other follow from invariant
![]() $(4)$
for index
$(4)$
for index
![]() $i$
, which is satisfied by our initial assumptions.
$i$
, which is satisfied by our initial assumptions.
Moving on, suppose that
![]() $C' \subseteq C$
. Then we clearly must have
$C' \subseteq C$
. Then we clearly must have
![]() $\mathcal{Q} \subseteq \{Q_1,\ldots,Q_k,H_{i+1}\}$
. Note that by invariant
$\mathcal{Q} \subseteq \{Q_1,\ldots,Q_k,H_{i+1}\}$
. Note that by invariant
![]() $(4)$
for index
$(4)$
for index
![]() $i$
(applied with the component
$i$
(applied with the component
![]() $C$
), the subgraphs
$C$
), the subgraphs
![]() $Q_1,\ldots,Q_k$
are pairwise adjacent in
$Q_1,\ldots,Q_k$
are pairwise adjacent in
![]() $G$
. Furthermore, since
$G$
. Furthermore, since
![]() $S=\{v_1,\ldots,v_k\} \subseteq V(H)=V(H_{i+1})$
by our choice of
$S=\{v_1,\ldots,v_k\} \subseteq V(H)=V(H_{i+1})$
by our choice of
![]() $H$
, we know that
$H$
, we know that
![]() $H_{i+1}$
is adjacent to each of
$H_{i+1}$
is adjacent to each of
![]() $Q_1,\ldots,Q_k$
in
$Q_1,\ldots,Q_k$
in
![]() $G$
. Hence, the members of
$G$
. Hence, the members of
![]() $\mathcal{Q}$
are pairwise adjacent to each other. It remains to be shown that
$\mathcal{Q}$
are pairwise adjacent to each other. It remains to be shown that
![]() $|\mathcal{Q}| \le t-2$
. Towards a contradiction, suppose that
$|\mathcal{Q}| \le t-2$
. Towards a contradiction, suppose that
![]() $|\mathcal{Q}| \ge t-1$
. We have
$|\mathcal{Q}| \ge t-1$
. We have
![]() $k \le t-2$
, and therefore this is only possible if
$k \le t-2$
, and therefore this is only possible if
![]() $k=t-2$
and
$k=t-2$
and
![]() $\mathcal{Q}=\{Q_1,\ldots,Q_{t-2},H_{i+1}\}$
.
$\mathcal{Q}=\{Q_1,\ldots,Q_{t-2},H_{i+1}\}$
.
We will now obtain the desired contradiction to the above assumption by constructing an odd
![]() $K_t$
-model which is a subgraph of
$K_t$
-model which is a subgraph of
![]() $G$
(clearly this does not exist by assumption on
$G$
(clearly this does not exist by assumption on
![]() $G$
). Let us denote by
$G$
). Let us denote by
![]() $i_1\lt i_2\lt \cdots \lt i_{t-1}=i+1$
the sequence of indices such that
$i_1\lt i_2\lt \cdots \lt i_{t-1}=i+1$
the sequence of indices such that
![]() $\{Q_1,\ldots,Q_{t-2},H_{i+1}\}=\{H_{i_1},\ldots,H_{i_{t-1}}\}$
. By invariant
$\{Q_1,\ldots,Q_{t-2},H_{i+1}\}=\{H_{i_1},\ldots,H_{i_{t-1}}\}$
. By invariant
![]() $(2)$
for
$(2)$
for
![]() $H_1, \ldots, H_i, H_{i+1}$
, for every
$H_1, \ldots, H_i, H_{i+1}$
, for every
![]() $s \in [i+1]$
we know that
$s \in [i+1]$
we know that
![]() $H_s[A_s,B_s]$
is connected, and therefore admits a spanning tree
$H_s[A_s,B_s]$
is connected, and therefore admits a spanning tree
![]() $T_s$
. This is a spanning tree of
$T_s$
. This is a spanning tree of
![]() $H_s$
which uses only edges spanned between
$H_s$
which uses only edges spanned between
![]() $A_s$
and
$A_s$
and
![]() $B_s$
, for every
$B_s$
, for every
![]() $s \in [i+1]$
. Furthermore, let
$s \in [i+1]$
. Furthermore, let
![]() $T$
be any fixed spanning tree of the connected graph
$T$
be any fixed spanning tree of the connected graph
![]() $G[C']$
. Finally, consider a
$G[C']$
. Finally, consider a
![]() $2$
-colour-assignment
$2$
-colour-assignment
![]() $c:\left (\bigcup _{j=1}^{t-1}{V(T_{i_j})}\right ) \cup V(T) \rightarrow \{1,2\}$
to the vertices in the
$c:\left (\bigcup _{j=1}^{t-1}{V(T_{i_j})}\right ) \cup V(T) \rightarrow \{1,2\}$
to the vertices in the
![]() $t$
disjoint trees
$t$
disjoint trees
![]() $T_{i_1},\ldots,T_{i_{t-1}}, T$
by piecing together proper
$T_{i_1},\ldots,T_{i_{t-1}}, T$
by piecing together proper
![]() $2$
-colourings of the individual trees. To finish the construction of the odd
$2$
-colourings of the individual trees. To finish the construction of the odd
![]() $K_t$
-model, we need the following claim.
$K_t$
-model, we need the following claim.
![]() $(\ast )$
Any pair of two distinct trees from the collection
$(\ast )$
Any pair of two distinct trees from the collection
![]() $T_{i_1},\ldots,T_{i_{t-1}}, T$
is joined by at least one edge
$T_{i_1},\ldots,T_{i_{t-1}}, T$
is joined by at least one edge
![]() $xy \in E(G)$
satisfying
$xy \in E(G)$
satisfying
![]() $c(x)=c(y)$
.
$c(x)=c(y)$
.
Proof of (*). Consider first the case that the pair of trees is of the form
![]() $T_{s_1}, T_{s_2}$
with
$T_{s_1}, T_{s_2}$
with
![]() $s_1\lt s_2$
and
$s_1\lt s_2$
and
![]() $s_1, s_2 \in \{i_1,\ldots,i_{t-1}\}$
. Then, since
$s_1, s_2 \in \{i_1,\ldots,i_{t-1}\}$
. Then, since
![]() $H_{s_1}, H_{s_2} \in \mathcal{Q}$
are adjacent, there exists a vertex
$H_{s_1}, H_{s_2} \in \mathcal{Q}$
are adjacent, there exists a vertex
![]() $y \in V(T_{s_2})=V(H_{s_2})$
which is adjacent to a vertex in
$y \in V(T_{s_2})=V(H_{s_2})$
which is adjacent to a vertex in
![]() $V(T_{s_1})=V(H_{s_1})$
. By invariant
$V(T_{s_1})=V(H_{s_1})$
. By invariant
![]() $(3)$
, applied for the index
$(3)$
, applied for the index
![]() $s_1$
and the vertex
$s_1$
and the vertex
![]() $y$
, we find that
$y$
, we find that
![]() $y$
must have neighbours
$y$
must have neighbours
![]() $a \in A_{s_1}$
and
$a \in A_{s_1}$
and
![]() $b \in B_{s_1}$
in
$b \in B_{s_1}$
in
![]() $G$
. Note that since
$G$
. Note that since
![]() $c$
restricted to
$c$
restricted to
![]() $V(T_{s_1})$
is a proper colouring, we must have
$V(T_{s_1})$
is a proper colouring, we must have
![]() $c(a) \neq c(b)$
. Hence, there exists
$c(a) \neq c(b)$
. Hence, there exists
![]() $x \in \{a,b\}$
with
$x \in \{a,b\}$
with
![]() $c(x)=c(y)$
, and the edge
$c(x)=c(y)$
, and the edge
![]() $xy \in E(G)$
connecting
$xy \in E(G)$
connecting
![]() $T_{s_1}$
and
$T_{s_1}$
and
![]() $T_{s_2}$
verifies
$T_{s_2}$
verifies
![]() $(\ast )$
in this case.
$(\ast )$
in this case.
Secondly, consider the case that the pair of trees is of the form
![]() $T_s, T$
for some
$T_s, T$
for some
![]() $s \in \{i_1,\ldots,i_{t-1}\}$
. Since
$s \in \{i_1,\ldots,i_{t-1}\}$
. Since
![]() $G[C']$
by definition is adjacent to every member of
$G[C']$
by definition is adjacent to every member of
![]() $\mathcal{Q}$
, which includes
$\mathcal{Q}$
, which includes
![]() $H_s$
, analogous to the previous case there exists a vertex
$H_s$
, analogous to the previous case there exists a vertex
![]() $y \in V(T)$
which is joined to
$y \in V(T)$
which is joined to
![]() $H_s$
. Applying the invariant
$H_s$
. Applying the invariant
![]() $(3)$
with the index
$(3)$
with the index
![]() $s$
and the vertex
$s$
and the vertex
![]() $y$
now yields that there are neighbours
$y$
now yields that there are neighbours
![]() $a \in A_s, b \in B_s$
of
$a \in A_s, b \in B_s$
of
![]() $y$
. As above, we conclude that since
$y$
. As above, we conclude that since
![]() $c(a)\neq c(b)$
there exists
$c(a)\neq c(b)$
there exists
![]() $x \in \{a,b\}$
with
$x \in \{a,b\}$
with
![]() $c(x)=c(y)$
. The edge
$c(x)=c(y)$
. The edge
![]() $xy$
is monochromatic and connects
$xy$
is monochromatic and connects
![]() $T_s$
and
$T_s$
and
![]() $T$
, thus
$T$
, thus
![]() $(\ast )$
is verified also in the second case.
$(\ast )$
is verified also in the second case.
This proves
![]() $(\ast )$
.
$(\ast )$
.
Now the collection of the
![]() $t$
disjoint trees
$t$
disjoint trees
![]() $T_{i_1},\ldots,T_{i_{t-1}}, T$
in
$T_{i_1},\ldots,T_{i_{t-1}}, T$
in
![]() $G$
, the colouring
$G$
, the colouring
![]() $c$
as well as the monochromatic edges guaranteed between each pair of trees by
$c$
as well as the monochromatic edges guaranteed between each pair of trees by
![]() $(\ast )$
certify that
$(\ast )$
certify that
![]() $G$
contains an odd
$G$
contains an odd
![]() $K_t$
-model. This is a contradiction to the assumption that
$K_t$
-model. This is a contradiction to the assumption that
![]() $G$
is odd
$G$
is odd
![]() $K_t$
-minor-free, and hence, our above assumption that
$K_t$
-minor-free, and hence, our above assumption that
![]() $|\mathcal{Q}| \ge t-1$
was wrong. This concludes the proof that also the invariant
$|\mathcal{Q}| \ge t-1$
was wrong. This concludes the proof that also the invariant
![]() $(4)$
remains satisfied after extending the sequence
$(4)$
remains satisfied after extending the sequence
![]() $H_1,\ldots,H_i$
of subgraphs by
$H_1,\ldots,H_i$
of subgraphs by
![]() $H_{i+1}$
.
$H_{i+1}$
.
Finally, since all the subgraphs
![]() $H_1, H_2, \ldots$
as defined above are non-empty, after finitely many steps the union of the subgraphs will cover all vertices of
$H_1, H_2, \ldots$
as defined above are non-empty, after finitely many steps the union of the subgraphs will cover all vertices of
![]() $G$
, i.e., we will find an integer
$G$
, i.e., we will find an integer
![]() $\ell \ge 1$
such that
$\ell \ge 1$
such that
![]() $V(H_1) \cup \cdots \cup V(H_\ell )=V(G)$
forms a partition of
$V(H_1) \cup \cdots \cup V(H_\ell )=V(G)$
forms a partition of
![]() $G$
, with all four invariants
$G$
, with all four invariants
![]() $(1)-(4)$
satisfied for each index
$(1)-(4)$
satisfied for each index
![]() $i \in [\ell ]$
. This concludes the proof of the theorem. □
$i \in [\ell ]$
. This concludes the proof of the theorem. □
After having done the main bulk of work in the previous proof, we can now easily conclude Theorem 1.3.
Proof of Theorem
1.3. Let
![]() $t \ge 3$
be an integer an let
$t \ge 3$
be an integer an let
![]() $G$
be any given odd
$G$
be any given odd
![]() $K_t$
-minor-free graph. W.l.o.g. we may assume that
$K_t$
-minor-free graph. W.l.o.g. we may assume that
![]() $G$
is connected. We apply Theorem 2.3 to obtain a collection
$G$
is connected. We apply Theorem 2.3 to obtain a collection
![]() $H_1, \ldots, H_\ell$
of connected induced subgraphs of
$H_1, \ldots, H_\ell$
of connected induced subgraphs of
![]() $G$
such that
$G$
such that
-
•
 $V(H_1), \ldots, V(H_\ell )$
forms a partition of
$V(H_1), \ldots, V(H_\ell )$
forms a partition of
 $V(G)$
,
$V(G)$
, -
• every graph
 $H_i$
with
$H_i$
with
 $i \in [\ell ]$
admits a
$i \in [\ell ]$
admits a
 $2$
-colouring
$2$
-colouring
 $f_i:V(H_i) \rightarrow \{1,2\}$
with monochromatic components of size at most
$f_i:V(H_i) \rightarrow \{1,2\}$
with monochromatic components of size at most
 $\lceil \frac{t-2}{2}\rceil$
(by property
$\lceil \frac{t-2}{2}\rceil$
(by property
 $(1)$
in Theorem 2.3), and
$(1)$
in Theorem 2.3), and -
• for every
 $1 \le i \lt \ell$
the subgraph
$1 \le i \lt \ell$
the subgraph
 $H_{i+1}$
is adjacent in
$H_{i+1}$
is adjacent in
 $G$
to at most
$G$
to at most
 $t-2$
among the subgraphs
$t-2$
among the subgraphs
 $H_1,\ldots,H_{i}$
(by property
$H_1,\ldots,H_{i}$
(by property
 $(4)$
in Theorem 2.3, applied to the connected component of
$(4)$
in Theorem 2.3, applied to the connected component of
 $G-(V(H_1) \cup \cdots \cup V(H_i))$
which contains
$G-(V(H_1) \cup \cdots \cup V(H_i))$
which contains
 $V(H_{i+1})$
).
$V(H_{i+1})$
).
Now define an auxiliary simple graph on the vertex-set
![]() $[\ell ]$
, in which two indices
$[\ell ]$
, in which two indices
![]() $i, j \in [\ell ]$
are made adjacent if and only if the subgraphs
$i, j \in [\ell ]$
are made adjacent if and only if the subgraphs
![]() $H_i$
and
$H_i$
and
![]() $H_j$
are adjacent in
$H_j$
are adjacent in
![]() $G$
. By the third item above, this graph is
$G$
. By the third item above, this graph is
![]() $(t-2)$
-degenerate, and hence, it has chromatic number at most
$(t-2)$
-degenerate, and hence, it has chromatic number at most
![]() $(t-2)+1=t-1$
. Fix a proper
$(t-2)+1=t-1$
. Fix a proper
![]() $(t-1)$
-colouring
$(t-1)$
-colouring
![]() $f:[\ell ]\rightarrow [t-1]$
of this auxiliary graph. Now consider the product colouring
$f:[\ell ]\rightarrow [t-1]$
of this auxiliary graph. Now consider the product colouring
![]() $g:V(G) \rightarrow [t-1] \times \{1,2\}$
, defined by
$g:V(G) \rightarrow [t-1] \times \{1,2\}$
, defined by
![]() $g(x)\;:\!=\;(f(i), f_i(x))$
for every
$g(x)\;:\!=\;(f(i), f_i(x))$
for every
![]() $x \in V(H_i)$
. From the definition of the auxiliary graph and since
$x \in V(H_i)$
. From the definition of the auxiliary graph and since
![]() $f$
is a proper colouring we have that every monochromatic component in
$f$
is a proper colouring we have that every monochromatic component in
![]() $G$
with respect to the colouring
$G$
with respect to the colouring
![]() $g$
must be fully included in
$g$
must be fully included in
![]() $V(H_i)$
for some
$V(H_i)$
for some
![]() $i \in [\ell ]$
. But then it is a monochromatic component also of the colouring
$i \in [\ell ]$
. But then it is a monochromatic component also of the colouring
![]() $f_i$
of
$f_i$
of
![]() $H_i$
. Hence, by the second item above it cannot be of size more than
$H_i$
. Hence, by the second item above it cannot be of size more than
![]() $\lceil \frac{t-2}{2}\rceil$
. Since
$\lceil \frac{t-2}{2}\rceil$
. Since
![]() $g$
uses a colour-set of size
$g$
uses a colour-set of size
![]() $2(t-1)$
, this proves the claim of the theorem. □
$2(t-1)$
, this proves the claim of the theorem. □