Observations of pumping and vortex dynamics due to a cylinder oscillating normal to a plane wall

Abstract

Understanding the fluid dynamics associated with a circular cylinder oscillating normal to a plane wall is important for safe design of offshore infrastructure, such as power cables and pipeline risers. This paper investigates the fluid dynamics of an oscillating cylinder with no imposed incident current experimentally using flow visualisation and force measurements where the ratio of the cylinder Reynolds number ($Re$) to Keulegan–Carpenter number ($KC$) is $\beta =500$ and $KC$ varies between 2 and 12. The minimum distance between the cylinder and wall was between 12.5 % and $50\,\%$ of the diameter. Across this parameter space three primary vortex flow regimes were observed: (i) for $KC\leq 5$, the flow field is approximately symmetric about the cylinder centreline and the velocity field between the cylinder and the wall resembled a pumping flow in phase with cylinder motion, which is well predicted by potential theory for most of the cycle; (ii) for $5< KC<8$, the flow field is increasingly asymmetric but with frequent switching of the side associated with vortex shedding; and (iii) for $KC\geq 8$, the flow field is consistently asymmetric due to vortex shedding. The in-line force increases when the cylinder is near the wall due to dynamic pressures associated with pumping. This increase can be estimated using potential theory superimposed onto the force time history for an isolated cylinder at the same $KC$ and $Re$. This study complements recent numerical modelling focused on low Reynolds number conditions and provides important insights into the fluid mechanics associated with trenching beneath cable and pipeline risers.

1. Introduction

The oscillation of a circular cylinder in otherwise still fluid induces flow patterns that differ with the amplitude and frequency of oscillations (e.g. Tatsuno & Bearman 1990). With the addition of a nearby solid boundary, these flow patterns are further modified, depending on the proximity of cylinder motions to the boundary. Understanding this modified fluid–structure interaction is important for a number of practical applications, including the near-seabed behaviour of power cables and pipeline risers, as well as the installation of cables and pipelines. In each of these applications the cables and risers can be excited by near-surface wave and current loading, resulting in oscillations close to the seabed despite the absence of near-bed flows. For example, significant trenches have been observed to develop in the seabed at the touchdown zone of steel catenary risers (Bridge 2005), which experience near-seabed motion amplitudes of up to two diameters. These motions and the trenches that are generated influence internal stresses in the riser, which complicates fatigue estimates (e.g. Shiri 2014; Clukey et al. 2017). Similar challenges also exist for electrical cables connected to offshore wind turbines (Rezaei 2017). Understanding the fluid dynamics near the seabed is therefore critical for predicting the development of trenches and, in turn, cable and pipeline fatigue.

To investigate the underlying physics, we can simplify the problem to that of a cylindrical object oscillating with sinusoidal motion near a flat, rigid seabed. Dimensional considerations suggest the following functional form for the flow field (figure 1):

(1.1)\begin{equation} \boldsymbol{u}(x,y,t)=f\left(D, T, A=\frac{V_mT}{2{\rm \pi}}, \nu, h_{min}\right), \end{equation}

where $\boldsymbol {u}(x,y,t)$ is the two-dimensional fluid velocity vector in time, $D$ is the cylinder diameter, $T$ is the period of oscillation, $A$ is the amplitude of motion (defined from the maximum vertical cylinder velocity for sinusoidal motion, $V_m$), $\nu$ is the fluid kinematic viscosity and $h_{min}$ is the minimum distance between the cylinder and the wall. Equation (1.1) can be rewritten in terms of three controlling non-dimensional groups

(1.2)\begin{equation} \frac{\boldsymbol{u}(x,y,t)}{V_{m}}=f\left(KC=\frac{2{\rm \pi} A}{D}, \beta=\frac{D^2}{T \nu}, \frac{h_{min}}{D}\right), \end{equation}

where $KC$ is the Keulegan–Carpenter number, the $\beta$ parameter represents the ratio of $Re$ to $KC$ (where $Re$ is the Reynolds number defined by $Re=V_mD/\nu$) and $h_{min}/D$ is the minimum gap between the cylinder and the wall.

Figure 1. Problem definition.

Various parts of the parameter space implied by (1.2) have been studied before. For example, the flow field around a sinusoidally oscillating cylinder far from any boundaries (i.e. an ‘isolated’ cylinder – $h_{min}/D \to \infty$) is a classical problem in fluid mechanics. For this scenario, Tatsuno & Bearman (1990) observed a family of different flow regimes, with the existence of each regime being dependent on both $KC$ and $\beta$ when $\beta \lesssim 160$. In contrast, for larger $\beta$, the different regimes depended predominantly on $KC$ only. Williamson (1985) explored the same problem across the parameter space $KC<60$ and $\beta <730$. For $KC<4$ a pair of symmetric vortices was shown to form on the trailing side of the cylinder, which vortices do not shed during motion but detach upon cylinder reversal. In the range $4< KC<7$, the vortices become increasingly asymmetric in strength and do not shed during a half-cycle. From $7< KC<13$, the oscillation amplitude is sufficient for vortex shedding to occur; and a transverse vortex street forms with two vortices per cycle convecting away at an angle from the oscillation axis. For $13\geq KC \geq 15$, the vortex street becomes oblique to the oscillation axis because the second vortex forming at the end of each half-cycle is sufficiently strong to detach upon reversal. At larger $KC$, additional vortices are shed during each half-cycle, leading to a family of additional flow regimes. Over the parameter space $100< \beta \lesssim 10\,000$, Sarpkaya (1976) and Justesen (1989) showed that $KC$ continues to be the dominant parameter. In these latter two studies, the threshold $KC$ values between regimes also remained relatively constant and similar to Williamson (1985) at least until $Re$ approaches ${O}(10^5)$.

The presence of a rigid wall close to an oscillating cylinder limits the flow normal to the boundary and changes the vortex dynamics around the cylinder. The effect of a wall has been explored theoretically assuming inviscid flow ($Re \to \infty$, e.g. Carpenter 1958; Yamamoto, Nath & Slotta 1974) or Stokes flow ($Re\ll 1$, e.g. Jeffrey & Onishi 1981; Clarke et al. 2005) and has been found to generally increase hydrodynamic forces. Sumer, Jensen & Fredsøe (1991) experimentally investigated a cylinder oscillating parallel to a rigid wall at intermediate Reynolds numbers more representative of subsea applications, where viscous effects and associated vortex dynamics are important. They noted that the symmetric and attached vortices that form for $KC<4$ for an isolated cylinder become increasingly asymmetric as the distance between the cylinder and the wall reduces. For $7< KC<15$, they found that the transverse street moves parallel to the wall as the cylinder approaches the wall. In contrast, for $KC>10$, vortex shedding was found to be suppressed when the cylinder is in close proximity to the wall ($h_{min}/D<0.1$).

Although the literature has historically focused on theoretical models and experiments, numerical models are increasingly employed to investigate flow regimes in detail for a range of scenarios. Justesen (1991), Dütsch et al. (1998), Tong et al. (2015) among others, have used computational fluid dynamics to simulate the oscillatory flow field around an isolated cylinder. These authors have demonstrated that the flow field and variations with $KC$ and $\beta$ described by Tatsuno & Bearman (1990) can be well reproduced for small $\beta$. Tom (2018) utilised direct numerical simulations to describe the oscillation of a circular cylinder normal to a rigid wall for $Re=150$. The presence of the wall (located at a minimum distance from the cylinder of less than 0.5 times the cylinder diameter) prevents vortices from convecting away from the cylinder in the direction of the wall. The vortex street was observed to wrap around upon itself, leading to local circulation cells near the wall, which are symmetric at low $KC$ and asymmetric above $KC>5.25$. The wall was also found to increase the maximum near-wall velocities above those predicted by potential flow for $KC>5.25$ and to lead to non-zero horizontal flows near the wall even when the cylinder is halted. Zhao (2020) used the same approach, $Re$ and $KC$ range to further explore the effect of a rigid wall on the flow field and Morison drag and inertia coefficients, with broadly similar findings to those previously described by Tom (2018). Zhao (2020) also studied the effect of the direction of oscillation relative to the wall.

For larger $\beta$, numerical analysis is complicated by the need for a suitable turbulence closure model (or onerously large computational requirements). While some authors (e.g. Saghafian et al. 2003) have demonstrated the potential for using nonlinear eddy-viscosity models to capture the general fluid mechanics of an oscillating cylinder, attaining realistic insight into the flow field at practical Reynolds numbers is complicated by uncertainties introduced by empirical turbulence models and the predominance of three-dimensional effects (Tong et al. 2015).

This study extends the previous experimental and numerical studies to investigate flow around cylinders oscillating normal to a wall at relatively large $\beta$. The experiments consider $KC<12$, which is representative of typical motions experienced by submarine risers, or cables and pipelines during lay (e.g. Tom, Draper & White 2018). A single $\beta$ (=500) is adopted on the basis that the vortex flow regimes are expected to be relatively insensitive to $\beta$ if it is large, at least for $Re<10^5$ (Sumer et al. 2006). Experiments were conducted for a range of minimum distances (or gaps) between the cylinder and the wall ($h_{min}/D$ as defined on figure 1). For flow visualisation a focus is placed on a gap of 0.125, whilst force measurements are compared for gaps ranging between 0.125 and 0.5. These distances are representative of tests described by Tom et al. (2018) to explore sediment transport beneath an oscillating cylinder. The current investigation is primarily focused on four aspects: (i) whether, for the considered parameter space, the presence of the wall notably changes the vortex shedding regimes; (ii) quantifying how the identified vortex regimes influence the near-wall velocity relevant for sediment transport; (iii) how the wall affects the in-line forces acting on the cylinder; and (iv) whether simplified potential flow arguments can be used to predict aspects of these velocities and forces.

2. Experimental methods

2.1. Facility and motion control

Experiments were conducted in a flume with a total length of 15 m and cross-section 0.4 m in width by 0.5 m in height. Clear acrylic cylinders of $D=$ 13, 25 or 40 cm were attached vertically to a belt-driven linear actuator attached to the top of the flume and translated along the flume (figure 2). Motion was computer controlled and capable of producing a minimum oscillation period of 0.8 s and maximum amplitude of 0.8 m. A harmonic displacement was prescribed

(2.1)\begin{equation} y_{cyl}(t)=h_{min}+A\left(1-\cos\left(\frac{2{\rm \pi} t}{T}\right)\right), \end{equation}

where $y_{cyl}(t)$ is the vertical distance from wall to the cylinder invert, $A$ is the oscillation amplitude, $T$ is the period, $h_{min}$ is the minimum distance from the cylinder invert to the wall and $t$ is time (see figure 1). Specific values of these parameters chosen for testing are given in table 1.

Figure 2. Experimental test set-up.

Table 1. Summary of visualisation and force measurement experiments.

Typical cylinder displacement time histories measured using a spring-loaded string potentiometer sampled at rate of 100 Hz are shown in figure 3. These data were filtered using a low pass sixth-order Butterworth filter with a cutoff frequency of 10 Hz. The motions are presented as phase-averaged results over at least 20 cycles with the prescribed input overlaid for comparison. This serves to demonstrate that the output motion was not perfectly sinusoidal but improved with increasing amplitude ($KC$). The implications of these motion variations on the measured flow field and forces are explored in later sections.

Figure 3. Measured experimental relative displacements for $KC$ 2 to 12. Dashed blue line – ideal motion. Solid lines – ensemble-averaged measured motions increasing in $KC$ with colour intensity.

A 20 mm thick Perspex plate was positioned across the tank and clamped in place during testing to form a plane, rigid wall. The water depth in each test was set at 0.385 m (giving a submerged cylinder length of 10$D$–30$D$). To eliminate end effects along the base of the flume, the gap between the cylinder end and the flume bottom wall was kept to a small value of 5 mm. A skimmer plate was not used at the free surface as any free surface water movements were observed to be less than approximately 5 mm, which is believed to have negligible influence on both the force measurements and visualisations. The set-up for the flow visualisation tests is schematically shown in figure 2, where the cylinder and rigid wall were oriented vertically and the cylinder was oscillated horizontally. Although the oscillation direction in the experiments was horizontal, when describing the results, we use the term ‘vertical’ to refer to the direction of oscillation and ‘horizontal’ to refer to the direction parallel to the wall and normal to the cylinder axis. These references are adopted herein for consistency with the primarily application of the results (i.e. a horizontally oriented pipeline oscillating vertically above the seabed). The same orientation was adopted for the force measurement experiments, with a shear load cell attached to the top of the cylinder.

There are some limitations to the experiments described. First, these experiments focused on an idealised plane cylinder and are not able to explicitly capture three-dimensional aspects of the infrastructure geometries (such as curvature in the longitudinal direction). This limitation may introduce some uncertainty, particularly in observations related to temporal consistency of vortices and near-wall asymmetry (§ 4). The influence of three-dimensionality would be an interesting topic of further study. The second limitation is that the experiments are limited to a constant $\beta$. This limitation is expected to have relatively little effect on the flow visualisation findings but may be more influential on the magnitude of hydrodynamic forces measured (Sarpkaya 1976; Sumer et al. 2006). Nevertheless, the relative trends in the force changes due to the wall are expected to remain relevant at other $\beta$, but this should be confirmed through further work.

2.2. Flow visualisation and velocity field measurements

Particle image velocimetry (PIV) was employed for flow visualisation and velocity field measurements. A 5 W continuous wave Argo-ion laser was utilised for illumination, producing an approximately 1–2 mm thick light sheet. The laser was directed horizontally across the flume and cylinder at a height of half the water depth (approximately 0.1925 m above the base). Synthetic polycrystalline particles with median particle diameter of approximately $5\, \mathrm {\mu }{\rm m}$ were suspended in the water for tracking. Images were captured using a high speed Photron camera (FASTCAM SA3) at a frame rate of 500 frames s⁻¹, an exposure time of 1/1000 s and a typical image size of 768 px × 512 px, corresponding to visual dimensions of 90 mm × 62 mm. This system was adopted for detailed investigation of the near-wall behaviour. Larger image sizes were used for cases where the overall flow field and vortex dynamics were of primary interest. The PIV measurement approach is consistent with other studies conducted at this facility (Sun et al. 2022), where expected PIV error of 3 % and 5 % for velocity and vorticity were approximated under similar conditions.

The PIV analyses were conducted using GeoPIV-RG (Stanier et al. 2016). This software incorporates first-order subset deformation shape functions and inverse compositional Gauss–Newton sub-pixel interpolation to examine cross-correlation of image pairs. For tests specifically focusing on the flow between the cylinder and the wall, consecutive image pairs (sampled at 500 Hz) were analysed with 32 px × 32 px interrogation patches and 50 % overlap. This corresponds to a patch size of approximately 3.3 mm with the adopted field of view, which is sufficient to describe the overall flow behaviour and velocity characteristics but not detailed information regarding boundary layers. For tests examining the larger flow field, 48 px × 48 px resolution was used.

Phase-averaged results were calculated by averaging the velocity at specified phases in the cycle over a number of cycles. For the two-dimensional velocity fields, the phase (ensemble) average of the field corresponds to the phase average at each spatial position. Long exposure images presented herein were artificially generated from the high speed images taken for PIV analysis. These were created by adding the image intensities of 10–20 consecutive images, with individual exposure times of 1/1000 s, covering relatively short portions of a cycle. The number of images and the time between selected images were varied for different experiments to achieve optimal visual clarity to illustrate the flow features.

2.3. Force measurements

Hydrodynamic forces were measured using a 3-axis piezo-electric load cell attached to the top of the cylinder. In-house software (De Catania et al. 2010) was used for data measurement and forces were recorded at a rate of 200 Hz. The two load axes of interest (i.e. parallel and perpendicular to the direction of motion) were first statically calibrated by applying known loads.

During post-processing, the resultant hydrodynamic force was assumed to act at the mid-depth of the immersed cylinder. Accounting for the load cell sensitivity to eccentric loading, the uncertainty due to this assumption is less than ${\pm }5\,\%$, depending on the assumption of where the force resultant acts within the middle half of the immersed cylinder. The force time histories were filtered in post-processing using a sixth-order Butterworth filter. A low-pass filter was first used to eliminate high-frequency noise, with a cutoff frequency of 4 times the oscillation frequency. A high-pass filter was subsequently used, with a cutoff frequency of half the oscillation frequency, to correct for long-term drift in the load measurements. Force measurements were not explicitly corrected for blockage or end effects.

3. General flow field characteristics

Observations of the general flow field for $2\leq KC\leq 12$ suggest the existence of three flow regimes based primarily on flow field symmetry about the $y$-axis (described in more detail in the following sections). In the following, qualitative observations about the general flow dynamics are described, and representative vortex schematics are presented, for each of these flow regimes. These observations were made based on visual observations of the flow patterns across a number of tests and cycles. The schematics and descriptions are therefore simplified interpretations of the flow field. While subjective, this approach is useful for understanding the general features consistently observed and is consistent with approaches taken by previous researchers (e.g. Williamson 1985; Tatsuno & Bearman 1990; Sumer et al. 1991). The interpretations are first presented and quantitative analysis in provided subsequently to differentiate the regimes in § 3.4 and further in § 4. Example supplementary movies for a range of $KC$ are included in the online version of this paper available at https://doi.org/10.1017/jfm.2022.872.

3.1. Approximately symmetric flow – $KC\leq 5$

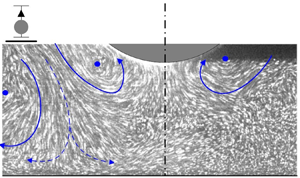
The vortex dynamics and flow patterns typically observed for $KC\leq 5$ are summarised schematically in figure 4. In this regime, two vortices remain attached during each half-cycle and only detach when the cylinder changes direction. This behaviour is similar to regime A for an isolated cylinder described by Tatsuno & Bearman (1990) and by Williamson (1985). The flow field remains generally symmetric about the cylinder axis of oscillation, such that $K_x$ symmetry (i.e. reflective about the $y$-axis – Elston, Blackburn & Sheridan 2006) is maintained, whilst $H_1$ and $H_2$ symmetries (Elston et al. 2006) are not maintained (i.e. the flow field at $t/T=0$ is not spatially reflective of $t/T=0.5$).

Figure 4. Sketches of the vortex dynamics for approximately symmetric flow ($KC\lesssim 5$) at different phases within one period. Solid lines represent vortices. Dashed lines represent pumping or overall circulation features.

When oscillating normal to a plane wall, several primary flow features can be observed. First, when the cylinder is close to the wall, a symmetric (about the $y$-axis) ‘pumping’ flow is observed in the gap between the cylinder and the wall. The velocity within this gap is horizontal along the wall and in phase with cylinder motion. Second, vortex pairs that detach towards the end of each cycle (e.g. vortices O, P, C and D at $t/T \sim 0, 1$ in figure 4) cannot convect vertically away from the cylinder and instead remain near to the wall or convect outward in opposite directions along the wall. Combined with the pumping flow and the formation of the newly attached vortices (A, B, E and F), these shed vortices form two counter-rotating circulation cells on either side of the cylinder (e.g. figure 4, $t/T = 0.6$). These cells induce flow directed outward from the centreline near the wall, as indicated in the long exposure images in figure 5, which represent different phases of cylinder oscillation. These circulation cells or zones that form are also evident from ensemble-averaged (phase averaged at the specified phases in the cycle) flow fields shown in figure 6(b,d). The remnant wall-parallel velocity (figure 6d) is indicative of second-order streaming, which is described in further detail in § 4 and figure 14.

Figure 5. Example long exposure images for $KC=4$. Solid lines represent vortices with cores denoted by dots. Dashed lines represent pumping or overall circulation features; (a) $t/T = 0.9$, (b) $t/T = 0.1$, (c) $t/T = 0.1$, (d) $t/T = 0.5$.

Figure 6. Ensemble (phase)-averaged flow fields. $KC=4$. (a) Isolated cylinder, $t/T=0.9$; (b) $h_{min}/D=0.125$, $t/T=0.9$; (c) isolated cylinder, $t/T=0.5$; (d) $h_{min}/D=0.125$, $t/T=0.5$. Colours represent horizontal velocity, $u/V_m$.

To illustrate further the effect of the wall, figure 6(b,d) shows comparable flow fields for an isolated cylinder without the wall for $KC=4$. For the isolated cylinder, there is significant vertical motion away from the cylinder as it moves downwards. By contrast, the wall prevents this movement. The motion is instead diverted horizontally along the wall, leading to ‘pumping’. Although the flow imaging shown in figure 5 indicates that the vortices are not perfectly symmetric on a given cycle at this $\beta$, the vortex features are broadly symmetric when phase averaged over a number of cycles (figure 6d).

3.2. Intermittently asymmetric flow – $5< KC<8$

As $KC$ increases, the vortices forming on the instantaneously trailing side of the cylinder become asymmetric but still only detach at the end of each half-cycle. Detached vortices convect obliquely away from the oscillation axis. For a free cylinder, these observations are representative of regime D/regime E, where $K_x$ symmetry is broken but $H_1$ mirror symmetry may (regime D) or may not (regime E) remain (Elston et al. 2006). However, with a nearby wall, all spatial and spatio-temporal symmetries are broken, as illustrated schematically in figure 7.

Figure 7. Vortex dynamics for intermittently asymmetric flow ($5< KC<8$). Solid lines represent vortices with cores denoted by dots. Dashed lines represent pumping or overall circulation features.

Dominant vortices form towards the end of each half-cycle (e.g. vortices B, E and H in figure 7) and tend to separate into two companion vortices of the same vorticity sign (e.g. B and C or E and F), which are bounded by strong, oppositely directed flows. For $t/T=0.0$ to 0.1 these companion vortices move past the cylinder and divert along the wall. The vortex asymmetry and impingement events to the side of the cylinder lead to locally asymmetric flow near the wall (i.e. non-zero horizontal velocities across the cylinder centreline; see figure 8). The strength and occurrence of this asymmetric flow increases with $KC$. However, over this $KC$ range, the direction of the near-wall centreline flow is typically inconsistent over many cycles because the side on which the dominant vortex forms switches frequently. Figure 9, for instance, shows results for 96 consecutive cycles where phase-averaged flow field results correspond to only cycles where the dominant vortex was on one side of the cylinder or the other. Mode selection was conducted by selecting cycles where the centreline horizontal velocity measured at $y/D=0.1$ (for $t/T=0.1$) was $|u/V_m|>0.05$. Using this criterion, approximately $15\,\%$ of the cycles were left side dominant and $47\,\%$ were right side dominant (the remaining $38\,\%$ did not satisfy the specified velocity criterion at $t/T=0.1$). The switching demonstrates the variable nature of the flow field in this $KC$ range. For the particular test in figure 9 ($KC=6$), the dominant vortex tended to appear on the right side of the cylinder. However, the preferential side was not consistent across all experiments or cylinder diameters and hence is believed to be sensitive to initial experimental conditions, although, as shown in § 3.4, the switching commonly occurred even during a continuous test.

Figure 8. Example occurrences of dominant vortex recirculation flows impinging on the wall on different sides. Here, $KC=6$ with cylinder close to wall; (a) $t/T \sim 0.12$, (b) $t/T \sim 0.1$.

Figure 9. Comparison of phase-averaged horizontal velocity (colour shading) and velocity vectors, mode selected for dominant vortex side. Here, $KC=6$. Left-hand side – left side dominant cycles. Right-hand side – right side dominant cycles; (a) $t/T = 0.5$, (b) $t/T = 0.5$, (c) $t/T = 0.75$, (d) $t/T = 0.75$, (e) $t/T = 0, 1$, ( f) $t/T = 0, 1$.

The observed irregular asymmetry is consistent with experimental observations of free cylinders (Williamson 1985) and numerical calculations for oscillation normal to a rigid wall (Tom 2018; Zhao 2020). In those studies, as in the current case, the observations of intermittent asymmetry were made for a single cross-section along a cylinder (i.e. two-dimensional intermittency). It is possible that spanwise migration of vortex cells may also contribute to the intermittency – i.e. low spanwise correlation (Obasaju, Bearman & Graham 1988; Kozakiewicz, Sumer & Fredsøe 1992). Detailed exploration of these three-dimensional aspects over this $KC$ range is an interesting area for further research but beyond the scope of the current work. Nevertheless, the general observations are also consistent with experimental observations of sediment transport on a movable sand bed beneath an oscillating cylinder in otherwise still fluid at similar $KC$ (Tom et al. 2018). In Tom et al. (2018) tests with similar $KC$ conditions, sediment movement was qualitatively observed to primarily occur sporadically in space along the cylinder and in time, for any given cycle of motion. However, a symmetric trench about the cylinder centreline eventuated at equilibrium, implying a long-term averaging of the asymmetry – a feature also present in the experimental study of Guan et al. (2019). These features are both qualitatively consistent with the current observations and quantitative measurements made later in this paper.

3.3. Asymmetric flow with vortex shedding – $8\leq KC<12$

In the range $8\leq KC < 12$, the amplitudes of cylinder displacement are sufficient for a vortex to shed completely during each half-cycle. The primary flow features for this $KC$ range are schematically described in figure 10. In contrast to previous regimes, a single dominant vortex (e.g. vortices A and D in figure 10) forms each half-cycle and has sufficient momentum to convect across the cylinder when it changes direction. The dominant vortex then detaches and convects away in a direction broadly transverse to the oscillation axis (as opposed to obliquely away). Due to the increased strength of vortices and their transverse direction of movement, the overall circulation in this regime comprises significantly more fluid moving from the far field transversely across the oscillation axis. This regime is similar to the isolated cylinder regime G described by Tatsuno & Bearman (1990) and that described by Williamson (1985) for $8\leq KC<13$.

Figure 10. Vortex dynamics for asymmetric flow with vortex shedding ($8\leq KC<12$). Solid lines represent vortices with cores denoted by dots. Dashed lines represent pumping or overall circulation features.

Interrogation of instantaneous flow fields and visual observation of the test videos (e.g. long exposure images such as figure 11) again reveal that the dominant vortex tends to separate into individual vortices (e.g. vortices A to A + C and B to B + C). The distinct movement of these vortices (e.g. vortex R in figure 10) appears to contribute to the tendency to asymmetric near-wall flows during the last quarter of the cycle (0.75 $\leq t/T \leq 1.0$). A particular feature of this $KC$ range is that asymmetric flow across the cylinder centreline in the range $0.8\leq t/T\leq 1.0$ is consistently observed.

Figure 11. Example long exposure images for $KC=10$. Solid lines represent vortices. Dashed lines represent pumping or overall circulation features; (a) $t/T = 0.5$, (b) $t/T = 0.8$, (c) $t/T = 0, 1$, (d) $t/T = 0.25$.

The direction of asymmetric gap flow and the direction of vortex shedding all appear to be more consistent between cycles when $8\leq KC < 12$ as compared with smaller $KC$. This is believed to be due to the increased secondary flow across the oscillation axis coincident with vortex shedding. The direction of shedding typically remained constant over at least ${O}(10)$ cycles. However, switching was still observed to occur occasionally.

3.4. Quantification of regime ranges

The three identified regimes can be interpreted analogously to the isolated cylinder regimes identified at lower Reynolds number by Tatsuno & Bearman (1990) based primarily on flow symmetry: (i) the symmetric regime similar to regime A; (ii) the intermittently asymmetric regime similar to regime E; and (iii) the predominantly asymmetric regime similar to regime G.

To quantify the flow symmetry and the regimes observed with a wall, we compare the horizontal velocity beneath the centreline of the cylinder when it is close to the wall (e.g. $t/T=0$). Figure 12(a) shows the root-mean-square (r.m.s.) value of the centreline velocity at $t/T=0$ for a range of $KC$. For purely symmetric flow, the centreline horizontal velocity is zero. The r.m.s. velocity thus represents the typical deviation from symmetry averaged over the total number of cycles. At low $KC$, there is relatively little asymmetry. For $KC>5$ there is an evident increase in asymmetry. This suggests that the threshold between regime A-like and regime E-like flow occurs at a $KC$ of approximately 5 to 6.

Figure 12. Variation in centreline horizontal velocity at $t/T=0$ ($u_{rms,t_0}/V_m$) at $y/D=0.07$. (a) Root-mean-square value. (b) Percentage of cycles for which $u_{t_0}/V_m$ switches direction over consecutive cycles.

To quantify the transition between regime E-like and G-like flow, the direction of horizontal flow on the centreline at $y/D=0.07$ and $t/T=0.0$ was tabulated for each cycle and compared between subsequent cycles. Figure 12(b) shows the percentage of cycles where the horizontal velocity changes sign between consecutive cycles. For $KC=6$, there is frequent switching between cycles. However, for $KC\geq 8$, the switching is less frequent. Although there is a lack of definition between 6 and 8, a clear change occurs for $KC\geq 8$ in terms of both the switching and the magnitude of asymmetric flows. This $KC$ threshold of 8 is similar to that qualitatively observed by Williamson (1985) for the initiation of vortex shedding for an isolated cylinder. The increased temporal regularity in asymmetry for $KC\geq 8$ is also consistent with the findings of Tom (2018) and Zhao (2020), wherein regime F-like flow (i.e. $KC=9$ and 12 in Zhao 2020) also demonstrated temporal regularity in the near-wall flow, although both of those numerical studies were conducted at a lower Reynolds number ($Re=150$).

4. Near-wall flow dynamics

Across the parameter space investigated, two primary flow mechanisms are observed close to the wall: a pumping flow and local flows associated with vortex dynamics. These features characterise the near-wall velocity response and in turn affect the formation of seabed trenches (Tom et al. 2018). Important physical insight may be attained by quantitatively exploring how the velocity response varies due to these observed flow features.

In the inviscid limit, Carpenter (1958) represented the potential flow solution for a cylinder oscillating near a wall as an infinite series of image doublets. The complex velocity potential can then be defined as

(4.1) \begin{gather} w= V\sum_{k=0}^{\infty}\beta_k(w_k+w_k^\prime)= V\sum_{k=0}^{\infty}\beta_k \left\{ \begin{array}{@{}ll} \dfrac{1}{z-f_k}+\dfrac{-1}{z-(f-f_k)} & \text{for }k\text{ even}, \\ \dfrac{-1}{z-f_k}+\dfrac{1}{z-(f-f_k)} & \text{for }k\text{ odd}, \end{array} \right. \end{gather}

(4.2)\begin{gather} f_k=\frac{b^2}{f-f_{k-1}}; \quad f_0=0, \end{gather}

(4.3)\begin{gather} \beta_k=\frac{(bb)^2}{(f-f_{k-2})^2(f-f_{k-1})^2}\beta_{k-2}; \quad \beta_1={-}b^2\left(\frac{b^2}{f^2}\right); \quad \beta_0=b^2, \end{gather}

where $w=\phi +{\rm i}\psi$ is the velocity potential, $f$ is twice the distance between the cylinder centres (i.e. $2[h_{min}+b+A-A \cos ({2{\rm \pi} t}/{T})]$), $b$ is the cylinder radius, $z^\prime =x^\prime +iy^\prime$ is the spatial coordinate and $k$ is the image doublet number. Note that this is the simplified potential solution for cylinders moving horizontally towards each other (i.e. in the coordinate space $z^\prime$ shifted $90^\circ$ from the actual vertical case). Thus, for the case of vertical oscillation of velocity $V$, the velocity field (in the real coordinate space of vertical oscillation $z=x+iy$)is calculated as

(4.4)\begin{equation} u-{\rm i}v=\frac{\partial \psi}{\partial x^\prime}-{\rm i}\frac{\partial \psi}{\partial y^\prime}=\frac{\partial \text{Im}(w)}{\partial x^{\prime}}-{\rm i}\frac{\partial \text{Im}(w)}{\partial y^{\prime}}, \end{equation}

where $\text {Im}(w)$ is the imaginary component of $w$. In this paper, the velocities were calculated numerically using a simple first-order finite difference method.

Figure 13 shows measurements of the horizontal velocity magnitude at $x/D=0.4$ and $y/D=0.07$ for different $KC$, compared with theoretical predictions from potential flow both with and without a nearby wall. This location was selected because it is close to where the near-wall horizontal velocity due to pumping is largest at $t/T\sim 0.75$ (figure 9), which is approximately 50 % larger with the wall than without. The experimental measurements correspond to the maximum value over a single (mode selected and phase averaged over at least 70 cycles each) period. It can be seen that the measured results are consistent with the general trends and approximate magnitudes from theory for $KC\leq 5$. However, for $KC\geq 6$, the measured horizontal velocities diverge from theory and generally become relatively larger, due to the increasing influence of vortices on the near-wall flow. For cylinder motions and near-wall location considered, the measured horizontal velocities are up to a factor 1.8 times larger than predicted by potential flow. This implies that the vortex-induced flows are likely to be more important for trenching for $KC\geq 6$.

Figure 13. Maximum phase-averaged horizontal velocity magnitude ($u_{max}/V_m$) at $x/D=0.4$ and $y/D=0.07$. Solid circles – experimental measurements. Solid line – potential flow with wall. Dashed line – potential flow without wall.

Figure 14 describes the overall intra-cycle response for the PIV results from a statistical perspective, again with each set comprising at least 70 cycles, at two points representative of the gap near the wall – $x/D=0$, $y/D=0.07$ and $x/D=0.4$, $y/D=0.07$. Here, the results have not been smoothed and hence show more irregularity in parts of the cycle. Statistical phase averages and $\pm 1$ standard deviation on the inter-cycle variation are shown for (i) all cycles (blue) and (ii) mode-selected cycles for left-side dominant vortices (green). For $x/D=0.4$, the potential flow theoretical predictions are also shown for (i) perfectly sinusoidal motion and (ii) the motion inferred from the experiments by tracking the cylinder position from the images. The latter uses the phase-averaged motion inferred from the cylinder position in the images for each set of tests.

Figure 14. Horizontal velocity time histories at $y/D=0.07$; (a) $x/D=0.0$, (b) $x/D=0.4$. Solid blue lines – phase-averaged result. Dashed blue lines – phase-average ${\pm }1$ standard deviation. Green lines – mode selected for left side dominant vortex. Solid black lines – sinusoidal motion, potential flow. Solid red lines – phase-averaged cylinder motion, potential flow.

From figure 14, the experimental response (at $x/D=0.4$ for all $KC$) is tracked reasonably well – at least the general trend if not the magnitude – by the potential flow prediction incorporating the inferred cylinder motion, especially when the cylinder is near the wall. This suggests that pumping remains a dominant driver of the near-wall response throughout this $KC$ range, at least for portions of the cycle, and that the irregular motion due to the vortex dynamics does not have a significant effect. This characteristic is demonstrated by the general trends of negative (inward-directed) velocity as the cylinder moves away from the wall and the reverse as it approaches.

Although most obvious for $KC\geq 8$, vortex interactions influence the near-wall velocities across this $KC$ range. For $KC\leq 6$, figure 14(b) indicates a velocity bias at $x/D=0.4$ directed away from the centreline when the cylinder is away from the wall ($t/T\sim 0.4$ to 0.6). This is the quantitative expression of the circulation cells described in § 3 and occurs on both sides of the cylinder. These features are not captured by theory since they arise from viscous effects due to vortex detachment. The relatively small centreline bias at small $KC$ is consistent with the circulation cells being approximately symmetric.

As $KC$ increases, the velocity bias becomes more strongly evident at the centreline. The phase-averaged results for $KC=6$ and 8 suggest an approximately zero centreline velocity throughout the cycle; however, inspection of the mode-selected results (figure 9) reveals that the flow field is typically asymmetric on individual cycles. The flow field only becomes symmetric when averaged over many cycles due to fluctuation in the dominant vortex side.

The near-wall response for $KC\geq 8$ indicates that large centreline velocities are common in the range $0.2< t/T<0.6$. These instances correspond to flow forced across the centreline following impingement of vortices/recirculation flow due to shed vortices. This response, which is conceptually consistent with the vortex dynamics described in figure 10, is quantitatively evident through probability distributions of the position and phase of maximum (negative) vertical velocity instances for $KC=10$ and 12, shown in figure 15. The distributions indicate that the maximum vertical velocity towards the wall typically occurred in these tests on the left side of the cylinder and for $t/T<0.4$. Hence, relatively high centreline velocities directed to the right of the cylinder (at least for $0.4< t/T<0.6$ – figure 13) are coincident with and preceded by strong vertical velocities occurring on the left of the cylinder.

Figure 15. Probability distribution functions of the horizontal location and phase of the maximum (negative) vertical velocity instances at $y/D=0.07$: (a) $KC=10$; horizontal location, (b) $KC=10$; phase, (c) $KC=12$, horizontal location, (d) $KC=12$; phase.

5. In-line forces

In this section, the influence of the wall on forces is examined. Figure 16 shows example force time series, phase averaged over at least 20 cycles for a range of $h_{min}/D$ and normalised as per

(5.1)\begin{equation} C_I=\frac{F_I}{0.5DV_m^2\rho}, \end{equation}

where $F_I$ is the measured in-line force per unit length. Experimental measurements in figure 16 are phase averaged but not mode selected for the dominant vortex side because the in-line force is not significantly affected by the traverse force direction (An, Cheng & Zhao 2015). Predictions based on potential flow theory are calculated by integrating around the circumference following the theorem of Blasius

(5.2)\begin{equation} X-{\rm i}Y=\frac{1}{2}{\rm i}\rho \oint \left(\frac{{\rm d}w}{{\rm d}z}\right)^2 \,{\rm d}z - {\rm i}\rho \frac{\partial}{\partial t} \oint \bar{w} \,{\rm d}\bar{z} , \end{equation}

where $X$ and $Y$ are the Cartesian components of the hydrodynamic force and the potential is calculated via (4.1) to (4.3). For oscillation perpendicular to a plane wall (2.1), $Y$ is the in-line force component. Potential flow predictions in figure 16 incorporate the instantaneous cylinder position and velocity measured in the experiments.

Figure 16. Example in-line force coefficients for various $h_{min}/D$; (a) $KC=4.7$, (b) $KC=7.9$, (c) $KC=11.1$. Solid lines – experimental results. Dashed lines – potential flow. Black lines – $h_{min}/D=\infty$. Blue lines – $h_{min}/D=0.5$. Green lines – $h_{min}/D=0.25$. Red lines – $h_{min}/D=0.125$.

With reference to figure 16, the force time series is primarily affected by the wall for $t/T<0.2$ and $t/T>0.8$ over this $KC$ range, for all $h_{min}/D$ tested. For $t/T<0.2$ and $t/T>0.8$, the in-line force increases compared with the isolated cylinder. These increases are likely to be due to changes in the pressure in the gap associated with pumping flow, as opposed to vortex effects. This inference is corroborated by comparison with the potential flow solution, which indicates a similar increase in force over the same fraction of the oscillation period. Both the experimental measurements and potential flow predictions indicate that the wall influence reduces with increasing $h_{min}/D$, limiting towards the isolated cylinder result.

A simple prediction of the in-line force increase due to the wall at a given $h_{min}/D$ can be attained by factoring the measured isolated cylinder time series by the relative increase predicted by potential flow

(5.3)\begin{equation} C_{I,corr}(t, h_{min}/D, KC)=C_{I,\infty}(t, KC)\frac{C_{I,P-h_{min}/D}(t, h_{min}/D, KC)}{C_{I,P-\infty}(t, KC)}, \end{equation}

where $C_{I,corr}(t, h_{min}/D, KC)$ is the corrected force time series for a given $h_{min}/D$ and $KC$, $C_{I,\infty }(t, KC)$ is the cylinder force time series for an isolated cylinder for a given $KC$, $C_{I,P-h_{min}/D}(t, h_{min}/D, KC)$ is the potential flow prediction at a given $h_{min}/D$ and $KC$ and $C_{I,P-\infty }(t, KC)$ is the potential flow prediction for an isolated cylinder for a given $KC$. This correction should be calculated at each instance in time to give a full time history accounting for the instantaneous position relative to the wall.

Figure 17(a) compares the maximum measured in-line force during the first half of the cycle with that inferred from (5.3) for three different $h_{min}/D$. For $KC>6$ the experiments only indicate small increases in the maximum in-line force, irrespective of $h_{min}/D$. As such, except for $KC=4.7$, (5.3) generally overpredicts the increase in maximum in-line force over the first half of the cycle due to the wall. The poor comparison occurs because as $KC$ increases, the phase when the maximum in-line force occurs increases (figure 17b) due to the increased influence of the separation-driven force component, which is less influenced by the wall. Conversely, figure 17(c) shows that, at $t/T=0$, there is generally an increase in the magnitude of the in-line force across the $KC$ range and that (5.3) predicts this increase relatively well. This is because the dominant pumping mechanism driving the suction force at this phase is well described by potential flow. This means that potential flow can be used to predict the in-line force increases, due to a nearby wall, for portions of the cycle where the component in phase with cylinder acceleration dominates.

Figure 17. Comparison of in-line force measurements and predictions as a function of $h_{min}/D$ and $KC$. (a) Maximum $C_I$ in first half of cycle; (b) $t/T$ of maximum $C_I$ in first half of cycle; (c) $C_I$ at $t/T=0.0$. Solid circles – measurements. Lines – predictions following (5.3). Black – $h_{min}/D=\infty$. Blue – $h_{min}/D=0.5$. Green – $h_{min}/D=0.25$. Red – $h_{min}/D=0.125$. Open symbols – isolated cylinder results from Yuan (2013) ($\circ$); Sarpkaya (1986) ($\square$); Obasaju et al. (1988) ($\vartriangle$).

The relatively good comparison of the increase due to pumping via (5.3) at the beginning of the cycle, even for relatively large $KC$ values, is consistent with the numerical findings of Tom (2018). Tom (2018) showed that potential flow estimates of the increase in in-line force near the wall at $t/T=0$ are accurate (compared with the numerical results) within $10\,\%$ for $Re=150$. The potential flow comparison by Tom (2018) were less accurate for measuring the peak in-line force because the time when the maximum force occurs shifts to $t/T>0$ as $KC$ increases, coincident to when the cylinder is located further from the wall and pumping is less prevalent.

Prediction of forces using (5.3) requires that the isolated cylinder force is known or can be calculated. Harmonic approaches, such as the Morison equation, could be used with (5.3). This could be done in practice by first estimating the in-line force time history using various empirical measurements of drag and inertia coefficients described by the Morison equation (e.g. Sarpkaya 1986; Obasaju et al. 1988) to compute the isolated cylinder force time history. Then, this force time history should be modified for various $h_{min}/D$ according to (5.3). The results shown in figure 17 suggest that such an approach is most applicable for relatively small $KC$ where the maximum force is closer to being in phase with cylinder acceleration, although it may be less appropriate for providing an indication of the maximum in-line force over the course of a cycle at larger $KC$. However, the asymmetric nature of the in-line force time history reflects that direct fitting of Morison drag ($C_d$) and inertia ($C_i$) coefficients is unlikely to accurately capture the force time history in the presence of oscillation near a wall.

6. Concluding remarks

A new series of flow visualisation and in-line force measurement experiments investigating the flow and forcing behaviour of a cylinder oscillating normal to a plane wall has been described in this paper. The motivation for the experiments is to better understand the fluid dynamics associated with offshore infrastructure oscillating near the seabed, such as idealised risers, pipelines or mooring chains. The findings provide insight into the physics that may drive trenching beneath such infrastructure and ultimately contribute to structural fatigue. They also provide an opportunity for comparison with recent work involving numerical simulations of the same problem by Tom (2018) and Zhao (2020), conducted at low Reynolds number, $Re=150$.

The presence of a nearby wall affects the flow field and the vortex dynamics. However, the observed flow regimes and their approximate $KC$ ranges are qualitatively similar to those identified by Williamson (1985) at a similar $\beta$. The key difference is how the wall influences the movement of shed vortices.

Confinement of flow between the cylinder and the wall causes pumping beneath the cylinder that is primarily horizontal along the wall at small $h_{min}/D$. This is approximately symmetric about the cylinder centreline and in phase with cylinder motion. The pumping flow is evident for portions of the cycle when the cylinder is close to the wall, and its magnitude is well captured by potential flow for $KC\leq 6$. As $KC$ increases, asymmetric vortex dynamics increasingly affects the near-wall flow field. This is characterised by asymmetric near-wall flow across the cylinder axis and instances of high velocity flows directed at the wall corresponding to vortex impingement (figure 8). Although the near-wall flow does become more asymmetric, for $KC\leq 12$ the time variation in pumping flow (when the cylinder is near the wall) is still captured by potential flow. However, the magnitude of pumping flow predicted by potential flow compares less well as $KC$ increases due to asymmetry associated with the vortex dynamics, with increases in the horizontal velocity above pumping flow of at least a factor of 1.8 for $KC>6$. This increase has implications for sediment transport beneath oscillating risers, pipelines and cables because this would suggest increases in bed shear stress of greater than 3 times that due to non-vortex-enhanced pumping flow.

The magnitude of the in-line force generally increases when the cylinder oscillates near to a wall, relative to the force for an isolated cylinder. The increase is in phase with cylinder acceleration and appears to be primarily due to suction caused by flow confinement from the wall. The force increases are limited to a relatively small portion of the cycle near the beginning of the cycle and increases with reducing $h_{min}/D$. A methodology is presented to account for these increases by factoring the isolated cylinder force time history by the increase predicted by inviscid potential flow theory. For relatively large $KC$ cases where vortex interactions drive the maximum magnitude of in-line force, the proposed methodology underpredicts the increase in in-line force. However, for small $KC$ cases, the trends in increasing in-line force (relative to the isolated cylinder case) are reasonably well predicted by inviscid theory. Therefore, inviscid theory modifications provide a useful estimation of the in-line force acting on near-seabed infrastructure that experiences relatively small oscillation amplitudes. Improved estimates in in-line force could enable more accurate estimations of infrastructure fatigue life, which could reduce project costs.