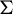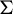1 Introduction
Let
![]() $\Gamma $
be a countable discrete group. Let
$\Gamma $
be a countable discrete group. Let
![]() $\alpha $
be a minimal action of
$\alpha $
be a minimal action of
![]() $\Gamma $
on a compact Hausdorff space C. The action
$\Gamma $
on a compact Hausdorff space C. The action
![]() $\alpha $
is topologically free if for every non-trivial element
$\alpha $
is topologically free if for every non-trivial element
![]() $\gamma \in \Gamma $
, the set
$\gamma \in \Gamma $
, the set
![]() $\{x\in C\mid \alpha (\gamma )x=x\}$
has empty interior. This notion of freeness can be characterized by the triviality of the uniformly recurrent subgroup (hereafter URS) associated with the action
$\{x\in C\mid \alpha (\gamma )x=x\}$
has empty interior. This notion of freeness can be characterized by the triviality of the uniformly recurrent subgroup (hereafter URS) associated with the action
![]() $\alpha $
as follows. Let
$\alpha $
as follows. Let
![]() $\mathrm {Sub}(\Gamma )$
be the space of subgroups of
$\mathrm {Sub}(\Gamma )$
be the space of subgroups of
![]() $\Gamma $
and let
$\Gamma $
and let
![]() $\mathrm {Stab}_{\alpha } : C\to \mathrm {Sub}(\Gamma )$
be the Borel map defined by
$\mathrm {Stab}_{\alpha } : C\to \mathrm {Sub}(\Gamma )$
be the Borel map defined by
Here
![]() $\mathrm {Sub}(\Gamma )$
is equipped with the topology of pointwise convergence which turns it into a compact totally disconnected topological space on which
$\mathrm {Sub}(\Gamma )$
is equipped with the topology of pointwise convergence which turns it into a compact totally disconnected topological space on which
![]() $\Gamma $
acts continuously by conjugation. Glasner and Weiss proved in [Reference Glasner and WeissGW15] that there exists a unique closed,
$\Gamma $
acts continuously by conjugation. Glasner and Weiss proved in [Reference Glasner and WeissGW15] that there exists a unique closed,
![]() $\Gamma $
-invariant, minimal subset in the closure of
$\Gamma $
-invariant, minimal subset in the closure of
![]() $\{\mathrm {Stab}_{\alpha }(x)\mid x\in C\}$
, called the stabilizer URS, associated with the minimal action
$\{\mathrm {Stab}_{\alpha }(x)\mid x\in C\}$
, called the stabilizer URS, associated with the minimal action
![]() $\alpha $
, which we denote by
$\alpha $
, which we denote by
![]() $\mathrm {URS}(\alpha )$
. The stabilizer URS is trivial if it is equal to
$\mathrm {URS}(\alpha )$
. The stabilizer URS is trivial if it is equal to
![]() $\{\{1\}\}$
. One of the features of the stabilizer URS associated with a minimal action
$\{\{1\}\}$
. One of the features of the stabilizer URS associated with a minimal action
![]() $\alpha $
is that its triviality is equivalent to the topological freeness of
$\alpha $
is that its triviality is equivalent to the topological freeness of
![]() $\alpha $
, see Lemma 2.1.
$\alpha $
, see Lemma 2.1.
Let
![]() $(X,\mu )$
be a standard probability measure space and let
$(X,\mu )$
be a standard probability measure space and let
![]() $\beta $
be a probability measure preserving (hereafter p.m.p.) action of a countable group
$\beta $
be a probability measure preserving (hereafter p.m.p.) action of a countable group
![]() $\Gamma $
on
$\Gamma $
on
![]() $(X,\mu )$
. The action
$(X,\mu )$
. The action
![]() $\beta $
is essentially free if for every non-trivial
$\beta $
is essentially free if for every non-trivial
![]() $\gamma \in \Gamma $
, the set
$\gamma \in \Gamma $
, the set
![]() $\{x\in X\mid \alpha (\gamma )x=x\}$
is
$\{x\in X\mid \alpha (\gamma )x=x\}$
is
![]() $\mu $
-negligible. The measurable counterpart of the stabilizer URS is the stabilizer invariant random subgroup, stabilizer IRS for short, associated with
$\mu $
-negligible. The measurable counterpart of the stabilizer URS is the stabilizer invariant random subgroup, stabilizer IRS for short, associated with
![]() $\beta $
. It is defined as the
$\beta $
. It is defined as the
![]() $\Gamma $
-invariant Borel probability measure
$\Gamma $
-invariant Borel probability measure
![]() $(\mathrm {Stab}_\beta )_*\mu $
on
$(\mathrm {Stab}_\beta )_*\mu $
on
![]() $\mathrm {Sub}(\Gamma )$
, and is denoted by
$\mathrm {Sub}(\Gamma )$
, and is denoted by
![]() $\mathrm {IRS}(\beta )$
. A stabilizer IRS is the prototype of an IRS, which is a Borel probability measure on
$\mathrm {IRS}(\beta )$
. A stabilizer IRS is the prototype of an IRS, which is a Borel probability measure on
![]() $\mathrm {Sub}(\Gamma )$
that is invariant under the conjugation action of
$\mathrm {Sub}(\Gamma )$
that is invariant under the conjugation action of
![]() $\Gamma $
. The trivial IRS is the Dirac measure at the trivial subgroup. Observe that
$\Gamma $
. The trivial IRS is the Dirac measure at the trivial subgroup. Observe that
![]() $\mathrm {IRS}(\beta )$
is trivial if and only if
$\mathrm {IRS}(\beta )$
is trivial if and only if
![]() $\beta $
is essentially free. Abért, Glasner and Virág proved that every IRS is in fact a stabilizer IRS for some p.m.p. action, see [Reference Abért, Glasner and VirágAGV14].
$\beta $
is essentially free. Abért, Glasner and Virág proved that every IRS is in fact a stabilizer IRS for some p.m.p. action, see [Reference Abért, Glasner and VirágAGV14].
An ergodic minimal action
![]() $\Gamma \curvearrowright (C,\mu )$
is a minimal action of
$\Gamma \curvearrowright (C,\mu )$
is a minimal action of
![]() $\Gamma $
on a compact Hausdorff space C together with a
$\Gamma $
on a compact Hausdorff space C together with a
![]() $\Gamma $
-invariant ergodic Borel probability measure
$\Gamma $
-invariant ergodic Borel probability measure
![]() $\mu $
. Thus, an ergodic minimal action has both a stabilizer URS and a stabilizer IRS. It is a classical result that the essential freeness of an ergodic minimal action implies its topological freeness, see Lemma 2.2. In other words, if the stabilizer IRS of an ergodic minimal action is trivial, then its stabilizer URS is trivial. The present article provides new counterexamples in the study of the converse.
$\mu $
. Thus, an ergodic minimal action has both a stabilizer URS and a stabilizer IRS. It is a classical result that the essential freeness of an ergodic minimal action implies its topological freeness, see Lemma 2.2. In other words, if the stabilizer IRS of an ergodic minimal action is trivial, then its stabilizer URS is trivial. The present article provides new counterexamples in the study of the converse.
Definition 1.1. An ergodic minimal action is allosteric (
![]() : other,
: other,
![]() : fix, firm, solid, rigid) if it is topologically free but not essentially free. A group is allosteric if it admits an allosteric action.
: fix, firm, solid, rigid) if it is topologically free but not essentially free. A group is allosteric if it admits an allosteric action.
Question 1.1. What is the class of allosteric groups?
First, let us discuss examples of groups that do not belong to this class. It is the case for groups whose ergodic IRSs are all atomic, that is, equal to the uniform measure on the set of conjugates of a subgroup which admits only finitely many conjugates. Indeed, we prove in Proposition 2.3 that the IRS of an ergodic minimal action which is topologically free is either trivial, or has no atoms. Thus, if
![]() $\mathrm {Sub}(\Gamma )$
is countable, then
$\mathrm {Sub}(\Gamma )$
is countable, then
![]() $\Gamma $
is not allosteric, see Corollary 2.4. Examples of groups with only countably many subgroups are finitely generated nilpotent groups, more generally polycyclic groups, extensions of Noetherian groups by groups with only countably many subgroups (e.g. solvable Baumslag-Solitar groups
$\Gamma $
is not allosteric, see Corollary 2.4. Examples of groups with only countably many subgroups are finitely generated nilpotent groups, more generally polycyclic groups, extensions of Noetherian groups by groups with only countably many subgroups (e.g. solvable Baumslag-Solitar groups
![]() $\mathrm {BS}(1,n)$
), see [Reference Becker, Lubotzky and ThomBLT19] or Tarski monsters.
$\mathrm {BS}(1,n)$
), see [Reference Becker, Lubotzky and ThomBLT19] or Tarski monsters.
There are also groups whose ergodic IRSs are all atomic for other reasons. For instance, this is the case for lattices in simple higher rank Lie groups [Reference Stuck and ZimmerSZ94], commutator subgroups of either a Higman–Thompson group or the full group of an irreducible shift of finite type [Reference Dudko and MedynetsDM14], and a projective special linear group
![]() $\mathrm {PSL}_n(k)$
over an infinite countable field k [Reference Peterson and ThomPT16]. See also [Reference CreutzCre17], [Reference Creutz and PetersonCP17] or [Reference BekkaBek20] for other examples of groups with few ergodic IRSs. Thus, none of these groups are allosteric, because of their lack of IRSs.
$\mathrm {PSL}_n(k)$
over an infinite countable field k [Reference Peterson and ThomPT16]. See also [Reference CreutzCre17], [Reference Creutz and PetersonCP17] or [Reference BekkaBek20] for other examples of groups with few ergodic IRSs. Thus, none of these groups are allosteric, because of their lack of IRSs.
More surprisingly, there exists non-allosteric groups with plenty of ergodic IRSs, such as countable abelian groups which admit uncountably many subgroups. Indeed, if
![]() $\Gamma $
is such a group, then any Borel probability measure on
$\Gamma $
is such a group, then any Borel probability measure on
![]() $\mathrm {Sub}(\Gamma )$
is an IRS, but
$\mathrm {Sub}(\Gamma )$
is an IRS, but
![]() $\Gamma $
is not allosteric since any minimal
$\Gamma $
is not allosteric since any minimal
![]() $\Gamma $
-action which is topologically free is actually essentially free for any invariant measure, see Remark 4.4. Another example is given by the group
$\Gamma $
-action which is topologically free is actually essentially free for any invariant measure, see Remark 4.4. Another example is given by the group
![]() $\text {FSym}(\mathbb N)$
of finitely supported permutations on
$\text {FSym}(\mathbb N)$
of finitely supported permutations on
![]() $\mathbb N$
, as well as its alternating subgroup
$\mathbb N$
, as well as its alternating subgroup
![]() $\text {Alt}(\mathbb N)$
. They both admit many ergodic IRSs, see [Reference Thomas and Tucker-DrobTTD18, Reference VershikVer12]. However, an argument similar to that of [Reference Thomas and Tucker-DrobTTD18, Lemma 10.4] implies that neither
$\text {Alt}(\mathbb N)$
. They both admit many ergodic IRSs, see [Reference Thomas and Tucker-DrobTTD18, Reference VershikVer12]. However, an argument similar to that of [Reference Thomas and Tucker-DrobTTD18, Lemma 10.4] implies that neither
![]() $\text {FSym}(\mathbb N)$
nor
$\text {FSym}(\mathbb N)$
nor
![]() $\text {Alt}(\mathbb N)$
is allosteric.
$\text {Alt}(\mathbb N)$
is allosteric.
Let us now discuss examples of allosteric groups. Bergeron and Gaboriau proved in [Reference Bergeron and GaboriauBG04] that if
![]() $\Gamma $
is non-amenable and isomorphic to a free product of two non-trivial residually finite groups, then
$\Gamma $
is non-amenable and isomorphic to a free product of two non-trivial residually finite groups, then
![]() $\Gamma $
is allosteric. We refer to Remark 2.12 for a more precise statement of their results. In [Reference Abért and ElekAE07], Abért and Elek independently proved that finitely generated non-abelian free groups are allosteric, and in [Reference Abért and ElekAE12], they proved that the free product of four copies of
$\Gamma $
is allosteric. We refer to Remark 2.12 for a more precise statement of their results. In [Reference Abért and ElekAE07], Abért and Elek independently proved that finitely generated non-abelian free groups are allosteric, and in [Reference Abért and ElekAE12], they proved that the free product of four copies of
![]() $\mathbb Z/2\mathbb Z$
admits an allosteric action whose orbit equivalence relation is measure hyperfinite. In all [Reference Abért and ElekAE07, Reference Abért and ElekAE12, Reference Bergeron and GaboriauBG04], the allosteric actions obtained are in fact profinite, see §2.2 for a definition. These were the first known examples answering a question of Grigorchuk, Nekrashevich and Sushchanskii in [Reference Grigorchuk, Nekrashevich and SushchanskiiGNS00, Problem 7.3.3] about the existence of profinite allosteric actions.
$\mathbb Z/2\mathbb Z$
admits an allosteric action whose orbit equivalence relation is measure hyperfinite. In all [Reference Abért and ElekAE07, Reference Abért and ElekAE12, Reference Bergeron and GaboriauBG04], the allosteric actions obtained are in fact profinite, see §2.2 for a definition. These were the first known examples answering a question of Grigorchuk, Nekrashevich and Sushchanskii in [Reference Grigorchuk, Nekrashevich and SushchanskiiGNS00, Problem 7.3.3] about the existence of profinite allosteric actions.
The main result of this article is to prove that non-amenable surface groups, that is, fundamental groups of closed surfaces other than the sphere, the torus, the projective plane or the Klein bottle, are allosteric. More precisely, we prove the following result.
Theorem 1.2. Any non-amenable surface group admits a continuum of profinite allosteric actions that are pairwise topologically and measurably non-isomorphic.
Moreover, we prove that the IRSs given by the non-isomorphic allosteric actions that we construct are pairwise distinct. We refer to Theorems 4.1 and 4.2 for a precise statement of our results. Let us mention that surface groups are known to have a large ‘zoo’ of IRSs. For instance, Bowen, Grigorchuk and Kravchenko proved in [Reference Bowen, Grigorchuk and KravchenkoBGK17] that any non-elementary Gromov hyperbolic group admits a continuum of IRSs which are weakly mixing when considered as dynamical systems on
![]() $\mathrm {Sub}(\Gamma )$
. In an upcoming work (personal communication), Carderi, Le Maître and Gaboriau prove that non-amenable surface groups admit a continuum of IRSs whose support coincides with the perfect kernel of
$\mathrm {Sub}(\Gamma )$
. In an upcoming work (personal communication), Carderi, Le Maître and Gaboriau prove that non-amenable surface groups admit a continuum of IRSs whose support coincides with the perfect kernel of
![]() $\Gamma $
, that is, the largest closed subset without isolated points in
$\Gamma $
, that is, the largest closed subset without isolated points in
![]() $\mathrm {Sub}(\Gamma )$
. However, our IRSs are drastically different from the latter ones: we show that they are not weakly mixing and that their support is strictly smaller than the perfect kernel, see Remarks 4.4 and 4.5.
$\mathrm {Sub}(\Gamma )$
. However, our IRSs are drastically different from the latter ones: we show that they are not weakly mixing and that their support is strictly smaller than the perfect kernel, see Remarks 4.4 and 4.5.
We develop in §2 the preliminary results needed about profinite actions and allosteric actions. In particular, we prove that allostery is invariant under commensurability. To build ergodic profinite allosteric actions of non-amenable surface groups, we rely on a residual property of non-amenable surface groups to prove in §3 that they admit special kinds of finite index subgroups. The proof of Theorem 1.2 is completed in §4.
2 Preliminaries
2.1 Topological dynamic and URS/IRS
Let C be a compact Hausdorff space and let
![]() $\alpha $
be an action by homeomorphisms of a countable discrete group
$\alpha $
be an action by homeomorphisms of a countable discrete group
![]() $\Gamma $
on C. The action
$\Gamma $
on C. The action
![]() $\alpha $
is minimal if the orbit of every
$\alpha $
is minimal if the orbit of every
![]() $x\in C$
is dense. Recall that
$x\in C$
is dense. Recall that
![]() $\alpha $
is topologically free if for every non-trivial element
$\alpha $
is topologically free if for every non-trivial element
![]() $\gamma \in \Gamma $
, the closed set
$\gamma \in \Gamma $
, the closed set
has empty interior. Since C is a Baire space, this is equivalent to saying that the set
![]() ${\{x\in C\mid \mathrm {Stab}_{\alpha }(x)\neq \{1\}\}}$
is meagre, that is, a countable union of nowhere dense sets.
${\{x\in C\mid \mathrm {Stab}_{\alpha }(x)\neq \{1\}\}}$
is meagre, that is, a countable union of nowhere dense sets.
The set
![]() $\mathrm {Sub}(\Gamma )$
of subgroups of
$\mathrm {Sub}(\Gamma )$
of subgroups of
![]() $\Gamma $
naturally identifies with a subset of
$\Gamma $
naturally identifies with a subset of
![]() $\{0,1\}^\Gamma $
. It is closed for the product topology. Thus, the induced topology on
$\{0,1\}^\Gamma $
. It is closed for the product topology. Thus, the induced topology on
![]() $\mathrm {Sub}(\Gamma )$
turns it into a compact totally disconnected space, on which
$\mathrm {Sub}(\Gamma )$
turns it into a compact totally disconnected space, on which
![]() $\Gamma $
acts continuously by conjugation. A URS of
$\Gamma $
acts continuously by conjugation. A URS of
![]() $\Gamma $
is a closed minimal
$\Gamma $
is a closed minimal
![]() $\Gamma $
-invariant subset of
$\Gamma $
-invariant subset of
![]() $\mathrm {Sub}(\Gamma )$
. The trivial URS is the URS that only contains the trivial subgroup. Recall that the stabilizer URS of a minimal action
$\mathrm {Sub}(\Gamma )$
. The trivial URS is the URS that only contains the trivial subgroup. Recall that the stabilizer URS of a minimal action
![]() $\alpha $
of
$\alpha $
of
![]() $\Gamma $
on C is the unique closed,
$\Gamma $
on C is the unique closed,
![]() $\Gamma $
-invariant minimal subset in the closure of
$\Gamma $
-invariant minimal subset in the closure of
![]() $\{\mathrm {Stab}_{\alpha }(x)\mid x\in C\}$
. It is straightforward to check that the map
$\{\mathrm {Stab}_{\alpha }(x)\mid x\in C\}$
. It is straightforward to check that the map
![]() $\mathrm {Stab}_{\alpha }$
is upper-semi continuous. Therefore, it is continuous on a
$\mathrm {Stab}_{\alpha }$
is upper-semi continuous. Therefore, it is continuous on a
![]() $G_\delta $
dense set. If
$G_\delta $
dense set. If
![]() $C_0\subset C$
denotes the locus of continuity of
$C_0\subset C$
denotes the locus of continuity of
![]() ${\mathrm {Stab}_{\alpha } : C\to \mathrm {Sub}(\Gamma )}$
, then one can prove that
${\mathrm {Stab}_{\alpha } : C\to \mathrm {Sub}(\Gamma )}$
, then one can prove that
![]() $\mathrm {URS}(\alpha )$
is equal to the closure of the set
$\mathrm {URS}(\alpha )$
is equal to the closure of the set
![]() $\{\mathrm {Stab}_{\alpha }(x)\mid x\in C_0\}$
, see [Reference Glasner and WeissGW15].
$\{\mathrm {Stab}_{\alpha }(x)\mid x\in C_0\}$
, see [Reference Glasner and WeissGW15].
A proof of the following classical result can be found in [Reference Le Boudec and Matte BonLBMB18, Proposition 2.7].
Lemma 2.1. Let
![]() $\alpha $
be a minimal
$\alpha $
be a minimal
![]() $\Gamma $
-action on a compact Hausdorff space C. Then
$\Gamma $
-action on a compact Hausdorff space C. Then
![]() $\alpha $
is topologically free if and only if its stabilizer URS is trivial, if and only if there exists
$\alpha $
is topologically free if and only if its stabilizer URS is trivial, if and only if there exists
![]() $x\in C$
such that
$x\in C$
such that
![]() $\mathrm {Stab}_{\alpha }(x)$
is trivial.
$\mathrm {Stab}_{\alpha }(x)$
is trivial.
The following lemma clarifies the relation between the stabilizer URS and the stabilizer IRS. Recall that the support of a Borel probability measure is the intersection of all closed subsets of full measure.
Lemma 2.2. Let
![]() $\alpha $
be a minimal
$\alpha $
be a minimal
![]() $\Gamma $
-action on a compact Hausdorff space C and
$\Gamma $
-action on a compact Hausdorff space C and
![]() $\mu $
be a
$\mu $
be a
![]() $\Gamma $
-invariant Borel probability measure on C. Then
$\Gamma $
-invariant Borel probability measure on C. Then
![]() $\mathrm {URS}(\alpha )$
is contained in the support of
$\mathrm {URS}(\alpha )$
is contained in the support of
![]() $\mathrm {IRS}(\alpha )$
. In particular, if
$\mathrm {IRS}(\alpha )$
. In particular, if
![]() $\mathrm {IRS}(\alpha )$
is trivial, then
$\mathrm {IRS}(\alpha )$
is trivial, then
![]() $\mathrm {URS}(\alpha )$
is trivial.
$\mathrm {URS}(\alpha )$
is trivial.
Proof. Let F be a closed subset of
![]() $\mathrm {Sub}(\Gamma )$
such that
$\mathrm {Sub}(\Gamma )$
such that
![]() $\mu (\mathrm {Stab}_{\alpha }^{-1}(F))=1$
. By minimality of
$\mu (\mathrm {Stab}_{\alpha }^{-1}(F))=1$
. By minimality of
![]() $\alpha $
, every non-empty open subset U of C satisfies
$\alpha $
, every non-empty open subset U of C satisfies
![]() $\mu (U)>0$
. Thus,
$\mu (U)>0$
. Thus,
![]() $\mathrm {Stab}_{\alpha }^{-1}(F)$
is dense in C. Let
$\mathrm {Stab}_{\alpha }^{-1}(F)$
is dense in C. Let
![]() $x\in C$
be a continuity point of
$x\in C$
be a continuity point of
![]() $\mathrm {Stab}_{\alpha }$
. Let
$\mathrm {Stab}_{\alpha }$
. Let
![]() $(x_n)_{n\geq 0}$
be a sequence of elements in
$(x_n)_{n\geq 0}$
be a sequence of elements in
![]() $\mathrm {Stab}_{\alpha }^{-1}(F)$
that converges to x. Then
$\mathrm {Stab}_{\alpha }^{-1}(F)$
that converges to x. Then
![]() $\mathrm {Stab}_{\alpha }(x)\in F$
and we thus obtain that
$\mathrm {Stab}_{\alpha }(x)\in F$
and we thus obtain that
![]() $\mathrm {URS}(\alpha )\subset F$
. By definition of the support of
$\mathrm {URS}(\alpha )\subset F$
. By definition of the support of
![]() $\mathrm {IRS}(\alpha )$
, this implies that
$\mathrm {IRS}(\alpha )$
, this implies that
![]() $\mathrm {URS}(\alpha )\subset \mathrm {supp}(\mathrm {IRS}(\alpha ))$
.
$\mathrm {URS}(\alpha )\subset \mathrm {supp}(\mathrm {IRS}(\alpha ))$
.
The following proposition gives a partial converse to Lemma 2.2.
Proposition 2.3. Let
![]() $\alpha $
be a minimal
$\alpha $
be a minimal
![]() $\Gamma $
-action on a compact Hausdorff space C and
$\Gamma $
-action on a compact Hausdorff space C and
![]() $\mu $
be a
$\mu $
be a
![]() $\Gamma $
-invariant Borel probability measure on C. If
$\Gamma $
-invariant Borel probability measure on C. If
![]() $\mathrm {URS}(\alpha )$
is trivial, then
$\mathrm {URS}(\alpha )$
is trivial, then
![]() $\mathrm {IRS}(\alpha )$
is either trivial or atomless.
$\mathrm {IRS}(\alpha )$
is either trivial or atomless.
Proof. Assume that
![]() $\mathrm {IRS}(\alpha )$
has a non-trivial atom
$\mathrm {IRS}(\alpha )$
has a non-trivial atom
![]() $\{\Lambda \}$
. By invariance, the atoms
$\{\Lambda \}$
. By invariance, the atoms
![]() $\{\gamma \Lambda \gamma ^{-1}\}$
have equal measure for all
$\{\gamma \Lambda \gamma ^{-1}\}$
have equal measure for all
![]() $\gamma \in \Gamma $
. Thus,
$\gamma \in \Gamma $
. Thus,
![]() $\Lambda $
has only finitely many conjugates. Thus, the closure in
$\Lambda $
has only finitely many conjugates. Thus, the closure in
![]() $\mathrm {Sub}(\Gamma )$
of the set
$\mathrm {Sub}(\Gamma )$
of the set
![]() $\{\mathrm {Stab}_{\alpha }(x)\mid x\in C\}$
contains the finite set
$\{\mathrm {Stab}_{\alpha }(x)\mid x\in C\}$
contains the finite set
![]() $\{\gamma \Lambda \gamma ^{-1}\mid \gamma \in \Gamma \}$
, which is closed,
$\{\gamma \Lambda \gamma ^{-1}\mid \gamma \in \Gamma \}$
, which is closed,
![]() $\Gamma $
-invariant and minimal. Thus,
$\Gamma $
-invariant and minimal. Thus,
![]() $\mathrm {URS}(\alpha )$
is non-trivial.
$\mathrm {URS}(\alpha )$
is non-trivial.
This last result implies that the converse of Lemma 2.2 is actually true for groups admitting only countably many subgroups.
Corollary 2.4. Let
![]() $\alpha $
be a minimal
$\alpha $
be a minimal
![]() $\Gamma $
-action on a compact Hausdorff space C and
$\Gamma $
-action on a compact Hausdorff space C and
![]() $\mu $
a
$\mu $
a
![]() $\Gamma $
-invariant Borel probability measure on C. If
$\Gamma $
-invariant Borel probability measure on C. If
![]() $\mathrm {Sub}(\Gamma )$
is countable, then
$\mathrm {Sub}(\Gamma )$
is countable, then
![]() $\mathrm {IRS}(\alpha )$
is trivial if and only if
$\mathrm {IRS}(\alpha )$
is trivial if and only if
![]() $\mathrm {URS}(\alpha )$
is trivial.
$\mathrm {URS}(\alpha )$
is trivial.
Thus, groups
![]() $\Gamma $
such that
$\Gamma $
such that
![]() $\mathrm {Sub}(\Gamma )$
is countable are not allosteric.
$\mathrm {Sub}(\Gamma )$
is countable are not allosteric.
2.2 Profinite actions and their URS/IRS
Let
![]() $\Gamma $
be a countable group. For every
$\Gamma $
be a countable group. For every
![]() $n\geq 0$
, let
$n\geq 0$
, let
![]() $\alpha _n$
be a
$\alpha _n$
be a
![]() $\Gamma $
-action on a finite set
$\Gamma $
-action on a finite set
![]() $X_n$
, and assume that for every
$X_n$
, and assume that for every
![]() $n\geq 0$
,
$n\geq 0$
,
![]() $\alpha _{n}$
is a quotient of
$\alpha _{n}$
is a quotient of
![]() $\alpha _{n+1}$
, that is, there exists a
$\alpha _{n+1}$
, that is, there exists a
![]() $\Gamma $
-equivariant onto map
$\Gamma $
-equivariant onto map
![]() $q_n : X_{n+1}\twoheadrightarrow X_n$
. The inverse limit of the finite spaces
$q_n : X_{n+1}\twoheadrightarrow X_n$
. The inverse limit of the finite spaces
![]() $X_n$
is the space
$X_n$
is the space
 $$ \begin{align*}\varprojlim X_n:=\bigg\{(x_n)_{n\geq 0}\in \prod_{n\geq 0}X_n\mid \text{for all } n\geq 0, q_n(x_{n+1})=x_n\bigg\}.\end{align*} $$
$$ \begin{align*}\varprojlim X_n:=\bigg\{(x_n)_{n\geq 0}\in \prod_{n\geq 0}X_n\mid \text{for all } n\geq 0, q_n(x_{n+1})=x_n\bigg\}.\end{align*} $$
This space is closed, thus compact, and totally disconnected in the product topology. Let
![]() $\alpha $
be the
$\alpha $
be the
![]() $\Gamma $
-action by homeomorphisms on
$\Gamma $
-action by homeomorphisms on
![]() $\varprojlim X_n$
defined by
$\varprojlim X_n$
defined by
If each
![]() $X_n$
is endowed with a
$X_n$
is endowed with a
![]() $\Gamma $
-invariant probability measure
$\Gamma $
-invariant probability measure
![]() $\mu _n$
, we let
$\mu _n$
, we let
![]() $\mu $
be the unique Borel probability measure on
$\mu $
be the unique Borel probability measure on
![]() $\varprojlim X_n$
that projects onto
$\varprojlim X_n$
that projects onto
![]() $\mu _k$
via the canonical projection
$\mu _k$
via the canonical projection
![]() $\pi _k : \varprojlim X_n\to X_k$
, for every
$\pi _k : \varprojlim X_n\to X_k$
, for every
![]() $k\geq 0$
. The
$k\geq 0$
. The
![]() $\Gamma $
-action
$\Gamma $
-action
![]() $\alpha $
preserves
$\alpha $
preserves
![]() $\mu $
and is called the inverse limit of the p.m.p.
$\mu $
and is called the inverse limit of the p.m.p.
![]() $\Gamma $
-actions
$\Gamma $
-actions
![]() $\alpha _n$
. A p.m.p. action of
$\alpha _n$
. A p.m.p. action of
![]() $\Gamma $
is profinite if it is measurably isomorphic to an inverse limit of p.m.p.
$\Gamma $
is profinite if it is measurably isomorphic to an inverse limit of p.m.p.
![]() $\Gamma $
-actions on finite sets. A proof of the following Lemma can be found in [Reference GrigorchukGri11, Proposition 4.1].
$\Gamma $
-actions on finite sets. A proof of the following Lemma can be found in [Reference GrigorchukGri11, Proposition 4.1].
Lemma 2.5. Let
![]() $\Gamma \curvearrowright ^\alpha \varprojlim (X_n,\mu _n)$
be the inverse limit of the p.m.p. finite actions
$\Gamma \curvearrowright ^\alpha \varprojlim (X_n,\mu _n)$
be the inverse limit of the p.m.p. finite actions
![]() $\Gamma \curvearrowright ^{\alpha _n} (X_n,\mu _n)$
and let
$\Gamma \curvearrowright ^{\alpha _n} (X_n,\mu _n)$
and let
![]() $\mu $
denotes the inverse limit of the
$\mu $
denotes the inverse limit of the
![]() $\mu _n$
. Then the following are equivalent.
$\mu _n$
. Then the following are equivalent.
-
(1) For every
 $n\geq 0$
,
$n\geq 0$
,
 $\alpha _n$
is transitive and
$\alpha _n$
is transitive and
 $\mu _n$
is the uniform measure on
$\mu _n$
is the uniform measure on
 $X_n$
.
$X_n$
. -
(2) The action
 $\alpha $
is minimal.
$\alpha $
is minimal. -
(3) The action
 $\alpha $
is
$\alpha $
is
 $\mu $
-ergodic.
$\mu $
-ergodic. -
(3) The action
 $\alpha $
is uniquely ergodic, that is,
$\alpha $
is uniquely ergodic, that is,
 $\mu $
is the unique
$\mu $
is the unique
 $\Gamma $
-invariant Borel probability measure on
$\Gamma $
-invariant Borel probability measure on
 $\varprojlim X_n$
.
$\varprojlim X_n$
.
With the above notation, the following lemma is useful to compute the measure of a closed subset in an inverse limit (here, no group action is involved).
Lemma 2.6. Let A be a closed subset of
![]() $\varprojlim X_n$
. Then,
$\varprojlim X_n$
. Then,
![]() $A=\bigcap _{n\geq 0}\pi _n^{-1}(\pi _n(A))$
. Thus,
$A=\bigcap _{n\geq 0}\pi _n^{-1}(\pi _n(A))$
. Thus,
Proof. First, A is contained in
![]() $\bigcap _{n\geq 0}\pi _n^{-1}(\pi _n(A))$
since it is contained in each
$\bigcap _{n\geq 0}\pi _n^{-1}(\pi _n(A))$
since it is contained in each
![]() $\pi _n^{-1}(\pi _n(A))$
. Conversely, let x be in
$\pi _n^{-1}(\pi _n(A))$
. Conversely, let x be in
![]() $\bigcap _{n\geq 0}\pi _n^{-1}(\pi _n(A))$
. For every
$\bigcap _{n\geq 0}\pi _n^{-1}(\pi _n(A))$
. For every
![]() $n\geq 0$
, there exists
$n\geq 0$
, there exists
![]() $y_n\in A$
such that
$y_n\in A$
such that
![]() $\pi _n(x)=\pi _n(y_n)$
. By compactness of A, let
$\pi _n(x)=\pi _n(y_n)$
. By compactness of A, let
![]() $y\in A$
be a limit of some subsequence of
$y\in A$
be a limit of some subsequence of
![]() $(y_n)_{n\geq 0}$
. By definition of the product topology, for every
$(y_n)_{n\geq 0}$
. By definition of the product topology, for every
![]() $n\geq 0, \pi _n(x)=\pi _n(y)$
, thus
$n\geq 0, \pi _n(x)=\pi _n(y)$
, thus
![]() $x=y$
and x belongs to A.
$x=y$
and x belongs to A.
Let
![]() $(\Gamma _n)_{n\geq 0}$
be a chain in
$(\Gamma _n)_{n\geq 0}$
be a chain in
![]() $\Gamma $
, that is, an infinite decreasing sequence
$\Gamma $
, that is, an infinite decreasing sequence
![]() $\Gamma =\Gamma _0\geq \Gamma _1\geq \ldots $
of finite index subgroups. If
$\Gamma =\Gamma _0\geq \Gamma _1\geq \ldots $
of finite index subgroups. If
![]() $X_n=\Gamma /\Gamma _n$
and
$X_n=\Gamma /\Gamma _n$
and
![]() $\mu _n$
is the uniform probability measure on
$\mu _n$
is the uniform probability measure on
![]() $X_n$
, then we get a profinite action that is ergodic by Lemma 2.5. Conversely, any ergodic (equivalently minimal) profinite
$X_n$
, then we get a profinite action that is ergodic by Lemma 2.5. Conversely, any ergodic (equivalently minimal) profinite
![]() $\Gamma $
-action
$\Gamma $
-action
![]() $\Gamma \curvearrowright \varprojlim X_n$
is measurably isomorphic to a profinite action of the form
$\Gamma \curvearrowright \varprojlim X_n$
is measurably isomorphic to a profinite action of the form
![]() $\Gamma \curvearrowright \varprojlim \Gamma /\Gamma _n$
for some chain
$\Gamma \curvearrowright \varprojlim \Gamma /\Gamma _n$
for some chain
![]() $(\Gamma _n)_{n\geq 0}$
, by fixing a point
$(\Gamma _n)_{n\geq 0}$
, by fixing a point
![]() $x\in \varprojlim X_n$
and letting
$x\in \varprojlim X_n$
and letting
![]() $\Gamma _n$
be the stabilizer of
$\Gamma _n$
be the stabilizer of
![]() $\pi _n(x)\in X_n$
.
$\pi _n(x)\in X_n$
.
Lemma 2.7. Let
![]() $(\Gamma _n)_{n\geq 0}$
be a chain in
$(\Gamma _n)_{n\geq 0}$
be a chain in
![]() $\Gamma $
and let
$\Gamma $
and let
![]() $\alpha $
be the corresponding ergodic profinite
$\alpha $
be the corresponding ergodic profinite
![]() $\Gamma $
-action. Then
$\Gamma $
-action. Then
![]() $\mathrm {URS}(\alpha )$
is trivial if and only if there exists
$\mathrm {URS}(\alpha )$
is trivial if and only if there exists
![]() $(\gamma _n\Gamma _n)_{n\geq 0}\in \varprojlim \Gamma /\Gamma _n$
such that
$(\gamma _n\Gamma _n)_{n\geq 0}\in \varprojlim \Gamma /\Gamma _n$
such that
Proof. For all
![]() $x\in \varprojlim \Gamma /\Gamma _n$
, if
$x\in \varprojlim \Gamma /\Gamma _n$
, if
![]() $x=(\gamma _n\Gamma _n)_{n\geq 0}$
, then
$x=(\gamma _n\Gamma _n)_{n\geq 0}$
, then
Thus, the result is a direct consequence of Lemma 2.1.
Proposition 2.8. Let
![]() $(\Gamma _n)_{n\geq 0}$
be a chain in
$(\Gamma _n)_{n\geq 0}$
be a chain in
![]() $\Gamma $
and let
$\Gamma $
and let
![]() $\alpha $
be the corresponding ergodic profinite
$\alpha $
be the corresponding ergodic profinite
![]() $\Gamma $
-action. If
$\Gamma $
-action. If
![]() $\mathrm {URS}(\alpha )$
is trivial, then either
$\mathrm {URS}(\alpha )$
is trivial, then either
![]() $\mathrm {IRS}(\alpha )$
is trivial or there exists a finite index subgroup
$\mathrm {IRS}(\alpha )$
is trivial or there exists a finite index subgroup
![]() $\Lambda \leq \Gamma $
such that the p.m.p.
$\Lambda \leq \Gamma $
such that the p.m.p.
![]() $\Lambda $
-action by conjugation on
$\Lambda $
-action by conjugation on
![]() $(\mathrm {Sub}(\Gamma ),\mathrm {IRS}(\alpha ))$
is not ergodic.
$(\mathrm {Sub}(\Gamma ),\mathrm {IRS}(\alpha ))$
is not ergodic.
Proof. Assume that the p.m.p.
![]() $\Gamma $
-action by conjugation on
$\Gamma $
-action by conjugation on
![]() $(\mathrm {Sub}(\Gamma ),\mathrm {IRS}(\alpha ))$
remains ergodic under any finite index subgroup of
$(\mathrm {Sub}(\Gamma ),\mathrm {IRS}(\alpha ))$
remains ergodic under any finite index subgroup of
![]() $\Gamma $
. Since
$\Gamma $
. Since
![]() $\mathrm {URS}(\alpha )$
is trivial, there exists by Lemma 2.7 a sequence
$\mathrm {URS}(\alpha )$
is trivial, there exists by Lemma 2.7 a sequence
![]() $(\gamma _n)_{n\geq 0}$
of elements in
$(\gamma _n)_{n\geq 0}$
of elements in
![]() $\Gamma $
such that
$\Gamma $
such that
For every
![]() $k\geq 0$
, if
$k\geq 0$
, if
![]() $\pi _k : \varprojlim \Gamma /\Gamma _n\to \Gamma /\Gamma _k$
denotes the projection onto the kth coordinate, then the set
$\pi _k : \varprojlim \Gamma /\Gamma _n\to \Gamma /\Gamma _k$
denotes the projection onto the kth coordinate, then the set
has positive measure for
![]() $\mathrm {IRS}(\alpha )$
, is contained in
$\mathrm {IRS}(\alpha )$
, is contained in
![]() $\mathrm {Sub}(\gamma _k\Gamma _k\gamma _k^{-1})$
and is invariant under the finite index subgroup
$\mathrm {Sub}(\gamma _k\Gamma _k\gamma _k^{-1})$
and is invariant under the finite index subgroup
![]() $\mathrm {Stab}_{\alpha _k}(\gamma _k\Gamma _k)=\gamma _k\Gamma _k\gamma _k^{-1} $
. By ergodicity, it is a full measure set. Thus, for almost every (a.e.)
$\mathrm {Stab}_{\alpha _k}(\gamma _k\Gamma _k)=\gamma _k\Gamma _k\gamma _k^{-1} $
. By ergodicity, it is a full measure set. Thus, for almost every (a.e.)
![]() $x\in \varprojlim \Gamma /\Gamma _n$
,
$x\in \varprojlim \Gamma /\Gamma _n$
,
![]() $\mathrm {Stab}_{\alpha }(x)$
is a subgroup of
$\mathrm {Stab}_{\alpha }(x)$
is a subgroup of
![]() $\gamma _k\Gamma _k\gamma _k^{-1}$
. Since this is true for every
$\gamma _k\Gamma _k\gamma _k^{-1}$
. Since this is true for every
![]() $k\geq 0$
, we conclude that
$k\geq 0$
, we conclude that
![]() $\mathrm {IRS}(\alpha )$
is trivial.
$\mathrm {IRS}(\alpha )$
is trivial.
2.3 Allostery and commensurability
Two groups
![]() $\Gamma _1$
and
$\Gamma _1$
and
![]() $\Gamma _2$
are commensurable if there exist finite index subgroups
$\Gamma _2$
are commensurable if there exist finite index subgroups
![]() $\Lambda _1\leq \Gamma _1$
and
$\Lambda _1\leq \Gamma _1$
and
![]() $\Lambda _2\leq \Gamma _2$
such that
$\Lambda _2\leq \Gamma _2$
such that
![]() $\Lambda _1$
is isomorphic to
$\Lambda _1$
is isomorphic to
![]() $\Lambda _2$
. In this section, we prove the following result.
$\Lambda _2$
. In this section, we prove the following result.
Theorem 2.9. Allostery is invariant under commensurability.
We prove Theorem 2.9 in two steps, by showing that allostery is inherited by finite index overgroups in Proposition 2.10 and by finite index subgroups in Proposition 2.11. Let
![]() $\Gamma $
be a countable group and
$\Gamma $
be a countable group and
![]() $\Lambda \leq \Gamma $
a finite index subgroup. Let
$\Lambda \leq \Gamma $
a finite index subgroup. Let
![]() $\alpha : \Lambda \curvearrowright (C,\mu )$
be an action by homeomorphisms on a compact Hausdorff space C with a
$\alpha : \Lambda \curvearrowright (C,\mu )$
be an action by homeomorphisms on a compact Hausdorff space C with a
![]() $\Lambda $
-invariant Borel probability measure
$\Lambda $
-invariant Borel probability measure
![]() $\mu $
on C. Let
$\mu $
on C. Let
![]() $\beta : \Gamma \curvearrowright C\times \Gamma $
be the action defined by
$\beta : \Gamma \curvearrowright C\times \Gamma $
be the action defined by
![]() $\beta (\gamma )(x,\delta )=(x,\gamma \delta )$
. Define an equivalence relation
$\beta (\gamma )(x,\delta )=(x,\gamma \delta )$
. Define an equivalence relation
![]() $\sim $
on a
$\sim $
on a
![]() $C\times \Gamma $
by declaring that
$C\times \Gamma $
by declaring that
![]() $(x,\gamma )\sim (x',\gamma ')$
if and only if there exists
$(x,\gamma )\sim (x',\gamma ')$
if and only if there exists
![]() $\unicode{x3bb} \in \Lambda $
such that
$\unicode{x3bb} \in \Lambda $
such that
![]() $(x',\gamma ')=(\alpha (\unicode{x3bb} )x,\gamma \unicode{x3bb} )$
. The
$(x',\gamma ')=(\alpha (\unicode{x3bb} )x,\gamma \unicode{x3bb} )$
. The
![]() $\Gamma $
-action
$\Gamma $
-action
![]() $\beta $
projects onto a
$\beta $
projects onto a
![]() $\Gamma $
-action by homeomorphisms on
$\Gamma $
-action by homeomorphisms on
![]() $C\times \Gamma /\!\sim $
which is called the
$C\times \Gamma /\!\sim $
which is called the
![]() $\Gamma $
-action induced by
$\Gamma $
-action induced by
![]() $\alpha $
. We denote it by
$\alpha $
. We denote it by
![]() $\mathrm {Ind}_\Lambda ^\Gamma \alpha $
. The product of
$\mathrm {Ind}_\Lambda ^\Gamma \alpha $
. The product of
![]() $\mu $
with the counting measure on
$\mu $
with the counting measure on
![]() $\Gamma $
projects onto a Borel probability measure on
$\Gamma $
projects onto a Borel probability measure on
![]() $C\times \Gamma /\!\sim $
which is invariant by
$C\times \Gamma /\!\sim $
which is invariant by
![]() $\mathrm {Ind}_\Lambda ^\Gamma \alpha $
.
$\mathrm {Ind}_\Lambda ^\Gamma \alpha $
.
Proposition 2.10. Let
![]() $\Gamma $
be a countable group and
$\Gamma $
be a countable group and
![]() $\Lambda \leq \Gamma $
a finite index subgroup. Then the
$\Lambda \leq \Gamma $
a finite index subgroup. Then the
![]() $\Gamma $
-action induced by any allosteric
$\Gamma $
-action induced by any allosteric
![]() $\Lambda $
-action is allosteric.
$\Lambda $
-action is allosteric.
Proof. Let
![]() $\alpha : \Lambda \curvearrowright (C,\mu )$
be an allosteric action. It is an exercise to prove that
$\alpha : \Lambda \curvearrowright (C,\mu )$
be an allosteric action. It is an exercise to prove that
![]() $\mathrm {Ind}_\Lambda ^\Gamma \alpha $
is ergodic and minimal. Moreover,
$\mathrm {Ind}_\Lambda ^\Gamma \alpha $
is ergodic and minimal. Moreover,
![]() $\mathrm {IRS}(\mathrm {Ind}_\Lambda ^\Gamma \alpha )$
is non-trivial since the restriction of
$\mathrm {IRS}(\mathrm {Ind}_\Lambda ^\Gamma \alpha )$
is non-trivial since the restriction of
![]() $\mathrm {Ind}_\Lambda ^\Gamma \alpha $
to
$\mathrm {Ind}_\Lambda ^\Gamma \alpha $
to
![]() $\Lambda $
is not essentially free. Finally,
$\Lambda $
is not essentially free. Finally,
![]() $\mathrm {URS}(\alpha )$
is trivial, thus there exists by Lemma 2.1 a point
$\mathrm {URS}(\alpha )$
is trivial, thus there exists by Lemma 2.1 a point
![]() $x\in C$
such that
$x\in C$
such that
![]() $\mathrm {Stab}_{\alpha }(x)=\{1\}$
. Let y be the projection of
$\mathrm {Stab}_{\alpha }(x)=\{1\}$
. Let y be the projection of
![]() $(x,1)$
onto the quotient
$(x,1)$
onto the quotient
![]() $(C\times \Gamma )/\!\sim $
, then
$(C\times \Gamma )/\!\sim $
, then
![]() $\mathrm {Stab}_{\mathrm {Ind}_\Lambda ^\Gamma \alpha }(y)=\{1\}$
. Since
$\mathrm {Stab}_{\mathrm {Ind}_\Lambda ^\Gamma \alpha }(y)=\{1\}$
. Since
![]() $\mathrm {Ind}_\Lambda ^\Gamma \alpha $
is minimal, this implies by Lemma 2.1 that
$\mathrm {Ind}_\Lambda ^\Gamma \alpha $
is minimal, this implies by Lemma 2.1 that
![]() $\mathrm {URS}(\mathrm {Ind}_\Lambda ^\Gamma \alpha )$
is trivial. Thus,
$\mathrm {URS}(\mathrm {Ind}_\Lambda ^\Gamma \alpha )$
is trivial. Thus,
![]() $\mathrm {Ind}_\Lambda ^\Gamma \alpha $
is allosteric.
$\mathrm {Ind}_\Lambda ^\Gamma \alpha $
is allosteric.
Proposition 2.11. Any finite index subgroup of an allosteric group is allosteric.
Proof. Let
![]() $\Lambda \leq \Gamma $
be a finite index subgroup. We recall the following two facts. If
$\Lambda \leq \Gamma $
be a finite index subgroup. We recall the following two facts. If
![]() $\Gamma \curvearrowright (X,\mu )$
is an ergodic action, then any
$\Gamma \curvearrowright (X,\mu )$
is an ergodic action, then any
![]() $\Lambda $
-invariant measurable set
$\Lambda $
-invariant measurable set
![]() $A\subset X$
of positive measure satisfies
$A\subset X$
of positive measure satisfies
![]() $\mu (A)\geq 1/[\Gamma :\Lambda ]$
. Moreover, for any
$\mu (A)\geq 1/[\Gamma :\Lambda ]$
. Moreover, for any
![]() $\Lambda $
-invariant measurable set
$\Lambda $
-invariant measurable set
![]() $B\subset X$
of positive measure, there exists a
$B\subset X$
of positive measure, there exists a
![]() $\Lambda $
-invariant measurable set
$\Lambda $
-invariant measurable set
![]() $A\subset B$
of positive measure on which
$A\subset B$
of positive measure on which
![]() $\Lambda $
acts ergodically.
$\Lambda $
acts ergodically.
Let
![]() $\Gamma $
be an allosteric group, and let
$\Gamma $
be an allosteric group, and let
![]() $\Lambda \leq \Gamma $
be a finite index subgroup. Let N be the normal core of
$\Lambda \leq \Gamma $
be a finite index subgroup. Let N be the normal core of
![]() $\Lambda $
(the intersection of the conjugates of
$\Lambda $
(the intersection of the conjugates of
![]() $\Lambda $
). It is a finite index normal subgroup of
$\Lambda $
). It is a finite index normal subgroup of
![]() $\Gamma $
which is contained in
$\Gamma $
which is contained in
![]() $\Lambda $
. We will prove that N is allosteric. Proposition 2.10 will then imply that
$\Lambda $
. We will prove that N is allosteric. Proposition 2.10 will then imply that
![]() $\Lambda $
is allosteric. We let
$\Lambda $
is allosteric. We let
![]() $d=[\Gamma :N]$
and we fix
$d=[\Gamma :N]$
and we fix
![]() $\gamma _1,\ldots ,\gamma _d\in \Gamma $
, a coset representative system for N in
$\gamma _1,\ldots ,\gamma _d\in \Gamma $
, a coset representative system for N in
![]() $\Gamma $
. Let
$\Gamma $
. Let
![]() $\Gamma \curvearrowright ^\alpha (C,\mu )$
be an allosteric action. For all
$\Gamma \curvearrowright ^\alpha (C,\mu )$
be an allosteric action. For all
![]() $x\in C$
, we define
$x\in C$
, we define
![]() $\mathcal {O}_N(x)=\overline {\{\alpha (\gamma )x\mid \gamma \in N\}}$
. This is a closed, N-invariant subset of C. By minimality of
$\mathcal {O}_N(x)=\overline {\{\alpha (\gamma )x\mid \gamma \in N\}}$
. This is a closed, N-invariant subset of C. By minimality of
![]() $\alpha $
, for all
$\alpha $
, for all
![]() $x\in C$
,
$x\in C$
,
 $$ \begin{align*}X=\bigcup_{i=1}^d\mathcal{O}_N(\alpha(\gamma_i)x).\end{align*} $$
$$ \begin{align*}X=\bigcup_{i=1}^d\mathcal{O}_N(\alpha(\gamma_i)x).\end{align*} $$
Moreover, since N is normal in
![]() $\Gamma $
, for all
$\Gamma $
, for all
![]() $x\in C$
and
$x\in C$
and
![]() $\gamma \in \Gamma $
, we have
$\gamma \in \Gamma $
, we have
![]() $\mathcal {O}_N(\alpha (\gamma )x)=\alpha (\gamma )\mathcal {O}_N(x)$
. This implies that
$\mathcal {O}_N(\alpha (\gamma )x)=\alpha (\gamma )\mathcal {O}_N(x)$
. This implies that
![]() $\mu (\mathcal {O}_N(\alpha (\gamma )x))=\mu (\mathcal {O}_N(x))$
and that
$\mu (\mathcal {O}_N(\alpha (\gamma )x))=\mu (\mathcal {O}_N(x))$
and that
![]() $\mu (\mathcal {O}_N(x))>0$
. Let y be a point in some closed, N-invariant and N-minimal set. Then
$\mu (\mathcal {O}_N(x))>0$
. Let y be a point in some closed, N-invariant and N-minimal set. Then
![]() $N\curvearrowright \mathcal {O}_N(y)$
is minimal. Let
$N\curvearrowright \mathcal {O}_N(y)$
is minimal. Let
![]() $A\subset \mathcal {O}_N(y)$
be an N-invariant measurable set of positive measure on which N acts ergodically. Let
$A\subset \mathcal {O}_N(y)$
be an N-invariant measurable set of positive measure on which N acts ergodically. Let
![]() $\mu _A$
be the Borel probability measure on A induced by
$\mu _A$
be the Borel probability measure on A induced by
![]() $\mu $
. Then
$\mu $
. Then
![]() $N\curvearrowright (\mathcal {O}_N(y),\mu _A)$
is an ergodic minimal action, which is still topologically free. Let us prove that it is not essentially free. Since
$N\curvearrowright (\mathcal {O}_N(y),\mu _A)$
is an ergodic minimal action, which is still topologically free. Let us prove that it is not essentially free. Since
![]() $\alpha $
is allosteric,
$\alpha $
is allosteric,
![]() $\mathrm {IRS}(\alpha )$
is atomless, see Proposition 2.3. Thus, for
$\mathrm {IRS}(\alpha )$
is atomless, see Proposition 2.3. Thus, for
![]() $\mu $
-a.e.
$\mu $
-a.e.
![]() $x\in C$
,
$x\in C$
,
![]() $\mathrm {Stab}_{\alpha }(x)$
is infinite. Since N has finite index in
$\mathrm {Stab}_{\alpha }(x)$
is infinite. Since N has finite index in
![]() $\Gamma $
, this implies that for
$\Gamma $
, this implies that for
![]() $\mu $
-a.e.
$\mu $
-a.e.
![]() $x\in C$
,
$x\in C$
,
![]() $\mathrm {Stab}_{\alpha }(x)\cap N$
is infinite. Thus,
$\mathrm {Stab}_{\alpha }(x)\cap N$
is infinite. Thus,
![]() $N\curvearrowright (\mathcal {O}_N(y),\mu _A)$
is not essentially free and thus is allosteric.
$N\curvearrowright (\mathcal {O}_N(y),\mu _A)$
is not essentially free and thus is allosteric.
Remark 2.12. It is proved in [Reference Bergeron and GaboriauBG04, Théorème
![]() $4.1$
] that if
$4.1$
] that if
![]() $\Gamma $
is isomorphic to a free product of two infinite residually finite groups, then
$\Gamma $
is isomorphic to a free product of two infinite residually finite groups, then
![]() $\Gamma $
admits a continuum of profinite allosteric actions. Let
$\Gamma $
admits a continuum of profinite allosteric actions. Let
![]() $\Gamma '$
be a non-amenable group which is isomorphic to a free product of two non-trivial residually finite groups. Then Kurosh’s theorem [Reference SerreSer77, §
$\Gamma '$
be a non-amenable group which is isomorphic to a free product of two non-trivial residually finite groups. Then Kurosh’s theorem [Reference SerreSer77, §
![]() $5.5$
] implies that
$5.5$
] implies that
![]() $\Gamma '$
admits a finite index subgroup
$\Gamma '$
admits a finite index subgroup
![]() $\Gamma $
isomorphic to a free product of finitely many (and at least two) residually finite infinite groups. Proposition 2.10 then implies that
$\Gamma $
isomorphic to a free product of finitely many (and at least two) residually finite infinite groups. Proposition 2.10 then implies that
![]() $\Gamma '$
is allosteric.
$\Gamma '$
is allosteric.
3 Finite index subgroups of surface groups
3.1 Residual properties of surface groups
A surface group is the fundamental group of a closed connected surface. If the surface is orientable, then its fundamental group is called an orientable surface group and a presentation is given by
for some
![]() $g\geq 1$
called the genus of the surface (if
$g\geq 1$
called the genus of the surface (if
![]() $g=0$
, then the surface is a sphere and its fundamental group is trivial). If the surface is non-orientable, we call its fundamental group a non-orientable surface group. It has a presentation given by
$g=0$
, then the surface is a sphere and its fundamental group is trivial). If the surface is non-orientable, we call its fundamental group a non-orientable surface group. It has a presentation given by
for some
![]() $g\geq 1$
, called the genus of the surface. A surface group is amenable if and only if it is the fundamental group of the sphere, the torus (orientable surfaces of genus
$g\geq 1$
, called the genus of the surface. A surface group is amenable if and only if it is the fundamental group of the sphere, the torus (orientable surfaces of genus
![]() $0$
and
$0$
and
![]() $1$
), the projective plane or the Klein bottle (non-orientable surfaces of genus
$1$
), the projective plane or the Klein bottle (non-orientable surfaces of genus
![]() $1$
and
$1$
and
![]() $2$
). These groups are respectively isomorphic to the trivial group for the sphere,
$2$
). These groups are respectively isomorphic to the trivial group for the sphere,
![]() $\mathbb {Z}^2$
for the torus,
$\mathbb {Z}^2$
for the torus,
![]() $\mathbb {Z}/2\mathbb {Z}$
for the projective plane and the non-trivial semi-direct product
$\mathbb {Z}/2\mathbb {Z}$
for the projective plane and the non-trivial semi-direct product
![]() $\mathbb {Z}\rtimes \mathbb {Z}$
for the Klein bottle.
$\mathbb {Z}\rtimes \mathbb {Z}$
for the Klein bottle.
Definition 3.1. Let p be a prime number. A group
![]() $\Gamma $
is a residually finite p-group if for every non-trivial element
$\Gamma $
is a residually finite p-group if for every non-trivial element
![]() $\gamma \in \Gamma $
, there exists a normal subgroup
$\gamma \in \Gamma $
, there exists a normal subgroup
![]() $N\trianglelefteq \Gamma $
such that
$N\trianglelefteq \Gamma $
such that
![]() $\Gamma /N$
is a finite p-group and
$\Gamma /N$
is a finite p-group and
![]() $\gamma \notin N$
. Equivalently,
$\gamma \notin N$
. Equivalently,
![]() $\Gamma $
is a residually finite p-group if and only if there exists a chain
$\Gamma $
is a residually finite p-group if and only if there exists a chain
![]() $(\Gamma _n)_{n\geq 0}$
in
$(\Gamma _n)_{n\geq 0}$
in
![]() $\Gamma $
consisting of normal subgroups such that for every
$\Gamma $
consisting of normal subgroups such that for every
![]() $n\geq 0$
, the quotient
$n\geq 0$
, the quotient
![]() $\Gamma /\Gamma _n$
is a finite p-group and
$\Gamma /\Gamma _n$
is a finite p-group and
Baumslag proved in [Reference BaumslagBau62] that orientable surface groups are residually free, that is, for every non-trivial element
![]() $\gamma $
, there exists a normal subgroup
$\gamma $
, there exists a normal subgroup
![]() $N\trianglelefteq \Gamma $
such that
$N\trianglelefteq \Gamma $
such that
![]() $\Gamma /N$
is a free group and
$\Gamma /N$
is a free group and
![]() $\gamma \notin N$
. Free groups are residually finite p-groups for every prime p, a result independently proved by Takahasi [Reference TakahasiTak51] and by Gruenberg in [Reference GruenbergGru57]. This implies the following well-known result: orientable surface groups are residually finite p-groups for every prime p.
$\gamma \notin N$
. Free groups are residually finite p-groups for every prime p, a result independently proved by Takahasi [Reference TakahasiTak51] and by Gruenberg in [Reference GruenbergGru57]. This implies the following well-known result: orientable surface groups are residually finite p-groups for every prime p.
Remark 3.1. By a result of Baumslag [Reference BaumslagBau67], non-amenable non-orientable surface groups are also residually p-finite groups for every prime p. However, we leave as an exercise to the interested reader the fact that the fundamental group of a Klein bottle is not residually p for some prime p. We will not require these results.
3.2 Special kind of finite index subgroups in surface groups
Let
![]() $A,B$
be two non-empty totally ordered finite sets. We let
$A,B$
be two non-empty totally ordered finite sets. We let
![]() $\Gamma _{A,B}$
be the group defined by the generators
$\Gamma _{A,B}$
be the group defined by the generators
![]() $a_i,\alpha _i,b_j,\beta _j$
for
$a_i,\alpha _i,b_j,\beta _j$
for
![]() $i\in A$
and
$i\in A$
and
![]() $j\in B$
and the relation
$j\in B$
and the relation
where
![]() $i_1\leq \cdots \leq i_n$
is an ascending enumeration of the elements in A and
$i_1\leq \cdots \leq i_n$
is an ascending enumeration of the elements in A and
![]() ${j_1\leq \cdots \leq j_m}$
an ascending enumeration of the elements in B. Then
${j_1\leq \cdots \leq j_m}$
an ascending enumeration of the elements in B. Then
![]() $\Gamma _{A,B}$
is isomorphic to a non-amenable orientable surface group, and every non-amenable orientable surface group is isomorphic to
$\Gamma _{A,B}$
is isomorphic to a non-amenable orientable surface group, and every non-amenable orientable surface group is isomorphic to
![]() $\Gamma _{A,B}$
for some non-empty totally ordered finite sets A and B (see Figure 1). The group
$\Gamma _{A,B}$
for some non-empty totally ordered finite sets A and B (see Figure 1). The group
![]() $\Gamma _{A,B}$
naturally splits as an amalgamated product
$\Gamma _{A,B}$
naturally splits as an amalgamated product
where
![]() $\Gamma _A=\langle a_i,\alpha _i, i\in A\rangle $
and
$\Gamma _A=\langle a_i,\alpha _i, i\in A\rangle $
and
![]() $\Gamma _B=\langle b_j,\beta _j, j\in B\rangle $
are free groups of rank
$\Gamma _B=\langle b_j,\beta _j, j\in B\rangle $
are free groups of rank
![]() $2\lvert A\rvert $
and
$2\lvert A\rvert $
and
![]() $2\lvert B\rvert $
.
$2\lvert B\rvert $
.

Figure 1 Illustration of
![]() $\Gamma _{A,B}$
with
$\Gamma _{A,B}$
with
![]() $\lvert A\rvert =1$
and
$\lvert A\rvert =1$
and
![]() $\lvert B\rvert =2$
as an orientable surface group.
$\lvert B\rvert =2$
as an orientable surface group.
If
![]() $A'\subset A$
and
$A'\subset A$
and
![]() $B'\subset B$
, there is a natural surjection
$B'\subset B$
, there is a natural surjection
![]() $\Gamma _{A,B}\twoheadrightarrow \Gamma _{A',B'}$
defined on the generators by
$\Gamma _{A,B}\twoheadrightarrow \Gamma _{A',B'}$
defined on the generators by
 $$ \begin{align*}\begin{array}{llll} a_i \mapsto a_i' &\text{ for every }i\in A',&\quad b_j\mapsto b_j' &\text{ for every }j\in B',\\ \alpha_i \mapsto \alpha_i' &\text{ for every }i\in A',&\quad \beta_j\mapsto \beta_j' &\text{ for every }j\in B',\\ a_i \mapsto 1 &\text{ for every }i\in A\setminus A', &\quad b_j\mapsto 1 &\text{ for every }j\in B\setminus B', \\ \alpha_i \mapsto 1 &\text{ for every }i\in A\setminus A', &\quad \beta_j\mapsto 1 &\text{ for every }j\in B\setminus B'. \end{array}\end{align*} $$
$$ \begin{align*}\begin{array}{llll} a_i \mapsto a_i' &\text{ for every }i\in A',&\quad b_j\mapsto b_j' &\text{ for every }j\in B',\\ \alpha_i \mapsto \alpha_i' &\text{ for every }i\in A',&\quad \beta_j\mapsto \beta_j' &\text{ for every }j\in B',\\ a_i \mapsto 1 &\text{ for every }i\in A\setminus A', &\quad b_j\mapsto 1 &\text{ for every }j\in B\setminus B', \\ \alpha_i \mapsto 1 &\text{ for every }i\in A\setminus A', &\quad \beta_j\mapsto 1 &\text{ for every }j\in B\setminus B'. \end{array}\end{align*} $$
We say that this morphism erases the generators
![]() $a_i,\alpha _i,b_j,\beta _j$
for
$a_i,\alpha _i,b_j,\beta _j$
for
![]() $i\in A\setminus A'$
and
$i\in A\setminus A'$
and
![]() ${j\in B\setminus B'}$
, see Figure 2. Algebraically,
${j\in B\setminus B'}$
, see Figure 2. Algebraically,
![]() $\Gamma _{A',B'}$
is isomorphic to the quotient of
$\Gamma _{A',B'}$
is isomorphic to the quotient of
![]() $\Gamma _{A,B}$
by the normal closure of the set
$\Gamma _{A,B}$
by the normal closure of the set
![]() $\{a_i,\alpha _i, b_j,\beta _j\mid i\in A\setminus A', j\in B\setminus B'\}$
in
$\{a_i,\alpha _i, b_j,\beta _j\mid i\in A\setminus A', j\in B\setminus B'\}$
in
![]() $\Gamma _{A,B}$
, and the homomorphism
$\Gamma _{A,B}$
, and the homomorphism
![]() $\Gamma _{A,B}\twoheadrightarrow \Gamma _{A',B'}$
corresponds to the quotient group homomorphism.
$\Gamma _{A,B}\twoheadrightarrow \Gamma _{A',B'}$
corresponds to the quotient group homomorphism.

Figure 2 An illustration of the morphism that erases generators.

Figure 3 Illustrations of the proof of Theorem 3.2. The above line illustrates the coverings corresponding to the inclusions
![]() $\Lambda \leq \Lambda _d\leq \Gamma $
. The bottom line illustrates the covering corresponding to the inclusion
$\Lambda \leq \Lambda _d\leq \Gamma $
. The bottom line illustrates the covering corresponding to the inclusion
![]() $N'\leq \Lambda _d/N$
.
$N'\leq \Lambda _d/N$
.
Here is the main theorem of this section. In what follows,
![]() $\mathbb Z[1/p]$
denotes the set of rational numbers of the form
$\mathbb Z[1/p]$
denotes the set of rational numbers of the form
![]() $k/p^n$
for
$k/p^n$
for
![]() $k,n\in \mathbb Z$
.
$k,n\in \mathbb Z$
.
Theorem 3.2. Let
![]() $\Gamma $
be a non-amenable orientable surface group and fix a decomposition
$\Gamma $
be a non-amenable orientable surface group and fix a decomposition
![]() $\Gamma =\Gamma _A*_{\mathbb Z}\Gamma _B$
as above. Let p be a prime number and
$\Gamma =\Gamma _A*_{\mathbb Z}\Gamma _B$
as above. Let p be a prime number and
![]() $r\in ]0,1[\cap \mathbb Z[1/p]$
. Let
$r\in ]0,1[\cap \mathbb Z[1/p]$
. Let
![]() $\langle \langle \mathbb Z\rangle \rangle ^{\Gamma _B}$
be the normal closure of the amalgamated subgroup
$\langle \langle \mathbb Z\rangle \rangle ^{\Gamma _B}$
be the normal closure of the amalgamated subgroup
![]() $\mathbb Z$
in
$\mathbb Z$
in
![]() $\Gamma _B$
. For every non-trivial
$\Gamma _B$
. For every non-trivial
![]() $\gamma \in \Gamma $
and for every element
$\gamma \in \Gamma $
and for every element
![]() $\delta \in \Gamma _B\setminus \langle \langle {\mathbb Z}\rangle \rangle ^{\Gamma _B}$
, there exists a finite index subgroup
$\delta \in \Gamma _B\setminus \langle \langle {\mathbb Z}\rangle \rangle ^{\Gamma _B}$
, there exists a finite index subgroup
![]() $\Lambda \leq \Gamma $
such that:
$\Lambda \leq \Gamma $
such that:
-
(1)
 $\gamma \notin \Lambda $
;
$\gamma \notin \Lambda $
; -
(2) the index
 $[\Gamma :\Lambda ]$
is a power of p;
$[\Gamma :\Lambda ]$
is a power of p; -
(3) the number of left cosets
 $x\in \Gamma /\Lambda $
that are fixed by every element in
$x\in \Gamma /\Lambda $
that are fixed by every element in
 $\Gamma _A$
is equal to
$\Gamma _A$
is equal to
 $r[\Gamma :\Lambda ]$
;
$r[\Gamma :\Lambda ]$
; -
(4) none of the left coset
 $x\in \Gamma /\Lambda $
is fixed by
$x\in \Gamma /\Lambda $
is fixed by
 $\delta $
.
$\delta $
.
Proof. Fix
![]() $A,B$
two non-empty totally ordered finite sets, such that
$A,B$
two non-empty totally ordered finite sets, such that
![]() $\Gamma $
is isomorphic to
$\Gamma $
is isomorphic to
![]() $\Gamma _{A,B}$
. Let
$\Gamma _{A,B}$
. Let
![]() $S=\{a_i,\alpha _i,b_j,\beta _j\mid i\in A, j\in B\}$
be the set of generators. Let
$S=\{a_i,\alpha _i,b_j,\beta _j\mid i\in A, j\in B\}$
be the set of generators. Let
![]() $j_0$
be the smallest element in B. Let
$j_0$
be the smallest element in B. Let
![]() $\gamma \in \Gamma \setminus \{1\}$
and
$\gamma \in \Gamma \setminus \{1\}$
and
![]() $\delta \in \Gamma _B\setminus \langle \langle \mathbb Z\rangle \rangle ^{\Gamma _B}$
. Let p be a prime number and
$\delta \in \Gamma _B\setminus \langle \langle \mathbb Z\rangle \rangle ^{\Gamma _B}$
. Let p be a prime number and
![]() $r \in\, ] 0,1 [\cap {\mathbb Z}[1/p]$
.
$r \in\, ] 0,1 [\cap {\mathbb Z}[1/p]$
.
Step 1: Cyclic covering. Let
![]() $\varphi : \Gamma _{A,B}\twoheadrightarrow \mathbb Z$
be the surjective homomorphism defined on the generators of
$\varphi : \Gamma _{A,B}\twoheadrightarrow \mathbb Z$
be the surjective homomorphism defined on the generators of
![]() $\Gamma _{A,B}$
by
$\Gamma _{A,B}$
by
For every
![]() $d\geq 1$
, we let
$d\geq 1$
, we let
![]() $\Lambda _d$
be the kernel of the homomorphism
$\Lambda _d$
be the kernel of the homomorphism
![]() $\Gamma \to \mathbb Z/d\mathbb Z$
obtained by composing
$\Gamma \to \mathbb Z/d\mathbb Z$
obtained by composing
![]() $\varphi $
with the homomorphism of reduction modulo d. Then
$\varphi $
with the homomorphism of reduction modulo d. Then
![]() $\Lambda _d$
is a surface group. Let us describe a generating set for
$\Lambda _d$
is a surface group. Let us describe a generating set for
![]() $\Lambda _d$
. For every
$\Lambda _d$
. For every
![]() $0\leq k\leq d-1$
and
$0\leq k\leq d-1$
and
![]() $i\in A$
, let
$i\in A$
, let
![]() $a_{i,k}$
and
$a_{i,k}$
and
![]() $\alpha _{i,k}$
be the conjugates of
$\alpha _{i,k}$
be the conjugates of
![]() $a_i$
and
$a_i$
and
![]() $\alpha _i$
respectively, by
$\alpha _i$
respectively, by
![]() $b_{j_0}^k$
. Similarly, let
$b_{j_0}^k$
. Similarly, let
![]() $b_{j,k}$
and
$b_{j,k}$
and
![]() $\beta _{j,k}$
be the conjugates of
$\beta _{j,k}$
be the conjugates of
![]() $b_j$
and
$b_j$
and
![]() $\beta _j$
respectively, by
$\beta _j$
respectively, by
![]() $b_{j_0}^k$
. Then
$b_{j_0}^k$
. Then
![]() $\Lambda _d$
is generated by the set
$\Lambda _d$
is generated by the set
 $$ \begin{align*} \bigcup_{k=0}^{d-1}\{a_{i,k},\alpha_{i,k}\mid i\in A\}\cup \bigcup_{k=0}^{d-1}\{b_{j,k},\beta_{j,k}\mid j\in B\setminus\{j_0\}\}\cup \{b_{j_0}^{d},\beta_{j_0}\}. \end{align*} $$
$$ \begin{align*} \bigcup_{k=0}^{d-1}\{a_{i,k},\alpha_{i,k}\mid i\in A\}\cup \bigcup_{k=0}^{d-1}\{b_{j,k},\beta_{j,k}\mid j\in B\setminus\{j_0\}\}\cup \{b_{j_0}^{d},\beta_{j_0}\}. \end{align*} $$
So far, every left coset
![]() $x\in \Gamma /\Lambda _d$
is fixed by every element of
$x\in \Gamma /\Lambda _d$
is fixed by every element of
![]() $\Gamma _A$
, and either every or none of the left coset
$\Gamma _A$
, and either every or none of the left coset
![]() $x\in \Gamma /\Lambda _d$
is fixed by
$x\in \Gamma /\Lambda _d$
is fixed by
![]() $\delta $
, depending on whether
$\delta $
, depending on whether
![]() $\delta \in \Lambda _d$
or not.
$\delta \in \Lambda _d$
or not.
Step 2: Erasing the right amount of generators. Let n be the length of
![]() $\gamma \in \Gamma \setminus \{1\}$
in the generating set S. In the following, we let d be a (large enough) power of the prime p such that
$\gamma \in \Gamma \setminus \{1\}$
in the generating set S. In the following, we let d be a (large enough) power of the prime p such that
![]() $rd$
is an integer and
$rd$
is an integer and
![]() $rd+n\leq d$
. Let
$rd+n\leq d$
. Let
![]() $E\subset \{n+1,\ldots ,d-1-n\}$
be a subset of cardinality
$E\subset \{n+1,\ldots ,d-1-n\}$
be a subset of cardinality
![]() $rd$
, so that
$rd$
, so that
![]() $\gamma $
does not belong to the normal closure N of the set
$\gamma $
does not belong to the normal closure N of the set
![]() $\bigcup _{k\in E}b_{j_0}^k\Gamma _Ab_{j_0}^{-k}$
in
$\bigcup _{k\in E}b_{j_0}^k\Gamma _Ab_{j_0}^{-k}$
in
![]() $\Lambda _d$
. Let us prove that none of the conjugate of
$\Lambda _d$
. Let us prove that none of the conjugate of
![]() $\delta $
by a power of
$\delta $
by a power of
![]() $b_{j_0}$
belongs to N. Assume this is not the case, then this would imply that
$b_{j_0}$
belongs to N. Assume this is not the case, then this would imply that
![]() $\delta $
belongs to the normal closure of
$\delta $
belongs to the normal closure of
![]() $\bigcup _{k=0}^{d-1}b_{j_0}^k\Gamma _Ab_{j_0}^{-k}$
in
$\bigcup _{k=0}^{d-1}b_{j_0}^k\Gamma _Ab_{j_0}^{-k}$
in
![]() $\Lambda _d$
, which is easily seen to be equal to the normal closure
$\Lambda _d$
, which is easily seen to be equal to the normal closure
![]() $\langle \langle \Gamma _A\rangle \rangle ^\Gamma $
of
$\langle \langle \Gamma _A\rangle \rangle ^\Gamma $
of
![]() $\Gamma _A$
in
$\Gamma _A$
in
![]() $\Gamma $
. However, the group
$\Gamma $
. However, the group
![]() $\Gamma /\langle \langle \Gamma _A\rangle \rangle ^\Gamma $
is naturally isomorphic to
$\Gamma /\langle \langle \Gamma _A\rangle \rangle ^\Gamma $
is naturally isomorphic to
![]() $\Gamma _B/\langle \langle \mathbb Z\rangle \rangle ^{\Gamma _B}$
, in such a way that the following diagram commutes:
$\Gamma _B/\langle \langle \mathbb Z\rangle \rangle ^{\Gamma _B}$
, in such a way that the following diagram commutes:

which implies that
![]() $\Gamma _B\cap \langle \langle \Gamma _A\rangle \rangle ^\Gamma $
is equal to
$\Gamma _B\cap \langle \langle \Gamma _A\rangle \rangle ^\Gamma $
is equal to
![]() $\langle \langle \mathbb Z\rangle \rangle ^{\Gamma _B}$
. This would thus imply that
$\langle \langle \mathbb Z\rangle \rangle ^{\Gamma _B}$
. This would thus imply that
![]() $\delta \in \langle \langle \mathbb Z\rangle \rangle ^{\Gamma _B}$
, which is a contradiction.
$\delta \in \langle \langle \mathbb Z\rangle \rangle ^{\Gamma _B}$
, which is a contradiction.
Step 3: The group
![]() $\Lambda _d/N$
is a residually finite p-group. We let
$\Lambda _d/N$
is a residually finite p-group. We let
![]() $\pi : \Lambda _d\twoheadrightarrow \Lambda _d/N$
be the quotient group homomorphism. As orientable surface groups are p-residually finite and since
$\pi : \Lambda _d\twoheadrightarrow \Lambda _d/N$
be the quotient group homomorphism. As orientable surface groups are p-residually finite and since
![]() $\Lambda _d/N$
is an orientable surface group, there exists a normal subgroup
$\Lambda _d/N$
is an orientable surface group, there exists a normal subgroup
![]() $N'\trianglelefteq \Lambda _d/N$
whose index is a power of p, such that for every
$N'\trianglelefteq \Lambda _d/N$
whose index is a power of p, such that for every
![]() $k\in \{0,\ldots ,d-1\}\setminus E$
, for every
$k\in \{0,\ldots ,d-1\}\setminus E$
, for every
![]() $i\in A$
,
$i\in A$
,
![]() $\pi (a_{i,k})\notin N'$
and
$\pi (a_{i,k})\notin N'$
and
![]() $\pi (\alpha _{i,k})\notin N'$
. If
$\pi (\alpha _{i,k})\notin N'$
. If
![]() $\gamma \in \Lambda _d$
, we also assume that
$\gamma \in \Lambda _d$
, we also assume that
![]() $\pi (\gamma )\notin N$
, and if
$\pi (\gamma )\notin N$
, and if
![]() $\delta \in \Lambda _d$
, we also assume that for all
$\delta \in \Lambda _d$
, we also assume that for all
![]() $k\in \{0,\ldots ,d-1\}$
,
$k\in \{0,\ldots ,d-1\}$
,
![]() $\pi (b_{j_0}^k\delta b_{j_0}^{-k})\notin N'$
. Let us prove that the subgroup
$\pi (b_{j_0}^k\delta b_{j_0}^{-k})\notin N'$
. Let us prove that the subgroup
![]() $\Lambda :=\pi ^{-1}(N')$
of
$\Lambda :=\pi ^{-1}(N')$
of
![]() $\Gamma $
satisfies the four conclusions of the theorem.
$\Gamma $
satisfies the four conclusions of the theorem.
Proof of
 $(1)$
$(1)$
Either
![]() $\gamma \notin \Lambda _d$
and thus
$\gamma \notin \Lambda _d$
and thus
![]() $\gamma \notin \Lambda $
, or
$\gamma \notin \Lambda $
, or
![]() $\gamma \in \Lambda _d$
and
$\gamma \in \Lambda _d$
and
![]() $\pi (\gamma )\notin N$
.
$\pi (\gamma )\notin N$
.
Proof of
 $(2)$
$(2)$
Since the index of
![]() $N'$
in
$N'$
in
![]() $\Lambda _d/N$
is a power of p,
$\Lambda _d/N$
is a power of p,
![]() $[\Lambda _d:\Lambda ]$
is also a power of p. Thus
$[\Lambda _d:\Lambda ]$
is also a power of p. Thus
![]() $[\Gamma :\Lambda ]=[\Gamma :\Lambda _d][\Lambda _d:\Lambda ]$
is a power of p.
$[\Gamma :\Lambda ]=[\Gamma :\Lambda _d][\Lambda _d:\Lambda ]$
is a power of p.
Proof of
 $(3)$
$(3)$
By construction,
![]() $x\in \Gamma /\Lambda $
is fixed by every element in
$x\in \Gamma /\Lambda $
is fixed by every element in
![]() $\Gamma _A$
if and only its image under the canonical
$\Gamma _A$
if and only its image under the canonical
![]() $[\Lambda _d:\Lambda ]$
-to-one map
$[\Lambda _d:\Lambda ]$
-to-one map
![]() $\Gamma /\Lambda \mapsto \Gamma /\Lambda _d$
is equal to
$\Gamma /\Lambda \mapsto \Gamma /\Lambda _d$
is equal to
![]() $b_{j_0}^k\Lambda _d$
for some
$b_{j_0}^k\Lambda _d$
for some
![]() $k\in E$
. Since
$k\in E$
. Since
![]() $\lvert E\rvert =rd$
, there are exactly
$\lvert E\rvert =rd$
, there are exactly
![]() $rd[\Lambda _d:\Lambda ]=r[\Gamma :\Lambda ]$
such
$rd[\Lambda _d:\Lambda ]=r[\Gamma :\Lambda ]$
such
![]() $x\in \Gamma /\Lambda $
.
$x\in \Gamma /\Lambda $
.
Proof of
 $(4)$
$(4)$
If
![]() $\delta \notin \Lambda _d$
, then none of the coset
$\delta \notin \Lambda _d$
, then none of the coset
![]() $x\in \Gamma /\Lambda $
is fixed by
$x\in \Gamma /\Lambda $
is fixed by
![]() $\delta $
. If
$\delta $
. If
![]() $\delta \in \Lambda _d$
, then for all
$\delta \in \Lambda _d$
, then for all
![]() $k\in \{0,\ldots ,d-1\}$
, we have
$k\in \{0,\ldots ,d-1\}$
, we have
![]() $\pi (b_{j_0}^k\delta b_{j_0}^{-k})\notin N'$
, and thus
$\pi (b_{j_0}^k\delta b_{j_0}^{-k})\notin N'$
, and thus
![]() $\delta b_{j_0}^{-k}\Lambda \neq b_{j_0}^{-k}\Lambda $
. By normality of
$\delta b_{j_0}^{-k}\Lambda \neq b_{j_0}^{-k}\Lambda $
. By normality of
![]() $\Lambda $
in
$\Lambda $
in
![]() $\Lambda _d$
, we deduce that none of the coset
$\Lambda _d$
, we deduce that none of the coset
![]() $x\in \Gamma /\Lambda $
is fixed by
$x\in \Gamma /\Lambda $
is fixed by
![]() $\delta $
(see Figure 3).
$\delta $
(see Figure 3).
4 Proof of the main theorem
In this section, we give the proof of Theorem 1.2. More precisely, we prove the following results.
Theorem 4.1. (Orientable case)
Let
![]() $\Gamma $
be a non-amenable orientable surface group and fix a decomposition
$\Gamma $
be a non-amenable orientable surface group and fix a decomposition
![]() $\Gamma =\Gamma _A*_{\mathbb Z}\Gamma _B$
as above. Let
$\Gamma =\Gamma _A*_{\mathbb Z}\Gamma _B$
as above. Let
![]() $\langle \langle \mathbb Z\rangle \rangle ^{\Gamma _B}$
be the normal closure of the amalgamated subgroup
$\langle \langle \mathbb Z\rangle \rangle ^{\Gamma _B}$
be the normal closure of the amalgamated subgroup
![]() $\mathbb Z$
in
$\mathbb Z$
in
![]() $\Gamma _B$
. Then there exists a continuum
$\Gamma _B$
. Then there exists a continuum
![]() $(\alpha ^t)_{0<t<1}$
of ergodic profinite allosteric actions of
$(\alpha ^t)_{0<t<1}$
of ergodic profinite allosteric actions of
![]() $\Gamma $
such that for all
$\Gamma $
such that for all
![]() $0<t<1$
:
$0<t<1$
:
-
(1) the set of points whose stabilizer for
 $\alpha ^t$
contains
$\alpha ^t$
contains
 $\Gamma _A$
has measure t;
$\Gamma _A$
has measure t; -
(2) each element of
 $\Gamma _B\setminus \langle \langle \mathbb Z\rangle \rangle ^{\Gamma _B}$
acts essentially freely for
$\Gamma _B\setminus \langle \langle \mathbb Z\rangle \rangle ^{\Gamma _B}$
acts essentially freely for
 $\alpha ^t$
.
$\alpha ^t$
.
In particular, for all
![]() $0<s<t<1$
, the actions
$0<s<t<1$
, the actions
![]() $\alpha ^s$
and
$\alpha ^s$
and
![]() $\alpha ^t$
are neither topologically nor measurably isomorphic, and the probability measures
$\alpha ^t$
are neither topologically nor measurably isomorphic, and the probability measures
![]() $\mathrm {IRS}(\alpha ^s)$
and
$\mathrm {IRS}(\alpha ^s)$
and
![]() $\mathrm {IRS}(\alpha ^t)$
are distinct.
$\mathrm {IRS}(\alpha ^t)$
are distinct.
Theorem 4.2. (Non-orientable case)
Let
![]() $\Gamma '$
be a non-amenable non-orientable surface group. Then there exists an index-two subgroup
$\Gamma '$
be a non-amenable non-orientable surface group. Then there exists an index-two subgroup
![]() $\Gamma \leq \Gamma '$
which is isomorphic to an orientable surface group and which decomposes as
$\Gamma \leq \Gamma '$
which is isomorphic to an orientable surface group and which decomposes as
![]() $\Gamma =\Gamma _A*_{\mathbb Z}\Gamma _B$
, and a continuum
$\Gamma =\Gamma _A*_{\mathbb Z}\Gamma _B$
, and a continuum
![]() $(\beta ^t)_{0<t<1}$
of ergodic profinite allosteric actions of
$(\beta ^t)_{0<t<1}$
of ergodic profinite allosteric actions of
![]() $\Gamma '$
such that for all
$\Gamma '$
such that for all
![]() $0<t<1$
, the set of points whose stabilizer for
$0<t<1$
, the set of points whose stabilizer for
![]() $\beta ^t$
contains
$\beta ^t$
contains
![]() $\Gamma _A$
has measure
$\Gamma _A$
has measure
![]() $t/2$
. In particular, for all
$t/2$
. In particular, for all
![]() $0<s<t<1$
, the actions
$0<s<t<1$
, the actions
![]() $\beta ^s$
and
$\beta ^s$
and
![]() $\beta ^t$
are neither topologically nor measurably isomorphic, and the probability measures
$\beta ^t$
are neither topologically nor measurably isomorphic, and the probability measures
![]() $\mathrm {IRS}(\beta ^s)$
and
$\mathrm {IRS}(\beta ^s)$
and
![]() $\mathrm {IRS}(\beta ^t)$
are distinct.
$\mathrm {IRS}(\beta ^t)$
are distinct.
During the proof of these theorems, we will need the following lemma.
Lemma 4.3. Let
![]() $\Gamma $
be a group, and
$\Gamma $
be a group, and
![]() $\Lambda _1,\ldots ,\Lambda _n$
be finite index subgroups of
$\Lambda _1,\ldots ,\Lambda _n$
be finite index subgroups of
![]() $\Gamma $
. If the indices
$\Gamma $
. If the indices
![]() $[\Gamma :\Lambda _i]$
,
$[\Gamma :\Lambda _i]$
,
![]() $i\in \{1,\ldots ,n\}$
, are pairwise coprime integers, then the left coset action
$i\in \{1,\ldots ,n\}$
, are pairwise coprime integers, then the left coset action
![]() $\Gamma \curvearrowright \Gamma /(\Lambda _1\cap \cdots \cap \Lambda _n)$
is isomorphic to the diagonal action
$\Gamma \curvearrowright \Gamma /(\Lambda _1\cap \cdots \cap \Lambda _n)$
is isomorphic to the diagonal action
![]() $\Gamma \curvearrowright \Gamma /\Lambda _1\times \cdots \times \Gamma /\Lambda _n$
of the left coset actions
$\Gamma \curvearrowright \Gamma /\Lambda _1\times \cdots \times \Gamma /\Lambda _n$
of the left coset actions
![]() $\Gamma \curvearrowright \Gamma /\Lambda _i$
.
$\Gamma \curvearrowright \Gamma /\Lambda _i$
.
Proof. The kernel of the group homomorphism
![]() $\Gamma \to \Gamma /\Lambda _1\times \cdots \times \Gamma /\Lambda _n$
defined by
$\Gamma \to \Gamma /\Lambda _1\times \cdots \times \Gamma /\Lambda _n$
defined by
![]() $\gamma \mapsto (\gamma \Lambda _1,\ldots ,\gamma \Lambda _n)$
is equal to
$\gamma \mapsto (\gamma \Lambda _1,\ldots ,\gamma \Lambda _n)$
is equal to
![]() $\Lambda _1\cap \cdots \cap \Lambda _n$
. Thus,
$\Lambda _1\cap \cdots \cap \Lambda _n$
. Thus,
![]() $\Gamma /(\Lambda _1\cap \cdots \cap \Lambda _n)$
is isomorphic to a subgroup of
$\Gamma /(\Lambda _1\cap \cdots \cap \Lambda _n)$
is isomorphic to a subgroup of
![]() $\Gamma /\Lambda _1\times \cdots \times \Gamma /\Lambda _n$
. Moreover, for every
$\Gamma /\Lambda _1\times \cdots \times \Gamma /\Lambda _n$
. Moreover, for every
![]() $1\leq i\leq n$
,
$1\leq i\leq n$
,
and since the indices
![]() $[\Gamma :\Lambda _i]$
are pairwise coprime, this implies that
$[\Gamma :\Lambda _i]$
are pairwise coprime, this implies that
![]() $[\Gamma :\Lambda _1\cap \cdots \cap \Lambda _n]$
is divisible by
$[\Gamma :\Lambda _1\cap \cdots \cap \Lambda _n]$
is divisible by
![]() $[\Gamma :\Lambda _1]\cdots [\Gamma :\Lambda _n]$
. Thus, the group homomorphism
$[\Gamma :\Lambda _1]\cdots [\Gamma :\Lambda _n]$
. Thus, the group homomorphism
![]() $\Gamma /\Lambda _1\cap \cdots \cap \Lambda _n\to \Gamma /\Lambda _1\times \cdots \times \Gamma /\Lambda _n$
is an isomorphism and it is
$\Gamma /\Lambda _1\cap \cdots \cap \Lambda _n\to \Gamma /\Lambda _1\times \cdots \times \Gamma /\Lambda _n$
is an isomorphism and it is
![]() $\Gamma $
-equivariant.
$\Gamma $
-equivariant.
We are now ready to prove Theorems 4.1 and 4.2.
Proof of Theorem 4.1
Let
![]() $\Gamma $
be a non-amenable orientable surface group, and we fix a decomposition
$\Gamma $
be a non-amenable orientable surface group, and we fix a decomposition
![]() $\Gamma =\Gamma _A*_{\mathbb Z}\Gamma _B$
. Let
$\Gamma =\Gamma _A*_{\mathbb Z}\Gamma _B$
. Let
![]() $0<t<1$
be a real number. Let
$0<t<1$
be a real number. Let
![]() $(p_n)_{n\geq 1}$
be a sequence of pairwise distinct prime numbers. We fix a sequence
$(p_n)_{n\geq 1}$
be a sequence of pairwise distinct prime numbers. We fix a sequence
![]() $(r_n)_{n\geq 1}$
such that each
$(r_n)_{n\geq 1}$
such that each
![]() $r_n$
belongs to
$r_n$
belongs to
![]() $]0,1[\cap \mathbb Z[1/p_n]$
and
$]0,1[\cap \mathbb Z[1/p_n]$
and
![]() $\prod _{n\geq 1}r_n=t$
. Such a sequence exists because each
$\prod _{n\geq 1}r_n=t$
. Such a sequence exists because each
![]() $\mathbb Z[1/p_n]$
is dense in
$\mathbb Z[1/p_n]$
is dense in
![]() $\mathbb R$
. Finally, let
$\mathbb R$
. Finally, let
![]() $(\gamma _n)_{n\geq 0}$
be an enumeration of the elements in
$(\gamma _n)_{n\geq 0}$
be an enumeration of the elements in
![]() $\Gamma $
with
$\Gamma $
with
![]() $\gamma _0=1$
, and
$\gamma _0=1$
, and
![]() $(\delta _n)_{n\geq 1}$
be an enumeration of the elements in
$(\delta _n)_{n\geq 1}$
be an enumeration of the elements in
![]() $\Gamma _B\setminus \langle \langle \mathbb Z\rangle \rangle ^{\Gamma _B}$
. For every
$\Gamma _B\setminus \langle \langle \mathbb Z\rangle \rangle ^{\Gamma _B}$
. For every
![]() $n\geq 1$
, there exists by Theorem 3.2 a finite index subgroup
$n\geq 1$
, there exists by Theorem 3.2 a finite index subgroup
![]() $\Lambda _n^t\leq \Gamma $
which does not contain
$\Lambda _n^t\leq \Gamma $
which does not contain
![]() $\gamma _n$
, whose index
$\gamma _n$
, whose index
![]() $[\Gamma :\Lambda _n^t]$
is a power of
$[\Gamma :\Lambda _n^t]$
is a power of
![]() $p_n$
, such that the number of left cosets
$p_n$
, such that the number of left cosets
![]() $x\in \Gamma /\Lambda _n^t$
that are fixed by any element of
$x\in \Gamma /\Lambda _n^t$
that are fixed by any element of
![]() $\Gamma _A$
is equal to
$\Gamma _A$
is equal to
![]() $r_n[\Gamma :\Lambda _n^t]$
, and such that none of the left coset
$r_n[\Gamma :\Lambda _n^t]$
, and such that none of the left coset
![]() $x\in \Gamma /\Lambda _n^t$
is fixed by
$x\in \Gamma /\Lambda _n^t$
is fixed by
![]() $\delta _n$
. For every
$\delta _n$
. For every
![]() $n\geq 1$
, let
$n\geq 1$
, let
![]() $\Gamma _n^t:=\Lambda _1^t\cap \cdots \cap \Lambda _n^t$
. The sequence
$\Gamma _n^t:=\Lambda _1^t\cap \cdots \cap \Lambda _n^t$
. The sequence
![]() $(\Gamma _n^t)_{n\geq 1}$
forms a chain in
$(\Gamma _n^t)_{n\geq 1}$
forms a chain in
![]() $\Gamma $
, and we denote by
$\Gamma $
, and we denote by
![]() $\alpha ^t$
the corresponding ergodic profinite action and by
$\alpha ^t$
the corresponding ergodic profinite action and by
![]() $\mu _t$
the profinite
$\mu _t$
the profinite
![]() $\Gamma $
-invariant probability measure on
$\Gamma $
-invariant probability measure on
![]() $\varprojlim \Gamma /\Gamma _n^t$
. This is a p.m.p. ergodic minimal action and we will prove that it is allosteric. By construction of
$\varprojlim \Gamma /\Gamma _n^t$
. This is a p.m.p. ergodic minimal action and we will prove that it is allosteric. By construction of
![]() $\Lambda _n^t$
, we have that
$\Lambda _n^t$
, we have that
This implies by Lemma 2.7 that
![]() $\mathrm {URS}(\alpha ^t)$
is trivial. Let us prove that each element of
$\mathrm {URS}(\alpha ^t)$
is trivial. Let us prove that each element of
![]() ${\Gamma _B\setminus \langle \langle \mathbb Z\rangle \rangle ^{\Gamma _B}}$
acts essentially freely for
${\Gamma _B\setminus \langle \langle \mathbb Z\rangle \rangle ^{\Gamma _B}}$
acts essentially freely for
![]() $\alpha ^t$
. Let
$\alpha ^t$
. Let
![]() $\delta \in \Gamma _B\setminus \langle \langle \mathbb Z\rangle \rangle ^{\Gamma _B}$
. By Lemma 4.3, the number of
$\delta \in \Gamma _B\setminus \langle \langle \mathbb Z\rangle \rangle ^{\Gamma _B}$
. By Lemma 4.3, the number of
![]() $x\in \Gamma /\Gamma _n^t$
such that
$x\in \Gamma /\Gamma _n^t$
such that
![]() $\delta x=x$
is equal to the number of
$\delta x=x$
is equal to the number of
![]() $(x_1,\ldots ,x_n)\in \Gamma /\Lambda _1^t\times \cdots \times \Gamma /\Lambda _n^t$
such that
$(x_1,\ldots ,x_n)\in \Gamma /\Lambda _1^t\times \cdots \times \Gamma /\Lambda _n^t$
such that
![]() $(\delta x_1,\ldots ,\delta x_n)=(x_1,\ldots ,x_n)$
. If n is large enough, then this last number is zero by construction of
$(\delta x_1,\ldots ,\delta x_n)=(x_1,\ldots ,x_n)$
. If n is large enough, then this last number is zero by construction of
![]() $\Lambda _n^t$
. Thus, Lemma 2.6 implies that
$\Lambda _n^t$
. Thus, Lemma 2.6 implies that
![]() $\mathrm {Fix}_{\alpha ^t}(\delta )$
is
$\mathrm {Fix}_{\alpha ^t}(\delta )$
is
![]() $\mu _t$
-negligible.
$\mu _t$
-negligible.
Finally, let us prove that the actions
![]() $\alpha ^t$
are not essentially free. By construction, the indices
$\alpha ^t$
are not essentially free. By construction, the indices
![]() $[\Gamma :\Lambda _i^t]$
are pairwise coprime. Thus, Lemma 4.3 implies that the number of
$[\Gamma :\Lambda _i^t]$
are pairwise coprime. Thus, Lemma 4.3 implies that the number of
![]() $x\in \Gamma /\Gamma _n^t$
that are fixed by every element in
$x\in \Gamma /\Gamma _n^t$
that are fixed by every element in
![]() $\Gamma _A$
is equal to the number of
$\Gamma _A$
is equal to the number of
![]() $(y_1,\ldots ,y_n)\in \Gamma /\Lambda _1^t\times \cdots \times \Gamma /\Lambda _n^t$
that are fixed for the diagonal action by every element in
$(y_1,\ldots ,y_n)\in \Gamma /\Lambda _1^t\times \cdots \times \Gamma /\Lambda _n^t$
that are fixed for the diagonal action by every element in
![]() $\Gamma _A$
. By construction of
$\Gamma _A$
. By construction of
![]() $\Lambda _i^t$
, this number is equal to
$\Lambda _i^t$
, this number is equal to
![]() $r_1[\Gamma :\Lambda _1^t]\times \cdots \times r_n[\Gamma :\Lambda _n^t]$
which is equal to
$r_1[\Gamma :\Lambda _1^t]\times \cdots \times r_n[\Gamma :\Lambda _n^t]$
which is equal to
![]() $r_1\ldots r_n[\Gamma :\Gamma _n^t]$
. Thus, Lemma 2.6 implies that the
$r_1\ldots r_n[\Gamma :\Gamma _n^t]$
. Thus, Lemma 2.6 implies that the
![]() $\mu _t$
-measure of the set of points whose stabilizer for
$\mu _t$
-measure of the set of points whose stabilizer for
![]() $\alpha ^t$
contains
$\alpha ^t$
contains
![]() $\Gamma _A$
is t. In particular, this implies that
$\Gamma _A$
is t. In particular, this implies that
![]() $\mathrm {IRS}(\alpha ^t)$
is non-trivial. Thus,
$\mathrm {IRS}(\alpha ^t)$
is non-trivial. Thus,
![]() $\alpha ^t$
is allosteric. Moreover, this also implies that for all
$\alpha ^t$
is allosteric. Moreover, this also implies that for all
![]() $0<s<t<1$
, the actions
$0<s<t<1$
, the actions
![]() $\alpha ^s$
and
$\alpha ^s$
and
![]() $\alpha ^t$
are not measurably isomorphic and thus not topologically isomorphic since every
$\alpha ^t$
are not measurably isomorphic and thus not topologically isomorphic since every
![]() $\alpha ^t$
is uniquely ergodic by Lemma 2.5, and this finally implies that the measures
$\alpha ^t$
is uniquely ergodic by Lemma 2.5, and this finally implies that the measures
![]() $\mathrm {IRS}(\alpha ^s)$
and
$\mathrm {IRS}(\alpha ^s)$
and
![]() $\mathrm {IRS}(\alpha ^t)$
are distinct.
$\mathrm {IRS}(\alpha ^t)$
are distinct.
Proof of Theorem 4.2
Let
![]() $\Sigma '$
be a non-orientable surface of genus
$\Sigma '$
be a non-orientable surface of genus
![]() $g\geq 3$
. Consider the usual embedding of an orientable surface
$g\geq 3$
. Consider the usual embedding of an orientable surface
![]() $\Sigma $
of genus
$\Sigma $
of genus
![]() $g-1$
into
$g-1$
into
![]() $\mathbb R^3$
in such a way that the reflexions in all three coordinate planes map the surface to itself, and let
$\mathbb R^3$
in such a way that the reflexions in all three coordinate planes map the surface to itself, and let
![]() $\iota $
to be the fixed-point free antipodal map
$\iota $
to be the fixed-point free antipodal map
![]() $x\mapsto -x$
. Then
$x\mapsto -x$
. Then
![]() $\Sigma '$
is homeomorphic to the quotient of
$\Sigma '$
is homeomorphic to the quotient of
![]() $\Sigma $
by
$\Sigma $
by
![]() $\iota $
, and the covering
$\iota $
, and the covering
![]() $\Sigma \mapsto \Sigma /\iota \approx \Sigma '$
is called the orientation covering. We decompose
$\Sigma \mapsto \Sigma /\iota \approx \Sigma '$
is called the orientation covering. We decompose
![]() $\Sigma $
as the union of two surfaces
$\Sigma $
as the union of two surfaces
![]() $\Sigma _A$
and
$\Sigma _A$
and
![]() $\Sigma _B$
with one boundary, of genus
$\Sigma _B$
with one boundary, of genus
![]() $\lvert A\rvert $
and
$\lvert A\rvert $
and
![]() $\lvert B\rvert $
respectively, with
$\lvert B\rvert $
respectively, with
![]() $\lvert A\rvert \leq \lvert B\rvert $
, so that
$\lvert A\rvert \leq \lvert B\rvert $
, so that
![]() $\iota (\Sigma _A)\subset \Sigma _B$
. Fix a point
$\iota (\Sigma _A)\subset \Sigma _B$
. Fix a point
![]() $p\in \Sigma _A\cap \Sigma _B$
, then Van Kampen’s theorem implies that the fundamental group
$p\in \Sigma _A\cap \Sigma _B$
, then Van Kampen’s theorem implies that the fundamental group
![]() $\Gamma $
of the surface
$\Gamma $
of the surface
![]() $\Sigma $
based at p is isomorphic to
$\Sigma $
based at p is isomorphic to
![]() $\Gamma _A*_{\mathbb Z}\Gamma _B$
with
$\Gamma _A*_{\mathbb Z}\Gamma _B$
with
![]() $\Gamma _A=\pi _1(\Sigma _A,p), \Gamma _B=\pi _1(\Sigma _B,p)$
and
$\Gamma _A=\pi _1(\Sigma _A,p), \Gamma _B=\pi _1(\Sigma _B,p)$
and
![]() $\mathbb Z\approx \pi _1(\Gamma _A\cap \Gamma _B,p)$
. The fundamental group
$\mathbb Z\approx \pi _1(\Gamma _A\cap \Gamma _B,p)$
. The fundamental group
![]() $\Gamma '$
of
$\Gamma '$
of
![]() $\Sigma '$
based at
$\Sigma '$
based at
![]() $p'=\iota (p)$
naturally contains the subgroup
$p'=\iota (p)$
naturally contains the subgroup
![]() $\Gamma $
as an index-two subgroup. Fix a curve contained in
$\Gamma $
as an index-two subgroup. Fix a curve contained in
![]() $\Sigma _B$
that joins p to
$\Sigma _B$
that joins p to
![]() $\iota (p)$
. This produces an element
$\iota (p)$
. This produces an element
![]() $\gamma _0\in \Gamma '\setminus \Gamma $
that satisfies
$\gamma _0\in \Gamma '\setminus \Gamma $
that satisfies
![]() $\gamma _0\Gamma _A\gamma _0^{-1}\leq \Gamma _B$
.
$\gamma _0\Gamma _A\gamma _0^{-1}\leq \Gamma _B$
.
Let
![]() $(\alpha ^t)_{0<t<1}$
be a continuum of allosteric
$(\alpha ^t)_{0<t<1}$
be a continuum of allosteric
![]() $\Gamma $
-actions on
$\Gamma $
-actions on
![]() $(X_t,\mu _t)$
given by Theorem 4.1. The actions
$(X_t,\mu _t)$
given by Theorem 4.1. The actions
![]() $\beta ^t: \Gamma '\curvearrowright (Y_t,\nu _t)$
induced by the
$\beta ^t: \Gamma '\curvearrowright (Y_t,\nu _t)$
induced by the
![]() $\Gamma $
-actions
$\Gamma $
-actions
![]() $\alpha ^t$
are allosteric, see Proposition 2.10. Let us prove that the set of points in
$\alpha ^t$
are allosteric, see Proposition 2.10. Let us prove that the set of points in
![]() $Y_t$
whose stabilizer for
$Y_t$
whose stabilizer for
![]() $\beta ^t$
contains
$\beta ^t$
contains
![]() $\Gamma _A$
has
$\Gamma _A$
has
![]() $\nu _t$
-measure
$\nu _t$
-measure
![]() $t/2$
. Since
$t/2$
. Since
![]() $\beta ^t$
is an induced action and
$\beta ^t$
is an induced action and
![]() $[\Gamma ':\Gamma ]=2$
, the
$[\Gamma ':\Gamma ]=2$
, the
![]() $\Gamma '$
-action
$\Gamma '$
-action
![]() $\beta ^t$
is measurably isomorphic to a p.m.p.
$\beta ^t$
is measurably isomorphic to a p.m.p.
![]() $\Gamma '$
-action on
$\Gamma '$
-action on
![]() $(X_t\times \{0,1\},\mu _t\times \text { unif})$
, still denoted by
$(X_t\times \{0,1\},\mu _t\times \text { unif})$
, still denoted by
![]() $\beta ^t$
, that satisfies the following two properties:
$\beta ^t$
, that satisfies the following two properties:
-
(1) for every
 $\gamma \in \Gamma '\setminus \Gamma $
, the sets
$\gamma \in \Gamma '\setminus \Gamma $
, the sets
 $X_t\times \{0\}$
and
$X_t\times \{0\}$
and
 $X_t\times \{1\}$
are switched by
$X_t\times \{1\}$
are switched by
 $\beta ^t(\gamma )$
;
$\beta ^t(\gamma )$
; -
(2) for every
 $\gamma \in \Gamma $
, for every
$\gamma \in \Gamma $
, for every
 $x\in X_t$
, we have
$x\in X_t$
, we have
 $\beta ^t(\gamma )(x,0)=(\alpha ^t(\gamma )x,0)$
and
$\beta ^t(\gamma )(x,0)=(\alpha ^t(\gamma )x,0)$
and
 $\beta ^t(\gamma )(x,1)=(\alpha ^t(\gamma _0\gamma \gamma _0^{-1})x,1)$
.
$\beta ^t(\gamma )(x,1)=(\alpha ^t(\gamma _0\gamma \gamma _0^{-1})x,1)$
.
This implies that for all
![]() $(x,\varepsilon )\in X_t\times \{0,1\}$
, the subgroup
$(x,\varepsilon )\in X_t\times \{0,1\}$
, the subgroup
![]() $\Gamma _A$
is contained in
$\Gamma _A$
is contained in
![]() $\mathrm {Stab}_{\beta ^t}(x,\varepsilon )$
if and only if either
$\mathrm {Stab}_{\beta ^t}(x,\varepsilon )$
if and only if either
![]() $\varepsilon =0$
and
$\varepsilon =0$
and
![]() $\Gamma _A$
is contained in
$\Gamma _A$
is contained in
![]() $\mathrm {Stab}_{\alpha ^t}(x)$
, or
$\mathrm {Stab}_{\alpha ^t}(x)$
, or
![]() $\varepsilon =1$
and
$\varepsilon =1$
and
![]() $\gamma _0\Gamma _A\gamma _0^{-1}$
is contained in
$\gamma _0\Gamma _A\gamma _0^{-1}$
is contained in
![]() $\mathrm {Stab}_{\alpha ^t}(x)$
. Thus, the set of points whose stabilizer for
$\mathrm {Stab}_{\alpha ^t}(x)$
. Thus, the set of points whose stabilizer for
![]() $\beta ^t$
contains
$\beta ^t$
contains
![]() $\Gamma _A$
has
$\Gamma _A$
has
![]() $\nu _t$
-measure
$\nu _t$
-measure
 $$ \begin{align*}\frac{t+\mu_t(\{x\in X_t\mid \gamma_0\Gamma_A\gamma_0^{-1}\leq\mathrm{Stab}_{\alpha^t}(x)\})}{2}.\end{align*} $$
$$ \begin{align*}\frac{t+\mu_t(\{x\in X_t\mid \gamma_0\Gamma_A\gamma_0^{-1}\leq\mathrm{Stab}_{\alpha^t}(x)\})}{2}.\end{align*} $$
To finish the proof, it is enough to prove that the intersection of
![]() $\gamma _0\Gamma _A\gamma _0^{-1}$
and
$\gamma _0\Gamma _A\gamma _0^{-1}$
and
![]() $\Gamma _B\setminus \langle \langle \mathbb Z\rangle \rangle ^{\Gamma _B}$
is non-trivial, since any element in
$\Gamma _B\setminus \langle \langle \mathbb Z\rangle \rangle ^{\Gamma _B}$
is non-trivial, since any element in
![]() $\Gamma _B\setminus \langle \langle \mathbb Z\rangle \rangle ^{\Gamma _B}$
acts essentially freely for
$\Gamma _B\setminus \langle \langle \mathbb Z\rangle \rangle ^{\Gamma _B}$
acts essentially freely for
![]() $\alpha ^t$
. The conjugation by
$\alpha ^t$
. The conjugation by
![]() $\gamma _0$
induces a group automorphism
$\gamma _0$
induces a group automorphism
![]() $\varphi :\Gamma \mapsto \Gamma $
, such that
$\varphi :\Gamma \mapsto \Gamma $
, such that
![]() $\varphi (\Gamma _A)\leq \Gamma _B$
. Since
$\varphi (\Gamma _A)\leq \Gamma _B$
. Since
![]() $\Gamma _A$
is not contained in the derived subgroup
$\Gamma _A$
is not contained in the derived subgroup
![]() $D(\Gamma )$
, so is
$D(\Gamma )$
, so is
![]() $\varphi (\Gamma _A)$
. However, the amalgamated subgroup
$\varphi (\Gamma _A)$
. However, the amalgamated subgroup
![]() $\mathbb Z$
is contained in
$\mathbb Z$
is contained in
![]() $D(\Gamma )$
, thus so is
$D(\Gamma )$
, thus so is
![]() $\langle \langle {\mathbb Z}\rangle \rangle ^{\Gamma _B}$
. This implies that the intersection
$\langle \langle {\mathbb Z}\rangle \rangle ^{\Gamma _B}$
. This implies that the intersection
![]() $\varphi (\Gamma _A)\cap (\Gamma _B\setminus \langle \langle {\mathbb Z}\rangle \rangle ^{\Gamma _B})$
is non-empty. We deduce that the set of points whose stabilizer for
$\varphi (\Gamma _A)\cap (\Gamma _B\setminus \langle \langle {\mathbb Z}\rangle \rangle ^{\Gamma _B})$
is non-empty. We deduce that the set of points whose stabilizer for
![]() $\beta ^t$
contains
$\beta ^t$
contains
![]() $\Gamma _A$
has
$\Gamma _A$
has
![]() $\nu _t$
-measure
$\nu _t$
-measure
![]() $t/2$
. We conclude that the actions
$t/2$
. We conclude that the actions
![]() $\beta ^t$
are neither measurably nor topologically pairwise isomorphic and that their IRS are pairwise disjoint as in Theorem 4.1.
$\beta ^t$
are neither measurably nor topologically pairwise isomorphic and that their IRS are pairwise disjoint as in Theorem 4.1.
Remark 4.4. Let
![]() $\alpha : \Gamma \curvearrowright (C,\mu )$
be an allosteric action. Then we have
$\alpha : \Gamma \curvearrowright (C,\mu )$
be an allosteric action. Then we have
This implies that the support of
![]() $\mathrm {IRS}(\alpha )$
does not contain any non-trivial subgroup with only finitely many conjugates, because otherwise, the closure of the set
$\mathrm {IRS}(\alpha )$
does not contain any non-trivial subgroup with only finitely many conjugates, because otherwise, the closure of the set
![]() $\{\mathrm {Stab}_{\alpha }(x)\mid x\in C\}$
would contain a closed minimal
$\{\mathrm {Stab}_{\alpha }(x)\mid x\in C\}$
would contain a closed minimal
![]() $\Gamma $
-invariant set
$\Gamma $
-invariant set
![]() $\neq \{\{1\}\}$
. Carderi, Gaboriau and Le Maître proved (personal communication) that the perfect kernel of a surface group coincides with the set of its infinite index subgroups. This implies that allosteric actions of surface groups are not totipotent (a p.m.p. action is totipotent if the support of its IRS coincides with the perfect kernel of the group, see [Reference Carderi, Gaboriau and Le MaîtreCGLM20]).
$\neq \{\{1\}\}$
. Carderi, Gaboriau and Le Maître proved (personal communication) that the perfect kernel of a surface group coincides with the set of its infinite index subgroups. This implies that allosteric actions of surface groups are not totipotent (a p.m.p. action is totipotent if the support of its IRS coincides with the perfect kernel of the group, see [Reference Carderi, Gaboriau and Le MaîtreCGLM20]).
Remark 4.5. A p.m.p. action
![]() $\Gamma \curvearrowright (X,\mu )$
is weakly mixing if for every
$\Gamma \curvearrowright (X,\mu )$
is weakly mixing if for every
![]() $\varepsilon>0$
and every finite collection
$\varepsilon>0$
and every finite collection
![]() $\Omega $
of measurable subsets of X, there exists a
$\Omega $
of measurable subsets of X, there exists a
![]() $\gamma \in \Gamma $
such that for every
$\gamma \in \Gamma $
such that for every
![]() $A,B\in \Omega $
,
$A,B\in \Omega $
,
With this definition, it is easily seen that the restriction of a weakly mixing action to a finite index subgroup remains weakly mixing. Thus, Proposition 2.8 implies that the IRSs of non-amenable surface groups we have constructed are not weakly mixing.
Remark 4.6. The proof of our main theorem applies mutatis mutandis to branched orientable surface groups, that is, fundamental groups of closed orientable branched surfaces (see Figure 4). These groups can be written as amalgams. Fix an integer
![]() $g\geq 2$
as well as
$g\geq 2$
as well as
![]() $2g$
letters
$2g$
letters
![]() $x_1,y_1,\ldots ,x_g,y_g$
. Fix a partition of
$x_1,y_1,\ldots ,x_g,y_g$
. Fix a partition of
![]() $\{1,\ldots ,g\}$
into n non-empty intervals
$\{1,\ldots ,g\}$
into n non-empty intervals
![]() $A_1,\ldots ,A_n$
. Let
$A_1,\ldots ,A_n$
. Let
![]() $\Gamma _k$
be the free group generated by
$\Gamma _k$
be the free group generated by
![]() $x_i$
and
$x_i$
and
![]() $y_i$
for every
$y_i$
for every
![]() $i\in A_k$
, and let
$i\in A_k$
, and let
![]() $\mathbb Z\to \Gamma _k$
be the injective homomorphism defined by sending the generator of
$\mathbb Z\to \Gamma _k$
be the injective homomorphism defined by sending the generator of
![]() $\mathbb Z$
to the product
$\mathbb Z$
to the product
![]() $\prod _{i\in A_k}[x_i,y_i]$
. Then the amalgam
$\prod _{i\in A_k}[x_i,y_i]$
. Then the amalgam
![]() $*_{\mathbb Z}\Gamma _i$
is a branched orientable surface group, and any branched orientable surface group can be obtained this way. The fundamental group of a closed orientable branched surface of genus
$*_{\mathbb Z}\Gamma _i$
is a branched orientable surface group, and any branched orientable surface group can be obtained this way. The fundamental group of a closed orientable branched surface of genus
![]() $\geq 2$
is a residually p-finite group for every prime p, see [Reference Kim and McCarronKM93, Theorem
$\geq 2$
is a residually p-finite group for every prime p, see [Reference Kim and McCarronKM93, Theorem
![]() $4.2$
]. Thus, our method of proof applies to branched orientable surface groups, with any
$4.2$
]. Thus, our method of proof applies to branched orientable surface groups, with any
![]() $\Gamma _k$
in the role played by
$\Gamma _k$
in the role played by
![]() $\Gamma _A$
during the proof of Theorem 4.1.
$\Gamma _A$
during the proof of Theorem 4.1.

Figure 4 A branched surface.
Question 4.7. Is the fundamental group of a compact hyperbolic
![]() $3$
-manifold allosteric? More generally, is the fundamental group of a compact orientable aspherical
$3$
-manifold allosteric? More generally, is the fundamental group of a compact orientable aspherical
![]() $3$
-manifold allosteric?
$3$
-manifold allosteric?
Acknowledgements
I would like to thank A. Le Boudec for various conversations related to this article, as well as T. Nagnibeda for letting me know that Vershik’s work implies that the group of finitely supported permutations of the integers is not allosteric. I wish to thank particularly D. Gaboriau for his constant encouragement and support, as well as for his numerous remarks on this article. I thank the anonymous referee for its numerous remarks and comments.