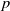1. Introduction
Let
![]() $G$
be a commutative algebraic group defined over the field of algebraic numbers
$G$
be a commutative algebraic group defined over the field of algebraic numbers
![]() $\overline{\mathbb{Q}}$
of positive dimension
$\overline{\mathbb{Q}}$
of positive dimension
![]() $d$
, and
$d$
, and
![]() $\mathrm{Lie}(G)$
denote the Lie algebra of
$\mathrm{Lie}(G)$
denote the Lie algebra of
![]() $G$
. By fixing a choice of
$G$
. By fixing a choice of
![]() $\overline{\mathbb{Q}}$
-basis for
$\overline{\mathbb{Q}}$
-basis for
![]() $\mathrm{Lie}(G)$
, one can identify
$\mathrm{Lie}(G)$
, one can identify
![]() $\mathrm{Lie}(G)$
with the
$\mathrm{Lie}(G)$
with the
![]() $\overline{\mathbb{Q}}$
-vector space
$\overline{\mathbb{Q}}$
-vector space
![]() $\overline{\mathbb{Q}}^d$
. The set of complex points
$\overline{\mathbb{Q}}^d$
. The set of complex points
![]() $G(\mathbb{C})$
of
$G(\mathbb{C})$
of
![]() $G$
has naturally the structure of a complex Lie group whose Lie algebra
$G$
has naturally the structure of a complex Lie group whose Lie algebra
![]() $\mathrm{Lie}(G(\mathbb{C}))$
is the complex vector space
$\mathrm{Lie}(G(\mathbb{C}))$
is the complex vector space
![]() $\mathrm{Lie}(G)\otimes _{\overline{\mathbb{Q}}}\mathbb{C}$
. This is identified with the
$\mathrm{Lie}(G)\otimes _{\overline{\mathbb{Q}}}\mathbb{C}$
. This is identified with the
![]() $\mathbb{C}$
-vector space
$\mathbb{C}$
-vector space
![]() $\mathbb{C}^d$
, and one has an analytic homomorphism, the so-called (complex) exponential map
$\mathbb{C}^d$
, and one has an analytic homomorphism, the so-called (complex) exponential map
![]() $\exp _{G(\mathbb{C})}\,:\,\mathbb{C}^d\rightarrow G(\mathbb{C}).$
A vector
$\exp _{G(\mathbb{C})}\,:\,\mathbb{C}^d\rightarrow G(\mathbb{C}).$
A vector
![]() $u\in \mathbb{C}^d$
is called a logarithm of an algebraic point of
$u\in \mathbb{C}^d$
is called a logarithm of an algebraic point of
![]() $G$
if
$G$
if
![]() $\exp _{G(\mathbb{C})}(u)$
is an algebraic point on
$\exp _{G(\mathbb{C})}(u)$
is an algebraic point on
![]() $G$
, that is
$G$
, that is
![]() $\exp _{G(\mathbb{C})}(u)\in G(\overline{\mathbb{Q}})$
. Transcendence result concerning the coordinates of a logarithm of algebraic points of abelian varieties was first given by S. Lang in 1962. Namely, he proved that if
$\exp _{G(\mathbb{C})}(u)\in G(\overline{\mathbb{Q}})$
. Transcendence result concerning the coordinates of a logarithm of algebraic points of abelian varieties was first given by S. Lang in 1962. Namely, he proved that if
![]() $A$
is an abelian variety defined over
$A$
is an abelian variety defined over
![]() $\overline{\mathbb{Q}}$
and
$\overline{\mathbb{Q}}$
and
![]() $u$
is a non-zero logarithm of an algebraic point of
$u$
is a non-zero logarithm of an algebraic point of
![]() $A$
, then at least one of the coordinates of
$A$
, then at least one of the coordinates of
![]() $u$
is transcendental (see [Reference Lang7, Theorem 2]). The
$u$
is transcendental (see [Reference Lang7, Theorem 2]). The
![]() $p$
-adic analogue of Lang’s result is due to D. Bertrand in 1977. Let
$p$
-adic analogue of Lang’s result is due to D. Bertrand in 1977. Let
![]() $\mathcal A_p\subseteq \mathbb{C}_p^d$
denote the
$\mathcal A_p\subseteq \mathbb{C}_p^d$
denote the
![]() $p$
-adic domain of the
$p$
-adic domain of the
![]() $p$
-adic exponential map
$p$
-adic exponential map
![]() $\exp _{A(\mathbb{C}_p)}$
of
$\exp _{A(\mathbb{C}_p)}$
of
![]() $A$
(see [Reference Bourbaki3]). If
$A$
(see [Reference Bourbaki3]). If
![]() $\mathfrak{u}$
is a non-zero vector in
$\mathfrak{u}$
is a non-zero vector in
![]() $\mathcal A_p$
such that
$\mathcal A_p$
such that
![]() $\exp _{A(\mathbb{C}_p)}(\mathfrak{u})\in A(\overline{\mathbb{Q}})$
, then there is at least one coordinate of
$\exp _{A(\mathbb{C}_p)}(\mathfrak{u})\in A(\overline{\mathbb{Q}})$
, then there is at least one coordinate of
![]() $\mathfrak{u}$
is transcendental (see [Reference Bertrand2, Proposition 2]). There are some extensions of these results in both complex and
$\mathfrak{u}$
is transcendental (see [Reference Bertrand2, Proposition 2]). There are some extensions of these results in both complex and
![]() $p$
-adic cases, among which D. H. Pham has recently obtained results on complex and
$p$
-adic cases, among which D. H. Pham has recently obtained results on complex and
![]() $p$
-adic linear independence concerning the coordinates of abelian logarithms of algebraic points (see [Reference Pham11]).
$p$
-adic linear independence concerning the coordinates of abelian logarithms of algebraic points (see [Reference Pham11]).
The first aim of this note is to establish results on complex and
![]() $p$
-adic linear independence on semiabelian varieties, which are determined by extensions of simple abelian varieties by the multiplicative group
$p$
-adic linear independence on semiabelian varieties, which are determined by extensions of simple abelian varieties by the multiplicative group
![]() $\mathbb{G}_m$
. To state the results, let
$\mathbb{G}_m$
. To state the results, let
![]() $S$
be a semiabelian variety defined over
$S$
be a semiabelian variety defined over
![]() $\overline{\mathbb{Q}}$
given by the exact sequence
$\overline{\mathbb{Q}}$
given by the exact sequence
where
![]() $A$
is an abelian variety defined over
$A$
is an abelian variety defined over
![]() $\overline{\mathbb{Q}}$
(not necessarily simple). It follows from [Reference Bertolin, Philippon, Saha and Saha1, Section 2] that the extension
$\overline{\mathbb{Q}}$
(not necessarily simple). It follows from [Reference Bertolin, Philippon, Saha and Saha1, Section 2] that the extension
![]() $S$
corresponds to an algebraic point
$S$
corresponds to an algebraic point
![]() $P$
in
$P$
in
![]() $A^*(\overline{\mathbb{Q}})$
via the canonical isomorphism Ext
$A^*(\overline{\mathbb{Q}})$
via the canonical isomorphism Ext
![]() $^1(A,\mathbb{G}_m)\cong$
Pic
$^1(A,\mathbb{G}_m)\cong$
Pic
![]() $^0(A)=A^*$
. Note that if
$^0(A)=A^*$
. Note that if
![]() $P$
is not a torsion point of
$P$
is not a torsion point of
![]() $A^*$
, the extension
$A^*$
, the extension
![]() $S$
is non-trivial (i.e. the semiabelian variety
$S$
is non-trivial (i.e. the semiabelian variety
![]() $S$
is not the direct product
$S$
is not the direct product
![]() $\mathbb{G}_m\times A$
of
$\mathbb{G}_m\times A$
of
![]() $\mathbb{G}_m$
and
$\mathbb{G}_m$
and
![]() $A$
). It is known that the exact sequence
$A$
). It is known that the exact sequence
induces naturally an exact sequence of
![]() $\overline{\mathbb{Q}}$
-vector spaces
$\overline{\mathbb{Q}}$
-vector spaces
In particular, this gives
![]() $\mathrm{Lie}(S)\cong \mathrm{Lie}(\mathbb{G}_m)\times \mathrm{Lie}(A)$
. Hence, by a choice of
$\mathrm{Lie}(S)\cong \mathrm{Lie}(\mathbb{G}_m)\times \mathrm{Lie}(A)$
. Hence, by a choice of
![]() $\overline{\mathbb{Q}}$
-basis for
$\overline{\mathbb{Q}}$
-basis for
![]() $\mathrm{Lie}(A)$
, one can identify the Lie algebra
$\mathrm{Lie}(A)$
, one can identify the Lie algebra
![]() $\mathrm{Lie}(S)$
with the
$\mathrm{Lie}(S)$
with the
![]() $\overline{\mathbb{Q}}$
-vector space
$\overline{\mathbb{Q}}$
-vector space
![]() $\overline{\mathbb{Q}}\times \overline{\mathbb{Q}}^g=\overline{\mathbb{Q}}^{g+1}$
, here
$\overline{\mathbb{Q}}\times \overline{\mathbb{Q}}^g=\overline{\mathbb{Q}}^{g+1}$
, here
![]() $g=\dim A$
. Our theorem now reads as follows:
$g=\dim A$
. Our theorem now reads as follows:
Theorem 1.1.
Let
![]() $S$
be a semiabelian variety defined over
$S$
be a semiabelian variety defined over
![]() $\overline{\mathbb{Q}}$
given by an extension
$\overline{\mathbb{Q}}$
given by an extension
![]() $1\rightarrow \mathbb{G}_m\rightarrow S\rightarrow A\rightarrow 1$
with
$1\rightarrow \mathbb{G}_m\rightarrow S\rightarrow A\rightarrow 1$
with
![]() $A$
a simple abelian variety defined over
$A$
a simple abelian variety defined over
![]() $\overline{\mathbb{Q}}$
of dimension
$\overline{\mathbb{Q}}$
of dimension
![]() $g$
. Let
$g$
. Let
![]() $\exp _{S(\mathbb{C})}$
and
$\exp _{S(\mathbb{C})}$
and
![]() $\exp _{S(\mathbb{C}_p)}$
be the complex and
$\exp _{S(\mathbb{C}_p)}$
be the complex and
![]() $p$
-adic exponential maps of
$p$
-adic exponential maps of
![]() $S$
, respectively.
$S$
, respectively.
(i) Let
![]() $u=(u_0, u_1,\ldots, u_g)$
be a vector in
$u=(u_0, u_1,\ldots, u_g)$
be a vector in
![]() $\mathbb{C}^{g+1}$
with
$\mathbb{C}^{g+1}$
with
![]() $u_0\ne 0$
and
$u_0\ne 0$
and
![]() $(u_1,\ldots, u_g)\ne (0,\ldots, 0)$
such that
$(u_1,\ldots, u_g)\ne (0,\ldots, 0)$
such that
![]() $\exp _{S(\mathbb{C})}(u)\in S(\overline{\mathbb{Q}})$
. Then
$\exp _{S(\mathbb{C})}(u)\in S(\overline{\mathbb{Q}})$
. Then
![]() $1, u_0, u_1,\ldots, u_{g}$
are linearly independent over
$1, u_0, u_1,\ldots, u_{g}$
are linearly independent over
![]() $\overline{\mathbb{Q}}$
.
$\overline{\mathbb{Q}}$
.
(ii) Let
![]() $\mathfrak{u}=(\mathfrak{u}_0,\mathfrak{u}_1,\ldots, \mathfrak{u}_g)$
be a vector in
$\mathfrak{u}=(\mathfrak{u}_0,\mathfrak{u}_1,\ldots, \mathfrak{u}_g)$
be a vector in
![]() $\mathcal S_p$
with
$\mathcal S_p$
with
![]() $\mathfrak{u}_0\ne 0$
and
$\mathfrak{u}_0\ne 0$
and
![]() $(\mathfrak{u}_1, \ldots, \mathfrak{u}_g)\ne (0, \ldots, 0)$
such that
$(\mathfrak{u}_1, \ldots, \mathfrak{u}_g)\ne (0, \ldots, 0)$
such that
![]() $\exp _{S(\mathbb{C}_p)}(\mathfrak{u})\in S(\overline{\mathbb{Q}})$
, where
$\exp _{S(\mathbb{C}_p)}(\mathfrak{u})\in S(\overline{\mathbb{Q}})$
, where
![]() $\mathcal S_p$
is the
$\mathcal S_p$
is the
![]() $p$
-adic domain of
$p$
-adic domain of
![]() $\exp _{S({\mathbb{C}}_p)}$
. Then
$\exp _{S({\mathbb{C}}_p)}$
. Then
![]() $1, \mathfrak{u}_0, \mathfrak{u}_1,\ldots, \mathfrak{u}_g$
are linearly independent over
$1, \mathfrak{u}_0, \mathfrak{u}_1,\ldots, \mathfrak{u}_g$
are linearly independent over
![]() $\overline{\mathbb{Q}}$
.
$\overline{\mathbb{Q}}$
.
2. Semiabelian varieties and algebraic subgroups
This section involves the structure of algebraic subgroups concerning semiabelian varieties defined over
![]() $\overline{\mathbb{Q}}$
, which plays a crucial point for the proofs in the next section. The following lemma describes the form of a connected algebraic subgroup of the direct product of the additive group
$\overline{\mathbb{Q}}$
, which plays a crucial point for the proofs in the next section. The following lemma describes the form of a connected algebraic subgroup of the direct product of the additive group
![]() $\mathbb{G}_a$
with a semiabelian variety defined over
$\mathbb{G}_a$
with a semiabelian variety defined over
![]() $\overline{\mathbb{Q}}$
.
$\overline{\mathbb{Q}}$
.
Lemma 2.1.
Let
![]() $S$
be a semiabelian variety defined over
$S$
be a semiabelian variety defined over
![]() $\overline{\mathbb{Q}}$
and
$\overline{\mathbb{Q}}$
and
![]() $H$
a connected algebraic subgroup of the algebraic group
$H$
a connected algebraic subgroup of the algebraic group
![]() $\mathbb{G}_a\times S$
defined over
$\mathbb{G}_a\times S$
defined over
![]() $\overline{\mathbb{Q}}$
. Then
$\overline{\mathbb{Q}}$
. Then
![]() $H$
is of the form
$H$
is of the form
![]() $H_a\times R$
, where
$H_a\times R$
, where
![]() $H_a$
and
$H_a$
and
![]() $R$
are connected algebraic subgroups of
$R$
are connected algebraic subgroups of
![]() $\mathbb{G}_a$
and
$\mathbb{G}_a$
and
![]() $S$
defined over
$S$
defined over
![]() $\overline{\mathbb{Q}}$
, respectively.
$\overline{\mathbb{Q}}$
, respectively.
Proof. Let
![]() $\pi _a$
and
$\pi _a$
and
![]() $\pi$
be the projections of
$\pi$
be the projections of
![]() $\mathbb{G}_a\times S$
on
$\mathbb{G}_a\times S$
on
![]() $\mathbb{G}_a$
and
$\mathbb{G}_a$
and
![]() $S$
, respectively. Put
$S$
, respectively. Put
where
![]() $e$
is the identity element of
$e$
is the identity element of
![]() $S$
. Then
$S$
. Then
![]() $H_a$
and
$H_a$
and
![]() $R$
are connected algebraic subgroups of
$R$
are connected algebraic subgroups of
![]() $\mathbb{G}_a$
and
$\mathbb{G}_a$
and
![]() $S$
defined over
$S$
defined over
![]() $\overline{\mathbb{Q}}$
, respectively. Let
$\overline{\mathbb{Q}}$
, respectively. Let
![]() $I$
be the image of
$I$
be the image of
![]() $H$
under the projection
$H$
under the projection
Denote by
![]() $p_a$
and
$p_a$
and
![]() $p$
the projections of
$p$
the projections of
![]() $(\mathbb{G}_a/H_a)\times (S/R)$
onto
$(\mathbb{G}_a/H_a)\times (S/R)$
onto
![]() $\mathbb{G}_a/H_a$
and onto
$\mathbb{G}_a/H_a$
and onto
![]() $S/R$
, respectively. One can show that
$S/R$
, respectively. One can show that
![]() $I\cong p_a(I)$
and
$I\cong p_a(I)$
and
![]() $I\cong p(I)$
, hence
$I\cong p(I)$
, hence
![]() $p_a(I)\cong p(I)$
. On the other hand,
$p_a(I)\cong p(I)$
. On the other hand,
![]() $H_a$
is either trivial or
$H_a$
is either trivial or
![]() $\mathbb{G}_a$
, and this leads to the algebraic subgroup
$\mathbb{G}_a$
, and this leads to the algebraic subgroup
![]() $p_a(I)$
of
$p_a(I)$
of
![]() $\mathbb{G}_a/H_a$
is either
$\mathbb{G}_a/H_a$
is either
![]() $\mathbb{G}_a$
or trivial. We claim that the first case cannot hold. In fact, if not, then this gives
$\mathbb{G}_a$
or trivial. We claim that the first case cannot hold. In fact, if not, then this gives
![]() $p(I)\cong \mathbb{G}_a$
. Since
$p(I)\cong \mathbb{G}_a$
. Since
![]() $p(I)$
is an algebraic subgroup of
$p(I)$
is an algebraic subgroup of
![]() $S/R$
defined over
$S/R$
defined over
![]() $\overline{\mathbb{Q}}$
, there exists a connected algebraic subgroup
$\overline{\mathbb{Q}}$
, there exists a connected algebraic subgroup
![]() $Q$
of
$Q$
of
![]() $S$
containing
$S$
containing
![]() $R$
defined over
$R$
defined over
![]() $\overline{\mathbb{Q}}$
such that
$\overline{\mathbb{Q}}$
such that
![]() $p(I)\cong Q/R$
, and then
$p(I)\cong Q/R$
, and then
![]() $Q/R\cong \mathbb{G}_a$
. Furthermore, it follows from [Reference Perucca10, Proposition 2.1.3] that
$Q/R\cong \mathbb{G}_a$
. Furthermore, it follows from [Reference Perucca10, Proposition 2.1.3] that
![]() $Q$
and
$Q$
and
![]() $R$
are semiabelian varieties. We therefore get the short exact sequences
$R$
are semiabelian varieties. We therefore get the short exact sequences
and
of
![]() $Q$
and
$Q$
and
![]() $R$
, respectively, for non-negative integers
$R$
, respectively, for non-negative integers
![]() $q,r$
and for abelian varieties
$q,r$
and for abelian varieties
![]() $B, C$
defined over
$B, C$
defined over
![]() $\overline{\mathbb{Q}}$
. Since
$\overline{\mathbb{Q}}$
. Since
![]() $Q/R$
is isomorphic to
$Q/R$
is isomorphic to
![]() $\mathbb{G}_a$
, the composition of the homomorphism of algebraic groups
$\mathbb{G}_a$
, the composition of the homomorphism of algebraic groups
![]() $\mathbb{G}_m^q\rightarrow Q$
(from the first exact sequence above) with the projection
$\mathbb{G}_m^q\rightarrow Q$
(from the first exact sequence above) with the projection
![]() $Q\rightarrow Q/R$
must be trivial. This means that
$Q\rightarrow Q/R$
must be trivial. This means that
![]() $G_m^q\hookrightarrow R$
. We now consider the cases:
$G_m^q\hookrightarrow R$
. We now consider the cases:
If
![]() $q\gt r$
, then
$q\gt r$
, then
If
![]() $q\lt r$
, then
$q\lt r$
, then
(since
![]() $\mathbb{G}_m^r\hookrightarrow R$
from the second exact sequence and
$\mathbb{G}_m^r\hookrightarrow R$
from the second exact sequence and
![]() $R$
is an algebraic subgroup of
$R$
is an algebraic subgroup of
![]() $Q$
).
$Q$
).
If
![]() $q=r$
, then
$q=r$
, then
But these cases cannot hold because of the fact that there is no non-trivial algebraic homomorphism from a linear algebraic group to an abelian variety defined over
![]() $\overline{\mathbb{Q}}$
(see [Reference Conrad5, Lemma 2.3]). Hence,
$\overline{\mathbb{Q}}$
(see [Reference Conrad5, Lemma 2.3]). Hence,
![]() $p_a(I)$
must be trivial, and this shows that so is
$p_a(I)$
must be trivial, and this shows that so is
![]() $I$
. From this, we are able to conclude that
$I$
. From this, we are able to conclude that
![]() $H=H_a\times R$
, which completes the proof of the lemma.
$H=H_a\times R$
, which completes the proof of the lemma.
3. Proof of the theorem
(i) Let
![]() $G$
be the commutative algebraic group defined by
$G$
be the commutative algebraic group defined by
![]() $G=\mathbb{G}_a\times S$
. Then
$G=\mathbb{G}_a\times S$
. Then
![]() $G$
is defined over
$G$
is defined over
![]() $\overline{\mathbb{Q}}$
and its Lie algebra
$\overline{\mathbb{Q}}$
and its Lie algebra
![]() $\mathrm{Lie}(G)$
is identified with
$\mathrm{Lie}(G)$
is identified with
![]() $\overline{\mathbb{Q}}\times \overline{\mathbb{Q}}^{g+1}=\overline{\mathbb{Q}}^{g+2}$
. Suppose by contradiction that the numbers
$\overline{\mathbb{Q}}\times \overline{\mathbb{Q}}^{g+1}=\overline{\mathbb{Q}}^{g+2}$
. Suppose by contradiction that the numbers
![]() $1, u_0,u_1,\ldots, u_g$
are linearly dependent over
$1, u_0,u_1,\ldots, u_g$
are linearly dependent over
![]() $\overline{\mathbb{Q}}$
, that is there is a non-zero linear form
$\overline{\mathbb{Q}}$
, that is there is a non-zero linear form
![]() $L$
in
$L$
in
![]() $g+2$
variables with coefficients in
$g+2$
variables with coefficients in
![]() $\overline{\mathbb{Q}}$
such that
$\overline{\mathbb{Q}}$
such that
![]() $L(1, u_0, u_1,\ldots, u_g)=0$
. Let
$L(1, u_0, u_1,\ldots, u_g)=0$
. Let
![]() $V$
be the
$V$
be the
![]() $\overline{\mathbb{Q}}$
-vector space defined by the zero set of
$\overline{\mathbb{Q}}$
-vector space defined by the zero set of
![]() $L$
in
$L$
in
![]() $\overline{\mathbb{Q}}^{g+2}$
. Then one has the vector
$\overline{\mathbb{Q}}^{g+2}$
. Then one has the vector
![]() $\tilde u\,:\!=\,(1,u)$
lies in the
$\tilde u\,:\!=\,(1,u)$
lies in the
![]() $\mathbb{C}$
-vector space
$\mathbb{C}$
-vector space
![]() $V\otimes _{\overline{\mathbb{Q}}}{\mathbb{C}}$
, and furthermore,
$V\otimes _{\overline{\mathbb{Q}}}{\mathbb{C}}$
, and furthermore,
Hence, thanks to the analytic subgroup theorem (see [Reference Wüstholz16] or [Reference Wüstholz17]), there exists a connected algebraic subgroup
![]() $H$
of
$H$
of
![]() $G$
of positive dimension defined over
$G$
of positive dimension defined over
![]() $\overline{\mathbb{Q}}$
for which
$\overline{\mathbb{Q}}$
for which
![]() $\mathrm{Lie}(H)$
is contained in
$\mathrm{Lie}(H)$
is contained in
![]() $V$
and
$V$
and
![]() $\tilde u$
lies in
$\tilde u$
lies in
![]() $\mathrm{Lie}(H({\mathbb{C}}))$
. The above lemma tells us that
$\mathrm{Lie}(H({\mathbb{C}}))$
. The above lemma tells us that
![]() $H$
must be of the form
$H$
must be of the form
![]() $H_a\times R$
with
$H_a\times R$
with
![]() $H_a$
an algebraic subgroup of
$H_a$
an algebraic subgroup of
![]() $\mathbb{G}_a$
and
$\mathbb{G}_a$
and
![]() $R$
an algebraic subgroup of
$R$
an algebraic subgroup of
![]() $S$
(defined over
$S$
(defined over
![]() $\overline{\mathbb{Q}}$
). Since
$\overline{\mathbb{Q}}$
). Since
it follows that
![]() $\mathrm{Lie}(H_a({\mathbb{C}}))$
is not trivial, and this leads to
$\mathrm{Lie}(H_a({\mathbb{C}}))$
is not trivial, and this leads to
![]() $H_a$
must be
$H_a$
must be
![]() $\mathbb{G}_a$
. In particular,
$\mathbb{G}_a$
. In particular,
![]() $\mathrm{Lie}(H_a)=\overline{\mathbb{Q}}$
and since
$\mathrm{Lie}(H_a)=\overline{\mathbb{Q}}$
and since
![]() $\mathrm{Lie}(H)\subseteq V$
, the linear form
$\mathrm{Lie}(H)\subseteq V$
, the linear form
![]() $L$
is given by
$L$
is given by
![]() $L=a_0X_0+a_1X_1+\cdots +a_gX_g$
with coefficients
$L=a_0X_0+a_1X_1+\cdots +a_gX_g$
with coefficients
![]() $a_0, a_1,\ldots, a_g\in \overline{\mathbb{Q}}$
not all zero. Let
$a_0, a_1,\ldots, a_g\in \overline{\mathbb{Q}}$
not all zero. Let
![]() $W$
denote the
$W$
denote the
![]() $\overline{\mathbb{Q}}$
-vector space defined by
$\overline{\mathbb{Q}}$
-vector space defined by
Then one has
![]() $\mathrm{Lie}(R)\subseteq W$
. Let
$\mathrm{Lie}(R)\subseteq W$
. Let
![]() $\pi\,:\, S\rightarrow A$
denote the projection from the extension
$\pi\,:\, S\rightarrow A$
denote the projection from the extension
![]() $1\rightarrow \mathbb{G}_m\rightarrow S\rightarrow A\rightarrow 1$
. Then we get an isomorphism of algebraic groups
$1\rightarrow \mathbb{G}_m\rightarrow S\rightarrow A\rightarrow 1$
. Then we get an isomorphism of algebraic groups
![]() $R/R\cap \mathbb{G}_m\cong \pi (R).$
On the other hand, since
$R/R\cap \mathbb{G}_m\cong \pi (R).$
On the other hand, since
![]() $A$
is a simple abelian variety, it follows that either
$A$
is a simple abelian variety, it follows that either
![]() $\pi (R)$
is trivial or
$\pi (R)$
is trivial or
![]() $\pi (R)$
is
$\pi (R)$
is
![]() $A$
. In the first case,
$A$
. In the first case,
![]() $R=Ker\pi \cong \mathbb{G}_m$
, and therefore
$R=Ker\pi \cong \mathbb{G}_m$
, and therefore
![]() $\mathrm{Lie}(R)$
is identified with the
$\mathrm{Lie}(R)$
is identified with the
![]() $\overline{\mathbb{Q}}$
-vector subspace
$\overline{\mathbb{Q}}$
-vector subspace
![]() $\overline{\mathbb{Q}}\times \{0\}\times \cdots \times \{0\}$
of
$\overline{\mathbb{Q}}\times \{0\}\times \cdots \times \{0\}$
of
![]() $\mathrm{Lie}(S)=\overline{\mathbb{Q}}\times \overline{\mathbb{Q}}^{g}$
. Since
$\mathrm{Lie}(S)=\overline{\mathbb{Q}}\times \overline{\mathbb{Q}}^{g}$
. Since
![]() $\mathrm{Lie}(R)\subseteq W$
, it follows that
$\mathrm{Lie}(R)\subseteq W$
, it follows that
![]() $a_0\alpha =0$
for all
$a_0\alpha =0$
for all
![]() $\alpha \in \overline{\mathbb{Q}}$
. This implies that
$\alpha \in \overline{\mathbb{Q}}$
. This implies that
![]() $a_0=0$
. By the expression of the exponential map
$a_0=0$
. By the expression of the exponential map
![]() $\exp _{S({\mathbb{C}})}$
given in [Reference Bertolin, Philippon, Saha and Saha1, Section 2.3], we obtain
$\exp _{S({\mathbb{C}})}$
given in [Reference Bertolin, Philippon, Saha and Saha1, Section 2.3], we obtain
![]() $\exp _{A({\mathbb{C}})}(u_1,\ldots, u_g)\in A(\overline{\mathbb{Q}})$
, and therefore by the analytic subgroup theorem again, one can find an algebraic subgroup
$\exp _{A({\mathbb{C}})}(u_1,\ldots, u_g)\in A(\overline{\mathbb{Q}})$
, and therefore by the analytic subgroup theorem again, one can find an algebraic subgroup
![]() $B$
of
$B$
of
![]() $A$
defined over
$A$
defined over
![]() $\overline{\mathbb{Q}}$
of positive dimension such that
$\overline{\mathbb{Q}}$
of positive dimension such that
![]() $\mathrm{Lie}(B)$
is contained in the
$\mathrm{Lie}(B)$
is contained in the
![]() $\overline{\mathbb{Q}}$
-vector space
$\overline{\mathbb{Q}}$
-vector space
![]() $\{(z_1,\ldots, z_g)\in \overline{\mathbb{Q}}^g\,:\, a_1z_1+\cdots +a_gz_g=0\}$
. Note that
$\{(z_1,\ldots, z_g)\in \overline{\mathbb{Q}}^g\,:\, a_1z_1+\cdots +a_gz_g=0\}$
. Note that
![]() $A$
is simple, this gives
$A$
is simple, this gives
![]() $B$
must be equal to
$B$
must be equal to
![]() $A$
. But this cannot happen since
$A$
. But this cannot happen since
![]() $\dim B=\dim _{\overline{\mathbb{Q}}}\mathrm{Lie}(B)\le g-1$
. Thus,
$\dim B=\dim _{\overline{\mathbb{Q}}}\mathrm{Lie}(B)\le g-1$
. Thus,
![]() $\pi (R)=A$
and this means that
$\pi (R)=A$
and this means that
![]() $R/R\cap \mathbb{G}_m\cong A$
. It is clear that
$R/R\cap \mathbb{G}_m\cong A$
. It is clear that
![]() $R\cap G_m$
is either trivial or
$R\cap G_m$
is either trivial or
![]() $\mathbb{G}_m$
, one can show that
$\mathbb{G}_m$
, one can show that
![]() $R\cong A$
(since
$R\cong A$
(since
![]() $R$
is a proper algebraic subgroup of
$R$
is a proper algebraic subgroup of
![]() $S$
). In this case, similarly, we obtain
$S$
). In this case, similarly, we obtain
![]() $L$
is of the form
$L$
is of the form
![]() $L=a_0X_0$
. In particular,
$L=a_0X_0$
. In particular,
![]() $u_0=0$
which is a contradiction, and this completes the proof for the first part of Theorem1.1.
$u_0=0$
which is a contradiction, and this completes the proof for the first part of Theorem1.1.
(ii) The proof of the second part follows directly from the
![]() $p$
-adic analytic subgroup theorem (see [Reference Fuchs and Pham6] or [Reference Matev9]) and from the same argument as in the proof of the first part above.
$p$
-adic analytic subgroup theorem (see [Reference Fuchs and Pham6] or [Reference Matev9]) and from the same argument as in the proof of the first part above.
4. Applications to complex and
 $\boldsymbol{p}$
-adic Weierstrass sigma functions
$\boldsymbol{p}$
-adic Weierstrass sigma functions
This last section is devoted to discuss applications concerning the complex and
![]() $p$
-adic Weierstrass sigma functions associated with elliptic curves. To begin with, let
$p$
-adic Weierstrass sigma functions associated with elliptic curves. To begin with, let
![]() $E$
be an elliptic curve defined over
$E$
be an elliptic curve defined over
![]() $\mathbb{C}$
characterised by the Weierstrass model
$\mathbb{C}$
characterised by the Weierstrass model
with
![]() $g_2, g_3\in \mathbb{C}$
such that
$g_2, g_3\in \mathbb{C}$
such that
![]() $g_2^3-27g_3^2\ne 0.$
Let
$g_2^3-27g_3^2\ne 0.$
Let
![]() $\Lambda$
denote the period lattice of
$\Lambda$
denote the period lattice of
![]() $E$
, and
$E$
, and
![]() $\wp$
the Weierstrass elliptic function associated with
$\wp$
the Weierstrass elliptic function associated with
![]() $E$
(or relative to
$E$
(or relative to
![]() $\Lambda$
), which is defined as:
$\Lambda$
), which is defined as:
where
![]() $\Lambda ^*=\Lambda \setminus \{0\}$
. There are two more Weierstrass functions associated with
$\Lambda ^*=\Lambda \setminus \{0\}$
. There are two more Weierstrass functions associated with
![]() $E$
, which are auxiliary to the function
$E$
, which are auxiliary to the function
![]() $\wp$
, called Weierstrass sigma and zeta functions, respectively. They play important roles in studying elliptic curves and are considered elliptic analogues of the classical trigonometric functions. In detail, the Weierstrass sigma function
$\wp$
, called Weierstrass sigma and zeta functions, respectively. They play important roles in studying elliptic curves and are considered elliptic analogues of the classical trigonometric functions. In detail, the Weierstrass sigma function
![]() $\sigma$
associated with
$\sigma$
associated with
![]() $E$
is defined as:
$E$
is defined as:
and the Weierstrass zeta function
![]() $\zeta$
associated with
$\zeta$
associated with
![]() $E$
is defined as:
$E$
is defined as:
These functions are related by:
It is convenient to recall that the corresponding Laurent expansions at the origin of these Weierstrass functions are given by:
where
![]() $G_k(\Lambda )=\displaystyle \sum _{w\in \Lambda ^*}w^{-k}$
for
$G_k(\Lambda )=\displaystyle \sum _{w\in \Lambda ^*}w^{-k}$
for
![]() $k\ge 3$
are the Eisenstein series (of weight
$k\ge 3$
are the Eisenstein series (of weight
![]() $k$
), and
$k$
), and
where the sequence
![]() $(a_{m,n})_{m,n\ge 0}$
is defined by the recurrence relation
$(a_{m,n})_{m,n\ge 0}$
is defined by the recurrence relation
with
![]() $a_{0,0}=1$
and
$a_{0,0}=1$
and
![]() $a_{m,n}=0$
for either
$a_{m,n}=0$
for either
![]() $m$
or
$m$
or
![]() $n$
is negative. One can show that
$n$
is negative. One can show that
![]() $g_2=60G_4(\Lambda )$
and
$g_2=60G_4(\Lambda )$
and
![]() $g_3=140G_6(\Lambda )$
, and by induction,
$g_3=140G_6(\Lambda )$
, and by induction,
![]() ${G}_{2k+2}(\Lambda )$
can be represented as polynomials
${G}_{2k+2}(\Lambda )$
can be represented as polynomials
![]() $P_{2k+2}$
in terms of
$P_{2k+2}$
in terms of
![]() $g_2, g_3$
with rational coefficients (see [Reference Chandrasekharan4, Chapter IV]).
$g_2, g_3$
with rational coefficients (see [Reference Chandrasekharan4, Chapter IV]).
Now, let
![]() $E$
be an elliptic curve defined over
$E$
be an elliptic curve defined over
![]() $\overline{\mathbb{Q}}$
and
$\overline{\mathbb{Q}}$
and
![]() $G$
an extension of
$G$
an extension of
![]() $E$
by
$E$
by
![]() $\mathbb{G}_m$
defined over
$\mathbb{G}_m$
defined over
![]() $\overline{\mathbb{Q}}$
. Recall that the group Ext
$\overline{\mathbb{Q}}$
. Recall that the group Ext
![]() $^1(E,\mathbb{G}_m)$
of extension classes of
$^1(E,\mathbb{G}_m)$
of extension classes of
![]() $E$
by
$E$
by
![]() $\mathbb{G}_m$
is isomorphic to the Picard group Pic
$\mathbb{G}_m$
is isomorphic to the Picard group Pic
![]() $^0(E)=E^*$
of divisors on
$^0(E)=E^*$
of divisors on
![]() $E$
modulo principal divisors. This means that the extension
$E$
modulo principal divisors. This means that the extension
![]() $G$
corresponds to an algebraic point
$G$
corresponds to an algebraic point
![]() $P$
in
$P$
in
![]() $E(\overline{\mathbb{Q}})$
(here we identify
$E(\overline{\mathbb{Q}})$
(here we identify
![]() $E$
with
$E$
with
![]() $E^*$
). Let
$E^*$
). Let
![]() $q\in{\mathbb{C}}$
be an elliptic logarithm of
$q\in{\mathbb{C}}$
be an elliptic logarithm of
![]() $P$
, that is
$P$
, that is
![]() $\exp _{E({\mathbb{C}})}(q)=P$
, here the exponential map
$\exp _{E({\mathbb{C}})}(q)=P$
, here the exponential map
![]() $\exp _{E({\mathbb{C}})}$
of the elliptic curve
$\exp _{E({\mathbb{C}})}$
of the elliptic curve
![]() $E$
is given by:
$E$
is given by:
The exponential map of
![]() $G$
is given by:
$G$
is given by:
where
![]() $f (z)=\dfrac{\sigma (z+q)}{\sigma (z)\sigma (q)}e^{-\zeta (q)z}$
is Serre’s function (see [Reference Bertolin, Philippon, Saha and Saha1, Section 6]). We now obtain the following theorem, which is an improvement of a previous result in transcendence given by M. Waldschmidt (see [Reference Waldschmidt13, Theorem 1] or [Reference Waldschmidt14, Theorem 3.2.10]).
$f (z)=\dfrac{\sigma (z+q)}{\sigma (z)\sigma (q)}e^{-\zeta (q)z}$
is Serre’s function (see [Reference Bertolin, Philippon, Saha and Saha1, Section 6]). We now obtain the following theorem, which is an improvement of a previous result in transcendence given by M. Waldschmidt (see [Reference Waldschmidt13, Theorem 1] or [Reference Waldschmidt14, Theorem 3.2.10]).
Theorem 4.1.
Let
![]() $E$
be an elliptic curve defined over
$E$
be an elliptic curve defined over
![]() $\overline{\mathbb{Q}}$
and
$\overline{\mathbb{Q}}$
and
![]() $\wp, \zeta, \sigma$
the Weierstrass elliptic, zeta, sigma functions associated with
$\wp, \zeta, \sigma$
the Weierstrass elliptic, zeta, sigma functions associated with
![]() $E$
, respectively. Let
$E$
, respectively. Let
![]() $\alpha, \beta$
be algebraic numbers and
$\alpha, \beta$
be algebraic numbers and
![]() $u, u_0$
complex numbers such that
$u, u_0$
complex numbers such that
![]() $\wp (u), \wp (u_0)$
are algebraic numbers. Suppose that
$\wp (u), \wp (u_0)$
are algebraic numbers. Suppose that
![]() $u_0$
is not a torsion point and that
$u_0$
is not a torsion point and that
![]() $u, u+u_0$
are not in the lattice of periods of
$u, u+u_0$
are not in the lattice of periods of
![]() $\wp$
. Then, the number
$\wp$
. Then, the number
is transcendental.
Proof. Consider the algebraic point
This algebraic point corresponds to a semiabelian variety
![]() $G$
in Ext
$G$
in Ext
![]() $^1(E,\mathbb{G}_m)$
. Then one has
$^1(E,\mathbb{G}_m)$
. Then one has
with
![]() $f(u)=\dfrac{\sigma (u+u_0)}{\sigma (u)\sigma (u_0)}e^{-\zeta (u_0)u}$
, and this gives
$f(u)=\dfrac{\sigma (u+u_0)}{\sigma (u)\sigma (u_0)}e^{-\zeta (u_0)u}$
, and this gives
Hence, if this number is algebraic then
![]() $\exp _{G({\mathbb{C}})}(u,\alpha u+\beta )\in G(\overline{\mathbb{Q}})$
. Applying the first part of Theorem1.1, we deduce that the elements
$\exp _{G({\mathbb{C}})}(u,\alpha u+\beta )\in G(\overline{\mathbb{Q}})$
. Applying the first part of Theorem1.1, we deduce that the elements
![]() $1, u, \alpha u+\beta$
are linearly independent over
$1, u, \alpha u+\beta$
are linearly independent over
![]() $\overline{\mathbb{Q}}$
. This contradiction proves the theorem.
$\overline{\mathbb{Q}}$
. This contradiction proves the theorem.
It is natural to obtain a
![]() $p$
-adic analogue of the above theorem, and in order to express such a result in the
$p$
-adic analogue of the above theorem, and in order to express such a result in the
![]() $p$
-adic setting, we first recall the
$p$
-adic setting, we first recall the
![]() $p$
-adic Weierstrass elliptic, zeta and sigma functions, respectively. By definition, the
$p$
-adic Weierstrass elliptic, zeta and sigma functions, respectively. By definition, the
![]() $p$
-adic Weierstrass elliptic function
$p$
-adic Weierstrass elliptic function
![]() $\wp _p$
is the (Lutz-Weil)
$\wp _p$
is the (Lutz-Weil)
![]() $p$
-adic elliptic function associated with the elliptic curve
$p$
-adic elliptic function associated with the elliptic curve
![]() $E$
(see [Reference Lutz8] and [Reference Weil15]). This function satisfies the relation (as the complex one)
$E$
(see [Reference Lutz8] and [Reference Weil15]). This function satisfies the relation (as the complex one)
![]() $\wp _p^{\prime}(z)= 4\wp _p^3(z)-g_2\wp _p-g_3,$
but only on the neighbourhood of the origin
$\wp _p^{\prime}(z)= 4\wp _p^3(z)-g_2\wp _p-g_3,$
but only on the neighbourhood of the origin
where
![]() $B(r_p)$
is the set of all
$B(r_p)$
is the set of all
![]() $p$
-adic numbers
$p$
-adic numbers
![]() $x$
in
$x$
in
![]() $\mathbb{C}_p$
with
$\mathbb{C}_p$
with
![]() $|x|_p\lt r_p\,:\!=\,p^{-\frac{1}{p-1}}$
. Note that
$|x|_p\lt r_p\,:\!=\,p^{-\frac{1}{p-1}}$
. Note that
![]() $\wp _p$
is analytic on
$\wp _p$
is analytic on
![]() $\mathcal E_p\setminus \{0\}$
and expressed by:
$\mathcal E_p\setminus \{0\}$
and expressed by:
Let
![]() $\zeta _p$
and
$\zeta _p$
and
![]() $\sigma _p$
be the
$\sigma _p$
be the
![]() $p$
-adic Weierstrass zeta and sigma functions, respectively. By definition,
$p$
-adic Weierstrass zeta and sigma functions, respectively. By definition,
![]() $\zeta _p$
and
$\zeta _p$
and
![]() $\sigma _p$
are meromorphic functions on the domain
$\sigma _p$
are meromorphic functions on the domain
![]() $\mathcal E_p\setminus \{0\}$
satisfying the followings:
$\mathcal E_p\setminus \{0\}$
satisfying the followings:
and their corresponding
![]() $p$
-adic expansions are also given by:
$p$
-adic expansions are also given by:
and
We obtain the following theorem.
Theorem 4.2.
Let
![]() $E$
be an elliptic curve defined over
$E$
be an elliptic curve defined over
![]() $\overline{\mathbb{Q}}$
and
$\overline{\mathbb{Q}}$
and
![]() $\wp _p, \zeta _p, \sigma _p$
the
$\wp _p, \zeta _p, \sigma _p$
the
![]() $p$
-adic Weierstrass elliptic, zeta, sigma functions associated with
$p$
-adic Weierstrass elliptic, zeta, sigma functions associated with
![]() $E$
, respectively. Let
$E$
, respectively. Let
![]() $\alpha$
and
$\alpha$
and
![]() $\beta$
be algebraic numbers and
$\beta$
be algebraic numbers and
![]() $\mathfrak{u}, \mathfrak{u}_0$
non-zero
$\mathfrak{u}, \mathfrak{u}_0$
non-zero
![]() $p$
-adic numbers in
$p$
-adic numbers in
![]() $\mathcal E_p$
such that
$\mathcal E_p$
such that
![]() $\wp _p(\mathfrak{u}), \wp _p(\mathfrak{u}_0)$
are algebraic numbers. If
$\wp _p(\mathfrak{u}), \wp _p(\mathfrak{u}_0)$
are algebraic numbers. If
![]() $\alpha \mathfrak{u} + \beta \in B(r_p)$
, then the number
$\alpha \mathfrak{u} + \beta \in B(r_p)$
, then the number
is transcendental.
Proof. As in the complex case, we first consider the algebraic point
and this algebraic point gives the corresponding semiabelian variety
![]() $G_p$
in Ext
$G_p$
in Ext
![]() $^1(E,\mathbb{G}_m)$
. Since we have seen from above that the
$^1(E,\mathbb{G}_m)$
. Since we have seen from above that the
![]() $p$
-adic functions
$p$
-adic functions
![]() $\wp _p, \zeta _p$
and
$\wp _p, \zeta _p$
and
![]() $\sigma _p$
are represented by the same power series as the complex functions
$\sigma _p$
are represented by the same power series as the complex functions
![]() $\wp, \zeta$
and
$\wp, \zeta$
and
![]() $\sigma$
, respectively, one can show that the
$\sigma$
, respectively, one can show that the
![]() $p$
-adic exponential map of
$p$
-adic exponential map of
![]() $G_p$
is also expressed as the same type as the complex exponential map. More precisely, the map
$G_p$
is also expressed as the same type as the complex exponential map. More precisely, the map
![]() $\exp _{G({\mathbb{C}}_p)}$
is given by:
$\exp _{G({\mathbb{C}}_p)}$
is given by:
with
![]() $\mathcal G_p=\mathcal E_p\times B(r_p)$
and
$\mathcal G_p=\mathcal E_p\times B(r_p)$
and
![]() $f_p(z)=\dfrac{\sigma _p(z+\mathfrak{u}_0)}{\sigma _p(z)\sigma _p(\mathfrak{u}_0)}e_p^{-\zeta _p(\mathfrak{u}_0)z}$
with
$f_p(z)=\dfrac{\sigma _p(z+\mathfrak{u}_0)}{\sigma _p(z)\sigma _p(\mathfrak{u}_0)}e_p^{-\zeta _p(\mathfrak{u}_0)z}$
with
![]() $e_p$
the usual
$e_p$
the usual
![]() $p$
-adic exponential function, and prolonged to a function on the whole
$p$
-adic exponential function, and prolonged to a function on the whole
![]() ${\mathbb{C}}_p$
(thanks to [Reference Robert12, Section 5.4.4]). Assume by contradiction as the complex case that the number
${\mathbb{C}}_p$
(thanks to [Reference Robert12, Section 5.4.4]). Assume by contradiction as the complex case that the number
is algebraic, then we also get
![]() $\exp _{G_p({\mathbb{C}}_p)}(\mathfrak{u},\alpha \mathfrak{u}+\beta )\in G_p(\overline{\mathbb{Q}}),$
and therefore we are able to deduce from the second part of Theorem1.1 that
$\exp _{G_p({\mathbb{C}}_p)}(\mathfrak{u},\alpha \mathfrak{u}+\beta )\in G_p(\overline{\mathbb{Q}}),$
and therefore we are able to deduce from the second part of Theorem1.1 that
![]() $1, \mathfrak{u}, \alpha \mathfrak{u} +\beta$
are linearly independent over
$1, \mathfrak{u}, \alpha \mathfrak{u} +\beta$
are linearly independent over
![]() $\overline{\mathbb{Q}}$
(a contradiction). This completes the proof of the theorem.
$\overline{\mathbb{Q}}$
(a contradiction). This completes the proof of the theorem.
Acknowledgements
The author would like to thank the editor and the anonymous referee for careful reading of this manuscript and useful comments.