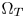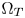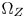Color-gamut mapping in the non-uniform CIE-1931 space with perceptual hue fidelity constraints for SMPTE ST.2094-40 standard

Abstract

As high-dynamic range (HDR) and wide-color gamut (WCG) contents become more and more popular in multimedia markets, color mapping of the distributed contents to different rendering devices plays a pivotal role in HDR distribution eco-systems. The widely used and economic gamut-clipping (GC)-based techniques perform poorly in mapping WCG contents to narrow gamut devices; and high-performance color-appearance model (CAM)-based techniques are computationally expensive to commercial applications. In this paper, we propose a novel color gamut mapping (CGM) algorithm to solve the problem. By introducing a color transition/protection zone (TPZ) and a set of perceptual hue fidelity constraints into the CIE-1931 space, the proposed algorithm directly carries out CGM in the perceptually non-uniform space, thus greatly decreases the computational complexity. The proposed TPZ effectively achieves a reasonable compromise between saturation preserving and details protection in out-of-gamut colors. The proposed hue fidelity constraints reference the measurements of human subjects' visual responses, thus effectively preserve the perceptual hue of the original colors. Experimental results show that the proposed algorithm clearly outperforms the GC-CGM, and performs similarly or better than the expensive CAM-CGM. The proposed algorithm is real-time and hardware friendly. It is an important supplement of the SMPTE ST.2094-40 standard.

I. INTRODUCTION

High-dynamic range (HDR) and wide-color gamut (WCG) contents become more and more popular in multimedia markets nowadays. The accuracy of rendering colors is one of the most important factors that determine the visual quality of the HDR and WCG contents on user-end rendering devices. However, due to the limits of color reproductions, a user-end device, e.g., a ultra-high definition television (UHDTV), may not match the HDR contents in both dynamic range and color gamut. Directly rendering HDR and WCG contents on a user-end display may lead to multiple artifacts, including detail loss, hue distortions, even high visual impacts such as banding, alien color spots, etc., thus seriously degrade the final visual quality. In recent years, HDR contents creators, especially studios, tend to directly master their materials in the Rec.2020 gamut, which covers 75.8% of the CIE-1931 space, and is the widest gamut in broadcasting industries but not supported by most TV products nowadays. This makes the mis-matching issues more serious.

SMPTE ST.2094-40 standard [1] specifies an effective solution to solve the problem of dynamic range mismatching between contents and rendering devices, referenced as tone-mapping, which projects the colors in a large dynamic range into a smaller dynamic range. However, it does not give the rules of color gamut mapping (CGM) that represents the colors of a source gamut, denoted $\Omega _S$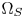, in a different target gamut, denoted $\Omega _T$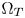. Although TV manufacturers may use their own intelligent properties to solve the problem, very few high-performance CGM techniques are suitable for commercial applications, which require very limited system resources, and need to be low-cost.

Due to lack of WCG contents, earlier HDR researches generally focus their works on improving the tone-mapped color quality without accurate gamut mapping [2–4]. For example, Johnson et al. [2] simply apply a clipping followed by scaling function to the linear RGB (luminance) components, thus avoid the colors that are unrepresentable to rendering devices. Mantiuk et al. [3] reduce the peak luminance of contents to avoid generating the colors that may be outside the rendering devices' gamut. As the fast developing HDR broadcasting industries, the techniques cannot provide customers with satisfied visual quality.

Most high-performance CGM techniques adopt color-appearance models (CAM) due to their good descriptions of the perceptual properties of human color vision [5]. A CAM-based CGM method generally models $\Omega _S$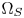 and $\Omega _T$ 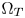in a perceptually uniform color space such as the CIELCH space, etc. Then, it represents the input colors of $\Omega _S$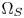, usually given as linear RGB components, as the coordinates in the perceptually uniform space, and moves the colors that are outside $\Omega _T$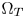, referenced as the out-of-gamut colors, to either the appropriate positions inside $\Omega _T$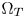, or to the boundaries of $\Omega _T$. Since the color gamut boundaries in a uniform space are generally non-linear, and complex computations such as exponential and trigonometric operators involve color representations, the CAM-based techniques are expensive in hardware implementations.

Recent researches have shown that the CAM-based CGM perform robustly to different contents. Sikudova et al. [6] propose to probe a scale vector consisting of the scale factor of each hue slice pair between $\Omega _S$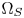 and $\Omega _T$ 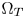in the CIELCH space by iteratively scaling the target gamut boundaries or moving the cusp of each hue slice in $\Omega _S$ 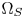toward the lightness axes until all colors are inside the new boundaries. The scaler vector is then applied to the source colors to obtain the mapped colors. The method is high-cost and iterative thus not suitable for hardware implementation.

Azimi et al. [7] propose a hybrid CGM method that adopts the toward white point algorithm [8] in multiple color spaces including CIELAB, CIELUV, etc., and the final results are obtained by choosing the mapped colors that lead to the minimum color difference CIE-$\Delta E$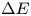 [9] compared to the original colors. The method is very expensive in both resource consuming and computations. Azimi et al. [10] also propose a simple toward white point-based CGM algorithm that introduces an inner gamut inside $\Omega _T$ 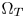in the CIELCH space. An out-of-gamut color is then proportionally moved to a position between the boundaries of $\Omega _T$ 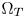and the inner gamut. The method effectively protects many details in out-of-gamut colors. However, it is sensitive to the size of the inner gamut, and its color-moving paths are not defined in luminance – chroma slices, thus it cannot guarantee the perceptual hue fidelity during color moving.

Yuan et al. [11] also move out-of-gamut colors in the CIELCH space. They move the out-of-gamut colors that are far away from the boundaries of $\Omega _T$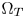 to the boundaries of $\Omega _T$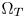, and gradually move the out-of-gamut colors that are near the $\Omega _T$ 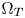boundaries inside $\Omega _T$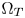. The method protects some details in out-of-gamut colors, but may generate serious banding artifacts in real Rec.2020 contents.

Masaoka et al. [12] propose a high-performance CIELCH space-based CGM that guarantees the hue fidelity of the mapped colors. In each hue slice, a lightness focal point and a chroma focal point are firstly located on the lightness and the chroma axis according to the cusps of $\Omega _S$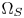 and $\Omega _T$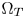. An out-of-gamut color thus can be moved toward either the lightness or the chroma focal point until it reaches a boundary of $\Omega _T$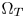. The method obtains natural and visually pleased colors from multiple WCG contents. However, it adopts a $129 \times 129 \times 129$ 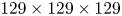lookup table (LUT) for obtaining high color accuracy. Over 2 million elements need to be saved in the LUT. This is too expensive for commercial applications such as UHDTV products.

In a word, although the CAM-based methods perform robustly in many applications, they are high-cost. In addition to their complex computations, the boundaries of $\Omega _S$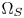 and $\Omega _T$ 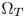are generally non-linear in perceptually uniform spaces such as the CIELCH space. This requires more gamut boundary descriptors (GBD) to well represent gamut boundaries [7, 12]. This significantly increases the costs. In fact, color moving can be carried out in any color space [13]. The GBD of standard gamuts such as Rec.2020 and DCI-P3 are all linear in the CIE-1931 xyY space. Moving colors in the CIE-1931 space is theoretically easier than moving colors in perceptually uniform spaces. However, the CIE-1931 space is perceptually non-uniform. Furthermore, lightness and chroma are not independent to each other in the space. Simply moving colors in the CEI-1931 space may lead to serious hue distortions. Therefore, few CGM algorithms are designed for the CIE-1931 space.

In practice, color-space conversion followed by gamut clipping (GC) in the CIE-1931 space [14] is the most popular CGM method in commercial applications due to its simplicity, efficiency, and low costs. It keeps the chromaticity coordinates of the non-out-of-gamut colors unchanged, and clips the out-of-gamut colors to the boundaries of $\Omega _T$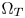. A color space conversion matrix between $\Omega _S$ 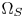and $\Omega _T$ 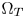is first computed from the gamut primaries and the reference white [14]. Then the matrix is applied to the colors of $\Omega _S$ 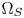to represent the colors in $\Omega _T$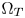. The negative and the bigger-than-one values (in the normalized domain), which come from the out-of-gamut colors, are respectively clipped to zero or one, thus mapping the colors to the boundaries of $\Omega _T$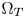. The GC-based CGM is very simple and hardware friendly. However, it only performs well when $\Omega _T \ge \Omega _S$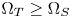, i.e., the colors of $\Omega _S$ 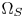can be totally represented by the colors of $\Omega _T$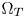. In the case of $\Omega _T < \Omega _S$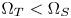, not all source colors can be represented in $\Omega _T$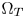. Directly clipping the out-of-gamut colors to the boundaries of $\Omega _T$ 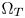may seriously lose color variations and smooth transitions, and lead to high visual impacts in the obtained colors.

In HDR and WCG contents distribution systems, the Rec.2020 gamut is widely adopted as the color container. Namely, contents creators can carry out color grading in a non-Rec.2020 target device gamut as $\Omega _T$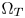, but convert the obtained contents to Rec.2020 gamut contents before packing and distributing. Since no out-of-gamut colors exist in the contents, the GC-based CGM performs well in this case. As the fast development of broadcasting technologies, HDR contents creators, especially studios, tend to directly master their contents in the Rec.2020 gamut to get better visual effects. GC-based CGM performs poorly in such a case. Modern broadcasting industries need a high-performance CGM technique that satisfies following important requirements:

1. (1) The colors that are inside $\Omega _T$ should keep their color fidelity as much as possible.

2. (2) The colors that are outside $\Omega _T$ should well keep their perceptual hue after CGM.

3. (3) Effectively preserves the abundant details and smooth transitions in out-of-gamut colors.

4. (4) No significant artifacts and no high visual impacts.

5. (5) Low-cost and hardware friendly.

In this paper, we propose a novel CGM algorithm that directly carries out CGM in the perceptually non-uniform CIE-1931 space, and satisfies the requirements listed above. Section II presents an overview of the proposed algorithm. Technical details are given in Sections III and IV. Section V presents the experimental results and performance evaluations. Finally, Section VI concludes this paper.

II. OVERVIEW

Although directly carrying out GC-based CGM in the CIE-xyY 1931 space has benefits in both of the computational complexity and the costs, hue distortions caused by the non-uniformness of the space and the high visual impacts caused by color-clipping limit its applications. We propose to solve the problems by introducing two important elements into the CIE-xyY space: (1) a color transition/protection zones (TPZ) inside $\Omega _T$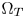, denoted $\Omega _Z$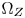, for preserving the accuracy of inside-gamut colors and maintaining the variations and smoothness in out-of-gamut colors after CGM; and (2) a set of strict color fidelity constraints to avoid serious perceptual hue distortions during color moving.

The key to move colors in the non-uniform CIE-xyY space without introducing serious hue distortions is to find their constant hue loci, along each of which, all colors have perceptually similar hues. The constant hue loci form the perceptual color fidelity constraints of color moving, called the color-moving constraints (CMC). In this paper, we adopt the Munsell Renotations [15] to define the CMC. The Munsell color system [16] is perceptually uniform and built from strict measurements of human subjects' visual responses. The Munsell Renotations present the chromaticity coordinates of the important Munsell colors in the CIE-xyY space. Constant hue loci thus can be directly obtained in the CIE-xyY space by connecting the colors sharing the same hue names. They are ideal references to define the CMC. Figure 1 shows the main structure of the proposed algorithm. Note that the Munsell colors are defined under Illuminant C, and modern UHDTVs use Illuminant D65. We need to adopt chromatic adaptation to obtain the Munsell constant hue loci under Illuminant D65.

Fig. 1. The main diagram of the proposed CGM algorithm.

As shown in Fig. 1, the proposed algorithm consists of two parts. One is the off-line processing (Section III), and the other is the in-line processing (Section IV). The off-line processing defines the GBD of both of $\Omega _S$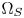 and $\Omega _T$ 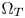(Section III-A), and the CMC between $\Omega _S$ 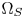and $\Omega _T$ 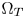(Section III-B). The obtained GBD and the CMC are then saved into a hardware friendly LUT for later in-line processing usages. The off-line processing is not necessarily hardware friendly, since it is not a part of products. We only perform the off-line processing for LUT updating.

The in-line processing adopts the GBD and the CMC obtained in the off-line processing, and carries out CGM in the perceptually non-uniform CIE-xyY space. A color TPZ $\Omega _Z$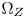 is firstly defined from the received ST.2094-40 metadata [1] (Section IV-A). The colors outside $\Omega _Z$ 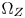are defined as the out-of-gamut colors in this paper. Note that we need not update $\Omega _Z$ 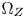frequently. It can be defined only once, or updated when contents statistics have great changes. Second, the input linear RGB colors are converted to the chromaticity coordinates in the CIE-xyY space with a simple conversion matrix [14]. We keep the positions of the inside-$\Omega _Z$ 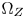colors unchanged, and estimate the constant hue loci of the out-of-$\Omega _Z$ 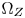colors (Section IV-B). The third, we move the out-of-$\Omega _Z$ 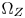colors along their constant hue loci to the appropriate positions between the boundaries of $\Omega _T$ 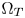and $\Omega _Z$ 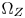(Section IV-C), and convert the obtained color coordinates back to linear RGB components. By avoiding mapping the out-of-gamut colors only to the target gamut boundaries, the proposed TPZ effectively preserves the abundant variations and smoothness of the colors, and with the constant hue loci, we avoid perceivable hue distortions in color moving. Note that the in-line processing will be parts of products. Therefore, it should be simple, real-time, and low-cost.

III. THE OFF-LINE PROCESSING

The off-line processing of the proposed CGM algorithm obtains a hardware friendly LUT that contains the necessary information, including the GBD of $\Omega _S$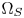 and $\Omega _T$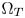, and the CMC, for carrying out CGM in the perceptually non-uniform CIE-xyY space. Section III-A introduces the computations of the GBD, and Section III-B presents the details of the CMC computations.

A) GBD generation

GBD are critical for accurate CGM. Morovic et al. [17] propose an universal Segment Maxima algorithm to compute the GBD for a given gamut. However, benefiting from the linear gamut boundaries in the CIE-xyY space, we can simplify the algorithm as locating the most saturated colors in different luminance as the boundary points. Let $w(x_w, y_w)$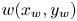 be the white point under a given illuminant condition, to a given color $c(x, y)$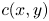, we approximate the hue and the saturation of c, denoted $h_c$ 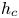and $\rho _c$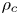, respectively, as

(1)\begin{equation} \begin{cases}h_c = {\rm atan}((y - y_w) / (x - x_w) ) \\ \rho_c = \sqrt{(x - x_w)^2 + (y - y_w)^2}. \end{cases}\end{equation}

Note that a color gamut is a 3D solid, and $c(x, y)$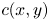 may represent many colors located in $(x, y)$ 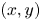with different luminance. Gamut boundary points are then obtained by,

(2)\begin{equation} b(h, l) = \arg \displaystyle \max_{\forall h, l; c \in \mathcal{C}} \rho_c, \end{equation}

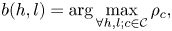
where l is a given luminance, and $\mathcal {C}$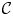 is the set of all possible colors of the gamut. Figure 2 shows the obtained Rec.2020 gamut boundaries sampled at several luminance with the peak luminance 4000 nits (normalized to 0.4). As shown in Fig. 2, only few GBD can well define the linear boundaries at a luminance layer l in the CIE-xyY space.

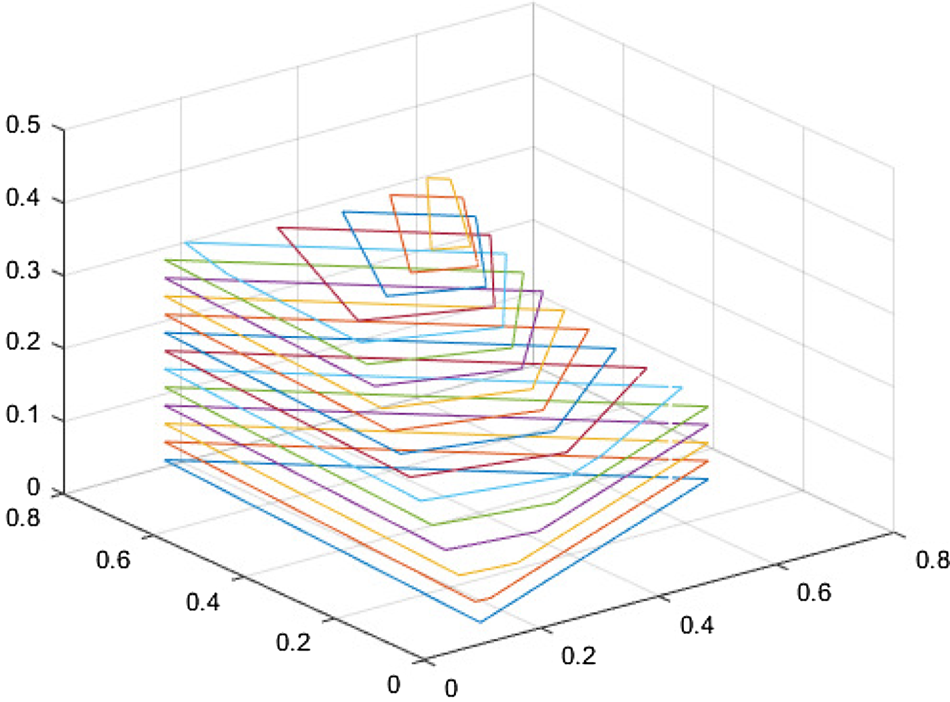
Fig. 2. An example of the sampled Rec.2020 gamut solid under the peak luminance 4000 nits (normalized to 0.4).

With (1) and (2), we can obtain the GBD of arbitrary RGB gamuts in the CIE-xyY space. Since the hue and the luminance are continuous, hue quantization and luminance sampling are necessary in GBD computations. The hue quantization level can be experimentally set to 1 to 2 degrees. The sampling rate of luminance is application-depended. The bit-depth of colors also greatly affects the quality of the GBD. Our simulations show that 12 or higher bit colors can generate satisfied GBD.

B) Computations of CMC

The Munsell color system adopts Value (lightness), Hue, and Chroma to present colors [16]. The colors having the same Value and Hue but different Chroma form the constant hue loci at a given luminance layer. From the Munsell Renotations [15], where 14 sets of Munsell colors are defined in different luminance layers, we interpolate the constant hue loci of different hues in arbitrary luminance layers. Figure 3 shows the examples of the obtained constant hue loci overlapped on the Rec.2020 gamut as $\Omega _S$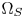, and the DCI-P3 gamut as $\Omega _T$ 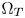at different luminance layers.

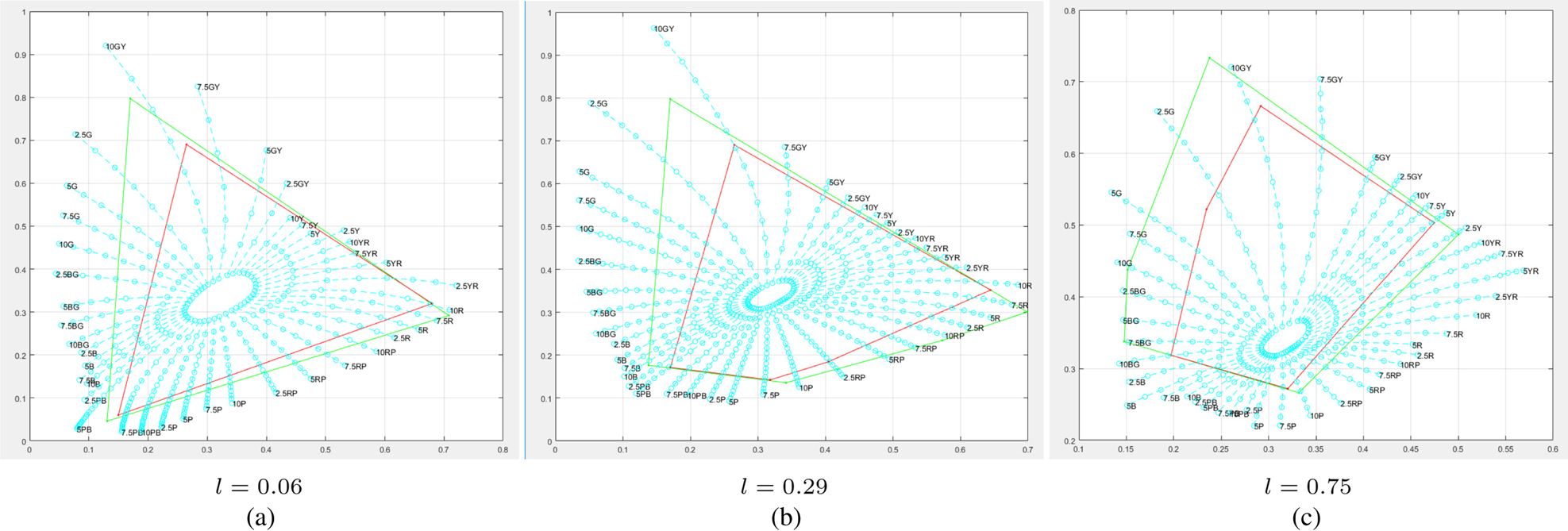
Fig. 3. Examples of the constant hue loci at different luminance layers (green: Rec.2020; red: DCI-P3; cyan: constant hue loci). (a) l=0.06. (b) l=0.29. (c) l=0.75.

Although we can directly adopt the constant hue loci segments between $\Omega _S$ and $\Omega _T$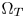 as the CMC, the segments are non-linear, and not convenient to either color-moving operators or CMC storage. We note that, as shown in Fig. 3, the constant hue loci near the green vertex have relative big curvatures, which may lead to relatively big errors if we linearize those loci. However, the MacAdam Ellipses [18] show that human vision system has relatively big tolerance of color differences in the region. The loci segments near the blue, the purple, and the red vertices have relatively small curvatures, and their length are also small. Although human vision system has relative small tolerance of color differences in those regions [18], linearizing those loci will lead to relatively small errors too.

After testing the perceptual color accuracy with many real-world images and test patterns, we conclude that the constant hue loci segments between $\Omega _S$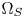 and $\Omega _T$ 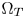can be linearized without greatly degrading the final visual quality. This greatly decreases the LUT size, and simplifies the color-moving computations. In this paper, we adopt the linearized loci segments as the CMC. Figure 4(a) shows the examples of the CMC between the Rec.2020 and the DCI-P3 gamut at layer l=0.06. Note that the paths connecting the vertices of $\Omega _S$ 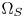and $\Omega _T$ do not follow the constant hue loci. A general rule of color moving is to move a vertex color of $\Omega _S$ to the corresponding vertex color of $\Omega _T$.

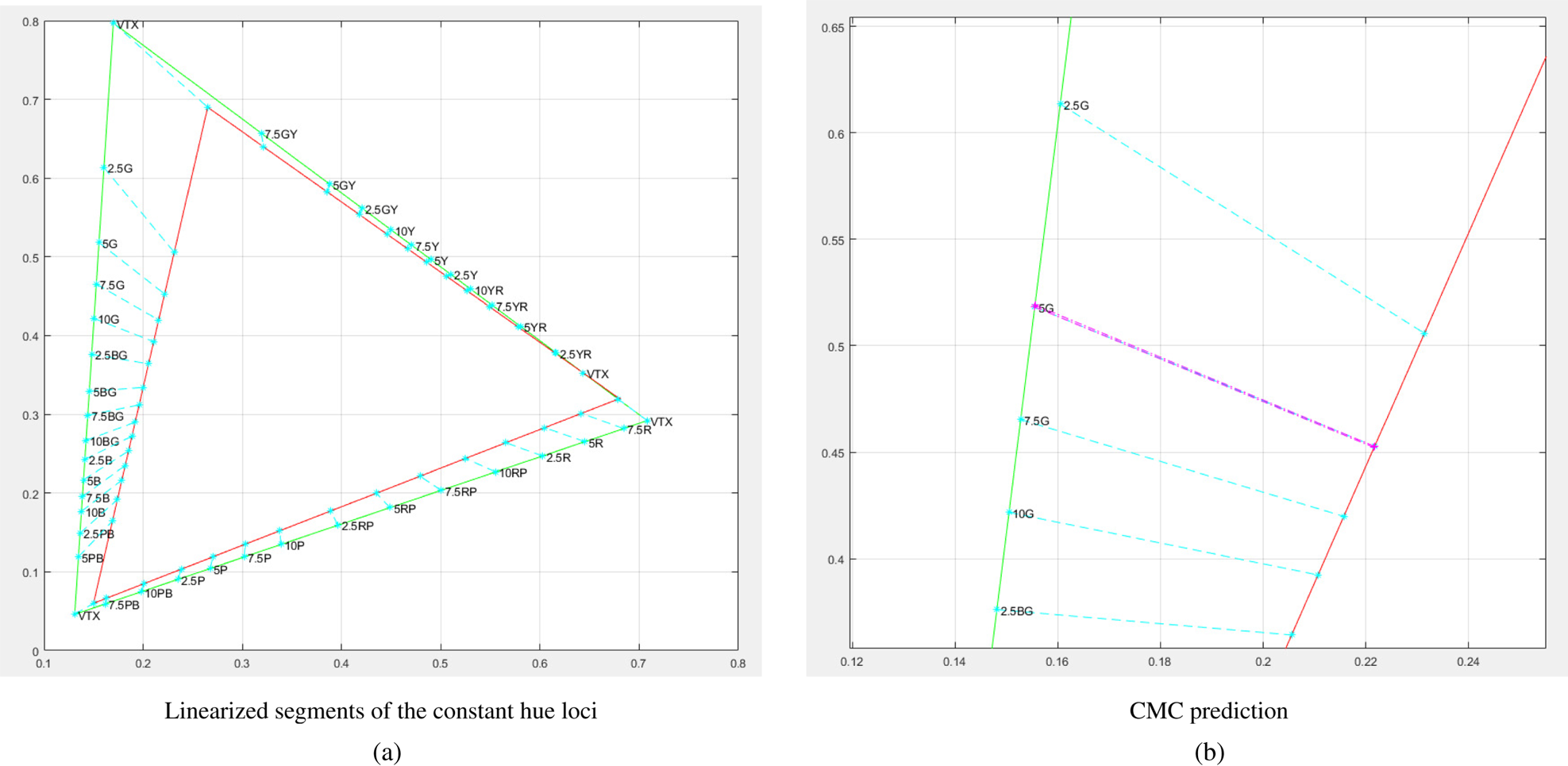
Fig. 4. Examples of the linearized constant hue loci and CMC redundancy removal (Rec.2020 to DCI-P3, l=0.06). (a) Linearized segments of the constant hue loci. (b) CMC prediction.

Analysis of the CMC shows that there are great redundancy existing among the CMC in the same luminance layer. For example, as shown in Fig. 4(b), the CMC of hue 5G can be well represented by its neighbors hue 2.5G and 7.5G with line interpolation, thus the CMC of hue 5G is redundant, and can be removed from the CMC list. By removing the redundant CMC, we further decrease the LUT size. Also, our simulations show that it is not necessary to save many layers' CMC. Few key luminance layers are enough to interpolate visually pleased mapped colors. Our simulations show that 6–15 key luminance layers are good enough for most real-world contents. This further decreases the total number of the CMC saved in the LUT size, thus decreases the hardware costs.

IV. THE IN-LINE PROCESSING

The in-line processing of the proposed algorithm carries out color moving in the perceptually non-uniform CIE-xyY space using the CMC obtained in Section III (saved as a LUT). A color TPZ, which is also a 3D solid, denoted $\Omega _Z$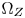, is firstly defined inside $\Omega _T$ 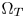(Section IV-A) to (1) preserve the original hue and saturation of the colors that are inside $\Omega _Z$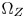, and (2) protect delicate details and natural color variations of the colors that are outside $\Omega _Z$ 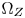in color moving. Then, the constant hue loci of arbitrary out-of-$\Omega _Z$ 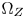colors are estimated with the CMC LUT (Section IV-B). Finally, according to their original positions in $\Omega _S$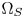, we move the out-of-$\Omega _Z$ 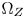colors along their constant hue loci to the appropriate positions between $\Omega _T$ 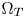and $\Omega _Z$ 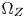(Section IV-C), and keep the chromaticity coordinates of the inside-$\Omega _Z$ 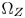colors unchanged. The in-line processing will be parts of products, thus it needs to be economic and real-time.

A) Definition of $\Omega _Z$

Most serious artifacts in GC-based CGM are caused by directly mapping the out-of-gamut colors to the boundaries of $\Omega _T$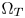, thus details and smooth transitions of those colors may be lost. An effective solution of the issue is to move the out-of-gamut colors proportionally inside $\Omega _T$ 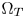according to their original positions in $\Omega _S$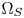. In such a way, we can preserve parts of the original color variations in the mapped colors. Furthermore, we also need to appropriately move small parts of the colors that are inside $\Omega _T$ 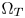but near its boundaries, thus we can maintain the smooth transition between the moved colors and unchanged colors. The TPZ $\Omega _Z$ 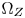is designed for this propose. The size of $\Omega _Z$ 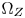determines the limits that the out-of-$\Omega _Z$ 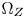colors can be moved inside $\Omega _T$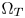. The bigger the $\Omega _Z$ 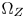is, the smaller the space between the boundaries of $\Omega _T$ 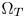and $\Omega _Z$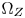, and the less the details in out-of-$\Omega _Z$ 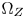colors are protected, but the more saturation are preserved. The smaller the $\Omega _Z$ 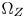is, the bigger the space between the boundaries of $\Omega _T$ 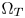and $\Omega _Z$ 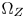is, the more details and color variations are protected, but the more saturation is sacrificed. Therefore, the size of $\Omega _Z$ 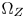should achieve a reasonable compromise between detail protection and saturation preserving.

In this paper, we define the $\Omega _Z$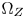 along the extensions of the vertex paths between $\Omega _S$ 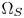and $\Omega _T$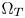. Let $v_s$ 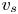and $v_t$ 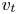be a pair of corresponding vertices of $\Omega _S$ 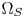and $\Omega _T$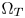, respectively. The corresponding vertex of $\Omega _Z$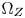, denoted $v_z$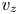, is such a point that satisfies (3),

(3)\begin{equation} \vert v_t v_z\vert = \alpha \vert v_s v_t\vert, \end{equation}

where α is a size control factor, and can be experimentally set as $\alpha \in [0, 0.4]$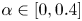. When $\alpha = 0$, $v_z$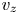 becomes $v_t$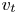, namely, $\Omega _Z$ 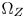achieves its maxima and is equal to $\Omega _T$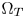. In such a case, the proposed algorithm performs similarly to the GC-based CGM. As α increases, $\Omega _Z$ 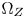becomes smaller, and more details are preserved, but more saturation is sacrificed. Depending on concrete applications, α can be either a constant for all gamut vertices, or a victor where each element corresponds a gamut vertex pair. We recommend to set α as a vector adaptively to the contents statistics¹ for preserving more saturation during CGM. Figure 5 shows the examples of the $\Omega _Z$ 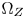defined at different luminance and overlapped by the CMC we obtained in Section III.

Fig. 5. Examples of the $\Omega _Z$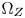 overlapped by CMC at different luminance layers (green: $\Omega _S$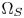, red: $\Omega _T$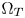, cyan: $\Omega _Z$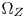, and “VTX” means vertex). (a) l=0.06. (b) l=0.415. (c) $l = 0.74$.

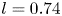Once $\Omega _Z$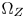 is determined, we extend the CMC, which are between the boundaries of $\Omega _S$ 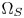and $\Omega _T$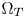, to the boundaries of $\Omega _Z$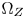. Such a CMC path consists of three points: (1) the start point on a boundary of $\Omega _S$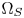, denoted s; (2) the inner point on the corresponding boundary of $\Omega _T$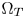, denoted t; and (3) the end point on the corresponding boundary of $\Omega _Z$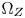, denoted z, and can be written as $\overline {stz}$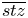. Note that the size of $\Omega _Z$ 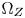should not be too small. First, a very small size $\Omega _Z$ 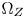may sacrifice too much saturation. Second, a very small size $\Omega _Z$ 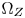will lead to bigger spaces between the boundaries of $\Omega _T$ 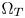and $\Omega _Z$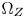. Since the real constant hue loci are non-linear, the big spaces may lead to relatively high linearization errors between the linearized CMC and the real constant hue loci. Our simulations show that controlling α of (3) in $[0.1, 0.4]$ 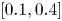can achieve good compromise between details protection and saturation preserving.

In practice, we need not update $\Omega _Z$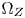 frequently. It can be either computed only one time at the stage of device initialization, or updated under the controls from the received ST.2094-40 metadata. For example, we may only update $\Omega _Z$ 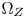when the statistics of contents has great changes. Since (3) only contains linear and simple operators, updating $\Omega _Z$ 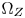is real-time and hardware friendly.

B) Constant hue loci estimation

Constant hue loci estimation for arbitrary out-of-$\Omega _Z$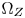 colors is crucial to correctly move the colors in the perceptual non-uniform CIE-xyY space without introducing visible hue distortions. In this section, we firstly introduce the conception of hue sector. In a given luminance layer, we define the polygon formed by two neighboring CMC paths and two corresponding boundaries of $\Omega _S$ 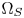and $\Omega _Z$ 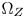as a hue sector. Figure 6 shows an example of the hue sector consisting of the CMC of hue 2.5G and 10G, and the boundary segments of $\Omega _S$ 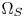and $\Omega _Z$ 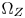between the two CMC paths in layer l = 0.06, i.e., $[s_1, z_1, z_2, s_2]$.

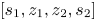Fig. 6. An example of the hue sectors and the estimated constant hue loci of an arbitrary color c at layer l=0.06.

To a given color c that is outside $\Omega _Z$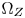, we firstly determine its hue sector. With the example shown in Fig. 6, assume that c is in the hue sector consisting of two neighboring CMC paths $\overline { s_1 t_1 z_1}$ 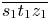and $\overline {s_2 t_2 z_2}$. We propose to estimate the constant hue locus of c from $\overline {s_1 z_1}$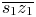 and $\overline {s_2 z_2}$ 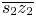with following two rules: (1) if c is on one of $\overline {s_1 z_1}$ 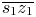and $\overline {s_2 z_2}$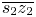, its constant hue locus is the CMC path; and (2) when c is between $\overline {s_1 z_1}$ 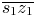and $\overline {s_2 z_2}$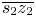, its constant hue locus should gradually change from $\overline {s_1 z_1}$ 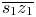to $\overline {s_2 z_2}$ 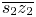depending on its position. According to the two rules, we propose an efficient but reliable anchor point-based strategy to estimate the constant hue locus that passes an arbitrary out-of-$\Omega _Z$ 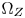color c. Let A be the intersection of $\overline {s_1 z_1}$ 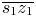and $\overline {s_2 z_2}$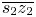, the vector from c to A, namely $\overrightarrow {cA}$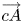, indicates the direction of the constant hue locus of c, and point A is thus called the anchor. The intersections of line $\overline {cA}$ 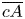and the corresponding boundaries of $\Omega _S$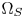, $\Omega _T$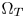, and $\Omega _Z$ 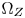form the constant hue locus of c, denoted $\overline {s_r t_r z_r}$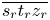. Figure 6 shows the details of this strategy.

C) Color moving along constant hue loci

The essential of the color-moving operator in the proposed algorithm is to compute an appropriate position, denoted $c'(x', y')$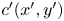, inside $\Omega _T$ 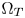for a given out-of-$\Omega _Z$ 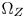color c on its constant hue locus $\overline {s_r t_r z_r}$ 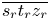(see Fig. 6). We propose to compute $c'$ 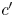by mapping $\overline {s_r z_r}$ 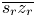to $\overline {t_r z_r}$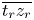, and keep the relative position of $c'$ 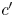on $\overline {t_r z_r}$ 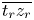unchanged as c is on $\overline {s_r z_r}$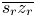. The relative position of c on $\overline {s_r z_r}$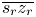, denoted γ, is defined as

(4)\begin{equation} \gamma = \frac{\vert \overline{c z_r}\vert }{\vert \overline{s_r z_r}\vert }. \end{equation}

To keep the γ unchanged after moving c to $c'$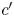 along its constant hue locus $\overline {s_r z_r}$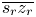, we have

(5)\begin{equation} \begin{cases} x' = x_{z_r} + \gamma ( x_{t_r} - x_{z_r} ) \\ y' = y_{z_r} + \gamma ( y_{t_r} - y_{z_r} ), \end{cases}\end{equation}

where $(x_{t_r}, y_{t_r})$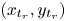 and $(x_{z_r}, y_{z_r})$ 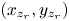are the coordinates of $t_r$ 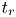and $z_r$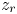, respectively (see the demonstration in Fig. 6).

In practice, due to the cost limits, the LUT only contains the CMC of few key luminance layers. An input color c may have no corresponding luminance layer in the LUT for directly carrying out color moving with (5). We propose a luminance-adaptive interpolation strategy to solve the problem. Let $Y_c$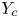 be the luminance of c. We firstly locate two available neighboring luminance layers, denoted $Y_L$ 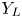and $Y_H$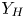, respectively, in the LUT, and $Y_L \le Y_c < Y_H$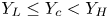. Thus the target colors of c in layers $Y_L$ 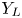and $Y_H$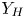, denoted $c'_L$ 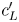and $c'_H$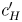, respectively, can be determined from (5). The output $c'$ 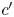is then interpolated as

(6)\begin{equation} \begin{cases} x' = x'_L + \beta ( x'_H - x'_L ) \\ y' = y'_L + \beta ( y'_H - y'_L ), \end{cases}\end{equation}

where $(x'_L, y'_L)$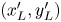 and $(x'_H, y'_H)$ 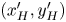are the coordinates of $c'_L$ 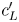and $c'_H$ 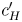in layers $Y_L$ 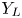and $Y_H$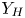, respectively; and

(7)\begin{equation} \beta = \frac{Y_c - Y_L}{Y_H - Y_L}. \end{equation}

As can be seen from (6) and (7), when $Y_c \approx Y_L$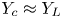, $\beta \approx 0$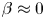, and $c'$ 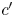is approximately equal to $c'_L$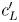; if $Y_c \approx Y_H$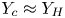, $\beta \approx 1$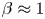, and $c'$ 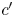is approximately equal to $c'_H$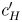. Otherwise, $c'$ 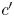smoothly varies along the cross-layer path $\overline {c'_L c'_H}$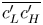. This guarantees the naturalness and smoothness of the obtained colors in $\Omega _T$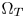. Also, as shown in (3)–(7), all computations in the proposed algorithm do not have complex computation such as exponential or Trigonometric operators. This is suitable for hardware implementations.

V. EXPERIMENTAL RESULTS

Two important CGM techniques, namely (1) the GC-based CGM method [14], which is the most popular method in commercial products, and (2) the recently published CAM-based Azimi CGM [10], which performs robustly to multiple WCG contents, are selected as the reference methods to evaluate the performance of the proposed algorithm. We also test the CGM technique proposed in [11]. However, it performs worse than the Azimi CGM, therefore we do not adopt it as a reference method. Section V-A introduces the test images and the experimental environment of our simulations. Section V-B describes the necessary parameters of the test algorithms. The CGM results comparisons and performance evaluations are given in Section V-C.

A) Test images and simulation environment

Considering the popularity of the Rec.2020 and the DCI-P3 gamut in HDR contents distribution eco-systems, we focus our tests on the CGM between the two gamuts. HDR contents creators may only adopt Rec.2020 as a color container, e.g., the DCI-P3 contents encapsulated in the Rec.2020 gamut. The contents are not suitable for testing CGM algorithms due to lack of the out-of-gamut colors. In this paper, we use the famous LUMA HDRV HDR contents database [19] as the test images. The contents are mastered in real Rec.2020 gamut for the purposes of HDR technique developing and testing, including tone-mapping, CGM, etc. Especially, the contents contain abundant details in the colors near the Rec.2020 gamut boundaries. This is very challenging to CGM algorithms. All the 14 videos containing over 14300 real Rec.2020 frames are tested in our simulations to comprehensively evaluate the proposed algorithm. Note that the test images we used in algorithm developing are independent of the test images of performance evaluations in this section.

All the test CGM algorithms are implemented with ${\rm C}/{\rm C}++$, and run on a 8-core 3.2M Hz CPU workstation with the Linux operation system. Experimental results are reviewed on a Samsung 9800 UHDTV under ${\rm HDR}+$ mode, which supports the PQ electronic-optical transform function (EOTF) [20].²

B) Parameters used in simulations

We adopt the Munsell Renotations published by The Munsell Science Laboratory of Rochester Institute of Technology³ to compute the CMC, and experimentally set α in (3) to $[0.3, 0.35, 0.3]$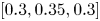 for the red, the green, and the blue vertices. Note that as luminance increases, the number of the gamut vertices changes too. The control factors of the new vertices can be interpolated from the three basic factors. Also, instead of directly saving all the coordinates of the CMC into the LUT, we pre-compute the direction vectors of the CMC (see Section III-B) at the quantized positions in the CIE-xyY space. Thus, we can estimate the constant hue loci of arbitrary out-of-$\Omega _Z$ 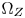colors from the direction vectors at quantized positions, and avoid going over all hue sectors for locating the hue sector of a given color. This further decreases the hardware costs and increases the efficiency. Our researches show that a $32 \times 32 \times 6$ 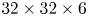LUT performs well in all simulations, where 32 is the number of the quantized positions along the x- and the y-axes, and 6 is the number of the sampled luminance layers.

Following the parameters given in [10], we set the inner gamut determining factor of the Azimi CGM to 0.5. The GC-CGM only need the Rec.2020 to DCI-P3 color-space conversion matrix.

C) Results analysis and performance evaluations

One of the basic requirements of a high-performance CGM method is that it should perform robustly to both of the contents where Rec.2020 is used as a color container and the real Rec.2020 contents. We firstly test the proposed and the reference algorithms with the DCI-P3 contents encapsulated in the Rec.2020 gamut. Color distribution analysis shows that in the LUMA data set, the colors of some scenes of video “Bistro”, “Fishing”, “Poker”, etc., are mostly inside DCI-P3 gamut. Figure 7 shows the comparisons of the three CGM methods with those contents.

Fig. 7. Examples of CGM comparison with DCI-P3 contents using Rec.2020 as a color container (from top to bottom: “Bistro”, “Fishing”, “Poker”, and “Show Girl”). (a) GC-CGM. (b) Azimi CGM. (c) Ours.

As shown in Fig. 7(a), the GC-CGM performs the best to the contents using the Rec.2020 as a color container, since few out-of-gamut colors exist in the contents. Both of the Azimi and the proposed methods perform similarly to the GC-CGM method, as shown in Figs 7(b) and 7(c), respectively. There is no significant visual difference in the results of the three methods. The tests show that both of the proposed and the Azimi methods are capable of replacing the GC-CGM method in the applications where DCI-P3 contents are encapsulated in the Rec.2020. However, the Azimi CGM is more expensive than the proposed method.

Video “Light Show” is with the real Rec.2020 gamut, and has abundant details in out-of-gamut colors. The three CGM methods perform very different to this video. Figure 8 shows the comparison examples.

Fig. 8. Examples of Rec.2020 to DCI-P3 CGM comparison with video ‘Light Show”. (a) GC-CGM. (b) Azimi CGM. (c) Ours.

As shown in Fig. 8(a), the GC-CGM performs poorly. It simply clips all out-of-gamut colors to the DCI-P3 gamut boundaries, thus loses many details and variations of the colors. This leads to serious banding artifacts and spots deficiency in the obtained colors. Also, without any constraint in color clipping, the method generates serious hue distortions. The Azimi method generates acceptable colors, and does not lead to high visual impacts, as shown in Fig. 8(b). However, the method loses too much saturation due to its relatively small inner gamut. Furthermore, the method moves colors toward the white point. This cannot guarantee that the moving paths follow constant hue loci, since the CIELCH space is not 100% perceptually uniform, especially, in the yellowish tones. As can be seen in Fig. 8(b), the method leads visible hue shifts in the yellow-green tones. The proposed method performs the best among the three methods. As shown in Fig. 8(c), it effectively protects both of the details and the saturation of the out-of-gamut colors in the mapped colors using the pre-defined color TPZ $\Omega _Z$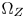. With the CMC obtained from the Munsell constant hue loci, the proposed method correctly estimates the constant hue loci of different colors, and obtains the natural and visually pleased outputs without introducing perceivable hue distortions. The proposed method is also very economic. It only adopts linear operators such as adding and multiplication in color moving. Thus, it is much cheaper than the CAM-based Azimi method.

The experimental results of video “Carousel” confirm the observations we got from video “Light Show”. The video has many out-of-gamut colors that are very close to or on the Rec.2020 gamut boundaries. Figure 9 shows the comparison examples of the three CGM methods.

Fig. 9. Examples of Rec.2020 to DCI-P3 CGM comparison with video ‘Carousel”. (a) GC-CGM. (b) Azimi CGM. (c) Ours.

As shown in Fig. 9(a), the GC-CGM gets serious banding artifacts in the resulted colors since it loses all natural color variations in out-of-gamut colors. It also over-saturates many colors in bright regions (see the bottom row, the light bulbs) due to clipping multiple colors into few even single color on the target gamut boundaries. The Azimi method, as shown in Fig. 9(b), outperforms the GC-CGM method, but it less-saturates the output colors. Also, it has slightly visible hue distortions since it always take the white point as the color-moving reference (see the middle row of Fig. 9(b)). The proposed algorithm performs well to the challenging contents. It is robust to both the bright and the dark colors, and obtains artifact-free, natural, and accurate output colors, as shown in Fig. 9(c).

Figure 10 shows the examples of the comparisons of the three CGM methods with video “Show Girl”. The GC-CGM performs the worst. It erases many smooth color transitions and details by mapping all out-of-gamut colors to the DCI-P3 gamut boundaries. The method also causes serious banding artifacts. The Azimi and the proposed methods perform similarly to each other in this test. They effectively preserve the natural variations of out-of-gamut colors. However, the Azimi method slightly less saturates the output colors, and loses some color smoothness. But it tends to preserve more details. The proposed method achieves a visually pleased compromise between saturation and details preserving, and it is much cheaper than the Azimi method.

Fig. 10. Examples of Rec.2020 to DCI-P3 CGM comparison with video ‘Show Girl”. (a) GC-CGM. (b) Azimi CGM. (c) Ours.

The experimental results obtained from the rest videos in the LUMA HDR database, including “Fire Place”, “Smith Welding”, “Smith Hammer”, etc., show the similar observations we have mentioned above. For the briefness of this paper, we will not list the results in this section. However, we notice that the Azimi method may preserve more details than the proposed and the GC-CAM methods in some scenes. Figure 11 shows the examples of such cases. As can be seen, the GC-CGM method loses details the most (Fig. 11(a)). The proposed algorithm effectively protects the details, but slightly decreases the contrast of the details (Fig. 11(c)). The Azimi method protects the details the best (Fig. 11(b)). This is because of its relatively small inner gamut. However, a small-size inner gamut usually leads to less-saturation issues, especially, the colors that are closed to or on the target gamut boundaries.

Fig. 11. Examples of the contrast comparison between the proposed and the reference CGM algorithms. (a) GC-CGM. (b) Azimi CGM. (c) Ours.

Generally speaking, the GC-CGM cannot satisfy the CGM tasks of mapping the real Rec.2020 colors to smaller gamuts such as the DCI-P3 gamut. It may seriously lose details and natural variations in out-of-gamut colors, and introduce serious hue distortions into the final outputs. The CAM-based Azimi method clearly outperforms the GC-CGM, and obtains the smoothest results among all the three algorithms, and it also well preserves the original details in its results. However, it cannot guarantee the perceptual hue fidelity in the output colors. Multiple hue shifting issues of the method are found in our simulations. The method is sensitive to its inner gamut size, and tends to less-saturate the resulted colors. The proposed algorithm generally performs the best in all the tests. By adopting the effective CMC of difference hues, the proposed method successfully avoids perceivable hue distortions; and with a content-adaptively defined color TPZ, it achieves a reasonable compromise between details protection and saturation preserving. Furthermore, the proposed algorithm does not have any complex computations, and it is much cheaper than the CAM-based CGM methods, including the reference Azimi method.

In all our simulations, the GC-CGM is the most efficient, followed by the proposed and the Azimi method. Table 1 shows the average relative efficiency comparisons of the three CGM algorithms, where the efficiency of the GC-CGM is regarded as 1. The lower the relative efficiency value is, the more efficient the CGM algorithm is. As can be seen from Table 1, the proposed algorithm is about fourtimes faster than the CAM-based Azimi method.

Table 1. Relative efficiency comparisons of the three CGM algorithms.

V. CONCLUSION

A real-time and content robust CGM algorithm is proposed for economic CGM in commercial applications such as UHDTV. By introducing a color TPZ inside the target gamut, and a set of perceptual hue fidelity constraints designed based on the Munsell constant hue loci in the color-moving operators, the proposed algorithm effectively preserves the perceptual hues and the natural variations of the original colors in CGM processing between a bigger source gamut and a smaller target gamut. Thus, reliable CGM can be directly carried out in the perceptually non-uniform CIE-1931 space. This greatly decreases the complexity of the GBD and simplifies color-moving computations, and significantly decreases the costs. Experimental results of the CGM between the Rec.2020 and the DCI-P3 gamut show that the proposed algorithm performs robustly to different HDR and WCG contents, and obtains natural and visually pleased colors without introducing any visible artifacts and hue distortions. Performance comparisons show that the proposed algorithm clearly outperforms the widely used GC-based CGM, and performs similarly or even better than the expensive CAM-based CGM. The proposed algorithm only adopts linear operators, and is much more economic than the CAM-based methods. One of the issues of the proposed algorithm is that it may slightly decrease the contrast of the delicate structures of out-of-gamut colors. We will further improve the proposed algorithm in our future works.

The proposed algorithm extends the SMPTE ST.2094-40 standard in color gamut transfer, and can be an important complement of the standard in theHDR and WCG contents distribution industries.