The general equations necessary for a basic theoretical interpretation of the physics of turbulence in ferrofluids are presented. The equations are examined and show multiple novel turbulence aspects that arise in ferrofluids. For example, two new modes of turbulent kinetic energy and turbulent kinetic energy dissipation rate occur, and unique modes of energy conversion (rotational to/from translational kinetic energy and magnetic energy to/from turbulent kinetic energy) are exhibited in turbulent ferrofluid flows. Furthermore, it is shown that potential models for turbulence in ferrofluids are complicated by additional closure requirements from the five additional nonlinear terms in the governing equations. The equations are applied to turbulence of a ferrofluid in the presence of a steady magnetic field (as well as the case of no magnetic field) in order to identify the importance of the new terms. Results are presented for the enhanced anisotropy in the presence of a magnetic field, and results show how turbulence properties (both classical ones and new ones) vary with the strength of the magnetic field. Three different equations for the magnetization are examined and lead to different results at large magnitudes of the applied magnetic field.

In this study, we investigate the stability of time-dependent zonal flows to two-dimensional (zonally symmetric) disturbances. While steady currents can only experience inertial instability (II) in this setting, unsteady ones may be destabilized in other ways. For example, time-periodic flows can be subject to parametric subharmonic instability (PSI). Motivated by observations of salinity interleaving patterns in the upper equatorial Pacific Ocean, our objective is to determine the basic properties of dominant instabilities (their generation mechanism, spatial and temporal characteristics, and finite-amplitude development) for background flows that are representative of those in the upper-equatorial ocean, yet still amenable to a computational sweep of parameter space. Our approach is to explore the stability of solutions to linear and nonlinear versions of a two-dimensional model for an idealized background flow with oscillating linear shear. To illustrate basic properties of the instabilities, the f-plane and equatorial β-plane scenarios are studied using a linear model. Stability regime diagrams show that on the f-plane there is a clear separation in dominant vertical scales between PSI- and II-dominated regimes, whereas on the equatorial β-plane the parameter space contains a region where dominant instability is a mixture of the two types. In general, PSI favours lower vertical modes than II. The finite-amplitude development of instabilities on the equatorial β-plane is explored using a nonlinear model, including cases illustrating the equilibration of pure II and the development of pure PSI and mixed instabilities. We find that unless the instabilities are weak enough to be equilibrated by viscosity at low amplitude, disturbances continue to grow until the vertical shear of their meridional velocity field becomes large enough to allow for Richardson numbers less than 1/4; as a consequence, PSI-favoured vertical modes are able to reach higher amplitudes than II-favoured modes before becoming susceptible to Kelvin–Helmholtz instability, and induce tracer intrusions of a considerably larger meridional extent.

Numerical simulations of the pulsating flow in a pipe of circular cross-section characterized by small imperfections are carried out to determine the conditions leading to the appearance of turbulence. The results show that in the oscillatory case (no steady velocity component of the basic flow), the critical value of the Reynolds number Rδ depends on the Womersley parameter α and, in particular, Rδ increases as α decreases. The critical value of Rδ of the plane wall case is recovered when α is larger than about 10. For moderate values of the Reynolds numbers but larger than the critical one, turbulence appears around flow reversal and breaks the symmetry of the flow, originating a steady velocity component. Moreover, turbulence is not present throughout the whole cycle and there are phases during which the flow relaminarizes. The presence of a steady pressure gradient tends to destabilize the flow and this destabilizing effect becomes larger as the steady velocity component is increased. When turbulence is present, its dynamics is similar to that of the steady case and a log-law layer can be identified both in the oscillatory and the pulsating case.

Gaseous detonation propagation in a bifurcated tube was experimentally and numerically studied for stoichiometric hydrogen and oxygen mixtures diluted with argon. Pressure detection, smoked foil recording and schlieren visualization were used in the experiments. Numerical simulation was carried out at low initial pressure (8.00kPa), based on the reactive Navier–Stokes equations in conjunction with a detailed chemical reaction model. The results show that the detonation wave is strongly disturbed by the wall geometry of the bifurcated tube and undergoes a successive process of attenuation, failure, re-initiation and the transition from regular reflection to Mach reflection. Detonation failure is attributed to the rarefaction waves from the left-hand corner by decoupling leading shock and reaction zones. Re-initiation is induced by the inert leading shock reflection on the right-hand wall in the vertical branch. The branched wall geometry has only a local effect on the detonation propagation. In the horizontal branch, the disturbed detonation wave recovers to a self-sustaining one earlier than that in the vertical branch. A critical case was found in the experiments where the disturbed detonation wave can be recovered to be self-sustaining downstream of the horizontal branch, but fails in the vertical branch, as the initial pressure drops to 2.00kPa. Numerical simulation also shows that complex vortex structures can be observed during detonation diffraction. The reflected shock breaks the vortices into pieces and its interaction with the unreacted recirculation region induces an embedded jet. In the vertical branch, owing to the strength difference at any point and the effect of chemical reactions, the Mach stem cannot be approximated as an arc. This is different from the case in non-reactive steady flow. Generally, numerical simulation qualitatively reproduces detonation attenuation, failure, re-initiation and the transition from regular reflection to Mach reflection observed in experiments.

We report high drag reduction in direct numerical simulations of controlled flows past circular cylinders at Reynolds numbers of 300 and 1000. The flow is controlled by the azimuthal component of the tangential velocity of the cylinder surface. Starting from a spanwise-uniform velocity profile that leads to high drag reduction, the optimization procedure identifies, for the same energy input, spanwise-varying velocity profiles that lead to higher drag reduction. The three-dimensional variations of the velocity field, corresponding to modes A and B of three-dimensional wake instabilities, are largely responsible for this drag reduction. The spanwise wall velocity variations introduce streamwise vortex braids in the wake that are responsible for reducing the drag induced by the primary spanwise vortices shed by the cylinder. The results demonstrate that extending two-dimensional controllers to three-dimensional flows is not optimal as three-dimensional control strategies can lead efficiently to higher drag reduction.

The hydrodynamics of the dense granular flow of rough inelastic particles down an inclined plane is analysed using constitutive relations derived from kinetic theory. The basic equations are the momentum and energy conservation equations, and the granular energy conservation equation contains a term which represents the dissipation of energy due to inelastic collisions. A fundamental length scale in the flow is the ‘conduction length’ δ=(d/(1-en)1/2), which is the length over which the rate of conduction of energy is comparable to the rate of dissipation. Here, d is the particle diameter and en is the normal coefficient of restitution. For a thick granular layer with height h ≫ δ, the flow in the bulk is analysed using an asymptotic analysis in the small parameter δ/h. In the leading approximation, the rate of conduction of energy is small compared to the rates of production and dissipation, and there is a balance between the rate of production due to mean shear and the rate of dissipation due to inelastic collisions. A direct consequence of this is that the volume fraction in the bulk is a constant in the leading approximation. The first correction due to the conduction of energy is determined using asymptotic analysis, and is found to be O(δ/h)2 smaller than the leading-order volume fraction. The numerical value of this correction is found to be negligible for systems of practical interest, resulting in a lack of variation of volume fraction with height in the bulk.

The flow in the ‘conduction boundary layers’ of thickness comparable to the conduction length at the bottom and top is analysed. Asymptotic analysis is used to simplify the governing equations to a second-order differential equation in the scaled cross-stream coordinate, and the resulting equation has the form of a diffusion equation. However, depending on the parameters in the constitutive model, it is found that the diffusion coefficient could be positive or negative. Domains in the parameter space where the diffusion coefficients are positive and negative are identified, and analytical solutions for the boundary layer equations, subject to appropriate boundary conditions, are obtained when the diffusion coefficient is positive. There is no boundary layer solution that matches the solution in the bulk for parameter regions where the diffusion coefficient is negative, indicating that a steady solution does not exist. An analytical result is derived showing that a boundary layer solution exists (diffusion coefficient is positive) if, and only if, the numerical values of the viscometric coefficients are such that volume fraction in the bulk decreases as the angle of inclination increases. If the numerical values of the viscometric coefficients are such that the volume fraction in the bulk increases as the angle of inclination increases, a boundary layer solution does not exist.

The results are extended to dense flows in thin layers using asymptotic analysis. Use is made of the fact that the pair distribution function is numerically large for dense flows, and the inverse of the pair distribution function is used as a small parameter. This approximation results in a nonlinear second-order differential equation for the pair distribution function, which is solved subject to boundary conditions. For a dissipative base, it is found that a flowing solution exists only when the height is larger than a critical value, whereas the temperature decreases to zero and the flow stops when the height becomes smaller than this critical value. This is because the dissipation at the base becomes a larger fraction of the total dissipation as the height is decreased, and there is a minimum height below which the rate of production due to shear is not sufficient to compensate for the rate of dissipation at the base. The scaling of the minimum height with dissipation in the base, the bulk volume fraction and the parameters in the constitutive relations are determined. From this, the variation of the minimum height on the angle of inclination is obtained, and this is found to be in qualitative agreement with previous experiments and simulations.

We have numerically investigated the interaction dynamics between two rigid spherical particles moving in a fluid-filled cylinder that is rotating at a constant speed. The cylinder rotation is about a horizontal axis. The particle densities are less than that of the fluid. The numerical procedure employed to solve the mathematical formulation is based on a three-dimensional arbitrary Larangian–Eulerian (ALE), moving mesh finite-element technique, described in a frame of reference rotating with the cylinder. Results are obtained in the ranges of particle Reynolds number, 1 <Rep≤60, and shear Reynolds number, 1≤Res<10. Two identical particles, depending on initial conditions at release, approach each other (‘drafting’ and ‘kissing’), tumble in the axial direction, and axially migrate towards opposing transverse planes on which they ‘settle’ (settling planes). Under some other initial conditions, the particles migrate directly onto their settling planes. For two identical particles, the settling planes are equidistant from the mid-transverse plane of the cylinder and the locations of the planes are determined by particle–particle and particle–wall force balances. Furthermore, for identical particles and given values of Rep and Res, the locations of such settling planes remain the same, independent of the initial conditions at release. While located on these settling planes, as viewed in an inertial frame, the particles may attain three possible distinct states depending on the values of the Reynolds numbers. In one state (low Rep, high Res), the particles attain and remain at fixed equilibrium points on their settling planes. In the second (all Rep, low Res), they execute spiralling motions about fixed points on their respective settling planes. These fixed points coincide with the locations of the equilibrium point which would occur on the mid-axial plane in the case of a single particle. In the third state (low Rep, moderate Res or high Rep, moderate to high Res), they execute near-circular orbital motion on their respective settling planes, again about fixed points. These fixed points also coincide with the locations of the equilibrium points corresponding to single-particle dynamics. Both the spiral and near-circular motions of the particles occur in an out-of-phase manner with regard to their radial positions about the fixed point; the near-circular out-of-phase motion resembles bicycle pedalling. Also, in the second and third states, the particles simultaneously experience very weak axial oscillations about their settling planes, the frequency of such oscillations coinciding with the frequency of rotation of the circular cylinder.

The behaviours of two non-identical particles (same density but different sizes, or same size but different densities) are different from those of identical particles. For example, non-identical particles may both end up settling on the mid-axial plane. This occurs when the locations of their corresponding single-particle equilibrium points are far apart. When such points are not far apart, particles may settle on planes that may not be symmetrical about the mid-axial plane. While located on their settling planes, their equilibrium states may not be similar. For example, for particles of the same density but of different sizes, the smaller of the two may execute a spiralling motion while the larger is in near-circular orbital motion. With particles of the same size but of different densities, while the lighter of the two approaches its equilibrium point on the mid-axial plane, the heavier one experiences a circular motion on the same plane about its equilibrium point. A major reason for the eventual attainment of these various states is noted to be the interplay between the particle–particle and particle–wall forces.

In this paper we present results on parametrically forced gravity waves in a circular cylinder in the limit of large fluid-depth approximation. The phase diagram that shows the stability-forcing-amplitude threshold and the wave-breaking threshold has been determined in the frequency range of existence of the lowest axisymmetric wave mode. The instability is shown to be supercritical for forcing frequencies at and above the natural frequency and subcritical below in a frequency range where the instability and breaking thresholds do not coincide. Above the instability threshold, the growth in wave amplitude is exponential, but with an initial time delay. The wave-amplitude response curve of stationary wave motions exhibits steady-state wave motion, amplitude modulations and bifurcations to other wave modes at frequencies where the parametric instability boundary of the axisymmetric mode overlaps with the neighbouring modes. The amplitude modulations are either on a slow time scale or exhibit period tripling and intermittent period tripling, without wave breaking. In the wave-breaking regime, a finite-time singularity may occur with intense jet formation, a phenomenon demonstrated by others in fluids of high viscosity and large surface tension. Here, this singular behaviour with jet formation is demonstrated for a low viscosity and low kinematic surface tension liquid. The results indicate that the jet is driven by inertial collapse of the cavity created at the wave trough. Therefore, the jet velocity is determined by the wave fluid velocity but depends, in addition, on kinematic surface tension and viscosity as these affect the last stable wave crest shape and the cavity size.

We present high-resolution direct numerical simulations of the nonlinear evolution of a pair of counter-rotating vertical vortices in a stratified fluid for various high Reynolds numbers Re and low Froude numbers Fh. The vortices are bent by the zigzag instability producing high vertical shear. There is no nonlinear saturation so that the exponential growth is stopped only when the viscous dissipation by vertical shear is of the same order as the horizontal transport, i.e. when /Re=O(1) where is the maximum horizontal enstrophy non-dimensionalized by the vortex turnover frequency. The zigzag instability therefore directly transfers the energy from large scales to the small dissipative vertical scales. However, for high Reynolds number, the vertical shear created by the zigzag instability is so intense that the minimum local Richardson number Ri decreases below a threshold of around 1/4 and small-scale Kelvin–Helmholtz instabilities develop. 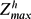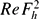We show that this can only occur when is above a threshold estimated as 340. Movies are available with the online version of the paper.

The evolution of an unstable baroclinic jet, subject to a small perturbation, is examined numerically in a quasi-geostrophic two-layer β-channel model. After a period of initial wave growth, wave breaking leads to turbulence within each layer, and to the eventual equilibration of the flow. The equilibrated flow must satisfy certain dynamical constraints: total momentum is conserved, the total energy is bounded and the flow must be realizable via some area-preserving (diffusive) rearrangement of the initial potential vorticity field in each layer. A theory is introduced that predicts the equilibrated flow in terms of the initial flow parameters. The idea is that the equilibrated state minimizes available potential energy, subject to the constraints on total momentum and total energy, and the further ‘kinematic’ constraint that the potential vorticity changes through a process of complete homogenization within well-delineated regions in each layer. Within a large region of parameter space, the theory accurately predicts the cross-channel structure and strength of the equilibrated jet, the regions where potential vorticity mixing takes place, and total eddy mass (temperature) fluxes. Results are compared with predictions from a maximum-entropy theory that allows for more general rearrangements of the initial potential vorticity field, subject to the known dynamical constraints. The maximum-entropy theory predicts that significantly more available potential energy is released than is observed in the simulations, and that an unphysical ‘exchange’ of bands of fluid will occur across the channel in the lower layer. The kinematic constraint of piecewise potential vorticity homogenization is therefore important in limiting the ‘efficiency’ of release of available potential energy in unstable baroclinic flows. For a typical initial flow, it is demonstrated that if the dynamical constraints alone are considered, then over twice as much potential energy is available for release compared to that actually released in the simulations.

Temporal and spatio-temporal instabilities of binary liquid films flowing down an inclined uniformly heated plate with Soret effect are investigated by using the Chebyshev collocation method to solve the full system of linear stability equations. Seven dimensionless parameters, i.e. the Kapitza, Galileo, Prandtl, Lewis, Soret, Marangoni, and Biot numbers (Ka, G, Pr, L, χ, M, B), as well as the inclination angle (β) are used to control the flow system. In the case of pure spanwise perturbations, thermocapillary S- and P-modes are obtained. It is found that the most dangerous modes are stationary for positive Soret numbers (χ≥0), and oscillatory for χ<0. Moreover, the P-mode which is short-wave unstable for χ=0 remains so for χ<0, but becomes long-wave unstable for χ>0 and even merges with the long-wave S-mode. In the case of streamwise perturbations, a long-wave surface mode (H-mode) is also obtained. From the neutral curves, it is found that larger Soret numbers make the film flow more unstable as do larger Marangoni numbers. The increase of these parameters leads to the merging of the long-wave H- and S-modes, making the situation long-wave unstable for any Galileo number. It also strongly influences the short-wave P-mode which becomes the most critical for large enough Galileo numbers. Furthermore, from the boundary curves between absolute and convective instabilities (AI/CI) calculated for both the long-wave instability (S- and H-modes) and the short-wave instability (P-mode), it is shown that for small Galileo numbers the AI/CI boundary curves are determined by the long-wave instability, while for large Galileo numbers they are determined by the short-wave instability.

The potential flow upstream from a contraction in a rectangular flume is analysed. In order to calculate the potential function, the flow is considered as the superposition of sinks uniformly distributed in the contraction. The effect of boundaries is taken into account by introducing virtual sinks. The calculation is performed in the complex plane and provides a closed-form solution of the complex potential function. As an illustration, the effect of contraction size and position is analysed, and the solution is compared to experimental measurements and other numerical solutions for vertical sluice gates.

Direct numerical simulations are performed to investigate the three-dimensional stability of compressible flow over open cavities. A linear stability analysis is conducted to search for three-dimensional global instabilities of the two-dimensional mean flow for cavities that are homogeneous in the spanwise direction. The presence of such instabilities is reported for a range of flow conditions and cavity aspect ratios. For cavities of aspect ratio (length to depth) of 2 and 4, the three-dimensional mode has a spanwise wavelength of approximately one cavity depth and oscillates with a frequency about one order of magnitude lower than two-dimensional Rossiter (flow/acoustics) instabilities. A steady mode of smaller spanwise wavelength is also identified for square cavities. The linear results indicate that the instability is hydrodynamic (rather than acoustic) in nature and arises from a generic centrifugal instability mechanism associated with the mean recirculating vortical flow in the downstream part of the cavity. These three-dimensional instabilities are related to centrifugal instabilities previously reported in flows over backward-facing steps, lid-driven cavity flows and Couette flows. Results from three-dimensional simulations of the nonlinear compressible Navier–Stokes equations are also reported. The formation of oscillating (and, in some cases, steady) spanwise structures is observed inside the cavity. The spanwise wavelength and oscillation frequency of these structures agree with the linear analysis predictions. When present, the shear-layer (Rossiter) oscillations experience a low-frequency modulation that arises from nonlinear interactions with the three-dimensional mode. The results are consistent with observations of low-frequency modulations and spanwise structures in previous experimental and numerical studies on open cavity flows.

We investigate the critical conditions for the onset of motion of a three-dimensional droplet on a wall in shear flows at moderate Reynolds number. A diffuse-interface method is used for this purpose, which also circumvents the stress singularity at the moving contact line, and the method allows for a density and viscosity contrast between the fluids. Contact-angle hysteresis is represented by the prescription of a receding contact angle θR and an advancing contact angle value θA. Critical conditions are determined by tracking the motion and deformation of a droplet (initially a spherical cap with a uniform contact angle θ0). At sufficiently low values of a Weber number, We (based on the applied shear rate and the drop volume), the drop deforms and translates for some time, but subsequently reaches a stationary position and attains a steady-state shape. At sufficiently large values of We no such steady state is found. We present results for the critical value of We as a function of Reynolds number Re for cases with the initial value of the contact angle θ0=θR as well as for θ0=θA. A scaling argument based on a force balance on the drop is shown to represent the results very accurately. Results are also presented for the static shape, transient motion and flow structure at criticality. It is shown that at low Re our results agree (with some qualifications) with those of Dimitrakopoulos & Higdon (1998, J. Fluid Mech. vol. 377, p. 189). Overall, the results indicate that the critical value of We is affected significantly by inertial effects at moderate Reynolds numbers, whereas the steady shape of droplets still shows some resemblance to that obtained previously for creeping flow conditions. The paper concludes with an investigation into the complex structure of a steady wake behind the droplet and the occurrence of a stagnation point at the upstream side of the droplet.

In the vapour phase and close to the liquid–vapour saturation curve, fluids made of complex molecules are expected to exhibit a thermodynamic region in which the fundamental derivative of gasdynamic Γ is negative. In this region, non-classical gasdynamic phenomena such as rarefaction shock waves are physically admissible, namely they obey the second law of thermodynamics and fulfil the speed-orienting condition for mechanical stability. Previous studies have demonstrated that the thermodynamic states for which rarefaction shock waves are admissible are however not limited to the Γ<0 region. In this paper, the conditions for admissibility of rarefaction shocks are investigated. This results in the definition of a new thermodynamic region – the rarefaction shocks region – which embeds the Γ<0 region. The rarefaction shocks region is bounded by the saturation curve and by the locus of the states connecting double-sonic rarefaction shocks, i.e. shock waves in which both the pre-shock and post-shock states are sonic. Only one double-sonic shock is shown to be admissible along a given isentrope, therefore the double-sonic states can be connected by a single curve in the volume–pressure plane. This curve is named the double sonic locus. The influence of molecular complexity on the shape and size of the rarefaction shocks region is also illustrated by using the van der Waals model; these results are confirmed by very accurate multi-parameter thermodynamic models applied to siloxane fluids and are therefore of practical importance in experiments aimed at proving the existence of rarefaction shock waves in the single-phase vapour region as well as in future industrial applications operating in the non-classical regime.

Sheet-like thermal plumes are investigated using time-dependent and three-dimensional flow fields obtained from direct numerical simulations and well-resolved large-eddy simulations of turbulent Rayleigh–Bénard convection in water (Prandtl number Pr=5.4) in a cylindrical container with the aspect ratio Γ=1 and for the Rayleigh numbers Ra=2×109 and 2×1010.

To analyse quantitatively the physical properties of the sheet-like thermal plumes and the turbulent background and to obtain the temperature threshold which separates these two different flow regions, the temperature dependences of the conditionally averaged local heat flux, thermal dissipation rate and selected components of the velocity and vorticity fields are studied. It is shown that the sheet-like plumes are characterized by high values of the local heat flux and relatively large absolute values of the vertical components of the vorticity and velocity fields. The borders of these plumes are indicated by large values of the thermal dissipation rate and large absolute values of the horizontal vorticity components. In contrast to the sheet-like thermal plumes, the turbulent background is characterized by low values of the thermal dissipation rate, local heat flux and vertical vorticity component. The highest values of the local heat flux and the highest absolute values of the vertical vorticity component are found in the regions where the sheet-like plumes strike against each other. Fluid swirling at these places forms the stems of the mushroom-like thermal plumes which develop in the bulk of the Rayleigh–Bénard cell.

Further, formulae to calculate the curvature, thickness and length of the plumes are introduced. Geometrical properties such as plume area, diameter, curvature, thickness and aspect ratio together with the physical properties of the sheet-like plumes such as temperature, heat flux, thermal dissipation rate, velocity and vorticity are investigated.

In this paper, we report experimental and theoretical results on the flow inside a precessing and rotating cylinder. Particle image velocimetry measurements have revealed the instantaneous structure of the flow and confirmed that it is the sum of forced inertial (Kelvin) modes, as predicted by the classical linear inviscid theory. But this theory predicts also that the amplitude of a mode diverges when its natural frequency equals the precession frequency. A viscous and weakly nonlinear theory has therefore been developed at the resonance. This theory has been compared to experimental results and shows a good quantitative agreement. For low Reynolds numbers, the mode amplitude scales as the square root of the Reynolds number owing to the presence of Ekman layers on the cylinder walls. When the Reynolds number is increased, the amplitude saturates at a value which scales as the precession angle to the power one-third for a given resonance. The nonlinear theory also predicts the forcing of a geostrophic (axisymmetric) mode which has been observed and measured in the experiments. These results allow the flow inside a precessing cylinder to be fully characterized in all regimes as long as there is no instability.

Vortex breakdown is a phenomenon inherent to many practical problems, such as leading-edge vortices on aircraft, atmospheric tornadoes, and flame-holders in combustion devices. The breakdown of these vortices is associated with the stagnation of the axial velocity on the vortex axis and the development of a near-axis recirculation zone. For large enough Reynolds number, the breakdown can be time-dependent. The unsteadiness can have serious consequences in some applications, such as tail-buffeting in aircraft flying at high angles of attack. There has been much interest in controlling the vortex breakdown phenomenon, but most efforts have focused on either shifting the threshold for the onset of steady breakdown or altering the spatial location of the recirculation zone. There has been much less attention paid to the problem of controlling unsteady vortex breakdown. Here we present results from a combined experimental and numerical investigation of vortex breakdown in an enclosed cylinder in which low-amplitude modulations of the rotating endwall that sets up the vortex are used as an open-loop control. As expected, for very low amplitudes of the modulation, variation of the modulation frequency reveals typical resonance tongues and frequency locking, so that the open-loop control allows us to drive the unsteady vortex breakdown to a prescribed periodicity within the resonance regions. For modulation amplitudes above a critical level that depends on the modulation frequency (but still very low), the result is a periodic state synchronous with the forcing frequency over an extensive range of forcing frequencies. Of particular interest is the spatial form of this forced periodic state: for modulation frequencies less than about twice the natural frequency of the unsteady breakdown, the oscillations of the near-axis recirculation zone are amplified, whereas for modulation frequencies larger than about twice the natural frequency the oscillations of the recirculation zone are quenched, and the near-axis flow is driven to the steady axisymmetric state. Movies are available with the online version of the paper.

We report on a series of experiments in which a Hele-Shaw cell containing aqueous solutions of NH4Cl was translated at prescribed rates through a steady temperature gradient. The salt formed the primary solid phase of a mushy layer as the solution solidified, with the salt-depleted residual fluid driving buoyancy-driven convection and the development of chimneys in the mushy layer. Depending on the operating conditions, several morphological transitions occurred. A regime diagram is presented quantifying these transitions as a function of freezing rate and the initial concentration of the solution. In general, for a given concentration, increasing the freezing rate caused the steady-state system to change from a convecting mushy layer with chimneys to a non-convecting mushy layer below a relatively quiescent liquid, and then to a much thinner mushy layer separated from the liquid by a region of active secondary nucleation. At higher initial concentrations the second of these states did not occur. At lower concentrations, but still above the eutectic, the mushy layer disappeared. A simple mathematical model of the system is developed which compares well with the experimental measurements of the intermediate, non-convecting state and serves as a benchmark against which to understand some of the effects of convection. Movies are available with the online version of the paper.