Let there be assigned to any term its symbolic number, to be used in calculation as the term itself is used in reasoning.
Leibniz (1679), p. 171 Introduction
According to the prevalent philosophical interpretation of Gödel’s Second Theorem, a sufficiently adequate and consistent theory T does not prove its consistency. Upon further examination however, it is not entirely clear how to justify this informal reading, as the formulation of the underlying mathematical theorem depends on several arbitrary implementation choices. Visser (Reference Visser2011) for instance locates three sources of indeterminacy in the formalisation of the consistency statement for a theory T:
-
I. the choice of a proof system;
-
II. the choice of a Gödel numbering;
-
III. the choice of a specific formula representing the axiom set of T.
By affirming the theorem’s prevalent interpretation we (implicitly) rely on its invariance regarding these formalisation choices. That is, we believe that any admissible choice yields a formal consistency sentence which is unprovable in T.
This belief is only partially supported by metamathematical results. While employing fixed choices for (I) and (II), Feferman (Reference Feferman1960) provides the invariance of Gödel’s theorem with respect to (III), i.e., regarding a certain class of formulæ which represent T’s axioms. Visser’s (2011) approach rests on fixed choices for (II) and (III) but is independent of (I). The aim of the present paper is to examine the theorem’s dependency regarding (II), which to the best of my knowledge has hitherto not been treated in the literature.
I follow the popular custom of basing the notion of provability on Löb’s conditions. It is widely believed that these conditions are already sufficient to derive the unprovability of the resulting consistency sentences. This is however not the case, as I will show in this paper, since Gödel’s theorem based on Löb’s conditions in fact depends on the underlying numbering. Consider for instance a numbering which assigns even numbers to theorems and odd numbers to all other expressions of a given language. The formula
![]() $\exists y \ x = \overline {2} \times y$
then serves as a binumeration of the codes of theorems, which in addition satisfies Löb’s conditions. However, the resulting consistency sentence is provable.
$\exists y \ x = \overline {2} \times y$
then serves as a binumeration of the codes of theorems, which in addition satisfies Löb’s conditions. However, the resulting consistency sentence is provable.
A similar construction shows that the set of true sentences is arithmetically definable, once such deviant numberings are employed. Thus also the prevalent interpretation of Tarski’s Theorem relies on a more careful choice of the underlying Gödel numbering.
I argue that these “counterexamples” do not threaten these theorems’ prevalent interpretations, since the employed numberings are inadmissible choices in the formalisation process. In fact, I show that once natural classes of admissible numberings are singled out, invariance of these theorems holds.
This work can be seen to provide further justification to the prevalent philosophical readings of these limitative results as sketched above. For instance, Detlefsen (Reference Detlefsen1986) famously argues that only once every sentence expressing T-consistency is shown to be unprovable in T, the prevalent philosophical reading of Gödel’s Second Theorem can be maintained. Under the assumption that Löb’s conditions are necessary for a formula to express T-provability,Footnote 1 the result obtained in this paper serves as a further step towards this goal. Namely, it establishes that no matter which admissible numbering is employed in the formulation of Löb’s conditions, every formula expressing T-provability results in a consistency sentence which is not provable in T. A fully satisfactory account along these lines clearly also requires consideration of other aspects of formalisation not treated here, such as the different ways consistency sentences are constructed from formulæ expressing provability.Footnote 2
The plan of this paper is as follows. §2 provides an introduction to the popular version of Gödel’s Second Theorem based on Löb’s conditions as well as “counterexamples” thereof which are based on deviant numberings. I discuss the notion of a numbering’s admissibility in §3, where I argue that computability is a necessary condition for the admissibility of a numbering. A precise and robust notion of computability then allows for a (meta-)mathematical restatement of the claim that Gödel’s theorem is invariant regarding admissible numberings, which is proved in §4. Finally, §5 contains some concluding remarks.
2 Dependency results
2.1 Technical preliminaries
Let the language
![]() $\mathcal {L}$
be given by the signature
$\mathcal {L}$
be given by the signature
![]() $\sigma (\mathcal {L}) = \{ ` \mathsf {0} \text{'} , ` \mathsf {S} \text{'} , ` + \text{'} , ` \times \text{'} , ` = \text{'} , ` \neg \text{'} , ` \wedge \text{'} , ` \forall \text{'} \}$
. Consider the alphabet A which consists of
$\sigma (\mathcal {L}) = \{ ` \mathsf {0} \text{'} , ` \mathsf {S} \text{'} , ` + \text{'} , ` \times \text{'} , ` = \text{'} , ` \neg \text{'} , ` \wedge \text{'} , ` \forall \text{'} \}$
. Consider the alphabet A which consists of
![]() $\sigma (\mathcal {L})$
together with the symbols
$\sigma (\mathcal {L})$
together with the symbols
![]() $` \mathsf {v} \text{'} $
,
$` \mathsf {v} \text{'} $
,
![]() $` \prime \text{'} $
,
$` \prime \text{'} $
,
![]() $` ( \text{'} $
and
$` ( \text{'} $
and
![]() $` ) \text{'} $
. Let
$` ) \text{'} $
. Let
![]() $A^\ast $
denote the set of finite strings over A (without the empty string), and let
$A^\ast $
denote the set of finite strings over A (without the empty string), and let
![]() $\ast $
and
$\ast $
and
![]() $\equiv $
denote the concatenation operation and the equality relation on
$\equiv $
denote the concatenation operation and the equality relation on
![]() $A^\ast $
respectively. For better readability, we often omit the use of quotation symbols and the concatenaton operation. For instance, for
$A^\ast $
respectively. For better readability, we often omit the use of quotation symbols and the concatenaton operation. For instance, for
![]() $s,t \in A^\ast $
we write
$s,t \in A^\ast $
we write
![]() $s \prime $
instead of
$s \prime $
instead of
![]() $s \ast ` \prime \text{'} $
and
$s \ast ` \prime \text{'} $
and
![]() $(\mathsf {S} t)$
instead of
$(\mathsf {S} t)$
instead of
![]() $ ` (\mathsf {S} \text{'} \ast t \ast ` ) \text{'} $
, etc. We take an
$ ` (\mathsf {S} \text{'} \ast t \ast ` ) \text{'} $
, etc. We take an
![]() $\mathcal {L}$
-expression to be any element of
$\mathcal {L}$
-expression to be any element of
![]() $A^\ast $
. The set
$A^\ast $
. The set
![]() $\mathit {Var}$
of
$\mathit {Var}$
of
![]() $\mathcal {L}$
-variables is generated from
$\mathcal {L}$
-variables is generated from
![]() $\mathsf {v}$
by appending a finite number of strokes. The sets
$\mathsf {v}$
by appending a finite number of strokes. The sets
![]() $\mathit {Term}, \mathit {Fml} \subseteq A^\ast $
contain the well-formed
$\mathit {Term}, \mathit {Fml} \subseteq A^\ast $
contain the well-formed
![]() $\mathcal {L}$
-terms and
$\mathcal {L}$
-terms and
![]() $\mathcal {L}$
-formulæ given in infix notation respectively.Footnote
3
Any used symbol not contained in
$\mathcal {L}$
-formulæ given in infix notation respectively.Footnote
3
Any used symbol not contained in
![]() $\mathcal {L}$
is to be understood as the usual abbreviation by symbols of
$\mathcal {L}$
is to be understood as the usual abbreviation by symbols of
![]() $\mathcal {L}$
. For instance, we define
$\mathcal {L}$
. For instance, we define
![]() $x \leq y \equiv \exists z \ z + x = y$
, where
$x \leq y \equiv \exists z \ z + x = y$
, where
![]() $x,y,z \in \mathit {Var}$
and
$x,y,z \in \mathit {Var}$
and
![]() $\exists $
is defined by means of
$\exists $
is defined by means of
![]() $\forall $
and
$\forall $
and
![]() $\neg $
as usual. Since the language
$\neg $
as usual. Since the language
![]() $\mathcal {L}$
is fixed, expressions, terms, formulæ and sentences are throughout the paper implicitly assumed to belong to
$\mathcal {L}$
is fixed, expressions, terms, formulæ and sentences are throughout the paper implicitly assumed to belong to
![]() $\mathcal {L}$
. For the sake of brevity, we sometimes use the symbols
$\mathcal {L}$
. For the sake of brevity, we sometimes use the symbols
![]() ${\Rightarrow }$
,
${\Rightarrow }$
,
![]() ,
, ![]() and
and
![]() ${{\exists\kern-0.45em\exists }}$
as abbreviations of the meta-theoretical connectives “implies”, “and”, “for all” and “there is” respectively.
${{\exists\kern-0.45em\exists }}$
as abbreviations of the meta-theoretical connectives “implies”, “and”, “for all” and “there is” respectively.
Corresponding to their alphabetical expressions, the following “constructor” operations on strings play an important role throughout this paper:
 $$ \begin{align*} \underline{\prime} & \colon \mathit{Var} \to \mathit{Var}, \text{ given by } x \mapsto x \prime ;\\ \underline{\mathsf{S}} & \colon \mathit{Term} \to \mathit{Term}, \text{ given by } t \mapsto (\mathsf{S} t);\\ \underline{+} & \colon \mathit{Term} \times \mathit{Term} \to \mathit{Term}, \text{ given by } (s,t) \mapsto (s + t);\\ \underline{\times} & \colon \mathit{Term} \times \mathit{Term} \to \mathit{Term}, \text{ given by } (s,t) \mapsto (s \times t);\\ \underline{=} & \colon \mathit{Term} \times \mathit{Term} \to \mathit{Fml}, \text{ given by } (s,t) \mapsto (s = t);\\ \underline{\neg} & \colon \mathit{Fml} \to \mathit{Fml}, \text{ given by } \varphi \mapsto (\neg \varphi);\\ \underline{\wedge} & \colon \mathit{Fml} \times \mathit{Fml} \to \mathit{Fml}, \text{ given by } (\varphi,\psi) \mapsto (\varphi \wedge \psi);\\ \underline{\forall} & \colon \mathit{Var} \times \mathit{Fml} \to \mathit{Fml}, \text{ given by } (x,\varphi) \mapsto ( \forall x \varphi ). \end{align*} $$
$$ \begin{align*} \underline{\prime} & \colon \mathit{Var} \to \mathit{Var}, \text{ given by } x \mapsto x \prime ;\\ \underline{\mathsf{S}} & \colon \mathit{Term} \to \mathit{Term}, \text{ given by } t \mapsto (\mathsf{S} t);\\ \underline{+} & \colon \mathit{Term} \times \mathit{Term} \to \mathit{Term}, \text{ given by } (s,t) \mapsto (s + t);\\ \underline{\times} & \colon \mathit{Term} \times \mathit{Term} \to \mathit{Term}, \text{ given by } (s,t) \mapsto (s \times t);\\ \underline{=} & \colon \mathit{Term} \times \mathit{Term} \to \mathit{Fml}, \text{ given by } (s,t) \mapsto (s = t);\\ \underline{\neg} & \colon \mathit{Fml} \to \mathit{Fml}, \text{ given by } \varphi \mapsto (\neg \varphi);\\ \underline{\wedge} & \colon \mathit{Fml} \times \mathit{Fml} \to \mathit{Fml}, \text{ given by } (\varphi,\psi) \mapsto (\varphi \wedge \psi);\\ \underline{\forall} & \colon \mathit{Var} \times \mathit{Fml} \to \mathit{Fml}, \text{ given by } (x,\varphi) \mapsto ( \forall x \varphi ). \end{align*} $$
By slight abuse of notation, both the standard interpretation of
![]() $\mathcal {L}$
and its domain is denoted by
$\mathcal {L}$
and its domain is denoted by
![]() $\mathbb {N}$
. As usual,
$\mathbb {N}$
. As usual,
![]() $\overline {n}$
denotes the (standard) numeral of the number n. Let
$\overline {n}$
denotes the (standard) numeral of the number n. Let
![]() $\varphi $
be an expression and let
$\varphi $
be an expression and let
![]() $\alpha $
be a numbering of
$\alpha $
be a numbering of
![]() $A^\ast $
, i.e.,
$A^\ast $
, i.e.,
![]() $\alpha \colon A^\ast \to \mathbb {N}$
is injective. We write
$\alpha \colon A^\ast \to \mathbb {N}$
is injective. We write ![]() for the numeral of the
for the numeral of the
![]() $\alpha $
-code
$\alpha $
-code
![]() $\alpha (\varphi )$
of
$\alpha (\varphi )$
of
![]() $\varphi $
and we write
$\varphi $
and we write ![]() if no specific numbering is indicated.
if no specific numbering is indicated.
We call a function
![]() $\alpha \colon B \to \mathbb {N}$
recursive, if
$\alpha \colon B \to \mathbb {N}$
recursive, if
![]() $B \subseteq \mathbb {N}$
is decidable and there exists a partial recursive function
$B \subseteq \mathbb {N}$
is decidable and there exists a partial recursive function
![]() $\alpha ' \colon \mathbb {N} \to \mathbb {N}$
with
$\alpha ' \colon \mathbb {N} \to \mathbb {N}$
with
![]() $\textrm{{dom}}(\alpha ') = B$
and
$\textrm{{dom}}(\alpha ') = B$
and
![]() $\alpha ' \upharpoonright B = \alpha $
. Let
$\alpha ' \upharpoonright B = \alpha $
. Let
![]() $\alpha _1$
and
$\alpha _1$
and
![]() $\alpha _2$
be numberings of given sets
$\alpha _2$
be numberings of given sets
![]() $S_1$
and
$S_1$
and
![]() $S_2$
respectively. We call a function
$S_2$
respectively. We call a function
![]() $f \colon S_1 \to S_2 $
recursive relative to
$f \colon S_1 \to S_2 $
recursive relative to
![]() $\langle \alpha _1, \alpha _2 \rangle $
if
$\langle \alpha _1, \alpha _2 \rangle $
if
![]() $\alpha _2 \circ f \circ \alpha _1^{-1}$
is recursive. If moreover
$\alpha _2 \circ f \circ \alpha _1^{-1}$
is recursive. If moreover
![]() $\alpha _1 = \alpha _2$
, we also say that f is recursive relative to
$\alpha _1 = \alpha _2$
, we also say that f is recursive relative to
![]() $\alpha _1$
.
$\alpha _1$
.
In this paper we consider consistent and “sufficiently adequate”
![]() $\mathcal {L}$
-theories. We take any “sufficiently adequate”
$\mathcal {L}$
-theories. We take any “sufficiently adequate”
![]() $\mathcal {L}$
-theory to be recursively enumerable and to extend the Tarski–Mostowski–Robinson theory
$\mathcal {L}$
-theory to be recursively enumerable and to extend the Tarski–Mostowski–Robinson theory
![]() $\mathsf {R}$
, which is given by the following axiom schemata:Footnote
4
$\mathsf {R}$
, which is given by the following axiom schemata:Footnote
4
-
R1.
 $\overline {m} + \overline {n} = \overline {m + n}$
$\overline {m} + \overline {n} = \overline {m + n}$
-
R2.
 $\overline {m} \times \overline {n} = \overline {m \cdot n}$
$\overline {m} \times \overline {n} = \overline {m \cdot n}$
-
R3.
 $\overline {m} \neq \overline {n}, \text { for } m \neq n$
$\overline {m} \neq \overline {n}, \text { for } m \neq n$
-
R4.
 $x \leq \overline {n} \rightarrow \bigvee _{k \leq n} x = \overline {k}$
$x \leq \overline {n} \rightarrow \bigvee _{k \leq n} x = \overline {k}$
-
R5.
 $x \leq \overline {n} \vee \overline {n} \leq x$
$x \leq \overline {n} \vee \overline {n} \leq x$
2.2 Löb’s conditions
Perhaps the most popular approach to abstracting away from specific formalisation choices regarding consistency sentences rests on the so-called Hilbert–Bernays–Löb derivability conditions, or for short: Löb’s conditions, which are defined as follows. A formula
![]() $\mathsf {Pr}(x)$
satisfies Löb’s conditions for T, in short: Löb(T), if for all sentences
$\mathsf {Pr}(x)$
satisfies Löb’s conditions for T, in short: Löb(T), if for all sentences
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
:
$\psi $
:
-
Löb1
 ;
; -
Löb2
 ;
; -
Löb3
 .
.
Let
![]() $\bot $
be some fixed T-contradiction, such as
$\bot $
be some fixed T-contradiction, such as
![]() $\mathsf {0} = \mathsf {S0}$
. This approach results in the following famous generalisation of Gödel’s Second Theorem due to Hilbert & Bernays (Reference Hilbert and Bernays1970) and Löb (Reference Löb1955), which constitutes the starting point of this study:
$\mathsf {0} = \mathsf {S0}$
. This approach results in the following famous generalisation of Gödel’s Second Theorem due to Hilbert & Bernays (Reference Hilbert and Bernays1970) and Löb (Reference Löb1955), which constitutes the starting point of this study:
Theorem 2.1
![]() , for all formulæ
, for all formulæ
![]() $\mathsf {Pr}(x)$
satisfying Löb(T).
$\mathsf {Pr}(x)$
satisfying Löb(T).
Indeed, this version of Gödel’s theorem neither resorts to the underlying proof system nor to the specific way T-provability and T’s axiom set are formalised.Footnote
5
However, its formulation employs a specific and arbitrarily chosen Gödel numbering. In order to also abstract away from this source of indeterminacy, we first make the numbering used in the formulation of Löb’s conditions explicit, where prima facie any injective function
![]() $\alpha \colon A^\ast \to \mathbb {N}$
qualifies as a numbering. We then take a formula
$\alpha \colon A^\ast \to \mathbb {N}$
qualifies as a numbering. We then take a formula
![]() $\mathsf {Pr}^\alpha (x)$
to satisfy Löb’s conditions relative to
$\mathsf {Pr}^\alpha (x)$
to satisfy Löb’s conditions relative to
![]() $\alpha $
for T, in short: Löb(
$\alpha $
for T, in short: Löb(
![]() $T, \alpha $
), if for all sentences
$T, \alpha $
), if for all sentences
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
:
$\psi $
:
-
 $\boldsymbol{L\ddot{o}b1}^{\boldsymbol{\alpha }}$
$\boldsymbol{L\ddot{o}b1}^{\boldsymbol{\alpha }}$
 ;
; -
 $\boldsymbol{L\ddot{o}b2}^{\boldsymbol{\alpha }}$
$\boldsymbol{L\ddot{o}b2}^{\boldsymbol{\alpha }}$
 ;
; -
 $\boldsymbol{L\ddot{o}b3}^{\boldsymbol{\alpha }}$
$\boldsymbol{L\ddot{o}b3}^{\boldsymbol{\alpha }}$
 .
.
It is widely believed that Löb’s conditions are sufficient to allow for the “modal reasoning” involved in the proof of Löb’s theorem, and thus in particular, of Theorem 2.1 (for such a proof see e.g., Smith, Reference Smith2007, p. 230). As this “modal reasoning” does not resort to the underlying numbering, one might expect Theorem 2.1 to be invariant in the following sense: whatever numbering
![]() $\alpha $
is chosen,
$\alpha $
is chosen,
![]() for every formula
for every formula
![]() $\mathsf {Pr}^{\alpha }(x)$
satisfying Löb(
$\mathsf {Pr}^{\alpha }(x)$
satisfying Löb(
![]() $T, \alpha $
).
$T, \alpha $
).
2.3 Deviant numberings
I now show that this invariance claim is false, as there exist highly artificial and deviant numberings. To start with, for any given set
![]() $S \subseteq A^\ast $
of expressions an injective function
$S \subseteq A^\ast $
of expressions an injective function
![]() $\alpha \colon A^\ast \to \mathbb {N}$
can be defined such that the set of
$\alpha \colon A^\ast \to \mathbb {N}$
can be defined such that the set of
![]() $\alpha $
-codes of S is
$\alpha $
-codes of S is
![]() $\Delta ^0_0$
-binumerable.Footnote
6
For instance, define
$\Delta ^0_0$
-binumerable.Footnote
6
For instance, define
![]() $\alpha $
such that
$\alpha $
such that
 $$ \begin{align*} \alpha(\varphi) \text{ is } \begin{cases} \text{even} & \text{ if } \varphi \in S,\\ \text{odd} & \text{ if } \varphi \not\in S. \end{cases} \end{align*} $$
$$ \begin{align*} \alpha(\varphi) \text{ is } \begin{cases} \text{even} & \text{ if } \varphi \in S,\\ \text{odd} & \text{ if } \varphi \not\in S. \end{cases} \end{align*} $$
This can simply be done by enumerating both S and
![]() $A^\ast \setminus S$
(without repetitions) and subsequently assigning the number
$A^\ast \setminus S$
(without repetitions) and subsequently assigning the number
![]() $2 \cdot k$
to the k-th element of the enumeration of S and the number
$2 \cdot k$
to the k-th element of the enumeration of S and the number
![]() $2 \cdot k +1$
to the k-th element of the enumeration of
$2 \cdot k +1$
to the k-th element of the enumeration of
![]() $A^\ast \setminus S$
. Clearly, these enumerations are possibly noneffective.
$A^\ast \setminus S$
. Clearly, these enumerations are possibly noneffective.
Let
![]() $S := T^{\vdash }$
be the deductive closure of T and let
$S := T^{\vdash }$
be the deductive closure of T and let
![]() $\alpha $
be defined as above, such that the set of
$\alpha $
be defined as above, such that the set of
![]() $\alpha $
-codes of T-theorems are exactly the even numbers. The formula
$\alpha $
-codes of T-theorems are exactly the even numbers. The formula
![]() $\mathsf {Pr}^\alpha (x) \equiv \exists y < x \ x = \overline {2} \times y$
then satisfies Löb(
$\mathsf {Pr}^\alpha (x) \equiv \exists y < x \ x = \overline {2} \times y$
then satisfies Löb(
![]() $T, \alpha $
) and we have
$T, \alpha $
) and we have
![]() by the
by the
![]() $\Sigma ^0_1$
-completeness of T, in violation of the above invariance claim. The reason for this is that in addition to Löb’s conditions, the fixed point construction is also a crucial ingredient in the “modal reasoning” towards Löb’s theorem. And indeed, the Diagonal Lemma fails with regard to
$\Sigma ^0_1$
-completeness of T, in violation of the above invariance claim. The reason for this is that in addition to Löb’s conditions, the fixed point construction is also a crucial ingredient in the “modal reasoning” towards Löb’s theorem. And indeed, the Diagonal Lemma fails with regard to
![]() $\alpha $
, i.e., there is no (
$\alpha $
, i.e., there is no (
![]() $\alpha $
-)fixpoint of
$\alpha $
-)fixpoint of
![]() $\neg \mathsf {Pr}^\alpha (x)$
. To see this, assume that there exists G such that
$\neg \mathsf {Pr}^\alpha (x)$
. To see this, assume that there exists G such that
![]() , which implies
, which implies
![]() $T \not \vdash G$
. But then
$T \not \vdash G$
. But then
![]() and therefore
and therefore
![]() $T \vdash G$
, yielding a contradiction.
$T \vdash G$
, yielding a contradiction.
Similarly, setting
![]() $S := \mathsf {Th}(\mathbb {N})$
yields a numbering
$S := \mathsf {Th}(\mathbb {N})$
yields a numbering
![]() $\beta $
such that
$\beta $
such that
![]() $\exists y < x \ x = \overline {2} \times y$
binumerates
$\exists y < x \ x = \overline {2} \times y$
binumerates
![]() $\{ \beta (\varphi ) \mid \mathbb {N} \models \varphi \}$
, thus violating (both the semantic and the syntactic version of) Tarski’s Theorem.
$\{ \beta (\varphi ) \mid \mathbb {N} \models \varphi \}$
, thus violating (both the semantic and the syntactic version of) Tarski’s Theorem.
While
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
appear to be highly deviant numberings which resist any arithmetisation of the usual syntactic properties, less artificial numberings can be constructed for certain theories
$\beta $
appear to be highly deviant numberings which resist any arithmetisation of the usual syntactic properties, less artificial numberings can be constructed for certain theories
![]() $T \supseteq \mathsf {R}$
which still violate Gödel’s Second Theorem and the two versions of Tarski’s Theorem respectively.Footnote
7
For instance, based on a more careful construction, both
$T \supseteq \mathsf {R}$
which still violate Gödel’s Second Theorem and the two versions of Tarski’s Theorem respectively.Footnote
7
For instance, based on a more careful construction, both
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
can be taken to be monotonic (see
$\beta $
can be taken to be monotonic (see
![]() $\zeta $
in Appendix 6). That is, the Gödel number of a string is larger than the Gödel numbers of its substrings. There also exists a numbering
$\zeta $
in Appendix 6). That is, the Gödel number of a string is larger than the Gödel numbers of its substrings. There also exists a numbering
![]() $\delta $
such that the functions
$\delta $
such that the functions
![]() $\underline {\mathsf {S}}$
,
$\underline {\mathsf {S}}$
,
![]() $\underline {+}$
,
$\underline {+}$
,
![]() $\underline {\times }$
,
$\underline {\times }$
,
![]() $\underline {\prime }$
,
$\underline {\prime }$
,
![]() $\underline {=}$
,
$\underline {=}$
,
![]() $\underline {\wedge }$
and
$\underline {\wedge }$
and
![]() $\underline {\forall }$
are recursive relative to
$\underline {\forall }$
are recursive relative to
![]() $\delta $
, yet the set of T-theorems is binumerable by a
$\delta $
, yet the set of T-theorems is binumerable by a
 $\Delta ^0_0(\mathsf {exp})$
-formula
$\Delta ^0_0(\mathsf {exp})$
-formula
![]() $\mathsf {Pr}^{\delta }(x)$
(see Appendix 6).Footnote
8
In particular,
$\mathsf {Pr}^{\delta }(x)$
(see Appendix 6).Footnote
8
In particular,
![]() $\mathsf {Pr}^{\delta }(x)$
once again satisfies Löb(
$\mathsf {Pr}^{\delta }(x)$
once again satisfies Löb(
![]() $T, \delta $
), but
$T, \delta $
), but ![]() .
.
There exists moreover a numbering
![]() $\eta $
such that all the functions
$\eta $
such that all the functions
![]() $\underline {\mathsf {S}}$
,
$\underline {\mathsf {S}}$
,
![]() $\underline {+}$
,
$\underline {+}$
,
![]() $\underline {\times }$
,
$\underline {\times }$
,
![]() $\underline {\prime }$
,
$\underline {\prime }$
,
![]() $\underline {=}$
,
$\underline {=}$
,
![]() $\underline {\neg }$
,
$\underline {\neg }$
,
![]() $\underline {\wedge }$
and
$\underline {\wedge }$
and
![]() $\underline {\rightarrow }$
are recursive relative to
$\underline {\rightarrow }$
are recursive relative to
![]() $\eta $
and the set
$\eta $
and the set
![]() $\{ \eta (\varphi ) \mid \mathcal {N} \models \varphi \}$
of true sentences is binumerable by a
$\{ \eta (\varphi ) \mid \mathcal {N} \models \varphi \}$
of true sentences is binumerable by a
 $\Delta ^0_0(\mathsf {exp})$
-formula
$\Delta ^0_0(\mathsf {exp})$
-formula
![]() $\mathsf {Pr}^{\eta }(x)$
(see Appendix 6). In particular, the formula
$\mathsf {Pr}^{\eta }(x)$
(see Appendix 6). In particular, the formula
![]() $\mathsf {Pr}^{\eta }(x)$
satisfies Löb(
$\mathsf {Pr}^{\eta }(x)$
satisfies Löb(
![]() $T, \eta $
) for sound theories
$T, \eta $
) for sound theories
![]() $T \supseteq \mathsf {R}$
, but
$T \supseteq \mathsf {R}$
, but ![]() .
.
Both numberings
![]() $\delta $
and
$\delta $
and
![]() $\eta $
thus yield deviant results, even though they allow for the arithmetisation of a large portion of syntactic properties and operations. For instance, the
$\eta $
thus yield deviant results, even though they allow for the arithmetisation of a large portion of syntactic properties and operations. For instance, the
![]() $\mathsf {num}$
-function (mapping numbers to their standard numerals) and the substitution function for terms as well as for atomic formulæ can be binumerated relative to both numberings. However, since
$\mathsf {num}$
-function (mapping numbers to their standard numerals) and the substitution function for terms as well as for atomic formulæ can be binumerated relative to both numberings. However, since
![]() $\underline {\neg }$
and
$\underline {\neg }$
and
![]() $\underline {\forall }$
are not recursive relative to
$\underline {\forall }$
are not recursive relative to
![]() $\delta $
and
$\delta $
and
![]() $\eta $
respectively, the arithmetisation of the substitution function for (complex) formulæ fails for both numberings. This can be seen as the reason why the Diagonal Lemma does not hold when employing these numberings, since its proof crucially relies on the arithmetisation of the substitution function.
$\eta $
respectively, the arithmetisation of the substitution function for (complex) formulæ fails for both numberings. This can be seen as the reason why the Diagonal Lemma does not hold when employing these numberings, since its proof crucially relies on the arithmetisation of the substitution function.
In what follows I will argue that these results do not refute Gödel and Tarski’s classical theorems, since the underlying numberings are inadmissible for the contexts they are employed in.Footnote 9 Our initial naïve approach to numberings is thus not tenable and has to be replaced by a refined account based on admissible numberings, ruling out such deviant constructions. This is precisely the aim of the next section.
3 Admissibility of numberings
It is notoriously difficult to make the informal notion of the admissibility of a numbering precise. However, for the purposes of this paper it is sufficient to isolate a necessary condition of admissibility, namely, the computability of a numbering. More specifically, computable numberings will here be characterised by computable simulations of the structure of strings together with the concatenation operation. Once the notion of computable simulation is made precise, I will discuss its adequacy and compare it to three other proposals found in the literature. I will conclude this section by considering other approaches to the admissibility of numberings based on compositionality and monotonicity rather than computational considerations.
3.1 Computable simulations
The reader is reminded that the set of expressions is given by the set
![]() $A^\ast $
of strings over the alphabet A. Let
$A^\ast $
of strings over the alphabet A. Let
![]() $\alpha \colon A^\ast \to \mathbb {N}$
be any injective function and let
$\alpha \colon A^\ast \to \mathbb {N}$
be any injective function and let
![]() $G := \alpha (A^\ast )$
be the set of Gödel numbers, or
$G := \alpha (A^\ast )$
be the set of Gödel numbers, or
![]() $\alpha $
-codes, of
$\alpha $
-codes, of
![]() $A^\ast $
. For any operation
$A^\ast $
. For any operation
![]() $e \colon (A^\ast )^k \to A^\ast $
, we call the function
$e \colon (A^\ast )^k \to A^\ast $
, we call the function ![]() given by
given by
the (
![]() $\alpha $
-)tracking function of e. To illustrate,
$\alpha $
-)tracking function of e. To illustrate, ![]() is defined such that the diagram
is defined such that the diagram

commutes, where
![]() $\alpha \times \cdots \times \alpha (a_1, \ldots , a_k) := (\alpha (a_1),\ldots , \alpha (a_k))$
. The function
$\alpha \times \cdots \times \alpha (a_1, \ldots , a_k) := (\alpha (a_1),\ldots , \alpha (a_k))$
. The function
![]() can thus be seen to simulate e on the set of
can thus be seen to simulate e on the set of
![]() $\alpha $
-codes. For this reason we also sometimes call
$\alpha $
-codes. For this reason we also sometimes call
![]() the e-simulating function (on G).
the e-simulating function (on G).
Intrinsic to the structure of strings is the concatenation operation
![]() $\ast $
, which allows to generate any string of
$\ast $
, which allows to generate any string of
![]() $A^\ast $
from elements of A. The operation
$A^\ast $
from elements of A. The operation
![]() can then be seen to simulate the concatenation operator on the set G of Gödel numbers. It is easy to check that the associativity of
can then be seen to simulate the concatenation operator on the set G of Gödel numbers. It is easy to check that the associativity of
![]() $\ast $
is inherited by
$\ast $
is inherited by
![]() . Moreover, as in the case of strings over A, each
. Moreover, as in the case of strings over A, each
![]() $\alpha $
-code in G can be finitely generated from the set
$\alpha $
-code in G can be finitely generated from the set
![]() $\alpha (A)$
of
$\alpha (A)$
of
![]() $\alpha $
-codes of A by the
$\alpha $
-codes of A by the
![]() $\ast $
-simulating operation
$\ast $
-simulating operation
![]() . For instance, for any string
. For instance, for any string
![]() $s \in A^\ast $
there are alphabetical expressions
$s \in A^\ast $
there are alphabetical expressions
![]() $s_1, \ldots , s_n \in A$
such that
$s_1, \ldots , s_n \in A$
such that
The
![]() $\alpha $
-code of s is then simply the result of “
$\alpha $
-code of s is then simply the result of “![]() -concatenating” the
-concatenating” the
![]() $\alpha $
-codes of the alphabetical expressions
$\alpha $
-codes of the alphabetical expressions
![]() $s_i$
, i.e.,
$s_i$
, i.e.,
This situation can be naturally described in algebraic terms, by conceiving of
![]() $A^\ast $
together with
$A^\ast $
together with
![]() $\ast $
as a semigroup. The above considerations then show that also
$\ast $
as a semigroup. The above considerations then show that also ![]() forms a semigroup and
forms a semigroup and
![]() $\alpha $
is a (semigroup) isomorphism.
$\alpha $
is a (semigroup) isomorphism.
Thus far, no requirements have been imposed on the numbering
![]() $\alpha $
. That
$\alpha $
. That
![]() $\alpha $
computably simulates
$\alpha $
computably simulates
![]() $A^\ast $
can now be informally expressed by (i) requiring that for each number it is decidable whether or not it
$A^\ast $
can now be informally expressed by (i) requiring that for each number it is decidable whether or not it
![]() $\alpha $
-codes an expression, and by (ii) requiring that Gödel numbers are mechanically generated from the
$\alpha $
-codes an expression, and by (ii) requiring that Gödel numbers are mechanically generated from the
![]() $\alpha $
-codes of alphabetic expressions in A. Since G is a set of natural numbers and
$\alpha $
-codes of alphabetic expressions in A. Since G is a set of natural numbers and
![]() is an arithmetical operation which generates G from
is an arithmetical operation which generates G from
![]() $\alpha (A)$
, both requirements can be explicated via the Church–Turing Thesis as follows:
$\alpha (A)$
, both requirements can be explicated via the Church–Turing Thesis as follows:
Definition 3.2. A numbering
![]() $\alpha \colon A^\ast \to \mathbb {N}$
is a computable simulation (of
$\alpha \colon A^\ast \to \mathbb {N}$
is a computable simulation (of
![]() $A^\ast $
), if G is decidable and
$A^\ast $
), if G is decidable and
![]() is recursive, where G and
is recursive, where G and
![]() are given as above.
are given as above.
This notion of a computable simulation can be traced back to Montague (Reference Montague1957, chap. IV) as well as to the foundational texts Rabin (Reference Rabin1960) and Mal’cev (Reference Mal’cev1961) of the field of computable algebra.Footnote
10
The reader who questions the need for such a notion is reminded that the explication of a numbering’s computability via the Church-Turing Thesis is not entirely straightforward. Turing machines for instance only operate over strings. A sensible application of Turing-computability to numberings thus requires a representation of their co-domain
![]() $\mathbb {N}$
by strings, which in general yields different sets of computable numberings (Montague, Reference Montague1960). The task of singling out admissible or natural representations has proven to be fraught with difficulty, purportedly even resulting in a circular conceptual analysis of (numerical) computability (see Boker & Dershowitz, Reference Boker, Dershowitz, Avron, Dershowitz and Rabinovich2008, Reference Boker, Dershowitz, Blass, Dershowitz and Reisig2010; Quinon, Reference Quinon, Manea, Miller and Nowotka2018; Rescorla, Reference Rescorla2007; Shapiro, Reference Shapiro1982, Reference Shapiro2017).
$\mathbb {N}$
by strings, which in general yields different sets of computable numberings (Montague, Reference Montague1960). The task of singling out admissible or natural representations has proven to be fraught with difficulty, purportedly even resulting in a circular conceptual analysis of (numerical) computability (see Boker & Dershowitz, Reference Boker, Dershowitz, Avron, Dershowitz and Rabinovich2008, Reference Boker, Dershowitz, Blass, Dershowitz and Reisig2010; Quinon, Reference Quinon, Manea, Miller and Nowotka2018; Rescorla, Reference Rescorla2007; Shapiro, Reference Shapiro1982, Reference Shapiro2017).
As will be shown in §4.1, computable simulations do not depend on such arbitrary representational choices, thus providing an adequate explication of computability for our purposes.
3.2 The epistemic role of numberings
While we have seen that computable simulations explicate the notion of computability adequately, the question remains why admissible numberings should be computable in the first place.
Recall the philosophical interpretation of Gödel’s Second Theorem, according to which T does not prove its consistency. This interpretation’s justification rests on the hypothesis that we can formulate the question whether or not T proves a sentence which expresses T’s consistency in a meaningful way. Indeed, the employed Gödel numbering enables us to interpret certain arithmetical closed terms and formulæ as (names of) syntactic objects and properties of syntactical objects respectively. Let us call this the semantic role of Gödel numberings. It allows us to not only reason in T about numbers but also about expressions via their Gödel codes.
The prevalent philosophical reading of Gödel’s theorem as a limitative result rests on yet another crucial feature of numberings. What we are essentially concerned with, is the question of whether or not the consistency sentence is derivable by using only the theory T’s resources. It is therefore pivotal in this context that admissible numberings ensure that reasoning about expressions via their representations in
![]() $\mathcal {L}$
requires no resources which lie outside the formal system T. Let us call this the epistemic role of Gödel numberings.
$\mathcal {L}$
requires no resources which lie outside the formal system T. Let us call this the epistemic role of Gödel numberings.
As we have seen in §3.1, every numbering induces a pair
![]() , where G is a set of codes and
, where G is a set of codes and ![]() is a
is a
![]() $\ast $
-simulating operation on G, which represents the structure of expressions. That this representation does not employ resources exceeding T can be understood in virtue of T “recognising” or “knowing” or “verifying” certain facts and properties concerning
$\ast $
-simulating operation on G, which represents the structure of expressions. That this representation does not employ resources exceeding T can be understood in virtue of T “recognising” or “knowing” or “verifying” certain facts and properties concerning ![]() . Since T is a formal theory, it can be seen to “recognise,” “know” and “verify” facts and properties by means of proving (formulæ which express) them.
. Since T is a formal theory, it can be seen to “recognise,” “know” and “verify” facts and properties by means of proving (formulæ which express) them.
So far, none of these facts and properties have been specified. A minimal approach is to require that T “recognises” the two constituents of the given representation, namely the set G and the operation
![]() . Accordingly, T “knows” whether or not
. Accordingly, T “knows” whether or not
![]() ${n \in G}$
, and whether or not
${n \in G}$
, and whether or not ![]() , for numbers l, m and n. That is, T binumerates both G and
, for numbers l, m and n. That is, T binumerates both G and
![]() (i.e., its graph). But this is tantamount to G being decidable and
(i.e., its graph). But this is tantamount to G being decidable and
![]() being recursive.Footnote
11
Hence by Definition 3.2, the underlying numbering is a computable simulation.
being recursive.Footnote
11
Hence by Definition 3.2, the underlying numbering is a computable simulation.
Note that even though the admissibility of a numbering is analysed in terms of T’s resources, the extracted notion of computable simulation is theory-independent. This rests on the fact that theories extending
![]() $\mathsf {R}$
binumerate exactly the same sets and functions, namely decidable and recursive ones respectively.
$\mathsf {R}$
binumerate exactly the same sets and functions, namely decidable and recursive ones respectively.
However, one might require T to recognise further properties regarding ![]() . For instance, T might reasonably be required to verify the functionality of
. For instance, T might reasonably be required to verify the functionality of ![]() , i.e., to prove that
, i.e., to prove that ![]() is total (cf. §4.3). Since different theories extending
is total (cf. §4.3). Since different theories extending
![]() $\mathsf {R}$
prove the totality of different classes of functions in general, this requirement yields a notion of admissibility which is sensitive to T.
$\mathsf {R}$
prove the totality of different classes of functions in general, this requirement yields a notion of admissibility which is sensitive to T.
As we will show in §4, even the minimal approach places enough restriction on admissible numberings to establish the invariance of Gödel’s Second Theorem (see Theorem 4.14). It is therefore sufficient for the purpose of this paper to conclude that admissible numberings are computable simulations.Footnote 12
In the context of the semantic version of Tarski’s Theorem, we are concerned with the question of whether the set of true sentences is definable in the language
![]() $\mathcal {L}$
, rather than with provability in a formal theory T. Accordingly, the epistemic role of numberings in this context is to ensure that reasoning about expressions does not resort to resources exceeding the language
$\mathcal {L}$
, rather than with provability in a formal theory T. Accordingly, the epistemic role of numberings in this context is to ensure that reasoning about expressions does not resort to resources exceeding the language
![]() $\mathcal {L}$
, rather than the theory T as in the context of Gödel’s theorem. This can be made precise by requiring that
$\mathcal {L}$
, rather than the theory T as in the context of Gödel’s theorem. This can be made precise by requiring that
![]() $\mathcal {L}$
“captures” or “expresses” relevant facts and properties about admissible representations
$\mathcal {L}$
“captures” or “expresses” relevant facts and properties about admissible representations ![]() by means of defining them. Once again resorting to a minimal approach then yields the requirement that both G and
by means of defining them. Once again resorting to a minimal approach then yields the requirement that both G and ![]() (i.e., its graph) are definable in the standard interpretation
(i.e., its graph) are definable in the standard interpretation
![]() $\mathbb {N}$
of
$\mathbb {N}$
of
![]() $\mathcal {L}$
. We call any numbering which gives rise to such a representation
$\mathcal {L}$
. We call any numbering which gives rise to such a representation
![]() an arithmetical simulation (of
an arithmetical simulation (of
![]() $A^\ast $
).
$A^\ast $
).
According to the proposed analysis, the notion of admissibility is thus sensitive to the considered metamathematical context. While admissible numberings are computable simulations in the context of Gödel’s Second Theorem and other limitative results which primarily pertain to provability-in-a-theory (such as the syntactic version of Tarski’s Theorem), they are required to be arithmetical simulations in the context of the semantic version of Tarski’s Theorem.
In the remainder of this paper I will consider the admissibility of numberings exclusively in the context of Gödel’s Second Theorem (with Theorem 4.8 and footnote 23 as exceptions):
-
Computable Simulativity. Every admissible numbering is a computable simulation.
I now turn briefly to other proposals found in the literature which tie computational considerations to the admissibility of numberings.
3.3 Other routes to admissibility
Let
![]() $\gamma $
denote the standard numbering introduced in Smith (Reference Smith2007, sec. 15.1).Footnote
13
According to Smith (Reference Smith2007) “the key feature of our Gödelian scheme [
$\gamma $
denote the standard numbering introduced in Smith (Reference Smith2007, sec. 15.1).Footnote
13
According to Smith (Reference Smith2007) “the key feature of our Gödelian scheme [
![]() $\gamma $
] is this: there is a pair of algorithms, one of which takes us from an expression to its code number, the other of which takes us back again from the code number to the original expression” (p. 126). Given any other comparable numbering
$\gamma $
] is this: there is a pair of algorithms, one of which takes us from an expression to its code number, the other of which takes us back again from the code number to the original expression” (p. 126). Given any other comparable numbering
![]() $\alpha $
, converting the
$\alpha $
, converting the
![]() $\alpha $
-code of a certain expression
$\alpha $
-code of a certain expression
![]() $\varphi $
into its
$\varphi $
into its
![]() $\gamma $
-code involves running through two algorithms (first mapping
$\gamma $
-code involves running through two algorithms (first mapping
![]() $\alpha (\varphi )$
to
$\alpha (\varphi )$
to
![]() $\varphi $
and then mapping
$\varphi $
and then mapping
![]() $\varphi $
to
$\varphi $
to
![]() $\gamma (\varphi )$
), which by assumption do not involve any open-ended searches (ibid.). Conversely,
$\gamma (\varphi )$
), which by assumption do not involve any open-ended searches (ibid.). Conversely,
![]() $\gamma $
-codes can be converted into
$\gamma $
-codes can be converted into
![]() $\alpha $
-codes in a similar fashion. Hence, “there is a p.r. function
$\alpha $
-codes in a similar fashion. Hence, “there is a p.r. function
![]() $tr$
which ‘translates’ code numbers according to [
$tr$
which ‘translates’ code numbers according to [
![]() $\alpha $
] into code numbers under our official Gödelian scheme [
$\alpha $
] into code numbers under our official Gödelian scheme [
![]() $\gamma $
], and another p.r. function
$\gamma $
], and another p.r. function
![]() $tr^{-1}$
which converts code numbers under our scheme back into code numbers under scheme [
$tr^{-1}$
which converts code numbers under our scheme back into code numbers under scheme [
![]() $\alpha $
]” (ibid.).Footnote
14
Let us call any numbering
$\alpha $
]” (ibid.).Footnote
14
Let us call any numbering
![]() $\alpha $
for which such a pair of p.r. translation functions exist, computably translatable to
$\alpha $
for which such a pair of p.r. translation functions exist, computably translatable to
![]() $\gamma $
. The following criterion of admissibility is thus extracted by Smith (Reference Smith2007):
$\gamma $
. The following criterion of admissibility is thus extracted by Smith (Reference Smith2007):
-
Computable Translatability. A numbering is admissible iff it is computably translatable to the standard numbering
 $\gamma $
.
$\gamma $
.
While I agree with Smith’s initial analysis that the key feature of admissibility consists essentially in intuitive computability, the proposed criterion fails to capture this feature in a conceptually satisfactory way. This deficiency can be seen to result from general difficulties in giving a precise account of the computability of numberings (see the remark following Definition 3.2). To circumvent these difficulties, Smith requires admissible numberings to be computably translatable to some designated standard numbering
![]() $\gamma $
. The conceptual adequacy of the resulting criterion thus crucially rests on the admissibility of
$\gamma $
. The conceptual adequacy of the resulting criterion thus crucially rests on the admissibility of
![]() $\gamma $
. For instance, employing one of the deviant numberings of §2.3 as a reference numbering instead of
$\gamma $
. For instance, employing one of the deviant numberings of §2.3 as a reference numbering instead of
![]() $\gamma $
, would clearly render the criterion inadequate. What justifies the choice of
$\gamma $
, would clearly render the criterion inadequate. What justifies the choice of
![]() $\gamma $
as the reference numbering is exactly its intuitive computability. Hence, instead of taking the conceptually prior feature of computability as characterising admissibility, a conceptual surrogate is employed.Footnote
15
Furthermore, Smith’s justification for the existence of p.r. translation functions between numberings which share the same “key feature” (i.e., come with a pair of encoding and decoding algorithms) crucially relies on informal reasoning about computability. A more satisfactory approach would be to first formally characterise the conceptually prior notion of intuitive computability of numberings (cf. Definition 3.2) and then mathematically prove the existence of respective translation functions between them (cf. Theorem 4.6 and Corollary 4.7 below), employing the Church–Turing Thesis only in its “interpretive use” (Smith, Reference Smith2007, p. 275).
$\gamma $
as the reference numbering is exactly its intuitive computability. Hence, instead of taking the conceptually prior feature of computability as characterising admissibility, a conceptual surrogate is employed.Footnote
15
Furthermore, Smith’s justification for the existence of p.r. translation functions between numberings which share the same “key feature” (i.e., come with a pair of encoding and decoding algorithms) crucially relies on informal reasoning about computability. A more satisfactory approach would be to first formally characterise the conceptually prior notion of intuitive computability of numberings (cf. Definition 3.2) and then mathematically prove the existence of respective translation functions between them (cf. Theorem 4.6 and Corollary 4.7 below), employing the Church–Turing Thesis only in its “interpretive use” (Smith, Reference Smith2007, p. 275).
A second approach can be found in Smullyan (Reference Smullyan1961), who bases the concept of admissibility of numberings on representability in elementary formal systems (for definitions see Smullyan, Reference Smullyan1961, p. 6). These systems can be seen as devices intended to “explicate the notion of ‘definability by recursion’” (Smullyan, Reference Smullyan1961, p. 2) directly operating on strings, without the usual recourse to numberings. A set S of strings which is definable by recursion in some elementary formal system is called formally representable. If in addition to S also the complement of S is formally representable, S is called solvable. The admissible numberings of S are then taken to be exactly those which preserve these recursion theoretic properties. More precisely, a numbering
![]() $\alpha \colon S \to \mathbb {N}$
is called EFS-admissible, if for every subset
$\alpha \colon S \to \mathbb {N}$
is called EFS-admissible, if for every subset
![]() $U \subseteq S$
the following holds: U is formally representable iff
$U \subseteq S$
the following holds: U is formally representable iff
![]() $\alpha (U)$
is recursively enumerable and U is solvable iff
$\alpha (U)$
is recursively enumerable and U is solvable iff
![]() $\alpha (U)$
is decidable. This yields:
$\alpha (U)$
is decidable. This yields:
-
EFS-Admissibility. A numbering is admissible iff it is EFS-admissible.
Once again this definition has a computational motivation, since the concept of formal representability is intended to capture the concept of computability, in the sense that formally representable sets characterise sets which are generated by a “computing machine” (Smullyan, Reference Smullyan1961, p. 9).
An account of admissibility which prima facie “strictly contains” the notion of computable simulativity is introduced in Manin (Reference Manin2009). A numbering
![]() $\alpha $
is called sequence-admissible, if the image of
$\alpha $
is called sequence-admissible, if the image of
![]() $\alpha $
is decidable and the length function, the projection function given by
$\alpha $
is decidable and the length function, the projection function given by
![]() $\langle i , \langle a_1, \ldots , a_n \rangle \rangle \mapsto a_i$
as well as the concatenation function are recursive.Footnote
16
This yields the following criterion:
$\langle i , \langle a_1, \ldots , a_n \rangle \rangle \mapsto a_i$
as well as the concatenation function are recursive.Footnote
16
This yields the following criterion:
-
Sequence-Admissibility. A numbering is admissible iff it is sequence-admissible.
Despite the different conceptions of computability underlying these proposals, all three notions will be shown in §4 to be extensionally equivalent to computable simulativity (see Corollary 4.7). This endows the criterion of computable simulativity with a desirable amount of robustness.
3.4 Compositionality and monotonicity
I conclude this section by discussing other approaches to the admissibility of numberings based on compositionality and monotonicity rather than computational considerations. As we have seen in §3.2, numberings have a semantic role as they represent strings by natural numbers. It thus seems reasonable to require admissible numberings to satisfy some principle of compositionality. Accordingly, the semantic value of every complex expression can be taken to be determined by its structure and the semantic values of its subexpressions.Footnote
17
Since for a given numbering
![]() $\alpha $
the semantic value of a string is its
$\alpha $
the semantic value of a string is its
![]() $\alpha $
-code, the compositionality of
$\alpha $
-code, the compositionality of
![]() $\alpha $
can be understood as
$\alpha $
can be understood as
![]() $\alpha \colon A^\ast \to G$
being an
$\alpha \colon A^\ast \to G$
being an
![]() $\Omega $
-homomorphism, where the signature
$\Omega $
-homomorphism, where the signature
![]() $\Omega $
contains a binary (concatenation) function symbol
$\Omega $
contains a binary (concatenation) function symbol
![]() . But as we have already seen in §3.1, every numbering
. But as we have already seen in §3.1, every numbering
![]() $\alpha $
induces such a homomorphism. Hence every numbering is compositional in this sense.
$\alpha $
induces such a homomorphism. Hence every numbering is compositional in this sense.
Even resorting to the “mode of presentation” does not yield any proper restriction on numberings. It is a common practice to first assign numbers to the alphabetical symbols and then to define the Gödel number of a string as a function of the Gödel numbers of its entries (e.g., based on prime factorisation in the tradition of Gödel, Reference Gödel1931 or on k-adic notation following Smullyan, Reference Smullyan1961, Reference Smullyan1992). In fact, any numbering
![]() $\alpha $
of
$\alpha $
of
![]() $A^\ast $
can be reconstructed in this standard “bottom-up” fashion: firstly, map each symbol s of the alphabet A to its
$A^\ast $
can be reconstructed in this standard “bottom-up” fashion: firstly, map each symbol s of the alphabet A to its
![]() $\alpha $
-code. Secondly, consider the
$\alpha $
-code. Secondly, consider the
![]() $\ast $
-simulating partial function
$\ast $
-simulating partial function
![]() , given in §3.1. These two steps then resemble the usual “bottom-up” definition of numberings and uniquely determine our initially given numbering, since
, given in §3.1. These two steps then resemble the usual “bottom-up” definition of numberings and uniquely determine our initially given numbering, since
![]() $\alpha $
is the unique function which extends the assignment given in step 1 and is compositional with regard to the partial function given in step 2, i.e., is an
$\alpha $
is the unique function which extends the assignment given in step 1 and is compositional with regard to the partial function given in step 2, i.e., is an
![]() $\Omega $
-homomorphism.Footnote
18
Every numbering irrespective of its presentation can thus be reconstructed in the above manner, which is the prevalent mode of presentation for standard Gödel numbers found in the literature.
$\Omega $
-homomorphism.Footnote
18
Every numbering irrespective of its presentation can thus be reconstructed in the above manner, which is the prevalent mode of presentation for standard Gödel numbers found in the literature.
In addition to the “bottom-up” fashion of defining numberings, it is ubiquitous in the literature to employ a monotonic partial operation ![]() in step 2. This gives rise to the following property of Gödel numberings:
in step 2. This gives rise to the following property of Gödel numberings:
Definition 3.3. A numbering
![]() $\alpha $
of
$\alpha $
of
![]() $A^\ast $
is called monotonic, if
$A^\ast $
is called monotonic, if
![]() $\alpha (s) \leq \alpha (t)$
for any
$\alpha (s) \leq \alpha (t)$
for any
![]() $s,t \in A^\ast $
such that s is a subexpression (i.e., a substring) of t.
$s,t \in A^\ast $
such that s is a subexpression (i.e., a substring) of t.
Monotonicity is a prevalent property shared by all standard numberings found in the literature (which are known to the author). One reason for this custom is that monotonicity ensures that the above bottom-up mode of presentation yields an injective function and hence a numbering. Monotonicity thus serves as a technical constraint warranting the intended output of a particular construction principle (see for instance Hilbert & Bernays, Reference Hilbert and Bernays1970, p. 220). Moreover, monotonicity provides a low arithmetical complexity of formulæ representing syntactic properties, allowing the use of convenient tools (such as
![]() $\Sigma ^0_1$
-completeness) when proving certain metamathematical theorems.
$\Sigma ^0_1$
-completeness) when proving certain metamathematical theorems.
Apart from these technical considerations, on which conceptual grounds can monotonicity be justified? Can monotonicity be extracted as a necessary condition by analysing the admissibility of numberings as we did in the case of computability?
As we have seen in §3.2, a crucial role of Gödel numberings is to allow reasoning about expressions in an arithmetical theory T. Admissible numberings were thus required to simulate certain structural properties of strings. As we have seen for instance, the operation ![]() induced by
induced by
![]() $\alpha $
simulates the concatenation operation
$\alpha $
simulates the concatenation operation
![]() $\ast $
on
$\ast $
on
![]() $A^\ast $
in virtue of the commutativity of diagram 1 (in §3.1). The subexpression-relation
$A^\ast $
in virtue of the commutativity of diagram 1 (in §3.1). The subexpression-relation
![]() ${\preceq }$
on
${\preceq }$
on
![]() $A^\ast $
can be reasonably taken as yet another important structural feature of strings. Hence for any admissible numbering, the induced semigroup
$A^\ast $
can be reasonably taken as yet another important structural feature of strings. Hence for any admissible numbering, the induced semigroup ![]() of Gödel numbers should simulate
of Gödel numbers should simulate
![]() ${\preceq }$
appropriately. This can be made precise by extending the signature
${\preceq }$
appropriately. This can be made precise by extending the signature
![]() $\Omega $
by a binary relation symbol
$\Omega $
by a binary relation symbol
![]() ${\sqsubseteq }$
, yielding
${\sqsubseteq }$
, yielding ![]() , and by construing
, and by construing
![]() $(A^\ast ,\ast ,\preceq )$
as an
$(A^\ast ,\ast ,\preceq )$
as an
![]() $\Omega ^+$
-structure. A numbering
$\Omega ^+$
-structure. A numbering
![]() $\alpha $
may then be called
$\alpha $
may then be called
![]() $\preceq $
-preserving if
$\preceq $
-preserving if
![]() $\alpha \colon A^\ast \to G$
is an
$\alpha \colon A^\ast \to G$
is an
![]() $\Omega ^+$
-isomorphism. It can be easily seen that in a similar way as in §3.1, for every
$\Omega ^+$
-isomorphism. It can be easily seen that in a similar way as in §3.1, for every
![]() $\alpha $
a “
$\alpha $
a “
![]() $\preceq $
-simulation”
$\preceq $
-simulation”
![]() on G can be defined, such that
on G can be defined, such that ![]() is an
is an
![]() $\Omega ^+$
-structure and
$\Omega ^+$
-structure and
![]() $\alpha $
is an
$\alpha $
is an
![]() $\Omega ^+$
-isomorphism. Hence, once again,
$\Omega ^+$
-isomorphism. Hence, once again,
![]() $\preceq $
-preservation does not impose any restriction on numberings.
$\preceq $
-preservation does not impose any restriction on numberings.
By additionally drawing on the epistemic role of numberings, the induced structure
![]() can be required to not exceed T’s resources, analogously to the analysis in §3.2. Accordingly, it can be required that T “recognises”, and thus binumerates, the relation
can be required to not exceed T’s resources, analogously to the analysis in §3.2. Accordingly, it can be required that T “recognises”, and thus binumerates, the relation ![]() , which is tantamount to
, which is tantamount to ![]() being decidable. Yet, as in the proof of Corollary 4.7 we can show that for every computable simulation
being decidable. Yet, as in the proof of Corollary 4.7 we can show that for every computable simulation
![]() $\alpha $
also the “
$\alpha $
also the “
![]() $\preceq $
-simulating relation”
$\preceq $
-simulating relation” ![]() is decidable. This condition therefore does not pose any additional constraint given the requirement of computable simulativity.
is decidable. This condition therefore does not pose any additional constraint given the requirement of computable simulativity.
As in the case of the
![]() $\ast $
-simulating operation
$\ast $
-simulating operation
![]() , one may require T to verify further principles regarding
, one may require T to verify further principles regarding
![]() $\preceq $
. For instance, T might be required to prove that any two strings
$\preceq $
. For instance, T might be required to prove that any two strings
![]() $s,t$
are subexpressions of
$s,t$
are subexpressions of
![]() $s \ast t$
. This results in a more restrictive notion of admissibility which is sensitive to the considered theory T. Since these principles are formulated in purely string-theoretical terms without access to the arithmetical properties of their codes, they result in limitations, for instance, regarding the growth rate of admissible numberings (cf. §4.3). However, the constraint of monotonicity cannot be obtained using this approach.
$s \ast t$
. This results in a more restrictive notion of admissibility which is sensitive to the considered theory T. Since these principles are formulated in purely string-theoretical terms without access to the arithmetical properties of their codes, they result in limitations, for instance, regarding the growth rate of admissible numberings (cf. §4.3). However, the constraint of monotonicity cannot be obtained using this approach.
As suggested by an anonymous referee, another route to obtain monotonicity may proceed by conceiving of
![]() $\leq $
and
$\leq $
and
![]() $\preceq $
as parthood relations on numbers and strings respectively. Taking parthood as an important structural feature of strings, admissible numberings may then be required to preserve structure in virtue of representing the parthood relation
$\preceq $
as parthood relations on numbers and strings respectively. Taking parthood as an important structural feature of strings, admissible numberings may then be required to preserve structure in virtue of representing the parthood relation
![]() $\preceq $
on strings by the parthood relation
$\preceq $
on strings by the parthood relation
![]() $\leq $
on numbers. I however do not think that this approach is satisfactory for our purposes, for the following reasons.
$\leq $
on numbers. I however do not think that this approach is satisfactory for our purposes, for the following reasons.
Firstly, assuming that both relations
![]() ${\preceq }$
and
${\preceq }$
and
![]() ${\leq }$
are indeed similar in structure by being parthood relations, they still significantly differ with regard to another important structural aspect. While
${\leq }$
are indeed similar in structure by being parthood relations, they still significantly differ with regard to another important structural aspect. While
![]() ${\leq }$
is a total order relation, there are strings which are incomparable with respect to
${\leq }$
is a total order relation, there are strings which are incomparable with respect to
![]() $\preceq $
. For this reason, there exists no numbering such that
$\preceq $
. For this reason, there exists no numbering such that
![]() ${\preceq }$
is represented by
${\preceq }$
is represented by
![]() ${\leq }$
, i.e., that
${\leq }$
, i.e., that ![]() , clearly rendering the above requirement absurd. To require that
, clearly rendering the above requirement absurd. To require that
![]() ${\preceq }$
is represented by
${\preceq }$
is represented by
![]() ${\leq }$
in virtue of
${\leq }$
in virtue of ![]() being contained in
being contained in
![]() ${\leq }$
, i.e., that the underlying numbering is monotonic, appears to be an ad-hoc reaction to this structural discrepancy rather than based on conceptual grounds.
${\leq }$
, i.e., that the underlying numbering is monotonic, appears to be an ad-hoc reaction to this structural discrepancy rather than based on conceptual grounds.
Secondly, even if the adequacy of this last step is granted, further problems arise by this conception of structure preservation. This can be illustrated by basing the structure of strings on so-called successor functions
![]() $\mathsf {S}_a$
, which append the alphabetical symbol
$\mathsf {S}_a$
, which append the alphabetical symbol
![]() $a \in A$
to any input string (see Corcoran et al., Reference Corcoran, Frank and Maloney1974). Instead of employing the concatenation operation
$a \in A$
to any input string (see Corcoran et al., Reference Corcoran, Frank and Maloney1974). Instead of employing the concatenation operation
![]() $\ast $
, the set of strings can be generated from the empty string by using successor functions
$\ast $
, the set of strings can be generated from the empty string by using successor functions
![]() $\mathsf {S}_a$
for each
$\mathsf {S}_a$
for each
![]() $a \in A$
. According to the above approach, admissible numberings can then be required to preserve this structure in virtue of representing the empty string and the successor functions
$a \in A$
. According to the above approach, admissible numberings can then be required to preserve this structure in virtue of representing the empty string and the successor functions
![]() $\mathsf {S}_a$
by their arithmetical counterparts, namely, by
$\mathsf {S}_a$
by their arithmetical counterparts, namely, by
![]() $0$
and the successor operation
$0$
and the successor operation
![]() ${n \mapsto n+1}$
. However, even the requirement that (the graph of) the tracking function of some
${n \mapsto n+1}$
. However, even the requirement that (the graph of) the tracking function of some
![]() $\mathsf {S}_a$
is contained in (the graph of) the arithmetical successor function cannot be satisfied by any Gödel numbering. As in the case of monotonicity, this requirement stems from a loose and almost metaphorical conception of structure similarity and preservation. In some sense, the empty string and the successor functions
$\mathsf {S}_a$
is contained in (the graph of) the arithmetical successor function cannot be satisfied by any Gödel numbering. As in the case of monotonicity, this requirement stems from a loose and almost metaphorical conception of structure similarity and preservation. In some sense, the empty string and the successor functions
![]() $\mathsf {S}_a$
indeed have the structure of
$\mathsf {S}_a$
indeed have the structure of
![]() $0$
and the arithmetical successor operation, namely in virtue of being generators and constructors respectively. However, they once again differ crucially in other structural respects, resulting in the absurdity of the extracted requirement.
$0$
and the arithmetical successor operation, namely in virtue of being generators and constructors respectively. However, they once again differ crucially in other structural respects, resulting in the absurdity of the extracted requirement.
Thirdly, while I agree that admissible numberings should preserve the structure of the subexpression relation
![]() $\preceq $
, it is not clear why structure preservation should entail constraints on the arithmetical content of
$\preceq $
, it is not clear why structure preservation should entail constraints on the arithmetical content of ![]() , such as the containment of
, such as the containment of ![]() in
in
![]() $\leq $
, in the first place. Rather, I take an admissible numbering
$\leq $
, in the first place. Rather, I take an admissible numbering
![]() $\alpha $
to preserve the structure of
$\alpha $
to preserve the structure of
![]() $\preceq $
in virtue of the decidability of whether or not a number
$\preceq $
in virtue of the decidability of whether or not a number
![]() $n \alpha $
-codes a subexpression with
$n \alpha $
-codes a subexpression with
![]() $\alpha $
-code m for any
$\alpha $
-code m for any
![]() $m,n \in \mathbb {N}$
, or that the arithmetisations of certain additional string-theoretic properties regarding
$m,n \in \mathbb {N}$
, or that the arithmetisations of certain additional string-theoretic properties regarding
![]() $\preceq $
are provable in T, as extracted from my initial analysis given above. As we have already seen, monotonicity can not however be derived from this conception of structure preservation.
$\preceq $
are provable in T, as extracted from my initial analysis given above. As we have already seen, monotonicity can not however be derived from this conception of structure preservation.
Finally, the very assumption that both
![]() ${\preceq }$
and
${\preceq }$
and
![]() ${\leq }$
are parthood relations appears to rely on specific and quite arbitrary representational choices of strings and numbers. While
${\leq }$
are parthood relations appears to rely on specific and quite arbitrary representational choices of strings and numbers. While
![]() $\preceq $
may be understood as a parthood relation on strings via their natural interpretation as geometric objects, it is less clear how
$\preceq $
may be understood as a parthood relation on strings via their natural interpretation as geometric objects, it is less clear how
![]() $\leq $
can be given such a mereological interpretation. One way is to represent numbers as strings of strokes. Another approach is to represent numbers as Von Neumann ordinals, and to understand the parthood relation on sets as the containment relation
$\leq $
can be given such a mereological interpretation. One way is to represent numbers as strings of strokes. Another approach is to represent numbers as Von Neumann ordinals, and to understand the parthood relation on sets as the containment relation
![]() $\subseteq $
(see e.g., Lewis, Reference Lewis1991). Then
$\subseteq $
(see e.g., Lewis, Reference Lewis1991). Then
![]() $\leq $
is indeed a parthood relation on numbers. However, this interpretation breaks down for other reasonable representations, such as Zermelo ordinals or equivalence classes of finite sets under the equivalence relation of equinumerosity. Yet another approach is to construe strings and numbers as free algebras and to extract a parthood relation from their underlying term algebras (see Burris & Sankappanavar, Reference Burris and Sankappanavar1981). In the case of numbers, this approach indeed yields
$\leq $
is indeed a parthood relation on numbers. However, this interpretation breaks down for other reasonable representations, such as Zermelo ordinals or equivalence classes of finite sets under the equivalence relation of equinumerosity. Yet another approach is to construe strings and numbers as free algebras and to extract a parthood relation from their underlying term algebras (see Burris & Sankappanavar, Reference Burris and Sankappanavar1981). In the case of numbers, this approach indeed yields
![]() $\leq $
as our parthood relation. If we take strings to be generated by the concatenation operation, then
$\leq $
as our parthood relation. If we take strings to be generated by the concatenation operation, then
![]() $A^\ast $
can be viewed as a free semigroup and we extract
$A^\ast $
can be viewed as a free semigroup and we extract
![]() $\preceq $
as a parthood relation on strings. However, as we have seen above, we can also take strings to be generated from the empty string by the successor functions
$\preceq $
as a parthood relation on strings. However, as we have seen above, we can also take strings to be generated from the empty string by the successor functions
![]() $\mathsf {S}_a$
. This results in a different free algebra, according to which the parts of any string are exactly its initial strings. Similarly, parthood holds between strings and their final strings if we conceive of
$\mathsf {S}_a$
. This results in a different free algebra, according to which the parts of any string are exactly its initial strings. Similarly, parthood holds between strings and their final strings if we conceive of
![]() $\mathsf {S}_a$
as prefixing, instead of appending, a to input strings.
$\mathsf {S}_a$
as prefixing, instead of appending, a to input strings.
In addition to these conceptual reservations, the obtained results also suggest that monotonicity is a property orthogonal to the invariance problems considered in this paper.Footnote
19
Namely, there exist both monotonic and nonmonotonic numberings which satisfy Gödel’s Second Theorem as well as Tarski’s theorems (take any standard numbering and Visser’s (Reference Visser, Gabbay and Guenthner1989) self-referential numbering ![]() respectively), as well as monotonic and nonmonotonic numberings which violate these theorems (e.g.,
respectively), as well as monotonic and nonmonotonic numberings which violate these theorems (e.g.,
![]() $\zeta $
and
$\zeta $
and
![]() $\delta $
respectively).
$\delta $
respectively).
Consequently, in what follows, admissible numberings are not required to be monotonic. This also permits a more general approach, since monotonicity constitutes a proper constraint on computable simulations.Footnote 20
4 Invariance of Gödel’s Second Theorem
Before we turn to the proofs of the desired invariance claims, it will be convenient to introduce an equivalence relation on numberings, which preserves important computational properties. By a powerful theorem due to Mal’cev (Reference Mal’cev1961), all admissible numberings will be shown to be equivalent in this sense. From this we can in particular conclude that computable simulativity is extensionally equivalent to the criteria of computable translatability, sequence-admissibility and EFS-admissibility, introduced in §3.3.
4.1 Equivalence of numberings
Definition 4.4 (Manin, Reference Manin2009)
Let S be a set. We call two numberings
![]() $\alpha $
,
$\alpha $
,
![]() $\beta $
of S equivalent (and write
$\beta $
of S equivalent (and write
![]() $\alpha \sim \beta $
), if
$\alpha \sim \beta $
), if
![]() $\alpha \circ \beta ^{-1} \colon \beta (S) \to \mathbb {N}$
and
$\alpha \circ \beta ^{-1} \colon \beta (S) \to \mathbb {N}$
and
![]() $\beta \circ \alpha ^{-1} \colon \alpha (S) \to \mathbb {N}$
are recursive.
$\beta \circ \alpha ^{-1} \colon \alpha (S) \to \mathbb {N}$
are recursive.
It can be easily checked that
![]() $\sim $
is a partial equivalence relation, i.e.,
$\sim $
is a partial equivalence relation, i.e.,
![]() $\sim $
is symmetric and transitive. If we require numberings to have a decidable image, then
$\sim $
is symmetric and transitive. If we require numberings to have a decidable image, then
![]() $\sim $
is also reflexive. In particular,
$\sim $
is also reflexive. In particular,
![]() $\sim $
is an equivalence relation on the set of computable simulations of S.
$\sim $
is an equivalence relation on the set of computable simulations of S.
A subset
![]() $R \subseteq S$
is called decidable, recursively enumerable, arithmetical relative to a numbering
$R \subseteq S$
is called decidable, recursively enumerable, arithmetical relative to a numbering
![]() $\alpha $
, if the set
$\alpha $
, if the set
![]() $\alpha (R)$
has the respective property. The following lemma shows that these properties are invariant with regard to equivalent computable simulations.Footnote
21
$\alpha (R)$
has the respective property. The following lemma shows that these properties are invariant with regard to equivalent computable simulations.Footnote
21
Lemma 4.5. Let
![]() $S_i$
be sets and let
$S_i$
be sets and let
![]() $\alpha _i$
and
$\alpha _i$
and
![]() $\beta _i$
be numberings of
$\beta _i$
be numberings of
![]() $S_i$
such that
$S_i$
such that
![]() ${\alpha _i \sim \beta _i}$
, for
${\alpha _i \sim \beta _i}$
, for
![]() $i \in \{1, \ldots ,k\}$
and
$i \in \{1, \ldots ,k\}$
and
![]() $k \in \mathbb {N}$
. Then for any subset
$k \in \mathbb {N}$
. Then for any subset
![]() $R \subseteq S_1 \times \ldots \times S_k$
the set
$R \subseteq S_1 \times \ldots \times S_k$
the set
![]() $\alpha _1 \times \ldots \times \alpha _k (R) := \{ \langle \alpha _1(s_1), \ldots , \alpha _k(s_k) \rangle \mid \langle s_1,\ldots ,s_k \rangle \in R \}$
is decidable, recursively enumerable, arithmetical iff
$\alpha _1 \times \ldots \times \alpha _k (R) := \{ \langle \alpha _1(s_1), \ldots , \alpha _k(s_k) \rangle \mid \langle s_1,\ldots ,s_k \rangle \in R \}$
is decidable, recursively enumerable, arithmetical iff
![]() $\beta _1 \times \ldots \times \beta _k (R)$
has the respective property.
$\beta _1 \times \ldots \times \beta _k (R)$
has the respective property.
The next theorem due to Mal’cev (Reference Mal’cev1961) serves as a powerful tool in proving invariance.Footnote 22
Theorem 4.6. Any two computable simulations
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
of
$\beta $
of
![]() $A^\ast $
are equivalent, i.e.,
$A^\ast $
are equivalent, i.e.,
![]() $\alpha \sim \beta $
.
$\alpha \sim \beta $
.
From Lemma 4.5 and Theorem 4.6 we can conclude the extensional equivalence of computable simulativity and the three criteria considered in §3.3.
Corollary 4.7. Let
![]() $\alpha $
be a numbering of
$\alpha $
be a numbering of
![]() $A^\ast $
. The following are equivalent:
$A^\ast $
. The following are equivalent:
-
1.
 $\alpha $
is a computable simulation of
$\alpha $
is a computable simulation of
 $A^\ast $
;
$A^\ast $
; -
2.
 $\alpha $
is computably translatable to the standard numbering
$\alpha $
is computably translatable to the standard numbering
 $\gamma $
;
$\gamma $
; -
3.
 $\alpha $
is sequence-admissible;
$\alpha $
is sequence-admissible; -
4.
 $\alpha $
is EFS-admissible.
$\alpha $
is EFS-admissible.
Proof.
![]() $(3 \Rightarrow 1)$
and
$(3 \Rightarrow 1)$
and
![]() $(4 \Rightarrow 1)$
are immediate.
$(4 \Rightarrow 1)$
are immediate.
![]() $(1 \Leftrightarrow 2)$
and
$(1 \Leftrightarrow 2)$
and
![]() $(1 \Rightarrow 4)$
follow from Theorem 4.6 and Lemma 4.5.
$(1 \Rightarrow 4)$
follow from Theorem 4.6 and Lemma 4.5.
![]() $(1 \Rightarrow 3)$
: It is easy to check that Smith’s (Reference Smith2007) numbering
$(1 \Rightarrow 3)$
: It is easy to check that Smith’s (Reference Smith2007) numbering
![]() $\gamma $
is a computable simulation as well as sequence-admissible. Then the length function and the concatenation function is recursive relative to
$\gamma $
is a computable simulation as well as sequence-admissible. Then the length function and the concatenation function is recursive relative to
![]() $\langle \gamma ,\operatorname {id} \rangle $
and
$\langle \gamma ,\operatorname {id} \rangle $
and
![]() $\langle \gamma \times \gamma , \gamma \rangle $
respectively (see footnote 16). For any computable simulation
$\langle \gamma \times \gamma , \gamma \rangle $
respectively (see footnote 16). For any computable simulation
![]() $\alpha $
of
$\alpha $
of
![]() $A^\ast $
, these functions are also recursive relative to
$A^\ast $
, these functions are also recursive relative to
![]() $\langle \alpha ,\operatorname {id} \rangle $
and
$\langle \alpha ,\operatorname {id} \rangle $
and
![]() $\langle \alpha \times \alpha , \alpha \rangle $
respectively, since
$\langle \alpha \times \alpha , \alpha \rangle $
respectively, since
![]() $\alpha \sim \gamma $
(Theorem 4.6) and r.e. sets are invariant with regard to equivalent numberings by Lemma 4.5. □
$\alpha \sim \gamma $
(Theorem 4.6) and r.e. sets are invariant with regard to equivalent numberings by Lemma 4.5. □
4.2 Invariance proofs
We start by proving the invariance of the semantic version of Tarski’s Theorem, which is also shown in Manin (Reference Manin2009, p. 240):Footnote 23
Theorem 4.8. For all computable simulations
![]() $\alpha $
(of
$\alpha $
(of
![]() $A^\ast $
), the set
$A^\ast $
), the set
![]() $\{ \alpha (\varphi ) \mid \mathbb {N} \models \varphi \}$
is not arithmetical.
$\{ \alpha (\varphi ) \mid \mathbb {N} \models \varphi \}$
is not arithmetical.
Proof. Let
![]() $\alpha $
be any computable simulation of
$\alpha $
be any computable simulation of
![]() $A^\ast $
. Since
$A^\ast $
. Since
![]() $\gamma $
is standard, Tarski’s Theorem holds with regard to
$\gamma $
is standard, Tarski’s Theorem holds with regard to
![]() $\gamma $
, i.e.,
$\gamma $
, i.e.,
![]() $\{ \gamma (\varphi ) \mid \mathbb {N} \models \varphi \}$
is not arithmetical. By Lemma 4.5 and Theorem 4.6 also
$\{ \gamma (\varphi ) \mid \mathbb {N} \models \varphi \}$
is not arithmetical. By Lemma 4.5 and Theorem 4.6 also
![]() $\{ \alpha (\varphi ) \mid \mathbb {N} \models \varphi \}$
is not arithmetical. □
$\{ \alpha (\varphi ) \mid \mathbb {N} \models \varphi \}$
is not arithmetical. □
In order to establish the invariance of Gödel’s Second Theorem, we first formalise certain properties of the equivalence of numberings in
![]() $\mathsf {R}$
.
$\mathsf {R}$
.
Definition 4.9. Let
![]() $\alpha \colon B \to \mathbb {N}$
be a function with
$\alpha \colon B \to \mathbb {N}$
be a function with
![]() $B \subseteq \mathbb {N}$
and let
$B \subseteq \mathbb {N}$
and let
![]() $f(x,y) \in \mathit {Fml}$
be a binumeration of (the graph of)
$f(x,y) \in \mathit {Fml}$
be a binumeration of (the graph of)
![]() $\alpha $
. We call
$\alpha $
. We call
![]() $f(x,y)$
an inj-binumeration of
$f(x,y)$
an inj-binumeration of
![]() $\alpha $
if
$\alpha $
if
![]() $\mathsf {R} \vdash \forall x, y\, ( f(x,\overline {m}) \wedge f(y,\overline {m}) \rightarrow x=y )$
, for all
$\mathsf {R} \vdash \forall x, y\, ( f(x,\overline {m}) \wedge f(y,\overline {m}) \rightarrow x=y )$
, for all
![]() $m \in \alpha (B)$
.
$m \in \alpha (B)$
.
Lemma 4.10. Let
![]() $B \subseteq \mathbb {N}$
. For each injective recursive function
$B \subseteq \mathbb {N}$
. For each injective recursive function
![]() $\alpha \colon B \to \mathbb {N}$
there exists an inj-binumeration thereof.
$\alpha \colon B \to \mathbb {N}$
there exists an inj-binumeration thereof.
Proof. Let
![]() $\alpha \colon B \to \mathbb {N}$
be an injective recursive function and let
$\alpha \colon B \to \mathbb {N}$
be an injective recursive function and let
![]() $\alpha '$
be a total recursive function extending
$\alpha '$
be a total recursive function extending
![]() $\alpha $
(see §2.1). By Theorem II.6 of Tarski et al. (Reference Tarski, Mostowski and Robinson1953) there is a binumeration
$\alpha $
(see §2.1). By Theorem II.6 of Tarski et al. (Reference Tarski, Mostowski and Robinson1953) there is a binumeration
![]() $g(x,y)$
of
$g(x,y)$
of
![]() $\alpha '$
and a binumeration
$\alpha '$
and a binumeration
![]() $\beta (x)$
of B. Then
$\beta (x)$
of B. Then
![]() ${f'(x,y) \equiv \beta (x) \wedge g(x,y)}$
is a binumeration of
${f'(x,y) \equiv \beta (x) \wedge g(x,y)}$
is a binumeration of
![]() $\alpha $
. We define
$\alpha $
. We define
In order to show that
![]() $f(x,y)$
numerates
$f(x,y)$
numerates
![]() $\alpha $
, let
$\alpha $
, let
![]() $n, m \in \mathbb {N}$
be such that
$n, m \in \mathbb {N}$
be such that
![]() $\alpha (n)=m$
. Since
$\alpha (n)=m$
. Since
![]() $f'(x,y)$
binumerates
$f'(x,y)$
binumerates
![]() $\alpha $
, we have
$\alpha $
, we have
![]() $ \mathsf {R} \vdash f'(\overline {n},\overline {m})$
and
$ \mathsf {R} \vdash f'(\overline {n},\overline {m})$
and
![]() $\mathsf {R} \vdash \neg f'(\overline {k},\overline {m})$
for all
$\mathsf {R} \vdash \neg f'(\overline {k},\overline {m})$
for all
![]() $k < n$
. Thus
$k < n$
. Thus
![]() $\mathsf {R} \vdash f'(\overline {k},\overline {m}) \rightarrow \overline {n} = \overline {k}$
for all
$\mathsf {R} \vdash f'(\overline {k},\overline {m}) \rightarrow \overline {n} = \overline {k}$
for all
![]() $k < n$
, which yields
$k < n$
, which yields
![]() $\mathsf {R} \vdash f'(\overline {k},\overline {m}) \rightarrow \overline {n} = \overline {k}$
for all
$\mathsf {R} \vdash f'(\overline {k},\overline {m}) \rightarrow \overline {n} = \overline {k}$
for all
![]() $k \leq n$
. Using
$k \leq n$
. Using
![]() $\mathsf {R4}$
yields (
$\mathsf {R4}$
yields (
![]() $\ast $
)
$\ast $
)
![]() $\mathsf {R} \vdash \forall z \leq \overline {n}\, (\;f'(z,\overline {m}) \rightarrow \overline {n} = z)$
. Thus
$\mathsf {R} \vdash \forall z \leq \overline {n}\, (\;f'(z,\overline {m}) \rightarrow \overline {n} = z)$
. Thus
![]() $\mathsf {R} \vdash f(\overline {n},\overline {m})$
. Since
$\mathsf {R} \vdash f(\overline {n},\overline {m})$
. Since
![]() $\mathsf {R} \vdash \neg f'(\overline {n},\overline {m}) \rightarrow \neg f(\overline {n},\overline {m})$
and
$\mathsf {R} \vdash \neg f'(\overline {n},\overline {m}) \rightarrow \neg f(\overline {n},\overline {m})$
and
![]() $\mathsf {R}$
is consistent,
$\mathsf {R}$
is consistent,
![]() $f(x,y)$
also binumerates
$f(x,y)$
also binumerates
![]() $\alpha $
.
$\alpha $
.
Let
![]() $m \in \alpha (B)$
. Let
$m \in \alpha (B)$
. Let
![]() $n \in \mathbb {N}$
be such that (
$n \in \mathbb {N}$
be such that (
![]() $\ast \ast $
)
$\ast \ast $
)
![]() $\mathsf {R} \vdash f(\overline {n},\overline {m})$
. In order to show that
$\mathsf {R} \vdash f(\overline {n},\overline {m})$
. In order to show that
![]() $f(x,y)$
is an inj-binumeration it suffices to show that
$f(x,y)$
is an inj-binumeration it suffices to show that
![]() $\mathsf {R} \vdash \forall x (\;f(x,\overline {m}) \rightarrow x = \overline {n})$
, which we prove in the following derivation in
$\mathsf {R} \vdash \forall x (\;f(x,\overline {m}) \rightarrow x = \overline {n})$
, which we prove in the following derivation in
![]() $\mathsf {R}$
:
$\mathsf {R}$
:

□
Lemma 4.11. Let
![]() $B \subseteq \mathbb {N}$
and
$B \subseteq \mathbb {N}$
and
![]() $\alpha \colon B \to \mathbb {N}$
be an injective recursive function. Let
$\alpha \colon B \to \mathbb {N}$
be an injective recursive function. Let
![]() $f(x,y)$
be an inj-binumeration of
$f(x,y)$
be an inj-binumeration of
![]() $\alpha $
and let
$\alpha $
and let
![]() $\varphi (x) \in \mathit {Fml}$
. Then there exists
$\varphi (x) \in \mathit {Fml}$
. Then there exists
![]() ${\psi (y) \in \mathit {Fml}}$
such that
${\psi (y) \in \mathit {Fml}}$
such that
![]() $\mathsf {R} \vdash f(\overline {n},\overline {m}) \rightarrow ( \varphi (\overline {n}) \leftrightarrow \psi (\overline {m}))$
, for all
$\mathsf {R} \vdash f(\overline {n},\overline {m}) \rightarrow ( \varphi (\overline {n}) \leftrightarrow \psi (\overline {m}))$
, for all
![]() $n \in \mathbb {N}$
and
$n \in \mathbb {N}$
and
![]() $m \in \alpha (B)$
.
$m \in \alpha (B)$
.
If moreover T is
![]() $\Sigma ^0_k$
-sound for some
$\Sigma ^0_k$
-sound for some
![]() $k \geq 1$
such that
$k \geq 1$
such that
 $f(x,y) \in \Sigma ^0_k$
and
$f(x,y) \in \Sigma ^0_k$
and
![]() $\varphi (x)$
is a
$\varphi (x)$
is a
![]() $\Sigma ^0_1$
-numeration of
$\Sigma ^0_1$
-numeration of
![]() $C \subseteq B$
in T, then
$C \subseteq B$
in T, then
![]() $\psi (y)$
numerates
$\psi (y)$
numerates
![]() $\alpha (C)$
in T.
$\alpha (C)$
in T.
Proof. Define
![]() $\psi (y) \equiv \exists z (\;f(z,y) \wedge \varphi (z ) )$
. Using the fact that
$\psi (y) \equiv \exists z (\;f(z,y) \wedge \varphi (z ) )$
. Using the fact that
![]() $f(x,y)$
is an inj-binumeration of
$f(x,y)$
is an inj-binumeration of
![]() $\alpha $
, it is straightforward to show that
$\alpha $
, it is straightforward to show that
![]() ${\mathsf {R} \vdash f(\overline {n},\overline {m}) \rightarrow ( \varphi (\overline {n}) \leftrightarrow \psi (\overline {m}))}$
.
${\mathsf {R} \vdash f(\overline {n},\overline {m}) \rightarrow ( \varphi (\overline {n}) \leftrightarrow \psi (\overline {m}))}$
.
Assume now that T is
![]() $\Sigma ^0_k$
-sound for some
$\Sigma ^0_k$
-sound for some
![]() $k \geq 1$
and
$k \geq 1$
and
 $f(x,y) \in \Sigma ^0_k$
. Let
$f(x,y) \in \Sigma ^0_k$
. Let
![]() $\varphi (x)$
be a
$\varphi (x)$
be a
![]() $\Sigma ^0_1$
-numeration of
$\Sigma ^0_1$
-numeration of
![]() $C \subseteq B$
in T. In order to show that
$C \subseteq B$
in T. In order to show that
![]() $\psi (y)$
numerates
$\psi (y)$
numerates
![]() $\alpha (C)$
in T, let
$\alpha (C)$
in T, let
![]() $m \in \mathbb {N}$
be such that
$m \in \mathbb {N}$
be such that
![]() $T \vdash \psi ( \overline {m})$
, i.e.,
$T \vdash \psi ( \overline {m})$
, i.e.,
![]() $T \vdash \exists z (\;f(z,\overline {m}) \wedge \varphi (z ) )$
by definition of
$T \vdash \exists z (\;f(z,\overline {m}) \wedge \varphi (z ) )$
by definition of
![]() $\psi $
. Since
$\psi $
. Since
 $\exists z (\;f(z,\overline {m}) \wedge \varphi (z ) ) \in \Sigma ^0_k$
, there exists
$\exists z (\;f(z,\overline {m}) \wedge \varphi (z ) ) \in \Sigma ^0_k$
, there exists
![]() $n \in \mathbb {N}$
such that
$n \in \mathbb {N}$
such that
![]() $\mathbb {N} \models f(\overline {n},\overline {m}) \wedge \varphi (\overline {n} )$
by the
$\mathbb {N} \models f(\overline {n},\overline {m}) \wedge \varphi (\overline {n} )$
by the
![]() $\Sigma ^0_k$
-soundness of T. Since
$\Sigma ^0_k$
-soundness of T. Since
![]() $f(x,y)$
is a binumeration of
$f(x,y)$
is a binumeration of
![]() $\alpha $
it also defines
$\alpha $
it also defines
![]() $\alpha $
, hence
$\alpha $
, hence
![]() $\alpha (n)=m$
. Since
$\alpha (n)=m$
. Since
![]() $\varphi $
is a
$\varphi $
is a
![]() $\Sigma ^0_1$
-numeration of C in T we get
$\Sigma ^0_1$
-numeration of C in T we get
![]() $n \in C$
by
$n \in C$
by
![]() $\Sigma ^0_1$
-completeness of T. Thus
$\Sigma ^0_1$
-completeness of T. Thus
![]() $m = \alpha (n) \in \alpha (C)$
obtains. The proof of the other direction is immediate. □
$m = \alpha (n) \in \alpha (C)$
obtains. The proof of the other direction is immediate. □
In addition to proving the invariance of Gödel’s Second Theorem, the above method can also be used to simplify proofs of metamathematical theorems. For instance, they provide a proof of the Diagonal Lemma which avoids the usual tedious process of arithmetisation (in particular of the numeral and the substitution functions).
Lemma 4.12. Let
![]() $T \supseteq \mathsf {R}$
, let
$T \supseteq \mathsf {R}$
, let
![]() $\alpha $
be an admissible numbering and let
$\alpha $
be an admissible numbering and let
![]() $\varphi (x) \in \mathit {Fml}$
with free variable x. Then there exists a sentence
$\varphi (x) \in \mathit {Fml}$
with free variable x. Then there exists a sentence
![]() $\lambda $
such that
$\lambda $
such that
![]() .
.
Proof. Let ![]() be the numbering introduced in Visser (Reference Visser, Gabbay and Guenthner1989, pp. 159f.). It can be easily checked that
be the numbering introduced in Visser (Reference Visser, Gabbay and Guenthner1989, pp. 159f.). It can be easily checked that
![]() is a computable simulation. Thus
is a computable simulation. Thus
![]() by Theorem 4.6. By Lemma 4.11 there exists a formula
by Theorem 4.6. By Lemma 4.11 there exists a formula
![]() $\psi (y)$
such that for all
$\psi (y)$
such that for all
![]() $n \in \mathbb {N}$
and
$n \in \mathbb {N}$
and ![]() we have
we have
![]() $(\ast ) \mathsf {R} \vdash f(\overline {n},\overline {m}) \rightarrow ( \varphi (\overline {n}) \leftrightarrow \psi (\overline {m})),$
where f binumerates
$(\ast ) \mathsf {R} \vdash f(\overline {n},\overline {m}) \rightarrow ( \varphi (\overline {n}) \leftrightarrow \psi (\overline {m})),$
where f binumerates
![]() . By definition of
. By definition of
![]() , for any given formula
, for any given formula
![]() $\psi (y)$
there exists
$\psi (y)$
there exists
![]() $k \in \mathbb {N}$
such that
$k \in \mathbb {N}$
such that
![]() (Visser, Reference Visser, Gabbay and Guenthner1989, p. 159). Hence
(Visser, Reference Visser, Gabbay and Guenthner1989, p. 159). Hence
 and therefore
and therefore
 . Setting
. Setting
![]() $\lambda \equiv \psi (\overline {k})$
,
$\lambda \equiv \psi (\overline {k})$
,
![]() $(\ast )$
yields
$(\ast )$
yields ![]() . Thus
. Thus
![]() . □
. □
Note that neither the definition of ![]() nor the proofs of Theorem 4.6 and Lemma 4.11 employ any arithmetisation of the usual syntactic properties and operations.
nor the proofs of Theorem 4.6 and Lemma 4.11 employ any arithmetisation of the usual syntactic properties and operations.
Corollary 4.13 (Syntactic version of Tarski’s Theorem)
Let
![]() $T \supseteq \mathsf {R}$
and let
$T \supseteq \mathsf {R}$
and let
![]() $\alpha $
be an admissible numbering. Then there exists no formula
$\alpha $
be an admissible numbering. Then there exists no formula
![]() $\tau (x) \in \mathit {Fml}$
with free variable x such that
$\tau (x) \in \mathit {Fml}$
with free variable x such that
![]() for every sentence
for every sentence
![]() $\varphi $
.
$\varphi $
.
Using Lemma 4.12 and the usual schematic “modal reasoning” we can also prove the invariance of Löb’s Theorem as well as its formalised version regarding admissible numberings. In particular, we can prove the desired
Theorem 4.14 (Invariance of Gödel’s Second Theorem)
![]() , for all admissible numberings
, for all admissible numberings
![]() $\alpha $
and arithmetical formulæ
$\alpha $
and arithmetical formulæ
![]() $\mathsf {Pr}^{\alpha }(x)$
satisfying Löb
$\mathsf {Pr}^{\alpha }(x)$
satisfying Löb
![]() $(T, \alpha $
).
$(T, \alpha $
).
The reader might observe that the formulation of Theorem 4.14 already presupposes the employed provability predicates to satisfy Löb’s conditions. Since these conditions allow for the schematic “modal reasoning” sufficient to prove Gödel’s Second Theorem (or more generally, Löb’s Theorem), the problem of the invariance of Gödel’s Second Theorem with regard to numberings was essentially reduced to establishing an invariant version of the Diagonal lemma (Lemma 4.12).
However, no information about the existence of provability predicates satisfying Löb’s conditions with regard to varying numberings is provided by Theorem 4.14. As a result, the reader might wonder how much Theorem 4.14 improves on the classical result by Hilbert, Bernays and Löb (Theorem 2.1). For it could be the case that only the typically employed, standard numberings yield nontrivialFootnote 24 provability predicates satisfying Löb’s conditions, rendering Theorem 4.14 a trivial extension of the standard Theorem 2.1 (at least from an extensional perspective).
The next theorem shows that in fact every admissible numbering
![]() $\alpha $
allows for the construction of a nontrivial provability predicate satisfying Löb’s conditions relative to
$\alpha $
allows for the construction of a nontrivial provability predicate satisfying Löb’s conditions relative to
![]() $\alpha $
. This establishes Theorem 4.14 as a proper extension of the classical results based on a specific numbering.
$\alpha $
. This establishes Theorem 4.14 as a proper extension of the classical results based on a specific numbering.
Let
![]() $\Omega _1 \equiv \forall x,y\, \exists z\, \mathsf {o}(x,y,z)$
where
$\Omega _1 \equiv \forall x,y\, \exists z\, \mathsf {o}(x,y,z)$
where
![]() $\mathsf {o}(x,y,z)$
is a standard binumeration of (the graph of) the polynomially growing function
$\mathsf {o}(x,y,z)$
is a standard binumeration of (the graph of) the polynomially growing function
![]() $\omega _1(x,y) = x^{\log y}$
, where
$\omega _1(x,y) = x^{\log y}$
, where
![]() $\log x = \max \{y \mid 2^y \leq x \}$
. Let
$\log x = \max \{y \mid 2^y \leq x \}$
. Let
![]() $\mathsf {Exp} \equiv \forall x,y\, \exists z\, \mathsf {e}(x,y,z)$
, where
$\mathsf {Exp} \equiv \forall x,y\, \exists z\, \mathsf {e}(x,y,z)$
, where
![]() $\mathsf {e}(x,y,z)$
is a standard binumeration of (the graph of) the exponentiation function given by
$\mathsf {e}(x,y,z)$
is a standard binumeration of (the graph of) the exponentiation function given by
![]() $(x,y) \mapsto x^y$
.Footnote
25
$(x,y) \mapsto x^y$
.Footnote
25
Theorem 4.15. For all admissible numberings
![]() $\alpha $
and
$\alpha $
and
![]() ${\Sigma }^{0}_{2}$
-sound theories T extending
${\Sigma }^{0}_{2}$
-sound theories T extending
![]() $\mathsf {I} \Delta _0 + \Omega _1$
or
$\mathsf {I} \Delta _0 + \Omega _1$
or
![]() $\mathsf {I} \Delta _0 + \mathsf {Exp}$
, there exists a formula
$\mathsf {I} \Delta _0 + \mathsf {Exp}$
, there exists a formula
![]() $\mathsf {Pr}_{T}^{\alpha }(x)$
satisfying Löb
$\mathsf {Pr}_{T}^{\alpha }(x)$
satisfying Löb
![]() $(T, \alpha) $
which numerates
$(T, \alpha) $
which numerates
![]() $\{ \alpha (\varphi ) \mid T \vdash \varphi \}$
in T.
$\{ \alpha (\varphi ) \mid T \vdash \varphi \}$
in T.
Before proving the theorem we show a useful auxiliary lemma.
Lemma 4.16. Let
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
be equivalent numberings. Then there exists a binumeration
$\beta $
be equivalent numberings. Then there exists a binumeration
![]() $f(x,y)$
of
$f(x,y)$
of
![]() $\beta \circ \alpha ^{-1}$
such that for each
$\beta \circ \alpha ^{-1}$
such that for each
![]() $\mathsf {Pr}^{\alpha }(x)$
satisfying Löb
$\mathsf {Pr}^{\alpha }(x)$
satisfying Löb
![]() $(T, \alpha) $
there exists
$(T, \alpha) $
there exists
![]() $\mathsf {Pr}^{\beta }(x)$
satisfying Löb
$\mathsf {Pr}^{\beta }(x)$
satisfying Löb
![]() $(T, \beta),$
such that for all
$(T, \beta),$
such that for all
![]() $n \in \mathbb {N}$
and
$n \in \mathbb {N}$
and
![]() $m \in \beta (A^\ast )$
$m \in \beta (A^\ast )$
If moreover T is
![]() $\Sigma ^0_2$
-sound and
$\Sigma ^0_2$
-sound and
![]() $\mathsf {Pr}^{\alpha }(x)$
is a
$\mathsf {Pr}^{\alpha }(x)$
is a
![]() $\Sigma ^0_1$
-numeration of
$\Sigma ^0_1$
-numeration of
![]() $\alpha (T^{\vdash } )$
in T, then
$\alpha (T^{\vdash } )$
in T, then
![]() $\mathsf {Pr}^{\beta }(x)$
numerates
$\mathsf {Pr}^{\beta }(x)$
numerates
![]() $\beta (T^{\vdash } ) $
in T.
$\beta (T^{\vdash } ) $
in T.
Proof. By Lemma 4.10 & 4.11 there exists a binumeration
![]() $f(x,y)$
of
$f(x,y)$
of
![]() $\beta \circ \alpha ^{-1}$
and a formula
$\beta \circ \alpha ^{-1}$
and a formula
![]() $\mathsf {Pr}^{\beta }(x)$
such that
$\mathsf {Pr}^{\beta }(x)$
such that
for all
![]() $n \in \mathbb {N}$
and
$n \in \mathbb {N}$
and
![]() $m \in \beta (A^\ast )$
. We show now that
$m \in \beta (A^\ast )$
. We show now that
![]() $\mathsf {Pr}^{\beta }(x)$
satisfies Löb(
$\mathsf {Pr}^{\beta }(x)$
satisfies Löb(
![]() $T, \beta $
):
$T, \beta $
):
-
i. If
 $T \vdash \varphi $
, then
$T \vdash \varphi $
, then
 , since
, since
 $\mathsf {Pr}^{\alpha }(x)$
satisfies Löb1
$\mathsf {Pr}^{\alpha }(x)$
satisfies Löb1
 $^\alpha $
. We havesince
$^\alpha $
. We havesince
 $f(x,y)$
binumerates
$f(x,y)$
binumerates
 $\beta \circ \alpha ^{-1}$
. It then follows from 2 thatThus
$\beta \circ \alpha ^{-1}$
. It then follows from 2 thatThus
 .
.
-
ii. Let
 $\varphi , \psi \in \mathit {Fml}$
. Since
$\varphi , \psi \in \mathit {Fml}$
. Since
 $f(x,y)$
binumerates
$f(x,y)$
binumerates
 $\beta \circ \alpha ^{-1}$
we haveUsing 2 we therefore get
$\beta \circ \alpha ^{-1}$
we haveUsing 2 we therefore get (3)Similarly, we show
(3)Similarly, we show (4)and
(4)and (5)Since
(5)Since
 $\mathsf {Pr}^{\alpha }(x)$
satisfies Löb2
$\mathsf {Pr}^{\alpha }(x)$
satisfies Löb2
 $^\alpha $
and using 3–5 we conclude that
$^\alpha $
and using 3–5 we conclude that
-
iii. Let
 $\varphi \in \mathit {Fml}$
. As in (ii) we show(6)Since
$\varphi \in \mathit {Fml}$
. As in (ii) we show(6)Since
 $\mathsf {Pr}^{\alpha }(x)$
satisfies Löb3
$\mathsf {Pr}^{\alpha }(x)$
satisfies Löb3
 $^\alpha $
and using 4 & 6 we get(7)Application of Löb1
$^\alpha $
and using 4 & 6 we get(7)Application of Löb1
 $^\beta $
to 4 then yieldsApplying Löb2
$^\beta $
to 4 then yieldsApplying Löb2
 $^\beta $
then yieldsIn combination with 7 we thus obtain
$^\beta $
then yieldsIn combination with 7 we thus obtain

Assume now that T is
![]() $\Sigma ^0_2$
-sound and that
$\Sigma ^0_2$
-sound and that
![]() $\mathsf {Pr}^{\alpha }(x)$
is a
$\mathsf {Pr}^{\alpha }(x)$
is a
![]() $\Sigma ^0_1$
-numeration of
$\Sigma ^0_1$
-numeration of
![]() $\alpha (T^{\vdash } )$
in T. Since
$\alpha (T^{\vdash } )$
in T. Since
![]() $\alpha (A^\ast )$
is decidable, inspection of the proof of Lemma 4.10 shows that we can choose
$\alpha (A^\ast )$
is decidable, inspection of the proof of Lemma 4.10 shows that we can choose
 $f(x,y) \in \Delta ^0_2$
. Then
$f(x,y) \in \Delta ^0_2$
. Then
![]() $\mathsf {Pr}^{\beta }(x)$
numerates
$\mathsf {Pr}^{\beta }(x)$
numerates
![]() $\beta (T^{\vdash } )$
in T by Lemma 4.11. □
$\beta (T^{\vdash } )$
in T by Lemma 4.11. □
Proof of Theorem 4.15
Let
![]() $\gamma $
be a standard numbering and let
$\gamma $
be a standard numbering and let
![]() $\mathsf {Pr}^{\gamma }(x)$
a standard
$\mathsf {Pr}^{\gamma }(x)$
a standard
![]() $\Sigma ^0_1$
-provability predicate satisfying Löb(
$\Sigma ^0_1$
-provability predicate satisfying Löb(
![]() $T, \gamma $
) and numerating
$T, \gamma $
) and numerating
![]() $\gamma (T^\vdash )$
in T (see for instance Wilkie & Paris, Reference Wilkie and Paris1987 if
$\gamma (T^\vdash )$
in T (see for instance Wilkie & Paris, Reference Wilkie and Paris1987 if
![]() $T \supseteq \mathsf {I} \Delta _0 + \Omega _1$
or Rautenberg, Reference Rautenberg2006, chap. 7 if
$T \supseteq \mathsf {I} \Delta _0 + \Omega _1$
or Rautenberg, Reference Rautenberg2006, chap. 7 if
![]() $T \supseteq \mathsf {I} \Delta _0 + \mathsf {Exp}$
). By Theorem 4.6,
$T \supseteq \mathsf {I} \Delta _0 + \mathsf {Exp}$
). By Theorem 4.6,
![]() $\alpha \sim \gamma $
. Lemma 4.16 then yields a formula
$\alpha \sim \gamma $
. Lemma 4.16 then yields a formula
![]() $\mathsf {Pr}^{\alpha }(x)$
satisfying Löb(
$\mathsf {Pr}^{\alpha }(x)$
satisfying Löb(
![]() $T, \alpha $
), numerating
$T, \alpha $
), numerating
![]() $\alpha (T^\vdash )$
in T. □
$\alpha (T^\vdash )$
in T. □
The above lemma also provides a different proof of Theorem 4.14.
Alternative Proof of Theorem 4.14
Since
![]() $\gamma $
is a computable simulation we have
$\gamma $
is a computable simulation we have
![]() $\alpha \sim \gamma $
, by Theorem 4.6. Applying Lemma 4.16 yields a binumeration
$\alpha \sim \gamma $
, by Theorem 4.6. Applying Lemma 4.16 yields a binumeration
![]() $f(x,y)$
of
$f(x,y)$
of
![]() $\gamma \circ \alpha ^{-1}$
and a formula
$\gamma \circ \alpha ^{-1}$
and a formula
![]() $\mathsf {Pr}^{\gamma }(x)$
satisfying Löb(
$\mathsf {Pr}^{\gamma }(x)$
satisfying Löb(
![]() $T, \gamma $
), such that
$T, \gamma $
), such that
Since
![]() $\gamma $
is standard,
$\gamma $
is standard,
![]() . Thus
. Thus
![]() .□
.□
4.3 A note on intensionality
Despite its satisfaction of Löb’s conditions as well as its numeration of T-theorems, I believe that even if
![]() $\mathsf {Pr}^{\gamma }(x)$
is constructed canonically, the provability predicate
$\mathsf {Pr}^{\gamma }(x)$
is constructed canonically, the provability predicate
![]() $\mathsf {Pr}^{\alpha }(x)$
obtained in Theorem 4.15 hardly qualifies as being intensionally correct. According to the proof of Lemma 4.11,
$\mathsf {Pr}^{\alpha }(x)$
obtained in Theorem 4.15 hardly qualifies as being intensionally correct. According to the proof of Lemma 4.11,
![]() $\mathsf {Pr}^{\alpha }(x)$
is of the form
$\mathsf {Pr}^{\alpha }(x)$
is of the form
![]() $\exists z (\;f(z,x) \wedge \mathsf {Pr}^{\gamma }(z) )$
, with f being a binumeration of
$\exists z (\;f(z,x) \wedge \mathsf {Pr}^{\gamma }(z) )$
, with f being a binumeration of
![]() ${\alpha \circ \gamma ^{-1}}$
. The intensional correctness of
${\alpha \circ \gamma ^{-1}}$
. The intensional correctness of
![]() $\mathsf {Pr}^{\alpha }(x)$
therefore presumably fails, if made precise by a version of the resemblance criterion (see Halbach & Visser, Reference Halbach and Visser2014, p. 676 and footnote 9). If intensional correctness is understood by recourse to meaning postulates (see Halbach & Visser, Reference Halbach and Visser2014, p. 676), it should be noted that computable equivalence is too weak to preserve proof-theoretic properties which are not merely schematic.
$\mathsf {Pr}^{\alpha }(x)$
therefore presumably fails, if made precise by a version of the resemblance criterion (see Halbach & Visser, Reference Halbach and Visser2014, p. 676 and footnote 9). If intensional correctness is understood by recourse to meaning postulates (see Halbach & Visser, Reference Halbach and Visser2014, p. 676), it should be noted that computable equivalence is too weak to preserve proof-theoretic properties which are not merely schematic.
For instance, any intensionally correct provability predicate might be taken to satisfy global versions of Löb’s conditions (see for instance D2
![]() $^{\text {G}}$
and D3
$^{\text {G}}$
and D3
![]() $^{\text {G}}$
in Kurahashi, Reference Kurahashi2020, sec. 2.3), as opposed to the local (i.e., schematic) conditions employed in this paper. While the invariance of Gödel’s Second Theorem with regard to these conditions remains unaffected, it can be shown that there is a computable simulation
$^{\text {G}}$
in Kurahashi, Reference Kurahashi2020, sec. 2.3), as opposed to the local (i.e., schematic) conditions employed in this paper. While the invariance of Gödel’s Second Theorem with regard to these conditions remains unaffected, it can be shown that there is a computable simulation
![]() $\alpha $
such that the provability predicate
$\alpha $
such that the provability predicate
![]() $\mathsf {Pr}^{\alpha }(x)$
obtained in Theorem 4.15 does not satisfy these global conditions.
$\mathsf {Pr}^{\alpha }(x)$
obtained in Theorem 4.15 does not satisfy these global conditions.
Furthermore, computability is in general too weak to enforce an intensionally correct arithmetisation of even basic syntactic operations. Before I illustrate this point for
![]() $T = \mathsf {PA}$
, the reader is reminded that
$T = \mathsf {PA}$
, the reader is reminded that
![]() $A^\ast $
denotes the set of strings over the alphabet A of our language
$A^\ast $
denotes the set of strings over the alphabet A of our language
![]() $\mathcal {L}$
. The operation
$\mathcal {L}$
. The operation
![]() $\underline {\neg }$
maps each well-formed formula
$\underline {\neg }$
maps each well-formed formula
![]() $\varphi \in A^\ast $
to its negation
$\varphi \in A^\ast $
to its negation
![]() $(\neg \varphi )$
. We may reasonably require that every intensionally correct arithmetisation of syntax is based on a numbering such that the tracking functions of
$(\neg \varphi )$
. We may reasonably require that every intensionally correct arithmetisation of syntax is based on a numbering such that the tracking functions of
![]() $\underline {\neg }$
and the other constructor operations introduced in §2.1 are provably total in
$\underline {\neg }$
and the other constructor operations introduced in §2.1 are provably total in
![]() $\mathsf {PA}$
(see also Halbach, Reference Halbach2014, p. 33).
$\mathsf {PA}$
(see also Halbach, Reference Halbach2014, p. 33).
Definition 4.17. Let T be an
![]() $\mathcal {L}$
-theory and let
$\mathcal {L}$
-theory and let
![]() $f \colon \mathbb {N}^k \to \mathbb {N}$
be a function. We say that f is
$f \colon \mathbb {N}^k \to \mathbb {N}$
be a function. We say that f is
![]() $\Sigma _n$
-definable in T, if there exists a
$\Sigma _n$
-definable in T, if there exists a
![]() $\Sigma _n$
-formula
$\Sigma _n$
-formula
![]() $\varphi (x_1, \ldots , x_k,y)$
which defines the graph of f such that
$\varphi (x_1, \ldots , x_k,y)$
which defines the graph of f such that
![]() $T \vdash \forall x_1, \ldots , x_k \exists ! y\, \varphi (x_1, \ldots , x_k,y)$
.
$T \vdash \forall x_1, \ldots , x_k \exists ! y\, \varphi (x_1, \ldots , x_k,y)$
.
The function f is called provably total in T if f is
![]() $\Sigma _1$
-definable in T.
$\Sigma _1$
-definable in T.
We now construct a computable simulation
![]() $\beta $
of the set of strings
$\beta $
of the set of strings
![]() $A^\ast $
, such that the tracking function of
$A^\ast $
, such that the tracking function of
![]() $\underline {\neg }$
is recursive but not provably total in
$\underline {\neg }$
is recursive but not provably total in
![]() $\mathsf {PA}$
. Suppose that the symbols of the alphabet A are ordered. We now effectively enumerate
$\mathsf {PA}$
. Suppose that the symbols of the alphabet A are ordered. We now effectively enumerate
![]() $A^\ast $
using the length-first ordering, according to which
$A^\ast $
using the length-first ordering, according to which
![]() $s < t$
, if the length of s is smaller than the length of t, or if s and t have the same length, s is lexicographically smaller than t. Let
$s < t$
, if the length of s is smaller than the length of t, or if s and t have the same length, s is lexicographically smaller than t. Let
![]() $\psi _i$
be the i-th string in this enumeration. Let
$\psi _i$
be the i-th string in this enumeration. Let
![]() $h \colon \mathbb {N} \to \mathbb {N}$
be a strictly increasing and recursive function which is not provably total in
$h \colon \mathbb {N} \to \mathbb {N}$
be a strictly increasing and recursive function which is not provably total in
![]() $\mathsf {PA}$
, such that
$\mathsf {PA}$
, such that
![]() $h(\mathbb {N})$
is decidable,
$h(\mathbb {N})$
is decidable,
![]() $0 \notin h(\mathbb {N})$
and
$0 \notin h(\mathbb {N})$
and
![]() $| h(\mathbb {N}) | = | \mathbb {N} \setminus h(\mathbb {N}) | = | \mathbb {N} | $
.Footnote
26
$| h(\mathbb {N}) | = | \mathbb {N} \setminus h(\mathbb {N}) | = | \mathbb {N} | $
.Footnote
26
We define
![]() $\beta \colon A^\ast \to \mathbb {N}$
recursively as follows. Let
$\beta \colon A^\ast \to \mathbb {N}$
recursively as follows. Let
![]() $\beta (\psi _0) = 0$
. Suppose now that
$\beta (\psi _0) = 0$
. Suppose now that
![]() $\beta (\psi _j)$
is defined for all
$\beta (\psi _j)$
is defined for all
![]() $j < i$
, then
$j < i$
, then

The resulting numbering
![]() $\beta $
is bijective, and
$\beta $
is bijective, and
![]() $\beta \sim \iota $
, where
$\beta \sim \iota $
, where
![]() $\iota \colon A^\ast \to \mathbb {N}$
is given by
$\iota \colon A^\ast \to \mathbb {N}$
is given by
![]() $\psi _i \mapsto i$
. Since
$\psi _i \mapsto i$
. Since
![]() $\iota $
is a computable simulation (see Smullyan, Reference Smullyan1961, chap. 9 and Corollary 4.7), also
$\iota $
is a computable simulation (see Smullyan, Reference Smullyan1961, chap. 9 and Corollary 4.7), also
![]() $\beta $
computably simulates
$\beta $
computably simulates
![]() $A^\ast $
, by Lemma 4.5. However, the
$A^\ast $
, by Lemma 4.5. However, the
![]() $\beta $
-tracking function of
$\beta $
-tracking function of
![]() $\underline {\neg }$
coincides with h and is therefore not provably total in
$\underline {\neg }$
coincides with h and is therefore not provably total in
![]() $\mathsf {PA}$
. That is, there is no
$\mathsf {PA}$
. That is, there is no
![]() $\Sigma _1$
-numeration
$\Sigma _1$
-numeration
![]() $\mathsf {Neg}(x,y)$
of the graph of the function
$\mathsf {Neg}(x,y)$
of the graph of the function
![]() ${\beta (\varphi ) \mapsto \beta ( (\neg \varphi ) )}$
such that
${\beta (\varphi ) \mapsto \beta ( (\neg \varphi ) )}$
such that
![]() $\mathsf {PA} \vdash \forall x\, \exists ! z\, \mathsf {Neg}(x,y)$
. The definition of
$\mathsf {PA} \vdash \forall x\, \exists ! z\, \mathsf {Neg}(x,y)$
. The definition of
![]() $\beta $
can be easily extended such that the
$\beta $
can be easily extended such that the
![]() $\beta $
-tracking functions of all the operations
$\beta $
-tracking functions of all the operations
![]() $\underline {=}$
,
$\underline {=}$
,
![]() $\underline {\wedge }$
,
$\underline {\wedge }$
,
![]() $\underline {\rightarrow }$
,
$\underline {\rightarrow }$
,
![]() $\underline {\forall }$
, etc. are recursive but not provably total in
$\underline {\forall }$
, etc. are recursive but not provably total in
![]() $\mathsf {PA}$
. However, as already mentioned above, this might reasonably be taken as a minimal requirement for an intensionally correct arithmetisation when resorting to the meaning postulate approach.
$\mathsf {PA}$
. However, as already mentioned above, this might reasonably be taken as a minimal requirement for an intensionally correct arithmetisation when resorting to the meaning postulate approach.
5 Summary and conclusions
The purpose of this paper has been to investigate the invariance of Gödel’s Second Theorem regarding numberings. More precisely, I have examined the extent to which one can abstract away from the choice of the employed numbering in the formulation of Gödel’s theorem which is based on Löb’s conditions (see Theorem 2.1).
I have shown that “counterexamples” to several metamathematical theorems can be constructed, based on a naïve approach to numberings. For instance, there exists a numbering
![]() $\delta $
and a formula
$\delta $
and a formula
![]() $\mathsf {Pr}^\delta (x)$
satisfying Löb’s conditions (relative to
$\mathsf {Pr}^\delta (x)$
satisfying Löb’s conditions (relative to
![]() $\delta $
) such that
$\delta $
) such that ![]() is a provable consistency sentence. Moreover, there is a numbering
is a provable consistency sentence. Moreover, there is a numbering
![]() $\eta $
and a formula
$\eta $
and a formula
![]() $\mathsf {Tr}^\eta (x)$
defining the set of (
$\mathsf {Tr}^\eta (x)$
defining the set of (
![]() $\eta $
-codes of) true sentences, such that
$\eta $
-codes of) true sentences, such that ![]() , for all sentences
, for all sentences
![]() $\varphi $
, violating both the semantic and syntactic version of Tarski’s Theorem (see §2.3 and set
$\varphi $
, violating both the semantic and syntactic version of Tarski’s Theorem (see §2.3 and set
![]() $\mathsf {Tr}^\eta (x) := \mathsf {Pr}^\eta (x)$
).
$\mathsf {Tr}^\eta (x) := \mathsf {Pr}^\eta (x)$
).
These examples suggest that the invariance problem regarding numberings comes with some subtleties which are typically overlooked. I have argued that they do not however refute the usual philosophical interpretations of these theorems, since the employed numberings resort to resources exceeding the relevant theoretical framework, and are therefore not admissible choices in the formalisation process. Since the relevant theoretical framework depends on the given metamathematical context, the admissibility of numberings has been analysed as a context-sensitive notion. In the context of Gödel’s Second Theorem and the syntactic version of Tarski’s Theorem for instance, the relevant theoretical framework consists of the considered formal theory T. Accordingly, admissible numberings are required to allow for T to verify, i.e., prove, certain basic properties of strings via their codes. Since the relevant theoretical framework in the context of the semantic version of Tarski’s Theorem consists of the considered language
![]() $\mathcal {L}$
rather than a theory, admissible numberings in this context are required to allow for
$\mathcal {L}$
rather than a theory, admissible numberings in this context are required to allow for
![]() $\mathcal {L}$
to express, i.e., define, certain properties of strings via their codes. By resorting to a minimal set of properties of strings, every admissible numbering in the context of Gödel’s Second Theorem has been shown to be a computable simulation, while in the context of the semantic version of Tarski’s Theorem every admissible numbering is an arithmetical simulation (see §3.2). It should be noted that admissible numberings are not required to be monotonic (a detailed discussion of monotonicity is contained in §3.4).
$\mathcal {L}$
to express, i.e., define, certain properties of strings via their codes. By resorting to a minimal set of properties of strings, every admissible numbering in the context of Gödel’s Second Theorem has been shown to be a computable simulation, while in the context of the semantic version of Tarski’s Theorem every admissible numbering is an arithmetical simulation (see §3.2). It should be noted that admissible numberings are not required to be monotonic (a detailed discussion of monotonicity is contained in §3.4).
Finally, I have formulated and proven (meta-)mathematical invariance claims relative to these two precise necessary conditions of admissibility (see §4), namely the invariance of Gödel’s Second Theorem and the syntactic version of Tarski’s Theorem regarding computable simulations (see Theorem 4.6 and Corollary 4.13) as well as the invariance of the semantic version of Tarski’s Theorem regarding arithmetical simulations (see Theorem 4.8 and footnote 23). Thus, once admissible numberings are singled out, invariance prevails and these theorems can be seen to be independent of the choice regarding their underlying numbering.
I conclude by pointing towards potential future research avenues. It should be noted that the notion of admissibility used in this paper is too weak to ensure the invariance of metamathematical theorems which do not only resort to schematic quantification. For instance, the parametric version of the Diagonal Lemma (see Hájek & Pudlák, Reference Hájek and Pudlák1998, theorem III.2.1) or the free-variable version of Löb’s Theorem (see Smorynski, Reference Smorynski and Barwise1977, theorem 4.1.7) appears to be outside the scope of this paper’s methods. While Lemma 4.11 can be converted into a uniform version such that
![]() $\mathsf {R} + ``{\leq \text {is a linear ordering''}} \vdash \forall x, y \, (\;f(x,y) \rightarrow ( \varphi (x) \leftrightarrow \psi (y)))$
, the translation function binumerated by f is not necessarily T-provably total. This is however a necessary ingredient for proving the invariance of these theorems along the lines of our proof of Lemma 4.12. These remarks suggest that invariance results of such theorems require a more restrictive notion of admissibility, allowing further properties of the resulting translation functions to be verified within T. A philosophically adequate account of admissibility of numberings relative to a theory is thus called for (cf. §3.2).
$\mathsf {R} + ``{\leq \text {is a linear ordering''}} \vdash \forall x, y \, (\;f(x,y) \rightarrow ( \varphi (x) \leftrightarrow \psi (y)))$
, the translation function binumerated by f is not necessarily T-provably total. This is however a necessary ingredient for proving the invariance of these theorems along the lines of our proof of Lemma 4.12. These remarks suggest that invariance results of such theorems require a more restrictive notion of admissibility, allowing further properties of the resulting translation functions to be verified within T. A philosophically adequate account of admissibility of numberings relative to a theory is thus called for (cf. §3.2).
This observation is closely related to another direction of research into which the study of invariance may be extended. For instance, in addition to Gödel’s Second Theorem itself being invariant, one might also require its proof and the process of arithmetisation to be independent of the employed numbering. This would rule out intensionally incorrect provability predicates such as those present in the proof of Theorem 4.15, as well as nonstandard proofs based on nonstandard numberings (cf. Lemma 4.12). As noted in §4.3, an invariance claim along these lines requires translation functions of numberings to preserve stronger than merely schematic proof-theoretic properties. Since computable equivalence is too weak for this purpose, once again a more restrictive and theory-dependent notion of admissibility of numberings is needed. I believe that future work in this direction may further elucidate to what extent the choice of numberings bears on intensionality phenomena in metamathematics.
6 Appendix: Constructions of deviant numberings
The Numbering
 ${\delta }$
${\delta }$
For technical convenience we add the constant symbol
![]() $\mathsf {1}$
to
$\mathsf {1}$
to
![]() $\mathcal {L}$
. The reader is reminded that the set of expressions is given by
$\mathcal {L}$
. The reader is reminded that the set of expressions is given by
![]() $A^\ast $
(with
$A^\ast $
(with
![]() $\mathsf {1} \in A$
). Let
$\mathsf {1} \in A$
). Let
![]() $T \supseteq \mathsf {PA}^-$
be any fixed consistent theory, where
$T \supseteq \mathsf {PA}^-$
be any fixed consistent theory, where
![]() $\mathsf {PA}^-$
is the theory of the non-negative parts of discretely ordered rings (see Kaye, Reference Kaye1991, pp. 16f.). We specify a numbering
$\mathsf {PA}^-$
is the theory of the non-negative parts of discretely ordered rings (see Kaye, Reference Kaye1991, pp. 16f.). We specify a numbering
![]() $\delta $
of
$\delta $
of
![]() $A^\ast $
such that the tracking functions of the operations
$A^\ast $
such that the tracking functions of the operations
![]() $\underline {\mathsf {S}}$
,
$\underline {\mathsf {S}}$
,
![]() $\underline {+}$
,
$\underline {+}$
,
![]() $\underline {\times }$
,
$\underline {\times }$
,
![]() $\underline {\prime }$
,
$\underline {\prime }$
,
![]() $\underline {=}$
,
$\underline {=}$
,
![]() $\underline {\wedge }$
and
$\underline {\wedge }$
and
![]() $\underline {\forall }$
are recursive relative to
$\underline {\forall }$
are recursive relative to
![]() $\delta $
and the set of (
$\delta $
and the set of (
![]() $\delta $
-codes of) T-theorems is decidable. For technical convenience, we employ a derivability relation such that for every formula
$\delta $
-codes of) T-theorems is decidable. For technical convenience, we employ a derivability relation such that for every formula
![]() $\varphi $
we have
$\varphi $
we have
![]() $T \vdash \varphi $
iff
$T \vdash \varphi $
iff
![]() $T \vdash \forall \varphi $
, where
$T \vdash \forall \varphi $
, where
![]() $\forall \varphi $
denotes the universal closure of
$\forall \varphi $
denotes the universal closure of
![]() $\varphi $
.
$\varphi $
.
The basic idea is to construct
![]() $\delta $
such that all (
$\delta $
such that all (
![]() $\delta $
-codes of) T-theorems can be isolated from the remaining (
$\delta $
-codes of) T-theorems can be isolated from the remaining (
![]() $\delta $
-codes of) strings of
$\delta $
-codes of) strings of
![]() $A^\ast $
by the decidable property of parity. In order to do so, we first partition the even and odd numbers into infinite decidable sets, each corresponding to a certain syntactic category. Let
$A^\ast $
by the decidable property of parity. In order to do so, we first partition the even and odd numbers into infinite decidable sets, each corresponding to a certain syntactic category. Let
 ${\langle x,y \rangle \equiv \frac {(x+y+1)(x+y+2)}{2}+y}$
be the usual pairing function. We define the following functions:
${\langle x,y \rangle \equiv \frac {(x+y+1)(x+y+2)}{2}+y}$
be the usual pairing function. We define the following functions:
 $$ \begin{align*} & & \Theta^{\mathsf{junk}}(x,y) & = 12 \cdot \langle x,y \rangle +1,\\ & & \Theta^{\mathsf{tm}}(x,y) & = 12 \cdot \langle x,y \rangle +3,\\ \Lambda^{=}(x,y) & = 8 \cdot \langle x,y \rangle, & \Theta^{=}(x,y) & = 12 \cdot \langle x,y \rangle +5,\\ \Lambda^{\neg}(x,y) & = 8 \cdot \langle x,y \rangle +2, & \Theta^{\neg}(x,y) & = 12 \cdot \langle x,y \rangle +7,\\ \Lambda^{\wedge}(x,y) & = 8 \cdot \langle x,y \rangle + 4, & \Theta^{\wedge}(x,y) & = 12 \cdot \langle x,y \rangle +9,\\ \Lambda^{\forall}(x,y) & = 8 \cdot \langle x,y \rangle +6, & \Theta^{\forall}(x,y) & = 12 \cdot \langle x,y \rangle +11. \end{align*} $$
$$ \begin{align*} & & \Theta^{\mathsf{junk}}(x,y) & = 12 \cdot \langle x,y \rangle +1,\\ & & \Theta^{\mathsf{tm}}(x,y) & = 12 \cdot \langle x,y \rangle +3,\\ \Lambda^{=}(x,y) & = 8 \cdot \langle x,y \rangle, & \Theta^{=}(x,y) & = 12 \cdot \langle x,y \rangle +5,\\ \Lambda^{\neg}(x,y) & = 8 \cdot \langle x,y \rangle +2, & \Theta^{\neg}(x,y) & = 12 \cdot \langle x,y \rangle +7,\\ \Lambda^{\wedge}(x,y) & = 8 \cdot \langle x,y \rangle + 4, & \Theta^{\wedge}(x,y) & = 12 \cdot \langle x,y \rangle +9,\\ \Lambda^{\forall}(x,y) & = 8 \cdot \langle x,y \rangle +6, & \Theta^{\forall}(x,y) & = 12 \cdot \langle x,y \rangle +11. \end{align*} $$
In what follows, we define
![]() $\delta $
such that all (
$\delta $
such that all (
![]() $\delta $
-codes of) terms are elements of
$\delta $
-codes of) terms are elements of
![]() $\Theta ^{\mathsf {tm}} (\mathbb {N},\mathbb {N}) = \{ \Theta ^{\mathsf {tm}} (m,n) \mid m,n \in \mathbb {N} \} = 12 \mathbb {N} + 3$
, all (
$\Theta ^{\mathsf {tm}} (\mathbb {N},\mathbb {N}) = \{ \Theta ^{\mathsf {tm}} (m,n) \mid m,n \in \mathbb {N} \} = 12 \mathbb {N} + 3$
, all (
![]() $\delta $
-codes of) T-theorems of the form
$\delta $
-codes of) T-theorems of the form
![]() $(s = t)$
are elements of
$(s = t)$
are elements of
![]() $\Lambda ^{=} (\mathbb {N},\mathbb {N}) = 8 \mathbb {N}$
, all (
$\Lambda ^{=} (\mathbb {N},\mathbb {N}) = 8 \mathbb {N}$
, all (
![]() $\delta $
-codes of) formulæ of the form
$\delta $
-codes of) formulæ of the form
![]() $(s = t)$
which are not T-theorems are elements of
$(s = t)$
which are not T-theorems are elements of
![]() $\Theta ^{=} (\mathbb {N},\mathbb {N}) = 12 \mathbb {N} +5$
, all (
$\Theta ^{=} (\mathbb {N},\mathbb {N}) = 12 \mathbb {N} +5$
, all (
![]() $\delta $
-codes of) of T-theorems of the form
$\delta $
-codes of) of T-theorems of the form
![]() $(\varphi \wedge \psi )$
are elements of
$(\varphi \wedge \psi )$
are elements of
![]() $\Lambda ^{\wedge } (\mathbb {N},\mathbb {N}) = 8 \mathbb {N} + 2$
, etc. Moreover, all (
$\Lambda ^{\wedge } (\mathbb {N},\mathbb {N}) = 8 \mathbb {N} + 2$
, etc. Moreover, all (
![]() $\delta $
-codes of) junk-expressions, i.e., strings which are not well-formed expressions, are elements of
$\delta $
-codes of) junk-expressions, i.e., strings which are not well-formed expressions, are elements of
![]() $\Theta ^{\mathsf {junk}} (\mathbb {N},\mathbb {N}) = 12 \mathbb {N} + 1$
. Since
$\Theta ^{\mathsf {junk}} (\mathbb {N},\mathbb {N}) = 12 \mathbb {N} + 1$
. Since
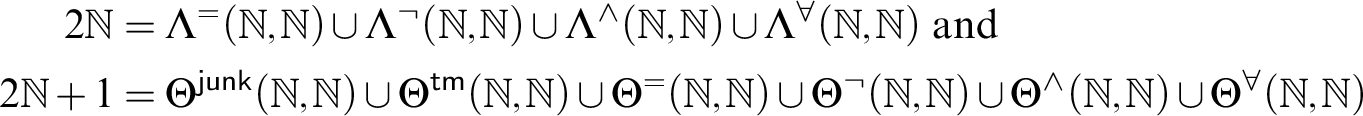 $$ \begin{align*} 2 \mathbb{N} & = \Lambda^{=} (\mathbb{N},\mathbb{N}) \cup \Lambda^{\neg} (\mathbb{N},\mathbb{N}) \cup \Lambda^{\wedge} (\mathbb{N},\mathbb{N}) \cup \Lambda^{\forall} (\mathbb{N},\mathbb{N}) \text{ and}\\ 2 \mathbb{N}+1 & = \Theta^{\mathsf{junk}}(\mathbb{N},\mathbb{N}) \cup \Theta^{\mathsf{tm}}(\mathbb{N},\mathbb{N}) \cup \Theta^{=} (\mathbb{N},\mathbb{N}) \cup \Theta^{\neg} (\mathbb{N},\mathbb{N}) \cup \Theta^{\wedge} (\mathbb{N},\mathbb{N}) \cup \Theta^{\forall} (\mathbb{N},\mathbb{N}) \end{align*} $$
$$ \begin{align*} 2 \mathbb{N} & = \Lambda^{=} (\mathbb{N},\mathbb{N}) \cup \Lambda^{\neg} (\mathbb{N},\mathbb{N}) \cup \Lambda^{\wedge} (\mathbb{N},\mathbb{N}) \cup \Lambda^{\forall} (\mathbb{N},\mathbb{N}) \text{ and}\\ 2 \mathbb{N}+1 & = \Theta^{\mathsf{junk}}(\mathbb{N},\mathbb{N}) \cup \Theta^{\mathsf{tm}}(\mathbb{N},\mathbb{N}) \cup \Theta^{=} (\mathbb{N},\mathbb{N}) \cup \Theta^{\neg} (\mathbb{N},\mathbb{N}) \cup \Theta^{\wedge} (\mathbb{N},\mathbb{N}) \cup \Theta^{\forall} (\mathbb{N},\mathbb{N}) \end{align*} $$
all
![]() $\delta $
-codes of T-theorems are even, while the
$\delta $
-codes of T-theorems are even, while the
![]() $\delta $
-codes of all other expressions are odd. Thus
$\delta $
-codes of all other expressions are odd. Thus
![]() $T \vdash \varphi \text { iff } \delta (\varphi ) \text { is even}$
, for every sentence
$T \vdash \varphi \text { iff } \delta (\varphi ) \text { is even}$
, for every sentence
![]() $\varphi $
. Using
$\varphi $
. Using
![]() $\Sigma ^0_1$
-completeness it is then easy to check that the
$\Sigma ^0_1$
-completeness it is then easy to check that the
![]() $\Delta ^0_0$
-formula
$\Delta ^0_0$
-formula
![]() $\mathsf {Pr}(x) \equiv \exists y < x \ x = \overline {2} \times y$
satisfies Löb(
$\mathsf {Pr}(x) \equiv \exists y < x \ x = \overline {2} \times y$
satisfies Löb(
![]() $T, \delta $
) and
$T, \delta $
) and ![]() . However,
. However,
![]() $\mathsf {Pr}(x)$
will not define the set of T-theorems, since not every even number will code a T-theorem. We construct a
$\mathsf {Pr}(x)$
will not define the set of T-theorems, since not every even number will code a T-theorem. We construct a
 $\Delta ^0_0(\mathsf {exp})$
-formula below which in addition to satisfying Löb’s conditions also binumerates the set of T-theorems.
$\Delta ^0_0(\mathsf {exp})$
-formula below which in addition to satisfying Löb’s conditions also binumerates the set of T-theorems.
In order to define the desired numbering
![]() $\delta $
, we first construct numberings
$\delta $
, we first construct numberings
![]() $\delta _i$
for every stage
$\delta _i$
for every stage
![]() ${i < \omega }$
. On the term level any standard numbering will do. In order to satisfy the aforementioned desired properties, we set
${i < \omega }$
. On the term level any standard numbering will do. In order to satisfy the aforementioned desired properties, we set
![]() $\delta _0(s) = \Theta ^{\mathsf {tm}}(0, \gamma (s) )$
, for each
$\delta _0(s) = \Theta ^{\mathsf {tm}}(0, \gamma (s) )$
, for each
![]() $s \in \mathit {Term}$
, where
$s \in \mathit {Term}$
, where
![]() $\gamma $
is Smith’s (Reference Smith2007) standard numbering. The arithmetisation of the syntactic properties of and operations on terms proceeds as usual. In particular, the properties of being a (
$\gamma $
is Smith’s (Reference Smith2007) standard numbering. The arithmetisation of the syntactic properties of and operations on terms proceeds as usual. In particular, the properties of being a (
![]() $\delta _0$
-code of a) variable and being a (
$\delta _0$
-code of a) variable and being a (
![]() $\delta _0$
-code of a) term are decidable. Moreover, the
$\delta _0$
-code of a) term are decidable. Moreover, the
![]() $\delta _0$
-tracking functions of
$\delta _0$
-tracking functions of
![]() $\underline {\mathsf {S}}$
,
$\underline {\mathsf {S}}$
,
![]() $\underline {+}$
,
$\underline {+}$
,
![]() $\underline {\times }$
,
$\underline {\times }$
,
![]() $\underline {\prime }$
are recursive.
$\underline {\prime }$
are recursive.
In order to extend
![]() $\delta _0$
such that also
$\delta _0$
such that also
![]() $\underline {=}$
has a recursive tracking function, we first show that for any given expressions
$\underline {=}$
has a recursive tracking function, we first show that for any given expressions
![]() $s,t$
, it is decidable whether or not
$s,t$
, it is decidable whether or not
![]() $T \vdash s=t$
(with
$T \vdash s=t$
(with
![]() $s,t$
being possibly open terms).
$s,t$
being possibly open terms).
Since T is
![]() $\Pi ^0_1$
-sound and proves the axioms of a commutative semiring, to each term
$\Pi ^0_1$
-sound and proves the axioms of a commutative semiring, to each term
![]() $s(x_1,\ldots ,x_l)$
there corresponds a unique polynomial
$s(x_1,\ldots ,x_l)$
there corresponds a unique polynomial
![]() $p_s \in \mathbb {N}[x_1,\ldots ,x_l]$
such that
$p_s \in \mathbb {N}[x_1,\ldots ,x_l]$
such that
![]() $p_s = p_t$
iff
$p_s = p_t$
iff
![]() $T \vdash s = t$
. In order to show the decidability of
$T \vdash s = t$
. In order to show the decidability of
![]() $T \vdash s = t$
, the rough idea is to define a rewriting system which effectively reduces each term
$T \vdash s = t$
, the rough idea is to define a rewriting system which effectively reduces each term
![]() $s(x_1,\ldots ,x_l)$
to its unique normal form
$s(x_1,\ldots ,x_l)$
to its unique normal form
![]() $p_s$
. Since commutativity blocks the termination of such systems, we instead define a class-rewriting system which essentially operates on AC-congruence classes of terms, with
$p_s$
. Since commutativity blocks the termination of such systems, we instead define a class-rewriting system which essentially operates on AC-congruence classes of terms, with
![]() $AC$
being the equational theory consisting of the associativity and commutativity axioms of both
$AC$
being the equational theory consisting of the associativity and commutativity axioms of both
![]() $+$
and
$+$
and
![]() $\cdot $
. This gives rise to a system with the following properties:
$\cdot $
. This gives rise to a system with the following properties:
-
1. for each term there exists a unique normal form up to permutations under associativity and commutativity,
-
2. each normal form
 $s'$
of s is a term and
$s'$
of s is a term and
 $T \vdash s = s'$
,
$T \vdash s = s'$
, -
3. normal forms of terms can be effectively computed,
-
4. for any two
 $s,t$
and respective normal forms
$s,t$
and respective normal forms
 $s',t'$
:
$s',t'$
:
 $T \vdash s = t$
iff
$T \vdash s = t$
iff
 $s' \sim _{AC} t'$
.
$s' \sim _{AC} t'$
.
We first define the ordinary term rewriting system R, consisting of the following rules:
-
i.
 $t \times (u + v) \rightarrow t \times u + t \times v$
$t \times (u + v) \rightarrow t \times u + t \times v$
-
ii.
 $\mathsf {S}t \rightarrow t + \mathsf {1}$
$\mathsf {S}t \rightarrow t + \mathsf {1}$
-
iii.
 $\mathsf {1} \times t \rightarrow t$
$\mathsf {1} \times t \rightarrow t$
-
iv.
 $\mathsf {0} \times t \rightarrow \mathsf {0}$
$\mathsf {0} \times t \rightarrow \mathsf {0}$
-
v.
 $t + \mathsf {0} \rightarrow t$
$t + \mathsf {0} \rightarrow t$
In allowing the rewriting of a term by means of rewriting any
![]() $AC$
-equivalent term, R is thus extended to the class-rewriting system
$AC$
-equivalent term, R is thus extended to the class-rewriting system
![]() $R / AC$
. In order to show that this system terminates, let
$R / AC$
. In order to show that this system terminates, let
![]() $A = \{ n \geq 2 \mid n \in \mathbb {N} \}$
and consider the following polynomial weight functions:
$A = \{ n \geq 2 \mid n \in \mathbb {N} \}$
and consider the following polynomial weight functions:
-
a.
 $\mathsf {0}_A = 2$
$\mathsf {0}_A = 2$
-
b.
 $\mathsf {1}_A = 2$
$\mathsf {1}_A = 2$
-
c.
 $\mathsf {S}_A = X + 4$
$\mathsf {S}_A = X + 4$
-
d.
 $+_A = X + Y +1$
$+_A = X + Y +1$
-
e.
 $\times _A = XY$
$\times _A = XY$
All polynomials (a)–(e) satisfy associativity and commutativity. Furthermore the polynomials
![]() $F_{l,r}$
(i.e., the result of subtracting the weight of the right hand side from the left hand side of a given rule) of the rules
$F_{l,r}$
(i.e., the result of subtracting the weight of the right hand side from the left hand side of a given rule) of the rules
![]() $\text {(i)-(v)}$
are
$\text {(i)-(v)}$
are
![]() $X-1$
,
$X-1$
,
![]() $1$
, X,
$1$
, X,
![]() $2X-2$
and
$2X-2$
and
![]() $3$
respectively, which are all strictly positive (over A). Thus
$3$
respectively, which are all strictly positive (over A). Thus
![]() $R / AC$
is terminating (see Terese, Reference Terese2003, chap. 6). Furthermore, R is left-linear. The critical pairs of R are of the form
$R / AC$
is terminating (see Terese, Reference Terese2003, chap. 6). Furthermore, R is left-linear. The critical pairs of R are of the form
![]() ${(u+v,\mathsf {1} \times u + \mathsf {1} \times v)}$
,
${(u+v,\mathsf {1} \times u + \mathsf {1} \times v)}$
,
![]() $(\mathsf {0},\mathsf {0} \times u + \mathsf {0} \times v)$
and
$(\mathsf {0},\mathsf {0} \times u + \mathsf {0} \times v)$
and
![]() $(t \times u, t \times u + t \times \mathsf {0})$
. It can easily be checked that they converge, for instance,
$(t \times u, t \times u + t \times \mathsf {0})$
. It can easily be checked that they converge, for instance,
![]() $\mathsf {1} \times u + \mathsf {1} \times v \rightarrow u + \mathsf {1} \times v \rightarrow u + v$
. Hence the class-rewriting system
$\mathsf {1} \times u + \mathsf {1} \times v \rightarrow u + \mathsf {1} \times v \rightarrow u + v$
. Hence the class-rewriting system
![]() $R / AC$
has the Church-Rosser property modulo
$R / AC$
has the Church-Rosser property modulo
![]() $AC$
(see Dershowitz & Jouannaud, Reference Dershowitz, Jouannaud and Leeuwen1990, chap. 7).
$AC$
(see Dershowitz & Jouannaud, Reference Dershowitz, Jouannaud and Leeuwen1990, chap. 7).
We may conclude that for each term,
![]() $R / AC$
effectively computes a unique normal form up to permutations under associativity and commutativity. In order to decide whether or not
$R / AC$
effectively computes a unique normal form up to permutations under associativity and commutativity. In order to decide whether or not
![]() $T \vdash s =t$
for two terms
$T \vdash s =t$
for two terms
![]() $s,t$
, one proceeds as follows: first effectively rewrite s and t into their respective normal forms
$s,t$
, one proceeds as follows: first effectively rewrite s and t into their respective normal forms
![]() $s'$
and
$s'$
and
![]() $t'$
. Then check whether or not
$t'$
. Then check whether or not
![]() $s' \sim _{AC} t'$
. Since the word problem for
$s' \sim _{AC} t'$
. Since the word problem for
![]() $AC$
is decidable and
$AC$
is decidable and
![]() $T \vdash s =t$
iff
$T \vdash s =t$
iff
![]() $s' \sim _{AC} t'$
, the decidability of
$s' \sim _{AC} t'$
, the decidability of
![]() $T \vdash s =t$
obtains. This decision process can be mimicked on the
$T \vdash s =t$
obtains. This decision process can be mimicked on the
![]() $\delta _0$
-codes of terms in the usual way, yielding a corresponding decidable arithmetical property, which is binumerated by the formula
$\delta _0$
-codes of terms in the usual way, yielding a corresponding decidable arithmetical property, which is binumerated by the formula
![]() $\mathsf {PrEqu}(x,y)$
.
$\mathsf {PrEqu}(x,y)$
.
In order to extend
![]() $\delta _0$
to a numbering of
$\delta _0$
to a numbering of
![]() $A^\ast $
satisfying the desired properties, we exploit the fact that for any given expressions
$A^\ast $
satisfying the desired properties, we exploit the fact that for any given expressions
![]() $\varphi $
,
$\varphi $
,
![]() $\psi $
and x, whether or not
$\psi $
and x, whether or not
![]() $\varphi \wedge \psi $
and
$\varphi \wedge \psi $
and
![]() $\forall x \varphi $
are T-provable is already fully determined by the T-provability of
$\forall x \varphi $
are T-provable is already fully determined by the T-provability of
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
(and by the decidable fact of whether or not x is a variable). Clearly this does not hold for
$\psi $
(and by the decidable fact of whether or not x is a variable). Clearly this does not hold for
![]() $\neg $
, as neither
$\neg $
, as neither
![]() $T \vdash \neg \varphi $
nor
$T \vdash \neg \varphi $
nor
![]() $T \not \vdash \neg \varphi $
are entailed by
$T \not \vdash \neg \varphi $
are entailed by
![]() $T \not \vdash \varphi $
. For this reason,
$T \not \vdash \varphi $
. For this reason,
![]() $\underline {\neg }$
will not have a recursive
$\underline {\neg }$
will not have a recursive
![]() $\delta $
-tracking function.
$\delta $
-tracking function.
Let
![]() $\mathit {Junk}$
denote all strings of
$\mathit {Junk}$
denote all strings of
![]() $A^\ast $
which are not well-formed expressions. Let
$A^\ast $
which are not well-formed expressions. Let
![]() $\{ \chi _n \mid n \in \mathbb {N} \}$
be an enumeration without repetitions of T-provable formulæ which are of the form
$\{ \chi _n \mid n \in \mathbb {N} \}$
be an enumeration without repetitions of T-provable formulæ which are of the form
![]() $(\neg \varphi )$
and let
$(\neg \varphi )$
and let
![]() $\{ \nu _n \mid n \in \mathbb {N} \}$
be an enumeration without repetitions of non-T-provable formulæ of the form
$\{ \nu _n \mid n \in \mathbb {N} \}$
be an enumeration without repetitions of non-T-provable formulæ of the form
![]() $(\neg \varphi )$
. Moreover, let
$(\neg \varphi )$
. Moreover, let
![]() $\{ \mu _n \mid n \in \mathbb {N} \}$
be an enumeration without repetitions of
$\{ \mu _n \mid n \in \mathbb {N} \}$
be an enumeration without repetitions of
![]() $\mathit {Junk}$
.
$\mathit {Junk}$
.
Set
![]() $\delta _0(\chi _n) = \Lambda ^{\neg }(0,n) $
,
$\delta _0(\chi _n) = \Lambda ^{\neg }(0,n) $
,
![]() $\delta _0(\nu _n)= \Theta ^{\neg }(0,n)$
and
$\delta _0(\nu _n)= \Theta ^{\neg }(0,n)$
and
![]() $\delta ^{\mathsf {junk}}(\mu _n)= \Theta ^{\mathsf {junk}}(0,n)$
. We now successively extend the numbering
$\delta ^{\mathsf {junk}}(\mu _n)= \Theta ^{\mathsf {junk}}(0,n)$
. We now successively extend the numbering
![]() $\delta _0$
of
$\delta _0$
of
![]() $\mathit {Term} \cup \{ (\neg \varphi ) \mid \varphi \in \mathit {Fml} \}$
in
$\mathit {Term} \cup \{ (\neg \varphi ) \mid \varphi \in \mathit {Fml} \}$
in
![]() $\omega $
-many steps to a numbering of
$\omega $
-many steps to a numbering of
![]() $A^\ast $
, by defining a function
$A^\ast $
, by defining a function
![]() $\delta _{i+1}$
for each
$\delta _{i+1}$
for each
![]() $i < \omega $
as follows:
$i < \omega $
as follows:
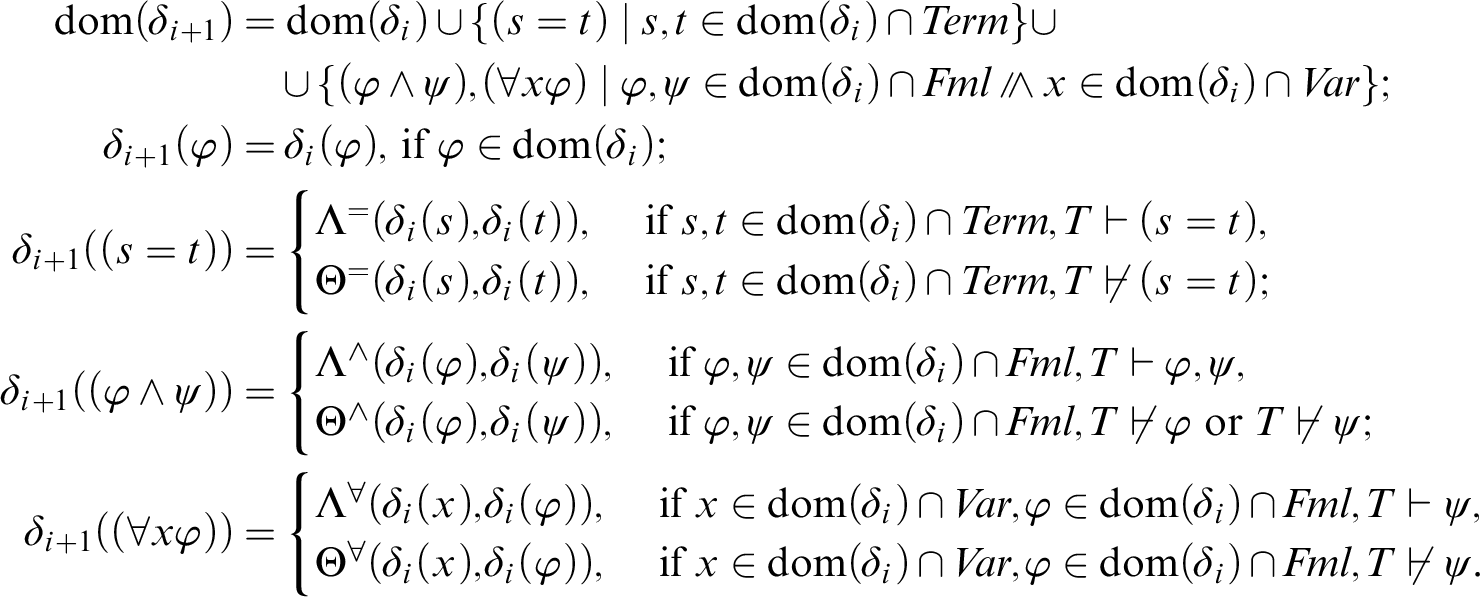
Finally, we set
 $\delta = \left ( \bigcup _{i < \omega } \delta _i \right ) \cup \delta ^{\mathsf {junk}}$
, with
$\delta = \left ( \bigcup _{i < \omega } \delta _i \right ) \cup \delta ^{\mathsf {junk}}$
, with
 $\textrm{{dom}}(\delta ) = \left ( \bigcup _{i < \omega } \textrm{{dom}}(\delta _i) \right ) \cup \mathit {Junk}$
. By definition of the functions
$\textrm{{dom}}(\delta ) = \left ( \bigcup _{i < \omega } \textrm{{dom}}(\delta _i) \right ) \cup \mathit {Junk}$
. By definition of the functions
![]() $\Theta ^{\mathsf {junk}}$
,
$\Theta ^{\mathsf {junk}}$
,
![]() $\Theta ^{\mathsf {tm}}$
,
$\Theta ^{\mathsf {tm}}$
,
![]() $\Lambda ^{=}$
,
$\Lambda ^{=}$
,
![]() $\Theta ^{=}$
, etc.,
$\Theta ^{=}$
, etc.,
![]() $\delta $
is an injective function and thus a numbering of
$\delta $
is an injective function and thus a numbering of
![]() $A^\ast $
. In order to show that
$A^\ast $
. In order to show that
![]() $\{ \delta (\varphi ) \mid T \vdash \varphi \}$
can be binumerated by a
$\{ \delta (\varphi ) \mid T \vdash \varphi \}$
can be binumerated by a
 $\Delta ^0_0(\mathsf {exp})$
-formula, we define
$\Delta ^0_0(\mathsf {exp})$
-formula, we define
 $$ \begin{align*} \mathsf{Pr}(x) \equiv & \exists s \ \mathsf{Seq}(s) \wedge x = (s)_{\mathsf{Lh}(s)} \wedge \forall i \leq \mathsf{Lh}(s) \big( \exists n \ (s)_i = \Lambda^{\neg}(0,n)\\ & \vee \exists p,q \ \mathsf{Term}(p) \wedge \mathsf{Term}(q) \wedge \mathsf{PrEqu}(p,q) \wedge (s)_i = \Lambda^{=}(p,q)\\ & \vee \exists j,k < i \ (s)_i = \Lambda^{\wedge}( (s)_j, (s)_k )\\ & \vee \exists j < i, y \leq (s)_i \ \mathsf{Var}(y) \wedge (s)_i = \Lambda^{\forall}(y, (s)_j ) \big). \end{align*} $$
$$ \begin{align*} \mathsf{Pr}(x) \equiv & \exists s \ \mathsf{Seq}(s) \wedge x = (s)_{\mathsf{Lh}(s)} \wedge \forall i \leq \mathsf{Lh}(s) \big( \exists n \ (s)_i = \Lambda^{\neg}(0,n)\\ & \vee \exists p,q \ \mathsf{Term}(p) \wedge \mathsf{Term}(q) \wedge \mathsf{PrEqu}(p,q) \wedge (s)_i = \Lambda^{=}(p,q)\\ & \vee \exists j,k < i \ (s)_i = \Lambda^{\wedge}( (s)_j, (s)_k )\\ & \vee \exists j < i, y \leq (s)_i \ \mathsf{Var}(y) \wedge (s)_i = \Lambda^{\forall}(y, (s)_j ) \big). \end{align*} $$
Clearly,
![]() $\mathsf {Pr}(x)$
defines
$\mathsf {Pr}(x)$
defines
![]() $\{ \delta (\varphi ) \mid T \vdash \varphi \}$
. As we have seen above,
$\{ \delta (\varphi ) \mid T \vdash \varphi \}$
. As we have seen above,
![]() $\mathsf {PrEqu}(x,y)$
can be taken to be a
$\mathsf {PrEqu}(x,y)$
can be taken to be a
 $\Delta ^0_0(\mathsf {exp})$
-formula, as well as
$\Delta ^0_0(\mathsf {exp})$
-formula, as well as
![]() $\mathsf {Seq}(x), \mathsf {Term}(x)$
and
$\mathsf {Seq}(x), \mathsf {Term}(x)$
and
![]() $\mathsf {Var}(x)$
. It remains to show that the variable s can be bounded. To do so, construct a
$\mathsf {Var}(x)$
. It remains to show that the variable s can be bounded. To do so, construct a
 $\Delta ^0_0(\mathsf {exp})$
-definable height function
$\Delta ^0_0(\mathsf {exp})$
-definable height function
![]() $h(x)$
such that
$h(x)$
such that
![]() $h( \delta (\varphi ) ) = \# \{ \psi \mid \psi \text { is a subformula of } \varphi \}$
. Then the length of the sequence (coded by) s can be bounded by the number of subformulæ of the theorem (coded by) x, i.e., by
$h( \delta (\varphi ) ) = \# \{ \psi \mid \psi \text { is a subformula of } \varphi \}$
. Then the length of the sequence (coded by) s can be bounded by the number of subformulæ of the theorem (coded by) x, i.e., by
![]() $h(x)$
. Thus
$h(x)$
. Thus
![]() $\mathsf {Pr}(x)$
can be taken to be
$\mathsf {Pr}(x)$
can be taken to be
 $\Delta ^0_0(\mathsf {exp})$
.
$\Delta ^0_0(\mathsf {exp})$
.
In a similar way, it can be shown that
![]() $\{ \delta (\varphi ) \mid \varphi \in \mathit {Fml} \}$
is
$\{ \delta (\varphi ) \mid \varphi \in \mathit {Fml} \}$
is
 $\Delta ^0_0(\mathsf {exp})$
-binumerable, by extending
$\Delta ^0_0(\mathsf {exp})$
-binumerable, by extending
![]() $\mathsf {Pr}(x)$
in each clause with the corresponding set
$\mathsf {Pr}(x)$
in each clause with the corresponding set
![]() $\Omega ^\neg $
,
$\Omega ^\neg $
,
![]() $\Omega ^{=}$
,
$\Omega ^{=}$
,
![]() $\Omega ^{\wedge }$
or
$\Omega ^{\wedge }$
or
![]() $\Omega ^\forall $
of nonprovable formulæ respectively.
$\Omega ^\forall $
of nonprovable formulæ respectively.
We conclude by showing the operations
![]() $\underline {=}$
,
$\underline {=}$
,
![]() $\underline {\wedge }$
and
$\underline {\wedge }$
and
![]() $\underline {\forall }$
are recursive relative to
$\underline {\forall }$
are recursive relative to
![]() $\delta $
. As above, it can be shown that
$\delta $
. As above, it can be shown that
![]() $\textrm{{dom}}(\delta _i)$
, for all
$\textrm{{dom}}(\delta _i)$
, for all
![]() $i < \omega $
as well as
$i < \omega $
as well as
![]() $\textrm{{dom}}(\delta )$
is decidable. Moreover, the sets
$\textrm{{dom}}(\delta )$
is decidable. Moreover, the sets
![]() $\mathit {Var}$
,
$\mathit {Var}$
,
![]() $\mathit {Term}$
,
$\mathit {Term}$
,
![]() $\mathit {Fml}$
as well as
$\mathit {Fml}$
as well as
![]() $T^\vdash $
are decidable relative to
$T^\vdash $
are decidable relative to
![]() $\delta $
. To then compute, for instance, the tracking function of
$\delta $
. To then compute, for instance, the tracking function of
![]() $\underline {\wedge }$
given by
$\underline {\wedge }$
given by
![]() , one first decides for a given input
, one first decides for a given input
![]() $(m,n)$
whether or not
$(m,n)$
whether or not
![]() $\mathsf {Pr}(m)$
and
$\mathsf {Pr}(m)$
and
![]() $\mathsf {Pr}(n)$
are true. If both hold, then the output is
$\mathsf {Pr}(n)$
are true. If both hold, then the output is
![]() $\Lambda ^{\wedge }(m,n)$
. If not, the output is
$\Lambda ^{\wedge }(m,n)$
. If not, the output is
![]() $\Theta ^{\wedge }(m,n)$
. Hence, the tracking function
$\Theta ^{\wedge }(m,n)$
. Hence, the tracking function
![]() $\underline {\wedge }$
is recursive. Showing the recursiveness of the remaining tracking functions proceeds in a similar way.
$\underline {\wedge }$
is recursive. Showing the recursiveness of the remaining tracking functions proceeds in a similar way.
Remark
The deviant numbering
![]() $\delta $
is optimal in the following sense.
$\delta $
is optimal in the following sense.
Lemma 6.18. There is no numbering
![]() $\delta '$
of
$\delta '$
of
![]() $A^\ast $
such that the set of (
$A^\ast $
such that the set of (
![]() $\delta '$
-codes of) T-theorems is decidable and all the constructor operations introduced in §2.1 are recursive relative to
$\delta '$
-codes of) T-theorems is decidable and all the constructor operations introduced in §2.1 are recursive relative to
![]() $\delta '$
.
$\delta '$
.
Proof sketch
Let
![]() $\delta '$
be a numbering of
$\delta '$
be a numbering of
![]() $A^\ast $
such that all the constructor operations introduced in §2.1 are recursive relative to
$A^\ast $
such that all the constructor operations introduced in §2.1 are recursive relative to
![]() $\delta '$
. Let
$\delta '$
. Let
![]() $\gamma $
be Smith’s (Reference Smith2007) standard numbering. Clearly, all the constructor operations introduced in §2.1 are also recursive relative to
$\gamma $
be Smith’s (Reference Smith2007) standard numbering. Clearly, all the constructor operations introduced in §2.1 are also recursive relative to
![]() $\gamma $
. By slightly generalising Mal’cev’s theorem (see Theorem 4.6 and Mal’cev, Reference Mal’cev1961, sec. 4), we can show that
$\gamma $
. By slightly generalising Mal’cev’s theorem (see Theorem 4.6 and Mal’cev, Reference Mal’cev1961, sec. 4), we can show that
![]() $\delta '$
and
$\delta '$
and
![]() $\gamma $
are equivalent numberings of
$\gamma $
are equivalent numberings of
![]() $\mathit {Term} \cup \mathit {Fml} \subset A^\ast $
, i.e., of the well-formed
$\mathit {Term} \cup \mathit {Fml} \subset A^\ast $
, i.e., of the well-formed
![]() $\mathcal {L}$
-expressions. Hence, by Lemma 4.5, the set of (
$\mathcal {L}$
-expressions. Hence, by Lemma 4.5, the set of (
![]() $\delta '$
-codes of) T-theorems cannot be decidable. □
$\delta '$
-codes of) T-theorems cannot be decidable. □
In short: invariance is maintained as long as all constructor operations are required to be recursive. The construction of
![]() $\delta $
shows that deviance lurks as soon as we drop the requirement of recursiveness for
$\delta $
shows that deviance lurks as soon as we drop the requirement of recursiveness for
![]() $\underline {\neg }$
. Similarly, deviant results can occur once the recursiveness requirement is given up for
$\underline {\neg }$
. Similarly, deviant results can occur once the recursiveness requirement is given up for
![]() $\underline {\forall }$
, as witnessed by the numbering
$\underline {\forall }$
, as witnessed by the numbering
![]() $\eta $
constructed below. However, we cannot expect to find a deviant analogue to
$\eta $
constructed below. However, we cannot expect to find a deviant analogue to
![]() $\delta $
and
$\delta $
and
![]() $\eta $
if we relax the requirement of recursiveness for
$\eta $
if we relax the requirement of recursiveness for
![]() $\underline {\wedge }$
.Footnote
27
$\underline {\wedge }$
.Footnote
27
Lemma 6.19. Let T be
![]() $\Sigma _1$
-sound. There is no numbering
$\Sigma _1$
-sound. There is no numbering
![]() $\delta '$
of
$\delta '$
of
![]() $A^\ast $
such that the set of (
$A^\ast $
such that the set of (
![]() $\delta '$
-codes of) T-theorems is decidable and the constructor operations
$\delta '$
-codes of) T-theorems is decidable and the constructor operations
![]() $\underline {\mathsf {S}}$
,
$\underline {\mathsf {S}}$
,
![]() $\underline {+}$
,
$\underline {+}$
,
![]() $\underline {\times }$
,
$\underline {\times }$
,
![]() $\underline {\prime }$
,
$\underline {\prime }$
,
![]() $\underline {=}$
,
$\underline {=}$
,
![]() $\underline {\neg }$
and
$\underline {\neg }$
and
![]() $\underline {\forall }$
are recursive relative to
$\underline {\forall }$
are recursive relative to
![]() $\delta '$
.
$\delta '$
.
Proof. Let
![]() $\delta '$
be a numbering of
$\delta '$
be a numbering of
![]() $A^\ast $
such that the set of (
$A^\ast $
such that the set of (
![]() $\delta '$
-codes of) T-theorems is decidable and the operations
$\delta '$
-codes of) T-theorems is decidable and the operations
![]() $\underline {\mathsf {S}}$
,
$\underline {\mathsf {S}}$
,
![]() $\underline {+}$
,
$\underline {+}$
,
![]() $\underline {\times }$
,
$\underline {\times }$
,
![]() $\underline {\prime }$
,
$\underline {\prime }$
,
![]() $\underline {=}$
,
$\underline {=}$
,
![]() $\underline {\neg }$
and
$\underline {\neg }$
and
![]() $\underline {\forall }$
are recursive relative to
$\underline {\forall }$
are recursive relative to
![]() $\delta '$
. Let
$\delta '$
. Let
![]() $\mathit {Term}^- \cup \mathit {Fml\,}^- \subset A^\ast $
denote the conjunction-free fragement of
$\mathit {Term}^- \cup \mathit {Fml\,}^- \subset A^\ast $
denote the conjunction-free fragement of
![]() $\mathcal {L}$
, i.e., the set of well-formed
$\mathcal {L}$
, i.e., the set of well-formed
![]() $\mathcal {L}$
-expressions without conjunction. As in the proof of Lemma 6.18 we can show that Smith’s
$\mathcal {L}$
-expressions without conjunction. As in the proof of Lemma 6.18 we can show that Smith’s
![]() $\gamma $
and
$\gamma $
and
![]() $\delta '$
are equivalent numberings of
$\delta '$
are equivalent numberings of
![]() $\mathit {Term}^- \cup \mathit {Fml\,}^-$
. Hence, by Lemma 4.5,
$\mathit {Term}^- \cup \mathit {Fml\,}^-$
. Hence, by Lemma 4.5,
![]() $\{ \varphi \in \mathit {Fml\,}^- \mid T \vdash \varphi \}$
is decidable relative to
$\{ \varphi \in \mathit {Fml\,}^- \mid T \vdash \varphi \}$
is decidable relative to
![]() $\gamma $
. It is therefore decidable (in the classical sense) whether or not
$\gamma $
. It is therefore decidable (in the classical sense) whether or not
![]() ${T \vdash \exists \vec {y} \, P(\vec {x},\vec {y}) = 0}$
, for each polynomial
${T \vdash \exists \vec {y} \, P(\vec {x},\vec {y}) = 0}$
, for each polynomial
![]() $P(\vec {x},\vec {y}) = 0$
with integer coefficients, since
$P(\vec {x},\vec {y}) = 0$
with integer coefficients, since
![]() $\exists \vec {y} \, P(\vec {x},\vec {y}) = 0 \in \mathit {Fml\,}^-$
. Since T is
$\exists \vec {y} \, P(\vec {x},\vec {y}) = 0 \in \mathit {Fml\,}^-$
. Since T is
![]() $\Sigma _1$
-sound, we conclude that every Diophantine set is decidable. Hence, by the DPRM-theorem (see Davis, Reference Davis1973), every recursively enumerable set is decidable. But this is absurd. □
$\Sigma _1$
-sound, we conclude that every Diophantine set is decidable. Hence, by the DPRM-theorem (see Davis, Reference Davis1973), every recursively enumerable set is decidable. But this is absurd. □
We can show similarly that there is no numbering
![]() $\delta '$
of
$\delta '$
of
![]() $A^\ast $
such that the set of (
$A^\ast $
such that the set of (
![]() $\delta '$
-codes of) true sentences is decidable and the operations
$\delta '$
-codes of) true sentences is decidable and the operations
![]() $\underline {\mathsf {S}}$
,
$\underline {\mathsf {S}}$
,
![]() $\underline {+}$
,
$\underline {+}$
,
![]() $\underline {\times }$
,
$\underline {\times }$
,
![]() $\underline {\prime }$
,
$\underline {\prime }$
,
![]() $\underline {=}$
,
$\underline {=}$
,
![]() $\underline {\neg }$
and
$\underline {\neg }$
and
![]() $\underline {\forall }$
are recursive relative to
$\underline {\forall }$
are recursive relative to
![]() $\delta '$
.
$\delta '$
.
The Numbering
 ${\theta }$
${\theta }$
We now construct a numbering
![]() $\theta $
of
$\theta $
of
![]() $A^\ast $
such that the tracking function of
$A^\ast $
such that the tracking function of
![]() $\underline {\neg }$
is recursive and the set of (
$\underline {\neg }$
is recursive and the set of (
![]() $\theta $
-codes of) T-theorems is decidable, for any fixed consistent theory
$\theta $
-codes of) T-theorems is decidable, for any fixed consistent theory
![]() $T \supseteq \mathsf {R}$
. As opposed to the above construction, we here employ the standard derivability relation such that only closed sentences are T-theorems. We then use the fact that membership of
$T \supseteq \mathsf {R}$
. As opposed to the above construction, we here employ the standard derivability relation such that only closed sentences are T-theorems. We then use the fact that membership of
![]() $\neg \varphi $
in the sets
$\neg \varphi $
in the sets
![]() ${\{ \varphi \mid T \vdash \varphi \}}$
,
${\{ \varphi \mid T \vdash \varphi \}}$
,
![]() $\{ \varphi \mid T \vdash \neg \varphi \}$
and
$\{ \varphi \mid T \vdash \neg \varphi \}$
and
![]() $\{ \varphi \mid T \not \vdash \varphi , T \not \vdash \neg \varphi \}$
is already fully determined by the respective membership of
$\{ \varphi \mid T \not \vdash \varphi , T \not \vdash \neg \varphi \}$
is already fully determined by the respective membership of
![]() $\varphi $
. This does however not hold for
$\varphi $
. This does however not hold for
![]() $\varphi \wedge \psi $
, since for instance
$\varphi \wedge \psi $
, since for instance
![]() ${T \vdash \neg (\varphi \wedge \neg \varphi )}$
but
${T \vdash \neg (\varphi \wedge \neg \varphi )}$
but
![]() $T \not \vdash \neg (\varphi \wedge \varphi )$
, for any T-independent
$T \not \vdash \neg (\varphi \wedge \varphi )$
, for any T-independent
![]() $\varphi $
. Hence, in what follows,
$\varphi $
. Hence, in what follows,
![]() $\theta (\varphi \wedge \psi )$
is not defined along the lines of
$\theta (\varphi \wedge \psi )$
is not defined along the lines of
![]() $\theta (\neg \varphi )$
and thus
$\theta (\neg \varphi )$
and thus
![]() $\underline {\wedge }$
does not have a recursive
$\underline {\wedge }$
does not have a recursive
![]() $\theta $
-tracking function.
$\theta $
-tracking function.
Let
![]() $\{ \chi _n \mid n \in \mathbb {N} \}$
be an enumeration without repetitions of T-theorems which are not of the form
$\{ \chi _n \mid n \in \mathbb {N} \}$
be an enumeration without repetitions of T-theorems which are not of the form
![]() $(\neg \varphi )$
, let
$(\neg \varphi )$
, let
![]() $\{ \mu _n \mid n \in \mathbb {N} \}$
be an enumeration without repetitions of T-refutable sentences which are not of the form
$\{ \mu _n \mid n \in \mathbb {N} \}$
be an enumeration without repetitions of T-refutable sentences which are not of the form
![]() $(\neg \varphi )$
and let
$(\neg \varphi )$
and let
![]() $\{ \nu _n \mid n \in \mathbb {N} \}$
be an enumeration without repetitions of expressions not of the form
$\{ \nu _n \mid n \in \mathbb {N} \}$
be an enumeration without repetitions of expressions not of the form
![]() $(\neg \varphi )$
which are neither T-provable nor T-refutable (including nonwell-formed expressions).
$(\neg \varphi )$
which are neither T-provable nor T-refutable (including nonwell-formed expressions).
First, we set
![]() $\theta _0(\chi _n) = 3 \cdot \langle 0, n \rangle $
,
$\theta _0(\chi _n) = 3 \cdot \langle 0, n \rangle $
,
![]() $\theta _0(\mu _n) = 3 \cdot \langle 0, n \rangle + 1$
and
$\theta _0(\mu _n) = 3 \cdot \langle 0, n \rangle + 1$
and
![]() $\theta _0(\nu _n) = 3 \cdot \langle 0, n \rangle +2$
, with
$\theta _0(\nu _n) = 3 \cdot \langle 0, n \rangle +2$
, with
![]() $\textrm{{dom}}(\theta _0) = A^\ast \setminus \{ (\neg \varphi ) \mid \varphi \in A^\ast \}$
. We then extend
$\textrm{{dom}}(\theta _0) = A^\ast \setminus \{ (\neg \varphi ) \mid \varphi \in A^\ast \}$
. We then extend
![]() $\theta _0$
to a numbering of
$\theta _0$
to a numbering of
![]() $A^\ast $
in
$A^\ast $
in
![]() $\omega $
-many steps by defining
$\omega $
-many steps by defining
![]() $\theta _{i+1}$
for each
$\theta _{i+1}$
for each
![]() $i < \omega $
:
$i < \omega $
:
 $$ \begin{align*} {\mathrm{dom}}(\theta_{i+1}) & = {\mathrm{dom}}(\theta_i) \cup \{ (\neg \varphi) \mid \varphi \in {\mathrm{dom}}(\theta_i) \}\\ \theta_{i+1}(\varphi) & = \theta_i(\varphi), \text{ if } \varphi \in {\mathrm{dom}}(\theta_i) \\ \theta_{i+1}((\neg \varphi)) & = \begin{cases} 3 \cdot \langle i+1,j \rangle, & \text{ if } T \vdash \neg \varphi \text{ and } \theta_i(\varphi)=3 \cdot \langle i,j \rangle +1\\ 3 \cdot \langle i+1,j \rangle + 1, & \text{ if } T \vdash \varphi \text{ and } \theta_i(\varphi)=3 \cdot \langle i,j \rangle\\ 3 \cdot \langle i+1,j \rangle + 2, & \text{ if } T \not\vdash \varphi, T \not\vdash \neg \varphi \text{ and } \theta_i(\varphi)=3 \cdot \langle i,j \rangle + 2 \end{cases} \end{align*} $$
$$ \begin{align*} {\mathrm{dom}}(\theta_{i+1}) & = {\mathrm{dom}}(\theta_i) \cup \{ (\neg \varphi) \mid \varphi \in {\mathrm{dom}}(\theta_i) \}\\ \theta_{i+1}(\varphi) & = \theta_i(\varphi), \text{ if } \varphi \in {\mathrm{dom}}(\theta_i) \\ \theta_{i+1}((\neg \varphi)) & = \begin{cases} 3 \cdot \langle i+1,j \rangle, & \text{ if } T \vdash \neg \varphi \text{ and } \theta_i(\varphi)=3 \cdot \langle i,j \rangle +1\\ 3 \cdot \langle i+1,j \rangle + 1, & \text{ if } T \vdash \varphi \text{ and } \theta_i(\varphi)=3 \cdot \langle i,j \rangle\\ 3 \cdot \langle i+1,j \rangle + 2, & \text{ if } T \not\vdash \varphi, T \not\vdash \neg \varphi \text{ and } \theta_i(\varphi)=3 \cdot \langle i,j \rangle + 2 \end{cases} \end{align*} $$
Finally, we set
![]() $\theta = \bigcup _{i < \omega } \theta _i$
, with
$\theta = \bigcup _{i < \omega } \theta _i$
, with
![]() $\textrm{{dom}}(\theta ) = \bigcup _{i < \omega } \textrm{{dom}}(\theta _i)$
. It is easy to check that
$\textrm{{dom}}(\theta ) = \bigcup _{i < \omega } \textrm{{dom}}(\theta _i)$
. It is easy to check that
![]() $\theta $
is indeed a numbering of
$\theta $
is indeed a numbering of
![]() $A^\ast $
. We now show that
$A^\ast $
. We now show that
![]() ${\mathsf {Pr}(x) \equiv \exists y < x \ x = \overline {3} \times y}$
defines
${\mathsf {Pr}(x) \equiv \exists y < x \ x = \overline {3} \times y}$
defines
![]() $\{ \theta (\varphi ) \mid T \vdash \varphi \}$
. First, we define the height function
$\{ \theta (\varphi ) \mid T \vdash \varphi \}$
. First, we define the height function
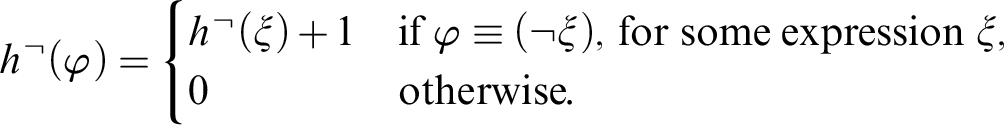 $$ \begin{align*} h^\neg(\varphi) = \begin{cases} h^\neg(\xi) + 1 & \text{if } \varphi \equiv (\neg \xi), \text{ for some expression } \xi,\\ 0 & \text{otherwise.} \end{cases} \end{align*} $$
$$ \begin{align*} h^\neg(\varphi) = \begin{cases} h^\neg(\xi) + 1 & \text{if } \varphi \equiv (\neg \xi), \text{ for some expression } \xi,\\ 0 & \text{otherwise.} \end{cases} \end{align*} $$
It is then easy to show by induction that for every T-theorem
![]() $\varphi $
the following holds:
$\varphi $
the following holds:
 $$ \begin{align*} \theta(\varphi) = 3 \cdot \langle h^\neg(\varphi),n \rangle \text{ and } \varphi \equiv \begin{cases} \underbrace{(\neg \cdots (\neg}_{h^\neg(\varphi)\text{-times}}\chi_n ) \cdots ) & \text{if } h^\neg(\varphi) \text{ is even},\\ \underbrace{(\neg \cdots (\neg}_{h^\neg(\varphi)\text{-times}} \mu_n ) \cdots ) & \text{if } h^\neg(\varphi) \text{ is odd}. \end{cases} \end{align*} $$
$$ \begin{align*} \theta(\varphi) = 3 \cdot \langle h^\neg(\varphi),n \rangle \text{ and } \varphi \equiv \begin{cases} \underbrace{(\neg \cdots (\neg}_{h^\neg(\varphi)\text{-times}}\chi_n ) \cdots ) & \text{if } h^\neg(\varphi) \text{ is even},\\ \underbrace{(\neg \cdots (\neg}_{h^\neg(\varphi)\text{-times}} \mu_n ) \cdots ) & \text{if } h^\neg(\varphi) \text{ is odd}. \end{cases} \end{align*} $$
Since there is a 1:1-correspondence between T-theorems
![]() $\varphi $
and pairs of natural numbers
$\varphi $
and pairs of natural numbers
![]() $\langle h^\neg (\varphi ),n \rangle $
, the set of
$\langle h^\neg (\varphi ),n \rangle $
, the set of
![]() $\theta $
-codes of T-theorems is exactly
$\theta $
-codes of T-theorems is exactly
![]() $3 \mathbb {N}$
. To show that the
$3 \mathbb {N}$
. To show that the
![]() $\theta $
-tracking function of
$\theta $
-tracking function of
![]() $\underline {\neg }$
is recursive proceeds as in the case of
$\underline {\neg }$
is recursive proceeds as in the case of
![]() $\delta $
.
$\delta $
.
The Numbering
 ${\eta }$
${\eta }$
Let T be given as in the construction of the numbering
![]() $\delta $
. We now construct a numbering
$\delta $
. We now construct a numbering
![]() $\eta $
of
$\eta $
of
![]() $A^\ast $
such that the tracking functions of the operations
$A^\ast $
such that the tracking functions of the operations
![]() $\underline {\mathsf {S}}$
,
$\underline {\mathsf {S}}$
,
![]() $\underline {+}$
,
$\underline {+}$
,
![]() $\underline {\times }$
,
$\underline {\times }$
,
![]() $\underline {\prime }$
,
$\underline {\prime }$
,
![]() $\underline {=}$
,
$\underline {=}$
,
![]() $\underline {\neg }$
,
$\underline {\neg }$
,
![]() $\underline {\wedge }$
and
$\underline {\wedge }$
and
![]() $\underline {\rightarrow }$
are recursive relative to
$\underline {\rightarrow }$
are recursive relative to
![]() $\eta $
and
$\eta $
and
![]() $\{ \eta (\chi ) \mid \mathbb {N} \models \chi \}$
is decidable. As in the case of
$\{ \eta (\chi ) \mid \mathbb {N} \models \chi \}$
is decidable. As in the case of
![]() $\delta $
, we partition the natural numbers into decidable infinite sets corresponding to certain syntactic categories:
$\delta $
, we partition the natural numbers into decidable infinite sets corresponding to certain syntactic categories:
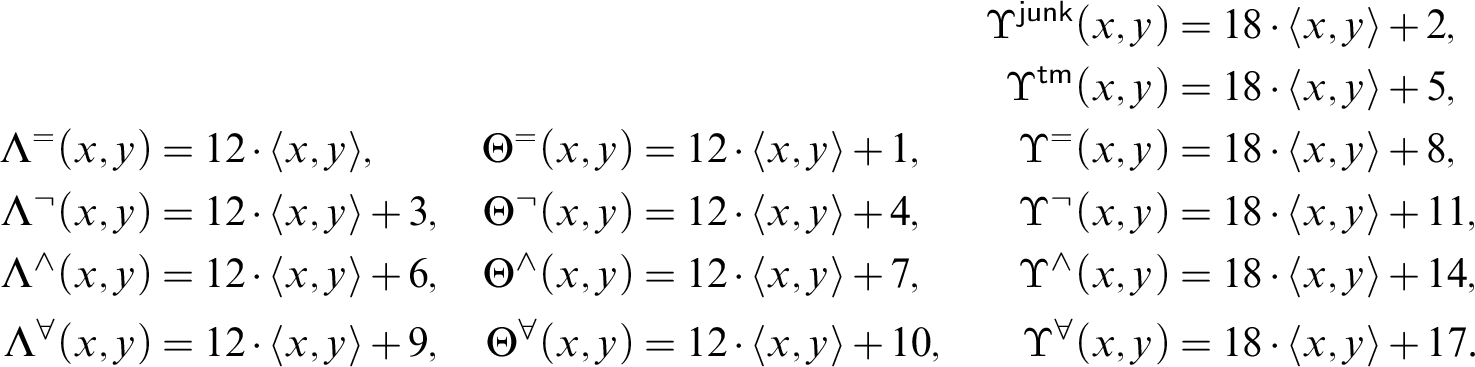 $$ \begin{align*} & & & & \Upsilon^{\mathsf{junk}}(x,y) & = 18 \cdot \langle x,y \rangle +2,\\ & & & & \Upsilon^{\mathsf{tm}}(x,y) & = 18 \cdot \langle x,y \rangle +5,\\ \Lambda^{=}(x,y) & = 12 \cdot \langle x,y \rangle, & \Theta^{=}(x,y) & = 12 \cdot \langle x,y \rangle +1, & \Upsilon^{=}(x,y) & = 18 \cdot \langle x,y \rangle +8,\\ \Lambda^{\neg}(x,y) & = 12 \cdot \langle x,y \rangle +3, & \Theta^{\neg}(x,y) & = 12 \cdot \langle x,y \rangle +4, & \Upsilon^{\neg}(x,y) & = 18 \cdot \langle x,y \rangle +11,\\ \Lambda^{\wedge}(x,y) & = 12 \cdot \langle x,y \rangle + 6, & \Theta^{\wedge}(x,y) & = 12 \cdot \langle x,y \rangle +7, & \Upsilon^{\wedge}(x,y) & = 18 \cdot \langle x,y \rangle +14,\\ \Lambda^{\forall}(x,y) & = 12 \cdot \langle x,y \rangle +9, & \Theta^{\forall}(x,y) & = 12 \cdot \langle x,y \rangle +10, & \Upsilon^{\forall}(x,y) & = 18 \cdot \langle x,y \rangle +17. \end{align*} $$
$$ \begin{align*} & & & & \Upsilon^{\mathsf{junk}}(x,y) & = 18 \cdot \langle x,y \rangle +2,\\ & & & & \Upsilon^{\mathsf{tm}}(x,y) & = 18 \cdot \langle x,y \rangle +5,\\ \Lambda^{=}(x,y) & = 12 \cdot \langle x,y \rangle, & \Theta^{=}(x,y) & = 12 \cdot \langle x,y \rangle +1, & \Upsilon^{=}(x,y) & = 18 \cdot \langle x,y \rangle +8,\\ \Lambda^{\neg}(x,y) & = 12 \cdot \langle x,y \rangle +3, & \Theta^{\neg}(x,y) & = 12 \cdot \langle x,y \rangle +4, & \Upsilon^{\neg}(x,y) & = 18 \cdot \langle x,y \rangle +11,\\ \Lambda^{\wedge}(x,y) & = 12 \cdot \langle x,y \rangle + 6, & \Theta^{\wedge}(x,y) & = 12 \cdot \langle x,y \rangle +7, & \Upsilon^{\wedge}(x,y) & = 18 \cdot \langle x,y \rangle +14,\\ \Lambda^{\forall}(x,y) & = 12 \cdot \langle x,y \rangle +9, & \Theta^{\forall}(x,y) & = 12 \cdot \langle x,y \rangle +10, & \Upsilon^{\forall}(x,y) & = 18 \cdot \langle x,y \rangle +17. \end{align*} $$
In what follows we define
![]() $\eta $
such that all numbers of true sentences of the form
$\eta $
such that all numbers of true sentences of the form
![]() $(s = t)$
are elements of
$(s = t)$
are elements of
![]() $\Lambda ^{=} (\mathbb {N},\mathbb {N}) = \{ \Lambda ^{=} (m,n) \mid m,n \in \mathbb {N} \} = 12 \mathbb {N}$
, all numbers of true sentences of the form
$\Lambda ^{=} (\mathbb {N},\mathbb {N}) = \{ \Lambda ^{=} (m,n) \mid m,n \in \mathbb {N} \} = 12 \mathbb {N}$
, all numbers of true sentences of the form
![]() $(\varphi \wedge \psi )$
are elements of
$(\varphi \wedge \psi )$
are elements of
![]() $\Lambda ^{\wedge } (\mathbb {N},\mathbb {N}) = 12 \mathbb {N} + 3$
, etc. Since
$\Lambda ^{\wedge } (\mathbb {N},\mathbb {N}) = 12 \mathbb {N} + 3$
, etc. Since
all (
![]() $\eta $
-codes of) true sentences are elements of
$\eta $
-codes of) true sentences are elements of
![]() $3 \mathbb {N} = \{ 3 \cdot n \mid n \in \mathbb {N} \}$
. Similarly, all (
$3 \mathbb {N} = \{ 3 \cdot n \mid n \in \mathbb {N} \}$
. Similarly, all (
![]() $\eta $
-codes of) false sentences are elements of
$\eta $
-codes of) false sentences are elements of
![]() $3 \mathbb {N} +1$
, and all (
$3 \mathbb {N} +1$
, and all (
![]() $\eta $
-codes of) expressions which are not sentences are elements of
$\eta $
-codes of) expressions which are not sentences are elements of
![]() $3 \mathbb {N} +2$
. Thus
$3 \mathbb {N} +2$
. Thus
![]() $\mathsf {Pr}(x) \equiv \exists y < x \ x = \overline {3} \times y$
satisfies Löb(
$\mathsf {Pr}(x) \equiv \exists y < x \ x = \overline {3} \times y$
satisfies Löb(
![]() $T, \eta $
) and
$T, \eta $
) and ![]() , for any sound T. Moreover, the set
, for any sound T. Moreover, the set
![]() $\{ \eta (\chi ) \mid \mathbb {N} \models \chi \}$
is definable by a
$\{ \eta (\chi ) \mid \mathbb {N} \models \chi \}$
is definable by a
 $\Delta ^0_0(\mathsf {exp})$
-formula.
$\Delta ^0_0(\mathsf {exp})$
-formula.
In a similar way to the above definitions of
![]() $\delta $
and
$\delta $
and
![]() $\theta $
, we define
$\theta $
, we define
![]() $\eta $
by exploiting the fact that the membership of
$\eta $
by exploiting the fact that the membership of
![]() $\neg \varphi $
and
$\neg \varphi $
and
![]() $\varphi \wedge \psi $
in
$\varphi \wedge \psi $
in
![]() $\{ \chi \mid \mathbb {N} \models \chi \}$
,
$\{ \chi \mid \mathbb {N} \models \chi \}$
,
![]() ${\{ \chi \mid \mathbb {N} \not \models \chi \}}$
and
${\{ \chi \mid \mathbb {N} \not \models \chi \}}$
and
![]() ${\{ \chi \mid \chi \text { is not a sentence} \}}$
is already fully determined by the respective memberships of
${\{ \chi \mid \chi \text { is not a sentence} \}}$
is already fully determined by the respective memberships of
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
.Footnote
28
This however does not hold for
$\psi $
.Footnote
28
This however does not hold for
![]() $\underline {\forall }$
, since there are expressions
$\underline {\forall }$
, since there are expressions
![]() $\varphi $
,
$\varphi $
,
![]() $\psi $
such that both
$\psi $
such that both
![]() $\mathbb {N} \models \forall x \varphi $
and
$\mathbb {N} \models \forall x \varphi $
and
![]() $\mathbb {N} \models \forall x \psi $
but
$\mathbb {N} \models \forall x \psi $
but
![]() $\varphi \in \{ \chi \mid \mathbb {N} \models \chi \}$
and
$\varphi \in \{ \chi \mid \mathbb {N} \models \chi \}$
and
![]() ${\psi \in \{ \chi \mid \chi \text { is not a sentence} \}}$
. Hence, in what follows,
${\psi \in \{ \chi \mid \chi \text { is not a sentence} \}}$
. Hence, in what follows,
![]() $\eta (\forall x \varphi )$
is not defined along the lines of
$\eta (\forall x \varphi )$
is not defined along the lines of
![]() $\eta (\neg \varphi )$
and
$\eta (\neg \varphi )$
and
![]() $\eta (\varphi \wedge \psi )$
, resulting in the nonrecursiveness of the
$\eta (\varphi \wedge \psi )$
, resulting in the nonrecursiveness of the
![]() $\eta $
-tracking function of
$\eta $
-tracking function of
![]() $\underline {\forall }$
.
$\underline {\forall }$
.
Let
![]() $\{ \chi _n \mid n \in \mathbb {N} \}$
be an enumeration without repetitions of true sentences which are of the form
$\{ \chi _n \mid n \in \mathbb {N} \}$
be an enumeration without repetitions of true sentences which are of the form
![]() $(\forall x \varphi )$
, let
$(\forall x \varphi )$
, let
![]() $\{ \nu _n \mid n \in \mathbb {N} \}$
be an enumeration without repetitions of false sentences which are of the form
$\{ \nu _n \mid n \in \mathbb {N} \}$
be an enumeration without repetitions of false sentences which are of the form
![]() $(\forall x \varphi )$
, and let
$(\forall x \varphi )$
, and let
![]() $\{ \mu _n \mid n \in \mathbb {N} \}$
be an enumeration without repetitions of formulæ of the form
$\{ \mu _n \mid n \in \mathbb {N} \}$
be an enumeration without repetitions of formulæ of the form
![]() $(\forall x \varphi )$
which are not sentences (with x and
$(\forall x \varphi )$
which are not sentences (with x and
![]() $\varphi $
being expressions). Moreover, let
$\varphi $
being expressions). Moreover, let
![]() $\{ \xi _n \mid n \in \mathbb {N} \}$
be an enumeration without repetitions of strings which are not well-formed expressions.
$\{ \xi _n \mid n \in \mathbb {N} \}$
be an enumeration without repetitions of strings which are not well-formed expressions.
We first define a numbering
![]() $\eta _0$
of
$\eta _0$
of
![]() $\mathit {Term} \cup \{ (\forall x \varphi ) \mid x \in \mathit {Var}, \varphi \in \mathit {Fml} \} $
by setting
$\mathit {Term} \cup \{ (\forall x \varphi ) \mid x \in \mathit {Var}, \varphi \in \mathit {Fml} \} $
by setting
![]() $\eta _0(s) = \Upsilon ^{\mathsf {tm}}(0,\gamma (s))$
for
$\eta _0(s) = \Upsilon ^{\mathsf {tm}}(0,\gamma (s))$
for
![]() $s \in \mathit {Term}$
, and
$s \in \mathit {Term}$
, and
![]() $\eta _0(\chi _n)= \Lambda ^{\forall }(0,n) $
,
$\eta _0(\chi _n)= \Lambda ^{\forall }(0,n) $
,
![]() $\eta _0(\nu _n)= \Theta ^{\forall }(0,n)$
and
$\eta _0(\nu _n)= \Theta ^{\forall }(0,n)$
and
![]() $\eta _0(\mu _n)= \Upsilon ^{\forall }(0,n)$
. Moreover, set
$\eta _0(\mu _n)= \Upsilon ^{\forall }(0,n)$
. Moreover, set
![]() $\eta ^{\mathsf {junk}}(\xi _n)= \Upsilon ^{\mathsf {junk}}(0,n) $
.
$\eta ^{\mathsf {junk}}(\xi _n)= \Upsilon ^{\mathsf {junk}}(0,n) $
.
As above we extend
![]() $\eta _0$
to a numbering of the well formed expressions, by defining
$\eta _0$
to a numbering of the well formed expressions, by defining
![]() $\eta _{i+1}$
for each
$\eta _{i+1}$
for each
![]() $i < \omega $
:
$i < \omega $
:
 $$ \begin{align*} {\mathrm{dom}}(\eta_{i+1}) & = {\mathrm{dom}}(\eta_i) \cup \{ (s = t) \mid s,t \in {\mathrm{dom}}(\eta_i) \cap \mathit{Term} \} \cup\\ & \quad \cup \{ (\neg \varphi), (\varphi \wedge \psi) \mid \varphi, \psi \in {\mathrm{dom}}(\eta_i) \cap Form\};\\ \eta_{i+1}(\varphi) & = \eta_i(\varphi), \text{ if } \varphi \in {\mathrm{dom}}(\eta_i);\\ \eta_{i+1}((s = t)) & = \begin{cases} \Lambda^{=}(\eta_i(s),\eta_i(t)), & \text{ if } s,t \in {\mathrm{dom}}(\eta_i), s,t \text{ are closed terms, } \mathbb{N} \models s=t,\\ \Theta^{=}(\eta_i(s),\eta_i(t)), & \text{ if } s,t \in {\mathrm{dom}}(\eta_i), s,t \text{ are closed terms, } \mathbb{N} \not\models s = t,\\ \Upsilon^{=}(\eta_i(s),\eta_i(t)), & \text{ if } s,t \in {\mathrm{dom}}(\eta_i) \cap \mathit{Term}, \\ & \;\,\,s \text{ or } t \text{ is not a closed term;} \end{cases}\\ \eta_{i+1}((\neg \varphi)) & = \begin{cases} \Lambda^{\neg}(0,\eta_i(\varphi)), & \text{ if } \varphi \in {\mathrm{dom}}(\eta_i), \mathbb{N} \not\models \varphi,\\ \Theta^{\neg}(0,\eta_i(\varphi)), & \text{ if } \varphi \in {\mathrm{dom}}(\eta_i), \mathbb{N} \models \varphi,\\ \Upsilon^{\neg}(0,\eta_i(\varphi)), & \text{ if } \varphi \in {\mathrm{dom}}(\eta_i) \cap Form, \varphi \text{ is not a sentence;} \end{cases}\\ \eta_{i+1}((\varphi \wedge \psi)) & = \begin{cases} \Lambda^{\wedge}(\eta_i(\varphi),\eta_i(\psi)), & \text{ if } \varphi, \psi \in {\mathrm{dom}}(\eta_i), \mathbb{N} \models \varphi, \psi,\\ \Theta^{\wedge}(\eta_i(\varphi),\eta_i(\psi)), & \text{ if } \varphi, \psi \in {\mathrm{dom}}(\eta_i), \mathbb{N} \not\models \varphi \text{ or } \mathbb{N} \not\models \psi,\\ \Upsilon^{\wedge}(\eta_i(\varphi),\eta_i(\psi)), & \text{ if } \varphi, \psi \in {\mathrm{dom}}(\eta_i) \cap Form, \\ & \,\varphi \text{ or } \psi \text{ is not a sentence.} \end{cases} \end{align*} $$
$$ \begin{align*} {\mathrm{dom}}(\eta_{i+1}) & = {\mathrm{dom}}(\eta_i) \cup \{ (s = t) \mid s,t \in {\mathrm{dom}}(\eta_i) \cap \mathit{Term} \} \cup\\ & \quad \cup \{ (\neg \varphi), (\varphi \wedge \psi) \mid \varphi, \psi \in {\mathrm{dom}}(\eta_i) \cap Form\};\\ \eta_{i+1}(\varphi) & = \eta_i(\varphi), \text{ if } \varphi \in {\mathrm{dom}}(\eta_i);\\ \eta_{i+1}((s = t)) & = \begin{cases} \Lambda^{=}(\eta_i(s),\eta_i(t)), & \text{ if } s,t \in {\mathrm{dom}}(\eta_i), s,t \text{ are closed terms, } \mathbb{N} \models s=t,\\ \Theta^{=}(\eta_i(s),\eta_i(t)), & \text{ if } s,t \in {\mathrm{dom}}(\eta_i), s,t \text{ are closed terms, } \mathbb{N} \not\models s = t,\\ \Upsilon^{=}(\eta_i(s),\eta_i(t)), & \text{ if } s,t \in {\mathrm{dom}}(\eta_i) \cap \mathit{Term}, \\ & \;\,\,s \text{ or } t \text{ is not a closed term;} \end{cases}\\ \eta_{i+1}((\neg \varphi)) & = \begin{cases} \Lambda^{\neg}(0,\eta_i(\varphi)), & \text{ if } \varphi \in {\mathrm{dom}}(\eta_i), \mathbb{N} \not\models \varphi,\\ \Theta^{\neg}(0,\eta_i(\varphi)), & \text{ if } \varphi \in {\mathrm{dom}}(\eta_i), \mathbb{N} \models \varphi,\\ \Upsilon^{\neg}(0,\eta_i(\varphi)), & \text{ if } \varphi \in {\mathrm{dom}}(\eta_i) \cap Form, \varphi \text{ is not a sentence;} \end{cases}\\ \eta_{i+1}((\varphi \wedge \psi)) & = \begin{cases} \Lambda^{\wedge}(\eta_i(\varphi),\eta_i(\psi)), & \text{ if } \varphi, \psi \in {\mathrm{dom}}(\eta_i), \mathbb{N} \models \varphi, \psi,\\ \Theta^{\wedge}(\eta_i(\varphi),\eta_i(\psi)), & \text{ if } \varphi, \psi \in {\mathrm{dom}}(\eta_i), \mathbb{N} \not\models \varphi \text{ or } \mathbb{N} \not\models \psi,\\ \Upsilon^{\wedge}(\eta_i(\varphi),\eta_i(\psi)), & \text{ if } \varphi, \psi \in {\mathrm{dom}}(\eta_i) \cap Form, \\ & \,\varphi \text{ or } \psi \text{ is not a sentence.} \end{cases} \end{align*} $$
Finally, we define
 $\eta = \left ( \bigcup _{i < \omega } \eta _i \right ) \cup \eta ^{\mathsf {junk}}$
, with
$\eta = \left ( \bigcup _{i < \omega } \eta _i \right ) \cup \eta ^{\mathsf {junk}}$
, with
 $\textrm{{dom}}(\eta ) = \left ( \bigcup _{i < \omega } \textrm{{dom}}(\eta _i) \right ) \cup \mathit {Junk}$
. Showing that
$\textrm{{dom}}(\eta ) = \left ( \bigcup _{i < \omega } \textrm{{dom}}(\eta _i) \right ) \cup \mathit {Junk}$
. Showing that
![]() $\eta $
is a numbering of
$\eta $
is a numbering of
![]() $A^\ast $
such that
$A^\ast $
such that
![]() $\{ \eta (\chi ) \mid \mathbb {N} \models \chi \}$
can be defined by a
$\{ \eta (\chi ) \mid \mathbb {N} \models \chi \}$
can be defined by a
 $\Delta ^0_0(\mathsf {exp})$
-formula and the
$\Delta ^0_0(\mathsf {exp})$
-formula and the
![]() $\eta $
-tracking functions of all operations operations
$\eta $
-tracking functions of all operations operations
![]() $\underline {\mathsf {S}}$
,
$\underline {\mathsf {S}}$
,
![]() $\underline {+}$
,
$\underline {+}$
,
![]() $\underline {\times }$
,
$\underline {\times }$
,
![]() $\underline {\prime }$
,
$\underline {\prime }$
,
![]() $\underline {=}$
,
$\underline {=}$
,
![]() $\underline {\neg }$
,
$\underline {\neg }$
,
![]() $\underline {\wedge }$
and
$\underline {\wedge }$
and
![]() $\underline {\rightarrow }$
are recursive proceeds as in the case of
$\underline {\rightarrow }$
are recursive proceeds as in the case of
![]() $\delta $
above.
$\delta $
above.
The Numbering
 ${\zeta }$
${\zeta }$
We conclude with a construction of a numbering
![]() $\zeta $
of
$\zeta $
of
![]() $A^\ast $
which is monotonic and such that
$A^\ast $
which is monotonic and such that
![]() $\zeta (T^\vdash ) = \{ n \mid {\exists\kern-0.45em\exists } m \geq 10 \ n = m^3 \}$
. Hence the formula
$\zeta (T^\vdash ) = \{ n \mid {\exists\kern-0.45em\exists } m \geq 10 \ n = m^3 \}$
. Hence the formula
![]() ${\mathsf {Pr}(x) \equiv \exists y < x (x = y \times y \times y \wedge y \geq \overline {10})}$
is a
${\mathsf {Pr}(x) \equiv \exists y < x (x = y \times y \times y \wedge y \geq \overline {10})}$
is a
![]() $\Delta ^0_0$
-binumeration of (
$\Delta ^0_0$
-binumeration of (
![]() $\zeta $
-codes) of T-theorems.
$\zeta $
-codes) of T-theorems.
Let
![]() $\alpha _0 \equiv ( \mathsf {0} = \mathsf {0} )$
and
$\alpha _0 \equiv ( \mathsf {0} = \mathsf {0} )$
and
![]() $\alpha _{i+1} \equiv ( \alpha _i \wedge (\mathsf {0} = \mathsf {0}))$
, for
$\alpha _{i+1} \equiv ( \alpha _i \wedge (\mathsf {0} = \mathsf {0}))$
, for
![]() $i < \omega $
. Let
$i < \omega $
. Let
![]() $(\beta _i)_{i < \omega }$
be an enumeration (without repetitions) of the substrings of elements of
$(\beta _i)_{i < \omega }$
be an enumeration (without repetitions) of the substrings of elements of
![]() $(\alpha _i)_{i < \omega }$
which are themselves not elements of
$(\alpha _i)_{i < \omega }$
which are themselves not elements of
![]() $(\alpha _i)_{i < \omega }$
. We assume that
$(\alpha _i)_{i < \omega }$
. We assume that
![]() $(\beta _i)_{i < \omega }$
is given in length-first ordering, i.e.,
$(\beta _i)_{i < \omega }$
is given in length-first ordering, i.e.,
![]() $i < j$
iff the length of
$i < j$
iff the length of
![]() $\beta _i$
is smaller than the length of
$\beta _i$
is smaller than the length of
![]() $\beta _j$
, or
$\beta _j$
, or
![]() $\beta _i$
and
$\beta _i$
and
![]() $\beta _j$
have the same length and
$\beta _j$
have the same length and
![]() $\beta _i$
is lexicographically (relative to some total order on A) smaller than
$\beta _i$
is lexicographically (relative to some total order on A) smaller than
![]() $\beta _j$
. Moreover, let
$\beta _j$
. Moreover, let
![]() $\gamma _0 \equiv ` \prime \text{'} $
and
$\gamma _0 \equiv ` \prime \text{'} $
and
![]() $\gamma _{i+1} \equiv \gamma _i \ast ` \prime \text{'} $
, for
$\gamma _{i+1} \equiv \gamma _i \ast ` \prime \text{'} $
, for
![]() $i < \omega $
.
$i < \omega $
.
Let
![]() $(\chi _i)_{i < \omega }$
be a monotonic enumeration of
$(\chi _i)_{i < \omega }$
be a monotonic enumeration of
![]() ${A^\ast \setminus ( (\alpha _i)_{i < \omega } \cup (\beta _i)_{i < \omega } \cup (\gamma _i)_{i < \omega } )}$
without repetitions. We thus have
${A^\ast \setminus ( (\alpha _i)_{i < \omega } \cup (\beta _i)_{i < \omega } \cup (\gamma _i)_{i < \omega } )}$
without repetitions. We thus have
![]() $j \leq i$
if
$j \leq i$
if
![]() $\chi _j$
is a subexpression of
$\chi _j$
is a subexpression of
![]() $\chi _i$
. This can for instance be achieved by starting with a surjective and monotonic standard numbering of
$\chi _i$
. This can for instance be achieved by starting with a surjective and monotonic standard numbering of
![]() $A^\ast $
.
$A^\ast $
.
We define a bijection
![]() $g \colon \mathbb {N} \to A^\ast $
by recursion as follows. Let
$g \colon \mathbb {N} \to A^\ast $
by recursion as follows. Let
![]() $\prec $
denote the strict substring relation on
$\prec $
denote the strict substring relation on
![]() $A^\ast $
. Let
$A^\ast $
. Let
![]() $n \in \mathbb {N}$
and assume that
$n \in \mathbb {N}$
and assume that
![]() $g(m)$
is already defined for all
$g(m)$
is already defined for all
![]() $m < n$
. Let
$m < n$
. Let
![]() $(\mu _i)_{i< \omega }$
be any given enumeration of strings. For the sake of brevity, we also write
$(\mu _i)_{i< \omega }$
be any given enumeration of strings. For the sake of brevity, we also write
![]() $\widetilde {\mu }$
instead of
$\widetilde {\mu }$
instead of
![]() $(\mu _i)_{i < \omega }$
. We first set
$(\mu _i)_{i < \omega }$
. We first set
That is, for a given enumeration
![]() $\widetilde {\mu }$
and input n, the function
$\widetilde {\mu }$
and input n, the function
![]() $\mathfrak {m}(\cdot ,\widetilde {\mu }) \colon \mathbb {N} \to \mathbb {N}$
outputs the smallest index k such that
$\mathfrak {m}(\cdot ,\widetilde {\mu }) \colon \mathbb {N} \to \mathbb {N}$
outputs the smallest index k such that
![]() $\mu _k$
is not the g-value of any
$\mu _k$
is not the g-value of any
![]() $m < n$
. We now define
$m < n$
. We now define
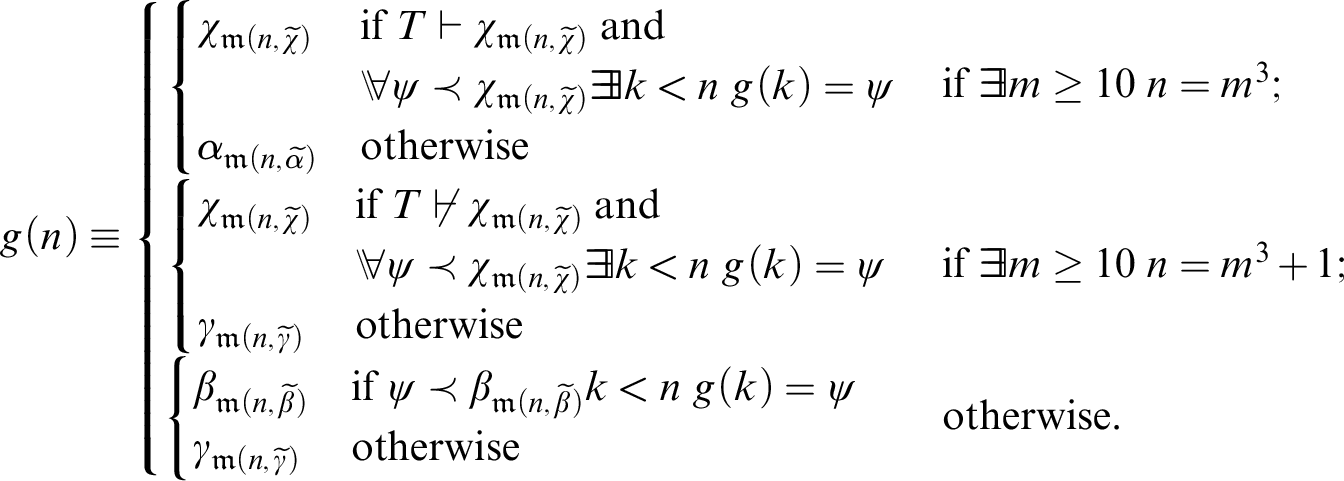
Since
![]() $\widetilde {\alpha }$
,
$\widetilde {\alpha }$
,
![]() $\widetilde {\beta }$
,
$\widetilde {\beta }$
,
![]() $\widetilde {\gamma }$
and
$\widetilde {\gamma }$
and
![]() $\widetilde {\chi }$
are pairwise disjoint enumerations without repetitions, g is injective. We now define
$\widetilde {\chi }$
are pairwise disjoint enumerations without repetitions, g is injective. We now define
![]() $\zeta := g^{-1}$
.
$\zeta := g^{-1}$
.
We show that
![]() $\zeta $
is indeed a function with domain
$\zeta $
is indeed a function with domain
![]() $A^*$
, i.e., we have to show that g is surjective. Informally speaking, this is tantamount to showing that there is no number from which on the values of g only belong to three or less of the four enumerations.
$A^*$
, i.e., we have to show that g is surjective. Informally speaking, this is tantamount to showing that there is no number from which on the values of g only belong to three or less of the four enumerations.
We first show that for each i there exists n such that
![]() $g(n) \equiv \alpha _i$
. Assume that this is not the case, and let
$g(n) \equiv \alpha _i$
. Assume that this is not the case, and let
![]() $i_0 = \max \{i \mid \exists\kern-0.45em\exists n \ g(n) \equiv \alpha _i \}$
. Then there exists an index
$i_0 = \max \{i \mid \exists\kern-0.45em\exists n \ g(n) \equiv \alpha _i \}$
. Then there exists an index
![]() $j_0$
such that for all
$j_0$
such that for all
![]() $j> j_0$
:
$j> j_0$
:
Let now
![]() $i> i_0$
be given such that
$i> i_0$
be given such that
![]() $(\alpha _{i} \vee \alpha _{i}) \equiv \chi _j$
for some
$(\alpha _{i} \vee \alpha _{i}) \equiv \chi _j$
for some
![]() $j> j_0$
(note that such numbers exists since there are infinitely many strings of the form
$j> j_0$
(note that such numbers exists since there are infinitely many strings of the form
![]() $(\alpha _{i} \vee \alpha _{i})$
). Then
$(\alpha _{i} \vee \alpha _{i})$
). Then
![]() $T \vdash (\alpha _{i} \vee \alpha _{i})$
and
$T \vdash (\alpha _{i} \vee \alpha _{i})$
and
![]() $\alpha _{i} \prec (\alpha _{i} \vee \alpha _{i})$
, but since
$\alpha _{i} \prec (\alpha _{i} \vee \alpha _{i})$
, but since
![]() $i> i_0$
there is no k such that
$i> i_0$
there is no k such that
![]() $g(\alpha _{i}) \equiv k$
, in contradiction to (8).
$g(\alpha _{i}) \equiv k$
, in contradiction to (8).
Analogously it can be shown that for each i there exists n such that
![]() $g(n) \equiv \gamma _i$
(for instance, by considering
$g(n) \equiv \gamma _i$
(for instance, by considering
![]() $` \mathsf {v} \text{'} \ast \gamma _i$
instead of
$` \mathsf {v} \text{'} \ast \gamma _i$
instead of
![]() $(\alpha _{i} \vee \alpha _{i})$
).
$(\alpha _{i} \vee \alpha _{i})$
).
We now show that each
![]() $\beta _i$
is the g-value of some number, by induction over i. Since
$\beta _i$
is the g-value of some number, by induction over i. Since
![]() $\widetilde {\beta }$
is length-first-ordered,
$\widetilde {\beta }$
is length-first-ordered,
![]() $\beta _0$
has no proper substrings and hence
$\beta _0$
has no proper substrings and hence
![]() $g(0) \equiv \beta _0$
. Let
$g(0) \equiv \beta _0$
. Let
![]() $i> 0$
, and assume that each
$i> 0$
, and assume that each
![]() $\beta _j$
with
$\beta _j$
with
![]() $j <i$
is the g-value of some number. If
$j <i$
is the g-value of some number. If
![]() $\psi \prec \beta _i$
, then
$\psi \prec \beta _i$
, then
![]() $\psi \equiv \beta _j$
for some
$\psi \equiv \beta _j$
for some
![]() $j < i$
or
$j < i$
or
![]() $\psi \equiv \alpha _l$
for some
$\psi \equiv \alpha _l$
for some
![]() $l \in \mathbb {N}$
. Since by induction hypothesis each
$l \in \mathbb {N}$
. Since by induction hypothesis each
![]() $\beta _j$
with
$\beta _j$
with
![]() $j < i$
is the g-value of a number, and we have seen above that each
$j < i$
is the g-value of a number, and we have seen above that each
![]() $\alpha _l$
is the g-value of a number, there exists a smallest number n such that n is not of the form
$\alpha _l$
is the g-value of a number, there exists a smallest number n such that n is not of the form
![]() $m^3$
or
$m^3$
or
![]() $m^3+1$
(for
$m^3+1$
(for
![]() $m \geq 10$
), and the g-value of each (proper) substring of
$m \geq 10$
), and the g-value of each (proper) substring of
![]() $\beta _i$
is smaller than n. Then
$\beta _i$
is smaller than n. Then
 $g(n) \equiv \beta _{\mathfrak {m}(n,\widetilde {\beta })} \equiv \beta _i$
.
$g(n) \equiv \beta _{\mathfrak {m}(n,\widetilde {\beta })} \equiv \beta _i$
.
We now show that each
![]() $\chi _i$
is the g-value of some number, by induction over i. Since
$\chi _i$
is the g-value of some number, by induction over i. Since
![]() $\widetilde {\chi }$
is monotonic,
$\widetilde {\chi }$
is monotonic,
![]() $\chi _0$
is a string of length
$\chi _0$
is a string of length
![]() $1$
. Hence
$1$
. Hence
![]() $g(10^3+1) \equiv \chi _0$
.
$g(10^3+1) \equiv \chi _0$
.
Let
![]() $i> 0$
be given and assume that each
$i> 0$
be given and assume that each
![]() $\chi _j$
with
$\chi _j$
with
![]() $j <i$
is the g-value of some number. If
$j <i$
is the g-value of some number. If
![]() $\psi \prec \chi _i$
, then either
$\psi \prec \chi _i$
, then either
![]() $\psi \equiv \chi _j$
with
$\psi \equiv \chi _j$
with
![]() $j < i$
, or
$j < i$
, or
![]() $\psi \equiv \alpha _l$
or
$\psi \equiv \alpha _l$
or
![]() $\psi \equiv \beta _l$
or
$\psi \equiv \beta _l$
or
![]() $\psi \equiv \gamma _l$
, for some
$\psi \equiv \gamma _l$
, for some
![]() $l \in \mathbb {N}$
. Once again, by induction hypothesis each
$l \in \mathbb {N}$
. Once again, by induction hypothesis each
![]() $\chi _j$
with
$\chi _j$
with
![]() $j < i$
is the g-value of a number, and we have seen above that each
$j < i$
is the g-value of a number, and we have seen above that each
![]() $\alpha _l$
,
$\alpha _l$
,
![]() $\beta _l$
and
$\beta _l$
and
![]() $\gamma _l$
is the g-value of a number. Hence
$\gamma _l$
is the g-value of a number. Hence
 $g(n) \equiv \chi _{\mathfrak {m}(n,\widetilde {\chi })} \equiv \chi _i$
, where n is the smallest number of the appropriate form, i.e.,
$g(n) \equiv \chi _{\mathfrak {m}(n,\widetilde {\chi })} \equiv \chi _i$
, where n is the smallest number of the appropriate form, i.e.,
![]() $m^3$
in case that
$m^3$
in case that
![]() $T \vdash \chi _i$
, and
$T \vdash \chi _i$
, and
![]() $m^3+1$
otherwise (for
$m^3+1$
otherwise (for
![]() $m \geq 10$
), such that the g-value of each (proper) substring of
$m \geq 10$
), such that the g-value of each (proper) substring of
![]() $\chi _i$
is smaller than n.
$\chi _i$
is smaller than n.
It remains to show that
![]() $\zeta $
is monotonic. Let
$\zeta $
is monotonic. Let
![]() $\varphi \prec \psi $
be given strings.
$\varphi \prec \psi $
be given strings.
If
![]() $\psi \equiv \gamma _i$
, for some
$\psi \equiv \gamma _i$
, for some
![]() $i \in \mathbb {N}$
. Then
$i \in \mathbb {N}$
. Then
![]() $\varphi \equiv \gamma _j$
, for some
$\varphi \equiv \gamma _j$
, for some
![]() $j < i$
. It follows immediately from the definition of g that if
$j < i$
. It follows immediately from the definition of g that if
![]() $\zeta (\gamma _i )=m $
, there exists
$\zeta (\gamma _i )=m $
, there exists
![]() $k < m$
such that
$k < m$
such that
![]() $g(k) \equiv \gamma _j$
. Hence
$g(k) \equiv \gamma _j$
. Hence
![]() $\zeta (\gamma _j) < \zeta (\gamma _i)$
.
$\zeta (\gamma _j) < \zeta (\gamma _i)$
.
If
![]() $\psi \equiv \beta _i$
or
$\psi \equiv \beta _i$
or
![]() $\psi \equiv \chi _i$
, for some
$\psi \equiv \chi _i$
, for some
![]() $i \in \mathbb {N}$
, the claim immediately follows from the defining clauses of g.
$i \in \mathbb {N}$
, the claim immediately follows from the defining clauses of g.
If
![]() $\psi \equiv \alpha _i$
, for some
$\psi \equiv \alpha _i$
, for some
![]() $i \in \mathbb {N}$
, then
$i \in \mathbb {N}$
, then
![]() $\varphi \equiv \alpha _j$
, for some
$\varphi \equiv \alpha _j$
, for some
![]() $j < i$
, or
$j < i$
, or
![]() $\varphi \equiv \beta _l$
for some
$\varphi \equiv \beta _l$
for some
![]() $l \in \mathbb {N}$
. By definition of g, we have
$l \in \mathbb {N}$
. By definition of g, we have
![]() $\zeta (\alpha _j) < \zeta (\alpha _i)$
. It remains to show that for all
$\zeta (\alpha _j) < \zeta (\alpha _i)$
. It remains to show that for all
![]() $i,l \in \mathbb {N}$
:
$i,l \in \mathbb {N}$
:
We first show that
![]() $A[i]$
implies
$A[i]$
implies
![]() , for any
, for any
![]() $i \in \mathbb {N}$
; where
$i \in \mathbb {N}$
; where
![]() $A[i]$
is the statement:
$A[i]$
is the statement:
“
![]() ”: Let
”: Let
![]() $g(m^3) \equiv \alpha _i$
for some m. By
$g(m^3) \equiv \alpha _i$
for some m. By
![]() $A[i]$
, we find n and l such that
$A[i]$
, we find n and l such that
![]() $g(n) \equiv \gamma _l$
and
$g(n) \equiv \gamma _l$
and
![]() $(m-1)^3+1 < n < m^3$
. Since n cannot be of the form
$(m-1)^3+1 < n < m^3$
. Since n cannot be of the form
![]() $s^3$
or
$s^3$
or
![]() $s^3+1$
, it follows that
$s^3+1$
, it follows that
![]() $g(n)$
is obtained by the second case of the third clause of the definition of g. Hence, there exists
$g(n)$
is obtained by the second case of the third clause of the definition of g. Hence, there exists
 $\psi \prec \beta _{\mathfrak {m}(n,\widetilde {\beta })}$
such that (
$\psi \prec \beta _{\mathfrak {m}(n,\widetilde {\beta })}$
such that (
![]() $\ast $
)
$\ast $
)
![]() $g(k) \not \equiv \psi $
for all
$g(k) \not \equiv \psi $
for all
![]() $k < n$
. Clearly,
$k < n$
. Clearly,
![]() $\psi $
is not contained in
$\psi $
is not contained in
![]() $\widetilde {\beta }$
. For otherwise,
$\widetilde {\beta }$
. For otherwise,
![]() $\psi \equiv \beta _j$
for some
$\psi \equiv \beta _j$
for some
![]() $j \in \mathbb {N}$
. Then
$j \in \mathbb {N}$
. Then
 $j < \beta _{\mathfrak {m}(n,\widetilde {\beta })}$
by definition of
$j < \beta _{\mathfrak {m}(n,\widetilde {\beta })}$
by definition of
![]() $\widetilde {\beta }$
. But since
$\widetilde {\beta }$
. But since
![]() $\beta _j$
is not the g-value of any number smaller than n, we have
$\beta _j$
is not the g-value of any number smaller than n, we have
 $\mathfrak {m}(n,\widetilde {\beta }) \leq j$
, resulting in a contradiction.
$\mathfrak {m}(n,\widetilde {\beta }) \leq j$
, resulting in a contradiction.
Hence,
![]() $\psi \equiv \alpha _j$
for some
$\psi \equiv \alpha _j$
for some
![]() $j \in \mathbb {N}$
. Since
$j \in \mathbb {N}$
. Since
![]() $g^{-1}(\alpha _i) \equiv m^3$
, we have
$g^{-1}(\alpha _i) \equiv m^3$
, we have
 $g^{-1}(\alpha _{j'}) \leq (m-1)^3$
for every
$g^{-1}(\alpha _{j'}) \leq (m-1)^3$
for every
![]() $j' < i$
. By (
$j' < i$
. By (
![]() $\ast $
),
$\ast $
),
![]() $\alpha _j$
is not the g-value of any number smaller than n. Since
$\alpha _j$
is not the g-value of any number smaller than n. Since
![]() $(m-1)^3 < n$
we thus conclude that
$(m-1)^3 < n$
we thus conclude that
![]() $i \leq j$
. Therefore
$i \leq j$
. Therefore
 $\alpha _i \preceq \alpha _j \prec \beta _{\mathfrak {m}(n,\widetilde {\beta })}$
.
$\alpha _i \preceq \alpha _j \prec \beta _{\mathfrak {m}(n,\widetilde {\beta })}$
.
We show now that
![]() $B[i,l]$
holds, for any given l. If
$B[i,l]$
holds, for any given l. If
![]() $\beta _l \prec \alpha _i$
, then also
$\beta _l \prec \alpha _i$
, then also
 $\beta _l \prec \beta _{\mathfrak {m}(n,\widetilde {\beta })}$
. Hence
$\beta _l \prec \beta _{\mathfrak {m}(n,\widetilde {\beta })}$
. Hence
 $l < \mathfrak {m}(n,\widetilde {\beta })$
, by definition of
$l < \mathfrak {m}(n,\widetilde {\beta })$
, by definition of
![]() $\widetilde {\beta }$
. But then there exists
$\widetilde {\beta }$
. But then there exists
![]() $k < n$
such that
$k < n$
such that
![]() $g(k) \equiv \beta _l$
. Since
$g(k) \equiv \beta _l$
. Since
![]() $k < n < m^3$
we conclude that
$k < n < m^3$
we conclude that
![]() $g^{-1}(\beta _l) < g^{-1}(\alpha _i)$
, as desired.
$g^{-1}(\beta _l) < g^{-1}(\alpha _i)$
, as desired.
“
![]() ”: We show now by induction that
”: We show now by induction that
![]() $A[i]$
holds for all
$A[i]$
holds for all
![]() $i \in \mathbb {N}$
.
$i \in \mathbb {N}$
.
Since
![]() $\alpha _0$
has length
$\alpha _0$
has length
![]() $5$
, it has not more than
$5$
, it has not more than
 $\frac {5 (5+1)}{2}$
substrings. By definition of g and
$\frac {5 (5+1)}{2}$
substrings. By definition of g and
![]() $\widetilde {\beta }$
, it is easy to check that there is a number
$\widetilde {\beta }$
, it is easy to check that there is a number
![]() $n < 10^3$
such that the g-value of each proper substring of
$n < 10^3$
such that the g-value of each proper substring of
![]() $\alpha _0$
is smaller than n. Hence
$\alpha _0$
is smaller than n. Hence
 $\alpha _0 \prec \beta _{\mathfrak {m}(n,\widetilde {\beta })}$
. But since
$\alpha _0 \prec \beta _{\mathfrak {m}(n,\widetilde {\beta })}$
. But since
![]() $g^{-1}(\alpha _0) \geq 10^3$
we have
$g^{-1}(\alpha _0) \geq 10^3$
we have
 $g(n) \equiv \gamma _{\mathfrak {m}(n,\widetilde {\beta })}$
.
$g(n) \equiv \gamma _{\mathfrak {m}(n,\widetilde {\beta })}$
.
Let now
![]() $i> 0$
be given, and assume that
$i> 0$
be given, and assume that
![]() $A[i-1]$
holds. Let
$A[i-1]$
holds. Let
![]() $g^{-1}(\alpha _i) = m^3$
. We assume that
$g^{-1}(\alpha _i) = m^3$
. We assume that
![]() $A[i]$
does not hold. Let n be fixed such that
$A[i]$
does not hold. Let n be fixed such that
![]() $(m-1)^3+1 < n < m^3$
. We then have
$(m-1)^3+1 < n < m^3$
. We then have
![]() $g(n) \equiv \beta _{l}$
for some l. Hence,
$g(n) \equiv \beta _{l}$
for some l. Hence,
If
![]() $\beta _{l} \prec \alpha _{i-1}$
, then
$\beta _{l} \prec \alpha _{i-1}$
, then
![]() $g^{-1}(\beta _l) < g^{-1}(\alpha _{i-1}) \leq (m-1)^3$
by
$g^{-1}(\beta _l) < g^{-1}(\alpha _{i-1}) \leq (m-1)^3$
by
![]() $B[i-1,l]$
(using the fact that
$B[i-1,l]$
(using the fact that
![]() and the induction hypothesis
and the induction hypothesis
![]() $A[i-1]$
). But since
$A[i-1]$
). But since
![]() $(m-1)^3 < n = g^{-1}(\beta _l)$
, we conclude that
$(m-1)^3 < n = g^{-1}(\beta _l)$
, we conclude that
![]() $\beta _{l} \prec \alpha _{i-1}$
does not hold. We now show that
$\beta _{l} \prec \alpha _{i-1}$
does not hold. We now show that
![]() $\beta _{l} \prec \alpha _{i}$
. Assume this is not the case, then
$\beta _{l} \prec \alpha _{i}$
. Assume this is not the case, then
![]() $\alpha _{i} \prec \beta _{l}$
by definition of
$\alpha _{i} \prec \beta _{l}$
by definition of
![]() $\widetilde {\beta }$
. Using (2) we can then derive the contradiction
$\widetilde {\beta }$
. Using (2) we can then derive the contradiction
![]() $g^{-1}(\alpha _i) < n < m^3 = g^{-1}(\alpha _i)$
.
$g^{-1}(\alpha _i) < n < m^3 = g^{-1}(\alpha _i)$
.
We thus have shown that
![]() $\beta _{l} \prec \alpha _{i}$
, but
$\beta _{l} \prec \alpha _{i}$
, but
![]() $\beta _{l} \not \prec \alpha _{i-1}$
. Since
$\beta _{l} \not \prec \alpha _{i-1}$
. Since
![]() $\beta _{l}$
is the g-value of any given number between
$\beta _{l}$
is the g-value of any given number between
![]() $(m-1)^3+1$
and
$(m-1)^3+1$
and
![]() $m^3$
, there are
$m^3$
, there are
![]() $\Delta $
-many substrings of
$\Delta $
-many substrings of
![]() $\alpha _l$
which are not substrings of
$\alpha _l$
which are not substrings of
![]() $\alpha _{i-1}$
, with
$\alpha _{i-1}$
, with
![]() $\Delta := (m^3 - ((m-1)^3+1) -1$
.
$\Delta := (m^3 - ((m-1)^3+1) -1$
.
We derive a contradiction by showing that
where
![]() $\#(s)$
denotes the number of substrings of s. Let
$\#(s)$
denotes the number of substrings of s. Let
![]() $\mathit {lh}(s)$
denote the length of s. Since
$\mathit {lh}(s)$
denote the length of s. Since
![]() $\mathit {lh}(\alpha _{i}) = 5 + 8i$
, it is easy to check that
$\mathit {lh}(\alpha _{i}) = 5 + 8i$
, it is easy to check that
Moreover
![]() $i \leq m - 10$
, since
$i \leq m - 10$
, since
![]() $(i + 10)^3 \leq g^{-1}(\alpha _i) = m^3$
. Hence
$(i + 10)^3 \leq g^{-1}(\alpha _i) = m^3$
. Hence
It remains to check that
![]() $64m - 600 < \Delta $
. But this is equivalent to
$64m - 600 < \Delta $
. But this is equivalent to
which in turn is equivalent to the true equation
This concludes the proof of (3), in contradiction to there being
![]() $\Delta $
-many substrings of
$\Delta $
-many substrings of
![]() $\alpha _l$
which are not substrings of
$\alpha _l$
which are not substrings of
![]() $\alpha _{i-1}$
. Thus
$\alpha _{i-1}$
. Thus
![]() $A[i]$
obtains.
$A[i]$
obtains.
Acknowledgments
I am indebted to Arnon Avron, Volker Halbach, Karl-Georg Niebergall, Lavinia Picollo, Dan Waxman and two anonymous referees for extensive and extremely helpful comments on earlier versions of this paper. Special thanks go to Albert Visser for his encouragement and many fruitful discussions on numberings over the last years, which greatly improved this paper. I would also like to thank Udi Boker, Luca Castaldo, Nachum Dershowitz, Mirko Engler, Michael Goldboim, David Kashtan, Ran Lanzet, Carlo Nicolai, Fedor Pakhomov, Carl Posy, Lorenzo Rossi and Gil Sagi for helpful conversations on topics presented in this paper. Finally, I am grateful to the audiences of my talks on this material for their valuable feedback. This research was supported by the Minerva Foundation of the Max Planck Society.













