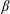1 Introduction
Magnetic reconnection in current sheets is present in many astrophysical and laboratory settings and is an important process for converting magnetic energy into thermal and non-thermal kinetic energy (Zweibel & Yamada Reference Zweibel and Yamada2009; Ji et al. Reference Ji, Alt, Antiochos, Baalrud, Bale, Bellan, Begelman, Beresnyak, Blackman and Brennan2019; Yamada, Kulsrud & Ji Reference Yamada, Kulsrud and Ji2010). In low- $\unicode[STIX]{x1D6FD}$ collisionless guide-field reconnection, field lines are broken within a microscopic electron diffusion region, of size comparable to the electron inertial length
$\unicode[STIX]{x1D6FD}$ collisionless guide-field reconnection, field lines are broken within a microscopic electron diffusion region, of size comparable to the electron inertial length  $d_{e}=c/\unicode[STIX]{x1D714}_{pe}$, where
$d_{e}=c/\unicode[STIX]{x1D714}_{pe}$, where  $\unicode[STIX]{x1D714}_{pe}=\sqrt{4\unicode[STIX]{x03C0}n_{e}e^{2}/m_{e}}$ is the electron plasma frequency. In the usual picture of (guide-field) reconnection, this electron region is embedded in a larger-scale ‘ion region’ of thickness of order the ion sound scale
$\unicode[STIX]{x1D714}_{pe}=\sqrt{4\unicode[STIX]{x03C0}n_{e}e^{2}/m_{e}}$ is the electron plasma frequency. In the usual picture of (guide-field) reconnection, this electron region is embedded in a larger-scale ‘ion region’ of thickness of order the ion sound scale  $\unicode[STIX]{x1D70C}_{s}=\unicode[STIX]{x1D70C}_{i}\sqrt{ZT_{e}/2T_{i}}$, where the ion gyroradius
$\unicode[STIX]{x1D70C}_{s}=\unicode[STIX]{x1D70C}_{i}\sqrt{ZT_{e}/2T_{i}}$, where the ion gyroradius  $\unicode[STIX]{x1D70C}_{i}=v_{\text{th}i}/\unicode[STIX]{x1D6FA}_{i}$, the ion thermal speed
$\unicode[STIX]{x1D70C}_{i}=v_{\text{th}i}/\unicode[STIX]{x1D6FA}_{i}$, the ion thermal speed  $v_{\text{th}i}=\sqrt{2T_{i}/m_{i}}$ and the ion gyrofrequency
$v_{\text{th}i}=\sqrt{2T_{i}/m_{i}}$ and the ion gyrofrequency  $\unicode[STIX]{x1D6FA}_{i}=ZeB_{0}/m_{i}c$. Associated with this region one expects bidirectional jets of plasma flowing away from the reconnection site at around the in-plane Alfvén speed
$\unicode[STIX]{x1D6FA}_{i}=ZeB_{0}/m_{i}c$. Associated with this region one expects bidirectional jets of plasma flowing away from the reconnection site at around the in-plane Alfvén speed  $v_{\text{A}y}=B_{y}/\sqrt{4\unicode[STIX]{x03C0}n_{i}m_{i}}$, where
$v_{\text{A}y}=B_{y}/\sqrt{4\unicode[STIX]{x03C0}n_{i}m_{i}}$, where  $B_{y}$ is the reconnecting (in-plane) magnetic field. We will term this standard picture ‘ion-coupled’ reconnection.
$B_{y}$ is the reconnecting (in-plane) magnetic field. We will term this standard picture ‘ion-coupled’ reconnection.
However, recent analysis of data from the MMS spacecraft (Phan et al. Reference Phan, Eastwood, Shay, Drake, Sonnerup, Fujimoto, Cassak, Øieroset, Burch and Torbert2018) has shown that, at least in Earth’s turbulent magnetosheath, one overwhelmingly finds current sheets with thicknesses of only a few  $d_{e}$ (i.e. much thinner than
$d_{e}$ (i.e. much thinner than  $\unicode[STIX]{x1D70C}_{s}$) without associated ion regions and ion jets, but with clear electron jets moving at appreciable fractions of the electron Alfvén velocity
$\unicode[STIX]{x1D70C}_{s}$) without associated ion regions and ion jets, but with clear electron jets moving at appreciable fractions of the electron Alfvén velocity  $v_{\text{A}ey}=B_{y}/\sqrt{4\unicode[STIX]{x03C0}n_{e}m_{e}}$. This new regime has also recently been reproduced in the numerical simulations of Sharma Pyakurel et al. (Reference Sharma Pyakurel, Shay, Phan, Matthaeus, Drake, TenBarge, Haggerty, Klein, Cassak and Parashar2019). A similar situation has been observed in the hybrid Vlasov–Maxwell turbulence simulations of Califano et al. (Reference Califano, Cerri, Faganello, Laveder and Kunz2018), who observed that when energy is injected at scales much larger than the ion scales, ion-coupled reconnection is observed, while if energy is injected closer to the ion scales, only electron jets and electron-scale sheets are observed. Reconnection of current sheets with thicknesses of a few
$v_{\text{A}ey}=B_{y}/\sqrt{4\unicode[STIX]{x03C0}n_{e}m_{e}}$. This new regime has also recently been reproduced in the numerical simulations of Sharma Pyakurel et al. (Reference Sharma Pyakurel, Shay, Phan, Matthaeus, Drake, TenBarge, Haggerty, Klein, Cassak and Parashar2019). A similar situation has been observed in the hybrid Vlasov–Maxwell turbulence simulations of Califano et al. (Reference Califano, Cerri, Faganello, Laveder and Kunz2018), who observed that when energy is injected at scales much larger than the ion scales, ion-coupled reconnection is observed, while if energy is injected closer to the ion scales, only electron jets and electron-scale sheets are observed. Reconnection of current sheets with thicknesses of a few  $d_{e}$ is also observed in the VINETA-II experiment (Jain et al. Reference Jain, von Stechow, Muñoz, Büchner, Grulke and Klinger2017). We will follow the terminology of Califano et al. (Reference Califano, Cerri, Faganello, Laveder and Kunz2018) and term this new regime ‘electron-only’ reconnection.
$d_{e}$ is also observed in the VINETA-II experiment (Jain et al. Reference Jain, von Stechow, Muñoz, Büchner, Grulke and Klinger2017). We will follow the terminology of Califano et al. (Reference Califano, Cerri, Faganello, Laveder and Kunz2018) and term this new regime ‘electron-only’ reconnection.
The goal of this paper is to develop a theoretical picture that can explain the onset of this new regime of electron-only reconnection, and under what circumstances it occurs in place of the standard ion-coupled reconnection. To achieve this, we will make use of a simplified model, rigorously derived from gyrokinetics in the limit  $\unicode[STIX]{x1D6FD}_{e}\sim m_{e}/m_{i}\ll 1$, the so-called ‘kinetic reduced electron heating model’, henceforth KREHM (Zocco & Schekochihin Reference Zocco and Schekochihin2011). The details of this model, as well as its utility and limitations, are described in § 2.
$\unicode[STIX]{x1D6FD}_{e}\sim m_{e}/m_{i}\ll 1$, the so-called ‘kinetic reduced electron heating model’, henceforth KREHM (Zocco & Schekochihin Reference Zocco and Schekochihin2011). The details of this model, as well as its utility and limitations, are described in § 2.
To make progress in understanding electron-only reconnection onset, there are two main questions which should be answered. First, can current sheets collapse to thicknesses of order a few  $d_{e}$, significantly below the ion scales? We answer this in § 3 by deriving a collapsing X-point solution analogous to Chapman–Kendall collapse (Chapman & Kendall Reference Chapman and Kendall1963; Biskamp Reference Biskamp2000), and showing that the solution is valid both above and below the ion scales. This means that ideal (i.e. with field lines frozen into an effective electron flow) sheets can indeed collapse well past the ion scale.
$d_{e}$, significantly below the ion scales? We answer this in § 3 by deriving a collapsing X-point solution analogous to Chapman–Kendall collapse (Chapman & Kendall Reference Chapman and Kendall1963; Biskamp Reference Biskamp2000), and showing that the solution is valid both above and below the ion scales. This means that ideal (i.e. with field lines frozen into an effective electron flow) sheets can indeed collapse well past the ion scale.
Second, at what sheet thickness do these collapsing sheets begin to reconnect, and under what conditions is this thickness above (obtaining ion-coupled reconnection) or well below (obtaining electron-only reconnection) the ion scales? We answer this in § 4, showing that the sheets are disrupted when they collapse to a critical thicknessFootnote 1 at which the linear tearing growth rateFootnote 2 is faster than the collapse or formation rate of the sheet derived in § 3. Our analysis allows us to derive relationships between  $\unicode[STIX]{x1D6FD}_{e}$ and the aspect ratio and thickness of the sheet at disruption (reconnection onset), and we thus determine the physical conditions under which one will observe ion-coupled or electron-only reconnection. The essential physical result is that if the initial collapsing solution is not sufficiently anisotropic when its thickness is above the ion scales, the collapse continues down to a thickness well below the ion scale, and electron-only reconnection will occur. Remarkably (considering the formal limitation of KREHM to low
$\unicode[STIX]{x1D6FD}_{e}$ and the aspect ratio and thickness of the sheet at disruption (reconnection onset), and we thus determine the physical conditions under which one will observe ion-coupled or electron-only reconnection. The essential physical result is that if the initial collapsing solution is not sufficiently anisotropic when its thickness is above the ion scales, the collapse continues down to a thickness well below the ion scale, and electron-only reconnection will occur. Remarkably (considering the formal limitation of KREHM to low  $\unicode[STIX]{x1D6FD}$), we will see that our model seems to agree rather well with the magnetosheath observations of electron-only reconnection (Phan et al. Reference Phan, Eastwood, Shay, Drake, Sonnerup, Fujimoto, Cassak, Øieroset, Burch and Torbert2018; Stawarz et al. Reference Stawarz, Eastwood, Phan, Gingell, Shay, Burch, Ergun, Giles, Gershman and Le Contel2019).
$\unicode[STIX]{x1D6FD}$), we will see that our model seems to agree rather well with the magnetosheath observations of electron-only reconnection (Phan et al. Reference Phan, Eastwood, Shay, Drake, Sonnerup, Fujimoto, Cassak, Øieroset, Burch and Torbert2018; Stawarz et al. Reference Stawarz, Eastwood, Phan, Gingell, Shay, Burch, Ergun, Giles, Gershman and Le Contel2019).
2 Equations
Our starting point is the KREHM derived by Zocco & Schekochihin (Reference Zocco and Schekochihin2011) (henceforth ZS11) from gyrokinetics for electron  $\unicode[STIX]{x1D6FD}$ of order the mass ratio
$\unicode[STIX]{x1D6FD}$ of order the mass ratio  $\unicode[STIX]{x1D6FD}_{e}\sim Zm_{e}/m_{i}$, where
$\unicode[STIX]{x1D6FD}_{e}\sim Zm_{e}/m_{i}$, where  $Z=q_{i}/e$ (and the temperature ratio
$Z=q_{i}/e$ (and the temperature ratio  $\unicode[STIX]{x1D70F}=T_{0i}/T_{0e}\sim 1$). The spatial scales of the fluctuations are ordered to be comparable to the relevant ion kinetic scales,
$\unicode[STIX]{x1D70F}=T_{0i}/T_{0e}\sim 1$). The spatial scales of the fluctuations are ordered to be comparable to the relevant ion kinetic scales,  $k_{\bot }\unicode[STIX]{x1D70C}_{i}\sim k_{\bot }\unicode[STIX]{x1D70C}_{s}\sim 1$, and so KREHM is able to capture both the large-scale (
$k_{\bot }\unicode[STIX]{x1D70C}_{i}\sim k_{\bot }\unicode[STIX]{x1D70C}_{s}\sim 1$, and so KREHM is able to capture both the large-scale ( $k_{\bot }\unicode[STIX]{x1D70C}_{s}\ll 1$) and small-scale (
$k_{\bot }\unicode[STIX]{x1D70C}_{s}\ll 1$) and small-scale ( $k_{\bot }\unicode[STIX]{x1D70C}_{s}\gg 1$) behaviour of the plasma, as well as the transition between them. This is essential for our present purposes, since we are attempting to diagnose the transition between ion-coupled and electron-only reconnection onset.
$k_{\bot }\unicode[STIX]{x1D70C}_{s}\gg 1$) behaviour of the plasma, as well as the transition between them. This is essential for our present purposes, since we are attempting to diagnose the transition between ion-coupled and electron-only reconnection onset.
KREHM is in some sense a minimal model for describing collisionless guide-field reconnection, since the equations incorporate the dispersive effects entering at the ion sound scale  $\unicode[STIX]{x1D70C}_{s}$ that are thought to be essential to enable fast reconnection (Rogers et al. Reference Rogers, Denton, Drake and Shay2001), a flux-unfreezing mechanism (electron inertia) entering at the electron inertial scale
$\unicode[STIX]{x1D70C}_{s}$ that are thought to be essential to enable fast reconnection (Rogers et al. Reference Rogers, Denton, Drake and Shay2001), a flux-unfreezing mechanism (electron inertia) entering at the electron inertial scale  $d_{e}$, and a rigorous treatment of the (electron) heating channel. The equations, written in terms of the electrostatic potential
$d_{e}$, and a rigorous treatment of the (electron) heating channel. The equations, written in terms of the electrostatic potential  $\unicode[STIX]{x1D719}$, the magnetic potential
$\unicode[STIX]{x1D719}$, the magnetic potential  $A_{\Vert }$ and the reduced electron distribution function
$A_{\Vert }$ and the reduced electron distribution function  $g_{e}$, are
$g_{e}$, are
 $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}}{\text{d}t}\frac{Z}{\unicode[STIX]{x1D70F}}(1-\hat{\unicode[STIX]{x1D6E4}}_{0})\frac{e\unicode[STIX]{x1D719}}{T_{0e}}=\hat{\boldsymbol{b}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\frac{e}{cm_{e}}d_{e}^{2}\unicode[STIX]{x1D735}_{\bot }^{2}A_{\Vert },\quad & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}}{\text{d}t}\frac{Z}{\unicode[STIX]{x1D70F}}(1-\hat{\unicode[STIX]{x1D6E4}}_{0})\frac{e\unicode[STIX]{x1D719}}{T_{0e}}=\hat{\boldsymbol{b}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\frac{e}{cm_{e}}d_{e}^{2}\unicode[STIX]{x1D735}_{\bot }^{2}A_{\Vert },\quad & \displaystyle\end{eqnarray}$$ $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}}{\text{d}t}(A_{\Vert }-d_{e}^{2}\unicode[STIX]{x1D735}_{\bot }^{2}A_{\Vert })=-c\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D719}}{\unicode[STIX]{x2202}z}-\frac{cT_{0e}}{e}\hat{\boldsymbol{b}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\left[\frac{Z}{\unicode[STIX]{x1D70F}}\left(1-\hat{\unicode[STIX]{x1D6E4}}_{0}\right)\frac{e\unicode[STIX]{x1D719}}{T_{0e}}-\frac{\unicode[STIX]{x1D6FF}T_{\Vert e}}{T_{0e}}\right],\quad & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}}{\text{d}t}(A_{\Vert }-d_{e}^{2}\unicode[STIX]{x1D735}_{\bot }^{2}A_{\Vert })=-c\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D719}}{\unicode[STIX]{x2202}z}-\frac{cT_{0e}}{e}\hat{\boldsymbol{b}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\left[\frac{Z}{\unicode[STIX]{x1D70F}}\left(1-\hat{\unicode[STIX]{x1D6E4}}_{0}\right)\frac{e\unicode[STIX]{x1D719}}{T_{0e}}-\frac{\unicode[STIX]{x1D6FF}T_{\Vert e}}{T_{0e}}\right],\quad & \displaystyle\end{eqnarray}$$ $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}g_{e}}{\text{d}t}+v_{\Vert }\hat{\boldsymbol{b}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\left(g_{e}-\frac{\unicode[STIX]{x1D6FF}T_{\Vert e}}{T_{0e}}F_{0\text{e}}\right)=C[g_{e}]+\left(1-\frac{2v_{\Vert }^{2}}{v_{\text{th}e}^{2}}\right)F_{0\text{e}}\hat{\boldsymbol{b}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\frac{e}{cm_{e}}d_{e}^{2}\unicode[STIX]{x1D735}_{\bot }^{2}A_{\Vert },\quad & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}g_{e}}{\text{d}t}+v_{\Vert }\hat{\boldsymbol{b}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\left(g_{e}-\frac{\unicode[STIX]{x1D6FF}T_{\Vert e}}{T_{0e}}F_{0\text{e}}\right)=C[g_{e}]+\left(1-\frac{2v_{\Vert }^{2}}{v_{\text{th}e}^{2}}\right)F_{0\text{e}}\hat{\boldsymbol{b}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\frac{e}{cm_{e}}d_{e}^{2}\unicode[STIX]{x1D735}_{\bot }^{2}A_{\Vert },\quad & \displaystyle\end{eqnarray}$$where
 $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}}{\text{d}t}=\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}+\frac{c}{B_{0}}\{\unicode[STIX]{x1D719},...\,\}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}}{\text{d}t}=\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}+\frac{c}{B_{0}}\{\unicode[STIX]{x1D719},...\,\}, & \displaystyle\end{eqnarray}$$ $$\begin{eqnarray}\displaystyle & \displaystyle \hat{\boldsymbol{b}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}=\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}z}-\frac{1}{B_{0}}\{A_{\Vert },...\,\}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \hat{\boldsymbol{b}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}=\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}z}-\frac{1}{B_{0}}\{A_{\Vert },...\,\}, & \displaystyle\end{eqnarray}$$ $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x1D6FF}T_{\Vert e}}{T_{0e}}=\frac{1}{n_{0\text{e}}}\int d^{3}\boldsymbol{v}\frac{2v_{\Vert }^{2}}{v_{\text{th}e}^{2}}g_{e}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x1D6FF}T_{\Vert e}}{T_{0e}}=\frac{1}{n_{0\text{e}}}\int d^{3}\boldsymbol{v}\frac{2v_{\Vert }^{2}}{v_{\text{th}e}^{2}}g_{e}, & \displaystyle\end{eqnarray}$$ and  $\hat{\unicode[STIX]{x1D6E4}}_{0}$, encoding the ion finite Larmor radius effects, is the inverse Fourier transform of
$\hat{\unicode[STIX]{x1D6E4}}_{0}$, encoding the ion finite Larmor radius effects, is the inverse Fourier transform of
 $$\begin{eqnarray}\unicode[STIX]{x1D6E4}_{0}\left({\textstyle \frac{1}{2}}k_{\bot }^{2}\unicode[STIX]{x1D70C}_{i}^{2}\right)=\text{I}_{0}\left({\textstyle \frac{1}{2}}k_{\bot }^{2}\unicode[STIX]{x1D70C}_{i}^{2}\right)\text{e}^{-1/2k_{\bot }^{2}\unicode[STIX]{x1D70C}_{i}^{2}},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E4}_{0}\left({\textstyle \frac{1}{2}}k_{\bot }^{2}\unicode[STIX]{x1D70C}_{i}^{2}\right)=\text{I}_{0}\left({\textstyle \frac{1}{2}}k_{\bot }^{2}\unicode[STIX]{x1D70C}_{i}^{2}\right)\text{e}^{-1/2k_{\bot }^{2}\unicode[STIX]{x1D70C}_{i}^{2}},\end{eqnarray}$$ where  $\text{I}_{0}$ is the modified Bessel function. The electron density perturbation
$\text{I}_{0}$ is the modified Bessel function. The electron density perturbation  $\unicode[STIX]{x1D6FF}n_{e}$ is related to
$\unicode[STIX]{x1D6FF}n_{e}$ is related to  $\unicode[STIX]{x1D719}$ via the relation
$\unicode[STIX]{x1D719}$ via the relation
 $$\begin{eqnarray}\frac{\unicode[STIX]{x1D6FF}n_{e}}{n_{0e}}=-\frac{Z}{\unicode[STIX]{x1D70F}}\left(1-\hat{\unicode[STIX]{x1D6E4}}_{0}\right)\frac{e\unicode[STIX]{x1D719}}{T_{0e}}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{\unicode[STIX]{x1D6FF}n_{e}}{n_{0e}}=-\frac{Z}{\unicode[STIX]{x1D70F}}\left(1-\hat{\unicode[STIX]{x1D6E4}}_{0}\right)\frac{e\unicode[STIX]{x1D719}}{T_{0e}}.\end{eqnarray}$$ The Poisson bracket appearing in the equations is  $\{f,g\}=\hat{\boldsymbol{z}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{\bot }f\times \unicode[STIX]{x1D735}_{\bot }g$. We have taken the limit
$\{f,g\}=\hat{\boldsymbol{z}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{\bot }f\times \unicode[STIX]{x1D735}_{\bot }g$. We have taken the limit  $\unicode[STIX]{x1D708}_{ei}\ll \unicode[STIX]{x1D714}$, which allows us to neglect a resistive term in (2.2) (but not the collisions
$\unicode[STIX]{x1D708}_{ei}\ll \unicode[STIX]{x1D714}$, which allows us to neglect a resistive term in (2.2) (but not the collisions  $C[g_{e}]$ in (2.3)).
$C[g_{e}]$ in (2.3)).
The function  $g_{e}$ is a mathematically convenient reduced electron-gyrocentre parallel velocity distribution function, which encodes the electron heating channel. This is perhaps all the information that is needed to understand the present paper: in more detail, it is related to the perturbed distribution function
$g_{e}$ is a mathematically convenient reduced electron-gyrocentre parallel velocity distribution function, which encodes the electron heating channel. This is perhaps all the information that is needed to understand the present paper: in more detail, it is related to the perturbed distribution function  $\unicode[STIX]{x1D6FF}f_{e}$ by
$\unicode[STIX]{x1D6FF}f_{e}$ by
 $$\begin{eqnarray}\unicode[STIX]{x1D6FF}f_{e}(\boldsymbol{r},\boldsymbol{v},t)=\left(1+\frac{\unicode[STIX]{x1D6FF}n_{e}}{n_{0e}}+\frac{2v_{\Vert }u_{\Vert e}}{v_{\text{th}e}^{2}}\right)F_{0e}+g_{e}(\boldsymbol{R}_{e},\boldsymbol{v},t),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FF}f_{e}(\boldsymbol{r},\boldsymbol{v},t)=\left(1+\frac{\unicode[STIX]{x1D6FF}n_{e}}{n_{0e}}+\frac{2v_{\Vert }u_{\Vert e}}{v_{\text{th}e}^{2}}\right)F_{0e}+g_{e}(\boldsymbol{R}_{e},\boldsymbol{v},t),\end{eqnarray}$$ where  $\boldsymbol{R}_{e}=\boldsymbol{r}+\boldsymbol{v}_{\bot }\times \hat{\boldsymbol{z}}/\unicode[STIX]{x1D6FA}_{e}$ is the electron gyrocentre. Integrating the zeroth and first
$\boldsymbol{R}_{e}=\boldsymbol{r}+\boldsymbol{v}_{\bot }\times \hat{\boldsymbol{z}}/\unicode[STIX]{x1D6FA}_{e}$ is the electron gyrocentre. Integrating the zeroth and first  $v_{\Vert }$-moments of
$v_{\Vert }$-moments of  $\unicode[STIX]{x1D6FF}f_{e}$ over all velocity (perturbed electron density and parallel flow), we can see that contribution from
$\unicode[STIX]{x1D6FF}f_{e}$ over all velocity (perturbed electron density and parallel flow), we can see that contribution from  $g_{e}$ to these vanishes, i.e.
$g_{e}$ to these vanishes, i.e.  $g_{e}$ contains the information of all higher moments, but not density or parallel flow. It turns out (see ZS11 for details) that the non-trivial
$g_{e}$ contains the information of all higher moments, but not density or parallel flow. It turns out (see ZS11 for details) that the non-trivial  $v_{\bot }$ dependence of
$v_{\bot }$ dependence of  $g_{e}$ can be safely ignored, and so
$g_{e}$ can be safely ignored, and so  $g_{e}$ can be considered a function of
$g_{e}$ can be considered a function of  $v_{\Vert }$, space and time only.
$v_{\Vert }$, space and time only.
We may write (2.2) as
 $$\begin{eqnarray}\frac{\unicode[STIX]{x2202}A_{\Vert }}{\unicode[STIX]{x2202}t}=-c\hat{\boldsymbol{b}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\left[\unicode[STIX]{x1D719}+\frac{Z}{\unicode[STIX]{x1D70F}}\left(1-\hat{\unicode[STIX]{x1D6E4}}_{0}\right)\unicode[STIX]{x1D719}-\frac{\unicode[STIX]{x1D6FF}T_{\Vert e}}{e}\right]+\frac{\text{d}}{\text{d}t}d_{e}^{2}\unicode[STIX]{x1D735}_{\bot }^{2}A_{\Vert },\end{eqnarray}$$
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}A_{\Vert }}{\unicode[STIX]{x2202}t}=-c\hat{\boldsymbol{b}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\left[\unicode[STIX]{x1D719}+\frac{Z}{\unicode[STIX]{x1D70F}}\left(1-\hat{\unicode[STIX]{x1D6E4}}_{0}\right)\unicode[STIX]{x1D719}-\frac{\unicode[STIX]{x1D6FF}T_{\Vert e}}{e}\right]+\frac{\text{d}}{\text{d}t}d_{e}^{2}\unicode[STIX]{x1D735}_{\bot }^{2}A_{\Vert },\end{eqnarray}$$which defines an effective velocity
 $$\begin{eqnarray}\boldsymbol{u}_{\text{eff}}=\hat{z}\times \unicode[STIX]{x1D735}_{\bot }\frac{c}{B_{0}}\left[\unicode[STIX]{x1D719}+\frac{Z}{\unicode[STIX]{x1D70F}}\left(1-\hat{\unicode[STIX]{x1D6E4}}_{0}\right)\unicode[STIX]{x1D719}-\frac{\unicode[STIX]{x1D6FF}T_{\Vert e}}{e}\right],\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{u}_{\text{eff}}=\hat{z}\times \unicode[STIX]{x1D735}_{\bot }\frac{c}{B_{0}}\left[\unicode[STIX]{x1D719}+\frac{Z}{\unicode[STIX]{x1D70F}}\left(1-\hat{\unicode[STIX]{x1D6E4}}_{0}\right)\unicode[STIX]{x1D719}-\frac{\unicode[STIX]{x1D6FF}T_{\Vert e}}{e}\right],\end{eqnarray}$$ into which the field lines are frozen, apart from the effects of electron inertia (Zocco & Schekochihin Reference Zocco and Schekochihin2011). Thus, field lines are only broken when gradients are of order  $d_{e}^{-1}$.
$d_{e}^{-1}$.
These equations have various interesting limits. First, for fluctuations on long length scales (compared to the ion gyroradius)  $k_{\bot }\unicode[STIX]{x1D70C}_{i}\ll 1$, and
$k_{\bot }\unicode[STIX]{x1D70C}_{i}\ll 1$, and  $\unicode[STIX]{x1D6E4}_{0}\approx 1-k_{\bot }^{2}\unicode[STIX]{x1D70C}_{i}^{2}/2$, and one can show that the equations reduce to those of RMHD, reduced magnetohydrodynamics (Strauss Reference Strauss1976), describing nonlinearly interacting Alfvénic fluctuations propagating up and down the magnetic field. Second, if one takes
$\unicode[STIX]{x1D6E4}_{0}\approx 1-k_{\bot }^{2}\unicode[STIX]{x1D70C}_{i}^{2}/2$, and one can show that the equations reduce to those of RMHD, reduced magnetohydrodynamics (Strauss Reference Strauss1976), describing nonlinearly interacting Alfvénic fluctuations propagating up and down the magnetic field. Second, if one takes  $k_{\bot }\unicode[STIX]{x1D70C}_{i}\gg 1$,
$k_{\bot }\unicode[STIX]{x1D70C}_{i}\gg 1$,  $\unicode[STIX]{x1D6E4}_{0}\approx 0$, and subsequently expand in the square root of the mass ratio
$\unicode[STIX]{x1D6E4}_{0}\approx 0$, and subsequently expand in the square root of the mass ratio  $\sqrt{m_{e}/m_{i}}$, i.e.
$\sqrt{m_{e}/m_{i}}$, i.e.  $k_{\bot }d_{e}\ll 1$, one obtains the equations of ERMHD, electron reduced magnetohydrodynamics (Schekochihin et al. Reference Schekochihin, Cowley, Dorland, Hammett, Howes, Quataert and Tatsuno2009), which involve nonlinearly interacting kinetic-Alfvén fluctuations propagating up and down the field.
$k_{\bot }d_{e}\ll 1$, one obtains the equations of ERMHD, electron reduced magnetohydrodynamics (Schekochihin et al. Reference Schekochihin, Cowley, Dorland, Hammett, Howes, Quataert and Tatsuno2009), which involve nonlinearly interacting kinetic-Alfvén fluctuations propagating up and down the field.
It is important to note that, as mentioned earlier, formally these equations are only valid for  $\unicode[STIX]{x1D6FD}_{i}\sim \unicode[STIX]{x1D6FD}_{e}\ll 1$. This rather limits their formal applicability to some physical regimes, including the magnetosheath, where electron-only reconnection has recently been observed (Phan et al. Reference Phan, Eastwood, Shay, Drake, Sonnerup, Fujimoto, Cassak, Øieroset, Burch and Torbert2018; Stawarz et al. Reference Stawarz, Eastwood, Phan, Gingell, Shay, Burch, Ergun, Giles, Gershman and Le Contel2019), where
$\unicode[STIX]{x1D6FD}_{i}\sim \unicode[STIX]{x1D6FD}_{e}\ll 1$. This rather limits their formal applicability to some physical regimes, including the magnetosheath, where electron-only reconnection has recently been observed (Phan et al. Reference Phan, Eastwood, Shay, Drake, Sonnerup, Fujimoto, Cassak, Øieroset, Burch and Torbert2018; Stawarz et al. Reference Stawarz, Eastwood, Phan, Gingell, Shay, Burch, Ergun, Giles, Gershman and Le Contel2019), where  $\unicode[STIX]{x1D6FD}_{i}\gtrsim 1$ and
$\unicode[STIX]{x1D6FD}_{i}\gtrsim 1$ and  $\unicode[STIX]{x1D6FD}_{e}\lesssim 1$. Nonetheless, we believe that their simplicity allows us to model the essential physics of current sheet collapse and reconnection onset in a useful way, for three main reasons. First, simulations of turbulence using KREHM have revealed that it seems to compare rather well with more complete models, even at higher
$\unicode[STIX]{x1D6FD}_{e}\lesssim 1$. Nonetheless, we believe that their simplicity allows us to model the essential physics of current sheet collapse and reconnection onset in a useful way, for three main reasons. First, simulations of turbulence using KREHM have revealed that it seems to compare rather well with more complete models, even at higher  $\unicode[STIX]{x1D6FD}$ than its formal regime of applicability (Grošelj et al. Reference Grošelj, Cerri, Bañón Navarro, Willmott, Told, Loureiro, Califano and Jenko2017). Second, we will show in § 3 that the Chapman–Kendall-like current sheet collapse solution also exists in ERMHD at arbitrary
$\unicode[STIX]{x1D6FD}$ than its formal regime of applicability (Grošelj et al. Reference Grošelj, Cerri, Bañón Navarro, Willmott, Told, Loureiro, Califano and Jenko2017). Second, we will show in § 3 that the Chapman–Kendall-like current sheet collapse solution also exists in ERMHD at arbitrary  $\unicode[STIX]{x1D6FD}_{i}$ and
$\unicode[STIX]{x1D6FD}_{i}$ and  $\unicode[STIX]{x1D70F}$, meaning that this part of the analysis remains true even without the formal
$\unicode[STIX]{x1D70F}$, meaning that this part of the analysis remains true even without the formal  $\unicode[STIX]{x1D6FD}_{i}\ll 1$ requirement. Finally, the collisionless tearing mode (which we will show enables the onset of reconnection in § 4) has a growth rate that decreases with
$\unicode[STIX]{x1D6FD}_{i}\ll 1$ requirement. Finally, the collisionless tearing mode (which we will show enables the onset of reconnection in § 4) has a growth rate that decreases with  $\unicode[STIX]{x1D6FD}_{e}$ (Numata & Loureiro Reference Numata and Loureiro2015) for constant ratio of sheet thickness to
$\unicode[STIX]{x1D6FD}_{e}$ (Numata & Loureiro Reference Numata and Loureiro2015) for constant ratio of sheet thickness to  $\unicode[STIX]{x1D70C}_{i}$, meaning that at higher
$\unicode[STIX]{x1D70C}_{i}$, meaning that at higher  $\unicode[STIX]{x1D6FD}_{e}$, the basic physics of our picture will remain, but with the sheets potentially attaining even smaller (relative to
$\unicode[STIX]{x1D6FD}_{e}$, the basic physics of our picture will remain, but with the sheets potentially attaining even smaller (relative to  $\unicode[STIX]{x1D70C}_{i}$) thicknesses.
$\unicode[STIX]{x1D70C}_{i}$) thicknesses.
We should also mention here that Boldyrev & Loureiro (Reference Boldyrev and Loureiro2019) have used a set of fluid equations derived for  $k_{\bot }\unicode[STIX]{x1D70C}_{i}\gg 1$,
$k_{\bot }\unicode[STIX]{x1D70C}_{i}\gg 1$,  $\unicode[STIX]{x1D6FD}_{i}\sim 1$,
$\unicode[STIX]{x1D6FD}_{i}\sim 1$,  $\unicode[STIX]{x1D6FD}_{e}\ll 1$ to study the small-scale tearing instability and its effect on turbulence, obtaining some results similar to ours (which is an additional source of reassurance that our low-
$\unicode[STIX]{x1D6FD}_{e}\ll 1$ to study the small-scale tearing instability and its effect on turbulence, obtaining some results similar to ours (which is an additional source of reassurance that our low- $\unicode[STIX]{x1D6FD}_{i}$ ordering does not invalidate the basic picture of tearing-induced reconnection onset): we have used KREHM instead because, first, we want a set of equations covering the ion-scale transition at
$\unicode[STIX]{x1D6FD}_{i}$ ordering does not invalidate the basic picture of tearing-induced reconnection onset): we have used KREHM instead because, first, we want a set of equations covering the ion-scale transition at  $k_{\bot }\unicode[STIX]{x1D70C}_{i}\sim 1$ to describe the transition between the ion-coupled and electron-only reconnection regimes, and second, the electron heating channel as encoded by (2.3) is important for a realistic picture of reconnection.
$k_{\bot }\unicode[STIX]{x1D70C}_{i}\sim 1$ to describe the transition between the ion-coupled and electron-only reconnection regimes, and second, the electron heating channel as encoded by (2.3) is important for a realistic picture of reconnection.
3 X-point collapse
For electron-only reconnection to occur, it must first be possible to form current sheets with thicknesses well below the ion scale. In ideal MHD (magnetohydrodynamics), it is well known that X-points tend to collapse into sheets (Syrovatskii Reference Syrovatskii1981). It turns out that this is still true in our system of equations, even at scales well below the ion gyroradius. If we require
 $$\begin{eqnarray}\hat{\boldsymbol{b}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D735}_{\bot }^{2}A_{\Vert }=0,\end{eqnarray}$$
$$\begin{eqnarray}\hat{\boldsymbol{b}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D735}_{\bot }^{2}A_{\Vert }=0,\end{eqnarray}$$ then  $g_{e}=0$ is a solution. Let us also impose a ‘vorticity-free’ condition on the system,
$g_{e}=0$ is a solution. Let us also impose a ‘vorticity-free’ condition on the system,
 $$\begin{eqnarray}\unicode[STIX]{x1D735}_{\bot }^{2}\unicode[STIX]{x1D719}=0.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D735}_{\bot }^{2}\unicode[STIX]{x1D719}=0.\end{eqnarray}$$ Under this condition,  $\hat{\unicode[STIX]{x1D6E4}}_{0}\unicode[STIX]{x1D719}=\unicode[STIX]{x1D719}$Footnote 3, and along with (3.1), the whole of (2.1) vanishes. Our flow must, of course, be consistent with maintaining the condition (3.1).
$\hat{\unicode[STIX]{x1D6E4}}_{0}\unicode[STIX]{x1D719}=\unicode[STIX]{x1D719}$Footnote 3, and along with (3.1), the whole of (2.1) vanishes. Our flow must, of course, be consistent with maintaining the condition (3.1).
3.1 Chapman–Kendall solution
One (two-dimensional) solution which satisfies the conditions (3.1), (3.2) is a slightly modified version of ‘Chapman–Kendall’ collapse (Chapman & Kendall Reference Chapman and Kendall1963; Biskamp Reference Biskamp2000), originally derived for MHD (but which turns out to still be applicable here),
 $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D719}=\frac{B_{0}}{c}\frac{\unicode[STIX]{x1D6EC}(t)}{2}xy, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D719}=\frac{B_{0}}{c}\frac{\unicode[STIX]{x1D6EC}(t)}{2}xy, & \displaystyle\end{eqnarray}$$ $$\begin{eqnarray}\displaystyle & \displaystyle A_{\Vert }=\frac{B_{\bot }}{2}\left(\frac{x^{2}+2d_{e}^{2}}{a(t)}-\frac{y^{2}+2d_{e}^{2}}{L(t)}\right), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle A_{\Vert }=\frac{B_{\bot }}{2}\left(\frac{x^{2}+2d_{e}^{2}}{a(t)}-\frac{y^{2}+2d_{e}^{2}}{L(t)}\right), & \displaystyle\end{eqnarray}$$ where  $a(t)$ and
$a(t)$ and  $L(t)$ are the thickness and length of the current sheet respectively. This solution is an approximation valid in the region close to the X-point in the interior of a realistic current sheet. Inserting this into (2.10), we obtain
$L(t)$ are the thickness and length of the current sheet respectively. This solution is an approximation valid in the region close to the X-point in the interior of a realistic current sheet. Inserting this into (2.10), we obtain
 $$\begin{eqnarray}\displaystyle & \displaystyle {\dot{a}}=-\unicode[STIX]{x1D6EC}(t)a, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\dot{a}}=-\unicode[STIX]{x1D6EC}(t)a, & \displaystyle\end{eqnarray}$$ $$\begin{eqnarray}\displaystyle & \displaystyle \dot{L}=\unicode[STIX]{x1D6EC}(t)L. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \dot{L}=\unicode[STIX]{x1D6EC}(t)L. & \displaystyle\end{eqnarray}$$ Thus, in the absence of reconnection, current sheets can thin to scales much smaller than the ion scales. However, this does not show that such thin sheets are always physically realisable: we will show in § 4 that, in fact, localised current configurations with  $L>a$ are disrupted by the onset of reconnection at scales larger than
$L>a$ are disrupted by the onset of reconnection at scales larger than  $d_{e}$ (but, importantly, sometimes smaller than
$d_{e}$ (but, importantly, sometimes smaller than  $\unicode[STIX]{x1D70C}_{s}$)Footnote 4. White, Hazeltine & Loureiro (Reference White, Hazeltine and Loureiro2018) have found that KREHM also allows a more general class of Chapman–Kendall-like solutions, for example a helically twisted version of the simple solution presented here.
$\unicode[STIX]{x1D70C}_{s}$)Footnote 4. White, Hazeltine & Loureiro (Reference White, Hazeltine and Loureiro2018) have found that KREHM also allows a more general class of Chapman–Kendall-like solutions, for example a helically twisted version of the simple solution presented here.
3.2 Choosing  $\unicode[STIX]{x1D6EC}(t)$
$\unicode[STIX]{x1D6EC}(t)$
It remains for us to decide a reasonable form for  $\unicode[STIX]{x1D6EC}(t)$. We do this in two limiting cases,
$\unicode[STIX]{x1D6EC}(t)$. We do this in two limiting cases,  $a\gg \unicode[STIX]{x1D70C}_{i}$ and
$a\gg \unicode[STIX]{x1D70C}_{i}$ and  $a\ll \unicode[STIX]{x1D70C}_{i}$, and ask that the outflows match the characteristic wave speed involved in maintaining the structure of the sheet in the
$a\ll \unicode[STIX]{x1D70C}_{i}$, and ask that the outflows match the characteristic wave speed involved in maintaining the structure of the sheet in the  $y$-direction in both cases. In the case where
$y$-direction in both cases. In the case where  $a\gg \unicode[STIX]{x1D70C}_{i}$, the outflows should attain the constant in-plane Alfvén speed
$a\gg \unicode[STIX]{x1D70C}_{i}$, the outflows should attain the constant in-plane Alfvén speed  $v_{\text{A}y}=B_{y}(a)/\sqrt{4\unicode[STIX]{x03C0}n_{0i}m_{i}}$ at
$v_{\text{A}y}=B_{y}(a)/\sqrt{4\unicode[STIX]{x03C0}n_{0i}m_{i}}$ at  $y\sim L(t)$. In the small-scale case where
$y\sim L(t)$. In the small-scale case where  $a\ll \unicode[STIX]{x1D70C}_{i}$, the outflow speed at
$a\ll \unicode[STIX]{x1D70C}_{i}$, the outflow speed at  $y\sim L(t)$ should be the in-plane kinetic-Alfvén wave speed (see ZS11 or Schekochihin et al. Reference Schekochihin, Cowley, Dorland, Hammett, Howes, Quataert and Tatsuno2009),
$y\sim L(t)$ should be the in-plane kinetic-Alfvén wave speed (see ZS11 or Schekochihin et al. Reference Schekochihin, Cowley, Dorland, Hammett, Howes, Quataert and Tatsuno2009),
 $$\begin{eqnarray}u_{\text{KAW}y}=\sqrt{\frac{1}{2}\left(1+\frac{Z}{\unicode[STIX]{x1D70F}}\right)}v_{\text{A}y}\frac{\unicode[STIX]{x1D70C}_{i}}{a(t)}.\end{eqnarray}$$
$$\begin{eqnarray}u_{\text{KAW}y}=\sqrt{\frac{1}{2}\left(1+\frac{Z}{\unicode[STIX]{x1D70F}}\right)}v_{\text{A}y}\frac{\unicode[STIX]{x1D70C}_{i}}{a(t)}.\end{eqnarray}$$ Importantly, this is inversely proportional to  $a$. Thus, it is physically reasonable to choose
$a$. Thus, it is physically reasonable to choose
 $$\begin{eqnarray}\unicode[STIX]{x1D6EC}(t)=\left\{\begin{array}{@{}ll@{}}{\displaystyle \frac{2v_{\text{A}y}}{L(t)}}, & a\gg \unicode[STIX]{x1D70C}_{i},\\[12.0pt] {\displaystyle \frac{\sqrt{2(1+Z/\unicode[STIX]{x1D70F})}v_{\text{A}y}\unicode[STIX]{x1D70C}_{i}}{a(t)L(t)}}, & a\ll \unicode[STIX]{x1D70C}_{i},\\ \end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6EC}(t)=\left\{\begin{array}{@{}ll@{}}{\displaystyle \frac{2v_{\text{A}y}}{L(t)}}, & a\gg \unicode[STIX]{x1D70C}_{i},\\[12.0pt] {\displaystyle \frac{\sqrt{2(1+Z/\unicode[STIX]{x1D70F})}v_{\text{A}y}\unicode[STIX]{x1D70C}_{i}}{a(t)L(t)}}, & a\ll \unicode[STIX]{x1D70C}_{i},\\ \end{array}\right.\end{eqnarray}$$ which defines (inverse) time scales associated with forming sheets of thickness  $a$ and length
$a$ and length  $L$. With these choices, equations (3.5) and (3.6) have the solutions
$L$. With these choices, equations (3.5) and (3.6) have the solutions
 $$\begin{eqnarray}\displaystyle & \displaystyle a\gg \unicode[STIX]{x1D70C}_{i}:\quad L=L_{0}+2v_{\text{A}y}t,\quad a=a_{0}L_{0}/L, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle a\gg \unicode[STIX]{x1D70C}_{i}:\quad L=L_{0}+2v_{\text{A}y}t,\quad a=a_{0}L_{0}/L, & \displaystyle\end{eqnarray}$$ $$\begin{eqnarray}\displaystyle & \displaystyle a\ll \unicode[STIX]{x1D70C}_{i}:\quad L=L_{0}\exp \left(\frac{\sqrt{2(1+Z/\unicode[STIX]{x1D70F})}v_{\text{A}y}\unicode[STIX]{x1D70C}_{i}}{a_{0}L_{0}}t\right),\quad a=a_{0}L_{0}/L. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle a\ll \unicode[STIX]{x1D70C}_{i}:\quad L=L_{0}\exp \left(\frac{\sqrt{2(1+Z/\unicode[STIX]{x1D70F})}v_{\text{A}y}\unicode[STIX]{x1D70C}_{i}}{a_{0}L_{0}}t\right),\quad a=a_{0}L_{0}/L. & \displaystyle\end{eqnarray}$$ The aspect ratio as a function of  $a$ is given by
$a$ is given by
 $$\begin{eqnarray}\frac{L}{a}=\frac{a_{0}L_{0}}{a^{2}},\end{eqnarray}$$
$$\begin{eqnarray}\frac{L}{a}=\frac{a_{0}L_{0}}{a^{2}},\end{eqnarray}$$ simply from continuity. It is important to note that, if the sheets are formed as part of turbulence, this scaling is not accurate, because structures will interact with each other as well as undergoing their own nonlinear evolution. Instead, one might expect, for  $a\gg \unicode[STIX]{x1D70C}_{i}$,
$a\gg \unicode[STIX]{x1D70C}_{i}$,  $L/a\propto a^{-1/4}$ (cf. Boldyrev Reference Boldyrev2006; Chandran, Schekochihin & Mallet Reference Chandran, Schekochihin and Mallet2015; Mallet & Schekochihin Reference Mallet and Schekochihin2017). The aspect ratio scaling for
$L/a\propto a^{-1/4}$ (cf. Boldyrev Reference Boldyrev2006; Chandran, Schekochihin & Mallet Reference Chandran, Schekochihin and Mallet2015; Mallet & Schekochihin Reference Mallet and Schekochihin2017). The aspect ratio scaling for  $a\ll \unicode[STIX]{x1D70C}_{i}$ in turbulence is as yet unknown.
$a\ll \unicode[STIX]{x1D70C}_{i}$ in turbulence is as yet unknown.
3.3 Collapse time
Let us start with a structure of thickness  $a_{0}>\unicode[STIX]{x1D70C}_{i}$, and ask how long it takes for it to collapse to a thickness
$a_{0}>\unicode[STIX]{x1D70C}_{i}$, and ask how long it takes for it to collapse to a thickness  $a_{\ast }<\unicode[STIX]{x1D70C}_{i}$. First, using (3.9), the time taken to collapse to
$a_{\ast }<\unicode[STIX]{x1D70C}_{i}$. First, using (3.9), the time taken to collapse to  $\unicode[STIX]{x1D70C}_{i}$ is
$\unicode[STIX]{x1D70C}_{i}$ is
 $$\begin{eqnarray}t_{\unicode[STIX]{x1D70C}}\sim \left(\frac{a_{0}}{\unicode[STIX]{x1D70C}_{i}}-1\right)\frac{L_{0}}{2v_{\text{A}y}}\approx \frac{a_{0}L_{0}}{2v_{\text{A}y}\unicode[STIX]{x1D70C}_{i}}.\end{eqnarray}$$
$$\begin{eqnarray}t_{\unicode[STIX]{x1D70C}}\sim \left(\frac{a_{0}}{\unicode[STIX]{x1D70C}_{i}}-1\right)\frac{L_{0}}{2v_{\text{A}y}}\approx \frac{a_{0}L_{0}}{2v_{\text{A}y}\unicode[STIX]{x1D70C}_{i}}.\end{eqnarray}$$ Subsequent collapse from  $\unicode[STIX]{x1D70C}_{i}$ down to
$\unicode[STIX]{x1D70C}_{i}$ down to  $a_{\ast }$ occurs according to (3.10) in a time
$a_{\ast }$ occurs according to (3.10) in a time
 $$\begin{eqnarray}t_{\ast }\sim \frac{a_{0}L_{0}\ln (\unicode[STIX]{x1D70C}_{i}/a_{\ast })}{\sqrt{2\left(1+\frac{Z}{\unicode[STIX]{x1D70F}}\right)}v_{\text{A}y}\unicode[STIX]{x1D70C}_{i}},\end{eqnarray}$$
$$\begin{eqnarray}t_{\ast }\sim \frac{a_{0}L_{0}\ln (\unicode[STIX]{x1D70C}_{i}/a_{\ast })}{\sqrt{2\left(1+\frac{Z}{\unicode[STIX]{x1D70F}}\right)}v_{\text{A}y}\unicode[STIX]{x1D70C}_{i}},\end{eqnarray}$$ which is, in practice, usually of order  $t_{\unicode[STIX]{x1D70C}}$. Thus, the total collapse time is of order
$t_{\unicode[STIX]{x1D70C}}$. Thus, the total collapse time is of order  $t_{\unicode[STIX]{x1D70C}}$, and mainly depends on the initial size and reconnecting field within the structure.
$t_{\unicode[STIX]{x1D70C}}$, and mainly depends on the initial size and reconnecting field within the structure.
3.4 Current sheet collapse at higher  $\unicode[STIX]{x1D6FD}$
$\unicode[STIX]{x1D6FD}$
Finally, the question of whether or not this collapse process depends crucially on the low- $\unicode[STIX]{x1D6FD}$ ordering used to derive KREHM may be of interest to the reader. First, for
$\unicode[STIX]{x1D6FD}$ ordering used to derive KREHM may be of interest to the reader. First, for  $k_{\bot }\unicode[STIX]{x1D70C}_{i}\ll 1$, the Chapman–Kendall collapse obviously works, since the RMHD equations are valid at arbitrary
$k_{\bot }\unicode[STIX]{x1D70C}_{i}\ll 1$, the Chapman–Kendall collapse obviously works, since the RMHD equations are valid at arbitrary  $\unicode[STIX]{x1D6FD}$ and can be derived from gyrokinetics under the assumption
$\unicode[STIX]{x1D6FD}$ and can be derived from gyrokinetics under the assumption  $k_{\bot }\unicode[STIX]{x1D70C}_{i}\ll 1$ (Schekochihin et al. Reference Schekochihin, Cowley, Dorland, Hammett, Howes, Quataert and Tatsuno2009). Second, for
$k_{\bot }\unicode[STIX]{x1D70C}_{i}\ll 1$ (Schekochihin et al. Reference Schekochihin, Cowley, Dorland, Hammett, Howes, Quataert and Tatsuno2009). Second, for  $k_{\bot }\unicode[STIX]{x1D70C}_{i}\gg 1$, we can examine the (two-dimensional) electron reduced MHD equations (Schekochihin et al. Reference Schekochihin, Cowley, Dorland, Hammett, Howes, Quataert and Tatsuno2009), which may be manipulated into the following form, chosen for their similarity to (2.1) and (2.2),
$k_{\bot }\unicode[STIX]{x1D70C}_{i}\gg 1$, we can examine the (two-dimensional) electron reduced MHD equations (Schekochihin et al. Reference Schekochihin, Cowley, Dorland, Hammett, Howes, Quataert and Tatsuno2009), which may be manipulated into the following form, chosen for their similarity to (2.1) and (2.2),
 $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}}{\text{d}t}\frac{Z}{\unicode[STIX]{x1D70F}}\frac{e\unicode[STIX]{x1D719}}{T_{0e}}=\frac{2}{2+\unicode[STIX]{x1D6FD}_{i}\left(1+\displaystyle \frac{Z}{\unicode[STIX]{x1D70F}}\right)}\hat{\boldsymbol{b}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\frac{e}{cm_{e}}d_{e}^{2}\unicode[STIX]{x1D735}_{\bot }^{2}A_{\Vert }, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}}{\text{d}t}\frac{Z}{\unicode[STIX]{x1D70F}}\frac{e\unicode[STIX]{x1D719}}{T_{0e}}=\frac{2}{2+\unicode[STIX]{x1D6FD}_{i}\left(1+\displaystyle \frac{Z}{\unicode[STIX]{x1D70F}}\right)}\hat{\boldsymbol{b}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\frac{e}{cm_{e}}d_{e}^{2}\unicode[STIX]{x1D735}_{\bot }^{2}A_{\Vert }, & \displaystyle\end{eqnarray}$$ $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}}{\text{d}t}A_{\Vert }=-\frac{cT_{0e}}{e}\hat{\boldsymbol{b}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\left[\frac{Z}{\unicode[STIX]{x1D70F}}\frac{e\unicode[STIX]{x1D719}}{T_{0e}}\right]. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}}{\text{d}t}A_{\Vert }=-\frac{cT_{0e}}{e}\hat{\boldsymbol{b}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\left[\frac{Z}{\unicode[STIX]{x1D70F}}\frac{e\unicode[STIX]{x1D719}}{T_{0e}}\right]. & \displaystyle\end{eqnarray}$$The effective velocity into which the field lines are frozen is
 $$\begin{eqnarray}\boldsymbol{u}_{\text{eff}}=\hat{z}\times \unicode[STIX]{x1D735}_{\bot }\frac{c}{B_{0}}\left(1+\frac{Z}{\unicode[STIX]{x1D70F}}\right)\unicode[STIX]{x1D719},\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{u}_{\text{eff}}=\hat{z}\times \unicode[STIX]{x1D735}_{\bot }\frac{c}{B_{0}}\left(1+\frac{Z}{\unicode[STIX]{x1D70F}}\right)\unicode[STIX]{x1D719},\end{eqnarray}$$ which can be compared with (2.11). Under the condition (3.1), equation (3.14) vanishesFootnote 5. Inserting (3.3) and (3.4) with  $d_{e}=0$ into (3.15), and requiring the outflow velocity to be the in-plane kinetic-Alfvén velocity (at larger
$d_{e}=0$ into (3.15), and requiring the outflow velocity to be the in-plane kinetic-Alfvén velocity (at larger  $\unicode[STIX]{x1D6FD}_{i}$, see Schekochihin et al. Reference Schekochihin, Cowley, Dorland, Hammett, Howes, Quataert and Tatsuno2009),
$\unicode[STIX]{x1D6FD}_{i}$, see Schekochihin et al. Reference Schekochihin, Cowley, Dorland, Hammett, Howes, Quataert and Tatsuno2009),
 $$\begin{eqnarray}u_{\text{KAW}y}=\sqrt{\frac{1+Z/\unicode[STIX]{x1D70F}}{2+\unicode[STIX]{x1D6FD}_{i}(1+Z/\unicode[STIX]{x1D70F})}}v_{\text{A}y}\frac{\unicode[STIX]{x1D70C}_{i}}{a(t)},\end{eqnarray}$$
$$\begin{eqnarray}u_{\text{KAW}y}=\sqrt{\frac{1+Z/\unicode[STIX]{x1D70F}}{2+\unicode[STIX]{x1D6FD}_{i}(1+Z/\unicode[STIX]{x1D70F})}}v_{\text{A}y}\frac{\unicode[STIX]{x1D70C}_{i}}{a(t)},\end{eqnarray}$$ we find that the solutions for  $a(t)$ and
$a(t)$ and  $L(t)$ are
$L(t)$ are
 $$\begin{eqnarray}\displaystyle L=L_{0}\exp \left(\frac{\sqrt{\displaystyle \frac{2(1+Z/\unicode[STIX]{x1D70F})}{1+\unicode[STIX]{x1D6FD}_{i}(1+Z/\unicode[STIX]{x1D70F})/2}}v_{\text{A}y}\unicode[STIX]{x1D70C}_{i}}{a_{0}L_{0}}t\right),\quad a=a_{0}L_{0}/L,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle L=L_{0}\exp \left(\frac{\sqrt{\displaystyle \frac{2(1+Z/\unicode[STIX]{x1D70F})}{1+\unicode[STIX]{x1D6FD}_{i}(1+Z/\unicode[STIX]{x1D70F})/2}}v_{\text{A}y}\unicode[STIX]{x1D70C}_{i}}{a_{0}L_{0}}t\right),\quad a=a_{0}L_{0}/L,\end{eqnarray}$$ only mildly different to the KREHM case. Thus, the fact that current sheets collapse even at thicknesses  $a\ll \unicode[STIX]{x1D70C}_{i}$ does not depend on the
$a\ll \unicode[STIX]{x1D70C}_{i}$ does not depend on the  $\unicode[STIX]{x1D6FD}\ll 1$ ordering of KREHM.
$\unicode[STIX]{x1D6FD}\ll 1$ ordering of KREHM.
Table 1. Scalings for the collisionless tearing mode in various limits, as discussed in appendix B. The final row,  $a/\unicode[STIX]{x1D70C}_{s}\ll 1$ and
$a/\unicode[STIX]{x1D70C}_{s}\ll 1$ and  $\unicode[STIX]{x1D6E5}^{\prime }\unicode[STIX]{x1D6FF}_{\text{in}}\gg 1$, is probably inaccurate since we do not have an analytic solution. The quantity
$\unicode[STIX]{x1D6E5}^{\prime }\unicode[STIX]{x1D6FF}_{\text{in}}\gg 1$, is probably inaccurate since we do not have an analytic solution. The quantity  $H=\sqrt{1+\unicode[STIX]{x1D70F}/Z}$; please see the appendix for details.
$H=\sqrt{1+\unicode[STIX]{x1D70F}/Z}$; please see the appendix for details.

4 Disruption of forming sheets by the tearing instability
A useful model of the disruption of forming current sheets by reconnection has been developed recently by Uzdensky & Loureiro (Reference Uzdensky and Loureiro2016). In this model, collapsing sheets are disrupted if their linear tearing mode is faster than their formation time scale, i.e.
 $$\begin{eqnarray}\unicode[STIX]{x1D6FE}/\unicode[STIX]{x1D6EC}(t)>1,\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FE}/\unicode[STIX]{x1D6EC}(t)>1,\end{eqnarray}$$assuming that the nonlinear stage of the tearing mode is at least as fast as the linear stage.
In general, the tearing mode that disrupts the sheet has the maximum tearing growth rate  $\unicode[STIX]{x1D6FE}_{\text{max}}$ if it fits into the sheet, i.e. if
$\unicode[STIX]{x1D6FE}_{\text{max}}$ if it fits into the sheet, i.e. if  $k_{\text{max}}L>1$, and by the growth rate of the longest-wavelength mode that fits in the sheet otherwise, i.e. the mode with
$k_{\text{max}}L>1$, and by the growth rate of the longest-wavelength mode that fits in the sheet otherwise, i.e. the mode with  $k_{y}L=1$. The relevant tearing growth rates for our system are summarised in table 1: the growth rates for the case
$k_{y}L=1$. The relevant tearing growth rates for our system are summarised in table 1: the growth rates for the case  $a\gg \unicode[STIX]{x1D70C}_{s}$ are derived in ZS11, while we derive the growth rates for the opposite case with
$a\gg \unicode[STIX]{x1D70C}_{s}$ are derived in ZS11, while we derive the growth rates for the opposite case with  $a\ll \unicode[STIX]{x1D70C}_{s}$ in appendix B.
$a\ll \unicode[STIX]{x1D70C}_{s}$ in appendix B.
4.1 Critical aspect ratio
One can show that for our choice of  $\unicode[STIX]{x1D6EC}(t)$, in the case
$\unicode[STIX]{x1D6EC}(t)$, in the case  $a\gg \unicode[STIX]{x1D70C}_{s}$,
$a\gg \unicode[STIX]{x1D70C}_{s}$,  $k_{\text{max}}$ becomes accessible before the mode with
$k_{\text{max}}$ becomes accessible before the mode with  $k_{y}L=1$ goes unstable, while in the case where
$k_{y}L=1$ goes unstable, while in the case where  $a\ll \unicode[STIX]{x1D70C}_{s}$, the sheet is disrupted when
$a\ll \unicode[STIX]{x1D70C}_{s}$, the sheet is disrupted when  $k_{\text{max}}L\sim 1$, and thus in practice we may always use
$k_{\text{max}}L\sim 1$, and thus in practice we may always use  $\unicode[STIX]{x1D6FE}_{\text{max}}$. Using (4.1), we find that sheets are disrupted for aspect ratios
$\unicode[STIX]{x1D6FE}_{\text{max}}$. Using (4.1), we find that sheets are disrupted for aspect ratios
 $$\begin{eqnarray}\displaystyle \frac{L}{a}>\left(\frac{L}{a}\right)_{\text{crit}}\sim \left\{\begin{array}{@{}ll@{}}{\displaystyle \frac{1}{\sqrt{1+\unicode[STIX]{x1D70F}/Z}}}\left({\displaystyle \frac{a}{d_{e}}}\right)^{1/n}\left({\displaystyle \frac{a}{\unicode[STIX]{x1D70C}_{s}}}\right)\left({\displaystyle \frac{\unicode[STIX]{x1D70C}_{s}}{d_{e}}}\right)^{(1-1/n)/3}, & a\gg \unicode[STIX]{x1D70C}_{s}\\[6.0pt] \left({\displaystyle \frac{a}{d_{e}}}\right)^{1/n}, & a\ll \unicode[STIX]{x1D70C}_{s}.\end{array}\right. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{L}{a}>\left(\frac{L}{a}\right)_{\text{crit}}\sim \left\{\begin{array}{@{}ll@{}}{\displaystyle \frac{1}{\sqrt{1+\unicode[STIX]{x1D70F}/Z}}}\left({\displaystyle \frac{a}{d_{e}}}\right)^{1/n}\left({\displaystyle \frac{a}{\unicode[STIX]{x1D70C}_{s}}}\right)\left({\displaystyle \frac{\unicode[STIX]{x1D70C}_{s}}{d_{e}}}\right)^{(1-1/n)/3}, & a\gg \unicode[STIX]{x1D70C}_{s}\\[6.0pt] \left({\displaystyle \frac{a}{d_{e}}}\right)^{1/n}, & a\ll \unicode[STIX]{x1D70C}_{s}.\end{array}\right. & & \displaystyle\end{eqnarray}$$ The  $a\gg \unicode[STIX]{x1D70C}_{s}$ expression was previously found by Del Sarto et al. (Reference Del Sarto, Pucci, Tenerani and Velli2016)Footnote 6.
$a\gg \unicode[STIX]{x1D70C}_{s}$ expression was previously found by Del Sarto et al. (Reference Del Sarto, Pucci, Tenerani and Velli2016)Footnote 6.
We have shown that there is a maximum achievable aspect ratio for sheets with both  $a\gg \unicode[STIX]{x1D70C}_{s}$ and
$a\gg \unicode[STIX]{x1D70C}_{s}$ and  $a\ll \unicode[STIX]{x1D70C}_{s}$. Inserting
$a\ll \unicode[STIX]{x1D70C}_{s}$. Inserting  $a\sim \unicode[STIX]{x1D70C}_{s}$ into (4.2), sheets will become unstable before they reach the ion scales (
$a\sim \unicode[STIX]{x1D70C}_{s}$ into (4.2), sheets will become unstable before they reach the ion scales ( $a\sim \unicode[STIX]{x1D70C}_{s}$) only if their aspect ratio becomes larger than
$a\sim \unicode[STIX]{x1D70C}_{s}$) only if their aspect ratio becomes larger than  $(\unicode[STIX]{x1D70C}_{s}/d_{e})^{\unicode[STIX]{x1D708}}$, where
$(\unicode[STIX]{x1D70C}_{s}/d_{e})^{\unicode[STIX]{x1D708}}$, where  $1/n\leqslant \unicode[STIX]{x1D708}\leqslant 1/3+2/3n$. Once the sheet reaches the thickness at which it disrupts, it reconnects at that thicknessFootnote 7 until all the available flux has been used up. Thus, if one observes a reconnecting (i.e. disrupting) sheet with length
$1/n\leqslant \unicode[STIX]{x1D708}\leqslant 1/3+2/3n$. Once the sheet reaches the thickness at which it disrupts, it reconnects at that thicknessFootnote 7 until all the available flux has been used up. Thus, if one observes a reconnecting (i.e. disrupting) sheet with length
 $$\begin{eqnarray}L>\frac{\unicode[STIX]{x1D70C}_{s}}{\sqrt{1+\unicode[STIX]{x1D70F}/Z}}\left(\frac{m_{e}}{m_{i}}\frac{Z}{\unicode[STIX]{x1D6FD}_{e}}\right)^{\unicode[STIX]{x1D708}/2},\end{eqnarray}$$
$$\begin{eqnarray}L>\frac{\unicode[STIX]{x1D70C}_{s}}{\sqrt{1+\unicode[STIX]{x1D70F}/Z}}\left(\frac{m_{e}}{m_{i}}\frac{Z}{\unicode[STIX]{x1D6FD}_{e}}\right)^{\unicode[STIX]{x1D708}/2},\end{eqnarray}$$ one expects to see that the sheet thickness is larger than the ion scale and that there should be bidirectional ion jets moving at  $v_{\text{A}y}$. This roughly agrees with the numerical simulations of Sharma Pyakurel et al. (Reference Sharma Pyakurel, Shay, Phan, Matthaeus, Drake, TenBarge, Haggerty, Klein, Cassak and Parashar2019), who found that to obtain fully ion-coupled guide-field reconnection,
$v_{\text{A}y}$. This roughly agrees with the numerical simulations of Sharma Pyakurel et al. (Reference Sharma Pyakurel, Shay, Phan, Matthaeus, Drake, TenBarge, Haggerty, Klein, Cassak and Parashar2019), who found that to obtain fully ion-coupled guide-field reconnection,  $L$ needed to be of order
$L$ needed to be of order  $10d_{i}$, and is reminiscent of the results of Mandt, Denton & Drake (Reference Mandt, Denton and Drake1994) for reconnection without a guide field, who observed a change in the scaling of the reconnection rate once the length of sheets became comparable to a few times the ion inertial length. In the magnetosheath interval studied by Phan et al. (Reference Phan, Eastwood, Shay, Drake, Sonnerup, Fujimoto, Cassak, Øieroset, Burch and Torbert2018) and subsequently Stawarz et al. (Reference Stawarz, Eastwood, Phan, Gingell, Shay, Burch, Ergun, Giles, Gershman and Le Contel2019),
$10d_{i}$, and is reminiscent of the results of Mandt, Denton & Drake (Reference Mandt, Denton and Drake1994) for reconnection without a guide field, who observed a change in the scaling of the reconnection rate once the length of sheets became comparable to a few times the ion inertial length. In the magnetosheath interval studied by Phan et al. (Reference Phan, Eastwood, Shay, Drake, Sonnerup, Fujimoto, Cassak, Øieroset, Burch and Torbert2018) and subsequently Stawarz et al. (Reference Stawarz, Eastwood, Phan, Gingell, Shay, Burch, Ergun, Giles, Gershman and Le Contel2019),  $\unicode[STIX]{x1D6FD}_{e}\approx 0.5$ and
$\unicode[STIX]{x1D6FD}_{e}\approx 0.5$ and  $\unicode[STIX]{x1D70F}/Z\approx 10$; choosing
$\unicode[STIX]{x1D70F}/Z\approx 10$; choosing  $\unicode[STIX]{x1D708}=1$ and using the
$\unicode[STIX]{x1D708}=1$ and using the  $a\gg \unicode[STIX]{x1D70C}_{s}$ expression gives the critical length for ion-coupled reconnection
$a\gg \unicode[STIX]{x1D70C}_{s}$ expression gives the critical length for ion-coupled reconnection  $L/\unicode[STIX]{x1D70C}_{s}\approx 10$ (this is also effectively the critical aspect ratio of such ion-coupled reconnecting sheets, since it is the point at which
$L/\unicode[STIX]{x1D70C}_{s}\approx 10$ (this is also effectively the critical aspect ratio of such ion-coupled reconnecting sheets, since it is the point at which  $a\approx \unicode[STIX]{x1D70C}_{s}$). In other words, the fact that ion-scale sheets and ion jets are not often observed in the magnetosheath means that the aspect ratios of the sheets formed (presumably by the turbulent dynamics) are not extremely high.
$a\approx \unicode[STIX]{x1D70C}_{s}$). In other words, the fact that ion-scale sheets and ion jets are not often observed in the magnetosheath means that the aspect ratios of the sheets formed (presumably by the turbulent dynamics) are not extremely high.
As  $a\rightarrow d_{e}$, current sheets of any appreciable aspect ratio greater than 1 are disrupted – so in practice, as one might have expected, the steady-state Sweet–Parker-like configuration, with width
$a\rightarrow d_{e}$, current sheets of any appreciable aspect ratio greater than 1 are disrupted – so in practice, as one might have expected, the steady-state Sweet–Parker-like configuration, with width  $d_{e}$ (which we derive in appendix A) is not accessible. Reconnecting sheets for
$d_{e}$ (which we derive in appendix A) is not accessible. Reconnecting sheets for  $a\ll \unicode[STIX]{x1D70C}_{s}$ should have the aspect ratio given by the second expression in (4.2), and so we can estimate the aspect ratio of the sheets observed by Phan et al. (Reference Phan, Eastwood, Shay, Drake, Sonnerup, Fujimoto, Cassak, Øieroset, Burch and Torbert2018), with thicknesses
$a\ll \unicode[STIX]{x1D70C}_{s}$ should have the aspect ratio given by the second expression in (4.2), and so we can estimate the aspect ratio of the sheets observed by Phan et al. (Reference Phan, Eastwood, Shay, Drake, Sonnerup, Fujimoto, Cassak, Øieroset, Burch and Torbert2018), with thicknesses  $a\approx 4d_{e}$, to be no more than
$a\approx 4d_{e}$, to be no more than  ${\approx}4$, using the
${\approx}4$, using the  $n=1$ expression.
$n=1$ expression.
A simple estimate of the disruption time scale of the current sheets observed by Phan et al. (Reference Phan, Eastwood, Shay, Drake, Sonnerup, Fujimoto, Cassak, Øieroset, Burch and Torbert2018) is possible using (3.13). Given that  $aL$ is constant during collapse, we can estimate
$aL$ is constant during collapse, we can estimate  $a_{0}L_{0}=aL\approx 64d_{e}^{2}$. Using
$a_{0}L_{0}=aL\approx 64d_{e}^{2}$. Using  $d_{e}\approx 1~\text{km}$,
$d_{e}\approx 1~\text{km}$,  $v_{\text{A}y}\approx 25~\text{kms}^{-1}$ and
$v_{\text{A}y}\approx 25~\text{kms}^{-1}$ and  $\unicode[STIX]{x1D70C}_{i}\approx 100~\text{km}$,
$\unicode[STIX]{x1D70C}_{i}\approx 100~\text{km}$,  $t_{\ast }\approx 0.06~\text{s}$, which suggests that these electron-only reconnection events are individually rather short lived.
$t_{\ast }\approx 0.06~\text{s}$, which suggests that these electron-only reconnection events are individually rather short lived.
4.2 Outflow velocity
One can obtain an estimate of the electron outflow velocity in the reconnecting sheets by a simple scaling argument. Our configuration is a current sheet of thickness  $a$ and length
$a$ and length  $L\gg a$, and a known upstream field
$L\gg a$, and a known upstream field  $B_{\text{in}}$. The electrons flow into the sheet at
$B_{\text{in}}$. The electrons flow into the sheet at  $u_{\text{in}}$, and out at
$u_{\text{in}}$, and out at  $u_{\text{out}}$ (which are related to
$u_{\text{out}}$ (which are related to  $\unicode[STIX]{x1D719}$ via (2.11)). We will assume that
$\unicode[STIX]{x1D719}$ via (2.11)). We will assume that  $g_{e}=0$ for simplicity; although this is not realistic, on the level of the scaling arguments presented here it is irrelevant.
$g_{e}=0$ for simplicity; although this is not realistic, on the level of the scaling arguments presented here it is irrelevant.
First, because upon inspecting (2.11),  $\unicode[STIX]{x1D735}_{\bot }\boldsymbol{\cdot }\boldsymbol{u}_{\text{eff}}=0$,
$\unicode[STIX]{x1D735}_{\bot }\boldsymbol{\cdot }\boldsymbol{u}_{\text{eff}}=0$,
 $$\begin{eqnarray}Lu_{\text{in}}\sim au_{\text{out}}.\end{eqnarray}$$
$$\begin{eqnarray}Lu_{\text{in}}\sim au_{\text{out}}.\end{eqnarray}$$ Second, because  $L\gg a$, the upstream energy is dominated by the magnetic field, while the energy downstream is dominated by the ion flow and the density perturbations (Zocco & Schekochihin Reference Zocco and Schekochihin2011). Balancing these,
$L\gg a$, the upstream energy is dominated by the magnetic field, while the energy downstream is dominated by the ion flow and the density perturbations (Zocco & Schekochihin Reference Zocco and Schekochihin2011). Balancing these,
 $$\begin{eqnarray}\frac{B_{\text{in}}^{2}}{8\unicode[STIX]{x03C0}}\sim \left[1+\frac{Z}{\unicode[STIX]{x1D70F}}(1-\hat{\unicode[STIX]{x1D6E4}}_{0})\right]\frac{Z}{\unicode[STIX]{x1D70F}}(1-\hat{\unicode[STIX]{x1D6E4}}_{0})\frac{e^{2}n_{0e}}{2T_{0e}}\unicode[STIX]{x1D719}_{\text{out}}^{2}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{B_{\text{in}}^{2}}{8\unicode[STIX]{x03C0}}\sim \left[1+\frac{Z}{\unicode[STIX]{x1D70F}}(1-\hat{\unicode[STIX]{x1D6E4}}_{0})\right]\frac{Z}{\unicode[STIX]{x1D70F}}(1-\hat{\unicode[STIX]{x1D6E4}}_{0})\frac{e^{2}n_{0e}}{2T_{0e}}\unicode[STIX]{x1D719}_{\text{out}}^{2}.\end{eqnarray}$$ In the limit  $\unicode[STIX]{x1D70C}_{i}\ll a$,
$\unicode[STIX]{x1D70C}_{i}\ll a$,  $Z/\unicode[STIX]{x1D70F}(1-\hat{\unicode[STIX]{x1D6E4}}_{0})\approx (\unicode[STIX]{x1D70C}_{s}/a)^{2}$, and using (2.11), this just results (reassuringly) in Alfvénic outflows,
$Z/\unicode[STIX]{x1D70F}(1-\hat{\unicode[STIX]{x1D6E4}}_{0})\approx (\unicode[STIX]{x1D70C}_{s}/a)^{2}$, and using (2.11), this just results (reassuringly) in Alfvénic outflows,  $u_{\text{out}}\sim v_{\text{A}y}$, where
$u_{\text{out}}\sim v_{\text{A}y}$, where  $v_{\text{A}y}=B_{\text{in}}/\sqrt{4\unicode[STIX]{x03C0}n_{0i}m_{i}}$. In the case where
$v_{\text{A}y}=B_{\text{in}}/\sqrt{4\unicode[STIX]{x03C0}n_{0i}m_{i}}$. In the case where  $\unicode[STIX]{x1D70C}_{i}\gg a$, using
$\unicode[STIX]{x1D70C}_{i}\gg a$, using  $\hat{\unicode[STIX]{x1D6E4}}_{0}\approx 0$, we find
$\hat{\unicode[STIX]{x1D6E4}}_{0}\approx 0$, we find
 $$\begin{eqnarray}u_{\text{out}}\sim \sqrt{\frac{1}{2}\left(1+\frac{Z}{\unicode[STIX]{x1D70F}}\right)}v_{\text{A}y}\frac{\unicode[STIX]{x1D70C}_{i}}{a},\end{eqnarray}$$
$$\begin{eqnarray}u_{\text{out}}\sim \sqrt{\frac{1}{2}\left(1+\frac{Z}{\unicode[STIX]{x1D70F}}\right)}v_{\text{A}y}\frac{\unicode[STIX]{x1D70C}_{i}}{a},\end{eqnarray}$$which is just the in-plane kinetic-Alfvén wave speed. So, rather different from the MHD case, the outflow velocity depends on the thickness of the sheet. Written in terms of the electron Alfvén speed, this is
 $$\begin{eqnarray}u_{\text{out}}\sim \sqrt{\frac{\unicode[STIX]{x1D6FD}_{i}}{2}\left(1+\frac{Z}{\unicode[STIX]{x1D70F}}\right)}v_{\text{A}ey}\frac{d_{e}}{a}.\end{eqnarray}$$
$$\begin{eqnarray}u_{\text{out}}\sim \sqrt{\frac{\unicode[STIX]{x1D6FD}_{i}}{2}\left(1+\frac{Z}{\unicode[STIX]{x1D70F}}\right)}v_{\text{A}ey}\frac{d_{e}}{a}.\end{eqnarray}$$ For the Phan et al. (Reference Phan, Eastwood, Shay, Drake, Sonnerup, Fujimoto, Cassak, Øieroset, Burch and Torbert2018) sheets, our model predicts (with  $\unicode[STIX]{x1D6FD}_{i}\approx 5$, cf. Stawarz et al. Reference Stawarz, Eastwood, Phan, Gingell, Shay, Burch, Ergun, Giles, Gershman and Le Contel2019)
$\unicode[STIX]{x1D6FD}_{i}\approx 5$, cf. Stawarz et al. Reference Stawarz, Eastwood, Phan, Gingell, Shay, Burch, Ergun, Giles, Gershman and Le Contel2019)  $u_{\text{out}}/v_{\text{A}ey}\approx 0.4$, while the observed outflow speed in Phan et al. (Reference Phan, Eastwood, Shay, Drake, Sonnerup, Fujimoto, Cassak, Øieroset, Burch and Torbert2018) is
$u_{\text{out}}/v_{\text{A}ey}\approx 0.4$, while the observed outflow speed in Phan et al. (Reference Phan, Eastwood, Shay, Drake, Sonnerup, Fujimoto, Cassak, Øieroset, Burch and Torbert2018) is  $u_{\text{out}}/v_{\text{A}ey}\approx 0.25-0.45$; given the idealisations involved (not to mention the fact that we are pushing our equations rather beyond their low-
$u_{\text{out}}/v_{\text{A}ey}\approx 0.25-0.45$; given the idealisations involved (not to mention the fact that we are pushing our equations rather beyond their low- $\unicode[STIX]{x1D6FD}$ regime of validity), this is reasonable agreement. More generally, we plot the dependence of the thickness at disruption,
$\unicode[STIX]{x1D6FD}$ regime of validity), this is reasonable agreement. More generally, we plot the dependence of the thickness at disruption,  $a_{\text{crit}}$, and the electron outflow velocity
$a_{\text{crit}}$, and the electron outflow velocity  $u_{\text{out},\text{crit}}$, as functions of
$u_{\text{out},\text{crit}}$, as functions of  $(L/a)_{\text{crit}}$ in figure 1.
$(L/a)_{\text{crit}}$ in figure 1.

Figure 1. In black, the disrupted thicknesses (a) and outflow velocities (b) of reconnecting sheets as a function of aspect ratio (cf. (4.2) and (4.6)). Because we have only derived scalings in the asymptotic limits  $a\gg \unicode[STIX]{x1D70C}_{s}$ and
$a\gg \unicode[STIX]{x1D70C}_{s}$ and  $a\ll \unicode[STIX]{x1D70C}_{s}$, for
$a\ll \unicode[STIX]{x1D70C}_{s}$, for  $0.5<a_{\text{crit}}/\unicode[STIX]{x1D70C}_{s}<2$ we have plotted these two scalings as dotted lines; the true scaling must lie between them. Red dashed lines show the positions of
$0.5<a_{\text{crit}}/\unicode[STIX]{x1D70C}_{s}<2$ we have plotted these two scalings as dotted lines; the true scaling must lie between them. Red dashed lines show the positions of  $\unicode[STIX]{x1D70C}_{s}$ and
$\unicode[STIX]{x1D70C}_{s}$ and  $d_{e}$ (a) and
$d_{e}$ (a) and  $v_{\text{A}ey}$ (b). We have used parameters taken from Stawarz et al. (Reference Stawarz, Eastwood, Phan, Gingell, Shay, Burch, Ergun, Giles, Gershman and Le Contel2019),
$v_{\text{A}ey}$ (b). We have used parameters taken from Stawarz et al. (Reference Stawarz, Eastwood, Phan, Gingell, Shay, Burch, Ergun, Giles, Gershman and Le Contel2019),  $\unicode[STIX]{x1D6FD}_{e}=0.5$,
$\unicode[STIX]{x1D6FD}_{e}=0.5$,  $\unicode[STIX]{x1D70F}=10$.
$\unicode[STIX]{x1D70F}=10$.
Finally, it is worth asking what the effect of relaxing the low- $\unicode[STIX]{x1D6FD}$ ordering of the KREHM equations would be on the tearing mode and on the critical aspect ratio we obtain here. We have shown in § 3.4 that
$\unicode[STIX]{x1D6FD}$ ordering of the KREHM equations would be on the tearing mode and on the critical aspect ratio we obtain here. We have shown in § 3.4 that  $\unicode[STIX]{x1D6FD}$ does not make a difference to the collapse process. Numata & Loureiro (Reference Numata and Loureiro2015) have shown that, if
$\unicode[STIX]{x1D6FD}$ does not make a difference to the collapse process. Numata & Loureiro (Reference Numata and Loureiro2015) have shown that, if  $\unicode[STIX]{x1D70C}_{i}/a$ and
$\unicode[STIX]{x1D70C}_{i}/a$ and  $\unicode[STIX]{x1D70C}_{s}/a$ are kept constant, the gyrokinetic tearing mode growth rate basically agrees with KREHM, i.e. proportional to
$\unicode[STIX]{x1D70C}_{s}/a$ are kept constant, the gyrokinetic tearing mode growth rate basically agrees with KREHM, i.e. proportional to  $\unicode[STIX]{x1D6FD}_{e}^{-1/2}$. Thus, we believe that using the KREHM tearing mode scalings is physically (if not quite mathematically) reasonable up to
$\unicode[STIX]{x1D6FD}_{e}^{-1/2}$. Thus, we believe that using the KREHM tearing mode scalings is physically (if not quite mathematically) reasonable up to  $\unicode[STIX]{x1D6FD}_{e}\sim 1$.
$\unicode[STIX]{x1D6FD}_{e}\sim 1$.
5 Conclusions
We have developed a theoretical model for low- $\unicode[STIX]{x1D6FD}$ current sheet formation and disruption by reconnection, and predict that sheets that are not sufficiently anisotropic will collapse to scales much smaller than the ion kinetic scales (
$\unicode[STIX]{x1D6FD}$ current sheet formation and disruption by reconnection, and predict that sheets that are not sufficiently anisotropic will collapse to scales much smaller than the ion kinetic scales ( $\unicode[STIX]{x1D70C}_{s}$ and
$\unicode[STIX]{x1D70C}_{s}$ and  $\unicode[STIX]{x1D70C}_{i}$), only reconnecting when their thickness is a few times the electron inertial scale
$\unicode[STIX]{x1D70C}_{i}$), only reconnecting when their thickness is a few times the electron inertial scale  $d_{e}$. For such sheets, we predict electron jets with velocities an appreciable fraction of the electron Alfvén velocity (i.e. much larger than the ion Alfvén velocity), and that there will be no ion-scale region and very slow or no ion outflows. As the aspect ratio of the sheets is varied, there is a gradual transition between the usual ‘ion-coupled’ regime and this new regime of ‘electron-only’ reconnection, with sheets reconnecting at thickness
$d_{e}$. For such sheets, we predict electron jets with velocities an appreciable fraction of the electron Alfvén velocity (i.e. much larger than the ion Alfvén velocity), and that there will be no ion-scale region and very slow or no ion outflows. As the aspect ratio of the sheets is varied, there is a gradual transition between the usual ‘ion-coupled’ regime and this new regime of ‘electron-only’ reconnection, with sheets reconnecting at thickness  $a\approx \unicode[STIX]{x1D70C}_{s}$ when their aspect ratio
$a\approx \unicode[STIX]{x1D70C}_{s}$ when their aspect ratio  $L/a\approx 10$. We find that in the magnetosheath, this means that the aspect ratio of reconnecting sheets, observed to be of thickness
$L/a\approx 10$. We find that in the magnetosheath, this means that the aspect ratio of reconnecting sheets, observed to be of thickness  $a\approx 4d_{e}$, is no more than a factor of
$a\approx 4d_{e}$, is no more than a factor of  ${\approx}4$. Our results may thus help to explain recent observations of electron-only reconnection in the magnetosheath (Phan et al. Reference Phan, Eastwood, Shay, Drake, Sonnerup, Fujimoto, Cassak, Øieroset, Burch and Torbert2018).
${\approx}4$. Our results may thus help to explain recent observations of electron-only reconnection in the magnetosheath (Phan et al. Reference Phan, Eastwood, Shay, Drake, Sonnerup, Fujimoto, Cassak, Øieroset, Burch and Torbert2018).
Our picture of reconnection onset is based on two phenomena. First, ideal current sheets tend to collapse (Syrovatskii Reference Syrovatskii1981; Chapman & Kendall Reference Chapman and Kendall1963; Biskamp Reference Biskamp2000), and we show in § 3 that this collapse does not have to stop at the ion scale. Second, this ideal collapse process breaks down when the tearing mode growth rate becomes larger than the collapse (or sheet formation) rate, an application of the ideas of Uzdensky & Loureiro (Reference Uzdensky and Loureiro2016) to a collisionless plasma. This implies a critical aspect ratio at which reconnection onset occurs, which we derive in § 4. Importantly, the sheet thickness at disruption can be above or below the ion scales, and so we can predict the physical conditions in which we expect ion-coupled reconnection to give way to electron-only reconnection.
Our analysis is based on the KREHM equations, which are derived from gyrokinetics for  $\unicode[STIX]{x1D6FD}_{e}\sim \unicode[STIX]{x1D6FD}_{i}\sim Zm_{e}/m_{i}\ll 1$. This low-
$\unicode[STIX]{x1D6FD}_{e}\sim \unicode[STIX]{x1D6FD}_{i}\sim Zm_{e}/m_{i}\ll 1$. This low- $\unicode[STIX]{x1D6FD}$ ordering is not usually formally valid in the magnetosheath. However, we can show that, in fact, the collapse process does not depend on the low
$\unicode[STIX]{x1D6FD}$ ordering is not usually formally valid in the magnetosheath. However, we can show that, in fact, the collapse process does not depend on the low  $\unicode[STIX]{x1D6FD}$, and KREHM does a surprisingly good job of predicting the full gyrokinetic tearing rates even at moderate
$\unicode[STIX]{x1D6FD}$, and KREHM does a surprisingly good job of predicting the full gyrokinetic tearing rates even at moderate  $\unicode[STIX]{x1D6FD}_{e}$. This perhaps explains why our estimates of electron outflow velocities agree reasonably well with the MMS observations. More generally, we believe that KREHM, while not always formally valid, is a useful minimal physical model of collisionless reconnection, which allows us to make theoretical progress in understanding electron-only reconnection and the transition from the ion-coupled to electron-only regimes.
$\unicode[STIX]{x1D6FD}_{e}$. This perhaps explains why our estimates of electron outflow velocities agree reasonably well with the MMS observations. More generally, we believe that KREHM, while not always formally valid, is a useful minimal physical model of collisionless reconnection, which allows us to make theoretical progress in understanding electron-only reconnection and the transition from the ion-coupled to electron-only regimes.
Boldyrev & Loureiro (Reference Boldyrev and Loureiro2019) use a different approach to the one used in this work: instead of studying a nonlinear collapsing solution, they show that if helicity in a structure is held constant, the nonlinear interaction is minimised by making the structure as sheet like as possible: thus, sheet-like structures last longer. They then argue that this means that the turbulence favours the creation of highly sheet-like structures, but that this is limited by the tearing instability, which then sets a particular critical aspect ratio (as does our analysis). Despite the overall similarity of the results, there are some important differences in the two pictures: in ours, the nonlinear interaction actively produces increasingly sheet-like structures, while in Boldyrev & Loureiro (Reference Boldyrev and Loureiro2019), its role is to rapidly remove non-sheet-like structures. Our method has the advantage that it also works for sheets thicker than the ion scales, and we can therefore predict when one expects to see electron-only versus ion-coupled reconnection, depending on the characteristic aspect ratios of sheets as a function of their thickness.
In turbulence models that include the phenomenon of dynamic alignment (Boldyrev Reference Boldyrev2006; Chandran et al. Reference Chandran, Schekochihin and Mallet2015; Mallet & Schekochihin Reference Mallet and Schekochihin2017), the turbulent structures at scale  $\unicode[STIX]{x1D706}$ are sheet like in the perpendicular plane, with aspect ratios
$\unicode[STIX]{x1D706}$ are sheet like in the perpendicular plane, with aspect ratios  $\propto (\unicode[STIX]{x1D706}/L_{\bot })^{-1/4}$, where
$\propto (\unicode[STIX]{x1D706}/L_{\bot })^{-1/4}$, where  $L_{\bot }$ is the outer scale at which energy is injected into the system. Thus, for electron-only reconnection to be observed in turbulence, energy must be injected relatively close to the ion scales: in the magnetosheath, this injection could potentially come in the form of Alfvén vortices (Alexandrova Reference Alexandrova2008), perhaps driven by density gradients (Sundkvist & Bale Reference Sundkvist and Bale2008). If this picture is correct, electron-only reconnection may be relevant in other astrophysical environments with large density inhomogeneities, for example close to shocks. The appearance of electron-only reconnection in turbulent systems where the driving scale is relatively close to the ion scales has been observed rather clearly in the (two-dimensional) hybrid turbulence simulations of Califano et al. (Reference Califano, Cerri, Faganello, Laveder and Kunz2018), who observed electron-only reconnection when
$L_{\bot }$ is the outer scale at which energy is injected into the system. Thus, for electron-only reconnection to be observed in turbulence, energy must be injected relatively close to the ion scales: in the magnetosheath, this injection could potentially come in the form of Alfvén vortices (Alexandrova Reference Alexandrova2008), perhaps driven by density gradients (Sundkvist & Bale Reference Sundkvist and Bale2008). If this picture is correct, electron-only reconnection may be relevant in other astrophysical environments with large density inhomogeneities, for example close to shocks. The appearance of electron-only reconnection in turbulent systems where the driving scale is relatively close to the ion scales has been observed rather clearly in the (two-dimensional) hybrid turbulence simulations of Califano et al. (Reference Califano, Cerri, Faganello, Laveder and Kunz2018), who observed electron-only reconnection when  $d_{i}/L_{\bot }\approx 0.6$, but ion-coupled reconnection when
$d_{i}/L_{\bot }\approx 0.6$, but ion-coupled reconnection when  $d_{i}/L_{\bot }\approx 0.3$. Our results therefore provide a theoretical context for these numerical results.
$d_{i}/L_{\bot }\approx 0.3$. Our results therefore provide a theoretical context for these numerical results.
Another low- $\unicode[STIX]{x1D6FD}_{e}$ environment of interest is the inner heliosphere and solar corona, currently being explored by the Parker Solar Probe (Fox et al. Reference Fox, Velli, Bale, Decker, Driesman, Howard, Kasper, Kinnison, Kusterer and Lario2016). Our results show that whether ion-coupled or electron-only reconnection, or a mixture of the two, occur in this turbulent setting depends crucially on the length of the inertial range between the injection scale and the ion scales.
$\unicode[STIX]{x1D6FD}_{e}$ environment of interest is the inner heliosphere and solar corona, currently being explored by the Parker Solar Probe (Fox et al. Reference Fox, Velli, Bale, Decker, Driesman, Howard, Kasper, Kinnison, Kusterer and Lario2016). Our results show that whether ion-coupled or electron-only reconnection, or a mixture of the two, occur in this turbulent setting depends crucially on the length of the inertial range between the injection scale and the ion scales.
However, a detailed picture of electron-only reconnection onset in turbulence in the range of scales between  $\unicode[STIX]{x1D70C}_{s}$ and
$\unicode[STIX]{x1D70C}_{s}$ and  $d_{e}$ requires a model of how the aspect ratios of typical turbulent structures evolve in this range in the absence of reconnection (or, indeed, after ion-coupled reconnection decreases the typical aspect ratio, see e.g. Mallet, Schekochihin & Chandran Reference Mallet, Schekochihin and Chandran2017): this will be the focus of future work.
$d_{e}$ requires a model of how the aspect ratios of typical turbulent structures evolve in this range in the absence of reconnection (or, indeed, after ion-coupled reconnection decreases the typical aspect ratio, see e.g. Mallet, Schekochihin & Chandran Reference Mallet, Schekochihin and Chandran2017): this will be the focus of future work.
Acknowledgements
We thank A. A. Schekochihin, T. D. Phan, R. Meyrand, D. Grošelj and P. Sharma Pyakurel for useful conversations, and the anonymous reviewers for their helpful comments. This work was supported by NASA grant NNX16AP95G.
Appendix A. Steady-state reconnecting sheet
Let us perform a scaling analysis of (2.1)–(2.3), similarly to Parker (Reference Parker1957) and Sweet (Reference Sweet and Lehnert1958), and find a steady-state reconnecting configuration. The existence of this hypothetical configuration is quite reassuring, but as we have shown in § 4, this steady-state configuration is not realisable, because it is violently unstable. This is reminiscent of the results of Loureiro, Schekochihin & Cowley (Reference Loureiro, Schekochihin and Cowley2007), Pucci & Velli (Reference Pucci and Velli2014) and Uzdensky & Loureiro (Reference Uzdensky and Loureiro2016) on the resistive plasmoid instability. We will work in two dimensions, i.e.  $\unicode[STIX]{x2202}/\unicode[STIX]{x2202}z=0$, and for simplicity set
$\unicode[STIX]{x2202}/\unicode[STIX]{x2202}z=0$, and for simplicity set  $g_{e}=0$. Our configuration will the same as in § 4.2, namely a current sheet of thickness
$g_{e}=0$. Our configuration will the same as in § 4.2, namely a current sheet of thickness  $a$ and a length
$a$ and a length  $L\gg a$, with upstream field
$L\gg a$, with upstream field  $B_{\text{in}}$, and electrons flowing into the sheet at
$B_{\text{in}}$, and electrons flowing into the sheet at  $u_{\text{in}}$, and out at
$u_{\text{in}}$, and out at  $u_{\text{out}}$. The analysis of (4.4)–(4.7) to determine the outflow velocity in terms of
$u_{\text{out}}$. The analysis of (4.4)–(4.7) to determine the outflow velocity in terms of  $a$ is therefore still valid.
$a$ is therefore still valid.
We additionally require a steady state,  $\unicode[STIX]{x2202}/\unicode[STIX]{x2202}t=0$. To achieve this, we balance the nonlinear terms in (2.2),
$\unicode[STIX]{x2202}/\unicode[STIX]{x2202}t=0$. To achieve this, we balance the nonlinear terms in (2.2),
 $$\begin{eqnarray}\left\{A_{\Vert },\left[1+\frac{Z}{\unicode[STIX]{x1D70F}}(1-\hat{\unicode[STIX]{x1D6E4}}_{0})\right]\unicode[STIX]{x1D719}\right\}\sim \{\unicode[STIX]{x1D719},d_{e}^{2}\unicode[STIX]{x1D735}_{\bot }^{2}A_{\Vert }\}.\end{eqnarray}$$
$$\begin{eqnarray}\left\{A_{\Vert },\left[1+\frac{Z}{\unicode[STIX]{x1D70F}}(1-\hat{\unicode[STIX]{x1D6E4}}_{0})\right]\unicode[STIX]{x1D719}\right\}\sim \{\unicode[STIX]{x1D719},d_{e}^{2}\unicode[STIX]{x1D735}_{\bot }^{2}A_{\Vert }\}.\end{eqnarray}$$This gives
 $$\begin{eqnarray}\displaystyle a\sim \left\{\begin{array}{@{}lc@{}}d_{e}, & d_{e}\gg \unicode[STIX]{x1D70C}_{i},\\ {\displaystyle \frac{d_{e}}{\sqrt{1+Z/\unicode[STIX]{x1D70F}}}}, & d_{e}\ll \unicode[STIX]{x1D70C}_{i},\\ \end{array}\right. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle a\sim \left\{\begin{array}{@{}lc@{}}d_{e}, & d_{e}\gg \unicode[STIX]{x1D70C}_{i},\\ {\displaystyle \frac{d_{e}}{\sqrt{1+Z/\unicode[STIX]{x1D70F}}}}, & d_{e}\ll \unicode[STIX]{x1D70C}_{i},\\ \end{array}\right. & & \displaystyle\end{eqnarray}$$ using the small- and large-argument expansions of  $\hat{\unicode[STIX]{x1D6E4}}_{0}$. Thus, these steady-state sheets have a constant thickness
$\hat{\unicode[STIX]{x1D6E4}}_{0}$. Thus, these steady-state sheets have a constant thickness  $a\sim d_{e}$, and an arbitrary length
$a\sim d_{e}$, and an arbitrary length  $L$, i.e.
$L$, i.e.
 $$\begin{eqnarray}\frac{u_{\text{in}}}{u_{\text{out}}}\sim \frac{d_{e}}{L}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{u_{\text{in}}}{u_{\text{out}}}\sim \frac{d_{e}}{L}.\end{eqnarray}$$The dimensionless reconnection rate as usually defined is
 $$\begin{eqnarray}R\sim \frac{u_{\text{in}}}{v_{\text{A}y}}\sim \left\{\begin{array}{@{}cc@{}}d_{e}/L, & d_{e}\gg \unicode[STIX]{x1D70C}_{i},\\ \unicode[STIX]{x1D70C}_{i}/L, & d_{e}\ll \unicode[STIX]{x1D70C}_{i}.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}R\sim \frac{u_{\text{in}}}{v_{\text{A}y}}\sim \left\{\begin{array}{@{}cc@{}}d_{e}/L, & d_{e}\gg \unicode[STIX]{x1D70C}_{i},\\ \unicode[STIX]{x1D70C}_{i}/L, & d_{e}\ll \unicode[STIX]{x1D70C}_{i}.\end{array}\right.\end{eqnarray}$$ We have managed to derive a Sweet–Parker-like scenario for collisionless reconnection. The result for  $d_{e}\gg \unicode[STIX]{x1D70C}_{i}$ has been previously discovered by Wesson (Reference Wesson1990), while Bulanov, Pegoraro & Sakharov (Reference Bulanov, Pegoraro and Sakharov1992) and Avinash et al. (Reference Avinash, Bulanov, Esirkepov, Kaw, Pegoraro, Sasorov and Sen1998) also derived the scaling (A 3) for electron MHD (i.e. in the whistler frequency range).
$d_{e}\gg \unicode[STIX]{x1D70C}_{i}$ has been previously discovered by Wesson (Reference Wesson1990), while Bulanov, Pegoraro & Sakharov (Reference Bulanov, Pegoraro and Sakharov1992) and Avinash et al. (Reference Avinash, Bulanov, Esirkepov, Kaw, Pegoraro, Sasorov and Sen1998) also derived the scaling (A 3) for electron MHD (i.e. in the whistler frequency range).
Note that in the case  $d_{e}\ll \unicode[STIX]{x1D70C}_{i}$, the outflow velocity is
$d_{e}\ll \unicode[STIX]{x1D70C}_{i}$, the outflow velocity is
 $$\begin{eqnarray}u_{\text{out}}\sim \sqrt{\frac{\unicode[STIX]{x1D6FD}_{i}}{2}\left(1+\frac{Z}{\unicode[STIX]{x1D70F}}\right)}v_{\text{A}ey},\end{eqnarray}$$
$$\begin{eqnarray}u_{\text{out}}\sim \sqrt{\frac{\unicode[STIX]{x1D6FD}_{i}}{2}\left(1+\frac{Z}{\unicode[STIX]{x1D70F}}\right)}v_{\text{A}ey},\end{eqnarray}$$ of order the electron Alfvén velocity  $v_{\text{A}ey}$. In § 4, we show that this steady-state configuration is not realisable, because reconnection onset occurs at a somewhat larger thickness.
$v_{\text{A}ey}$. In § 4, we show that this steady-state configuration is not realisable, because reconnection onset occurs at a somewhat larger thickness.
Appendix B. Tearing mode in a sheet with thickness below the ion scales
Let us analyse the tearing mode of (2.1)–(2.3) – we will study the two-dimensional case,  $\unicode[STIX]{x2202}/\unicode[STIX]{x2202}z=0$, and use as our equilibrium
$\unicode[STIX]{x2202}/\unicode[STIX]{x2202}z=0$, and use as our equilibrium
 $$\begin{eqnarray}\unicode[STIX]{x1D719}_{0}=0,\quad g_{e0}=0,\quad A_{\Vert 0}=A_{\Vert 0}(x),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D719}_{0}=0,\quad g_{e0}=0,\quad A_{\Vert 0}=A_{\Vert 0}(x),\end{eqnarray}$$ where  $A_{\Vert 0}(x)$ is controlled by a dimensionless function
$A_{\Vert 0}(x)$ is controlled by a dimensionless function  $f(x)$, varying on the equilibrium scale length
$f(x)$, varying on the equilibrium scale length  $a$,
$a$,
 $$\begin{eqnarray}B_{y0}=-\frac{\text{d}A_{\Vert 0}}{\text{d}x}=b_{a}f(x).\end{eqnarray}$$
$$\begin{eqnarray}B_{y0}=-\frac{\text{d}A_{\Vert 0}}{\text{d}x}=b_{a}f(x).\end{eqnarray}$$Due to the symmetry of this equilibrium, our perturbations take the form
 $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\unicode[STIX]{x1D719}_{1}\\ A_{\Vert 1}\\ g_{e1}\end{array}\!\right\}=\left\{\begin{array}{@{}c@{}}\unicode[STIX]{x1D719}(x)\\ A_{\Vert }(x)\\ g_{e}(x)\end{array}\!\right\}\text{e}^{\text{i}k_{y}+\unicode[STIX]{x1D6FE}t}. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\unicode[STIX]{x1D719}_{1}\\ A_{\Vert 1}\\ g_{e1}\end{array}\!\right\}=\left\{\begin{array}{@{}c@{}}\unicode[STIX]{x1D719}(x)\\ A_{\Vert }(x)\\ g_{e}(x)\end{array}\!\right\}\text{e}^{\text{i}k_{y}+\unicode[STIX]{x1D6FE}t}. & & \displaystyle\end{eqnarray}$$We will discuss two different regimes,
 $$\begin{eqnarray}\displaystyle & \displaystyle \text{(i)}\quad a\gg \unicode[STIX]{x1D70C}_{s}\gg d_{e}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \text{(i)}\quad a\gg \unicode[STIX]{x1D70C}_{s}\gg d_{e}, & \displaystyle\end{eqnarray}$$ $$\begin{eqnarray}\displaystyle & \displaystyle \text{(ii)}\quad \unicode[STIX]{x1D70C}_{s}\gg a\gg d_{e}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \text{(ii)}\quad \unicode[STIX]{x1D70C}_{s}\gg a\gg d_{e}, & \displaystyle\end{eqnarray}$$where (i) has already been treated by ZS11 (and references therein), while (ii) represents the tearing of sub-ion-scale sheets we are interested in the present work.
The linearised equations may be writtenFootnote 8
 $$\begin{eqnarray}\displaystyle & \displaystyle \frac{2}{d_{e}^{2}}\frac{\unicode[STIX]{x1D6FF}}{af}\frac{Z}{\unicode[STIX]{x1D70F}}(1-\hat{\unicode[STIX]{x1D6E4}}_{0})\tilde{\unicode[STIX]{x1D719}}=\left[\unicode[STIX]{x2202}_{x}^{2}-k_{y}^{2}-\frac{f^{\prime \prime }}{f}\right]A_{\Vert }, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{2}{d_{e}^{2}}\frac{\unicode[STIX]{x1D6FF}}{af}\frac{Z}{\unicode[STIX]{x1D70F}}(1-\hat{\unicode[STIX]{x1D6E4}}_{0})\tilde{\unicode[STIX]{x1D719}}=\left[\unicode[STIX]{x2202}_{x}^{2}-k_{y}^{2}-\frac{f^{\prime \prime }}{f}\right]A_{\Vert }, & \displaystyle\end{eqnarray}$$ $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x1D6FF}}{af}(1-d_{e}^{2}\unicode[STIX]{x2202}_{x}^{2})A_{\Vert }=\left[1+G\frac{Z}{\unicode[STIX]{x1D70F}}(1-\hat{\unicode[STIX]{x1D6E4}}_{0})\right]\tilde{\unicode[STIX]{x1D719}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x1D6FF}}{af}(1-d_{e}^{2}\unicode[STIX]{x2202}_{x}^{2})A_{\Vert }=\left[1+G\frac{Z}{\unicode[STIX]{x1D70F}}(1-\hat{\unicode[STIX]{x1D6E4}}_{0})\right]\tilde{\unicode[STIX]{x1D719}}, & \displaystyle\end{eqnarray}$$where
 $$\begin{eqnarray}\unicode[STIX]{x1D6FF}=\frac{\unicode[STIX]{x1D6FE}aB_{0}}{k_{y}b_{a}v_{\text{th}e}},\quad \tilde{\unicode[STIX]{x1D719}}=-\frac{c}{v_{\text{th}e}}i\unicode[STIX]{x1D719},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FF}=\frac{\unicode[STIX]{x1D6FE}aB_{0}}{k_{y}b_{a}v_{\text{th}e}},\quad \tilde{\unicode[STIX]{x1D719}}=-\frac{c}{v_{\text{th}e}}i\unicode[STIX]{x1D719},\end{eqnarray}$$ and the function  $G$, which results from solving the linearised
$G$, which results from solving the linearised  $g_{e}$ equation (Zocco & Schekochihin Reference Zocco and Schekochihin2011), is
$g_{e}$ equation (Zocco & Schekochihin Reference Zocco and Schekochihin2011), is
 $$\begin{eqnarray}G\left(\frac{a|f|}{\unicode[STIX]{x1D6FF}}\right)=-2\left[\frac{\unicode[STIX]{x1D6FF}^{2}}{a^{2}f^{2}}+\frac{1}{Z^{\prime }(i\unicode[STIX]{x1D6FF}/a|f|)}\right],\end{eqnarray}$$
$$\begin{eqnarray}G\left(\frac{a|f|}{\unicode[STIX]{x1D6FF}}\right)=-2\left[\frac{\unicode[STIX]{x1D6FF}^{2}}{a^{2}f^{2}}+\frac{1}{Z^{\prime }(i\unicode[STIX]{x1D6FF}/a|f|)}\right],\end{eqnarray}$$ $Z$ here being the plasma dispersion function. This has limiting values
$Z$ here being the plasma dispersion function. This has limiting values  $G(0)=3$,
$G(0)=3$,  $G(\infty )=1$. We will make further progress by, as usual, solving separately in an ‘outer region’ where
$G(\infty )=1$. We will make further progress by, as usual, solving separately in an ‘outer region’ where  $x\sim a$ and an ‘inner region’ where
$x\sim a$ and an ‘inner region’ where  $x\ll a$.
$x\ll a$.
B.1 Outer region
Here,  $x\sim a$ and
$x\sim a$ and  $G\approx 1$, and
$G\approx 1$, and  $\unicode[STIX]{x2202}_{x}^{2}\sim f^{\prime \prime }/f\sim 1/a$. We may therefore neglect
$\unicode[STIX]{x2202}_{x}^{2}\sim f^{\prime \prime }/f\sim 1/a$. We may therefore neglect  $d_{e}^{2}\unicode[STIX]{x2202}_{x}^{2}\ll 1$ in (B 7). The structure of the equation depends on
$d_{e}^{2}\unicode[STIX]{x2202}_{x}^{2}\ll 1$ in (B 7). The structure of the equation depends on  $a/\unicode[STIX]{x1D70C}_{s}$. In case (i),
$a/\unicode[STIX]{x1D70C}_{s}$. In case (i),  $a\gg \unicode[STIX]{x1D70C}_{s}$, one can expand
$a\gg \unicode[STIX]{x1D70C}_{s}$, one can expand  $\hat{\unicode[STIX]{x1D6E4}}_{0}$ for small argument and show that the left-hand side of (B 6) is smaller than the right-hand side by
$\hat{\unicode[STIX]{x1D6E4}}_{0}$ for small argument and show that the left-hand side of (B 6) is smaller than the right-hand side by  $\unicode[STIX]{x1D6FE}/\unicode[STIX]{x1D714}_{Ay}$, where
$\unicode[STIX]{x1D6FE}/\unicode[STIX]{x1D714}_{Ay}$, where  $\unicode[STIX]{x1D714}_{Ay}=k_{y}b_{a}f/\sqrt{4\unicode[STIX]{x03C0}n_{0i}m_{i}}$ is the in-plane Alfvén frequency; assuming this is small (which may be checked afterwards), one just obtains the same outer region equation as in the MHD tearing mode,
$\unicode[STIX]{x1D714}_{Ay}=k_{y}b_{a}f/\sqrt{4\unicode[STIX]{x03C0}n_{0i}m_{i}}$ is the in-plane Alfvén frequency; assuming this is small (which may be checked afterwards), one just obtains the same outer region equation as in the MHD tearing mode,
 $$\begin{eqnarray}\left[\unicode[STIX]{x2202}_{x}^{2}-k_{y}^{2}-\frac{f^{\prime \prime }}{f}\right]A_{\Vert }=0.\end{eqnarray}$$
$$\begin{eqnarray}\left[\unicode[STIX]{x2202}_{x}^{2}-k_{y}^{2}-\frac{f^{\prime \prime }}{f}\right]A_{\Vert }=0.\end{eqnarray}$$ In case (ii), however, where  $a\ll \unicode[STIX]{x1D70C}_{s}$,
$a\ll \unicode[STIX]{x1D70C}_{s}$,  $\hat{\unicode[STIX]{x1D6E4}}_{0}\approx 0$ and (B 7) becomes
$\hat{\unicode[STIX]{x1D6E4}}_{0}\approx 0$ and (B 7) becomes
 $$\begin{eqnarray}\frac{\unicode[STIX]{x1D6FF}}{af}A_{\Vert }=\left[1+\frac{Z}{\unicode[STIX]{x1D70F}}\right]\tilde{\unicode[STIX]{x1D719}}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{\unicode[STIX]{x1D6FF}}{af}A_{\Vert }=\left[1+\frac{Z}{\unicode[STIX]{x1D70F}}\right]\tilde{\unicode[STIX]{x1D719}}.\end{eqnarray}$$ Substituting this into (B 6) (again taking  $\hat{\unicode[STIX]{x1D6E4}}_{0}\approx 0$),
$\hat{\unicode[STIX]{x1D6E4}}_{0}\approx 0$),
 $$\begin{eqnarray}\unicode[STIX]{x1D706}^{2}\frac{2}{f^{2}}\frac{1}{\frac{\unicode[STIX]{x1D70F}}{Z}+1}A_{\Vert }=a^{2}\left(\unicode[STIX]{x2202}_{x}^{2}-k_{y}^{2}-\frac{f^{\prime \prime }}{f}\right)A_{\Vert },\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D706}^{2}\frac{2}{f^{2}}\frac{1}{\frac{\unicode[STIX]{x1D70F}}{Z}+1}A_{\Vert }=a^{2}\left(\unicode[STIX]{x2202}_{x}^{2}-k_{y}^{2}-\frac{f^{\prime \prime }}{f}\right)A_{\Vert },\end{eqnarray}$$ where  $\unicode[STIX]{x1D706}^{2}=\unicode[STIX]{x1D6FF}^{2}/d_{e}^{2}$. The left-hand side may only be neglected in the outer region (where
$\unicode[STIX]{x1D706}^{2}=\unicode[STIX]{x1D6FF}^{2}/d_{e}^{2}$. The left-hand side may only be neglected in the outer region (where  $f\sim 1$) if
$f\sim 1$) if  $\unicode[STIX]{x1D706}^{2}\ll 1$. In this case, one can see that, because
$\unicode[STIX]{x1D706}^{2}\ll 1$. In this case, one can see that, because  $\unicode[STIX]{x1D6FF}B_{y}=-\unicode[STIX]{x2202}_{x}A_{\Vert }$ must change sign at
$\unicode[STIX]{x1D6FF}B_{y}=-\unicode[STIX]{x2202}_{x}A_{\Vert }$ must change sign at  $x=0$,
$x=0$,
 $$\begin{eqnarray}A_{\Vert }^{\text{outer}}=A_{\Vert }(0)\left(1+\frac{1}{2}\unicode[STIX]{x1D6E5}^{\prime }|x|\right)\quad \text{for }x\ll a.\end{eqnarray}$$
$$\begin{eqnarray}A_{\Vert }^{\text{outer}}=A_{\Vert }(0)\left(1+\frac{1}{2}\unicode[STIX]{x1D6E5}^{\prime }|x|\right)\quad \text{for }x\ll a.\end{eqnarray}$$ We will determine when this is valid later. For  $k_{y}a\ll 1$,
$k_{y}a\ll 1$,  $\unicode[STIX]{x1D6E5}^{\prime }a\propto (k_{y}a)^{-n}$ with
$\unicode[STIX]{x1D6E5}^{\prime }a\propto (k_{y}a)^{-n}$ with  $1\leqslant n\leqslant 2$Footnote 9.
$1\leqslant n\leqslant 2$Footnote 9.
B.2 Inner region
Here,  $x\ll a$,
$x\ll a$,  $\unicode[STIX]{x2202}_{x}^{2}\gg k_{y}^{2},f^{\prime \prime }/f$ and
$\unicode[STIX]{x2202}_{x}^{2}\gg k_{y}^{2},f^{\prime \prime }/f$ and  $f\approx x/a$. Our analysis will at first follow ZS11 exactly. The equations become
$f\approx x/a$. Our analysis will at first follow ZS11 exactly. The equations become
 $$\begin{eqnarray}\displaystyle & \displaystyle \frac{2}{d_{e}^{2}}\frac{\unicode[STIX]{x1D6FF}}{x}\frac{Z}{\unicode[STIX]{x1D70F}}(1-\hat{\unicode[STIX]{x1D6E4}}_{0})\tilde{\unicode[STIX]{x1D719}}=\unicode[STIX]{x2202}_{x}^{2}A_{\Vert }, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{2}{d_{e}^{2}}\frac{\unicode[STIX]{x1D6FF}}{x}\frac{Z}{\unicode[STIX]{x1D70F}}(1-\hat{\unicode[STIX]{x1D6E4}}_{0})\tilde{\unicode[STIX]{x1D719}}=\unicode[STIX]{x2202}_{x}^{2}A_{\Vert }, & \displaystyle\end{eqnarray}$$ $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x1D6FF}}{x}(1-d_{e}^{2}\unicode[STIX]{x2202}_{x}^{2})A_{\Vert }=\left[1+G\frac{Z}{\unicode[STIX]{x1D70F}}(1-\hat{\unicode[STIX]{x1D6E4}}_{0})\right]\tilde{\unicode[STIX]{x1D719}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x1D6FF}}{x}(1-d_{e}^{2}\unicode[STIX]{x2202}_{x}^{2})A_{\Vert }=\left[1+G\frac{Z}{\unicode[STIX]{x1D70F}}(1-\hat{\unicode[STIX]{x1D6E4}}_{0})\right]\tilde{\unicode[STIX]{x1D719}}, & \displaystyle\end{eqnarray}$$ where  $\hat{\unicode[STIX]{x1D6E4}}_{0}=\hat{\unicode[STIX]{x1D6E4}}_{0}(\unicode[STIX]{x2202}_{x}^{2})$. Let us rescale the coordinate to
$\hat{\unicode[STIX]{x1D6E4}}_{0}=\hat{\unicode[STIX]{x1D6E4}}_{0}(\unicode[STIX]{x2202}_{x}^{2})$. Let us rescale the coordinate to  $\unicode[STIX]{x1D709}=x/\unicode[STIX]{x1D6FF}_{\text{in}}$, where
$\unicode[STIX]{x1D709}=x/\unicode[STIX]{x1D6FF}_{\text{in}}$, where  $\unicode[STIX]{x1D6FF}_{\text{in}}$ will be chosen later. Replacing the term involving
$\unicode[STIX]{x1D6FF}_{\text{in}}$ will be chosen later. Replacing the term involving  $\hat{\unicode[STIX]{x1D6E4}}_{0}$ in (B 15),
$\hat{\unicode[STIX]{x1D6E4}}_{0}$ in (B 15),
 $$\begin{eqnarray}\displaystyle & \displaystyle \frac{2\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D6FF}_{\text{in}}}{d_{e}^{2}}\frac{Z}{\unicode[STIX]{x1D70F}}(1-\hat{\unicode[STIX]{x1D6E4}}_{0})\tilde{\unicode[STIX]{x1D719}}=\unicode[STIX]{x1D709}A_{\Vert }^{\prime \prime }, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{2\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D6FF}_{\text{in}}}{d_{e}^{2}}\frac{Z}{\unicode[STIX]{x1D70F}}(1-\hat{\unicode[STIX]{x1D6E4}}_{0})\tilde{\unicode[STIX]{x1D719}}=\unicode[STIX]{x1D709}A_{\Vert }^{\prime \prime }, & \displaystyle\end{eqnarray}$$ $$\begin{eqnarray}\displaystyle & \displaystyle \frac{A_{\Vert }}{\unicode[STIX]{x1D709}}-\frac{\unicode[STIX]{x1D6FF}_{\text{in}}}{\unicode[STIX]{x1D6FF}}\tilde{\unicode[STIX]{x1D719}}=\frac{d_{e}^{2}}{\unicode[STIX]{x1D6FF}_{\text{in}}^{2}}\left(1+\frac{\unicode[STIX]{x1D6FF}_{\text{in}}^{2}}{2\unicode[STIX]{x1D6FF}^{2}}G\unicode[STIX]{x1D709}^{2}\right)\frac{A_{\Vert }^{\prime \prime }}{\unicode[STIX]{x1D709}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{A_{\Vert }}{\unicode[STIX]{x1D709}}-\frac{\unicode[STIX]{x1D6FF}_{\text{in}}}{\unicode[STIX]{x1D6FF}}\tilde{\unicode[STIX]{x1D719}}=\frac{d_{e}^{2}}{\unicode[STIX]{x1D6FF}_{\text{in}}^{2}}\left(1+\frac{\unicode[STIX]{x1D6FF}_{\text{in}}^{2}}{2\unicode[STIX]{x1D6FF}^{2}}G\unicode[STIX]{x1D709}^{2}\right)\frac{A_{\Vert }^{\prime \prime }}{\unicode[STIX]{x1D709}}, & \displaystyle\end{eqnarray}$$ where primes denote derivative with respect to  $\unicode[STIX]{x1D709}$. If one wants to include the case where
$\unicode[STIX]{x1D709}$. If one wants to include the case where  $\unicode[STIX]{x1D6FF}_{\text{in}}\sim \unicode[STIX]{x1D70C}_{s}$, the operator
$\unicode[STIX]{x1D6FF}_{\text{in}}\sim \unicode[STIX]{x1D70C}_{s}$, the operator  $\hat{\unicode[STIX]{x1D6E4}}_{0}$ is difficult to deal with analytically: we will follow ZS11 and use the Padé approximant
$\hat{\unicode[STIX]{x1D6E4}}_{0}$ is difficult to deal with analytically: we will follow ZS11 and use the Padé approximant
 $$\begin{eqnarray}\frac{Z}{\unicode[STIX]{x1D70F}}\left(1-\hat{\unicode[STIX]{x1D6E4}}_{0}\right)\approx -\frac{\unicode[STIX]{x1D70C}_{s}^{2}\unicode[STIX]{x2202}_{x}^{2}}{1-(1/2)\unicode[STIX]{x1D70C}_{i}^{2}\unicode[STIX]{x2202}_{x}^{2}}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{Z}{\unicode[STIX]{x1D70F}}\left(1-\hat{\unicode[STIX]{x1D6E4}}_{0}\right)\approx -\frac{\unicode[STIX]{x1D70C}_{s}^{2}\unicode[STIX]{x2202}_{x}^{2}}{1-(1/2)\unicode[STIX]{x1D70C}_{i}^{2}\unicode[STIX]{x2202}_{x}^{2}}.\end{eqnarray}$$ Let us make the helpful substitution  $\unicode[STIX]{x1D712}=\unicode[STIX]{x1D709}A_{\Vert }^{\prime }-A_{\Vert }=\unicode[STIX]{x1D709}^{2}(A_{\Vert }/\unicode[STIX]{x1D709})^{\prime }$, so that
$\unicode[STIX]{x1D712}=\unicode[STIX]{x1D709}A_{\Vert }^{\prime }-A_{\Vert }=\unicode[STIX]{x1D709}^{2}(A_{\Vert }/\unicode[STIX]{x1D709})^{\prime }$, so that  $\unicode[STIX]{x1D712}^{\prime }=\unicode[STIX]{x1D709}A_{\Vert }^{\prime \prime }$. Differentiating (B 17), using the approximant (B 18) in (B 16) and integrating once, the equations in terms of
$\unicode[STIX]{x1D712}^{\prime }=\unicode[STIX]{x1D709}A_{\Vert }^{\prime \prime }$. Differentiating (B 17), using the approximant (B 18) in (B 16) and integrating once, the equations in terms of  $\unicode[STIX]{x1D712}$ are
$\unicode[STIX]{x1D712}$ are
 $$\begin{eqnarray}\displaystyle & \displaystyle -\frac{2\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D70C}_{s}^{2}}{d_{e}^{2}\unicode[STIX]{x1D6FF}_{\text{in}}}\tilde{\unicode[STIX]{x1D719}}^{\prime }=\unicode[STIX]{x1D712}-\unicode[STIX]{x1D712}_{0}-\frac{\unicode[STIX]{x1D70C}_{i}^{2}}{2\unicode[STIX]{x1D6FF}_{\text{in}}^{2}}\unicode[STIX]{x1D712}^{\prime \prime }, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle -\frac{2\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D70C}_{s}^{2}}{d_{e}^{2}\unicode[STIX]{x1D6FF}_{\text{in}}}\tilde{\unicode[STIX]{x1D719}}^{\prime }=\unicode[STIX]{x1D712}-\unicode[STIX]{x1D712}_{0}-\frac{\unicode[STIX]{x1D70C}_{i}^{2}}{2\unicode[STIX]{x1D6FF}_{\text{in}}^{2}}\unicode[STIX]{x1D712}^{\prime \prime }, & \displaystyle\end{eqnarray}$$ $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}}{\text{d}\unicode[STIX]{x1D709}}\left(\frac{1}{\unicode[STIX]{x1D709}^{2}}+\frac{\unicode[STIX]{x1D6FF}_{\text{in}}^{2}}{2\unicode[STIX]{x1D6FF}^{2}}G\right)\unicode[STIX]{x1D712}^{\prime }=\frac{\unicode[STIX]{x1D6FF}_{\text{in}}^{2}}{d_{e}^{2}}\frac{\unicode[STIX]{x1D712}}{\unicode[STIX]{x1D709}^{2}}-\frac{\unicode[STIX]{x1D6FF}_{\text{in}}^{3}}{d_{e}^{2}\unicode[STIX]{x1D6FF}}\tilde{\unicode[STIX]{x1D719}}^{\prime }. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}}{\text{d}\unicode[STIX]{x1D709}}\left(\frac{1}{\unicode[STIX]{x1D709}^{2}}+\frac{\unicode[STIX]{x1D6FF}_{\text{in}}^{2}}{2\unicode[STIX]{x1D6FF}^{2}}G\right)\unicode[STIX]{x1D712}^{\prime }=\frac{\unicode[STIX]{x1D6FF}_{\text{in}}^{2}}{d_{e}^{2}}\frac{\unicode[STIX]{x1D712}}{\unicode[STIX]{x1D709}^{2}}-\frac{\unicode[STIX]{x1D6FF}_{\text{in}}^{3}}{d_{e}^{2}\unicode[STIX]{x1D6FF}}\tilde{\unicode[STIX]{x1D719}}^{\prime }. & \displaystyle\end{eqnarray}$$Combining these two equations, we get
 $$\begin{eqnarray}\unicode[STIX]{x1D709}^{2}\frac{\text{d}}{\text{d}\unicode[STIX]{x1D709}}\left[\frac{1}{\unicode[STIX]{x1D709}^{2}}+\frac{\unicode[STIX]{x1D6FF}_{\text{in}}^{2}}{2\unicode[STIX]{x1D6FF}^{2}}\left(G+\frac{\unicode[STIX]{x1D70F}}{Z}\right)\right]\unicode[STIX]{x1D712}^{\prime }=\frac{\unicode[STIX]{x1D6FF}_{\text{in}}^{2}}{\unicode[STIX]{x1D6FF}^{2}}\left[\unicode[STIX]{x1D706}^{2}\unicode[STIX]{x1D712}+\frac{1}{2}\unicode[STIX]{x1D709}^{2}\frac{\unicode[STIX]{x1D6FF}_{\text{in}}^{2}}{\unicode[STIX]{x1D70C}_{s}^{2}}\left(\unicode[STIX]{x1D712}-\unicode[STIX]{x1D712}_{0}\right)\right].\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D709}^{2}\frac{\text{d}}{\text{d}\unicode[STIX]{x1D709}}\left[\frac{1}{\unicode[STIX]{x1D709}^{2}}+\frac{\unicode[STIX]{x1D6FF}_{\text{in}}^{2}}{2\unicode[STIX]{x1D6FF}^{2}}\left(G+\frac{\unicode[STIX]{x1D70F}}{Z}\right)\right]\unicode[STIX]{x1D712}^{\prime }=\frac{\unicode[STIX]{x1D6FF}_{\text{in}}^{2}}{\unicode[STIX]{x1D6FF}^{2}}\left[\unicode[STIX]{x1D706}^{2}\unicode[STIX]{x1D712}+\frac{1}{2}\unicode[STIX]{x1D709}^{2}\frac{\unicode[STIX]{x1D6FF}_{\text{in}}^{2}}{\unicode[STIX]{x1D70C}_{s}^{2}}\left(\unicode[STIX]{x1D712}-\unicode[STIX]{x1D712}_{0}\right)\right].\end{eqnarray}$$ Noting that  $\unicode[STIX]{x1D709}\sim 1$ in the inner region, we can compare the size of the two terms on the right-hand side.
$\unicode[STIX]{x1D709}\sim 1$ in the inner region, we can compare the size of the two terms on the right-hand side.
In case (i),  $a\gg \unicode[STIX]{x1D70C}_{s}$, we must allow a finite
$a\gg \unicode[STIX]{x1D70C}_{s}$, we must allow a finite  $\unicode[STIX]{x1D6FF}_{\text{in}}/\unicode[STIX]{x1D70C}_{s}$ and must keep both of them. It therefore makes sense to define
$\unicode[STIX]{x1D6FF}_{\text{in}}/\unicode[STIX]{x1D70C}_{s}$ and must keep both of them. It therefore makes sense to define  $\unicode[STIX]{x1D6FF}_{\text{in}}=(\sqrt{2}\unicode[STIX]{x1D70C}_{s}\unicode[STIX]{x1D6FF})^{1/2}$,
$\unicode[STIX]{x1D6FF}_{\text{in}}=(\sqrt{2}\unicode[STIX]{x1D70C}_{s}\unicode[STIX]{x1D6FF})^{1/2}$,  $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FF}_{\text{in}}/\sqrt{2}\unicode[STIX]{x1D6FF}$,
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FF}_{\text{in}}/\sqrt{2}\unicode[STIX]{x1D6FF}$,  $\tilde{\unicode[STIX]{x1D706}}^{2}=\unicode[STIX]{x1D706}^{2}\unicode[STIX]{x1D6FC}^{2}$ and we obtain the same equations as in ZS11,
$\tilde{\unicode[STIX]{x1D706}}^{2}=\unicode[STIX]{x1D706}^{2}\unicode[STIX]{x1D6FC}^{2}$ and we obtain the same equations as in ZS11,
 $$\begin{eqnarray}\unicode[STIX]{x1D709}^{2}\frac{\text{d}}{\text{d}\unicode[STIX]{x1D709}}\left[\frac{1}{\unicode[STIX]{x1D709}^{2}}+\frac{\unicode[STIX]{x1D6FC}^{2}}{2}\left(G+\frac{\unicode[STIX]{x1D70F}}{Z}\right)\right]\unicode[STIX]{x1D712}^{\prime }=\tilde{\unicode[STIX]{x1D706}}^{2}\unicode[STIX]{x1D712}+\unicode[STIX]{x1D709}^{2}(\unicode[STIX]{x1D712}-\unicode[STIX]{x1D712}_{0}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D709}^{2}\frac{\text{d}}{\text{d}\unicode[STIX]{x1D709}}\left[\frac{1}{\unicode[STIX]{x1D709}^{2}}+\frac{\unicode[STIX]{x1D6FC}^{2}}{2}\left(G+\frac{\unicode[STIX]{x1D70F}}{Z}\right)\right]\unicode[STIX]{x1D712}^{\prime }=\tilde{\unicode[STIX]{x1D706}}^{2}\unicode[STIX]{x1D712}+\unicode[STIX]{x1D709}^{2}(\unicode[STIX]{x1D712}-\unicode[STIX]{x1D712}_{0}).\end{eqnarray}$$It is then possible to solve this analytically in terms of a nested ‘ion inner region’ and ‘electron inner region’, matched to each other and to the outer solution, via the matching condition
 $$\begin{eqnarray}\frac{1}{\unicode[STIX]{x1D712}_{0}}\int _{0}^{\infty }\frac{\unicode[STIX]{x1D712}^{\prime }}{\unicode[STIX]{x1D709}}\text{d}\unicode[STIX]{x1D709}=-\frac{1}{2}\unicode[STIX]{x1D6E5}^{\prime }\unicode[STIX]{x1D6FF}_{\text{in}}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{1}{\unicode[STIX]{x1D712}_{0}}\int _{0}^{\infty }\frac{\unicode[STIX]{x1D712}^{\prime }}{\unicode[STIX]{x1D709}}\text{d}\unicode[STIX]{x1D709}=-\frac{1}{2}\unicode[STIX]{x1D6E5}^{\prime }\unicode[STIX]{x1D6FF}_{\text{in}}.\end{eqnarray}$$ One can also (again, following ZS11) guess the scalings of the solution on dimensional grounds. The width of  $\unicode[STIX]{x1D712}^{\prime }/\unicode[STIX]{x1D709}$ in the integral above is
$\unicode[STIX]{x1D712}^{\prime }/\unicode[STIX]{x1D709}$ in the integral above is  $x\sim \unicode[STIX]{x1D6FF}$, or
$x\sim \unicode[STIX]{x1D6FF}$, or  $\unicode[STIX]{x1D709}\sim 1/\unicode[STIX]{x1D6FC}$. From (B 22),
$\unicode[STIX]{x1D709}\sim 1/\unicode[STIX]{x1D6FC}$. From (B 22),  $\unicode[STIX]{x1D712}^{\prime }/\unicode[STIX]{x1D709}\sim \tilde{\unicode[STIX]{x1D706}}^{2}\unicode[STIX]{x1D712}$, whence
$\unicode[STIX]{x1D712}^{\prime }/\unicode[STIX]{x1D709}\sim \tilde{\unicode[STIX]{x1D706}}^{2}\unicode[STIX]{x1D712}$, whence  $\tilde{\unicode[STIX]{x1D706}}^{2}\sim \unicode[STIX]{x1D6E5}^{\prime }\unicode[STIX]{x1D6FF}_{\text{in}}\unicode[STIX]{x1D6FC}$. For
$\tilde{\unicode[STIX]{x1D706}}^{2}\sim \unicode[STIX]{x1D6E5}^{\prime }\unicode[STIX]{x1D6FF}_{\text{in}}\unicode[STIX]{x1D6FC}$. For  $\unicode[STIX]{x1D6E5}^{\prime }\unicode[STIX]{x1D6FF}_{\text{in}}\gg 1$, the current cannot depend on
$\unicode[STIX]{x1D6E5}^{\prime }\unicode[STIX]{x1D6FF}_{\text{in}}\gg 1$, the current cannot depend on  $\unicode[STIX]{x1D6E5}^{\prime }$, and we cannot use (B 23); instead
$\unicode[STIX]{x1D6E5}^{\prime }$, and we cannot use (B 23); instead  $\unicode[STIX]{x1D712}^{\prime }/\unicode[STIX]{x1D709}\sim \unicode[STIX]{x1D712}$ (the current is limited by
$\unicode[STIX]{x1D712}^{\prime }/\unicode[STIX]{x1D709}\sim \unicode[STIX]{x1D712}$ (the current is limited by  $\unicode[STIX]{x1D6FF}_{\text{in}}$,
$\unicode[STIX]{x1D6FF}_{\text{in}}$,  $A_{\Vert }^{\prime \prime }\sim A_{\Vert }/\unicode[STIX]{x1D6FF}_{\text{in}}^{2}$), and so
$A_{\Vert }^{\prime \prime }\sim A_{\Vert }/\unicode[STIX]{x1D6FF}_{\text{in}}^{2}$), and so  $\tilde{\unicode[STIX]{x1D706}}^{2}\sim \unicode[STIX]{x1D6FC}$. The resulting growth rates
$\tilde{\unicode[STIX]{x1D706}}^{2}\sim \unicode[STIX]{x1D6FC}$. The resulting growth rates  $\unicode[STIX]{x1D6FE}$, inner widths
$\unicode[STIX]{x1D6FE}$, inner widths  $\unicode[STIX]{x1D6FF}_{\text{in}}$, and electron region widths
$\unicode[STIX]{x1D6FF}_{\text{in}}$, and electron region widths  $\unicode[STIX]{x1D6FF}$ are shown in table 1. The maximum growth rate, obtained by inserting
$\unicode[STIX]{x1D6FF}$ are shown in table 1. The maximum growth rate, obtained by inserting  $\unicode[STIX]{x1D6E5}^{\prime }\unicode[STIX]{x1D6FF}_{\text{in}}\sim 1$ into the small-
$\unicode[STIX]{x1D6E5}^{\prime }\unicode[STIX]{x1D6FF}_{\text{in}}\sim 1$ into the small- $\unicode[STIX]{x1D6E5}^{\prime }$ expression (or alternatively by balancing the small- and large-
$\unicode[STIX]{x1D6E5}^{\prime }$ expression (or alternatively by balancing the small- and large- $\unicode[STIX]{x1D6E5}^{\prime }$ growth rates), is also shown.
$\unicode[STIX]{x1D6E5}^{\prime }$ growth rates), is also shown.
One might also be interested in the dependence of the growth rates on  $\unicode[STIX]{x1D70F}/Z$. It is possible to solve this equation analytically (see ZS11), showing that in fact, the growth rates are proportional to
$\unicode[STIX]{x1D70F}/Z$. It is possible to solve this equation analytically (see ZS11), showing that in fact, the growth rates are proportional to
 $$\begin{eqnarray}H(\unicode[STIX]{x1D70F}/Z)=\sqrt{1+\unicode[STIX]{x1D70F}/Z}.\end{eqnarray}$$
$$\begin{eqnarray}H(\unicode[STIX]{x1D70F}/Z)=\sqrt{1+\unicode[STIX]{x1D70F}/Z}.\end{eqnarray}$$This factor is also shown in table 1.
In case (ii),  $a\ll \unicode[STIX]{x1D70C}_{s}$, there is no space for the ion inner region to form, and we must instead match the solution in the electron inner region directly onto the outer solution. Going back to (B 21), if
$a\ll \unicode[STIX]{x1D70C}_{s}$, there is no space for the ion inner region to form, and we must instead match the solution in the electron inner region directly onto the outer solution. Going back to (B 21), if  $\unicode[STIX]{x1D6FF}_{\text{in}}\ll \unicode[STIX]{x1D70C}_{s}$ (as it must be since
$\unicode[STIX]{x1D6FF}_{\text{in}}\ll \unicode[STIX]{x1D70C}_{s}$ (as it must be since  $\unicode[STIX]{x1D70C}_{s}\gg a\gg \unicode[STIX]{x1D6FF}_{\text{in}}$), we can neglect the second term on the right-hand side, and set
$\unicode[STIX]{x1D70C}_{s}\gg a\gg \unicode[STIX]{x1D6FF}_{\text{in}}$), we can neglect the second term on the right-hand side, and set  $\unicode[STIX]{x1D6FF}_{\text{in}}=\unicode[STIX]{x1D6FF}$, obtaining
$\unicode[STIX]{x1D6FF}_{\text{in}}=\unicode[STIX]{x1D6FF}$, obtaining
 $$\begin{eqnarray}\unicode[STIX]{x1D709}^{2}\frac{\text{d}}{\text{d}\unicode[STIX]{x1D709}}\left[\frac{1}{\unicode[STIX]{x1D709}^{2}}+\frac{1}{2}\left(G+\frac{\unicode[STIX]{x1D70F}}{Z}\right)\right]\unicode[STIX]{x1D712}^{\prime }=\unicode[STIX]{x1D706}^{2}\unicode[STIX]{x1D712}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D709}^{2}\frac{\text{d}}{\text{d}\unicode[STIX]{x1D709}}\left[\frac{1}{\unicode[STIX]{x1D709}^{2}}+\frac{1}{2}\left(G+\frac{\unicode[STIX]{x1D70F}}{Z}\right)\right]\unicode[STIX]{x1D712}^{\prime }=\unicode[STIX]{x1D706}^{2}\unicode[STIX]{x1D712}.\end{eqnarray}$$ We can again guess the scalings on dimensional grounds, similarly to case (i). For  $\unicode[STIX]{x1D6E5}^{\prime }\unicode[STIX]{x1D6FF}\ll 1$,
$\unicode[STIX]{x1D6E5}^{\prime }\unicode[STIX]{x1D6FF}\ll 1$,  $\unicode[STIX]{x1D706}^{2}\sim \unicode[STIX]{x1D6E5}^{\prime }\unicode[STIX]{x1D6FF}$. Therefore, we may solve (B 25) perturbatively in powers of
$\unicode[STIX]{x1D706}^{2}\sim \unicode[STIX]{x1D6E5}^{\prime }\unicode[STIX]{x1D6FF}$. Therefore, we may solve (B 25) perturbatively in powers of  $\unicode[STIX]{x1D706}^{2}\ll 1$, to first order, i.e.
$\unicode[STIX]{x1D706}^{2}\ll 1$, to first order, i.e.  $\unicode[STIX]{x1D712}=\unicode[STIX]{x1D712}_{0}+\unicode[STIX]{x1D712}_{1}$, with the boundary condition that the current
$\unicode[STIX]{x1D712}=\unicode[STIX]{x1D712}_{0}+\unicode[STIX]{x1D712}_{1}$, with the boundary condition that the current  $\unicode[STIX]{x1D712}^{\prime }/\unicode[STIX]{x1D709}$ is even as
$\unicode[STIX]{x1D712}^{\prime }/\unicode[STIX]{x1D709}$ is even as  $\unicode[STIX]{x1D709}\rightarrow 0$. Setting the right-hand side to zero, the zeroth-order solution
$\unicode[STIX]{x1D709}\rightarrow 0$. Setting the right-hand side to zero, the zeroth-order solution  $\unicode[STIX]{x1D712}_{0}$ is just a constant. This means our solution is equivalent to taking a ‘constant-
$\unicode[STIX]{x1D712}_{0}$ is just a constant. This means our solution is equivalent to taking a ‘constant- $\unicode[STIX]{x1D713}$’ approximation (Furth, Killeen & Rosenbluth Reference Furth, Killeen and Rosenbluth1963). At the next order, using
$\unicode[STIX]{x1D713}$’ approximation (Furth, Killeen & Rosenbluth Reference Furth, Killeen and Rosenbluth1963). At the next order, using  $\unicode[STIX]{x1D712}_{0}$ on the right-hand side and the boundary condition, we obtain
$\unicode[STIX]{x1D712}_{0}$ on the right-hand side and the boundary condition, we obtain
 $$\begin{eqnarray}\frac{\unicode[STIX]{x1D712}_{1}^{\prime }}{\unicode[STIX]{x1D709}}=-\frac{\unicode[STIX]{x1D706}^{2}\unicode[STIX]{x1D712}_{0}}{1+\unicode[STIX]{x1D709}^{2}/2(G+\unicode[STIX]{x1D70F}/Z)},\end{eqnarray}$$
$$\begin{eqnarray}\frac{\unicode[STIX]{x1D712}_{1}^{\prime }}{\unicode[STIX]{x1D709}}=-\frac{\unicode[STIX]{x1D706}^{2}\unicode[STIX]{x1D712}_{0}}{1+\unicode[STIX]{x1D709}^{2}/2(G+\unicode[STIX]{x1D70F}/Z)},\end{eqnarray}$$and matching this to the outer solution using (B 23),
 $$\begin{eqnarray}\unicode[STIX]{x1D706}^{2}=\frac{\unicode[STIX]{x1D6E5}^{\prime }\unicode[STIX]{x1D6FF}}{2I},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D706}^{2}=\frac{\unicode[STIX]{x1D6E5}^{\prime }\unicode[STIX]{x1D6FF}}{2I},\end{eqnarray}$$where
 $$\begin{eqnarray}I=\int _{0}^{\infty }\frac{\text{d}\unicode[STIX]{x1D709}}{1+\unicode[STIX]{x1D709}^{2}/2(G+\unicode[STIX]{x1D70F}/Z)}.\end{eqnarray}$$
$$\begin{eqnarray}I=\int _{0}^{\infty }\frac{\text{d}\unicode[STIX]{x1D709}}{1+\unicode[STIX]{x1D709}^{2}/2(G+\unicode[STIX]{x1D70F}/Z)}.\end{eqnarray}$$ This is precisely the same growth rate, including the prefactor, as for the small- $\unicode[STIX]{x1D6E5}^{\prime }$ case with
$\unicode[STIX]{x1D6E5}^{\prime }$ case with  $a\gg \unicode[STIX]{x1D70C}_{s}$ (cf. Zocco & Schekochihin (Reference Zocco and Schekochihin2011), equation B71). For
$a\gg \unicode[STIX]{x1D70C}_{s}$ (cf. Zocco & Schekochihin (Reference Zocco and Schekochihin2011), equation B71). For  $\unicode[STIX]{x1D70F}/Z\gg 1$, we can neglect
$\unicode[STIX]{x1D70F}/Z\gg 1$, we can neglect  $G$ and
$G$ and  $I\sim \sqrt{Z/\unicode[STIX]{x1D70F}}$, while for
$I\sim \sqrt{Z/\unicode[STIX]{x1D70F}}$, while for  $\unicode[STIX]{x1D70F}/Z\ll 1$,
$\unicode[STIX]{x1D70F}/Z\ll 1$,  $I\sim 1$. We include this effect in table 1 by amending the scalings by the factor
$I\sim 1$. We include this effect in table 1 by amending the scalings by the factor  $H(\unicode[STIX]{x1D70F}/Z)$ defined in (B 24).
$H(\unicode[STIX]{x1D70F}/Z)$ defined in (B 24).
For  $\unicode[STIX]{x1D6E5}^{\prime }\unicode[STIX]{x1D6FF}\gg 1$, on dimensional grounds,
$\unicode[STIX]{x1D6E5}^{\prime }\unicode[STIX]{x1D6FF}\gg 1$, on dimensional grounds,  $\unicode[STIX]{x1D706}^{2}\sim 1$: unfortunately, this invalidates the neglect of the left-hand side in (B 12), meaning that our matching condition (B 23) is no longer valid. We have not yet obtained an analytic solution to the equations in this case. However, since on physical grounds the growth rate must decrease as
$\unicode[STIX]{x1D706}^{2}\sim 1$: unfortunately, this invalidates the neglect of the left-hand side in (B 12), meaning that our matching condition (B 23) is no longer valid. We have not yet obtained an analytic solution to the equations in this case. However, since on physical grounds the growth rate must decrease as  $k_{y}\rightarrow 0$, it is reasonable to assume that the maximum growth rate of the tearing mode may be estimated by setting
$k_{y}\rightarrow 0$, it is reasonable to assume that the maximum growth rate of the tearing mode may be estimated by setting  $\unicode[STIX]{x1D6E5}^{\prime }\unicode[STIX]{x1D6FF}\sim 1$ in the scalings obtained for the
$\unicode[STIX]{x1D6E5}^{\prime }\unicode[STIX]{x1D6FF}\sim 1$ in the scalings obtained for the  $\unicode[STIX]{x1D6E5}^{\prime }\unicode[STIX]{x1D6FF}\ll 1$ limit. The scalings derived here for the tearing mode with
$\unicode[STIX]{x1D6E5}^{\prime }\unicode[STIX]{x1D6FF}\ll 1$ limit. The scalings derived here for the tearing mode with  $a\ll \unicode[STIX]{x1D70C}_{s}$ are also shown in table 1.
$a\ll \unicode[STIX]{x1D70C}_{s}$ are also shown in table 1.
Boldyrev & Loureiro (Reference Boldyrev and Loureiro2019) have derived a somewhat similar tearing mode for the ‘inertial kinetic-Alfvén’ regime (Chen & Boldyrev Reference Chen and Boldyrev2017). The difference between their equations and the KREHM equations (Zocco & Schekochihin Reference Zocco and Schekochihin2011) is that theirs are fluid (i.e. they do not contain heating), and, secondly, they order  $\unicode[STIX]{x1D6FD}_{i}\sim 1$, which introduces an additional term in our (B 16) (their equation 18) proportional to
$\unicode[STIX]{x1D6FD}_{i}\sim 1$, which introduces an additional term in our (B 16) (their equation 18) proportional to  $\unicode[STIX]{x1D6FD}_{i}\unicode[STIX]{x1D719}^{\prime \prime }$ (
$\unicode[STIX]{x1D6FD}_{i}\unicode[STIX]{x1D719}^{\prime \prime }$ ( $b_{z}^{\prime \prime }$ in their variables). This means they can neglect the term on the right-hand side in our equation, because in the inner region the gradients are large, and then makes their equations structurally identical to the MHD tearing equations. They therefore obtain different maximum growth rates
$b_{z}^{\prime \prime }$ in their variables). This means they can neglect the term on the right-hand side in our equation, because in the inner region the gradients are large, and then makes their equations structurally identical to the MHD tearing equations. They therefore obtain different maximum growth rates  $\unicode[STIX]{x1D6FE}_{\text{max}}\sim (d_{e}/a)^{1+1/n}v_{\text{A}ey}/a$ that are a multiplied by a factor
$\unicode[STIX]{x1D6FE}_{\text{max}}\sim (d_{e}/a)^{1+1/n}v_{\text{A}ey}/a$ that are a multiplied by a factor  $\unicode[STIX]{x1D6FD}_{i}^{1/2}$ compared to ours.
$\unicode[STIX]{x1D6FD}_{i}^{1/2}$ compared to ours.