1. Introduction
Persistence of spectral projections under perturbations, for linear operators on large tensor products, is crucial in many domains. Perhaps the most significant one is many-particle quantum systems, but a parallel problem occurs for stochastic systems with many components, like interacting particle systems and probabilistic cellular automata (PCA). In particular, we would like to know whether the subspace corresponding to an isolated part of the spectrum is robust to small perturbations, meaning that it has a smooth continuation as the subspace corresponding to the part of the spectrum near the original. We call this ‘persistence of spectral projections’.
As a toy example, consider a PCA with three states
![]() $\{+,0,-\}$
per site of a graph with N nodes and bounded degree. For parameter
$\{+,0,-\}$
per site of a graph with N nodes and bounded degree. For parameter
![]() $\varepsilon=0$
, suppose the state on each site evolves independently of the others, with
$\varepsilon=0$
, suppose the state on each site evolves independently of the others, with
![]() $\{+,-\}$
being absorbing and 0 going to
$\{+,-\}$
being absorbing and 0 going to
![]() $\{+,-\}$
with probabilities
$\{+,-\}$
with probabilities
![]() $\frac12,\frac12$
. Then the subset
$\frac12,\frac12$
. Then the subset
![]() $\{+,-\}^N$
consists of absorbing states, so produces an eigenspace of the transition operator (on functions on the state space), with eigenvalue
$\{+,-\}^N$
consists of absorbing states, so produces an eigenspace of the transition operator (on functions on the state space), with eigenvalue
![]() $+1$
and dimension
$+1$
and dimension
![]() $2^N$
. The subset where at least one node is in state 0 produces an eigenspace of eigenvalue 0 and the complementary dimension
$2^N$
. The subset where at least one node is in state 0 produces an eigenspace of eigenvalue 0 and the complementary dimension
![]() $3^N-2^N$
. When an interaction of strength
$3^N-2^N$
. When an interaction of strength
![]() $\varepsilon>0$
along the edges of the graph is introduced, for example favouring alignment of
$\varepsilon>0$
along the edges of the graph is introduced, for example favouring alignment of
![]() $\{+,-\}$
, do these two spectral projections persist? That is, are there nearby invariant subspaces for the perturbed transition operator, with spectra contained in neighbourhoods of
$\{+,-\}$
, do these two spectral projections persist? That is, are there nearby invariant subspaces for the perturbed transition operator, with spectra contained in neighbourhoods of
![]() $+1$
and 0 respectively?
$+1$
and 0 respectively?
Liggett’s statement that ‘total variation convergence essentially never occurs for particle systems’ [Reference Liggett11, p. 70] makes the persistence of spectral projections look unlikely, but our solution is to use a different metric than total variation.
This paper specialises to Markov processes, mostly in discrete time, such as PCA. The transition operator T for updating a probability distribution in one time-step acts dually on the space of real-valued continuous functions of the state of the whole system. This space can be considered to be the tensor product of the spaces of real-valued continuous functions of the state of the individual units. To see this, recall that the tensor product
![]() $\otimes_{s \in S} V_s$
of a finite set of vector spaces
$\otimes_{s \in S} V_s$
of a finite set of vector spaces
![]() $V_s$
is the set of multilinear forms on the product
$V_s$
is the set of multilinear forms on the product
![]() $\times_{s\in S} V_s^*$
of the dual spaces
$\times_{s\in S} V_s^*$
of the dual spaces
![]() $V_s^*$
. Taking
$V_s^*$
. Taking
![]() $V_s = C(X_s,\mathbb{R})$
(continuous functions from
$V_s = C(X_s,\mathbb{R})$
(continuous functions from
![]() $X_s$
to
$X_s$
to
![]() $\mathbb{R}$
) then (modulo assumptions that we’ll specify)
$\mathbb{R}$
) then (modulo assumptions that we’ll specify)
![]() $V_s^*$
is the space of measures
$V_s^*$
is the space of measures
![]() $\mathcal{M}_s$
on
$\mathcal{M}_s$
on
![]() $X_s$
. Define
$X_s$
. Define
![]() $\delta_{x_s}$
to be the atomic probability at
$\delta_{x_s}$
to be the atomic probability at
![]() $x_s \in X_s$
. To a continuous function
$x_s \in X_s$
. To a continuous function
![]() $f\colon\times_{s\in S} X_s \to \mathbb{R}$
associate the element
$f\colon\times_{s\in S} X_s \to \mathbb{R}$
associate the element
![]() $\hat{f}$
of the tensor product
$\hat{f}$
of the tensor product
![]() $\otimes_{s\in S} V_s$
defined by
$\otimes_{s\in S} V_s$
defined by
![]() $\hat{f}((\delta_{x_s})_{s \in S}) = f(x)$
for all
$\hat{f}((\delta_{x_s})_{s \in S}) = f(x)$
for all
![]() $x=(x_s)_{s\in S} \in \times_{s\in S} X_s$
. Thus, the problem is about stochastic operators on large tensor products.
$x=(x_s)_{s\in S} \in \times_{s\in S} X_s$
. Thus, the problem is about stochastic operators on large tensor products.
Even if the system is geometrically ergodic (meaning there is a unique stationary probability and it attracts every probability exponentially in an appropriate metric) and the update of each unit is independent of the state outside a bounded neighbourhood, when we change parameters in a reasonable way the stationary probability may move at a speed going to infinity with the number of units if distances between probability distributions are measured in any of the standard ways (e.g. total variation, Jensen–Shannon, Hellinger, Kantorovich, Fisher information [Reference MacKay13], and Prokhorov [Reference MacKay14]). The solution proposed in [Reference MacKay13] was to introduce a new metric for probabilities on large product systems, christened the ‘Dobrushin metric’ as most of the ingredients were already in Dobrushin’s work [Reference Dobrushin7], but credit should also be given to Vasershtein [Reference Vasershtein22] (more commonly transliterated now as Wasserstein). Furthermore, as neither paper actually introduced it, I will now just call it the D-metric. After the publication of [Reference MacKay13], I found that Steif had proposed a solution 20 years earlier [Reference Steif19]. Although his metric is defined differently and in a restricted context, it is in fact equal to mine in the finite case [Reference MacKay14, Appendix], and with Armstrong-Goodall we have proved they are equal under the general conditions for definition of mine [Reference Armstrong-Goodall and MacKay3]; it is a case of ‘strong duality’.
With respect to the D-metric, the stationary probability of a family of PCA with non-degenerate stationary probability varies smoothly, uniformly in the size of the system [Reference MacKay13]; the proof there is defective but it is rectified here in Appendix B. A slightly more sophisticated way of viewing this result is as persistence of a (rank-1) projection P onto the space of stationary measures, and its complementary projection
![]() $Q=I-P$
to the subspace of neutral measures (for the terminology, see Definition 3), between which there is a spectral gap. Thus, P is a spectral projection (a projection operator onto a subspace corresponding to a closed subset of the spectrum of T, whose complementary projection
$Q=I-P$
to the subspace of neutral measures (for the terminology, see Definition 3), between which there is a spectral gap. Thus, P is a spectral projection (a projection operator onto a subspace corresponding to a closed subset of the spectrum of T, whose complementary projection
![]() $Q=I-P$
is onto a complementary subspace corresponding to the disjoint closed complement of the spectrum).
$Q=I-P$
is onto a complementary subspace corresponding to the disjoint closed complement of the spectrum).
A question that the work of [Reference MacKay13] prompted is whether other spectral projections for stochastic operators might also persist uniformly smoothly in the size of the system. Here, suitable conditions are formulated and a proof of persistence is given. Furthermore, a perturbation theory is developed to derive effective dynamics on the image of a spectral projection.
Here is an outline of the paper. First, the D-metric is reviewed (Section 2). Then, the continuation problem for spectral projections of a class of stochastic operators is formulated and solved (Section 3). An illustration of the result is given (Section 4), followed by a general development of second-order perturbation theory for stochastic operators (Section 5) and then a discussion of further potential applications, including to metastability (Section 6). The paper ends with a short summary (Section 7) and two Appendices.
2. The D-metric
The exposition of this section follows [Reference MacKay13] but fills some gaps.
Let X be the product of a set of metric spaces
![]() $(X_s, d_s)$
, for ‘sites’ s in a countable set S (countable includes finite). The spaces
$(X_s, d_s)$
, for ‘sites’ s in a countable set S (countable includes finite). The spaces
![]() $(X_s, d_s)$
are assumed to be Polish (complete separable metric spaces) with bounded diameter,
$(X_s, d_s)$
are assumed to be Polish (complete separable metric spaces) with bounded diameter,
![]() $\Omega = \sup_{s\in S} \mbox{diam}_s(X_s) < \infty$
, and to have at least two points each. The product X is endowed with product topology and the resulting Borel sets. By a measure I mean a finite signed real Borel measure.
$\Omega = \sup_{s\in S} \mbox{diam}_s(X_s) < \infty$
, and to have at least two points each. The product X is endowed with product topology and the resulting Borel sets. By a measure I mean a finite signed real Borel measure.
With the above assumptions, X is compact and the space
![]() $\mathcal{M}$
of measures is the dual of the space
$\mathcal{M}$
of measures is the dual of the space
![]() $C(X,\mathbb{R})$
of continuous functions from X to
$C(X,\mathbb{R})$
of continuous functions from X to
![]() $\mathbb{R}$
with supremum norm
$\mathbb{R}$
with supremum norm
![]() $|\ |_\infty$
. Given a measure m and a continuous function
$|\ |_\infty$
. Given a measure m and a continuous function
![]() $f\colon X \to \mathbb{R}$
, m(f) (or just mf) denotes the integral of f with respect to m. Define
$f\colon X \to \mathbb{R}$
, m(f) (or just mf) denotes the integral of f with respect to m. Define
![]() $|m|_1 = \sup \{m(f); f \in C(X,\mathbb{R}), |f|_\infty \le 1\}$
.
$|m|_1 = \sup \{m(f); f \in C(X,\mathbb{R}), |f|_\infty \le 1\}$
.
The set
![]() $\mathcal{P}$
of probabilities on X consists of the measures p satisfying
$\mathcal{P}$
of probabilities on X consists of the measures p satisfying
![]() $p(X)=1$
and
$p(X)=1$
and
![]() $p(Y)\ge 0$
for all Borel subsets Y. In particular,
$p(Y)\ge 0$
for all Borel subsets Y. In particular,
![]() $p \in \mathcal{P}$
implies
$p \in \mathcal{P}$
implies
![]() $p(\textbf{1})=1$
, where
$p(\textbf{1})=1$
, where
![]() $\textbf{1}$
is the function taking the value 1 everywhere on X. Also,
$\textbf{1}$
is the function taking the value 1 everywhere on X. Also,
![]() $|p|_1 = 1$
.
$|p|_1 = 1$
.
Definition 1. For a function
![]() $f \colon X \to \mathbb{R}$
, its Lipschitz constant with respect to variations on site
$f \colon X \to \mathbb{R}$
, its Lipschitz constant with respect to variations on site
![]() $s\in S$
is
$s\in S$
is
over
![]() $x,x' \in X$
differing at site s and agreeing elsewhere.
$x,x' \in X$
differing at site s and agreeing elsewhere.
Note that
![]() $\Delta_s(f)\ge 0$
and may be
$\Delta_s(f)\ge 0$
and may be
![]() $+\infty$
.
$+\infty$
.
Definition 2. The set F of Dobrushin smooth functions consists of those
![]() $f\colon X\to \mathbb{R}$
for which the semi-norm
$f\colon X\to \mathbb{R}$
for which the semi-norm
![]() $|f|_F = \sum_{s\in S} \Delta_s(f)$
is finite.
$|f|_F = \sum_{s\in S} \Delta_s(f)$
is finite.
Note that Dobrushin smooth functions are automatically continuous: firstly,
secondly, given
![]() $\varepsilon>0$
, there exists a finite (possibly empty) subset
$\varepsilon>0$
, there exists a finite (possibly empty) subset
![]() $K\subset S$
such that
$K\subset S$
such that
![]() $\sum_{s\in S\setminus K} \Delta_s(f) <\varepsilon/\Omega$
and
$\sum_{s\in S\setminus K} \Delta_s(f) <\varepsilon/\Omega$
and
![]() $\Delta_s(f)>0$
for
$\Delta_s(f)>0$
for
![]() $s \in K$
. For
$s \in K$
. For
![]() $s \in K$
, let
$s \in K$
, let
![]() $A_s \subset X_s$
be the open ball of radius
$A_s \subset X_s$
be the open ball of radius
![]() $\varepsilon /(|K|\Delta_s(f))$
about
$\varepsilon /(|K|\Delta_s(f))$
about
![]() $y_s$
, and for
$y_s$
, and for
![]() $s \in S\setminus K$
, let
$s \in S\setminus K$
, let
![]() $A_s = X_s$
. Then
$A_s = X_s$
. Then
![]() $\prod_{s\in S} A_s$
is an open neighbourhood of y in X, and
$\prod_{s\in S} A_s$
is an open neighbourhood of y in X, and
![]() $x \in \prod_{s\in S} A_s$
implies
$x \in \prod_{s\in S} A_s$
implies
![]() $|f(x)-f(y)| < \varepsilon$
.
$|f(x)-f(y)| < \varepsilon$
.
Also, letting C be the set of constant functions, then
![]() $|\cdot |_F$
is a norm on the quotient space
$|\cdot |_F$
is a norm on the quotient space
![]() $F/C$
(F modulo addition of constants).
$F/C$
(F modulo addition of constants).
Definition 3. The space Z of neutral (or zero-charge) measures on X is the set of measures
![]() $\mu$
for which
$\mu$
for which
![]() $\mu(X)=0$
. Equivalently,
$\mu(X)=0$
. Equivalently,
![]() $\mu(\textbf{1}) = 0$
.
$\mu(\textbf{1}) = 0$
.
Definition 4. The norm
![]() $|\mu |_Z$
of
$|\mu |_Z$
of
![]() $\mu \in Z$
is
$\mu \in Z$
is
![]() $|\mu|_Z = \sup \{\mu(f)\colon |f|_F \le 1\}$
.
$|\mu|_Z = \sup \{\mu(f)\colon |f|_F \le 1\}$
.
It is a norm on Z; see [Reference MacKay13]. With this norm, the dual space
![]() $Z^*$
is
$Z^*$
is
![]() $F/C$
(proved in Appendix A).
$F/C$
(proved in Appendix A).
Definition 5. The D-metric on
![]() $\mathcal{P}$
is defined by
$\mathcal{P}$
is defined by
![]() $ D(\rho, \sigma) = |\rho-\sigma|_Z$
for any two
$ D(\rho, \sigma) = |\rho-\sigma|_Z$
for any two
![]() $\rho, \sigma \in {\mathcal{P}}$
.
$\rho, \sigma \in {\mathcal{P}}$
.
The D-metric makes
![]() ${\mathcal{P}}$
into a complete metric space, with diameter
${\mathcal{P}}$
into a complete metric space, with diameter
![]() $\Omega=\sup_{s\in S} \mbox{diam}_s(X_s)$
. The proof of completeness in [Reference MacKay13] is wrong (the direction of duality above was mistaken), but a proof is provided here in Appendix B.
$\Omega=\sup_{s\in S} \mbox{diam}_s(X_s)$
. The proof of completeness in [Reference MacKay13] is wrong (the direction of duality above was mistaken), but a proof is provided here in Appendix B.
Definition 6. For
![]() $m \in \mathcal{M}$
, define
$m \in \mathcal{M}$
, define
![]() $|m|_\mathcal{M} = \sup \{m(f)\colon |f|_F \le 1, |f|_\infty \le \Omega\}$
.
$|m|_\mathcal{M} = \sup \{m(f)\colon |f|_F \le 1, |f|_\infty \le \Omega\}$
.
It is a norm on
![]() $\mathcal{M}$
, and satisfies
$\mathcal{M}$
, and satisfies
![]() $|m|_\mathcal{M} \le \Omega |m|_1$
. Note that for
$|m|_\mathcal{M} \le \Omega |m|_1$
. Note that for
![]() $\mu \in Z$
,
$\mu \in Z$
,
![]() $|\mu|_\mathcal{M} = |\mu|_Z$
, because if
$|\mu|_\mathcal{M} = |\mu|_Z$
, because if
![]() $|f|_F \le 1$
, we can add a constant to f to achieve
$|f|_F \le 1$
, we can add a constant to f to achieve
![]() $|f|_\infty \le \Omega$
and it does not change
$|f|_\infty \le \Omega$
and it does not change
![]() $\mu(f)$
.
$\mu(f)$
.
Definition 7. A transition operator T is a bounded linear operator on
![]() $\mathcal{M}$
, written as acting to the left, such that
$\mathcal{M}$
, written as acting to the left, such that
![]() $p\in \mathcal{P}$
implies
$p\in \mathcal{P}$
implies
![]() $pT \in \mathcal{P}$
.
$pT \in \mathcal{P}$
.
Note that a transition operator maps Z to Z (write
![]() $\mu \in Z$
as
$\mu \in Z$
as
![]() $\mu^+-\mu^-$
with
$\mu^+-\mu^-$
with
![]() $\mu^\pm$
non-negative;
$\mu^\pm$
non-negative;
![]() $\mu \textbf{1} = 0$
so
$\mu \textbf{1} = 0$
so
![]() $\mu^\pm \textbf{1}$
are equal; if
$\mu^\pm \textbf{1}$
are equal; if
![]() $\mu \ne 0$
then the common value
$\mu \ne 0$
then the common value
![]() $k>0$
; then
$k>0$
; then
![]() $\mu^\pm/k \in \mathcal{P}$
and it follows that
$\mu^\pm/k \in \mathcal{P}$
and it follows that
![]() $(\mu T) \textbf{1} = 0$
). Furthermore, to check T is bounded it is enough to check that its restriction
$(\mu T) \textbf{1} = 0$
). Furthermore, to check T is bounded it is enough to check that its restriction
![]() $T_Z\colon Z \to Z$
is bounded. This is because, choosing a
$T_Z\colon Z \to Z$
is bounded. This is because, choosing a
![]() $p \in \mathcal{P}$
, any
$p \in \mathcal{P}$
, any
![]() $m \in \mathcal{M}$
can be written as
$m \in \mathcal{M}$
can be written as
![]() $kp + \mu$
for some
$kp + \mu$
for some
![]() $k \in \mathbb{R}$
,
$k \in \mathbb{R}$
,
![]() $\mu \in Z$
(simply let
$\mu \in Z$
(simply let
![]() $k = m\textbf{1}$
and
$k = m\textbf{1}$
and
![]() $\mu = m-kp$
). Then, for
$\mu = m-kp$
). Then, for
![]() $|f|_F \le 1$
,
$|f|_F \le 1$
,
![]() $|f|_\infty \le \Omega$
,
$|f|_\infty \le \Omega$
,
Definition 8. For
![]() $f\in F$
, let
$f\in F$
, let
![]() $\|f\| = \max\!(|f|_F, |f|_\infty /\Omega)$
.
$\|f\| = \max\!(|f|_F, |f|_\infty /\Omega)$
.
It is a complete norm on F.
A transition operator T has a dual acting on F that we denote by the same symbol but acting to the right.
Proposition 2.1. Given a transition operator T on
![]() $\mathcal{M}$
, there is a unique linear operator on F such that
$\mathcal{M}$
, there is a unique linear operator on F such that
![]() $p(Tf) = (pT)f$
for all
$p(Tf) = (pT)f$
for all
![]() $f \in F$
,
$f \in F$
,
![]() $p \in \mathcal{M}$
.
$p \in \mathcal{M}$
.
Proof. First, prove the uniqueness of Tf. If there are
![]() $g_1,g_2 \in F$
such that, for all
$g_1,g_2 \in F$
such that, for all
![]() $p \in \mathcal{M}$
,
$p \in \mathcal{M}$
,
![]() $p(g_1)=(pT)f=p(g_2)$
, let
$p(g_1)=(pT)f=p(g_2)$
, let
![]() $g = g_1-g_2$
. Then, for all
$g = g_1-g_2$
. Then, for all
![]() $\mu\in Z$
,
$\mu\in Z$
,
![]() $\mu(g) = 0$
, which implies that g is constant. Then, choosing a
$\mu(g) = 0$
, which implies that g is constant. Then, choosing a
![]() $\pi \in \mathcal{P}$
,
$\pi \in \mathcal{P}$
,
![]() $\pi(\textbf{1})=1$
, so
$\pi(\textbf{1})=1$
, so
![]() $\pi(g)=0$
implies
$\pi(g)=0$
implies
![]() $g=0$
.
$g=0$
.
Next, prove the existence of Tf. Given
![]() $x \in X$
, let
$x \in X$
, let
![]() $g(x) = (\delta_x T)f$
(recall that
$g(x) = (\delta_x T)f$
(recall that
![]() $\delta_x$
is the atomic probability at x). We have to check that the function g is in F. Making a change in x at a single site s, we obtain
$\delta_x$
is the atomic probability at x). We have to check that the function g is in F. Making a change in x at a single site s, we obtain
![]() $g(x')-g(x) \le |\delta_{x'}-\delta_x|_Z |T|_Z |f|_F$
. Noting that
$g(x')-g(x) \le |\delta_{x'}-\delta_x|_Z |T|_Z |f|_F$
. Noting that
![]() $|\delta_{x'}-\delta_x|_Z = d_s(x'_s,x_s)$
, we obtain
$|\delta_{x'}-\delta_x|_Z = d_s(x'_s,x_s)$
, we obtain
![]() $\Delta_s(g) \le |T|_Z |f|_F$
. To bound the sum of the
$\Delta_s(g) \le |T|_Z |f|_F$
. To bound the sum of the
![]() $\Delta_s(g)$
, let
$\Delta_s(g)$
, let
![]() $\gamma \in (0,1)$
. For each
$\gamma \in (0,1)$
. For each
![]() $s \in S$
, let
$s \in S$
, let
![]() $x^{(s)}, y^{(s)}$
be points of X differing only at site s and that achieve
$x^{(s)}, y^{(s)}$
be points of X differing only at site s and that achieve
![]() $g(x^{(s)})-g(y^{(s)}) \ge \gamma \Delta_s(g) d_s(x^{(s)},y^{(s)})$
. Let
$g(x^{(s)})-g(y^{(s)}) \ge \gamma \Delta_s(g) d_s(x^{(s)},y^{(s)})$
. Let
![]() $\mu \in Z$
be the sum of ‘dipoles’
$\mu \in Z$
be the sum of ‘dipoles’
over a finite subset
![]() $S'\subset S$
. Then
$S'\subset S$
. Then
![]() $|\mu|_Z=1$
and
$|\mu|_Z=1$
and
This is true for all finite
![]() $S'\subset S$
, hence
$S'\subset S$
, hence
![]() $\gamma\sum_{s\in S}\Delta_s(g) \le |T|_Z|f|_F$
. So
$\gamma\sum_{s\in S}\Delta_s(g) \le |T|_Z|f|_F$
. So
![]() $g \in F$
.
$g \in F$
.
Elaborating on the proof, we can obtain useful bounds. Specifically, taking
![]() $\gamma\to 1$
we obtain
$\gamma\to 1$
we obtain
![]() $|Tf|_F \le |T|_Z |f|_F$
. Also,
$|Tf|_F \le |T|_Z |f|_F$
. Also,
![]() $|Tf|_\infty = \sup_x |(\delta_xT)f | \le |f|_\infty$
. We quantify the size of a transition operator T by its operator norm on F:
$|Tf|_\infty = \sup_x |(\delta_xT)f | \le |f|_\infty$
. We quantify the size of a transition operator T by its operator norm on F:
Note that
![]() $\|T\| \le \max\!(|T|_Z,1)$
.
$\|T\| \le \max\!(|T|_Z,1)$
.
It will be convenient in much of this paper to consider the action of T on F rather than
![]() $\mathcal{M}$
, because F is complete. The property that T preserves probability can be written as
$\mathcal{M}$
, because F is complete. The property that T preserves probability can be written as
![]() $T\textbf{1} =\textbf{1}$
.
$T\textbf{1} =\textbf{1}$
.
Definition 9. A parametrised family of transition operators
![]() $T_\nu, \nu \in \mathbb{R}^m$
, is smooth if it depends
$T_\nu, \nu \in \mathbb{R}^m$
, is smooth if it depends
![]() $C^r$
on
$C^r$
on
![]() $\nu$
for some
$\nu$
for some
![]() $r\ge 1$
, using the operator norm (1). A family of probability distributions
$r\ge 1$
, using the operator norm (1). A family of probability distributions
![]() $p_\nu$
is smooth if it depends
$p_\nu$
is smooth if it depends
![]() $C^r$
on
$C^r$
on
![]() $\nu$
, using the norm
$\nu$
, using the norm
![]() $|\cdot |_Z$
on differences of probabilities.
$|\cdot |_Z$
on differences of probabilities.
The reason for introducing the Dobrushin metric and the concept of smoothness in [Reference MacKay13] was to derive the following theorem.
Theorem 1. Let T be a transition operator. If
![]() $(I-T)$
is invertible on Z with bounded inverse then T has a unique stationary probability
$(I-T)$
is invertible on Z with bounded inverse then T has a unique stationary probability
![]() $p \in \mathcal{P}$
(i.e.
$p \in \mathcal{P}$
(i.e.
![]() $pT=p$
) and it varies smoothly with respect to smooth changes in T, with
$pT=p$
) and it varies smoothly with respect to smooth changes in T, with
![]() $p' = p T' (I-T)_Z^{-1}$
, where ′ denotes the derivative with respect to parameters and
$p' = p T' (I-T)_Z^{-1}$
, where ′ denotes the derivative with respect to parameters and
![]() $(I-T)_Z$
is the restriction of
$(I-T)_Z$
is the restriction of
![]() $I-T$
to Z.
$I-T$
to Z.
A different norm on transition operators was used in [Reference MacKay13], but it is equivalent to the operator norm (1). Also, it was mistakenly assumed in [Reference MacKay13] that Z is complete and hence that if a bounded operator on Z is invertible then its inverse is bounded; it is not clear that this always holds for
![]() $(I-T)_Z$
so we include the requirement for its inverse to be bounded in the statement of the theorem. With this addition, the proof in [Reference MacKay13] goes through. There are sufficient conditions for bounded invertibility of
$(I-T)_Z$
so we include the requirement for its inverse to be bounded in the statement of the theorem. With this addition, the proof in [Reference MacKay13] goes through. There are sufficient conditions for bounded invertibility of
![]() $(I-T)_Z$
in terms of Dobrushin’s ‘dependency matrix’ [Reference Dobrushin7], which are verifiable in relevant classes of system, so this is a useable result [Reference MacKay13].
$(I-T)_Z$
in terms of Dobrushin’s ‘dependency matrix’ [Reference Dobrushin7], which are verifiable in relevant classes of system, so this is a useable result [Reference MacKay13].
3. Spectral projections
We begin the discussion of spectral projections in the general context of bounded linear operators on Banach spaces.
Definition 10. Given a bounded linear operator T on a Banach space F, a spectral projection for T is a bounded linear operator P on F such that
![]() $P^2 = P$
,
$P^2 = P$
,
![]() $PT=TP$
, and the parts of the spectrum of T corresponding to the restrictions of T to the image (commonly called the ‘range’, but we reserve ‘range’ for the whole space into which P is defined to map) of P and the image of
$PT=TP$
, and the parts of the spectrum of T corresponding to the restrictions of T to the image (commonly called the ‘range’, but we reserve ‘range’ for the whole space into which P is defined to map) of P and the image of
![]() $Q=I-P$
(which are invariant under T) are disjoint.
$Q=I-P$
(which are invariant under T) are disjoint.
Because the two parts of the spectrum are closed and bounded, it follows that the distance between them is positive, called a spectral gap.
An example of a spectral projection is
![]() $P= \textbf{1} p$
for the stationary probability p for a geometrically ergodic transition operator T. This is because
$P= \textbf{1} p$
for the stationary probability p for a geometrically ergodic transition operator T. This is because
![]() $p \textbf{1} = 1$
for any probability p,
$p \textbf{1} = 1$
for any probability p,
![]() $T \textbf{1} = \textbf{1}$
by the definition of a transition operator,
$T \textbf{1} = \textbf{1}$
by the definition of a transition operator,
![]() $p T = p$
for a stationary measure, and geometric ergodicity implies the eigenspace for eigenvalue 1 is one-dimensional and the rest of the spectrum is in a disk of radius less than 1 around 0. Theorem 1 gives smooth dependence of p on T. Using the norm (1) on spectral projections we find that
$p T = p$
for a stationary measure, and geometric ergodicity implies the eigenspace for eigenvalue 1 is one-dimensional and the rest of the spectrum is in a disk of radius less than 1 around 0. Theorem 1 gives smooth dependence of p on T. Using the norm (1) on spectral projections we find that
![]() $\|\textbf{1} p'\| = |p'|_Z / \Omega$
, so we see that Theorem 1 gives smooth dependence of the spectral projection
$\|\textbf{1} p'\| = |p'|_Z / \Omega$
, so we see that Theorem 1 gives smooth dependence of the spectral projection
![]() $\textbf{1} p$
on T. The goal of this section is to extend this result to arbitrary spectral projections for T.
$\textbf{1} p$
on T. The goal of this section is to extend this result to arbitrary spectral projections for T.
Returning to the general context of bounded linear operators on a Banach space F, the set M of (bounded) projections on F is a smooth manifold (a variant of a Grassmann manifold). One way to see this is that projections are equivalent to direct sum decompositions
![]() $R\oplus K$
of F into two closed subspaces, namely the projection onto R along K. The space of closed subspaces is the Grassmann manifold. The space of complementary pairs of closed subspaces is also a manifold.
$R\oplus K$
of F into two closed subspaces, namely the projection onto R along K. The space of closed subspaces is the Grassmann manifold. The space of complementary pairs of closed subspaces is also a manifold.
Here is an outline proof that M is a manifold, from the definition as the set of projections, because the ingredients are useful later. Let B(F) be the space of bounded linear operators P on the space F, with operator norm, which makes B(F) a Banach space. Define
![]() $\Phi$
on B(F) by
$\Phi$
on B(F) by
![]() $\Phi(P) = P^2-P$
, so
$\Phi(P) = P^2-P$
, so
![]() $M= \Phi^{-1}(0)$
. Given
$M= \Phi^{-1}(0)$
. Given
![]() ${P_0}\in M$
, let
${P_0}\in M$
, let
![]() $R = \mbox{im}\,{P_0}$
and
$R = \mbox{im}\,{P_0}$
and
![]() $K=\ker {P_0}$
. Both are closed. Then
$K=\ker {P_0}$
. Both are closed. Then
![]() $F = R \oplus K$
. Relative to this direct-sum decomposition,
$F = R \oplus K$
. Relative to this direct-sum decomposition,
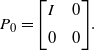 \begin{equation} {P_0} = \Bigg[\begin{array}{c@{\quad}c} I & 0 \\[5pt] 0 & 0 \end{array}\Bigg].\end{equation}
\begin{equation} {P_0} = \Bigg[\begin{array}{c@{\quad}c} I & 0 \\[5pt] 0 & 0 \end{array}\Bigg].\end{equation}
For an arbitrary operator
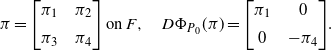 \begin{equation*} \pi = \Bigg[\begin{array}{c@{\quad}c} \pi_1 & \pi_2 \\[5pt] \pi_3 & \pi_4 \end{array} \Bigg]\ \mathrm{ on }\; F, \quad D\Phi_{{P_0}} (\pi) = \Bigg[\begin{array}{c@{\quad}c} \pi_1 & 0 \\[5pt] 0 & -\pi_4 \end{array} \Bigg].\end{equation*}
\begin{equation*} \pi = \Bigg[\begin{array}{c@{\quad}c} \pi_1 & \pi_2 \\[5pt] \pi_3 & \pi_4 \end{array} \Bigg]\ \mathrm{ on }\; F, \quad D\Phi_{{P_0}} (\pi) = \Bigg[\begin{array}{c@{\quad}c} \pi_1 & 0 \\[5pt] 0 & -\pi_4 \end{array} \Bigg].\end{equation*}
With respect to the same direct-sum decomposition, let
![]() $T_{{P_0}}M$
(note the reuse of the symbol T, which will signify tangent space instead of transition operator) be the space of operators on F of the form
$T_{{P_0}}M$
(note the reuse of the symbol T, which will signify tangent space instead of transition operator) be the space of operators on F of the form
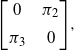 \begin{equation} \Bigg[\begin{array}{c@{\quad}c} 0 & \pi_2 \\[5pt] \pi_3 & 0 \end{array}\Bigg],\end{equation}
\begin{equation} \Bigg[\begin{array}{c@{\quad}c} 0 & \pi_2 \\[5pt] \pi_3 & 0 \end{array}\Bigg],\end{equation}
and
![]() $N_{{P_0}}M$
be those of the form
$N_{{P_0}}M$
be those of the form
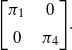 \begin{align*}\Bigg[\begin{array}{c@{\quad}c} \pi_1 & 0 \\[5pt] 0 & \pi_4 \end{array} \Bigg].\end{align*}
\begin{align*}\Bigg[\begin{array}{c@{\quad}c} \pi_1 & 0 \\[5pt] 0 & \pi_4 \end{array} \Bigg].\end{align*}
Consequently,
![]() $D\Phi_{{P_0}}$
maps
$D\Phi_{{P_0}}$
maps
![]() $N_{{P_0}}M$
to itself by
$N_{{P_0}}M$
to itself by
![]() $(\pi_1,\pi_4) \mapsto (\pi_1,-\pi_4)$
, which has bounded inverse, namely itself. So the implicit function theorem shows that the set of P for which the diagonal blocks of
$(\pi_1,\pi_4) \mapsto (\pi_1,-\pi_4)$
, which has bounded inverse, namely itself. So the implicit function theorem shows that the set of P for which the diagonal blocks of
![]() $P^2-P$
in the decomposition
$P^2-P$
in the decomposition
![]() $R\oplus K$
are zero is locally the graph of a
$R\oplus K$
are zero is locally the graph of a
![]() $C^1$
function
$C^1$
function
![]() $\psi\colon T_{P_0}M \to N_{P_0}M$
.
$\psi\colon T_{P_0}M \to N_{P_0}M$
.
To complete the outline proof, we have to check that the off-diagonal blocks of
![]() $P^2-P$
automatically evaluate to zero too. The way we found to do this is via an explicit formula for
$P^2-P$
automatically evaluate to zero too. The way we found to do this is via an explicit formula for
![]() $\psi$
, as follows. Writing
$\psi$
, as follows. Writing
![]() $P=P_0+\pi$
, the equations for the diagonal blocks of
$P=P_0+\pi$
, the equations for the diagonal blocks of
![]() $P^2-P$
to be zero are
$P^2-P$
to be zero are
![]() $\pi_1+\pi_1^2 = -\pi_2\pi_3$
,
$\pi_1+\pi_1^2 = -\pi_2\pi_3$
,
![]() $\pi_4-\pi_4^2 = \pi_3\pi_2$
. The unique solution
$\pi_4-\pi_4^2 = \pi_3\pi_2$
. The unique solution
![]() $\psi$
for
$\psi$
for
![]() $\pi$
small is
$\pi$
small is
where the square roots are defined by their binomial expansions. Then the off-diagonal blocks
![]() $\pi_1\pi_2+\pi_2\pi_4$
,
$\pi_1\pi_2+\pi_2\pi_4$
,
![]() $\pi_3\pi_1 + \pi_4 \pi_3$
can be seen to evaluate to 0. Note that this explicit formula for
$\pi_3\pi_1 + \pi_4 \pi_3$
can be seen to evaluate to 0. Note that this explicit formula for
![]() $\psi$
gives a direct proof that M is a manifold, rendering use of the implicit function theorem redundant. Perhaps there is a simpler way to show the off-diagonal blocks are zero.
$\psi$
gives a direct proof that M is a manifold, rendering use of the implicit function theorem redundant. Perhaps there is a simpler way to show the off-diagonal blocks are zero.
Note that
![]() $\Phi(P_0+\tilde{\pi} + \psi(\tilde{\pi}))=0$
for
$\Phi(P_0+\tilde{\pi} + \psi(\tilde{\pi}))=0$
for
![]() $\tilde{\pi} \in T_{P_0}M$
near 0 (or the explicit formula for
$\tilde{\pi} \in T_{P_0}M$
near 0 (or the explicit formula for
![]() $\psi$
) implies
$\psi$
) implies
![]() $D\psi{(0)} = 0$
, so
$D\psi{(0)} = 0$
, so
![]() $T_{P_0}M$
is the tangent space to M at
$T_{P_0}M$
is the tangent space to M at
![]() ${P_0}$
(hence the notation). Note also that the manifold M of projections has many components of different dimensions, corresponding to the similarity class (rank in finite dimensions) of the projection.
${P_0}$
(hence the notation). Note also that the manifold M of projections has many components of different dimensions, corresponding to the similarity class (rank in finite dimensions) of the projection.
Then we have the following classical theorem. It is often proved by contour integration of the resolvent operator, e.g. [Reference Kato10], but we prefer our own proof.
Theorem 2. Given a family of bounded linear operators
![]() $T_\mu$
on a Banach space F, depending
$T_\mu$
on a Banach space F, depending
![]() $C^r$
(
$C^r$
(
![]() $r\ge 1$
) on
$r\ge 1$
) on
![]() $\mu \in \mathbb{R}^n$
, and
$\mu \in \mathbb{R}^n$
, and
![]() $P_0$
a spectral projection for
$P_0$
a spectral projection for
![]() $T_0$
, there is a neighbourhood of
$T_0$
, there is a neighbourhood of
![]() $P_0$
containing a unique spectral projection
$P_0$
containing a unique spectral projection
![]() $P_\mu$
for
$P_\mu$
for
![]() $T_\mu$
for all
$T_\mu$
for all
![]() $\mu$
near 0 and it depends
$\mu$
near 0 and it depends
![]() $C^r$
on
$C^r$
on
![]() $\mu$
.
$\mu$
.
Proof. Define a map
![]() $G\colon M \times B(F) \to B(F)$
by the commutator
$G\colon M \times B(F) \to B(F)$
by the commutator
![]() $G(P,T) = [P,T] = PT-TP$
. Note that the image lies in
$G(P,T) = [P,T] = PT-TP$
. Note that the image lies in
![]() $T_PM$
, because in the direct sum decomposition
$T_PM$
, because in the direct sum decomposition
![]() $F=R\oplus K$
above, where P has the form (2), then [P, T] has the form (3). Thus G can be considered as a map from B(F) to sections of TM.
$F=R\oplus K$
above, where P has the form (2), then [P, T] has the form (3). Thus G can be considered as a map from B(F) to sections of TM.
Now we apply the implicit function theorem to G. We have
![]() $G(P_0,T_0)=0$
, and G is
$G(P_0,T_0)=0$
, and G is
![]() $C^r$
. It remains to check that the derivative
$C^r$
. It remains to check that the derivative
![]() ${\partial G}/{\partial P}$
at
${\partial G}/{\partial P}$
at
![]() $(P_0,T_0)$
, mapping
$(P_0,T_0)$
, mapping
![]() $T_{P_0}M$
to itself, is invertible with bounded inverse. We denote it for short by L.
$T_{P_0}M$
to itself, is invertible with bounded inverse. We denote it for short by L.
Applied to a tangent vector
![]() $P' \in T_PM$
,
$P' \in T_PM$
,
![]() $L(P') = P'T-TP' \in T_PM$
. In the direct sum decomposition
$L(P') = P'T-TP' \in T_PM$
. In the direct sum decomposition
![]() $F=R \oplus K$
,
$F=R \oplus K$
,
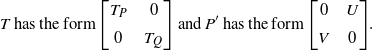 \begin{align*} T \;\mathrm{ has\; the\; form\ } \Bigg[\begin{array}{c@{\quad}c} T_P & 0 \\[5pt] 0 & T_Q\end{array}\Bigg]\ \mathrm{ and }\; P'\; \mathrm{ has\; the\; form\ } \Bigg[\begin{array}{c@{\quad}c} 0 & U \\[5pt] V & 0\end{array}\Bigg]. \end{align*}
\begin{align*} T \;\mathrm{ has\; the\; form\ } \Bigg[\begin{array}{c@{\quad}c} T_P & 0 \\[5pt] 0 & T_Q\end{array}\Bigg]\ \mathrm{ and }\; P'\; \mathrm{ has\; the\; form\ } \Bigg[\begin{array}{c@{\quad}c} 0 & U \\[5pt] V & 0\end{array}\Bigg]. \end{align*}
So
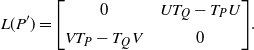 \begin{equation*} L(P') = \Bigg[ \begin{array}{c@{\quad}c} 0 & UT_Q-T_PU \\[5pt] VT_P - T_Q V & 0 \end{array} \Bigg]. \end{equation*}
\begin{equation*} L(P') = \Bigg[ \begin{array}{c@{\quad}c} 0 & UT_Q-T_PU \\[5pt] VT_P - T_Q V & 0 \end{array} \Bigg]. \end{equation*}
A general element of
![]() $T_PM$
has the form
$T_PM$
has the form
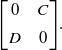 \begin{align*}\Bigg[\begin{array}{c@{\quad}c} 0 & C \\[5pt] D & 0 \end{array}\Bigg].\end{align*}
\begin{align*}\Bigg[\begin{array}{c@{\quad}c} 0 & C \\[5pt] D & 0 \end{array}\Bigg].\end{align*}
We claim that L considered as mapping
![]() $T_PM$
to itself is invertible, because inverting L reduces to solving two ‘Sylvester equations’
$T_PM$
to itself is invertible, because inverting L reduces to solving two ‘Sylvester equations’
![]() $UT_Q-T_PU = C$
,
$UT_Q-T_PU = C$
,
![]() $VT_P-T_QV = D$
, for operators U, V. There is a unique bounded solution to each of the Sylvester equations if and only if the spectra of
$VT_P-T_QV = D$
, for operators U, V. There is a unique bounded solution to each of the Sylvester equations if and only if the spectra of
![]() $T_P$
and
$T_P$
and
![]() $T_Q$
are disjoint [Reference Bhatia and Rosenthal4]. It is automatic that the resulting inverse operators
$T_Q$
are disjoint [Reference Bhatia and Rosenthal4]. It is automatic that the resulting inverse operators
![]() $C \mapsto U, D \mapsto V$
are bounded, because the inverse of an invertible bounded linear operator between Banach spaces is bounded [Reference Kato10].
$C \mapsto U, D \mapsto V$
are bounded, because the inverse of an invertible bounded linear operator between Banach spaces is bounded [Reference Kato10].
Thus, L has bounded inverse and the result follows by the implicit function theorem.
Note that the result does not preclude existence of other spectral projections further away from
![]() $P_0$
, for example of different rank.
$P_0$
, for example of different rank.
Denoting derivatives with respect to
![]() $\mu$
by ′, we note the useful formula
$\mu$
by ′, we note the useful formula
![]() $P' = -L^{-1} [P,T']$
. This results from applying the chain rule to the equation
$P' = -L^{-1} [P,T']$
. This results from applying the chain rule to the equation
![]() $G(P_\mu, T_\mu) = 0$
at
$G(P_\mu, T_\mu) = 0$
at
![]() $\mu=0$
, but holds more generally if L is evaluated at
$\mu=0$
, but holds more generally if L is evaluated at
![]() $(P_\mu,T_\mu)$
. If we have bounds on
$(P_\mu,T_\mu)$
. If we have bounds on
![]() $L^{-1}$
and T
′, it allows us to deduce bounds on
$L^{-1}$
and T
′, it allows us to deduce bounds on
![]() $P_\mu-P_0$
.
$P_\mu-P_0$
.
We now apply Theorem 2 to the case of F being the Dobrushin smooth functions on a countable product of Polish spaces with bounded diameter, with the norm of Definition 8 and the associated norm (1) on linear operators on F, such as transition operators T, projections P, and infinitesimal changes to each, and smoothness as in Definition 9.
Theorem 3. Given a smooth family of transition operators
![]() $T_\mu$
, for each spectral projection
$T_\mu$
, for each spectral projection
![]() $P_0$
of
$P_0$
of
![]() $T_0$
there is
$T_0$
there is
![]() $\varepsilon>0$
such that
$\varepsilon>0$
such that
![]() $P_0$
persists smoothly to a spectral projection
$P_0$
persists smoothly to a spectral projection
![]() $P_\mu$
for all
$P_\mu$
for all
![]() $|\mu| < \varepsilon$
.
$|\mu| < \varepsilon$
.
For practical purposes, we need a bound on the solutions of the Sylvester equations.
Definition 11. For bounded linear maps
![]() $A\colon K \to K$
,
$A\colon K \to K$
,
![]() $B\colon H \to H$
between normed spaces, their separation is
$B\colon H \to H$
between normed spaces, their separation is
over bounded linear
![]() $X\colon H\to K$
.
$X\colon H\to K$
.
This generalises the concept of the separation of two matrices A, B, which is usually defined using the Frobenius norm [Reference Stewart20, Reference Varah21]. Note that
![]() $\mbox{sep}(B,A)$
is not necessarily equal to
$\mbox{sep}(B,A)$
is not necessarily equal to
![]() $\mbox{sep}(A,B)$
. From the definition,
$\mbox{sep}(A,B)$
. From the definition,
![]() $\mbox{sep}(A,B) >0$
if and only if the Sylvester equation
$\mbox{sep}(A,B) >0$
if and only if the Sylvester equation
![]() $AX-XB = C$
has a unique solution X for each C, and by the theory of Sylvester equations already used, this is true if and only if the spectra of A and B are disjoint. Then
$AX-XB = C$
has a unique solution X for each C, and by the theory of Sylvester equations already used, this is true if and only if the spectra of A and B are disjoint. Then
![]() $\| X \| \le \| C \| /\mbox{sep}(A,B)$
. Thus, taking
$\| X \| \le \| C \| /\mbox{sep}(A,B)$
. Thus, taking
![]() $A=T_P$
and
$A=T_P$
and
![]() $B=T_Q$
,
$B=T_Q$
,
In some cases we can give explicit lower bounds on
![]() $\mbox{sep}(A,B)$
. For example, if the spectral radii
$\mbox{sep}(A,B)$
. For example, if the spectral radii
![]() $\rho_A, \rho_{B^{-1}}$
of A and
$\rho_A, \rho_{B^{-1}}$
of A and
![]() $B^{-1}$
satisfy
$B^{-1}$
satisfy
![]() $\rho_A \rho_{B^{-1}} < 1$
then for
$\rho_A \rho_{B^{-1}} < 1$
then for
![]() $\lambda>1$
there exist
$\lambda>1$
there exist
![]() $C_A,C_{B^{-1}}$
(dependent on
$C_A,C_{B^{-1}}$
(dependent on
![]() $\lambda$
) such that, for
$\lambda$
) such that, for
![]() $n\ge 0$
,
$n\ge 0$
,
![]() $\|A^n\| \le C_A (\lambda\rho_A)^n$
and
$\|A^n\| \le C_A (\lambda\rho_A)^n$
and
![]() $\|B^{-n}\| \le C_{B^{-1}} (\lambda\rho_{B^{-1}})^n$
. The explicit (convergent) solution
$\|B^{-n}\| \le C_{B^{-1}} (\lambda\rho_{B^{-1}})^n$
. The explicit (convergent) solution
![]() $X=-\sum_{n=0}^\infty A^n C B^{-n-1}$
of the Sylvester equation shows that
$X=-\sum_{n=0}^\infty A^n C B^{-n-1}$
of the Sylvester equation shows that
Similarly, for
![]() $YA-BY=D$
the explicit solution
$YA-BY=D$
the explicit solution
![]() $Y=-\sum_{n\ge 0} B^{-n-1}DA^n$
provides the same bound on
$Y=-\sum_{n\ge 0} B^{-n-1}DA^n$
provides the same bound on
![]() $\mbox{sep}(B,A)$
. A method to obtain similar bounds for some more general forms of separation of the spectra is described in [Reference Nevanlinna16].
$\mbox{sep}(B,A)$
. A method to obtain similar bounds for some more general forms of separation of the spectra is described in [Reference Nevanlinna16].
The important point is that for a family of examples with growing system size N, if the separation is bounded away from zero then the continuation in Theorem 3 is uniform in N. Furthermore, it can apply to infinite systems.
The same can be done in continuous time, with the transition operator replaced by a transition generator, but we do not spell it out here, save to mention that if the spectra of A and B lie in
![]() ${\mathrm{Re}\,} z \ge r_A$
,
${\mathrm{Re}\,} z \ge r_A$
,
![]() ${\mathrm{Re}\,} z \le r_B$
respectively, with
${\mathrm{Re}\,} z \le r_B$
respectively, with
![]() $r_A>r_B$
, the explicit (convergent) solution
$r_A>r_B$
, the explicit (convergent) solution
![]() $X=\int_0^\infty {\mathrm{e}}^{(-A+r)t}C{\mathrm{e}}^{(B-r)t}\,{\mathrm{d}} t$
for
$X=\int_0^\infty {\mathrm{e}}^{(-A+r)t}C{\mathrm{e}}^{(B-r)t}\,{\mathrm{d}} t$
for
![]() $r \in (r_B,r_A)$
provides a bound of the form
$r \in (r_B,r_A)$
provides a bound of the form
for any
![]() $\varepsilon>0$
, with
$\varepsilon>0$
, with
![]() $c_A,c_B$
depending on
$c_A,c_B$
depending on
![]() $\varepsilon$
.
$\varepsilon$
.
4. An illustration
As an example, consider a three-state PCA, with local state space
![]() $\{+,0,-\}$
at each site of a finite undirected graph with N nodes and bounded degree, say by m. The transition probabilities for the state at a given site are taken to be
$\{+,0,-\}$
at each site of a finite undirected graph with N nodes and bounded degree, say by m. The transition probabilities for the state at a given site are taken to be
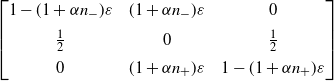 \begin{equation} \left[ \begin{array}{c@{\quad}c@{\quad}c} 1-(1+\alpha n_- )\varepsilon & (1+\alpha n_-)\varepsilon & 0 \\[5pt] \frac12 & 0 & \frac12 \\[5pt] 0 & (1+\alpha n_+)\varepsilon & 1- (1+\alpha n_+)\varepsilon \end{array} \right] \end{equation}
\begin{equation} \left[ \begin{array}{c@{\quad}c@{\quad}c} 1-(1+\alpha n_- )\varepsilon & (1+\alpha n_-)\varepsilon & 0 \\[5pt] \frac12 & 0 & \frac12 \\[5pt] 0 & (1+\alpha n_+)\varepsilon & 1- (1+\alpha n_+)\varepsilon \end{array} \right] \end{equation}
in basis
![]() $(+,0,-)$
, where
$(+,0,-)$
, where
![]() $n_\pm$
are the numbers of neighbours in states
$n_\pm$
are the numbers of neighbours in states
![]() $\pm$
respectively,
$\pm$
respectively,
![]() $\alpha \ge 0$
, and
$\alpha \ge 0$
, and
![]() $\varepsilon \in [0,(1+\alpha m)^{-1}]$
. For
$\varepsilon \in [0,(1+\alpha m)^{-1}]$
. For
![]() $\varepsilon=0$
the system has eigenvalue 1 with multiplicity
$\varepsilon=0$
the system has eigenvalue 1 with multiplicity
![]() $2^N$
and eigenvalue 0 with multiplicity
$2^N$
and eigenvalue 0 with multiplicity
![]() $3^N-2^N$
.
$3^N-2^N$
.
From the above theory, the spectral projection to the subspace for eigenvalue 1 has a continuation for
![]() $\varepsilon$
small. The continuation is uniform in N because the separation of the relevant operators can be bounded away from 0 uniformly in N. The dynamics on the image of the projection is slow because the spectrum moves from
$\varepsilon$
small. The continuation is uniform in N because the separation of the relevant operators can be bounded away from 0 uniformly in N. The dynamics on the image of the projection is slow because the spectrum moves from
![]() $\{1\}$
by at most
$\{1\}$
by at most
![]() $O(\varepsilon)$
. It is still Markovian. It might loosely be considered as an effective PCA with two states
$O(\varepsilon)$
. It is still Markovian. It might loosely be considered as an effective PCA with two states
![]() $\{+,-\}$
on each site but
$\{+,-\}$
on each site but
![]() $R=\mbox{im}\, P$
is not spanned by
$R=\mbox{im}\, P$
is not spanned by
![]() $\delta$
-functions on states, so such a description requires interpretation analogous to quasiparticles in quantum mechanics.
$\delta$
-functions on states, so such a description requires interpretation analogous to quasiparticles in quantum mechanics.
If
![]() $\alpha < 1/m$
and
$\alpha < 1/m$
and
![]() $\varepsilon>0$
, the dynamics on R is geometrically ergodic, because the whole system is. The latter can be proved using Dobrushin’s dependency matrix, as follows (compare an example of its use in [Reference MacKay13]). Take the discrete metric on the local state spaces. Then the update probability distributions
$\varepsilon>0$
, the dynamics on R is geometrically ergodic, because the whole system is. The latter can be proved using Dobrushin’s dependency matrix, as follows (compare an example of its use in [Reference MacKay13]). Take the discrete metric on the local state spaces. Then the update probability distributions
![]() $p(\sigma)$
for the state at a site given its current state
$p(\sigma)$
for the state at a site given its current state
![]() $\sigma$
and the numbers
$\sigma$
and the numbers
![]() $n_\pm$
are the rows of the matrix (4) and so the variation distance for a change of state on the given site is at most
$n_\pm$
are the rows of the matrix (4) and so the variation distance for a change of state on the given site is at most
![]() $(1-\varepsilon)$
, and for a change on a neighbouring site is at most
$(1-\varepsilon)$
, and for a change on a neighbouring site is at most
![]() $\alpha \varepsilon$
. Thus the dependency matrix has
$\alpha \varepsilon$
. Thus the dependency matrix has
![]() $\ell_\infty$
-norm at most
$\ell_\infty$
-norm at most
![]() $1-(1-m\alpha)\varepsilon$
. If
$1-(1-m\alpha)\varepsilon$
. If
![]() $\alpha < 1/m$
and
$\alpha < 1/m$
and
![]() $\varepsilon>0$
, this is less than 1 and so the system is geometrically ergodic.
$\varepsilon>0$
, this is less than 1 and so the system is geometrically ergodic.
5. Second-order perturbation theory
We might ask what the dynamics of the above example look like on the image of the projection corresponding to the spectrum near 1. This can be answered by analogy to second-order perturbation theory computations in quantum mechanics, e.g. the derivation of the
![]() $t-J$
model from the Hubbard model [Reference Spalek17]. In the above example, the 0 state mediates interactions between the
$t-J$
model from the Hubbard model [Reference Spalek17]. In the above example, the 0 state mediates interactions between the
![]() $\pm$
states. Here, a general treatment of second-order perturbation theory for families of stochastic operators is given and applied to this example.
$\pm$
states. Here, a general treatment of second-order perturbation theory for families of stochastic operators is given and applied to this example.
Under the spectral gap condition at
![]() $\varepsilon=0$
and with the norm (1), it has been proved above that for a smooth family of stochastic operators
$\varepsilon=0$
and with the norm (1), it has been proved above that for a smooth family of stochastic operators
![]() $T_\varepsilon$
and a spectral projection
$T_\varepsilon$
and a spectral projection
![]() $P_0$
for
$P_0$
for
![]() $T_0$
, there is an open neighbourhood in
$T_0$
, there is an open neighbourhood in
![]() $\varepsilon$
for which
$\varepsilon$
for which
![]() $P_0$
continues smoothly to a spectral projection
$P_0$
continues smoothly to a spectral projection
![]() $P_\varepsilon$
for
$P_\varepsilon$
for
![]() $T_\varepsilon$
. It is convenient to write
$T_\varepsilon$
. It is convenient to write
![]() $P_\varepsilon = \psi_\varepsilon P_0 {\psi_\varepsilon}^{-1}$
for an
$P_\varepsilon = \psi_\varepsilon P_0 {\psi_\varepsilon}^{-1}$
for an
![]() $\varepsilon$
-dependent invertible bounded linear map
$\varepsilon$
-dependent invertible bounded linear map
![]() $\psi$
, with
$\psi$
, with
![]() $\psi_0$
the identity. There is a lot of freedom in the choice of
$\psi_0$
the identity. There is a lot of freedom in the choice of
![]() $\psi$
, the only constraints being that
$\psi$
, the only constraints being that
![]() $\psi_\varepsilon(\mbox{im}\,P_\varepsilon) = \mbox{im}\,P_0$
and
$\psi_\varepsilon(\mbox{im}\,P_\varepsilon) = \mbox{im}\,P_0$
and
![]() $\psi_\varepsilon(\ker P_\varepsilon)= \ker P_0$
, but it is good also to take
$\psi_\varepsilon(\ker P_\varepsilon)= \ker P_0$
, but it is good also to take
![]() $\psi$
to be as smooth in
$\psi$
to be as smooth in
![]() $\varepsilon$
as is T. Then we can define
$\varepsilon$
as is T. Then we can define
![]() $S = \psi' \psi^{-1}$
, where ′ denotes
$S = \psi' \psi^{-1}$
, where ′ denotes
![]() ${{\mathrm{d}}}/{{\mathrm{d}}\varepsilon}$
, and the above conditions reduce to
${{\mathrm{d}}}/{{\mathrm{d}}\varepsilon}$
, and the above conditions reduce to
where
![]() $[\,\cdot\,,\cdot\,]$
again denotes the commutator. A convenient solution is
$[\,\cdot\,,\cdot\,]$
again denotes the commutator. A convenient solution is
![]() $S = P'(P-Q)$
, which can be checked to satisfy the condition (5).
$S = P'(P-Q)$
, which can be checked to satisfy the condition (5).
Then it is desired to compute
![]() $\hat{T} = \psi^{-1}T\psi$
on
$\hat{T} = \psi^{-1}T\psi$
on
![]() $\mbox{im}\,P_0$
. This is the stochastic operator that represents the dynamics of
$\mbox{im}\,P_0$
. This is the stochastic operator that represents the dynamics of
![]() $T_\varepsilon$
on
$T_\varepsilon$
on
![]() $\mbox{im}\,P_\varepsilon$
, using the coordinate system
$\mbox{im}\,P_\varepsilon$
, using the coordinate system
![]() $\psi_\varepsilon$
.
$\psi_\varepsilon$
.
Start from
![]() $\hat{T}_0 = T_0$
. The first derivative is
$\hat{T}_0 = T_0$
. The first derivative is
![]() $\hat{T}' = \psi^{-1}(T'+[T,S])\psi$
. Using the above choice of S, we obtain
$\hat{T}' = \psi^{-1}(T'+[T,S])\psi$
. Using the above choice of S, we obtain
![]() $\hat{T}' = \psi^{-1}J\psi$
, where
$\hat{T}' = \psi^{-1}J\psi$
, where
![]() $J = PT'P+QT'Q$
. The second derivative can be evaluated to
$J = PT'P+QT'Q$
. The second derivative can be evaluated to
![]() $\hat{T}'' = \psi^{-1}(PT''P+QT''Q + [[T,P'],P'])\psi$
.
$\hat{T}'' = \psi^{-1}(PT''P+QT''Q + [[T,P'],P'])\psi$
.
Evaluating these at
![]() $\varepsilon=0$
, we obtain
$\varepsilon=0$
, we obtain
![]() $\hat{T}$
to second order in
$\hat{T}$
to second order in
![]() $\varepsilon$
as
$\varepsilon$
as
It is perhaps more useful to substitute
![]() $[T,P'] = [T',P]$
, since the right-hand side of this is readily computable, but the second occurrence of P
′ above means that solution of this equation for P
′ is required.
$[T,P'] = [T',P]$
, since the right-hand side of this is readily computable, but the second occurrence of P
′ above means that solution of this equation for P
′ is required.
For the example of Section 4, there is already an effect at first order in
![]() $\varepsilon$
, so second-order perturbation theory is perhaps unnecessary, but it still serves as an illustration of the procedure.
$\varepsilon$
, so second-order perturbation theory is perhaps unnecessary, but it still serves as an illustration of the procedure.
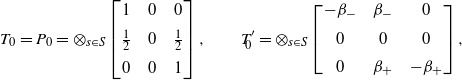 \begin{align*}T_0 = P_0 = \otimes_{s\in S} \left[\begin{array}{c@{\quad}c@{\quad}c} 1 & 0 & 0 \\[5pt] \frac12 & 0 & \frac12 \\[5pt] 0 & 0 & 1 \end{array} \right], \qquad T'_{\!\!0} = \otimes_{s\in S} \left[\begin{array}{c@{\quad}c@{\quad}c} -\beta_- & \beta_- & 0\\[5pt] 0 & 0 & 0 \\[5pt] 0 & \beta_+ & -\beta_+ \end{array} \right],\end{align*}
\begin{align*}T_0 = P_0 = \otimes_{s\in S} \left[\begin{array}{c@{\quad}c@{\quad}c} 1 & 0 & 0 \\[5pt] \frac12 & 0 & \frac12 \\[5pt] 0 & 0 & 1 \end{array} \right], \qquad T'_{\!\!0} = \otimes_{s\in S} \left[\begin{array}{c@{\quad}c@{\quad}c} -\beta_- & \beta_- & 0\\[5pt] 0 & 0 & 0 \\[5pt] 0 & \beta_+ & -\beta_+ \end{array} \right],\end{align*}
where
![]() $\beta_\pm = 1+ \alpha n_\pm$
. Thus
$\beta_\pm = 1+ \alpha n_\pm$
. Thus
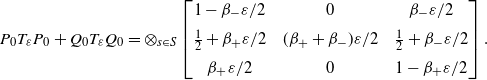 \begin{align*}P_0 T_\varepsilon P_0 + Q_0 T_\varepsilon Q_0 = \otimes_{s\in S} \left[\begin{array}{c@{\quad}c@{\quad}c} 1-\beta_-\varepsilon/2 & 0 & \beta_-\varepsilon/2 \\[5pt] \tfrac12 + \beta_+\varepsilon/2 & (\beta_++\beta_-)\varepsilon/2 & \tfrac12 + \beta_-\varepsilon/2 \\[5pt] \beta_+\varepsilon/2 & 0 & 1-\beta_+\varepsilon/2 \end{array}\right].\end{align*}
\begin{align*}P_0 T_\varepsilon P_0 + Q_0 T_\varepsilon Q_0 = \otimes_{s\in S} \left[\begin{array}{c@{\quad}c@{\quad}c} 1-\beta_-\varepsilon/2 & 0 & \beta_-\varepsilon/2 \\[5pt] \tfrac12 + \beta_+\varepsilon/2 & (\beta_++\beta_-)\varepsilon/2 & \tfrac12 + \beta_-\varepsilon/2 \\[5pt] \beta_+\varepsilon/2 & 0 & 1-\beta_+\varepsilon/2 \end{array}\right].\end{align*}
To compute the second-order term, begin with
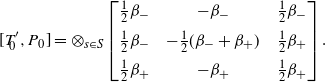 \begin{align*}[T'_{\!\!0},P_0] = \otimes_{s \in S} \left[\begin{array}{c@{\quad}c@{\quad}c} \frac12 \beta_- &-\beta_- &\frac12 \beta_- \\[5pt] \frac12\beta_- &-\frac12 (\beta_-+\beta_+) & \frac12 \beta_+ \\[5pt] \frac12 \beta_+ & -\beta_+ & \frac12 \beta_+ \end{array} \right].\end{align*}
\begin{align*}[T'_{\!\!0},P_0] = \otimes_{s \in S} \left[\begin{array}{c@{\quad}c@{\quad}c} \frac12 \beta_- &-\beta_- &\frac12 \beta_- \\[5pt] \frac12\beta_- &-\frac12 (\beta_-+\beta_+) & \frac12 \beta_+ \\[5pt] \frac12 \beta_+ & -\beta_+ & \frac12 \beta_+ \end{array} \right].\end{align*}
Using
![]() $P_0P'_{\!\!0}=P'_{\!\!0}Q_0$
,
$P_0P'_{\!\!0}=P'_{\!\!0}Q_0$
,
![]() $P'_{\!\!0}$
has just four independent parameters on each site, and solving
$P'_{\!\!0}$
has just four independent parameters on each site, and solving
![]() $[T,P']=[T',P]$
for them yields
$[T,P']=[T',P]$
for them yields
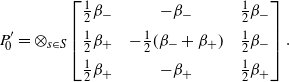 \begin{align*}P'_{\!\!0} =\otimes_{s\in S} \left[ \begin{array}{c@{\quad}c@{\quad}c} \frac12 \beta_- & -\beta_- & \frac12 \beta_- \\[5pt] \frac12 \beta_+ & -\frac12 (\beta_-+\beta_+) & \frac12 \beta_- \\[5pt] \frac12 \beta_+ & -\beta_+ & \frac12 \beta_+ \end{array} \right].\end{align*}
\begin{align*}P'_{\!\!0} =\otimes_{s\in S} \left[ \begin{array}{c@{\quad}c@{\quad}c} \frac12 \beta_- & -\beta_- & \frac12 \beta_- \\[5pt] \frac12 \beta_+ & -\frac12 (\beta_-+\beta_+) & \frac12 \beta_- \\[5pt] \frac12 \beta_+ & -\beta_+ & \frac12 \beta_+ \end{array} \right].\end{align*}
To compute the
![]() $\varepsilon^2$
term in (6), we can first subtract
$\varepsilon^2$
term in (6), we can first subtract
![]() $[T'_{\!\!0},P_0]$
from
$[T'_{\!\!0},P_0]$
from
![]() $P'_{\!\!0}$
, leaving, site-wise,
$P'_{\!\!0}$
, leaving, site-wise,
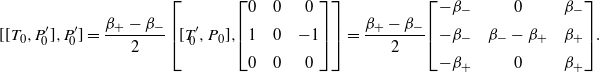 \begin{align*}[[T_0,P'_{\!\!0}],P'_{\!\!0}] = \frac{\beta_+-\beta_-}{2}\left[\![T'_{\!\!0},P_0],\! \left[\begin{array}{c@{\quad}c@{\quad}c} 0 & 0 & 0 \\[5pt] 1 & 0 & -1\\[5pt] 0 & 0 & 0\end{array}\right]\right] =\frac{\beta_+-\beta_-}{2} \!\left[\begin{array}{c@{\quad}c@{\quad}c} -\beta_- & 0 & \beta_-\\[5pt] -\beta_- & \beta_- - \beta_+ & \beta_+ \\[5pt] -\beta_+ & 0 & \beta_+ \end{array}\right]\!.\end{align*}
\begin{align*}[[T_0,P'_{\!\!0}],P'_{\!\!0}] = \frac{\beta_+-\beta_-}{2}\left[\![T'_{\!\!0},P_0],\! \left[\begin{array}{c@{\quad}c@{\quad}c} 0 & 0 & 0 \\[5pt] 1 & 0 & -1\\[5pt] 0 & 0 & 0\end{array}\right]\right] =\frac{\beta_+-\beta_-}{2} \!\left[\begin{array}{c@{\quad}c@{\quad}c} -\beta_- & 0 & \beta_-\\[5pt] -\beta_- & \beta_- - \beta_+ & \beta_+ \\[5pt] -\beta_+ & 0 & \beta_+ \end{array}\right]\!.\end{align*}
Thus, the final result to second order, using the
![]() $(+,-)$
part of the
$(+,-)$
part of the
![]() $\psi_\varepsilon$
basis, is the effective PCA
$\psi_\varepsilon$
basis, is the effective PCA
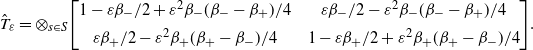 \begin{align*}\hat{T}_\varepsilon = \otimes_{s\in S} \Bigg[\begin{array}{c@{\quad}c} 1-\varepsilon\beta_-/2+\varepsilon^2\beta_-(\beta_- -\beta_+)/4 & \varepsilon\beta_-/2-\varepsilon^2\beta_-(\beta_- -\beta_+)/4 \\[5pt] \varepsilon \beta_+/2-\varepsilon^2\beta_+(\beta_+ -\beta_-)/4 & 1-\varepsilon \beta_+/2 + \varepsilon^2\beta_+(\beta_+ -\beta_-)/4 \end{array} \Bigg].\end{align*}
\begin{align*}\hat{T}_\varepsilon = \otimes_{s\in S} \Bigg[\begin{array}{c@{\quad}c} 1-\varepsilon\beta_-/2+\varepsilon^2\beta_-(\beta_- -\beta_+)/4 & \varepsilon\beta_-/2-\varepsilon^2\beta_-(\beta_- -\beta_+)/4 \\[5pt] \varepsilon \beta_+/2-\varepsilon^2\beta_+(\beta_+ -\beta_-)/4 & 1-\varepsilon \beta_+/2 + \varepsilon^2\beta_+(\beta_+ -\beta_-)/4 \end{array} \Bigg].\end{align*}
The outcome is a two-state model in which to leading order there is a small probability
![]() $\varepsilon \beta_\mp/2 = \varepsilon (1+\alpha n_\mp)/2$
per timestep for transition from state
$\varepsilon \beta_\mp/2 = \varepsilon (1+\alpha n_\mp)/2$
per timestep for transition from state
![]() $+$
to
$+$
to
![]() $-$
, respectively
$-$
, respectively
![]() $-$
to
$-$
to
![]() $+$
.
$+$
.
Perhaps a reader can suggest (and apply the method to) a more significant example.
6. Further potential applications
One area to which the above results might be usefully applied is metastability. Metastability is the phenomenon that an ergodic process may spend long times exploring restricted subsets of the support of the probability distribution, switching between them infrequently but sufficiently to achieve ergodicity in the long run. For an infinite limit, there may be more than one stationary distribution. One reference is [Reference Bovier and den Hollander5].
As an application of the result, we can start from [Reference Davies6] in which the hypothesis is a reversible Markov process in continuous time with spectrum in
![]() $[\!-\!\varepsilon,0] \cup [\!-\!\infty,-1]$
such that each function in the image of the spectral projection P for
$[\!-\!\varepsilon,0] \cup [\!-\!\infty,-1]$
such that each function in the image of the spectral projection P for
![]() $[\!-\!\varepsilon,0]$
is bounded, and it is proved that there is a partition of the state spaces into ‘metastable regions’. It is not clear to me, however, whether there are relevant examples satisfying the hypotheses. We might think that Glauber dynamics of the 2D Ising model below the critical temperature would qualify, but I am not aware that it is proved to have a spectral gap. Nevertheless, if there are examples on product spaces then the result of the present paper proves robustness of spectral gap and hence of the phenomenon of metastability.
$[\!-\!\varepsilon,0]$
is bounded, and it is proved that there is a partition of the state spaces into ‘metastable regions’. It is not clear to me, however, whether there are relevant examples satisfying the hypotheses. We might think that Glauber dynamics of the 2D Ising model below the critical temperature would qualify, but I am not aware that it is proved to have a spectral gap. Nevertheless, if there are examples on product spaces then the result of the present paper proves robustness of spectral gap and hence of the phenomenon of metastability.
We could envisage the result also being useful to treat perturbation of Markov dynamics with more than one stationary distribution, for example with more than one communicating component. Addition of some interaction between the communicating components typically reduces the system to a single communicating component, but the result of this paper shows there is a continuation of the spectral projection to a spectral projection with spectrum contained near 1 and the same rank (equal to the original number of communicating components), and it gives strong control over the resulting continuation. More substantially, we would like to deduce something about metastability in ergodic finite versions of infinite PCA with non-unique stationary distribution.
Another possible application is to perturbations of product systems in which the units all have simple eigenvalue +1 and isolated spectrum near some
![]() $\lambda$
in the open unit disk. The conclusion is that there persists an invariant subspace with decay constant near
$\lambda$
in the open unit disk. The conclusion is that there persists an invariant subspace with decay constant near
![]() $\lambda$
.
$\lambda$
.
7. Discussion
It has been proved here that every spectral projection of a stochastic operator on a product space persists
![]() $C^r$
-smoothly with respect to the norm (1) for
$C^r$
-smoothly with respect to the norm (1) for
![]() $C^r$
-smooth changes in the transition operator, again measured using (1). This generalises the case of the rank-one projection onto a stationary distribution, treated in [Reference MacKay13].
$C^r$
-smooth changes in the transition operator, again measured using (1). This generalises the case of the rank-one projection onto a stationary distribution, treated in [Reference MacKay13].
Second-order perturbation theory has been developed for families of such operators and an example treated. Potential applications have also been suggested to robustness of metastability and some other uses for multi-component stochastic processes.
A reviewer raised the question of relations to some other literature. In particular, linear operators on a general class of Banach spaces with a positive cone and a multiple eigenvalue
![]() $+1$
are considered in [Reference Erkurşun-Özcan and Mukhamedov8, Reference Mukhamedov and Al-Rawashdeh15]. It appears, however, that our space does not satisfy the additivity property that they require for the norm on vectors in the positive cone. Furthermore, those papers do not consider the question of persistence of the spectral projection for the multiple eigenvalue, nor treat any other spectral projections. Nor do they address the difficulties with making useful norms on large tensor products.
$+1$
are considered in [Reference Erkurşun-Özcan and Mukhamedov8, Reference Mukhamedov and Al-Rawashdeh15]. It appears, however, that our space does not satisfy the additivity property that they require for the norm on vectors in the positive cone. Furthermore, those papers do not consider the question of persistence of the spectral projection for the multiple eigenvalue, nor treat any other spectral projections. Nor do they address the difficulties with making useful norms on large tensor products.
Looking to the future, an additional benefit of the work of this paper is to gain some understanding of spectral projections on large tensor products with a view to tackling the quantum case. In addition to its clear role in condensed matter physics, the quantum case has taken on enhanced interest because of the problem of designing quantum registers for quantum computing. In many quantum contexts, we want the subspace corresponding to an isolated part of the spectrum to be robust to small perturbations. Yet, the Anderson orthogonalisation catastrophe [Reference Anderson1] apparently precludes this. The approach here suggests that with a suitable new norm, we could nonetheless prove persistence of spectral projections for Hermitian operators on large tensor products.
Appendix A. Dual of space Z of neutral measures
Here it is proved that the dual space
![]() $Z^*$
of the space Z of neutral measures with the
$Z^*$
of the space Z of neutral measures with the
![]() $|\cdot |_Z$
-norm can be regarded naturally as the quotient
$|\cdot |_Z$
-norm can be regarded naturally as the quotient
![]() $F/C$
of the space F of Dobrushin smooth functions by the constant ones C.
$F/C$
of the space F of Dobrushin smooth functions by the constant ones C.
Given
![]() $f \in F$
, define
$f \in F$
, define
![]() $\hat{f}\colon Z \to \mathbb{R}$
by
$\hat{f}\colon Z \to \mathbb{R}$
by
![]() $\hat{f}(\mu) = \mu(f)$
. Then
$\hat{f}(\mu) = \mu(f)$
. Then
![]() $\hat{f}$
is linear. Also, it is bounded:
$\hat{f}$
is linear. Also, it is bounded:
![]() $\hat{f}(\mu) = \mu(f) \le |\mu|_Z |f|_F$
. Thus,
$\hat{f}(\mu) = \mu(f) \le |\mu|_Z |f|_F$
. Thus,
![]() $\hat{f} \in Z^*$
with
$\hat{f} \in Z^*$
with
![]() $|\hat{f}|_{Z^*} \le |f|_F$
. Adding a constant to f does not change
$|\hat{f}|_{Z^*} \le |f|_F$
. Adding a constant to f does not change
![]() $\hat{f}$
so we can consider
$\hat{f}$
so we can consider
![]() $F/C \subset Z^*$
.
$F/C \subset Z^*$
.
Conversely, given
![]() $u \in Z^*$
, choose a reference point
$u \in Z^*$
, choose a reference point
![]() $a\in X$
and define
$a\in X$
and define
![]() $\check{u}\colon X \to \mathbb{R}$
by
$\check{u}\colon X \to \mathbb{R}$
by
![]() $\check{u}(x) = u(\delta_{xa}) + c$
for arbitrary
$\check{u}(x) = u(\delta_{xa}) + c$
for arbitrary
![]() $c \in \mathbb{R}$
, where, for
$c \in \mathbb{R}$
, where, for
![]() $x,y \in X$
,
$x,y \in X$
,
![]() $\delta_{xy}$
is the dipole measure
$\delta_{xy}$
is the dipole measure
![]() $\delta_x - \delta_y \in Z$
. Then
$\delta_x - \delta_y \in Z$
. Then
![]() $\check{u}(x)-\check{u}(y) = u(\delta_{xy}) \le |u|_{Z^*} |\delta_{xy}|_Z$
. Taking x, y to differ at only site s, we obtain that
$\check{u}(x)-\check{u}(y) = u(\delta_{xy}) \le |u|_{Z^*} |\delta_{xy}|_Z$
. Taking x, y to differ at only site s, we obtain that
![]() $|\delta_{xy}|_Z = \sup_{f \in F\setminus C} ({f(x)-f(y)}/{|f|_F})$
is attained for
$|\delta_{xy}|_Z = \sup_{f \in F\setminus C} ({f(x)-f(y)}/{|f|_F})$
is attained for
![]() $f(z) = d_s(z_s,y_s)$
, giving value
$f(z) = d_s(z_s,y_s)$
, giving value
![]() $d_s(x_s,y_s)$
. Hence
$d_s(x_s,y_s)$
. Hence
![]() $\Delta_s(\check{u}) \le |u|_{Z^*}$
. Given
$\Delta_s(\check{u}) \le |u|_{Z^*}$
. Given
![]() $\gamma \in (0,1)$
, for each
$\gamma \in (0,1)$
, for each
![]() $s\in S$
there exist
$s\in S$
there exist
![]() $x^{(s)}, y^{(s)}$
, differing only on site s, such that
$x^{(s)}, y^{(s)}$
, differing only on site s, such that
![]() $\check{u}(x^{(s)})-\check{u}(y^{(s)}) \ge \gamma \Delta_s(\check{u}) d_s\big(x^{(s)}_s,y^{(s)}_s\big)$
. Choose
$\check{u}(x^{(s)})-\check{u}(y^{(s)}) \ge \gamma \Delta_s(\check{u}) d_s\big(x^{(s)}_s,y^{(s)}_s\big)$
. Choose
where S
′ is any finite subset of S. Then
![]() $\mu \in Z$
and
$\mu \in Z$
and
![]() $|\mu|_Z\le 1$
by using the Lipschitz bounds for
$|\mu|_Z\le 1$
by using the Lipschitz bounds for
![]() $f \in F$
on
$f \in F$
on
![]() $\mu(f)$
; furthermore,
$\mu(f)$
; furthermore,
![]() $|\mu|_Z \ge 1$
by choosing
$|\mu|_Z \ge 1$
by choosing
![]() $f(x) = \sum_{s\in S'} \alpha_s d_s\big(x_s,y^{(s)}_s\big)$
, any
$f(x) = \sum_{s\in S'} \alpha_s d_s\big(x_s,y^{(s)}_s\big)$
, any
![]() $\alpha_s>0$
. Thus
$\alpha_s>0$
. Thus
![]() $|\mu|_Z=1$
. It follows that
$|\mu|_Z=1$
. It follows that
![]() $\sum_{s\in S'} \Delta_s(\check{u}) \le \gamma |u|_{Z^*}$
for all
$\sum_{s\in S'} \Delta_s(\check{u}) \le \gamma |u|_{Z^*}$
for all
![]() $\gamma<1$
and
$\gamma<1$
and
![]() $S'\subset S$
. So
$S'\subset S$
. So
![]() $\check{u} \in F$
and
$\check{u} \in F$
and
![]() $|\check{u}|_F \le |u|_{Z^*}$
. So we can consider
$|\check{u}|_F \le |u|_{Z^*}$
. So we can consider
![]() $Z^* \subset F/C$
.
$Z^* \subset F/C$
.
From the bounds on the norms in the two directions, we deduce equality:
![]() $|\hat{f}|_{Z^*} = |f|_F$
and
$|\hat{f}|_{Z^*} = |f|_F$
and
![]() $|\check{u}|_F = |u|_{Z^*}$
.
$|\check{u}|_F = |u|_{Z^*}$
.
Note, however, that the dual of
![]() $F/C$
is strictly larger than Z. It contains limits of sequences of dipoles, for example [Reference Arens and Eells2].
$F/C$
is strictly larger than Z. It contains limits of sequences of dipoles, for example [Reference Arens and Eells2].
Appendix B. Completeness of
 $\mathcal{P}$
in the D-metric
$\mathcal{P}$
in the D-metric
We prove this via a few artificial constructions for which precursors occur in [Reference Föllmer and Horst9, Reference Steif18].
We first metrise product-topology on X, by choosing an enumeration of S (i.e. label the sites by non-negative integers) and an
![]() $\eta>1$
, and using
$\eta>1$
, and using
![]() $d_\eta (x,y) = \sum_j \eta^{-j} d_j(x_j,y_j)$
for some
$d_\eta (x,y) = \sum_j \eta^{-j} d_j(x_j,y_j)$
for some
![]() $\eta>1$
. The sum converges because the diameters of the
$\eta>1$
. The sum converges because the diameters of the
![]() $X_j$
are bounded.
$X_j$
are bounded.
Next, we define the Kantorovich–Rubinstein (KR) metric on
![]() $\mathcal{P}$
with respect to
$\mathcal{P}$
with respect to
![]() $d_\eta$
on X:
$d_\eta$
on X:
As a countable product of complete separable metric spaces, X is a complete separable metric space. For any complete separable metric space X, the space
![]() $\mathcal{M}(X)$
of real-valued Borel measures on X is the dual of the space of continuous functions
$\mathcal{M}(X)$
of real-valued Borel measures on X is the dual of the space of continuous functions
![]() $X \to \mathbb{R}$
with
$X \to \mathbb{R}$
with
![]() $\sup$
-norm
$\sup$
-norm
![]() $|\cdot |_\infty$
, and the KR metric metrises weak
$|\cdot |_\infty$
, and the KR metric metrises weak
![]() $^*$
convergence on
$^*$
convergence on
![]() $\mathcal{P} (X)$
[Reference Villani23], denoted by
$\mathcal{P} (X)$
[Reference Villani23], denoted by
![]() $\rightharpoonup$
(confusingly, weak
$\rightharpoonup$
(confusingly, weak
![]() $^*$
convergence on
$^*$
convergence on
![]() $\mathcal{M}$
is often called weak convergence).
$\mathcal{M}$
is often called weak convergence).
Then we define an auxiliary metric
![]() $\rho$
on
$\rho$
on
![]() $\mathcal{P}$
:
$\mathcal{P}$
:
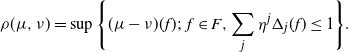 \begin{align*}\rho(\mu,\nu) = \sup \Bigg\{(\mu-\nu)(f);\;\; f \in F, \sum_j \eta^j \Delta_j(f) \le 1\Bigg\}.\end{align*}
\begin{align*}\rho(\mu,\nu) = \sup \Bigg\{(\mu-\nu)(f);\;\; f \in F, \sum_j \eta^j \Delta_j(f) \le 1\Bigg\}.\end{align*}
This is clearly a semi-metric. To prove it is a metric, if
![]() $\mu \ne \nu$
there exists a continuous f with
$\mu \ne \nu$
there exists a continuous f with
![]() $(\mu-\nu)f \ne 0$
; approximate f by g with
$(\mu-\nu)f \ne 0$
; approximate f by g with
![]() $\sum_j \eta^j \Delta_j g < \infty$
and
$\sum_j \eta^j \Delta_j g < \infty$
and
![]() $|f-g|_\infty$
small enough that
$|f-g|_\infty$
small enough that
![]() $(\mu-\nu)g \ne 0$
.
$(\mu-\nu)g \ne 0$
.
We show that
![]() $\rho \le d_\mathrm{KR}$
. If
$\rho \le d_\mathrm{KR}$
. If
![]() $\sum_j \eta^j \Delta_j f \le 1$
then, for any
$\sum_j \eta^j \Delta_j f \le 1$
then, for any
![]() $x,y \in X$
,
$x,y \in X$
,
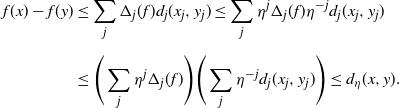 \begin{align*} f(x)-f(y) & \le \sum_j \Delta_j (f) d_j(x_j,y_j) \le \sum_j \eta^j \Delta_j(f) \eta^{-j} d_j(x_j,y_j) \\[5pt] & \le \Bigg(\sum_j \eta^j \Delta_j(f)\Bigg) \Bigg(\sum_j \eta^{-j} d_j(x_j,y_j)\Bigg) \le d_\eta (x,y).\end{align*}
\begin{align*} f(x)-f(y) & \le \sum_j \Delta_j (f) d_j(x_j,y_j) \le \sum_j \eta^j \Delta_j(f) \eta^{-j} d_j(x_j,y_j) \\[5pt] & \le \Bigg(\sum_j \eta^j \Delta_j(f)\Bigg) \Bigg(\sum_j \eta^{-j} d_j(x_j,y_j)\Bigg) \le d_\eta (x,y).\end{align*}
So the set of f in the definition of
![]() $\rho$
is a subset of that for
$\rho$
is a subset of that for
![]() $d_\mathrm{KR}$
, so
$d_\mathrm{KR}$
, so
![]() $\rho(\mu,\nu) \le d_\mathrm{KR}(\mu,\nu)$
.
$\rho(\mu,\nu) \le d_\mathrm{KR}(\mu,\nu)$
.
It follows that if
![]() $\mu_n \rightharpoonup \mu$
then
$\mu_n \rightharpoonup \mu$
then
![]() $\rho(\mu_n,\mu) \to 0$
. Although not needed, the converse is also true: if
$\rho(\mu_n,\mu) \to 0$
. Although not needed, the converse is also true: if
![]() $\rho(\mu_n,\mu)\to 0$
then, given f continuous and
$\rho(\mu_n,\mu)\to 0$
then, given f continuous and
![]() $\varepsilon>0$
, there exists
$\varepsilon>0$
, there exists
![]() $K\subset S$
such that
$K\subset S$
such that
![]() $f=f_K+\tilde{f}$
with
$f=f_K+\tilde{f}$
with
![]() $f_K$
independent of coordinates outside K and
$f_K$
independent of coordinates outside K and
![]() $|\tilde{f}|\le \varepsilon/4$
. So there exists N such that
$|\tilde{f}|\le \varepsilon/4$
. So there exists N such that
![]() $(\mu_n-\mu)(f_K) < \varepsilon/2$
for
$(\mu_n-\mu)(f_K) < \varepsilon/2$
for
![]() $n\ge N$
. Also, for all n,
$n\ge N$
. Also, for all n,
![]() $(\mu_n-\mu)(\tilde{f}) < \varepsilon/2$
. Thus,
$(\mu_n-\mu)(\tilde{f}) < \varepsilon/2$
. Thus,
![]() $(\mu_n-\mu)(f) <\varepsilon$
for
$(\mu_n-\mu)(f) <\varepsilon$
for
![]() $n\ge N$
. So
$n\ge N$
. So
![]() $\mu_n\rightharpoonup \mu$
. So
$\mu_n\rightharpoonup \mu$
. So
![]() $\rho$
metrises weak
$\rho$
metrises weak
![]() $^*$
convergence in
$^*$
convergence in
![]() $\mathcal{P}$
.
$\mathcal{P}$
.
It follows that
![]() $\mathcal{P}$
is complete in
$\mathcal{P}$
is complete in
![]() $\rho$
, because suppose
$\rho$
, because suppose
![]() $\mu_n$
is Cauchy in
$\mu_n$
is Cauchy in
![]() $\rho$
. Given
$\rho$
. Given
![]() $\varepsilon>0$
there exists N such that
$\varepsilon>0$
there exists N such that
![]() $n,m\ge N$
imply
$n,m\ge N$
imply
![]() $\rho(\mu_n,\mu_m) < \varepsilon$
.
$\rho(\mu_n,\mu_m) < \varepsilon$
.
![]() $\mathcal{P}$
is weak
$\mathcal{P}$
is weak
![]() $^*$
sequentially compact in the usual topology. Thus there is a weak
$^*$
sequentially compact in the usual topology. Thus there is a weak
![]() $^*$
-convergent subsequence to some
$^*$
-convergent subsequence to some
![]() $\mu \in \mathcal{P}$
:
$\mu \in \mathcal{P}$
:
![]() $\mu_{n_k} \rightharpoonup \mu$
. Then
$\mu_{n_k} \rightharpoonup \mu$
. Then
![]() $\rho(\mu_{n_k},\mu) \to 0$
so, given
$\rho(\mu_{n_k},\mu) \to 0$
so, given
![]() $\varepsilon>0$
,
$\varepsilon>0$
,
![]() $\rho(\mu_n,\mu) \le \rho(\mu_n,\mu_{n_k}) + \rho(\mu_{n_k},\mu) < 2\varepsilon$
for
$\rho(\mu_n,\mu) \le \rho(\mu_n,\mu_{n_k}) + \rho(\mu_{n_k},\mu) < 2\varepsilon$
for
![]() $n\ge N$
and sufficiently large k. Thus,
$n\ge N$
and sufficiently large k. Thus,
![]() $\rho(\mu_n,\mu) \to 0$
.
$\rho(\mu_n,\mu) \to 0$
.
We also have
![]() $\rho \le D$
: if
$\rho \le D$
: if
![]() $\sum_j \eta^j \Delta_j(f) \le 1$
then
$\sum_j \eta^j \Delta_j(f) \le 1$
then
So, given a Cauchy sequence
![]() $\mu_n$
in D, it is Cauchy in
$\mu_n$
in D, it is Cauchy in
![]() $\rho$
, thus
$\rho$
, thus
![]() $\rho$
-converges to some
$\rho$
-converges to some
![]() $\mu \in \mathcal{P}$
. Given
$\mu \in \mathcal{P}$
. Given
![]() $\varepsilon>0$
there exists
$\varepsilon>0$
there exists
![]() $N(\varepsilon)$
such that
$N(\varepsilon)$
such that
![]() $D(\mu_n,\mu_m)<\varepsilon/4$
for
$D(\mu_n,\mu_m)<\varepsilon/4$
for
![]() $n,m \ge N(\varepsilon)$
; it also follows that
$n,m \ge N(\varepsilon)$
; it also follows that
![]() $\rho(\mu_m,\mu) <\varepsilon/4$
for
$\rho(\mu_m,\mu) <\varepsilon/4$
for
![]() $m \ge N(\varepsilon)$
. Given
$m \ge N(\varepsilon)$
. Given
![]() $f\in F$
, a reference point
$f\in F$
, a reference point
![]() $0 \in X$
and a finite subset
$0 \in X$
and a finite subset
![]() $K\subset S$
, let
$K\subset S$
, let
![]() $f_K(x) = f(x_K,0_{S\setminus K})$
and
$f_K(x) = f(x_K,0_{S\setminus K})$
and
![]() $\tilde{f}=f-f_K$
. Then
$\tilde{f}=f-f_K$
. Then
![]() $\Delta_j f_K \le \Delta_j f$
for
$\Delta_j f_K \le \Delta_j f$
for
![]() $j \in K$
and is 0 otherwise. There exists
$j \in K$
and is 0 otherwise. There exists
![]() $K\subset S$
such that
$K\subset S$
such that
![]() $|\tilde{f}| \le \frac14 \varepsilon |f|_F$
. So
$|\tilde{f}| \le \frac14 \varepsilon |f|_F$
. So
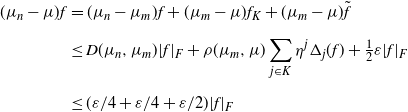 \begin{align*} (\mu_n-\mu)f & = (\mu_n-\mu_m)f + (\mu_m-\mu)f_K + (\mu_m-\mu)\tilde{f} \\[5pt] & \le D(\mu_n,\mu_m) |f|_F + \rho(\mu_m,\mu) \sum_{j\in K} \eta^j \Delta_j(f) + \tfrac12 \varepsilon |f|_F \\[5pt] & \le (\varepsilon/4 + \varepsilon/4 + \varepsilon/2)|f|_F\end{align*}
\begin{align*} (\mu_n-\mu)f & = (\mu_n-\mu_m)f + (\mu_m-\mu)f_K + (\mu_m-\mu)\tilde{f} \\[5pt] & \le D(\mu_n,\mu_m) |f|_F + \rho(\mu_m,\mu) \sum_{j\in K} \eta^j \Delta_j(f) + \tfrac12 \varepsilon |f|_F \\[5pt] & \le (\varepsilon/4 + \varepsilon/4 + \varepsilon/2)|f|_F\end{align*}
for
![]() $n \ge N(\varepsilon)$
and
$n \ge N(\varepsilon)$
and
![]() $m\ge \max\!(N(\varepsilon),N(\varepsilon \eta^{-k}))$
, where k is the largest label of K. Thus,
$m\ge \max\!(N(\varepsilon),N(\varepsilon \eta^{-k}))$
, where k is the largest label of K. Thus,
![]() $D(\mu_n,\mu) \to 0$
as
$D(\mu_n,\mu) \to 0$
as
![]() $n \to \infty$
. So
$n \to \infty$
. So
![]() $(\mathcal{P},D)$
is complete.
$(\mathcal{P},D)$
is complete.
Acknowledgements
I am grateful to Nick Higham for pointers to the literature on Sylvester equations. I dedicate this paper to his memory. I am also grateful to a reviewer who insisted that I give more complete proofs, which led me to realise that my statement in [Reference MacKay13] that
![]() $\mathcal{P}$
is complete with respect to the D-metric required proof (given here in Appendix B).
$\mathcal{P}$
is complete with respect to the D-metric required proof (given here in Appendix B).
Funding information
There are no funding bodies to thank relating to the creation of this article.
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this article.



