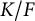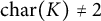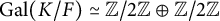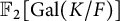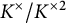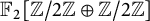1 Introduction
1.1 Background and motivation
Let K be a field, and write
![]() $\xi _{p}$
for a primitive pth root of unity. We write
$\xi _{p}$
for a primitive pth root of unity. We write
![]() $K_{\text {sep}}$
for a separable closure of K, and
$K_{\text {sep}}$
for a separable closure of K, and
![]() $K(p)$
for the maximal p-extension within
$K(p)$
for the maximal p-extension within
![]() $K_{\text {sep}}$
. Each of these extensions is Galois. The absolute Galois group of K is the group
$K_{\text {sep}}$
. Each of these extensions is Galois. The absolute Galois group of K is the group
![]() $G_{K}:=\mathrm {Gal}(K_{\text {sep}}/K)$
. The group
$G_{K}:=\mathrm {Gal}(K_{\text {sep}}/K)$
. The group
![]() $G_{K}(p):=\mathrm {Gal}(K(p)/K)$
is the maximal pro-p quotient of
$G_{K}(p):=\mathrm {Gal}(K(p)/K)$
is the maximal pro-p quotient of
![]() $G_{K}$
. For convenience, we will call
$G_{K}$
. For convenience, we will call
![]() $G_{K}(p)$
the absolute p-Galois group of K. One of the major open problems in Galois theory is to determine those profinite groups G for which there exists some field K with
$G_{K}(p)$
the absolute p-Galois group of K. One of the major open problems in Galois theory is to determine those profinite groups G for which there exists some field K with
![]() $G_{K} \simeq G$
, i.e., to distinguish absolute Galois groups within the class of profinite groups. This problem is very difficult. The analogous question for pro-p groups—to distinguish absolute p-Galois groups within the class of pro-p groups—is also unsolved and extremely difficult.
$G_{K} \simeq G$
, i.e., to distinguish absolute Galois groups within the class of profinite groups. This problem is very difficult. The analogous question for pro-p groups—to distinguish absolute p-Galois groups within the class of pro-p groups—is also unsolved and extremely difficult.
How does one look for those properties that distinguish absolute p-Galois groups from the broader class of pro-p groups? To motivate the perspective pursued in this paper, note that since
![]() $G_{K}(p)$
is a pro-p group, it is natural to study it recursively through its Frattini subgroup and its quotient. This quotient is the maximal elementary p-abelian quotient of
$G_{K}(p)$
is a pro-p group, it is natural to study it recursively through its Frattini subgroup and its quotient. This quotient is the maximal elementary p-abelian quotient of
![]() $G_{K}(p)$
, which by Kummer theory (assuming
$G_{K}(p)$
, which by Kummer theory (assuming
![]() $\xi _{p} \in K$
) corresponds to
$\xi _{p} \in K$
) corresponds to
![]() $J(K):=K^{\times }/K^{\times p}$
. In the case that K is itself a Galois extension of a field F, one then has a natural action of
$J(K):=K^{\times }/K^{\times p}$
. In the case that K is itself a Galois extension of a field F, one then has a natural action of
![]() $\text {Gal}(K/F)$
on
$\text {Gal}(K/F)$
on
![]() $J(K)$
. (Throughout the remainder of this discussion, we will assume that
$J(K)$
. (Throughout the remainder of this discussion, we will assume that
![]() $\mathrm {Gal}(K/F)$
is a p-group, just to stay firmly planted in the context of p-groups.) One field-theoretic lens for studying
$\mathrm {Gal}(K/F)$
is a p-group, just to stay firmly planted in the context of p-groups.) One field-theoretic lens for studying
![]() $G_{K}(p)$
, therefore, is to determine the structure of
$G_{K}(p)$
, therefore, is to determine the structure of
![]() $J(K)$
as a module over
$J(K)$
as a module over
![]() $\mathbb {F}_{p}[\mathrm {Gal}(K/F)]$
. It is worth noting that the submodules of
$\mathbb {F}_{p}[\mathrm {Gal}(K/F)]$
. It is worth noting that the submodules of
![]() $J(K)$
are in bijection with the elementary p-abelian extensions of K that are additionally Galois over F (see [Reference Waterhouse31]), again assuming
$J(K)$
are in bijection with the elementary p-abelian extensions of K that are additionally Galois over F (see [Reference Waterhouse31]), again assuming
![]() $\xi _{p} \in K$
.
$\xi _{p} \in K$
.
Given that the modular representation theory of
![]() $\mathbb {F}_{p}[\mathrm {Gal}(K/F)]$
is most tractable when
$\mathbb {F}_{p}[\mathrm {Gal}(K/F)]$
is most tractable when
![]() $\mathrm {Gal}(K/F)$
is cyclic, this is a natural place to begin. Some early work by Borevič and Fadeev (see [Reference Borevič7, Reference Faddeev12]) examined the module structure of
$\mathrm {Gal}(K/F)$
is cyclic, this is a natural place to begin. Some early work by Borevič and Fadeev (see [Reference Borevič7, Reference Faddeev12]) examined the module structure of
![]() $J(K)$
when K is a local field and
$J(K)$
when K is a local field and
![]() $\mathrm {Gal}(K/F) \simeq \mathbb {Z}/p\mathbb {Z}$
using local class field theory. Subsequently, Mináč and Swallow [Reference Mináč and Swallow26] showed that the module
$\mathrm {Gal}(K/F) \simeq \mathbb {Z}/p\mathbb {Z}$
using local class field theory. Subsequently, Mináč and Swallow [Reference Mináč and Swallow26] showed that the module
![]() $J(K)$
can be computed when
$J(K)$
can be computed when
![]() $\mathrm {Gal}(K/F) \simeq \mathbb {Z}/p\mathbb {Z}$
assuming only
$\mathrm {Gal}(K/F) \simeq \mathbb {Z}/p\mathbb {Z}$
assuming only
![]() $\xi _{p} \in K$
and without such heavy machinery.
$\xi _{p} \in K$
and without such heavy machinery.
The surprise from this result is twofold. First, despite the fact that the field K is completely general, the
![]() $\mathbb {F}_{p}[\mathrm {Gal}(K/F)]$
-module
$\mathbb {F}_{p}[\mathrm {Gal}(K/F)]$
-module
![]() $J(K)$
is far more stratified than a “random”
$J(K)$
is far more stratified than a “random”
![]() $\mathbb {F}_{p}[\mathbb {Z}/p\mathbb {Z}]$
-module: whereas a general
$\mathbb {F}_{p}[\mathbb {Z}/p\mathbb {Z}]$
-module: whereas a general
![]() $\mathbb {F}_{p}[\mathbb {Z}/p\mathbb {Z}]$
-module can have summands drawn from any one of p possible isomorphism types, the decomposition of
$\mathbb {F}_{p}[\mathbb {Z}/p\mathbb {Z}]$
-module can have summands drawn from any one of p possible isomorphism types, the decomposition of
![]() $J(K)$
as an
$J(K)$
as an
![]() $\mathbb {F}_{p}[\mathrm {Gal}(K/F)]$
-module involves at most three isomorphism classes of indecomposable summands (free cyclic modules, trivial cyclic modules, and at most one cyclic module of dimension
$\mathbb {F}_{p}[\mathrm {Gal}(K/F)]$
-module involves at most three isomorphism classes of indecomposable summands (free cyclic modules, trivial cyclic modules, and at most one cyclic module of dimension
![]() $2$
). The second surprise comes from the proof of the result itself. Although this decomposition requires a lot of careful work, the machinery needed for the proof is actually quite elementary. Indeed, the key theoretical tool in the proof is Hilbert’s Satz 90.
$2$
). The second surprise comes from the proof of the result itself. Although this decomposition requires a lot of careful work, the machinery needed for the proof is actually quite elementary. Indeed, the key theoretical tool in the proof is Hilbert’s Satz 90.
The benefit of an elementary approach to the decomposition of
![]() $J(K)$
when
$J(K)$
when
![]() $\mathrm {Gal}(K/F) \simeq \mathbb {Z}/p\mathbb {Z}$
and
$\mathrm {Gal}(K/F) \simeq \mathbb {Z}/p\mathbb {Z}$
and
![]() $\xi _{p} \in K$
is not just that it lets one compute this module for arbitrary K, but also that it provides a road map for how one might generalize this decomposition to a broader class of Galois modules. Indeed, generalizations of this type have been carried out in a variety of contexts. In [Reference Mináč, Schultz and Swallow23], three of the authors gave the decomposition of
$\xi _{p} \in K$
is not just that it lets one compute this module for arbitrary K, but also that it provides a road map for how one might generalize this decomposition to a broader class of Galois modules. Indeed, generalizations of this type have been carried out in a variety of contexts. In [Reference Mináč, Schultz and Swallow23], three of the authors gave the decomposition of
![]() $J(K)$
whenever
$J(K)$
whenever
![]() $\mathrm {Gal}(K/F) \simeq \mathbb {Z}/p^{n}\mathbb {Z}$
. Looking past power classes, observe that when
$\mathrm {Gal}(K/F) \simeq \mathbb {Z}/p^{n}\mathbb {Z}$
. Looking past power classes, observe that when
![]() $i = 1$
and
$i = 1$
and
![]() $\xi _{p} \in K$
, we have
$\xi _{p} \in K$
, we have
![]() $H^{i}(G_{K}(p),\mathbb {F}_{p}) \simeq K^{\times }/K^{\times p}$
as Galois modules, so higher cohomology groups provide a new family of Galois modules to investigate. Using the connection between Milnor K-theory and Galois cohomology—together with the generalization of Hilbert 90 to this context—two of the authors and Lemire gave a decomposition of the Galois cohomology groups
$H^{i}(G_{K}(p),\mathbb {F}_{p}) \simeq K^{\times }/K^{\times p}$
as Galois modules, so higher cohomology groups provide a new family of Galois modules to investigate. Using the connection between Milnor K-theory and Galois cohomology—together with the generalization of Hilbert 90 to this context—two of the authors and Lemire gave a decomposition of the Galois cohomology groups
![]() $H^{i}(G_{K}(p),\mathbb {F}_{p})$
in [Reference Lemire, Mináč and Swallow20] under the assumption that
$H^{i}(G_{K}(p),\mathbb {F}_{p})$
in [Reference Lemire, Mináč and Swallow20] under the assumption that
![]() $\mathrm {Gal}(K/F) \simeq \mathbb {Z}/p\mathbb {Z}$
and
$\mathrm {Gal}(K/F) \simeq \mathbb {Z}/p\mathbb {Z}$
and
![]() $\xi _{p} \in K$
. Some partial results for the structure of
$\xi _{p} \in K$
. Some partial results for the structure of
![]() $H^{i}(G_{K}(p),\mathbb {F}_{p})$
when
$H^{i}(G_{K}(p),\mathbb {F}_{p})$
when
![]() $\mathrm {Gal}(K/F) \simeq \mathbb {Z}/p^{n}\mathbb {Z}$
are given in [Reference Lemire, Mináč, Schultz and Swallow19]. Generalizations to the case where K is characteristic p (but
$\mathrm {Gal}(K/F) \simeq \mathbb {Z}/p^{n}\mathbb {Z}$
are given in [Reference Lemire, Mináč, Schultz and Swallow19]. Generalizations to the case where K is characteristic p (but
![]() $\mathrm {Gal}(K/F)$
is still assumed to be a cyclic p-group) have also been explored in [Reference Berg and Schultz5, Reference Bhandari, Lemire, Mináč and Swallow6, Reference Mináč, Schultz and Swallow25, Reference Schultz29].
$\mathrm {Gal}(K/F)$
is still assumed to be a cyclic p-group) have also been explored in [Reference Berg and Schultz5, Reference Bhandari, Lemire, Mináč and Swallow6, Reference Mináč, Schultz and Swallow25, Reference Schultz29].
As with the original decomposition of
![]() $J(K)$
in [Reference Mináč and Swallow26], these subsequent module decompositions contain far fewer isomorphism classes of indecomposables than one might expect a priori. These stratified decompositions have, in turn, been translated into properties that distinguish absolute p-Galois groups within the larger class of pro-p groups. For example, using the structure of
$J(K)$
in [Reference Mináč and Swallow26], these subsequent module decompositions contain far fewer isomorphism classes of indecomposables than one might expect a priori. These stratified decompositions have, in turn, been translated into properties that distinguish absolute p-Galois groups within the larger class of pro-p groups. For example, using the structure of
![]() $J(K)$
, a variety of automatic realization and realization multiplicity results have been proved (see [Reference Berg and Schultz5, Reference Chebolu, Mináč and Schultz8, Reference Mináč, Schultz and Swallow24, Reference Mináč and Swallow27, Reference Schultz29]). The module structure for cohomology groups computed in [Reference Lemire, Mináč and Swallow20] was used in [Reference Benson, Lemire, Mináč and Swallow4] to find a number of pro-p groups that are not absolute p-Galois groups.
$J(K)$
, a variety of automatic realization and realization multiplicity results have been proved (see [Reference Berg and Schultz5, Reference Chebolu, Mináč and Schultz8, Reference Mináč, Schultz and Swallow24, Reference Mináč and Swallow27, Reference Schultz29]). The module structure for cohomology groups computed in [Reference Lemire, Mináč and Swallow20] was used in [Reference Benson, Lemire, Mináč and Swallow4] to find a number of pro-p groups that are not absolute p-Galois groups.
It would be natural to assume that the previous module computations are possible because the modular representation theory for the group ring
![]() $\mathbb {F}_{p}[\mathrm {Gal}(K/F)]$
is simple when
$\mathbb {F}_{p}[\mathrm {Gal}(K/F)]$
is simple when
![]() $\mathrm {Gal}(K/F)$
is cyclic—namely, in this case, there are
$\mathrm {Gal}(K/F)$
is cyclic—namely, in this case, there are
![]() $|\mathrm {Gal}(K/F)|$
isomorphism classes of indecomposables, and each of them is cyclic. In contrast, if G is a noncyclic elementary p-abelian group, then there are infinitely many isomorphism classes of indecomposable
$|\mathrm {Gal}(K/F)|$
isomorphism classes of indecomposables, and each of them is cyclic. In contrast, if G is a noncyclic elementary p-abelian group, then there are infinitely many isomorphism classes of indecomposable
![]() $\mathbb {F}_{p}[G]$
-modules (and often it is impossible to give a full classification of indecomposables). There has been some work which provides partial information about Galois modules in these more complicated settings, recovering information about the Socle series or arguing that the modules are constant Jordan type in special cases [Reference Adem, Gao, Karagueuzian and Mináč1, Reference Eimer11, Reference Mináč, Swallow and Topaz28]. However, these modules were not determined completely.
$\mathbb {F}_{p}[G]$
-modules (and often it is impossible to give a full classification of indecomposables). There has been some work which provides partial information about Galois modules in these more complicated settings, recovering information about the Socle series or arguing that the modules are constant Jordan type in special cases [Reference Adem, Gao, Karagueuzian and Mináč1, Reference Eimer11, Reference Mináč, Swallow and Topaz28]. However, these modules were not determined completely.
In this paper, we provide a decomposition for
![]() $J(K)$
as an
$J(K)$
as an
![]() $\mathbb {F}_{2}[\mathrm {Gal}(K/F)]$
-module when
$\mathbb {F}_{2}[\mathrm {Gal}(K/F)]$
-module when
![]() $\mathrm {Gal}(K/F) \simeq \mathbb {Z}/2\mathbb {Z} \oplus \mathbb {Z}/2\mathbb {Z}$
, without any restriction on K other than
$\mathrm {Gal}(K/F) \simeq \mathbb {Z}/2\mathbb {Z} \oplus \mathbb {Z}/2\mathbb {Z}$
, without any restriction on K other than
![]() $\text {char}(K) \neq 2$
. The decomposition follows the two themes that have arisen in the context of cyclic Galois groups: the module structure is far more stratified than one would expect for a general module (across all fields K, the summands are drawn from at most nine indecomposable types), and the decomposition can be determined using relatively concrete techniques and the assistance of Hilbert 90 (see [Reference Dwilewicz, Mináč, Schultz and Swallow10] for a discussion on how one interprets Hilbert 90 for biquadratic extensions). Undoubtedly, this stratified decomposition—both the appearance of some summand types and the exclusion of others—can be translated into new and exciting group-theoretic properties of absolute
$\text {char}(K) \neq 2$
. The decomposition follows the two themes that have arisen in the context of cyclic Galois groups: the module structure is far more stratified than one would expect for a general module (across all fields K, the summands are drawn from at most nine indecomposable types), and the decomposition can be determined using relatively concrete techniques and the assistance of Hilbert 90 (see [Reference Dwilewicz, Mináč, Schultz and Swallow10] for a discussion on how one interprets Hilbert 90 for biquadratic extensions). Undoubtedly, this stratified decomposition—both the appearance of some summand types and the exclusion of others—can be translated into new and exciting group-theoretic properties of absolute
![]() $2$
-Galois groups. The authors are currently looking into such results.
$2$
-Galois groups. The authors are currently looking into such results.
A decomposition of
![]() $J(K)$
when
$J(K)$
when
![]() $\mathrm {Gal}(K/F) \simeq \mathbb {Z}/2\mathbb {Z} \oplus \mathbb {Z}/2\mathbb {Z}$
was completed by the first, second, and fourth authors in 2005 using more technical machinery. (This previous work is not publicly available, but we believe that the results and exposition in the current article supersede and enhance the 2005 work.) A deeper dive into the module from this perspective was explored in [Reference Ferguson13] under the joint supervision of Minač and Swallow. The impetus for revisiting this problem using more ubiquitous tools was to give greater insight into how decompositions for
$\mathrm {Gal}(K/F) \simeq \mathbb {Z}/2\mathbb {Z} \oplus \mathbb {Z}/2\mathbb {Z}$
was completed by the first, second, and fourth authors in 2005 using more technical machinery. (This previous work is not publicly available, but we believe that the results and exposition in the current article supersede and enhance the 2005 work.) A deeper dive into the module from this perspective was explored in [Reference Ferguson13] under the joint supervision of Minač and Swallow. The impetus for revisiting this problem using more ubiquitous tools was to give greater insight into how decompositions for
![]() $J(K)$
(and its ilk) could be carried out when
$J(K)$
(and its ilk) could be carried out when
![]() $\mathrm {Gal}(K/F)$
is some other elementary p-abelian group. This approach has already met with success: it has allowed us to exclude one summand type that appeared in the original decomposition from 2005, and it inspired the recent decomposition of the parameterizing space of elementary p-abelian extensions of K as a module over
$\mathrm {Gal}(K/F)$
is some other elementary p-abelian group. This approach has already met with success: it has allowed us to exclude one summand type that appeared in the original decomposition from 2005, and it inspired the recent decomposition of the parameterizing space of elementary p-abelian extensions of K as a module over
![]() $\mathbb {F}_{p}[\mathrm {Gal}(K/F)]$
whenever
$\mathbb {F}_{p}[\mathrm {Gal}(K/F)]$
whenever
![]() $G_{F}(p)$
is a free, finitely generated pro-p group and
$G_{F}(p)$
is a free, finitely generated pro-p group and
![]() $\mathrm {Gal}(K/F)$
is any finite p-group (see the remark after Theorem 1.1). We are hopeful that the techniques we develop here can inspire the next steps toward investigations of a broader class of elementary p-abelian Galois modules.
$\mathrm {Gal}(K/F)$
is any finite p-group (see the remark after Theorem 1.1). We are hopeful that the techniques we develop here can inspire the next steps toward investigations of a broader class of elementary p-abelian Galois modules.
1.2 Statement of the main result
We first set terminology that will hold for the rest of the paper. Suppose that F is a field with
![]() $\text {char}(F) \neq 2$
and that
$\text {char}(F) \neq 2$
and that
![]() $K/F$
is an extension with
$K/F$
is an extension with
![]() $G:=\mathrm {Gal}(K/F) \simeq \mathbb {Z}/2\mathbb {Z}\oplus \mathbb {Z}/2\mathbb {Z}$
. Let
$G:=\mathrm {Gal}(K/F) \simeq \mathbb {Z}/2\mathbb {Z}\oplus \mathbb {Z}/2\mathbb {Z}$
. Let
![]() $a_{1},a_{2} \in F$
be given so that
$a_{1},a_{2} \in F$
be given so that
![]() $K = F(\sqrt {a_{1}},\sqrt {a_{2}})$
, and let
$K = F(\sqrt {a_{1}},\sqrt {a_{2}})$
, and let
![]() $\sigma _{1},\sigma _{2} \in \text {Gal}(K/F)$
be their duals; that is, we have
$\sigma _{1},\sigma _{2} \in \text {Gal}(K/F)$
be their duals; that is, we have
![]() $\sigma _{i}(\sqrt {a_{j}}) = (-1)^{\delta _{ij}}\sqrt {a_{j}}$
. For
$\sigma _{i}(\sqrt {a_{j}}) = (-1)^{\delta _{ij}}\sqrt {a_{j}}$
. For
![]() $i \in \{1,2\}$
, we define
$i \in \{1,2\}$
, we define
![]() $K_{i} = F(\sqrt {a_{i}})$
. Write
$K_{i} = F(\sqrt {a_{i}})$
. Write
![]() $H_{i}$
for the subgroup of
$H_{i}$
for the subgroup of
![]() $\mathrm {Gal}(K/F)$
which fixes elements in
$\mathrm {Gal}(K/F)$
which fixes elements in
![]() $K_{i}$
, and
$K_{i}$
, and
![]() $\overline {G_{i}}$
for the corresponding quotient group:
$\overline {G_{i}}$
for the corresponding quotient group:
![]() $\overline {G_{i}} := \mathrm {Gal}(K_{i}/F) = \{\overline {\text {id}},\overline {\sigma _{i}}\}.$
In the same spirit, write
$\overline {G_{i}} := \mathrm {Gal}(K_{i}/F) = \{\overline {\text {id}},\overline {\sigma _{i}}\}.$
In the same spirit, write
![]() $K_{3} = F(\sqrt {a_{1}a_{2}})$
, denote the subgroup of
$K_{3} = F(\sqrt {a_{1}a_{2}})$
, denote the subgroup of
![]() $\mathrm {Gal}(K/F)$
which fixes
$\mathrm {Gal}(K/F)$
which fixes
![]() $K_{3}$
as
$K_{3}$
as
![]() $H_{3}$
, and use
$H_{3}$
, and use
![]() $\overline {G_{3}}$
for the corresponding quotient
$\overline {G_{3}}$
for the corresponding quotient
![]() $G/H_{3} = \mathrm {Gal}(K_{3}/F)$
. To round out the notation, let
$G/H_{3} = \mathrm {Gal}(K_{3}/F)$
. To round out the notation, let
![]() $H_{0} = \{\text {id}\}$
(the elements which fix the extension
$H_{0} = \{\text {id}\}$
(the elements which fix the extension
![]() $K/F$
) and
$K/F$
) and
![]() $H_{4} = \mathrm {Gal}(K/F)$
(the elements which fix the extension
$H_{4} = \mathrm {Gal}(K/F)$
(the elements which fix the extension
![]() $F/F$
), and use
$F/F$
), and use
![]() $\overline {G_{0}}$
and
$\overline {G_{0}}$
and
![]() $\overline {G_{4}}$
for their quotients. (See Figure 1.)
$\overline {G_{4}}$
for their quotients. (See Figure 1.)

Figure 1: The lattice of fields for
![]() $K/F$
, with corresponding Galois groups.
$K/F$
, with corresponding Galois groups.
In our result below, we use
![]() $\Omega ^{-n}$
and
$\Omega ^{-n}$
and
![]() $\Omega ^{n}$
to denote certain indecomposable modules of dimension
$\Omega ^{n}$
to denote certain indecomposable modules of dimension
![]() $2n+1$
; more information on these modules can be found in Section 2.
$2n+1$
; more information on these modules can be found in Section 2.
Theorem 1.1 Suppose that
![]() $\text {char}(K) \neq 2$
and that
$\text {char}(K) \neq 2$
and that
![]() $\mathrm {Gal}(K/F) \simeq \mathbb {Z}/2\mathbb {Z}\oplus \mathbb {Z}/2\mathbb {Z}$
. Let
$\mathrm {Gal}(K/F) \simeq \mathbb {Z}/2\mathbb {Z}\oplus \mathbb {Z}/2\mathbb {Z}$
. Let
![]() $J(K) = K^{\times }/K^{\times 2}$
. Then, as an
$J(K) = K^{\times }/K^{\times 2}$
. Then, as an
![]() $\mathbb {F}_{2}[\mathrm {Gal}(K/F)]$
-module, we have
$\mathbb {F}_{2}[\mathrm {Gal}(K/F)]$
-module, we have
where
-
• X is isomorphic to one of the following:
 $\{0\}, \mathbb {F}_{2},\mathbb {F}_{2}\oplus \mathbb {F}_{2}, \Omega ^{-1}, \Omega ^{-2},$
or
$\{0\}, \mathbb {F}_{2},\mathbb {F}_{2}\oplus \mathbb {F}_{2}, \Omega ^{-1}, \Omega ^{-2},$
or
 $\Omega ^{-1}\oplus \Omega ^{-1}$
;
$\Omega ^{-1}\oplus \Omega ^{-1}$
; -
• for each
 $i \in \{0,1,2,3,4\}$
, the summand
$i \in \{0,1,2,3,4\}$
, the summand
 $Y_{i}$
is a direct sum of modules isomorphic to
$Y_{i}$
is a direct sum of modules isomorphic to
 $\mathbb {F}_{2}[\overline {G_{i}}]$
; and
$\mathbb {F}_{2}[\overline {G_{i}}]$
; and -
• for each
 $i \in \{1,2\}$
, the summand
$i \in \{1,2\}$
, the summand
 $Z_{i}$
is a direct sum of modules isomorphic to
$Z_{i}$
is a direct sum of modules isomorphic to
 $\Omega ^{i}$
.
$\Omega ^{i}$
.
Remark 1.2 When
![]() $\text {char}(K) = 2$
, elementary
$\text {char}(K) = 2$
, elementary
![]() $2$
-abelian extensions of K are parameterized by
$2$
-abelian extensions of K are parameterized by
![]() $\mathbb {F}_{2}$
-subspaces of
$\mathbb {F}_{2}$
-subspaces of
![]() $K/\wp {K}$
, where
$K/\wp {K}$
, where
![]() $\wp {K} = \{k^{2}-k: k \in K\}$
. It is therefore natural to ask whether
$\wp {K} = \{k^{2}-k: k \in K\}$
. It is therefore natural to ask whether
![]() $K/\wp (K)$
can be decomposed as an
$K/\wp (K)$
can be decomposed as an
![]() $\mathbb {F}_{2}[\mathrm {Gal}(K/F)]$
-module as well. The answer is a resounding “yes.” Indeed, when p is any prime number and
$\mathbb {F}_{2}[\mathrm {Gal}(K/F)]$
-module as well. The answer is a resounding “yes.” Indeed, when p is any prime number and
![]() $\text {char}(K)=p$
, the thesis [Reference Heller14] gives the structure of
$\text {char}(K)=p$
, the thesis [Reference Heller14] gives the structure of
![]() $K/\{k^{p}-k:k \in K\}$
as an
$K/\{k^{p}-k:k \in K\}$
as an
![]() $\mathbb {F}_{p}[\mathrm {Gal}(K/F)]$
-module whenever
$\mathbb {F}_{p}[\mathrm {Gal}(K/F)]$
-module whenever
![]() $\mathrm {Gal}(K/F) \simeq \mathbb {Z}/p\mathbb {Z}\oplus \mathbb {Z}/p\mathbb {Z}$
. This decomposition reveals that the only nonfree summand is isomorphic to
$\mathrm {Gal}(K/F) \simeq \mathbb {Z}/p\mathbb {Z}\oplus \mathbb {Z}/p\mathbb {Z}$
. This decomposition reveals that the only nonfree summand is isomorphic to
![]() $\Omega ^{-2}_{\mathrm {Gal}(K/F)}$
. This result is extended considerably in the forthcoming paper [Reference Heller, Mináč, Nguyen, Schultz and Tan15]: for any prime p and any Galois extension
$\Omega ^{-2}_{\mathrm {Gal}(K/F)}$
. This result is extended considerably in the forthcoming paper [Reference Heller, Mináč, Nguyen, Schultz and Tan15]: for any prime p and any Galois extension
![]() $K/F$
so that
$K/F$
so that
![]() $\mathrm {Gal}(K/F)$
is a finite p-group, if
$\mathrm {Gal}(K/F)$
is a finite p-group, if
![]() $G_{F}(p)$
is a free pro-p group that is finitely generated, then the parameterizing space of elementary p-abelian extensions of K decomposes into a free summand and a single summand isomorphic to
$G_{F}(p)$
is a free pro-p group that is finitely generated, then the parameterizing space of elementary p-abelian extensions of K decomposes into a free summand and a single summand isomorphic to
![]() $\Omega ^{-2}_{\mathrm {Gal}(K/F)}$
.
$\Omega ^{-2}_{\mathrm {Gal}(K/F)}$
.
Theorem 1.1 helps give new insight into the question of what distinguishes absolute
![]() $2$
-Galois groups from the broader class of pro-
$2$
-Galois groups from the broader class of pro-
![]() $2$
groups. By equivariant Kummer theory, we know that
$2$
groups. By equivariant Kummer theory, we know that
![]() $J(K)$
is dual to the maximal elementary
$J(K)$
is dual to the maximal elementary
![]() $2$
-abelian quotient of
$2$
-abelian quotient of
![]() $G_{K}(2)$
. Theorem 1.1 (together with the main result of [Reference Heller14] to address the characteristic
$G_{K}(2)$
. Theorem 1.1 (together with the main result of [Reference Heller14] to address the characteristic
![]() $2$
case) tells us that whenever G is the absolute
$2$
case) tells us that whenever G is the absolute
![]() $2$
-Galois group of a field F, then for every continuous surjection
$2$
-Galois group of a field F, then for every continuous surjection
![]() $G \twoheadrightarrow \mathbb {Z}/2\mathbb {Z}\oplus \mathbb {Z}/2\mathbb {Z}$
, the maximal elementary p-abelian quotient of the kernel of this surjection has a particular module structure attached to it.
$G \twoheadrightarrow \mathbb {Z}/2\mathbb {Z}\oplus \mathbb {Z}/2\mathbb {Z}$
, the maximal elementary p-abelian quotient of the kernel of this surjection has a particular module structure attached to it.
Alternatively, one could attempt to use this result to uncover specific information about embedding problems over
![]() $\mathbb {Z}/2\mathbb {Z}\oplus \mathbb {Z}/2\mathbb {Z}$
extensions. To do this, one needs a dictionary that translates module- and field-theoretic information associated to submodules of
$\mathbb {Z}/2\mathbb {Z}\oplus \mathbb {Z}/2\mathbb {Z}$
extensions. To do this, one needs a dictionary that translates module- and field-theoretic information associated to submodules of
![]() $J(K)$
into structural properties of the Galois groups to which they correspond. Such a dictionary already exists in the case where
$J(K)$
into structural properties of the Galois groups to which they correspond. Such a dictionary already exists in the case where
![]() $\mathrm { Gal}(K/F) \simeq \mathbb {Z}/p\mathbb {Z}$
(see [Reference Schultz29, Reference Waterhouse31]) and has been used to great effect to show how the Galois module structure of
$\mathrm { Gal}(K/F) \simeq \mathbb {Z}/p\mathbb {Z}$
(see [Reference Schultz29, Reference Waterhouse31]) and has been used to great effect to show how the Galois module structure of
![]() $J(K)$
in this case reveals distinguishing properties of absolute p-Galois groups (e.g., automatic realization results that one would not expect from group theory alone; see [Reference Mináč, Schultz and Swallow24, Reference Mináč and Swallow27, Reference Schultz29]).
$J(K)$
in this case reveals distinguishing properties of absolute p-Galois groups (e.g., automatic realization results that one would not expect from group theory alone; see [Reference Mináč, Schultz and Swallow24, Reference Mináč and Swallow27, Reference Schultz29]).
Indeed, such a dictionary in the biquadratic case can be used to calculate all information about
![]() $J(K)$
simultaneously: for a given biquadratic extension
$J(K)$
simultaneously: for a given biquadratic extension
![]() $K/F$
, one creates a pro-
$K/F$
, one creates a pro-
![]() $2$
extension
$2$
extension
![]() $L/F$
by defining
$L/F$
by defining
![]() $L = K(\sqrt {\gamma }: \gamma \in J(K))$
, and the aforementioned dictionary would allow us to compute
$L = K(\sqrt {\gamma }: \gamma \in J(K))$
, and the aforementioned dictionary would allow us to compute
![]() $\mathrm {Gal}(L/F)$
. This would give an important invariant attached to any biquadratic extension of F, and exhibit some critical distinctions between absolute
$\mathrm {Gal}(L/F)$
. This would give an important invariant attached to any biquadratic extension of F, and exhibit some critical distinctions between absolute
![]() $2$
-Galois groups and the larger class of pro-
$2$
-Galois groups and the larger class of pro-
![]() $2$
groups. The authors of this manuscript are already working to provide this dictionary, an effort that should produce yet more explicit manifestations for the “specialness” of absolute
$2$
groups. The authors of this manuscript are already working to provide this dictionary, an effort that should produce yet more explicit manifestations for the “specialness” of absolute
![]() $2$
-Galois groups.
$2$
-Galois groups.
1.3 Outline of the paper
In Section 2, we review some basic facts concerning modules over
![]() $\mathbb {F}_{2}[\mathbb {Z}/2\mathbb {Z}\oplus \mathbb {Z}/2\mathbb {Z}]$
. Section 3 is devoted to producing a “large” module whose fixed part is the “obvious” component
$\mathbb {F}_{2}[\mathbb {Z}/2\mathbb {Z}\oplus \mathbb {Z}/2\mathbb {Z}]$
. Section 3 is devoted to producing a “large” module whose fixed part is the “obvious” component
![]() $[F^{\times }]$
within
$[F^{\times }]$
within
![]() $J(K)^{G}$
; the key is to give a filtration of
$J(K)^{G}$
; the key is to give a filtration of
![]() $[F^{\times }]$
that is sensitive to image subspaces coming from particular elements of
$[F^{\times }]$
that is sensitive to image subspaces coming from particular elements of
![]() $\mathbb {F}_{2}[G]$
. Section 4 aims to find a module whose fixed part spans a complement to
$\mathbb {F}_{2}[G]$
. Section 4 aims to find a module whose fixed part spans a complement to
![]() $[F^{\times }]$
in
$[F^{\times }]$
in
![]() $J(K)^{G}$
. This requires a deeper understanding of how
$J(K)^{G}$
. This requires a deeper understanding of how
![]() $J(K)^{G}$
behaves under the norm maps associated to the intermediate extensions
$J(K)^{G}$
behaves under the norm maps associated to the intermediate extensions
![]() $K/K_{i}$
(for
$K/K_{i}$
(for
![]() $i \in \{1,2,3\}$
). The proof of Lemma 4.6 gives our first appearance of a Hilbert 90 result for biquadratic extensions. Section 5 has another result related to Hilbert 90 for biquadratic extensions (Lemma 5.1), as well as the proof of Theorem 1.1. In Section 6, we discuss the realizability of some of the possibilities for the X summand in terms of the solvability (or nonsolvability) of particular embedding problems.
$i \in \{1,2,3\}$
). The proof of Lemma 4.6 gives our first appearance of a Hilbert 90 result for biquadratic extensions. Section 5 has another result related to Hilbert 90 for biquadratic extensions (Lemma 5.1), as well as the proof of Theorem 1.1. In Section 6, we discuss the realizability of some of the possibilities for the X summand in terms of the solvability (or nonsolvability) of particular embedding problems.
2 A primer in diagrammatic thinking in module theory
We will use G to denote the Klein
![]() $4$
-group with generators
$4$
-group with generators
![]() $\sigma _{1}$
and
$\sigma _{1}$
and
![]() $\sigma _{2}$
. When M is an
$\sigma _{2}$
. When M is an
![]() $\mathbb {F}_{2}[G]$
-module, we assume that M’s structure is multiplicative, so that the module action is written exponentially. Despite this, if
$\mathbb {F}_{2}[G]$
-module, we assume that M’s structure is multiplicative, so that the module action is written exponentially. Despite this, if
![]() $U,V$
are submodules of a larger
$U,V$
are submodules of a larger
![]() $\mathbb {F}_{2}[G]$
-module W, we will still write
$\mathbb {F}_{2}[G]$
-module W, we will still write
![]() $U+V$
for the set
$U+V$
for the set
![]() $\{uv: u \in U, v \in V\}$
, and we will use
$\{uv: u \in U, v \in V\}$
, and we will use
![]() $U \oplus V$
to indicate this set when
$U \oplus V$
to indicate this set when
![]() $U \cap V$
is trivial.
$U \cap V$
is trivial.
Throughout this paper, we will be considering the solvability of certain systems of equations within various
![]() $\mathbb {F}_{2}[G]$
-modules. Although one could of course write these systems out, it will often be convenient to have graphical representations for the equations. We adopt the convention that an arrow between elements denotes that one is the image of another through some given element of
$\mathbb {F}_{2}[G]$
-modules. Although one could of course write these systems out, it will often be convenient to have graphical representations for the equations. We adopt the convention that an arrow between elements denotes that one is the image of another through some given element of
![]() $F_{2}[G]$
, with the direction of the arrow indicating the acting element from
$F_{2}[G]$
, with the direction of the arrow indicating the acting element from
![]() $\mathbb {F}_{2}[G]$
. If the arrow points down and to the left, this indicates that the bottom element is the image of the upper element under
$\mathbb {F}_{2}[G]$
. If the arrow points down and to the left, this indicates that the bottom element is the image of the upper element under
![]() $1+\sigma _{2}$
, and likewise if the arrow points down and to the right, this means the lower element is the image of the upper element under
$1+\sigma _{2}$
, and likewise if the arrow points down and to the right, this means the lower element is the image of the upper element under
![]() $1+\sigma _{1}$
. In the event that the action of
$1+\sigma _{1}$
. In the event that the action of
![]() $1+\sigma _{1}$
and
$1+\sigma _{1}$
and
![]() $1+\sigma _{2}$
is the same on a given element, then we write the image immediately below, and use two bent arrows to signify the equality of the two actions. Figure 2 gives some basic examples.
$1+\sigma _{2}$
is the same on a given element, then we write the image immediately below, and use two bent arrows to signify the equality of the two actions. Figure 2 gives some basic examples.

Figure 2: A sampling of linear equations. On the left, we have the relation
![]() $\alpha ^{1+\sigma _{2}} = \alpha _{1}$
; in the middle, we have the simultaneous equations in
$\alpha ^{1+\sigma _{2}} = \alpha _{1}$
; in the middle, we have the simultaneous equations in
![]() $\beta $
and
$\beta $
and
![]() $\beta _{1}$
given by
$\beta _{1}$
given by
![]() $\beta ^{1+\sigma _{1}} = \beta ^{1+\sigma _{2}} = \beta _{1}$
; and on the right, we have the simultaneous equations in
$\beta ^{1+\sigma _{1}} = \beta ^{1+\sigma _{2}} = \beta _{1}$
; and on the right, we have the simultaneous equations in
![]() $\gamma ,\gamma _{1},\gamma _{2}$
given by
$\gamma ,\gamma _{1},\gamma _{2}$
given by
![]() $\gamma ^{1+\sigma _{2}} = \gamma _{1}$
and
$\gamma ^{1+\sigma _{2}} = \gamma _{1}$
and
![]() $\gamma ^{1+\sigma _{1}} = \gamma _{2}$
.
$\gamma ^{1+\sigma _{1}} = \gamma _{2}$
.
Since these diagrams represent simultaneous linear equations in the module, we will say that a solution to a system of equations is a solution to the corresponding diagram; if we have some fixed values for particular parameters in a system of equations, and there exist values for the remaining parameters so that the underlying system is solved, then we will say that the diagram is solvable for those (original) fixed values. For example, to say that the diagram on the left side of Figure 2 is solvable for some particular
![]() $\alpha _{1}$
is equivalent to saying that
$\alpha _{1}$
is equivalent to saying that
![]() $\alpha _{1}$
is in the image of
$\alpha _{1}$
is in the image of
![]() $1+\sigma _{1}$
.
$1+\sigma _{1}$
.
Our decomposition will not require us to have a classification of indecomposable
![]() $\mathbb {F}_{2}[G]$
-modules, but for the reader’s benefit, we review some basic information about these modules. For a full treatment, the reader can consult [Reference Benson3, Theorem 4.3.3]. There are seven ideals in the ring
$\mathbb {F}_{2}[G]$
-modules, but for the reader’s benefit, we review some basic information about these modules. For a full treatment, the reader can consult [Reference Benson3, Theorem 4.3.3]. There are seven ideals in the ring
![]() $\mathbb {F}_{2}[\mathbb {Z}/2\mathbb {Z}\oplus \mathbb {Z}/2\mathbb {Z}]$
, and hence six cyclic, nontrivial indecomposable submodule classes. Aside from the even-dimensional cyclic modules, there are also families of indecomposable even-dimensional
$\mathbb {F}_{2}[\mathbb {Z}/2\mathbb {Z}\oplus \mathbb {Z}/2\mathbb {Z}]$
, and hence six cyclic, nontrivial indecomposable submodule classes. Aside from the even-dimensional cyclic modules, there are also families of indecomposable even-dimensional
![]() $\mathbb {F}_{2}[G]$
-modules that correspond to certain rational canonical form matrices. These will not appear in our decomposition. There are also odd-dimensional indecomposable
$\mathbb {F}_{2}[G]$
-modules that correspond to certain rational canonical form matrices. These will not appear in our decomposition. There are also odd-dimensional indecomposable
![]() $\mathbb {F}_{2}[G]$
-modules: for each odd number
$\mathbb {F}_{2}[G]$
-modules: for each odd number
![]() $2n+1$
with
$2n+1$
with
![]() $n\geq 1$
, there are two irreducible
$n\geq 1$
, there are two irreducible
![]() $\mathbb {F}_{2}[G]$
-modules of dimension n, denoted
$\mathbb {F}_{2}[G]$
-modules of dimension n, denoted
![]() $\Omega ^{n}$
and
$\Omega ^{n}$
and
![]() $\Omega ^{-n}$
. As it happens, our decomposition of
$\Omega ^{-n}$
. As it happens, our decomposition of
![]() $J(K)$
will only require the cyclic modules we have already introduced together with
$J(K)$
will only require the cyclic modules we have already introduced together with
![]() $\Omega ^{1}, \Omega ^{2}, \Omega ^{-1}$
, and
$\Omega ^{1}, \Omega ^{2}, \Omega ^{-1}$
, and
![]() $\Omega ^{-2}$
. We will need formal definitions for these latter modules, but there is no additional cost to define
$\Omega ^{-2}$
. We will need formal definitions for these latter modules, but there is no additional cost to define
![]() $\Omega ^{n}$
and
$\Omega ^{n}$
and
![]() $\Omega ^{-n}$
in general. Using our depiction scheme, these modules are shown in Figure 3.
$\Omega ^{-n}$
in general. Using our depiction scheme, these modules are shown in Figure 3.

Figure 3: The two indecomposable
![]() $\mathbb {F}_{2}[G]$
-modules of odd dimension
$\mathbb {F}_{2}[G]$
-modules of odd dimension
![]() $2n+1$
:
$2n+1$
:
![]() $\Omega ^{-n}$
(depicted above) and
$\Omega ^{-n}$
(depicted above) and
![]() $\Omega ^{n}$
(depicted below). Although it is not explicit in the diagram, each of the
$\Omega ^{n}$
(depicted below). Although it is not explicit in the diagram, each of the
![]() $\beta _{i}$
and
$\beta _{i}$
and
![]() $\delta _{i}$
is fixed by the action of G.
$\delta _{i}$
is fixed by the action of G.
One key fact we will use about
![]() $\mathbb {F}_{2}[G]$
-module is that we can detect independence of two
$\mathbb {F}_{2}[G]$
-module is that we can detect independence of two
![]() $\mathbb {F}_{2}[G]$
-modules by examining the independence of their fixed parts. We follow the standard convention of writing
$\mathbb {F}_{2}[G]$
-modules by examining the independence of their fixed parts. We follow the standard convention of writing
![]() $M^{G}$
for the fixed submodule of an
$M^{G}$
for the fixed submodule of an
![]() $\mathbb {F}_{2}[G]$
-module M.
$\mathbb {F}_{2}[G]$
-module M.
Lemma 2.1 Suppose that M and N are submodules of a larger
![]() $\mathbb {F}_{2}[G]$
-module W. Then
$\mathbb {F}_{2}[G]$
-module W. Then
![]() $M \cap N = \{1\}$
if and only if
$M \cap N = \{1\}$
if and only if
![]() $M^{G} \cap N^{G} = \{1\}$
.
$M^{G} \cap N^{G} = \{1\}$
.
Proof Of course, if
![]() $M \cap N = \{1\}$
, then
$M \cap N = \{1\}$
, then
![]() $M^{G} \cap N^{G} = \{1\}$
as well. Suppose, then, that
$M^{G} \cap N^{G} = \{1\}$
as well. Suppose, then, that
![]() $M^{G} \cap N^{G} = \{1\}$
, and let
$M^{G} \cap N^{G} = \{1\}$
, and let
![]() $w \in M \cap N$
be given. If w is nontrivial, then
$w \in M \cap N$
be given. If w is nontrivial, then
![]() $\langle w \rangle $
is isomorphic to precisely one of the following:
$\langle w \rangle $
is isomorphic to precisely one of the following:
![]() $\mathbb {F}_{2}$
,
$\mathbb {F}_{2}$
,
![]() $\mathbb {F}_{2}[\overline {G_{1}}]$
,
$\mathbb {F}_{2}[\overline {G_{1}}]$
,
![]() $\mathbb {F}_{2}[\overline {G_{2}}]$
,
$\mathbb {F}_{2}[\overline {G_{2}}]$
,
![]() $\mathbb {F}_{2}[\overline {G_{3}}]$
,
$\mathbb {F}_{2}[\overline {G_{3}}]$
,
![]() $\Omega ^{-1}$
, or
$\Omega ^{-1}$
, or
![]() $\mathbb {F}_{2}[G]$
. In the first case, we have
$\mathbb {F}_{2}[G]$
. In the first case, we have
![]() $w \in W^{G}$
, and so
$w \in W^{G}$
, and so
![]() $w \in M^{G} \cap N^{G} = \{1\}$
; this is a contraction. If either
$w \in M^{G} \cap N^{G} = \{1\}$
; this is a contraction. If either
![]() $\langle w \rangle \simeq \mathbb {F}_{2}[\overline {G_{1}}]$
,
$\langle w \rangle \simeq \mathbb {F}_{2}[\overline {G_{1}}]$
,
![]() $\langle w\rangle \simeq \mathbb {F}_{2}[\overline {G_{3}}]$
, or
$\langle w\rangle \simeq \mathbb {F}_{2}[\overline {G_{3}}]$
, or
![]() $\langle w\rangle \simeq \Omega ^{-1}$
, then
$\langle w\rangle \simeq \Omega ^{-1}$
, then
![]() $w^{1+\sigma _{1}}$
is a nontrivial element in
$w^{1+\sigma _{1}}$
is a nontrivial element in
![]() $W^{G}$
; but this again leads to a contradiction, since then we again have
$W^{G}$
; but this again leads to a contradiction, since then we again have
![]() $w^{1+\sigma _{1}} \in M^{G} \cap N^{G} = \{1\}$
. If
$w^{1+\sigma _{1}} \in M^{G} \cap N^{G} = \{1\}$
. If
![]() $\langle w \rangle \simeq \mathbb {F}_{2}[\overline {G_{2}}]$
, then
$\langle w \rangle \simeq \mathbb {F}_{2}[\overline {G_{2}}]$
, then
![]() $w^{1+\sigma _{2}}$
is the nontrivial element in
$w^{1+\sigma _{2}}$
is the nontrivial element in
![]() $W^{G}$
, which leads to a contradiction, and if
$W^{G}$
, which leads to a contradiction, and if
![]() $\langle w \rangle \simeq \mathbb {F}_{2}[G]$
, then the contradictory nontrivial element of
$\langle w \rangle \simeq \mathbb {F}_{2}[G]$
, then the contradictory nontrivial element of
![]() $W^{G}$
is
$W^{G}$
is
![]() $w^{(1+\sigma _{1})(1+\sigma _{2})}$
.▪
$w^{(1+\sigma _{1})(1+\sigma _{2})}$
.▪
3 A maximal submodule with fixed part
 $[F^{\times }]$
$[F^{\times }]$
In Section 2, we saw that fixed submodules play an important role in determining independence among
![]() $\mathbb {F}_{2}[G]$
-modules. Of course, the most natural fixed submodule of
$\mathbb {F}_{2}[G]$
-modules. Of course, the most natural fixed submodule of
![]() $J(K)$
is
$J(K)$
is
![]() $[F^{\times }]$
. Our objective in this section will be to find a “sufficiently large” submodule
$[F^{\times }]$
. Our objective in this section will be to find a “sufficiently large” submodule
![]() $\widehat {J}$
of
$\widehat {J}$
of
![]() $J(K)$
for which
$J(K)$
for which
![]() $\widehat {J}^{G} = [F^{\times }]$
. For the purposes of the decomposition that we are building, being “sufficiently large” will mean that
$\widehat {J}^{G} = [F^{\times }]$
. For the purposes of the decomposition that we are building, being “sufficiently large” will mean that
![]() $\widehat {J}$
contains solutions to certain systems of equations, assuming such equations have solutions within the full module
$\widehat {J}$
contains solutions to certain systems of equations, assuming such equations have solutions within the full module
![]() $J(K)$
.
$J(K)$
.
In a certain sense, we are most interested in finding free summands—by which we mean free over
![]() $\mathbb {F}_{2}[\overline {G_{i}}]$
for some
$\mathbb {F}_{2}[\overline {G_{i}}]$
for some
![]() $i \in \{0,1,2,3,4\}$
—with the general philosophy that larger submodules are preferable. Hence, primary preference goes to free (cyclic)
$i \in \{0,1,2,3,4\}$
—with the general philosophy that larger submodules are preferable. Hence, primary preference goes to free (cyclic)
![]() $\mathbb {F}_{2}[G]$
-modules, and secondary preference goes to free (cyclic)
$\mathbb {F}_{2}[G]$
-modules, and secondary preference goes to free (cyclic)
![]() $\mathbb {F}_{2}[\overline {G_{i}}]$
-modules for
$\mathbb {F}_{2}[\overline {G_{i}}]$
-modules for
![]() $i \in \{1,2,3\}$
; for concreteness, we give preference to
$i \in \{1,2,3\}$
; for concreteness, we give preference to
![]() $i=1$
over
$i=1$
over
![]() $i=2$
, and
$i=2$
, and
![]() $i=2$
over
$i=2$
over
![]() $i=3$
. We finish with free
$i=3$
. We finish with free
![]() $\mathbb {F}_{2}[\overline {G_{4}}]$
-modules (i.e., trivial modules).
$\mathbb {F}_{2}[\overline {G_{4}}]$
-modules (i.e., trivial modules).
The issue in pursuing this agenda is that there are potential interrelations between these free modules. For example, suppose a free cyclic
![]() $\mathbb {F}_{2}[\overline {G_{1}}]$
-module
$\mathbb {F}_{2}[\overline {G_{1}}]$
-module
![]() $\langle [\gamma _{1}]\rangle $
and a free cyclic
$\langle [\gamma _{1}]\rangle $
and a free cyclic
![]() $\mathbb {F}_{2}[\overline {G_{2}}]$
-module
$\mathbb {F}_{2}[\overline {G_{2}}]$
-module
![]() $\langle [\gamma _{2}]\rangle $
share the same fixed submodule
$\langle [\gamma _{2}]\rangle $
share the same fixed submodule
![]() $\langle [f]\rangle $
. This means that
$\langle [f]\rangle $
. This means that
![]() $[f],[\gamma _{1}],$
and
$[f],[\gamma _{1}],$
and
![]() $[\gamma _{2}]$
satisfy the system of equations
$[\gamma _{2}]$
satisfy the system of equations

Hence, in our pursuit of free submodules, we are obliged to look for solutions to this type of system and ensure our decomposition of
![]() $[F^{\times }]$
captures these elements.
$[F^{\times }]$
captures these elements.
With all this in mind, let us move toward statements that are more precise. In Figure 4, we introduce five subspaces of
![]() $[F^{\times }]$
that capture the ideas we alluded to in the previous paragraphs. We denote these spaces
$[F^{\times }]$
that capture the ideas we alluded to in the previous paragraphs. We denote these spaces
![]() $\mathscr {A},\mathscr {V},\mathscr {B},\mathscr {C},$
and
$\mathscr {A},\mathscr {V},\mathscr {B},\mathscr {C},$
and
![]() $\mathscr {D}$
. For
$\mathscr {D}$
. For
![]() $\mathscr {M} \in \{\mathscr {A},\mathscr {V},\mathscr {B},\mathscr {C},\mathscr {D}\}$
, the space
$\mathscr {M} \in \{\mathscr {A},\mathscr {V},\mathscr {B},\mathscr {C},\mathscr {D}\}$
, the space
![]() $\mathscr {M}$
is the set of all
$\mathscr {M}$
is the set of all
![]() $[f] \in [F^{\times }]$
for which the corresponding diagram from Figure 4 is solvable for
$[f] \in [F^{\times }]$
for which the corresponding diagram from Figure 4 is solvable for
![]() $[f]$
. For example, an element
$[f]$
. For example, an element
![]() $[f] \in [F^{\times }]$
is an element of
$[f] \in [F^{\times }]$
is an element of
![]() $\mathscr {A}$
if and only if
$\mathscr {A}$
if and only if
![]() $[f] \in [N_{K/F}(K^{\times })]$
(since
$[f] \in [N_{K/F}(K^{\times })]$
(since
![]() $N_{K/F}$
is given by applying
$N_{K/F}$
is given by applying
![]() $(1+\sigma _{1})(1+\sigma _{2})$
).
$(1+\sigma _{1})(1+\sigma _{2})$
).

Figure 4: Diagrams that represent the various systems of equations that are solvable in order for
![]() $[f]$
to be an element of the subspaces
$[f]$
to be an element of the subspaces
![]() $\mathscr {A},\mathscr {V},\mathscr {B},\mathscr {C}$
, or
$\mathscr {A},\mathscr {V},\mathscr {B},\mathscr {C}$
, or
![]() $\mathscr {D}$
.
$\mathscr {D}$
.
It is readily apparent that
![]() $\mathscr {A} \subseteq \mathscr {V}$
, and furthermore that
$\mathscr {A} \subseteq \mathscr {V}$
, and furthermore that
![]() $\mathscr {V}$
is a subspace of both
$\mathscr {V}$
is a subspace of both
![]() $\mathscr {B}$
and
$\mathscr {B}$
and
![]() $\mathscr {C}$
. We just observed that
$\mathscr {C}$
. We just observed that
![]() $\mathscr {B} \cap \mathscr {C} = \mathscr {V}$
. Continuing in the theme of being careful about interrelations that exist between these subspaces, the following lemma considers how elements of
$\mathscr {B} \cap \mathscr {C} = \mathscr {V}$
. Continuing in the theme of being careful about interrelations that exist between these subspaces, the following lemma considers how elements of
![]() $\mathscr {D}$
are related to elements from
$\mathscr {D}$
are related to elements from
![]() $\mathscr {B}+\mathscr {C}$
.
$\mathscr {B}+\mathscr {C}$
.
Lemma 3.1 Let
![]() $\mathscr {B},\mathscr {C}$
, and
$\mathscr {B},\mathscr {C}$
, and
![]() $\mathscr {D}$
be defined as in Figure 4. Then
$\mathscr {D}$
be defined as in Figure 4. Then
![]() $[b][c] \in (\mathscr {B}+\mathscr {C}) \cap \mathscr {D}$
if and only if
$[b][c] \in (\mathscr {B}+\mathscr {C}) \cap \mathscr {D}$
if and only if

is solvable for some
![]() $[\gamma _{1}],[\gamma _{2}],[\gamma _{3}] \in J(K)$
.
$[\gamma _{1}],[\gamma _{2}],[\gamma _{3}] \in J(K)$
.
Proof Suppose first that equation (3.1) holds. From this, we see that
 $$ \begin{align*} \left([\gamma_{1}][\gamma_{2}][\gamma_{3}]\right)^{1+\sigma_{2}} &= [1][b][c],\\ \left([\gamma_{1}][\gamma_{2}][\gamma_{3}]\right)^{1+\sigma_{1}} &= [b][c][1]. \end{align*} $$
$$ \begin{align*} \left([\gamma_{1}][\gamma_{2}][\gamma_{3}]\right)^{1+\sigma_{2}} &= [1][b][c],\\ \left([\gamma_{1}][\gamma_{2}][\gamma_{3}]\right)^{1+\sigma_{1}} &= [b][c][1]. \end{align*} $$
Hence,
![]() $[b][c] \in (\mathscr {B}+\mathscr {C})\cap \mathscr {D}$
.
$[b][c] \in (\mathscr {B}+\mathscr {C})\cap \mathscr {D}$
.
For the other direction, suppose there exists
![]() $[\gamma ] \in J(K)$
so that the diagram for
$[\gamma ] \in J(K)$
so that the diagram for
![]() $\mathscr {D}$
holds with
$\mathscr {D}$
holds with
![]() $[\gamma ]$
and
$[\gamma ]$
and
![]() $[f] = [b][c]$
. Since
$[f] = [b][c]$
. Since
![]() $[b] \in \mathscr {B}$
and
$[b] \in \mathscr {B}$
and
![]() $[c] \in \mathscr {C}$
, we also have elements
$[c] \in \mathscr {C}$
, we also have elements
![]() $[\gamma _{L}],[\gamma _{R}] \in J(K)$
so that
$[\gamma _{L}],[\gamma _{R}] \in J(K)$
so that
![]() $[\gamma _{L}]$
and
$[\gamma _{L}]$
and
![]() $[b]$
satisfy the diagram for
$[b]$
satisfy the diagram for
![]() $\mathscr {B}$
, and
$\mathscr {B}$
, and
![]() $[\gamma _{R}]$
and
$[\gamma _{R}]$
and
![]() $[c]$
satisfy the diagram for
$[c]$
satisfy the diagram for
![]() $\mathscr {C}$
. From these relations, we find that equation (3.1) is satisfied with
$\mathscr {C}$
. From these relations, we find that equation (3.1) is satisfied with
![]() $[\gamma _{1}] = [\gamma _{L}]$
,
$[\gamma _{1}] = [\gamma _{L}]$
,
![]() $[\gamma _{2}] = [\gamma _{L}][\gamma ][\gamma _{R}]$
, and
$[\gamma _{2}] = [\gamma _{L}][\gamma ][\gamma _{R}]$
, and
![]() $[\gamma _{3}] = [\gamma _{R}]$
.▪
$[\gamma _{3}] = [\gamma _{R}]$
.▪
Notice that if
![]() $[f]$
and
$[f]$
and
![]() $[\hat f]$
are elements of
$[\hat f]$
are elements of
![]() $\mathscr {V}$
(with corresponding elements
$\mathscr {V}$
(with corresponding elements
![]() $[\gamma _{L}],[\gamma _{R}]$
solving the diagram with
$[\gamma _{L}],[\gamma _{R}]$
solving the diagram with
![]() $[f]$
, and
$[f]$
, and
![]() $[\widehat {\gamma _{L}}],[\widehat {\gamma _{R}}]$
solving the diagram for
$[\widehat {\gamma _{L}}],[\widehat {\gamma _{R}}]$
solving the diagram for
![]() $[\hat f]$
), then equation (3.1) is solvable for
$[\hat f]$
), then equation (3.1) is solvable for
![]() $[b]=[f]$
and
$[b]=[f]$
and
![]() $[c]=[\hat f]$
:
$[c]=[\hat f]$
:

Hence, we will be particularly interested in understanding solutions to equation (3.1) that come from outside
![]() $\mathscr {V}$
. The following lemma characterizes such solutions.
$\mathscr {V}$
. The following lemma characterizes such solutions.
Lemma 3.2 Suppose that B is a complement to
![]() $\mathscr {V}$
within
$\mathscr {V}$
within
![]() $\mathscr {B}$
, and that C is a complement to
$\mathscr {B}$
, and that C is a complement to
![]() $\mathscr {V}$
within
$\mathscr {V}$
within
![]() $\mathscr {C}$
. Define subspaces
$\mathscr {C}$
. Define subspaces
![]() $B_{W}$
of B and
$B_{W}$
of B and
![]() $C_{W}$
of C by
$C_{W}$
of C by
 $$ \begin{align*} B_{W} &= \{[b] \in B: \exists [c] \in C \textit{ so that equation } \textrm{(3.1)} \textit{ is solvable}\},\\ C_{W} &= \{[c] \in C: \exists [b] \in B \textit{ so that equation } \textrm{(3.1)} \textit{ is solvable}\}. \end{align*} $$
$$ \begin{align*} B_{W} &= \{[b] \in B: \exists [c] \in C \textit{ so that equation } \textrm{(3.1)} \textit{ is solvable}\},\\ C_{W} &= \{[c] \in C: \exists [b] \in B \textit{ so that equation } \textrm{(3.1)} \textit{ is solvable}\}. \end{align*} $$
Then there exists an
![]() $\mathbb {F}_{2}$
-linear bijection
$\mathbb {F}_{2}$
-linear bijection
![]() $\phi _{W}:B_{W} \to C_{W}$
which takes each
$\phi _{W}:B_{W} \to C_{W}$
which takes each
![]() $[b] \in B_{W}$
to the unique
$[b] \in B_{W}$
to the unique
![]() $[c] \in C_{W}$
for which equation (3.1) is solvable for
$[c] \in C_{W}$
for which equation (3.1) is solvable for
![]() $[b]$
and
$[b]$
and
![]() $[c]$
.
$[c]$
.
Proof That
![]() $B_{W}$
and
$B_{W}$
and
![]() $C_{W}$
are subspaces follows since equation (3.1) is linear. Now, we claim that, for each
$C_{W}$
are subspaces follows since equation (3.1) is linear. Now, we claim that, for each
![]() $[b] \in B_{W}$
, there exists a unique
$[b] \in B_{W}$
, there exists a unique
![]() $[c] \in C_{W}$
for which the equations represented by equation (3.1) are solvable. Suppose instead we had some
$[c] \in C_{W}$
for which the equations represented by equation (3.1) are solvable. Suppose instead we had some
![]() $[b] \in B_{W}$
so that there exist
$[b] \in B_{W}$
so that there exist
![]() $[c],[\hat c] \in C_{W}$
which make equation (3.1) solvable; we will write
$[c],[\hat c] \in C_{W}$
which make equation (3.1) solvable; we will write
![]() $[\gamma _{1}],[\gamma _{2}],[\gamma _{3}]$
for the additional terms that solve the system with
$[\gamma _{1}],[\gamma _{2}],[\gamma _{3}]$
for the additional terms that solve the system with
![]() $[b]$
and
$[b]$
and
![]() $[c]$
, and we will write
$[c]$
, and we will write
![]() $[\gamma _{1}],[\widehat {\gamma _{2}}],[\widehat {\gamma _{3}}]$
for the additional terms that solve the system with
$[\gamma _{1}],[\widehat {\gamma _{2}}],[\widehat {\gamma _{3}}]$
for the additional terms that solve the system with
![]() $[b]$
and
$[b]$
and
![]() $[\hat c]$
. By multiplying the two systems, we are left with
$[\hat c]$
. By multiplying the two systems, we are left with

and so we see that
![]() $[c][\hat c] \in \mathscr {V}$
. However, since
$[c][\hat c] \in \mathscr {V}$
. However, since
![]() $[c]$
and
$[c]$
and
![]() $[\hat c]$
are contained in a complement C of
$[\hat c]$
are contained in a complement C of
![]() $\mathscr {V}$
within
$\mathscr {V}$
within
![]() $\mathscr {C}$
, this implies
$\mathscr {C}$
, this implies
![]() $[c][\hat c] =[1]$
. Hence,
$[c][\hat c] =[1]$
. Hence,
![]() $[c]=[\hat c]$
.
$[c]=[\hat c]$
.
The same argument, of course, shows that, for a given
![]() $[c] \in C_{W}$
, there exists a unique
$[c] \in C_{W}$
, there exists a unique
![]() $[b] \in B_{W}$
for which equation (3.1) is solvable. We define
$[b] \in B_{W}$
for which equation (3.1) is solvable. We define
![]() $\phi _{W}$
as the function which associates to each
$\phi _{W}$
as the function which associates to each
![]() $[b] \in B_{W}$
its corresponding
$[b] \in B_{W}$
its corresponding
![]() $[c] \in C_{W}$
. The fact that the equations represented by equation (3.1) are linear implies that
$[c] \in C_{W}$
. The fact that the equations represented by equation (3.1) are linear implies that
![]() $\phi _{W}$
is linear as well, and hence an isomorphism of
$\phi _{W}$
is linear as well, and hence an isomorphism of
![]() $\mathbb {F}_{2}$
-spaces.▪
$\mathbb {F}_{2}$
-spaces.▪
We are now prepared to state and prove the main result in this section.
Theorem 3.3 There exists a submodule
![]() $\widehat {J}$
of
$\widehat {J}$
of
![]() $J(K)$
so that
$J(K)$
so that
![]() $\widehat {J}^{G} = [F^{\times }]$
, and for which
$\widehat {J}^{G} = [F^{\times }]$
, and for which
where
-
•
 $Y_{A}$
is a direct sum of submodules isomorphic to
$Y_{A}$
is a direct sum of submodules isomorphic to
 $\mathbb {F}_{2}[G]$
;
$\mathbb {F}_{2}[G]$
; -
•
 $Y_{V}$
is a direct sum of submodules isomorphic to
$Y_{V}$
is a direct sum of submodules isomorphic to
 $\Omega ^{1}$
;
$\Omega ^{1}$
; -
•
 $Y_{W}$
is a direct sum of submodules isomorphic to
$Y_{W}$
is a direct sum of submodules isomorphic to
 $\Omega ^{2}$
;
$\Omega ^{2}$
; -
•
 $Y_{B}$
is a direct sum of submodules isomorphic to
$Y_{B}$
is a direct sum of submodules isomorphic to
 $\mathbb {F}_{2}[\overline {G_{1}}]$
;
$\mathbb {F}_{2}[\overline {G_{1}}]$
; -
•
 $Y_{C}$
is a direct sum of submodules isomorphic to
$Y_{C}$
is a direct sum of submodules isomorphic to
 $\mathbb {F}_{2}[\overline {G_{2}}]$
;
$\mathbb {F}_{2}[\overline {G_{2}}]$
; -
•
 $Y_{D}$
is a direct sum of submodules isomorphic to
$Y_{D}$
is a direct sum of submodules isomorphic to
 $\mathbb {F}_{2}[\overline {G_{3}}]$
; and
$\mathbb {F}_{2}[\overline {G_{3}}]$
; and -
•
 $Y_{F}$
is a direct sum of submodules isomorphic to
$Y_{F}$
is a direct sum of submodules isomorphic to
 $\mathbb {F}_{2}$
.
$\mathbb {F}_{2}$
.
Proof Choose
![]() $\mathcal {A}$
to be an
$\mathcal {A}$
to be an
![]() $\mathbb {F}_{2}$
-basis for
$\mathbb {F}_{2}$
-basis for
![]() $\mathscr {A}$
. By the definition of
$\mathscr {A}$
. By the definition of
![]() $\mathscr {A}$
, for each
$\mathscr {A}$
, for each
![]() $[f] \in \mathcal {A}$
, there exists some
$[f] \in \mathcal {A}$
, there exists some
![]() $[\gamma _{f}] \in [K^{\times }]$
so that
$[\gamma _{f}] \in [K^{\times }]$
so that
![]() $[N_{K/F}(\gamma _{f})] = [f]$
. We define
$[N_{K/F}(\gamma _{f})] = [f]$
. We define
![]() $M_{[f]} := \langle [\gamma _{f}]\rangle $
, and observe that
$M_{[f]} := \langle [\gamma _{f}]\rangle $
, and observe that
![]() $M_{[f]} \simeq \mathbb {F}_{2}[G]$
and
$M_{[f]} \simeq \mathbb {F}_{2}[G]$
and
![]() $M_{[f]}^{G} = \langle [f]\rangle $
. Let
$M_{[f]}^{G} = \langle [f]\rangle $
. Let
![]() $Y_{A} = \sum _{[f]\in \mathcal {A}}M_{[f]}.$
Observe that
$Y_{A} = \sum _{[f]\in \mathcal {A}}M_{[f]}.$
Observe that
![]() $Y_{A} = \bigoplus _{[f]\in \mathcal {A}}M_{[f]}$
by Lemma 2.1, and that
$Y_{A} = \bigoplus _{[f]\in \mathcal {A}}M_{[f]}$
by Lemma 2.1, and that
![]() $Y_{A}^{G} = \bigoplus _{[f] \in \mathcal {A}} \langle [f] \rangle = \langle \mathcal {A} \rangle = \mathscr {A}$
by construction.
$Y_{A}^{G} = \bigoplus _{[f] \in \mathcal {A}} \langle [f] \rangle = \langle \mathcal {A} \rangle = \mathscr {A}$
by construction.
Let
![]() $\mathcal {V}$
be an
$\mathcal {V}$
be an
![]() $\mathbb {F}_{2}$
-basis for a complement of
$\mathbb {F}_{2}$
-basis for a complement of
![]() $\mathscr {A}$
in
$\mathscr {A}$
in
![]() $\mathscr {V}$
. By definition of
$\mathscr {V}$
. By definition of
![]() $\mathscr {V}$
, for each
$\mathscr {V}$
, for each
![]() $[f] \in \mathcal {V}$
, we can choose
$[f] \in \mathcal {V}$
, we can choose
![]() $[\gamma _{1,f}],[\gamma _{2,f}] \in [K^{\times }]$
so that, for
$[\gamma _{1,f}],[\gamma _{2,f}] \in [K^{\times }]$
so that, for
![]() $\{i,j\} = \{1,2\}$
, we have
$\{i,j\} = \{1,2\}$
, we have
![]() $[\gamma _{i,f}]^{1+\sigma _{i}} = [f]$
and
$[\gamma _{i,f}]^{1+\sigma _{i}} = [f]$
and
![]() $[\gamma _{i,f}]^{1+\sigma _{j}} = [1]$
. For each
$[\gamma _{i,f}]^{1+\sigma _{j}} = [1]$
. For each
![]() $[f] \in \mathcal {V}$
, we define
$[f] \in \mathcal {V}$
, we define
![]() $M_{[f]} := \langle [\gamma _{1,f}],[\gamma _{2,f}]\rangle $
. We claim that
$M_{[f]} := \langle [\gamma _{1,f}],[\gamma _{2,f}]\rangle $
. We claim that
![]() $M_{[f]} \simeq \Omega ^{1}$
and that
$M_{[f]} \simeq \Omega ^{1}$
and that
![]() $M_{[f]}^{G} = \langle [f]\rangle $
. By construction, the appropriate
$M_{[f]}^{G} = \langle [f]\rangle $
. By construction, the appropriate
![]() $\Omega ^{1}$
-relations are satisfied for
$\Omega ^{1}$
-relations are satisfied for
![]() $M_{[f]}$
, so we need only check that there are not additional relations. For this, observe that any nontrivial relation among
$M_{[f]}$
, so we need only check that there are not additional relations. For this, observe that any nontrivial relation among
![]() $\{[f],[\gamma _{1,f}],[\gamma _{2,f}]\}$
must involve at least one of
$\{[f],[\gamma _{1,f}],[\gamma _{2,f}]\}$
must involve at least one of
![]() $[\gamma _{1,f}]$
or
$[\gamma _{1,f}]$
or
![]() $[\gamma _{2,f}]$
since we know that
$[\gamma _{2,f}]$
since we know that
![]() $[f]$
is nontrivial. On the one hand, if we had a nontrivial relation involving
$[f]$
is nontrivial. On the one hand, if we had a nontrivial relation involving
![]() $[\gamma _{1,f}]$
, then an application of
$[\gamma _{1,f}]$
, then an application of
![]() $1+\sigma _{1}$
to this relation would tell us that
$1+\sigma _{1}$
to this relation would tell us that
![]() $[f]=[1]$
; on the other hand, a nontrivial relation involving
$[f]=[1]$
; on the other hand, a nontrivial relation involving
![]() $[\gamma _{2,f}]$
would tell us that
$[\gamma _{2,f}]$
would tell us that
![]() $[f]=[1]$
after an application of
$[f]=[1]$
after an application of
![]() $1+\sigma _{2}$
. Hence, our set is independent, and so
$1+\sigma _{2}$
. Hence, our set is independent, and so
![]() $M_{[f]} \simeq \Omega ^{1}$
. This gives
$M_{[f]} \simeq \Omega ^{1}$
. This gives
![]() $M_{[f]}^{G} = \langle [f]\rangle $
as well. Let
$M_{[f]}^{G} = \langle [f]\rangle $
as well. Let
![]() $Y_{V} = \sum _{[f]\in \mathcal {V}}M_{[f]}.$
Indeed, we have
$Y_{V} = \sum _{[f]\in \mathcal {V}}M_{[f]}.$
Indeed, we have
![]() $Y_{V} = \bigoplus _{[f]\in \mathcal {V}}M_{[f]}$
by Lemma 2.1. We also have
$Y_{V} = \bigoplus _{[f]\in \mathcal {V}}M_{[f]}$
by Lemma 2.1. We also have
![]() $Y_{V}^{G} = \bigoplus _{[f] \in \mathcal {V}} M_{[f]}^{G} =\bigoplus _{[f] \in \mathcal {V}} \langle [f] \rangle = \langle \mathcal {V} \rangle $
by construction.
$Y_{V}^{G} = \bigoplus _{[f] \in \mathcal {V}} M_{[f]}^{G} =\bigoplus _{[f] \in \mathcal {V}} \langle [f] \rangle = \langle \mathcal {V} \rangle $
by construction.
Now, let B be a complement to
![]() $\mathscr {V}$
within
$\mathscr {V}$
within
![]() $\mathscr {B}$
, and let C a complement to
$\mathscr {B}$
, and let C a complement to
![]() $\mathscr {V}$
within
$\mathscr {V}$
within
![]() $\mathscr {C}$
. Let
$\mathscr {C}$
. Let
![]() $B_{W}$
and
$B_{W}$
and
![]() $C_{W}$
be the subspaces defined in Lemma 3.2. Let
$C_{W}$
be the subspaces defined in Lemma 3.2. Let
![]() $\mathcal {B}_{W}$
be an
$\mathcal {B}_{W}$
be an
![]() $\mathbb {F}_{2}$
-basis for
$\mathbb {F}_{2}$
-basis for
![]() $B_{W}$
. For each
$B_{W}$
. For each
![]() $[b] \in \mathcal {B}_{W}$
, we know that there exist
$[b] \in \mathcal {B}_{W}$
, we know that there exist
![]() $[\gamma _{1}],[\gamma _{2}],[\gamma _{3}] \in J(K)$
and
$[\gamma _{1}],[\gamma _{2}],[\gamma _{3}] \in J(K)$
and
![]() $\phi _{W}([b]) =[c]\in C_{W}$
which solve equation (3.1). Let
$\phi _{W}([b]) =[c]\in C_{W}$
which solve equation (3.1). Let
![]() $M_{[b]} = \langle [b],[c],[\gamma _{1}],[\gamma _{2}],[\gamma _{3}]\rangle $
. We claim that
$M_{[b]} = \langle [b],[c],[\gamma _{1}],[\gamma _{2}],[\gamma _{3}]\rangle $
. We claim that
![]() $M_{[b]} \simeq \Omega ^{2}$
. Certainly, the appropriate
$M_{[b]} \simeq \Omega ^{2}$
. Certainly, the appropriate
![]() $\Omega ^{2}$
relations hold by construction, so we simply need to ensure that there are no additional relations. The elements
$\Omega ^{2}$
relations hold by construction, so we simply need to ensure that there are no additional relations. The elements
![]() $[b]$
and
$[b]$
and
![]() $[c]$
are independent since
$[c]$
are independent since
![]() $[b]$
and
$[b]$
and
![]() $[c]$
are each drawn from a complement to
$[c]$
are each drawn from a complement to
![]() $\mathscr {V} = \mathscr {B} \cap \mathscr {C}$
in their respective spaces. Now, if we had a nontrivial
$\mathscr {V} = \mathscr {B} \cap \mathscr {C}$
in their respective spaces. Now, if we had a nontrivial
![]() $\mathbb {F}_{2}$
-dependence that involved any of
$\mathbb {F}_{2}$
-dependence that involved any of
![]() $[\gamma _{1}]$
or
$[\gamma _{1}]$
or
![]() $[\gamma _{2}]$
, then an application of
$[\gamma _{2}]$
, then an application of
![]() $1+\sigma _{1}$
would force a nontrivial
$1+\sigma _{1}$
would force a nontrivial
![]() $\mathbb {F}_{2}$
-dependence on
$\mathbb {F}_{2}$
-dependence on
![]() $[b]$
and
$[b]$
and
![]() $[c]$
, which we have just seen is not possible. Likewise, a nontrivial
$[c]$
, which we have just seen is not possible. Likewise, a nontrivial
![]() $\mathbb {F}_{2}$
-dependence that involves
$\mathbb {F}_{2}$
-dependence that involves
![]() $[\gamma _{3}]$
would force a nontrivial
$[\gamma _{3}]$
would force a nontrivial
![]() $\mathbb {F}_{2}$
-dependence between
$\mathbb {F}_{2}$
-dependence between
![]() $[b]$
and
$[b]$
and
![]() $[c]$
. Hence, the set is independent, and so
$[c]$
. Hence, the set is independent, and so
![]() $M_{[b]} \simeq \Omega ^{2}$
. Note this also forces
$M_{[b]} \simeq \Omega ^{2}$
. Note this also forces
![]() $M_{[b]}^{G} = \langle [b],[c]\rangle = \langle [b],\phi _{W}([b])\rangle $
. Let
$M_{[b]}^{G} = \langle [b],[c]\rangle = \langle [b],\phi _{W}([b])\rangle $
. Let
![]() $Y_{W} = \sum _{[b] \in \mathcal {B}_{W}} M_{[b]}.$
As before, we in fact have
$Y_{W} = \sum _{[b] \in \mathcal {B}_{W}} M_{[b]}.$
As before, we in fact have
![]() $Y_{W} = \bigoplus _{[b] \in \mathcal {B}_{W}} M_{[b]}$
, and furthermore
$Y_{W} = \bigoplus _{[b] \in \mathcal {B}_{W}} M_{[b]}$
, and furthermore
by Lemma 3.2.
Let
![]() $\mathcal {B}_{0}$
be a basis for a complement to
$\mathcal {B}_{0}$
be a basis for a complement to
![]() $B_{W}$
within B. Since
$B_{W}$
within B. Since
![]() $B \subseteq \mathscr {B}$
, each
$B \subseteq \mathscr {B}$
, each
![]() $[f] \in \mathcal {B}_{0}$
has some
$[f] \in \mathcal {B}_{0}$
has some
![]() $[\gamma _{f}] \in [K^{\times }]$
so that
$[\gamma _{f}] \in [K^{\times }]$
so that
![]() $[\gamma _{f}]^{1+\sigma _{1}} = [f]$
and
$[\gamma _{f}]^{1+\sigma _{1}} = [f]$
and
![]() $[\gamma _{f}]^{1+\sigma _{2}} = [1]$
. Since
$[\gamma _{f}]^{1+\sigma _{2}} = [1]$
. Since
![]() $[f] \neq [1]$
, we get
$[f] \neq [1]$
, we get
![]() $M_{[f]}:=\langle [\gamma _{f}]\rangle $
is isomorphic to
$M_{[f]}:=\langle [\gamma _{f}]\rangle $
is isomorphic to
![]() $\mathbb {F}_{2}[\overline {G_{1}}]$
, and
$\mathbb {F}_{2}[\overline {G_{1}}]$
, and
![]() $M_{[f]}^{G} = \langle [f]\rangle $
. Let
$M_{[f]}^{G} = \langle [f]\rangle $
. Let
![]() $Y_{B} = \sum _{[f] \in \mathcal {B}_{0}}M_{[f]}.$
Lemma 2.1 again gives
$Y_{B} = \sum _{[f] \in \mathcal {B}_{0}}M_{[f]}.$
Lemma 2.1 again gives
![]() $Y_{B} = \bigoplus _{[f] \in \mathcal {B}_{0}} M_{[f]}$
, and furthermore we have
$Y_{B} = \bigoplus _{[f] \in \mathcal {B}_{0}} M_{[f]}$
, and furthermore we have
![]() $Y_{B}^{G} = \bigoplus _{[f] \in \mathcal {B}_{0}} M_{[f]}^{G} = \bigoplus _{[f] \in \mathcal {B}_{0}} \langle [f] \rangle = \langle \mathcal {B}_{0}\rangle $
.
$Y_{B}^{G} = \bigoplus _{[f] \in \mathcal {B}_{0}} M_{[f]}^{G} = \bigoplus _{[f] \in \mathcal {B}_{0}} \langle [f] \rangle = \langle \mathcal {B}_{0}\rangle $
.
Let
![]() $\mathcal {C}_{0}$
be a basis for a complement to
$\mathcal {C}_{0}$
be a basis for a complement to
![]() $C_{W}$
within C. Since
$C_{W}$
within C. Since
![]() $C \subseteq \mathscr {C}$
, for each
$C \subseteq \mathscr {C}$
, for each
![]() $[f] \in \mathcal {C}_{0}$
, there exists some
$[f] \in \mathcal {C}_{0}$
, there exists some
![]() $[\gamma _{f}] \in [K^{\times }]$
so that
$[\gamma _{f}] \in [K^{\times }]$
so that
![]() $[\gamma _{f}]^{1+\sigma _{2}} = [f]$
and
$[\gamma _{f}]^{1+\sigma _{2}} = [f]$
and
![]() $[\gamma _{f}]^{1+\sigma _{1}} = [1]$
. Since
$[\gamma _{f}]^{1+\sigma _{1}} = [1]$
. Since
![]() $[f] \neq [1]$
, we get
$[f] \neq [1]$
, we get
![]() $M_{[f]}:=\langle [\gamma _{f}]\rangle $
is isomorphic to
$M_{[f]}:=\langle [\gamma _{f}]\rangle $
is isomorphic to
![]() $\mathbb {F}_{2}[\overline {G_{2}}]$
, and
$\mathbb {F}_{2}[\overline {G_{2}}]$
, and
![]() $M_{[f]}^{G} = \langle [f]\rangle $
. Let
$M_{[f]}^{G} = \langle [f]\rangle $
. Let
![]() $Y_{C} = \sum _{[f] \in \mathcal {C}_{0}}M_{[f]}.$
Once again, we have
$Y_{C} = \sum _{[f] \in \mathcal {C}_{0}}M_{[f]}.$
Once again, we have
![]() $Y_{C} = \bigoplus _{[f] \in \mathcal {C}_{0}} M_{[f]}$
by Lemma 2.1, and
$Y_{C} = \bigoplus _{[f] \in \mathcal {C}_{0}} M_{[f]}$
by Lemma 2.1, and
![]() $Y_{C}^{G} = \bigoplus _{[f] \in \mathcal {C}_{0}} M_{[f]}^{G} = \bigoplus _{[f] \in \mathcal {C}_{0}} \langle [f] \rangle = \langle \mathcal {C}_{0}\rangle $
.
$Y_{C}^{G} = \bigoplus _{[f] \in \mathcal {C}_{0}} M_{[f]}^{G} = \bigoplus _{[f] \in \mathcal {C}_{0}} \langle [f] \rangle = \langle \mathcal {C}_{0}\rangle $
.
Let
![]() $\mathcal {D}_{0}$
be a basis for a complement to
$\mathcal {D}_{0}$
be a basis for a complement to
![]() $(\mathscr {B}+\mathscr {C}) \cap \mathscr {D}$
within
$(\mathscr {B}+\mathscr {C}) \cap \mathscr {D}$
within
![]() $\mathscr {D}$
. By the definition of
$\mathscr {D}$
. By the definition of
![]() $\mathscr {D}$
, for each
$\mathscr {D}$
, for each
![]() $[f] \in \mathcal {D}_{0}$
, there exists some
$[f] \in \mathcal {D}_{0}$
, there exists some
![]() $[\gamma _{f}] \in [K^{\times }]$
so that
$[\gamma _{f}] \in [K^{\times }]$
so that
![]() $[\gamma _{f}]^{1+\sigma _{2}} = [\gamma _{f}]^{1+\sigma _{1}} = [f]$
. Since
$[\gamma _{f}]^{1+\sigma _{2}} = [\gamma _{f}]^{1+\sigma _{1}} = [f]$
. Since
![]() $[f] \neq [1]$
, we get
$[f] \neq [1]$
, we get
![]() $M_{[f]}:=\langle [\gamma _{f}]\rangle $
is isomorphic to
$M_{[f]}:=\langle [\gamma _{f}]\rangle $
is isomorphic to
![]() $\mathbb {F}_{2}[\overline {G_{3}}]$
, and
$\mathbb {F}_{2}[\overline {G_{3}}]$
, and
![]() $M_{[f]}^{G} = \langle [f]\rangle $
. Let
$M_{[f]}^{G} = \langle [f]\rangle $
. Let
![]() $Y_{D} = \sum _{[f] \in \mathcal {D}_{0}}M_{[f]}.$
Again, we get
$Y_{D} = \sum _{[f] \in \mathcal {D}_{0}}M_{[f]}.$
Again, we get
![]() $Y_{D} = \bigoplus _{[f] \in \mathcal {D}_{0}} M_{[f]}$
, and
$Y_{D} = \bigoplus _{[f] \in \mathcal {D}_{0}} M_{[f]}$
, and
![]() $Y_{D}^{G} = \bigoplus _{[f] \in \mathcal {D}_{0}} M_{[f]}^{G} = \bigoplus _{[f] \in \mathcal {D}_{0}} \langle [f] \rangle = \langle \mathcal {D}_{0}\rangle $
.
$Y_{D}^{G} = \bigoplus _{[f] \in \mathcal {D}_{0}} M_{[f]}^{G} = \bigoplus _{[f] \in \mathcal {D}_{0}} \langle [f] \rangle = \langle \mathcal {D}_{0}\rangle $
.
Finally, define
![]() $\mathcal {F}_{0}$
to be a basis for a complement to
$\mathcal {F}_{0}$
to be a basis for a complement to
![]() $\mathscr {B}+\mathscr {C}+\mathscr {D}$
within
$\mathscr {B}+\mathscr {C}+\mathscr {D}$
within
![]() $[F^{\times }]$
. For each
$[F^{\times }]$
. For each
![]() $[f] \in \mathcal {F}_{0}$
, we define
$[f] \in \mathcal {F}_{0}$
, we define
![]() $M_{[f]} = \langle [f]\rangle $
, which is clearly isomorphic to
$M_{[f]} = \langle [f]\rangle $
, which is clearly isomorphic to
![]() $\mathbb {F}_{2}$
. We let
$\mathbb {F}_{2}$
. We let
![]() $Y_{F} = \bigoplus _{[f] \in \mathcal {F}_{0}} M_{[f]}.$
$Y_{F} = \bigoplus _{[f] \in \mathcal {F}_{0}} M_{[f]}.$
We have already detailed the fixed parts of each submodule, and we will use this to show that the sum is direct. First, recall that
![]() $Y_{A}^{G} = \mathscr {A}$
and
$Y_{A}^{G} = \mathscr {A}$
and
![]() $Y_{V}^{G} = \langle \mathcal {V}\rangle $
, where
$Y_{V}^{G} = \langle \mathcal {V}\rangle $
, where
![]() $\mathcal {V}$
is chosen to be a complement to
$\mathcal {V}$
is chosen to be a complement to
![]() $\mathscr {A}$
in
$\mathscr {A}$
in
![]() $\mathscr {V}$
. Then Lemma 2.1 gives
$\mathscr {V}$
. Then Lemma 2.1 gives
![]() $Y_{A}+Y_{V} = Y_{A}\oplus Y_{V}$
, and additionally we have
$Y_{A}+Y_{V} = Y_{A}\oplus Y_{V}$
, and additionally we have
![]() $(Y_{A}\oplus Y_{V})^{G} = \mathscr {V}$
.
$(Y_{A}\oplus Y_{V})^{G} = \mathscr {V}$
.
Next, since
![]() $Y_{W}^{G} = B_{W}\oplus C_{W}$
—where
$Y_{W}^{G} = B_{W}\oplus C_{W}$
—where
![]() $B_{W}$
and
$B_{W}$
and
![]() $C_{W}$
are complements to
$C_{W}$
are complements to
![]() $\mathscr {V}$
in their respective spaces—Lemma 2.1 gives
$\mathscr {V}$
in their respective spaces—Lemma 2.1 gives
![]() $(Y_{A} \oplus Y_{V})+Y_{W} = Y_{A} \oplus Y_{V} \oplus Y_{W}$
, and indeed
$(Y_{A} \oplus Y_{V})+Y_{W} = Y_{A} \oplus Y_{V} \oplus Y_{W}$
, and indeed
![]() $(Y_{A}\oplus Y_{V} \oplus Y_{W})^{G} = \mathscr {V} \oplus B_{W} \oplus C_{W}$
.
$(Y_{A}\oplus Y_{V} \oplus Y_{W})^{G} = \mathscr {V} \oplus B_{W} \oplus C_{W}$
.
Next, we know that
![]() $\mathscr {B} = \mathscr {V} \oplus B_{W} \oplus \langle \mathcal {B}_{0}\rangle $
, and since
$\mathscr {B} = \mathscr {V} \oplus B_{W} \oplus \langle \mathcal {B}_{0}\rangle $
, and since
![]() $Y_{B}^{G} = \langle \mathcal {B}_{0}\rangle $
, this means that
$Y_{B}^{G} = \langle \mathcal {B}_{0}\rangle $
, this means that
![]() $Y_{A}\oplus Y_{V} \oplus Y_{W} + Y_{B} = Y_{A}\oplus Y_{V} \oplus Y_{W} \oplus Y_{B}$
, and
$Y_{A}\oplus Y_{V} \oplus Y_{W} + Y_{B} = Y_{A}\oplus Y_{V} \oplus Y_{W} \oplus Y_{B}$
, and
![]() $(Y_{A}\oplus Y_{V} \oplus Y_{W} \oplus Y_{B})^{G} = \mathscr {B} \oplus C_{W}$
. Using the facts that
$(Y_{A}\oplus Y_{V} \oplus Y_{W} \oplus Y_{B})^{G} = \mathscr {B} \oplus C_{W}$
. Using the facts that
![]() $\mathscr {B} \cap \mathscr {C} = \mathscr {V}$
, that
$\mathscr {B} \cap \mathscr {C} = \mathscr {V}$
, that
![]() $Y_{C}^{G} = \langle \mathcal {C}_{0}\rangle $
, and that
$Y_{C}^{G} = \langle \mathcal {C}_{0}\rangle $
, and that
![]() $\mathscr {C} = \mathscr {V} \oplus C_{W} \oplus \langle \mathcal {C}_{0} \rangle $
, Lemma 2.1 gives
$\mathscr {C} = \mathscr {V} \oplus C_{W} \oplus \langle \mathcal {C}_{0} \rangle $
, Lemma 2.1 gives
![]() $Y_{A}\oplus Y_{V} \oplus Y_{W} \oplus Y_{B} + Y_{C}= Y_{A} \oplus Y_{V} \oplus Y_{W} \oplus Y_{B} \oplus Y_{C}$
, and
$Y_{A}\oplus Y_{V} \oplus Y_{W} \oplus Y_{B} + Y_{C}= Y_{A} \oplus Y_{V} \oplus Y_{W} \oplus Y_{B} \oplus Y_{C}$
, and
![]() $(Y_{A} \oplus Y_{V} \oplus Y_{W} \oplus Y_{B} \oplus Y_{C})^{G} = \mathscr {B}+\mathscr {C}$
.
$(Y_{A} \oplus Y_{V} \oplus Y_{W} \oplus Y_{B} \oplus Y_{C})^{G} = \mathscr {B}+\mathscr {C}$
.
For the next term, since
![]() $Y_{D}^{G} = \langle \mathcal {D}_{0} \rangle $
, where
$Y_{D}^{G} = \langle \mathcal {D}_{0} \rangle $
, where
![]() $\mathcal {D}_{0}$
is a complement to
$\mathcal {D}_{0}$
is a complement to
![]() $(\mathscr {B}+\mathscr {C})\cap \mathscr {D}$
, Lemma 2.1 gives us
$(\mathscr {B}+\mathscr {C})\cap \mathscr {D}$
, Lemma 2.1 gives us
![]() $Y_{A}\oplus Y_{V} \oplus Y_{W} \oplus Y_{B} \oplus Y_{C} + Y_{D} = Y_{A} \oplus Y_{V} \oplus Y_{W} \oplus Y_{B} \oplus Y_{C} \oplus Y_{D}$
, and indeed
$Y_{A}\oplus Y_{V} \oplus Y_{W} \oplus Y_{B} \oplus Y_{C} + Y_{D} = Y_{A} \oplus Y_{V} \oplus Y_{W} \oplus Y_{B} \oplus Y_{C} \oplus Y_{D}$
, and indeed
![]() $(Y_{A} \oplus Y_{V} \oplus Y_{W} \oplus Y_{B} \oplus Y_{C} \oplus Y_{D})^{G} = \mathscr {B}+\mathscr {C}+\mathscr {D}$
.
$(Y_{A} \oplus Y_{V} \oplus Y_{W} \oplus Y_{B} \oplus Y_{C} \oplus Y_{D})^{G} = \mathscr {B}+\mathscr {C}+\mathscr {D}$
.
Finally, since
![]() $Y_{F}^{G} = \langle \mathcal {F}_{0}\rangle $
, where
$Y_{F}^{G} = \langle \mathcal {F}_{0}\rangle $
, where
![]() $\mathcal {F}_{0}$
is a complement to
$\mathcal {F}_{0}$
is a complement to
![]() $\mathscr {B}+\mathscr {C}+\mathscr {D}$
in
$\mathscr {B}+\mathscr {C}+\mathscr {D}$
in
![]() $[F^{\times }]$
, one final application of Lemma 2.1 gives
$[F^{\times }]$
, one final application of Lemma 2.1 gives
![]() $\widehat {J}^{G} = [F^{\times }]$
and
$\widehat {J}^{G} = [F^{\times }]$
and
▪
Corollary 3.4 Suppose that
![]() $[f] \in \mathscr {M}$
for
$[f] \in \mathscr {M}$
for
![]() $\mathscr {M} \in \{\mathscr {A},\mathscr {B},\mathscr {C},\mathscr {D}\}$
. Then the diagram corresponding to
$\mathscr {M} \in \{\mathscr {A},\mathscr {B},\mathscr {C},\mathscr {D}\}$
. Then the diagram corresponding to
![]() $\mathscr {M}$
has a solution for
$\mathscr {M}$
has a solution for
![]() $[f]$
in which each term of the solution comes from
$[f]$
in which each term of the solution comes from
![]() $\widehat {J}$
.
$\widehat {J}$
.
Proof Suppose first that
![]() $[f] \in \mathscr {A}$
. Since
$[f] \in \mathscr {A}$
. Since
![]() $\mathcal {A}$
is a basis for
$\mathcal {A}$
is a basis for
![]() $\mathscr {A}$
, we have
$\mathscr {A}$
, we have
![]() $[f] = \prod _{i=1}^{n} [f_{i}]$
for appropriately chosen
$[f] = \prod _{i=1}^{n} [f_{i}]$
for appropriately chosen
![]() $[f_{i}] \in \mathcal {A}$
. By construction, there exist
$[f_{i}] \in \mathcal {A}$
. By construction, there exist
![]() $[k_{i}] \in J(K)$
so that
$[k_{i}] \in J(K)$
so that
![]() $[N_{K/F}(k_{i})]=[f_{i}]$
, and so we get
$[N_{K/F}(k_{i})]=[f_{i}]$
, and so we get
![]() $k = \prod _{i=1}^{n} [k_{i}]$
has
$k = \prod _{i=1}^{n} [k_{i}]$
has
![]() $[N_{K/F}(k)] = [f]$
. Hence, the diagram corresponding to
$[N_{K/F}(k)] = [f]$
. Hence, the diagram corresponding to
![]() $\mathscr {A}$
is solvable for
$\mathscr {A}$
is solvable for
![]() $[f]$
with terms drawn from
$[f]$
with terms drawn from
![]() $\widehat {J}$
.
$\widehat {J}$
.
Now, suppose that
![]() $[f] \in \mathscr {B}$
. Since we know
$[f] \in \mathscr {B}$
. Since we know
![]() $\mathscr {B} = \mathscr {V} \oplus B_{W} \oplus \langle \mathcal {B}_{0}\rangle $
, we can write
$\mathscr {B} = \mathscr {V} \oplus B_{W} \oplus \langle \mathcal {B}_{0}\rangle $
, we can write
![]() $[f] = \prod _{i=1}^{n} [f_{i}] \prod _{j=1}^{m} [\widehat {f_{j}}] \prod _{k=1}^{\ell } [\widetilde {f_{k}}]$
, where
$[f] = \prod _{i=1}^{n} [f_{i}] \prod _{j=1}^{m} [\widehat {f_{j}}] \prod _{k=1}^{\ell } [\widetilde {f_{k}}]$
, where
![]() $f_{i} \in \mathcal {A} \cup \mathcal {V}$
,
$f_{i} \in \mathcal {A} \cup \mathcal {V}$
,
![]() $\widehat {f_{j}} \in \mathcal {B}_{W}$
, and
$\widehat {f_{j}} \in \mathcal {B}_{W}$
, and
![]() $\widetilde {f_{k}} \in \mathcal {B}_{0}$
are appropriately chosen. Based on the construction of the terms from
$\widetilde {f_{k}} \in \mathcal {B}_{0}$
are appropriately chosen. Based on the construction of the terms from
![]() $Y_{A}$
,
$Y_{A}$
,
![]() $Y_{V}$
,
$Y_{V}$
,
![]() $Y_{W}$
, and
$Y_{W}$
, and
![]() $Y_{B}$
, we have elements
$Y_{B}$
, we have elements
![]() $[\gamma _{i}],[\widehat {\gamma _{j}}],[\widetilde {\gamma _{k}}] \in \widehat {J}$
that solve the diagram corresponding to
$[\gamma _{i}],[\widehat {\gamma _{j}}],[\widetilde {\gamma _{k}}] \in \widehat {J}$
that solve the diagram corresponding to
![]() $\mathscr {B}$
. Hence, if we let
$\mathscr {B}$
. Hence, if we let
![]() $[\gamma ] = \prod _{i=1}^{n} [\gamma _{i}] \prod _{j=1}^{m} [\widehat {\gamma _{j}}] \prod _{k=1}^{\ell } [\widetilde {\gamma _{k}}]$
, then the diagram corresponding to
$[\gamma ] = \prod _{i=1}^{n} [\gamma _{i}] \prod _{j=1}^{m} [\widehat {\gamma _{j}}] \prod _{k=1}^{\ell } [\widetilde {\gamma _{k}}]$
, then the diagram corresponding to
![]() $\mathscr {B}$
is solved with
$\mathscr {B}$
is solved with
![]() $[\gamma ]$
and
$[\gamma ]$
and
![]() $[f]$
. An analogous argument settles the case where
$[f]$
. An analogous argument settles the case where
![]() $[f] \in \mathscr {C}$
.
$[f] \in \mathscr {C}$
.
We have left to settle the statement for
![]() $\mathscr {M}=\mathscr {D}$
. This will take a bit more work. Since
$\mathscr {M}=\mathscr {D}$
. This will take a bit more work. Since
![]() $\mathcal {D}_{0}$
is a basis for a complement to
$\mathcal {D}_{0}$
is a basis for a complement to
![]() $(\mathscr {B}+\mathscr {C})\cap \mathscr {D}$
within
$(\mathscr {B}+\mathscr {C})\cap \mathscr {D}$
within
![]() $\mathscr {D}$
, we can write
$\mathscr {D}$
, we can write
![]() $[f] = [\hat f] \prod _{i=1}^{n}[f_{i}]$
, where
$[f] = [\hat f] \prod _{i=1}^{n}[f_{i}]$
, where
![]() $[\hat f] \in (\mathscr {B}+\mathscr {C})\cap \mathscr {D}$
, and with
$[\hat f] \in (\mathscr {B}+\mathscr {C})\cap \mathscr {D}$
, and with
![]() $[f_{i}] \in \mathcal {D}_{0}$
appropriately chosen. By construction of
$[f_{i}] \in \mathcal {D}_{0}$
appropriately chosen. By construction of
![]() $Y_{D}$
, for each i, we have an element
$Y_{D}$
, for each i, we have an element
![]() $[\gamma _{i}]$
so that the diagram for
$[\gamma _{i}]$
so that the diagram for
![]() $\mathscr {D}$
is solved with
$\mathscr {D}$
is solved with
![]() $[\gamma _{i}]$
and
$[\gamma _{i}]$
and
![]() $[f_{i}]$
. Furthermore, since
$[f_{i}]$
. Furthermore, since
![]() $[\hat f] \in (\mathscr {B}+\mathscr {C}) \cap \mathscr {D}$
, Lemma 3.1 tells us that
$[\hat f] \in (\mathscr {B}+\mathscr {C}) \cap \mathscr {D}$
, Lemma 3.1 tells us that
![]() $[\hat f] = [b][c]$
has the property that equation (3.1) is solvable for
$[\hat f] = [b][c]$
has the property that equation (3.1) is solvable for
![]() $[b]$
and
$[b]$
and
![]() $[c]$
:
$[c]$
:

Since B is a complement to
![]() $\mathscr {V}$
in
$\mathscr {V}$
in
![]() $\mathscr {B}$
and C is a complement to
$\mathscr {B}$
and C is a complement to
![]() $\mathscr {V}$
in
$\mathscr {V}$
in
![]() $\mathscr {C}$
, we can write
$\mathscr {C}$
, we can write
![]() $[b] = [v_{1}][b_{W}]$
and
$[b] = [v_{1}][b_{W}]$
and
![]() $[c] = [v_{2}][c_{W}]$
for
$[c] = [v_{2}][c_{W}]$
for
![]() $[v_{1}],[v_{2}] \in \mathscr {V}$
and
$[v_{1}],[v_{2}] \in \mathscr {V}$
and
![]() $[b_{W}] \in B$
and
$[b_{W}] \in B$
and
![]() $[c_{W}] \in C$
. For
$[c_{W}] \in C$
. For
![]() $i \in \{1,2\}$
, the construction of
$i \in \{1,2\}$
, the construction of
![]() $Y_{A}$
and
$Y_{A}$
and
![]() $Y_{V}$
give
$Y_{V}$
give
![]() $[\widetilde {\gamma _{L,i}}],[\widetilde {\gamma _{R,i}}] \in \widehat {J}$
that accompany
$[\widetilde {\gamma _{L,i}}],[\widetilde {\gamma _{R,i}}] \in \widehat {J}$
that accompany
![]() $[v_{i}]$
in solving the diagram for
$[v_{i}]$
in solving the diagram for
![]() $\mathscr {V}$
. Note in particular this means that the diagram corresponding to
$\mathscr {V}$
. Note in particular this means that the diagram corresponding to
![]() $\mathscr {D}$
is solved for
$\mathscr {D}$
is solved for
![]() $[\widetilde {\gamma _{L,i}}][\widetilde {\gamma _{R,i}}]$
and
$[\widetilde {\gamma _{L,i}}][\widetilde {\gamma _{R,i}}]$
and
![]() $[v_{i}]$
. We have left to deal with the
$[v_{i}]$
. We have left to deal with the
![]() $[b_{W}]$
and
$[b_{W}]$
and
![]() $[c_{W}]$
terms.
$[c_{W}]$
terms.
From our previous equations, we get

This means that
![]() $[b_{W}] \in B_{W}$
, and, by Lemma 3.2, we have
$[b_{W}] \in B_{W}$
, and, by Lemma 3.2, we have
![]() $\phi _{W}([b_{W}]) = c_{W} \in C_{W}$
. Hence,
$\phi _{W}([b_{W}]) = c_{W} \in C_{W}$
. Hence,
![]() $[b_{W}] = \prod _{j=1}^{m} [b_{j}]$
for
$[b_{W}] = \prod _{j=1}^{m} [b_{j}]$
for
![]() $[b_{j}]$
appropriately chosen from
$[b_{j}]$
appropriately chosen from
![]() $\mathcal {B}_{W}$
. By the construction of
$\mathcal {B}_{W}$
. By the construction of
![]() $Y_{W}$
, we have elements
$Y_{W}$
, we have elements
![]() $[\gamma _{1,j}],[\gamma _{2,j}],[\gamma _{3,j}] \in \widehat {J}$
which solve equation (3.1) for
$[\gamma _{1,j}],[\gamma _{2,j}],[\gamma _{3,j}] \in \widehat {J}$
which solve equation (3.1) for
![]() $[b_{j}]$
and
$[b_{j}]$
and
![]() $\phi _{W}([b_{j}])$
. Hence,
$\phi _{W}([b_{j}])$
. Hence,
![]() $\prod _{j=1}^{m} [\gamma _{1,j}]$
,
$\prod _{j=1}^{m} [\gamma _{1,j}]$
,
![]() $\prod _{j=1}^{m}[\gamma _{2,j}]$
, and
$\prod _{j=1}^{m}[\gamma _{2,j}]$
, and
![]() $\prod _{j=1}^{m} [\gamma _{3,j}]$
solve equation (3.1) for
$\prod _{j=1}^{m} [\gamma _{3,j}]$
solve equation (3.1) for
![]() $[b_{W}]$
and
$[b_{W}]$
and
![]() $\prod _{j=1}^{m} \phi _{W}([b_{j}]) = \phi _{W}(\prod _{j=1}^{m} [b_{j}]) = [c_{W}]$
. In particular, the equation corresponding to
$\prod _{j=1}^{m} \phi _{W}([b_{j}]) = \phi _{W}(\prod _{j=1}^{m} [b_{j}]) = [c_{W}]$
. In particular, the equation corresponding to
![]() $\mathscr {D}$
is solved by
$\mathscr {D}$
is solved by
![]() $\prod _{j=1}^{m} [\gamma _{1,j}][\gamma _{2,j}][\gamma _{3,j}]$
and
$\prod _{j=1}^{m} [\gamma _{1,j}][\gamma _{2,j}][\gamma _{3,j}]$
and
![]() $[b_{W}][c_{W}]$
.
$[b_{W}][c_{W}]$
.
In all, our original element
![]() $[f] \in \mathscr {D}$
has now been expressed as
$[f] \in \mathscr {D}$
has now been expressed as
![]() $[f] = [\hat f]\prod _{i=1}^{n}[f_{i}] = [b][c] \prod _{i=1}^{n} [f_{i}] = [v_{1}][b_{W}][v_{2}][c_{W}]\prod _{i=1}^{n}[f_{i}]$
, where each of
$[f] = [\hat f]\prod _{i=1}^{n}[f_{i}] = [b][c] \prod _{i=1}^{n} [f_{i}] = [v_{1}][b_{W}][v_{2}][c_{W}]\prod _{i=1}^{n}[f_{i}]$
, where each of
![]() $[v_{1}],[v_{2}],[b_{W}][c_{W}],$
and
$[v_{1}],[v_{2}],[b_{W}][c_{W}],$
and
![]() $\prod _{i=1}^{n}[f_{i}]$
have some corresponding element
$\prod _{i=1}^{n}[f_{i}]$
have some corresponding element
![]() $[\gamma ] \in \widehat {J}$
which solves the diagram corresponding to
$[\gamma ] \in \widehat {J}$
which solves the diagram corresponding to
![]() $\mathscr {D}$
.▪
$\mathscr {D}$
.▪
4 A module whose fixed part complements
 $[F^{\times }]$
in
$[F^{\times }]$
in
 $J(K)^{G}$
$J(K)^{G}$
Lemma 2.1 tells us that independent summands of
![]() $J(K)$
have independent fixed parts. Since we have already constructed a module whose fixed part is
$J(K)$
have independent fixed parts. Since we have already constructed a module whose fixed part is
![]() $[F^{\times }]$
, we now are interested in finding a complementary module whose fixed part spans a complement to
$[F^{\times }]$
, we now are interested in finding a complementary module whose fixed part spans a complement to
![]() $[F^{\times }]$
in
$[F^{\times }]$
in
![]() $J(K)^{G}$
—at least to the degree that such a goal is achievable at all. Ultimately, this search will culminate in Theorem 4.8 at the end of this section, but to work toward this result, we must first determine precisely which elements from
$J(K)^{G}$
—at least to the degree that such a goal is achievable at all. Ultimately, this search will culminate in Theorem 4.8 at the end of this section, but to work toward this result, we must first determine precisely which elements from
![]() $J(K)^{G}$
come from
$J(K)^{G}$
come from
![]() $[F^{\times }]$
.
$[F^{\times }]$
.
Kummer theory tells us that we can determine whether an element
![]() $[\gamma ] \in J(K)^{G}$
comes from
$[\gamma ] \in J(K)^{G}$
comes from
![]() $[F^{\times }]$
by examining the Galois group of the extension it generates over F:
$[F^{\times }]$
by examining the Galois group of the extension it generates over F:
The following result gives a slightly more nuanced view of this phenomenon. Note that in this result—and hence for much of the duration of this section—we use the notation
![]() $[\gamma ]_{i}$
to indicate the class of an element
$[\gamma ]_{i}$
to indicate the class of an element
![]() $\gamma \in K_{i}^{\times } \cap K^{\times 2}$
considered in the set
$\gamma \in K_{i}^{\times } \cap K^{\times 2}$
considered in the set
![]() $(K_{i}^{\times } \cap K^{\times 2})/K_{i}^{\times 2}$
for
$(K_{i}^{\times } \cap K^{\times 2})/K_{i}^{\times 2}$
for
![]() $i \in \{1,2,3\}$
.
$i \in \{1,2,3\}$
.
Lemma 4.1 Suppose that
![]() $[\gamma ] \in J(K)^{G} \setminus \{[1]\}$
. Then
$[\gamma ] \in J(K)^{G} \setminus \{[1]\}$
. Then
![]() $K(\sqrt {\gamma })/F$
is Galois, and if
$K(\sqrt {\gamma })/F$
is Galois, and if
![]() $\widehat { \sigma _{1}}$
and
$\widehat { \sigma _{1}}$
and
![]() $\widehat {\sigma _{2}}$
represent lifts of
$\widehat {\sigma _{2}}$
represent lifts of
![]() $\sigma _{1},\sigma _{2} \in \mathrm {Gal}(K/F)$
to the group
$\sigma _{1},\sigma _{2} \in \mathrm {Gal}(K/F)$
to the group
![]() $\mathrm {Gal}(K(\sqrt {\gamma })/F)$
, then we have
$\mathrm {Gal}(K(\sqrt {\gamma })/F)$
, then we have
 $$ \begin{align*} [N_{K/K_{1}}(\gamma)]_{1} &= [1]_{1} \Leftrightarrow \hat\sigma_{2}^{2} = \text{id},\\ [N_{K/K_{2}}(\gamma)]_{2} &= [1]_{2} \Leftrightarrow \hat\sigma_{1}^{2} = \text{id},\\ [N_{K/K_{3}}(\gamma)]_{3} &= [1]_{3} \Leftrightarrow \left(\hat\sigma_{1}\hat\sigma_{2}\right)^{2} = \text{id}. \end{align*} $$
$$ \begin{align*} [N_{K/K_{1}}(\gamma)]_{1} &= [1]_{1} \Leftrightarrow \hat\sigma_{2}^{2} = \text{id},\\ [N_{K/K_{2}}(\gamma)]_{2} &= [1]_{2} \Leftrightarrow \hat\sigma_{1}^{2} = \text{id},\\ [N_{K/K_{3}}(\gamma)]_{3} &= [1]_{3} \Leftrightarrow \left(\hat\sigma_{1}\hat\sigma_{2}\right)^{2} = \text{id}. \end{align*} $$
Proof We consider the first statement first. Observe that we already know that
![]() $\hat \sigma _{2}^{2}$
acts trivially on
$\hat \sigma _{2}^{2}$
acts trivially on
![]() $\sqrt {a_{1}}$
and
$\sqrt {a_{1}}$
and
![]() $\sqrt {a_{2}}$
, so we only need to determine the action of
$\sqrt {a_{2}}$
, so we only need to determine the action of
![]() $\hat \sigma _{2}^{2}$
on
$\hat \sigma _{2}^{2}$
on
![]() $\sqrt {\gamma }$
. For this, note that
$\sqrt {\gamma }$
. For this, note that
Since
![]() $[\gamma ] \in J(K)^{G}$
, we have that
$[\gamma ] \in J(K)^{G}$
, we have that
![]() $[\gamma ]^{\sigma _{2}+1} = [N_{K/K_{1}}(\gamma )]=[1]$
. Hence, we have
$[\gamma ]^{\sigma _{2}+1} = [N_{K/K_{1}}(\gamma )]=[1]$
. Hence, we have
![]() $N_{K/K_{1}}(\gamma ) \in K_{1}^{\times } \cap K^{\times 2}$
, and, by Kummer theory, this means that
$N_{K/K_{1}}(\gamma ) \in K_{1}^{\times } \cap K^{\times 2}$
, and, by Kummer theory, this means that
![]() $N_{K/K_{1}}(\gamma ) = a_{2}^{\varepsilon }k_{1}^{2}$
for some
$N_{K/K_{1}}(\gamma ) = a_{2}^{\varepsilon }k_{1}^{2}$
for some
![]() $\varepsilon \in \{0,1\}$
and
$\varepsilon \in \{0,1\}$
and
![]() $k_{1} \in K_{1}^{\times }$
. Note that
$k_{1} \in K_{1}^{\times }$
. Note that
![]() $\varepsilon = 0$
if and only if
$\varepsilon = 0$
if and only if
![]() $N_{K/K_{1}}(\gamma ) \in K_{1}^{\times 2}$
, which is equivalent to
$N_{K/K_{1}}(\gamma ) \in K_{1}^{\times 2}$
, which is equivalent to
![]() $[N_{K/K_{1}}(\gamma )]_{1} = [1]_{1}$
. Hence, our previous calculation continues
$[N_{K/K_{1}}(\gamma )]_{1} = [1]_{1}$
. Hence, our previous calculation continues
This gives the desired result.
Similar calculations give the other two results.▪
Corollary 4.2 Define
![]() $T:J(K)^{G} \to \bigoplus _{i=1}^{3} (K_{i}^{\times }\cap K^{\times 2})/K_{i}^{\times 2}$
by
$T:J(K)^{G} \to \bigoplus _{i=1}^{3} (K_{i}^{\times }\cap K^{\times 2})/K_{i}^{\times 2}$
by
Then
![]() $\ker (T)=[F^{\times }]$
.
$\ker (T)=[F^{\times }]$
.
Remark 4.3 Note that Kummer theory tells us that each
![]() $(K_{i}^{\times } \cap K^{\times 2})/K_{i}^{\times 2}$
consists of only two distinct classes, with representatives drawn from
$(K_{i}^{\times } \cap K^{\times 2})/K_{i}^{\times 2}$
consists of only two distinct classes, with representatives drawn from
![]() $\{1,a_{1},a_{2},a_{1}a_{2}\}$
. For example,
$\{1,a_{1},a_{2},a_{1}a_{2}\}$
. For example,
![]() $(K_{3}^{\times } \cap K^{\times 2})/K_{3}^{\times 2}$
has
$(K_{3}^{\times } \cap K^{\times 2})/K_{3}^{\times 2}$
has
![]() $[1]_{3}=[a_{1}a_{2}]_{3}$
and
$[1]_{3}=[a_{1}a_{2}]_{3}$
and
![]() $[a_{1}]_{3}=[a_{2}]_{3}$
as its elements. For the sake of lightening what would otherwise be fairly weighty notation, when considering elements in the image of T, we will suppress the bracket notation in its coordinates; that is to say, if
$[a_{1}]_{3}=[a_{2}]_{3}$
as its elements. For the sake of lightening what would otherwise be fairly weighty notation, when considering elements in the image of T, we will suppress the bracket notation in its coordinates; that is to say, if
![]() $T([\gamma ]) = ([u]_{1},[v]_{2},[w]_{3})$
, then we will instead write
$T([\gamma ]) = ([u]_{1},[v]_{2},[w]_{3})$
, then we will instead write
![]() $T([\gamma ]) = (u,v,w)$
.
$T([\gamma ]) = (u,v,w)$
.
Our goal, then, is to build a module whose fixed part spans the image of T, ideally while avoiding
![]() $[F^{\times }]$
as much as possible. The first question we consider when looking for such a module is to determine when elements with a nontrivial image under T are themselves in the image of either
$[F^{\times }]$
as much as possible. The first question we consider when looking for such a module is to determine when elements with a nontrivial image under T are themselves in the image of either
![]() $1+\sigma _{1}$
or
$1+\sigma _{1}$
or
![]() $1+\sigma _{2}$
. We start with the following result.
$1+\sigma _{2}$
. We start with the following result.
Lemma 4.4 If
![]() $\gamma \in K^{\times }$
has
$\gamma \in K^{\times }$
has
![]() $[N_{K/F}(\gamma )]= [1]$
, then
$[N_{K/F}(\gamma )]= [1]$
, then
![]() $[N_{K/K_{1}}(\gamma )],[N_{K/K_{2}}(\gamma )] \in J(K)^{G}$
, and
$[N_{K/K_{1}}(\gamma )],[N_{K/K_{2}}(\gamma )] \in J(K)^{G}$
, and
-
•
 $[N_{K/F}(\gamma )]_{F} = [1]_{F} \Leftrightarrow T([N_{K/K_{1}}(\gamma )]) = (1,1,1) \Leftrightarrow T([N_{K/K_{2}}(\gamma )]) = (1,1,1)$
;
$[N_{K/F}(\gamma )]_{F} = [1]_{F} \Leftrightarrow T([N_{K/K_{1}}(\gamma )]) = (1,1,1) \Leftrightarrow T([N_{K/K_{2}}(\gamma )]) = (1,1,1)$
; -
•
 $[N_{K/F}(\gamma )]_{F} = [a_{1}]_{F} \Leftrightarrow T([N_{K/K_{1}}(\gamma )]) = (1,a_{1},a_{1}) \Leftrightarrow T([N_{K/K_{2}}(\gamma )]) = (1,1,a_{1})$
;
$[N_{K/F}(\gamma )]_{F} = [a_{1}]_{F} \Leftrightarrow T([N_{K/K_{1}}(\gamma )]) = (1,a_{1},a_{1}) \Leftrightarrow T([N_{K/K_{2}}(\gamma )]) = (1,1,a_{1})$
; -
•
 $[N_{K/F}(\gamma )]_{F} = [a_{2}]_{F} \Leftrightarrow T([N_{K/K_{1}}(\gamma )]) = (1,1,a_{1}) \Leftrightarrow T([N_{K/K_{2}}(\gamma )]) = (a_{2},1,a_{1})$
; and
$[N_{K/F}(\gamma )]_{F} = [a_{2}]_{F} \Leftrightarrow T([N_{K/K_{1}}(\gamma )]) = (1,1,a_{1}) \Leftrightarrow T([N_{K/K_{2}}(\gamma )]) = (a_{2},1,a_{1})$
; and -
•
 $[N_{K/F}(\gamma )]_{F} = [a_{1}a_{2}]_{F} \Leftrightarrow T([N_{K/K_{1}}(\gamma )]) = (1,a_{1},1) \Leftrightarrow T([N_{K/K_{2}}(\gamma )]) = (a_{2},1,1)$
.
$[N_{K/F}(\gamma )]_{F} = [a_{1}a_{2}]_{F} \Leftrightarrow T([N_{K/K_{1}}(\gamma )]) = (1,a_{1},1) \Leftrightarrow T([N_{K/K_{2}}(\gamma )]) = (a_{2},1,1)$
.
Proof Observe first that since
![]() $[N_{K/F}(\gamma )] = [1]$
, Kummer theory tells us that
$[N_{K/F}(\gamma )] = [1]$
, Kummer theory tells us that
![]() $[N_{K/F}(\gamma )]_{F} \in \{[1]_{F},[a_{1}]_{F},[a_{2}]_{F},[a_{1}a_{2}]_{F}\}$
. So let us write
$[N_{K/F}(\gamma )]_{F} \in \{[1]_{F},[a_{1}]_{F},[a_{2}]_{F},[a_{1}a_{2}]_{F}\}$
. So let us write
![]() $N_{K/F}(\gamma ) = f^{2} a_{1}^{\varepsilon _{1}}a_{2}^{\varepsilon _{2}}$
. The result then follows from the following calculations:
$N_{K/F}(\gamma ) = f^{2} a_{1}^{\varepsilon _{1}}a_{2}^{\varepsilon _{2}}$
. The result then follows from the following calculations:
 $$ \begin{align*} [N_{K/K_{1}}(N_{K/K_{1}}(\gamma))]_{1} &= [N_{K/K_{1}}(\gamma)^{2}]_{1} = [1]_{1},\\ [N_{K/K_{2}}(N_{K/K_{1}}(\gamma))]_{2} &= [N_{K/F}(\gamma)]_{2} = [f^{2}a_{1}^{\varepsilon_{1}}a_{2}^{\varepsilon_{2}}]_{2} = [a_{1}]_{2}^{\varepsilon_{1}},\\ [N_{K/K_{3}}(N_{K/K_{1}}(\gamma))]_{3} &= [N_{K/F}(\gamma)]_{3} = [f^{2}a_{1}^{\varepsilon_{1}}a_{2}^{\varepsilon_{2}}]_{3} = [a_{1}]_{3}^{\varepsilon_{1}+\varepsilon_{2}},\\ [N_{K/K_{1}}(N_{K/K_{2}}(\gamma))]_{1} &= [N_{K/F}(\gamma)]_{1} = [f^{2}a_{1}^{\varepsilon_{1}}a_{2}^{\varepsilon_{2}}]_{1} = [a_{2}]_{1}^{\varepsilon_{2}},\\ [N_{K/K_{2}}(N_{K/K_{2}}(\gamma))]_{2} &= [N_{K/K_{2}}(\gamma)^{2}]_{2} = [1]_{2},\\ [N_{K/K_{3}}(N_{K/K_{2}}(\gamma))]_{3} &= [N_{K/F}(\gamma)]_{3} = [f^{2}a_{1}^{\varepsilon_{1}}a_{2}^{\varepsilon_{2}}]_{3} = [a_{1}]_{3}^{\varepsilon_{1}+\varepsilon_{2}}.\\[-36pt] \end{align*} $$
$$ \begin{align*} [N_{K/K_{1}}(N_{K/K_{1}}(\gamma))]_{1} &= [N_{K/K_{1}}(\gamma)^{2}]_{1} = [1]_{1},\\ [N_{K/K_{2}}(N_{K/K_{1}}(\gamma))]_{2} &= [N_{K/F}(\gamma)]_{2} = [f^{2}a_{1}^{\varepsilon_{1}}a_{2}^{\varepsilon_{2}}]_{2} = [a_{1}]_{2}^{\varepsilon_{1}},\\ [N_{K/K_{3}}(N_{K/K_{1}}(\gamma))]_{3} &= [N_{K/F}(\gamma)]_{3} = [f^{2}a_{1}^{\varepsilon_{1}}a_{2}^{\varepsilon_{2}}]_{3} = [a_{1}]_{3}^{\varepsilon_{1}+\varepsilon_{2}},\\ [N_{K/K_{1}}(N_{K/K_{2}}(\gamma))]_{1} &= [N_{K/F}(\gamma)]_{1} = [f^{2}a_{1}^{\varepsilon_{1}}a_{2}^{\varepsilon_{2}}]_{1} = [a_{2}]_{1}^{\varepsilon_{2}},\\ [N_{K/K_{2}}(N_{K/K_{2}}(\gamma))]_{2} &= [N_{K/K_{2}}(\gamma)^{2}]_{2} = [1]_{2},\\ [N_{K/K_{3}}(N_{K/K_{2}}(\gamma))]_{3} &= [N_{K/F}(\gamma)]_{3} = [f^{2}a_{1}^{\varepsilon_{1}}a_{2}^{\varepsilon_{2}}]_{3} = [a_{1}]_{3}^{\varepsilon_{1}+\varepsilon_{2}}.\\[-36pt] \end{align*} $$
▪
Corollary 4.5 Suppose that
![]() $[\gamma ] \in J(K)$
generates a module isomorphic to
$[\gamma ] \in J(K)$
generates a module isomorphic to
![]() $\mathbb {F}_{2}[\overline {G_{i}}]$
for some
$\mathbb {F}_{2}[\overline {G_{i}}]$
for some
![]() $i \in \{1,2,3\}$
. Then
$i \in \{1,2,3\}$
. Then
![]() $T(\langle [\gamma ]\rangle ^{G}) = \{(1,1,1)\}$
.
$T(\langle [\gamma ]\rangle ^{G}) = \{(1,1,1)\}$
.
Proof We proceed by cases. If
![]() $\langle [\gamma ]\rangle \simeq \mathbb {F}_{2}[\overline {G_{1}}]$
, then we have
$\langle [\gamma ]\rangle \simeq \mathbb {F}_{2}[\overline {G_{1}}]$
, then we have
![]() $[\gamma ]^{1+\sigma _{2}} = [1]$
, so that
$[\gamma ]^{1+\sigma _{2}} = [1]$
, so that
![]() $[N_{K/F}(\gamma )] = [1]$
. Since
$[N_{K/F}(\gamma )] = [1]$
. Since
![]() $\langle [\gamma ]\rangle ^{G} = \langle [\gamma ]^{1+\sigma _{1}}\rangle $
, in this case, our objective is to show that
$\langle [\gamma ]\rangle ^{G} = \langle [\gamma ]^{1+\sigma _{1}}\rangle $
, in this case, our objective is to show that
![]() $T([\gamma ]^{1+\sigma _{1}}) = (1,1,1)$
. But since
$T([\gamma ]^{1+\sigma _{1}}) = (1,1,1)$
. But since
![]() $[\gamma ]^{1+\sigma _{1}} = [N_{K/K_{2}}(\gamma )]$
, the previous lemma tells us that if we have
$[\gamma ]^{1+\sigma _{1}} = [N_{K/K_{2}}(\gamma )]$
, the previous lemma tells us that if we have
![]() $T([\gamma ]^{1+\sigma _{1}}) \neq (1,1,1)$
, then we have
$T([\gamma ]^{1+\sigma _{1}}) \neq (1,1,1)$
, then we have
![]() $(1,1,1) \neq T([N_{K/K_{1}}(\gamma )]) = T([\gamma ]^{1+\sigma _{2}}) = T([1])$
as well, a contradiction. The same argument gives the result for
$(1,1,1) \neq T([N_{K/K_{1}}(\gamma )]) = T([\gamma ]^{1+\sigma _{2}}) = T([1])$
as well, a contradiction. The same argument gives the result for
![]() $i=2$
.
$i=2$
.
For
![]() $i=3$
, a variation on this argument works: we know we have
$i=3$
, a variation on this argument works: we know we have
![]() $[N_{K/K_{1}}(\gamma )] = [N_{K/K_{2}}(\gamma )]$
, and yet the lemma above provides no nontrivial case in which
$[N_{K/K_{1}}(\gamma )] = [N_{K/K_{2}}(\gamma )]$
, and yet the lemma above provides no nontrivial case in which
![]() $T([N_{K/K_{1}}(\gamma )]) = T([N_{K/K_{2}}(\gamma )])$
.▪
$T([N_{K/K_{1}}(\gamma )]) = T([N_{K/K_{2}}(\gamma )])$
.▪
Lemma 4.4 tells us a relationship between the possible values under T for elements from
![]() $J(K)^{G}$
which are in the image of a common element; if two elements
$J(K)^{G}$
which are in the image of a common element; if two elements
![]() $[x]$
and
$[x]$
and
![]() $[y]$
have “compatible” images under T (i.e., allowable in light of Lemma 4.4), is it the case that there exists some
$[y]$
have “compatible” images under T (i.e., allowable in light of Lemma 4.4), is it the case that there exists some
![]() $[\gamma ]$
so that
$[\gamma ]$
so that
![]() $[x] = [N_{K/K_{1}}(\gamma )]$
and
$[x] = [N_{K/K_{1}}(\gamma )]$
and
![]() $[y] = [N_{K/K_{2}}(\gamma )]$
? The answer to this is generally “no,” but there is a weaker version which we will take advantage of.
$[y] = [N_{K/K_{2}}(\gamma )]$
? The answer to this is generally “no,” but there is a weaker version which we will take advantage of.
Lemma 4.6 Suppose that
![]() $[x],[y]\in J(K)^{G}$
are given, and that
$[x],[y]\in J(K)^{G}$
are given, and that
![]() $(T([x]),T([y]))$
is either
$(T([x]),T([y]))$
is either
![]() $\left ((1,a_{1},a_{1}),(1,1,a_{1})\right )$
or
$\left ((1,a_{1},a_{1}),(1,1,a_{1})\right )$
or
![]() $\left ((1,1,a_{1}),(a_{2},1,a_{1})\right )$
or
$\left ((1,1,a_{1}),(a_{2},1,a_{1})\right )$
or
![]() $\left ((1,a_{1},1),(a_{1},1,1)\right )$
. Then there exists some
$\left ((1,a_{1},1),(a_{1},1,1)\right )$
. Then there exists some
![]() $[\gamma ]$
with
$[\gamma ]$
with
![]() $[N_{K/F}(\gamma )]=[1]$
so that
$[N_{K/F}(\gamma )]=[1]$
so that
![]() $T([N_{K/K_{1}}(\gamma )]) = T([x])$
and
$T([N_{K/K_{1}}(\gamma )]) = T([x])$
and
![]() $T([N_{K/K_{2}}(\gamma )]) = T([y])$
.
$T([N_{K/K_{2}}(\gamma )]) = T([y])$
.
Proof Our approach will be to argue that the appearance of these elements in the image of T guarantees the solvability of certain embedding problems, from which we deduce the solvability of certain equations involving norms.
We first handle the case where
![]() $\mathrm {im}(T)$
contains
$\mathrm {im}(T)$
contains
![]() $\{(1,a_{1},a_{1}),(1,1,a_{1})\}$
. Since
$\{(1,a_{1},a_{1}),(1,1,a_{1})\}$
. Since
![]() $T([x]) = (1,a_{1},a_{1})$
, we know from Lemma 4.1 that in
$T([x]) = (1,a_{1},a_{1})$
, we know from Lemma 4.1 that in
![]() $K(\sqrt {x})/F$
the generators
$K(\sqrt {x})/F$
the generators
![]() $\sigma _{1},\sigma _{2} \in \mathrm {Gal}(K/F)$
extend to elements
$\sigma _{1},\sigma _{2} \in \mathrm {Gal}(K/F)$
extend to elements
![]() $\hat \sigma _{1},\hat \sigma _{2} \in \mathrm {Gal}(K(\sqrt {x})/F)$
which satisfy the relations
$\hat \sigma _{1},\hat \sigma _{2} \in \mathrm {Gal}(K(\sqrt {x})/F)$
which satisfy the relations
Hence,
![]() $\mathrm {Gal}(K(\sqrt {x})/F)\twoheadrightarrow \mathrm {Gal}(K/F)$
solves the embedding problem
$\mathrm {Gal}(K(\sqrt {x})/F)\twoheadrightarrow \mathrm {Gal}(K/F)$
solves the embedding problem
![]() $\mathbb {Z}/4\mathbb {Z}\oplus \mathbb {Z}/2\mathbb {Z} \twoheadrightarrow \mathbb {Z}/2\mathbb {Z}\oplus \mathbb {Z}/2\mathbb {Z}$
, and in particular
$\mathbb {Z}/4\mathbb {Z}\oplus \mathbb {Z}/2\mathbb {Z} \twoheadrightarrow \mathbb {Z}/2\mathbb {Z}\oplus \mathbb {Z}/2\mathbb {Z}$
, and in particular
![]() $K_{1}/F$
embeds in a cyclic extension of degree
$K_{1}/F$
embeds in a cyclic extension of degree
![]() $4$
. By [Reference Albert2, Theorem 3], we have
$4$
. By [Reference Albert2, Theorem 3], we have
![]() $-1\in N_{K_{1}/F}(K_{1}^{\times })$
; since we have
$-1\in N_{K_{1}/F}(K_{1}^{\times })$
; since we have
![]() $-a_{1} = (\sqrt {a_{1}})^{1+\sigma _{1}}=N_{K_{1}/F}(\sqrt {a_{1}})$
, it therefore follows that
$-a_{1} = (\sqrt {a_{1}})^{1+\sigma _{1}}=N_{K_{1}/F}(\sqrt {a_{1}})$
, it therefore follows that
![]() $a_{1} \in N_{K_{1}/F}(K_{1}^{\times })$
, say
$a_{1} \in N_{K_{1}/F}(K_{1}^{\times })$
, say
![]() $a_{1} = N_{K_{1}/F}(k_{1})$
for
$a_{1} = N_{K_{1}/F}(k_{1})$
for
![]() $k_{1} \in K_{1}^{\times }$
.
$k_{1} \in K_{1}^{\times }$
.
On the other hand, since
![]() $T([y]) = (1,1,a_{1})$
, we know from Lemma 4.1 that the generators
$T([y]) = (1,1,a_{1})$
, we know from Lemma 4.1 that the generators
![]() $\sigma _{1},\sigma _{2} \in \mathrm {Gal}(K/F)$
extend to elements
$\sigma _{1},\sigma _{2} \in \mathrm {Gal}(K/F)$
extend to elements
![]() $\tilde \sigma _{1},\tilde \sigma _{2} \in \mathrm {Gal}(K(\sqrt {y})/F)$
that satisfy
$\tilde \sigma _{1},\tilde \sigma _{2} \in \mathrm {Gal}(K(\sqrt {y})/F)$
that satisfy
From this, we see that
![]() $\mathrm {Gal}(K(\sqrt {y})/F) \twoheadrightarrow \mathrm {Gal}(K/F)$
solves the embedding problem
$\mathrm {Gal}(K(\sqrt {y})/F) \twoheadrightarrow \mathrm {Gal}(K/F)$
solves the embedding problem
![]() $D_{4} \twoheadrightarrow \mathbb {Z}/2\mathbb {Z}\oplus \mathbb {Z}/2\mathbb {Z}$
, where the kernel of the latter surjection is
$D_{4} \twoheadrightarrow \mathbb {Z}/2\mathbb {Z}\oplus \mathbb {Z}/2\mathbb {Z}$
, where the kernel of the latter surjection is
![]() $\langle (\tilde \sigma _{1}\tilde \sigma _{2})^{2}\rangle $
. By a well-known result for the solvability of such embedding problems (see, e.g., [Reference Jensen and Yui16, Proposition III.3.3]), we therefore have
$\langle (\tilde \sigma _{1}\tilde \sigma _{2})^{2}\rangle $
. By a well-known result for the solvability of such embedding problems (see, e.g., [Reference Jensen and Yui16, Proposition III.3.3]), we therefore have
![]() $a_{1} \in N_{K_{2}/F}(K_{2}^{\times })$
, say
$a_{1} \in N_{K_{2}/F}(K_{2}^{\times })$
, say
![]() $a_{1} = N_{K_{2}/F}(k_{2})$
for
$a_{1} = N_{K_{2}/F}(k_{2})$
for
![]() $k_{2} \in K_{2}^{\times }$
.
$k_{2} \in K_{2}^{\times }$
.
By [Reference Wadsworth30, Lemma 2.14], there exists some
![]() $\gamma \in K^{\times }$
and
$\gamma \in K^{\times }$
and
![]() $f \in F^{\times }$
so that
$f \in F^{\times }$
so that
![]() $N_{K/K_{1}}(\gamma ) = fk_{1}$
and
$N_{K/K_{1}}(\gamma ) = fk_{1}$
and
![]() $N_{K/K_{2}}(\gamma ) = fk_{2}$
. In particular, we have
$N_{K/K_{2}}(\gamma ) = fk_{2}$
. In particular, we have
![]() $[N_{K/F}(\gamma )]_{F} = [f^{2}a_{1}]_{F} = [a_{1}]_{F}$
. An application of Lemma 4.4 finishes this case.
$[N_{K/F}(\gamma )]_{F} = [f^{2}a_{1}]_{F} = [a_{1}]_{F}$
. An application of Lemma 4.4 finishes this case.
The second case is effectively identical to the first. For the last case, note that the images we are given provide two
![]() $D_{4}$
-extensions over
$D_{4}$
-extensions over
![]() $K/F$
, one in which
$K/F$
, one in which
![]() $\sigma _{1}$
extends to an element of order
$\sigma _{1}$
extends to an element of order
![]() $4$
, and another where
$4$
, and another where
![]() $\sigma _{2}$
extends to an element of order
$\sigma _{2}$
extends to an element of order
![]() $4$
. In the former case, we then get
$4$
. In the former case, we then get
![]() $a_{1}a_{2} \in N_{K_{2}/F}(K_{2}^{\times })$
, and in the latter, we get
$a_{1}a_{2} \in N_{K_{2}/F}(K_{2}^{\times })$
, and in the latter, we get
![]() $a_{1}a_{2} \in N_{K_{1}/F}(K_{1}^{\times })$
. From here, the proof proceeds as before.▪
$a_{1}a_{2} \in N_{K_{1}/F}(K_{1}^{\times })$
. From here, the proof proceeds as before.▪
Remark 4.7 The use of [Reference Wadsworth30, Lemma 2.14] amounts to an appeal to Hilbert 90 for biquadratic extensions. See [Reference Dwilewicz, Mináč, Schultz and Swallow10].
We are now prepared for the main result of this section.
Theorem 4.8 There exists
![]() $X \subseteq J(K)$
with
$X \subseteq J(K)$
with
![]() $T(X^{G}) = \mathrm {im}(T)$
, so that
$T(X^{G}) = \mathrm {im}(T)$
, so that
 $$ \begin{align*} & X \simeq \\ & \left\{\!\!\begin{array}{l@{}l} \{[1]\},&\text{ if }\dim(\mathrm{im}(T)) = 0,\\ \mathbb{F}_{2},&\text{ if }\dim(\mathrm{im}(T)) = 1,\\ \Omega^{-1},&\text{ if }\dim(\mathrm{im}(T)) = 2\text{ and }\mathrm{im}(T)\text{ is one of the ``coordinate planes,''}\\ \mathbb{F}_{2}\oplus \mathbb{F}_{2},&\text{ if }\dim(\mathrm{im}(T)) = 2\text{ and }\mathrm{im}(T)\text{ is not one of the ``coordinate planes,''}\\ \Omega^{-2},&\text{ if }\dim(\mathrm{im}(T)) = 3\text{ and }T\left([N_{K/K_{1}}(K^{\times})] \cap [N_{K/K_{2}}(K^{\times})]\right) \neq \{(1,1,1)\},\\ \Omega^{-1}\oplus\Omega^{-1},&\text{ if }\dim(\mathrm{im}(T)) = 3\text{ and }T\left([N_{K/K_{1}}(K^{\times})] \cap [N_{K/K_{2}}(K^{\times})]\right) = \{(1,1,1)\}\text{.} \end{array} \right. \end{align*} $$
$$ \begin{align*} & X \simeq \\ & \left\{\!\!\begin{array}{l@{}l} \{[1]\},&\text{ if }\dim(\mathrm{im}(T)) = 0,\\ \mathbb{F}_{2},&\text{ if }\dim(\mathrm{im}(T)) = 1,\\ \Omega^{-1},&\text{ if }\dim(\mathrm{im}(T)) = 2\text{ and }\mathrm{im}(T)\text{ is one of the ``coordinate planes,''}\\ \mathbb{F}_{2}\oplus \mathbb{F}_{2},&\text{ if }\dim(\mathrm{im}(T)) = 2\text{ and }\mathrm{im}(T)\text{ is not one of the ``coordinate planes,''}\\ \Omega^{-2},&\text{ if }\dim(\mathrm{im}(T)) = 3\text{ and }T\left([N_{K/K_{1}}(K^{\times})] \cap [N_{K/K_{2}}(K^{\times})]\right) \neq \{(1,1,1)\},\\ \Omega^{-1}\oplus\Omega^{-1},&\text{ if }\dim(\mathrm{im}(T)) = 3\text{ and }T\left([N_{K/K_{1}}(K^{\times})] \cap [N_{K/K_{2}}(K^{\times})]\right) = \{(1,1,1)\}\text{.} \end{array} \right. \end{align*} $$
In all cases except the last, we have
![]() $[F^{\times }] \cap X^{G} = \{[1]\}$
; in the last case, we have
$[F^{\times }] \cap X^{G} = \{[1]\}$
; in the last case, we have
![]() $\dim (X^{G} \cap [F^{\times }]) = 1$
and
$\dim (X^{G} \cap [F^{\times }]) = 1$
and
![]() $X^{G} \cap (\mathscr {B}+\mathscr {C}+\mathscr {D}) =\{[1]\}$
.
$X^{G} \cap (\mathscr {B}+\mathscr {C}+\mathscr {D}) =\{[1]\}$
.
Proof We proceed by cases based on
![]() $\dim (\mathrm {im}(T))$
. First, if
$\dim (\mathrm {im}(T))$
. First, if
![]() $\dim (\mathrm {im}(T)) = 1$
, then let
$\dim (\mathrm {im}(T)) = 1$
, then let
![]() $[x] \in J(K)^{G}$
be given so that
$[x] \in J(K)^{G}$
be given so that
![]() $T([x]) \neq (1,1,1)$
. Then
$T([x]) \neq (1,1,1)$
. Then
![]() $X:=\langle [x]\rangle $
has the desired properties.
$X:=\langle [x]\rangle $
has the desired properties.
Now, suppose that
![]() $\dim (\mathrm {im}(T)) = 2$
. By Lemma 4.6, we know that if
$\dim (\mathrm {im}(T)) = 2$
. By Lemma 4.6, we know that if
![]() $\mathrm {im}(T)$
is any of
$\mathrm {im}(T)$
is any of
 $$ \begin{align*} \langle (1,a_{1},a_{1}),(1,1,a_{1})\rangle &= \{(1,w,z):w \in (K_{2}^{\times}\cap K^{\times 2})/K_{2}^{\times 2},z \in (K_{3}^{\times} \cap K^{\times 2})/K_{3}^{\times 2}\},\\ \langle (1,1,a_{1}),(a_{2},1,a_{1})\rangle &= \{(w,1,z):w \in (K_{1}^{\times}\cap K^{\times 2})/K_{1}^{\times 2},z \in (K_{3}^{\times} \cap K^{\times 2})/K_{3}^{\times 2}\}\text{, or}\\ \langle (1,a_{1},1),(a_{1},1,1)\rangle &= \{(w,z,1):w \in (K_{1}^{\times}\cap K^{\times 2})/K_{1}^{\times 2},z \in (K_{2}^{\times} \cap K^{\times 2})/K_{2}^{\times 2}\}, \end{align*} $$
$$ \begin{align*} \langle (1,a_{1},a_{1}),(1,1,a_{1})\rangle &= \{(1,w,z):w \in (K_{2}^{\times}\cap K^{\times 2})/K_{2}^{\times 2},z \in (K_{3}^{\times} \cap K^{\times 2})/K_{3}^{\times 2}\},\\ \langle (1,1,a_{1}),(a_{2},1,a_{1})\rangle &= \{(w,1,z):w \in (K_{1}^{\times}\cap K^{\times 2})/K_{1}^{\times 2},z \in (K_{3}^{\times} \cap K^{\times 2})/K_{3}^{\times 2}\}\text{, or}\\ \langle (1,a_{1},1),(a_{1},1,1)\rangle &= \{(w,z,1):w \in (K_{1}^{\times}\cap K^{\times 2})/K_{1}^{\times 2},z \in (K_{2}^{\times} \cap K^{\times 2})/K_{2}^{\times 2}\}, \end{align*} $$
then we can find some
![]() $[\gamma ] \in J(K)$
with
$[\gamma ] \in J(K)$
with
![]() $[N_{K/F}(\gamma )]=[1]$
so that
$[N_{K/F}(\gamma )]=[1]$
so that
![]() $\left \langle T\left ([N_{K/K_{1}}(\gamma )]\right ),T\left ([N_{K/K_{2}}(\gamma )]\right )\right \rangle = \mathrm {im}(T)$
. It is easy to see that
$\left \langle T\left ([N_{K/K_{1}}(\gamma )]\right ),T\left ([N_{K/K_{2}}(\gamma )]\right )\right \rangle = \mathrm {im}(T)$
. It is easy to see that
![]() $X:=\langle [\gamma ]\rangle \simeq \Omega ^{-1}$
, and since the nontrivial fixed elements in this module have nontrivial images under T, we get
$X:=\langle [\gamma ]\rangle \simeq \Omega ^{-1}$
, and since the nontrivial fixed elements in this module have nontrivial images under T, we get
![]() $X^{G} \cap [F^{\times }] = \{[1]\}$
.
$X^{G} \cap [F^{\times }] = \{[1]\}$
.
On the other hand, if
![]() $\dim (\mathrm {im}(T)) = 2$
but
$\dim (\mathrm {im}(T)) = 2$
but
![]() $\mathrm {im}(T)$
is none of the three subspaces above, then let
$\mathrm {im}(T)$
is none of the three subspaces above, then let
![]() $[x_{1}],[x_{2}] \in J(K)^{G}$
be given so that
$[x_{1}],[x_{2}] \in J(K)^{G}$
be given so that
![]() $\{T([x_{1}]),T([x_{2}])\}$
forms a basis for
$\{T([x_{1}]),T([x_{2}])\}$
forms a basis for
![]() $\mathrm {im}(T)$
; we then set
$\mathrm {im}(T)$
; we then set
![]() $X:=\langle [x_{1}],[x_{2}]\rangle \simeq \mathbb {F}_{2}\oplus \mathbb {F}_{2}$
, with
$X:=\langle [x_{1}],[x_{2}]\rangle \simeq \mathbb {F}_{2}\oplus \mathbb {F}_{2}$
, with
![]() $X \cap [F^{\times }] = \{[1]\}$
.
$X \cap [F^{\times }] = \{[1]\}$
.
Now, suppose that
![]() $\dim (\mathrm {im}(T)) = 3$
. First, consider the case where
$\dim (\mathrm {im}(T)) = 3$
. First, consider the case where
![]() $T([N_{K/K_{1}}(K^{\times })]\cap [N_{K/K_{2}}(K^{\times })]) \neq \{(1,1,1)\}$
, and let
$T([N_{K/K_{1}}(K^{\times })]\cap [N_{K/K_{2}}(K^{\times })]) \neq \{(1,1,1)\}$
, and let
![]() $[x]$
be given so that
$[x]$
be given so that
![]() $[N_{K/K_{1}}(\gamma _{2})] = [x] = [N_{K/K_{2}}(\gamma _{1})]$
for some
$[N_{K/K_{1}}(\gamma _{2})] = [x] = [N_{K/K_{2}}(\gamma _{1})]$
for some
![]() $[\gamma _{1}],[\gamma _{2}] \in J(K)$
and with
$[\gamma _{1}],[\gamma _{2}] \in J(K)$
and with
![]() $T([x]) \neq (1,1,1)$
. (Note that since
$T([x]) \neq (1,1,1)$
. (Note that since
![]() $[x]$
is in the image of
$[x]$
is in the image of
![]() $N_{K/K_{1}}$
and
$N_{K/K_{1}}$
and
![]() $N_{K/K_{2}}$
, it is automatically in
$N_{K/K_{2}}$
, it is automatically in
![]() $J(K)^{G}$
; hence, it makes sense to evaluate its image under T.) Lemma 4.4 tells us that
$J(K)^{G}$
; hence, it makes sense to evaluate its image under T.) Lemma 4.4 tells us that
![]() $T([x]) = (1,1,a_{1})$
, and furthermore that
$T([x]) = (1,1,a_{1})$
, and furthermore that
![]() $T([N_{K/K_{1}}(\gamma _{1})]) = (1,a_{1},a_{1})$
and
$T([N_{K/K_{1}}(\gamma _{1})]) = (1,a_{1},a_{1})$
and
![]() $T([N_{K/K_{2}}(\gamma _{2})]) = (a_{2},1,a_{1})$
. We claim that
$T([N_{K/K_{2}}(\gamma _{2})]) = (a_{2},1,a_{1})$
. We claim that
![]() $X:=\langle [\gamma _{1}],[\gamma _{2}]\rangle \simeq \Omega ^{-2}$
; certainly, the appropriate relations hold, so we only need to check that the module is five-dimensional. Note that
$X:=\langle [\gamma _{1}],[\gamma _{2}]\rangle \simeq \Omega ^{-2}$
; certainly, the appropriate relations hold, so we only need to check that the module is five-dimensional. Note that
![]() $\{[N_{K/K_{1}}(\gamma _{1})],[x],[N_{K/K_{2}}(\gamma _{2})]\}$
must be independent since their images under T are independent, and hence any nontrivial dependence must involve
$\{[N_{K/K_{1}}(\gamma _{1})],[x],[N_{K/K_{2}}(\gamma _{2})]\}$
must be independent since their images under T are independent, and hence any nontrivial dependence must involve
![]() $[\gamma _{1}]$
or
$[\gamma _{1}]$
or
![]() $[\gamma _{2}]$
. However, an application of
$[\gamma _{2}]$
. However, an application of
![]() $1+\sigma _{1}$
(or
$1+\sigma _{1}$
(or
![]() $1+\sigma _{2}$
) to such a relation creates a nontrivial relation among
$1+\sigma _{2}$
) to such a relation creates a nontrivial relation among
![]() $\{[N_{K/K_{1}}(\gamma _{1})],[x],[N_{K/K_{2}}(\gamma _{2})]\}$
, contrary to their independence. Since we have
$\{[N_{K/K_{1}}(\gamma _{1})],[x],[N_{K/K_{2}}(\gamma _{2})]\}$
, contrary to their independence. Since we have
![]() $X \simeq \Omega ^{-2}$
, we get
$X \simeq \Omega ^{-2}$
, we get
![]() $X^{G} = \langle [N_{K/K_{1}}(\gamma _{1})],[x],[N_{K/K_{2}}(\gamma _{2})]\rangle $
, whence
$X^{G} = \langle [N_{K/K_{1}}(\gamma _{1})],[x],[N_{K/K_{2}}(\gamma _{2})]\rangle $
, whence
![]() $X^{G} \cap [F^{\times }] = \{[1]\}$
.
$X^{G} \cap [F^{\times }] = \{[1]\}$
.
Alternatively, suppose that
![]() $\dim (\mathrm {im}(T)) = 3$
, but
$\dim (\mathrm {im}(T)) = 3$
, but
![]() $T([N_{K/K_{1}}(K^{\times }) \cap [N_{K/K_{2}}(K^{\times })]) = \{(1,1,1)\}$
. Lemma 4.6 gives us elements
$T([N_{K/K_{1}}(K^{\times }) \cap [N_{K/K_{2}}(K^{\times })]) = \{(1,1,1)\}$
. Lemma 4.6 gives us elements
![]() $[\gamma _{1}],[\gamma _{2}] \in J(K)$
so that
$[\gamma _{1}],[\gamma _{2}] \in J(K)$
so that
 $$ \begin{align*} T([N_{K/K_{1}}(\gamma_{1})])&=(1,a_{1},a_{1}),\\ T([N_{K/K_{2}}(\gamma_{1})])&=(1,1,a_{1}) = T([N_{K/K_{1}}(\gamma_{2})]),\\ T([N_{K/K_{2}}(\gamma_{2})])&=(a_{2},1,a_{1}). \end{align*} $$
$$ \begin{align*} T([N_{K/K_{1}}(\gamma_{1})])&=(1,a_{1},a_{1}),\\ T([N_{K/K_{2}}(\gamma_{1})])&=(1,1,a_{1}) = T([N_{K/K_{1}}(\gamma_{2})]),\\ T([N_{K/K_{2}}(\gamma_{2})])&=(a_{2},1,a_{1}). \end{align*} $$
We define
![]() $X = \langle [\gamma _{1}],[\gamma _{2}]\rangle $
. One sees that
$X = \langle [\gamma _{1}],[\gamma _{2}]\rangle $
. One sees that
![]() $\langle [\gamma _{1}]\rangle \simeq \langle [\gamma _{2}]\rangle \simeq \Omega ^{-1}$
in the same manner as above (these modules satisfy the appropriate relations by definition, and one can argue they generate a module of the appropriate dimension by leveraging the independence of the image of their fixed components under T). We claim that
$\langle [\gamma _{1}]\rangle \simeq \langle [\gamma _{2}]\rangle \simeq \Omega ^{-1}$
in the same manner as above (these modules satisfy the appropriate relations by definition, and one can argue they generate a module of the appropriate dimension by leveraging the independence of the image of their fixed components under T). We claim that
![]() $X \simeq \Omega ^{-1}\oplus \Omega ^{-1}$
; for the sake of contradiction, then, assume instead that
$X \simeq \Omega ^{-1}\oplus \Omega ^{-1}$
; for the sake of contradiction, then, assume instead that
![]() $\langle [\gamma _{1}]\rangle \cap \langle [\gamma _{2}]\rangle \neq \{[1]\}$
. By Lemma 2.1, this implies that there is some
$\langle [\gamma _{1}]\rangle \cap \langle [\gamma _{2}]\rangle \neq \{[1]\}$
. By Lemma 2.1, this implies that there is some
![]() $[x]\neq [1]$
with
$[x]\neq [1]$
with
![]() $[x] \in \langle [\gamma _{1}]\rangle ^{G} \cap \langle [\gamma _{2}]\rangle ^{G} $
. Considering images under T and using Lemma 4.4, we must have
$[x] \in \langle [\gamma _{1}]\rangle ^{G} \cap \langle [\gamma _{2}]\rangle ^{G} $
. Considering images under T and using Lemma 4.4, we must have
![]() $[N_{K/K_{2}}(\gamma _{1})] = [x] = [N_{K/K_{1}}(\gamma _{2})]$
, contrary to the assumption in this case that
$[N_{K/K_{2}}(\gamma _{1})] = [x] = [N_{K/K_{1}}(\gamma _{2})]$
, contrary to the assumption in this case that
![]() $T([N_{K/K_{1}}(K^{\times })] \cap [N_{K/K_{2}}(K^{\times })]) = \{(1,1,1)\}$
. Hence, we get
$T([N_{K/K_{1}}(K^{\times })] \cap [N_{K/K_{2}}(K^{\times })]) = \{(1,1,1)\}$
. Hence, we get
![]() $X \simeq \Omega ^{-1} \oplus \Omega ^{-1}$
.
$X \simeq \Omega ^{-1} \oplus \Omega ^{-1}$
.
Finally, we check that
![]() $\dim (X^{G} \cap [F^{\times }]) = 1$
with
$\dim (X^{G} \cap [F^{\times }]) = 1$
with
![]() $X^{G} \cap (\mathscr {B}+\mathscr {C}+\mathscr {D}) = \{[1]\}$
. The former follows from the rank-nullity theorem applied to the function T; in fact, we see that
$X^{G} \cap (\mathscr {B}+\mathscr {C}+\mathscr {D}) = \{[1]\}$
. The former follows from the rank-nullity theorem applied to the function T; in fact, we see that
![]() $X^{G} \cap [F^{\times }] = \{[1],[N_{K/K_{2}}(\gamma _{1})][N_{K/K_{1}}(\gamma _{2})]\}$
. For the latter, suppose instead that
$X^{G} \cap [F^{\times }] = \{[1],[N_{K/K_{2}}(\gamma _{1})][N_{K/K_{1}}(\gamma _{2})]\}$
. For the latter, suppose instead that
![]() $[N_{K/K_{2}}(\gamma _{1})][N_{K/K_{1}}(\gamma _{2})] \in \mathscr {B}+\mathscr {C}+\mathscr {D}$
. Then we get
$[N_{K/K_{2}}(\gamma _{1})][N_{K/K_{1}}(\gamma _{2})] \in \mathscr {B}+\mathscr {C}+\mathscr {D}$
. Then we get
![]() $[N_{K/K_{2}}(\gamma _{1})][N_{K/K_{1}}(\gamma _{2})] = [f_{\mathscr {B}}][f_{\mathscr {C}}][f_{\mathscr {D}}]$
for some
$[N_{K/K_{2}}(\gamma _{1})][N_{K/K_{1}}(\gamma _{2})] = [f_{\mathscr {B}}][f_{\mathscr {C}}][f_{\mathscr {D}}]$
for some
![]() $[f_{\mathscr {B}}]\in \mathscr {B},[f_{\mathscr {C}]}\in \mathscr {C}$
and
$[f_{\mathscr {B}}]\in \mathscr {B},[f_{\mathscr {C}]}\in \mathscr {C}$
and
![]() $[f_{\mathscr {D}}]\in \mathscr {D}$
; in particular, this means we have elements
$[f_{\mathscr {D}}]\in \mathscr {D}$
; in particular, this means we have elements
![]() $[\gamma _{\mathscr {B}}],[\gamma _{\mathscr {C}}],[\gamma _{\mathscr {D}}] \in J(K)$
which solve the relevant diagrams from Figure 4. One can then check that
$[\gamma _{\mathscr {B}}],[\gamma _{\mathscr {C}}],[\gamma _{\mathscr {D}}] \in J(K)$
which solve the relevant diagrams from Figure 4. One can then check that
 $$ \begin{align*} N_{K/K_{1}}([\gamma_{2}][\gamma_{\mathscr{C}}]) &= [N_{K/K_{1}}(\gamma_{2})][f_{\mathscr{C}}] = [N_{K/K_{2}}(\gamma_{1})][f_{\mathscr{B}}][f_{\mathscr{D}}] \\&= N_{K/K_{2}}([\gamma_{1}][\gamma_{\mathscr{B}}][\gamma_{\mathscr{D}}]). \end{align*} $$
$$ \begin{align*} N_{K/K_{1}}([\gamma_{2}][\gamma_{\mathscr{C}}]) &= [N_{K/K_{1}}(\gamma_{2})][f_{\mathscr{C}}] = [N_{K/K_{2}}(\gamma_{1})][f_{\mathscr{B}}][f_{\mathscr{D}}] \\&= N_{K/K_{2}}([\gamma_{1}][\gamma_{\mathscr{B}}][\gamma_{\mathscr{D}}]). \end{align*} $$
This element is conspicuously an element in
![]() $[N_{K/K_{1}}(K^{\times })] \cap [N_{K/K_{2}}(K^{\times })]$
, and since
$[N_{K/K_{1}}(K^{\times })] \cap [N_{K/K_{2}}(K^{\times })]$
, and since
![]() $\ker (T) = [F^{\times }]$
, we get that
$\ker (T) = [F^{\times }]$
, we get that
![]() $T([N_{K/K_{2}}(\gamma _{1})][f_{\mathscr {B}}][f_{\mathscr {D}}]) = T([N_{K/K_{2}}(\gamma _{1})]) \neq \{(1,1,1)\}$
. This runs contrary to the overriding assumption in this case, that
$T([N_{K/K_{2}}(\gamma _{1})][f_{\mathscr {B}}][f_{\mathscr {D}}]) = T([N_{K/K_{2}}(\gamma _{1})]) \neq \{(1,1,1)\}$
. This runs contrary to the overriding assumption in this case, that
![]() $T([N_{K/K_{1}}(K^{\times })] \cap [N_{K/K_{2}}(K^{\times })]) = \{(1,1,1)\}$
.▪
$T([N_{K/K_{1}}(K^{\times })] \cap [N_{K/K_{2}}(K^{\times })]) = \{(1,1,1)\}$
.▪
5 Proof of Theorem 1.1
We need one final preparatory result, which is again a manifestation of Hilbert 90 in the biquadratic case.
Lemma 5.1 Let
![]() $\{\ell ,m,n\}=\{1,2,3\}$
. If
$\{\ell ,m,n\}=\{1,2,3\}$
. If
![]() $f \in F^{\times }$
has
$f \in F^{\times }$
has
![]() $[f] \in [N_{K/K_{\ell }}(K^{\times })]$
, then
$[f] \in [N_{K/K_{\ell }}(K^{\times })]$
, then
![]() $[f] \in [N_{K_{m}/F}(K_{m}^{\times })][N_{K_{n}/F}(K_{n}^{\times })]$
.
$[f] \in [N_{K_{m}/F}(K_{m}^{\times })][N_{K_{n}/F}(K_{n}^{\times })]$
.
Proof We prove the result when
![]() $\ell = 3$
,
$\ell = 3$
,
![]() $m = 1$
, and
$m = 1$
, and
![]() $n=2$
; the other results follow by the symmetry of the fields
$n=2$
; the other results follow by the symmetry of the fields
![]() $K_{1},K_{2}$
, and
$K_{1},K_{2}$
, and
![]() $K_{3}$
.
$K_{3}$
.
First, we argue that if
![]() $f \in F^{\times }$
has
$f \in F^{\times }$
has
![]() $[f] \in [N_{K/K_{3}}(K^{\times })]$
, then
$[f] \in [N_{K/K_{3}}(K^{\times })]$
, then
for some
![]() $\tilde k \in K^{\times }$
and
$\tilde k \in K^{\times }$
and
![]() $\varepsilon \in \{0,1\}$
. To see this, note that
$\varepsilon \in \{0,1\}$
. To see this, note that
![]() $f = k^{1+\sigma _{1} \sigma _{1}} \hat k^{2}$
for some
$f = k^{1+\sigma _{1} \sigma _{1}} \hat k^{2}$
for some
![]() $k,\hat k \in K$
. Solving for
$k,\hat k \in K$
. Solving for
![]() $\hat k^{2}$
and using the fact that
$\hat k^{2}$
and using the fact that
![]() $F \subseteq K_{3}$
, we then have
$F \subseteq K_{3}$
, we then have
![]() $\hat k^{2} \in K_{3}$
. However, this means
$\hat k^{2} \in K_{3}$
. However, this means
![]() $\hat k^{2} \in K^{\times 2} \cap K_{3}^{\times }$
, so by Kummer theory, we get
$\hat k^{2} \in K^{\times 2} \cap K_{3}^{\times }$
, so by Kummer theory, we get
![]() $\hat k^{2}=k_{3}^{2} a_{1}^{\varepsilon }$
, where
$\hat k^{2}=k_{3}^{2} a_{1}^{\varepsilon }$
, where
![]() $k_{3} \in K_{3}^{\times }$
and
$k_{3} \in K_{3}^{\times }$
and
![]() $\varepsilon \in \{0,1\}$
. Naturally, we have
$\varepsilon \in \{0,1\}$
. Naturally, we have
![]() $k_{3}^{2} = N_{K/K_{3}}(k_{3})$
, so that our original expression becomes
$k_{3}^{2} = N_{K/K_{3}}(k_{3})$
, so that our original expression becomes
Setting
![]() $\tilde k = k k_{3}$
and dividing through by
$\tilde k = k k_{3}$
and dividing through by
![]() $a_{1}^{\varepsilon }$
gives equation (5.1).
$a_{1}^{\varepsilon }$
gives equation (5.1).
Now, we argue that
For this, suppose that we have elements
![]() $g \in F^{\times }$
and
$g \in F^{\times }$
and
![]() $k \in K^{\times }$
so that
$k \in K^{\times }$
so that
![]() $g = N_{K/K_{3}}(k)$
. Now,
$g = N_{K/K_{3}}(k)$
. Now,
![]() $k = f_{1} +f_{2}\sqrt {a_{1}}+f_{3}\sqrt {a_{2}}+f_{4}\sqrt {a_{1}a_{2}}$
for some
$k = f_{1} +f_{2}\sqrt {a_{1}}+f_{3}\sqrt {a_{2}}+f_{4}\sqrt {a_{1}a_{2}}$
for some
![]() $f_{1},f_{2},f_{3},f_{4} \in F^{\times }$
, and so by assumption we get
$f_{1},f_{2},f_{3},f_{4} \in F^{\times }$
, and so by assumption we get
However, since
![]() $g \in F^{\times }$
, we must have
$g \in F^{\times }$
, we must have
![]() $f_{1}f_{4} = f_{2}f_{3}$
. Our goal is to write g as an element of
$f_{1}f_{4} = f_{2}f_{3}$
. Our goal is to write g as an element of
![]() $N_{K_{1}/F}(K_{1}^{\times })\cdot N_{K_{2}/F}(K_{2}^{\times })$
, which means we would like to find
$N_{K_{1}/F}(K_{1}^{\times })\cdot N_{K_{2}/F}(K_{2}^{\times })$
, which means we would like to find
![]() $h_{1},h_{2},h_{3},h_{4} \in F$
so that
$h_{1},h_{2},h_{3},h_{4} \in F$
so that
![]() $h_{1} +h_{2} \sqrt {a_{1}} \in K_{1}$
and
$h_{1} +h_{2} \sqrt {a_{1}} \in K_{1}$
and
![]() $h_{3}+h_{4}\sqrt {a_{2}} \in K_{2}$
yield
$h_{3}+h_{4}\sqrt {a_{2}} \in K_{2}$
yield
In other words, we need to solve
We proceed by cases. First, suppose that
![]() $f_{1}=0$
. Hence, we must have either
$f_{1}=0$
. Hence, we must have either
![]() $f_{2} = 0$
or
$f_{2} = 0$
or
![]() $f_{3} = 0$
. Note if
$f_{3} = 0$
. Note if
![]() $f_{2} = 0$
, then our expression for g becomes
$f_{2} = 0$
, then our expression for g becomes
A similar computation settles the case where
![]() $f_{3} = 0$
. So now suppose that
$f_{3} = 0$
. So now suppose that
![]() $f_{1} \neq 0$
, and observe that since
$f_{1} \neq 0$
, and observe that since
![]() $f_{4} = \frac {f_{2}f_{3}}{f_{1}}$
, we have
$f_{4} = \frac {f_{2}f_{3}}{f_{1}}$
, we have
 $$ \begin{align*}f_{1}^{2}-f_{2}^{2} a_{1} - f_{3}^{2} a_{2}+f_{4}^{2} a_{1}a_{2} = \left(f_{1}^{2}-f_{2}^{2} a_{1}\right)\left(1^{2}-\frac{f_{3}^{2}}{f_{1}^{2}}a_{2}\right).\end{align*} $$
$$ \begin{align*}f_{1}^{2}-f_{2}^{2} a_{1} - f_{3}^{2} a_{2}+f_{4}^{2} a_{1}a_{2} = \left(f_{1}^{2}-f_{2}^{2} a_{1}\right)\left(1^{2}-\frac{f_{3}^{2}}{f_{1}^{2}}a_{2}\right).\end{align*} $$
With both (5.1) and (5.2) in hand, we can prove the lemma. If we apply (5.2) to
![]() $\frac {f}{a_{1}^{\varepsilon }}$
from (5.1), then we see that
$\frac {f}{a_{1}^{\varepsilon }}$
from (5.1), then we see that
However, since
![]() $[a_{1}]=[1]$
, we get the desired result.▪
$[a_{1}]=[1]$
, we get the desired result.▪
We are now ready for the proof of the main result of this paper. Our basic strategy is to show that the modules
![]() $\widehat {J}$
and X from Theorems 3.3 and 4.8 provide the desired decomposition, although in the case where
$\widehat {J}$
and X from Theorems 3.3 and 4.8 provide the desired decomposition, although in the case where
![]() $\dim (\mathrm {im}(T)) = 3$
and
$\dim (\mathrm {im}(T)) = 3$
and
![]() $T([N_{K/K_{1}}(K^{\times })] \cap [N_{K/K_{2}}(K^{\times })]) = \{(1,1,1)\}$
we will need to make a small adjustment to
$T([N_{K/K_{1}}(K^{\times })] \cap [N_{K/K_{2}}(K^{\times })]) = \{(1,1,1)\}$
we will need to make a small adjustment to
![]() $\widehat {J}$
—removing a single trivial summand—to achieve our result.
$\widehat {J}$
—removing a single trivial summand—to achieve our result.
Proof Let
![]() $\widehat {J}\, $
be the module from Theorem 3.3, and let X be the module from Theorem 4.8.
$\widehat {J}\, $
be the module from Theorem 3.3, and let X be the module from Theorem 4.8.
If we are not in the case where
![]() $\dim (\mathrm {im}(T)) = 3$
and
$\dim (\mathrm {im}(T)) = 3$
and
![]() $T([N_{K/K_{1}}(K^{\times })] \cap [N_{K/K_{2}}(K^{\times })]) = \{(1,1,1)\}$
, then define
$T([N_{K/K_{1}}(K^{\times })] \cap [N_{K/K_{2}}(K^{\times })]) = \{(1,1,1)\}$
, then define
![]() $\widetilde {J} = \widehat {J}$
. Otherwise, note that, in the final case of Theorem 4.8, we have a unique
$\widetilde {J} = \widehat {J}$
. Otherwise, note that, in the final case of Theorem 4.8, we have a unique
![]() $[x_{0}] \in X^{G} \cap [F^{\times }]$
, and that
$[x_{0}] \in X^{G} \cap [F^{\times }]$
, and that
![]() $[x_{0}] \not \in \mathscr {B}+\mathscr {C}+\mathscr {D}$
. Now, in the construction of
$[x_{0}] \not \in \mathscr {B}+\mathscr {C}+\mathscr {D}$
. Now, in the construction of
![]() $\widehat {J}$
, the summand
$\widehat {J}$
, the summand
![]() $Y_{F}$
is chosen as the span of
$Y_{F}$
is chosen as the span of
![]() $\mathcal {F}_{0}$
, where
$\mathcal {F}_{0}$
, where
![]() $\mathcal {F}_{0}$
is an arbitrary basis for a complement of
$\mathcal {F}_{0}$
is an arbitrary basis for a complement of
![]() $\mathscr {B}+\mathscr {C}+\mathscr {D}$
within
$\mathscr {B}+\mathscr {C}+\mathscr {D}$
within
![]() $[F^{\times }]$
(see the definition of
$[F^{\times }]$
(see the definition of
![]() $\mathcal {F}_{0}$
in Theorem 3.3). Since
$\mathcal {F}_{0}$
in Theorem 3.3). Since
![]() $[x_{0}] \in [F^{\times }] \setminus (\mathscr {B}+\mathscr {C}+\mathscr {D})$
, we can assume that
$[x_{0}] \in [F^{\times }] \setminus (\mathscr {B}+\mathscr {C}+\mathscr {D})$
, we can assume that
![]() $[x_{0}] \in \mathcal {F}_{0}$
. In this case, we define
$[x_{0}] \in \mathcal {F}_{0}$
. In this case, we define
![]() $\tilde Y_{F} = \sum _{[f] \in \mathcal {F}_{0}\setminus \{[x_{0}]\}} \langle [f]\rangle = \bigoplus _{[f] \in \mathcal {F}_{0}\setminus \{[x_{0}]\}} \langle [f] \rangle $
, and set
$\tilde Y_{F} = \sum _{[f] \in \mathcal {F}_{0}\setminus \{[x_{0}]\}} \langle [f]\rangle = \bigoplus _{[f] \in \mathcal {F}_{0}\setminus \{[x_{0}]\}} \langle [f] \rangle $
, and set
(That is, the module
![]() $\widetilde {J}$
is just the result of removing the summand
$\widetilde {J}$
is just the result of removing the summand
![]() $\langle [x_{0}]\rangle $
from
$\langle [x_{0}]\rangle $
from
![]() $\widehat {J}$
.)
$\widehat {J}$
.)
In either case, we will show that
![]() $J(K) = \widetilde {J} \oplus X$
. Of course, we have
$J(K) = \widetilde {J} \oplus X$
. Of course, we have
![]() $\widetilde {J} + X \subseteq J(K)$
; furthermore, our construction of
$\widetilde {J} + X \subseteq J(K)$
; furthermore, our construction of
![]() $\widetilde {J}$
gives
$\widetilde {J}$
gives
![]() $X^{G} \cap \widetilde {J} = \{[1]\}$
, so that
$X^{G} \cap \widetilde {J} = \{[1]\}$
, so that
![]() $\widetilde {J} + X = \widetilde {J} \oplus X$
. Hence, we only need to verify that
$\widetilde {J} + X = \widetilde {J} \oplus X$
. Hence, we only need to verify that
![]() $J(K) \subseteq \widetilde {J} + X$
. We do this by examining the possible isomorphism classes for
$J(K) \subseteq \widetilde {J} + X$
. We do this by examining the possible isomorphism classes for
![]() $\langle [\gamma ]\rangle $
, where
$\langle [\gamma ]\rangle $
, where
![]() $[\gamma ] \in J(K)$
.
$[\gamma ] \in J(K)$
.
First, suppose that
![]() $\langle [\gamma ]\rangle \simeq \mathbb {F}_{2}$
, so that
$\langle [\gamma ]\rangle \simeq \mathbb {F}_{2}$
, so that
![]() $[\gamma ] \in J(K)^{G}$
. If
$[\gamma ] \in J(K)^{G}$
. If
![]() $[\gamma ] \in [F^{\times }]$
, then since
$[\gamma ] \in [F^{\times }]$
, then since
![]() $[F^{\times }] = \widehat {J}^{G} \subseteq \widetilde {J}^{G} \oplus X^{G}$
, we have
$[F^{\times }] = \widehat {J}^{G} \subseteq \widetilde {J}^{G} \oplus X^{G}$
, we have
![]() $[\gamma ] \in \widetilde {J}+X$
. Otherwise, we have
$[\gamma ] \in \widetilde {J}+X$
. Otherwise, we have
![]() $T([\gamma ]) \neq (1,1,1)$
, in which case by Theorem 4.8 there exists some
$T([\gamma ]) \neq (1,1,1)$
, in which case by Theorem 4.8 there exists some
![]() $[x] \in X^{G}$
with
$[x] \in X^{G}$
with
![]() $T([\gamma ]) = T([x])$
. We then have
$T([\gamma ]) = T([x])$
. We then have
![]() $[\gamma ][x] \in [F^{\times }]$
, and from the previous case, this gives
$[\gamma ][x] \in [F^{\times }]$
, and from the previous case, this gives
![]() $[\gamma ][x] \in \widetilde {J}+X$
. Since
$[\gamma ][x] \in \widetilde {J}+X$
. Since
![]() $[x] \in \widetilde {J}+X$
, we get
$[x] \in \widetilde {J}+X$
, we get
![]() $[\gamma ] \in \widetilde {J}+X$
.
$[\gamma ] \in \widetilde {J}+X$
.
Now, suppose that
![]() $\langle [\gamma ] \rangle \simeq \mathbb {F}_{2}[\overline {G_{1}}]$
. Corollary 4.5 tells us that
$\langle [\gamma ] \rangle \simeq \mathbb {F}_{2}[\overline {G_{1}}]$
. Corollary 4.5 tells us that
![]() $[\gamma ]^{1+\sigma _{1}} \in [F^{\times }]$
, and so
$[\gamma ]^{1+\sigma _{1}} \in [F^{\times }]$
, and so
![]() $[\gamma ]^{1+\sigma _{1}} \in \mathscr {B}$
. Corollary 3.4 tells us that there exists some
$[\gamma ]^{1+\sigma _{1}} \in \mathscr {B}$
. Corollary 3.4 tells us that there exists some
![]() $[\tilde \gamma ] \in \widehat {J}$
so that
$[\tilde \gamma ] \in \widehat {J}$
so that
![]() $[\tilde \gamma ]^{1+\sigma _{2}} = [1]$
and
$[\tilde \gamma ]^{1+\sigma _{2}} = [1]$
and
![]() $[\tilde \gamma ]^{1+\sigma _{1}} = [\gamma ]^{1+\sigma _{1}}$
; in fact, since
$[\tilde \gamma ]^{1+\sigma _{1}} = [\gamma ]^{1+\sigma _{1}}$
; in fact, since
![]() $\widehat {J}$
and
$\widehat {J}$
and
![]() $\widetilde {J}$
differ by only a trivial summand, we can assume
$\widetilde {J}$
differ by only a trivial summand, we can assume
![]() $[\tilde \gamma ] \in \widetilde {J}$
as well. However, then, we get
$[\tilde \gamma ] \in \widetilde {J}$
as well. However, then, we get
![]() $[\gamma ][\tilde \gamma ] \in J(K)^{G}$
, so by the previous case we have
$[\gamma ][\tilde \gamma ] \in J(K)^{G}$
, so by the previous case we have
![]() $[\gamma ][\tilde \gamma ] \in \widetilde {J}+X$
. Since
$[\gamma ][\tilde \gamma ] \in \widetilde {J}+X$
. Since
![]() $[\tilde \gamma ] \in \widetilde {J}+X$
already, this gives
$[\tilde \gamma ] \in \widetilde {J}+X$
already, this gives
![]() $[\gamma ] \in \widetilde {J}+X$
.
$[\gamma ] \in \widetilde {J}+X$
.
The cases where
![]() $\langle [\gamma ] \rangle $
is isomorphic to either
$\langle [\gamma ] \rangle $
is isomorphic to either
![]() $\mathbb {F}_{2}[\overline {G_{2}}]$
or
$\mathbb {F}_{2}[\overline {G_{2}}]$
or
![]() $\mathbb {F}_{2}[\overline {G_{3}}]$
follow the same argument as the case
$\mathbb {F}_{2}[\overline {G_{3}}]$
follow the same argument as the case
![]() $\mathbb {F}_{2}[\overline {G_{1}}]$
above.
$\mathbb {F}_{2}[\overline {G_{1}}]$
above.
Now, suppose that
![]() $\langle [\gamma ]\rangle \simeq \Omega ^{-1}$
, and first consider the case where
$\langle [\gamma ]\rangle \simeq \Omega ^{-1}$
, and first consider the case where
![]() $T(\langle [\gamma ]\rangle ^{G}) = \{(1,1,1)\}$
. By Corollary 4.2 and Lemma 5.1, we have
$T(\langle [\gamma ]\rangle ^{G}) = \{(1,1,1)\}$
. By Corollary 4.2 and Lemma 5.1, we have
![]() $[N_{K/K_{1}}(\gamma )] \in [N_{K/K_{1}}(K^{\times })] \cap [F^{\times }] = [N_{K_{2}/F}(K_{2}^{\times })][N_{K_{3}/F}(K_{3}^{\times })]$
, say
$[N_{K/K_{1}}(\gamma )] \in [N_{K/K_{1}}(K^{\times })] \cap [F^{\times }] = [N_{K_{2}/F}(K_{2}^{\times })][N_{K_{3}/F}(K_{3}^{\times })]$
, say
![]() $[N_{K/K_{1}}(\gamma )] = [f_{1,2}][f_{1,3}]$
, where for
$[N_{K/K_{1}}(\gamma )] = [f_{1,2}][f_{1,3}]$
, where for
![]() $i \in \{2,3\}$
we have
$i \in \{2,3\}$
we have
![]() $[f_{1,i}] = [N_{K_{i}/F}(k_{i})]$
for some
$[f_{1,i}] = [N_{K_{i}/F}(k_{i})]$
for some
![]() $k_{i} \in K_{i}^{\times }$
. This means that
$k_{i} \in K_{i}^{\times }$
. This means that
![]() $[f_{1,2}] \in \mathscr {C}$
and
$[f_{1,2}] \in \mathscr {C}$
and
![]() $[f_{1,3}] \in \mathscr {D}$
, so by Corollary 3.4 there exists
$[f_{1,3}] \in \mathscr {D}$
, so by Corollary 3.4 there exists
![]() $[\gamma _{1,i}] \in \widehat {J}$
with
$[\gamma _{1,i}] \in \widehat {J}$
with
![]() $[\gamma _{1,i}]$
and
$[\gamma _{1,i}]$
and
![]() $[f_{1,i}]$
providing a solution to the appropriate diagram; since
$[f_{1,i}]$
providing a solution to the appropriate diagram; since
![]() $\widehat {J}$
and
$\widehat {J}$
and
![]() $\widetilde {J}$
differ only by a trivial summand, we can assume that
$\widetilde {J}$
differ only by a trivial summand, we can assume that
![]() $[\gamma _{1,i}] \in \widetilde {J}$
for
$[\gamma _{1,i}] \in \widetilde {J}$
for
![]() $i \in \{2,3\}$
. (See Figure 5 for a graphical description of these relationships.)
$i \in \{2,3\}$
. (See Figure 5 for a graphical description of these relationships.)

Figure 5: Decomposing
![]() $[N_{K/K_{1}}(\gamma )]$
in terms of solutions to the diagrams for
$[N_{K/K_{1}}(\gamma )]$
in terms of solutions to the diagrams for
![]() $\mathscr {C}$
and
$\mathscr {C}$
and
![]() $\mathscr {D}$
.
$\mathscr {D}$
.
Consider the element
![]() $[\tilde \gamma ] = [\gamma ][\gamma _{1,2}][\gamma _{1,3}]$
. One sees that
$[\tilde \gamma ] = [\gamma ][\gamma _{1,2}][\gamma _{1,3}]$
. One sees that
![]() $[\tilde \gamma ]^{1+\sigma _{2}} = [1]$
, and that
$[\tilde \gamma ]^{1+\sigma _{2}} = [1]$
, and that
![]() $[\tilde \gamma ]^{1+\sigma _{1}} = [N_{K/K_{2}}(\gamma )][f_{1,3}]$
. Hence,
$[\tilde \gamma ]^{1+\sigma _{1}} = [N_{K/K_{2}}(\gamma )][f_{1,3}]$
. Hence,
![]() $\langle [\tilde \gamma ] \rangle $
is isomorphic to either
$\langle [\tilde \gamma ] \rangle $
is isomorphic to either
![]() $\{[1]\}$
or
$\{[1]\}$
or
![]() $\mathbb {F}_{2}$
or
$\mathbb {F}_{2}$
or
![]() $\mathbb {F}_{2}[\overline {G_{1}}]$
. Our previous cases, therefore, allow us to conclude
$\mathbb {F}_{2}[\overline {G_{1}}]$
. Our previous cases, therefore, allow us to conclude
![]() $[\tilde \gamma ] \in \widetilde {J}+X$
. Since
$[\tilde \gamma ] \in \widetilde {J}+X$
. Since
![]() $[\gamma _{1,2}],[\gamma _{1,3}] \in \widetilde {J}$
, we have
$[\gamma _{1,2}],[\gamma _{1,3}] \in \widetilde {J}$
, we have
![]() $[\gamma ] \in \widetilde {J}+X$
.
$[\gamma ] \in \widetilde {J}+X$
.
If
![]() $T(\langle [\gamma ]\rangle ^{G}) \neq \{(1,1,1)\}$
, then Lemma 4.4 gives us that precisely one of the following holds:
$T(\langle [\gamma ]\rangle ^{G}) \neq \{(1,1,1)\}$
, then Lemma 4.4 gives us that precisely one of the following holds:
-
•
 $T([N_{K/K_{1}}(\gamma )]) = (1,a_{1},a_{1})$
and
$T([N_{K/K_{1}}(\gamma )]) = (1,a_{1},a_{1})$
and
 $T([N_{K/K_{2}}(\gamma )]) = (1,1,a_{1})$
; or
$T([N_{K/K_{2}}(\gamma )]) = (1,1,a_{1})$
; or -
•
 $T([N_{K/K_{1}}(\gamma )]) = (1,1,a_{1})$
and
$T([N_{K/K_{1}}(\gamma )]) = (1,1,a_{1})$
and
 $T([N_{K/K_{2}}(\gamma )]) = (a_{2},1,a_{1})$
; or
$T([N_{K/K_{2}}(\gamma )]) = (a_{2},1,a_{1})$
; or -
•
 $T([N_{K/K_{1}}(\gamma )]) = (1,a_{1},1)$
and
$T([N_{K/K_{1}}(\gamma )]) = (1,a_{1},1)$
and
 $T([N_{K/K_{2}}(\gamma )]) = (a_{2},1,1)$
.
$T([N_{K/K_{2}}(\gamma )]) = (a_{2},1,1)$
.
In any of these cases, our construction for X (see the second case in Theorem 4.8) gives an element
![]() $[x] \in X$
so that
$[x] \in X$
so that
![]() $T([N_{K/K_{1}}(\gamma )]) = T([N_{K/K_{1}}(x)])$
and
$T([N_{K/K_{1}}(\gamma )]) = T([N_{K/K_{1}}(x)])$
and
![]() $T([N_{K/K_{2}}(\gamma )]) =T([N_{K/K_{2}}(x)])$
. Hence, the images of
$T([N_{K/K_{2}}(\gamma )]) =T([N_{K/K_{2}}(x)])$
. Hence, the images of
![]() $[\gamma ][x]$
under
$[\gamma ][x]$
under
![]() $1+\sigma _{1}$
and
$1+\sigma _{1}$
and
![]() $1+\sigma _{2}$
both lie in
$1+\sigma _{2}$
both lie in
![]() $[F^{\times }]$
, and so
$[F^{\times }]$
, and so
![]() $\langle [\gamma ][x] \rangle $
falls into one of the previous cases. (For example, if
$\langle [\gamma ][x] \rangle $
falls into one of the previous cases. (For example, if
![]() $([\gamma ][x])^{1+\sigma _{1}}$
and
$([\gamma ][x])^{1+\sigma _{1}}$
and
![]() $([\gamma ][x])^{1+\sigma _{2}}$
are independent, then
$([\gamma ][x])^{1+\sigma _{2}}$
are independent, then
![]() $\langle [\gamma ][x]\rangle \simeq \Omega ^{-1}$
and
$\langle [\gamma ][x]\rangle \simeq \Omega ^{-1}$
and
![]() $T(\langle [\gamma ][x]\rangle ^{G})=\{(1,1,1)\}$
. This is precisely the previous case.) We therefore get
$T(\langle [\gamma ][x]\rangle ^{G})=\{(1,1,1)\}$
. This is precisely the previous case.) We therefore get
![]() $[\gamma ][x] \in \widetilde {J}+X$
, whence
$[\gamma ][x] \in \widetilde {J}+X$
, whence
![]() $[\gamma ] \in \widetilde {J}+X$
.
$[\gamma ] \in \widetilde {J}+X$
.
The final case to consider is when
![]() $\langle [\gamma ]\rangle \simeq \mathbb {F}_{2}[G]$
. In this case, note that
$\langle [\gamma ]\rangle \simeq \mathbb {F}_{2}[G]$
. In this case, note that
![]() $[N_{K/F}(\gamma )] \in \mathscr {A}$
, and Corollary 3.4 gives us some element
$[N_{K/F}(\gamma )] \in \mathscr {A}$
, and Corollary 3.4 gives us some element
![]() $[\tilde \gamma ] \in \widehat {J}$
(which we may assume is in
$[\tilde \gamma ] \in \widehat {J}$
(which we may assume is in
![]() $\widetilde {J}$
since
$\widetilde {J}$
since
![]() $\widetilde {J}$
and
$\widetilde {J}$
and
![]() $\widehat {J}$
differ only by a trivial summand) so that
$\widehat {J}$
differ only by a trivial summand) so that
![]() $[N_{K/F}(\tilde \gamma )] = [N_{K/F}(\gamma )]$
. From this, we get that
$[N_{K/F}(\tilde \gamma )] = [N_{K/F}(\gamma )]$
. From this, we get that
![]() $\langle [\gamma ][\tilde \gamma ]\rangle $
is not free, and so is one of the previous isomorphism types. As usual, this gives us
$\langle [\gamma ][\tilde \gamma ]\rangle $
is not free, and so is one of the previous isomorphism types. As usual, this gives us
![]() $[\gamma ] \in \widetilde {J}+X$
.▪
$[\gamma ] \in \widetilde {J}+X$
.▪
6 Some realizability results
Theorem 1.1 tells us that there are a limited number of summands that could possibly appear in a decomposition of
![]() $J(K)$
, but is it the case that each of these summand types occurs for at least one biquadratic extension
$J(K)$
, but is it the case that each of these summand types occurs for at least one biquadratic extension
![]() $K/F$
? In this section, we offer some partial results concerning this kind of realizability question, focusing particularly on the possible structures for the X summand from Theorem 1.1. For a more complete treatment of this problem of realizing the various summands, the reader is encouraged to consult [Reference Chemotti, Mináč, Nguyen, Schultz, Swallow and Tan9], which enhances the current work by exploring its connection to the Brauer group
$K/F$
? In this section, we offer some partial results concerning this kind of realizability question, focusing particularly on the possible structures for the X summand from Theorem 1.1. For a more complete treatment of this problem of realizing the various summands, the reader is encouraged to consult [Reference Chemotti, Mináč, Nguyen, Schultz, Swallow and Tan9], which enhances the current work by exploring its connection to the Brauer group
![]() $\text {Br}(F)$
.
$\text {Br}(F)$
.
The X summand takes on one of six possible structures, with the various possibilities determined by the image of the function T from Section 4 (as detailed in Theorem 4.8). To determine whether these structures are realizable, we will view the conditions found in Theorem 4.8 through the lens of Galois embedding problems via Lemma 4.1.
First, we introduce some terminology. Note that since
![]() $K/F$
is a biquadratic extension with intermediate fields
$K/F$
is a biquadratic extension with intermediate fields
![]() $K_{1}, K_{2}$
, and
$K_{1}, K_{2}$
, and
![]() $K_{3}$
, if there exists some extension
$K_{3}$
, if there exists some extension
![]() $L/K$
which is Galois over F with
$L/K$
which is Galois over F with
![]() $\mathrm {Gal}(L/F) \simeq D_{4}$
, then there is a unique
$\mathrm {Gal}(L/F) \simeq D_{4}$
, then there is a unique
![]() $i \in \{1,2,3\}$
so that
$i \in \{1,2,3\}$
so that
![]() $\mathrm {Gal}(L/K_{i}) \simeq \mathbb {Z}/4\mathbb {Z}$
. We will refer to such an extension as a
$\mathrm {Gal}(L/K_{i}) \simeq \mathbb {Z}/4\mathbb {Z}$
. We will refer to such an extension as a
![]() $D_{4}$
-extension of type i. Likewise, if there is an extension
$D_{4}$
-extension of type i. Likewise, if there is an extension
![]() $L/K$
with
$L/K$
with
![]() $\mathrm {Gal}(L/F) \simeq \mathbb {Z}/4\mathbb {Z} \oplus \mathbb {Z}/2\mathbb {Z}$
, then there is a unique
$\mathrm {Gal}(L/F) \simeq \mathbb {Z}/4\mathbb {Z} \oplus \mathbb {Z}/2\mathbb {Z}$
, then there is a unique
![]() $i \in \{1,2,3\}$
so that there exists some field
$i \in \{1,2,3\}$
so that there exists some field
![]() $\widetilde {L}$
with
$\widetilde {L}$
with
![]() $K_{i} \subsetneq \widetilde {L} \subsetneq L$
and
$K_{i} \subsetneq \widetilde {L} \subsetneq L$
and
![]() $\mathrm {Gal}(\widetilde {L}/F) \simeq \mathbb {Z}/4\mathbb {Z}$
. We will refer to such an extension as a
$\mathrm {Gal}(\widetilde {L}/F) \simeq \mathbb {Z}/4\mathbb {Z}$
. We will refer to such an extension as a
![]() $\mathbb {Z}/4\mathbb {Z}\oplus \mathbb {Z}/2\mathbb {Z}$
-extension of type i.
$\mathbb {Z}/4\mathbb {Z}\oplus \mathbb {Z}/2\mathbb {Z}$
-extension of type i.
Lemma 4.1 tells us that if
![]() $[\gamma ] \in J(K)^{G}$
, then the Galois group of
$[\gamma ] \in J(K)^{G}$
, then the Galois group of
![]() $K(\sqrt {\gamma })/F$
can be computed entirely in terms of
$K(\sqrt {\gamma })/F$
can be computed entirely in terms of
![]() $T([\gamma ])$
. For example, suppose that
$T([\gamma ])$
. For example, suppose that
![]() $T([\gamma ]) = (a_{2},1,1)$
. By Lemma 4.1, we see that
$T([\gamma ]) = (a_{2},1,1)$
. By Lemma 4.1, we see that
![]() $K(\sqrt {\gamma })/F$
is a
$K(\sqrt {\gamma })/F$
is a
![]() $D_{4}$
-extension of type
$D_{4}$
-extension of type
![]() $1$
. Similarly, if
$1$
. Similarly, if
![]() $T([\gamma ]) = (1,a_{1},1)$
or
$T([\gamma ]) = (1,a_{1},1)$
or
![]() $T([\gamma ]) = (1,1,a_{1})$
, then
$T([\gamma ]) = (1,1,a_{1})$
, then
![]() $K(\sqrt {\gamma })/F$
is a
$K(\sqrt {\gamma })/F$
is a
![]() $D_{4}$
-extension of type
$D_{4}$
-extension of type
![]() $2$
or
$2$
or
![]() $3$
(respectively). We also have that
$3$
(respectively). We also have that
![]() $T([\gamma ]) \in \{(a_{2},a_{1},1),(a_{2},1,a_{1}),(1,a_{1},a_{1})\}$
implies that
$T([\gamma ]) \in \{(a_{2},a_{1},1),(a_{2},1,a_{1}),(1,a_{1},a_{1})\}$
implies that
![]() $K(\sqrt {\gamma })/F$
is a
$K(\sqrt {\gamma })/F$
is a
![]() $\mathbb {Z}/4\mathbb {Z}\oplus \mathbb {Z}/2\mathbb {Z}$
-extension (of types
$\mathbb {Z}/4\mathbb {Z}\oplus \mathbb {Z}/2\mathbb {Z}$
-extension (of types
![]() $3$
,
$3$
,
![]() $2$
, and
$2$
, and
![]() $1$
, respectively). If
$1$
, respectively). If
![]() $T([\gamma ]) = (a_{2},a_{1},a_{1})$
, then
$T([\gamma ]) = (a_{2},a_{1},a_{1})$
, then
![]() $K(\sqrt {\gamma })/F$
is a
$K(\sqrt {\gamma })/F$
is a
![]() $Q_{8}$
-extension. Finally, if
$Q_{8}$
-extension. Finally, if
![]() $T([\gamma ]) = (1,1,1)$
, then
$T([\gamma ]) = (1,1,1)$
, then
![]() $\mathrm { Gal}(K(\sqrt {\gamma })/F)$
is elementary
$\mathrm { Gal}(K(\sqrt {\gamma })/F)$
is elementary
![]() $2$
-abelian of rank
$2$
-abelian of rank
![]() $3$
. Since each of the possible values of
$3$
. Since each of the possible values of
![]() $T([\gamma ])$
yields a distinct Galois group, this dictionary works both ways: the structure of the Galois group of a given
$T([\gamma ])$
yields a distinct Galois group, this dictionary works both ways: the structure of the Galois group of a given
![]() $K(\sqrt {\gamma })/F$
determines the value of
$K(\sqrt {\gamma })/F$
determines the value of
![]() $T([\gamma ])$
.
$T([\gamma ])$
.
Happily, these types of embedding problems have already been studied extensively. For example, in [Reference Kiming17], one finds that a quadratic extension
![]() $E(\sqrt {a})/E$
embeds in a
$E(\sqrt {a})/E$
embeds in a
![]() $\mathbb {Z}_{4}$
-extension if and only if
$\mathbb {Z}_{4}$
-extension if and only if
![]() $a=x^{2}+y^{2}$
for
$a=x^{2}+y^{2}$
for
![]() $x,y \in E$
. Likewise, a biquadratic extension
$x,y \in E$
. Likewise, a biquadratic extension
![]() $E(\sqrt {a},\sqrt {b})/E$
embeds in a
$E(\sqrt {a},\sqrt {b})/E$
embeds in a
![]() $D_{4}$
-extension
$D_{4}$
-extension
![]() $L/E$
for which
$L/E$
for which
![]() $\mathrm {Gal}(L/E(\sqrt {b})) \simeq \mathbb {Z}/4\mathbb {Z}$
if and only if
$\mathrm {Gal}(L/E(\sqrt {b})) \simeq \mathbb {Z}/4\mathbb {Z}$
if and only if
![]() $b = ay^{2}-x^{2}$
for some
$b = ay^{2}-x^{2}$
for some
![]() $x,y \in E$
. Finally, a biquadratic extension
$x,y \in E$
. Finally, a biquadratic extension
![]() $E(\sqrt {a},\sqrt {b})/E$
embeds in a
$E(\sqrt {a},\sqrt {b})/E$
embeds in a
![]() $Q_{8}$
-extension if and only if there are
$Q_{8}$
-extension if and only if there are
![]() $e_{1},e_{2},e_{3},f_{1},f_{2},f_{3} \in E$
with
$e_{1},e_{2},e_{3},f_{1},f_{2},f_{3} \in E$
with
![]() $a = \sum _{i=1}^{3} e_{i}^{2}$
and
$a = \sum _{i=1}^{3} e_{i}^{2}$
and
![]() $b = \sum _{i=1}^{3} f_{i}^{2}$
and
$b = \sum _{i=1}^{3} f_{i}^{2}$
and
![]() $\sum _{i=1}^{3} e_{i}f_{i}=0$
. Hence, we can determine if a given biquadratic extension
$\sum _{i=1}^{3} e_{i}f_{i}=0$
. Hence, we can determine if a given biquadratic extension
![]() $K/F$
has elements
$K/F$
has elements
![]() $[\gamma ] \in J(K)^{G}$
with prescribed values under T by determining whether certain equations hold over F.
$[\gamma ] \in J(K)^{G}$
with prescribed values under T by determining whether certain equations hold over F.
Example 6.1 Let
![]() $F = \mathbb {Q}$
and
$F = \mathbb {Q}$
and
![]() $K = \mathbb {Q}(\sqrt {7},\sqrt {-5})$
. (Following our previous conventions, this means
$K = \mathbb {Q}(\sqrt {7},\sqrt {-5})$
. (Following our previous conventions, this means
![]() $a_{1} = 7$
and
$a_{1} = 7$
and
![]() $a_{2} = -5$
.) None of the elements from
$a_{2} = -5$
.) None of the elements from
![]() $\{7,-5,-35\}$
be written as a sum of two rational squares, and hence
$\{7,-5,-35\}$
be written as a sum of two rational squares, and hence
![]() $K/F$
does not embed in any type of
$K/F$
does not embed in any type of
![]() $\mathbb {Z}/4\mathbb {Z}\oplus \mathbb {Z}/2\mathbb {Z}$
-extension. Hence, no element from
$\mathbb {Z}/4\mathbb {Z}\oplus \mathbb {Z}/2\mathbb {Z}$
-extension. Hence, no element from
![]() $\{(a_{2},a_{1},1),(a_{2},1,a_{1}),(1,a_{1},a_{1})\}$
is in
$\{(a_{2},a_{1},1),(a_{2},1,a_{1}),(1,a_{1},a_{1})\}$
is in
![]() $\text {im}(T)$
. We can also clearly see that
$\text {im}(T)$
. We can also clearly see that
![]() $7=-5y^{2}-x^{2}$
has no rational solutions, so
$7=-5y^{2}-x^{2}$
has no rational solutions, so
![]() $K/F$
does not embed in a
$K/F$
does not embed in a
![]() $D_{4}$
-extension of type
$D_{4}$
-extension of type
![]() $1$
; therefore,
$1$
; therefore,
![]() $(a_{2},1,1) \not \in \text {im}(T)$
. Likewise
$(a_{2},1,1) \not \in \text {im}(T)$
. Likewise
![]() $-5 = -35y^{2}-x^{2}$
and
$-5 = -35y^{2}-x^{2}$
and
![]() $-35 = -5y^{2}-x^{2}$
have no rational solutions. For example, a rational solution to
$-35 = -5y^{2}-x^{2}$
have no rational solutions. For example, a rational solution to
![]() $-5=-35y^{2}-x^{2}$
would imply an integral solution to
$-5=-35y^{2}-x^{2}$
would imply an integral solution to
![]() $u^{2}=7v^{2}+5w^{2}$
for which
$u^{2}=7v^{2}+5w^{2}$
for which
![]() $5 \nmid u$
and
$5 \nmid u$
and
![]() $5\nmid v$
. One sees this is impossible by examining this equation modulo
$5\nmid v$
. One sees this is impossible by examining this equation modulo
![]() $5$
. Because these equations have no rational solutions, it follows that
$5$
. Because these equations have no rational solutions, it follows that
![]() $K/F$
does not embed in a
$K/F$
does not embed in a
![]() $D_{4}$
-extension of type
$D_{4}$
-extension of type
![]() $2$
or
$2$
or
![]() $3$
either. Hence,
$3$
either. Hence,
![]() $\{(1,a_{1},1),(1,1,a_{1})\} \not \in \text {im}(T)$
. Finally, since
$\{(1,a_{1},1),(1,1,a_{1})\} \not \in \text {im}(T)$
. Finally, since
![]() $-5$
is conspicuously not a sum of three rational squares, we have that
$-5$
is conspicuously not a sum of three rational squares, we have that
![]() $K/F$
does not embed in a
$K/F$
does not embed in a
![]() $Q_{8}$
-extension, and so
$Q_{8}$
-extension, and so
![]() $(a_{2},a_{1},a_{1}) \not \in \text {im}(T)$
. Hence,
$(a_{2},a_{1},a_{1}) \not \in \text {im}(T)$
. Hence,
![]() $\text {im}(T) = \{(1,1,1)\}$
, and by Theorem 4.8, we have
$\text {im}(T) = \{(1,1,1)\}$
, and by Theorem 4.8, we have
![]() $X = \{[1]\}$
.
$X = \{[1]\}$
.
Example 6.2 Let
![]() $F = \mathbb {Q}$
and
$F = \mathbb {Q}$
and
![]() $K = \mathbb {Q}(\sqrt {7},\sqrt {-1})$
. We see that
$K = \mathbb {Q}(\sqrt {7},\sqrt {-1})$
. We see that
![]() $K/F$
does not embed in any
$K/F$
does not embed in any
![]() $\mathbb {Z}/4\mathbb {Z}\oplus \mathbb {Z}/2\mathbb {Z}$
-extension since none of
$\mathbb {Z}/4\mathbb {Z}\oplus \mathbb {Z}/2\mathbb {Z}$
-extension since none of
![]() $7,-1$
, nor
$7,-1$
, nor
![]() $-7$
is a sum of two rational squares; it does not embed in a
$-7$
is a sum of two rational squares; it does not embed in a
![]() $D_{4}$
-extension of type
$D_{4}$
-extension of type
![]() $1$
or
$1$
or
![]() $3$
since
$3$
since
![]() $7 = -y^{2}-x^{2}$
and
$7 = -y^{2}-x^{2}$
and
![]() $-7 = -y^{2}-x^{2}$
have no rational solutions; and it does not embed in a
$-7 = -y^{2}-x^{2}$
have no rational solutions; and it does not embed in a
![]() $Q_{8}$
-extension since
$Q_{8}$
-extension since
![]() $-1$
is not a sum of three rational squares. It does, however, embed in a
$-1$
is not a sum of three rational squares. It does, however, embed in a
![]() $D_{4}$
-extension of type
$D_{4}$
-extension of type
![]() $2$
since
$2$
since
![]() $-1 = -7y^{2}-x^{2}$
has a rational solution. Hence,
$-1 = -7y^{2}-x^{2}$
has a rational solution. Hence,
![]() $\text {im}(T) = \{(1,1,1),(1,a_{1},1)\}$
, and so
$\text {im}(T) = \{(1,1,1),(1,a_{1},1)\}$
, and so
![]() $X \simeq \mathbb {F}_{2}$
.
$X \simeq \mathbb {F}_{2}$
.
Example 6.3 Let
![]() $F = \mathbb {Q}$
and
$F = \mathbb {Q}$
and
![]() $K = \mathbb {Q}(\sqrt {2},\sqrt {-1})$
. Since
$K = \mathbb {Q}(\sqrt {2},\sqrt {-1})$
. Since
![]() $2$
is a sum of two rational squares but
$2$
is a sum of two rational squares but
![]() $-1$
and
$-1$
and
![]() $-2$
are not, we see that
$-2$
are not, we see that
![]() $K/F$
embeds in a
$K/F$
embeds in a
![]() $\mathbb {Z}/4\mathbb {Z}\oplus \mathbb {Z}/2\mathbb {Z}$
-extension of type
$\mathbb {Z}/4\mathbb {Z}\oplus \mathbb {Z}/2\mathbb {Z}$
-extension of type
![]() $1$
, but not of type
$1$
, but not of type
![]() $2$
or
$2$
or
![]() $3$
. It is also the case that
$3$
. It is also the case that
![]() $2 = -y^{2}-x^{2}$
has no rational solutions, but
$2 = -y^{2}-x^{2}$
has no rational solutions, but
![]() $-1 = 2y^{2}-x^{2}$
and
$-1 = 2y^{2}-x^{2}$
and
![]() $-2 = 2y^{2}-x^{2}$
do have rational solutions, and hence
$-2 = 2y^{2}-x^{2}$
do have rational solutions, and hence
![]() $K/F$
embeds in
$K/F$
embeds in
![]() $D_{4}$
-extensions of types
$D_{4}$
-extensions of types
![]() $2$
and
$2$
and
![]() $3$
, but not type
$3$
, but not type
![]() $1$
. We also have that
$1$
. We also have that
![]() $-1$
is not a sum of three rational squares, so
$-1$
is not a sum of three rational squares, so
![]() $K/F$
does not embed in a
$K/F$
does not embed in a
![]() $Q_{8}$
-extension. Taken together, this means that
$Q_{8}$
-extension. Taken together, this means that
![]() $\text {im}(T) = \{(1,1,1),(1,a_{1},a_{1}),(1,a_{1},1),(1,1,a_{1})\}$
, which is one of the coordinate planes (the “
$\text {im}(T) = \{(1,1,1),(1,a_{1},a_{1}),(1,a_{1},1),(1,1,a_{1})\}$
, which is one of the coordinate planes (the “
![]() $yz$
-plane”). Hence, from Theorem 4.8, we have
$yz$
-plane”). Hence, from Theorem 4.8, we have
![]() $X \simeq \Omega ^{-1}$
.
$X \simeq \Omega ^{-1}$
.
Example 6.4 Let
![]() $F = \mathbb {Q}$
and
$F = \mathbb {Q}$
and
![]() $K = \mathbb {Q}(\sqrt {5},\sqrt {13})$
. We know that each of
$K = \mathbb {Q}(\sqrt {5},\sqrt {13})$
. We know that each of
![]() $5$
,
$5$
,
![]() $13$
, and
$13$
, and
![]() $65$
can be written as a sum of two rational (indeed, integral) squares, and hence
$65$
can be written as a sum of two rational (indeed, integral) squares, and hence
![]() $K/F$
embeds in
$K/F$
embeds in
![]() $\mathbb {Z}/4\mathbb {Z}\oplus \mathbb {Z}/2\mathbb {Z}$
-extensions of types
$\mathbb {Z}/4\mathbb {Z}\oplus \mathbb {Z}/2\mathbb {Z}$
-extensions of types
![]() $1$
–
$1$
–
![]() $3$
. Therefore,
$3$
. Therefore,
![]() $\{(1,1,1),(a_{2},a_{1},1),(a_{2},1,a_{1}),(1,a_{1},a_{1})\} \subseteq \text {im}(T)$
. On the other hand, there is no rational solution to
$\{(1,1,1),(a_{2},a_{1},1),(a_{2},1,a_{1}),(1,a_{1},a_{1})\} \subseteq \text {im}(T)$
. On the other hand, there is no rational solution to
![]() $5 = 13y^{2}-x^{2}$
, since such a solution would imply an integral solution to
$5 = 13y^{2}-x^{2}$
, since such a solution would imply an integral solution to
![]() $5u^{2} = 13v^{2}-w^{2}$
. (After ensuring that
$5u^{2} = 13v^{2}-w^{2}$
. (After ensuring that
![]() $5$
does not divide all of u, v, and w, one examines the equation modulo
$5$
does not divide all of u, v, and w, one examines the equation modulo
![]() $5$
.) Hence,
$5$
.) Hence,
![]() $K/F$
does not embed in a
$K/F$
does not embed in a
![]() $D_{4}$
-extension of type
$D_{4}$
-extension of type
![]() $1$
, and so
$1$
, and so
![]() $(a_{2},1,1) \not \in \text {im}(T)$
. Since T is an
$(a_{2},1,1) \not \in \text {im}(T)$
. Since T is an
![]() $\mathbb {F}_{2}$
-space, we get
$\mathbb {F}_{2}$
-space, we get
![]() $\{(1,1,1),(a_{2},a_{1},1),(a_{2},1,a_{1}),(1,a_{1},a_{1})\} = \text {im}(T)$
. By Theorem 4.8, we have
$\{(1,1,1),(a_{2},a_{1},1),(a_{2},1,a_{1}),(1,a_{1},a_{1})\} = \text {im}(T)$
. By Theorem 4.8, we have
![]() $X \simeq \mathbb {F}_{2}\oplus \mathbb {F}_{2}$
.
$X \simeq \mathbb {F}_{2}\oplus \mathbb {F}_{2}$
.
Example 6.5 Let
![]() $F = \mathbb {Q}$
and
$F = \mathbb {Q}$
and
![]() $K = \mathbb {Q}(\sqrt {5},\sqrt {41})$
. Since
$K = \mathbb {Q}(\sqrt {5},\sqrt {41})$
. Since
![]() $5$
,
$5$
,
![]() $41$
, and
$41$
, and
![]() $205$
are all expressible as sums of two rational squares, and since we can write
$205$
are all expressible as sums of two rational squares, and since we can write
![]() $5 = (2)^{2}+(1)^{2}+0^{2}$
and
$5 = (2)^{2}+(1)^{2}+0^{2}$
and
![]() $41 = (-1)^{2}+(2)^{2}+(6)^{2}$
, we see that
$41 = (-1)^{2}+(2)^{2}+(6)^{2}$
, we see that
![]() $\{(a_{2},a_{1},1),(a_{2},1,a_{1}),(1,a_{1},a_{1}),(a_{2},a_{1},a_{1})\} \subseteq \text {im}(T)$
. Hence,
$\{(a_{2},a_{1},1),(a_{2},1,a_{1}),(1,a_{1},a_{1}),(a_{2},a_{1},a_{1})\} \subseteq \text {im}(T)$
. Hence,
![]() $\dim (\text {im}(T)) = 3$
in this case, and we have either
$\dim (\text {im}(T)) = 3$
in this case, and we have either
![]() $X \simeq \Omega ^{-1}\oplus \Omega ^{-1}$
or
$X \simeq \Omega ^{-1}\oplus \Omega ^{-1}$
or
![]() $X \simeq \Omega ^{-2}$
(depending on whether
$X \simeq \Omega ^{-2}$
(depending on whether
![]() $[N_{K/K_{1}}(K^{\times })] \cap [N_{K/K_{2}}(K^{\times })] \subseteq [\mathbb {Q}^{\times }])$
.
$[N_{K/K_{1}}(K^{\times })] \cap [N_{K/K_{2}}(K^{\times })] \subseteq [\mathbb {Q}^{\times }])$
.
The reader will notice that we have connected the solvability of particular embedding problems to the existence of certain points on rational conics
![]() $1=by^{2}-ax^{2}$
. These are in turn connected to the splitting of quaternion algebras
$1=by^{2}-ax^{2}$
. These are in turn connected to the splitting of quaternion algebras
![]() $(a,b)_{\mathbb {Q}}$
(see [Reference Lam18, Theorem 2.7]). However, this connection—and the well-established track record that the Brauer group has in encoding the solvability of certain Galois embedding problems (see [Reference Jensen and Yui16, Reference Kiming17, Reference Michailov21, Reference Michailov22])—might suggest that there is something deeper to explore in this vein. Indeed, the solvability of each of the embedding problems we have discussed is encoded in the vanishing of certain element(s) drawn from
$(a,b)_{\mathbb {Q}}$
(see [Reference Lam18, Theorem 2.7]). However, this connection—and the well-established track record that the Brauer group has in encoding the solvability of certain Galois embedding problems (see [Reference Jensen and Yui16, Reference Kiming17, Reference Michailov21, Reference Michailov22])—might suggest that there is something deeper to explore in this vein. Indeed, the solvability of each of the embedding problems we have discussed is encoded in the vanishing of certain element(s) drawn from
![]() $\langle (a_{1},a_{1}),(a_{1},a_{2}),(a_{2},a_{2})\rangle \subseteq \text {Br}(\mathbb {Q})$
. The focus of the follow-up paper [Reference Chemotti, Mináč, Nguyen, Schultz, Swallow and Tan9] is to reinterpret the decomposition of
$\langle (a_{1},a_{1}),(a_{1},a_{2}),(a_{2},a_{2})\rangle \subseteq \text {Br}(\mathbb {Q})$
. The focus of the follow-up paper [Reference Chemotti, Mináč, Nguyen, Schultz, Swallow and Tan9] is to reinterpret the decomposition of
![]() $J(K)$
provided by Theorem 1.1 through the lens of certain equations in
$J(K)$
provided by Theorem 1.1 through the lens of certain equations in
![]() $\text {Br}(F)$
. In particular, this will allow us to compute the multiplicities of the various summands by analyzing subspaces within
$\text {Br}(F)$
. In particular, this will allow us to compute the multiplicities of the various summands by analyzing subspaces within
![]() $\text {Br}(F)$
, and ultimately show that all listed “unexceptional” summand types (i.e.,
$\text {Br}(F)$
, and ultimately show that all listed “unexceptional” summand types (i.e.,
![]() $\mathbb {F}_{2}[\overline {G_{i}}]$
for
$\mathbb {F}_{2}[\overline {G_{i}}]$
for
![]() $i \in \{0,1,2,3,4\}$
, as well as
$i \in \{0,1,2,3,4\}$
, as well as
![]() $\Omega ^{1}$
and
$\Omega ^{1}$
and
![]() $\Omega ^{2}$
) from Theorem 1.1 are realizable.
$\Omega ^{2}$
) from Theorem 1.1 are realizable.
Acknowledgment
We gratefully acknowledge discussions and collaborations with our friends and colleagues D. Benson, B. Brubaker, J. Carlson, S. Chebolu, I. Efrat, J. Gärtner, S. Gille, L. Heller, D. Hoffmann, J. Labute, T.-Y. Lam, R. Sharifi, N.D. Tan, A. Topaz, R. Vakil, K. Wickelgren, and O. Wittenberg, which have influenced our work in this and related papers. We are particularly grateful to A. Eimer and P. Guillot for their careful consideration of a previous draft of this manuscript which omitted
![]() $\Omega ^{2}$
summands. Finally, we are grateful for the careful attention that our manuscript received from two anonymous referees. The encouraging suggestions they made have helped improve both the expositional quality of the manuscript and its accuracy.
$\Omega ^{2}$
summands. Finally, we are grateful for the careful attention that our manuscript received from two anonymous referees. The encouraging suggestions they made have helped improve both the expositional quality of the manuscript and its accuracy.