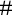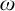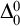1 Introduction
1.1 The project
The axiomatic study on the notion of truth has extensively been pursued in the framework of first-order arithmetic since the beginning of axiomatic truth theory by Feferman [Reference Feferman5]. Overviews on the axiomatic studies of truth along this line can be found in the monographs by Halbach [Reference Halbach11] and by Horsten [Reference Horsten12].
First-order arithmetic is a natural formal theory for the mathematical structure
![]() $\omega $
of the natural numbers and is favoured because of its simplicity. Nonetheless, it is not a natural framework for the entire mathematics. In ordinary mathematics, not only natural numbers but also higher-order objects are commonly used: sets of natural numbers, functions on natural numbers, sets of or functions on those objects, and so on. Thus, other frameworks, for example, second-order arithmetic, higher-order arithmetic, or first-order set theory, seem to be better suited as natural formal frameworks for ordinary mathematics.
$\omega $
of the natural numbers and is favoured because of its simplicity. Nonetheless, it is not a natural framework for the entire mathematics. In ordinary mathematics, not only natural numbers but also higher-order objects are commonly used: sets of natural numbers, functions on natural numbers, sets of or functions on those objects, and so on. Thus, other frameworks, for example, second-order arithmetic, higher-order arithmetic, or first-order set theory, seem to be better suited as natural formal frameworks for ordinary mathematics.
Philosophical motivations to develop (significant parts of) mathematics in the framework of arithmetic are mainly foundational and minimalistic, namely, to minimize the ontological commitment. Among them, the best known is what we call Hilbert’s Finitism, the finitism in Hilbert’s programme. Differently from Hilbert’s original intention, Tait [Reference Tait27] describes it as follows.
Rather, the special role of finitism consists in the circumstance that is a minimal kind of reasoning presupposed by all nontrivial mathematical reasoning about numbers. And for this reason it is indubitable in a Cartesian sense that there is no preferred or even equally preferable ground on which to stand and criticize it. (p. 525)
Although there have been unsettled philosophical and historical discussions on exactly what is allowed in Hilbert’s Finitism (see, e.g., [Reference Tait, Sommer, Sieg and Talcott28, Reference Zach31]), it seems to be a common perception that the finitist rejects any kind of infinite totality, including the totality of
![]() $\omega $
. Because the quantifiers varying over
$\omega $
. Because the quantifiers varying over
![]() $\omega $
are considered to presuppose the totality of
$\omega $
are considered to presuppose the totality of
![]() $\omega $
, the axiomatic systems intended for Hilbert’s Finitism and those for other variants of finitism should be formulated in the language without unbounded quantifiers over infinite domains.Footnote
1
In particular, Primitive Recursive Arithmetic
$\omega $
, the axiomatic systems intended for Hilbert’s Finitism and those for other variants of finitism should be formulated in the language without unbounded quantifiers over infinite domains.Footnote
1
In particular, Primitive Recursive Arithmetic
![]() $\mathbb {PRA}$
, also called Skolem Arithmetic, with which Tait [Reference Tait27] identifies Hilbert’s Finitism, is formulated in the language of arithmetic that does not allow (unbounded) quantifiers, and hence it is not formulated in the first-order language of arithmetic.Footnote
2
$\mathbb {PRA}$
, also called Skolem Arithmetic, with which Tait [Reference Tait27] identifies Hilbert’s Finitism, is formulated in the language of arithmetic that does not allow (unbounded) quantifiers, and hence it is not formulated in the first-order language of arithmetic.Footnote
2
Therefore, even though first-order arithmetic may be a natural theory of the structure
![]() $\omega $
, it does not appear more natural nor more philosophically motivated than other frameworks of mathematics: systems stronger or weaker than first-order arithmetic. Accordingly, the axiomatic study on the notion of truth in such stronger and weaker frameworks is as much worthwhile as respective studies in the first-order arithmetic. As for stronger frameworks, we should mention Fujimoto’s works [Reference Fujimoto6, Reference Fujimoto7] in which axiomatic truth theories over Zermelo–Fraenkel set theory have been investigated. Philosophical discussions of this direction of research can also be found in [Reference Fujimoto8]. The present paper, on the other hand, initiates a study of axiomatic truth theories over weaker systems, especially finitist arithmetic without unbounded quantifiers.
$\omega $
, it does not appear more natural nor more philosophically motivated than other frameworks of mathematics: systems stronger or weaker than first-order arithmetic. Accordingly, the axiomatic study on the notion of truth in such stronger and weaker frameworks is as much worthwhile as respective studies in the first-order arithmetic. As for stronger frameworks, we should mention Fujimoto’s works [Reference Fujimoto6, Reference Fujimoto7] in which axiomatic truth theories over Zermelo–Fraenkel set theory have been investigated. Philosophical discussions of this direction of research can also be found in [Reference Fujimoto8]. The present paper, on the other hand, initiates a study of axiomatic truth theories over weaker systems, especially finitist arithmetic without unbounded quantifiers.
1.2 Summary of this article
Our main result is that the finitist analogues of theories of Tarski compositional truth, of Tarski ramified truth (up to rank
![]() $\omega $
), of Kripke–Feferman truth, and of Friedman–Sheard truth are all equivalent, that is, they prove the same finitist formulae not containing any truth predicates. Thus, in this regard, finitist truth theories behave significantly differently than those over first-order arithmetic and over first-order set theory.
$\omega $
), of Kripke–Feferman truth, and of Friedman–Sheard truth are all equivalent, that is, they prove the same finitist formulae not containing any truth predicates. Thus, in this regard, finitist truth theories behave significantly differently than those over first-order arithmetic and over first-order set theory.
Below, we first outline the finitist analogues of well-known axiomatizations of truth and indicate in which sense they are equivalent.
Finitist language and finitist logic
As discussed above, the finitist view is well formulated in an arithmetical language which does not allow unbounded quantification. We call languages without unbounded quantifiers finitist languages and denote them by Fraktur letters (e.g.,
![]() $\mathfrak {L}(\mathcal {S}^n)$
) in order to distinguish them from first-order languages which we denote by calligraphic letters (e.g.,
$\mathfrak {L}(\mathcal {S}^n)$
) in order to distinguish them from first-order languages which we denote by calligraphic letters (e.g.,
![]() $\mathcal {L}_1(\mathcal {S}^n)$
). Finitist languages allow us to express universal quantification (if located at the outer-most position) implicitly by means of free variables. Similarly to first-order languages, there are many different finitist languages, depending on the choice of vocabulary: constant, function, and relation symbols.
$\mathcal {L}_1(\mathcal {S}^n)$
). Finitist languages allow us to express universal quantification (if located at the outer-most position) implicitly by means of free variables. Similarly to first-order languages, there are many different finitist languages, depending on the choice of vocabulary: constant, function, and relation symbols.
Our investigation will be on formal theories of truth formulated in finitist languages with unary relation symbols
![]() $T_i(x)$
with indices i, where
$T_i(x)$
with indices i, where
![]() $T_i(x)$
is intended to mean that (the sentence whose Gödel number is) x is true. All the finitist languages in the present paper are arithmetic, in the sense that they have, at least, constants 0 and 1, binary function symbols
$T_i(x)$
is intended to mean that (the sentence whose Gödel number is) x is true. All the finitist languages in the present paper are arithmetic, in the sense that they have, at least, constants 0 and 1, binary function symbols
![]() $+$
and
$+$
and
![]() $\cdot $
, and a binary relation symbol
$\cdot $
, and a binary relation symbol
![]() $<$
as well as the equality
$<$
as well as the equality
![]() $=$
. The difference of vocabulary is only in whether and how many of the truth predicates
$=$
. The difference of vocabulary is only in whether and how many of the truth predicates
![]() $T_i(x)$
and further function symbols are included.
$T_i(x)$
and further function symbols are included.
Similarly to logical axioms and rules for first-order theories, we have logical axioms and rules for finitist theories. The axioms and rules for propositional connectives and the equality axioms are the same as for classical first-order logic. The axioms and rules for quantifiers are replaced in the obvious manner.
It is worth mentioning that almost all variants of intuitionism and constructivism accept classical reasoning for finitary statements. Thus, even if we want to take into account these philosophical standpoints, it is natural to consider theories over classical logic (formulated in the finitist languages).Footnote 3
Finitist truth theories
One of the significant features of truth in the finitist setting is that, even in the presence of addition
![]() $+$
and multiplication
$+$
and multiplication
![]() $\cdot $
, a liar sentence does not always emerge and hence the notion of naïve truth is not necessarily contradictory. In order to have a liar sentence (in the sense of some “standard” or reasonable coding), we need more function symbols: exponentiation
$\cdot $
, a liar sentence does not always emerge and hence the notion of naïve truth is not necessarily contradictory. In order to have a liar sentence (in the sense of some “standard” or reasonable coding), we need more function symbols: exponentiation
![]() $\exp $
suffices; even smash function
$\exp $
suffices; even smash function
![]() $x\# y\,{=}\,2^{|x|\cdot |y|}$
(where
$x\# y\,{=}\,2^{|x|\cdot |y|}$
(where
![]() $|x|\,{=}\,\min \{z\,{:}\,x\,{<}\,2^z\}$
) is enough. While the finitist theory of naïve truth (in a language not containing
$|x|\,{=}\,\min \{z\,{:}\,x\,{<}\,2^z\}$
) is enough. While the finitist theory of naïve truth (in a language not containing
![]() $\exp $
nor
$\exp $
nor
![]() $\#$
) is one of the themes of another article [Reference Sato and Walker23] of the authors, in the present article we concentrate on theories in languages with at least
$\#$
) is one of the themes of another article [Reference Sato and Walker23] of the authors, in the present article we concentrate on theories in languages with at least
![]() $\#$
, where the construction of a liar sentence is possible.
$\#$
, where the construction of a liar sentence is possible.
In the presence of a liar sentence, say,
![]() $\mathrm {liar}$
is a term such that
$\mathrm {liar}$
is a term such that
![]() $\mathrm {liar}\,{=}\, \ulcorner \neg T(\mathrm {liar})\urcorner $
(where
$\mathrm {liar}\,{=}\, \ulcorner \neg T(\mathrm {liar})\urcorner $
(where
![]() $\ulcorner A\urcorner $
denotes the Gödel number of a formula A), the two axiom schemata for the truth predicate
$\ulcorner A\urcorner $
denotes the Gödel number of a formula A), the two axiom schemata for the truth predicate
-
(
 $\mathit {Truth}\text{-}\mathit{Negation}$
):
$\mathit {Truth}\text{-}\mathit{Negation}$
):
 $T(\ulcorner \neg A\urcorner ) \,{\leftrightarrow }\,\neg T(\ulcorner A\urcorner )$
for any standard sentence A,
$T(\ulcorner \neg A\urcorner ) \,{\leftrightarrow }\,\neg T(\ulcorner A\urcorner )$
for any standard sentence A, -
(
 $\mathit{Truth}\text{-}\mathit{Truth}$
):
$\mathit{Truth}\text{-}\mathit{Truth}$
):
 $T(\ulcorner T(t) \urcorner ) \,{\leftrightarrow }\,T(t)$
for any term t
$T(\ulcorner T(t) \urcorner ) \,{\leftrightarrow }\,T(t)$
for any term t
cannot consistently coexist, because they imply
Among strategies to formulate consistent truth theories, the four most popular ones are the following.
-
Compositional truth: prohibiting the truth predicate from being applied to (Gödel numbers of) sentences that involve the truth predicate itself (this is a special case of the next, with only one rank allowed).
-
Ramified truth: ramifying the truth predicate into several ranks, and considering only the well-typed applications of truth predicates, namely, ignoring ill-typed ones, like
 $T_i(\ulcorner T_j(u)\urcorner )$
for
$T_i(\ulcorner T_j(u)\urcorner )$
for
 $j\,{\geq }\,i$
.
$j\,{\geq }\,i$
. -
Kripke–Feferman truth: replacing the aforementioned (Truth-Negation) by
 $T(\ulcorner \neg T (\ulcorner A\urcorner )\urcorner ) \,{\leftrightarrow }\, T(\ulcorner \neg A\urcorner )$
(more precisely, the extension of it to possibly non-standard formulae A).
$T(\ulcorner \neg T (\ulcorner A\urcorner )\urcorner ) \,{\leftrightarrow }\, T(\ulcorner \neg A\urcorner )$
(more precisely, the extension of it to possibly non-standard formulae A). -
Friedman–Sheard truth: replacing the axiom (Truth-Truth) by the following analogous rules:

We take all of these four popular strategies into account. For the second strategy, the typed truth, we consider only finite ranks. For, in order to formulate truth of transfinite ranks
![]() $\alpha $
, we need to assume the well-foundedness of
$\alpha $
, we need to assume the well-foundedness of
![]() $\alpha $
, which seems not expressible without unbounded quantifiers.
$\alpha $
, which seems not expressible without unbounded quantifiers.
In the finitist setting, we face a difficulty in the formulation of the very basic axioms for the truth predicates. In the standard formulations, almost all truth theories over first-order arithmetic contain
where
![]() $\mathrm {CTerm}(u)$
means that u is (a Gödel number of) a closed term. While, in the first-order setting, valuation may be expressed by means of the unbounded existential quantifier, the situation is entirely different in our finitist setting, where no unbounded quantifiers are available. In our setting, we might rather try to augment a finitist language by a new symbol
$\mathrm {CTerm}(u)$
means that u is (a Gödel number of) a closed term. While, in the first-order setting, valuation may be expressed by means of the unbounded existential quantifier, the situation is entirely different in our finitist setting, where no unbounded quantifiers are available. In our setting, we might rather try to augment a finitist language by a new symbol
![]() $\mathrm {val}$
for the valuation function. However, by a diagonalization argument similar to the one for the liar paradox, we see that
$\mathrm {val}$
for the valuation function. However, by a diagonalization argument similar to the one for the liar paradox, we see that
![]() $\mathrm {val}$
cannot be used for valuating all terms in the augmented language, including those terms in which the symbol
$\mathrm {val}$
cannot be used for valuating all terms in the augmented language, including those terms in which the symbol
![]() $\mathrm {val}$
itself occurs. Therefore, we have to give up certain requirements concerning valuation of terms and must conceive alternative ways of formulating axioms, similarly to the alternative axioms that we consider for truth predicates. For typed truth, it seems reasonable to have typed valuation functions, namely
$\mathrm {val}$
itself occurs. Therefore, we have to give up certain requirements concerning valuation of terms and must conceive alternative ways of formulating axioms, similarly to the alternative axioms that we consider for truth predicates. For typed truth, it seems reasonable to have typed valuation functions, namely
![]() $\mathrm {val}_0$
,
$\mathrm {val}_0$
,
![]() $\mathrm {val}_1$
, …, (as we will consider in Section 11), but for self-referential truth, we have to formulate axioms without valuation function. How to do this? We propose to formulate the axioms without valuation function in the following way:
$\mathrm {val}_1$
, …, (as we will consider in Section 11), but for self-referential truth, we have to formulate axioms without valuation function. How to do this? We propose to formulate the axioms without valuation function in the following way:

where
![]() $\mathrm {num}(x)$
is (the Gödel number of) the x-th numeral (and x might be non-standard). Here
$\mathrm {num}(x)$
is (the Gödel number of) the x-th numeral (and x might be non-standard). Here
stands for
![]() $\mathrm {val}(u)\,{=}\,x$
but does not use
$\mathrm {val}(u)\,{=}\,x$
but does not use
![]() $\mathrm {val}$
. For uniformity, we follow this strategy also for typed truth.
$\mathrm {val}$
. For uniformity, we follow this strategy also for typed truth.
However, for example, how can we obtain the following in Kripke–Feferman truth theories?
If there are x and y such that
and
, then this is easy via
![]() $\neg (x\,{=}\,y)$
, but how do we guarantee or even express the existence of such x and y without (unbounded) existential quantifier?
$\neg (x\,{=}\,y)$
, but how do we guarantee or even express the existence of such x and y without (unbounded) existential quantifier?
Our trick is the addition of the following rule, where x must not occur in a formula A nor in a term t (i.e., x is the eigenvariable).

This is analogous to the logical rule for existential quantification in the first-order setting and, in this sense, expresses the existence of the value
![]() $\mathrm {val}(u)$
without unbounded quantifiers and without adding new function symbols. As it avoids the expansion of the language, this allows us to sustain self-referentiality, namely, that the language to which the truth predicate applies is the same as the language in which the theory of truth is formulated. Such self-referentiality seems essential for Kripke–Feferman and Friedman–Sheard truth.
$\mathrm {val}(u)$
without unbounded quantifiers and without adding new function symbols. As it avoids the expansion of the language, this allows us to sustain self-referentiality, namely, that the language to which the truth predicate applies is the same as the language in which the theory of truth is formulated. Such self-referentiality seems essential for Kripke–Feferman and Friedman–Sheard truth.
Our main results
The most standard choice of function symbols for arithmetic is
![]() $\{{+},{\cdot }\,\}$
. As mentioned above, however, as we concentrate on finitist settings with liar sentences, this is not appropriate for our purpose. Another standard is the class
$\{{+},{\cdot }\,\}$
. As mentioned above, however, as we concentrate on finitist settings with liar sentences, this is not appropriate for our purpose. Another standard is the class
![]() $\mathcal {PR}$
of all primitive recursive functions, but by adding
$\mathcal {PR}$
of all primitive recursive functions, but by adding
![]() $(\exists \mbox {-val})$
for all (codes of) terms built up from function symbols in
$(\exists \mbox {-val})$
for all (codes of) terms built up from function symbols in
![]() $\mathcal {PR}$
, we would make the resulting theory stronger than
$\mathcal {PR}$
, we would make the resulting theory stronger than
![]() $\mathbb {PRA}$
, with which Tait identified Hilbert’s Finitism. Although there seems to be no “standard” choice of function symbols in between
$\mathbb {PRA}$
, with which Tait identified Hilbert’s Finitism. Although there seems to be no “standard” choice of function symbols in between
![]() $\{+,\cdot \}$
and
$\{+,\cdot \}$
and
![]() $\mathcal {PR}$
, the standard of slicing up
$\mathcal {PR}$
, the standard of slicing up
![]() $\mathcal {PR}$
is Grzegorczyk hierarchy
$\mathcal {PR}$
is Grzegorczyk hierarchy
![]() $\mathcal {E}^n$
.
$\mathcal {E}^n$
.
For these reasons, we consider languages
![]() $\mathfrak {L}(\mathcal {S}^n)$
, whose function symbols are
$\mathfrak {L}(\mathcal {S}^n)$
, whose function symbols are
![]() ${+},{\cdot },{\#}, \gamma _3,\ldots ,\gamma _n$
where
${+},{\cdot },{\#}, \gamma _3,\ldots ,\gamma _n$
where

because, for
![]() $n\,{\geq }\,3$
, within
$n\,{\geq }\,3$
, within
![]() $\mathfrak {L}(\mathcal {S}^n)$
the use of functions from
$\mathfrak {L}(\mathcal {S}^n)$
the use of functions from
![]() $\mathcal {E}^n$
can be conceived as abbreviations.
$\mathcal {E}^n$
can be conceived as abbreviations.
Let
![]() $\mathbb {FA}(\mathcal {S}^n)$
be the finitist arithmetic generated from the axioms of Robinson Arithmetic, the basic axioms for the function symbols
$\mathbb {FA}(\mathcal {S}^n)$
be the finitist arithmetic generated from the axioms of Robinson Arithmetic, the basic axioms for the function symbols
![]() ${\#}, \gamma _3,\ldots ,\gamma _n$
, and the induction schema
${\#}, \gamma _3,\ldots ,\gamma _n$
, and the induction schema
![]() $A(0)\,{\land }\, (\forall y\,{<}\,x)(A(y)\,{\to }\,A(y{+}1)) \,{\to }\,A(x)$
for any
$A(0)\,{\land }\, (\forall y\,{<}\,x)(A(y)\,{\to }\,A(y{+}1)) \,{\to }\,A(x)$
for any
![]() $\mathfrak {L}(\mathcal {S}^n)$
formula A. Here we choose blackboard bold letters to denote finitist theories and to distinguish them from first-order theories denoted by bold ones (e.g.,
$\mathfrak {L}(\mathcal {S}^n)$
formula A. Here we choose blackboard bold letters to denote finitist theories and to distinguish them from first-order theories denoted by bold ones (e.g.,
![]() and
and
![]() $\mathbf {WKL}_0^*(\mathcal {S}^n)$
). Moreover let
$\mathbf {WKL}_0^*(\mathcal {S}^n)$
). Moreover let
![]() $\mathbb {FCT}(\mathcal {S}^n)$
,
$\mathbb {FCT}(\mathcal {S}^n)$
,
![]() $\mathbb {FRT}_{m}(\mathcal {S}^n)$
,
$\mathbb {FRT}_{m}(\mathcal {S}^n)$
,
![]() $\mathbb {FFS}(\mathcal {S}^n)$
, and
$\mathbb {FFS}(\mathcal {S}^n)$
, and
![]() $\mathbb {FKF}(\mathcal {S}^n)$
be, respectively, the theories of Tarski compositional truth, Tarski ramified truth, Friedman–Sheard truth, and Kripke–Feferman truth, all formulated over
$\mathbb {FKF}(\mathcal {S}^n)$
be, respectively, the theories of Tarski compositional truth, Tarski ramified truth, Friedman–Sheard truth, and Kripke–Feferman truth, all formulated over
![]() $\mathbb {FA}(\mathcal {S}^n)$
, where m means that
$\mathbb {FA}(\mathcal {S}^n)$
, where m means that
![]() $\mathbb {FRT}_{m}(\mathcal {S}^n)$
is formulated in the language
$\mathbb {FRT}_{m}(\mathcal {S}^n)$
is formulated in the language
![]() $\mathfrak {L}(\mathcal {S}^n,T_0,\ldots ,T_{m-1})$
with m truth predicates
$\mathfrak {L}(\mathcal {S}^n,T_0,\ldots ,T_{m-1})$
with m truth predicates
![]() $T_0,\ldots ,T_{m-1}$
.
$T_0,\ldots ,T_{m-1}$
.
Our main theorem is that, for
![]() $n\,{\geq }\,2$
,
$n\,{\geq }\,2$
,
![]() $\mathbb {FCT}(\mathcal {S}^n)$
,
$\mathbb {FCT}(\mathcal {S}^n)$
,
![]() $\mathbb {FRT}_{m+1}(\mathcal {S}^n)$
,
$\mathbb {FRT}_{m+1}(\mathcal {S}^n)$
,
![]() $\mathbb {FFS}(\mathcal {S}^n)$
, and
$\mathbb {FFS}(\mathcal {S}^n)$
, and
![]() $\mathbb {FKF}(\mathcal {S}^n)$
prove the same
$\mathbb {FKF}(\mathcal {S}^n)$
prove the same
![]() $\mathfrak {L}(\mathcal {S}^n)$
formulae as
$\mathfrak {L}(\mathcal {S}^n)$
formulae as
![]() $\mathbb {FA}(\mathcal {S}^{n+1})$
, independently of m. Here we need to consider all formulae not only sentences, as all these theories are complete for
$\mathbb {FA}(\mathcal {S}^{n+1})$
, independently of m. Here we need to consider all formulae not only sentences, as all these theories are complete for
![]() $\mathfrak {L}(\mathcal {S}^n)$
sentences (cf. the
$\mathfrak {L}(\mathcal {S}^n)$
sentences (cf. the
![]() $\Sigma _1$
completeness of first-order arithmetic).
$\Sigma _1$
completeness of first-order arithmetic).
Since the valuation function for
![]() $\mathcal {S}^n$
terms generates
$\mathcal {S}^n$
terms generates
![]() $\mathcal {S}^{n+1}$
, any theory closed under the rule (
$\mathcal {S}^{n+1}$
, any theory closed under the rule (
![]() $\exists \mbox {-val}$
) is naturally expected to have, at least, the strength of
$\exists \mbox {-val}$
) is naturally expected to have, at least, the strength of
![]() $\mathbb {FA}(\mathcal {S}^{n+1})$
. The import of our theorem is that the other truth-theoretic axioms and rules do not strengthen the theories any further. In other words, the strength of the other truth-theoretic axioms and rules is absorbed by the strength added by the valuation function.
$\mathbb {FA}(\mathcal {S}^{n+1})$
. The import of our theorem is that the other truth-theoretic axioms and rules do not strengthen the theories any further. In other words, the strength of the other truth-theoretic axioms and rules is absorbed by the strength added by the valuation function.
On the other hand, we will also see that the finitist Kripke–Feferman–Burgess truth theory
![]() $\mathbb {FKFB}(\mathcal {S}^n)$
, which extends
$\mathbb {FKFB}(\mathcal {S}^n)$
, which extends
![]() $\mathbb {FKF}(\mathcal {S}^n)$
with the so-called axioms of grounded truth, proves the same
$\mathbb {FKF}(\mathcal {S}^n)$
with the so-called axioms of grounded truth, proves the same
![]() $\mathfrak {L}(\mathcal {S}^n)$
formulae as
$\mathfrak {L}(\mathcal {S}^n)$
formulae as
![]() $\mathbb {PRA}$
. Therefore, the groundedness of truth, in this sense, exceeds the strength added by the valuation function.
$\mathbb {PRA}$
. Therefore, the groundedness of truth, in this sense, exceeds the strength added by the valuation function.
We can compare these results with the other aforementioned contexts, namely well-known results over Peano Arithmetic (summarized in [Reference Halbach11]) and those from [Reference Fujimoto6, Reference Fujimoto7] over Zermelo–Fraenkel set theory as follows.

Remarks on the measurement
In our main result, the strengths of our finitist truth theories
![]() $\mathbb {FCT}(\mathcal {S}^n)$
,
$\mathbb {FCT}(\mathcal {S}^n)$
,
![]() $\mathbb {FRT}_{m+1}(\mathcal {S}^n)$
,
$\mathbb {FRT}_{m+1}(\mathcal {S}^n)$
,
![]() $\mathbb {FFS}(\mathcal {S}^n)$
, and
$\mathbb {FFS}(\mathcal {S}^n)$
, and
![]() $\mathbb {FKF}(\mathcal {S}^n)$
are measured as being
$\mathbb {FKF}(\mathcal {S}^n)$
are measured as being
![]() $\mathfrak {L}(\mathcal {S}^n)$
equivalent to
$\mathfrak {L}(\mathcal {S}^n)$
equivalent to
![]() $\mathbb {FA}(\mathcal {S}^{n+1})$
and that of
$\mathbb {FA}(\mathcal {S}^{n+1})$
and that of
![]() $\mathbb {FKFB}(\mathcal {S}^n)$
as being
$\mathbb {FKFB}(\mathcal {S}^n)$
as being
![]() $\mathfrak {L}(\mathcal {S}^n)$
equivalent to
$\mathfrak {L}(\mathcal {S}^n)$
equivalent to
![]() $\mathbb {PRA}\,{\equiv }\, \bigcup _{k\in \omega }\mathbb {FA}(\mathcal {S}^{k})$
. In the present authors’ next work [Reference Sato and Walker23],
$\mathbb {PRA}\,{\equiv }\, \bigcup _{k\in \omega }\mathbb {FA}(\mathcal {S}^{k})$
. In the present authors’ next work [Reference Sato and Walker23],
![]() $\mathbb {FA}(\mathcal {S}^{n})\not \vdash \mathrm {Con}(\mathbb {FA}(\mathcal {S}^{n}))$
(i.e., Gödel second incompleteness for
$\mathbb {FA}(\mathcal {S}^{n})\not \vdash \mathrm {Con}(\mathbb {FA}(\mathcal {S}^{n}))$
(i.e., Gödel second incompleteness for
![]() $\mathbb {FA}(\mathcal {S}^{n})$
) and
$\mathbb {FA}(\mathcal {S}^{n})$
) and
![]() $\mathbb {FA}(\mathcal {S}^{n+1})\vdash \mathrm {Con}(\mathbb {FA}(\mathcal {S}^{n}))$
will be shown, which yield the inequivalences
$\mathbb {FA}(\mathcal {S}^{n+1})\vdash \mathrm {Con}(\mathbb {FA}(\mathcal {S}^{n}))$
will be shown, which yield the inequivalences
![]() ${\lneq }_{\mathfrak {L}(\mathcal {S}^n)}$
on the first line of the table above. Here
${\lneq }_{\mathfrak {L}(\mathcal {S}^n)}$
on the first line of the table above. Here
![]() $\mathrm {Con}(\mathbb {FA}(\mathcal {S}^{n}))$
is the Gödel formula (rather than Gödel sentence) asserting the consistency of
$\mathrm {Con}(\mathbb {FA}(\mathcal {S}^{n}))$
is the Gödel formula (rather than Gödel sentence) asserting the consistency of
![]() $\mathbb {FA}(\mathcal {S}^{n})$
with a free variable intended to vary over (Gödel codes of) proofs. Note that, for
$\mathbb {FA}(\mathcal {S}^{n})$
with a free variable intended to vary over (Gödel codes of) proofs. Note that, for
![]() $n\,{\geq }\,3$
, these easily follow from the first-order Gödel second incompleteness theorem and
$n\,{\geq }\,3$
, these easily follow from the first-order Gödel second incompleteness theorem and
![]() since partial cut elimination yields both the
since partial cut elimination yields both the
![]() $\mathfrak {L}(\mathcal {S}^n)$
equivalence and the equiconsistency between
$\mathfrak {L}(\mathcal {S}^n)$
equivalence and the equiconsistency between
![]() and
and
![]() $\mathbb {FA}(\mathcal {S}^{n})$
.
$\mathbb {FA}(\mathcal {S}^{n})$
.
Traditionally, the strengths of truth theories over Peano Arithmetic
![]() $\mathbf {PA}$
have also been measured by the notion of proof-theoretic ordinal. While this notion is usually defined for theories over
$\mathbf {PA}$
have also been measured by the notion of proof-theoretic ordinal. While this notion is usually defined for theories over
![]() $\mathbf {PA}$
, it can be extended somehow naturally to weaker ones but over
$\mathbf {PA}$
, it can be extended somehow naturally to weaker ones but over
![]() $\mathbf {I}\boldsymbol {\Sigma }_1$
(see the first author’s recent surveys [Reference Sato18, Reference Sato20]). Although there seems to be no standard way to extend the notion further below, one of plausible approaches is by provable total functions (e.g.,
$\mathbf {I}\boldsymbol {\Sigma }_1$
(see the first author’s recent surveys [Reference Sato18, Reference Sato20]). Although there seems to be no standard way to extend the notion further below, one of plausible approaches is by provable total functions (e.g.,
![]() $|\mathbf {T}|_{\mathrm {prt}}$
and
$|\mathbf {T}|_{\mathrm {prt}}$
and
![]() $|\mathbf {T}|_{\mathrm {Har}}$
in the notation of [Reference Sato18]), by which the proof-theoretic ordinal (in the accordingly extended sense) of
$|\mathbf {T}|_{\mathrm {Har}}$
in the notation of [Reference Sato18]), by which the proof-theoretic ordinal (in the accordingly extended sense) of
![]() $\mathbb {FA}(\mathcal {S}^n)$
would be
$\mathbb {FA}(\mathcal {S}^n)$
would be
![]() $\omega ^{n+m}$
or
$\omega ^{n+m}$
or
![]() $\omega ^{n-m}$
for large enough n (cf. [Reference Sato18, Section 10]), for some uniform constant m depending on the precise formulation.
$\omega ^{n-m}$
for large enough n (cf. [Reference Sato18, Section 10]), for some uniform constant m depending on the precise formulation.
1.3 Side results on finitist inductive definitions
As technical intermediate steps toward our main results, we will obtain several results on variants of inductive definition of finitist or
![]() positive operators, in a manner comparable with those of arithmetical positive operators, on which characterizations of the proof-theoretic strengths of
positive operators, in a manner comparable with those of arithmetical positive operators, on which characterizations of the proof-theoretic strengths of
![]() $\mathbf {KF}[\![\mathbf {PA}]\!]$
and
$\mathbf {KF}[\![\mathbf {PA}]\!]$
and
![]() $\mathbf {KFB}[\![\mathbf {PA}]\!]$
rely, and with those of set-theoretic positive operators from [Reference Sato16, Reference Sato17], on which the analysis by Fujimoto [Reference Fujimoto6, Reference Fujimoto7] relies. Correspondingly to the previous table, we can compare them as in the next table, where
$\mathbf {KFB}[\![\mathbf {PA}]\!]$
rely, and with those of set-theoretic positive operators from [Reference Sato16, Reference Sato17], on which the analysis by Fujimoto [Reference Fujimoto6, Reference Fujimoto7] relies. Correspondingly to the previous table, we can compare them as in the next table, where
![]() $n\,{\geq }\,3$
. Moreover, full finitist inductive definition
$n\,{\geq }\,3$
. Moreover, full finitist inductive definition
![]() $\mathbb {ID}_1(\mathcal {S}^{n})$
will turn out to be
$\mathbb {ID}_1(\mathcal {S}^{n})$
will turn out to be
![]() $\mathfrak {L}(\mathcal {S}^{n})$
equivalent to
$\mathfrak {L}(\mathcal {S}^{n})$
equivalent to
![]() $\mathbb {PRA}$
and hence to
$\mathbb {PRA}$
and hence to
![]() $\mathbf {I}\boldsymbol {\Sigma }_1$
.
$\mathbf {I}\boldsymbol {\Sigma }_1$
.

In view of
![]() $\mathbf {WKL}_0^*(\mathcal {S}^{n}) \,{=}_{\mathfrak {L}(\mathcal {S}^n)} \mathbb {FA}(\mathcal {S}^{n})$
, a variant of famous Parson’s theorem,
$\mathbf {WKL}_0^*(\mathcal {S}^{n}) \,{=}_{\mathfrak {L}(\mathcal {S}^n)} \mathbb {FA}(\mathcal {S}^{n})$
, a variant of famous Parson’s theorem,
![]() $\mathbb {FA}(\mathcal {S}^{n}) \,{=}_{\mathfrak {L}(\mathcal {S}^{n})} \,\widehat {\mathbb {ID}}_1(\mathcal {S}^{n})$
will follow from
$\mathbb {FA}(\mathcal {S}^{n}) \,{=}_{\mathfrak {L}(\mathcal {S}^{n})} \,\widehat {\mathbb {ID}}_1(\mathcal {S}^{n})$
will follow from
Here
asserts the existence of (not necessarily least) fixed point for any
positive operator, and so the latter equivalence is the superscript-0 analogue of
due to Avigad [Reference Avigad2]. In the first author’s recent paper [Reference Sato19], he has introduced the schema of strengthened inductive dichotomy
![]() $(\mathcal {C}\mathsf {-SIDic}$
), another weak variant of inductive definition, and he proved
$(\mathcal {C}\mathsf {-SIDic}$
), another weak variant of inductive definition, and he proved
. The superscript-0 analogues of this equivalence and famous
, where
![]() $(\mathcal {C}\mathsf {-SLFP})$
asserts the existence of stage comparison (cf. [Reference Sato17, Reference Sato19]), are proved in [Reference Sato21]. These reverse-mathematical results can be summarized as in the following table, where we omit “
$(\mathcal {C}\mathsf {-SLFP})$
asserts the existence of stage comparison (cf. [Reference Sato17, Reference Sato19]), are proved in [Reference Sato21]. These reverse-mathematical results can be summarized as in the following table, where we omit “
![]() $\mathbf {RCA}_0^*(\mathcal {S}^{n})\,{+}$
” as usual.
$\mathbf {RCA}_0^*(\mathcal {S}^{n})\,{+}$
” as usual.

1.4 Outline and prerequisites
Section 2 introduces finitist theories of arithmetic over which we will formulate truth theories and shows some fundamental results. Section 3 presents our way of coding syntax, and core truth theories
![]() $\mathbb {FET}(\mathcal {S}^n)$
with lower bounds. Section 4 introduces our target theories, i.e., various finitist theories of truth, and shows basic results on them. Section 5 shows the interrelations among these finitist truth theories. Section 6 gives upper bounds, by finitist fixed-point theories
$\mathbb {FET}(\mathcal {S}^n)$
with lower bounds. Section 4 introduces our target theories, i.e., various finitist theories of truth, and shows basic results on them. Section 5 shows the interrelations among these finitist truth theories. Section 6 gives upper bounds, by finitist fixed-point theories
![]() $\widehat {\mathbb {ID}}(\mathcal {S}^{n+1})$
, whose upper bounds are given in Section 7 by known techniques from second-order arithmetic. Section 8 investigates briefly the groundedness of truth. The proof of
$\widehat {\mathbb {ID}}(\mathcal {S}^{n+1})$
, whose upper bounds are given in Section 7 by known techniques from second-order arithmetic. Section 8 investigates briefly the groundedness of truth. The proof of
![]() $\mathbb {FFS}(\mathcal {S}^{n}) \,{\leq }_{\mathfrak {L}(\mathcal {S}^n)}\, \mathbb {FRT}_{<\omega }(\mathcal {S}^{n}) \,{\leq }_{\mathfrak {L}(\mathcal {S}^n)}\, \mathbb {FKF}(\mathcal {S}^{n}) \,{\leq }_{\mathfrak {L}(\mathcal {S}^n)}\, \widehat {\mathbb {ID}}(\mathcal {S}^{n+1})$
in Sections 5 and 6 should be familiar to axiomatic-truth-theorists, who may proceed directly to the reduction of
$\mathbb {FFS}(\mathcal {S}^{n}) \,{\leq }_{\mathfrak {L}(\mathcal {S}^n)}\, \mathbb {FRT}_{<\omega }(\mathcal {S}^{n}) \,{\leq }_{\mathfrak {L}(\mathcal {S}^n)}\, \mathbb {FKF}(\mathcal {S}^{n}) \,{\leq }_{\mathfrak {L}(\mathcal {S}^n)}\, \widehat {\mathbb {ID}}(\mathcal {S}^{n+1})$
in Sections 5 and 6 should be familiar to axiomatic-truth-theorists, who may proceed directly to the reduction of
![]() $\widehat {\mathbb {ID}}(\mathcal {S}^{n+1})$
in Section 7, but even for whom Sections 5 and 6 may shed light on the new aspects of the results.
$\widehat {\mathbb {ID}}(\mathcal {S}^{n+1})$
in Section 7, but even for whom Sections 5 and 6 may shed light on the new aspects of the results.
Readers are supposed to be familiar with truth theories over first-order arithmetic (studied, e.g., in [Reference Halbach11, Reference Horsten12]) and with coding of syntax in weak arithmetic (explained, e.g., in [Reference Buss4, Reference Hájek and Pudlák9]). Moreover, familiarity with second-order arithmetic (studied in, e.g., [Reference Simpson25]) and with (partial) cut elimination simplifies the reading of Sections 7 and 7.3 respectively. It is also essential to know the difference between admissibility and derivability of inference rules.
2 Finitist arithmetic
While the main topic of this paper is truth theory, we devote one section to the explanation of finitist arithmetic, the reason being that the study of arithmetic in finitist languages is not standard in the field.
2.1 Definitions
A finitist language is determined by its vocabulary. Besides sets of constant, function, and relation symbols, we also specify a set of designated binary (or n-ary, for
![]() $n\,{\geq }\,2$
) relation symbols with distinct relata. For all the examples treated in the present article, the vocabulary contains, at least, two constants
$n\,{\geq }\,2$
) relation symbols with distinct relata. For all the examples treated in the present article, the vocabulary contains, at least, two constants
![]() $0$
and
$0$
and
![]() $1$
, two binary function symbols
$1$
, two binary function symbols
![]() $+$
and
$+$
and
![]() $\cdot $
, and two binary relation symbols
$\cdot $
, and two binary relation symbols
![]() $=$
and
$=$
and
![]() $<$
, where only
$<$
, where only
![]() $<$
is designated with the first relatum being distinct. The well formed formulae of a finitist language are defined in the same way as those of a first-order language, except that the clauses for (unbounded) quantifiers are replaced by those for quantifiers bounded by designated relation symbols. In our case, the clauses are:
$<$
is designated with the first relatum being distinct. The well formed formulae of a finitist language are defined in the same way as those of a first-order language, except that the clauses for (unbounded) quantifiers are replaced by those for quantifiers bounded by designated relation symbols. In our case, the clauses are:
-
• if
 $A(x)$
is a well formed formula and t is a term in which x does not occur, then both
$A(x)$
is a well formed formula and t is a term in which x does not occur, then both
 $(\forall x\,{<}\,t)A(x)$
and
$(\forall x\,{<}\,t)A(x)$
and
 $(\exists x\,{<}\,t)A(x)$
are well formed formulae.
$(\exists x\,{<}\,t)A(x)$
are well formed formulae.
The term “formula” often refers to “well formed formula”. As we consider only theories over classical logic, the negation symbol
![]() $\neg $
applies only to atomic formulae, and we define the negation
$\neg $
applies only to atomic formulae, and we define the negation
![]() $\sim $
of arbitrary formulae as the usual syntactical operation according to De Morgan’s law. Accordingly,
$\sim $
of arbitrary formulae as the usual syntactical operation according to De Morgan’s law. Accordingly,
![]() $A\,{\to }\,B$
stands for
$A\,{\to }\,B$
stands for
![]() ${\sim }A\,{\lor }\,B$
.
${\sim }A\,{\lor }\,B$
.
The logical axioms and rules are the same as those of first-order logic, except that the axioms and rules for bounded quantifiers are as follows, where x is an eigenvariable, namely, x must not occur in B.

Because of our treatment of
![]() $\to $
, these rules are equivalent to the following.
$\to $
, these rules are equivalent to the following.

Furthermore, though in many cases it is admissible, we consider the following instantiating rule as a logical rule, namely, we assume that all finitist theories are closed under the following rule, where x is an eigenvariable.

It is particularly important to keep this rule in mind when we define theories not only with non-logical axioms but also with non-logical rules.
As we cannot form universal closure, we define partial conservation in terms of provable formulae, not only provable sentences.
Definition 2.1 (Partial conservation,
 $\leq _{\mathfrak {C}}$
)
$\leq _{\mathfrak {C}}$
)
For theories
![]() $\mathbb {T}_1$
and
$\mathbb {T}_1$
and
![]() $\mathbb {T}_2$
and a class
$\mathbb {T}_2$
and a class
![]() $\mathfrak {C}$
of formulae from the intersection of the languages of
$\mathfrak {C}$
of formulae from the intersection of the languages of
![]() $\mathbb {T}_1$
and
$\mathbb {T}_1$
and
![]() $\mathbb {T}_2$
, we say that
$\mathbb {T}_2$
, we say that
![]() $\mathbb {T}_1$
is
$\mathbb {T}_1$
is
![]() $\mathfrak {C}$
conservative over
$\mathfrak {C}$
conservative over
![]() $\mathbb {T}_2$
(in symbols,
$\mathbb {T}_2$
(in symbols,
![]() $\mathbb {T}_1\, {\leq }_{\mathfrak {C}}\,\mathbb {T}_2$
) if
$\mathbb {T}_1\, {\leq }_{\mathfrak {C}}\,\mathbb {T}_2$
) if
![]() $\mathbb {T}_1\vdash A$
implies
$\mathbb {T}_1\vdash A$
implies
![]() $\mathbb {T}_2\vdash A$
for any
$\mathbb {T}_2\vdash A$
for any
![]() $\mathfrak {C}$
formula A. Moreover,
$\mathfrak {C}$
formula A. Moreover,
![]() $\mathbb {T}_1\, {=}_{\mathfrak {C}}\,\mathbb {T}_2$
stands for
$\mathbb {T}_1\, {=}_{\mathfrak {C}}\,\mathbb {T}_2$
stands for
![]() $\mathbb {T}_1\, {\leq }_{\mathfrak {C}}\,\mathbb {T}_2$
and
$\mathbb {T}_1\, {\leq }_{\mathfrak {C}}\,\mathbb {T}_2$
and
![]() $\mathbb {T}_2\, {\leq }_{\mathfrak {C}}\,\mathbb {T}_1$
.
$\mathbb {T}_2\, {\leq }_{\mathfrak {C}}\,\mathbb {T}_1$
.
All the finitist theories in this article are formulated in extensions of the finitist language of arithmetic. As already discussed in the Introduction, it is important which function symbols are included.
Definition 2.2 (
 $\mathfrak {L}(\mathcal {S}^n)$
,
$\mathfrak {L}(\mathcal {S}^n)$
,
 $\mathbb {FA}(\mathcal {S}^n)$
)
$\mathbb {FA}(\mathcal {S}^n)$
)
Let
![]() $\mathfrak {L}(\mathcal {S}^n)$
be the finitist language determined by the following vocabulary: two constants
$\mathfrak {L}(\mathcal {S}^n)$
be the finitist language determined by the following vocabulary: two constants
![]() $0$
and
$0$
and
![]() $1$
; three binary function symbols
$1$
; three binary function symbols
![]() $+$
,
$+$
,
![]() $\cdot $
, and
$\cdot $
, and
![]() $\#$
; unary function symbols
$\#$
; unary function symbols
![]() $\gamma _3,\ldots , \gamma _{n}$
if
$\gamma _3,\ldots , \gamma _{n}$
if
![]() $n\,{\geq }\,3$
; and two binary relation symbols
$n\,{\geq }\,3$
; and two binary relation symbols
![]() $=$
and
$=$
and
![]() $<$
. By an
$<$
. By an
![]() $\mathcal {S}^n$
term, we mean an
$\mathcal {S}^n$
term, we mean an
![]() $\mathfrak {L}(\mathcal {S}^n)$
term.
$\mathfrak {L}(\mathcal {S}^n)$
term.
Let
![]() $\mathbb {FA}(\mathcal {S}^n)$
be the
$\mathbb {FA}(\mathcal {S}^n)$
be the
![]() $\mathfrak {L}(\mathcal {S}^n)$
theory generated by (the equality axioms and) the following non-logical axioms.
$\mathfrak {L}(\mathcal {S}^n)$
theory generated by (the equality axioms and) the following non-logical axioms.
-
Axioms of discrete order:
 $\neg (x\,{<}\,x)$
;
$\neg (x\,{<}\,x)$
;
 $(x\,{<}\,y\,{\land }\,y\,{<}\,z) \,{\to }\,x\,{<}\,z$
;
$(x\,{<}\,y\,{\land }\,y\,{<}\,z) \,{\to }\,x\,{<}\,z$
;
 $x\,{<}\,x{+}1$
; and
$x\,{<}\,x{+}1$
; and
 $x\,{<}\,y\,{\to }\,(x{+}1\,{=}\,y\,{\lor }\, x{+}1\,{<}\,y)$
.
$x\,{<}\,y\,{\to }\,(x{+}1\,{=}\,y\,{\lor }\, x{+}1\,{<}\,y)$
. -
Axioms of addition and multiplication:
 $x{+}0\,{=}\,x$
;
$x{+}0\,{=}\,x$
;
 $x{+}(y{+}1)\,{=}\,(x{+}y){+}1$
;
$x{+}(y{+}1)\,{=}\,(x{+}y){+}1$
;
 $x{\cdot }0\,{=}\,0$
; and
$x{\cdot }0\,{=}\,0$
; and
 $x{\cdot }(y{+}1)\,{=}\,(x{\cdot }y){+}x$
.
$x{\cdot }(y{+}1)\,{=}\,(x{\cdot }y){+}x$
. -
Axioms of smash function
 $\#$
:
$\#$
:
 $x\,{\#}\,0\,{=}\,1$
;
$x\,{\#}\,0\,{=}\,1$
;
 $x\,{<}\,x\,{\#}\,1$
;
$x\,{<}\,x\,{\#}\,1$
;
 $x\,{\#}\,1\,{<}\,2{\cdot }(x{+}1)$
;
$x\,{\#}\,1\,{<}\,2{\cdot }(x{+}1)$
;
 $x\,{\#}\,(2{\cdot } y{+}2)\,{=}\, x\,{\#}\,(2{\cdot } y{+}3)\,{=}\, (x\,{\#}\,(y{+}1))\,{\cdot }\,(x\,{\#}\,1)$
; and
$x\,{\#}\,(2{\cdot } y{+}2)\,{=}\, x\,{\#}\,(2{\cdot } y{+}3)\,{=}\, (x\,{\#}\,(y{+}1))\,{\cdot }\,(x\,{\#}\,1)$
; and
 $\mathrm {Pow2}(x\,{\#}\,y)$
, where
$\mathrm {Pow2}(x\,{\#}\,y)$
, where
 $\mathrm {Pow2}(z)\,{\equiv }\, \neg (z\,{=}\,0)\,{\land }\, (\forall u,v\,{<}\,z) (1\,{<}\,u\,{\land }\,u{\cdot }v\,{=}\,z \,{\to }\,(\exists w\,{<}\,u)(u\,{=}\,2{\cdot }w))$
and
$\mathrm {Pow2}(z)\,{\equiv }\, \neg (z\,{=}\,0)\,{\land }\, (\forall u,v\,{<}\,z) (1\,{<}\,u\,{\land }\,u{\cdot }v\,{=}\,z \,{\to }\,(\exists w\,{<}\,u)(u\,{=}\,2{\cdot }w))$
and
 $2\,{:\equiv }\,1{+}1$
.
$2\,{:\equiv }\,1{+}1$
. -
Axioms of
 $\gamma _{k+1}$
:
$\gamma _{k+1}$
:
 $\gamma _{k+1}(0)\,{=}\,1$
; and
$\gamma _{k+1}(0)\,{=}\,1$
; and
 $\gamma _{k+1}(x{+}1)\,{=}\, \gamma _k(\gamma _{k+1}(x))$
, if
$\gamma _{k+1}(x{+}1)\,{=}\, \gamma _k(\gamma _{k+1}(x))$
, if
 $n\,{\geq }\,k{+}1\,{\geq }\,3$
, where
$n\,{\geq }\,k{+}1\,{\geq }\,3$
, where
 $\gamma _2(x)\,{=}\,2\cdot x$
.
$\gamma _2(x)\,{=}\,2\cdot x$
. -
Axiom schema of induction:
 $A(0)\,{\land }\,(\forall y\,{<}\,x) (A(y)\,{\to }\,A(y{+}1))\,{\to }\,A(x)$
for any
$A(0)\,{\land }\,(\forall y\,{<}\,x) (A(y)\,{\to }\,A(y{+}1))\,{\to }\,A(x)$
for any
 $\mathfrak {L}(\mathcal {S}^n)$
formula A.
$\mathfrak {L}(\mathcal {S}^n)$
formula A.
Remark 2.3. In the cases of
![]() $\mathbb {FA}(\mathcal {S}^n)$
and extensions, we can restrict the rule (Inst) only to
$\mathbb {FA}(\mathcal {S}^n)$
and extensions, we can restrict the rule (Inst) only to
![]() $x\,{<}\,x{+}1$
: from
$x\,{<}\,x{+}1$
: from
![]() $A(x)$
we can infer
$A(x)$
we can infer
![]() $x\,{<}\,t{+}1\,{\to }\,A(x)$
and so
$x\,{<}\,t{+}1\,{\to }\,A(x)$
and so
![]() $(\forall x\,{<}\,t{+}1)A(x)$
, which yields
$(\forall x\,{<}\,t{+}1)A(x)$
, which yields
![]() $t\,{<}\,t{+}1 \,{\to }\,A(t)$
.
$t\,{<}\,t{+}1 \,{\to }\,A(t)$
.
Remark 2.4. Any
![]() $\mathfrak {L}(\mathcal {S}^n)$
term t is monotone in the sense of
$\mathfrak {L}(\mathcal {S}^n)$
term t is monotone in the sense of
![]() $x\,{\leq }\,y\,{\to }\,t(x)\,{\leq }\,t(y)$
. Thus, for any
$x\,{\leq }\,y\,{\to }\,t(x)\,{\leq }\,t(y)$
. Thus, for any
![]() $\mathfrak {L}(\mathcal {S}^n)$
formula A, we can define an
$\mathfrak {L}(\mathcal {S}^n)$
formula A, we can define an
![]() $\mathfrak {L}(\mathcal {S}^n)$
term
$\mathfrak {L}(\mathcal {S}^n)$
term
![]() $\mathrm {bd}_A$
, whose variables all occur freely in A, that bounds the bounding terms of all quantifiers hereditarily in A: if A is atomic,
$\mathrm {bd}_A$
, whose variables all occur freely in A, that bounds the bounding terms of all quantifiers hereditarily in A: if A is atomic,
![]() $\mathrm {bd}_A$
is the summation of all the terms occurring in A;
$\mathrm {bd}_A$
is the summation of all the terms occurring in A;
![]() $\mathrm {bd}_{A\land B} \,{\equiv }\,\mathrm {bd}_{A\lor B} \,{:\equiv }\,\mathrm {bd}_A\,{+}\,\mathrm {bd}_B$
; and
$\mathrm {bd}_{A\land B} \,{\equiv }\,\mathrm {bd}_{A\lor B} \,{:\equiv }\,\mathrm {bd}_A\,{+}\,\mathrm {bd}_B$
; and
![]() $\mathrm {bd}_{(\forall x < t)A(x)} \,{\equiv }\,\mathrm {bd}_{(\exists x < t)A(x)} \,{:\equiv }\,\mathrm {bd}_{A(x)}(t)$
.
$\mathrm {bd}_{(\forall x < t)A(x)} \,{\equiv }\,\mathrm {bd}_{(\exists x < t)A(x)} \,{:\equiv }\,\mathrm {bd}_{A(x)}(t)$
.
One significant feature of arithmetic with
![]() $+$
and
$+$
and
![]() $\cdot $
is that it allows us to encode any finite sequence of numbers by a single number. While various ways to achieve this are known, we take the one from [Reference Hájek and Pudlák9, Chapter V], because it seems to be one of the most efficient ways in the literature. It starts with encoding finite sets of numbers. The following lemma is proved in [Reference Hájek and Pudlák9, Chapter V.3.b] or [Reference Walker29, Section 3.2] and shows that
$\cdot $
is that it allows us to encode any finite sequence of numbers by a single number. While various ways to achieve this are known, we take the one from [Reference Hájek and Pudlák9, Chapter V], because it seems to be one of the most efficient ways in the literature. It starts with encoding finite sets of numbers. The following lemma is proved in [Reference Hájek and Pudlák9, Chapter V.3.b] or [Reference Walker29, Section 3.2] and shows that
![]() $1$
encodes the empty set and that any finite set can be extended with one new element.
$1$
encodes the empty set and that any finite set can be extended with one new element.
Lemma 2.5. There are
![]() $\mathfrak {L}(\mathcal {S}^2)$
formulae
$\mathfrak {L}(\mathcal {S}^2)$
formulae
![]() $\mathrm {Seq}$
and
$\mathrm {Seq}$
and
![]() $\in $
such that
$\in $
such that
 $$ \begin{align*} \mathbb{FA}(\mathcal{S}^2) \vdash \mathrm{Seq}(u)\,{\to}\, (\exists v\,{<}\,9{\cdot}u{\cdot}(x{+}1)^2{+}1) \begin{pmatrix} u\,{\leq}\,v\,{\land}\, \mathrm{Seq}(v)\,{\land}\\ (\forall y\,{<}\,v)(y\,{\in}\,v\, {\leftrightarrow}\,y\,{\in}\,u\,{\lor}\,y\,{=}\,x)) \end{pmatrix} \end{align*} $$
$$ \begin{align*} \mathbb{FA}(\mathcal{S}^2) \vdash \mathrm{Seq}(u)\,{\to}\, (\exists v\,{<}\,9{\cdot}u{\cdot}(x{+}1)^2{+}1) \begin{pmatrix} u\,{\leq}\,v\,{\land}\, \mathrm{Seq}(v)\,{\land}\\ (\forall y\,{<}\,v)(y\,{\in}\,v\, {\leftrightarrow}\,y\,{\in}\,u\,{\lor}\,y\,{=}\,x)) \end{pmatrix} \end{align*} $$
with
![]() $\mathbb {FA}(\mathcal {S}^2) \vdash (x\,{\in }\,u\,{\to }\,x\,{<}\,u)\,{\land }\, \mathrm {Seq}(1)\,{\land }\, \neg (z\,{\in }\,1)$
.
$\mathbb {FA}(\mathcal {S}^2) \vdash (x\,{\in }\,u\,{\to }\,x\,{<}\,u)\,{\land }\, \mathrm {Seq}(1)\,{\land }\, \neg (z\,{\in }\,1)$
.
2.2 Extension by definition and bounded
 $\mu $
algebra
$\mu $
algebra
In the language
![]() $\mathfrak {L}(\mathcal {S}^n)$
of the finitist arithmetic
$\mathfrak {L}(\mathcal {S}^n)$
of the finitist arithmetic
![]() $\mathbb {FA}(\mathcal {S}^n)$
, we only have function symbols
$\mathbb {FA}(\mathcal {S}^n)$
, we only have function symbols
![]() $0,1,{+},{\cdot },{\#}$
,
$0,1,{+},{\cdot },{\#}$
,
![]() $\gamma _3,\ldots ,\gamma _n$
. However, similarly as in first-order arithmetic, we may also use additional function symbols in
$\gamma _3,\ldots ,\gamma _n$
. However, similarly as in first-order arithmetic, we may also use additional function symbols in
![]() $\mathfrak {L}(\mathcal {S}^n)$
formulae and treat them as mere abbreviations. What we have to keep in mind is that we need a term (in the official language) which bounds the value of such an additional function symbol.
$\mathfrak {L}(\mathcal {S}^n)$
formulae and treat them as mere abbreviations. What we have to keep in mind is that we need a term (in the official language) which bounds the value of such an additional function symbol.
Definition 2.6 (Bounded definable functions)
Let
![]() $\mathbb {T}$
expand
$\mathbb {T}$
expand
![]() $\mathbb {FA}(\mathcal {S}^n)$
. A pair of an
$\mathbb {FA}(\mathcal {S}^n)$
. A pair of an
![]() $\mathcal {S}^n$
term
$\mathcal {S}^n$
term
![]() $t(x_0,\ldots ,x_{k-1})$
and an
$t(x_0,\ldots ,x_{k-1})$
and an
![]() $\mathfrak {L}(\mathcal {S}^n)$
formula
$\mathfrak {L}(\mathcal {S}^n)$
formula
![]() $A(x_0,\ldots ,x_{k-1},y)$
, both without free variables other than displayed, is said to define a total k-ary function in
$A(x_0,\ldots ,x_{k-1},y)$
, both without free variables other than displayed, is said to define a total k-ary function in
![]() $\mathbb {T}$
if
$\mathbb {T}$
if
where
![]() $(\exists !y\,{<}\,t)A(y)$
is short for
$(\exists !y\,{<}\,t)A(y)$
is short for
![]() $(\exists y\,{<}\,t)(A(y) \,{\land }\,(\forall z\,{<}\,t)(A(z)\,{\to }\,z\,{=}\,y))$
.
$(\exists y\,{<}\,t)(A(y) \,{\land }\,(\forall z\,{<}\,t)(A(z)\,{\to }\,z\,{=}\,y))$
.
We loosely say that a k-ary function f (with the implicitly intended formula
![]() $\mathrm {Gr}_f (x_0,\ldots ,x_{k-1},y)$
for its graph) is bounded definable in
$\mathrm {Gr}_f (x_0,\ldots ,x_{k-1},y)$
for its graph) is bounded definable in
![]() $\mathbb {T}$
if there is a term t (called the bounding term) such that the pair of t and
$\mathbb {T}$
if there is a term t (called the bounding term) such that the pair of t and
![]() $\mathrm {Gr}_f$
defines a total k-ary function in
$\mathrm {Gr}_f$
defines a total k-ary function in
![]() $\mathbb {T}$
.
$\mathbb {T}$
.
The first-order analogue of this notion is called bounded
![]() definability in [Reference Nemoto and Sato15, Notation 2.9
definability in [Reference Nemoto and Sato15, Notation 2.9
![]() $(1)$
].
$(1)$
].
Proposition 2.7. The following functions (with the obvious intended formulae for their graphs) are bounded definable in any extension
![]() $\mathbb {T}$
of
$\mathbb {T}$
of
![]() $\mathbb {FA}(\mathcal {S}^2)$
, so that the attached formulae are provable in
$\mathbb {FA}(\mathcal {S}^2)$
, so that the attached formulae are provable in
![]() $\mathbb {T}$
:
$\mathbb {T}$
:
-
• subtraction
 $x{-}y$
with
$x{-}y$
with
 $y\,{\leq }\,x\,{\to }\,(x{-}y){+}y\,{=}\,x$
and
$y\,{\leq }\,x\,{\to }\,(x{-}y){+}y\,{=}\,x$
and
 $y\,{>}\,x\,{\to }\,x{-}y\,{=}\,0$
;
$y\,{>}\,x\,{\to }\,x{-}y\,{=}\,0$
; -
• division
 $x/y$
with
$x/y$
with
 $0\,{<}\,y\,{\to }\, (\exists z\,{<}\,y)(x\,{=}\,(x/y){\cdot }y{+}z)$
;
$0\,{<}\,y\,{\to }\, (\exists z\,{<}\,y)(x\,{=}\,(x/y){\cdot }y{+}z)$
; -
• pairing function
 $\mathrm {pair}(x,y)$
with
$\mathrm {pair}(x,y)$
with
 $2{\cdot }\mathrm {pair}(x,y) \,{=}\,(x{+}y){\cdot }(x{+}y{+}1){+}2{\cdot }x$
;
$2{\cdot }\mathrm {pair}(x,y) \,{=}\,(x{+}y){\cdot }(x{+}y{+}1){+}2{\cdot }x$
; -
• depairing functions
 $\mathrm {dep}_0$
and
$\mathrm {dep}_0$
and
 $\mathrm {dep}_1$
with
$\mathrm {dep}_1$
with
 $\mathrm {dep}_i(\mathrm {pair}(x_0,x_1))\,{=}\,x_i$
for
$\mathrm {dep}_i(\mathrm {pair}(x_0,x_1))\,{=}\,x_i$
for
 $i\,{<}\,2$
.
$i\,{<}\,2$
.
If a function is bounded definable in
![]() $\mathbb {T}$
with a bounding term t, then the use of an additional function symbol f for that function can be justified as follows: a formula of form
$\mathbb {T}$
with a bounding term t, then the use of an additional function symbol f for that function can be justified as follows: a formula of form
![]() $B(f(s_0,\ldots ,s_{k-1}))$
can be rewritten as
$B(f(s_0,\ldots ,s_{k-1}))$
can be rewritten as
and by iterating this process (backward along the construction of the subterms
![]() $s_i$
’s) we can eventually obtain a formula without occurrences of f.
$s_i$
’s) we can eventually obtain a formula without occurrences of f.
Lemma 2.8. Let
![]() $\mathbb {T}$
expand
$\mathbb {T}$
expand
![]() $\mathbb {FA}(\mathcal {S}^2)$
. The class of all bounded definable functions in
$\mathbb {FA}(\mathcal {S}^2)$
. The class of all bounded definable functions in
![]() $\mathbb {T}$
is closed under composition and under bounded minimization, where the latter means that if f is
$\mathbb {T}$
is closed under composition and under bounded minimization, where the latter means that if f is
![]() $k{+}1$
-ary and bounded definable in
$k{+}1$
-ary and bounded definable in
![]() $\mathbb {T}$
then so is the
$\mathbb {T}$
then so is the
![]() $k{+}1$
-ary function g with
$k{+}1$
-ary function g with
![]() $g(x_0,\ldots ,x_{k-1},y) \,{=}\,\min \{z\,{:}\,z\,{=}\,y \,{\lor }\,f(x_0,\ldots ,x_{k-1},z)\,{=}\,0\}$
.
$g(x_0,\ldots ,x_{k-1},y) \,{=}\,\min \{z\,{:}\,z\,{=}\,y \,{\lor }\,f(x_0,\ldots ,x_{k-1},z)\,{=}\,0\}$
.
Definition 2.9 (Bounded
 $\mu $
algebra,
$\mu $
algebra,
 $\mathcal {S}^n$
)
$\mathcal {S}^n$
)
A class of numerical functions is called a bounded
![]() $\mu $
algebra if it contains constant functions, projection functions,
$\mu $
algebra if it contains constant functions, projection functions,
![]() $+$
and
$+$
and
![]() $\cdot $
, and it is closed under composition and under bounded minimization. The bounded
$\cdot $
, and it is closed under composition and under bounded minimization. The bounded
![]() $\mu $
algebra generated by a class
$\mu $
algebra generated by a class
![]() $\mathcal {F}$
of numerical functions is the smallest bounded
$\mathcal {F}$
of numerical functions is the smallest bounded
![]() $\mu $
algebra that includes
$\mu $
algebra that includes
![]() $\mathcal {F}$
. Let
$\mathcal {F}$
. Let
![]() $\mathcal {S}^n$
denote the bounded
$\mathcal {S}^n$
denote the bounded
![]() $\mu $
algebra generated by
$\mu $
algebra generated by
![]() $\{{+},{\cdot },{\#},\gamma _3,\ldots ,\gamma _n\}$
.
$\{{+},{\cdot },{\#},\gamma _3,\ldots ,\gamma _n\}$
.
Thus, for the concern of justified use of function symbols, what is important is not the class of function symbols but the bounded
![]() $\mu $
algebra generated by it. In combination with Lemma 2.8, the next lemma justifies us to call
$\mu $
algebra generated by it. In combination with Lemma 2.8, the next lemma justifies us to call
![]() $\mathbb {FA}(\mathcal {S}^n)$
the finitist arithmetic for
$\mathbb {FA}(\mathcal {S}^n)$
the finitist arithmetic for
![]() $\mathcal {S}^n$
. In what follows, however, we do not add symbols for all the functions in
$\mathcal {S}^n$
. In what follows, however, we do not add symbols for all the functions in
![]() $\mathcal {S}^n$
to
$\mathcal {S}^n$
to
![]() $\mathfrak {L}(\mathcal {S}^n)$
as full-fledged symbols, but just as abbreviations (but see also Remark 3.6). For a term s in the expanded language we can define a term t in the original such that
$\mathfrak {L}(\mathcal {S}^n)$
as full-fledged symbols, but just as abbreviations (but see also Remark 3.6). For a term s in the expanded language we can define a term t in the original such that
![]() $s\,{\leq }\,t$
, by replacing bounded definable functions with their bounding terms. We call this t the bounding term of s.
$s\,{\leq }\,t$
, by replacing bounded definable functions with their bounding terms. We call this t the bounding term of s.
Lemma 2.10. Any function that is bounded definable in an
![]() $\mathfrak {L}(\mathcal {S}^n)$
theory
$\mathfrak {L}(\mathcal {S}^n)$
theory
![]() $\mathbb {T}$
is contained in
$\mathbb {T}$
is contained in
![]() $\mathcal {S}^n$
.
$\mathcal {S}^n$
.
Proof First, by meta-induction on an
![]() $\mathfrak {L}(\mathcal {S}^n)$
formula A, we can show that the characteristic function
$\mathfrak {L}(\mathcal {S}^n)$
formula A, we can show that the characteristic function
![]() $\mathrm {char}_A$
of A is in
$\mathrm {char}_A$
of A is in
![]() $\mathcal {S}^n$
. The non-trivial case is as follows. Let
$\mathcal {S}^n$
. The non-trivial case is as follows. Let
![]() $A(x_0,\ldots ,x_{k-1})$
be
$A(x_0,\ldots ,x_{k-1})$
be
![]() $(\exists y\,{<}\,t(x_0,\ldots ,x_{k-1}))B(y,x_0,\ldots ,x_{k-1})$
. Then
$(\exists y\,{<}\,t(x_0,\ldots ,x_{k-1}))B(y,x_0,\ldots ,x_{k-1})$
. Then
 $$\begin{align*}\mathrm{char}_A(x_0,\ldots,x_{k-1}) \,{=}\,\mathrm{char}_<\left( \min\left\{z\,{:}\,\begin{matrix} z\,{=}\,t(x_0,\ldots,x_{k-1}) \,{\lor}\\ \mathrm{char}_B(z,x_0,\ldots,x_{k-1}) \end{matrix} \right\}, t(x_0,\ldots,x_{k-1})\right).\end{align*}$$
$$\begin{align*}\mathrm{char}_A(x_0,\ldots,x_{k-1}) \,{=}\,\mathrm{char}_<\left( \min\left\{z\,{:}\,\begin{matrix} z\,{=}\,t(x_0,\ldots,x_{k-1}) \,{\lor}\\ \mathrm{char}_B(z,x_0,\ldots,x_{k-1}) \end{matrix} \right\}, t(x_0,\ldots,x_{k-1})\right).\end{align*}$$
Thus, if the pair of t and A defines f, then
Now we are in a position to see the background of our somewhat strange choice of function symbols in
![]() $\mathfrak {L}(\mathcal {S}^n)$
. On the one hand, as discussed in the Introduction, the most standard way to slice the class
$\mathfrak {L}(\mathcal {S}^n)$
. On the one hand, as discussed in the Introduction, the most standard way to slice the class
![]() $\mathcal {PR}$
of primitive recursive functions is Grzegorczyk hierarchy
$\mathcal {PR}$
of primitive recursive functions is Grzegorczyk hierarchy
![]() $\mathcal {E}^n$
, and
$\mathcal {E}^n$
, and
![]() $\mathcal {E}^n$
is the bounded
$\mathcal {E}^n$
is the bounded
![]() $\mu $
algebra generated by
$\mu $
algebra generated by
![]() $\{{+},{\cdot },\gamma _3,\ldots ,\gamma _n\}$
for
$\{{+},{\cdot },\gamma _3,\ldots ,\gamma _n\}$
for
![]() $n\,{\geq }\,2$
. Here
$n\,{\geq }\,2$
. Here
![]() $\cdot $
is the iteration of
$\cdot $
is the iteration of
![]() $+$
,
$+$
,
![]() $\gamma _3$
is that of
$\gamma _3$
is that of
![]() $\cdot $
, and so on, where
$\cdot $
, and so on, where
![]() $\gamma _3,\ldots ,\gamma _n$
could also be replaced by their binary counterparts
$\gamma _3,\ldots ,\gamma _n$
could also be replaced by their binary counterparts
![]() $x^y,\ldots $
as they generate the same bounded
$x^y,\ldots $
as they generate the same bounded
![]() $\mu $
algebras. On the other hand, in our truth-theoretic study we use arithmetic primarily for the coding of syntax, and in most efficient codings the required recursions and inductions are not along sequence codes (numbers denoting strings), but rather along the length of sequences (the lengths of strings). And, indeed,
$\mu $
algebras. On the other hand, in our truth-theoretic study we use arithmetic primarily for the coding of syntax, and in most efficient codings the required recursions and inductions are not along sequence codes (numbers denoting strings), but rather along the length of sequences (the lengths of strings). And, indeed,
![]() $\mathcal {S}^n$
was defined in accordance with the requirements for such length-recursions and -inductions. It can alternatively be conceived as the bounded
$\mathcal {S}^n$
was defined in accordance with the requirements for such length-recursions and -inductions. It can alternatively be conceived as the bounded
![]() $\mu $
algebra generated by
$\mu $
algebra generated by
![]() $\{(x_0,\ldots ,x_{k-1}) \mapsto 2^{f(|x_0|,\ldots ,|x_{k-1}|)}\,{:}\, f\,{\in }\,\mathcal {E}^n\}$
, which we call smashed Grzegorczyk hierarchy. From this perspective, we naturally let
$\{(x_0,\ldots ,x_{k-1}) \mapsto 2^{f(|x_0|,\ldots ,|x_{k-1}|)}\,{:}\, f\,{\in }\,\mathcal {E}^n\}$
, which we call smashed Grzegorczyk hierarchy. From this perspective, we naturally let
![]() $\mathcal {S}^1$
be generated by
$\mathcal {S}^1$
be generated by
![]() $\{{+},{\cdot }\,\}$
, i.e.,
$\{{+},{\cdot }\,\}$
, i.e.,
![]() $\mathcal {E}^2$
.
$\mathcal {E}^2$
.
A careful reader might consider that, from this perspective, it would be more natural to replace the number-induction
![]() $A(0)\,{\land }\,(\forall y\,{<}\,x)(A(y)\,{\to }\, A(y{+}1))\,{\to }\,A(x)$
by the length-induction
$A(0)\,{\land }\,(\forall y\,{<}\,x)(A(y)\,{\to }\, A(y{+}1))\,{\to }\,A(x)$
by the length-induction
This is right, but, as far as we accept the schemata unrestrictedly for all formulae, they are equivalent. For the direction from length-induction to number-induction, take
![]() $B(y)\,{:\equiv }\, (\forall z\,{<}\,x{-}y)(A(z)\,{\to }\,A(z{+}y))$
and it suffices to see
$B(y)\,{:\equiv }\, (\forall z\,{<}\,x{-}y)(A(z)\,{\to }\,A(z{+}y))$
and it suffices to see
assuming
![]() $(\forall y\,{<}\,x)(A(y)\,{\to }\, A(y{+}1))$
. Let
$(\forall y\,{<}\,x)(A(y)\,{\to }\, A(y{+}1))$
. Let
![]() $y\,{<}\,x$
and
$y\,{<}\,x$
and
![]() $B(y)$
. For
$B(y)$
. For
![]() $z\,{<}\,x{-}2{\cdot }y$
, since
$z\,{<}\,x{-}2{\cdot }y$
, since
![]() $z\,{+}\,y\,{<}\,x{-}y$
, by
$z\,{+}\,y\,{<}\,x{-}y$
, by
![]() $B(y)$
we have
$B(y)$
we have
![]() $A(z)\,{\to }\,A(z{+}y)$
and
$A(z)\,{\to }\,A(z{+}y)$
and
![]() $A(z{+}y)\,{\to }\,A(z{+}2{\cdot }y)$
, which imply
$A(z{+}y)\,{\to }\,A(z{+}2{\cdot }y)$
, which imply
![]() $A(z)\,{\to }\,A(z{+}2{\cdot }y)$
. For
$A(z)\,{\to }\,A(z{+}2{\cdot }y)$
. For
![]() $z\,{<}\,x{-}2{\cdot }y{-}1$
we have
$z\,{<}\,x{-}2{\cdot }y{-}1$
we have
![]() $A(z{+}2{\cdot }y)\,{\to }\,A(z{+}2{\cdot }y{+}1)$
and similarly
$A(z{+}2{\cdot }y)\,{\to }\,A(z{+}2{\cdot }y{+}1)$
and similarly
![]() $A(z)\,{\to }\,A(z{+}2{\cdot }y{+}1)$
. Let us mention that this proof requires an increase of the complexity of formula: known as the implications from
$A(z)\,{\to }\,A(z{+}2{\cdot }y{+}1)$
. Let us mention that this proof requires an increase of the complexity of formula: known as the implications from
![]() $\Sigma ^b_{n+1}\mathsf {-PIND}$
to
$\Sigma ^b_{n+1}\mathsf {-PIND}$
to
![]() $\Sigma ^b_{n}\mathsf {-IND}$
, and from
$\Sigma ^b_{n}\mathsf {-IND}$
, and from
![]() $\Sigma ^b_{n}\mathsf {-IND}$
to
$\Sigma ^b_{n}\mathsf {-IND}$
to
![]() $\Sigma ^b_{n}\mathsf {-PIND}$
for
$\Sigma ^b_{n}\mathsf {-PIND}$
for
![]() $n\,{\geq }\,1$
in the notation of [Reference Buss4].
$n\,{\geq }\,1$
in the notation of [Reference Buss4].
2.3 Bounded recursion
So far, the smash function
![]() $\#$
played no particular role. The significance of
$\#$
played no particular role. The significance of
![]() $\#$
is that, if it is included among the generators of a bounded
$\#$
is that, if it is included among the generators of a bounded
![]() $\mu $
algebra, then the algebra is closed under some form of recursion.
$\mu $
algebra, then the algebra is closed under some form of recursion.
Theorem 2.11 (Bounded binary recursion)
Let
![]() $\mathbb {T}$
expand
$\mathbb {T}$
expand
![]() $\mathbb {FA}(\mathcal {S}^2)$
, let
$\mathbb {FA}(\mathcal {S}^2)$
, let
![]() $h,g,p$
be bounded definable functions in
$h,g,p$
be bounded definable functions in
![]() $\mathbb {T}$
whose arities are k,
$\mathbb {T}$
whose arities are k,
![]() $k{+}2$
, and
$k{+}2$
, and
![]() $k{+}1$
respectively, and let
$k{+}1$
respectively, and let
![]() $t(y,x_0,\ldots ,x_{k-1})$
be a
$t(y,x_0,\ldots ,x_{k-1})$
be a
![]() $\mathbb {T}$
term.
$\mathbb {T}$
term.
If
![]() $\mathbb {T}$
proves
$\mathbb {T}$
proves
![]() $h(x_0,\ldots ,x_{k-1})\,{<}\,t(0,x_0,\ldots ,x_{k-1}) \;{\land }\;p(y,x_0,\ldots ,x_{k-1})\,{\leq }\,y/2$
and
$h(x_0,\ldots ,x_{k-1})\,{<}\,t(0,x_0,\ldots ,x_{k-1}) \;{\land }\;p(y,x_0,\ldots ,x_{k-1})\,{\leq }\,y/2$
and
then there is a (
![]() $k{+}1$
)-ary function f that is bounded definable in
$k{+}1$
)-ary function f that is bounded definable in
![]() $\mathbb {T}$
such that
$\mathbb {T}$
such that
![]() $\mathbb {T}$
proves both
$\mathbb {T}$
proves both
![]() $f(0,x_0,\ldots ,x_{k-1}) \,{=}\,h(x_0,\ldots ,x_{k-1})$
and
$f(0,x_0,\ldots ,x_{k-1}) \,{=}\,h(x_0,\ldots ,x_{k-1})$
and
Proof For the graph, define
![]() $\max(x,y):=(x-y)+y$
and let
$\max(x,y):=(x-y)+y$
and let
 $$\begin{align*}&\mathrm{Gr}_f(x_0,\ldots,x_{k-1},y,z) \,{:\equiv}\\ &\quad(\exists u\,{<}\,s(y,x_0,\ldots,x_{k-1}) \,{\#}\,\max(2{\cdot} y,1)) A(u,x_0,\ldots,x_{k-1},y,z),\end{align*}$$
$$\begin{align*}&\mathrm{Gr}_f(x_0,\ldots,x_{k-1},y,z) \,{:\equiv}\\ &\quad(\exists u\,{<}\,s(y,x_0,\ldots,x_{k-1}) \,{\#}\,\max(2{\cdot} y,1)) A(u,x_0,\ldots,x_{k-1},y,z),\end{align*}$$
where
![]() $s(y,x_0,\ldots ,x_{k-1})\,{\equiv }\, 3^4{\cdot }(y\,{+}\,t(y,x_0,\ldots ,x_{k-1}))^4$
and
$s(y,x_0,\ldots ,x_{k-1})\,{\equiv }\, 3^4{\cdot }(y\,{+}\,t(y,x_0,\ldots ,x_{k-1}))^4$
and
![]() $A(u,x_0,\ldots ,x_{k-1},y,z)$
is
$A(u,x_0,\ldots ,x_{k-1},y,z)$
is
 $$ \begin{align*} &\mathrm{Seq}(u) \,{\land}\, (\forall a,j\,{<}\,u)(\mathrm{pair}(j,a)\,{\in}\,u \,{\to}\,j\,{\leq}\,y) \,{\land}\, \mathrm{pair}(y,z)\,{\in}\,u\\ &\,{\land}\, (\forall j\,{\leq}\,y)(\forall b\,{<}\,u) (\exists c\,{<}\,u) \left(\begin{matrix} j\,{>}\,0\,{\land}\\ \mathrm{pair}(j,b)\,{\in}\,u \end{matrix} \;{\to}\quad\begin{matrix} \mathrm{pair}(p(j,x_0,\ldots,x_{k-1}),c)\,{\in}\,u \\{\land}\,b\,{=}\, g(j{-}1,x_0,\ldots,x_{k-1},c) \end{matrix}\right)\\ &\,{\land}\, (\forall a\,{<}\,u)(\mathrm{pair}(0,a)\,{\in}\,u \,{\to}\,a\,{=}\,h(x_0,\ldots,x_{k-1})). \end{align*} $$
$$ \begin{align*} &\mathrm{Seq}(u) \,{\land}\, (\forall a,j\,{<}\,u)(\mathrm{pair}(j,a)\,{\in}\,u \,{\to}\,j\,{\leq}\,y) \,{\land}\, \mathrm{pair}(y,z)\,{\in}\,u\\ &\,{\land}\, (\forall j\,{\leq}\,y)(\forall b\,{<}\,u) (\exists c\,{<}\,u) \left(\begin{matrix} j\,{>}\,0\,{\land}\\ \mathrm{pair}(j,b)\,{\in}\,u \end{matrix} \;{\to}\quad\begin{matrix} \mathrm{pair}(p(j,x_0,\ldots,x_{k-1}),c)\,{\in}\,u \\{\land}\,b\,{=}\, g(j{-}1,x_0,\ldots,x_{k-1},c) \end{matrix}\right)\\ &\,{\land}\, (\forall a\,{<}\,u)(\mathrm{pair}(0,a)\,{\in}\,u \,{\to}\,a\,{=}\,h(x_0,\ldots,x_{k-1})). \end{align*} $$
For the uniqueness of z, if
![]() $A(u,x_0,\ldots ,x_{k-1},y,z) \,{\land }\,A(v,x_0,\ldots ,x_{k-1},y,z')$
then we have
$A(u,x_0,\ldots ,x_{k-1},y,z) \,{\land }\,A(v,x_0,\ldots ,x_{k-1},y,z')$
then we have
![]() $(\forall a\,{<}\,u)(\forall b\,{<}\,v) (\mathrm {pair}(j,a)\,{\in }\,u \,{\land }\,\mathrm {pair}(j,b)\,{\in }\,v \,{\to }\,a\,{=}\,b)$
by induction on j with
$(\forall a\,{<}\,u)(\forall b\,{<}\,v) (\mathrm {pair}(j,a)\,{\in }\,u \,{\land }\,\mathrm {pair}(j,b)\,{\in }\,v \,{\to }\,a\,{=}\,b)$
by induction on j with
![]() $0\,{<}\,j\,{\leq }\,y$
and hence
$0\,{<}\,j\,{\leq }\,y$
and hence
![]() $z\,{=}\,z'$
.
$z\,{=}\,z'$
.
We show
![]() $B(p(y,x_0,\ldots ,x_{k-1}))\,{\to }\,B(y)$
for
$B(p(y,x_0,\ldots ,x_{k-1}))\,{\to }\,B(y)$
for
![]() $y\,{>}\,0$
, where
$y\,{>}\,0$
, where
Here and below, for better readability, we omit
![]() $x_0,\ldots ,x_{k-1}$
.
$x_0,\ldots ,x_{k-1}$
.
Let
![]() $z\,{<}\,t(p(y))$
and
$z\,{<}\,t(p(y))$
and
![]() $u\,{<}\,s(p(y))\,{\#}\, \max(2{\cdot} p(y),1)$
witness
$u\,{<}\,s(p(y))\,{\#}\, \max(2{\cdot} p(y),1)$
witness
![]() $B(p(y))$
. Lemma 2.5 yields
$B(p(y))$
. Lemma 2.5 yields
![]() $v$
with:
$v$
with:
-
(a)
 $v\,{<}\,9{\cdot }u{\cdot } (\mathrm {pair}(y,g(y{-}1,z)){+}1)^2{+}1$
, and
$v\,{<}\,9{\cdot }u{\cdot } (\mathrm {pair}(y,g(y{-}1,z)){+}1)^2{+}1$
, and -
(b)
 $(\forall w\,{<}\,v)( w\,{\in }\,v\,{\leftrightarrow }\, w\,{\in }\,u \,{\lor }\, w\,{=}\,\mathrm {pair}(y,g(y{-}1,z)))$
.
$(\forall w\,{<}\,v)( w\,{\in }\,v\,{\leftrightarrow }\, w\,{\in }\,u \,{\lor }\, w\,{=}\,\mathrm {pair}(y,g(y{-}1,z)))$
.
Obviously
![]() $A(v,y,g(y{-}1,z))$
. It remains to bound
$A(v,y,g(y{-}1,z))$
. It remains to bound
![]() $v$
. By
$v$
. By
![]() $z\,{<}\,t(p(y))$
and the premise of the theorem, we have
$z\,{<}\,t(p(y))$
and the premise of the theorem, we have
![]() $\mathrm {pair}(y,g(y{-}1,z)) \,{<}\,3{\cdot }(y{+}t(y))^2$
and, by (a), also
$\mathrm {pair}(y,g(y{-}1,z)) \,{<}\,3{\cdot }(y{+}t(y))^2$
and, by (a), also
![]() $v\,{\leq }\,9{\cdot }3^2{\cdot }u{\cdot } (y{+}t(y))^4 \,{=}\, u{\cdot }s(y)$
. Now
$v\,{\leq }\,9{\cdot }3^2{\cdot }u{\cdot } (y{+}t(y))^4 \,{=}\, u{\cdot }s(y)$
. Now
![]() $u\,{<}\,s(p(y))\,{\#}\,\max(2{\cdot} p(y),1)\,{\leq }\,s(y)\,{\#}\, y$
as s is monotone. Then
$u\,{<}\,s(p(y))\,{\#}\,\max(2{\cdot} p(y),1)\,{\leq }\,s(y)\,{\#}\, y$
as s is monotone. Then
![]() $v\,{\leq }\,u{\cdot }s(y) \,{<}\, (s(y){\#}y) \,{\cdot }\, (s(y){\#}1)\,{=}\, s(y)\,{\#}(2{\cdot} y)$
by the axioms for
$v\,{\leq }\,u{\cdot }s(y) \,{<}\, (s(y){\#}y) \,{\cdot }\, (s(y){\#}1)\,{=}\, s(y)\,{\#}(2{\cdot} y)$
by the axioms for
![]() $\#$
.
$\#$
.
Since
![]() $B(0)$
is obvious, we can show
$B(0)$
is obvious, we can show
![]() $(\forall y\,{\leq }\,x)B(y)$
by induction on x.
$(\forall y\,{\leq }\,x)B(y)$
by induction on x.
Corollary 2.12. The following functions (with the obvious intended formulae expressing the graphs) are bounded definable in the respectively mentioned theories, so that the attached formulae are provable:
-
• in
 $\mathbb {FA}(\mathcal {S}^2)$
, (modified) logarithm
$\mathbb {FA}(\mathcal {S}^2)$
, (modified) logarithm
 $|x|$
with
$|x|$
with
 $|0|\,{=}\,0$
and
$|0|\,{=}\,0$
and
 $x\,{>}\,0\,{\to }\, |x|\,{=}\,|x/2|{+}1$
;
$x\,{>}\,0\,{\to }\, |x|\,{=}\,|x/2|{+}1$
; -
• in
 $\mathbb {FA}(\mathcal {S}^n)$
for
$\mathbb {FA}(\mathcal {S}^n)$
for
 $n\,{\geq }\,3$
, cut-off
$n\,{\geq }\,3$
, cut-off
 $\gamma _{n+1}$
, denoted by
$\gamma _{n+1}$
, denoted by
 $\mathrm {cg}_{n+1}(x,y)$
, with
$\mathrm {cg}_{n+1}(x,y)$
, with
 $\gamma _n(\mathrm {cg}_{n+1}(x,y)) \,{>}\,y\,{\to }\,\mathrm {cg}_{n+1}(x{+}1,y) \,{=}\,y{+}1$
,
$\gamma _n(\mathrm {cg}_{n+1}(x,y)) \,{>}\,y\,{\to }\,\mathrm {cg}_{n+1}(x{+}1,y) \,{=}\,y{+}1$
,
 $\gamma _n(\mathrm {cg}_{n+1}(x,y)) \,{\leq }\,y\,{\to }\,\mathrm {cg}_{n+1}(x{+}1,y) \,{=}\,\gamma _n(\mathrm {cg}_{n+1}(x,y))$
and
$\gamma _n(\mathrm {cg}_{n+1}(x,y)) \,{\leq }\,y\,{\to }\,\mathrm {cg}_{n+1}(x{+}1,y) \,{=}\,\gamma _n(\mathrm {cg}_{n+1}(x,y))$
and
 $\mathrm {cg}_{n+1}(0,y)\,{=}\,1$
.
$\mathrm {cg}_{n+1}(0,y)\,{=}\,1$
.
In more intuitive terms,
![]() $|x|$
is
$|x|$
is
![]() $\lceil \log _2(x{+}1)\rceil $
, the length of the shortest binary expression of x, and
$\lceil \log _2(x{+}1)\rceil $
, the length of the shortest binary expression of x, and
![]() $\mathrm {cg}_{n+1}(x,y)\,{=}\,\min \{\gamma _{n+1}(x),y{+}1\}$
. Thus, for
$\mathrm {cg}_{n+1}(x,y)\,{=}\,\min \{\gamma _{n+1}(x),y{+}1\}$
. Thus, for
![]() $n\,{\geq }\,2$
, we can express the graph
$n\,{\geq }\,2$
, we can express the graph
![]() $\mathrm {Gr}_{\gamma _{n+1}}$
of
$\mathrm {Gr}_{\gamma _{n+1}}$
of
![]() $\gamma _{n+1}$
in
$\gamma _{n+1}$
in
![]() $\mathfrak {L}(\mathcal {S}^n)$
as follows. (Actually,
$\mathfrak {L}(\mathcal {S}^n)$
as follows. (Actually,
![]() $\mathrm {Gr}_{\gamma _3}(y,z)$
is known to be expressible only with
$\mathrm {Gr}_{\gamma _3}(y,z)$
is known to be expressible only with
![]() $+$
and
$+$
and
![]() $\cdot $
, without
$\cdot $
, without
![]() $\#$
. Furthermore, as will be shown in [Reference Sato22], we do not need
$\#$
. Furthermore, as will be shown in [Reference Sato22], we do not need
![]() $+$
and
$+$
and
![]() $\cdot $
as functions but only their graphs.)
$\cdot $
as functions but only their graphs.)
Definition 2.13. Define
![]() $\mathrm {Gr}_{\gamma _n}(x,y)$
for
$\mathrm {Gr}_{\gamma _n}(x,y)$
for
![]() $n\,{\geq }\,3$
as follows:
$n\,{\geq }\,3$
as follows:
Corollary 2.14 (Bounded recursion)
Let
![]() $\mathbb {T}$
expand
$\mathbb {T}$
expand
![]() $\mathbb {FA}(\mathcal {S}^3)$
, let
$\mathbb {FA}(\mathcal {S}^3)$
, let
![]() $h,g$
be bounded definable functions in
$h,g$
be bounded definable functions in
![]() $\mathbb {T}$
whose arities are k and
$\mathbb {T}$
whose arities are k and
![]() $k{+}2$
respectively, and let
$k{+}2$
respectively, and let
![]() $t(y,x_0,\ldots ,x_{k-1})$
be a
$t(y,x_0,\ldots ,x_{k-1})$
be a
![]() $\mathbb {T}$
term.
$\mathbb {T}$
term.
If
![]() $\mathbb {T}$
proves
$\mathbb {T}$
proves
![]() $h(x_0,\ldots ,x_{k-1})\,{<}\,t(0,x_0,\ldots ,x_{k-1})$
and
$h(x_0,\ldots ,x_{k-1})\,{<}\,t(0,x_0,\ldots ,x_{k-1})$
and
then there is a (
![]() $k{+}1$
)-ary function f that is bounded definable in
$k{+}1$
)-ary function f that is bounded definable in
![]() $\mathbb {T}$
such that
$\mathbb {T}$
such that
![]() $\mathbb {T}$
proves
$\mathbb {T}$
proves
![]() $f(0,x_0,\ldots ,x_{k-1}) \,{=}\,h(x_0,\ldots ,x_{k-1})$
and
$f(0,x_0,\ldots ,x_{k-1}) \,{=}\,h(x_0,\ldots ,x_{k-1})$
and
Proof Let
![]() $g'(y,z)\,{:=}\, g(|y{+}1|{-}1,x_0,\ldots ,x_{k-1},z)$
and
$g'(y,z)\,{:=}\, g(|y{+}1|{-}1,x_0,\ldots ,x_{k-1},z)$
and
![]() $t'(y)\,{:=}\, t(|y|,x_0,\ldots ,x_{k-1})$
.
$t'(y)\,{:=}\, t(|y|,x_0,\ldots ,x_{k-1})$
.
The last theorem applied to h,
![]() $\mbox {-}/2$
,
$\mbox {-}/2$
,
![]() $g'$
, and
$g'$
, and
![]() $t'$
yields a bounded definable
$t'$
yields a bounded definable
![]() $f'$
such that
$f'$
such that
![]() $f'(y,x_0,\ldots ,x_{k-1}) \,{=}\,g(|y{+}1|{-}1,x_0,\ldots ,x_{k-1},f'(y/2,x_0,\ldots ,x_{k-1}))$
for
$f'(y,x_0,\ldots ,x_{k-1}) \,{=}\,g(|y{+}1|{-}1,x_0,\ldots ,x_{k-1},f'(y/2,x_0,\ldots ,x_{k-1}))$
for
![]() $y\,{>}\,0$
starting with
$y\,{>}\,0$
starting with
![]() $f'(0,x_0,\ldots ,x_{k-1}) \,{=}\,h(x_0,\ldots ,x_{k-1})$
.
$f'(0,x_0,\ldots ,x_{k-1}) \,{=}\,h(x_0,\ldots ,x_{k-1})$
.
Define f by
![]() $f(y,x_0,\ldots ,x_{k-1}) \,{=}\,f'(\gamma _3(y){-}1,x_0,\ldots ,x_{k-1})$
.
$f(y,x_0,\ldots ,x_{k-1}) \,{=}\,f'(\gamma _3(y){-}1,x_0,\ldots ,x_{k-1})$
.
With bounded binary recursion (Theorem 2.11), we can introduce fundamental operations on (codes of) finite sequences and, hence, on syntactical objects. The following is proved in [Reference Hájek and Pudlák9, Chapter V] or [Reference Walker29, Chapter 4].
Lemma 2.15. There are bounded definable functions
![]() $\mathrm {lh}$
,
$\mathrm {lh}$
,
![]() $\mathrm {ev}$
,
$\mathrm {ev}$
,
![]() $\mathrm {slo}$
, and
$\mathrm {slo}$
, and
![]() $\mathrm {conc}$
in
$\mathrm {conc}$
in
![]() $\mathbb {FA}(\mathcal {S}^2)$
such that it proves
$\mathbb {FA}(\mathcal {S}^2)$
such that it proves
 $$\begin{align*}\begin{matrix} \mathrm{lh}(1)\,{=}\,0 \;{\land}\; \mathrm{Seq}(\mathrm{slo}(x)) \;{\land}\; \mathrm{lh}(\mathrm{slo}(x))\,{=}\,1\; {\land}\; \mathrm{ev}(\mathrm{slo}(x),0)\,{=}\,x \\ {\land}\;(\mathrm{Seq}(u)\,{\land}\,\mathrm{Seq}(v) \,{\to}\, \mathrm{Seq}(\mathrm{conc}(u,v)) \;{\land}\; \mathrm{lh}(\mathrm{conc}(u,v))\,{=}\, \mathrm{lh}(u){+}\mathrm{lh}(u)) \\ {\land}\;(\forall y\,{<}\,\mathrm{lh}(u)) (\mathrm{ev}(u,y)\,{=}\, \mathrm{ev}(\mathrm{conc}(u,v),y)) \\{\land}\; (\forall y\,{<}\,\mathrm{lh}(v)) (\mathrm{ev}(v,y)\,{=}\, \mathrm{ev}(\mathrm{conc}(u,v),\mathrm{lh}(u){+}y))\\ {\land}\; \mathrm{conc}(u,\mathrm{slo}(x))\,{\leq}\,9{\cdot}u {\cdot}(x{+}1)^2 \\{\land}\;(\mathrm{lh}(v)\,{>}\,0\,{\to}\, \mathrm{conc}(v,u)\,{\geq}\,2{\cdot}u) \;{\land}\;(\mathrm{lh}(v)\,{>}\,0\,{\land}\,\mathrm{ev}(v,0)\,{>}\,1\,{\to}\, \mathrm{conc}(u,v)\,{>}\,2{\cdot}u). \end{matrix} \end{align*}$$
$$\begin{align*}\begin{matrix} \mathrm{lh}(1)\,{=}\,0 \;{\land}\; \mathrm{Seq}(\mathrm{slo}(x)) \;{\land}\; \mathrm{lh}(\mathrm{slo}(x))\,{=}\,1\; {\land}\; \mathrm{ev}(\mathrm{slo}(x),0)\,{=}\,x \\ {\land}\;(\mathrm{Seq}(u)\,{\land}\,\mathrm{Seq}(v) \,{\to}\, \mathrm{Seq}(\mathrm{conc}(u,v)) \;{\land}\; \mathrm{lh}(\mathrm{conc}(u,v))\,{=}\, \mathrm{lh}(u){+}\mathrm{lh}(u)) \\ {\land}\;(\forall y\,{<}\,\mathrm{lh}(u)) (\mathrm{ev}(u,y)\,{=}\, \mathrm{ev}(\mathrm{conc}(u,v),y)) \\{\land}\; (\forall y\,{<}\,\mathrm{lh}(v)) (\mathrm{ev}(v,y)\,{=}\, \mathrm{ev}(\mathrm{conc}(u,v),\mathrm{lh}(u){+}y))\\ {\land}\; \mathrm{conc}(u,\mathrm{slo}(x))\,{\leq}\,9{\cdot}u {\cdot}(x{+}1)^2 \\{\land}\;(\mathrm{lh}(v)\,{>}\,0\,{\to}\, \mathrm{conc}(v,u)\,{\geq}\,2{\cdot}u) \;{\land}\;(\mathrm{lh}(v)\,{>}\,0\,{\land}\,\mathrm{ev}(v,0)\,{>}\,1\,{\to}\, \mathrm{conc}(u,v)\,{>}\,2{\cdot}u). \end{matrix} \end{align*}$$
Definition 2.16. We write
![]() $\langle \,\rangle $
,
$\langle \,\rangle $
,
![]() $u(x)$
,
$u(x)$
,
![]() $\langle x\rangle $
, and
$\langle x\rangle $
, and
![]() $u{*}v$
for
$u{*}v$
for
![]() $1$
,
$1$
,
![]() $\mathrm {ev}(u,x)$
,
$\mathrm {ev}(u,x)$
,
![]() $\mathrm {slo}(x)$
, and
$\mathrm {slo}(x)$
, and
![]() $\mathrm {conc}(u,v)$
, respectively, where
$\mathrm {conc}(u,v)$
, respectively, where
![]() $\mathrm {conc}$
,
$\mathrm {conc}$
,
![]() $\mathrm {ev}$
, and
$\mathrm {ev}$
, and
![]() $\mathrm {slo}$
are from the last lemma.
$\mathrm {slo}$
are from the last lemma.
2.4 Totality rule and the use of function symbols
It is known that, in first-order arithmetic
![]() , the totality of exponentiation
, the totality of exponentiation
![]() $\forall y\exists z\mathrm {Gr}_{\gamma _3}(y,z)$
justifies the use of the function symbol
$\forall y\exists z\mathrm {Gr}_{\gamma _3}(y,z)$
justifies the use of the function symbol
![]() $\gamma _3$
even in the
$\gamma _3$
even in the
![]() induction schema. However, the straightforward rewriting of
induction schema. However, the straightforward rewriting of
![]() $A(\gamma _3(t))$
by
$A(\gamma _3(t))$
by
![]() $\exists z( \mathrm {Gr}_{\gamma _3}(t,z) \,{\land }\,A(z))$
or by
$\exists z( \mathrm {Gr}_{\gamma _3}(t,z) \,{\land }\,A(z))$
or by
![]() $\forall z( \mathrm {Gr}_{\gamma _3}(t,z) \,{\to }\,A(z))$
does not justify the use of induction for
$\forall z( \mathrm {Gr}_{\gamma _3}(t,z) \,{\to }\,A(z))$
does not justify the use of induction for
![]() $A(\gamma _3(t))$
. What we need to show is, for any
$A(\gamma _3(t))$
. What we need to show is, for any
![]() formula A with occurrences of
formula A with occurrences of
![]() $\gamma _3$
, the existence of a finite fragment
$\gamma _3$
, the existence of a finite fragment
![]() $u\,{=}\,\gamma _3{\upharpoonright }k$
(a finite sequence coded by a number) that is long enough to contain all the values of
$u\,{=}\,\gamma _3{\upharpoonright }k$
(a finite sequence coded by a number) that is long enough to contain all the values of
![]() $\gamma _3$
referred to in subformulae of A. A similar idea was used to prove the formalized version of Kleene’s Normal Form Theorem in the function-based second-order arithmetic in [Reference Nemoto and Sato15, Lemma 2.13].
$\gamma _3$
referred to in subformulae of A. A similar idea was used to prove the formalized version of Kleene’s Normal Form Theorem in the function-based second-order arithmetic in [Reference Nemoto and Sato15, Lemma 2.13].
In this subsection, we prove the same result in our finitist setting. As we cannot form totality assertions in the language
![]() $\mathfrak {L}(\mathcal {S}^n)$
, we express the totality by a non-logical rule, similarly to the non-logical rule (
$\mathfrak {L}(\mathcal {S}^n)$
, we express the totality by a non-logical rule, similarly to the non-logical rule (
![]() $\exists \mbox {-val}$
) discussed in the Introduction.
$\exists \mbox {-val}$
) discussed in the Introduction.
Definition 2.17. The rule
![]() $(\mathrm{Tot}{\text{-}}\gamma _{n+1})$
is as follows, where x must not occur in A (i.e., x is an eigenvariable) nor in t.
$(\mathrm{Tot}{\text{-}}\gamma _{n+1})$
is as follows, where x must not occur in A (i.e., x is an eigenvariable) nor in t.
In this subsection we locally interpret
![]() $\mathbb {FA}(\mathcal {S}^{n+1})$
in
$\mathbb {FA}(\mathcal {S}^{n+1})$
in
![]() $\mathbb {FA}(\mathcal {S}^n)\,{+}\, (\mathrm{Tot}{\text{-}}\gamma _{n+1})$
. We first define the formulae
$\mathbb {FA}(\mathcal {S}^n)\,{+}\, (\mathrm{Tot}{\text{-}}\gamma _{n+1})$
. We first define the formulae
![]() $\mathrm {FLE}_{n,t}(u)$
and
$\mathrm {FLE}_{n,t}(u)$
and
![]() $\mathrm {FLE}_{n,A}(u)$
meaning that u is a long enough fragment of
$\mathrm {FLE}_{n,A}(u)$
meaning that u is a long enough fragment of
![]() $\gamma _{n+1}$
for all references in a term t or a formula A, respectively.
$\gamma _{n+1}$
for all references in a term t or a formula A, respectively.
Definition 2.18. Define
![]() $\mathrm {Frag}_{\gamma _{n+1}}(u)\;{:\equiv }\; \mathrm {Seq}(u) \,{\land }\, (\forall x\,{<}\,\mathrm {lh}(u)) \mathrm {Gr}_{\gamma _{n+1}}(x,u(x))$
.
$\mathrm {Frag}_{\gamma _{n+1}}(u)\;{:\equiv }\; \mathrm {Seq}(u) \,{\land }\, (\forall x\,{<}\,\mathrm {lh}(u)) \mathrm {Gr}_{\gamma _{n+1}}(x,u(x))$
.
For any
![]() $\mathcal {S}^{n+1}$
term t (without added symbols for bounded definable functions) whose variables are among
$\mathcal {S}^{n+1}$
term t (without added symbols for bounded definable functions) whose variables are among
![]() $x_0,\ldots ,x_{k-1}$
, we define the
$x_0,\ldots ,x_{k-1}$
, we define the
![]() $\mathfrak {L}(\mathcal {S}^n)$
formula
$\mathfrak {L}(\mathcal {S}^n)$
formula
![]() $\mathrm {FLE}_{n,t}(u,x_0,\ldots ,x_{k-1})$
by meta-recursion on t as follows.
$\mathrm {FLE}_{n,t}(u,x_0,\ldots ,x_{k-1})$
by meta-recursion on t as follows.
 $$ \begin{align*} &\mathrm{FLE}_{n,t}(u,x_0,\ldots,x_{k-1})\, {:\equiv}\\ &\begin{cases} \mathrm{Frag}_{\gamma_{n+1}}(u), &\!\!\!\!\!\!\!\!\!\!\mbox{ if}\ t\ \mbox{is a variable or constant},\\ {\bigwedge}_{i<\ell}\mathrm{FLE}_{n,t_i}(u,x_0,\ldots,x_{k-1}), &\hspace{-20pt}\!\!\!\!\!\!\!\!\!\!\mbox{ if }t\,{\equiv}\,\mathrm{f}(t_0,\ldots,t_{\ell-1}) \mbox{ for some f from }\mathcal{S}^n,\\ \mathrm{FLE}_{n,s}(u,x_0,\ldots,x_{k-1}) \,{\land}\, s^u(x_0,\ldots,x_{k-1})\,{<}\,\mathrm{lh}(u),\hspace{-40pt} &\!\!\!\!\!\!\!\!\!\!\hspace{55pt}\mbox{ if }t\,{\equiv}\,\gamma_{n+1}(s), \end{cases} \end{align*} $$
$$ \begin{align*} &\mathrm{FLE}_{n,t}(u,x_0,\ldots,x_{k-1})\, {:\equiv}\\ &\begin{cases} \mathrm{Frag}_{\gamma_{n+1}}(u), &\!\!\!\!\!\!\!\!\!\!\mbox{ if}\ t\ \mbox{is a variable or constant},\\ {\bigwedge}_{i<\ell}\mathrm{FLE}_{n,t_i}(u,x_0,\ldots,x_{k-1}), &\hspace{-20pt}\!\!\!\!\!\!\!\!\!\!\mbox{ if }t\,{\equiv}\,\mathrm{f}(t_0,\ldots,t_{\ell-1}) \mbox{ for some f from }\mathcal{S}^n,\\ \mathrm{FLE}_{n,s}(u,x_0,\ldots,x_{k-1}) \,{\land}\, s^u(x_0,\ldots,x_{k-1})\,{<}\,\mathrm{lh}(u),\hspace{-40pt} &\!\!\!\!\!\!\!\!\!\!\hspace{55pt}\mbox{ if }t\,{\equiv}\,\gamma_{n+1}(s), \end{cases} \end{align*} $$
where
![]() $s^u$
is the result of replacing all the subterms of the form
$s^u$
is the result of replacing all the subterms of the form
![]() $\gamma _{n+1}(t)$
by
$\gamma _{n+1}(t)$
by
![]() $u(t^u)$
in s.
$u(t^u)$
in s.
Next, for any
![]() $\mathfrak {L}(\mathcal {S}^{n+1})$
formula A whose free variables are among
$\mathfrak {L}(\mathcal {S}^{n+1})$
formula A whose free variables are among
![]() $x_0,\ldots ,x_{k-1}$
, we define the
$x_0,\ldots ,x_{k-1}$
, we define the
![]() $\mathfrak {L}(\mathcal {S}^n)$
formula
$\mathfrak {L}(\mathcal {S}^n)$
formula
![]() $\mathrm {FLE}_{n,A}(u,x_0,\ldots ,x_{k-1})$
by meta-recursion on A as follows.
$\mathrm {FLE}_{n,A}(u,x_0,\ldots ,x_{k-1})$
by meta-recursion on A as follows.
 $$ \begin{align*} & \mathrm{FLE}_{n,A}(u,x_0,\ldots,x_{k-1}) \,{:\equiv}\\ &\begin{cases} {\bigwedge}_{i<2}\mathrm{FLE}_{n,t_i}(u,x_0,\ldots,x_{k-1}), &\hspace{-110pt}\mbox{ if}\ A\ \mbox{is }t_0\,{=}\,t_1,\;t_0\,{<}\,t_1,\; \neg\, t_0\,{=}\,t_1,\;\neg\, t_0\,{<}\,t_1.\\ {\bigwedge}_{i<2}\mathrm{FLE}_{n,B_i}(u,x_0,\ldots,x_{k-1}), &\hspace{-110pt}\mbox{ if}\ A\ \mbox{is }B_0\,{\land}\,B_1 \mbox{ or }B_0\,{\lor}\,B_1,\\ (\exists v\,{\leq}\,u) (\mathrm{FLE}_{n,B}(u,t^v,x_0,\ldots,x_{k-1}) \,{\land}\, \mathrm{FLE}_{n,t}(v,x_0,\ldots,x_{k-1})), \\ & \hspace{-200pt} \mbox{ if}\ A\ \mbox{is }(\forall y\,{<}\,t)B(y,x_0,\ldots,x_{k-1})\mbox{ or }(\exists y\,{<}\,t)B(y,x_0,\ldots,x_{k-1}). \end{cases} \end{align*} $$
$$ \begin{align*} & \mathrm{FLE}_{n,A}(u,x_0,\ldots,x_{k-1}) \,{:\equiv}\\ &\begin{cases} {\bigwedge}_{i<2}\mathrm{FLE}_{n,t_i}(u,x_0,\ldots,x_{k-1}), &\hspace{-110pt}\mbox{ if}\ A\ \mbox{is }t_0\,{=}\,t_1,\;t_0\,{<}\,t_1,\; \neg\, t_0\,{=}\,t_1,\;\neg\, t_0\,{<}\,t_1.\\ {\bigwedge}_{i<2}\mathrm{FLE}_{n,B_i}(u,x_0,\ldots,x_{k-1}), &\hspace{-110pt}\mbox{ if}\ A\ \mbox{is }B_0\,{\land}\,B_1 \mbox{ or }B_0\,{\lor}\,B_1,\\ (\exists v\,{\leq}\,u) (\mathrm{FLE}_{n,B}(u,t^v,x_0,\ldots,x_{k-1}) \,{\land}\, \mathrm{FLE}_{n,t}(v,x_0,\ldots,x_{k-1})), \\ & \hspace{-200pt} \mbox{ if}\ A\ \mbox{is }(\forall y\,{<}\,t)B(y,x_0,\ldots,x_{k-1})\mbox{ or }(\exists y\,{<}\,t)B(y,x_0,\ldots,x_{k-1}). \end{cases} \end{align*} $$
For the last clause, it might help to remind that, according to the standard abbreviation in first-order setting, both
![]() $y\,{<}\,t$
and
$y\,{<}\,t$
and
![]() $B(y,x_0,\ldots ,x_{k-1})$
are subformulae of
$B(y,x_0,\ldots ,x_{k-1})$
are subformulae of
![]() $(Q y\,{<}\,t)B(y,x_0,\ldots ,x_{k-1})$
.
$(Q y\,{<}\,t)B(y,x_0,\ldots ,x_{k-1})$
.
Lemma 2.19. For any
![]() $\mathcal {S}^{n+1}$
term t and
$\mathcal {S}^{n+1}$
term t and
![]() $\mathfrak {L}(\mathcal {S}^{n+1})$
formula A whose free variables are among
$\mathfrak {L}(\mathcal {S}^{n+1})$
formula A whose free variables are among
![]() $x_0,\ldots ,x_{k-1}$
, the following are provable in
$x_0,\ldots ,x_{k-1}$
, the following are provable in
![]() $\mathbb {FA}(\mathcal {S}^n)$
:
$\mathbb {FA}(\mathcal {S}^n)$
:
-
(i)
 $\qquad \begin {matrix} \mathrm {FLE}_{n,t}(v,x_0,\ldots ,x_{k-1}) \,{\land }\,v\,{\leq }\,u\,{\land }\, \mathrm {Frag}_{\gamma _{n+1}}(u) \hspace {90pt}\\ \hspace {130pt}{\to }\, t^v(x_0,\ldots ,x_{k-1})\,{=}\,t^u(x_0,\ldots ,x_{k-1}) \end {matrix}$
;
$\qquad \begin {matrix} \mathrm {FLE}_{n,t}(v,x_0,\ldots ,x_{k-1}) \,{\land }\,v\,{\leq }\,u\,{\land }\, \mathrm {Frag}_{\gamma _{n+1}}(u) \hspace {90pt}\\ \hspace {130pt}{\to }\, t^v(x_0,\ldots ,x_{k-1})\,{=}\,t^u(x_0,\ldots ,x_{k-1}) \end {matrix}$
; -
(ii)
 $\qquad \begin {matrix} \mathrm {FLE}_{n,t}(v,x_0,\ldots ,x_{k-1})\,{\land }\, v\,{\leq }\,u\,{\land }\,{\bigwedge }_{i<k}y_i\,{\leq }\,x_i \,{\land }\, \mathrm {Frag}_{\gamma _{n+1}}(u)\hspace {20pt}\\ \hspace {170pt}{\to }\, \mathrm {FLE}_{n,t}(u,y_0,\ldots ,y_{k-1}) \end {matrix}$
;
$\qquad \begin {matrix} \mathrm {FLE}_{n,t}(v,x_0,\ldots ,x_{k-1})\,{\land }\, v\,{\leq }\,u\,{\land }\,{\bigwedge }_{i<k}y_i\,{\leq }\,x_i \,{\land }\, \mathrm {Frag}_{\gamma _{n+1}}(u)\hspace {20pt}\\ \hspace {170pt}{\to }\, \mathrm {FLE}_{n,t}(u,y_0,\ldots ,y_{k-1}) \end {matrix}$
; -
(iii)
 $\qquad \begin {matrix} \mathrm {FLE}_{n,A}(v,x_0,\ldots ,x_{k-1})\,{\land }\, v\,{\leq }\,u\,{\land }\,{\bigwedge }_{i<k}y_i\,{\leq }\,x_i \,{\land }\, \mathrm {Frag}_{\gamma _{n+1}}(u) \hspace {20pt}\\ \hspace {170pt}{\to }\, \mathrm {FLE}_{n,A}(u,y_0,\ldots ,y_{k-1}) \end {matrix}$
.
$\qquad \begin {matrix} \mathrm {FLE}_{n,A}(v,x_0,\ldots ,x_{k-1})\,{\land }\, v\,{\leq }\,u\,{\land }\,{\bigwedge }_{i<k}y_i\,{\leq }\,x_i \,{\land }\, \mathrm {Frag}_{\gamma _{n+1}}(u) \hspace {20pt}\\ \hspace {170pt}{\to }\, \mathrm {FLE}_{n,A}(u,y_0,\ldots ,y_{k-1}) \end {matrix}$
.
Lemma 2.20. The following are provable in
![]() $\mathbb {FA}(\mathcal {S}^n)$
:
$\mathbb {FA}(\mathcal {S}^n)$
:
(1)
![]() $\mathrm {cg}_{n+1}(x{+}y,z)\,{\leq }\,z\;{\to }\; \mathrm {cg}_{n+1}(x,z){\cdot } \mathrm {cg}_{n+1}(y,z) \,{\leq }\, \mathrm {cg}_{n+1}(x{+}y,z)$
for
$\mathrm {cg}_{n+1}(x{+}y,z)\,{\leq }\,z\;{\to }\; \mathrm {cg}_{n+1}(x,z){\cdot } \mathrm {cg}_{n+1}(y,z) \,{\leq }\, \mathrm {cg}_{n+1}(x{+}y,z)$
for
![]() $n\,{\geq }\,3$
;
$n\,{\geq }\,3$
;
(2)
![]() $\mathrm {Gr}_{\gamma _{n+1}}(6{\cdot }y^2{+}4,z) \,{\to }\,(\exists u\,{<}\,z) (y\,{\leq }\,\mathrm {lh}(u)\,{\land }\, \mathrm {Frag}_{\gamma _{n+1}}(u))$
for
$\mathrm {Gr}_{\gamma _{n+1}}(6{\cdot }y^2{+}4,z) \,{\to }\,(\exists u\,{<}\,z) (y\,{\leq }\,\mathrm {lh}(u)\,{\land }\, \mathrm {Frag}_{\gamma _{n+1}}(u))$
for
![]() $n\,{\geq }\,2$
.
$n\,{\geq }\,2$
.
Proof (1) We prove this by meta-induction on
![]() $n\,{\geq }\,3$
and internal induction on y in
$n\,{\geq }\,3$
and internal induction on y in
![]() $\mathbb {FA}(\mathcal {S}^n)$
. If
$\mathbb {FA}(\mathcal {S}^n)$
. If
![]() $x\,{\cdot }\,y\,{=}\,0$
or
$x\,{\cdot }\,y\,{=}\,0$
or
![]() $y\,{=}\,1$
, this can be seen easily by
$y\,{=}\,1$
, this can be seen easily by
![]() $\mathrm{cg}_n(0,z) = 1$
and
$\mathrm{cg}_n(0,z) = 1$
and
![]() $\mathrm{cg}_n(x,z) \geq \min(x\cdot 2,z)$
. So, assume
$\mathrm{cg}_n(x,z) \geq \min(x\cdot 2,z)$
. So, assume
![]() $\mathrm {cg}_{n+1}(x{+}y{+}1,z)\,{\leq }\,z$
with
$\mathrm {cg}_{n+1}(x{+}y{+}1,z)\,{\leq }\,z$
with
![]() $x,\, y\,\geq\, 1$
. Then
$x,\, y\,\geq\, 1$
. Then
![]() $\mathrm {cg}_{n+1}(x{+}y,z)\,{\leq }\,z$
and so
$\mathrm {cg}_{n+1}(x{+}y,z)\,{\leq }\,z$
and so
 $$ \begin{align*} \mathrm{cg}_{n+1}(x,z){\cdot} \mathrm{cg}_{n+1}(y{+}1,z) \,&{<}\, \gamma_n(\mathrm{cg}_{n+1}(x,z)){\cdot} \gamma_n(\mathrm{cg}_{n+1}(y,z))\\ \,&{\leq}\, \gamma_n(\mathrm{cg}_{n+1}(x,z) {+} \mathrm{cg}_{n+1}(y,z))\\ \,&{\leq}\, \gamma_n(\mathrm{cg}_{n+1}(x,z) {\cdot} \mathrm{cg}_{n+1}(y,z))\\ \,&{\leq}\, \gamma_n(\mathrm{cg}_{n+1}(x{+}y,z)) \,{=}\,\mathrm{cg}_{n+1}(x{+}y{+}1,z), \end{align*} $$
$$ \begin{align*} \mathrm{cg}_{n+1}(x,z){\cdot} \mathrm{cg}_{n+1}(y{+}1,z) \,&{<}\, \gamma_n(\mathrm{cg}_{n+1}(x,z)){\cdot} \gamma_n(\mathrm{cg}_{n+1}(y,z))\\ \,&{\leq}\, \gamma_n(\mathrm{cg}_{n+1}(x,z) {+} \mathrm{cg}_{n+1}(y,z))\\ \,&{\leq}\, \gamma_n(\mathrm{cg}_{n+1}(x,z) {\cdot} \mathrm{cg}_{n+1}(y,z))\\ \,&{\leq}\, \gamma_n(\mathrm{cg}_{n+1}(x{+}y,z)) \,{=}\,\mathrm{cg}_{n+1}(x{+}y{+}1,z), \end{align*} $$
where the second inequality is obvious for
![]() $n\,{=}\,3$
and by the meta-induction hypothesis otherwise since
$n\,{=}\,3$
and by the meta-induction hypothesis otherwise since
![]() $\gamma _n(x)\,{=}\,\mathrm {cg}_n(x,\gamma _n(x))$
, and where the fourth inequality is by the induction hypothesis.
$\gamma _n(x)\,{=}\,\mathrm {cg}_n(x,\gamma _n(x))$
, and where the fourth inequality is by the induction hypothesis.
(2) For uniformity, let
![]() $\gamma _2(x)\,{=}\,2{\cdot }x$
. We prove
$\gamma _2(x)\,{=}\,2{\cdot }x$
. We prove
![]() $A(x)$
by induction on x, where
$A(x)$
by induction on x, where
Again
![]() $A(0)$
is obvious. Assume
$A(0)$
is obvious. Assume
![]() $A(x)$
. To show
$A(x)$
. To show
![]() $A(x{+}1)$
, fix
$A(x{+}1)$
, fix
![]() $y,z\,{<}\,x{+}1$
and assume
$y,z\,{<}\,x{+}1$
and assume
![]() $\mathrm {Gr}_{\gamma _{n+1}}(6{\cdot }y^2{+}4,z)$
. If
$\mathrm {Gr}_{\gamma _{n+1}}(6{\cdot }y^2{+}4,z)$
. If
![]() $y\,{=}\,0$
, then the statement is obvious. Thus we may assume
$y\,{=}\,0$
, then the statement is obvious. Thus we may assume
![]() $y\,{\neq }\,0$
. By
$y\,{\neq }\,0$
. By
![]() $\mathrm {cg}_{n+1}(6{\cdot }(y{-}1)^2{+}4,z) \,{<}\,z\,{\leq }\,x$
, the induction hypothesis yields
$\mathrm {cg}_{n+1}(6{\cdot }(y{-}1)^2{+}4,z) \,{<}\,z\,{\leq }\,x$
, the induction hypothesis yields
![]() $w\,{<}\, \mathrm {cg}_{n+1}(6{\cdot }(y{-}1)^2{+}4,z)$
with
$w\,{<}\, \mathrm {cg}_{n+1}(6{\cdot }(y{-}1)^2{+}4,z)$
with
![]() $y{-}1\,{\leq }\,\mathrm {lh}(w) \,{\land }\,\mathrm {Frag}_{\gamma _{n+1}}(w)$
. We may assume
$y{-}1\,{\leq }\,\mathrm {lh}(w) \,{\land }\,\mathrm {Frag}_{\gamma _{n+1}}(w)$
. We may assume
![]() $\mathrm {lh}(w)\,{=}\,y{-}1$
. Let
$\mathrm {lh}(w)\,{=}\,y{-}1$
. Let
![]() $u\,{:=}\,w{*}\langle \mathrm {cg}_{n+1}(y{-}1,z)\rangle $
. As
$u\,{:=}\,w{*}\langle \mathrm {cg}_{n+1}(y{-}1,z)\rangle $
. As
![]() $9\,{<}\,2^4\,{\leq }\, \mathrm {cg}_{n+1}(4,z)$
, we have
$9\,{<}\,2^4\,{\leq }\, \mathrm {cg}_{n+1}(4,z)$
, we have
and, by (1),
![]() $u\,{<}\,\mathrm {cg}_{n+1}(4{+}6{\cdot }(y{-}1)^2{+}4 {+}2{\cdot }y,z) \,{\leq }\,\mathrm {cg}_{n+1}(6{\cdot }y^2{+}4,z) \,{=}\,z$
.
$u\,{<}\,\mathrm {cg}_{n+1}(4{+}6{\cdot }(y{-}1)^2{+}4 {+}2{\cdot }y,z) \,{\leq }\,\mathrm {cg}_{n+1}(6{\cdot }y^2{+}4,z) \,{=}\,z$
.
Lemma 2.21. For
![]() $n\,{\geq }\,2$
, any
$n\,{\geq }\,2$
, any
![]() $\mathcal {S}^{n+1}$
term t, and any
$\mathcal {S}^{n+1}$
term t, and any
![]() $\mathfrak {L}(\mathcal {S}^{n+1})$
formula A, the following rules are derivable in
$\mathfrak {L}(\mathcal {S}^{n+1})$
formula A, the following rules are derivable in
![]() $\mathbb {FA}(\mathcal {S}^{n}) \,{+}\,(\mathrm{Tot}{\text{-}}\gamma _{n+1})$
, where u is a variable that does not appear in terms t,
$\mathbb {FA}(\mathcal {S}^{n}) \,{+}\,(\mathrm{Tot}{\text{-}}\gamma _{n+1})$
, where u is a variable that does not appear in terms t,
![]() $t_0,\ldots ,t_{k-1}$
nor in a formula D (but t,
$t_0,\ldots ,t_{k-1}$
nor in a formula D (but t,
![]() $t_0,\ldots ,t_{k-1}$
may occur in D).
$t_0,\ldots ,t_{k-1}$
may occur in D).
Proof We prove the derivability by meta-induction on t and A respectively.
The only non-trivial case for the former rule is where
![]() $t\,{\equiv }\,\gamma _{n+1}(s)$
.
$t\,{\equiv }\,\gamma _{n+1}(s)$
.

The other cases for the former rule are similar to the cases where
![]() $A\,{\equiv }\, B\,{\land }\,C$
and
$A\,{\equiv }\, B\,{\land }\,C$
and
![]() $A\,{\equiv }\, B\,{\lor }\,C$
for the latter rule. The cases of bounded quantifiers can be treated similarly.
$A\,{\equiv }\, B\,{\lor }\,C$
for the latter rule. The cases of bounded quantifiers can be treated similarly.

Definition 2.22 (
 $A^u$
)
$A^u$
)
For any
![]() $\mathfrak {L}(\mathcal {S}^{n+1})$
formula A, define
$\mathfrak {L}(\mathcal {S}^{n+1})$
formula A, define
![]() $A^u$
as the result of replacing all the subformulae of the forms
$A^u$
as the result of replacing all the subformulae of the forms
![]() $s\,{=}\,t$
and
$s\,{=}\,t$
and
![]() $s\,{<}\,t$
by
$s\,{<}\,t$
by
![]() $s^u\,{=}\,t^u$
and
$s^u\,{=}\,t^u$
and
![]() $s^u\,{<}\,t^u$
, respectively, in A.
$s^u\,{<}\,t^u$
, respectively, in A.
Lemma 2.23. For
![]() $n\,{\geq }\,2$
,
$n\,{\geq }\,2$
,
Theorem 2.24. For
![]() $n\,{\geq }\,2$
and any
$n\,{\geq }\,2$
and any
![]() $\mathfrak {L}(\mathcal {S}^{n+1})$
formula A whose free variables are among
$\mathfrak {L}(\mathcal {S}^{n+1})$
formula A whose free variables are among
![]() $x_0,\ldots ,x_{k-1}$
, if
$x_0,\ldots ,x_{k-1}$
, if
![]() $\mathbb {FA}(\mathcal {S}^{n+1}) \vdash A(x_0,\ldots ,x_{k-1})$
then
$\mathbb {FA}(\mathcal {S}^{n+1}) \vdash A(x_0,\ldots ,x_{k-1})$
then
Proof We can prove this by meta-induction on the derivation of
![]() $A(x_0,\ldots ,x_{k-1})$
in
$A(x_0,\ldots ,x_{k-1})$
in
![]() $\mathbb {FA}(\mathcal {S}^{n+1})$
. For better readability, we omit the parameters
$\mathbb {FA}(\mathcal {S}^{n+1})$
. For better readability, we omit the parameters
![]() $x_0,\ldots , x_{k-1}$
. The non-trivial case is modus ponens (MP): A is inferred from B and
$x_0,\ldots , x_{k-1}$
. The non-trivial case is modus ponens (MP): A is inferred from B and
![]() $B\,{\to }\,A$
. By the meta-induction hypothesis,
$B\,{\to }\,A$
. By the meta-induction hypothesis,
![]() $\mathbb {FA}(\mathcal {S}^n)\,{+}\, (\mathrm{Tot}{\text{-}}\gamma _{n+1})$
proves both
$\mathbb {FA}(\mathcal {S}^n)\,{+}\, (\mathrm{Tot}{\text{-}}\gamma _{n+1})$
proves both
![]() $\mathrm {FLE}_{n,B}(v) \,{\to }\,B^v$
and
$\mathrm {FLE}_{n,B}(v) \,{\to }\,B^v$
and
![]() $\mathrm {FLE}_{n,B\to A}(w) \,{\to }\,(B^w\,{\to }\,A^w)$
. By Lemma 2.23,
$\mathrm {FLE}_{n,B\to A}(w) \,{\to }\,(B^w\,{\to }\,A^w)$
. By Lemma 2.23,
![]() $\mathbb {FA}(\mathcal {S}^n)\,{+}\, (\mathrm{Tot}{\text{-}}\gamma _{n+1})$
also proves
$\mathbb {FA}(\mathcal {S}^n)\,{+}\, (\mathrm{Tot}{\text{-}}\gamma _{n+1})$
also proves
![]() $ v\,{\leq }\,w\,{\land }\,\mathrm {FLE}_{n,B\to A}(w) \,{\to }\, ( \mathrm {FLE}_{n,B}(v)\,{\to }\, (B^v\,{\to }\,A^w))$
. We finally obtain
$ v\,{\leq }\,w\,{\land }\,\mathrm {FLE}_{n,B\to A}(w) \,{\to }\, ( \mathrm {FLE}_{n,B}(v)\,{\to }\, (B^v\,{\to }\,A^w))$
. We finally obtain
to which we can apply Lemma 2.21 twice.
Corollary 2.25.
![]() $\mathbb {FA}(\mathcal {S}^{n+1}) \,{\leq }_{\mathfrak {L}(\mathcal {S}^n)}\, \mathbb {FA}(\mathcal {S}^{n})\,{+}\, (\mathrm{Tot}{\text{-}}\gamma _{n+1})$
for
$\mathbb {FA}(\mathcal {S}^{n+1}) \,{\leq }_{\mathfrak {L}(\mathcal {S}^n)}\, \mathbb {FA}(\mathcal {S}^{n})\,{+}\, (\mathrm{Tot}{\text{-}}\gamma _{n+1})$
for
![]() $n\,{\geq }\,2$
.
$n\,{\geq }\,2$
.
Proof For an
![]() $\mathfrak {L}(\mathcal {S}^n)$
formula A, because
$\mathfrak {L}(\mathcal {S}^n)$
formula A, because
![]() $A^u\,{\equiv }\,A$
, if
$A^u\,{\equiv }\,A$
, if
![]() $\mathbb {FA}(\mathcal {S}^{n+1})\vdash A$
then
$\mathbb {FA}(\mathcal {S}^{n+1})\vdash A$
then
![]() $\mathbb {FA}(\mathcal {S}^{n})\,{+}\, (\mathrm{Tot}{\text{-}}\gamma _{n+1})\vdash \mathrm {FLE}_{n,A}(u)\,{\to }\,A$
by the last lemma, and so, by (Inst),
$\mathbb {FA}(\mathcal {S}^{n})\,{+}\, (\mathrm{Tot}{\text{-}}\gamma _{n+1})\vdash \mathrm {FLE}_{n,A}(u)\,{\to }\,A$
by the last lemma, and so, by (Inst),
![]() $\mathbb {FA}(\mathcal {S}^{n})\,{+}\, (\mathrm{Tot}{\text{-}}\gamma _{n+1})\vdash \mathrm {FLE}_{n,A}(\langle \,\rangle )\,{\to }\,A$
where
$\mathbb {FA}(\mathcal {S}^{n})\,{+}\, (\mathrm{Tot}{\text{-}}\gamma _{n+1})\vdash \mathrm {FLE}_{n,A}(\langle \,\rangle )\,{\to }\,A$
where
![]() $\mathbb {FA}(\mathcal {S}^{n})\vdash \mathrm {FLE}_{n,A}(\langle \,\rangle )$
.
$\mathbb {FA}(\mathcal {S}^{n})\vdash \mathrm {FLE}_{n,A}(\langle \,\rangle )$
.
3 Towards truth theory
3.1 Syntax coding
We now show how to encode syntax. Our theories will be formulated in the following finitist languages.
Definition 3.1. Let
![]() $\mathfrak {L}(\mathcal {S}^n,T_0,\ldots ,T_{m-1})$
denote the finitist language that expands
$\mathfrak {L}(\mathcal {S}^n,T_0,\ldots ,T_{m-1})$
denote the finitist language that expands
![]() $\mathfrak {L}(\mathcal {S}^n)$
by unary relation symbols
$\mathfrak {L}(\mathcal {S}^n)$
by unary relation symbols
![]() $T_0,\ldots ,T_{m-1}$
. In the case of
$T_0,\ldots ,T_{m-1}$
. In the case of
![]() $m\,{=}\,1$
, we write T for
$m\,{=}\,1$
, we write T for
![]() $T_0$
.
$T_0$
.
We first assign different numbers to primitive symbols (including parenthesis), for example,
 $$ \begin{align*} &\lceil (\rceil\,{:=}\,1; \;\; \lceil )\rceil\,{:=}\,3; \;\; \lceil 0\rceil\,{:=}\,5; \;\; \lceil 1\rceil\,{:=}\,7; \;\; \lceil {+}\rceil\,{:=}\,9; \;\; \lceil {\cdot}\rceil\,{:=}\,11; \;\; \lceil {\#}\rceil\,{:=}\,13; \\ & \lceil {=}\rceil\,{:=}\,15; \;\; \lceil {<}\rceil\,{:=}\,17; \;\;\lceil {\neg}\rceil\,{:=}\,19; \;\; \lceil {\land}\rceil\,{:=}\,21; \;\; \lceil {\lor}\rceil\,{:=}\,23; \;\; \lceil {\forall}\rceil\,{:=}\,25; \;\; \lceil {\exists}\rceil\,{:=}\,27; \\ &\lceil x_j\rceil\,{:=}\,29{+}6j; \;\; \lceil\gamma_{j+3}\rceil\,{:=}\,31{+}6j; \;\; \lceil T_j\rceil\,{:=}\,33{+}6j, \end{align*} $$
$$ \begin{align*} &\lceil (\rceil\,{:=}\,1; \;\; \lceil )\rceil\,{:=}\,3; \;\; \lceil 0\rceil\,{:=}\,5; \;\; \lceil 1\rceil\,{:=}\,7; \;\; \lceil {+}\rceil\,{:=}\,9; \;\; \lceil {\cdot}\rceil\,{:=}\,11; \;\; \lceil {\#}\rceil\,{:=}\,13; \\ & \lceil {=}\rceil\,{:=}\,15; \;\; \lceil {<}\rceil\,{:=}\,17; \;\;\lceil {\neg}\rceil\,{:=}\,19; \;\; \lceil {\land}\rceil\,{:=}\,21; \;\; \lceil {\lor}\rceil\,{:=}\,23; \;\; \lceil {\forall}\rceil\,{:=}\,25; \;\; \lceil {\exists}\rceil\,{:=}\,27; \\ &\lceil x_j\rceil\,{:=}\,29{+}6j; \;\; \lceil\gamma_{j+3}\rceil\,{:=}\,31{+}6j; \;\; \lceil T_j\rceil\,{:=}\,33{+}6j, \end{align*} $$
and even numbers to the bounded definable functions, which we loosely consider to be in the languages.
Definition 3.2 (Dot notation)
For a function symbol
![]() $\mathrm {f}$
of arity
$\mathrm {f}$
of arity
![]() $\ell $
(which might be 0, i.e.,
$\ell $
(which might be 0, i.e.,
![]() $\mathrm {f}$
might be constant), let
$\mathrm {f}$
might be constant), let
For any
![]() $\mathfrak {L}(\mathcal {S}^n)$
term
$\mathfrak {L}(\mathcal {S}^n)$
term
![]() $t(x_0,\ldots ,x_{k-1})$
, define the
$t(x_0,\ldots ,x_{k-1})$
, define the
![]() $\mathfrak {L}(\mathcal {S}^2)$
term
$\mathfrak {L}(\mathcal {S}^2)$
term
whose variables are those of
![]() $t(x_0,\ldots ,x_{k-1})$
by meta-recursion on t as follows.
$t(x_0,\ldots ,x_{k-1})$
by meta-recursion on t as follows.

Let
. In particular,
![]() $\ulcorner x_j\urcorner \,{=}\,\langle \lceil x_j\rceil \rangle $
and
$\ulcorner x_j\urcorner \,{=}\,\langle \lceil x_j\rceil \rangle $
and
for any constant c.
For any
![]() $\mathfrak {L}(\mathcal {S}^n)$
formula
$\mathfrak {L}(\mathcal {S}^n)$
formula
![]() $A(x_0,\ldots ,x_{k-1})$
, define an
$A(x_0,\ldots ,x_{k-1})$
, define an
![]() $\mathfrak {L}(\mathcal {S}^2)$
term
$\mathfrak {L}(\mathcal {S}^2)$
term
(in the expanded language) whose variables are the same as the free variables of
![]() $A(x_0,\ldots ,x_{k-1})$
by meta-recursion on A as follows.
$A(x_0,\ldots ,x_{k-1})$
by meta-recursion on A as follows.

Here
stands for
![]() $\langle \lceil (\rceil \rangle \,{*}\,\langle \lceil {\neg }\rceil \rangle \,{*}\,t\,{*}\, \langle \lceil )\rceil \rangle $
, and
$\langle \lceil (\rceil \rangle \,{*}\,\langle \lceil {\neg }\rceil \rangle \,{*}\,t\,{*}\, \langle \lceil )\rceil \rangle $
, and
for
![]() $\langle \lceil (\rceil \rangle \,{*}\,s \,{*}\,\langle \lceil \Box \rceil \rangle \,{*}\,t\,{*}\, \langle \lceil )\rceil \rangle $
for
$\langle \lceil (\rceil \rangle \,{*}\,s \,{*}\,\langle \lceil \Box \rceil \rangle \,{*}\,t\,{*}\, \langle \lceil )\rceil \rangle $
for
![]() $\Box \,{\equiv }\,{\land },{\lor }$
, and
$\Box \,{\equiv }\,{\land },{\lor }$
, and
for
![]() $\langle \lceil (\rceil \rangle \,{*}\,\langle \lceil Q\rceil \rangle \,{*}\, x \,{*}\,s \,{*}\,t\,{*}\, \langle \lceil )\rceil \rangle $
for
$\langle \lceil (\rceil \rangle \,{*}\,\langle \lceil Q\rceil \rangle \,{*}\, x \,{*}\,s \,{*}\,t\,{*}\, \langle \lceil )\rceil \rangle $
for
![]() $Q\,{\equiv }\,\forall ,\exists $
. Let
$Q\,{\equiv }\,\forall ,\exists $
. Let
![]() $\ulcorner A(x_0,\ldots ,x_{k-1})\urcorner $
denote
$\ulcorner A(x_0,\ldots ,x_{k-1})\urcorner $
denote
.
To avoid ambiguity, we apply the dot notation only to minimum units (which might consist of several letters, e.g.,
![]() $\mathrm {num}$
or
$\mathrm {num}$
or
![]() $\mathrm {CTerm}_n$
). Thus, if we apply dot to
$\mathrm {CTerm}_n$
). Thus, if we apply dot to
![]() $\lambda x.A(t(x))$
, we must first introduce
$\lambda x.A(t(x))$
, we must first introduce
![]() $B(x)\,{\equiv }\,A(t(x))$
.
$B(x)\,{\equiv }\,A(t(x))$
.
We define
![]() $\mathfrak {L}(\mathcal {S}^2)$
formulae for syntactical notions, e.g.,
$\mathfrak {L}(\mathcal {S}^2)$
formulae for syntactical notions, e.g.,
![]() $\mathrm {Var}(u)$
,
$\mathrm {Var}(u)$
,
![]() $\mathrm {Term}_n(u)$
,
$\mathrm {Term}_n(u)$
,
![]() $\mathrm {CTerm}_n(u)$
,
$\mathrm {CTerm}_n(u)$
,
![]() $\mathrm {AtForm}_{n,T_{<m}}(u)$
, and
$\mathrm {AtForm}_{n,T_{<m}}(u)$
, and
![]() $\mathrm {Form}_{n,T_{<m}}(u)$
which mean that u is a code of variable, term, closed term, atomic formula, and formula, respectively, all in the sense of
$\mathrm {Form}_{n,T_{<m}}(u)$
which mean that u is a code of variable, term, closed term, atomic formula, and formula, respectively, all in the sense of
![]() $\mathfrak {L}(\mathcal {S}^n,T_0,\ldots ,T_{m-1})$
.
$\mathfrak {L}(\mathcal {S}^n,T_0,\ldots ,T_{m-1})$
.
![]() $\mathrm {Form}^k_{n,T_{<m}}(u, \ulcorner x_0\urcorner ,\ldots ,\ulcorner x_{k-1}\urcorner )$
means additionally that free variables are among
$\mathrm {Form}^k_{n,T_{<m}}(u, \ulcorner x_0\urcorner ,\ldots ,\ulcorner x_{k-1}\urcorner )$
means additionally that free variables are among
![]() $x_0,\ldots ,x_{k-1}$
. Let
$x_0,\ldots ,x_{k-1}$
. Let
![]() $\mathrm {Sent}_{n,T_{<m}}(u)\,{:\equiv }\,\mathrm {Form}^0_{n,T_{<m}}(u)$
. We omit “k” and “
$\mathrm {Sent}_{n,T_{<m}}(u)\,{:\equiv }\,\mathrm {Form}^0_{n,T_{<m}}(u)$
. We omit “k” and “
![]() ${<}\,m$
” if
${<}\,m$
” if
![]() $k,m\,{=}\,1$
.
$k,m\,{=}\,1$
.
Definition 3.3 (Dyadic numeral
 $\mathrm {num}(x)$
)
$\mathrm {num}(x)$
)
By bounded binary recursion, we define a bounded definable function
![]() $\mathrm {num}$
as follows, where
$\mathrm {num}$
as follows, where
![]() $\times $
denotes
$\times $
denotes
![]() $\cdot $
for better readability:
$\cdot $
for better readability:
![]() $\mathrm {num}(0)\,{=}\,\ulcorner 0\urcorner $
;
$\mathrm {num}(0)\,{=}\,\ulcorner 0\urcorner $
;
![]() $\mathrm {num}(1)\,{=}\,\ulcorner 1\urcorner $
;
$\mathrm {num}(1)\,{=}\,\ulcorner 1\urcorner $
;
;

Definition 3.4. By bounded binary recursion, we have bounded definable functions
![]() $\mathrm {sbst}$
and
$\mathrm {sbst}$
and
in
![]() $\mathbb {FA}(\mathcal {S}^2)$
for the syntactical operations of substitution and negation, respectively, with the following defining axioms.
$\mathbb {FA}(\mathcal {S}^2)$
for the syntactical operations of substitution and negation, respectively, with the following defining axioms.

Our
![]() $\mathrm {sbst}$
does not prevent variable collisions. Moreover,
$\mathrm {sbst}$
does not prevent variable collisions. Moreover,
![]() $\mathrm {Term}_n(u)$
does not necessarily imply
$\mathrm {Term}_n(u)$
does not necessarily imply
![]() $\mathrm {Form}_{n,T_{<m}}(w)\,{\land }\,\mathrm {Var}(x) \,{\to }\,\mathrm {Form}_{n,T_{<m}}(\mathrm {sbst}(w,x,u))$
: if a term u contains a variable y then
$\mathrm {Form}_{n,T_{<m}}(w)\,{\land }\,\mathrm {Var}(x) \,{\to }\,\mathrm {Form}_{n,T_{<m}}(\mathrm {sbst}(w,x,u))$
: if a term u contains a variable y then
![]() is not a well formed formula (as far as x occurs in
is not a well formed formula (as far as x occurs in
![]() $v$
). However, in what follows, these do not matter for us, as we basically substitute closed terms only. Note also that the bound for
$v$
). However, in what follows, these do not matter for us, as we basically substitute closed terms only. Note also that the bound for
![]() $\mathrm {sbst}$
essentially requires
$\mathrm {sbst}$
essentially requires
![]() $\#$
while
$\#$
while
![]() $\mathrm {sbst}$
is crucial for a liar sentence.
$\mathrm {sbst}$
is crucial for a liar sentence.
We can also introduce a uniform version of
![]() $\mathrm {sbst}$
. For an assignment a of terms to variables, let the substitution by a applied to
$\mathrm {sbst}$
. For an assignment a of terms to variables, let the substitution by a applied to
![]() $w$
result in
$w$
result in
![]() $\mathrm {usbs}(w,a)$
. The following definition is by bounded binary recursion on
$\mathrm {usbs}(w,a)$
. The following definition is by bounded binary recursion on
![]() $u{*}\langle a\rangle $
, since
$u{*}\langle a\rangle $
, since
![]() $\mathrm {ovw}(a,x,0)\,{\leq }\,a$
implies
$\mathrm {ovw}(a,x,0)\,{\leq }\,a$
implies
![]() . Note
. Note
![]() $\neg \mathrm {Term}_n(0)$
.
$\neg \mathrm {Term}_n(0)$
.
Definition 3.5. Define
![]() $\mathrm {ovw}(a,x,u)$
by the defining axioms
$\mathrm {ovw}(a,x,u)$
by the defining axioms
 $$ \begin{align*} \mathrm{ovw}(a,x,u)(x)\,{=}\,u, \qquad \mathrm{lh}(\mathrm{ovw}(a,x,u))\,{=}\,\mathrm{lh}(a),\\ \mbox{ and }(\forall y\,{<}\,\mathrm{lh}(a)) (y\,{\neq}\,x\,{\to}\,\mathrm{ovw}(a,x,u)(y)\,{=}\,a(y)). \end{align*} $$
$$ \begin{align*} \mathrm{ovw}(a,x,u)(x)\,{=}\,u, \qquad \mathrm{lh}(\mathrm{ovw}(a,x,u))\,{=}\,\mathrm{lh}(a),\\ \mbox{ and }(\forall y\,{<}\,\mathrm{lh}(a)) (y\,{\neq}\,x\,{\to}\,\mathrm{ovw}(a,x,u)(y)\,{=}\,a(y)). \end{align*} $$
We introduce
![]() $\mathrm {usbs}$
with the same defining axioms as
$\mathrm {usbs}$
with the same defining axioms as
![]() $\mathrm {sbst}$
except:
$\mathrm {sbst}$
except:

Remark 3.6. We apply the dot notation
![]() not only to terms generated by the official symbols
not only to terms generated by the official symbols
![]() ${+},{\cdot },{\#},\gamma _3,\ldots ,\gamma _n$
but also to those generated by “unofficial” ones for bounded definable functions (whence the arity of
${+},{\cdot },{\#},\gamma _3,\ldots ,\gamma _n$
but also to those generated by “unofficial” ones for bounded definable functions (whence the arity of
![]() $\mathrm {f}$
is not restricted to 1 or 2 in Definition 3.2). More precisely, fixing a sufficiently large standard number k and k many “unofficial” function symbols, we expand the language
$\mathrm {f}$
is not restricted to 1 or 2 in Definition 3.2). More precisely, fixing a sufficiently large standard number k and k many “unofficial” function symbols, we expand the language
![]() $\mathfrak {L}(\mathcal {S}^n,T_0,\ldots ,T_{m-1})$
with terms (or formulae) comprising less than k occurrences of such symbols. A translation of the expanded language into the original is formalizable in
$\mathfrak {L}(\mathcal {S}^n,T_0,\ldots ,T_{m-1})$
with terms (or formulae) comprising less than k occurrences of such symbols. A translation of the expanded language into the original is formalizable in
![]() $\mathbb {FA}(\mathcal {S}^2)$
, by which we identify codes of formulae in the expanded language with those in the original. We do not add such symbols as full-fledged function symbols, as
$\mathbb {FA}(\mathcal {S}^2)$
, by which we identify codes of formulae in the expanded language with those in the original. We do not add such symbols as full-fledged function symbols, as
![]() $\mathbb {FA}(\mathcal {S}^2)$
cannot always handle non-standardly many occurrences. For example, while
$\mathbb {FA}(\mathcal {S}^2)$
cannot always handle non-standardly many occurrences. For example, while
![]() $\omega _1(x)\,{:=}\,x{\#}x$
is bounded definable in
$\omega _1(x)\,{:=}\,x{\#}x$
is bounded definable in
![]() $\mathbb {FA}(\mathcal {S}^2)$
, the y-th iterate
$\mathbb {FA}(\mathcal {S}^2)$
, the y-th iterate
![]() $\omega _1(\ldots (\omega _1(x))\ldots )$
is translated into a term that has
$\omega _1(\ldots (\omega _1(x))\ldots )$
is translated into a term that has
![]() $\exp (y)$
many occurrences of x. Note that this problem is specific to the syntax-coding by linear strings, but does not emerge for coding by binary trees employed in the authors’ next work [Reference Sato and Walker23].
$\exp (y)$
many occurrences of x. Note that this problem is specific to the syntax-coding by linear strings, but does not emerge for coding by binary trees employed in the authors’ next work [Reference Sato and Walker23].
3.2 Finitist equational truth, lower bounds, and sentence induction
Definition 3.7.
![]() $\mathbb {FET}(\mathcal {S}^n)$
with
$\mathbb {FET}(\mathcal {S}^n)$
with
![]() $n\,{\geq }\,2$
is the
$n\,{\geq }\,2$
is the
![]() $\mathfrak {L}(\mathcal {S}^n,T)$
theory generated by the following non-logical axioms:
$\mathfrak {L}(\mathcal {S}^n,T)$
theory generated by the following non-logical axioms:
-
(
 $\mathbb {FA}(\mathcal {S}^n)$
): all the axioms of
$\mathbb {FA}(\mathcal {S}^n)$
): all the axioms of
 $\mathbb {FA}(\mathcal {S}^n)$
with the schema of induction extended to
$\mathbb {FA}(\mathcal {S}^n)$
with the schema of induction extended to
 $\mathfrak {L}(\mathcal {S}^n,T)$
formulae;
$\mathfrak {L}(\mathcal {S}^n,T)$
formulae; -
(
 $T\mathrm {term}$
):
$T\mathrm {term}$
):

 for any k-ary
for any k-ary
 $\mathcal {S}^n$
function symbol
$\mathcal {S}^n$
function symbol
 $\mathrm {f}$
(including
$\mathrm {f}$
(including
 $k\,{=}\,0$
, i.e., constant symbols);
$k\,{=}\,0$
, i.e., constant symbols); -
(
 $T{=}$
):
$T{=}$
):

and the following non-logical rule, where x must not appear in A nor in t.

The preparatory truth theory
![]() $\mathbb {FET}(\mathcal {S}^n)$
only has the axioms and a rule which govern the behaviour of the truth predicate on equations. The motivation behind the rule (
$\mathbb {FET}(\mathcal {S}^n)$
only has the axioms and a rule which govern the behaviour of the truth predicate on equations. The motivation behind the rule (
![]() $\exists \mbox {-val}$
) was explained already in the Introduction.
$\exists \mbox {-val}$
) was explained already in the Introduction.
Lemma 3.8. For any
![]() $\mathcal {S}^n$
term t whose variables are among
$\mathcal {S}^n$
term t whose variables are among
![]() $x_0,\ldots ,x_{k-1}$
, the theory
$x_0,\ldots ,x_{k-1}$
, the theory
![]() $\mathbb {FET}(\mathcal {S}^n)$
proves:
$\mathbb {FET}(\mathcal {S}^n)$
proves:
-
(i)
 ,
, -
(ii)
 ,
, -
(iii)

 .
.
Proof (i) By the rule (
![]() $\exists \mbox {-val}$
), it suffices to show
$\exists \mbox {-val}$
), it suffices to show
![]() , which follows from (
, which follows from (
![]() $T{=}$
).
$T{=}$
).
(ii) We prove this by meta-induction on t. If t is a variable, this is trivial. If
![]() $t\,{\equiv }\,\mathrm {f}(t_0,\ldots ,t_{\ell -1})$
(possibly
$t\,{\equiv }\,\mathrm {f}(t_0,\ldots ,t_{\ell -1})$
(possibly
![]() $\ell \,{=}\,0$
), by (Inst) we substitute
$\ell \,{=}\,0$
), by (Inst) we substitute
![]() $t_i(x_0,\ldots ,x_{k-1})$
and
$t_i(x_0,\ldots ,x_{k-1})$
and
to
![]() $x_i$
and
$x_i$
and
![]() $u_i$
in (
$u_i$
in (
![]() $T\mbox {term}$
), i.e.,
$T\mbox {term}$
), i.e.,

in which we can replace the premises with
by the meta-induction hypothesis.
(iii) We prove this again by meta-induction on t. If t is a constant or variable, this is by (i). Otherwise, it suffices to see
for a function symbol
![]() $\mathrm {f}$
, provided
$\mathrm {f}$
, provided
![]() ${\bigwedge }_{i<2k}\mathrm {CTerm}_n(w_i)$
. By (
${\bigwedge }_{i<2k}\mathrm {CTerm}_n(w_i)$
. By (
![]() $\exists \mbox {-val}$
) we may assume
$\exists \mbox {-val}$
) we may assume
for fresh
![]() $z_i$
. Use (ii) and (
$z_i$
. Use (ii) and (
![]() $T{=}$
).
$T{=}$
).
We may extend (iii) for non-standard terms with non-standardly many variables: by induction on
![]() $w$
,
$w$
,

We next show
![]() $\mathbb {FA}(\mathcal {S}^{n+1}) \,{\leq }_{\mathfrak {L}(\mathcal {S}^n)}\, \mathbb {FET}(\mathcal {S}^n)$
. This yields the lower bounds of all our truth theories, since they all include
$\mathbb {FA}(\mathcal {S}^{n+1}) \,{\leq }_{\mathfrak {L}(\mathcal {S}^n)}\, \mathbb {FET}(\mathcal {S}^n)$
. This yields the lower bounds of all our truth theories, since they all include
![]() $\mathbb {FET}(\mathcal {S}^n)$
. By Corollary 2.25 it suffices to show
$\mathbb {FET}(\mathcal {S}^n)$
. By Corollary 2.25 it suffices to show
![]() $\mathbb {FA}(\mathcal {S}^{n})\,{+}\, (\mathrm{Tot}{\text{-}}\gamma _{n+1}) \,{\leq }_{\mathfrak {L}(\mathcal {S}^n)}\, \mathbb {FET}(\mathcal {S}^n)$
.
$\mathbb {FA}(\mathcal {S}^{n})\,{+}\, (\mathrm{Tot}{\text{-}}\gamma _{n+1}) \,{\leq }_{\mathfrak {L}(\mathcal {S}^n)}\, \mathbb {FET}(\mathcal {S}^n)$
.
Lemma 3.9.
![]() $\mathbb {FET}(\mathcal {S}^2)$
proves (i)
$\mathbb {FET}(\mathcal {S}^2)$
proves (i)
and (ii)
for
![]() $n\,{\geq }\,3$
, where
$n\,{\geq }\,3$
, where
![]() $\mathcal {S}^2$
functions
$\mathcal {S}^2$
functions
![]() $\mathrm {cgr}_n$
are introduced with the following defining axioms.
$\mathrm {cgr}_n$
are introduced with the following defining axioms.

Proof We first prove (ii). As
![]() $A(0)$
is obvious, by induction, it suffices to show
$A(0)$
is obvious, by induction, it suffices to show
![]() $A(x)\,{\to }\,A(x{+}1)$
, where
$A(x)\,{\to }\,A(x{+}1)$
, where
Assume
![]() $A(x)$
. To show
$A(x)$
. To show
![]() $A(x{+}1)$
, take
$A(x{+}1)$
, take
![]() $y,z\,{<}\,x{+}1$
. Since the claim is obvious for
$y,z\,{<}\,x{+}1$
. Since the claim is obvious for
![]() $y\,{=}\,0$
, we assume
$y\,{=}\,0$
, we assume
![]() $y\,{>}\,0$
. What we have to show is
$y\,{>}\,0$
. What we have to show is
By (
![]() $\exists \mbox {-val}$
), for fresh
$\exists \mbox {-val}$
), for fresh
![]() $v$
we may assume
$v$
we may assume
which implies
by (
![]() $T\mathrm {term}$
). Hence, by (
$T\mathrm {term}$
). Hence, by (
![]() $T{=}$
), what we have to show now is
$T{=}$
), what we have to show now is
If
![]() $z\,{=}\,\gamma _{n}(v)$
, then
$z\,{=}\,\gamma _{n}(v)$
, then
![]() $v\,{<}\,z\,{\leq }\,x$
, and so the induction hypothesis and (
$v\,{<}\,z\,{\leq }\,x$
, and so the induction hypothesis and (
![]() $*$
) yield
$*$
) yield
![]() $\mathrm {Gr}_{\gamma _{n+1}}(|y|{-}1,v)$
which implies
$\mathrm {Gr}_{\gamma _{n+1}}(|y|{-}1,v)$
which implies
![]() $(\exists v\,{<}\,z) (\mathrm {Gr}_{\gamma _{n+1}}(|y|{-}1,v) \,{\land }\,z\,{=}\,\gamma _{n}(v))$
, namely,
$(\exists v\,{<}\,z) (\mathrm {Gr}_{\gamma _{n+1}}(|y|{-}1,v) \,{\land }\,z\,{=}\,\gamma _{n}(v))$
, namely,
![]() $\mathrm {Gr}_{\gamma _{n+1}}(|y|,z)$
.
$\mathrm {Gr}_{\gamma _{n+1}}(|y|,z)$
.
Conversely, assume
![]() $\mathrm {Gr}_{\gamma _{n+1}}(|y|,z)$
, say
$\mathrm {Gr}_{\gamma _{n+1}}(|y|,z)$
, say
![]() $\mathrm {Gr}_{\gamma _{n+1}}(|y|{-}1,w) \,{\land }\,z\,{=}\,\gamma _{n}(w)$
. It suffices to show
$\mathrm {Gr}_{\gamma _{n+1}}(|y|{-}1,w) \,{\land }\,z\,{=}\,\gamma _{n}(w)$
. It suffices to show
![]() $w\,{=}\,v$
. The induction hypothesis yields
$w\,{=}\,v$
. The induction hypothesis yields
![]() by
by
![]() $w\,{<}\,z\,{\leq }\,x$
. By Lemma 3.8(i) and the assumption (
$w\,{<}\,z\,{\leq }\,x$
. By Lemma 3.8(i) and the assumption (
![]() $*$
),
$*$
),
![]() $w\,{=}\,v$
follows from (
$w\,{=}\,v$
follows from (
![]() $T{=}$
).
$T{=}$
).
We can show (i) similarly. Notice
since
![]() $(1{\#}y)\,{=}\,(1{\#}(y/2)){\cdot }2$
for
$(1{\#}y)\,{=}\,(1{\#}(y/2)){\cdot }2$
for
![]() $y\,{>}\,0$
and
$y\,{>}\,0$
and
![]() $\mathrm {Gr}_{\gamma _3}(x,v) \,{\land }\,z\,{=}\,v\,{\#}\,2\,{\to }\, \mathrm {Gr}_{\gamma _3}(x{\cdot }2{+}2,z)$
.
$\mathrm {Gr}_{\gamma _3}(x,v) \,{\land }\,z\,{=}\,v\,{\#}\,2\,{\to }\, \mathrm {Gr}_{\gamma _3}(x{\cdot }2{+}2,z)$
.
Corollary 3.10.
![]() $(\mathrm{Tot}{\text{-}}\gamma _{n+1})$
is a derivable rule in
$(\mathrm{Tot}{\text{-}}\gamma _{n+1})$
is a derivable rule in
![]() $\mathbb {FET}(\mathcal {S}^n)$
.
$\mathbb {FET}(\mathcal {S}^n)$
.
Therefore,
![]() $\mathbb {FA}(\mathcal {S}^{n+1}) \,{\leq }_{\mathfrak {L}(\mathcal {S}^n)}\, \mathbb {FET}(\mathcal {S}^n)$
.
$\mathbb {FA}(\mathcal {S}^{n+1}) \,{\leq }_{\mathfrak {L}(\mathcal {S}^n)}\, \mathbb {FET}(\mathcal {S}^n)$
.
Proof By
![]() $\mathbb {FA}(\mathcal {S}^2) \vdash \mathrm {Gr}_{\gamma _3}((1{\#}y){\cdot }2{-}2,z) \,{\to }\,(\exists v\,{\leq }\,z)\mathrm {Gr}_{\gamma _3}(y,v)$
and the last lemma, (
$\mathbb {FA}(\mathcal {S}^2) \vdash \mathrm {Gr}_{\gamma _3}((1{\#}y){\cdot }2{-}2,z) \,{\to }\,(\exists v\,{\leq }\,z)\mathrm {Gr}_{\gamma _3}(y,v)$
and the last lemma, (
![]() $\exists \mbox {-val}$
) implies
$\exists \mbox {-val}$
) implies
![]() $(\mathrm{Tot}{\text{-}}\gamma _{3})$
.
$(\mathrm{Tot}{\text{-}}\gamma _{3})$
.
Similarly
![]() $\mathbb {FA}(\mathcal {S}^2) \vdash \mathrm {Gr}_{\gamma _3}(y,x) \,{\land }\,\mathrm {Gr}_{\gamma _{n+1}}(|x|,z) \,{\to }\,(\exists v\,{<}\,z)\mathrm {Gr}_{\gamma _{n+1}}(y,v)$
yields
$\mathbb {FA}(\mathcal {S}^2) \vdash \mathrm {Gr}_{\gamma _3}(y,x) \,{\land }\,\mathrm {Gr}_{\gamma _{n+1}}(|x|,z) \,{\to }\,(\exists v\,{<}\,z)\mathrm {Gr}_{\gamma _{n+1}}(y,v)$
yields
![]() $(\mathrm{Tot}{\text{-}}\gamma _{n+1})$
for
$(\mathrm{Tot}{\text{-}}\gamma _{n+1})$
for
![]() $n\,{\geq }\,3$
.
$n\,{\geq }\,3$
.
We can now justify sentence induction. In first-order truth theories, induction on the complexity of sentence is a fundamental tool, but it involves a
![]() $\Pi _1$
induction formula. Note that
$\Pi _1$
induction formula. Note that
![]() does not imply
does not imply
![]() $\mathrm {Sent}_{n,T}(v)$
but only
$\mathrm {Sent}_{n,T}(v)$
but only
![]() $\mathrm {Sent}_{n,T}(\mathrm {sbst}(v,x, \mathrm {num}(z)))$
, whereas
$\mathrm {Sent}_{n,T}(\mathrm {sbst}(v,x, \mathrm {num}(z)))$
, whereas
![]() is not guaranteed.
is not guaranteed.
Theorem 3.11 (Sentence induction)
The following rule, with eigenvariables
![]() $u,v,y$
, is derivable in
$u,v,y$
, is derivable in
![]() $\mathbb {FET}(\mathcal {S}^n)$
.
$\mathbb {FET}(\mathcal {S}^n)$
.

Proof Define
![]() $\mathrm {AssBd}(a,p)$
as follows, meaning that a substitutes variables by either themselves or numerals for numbers
$\mathrm {AssBd}(a,p)$
as follows, meaning that a substitutes variables by either themselves or numerals for numbers
![]() ${<}\,p$
:
${<}\,p$
:
We have an
![]() $\mathcal {S}^3$
term
$\mathcal {S}^3$
term
![]() $\mathrm {boa}(p,q)$
which bounds all such a’s of length q, i.e.,
$\mathrm {boa}(p,q)$
which bounds all such a’s of length q, i.e.,
where a is free. Moreover, we bound the value of
![]() $\mathrm {usbs}(v,a)$
by
$\mathrm {usbs}(v,a)$
by
![]() $\gamma _{n+1}$
together with
$\gamma _{n+1}$
together with
![]() $\mathrm {ht}$
, defined as follows, where
$\mathrm {ht}$
, defined as follows, where
![]() $\star \,{\equiv }\,{+},{\cdot },{\#} \mbox { and }\Box \,{\equiv }\,{\land },{\lor } \mbox { and }Q\,{\equiv }\,\forall ,\exists $
.
$\star \,{\equiv }\,{+},{\cdot },{\#} \mbox { and }\Box \,{\equiv }\,{\land },{\lor } \mbox { and }Q\,{\equiv }\,\forall ,\exists $
.

Fix possibly non-standard p and q. Since we may assume to have
![]() $w'$
with
$w'$
with
![]() $\mathrm {Frag}_{\gamma _{n+1}}(w') \,{\land }\,\mathrm {lh}(w')\,{\geq }\,p$
by Lemma 2.21, induction on
$\mathrm {Frag}_{\gamma _{n+1}}(w') \,{\land }\,\mathrm {lh}(w')\,{\geq }\,p$
by Lemma 2.21, induction on
![]() $v$
shows
$v$
shows

By
![]() $(\mathrm{Tot}{\text{-}}\gamma _{3})$
we may assume the existence of
$(\mathrm{Tot}{\text{-}}\gamma _{3})$
we may assume the existence of
![]() $r\,{=}\,\mathrm {boa}(\gamma _{n+1}(p),q)$
. By definition, this implies
$r\,{=}\,\mathrm {boa}(\gamma _{n+1}(p),q)$
. By definition, this implies
![]() $\mathrm {AssBd}(a,\gamma _{n+1}(p))\,{\to }\, (\exists b\,{<}\,r)(\forall x\,{<}\,q)(b(x)\,{=}\,a(x))$
. By induction on
$\mathrm {AssBd}(a,\gamma _{n+1}(p))\,{\to }\, (\exists b\,{<}\,r)(\forall x\,{<}\,q)(b(x)\,{=}\,a(x))$
. By induction on
![]() $w$
, we now prove
$w$
, we now prove
 $$\begin{align*}(\forall a\,{<}\,r)\begin{pmatrix}\begin{pmatrix} \mathrm{lh}(a)\,{\leq}\,q\,{\land}\, \mathrm{Form}_{n,T}(w)\,{\land}\, \mathrm{lh}(w)\,{\leq}\,p\\{\land}\,w\,{\leq}\,q\,{\land}\, \mathrm{AssBd}(a,\gamma_{n+1}(p{-}\mathrm{ht}(w))) \end{pmatrix}{\to}\,A(\mathrm{usbs}(w,a))\end{pmatrix}.\end{align*}$$
$$\begin{align*}(\forall a\,{<}\,r)\begin{pmatrix}\begin{pmatrix} \mathrm{lh}(a)\,{\leq}\,q\,{\land}\, \mathrm{Form}_{n,T}(w)\,{\land}\, \mathrm{lh}(w)\,{\leq}\,p\\{\land}\,w\,{\leq}\,q\,{\land}\, \mathrm{AssBd}(a,\gamma_{n+1}(p{-}\mathrm{ht}(w))) \end{pmatrix}{\to}\,A(\mathrm{usbs}(w,a))\end{pmatrix}.\end{align*}$$
For example, consider
![]() . (
. (
![]() ) yields
) yields
![]() for some
for some
![]() $z\,{\leq }\,\gamma _{n+1}(p{-}\mathrm {ht}(w){+}\mathrm {ht}(u)) \,{=}\,\gamma _{n+1}(p{-}\mathrm {ht}(v))$
. Let
$z\,{\leq }\,\gamma _{n+1}(p{-}\mathrm {ht}(w){+}\mathrm {ht}(u)) \,{=}\,\gamma _{n+1}(p{-}\mathrm {ht}(v))$
. Let
![]() $b\,{:=}\,\mathrm {ovw}(a,x,\mathrm {num}(y))\,{<}\,r$
for any
$b\,{:=}\,\mathrm {ovw}(a,x,\mathrm {num}(y))\,{<}\,r$
for any
![]() $y\,{<}\,z$
. Then we have
$y\,{<}\,z$
. Then we have
![]() $\mathrm {AssBd}(b,\gamma _{n+1}(p{-}\mathrm {ht}(v)))$
and
$\mathrm {AssBd}(b,\gamma _{n+1}(p{-}\mathrm {ht}(v)))$
and
![]() $A(\mathrm {usbs}(v,b))$
by induction hypothesis. By
$A(\mathrm {usbs}(v,b))$
by induction hypothesis. By
![]() $\mathrm {usbs}(v,b)\,{=}\, \mathrm {sbst}(\mathrm {usbs}(v,\mathrm {ovw}(a,x,0)),x,\mathrm {num}(y))$
, since
$\mathrm {usbs}(v,b)\,{=}\, \mathrm {sbst}(\mathrm {usbs}(v,\mathrm {ovw}(a,x,0)),x,\mathrm {num}(y))$
, since
![]() $y\,{<}\,z$
is arbitrary, the third premise of the rule yields
$y\,{<}\,z$
is arbitrary, the third premise of the rule yields
![]() $A(\mathrm {usbs}(w,a))$
.
$A(\mathrm {usbs}(w,a))$
.
Since p and q are arbitrary, setting
![]() $p\,{:=}\,\mathrm {lh}(u)$
,
$p\,{:=}\,\mathrm {lh}(u)$
,
![]() $q\,{:=}\,u$
and
$q\,{:=}\,u$
and
![]() $a\,{:=}\,\langle \,\rangle $
, we have
$a\,{:=}\,\langle \,\rangle $
, we have
![]() $\mathrm {Sent}_{n,T}(u)\,{\to }\,A(u)$
.
$\mathrm {Sent}_{n,T}(u)\,{\to }\,A(u)$
.
4 Finitist truth theories of our main interest
4.1 Finitist typed truth
The finitist theory of compositional truth
![]() $\mathbb {FCT}(\mathcal {S}^n)$
extends
$\mathbb {FCT}(\mathcal {S}^n)$
extends
![]() $\mathbb {FET}(\mathcal {S}^n)$
by the axioms which govern the behaviour of the truth predicate on compound formulae generated by propositional connectives and bounded quantifiers. However, in the scope of the truth predicate, only (codes of) those formulae without truth predicate can occur. In other words, the truth predicate cannot occur in the scope of itself. (More precisely, although we have such self-applied formulae in the language, we exclude their codes from the scope of our truth axioms.)
$\mathbb {FET}(\mathcal {S}^n)$
by the axioms which govern the behaviour of the truth predicate on compound formulae generated by propositional connectives and bounded quantifiers. However, in the scope of the truth predicate, only (codes of) those formulae without truth predicate can occur. In other words, the truth predicate cannot occur in the scope of itself. (More precisely, although we have such self-applied formulae in the language, we exclude their codes from the scope of our truth axioms.)
Definition 4.1 (Finitist compositional truth)
For
![]() $n\,{\geq }\,2$
, let
$n\,{\geq }\,2$
, let
![]() $\mathbb {FCT}(\mathcal {S}^n)$
extend
$\mathbb {FCT}(\mathcal {S}^n)$
extend
![]() $\mathbb {FET}(\mathcal {S}^n)$
by the following non-logical axioms, where
$\mathbb {FET}(\mathcal {S}^n)$
by the following non-logical axioms, where
![]() $\mathrm {Sent}_n$
and
$\mathrm {Sent}_n$
and
![]() $\mathrm {Form}_n$
stand for
$\mathrm {Form}_n$
stand for
![]() $\mathrm {Sent}_{n,T_{<0}}$
and
$\mathrm {Sent}_{n,T_{<0}}$
and
![]() $\mathrm {Form}_{n,T_{<0}}$
respectively:
$\mathrm {Form}_{n,T_{<0}}$
respectively:
-
(
 $T{<}$
):
$T{<}$
):
 ;
; -
(
 $T{\neg }\mathrm {Atom}$
):
$T{\neg }\mathrm {Atom}$
):

 ;
; -
(
 $T{\land }^{}_{\mathrm {tp}}$
):
$T{\land }^{}_{\mathrm {tp}}$
):
 ;
; -
(
 $T{\lor }^{}_{\mathrm {tp}}$
):
$T{\lor }^{}_{\mathrm {tp}}$
):
 ;
; -
(
 $T\forall ^{}_{\mathrm {tp}}$
):
$T\forall ^{}_{\mathrm {tp}}$
):

 ;
; -
(
 $T\exists ^{}_{\mathrm {tp}}$
):
$T\exists ^{}_{\mathrm {tp}}$
):

 .
.
The last four axioms are for (possibly) non-standard sentences, while the schemata (Truth-Negation) and (Truth-Truth) in the Introduction were only for standard ones. The subscript “tp” stands for “typed” truth.
Remark 4.2. In the first-order setting, it is also common to formulate the truth axiom for
![]() $\forall $
as follows:
$\forall $
as follows:

A discussion on the difference between the two alternative formulations can be found in [Reference Wcisło and Łełyk30, Section 1]. However, since there seems to be no way to bound
![]() $w$
in truth axioms for bounded quantifiers, we consider only substitutions by numerals.
$w$
in truth axioms for bounded quantifiers, we consider only substitutions by numerals.
Within
![]() $\mathbb {FCT}(\mathcal {S}^n)$
, we can prove the uniform Tarski biconditional in our setting.
$\mathbb {FCT}(\mathcal {S}^n)$
, we can prove the uniform Tarski biconditional in our setting.
Theorem 4.3. For any
![]() $\mathfrak {L}(\mathcal {S}^n)$
formula
$\mathfrak {L}(\mathcal {S}^n)$
formula
![]() $A(x_0,\ldots ,x_{k-1})$
whose free variables are among
$A(x_0,\ldots ,x_{k-1})$
whose free variables are among
![]() $x_0,\ldots ,x_{k-1}$
,
$x_0,\ldots ,x_{k-1}$
,
Proof We prove the statement by meta-induction on A. We make a case distinction based on the outer-most connective of A. In all the cases, we work in
![]() $\mathbb {FCT}(\mathcal {S}^n)$
, and assume
$\mathbb {FCT}(\mathcal {S}^n)$
, and assume
![]() for
for
![]() $i\,{<}\,k$
. Then, by Lemma 3.8(ii),
$i\,{<}\,k$
. Then, by Lemma 3.8(ii),
![]() for any term
for any term
![]() $t_i$
.
$t_i$
.
First consider the cases where A is an atomic formula or the negation of an atomic formula. Take the case of
![]() $A\,{\equiv }\,\neg (t_0\,{<}\,t_1)$
. Now (
$A\,{\equiv }\,\neg (t_0\,{<}\,t_1)$
. Now (
![]() $T{\neg }\mbox {Atom}$
) implies that
$T{\neg }\mbox {Atom}$
) implies that
![]() and
and
![]() $\neg (t_0(x_0,\ldots ,x_{k-1}) \,{<}\,t_1(x_0,\ldots ,x_{k-1}))$
are equivalent.
$\neg (t_0(x_0,\ldots ,x_{k-1}) \,{<}\,t_1(x_0,\ldots ,x_{k-1}))$
are equivalent.
The cases of conjunction and disjunction are easy by (
![]() $T{\land }_{\mathrm {tp}}$
) and (
$T{\land }_{\mathrm {tp}}$
) and (
![]() $T{\lor }_{\mathrm {tp}}$
).
$T{\lor }_{\mathrm {tp}}$
).
Finally, in the case of bounded quantifiers, let
Then
![]() is equivalent to
is equivalent to
![]() $(\forall y\,{<}\,t_0(x_0,\ldots ,x_{k-1})) B(x_0,\ldots ,x_{k-1},y))$
by (
$(\forall y\,{<}\,t_0(x_0,\ldots ,x_{k-1})) B(x_0,\ldots ,x_{k-1},y))$
by (
![]() $T\forall _{\mathrm {tp}}$
) and by the meta-induction hypothesis.
$T\forall _{\mathrm {tp}}$
) and by the meta-induction hypothesis.
We now show the formula version of Lemma 3.8(iii) (but without T).
Lemma 4.4. For any
![]() $\mathfrak {L}(\mathcal {S}^n)$
formula A whose free variables are among
$\mathfrak {L}(\mathcal {S}^n)$
formula A whose free variables are among
![]() $x_0,\ldots ,x_{k-1}$
,
$x_0,\ldots ,x_{k-1}$
,
Proof By (
![]() $\exists \mbox {-val}$
), it suffices to show
$\exists \mbox {-val}$
), it suffices to show

By (
![]() $T{=}$
) the premise implies
$T{=}$
) the premise implies
![]() ${\bigwedge }_{i<k}x_i\,{=}\,y_i$
, and so
${\bigwedge }_{i<k}x_i\,{=}\,y_i$
, and so
![]() $A(x_0,\ldots ,x_{k-1})\,{\leftrightarrow }\,A(y_0,\ldots ,y_{k-1})$
. Apply Theorem 4.3.
$A(x_0,\ldots ,x_{k-1})\,{\leftrightarrow }\,A(y_0,\ldots ,y_{k-1})$
. Apply Theorem 4.3.
This lemma may also be proved by meta-induction on the formula A. As opposed to the proof above, the proof by meta-induction can be extended to (the codes of) non-standard formulae A similarly to Lemma 3.8(iii) by sentence induction, where the number k of arguments can also be non-standard.
In
![]() $\mathbb {FCT}(\mathcal {S}^n)$
, we ignored those formulae in which the truth predicate T has itself (or, more precisely, its code
$\mathbb {FCT}(\mathcal {S}^n)$
, we ignored those formulae in which the truth predicate T has itself (or, more precisely, its code
![]() $\ulcorner T\urcorner $
) in its scope. One way to consider such formulae consistently is to ramify T into several different ones
$\ulcorner T\urcorner $
) in its scope. One way to consider such formulae consistently is to ramify T into several different ones
![]() $T_0$
,
$T_0$
,
![]() $T_1$
,…. This leads us to the next kind of truth theory, the finitist theories of ramified truth.
$T_1$
,…. This leads us to the next kind of truth theory, the finitist theories of ramified truth.
Definition 4.5 (Finitist ramified truth)
For
![]() $n\,{\geq }\,2$
, the
$n\,{\geq }\,2$
, the
![]() $\mathfrak {L}(\mathcal {S}^n,T_0,\ldots ,T_{m-1})$
theory
$\mathfrak {L}(\mathcal {S}^n,T_0,\ldots ,T_{m-1})$
theory
![]() $\mathbb {FRT}_m(\mathcal {S}^n)$
is generated by the following non-logical axioms:
$\mathbb {FRT}_m(\mathcal {S}^n)$
is generated by the following non-logical axioms:
-
(
 $\mathbb {FA}(\mathcal {S}^n)$
): all the axioms of
$\mathbb {FA}(\mathcal {S}^n)$
): all the axioms of
 $\mathbb {FA}(\mathcal {S}^n)$
with the schema of induction extended to
$\mathbb {FA}(\mathcal {S}^n)$
with the schema of induction extended to
 $\mathfrak {L}(\mathcal {S}^n,T_0,\ldots ,T_{m-1})$
formulae;
$\mathfrak {L}(\mathcal {S}^n,T_0,\ldots ,T_{m-1})$
formulae; -
(
 $T\mathrm {term}$
):
$T\mathrm {term}$
):

 for any k-ary
for any k-ary
 $\mathcal {S}^n$
function symbol
$\mathcal {S}^n$
function symbol
 $\mathrm {f}$
(including
$\mathrm {f}$
(including
 $k\,{=}\,0$
, i.e., constant symbols);
$k\,{=}\,0$
, i.e., constant symbols); -
(
 $T\mathrm {Atom}$
):
$T\mathrm {Atom}$
):

 ;
; -
(
 $T{\neg }\mathrm {Atom}$
):
$T{\neg }\mathrm {Atom}$
):

 ;
; -
(
 $TT^{}_{\mathrm {tp}}$
):
$TT^{}_{\mathrm {tp}}$
):
 for
for
 $i\,{<}\,j$
;
$i\,{<}\,j$
; -
(
 $T\neg T^{}_{\mathrm {tp}}$
):
$T\neg T^{}_{\mathrm {tp}}$
):
 for
for
 $i\,{<}\,j$
;
$i\,{<}\,j$
; -
(
 $T{\land }^{}_{\mathrm {tp}}$
):
$T{\land }^{}_{\mathrm {tp}}$
):
 ;
; -
(
 $T{\lor }^{}_{\mathrm {tp}}$
):
$T{\lor }^{}_{\mathrm {tp}}$
):
 ;
; -
(
 $T\forall ^{}_{\mathrm {tp}}$
):
$T\forall ^{}_{\mathrm {tp}}$
):

 ;
; -
(
 $T\exists ^{}_{\mathrm {tp}}$
):
$T\exists ^{}_{\mathrm {tp}}$
):

 ,
,
and the following non-logical rules: for any
![]() $\mathfrak {L}(\mathcal {S}^n,T_0,\ldots ,T_{m-1})$
formula A and
$\mathfrak {L}(\mathcal {S}^n,T_0,\ldots ,T_{m-1})$
formula A and
![]() $\mathcal {S}^n$
term t in both of which x does not occur.
$\mathcal {S}^n$
term t in both of which x does not occur.

Lemma 4.6. For any
![]() $i,j\,{<}\,m$
,
$i,j\,{<}\,m$
,
Proof Let
![]() $\mathrm {SubTerm}(v,u)$
express that
$\mathrm {SubTerm}(v,u)$
express that
![]() $v$
is a subterm of u. For any fixed p, by induction on u we can prove
$v$
is a subterm of u. For any fixed p, by induction on u we can prove

Let
![]() $w$
be the bounding term of u (in the sense defined before Lemma 2.10). By
$w$
be the bounding term of u (in the sense defined before Lemma 2.10). By
![]() $(\exists \mbox {-val})$
we have p with
$(\exists \mbox {-val})$
we have p with
![]() , which implies the second premise. If
, which implies the second premise. If
![]() then
then
![]() $x\,{\leq }\,p$
and so
$x\,{\leq }\,p$
and so
![]() .
.
Lemma 4.7. For
![]() $j\,{\leq }\,i\,{\leq }\,m$
,
$j\,{\leq }\,i\,{\leq }\,m$
,
Proof We can show this by sentence induction (Theorem 3.11). Use Lemma 4.6 for the latter conjunct at the base case.
In
![]() $\mathbb {FRT}_{m+1}(\mathcal {S}^n)$
, we can extend the uniform Tarski biconditional (Theorem 4.3) and internal reflection of equality (Lemma 4.4) to
$\mathbb {FRT}_{m+1}(\mathcal {S}^n)$
, we can extend the uniform Tarski biconditional (Theorem 4.3) and internal reflection of equality (Lemma 4.4) to
![]() $\mathfrak {L}(\mathcal {S}^n,T_0,\ldots ,T_{m-1})$
.
$\mathfrak {L}(\mathcal {S}^n,T_0,\ldots ,T_{m-1})$
.
Theorem 4.8. For any
![]() $\mathfrak {L}(\mathcal {S}^n,T_0,\ldots ,T_{m-1})$
formula
$\mathfrak {L}(\mathcal {S}^n,T_0,\ldots ,T_{m-1})$
formula
![]() $A(x_0,\ldots ,x_{k-1})$
whose free variables are among
$A(x_0,\ldots ,x_{k-1})$
whose free variables are among
![]() $x_0,\ldots ,x_{k-1}$
,
$x_0,\ldots ,x_{k-1}$
,

Proof We can prove this by replacing T with
![]() $T_m$
in the proof of Theorem 4.3 and by adding two more cases which are covered by (
$T_m$
in the proof of Theorem 4.3 and by adding two more cases which are covered by (
![]() $TT^{}_{\mathrm {tp}}$
) and (
$TT^{}_{\mathrm {tp}}$
) and (
![]() $T\neg T^{}_{\mathrm {tp}}$
).
$T\neg T^{}_{\mathrm {tp}}$
).
Theorem 4.8 implies the following lemma, the internal reflection of equality. This can, as Lemma 4.4, be extended to non-standard formulae A with non-standardly many arguments.
Lemma 4.9. For any
![]() $\mathfrak {L}(\mathcal {S}^n,T_0,\ldots ,T_{m-1})$
formula A whose free variables are among
$\mathfrak {L}(\mathcal {S}^n,T_0,\ldots ,T_{m-1})$
formula A whose free variables are among
![]() $x_0,\ldots ,x_{k-1}$
,
$x_0,\ldots ,x_{k-1}$
,

Note that
![]() $\mathbb {FRT}_0(\mathcal {S}^n)$
is identical with
$\mathbb {FRT}_0(\mathcal {S}^n)$
is identical with
![]() $\mathbb {FA}(\mathcal {S}^n)$
and that
$\mathbb {FA}(\mathcal {S}^n)$
and that
![]() $\mathbb {FRT}_1(\mathcal {S}^n)$
is identical with
$\mathbb {FRT}_1(\mathcal {S}^n)$
is identical with
![]() $\mathbb {FCT}(\mathcal {S}^n)$
. Also,
$\mathbb {FCT}(\mathcal {S}^n)$
. Also,
![]() $\mathbb {FRT}_m(\mathcal {S}^n)$
is included in
$\mathbb {FRT}_m(\mathcal {S}^n)$
is included in
![]() $\mathbb {FRT}_{m+1}(\mathcal {S}^n)$
along the obvious inclusion. Let us also consider the “limit” of these inclusions.
$\mathbb {FRT}_{m+1}(\mathcal {S}^n)$
along the obvious inclusion. Let us also consider the “limit” of these inclusions.
Definition 4.10. Let
![]() $\mathbb {FRT}_{<\omega }(\mathcal {S}^n)$
be the union of
$\mathbb {FRT}_{<\omega }(\mathcal {S}^n)$
be the union of
![]() $\mathbb {FRT}_m(\mathcal {S}^n)$
for
$\mathbb {FRT}_m(\mathcal {S}^n)$
for
![]() $m\,{\in }\,\omega $
, formulated in
$m\,{\in }\,\omega $
, formulated in
![]() $\bigcup _{m\in \omega }\mathfrak {L}(\mathcal {S}^n, T_0,\ldots ,T_{m-1})$
.
$\bigcup _{m\in \omega }\mathfrak {L}(\mathcal {S}^n, T_0,\ldots ,T_{m-1})$
.
We may go even further. For any ordinal
![]() $\alpha $
in some standard ordinal notation system, we may define
$\alpha $
in some standard ordinal notation system, we may define
![]() $\mathbb {FRT}_\alpha (\mathcal {S}^n)$
. Nonetheless, we do not consider these theories for the following reasons. First, we cannot even state the well-foundedness of
$\mathbb {FRT}_\alpha (\mathcal {S}^n)$
. Nonetheless, we do not consider these theories for the following reasons. First, we cannot even state the well-foundedness of
![]() $\alpha $
. For example, even if we try to formulate it by a transfinite induction rule, there is no way to express the induction hypothesis without unbounded quantifiers. Second,
$\alpha $
. For example, even if we try to formulate it by a transfinite induction rule, there is no way to express the induction hypothesis without unbounded quantifiers. Second,
![]() $\mathbb {FRT}_{<\omega }(\mathcal {S}^n)$
suffices for the following comparison to finitist analogues of two other famous truth theories.
$\mathbb {FRT}_{<\omega }(\mathcal {S}^n)$
suffices for the following comparison to finitist analogues of two other famous truth theories.
4.2 Finitist self-referential truth
To obtain consistent theories of untyped or self-referential truth, certain naïve truth axioms have to be dropped. Two theories are particularly well known from the first-order setting: Kripke–Feferman truth and Friedman–Sheard truth, as discussed in the Introduction.
Let us start with the finitist theory of Kripke–Feferman truth.
Definition 4.11 (Finitist Kripke–Feferman truth)
For
![]() $n\,{\geq }\,2$
, the
$n\,{\geq }\,2$
, the
![]() $\mathfrak {L}(\mathcal {S}^n,T)$
theory
$\mathfrak {L}(\mathcal {S}^n,T)$
theory
![]() $\mathbb {FKF}(\mathcal {S}^n)$
is generated by the following non-logical axioms:
$\mathbb {FKF}(\mathcal {S}^n)$
is generated by the following non-logical axioms:
-
(
 $\mathbb {FCT}(\mathcal {S}^n)$
): all the axioms of
$\mathbb {FCT}(\mathcal {S}^n)$
): all the axioms of
 $\mathbb {FCT}(\mathcal {S}^n)$
;
$\mathbb {FCT}(\mathcal {S}^n)$
; -
(
 $TT^{}_{\mathrm {sr}}$
):
$TT^{}_{\mathrm {sr}}$
):
 ;
; -
(
 $T{\neg }T^{}_{\mathrm {kf}}$
):
$T{\neg }T^{}_{\mathrm {kf}}$
):
 ;
; -
(
 $T{\land }^{}_{\mathrm {sr}}$
):
$T{\land }^{}_{\mathrm {sr}}$
):
 ;
; -
(
 $T{\lor }^{}_{\mathrm {sr}}$
):
$T{\lor }^{}_{\mathrm {sr}}$
):
 ;
; -
(
 $T\forall ^{}_{\mathrm {sr}}$
):
$T\forall ^{}_{\mathrm {sr}}$
):

 ;
; -
(
 $T\exists ^{}_{\mathrm {sr}}$
):
$T\exists ^{}_{\mathrm {sr}}$
):

 ,
,
and the non-logical rule (
![]() $\exists \mbox {-val}$
) as in
$\exists \mbox {-val}$
) as in
![]() $\mathbb {FET}(\mathcal {S}^n)$
.
$\mathbb {FET}(\mathcal {S}^n)$
.
In other words, we define
![]() $\mathbb {FKF}(\mathcal {S}^n)$
from
$\mathbb {FKF}(\mathcal {S}^n)$
from
![]() $\mathbb {FCT}(\mathcal {S}^n)$
by strengthening the truth axioms for
$\mathbb {FCT}(\mathcal {S}^n)$
by strengthening the truth axioms for
![]() $\land $
,
$\land $
,
![]() $\lor $
,
$\lor $
,
![]() $\forall $
,
$\forall $
,
![]() $\exists $
to codes of non-typed formulae and by adding (
$\exists $
to codes of non-typed formulae and by adding (
![]() $TT^{}_{\mathrm {sr}}$
) and (
$TT^{}_{\mathrm {sr}}$
) and (
![]() $T\neg T^{}_{\mathrm {kf}}$
). Since the axiom (
$T\neg T^{}_{\mathrm {kf}}$
). Since the axiom (
![]() $T\neg T^{}_{\mathrm {kf}}$
) is specific to Kripke–Feferman truth, we write “kf” for its subscript, while “sr” of the others stands for “self-referential”.
$T\neg T^{}_{\mathrm {kf}}$
) is specific to Kripke–Feferman truth, we write “kf” for its subscript, while “sr” of the others stands for “self-referential”.
Now the uniform Tarski biconditional schema (Theorem 4.8) can be extended to formulae with the truth predicate T, but with a restriction: T appears only positively, i.e., not in the scope of
![]() $\neg $
. (Recall that
$\neg $
. (Recall that
![]() $\neg $
applies only to atomic formulae.)
$\neg $
applies only to atomic formulae.)
Lemma 4.12 (Uniform Tarski biconditional for T-positive formulae)
For any
![]() $\mathfrak {L}(\mathcal {S}^n,T)$
formula
$\mathfrak {L}(\mathcal {S}^n,T)$
formula
![]() $A(x_0,\ldots ,x_{k-1})$
whose free variables are among
$A(x_0,\ldots ,x_{k-1})$
whose free variables are among
![]() $x_0,\ldots ,x_{k-1}$
and in which the relation symbol T occurs only positively,
$x_0,\ldots ,x_{k-1}$
and in which the relation symbol T occurs only positively,
Before moving to the next truth theory, we explain the
![]() $\omega $
-soundness of our finitist theories due to the linguistic restriction. Any finitist formula is absolute between the standard model
$\omega $
-soundness of our finitist theories due to the linguistic restriction. Any finitist formula is absolute between the standard model
![]() $\omega $
and any non-standard model. Let us explain this more precisely. First, for any
$\omega $
and any non-standard model. Let us explain this more precisely. First, for any
![]() $\mathfrak {L}(\mathcal {S}^n,T)$
structure
$\mathfrak {L}(\mathcal {S}^n,T)$
structure
![]() $(M,T^M)$
, we know that
$(M,T^M)$
, we know that
![]() $(M,T^M)\models A(k_0,\ldots ,k_{\ell -1}) \,{\leftrightarrow }\, (\omega ,T^M{\cap }\,\omega )\models A(k_0,\ldots ,k_{\ell -1})$
for any
$(M,T^M)\models A(k_0,\ldots ,k_{\ell -1}) \,{\leftrightarrow }\, (\omega ,T^M{\cap }\,\omega )\models A(k_0,\ldots ,k_{\ell -1})$
for any
![]() $\mathfrak {L}(\mathcal {S}^n,T)$
formula A and
$\mathfrak {L}(\mathcal {S}^n,T)$
formula A and
![]() $k_0,\ldots ,k_{\ell -1}\,{\in }\,\omega $
. Hence, if an
$k_0,\ldots ,k_{\ell -1}\,{\in }\,\omega $
. Hence, if an
![]() $\mathfrak {L}(\mathcal {S}^n,T)$
theory
$\mathfrak {L}(\mathcal {S}^n,T)$
theory
![]() $\mathbb {T}$
has a model, then it has a standard model, i.e., a model whose elements are only standard natural numbers. This means that the consistency of
$\mathbb {T}$
has a model, then it has a standard model, i.e., a model whose elements are only standard natural numbers. This means that the consistency of
![]() $\mathbb {T}$
implies the
$\mathbb {T}$
implies the
![]() $\omega $
-soundness of
$\omega $
-soundness of
![]() $\mathbb {T}$
.
$\mathbb {T}$
.
Hence, the finitist theory of Friedman–Sheard truth, which we introduce next, is
![]() $\omega $
-sound (if consistent), contrastingly to the well known fact that the first-order Friedman–Sheard truth theory is
$\omega $
-sound (if consistent), contrastingly to the well known fact that the first-order Friedman–Sheard truth theory is
![]() $\omega $
-inconsistent.
$\omega $
-inconsistent.
Definition 4.13 (Finitist Friedman–Sheard truth)
For
![]() $n\,{\geq }\,2$
, the
$n\,{\geq }\,2$
, the
![]() $\mathfrak {L}(\mathcal {S}^n,T)$
theory
$\mathfrak {L}(\mathcal {S}^n,T)$
theory
![]() $\mathbb {FFS}(\mathcal {S}^n)$
is generated by the following non-logical axioms:
$\mathbb {FFS}(\mathcal {S}^n)$
is generated by the following non-logical axioms:
-
(
 $\mathbb {FCT}(\mathcal {S}^n)$
): all the axioms of
$\mathbb {FCT}(\mathcal {S}^n)$
): all the axioms of
 $\mathbb {FCT}(\mathcal {S}^n)$
;
$\mathbb {FCT}(\mathcal {S}^n)$
; -
(
 $TT{=}$
):
$TT{=}$
):
 $\mathrm {CTerm}_n(u)\,{\land }\, \mathrm {CTerm}_n(v)\,{\land }\, \mathrm {CTerm}_n(x)\,{\land }\, \mathrm {CTerm}_n(y)$
$\mathrm {CTerm}_n(u)\,{\land }\, \mathrm {CTerm}_n(v)\,{\land }\, \mathrm {CTerm}_n(x)\,{\land }\, \mathrm {CTerm}_n(y)$
 ;
; -
(
 $T{\land }^{}_{\mathrm {sr}}$
):
$T{\land }^{}_{\mathrm {sr}}$
):
 ;
; -
(
 $T{\lor }^{}_{\mathrm {sr}}$
):
$T{\lor }^{}_{\mathrm {sr}}$
):
 ;
; -
(
 $T{\neg }^{}_{\mathrm {sr}}$
):
$T{\neg }^{}_{\mathrm {sr}}$
):
 ;
; -
(
 $T\forall ^{}_{\mathrm {sr}}$
):
$T\forall ^{}_{\mathrm {sr}}$
):

 ;
; -
(
 $T\exists ^{}_{\mathrm {sr}}$
):
$T\exists ^{}_{\mathrm {sr}}$
):

 ,
,
with (
![]() $\exists \mbox {-val}$
) and the following, where B is any
$\exists \mbox {-val}$
) and the following, where B is any
![]() $\mathfrak {L}(\mathcal {S}^n,T)$
formula whose free variables are among
$\mathfrak {L}(\mathcal {S}^n,T)$
formula whose free variables are among
![]() $y_0,\ldots ,y_{k-1}$
.
$y_0,\ldots ,y_{k-1}$
.


We write
![]() $\mathbb {FFS}_m(\mathcal {S}^n)\vdash A$
if there is an
$\mathbb {FFS}_m(\mathcal {S}^n)\vdash A$
if there is an
![]() $\mathbb {FFS}(\mathcal {S}^n)$
proof of A in any path through which the rule (
$\mathbb {FFS}(\mathcal {S}^n)$
proof of A in any path through which the rule (
![]() $T\mbox {-Intr}$
) is used at most m times and (
$T\mbox {-Intr}$
) is used at most m times and (
![]() $T\mbox {-Elim}$
) is not used at all.
$T\mbox {-Elim}$
) is not used at all.
(
![]() $TT{=}$
) is a special case of (
$TT{=}$
) is a special case of (
![]() $TT_{\mathrm {sr}}$
) in
$TT_{\mathrm {sr}}$
) in
![]() $\mathbb {FKF}(\mathcal {S}^n)$
, with x being a code of equality. Here to
$\mathbb {FKF}(\mathcal {S}^n)$
, with x being a code of equality. Here to
![]() $=$
we apply the dot notation iteratedly:
$=$
we apply the dot notation iteratedly:
![]() is an
is an
![]() $\mathcal {S}^2$
term with two arguments, to which we apply Definition 3.2 again. Recall Remark 3.6 for the use of dot notation on the “unofficial” function symbols
$\mathcal {S}^2$
term with two arguments, to which we apply Definition 3.2 again. Recall Remark 3.6 for the use of dot notation on the “unofficial” function symbols
![]() .
.
In
![]() $\mathbb {FFS}_m(\mathcal {S}^n)\vdash A$
, we count the number of applications of rules only along paths. Thus,
$\mathbb {FFS}_m(\mathcal {S}^n)\vdash A$
, we count the number of applications of rules only along paths. Thus,
![]() $\mathbb {FFS}_m(\mathcal {S}^n)$
is closed under modus ponens (MP): if
$\mathbb {FFS}_m(\mathcal {S}^n)$
is closed under modus ponens (MP): if
![]() $\mathbb {FFS}_m(\mathcal {S}^n)\vdash A$
and
$\mathbb {FFS}_m(\mathcal {S}^n)\vdash A$
and
![]() $\mathbb {FFS}_m(\mathcal {S}^n)\vdash A\,{\to }\,B$
then
$\mathbb {FFS}_m(\mathcal {S}^n)\vdash A\,{\to }\,B$
then
![]() $\mathbb {FFS}_m(\mathcal {S}^n)\vdash B$
. Not only by this but also by the prohibition of (
$\mathbb {FFS}_m(\mathcal {S}^n)\vdash B$
. Not only by this but also by the prohibition of (
![]() $T\mbox {-Elim}$
), our way of restricting
$T\mbox {-Elim}$
), our way of restricting
![]() $\mathbb {FFS}_m(\mathcal {S}^n)$
differs from Halbach’s
$\mathbb {FFS}_m(\mathcal {S}^n)$
differs from Halbach’s
![]() $\mathbf {FS}_m$
in [Reference Halbach11].
$\mathbf {FS}_m$
in [Reference Halbach11].
We define
![]() $\mathbb {FFS}(\mathcal {S}^n)$
from
$\mathbb {FFS}(\mathcal {S}^n)$
from
![]() $\mathbb {FCT}(\mathcal {S}^n)$
by strengthening the truth axioms for
$\mathbb {FCT}(\mathcal {S}^n)$
by strengthening the truth axioms for
![]() $\land $
,
$\land $
,
![]() $\lor $
,
$\lor $
,
![]() $\forall $
,
$\forall $
,
![]() $\exists $
to codes of non-typed formulae and by adding (
$\exists $
to codes of non-typed formulae and by adding (
![]() $TT{=}$
) and the truth axiom for
$TT{=}$
) and the truth axiom for
![]() $\sim $
as well as the rules (T-Intr) and (T-Elim). The asymmetry between the two rules is not essential because of (
$\sim $
as well as the rules (T-Intr) and (T-Elim). The asymmetry between the two rules is not essential because of (
![]() $\exists \mbox {-val}$
), but has some practical convenience.
$\exists \mbox {-val}$
), but has some practical convenience.
Our rules differ from
![]() $(\mbox {truth-rule})$
in the Introduction, restricted to sentences, which was employed in Halbach’s [Reference Halbach11] formulation of first-order Friedman–Sheard truth theory and derives our strengthened versions as follows.
$(\mbox {truth-rule})$
in the Introduction, restricted to sentences, which was employed in Halbach’s [Reference Halbach11] formulation of first-order Friedman–Sheard truth theory and derives our strengthened versions as follows.


However, in our finitist setting, we cannot form
![]() $\forall y_0,\ldots ,y_{k-1}B(y_0,\ldots ,y_{k-1})$
nor these derivations. Recall also the weakness of our truth axioms for quantifiers, as mentioned in Remark 4.2.
$\forall y_0,\ldots ,y_{k-1}B(y_0,\ldots ,y_{k-1})$
nor these derivations. Recall also the weakness of our truth axioms for quantifiers, as mentioned in Remark 4.2.
Another difference from Halbach’s axiomatization of first-order Friedman–Sheard truth theory is that (
![]() $TT{=}$
) is explicitly included. In the first-order setting, or more precisely, in the presence (or with the justification) of a term for valuation function, (
$TT{=}$
) is explicitly included. In the first-order setting, or more precisely, in the presence (or with the justification) of a term for valuation function, (
![]() $TT{=}$
) and (
$TT{=}$
) and (
![]() $TT{<}$
), the latter being similarly defined, are provable from the other axioms and rules as follows, where we omit the antecedent “
$TT{<}$
), the latter being similarly defined, are provable from the other axioms and rules as follows, where we omit the antecedent “
![]() $\mathrm {CTerm}_n(u)\,{\land }\, \mathrm {CTerm}_n(v)\,{\to }$
”.
$\mathrm {CTerm}_n(u)\,{\land }\, \mathrm {CTerm}_n(v)\,{\to }$
”.

One can see the essential use of
in this proof. Since we do not officially have nor justify
![]() $\mathrm {val}$
as a bounded definable function in our setting, we have to simulate the use of
$\mathrm {val}$
as a bounded definable function in our setting, we have to simulate the use of
by a further rule as follows.
Proposition 4.14. For
![]() $n\,{\geq }\,2$
, the following rule is derivable in
$n\,{\geq }\,2$
, the following rule is derivable in
![]() $\mathbb {FFS}_0(\mathcal {S}^n)$
, where x does not occur in A.
$\mathbb {FFS}_0(\mathcal {S}^n)$
, where x does not occur in A.

We postpone the proof until the end of this section. As we do not know if we can derive this rule without (
![]() $TT{=}$
), we added (
$TT{=}$
), we added (
![]() $TT{=}$
) as an axiom, and it suffices to derive the respective assertions for
$TT{=}$
) as an axiom, and it suffices to derive the respective assertions for
![]() $<$
,
$<$
,
![]() $\neq $
, and
$\neq $
, and
![]() $\not <$
. These are necessary for the interpretability in Section 5.2, whose first-order analogue is due to Halbach [Reference Halbach10] and which is, we think, inevitable for any formulation of Friedman–Sheard truth to be called appropriate.
$\not <$
. These are necessary for the interpretability in Section 5.2, whose first-order analogue is due to Halbach [Reference Halbach10] and which is, we think, inevitable for any formulation of Friedman–Sheard truth to be called appropriate.
Lemma 4.15. (1)
![]() .
.
Thus (2)
![]() .
.
Proof
![]() implies
implies
![]() by Lemma 3.8(iii). Since Lemma 3.8(ii) yields
by Lemma 3.8(iii). Since Lemma 3.8(ii) yields
![]() , again by Lemma 3.8(iii),
, again by Lemma 3.8(iii),
![]() implies
implies
![]() . Thus, (
. Thus, (
![]() $TT{=}$
) yields
$TT{=}$
) yields
![]() which is equivalent to
which is equivalent to
![]() , to which we apply (
, to which we apply (
![]() $\exists \mbox {-val}$
).
$\exists \mbox {-val}$
).
(1) below allows us to exchange
![]() and
and
![]() $\mathrm {num}(x)$
in the scope of
$\mathrm {num}(x)$
in the scope of
![]() under
under
![]() $\mathrm {CTerm}(x)$
. By (
$\mathrm {CTerm}(x)$
. By (
![]() $\exists \mbox {-val}$
), we may assume
$\exists \mbox {-val}$
), we may assume
![]() for fresh z, and replace
for fresh z, and replace
![]() by
by
![]() and by
and by
![]() $\mathrm {num}(\mathrm {num}(z))$
by Lemmata 4.4 and 3.8(ii). However, to replace
$\mathrm {num}(\mathrm {num}(z))$
by Lemmata 4.4 and 3.8(ii). However, to replace
![]() $\mathrm {num}(\mathrm {num}(z))$
by
$\mathrm {num}(\mathrm {num}(z))$
by
![]() $\mathrm {num}(x)$
, we need the argument here.
$\mathrm {num}(x)$
, we need the argument here.
Lemma 4.16. For
![]() $n\,{\geq }\,2$
and any
$n\,{\geq }\,2$
and any
![]() $\mathfrak {L}(\mathcal {S}^n)$
formula A whose free variables are
$\mathfrak {L}(\mathcal {S}^n)$
formula A whose free variables are
![]() $x_0,\ldots ,x_{k-1}$
,
$x_0,\ldots ,x_{k-1}$
,
![]() $\mathbb {FFS}_1(\mathcal {S}^n)$
proves
$\mathbb {FFS}_1(\mathcal {S}^n)$
proves
-
(1)
 ,
, -
(2)
 .
.
Proof (1) We can derive this as follows.

(2) By Lemma 4.15(1), the following derivation suffices for the third conjunct.

At this point, one can see the reason why we do not employ the standard upper-dot notation to denote
![]() $\mathrm {num}(x)$
by
$\mathrm {num}(x)$
by
![]() , with which it is not easy to distinct
, with which it is not easy to distinct
![]() and
and
![]() $\mathrm {num}(\mathrm {num}(z))$
. On the other hand, we need extensive use of the other standard notation of lower-dot. For example, we have to be able to denote
$\mathrm {num}(\mathrm {num}(z))$
. On the other hand, we need extensive use of the other standard notation of lower-dot. For example, we have to be able to denote
![]() and the iterated applications in
and the iterated applications in
![]() ,
,
![]() ,
,
![]() , and so on.
, and so on.
Proof of Proposition 4.14. We can consider the following derivation.

We will also consider one more self-referential truth theory, the finitist Kripke–Feferman–Burgess truth theory
![]() $\mathbb {FKFB}(\mathcal {S}^n)$
. We do not give the definition of
$\mathbb {FKFB}(\mathcal {S}^n)$
. We do not give the definition of
![]() $\mathbb {FKFB}(\mathcal {S}^n)$
here but postpone it to Section 8.
$\mathbb {FKFB}(\mathcal {S}^n)$
here but postpone it to Section 8.
5 Interrelation between finitist truth theories
We now clarify the interrelationship among our finitist truth theories. Obviously
![]() $\mathbb {FET}(\mathcal {S}^n)$
is included in
$\mathbb {FET}(\mathcal {S}^n)$
is included in
![]() $\mathbb {FCT}(\mathcal {S}^n)$
, i.e.,
$\mathbb {FCT}(\mathcal {S}^n)$
, i.e.,
![]() $\mathbb {FRT}_1(\mathcal {S}^n)$
, and
$\mathbb {FRT}_1(\mathcal {S}^n)$
, and
![]() $\mathbb {FCT}(\mathcal {S}^n)$
is in
$\mathbb {FCT}(\mathcal {S}^n)$
is in
![]() $\mathbb {FRT}_m(\mathcal {S}^n)$
for
$\mathbb {FRT}_m(\mathcal {S}^n)$
for
![]() $m\,{>}\,1$
, in
$m\,{>}\,1$
, in
![]() $\mathbb {FFS}(\mathcal {S}^n)$
, and in
$\mathbb {FFS}(\mathcal {S}^n)$
, and in
![]() $\mathbb {FKF}(\mathcal {S}^n)$
. We will show
$\mathbb {FKF}(\mathcal {S}^n)$
. We will show
![]() $\mathbb {FFS}(\mathcal {S}^n) \,{\leq }_{\mathfrak {L}(\mathcal {S}^n)}\, \mathbb {FRT}_{<\omega }(\mathcal {S}^n)$
and
$\mathbb {FFS}(\mathcal {S}^n) \,{\leq }_{\mathfrak {L}(\mathcal {S}^n)}\, \mathbb {FRT}_{<\omega }(\mathcal {S}^n)$
and
![]() $\mathbb {FRT}_{<\omega }(\mathcal {S}^n) \,{\leq }_{\mathfrak {L}(\mathcal {S}^n)}\, \mathbb {FFS}(\mathcal {S}^n)$
and
$\mathbb {FRT}_{<\omega }(\mathcal {S}^n) \,{\leq }_{\mathfrak {L}(\mathcal {S}^n)}\, \mathbb {FFS}(\mathcal {S}^n)$
and
![]() $\mathbb {FRT}_{<\omega }(\mathcal {S}^n) \,{\leq }_{\mathfrak {L}(\mathcal {S}^n)}\, \mathbb {FKF}(\mathcal {S}^n)$
. The first two are analogous to the known results on the corresponding first-order truth theories from [Reference Halbach10].
$\mathbb {FRT}_{<\omega }(\mathcal {S}^n) \,{\leq }_{\mathfrak {L}(\mathcal {S}^n)}\, \mathbb {FKF}(\mathcal {S}^n)$
. The first two are analogous to the known results on the corresponding first-order truth theories from [Reference Halbach10].
5.1 Ramifying interpretation
To “embed”
![]() $\mathbb {FFS}(\mathcal {S}^n)$
in
$\mathbb {FFS}(\mathcal {S}^n)$
in
![]() $\mathbb {FRT}_{<\omega }(\mathcal {S}^n)$
, we ramify the truth predicate T into different truth predicates
$\mathbb {FRT}_{<\omega }(\mathcal {S}^n)$
, we ramify the truth predicate T into different truth predicates
![]() $T_j$
’s. For this, we introduce the ramifying interpretation
$T_j$
’s. For this, we introduce the ramifying interpretation
![]() $\mathfrak {r}(m)$
of rank m, which replaces the truth predicate T with
$\mathfrak {r}(m)$
of rank m, which replaces the truth predicate T with
![]() $T_{m-1}$
and any coded occurrence of T, at the depth j in the (iterated) scope of T, with
$T_{m-1}$
and any coded occurrence of T, at the depth j in the (iterated) scope of T, with
![]() $T_{m-j-1}$
. Since T may apply to codes of non-standard formulae, we also need the coded version
$T_{m-j-1}$
. Since T may apply to codes of non-standard formulae, we also need the coded version
![]() $\mathrm {ram}^m$
of the interpretation.
$\mathrm {ram}^m$
of the interpretation.
Definition 5.1 (
 $A^{\mathfrak {r}(m)}$
,
$A^{\mathfrak {r}(m)}$
,
 $\mathrm {ram}^m$
)
$\mathrm {ram}^m$
)
For any natural number m, we define an interpretation
![]() $\mathfrak {r}(m)$
of
$\mathfrak {r}(m)$
of
![]() $\mathfrak {L}(\mathcal {S}^n,T)$
in
$\mathfrak {L}(\mathcal {S}^n,T)$
in
![]() $\mathfrak {L}(\mathcal {S}^n,T_0,\ldots ,T_{m-1})$
by meta-recursion on m as follows. Let
$\mathfrak {L}(\mathcal {S}^n,T_0,\ldots ,T_{m-1})$
by meta-recursion on m as follows. Let
![]() $A^{\mathfrak {r}(m)} \,{:\equiv }\,A$
for any atomic
$A^{\mathfrak {r}(m)} \,{:\equiv }\,A$
for any atomic
![]() $\mathfrak {L}(\mathcal {S}^n)$
formula A;
$\mathfrak {L}(\mathcal {S}^n)$
formula A;
 $$ \begin{align*} (T(t))^{\mathfrak{r}(m)} \;&{:\equiv} \begin{cases} 0\,{=}\,0, & \mbox{ for }m\,{=}\,0,\\ T_{m-1}(\mathrm{ram}^{m-1}(t)), & \mbox{ for }m\,{>}\,0; \end{cases} \end{align*} $$
$$ \begin{align*} (T(t))^{\mathfrak{r}(m)} \;&{:\equiv} \begin{cases} 0\,{=}\,0, & \mbox{ for }m\,{=}\,0,\\ T_{m-1}(\mathrm{ram}^{m-1}(t)), & \mbox{ for }m\,{>}\,0; \end{cases} \end{align*} $$
and let
![]() $\mathfrak {r}(m)$
commute with
$\mathfrak {r}(m)$
commute with
![]() $\neg $
(applied to atomic formulae),
$\neg $
(applied to atomic formulae),
![]() $\land $
,
$\land $
,
![]() $\lor $
, and bounded quantifiers; where by meta-recursion on m and Theorem 2.11 we introduce an
$\lor $
, and bounded quantifiers; where by meta-recursion on m and Theorem 2.11 we introduce an
![]() $\mathcal {S}^2$
function
$\mathcal {S}^2$
function
![]() $\mathrm {ram}^m$
with the following defining axioms.
$\mathrm {ram}^m$
with the following defining axioms.

We easily see
![]() $\mathbb {FA}(\mathcal {S}^2) \vdash \ulcorner A^{\mathfrak {r}(m)}\urcorner \,{=}\,\mathrm {ram}^m(\ulcorner A\urcorner )$
for any
$\mathbb {FA}(\mathcal {S}^2) \vdash \ulcorner A^{\mathfrak {r}(m)}\urcorner \,{=}\,\mathrm {ram}^m(\ulcorner A\urcorner )$
for any
![]() $\mathfrak {L}(\mathcal {S}^n,T)$
formula A, and generalize it as follows.
$\mathfrak {L}(\mathcal {S}^n,T)$
formula A, and generalize it as follows.
Lemma 5.2. For any
![]() $\mathfrak {L}(\mathcal {S}^n,T)$
formula B,
$\mathfrak {L}(\mathcal {S}^n,T)$
formula B,
Theorem 5.3. For
![]() $n\,{\geq }\,2$
and any
$n\,{\geq }\,2$
and any
![]() $\mathfrak {L}(\mathcal {S}^n,T)$
formula A, (1) if
$\mathfrak {L}(\mathcal {S}^n,T)$
formula A, (1) if
![]() $\mathbb {FFS}_m(\mathcal {S}^n)\vdash A$
then
$\mathbb {FFS}_m(\mathcal {S}^n)\vdash A$
then
![]() $\mathbb {FRT}_m(\mathcal {S}^n)\vdash A^{\mathfrak {r}(m)}$
; and (2) if
$\mathbb {FRT}_m(\mathcal {S}^n)\vdash A^{\mathfrak {r}(m)}$
; and (2) if
![]() $\mathbb {FFS}(\mathcal {S}^n)\vdash A$
then there are k and
$\mathbb {FFS}(\mathcal {S}^n)\vdash A$
then there are k and
![]() $\ell $
such that, for any
$\ell $
such that, for any
![]() $m\,{\geq }\,\ell $
, we have
$m\,{\geq }\,\ell $
, we have
![]() $\mathbb {FRT}_{m+k}(\mathcal {S}^n) \vdash A^{\mathfrak {r}(m)}$
.
$\mathbb {FRT}_{m+k}(\mathcal {S}^n) \vdash A^{\mathfrak {r}(m)}$
.
Proof We prove (2) by meta-induction on the proof of
![]() $\mathbb {FFS}(\mathcal {S}^n)\vdash A$
, because (1) is easier. We focus only on the two non-obvious cases where the last inference is either (
$\mathbb {FFS}(\mathcal {S}^n)\vdash A$
, because (1) is easier. We focus only on the two non-obvious cases where the last inference is either (
![]() $T\mbox {-Intr}$
) or (
$T\mbox {-Intr}$
) or (
![]() $T\mbox {-Elim}$
).
$T\mbox {-Elim}$
).
First consider the case of (
![]() $T\mbox {-Intr}$
), say the last inference is the upper below. The induction hypothesis yields
$T\mbox {-Intr}$
), say the last inference is the upper below. The induction hypothesis yields
![]() $k,\ell $
such that
$k,\ell $
such that
![]() $\mathbb {FRT}_{m+k}(\mathcal {S}^n) \vdash B^{\mathfrak {r}(m)} (x_0,\ldots ,x_{k-1})$
for
$\mathbb {FRT}_{m+k}(\mathcal {S}^n) \vdash B^{\mathfrak {r}(m)} (x_0,\ldots ,x_{k-1})$
for
![]() $m\,{\geq }\,\ell $
. For such m, we can construct the lower derivation below, which is a proof in
$m\,{\geq }\,\ell $
. For such m, we can construct the lower derivation below, which is a proof in
![]() $\mathbb {FRT}_{m+1+k}(\mathcal {S}^n)$
. Thus we can take k and
$\mathbb {FRT}_{m+1+k}(\mathcal {S}^n)$
. Thus we can take k and
![]() $\ell {+}1$
.
$\ell {+}1$
.


Next consider the case of (
![]() $T\mbox {-Elim}$
), say the last inference is (
$T\mbox {-Elim}$
), say the last inference is (
![]() $T\mbox {-Elim}$
) as in Definition 4.13. Then the induction hypothesis yields k and
$T\mbox {-Elim}$
) as in Definition 4.13. Then the induction hypothesis yields k and
![]() $\ell $
such that
$\ell $
such that
![]() for
for
![]() $m\,{\geq }\,\ell $
, where we may assume
$m\,{\geq }\,\ell $
, where we may assume
![]() $\ell \,{>}\,0$
. Then
$\ell \,{>}\,0$
. Then
![]() $\mathbb {FRT}_{m+k}(\mathcal {S}^n)\vdash B^{\mathfrak {r}(m-1)}(x_0,\ldots ,x_{k-1})$
by Lemma 5.2 and Theorem 4.8, and we can take
$\mathbb {FRT}_{m+k}(\mathcal {S}^n)\vdash B^{\mathfrak {r}(m-1)}(x_0,\ldots ,x_{k-1})$
by Lemma 5.2 and Theorem 4.8, and we can take
![]() $k{+}1$
and
$k{+}1$
and
![]() $\ell {-}1$
.
$\ell {-}1$
.
Corollary 5.4. For
![]() $n\,{\geq }\,2$
, we have
$n\,{\geq }\,2$
, we have
![]() $\mathbb {FFS}(\mathcal {S}^n) \,{\leq }_{\mathfrak {L}(\mathcal {S}^n)}\, \mathbb {FRT}_{<\omega }(\mathcal {S}^n)$
.
$\mathbb {FFS}(\mathcal {S}^n) \,{\leq }_{\mathfrak {L}(\mathcal {S}^n)}\, \mathbb {FRT}_{<\omega }(\mathcal {S}^n)$
.
Proof Let A be an
![]() $\mathfrak {L}(\mathcal {S}^n)$
formula. Assume
$\mathfrak {L}(\mathcal {S}^n)$
formula. Assume
![]() $\mathbb {FFS}(\mathcal {S}^n)\vdash A$
. By the last theorem, there is m such that
$\mathbb {FFS}(\mathcal {S}^n)\vdash A$
. By the last theorem, there is m such that
![]() $\mathbb {FRT}_{<\omega } (\mathcal {S}^n)\vdash A^{\mathfrak {r}(m)}$
. Since A is an
$\mathbb {FRT}_{<\omega } (\mathcal {S}^n)\vdash A^{\mathfrak {r}(m)}$
. Since A is an
![]() $\mathfrak {L}(\mathcal {S}^n)$
formula, we have
$\mathfrak {L}(\mathcal {S}^n)$
formula, we have
![]() $A^{\mathfrak {r}(m)}\,{\equiv }\,A$
.
$A^{\mathfrak {r}(m)}\,{\equiv }\,A$
.
5.2 Ignoring interpretation
To interpret
![]() $\mathbb {FRT}_{<\omega }(\mathcal {S}^n)$
in
$\mathbb {FRT}_{<\omega }(\mathcal {S}^n)$
in
![]() $\mathbb {FKF}(\mathcal {S}^n)$
and in
$\mathbb {FKF}(\mathcal {S}^n)$
and in
![]() $\mathbb {FFS}(\mathcal {S}^n)$
, we can just forget the ramification. As in the definition of
$\mathbb {FFS}(\mathcal {S}^n)$
, we can just forget the ramification. As in the definition of
![]() $\mathfrak {r}(m)$
, we have to consider that T may apply to codes of non-standard formulae. This is why we need also the coded version of the interpretation.
$\mathfrak {r}(m)$
, we have to consider that T may apply to codes of non-standard formulae. This is why we need also the coded version of the interpretation.
Definition 5.5. For any natural number m, we define an interpretation
![]() $\mathfrak {i}(m)$
of
$\mathfrak {i}(m)$
of
![]() $\mathfrak {L}(\mathcal {S}^n,T_0,\ldots ,T_{m-1})$
in
$\mathfrak {L}(\mathcal {S}^n,T_0,\ldots ,T_{m-1})$
in
![]() $\mathfrak {L}(\mathcal {S}^n,T)$
by meta-recursion on m as follows.
$\mathfrak {L}(\mathcal {S}^n,T)$
by meta-recursion on m as follows.
Let
![]() $A^{\mathfrak {i}(m)} \,{:\equiv }\,A$
for any atomic
$A^{\mathfrak {i}(m)} \,{:\equiv }\,A$
for any atomic
![]() $\mathfrak {L}(\mathcal {S}^n)$
formula A;
$\mathfrak {L}(\mathcal {S}^n)$
formula A;
and let
![]() $\mathfrak {i}(m)$
commute with
$\mathfrak {i}(m)$
commute with
![]() $\neg $
(applied to atomic formulae),
$\neg $
(applied to atomic formulae),
![]() $\land $
,
$\land $
,
![]() $\lor $
, and bounded quantifiers; where by meta-recursion on m and Theorem 2.11, we introduce
$\lor $
, and bounded quantifiers; where by meta-recursion on m and Theorem 2.11, we introduce
![]() $\mathrm {ign}^m$
so that
$\mathrm {ign}^m$
so that
![]() $\neg \mathrm {Sent}_{n,T_0,\ldots ,T_{m-1}}(w) \,{\to }\,\mathrm {ign}^m(w)\,{=}\,\ulcorner 0\,{=}\,0\urcorner $
and else
$\neg \mathrm {Sent}_{n,T_0,\ldots ,T_{m-1}}(w) \,{\to }\,\mathrm {ign}^m(w)\,{=}\,\ulcorner 0\,{=}\,0\urcorner $
and else

Let us start with interpreting in
![]() $\mathbb {FKF}(\mathcal {S}^n)$
. The only axiom of
$\mathbb {FKF}(\mathcal {S}^n)$
. The only axiom of
![]() $\mathbb {FRT}_m(\mathcal {S}^n)$
whose ignoring version is missed in
$\mathbb {FRT}_m(\mathcal {S}^n)$
whose ignoring version is missed in
![]() $\mathbb {FKF}(\mathcal {S}^n)$
is
$\mathbb {FKF}(\mathcal {S}^n)$
is
![]() $(T{\neg }T^{}_{\mathrm {tp}})$
. Therefore, the next lemma is the key for the interpretability.
$(T{\neg }T^{}_{\mathrm {tp}})$
. Therefore, the next lemma is the key for the interpretability.
Lemma 5.6.
![]() .
.
Proof We proceed by meta-induction on m. We reason in
![]() $\mathbb {FKF}(\mathcal {S}^n)$
by sentence induction on
$\mathbb {FKF}(\mathcal {S}^n)$
by sentence induction on
![]() $w$
(cf. Theorem 3.11). We may assume
$w$
(cf. Theorem 3.11). We may assume
![]() $\mathrm {Sent}_{n,T_0,\ldots ,T_{m-1}}(w)$
.
$\mathrm {Sent}_{n,T_0,\ldots ,T_{m-1}}(w)$
.
Consider the case where
. Then
. Thus by
![]() $(T{=})$
and
$(T{=})$
and
![]() $(T\neg \mbox {Atom})$
, we have
$(T\neg \mbox {Atom})$
, we have

and so
, to which we apply (
![]() $\exists \mbox {-val}$
).
$\exists \mbox {-val}$
).
In the cases where
![]() ,
,
![]() or
or
![]() , we reason similarly.
, we reason similarly.
Next consider the case of
with
![]() $j\,{<}\,m$
. Then
$j\,{<}\,m$
. Then
. Since
, by (
![]() $T\neg T^{}_{\mathrm {kf}}$
) and (
$T\neg T^{}_{\mathrm {kf}}$
) and (
![]() $TT^{}_{\mathrm {tp}}$
), we obtain
$TT^{}_{\mathrm {tp}}$
), we obtain
By meta-induction hypothesis,
, to which we apply (
![]() $\exists \mbox {-val}$
).
$\exists \mbox {-val}$
).
In the case where
![]() with
with
![]() $j\,{<}\,m$
, we reason similarly.
$j\,{<}\,m$
, we reason similarly.
The other cases are immediate by induction hypothesis.
Theorem 5.7. For
![]() $n\,{\geq }\,2$
and any
$n\,{\geq }\,2$
and any
![]() $\mathfrak {L}(\mathcal {S}^n,T_0,\ldots ,T_{m-1})$
formula A whose free variables are among
$\mathfrak {L}(\mathcal {S}^n,T_0,\ldots ,T_{m-1})$
formula A whose free variables are among
![]() $x_0,\ldots ,x_{k-1}$
, if
$x_0,\ldots ,x_{k-1}$
, if
![]() $\mathbb {FRT}_m(\mathcal {S}^n)\vdash A(x_0,\ldots ,x_{k-1})$
then
$\mathbb {FRT}_m(\mathcal {S}^n)\vdash A(x_0,\ldots ,x_{k-1})$
then
Proof This is by meta-induction on a proof of
![]() $\mathbb {FRT}_m(\mathcal {S}^n)\vdash A(x_0,\ldots ,x_{k-1})$
, applying the last lemma.
$\mathbb {FRT}_m(\mathcal {S}^n)\vdash A(x_0,\ldots ,x_{k-1})$
, applying the last lemma.
Next let us interpret
![]() $\mathbb {FRT}_m(\mathcal {S}^n)$
in
$\mathbb {FRT}_m(\mathcal {S}^n)$
in
![]() $\mathbb {FFS}_m(\mathcal {S}^n)$
by
$\mathbb {FFS}_m(\mathcal {S}^n)$
by
![]() $\mathfrak {i}(m)$
. Although this is not necessary for the final result on the
$\mathfrak {i}(m)$
. Although this is not necessary for the final result on the
![]() $\mathfrak {L}(\mathcal {S}^n)$
conservations (except for the claim we will make in connection with [Reference Sato and Walker24]), we claimed that the axiom
$\mathfrak {L}(\mathcal {S}^n)$
conservations (except for the claim we will make in connection with [Reference Sato and Walker24]), we claimed that the axiom
![]() $(TT{=})$
should be included in
$(TT{=})$
should be included in
![]() $\mathbb {FFS}(\mathcal {S}^n)$
because we think this interpretability should be feasible. The only axiom of
$\mathbb {FFS}(\mathcal {S}^n)$
because we think this interpretability should be feasible. The only axiom of
![]() $\mathbb {FRT}_m(\mathcal {S}^n)$
whose ignoring version is missed in
$\mathbb {FRT}_m(\mathcal {S}^n)$
whose ignoring version is missed in
![]() $\mathbb {FFS}(\mathcal {S}^n)$
is
$\mathbb {FFS}(\mathcal {S}^n)$
is
![]() $(TT^{}_{\mathrm {tp}})$
. Therefore the next lemma is the key for the interpretability.
$(TT^{}_{\mathrm {tp}})$
. Therefore the next lemma is the key for the interpretability.
Lemma 5.8.
![]() .
.
Proof We prove this statement by meta-induction on m. By applying
![]() $(T\mbox {-Intr})$
to the equality axiom, we can extend Lemma 4.4 to
$(T\mbox {-Intr})$
to the equality axiom, we can extend Lemma 4.4 to
![]() $\mathfrak {L} (\mathcal {S}^n,T_0,\ldots ,T_{m-1})$
formulae A. Hence, we have to show
$\mathfrak {L} (\mathcal {S}^n,T_0,\ldots ,T_{m-1})$
formulae A. Hence, we have to show
. By Lemma 3.8(ii), this is equivalent to
which we now prove by sentence induction on
![]() $w$
.
$w$
.
If
![]() $w$
does not code any
$w$
does not code any
![]() $\mathfrak {L} (\mathcal {S}^n,T_0,\ldots ,T_{m-1})$
formula or if it codes an atomic
$\mathfrak {L} (\mathcal {S}^n,T_0,\ldots ,T_{m-1})$
formula or if it codes an atomic
![]() $\mathfrak {L}(\mathcal {S}^n)$
formula, this follows from (
$\mathfrak {L}(\mathcal {S}^n)$
formula, this follows from (
![]() $TT{=}$
) and Lemma 4.16(2) by Lemma 3.8(i). Below we assume
$TT{=}$
) and Lemma 4.16(2) by Lemma 3.8(i). Below we assume
![]() $\mathrm {Sent}_{n,T_0,\ldots ,T_{m-1}}(w)$
.
$\mathrm {Sent}_{n,T_0,\ldots ,T_{m-1}}(w)$
.
If
with
![]() $j\,{<}\,m$
, then
$j\,{<}\,m$
, then
![]() $ \mathrm {CTerm}_n(v) $
and so we can derive the following.
$ \mathrm {CTerm}_n(v) $
and so we can derive the following.

If
with
![]() $v$
being a code of atomic formula, we have the following derivation, where we omit “
$v$
being a code of atomic formula, we have the following derivation, where we omit “
![]() $\mathit {AtSent}_{n,T_0,\ldots ,T_{m-1}}(v) \,{\to }$
”.
$\mathit {AtSent}_{n,T_0,\ldots ,T_{m-1}}(v) \,{\to }$
”.

If
![]() or
or
![]() , we proceed similarly.
, we proceed similarly.
Finally assume
or
. For the former, consider the following derivation, where
![]() $(\mathrm {IH})$
is the induction hypothesis for
$(\mathrm {IH})$
is the induction hypothesis for
![]() $v$
and where we omit “
$v$
and where we omit “
![]() $\mathrm {Var}(x)\,{\land }\,\mathrm {CTerm}_n(u) \,{\land }\,\mathrm {Sent}_{n,T_0,\ldots ,T_{m-1}}(w) \,{\to }$
”. Note that another sentence induction shows
$\mathrm {Var}(x)\,{\land }\,\mathrm {CTerm}_n(u) \,{\land }\,\mathrm {Sent}_{n,T_0,\ldots ,T_{m-1}}(w) \,{\to }$
”. Note that another sentence induction shows
.

Theorem 5.9. For
![]() $n\,{\geq }\,2$
and for any
$n\,{\geq }\,2$
and for any
![]() $\mathfrak {L}(\mathcal {S}^n,T_0,\ldots ,T_{m-1})$
formula A whose free variables are among
$\mathfrak {L}(\mathcal {S}^n,T_0,\ldots ,T_{m-1})$
formula A whose free variables are among
![]() $x_0,\ldots ,x_{k-1}$
, if
$x_0,\ldots ,x_{k-1}$
, if
![]() $\mathbb {FRT}_m(\mathcal {S}^n) \vdash A(x_0,\ldots ,x_{k-1})$
then we have
$\mathbb {FRT}_m(\mathcal {S}^n) \vdash A(x_0,\ldots ,x_{k-1})$
then we have
![]() $\mathbb {FFS}_m(\mathcal {S}^n)\vdash A^{\mathfrak {i}(m)}(x_0,\ldots ,x_{k-1})$
.
$\mathbb {FFS}_m(\mathcal {S}^n)\vdash A^{\mathfrak {i}(m)}(x_0,\ldots ,x_{k-1})$
.
Lemma 5.10. For
![]() $n\,{\geq }\,2$
and for any
$n\,{\geq }\,2$
and for any
![]() $\mathfrak {L}(\mathcal {S}^n)$
formula A whose free variables are among
$\mathfrak {L}(\mathcal {S}^n)$
formula A whose free variables are among
![]() $x_0,\ldots ,x_{k-1}$
, the equivalence
$x_0,\ldots ,x_{k-1}$
, the equivalence
![]() $A^{\mathfrak {i}(m)}(x_0,\ldots ,x_{k-1}) \,{\leftrightarrow }\, A(x_0,\ldots ,x_{k-1})$
is provable in both
$A^{\mathfrak {i}(m)}(x_0,\ldots ,x_{k-1}) \,{\leftrightarrow }\, A(x_0,\ldots ,x_{k-1})$
is provable in both
![]() $\mathbb {FKF}(\mathcal {S}^n)$
and
$\mathbb {FKF}(\mathcal {S}^n)$
and
![]() $\mathbb {FFS}(\mathcal {S}^n)$
.
$\mathbb {FFS}(\mathcal {S}^n)$
.
What we have obtained can be summarized as follows.
-
(1)
 $\mathbb {FRT}_m(\mathcal {S}^n) \,{\leq }_{\mathfrak {L}(\mathcal {S}^n)}\, \mathbb {FKF}(\mathcal {S}^n)$
and
$\mathbb {FRT}_m(\mathcal {S}^n) \,{\leq }_{\mathfrak {L}(\mathcal {S}^n)}\, \mathbb {FKF}(\mathcal {S}^n)$
and
 $\mathbb {FRT}_m(\mathcal {S}^n) \,{\leq }_{\mathfrak {L}(\mathcal {S}^n)}\, \mathbb {FFS}_m(\mathcal {S}^n)$
for any
$\mathbb {FRT}_m(\mathcal {S}^n) \,{\leq }_{\mathfrak {L}(\mathcal {S}^n)}\, \mathbb {FFS}_m(\mathcal {S}^n)$
for any
 $m\,{\geq }\,0$
and
$m\,{\geq }\,0$
and
 $n\,{\geq }\,2$
.
$n\,{\geq }\,2$
. -
(2) Thus
 $\mathbb {FRT}_{<\omega }(\mathcal {S}^n) \,{\leq }_{\mathfrak {L}(\mathcal {S}^n)}\, \mathbb {FKF}(\mathcal {S}^n)$
and
$\mathbb {FRT}_{<\omega }(\mathcal {S}^n) \,{\leq }_{\mathfrak {L}(\mathcal {S}^n)}\, \mathbb {FKF}(\mathcal {S}^n)$
and
 $\mathbb {FRT}_{<\omega }(\mathcal {S}^n) \,{\leq }_{\mathfrak {L}(\mathcal {S}^n)}\, \mathbb {FFS}(\mathcal {S}^n)$
for
$\mathbb {FRT}_{<\omega }(\mathcal {S}^n) \,{\leq }_{\mathfrak {L}(\mathcal {S}^n)}\, \mathbb {FFS}(\mathcal {S}^n)$
for
 $n\,{\geq }\,2$
.
$n\,{\geq }\,2$
.
5.3 Summary of this section
We close this section by summarizing the
![]() $\mathfrak {L}(\mathcal {S}^n)$
conservations that we have shown.
$\mathfrak {L}(\mathcal {S}^n)$
conservations that we have shown.
 $$ \begin{align*} &\mathbb{FA}(\mathcal{S}^{n+1}) \;{\leq}_{\mathfrak{L}(\mathcal{S}^n)}\; \mathbb{FET}(\mathcal{S}^n)\\&\quad {\leq}_{\mathfrak{L}(\mathcal{S}^n)}\; \mathbb{FCT}(\mathcal{S}^n) \,{\equiv}\, \mathbb{FRT}_1(\mathcal{S}^n) \;{\leq}_{\mathfrak{L}(\mathcal{S}^n)}\; \mathbb{FRT}_2(\mathcal{S}^n) \;{\leq}_{\mathfrak{L}(\mathcal{S}^n)}\; \ldots\\&\quad {\leq}_{\mathfrak{L}(\mathcal{S}^n)}\; \mathbb{FRT}_{<\omega}(\mathcal{S}^n) \;{=}_{\mathfrak{L}(\mathcal{S}^n)}\; \mathbb{FFS}(\mathcal{S}^n) \;{\leq}_{\mathfrak{L}(\mathcal{S}^n)}\; \mathbb{FKF}(\mathcal{S}^n) \end{align*} $$
$$ \begin{align*} &\mathbb{FA}(\mathcal{S}^{n+1}) \;{\leq}_{\mathfrak{L}(\mathcal{S}^n)}\; \mathbb{FET}(\mathcal{S}^n)\\&\quad {\leq}_{\mathfrak{L}(\mathcal{S}^n)}\; \mathbb{FCT}(\mathcal{S}^n) \,{\equiv}\, \mathbb{FRT}_1(\mathcal{S}^n) \;{\leq}_{\mathfrak{L}(\mathcal{S}^n)}\; \mathbb{FRT}_2(\mathcal{S}^n) \;{\leq}_{\mathfrak{L}(\mathcal{S}^n)}\; \ldots\\&\quad {\leq}_{\mathfrak{L}(\mathcal{S}^n)}\; \mathbb{FRT}_{<\omega}(\mathcal{S}^n) \;{=}_{\mathfrak{L}(\mathcal{S}^n)}\; \mathbb{FFS}(\mathcal{S}^n) \;{\leq}_{\mathfrak{L}(\mathcal{S}^n)}\; \mathbb{FKF}(\mathcal{S}^n) \end{align*} $$
These are familiar for experts of axiomatic truth theories, except the first conservation
![]() $\mathbb {FA}(\mathcal {S}^{n+1}) \,{\leq }_{\mathfrak {L}(\mathcal {S}^n)}\, \mathbb {FET}(\mathcal {S}^n)$
.
$\mathbb {FA}(\mathcal {S}^{n+1}) \,{\leq }_{\mathfrak {L}(\mathcal {S}^n)}\, \mathbb {FET}(\mathcal {S}^n)$
.
Our next goal is to show that all these theories are
![]() $\mathfrak {L}(\mathcal {S}^n)$
equivalent to
$\mathfrak {L}(\mathcal {S}^n)$
equivalent to
![]() $\mathbb {FA}(\mathcal {S}^{n+1})$
. What remains to be shown is
$\mathbb {FA}(\mathcal {S}^{n+1})$
. What remains to be shown is
![]() $\mathbb {FKF}(\mathcal {S}^n) \,{\leq }_{\mathfrak {L}(\mathcal {S}^n)}\, \mathbb {FA}(\mathcal {S}^{n+1})$
, which we will establish in the next two sections.
$\mathbb {FKF}(\mathcal {S}^n) \,{\leq }_{\mathfrak {L}(\mathcal {S}^n)}\, \mathbb {FA}(\mathcal {S}^{n+1})$
, which we will establish in the next two sections.
6 Upper bound by fixed point theory
For our goal, it remains to show
![]() $\mathbb {FKF}(\mathcal {S}^{n}) \,{\leq }_{\mathfrak {L}(\mathcal {S}^n)}\, \mathbb {FA}(\mathcal {S}^{n+1})$
. In the first-order setting, the upper bound of the theory
$\mathbb {FKF}(\mathcal {S}^{n}) \,{\leq }_{\mathfrak {L}(\mathcal {S}^n)}\, \mathbb {FA}(\mathcal {S}^{n+1})$
. In the first-order setting, the upper bound of the theory
![]() $\mathbf {KF}$
of Kripke–Feferman truth can be given by interpreting the truth predicate as a fixed point of a positive operator in the fixed point theory
$\mathbf {KF}$
of Kripke–Feferman truth can be given by interpreting the truth predicate as a fixed point of a positive operator in the fixed point theory
![]() $\widehat {\mathbf {ID}}_1$
. Similarly, we consider the finitist analogue
$\widehat {\mathbf {ID}}_1$
. Similarly, we consider the finitist analogue
![]() $\widehat {\mathbb {ID}}_1(\mathcal {S}^{n+1})$
. As opposed to the first-order case, the shift along the smashed Grzegorczyk hierarchy is inevitable. The reduction of
$\widehat {\mathbb {ID}}_1(\mathcal {S}^{n+1})$
. As opposed to the first-order case, the shift along the smashed Grzegorczyk hierarchy is inevitable. The reduction of
![]() $\widehat {\mathbb {ID}}_1 (\mathcal {S}^{n+1})$
to
$\widehat {\mathbb {ID}}_1 (\mathcal {S}^{n+1})$
to
![]() $\mathbb {FA}(\mathcal {S}^{n+1})$
will be given via some first-order theories in the next section.
$\mathbb {FA}(\mathcal {S}^{n+1})$
will be given via some first-order theories in the next section.
Definition 6.1. Let U be a unary relation symbol and
![]() $\mathfrak {L}(\mathcal {S}^n,U)$
the expansion of the arithmetical language
$\mathfrak {L}(\mathcal {S}^n,U)$
the expansion of the arithmetical language
![]() $\mathfrak {L}(\mathcal {S}^n)$
with U. An
$\mathfrak {L}(\mathcal {S}^n)$
with U. An
![]() $\mathfrak {L}(\mathcal {S}^n)$
operator form is an
$\mathfrak {L}(\mathcal {S}^n)$
operator form is an
![]() $\mathfrak {L}(\mathcal {S}^n,U)$
formula with at most one free variable, and it is called positive if U occurs only positively in the formula.
$\mathfrak {L}(\mathcal {S}^n,U)$
formula with at most one free variable, and it is called positive if U occurs only positively in the formula.
For any
![]() $\mathfrak {L}(\mathcal {S}^n)$
operator form
$\mathfrak {L}(\mathcal {S}^n)$
operator form
![]() $O(x,U)$
and formula
$O(x,U)$
and formula
![]() $A(y)$
, let
$A(y)$
, let
![]() $O(x,\{y\,{:}\,A(y)\})$
denote the result of replacing all the subformulae of the forms
$O(x,\{y\,{:}\,A(y)\})$
denote the result of replacing all the subformulae of the forms
![]() $U(t)$
and
$U(t)$
and
![]() ${\neg }\, U(t)$
by
${\neg }\, U(t)$
by
![]() $A(t)$
and
$A(t)$
and
![]() ${\sim }\,A(t)$
, respectively, in the formula
${\sim }\,A(t)$
, respectively, in the formula
![]() $O(x,U)$
.
$O(x,U)$
.
Note that, if A is free from U, then so is
![]() $O(x,\{y\,{:}\,A(y)\})$
: the relation symbol U is just a place holder.
$O(x,\{y\,{:}\,A(y)\})$
: the relation symbol U is just a place holder.
We now define the finitist analogue of the first-order theory
![]() $\widehat {\mathbf {ID}}_1$
of non-iterated hat inductive definition. The characteristic axiom asserts that the new predicate defines a fixed point of a positive operator.
$\widehat {\mathbf {ID}}_1$
of non-iterated hat inductive definition. The characteristic axiom asserts that the new predicate defines a fixed point of a positive operator.
Definition 6.2 (
 $\widehat {\mathbb {ID}}_1(\mathcal {S}^n)$
)
$\widehat {\mathbb {ID}}_1(\mathcal {S}^n)$
)
Let
![]() $\mathfrak {L}_{\mathrm {fix}}(\mathcal {S}^n)$
be the expansion of the language
$\mathfrak {L}_{\mathrm {fix}}(\mathcal {S}^n)$
be the expansion of the language
![]() $\mathfrak {L}(\mathcal {S}^n)$
with a new unary relation symbol
$\mathfrak {L}(\mathcal {S}^n)$
with a new unary relation symbol
![]() $F_O$
for any positive
$F_O$
for any positive
![]() $\mathfrak {L}(\mathcal {S}^n)$
operator form
$\mathfrak {L}(\mathcal {S}^n)$
operator form
![]() $O(x,U)$
.
$O(x,U)$
.
![]() $\widehat {\mathbb {ID}}_1(\mathcal {S}^n)$
is the
$\widehat {\mathbb {ID}}_1(\mathcal {S}^n)$
is the
![]() $\mathfrak {L}_{\mathrm {fix}}(\mathcal {S}^n)$
theory generated by the following:
$\mathfrak {L}_{\mathrm {fix}}(\mathcal {S}^n)$
theory generated by the following:
-
(
 $\mathbb {FA}(\mathcal {S}^n)$
): all axioms of
$\mathbb {FA}(\mathcal {S}^n)$
): all axioms of
 $\mathbb {FA}(\mathcal {S}^n)$
with the schema of induction extended to
$\mathbb {FA}(\mathcal {S}^n)$
with the schema of induction extended to
 $\mathfrak {L}_{\mathrm {fix}}(\mathcal {S}^n)$
formulae;
$\mathfrak {L}_{\mathrm {fix}}(\mathcal {S}^n)$
formulae; -
(FP):
 $F_O(x)\,{\leftrightarrow }\,O(x,\{y\,{:}\,F_O(y)\})$
for any positive
$F_O(x)\,{\leftrightarrow }\,O(x,\{y\,{:}\,F_O(y)\})$
for any positive
 $\mathfrak {L}(\mathcal {S}^n)$
operator form
$\mathfrak {L}(\mathcal {S}^n)$
operator form
 $O(x,U)$
.
$O(x,U)$
.
The theories
![]() $\widehat {\mathbb {ID}}_m(\mathcal {S}^n)$
of m-th iterated hat inductive definition are defined by iterating this procedure: operator forms O for
$\widehat {\mathbb {ID}}_m(\mathcal {S}^n)$
of m-th iterated hat inductive definition are defined by iterating this procedure: operator forms O for
![]() $\widehat {\mathbb {ID}}_{m+1}(\mathcal {S}^n)$
can contain the fixed point predicates introduced in
$\widehat {\mathbb {ID}}_{m+1}(\mathcal {S}^n)$
can contain the fixed point predicates introduced in
![]() $\widehat {\mathbb {ID}}_m(\mathcal {S}^n)$
.
$\widehat {\mathbb {ID}}_m(\mathcal {S}^n)$
.
Another tool for our upper bound is the valuation function. As mentioned already in the Introduction, to define it, we need to ascend one level up along (smashed) Grzegorczyk hierarchy.
Lemma 6.3 (
 $\mathrm {val}^{n}$
)
$\mathrm {val}^{n}$
)
The function
![]() $\mathrm {val}^n$
with the following defining axioms is bounded definable in
$\mathrm {val}^n$
with the following defining axioms is bounded definable in
![]() $\mathbb {FA}(\mathcal {S}^{n+1})$
.
$\mathbb {FA}(\mathcal {S}^{n+1})$
.

Proof We apply bounded recursion. The bounding term is
![]() $\gamma _3(\gamma _3(z)) \,{=}\,2^{2^z}$
for
$\gamma _3(\gamma _3(z)) \,{=}\,2^{2^z}$
for
![]() $n\,{=}\,2$
and
$n\,{=}\,2$
and
![]() $\gamma _{n+1}(z)$
for
$\gamma _{n+1}(z)$
for
![]() $n\,{\geq }\,3$
.
$n\,{\geq }\,3$
.
If
![]() $x,y<2^{2^z}$
then
$x,y<2^{2^z}$
then
![]() $x\,{\star }\,y\,{\leq }\,2^{2^{z}{\cdot }2^{z}}\,{=}\, 2^{2^{2{\cdot }z}} \,{<}\,\gamma _3(\gamma _3(2{\cdot }z{+}1))$
, and if
$x\,{\star }\,y\,{\leq }\,2^{2^{z}{\cdot }2^{z}}\,{=}\, 2^{2^{2{\cdot }z}} \,{<}\,\gamma _3(\gamma _3(2{\cdot }z{+}1))$
, and if
![]() $x,y<\gamma _{n+1}(z)$
then
$x,y<\gamma _{n+1}(z)$
then
![]() $x\,{\star }\,y\,{<}\,\gamma _{n+1}(2{\cdot }z{+}1)$
for
$x\,{\star }\,y\,{<}\,\gamma _{n+1}(2{\cdot }z{+}1)$
for
![]() $n\,{\geq }\,3$
, where
$n\,{\geq }\,3$
, where
![]() . If
. If
![]() $x\,{<}\,\gamma _{n+1}(z)$
then
$x\,{<}\,\gamma _{n+1}(z)$
then
![]() $\gamma _n(x)\,{<}\,\gamma _{n+1}(z{+}1) \,{\leq }\,\gamma _{n+1}(2{\cdot }z{+}1)$
.
$\gamma _n(x)\,{<}\,\gamma _{n+1}(z{+}1) \,{\leq }\,\gamma _{n+1}(2{\cdot }z{+}1)$
.
Definition 6.4. Let
![]() $K_n(u,U)$
be the following positive operator form.
$K_n(u,U)$
be the following positive operator form.

Theorem 6.5. Let
![]() $n\,{\geq }\,2$
. For any
$n\,{\geq }\,2$
. For any
![]() $\mathfrak {L}(\mathcal {S}^n,T)$
formula A, if
$\mathfrak {L}(\mathcal {S}^n,T)$
formula A, if
![]() $\mathbb {FKF}(\mathcal {S}^n) \vdash A$
then
$\mathbb {FKF}(\mathcal {S}^n) \vdash A$
then
![]() $\widehat {\mathbb {ID}}_1(\mathcal {S}^{n+1}) \vdash A^{K_n}$
, where
$\widehat {\mathbb {ID}}_1(\mathcal {S}^{n+1}) \vdash A^{K_n}$
, where
![]() $A^{K_n}$
is the result of replacing all the subformulae of the form
$A^{K_n}$
is the result of replacing all the subformulae of the form
![]() $T(t)$
by
$T(t)$
by
![]() $F_{K_n}(t)$
in A. Thus
$F_{K_n}(t)$
in A. Thus
![]() $\mathbb {FKF}(\mathcal {S}^n) \,{\leq }_{\mathfrak {L}(\mathcal {S}^n)}\, \widehat {\mathbb {ID}}_1(\mathcal {S}^{n+1})$
.
$\mathbb {FKF}(\mathcal {S}^n) \,{\leq }_{\mathfrak {L}(\mathcal {S}^n)}\, \widehat {\mathbb {ID}}_1(\mathcal {S}^{n+1})$
.
Remark 6.6. We can also interpret
![]() $T(t)$
by
$T(t)$
by
. Together with the following fixed-point construction induction where U occurs only negatively in B, we can add either the consistency
or the completeness
.

7
 Hat inductive definition in second order arithmetic
Hat inductive definition in second order arithmetic
For our final goal, what remains to be shown is
![]() $\widehat {\mathbb {ID}}_1(\mathcal {S}^{n+1}) \,{\leq }_{\mathfrak {L}(\mathcal {S}^{n})} \,\mathbb {FA}(\mathcal {S}^{n+1})$
for
$\widehat {\mathbb {ID}}_1(\mathcal {S}^{n+1}) \,{\leq }_{\mathfrak {L}(\mathcal {S}^{n})} \,\mathbb {FA}(\mathcal {S}^{n+1})$
for
![]() $n\,{\geq }\,2$
. In this section, we prove this conservation, with
$n\,{\geq }\,2$
. In this section, we prove this conservation, with
![]() ${\leq }_{\mathfrak {L}(\mathcal {S}^{n})}$
being actually enhanced to
${\leq }_{\mathfrak {L}(\mathcal {S}^{n})}$
being actually enhanced to
![]() ${\leq }_{\mathfrak {L}(\mathcal {S}^{n+1})}$
(and also
${\leq }_{\mathfrak {L}(\mathcal {S}^{n+1})}$
(and also
![]() $\widehat {\mathbb {ID}}_1(\mathcal {S}^{n+1})$
to
$\widehat {\mathbb {ID}}_1(\mathcal {S}^{n+1})$
to
![]() $\widehat {\mathbb {ID}}_{<\omega }(\mathcal {S}^{n+1})$
). Our strategy is to use well known first-order theories at intermediate steps.
$\widehat {\mathbb {ID}}_{<\omega }(\mathcal {S}^{n+1})$
). Our strategy is to use well known first-order theories at intermediate steps.
![]() $\widehat {\mathbb {ID}}_1(\mathcal {S}^n)$
is defined in the finitist setting in the same way as the fixed point theory
$\widehat {\mathbb {ID}}_1(\mathcal {S}^n)$
is defined in the finitist setting in the same way as the fixed point theory
![]() $\widehat {\mathbf {ID}}_1$
is in the first-order setting. The linguistic limitation amounts to the restriction that operators be
$\widehat {\mathbf {ID}}_1$
is in the first-order setting. The linguistic limitation amounts to the restriction that operators be
![]() in terms of first-order arithmetic. Thus,
in terms of first-order arithmetic. Thus,
![]() $\widehat {\mathbb {ID}}_1(\mathcal {S}^n)$
is the finitist part of
$\widehat {\mathbb {ID}}_1(\mathcal {S}^n)$
is the finitist part of
![]() , the fixed point theory restricted to positive
, the fixed point theory restricted to positive
![]() operators. The restricted and unrestricted fixed point theories
operators. The restricted and unrestricted fixed point theories
![]() and
and
![]() $\widehat {\mathbf {ID}}_1$
are the first-order parts of the second-order arithmetic generated by the fixed point axioms
$\widehat {\mathbf {ID}}_1$
are the first-order parts of the second-order arithmetic generated by the fixed point axioms
![]() and
and
![]() respectively, where the superscript “
respectively, where the superscript “
![]() $-$
” means that the schemata are free from second-order parameters.
$-$
” means that the schemata are free from second-order parameters.
There have been extensive studies on second-order arithmetic (see [Reference Simpson25]), especially on the so-called big five:
![]() $\mathbf {RCA}_0$
,
$\mathbf {RCA}_0$
,
![]() $\mathbf {WKL}_0$
,
$\mathbf {WKL}_0$
,
![]() $\mathbf {ACA}_0$
,
$\mathbf {ACA}_0$
,
![]() $\mathbf {ATR}_0$
, and
$\mathbf {ATR}_0$
, and
![]() $\Pi ^1_1{\text{-}}\mathbf {CA}_0$
, where the last four extend
$\Pi ^1_1{\text{-}}\mathbf {CA}_0$
, where the last four extend
![]() $\mathbf {RCA}_0$
with
$\mathbf {RCA}_0$
with
![]() $(\mathsf {WKL})$
,
$(\mathsf {WKL})$
,
,
![]() $(\mathsf {ATR})$
, and
$(\mathsf {ATR})$
, and
![]() $(\Pi ^1_1\mathsf {-}\mathsf {CA})$
, respectively. The following three known facts are important for us. Firstly, as Avigad [Reference Avigad2] showed, the parameter-allowing fixed point axiom
$(\Pi ^1_1\mathsf {-}\mathsf {CA})$
, respectively. The following three known facts are important for us. Firstly, as Avigad [Reference Avigad2] showed, the parameter-allowing fixed point axiom
is equivalent to
![]() $(\mathsf {ATR})$
. Secondly, the relationship of
$(\mathsf {ATR})$
. Secondly, the relationship of
![]() $\mathbf {RCA}_0$
and
$\mathbf {RCA}_0$
and
![]() $\mathbf {WKL}_0$
and that of
$\mathbf {WKL}_0$
and that of
and
![]() $\mathbf {ATR}_0$
are strongly analogous as described informally as follows (see [Reference Simpson25, Remark I.11.8]):
$\mathbf {ATR}_0$
are strongly analogous as described informally as follows (see [Reference Simpson25, Remark I.11.8]):

For example,
![]() $(\mathsf {WKL})$
and
$(\mathsf {WKL})$
and
![]() $(\mathsf {ATR})$
are equivalent, over some base theory, to
$(\mathsf {ATR})$
are equivalent, over some base theory, to
![]() $(\Sigma ^0_1\mathsf {-Sep})$
and
$(\Sigma ^0_1\mathsf {-Sep})$
and
![]() $(\Sigma ^1_1\mathsf {-Sep})$
respectively, while the characteristic axioms of
$(\Sigma ^1_1\mathsf {-Sep})$
respectively, while the characteristic axioms of
![]() $\mathbf {RCA}_0$
and
$\mathbf {RCA}_0$
and
are
and
. This analogy survives, in the presence of
![]() $\gamma _3\,{\equiv } \,\exp $
, even if we drop
$\gamma _3\,{\equiv } \,\exp $
, even if we drop
![]() $(\Sigma ^0_1\mathsf {-Ind})$
from
$(\Sigma ^0_1\mathsf {-Ind})$
from
![]() $\mathbf {WKL}_0$
and
$\mathbf {WKL}_0$
and
![]() $\mathbf {RCA}_0$
, namely
$\mathbf {RCA}_0$
, namely

Thirdly,
![]() $\mathbf {WKL}^*_0$
is known to be
$\mathbf {WKL}^*_0$
is known to be
![]() $\Pi ^1_1$
conservative over
$\Pi ^1_1$
conservative over
![]() $\mathbf {RCA}^*_0$
and
$\mathbf {RCA}^*_0$
and
![]() $\Pi ^0_2$
conservative over
$\Pi ^0_2$
conservative over
, whose finitist part is our
![]() $\mathbb {FA}(\mathcal {S}^3)$
. This is in contrast to the strong analogy mentioned just above, because
$\mathbb {FA}(\mathcal {S}^3)$
. This is in contrast to the strong analogy mentioned just above, because
![]() $\mathbf {ATR}_0$
is not conservative over
$\mathbf {ATR}_0$
is not conservative over
. Because of the first and the second facts, one can expect that
is equivalent to
![]() $(\mathsf {WKL})$
and that, if so, the third fact yields the conservation of
$(\mathsf {WKL})$
and that, if so, the third fact yields the conservation of
over
, and hence of the set-parameter-free variant
. We show that this expectation is actually the case.
7.1 First-order and second-order arithmetic
As mentioned above, in this section we use first-order theories as auxiliary tools.
Definition 7.1 (
 $\mathcal {L}_1(\mathcal {S}^n)$
and
$\mathcal {L}_1(\mathcal {S}^n)$
and
 )
)
Let
![]() $\mathcal {L}_1(\mathcal {S}^n)$
be the one-sorted first-order language of first-order arithmetic which has the same constant, function, and relation symbols as the finitist language
$\mathcal {L}_1(\mathcal {S}^n)$
be the one-sorted first-order language of first-order arithmetic which has the same constant, function, and relation symbols as the finitist language
![]() $\mathfrak {L}(\mathcal {S}^n)$
.
$\mathfrak {L}(\mathcal {S}^n)$
.
Let
![]() be the
be the
![]() $\mathcal {L}_1(\mathcal {S}^n)$
theory generated from the same non-logical axioms as
$\mathcal {L}_1(\mathcal {S}^n)$
theory generated from the same non-logical axioms as
![]() $\mathbb {FA}(\mathcal {S}^n)$
.
$\mathbb {FA}(\mathcal {S}^n)$
.
Recall that first-order languages and theories are denoted by calligraphic and bold letters, and that negation
![]() $\neg $
applies only to atomic formulae, but a syntactic operation
$\neg $
applies only to atomic formulae, but a syntactic operation
![]() $\sim $
is defined by De Morgan’s Law.
$\sim $
is defined by De Morgan’s Law.
As non-logical axioms of
![]() are only those of
are only those of
![]() $\mathbb {FA}(\mathcal {S}^n)$
, in
$\mathbb {FA}(\mathcal {S}^n)$
, in
![]() we have induction schema only for
we have induction schema only for
![]() $\mathfrak {L}(\mathcal {S}^n)$
formulae, which are called
$\mathfrak {L}(\mathcal {S}^n)$
formulae, which are called
![]() formulae in the context of first-order arithmetic. We use lower-case Greek letters
formulae in the context of first-order arithmetic. We use lower-case Greek letters
![]() $\varphi $
,
$\varphi $
,
![]() $\psi $
to denote first-order formulae (whereas we used capital Roman letters A, B, C, …to denote finitist formulae, which are, at the same time,
$\psi $
to denote first-order formulae (whereas we used capital Roman letters A, B, C, …to denote finitist formulae, which are, at the same time,
![]() first-order formulae).
first-order formulae).
By the standard cut-elimination argument, we can show the following.
Theorem 7.2.
![]() .
.
Proof Trivially
![]() . For the converse, let A be any
. For the converse, let A be any
![]() $\mathfrak {L}(\mathcal {S}^n)$
formula with
$\mathfrak {L}(\mathcal {S}^n)$
formula with
![]() . Then, there is a finite set
. Then, there is a finite set
![]() $\Gamma $
of non-logical axioms of
$\Gamma $
of non-logical axioms of
![]() such that the sequent
such that the sequent
![]() $\neg \Gamma ,A$
is provable in the sequent-calculus of classical logic. By cut-elimination, we have a proof of this sequent in which only subformulae of
$\neg \Gamma ,A$
is provable in the sequent-calculus of classical logic. By cut-elimination, we have a proof of this sequent in which only subformulae of
![]() $\neg \Gamma ,A$
occur. All these subformulae are in
$\neg \Gamma ,A$
occur. All these subformulae are in
![]() $\mathfrak {L}(\mathcal {S}^n)$
and so this shows
$\mathfrak {L}(\mathcal {S}^n)$
and so this shows
![]() $\mathbb {FA}(\mathcal {S}^n)\vdash A$
.
$\mathbb {FA}(\mathcal {S}^n)\vdash A$
.
We also need another family of first-order theories, called second-order arithmetic. The name seems to contradict the fact that they are not theories over second-order logic but only over (two-sorted) first-order logic. However, this is an established standard terminology, and we have to get along with it.
Definition 7.3. Let
![]() $\mathcal {L}_2(\mathcal {S}^n)$
be the two-sorted first-order language of second-order arithmetic that extends
$\mathcal {L}_2(\mathcal {S}^n)$
be the two-sorted first-order language of second-order arithmetic that extends
![]() $\mathcal {L}_1(\mathcal {S}^n)$
. Namely, it has two sorts, called number and set; the number-sort fragment is exactly
$\mathcal {L}_1(\mathcal {S}^n)$
. Namely, it has two sorts, called number and set; the number-sort fragment is exactly
![]() $\mathcal {L}_1(\mathcal {S}^n)$
; terms of set-sort are only variables; and the only relation symbol beyond
$\mathcal {L}_1(\mathcal {S}^n)$
; terms of set-sort are only variables; and the only relation symbol beyond
![]() $\mathcal {L}_1(\mathcal {S}^n)$
is
$\mathcal {L}_1(\mathcal {S}^n)$
is
![]() $\in $
, whose first argument is of number-sort and whose second argument is of set-sort. Number-variables are denoted by lower-case Latin letters
$\in $
, whose first argument is of number-sort and whose second argument is of set-sort. Number-variables are denoted by lower-case Latin letters
![]() $x,y,z,\ldots $
and set-variables by capital ones
$x,y,z,\ldots $
and set-variables by capital ones
![]() $X,Y,Z,\ldots $
, both possibly with subscripts.
$X,Y,Z,\ldots $
, both possibly with subscripts.
The equality between set-variables is not a primitive symbol, but can be defined:
![]() $X\,{=}\,Y\,{:\equiv }\,\forall x(x\,{\in }\,X \,{\leftrightarrow }\,x\,{\in }\,Y)$
.
$X\,{=}\,Y\,{:\equiv }\,\forall x(x\,{\in }\,X \,{\leftrightarrow }\,x\,{\in }\,Y)$
.
Definition 7.4 (Class notation)
For
![]() $\mathcal {L}_2(\mathcal {S}^n)$
formulae
$\mathcal {L}_2(\mathcal {S}^n)$
formulae
![]() $\varphi (X)$
and
$\varphi (X)$
and
![]() $\psi (x)$
with distinguished set- and number-variables X and x, let
$\psi (x)$
with distinguished set- and number-variables X and x, let
![]() $\varphi (\{x\,{:}\,\psi (x)\})$
denote the result of replacing all the subformulae of the forms
$\varphi (\{x\,{:}\,\psi (x)\})$
denote the result of replacing all the subformulae of the forms
![]() $t\,{\in }\,X$
and
$t\,{\in }\,X$
and
![]() $\neg (t\,{\in }\,X)$
, in
$\neg (t\,{\in }\,X)$
, in
![]() $\varphi (X)$
, by
$\varphi (X)$
, by
![]() $\psi (t)$
and
$\psi (t)$
and
![]() ${\sim }\,\psi (t)$
respectively.
${\sim }\,\psi (t)$
respectively.
Definition 7.5 (
 ,
,
 $\Sigma _1(\mathcal {S}^n)$
,
$\Sigma _1(\mathcal {S}^n)$
,
 $\Pi _1(\mathcal {S}^n)$
,
$\Pi _1(\mathcal {S}^n)$
,
 $\Pi _2(\mathcal {S}^n)$
)
$\Pi _2(\mathcal {S}^n)$
)
An
![]() $\mathcal {L}_2(\mathcal {S}^n)$
formula is called
$\mathcal {L}_2(\mathcal {S}^n)$
formula is called
![]() if it has no set-quantifiers and called
if it has no set-quantifiers and called
![]() if, additionally, all the number-quantifiers in it are bounded. It is called
if, additionally, all the number-quantifiers in it are bounded. It is called
![]() $\Sigma ^0_1(\mathcal {S}^n)$
,
$\Sigma ^0_1(\mathcal {S}^n)$
,
![]() $\Pi ^0_1(\mathcal {S}^n)$
, or
$\Pi ^0_1(\mathcal {S}^n)$
, or
![]() $\Pi ^0_2(\mathcal {S}^n)$
if it is of the form
$\Pi ^0_2(\mathcal {S}^n)$
if it is of the form
![]() $\exists x\psi (x)$
,
$\exists x\psi (x)$
,
![]() $\forall x\psi (x)$
, or
$\forall x\psi (x)$
, or
![]() $\forall x\exists y\psi (x,y)$
, respectively, with
$\forall x\exists y\psi (x,y)$
, respectively, with
![]() $\psi $
being
$\psi $
being
![]() .
.
![]() ,
,
![]() $\Sigma _1(\mathcal {S}^n)$
,
$\Sigma _1(\mathcal {S}^n)$
,
![]() $\Pi _1(\mathcal {S}^n)$
, and
$\Pi _1(\mathcal {S}^n)$
, and
![]() $\Pi _2(\mathcal {S}^n)$
are defined in the same way for the language
$\Pi _2(\mathcal {S}^n)$
are defined in the same way for the language
![]() $\mathcal {L}_1(\mathcal {S}^n)$
.
$\mathcal {L}_1(\mathcal {S}^n)$
.
Definition 7.6. Let
![]() be the
be the
![]() $\mathcal {L}_2(\mathcal {S}^n)$
theory extending
$\mathcal {L}_2(\mathcal {S}^n)$
theory extending
![]() by the following further axiom and axiom schema:
by the following further axiom and axiom schema:
-
(Ind):
 $0\,{\in }\,X\,{\land }\,(\forall y\,{<}\,x) (y\,{\in }\,X\,{\to }\,y{+}1\,{\in }\,X) \,{\to }\,x\,{\in }\,X$
;
$0\,{\in }\,X\,{\land }\,(\forall y\,{<}\,x) (y\,{\in }\,X\,{\to }\,y{+}1\,{\in }\,X) \,{\to }\,x\,{\in }\,X$
; -
(
 ):
):
 $\exists X(X\,{=}\,\{x\,{:}\,\varphi (x)\})$
for any
$\exists X(X\,{=}\,\{x\,{:}\,\varphi (x)\})$
for any
 formula
formula
 $\varphi $
in which X does not occur.
$\varphi $
in which X does not occur.
Here we employ sans serif letters to denote axiom schemata in first-order languages.
Let
![]() $\mathbf {RCA}_0^*(\mathcal {S}^n)$
the extension of
$\mathbf {RCA}_0^*(\mathcal {S}^n)$
the extension of
![]() by
by
![]() , which is defined as follows:
, which is defined as follows:
-
(
 ):
):
 $\forall x(\varphi (x)\,{\leftrightarrow }\,{\sim }\psi (x)) \,{\to }\,\exists X(X\,{=}\,\{x\,{:}\,\varphi (x)\})$
for any
$\forall x(\varphi (x)\,{\leftrightarrow }\,{\sim }\psi (x)) \,{\to }\,\exists X(X\,{=}\,\{x\,{:}\,\varphi (x)\})$
for any
 $\Pi ^0_1(\mathcal {S}^n)$
formulae
$\Pi ^0_1(\mathcal {S}^n)$
formulae
 $\varphi $
and
$\varphi $
and
 $\psi $
in both of which X does not occur.
$\psi $
in both of which X does not occur.
The theory denoted by
![]() $\mathbf {RCA}_0^*$
(without “
$\mathbf {RCA}_0^*$
(without “
![]() $(\mathcal {S}^n)$
”) in the literature is thus
$(\mathcal {S}^n)$
”) in the literature is thus
![]() $\mathbf {RCA}_0^*(\mathcal {S}^3)$
in our notation. It is known to prove
$\mathbf {RCA}_0^*(\mathcal {S}^3)$
in our notation. It is known to prove
![]() $\Sigma ^0_1$
bounding schema (also called
$\Sigma ^0_1$
bounding schema (also called
![]() $\Sigma ^0_1$
collection schema):
$\Sigma ^0_1$
collection schema):
![]() $(\forall x\,{<}\,u)\exists y \varphi (x,y) \,{\to }\, \exists v (\forall x\,{<}\,u)(\exists y\,{<}\,v) \varphi (x,y)$
for any
$(\forall x\,{<}\,u)\exists y \varphi (x,y) \,{\to }\, \exists v (\forall x\,{<}\,u)(\exists y\,{<}\,v) \varphi (x,y)$
for any
![]() $\varphi $
in
$\varphi $
in
![]() $\Sigma ^0_1$
.
$\Sigma ^0_1$
.
Definition 7.7. In (extensions of)
![]() , we use the following abbreviations:
, we use the following abbreviations:
 $$ \begin{align*} \mathrm{BinSeq}(u)\,{:\equiv}\,& \mathrm{Seq}(u)\,{\land}\, (\forall x\,{<}\,\mathrm{lh}(u))(u(x)\,{<}\,2);\\ \mathrm{ExtOnSeq}(X)\,{:\equiv}\, &\forall u,v\left(\begin{pmatrix} \mathrm{Seq}(u)\,{\land}\,\mathrm{Seq}(v)\,{\land}\, \mathrm{lh}(u)\,{=}\,\mathrm{lh}(v)\\ {\land}\, (\forall x\,{<}\,\mathrm{lh}(u))(u(x)\,{=}\,v(x)) \end{pmatrix} {\to}\,(u\,{\in}\,X\,{\leftrightarrow}\,v\,{\in}\,X) \right)\!;\\ \mathrm{BinTree}(T)\,{:\equiv}\, &\begin{matrix} \mathrm{ExtOnSeq}(T)\,{\land}\, \langle\,\rangle\,{\in}\,T \,{\land}\, \forall u(u\,{\in}\,T\,{\to}\, \mathrm{BinSeq}(u)\\{\land}\, (\forall x\,{<}\,\mathrm{lh}(u)) (u{\upharpoonright}x\,{\in}\,T)) \end{matrix}. \end{align*} $$
$$ \begin{align*} \mathrm{BinSeq}(u)\,{:\equiv}\,& \mathrm{Seq}(u)\,{\land}\, (\forall x\,{<}\,\mathrm{lh}(u))(u(x)\,{<}\,2);\\ \mathrm{ExtOnSeq}(X)\,{:\equiv}\, &\forall u,v\left(\begin{pmatrix} \mathrm{Seq}(u)\,{\land}\,\mathrm{Seq}(v)\,{\land}\, \mathrm{lh}(u)\,{=}\,\mathrm{lh}(v)\\ {\land}\, (\forall x\,{<}\,\mathrm{lh}(u))(u(x)\,{=}\,v(x)) \end{pmatrix} {\to}\,(u\,{\in}\,X\,{\leftrightarrow}\,v\,{\in}\,X) \right)\!;\\ \mathrm{BinTree}(T)\,{:\equiv}\, &\begin{matrix} \mathrm{ExtOnSeq}(T)\,{\land}\, \langle\,\rangle\,{\in}\,T \,{\land}\, \forall u(u\,{\in}\,T\,{\to}\, \mathrm{BinSeq}(u)\\{\land}\, (\forall x\,{<}\,\mathrm{lh}(u)) (u{\upharpoonright}x\,{\in}\,T)) \end{matrix}. \end{align*} $$
The notion of bounded definability of functions in the finitist setting can be transferred to the first-order setting, where it should be called bounded
![]() definability. This can further be extended to allow set variables in arguments. As an instance of the so extended notion, we introduce
definability. This can further be extended to allow set variables in arguments. As an instance of the so extended notion, we introduce
![]() $X{\upharpoonright }t$
, which refers to the least u such that
$X{\upharpoonright }t$
, which refers to the least u such that
![]() $\mathrm {BinSeq}(u)$
,
$\mathrm {BinSeq}(u)$
,
![]() $\mathrm {lh}(u)\,{=}\,t$
and
$\mathrm {lh}(u)\,{=}\,t$
and
![]() $(\forall y\,{<}\,t)(u(y)\,{=}\,0 \,{\leftrightarrow }\,y\,{\in }\,X)$
. Thus,
$(\forall y\,{<}\,t)(u(y)\,{=}\,0 \,{\leftrightarrow }\,y\,{\in }\,X)$
. Thus,
![]() $\varphi (X{\upharpoonright }t)$
should be seen as an abbreviation of
$\varphi (X{\upharpoonright }t)$
should be seen as an abbreviation of
 $$\begin{align*}\exists u \begin{pmatrix} \varphi(u)\,{\land}\, \mathrm{BinSeq}(u)\,{\land}\, \mathrm{lh}(u)\,{=}\,t\,{\land}\, (\forall y\,{<}\,t)(u(y)\,{=}\,0 \,{\leftrightarrow}\,y\,{\in}\,X) \,{\land}\\ {\sim}\,(\exists v\,{<}\,u) (\mathrm{BinSeq}(v)\,{\land}\, \mathrm{lh}(v)\,{=}\,t\,{\land}\, (\forall y\,{<}\,t)(v(y)\,{=}\,0 \,{\leftrightarrow}\,y\,{\in}\,X)) \end{pmatrix}. \end{align*}$$
$$\begin{align*}\exists u \begin{pmatrix} \varphi(u)\,{\land}\, \mathrm{BinSeq}(u)\,{\land}\, \mathrm{lh}(u)\,{=}\,t\,{\land}\, (\forall y\,{<}\,t)(u(y)\,{=}\,0 \,{\leftrightarrow}\,y\,{\in}\,X) \,{\land}\\ {\sim}\,(\exists v\,{<}\,u) (\mathrm{BinSeq}(v)\,{\land}\, \mathrm{lh}(v)\,{=}\,t\,{\land}\, (\forall y\,{<}\,t)(v(y)\,{=}\,0 \,{\leftrightarrow}\,y\,{\in}\,X)) \end{pmatrix}. \end{align*}$$
To bound
![]() $X{\upharpoonright }t$
, the use of
$X{\upharpoonright }t$
, the use of
![]() $\exp \,{\equiv }\,\gamma _3$
is essential (otherwise we could only define
$\exp \,{\equiv }\,\gamma _3$
is essential (otherwise we could only define
![]() $X{\upharpoonright }|t|$
).
$X{\upharpoonright }|t|$
).
Now we can introduce the theory
![]() $\mathbf {WKL}_0^*(\mathcal {S}^n)$
, which extends
$\mathbf {WKL}_0^*(\mathcal {S}^n)$
, which extends
![]() $\mathbf {RCA}_0^*(\mathcal {S}^n)$
by a single
$\mathbf {RCA}_0^*(\mathcal {S}^n)$
by a single
![]() $\mathcal {L}_2(\mathcal {S}^3)$
assertion.
$\mathcal {L}_2(\mathcal {S}^3)$
assertion.
Definition 7.8. For
![]() $n\,{\geq }\,3$
, let
$n\,{\geq }\,3$
, let
![]() $\mathbf {WKL}_0^*(\mathcal {S}^n)$
be the extension of
$\mathbf {WKL}_0^*(\mathcal {S}^n)$
be the extension of
![]() $\mathbf {RCA}_0^*(\mathcal {S}^n)$
by (
$\mathbf {RCA}_0^*(\mathcal {S}^n)$
by (
![]() $\mathsf {WKL}$
), which is defined as follows:
$\mathsf {WKL}$
), which is defined as follows:
-
(
 $\mathsf {WKL}$
):
$\mathsf {WKL}$
):
 $\mathrm {BinTree}(T)\,{\land }\, \forall x\exists u(\mathrm {lh}(u)\,{=}\,x\,{\land }\,u\,{\in }\,T) \,{\to }\, \exists P\forall x(P{\upharpoonright }x\,{\in }\,T)$
.
$\mathrm {BinTree}(T)\,{\land }\, \forall x\exists u(\mathrm {lh}(u)\,{=}\,x\,{\land }\,u\,{\in }\,T) \,{\to }\, \exists P\forall x(P{\upharpoonright }x\,{\in }\,T)$
.
The following theorem is known. For example, [Reference Simpson and Smith26, Corollary 4.9] gave a model-theoretic proof of it for
![]() $n\,{=}\,3$
(where
$n\,{=}\,3$
(where
![]() is denoted by
is denoted by
![]() $\mathbf {EFA}$
), and no essential change is needed for
$\mathbf {EFA}$
), and no essential change is needed for
![]() $n\,{\geq }\,4$
.
$n\,{\geq }\,4$
.
Theorem 7.9.
![]() for
for
![]() $n\,{\geq }\,3$
.
$n\,{\geq }\,3$
.
By combining this with Theorem 7.2, we have
![]() $\mathbf {WKL}^*_0(\mathcal {S}^n) \,{=}_{\mathfrak {L}(\mathcal {S}^n)}\, \mathbb {FA}(\mathcal {S}^n)$
for
$\mathbf {WKL}^*_0(\mathcal {S}^n) \,{=}_{\mathfrak {L}(\mathcal {S}^n)}\, \mathbb {FA}(\mathcal {S}^n)$
for
![]() $n\,{\geq }\,3$
. In Section 7.3, we will give a direct proof-theoretic proof of this (as Corollary 7.23) due to Arai.
$n\,{\geq }\,3$
. In Section 7.3, we will give a direct proof-theoretic proof of this (as Corollary 7.23) due to Arai.
7.2 Equivalents of WKL
In this subsection, we show that
![]() $\mathbf {WKL}_0^*(\mathcal {S}^n)$
can be axiomatized over
$\mathbf {WKL}_0^*(\mathcal {S}^n)$
can be axiomatized over
by either (
![]() $\Sigma ^0_1(\mathcal {S}^n)\mathsf {-Sep}$
) or (
$\Sigma ^0_1(\mathcal {S}^n)\mathsf {-Sep}$
) or (
) instead of (
![]() $\mathsf {WKL}$
). The former was well known over
$\mathsf {WKL}$
). The former was well known over
![]() $\mathbf {RCA}_0(\mathcal {S}^n)$
(e.g., [Reference Simpson25, Lemma IV.4.4]), i.e., in the presence of
$\mathbf {RCA}_0(\mathcal {S}^n)$
(e.g., [Reference Simpson25, Lemma IV.4.4]), i.e., in the presence of
![]() $\Sigma ^0_1$
induction and (
$\Sigma ^0_1$
induction and (
. As
![]() $\mathbf {ATR}_0$
is known to be axiomatizable by either (
$\mathbf {ATR}_0$
is known to be axiomatizable by either (
![]() $\Sigma ^1_1\mathsf {-Sep}$
) or (
$\Sigma ^1_1\mathsf {-Sep}$
) or (
) over
![]() $\mathbf {ACA}_0$
, our result enhances the aforementioned analogy as follows.
$\mathbf {ACA}_0$
, our result enhances the aforementioned analogy as follows.

Definition 7.10. For any class
![]() $\mathcal {C}$
of
$\mathcal {C}$
of
![]() $\mathcal {L}_2(\mathcal {S}^n)$
formulae, we define the following axiom schemata:
$\mathcal {L}_2(\mathcal {S}^n)$
formulae, we define the following axiom schemata:
-
(
 $\mathcal {C}\mathsf {-Sep}$
):
$\mathcal {C}\mathsf {-Sep}$
):
 $\forall x{\sim }(\varphi (x)\,{\land }\,\psi (x)) \,{\to }\,\exists X\forall x ((\varphi (x)\,{\to }\,x\,{\in }\,X) \,{\land }\, (\psi (x)\,{\to }\,\neg \,x\,{\in }\,X))$
for any
$\forall x{\sim }(\varphi (x)\,{\land }\,\psi (x)) \,{\to }\,\exists X\forall x ((\varphi (x)\,{\to }\,x\,{\in }\,X) \,{\land }\, (\psi (x)\,{\to }\,\neg \,x\,{\in }\,X))$
for any
 $\mathcal {C}$
formulae
$\mathcal {C}$
formulae
 $\varphi $
and
$\varphi $
and
 $\psi $
in both of which X does not occur;
$\psi $
in both of which X does not occur; -
(
 $\mathcal {C}\mathsf {-FP}$
):
$\mathcal {C}\mathsf {-FP}$
):
 $\exists X(X\,{=}\,\{x\,{:}\,\varphi (x,X)\})$
for any
$\exists X(X\,{=}\,\{x\,{:}\,\varphi (x,X)\})$
for any
 $\mathcal {C}$
formula
$\mathcal {C}$
formula
 $\varphi (x,X)$
in which X occurs only positively.
$\varphi (x,X)$
in which X occurs only positively.
For
![]() , the class of
, the class of
![]() formulae without set parameters, it is easy to see, by partial cut elimination, that
formulae without set parameters, it is easy to see, by partial cut elimination, that
![]() is
is
![]() $\mathcal {L}_1(\mathcal {S}^n)$
conservative over
$\mathcal {L}_1(\mathcal {S}^n)$
conservative over
![]() $\widehat {\mathbf {ID}}_1(\mathcal {S}^n)$
, and for
$\widehat {\mathbf {ID}}_1(\mathcal {S}^n)$
, and for
![]() ,
,
![]() is
is
![]() $\mathcal {L}_1(\mathcal {S}^n)$
conservative over the finitary iterated version
$\mathcal {L}_1(\mathcal {S}^n)$
conservative over the finitary iterated version
![]() $\widehat {\mathbf {ID}}_{<\omega }(\mathcal {S}^n)$
, as shown in [Reference Avigad2]. Similarly, we can show that
$\widehat {\mathbf {ID}}_{<\omega }(\mathcal {S}^n)$
, as shown in [Reference Avigad2]. Similarly, we can show that
![]() is
is
![]() $\mathcal {L}_1(\mathcal {S}^n)$
conservative over
$\mathcal {L}_1(\mathcal {S}^n)$
conservative over
![]() and
and
![]() $\mathfrak {L}(\mathcal {S}^n)$
conservative over
$\mathfrak {L}(\mathcal {S}^n)$
conservative over
![]() $\widehat {\mathbb {ID}}_1(\mathcal {S}^n)$
. What we will actually need is weaker than these, namely, that our finitist fixed point theory
$\widehat {\mathbb {ID}}_1(\mathcal {S}^n)$
. What we will actually need is weaker than these, namely, that our finitist fixed point theory
![]() $\widehat {\mathbb {ID}}_1(\mathcal {S}^n)$
is included in
$\widehat {\mathbb {ID}}_1(\mathcal {S}^n)$
is included in
![]() (with set parameters being allowed).
(with set parameters being allowed).
Corollary 7.11.
![]() .
.
Because we will see
![]() , in order to have
, in order to have
![]() $\widehat {\mathbb {ID}}_1(\mathcal {S}^n) \,{\leq }_{\mathfrak {L}(\mathcal {S}^n)}\, \mathbb {FA}(\mathcal {S}^n)$
, it suffices to show the equivalence of the three axiomatizations, especially
$\widehat {\mathbb {ID}}_1(\mathcal {S}^n) \,{\leq }_{\mathfrak {L}(\mathcal {S}^n)}\, \mathbb {FA}(\mathcal {S}^n)$
, it suffices to show the equivalence of the three axiomatizations, especially
![]() .
.
Let us start with going from
![]() to
to
![]() $\mathbf {WKL}_0^*(\mathcal {S}^n)$
. Trivially (
$\mathbf {WKL}_0^*(\mathcal {S}^n)$
. Trivially (
![]() ) follows from (
) follows from (
![]() $\Sigma ^0_1(\mathcal {S}^n)\mathsf {-Sep}$
). As (
$\Sigma ^0_1(\mathcal {S}^n)\mathsf {-Sep}$
). As (
![]() $\mathsf {WKL}$
) is a single axiom formulated in
$\mathsf {WKL}$
) is a single axiom formulated in
![]() $\mathcal {L}_2(\mathcal {S}^3)$
, the well known fact
$\mathcal {L}_2(\mathcal {S}^3)$
, the well known fact
![]() $\mathbf {RCA}_0^* (\mathcal {S}^3) \,{+}\, (\Sigma ^0_1(\mathcal {S}^3)\mathsf {-Sep}) \vdash (\mathsf {WKL})$
suffices. Let us recall the proof.
$\mathbf {RCA}_0^* (\mathcal {S}^3) \,{+}\, (\Sigma ^0_1(\mathcal {S}^3)\mathsf {-Sep}) \vdash (\mathsf {WKL})$
suffices. Let us recall the proof.
Theorem 7.12.
![]() for
for
![]() $n\,{\geq }\,3$
.
$n\,{\geq }\,3$
.
Proof Define the following, with the former being equivalent to a
![]() formula under
formula under
![]() $\mathrm {ExtOnSeq}(T)$
:
$\mathrm {ExtOnSeq}(T)$
:
 $$ \begin{align*} \theta(u,x,T)\,{:\equiv}\, \exists v(\mathrm{BinSeq}(v) \,{\land}\,\mathrm{lh}(v)\,{=}\,x\,{\land}\, u{*}v\,{\in}\,T), \\ \varphi_i(u,T) \,{:\equiv}\, \exists x(\theta(u{*}\langle i\rangle,x,T) \,{\land}\,{\sim}\theta(u{*}\langle 1{-}i\rangle,x,T)). \end{align*} $$
$$ \begin{align*} \theta(u,x,T)\,{:\equiv}\, \exists v(\mathrm{BinSeq}(v) \,{\land}\,\mathrm{lh}(v)\,{=}\,x\,{\land}\, u{*}v\,{\in}\,T), \\ \varphi_i(u,T) \,{:\equiv}\, \exists x(\theta(u{*}\langle i\rangle,x,T) \,{\land}\,{\sim}\theta(u{*}\langle 1{-}i\rangle,x,T)). \end{align*} $$
![]() $\varphi _i(u,T)$
asserts
$\varphi _i(u,T)$
asserts
![]() $u{*}\langle i\rangle $
has a longer extension than
$u{*}\langle i\rangle $
has a longer extension than
![]() $u{*}\langle 1{-}i\rangle $
. Thus, if
$u{*}\langle 1{-}i\rangle $
. Thus, if
![]() $\mathrm{BinTree}(\mathrm{T})$
, then
$\mathrm{BinTree}(\mathrm{T})$
, then
![]() $\forall u{\sim }(\varphi _0(u,T)\,{\land }\,\varphi _1(u,T))$
. Now
$\forall u{\sim }(\varphi _0(u,T)\,{\land }\,\varphi _1(u,T))$
. Now
![]() $(\Sigma ^0_1(\mathcal {S}^3)\mathsf {-Sep})$
yields X with
$(\Sigma ^0_1(\mathcal {S}^3)\mathsf {-Sep})$
yields X with
By recursion on x, define P by
![]() $x\,{\in }\,P \,{\leftrightarrow }\, P{\upharpoonright }x\,{\in }\,X$
. Then
$x\,{\in }\,P \,{\leftrightarrow }\, P{\upharpoonright }x\,{\in }\,X$
. Then
We show
![]() $\mathrm {BinTree}(T)\,{\land }\, \forall x\theta (\langle \,\rangle ,x,T) \,{\to }\,\forall x(P{\upharpoonright }x\,{\in }\,T)$
.
$\mathrm {BinTree}(T)\,{\land }\, \forall x\theta (\langle \,\rangle ,x,T) \,{\to }\,\forall x(P{\upharpoonright }x\,{\in }\,T)$
.
Assume
![]() $\mathrm {BinTree}(T)$
. We prove
$\mathrm {BinTree}(T)$
. We prove
![]() $\theta (P{\upharpoonright }(x{-}y),y,T) \,{\to }\,P{\upharpoonright }x\,{\in }\,T$
by induction on y. If
$\theta (P{\upharpoonright }(x{-}y),y,T) \,{\to }\,P{\upharpoonright }x\,{\in }\,T$
by induction on y. If
![]() $y\,{=}\,0$
, this is obvious. We show
$y\,{=}\,0$
, this is obvious. We show
![]() $\theta (P{\upharpoonright }(x{-}(y{+}1)),y{+}1,T) \,{\to }\,\theta (P{\upharpoonright }(x{-}y),y,T)$
. Let
$\theta (P{\upharpoonright }(x{-}(y{+}1)),y{+}1,T) \,{\to }\,\theta (P{\upharpoonright }(x{-}y),y,T)$
. Let
![]() $v$
witness
$v$
witness
![]() $\theta (P{\upharpoonright }(x{-}(y{+}1)),y{+}1,T)$
. Then
$\theta (P{\upharpoonright }(x{-}(y{+}1)),y{+}1,T)$
. Then
![]() $\theta (P{\upharpoonright }(x{-}(y{+}1)) {*}\langle v(0)\rangle ,y,T)$
. Let
$\theta (P{\upharpoonright }(x{-}(y{+}1)) {*}\langle v(0)\rangle ,y,T)$
. Let
![]() $i\,{:=}\,(P{\upharpoonright }(x{-}y))(x{-}(y{+}1))$
. If
$i\,{:=}\,(P{\upharpoonright }(x{-}y))(x{-}(y{+}1))$
. If
![]() $v(0)\,{=}\,i$
, we are done. Assume otherwise, i.e.,
$v(0)\,{=}\,i$
, we are done. Assume otherwise, i.e.,
![]() $v(0)\,{=}\,1{-}i$
. Since
$v(0)\,{=}\,1{-}i$
. Since
![]() $(P{\upharpoonright }(x{-}y))(x{-}(y{+}1)) \,{\neq }\,1{-}i$
we have
$(P{\upharpoonright }(x{-}y))(x{-}(y{+}1)) \,{\neq }\,1{-}i$
we have
![]() ${\sim }\varphi _{1-i}(P{\upharpoonright } (x{-}(y{+}1)),T)$
and
${\sim }\varphi _{1-i}(P{\upharpoonright } (x{-}(y{+}1)),T)$
and
![]() $\theta (P{\upharpoonright } (x{-}(y{+}1)){*}\langle i\rangle ,y,T)$
.
$\theta (P{\upharpoonright } (x{-}(y{+}1)){*}\langle i\rangle ,y,T)$
.
Next we show
![]() . The key observation is the following, whose second conjunct means that, if
. The key observation is the following, whose second conjunct means that, if
![]() $v$
encodes a larger finite set than u does, then
$v$
encodes a larger finite set than u does, then
![]() $\theta (x,u)\,{\to }\,\theta (x,v)$
. We call it monotonicity.
$\theta (x,u)\,{\to }\,\theta (x,v)$
. We call it monotonicity.
Lemma 7.13 (
 Normal Form Theorem)
Normal Form Theorem)
Let
![]() $n\,{\geq }\,3$
. For any
$n\,{\geq }\,3$
. For any
formula
![]() $\varphi (x,X)$
in which X occurs only positively, we have an
$\varphi (x,X)$
in which X occurs only positively, we have an
![]() $\mathcal {L}_2(\mathcal {S}^n)$
term
$\mathcal {L}_2(\mathcal {S}^n)$
term
![]() $t(x)$
and a
$t(x)$
and a
formula
![]() $\theta (x,u)$
without occurrences of X such that
$\theta (x,u)$
without occurrences of X such that
Proof By meta-induction on
![]() $\varphi $
. The non-trivial cases are those of bounded quantifiers.
$\varphi $
. The non-trivial cases are those of bounded quantifiers.
Let
![]() $\varphi (x,X)\,{\equiv }\, (\forall y\,{<}\,t(x))\psi (y,x,X)$
. By induction hypothesis, there are a term s and a
$\varphi (x,X)\,{\equiv }\, (\forall y\,{<}\,t(x))\psi (y,x,X)$
. By induction hypothesis, there are a term s and a
![]() formula
formula
![]() $\chi $
with
$\chi $
with
![]() $\psi (y,x,X)\,{\leftrightarrow }\, \chi (y,x,X{\upharpoonright }z)$
for
$\psi (y,x,X)\,{\leftrightarrow }\, \chi (y,x,X{\upharpoonright }z)$
for
![]() $z\,{\geq }\,s(y,x)$
. Hence we have
$z\,{\geq }\,s(y,x)$
. Hence we have
![]() $(\forall y\,{<}\,t(x))\psi (y,x,X) \,{\leftrightarrow }\, (\forall y\,{<}\,t(x))\chi (y,x,X{\upharpoonright }z)$
for
$(\forall y\,{<}\,t(x))\psi (y,x,X) \,{\leftrightarrow }\, (\forall y\,{<}\,t(x))\chi (y,x,X{\upharpoonright }z)$
for
![]() $z\,{\geq }\,s(t(x),x)$
, because
$z\,{\geq }\,s(t(x),x)$
, because
![]() $y\,{<}\,t(x)\,{\to }\,s(y,x)\,{<}\,s(t(x),x)$
. Thus
$y\,{<}\,t(x)\,{\to }\,s(y,x)\,{<}\,s(t(x),x)$
. Thus
![]() $s(t(x),x)$
and
$s(t(x),x)$
and
![]() $\theta (x,u)\,{\equiv }\,(\forall y\,{<}\,t(x)) \chi (y,x,u)$
are the required term and formula.
$\theta (x,u)\,{\equiv }\,(\forall y\,{<}\,t(x)) \chi (y,x,u)$
are the required term and formula.
This lemma without positivity and monotonicity is the set-based analogue of Kleene’s Normal Form Theorem and was proved in detail in [Reference Nemoto14, Lemma 2.13].
Another lemma that we will need is a form of pigeon-hole principle.
Lemma 7.14.
![]() .
.
Proof Since we have an
![]() $\mathcal {S}^3$
term
$\mathcal {S}^3$
term
![]() $t(y,z)$
such that
$t(y,z)$
such that

we can prove the statement by induction on y. If
![]() $y\,{=}\,0$
, this is obvious.
$y\,{=}\,0$
, this is obvious.
Assume
![]() $\mathrm {Seq}(u) \,{\land }\,(\forall x\,{<}\,y{+}3)(u(x)\,{<}\,y{+}2)$
. If
$\mathrm {Seq}(u) \,{\land }\,(\forall x\,{<}\,y{+}3)(u(x)\,{<}\,y{+}2)$
. If
![]() $(\forall x\,{<}\,y{+}3)(u(x)\,{<}\,y{+}1)$
, the induction hypothesis yields
$(\forall x\,{<}\,y{+}3)(u(x)\,{<}\,y{+}1)$
, the induction hypothesis yields
![]() $x_0,x_1\,{<}\,y{+}2$
with
$x_0,x_1\,{<}\,y{+}2$
with
![]() $x_0\,{\neq }\,x_1$
and
$x_0\,{\neq }\,x_1$
and
![]() $u(x_0)\,{=}\,u(x_1)$
, which yields a conclusion of the lemma. Thus we may assume
$u(x_0)\,{=}\,u(x_1)$
, which yields a conclusion of the lemma. Thus we may assume
![]() $x_3\,{<}\,y{+}3$
,
$x_3\,{<}\,y{+}3$
,
![]() $u(x_3)\,{=}\,y{+}1$
and
$u(x_3)\,{=}\,y{+}1$
and
![]() $(\forall x\,{<}\,y{+}3)(x\,{\neq }\,x_3 \,{\to }\,u(x)\,{<}\,y{+}1)$
. Define
$(\forall x\,{<}\,y{+}3)(x\,{\neq }\,x_3 \,{\to }\,u(x)\,{<}\,y{+}1)$
. Define
![]() $v$
with
$v$
with
![]() $\mathrm {lh}(v)\,{=}\,y{+}2$
by
$\mathrm {lh}(v)\,{=}\,y{+}2$
by
![]() $v(x)\,{=}\,u(x)$
for
$v(x)\,{=}\,u(x)$
for
![]() $x\,{<}\,x_3$
and
$x\,{<}\,x_3$
and
![]() $v(x)\,{=}\,u(x{+}1)$
for
$v(x)\,{=}\,u(x{+}1)$
for
![]() $x\,{\geq }\,x_3$
. Apply the induction hypothesis to
$x\,{\geq }\,x_3$
. Apply the induction hypothesis to
![]() $v$
.
$v$
.
Theorem 7.15.
![]() and therefore we have
and therefore we have
![]() for
for
![]() $n\,{\geq }\,3$
.
$n\,{\geq }\,3$
.
Proof Let
![]() $\varphi (X)$
be any
$\varphi (X)$
be any
![]() formula in which X occurs only positively. Let t and
formula in which X occurs only positively. Let t and
![]() $\theta $
be as in Lemma 7.13 (
$\theta $
be as in Lemma 7.13 (
![]() Normal Form Theorem). We may assume
Normal Form Theorem). We may assume
![]() $t(x)\,{>}\,x$
. Define T by
$t(x)\,{>}\,x$
. Define T by
First we show
![]() $\mathrm {BinTree}(T)$
. Let
$\mathrm {BinTree}(T)$
. Let
![]() $u\,{\in }\,T$
and
$u\,{\in }\,T$
and
![]() $y\,{<}\,\mathrm {lh}(u)$
. We have to show
$y\,{<}\,\mathrm {lh}(u)$
. We have to show
![]() $u{\upharpoonright }y\,{\in }\,T$
. For
$u{\upharpoonright }y\,{\in }\,T$
. For
![]() $x\,{<}\,\mathrm {lh}(u{\upharpoonright }y)\,{=}\,y$
, if
$x\,{<}\,\mathrm {lh}(u{\upharpoonright }y)\,{=}\,y$
, if
![]() $t(x)\,{\leq }\,y$
then
$t(x)\,{\leq }\,y$
then
![]() $t(x)\,{\leq }\,\mathrm {lh}(u)$
and so
$t(x)\,{\leq }\,\mathrm {lh}(u)$
and so
![]() $\theta (x,u)\,{\leftrightarrow }\,u(x)\,{=}\,0$
. It remains to show
$\theta (x,u)\,{\leftrightarrow }\,u(x)\,{=}\,0$
. It remains to show
![]() $\forall x(t(x)\,{\leq }\,y \,{\to }\,(\theta (x,u)\,{\leftrightarrow }\, \theta (x,u{\upharpoonright }y)))$
. If
$\forall x(t(x)\,{\leq }\,y \,{\to }\,(\theta (x,u)\,{\leftrightarrow }\, \theta (x,u{\upharpoonright }y)))$
. If
![]() $t(x)\,{\leq }\,y$
, then we have
$t(x)\,{\leq }\,y$
, then we have
![]() $\theta (x,u)\,{\leftrightarrow }\, \varphi (x,\{z\,{<}\,\mathrm {lh}(u)\,{:}\,u(z)\,{=}\,0\}) \,{\leftrightarrow }\,\theta (x,u{\upharpoonright }y)$
.
$\theta (x,u)\,{\leftrightarrow }\, \varphi (x,\{z\,{<}\,\mathrm {lh}(u)\,{:}\,u(z)\,{=}\,0\}) \,{\leftrightarrow }\,\theta (x,u{\upharpoonright }y)$
.
If T is an infinite tree, then
![]() $(\mathsf {WKL})$
yields an infinite path P, which means
$(\mathsf {WKL})$
yields an infinite path P, which means
![]() $P{\upharpoonright }t(x)\,{\in }\,T$
for any x, implying
$P{\upharpoonright }t(x)\,{\in }\,T$
for any x, implying
It remains to show that T is an infinite tree. We have to show that, for given
![]() $y\,{>}\,0$
, there is
$y\,{>}\,0$
, there is
![]() $u\,{\in }\,T$
with
$u\,{\in }\,T$
with
![]() $\mathrm {lh}(u)\,{=}\,y$
. Define
$\mathrm {lh}(u)\,{=}\,y$
. Define
![]() $v$
such that
$v$
such that
![]() $(\forall x\,{<}\,y)(v(0)(x)\,{=}\,1)$
, that
$(\forall x\,{<}\,y)(v(0)(x)\,{=}\,1)$
, that
![]() $(\forall z\,{<}\,y{+}2)( \mathrm {BinSeq}(v(z))\,{\land }\, \mathrm {lh}(v(z))\,{=}\,y)$
and that
$(\forall z\,{<}\,y{+}2)( \mathrm {BinSeq}(v(z))\,{\land }\, \mathrm {lh}(v(z))\,{=}\,y)$
and that
Intuitively,
![]() $v(z)$
encodes the result of the z-th iterated application of the operator, but truncated at y, to
$v(z)$
encodes the result of the z-th iterated application of the operator, but truncated at y, to
![]() . By induction on
. By induction on
![]() $z\,{\leq }\,y$
we can easily show
$z\,{\leq }\,y$
we can easily show
![]() $(\forall x\,{<}\,y)(v(z)(x)\,{=}\,0 \,{\to }\,v(z{+}1)(x)\,{=}\,0)$
using the monotonicity of
$(\forall x\,{<}\,y)(v(z)(x)\,{=}\,0 \,{\to }\,v(z{+}1)(x)\,{=}\,0)$
using the monotonicity of
![]() $\theta $
. If there is
$\theta $
. If there is
![]() $z\,{\leq }\,y$
with
$z\,{\leq }\,y$
with
![]() $(\forall x\,{<}\,y)(v(z)(x)\,{=}\,v(z{+}1)(x))$
, i.e.,
$(\forall x\,{<}\,y)(v(z)(x)\,{=}\,v(z{+}1)(x))$
, i.e.,
![]() $(\forall x\,{<}\,y)(v(z)(x)\,{=}\,0 \,{\leftrightarrow }\,\theta (x,v(z))$
, then
$(\forall x\,{<}\,y)(v(z)(x)\,{=}\,0 \,{\leftrightarrow }\,\theta (x,v(z))$
, then
![]() $v(z)\,{\in }\,T$
.
$v(z)\,{\in }\,T$
.
We derive a contradiction assuming
![]() ${\sim }(\exists z\,{\leq }\,y) (\forall x\,{<}\,y)(v(z)(x)\,{=}\,v(z{+}1)(x))$
. Now define
${\sim }(\exists z\,{\leq }\,y) (\forall x\,{<}\,y)(v(z)(x)\,{=}\,v(z{+}1)(x))$
. Now define
![]() $w$
with
$w$
with
![]() $\mathrm {lh}(w)\,{=}\,y{+}1$
such that
$\mathrm {lh}(w)\,{=}\,y{+}1$
such that
![]() $(\forall z\,{\leq }\,y) (v(z)(w(z))\,{\neq }\,v(z{+}1)(w(z)))$
. Then we have
$(\forall z\,{\leq }\,y) (v(z)(w(z))\,{\neq }\,v(z{+}1)(w(z)))$
. Then we have
![]() $(\forall z_0\,{\leq }\,z)(v(z_0)(w(z))\,{=}\,1)$
and
$(\forall z_0\,{\leq }\,z)(v(z_0)(w(z))\,{=}\,1)$
and
![]() $(\forall z_1\,{\leq }\,y) (z_1\,{>}\,z\,{\to }\,v(z_1)(w(z))\,{=}\,0)$
. Hence
$(\forall z_1\,{\leq }\,y) (z_1\,{>}\,z\,{\to }\,v(z_1)(w(z))\,{=}\,0)$
. Hence
![]() $z_0\,{<}\,z_1\,{\leq }\,y\,{\to }\, w(z_0)\,{\neq }\,w(z_1)$
, contradicting Lemma 7.14.
$z_0\,{<}\,z_1\,{\leq }\,y\,{\to }\, w(z_0)\,{\neq }\,w(z_1)$
, contradicting Lemma 7.14.
The proof of
![]() $\forall y\exists u(\mathrm {lh}(u)\,{=}\,y \,{\land }\,u\,{\in }\,T)$
above is quite parallel to the standard bottom-up proof of the Knaster–Tarski fixed point theorem. Specifically, the last paragraph is the cardinality argument.
$\forall y\exists u(\mathrm {lh}(u)\,{=}\,y \,{\land }\,u\,{\in }\,T)$
above is quite parallel to the standard bottom-up proof of the Knaster–Tarski fixed point theorem. Specifically, the last paragraph is the cardinality argument.
We can replace (
) with
for any
formula
![]() $\psi (X)$
in which X occurs only negatively, by adding a conjunct “
$\psi (X)$
in which X occurs only negatively, by adding a conjunct “
![]() ${\land }\,\psi (\{x\,{<}\,\mathrm {lh}(u) \,{:}\,u(x)\,{=}\,0\})$
” to the definition of T. This allows us to add finitely many applications of
${\land }\,\psi (\{x\,{<}\,\mathrm {lh}(u) \,{:}\,u(x)\,{=}\,0\})$
” to the definition of T. This allows us to add finitely many applications of
![]() $\mbox {(FCI)}$
from Remark 6.6 in Corollary 7.11.
$\mbox {(FCI)}$
from Remark 6.6 in Corollary 7.11.
Finally, we prove that (
![]() ) implies (
) implies (
![]() $\Sigma ^0_1(\mathcal {S}^n)\mathsf {-Sep}$
). Although we do not need this implication, it is relatively easy and does not require
$\Sigma ^0_1(\mathcal {S}^n)\mathsf {-Sep}$
). Although we do not need this implication, it is relatively easy and does not require
![]() $n\,{\geq }\,3$
.
$n\,{\geq }\,3$
.
Proposition 7.16.
![]() .
.
Proof Let
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
be
$\psi $
be
![]() . Assume
. Assume
![]() $\forall x{\sim }(\exists y\varphi (x,y) \,{\land }\,\exists y\psi (x,y))$
. Consider the following positive
$\forall x{\sim }(\exists y\varphi (x,y) \,{\land }\,\exists y\psi (x,y))$
. Consider the following positive
![]() operator:
operator:
 $$\begin{align*}\theta(z,X)\,{:\equiv}\, (\exists x,y\,{<}\,z{+}1) \left (\mathrm{pair}(x,y)\,{=}\,z \,{\land} \left(\varphi(x,y) \,{\lor} \begin{pmatrix} {\sim}\psi(x,y) \,{\land}\\ \mathrm{pair}(x,y{+}1)\,{\in}\,X \end{pmatrix} \right)\right). \end{align*}$$
$$\begin{align*}\theta(z,X)\,{:\equiv}\, (\exists x,y\,{<}\,z{+}1) \left (\mathrm{pair}(x,y)\,{=}\,z \,{\land} \left(\varphi(x,y) \,{\lor} \begin{pmatrix} {\sim}\psi(x,y) \,{\land}\\ \mathrm{pair}(x,y{+}1)\,{\in}\,X \end{pmatrix} \right)\right). \end{align*}$$
![]() yields F with
yields F with
![]() $z\,{\in }\,F\,{\leftrightarrow }\,\theta (z,F)$
. By induction on k we can show both
$z\,{\in }\,F\,{\leftrightarrow }\,\theta (z,F)$
. By induction on k we can show both
![]() $\varphi (x,y)\,{\to }\, \mathrm {pair}(x,y{-}k)\,{\in }\,F$
and
$\varphi (x,y)\,{\to }\, \mathrm {pair}(x,y{-}k)\,{\in }\,F$
and
![]() $\psi (x,y)\,{\to }\,{\sim }\varphi (x,y{-}k)\,{\land }\, \mathrm {pair}(x,y{-}k)\,{\notin }\,F$
using the assumption. Therefore,
$\psi (x,y)\,{\to }\,{\sim }\varphi (x,y{-}k)\,{\land }\, \mathrm {pair}(x,y{-}k)\,{\notin }\,F$
using the assumption. Therefore,
![]() $\exists y\varphi (x,y)\,{\to }\,\mathrm {pair}(x,0)\,{\in }\,F$
and
$\exists y\varphi (x,y)\,{\to }\,\mathrm {pair}(x,0)\,{\in }\,F$
and
![]() $\exists y\psi (x,y)\,{\to }\,\mathrm {pair}(x,0)\,{\notin }\,F$
. By (
$\exists y\psi (x,y)\,{\to }\,\mathrm {pair}(x,0)\,{\notin }\,F$
. By (
![]() ), we can take
), we can take
![]() $X\,{=}\,\{x\,{:}\, \mathrm {pair}(x,0)\,{\in }\,F\}$
.
$X\,{=}\,\{x\,{:}\, \mathrm {pair}(x,0)\,{\in }\,F\}$
.
Corollary 7.17. The following are all equivalent formulations of the
![]() $\mathcal {L}_2(\mathcal {S}^n)$
theory
$\mathcal {L}_2(\mathcal {S}^n)$
theory
![]() $\mathbf {WKL}_0^*(\mathcal {S}^n)$
for
$\mathbf {WKL}_0^*(\mathcal {S}^n)$
for
![]() $n\,{\geq }\,3$
:
$n\,{\geq }\,3$
:
-
•
 ;
; -
•
 ; and
; and -
•
 .
.
Remark 7.18. With
![]() $\sim $
replaced by the intuitionistic negation, all the arguments and hence all the results in this subsection survive in intuitionistic or constructive settings, where we have the law of excluded middle (and double negation elimination) for
$\sim $
replaced by the intuitionistic negation, all the arguments and hence all the results in this subsection survive in intuitionistic or constructive settings, where we have the law of excluded middle (and double negation elimination) for
![]() formulae.
formulae.
7.3 Arai’s proof
As announced before, we give a proof-theoretic proof of
![]() $\mathbf {WKL}^*_0(\mathcal {S}^n) \,{=}_{\mathfrak {L}(\mathcal {S}^n)}\, \mathbb {FA}(\mathcal {S}^n)$
for
$\mathbf {WKL}^*_0(\mathcal {S}^n) \,{=}_{\mathfrak {L}(\mathcal {S}^n)}\, \mathbb {FA}(\mathcal {S}^n)$
for
![]() $n\,{\geq }\,3$
and of Theorem 7.9. With Corollaries 7.11 and 7.17, this shows
$n\,{\geq }\,3$
and of Theorem 7.9. With Corollaries 7.11 and 7.17, this shows
![]() $\widehat {\mathbb {ID}}_1(\mathcal {S}^n) \,{\leq }_{\mathfrak {L}(\mathcal {S}^n)} \,\mathbb {FA}(\mathcal {S}^n)$
. Our proof is taken from [Reference Arai1, Corollary 2.6], which is however for
$\widehat {\mathbb {ID}}_1(\mathcal {S}^n) \,{\leq }_{\mathfrak {L}(\mathcal {S}^n)} \,\mathbb {FA}(\mathcal {S}^n)$
. Our proof is taken from [Reference Arai1, Corollary 2.6], which is however for
![]() $\mathbf {WKL}_0\,{=}_{\Pi ^0_2}\,\mathbf {I}\boldsymbol {\Sigma }_1$
, namely in the presence of the induction schema for
$\mathbf {WKL}_0\,{=}_{\Pi ^0_2}\,\mathbf {I}\boldsymbol {\Sigma }_1$
, namely in the presence of the induction schema for
![]() $\Sigma _1$
formulae.
$\Sigma _1$
formulae.
We employ a sequent calculus. We use capital Greek letters
![]() $\Gamma ,\Lambda ,\ldots $
to denote sequents, namely, finite sets of formulae, and adapt the usual notions for sequents:
$\Gamma ,\Lambda ,\ldots $
to denote sequents, namely, finite sets of formulae, and adapt the usual notions for sequents:
![]() $\Gamma ,\varphi $
stands for
$\Gamma ,\varphi $
stands for
![]() $\Gamma \,{\cup }\, \{\varphi \}$
, and so on.
$\Gamma \,{\cup }\, \{\varphi \}$
, and so on.
Definition 7.19. Let
![]() $\mathbf {G}(\mathcal {S}^n)$
be the usual sequent calculus on
$\mathbf {G}(\mathcal {S}^n)$
be the usual sequent calculus on
![]() $\mathcal {L}_2$
sequents with the following axioms.
$\mathcal {L}_2$
sequents with the following axioms.

This calculus is, optionally, extended by the following rule, a sequent-style counterpart of
![]() $(\Sigma ^0_1(\mathcal {S}^n)\mathsf {-Sep})$
, with eigenvariables
$(\Sigma ^0_1(\mathcal {S}^n)\mathsf {-Sep})$
, with eigenvariables
![]() $x,y,z$
and X.
$x,y,z$
and X.

Definition 7.20. For any
![]() formula
formula
![]() $\varphi (x_0,\ldots ,x_{k-1},y)$
, let
$\varphi (x_0,\ldots ,x_{k-1},y)$
, let
 $$ \begin{align*} &(\exists y_0,\ldots,y_{\ell-1}\varphi(x_0,\ldots,x_{k-1},y_0,\ldots,y_{\ell-1}))^{(z)} \\ &{:\equiv}\, (\exists y_0,\ldots,y_{\ell-1}\,{<}\,z)\varphi(x_0,\ldots,x_{k-1},y_0,\ldots,y_{\ell-1}). \end{align*} $$
$$ \begin{align*} &(\exists y_0,\ldots,y_{\ell-1}\varphi(x_0,\ldots,x_{k-1},y_0,\ldots,y_{\ell-1}))^{(z)} \\ &{:\equiv}\, (\exists y_0,\ldots,y_{\ell-1}\,{<}\,z)\varphi(x_0,\ldots,x_{k-1},y_0,\ldots,y_{\ell-1}). \end{align*} $$
Define
![]() $\Gamma ^{(z)} \,{=}\,\{\psi ^{(z)}\,{:}\,\psi \,{\in }\,\Gamma \}$
for any sequent
$\Gamma ^{(z)} \,{=}\,\{\psi ^{(z)}\,{:}\,\psi \,{\in }\,\Gamma \}$
for any sequent
![]() $\Gamma $
of
$\Gamma $
of
![]() $\Sigma ^0_1(\mathcal {S}^n)$
formulae.
$\Sigma ^0_1(\mathcal {S}^n)$
formulae.
Lemma 7.21. The following rules are admissible in
![]() $\mathbf {G}(\mathcal {S}^n)$
.
$\mathbf {G}(\mathcal {S}^n)$
.


Theorem 7.22. Let
![]() $\Gamma $
be any sequent of
$\Gamma $
be any sequent of
![]() $\Sigma ^0_1(\mathcal {S}^n)$
formulae.
$\Sigma ^0_1(\mathcal {S}^n)$
formulae.
If
![]() $\mathbf {G}(\mathcal {S}^n) \,{+}\,(\Pi ^0_1{\text{-}}\mathrm{Red})\vdash \Gamma $
, then there is an
$\mathbf {G}(\mathcal {S}^n) \,{+}\,(\Pi ^0_1{\text{-}}\mathrm{Red})\vdash \Gamma $
, then there is an
![]() $\mathcal {S}^n$
term t whose free variables are among those of formulae in
$\mathcal {S}^n$
term t whose free variables are among those of formulae in
![]() $\Gamma $
such that
$\Gamma $
such that
![]() $\mathbf {G}(\mathcal {S}^n)\vdash \Gamma ^{(t)}$
.
$\mathbf {G}(\mathcal {S}^n)\vdash \Gamma ^{(t)}$
.
Proof Assume
![]() $\mathbf {G}(\mathcal {S}^n) \,{+}\,(\Pi ^0_1{\text{-}}\mathrm{Red})\vdash \Gamma $
. By partial cut elimination, we may assume that in this proof (Cut) applies only to
$\mathbf {G}(\mathcal {S}^n) \,{+}\,(\Pi ^0_1{\text{-}}\mathrm{Red})\vdash \Gamma $
. By partial cut elimination, we may assume that in this proof (Cut) applies only to
![]() formulae. We prove the conclusion by meta-induction on such a proof. We make a case distinction based on the last inference.
formulae. We prove the conclusion by meta-induction on such a proof. We make a case distinction based on the last inference.
We consider only two cases: (
![]() $\exists \mbox {-Intr}$
) and (
$\exists \mbox {-Intr}$
) and (
![]() $\Pi ^0_1\mbox {-Red}$
).
$\Pi ^0_1\mbox {-Red}$
).
Assume that the last inference is (
![]() $\exists \mbox {-Intr}$
). We may assume the upper sequent is
$\exists \mbox {-Intr}$
). We may assume the upper sequent is
![]() $\Gamma ,\varphi (s)$
with
$\Gamma ,\varphi (s)$
with
![]() $\exists x\varphi (x)\,{\in }\,\Gamma $
. Thus
$\exists x\varphi (x)\,{\in }\,\Gamma $
. Thus
![]() $\varphi $
is a
$\varphi $
is a
![]() formula. By induction hypothesis, there is an
formula. By induction hypothesis, there is an
![]() $\mathcal {S}^n$
term t such that
$\mathcal {S}^n$
term t such that
![]() $\mathbf {G}(\mathcal {S}^n) \vdash \Gamma ^{(t)},\varphi (s)$
. By substituting
$\mathbf {G}(\mathcal {S}^n) \vdash \Gamma ^{(t)},\varphi (s)$
. By substituting
![]() $0$
if necessary, we may assume that the free variables of s and t are only among those of
$0$
if necessary, we may assume that the free variables of s and t are only among those of
![]() $\Gamma $
. Then we have
$\Gamma $
. Then we have
![]() $\mathbf {G}(\mathcal {S}^n)\vdash \Gamma ^{(t)}, (\exists x\,{<}\,s{+}1)\varphi (x)$
and hence
$\mathbf {G}(\mathcal {S}^n)\vdash \Gamma ^{(t)}, (\exists x\,{<}\,s{+}1)\varphi (x)$
and hence
![]() $\mathbf {G}(\mathcal {S}^n) \vdash \Gamma ^{(t+s+1)}$
.
$\mathbf {G}(\mathcal {S}^n) \vdash \Gamma ^{(t+s+1)}$
.
Assume finally that the last inference is (
![]() $\Pi ^0_1\mbox {-Red}$
). Below, we apply (Subst) to
$\Pi ^0_1\mbox {-Red}$
). Below, we apply (Subst) to
![]() $(\forall y\,{<}\,t)\varphi (x,y)$
.
$(\forall y\,{<}\,t)\varphi (x,y)$
.

Up to now in this subsection, we did not need
![]() $n\,{\geq }\,3$
. Below we need
$n\,{\geq }\,3$
. Below we need
![]() $n\,{\geq }\,3$
through Corollary 7.17.
$n\,{\geq }\,3$
through Corollary 7.17.
Corollary 7.23. Let
![]() $n\,{\geq }\,3$
. Then
$n\,{\geq }\,3$
. Then
![]() and also
and also
![]() $\mathbf {WKL}_0^*(\mathcal {S}^n) \,{=}_{\mathfrak {L}(\mathcal {S}^n)}\, \mathbb {FA}(\mathcal {S}^n)$
.
$\mathbf {WKL}_0^*(\mathcal {S}^n) \,{=}_{\mathfrak {L}(\mathcal {S}^n)}\, \mathbb {FA}(\mathcal {S}^n)$
.
Proof For any
![]() formula
formula
![]() $\varphi (x,y)$
in which no set variables occur, if
$\varphi (x,y)$
in which no set variables occur, if
![]() $\mathbf {WKL}_0^*(\mathcal {S}^n) \vdash \forall x\exists y\varphi (x,y)$
, then clearly
$\mathbf {WKL}_0^*(\mathcal {S}^n) \vdash \forall x\exists y\varphi (x,y)$
, then clearly
![]() $\mathbf {G}(\mathcal {S}^n) \,{+}\,(\Pi ^0_1{\text{-}}\mathrm{Red}) \vdash \exists y\varphi (x,y)$
and, the last theorem gives us an
$\mathbf {G}(\mathcal {S}^n) \,{+}\,(\Pi ^0_1{\text{-}}\mathrm{Red}) \vdash \exists y\varphi (x,y)$
and, the last theorem gives us an
![]() $\mathcal {S}^n$
term
$\mathcal {S}^n$
term
![]() $t(x)$
with
$t(x)$
with
![]() $\mathbf {G}(\mathcal {S}^n)\vdash (\exists y\,{<}\,t(x))\varphi (x,y)$
. By partial cut elimination, we may assume that (Cut) applies only to
$\mathbf {G}(\mathcal {S}^n)\vdash (\exists y\,{<}\,t(x))\varphi (x,y)$
. By partial cut elimination, we may assume that (Cut) applies only to
![]() formulae in the
formulae in the
![]() $\mathbf {G}(\mathcal {S}^n)$
proof of
$\mathbf {G}(\mathcal {S}^n)$
proof of
![]() $(\exists y\,{<}\,t(x))\varphi (x,y)$
and, by Substitution (if set variables occur in some part of the proof), we can conclude
$(\exists y\,{<}\,t(x))\varphi (x,y)$
and, by Substitution (if set variables occur in some part of the proof), we can conclude
![]() $\mathbb {FA}(\mathcal {S}^n) \vdash (\exists y\,{<}\,t(x))\varphi (x,y)$
.
$\mathbb {FA}(\mathcal {S}^n) \vdash (\exists y\,{<}\,t(x))\varphi (x,y)$
.
8 Grounded truth and inductive definition
Among other well motivated truth theories is the so-called theory of grounded truth from [Reference Burgess and Tennant3]. It is called Kripke–Feferman–Burgess truth theory in [Reference Halbach11, Chapter 17] and extends Kripke–Feferman truth theory by the schema asserting that the truth predicate denotes the least fixed point of the first-order analogue of
![]() $K_n$
from Definition 6.4. However,
$K_n$
from Definition 6.4. However,
![]() $K_n$
involves the valuation function and the schema needs unbounded quantifiers, both of which are not available in the finitist setting. Thus we make the following modifications.
$K_n$
involves the valuation function and the schema needs unbounded quantifiers, both of which are not available in the finitist setting. Thus we make the following modifications.
Definition 8.1 (Finitist Kripke–Feferman–Burgess truth)
For
![]() $n\,{\geq }\,2$
, let
$n\,{\geq }\,2$
, let
![]() $\mathbb {FKFB}(\mathcal {S}^n)$
extend
$\mathbb {FKFB}(\mathcal {S}^n)$
extend
![]() $\mathbb {FKF}(\mathcal {S}^n)$
by the following non-logical rule:
$\mathbb {FKF}(\mathcal {S}^n)$
by the following non-logical rule:

for eigenvariables
![]() $y,z,v,w$
and any
$y,z,v,w$
and any
![]() $\mathfrak {L}(\mathcal {S}^n,T)$
formula
$\mathfrak {L}(\mathcal {S}^n,T)$
formula
![]() $A(u,x_0,\ldots ,x_{k-1})$
, where
$A(u,x_0,\ldots ,x_{k-1})$
, where

Intuitively,
![]() $\mathrm {Clos}_n(y,z,v,w,U)$
means that U is a closed set of the operator
$\mathrm {Clos}_n(y,z,v,w,U)$
means that U is a closed set of the operator
![]() $K_n$
from Section 6.
$K_n$
from Section 6.
In the first-order setting, Kripke–Feferman–Burgess truth theory is known to be equivalent to the first-order theory
![]() $\mathbf {ID}_1$
of non-iterated inductive definition. We define
$\mathbf {ID}_1$
of non-iterated inductive definition. We define
![]() $\mathbb {ID}_1(\mathcal {S}^n)$
similarly to
$\mathbb {ID}_1(\mathcal {S}^n)$
similarly to
![]() $\mathbf {ID}_1$
but with a rule.
$\mathbf {ID}_1$
but with a rule.
Definition 8.2.
![]() $\mathbb {ID}_1(\mathcal {S}^n)$
is the
$\mathbb {ID}_1(\mathcal {S}^n)$
is the
![]() $\mathfrak {L}_{\mathrm {fix}}(\mathcal {S}^n)$
theory extending
$\mathfrak {L}_{\mathrm {fix}}(\mathcal {S}^n)$
theory extending
![]() $\widehat {\mathbb {ID}}_1(\mathcal {S}^n)$
with the following non-logical rule, for any
$\widehat {\mathbb {ID}}_1(\mathcal {S}^n)$
with the following non-logical rule, for any
![]() $\mathfrak {L}(\mathcal {S}^n)$
operator form
$\mathfrak {L}(\mathcal {S}^n)$
operator form
![]() $O(x,U)$
and any
$O(x,U)$
and any
![]() $\mathfrak {L}_{\mathrm {fix}}(\mathcal {S}^n)$
formula
$\mathfrak {L}_{\mathrm {fix}}(\mathcal {S}^n)$
formula
![]() $A(x,z_0,\ldots ,z_{k-1})$
, where y is an eigenvariable.
$A(x,z_0,\ldots ,z_{k-1})$
, where y is an eigenvariable.

We can easily see
![]() $\mathbb {FKFB}(\mathcal {S}^n) \,{\leq }_{\mathfrak {L}(\mathcal {S}^n)}\, \mathbb {ID}_1(\mathcal {S}^{n+1})$
for
$\mathbb {FKFB}(\mathcal {S}^n) \,{\leq }_{\mathfrak {L}(\mathcal {S}^n)}\, \mathbb {ID}_1(\mathcal {S}^{n+1})$
for
![]() $n\,{\geq }\,2$
by extending the argument in Section 6.
$n\,{\geq }\,2$
by extending the argument in Section 6.
The lower bound for
![]() $\mathbb {FKFB}(\mathcal {S}^n)$
can be given without significant difference from the first-order analogue. It is convenient to extend the dot notation for operator forms, or, more generally, for
$\mathbb {FKFB}(\mathcal {S}^n)$
can be given without significant difference from the first-order analogue. It is convenient to extend the dot notation for operator forms, or, more generally, for
![]() $\mathfrak {L}(\mathcal {S}^n,U)$
formulae.
$\mathfrak {L}(\mathcal {S}^n,U)$
formulae.
Definition 8.3. For any
![]() $\mathfrak {L}(\mathcal {S}^n,U)$
formula
$\mathfrak {L}(\mathcal {S}^n,U)$
formula
![]() $P(x_0,\ldots ,x_{k-1},U)$
, define an
$P(x_0,\ldots ,x_{k-1},U)$
, define an
![]() $\mathcal {S}^2$
term
$\mathcal {S}^2$
term
by meta-recursion on P similarly to
in Definition 3.2 except the following additional clause for atomic formulae with U:

Lemma 8.4. For any
![]() $\mathfrak {L}(\mathcal {S}^n,U)$
formula
$\mathfrak {L}(\mathcal {S}^n,U)$
formula
![]() $P(x_0,\ldots ,x_{k-1},U)$
in which U occurs only positively and for any
$P(x_0,\ldots ,x_{k-1},U)$
in which U occurs only positively and for any
![]() $\mathfrak {L}(\mathcal {S}^n,T)$
formula
$\mathfrak {L}(\mathcal {S}^n,T)$
formula
![]() $A(x)$
in which T occurs only positively and
$A(x)$
in which T occurs only positively and
![]() $y,z_0,\ldots ,z_{k-1}$
do not occur,
$y,z_0,\ldots ,z_{k-1}$
do not occur,
Proof We prove this lemma by meta-induction on P. We consider only the case of
![]() $P(x_0,\ldots ,x_{k-1},U)\,{\equiv }\,U(t(x_0,\ldots ,x_{k-1}))$
. We reason in
$P(x_0,\ldots ,x_{k-1},U)\,{\equiv }\,U(t(x_0,\ldots ,x_{k-1}))$
. We reason in
![]() $\mathbb {FKF}(\mathcal {S}^n)$
. Since
$\mathbb {FKF}(\mathcal {S}^n)$
. Since
![]() is
is
![]() by definition, we can see by Theorem 4.12 that
by definition, we can see by Theorem 4.12 that
![]() is equivalent to
is equivalent to
![]() $A(t(z_0,\ldots ,z_{k-1}))$
, that is,
$A(t(z_0,\ldots ,z_{k-1}))$
, that is,
![]() $P(z_0,\ldots ,z_{k-1},\{x\,{:}\,A(x)\})$
.
$P(z_0,\ldots ,z_{k-1},\{x\,{:}\,A(x)\})$
.
The next shows that Gödel’s self-referential (fixed point) lemma follows from “fixed point” in our sense.
Theorem 8.5. For any positive
![]() $\mathfrak {L}(\mathcal {S}^n)$
operator form
$\mathfrak {L}(\mathcal {S}^n)$
operator form
![]() $O(x,U)$
, there is a standard number o such that:
$O(x,U)$
, there is a standard number o such that:
-
(i)
 , where
, where
 $\overline {o}$
is the numeral for o;
$\overline {o}$
is the numeral for o; -
(ii) the following rule is derivable in
 $\mathbb {FKFB}(\mathcal {S}^n)$
: for any
$\mathbb {FKFB}(\mathcal {S}^n)$
: for any
 $\mathfrak {L}(\mathcal {S}^n,T)$
formula
$\mathfrak {L}(\mathcal {S}^n,T)$
formula
 $A(y)$
which might have free variables other than y.
$A(y)$
which might have free variables other than y. 
Proof Let
![]() $\mathrm {diag}$
be a definable function in
$\mathrm {diag}$
be a definable function in
![]() $\mathbb {FA}(\mathcal {S}^2)$
with the defining axiom
$\mathbb {FA}(\mathcal {S}^2)$
with the defining axiom
and let k be such that
![]() . Let
. Let
![]() $o\,{=}\,\mathrm {diag}(k)$
. Then
$o\,{=}\,\mathrm {diag}(k)$
. Then
![]() .
.
(i) By Lemma 8.4,
![]() is equivalent to
is equivalent to
![]() .
.
(ii) Define B as follows, where
![]() $y_0,\ldots ,y_{k-1}$
do not occur in
$y_0,\ldots ,y_{k-1}$
do not occur in
![]() $A(x)$
:
$A(x)$
:

We reason in
![]() $\mathbb {FKFB}(\mathcal {S}^n)$
. Assume
$\mathbb {FKFB}(\mathcal {S}^n)$
. Assume
![]() $O(y,\{x\,{:}\,A(x)\}) \,{\to }\,A(y)$
. It suffices to show
$O(y,\{x\,{:}\,A(x)\}) \,{\to }\,A(y)$
. It suffices to show
![]() $\mathrm {Clos}_n(x,y,v,w,\{u\,{:}\,B(u)\})$
, as
$\mathrm {Clos}_n(x,y,v,w,\{u\,{:}\,B(u)\})$
, as
is equivalent to
![]() $O(y,\{x\,{:}\,A(x)\})$
.
$O(y,\{x\,{:}\,A(x)\})$
.
First assume
![]() $\mathrm {AtForm}_n(v)\,{\land }\, \mathrm {Sent}_n(v)\,{\land }\,T(v)$
. If
$\mathrm {AtForm}_n(v)\,{\land }\, \mathrm {Sent}_n(v)\,{\land }\,T(v)$
. If
![]() , then U does not occur in P, and so
, then U does not occur in P, and so
![]() $T(v)$
implies
$T(v)$
implies
![]() $P(y_0,\ldots ,y_{k-1})$
. Thus,
$P(y_0,\ldots ,y_{k-1})$
. Thus,
![]() $B(v)$
.
$B(v)$
.
Next assume
![]() $\mathrm {Sent}_{n,T}(v)\,{\land }\,\mathrm {Sent}_{n,T}(w)$
. In order to show
$\mathrm {Sent}_{n,T}(v)\,{\land }\,\mathrm {Sent}_{n,T}(w)$
. In order to show
, we let
. Then
![]() $P\,{\equiv }\,Q\,{\land }\,R$
and
$P\,{\equiv }\,Q\,{\land }\,R$
and
![]() $B(v)\,{\land }\,B(w)$
implies
$B(v)\,{\land }\,B(w)$
implies
![]() $Q(y_0,\ldots ,y_{k-1},\overline {o}) \,{\land }\,R(y_0,\ldots ,y_{k-1},\overline {o})$
. Similarly
$Q(y_0,\ldots ,y_{k-1},\overline {o}) \,{\land }\,R(y_0,\ldots ,y_{k-1},\overline {o})$
. Similarly
, and

Assume
and
![]() $B(z)$
. In order to show
$B(z)$
. In order to show
, let
for a subformula P of O. As O does not contain T, we have
![]() $P(x_0,\ldots ,x_{k-1},U)\,{\equiv }\,U(t(x_0,\ldots ,x_{k-1}))$
and
$P(x_0,\ldots ,x_{k-1},U)\,{\equiv }\,U(t(x_0,\ldots ,x_{k-1}))$
and

and so
.
![]() $B(z)$
implies
$B(z)$
implies
![]() $O(t(y_0,\ldots ,y_{k-1}),\{x\,{:}\,A(x)\})$
and
$O(t(y_0,\ldots ,y_{k-1}),\{x\,{:}\,A(x)\})$
and
![]() $A(t(y_0,\ldots ,y_{k-1}))$
, i.e.,
$A(t(y_0,\ldots ,y_{k-1}))$
, i.e.,
.
Note that
![]() is vacuous, since U must be positive in P. Thus we have covered all the cases.
is vacuous, since U must be positive in P. Thus we have covered all the cases.
Corollary 8.6. (1)
![]() $\widehat {\mathbb {ID}}_1(\mathcal {S}^n) +(\mathrm{Tot}{\text{-}}\gamma _{n+1}) \,{\leq }_{\mathfrak {L}(\mathcal {S}^n)}\, \mathbb {FKF}(\mathcal {S}^n)$
.
$\widehat {\mathbb {ID}}_1(\mathcal {S}^n) +(\mathrm{Tot}{\text{-}}\gamma _{n+1}) \,{\leq }_{\mathfrak {L}(\mathcal {S}^n)}\, \mathbb {FKF}(\mathcal {S}^n)$
.
(2)
![]() $\mathbb {ID}_1(\mathcal {S}^n) +(\mathrm{Tot}{\text{-}}\gamma _{n+1}) \,{\leq }_{\mathfrak {L}(\mathcal {S}^n)}\, \mathbb {FKFB}(\mathcal {S}^n)$
.
$\mathbb {ID}_1(\mathcal {S}^n) +(\mathrm{Tot}{\text{-}}\gamma _{n+1}) \,{\leq }_{\mathfrak {L}(\mathcal {S}^n)}\, \mathbb {FKFB}(\mathcal {S}^n)$
.
In the first-order setting, the analogues of (1) and of Section 6 show the equivalence
![]() $\widehat {\mathbf {ID}}_1\,{=}_{\mathcal {L}_1}\,\mathbf {KF}$
directly. We do not know if the argument of Section 2.4 can be extended to
$\widehat {\mathbf {ID}}_1\,{=}_{\mathcal {L}_1}\,\mathbf {KF}$
directly. We do not know if the argument of Section 2.4 can be extended to
![]() $\widehat {\mathbb {ID}}_1(\mathcal {S}^{n+1}) \,{\leq }_{\mathfrak {L}(\mathcal {S}^n)}\, \widehat {\mathbb {ID}}_1(\mathcal {S}^n)+(\mathrm{Tot}{\text{-}}\gamma _{n+1})$
nor to
$\widehat {\mathbb {ID}}_1(\mathcal {S}^{n+1}) \,{\leq }_{\mathfrak {L}(\mathcal {S}^n)}\, \widehat {\mathbb {ID}}_1(\mathcal {S}^n)+(\mathrm{Tot}{\text{-}}\gamma _{n+1})$
nor to
![]() $\mathbb {ID}_1(\mathcal {S}^{n+1}) \,{\leq }_{\mathfrak {L}(\mathcal {S}^n)}\, \mathbb {ID}_1(\mathcal {S}^n)+(\mathrm{Tot}{\text{-}}\gamma _{n+1})$
. Instead,
$\mathbb {ID}_1(\mathcal {S}^{n+1}) \,{\leq }_{\mathfrak {L}(\mathcal {S}^n)}\, \mathbb {ID}_1(\mathcal {S}^n)+(\mathrm{Tot}{\text{-}}\gamma _{n+1})$
. Instead,
![]() $\mathbb {ID}_1(\mathcal {S}^{n+1})\,{=}_{\mathfrak {L}(\mathcal {S}^n)}\, \mathbb {ID}_1(\mathcal {S}^{n})$
can be shown as follows.
$\mathbb {ID}_1(\mathcal {S}^{n+1})\,{=}_{\mathfrak {L}(\mathcal {S}^n)}\, \mathbb {ID}_1(\mathcal {S}^{n})$
can be shown as follows.
Definition 8.7. Let
![]() $\mathbf {I}\boldsymbol {\Sigma }_1(\mathcal {S}^n)$
be the extension of
$\mathbf {I}\boldsymbol {\Sigma }_1(\mathcal {S}^n)$
be the extension of
![]() by
by
We will omit “
![]() $(\mathcal {S}^n)$
”, as
$(\mathcal {S}^n)$
”, as
![]() $\mathbf {I}\boldsymbol {\Sigma }_1(\mathcal {S}^n)$
and
$\mathbf {I}\boldsymbol {\Sigma }_1(\mathcal {S}^n)$
and
![]() $\mathbf {I}\boldsymbol {\Sigma }_1(\mathcal {S}^m)$
are known to be mutually interpretable for
$\mathbf {I}\boldsymbol {\Sigma }_1(\mathcal {S}^m)$
are known to be mutually interpretable for
![]() $n,m\,{\geq }\,2$
.
$n,m\,{\geq }\,2$
.
Theorem 8.8.
![]() $\mathbb {ID}_1(\mathcal {S}^n) \,{=}_{\mathfrak {L}(\mathcal {S}^n)}\, \mathbf {I}\boldsymbol {\Sigma }_1$
for
$\mathbb {ID}_1(\mathcal {S}^n) \,{=}_{\mathfrak {L}(\mathcal {S}^n)}\, \mathbf {I}\boldsymbol {\Sigma }_1$
for
![]() $n\,{\geq }\,2$
.
$n\,{\geq }\,2$
.
Proof First we embed
![]() $\mathbb {ID}_1(\mathcal {S}^n)$
in
$\mathbb {ID}_1(\mathcal {S}^n)$
in
![]() $\mathbf {I}\boldsymbol {\Sigma }_1$
. For any positive operator
$\mathbf {I}\boldsymbol {\Sigma }_1$
. For any positive operator
![]() $O(x,U)$
, define the following first-order formulae, where
$O(x,U)$
, define the following first-order formulae, where
![]() $\mathrm{ES}_O(u)$
means that finite sets
$\mathrm{ES}_O(u)$
means that finite sets
![]() $X_j\,{=}\, \{y\,{<}\,\mathrm {lh}(u(j))\,{:}\,u(j)(y)\,{=}\,0\}$
satisfy
$X_j\,{=}\, \{y\,{<}\,\mathrm {lh}(u(j))\,{:}\,u(j)(y)\,{=}\,0\}$
satisfy
![]() $X_j\,{\subseteq }\,\{x\,{:}\,O(x,\bigcup _{i<j}X_i)\}$
.
$X_j\,{\subseteq }\,\{x\,{:}\,O(x,\bigcup _{i<j}X_i)\}$
.
 $$ \begin{align*} &\mathrm{ES}_O(u)\,{:\equiv}\, (\forall j\,{<}\,\mathrm{lh}(u)) (\mathrm{BinSeq}(u(j))\,{\land}\\ &\hspace{20pt}(\forall y\,{<}\,\mathrm{lh}(u(j)) (u(j)(y)\kern1.3pt{=}\kern1.3pt0\kern1.3pt{\to}\kern1.3pt O(y,\{x\kern1.3pt{:}\kern1.3pt(\exists i\kern1.3pt{<}\kern1.3pt j)( x\kern1.3pt{<}\kern1.3pt\mathrm{lh}(u(i))\kern1.3pt{\land}\kern1.3pt u(i)(x) \kern1.3pt{=}\kern1.3pt 0)\}) ),\\ &\mathrm{Fix}_O(x)\,{:\equiv}\, \exists u (\mathrm{lh}(u)\,{>}\,0 \,{\land}\, \mathrm{lh}(u(\mathrm{lh}(u){-}1))\,{>}\,x \,{\land}\, u(\mathrm{lh}(u){-}1)(x)\,{=}\,0\,{\land}\, \mathrm{ES}_O(u)). \end{align*} $$
$$ \begin{align*} &\mathrm{ES}_O(u)\,{:\equiv}\, (\forall j\,{<}\,\mathrm{lh}(u)) (\mathrm{BinSeq}(u(j))\,{\land}\\ &\hspace{20pt}(\forall y\,{<}\,\mathrm{lh}(u(j)) (u(j)(y)\kern1.3pt{=}\kern1.3pt0\kern1.3pt{\to}\kern1.3pt O(y,\{x\kern1.3pt{:}\kern1.3pt(\exists i\kern1.3pt{<}\kern1.3pt j)( x\kern1.3pt{<}\kern1.3pt\mathrm{lh}(u(i))\kern1.3pt{\land}\kern1.3pt u(i)(x) \kern1.3pt{=}\kern1.3pt 0)\}) ),\\ &\mathrm{Fix}_O(x)\,{:\equiv}\, \exists u (\mathrm{lh}(u)\,{>}\,0 \,{\land}\, \mathrm{lh}(u(\mathrm{lh}(u){-}1))\,{>}\,x \,{\land}\, u(\mathrm{lh}(u){-}1)(x)\,{=}\,0\,{\land}\, \mathrm{ES}_O(u)). \end{align*} $$
We can show
![]() $O(z,\{x\,{:}\,\mathrm {Fix}_O(x)\}) \,{\to }\,\mathrm {Fix}_O(z)$
by
$O(z,\{x\,{:}\,\mathrm {Fix}_O(x)\}) \,{\to }\,\mathrm {Fix}_O(z)$
by
![]() Normal Form Theorem and
Normal Form Theorem and
![]() $\Sigma _1$
bounding schema, provable in
$\Sigma _1$
bounding schema, provable in
![]() $\mathbf {I}\boldsymbol {\Sigma }_1$
(cf. [Reference Sato17, Lemma 5]). Since we have the induction schema for
$\mathbf {I}\boldsymbol {\Sigma }_1$
(cf. [Reference Sato17, Lemma 5]). Since we have the induction schema for
![]() formulae (
formulae (
![]() relative to
relative to
![]() $\Sigma _1$
, i.e., generated from
$\Sigma _1$
, i.e., generated from
![]() $\Sigma _1$
formulae by propositional connectives and bounded quantifiers), for any
$\Sigma _1$
formulae by propositional connectives and bounded quantifiers), for any
![]() formula
formula
![]() $\varphi $
, from
$\varphi $
, from
![]() $\forall x(O(x,\{y\,{:}\,\varphi (y)\}) \,{\to }\,\varphi (x))$
, by induction on j we obtain
$\forall x(O(x,\{y\,{:}\,\varphi (y)\}) \,{\to }\,\varphi (x))$
, by induction on j we obtain
![]() $\mathrm {ES}_O(u) \,{\to }\, (\forall x\,{<}\,\mathrm {lh}(u(j))) (u(j)(x)\,{=}\,0\,{\to }\,\varphi (x))$
. Thus, by interpreting
$\mathrm {ES}_O(u) \,{\to }\, (\forall x\,{<}\,\mathrm {lh}(u(j))) (u(j)(x)\,{=}\,0\,{\to }\,\varphi (x))$
. Thus, by interpreting
![]() $F_O(t)$
as the
$F_O(t)$
as the
![]() $\Sigma _1$
formula
$\Sigma _1$
formula
![]() $\mathrm {Fix}_O(t)$
, we can interpret
$\mathrm {Fix}_O(t)$
, we can interpret
![]() $\mathbb {ID}_1(\mathcal {S}^n)$
in
$\mathbb {ID}_1(\mathcal {S}^n)$
in
![]() $\mathbf {I}\boldsymbol {\Sigma }_1$
.
$\mathbf {I}\boldsymbol {\Sigma }_1$
.
Next consider the converse. For any
![]() formula
formula
![]() $C(x,y_0,\ldots ,y_{k-1})$
, define an operator
$C(x,y_0,\ldots ,y_{k-1})$
, define an operator
We can show
![]() $C(x,y_0,\ldots ,y_{k-1})\,{\to }\, F_O(\langle x{-}z,y_0,\ldots ,y_{k-1}\rangle )$
by induction on z. For any
$C(x,y_0,\ldots ,y_{k-1})\,{\to }\, F_O(\langle x{-}z,y_0,\ldots ,y_{k-1}\rangle )$
by induction on z. For any
![]() $\mathfrak {L}_{\mathrm {fix}}(\mathcal {S}^n)$
formula
$\mathfrak {L}_{\mathrm {fix}}(\mathcal {S}^n)$
formula
![]() $D(y_0,\ldots ,y_{k-1})$
in which x does not occur, if
$D(y_0,\ldots ,y_{k-1})$
in which x does not occur, if
![]() $\mathbb {ID}_1(\mathcal {S}^n)$
proves
$\mathbb {ID}_1(\mathcal {S}^n)$
proves
![]() $C(x,y_0,\ldots ,y_{k-1})\,{\to }\,D(y_0,\ldots ,y_{k-1})$
, then
$C(x,y_0,\ldots ,y_{k-1})\,{\to }\,D(y_0,\ldots ,y_{k-1})$
, then
![]() $\mathbb {ID}_1(\mathcal {S}^n)$
also proves
$\mathbb {ID}_1(\mathcal {S}^n)$
also proves
and
![]() $F_O(\langle x,y_0,\ldots ,y_{k-1}\rangle )\,{\to }\,D(y_0,\ldots ,y_{k-1})$
by (FI). Therefore, by interpreting
$F_O(\langle x,y_0,\ldots ,y_{k-1}\rangle )\,{\to }\,D(y_0,\ldots ,y_{k-1})$
by (FI). Therefore, by interpreting
![]() $\exists xC(x,y_0,\ldots ,y_{k-1})$
as
$\exists xC(x,y_0,\ldots ,y_{k-1})$
as
![]() $F_O(\langle 0,y_0,\ldots ,y_{k-1}\rangle )$
in
$F_O(\langle 0,y_0,\ldots ,y_{k-1}\rangle )$
in
![]() $\mathbb {ID}_1(\mathcal {S}^n)$
we can interpret the
$\mathbb {ID}_1(\mathcal {S}^n)$
we can interpret the
![]() fragment of
fragment of
![]() $\mathbf {I}\boldsymbol {\Sigma }_1$
. Since all the non-logical axioms are
$\mathbf {I}\boldsymbol {\Sigma }_1$
. Since all the non-logical axioms are
![]() , cut-elimination yields
, cut-elimination yields
![]() $\mathbb {ID}_1(\mathcal {S}^n) \,{\geq }_{\mathfrak {L}(\mathcal {S}^n)}\, \mathbf {I}\boldsymbol {\Sigma }_1$
.
$\mathbb {ID}_1(\mathcal {S}^n) \,{\geq }_{\mathfrak {L}(\mathcal {S}^n)}\, \mathbf {I}\boldsymbol {\Sigma }_1$
.
In relation to this theorem, the equivalence between
![]() and
and
![]() $(\Sigma ^0_1\mathsf {-CA})$
is proved in [Reference Sato21, Proposition 5].
$(\Sigma ^0_1\mathsf {-CA})$
is proved in [Reference Sato21, Proposition 5].
We define
![]() $\mathbb {ID}_1^-(\mathcal {S}^n)$
by requiring A in (FI) to be equivalent both to a formula in which
$\mathbb {ID}_1^-(\mathcal {S}^n)$
by requiring A in (FI) to be equivalent both to a formula in which
![]() $F_O$
occurs only positively and to one in which
$F_O$
occurs only positively and to one in which
![]() $F_O$
occurs only negatively. Then, as the first half of the proof shows, the modified schema is interpretable in
$F_O$
occurs only negatively. Then, as the first half of the proof shows, the modified schema is interpretable in
![]() $\mathbf {RCA}_0^*(\mathcal {S}^n)$
.
$\mathbf {RCA}_0^*(\mathcal {S}^n)$
.
By applying Parson’s theorem
![]() $\mathbf {I}\boldsymbol {\Sigma }_1\,{=}_{\mathfrak {L}(\mathcal {S}^n)} \,\mathbb {PRA}$
, which can also be proved similarly to Section 7.3, we can conclude that
$\mathbf {I}\boldsymbol {\Sigma }_1\,{=}_{\mathfrak {L}(\mathcal {S}^n)} \,\mathbb {PRA}$
, which can also be proved similarly to Section 7.3, we can conclude that
![]() $\mathbb {FKFB}(\mathcal {S}^n)$
is equivalent to
$\mathbb {FKFB}(\mathcal {S}^n)$
is equivalent to
![]() $\mathbb {PRA}$
with which Tait identified Hilbert’s Finitism.
$\mathbb {PRA}$
with which Tait identified Hilbert’s Finitism.
Corollary 8.9.
![]() $\mathbb {FKFB}(\mathcal {S}^n) \,{=}_{\mathfrak {L}(\mathcal {S}^n)}\, \mathbb {ID}_1(\mathcal {S}^n) \,{=}_{\mathfrak {L}(\mathcal {S}^n)}\, \mathbb {PRA}$
for
$\mathbb {FKFB}(\mathcal {S}^n) \,{=}_{\mathfrak {L}(\mathcal {S}^n)}\, \mathbb {ID}_1(\mathcal {S}^n) \,{=}_{\mathfrak {L}(\mathcal {S}^n)}\, \mathbb {PRA}$
for
![]() $n\,{\geq }\,2$
.
$n\,{\geq }\,2$
.
9 Concluding remarks
We have shown that, for
![]() $n\,{\geq }\,2$
, finitist versions of Tarski ramified truth (including Tarski compositional truth), Kripke–Feferman truth, and Friedman–Sheard truth, all formulated over
$n\,{\geq }\,2$
, finitist versions of Tarski ramified truth (including Tarski compositional truth), Kripke–Feferman truth, and Friedman–Sheard truth, all formulated over
![]() $\mathbb {FA}(\mathcal {S}^n)$
, have the same
$\mathbb {FA}(\mathcal {S}^n)$
, have the same
![]() $\mathfrak {L}(\mathcal {S}^n)$
theorems as
$\mathfrak {L}(\mathcal {S}^n)$
theorems as
![]() $\mathbb {FA}(\mathcal {S}^{n+1})$
and as
$\mathbb {FA}(\mathcal {S}^{n+1})$
and as
![]() $\mathbb {FA}(\mathcal {S}^{n})\,{+}\, (\mathrm{Tot}{\text{-}}\gamma _{n+1})$
, namely
$\mathbb {FA}(\mathcal {S}^{n})\,{+}\, (\mathrm{Tot}{\text{-}}\gamma _{n+1})$
, namely
 $$ \begin{align*} &\mathbb{FET}(\mathcal{S}^n) \,{=}_{\mathfrak{L}(\mathcal{S}^n)}\, \mathbb{FCT}(\mathcal{S}^n) \,{=}_{\mathfrak{L}(\mathcal{S}^n)}\, \mathbb{FRT}_{m+1}(\mathcal{S}^n)\\ &\,{=}_{\mathfrak{L}(\mathcal{S}^n)}\, \mathbb{FRT}_{<\omega}(\mathcal{S}^n) \,{=}_{\mathfrak{L}(\mathcal{S}^n)}\, \mathbb{FFS}(\mathcal{S}^n) \,{=}_{\mathfrak{L}(\mathcal{S}^n)}\, \mathbb{FKF}(\mathcal{S}^n)\\ &\,{=}_{\mathfrak{L}(\mathcal{S}^n)}\, \mathbb{FA}(\mathcal{S}^{n+1}) \,{=}_{\mathfrak{L}(\mathcal{S}^n)}\, \mathbb{FA}(\mathcal{S}^{n})\,{+}\, (\mbox{Tot-}\gamma_{n+1}) \,{=}_{\mathfrak{L}(\mathcal{S}^n)}\, \widehat{\mathbb{ID}}_1(\mathcal{S}^{n+1}). \end{align*} $$
$$ \begin{align*} &\mathbb{FET}(\mathcal{S}^n) \,{=}_{\mathfrak{L}(\mathcal{S}^n)}\, \mathbb{FCT}(\mathcal{S}^n) \,{=}_{\mathfrak{L}(\mathcal{S}^n)}\, \mathbb{FRT}_{m+1}(\mathcal{S}^n)\\ &\,{=}_{\mathfrak{L}(\mathcal{S}^n)}\, \mathbb{FRT}_{<\omega}(\mathcal{S}^n) \,{=}_{\mathfrak{L}(\mathcal{S}^n)}\, \mathbb{FFS}(\mathcal{S}^n) \,{=}_{\mathfrak{L}(\mathcal{S}^n)}\, \mathbb{FKF}(\mathcal{S}^n)\\ &\,{=}_{\mathfrak{L}(\mathcal{S}^n)}\, \mathbb{FA}(\mathcal{S}^{n+1}) \,{=}_{\mathfrak{L}(\mathcal{S}^n)}\, \mathbb{FA}(\mathcal{S}^{n})\,{+}\, (\mbox{Tot-}\gamma_{n+1}) \,{=}_{\mathfrak{L}(\mathcal{S}^n)}\, \widehat{\mathbb{ID}}_1(\mathcal{S}^{n+1}). \end{align*} $$
Especially, the hierarchy of Tarski ramified truth theories
![]() $\mathbb {FRT}_m$
’s collapses for
$\mathbb {FRT}_m$
’s collapses for
![]() $m\,{\geq }\,1$
, and the difference of strength between Friedman–Sheard truth and Kripke–Feferman truth is dissolved. These are completely opposed to the corresponding results on the analogous first-order truth theories.
$m\,{\geq }\,1$
, and the difference of strength between Friedman–Sheard truth and Kripke–Feferman truth is dissolved. These are completely opposed to the corresponding results on the analogous first-order truth theories.
The strength is due to the adaption of the rule (
![]() $\exists \mbox {-val}$
), which essentially asserts the totality of
$\exists \mbox {-val}$
), which essentially asserts the totality of
![]() $\gamma _{n+1}$
, the function on the next level of (smashed) Grzegorczyk hierarchy. What we have shown is that no further strength is added by any other truth-theoretic axiom or rule in these theories. An alternative formulation of finitist Tarski compositional truth in Section 11, avoiding (
$\gamma _{n+1}$
, the function on the next level of (smashed) Grzegorczyk hierarchy. What we have shown is that no further strength is added by any other truth-theoretic axiom or rule in these theories. An alternative formulation of finitist Tarski compositional truth in Section 11, avoiding (
![]() $\exists $
-val) but with ramified valuation functions, has at least the same strength. This might suggest that the strengths of finitist Tarski ramified truth of finite ranks do not rely on (
$\exists $
-val) but with ramified valuation functions, has at least the same strength. This might suggest that the strengths of finitist Tarski ramified truth of finite ranks do not rely on (
![]() $\exists $
-val). Moreover, in the forthcoming [Reference Sato and Walker24], we will substantiate the claim that the strengths of
$\exists $
-val). Moreover, in the forthcoming [Reference Sato and Walker24], we will substantiate the claim that the strengths of
![]() $\mathbb {FRT}_{<\omega }(\mathcal {S}^n)$
, of
$\mathbb {FRT}_{<\omega }(\mathcal {S}^n)$
, of
![]() $\mathbb {FFS}(\mathcal {S}^n)$
, and of
$\mathbb {FFS}(\mathcal {S}^n)$
, and of
![]() $\mathbb {FKF}(\mathcal {S}^n)$
do not rely on (
$\mathbb {FKF}(\mathcal {S}^n)$
do not rely on (
![]() $\exists $
-val) either, since the proof will rely only on a natural property of truth theory.
$\exists $
-val) either, since the proof will rely only on a natural property of truth theory.
On the other hand, as seen in Section 8, the finitist version
![]() $\mathbb {FKFB}(\mathcal {S}^n)$
of Kripke–Feferman–Burgess truth has the same
$\mathbb {FKFB}(\mathcal {S}^n)$
of Kripke–Feferman–Burgess truth has the same
![]() $\mathfrak {L}(\mathcal {S}^n)$
theorems as
$\mathfrak {L}(\mathcal {S}^n)$
theorems as
![]() $\mathbb {PRA}$
, with which Tait identified the limit of Hilbert’s Finitism. In this sense, the groundedness adds more strength than the other truth-theoretic axioms and rules.
$\mathbb {PRA}$
, with which Tait identified the limit of Hilbert’s Finitism. In this sense, the groundedness adds more strength than the other truth-theoretic axioms and rules.
As technical intermediate steps, we obtained several basic results on finitist theories and second-order axioms of full and hat inductive definitions for bounded (i.e.,
![]() ) positive operators, in a manner comparable to more popular arithmetical (i.e.,
) positive operators, in a manner comparable to more popular arithmetical (i.e.,
![]() ) ones. The reader may want to review the tables in Section 1.3.
) ones. The reader may want to review the tables in Section 1.3.
10 Open problems
Minor questions already raised
(i) Are the rule
![]() $(T\exists \mbox {-val})$
(from Proposition 4.14) and the axiom
$(T\exists \mbox {-val})$
(from Proposition 4.14) and the axiom
![]() $(TT{=})$
derivable in
$(TT{=})$
derivable in
![]() $\mathbb {FFS}(\mathcal {S}^n)$
minus
$\mathbb {FFS}(\mathcal {S}^n)$
minus
![]() $(TT{=})$
?
$(TT{=})$
?
(ii) Can the argument of Section 2.4 be extended to operators so that it would yield
-
•
 $\widehat {\mathbb {ID}}_1(\mathcal {S}^{n+1}) \,{\leq }_{\mathfrak {L}(\mathcal {S}^n)}\, \widehat {\mathbb {ID}}_1(\mathcal {S}^n) +(\mathrm{Tot}{\text{-}}\gamma _{n+1})$
and
$\widehat {\mathbb {ID}}_1(\mathcal {S}^{n+1}) \,{\leq }_{\mathfrak {L}(\mathcal {S}^n)}\, \widehat {\mathbb {ID}}_1(\mathcal {S}^n) +(\mathrm{Tot}{\text{-}}\gamma _{n+1})$
and -
•
 $\mathbb {ID}_1(\mathcal {S}^{n+1}) \,{\leq }_{\mathfrak {L}(\mathcal {S}^n)}\, \mathbb {ID}_1(\mathcal {S}^n) +(\mathrm{Tot}{\text{-}}\gamma _{n+1})$
?
$\mathbb {ID}_1(\mathcal {S}^{n+1}) \,{\leq }_{\mathfrak {L}(\mathcal {S}^n)}\, \mathbb {ID}_1(\mathcal {S}^n) +(\mathrm{Tot}{\text{-}}\gamma _{n+1})$
?
Mutual interpretability and speed-up
In our main series of results,
![]() $\widehat {\mathbb {ID}}_1(\mathcal {S}^{n+1}) {\leq }_{\mathfrak {L}(\mathcal {S}^n)}\,\mathbb {FA}(\mathcal {S}^{n+1})$
was proved through (at least, a finite fragment of) first-order theories by partial cut elimination (which can be replaced by some model-theoretic methods). Corollary 8.6, on the other hand, reduces
$\widehat {\mathbb {ID}}_1(\mathcal {S}^{n+1}) {\leq }_{\mathfrak {L}(\mathcal {S}^n)}\,\mathbb {FA}(\mathcal {S}^{n+1})$
was proved through (at least, a finite fragment of) first-order theories by partial cut elimination (which can be replaced by some model-theoretic methods). Corollary 8.6, on the other hand, reduces
![]() $\widehat {\mathbb {ID}}_1(\mathcal {S}^{n}) +(\mathrm{Tot}{\text{-}}\gamma _{n+1})$
directly to
$\widehat {\mathbb {ID}}_1(\mathcal {S}^{n}) +(\mathrm{Tot}{\text{-}}\gamma _{n+1})$
directly to
![]() $\mathbb {FKF}(\mathcal {S}^n)$
in a similar way as the proof of
$\mathbb {FKF}(\mathcal {S}^n)$
in a similar way as the proof of
![]() $\mathbb {FKF}(\mathcal {S}^n) \,{\leq }_{\mathfrak {L}(\mathcal {S}^n)}\, \widehat {\mathbb {ID}}_1(\mathcal {S}^{n+1})$
from Section 6. This is crucial from the perspective of speed-up, since reducing finite fragments of first-order theories to finitist ones usually yields exponential speed-up. A natural question is whether
$\mathbb {FKF}(\mathcal {S}^n) \,{\leq }_{\mathfrak {L}(\mathcal {S}^n)}\, \widehat {\mathbb {ID}}_1(\mathcal {S}^{n+1})$
from Section 6. This is crucial from the perspective of speed-up, since reducing finite fragments of first-order theories to finitist ones usually yields exponential speed-up. A natural question is whether
![]() $\widehat {\mathbb {ID}}_1(\mathcal {S}^{n+1}) \,{\leq }_{\mathfrak {L}(\mathcal {S}^n)}\, \mathbb {FKF}(\mathcal {S}^n)$
can be direct in this sense. Similarly, can we make
$\widehat {\mathbb {ID}}_1(\mathcal {S}^{n+1}) \,{\leq }_{\mathfrak {L}(\mathcal {S}^n)}\, \mathbb {FKF}(\mathcal {S}^n)$
can be direct in this sense. Similarly, can we make
![]() $\widehat {\mathbb {ID}}_1(\mathcal {S}^{n+1}) \,{\leq }_{\mathfrak {L}(\mathcal {S}^n)}\,\mathbb {FA}(\mathcal {S}^{n+1})$
direct? Since we have shown that
$\widehat {\mathbb {ID}}_1(\mathcal {S}^{n+1}) \,{\leq }_{\mathfrak {L}(\mathcal {S}^n)}\,\mathbb {FA}(\mathcal {S}^{n+1})$
direct? Since we have shown that
![]() $\mathbb{FA}(\mathcal{S}^{n+1}) \leq_{\mathfrak{L}(\mathcal{S}^n)} \mathbb{FCT}(\mathcal{S}^n)$
is direct, the latter would make
$\mathbb{FA}(\mathcal{S}^{n+1}) \leq_{\mathfrak{L}(\mathcal{S}^n)} \mathbb{FCT}(\mathcal{S}^n)$
is direct, the latter would make
![]() $\mathbb {FKF}(\mathcal {S}^{n}) \,{\leq }_{\mathfrak {L}(\mathcal {S}^n)}\,\mathbb{FCT}(\mathcal {S}^{n})$
direct.
$\mathbb {FKF}(\mathcal {S}^{n}) \,{\leq }_{\mathfrak {L}(\mathcal {S}^n)}\,\mathbb{FCT}(\mathcal {S}^{n})$
direct.
Natural truth theory over
 $\mathbb {PRA}$
$\mathbb {PRA}$
The referee has raised the question whether a natural truth theory for
![]() $\mathbb {PRA}$
can be defined. Although
$\mathbb {PRA}$
can be defined. Although
![]() $\mathbb {FKFB}(\mathcal {S}^n)$
is
$\mathbb {FKFB}(\mathcal {S}^n)$
is
![]() $\mathfrak {L}(\mathcal {S}^n)$
equivalent to
$\mathfrak {L}(\mathcal {S}^n)$
equivalent to
![]() $\mathbb {PRA}$
, it does not have function symbols for primitive recursive functions beyond
$\mathbb {PRA}$
, it does not have function symbols for primitive recursive functions beyond
![]() $\mathcal {S}^n$
, i.e., the language is not a superlanguage of that of
$\mathcal {S}^n$
, i.e., the language is not a superlanguage of that of
![]() $\mathbb {PRA}$
. Taking the union, e.g.,
$\mathbb {PRA}$
. Taking the union, e.g.,
![]() $\bigcup _{k\in \omega } \mathbb {FRT}_{<\omega }(\mathcal {S}^k)$
, results in theories which have all primitive recursive functions and are conservative over
$\bigcup _{k\in \omega } \mathbb {FRT}_{<\omega }(\mathcal {S}^k)$
, results in theories which have all primitive recursive functions and are conservative over
![]() $\mathbb {PRA}$
, but they do not appear natural, as the truth axioms for connectives are not uniform.
$\mathbb {PRA}$
, but they do not appear natural, as the truth axioms for connectives are not uniform.
Truth theories over weaker finitist arithmetic
It is natural to investigate similar truth theories over finitist arithmetic
![]() $\mathbb {FA}(\mathcal {S}^1)$
without the totality of smash
$\mathbb {FA}(\mathcal {S}^1)$
without the totality of smash
![]() ${\#}$
, or over
${\#}$
, or over
![]() $\mathbb {FA}$
without the totality of any functions (but with the graphs of them as relations). These are considered in the authors’ next works [Reference Sato22, Reference Sato and Walker23]. As mentioned already in Section 1.2.2, in such arithmetic diagonalization is not available. Actually, the finitist naïve truth theory over
$\mathbb {FA}$
without the totality of any functions (but with the graphs of them as relations). These are considered in the authors’ next works [Reference Sato22, Reference Sato and Walker23]. As mentioned already in Section 1.2.2, in such arithmetic diagonalization is not available. Actually, the finitist naïve truth theory over
![]() $\mathbb {FA}(\mathcal {S}^1)$
is consistent, and in
$\mathbb {FA}(\mathcal {S}^1)$
is consistent, and in
![]() $\mathbb {FA}$
the naïve truth is even definable, while both the theories are still (arguably) capable of formalizing syntax. However, we do not know if the former is conservative over
$\mathbb {FA}$
the naïve truth is even definable, while both the theories are still (arguably) capable of formalizing syntax. However, we do not know if the former is conservative over
![]() $\mathbb {FA}(\mathcal {S}^1)$
, nor if so are the respective Tarski ramified, Friedman–Sheard, and Kripke–Feferman truth theories.
$\mathbb {FA}(\mathcal {S}^1)$
, nor if so are the respective Tarski ramified, Friedman–Sheard, and Kripke–Feferman truth theories.
11 Appendix. Tarski ramified truth with ramified valuations
In the Introduction, we mentioned the possibility of formulating theories of typed truth with typed valuation functions. In this section, we briefly realize this possibility.
Since
![]() $\mathrm {val}^n$
was not primitive but a defined function, we first reformulate
$\mathrm {val}^n$
was not primitive but a defined function, we first reformulate
![]() $\mathbb {FA}(\mathcal {S}^{n+1})$
with primitive
$\mathbb {FA}(\mathcal {S}^{n+1})$
with primitive
![]() $\mathit {val}^n$
. The lower bound proof by
$\mathit {val}^n$
. The lower bound proof by
![]() $\mathrm {cgr}_n$
in Section 3.2 and the upper bound proof by
$\mathrm {cgr}_n$
in Section 3.2 and the upper bound proof by
![]() $\mathrm {val}^n$
in Section 6 revealed that
$\mathrm {val}^n$
in Section 6 revealed that
![]() $\mathcal {S}^{n+1}$
is generated by
$\mathcal {S}^{n+1}$
is generated by
![]() $\mathcal {S}^{n}\,{\cup }\, \{\mathrm {val}^n\}$
. Our reformulation is based on this set of generators.
$\mathcal {S}^{n}\,{\cup }\, \{\mathrm {val}^n\}$
. Our reformulation is based on this set of generators.
Definition 11.1 (Finitist theory of compositional valuation)
For
![]() $n\,{\geq }\,2$
, let
$n\,{\geq }\,2$
, let
![]() $\mathit {val}^n$
be a new unary function symbol. The
$\mathit {val}^n$
be a new unary function symbol. The
![]() $\mathfrak {L}(\mathcal {S}^{n},\mathit {val}^n)$
theory
$\mathfrak {L}(\mathcal {S}^{n},\mathit {val}^n)$
theory
![]() $\mathbb {FCV}(\mathcal {S}^{n})$
extends
$\mathbb {FCV}(\mathcal {S}^{n})$
extends
![]() $\mathbb {FA}(\mathcal {S}^n)$
by the defining axioms for
$\mathbb {FA}(\mathcal {S}^n)$
by the defining axioms for
![]() $\mathrm {val}^n$
from Lemma 6.3 (with
$\mathrm {val}^n$
from Lemma 6.3 (with
![]() $\mathrm {val}^n$
replaced by
$\mathrm {val}^n$
replaced by
![]() $\mathit {val}^n$
) and the induction schema extended to all
$\mathit {val}^n$
) and the induction schema extended to all
![]() $\mathfrak {L}(\mathcal {S}^{n},\mathit {val}^n)$
formulae.
$\mathfrak {L}(\mathcal {S}^{n},\mathit {val}^n)$
formulae.
With this reformulation, we can ramify the valuation function
![]() $\mathit {val}^n$
in the same way as the ramification of the truth predicate. In the reformulation above, we have already seen typed valuation functions
$\mathit {val}^n$
in the same way as the ramification of the truth predicate. In the reformulation above, we have already seen typed valuation functions
![]() $\mathit {val}^n$
along Grzegorczyk hierarchy. However, the types which we now assign to the valuation function play different roles, and so we indicate them by subscripts.
$\mathit {val}^n$
along Grzegorczyk hierarchy. However, the types which we now assign to the valuation function play different roles, and so we indicate them by subscripts.
Definition 11.2 (Finitist theory of ramified valuation and truth)
For
![]() $n\,{\geq }\,2$
, let
$n\,{\geq }\,2$
, let
![]() $\mathfrak {L}(\mathcal {S}^n,T_{<m}, \mathit {val}^n_{<m})$
be the expansion of
$\mathfrak {L}(\mathcal {S}^n,T_{<m}, \mathit {val}^n_{<m})$
be the expansion of
![]() $\mathfrak {L}(\mathcal {S}^n,T_0,\ldots ,T_{m-1})$
with unary function symbols
$\mathfrak {L}(\mathcal {S}^n,T_0,\ldots ,T_{m-1})$
with unary function symbols
![]() $\mathit {val}^n_0, \ldots ,\mathit {val}^n_{m-1}$
. The
$\mathit {val}^n_0, \ldots ,\mathit {val}^n_{m-1}$
. The
![]() $\mathfrak {L}(\mathcal {S}^n,T_{<m}, \mathit {val}^n_{<m})$
theory
$\mathfrak {L}(\mathcal {S}^n,T_{<m}, \mathit {val}^n_{<m})$
theory
![]() $\mathbb {FRVT}_m(\mathcal {S}^n)$
is generated by the following non-logical axioms for
$\mathbb {FRVT}_m(\mathcal {S}^n)$
is generated by the following non-logical axioms for
![]() $j\,{<}\,m$
:
$j\,{<}\,m$
:
-
(
 $\mathbb {FCV}(\mathcal {S}^n)$
): all the axioms of
$\mathbb {FCV}(\mathcal {S}^n)$
): all the axioms of
 $\mathbb {FCV}(\mathcal {S}^n)$
(defined in the obvious manner) with
$\mathbb {FCV}(\mathcal {S}^n)$
(defined in the obvious manner) with
 $\mathit {val}^n$
replaced by
$\mathit {val}^n$
replaced by
 $\mathit {val}^n_j$
for any
$\mathit {val}^n_j$
for any
 $j\,{<}\,m$
and the schema of induction extended to
$j\,{<}\,m$
and the schema of induction extended to
 $\mathfrak {L}(\mathcal {S}^n,T_{<m}, \mathit {val}^n_{<m})$
formulae;
$\mathfrak {L}(\mathcal {S}^n,T_{<m}, \mathit {val}^n_{<m})$
formulae; -
(
 $\mathrm {Val}_{\mathrm {tp}}$
):
$\mathrm {Val}_{\mathrm {tp}}$
):
 for
for
 $i\,{<}\,j$
;
$i\,{<}\,j$
; -
(
 $T\mathrm {Atom}^*$
):
$T\mathrm {Atom}^*$
):
 ;
; -
(
 $T\neg \mathrm {Atom}^*$
): defined similarly;
$T\neg \mathrm {Atom}^*$
): defined similarly; -
(
 $TT^{}_{\mathrm {tp}}$
), (
$TT^{}_{\mathrm {tp}}$
), (
 $T\neg T^{}_{\mathrm {tp}}$
), (
$T\neg T^{}_{\mathrm {tp}}$
), (
 $T{\land }^{}_{\mathrm {tp}}$
), (
$T{\land }^{}_{\mathrm {tp}}$
), (
 $T{\lor }^{}_{\mathrm {tp}}$
): as in
$T{\lor }^{}_{\mathrm {tp}}$
): as in
 $\mathbb {FRT}_m(\mathcal {S}^n)$
but with
$\mathbb {FRT}_m(\mathcal {S}^n)$
but with
 $\mathrm {Sent}_{n,T_{<j}}$
replaced by
$\mathrm {Sent}_{n,T_{<j}}$
replaced by
 $\mathrm {Sent}_{n,T_{<j}, \mathit {val}^n_{<j}}$
;
$\mathrm {Sent}_{n,T_{<j}, \mathit {val}^n_{<j}}$
; -
(
 $T\forall ^*_{\mathrm {tp}}$
):
$T\forall ^*_{\mathrm {tp}}$
):
 $\mathrm {Var}(x)\,{\land }\, \mathrm {CTerm}_{n,\mathit {val}^n_{<j}}(v) \,{\land }\,\mathrm {Form}_{n,T_{<j}, \mathit {val}^n_{<j}} (u,x)$
$\mathrm {Var}(x)\,{\land }\, \mathrm {CTerm}_{n,\mathit {val}^n_{<j}}(v) \,{\land }\,\mathrm {Form}_{n,T_{<j}, \mathit {val}^n_{<j}} (u,x)$
 ;
; -
(
 $T\exists ^*_{\mathrm {tp}}$
): defined similarly.
$T\exists ^*_{\mathrm {tp}}$
): defined similarly.
We can see
![]() $\mathbb {FA}(\mathcal {S}^{n+1})\,{=}_{\mathfrak {L}(\mathcal {S}^n)}\, \mathbb {FCV}(\mathcal {S}^n)\,{\leq }_{\mathfrak {L}(\mathcal {S}^n)}\, \mathbb {FRVT}_{1}(\mathcal {S}^n)$
easily by interpreting
$\mathbb {FA}(\mathcal {S}^{n+1})\,{=}_{\mathfrak {L}(\mathcal {S}^n)}\, \mathbb {FCV}(\mathcal {S}^n)\,{\leq }_{\mathfrak {L}(\mathcal {S}^n)}\, \mathbb {FRVT}_{1}(\mathcal {S}^n)$
easily by interpreting
![]() $\mathit {val}^n$
as
$\mathit {val}^n$
as
![]() $\mathit {val}^n_0$
. Conversely, a modification of the proof of sentence induction (Theorem 3.11) shows that, for
$\mathit {val}^n_0$
. Conversely, a modification of the proof of sentence induction (Theorem 3.11) shows that, for
![]() $n\,{\geq }\,3$
, the characteristic function of
$n\,{\geq }\,3$
, the characteristic function of
![]() $T_0$
is defined by a formula of the form
$T_0$
is defined by a formula of the form
where
![]() $t,s_0,\ldots ,s_\ell $
are
$t,s_0,\ldots ,s_\ell $
are
![]() $\mathcal {S}^n$
terms, and A is an
$\mathcal {S}^n$
terms, and A is an
![]() $\mathfrak {L}(\mathcal {S}^n)$
formula, namely they do not involve
$\mathfrak {L}(\mathcal {S}^n)$
formula, namely they do not involve
![]() $\mathit {val}^n$
. More precisely, as in the proof of Theorem 3.11, we fix
$\mathit {val}^n$
. More precisely, as in the proof of Theorem 3.11, we fix
![]() $w$
with
$w$
with
![]() $\mathrm {Frag}_{{\gamma }_{n+1}}(w)\,{\land }\, \mathrm {lh}(w)\,{\geq }\,p$
and
$\mathrm {Frag}_{{\gamma }_{n+1}}(w)\,{\land }\, \mathrm {lh}(w)\,{\geq }\,p$
and
![]() $r\,{=}\,\mathrm {boa}(\gamma _{n+1}(p),q)$
for given p and q, and, instead of the induction for the formula
$r\,{=}\,\mathrm {boa}(\gamma _{n+1}(p),q)$
for given p and q, and, instead of the induction for the formula
![]() $(\forall a\,{<}\,r)(\ldots )$
, by recursion on
$(\forall a\,{<}\,r)(\ldots )$
, by recursion on
![]() $w$
we define the binary sequence of length r which encodes that
$w$
we define the binary sequence of length r which encodes that
![]() $T_0(\mathrm {usbs}(w,a))$
holds or not for
$T_0(\mathrm {usbs}(w,a))$
holds or not for
![]() $a\,{<}\,r$
. Thus, we can define an
$a\,{<}\,r$
. Thus, we can define an
![]() $\mathcal {S}^{n+1}$
function
$\mathcal {S}^{n+1}$
function
![]() $\mathrm {chi}_0$
so that
$\mathrm {chi}_0$
so that
![]() $T_0(u)$
is interpreted as
$T_0(u)$
is interpreted as
![]() $\mathrm {chi}_0(u)\,{=}\,0$
, concluding
$\mathrm {chi}_0(u)\,{=}\,0$
, concluding
Thus
![]() $\mathbb {FRVT}_{1}(\mathcal {S}^n)$
, an alternative axiomatization of Tarski compositional truth, also has the same strength as all our other finitist truth theories except
$\mathbb {FRVT}_{1}(\mathcal {S}^n)$
, an alternative axiomatization of Tarski compositional truth, also has the same strength as all our other finitist truth theories except
![]() $\mathbb {FKFB}(\mathcal {S}^n)$
.
$\mathbb {FKFB}(\mathcal {S}^n)$
.
We can extend these interpretations by relating
![]() $T_{j+1}$
and
$T_{j+1}$
and
![]() $\mathit {val}^n_{j+1}$
in
$\mathit {val}^n_{j+1}$
in
![]() $\mathbb {FRVT}_{m+1}(\mathcal {S}^n)$
with
$\mathbb {FRVT}_{m+1}(\mathcal {S}^n)$
with
![]() $T_{j}$
and
$T_{j}$
and
![]() $\mathit {val}^{n+1}_{j}$
in
$\mathit {val}^{n+1}_{j}$
in
![]() $\mathbb {FRVT}_{m}(\mathcal {S}^{n+1})$
, and get
$\mathbb {FRVT}_{m}(\mathcal {S}^{n+1})$
, and get
![]() $\mathbb {FRVT}_{m+1}(\mathcal {S}^n) \,{=}_{\mathfrak {L}(\mathcal {S}^n)}\,\mathbb {FRVT}_m(\mathcal {S}^{n+1})$
. By composing this equivalence with different n and m, we obtain
$\mathbb {FRVT}_{m+1}(\mathcal {S}^n) \,{=}_{\mathfrak {L}(\mathcal {S}^n)}\,\mathbb {FRVT}_m(\mathcal {S}^{n+1})$
. By composing this equivalence with different n and m, we obtain
and therefore
![]() $\mathbb {FRVT}_{<\omega }(\mathcal {S}^n)\,{=}_{\mathfrak {L}(\mathcal {S}^n)}\, \mathbb {PRA}$
.
$\mathbb {FRVT}_{<\omega }(\mathcal {S}^n)\,{=}_{\mathfrak {L}(\mathcal {S}^n)}\, \mathbb {PRA}$
.
Acknowledgements
The authors would like to express their deep gratitude to Thomas Strahm who moved the second author to work on axiomatic truth theories of finitist strength in his PhD study, and to the anonymous referee for very careful reading and invaluable comments which helped to improve the article. In addition, they are very grateful for the guidance the second author received from his PhD supervisors, Fabrice Correia and Thomas Strahm. They would also like to thank the other referees of the thesis (besides the first author): Andrea Cantini, Volker Halbach, and Reinhard Kahle, for invaluable feedbacks.
The first author was partially supported by the John Templeton Foundation, during a part of the period of his joint work with the second author. This publication was made possible through the support of a grant from the John Templeton Foundation. The opinions expressed in this publication are those of the authors and do not necessarily reflect the views of the John Templeton Foundation. The PhD study of the second author was generously supported by the Swiss National Science Foundation.