1 Introduction
Since the early 2000s, graphics processing units (GPUs) have emerged as the architecture of choice for scientific computing, owing to their increased computational throughput, parallelism and energy efficiency relative to central processing units (CPUs) (Owens et al. Reference Owens, Houston, Luebke, Green, Stone and Phillips2008; Huang, Xiao & Feng Reference Huang, Xiao and Feng2009; Brodtkorb, Hagen & Sætra Reference Brodtkorb, Hagen and Sætra2013). Modern supercomputers increasingly rely on GPUs for acceleration: at the time of writing, TOP500 rankings report that GPU hardware is used by 66 of the 100 fastest and 79 of the 100 most energy-efficient supercomputers in the world (TOP500 2024).
In order to leverage these computational resources, scientists have been faced with the challenge of rethinking the implementation of many simulation algorithms. Among these are particle-mesh simulation algorithms. In particular, the particle-in-cell (PIC) plasma simulation algorithm is the tool of choice for fully self-consistent simulation of nonlinear plasma physics where kinetic physics is important (Birdsall & Langdon Reference Birdsall and Langdon2004; Hockney & Eastwood Reference Hockney and Eastwood2021). PIC simulations have played an essential role in advancing the understanding of laser–plasma interactions, plasma-based acceleration, space physics, plasma astrophysics and basic kinetic plasma physics (Van Dijk, Kroesen & Bogaerts Reference Van Dijk, Kroesen and Bogaerts2009; Arber et al. Reference Arber, Bennett, Brady, Lawrence-Douglas, Ramsay, Sircombe, Gillies, Evans, Schmitz and Bell2015; Nishikawa et al. Reference Nishikawa, Duţan, Köhn and Mizuno2021). In spite of the relative simplicity of the PIC algorithm, its implementation on GPU hardware is complicated by the use of particles, which result in irregular patterns of memory access and movement. Coupled with evolving GPU capabilities and the growing number of available software paths to GPU acceleration, many questions remain about best practices and paths toward GPU acceleration of PIC codes.
The GPU acceleration of PIC codes is an ongoing effort by the plasma simulation community. Early algorithms were constrained by limited device memory capacity and the need to circumvent the relatively poor performance of global atomic writes during current deposition on older hardware (Stantchev, Dorland & Gumerov Reference Stantchev, Dorland and Gumerov2008; Burau et al. Reference Burau, Widera, Hönig, Juckeland, Debus, Kluge, Schramm, Cowan, Sauerbrey and Bussmann2010; Decyk & Singh Reference Decyk and Singh2011; Joseph et al. Reference Joseph, Ravunnikutty, Ranka, D'Azevedo and Klasky2011; Kong et al. Reference Kong, Huang, Ren and Decyk2011; Bastrakov et al. Reference Bastrakov, Donchenko, Gonoskov, Efimenko, Malyshev, Meyerov and Surmin2012; Chen, Chacón & Barnes Reference Chen, Chacón and Barnes2012; Rossi et al. Reference Rossi, Londrillo, Sgattoni, Sinigardi and Turchetti2012; Decyk & Singh Reference Decyk and Singh2014). More recently, feature-rich, user-oriented PIC codes targeting modern GPU architectures have begun to emerge, including WarpX (Myers et al. Reference Myers, Almgren, Amorim, Bell, Fedeli, Ge, Gott, Grote, Hogan and Huebl2021; Vay et al. Reference Vay, Huebl, Almgren, Amorim, Bell, Fedeli, Ge, Gott, Grote and Hogan2021; Fedeli et al. Reference Fedeli, Huebl, Boillod-Cerneux, Clark, Gott, Hillairet, Jaure, Leblanc, Lehe and Myers2022), HiPACE++ (Diederichs et al. Reference Diederichs, Benedetti, Huebl, Lehe, Myers, Sinn, Vay, Zhang and Thévenet2022), VPIC (Bird et al. Reference Bird, Tan, Luedtke, Harrell, Taufer and Albright2021), PIConGPU (Zenker et al. Reference Zenker, Widera, Huebl, Juckeland, Knüpfer, Nagel and Bussmann2016), Smilei (Derouillat et al. Reference Derouillat, Beck, Pérez, Vinci, Chiaramello, Grassi, Flé, Bouchard, Plotnikov and Aunai2018) and Osiris 2.0 (Kong, Huang & Ren Reference Kong, Huang and Ren2009) and Osiris 3.0 (Tableman Reference Tableman2019).
In this paper, we discuss the approach we have taken to enable GPU acceleration of the fully electromagnetic PIC code Osiris 4.0. Osiris (Fonseca et al. Reference Fonseca, Silva, Tsung, Decyk, Lu, Ren, Mori, Deng, Lee, Katsouleas and Adam2002) is widely used by the plasma simulation community because of its maturity, speed and parallel scalability, and extensive suite of simulation capabilities, including customized field solvers for suppression of numerical dispersion (Li et al. Reference Li, Yu, Xu, Fiuza, Decyk, Dalichaouch, Davidson, Tableman, An and Tsung2017; Xu et al. Reference Xu, Li, Tsung, Dalichaouch, An, Wen, Decyk, Fonseca, Hogan and Mori2020; Li et al. Reference Li, Miller, Xu, Tsung, Decyk, An, Fonseca and Mori2021b), Cartesian and quasi-three-dimensional geometries (Davidson et al. Reference Davidson, Tableman, An, Tsung, Lu, Vieira, Fonseca, Silva and Mori2015), analytic pushers including radiation reaction (Li et al. Reference Li, Decyk, Miller, Tableman, Tsung, Vranic, Fonseca and Mori2021a), Monte Carlo modelling of Coulomb collisions (Nanbu & Yonemura Reference Nanbu and Yonemura1998), tile-based dynamic load balancing (Miller et al. Reference Miller, Lee, Tableman, Helm, Fonseca, Decyk and Mori2021a), particle damping for laser–solid interactions (Miller et al. Reference Miller, May, Fiuza and Mori2021b), field ionization (Deng et al. Reference Deng, Tsung, Lee, Lu, Mori, Katsouleas, Muggli, Blue, Clayton, O Connell, Clayton and Muggli2002), real-time subgrid radiation calculation (Pardal et al. Reference Pardal, Sainte-Marie, Reboul-Salze, Fonseca and Vieira2023) and semiclassical prescriptions for modelling effects of quantum electrodynamics (QED) (Vranic et al. Reference Vranic, Grismayer, Martins, Fonseca and Silva2015). Graphics processing unit acceleration was implemented in previous versions of Osiris, and was used in some physics studies. However, these versions were stand-alone, and due to the new data structures in Osiris 4.0 and developments in GPU hardware, a new algorithm was needed. Our new implementation, which improves upon previous versions, provides robust and performant acceleration of the base code via NVIDIA's Compute Unified Device Architecture (CUDA) in all Cartesian geometries (one, two, and three spatial dimensions). This is a step toward the larger software challenge of incorporating all the features listed above.
The outline of this paper is as follows. In § 2, we discuss the details of our algorithm and software implementation in CUDA. In § 3, we present simulations run on NERSC's Perlmutter system, which demonstrate (i) characterization of the absolute performance and weak scaling of the code on thermal plasmas, (ii) capability of the code to model more complex physics problems such as Weibel filamentation and laser-wakefield acceleration and (iii) 7${\times }$![]() improved energy efficiency relative to the CPU algorithm on a node-to-node basis. Finally, in § 4, we conclude and offer perspectives on future development.
improved energy efficiency relative to the CPU algorithm on a node-to-node basis. Finally, in § 4, we conclude and offer perspectives on future development.
2 Methodology
2.1 Graphics processing unit programming framework
A variety of software approaches have been taken to implement the PIC algorithm on GPUs, including those designed in CUDA (Stantchev et al. Reference Stantchev, Dorland and Gumerov2008; Burau et al. Reference Burau, Widera, Hönig, Juckeland, Debus, Kluge, Schramm, Cowan, Sauerbrey and Bussmann2010; Decyk & Singh Reference Decyk and Singh2011; Joseph et al. Reference Joseph, Ravunnikutty, Ranka, D'Azevedo and Klasky2011; Kong et al. Reference Kong, Huang, Ren and Decyk2011; Chen et al. Reference Chen, Chacón and Barnes2012; Rossi et al. Reference Rossi, Londrillo, Sgattoni, Sinigardi and Turchetti2012; Decyk & Singh Reference Decyk and Singh2014; Decyk Reference Decyk2015; Myers et al. Reference Myers, Almgren, Amorim, Bell, Fedeli, Ge, Gott, Grote, Hogan and Huebl2021), HIP (Myers et al. Reference Myers, Almgren, Amorim, Bell, Fedeli, Ge, Gott, Grote, Hogan and Huebl2021; Burau et al. Reference Burau, Widera, Hönig, Juckeland, Debus, Kluge, Schramm, Cowan, Sauerbrey and Bussmann2010), SYCL (Myers et al. Reference Myers, Almgren, Amorim, Bell, Fedeli, Ge, Gott, Grote, Hogan and Huebl2021), OpenCL (Bastrakov et al. Reference Bastrakov, Donchenko, Gonoskov, Efimenko, Malyshev, Meyerov and Surmin2012), Kokkos (Bird et al. Reference Bird, Tan, Luedtke, Harrell, Taufer and Albright2021), AMRex (Myers et al. Reference Myers, Almgren, Amorim, Bell, Fedeli, Ge, Gott, Grote, Hogan and Huebl2021; Diederichs et al. Reference Diederichs, Benedetti, Huebl, Lehe, Myers, Sinn, Vay, Zhang and Thévenet2022), Alpaka (Zenker et al. Reference Zenker, Widera, Huebl, Juckeland, Knüpfer, Nagel and Bussmann2016), OpenACC (Hariri et al. Reference Hariri, Tran, Jocksch, Lanti, Progsch, Messmer, Brunner, Gheller and Villard2016) and OpenMP (Derouillat et al. Reference Derouillat, Beck, Pérez, Vinci, Chiaramello, Grassi, Flé, Bouchard, Plotnikov and Aunai2018). Also, RAJA is another approach that has, to our knowledge, not been used. These frameworks have different levels of maturity and developer support, as well as differing implications for performance, supported GPU architectures and implementation flexibility. The choice of which software approach to take is a significant and non-trivial developer decision that must consider these aspects of the available frameworks. For example, CUDA is the most mature general-purpose GPU programming language, is generally regarded to give the highest performance and provides the greatest control over the GPU hardware. However, its greater level of control can come at the cost of greater quantity and complexity of code. This is especially true if cross-platform portability is required, since CUDA must be combined with other frameworks in order to support non-NVIDIA GPUs.
At the other end of the spectrum, a high-level approach abstracts hardware details, freeing application developers from the burden of supporting specialized, rapidly evolving systems. For example, OpenMP and OpenACC provide cross-platform portability through a set of compiler directives. While perhaps the simplest to implement, these approaches offer the least amount of flexibility, hardware control and performance. High-level abstraction layers, like Kokkos, are somewhere in between. These provide cross-platform portability and some degree of control over device memory, but to a lesser extent than CUDA.
Weighing the options led us to write our implementation in CUDA C through Fortran-C interoperability. This was informed by our goal of obtaining maximal performance. The low-level exposure of the code allowed us to optimize the particle-pushing kernels. The natural access to raw device memory pointers was also helpful for parts of the code with lower computational cost but greater algorithmic complexity, including particle sorting, management of the memory pool (discussed in § 2.3) and buffered data movements. These aspects of the algorithm may have been significantly more difficult to implement in a higher-level framework. As a production code supporting a large user community, the stability and maturity of CUDA also weighed heavily in our decision. Restriction to NVIDIA hardware is not a significant limitation because many supercomputers in the modern supercomputing ecosystem use NVIDIA GPUs. Furthermore, we have demonstrated with a preliminary HIP version of our code that translation from CUDA is relatively straightforward. This provides a reasonable path to supporting AMD GPUs as well, and thereby the vast majority of top supercomputers.
2.2 Tile-based domain decomposition
Most implementations of the PIC algorithm on GPUs have used some form of domain decomposition with more subdomains than GPUs. The resulting subdomains have been referred to in the literature as tiles, bins, clusters and supercells. Here, we refer to these subdomains as tiles. Tiles provide increased memory localization. In particular, they enable the use of shared memory as a developer-controlled cache by partitioning the computational domain into subdomains whose field and current arrays fit into shared memory. This gives higher performance for read, write and atomic operations in both the field interpolation and current deposit. Shared-memory capacity determines the maximum tile size.
Our GPU implementation is built on top of the existing tile data structure in Osiris, which was originally implemented to enable tile-based dynamic load balancing. The details of this implementation are discussed in Miller et al. (Reference Miller, Lee, Tableman, Helm, Fonseca, Decyk and Mori2021a). In essence, different Message Passing Interface (MPI) ranks can freely exchange tiles in order to ensure that the computational load is balanced. In addition to enabling the benefits for GPU performance previously discussed, the GPU implementation inherits the capacity for tile-based dynamic load balancing from the CPU code. This enables the GPU algorithm, like the CPU algorithm, to potentially run faster or with a lower memory footprint on load-imbalanced problems. The use of this tile data structure as the foundation of the algorithm is one of the main differences between this new implementation of GPU acceleration in Osiris and previous implementations.
In our implementation, each MPI rank has access to one GPU, and as many shared-memory CPU cores as available on the compute node on which the code is running. For example, a Perlmutter GPU node has 64 CPU cores, and 4 GPUs. Therefore, a typical configuration would be 1 GPU and 16 CPU cores per MPI rank.
The use of tiles makes it more difficult to efficiently transfer memory between CPU and GPU. Naively calling CUDA memory copying operations within a loop over tiles results in a bottleneck due to function launch overhead. We work around this issue through the implementation of a memory transfer class which buffers unidirectional data movements of both particle and field data. The size of the buffer (typically several gigabytes) is specified by the user. The memory manager performs a data transfer only when the buffer is full or the source code explicitly flushes the buffer.
2.3 Particle chunk pool
The use of tiles also introduces the problem of inter-tile memory management. Naively allocating a fixed-size particle buffer for each tile leads to the possibility of buffer overflow as load fluctuates. Allowing the size of each tile's particle buffer to vary through reallocation can overcome this issue. However, reallocation of device memory is not possible within kernels, may not be possible if the GPU operates at full memory capacity and can otherwise become a bottleneck.
We addressed these issues by using a memory pool of preallocated chunks of particle data. A similar approach was used in Myers et al. (Reference Myers, Almgren, Amorim, Bell, Fedeli, Ge, Gott, Grote, Hogan and Huebl2021). The data structures are shown in figure 1. Each MPI rank has its own chunk pool object, which allocates the majority of device memory as particle chunks at the beginning of the simulation. Each chunk contiguously stores the position, momentum and charge for a fixed number of particles. The chunk pool stores pointers to these chunks in a circular buffer in device memory. Chunk pointers can be retrieved from or returned to the circular buffer through buffered device-to-device memory transfers. The memory for the chunks themselves is preallocated, and never moved or deleted. The state of the circular buffer is maintained on both the host and device so that chunk pointers can be retrieved from or returned to the queue within either host functions or device kernels.
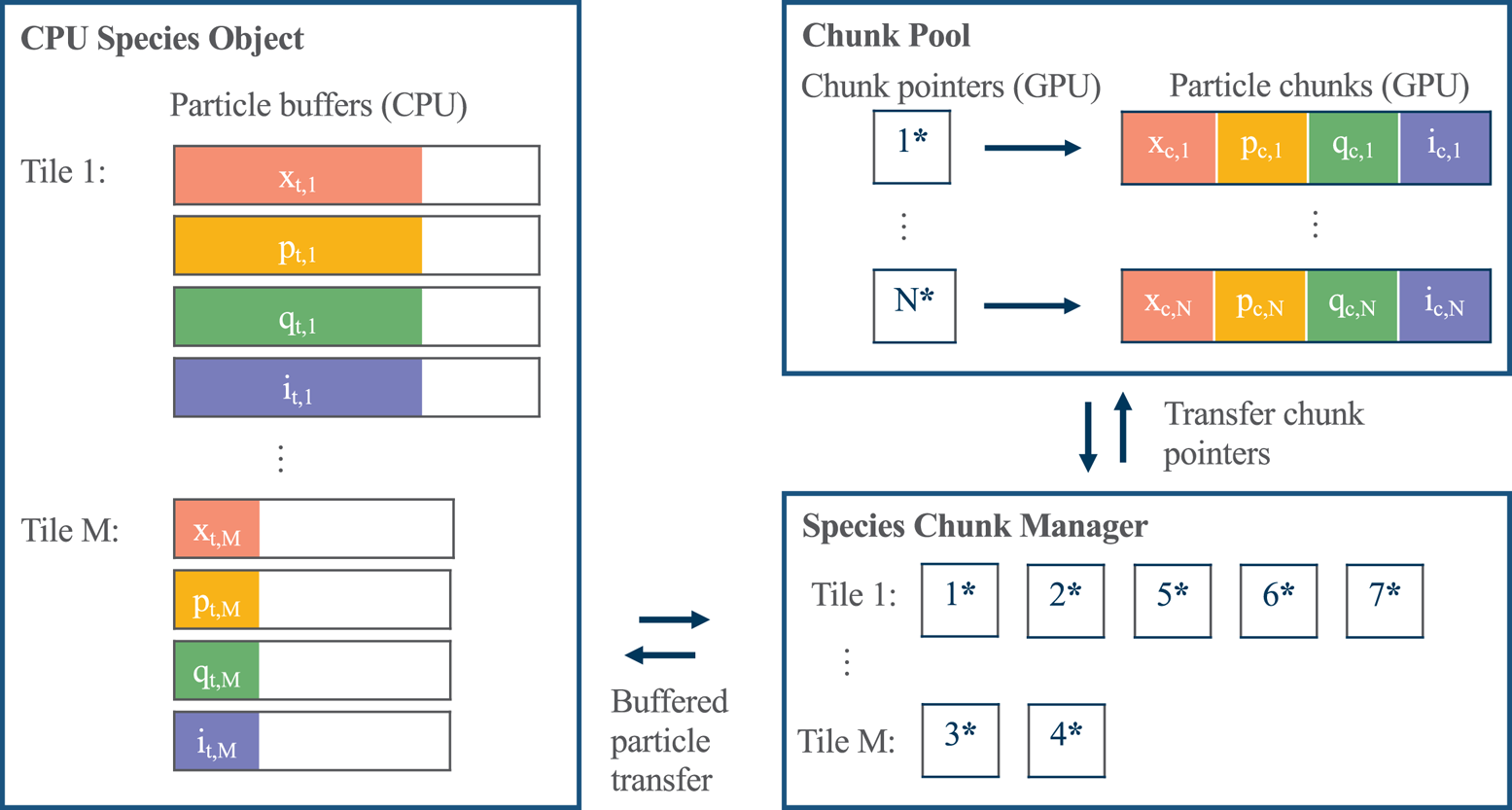
Figure 1. Schematic of the CPU memory layout, chunk pool data structure and species chunk manager. The CPU species object stores contiguous arrays of particle position relative to nearest cell, momentum, charge and cell index (x, p, q and i) for each tile. Note that, generally, particle data are maintained only on the GPU. The figure depicts the state immediately after particles have been copied from device to host for particle diagnostics. The species chunk manager, whose state is maintained on both CPU and GPU, stores pointers to chunks of device memory for each tile. Chunks contiguously store all four data fields for a fixed number of particles. Each species chunk manager may transfer pointers to chunks to and from the chunk pool with nearly zero overhead, enabling arbitrary load balancing between tiles with nearly zero overhead. Particle transfer between the CPU species object and species chunk manager is achieved through an object for buffered data movements, discussed in § 2.2.
Each particle species has a species chunk manager object, which is responsible for ensuring that there is an appropriate number of chunks to store the particles on each tile. All species chunk managers on a given GPU share the same chunk pool and may store a different number of chunks for each tile. During each timestep, the species chunk managers transfer chunk pointers to and from the chunk pool so that each tile retains a specified number of empty chunks prior to the particle push. The number of empty chunks is chosen to be large enough to avoid overflow during the sort, but small enough to avoid under-utilization of device memory. When particles are sent to and from the host for communication or diagnostics, buffered particle transfers are used to move the data. Each CPU species object for each tile stores particles in one contiguous buffer instead of a memory pool. A CPU memory pool is not necessary because of the typically abundant levels of CPU memory.
The overhead of using particle chunks compared with larger contiguous blocks of memory is negligible. This was confirmed by tests with a large chunk size. Within kernels that loop through particles, only a few additional variables and operations are required to also loop through the chunks. Furthermore, memory accesses of chunks within a kernel occur with the same performance as when accessing a larger contiguous block of memory. This is because, by choosing the number of particles per chunk to be greater than or equal to the warp size, each warp sees contiguous memory. For best performance, the chunk size is chosen to be a multiple of the warp size. Outside of kernels, the overhead of the species chunk managers exchanging chunks with the chunk pool is negligible because only pointers to chunks are passed. Occasional reallocation of a species chunk manager's chunk buffer for a particular tile is not a problem; these buffers can be much larger than necessary because they contain significantly less memory than the memory stored by the chunks themselves.
The particle chunk pool enables load to fluctuate between tiles with little wasted memory. When combined with dynamic load balancing for inter-GPU load imbalances, which ensures that total memory load per GPU remains roughly fixed, this enables simulations which nearly max out available system memory. This could be useful for running as large a simulation as possible given limited device memory resources, as in Tan et al. (Reference Tan, Bird, Chen and Taufer2021).
2.4 Particle pushing and current deposition
Particle pushing and current deposition typically constitute the most computationally expensive part of a PIC code. Thus, significant effort went into profiling and optimizing this part of the code, which we break into two separate kernels. In the first kernel, which we will refer to as update_velocity, electric and magnetic fields are interpolated onto the particle positions, then particle momenta are updated. In the second kernel, which we will refer to as advance_deposit, particles positions are advanced, and a charge-conserving current deposition is performed.
While the update_velocity kernel is straightforward to parallelize – particles can be processed individually in parallel – advance_deposit is not; a simple loop in parallel over particles could result in a memory collision when depositing their current onto the grid. To circumvent this we deposit current via atomic addition. On modern architectures, atomic addition of both single and double precision floats is natively supported and therefore fast enough that this is the typical solution (see Decyk & Singh Reference Decyk and Singh2014; Zenker et al. Reference Zenker, Widera, Huebl, Juckeland, Knüpfer, Nagel and Bussmann2016; Bird et al. Reference Bird, Tan, Luedtke, Harrell, Taufer and Albright2021; Myers et al. Reference Myers, Almgren, Amorim, Bell, Fedeli, Ge, Gott, Grote, Hogan and Huebl2021; Vay et al. Reference Vay, Huebl, Almgren, Amorim, Bell, Fedeli, Ge, Gott, Grote and Hogan2021; Fedeli et al. Reference Fedeli, Huebl, Boillod-Cerneux, Clark, Gott, Hillairet, Jaure, Leblanc, Lehe and Myers2022).
Both kernels saw a significant speedup when fields were explicitly loaded into shared memory. This includes both the electric and magnetic field arrays in update_velocity, and the current array in advance_deposit. With fields and currents instead simply stored in global memory, both kernels (in particular advance_deposit) suffered from high latency due to an L2 cache bottleneck, which was alleviated by using shared memory.
Best performance with shared memory came when using one CUDA thread block per tile with a block size of 512. Using more than one block added additional overhead related to shared memory without increasing occupancy. However, we anticipate situations where this would not give best performance. For example, in problems with severe load imbalance, one MPI rank can sometimes be responsible for a small number of tiles (order 1), each with many more particles than average. With one block per tile, far fewer warps would be launched than is sufficient to achieve high device occupancy. In these situations, the benefits of minimizing data duplication could be outweighed by the benefits of launching multiple blocks per tile. This is something we plan to explore in the future.
In addition to using shared memory, kernels benefited from other optimizations. This applies particularly to advance_deposit, which has more complicated logic and flow control. Memory transactions (both to global and shared) were minimized, arithmetic was streamlined to minimize instructions executed and register usage was optimized to ensure maximal warp occupancy. The NVIDIA profiling tool, Nsight Compute, played an important role in this process.
We also explored the possibility of enhancing performance by optimizing the memory layout of particle data. Based on the discussion of coalesced memory access in the CUDA programming guide (NVIDIA 2024), one might expect that while an ‘array of structs’ (AoS) layout for particle data is best on CPU architectures, a ‘struct of arrays’ (SoA) is best on GPUs. For example, for $N$![]() particles, each with position $(x_i,y_i)$
particles, each with position $(x_i,y_i)$![]() , where $i\in [1,N]$
, where $i\in [1,N]$![]() is the particle index, optimal performance on a GPU would be obtained by storing particle data as $(x_1, x_2,\ldots, x_N, y_1, y_2,\ldots, y_N)$
is the particle index, optimal performance on a GPU would be obtained by storing particle data as $(x_1, x_2,\ldots, x_N, y_1, y_2,\ldots, y_N)$![]() , instead of $(x_1, y_1, x_2, y_2,\ldots, x_N, y_N)$
, instead of $(x_1, y_1, x_2, y_2,\ldots, x_N, y_N)$![]() . This layout is used in Bird et al. (Reference Bird, Tan, Luedtke, Harrell, Taufer and Albright2021). We also store particle data in this manner, however, we found that there was no measurable difference between SoA and AoS.
. This layout is used in Bird et al. (Reference Bird, Tan, Luedtke, Harrell, Taufer and Albright2021). We also store particle data in this manner, however, we found that there was no measurable difference between SoA and AoS.
Finally, we make use of a distinct particle initialization scheme compared with what is done for CPU simulations. Particles that are close together in simulation space are staggered in memory upon initialization. This results in a speedup in advance_deposit by reducing the likelihood of memory collisions in the current deposition. This is particularly important for simulations with a cold plasma (e.g. plasma-based acceleration) where particle position evolves slowly after initialization. Benefit is also seen for warm plasmas over the first few 100 simulation iterations, until particle positions become sufficiently scrambled. A small slowdown occurs in update_velocity due to decreased data locality when interpolating fields onto particles, but this is outweighed by the speedup in advance_deposit.
In aggregate, the optimizations above resulted in a roughly 5–6${\times }$![]() speedup relative to our initial implementation. As we have stressed above, this level of optimization may not have been possible had we taken a higher-level approach using a framework such as OpenMP, OpenACC or Kokkos. Nevertheless, we expect these optimizations apply to other GPU programming frameworks.
speedup relative to our initial implementation. As we have stressed above, this level of optimization may not have been possible had we taken a higher-level approach using a framework such as OpenMP, OpenACC or Kokkos. Nevertheless, we expect these optimizations apply to other GPU programming frameworks.
2.5 Particle sorting and boundary conditions
The literature refers to spatial grouping of particles as particle sorting. This includes organizing particles by MPI rank, by tile or by any other grouping of cells. Formally this is a bucket sort. The order of the particles within buckets typically does not matter, and one can make the additional assumption that particles are mainly presorted – only a fraction of the particles will move between buckets on any given timestep. Particle sorting is required when any form of domain decomposition is used, or in special cases such as particle–particle collisions (Takizuka & Abe Reference Takizuka and Abe1977; Nanbu & Yonemura Reference Nanbu and Yonemura1998; Alves, Mori & Fiuza Reference Alves, Mori and Fiuza2021).
Efficient particle sorting in PIC codes on the GPU is non-trivial. Particle arrays must be compact; both in order to make efficient use of memory, and because a particle array with holes scattered throughout would result in poor performance during particle push and current deposition due to complicated control flow, warp divergence and non-coalesced memory access. In general, sorting is achieved by making use of some combination of atomic operations to resolve memory collisions, prefix scans and stream compaction to obtain ordered arrays and temporary buffers to store moving particles and counting integers. Many algorithms have been proposed by others (Stantchev et al. Reference Stantchev, Dorland and Gumerov2008; Joseph et al. Reference Joseph, Ravunnikutty, Ranka, D'Azevedo and Klasky2011; Kong et al. Reference Kong, Huang, Ren and Decyk2011; Mertmann et al. Reference Mertmann, Eremin, Mussenbrock, Brinkmann and Awakowicz2011; Decyk & Singh Reference Decyk and Singh2014; Hariri et al. Reference Hariri, Tran, Jocksch, Lanti, Progsch, Messmer, Brunner, Gheller and Villard2016; Jocksch et al. Reference Jocksch, Hariri, Tran, Brunner, Gheller and Villard2016; Myers et al. Reference Myers, Almgren, Amorim, Bell, Fedeli, Ge, Gott, Grote, Hogan and Huebl2021). Differences between algorithms in the literature arise because different codes face different constraints.
Our aim was to design a sorting algorithm with robust fault tolerance to memory overflow to handle the variety of physical systems modelled by the Osiris user community. Memory overflow can occur in a particle sorting kernel due to buffering of particles moving between tiles. We prevent this from occurring by using the chunk pool, as discussed in § 2.3, and by minimizing the memory footprint of the sort algorithm altogether. We tried to make the sort kernel as performant as possible given these constraints. Ultimately, we were justified in the choice of prioritizing fault tolerance over performance because performance was sufficient: kernel duration was dwarfed by CPU MPI communications of the particle data. For this reason, we expect that, at this stage, the only worthwhile way to improve the performance of the sort would be by taking advantage of remote direct memory access via CUDA-aware MPI.
In the remaining paragraphs of this section our algorithm is described in detail. Our algorithm takes place in three steps. First, a kernel is called where threads loop over all particles on a given tile, identify those departing and buffer them according to their destination. Particles whose destination tile is local (i.e. on the same MPI rank) are appended to the destination tile's particle buffer directly, which is made up of globally accessible chunks. Particles crossing an MPI rank boundary or the simulation boundary (e.g. absorbing wall) are buffered in a dedicated array of chunks also stored in global memory. An additional buffer for each tile, i_hole, is required to store the array indices of departing particles, which we refer to as ‘holes’. In the current implementation, this buffer is of fixed size. But it could be implemented using chunks as well. Three integers are required to count the number of particles: departing a given tile; being received by a given tile locally; and crossing an MPI rank or simulation boundary. These are stored in global memory and are incremented atomically.
Second, particles crossing an MPI rank or simulation boundary are copied from device to host. The host handles processing of particle boundary conditions (e.g. thermal-bath, open or reflecting particle boundaries), as well as exchange of particles with other MPI ranks. Then, the new set of particles is copied from host back to device.
Finally, a kernel is called to compact the buffers for each tile: holes left by particles that have departed are filled so that particles are stored contiguously. Mainly, this kernel is embarrassingly parallel. Threads loop over particles (that previously were either received locally from other tiles, or copied from the host) and move them into holes specified by i_hole. However, special care must be taken for the case where the new number of particles on a given tile, n_p_new, is less than its old number of particles, n_p_old. This is because, in this case, some of the holes specified by i_hole are ‘invalid’, i.e. they have index greater than n_p_new. Since the holes in i_hole are in no particular order, we require an initial step where i_hole is compacted into a smaller array containing only valid holes. This process is known as stream compaction and relies on parallel prefix scans (Blelloch Reference Blelloch1990). A similar compaction step is required when moving particles with index between n_p_new and n_p_old into holes, since that part of the array contains the invalid holes that must be filtered out. No atomic operations are necessary in this kernel.
3 Results
In this section, we present examples of simulations run on NERSC's Perlmutter system. Each Perlmutter GPU node has four NVIDIA A100 GPUs with 40 GB of device memory and a single AMD EPYC 7763 CPU. Each CPU node has two AMD EPYC 7763 CPUs. Each AMD EPYC 7763 CPU has 64 cores.
In all of our results, we define the absolute throughput as the total number of particle pushes divided by the total simulation time minus the time required to initialize the simulation. This metric is the average number of particles pushed per unit time when including the additional costs of particle communication, grid communication and field evolution. No additional normalization is used if more than one GPU is used.
3.1 Thermal plasma benchmarks
Figure 2 shows several performance tests from simulations of thermal plasmas. We begin by considering weak scaling, shown in figure 2(a). To understand the effect of different configuration settings on performance, we derive all of our simulations from a single base case, which serves as a control. We ran weak scaling tests of the following computational problems, which can be extrapolated to understand a variety of use cases:
(i) Base: three-dimensional simulation of a uniform plasma using our GPU algorithm run on 64 GPUs. The plasma is warm (the thermal momentum in all directions is $u_\text {th} = 0.1 m_e c$
 where $m_e$
where $m_e$ is the electron mass and c is the speed of light) and is represented by 512 particles per cell. Quadratic particle shapes are used. Single precision is used for both field and particle data. We note that particle positions are referenced with respect to cells, as depicted in figure 1, so that the use of single precision does not limit accuracy for large position values. The box is fully periodic with no moving window. The grid dimensions are $512 \times 512 \times 256$
is the electron mass and c is the speed of light) and is represented by 512 particles per cell. Quadratic particle shapes are used. Single precision is used for both field and particle data. We note that particle positions are referenced with respect to cells, as depicted in figure 1, so that the use of single precision does not limit accuracy for large position values. The box is fully periodic with no moving window. The grid dimensions are $512 \times 512 \times 256$ cells. The tile dimensions are $8 \times 8 \times 8$
cells. The tile dimensions are $8 \times 8 \times 8$ cells. The resolution is $k_p \varDelta _x = 0.1$
cells. The resolution is $k_p \varDelta _x = 0.1$ in all directions and $\omega_p \Delta t = 0.05$
in all directions and $\omega_p \Delta t = 0.05$ , where $\omega_p$
, where $\omega_p$ is the plasma frequency and $k_p \equiv \omega _p / c$
is the plasma frequency and $k_p \equiv \omega _p / c$ is the plasma wavenumber. The simulation is run for 1000 timesteps. One MPI rank is used per GPU and one CUDA thread block per tile with 512 threads.
is the plasma wavenumber. The simulation is run for 1000 timesteps. One MPI rank is used per GPU and one CUDA thread block per tile with 512 threads.(ii) Cold: same as base with $u_\text {th} = 0$
 . Particle communication vanishes aside from pings between neighbouring ranks.
. Particle communication vanishes aside from pings between neighbouring ranks.(iii) Drift: same as cold but with a moving window in the $\hat {\boldsymbol{x}}_1$
 direction. Particles are stationary but move relative to MPI partitions. This problem has the most particle communication and approximates the data movement for simulations of plasma-based acceleration.
direction. Particles are stationary but move relative to MPI partitions. This problem has the most particle communication and approximates the data movement for simulations of plasma-based acceleration.(iv) Two-dimensional: a two-dimensional version of base. The number of particles per cell and thermal velocity are the same. The grid size of $8192 \times 8192$
 cells gives the same number of total grid points and total number of particles. The tile dimensions are $32 \times 32$
cells gives the same number of total grid points and total number of particles. The tile dimensions are $32 \times 32$ cells.
cells.
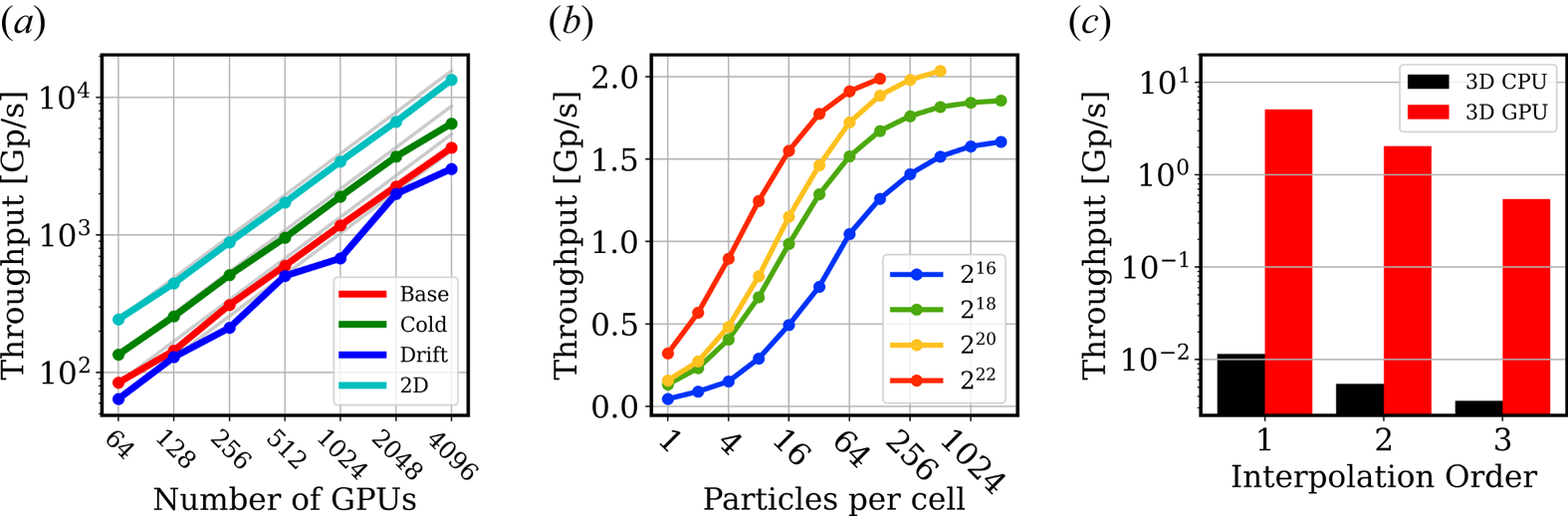
Figure 2. Comprehensive thermal plasma benchmarks run on Perlmutter. (a) Weak scaling tests for the cases described in the text, showing near-perfect scaling up to 4096 GPUs on Perlmutter. (b) Parameter scan showing dependence of throughput on particles per cell and grid sizes. (c) Comparison of absolute performance on one GPU and one core of one CPU for different interpolation orders. All simulations are run in three dimensions with quadratic interpolation and 512 particles per cell unless otherwise specified.
Figure 2(a) shows weak scaling tests for the four test problems. In each test, the grid dimensions are scaled proportionately to the number of MPI ranks used to decompose the problem. For ideal scaling, depicted by solid grey lines, the total throughput is proportional to the number of MPI ranks. In each case, weak scaling is nearly perfect up to 4096 GPUs, the highest power of two below the full system size of 6144. The drift case is slower than cold because of increased communication cost. It exhibits jitter due to variation in communication cost. Cold is faster than base due to the use of the staggered initialization discussed in § 2.4 and reduced communication costs. Without the staggered initialization, cold is several times slower than base.
Figure 2(b) shows the dependence of the absolute throughput on the number of gridpoints and particles per cell. All simulations are run on one GPU with the same parameters as the three-dimensional base simulation other than the number of gridpoints and particles per cell. The tile size is decreased for smaller grid sizes to maintain a sufficient number of blocks to saturate performance.
For a fixed total grid size, performance increases with particles per cell for two reasons. First, particle pushing contributes a greater fraction of the total simulation cost relative to the field solver and grid communication, and particle communication. Second, similarly, the kernels update_velocity and advance_deposit are both more efficient since they also have fixed costs, and particle pushing contributes a greater fraction of total kernel time when more particles per cell are used. The update_velocity kernel has the fixed cost of loading fields into shared-memory arrays. It also likely benefits from caching of field values. The advance_deposit kernel has the fixed cost of zeroing the shared-memory current array, and adding that array back to global memory after deposition. On the other hand, for a fixed number of particles per cell, performance decreases with decreasing grid size. This is because the relative cost of pushing to communication scales as the ratio of volume to surface area of the grid and because kernels are less efficient with smaller grid size.
While performance decreases with decreasing either particles per cell or gridpoints per GPU, the performance is still within a factor of two of the maximum with $2^{18}$![]() or more gridpoints and ${\sim }16$
or more gridpoints and ${\sim }16$![]() or more particles per cell. Note that the performance does not depend only on the total number of particles (i.e. particles per cell times grid points). For example, the cases with $2^{16}$
or more particles per cell. Note that the performance does not depend only on the total number of particles (i.e. particles per cell times grid points). For example, the cases with $2^{16}$![]() gridpoints and 128 particles per cell has the same number of particles as the case with $2^{20}$
gridpoints and 128 particles per cell has the same number of particles as the case with $2^{20}$![]() gridpoints and 8 particles per cell, but has approximately double the performance.
gridpoints and 8 particles per cell, but has approximately double the performance.
Finally, we compare the GPU code with the CPU code. There are three natural ways in which these can be compared: 1 GPU node vs 1 CPU node; 1 GPU vs 1 (many-core) CPU; and 1 GPU vs 1 core of 1 CPU. Each comparison is relevant and informative. In this test, in order to control for the confounding effect of communication, we compare performance on a single GPU with performance on a single core (instead of all 64 cores) of one CPU. Both CPU and GPU tests are run with one MPI rank. Figure 2(c) shows the absolute performances for different particle interpolation orders on a version of the base GPU case scaled to fit one GPU. The CPU code uses an optimized single instruction, multiple data (SIMD) pusher (Fonseca et al. Reference Fonseca, Vieira, Fiúza, Davidson, Tsung, Mori and Silva2013). The orders 1, 2 and 3 are linear, quadratic and cubic interpolations. For these three cases, the GPU algorithm on one GPU is approximately 300 times faster than the CPU algorithm on one core of one CPU. In table 1, the three-dimensional (3-D) timings from figure 2(c) are tabulated along with 2-D timings. We note that the 2-D CPU algorithm shares the same cost for 2nd- and 3rd-order interpolations because of specific memory alignment requirements for the SIMD pusher.
Table 1. Absolute throughput in gigaparticles per second and speedup for the GPU and CPU algorithms on one GPU and one core of one CPU on Perlmutter with different interpolation orders. The benchmarks are measured on a thermal plasma. The 3-D CPU and GPU performances are plotted in figure 2(c).

3.2 Simulations of more complex plasma systems
Here, we demonstrate the ability of our code to simulate commonly studied plasma systems with higher degrees of spatial inhomogeneity and more complex particle movement patterns. The level of robustness of the code required to handle these problems is significantly higher than that required to simulate the thermal plasma cases shown in § 3.1. Anecdotally, many bugs concerning edge cases outside particle-pushing kernels were exposed in these cases which did not manifest for thermal problems. Furthermore, these problems stress the performance of the code because they depart from several factors which led to best performance in thermal plasma tests from figure 2. Namely, they have fewer particles per cell, higher communication levels and greater degrees of spatial inhomogeneity.
Figure 3 shows two examples. Figure 3(a) shows tangling of magnetic filaments generated in a 3-D simulation of the Weibel instability (Weibel Reference Weibel1959; Fonseca et al. Reference Fonseca, Silva, Tonge, Mori and Dawson2003; Silva et al. Reference Silva, Fonseca, Tonge, Dawson, Mori and Medvedev2003). The simulation features two pairs of relativistically counterstreaming electron–positron plasmas with $u_\text {th} = 0.1$![]() , $u_\text {drift} = 0.75$
, $u_\text {drift} = 0.75$![]() and 32 particles per cell per species with quadratic interpolation. The grid dimensions are $2048 \times 2048 \times 1024$
and 32 particles per cell per species with quadratic interpolation. The grid dimensions are $2048 \times 2048 \times 1024$![]() . The resolution is $k_p \varDelta _x = 0.1$
. The resolution is $k_p \varDelta _x = 0.1$![]() . The simulation was run on 4096 GPUs on Perlmutter up to $\omega _p t = 50$
. The simulation was run on 4096 GPUs on Perlmutter up to $\omega _p t = 50$![]() . The turbulence, relativistic streaming and moving plasma structures with densities varying from $0$
. The turbulence, relativistic streaming and moving plasma structures with densities varying from $0$![]() to $8n_0$
to $8n_0$![]() stress the code more than the thermal plasmas in § 3.1. The code is robust to these stresses and the performance is $0.4\,{\rm Gp}\,{\rm s}^{-1}$
stress the code more than the thermal plasmas in § 3.1. The code is robust to these stresses and the performance is $0.4\,{\rm Gp}\,{\rm s}^{-1}$![]() , slightly less than 2 times lower than for an analogous thermal case (with 32 particles per cell, $2^{20}$
, slightly less than 2 times lower than for an analogous thermal case (with 32 particles per cell, $2^{20}$![]() gridpoints per GPU, on 4096 GPUs) based on extrapolation from figure 2(a,b).
gridpoints per GPU, on 4096 GPUs) based on extrapolation from figure 2(a,b).

Figure 3. Examples of spatially inhomogeneous plasma simulations run on Perlmutter. (a) Three-dimensional simulation of the Weibel instability on 4096 GPUs, demonstrating the tangling of magnetic field lines. (b) Charge density from a 2-D simulation of a laser-wakefield accelerator (LWFA) in the nonlinear regime with dynamic load balancing. The black lines indicate the computational boundaries of different MPI ranks.
Shown in figure 3(b) is a 2-D simulation with dynamic load balancing of a LWFA with a frequency ratio of $\omega _0 / \omega _p = 80$![]() , corresponding to an $800$
, corresponding to an $800$![]() nm laser pulse incident on a plasma of density $2.7 \times 10^{17}\,{\rm cm}^{-3}$
nm laser pulse incident on a plasma of density $2.7 \times 10^{17}\,{\rm cm}^{-3}$![]() . The laser and plasma are matched according to the scaling in Lu et al. (Reference Lu, Tzoufras, Joshi, Tsung, Mori, Vieira, Fonseca and Silva2007) with $a_0 = 4$
. The laser and plasma are matched according to the scaling in Lu et al. (Reference Lu, Tzoufras, Joshi, Tsung, Mori, Vieira, Fonseca and Silva2007) with $a_0 = 4$![]() and $k_p w_0 = 4$
and $k_p w_0 = 4$![]() . The simulation dimensions are $(6400 \times 9600 )$
. The simulation dimensions are $(6400 \times 9600 )$![]() with $k_p \varDelta _x = 0.0025$
with $k_p \varDelta _x = 0.0025$![]() in all directions and $\omega _p \varDelta _t = 0.0015$
in all directions and $\omega _p \varDelta _t = 0.0015$![]() . The simulation uses a moving window in the $\hat{\boldsymbol x}_1$
. The simulation uses a moving window in the $\hat{\boldsymbol x}_1$![]() direction and 64 particles per cell with quadratic interpolation for the plasma. The simulation was run on Perlmutter on 256 GPUs. The electron charge density is shown in colour. The black lines outline the domain boundaries processed by different GPUs. The domains are formed by free exchange of tiles between different MPI ranks, as described in § 2.2, to ensure load balance of simulation particles. Due to the particle communication associated with the moving window, this problem stresses the code similarly to the Weibel problem, but with a greater particle imbalance among GPUs. In this case, the performance is $0.2\,{\rm Gp}\,{\rm s}^{-1}$
direction and 64 particles per cell with quadratic interpolation for the plasma. The simulation was run on Perlmutter on 256 GPUs. The electron charge density is shown in colour. The black lines outline the domain boundaries processed by different GPUs. The domains are formed by free exchange of tiles between different MPI ranks, as described in § 2.2, to ensure load balance of simulation particles. Due to the particle communication associated with the moving window, this problem stresses the code similarly to the Weibel problem, but with a greater particle imbalance among GPUs. In this case, the performance is $0.2\,{\rm Gp}\,{\rm s}^{-1}$![]() , roughly 8 times lower than for an analogous 2-D thermal case (with 64 particles per cell, $2^{18}$
, roughly 8 times lower than for an analogous 2-D thermal case (with 64 particles per cell, $2^{18}$![]() gridpoints per GPU, on 256 GPUs) based on extrapolation from figure 2(a,b), and table 1. The discrepancy may be attributable to the fact that communication in this simulation is significantly higher relative to particle pushing (4 times higher) than in the thermal plasma benchmarks from figure 2(a,b), limiting the accuracy of the extrapolation.
gridpoints per GPU, on 256 GPUs) based on extrapolation from figure 2(a,b), and table 1. The discrepancy may be attributable to the fact that communication in this simulation is significantly higher relative to particle pushing (4 times higher) than in the thermal plasma benchmarks from figure 2(a,b), limiting the accuracy of the extrapolation.
This example illustrates the functionality of dynamic load balancing in Osiris. Despite the existence of a particle load imbalance, the performance is roughly identical with and without dynamic load balancing. This is because the simulation is dominated by communication; load balancing can only lead to a speedup when the simulation is dominated by particle pushing. Nevertheless, we anticipate that this feature could provide a significant speedup on other problems, other systems or as the code and hardware evolves (e.g. with the incorporation of CUDA-aware MPI, which could lower communication costs). Load balancing also ensures efficient use of limited device memory, which could enable running very large problems as discussed in § 2.3.
3.3 Energy efficiency
A major motivation for the transition of supercomputers from CPU to GPU hardware is the higher energy efficiency of GPUs. However, the energy efficiency of specific applications may vary because of different patterns of computation and data movement. Here, we measure the energy efficiency of CPU and GPU implementations of Osiris. To our knowledge, these are the first published measurements of energy consumption of the PIC algorithm.
A node-to-node comparison was run for a thermal plasma. The codes were used to simulate a thermal plasma just as in the base weak scaling test scaled to one GPU node. The CPU code was run with 128 MPI ranks and 128 cores on a Perlmutter CPU node, while the GPU code was run with 4 MPI ranks and 4 GPUs on a Perlmutter GPU node. Both the CPU and the GPU simulation were allowed to progress indefinitely and were terminated after 4 h.
For both simulations, the total energy was measured using the Slurm sacct command, which reports energy consumption as measured by Cray's Power Management System. The estimate provides a comprehensive measurement of energy consumption for the entire node. This includes power required for data movement, floating point operations and baseline power needed to keep the node running. For GPU nodes, the measurement includes the energy consumption of the CPUs and the GPUs. Zhao et al. (Reference Zhao, Rrapaj, Bhalachandra, Austin, Nam and Wright2023) provides more information on power consumption measurements on Perlmutter.
Performance on the GPU node was higher on a node-to-node basis: over the 4 h, a factor of 13.7 times more simulation iterations were performed, higher than the value of 11.3 expected from extrapolating single-GPU and single-CPU benchmarks. The GPU node also consumed 1.9 times the energy of the CPU node. Dividing these numbers, we find that the simulation was 7.2 times more energy efficient when run on the GPU node. The results are shown in absolute units of nanoJoules per push in figure 4.
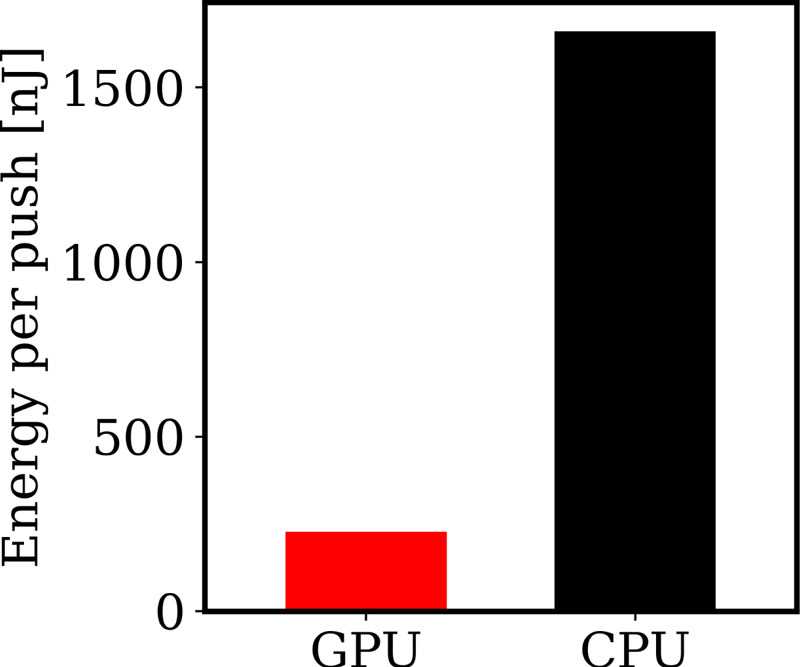
Figure 4. Energy consumption per particle push for the GPU algorithm and for the CPU algorithm. The comparison is between a simulation for 4 h on a Perlmutter GPU node with 4 GPUs and a Perlmutter CPU node with 128 CPU cores. The GPU node is ${\sim }14$![]() times faster than the CPU node and uses ${\sim }2$
times faster than the CPU node and uses ${\sim }2$![]() times more energy, leading to an overall energy efficiency ${\sim }7$
times more energy, leading to an overall energy efficiency ${\sim }7$![]() times higher. Further detail of what is being measured is in the text.
times higher. Further detail of what is being measured is in the text.
This simple test does not account for heating costs from inter-node communication or the potentially differing energy costs for creation and maintenance of CPU and GPU devices. Results may also vary significantly on different systems and hardware, or on different physics problems where the GPU is less performant (e.g. with fewer particles per cell). Nonetheless, the test suggests that GPU architectures may be the more environmentally sustainable choice for PIC simulations. Alternatively, increased efficiency could result in greater demand, resulting in increased overall energy consumption due to the Jevons paradox.
4 Conclusion
In this paper, we have described the new implementation of GPU acceleration in the PIC code Osiris. The code, written in CUDA, is built upon a tile-based domain decomposition in order to enable shared-memory storage of grid quantities, enhance memory localization and enable tile-based dynamic load balancing. For efficient memory usage when using tiles, we have implemented a memory pool for particle data. We have described aspects of the optimization of the particle push in detail, along with details about the implementation of the particle sort. We have discussed the pros and cons of using CUDA.
We have presented a comprehensive picture of the performance, capabilities and energy efficiency of the code through several tests. A variety of thermal plasma simulations demonstrate strong absolute performance (e.g. 5.0 gigaparticles per second in three dimensions with linear interpolation) and excellent weak scaling up to 4096 GPUs on Perlmutter. Simulations of Weibel filamentation and laser-wakefield acceleration illustrate the capacity of the code to run on more complex physical systems. Finally, node-to-node energy consumption measurements indicated that, on a node-to-node basis on Perlmutter, the GPU code is up to ${\sim }14$![]() times faster and ${\sim }7$
times faster and ${\sim }7$![]() times more energy efficient than the heavily optimized CPU code on a thermal plasma problem. These numbers may be lower on other problems where the GPU code is less performant.
times more energy efficient than the heavily optimized CPU code on a thermal plasma problem. These numbers may be lower on other problems where the GPU code is less performant.
Within our implementation, several areas of improvement remain. The degraded performance when running with few particles per cell (${\lesssim }16$![]() ) is likely caused by bottlenecks which could be identified by NSight Systems and subsequently alleviated. CUDA-aware MPI could also be used for particle and field communication, which is currently a bottleneck in cases such as the drifting plasma in figure 2.
) is likely caused by bottlenecks which could be identified by NSight Systems and subsequently alleviated. CUDA-aware MPI could also be used for particle and field communication, which is currently a bottleneck in cases such as the drifting plasma in figure 2.
Fault tolerance in the particle sort could also be improved. In the current implementation, fixed-size temporary buffers are allocated for to store the array indices of departing particles (i_hole). Overflowing these buffers causes a crash, and reallocation is not possible within the sort kernel. These buffers could be replaced by spare particle chunks from the memory pool. This would remove the need for preallocation of the fixed-size buffers and would make any overflow impossible during the sort as long as the chunk pool does not become empty.
The final major area of improvement is GPU acceleration of other Osiris simulation modes, such as quasi-three-dimensional geometry, QED and general relativity. Our current implementation, which accelerates the base Cartesian simulation modes in, one, two, and three spatial dimensions, is the first step in accelerating the entire codebase.
In conclusion, our GPU implementation of Osiris provides excellent performance, supports a variety of use cases and provides backward compatibility with existing CPU code. This poses Osiris to continue to serve the PIC simulation community's computational demands. The details of our implementation may also be fruitful for the development of other feature-rich GPU-accelerated PIC codes.
Acknowledgements
The authors graciously thank B. Cook, J. Blaschke and E. Palmer for their insight at NERSC GPU hackathons, H. Wen for his insights on particle sorting in PIC codes on GPUs, both reviewers for their helpful suggestions, and NERSC employees R. Gayatri, S. Bhalachandra and C. Lively for estimates of power consumption for our simulations on Perlmutter.
Editor V. Malka thanks the referees for their advice in evaluating this article.
Funding
This work was supported in parts by the US Department of Energy National Nuclear Security Administration (grant numbers DE-NA0004147, DE-NA0003842, DE-NA0004131, DE-NA0004144), Office of Science [grant number DE-SC001006], and Scientific Discovery through Advanced Computing Program [Lawrence Berkeley National Laboratory subcontract 7350365:1]; the Laboratory for Laser Energetics (subcontract number SUB00000211/GR531765); US National Science Foundation (grant number 2108970); Fundação para a Ciência e Tecnologia, Portugal (grant number PTDC-FIS-PLA-2940-2014); and European Research Council (ERC-2015-AdG, grant number 695008). The code was developed and tested on NERSC's Perlmutter system (accounts mp113 and m1157). The code was also developed and tested in part on the ALCF's Polaris system through an INCITE allocation. This work was completed in part at the NERSC Open Hackathon, part of the Open Hackathons program. The authors would like to acknowledge OpenACC-Standard.org for their support as well as the use resources at the National Energy Research Scientific Computing Center (NERSC). NERSC is a U.S. Department of Energy Office of Science User Facility located at Lawrence Berkeley National Laboratory, operated under Contract No. DE-AC02-05CH11231.
Declaration of interests
The authors report no conflict of interest.













