1 Notation
Dimensionless counterparts are indicated with a tilde, e.g. ![]() when they exist. Axis labelling in figures is of dimensionless quantities.
when they exist. Axis labelling in figures is of dimensionless quantities.

2 Drumlin Theories
The swarms of drumlins left behind by the great mid-latitude ice sheets have provided a source of debate (Reference Menzies and RoseMenzies and Rose, 1987) regarding their genesis. Two theories seem particularly in favour at the moment; ones based on the dilation, deformation and sliding of till (Reference Smalley and UnwinSmalley and Unwin, 1968; Reference MenziesMenzies, 1979; Reference Boulton, Menzies, Rose and BalkemaBoulton, 1987; Reference HindmarshHindmarsh, 1996; Reference HartHart 1997, Hindmarsh, in press a), and an alternative set of theories which argue that some drumlins are hydraulic features caused by subglacial outburst floods (Reference ShawShaw and others, 1989). The argument regarding their genesis extends beyond the parochial, because if these drumlins are the product of outburst floods, sedimentological evidence suggests that these floods were massive to the extent that they could have left a signal in the global climate (Reference Blanchon and ShawBlanchon and Shaw, 1995), although Reference ShoemakerShoemaker (1995) has argued that much smaller floods are adequate. In contrast, if much drumlin genesis can lie explained by viscous models of subglacial deformation, this is a significant consideration in the debate opening up regarding the plastic and viscous nature of till deformation (Reference Boulton and HindmarshBoulton and Hindmarsh, 1987; Reference KambKamb, 1991; Murrray and Clarke, 1995; Reference Iverson, Hanson, Hooke and JanssonIverson and others, 1995; Reference HindmarshHindmarsh, 1997).
Arguments in favour of the flood hypothesis come from sedimentological evidence and from macro-morphological evidence. The sedimentological evidence relates to combinations of fluvial and glacial working of these drumlins, and will not be commented on further other than to mention that proglacial streams are typically powerful, alter their drainage patterns catastrophically and fluctuations in margin position can produce complex combinations of fluvial and sedimentological evidence without there having been subglacial outburst floods. Postulated mechanisms for the creation of storage areas needed for such floods (Reference ShoemakerShoemaker, 1991) and mechanisms for the subsequent release are also controversial (Reference ShoemakerShoemaker, 1992; Reference Walder and ShoemakerWalder, 1994). The macro-morphological evidence relates to drumlin form, the argument being that certain shapes are far too much like dunes not to be dunes, and there is no glacial theory which predicts their formation.
The till-deformation model in its modern form is essentially based on continuity, that is the conservation of mass of deforming till. Relief is amplified where till flow is retarded (Reference MenziesMenzies, 1979; Reference Boulton, Menzies, Rose and BalkemaBoulton, 1987; Reference HartHart, 1997). We shall be seeking to show how well this theory explains aspects of drumlin formation in this paper. We shall be considering two aspects of drumlin formation; drumlinization, the production of typical drumlin shapes once sediment relief has been formed, and questions of how sediment relief might be amplified. At the moment, the former question can be discussed without great recourse to mathematics, and can be illustrated through computation. This is dune in this paper. The latter question has recently been partly answered by linear stability analyses (Hindmarsh, in press a, b). Regions in parameter space where sediment-thickness instabilities occur are found but the full non-linear problem of determining whether growing infinitesimal perturbations produce sufficiently large mounds remains to be solved.
Arguments in this paper in favour of the viscous theory are not mutually exclusive to Shaw’s thesis, as they represent a theory of the operation of the subglacial system over much longer time-scales than those characteristic of floods.
2.1. Some characteristics of drumlins
Discussions of drumlin morphology may be found in Reference ChorleyChorley (1959), Reference Smalley and UnwinSmalley and Unwin (1968) and Reference Rose and LetzerRose and Letzer (1975, Reference Rose and Letzer1977), as well as in many textbooks, for example Reference Sugden and JohnSugden and John (1976), Reference SharpSharp (1991), Reference HambreyHambrey (1994) and Reference Bennett and GlasserBennett and Glasser (1996). A recent bibliography is due to Reference MenziesMenzies (1984). Aerial photography and large-scale mapping techniques have made the features associated with drumlin swarms rather clearer in recent years. Recent discussions can be found in Reference ShawShaw and others (1989), Reference ClarkClark (1993) and Reference Bennett and GlasserBennett and Glasser (1996). Drumlins typically have a non-unit plan aspect-ratio. The longer axis can be in any direction but is usually oriented in the direction of ice flow. Such a property is regarded as a sign of maturity. It is thus generally supposed that drumlins not aligned with the most recent flow direction have not been heavily reworked. Blunt faces are typical, most commonly on the upstream side, but many drumlins also possess blunt downstream faces and some possess blunt downstream faces only (Reference Rose and LetzerRose and Letzer, 1975, table 3; Reference HambreyHambrey, 1994, fig. 4.15; personal communication from C. D. Clark, 1996). Blunt faces seem to be typical and are therefore presumably formed early.
It appears that like drumlins swarm; for example, if a drumlin is aligned in the flow direction, its neighbour is also likely to be. This implies that conditions necessary for drumlin generation were constant over a large glacier area and over a relatively long time period. There have been some recent discussions which attempt to relate drumlin-field characteristics to inferred subglacial physical conditions. Reference Patterson and HookePatterson and Hooke (1995) found that drumlins were associated with thin ice, longitudinal stretching and high pore-water pressures, while Reference Colgan and MickelsonColgan and Mickelson (1997) inferred that the Green Bay lobe drumlins formed under sleep margins, where shear stresses were between 15 and 25 kPa.
Fur reference, two classic aerial photographs of drumlins are presented, which are well known from textbooks (Reference SharpSharp, 1991; Reference Bennett and GlasserBennett, and Glasser, 1996). Good descriptions of drumlins may be found in these textbooks. Figure 1 shows a swarm of well-aligned, elongated drumlins. They have the characteristic blunt upstream face and long tail, which sometimes tapers out and sometimes ends in a downstream shock. A few of them have ridges running along their flanks. These flanking ridges are also characteristic of the horseshoe or barchan drumlins shown in Figure 2. These drumlins are not elongated and have been explained by Reference ShawShaw and others (1989) as the results of subglacial floods.
The theory presented below assumes that the sedimentology of drumlins is homogeneous. This is a simplification, as many drumlins are sheathed in till, presumably an overriding deforming bed, but have a competent core, consisting typically of gravel or other proglacially dumped material. Whereas observations of drumlin morphology are sufficient for workers to be generally agreed about descriptions of shape, excavations natural or anthropogenic of drumlins are less frequent, making it difficult to make generalizations about the internal geometry of drumlins. We point out that (i) some of the theory below either depends on sediments being slid over bedrock, which can happen to competent cores as well as to uniform drumlins, and (ii) that the kinematic wave theory presented below for internal deformation could easily be extended to include more complex sedimentologies. The particular prediction of backward-facing shocks rests essentially on internal deformation not being present at depth, owing to the increase of effective pressure with depth. One could argue that all drumlins are competently cored owing to the increase of strength with depth, which originates from the increase of effective pressure with depth. In short, we expect the theory to apply to homogeneous drumlins as well as competently cored drumlins.
2.2. Drumlinization and subglacial sediment deformation
The reasons why drumlins form comprise one of the great areas of debate in glacial geological science, and any theory of drumlin formation must explain how sediment relief comes to be amplified. Nevertheless, it has been understood for some time that amplification of relief, although common and probably forming the majority of cases, is not a necessary component of drumlin formation (e.g. Reference GravenorGravenor, 1953). On occasions, drumlinized forms are observed where pre-existent relief, not formed under an ice sheet, has been moulded into shapes more drumlin-like. For example, in land-based glaciers, sediment mounds are typically produced at the glacier margin, and a “noisy”, non-monotone retreat will produce drumlinization of ice-contact features, where the original relief of the sediment mounds was created by marginal or glaciofluvial processes. Certain drumlins, for example those with gravel cores (Reference Boulton, Menzies, Rose and BalkemaBoulton, 1987), clearly originate in this fashion. Reference GravenorGravenor (1953) called these depositional drumlins. They are a manifestation of the process of drumlinization.
This paper argues the case for drumlinization and relief amplification being consequences of the viscous deformation of till. The model of till mechanics used in this paper is called the hydrostatic thin-till approximation (HTTA), and represents a combination of the idea of static pressure gradients in till with the thin-till approximation (Reference AlleyAlley, 1989). It is supposed that the glacier simply transmits a shear stress to the till, that gradients in the till surface do not affect the shear stress and that there is no small-scale till-ice interaction which affects the mechanical coupling. Most crucially, effective pressures are controlled by static gradients. It was developed in the late 1980s by several glaciologists (Reference Boulton and HindmarshBoulton and Hindmarsh, 1987; Reference ClarkeClarke. 1987; Reference AlleyAlley, 1989. The present paper represents an examination of how well the HTTA theory ran explain drumlinization and relief amplification.

Fig. 1. Swarm of tapered drumlins. A discussion of this image may be found in Reference SharpSharp (1991). (Photograph: Air Photograph A-14509-5 from the National Air Photograph Library, Department of Energy, Mines and Resources Canada.)
Existing deforming-till theories of drumlin formation (Reference MenziesMenzies, 1979; Reference Boulton, Menzies, Rose and BalkemaBoulton, 1987) explain drumlin formation through variations in till deformation, but do not explicitly address the provenance of the two necessary components of a theory of drumlin formation. It is already known that a HTTA theory, which incorporates till sliding, can explain some of the macro-morphological features of drumlins (Reference HindmarshHindmarsh, 1996). For example, the HTTA model can produce a theory of drumlinization; pre-existing sediment bodies can be made to become more drumlin-like. Hindmarsh (in press a), using a linearized model, has shown how a flow of ice coupled to a flow of till can produce amplification of relief on wavelengths smaller than the ice-sheet thickness but larger than the deforming bed thickness.
These properties exist because the HTTA theory is a viscous theory. For a given shear stress and hydraulic conditions, flux–depth relationships can be computed for till. These flux–depth relations are non-linear and can be analysed by kinematic wave theory and shock theory. The basic idea is that the blunt faces of drumlins are “shocks”, directly analogous to hydraulic jumps, breaking surf and weather fronts, and that drumlinization is in essence a process of shock formation. The manifestai ion of the shock is a jump in the drumlin thickness (i.e. a cliff). Drumlins are rarely so steep-flanked as to contain cliffs but in the present HTTA theory that is not important; the theoretical difficulty in drumlinization is the creation of the steeper slopes and there are a large number of processes not treated in the present analysis which can act to reduce the slope once it has formed.
The theory of drumlinization in the present paper is a development of one due to Reference HindmarshHindmarsh (1996), which is itself a development of deformation theories due to Reference Smalley and UnwinSmalley and Unwin (1968), Reference MenziesMenzies (1979) and Reference Boulton, Menzies, Rose and BalkemaBoulton (1987). There are observations of sediment deformation which appear to be associated with drumlin formation (Reference Menzies, Zaniewski and DregerMenzies and others, 1997). Reference HindmarshHindmarsh (1996) restricted his consideration to till-sliding over bedrock, which has received interest owing to its possible role as an abrasion mechanism (Reference GjessingGjessing, 1965; Reference Cuffey and AlleyCuffey and Alley, 1996). Wet till-sliding has not been directly observed but Reference GjessingGjessing (1965) argued that polished surfaces were good evidence of this process occurring. If a sediment body is resting on a polished surface, failure is likely to Occur along the smooth base rather than within the body. In this paper, the effect of deformation within the till is considered as well; evolutions are considered in two horizontal dimensions and an analysis of the processes of shock formation is carried out.

Fig. 2. Barchan or horseshoe drumlins. Discussions of this image may be found in Reference ShawShaw and others (1989) and in Reference Bennett and GlasserBennett and Glasser (1996). (Photograph: Air Photograph A-13542-35 from the National Air Photograph Library, Department of Energy, Mines and Resources Canada.)
These ideas rely upon the deformation of wet sediment, in turn requiring the marginal areas of these ice sheets to have been warm-based at some point in the drumlin development. This is in accordance with some theoretical predictions (e.g. Reference Hindmarsh and BoultonHindmarsh and others, 1989) which suggest that ice-sheet margins are shear-heated to melting point. The very margins may have been cold-based but this is not a fundamental objection; drumlin development would have occurred under deeper ice. We shall proceed by assuming a warm-based bed.
This HTTA theory is one of a very small number of physically based models which can produce drumlinization. Reference Boulton, Menzies, Rose and BalkemaBoulton (1987) modelled drumlinization representing till as a linear fluid, while the model of Reference Smalley and UnwinSmalley and Unwin (1968) does not consider continuity. Other theories are more qualitative and lack the quantitative modelling presented in this paper. The arguments in this paper are not intended to supersede more qualitatively based geological models, which describe what is occurring in a more detailed fashion. It is intended as a counter point, yielding analogous descriptions of drumlin formation from a viewpoint which is essentially fluid–mechanical. It is thus hoped that there are analogous descriptions of all the processes in the geological literature; for example, Reference Evenson and GoldthwaitEvenson (1971) described the accretion of sediment on the upstream ends of drumlins, which is directly analogous to the upstream shock migration process described in this paper.
2.3. Drumlin growth: unstable thickening of sediment or the amplification of relief?
A theory of drumlinization which can only drumlinize preexistent relief is not adequate (e.g. Reference GravenorGravenor, 1953; Reference MenziesMenzies, 1989). Gravenor rejected the wide-scale operation of the processes forming what lie termed “depositional drumlins” (i.e. drumlinized pre-existent relief comprising a variety of sedimentary sequences) and suggested that most drumlins were “erosional” (i.e. formed out of previously deposited till that was selectively eroded).
In its original form, Gravenor’s theory does not distinguish between unstable till thickening and amplification of relief. As we shall see, this is a distinction of some mathematical importance. If till is thickening unstably, its maximum thickness increases and/or its minimum thickness decreases. If till relief is being amplified, then the range of sediment thicknesses is increasing but no statement is made about the dynamics of the maximum till thickness; it could be, and in cases to be considered later, is decreasing.
A sediment-thickness instability would occur when a till sheet flowing under a glacier were unstable in the sense that a steady thickness is not maintainable. This is essentially the argument proposed by Reference Smalley and UnwinSmalley and Unwin (1968), although few today agree with their particular instability mechanism. Reference MenziesMenzies (1979) and Reference Boulton, Menzies, Rose and BalkemaBoulton (1987) have also discussed how the flow of till can lead to preferential deposition but fall short of presenting a model for the unstable thickening of homogeneous till. Reference HartHart (1997) discussed the significance of till conservation in relation to drumlin formation and has extended Gravenor’s definition to include “deformational drumlins”.
In this paper, it is shown how relief amplification might operate and time-scales for the operation of this process are discussed. This process is contrasted with recently discovered instabilities in the sheet flow of till when it couples with the ice flow, both on wavelengths shorter than the ice-sheet thickness (Hindmarsh, in press a) and on wavelengths longer than the ice-sheet thickness (Hindmarsh, in press b).
2.4. Paper plan
The main aim of this paper is to establish, through numerical computation, that shock formation is a convincing explanation for certain aspects of drumlin form. This requires some argument on behalf of the viscous theory of till deformation (section 3), an informal presentation of till kinematics which also covers shock formation (section 4) and the presentation of computations of drumlinization of shapes with an emphasis on shock formation (section 5). These computations ignore the influence of till distribution on ice flow. How ice flow and tilt flow couple to produce unstable flow is discussed in section 6.
3 Plastic and Viscous Behaviour of Till
3.1. Relationship to till rheology
The ideas of till deformation in this paper rest upon the notion of a viscous rheology for till, which is becoming increasingly controversial; event-dominated behaviour has been reported from subglacial observations at hydraulically sealed sites (Reference Blake and ClarkeBlake and others, 1992: Reference Iverson, Hanson, Hooke and JanssonIverson and others, 1995; Reference Murray and ClarkeMurray and Clarke, 1995), while laboratory observations and point measurements, confirming several decades of soil-mechanical investigation (e.g. Reference WoodWood, 1990), indicate plastic-type behaviour (Reference KambKamb, 1991). This is consistent with, but not exclusive evidence for, a picture of small-scale failure, with sediment moving in flows of very low viscosity in-capable of supporting shear stresses typical of those found in glaciers. Reference Iverson, Jansson and HookeIverson and others (1994, Reference Iverson, Hanson, Hooke and Jansson1995) in particular have questioned the idea of viscous deformation occurring at small scales and whether “pervasive” deformation exists under Storglaciären at least.
Reference HindmarshHindmarsh (1997) has reviewed this controversy, arguing that while on the small scale till behaves plastically, with the successive failures leading to fluctuating behaviour, while on the larger scale the net effect of failure events is that of viscous behaviour. In support, he cited the ability of viscous sliding theories to predict drumlinization. Thus, the choice of viscous flow and sliding laws in this paper is not dictated by small-scale laboratory or field measurements but by whether they are successful in predicting drumlinization. The fact that till thus appears to behave viscously on the large scale despite its small-scale plastic behaviour has significant implications for ice-sheet modelling. Reference Bahr and RundleBahr and Rundle (1996) have presented a mathematical model of stick-slip behaviour at the glacier bed.
3.2. The plastic/viscous transition
The base of deformation D d (Reference Boulton and HindmarshBoulton and Hindmarsh, 1987; Reference Hart, Hindmarsh and BoultonHart and others, 1990) occurs at the point where the strength of the till, which increases with depth, equals the applied shear stress, which docs not change significantly with depth. This is written in terms of the Mohr–Coulomb criterion:

where κ is the cohesion, τ is the applied shear stress, ![]() is the angle of friction, φ is the porosity, g is the acceleration due to gravity and ρ s, ρ w are the densities of the sediment grains and water, respectively. The interfacial effective pressure p f > 0. This plastic Formula has a viscous interpretation; at depths beneath D d, we do not expect appreciable viscous deformation, while above this depth we expect appreciable deformation. More refined models (Reference Boulton and HindmarshBoulton and Hindmarsh, 1987; Reference AlleyAlley, 1989) have rates of deformation increasing towards the surface. The depth of the base of deformation thus provides a qualitative indication of till flux.
is the angle of friction, φ is the porosity, g is the acceleration due to gravity and ρ s, ρ w are the densities of the sediment grains and water, respectively. The interfacial effective pressure p f > 0. This plastic Formula has a viscous interpretation; at depths beneath D d, we do not expect appreciable viscous deformation, while above this depth we expect appreciable deformation. More refined models (Reference Boulton and HindmarshBoulton and Hindmarsh, 1987; Reference AlleyAlley, 1989) have rates of deformation increasing towards the surface. The depth of the base of deformation thus provides a qualitative indication of till flux.
The horizontal length scales of subglacial variability are quite small, of the order of a few metres (Reference Murray and ClarkeMurray and Clarke, 1995), and this leads us to ask what the properties of the physical system are which determine this length scale. It is unlikely to be the thickness of the glacier, which leads to the conjecture made by Reference HindmarshHindmarsh (1997), and followed in this paper, that the horizontal length scale of variability (the “fluctuation length scale”) is, to order of magnitude, the vertical length scale which determines the depth of the base of deformation under static conditions. This is generally of the order of some tens of centimetres to the order of a few metres. Over horizontal length scales comparable with the depth of the base of deformation, till behaves plastically, while over length scales much greater than this length scale, the aggregate effect of these plastic events is a viscous behaviour.
Small-scale observations of till behaving plastically are not evidence against the viscous theory of till. On occasions, it is illuminatory to consider the behaviour of materials from a plastic perspective and a viscous perspective (e.g. the perfectly plastic theory of ice-sheet behaviour). This procedure is followed in this paper and is called the ‘“plastic interpretation”. This refers to the large-scale behaviour of sediment and is a didactic device, usually set in comparison to the “viscous interpretation”. This is the model that on the large scale till behaves viscously.
We now ask whether the scale ranges occupied by forms such as flutes and drumlins are consistent with the small-scale plastic/large-scale viscous behaviour outlined above. There appears to be a sufficient paucity of evidence to be able to assert that drumlins do not exist in large numbers on very small scales (Reference ClarkClark, 1993; Reference Bennett and GlasserBennett and Glasser, 1996). Clark, in particular, has argued that there are three distinct populations of glacial depositional land forms: flutes, which have a maximum horizontal dimension of 100 m or so; drumlins, with a typical span of 1000 m and a span range of more than two orders of magnitude; and mega-lineations. Flutes have been very well described by a plastic theory (Reference BoultonBoulton, 1976; Reference Morris and MorlandMorris and Morland, 1976) where deformation is occurring perpendicular to the flutes and they thus belting to the sub-viscous scale, plastic scale. The present paper concludes that drumlins form when till is behaving viscously. Under typical sub-ice-sheet conditions, this means that drumlins will generally be greater than 10 m in plan size but this does not rule out smaller drumlins when the depth of the base of deformation is less than 10 m. The present theory does not explain why there should be a population difference between drumlins and mega-lineations.
Reference HartHart (1995) also identified three scales of features on a somewhat smaller scale—mini-lineations, flutes and drumlins. These are from a modern glacier forefield. She saw no difference in the flow processes on the small scale. This is not evidence against the formation of drumlins being an essentially viscous phenomenon, with the viscosity emerging at a larger scale.
3.3. Pressure and stress fields
Stress and effective pressure fields have been discussed in more detail by Hindmarsh (in press b), who contrasted regions where effective pressure at the interface is statically determined and thus increases with elevation, with regions where the interfacial effective pressure is determined by hydraulic considerations. The former case can occur when drainage can occur through the bed but there is also a significant dependence on length scale. Over wavelengths shorter than this length scale, interfacial effective pressures are statically controlled. This length scale depends on the local hydrogeology; for very thin and impermeable aquifers, it is smaller than typical drumlin lengths but for even relatively impermeable aquifers (e.g. 10 m thick layer with permeability 10−l5 m2) the length scale is several hundred metres. In this paper, we assume that interracial effective pressures are statically determined except where otherwise stated. The significance of this assumption is considered in section 4.3.
We now express these ideas more formally. Consider a sediment body lying on a bedrock surface. The sediment may be tens of centimetres to metres thick or may be a very thick body of potentially deformable sediment, and may be tens to hundreds of metres long or broad, or even cover the whole area of interest — the dimensions are not crucial. The effective pressure is defined by p c = p – p w where p = φp s + (1 – φ)p w is the bulk pressure of the soil, φ is the porosity of the soil, p w is the water pressure and p s is the pressure in the sediment grains. We assume that the water and soil pressures are hydrostatic in the sediment-flow theory.
We let (x, y) be the horizontal coordinates, z is the vertical coordinate and t represents time. Under static conditions, the bulk stress p = p i(D) + ρg(D – z) where ρ is the bulk density of the soil, g is the acceleration due to gravity and D represents the upper surface and thickness of the till body. The water pressure is given by p w = p i(D) – p f where ρ w is the density of water and p f = p e(D) is the effective pressure at the ice–till interface. The effective pressure within the body is given by p e = p f + (1 – φ) (ρ s – ρ w) g(D – z) and at the base of the body by
while effective pressure along the interface are given by
where
that is, elevation causes an increase in the interfacial effective pressure. The quantity p c is the datum ice–bed interface effective pressure. This represents the way this theory couples with a basal hydraulic theory, and has been discussed further by Hindmarsh (in press b). The effective pressure at the base of the till body (i.e. at z = 0) is given by combining Equations (4) and (2) to obtain
where
It must be emphasized that static variations of interfacial effective pressure are only expected to occur over wavelengths smaller than the wavelength over which glacial melt can be discharged by ground water. We can also retrieve the case where the interfacial effective pressure is independent of elevation by setting α = 0.
We can substitute the expression for interfacial effective pressure (4) into the deformation–base-depth expression (1) to compute how the base of deformation varies with elevation of the till-body surface. This shows that

An analogous idea exists for till sliding. Here, there is a critical depth, F s; if the sediment is thicker than this, then the weight of the sediment is too great for sliding to occur, whereas if the sediment is thinner, sliding can occur along the interface. We can thus say till sliding will occur under the plastic interpretation if

where tan ![]() and κ s are the constants defining the Mohr–Coulomb criterion for failure along the interface. On polished bedrock, we anticipate the failure will be much easier along the till-bed interface than within the till, for a given effective pressure. These ideas are illustrated in Figure 3. It can be seen that the depth of deformation decreases as the till-body elevation increases, owing to the increased interfacial effective pressure. Under the plastic interpretation, a sediment body can become so thick (around 300 m) that no deformation can occur at the top, but some can occur along the flanks. Likewise, sliding will be more likely to happen near the flanks.
and κ s are the constants defining the Mohr–Coulomb criterion for failure along the interface. On polished bedrock, we anticipate the failure will be much easier along the till-bed interface than within the till, for a given effective pressure. These ideas are illustrated in Figure 3. It can be seen that the depth of deformation decreases as the till-body elevation increases, owing to the increased interfacial effective pressure. Under the plastic interpretation, a sediment body can become so thick (around 300 m) that no deformation can occur at the top, but some can occur along the flanks. Likewise, sliding will be more likely to happen near the flanks.

Fig. 3. Dependence of the depth of the base of deformation and areas of till sliding upon drumlin-surface elevation. Upper half of the figure represents a sediment body. Internal deformation occurs in stippled area, which thins as elevation increases. Sliding occurs (horizontally lined rectangles) where the base of the sliding is lower than the base of the sediment body. Lower half of the figure illustrates the variation in the depths of the bases of deformation and sliding with position. This diagram was constructed using τ = 105 kPa, p c = 10 4 kPa, tan ![]() = 0.5, tan
= 0.5, tan ![]() = 0.25. The height of the sediment body is 40 m.
= 0.25. The height of the sediment body is 40 m.
Under the plastic interpretation, the zone of Failure will be transported away, uncovering the underlying layers which will then also fail. Under these conditions the drumlin will be thinned fairly uniformly. If failure along the sediment–bedrock face occurs, it will occur fore and aft, leading to the central part being left behind. These predictions do not lead to particularly convincing drumlinoid forms, while viscous theories lead to much more realistically drumlinoid forms. We shall therefore seek to argue that viscous behaviour of till on the drumlin scale leads to the process of drumlinization. The perfect plasticity interpretation leads to qualitative understanding of where deformation is more likely to occur but fails to represent the deformation processes on the drumlin scale, because the relative rates at which sediment is transported away from different parts of the sediment body are important.
The numerical experiments in this paper are carried out on flat or nearly flat beds and a free parameter representing the far-field effective pressure is used. This can be viewed as an effective pressure appropriate to the area being modelled. More specifically, since we are dealing with static gradients, it can be defined as the effective pressure at a datum level. It is often convenient, but not necessary, to set this datum at an elevation corresponding to zero sediment thickness. Interfacial effective-pressure gradients are set to be static.
4 Kinematics of Subglacial Till
The kinematics of till flow have been investigated more fully and more mathematically by Hindmarsh (in press b). Here, we present the main results, which are necessary for an understanding of drumlinization.
Internal deformation–flux relationshipThe flux contribution arising from internal deformation can be computed from a postulated viscous relationship for till (Reference Boulton and HindmarshBoulton and Hindmarsh, 1987)

whence


These relationships were derived by Reference AlleyAlley (1989). Sliding Two till-sliding laws have recently been proposed, a quasi-plastic one (Reference Cuffey and AlleyCuffey and Alley, 1996) and a viscous one (Reference HindmarshHindmarsh, 1996), which is the form used here. The till-sliding velocity is given by

We shall be investigating the influence of the unknown parameters on drumlinization. This is very computer-intensive, and the large number of free parameters means that, if we wish to explore parameter space in numerical simulations, we must introduce a scaling, which reduces the number of free parameters. The scaling and development below have been discussed in more detail by Hindmarsh (in press b). The exploration of parameter space reported below would not have been possible without the scaling.
Scaling is an operation to define a set of natural measures for the variables in a physical model. For example, glaciologists are familiar with scaling stresses by 105 Pa. Let us denote dimensionless variables by a tilde and write down
etc. where quantities in square brackets mean the scale magnitudes. Thus, to obtain the physical value, one multiplies the dimensionless value (quantity with tilde) by the scale magnitude.
The scale of the glacially applied shear stress [τ] is regarded as an externally determined parameter. Typically it is the basal shear stress of a glacier, 105 Pa. We expect this to a sensible unit for measuring shear stresses and effective pressures. We set the depth scale
i.e. setting the depth scale equal to the scale of the depth of the base of deformation, typically 10 m. Thus, dimensionless depths can be regarded as being in units of approximately 10 m.
If we have scaled the rate Factors

and, after defining
we can write the flux relation in scaled form as

We choose the discharge scale [q] so that the maximum of ![]() is 1. The parameters δ and Ψ depend upon densities and the acceleration due to gravity, which are well known, and the porosity φ, which can reasonably be expected to vary between 0.2 and 0.4, which is a small variation when compared with that conceivable in the other parameters. With ρ s = 2700kg m−3, ρ w = 1000 kg m−3, ρ i = 917 kg m−3, φ = (0.2 → 0.4) gives δ = (0.06 → 0.08) and we shall lake δ = 0.07 in this paper, which roughly corresponds to φ = 0.3. It is of significance to have δ non-zero, as this (i) leads to reverse shock motion when internal deformation only is occurring and the till thickness is sufficiently large, and (ii) leads to the possibility of relief amplification when internal deformation only is occurring and the till thickness is sufficiently large. These processes ran occur when the till is sliding even when δ = 0. We see now that the parameters are the exponents b, d, the datum effective pressure
is 1. The parameters δ and Ψ depend upon densities and the acceleration due to gravity, which are well known, and the porosity φ, which can reasonably be expected to vary between 0.2 and 0.4, which is a small variation when compared with that conceivable in the other parameters. With ρ s = 2700kg m−3, ρ w = 1000 kg m−3, ρ i = 917 kg m−3, φ = (0.2 → 0.4) gives δ = (0.06 → 0.08) and we shall lake δ = 0.07 in this paper, which roughly corresponds to φ = 0.3. It is of significance to have δ non-zero, as this (i) leads to reverse shock motion when internal deformation only is occurring and the till thickness is sufficiently large, and (ii) leads to the possibility of relief amplification when internal deformation only is occurring and the till thickness is sufficiently large. These processes ran occur when the till is sliding even when δ = 0. We see now that the parameters are the exponents b, d, the datum effective pressure ![]() and the rate-factor ratio
and the rate-factor ratio ![]() . In this paper, we shall not vary b and d independently. The fourth free parameter is
. In this paper, we shall not vary b and d independently. The fourth free parameter is ![]() , the initial thickness of the sediment body.
, the initial thickness of the sediment body.
One further construction is to define an effective depth ![]() ; we find from Equation (16) that we can write the flux relationships in an alternative form as
; we find from Equation (16) that we can write the flux relationships in an alternative form as

and we can construct

The construction P = D/γp c is significant because the geometric properties of Q depend upon P, and Q is proportional to both ![]() and q, while P is proportional to the depth of sediment. Since the kinematic-wave analysis depends upon how discharge varies with thickness, investigating the dependence of Q upon P is equivalent to considering the relationship between q and D, but with the influence of p c as an additional parameter removed.
and q, while P is proportional to the depth of sediment. Since the kinematic-wave analysis depends upon how discharge varies with thickness, investigating the dependence of Q upon P is equivalent to considering the relationship between q and D, but with the influence of p c as an additional parameter removed.
Figure 4 shows that, for small thickness, sediment flux increases with thickness in both cases. For sliding, a maximum flux is reached for all cases of d considered, and there-after the flux declines with thickness, and asymptotes to zero. The flux increases because more sediment is being transported in a plug flow, despite the decrease in the sliding velocity. Eventually, the decrease in sliding velocity with thickness (effective pressure at the base) becomes a significant factor. A maximum flux is reached and thereafter the flux declines asymptotically to zero if there is no internal deformation present. For internal deformation, the situation is more complex. The flux increases but the rate of increase falls as sediment thickness increases. This is because the average viscosity increases with sediment thicknesses, since the effective pressure and till viscosity are high at depth. Moreover, as sediment-body elevation increases, the effective pressure at the interface increases owing to the density difference between ice and water. This eventually causes a decrease in the flux for b > 2.

Fig. 4. Dependence of Q(P) ![]() flux q and W(P)
flux q and W(P) ![]() kinematic-wave velocity v on thickness for internal deformation (a–c) and sliding (d–f). Parameters are b (internal deformation), d (sliding) and P = D/pc. (a and d) Graphs of Q (never negative) and W for internal deformation (a) and sliding (d). b, d = 3. (b and e) Three-dimensional plots of Q on P and b or d for internal deformation (b) and sliding (e). Note viewing angles differ, (c and f) Three-dimensional plots of W on P and b or d for internal deformation (b) and sliding (e). Note viewing angles differ. Note that the kinematic-wave velocities are negative in some regions of the parameter space.
kinematic-wave velocity v on thickness for internal deformation (a–c) and sliding (d–f). Parameters are b (internal deformation), d (sliding) and P = D/pc. (a and d) Graphs of Q (never negative) and W for internal deformation (a) and sliding (d). b, d = 3. (b and e) Three-dimensional plots of Q on P and b or d for internal deformation (b) and sliding (e). Note viewing angles differ, (c and f) Three-dimensional plots of W on P and b or d for internal deformation (b) and sliding (e). Note viewing angles differ. Note that the kinematic-wave velocities are negative in some regions of the parameter space.
4.1. Kinematic waves and shocks
Kinematic waves are waves of constant fluid surface elevation, which in general propagate at different speeds to the fluid speed. If the flux ![]() is a non-linear function of the thickness
is a non-linear function of the thickness ![]() , shocks are liable to form. A shock occurs when a faster moving wave catches up with a slower moving wave. Shocks are familiar to earth scientists in the context of channelled flow of water, where hydraulic jumps represent standing shocks. In this case, the shock is a discontinuity in the water thickness. In reality, the shock is spread over a width of the same order as the depth of the flow, as a result of physical processes not included in the model. The till-evolution equation leads to shock formation and we thus find jumps in thickness of the till: drumlinization and shock formation will be argued to be closely related processes.
, shocks are liable to form. A shock occurs when a faster moving wave catches up with a slower moving wave. Shocks are familiar to earth scientists in the context of channelled flow of water, where hydraulic jumps represent standing shocks. In this case, the shock is a discontinuity in the water thickness. In reality, the shock is spread over a width of the same order as the depth of the flow, as a result of physical processes not included in the model. The till-evolution equation leads to shock formation and we thus find jumps in thickness of the till: drumlinization and shock formation will be argued to be closely related processes.
Standard kinematic wave theory (Reference LaxLax, 1973; Reference WhithamWhitham, 1974) yields the following expression for the kinematic-wave velocity

and wc can construct

thus, W is proportional to the wave velocity ![]() . This fact is used in Figure 8; which illustrates the dependence of W and thus
. This fact is used in Figure 8; which illustrates the dependence of W and thus ![]() on
on ![]() .
.
Hindmarsh (in press b) has shown how the flux and wave-velocity function may be analysed to reach the following conclusions. The following conclusions are derived more formally there but may be deduced qualitatively from Figure 4. Sliding If d > 1, this expression permits kinematic waves which move both forwards and backwards, with velocities becoming more negative as the till becomes thicker. This can be seen in Figure 4. The implication of this is that shucks will form on the upstream side of the bodies, which will therefore have blunt upstream ends, as do drumlins.
Internal deformation
Kinematic wave velocities are illustrated in Figure 4. This shows that kinematic-wave velocities increase with P (thickness) up to a point, whereafter they decline, sometimes reaching negative values.
Analysis of conditions for negative wave velocities, internal deformation
Negative wave velocities occur when the flux maximum has been reached. This can occur for reasonable sediment thicknesses and is thus expected, especially for higher P.
Determination of the thickness of maximum kinematic-wave velocity
In a similar way, the thickness ![]() corresponding to the maximum kinematic-wave velocity may be computed. Where a maximum exists, again we expect reverse-facing shocks, as kinematic waves from thinner, faster regions catch up with those from thicker, slower regions. The significance of
corresponding to the maximum kinematic-wave velocity may be computed. Where a maximum exists, again we expect reverse-facing shocks, as kinematic waves from thinner, faster regions catch up with those from thicker, slower regions. The significance of ![]() is that any sediment body which has an initial thickness less than
is that any sediment body which has an initial thickness less than ![]() will not form upstream-facing shocks. This is favoured by low effective pressures and high b. The maximum kinematic-wave velocity for sliding occurs when
will not form upstream-facing shocks. This is favoured by low effective pressures and high b. The maximum kinematic-wave velocity for sliding occurs when ![]() . Upstream-facing shocks are therefore inevitable for sliding.
. Upstream-facing shocks are therefore inevitable for sliding.
Downstream edge shocks
For deformation by internal deformation, the flux fund ion is concave and up to a certain thickness we expect shocks to form at the downstream edge whatever the rheological index might be. In the case of sliding, no shocks are expected at the downstream edge.
Equality of kinematic-wave speed and shock speeds
It is of interest to know if there is any thickness where the kinematic wave velocity is equal to the shock speed, where the till thickness on the other side of the shock vanishes. It is easy to show for sliding that this does not occur at any finite thickness. For internal deformation, equality does occur and has been analysed in Hindmarsh (in press b). For 1.5 ≤ b ≤ 4, P declines from about 4 to slightly less than 1. For example, if ![]() were 0.1, P would range from 0.4 units to 0.1 units — roughly 4 m to 1 m. For values of b less than about 1.5, P increases very rapidly, above likely original thicknesses.
were 0.1, P would range from 0.4 units to 0.1 units — roughly 4 m to 1 m. For values of b less than about 1.5, P increases very rapidly, above likely original thicknesses.
4.2. Illustrations of shock formation
We illustrate some of the processes of shock formation in Figure 5. This shows characteristic diagrams, i.e. the motion of kinematic waves in the (![]() ) plane, the initial body shape and
) plane, the initial body shape and ![]() for certain cases. Both cases show shock formation at both edges. The case of internal deformation shows shocks moving downstream, arising from the meeting of downstream-moving waves. The case of sliding shows shocks moving in a different direction, and coalescing, both arising from the meeting of upstream-moving waves. Had there been an upstream sediment supply, the upstream wave in this case would have moved upstream as well and coalescence would have been delayed.
for certain cases. Both cases show shock formation at both edges. The case of internal deformation shows shocks moving downstream, arising from the meeting of downstream-moving waves. The case of sliding shows shocks moving in a different direction, and coalescing, both arising from the meeting of upstream-moving waves. Had there been an upstream sediment supply, the upstream wave in this case would have moved upstream as well and coalescence would have been delayed.
We can classify the shocks more systematically by considering four types: DD, DU, UD and UU. “U” and “D’’ refer to upstream or downstream, the first letter refers to the direction the shock is facing and the second to the direction it is moving. DD shocks occur when kinematic waves from thicker, upstream parts catch up with those from slower, thinner parts. This happens when kinematic-wave velocity increases with thickness. This only occurs for internal deformation for small thicknesses. DU shocks occur when there are upstream-moving kinematic waves, with thinner waves moving upstream faster. This occurs when there is a minimum in the negative kinematic-wave velocity. Since the flux always asymptotes to zero if it is non-monotone, there must be a minimum in the kinematic-wave velocity. DU shocks can thus occur for both discharge mechanisms. UD shocks occur when thinner, faster-moving downstream waves catch-up with thicker waves of lesser velocity. This happens very often with internal deformation and occurs technically at the upstream edge of sliding bodies when there is no till upstream, as the kinematic-wave velocity remains finite as the till thickness vanishes. UU shocks occur when upstream-moving waves of a greater thickness catch up with upstream waves of thinner sediment moving more slowly. This can occur for sliding and internal deformation when b > 2 and δ > 0.

Fig. 5. Typical shock-formation mechanisms for sliding (lefthand side) and internal deformation (righthand side). Upper diagrams indicate characteristic lines, along which the elevation is constant. Once characteristics join, a shock forms, indicated by a heavy line. Initial conditions of an inverse parabola are illustrated in the lefthand part of the lower diagram for sliding and for internal deformation. The righthand parts of the lower diagrams are representations of the flux (solid line) and wave velocity (dotted line), forming the horizontal axis, plotted against sediment-body thickness (vertical axis). Significant points (zero wave velocity and least wave velocity for sliding, greatest wave velocity for intern at deformation) are joined by lines to the corresponding points on the initial condition curve and thence to the characteristic diagram. See text for explanation of the mechanisms for the formation of upstream and downstream, shocks.
4.3. Influence of interfacial effective-pressure regime
We have assumed in the above analysis that interfacial effective pressures are statically controlled. If instead they are constant, this is equivalent to δ = 0 and we retrieve the flux-thickness relationships due to Reference AlleyAlley (1989). The main qualitative difference is that, for internal deformation, there is no regime where flux decreases with thickness, with the consequence that there can be no backward-moving kinematic waves and no UU shocks. In all the cases below, any UU shocks are transient features and not main features of the evolution. Thus, in the context of drumlinization, the hydraulic regime is not crucial. This is not the case for the stability question, where hydraulic regime is crucial.
5 Numerical Computations
In 1HD (one horizontal dimension), a convenient solution method is by characteristics but, in 2HD, finite-difference methods are appropriate. Solutions of non-linear hyperbolic scalar differential equations are now reasonably well understood (Reference LeVequeLeVeque, 1992), although numerical methods for “non-convex” (i.e. the curvature changes sign) discharge functions are still an active area of research.
In this section, we consider testing of the finite-difference algorithm and carry out a parameter study, using the scaling properties of the equation to avoid repetition.
5.1. Testing
Reference HindmarshHindmarsh (1996) solved the 1HD equations using the method of characteristics. This method is particularly effective at shock-capturing (i.e. computing the shape of the blunt upstream face! but it is inconvenient in 2HD. We therefore use finite-difference techniques. The finite-difference computations were carried out using the public-domain hyperbolic solver CLAWPACK (Reference LeVequeLeVeque, 1992). Periodic boundary conditions were specified, which means that material leaving the outlets re-enters at the inlet; thus, the initial sediment body can be regarded as one of an infinite series of clones, spaced according to the grid dimensions. Downstream edges of drumlins can catch up with the upstream edge of the drumlin downstream. For completeness, we record that the “entropy-fix” was not used (Reference LeVequeLeVeque, 1992).
Most of the problems discussed below are non-convex, i.e. the curvature of the flux–depth relation changes sign. Such problems are severe tests of hyperbolic conservation-law sobers (personal communication from R. LeVeque, 1996) and, in certain cases, associated almost exclusively with till discharge by internal deformation, the finite-difference solver failed. Nevertheless, the comparison tests reported below give us confidence that when the finite-difference solver worked, it gave the correct answers. It simply appears that the numerical demands of drumlinization can be beyond the best numerical practice.
To test the finite-difference hyperbolic solver CLAWPACK solutions were compared with the IHD characteristic solver described by Reference HindmarshHindmarsh (1996). Here, the parameters are ![]() and b = 2. It is initialized with a body of parabolic form such that
and b = 2. It is initialized with a body of parabolic form such that
The evolution was computed over 20 time units, by which time the downstream edge of the sediment had reached ![]() = 8 × 101 (Fig. 6). As shown in Reference HindmarshHindmarsh (1996), a shock forms very rapidly on the upstream side and thereafter the patch moves as a wedge with the blunt face on the upstream side and gradually lengthens and thins. This figure shows calculations using both methods and in general the agreement is excellent, although the shock is smeared over a few gridpoints in the finite-difference calculations as is expected. The shock resolution of the finite-difference solver is very good and, as predicted by theory (Reference LaxLax, 1973; Reference LeVequeLeVeque, 1992), the conservative finite-difference scheme has ensured that the shock is more or less in the right place.
= 8 × 101 (Fig. 6). As shown in Reference HindmarshHindmarsh (1996), a shock forms very rapidly on the upstream side and thereafter the patch moves as a wedge with the blunt face on the upstream side and gradually lengthens and thins. This figure shows calculations using both methods and in general the agreement is excellent, although the shock is smeared over a few gridpoints in the finite-difference calculations as is expected. The shock resolution of the finite-difference solver is very good and, as predicted by theory (Reference LaxLax, 1973; Reference LeVequeLeVeque, 1992), the conservative finite-difference scheme has ensured that the shock is more or less in the right place.
5.2. Implications of the scaling
The scaling has reduced the number of free parameters to four. It means that we do not have to consider explicitly the role of shear stress, the length scale of the drumlin or the absolute values of the rate constants, only their ratio, as the dependence of the results on variation of these parameters can be deduced from the scaling rather than needing to be explicitly computed.
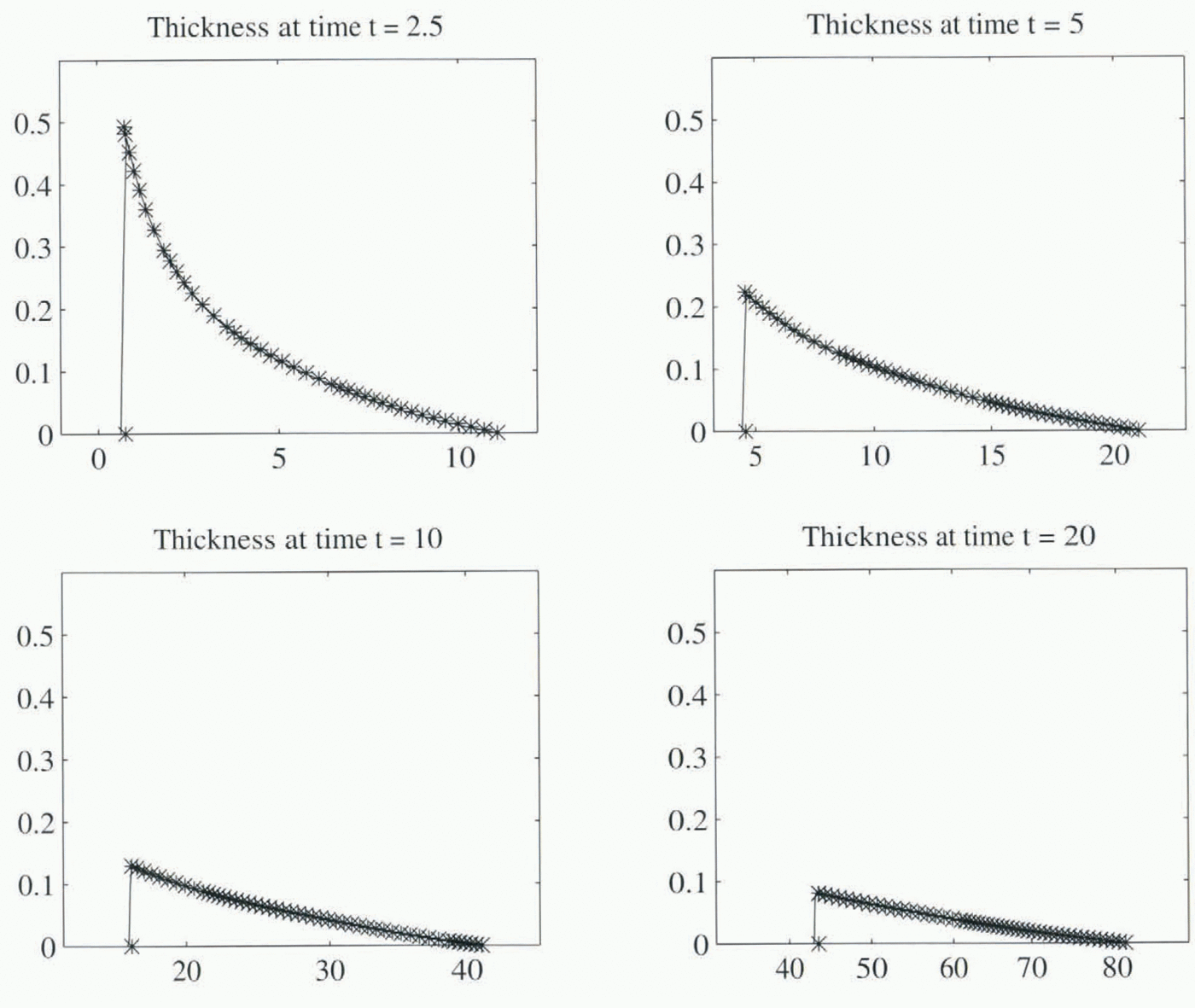
Fig. 6. A comparison of the evolution of a sliding sediment body using finite differences (1000 points) (solid line) and the method of characteristics (51 points) (*). Vertical axis thickness in dimensionless units, horizontal axis position in dimensional units. Good agreement between the two methods is obtained. Although the shock is smeared slightly by the finite-difference method, its position is approximately correct.
Consider the unsealed continuity equation

Sealing shows that for balance

and using our scale definition for the depth and the fluxes, we see that

Note that the lefthand sides are independent of the right-hand side in both cases. This means that, if we double the horizontal length scale, we double the time-scale; a drumlin twice as long takes twice as long to evolve.
These relationships also show the obvious linear relationships between the time-scale and the rate factors A s, A d. The dependence on τ is less direct, because the depth scale and effective-pressure scales depend also on this quantity.
Initial shape (i.e. the geometry once the overall dimensions have been set) is unlikely to affect significantly the outcome. This is because of information loss in shocks (a positive entropy jump).
5.3. Interpretation of units in the diagrams
The results below are presented in dimensionless units. As explained, we cannot say anything about the length and time-scales, because they are set by the unknown rate factors. We have assumed that [x] ![]() [D], by virtue of using the thin-till assumption, and we also assume that horizontal length scales are less than the length scale at which hydraulic gradients become important. Within these limits, the horizontal length scale could be anything provided that static interfacial effective-pressure gradients still occur.
[D], by virtue of using the thin-till assumption, and we also assume that horizontal length scales are less than the length scale at which hydraulic gradients become important. Within these limits, the horizontal length scale could be anything provided that static interfacial effective-pressure gradients still occur.
The vertical length scale is much more firmly fixed. We have γ ≈ 10 kPa m−1 which for a shear stress scale of [τ] = 100 kPa implies that the depth scale [D] = [τ]/γ ≈ 10 m. Where the shear stress is less, the depth scale will be correspondingly less. The initial thickness B is of course scaled in the same way as other thicknesses.
Datum-effective pressures are sealed by the shear stress. Thus, if ![]() = 0.1 and [τ] = 100 kPa, this implies that in dimensional form p c = 10 kPa. The indices b, d are dimensionless and the dimensionless rate factors
= 0.1 and [τ] = 100 kPa, this implies that in dimensional form p c = 10 kPa. The indices b, d are dimensionless and the dimensionless rate factors ![]() only play a role in determining the relative contributions of deformation and sliding in the experiments described below, as we have constructed max (
only play a role in determining the relative contributions of deformation and sliding in the experiments described below, as we have constructed max (![]() ) = 1.
) = 1.
5.4. 1HD parameter study
It is an open question whether till sliding is the fundamental means of sediment transport in shield areas. A typical evolution is similar to the one described in the testing section above, with shocks rapidly forming on the upstream and downstream side and the resultant wedge gradually lengthening and thinning. Interest thus resides in the effect the parameters have on the rate of drumlinization and more specifically how rapidly drumlinization occurs in terms of the distance slid. A three-dimensional plot of a typical evolution is shown in figure 7a; clearer examples of downstream shock formation and shock coalescence may be found in Reference HindmarshHindmarsh (1996).
Datum-effective pressure ![]() c. Physically, the scaled parameter p c represents the ratio of the datum-effective pressure to the shear stress. In the absence of shear-stress variations, a low datum-effective pressure represents high water pressures. A parameter study on
c. Physically, the scaled parameter p c represents the ratio of the datum-effective pressure to the shear stress. In the absence of shear-stress variations, a low datum-effective pressure represents high water pressures. A parameter study on ![]() is shown in figure 7b. This shows that low effective pressures (high water pressures) lead to more rapid thinning and lengthening; but that it seems too difficult to distinguish between the effects of time as a parameter and effective pressure; i.e. from observing one drumlin, we cannot say whether its degree of drumlinization is due to length of time of working or of effective pressure. This property arises from the role of
is shown in figure 7b. This shows that low effective pressures (high water pressures) lead to more rapid thinning and lengthening; but that it seems too difficult to distinguish between the effects of time as a parameter and effective pressure; i.e. from observing one drumlin, we cannot say whether its degree of drumlinization is due to length of time of working or of effective pressure. This property arises from the role of ![]() c as an inverse-rate factor.
c as an inverse-rate factor.
Flow-law exponent b. A parameter study on b ε [1.5, 4] (i.e. the range of b is 1.5–4) is shown in figure 7c. This shows the rate of drumlinization increasing with b. The larger b is, the larger the contrast between the rates of flow of thick and thin sections; this seems to account for the computed differences between the cases.
Initial thickness B. A parameter study on ![]() ε [0.5,5] is shown in figure 7d. Thick drumlins deform more slowly owing to the increased basal effective pressure, leading to the differences in the rate of drumlinization observable in the figure. The evolution of shape does not seem related to the initial thickness.
ε [0.5,5] is shown in figure 7d. Thick drumlins deform more slowly owing to the increased basal effective pressure, leading to the differences in the rate of drumlinization observable in the figure. The evolution of shape does not seem related to the initial thickness.
Some evolutions by internal deformation are shown in Figure 8. figure 8a is computed using the method of characteristics and is typical of a two-shock form. Shocks form front and rear, and the sediment body is moving slowly forward, thinning and lengthening. The thickness of the quasi-persistent form is round about the thickness for equality of shock and wave speed. During the persistent phase, the two shocks approach one another as the upstream, thicker, faster-moving shock approaches the downstream shock, and would have eventually coalesced. An unusually persistent form, computed using finite differences, is shown in figure 8b. The finite-difference calculations have periodic boundary conditions, meaning that there are an infinity of clones upstream and downstream. The first upstream clone can be seen arriving in the figure.
figure 8c and d are three-dimensional and two-dimensional plots of another evolution. The sediment body evolves into a quasi-persistent form, again round about the thickness where shock and wave speeds are equal. The near geometric similarity of the evolving form is clearly shown in figure 8d.
figure 8e and f show the evolution of a form where the shock coalescence occurs relatively early. Two downstream-moving shocks form to begin with, which coalesce rapidly, leaving a relatively thick “slime trail” behind them. As the shocks approach each other, a very thin sediment column is observed. This is almost certainly non-physical and would be removed by till-weight diffusion and other ice–till mechanical coupling effects, and result in earlier coalescence of the shocks.
The finite-difference algorithm experienced certain difficulties when attempting to compute evolutions where till discharge was affected by internal deformation. In some of the cases, the following happened. Immediately upstream of the upstream shock, relatively small wiggles (amplitude up to about 5% of the shuck thickness) were observed to form and then to decay. On occasions, negative thicknesses were found; these still corresponded to positive effective pressures. Nevertheless, we can have some confidence in the qualitative aspects of the results (the shocks fore and aft), as these were reproduced by the stable method of characteristics, predicted by the analysis, and it was precisely these qualitative features which anyhow caused the numerical problems.

Fig. 7. (a) Time–space diagram of the evolution of a 1HD sliding till body. The body lengthens and thins, and a UD shock forms by coalescence of DU and UD shocks. This wedge form persists. (b, c and d) are parameter studies. Horizontal axes are position, varied parameter and vertical axis is thickness. (b) Parameter study of sliding till body. Parameter varied is ![]() . Cases
. Cases ![]() = 0.1, 0.2 and 0.3 are till bodies which have entered from the virtual cells upstream. In case
= 0.1, 0.2 and 0.3 are till bodies which have entered from the virtual cells upstream. In case ![]() = 0.3, the body has entered from the first cell upstream, for
= 0.3, the body has entered from the first cell upstream, for ![]() = 0.2, the body has entered from the second cell upstream. Case
= 0.2, the body has entered from the second cell upstream. Case ![]() = 0.1 has the sediment almost flat. (c) Parameter study of sliding till body. Parameter varied is b. Drumlinization occurs more rapidly for higher b. (d) Parameter study of sliding till body. Parameter varied is
= 0.1 has the sediment almost flat. (c) Parameter study of sliding till body. Parameter varied is b. Drumlinization occurs more rapidly for higher b. (d) Parameter study of sliding till body. Parameter varied is ![]() , the initial thickness. Drumlinization occurs more rapidly for smaller bodies.
, the initial thickness. Drumlinization occurs more rapidly for smaller bodies.
Datum-effective pressure ![]() . The effect of p c on internal deformation is shown in figure 9a and b. figure 9a shows how lower effective pressure delays the coalescence of shocks. This is because, at higher effective pressures, the thickness of maximum kinematic-wave velocity is greater, meaning that it is nearer the centre of the original body, or may even be thicker than the original sediment body. In the first case, the UD shock forms further downstream and catches up with the DD shock sooner; in the second case, it never forms at all. figure 9b shows sediment bodies with only a DD shock remaining. Here, effective pressure is simply affecting matters by altering the viscosity of the sediment bodies; lower effective pressure leads to tower viscosity and a more rapid evolution.
. The effect of p c on internal deformation is shown in figure 9a and b. figure 9a shows how lower effective pressure delays the coalescence of shocks. This is because, at higher effective pressures, the thickness of maximum kinematic-wave velocity is greater, meaning that it is nearer the centre of the original body, or may even be thicker than the original sediment body. In the first case, the UD shock forms further downstream and catches up with the DD shock sooner; in the second case, it never forms at all. figure 9b shows sediment bodies with only a DD shock remaining. Here, effective pressure is simply affecting matters by altering the viscosity of the sediment bodies; lower effective pressure leads to tower viscosity and a more rapid evolution.
Rheological index b. figure 9c shows that higher b leads to a faster evolution and a thinner trail. The greater b, the lower the thickness of maximum kinematic-wave velocity, meaning the further upstream the UD shock forms. This causes the thinner trail, leaving more mass in the main body and thus permitting its form to be more persistent.
Initial thickness ![]() . Since the properties of drumlinization depend upon the parameter P =
. Since the properties of drumlinization depend upon the parameter P = ![]() when only one discharge mechanism operates, we expect greater thickness to correspond in some ways to lower effective pressure. This is confirmed in figure 9d, where the same effect of earlier coalescence is shown for the smaller initial thicknesses as for higher effective pressure.
when only one discharge mechanism operates, we expect greater thickness to correspond in some ways to lower effective pressure. This is confirmed in figure 9d, where the same effect of earlier coalescence is shown for the smaller initial thicknesses as for higher effective pressure.
Computations not presented here in detail show that the main influence of combining two discharge mechanisms is on the disappearance of the DD shock. Since sliding permits easier discharge and kinematic-wave velocities to decrease with thickness at low thicknesses, the conditions for DD shock formation can be removed. As the sliding contribution is removed, the dependence of ![]() upon
upon ![]() becomes sigmoidal and kinematic-wave velocity starts to increase with thickness, re-establishing conditions for DD shock formation.
becomes sigmoidal and kinematic-wave velocity starts to increase with thickness, re-establishing conditions for DD shock formation.
5.5. 2HD parameter study
In this section, we consider the evolution of drumlin form in 2HD (two horizontal dimensions). These calculations were also carried out using CLAWPACK. Velocity fields can be oriented arbitrarily and the direction specified is obvious from the figures. Physically, no terms relating to gradients across the direction of flow enter the evolution equation, sothe parameter studies for 1HD also apply to 2HD. Thus, this section considers the extent to which the original shape of the sediment body affects the resultant drumlinoid feature. Plan-aspect ratio is one shape descriptor which has long been recognized as having an important effect on drumlin shape (Reference Boulton, Menzies, Rose and BalkemaBoulton, 1987; Reference ClarkClark, 1993). We also investigate whether, for a given plan-aspect ratio, variations in shape have a significant effect on drumlin form.

Fig. 8. Evolution of sediment bodies by internal deformation. (a) Computed using the method of characteristics. It is typical of internal deformation to have shocks formed at upstream (low ![]() ) and downstream ends. A thin “slime trail” of sediment is left behind the moving drumlin, which does not lengthen as fast as an equivalent sliding body. (b) Unusually persistent form computed using finite differences. Periodic boundary conditions, with clones up- and downstream. Thickness in later parts of evolution is approximately that for kinematic-wave/shock-wave velocity equality. (c and d) Thicker persistent form, with thickness of 1 unit (roughtly 10 m). The greater thickness compared with (b) arises from the higher effective pressure (pc). (c) is a three-dimensional time–space diagram, (d) is profiles at selected time intervals, (e and f) Form where upstream and downstream shocks coalesce relatively quicly, leaving a DD shock. (e) is a three-dimensional time–space diagram, (f) is profiles at selected time intervals.
) and downstream ends. A thin “slime trail” of sediment is left behind the moving drumlin, which does not lengthen as fast as an equivalent sliding body. (b) Unusually persistent form computed using finite differences. Periodic boundary conditions, with clones up- and downstream. Thickness in later parts of evolution is approximately that for kinematic-wave/shock-wave velocity equality. (c and d) Thicker persistent form, with thickness of 1 unit (roughtly 10 m). The greater thickness compared with (b) arises from the higher effective pressure (pc). (c) is a three-dimensional time–space diagram, (d) is profiles at selected time intervals, (e and f) Form where upstream and downstream shocks coalesce relatively quicly, leaving a DD shock. (e) is a three-dimensional time–space diagram, (f) is profiles at selected time intervals.
In general, calculations were more troublesome for internal deformation than for sliding. Shapes with sleeper edges (hemispheres and cubes) could be evolved when sliding was occurring but, for internal deformation, parabolic bowls were used.
Figure 10(1) shows a hemisphere evolving under sliding. As with 1HD, the thinner parts move faster. Upstream and downstream shocks form, the downstream shock at a relatively high elevation and the shocks eventually coalesce, leaving a tapered form with a blunt upstream face.
Figure 10(2) shows a parabolic bowl evolving under deformation. As with 1HD, shocks form upstream and downstream, and the form gradually lengthens and thins. The upstream clone enters the figure at ![]() = 6.
= 6.
Figure 10(3) shows the same experiment but with a thicker body. There are differences in the plan-view evolution. Contour interval scales with the original thickness.
Figure 10(4) shows a cube evolving under sliding. The cube is a difficult shape to evolve, because it can create rarefaction shocks (which are ill-posed). Again, there is a strong suggestion of upstream and downstream shocks, and the form is drawn out, steadily losing evidence of its original cubic form.

Fig. 9. Parameter study of an internally deforming till body. Horizontal axes are position, varied parameter and vertical axis is thickness. (a and b) Parameter varied is ![]() c. Note times are different. (a) has forms with two shocks and other forms with higher effective pressure where the two shocks have coalsced. (b) are forms where all the shocks have coalsced and the cases with high effective pressure result in more viscous, slower-evolving sediment bodies. (c) Parameter varied is b. Higher b leads to a faster evolution and a thinner trail. This permits the drumlin form to be more persistent. (d) Parameter varied is
c. Note times are different. (a) has forms with two shocks and other forms with higher effective pressure where the two shocks have coalsced. (b) are forms where all the shocks have coalsced and the cases with high effective pressure result in more viscous, slower-evolving sediment bodies. (c) Parameter varied is b. Higher b leads to a faster evolution and a thinner trail. This permits the drumlin form to be more persistent. (d) Parameter varied is ![]() , the initial thickness. Thicker initial forms lead to slower evolution.
, the initial thickness. Thicker initial forms lead to slower evolution.
Figure 11 shows the evolution of ridges perpendicular to the original flow under deformation and sliding. Figure 11(1) shows the evolution of a ridge under sliding. The thinner parts move faster, causing the upstream shock edge to become convex in plan form, one part of the generation of a barchan form.
Figure 11 (2 and 3) shows the evolution of a ridge under deformation; the first is a thick initial ridge and the second is a relatively thin one. The upstream shock face is convex in plan form in both cases, while the thinner case (Fig. 11(3)) has a more pronounced downstream shock and leaves a more obvious “slime trail”. Figure 11(4) shows a case with exactly the same parameter as Figure 11(3) but with the initial form slightly different. There is little difference in the final outcome.
These results are of interest, because they suggest that the viscous model can act so as to produce barchan forms, although the results of the calculations are not really of the form discussed by Reference ShawShaw and others (1989), which has a hollow downstream edge.
Differently directed re-advances can rework drumlins into interesting forms (Reference ClarkClark, 1993; Reference Bennett and GlasserBennett and Glasser, 1996). Figure 12(1) shows the evolution under sliding of a ridge angled to the direction of ice flow. The results are rather typical of the reworked forms discussed by these authors.
The remaining cases are designed to show that even rather unpromising original forms end up, under the action of viscous deformation or sliding, looking rather more drumlinoid. Figure 12(2 and 3) show the evolution of intersecting ridges under sliding and deformation, respectively. The ridges rapidly become asymmetrical in the direction of ice flow, with shocks forming on the upstream side for the sliding case, and on both sides for the deformation case. The end form seems more drumlinoid than the initial form. Figure 12(4) shows the under deformation of intersecting ridges with an increased sediment thickness at the point of intersection. The parameters are otherwise the same as in Figure 12(3). The end result is somewhat different but again more drumlinoid than the initial form.
6 The Amplification of Relief of Sediment and Bedrock
A simple but rigorous argument shows that spatially constant stress and effective-pressure fields can produce neither unstable thickening not amplification of relief. In consequence, stress gradients must be a present (necessary but not sufficient) condition to produce either of these effects.
In order to discuss sediment thickness instabilities and relief amplification, it is necessary to consider how the stress fields in the ice couple with the bed. We shall discuss three ways that spatial gradients in the stress fields can occur. First, the large-scale structure leads to longitudinal gradients in stress fields. If one further accepts that interfacial effective pressure does increase with elevation, then the HTTA theory permits there is a decreasing flux of till with sediment thickness. If this is associated with net erosion of till, which arises from these large-scale gradients in the stress fields, it can be shown that a consequence is amplification of relief if the till is sufficiently thick. Numerical models which demonstrate this feature are given in section 6.1. This amplification is not a true instability as there is no exponential growth of relief.

Fig. 10. Plan views of evolving sediment bodies. Lines represent contours spaced at one-tenth of the original evolution. Rows of figures represent evolving cases, with the time written above. (1) Sliding hemisphere, d = < 2.0, ![]() c = 0.5,
c = 0.5, ![]() = 1. (2) Deforming parabolic bowl, b = 2.0,
= 1. (2) Deforming parabolic bowl, b = 2.0, ![]() c = 0.1,
c = 0.1, ![]() = 1. (3) Deforming parabolic bowl, b = 2.0,
= 1. (3) Deforming parabolic bowl, b = 2.0, ![]() c = 0.1,
c = 0.1, ![]() = 5. (4) Sliding cube, d = 2.0,
= 5. (4) Sliding cube, d = 2.0, ![]() c = 0.5,
c = 0.5, ![]() = 1.
= 1.
Reference GravenorGravenor’s (1953) theory of erosional drumlins appears to be a description of sediment-relief amplification and does not seem to require unstable thickening of sediment, while it is not clear whether Reference HartHart’s (1997) further definition of “de-positional drumlins” requires unstable thickening. It is thus not clear whether the field evidence implies a true instability (exponential growth) or simply growth of relief.
Consider the conservation equation
Let us suppose that q, the discharge, is a function of the thickness and of a field variable f(x). This field variable might be the effective pressure or the shear stress. Evolutions with these varying in space have been computed by Reference HindmarshHindmarsh (1996). Then, we can rewrite this equation

and, using the fact that the kinematic-wave velocity v is given by dq/dD, write

Thus, if the field variable is constant in space, thickness along a kinematic wave does not change, meaning that in the absence of shock formation the range of the initial till distribution does not change. Where shock formation occurs, the range can never increase and may decrease if maxima or minima are swallowed up in shocks.
Now, consider the case where the field variable varies in space. We restrict consideration to the case where dq/d f > 0. (The other cases are easy to work out.) This is the case, for example, where the field variable is τ, the shear stress. Then, if ∂ xf > 0, we expect there to be thinning following a characteristic. There is nothing particularly new in this statement; it forms the basis of the deformational erosional theory proposed by Reference BoultonBoulton (1996a, Reference Boultonb), where an increasing downstream shear stress in an ice sheet causes large-scale erosion.

Fig. 11. Plan views of evolving sediment bodies. Lines represent contours spaced at one-tenth of the original evolution. Rows of figures represent evolving cases, with the time written above. (1) Sliding ridge, d = 2.0, ![]() c = 0.5,
c = 0.5, ![]() = 1. (2) Deforming ridge, b = 2.0,
= 1. (2) Deforming ridge, b = 2.0, ![]() c = 0.1,
c = 0.1, ![]() = 5. (3) Deforming ridge, b = 20,
= 5. (3) Deforming ridge, b = 20, ![]() c = 0.1,
c = 0.1, ![]() = 0.5. (4) Deforming ridge, initial form less tapered than the other three, d = 2.0,
= 0.5. (4) Deforming ridge, initial form less tapered than the other three, d = 2.0, ![]() c = 0.1,
c = 0.1, ![]() = 0.5.
= 0.5.
Consider now how the range of thicknesses can evolve. We consider two thicknesses D 1, D 2, D 1 < D 2 but q 1 > q 2, q 1 = q(D 1, f), q 2 = q(D 2, f). Substituting these into Equation (21) and subtracting yields

Where q 2 < q 1, it is also true that

so we see that the range-evolution equations admit the possibility of relief being amplified while net erosion is occurring. The same can occur when q 2 > q 1 and net deposition is occurring. To summarize, relief amplification can occur when there is net erosion and sediment is sufficiently thick for the discharge to decrease with thickness, or when there is net deposition and the sediment is sufficiently thin for the discharge to increase with thickness. This does not necessarily occur, as the analysis has neglected the influence of shock formation, which needs to be considered on a case-by-case basis.
We illustrate such an evolution as follows. The results are presented in dimensionless units. A till body of unit thickness between ![]() = 0 and 1, with a bump in the middle is allowed to evolve under a shear-stress gradient which causes the shear stress to increase from 0.01 at
= 0 and 1, with a bump in the middle is allowed to evolve under a shear-stress gradient which causes the shear stress to increase from 0.01 at ![]() = 0 to 1.01 at
= 0 to 1.01 at ![]() = 1.01. This is shown in Figure 13. There is, in fact, some lee-side shock formation, although this is not very obvious from the diagram. Projected on to the
= 1.01. This is shown in Figure 13. There is, in fact, some lee-side shock formation, although this is not very obvious from the diagram. Projected on to the ![]() = 0 plane are three lines. The upper one is the envelope of the till-thickness maxima, plotted against time; the lower one is the the envelope of the non-zero till-thickness minima, while the middle one is the total relief (i.e. the difference between the first and second lines). This can be seen to increase rallier slowly for much of the evolution and then to decrease. More detailed examination of the results shows that this decrease is related to maxima being swallowed into shocks.
= 0 plane are three lines. The upper one is the envelope of the till-thickness maxima, plotted against time; the lower one is the the envelope of the non-zero till-thickness minima, while the middle one is the total relief (i.e. the difference between the first and second lines). This can be seen to increase rallier slowly for much of the evolution and then to decrease. More detailed examination of the results shows that this decrease is related to maxima being swallowed into shocks.
In areas where net erosion is occurring drumlin fields should form by relief amplification where the sediment thickness exceeds the thickness corresponding to the maximum flux. This depends on the quantity P = D/γp c and the parameter δ, which represents the interfacial effective-pressure gradient, as well as the rheological indices. If the sediment is flowing through sliding on bedrock, then a flux maximum occurs, but if the till is flowing through internal deformation, a flux maximum occurs only when δ > 0. In both cases, the critical thickness D ![]() p c. Thus, large sediment thicknesses and low effective pressures favour the amplification of relief, implying that they might be expected to form in basins, where the sediment is thick and interfacial effective pressures can be lower if they are determined primarily by static gradients. Note the implication that aquifer hydrogeology can play an important role in whether drumlin fields form or not.
p c. Thus, large sediment thicknesses and low effective pressures favour the amplification of relief, implying that they might be expected to form in basins, where the sediment is thick and interfacial effective pressures can be lower if they are determined primarily by static gradients. Note the implication that aquifer hydrogeology can play an important role in whether drumlin fields form or not.

Fig. 12. Plan views of evolving sediment bodies. Lines represent contours spaced at one-tenth of the original evolution. Rows of figures represent evolving cases, with the time written above. (1) Sliding ridge angled to direction of ice flow, d = 2.0, ![]() c = 0.5,
c = 0.5, ![]() = 1. (2) Sliding intersecting ridges, b = 2.0,
= 1. (2) Sliding intersecting ridges, b = 2.0, ![]() c = 0.5,
c = 0.5, ![]() = 1. (3) Deforming intersecting ridges, b = 2.0,
= 1. (3) Deforming intersecting ridges, b = 2.0, ![]() c = 0.3,
c = 0.3, ![]() = 1. (4) Deforming intersecting ridges with increased thickness at crossing point, d = 2.0,
= 1. (4) Deforming intersecting ridges with increased thickness at crossing point, d = 2.0, ![]() c = 0.3,
c = 0.3, ![]() = 1.
= 1.

Fig. 13. Relief amplification. A 1HD body evolves under the action of a shear stress increasing with . Plotted on the = 0 plane are till-thickness maximum (upper line), till-thickness minimum (lower line) and total relief (middle line). The relief grows slowly even thought the till is thinning but this is not a true instability.
The major problem with this idea of relief amplification is that it lakes too long and that relief is not amplified very much; it is not a true instability with exponential growth. While this mechanism of relief amplification cannot be excluded as a mechanism fur drumlin formation, it is more likely that true sediment-thickness instabilities are responsible. These would be aided by relief amplification.
6.2. Sediment-thickness instabilities
More rapid growth can occur if true sediment-thickness instabilities arise. Consider again Equation (21)

Table 1. Dependence of length scale [L] of hydraulic/static equality on the hydrogeology kΔ and the relief [R]

The potential for instability arises it ∂ x f is in some way related to D. Field variables of significance are the applied shear stress or the normal pressure, both determined by the ice flow which is in turn determined by the flow of the sediment in cases of interest for drumlin formation.
There are two cases where the linear stability has been investigated: the short wavelength theory, where interfacial pressures are statically determined and wavelengths lie between the thickness of the ice and the thickness of the deforming sediment (Hindmarsh, in press a) and the long wavelength theory (Hindmarsh, in press c), where wavelength is greater than the ice-sheet thickness. In the former case, mechanics are computed using the Nye–Kamb perturbation (Reference NyeNye, 1969; Reference KambKamb, 1970), while in the latter case the mechanics are computed using the shallow-ice approximation (Hutter, 1983) and effective pressures are affected by subglacial hydraulics.
In both cases, unstable thickening of sediment is found to occur. Bifurcations occur by varying the basal velocity, wavelength, sediment thickness, shear stress, datum-effective pressure and flow-law indices for both cases, and the ice thickness for the long wavelength case. Thus, extensive regions with and without unstable growth are found, which is a highly desirable property for any drumlin-formation mechanism, since drumlins are not ubiquitous. The geometry of the separatrices is not known; certainly the separatrices are not the same for short- and long-wavelength theories.
Table 2. Table 2. Dependence of thickness of maximum flux D q on the parameters b and p c when a sediment body is deforming internally. The maximum was sought for in the range 0 < D < 40; where it was not found in this range, a NaN (i.e. the IEEE undefined number) is specified. The search range is a plausible upper limit to the range of scaled drumlin thicknesses

Table 3. Dependence of thickness Dv at which the maximum kinematic-wave velocity occurs on the parameters b and p c. It depends on p c, b and δ, and no other parameters

In practical terms, the linear instability means that small perturbations (mounds of sediment) can grow under appropriate conditions. Once the mounds of sediment become large (i.e. an elevation which is an appreciable thickness of the deforming sediment), the linear approximation breaks down. In the first instance, we should be seeking mechanisms which quench the instability and cause mound growth to cease. One mechanism certain to play a role, and which may be all that is necessary, is shock formation.
In the linear approximation, shock formation does not occur. Once mounds become sufficiently large, then shocks start to form and sediment maxima or minima are inevitably annihilated in these shocks, as demonstrated extensively in the numerical computations in this paper. The idea that shock formation is a significant quenching mechanism is consistent with numerical evidence. A further quenching mechanism of likely importance is lack of sediment supply.
The stability characteristics of intermediate-wavelength drumlins have not been investigated, so it is not known whether there is a wavelength range of stability between the short- and long-wavelength case, or whether there is an overlap.
6.3. Time-scales for relief amplification and sediment-thickness instabilities
Sediment relief amplification according to the mechanisms described above requires there is a large-scale gradient in one or more of the pertinent subglacial fields. Horizontal velocity gradients in the till will be of the same magnitude as those in the ice. Where this gradient is a large-scale gradient imposed by the large-scale ice flow, erosion rates are easily calculable to order of magnitude.
In the ice

where a c is the accumulation rate and subscript i implies consideration of the ice. We assume
and since

where subscript s implies consideration of the sediment, we see

With [a c] = 0.1 m a−1, [H] = 1000 m, [D] = 10 m, implying [D] = 10 mm a−1. These may be conservative calculations and [D] may be an order of magnitude larger but, given that relief amplification can proceed no faster than [D], drumlin formation by these large-scale patterns could easily take 1000 years or appreciably longer. This seems to be far too long.
In contrast, a thickness instability could take a very much shorter time. The time constant for a sediment body of length [L] is [u]/[L]. With ice velocities of several hundred m a−1 and drumlin lengths of a few kilometres, this implies minimum formation time-scales of a few decades. Such fast rates are exhibited in the linearized stability analysis due to Hindmarsh (in press a).
7 Discussion
A theory of drumlin form must have three ingredients: (i) a mechanism for producing drumlinoid forms, (ii) a mechanism for promoting the unstable amplification of relief and (iii) a mechanism for quenching the unstable amplification once drumlins have reached a critical size.
7.1. Drumlinization theory
Using the assumptions of static pressure fields, viscous deformation and sliding laws, and a simple model of stress transmission from glacier to sediment body, allows seemingly arbitrarily shaped bodies to be drumlinized; that is, blunt faces are formed, upstream, downstream or both. Various drumlinized geometries can be created, ranging from long tapered forms to barchan forms and it is possible under certain circumstances to produce the downstream blunt forms found in some drumlins.
The theory is essentially a kinematic-wave theory. It predicts general thinning of drumlins, as the points of greatest elevation disappear into reverse-moving shocks, which are the blunt upstream faces of drumlins. A theory of drumlinization is not a complete theory of drumlin formation, as one also needs mechanisms for amplifying relief. The extent to which the theory can do this is discussed further in section 7.2.
It is a theory of sediment deformation in the tradition of Reference Smalley and UnwinSmalley and Unwin (1968) and Reference Boulton, Menzies, Rose and BalkemaBoulton (1987). It demonstrates the variety of shapes that can be created by a few simple assumptions and it also appears that all of these shapes are drumlinoid. No shapes have been created which did not look drumlinoid. This is not, of course, proof that all drumlinoid shapes are produced by sediment-deformation processes.
This model is based on viscous theories of sediment sliding and deformation. There is increasing evidence that such models are not typical of behaviour on the small scale but the case with which viscous models produce a meso-scale phenomenon, drumlins, suggests that on this scale till behaves viscously. This scale-dependent behaviour is not obvious; for example, it is conceivable that a model of self-organized criticality could apply (Reference HindmarshHindmarsh, 1997).
The plane-flow model has four independent parameters; b or d, A s, or A d, p t and B, the original thickness. The viscosity, shear stress and body length only affect the rate of drumlinization, which is not really observable in most cases.
The point is that, whatever sediment body is put into the model, it looks more drumlin-like until it is flattened out of recognition; drumlinization is a process of shock-wave formation. Different parameters produce different types of drumlins. The great heterogeneity of drumlins indicates that, if one theory is to suffice, it must be capable of producing a great variety of drumlins, including upstream and downstream blunt ends as well as both. Many complexities of plan evolution can potentially be explained by the topological complexities of 2HD-shock coalescence (e.g. Reference Arnol’dArnol’d, 1992). This matter is also related to a discussion of moraine “catastrophes” due to Reference NyeNye (1990).
This variability occurs because of the ability of the system to create shocks facing both ways and moving both ways. This property arises chiefly from the increased viscosity of till with effective pressure.
In many of the cases described above, the sediment bodies are not particularly thick — less than one unit, i.e. only a few metres thick. Does this mean that the theory is predicting drumlins which are too small in general?
The calculations which could deal with the process of shock formal ion were unable to deal with configurations where till-thickness instability occurred. The calculations will therefore have selected against thicker forms.
7.1.5. Specific predictions which could be tested in the field Specific predictions are:
1. Drumlins with only downstream shocks can only be formed when the till is deforming internally. If the till is residing on a polished cratonic surface, we might well expect sliding to be easy; and drumlins with upstream shocks only (i.e. tapered forms) to be seen. These predictions assume that other geomorphic processes have not significantly affected drumlin form.
2. There should be a tendency for drumlins with downstream shocks only to be flatter than other drumlins in the region, as the coalescence of the upstream and downstream shocks occurs relatively late in the drumlin evolution. Also, the thinner the drumlin, the less likely reverse shocks are to form. This is because the drumlin is more likely to be thinner or largely thinner than the thickness of maximum kinematic-wave velocity, which means that reverse shocks either cannot form or form relatively close to the forward-moving shock. The thickness of maximum kinematic-wave velocity depends on the datum-effective pressure and on the effective-pressure exponent in the deformation or sliding relations. Thus, we should not be surprised to see some randomness in the occurrence of drumlins with downstream blunt faces only and, where there are fields of such forms, this indicates some uniformity in the effective pressure.
3. The distance over which a shape is drumlinized depends quite sensitively on b and p c. It is not beyond the bounds of possibility that field observations could reveal the distance a drumlin has moved, which could constrain these parameters. If this could be done with a drumlin with a downstream face only, this would be particularly useful. A particularly useful feature is the length of the “slime trail”, that is the trail of sediment left behind the upstream shock by an internally deforming sediment body. The ratio of slime-trail volume to drumlin volume seems to be quite dependent on b. Organic deposits beneath a slime trail and dating of a drumlin exposure might well reveal the time period of drumlinization, which is needed to determine the rate factor.
4. The sliding–internal deformation contrast could be illuminated by measuring the angle of friction of till and of the till–bed contact for drumlins which appear to have slid.
5. If it could be shown that an internally deforming drumlin had a backwardly moving shock face (perhaps through consolidation pressures), this would be a definite indication that interfacial pressures were controlled statically.
The viscous theory can produce one part of the horseshoe shapes regarded as diagnostic by Reference ShawShaw and others (1989) (see Fig. 2), namely the convex-upstream plan form. It does not produce the concave-downstream form; in other words, it produces a half-moon rather than a new moon. It is likely that sufficiently contrived initial conditions or prescription of lateral variations in effective pressure could produce horseshoe shapes. Whether this would be over-contrived is the key question.
A lot of drumlinology (see Reference HartHart (1997) for a review) has considered the tectonic structures within drumlins. No predictions about this have been made with the present model. It could be extended by following tracers within the tilt and predictions tested against field observations.
7.2. Relief amplification and basal erosion
A distinction has been drawn in this paper between unstable thickening of sediment and amplification of relief, which is not a true instability process and can occur when a depositional basin is undergoing net erosion. Some of the classical glacial–geological evidence (Gravenor’s erosional drumlins) can be explained in terms of relief amplification in eroding basins; however, the rate of formation of these features is likely to be so slow that some other mechanisms, which might include unstable thickening, are likely to be necessary. Some recent mathematical investigations of till-sheet stability show the potential of the HTTA theory to produce at least some drumlin forms.
7.3. Quenching the instability
There is no shortage of candidates for quenching the linear instability, in order that the drumlins do not become too large. They are shock formation and various forms of coupling between the flows of ice, till and water. Such couplings may, of course, introduce further instabilities, while shock formation inevitably leads to loss of relief. These considerations can only be investigated by solving the non-linear problem computationally. This is likely to be a formidable task, in view of the difficulties inherent in distinguishing real dynamical effects from artefacts introduced by numerical methods.
Acknowledgements
G. Boullon’s obsession with drumlins has been the source of my interest in them. I should, in particular, like to thank A. Fowler for pointing out that a numerical scheme I used was necessarily unstable in view of the properties of first-order hyperbolic equations discussed in this paper. I should also like to acknowledge instructive conversations with M. Bennett, C. Clark, I. Evans, J. Hart, R. LeVeque and A. Smith. Anonymous reviews of this paper, as well as reviews of previous papers, provided considerable help in the writing.


















