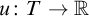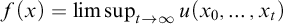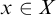1 Introduction
Throughout the paper, let T be a pruned tree on a non-empty countable set A, and X be the set of its infinite branches. We say that
![]() $f : X \to \mathbb {R}$
is a limsup function if there exists a function
$f : X \to \mathbb {R}$
is a limsup function if there exists a function
![]() $u : T \to \mathbb {R}$
such that, for every
$u : T \to \mathbb {R}$
such that, for every
![]() $x \in X$
,
$x \in X$
,
Payoff evaluations of limsup type are ubiquitous in gambling theory [Reference Dubins and Savage3], in the theory of dynamic games [Reference Levy, Solan and Meyers10], and in computer science [Reference Bruyère, Charlier, Leroy and Rigo1]. Limsup payoff evaluation expresses the decision maker’s preference to receive high payoff infinitely often.
We first relate limsup functions to certain well-known classes of functions. In fact, f is a limsup function precisely if it is a pointwise limit of a descending sequence of lower semicontinuous functions. Pointwise limits of a descending sequence of lower semicontinuous functions have been studied, e.g., in [Reference Hausdorff5]. In particular, it is known that f is a limsup function exactly if its subgraph is a
![]() $\mathbf {\Pi }_{2}^{0}$
set (i.e., a
$\mathbf {\Pi }_{2}^{0}$
set (i.e., a
![]() $G_{\delta }$
set), and that the sum, the minimum, and the maximum of two limsup functions is a limsup function. We also deduce a characterization of Baire class 1 functions
$G_{\delta }$
set), and that the sum, the minimum, and the maximum of two limsup functions is a limsup function. We also deduce a characterization of Baire class 1 functions
![]() $f: X \to \mathbb {R}$
: these are exactly the functions such that both f and
$f: X \to \mathbb {R}$
: these are exactly the functions such that both f and
![]() $-f$
are limsup functions.
$-f$
are limsup functions.
The core of the paper is devoted to the study of two related games. The first one is the following:
The moves
![]() $x_{0},x_{1},\dots $
of Player I are points of A such that
$x_{0},x_{1},\dots $
of Player I are points of A such that
![]() $(x_{0},\dots ,x_{t}) \in T$
for each
$(x_{0},\dots ,x_{t}) \in T$
for each
![]() $t \in \mathbb {N}$
. The moves
$t \in \mathbb {N}$
. The moves
![]() $v_{0},v_{1},\dots $
of Player II are real numbers (the results go through as stated or with obvious modifications for a version of the game where Player II is restricted to play rational numbers). The game starts with a move of Player I,
$v_{0},v_{1},\dots $
of Player II are real numbers (the results go through as stated or with obvious modifications for a version of the game where Player II is restricted to play rational numbers). The game starts with a move of Player I,
![]() $x_{0}$
. Having observed
$x_{0}$
. Having observed
![]() $x_{0}$
, Player II chooses
$x_{0}$
, Player II chooses
![]() $v_{0}$
. Having observed
$v_{0}$
. Having observed
![]() $v_{0}$
, Player I chooses
$v_{0}$
, Player I chooses
![]() $x_{1}$
, and so on. In this fashion the players produce a run of the game,
$x_{1}$
, and so on. In this fashion the players produce a run of the game,
![]() $(x_{0},v_{0},x_{1},v_{1},\dots )$
. Player II wins the run if
$(x_{0},v_{0},x_{1},v_{1},\dots )$
. Player II wins the run if
![]() $f(x_{0},x_{1},\dots ) = \limsup v_{t}$
. We denote this game by
$f(x_{0},x_{1},\dots ) = \limsup v_{t}$
. We denote this game by
![]() $\Gamma (f)$
.
$\Gamma (f)$
.
As we will see in Lemma 3.1, Player II has a winning strategy in
![]() $\Gamma (f)$
precisely when f is a limsup function. Whether Player I has a winning strategy in
$\Gamma (f)$
precisely when f is a limsup function. Whether Player I has a winning strategy in
![]() $\Gamma (f)$
turns out to be a more subtle question. We give a sufficient condition for Player I to have a winning strategy in
$\Gamma (f)$
turns out to be a more subtle question. We give a sufficient condition for Player I to have a winning strategy in
![]() $\Gamma (f)$
, a condition that is also necessary if either f is Borel measurable (more precisely, it suffices if the sets of the form
$\Gamma (f)$
, a condition that is also necessary if either f is Borel measurable (more precisely, it suffices if the sets of the form
![]() $\{x \in X : f(x) \ge r \}$
are co-analytic), or if the range of f contains no infinite strictly increasing sequence, in particular if f takes only finitely many values. We also show that the game
$\{x \in X : f(x) \ge r \}$
are co-analytic), or if the range of f contains no infinite strictly increasing sequence, in particular if f takes only finitely many values. We also show that the game
![]() $\Gamma (f)$
is determined if f is Borel measurable (again, it suffices if the sets of the form
$\Gamma (f)$
is determined if f is Borel measurable (again, it suffices if the sets of the form
![]() $\{x \in X : f(x) \ge r \}$
are co-analytic), but not in general.
$\{x \in X : f(x) \ge r \}$
are co-analytic), but not in general.
The second game, denoted by
![]() $\Gamma '(f)$
, is as follows:
$\Gamma '(f)$
, is as follows:
This game is similar to
![]() $\Gamma (f)$
except that now the moves
$\Gamma (f)$
except that now the moves
![]() $(v_{0},w_{0}),(v_{1},w_{1}),\dots $
of Player II are pairs of real numbers. Player II wins in
$(v_{0},w_{0}),(v_{1},w_{1}),\dots $
of Player II are pairs of real numbers. Player II wins in
![]() $\Gamma '(f)$
if
$\Gamma '(f)$
if
![]() $f(x_{0},x_{1},\dots ) = \limsup v_{t} = \liminf w_{t}$
. We denote this game by
$f(x_{0},x_{1},\dots ) = \limsup v_{t} = \liminf w_{t}$
. We denote this game by
![]() $\Gamma '(f)$
.
$\Gamma '(f)$
.
Player II has a winning strategy in the game
![]() $\Gamma '(f)$
precisely when he has a winning strategy in both games
$\Gamma '(f)$
precisely when he has a winning strategy in both games
![]() $\Gamma (f)$
and
$\Gamma (f)$
and
![]() $\Gamma (-f)$
, which is the case exactly when f is in Baire class 1. Moreover, the game
$\Gamma (-f)$
, which is the case exactly when f is in Baire class 1. Moreover, the game
![]() $\Gamma '(f)$
is always determined. This result holds for any function f, whether or not f is Borel measurable, and is established without the aid of Martin’s determinacy.
$\Gamma '(f)$
is always determined. This result holds for any function f, whether or not f is Borel measurable, and is established without the aid of Martin’s determinacy.
The so-called eraser game characterizing Baire class 1 functions from the Baire space to itself was constructed in [Reference Duparc4]. Carroy [Reference Carroy2] showed that the eraser game is determined, and Kiss [Reference Kiss8] generalized the characterization to functions of arbitrary Polish spaces. Game characterizations of several other classes of functions have been considered in [Reference Carroy2, Reference Nobrega11, Reference Semmes12].
Section 2 discusses characterizations of limsup functions. Sections 3 and 4 are devoted to the analysis of the games
![]() $\Gamma (f)$
and
$\Gamma (f)$
and
![]() $\Gamma '(f)$
, respectively.
$\Gamma '(f)$
, respectively.
Unless stated otherwise, proofs are conducted within ZFC.
2 Characterizations of limsup functions
For
![]() $s \in T$
, we let
$s \in T$
, we let
![]() $O(s)$
denote the set of
$O(s)$
denote the set of
![]() $x \in X$
such that s is an initial segment of x. We refer to
$x \in X$
such that s is an initial segment of x. We refer to
![]() $O(s)$
as a cylinder set. We endow X with its usual topology, generated by the base consisting of all cylinder sets. For a function
$O(s)$
as a cylinder set. We endow X with its usual topology, generated by the base consisting of all cylinder sets. For a function
![]() $f : X \to \mathbb {R}$
write
$f : X \to \mathbb {R}$
write
![]() $\mathop {subgr}(f) = \{(x,r) \in X \times \mathbb {R}: f(x) \ge r\}$
to denote the subgraph of f. For
$\mathop {subgr}(f) = \{(x,r) \in X \times \mathbb {R}: f(x) \ge r\}$
to denote the subgraph of f. For
![]() $r \in \mathbb {R}$
, we write
$r \in \mathbb {R}$
, we write
![]() $\{f \ge r\} = \{x \in X: f(x) \ge r\}$
,
$\{f \ge r\} = \{x \in X: f(x) \ge r\}$
,
![]() $\{f> r\} = \{x \in X: f(x) > r\}$
, and
$\{f> r\} = \{x \in X: f(x) > r\}$
, and
![]() $\{f=r\} = \{x\in X: f(x)= r\}$
.
$\{f=r\} = \{x\in X: f(x)= r\}$
.
Theorem 2.1. Consider a function
![]() $f : X \to \mathbb {R}$
. The following conditions are equivalent:
$f : X \to \mathbb {R}$
. The following conditions are equivalent:
-
[C1] The function f is a limsup function.
-
[C2] There is a sequence
 $g_{0}, g_{1},\dots$
of lower semicontinuous functions converging pointwise to f.
$g_{0}, g_{1},\dots$
of lower semicontinuous functions converging pointwise to f. -
[C3] There is a non-increasing sequence
 $g_{0} \geq g_{1} \geq \cdots$
of lower semicontinuous functions converging pointwise to f.
$g_{0} \geq g_{1} \geq \cdots$
of lower semicontinuous functions converging pointwise to f. -
[C4] The set
 $\mathop {subgr}(f)$
is a
$\mathop {subgr}(f)$
is a
 $\mathbf {\Pi }_{2}^{0}$
subset of
$\mathbf {\Pi }_{2}^{0}$
subset of
 $X \times \mathbb {R}$
.
$X \times \mathbb {R}$
. -
[C5] For each
 $r \in \mathbb {R}$
,
$r \in \mathbb {R}$
,
 $\{f \ge r \}$
is a
$\{f \ge r \}$
is a
 $\mathbf {\Pi }_{2}^{0}$
subset of X.
$\mathbf {\Pi }_{2}^{0}$
subset of X.
We remark that the functions satisfying condition [C5] are sometimes called semi-Borel class 2 (see [Reference Kiss7]) or upper semi-Baire class 1 functions. The equivalence of the conditions [C2]–[C5] is in fact well known (see [Reference Hausdorff5]). Below we prove the equivalence of conditions [C1]–[C3].
Proof that [C1] implies [C2]. Let f be a limsup function, and let u be a function as in (1.1). For
![]() $n \in \mathbb {N}$
let
$n \in \mathbb {N}$
let
![]() $g_{n}(x) = \sup \{u(x_{0},\dots ,x_{t}):t \geq n\}$
. ⊣
$g_{n}(x) = \sup \{u(x_{0},\dots ,x_{t}):t \geq n\}$
. ⊣
Proof that [C2] implies [C3]. Let
![]() $g_{n}$
be a sequence of lower semicontinuous functions converging pointwise to f. Define
$g_{n}$
be a sequence of lower semicontinuous functions converging pointwise to f. Define
![]() $g_{n}'(x) = \sup \{g_{m}(x):m \geq n\}$
. This gives a non-increasing sequence of lower semicontinuous functions converging pointwise to f. ⊣
$g_{n}'(x) = \sup \{g_{m}(x):m \geq n\}$
. This gives a non-increasing sequence of lower semicontinuous functions converging pointwise to f. ⊣
Proof that [C3] implies [C1]. Consider a non-increasing sequence
![]() $g_{0} \geq g_{1} \geq \cdots $
of lower semicontinuous functions converging pointwise to f. We will also assume that for each
$g_{0} \geq g_{1} \geq \cdots $
of lower semicontinuous functions converging pointwise to f. We will also assume that for each
![]() $n \in \mathbb {N}$
, the range of
$n \in \mathbb {N}$
, the range of
![]() $g_{n}$
contains only reals of the form
$g_{n}$
contains only reals of the form
![]() $z2^{-n}$
for
$z2^{-n}$
for
![]() $z \in \mathbb {Z}$
. To see that this could be imposed without loss of generality, consider the functions
$z \in \mathbb {Z}$
. To see that this could be imposed without loss of generality, consider the functions
![]() $g_{n}'(x) = \min \{z2^{-n}: z \in \mathbb {Z}, g_{n}(x) \leq z2^{-n}\}$
. Then,
$g_{n}'(x) = \min \{z2^{-n}: z \in \mathbb {Z}, g_{n}(x) \leq z2^{-n}\}$
. Then,
![]() $\{g_{n}'> z2^{-n}\}$
is the same as the set
$\{g_{n}'> z2^{-n}\}$
is the same as the set
![]() $\{g_{n}> z2^{-n}\}$
, implying that
$\{g_{n}> z2^{-n}\}$
, implying that
![]() $g_{n}'$
is lower semicontinuous. It is easy to see that
$g_{n}'$
is lower semicontinuous. It is easy to see that
![]() $g_{0}'\geq g_{1}' \geq \cdots $
is a non-increasing sequence, and that it converges pointwise to f.
$g_{0}'\geq g_{1}' \geq \cdots $
is a non-increasing sequence, and that it converges pointwise to f.
We define the function
![]() $u : T \rightarrow \mathbb {R}$
. For
$u : T \rightarrow \mathbb {R}$
. For
![]() $n \in \mathbb {N}$
and
$n \in \mathbb {N}$
and
![]() $r \in \mathbb {R}$
note that the set
$r \in \mathbb {R}$
note that the set
![]() $\{g_n> r\}$
is an open set, because
$\{g_n> r\}$
is an open set, because
![]() $g_{n}$
is assumed to be lower semicontinuous. Take a sequence
$g_{n}$
is assumed to be lower semicontinuous. Take a sequence
![]() $s \in T$
. Define
$s \in T$
. Define
![]() $R_{*}(s)$
to be the set of real numbers
$R_{*}(s)$
to be the set of real numbers
![]() $r \in \mathbb {R}$
such that
$r \in \mathbb {R}$
such that
![]() $O(s) \subseteq \bigcap _{n \in \mathbb {N}}\{g_n> r\}$
. For
$O(s) \subseteq \bigcap _{n \in \mathbb {N}}\{g_n> r\}$
. For
![]() $n \in \mathbb {N}$
define
$n \in \mathbb {N}$
define
![]() $R_{n}(s)$
to be the set of real numbers
$R_{n}(s)$
to be the set of real numbers
![]() $r \in \mathbb {R}$
such that
$r \in \mathbb {R}$
such that
![]() $O(s) \subseteq \{g_n>r\}$
, and such that for no proper initial segment
$O(s) \subseteq \{g_n>r\}$
, and such that for no proper initial segment
![]() $s'$
of s does it holds that
$s'$
of s does it holds that
![]() $O(s') \subseteq \{g_n>r\}$
. (We remark that
$O(s') \subseteq \{g_n>r\}$
. (We remark that
![]() $R_{*}(s)$
is a half-line and the sets
$R_{*}(s)$
is a half-line and the sets
![]() $R_{n}(s)$
are intervals.) Let
$R_{n}(s)$
are intervals.) Let
![]() $R(s)$
be the union of the sets
$R(s)$
be the union of the sets
![]() $R_{*}(s),R_{0}(s),R_{1}(s),\dots $
. Notice that the set
$R_{*}(s),R_{0}(s),R_{1}(s),\dots $
. Notice that the set
![]() $R(s)$
is bounded above by
$R(s)$
is bounded above by
![]() $\inf \{g_{0}(y):y \in O(s)\}$
. If
$\inf \{g_{0}(y):y \in O(s)\}$
. If
![]() $R(s)$
is non-empty, we define
$R(s)$
is non-empty, we define
![]() $u(s) = \sup R(s)$
. If
$u(s) = \sup R(s)$
. If
![]() $R(s)$
is empty, we let
$R(s)$
is empty, we let
![]() $u(s) = -\mathrm {length}(s)$
.
$u(s) = -\mathrm {length}(s)$
.
We show that u satisfies (1.1). Thus fix an
![]() $x \in X$
. We write
$x \in X$
. We write
![]() $s_{t}$
to denote
$s_{t}$
to denote
![]() $(x_{0},\dots ,x_{t})$
and let
$(x_{0},\dots ,x_{t})$
and let
![]() $\alpha = \limsup _{t \rightarrow \infty }u(s_{t})$
. We must show that
$\alpha = \limsup _{t \rightarrow \infty }u(s_{t})$
. We must show that
![]() $f(x) = \alpha $
.
$f(x) = \alpha $
.
We first show that
![]() $f(x) \leq \alpha $
.
$f(x) \leq \alpha $
.
Take a real number r with
![]() $r < f(x)$
. We argue that
$r < f(x)$
. We argue that
![]() $r \leq \alpha $
.
$r \leq \alpha $
.
For every
![]() $n \in \mathbb {N}$
it holds that
$n \in \mathbb {N}$
it holds that
![]() $r < g_{n}(x)$
, so
$r < g_{n}(x)$
, so
![]() $x \in \{g_n> r\}$
. Let
$x \in \{g_n> r\}$
. Let
![]() $t_{n}$
be the smallest
$t_{n}$
be the smallest
![]() $t \in \mathbb {N}$
for which
$t \in \mathbb {N}$
for which
![]() $O(s_{t_{n}}) \subseteq \{g_n>r\}$
. We distinguish between two cases, depending on whether the sequence
$O(s_{t_{n}}) \subseteq \{g_n>r\}$
. We distinguish between two cases, depending on whether the sequence
![]() $t_{0}, t_{1},\dots $
is bounded or not. Suppose first the sequence
$t_{0}, t_{1},\dots $
is bounded or not. Suppose first the sequence
![]() $t_{0}, t_{1},\dots $
is unbounded. By the choice of
$t_{0}, t_{1},\dots $
is unbounded. By the choice of
![]() $t_{n}$
, we have
$t_{n}$
, we have
![]() $r \in R_{n}(s_{t_{n}})$
, and hence
$r \in R_{n}(s_{t_{n}})$
, and hence
![]() $r \leq u(s_{t_{n}})$
. We obtain
$r \leq u(s_{t_{n}})$
. We obtain
![]() $r \leq \alpha $
, as desired. Suppose now that the sequence
$r \leq \alpha $
, as desired. Suppose now that the sequence
![]() $t_{0}, t_{1},\dots $
is bounded, say
$t_{0}, t_{1},\dots $
is bounded, say
![]() $t_{n} \leq t$
for each
$t_{n} \leq t$
for each
![]() $n \in \mathbb {N}$
. Then,
$n \in \mathbb {N}$
. Then,
![]() $O(s_{t}) \subseteq \bigcap _{n \in \mathbb {N}}\{g_n>r\}$
. Since for
$O(s_{t}) \subseteq \bigcap _{n \in \mathbb {N}}\{g_n>r\}$
. Since for
![]() $k \geq t$
the cylinder
$k \geq t$
the cylinder
![]() $O(s_{k})$
is contained in
$O(s_{k})$
is contained in
![]() $O(s_{t})$
, we have
$O(s_{t})$
, we have
![]() $r \in R_{*}(s_{k})$
, and consequently
$r \in R_{*}(s_{k})$
, and consequently
![]() $r \leq u(s_{k})$
. We conclude that
$r \leq u(s_{k})$
. We conclude that
![]() $r \leq \alpha $
, as desired.
$r \leq \alpha $
, as desired.
We now show that
![]() $\alpha \leq f(x)$
.
$\alpha \leq f(x)$
.
We know that
![]() $-\infty < \alpha $
. Take a real number
$-\infty < \alpha $
. Take a real number
![]() $r < \alpha $
. We now argue that
$r < \alpha $
. We now argue that
![]() $r \leq f(x)$
.
$r \leq f(x)$
.
There exists an increasing sequence
![]() $t_{0} < t_{1} < \cdots $
such that
$t_{0} < t_{1} < \cdots $
such that
![]() $r < u(s_{t_{k}})$
. By discarding finitely many elements of the sequence, we may assume that
$r < u(s_{t_{k}})$
. By discarding finitely many elements of the sequence, we may assume that
![]() $-t_{0} < r$
. The definition of u now implies that the set
$-t_{0} < r$
. The definition of u now implies that the set
![]() $R(s_{t_{k}})$
is not empty for each
$R(s_{t_{k}})$
is not empty for each
![]() $k \in \mathbb {N}$
, and hence we can take an
$k \in \mathbb {N}$
, and hence we can take an
![]() $r_{k} \in R(s_{t_{k}})$
such that
$r_{k} \in R(s_{t_{k}})$
such that
![]() $r < r_{k}$
.
$r < r_{k}$
.
Suppose first there exists some
![]() $k \in \mathbb {N}$
for which
$k \in \mathbb {N}$
for which
![]() $r_{k} \in R_{*}(s_{t_{k}})$
. In that case,
$r_{k} \in R_{*}(s_{t_{k}})$
. In that case,
![]() $x \in O(s_{t_{k}}) \subseteq \bigcap _{n \in \mathbb {N}}\{g_n>r_{k}\}$
. It follows that
$x \in O(s_{t_{k}}) \subseteq \bigcap _{n \in \mathbb {N}}\{g_n>r_{k}\}$
. It follows that
![]() $r < r_{k} < g_{n}(x)$
for each
$r < r_{k} < g_{n}(x)$
for each
![]() $n \in \mathbb {N}$
and consequently that
$n \in \mathbb {N}$
and consequently that
![]() $r \leq f(x)$
.
$r \leq f(x)$
.
Otherwise, for each
![]() $k \in \mathbb {N}$
choose an
$k \in \mathbb {N}$
choose an
![]() $n_{k} \in \mathbb {N}$
such that
$n_{k} \in \mathbb {N}$
such that
![]() $r_{k} \in R_{n_{k}}(s_{t_{k}})$
. We have
$r_{k} \in R_{n_{k}}(s_{t_{k}})$
. We have
![]() $x \in O(s_{t_{k}}) \subseteq \{g_{n_{k}}>r_{k}\}$
and hence
$x \in O(s_{t_{k}}) \subseteq \{g_{n_{k}}>r_{k}\}$
and hence
![]() $r < r_{k} < g_{n_{k}}(x)$
. It is therefore enough to show that the sequence
$r < r_{k} < g_{n_{k}}(x)$
. It is therefore enough to show that the sequence
![]() $n_{0},n_{1},\dots $
is unbounded: for then the numbers
$n_{0},n_{1},\dots $
is unbounded: for then the numbers
![]() $g_{n_{0}}(x), g_{n_{1}}(x), \dots $
form a sequence converging to
$g_{n_{0}}(x), g_{n_{1}}(x), \dots $
form a sequence converging to
![]() $f(x)$
, and we are able to conclude that
$f(x)$
, and we are able to conclude that
![]() $r \leq f(x)$
.
$r \leq f(x)$
.
We argue that the sequence
![]() $n_{0},n_{1},\dots $
is unbounded. Assume the contrary. By passing to a subsequence, we can then assume that
$n_{0},n_{1},\dots $
is unbounded. Assume the contrary. By passing to a subsequence, we can then assume that
![]() $n_{0} = n_{1} = \cdots $
. Now the sequence
$n_{0} = n_{1} = \cdots $
. Now the sequence
![]() $r_{0},r_{1},\dots $
is bounded, because
$r_{0},r_{1},\dots $
is bounded, because
![]() $r < r_{k} \leq \inf \{g_{0}(y):y \in O(s_{t_{k}})\} \leq g_{0}(x)$
, for each
$r < r_{k} \leq \inf \{g_{0}(y):y \in O(s_{t_{k}})\} \leq g_{0}(x)$
, for each
![]() $k \in \mathbb {N}$
. Since only finitely many points in the range of
$k \in \mathbb {N}$
. Since only finitely many points in the range of
![]() $g_{n_{0}}$
fall in the interval
$g_{n_{0}}$
fall in the interval
![]() $[r,g_{0}(x)]$
, only finitely many of the sets
$[r,g_{0}(x)]$
, only finitely many of the sets
![]() $\{\{g_{n_{0}}>r_{k}\}:k \in \mathbb {N}\}$
are distinct. Thus, at least two of these sets are the same, say
$\{\{g_{n_{0}}>r_{k}\}:k \in \mathbb {N}\}$
are distinct. Thus, at least two of these sets are the same, say
![]() $\{g_{n_{0}}>r_{0}\} = \{g_{n_{0}}>r_{1}\}$
. But
$\{g_{n_{0}}>r_{0}\} = \{g_{n_{0}}>r_{1}\}$
. But
![]() $s_{t_{1}}$
is a minimal sequence satisfying
$s_{t_{1}}$
is a minimal sequence satisfying
![]() $O(s_{t_{1}}) \subseteq \{g_{n_{0}}>r_{1}\}$
, while
$O(s_{t_{1}}) \subseteq \{g_{n_{0}}>r_{1}\}$
, while
![]() $s_{t_{0}}$
is a proper initial segment of
$s_{t_{0}}$
is a proper initial segment of
![]() $s_{t_{1}}$
satisfying
$s_{t_{1}}$
satisfying
![]() $O(s_{t_{0}}) \subseteq \{g_{n_{0}}> r_{0}\}$
, contradicting
$O(s_{t_{0}}) \subseteq \{g_{n_{0}}> r_{0}\}$
, contradicting
![]() $r_1 \in R_{n_1}(s_{t_1})$
. ⊣
$r_1 \in R_{n_1}(s_{t_1})$
. ⊣
We conclude this section with a list of some properties of the limsup functions that follow easily from the above characterization.
Corollary 2.2. The sum, the minimum, and the maximum of two limsup functions is a limsup function.
We say that a collection
![]() $\mathcal {C}$
of real-valued functions on X is closed under pointwise limits from above if for each sequence
$\mathcal {C}$
of real-valued functions on X is closed under pointwise limits from above if for each sequence
![]() $f_{0} \geq f_{1} \geq \cdots $
of functions in
$f_{0} \geq f_{1} \geq \cdots $
of functions in
![]() $\mathcal {C}$
converging pointwise to a function f, the function f is an element of
$\mathcal {C}$
converging pointwise to a function f, the function f is an element of
![]() $\mathcal {C}$
.
$\mathcal {C}$
.
Corollary 2.3. The set of limsup functions is the smallest collection of functions that (a) contains all lower semicontinuous functions and (b) is closed under pointwise limits from above.
Corollary 2.4. A uniform limit of limsup functions is a limsup function.
Corollary 2.5. A function f is of Baire class 1 if and only if both f and
![]() ${-}f$
are limsup functions.
${-}f$
are limsup functions.
3 A game for limsup functions
In this section we turn to the analysis of the game
![]() $\Gamma (f)$
. Let us begin with the following observation.
$\Gamma (f)$
. Let us begin with the following observation.
Lemma 3.1. Player II has a winning strategy in
![]() $\Gamma (f)$
precisely when f is a limsup function.
$\Gamma (f)$
precisely when f is a limsup function.
The result is obvious: the rules of the game
![]() $\Gamma (f)$
are designed so that any function
$\Gamma (f)$
are designed so that any function
![]() $u : T \to \mathbb {R}$
witnessing that f is a limsup function is a winning strategy for Player II, and vice versa.
$u : T \to \mathbb {R}$
witnessing that f is a limsup function is a winning strategy for Player II, and vice versa.
Unlike the eraser game (see [Reference Kiss8]), as we will show below, the game
![]() $\Gamma (f)$
need not be determined.
$\Gamma (f)$
need not be determined.
Recall that a set
![]() $B \subseteq X$
is called a Bernstein set if neither B nor
$B \subseteq X$
is called a Bernstein set if neither B nor
![]() $X \setminus B$
contains a non-empty perfect set. Under the axiom of choice, every uncountable Polish space contains a Bernstein set; moreover, every uncountable analytic set (in a Polish space) contains a non-empty perfect set.
$X \setminus B$
contains a non-empty perfect set. Under the axiom of choice, every uncountable Polish space contains a Bernstein set; moreover, every uncountable analytic set (in a Polish space) contains a non-empty perfect set.
Theorem 3.2. If X is uncountable and
![]() $B \subseteq X$
is a Bernstein set, then
$B \subseteq X$
is a Bernstein set, then
![]() $\Gamma (1_{B})$
is not determined.
$\Gamma (1_{B})$
is not determined.
Proof Notice first that B is not a Borel set: for if it were, either B or
![]() $X \setminus B$
would contain a non-empty perfect set. And since B is not Borel, the function
$X \setminus B$
would contain a non-empty perfect set. And since B is not Borel, the function
![]() $1_{B}$
is not a limsup function, and hence Player II has no winning strategy in
$1_{B}$
is not a limsup function, and hence Player II has no winning strategy in
![]() $\Gamma (1_{B})$
.
$\Gamma (1_{B})$
.
Suppose that Player I does.
Let
![]() $E = \{v \in 2^{\mathbb {N}}:v_{n} = 1\text { for infinitely many }n\in \mathbb {N}\}$
, where we write
$E = \{v \in 2^{\mathbb {N}}:v_{n} = 1\text { for infinitely many }n\in \mathbb {N}\}$
, where we write
![]() $2 = \{0,1\}$
. Notice that E is not a
$2 = \{0,1\}$
. Notice that E is not a
![]() $\mathbf {\Sigma }_{2}^{0}$
subset of
$\mathbf {\Sigma }_{2}^{0}$
subset of
![]() $2^{\mathbb {N}}$
. For it were, we would be able to express
$2^{\mathbb {N}}$
. For it were, we would be able to express
![]() $2^{\mathbb {N}}$
as a countable union of meagre sets, contradicting the Baire category theorem.
$2^{\mathbb {N}}$
as a countable union of meagre sets, contradicting the Baire category theorem.
Now, consider the continuous function
![]() $g : 2^{\mathbb {N}} \to X$
induced by Player I’s winning strategy. Then,
$g : 2^{\mathbb {N}} \to X$
induced by Player I’s winning strategy. Then,
![]() $g(E) \subseteq X \setminus B$
and
$g(E) \subseteq X \setminus B$
and
![]() $g(2^{\mathbb {N}} \setminus E) \subseteq B$
. Since
$g(2^{\mathbb {N}} \setminus E) \subseteq B$
. Since
![]() $g(E)$
is an analytic subset of X, it is either countable, or it contains a perfect subset. But
$g(E)$
is an analytic subset of X, it is either countable, or it contains a perfect subset. But
![]() $X \setminus B$
contains no perfect subset. Thus
$X \setminus B$
contains no perfect subset. Thus
![]() $g(E)$
is countable, hence a
$g(E)$
is countable, hence a
![]() $\mathbf {\Sigma }_{2}^{0}$
subset of X. But then,
$\mathbf {\Sigma }_{2}^{0}$
subset of X. But then,
![]() $E = g^{-1}(g(E))$
is a
$E = g^{-1}(g(E))$
is a
![]() $\mathbf {\Sigma }_{2}^{0}$
subset of
$\mathbf {\Sigma }_{2}^{0}$
subset of
![]() $2^{\mathbb {N}}$
, yielding a contradiction.
$2^{\mathbb {N}}$
, yielding a contradiction.
We now turn to a sufficient condition for Player I to have a winning strategy. This sufficient condition will also turn out to be necessary under various assumptions.
Recall that a set is called a Cantor set if it is homeomorphic to the classical middle-thirds Cantor set.
Theorem 3.3. Let
![]() $f : X \to \mathbb {R}$
be arbitrary and suppose that there is a number
$f : X \to \mathbb {R}$
be arbitrary and suppose that there is a number
![]() $r \in \mathbb {R}$
and a Cantor set
$r \in \mathbb {R}$
and a Cantor set
![]() $C \subseteq X$
such that, in the subspace topology of C, the set
$C \subseteq X$
such that, in the subspace topology of C, the set
![]() $C \cap \{f \ge r\}$
is meagre and dense. Then, Player I has a winning strategy in
$C \cap \{f \ge r\}$
is meagre and dense. Then, Player I has a winning strategy in
![]() $\Gamma (f)$
.
$\Gamma (f)$
.
Proof Let
![]() $Y = C \cap \{f \ge r\}$
, and let
$Y = C \cap \{f \ge r\}$
, and let
![]() $\{S_{0},S_{1},\dots \}$
be a cover of Y by closed nowhere dense subsets of C. We presently construct a winning strategy for Player I.
$\{S_{0},S_{1},\dots \}$
be a cover of Y by closed nowhere dense subsets of C. We presently construct a winning strategy for Player I.
Fix some sequence
![]() $v_{0},v_{1},\dots $
of Player II’s moves.
$v_{0},v_{1},\dots $
of Player II’s moves.
Let
![]() $y(0)$
be any point of the set
$y(0)$
be any point of the set
![]() $Y \setminus S_{0}$
. Notice that the set
$Y \setminus S_{0}$
. Notice that the set
![]() $C \setminus S_{0}$
is not empty because
$C \setminus S_{0}$
is not empty because
![]() $S_{0}$
is nowhere dense in C, and
$S_{0}$
is nowhere dense in C, and
![]() $Y \setminus S_{0}$
is not empty since Y is dense in C. Set
$Y \setminus S_{0}$
is not empty since Y is dense in C. Set
![]() $m_{0} = 0$
.
$m_{0} = 0$
.
Player I starts with a move
![]() $x_{0} = y(0)_{0}$
. Take an
$x_{0} = y(0)_{0}$
. Take an
![]() $n \in \mathbb {N}$
and suppose that Player I’s moves
$n \in \mathbb {N}$
and suppose that Player I’s moves
![]() $x_{0}, \dots , x_{n}$
have been defined, along with a point
$x_{0}, \dots , x_{n}$
have been defined, along with a point
![]() $y(n) \in Y$
and a number
$y(n) \in Y$
and a number
![]() $m_{n} \in \mathbb {N}$
, such that
$m_{n} \in \mathbb {N}$
, such that
To define the next move of Player I,
![]() $x_{n+1}$
, we distinguish two cases:
$x_{n+1}$
, we distinguish two cases:
Case 1:
![]() $v_{n}> r - 2^{-m_{n}}$
and
$v_{n}> r - 2^{-m_{n}}$
and
![]() $O(x_{0},\dots ,x_{n}) \cap S_{m_{n}} = \emptyset $
. Let
$O(x_{0},\dots ,x_{n}) \cap S_{m_{n}} = \emptyset $
. Let
![]() $y(n+1)$
be any point of the set
$y(n+1)$
be any point of the set
![]() $(O(x_{0},\dots ,x_{n}) \cap Y) \setminus S_{m_{n}+1}$
. Notice that the set
$(O(x_{0},\dots ,x_{n}) \cap Y) \setminus S_{m_{n}+1}$
. Notice that the set
![]() $(O(x_{0},\dots ,x_{n}) \cap C) \setminus S_{m_{n}+1}$
is not empty because
$(O(x_{0},\dots ,x_{n}) \cap C) \setminus S_{m_{n}+1}$
is not empty because
![]() $S_{m_{n}+1}$
is nowhere dense in C, and
$S_{m_{n}+1}$
is nowhere dense in C, and
![]() $(O(x_{0},\dots ,x_{n}) \cap Y) \setminus S_{m_{n}+1}$
is not empty since Y is dense in C. Let
$(O(x_{0},\dots ,x_{n}) \cap Y) \setminus S_{m_{n}+1}$
is not empty since Y is dense in C. Let
![]() $m_{n+1} = m_{n} + 1$
, and define Player I’s move as
$m_{n+1} = m_{n} + 1$
, and define Player I’s move as
![]() $x_{n+1} = y(n+1)_{n+1}$
.
$x_{n+1} = y(n+1)_{n+1}$
.
Case 2: otherwise. In this case we let
![]() $y(n+1) = y(n)$
,
$y(n+1) = y(n)$
,
![]() $m_{n+1} = m_{n}$
, and define Player I’s move as
$m_{n+1} = m_{n}$
, and define Player I’s move as
![]() $x_{n+1} = y(n+1)_{n+1}$
.
$x_{n+1} = y(n+1)_{n+1}$
.
Notice that in either case (3.1) holds for
![]() $n+1$
. This completes the definition of Player I’s strategy.
$n+1$
. This completes the definition of Player I’s strategy.
The intuition behind this definition could be explained as follows: Player I starts by zooming in on the point
![]() $y(0)$
chosen to be in Y but not in
$y(0)$
chosen to be in Y but not in
![]() $S_{0}$
. Player I awaits a stage n where Player II would make a move
$S_{0}$
. Player I awaits a stage n where Player II would make a move
![]() $v_{n}> r - 1$
, and where the set
$v_{n}> r - 1$
, and where the set
![]() $S_{0}$
would be “excluded.” As soon as such a stage is reached, Player I switches to an element
$S_{0}$
would be “excluded.” As soon as such a stage is reached, Player I switches to an element
![]() $y(1)$
, chosen to be in Y but not in
$y(1)$
, chosen to be in Y but not in
![]() $S_{1}$
. He then zooms in on
$S_{1}$
. He then zooms in on
![]() $y(1)$
, awaiting a stage where Player I would make a move
$y(1)$
, awaiting a stage where Player I would make a move
![]() $v_{n}> r - 1/2$
, and where
$v_{n}> r - 1/2$
, and where
![]() $S_{1}$
would be “excluded.” As soon as such a stage occurs, Player I switches to an element
$S_{1}$
would be “excluded.” As soon as such a stage occurs, Player I switches to an element
![]() $y(2)$
chosen to be in Y but not in
$y(2)$
chosen to be in Y but not in
![]() $S_{2}$
. And so on.
$S_{2}$
. And so on.
We argue that Player I’s strategy is winning.
Suppose first that
![]() $\limsup v_{n} \leq r - 2^{-m}$
for some
$\limsup v_{n} \leq r - 2^{-m}$
for some
![]() $m \in \mathbb {N}$
. Then, Case 1 occurs at most finitely many times. Let N be the last stage when Case 1 occurs (or
$m \in \mathbb {N}$
. Then, Case 1 occurs at most finitely many times. Let N be the last stage when Case 1 occurs (or
![]() $N = 0$
if Case 1 never occurs). Then, the point x produced by Player I equals to
$N = 0$
if Case 1 never occurs). Then, the point x produced by Player I equals to
![]() $y(N)$
. We thus have
$y(N)$
. We thus have
![]() $\limsup v_{n} \leq r - 2^{-m} < r \leq f(y(N)) = f(x)$
.
$\limsup v_{n} \leq r - 2^{-m} < r \leq f(y(N)) = f(x)$
.
Suppose now that
![]() $\limsup v_{n} \geq r$
. We argue that Case 1 occurs infinitely many times. Suppose to the contrary and let N be the last stage when Case 1 occurs (or
$\limsup v_{n} \geq r$
. We argue that Case 1 occurs infinitely many times. Suppose to the contrary and let N be the last stage when Case 1 occurs (or
![]() $0$
if Case 1 never occurs). Then,
$0$
if Case 1 never occurs). Then,
![]() $m_{N} = m_{N+1} = \cdots $
and
$m_{N} = m_{N+1} = \cdots $
and
![]() $y(N) = y(N+1) = \cdots = x$
. There are infinitely many
$y(N) = y(N+1) = \cdots = x$
. There are infinitely many
![]() $n> N$
with
$n> N$
with
![]() $v_{n}> r - 2^{-m_{N}}$
, and for each such n the neighborhood
$v_{n}> r - 2^{-m_{N}}$
, and for each such n the neighborhood
![]() $O(x_{0},\dots , x_{n})$
of x has a point in common with
$O(x_{0},\dots , x_{n})$
of x has a point in common with
![]() $S_{m_{N}}$
. This implies that
$S_{m_{N}}$
. This implies that
![]() $x \in S_{m_{N}}$
. This, however, contradicts the choice of
$x \in S_{m_{N}}$
. This, however, contradicts the choice of
![]() $y(N)$
. This establishes that Case 1 occurs infinitely many times.
$y(N)$
. This establishes that Case 1 occurs infinitely many times.
Let x be the point constructed by Player I. We argue that
![]() $x \in C \setminus Y$
. In view of (3.1), x is a limit of the sequence
$x \in C \setminus Y$
. In view of (3.1), x is a limit of the sequence
![]() $y(0),y(1),\dots $
. Since each
$y(0),y(1),\dots $
. Since each
![]() $y(n)$
is an element of the closed set C, so is x. To see that x is not an element of Y, suppose to the contrary. Then,
$y(n)$
is an element of the closed set C, so is x. To see that x is not an element of Y, suppose to the contrary. Then,
![]() $x \in S_{m}$
for some
$x \in S_{m}$
for some
![]() $m \in \mathbb {N}$
. Since Case 1 occurs infinitely often, the sequence
$m \in \mathbb {N}$
. Since Case 1 occurs infinitely often, the sequence
![]() $m_{0},m_{1},\dots $
runs through all natural numbers, so we can choose
$m_{0},m_{1},\dots $
runs through all natural numbers, so we can choose
![]() $n \in \mathbb {N}$
to be the largest number such that
$n \in \mathbb {N}$
to be the largest number such that
![]() $m_{n} = m$
. This choice implies that Case 1 occurs at stage n, and hence
$m_{n} = m$
. This choice implies that Case 1 occurs at stage n, and hence
![]() $O(x_{0},\dots ,x_{n})$
is disjoint from
$O(x_{0},\dots ,x_{n})$
is disjoint from
![]() $S_{m_{n}}$
, leading to a contradiction.
$S_{m_{n}}$
, leading to a contradiction.
It follows that x is not an element of
![]() $\{f \ge r\}$
. Thus
$\{f \ge r\}$
. Thus
![]() $\limsup v_{n} \geq r> f(x)$
, which completes the proof.
$\limsup v_{n} \geq r> f(x)$
, which completes the proof.
Remark 3.4. For an arbitrary set
![]() $H \subseteq X$
the existence of a Cantor set
$H \subseteq X$
the existence of a Cantor set
![]() $C \subseteq X$
such that
$C \subseteq X$
such that
![]() $C \cap H$
is meager and dense in C is equivalent to the existence of a Cantor set
$C \cap H$
is meager and dense in C is equivalent to the existence of a Cantor set
![]() $C \subseteq X$
such that
$C \subseteq X$
such that
![]() $C \cap H$
is countable and dense in C. This either follows from Theorems 3.3 and 3.6 applied to
$C \cap H$
is countable and dense in C. This either follows from Theorems 3.3 and 3.6 applied to
![]() $1_H$
and
$1_H$
and
![]() $r=\frac 12$
, or can also be proved directly by a standard Cantor scheme construction.
$r=\frac 12$
, or can also be proved directly by a standard Cantor scheme construction.
If the range of the function f does not contain a strictly increasing sequence, the condition of Theorem 3.3 is both sufficient and necessary for Player I to have a winning strategy. The proof relies on a Kechris–Louveau–Woodin separation theorem [Reference Kechris6, Theorem 21.22].
For a set
![]() $R \subseteq \mathbb {R}$
, and function
$R \subseteq \mathbb {R}$
, and function
![]() $f: X \to \mathbb {R}$
define the game
$f: X \to \mathbb {R}$
define the game
![]() $\Gamma _R(f)$
similarly to
$\Gamma _R(f)$
similarly to
![]() $\Gamma (f)$
, but allowing Player II to choose
$\Gamma (f)$
, but allowing Player II to choose
![]() $v_i$
’s from R instead of the whole real line.
$v_i$
’s from R instead of the whole real line.
Lemma 3.5. Let
![]() $R \subseteq \mathbb {R}$
and
$R \subseteq \mathbb {R}$
and
![]() $f: X \to R$
. Then, Player I has a winning strategy in the game
$f: X \to R$
. Then, Player I has a winning strategy in the game
![]() $\Gamma _R(f)$
if and only if Player I has a winning strategy in
$\Gamma _R(f)$
if and only if Player I has a winning strategy in
![]() $\Gamma (f)$
.
$\Gamma (f)$
.
Proof It is straightforward to check that if Player I has a winning strategy in
![]() $\Gamma (f)$
, then the restriction of this strategy is winning for Player I in
$\Gamma (f)$
, then the restriction of this strategy is winning for Player I in
![]() $\Gamma _R(f)$
.
$\Gamma _R(f)$
.
Conversely, fix a winning strategy
![]() $\sigma _R$
of Player I for the game
$\sigma _R$
of Player I for the game
![]() $\Gamma _R(f)$
. For each
$\Gamma _R(f)$
. For each
![]() $n \in \mathbb {N}$
define
$n \in \mathbb {N}$
define
![]() $F_n: \mathbb {R} \to R$
so that
$F_n: \mathbb {R} \to R$
so that
holds. Now define Player I’s strategy
![]() $\sigma $
in
$\sigma $
in
![]() $\Gamma (f)$
as follows: let
$\Gamma (f)$
as follows: let
![]() $\sigma (\emptyset ) = \sigma _R(\emptyset )$
, and let
$\sigma (\emptyset ) = \sigma _R(\emptyset )$
, and let
whenever
![]() $n \in \mathbb {N}$
and
$n \in \mathbb {N}$
and
![]() $(x_0, \dots , x_n) \in T\!$
.
$(x_0, \dots , x_n) \in T\!$
.
It remains to check that
![]() $\sigma $
is a winning strategy for Player I in
$\sigma $
is a winning strategy for Player I in
![]() $\Gamma (f)$
. Fix a run
$\Gamma (f)$
. Fix a run
![]() $x_0,v_0,x_1,v_1, \dots $
of the game
$x_0,v_0,x_1,v_1, \dots $
of the game
![]() $\Gamma (f)$
consistent with
$\Gamma (f)$
consistent with
![]() $\sigma $
, i.e., such that for each
$\sigma $
, i.e., such that for each
![]() $n \in \mathbb {N}$
,
$n \in \mathbb {N}$
,
![]() $\sigma (x_0,v_0, \dots , x_n,v_n) = x_{n+1}$
. Then, (3.3) implies that for each n
$\sigma (x_0,v_0, \dots , x_n,v_n) = x_{n+1}$
. Then, (3.3) implies that for each n
and as
![]() $\sigma _R$
is a winning strategy for Player I in
$\sigma _R$
is a winning strategy for Player I in
![]() $\Gamma _{R}(f)$
, we obtain that
$\Gamma _{R}(f)$
, we obtain that
We have to check that
![]() $f(x_0,x_1,x_2, \dots ) \neq \limsup _{n \to \infty } v_n$
. First, if
$f(x_0,x_1,x_2, \dots ) \neq \limsup _{n \to \infty } v_n$
. First, if
![]() $\limsup _{n \to \infty } v_n \notin R \supseteq \text {ran}(f)$
, we are done. Otherwise
$\limsup _{n \to \infty } v_n \notin R \supseteq \text {ran}(f)$
, we are done. Otherwise
![]() $\limsup _{n \to \infty } v_n = r \in R$
, therefore for each
$\limsup _{n \to \infty } v_n = r \in R$
, therefore for each
![]() $\varepsilon> 0$
, for all but finitely many k we have
$\varepsilon> 0$
, for all but finitely many k we have
![]() $v_k < r + \varepsilon $
, thus (3.2) implies
$v_k < r + \varepsilon $
, thus (3.2) implies
![]() $F_k(v_k) < r + 2\varepsilon + \frac {1}{k}$
for these cofinitely many k’s, therefore
$F_k(v_k) < r + 2\varepsilon + \frac {1}{k}$
for these cofinitely many k’s, therefore
![]() $\limsup _{k \to \infty } F_k(v_k) \leq r$
. Since
$\limsup _{k \to \infty } F_k(v_k) \leq r$
. Since
![]() $r - \varepsilon < v_k$
holds for infinitely many k, this argument also shows that
$r - \varepsilon < v_k$
holds for infinitely many k, this argument also shows that
![]() $r - 2\varepsilon - \tfrac {1}{k} < F_k(v_k)$
for infinitely many k too, thus
$r - 2\varepsilon - \tfrac {1}{k} < F_k(v_k)$
for infinitely many k too, thus
as desired.
Theorem 3.6. Consider a function
![]() $f : X \to \mathbb {R}$
such that the range of f contains no infinite strictly increasing sequence. If Player I has a winning strategy in
$f : X \to \mathbb {R}$
such that the range of f contains no infinite strictly increasing sequence. If Player I has a winning strategy in
![]() $\Gamma (f)$
, then there is a number
$\Gamma (f)$
, then there is a number
![]() $r \in \mathbb {R}$
and a Cantor set
$r \in \mathbb {R}$
and a Cantor set
![]() $C \subseteq X$
such that the set
$C \subseteq X$
such that the set
![]() $C \cap \{f \ge r\}$
is countable and dense in C.
$C \cap \{f \ge r\}$
is countable and dense in C.
Proof Define R to be the closure of the range of f. Then, it is easy to verify that R contains no infinite strictly increasing sequence. Hence, the usual order
![]() $>$
of the reals is a well ordering of R. Let
$>$
of the reals is a well ordering of R. Let
![]() $\rho $
be the order type of
$\rho $
be the order type of
![]() $(R,>)$
, and let
$(R,>)$
, and let
![]() $\alpha \mapsto r_{\alpha }$
be the bijective map from
$\alpha \mapsto r_{\alpha }$
be the bijective map from
![]() $\rho $
to R such that
$\rho $
to R such that
![]() $r_{\alpha }> r_{\beta }$
whenever
$r_{\alpha }> r_{\beta }$
whenever
![]() $\alpha < \beta $
. Notice that
$\alpha < \beta $
. Notice that
![]() $\rho $
is a countable ordinal.
$\rho $
is a countable ordinal.
Assume that Player I has a winning strategy in
![]() $\Gamma (f)$
. Then, by Lemma 3.5 Player I also has a winning strategy in
$\Gamma (f)$
. Then, by Lemma 3.5 Player I also has a winning strategy in
![]() $\Gamma _R (f)$
. Let
$\Gamma _R (f)$
. Let
![]() $\sigma _R$
be such a strategy. Let
$\sigma _R$
be such a strategy. Let
![]() $g : R^{\mathbb {N}} \to X$
be the continuous function induced by
$g : R^{\mathbb {N}} \to X$
be the continuous function induced by
![]() $\sigma _R$
. Here R is given its discrete topology; since R is countable,
$\sigma _R$
. Here R is given its discrete topology; since R is countable,
![]() $R^{\mathbb {N}}$
is a Polish space. For each
$R^{\mathbb {N}}$
is a Polish space. For each
![]() $r \in R$
let
$r \in R$
let
![]() $L_{r} = \{v \in R^{\mathbb {N}}: \limsup _{t \to \infty }v_{t} = r\}$
, and let
$L_{r} = \{v \in R^{\mathbb {N}}: \limsup _{t \to \infty }v_{t} = r\}$
, and let
![]() $A_{r} = g(L_{r})$
. The set
$A_{r} = g(L_{r})$
. The set
![]() $A_{r}$
is analytic. Moreover,
$A_{r}$
is analytic. Moreover,
Suppose that the function f fails to satisfy the conclusion of the theorem, that is, there is no number
![]() $r\in \mathbb {R}$
and Cantor set
$r\in \mathbb {R}$
and Cantor set
![]() $C\subseteq X$
such that
$C\subseteq X$
such that
![]() $C\cap \{f\ge r\}$
is countable and dense in C. We obtain a contradiction by showing that there exists a limsup function
$C\cap \{f\ge r\}$
is countable and dense in C. We obtain a contradiction by showing that there exists a limsup function
![]() $e : X \to R$
such that Player I has a winning strategy in the game
$e : X \to R$
such that Player I has a winning strategy in the game
![]() $\Gamma (e)$
. More precisely, we show that
$\Gamma (e)$
. More precisely, we show that
![]() $\sigma _R$
is a winning strategy for Player I in
$\sigma _R$
is a winning strategy for Player I in
![]() $\Gamma _R(e)$
, which suffices by Lemma 3.5.
$\Gamma _R(e)$
, which suffices by Lemma 3.5.
Note that a function
![]() $e : X \to R$
is a limsup function if and only if
$e : X \to R$
is a limsup function if and only if
![]() $\{e \ge r\}$
is a
$\{e \ge r\}$
is a
![]() $\mathbf {\Pi }_{2}^{0}$
set for each
$\mathbf {\Pi }_{2}^{0}$
set for each
![]() $r \in R$
, using that R is closed.
$r \in R$
, using that R is closed.
We define recursively a sequence
![]() $(G_{\alpha }:\alpha < \rho )$
of
$(G_{\alpha }:\alpha < \rho )$
of
![]() $\mathbf {\Pi }_{2}^{0}$
subsets of X such that
$\mathbf {\Pi }_{2}^{0}$
subsets of X such that
![]() $\{f \ge r_\alpha \} \subseteq G_{\alpha }$
. Let
$\{f \ge r_\alpha \} \subseteq G_{\alpha }$
. Let
![]() $\beta < \rho $
be an ordinal such that the sets
$\beta < \rho $
be an ordinal such that the sets
![]() $(G_{\alpha }:\alpha < \beta )$
have been defined. In particular, notice that
$(G_{\alpha }:\alpha < \beta )$
have been defined. In particular, notice that
Since f fails to satisfy the condition of the theorem, there exists no Cantor set
![]() $C \subseteq X$
such that
$C \subseteq X$
such that
![]() $C \cap \{f \ge r_\beta \}$
is countable and dense in C. This implies (using [Reference Kechris6, Theorem 21.22]) that
$C \cap \{f \ge r_\beta \}$
is countable and dense in C. This implies (using [Reference Kechris6, Theorem 21.22]) that
![]() $\{f \ge r_\beta \}$
can be separated from any disjoint analytic subset of X by a
$\{f \ge r_\beta \}$
can be separated from any disjoint analytic subset of X by a
![]() $\mathbf {\Pi }_{2}^{0}$
set. Consider the set
$\mathbf {\Pi }_{2}^{0}$
set. Consider the set
 $$ \begin{align} A_{r_{\beta}} \Big\backslash \bigcup_{\alpha < \beta}\, \bigcap_{\gamma:\, \alpha \leq \gamma <\beta} G_{\gamma}. \end{align} $$
$$ \begin{align} A_{r_{\beta}} \Big\backslash \bigcup_{\alpha < \beta}\, \bigcap_{\gamma:\, \alpha \leq \gamma <\beta} G_{\gamma}. \end{align} $$
It is analytic, since
![]() $\beta $
is a countable ordinal. Moreover, it is disjoint from
$\beta $
is a countable ordinal. Moreover, it is disjoint from
![]() $\{f \ge r_\beta \}$
as can be seen from (3.5) and (3.6). Hence there exists a
$\{f \ge r_\beta \}$
as can be seen from (3.5) and (3.6). Hence there exists a
![]() $\mathbf {\Pi }_{2}^{0}$
subset
$\mathbf {\Pi }_{2}^{0}$
subset
![]() $G_{\beta }$
of X containing
$G_{\beta }$
of X containing
![]() $\{f \ge r_\beta \}$
and disjoint from (3.7). Thus
$\{f \ge r_\beta \}$
and disjoint from (3.7). Thus
![]() $\{f \ge r_\beta \} \subseteq G_{\beta }$
and
$\{f \ge r_\beta \} \subseteq G_{\beta }$
and
This concludes the recursive definition of the sequence
![]() $(G_\alpha : \alpha <\rho )$
.
$(G_\alpha : \alpha <\rho )$
.
Now, for an arbitrary
![]() $\beta < \rho $
define the set
$\beta < \rho $
define the set
This is a
![]() $\mathbf {\Pi }_{2}^{0}$
set, since
$\mathbf {\Pi }_{2}^{0}$
set, since
![]() $\rho $
is a countable ordinal. Moreover,
$\rho $
is a countable ordinal. Moreover,
![]() $\{f \ge r_\beta \} \subseteq E_{\beta }$
for each
$\{f \ge r_\beta \} \subseteq E_{\beta }$
for each
![]() $\beta < \rho $
, hence
$\beta < \rho $
, hence
![]() $X = \bigcup _{\beta <\rho }E_{\beta }$
. In view of (3.8), we have
$X = \bigcup _{\beta <\rho }E_{\beta }$
. In view of (3.8), we have
Define
![]() $e \colon X \to R$
by letting
$e \colon X \to R$
by letting
![]() $e(x) = r_{\beta }$
, where
$e(x) = r_{\beta }$
, where
![]() $\beta < \rho $
is the least ordinal such that
$\beta < \rho $
is the least ordinal such that
![]() $x \in E_{\beta }$
. Then,
$x \in E_{\beta }$
. Then,
![]() $\{e \ge r_\beta \} = E_{\beta }$
for each
$\{e \ge r_\beta \} = E_{\beta }$
for each
![]() $\beta <\rho $
, so e is a limsup function. Moreover,
$\beta <\rho $
, so e is a limsup function. Moreover,
![]() $\{e = r_{\beta }\}$
equals the set
$\{e = r_{\beta }\}$
equals the set
![]() $E_{\beta } \setminus \bigcup _{\alpha < \beta }E_{\alpha }$
, which is disjoint from
$E_{\beta } \setminus \bigcup _{\alpha < \beta }E_{\alpha }$
, which is disjoint from
![]() $A_{r_{\beta }}$
by (3.9). This shows that Player I’s strategy
$A_{r_{\beta }}$
by (3.9). This shows that Player I’s strategy
![]() $\sigma _R$
remains winning in the game
$\sigma _R$
remains winning in the game
![]() $\Gamma _{R}(e)$
, yielding the desired contradiction.
$\Gamma _{R}(e)$
, yielding the desired contradiction.
Next we show that the above necessary and sufficient condition for the existence of a winning strategy for Player I also holds if we assume that f is sufficiently definable, e.g., Borel measurable.
We say that the function f is semi-Borel if for each
![]() $r \in \mathbb {R}$
, the set
$r \in \mathbb {R}$
, the set
![]() $\{f \ge r \}$
is co-analytic.
$\{f \ge r \}$
is co-analytic.
Theorem 3.7. Let
![]() $f : X \to \mathbb {R}$
be semi-Borel. If Player I has a winning strategy in
$f : X \to \mathbb {R}$
be semi-Borel. If Player I has a winning strategy in
![]() $\Gamma (f)$
, then there is a number
$\Gamma (f)$
, then there is a number
![]() $r \in \mathbb {R}$
and a Cantor set
$r \in \mathbb {R}$
and a Cantor set
![]() $C \subseteq X$
such that the set
$C \subseteq X$
such that the set
![]() $C \cap \{f \ge r\}$
is countable and dense in C.
$C \cap \{f \ge r\}$
is countable and dense in C.
Proof If for each
![]() $r \in \mathbb {R}$
,
$r \in \mathbb {R}$
,
![]() $\{f \ge r \}$
is a
$\{f \ge r \}$
is a
![]() $\mathbf {\Pi }_{2}^{0}$
set, then f is a limsup function, hence Player II has a winning strategy in
$\mathbf {\Pi }_{2}^{0}$
set, then f is a limsup function, hence Player II has a winning strategy in
![]() $\Gamma (f)$
, a contradiction. Hence
$\Gamma (f)$
, a contradiction. Hence
![]() $\{f \ge r \}$
is not a
$\{f \ge r \}$
is not a
![]() $\mathbf {\Pi }_{2}^{0}$
set for some
$\mathbf {\Pi }_{2}^{0}$
set for some
![]() $r \in \mathbb {R}$
. Then, the Hurewicz theorem (see, e.g., [Reference Kechris6, Theorem 21.18]) implies that there is a Cantor set C such that the set
$r \in \mathbb {R}$
. Then, the Hurewicz theorem (see, e.g., [Reference Kechris6, Theorem 21.18]) implies that there is a Cantor set C such that the set
![]() $C \cap \{f \ge r\}$
is countable and dense in C.
$C \cap \{f \ge r\}$
is countable and dense in C.
Corollary 3.8. If f is semi-Borel, then the game
![]() $\Gamma (f)$
is determined.
$\Gamma (f)$
is determined.
Proof If for each
![]() $r \in \mathbb {R}$
,
$r \in \mathbb {R}$
,
![]() $\{f \ge r \}$
is a
$\{f \ge r \}$
is a
![]() $\mathbf {\Pi }_{2}^{0}$
set, then f is a limsup function, hence Player II has a winning strategy in
$\mathbf {\Pi }_{2}^{0}$
set, then f is a limsup function, hence Player II has a winning strategy in
![]() $\Gamma (f)$
. Otherwise,
$\Gamma (f)$
. Otherwise,
![]() $\{f \ge r \}$
is not a
$\{f \ge r \}$
is not a
![]() $\mathbf {\Pi }_{2}^{0}$
set for some
$\mathbf {\Pi }_{2}^{0}$
set for some
![]() $r \in \mathbb {R}$
, and as above, the Hurewicz theorem implies that there is a Cantor set C such that the set
$r \in \mathbb {R}$
, and as above, the Hurewicz theorem implies that there is a Cantor set C such that the set
![]() $C \cap \{f \ge r\}$
is countable and dense in C, therefore Player I has a winning strategy by Theorem 3.3.
$C \cap \{f \ge r\}$
is countable and dense in C, therefore Player I has a winning strategy by Theorem 3.3.
Next we will show that in general the condition of Theorem 3.3 is not equivalent to the existence of a winning strategy for Player I. More precisely, we will show in Corollary 3.10 that the restriction on the range of f in Theorem 3.6 is optimal; if
![]() $R \subseteq \mathbb {R}$
contains an infinite strictly increasing sequence, then there exists a function
$R \subseteq \mathbb {R}$
contains an infinite strictly increasing sequence, then there exists a function
![]() $f : \mathbb {N}^{\mathbb {N}} \to R$
such that Player I has a winning strategy in
$f : \mathbb {N}^{\mathbb {N}} \to R$
such that Player I has a winning strategy in
![]() $\Gamma (f)$
, and
$\Gamma (f)$
, and
![]() $C \cap \{f \ge r\}$
is either uncountable or empty for each
$C \cap \{f \ge r\}$
is either uncountable or empty for each
![]() $r \in \mathbb {R}$
and each Cantor set
$r \in \mathbb {R}$
and each Cantor set
![]() $C \subseteq \mathbb {N}^{\mathbb {N}}$
.
$C \subseteq \mathbb {N}^{\mathbb {N}}$
.
Theorem 3.9. There exists a function
![]() $f : \mathbb {N}^{\mathbb {N}} \to \mathbb {N}$
such that Player I has a winning strategy in
$f : \mathbb {N}^{\mathbb {N}} \to \mathbb {N}$
such that Player I has a winning strategy in
![]() $\Gamma (f)$
, and
$\Gamma (f)$
, and
![]() $C \cap \{f \ge r\}$
is uncountable for each
$C \cap \{f \ge r\}$
is uncountable for each
![]() $r \in \mathbb {R}$
and each Cantor set
$r \in \mathbb {R}$
and each Cantor set
![]() $C \subseteq \mathbb {N}^{\mathbb {N}}$
.
$C \subseteq \mathbb {N}^{\mathbb {N}}$
.
Proof First note that every Cantor set can be written as a disjoint union of uncountably many (in fact, continuum many) Cantor sets, since it is well-known that a Cantor set is homeomorphic to
![]() $2^I$
for every countably infinite set I, in particular to
$2^I$
for every countably infinite set I, in particular to
![]() $2^{\mathbb {N} \times \mathbb {N}}$
, which is homeomorphic to
$2^{\mathbb {N} \times \mathbb {N}}$
, which is homeomorphic to
![]() $2^{\mathbb {N}} \times 2^{\mathbb {N}} = \bigcup _{c \in 2^{\mathbb {N}}} \left (\{c\} \times 2^{\mathbb {N}} \right )$
.
$2^{\mathbb {N}} \times 2^{\mathbb {N}} = \bigcup _{c \in 2^{\mathbb {N}}} \left (\{c\} \times 2^{\mathbb {N}} \right )$
.
This implies that if H is an arbitrary set, then in order to show that
![]() $C \cap H$
is uncountable for each Cantor set
$C \cap H$
is uncountable for each Cantor set
![]() $C \subseteq \mathbb {N}^{\mathbb {N}}$
, it suffices to show that
$C \subseteq \mathbb {N}^{\mathbb {N}}$
, it suffices to show that
![]() $C \cap H \neq \emptyset $
for each Cantor set
$C \cap H \neq \emptyset $
for each Cantor set
![]() $C \subseteq \mathbb {N}^{\mathbb {N}}$
.
$C \subseteq \mathbb {N}^{\mathbb {N}}$
.
Let
![]() $X = \mathbb {N}^{\mathbb {N}}$
and let
$X = \mathbb {N}^{\mathbb {N}}$
and let
![]() $\varphi : X \to \mathbb {N} \cup \{+\infty \}$
be given by
$\varphi : X \to \mathbb {N} \cup \{+\infty \}$
be given by
![]() $\varphi (x) = \limsup _{n \to \infty }x_{n}$
. We first argue that there exists a function
$\varphi (x) = \limsup _{n \to \infty }x_{n}$
. We first argue that there exists a function
![]() $f : X \to \mathbb {N}$
such that (a)
$f : X \to \mathbb {N}$
such that (a)
![]() $f(x) \neq \varphi (x)$
for each
$f(x) \neq \varphi (x)$
for each
![]() $x \in X$
, and (b)
$x \in X$
, and (b)
![]() $C \cap \{f \ge r\} \neq \emptyset $
for each
$C \cap \{f \ge r\} \neq \emptyset $
for each
![]() $r \in \mathbb {R}$
and each Cantor set
$r \in \mathbb {R}$
and each Cantor set
![]() $C \subseteq X$
. We will then show that condition (a) implies that Player I has a winning strategy in
$C \subseteq X$
. We will then show that condition (a) implies that Player I has a winning strategy in
![]() $\Gamma (f)$
, while we already argued that (b) implies that
$\Gamma (f)$
, while we already argued that (b) implies that
![]() $C \cap \{f \ge r\}$
is uncountable for each
$C \cap \{f \ge r\}$
is uncountable for each
![]() $r \in \mathbb {R}$
and each Cantor set
$r \in \mathbb {R}$
and each Cantor set
![]() $C \subseteq \mathbb {N}^{\mathbb {N}}$
.
$C \subseteq \mathbb {N}^{\mathbb {N}}$
.
Let
![]() $(r_{\alpha }:\alpha <\mathfrak {c})$
,
$(r_{\alpha }:\alpha <\mathfrak {c})$
,
![]() $(z_{\alpha }:\alpha <\mathfrak {c})$
, and
$(z_{\alpha }:\alpha <\mathfrak {c})$
, and
![]() $(C_{\alpha }:\alpha <\mathfrak {c})$
be enumerations of the real numbers, of the points of X, and of the Cantor subsets of X, respectively. We define the pairs
$(C_{\alpha }:\alpha <\mathfrak {c})$
be enumerations of the real numbers, of the points of X, and of the Cantor subsets of X, respectively. We define the pairs
![]() $(z_{\alpha }, f(z_{\alpha })) \in X \times \mathbb {N}$
recursively as follows. Take an ordinal
$(z_{\alpha }, f(z_{\alpha })) \in X \times \mathbb {N}$
recursively as follows. Take an ordinal
![]() $\alpha < \mathfrak {c}$
and suppose that
$\alpha < \mathfrak {c}$
and suppose that
![]() $(z_{\beta },f(z_{\beta }))$
has been defined for every
$(z_{\beta },f(z_{\beta }))$
has been defined for every
![]() $\beta < \alpha $
. Let
$\beta < \alpha $
. Let
![]() $z_{\alpha }$
be any point of
$z_{\alpha }$
be any point of
![]() $C_{\alpha } \setminus \{z_{\beta }:\beta <\alpha \}$
. Define
$C_{\alpha } \setminus \{z_{\beta }:\beta <\alpha \}$
. Define
![]() $f(z_{\alpha })$
to be the smallest natural number such that
$f(z_{\alpha })$
to be the smallest natural number such that
![]() $f(z_{\alpha }) \geq r_{\alpha }$
and
$f(z_{\alpha }) \geq r_{\alpha }$
and
![]() $f(z_{\alpha }) \neq \varphi (z_{\alpha })$
. To complete the definition of f, for each point
$f(z_{\alpha }) \neq \varphi (z_{\alpha })$
. To complete the definition of f, for each point
![]() $x \in X \setminus \{z_{\beta }:\beta <\mathfrak {c}\}$
let
$x \in X \setminus \{z_{\beta }:\beta <\mathfrak {c}\}$
let
![]() $f(x)$
be the smallest natural number such that
$f(x)$
be the smallest natural number such that
![]() $f(x) \neq \varphi (x)$
.
$f(x) \neq \varphi (x)$
.
Now we show that Player I has a winning strategy in
![]() $\Gamma (f)$
. Using Lemma 3.5, it is enough to show that Player I has a winning strategy in
$\Gamma (f)$
. Using Lemma 3.5, it is enough to show that Player I has a winning strategy in
![]() $\Gamma _{\mathbb {N}}(f)$
. Let Player I start by playing
$\Gamma _{\mathbb {N}}(f)$
. Let Player I start by playing
![]() $x_{0} = 0$
. To a move
$x_{0} = 0$
. To a move
![]() $v_{n} \in \mathbb {N}$
of Player II in round n, Player I responds with
$v_{n} \in \mathbb {N}$
of Player II in round n, Player I responds with
![]() $x_{n+1} = v_n$
. Then, for a run
$x_{n+1} = v_n$
. Then, for a run
![]() $x_{0},v_{0},x_{1},v_{1},\dots $
of the game, it holds that
$x_{0},v_{0},x_{1},v_{1},\dots $
of the game, it holds that
![]() $\varphi (x) = \limsup _{n \to \infty }x_{n} = \limsup _{n \to \infty }v_n$
. Since
$\varphi (x) = \limsup _{n \to \infty }x_{n} = \limsup _{n \to \infty }v_n$
. Since
![]() $f(x) \neq \varphi (x)$
holds, we have
$f(x) \neq \varphi (x)$
holds, we have
![]() $f(x) \neq \limsup _{n \to \infty } v_n $
, hence the run is won by Player I.
$f(x) \neq \limsup _{n \to \infty } v_n $
, hence the run is won by Player I.
Corollary 3.10. If
![]() $R \subseteq \mathbb {R}$
contains an infinite strictly increasing sequence, then there exists a function
$R \subseteq \mathbb {R}$
contains an infinite strictly increasing sequence, then there exists a function
![]() $f : \mathbb {N}^{\mathbb {N}} \to R$
such that Player I has a winning strategy in
$f : \mathbb {N}^{\mathbb {N}} \to R$
such that Player I has a winning strategy in
![]() $\Gamma (f)$
, and
$\Gamma (f)$
, and
![]() $C \cap \{f \ge r\}$
is either uncountable or empty for each
$C \cap \{f \ge r\}$
is either uncountable or empty for each
![]() $r \in \mathbb {R}$
and each Cantor set
$r \in \mathbb {R}$
and each Cantor set
![]() $C \subseteq \mathbb {N}^{\mathbb {N}}$
.
$C \subseteq \mathbb {N}^{\mathbb {N}}$
.
Proof Let
![]() $i : \mathbb {N} \to R$
be a strictly increasing map. Let
$i : \mathbb {N} \to R$
be a strictly increasing map. Let
![]() $f_0 : \mathbb {N}^{\mathbb {N}} \to \mathbb {N}$
be a function as in Theorem 3.9, that is, such that Player I has a winning strategy in
$f_0 : \mathbb {N}^{\mathbb {N}} \to \mathbb {N}$
be a function as in Theorem 3.9, that is, such that Player I has a winning strategy in
![]() $\Gamma (f_0)$
, and
$\Gamma (f_0)$
, and
![]() $C \cap \{f_0 \ge r\}$
is uncountable for each
$C \cap \{f_0 \ge r\}$
is uncountable for each
![]() $r \in \mathbb {R}$
and each Cantor set
$r \in \mathbb {R}$
and each Cantor set
![]() $C \subseteq \mathbb {N}^{\mathbb {N}}$
. We claim that the function defined as
$C \subseteq \mathbb {N}^{\mathbb {N}}$
. We claim that the function defined as
![]() $f = i \circ f_0$
works. Clearly,
$f = i \circ f_0$
works. Clearly,
![]() $f : \mathbb {N}^{\mathbb {N}} \to R$
, and it is also clear that
$f : \mathbb {N}^{\mathbb {N}} \to R$
, and it is also clear that
![]() $C \cap \{f \ge r\}$
is either uncountable or empty for each
$C \cap \{f \ge r\}$
is either uncountable or empty for each
![]() $r \in \mathbb {R}$
and each Cantor set
$r \in \mathbb {R}$
and each Cantor set
![]() $C \subseteq \mathbb {N}^{\mathbb {N}}$
, hence we only have to show that Player I has a winning strategy in
$C \subseteq \mathbb {N}^{\mathbb {N}}$
, hence we only have to show that Player I has a winning strategy in
![]() $\Gamma (f)$
. By Lemma 3.5 it suffices to check that Player I has a winning strategy in
$\Gamma (f)$
. By Lemma 3.5 it suffices to check that Player I has a winning strategy in
![]() $\Gamma _{i(\mathbb {N})}(f)$
. Let
$\Gamma _{i(\mathbb {N})}(f)$
. Let
![]() $\sigma _0$
be a winning strategy for Player I in
$\sigma _0$
be a winning strategy for Player I in
![]() $\Gamma (f_0)$
, and define for each
$\Gamma (f_0)$
, and define for each
![]() $n \in \mathbb {N}$
$n \in \mathbb {N}$
Since i is order-preserving, it is easy to check that
![]() $\sigma _{i (\mathbb {N} )}$
is a winning strategy for Player I in
$\sigma _{i (\mathbb {N} )}$
is a winning strategy for Player I in
![]() $\Gamma _{i(\mathbb {N})}(f)$
.
$\Gamma _{i(\mathbb {N})}(f)$
.
Next we state another result of similar sort. We will strengthen the above counterexamples by showing that such an f can have a co-analytic graph, but on the other hand we have to sacrifice that the range is countable. Note that the complexity of the graph of f is optimal, since if the graph of a function is analytic, then it is well-known that the function is actually Borel measurable, hence by Theorem 3.7 it cannot be a counterexample, and similarly, the range cannot be countable, since it is easy to show that a function with co-analytic graph and countable range is semi-Borel.
Recall that the statement “
![]() $V=L$
” is the Axiom of Constructibility due to K. Gödel. It is known that it is consistent with
$V=L$
” is the Axiom of Constructibility due to K. Gödel. It is known that it is consistent with
![]() $ZFC$
, and that it implies the Continuum Hypothesis.
$ZFC$
, and that it implies the Continuum Hypothesis.
Theorem 3.11. Assume
![]() $V=L$
. Then, there exists a function
$V=L$
. Then, there exists a function
![]() $f : \mathbb {N}^{\mathbb {N}} \to \mathbb {R}$
with co-analytic graph such that Player I has a winning strategy in
$f : \mathbb {N}^{\mathbb {N}} \to \mathbb {R}$
with co-analytic graph such that Player I has a winning strategy in
![]() $\Gamma (f)$
, and
$\Gamma (f)$
, and
![]() $C \cap \{f \ge r\}$
is uncountable for each
$C \cap \{f \ge r\}$
is uncountable for each
![]() $r \in \mathbb {R}$
and each Cantor set
$r \in \mathbb {R}$
and each Cantor set
![]() $C \subseteq \mathbb {N}^{\mathbb {N}}$
.
$C \subseteq \mathbb {N}^{\mathbb {N}}$
.
Proof Let
![]() $X = \mathbb {N}^{\mathbb {N}}$
. Let
$X = \mathbb {N}^{\mathbb {N}}$
. Let
![]() $q(0), q(1), \dots $
be an enumeration of the rational numbers, and let
$q(0), q(1), \dots $
be an enumeration of the rational numbers, and let
![]() $\varphi : X \to \mathbb {R}\cup \{+\infty \}$
be given by
$\varphi : X \to \mathbb {R}\cup \{+\infty \}$
be given by
![]() $\varphi (x) = \limsup _{n \to \infty } q(x_n)$
. In order to construct
$\varphi (x) = \limsup _{n \to \infty } q(x_n)$
. In order to construct
![]() $f : X \to \mathbb {R}$
with co-analytic graph, we use a result of Vidnyánszky [Reference Vidnyánszky13, Theorem 1.3]. Let
$f : X \to \mathbb {R}$
with co-analytic graph, we use a result of Vidnyánszky [Reference Vidnyánszky13, Theorem 1.3]. Let
![]() $B_1 = \{ (C, t) \in \mathcal {K}(X) \times \mathbb {R} : C$
is a Cantor set
$B_1 = \{ (C, t) \in \mathcal {K}(X) \times \mathbb {R} : C$
is a Cantor set
![]() $\}$
, where
$\}$
, where
![]() $\mathcal {K}(X)$
is the family of non-empty compact sets in X equipped with the Hausdorff metric. Let
$\mathcal {K}(X)$
is the family of non-empty compact sets in X equipped with the Hausdorff metric. Let
![]() $B_2 = \mathbb {R}$
and
$B_2 = \mathbb {R}$
and
![]() $B = B_1 \sqcup B_2$
be the disjoint union of
$B = B_1 \sqcup B_2$
be the disjoint union of
![]() $B_1$
and
$B_1$
and
![]() $B_2$
making B a subset of the Polish space
$B_2$
making B a subset of the Polish space
![]() $(\mathcal {K}(X)\times \mathbb {R}) \sqcup \mathbb {R}$
. Let
$(\mathcal {K}(X)\times \mathbb {R}) \sqcup \mathbb {R}$
. Let
![]() $i : X \to \mathbb {R}$
be a Borel bijection,
$i : X \to \mathbb {R}$
be a Borel bijection,
![]() $M = \mathbb {R}^2$
, and let
$M = \mathbb {R}^2$
, and let
 $$ \begin{align*}F_1 = &\Big\{\big(A, (C, r), (y, t)\big) \in M^{\le \omega} \times B_1 \\&\quad\times M : y \in i(C) \setminus \textrm{pr}_1(\textrm{ran}(A)), t \ge r, t \neq \varphi(i^{-1}(y))\Big\},\end{align*} $$
$$ \begin{align*}F_1 = &\Big\{\big(A, (C, r), (y, t)\big) \in M^{\le \omega} \times B_1 \\&\quad\times M : y \in i(C) \setminus \textrm{pr}_1(\textrm{ran}(A)), t \ge r, t \neq \varphi(i^{-1}(y))\Big\},\end{align*} $$
where
![]() $\textrm {pr}_1(\textrm {ran}(A))$
is the projection of the range of the sequence A onto the first coordinate. Let
$\textrm {pr}_1(\textrm {ran}(A))$
is the projection of the range of the sequence A onto the first coordinate. Let
 $$ \begin{align*} F_2 = \Big\{\!\big(A, y', (y, t)\big) \in M^{\le \omega} \times B_2 \times M : \; & t \neq \varphi\big(i^{-1}(y)\big), y' \not\in \textrm{pr}_1\big(\textrm{ran}(A)\big) \kern1.5pt{\Rightarrow}\kern1.5pt y' \kern1.5pt{=}\kern1.5pt y, \\ & y' \in \textrm{pr}_1\big(\textrm{ran}(A)\big) \Rightarrow y \not\in \textrm{pr}_1\big(\textrm{ran}(A) \big)\Big\}, \end{align*} $$
$$ \begin{align*} F_2 = \Big\{\!\big(A, y', (y, t)\big) \in M^{\le \omega} \times B_2 \times M : \; & t \neq \varphi\big(i^{-1}(y)\big), y' \not\in \textrm{pr}_1\big(\textrm{ran}(A)\big) \kern1.5pt{\Rightarrow}\kern1.5pt y' \kern1.5pt{=}\kern1.5pt y, \\ & y' \in \textrm{pr}_1\big(\textrm{ran}(A)\big) \Rightarrow y \not\in \textrm{pr}_1\big(\textrm{ran}(A) \big)\Big\}, \end{align*} $$
and let
![]() $F = F_1 \sqcup F_2 \subseteq M^{\le \omega } \times B \times M$
.
$F = F_1 \sqcup F_2 \subseteq M^{\le \omega } \times B \times M$
.
We now check that the conditions of Vidnyánszky’s theorem are satisfied. First, a non-empty compact set
![]() $C \subseteq \mathbb {N}^{\mathbb {N}}$
is a Cantor set if and only if it is perfect. Using [Reference Kechris6, Exercise 4.31] one can easily see that
$C \subseteq \mathbb {N}^{\mathbb {N}}$
is a Cantor set if and only if it is perfect. Using [Reference Kechris6, Exercise 4.31] one can easily see that
![]() $B_1$
is a Borel subset of
$B_1$
is a Borel subset of
![]() $\mathcal {K}(X) \times \mathbb {R}$
. Therefore B is a Borel subset of
$\mathcal {K}(X) \times \mathbb {R}$
. Therefore B is a Borel subset of
![]() $(\mathcal {K}(X) \times \mathbb {R}) \sqcup \mathbb {R}$
. The set
$(\mathcal {K}(X) \times \mathbb {R}) \sqcup \mathbb {R}$
. The set
![]() $F_1$
is clearly co-analytic, and since
$F_1$
is clearly co-analytic, and since
![]() $A \in M^{\le \omega }$
is a countable sequence, conditions of the form
$A \in M^{\le \omega }$
is a countable sequence, conditions of the form
![]() $y' \in \textrm {pr}_1(\textrm {ran}(A))$
are Borel. Therefore
$y' \in \textrm {pr}_1(\textrm {ran}(A))$
are Borel. Therefore
![]() $F_2$
is even Borel, making
$F_2$
is even Borel, making
![]() $F = F_1 \sqcup F_2$
co-analytic. For each
$F = F_1 \sqcup F_2$
co-analytic. For each
![]() $(A, b) \in M^{\le \omega } \times B$
, no matter whether
$(A, b) \in M^{\le \omega } \times B$
, no matter whether
![]() $b \in \mathcal {K}(X) \times \mathbb {R}$
or
$b \in \mathcal {K}(X) \times \mathbb {R}$
or
![]() $b \in \mathbb {R}$
, the section
$b \in \mathbb {R}$
, the section
contains
![]() $\{x_1\} \times \{t : t \ge x_2\}$
for some
$\{x_1\} \times \{t : t \ge x_2\}$
for some
![]() $(x_1, x_2) \in \mathbb {R}^2$
, hence it is cofinal in the Turing degrees (for this notion, see Definition 1.1 of [Reference Vidnyánszky13]). Therefore the conditions of the theorem are satisfied.
$(x_1, x_2) \in \mathbb {R}^2$
, hence it is cofinal in the Turing degrees (for this notion, see Definition 1.1 of [Reference Vidnyánszky13]). Therefore the conditions of the theorem are satisfied.
The conclusion of the theorem assures that there is a co-analytic set
![]() $G \subseteq M = \mathbb {R}^2$
and enumerations
$G \subseteq M = \mathbb {R}^2$
and enumerations
![]() $B = \{b_\alpha : \alpha < \omega _1\}$
,
$B = \{b_\alpha : \alpha < \omega _1\}$
,
![]() $G = \{g_\alpha : \alpha < \omega _1\}$
and for every
$G = \{g_\alpha : \alpha < \omega _1\}$
and for every
![]() $\alpha < \omega _1$
a sequence
$\alpha < \omega _1$
a sequence
![]() $A_\alpha \in M^{\le \omega }$
that is an enumeration of
$A_\alpha \in M^{\le \omega }$
that is an enumeration of
![]() $\{g_\beta : \beta < \alpha \}$
such that
$\{g_\beta : \beta < \alpha \}$
such that
![]() $g_\alpha \in F_{(A_\alpha , b_\alpha )}$
for every
$g_\alpha \in F_{(A_\alpha , b_\alpha )}$
for every
![]() $\alpha < \omega _1$
. We note here that the assumption
$\alpha < \omega _1$
. We note here that the assumption
![]() $V = L$
implies the continuum hypothesis.
$V = L$
implies the continuum hypothesis.
First we check that G is the graph of a function with domain
![]() $\mathbb {R}$
. Notice that for
$\mathbb {R}$
. Notice that for
![]() $\beta < \alpha $
, if
$\beta < \alpha $
, if
![]() $g_\alpha = (y_1, t_1)$
and
$g_\alpha = (y_1, t_1)$
and
![]() $g_\beta = (y_2, t_2)$
, then
$g_\beta = (y_2, t_2)$
, then
![]() $y_1 \neq y_2$
. Indeed,
$y_1 \neq y_2$
. Indeed,
![]() $g_\alpha \in F_{(A_\alpha , b_\alpha )}$
implies that
$g_\alpha \in F_{(A_\alpha , b_\alpha )}$
implies that
![]() $y_1 \not \in \textrm {pr}_1(\textrm {ran}(A_\alpha ))$
, and since
$y_1 \not \in \textrm {pr}_1(\textrm {ran}(A_\alpha ))$
, and since
![]() $y_2 \in \textrm {pr}_1(\textrm {ran}(A_\alpha ))$
,
$y_2 \in \textrm {pr}_1(\textrm {ran}(A_\alpha ))$
,
![]() $y_1 \neq y_2$
easily follows. To see that for each
$y_1 \neq y_2$
easily follows. To see that for each
![]() $y \in \mathbb {R}$
,
$y \in \mathbb {R}$
,
![]() $(y, t) \in G$
for some
$(y, t) \in G$
for some
![]() $t \in \mathbb {R}$
, let
$t \in \mathbb {R}$
, let
![]() $\alpha < \omega _1$
be chosen with
$\alpha < \omega _1$
be chosen with
![]() $b_\alpha = y \in B_2$
. Then, either
$b_\alpha = y \in B_2$
. Then, either
![]() $y \in \textrm {pr}_1(\textrm {ran}(A_\alpha ))$
and we are done, or
$y \in \textrm {pr}_1(\textrm {ran}(A_\alpha ))$
and we are done, or
![]() $g_\alpha $
is chosen to be
$g_\alpha $
is chosen to be
![]() $(y, t)$
for some
$(y, t)$
for some
![]() $t \in \mathbb {R}$
. Therefore G is indeed a graph of a function with domain
$t \in \mathbb {R}$
. Therefore G is indeed a graph of a function with domain
![]() $\mathbb {R}$
.
$\mathbb {R}$
.
Now we define the function
![]() $f : X \to \mathbb {R}$
in the following way: for each
$f : X \to \mathbb {R}$
in the following way: for each
![]() $(y, t) \in G$
, let
$(y, t) \in G$
, let
![]() $f(i^{-1}(y)) = t$
. Clearly, the graph of f is
$f(i^{-1}(y)) = t$
. Clearly, the graph of f is
![]() $(i, \textrm {id})^{-1}(G)$
, hence it is co-analytic.
$(i, \textrm {id})^{-1}(G)$
, hence it is co-analytic.
We now show that the defined function f has properties (a)
![]() $f(x) \neq \varphi (x)$
for each
$f(x) \neq \varphi (x)$
for each
![]() $x \in X$
, and (b)
$x \in X$
, and (b)
![]() $C \cap \{f \ge r\} \neq \emptyset $
for each
$C \cap \{f \ge r\} \neq \emptyset $
for each
![]() $r \in \mathbb {R}$
and each Cantor set
$r \in \mathbb {R}$
and each Cantor set
![]() $C \subseteq X$
. Then, we will show that (a) implies that Player I has a winning strategy in
$C \subseteq X$
. Then, we will show that (a) implies that Player I has a winning strategy in
![]() $\Gamma (f)$
. The proof that (b) implies that
$\Gamma (f)$
. The proof that (b) implies that
![]() $C \cap \{f \ge r\}$
is uncountable for each
$C \cap \{f \ge r\}$
is uncountable for each
![]() $r \in \mathbb {R}$
and each Cantor set C is exactly the same as in the proof of Theorem 3.9.
$r \in \mathbb {R}$
and each Cantor set C is exactly the same as in the proof of Theorem 3.9.
To show (a), let
![]() $(x, t) \in X \times \mathbb {R}$
be a pair with
$(x, t) \in X \times \mathbb {R}$
be a pair with
![]() $(i(x), t) = g_\alpha \in G$
. Then,
$(i(x), t) = g_\alpha \in G$
. Then,
![]() $g_\alpha \in F_{(A_\alpha , b_\alpha )}$
implies
$g_\alpha \in F_{(A_\alpha , b_\alpha )}$
implies
![]() $t \neq \varphi (x)$
, hence
$t \neq \varphi (x)$
, hence
![]() $f(x) = t \neq \varphi (x)$
. To show (b), let
$f(x) = t \neq \varphi (x)$
. To show (b), let
![]() $C \subseteq X$
be a Cantor set and let
$C \subseteq X$
be a Cantor set and let
![]() $r \in \mathbb {R}$
. Let
$r \in \mathbb {R}$
. Let
![]() $\alpha < \omega _1$
be the ordinal with
$\alpha < \omega _1$
be the ordinal with
![]() $b_\alpha = (C, r)$
. Then, for
$b_\alpha = (C, r)$
. Then, for
![]() $g_\alpha = (y, t)$
, using again that
$g_\alpha = (y, t)$
, using again that
![]() $g_\alpha \in F_{(A_\alpha , b_\alpha )}$
,
$g_\alpha \in F_{(A_\alpha , b_\alpha )}$
,
![]() $y \in i(C)$
and
$y \in i(C)$
and
![]() $t \ge r$
, hence
$t \ge r$
, hence
![]() $i^{-1}(y) \in C$
and
$i^{-1}(y) \in C$
and
![]() $f(i^{-1}(y)) = t \ge r$
.
$f(i^{-1}(y)) = t \ge r$
.
It remains to show that Player I has a winning strategy in
![]() $\Gamma (f)$
. Let Player I start by playing
$\Gamma (f)$
. Let Player I start by playing
![]() $x_{0} = 0$
. To a move
$x_{0} = 0$
. To a move
![]() $v_{n}$
of Player II, Player I responds with an
$v_{n}$
of Player II, Player I responds with an
![]() $x_{n+1} \in \mathbb {N}$
chosen to be the smallest natural number satisfying
$x_{n+1} \in \mathbb {N}$
chosen to be the smallest natural number satisfying
![]() $|v_{n} - q(x_{n+1})| \leq 2^{-n}$
. Then, for a run
$|v_{n} - q(x_{n+1})| \leq 2^{-n}$
. Then, for a run
![]() $x_{0},v_{0},x_{1},v_{1},\dots $
of the game, it holds that
$x_{0},v_{0},x_{1},v_{1},\dots $
of the game, it holds that
![]() $\varphi (x) = \limsup _{n \to \infty }v_{n}$
. Since
$\varphi (x) = \limsup _{n \to \infty }v_{n}$
. Since
![]() $f(x) \neq \varphi (x)$
, the run is won by Player I.
$f(x) \neq \varphi (x)$
, the run is won by Player I.
We note that the assumption
![]() $V=L$
cannot be simply dropped from the above theorem. Indeed, it can be derived using the standard proof that Projective Determinacy implies that the Hurewicz theorem holds for all projective sets; moreover, if the graph of f is projective, then so is
$V=L$
cannot be simply dropped from the above theorem. Indeed, it can be derived using the standard proof that Projective Determinacy implies that the Hurewicz theorem holds for all projective sets; moreover, if the graph of f is projective, then so is
![]() $\{f \ge r\}$
for every
$\{f \ge r\}$
for every
![]() $r\in \mathbb {R}$
. Thus one could derive an analogue to Theorem 3.7 under Projective Determinacy, assuming only that f has a projective graph.
$r\in \mathbb {R}$
. Thus one could derive an analogue to Theorem 3.7 under Projective Determinacy, assuming only that f has a projective graph.
Despite all the partial results above, we still do not know the answer to the following interesting question.
Question 3.12. For which
![]() $f : X \to \mathbb {R}$
does Player I have a winning strategy in
$f : X \to \mathbb {R}$
does Player I have a winning strategy in
![]() $\Gamma (f)$
?
$\Gamma (f)$
?
4 A game for Baire class 1 functions
Recall the definition of the game
![]() $\Gamma '(f)$
from the Introduction. Corollary 2.5 immediately yields the following result:
$\Gamma '(f)$
from the Introduction. Corollary 2.5 immediately yields the following result:
Corollary 4.1. Player II has a winning strategy in
![]() $\Gamma '(f)$
if and only if Player II has winning strategies in both games
$\Gamma '(f)$
if and only if Player II has winning strategies in both games
![]() $\Gamma (f)$
and
$\Gamma (f)$
and
![]() $\Gamma ({-}f)$
, if and only if f is of Baire class 1.
$\Gamma ({-}f)$
, if and only if f is of Baire class 1.
New we turn to the existence of a winning strategy for Player I.
Let
![]() $C \subseteq X$
be a closed set, and consider the restriction of f to C. The oscillation of
$C \subseteq X$
be a closed set, and consider the restriction of f to C. The oscillation of
![]() $f|_{C}$
at a point
$f|_{C}$
at a point
![]() $x \in C$
is defined as
$x \in C$
is defined as
Lemma 4.2. Suppose that there is a closed set
![]() $C \subseteq X$
such that the oscillation of
$C \subseteq X$
such that the oscillation of
![]() $f|_{C}$
is bounded away from zero:
$f|_{C}$
is bounded away from zero:
![]() $\inf _{x \in C}\mathrm {osc}_f(C,x)> 0$
. Then, Player I has a winning strategy in
$\inf _{x \in C}\mathrm {osc}_f(C,x)> 0$
. Then, Player I has a winning strategy in
![]() $\Gamma '(f)$
.
$\Gamma '(f)$
.
Proof Assume that
![]() $\mathrm {osc}_f(C,x) \geq 5\epsilon> 0$
for each
$\mathrm {osc}_f(C,x) \geq 5\epsilon> 0$
for each
![]() $x \in C$
. We will first describe a strategy of Player I and then we will show that it is a winning strategy. To define the moves of Player I in a particular run, we will use recursion to define natural numbers
$x \in C$
. We will first describe a strategy of Player I and then we will show that it is a winning strategy. To define the moves of Player I in a particular run, we will use recursion to define natural numbers
![]() $n_0<n_1<n_2<\cdots $
and sequences
$n_0<n_1<n_2<\cdots $
and sequences
![]() $s_0, s_1, s_2, \ldots \in T$
(these may depend on the moves of Player II).
$s_0, s_1, s_2, \ldots \in T$
(these may depend on the moves of Player II).
Let
![]() $n_{0} = 0$
, and let
$n_{0} = 0$
, and let
![]() $s_{0}$
be the empty sequence. Suppose that, for some even number
$s_{0}$
be the empty sequence. Suppose that, for some even number
![]() $k \in \mathbb {N}$
, Player I’s moves prior to the stage
$k \in \mathbb {N}$
, Player I’s moves prior to the stage
![]() $n_{k}$
have been defined.
$n_{k}$
have been defined.
Let
![]() $s_{k} \in T$
denote the sequence of Player I’s moves prior to the stage
$s_{k} \in T$
denote the sequence of Player I’s moves prior to the stage
![]() $n_{k}$
. Define
$n_{k}$
. Define
![]() $\alpha _{k} = \sup \{f(x): x \in O(s_{k}) \cap C\}$
, and choose a point
$\alpha _{k} = \sup \{f(x): x \in O(s_{k}) \cap C\}$
, and choose a point
![]() $x(k) \in O(s_{k}) \cap C$
so that
$x(k) \in O(s_{k}) \cap C$
so that
![]() $\alpha _{k} - \epsilon < f(x(k))$
. Starting with the stage
$\alpha _{k} - \epsilon < f(x(k))$
. Starting with the stage
![]() $n_{k}$
, Player I produces his moves using the point
$n_{k}$
, Player I produces his moves using the point
![]() $x(k)$
, that is, he plays
$x(k)$
, that is, he plays
![]() $x_{n} = x(k)_n$
at a stage
$x_{n} = x(k)_n$
at a stage
![]() $n \geq n_{k}$
. He continues doing so until the first stage, say
$n \geq n_{k}$
. He continues doing so until the first stage, say
![]() $n_{k+1}> n_{k}$
, that Player II makes a move
$n_{k+1}> n_{k}$
, that Player II makes a move
![]() $(v_{n_{k+1}}, w_{n_{k+1}})$
such that
$(v_{n_{k+1}}, w_{n_{k+1}})$
such that
![]() $|v_{n_{k+1}} - f(x(k))| < \epsilon $
. If no such stage occurs, then Player I goes on using the point
$|v_{n_{k+1}} - f(x(k))| < \epsilon $
. If no such stage occurs, then Player I goes on using the point
![]() $x(k)$
to make his moves until the end of the game.
$x(k)$
to make his moves until the end of the game.
Let
![]() $s_{k+1} \in T$
denote the sequence of moves produced by Player I prior to the stage
$s_{k+1} \in T$
denote the sequence of moves produced by Player I prior to the stage
![]() $n_{k+1}$
. Define
$n_{k+1}$
. Define
![]() $\beta _{k+1} = \inf \{f(x): x \in O(s_{k+1}) \cap C\}$
, and choose a point
$\beta _{k+1} = \inf \{f(x): x \in O(s_{k+1}) \cap C\}$
, and choose a point
![]() $x(k+1) \in O(s_{k+1}) \cap C$
so that
$x(k+1) \in O(s_{k+1}) \cap C$
so that
![]() $f(x(k+1)) < \beta _{k+1} + \epsilon $
. Starting with the stage
$f(x(k+1)) < \beta _{k+1} + \epsilon $
. Starting with the stage
![]() $n_{k+1}$
, Player I produces the moves using
$n_{k+1}$
, Player I produces the moves using
![]() $x(k+1)$
, that is he plays
$x(k+1)$
, that is he plays
![]() $x_{n} = x(k+1)_n$
at a stage
$x_{n} = x(k+1)_n$
at a stage
![]() $n \geq n_{k+1}$
. He continues doing so until the first stage, say
$n \geq n_{k+1}$
. He continues doing so until the first stage, say
![]() $n_{k+2}> n_{k+1}$
, that Player II makes a move
$n_{k+2}> n_{k+1}$
, that Player II makes a move
![]() $(v_{n_{k+2}},w_{n_{k+2}})$
such that
$(v_{n_{k+2}},w_{n_{k+2}})$
such that
![]() $|w_{n_{k+2}} - f(x(k+1))| < \epsilon $
. If no such stage occurs, then Player I goes on using the point
$|w_{n_{k+2}} - f(x(k+1))| < \epsilon $
. If no such stage occurs, then Player I goes on using the point
![]() $x(k+1)$
until the end of the game.
$x(k+1)$
until the end of the game.
We show that the strategy thus defined is winning.
Suppose first that only finitely many stages
![]() $n_{0},n_{1},\dots $
occur, the last one being
$n_{0},n_{1},\dots $
occur, the last one being
![]() $n_{k}$
. For concreteness, suppose that k is even. In this case Player I uses the point
$n_{k}$
. For concreteness, suppose that k is even. In this case Player I uses the point
![]() $x(k)$
to generate his moves until the end of the game. Moreover, there is no
$x(k)$
to generate his moves until the end of the game. Moreover, there is no
![]() $n> n_{k}$
such that
$n> n_{k}$
such that
![]() $|v_{n} - f(x(k))| < \epsilon $
. This implies that
$|v_{n} - f(x(k))| < \epsilon $
. This implies that
![]() $\limsup v_{n} \neq f(x(k))$
, and hence the run is won by Player I. Likewise, if the last one of the sequence
$\limsup v_{n} \neq f(x(k))$
, and hence the run is won by Player I. Likewise, if the last one of the sequence
![]() $n_{0},n_{1},\dots $
is the stage
$n_{0},n_{1},\dots $
is the stage
![]() $n_{k+1}$
where k is even, then Player I generates the point
$n_{k+1}$
where k is even, then Player I generates the point
![]() $x(k+1)$
, and there is no
$x(k+1)$
, and there is no
![]() $n> n_{k+1}$
such that
$n> n_{k+1}$
such that
![]() $|w_{n} - f(x(k+1))| < \epsilon $
. Therefore
$|w_{n} - f(x(k+1))| < \epsilon $
. Therefore
![]() $\liminf w_{n} \neq f(x(k+1))$
, and hence the run is won by Player I.
$\liminf w_{n} \neq f(x(k+1))$
, and hence the run is won by Player I.
Suppose that infinitely many stages
![]() $n_{0},n_{1},\dots $
occur. From the above definitions we get for each even
$n_{0},n_{1},\dots $
occur. From the above definitions we get for each even
![]() $k \in \mathbb {N}$
$k \in \mathbb {N}$
 $$ \begin{align*} v_{n_{k+1}} &> f(x(k)) - \epsilon\\ &> \alpha_{k} - 2\epsilon\\ &=(\alpha_{k} - \beta_{k+1}) + \beta_{k+1} - 2\epsilon\\ &\geq (\alpha_{k} - \beta_{k+1}) + f(x(k+1)) - 3\epsilon\\ &\geq (\alpha_{k} - \beta_{k+1}) + w_{n_{k+2}} - 4\epsilon. \end{align*} $$
$$ \begin{align*} v_{n_{k+1}} &> f(x(k)) - \epsilon\\ &> \alpha_{k} - 2\epsilon\\ &=(\alpha_{k} - \beta_{k+1}) + \beta_{k+1} - 2\epsilon\\ &\geq (\alpha_{k} - \beta_{k+1}) + f(x(k+1)) - 3\epsilon\\ &\geq (\alpha_{k} - \beta_{k+1}) + w_{n_{k+2}} - 4\epsilon. \end{align*} $$
Let
![]() $\alpha _{k+1} = \sup \{f(x):x \in C \cap O(s_{k+1})\}$
. Since the sequence
$\alpha _{k+1} = \sup \{f(x):x \in C \cap O(s_{k+1})\}$
. Since the sequence
![]() $s_{k+1}$
extends
$s_{k+1}$
extends
![]() $s_{k}$
, we have
$s_{k}$
, we have
![]() $\alpha _{k} \geq \alpha _{k+1}$
. By the assumption, the oscillation of
$\alpha _{k} \geq \alpha _{k+1}$
. By the assumption, the oscillation of
![]() $f|_{C}$
at the point
$f|_{C}$
at the point
![]() $x(k+1) \in C$
is at least
$x(k+1) \in C$
is at least
![]() $5\epsilon $
, hence
$5\epsilon $
, hence
![]() $\alpha _{k+1} - \beta _{k+1} \geq 5\epsilon $
. Combining these facts we obtain that for each even
$\alpha _{k+1} - \beta _{k+1} \geq 5\epsilon $
. Combining these facts we obtain that for each even
![]() $k \in \mathbb {N}$
it holds that
$k \in \mathbb {N}$
it holds that
![]() $v_{n_{k+1}} \geq w_{n_{k+2}} + \epsilon $
. This, however, means that
$v_{n_{k+1}} \geq w_{n_{k+2}} + \epsilon $
. This, however, means that
![]() $\limsup v_{n}> \liminf w_{n}$
, implying a win for Player I.
$\limsup v_{n}> \liminf w_{n}$
, implying a win for Player I.
Remark 4.3. The above construction of the winning strategy for Player I is similar to that in [Reference Kiss8]. In both cases Player I zooms in on a particular element of C until Player II triggers a switch to another element. The main difference is that here Player I undergoes two alternating types of switches: even switches are different from the odd ones. An odd switch, say
![]() $(k+1)$
st (where k is even) is triggered when Player II makes a move such that
$(k+1)$
st (where k is even) is triggered when Player II makes a move such that
![]() $v_{n}$
is close to
$v_{n}$
is close to
![]() $f(x(k))$
. Player I reacts by switching to a point
$f(x(k))$
. Player I reacts by switching to a point
![]() $x(k+1)$
with a low value of f. Even switches, say
$x(k+1)$
with a low value of f. Even switches, say
![]() $(k+2)$
nd, are triggered when Player II makes a move such that
$(k+2)$
nd, are triggered when Player II makes a move such that
![]() $w_{n}$
is close to
$w_{n}$
is close to
![]() $f(x(k+1))$
. Player I reacts by switching to a point
$f(x(k+1))$
. Player I reacts by switching to a point
![]() $x(k+2)$
of C with a high value of f.
$x(k+2)$
of C with a high value of f.
Theorem 4.4. Let
![]() $f : X \to \mathbb {R}$
be an arbitrary function. The game
$f : X \to \mathbb {R}$
be an arbitrary function. The game
![]() $\Gamma '(f)$
is determined.
$\Gamma '(f)$
is determined.
Proof If f is a function in Baire class 1, then Player II has a winning strategy by Lemma 4.1. Suppose that f is not a function in Baire class 1. Then (see [Reference Kuratowski9, Theorem 2 and Remark 1, p. 395]) there exists a non-empty closed set
![]() $K \subseteq X$
such that the set of discontinuity points of
$K \subseteq X$
such that the set of discontinuity points of
![]() $f|_{K}$
contains an open subset of K. Using the Baire category theorem and the arguments as in [Reference Kiss8, p. 9] one can show that there is a non-empty closed set
$f|_{K}$
contains an open subset of K. Using the Baire category theorem and the arguments as in [Reference Kiss8, p. 9] one can show that there is a non-empty closed set
![]() $C \subseteq K$
such that the oscillation of
$C \subseteq K$
such that the oscillation of
![]() $f|_{C}$
is bounded away from zero. The preceding lemma then implies that Player I has a winning strategy.
$f|_{C}$
is bounded away from zero. The preceding lemma then implies that Player I has a winning strategy.
Remark 4.5. It is not completely clear which results of the paper use the countability of A in an essential way. It seems to us that almost all results go through without the assumption that A is countable, and the only really problematic issues are the applications of the Hurewicz theorem and the Kechris–Louveau–Woodin theorem in the proofs of Theorems 3.6–3.8.
Acknowledgments
The first, third, fourth, and fifth authors were supported by the National Research, Development and Innovation Office—NKFIH, grant nos. 113047, 129211, and 124749. The third author was supported by the National Research, Development and Innovation Office—NKFIH, grant no. 128273. The fifth author was supported by the ÚNKP-19-3 New National Excellence Program of the Ministry for Innovation and Technology.