Design and analysis of a thick-panel origami-inspired soft crawling robot with multiple locomotion patterns

Abstract

Due to the flexibility obtained through both materials and structures, soft robots have wide potential applications in complicated internal and external environments. This paper presents a new soft crawling robot with multiple locomotion patterns that integrate inchworm motion and various turning motions. First, the conceptual design of the proposed robot is presented by introducing thick-panel origami into the synthesis of a crawling robot, resulting in a Waterbomb-structure-inspired hybrid mechanism. Second, all locomotion patterns of the robot are precisely described and analyzed by screw theory in an algebraic manner, which include inchworm motion, restricted planar motion, quantitative turning motion, and marginal exploration motion. Then, the output motion parameter for each locomotion pattern is analytically modeled as a function of the robotic dimensional parameters, and the robot can thus be designed and controlled in a customized way for the expected output motion. Finally, the theoretical analysis and derivations are validated by simulation and physical prototype building, which lay the foundations for the design and manufacture of small-scale soft crawling robots with precise output motions in a complex planar environment.

1. Introduction

The soft robot is composed of soft parts, which will not cause harmful stress [1] or damage to the task environment and objects when performing the motion and force transfer [2]. For this reason, soft robots, which have flexible body structures [3–5] and diverse motions [5–9], have the potential to perform tasks such as manipulation [10, 11] and transport [12, 13] within confined internal environments [14] as well as narrow external spaces [15]. In recent years, an increasing number of researchers have developed soft crawling robots [16–18] capable of executing various motions and being deployed across diverse work scenarios through exploration of new material properties and optimization of robot structures.

Soft robots built from new materials primarily utilize the feedback effect of the material itself to respond to various external stimuli, including electricity [19], heat [20], light [21], and chemical energy [22], enabling control over robot motions. For instance, Liwei Lin’s team utilized piezoelectric materials to develop a bionic, agile insect robot with exceptional mobility and agility [23]. Similarly, Shuang Wu and Yong Zhu employed thermo-responsive materials to devise a bidirectional crawling robot capable of multiple motion modes through a distributed and programmable heating strategy [24].

The design of soft robots through structure optimization involves integrating actuation strategies with robot structure to develop robots capable of executing one or more specific motions. Furthermore, the resultant robots can exhibit diverse motions efficiently. In contemporary research, origami structures [25–27] are widely employed in the design of soft robot structures. For example, Shuhei Miyashita and Daniela Rus have proposed a mobile robot that can self-fold into a 3D structure from a single planar material and is capable of walking, swimming, and performing some basic tasks [28]. Fuwen Hu and Chun Zhang utilized thermoplastic polyurethane as the material and adopted the rhombic dodecahedron origami structure to construct a soft multicellular robot with multimodal motions [29]. Origami robots impose structural constraints [30, 31] on robot motions through prescribed creases on the robot bodies. This allows the designed robots to realize ideal configuration transformations [32, 33] and execute the intended motions [34, 35] in collaboration with the actuation strategies. However, the motions of origami robots are also affected by the bending effect [36, 37] of planar sheet materials due to the material characteristics of origami. This makes robot motion unstable and challenges control.

Origami robots have attracted lots of attention and interest in both academia and industry in recent years. By processing two-dimensional materials, a moving, three-dimensional structure can be constructed using the crease of origami paper as a revolute joint. This resulted in the development of several folding structures with practical applications, including origami robots used in a variety of industries such as food packaging [38, 39], space exploration, micro- and nanostructure manufacture, and medical care. And thick-panel origami [40] developed as a branch of origami. The thick-panel origami structure considers the thickness of the panel and arranges creases on the top and bottom surfaces of the thick-panel material [41, 42] to make the obtained structure suitable for engineering applications [43, 44]. In this paper, the thick-panel origami structure is incorporated into the design of a soft crawling robot, and planar thin-panel material with prescribed creases is adhered to the corresponding soft material component, leading to the creases folding on the top and bottom surfaces of the soft material component. The thick-panel origami structure is integrated into the design of the soft crawling robot, and the body of the soft robot is composed of soft material components with thickness. The movement of the soft robot is accomplished by creases of thin sheet material attached to the soft material parts. This design method can simplify the motion design of a soft robot on the premise of retaining good environmental interaction ability.

Precise control and motion modeling of robots are always challenging when designing small-scale soft robots. By adopting techniques like anisotropic friction force and real-time excitation condition adjustment, small-scale robots made of hard materials can accomplish precise multimodal motions. For instance, Qing Lu created a multi-legged, high-speed moving microrobot that was 3D printed [45, 46]. The robot utilizes biologically inspired tilting legs to effectively manipulate the four motion modes of the millimeter robot: sticky, stick-slip, pure-slip, and jumping, with a step resolution of 2 μm in micromotion and a maximum movement speed of 800 mm/s in macromotion. In recent years, many research teams have been working to precisely predict and control the movements of soft robots, like the group led by Charlie C. L. Wang [47], who proposes a method for precise proprioception and real-time 3D shape reconstruction with low-cost sensors. Closed-loop control allows for accurate control and modeling of the robot, while sensor layout and actuator design enable machine learning [48] to model the 3D shape of the soft robot in real time. However, this control method needs to integrate a large number of sensors and is not suitable for small-scale soft robots. Small-scale soft robots comprising the material with exclusively low elastic inertia are difficult to accurately control [49] and model due to the continuum nonlinear deformation qualities [50] of the material. The precise control and motion design of a small-scale soft robot are always difficult points in its design. The planar sheets can be made less prone to bending by combining soft materials with origami. Instead of the high-energy nonlinear deformation of the soft material, the robot motion will primarily be generated by the low-energy crease folding [51] of the planar sheet. The difficulty of precise movement and motion control for the robot is reduced.

In rigid origami designs without thickness, the panel can be considered as a link [52, 53], and the crease can be regarded as a revolute joint [54]. In this paper, a soft, thick-panel 6R-Waterbomb [55–58] robot is designed. Here, motion [59] is primarily generated by the low-energy consumption of crease folding, which can be approximately regarded as a revolute joint. Furthermore, the components connecting the creases can be treated as links. In this way, the robot motion can be modeled as a cooperative motion of revolute joints with certain spatial relations [60, 61]. Specifically, the robot motion can be analyzed by modeling the robot structure in various configurations [62] as a hybrid mechanism [63] using screw theory [64–68]. This type of soft robot, which is based on the thick-panel origami structure, may in the future also use topology optimization [69, 70] to optimize the structure of the creases—which can be thought of as a flexure hinge [71, 72], and the soft material components—which can be thought of as beams [73], in order to enhance the structure’s rationality [74, 75]. The robot’s design may be optimized to enhance motion performance and environment adaptability in the future by including the selection of materials and body structures in the optimization range [76–78].

The research work presented in this paper contains the following:

1. 1. The Waterbomb thick-panel origami is adapted to design a soft crawling robot for complex planar environments.

2. 2. Motion modeling of the designed robot is carried out, and the feasible motion design of the robot is completed.

3. 3. The relationship between the output motions and the dimensional parameters of the robot is defined.

4. 4. The validity of the designed structure and motion is verified by simulation as well as physical model building.

The remainder of the paper is organized as follows: Section 2 introduces the design concept and main structure of the robot. Section 3 analyzes its feasible motions in different configurations and completes the motion design of the robot. The outputs generated by different motions of the robot are analyzed in Section 4. In Section 5, the validity of the designed structure and motions is verified through simulation and experiments. Finally, the conclusions are drawn in Section 6.

2. Concept design

The thick-panel Waterbomb is obtained by projecting the Waterbomb pattern onto the thick panel and arranging the creases on the top or bottom of the panel surfaces. Hereinafter, the red dashed lines and the blue solid lines represent valley and mountain creases, respectively. The folding path of the thick-panel Waterbomb is shown in Figure 1(a–d), and the kinematic relationships of its dihedral angles are

(1) \begin{align} \varphi _{2}=\varphi _{3}=\varphi _{5}=\varphi _{6}, \varphi _{1}=\varphi _{4}, \tan \frac{\varphi _{1}}{2}=\sqrt{2}\tan \frac{\varphi _{2}}{2} . \end{align}

In order to improve the adaptability of the robot in diverse motions and complex planar environments, the designed robot should have the ability to complete turning motions. As shown in Figure 1(a–d), the thick-panel Waterbomb structure can only be deformed in one path. The robot with the thick-panel Waterbomb structure cannot complete turning movements as the points M cannot rotate around the points N. To enable turning capability in the crawling robot, the offset valley crease on the thick-panel Waterbomb structure is replaced by a set of offset creases, which consists of a valley crease and two mountain creases. And the directions of the valley crease and mountain crease are parallel with the offset valley crease. The modification process of the Waterbomb structure is shown in Figure 1(c, e, f).

Figure 1. The structure based on Waterbomb thick-panel origami.

Figure 2. The robot’s manufacturing process and dimensional parameters.

Figure 1(f–h) shows the turning process of the modified thick-panel Waterbomb structure, that is, the rotation of points M around points N at a given distance d ₀. It can be observed that as the rotation amplitude gradually increases, there is a compression of the side offset crease set and a tension of the side offset crease set. When the offset crease set on the compression side is converted back into an offset valley crease and the center valley crease of the offset crease set on the tension side has a dihedral angle of 180°, both the thick-panel material component on the compression side and the planar panel material component arranged diagonally on the tension side constrain the robot’s turning motion. This prevents the points M from further increasing the rotational amplitude around the points N at the given distance d ₀, providing a structural constraint on the robot’s turning motion. The robot is considered to be in its “constrained state” when the Waterbomb structure imposes structural constraints on it.

By using the following two design methods: (1) combining soft material components with creased planar sheet material components and (2) setting offset crease sets, the designed robot has improved stiffness of the body, and the low-energy consumption of crease folding occurs instead of the high-energy consumption of planar sheet material bending and soft material deformation during the robot motion. The robot motion is mainly generated by the configuration transformation due to the designed crease folding, which reduces the unpredictable motion because of the insufficient stiffness of the planar sheet and the nonlinear deformation of the soft material. At the same time, structural constraints are provided for the turning motion of the robot, which are essential for subsequent motion design.

The robot manufacturing process is shown in Figure 2(a). The creases need to be prearranged on the planar sheet material part, and the dashed arrows indicate that the top and bottom surfaces are bonded. The initial state of the robot with all creases at a dihedral angle of 180° is shown in Figure 2(b). As shown in Figure 2(c), the part that contacts the planar environment and actuates the robot movement is named the leg, the part connected to the leg is the thorax, and the part connecting the two sides of the thorax is the dorsal. The two thorax and two dorsal parts of the designed robot, as seen in Figure 2, make up the thick-panel Waterbomb origami structure. In order to better reflect the advantages of this structural design, the robot designed in this paper is actuated by embedding permanent magnets in the robot leg. The internal permanent magnets are remotely actuated to change the anterior and posterior leg planar positions through external permanent magnets.

Each dimensional parameter in the robot design is defined as follows: a, leg length; b, adjacent parallel crease distance in the offset crease set; c, thickness of the dorsal part (spatial offset magnitude of the offset crease); d, thickness of the thorax; e, length of the lower part of the thorax; f, leg height; g, leg width; j, distance between the center of the posterior leg magnet and the front of the posterior leg and also the distance between the center of the anterior leg magnet and the rear of the anterior leg; k, distance between the left and right mountain creases in the offset crease set; and I, input variable, that is, the distance between the centers of anterior and posterior leg magnets.

3. Locomotion design

The inchworm, through the deformation of its flexible body and the “push–pull cycle” of the two pairs of legs, can perform linear and turning movements in a simple and efficient way. Like many robots with inchworm-like locomotion, the robot designed in this paper is powered by alternately actuating two leg parts that are in contact with the planar environment and can perform inchworm and turning locomotion by regulating the relative positions of the leg parts. The detailed motion analysis is as follows.

3.1. Inchworm motion

In the inchworm motion of the robot, the Waterbomb structure that determines the motion of the robot is shown in Figure 3(a). Due to the symmetrical design of the robot, the force and torque transmitted between the parts will be evenly distributed. And the dihedral angles of creases on both sides of the red dashed line will have the same value in Figure 3(b).

Figure 3. The Waterbomb structure in the inchworm motion.

Simplifying the offset crease set of the Waterbomb structure and abstracting the robot structure, resulting in a thick-panel Waterbomb mechanism as shown in Figure 3(c), the motion of the Waterbomb mechanism can be resolved by analyzing the dihedral angle of the thick-panel origami crease. To conduct the motion analysis explicitly, the thickness of the thick-panel Waterbomb is simplified and abstracted to a rigid origami Waterbomb structure without thickness, yielding a more simplified motion model in Figure 3(d). The creases and plates in Figure 3(d) can be abstracted into revolute joints and links using origami theory. Then, the equivalent kinematic model consisting of the revolute joint and the link can be obtained, that is, Figure 3(e). Based on this model, the overall inchworm motion of the robot can be designed and analyzed through screw theory.

Based on modeling the motion output of each crease on the robot body as a 6R mechanism, the robot inchworm motion can be equated to a (R + 2S+R)−PRP hybrid mechanism. And the anterior leg and the posterior leg alternately serve as fixed base and moving platform, as shown in Figure 4.

Figure 4. The mechanism schematic diagram during the inchworm motion.

In Figure 4, the directions of the revolute joint axes and the directions of the prismatic joints are indicated by $\boldsymbol{s}_{i}$ ( $i=1,2,3\ldots, \| \boldsymbol{s}_{i}\| =1$ ), and the positions of the revolute joints are labeled as A _i ( $i=1,2,3\ldots$ ). The reference coordinate system $O-xyz$ is set on the fixed base, the origin O is located on the center of the fixed base, the y-axis direction is along the straight line $OA_{9}$ , the z-axis is along the straight line $OA_{7}$ , the x-axis direction refers to the Cartesian coordinate system, and the directions of the x-axis, the y-axis, and the z-axis are represented by the unit vectors $\boldsymbol{s}_{x}, \boldsymbol{s}_{y}$ , and $\boldsymbol{s}_{z}$ , respectively. The point $O^{\prime}$ is located at the center of the moving platform. Hereinafter, the revolute joint i and prismatic joint i will be abbreviated as $R_{i}$ and $P_{i}$ ( $i=1,2,3\ldots$ ), and the position of each revolute joint relative to point O is indicated by $\boldsymbol{r}_{i}$ . The direction of the revolute joint axis and the direction of the prismatic joint are indicated by $\boldsymbol{s}_{i}$ ( $i=1,2,3\ldots, \| \boldsymbol{s}_{i}\| =1$ ). The labels of the revolute and prismatic joints are determined by the subscripts of their directions; that is, revolute joints are labeled from 1 to 9, while prismatic joints include only 10 and 11.

The sub-chain 1 is an R + 2S+R hybrid structure, where 2S is a parallel mechanism, abstracted from the Waterbomb structure in the robot. The outputs of $R_{1}$ and $R_{4}$ represent the angles of the planes on the left and right sides of the sheet material of the dorsal part, while those of $R_{7}$ and $R_{8}$ represent the angles of the creases connecting the thorax and the leg. The axis of each revolute joint is in the same direction as the direction of the crease. And the corresponding crease of $R_{i}$ is named Crease i. The $R_{7}$ and $R_{8}$ are always parallel to the x-axis direction, and the axes of $R_{1} R_{2} R_{3} R_{4} R_{5} R_{6}$ and $R_{9}$ intersect at point C, and the position of point C to point O is indicated by $\boldsymbol{r}_{C}$ .

The sub-chain 2, PRP, results from the interaction of its leg with the planar environment. The axis of $R_{9}$ is always parallel to the z-axis, and the directions of $P_{10}$ and $P_{11}$ are always parallel to the y-axis in this configuration.

The twist subspace of the R + 2S+R sub-chain can be obtained as

(2a) \begin{align} \boldsymbol{T}_{\alpha }& =\text{span} \left\{\begin{array}{c} \boldsymbol{s}_{x}\\ \boldsymbol{r}_{7}\times \boldsymbol{s}_{x} \end{array},\, \begin{array}{c} \boldsymbol{s}_{x}\\ \boldsymbol{r}_{C}\times \boldsymbol{s}_{x} \end{array},\, \begin{array}{c} \boldsymbol{s}_{y}\\ \boldsymbol{r}_{C}\times \boldsymbol{s}_{y} \end{array},\, \begin{array}{c} \boldsymbol{s}_{z}\\ \boldsymbol{r}_{C}\times \boldsymbol{s}_{z} \end{array},\, \begin{array}{c} \boldsymbol{s}_{x}\\ \boldsymbol{r}_{8}\times \boldsymbol{s}_{x} \end{array}\right\}\nonumber\\& = \text{span}\left\{\begin{array}{c} \boldsymbol{s}_{x}\\ \boldsymbol{r}_{C}\times \boldsymbol{s}_{x} \end{array},\, \begin{array}{c} \boldsymbol{s}_{y}\\ \boldsymbol{r}_{C}\times \boldsymbol{s}_{y} \end{array},\, \begin{array}{c} \boldsymbol{s}_{z}\\ \boldsymbol{r}_{C}\times \boldsymbol{s}_{z} \end{array},\, \begin{array}{c} \mathbf{0}\\ \boldsymbol{s}_{y} \end{array},\, \begin{array}{c} \mathbf{0}\\ \boldsymbol{s}_{z} \end{array}\right\} . \end{align}

The twist subspace of the PRP sub-chain can be defined as

(2b) \begin{align} \boldsymbol{T}_{\beta }=\text{span} \left\{\begin{array}{c} \mathbf{0}\\ \boldsymbol{s}_{y} \end{array},\, \begin{array}{c} \boldsymbol{s}_{z}\\ \boldsymbol{r}_{C}\times \boldsymbol{s}_{z} \end{array},\, \begin{array}{c} \mathbf{0}\\ \boldsymbol{s}_{y} \end{array}\right\} . \end{align}

It can be computed that the twist subspace for the (R + 2S+R)−PRP hybrid mechanism in Figure 4,

(2c) \begin{align} \boldsymbol{T}_{p}=\boldsymbol{T}_{\alpha }\cap \boldsymbol{T}_{\beta }=\text{span}\left\{\begin{array}{c} \boldsymbol{s}_{z}\\ \boldsymbol{r}_{C}\times \boldsymbol{s}_{z} \end{array},\, \begin{array}{c} \mathbf{0}\\ \boldsymbol{s}_{y} \end{array}\right\} . \end{align}

The specific details of the derivation process are shown in Appendix.

It is shown that the moving platform can realize translation in the y-axis direction relative to the fixed base and rotation around the axis whose direction is $\boldsymbol{s}_{z}$ and passes through point C.

The robot inchworm motion is conducted by continuously actuating the leg parts in the y-axis direction. First, keep the position of the anterior leg anchored, with the anterior leg as a fixed base and the posterior leg as a moving platform. The robot body will arch upward when the posterior leg is actuated to move linearly along the motion direction. Then, maintain the position of the posterior leg anchored, with the posterior leg as a fixed base and the anterior leg as a moving platform. Actuate the anterior leg to move linearly along the direction of motion to complete the inchworm motion. The robot’s inchworm motion process is shown in Figure 5(I–III).

Figure 5. The motion of the simulation model.

3.2. Turning motion

The structural modifications that enable the robot to perform turning motions are described in Section 2. The obtained robot is capable of executing turning motions progressively, categorized into three types: (1) restricted planar motion, (2) quantitative turning motion, and (3) marginal exploration motion.

Figure 6(a) exhibits the robot’s body structure during turning motion. Simplifying the offset crease set and the thickness of the thick panel as depicted in Figure 6(b), the Waterbomb structure is abstracted as the Waterbomb origami, with $\varphi _{1}\neq \varphi _{4}, \varphi _{2}\neq \varphi _{3}$ , and $\varphi _{5}\neq \varphi _{6}$ , as illustrated in Figure 6(c). Subsequently, the equivalent kinematic model of the Waterbomb structure is formulated by analyzing this rigid origami, as depicted in Figure 6(d). The robot’s turning motion in the unconstrained state can be equated to a (R + 2S+R)-PRP hybrid mechanism in Figure 7.

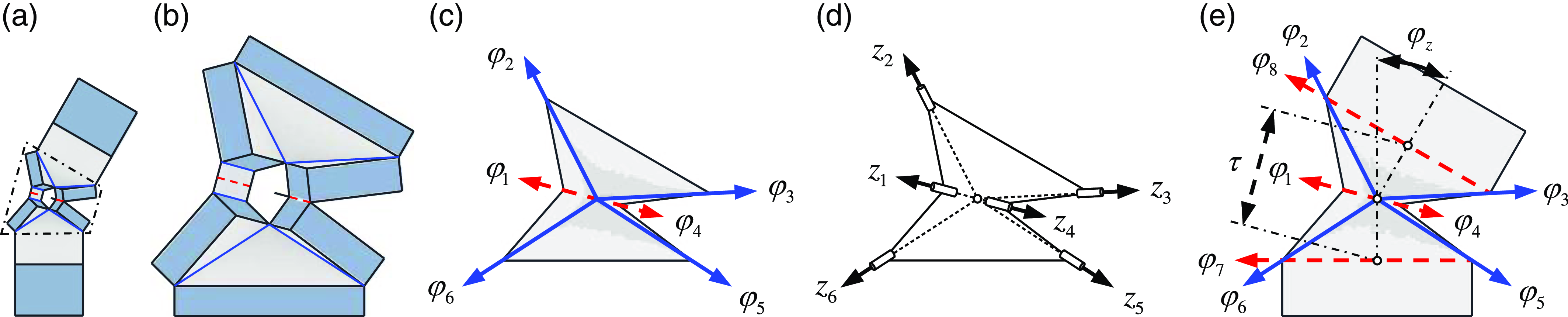
Figure 6. The Waterbomb structure in the turning motion.

Figure 7. The mechanism schematic diagram during the unconstrained turning motion.

In the R + 2S+R sub-chain shown in Figure 7, the axis of $R_{7}$ intersects with the axis of $R_{8}$ at point D, the position of point D relative to point O is indicated by $\boldsymbol{r}_{D}$ , and the direction of $P_{11}$ is perpendicular to the moving platform.

The constraint wrench subspace of the R + 2S+R sub-chain is computed as

(3a) \begin{align} \boldsymbol{W}_{\alpha }=\text{span}\left\{\begin{array}{c} \frac{\boldsymbol{r}_{D}-\boldsymbol{r}_{C}}{\left| \boldsymbol{r}_{D}-\boldsymbol{r}_{C}\right| }\\[3pt] \boldsymbol{r}_{C}\times \frac{\boldsymbol{r}_{D}-\boldsymbol{r}_{C}}{\left| \boldsymbol{r}_{D}-\boldsymbol{r}_{C}\right| } \end{array}\right\} . \end{align}

The constraint wrench subspace of the PRP sub-chain can be obtained as

(3b) \begin{align} \boldsymbol{W}_{\beta }=\text{span}\left\{\begin{array}{c} \mathbf{0}\\ \boldsymbol{s}_{y} \end{array},\, \begin{array}{c} \mathbf{0}\\ \boldsymbol{s}_{11} \end{array},\, \begin{array}{c} \boldsymbol{s}_{z}\\ \boldsymbol{r}_{C}\times \boldsymbol{s}_{z} \end{array}\right\} . \end{align}

By solving the reciprocal screw for the union of Eq. (3a) and Eq. (3b), the twist subspace for the (R + 2S+R)−PRP hybrid mechanism after turning is computed as

(3c) \begin{align} \boldsymbol{T}_{P}=\text{span}\left\{\begin{array}{c} \boldsymbol{s}_{z}\\ \boldsymbol{r}_{C}\times \boldsymbol{s}_{z} \end{array},\, \begin{array}{c} \mathbf{0}\\ \frac{\boldsymbol{r}_{8}-\boldsymbol{r}_{7}}{\left| \boldsymbol{r}_{8}-\boldsymbol{r}_{7}\right| } \end{array}\right\} . \end{align}

The specific details of the derivation process are shown in Appendix.

Analyzing the twist subspace and displacement manifold, it is revealed that the robot can realize translation along the line $OO^{\prime}$ and rotation around the axis whose direction is $\boldsymbol{s}_{z}$ and passes through point C during the turning motion.

3.2.1. Restricted plane motion

The analysis for the equivalent kinematic model reveals that the designed robot has two degrees of freedom (DoFs) during the unconstrained state. The anterior and posterior legs of the robot can achieve two DoFs relative movement within a restricted planar environment, as illustrated in Figure 5(III–V). And the turning amplitude can be computed by the relative positions of the centers of the anterior and posterior legs, as depicted in Figure 5(IV) and Eq. (4).

(4) \begin{align} \varphi _{z}=2\arctan \left(\frac{I_{x}}{I_{y}}\right) . \end{align}

3.2.2. Quantitative turning motion

When aiming the robot outputs a specific turning amplitude, the I that corresponds with the specific turning amplitude should be computed first. It is maintained that the magnet centers of the anterior and posterior legs have the calculated distance, while actuating the anterior leg continuously rotates around the center of the posterior leg. When the robot’s Waterbomb structure reaches the constrained state, the structure will constrain the robot, causing it to output the ideal rotation amplitude. The motion process is depicted in Figure 5(V–VII).

The robot motion in the constrained state can no longer be analyzed by the (R + 2S+R)-PRP hybrid mechanism but rather by the (R + 3R-4R+R)-PRP hybrid mechanism. The (R + 3R-4R+R)-PRP mechanism is illustrated in Figure 8.

Figure 8. The mechanism schematic diagram during the constrained turning motion.

In the R + 3R-4R+R sub-chain depicted in Figure 8, the intersection of the axes of $R_{2}$ and $R_{6}$ is point A, and point B is identified as the intersection of the $R_{3}$ axis and $R_{5}$ axis; the position of points A and B relative to point O is indicated by $\boldsymbol{r}_{A}$ and $\boldsymbol{r}_{B}$ . The $R_{4}$ in Figure 4 and Figure 7 has been reduced to three parallel revolute joints labeled as $4^{^{\prime}}, 4^{\prime\prime}$ , and $4^{\prime\prime\prime}$ . The axis of $R_{{4^{\prime\prime\prime}}}$ lies in the plane that is determined by the axes of $R_{{4^{^{\prime}}}}$ and $R_{{4^{\prime\prime}}}$ , which is parallel to and equidistant from them, maintaining a rotational angle of 180°, represented as a rigid body in the model.

The constraint wrench subspace for the 3R-chain is

(5a) \begin{align} \boldsymbol{W}_{1}=\text{span}\left\{\begin{array}{c} \boldsymbol{s}_{1}\\ \boldsymbol{r}_{A}\times \boldsymbol{s}_{1} \end{array},\, \begin{array}{c} \boldsymbol{s}_{a}\\ \boldsymbol{r}_{A}\times \boldsymbol{s}_{a} \end{array},\, \begin{array}{c} \boldsymbol{s}_{b}\\ \boldsymbol{r}_{A}\times \boldsymbol{s}_{b}+h_{b}\boldsymbol{s}_{b} \end{array}\right\}, \end{align}

where $(\boldsymbol{s}_{a};\, \boldsymbol{r}_{A}\times \boldsymbol{s}_{a})$ represents an arbitrary straight line lying within the plane defined by axes $(\boldsymbol{s}_{1};\, \boldsymbol{r}_{1}\times \boldsymbol{s}_{1})$ and $(\boldsymbol{s}_{4};\, \boldsymbol{r}^{\prime\prime\prime}_{4}\times \boldsymbol{s}_{4})$ and $\boldsymbol{s}_{a}\neq \boldsymbol{s}_{1}$ . And it is set that $\boldsymbol{s}_{a}=(\boldsymbol{r}_{1}-\boldsymbol{r}^{\prime\prime\prime}_{4})/| \boldsymbol{r}_{1}-\boldsymbol{r}^{\prime\prime\prime}_{4}|$ and $h_{b}=\frac{-\boldsymbol{s}_{1}^{\mathrm{T}}\left(\boldsymbol{r}_{A}\times \boldsymbol{s}_{b}\right)-\boldsymbol{s}_{b}^{\mathrm{T}}\left(\boldsymbol{r}_{\mathrm{1}}\times \boldsymbol{s}_{\mathrm{1}}\right)}{\boldsymbol{s}_{1}^{\mathrm{T}}\boldsymbol{s}_{b}}$ .

The constraint wrench subspace of the 4R-chain is

(5b) \begin{align} \boldsymbol{W}_{2}=\text{span}\left\{\begin{array}{c} \boldsymbol{s}_{4}\\ \boldsymbol{r}_{B}\times \boldsymbol{s}_{4} \end{array},\, \begin{array}{c} \boldsymbol{s}_{c}\\ \boldsymbol{r}_{B}\times \boldsymbol{s}_{c}+h_{d}\boldsymbol{s}_{d} \end{array}\right\}=\text{span}\left\{\begin{array}{c} \boldsymbol{s}_{4}\\ \boldsymbol{r}_{B}\times \boldsymbol{s}_{4} \end{array},\, \begin{array}{c} \boldsymbol{s}_{c}\\ \left(\boldsymbol{r}_{B}-h_{d}\left(\boldsymbol{s}_{d}\times \boldsymbol{s}_{c}\right)\right)\times \boldsymbol{s}_{c}+h_{c}\boldsymbol{s}_{c} \end{array}\right\}, \end{align}

where $h_{c}=h_{d}\boldsymbol{s}_{d}^{\mathrm{T}}\boldsymbol{s}_{c}$ .

The constraint wrench subspaces of the 3R−4R structure and the PRP sub-chain are computed as

(5c) \begin{align} \boldsymbol{W}_{\alpha }=\text{span}\left\{\begin{array}{c} \left(\boldsymbol{s}_{1}\times \boldsymbol{s}_{4}\right)\times \boldsymbol{s}_{z}\\ \boldsymbol{r}_{D}\times \left(\left(\boldsymbol{s}_{1}\times \boldsymbol{s}_{4}\right)\times \boldsymbol{s}_{z}\right) \end{array},\, \begin{array}{c} \mathbf{0}\\ \boldsymbol{s}_{z} \end{array},\, \begin{array}{c} \boldsymbol{s}_{z}\\ \boldsymbol{r}_{D}\times \boldsymbol{s}_{z} \end{array}\right\}, \boldsymbol{W}_{\beta }=\text{span}\left\{\begin{array}{c} \mathbf{0}\\ \boldsymbol{s}_{y} \end{array},\, \begin{array}{c} \mathbf{0}\\ \boldsymbol{s}_{11} \end{array},\, \begin{array}{c} \boldsymbol{s}_{z}\\ \boldsymbol{r}_{9}\times \boldsymbol{s}_{z} \end{array}\right\} . \end{align}

Finally, the twist subspace of the (R + 3R−4R+R)−PRP hybrid mechanism is computed as

(5d) \begin{align} \boldsymbol{T}_{p}=\left\{\begin{array}{c} \mathbf{0}\\ \left(\left(\boldsymbol{s}_{1}\times \boldsymbol{s}_{4}\right)\times \boldsymbol{s}_{z}\right)\times \boldsymbol{s}_{z} \end{array}\right\}=\left\{\begin{array}{c} \mathbf{0}\\ \boldsymbol{s}_{1}\times \boldsymbol{s}_{4} \end{array}\right\} . \end{align}

The specific details of the derivation process are shown in Appendix.

It is demonstrated that in the constrained state, the robot has only one DoF. The I corresponds to the amplitude of the robot’s turning in the constraint state.

3.2.3. Marginal exploration motion

In the case that the robot reaches the constrained state but fails to turn to the intended degree, the I can be adjusted to control the turning amplitude along a fixed trajectory while still keeping the constrained state. The motion process is illustrated in Figure 5(VII–IX).

4. Motion output

The robot motion is achieved through configuration transformation, which originates from the folding of creases. The dihedral angle of the creases can be used to calculate the motion output of the robot.

4.1. Inchworm motion output

Based on the analysis of the 6R mechanism, the relationship among the outputs of the creases on the robot’s body during the inchworm motion is obtained as

(6a) \begin{align} \varphi _{2}=\varphi _{3}=\varphi _{5}=\varphi _{6}, \varphi _{1}=\varphi _{4}, \tan \frac{\varphi _{1}}{2}=\sqrt{2}\tan \frac{\varphi _{2}}{2}, \varphi _{7}=\varphi _{8}, \varphi _{7}=\frac{\pi +\varphi _{1}}{2} . \end{align}

Three output variables are produced by the inchworm motion of the robot, as shown in Figure 9(a): body height (H), body width (W), and body length (L).

Figure 9. The robot’s motion outputs.

The H is dictated by the outputs of Creases 7 and 8,

(6b) \begin{align} H=\left(\frac{a}{2}+e\right)\cdot \sin \left(\varphi _{7}\right)+d\cdot \sin \left(\varphi _{7}-\frac{\pi }{2}\right)+f, \end{align}

and the maximum value is $H_{h}=\sqrt{d^{2}+(0.5a+e)^{2}}+f$ .

The W is determined by the outputs of Crease 2, 3, 5, and 6,

(6c) \begin{align} W=\sqrt{2}\cdot c\cdot \sin \left(\varphi _{2}\right)+a, \end{align}

and the maximum value is $W_{h}=\sqrt{2}\cdot c+a$ .

It is difficult to analyze the synchronous dihedral angle of each crease because of the offset crease sets. By assuming a value of k, the L can be calculated as

(6d) \begin{align} L=2\cdot c\cdot \sin \left(\frac{180-\varphi _{1}}{2}\right)+2\cdot \left(e+\frac{a}{2}\right)\cdot \cos \left(\frac{\varphi _{1}-\pi }{2}\right)+k+2\cdot g . \end{align}

Consequently, the input for the inchworm motion of this robot is

(6e) \begin{align} I=L+2\cdot \left(j-g\right) . \end{align}

When the robot tends to the maximum L, the dihedral angles of center creases in offset crease sets are close to 180°. In this configuration, $k=2b$ . The maximum of L is computed by

(6f) \begin{align} L=2\cdot c\cdot \sin \left(\frac{180-\varphi _{1}}{2}\right)+2\cdot \left(e+\frac{a}{2}\right)\cdot \cos \left(\frac{\varphi _{1}-\pi }{2}\right)+2\cdot b+2\cdot g . \end{align}

4.2. Turning motion output

Since the robot has two degrees of freedom in the turning configuration, as shown in Figure 7, figuring out the position and direction of the anterior leg relative to the posterior leg requires information of two motion parameters. To establish the relationship between each crease dihedral angle and the output of turning motion, the robot structure is simplified to the rigid origami depicted in Figure 6(e). The variables $\tau$ and $\varphi _{z}$ are assigned to represent the two DoFs associated with translational and rotational motion, respectively.

The specific relationships between the dihedral angles are shown in Appendix.

In the robot turning motion, the motion outputs include the H, W, and L, as well as the turning amplitude ( $\varphi _{z}$ ), and the details are illustrated in Figure 9(b).

The H of the turning motion can also be dictated by the outputs of Creases 7 and 8,

(7a) \begin{align} H=\left(\frac{a}{2}+e\right)\cdot \sin \left(\varphi _{7}\right)+d\cdot \sin \left(\varphi _{7}-\frac{\pi }{2}\right)+f, \end{align}

and $H_{h}=\sqrt{d^{2}+\left(\frac{a}{2}+e\right)^{2}}+f$ .

The W is determined by the outputs of Creases 2, 3, 5, and 6, as

(7b) \begin{align} W=\frac{\sqrt{2}}{2}\cdot c\cdot \sin \left(\varphi _{2}\right)+\frac{\sqrt{2}}{2}\cdot c\cdot \sin \left(\varphi _{3}\right)+a . \end{align}

The L is defined as the distance between the center point in front of the anterior leg and the center point behind the posterior leg during the turning motion. The equation describing the relationship between L and $\varphi _{z}$ as

(7c) \begin{align} L=2\cdot c\cdot \sin \left(\frac{180-\varphi _{4}}{2}\right)+2\cdot \cos \frac{\varphi _{z}}{2}\cdot \left(\cos \varphi _{7}\cdot \left(e+\frac{a}{2}\right)+g\right)+k, \end{align}

where both k and $\varphi _{4}$ are the corresponding outputs of the tension side.

The input variable is computed as

(7d) \begin{align} I=2\cdot c\cdot \sin \left(\frac{180-\varphi _{4}}{2}\right)+2\cdot \cos \frac{\varphi _{z}}{2}\cdot \left(\cos \varphi _{7}\cdot \left(e+\frac{a}{2}\right)+j\right)+k . \end{align}

As illustrated in Figure 9(b), the robot’s motion in the constrained state can be characterized as a specific turning motion state. In this state, the H, W, L, and $\varphi _{z}$ are calculated using the same equation as the turning motion, but with two conditions,

(7e) \begin{align} \tau =\frac{2\cdot a\cdot b}{4\cdot c}\cdot \sqrt{\frac{-16\cdot c^{2}\cdot \sin ^{2}\left(\frac{\varphi _{z}}{2}\right)-4\cdot b^{2}+16\cdot c^{2}}{16\cdot c^{2}\cdot \sin ^{2}\left(\frac{\varphi _{z}}{2}\right)+4\cdot b^{2}}}, k=2\cdot b . \end{align}

If either $\varphi _{z}$ or I is known, the corresponding I and $\varphi _{z}$ values, along with the dihedral angle of each crease on the body and the output parameter, can be determined using Eq. (7d). The output of the anterior leg relative to the posterior leg in the constrained state is a fixed trajectory. In a specific motion design of the robot, this trajectory is determined by the five design parameters of the robot body, that is, a, b, c, e, and j. By adjusting the specific values of these parameters, the ideal outputs of the motion in the constrained state can be customized.

The robot design allows for the creation of robots tailored to various target environments by adjusting output motions.

5. Simulations and validation

5.1. Verified by simulation

To verify the feasibility of the designed motion and the correctness of the equivalent kinematic model, the robot’s motion is simulated using CAD software. During the validation, as shown in Figs. 10–12, the right-side schematics show the rigid model of the design robot structure in motion. The schematics on the left are the mechanism model for the motion of the robot analyzed above. The parameter ratio of the rigid model on the right side is a: b: c: d: e: f: g = 6: 0.5: 1.08: 1.2: 4.5: 2.25: 4.5. The mechanism model has to match the rigid model’s a: e or a: b: c: e ratio, as can be seen on the left side of Figs. 10(a), 11(a), and 12(a). The above kinematic analysis may be demonstrated to be reliable if the rigid model and the mechanism model generate the same outcome when given the same input.

Figure 10. (a) Comparison of mechanism model and simulation model during the inchworm motion. (b–d) The inchworm motion process.

Figure 11. (a) Comparison of mechanism model and simulation model during the unconstrained turning motion. (b–d) The restricted planar motion process.

The output of $R_{7}$ in the mechanism model matches Crease 7 output in the simulation model when it comes to the simulation of inchworm motion. It is confirmed that the dihedral angles of the remaining creases and the output of the rest revolute joints are consistent. The verification process is shown in Figure 10, and specific data are presented in Table I.

In Table I, the angle formed by the dorsal part’s left and right planar sheets is set as Crease 2. Table I analysis indicates that the dihedral angles of Creases 1, 2, and 7 increase with an increase in L, ultimately reaching an extreme value that is constrained by the body parameters.

Table I. The table of revolute joint output and crease dihedral angle in inchworm motion.

Figure 12. (a) Comparison of mechanism model and simulation model during the constrained turning motion. (b–d) The marginal exploration motion process.

During the simulation of turning motion in the unconstrained state, the output of the $R_{7}$ is aligned with Crease 7 output, and the output of the $R_{9}$ is keeping with the turning amplitude of the simulation model. Subsequently, the alignment of the remaining revolute joint outputs with the crease outputs is verified, as detailed in Figure 11 and Table II.

Table II. The table of revolute joint output and crease dihedral angle in restricted planar motion.

The anterior leg exhibits flexible turning motion relative to the posterior leg within the black curve during the validation process, as depicted in Figure 11. And the black curve represents the trajectory of the center of the anterior leg’s upper surface in the constrained state.

The output of $R_{7}$ is adjusted to fit the dihedral angle of Crease 7 while simulating the marginal exploration motion. The alignment between the revolute joint output and the crease outputs is verified, as depicted in Figure 12 and Table III.

Table III. The table of revolute joint output and crease dihedral angle in marginal exploration motion.

Table III analysis shows that the dihedral angles of Creases 1, 2, 3, and 4 decrease with decreasing anterior–posterior leg distance, while the robot’s turning amplitude increases. As Figure 12(d) illustrates, the maximum turning amplitude in the constrained condition occurs when the output of the reacquired offset valley crease becomes 0°.

5.2. Verified by physical model

The large-scale physical model was fabricated using thick-panel material and planar sheet material, and the designed motions were then physically validated. The motion process of the physical model in the verification process is consistent with Figure 5, and the motion validation process is depicted in Figure 13.

Figure 13. The motion of the physical model.

5.3. Verified by prototype

A prototype is fabricated and tested for the desired motion based on the designed structure. Regarding material selection, PP synthetic paper with a thickness of 0.08 mm was utilized for planar sheet components, and SORTA-Clear™ 40 was employed for thick-panel components. The PP synthetic paper was chosen as the plane material because of its waterproof, abrasion-resistant, tear- and bend-resistant properties. The reason for choosing SORTA-Clear™ 40 as the material for thick panels is its high modulus of elasticity among silicone materials. The robot settings for the test were a = 6 mm, b = 0.5 mm, c = 1 mm, d = 1.2 mm, e = 3 mm, f = 4 mm, and j = 2.5 mm, and the driving and leg magnets are NdFeB42 with a size of 3 × 3 × 3 mm. The soft material parts were obtained through the mold reversal step, while the planar sheet material parts were obtained by cutting and folding.

Figure 14 displays the prototype and the control mechanism of the prototype. The displacement curve of the magnet when the driving magnet completes the marginal exploratory movement in a plane 6 mm vertical from the leg magnet’s center is shown by the red line in the picture. The red line is obtained by repeating the quantitative rotational motion. After the theoretical marginal exploration motion is finished, the curve of the front leg’s center is shown by the black dashed line. The robot can do the restricted planar motion when the driving magnet travels within the red line range and in a plane that is 6 mm vertical from the leg magnet’s center. The robot completes the quantitative turning motion when the driving magnet reaches the position indicated by the red line.

A sodium-calcium glass table served as the test motion for two different types of testing on the robot’s mobility capability. In the first experiment, the inchworm motion was examined. The maximum stride length L of the prototype was 23.2 mm, based on the parameters of the prototype and the calculation mentioned above. On this basis, the maximum step size of the prototype was tested 10 times, and the average result of the trials was 23.18 mm. And the speed of the prototype is about 4.6 mm/s, or 0.2 body/s. In experiment two, the rotation amplitude of the magnet center of the anterior and posterior legs was examined when it reached the constrained states at five different distances, and the experiment was repeated 10 times to assess the quantitative turning motion. Less than 0.5° separated the predicted turning amplitude from the actual turning amplitude. The tested three performance metrics are detailed in Table IV.

Table IV. The table of prototype performance.

Figure 14. The control mechanism of designed robot.

This section begins by comparing the simulation model with the mechanism model to demonstrate that the designed robot structure and motion are feasible in theory. Then, by building the physical model and prototype, it is shown that the robot structure’s actual mobility agrees with the outcomes of the simulation. Through the verification of the simulation model, the physical model, and the prototype, it is finally proved that the method of designing the crawling robot through the mechanism theory in this paper is correct. This lays the foundation for the development of crawling robots with precise output motions.

6. Conclusions

A new soft crawling robot with multiple locomotion patterns is presented in this paper. Through the design and analysis of the proposed robot, the following conclusions are drawn:

1. 1. The thick-panel origami is integrated into the design of a soft crawling robot for the first time. By locating creases on the surfaces of soft material, the bending effect of the thin panel is decreased. The robotic locomotion is archived by crease folding.

2. 2. In order to make the designed robot applicable for crawling in a complicated planar environment, the offset valley creases in the thick-panel Waterbomb origami are replaced by offset crease sets.

3. 3. Considering the structural equivalence between the robot and the corresponding hybrid mechanism, each locomotion pattern of the robot is analytically modeled by screw subspace. In this way, an approach for precisely describing the soft robot’s locomotion is put forward.

4. 4. The algebraic mapping between the output motions and the dimensional parameters of the robot is formulated. This enables the output motions to be arbitrarily customized to some extent by adjusting the robotic dimensional parameters.

In this paper, a single part of the Waterbomb thick-panel origami structure has been used to design a crawling soft robot. The origami pattern is a treasure trove, and a large number of origami patterns have the potential to be thickened and applied to soft robot design. And, to develop soft robots based on thick-panel origami structures with more intricate motion characteristics, it is also feasible to combine several thick-panel origami structures. The research work in this paper lays theoretical foundations for the design and manufacture of small-scale soft robots based upon the thick-panel origami structure.