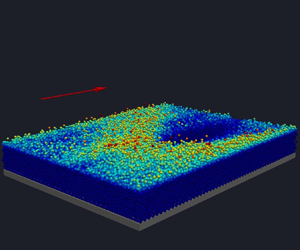
1. Introduction
Sediment beds under streaming water bodies often exhibit characteristic bedforms which can significantly affect the transport properties of the flow. Among these various bedforms, transverse bedforms are usually classified as ripples, dunes or antidunes (Yalin Reference Yalin1977). Ripples and dunes both exhibit a roughly triangular shape with a gentle slope on the upstream surface and a steeper downstream face, the latter approximately inclined at the angle of repose (Best Reference Best2005). However, these two bedforms differ in their scaling properties: while ripples are small compared to the fluid height and thus their wavelength is believed to scale with the particle diameter, the height of dunes is large enough to distinctly modify the flow field over the entire flow depth. As a consequence, the amplitude of dunes should scale with the fluid height (Engelund & Fredsoe Reference Engelund and Fredsoe1982). In contrast to the remaining bedform types, antidunes exhibit a symmetric cross-section and they can, depending on the hydraulic conditions, travel in the upstream or the downstream direction. Antidunes can only form in free-surface flows, whereas ripples and dunes can form in configurations without a free surface as well, such as pipe flows (see e.g. Ouriemi, Aussillous & Guazzelli Reference Ouriemi, Aussillous and Guazzelli2009) or closed-conduit flows (see e.g. Coleman, Fedele & Garcia Reference Coleman, Fedele and Garcia2003; Cardona Florez& Franklin Reference Cardona Florez and Franklin2016).
The origin of these transverse bedforms has been found to be an instability process in which an initially flat sediment bed deforms after an initial perturbation in the flow system, leading to the formation of transverse patterns (Yalin Reference Yalin1977). Inglis (Reference Inglis1949) proposed that inhomogeneities of the sediment bed such as small particle agglomerations could act as initial perturbations that trigger subsequent bedform evolution. In a more recent paper, Coleman & Melville (Reference Coleman and Melville1996) proposed an instability process originating in an isolated random pileup that grows with time and, once it has reached a critical height of approximately 3–4 times the particle diameter ![]() $D$, induces the generation of further pileups downstream. Coleman & Nikora (Reference Coleman and Nikora2009, Reference Coleman and Nikora2011) describe the formation of the initial bedforms as a two-stage formation process. In a first stage, random sediment patches with a typical length of (7–15)
$D$, induces the generation of further pileups downstream. Coleman & Nikora (Reference Coleman and Nikora2009, Reference Coleman and Nikora2011) describe the formation of the initial bedforms as a two-stage formation process. In a first stage, random sediment patches with a typical length of (7–15)![]() $D$ interact on an active (but still planar) sediment bed due to sediment transport events that are believed to be related to coherent turbulent structures. Once the height of these initial random patches exceeds some threshold height, the initial disturbance stabilizes by agglomerating sediment particles, with the consequence that further downstream regular patterns of sand-wavelets form. Venditti, Church & Bennett (Reference Venditti, Church and Bennett2005) observed different modes of bedform initiation in their experiments depending on the flow rate and, consequently, on the Reynolds and Froude number. At lower flow rates, local defects are seen to initiate a similar formation cycle as that described by Coleman & Melville (Reference Coleman and Melville1996), whereas at higher flow rates, the authors observed patterns to spontaneously evolve over the entire bed, leading to a regular ‘cross-hatch pattern’.
$D$ interact on an active (but still planar) sediment bed due to sediment transport events that are believed to be related to coherent turbulent structures. Once the height of these initial random patches exceeds some threshold height, the initial disturbance stabilizes by agglomerating sediment particles, with the consequence that further downstream regular patterns of sand-wavelets form. Venditti, Church & Bennett (Reference Venditti, Church and Bennett2005) observed different modes of bedform initiation in their experiments depending on the flow rate and, consequently, on the Reynolds and Froude number. At lower flow rates, local defects are seen to initiate a similar formation cycle as that described by Coleman & Melville (Reference Coleman and Melville1996), whereas at higher flow rates, the authors observed patterns to spontaneously evolve over the entire bed, leading to a regular ‘cross-hatch pattern’.
Unfortunately, up to the present date, accurate measurements of the initial bedform dimensions remain challenging. On the one hand, this is due to the very short time window in which the initial bedform evolution can be observed, and, on the other hand, due to the small height of the initial patterns of only a few particle diameters which makes them hard to detect. It is for this reason that most of the experimental studies in the last decades have focused on the description of fully developed patterns in the equilibrium state (cf. Yalin Reference Yalin1985; Lapotre, Lamb & McElroy Reference Lapotre, Lamb and McElroy2017), where the wavelength of the initial bedforms is typically much larger than in the initial phase (Langlois & Valance Reference Langlois and Valance2007). On the other hand, only a small number of experimentalists were able to quantitatively describe the wavelength of the initial bedforms. In turbulent open channel flow, Coleman & Melville (Reference Coleman and Melville1996) and Coleman & Nikora (Reference Coleman and Nikora2009) observed the initial wavelength to scale mainly with the sediment size in terms of the median grain size and to be rather unaffected by the flow conditions. Similar observations were made by Coleman et al. (Reference Coleman, Fedele and Garcia2003) in turbulent closed-conduit flows as well as by Coleman & Eling (Reference Coleman and Eling2000) in laminar open channel flows, the latter indicating in particular that the formation of initial bedforms is not restricted to the turbulent regime and the accompanying turbulent bursts, as earlier suggested by Raudkivi (Reference Raudkivi1997). Similarly, Langlois & Valance (Reference Langlois and Valance2007) and Cardona Florez & Franklin (Reference Cardona Florez and Franklin2016) both report under turbulent channel flow conditions that the initial wavelength depends mainly on the particle diameter, while the influence of the shear velocity and the flow conditions is rather weak. Ouriemi et al. (Reference Ouriemi, Aussillous and Guazzelli2009), on the contrary, measured initial wavelengths of the order of the fluid height in pipe flows, while Franklin (Reference Franklin2008) observed a dependence of the initial wavelength on both the particle diameter and the shear velocity in experimental measurements of turbulent closed-conduit flows.
In theoretical studies based on linear stability analysis, the flow system is usually described by a simplified model for the driving flow (such as Reynolds-averaged Navier–Stokes (RANS) models or potential flow solutions) combined with a sediment bed continuity equation for the evolution of the bed (see e.g. Kennedy Reference Kennedy1963, Reference Kennedy1969; Charru Reference Charru2006). In order to close the system of equations, a formulation for the particle flux is required. In most stability analyses, it is assumed that the particle flux and the local bed shear stress are in phase, which allows then to express the particle flux as a function of the local bed shear stress (Charru, Andreotti& Claudin Reference Charru, Andreotti and Claudin2013). In recent studies, this assumption has been removed and additional relaxation equations are used to take into account a possible phase lag between both quantities (Charru Reference Charru2006). A linear stability analysis is then performed in order to determine regions of instability in the parameter space as well as the most amplified wavelength for a given flow configuration. During the past decades, a large number of stability analyses for different flow configurations including different stabilizing and destabilizing effects has been presented for turbulent (see e.g. Richards Reference Richards1980; Sumer & Bakioglu Reference Sumer and Bakioglu1984; Colombini Reference Colombini2004; Fourriere, Claudin & Andreotti Reference Fourriere, Claudin and Andreotti2010; Colombini & Stocchino Reference Colombini and Stocchino2011) as well as for laminar flows (see e.g. Charru & Mouilleron-Arnould Reference Charru and Mouilleron-Arnould2002; Charru & Hinch Reference Charru and Hinch2006). A detailed overview of the different approaches used in linear stability analysis can be found in the reviews of Engelund & Fredsoe (Reference Engelund and Fredsoe1982), Seminara (Reference Seminara2010) and Charru et al. (Reference Charru, Andreotti and Claudin2013). Recently, Zgheib & Balachandar (Reference Zgheib and Balachandar2019) have presented a combined numerical–theoretical stability analysis, in which the bed shear stress for the linear stability analysis is computed by means of direct numerical simulations (DNS) in which the sediment bed is represented in a continuous and impermeable fashion.
However, despite an increasing complexity of the used models, the wavelengths predicted by most linear stability analyses still differ by more than one order of magnitude from the wavelengths observed in experiments (Langlois & Valance Reference Langlois and Valance2007; Ouriemi et al. Reference Ouriemi, Aussillous and Guazzelli2009). Furthermore, the observations concerning the scaling of the initial wavelengths differ markedly between the different studies. For instance, Fourriere et al. (Reference Fourriere, Claudin and Andreotti2010) found a single region with unstable wavelengths independent of the fluid height, leading them to the conclusion that only ripples can form directly from a flat bed, while dunes develop by a ripple coarsening processes only. Colombini & Stocchino (Reference Colombini and Stocchino2011), in contrast, observed two separate regions of instability with most amplified wavelengths of the size of the fluid height and of the particle diameter, respectively, which suggests that either ripples or dunes may form out of the same instability mechanism.
It should be kept in mind that the validity of linear stability investigations is limited to the very first instances of sediment bed evolution (Coleman & Melville Reference Coleman and Melville1996), i.e. the theory is not able to predict the bedform dimensions correctly, once nonlinear effects become dominant. In more recent studies, thus, weakly nonlinear analyses have been presented (e.g. Colombini & Stocchino Reference Colombini and Stocchino2008) to take into account also nonlinear effects.
In recent years an alternative method for the investigation of sediment transport in its early stages has become available in the form of DNS featuring fully resolved particles, which allow to resolve all relevant flow scales even below the particle length scale (e.g. Kidanemariam & Uhlmann Reference Kidanemariam and Uhlmann2014a,Reference Kidanemariam and Uhlmannb; Vowinckel, Kempe & Fröhlich Reference Vowinckel, Kempe and Fröhlich2014; Derksen Reference Derksen2015; Kidanemariam & Uhlmann Reference Kidanemariam and Uhlmann2017; Vowinckel et al. Reference Vowinckel, Nikora, Kempe and Fröhlich2017; Mazzuoli, Kidanemariam & Uhlmann Reference Mazzuoli, Kidanemariam and Uhlmann2019). In a set of numerical experiments, Kidanemariam & Uhlmann (Reference Kidanemariam and Uhlmann2017) (henceforth denoted KU2017) have recently determined a lower bound for the minimal unstable wavelength, ![]() $\lambda _{th}$, by reducing the streamwise domain length
$\lambda _{th}$, by reducing the streamwise domain length ![]() $L_x$ successively in a comparable concept as the minimal flow unit of Jiménez & Moin (Reference Jiménez and Moin1991). It was observed that, below a threshold
$L_x$ successively in a comparable concept as the minimal flow unit of Jiménez & Moin (Reference Jiménez and Moin1991). It was observed that, below a threshold ![]() $L_x = \lambda _{th}$, the formation of transverse bedforms is effectively hindered and a perturbed bed remains stable as a consequence of the limited domain size, even though the conditions would otherwise allow the bed to become unstable. For the considered parameter values, KU2017 found
$L_x = \lambda _{th}$, the formation of transverse bedforms is effectively hindered and a perturbed bed remains stable as a consequence of the limited domain size, even though the conditions would otherwise allow the bed to become unstable. For the considered parameter values, KU2017 found ![]() $\lambda _{th}/D$ to be in the range 75–100, which is equivalent to a range of
$\lambda _{th}/D$ to be in the range 75–100, which is equivalent to a range of ![]() $\lambda _{th}/H_f = 3\text {-}4$ in their cases, where
$\lambda _{th}/H_f = 3\text {-}4$ in their cases, where ![]() $H_f$ denotes the mean fluid height. Since, however, the relative fluid height
$H_f$ denotes the mean fluid height. Since, however, the relative fluid height ![]() $H_f/D$ was kept constant over all simulations, it was not possible to further distinguish between the two alternative scaling relations.
$H_f/D$ was kept constant over all simulations, it was not possible to further distinguish between the two alternative scaling relations.
The purpose of the present work is to investigate the scaling of the lower threshold for the minimal unstable wavelength. In order to be able to distinguish between the two alternative scalings, i.e. either with the particle diameter ![]() $D$ or the fluid height
$D$ or the fluid height ![]() $H_f$, two new series of numerical experiments are performed in which the relative streamwise domain lengths
$H_f$, two new series of numerical experiments are performed in which the relative streamwise domain lengths ![]() $L_x/D$ and
$L_x/D$ and ![]() $L_x/H_f$ are varied independently. In the subsequent analysis, we investigate the influence of both length scales on the stability of the subaqueous bedforms using the newly computed DNS data.
$L_x/H_f$ are varied independently. In the subsequent analysis, we investigate the influence of both length scales on the stability of the subaqueous bedforms using the newly computed DNS data.
The present manuscript is organized as follows. In § 2, we briefly describe the numerical method which we use for the simulation of subaqueous sediment transport in this work. An overview over the relevant physical and numerical parameters as well as the chosen flow configurations is given in § 3. Subsequently, in § 4, we shortly present two different ways of defining the fluid–bed interface, depending on whether the sediment bed is analysed in a spanwise-averaged framework or in its full extent. In § 5, we analyse the data obtained in the context of the two simulation series separately, focussing on the bedform geometry and its temporal evolution. A discussion of the results as well as a comparison with experimental and theoretical studies follows in § 6. We conclude the study with a summary of the main findings in § 7.
2. Numerical method
We use the same numerical method used in Kidanemariam & Uhlmann (Reference Kidanemariam and Uhlmann2014a,Reference Kidanemariam and Uhlmannb, Reference Kidanemariam and Uhlmann2017) to solve the coupled fluid–solid problem. For the simulation of the fluid phase, the Navier–Stokes equations for incompressible fluids are solved numerically in the entire computational domain using a second-order finite difference scheme together with a fractional step algorithm on a uniform Cartesian grid. Time integration of the governing equations is done in a semi-implicit way, including a Crank–Nicholson scheme for the viscous terms and a low-storage three-step Runge–Kutta scheme for the nonlinear terms. The immersed boundary formulation of Uhlmann (Reference Uhlmann2005) is then used to couple the flow field with the solid phase: localized force terms are introduced into the Navier–Stokes equations which impose the no-slip condition at the interface between the fluid and the solid phase. The motion of the particles is obtained by time integration of the Newton–Euler equations for rigid-body motion. The driving force and torque comprises hydrodynamic and gravitational contributions as well as those resulting from particle–particle and particle–wall contact. Owing to the fact that the characteristic time scale of particle collisions is typically several orders of magnitude smaller than those of the turbulent fluid motion, a sub-stepping method is used for the numerical time integration of the Newton–Euler equations (Kidanemariam & Uhlmann Reference Kidanemariam and Uhlmann2014b).
Momentum exchange due to particle collisions is computed using a soft-sphere discrete-element model (DEM). In the framework of the chosen approach, two particles are defined as ‘being in contact’, if the minimal distance between their surfaces ![]() $\varDelta$ falls below a force range
$\varDelta$ falls below a force range ![]() $\varDelta _c$. In this case, a contact force and torque act on both particles which are defined as the sum of three individual contributions, i.e. an elastic normal force, a normal damping force and a tangential frictional force. The elastic normal force is a linear function of the penetration length
$\varDelta _c$. In this case, a contact force and torque act on both particles which are defined as the sum of three individual contributions, i.e. an elastic normal force, a normal damping force and a tangential frictional force. The elastic normal force is a linear function of the penetration length ![]() $\delta _c = \Delta _c -\Delta$ with a constant stiffness coefficient
$\delta _c = \Delta _c -\Delta$ with a constant stiffness coefficient ![]() $k_n$. The normal damping force is a linear function of the normal component of the relative particle velocity between the two particles at the contact point, with a constant normal damping coefficient
$k_n$. The normal damping force is a linear function of the normal component of the relative particle velocity between the two particles at the contact point, with a constant normal damping coefficient ![]() $c_n$. Similarly, the tangential frictional force is defined as a linear function of the tangential component of the relative particle velocity at the contact point, with a constant tangential friction coefficient
$c_n$. Similarly, the tangential frictional force is defined as a linear function of the tangential component of the relative particle velocity at the contact point, with a constant tangential friction coefficient ![]() $c_t$. Note that the magnitude of the tangential frictional force has an upper traction limit in the form of the Coulomb friction limit with a friction coefficient
$c_t$. Note that the magnitude of the tangential frictional force has an upper traction limit in the form of the Coulomb friction limit with a friction coefficient ![]() $\mu _c$. A detailed description of the collision model and extensive validation can be found in Kidanemariam & Uhlmann (Reference Kidanemariam and Uhlmann2014b).
$\mu _c$. A detailed description of the collision model and extensive validation can be found in Kidanemariam & Uhlmann (Reference Kidanemariam and Uhlmann2014b).
For each simulation, the model thus requires the choice of the four force parameters (![]() $k_n, c_n, c_t, \mu _c$) as well as the force range
$k_n, c_n, c_t, \mu _c$) as well as the force range ![]() $\Delta _c$. Introducing a dry restitution coefficient
$\Delta _c$. Introducing a dry restitution coefficient ![]() $\varepsilon _d$, which is defined as the absolute value of the ratio between the normal components of the relative velocity before and after a dry collision, allows us to relate the normal stiffness coefficient
$\varepsilon _d$, which is defined as the absolute value of the ratio between the normal components of the relative velocity before and after a dry collision, allows us to relate the normal stiffness coefficient ![]() $k_n$ and the normal damping coefficient
$k_n$ and the normal damping coefficient ![]() $c_n$, and to formulate the model depending on the alternative set of force parameters (
$c_n$, and to formulate the model depending on the alternative set of force parameters (![]() $k_n, \varepsilon _d, c_t, \mu _c$). Due to the varying particle size and submerged weight in the present simulations, the set of parameters used in Kidanemariam & Uhlmann (Reference Kidanemariam and Uhlmann2014a, Reference Kidanemariam and Uhlmann2017) has been adapted to the respective cases. The force range
$k_n, \varepsilon _d, c_t, \mu _c$). Due to the varying particle size and submerged weight in the present simulations, the set of parameters used in Kidanemariam & Uhlmann (Reference Kidanemariam and Uhlmann2014a, Reference Kidanemariam and Uhlmann2017) has been adapted to the respective cases. The force range ![]() $\Delta _c$ is set equal to the uniform grid spacing
$\Delta _c$ is set equal to the uniform grid spacing ![]() ${\rm \Delta} x$ for all cases with a particle diameter
${\rm \Delta} x$ for all cases with a particle diameter ![]() $D \leq 15 {\rm \Delta} x$ and equal to
$D \leq 15 {\rm \Delta} x$ and equal to ![]() $2{\rm \Delta} x$ for all cases with larger particles. The stiffness parameter
$2{\rm \Delta} x$ for all cases with larger particles. The stiffness parameter ![]() $k_n$ has a value between approximately
$k_n$ has a value between approximately ![]() $8400$ and 17 000 times the submerged weight of a single particle, divided by the particle diameter in the respective case. The parameters are chosen such that the maximum overlap
$8400$ and 17 000 times the submerged weight of a single particle, divided by the particle diameter in the respective case. The parameters are chosen such that the maximum overlap ![]() $\delta _c$ is within a few per cent of
$\delta _c$ is within a few per cent of ![]() $\Delta _c$. The dry restitution coefficient is set to
$\Delta _c$. The dry restitution coefficient is set to ![]() $\varepsilon _d=0.3$, which determines, together with the chosen value of
$\varepsilon _d=0.3$, which determines, together with the chosen value of ![]() $k_n$, the constant normal damping coefficient
$k_n$, the constant normal damping coefficient ![]() $c_n$. The constant tangential friction coefficient is set to the same value
$c_n$. The constant tangential friction coefficient is set to the same value ![]() $c_t = c_n$. Finally, the Coulomb friction coefficient was fixed at
$c_t = c_n$. Finally, the Coulomb friction coefficient was fixed at ![]() $\mu _c = 0.4$ except for cases
$\mu _c = 0.4$ except for cases ![]() $H2D052$ and
$H2D052$ and ![]() $H6D102$, in which a slightly higher value
$H6D102$, in which a slightly higher value ![]() $\mu _c = 0.5$ was unintentionally used. In appendix A we show, however, that this difference in the limiting Coulomb friction has only a minor influence on the eventually developed bedform and that it does not affect the stability or instability of the sediment bed. In addition to the influence of
$\mu _c = 0.5$ was unintentionally used. In appendix A we show, however, that this difference in the limiting Coulomb friction has only a minor influence on the eventually developed bedform and that it does not affect the stability or instability of the sediment bed. In addition to the influence of ![]() $\mu _c$, we have also investigated the sensitivity of the sediment bed evolution on the values chosen for the dry restitution coefficient
$\mu _c$, we have also investigated the sensitivity of the sediment bed evolution on the values chosen for the dry restitution coefficient ![]() $\varepsilon _d$ and the force range
$\varepsilon _d$ and the force range ![]() $\Delta _c$. It was observed that the formation and the final shape of the developing sediment patterns are not significantly modified when changing
$\Delta _c$. It was observed that the formation and the final shape of the developing sediment patterns are not significantly modified when changing ![]() $\varepsilon _d$ from its current value of 0.3 to 0.9. Similarly, it can be stated that a change of the relative force range
$\varepsilon _d$ from its current value of 0.3 to 0.9. Similarly, it can be stated that a change of the relative force range ![]() $\Delta _c/\Delta _x$, which is achieved by refining the fluid grid by a factor of
$\Delta _c/\Delta _x$, which is achieved by refining the fluid grid by a factor of ![]() $1.5$, has no significant influence on the bedform evolution. It should be noted that the latter validation also serves as an additional grid convergence study, highlighting the fact that the chosen spatial resolution is sufficient for the purpose of capturing all relevant flow scales.
$1.5$, has no significant influence on the bedform evolution. It should be noted that the latter validation also serves as an additional grid convergence study, highlighting the fact that the chosen spatial resolution is sufficient for the purpose of capturing all relevant flow scales.
3. Flow configuration and parameter values
In the course of the current study, we have performed seven new independent direct numerical simulations of bedform evolution over an erodible subaqueous sediment bed in a turbulent open channel. Two additional cases from KU2017 have been included in our analysis. The studied flow configuration is shown in figure 1. As can be seen, a Cartesian coordinate system with ![]() $\boldsymbol {x}=( x,y,z )^{{\rm T}}$ is centred at the lower boundary of the open channel such that the
$\boldsymbol {x}=( x,y,z )^{{\rm T}}$ is centred at the lower boundary of the open channel such that the ![]() $x$-,
$x$-, ![]() $y$- and
$y$- and ![]() $z$-directions are the streamwise, wall-normal and spanwise directions, respectively. Mean flow is directed in the positive
$z$-directions are the streamwise, wall-normal and spanwise directions, respectively. Mean flow is directed in the positive ![]() $x$-direction and gravity in the negative
$x$-direction and gravity in the negative ![]() $y$-direction. In the streamwise and spanwise directions, periodic boundary conditions are imposed, whereas no-slip and free-slip conditions are imposed at the bottom and top planes of the channel, respectively.
$y$-direction. In the streamwise and spanwise directions, periodic boundary conditions are imposed, whereas no-slip and free-slip conditions are imposed at the bottom and top planes of the channel, respectively.

Figure 1. Schematic of the open channel flow configuration. Flow is in the positive ![]() $x$-direction. The computational domain is periodic along the
$x$-direction. The computational domain is periodic along the ![]() $x$- and
$x$- and ![]() $z$-directions. No-slip and free-slip boundary conditions are imposed at the bottom (
$z$-directions. No-slip and free-slip boundary conditions are imposed at the bottom (![]() $y=0$) and top (
$y=0$) and top (![]() $y=L_y$), respectively.
$y=L_y$), respectively.
As characteristic length scales, we define the mean fluid height ![]() $H_f$ and the mean sediment bed height
$H_f$ and the mean sediment bed height ![]() $H_b$ as averages over both spatial directions (streamwise and spanwise) as well as over time, i.e.
$H_b$ as averages over both spatial directions (streamwise and spanwise) as well as over time, i.e. ![]() $H_f=\langle h_f \rangle_{\textit{xzt}}$ and
$H_f=\langle h_f \rangle_{\textit{xzt}}$ and ![]() $H_b=\langle h_b \rangle_{\textit{xzt}}$, respectively. A precise definition of
$H_b=\langle h_b \rangle_{\textit{xzt}}$, respectively. A precise definition of ![]() $h_f(x,z,t)$ and
$h_f(x,z,t)$ and ![]() $h_b(x,z,t)$ will be given in § 4.1. Before the simulations with mobile particles are started, the sediment bed is left to settle without any fluid forces. Subsequently, turbulent flow is established while keeping the particles fixed. Finally, the particles are released at a time which will henceforth be defined as
$h_b(x,z,t)$ will be given in § 4.1. Before the simulations with mobile particles are started, the sediment bed is left to settle without any fluid forces. Subsequently, turbulent flow is established while keeping the particles fixed. Finally, the particles are released at a time which will henceforth be defined as ![]() $t=0$. More details can be found in Kidanemariam & Uhlmann (Reference Kidanemariam and Uhlmann2014a). The names of the individual simulations are chosen according to their streamwise domain length in terms of the mean fluid height and in terms of the particle diameter. For instance, in case
$t=0$. More details can be found in Kidanemariam & Uhlmann (Reference Kidanemariam and Uhlmann2014a). The names of the individual simulations are chosen according to their streamwise domain length in terms of the mean fluid height and in terms of the particle diameter. For instance, in case ![]() $H4D052$, the relative streamwise box length is
$H4D052$, the relative streamwise box length is ![]() $L_x/H_f \approx 4$ and
$L_x/H_f \approx 4$ and ![]() $L_x/D = 51.2$, respectively (cf. tables 1 and 2).
$L_x/D = 51.2$, respectively (cf. tables 1 and 2).
Table 1. Physical parameters of the simulations. ![]() $Re_b$,
$Re_b$, ![]() $Re_{\tau }$ and
$Re_{\tau }$ and ![]() $D^{+}$ are the bulk Reynolds number, the friction Reynolds number and the particle Reynolds number, respectively. The density ratio
$D^{+}$ are the bulk Reynolds number, the friction Reynolds number and the particle Reynolds number, respectively. The density ratio ![]() $\rho _p/\rho _f$ and the Galileo number
$\rho _p/\rho _f$ and the Galileo number ![]() $Ga$ are imposed in each simulation, whereas the Shields number
$Ga$ are imposed in each simulation, whereas the Shields number ![]() $\theta$, the relative submergence
$\theta$, the relative submergence ![]() $H_f/D$ and the relative sediment bed height
$H_f/D$ and the relative sediment bed height ![]() $H_b/D$ are computed a posteriori (cf. table 2). The last column provides information about the source of the listed cases, distinguishing between simulations that have been computed in the course of the current study (present) and cases that are from Kidanemariam & Uhlmann (Reference Kidanemariam and Uhlmann2017) (KU2017). It should be further mentioned that the physical parameters presented for case H4D1021,2,3 have been averaged over the three individual simulations. A list of the physical parameters for each individual run can be found in KU2017.
$H_b/D$ are computed a posteriori (cf. table 2). The last column provides information about the source of the listed cases, distinguishing between simulations that have been computed in the course of the current study (present) and cases that are from Kidanemariam & Uhlmann (Reference Kidanemariam and Uhlmann2017) (KU2017). It should be further mentioned that the physical parameters presented for case H4D1021,2,3 have been averaged over the three individual simulations. A list of the physical parameters for each individual run can be found in KU2017.

Table 2. Numerical parameters of the simulations. The computational domain has dimensions ![]() $L_i$ in the
$L_i$ in the ![]() $i$th direction and is discretized using a uniform grid with mesh width
$i$th direction and is discretized using a uniform grid with mesh width ![]() ${\rm \Delta} x$,
${\rm \Delta} x$, ![]() ${\rm \Delta} x^{+}$ denoting the grid width in wall units.
${\rm \Delta} x^{+}$ denoting the grid width in wall units. ![]() $N_p$ is the total number of particles in the respective case. The time is scaled in bulk time units
$N_p$ is the total number of particles in the respective case. The time is scaled in bulk time units ![]() $T_b=H_f/u_b$.
$T_b=H_f/u_b$. ![]() $T_{obs}$ is the total observation time of each simulation starting from the release of the moving particles. Time-dependent physical and numerical parameters in tables 1 and 2 (
$T_{obs}$ is the total observation time of each simulation starting from the release of the moving particles. Time-dependent physical and numerical parameters in tables 1 and 2 (![]() $Re_{\tau }$,
$Re_{\tau }$, ![]() $D^{+}$,
$D^{+}$, ![]() $H_f$,
$H_f$, ![]() $H_b$,
$H_b$, ![]() $\theta$,
$\theta$, ![]() ${\rm \Delta} x^{+}$) are computed as an average over a final time interval
${\rm \Delta} x^{+}$) are computed as an average over a final time interval ![]() $T^{s}_{obs}$.
$T^{s}_{obs}$.

In all cases, the flow is driven by a time-dependent streamwise pressure gradient, that is adjusted at each time step to ensure a constant flow rate ![]() $q_f$. Therefore, the bulk Reynolds number can be computed a priori as
$q_f$. Therefore, the bulk Reynolds number can be computed a priori as ![]() ${Re_b = u_b H_f/\nu }$, where the bulk velocity is defined as
${Re_b = u_b H_f/\nu }$, where the bulk velocity is defined as ![]() $u_b \equiv q_f/H_f$. The friction Reynolds number is defined as
$u_b \equiv q_f/H_f$. The friction Reynolds number is defined as ![]() ${Re_{\tau } = u_{\tau } H_f/\nu }$, where the friction velocity
${Re_{\tau } = u_{\tau } H_f/\nu }$, where the friction velocity ![]() $u_{\tau }$ is computed a posteriori from the streamwise and spanwise-averaged total mean shear stress, which is composed of viscous stresses, turbulent Reynolds stresses and the stresses resulting from the fluid–particle interaction. Due to the absence of a horizontal bottom wall, we evaluate the mean friction velocity
$u_{\tau }$ is computed a posteriori from the streamwise and spanwise-averaged total mean shear stress, which is composed of viscous stresses, turbulent Reynolds stresses and the stresses resulting from the fluid–particle interaction. Due to the absence of a horizontal bottom wall, we evaluate the mean friction velocity ![]() $u_{\tau }$ at the location of the mean fluid–bed interface
$u_{\tau }$ at the location of the mean fluid–bed interface ![]() $y=H_b$, which can be interpreted as a virtual wall. For a more detailed description of the determination of the shear stress distribution, the reader is referred to KU2017.
$y=H_b$, which can be interpreted as a virtual wall. For a more detailed description of the determination of the shear stress distribution, the reader is referred to KU2017.
From dimensional analysis, it can be concluded that, by adding sediment to a turbulent flow, the parameter space increases and in total, four non-dimensional numbers are required to fully describe a given system. In addition to ![]() $Re_b$, we choose the density ratio
$Re_b$, we choose the density ratio ![]() $\rho _p/\rho _f$, the non-dimensional length scale
$\rho _p/\rho _f$, the non-dimensional length scale ![]() $H_f/D$ as well as the Galileo number
$H_f/D$ as well as the Galileo number ![]() ${Ga = u_{g} D/\nu }$, which expresses the ratio between gravity and viscous forces, where the gravitational velocity scale is
${Ga = u_{g} D/\nu }$, which expresses the ratio between gravity and viscous forces, where the gravitational velocity scale is ![]() $u_g= \sqrt {(\rho _{p}/\rho _{f}-1)|\boldsymbol {g}| D}$.
$u_g= \sqrt {(\rho _{p}/\rho _{f}-1)|\boldsymbol {g}| D}$.
In the present simulations, we set the density ratio at ![]() $\rho _p/\rho _f = 2.5$ which is comparable to the values reported for glass in water. To allow pattern formation, the non-dimensional boundary shear stress, expressed by the Shields number
$\rho _p/\rho _f = 2.5$ which is comparable to the values reported for glass in water. To allow pattern formation, the non-dimensional boundary shear stress, expressed by the Shields number ![]() ${\theta = u_{\tau }^{2}/u_{g}^{2}= ( D^{+} /Ga)^{2}}$, is chosen larger than the critical value for incipient sediment motion. Note that quantities marked as
${\theta = u_{\tau }^{2}/u_{g}^{2}= ( D^{+} /Ga)^{2}}$, is chosen larger than the critical value for incipient sediment motion. Note that quantities marked as ![]() $(\cdot )^{+}$ are scaled in wall units. In turbulent flows, the critical Shields number has been observed to be in a range
$(\cdot )^{+}$ are scaled in wall units. In turbulent flows, the critical Shields number has been observed to be in a range ![]() $\theta _c = 0.03\text {-}0.05$, slightly depending on the Galileo number (Soulsby & Whitehouse Reference Soulsby and Whitehouse1997; Wong & Parker Reference Wong and Parker2006; Franklin & Charru Reference Franklin and Charru2011).
$\theta _c = 0.03\text {-}0.05$, slightly depending on the Galileo number (Soulsby & Whitehouse Reference Soulsby and Whitehouse1997; Wong & Parker Reference Wong and Parker2006; Franklin & Charru Reference Franklin and Charru2011).
The non-dimensional mean fluid height ![]() $H_f/D$ is varied in the different simulations to elucidate the relevant length scales that dominate the scaling of subaqueous bedforms by either increasing the particle diameter or the mean fluid height while keeping the same dimensions for the domain. As a consequence, the number of fully resolved particles lies in a range between
$H_f/D$ is varied in the different simulations to elucidate the relevant length scales that dominate the scaling of subaqueous bedforms by either increasing the particle diameter or the mean fluid height while keeping the same dimensions for the domain. As a consequence, the number of fully resolved particles lies in a range between ![]() $ {O}(10^{3})$ in the case with the largest particles and up to
$ {O}(10^{3})$ in the case with the largest particles and up to ![]() $ {O}(10^{5})$ in the case with the smallest particles.
$ {O}(10^{5})$ in the case with the smallest particles.
Note that, in all cases, the dimensions of the computational domain are sufficiently large to allow self-sustained turbulence. In particular, the cases with the shortest streamwise and spanwise dimensions (scaled in viscous lengths) are case ![]() $H2D052$ with
$H2D052$ with ![]() $L_x^{+} \approx 490$ and case H2D1022 with
$L_x^{+} \approx 490$ and case H2D1022 with ![]() $L_z^{+} \approx 555$, respectively. By comparison, Jiménez & Moin (Reference Jiménez and Moin1991) report the dimensions of their minimal flow unit as
$L_z^{+} \approx 555$, respectively. By comparison, Jiménez & Moin (Reference Jiménez and Moin1991) report the dimensions of their minimal flow unit as ![]() $L_x^{+} \approx 250\text {-}350$ and
$L_x^{+} \approx 250\text {-}350$ and ![]() $L_x^{+} \approx 100$, respectively.
$L_x^{+} \approx 100$, respectively.
In § 5, we will analyse the two simulation series separately: while in the first series (including cases ![]() $H6D052$,
$H6D052$, ![]() $H6D077$,
$H6D077$, ![]() $H6D102$ and
$H6D102$ and ![]() $H6D154$), the
$H6D154$), the ![]() $L_x/D$ ratio has been varied keeping
$L_x/D$ ratio has been varied keeping ![]() $L_x/H_f$ constant,
$L_x/H_f$ constant, ![]() $L_x/D$ is fixed in the second series (including cases H4D1021,2,3, H2D1021 and H2D1022) and
$L_x/D$ is fixed in the second series (including cases H4D1021,2,3, H2D1021 and H2D1022) and ![]() $L_x/H_f$ is varied instead. It should be noted that we have performed two additional simulations,
$L_x/H_f$ is varied instead. It should be noted that we have performed two additional simulations, ![]() $H2D052$ and
$H2D052$ and ![]() $H4D052$, which do not fit into either of these two series. Therefore, we discuss the results obtained in these latter cases in § 6 only.
$H4D052$, which do not fit into either of these two series. Therefore, we discuss the results obtained in these latter cases in § 6 only.
4. Extraction of bedform dimensions
For the following definition of the fluid–bed interface, we will consider the domain as composed of two distinct regions that are a lower particle-dominated region, hereafter termed the sediment bed, and the overlaying fluid-dominated region. Hence, the wall-normal dimension of the channel ![]() $L_y$ can be written as the sum of the instantaneous local height of the fluid phase
$L_y$ can be written as the sum of the instantaneous local height of the fluid phase ![]() $h_f(x,z,t)$ and that of the sediment bed
$h_f(x,z,t)$ and that of the sediment bed ![]() $h_b(x,z,t)$, viz.
$h_b(x,z,t)$, viz.
In the chosen Cartesian coordinate system, the wall-normal location of the fluid–bed interface is identical to the value of the function ![]() $h_b(x,z,t)$. In the following, we will present two different approaches to define the instantaneous fluid–bed interface. The first method defines the fluid–bed interface through a spanwise averaging, whereas the second extracts the sediment bed as a two-dimensional surface.
$h_b(x,z,t)$. In the following, we will present two different approaches to define the instantaneous fluid–bed interface. The first method defines the fluid–bed interface through a spanwise averaging, whereas the second extracts the sediment bed as a two-dimensional surface.
4.1. Definition and analysis of the spanwise-averaged fluid–bed interface
Assuming statistical homogeneity of the observed system, (4.1) can be averaged in the spanwise direction as
The spanwise-averaged sediment bed height ![]() $\langle h_b \rangle _{z}$ is determined depending on a threshold for the solid volume fraction. Since the method is presented in detail in our previous works (Kidanemariam & Uhlmann Reference Kidanemariam and Uhlmann2014a, Reference Kidanemariam and Uhlmann2017), we restrict ourselves to a short summary of the most important points. First, a solid-phase indicator function
$\langle h_b \rangle _{z}$ is determined depending on a threshold for the solid volume fraction. Since the method is presented in detail in our previous works (Kidanemariam & Uhlmann Reference Kidanemariam and Uhlmann2014a, Reference Kidanemariam and Uhlmann2017), we restrict ourselves to a short summary of the most important points. First, a solid-phase indicator function ![]() $\phi _p(\boldsymbol {x},t)$ is defined, which attains the value of unity for Eulerian grid points located inside the particle domain
$\phi _p(\boldsymbol {x},t)$ is defined, which attains the value of unity for Eulerian grid points located inside the particle domain ![]() $\Omega _p$ and zero elsewhere. Second, the spanwise-averaged sediment bed height
$\Omega _p$ and zero elsewhere. Second, the spanwise-averaged sediment bed height ![]() $\langle h_b \rangle _{z}$ is defined as the wall-normal location, at which the spanwise-averaged solid indicator function
$\langle h_b \rangle _{z}$ is defined as the wall-normal location, at which the spanwise-averaged solid indicator function ![]() $\langle \phi _p \rangle _{z}$ attains a threshold of
$\langle \phi _p \rangle _{z}$ attains a threshold of ![]() $\langle \phi _p \rangle _{z}^{thresh}=0.1$ (Kidanemariam & Uhlmann Reference Kidanemariam and Uhlmann2014b), i.e.
$\langle \phi _p \rangle _{z}^{thresh}=0.1$ (Kidanemariam & Uhlmann Reference Kidanemariam and Uhlmann2014b), i.e.
The spanwise-averaged fluid height ![]() $\langle h_f \rangle _{z}$ is computed using relation (4.2). Eventually, we perform another decomposition in the streamwise direction, similar to the spanwise decomposition used in (4.2). The resulting expression
$\langle h_f \rangle _{z}$ is computed using relation (4.2). Eventually, we perform another decomposition in the streamwise direction, similar to the spanwise decomposition used in (4.2). The resulting expression
divides the spanwise-averaged interface in an instantaneous mean height ![]() $\langle h_b \rangle _{xz} (t)$ and a fluctuation
$\langle h_b \rangle _{xz} (t)$ and a fluctuation ![]() $\langle h_b \rangle _{z}^{\prime } (x,t)$ with respect to the former. In the following, the fluctuation will form the basis for the analysis of the bedform evolution. The size and shape of two-dimensional transverse patterns are usually quantified by the pattern length and height. Over the last decades, a variety of different approaches has been developed to define these length scales. An overview over some of these methods is presented in Coleman & Nikora (Reference Coleman and Nikora2011). In the current work, we choose a statistical definition for the pattern height as well as for the wavelength of the bedforms (Langlois & Valance Reference Langlois and Valance2007). As a measure for the pattern height, we use the root mean square of the sediment bed height fluctuation
$\langle h_b \rangle _{z}^{\prime } (x,t)$ with respect to the former. In the following, the fluctuation will form the basis for the analysis of the bedform evolution. The size and shape of two-dimensional transverse patterns are usually quantified by the pattern length and height. Over the last decades, a variety of different approaches has been developed to define these length scales. An overview over some of these methods is presented in Coleman & Nikora (Reference Coleman and Nikora2011). In the current work, we choose a statistical definition for the pattern height as well as for the wavelength of the bedforms (Langlois & Valance Reference Langlois and Valance2007). As a measure for the pattern height, we use the root mean square of the sediment bed height fluctuation
In order to determine the average pattern wavelength, let us define the instantaneous two-point correlation coefficient of the sediment bed height fluctuation
where ![]() $\delta x$ expresses the streamwise separation length between two points. With increasing
$\delta x$ expresses the streamwise separation length between two points. With increasing ![]() $\delta x$, the evolution of
$\delta x$, the evolution of ![]() $R_{h}(\delta x,t)$ at a given time
$R_{h}(\delta x,t)$ at a given time ![]() $t$ behaves similarly to a damped oscillation curve around a zero mean. The global (and first) minimum of the curve occurs at a separation
$t$ behaves similarly to a damped oscillation curve around a zero mean. The global (and first) minimum of the curve occurs at a separation ![]() $\delta x_{\textit{min}}$, i.e.
$\delta x_{\textit{min}}$, i.e.
The mean wavelength is finally obtained as twice this separation length, i.e. ![]() ${\lambda _h(t) = 2 \delta x_{\textit{min}}}$.
${\lambda _h(t) = 2 \delta x_{\textit{min}}}$.
4.2. Definition and analysis of the two-dimensional fluid–bed interface
The spanwise-averaged definition and analysis, as described in the previous section, is restricted to a fluid–bed interface that is statistically homogeneous in the spanwise direction. However, in the general case, this procedure may be not adequate to describe possible three-dimensional sediment patterning.
Here, we use a criterion based on determining the top-layer particles of the fluid–bed interface. In classical morphodynamics, the sediment bed is distinguished from the bedload and suspended load (Bagnold Reference Bagnold1956; van Rijn Reference van Rijn1984). Following this classification, we have developed an algorithm which sorts out the latter two categories, leaving only the particles that are part of the sediment bed itself. First, single suspended particles are detected based on the wall-normal collision force component ![]() $F_{c,y}$. While particles inside the bed are exposed to a permanent wall-normal contact force of the order of their submerged weight
$F_{c,y}$. While particles inside the bed are exposed to a permanent wall-normal contact force of the order of their submerged weight ![]() $F_w=(\rho _p-\rho _f) \pi D^{3}/6 |\boldsymbol {g}|$, single suspended particles are typically not in contact with surrounding particles and, accordingly, only a small contact force acts on them. Thus, particles that are only exposed to a negligible wall-normal contact force will not be considered as ‘bed particles’ (where we have used a threshold
$F_w=(\rho _p-\rho _f) \pi D^{3}/6 |\boldsymbol {g}|$, single suspended particles are typically not in contact with surrounding particles and, accordingly, only a small contact force acts on them. Thus, particles that are only exposed to a negligible wall-normal contact force will not be considered as ‘bed particles’ (where we have used a threshold ![]() $|F_{c,y}|/F_w < 10^{-5}$ in practice, the precise value of which was not found to have any significant consequence for the extracted bed height).
$|F_{c,y}|/F_w < 10^{-5}$ in practice, the precise value of which was not found to have any significant consequence for the extracted bed height).
The remaining particles include both the actual sediment bed and the bedload layer. Particles inside the latter are in motion close to the bed, such that they lose contact to the bed only for short time intervals (Yalin Reference Yalin1977). In order to separate the bedload transport particles from the bed particles, a criterion based upon the particle speed is employed, eliminating all particles which exceed a threshold value. The threshold value can be chosen by defining a non-dimensional particle Shields number ![]() $\theta _p = (|\boldsymbol {u_p}|/u_g)^{2}$ with the norm of the particle velocity
$\theta _p = (|\boldsymbol {u_p}|/u_g)^{2}$ with the norm of the particle velocity ![]() $|\boldsymbol {u_p}|$ and the gravitational velocity scale
$|\boldsymbol {u_p}|$ and the gravitational velocity scale ![]() $u_g$. The sediment bed particles are then found as the set of all particles for which
$u_g$. The sediment bed particles are then found as the set of all particles for which ![]() $\theta _p \leq \theta _c$. Here, we choose as the critical value
$\theta _p \leq \theta _c$. Here, we choose as the critical value ![]() $\theta _c=0.05$ (Wong & Parker Reference Wong and Parker2006). Note that the particle velocity criterion also eliminates suspended particle pairs which might instantaneously experience collision forces above the chosen threshold of the wall-normal contact force.
$\theta _c=0.05$ (Wong & Parker Reference Wong and Parker2006). Note that the particle velocity criterion also eliminates suspended particle pairs which might instantaneously experience collision forces above the chosen threshold of the wall-normal contact force.
The fluid–bed interface is then defined through a three-dimensional ![]() $\alpha$-shape (Edelsbrunner & Mücke Reference Edelsbrunner and Mücke1994) enclosing the set of sediment bed particles. This enclosing surface can be thought of as a generalization of a convex hull, with an imposed radius
$\alpha$-shape (Edelsbrunner & Mücke Reference Edelsbrunner and Mücke1994) enclosing the set of sediment bed particles. This enclosing surface can be thought of as a generalization of a convex hull, with an imposed radius ![]() $\alpha$ (here taken as
$\alpha$ (here taken as ![]() $1.1$ times the particle diameter) that defines the length scale above which non-convexity is allowed. The fluid–bed interface is then made up of those triangular faces of the
$1.1$ times the particle diameter) that defines the length scale above which non-convexity is allowed. The fluid–bed interface is then made up of those triangular faces of the ![]() $\alpha$-shape which have an outward-pointing face normal with a positive
$\alpha$-shape which have an outward-pointing face normal with a positive ![]() $y$-component. The data consist of a function
$y$-component. The data consist of a function ![]() $h(x,z)$ which is sampled at the projection of the vertex points of the surface triangulation upon the
$h(x,z)$ which is sampled at the projection of the vertex points of the surface triangulation upon the ![]() $(x,z)$-plane at a given time. In a final step, this function
$(x,z)$-plane at a given time. In a final step, this function ![]() $h(x,z)$ is interpolated to a uniform Eulerian grid with a mesh width equal to one particle diameter and the result is smoothed using a two-dimensional box filter with a width of
$h(x,z)$ is interpolated to a uniform Eulerian grid with a mesh width equal to one particle diameter and the result is smoothed using a two-dimensional box filter with a width of ![]() $5$ particle diameters.
$5$ particle diameters.
For the analysis of this two-dimensional interface, let us extend our definition of the root mean square of the sediment bed height fluctuation, as defined in (4.5), to the multidimensional case in the following form:
including the two-dimensional sediment bed height fluctuation ![]() $h_b^{\prime } (x,z,t)$ with respect to the streamwise- and spanwise-averaged mean
$h_b^{\prime } (x,z,t)$ with respect to the streamwise- and spanwise-averaged mean ![]() $\langle h_b \rangle _{xz} (t)$.
$\langle h_b \rangle _{xz} (t)$.
5. Results
5.1. Variation of the particle diameter
In a first series, the influence of the particle diameter ![]() $D$ on the minimal unstable wavelength
$D$ on the minimal unstable wavelength ![]() $\lambda _{th}$ at a given parameter point is investigated. To this end, a series of four simulations with different particle size is performed, in which the particle diameter
$\lambda _{th}$ at a given parameter point is investigated. To this end, a series of four simulations with different particle size is performed, in which the particle diameter ![]() $D$ is successively increased from
$D$ is successively increased from ![]() $D/H_f \approx 0.04$ in case
$D/H_f \approx 0.04$ in case ![]() $H6D154$ to
$H6D154$ to ![]() $D/H_f \approx 0.13$ in case
$D/H_f \approx 0.13$ in case ![]() $H6D052$. It should be stressed that, in all four simulations, the streamwise domain length
$H6D052$. It should be stressed that, in all four simulations, the streamwise domain length ![]() $L_x$ is almost constant in the range
$L_x$ is almost constant in the range ![]() $(6.04\text {-}6.52) H_f$ and thus clearly above the critical value observed in KU2017. Note that case
$(6.04\text {-}6.52) H_f$ and thus clearly above the critical value observed in KU2017. Note that case ![]() $H6D154$ with the smallest particle diameter is identical to case
$H6D154$ with the smallest particle diameter is identical to case ![]() $H6$ presented in KU2017, in which a single bedform has been observed to evolve and to eventually reach a quasi-equilibrium state.
$H6$ presented in KU2017, in which a single bedform has been observed to evolve and to eventually reach a quasi-equilibrium state.
Figure 2 shows instantaneous snapshots of the sediment bed in the different cases after a simulation period of approximately ![]() $300$ bulk time units. It is seen that in case
$300$ bulk time units. It is seen that in case ![]() $H6D052$, no transverse pattern has formed. Instead, the bed has remained essentially flat and eroded sediment seems to distribute over the entire channel length and width, without accumulating in specific locations. In particular, case
$H6D052$, no transverse pattern has formed. Instead, the bed has remained essentially flat and eroded sediment seems to distribute over the entire channel length and width, without accumulating in specific locations. In particular, case ![]() $H6D052$ does not exhibit a similar regular pattern of streamwise aligned alternating ridges and troughs as those KU2017 found in the stable sediment bed of their case
$H6D052$ does not exhibit a similar regular pattern of streamwise aligned alternating ridges and troughs as those KU2017 found in the stable sediment bed of their case ![]() $H3$. On the other hand, the remaining new cases with a domain length
$H3$. On the other hand, the remaining new cases with a domain length ![]() $L_x \geq 76.8D$ are unstable, each featuring one single transverse bedform with an initial wavelength of the order of the streamwise box length. This indicates that, at the given parameter point, there is indeed a lower limit for
$L_x \geq 76.8D$ are unstable, each featuring one single transverse bedform with an initial wavelength of the order of the streamwise box length. This indicates that, at the given parameter point, there is indeed a lower limit for ![]() $\lambda _{th}$, which depends on the particle diameter and which is found in the range
$\lambda _{th}$, which depends on the particle diameter and which is found in the range ![]() $(51.2\text {-}76.8)D$. As can already be inferred from the top-view visualizations of the sediment bed (cf. figure 2), the shape of those bedforms which do emerge differs, in particular in the vicinity of the threshold.
$(51.2\text {-}76.8)D$. As can already be inferred from the top-view visualizations of the sediment bed (cf. figure 2), the shape of those bedforms which do emerge differs, in particular in the vicinity of the threshold.

Figure 2. Instantaneous snapshots of the sediment bed of the cases varying the particle diameter, seen from the top of the channel. Particles are coloured depending on the wall-normal location of their centre, as shown in the global colour code. The bedforms shown in the figures have been observed at ![]() $t \approx 300 T_b$ for all cases: (a)
$t \approx 300 T_b$ for all cases: (a) ![]() $H6D052$, (b)
$H6D052$, (b) ![]() $H6D077$, (c)
$H6D077$, (c) ![]() $H6D102$, (d)
$H6D102$, (d) ![]() $H6D154$. See also the supplementary movies available at https://dx.doi.org/10.4121/uuid:7eb6a0be-ff83-4883-9d99-31daaa6a2863.
$H6D154$. See also the supplementary movies available at https://dx.doi.org/10.4121/uuid:7eb6a0be-ff83-4883-9d99-31daaa6a2863.
In order to provide a quantitative description of these patterns, we will now discuss various geometrical measures. First, we will focus on the pattern height evolution by studying the root mean square sediment bed height fluctuation ![]() $\sigma _h$, which can be seen as a measure for the inhomogeneity of the sediment bed height (Kidanemariam & Uhlmann Reference Kidanemariam and Uhlmann2014a, Reference Kidanemariam and Uhlmann2017; Zgheib et al. Reference Zgheib, Fedele, Hoyal, Perillo and Balachandar2018). In a case in which no transverse bedforms evolve,
$\sigma _h$, which can be seen as a measure for the inhomogeneity of the sediment bed height (Kidanemariam & Uhlmann Reference Kidanemariam and Uhlmann2014a, Reference Kidanemariam and Uhlmann2017; Zgheib et al. Reference Zgheib, Fedele, Hoyal, Perillo and Balachandar2018). In a case in which no transverse bedforms evolve, ![]() $\sigma _h$ will show some fluctuations due to random uncorrelated bed undulations, but it will remain bounded by a small value in the course of the simulation. A sediment bed that shows such evolution will be classified as stable. In unstable systems, on the other hand,
$\sigma _h$ will show some fluctuations due to random uncorrelated bed undulations, but it will remain bounded by a small value in the course of the simulation. A sediment bed that shows such evolution will be classified as stable. In unstable systems, on the other hand, ![]() $\sigma _h$ will grow more or less monotonically during the initial phase of the simulation and, in particular, it will exceed the aforementioned threshold that bounds the stable cases. Figure 3 shows the time evolution of
$\sigma _h$ will grow more or less monotonically during the initial phase of the simulation and, in particular, it will exceed the aforementioned threshold that bounds the stable cases. Figure 3 shows the time evolution of ![]() $\sigma _h$. After a short initial transient of a few bulk time units during which the chaotic particle motion leads to small finite values of
$\sigma _h$. After a short initial transient of a few bulk time units during which the chaotic particle motion leads to small finite values of ![]() $\sigma _h$, we observe that in all cases with
$\sigma _h$, we observe that in all cases with ![]() $L_x \geq 76.8D$,
$L_x \geq 76.8D$, ![]() $\sigma _h$ increases with time starting at
$\sigma _h$ increases with time starting at ![]() $t \approx 20 T_b$, indicating that the chosen relative box length is sufficiently long to cover at least one unstable mode and thus to allow the bed to evolve transverse patterns. On the contrary,
$t \approx 20 T_b$, indicating that the chosen relative box length is sufficiently long to cover at least one unstable mode and thus to allow the bed to evolve transverse patterns. On the contrary, ![]() $\sigma _h$ in case
$\sigma _h$ in case ![]() $H6D052$ does not exhibit any substantial growth period. Instead, it remains around a value of
$H6D052$ does not exhibit any substantial growth period. Instead, it remains around a value of ![]() $\sigma _h \approx 0.3D$, only featuring fluctuations of small amplitude, bounded by an upper value of approximately
$\sigma _h \approx 0.3D$, only featuring fluctuations of small amplitude, bounded by an upper value of approximately ![]() $0.47D$. This value is in good agreement with the results of Coleman & Nikora (Reference Coleman and Nikora2009), who observed ‘mobile sediments on planar but active bed’ for
$0.47D$. This value is in good agreement with the results of Coleman & Nikora (Reference Coleman and Nikora2009), who observed ‘mobile sediments on planar but active bed’ for ![]() $\sigma _h$ in the range
$\sigma _h$ in the range ![]() $(0.40\text {-}0.50)D$. Unstable bedforms are usually observed to run through different phases of bedform evolution (KU2017). During an initial growth period, the bed increases exponentially as predicted by linear stability theory. After some time, nonlinear contributions become relevant and let the bed height tend to its quasi-steady equilibrium value (Charru et al. Reference Charru, Andreotti and Claudin2013). KU2017 observed that all their unstable cases exhibited an exponential growth at a very similar growth rate, apparently independent of the streamwise box length of the respective case. They found an exponential function
$(0.40\text {-}0.50)D$. Unstable bedforms are usually observed to run through different phases of bedform evolution (KU2017). During an initial growth period, the bed increases exponentially as predicted by linear stability theory. After some time, nonlinear contributions become relevant and let the bed height tend to its quasi-steady equilibrium value (Charru et al. Reference Charru, Andreotti and Claudin2013). KU2017 observed that all their unstable cases exhibited an exponential growth at a very similar growth rate, apparently independent of the streamwise box length of the respective case. They found an exponential function
with amplitude ![]() $A=0.0668$ and growth rate
$A=0.0668$ and growth rate ![]() $B=0.0140$ to best fit the initial increase of
$B=0.0140$ to best fit the initial increase of ![]() $\sigma _h$ with time over an interval of approximately
$\sigma _h$ with time over an interval of approximately ![]() $150$ bulk time units. In contrast, the temporal evolution in the first instances of the current unstable cases strongly varies from case to case. While the initial growth of case
$150$ bulk time units. In contrast, the temporal evolution in the first instances of the current unstable cases strongly varies from case to case. While the initial growth of case ![]() $H6D154$ follows the above described exponential function of KU2017, the remaining two cases
$H6D154$ follows the above described exponential function of KU2017, the remaining two cases ![]() $H6D102$ and
$H6D102$ and ![]() $H6D077$ grow more slowly. In the subsequent phase, case
$H6D077$ grow more slowly. In the subsequent phase, case ![]() $H6D154$ and
$H6D154$ and ![]() $H6D102$ attain what could be called as asymptotic state after approximately
$H6D102$ attain what could be called as asymptotic state after approximately ![]() $280$ and
$280$ and ![]() $350$ bulk time units, respectively. Case
$350$ bulk time units, respectively. Case ![]() $H6D077$ exhibits stronger oscillations with higher amplitude compared to the previous two cases, a behaviour similar to that of case H4D1023 from KU2017. Averaging
$H6D077$ exhibits stronger oscillations with higher amplitude compared to the previous two cases, a behaviour similar to that of case H4D1023 from KU2017. Averaging ![]() $\sigma _h$ over the final time interval
$\sigma _h$ over the final time interval ![]() $T^{s}_{obs}$ leads to values of
$T^{s}_{obs}$ leads to values of ![]() $\langle \sigma _h \rangle _t/D \approx 2.08$,
$\langle \sigma _h \rangle _t/D \approx 2.08$, ![]() $\langle \sigma _h \rangle _t/D \approx 0.89$ and
$\langle \sigma _h \rangle _t/D \approx 0.89$ and ![]() $\langle \sigma _h \rangle _t/D \approx 0.67$ for cases
$\langle \sigma _h \rangle _t/D \approx 0.67$ for cases ![]() $H6D154$,
$H6D154$, ![]() $H6D102$ and
$H6D102$ and ![]() $H6D077$, respectively. It is remarkable that the mean values in the final interval differ by more than a factor of two between cases
$H6D077$, respectively. It is remarkable that the mean values in the final interval differ by more than a factor of two between cases ![]() $H6D154$ and
$H6D154$ and ![]() $H6D102$, which possess a comparable relative domain length of
$H6D102$, which possess a comparable relative domain length of ![]() $L_x/H_f \approx 6$. On the other hand, cases
$L_x/H_f \approx 6$. On the other hand, cases ![]() $H6D102$ and H4D1021,2,3 attain very similar values of
$H6D102$ and H4D1021,2,3 attain very similar values of ![]() $\langle \sigma _h \rangle _t/D \approx 0.89$ and
$\langle \sigma _h \rangle _t/D \approx 0.89$ and ![]() $\langle \sigma _h \rangle _t/D \approx 0.96$, respectively, although case H4D1021,2,3 has a smaller relative box length
$\langle \sigma _h \rangle _t/D \approx 0.96$, respectively, although case H4D1021,2,3 has a smaller relative box length ![]() $L_x/H_f \approx 4$. This indicates that the attained mean value of
$L_x/H_f \approx 4$. This indicates that the attained mean value of ![]() $\sigma _h$ in the final interval mainly depends on the chosen
$\sigma _h$ in the final interval mainly depends on the chosen ![]() $L_x/D$ ratio, whereas it is not very sensitive to a variation of the mean fluid height
$L_x/D$ ratio, whereas it is not very sensitive to a variation of the mean fluid height ![]() $H_f$.
$H_f$.

Figure 3. (a) Time evolution of the root mean square of the bedform amplitude in cases ![]() $H6D052, H6D077, H6D102 \hbox{ and } H6D154$ normalized by the particle diameter
$H6D052, H6D077, H6D102 \hbox{ and } H6D154$ normalized by the particle diameter ![]() $\sigma _h /D$. Time is scaled in bulk time units
$\sigma _h /D$. Time is scaled in bulk time units ![]() $T_b$. The data of case H4D1021,2,3 are presented as an ensemble average over the three simulations. Additionally, the individual evolution of run H4D1023 is presented. The horizontal dotted and dashed lines indicate values reported by Coleman & Nikora (Reference Coleman and Nikora2009) for a ‘static plane bed’ (
$T_b$. The data of case H4D1021,2,3 are presented as an ensemble average over the three simulations. Additionally, the individual evolution of run H4D1023 is presented. The horizontal dotted and dashed lines indicate values reported by Coleman & Nikora (Reference Coleman and Nikora2009) for a ‘static plane bed’ (![]() $\sigma _h \approx 0.17D$) and ‘mobile sediments on planar but active beds’ (
$\sigma _h \approx 0.17D$) and ‘mobile sediments on planar but active beds’ (![]() $\sigma _h \approx 0.40\text {-}0.50D$, here
$\sigma _h \approx 0.40\text {-}0.50D$, here ![]() $\sigma _h \approx 0.47D$). The dashed-dotted line represents the exponential curve
$\sigma _h \approx 0.47D$). The dashed-dotted line represents the exponential curve ![]() $\sigma _h/D = 0.0668 \exp (0.0140t/T_b)$ found by KU2017 as the best fit for the initial growth of
$\sigma _h/D = 0.0668 \exp (0.0140t/T_b)$ found by KU2017 as the best fit for the initial growth of ![]() $\sigma _h$ in their cases (including the present case
$\sigma _h$ in their cases (including the present case ![]() $H6D154$). Mean values of
$H6D154$). Mean values of ![]() $\sigma _h$ averaged over the final time interval
$\sigma _h$ averaged over the final time interval ![]() $T^{s}_{obs}$ are as follows:
$T^{s}_{obs}$ are as follows: ![]() $H6D052$:
$H6D052$: ![]() $\langle \sigma _h \rangle _t/D \approx 0.30$,
$\langle \sigma _h \rangle _t/D \approx 0.30$, ![]() $H6D077$:
$H6D077$: ![]() $\langle \sigma _h \rangle _t/D \approx 0.67$,
$\langle \sigma _h \rangle _t/D \approx 0.67$, ![]() $H6D102$:
$H6D102$: ![]() $\langle \sigma _h \rangle _t/D \approx 0.89$,
$\langle \sigma _h \rangle _t/D \approx 0.89$, ![]() $H6D154$:
$H6D154$: ![]() $\langle \sigma _h \rangle _t/D \approx 2.08$, H4D1021,2,3:
$\langle \sigma _h \rangle _t/D \approx 2.08$, H4D1021,2,3: ![]() $\langle \sigma _h \rangle _t/D \approx 0.96$. (b) Same data as (a), but represented in semi-logarithmical scale.
$\langle \sigma _h \rangle _t/D \approx 0.96$. (b) Same data as (a), but represented in semi-logarithmical scale.
Figure 4 shows the time evolution of the mean pattern wavelength ![]() $\lambda _h$. It can be observed that the chosen mean wavelength for all cases with
$\lambda _h$. It can be observed that the chosen mean wavelength for all cases with ![]() $L_x \geq 76.8D$ settles, after some fluctuation in the first
$L_x \geq 76.8D$ settles, after some fluctuation in the first ![]() $100\text {-}200$ bulk time units, at the maximum possible wavelength, i.e.
$100\text {-}200$ bulk time units, at the maximum possible wavelength, i.e. ![]() $\lambda _h = L_x$, and maintains this value until the end of the simulation. KU2017 observed a similar evolution of the mean wavelength settling at
$\lambda _h = L_x$, and maintains this value until the end of the simulation. KU2017 observed a similar evolution of the mean wavelength settling at ![]() $\lambda _h = L_x$ for their shorter cases up to a box length
$\lambda _h = L_x$ for their shorter cases up to a box length ![]() $L_x = 179.2D$. The current observations further support their findings that these systems cannot freely choose their initial wavelength, but that they are constrained by the limitation of the streamwise domain size. As a consequence, the system chooses the maximum possible unstable wavelength as the dominant one, which, however, is not necessarily the same as the one it would choose in a system without spatial limitations (cf. the very long box with
$L_x = 179.2D$. The current observations further support their findings that these systems cannot freely choose their initial wavelength, but that they are constrained by the limitation of the streamwise domain size. As a consequence, the system chooses the maximum possible unstable wavelength as the dominant one, which, however, is not necessarily the same as the one it would choose in a system without spatial limitations (cf. the very long box with ![]() $L_x/H_f=48$ simulated by KU2017). In contrast to the observed unstable cases,
$L_x/H_f=48$ simulated by KU2017). In contrast to the observed unstable cases, ![]() $\lambda _h$ in case
$\lambda _h$ in case ![]() $H6D052$ jumps between the first three harmonics
$H6D052$ jumps between the first three harmonics ![]() $\lambda _1 = L_x$,
$\lambda _1 = L_x$, ![]() $\lambda _2 = L_x/2$ and
$\lambda _2 = L_x/2$ and ![]() $\lambda _3 = L_x/3$ for the entire observation interval. This behaviour is caused by random uncorrelated bed disturbances and it indicates that the system is not able to develop a pattern at a finite wavelength.
$\lambda _3 = L_x/3$ for the entire observation interval. This behaviour is caused by random uncorrelated bed disturbances and it indicates that the system is not able to develop a pattern at a finite wavelength.

Figure 4. Time evolution of the mean wavelength of the sediment bed height in cases ![]() $H6D052, H6D077, H6D102 \hbox{ and } H6D154 $ normalized by the particle diameter
$H6D052, H6D077, H6D102 \hbox{ and } H6D154 $ normalized by the particle diameter ![]() $\lambda _h /D$. Colour coding similar to figure 3.
$\lambda _h /D$. Colour coding similar to figure 3.
In the following, we will investigate the fully developed spanwise-averaged profile of the sediment pattern along the streamwise direction. To this end, we compute the phase-averaged bed height ![]() $\skew2\tilde {H}_b(\tilde {x})$ as defined in KU2017. For this purpose we use a constant pattern migration velocity
$\skew2\tilde {H}_b(\tilde {x})$ as defined in KU2017. For this purpose we use a constant pattern migration velocity ![]() $u_D$ which is determined from a linear fit of the space–time correlation. Phase averaging is performed over the final time interval
$u_D$ which is determined from a linear fit of the space–time correlation. Phase averaging is performed over the final time interval ![]() $T^{s}_{obs}$ (as indicated in table 2). We further introduce the aspect ratio
$T^{s}_{obs}$ (as indicated in table 2). We further introduce the aspect ratio ![]() $AR$ and the degree of asymmetry
$AR$ and the degree of asymmetry ![]() $LR$ of the pattern as (KU2017)
$LR$ of the pattern as (KU2017)
where ![]() $H_D=\max (\skew2\tilde {H}_b)-\min (\skew2\tilde {H}_b)$ is the pattern height,
$H_D=\max (\skew2\tilde {H}_b)-\min (\skew2\tilde {H}_b)$ is the pattern height, ![]() $l_D$ is the streamwise distance from the crest to the neighbouring downstream trough and
$l_D$ is the streamwise distance from the crest to the neighbouring downstream trough and ![]() $\lambda _h$ is the mean wavelength.
$\lambda _h$ is the mean wavelength.
Figure 5 shows the mean pattern profile averaged over the final time interval of all simulations as well as the attained aspect ratio of the bedforms. It can be seen that the profiles of cases with ![]() $L_x/D \geq 153.6$ almost collapse upon a self-similar profile exhibiting a strong asymmetry (
$L_x/D \geq 153.6$ almost collapse upon a self-similar profile exhibiting a strong asymmetry (![]() $LR \approx 0.28$) and an aspect ratio of
$LR \approx 0.28$) and an aspect ratio of ![]() $AR \approx 0.037$ (KU2017). Some experimental studies report higher values for the steady-state aspect ratio, i.e.
$AR \approx 0.037$ (KU2017). Some experimental studies report higher values for the steady-state aspect ratio, i.e. ![]() $AR \approx 0.045$ (Fourriere et al. Reference Fourriere, Claudin and Andreotti2010),
$AR \approx 0.045$ (Fourriere et al. Reference Fourriere, Claudin and Andreotti2010), ![]() $AR \approx 0.05$ (Andreotti & Claudin Reference Andreotti and Claudin2013) and
$AR \approx 0.05$ (Andreotti & Claudin Reference Andreotti and Claudin2013) and ![]() $AR \approx 0.067$ (Charru etal. Reference Charru, Andreotti and Claudin2013). KU2017 explain their lower value with the fact, that in their cases, ‘the “natural” steady-state regime is not yet reached’ and thus, a larger aspect ratio might be attained in a later phase, whereas the experimental data reflect the long-time state of the system which in those cases has evolved for at least one order of magnitude longer times. On the other hand, the pattern profiles in cases
$AR \approx 0.067$ (Charru etal. Reference Charru, Andreotti and Claudin2013). KU2017 explain their lower value with the fact, that in their cases, ‘the “natural” steady-state regime is not yet reached’ and thus, a larger aspect ratio might be attained in a later phase, whereas the experimental data reflect the long-time state of the system which in those cases has evolved for at least one order of magnitude longer times. On the other hand, the pattern profiles in cases ![]() $H6D102$ and H4D1021,2,3 with
$H6D102$ and H4D1021,2,3 with ![]() $L_x = 102.4D$ are characterized by a smaller aspect ratio of
$L_x = 102.4D$ are characterized by a smaller aspect ratio of ![]() $AR \approx 0.024 - 0.028$ and a more symmetric shape (
$AR \approx 0.024 - 0.028$ and a more symmetric shape (![]() $LR \approx 0.33 - 0.036$). Important to note is, however, that all four profiles with
$LR \approx 0.33 - 0.036$). Important to note is, however, that all four profiles with ![]() $L_x = 102.4D$ are again nearly self-similar, despite the fact that
$L_x = 102.4D$ are again nearly self-similar, despite the fact that ![]() $L_x/H_f$ varies by up to a factor of
$L_x/H_f$ varies by up to a factor of ![]() $1.5$. This is another indication that the pattern shape is mainly controlled by the particle diameter
$1.5$. This is another indication that the pattern shape is mainly controlled by the particle diameter ![]() $D$, but almost unaffected by the mean fluid height
$D$, but almost unaffected by the mean fluid height ![]() $H_f$. Further reducing the relative domain length to a value
$H_f$. Further reducing the relative domain length to a value ![]() $L_x/D=76.8$ in case
$L_x/D=76.8$ in case ![]() $H6D077$ leads to an even more symmetric profile (
$H6D077$ leads to an even more symmetric profile (![]() $LR \approx 0.41$), whereas the aspect ratio still attains a value
$LR \approx 0.41$), whereas the aspect ratio still attains a value ![]() $AR \approx 0.024$, comparable to the cases with
$AR \approx 0.024$, comparable to the cases with ![]() $L_x = 102.4D$. An additional observation in case
$L_x = 102.4D$. An additional observation in case ![]() $H6D077$ is that, in contrast to the previous cases, the curve representing the pattern profile is not smooth, but exhibits wavy disturbances. This is a direct consequence of the lower amount of particles in case
$H6D077$ is that, in contrast to the previous cases, the curve representing the pattern profile is not smooth, but exhibits wavy disturbances. This is a direct consequence of the lower amount of particles in case ![]() $H6D077$, which leads to stronger disturbances of the spanwise-averaged pattern profile.
$H6D077$, which leads to stronger disturbances of the spanwise-averaged pattern profile.

Figure 5. (a) Mean two-dimensional profile of the sedimentary patterns in cases ![]() $H6D077, H6D102, H6D154 \hbox{ and } H4D102^{1,2,3}$, averaged over the time period
$H6D077, H6D102, H6D154 \hbox{ and } H4D102^{1,2,3}$, averaged over the time period ![]() $T^{s}_{obs}$ at the end of each simulation. The filled circles indicate the location, where each profile attains its maximal value. Note that for the sake of visualization, the vertical and the horizontal axes are shown in different scales, i.e. the aspect ratio is exaggerated. The black line shows the same quantity for case
$T^{s}_{obs}$ at the end of each simulation. The filled circles indicate the location, where each profile attains its maximal value. Note that for the sake of visualization, the vertical and the horizontal axes are shown in different scales, i.e. the aspect ratio is exaggerated. The black line shows the same quantity for case ![]() $H7$ from KU2017, with
$H7$ from KU2017, with ![]() $L_x/D=179.2$ and
$L_x/D=179.2$ and ![]() $L_x/H_f=7.08$. (b) Aspect ratio (
$L_x/H_f=7.08$. (b) Aspect ratio (![]() $AR$) of the mean two-dimensional profiles presented in (a) as a function of the mean wavelength
$AR$) of the mean two-dimensional profiles presented in (a) as a function of the mean wavelength ![]() $\lambda _h$ (averaged over the final time interval
$\lambda _h$ (averaged over the final time interval ![]() $T^{s}_{obs}$). Round symbols represent case
$T^{s}_{obs}$). Round symbols represent case ![]() $H7$ as well as the three individual runs of case
$H7$ as well as the three individual runs of case ![]() $H12$ from KU2017.
$H12$ from KU2017.
5.2. Variation of the mean fluid height
In order to study the dependence of the minimal unstable wavelength ![]() $\lambda _{th}$ on the mean fluid height
$\lambda _{th}$ on the mean fluid height ![]() $H_f$, a second set of three simulations will be analysed in the following, including case H4D1021,2,3 of KU2017 as well as two new simulations H2D1021 and H2D1022. All three cases have the same initial sediment bed configuration and the streamwise and spanwise box dimensions match. However, in cases H2D1021 and H2D1022,
$H_f$, a second set of three simulations will be analysed in the following, including case H4D1021,2,3 of KU2017 as well as two new simulations H2D1021 and H2D1022. All three cases have the same initial sediment bed configuration and the streamwise and spanwise box dimensions match. However, in cases H2D1021 and H2D1022, ![]() $H_f$ has been increased by a factor of two compared to case H4D1021,2,3. Consequently, the bulk and friction Reynolds numbers are higher in the former two cases (cf. table1). In cases H2D1021 and H2D1022, two different values have been chosen for the Shields number, i.e.
$H_f$ has been increased by a factor of two compared to case H4D1021,2,3. Consequently, the bulk and friction Reynolds numbers are higher in the former two cases (cf. table1). In cases H2D1021 and H2D1022, two different values have been chosen for the Shields number, i.e. ![]() $\theta =0.18$ in the former and
$\theta =0.18$ in the former and ![]() $\theta =0.13$ in the latter, by adjusting the Galileo number, while the remaining parameters are identical. The dimensions of the channel configuration in the new simulations have been chosen in such a way, that their relative domain length (
$\theta =0.13$ in the latter, by adjusting the Galileo number, while the remaining parameters are identical. The dimensions of the channel configuration in the new simulations have been chosen in such a way, that their relative domain length (![]() $L_x/H_f \approx 2$) lies below the lower bound for the most unstable wavelength as initially reported by KU2017. As a consequence, none of the two cases should allow the sediment bed to become unstable and transverse patterns to evolve, if the minimal unstable wavelength scales with the mean fluid height. Note, however, that in the study of KU2017 the values of
$L_x/H_f \approx 2$) lies below the lower bound for the most unstable wavelength as initially reported by KU2017. As a consequence, none of the two cases should allow the sediment bed to become unstable and transverse patterns to evolve, if the minimal unstable wavelength scales with the mean fluid height. Note, however, that in the study of KU2017 the values of ![]() $L_x/D$ and
$L_x/D$ and ![]() $L_x/H_f$ were not varied independently, and, therefore, it was not possible to distinguish between the two alternative scaling relations. Here, we are now in a position to do this.
$L_x/H_f$ were not varied independently, and, therefore, it was not possible to distinguish between the two alternative scaling relations. Here, we are now in a position to do this.
Figures 6 and 7 show selected instantaneous snapshots of the particle bed evolution for the new cases H2D1021 and H2D1022, respectively. The sediment bed surface of case H2D1021 is deformed, showing streamwise and spanwise elongated crestlines. In some phases, the system alternates between patterns at either of the two orientations (cf. figure 6b,c), whereas in figure 6(a), for instance, streamwise and spanwise oriented crestlines appear at the same time. Similarly, the sediment bed of case H2D1022 exhibits one crest line parallel and one perpendicular to the mean flow direction in figure 7(a). In contrast, a later snapshot in figure 7(b) shows a three-dimensional bedform with a horseshoe-like shape with horns on both sides pointing downstream. This pattern resembles in its geometry a barchan dune (Franklin & Charru Reference Franklin and Charru2011). In the last snapshot provided in figure 7(c) a diagonal crest line has evolved crossing the whole extent of the ![]() $(x,z)$-plane from the lower left to the upper right corner. These observations represent a marked difference between the systems with larger clear fluid height (
$(x,z)$-plane from the lower left to the upper right corner. These observations represent a marked difference between the systems with larger clear fluid height (![]() $H_f/D \approx 50$) and those with smaller relative submergences (
$H_f/D \approx 50$) and those with smaller relative submergences (![]() $H_f/D \approx 25$). In the latter case (simulations H4D1021,2,3 of KU2017 -- images not shown), regular streamwise-aligned ridges are either displaced by the higher, dominating transverse bedforms or do exist superimposed to the former ones.
$H_f/D \approx 25$). In the latter case (simulations H4D1021,2,3 of KU2017 -- images not shown), regular streamwise-aligned ridges are either displaced by the higher, dominating transverse bedforms or do exist superimposed to the former ones.

Figure 6. Instantaneous snapshots of the sediment bed of case H2D1021 at (a) ![]() $t \approx 471 T_b$, (b)
$t \approx 471 T_b$, (b) ![]() $t \approx 619 T_b$ and (c)
$t \approx 619 T_b$ and (c) ![]() $t \approx 687 T_b$, seen from the top of the channel. Colour scheme is the same as in figure 2.
$t \approx 687 T_b$, seen from the top of the channel. Colour scheme is the same as in figure 2.

Figure 7. Instantaneous snapshots of the sediment bed of case H2D1022 at (a) ![]() $t \approx 300 T_b$, (b)
$t \approx 300 T_b$, (b) ![]() $t \approx 352 T_b$ and (c)
$t \approx 352 T_b$ and (c) ![]() $t \approx 490 T_b$, seen from the top of the channel. Colour scheme is the same as in figure 2.
$t \approx 490 T_b$, seen from the top of the channel. Colour scheme is the same as in figure 2.
An important consequence of the observed behaviour in cases H2D1021 and H2D1022 is that the bed height is clearly two-dimensional. This means that the spanwise-averaged sediment bed and flow field will not correctly describe the physical processes that lead to the formation of these type of bedforms. In the remainder of the current work, we will therefore analyse the sediment bed in its entire streamwise and spanwise dimensions and omit the spanwise averaging (cf. the definition in § 4.2).
Figure 8 shows the time evolution of the root mean square of the two-dimensional sediment bed height fluctuation ![]() $\sigma _h^{2D}$. All cases exhibit an exponential growth interval, but with clearly different growth rates, as indicated by the fitted exponential curves presented in figure 8. It is important to keep in mind that in contrast to the spanwise-averaged case, the two-dimensional measure
$\sigma _h^{2D}$. All cases exhibit an exponential growth interval, but with clearly different growth rates, as indicated by the fitted exponential curves presented in figure 8. It is important to keep in mind that in contrast to the spanwise-averaged case, the two-dimensional measure ![]() $\sigma _h^{2D}$ takes into account streamwise and spanwise variations of the fluid–bed interface, which means that a change in
$\sigma _h^{2D}$ takes into account streamwise and spanwise variations of the fluid–bed interface, which means that a change in ![]() $\sigma _h^{2D}$ with time can be a sign of evolving ridges or transverse patterns likewise. Indeed, the detailed analysis of a two-dimensional Fourier decomposition of the bed height perturbation which is presented below shows that the amplitude of variations in both directions is of similar order. In order to determine the scaling of the initial growth rate of the sediment bed height fluctuation, however, one would require a larger database and a larger number of individual runs at each parameter point to allow for ensemble averaging similar to case H4D1021,2,3. Nevertheless, it would be of great interest to elucidate the influence of the relevant parameters on the initial growth rate of
$\sigma _h^{2D}$ with time can be a sign of evolving ridges or transverse patterns likewise. Indeed, the detailed analysis of a two-dimensional Fourier decomposition of the bed height perturbation which is presented below shows that the amplitude of variations in both directions is of similar order. In order to determine the scaling of the initial growth rate of the sediment bed height fluctuation, however, one would require a larger database and a larger number of individual runs at each parameter point to allow for ensemble averaging similar to case H4D1021,2,3. Nevertheless, it would be of great interest to elucidate the influence of the relevant parameters on the initial growth rate of ![]() $\sigma _h^{2D}$ such as the Reynolds number
$\sigma _h^{2D}$ such as the Reynolds number ![]() $Re_b$ (
$Re_b$ (![]() $Re_{\tau }$, respectively) and the relative submergence
$Re_{\tau }$, respectively) and the relative submergence ![]() $H_f/D$ in a future study. After approximately
$H_f/D$ in a future study. After approximately ![]() $300$ bulk time units, all cases eventually reach what could be called an asymptotic state. We observe that the pattern amplitude attains fully developed averaged values of order comparable to one particle diameter for all cases, which suggests that at the given parameter point shown in figure 8, the averaged value of
$300$ bulk time units, all cases eventually reach what could be called an asymptotic state. We observe that the pattern amplitude attains fully developed averaged values of order comparable to one particle diameter for all cases, which suggests that at the given parameter point shown in figure 8, the averaged value of ![]() $\sigma _h^{2D}$ in the final interval does not strongly depend on the value of the mean fluid height
$\sigma _h^{2D}$ in the final interval does not strongly depend on the value of the mean fluid height ![]() $H_f$.
$H_f$.

Figure 8. (a) Time evolution of the two-dimensional root mean square of the bedform amplitude in cases ![]() $H4D102^{1,2,3}, H2D102^{1} \hbox{ and } H2D102^{2}$ normalized by the particle diameter
$H4D102^{1,2,3}, H2D102^{1} \hbox{ and } H2D102^{2}$ normalized by the particle diameter ![]() $\sigma _h^{2D}/D$. Time is scaled in bulk time units
$\sigma _h^{2D}/D$. Time is scaled in bulk time units ![]() $T_b$. The data of case H4D1021,2,3 are presented as an ensemble average over the three simulations. Additionally, the individual evolution of run H4D1023 is presented. The dashed-dotted lines represent exponential curves of the form
$T_b$. The data of case H4D1021,2,3 are presented as an ensemble average over the three simulations. Additionally, the individual evolution of run H4D1023 is presented. The dashed-dotted lines represent exponential curves of the form ![]() $\sigma _h/D = A\exp (Bt/T_b)$ which have been found to best fit the evolution of
$\sigma _h/D = A\exp (Bt/T_b)$ which have been found to best fit the evolution of ![]() $\sigma _h^{2D}$ during the initial growth period of the respective case. The coefficients are as follows: H4D1021,2,3:
$\sigma _h^{2D}$ during the initial growth period of the respective case. The coefficients are as follows: H4D1021,2,3: ![]() $A=0.2215$,
$A=0.2215$, ![]() $B=0.0070$; H2D1021:
$B=0.0070$; H2D1021: ![]() $A=0.2441$,
$A=0.2441$, ![]() $B=0.0266$; H2D1022:
$B=0.0266$; H2D1022: ![]() $A=0.1926$,
$A=0.1926$, ![]() $B=0.0130$. Note that in case H4D1021,2,3, the exponential curve best fits the ensemble average over the three runs. (b) Same data as (a), but represented in semi-logarithmical scale.
$B=0.0130$. Note that in case H4D1021,2,3, the exponential curve best fits the ensemble average over the three runs. (b) Same data as (a), but represented in semi-logarithmical scale.
The analysis of ![]() $\sigma _h^{2D}$ has shown that the sediment bed becomes unstable in all three cases. However, as
$\sigma _h^{2D}$ has shown that the sediment bed becomes unstable in all three cases. However, as ![]() $\sigma _h^{2D}$ is an integral measure for the bed evolution, it cannot provide further information about the evolution and interaction of single unstable modes. In particular, it does not allow us to determine the role of streamwise and transverse modes separately. For this reason, the evolution of the bed height perturbation will be further analysed in Fourier space for the different streamwise and spanwise wavenumbers. To this end, we compute the single-sided amplitude spectra
$\sigma _h^{2D}$ is an integral measure for the bed evolution, it cannot provide further information about the evolution and interaction of single unstable modes. In particular, it does not allow us to determine the role of streamwise and transverse modes separately. For this reason, the evolution of the bed height perturbation will be further analysed in Fourier space for the different streamwise and spanwise wavenumbers. To this end, we compute the single-sided amplitude spectra ![]() $\ \hat {A}_{(k,l)}$ (for the physically relevant non-negative wavenumbers
$\ \hat {A}_{(k,l)}$ (for the physically relevant non-negative wavenumbers ![]() $k,l \geq 0$) as twice the absolute value of the coefficient
$k,l \geq 0$) as twice the absolute value of the coefficient ![]() $\hat {h}_{b(k,l)} (\kappa ^{1}_k,\kappa ^{3}_l,t)$, which is the discrete Fourier transform of the sediment bed height perturbation in physical space,
$\hat {h}_{b(k,l)} (\kappa ^{1}_k,\kappa ^{3}_l,t)$, which is the discrete Fourier transform of the sediment bed height perturbation in physical space, ![]() $h_b^{\prime } (x,z,t)$. In the above expression,
$h_b^{\prime } (x,z,t)$. In the above expression, ![]() $\kappa ^{d}_k$ is the wavenumber of the
$\kappa ^{d}_k$ is the wavenumber of the ![]() $k$th mode in spatial direction
$k$th mode in spatial direction ![]() $d$ (where
$d$ (where ![]() $d=1,3$ corresponds to the
$d=1,3$ corresponds to the ![]() $x$- and
$x$- and ![]() $z$-direction, respectively).
$z$-direction, respectively).
Figure 9 shows the time evolution of the single-sided amplitude spectra for the most dominant modes in case H4D1023, H2D1021 and H2D1022, respectively. In case H4D1023, the wave with modes ![]() $(1,0)$ (first harmonic in the streamwise, constant in the spanwise direction) attains the highest amplitudes and thus clearly dominates the spectra. In good agreement with the evolution of
$(1,0)$ (first harmonic in the streamwise, constant in the spanwise direction) attains the highest amplitudes and thus clearly dominates the spectra. In good agreement with the evolution of ![]() $\sigma _h^{2D}$, this mode first increases exponentially during the initial 200–250 bulk time units, before it settles at values which fluctuate somewhat around an asymptotic mean. Note that only the first two harmonics of the pure streamwise waves
$\sigma _h^{2D}$, this mode first increases exponentially during the initial 200–250 bulk time units, before it settles at values which fluctuate somewhat around an asymptotic mean. Note that only the first two harmonics of the pure streamwise waves ![]() $\lambda _{(1,0)}$ and
$\lambda _{(1,0)}$ and ![]() $\lambda _{(2,0)}$ exceed a value of
$\lambda _{(2,0)}$ exceed a value of ![]() $\hat {A}_{(k,l)} = 0.30D$ during the observation interval, highlighting that, in these cases with a comparably short domain, a very sparse range of wavenumbers is amplified, and is then available to form the sediment pattern. On the other hand, waves of the first three pure spanwise harmonics
$\hat {A}_{(k,l)} = 0.30D$ during the observation interval, highlighting that, in these cases with a comparably short domain, a very sparse range of wavenumbers is amplified, and is then available to form the sediment pattern. On the other hand, waves of the first three pure spanwise harmonics ![]() $\lambda _{(0,1 \ldots 3)}$ are found to be significant. In the first approximately 100–150 bulk time units, these pure spanwise modes dominate the amplitude spectra, which reflects the formation of initial streamwise aligned ridges that has been observed by KU2017. In the subsequent quasi-steady phase of bedform evolution, pure spanwise modes are still present with finite but smaller amplitudes compared to
$\lambda _{(0,1 \ldots 3)}$ are found to be significant. In the first approximately 100–150 bulk time units, these pure spanwise modes dominate the amplitude spectra, which reflects the formation of initial streamwise aligned ridges that has been observed by KU2017. In the subsequent quasi-steady phase of bedform evolution, pure spanwise modes are still present with finite but smaller amplitudes compared to ![]() $\hat {A}_{(1,0)}$, reaching maximum values
$\hat {A}_{(1,0)}$, reaching maximum values ![]() $\hat {A}_{(0,1)} = 0.80D$. This is in good agreement with the observation of the aforementioned authors, that streamwise elongated patterns are still visible on the upstream face of the transverse bedforms, once these latter have reached a quasi-steady state. In addition, several diagonal waves including modes larger than zero in both directions evolve, but they do not reach amplitudes higher than
$\hat {A}_{(0,1)} = 0.80D$. This is in good agreement with the observation of the aforementioned authors, that streamwise elongated patterns are still visible on the upstream face of the transverse bedforms, once these latter have reached a quasi-steady state. In addition, several diagonal waves including modes larger than zero in both directions evolve, but they do not reach amplitudes higher than ![]() $\hat {A} = 0.5D$. The time evolution of the amplitude spectra in the new simulations H2D1021 and H2D1022 (cf. figure 9b,c, respectively), on the other hand, is dominated by the first pure spanwise oscillating wave mode
$\hat {A} = 0.5D$. The time evolution of the amplitude spectra in the new simulations H2D1021 and H2D1022 (cf. figure 9b,c, respectively), on the other hand, is dominated by the first pure spanwise oscillating wave mode ![]() $(0,1)$ during almost the whole observation interval, attaining maximum values of
$(0,1)$ during almost the whole observation interval, attaining maximum values of ![]() $\hat {A}_{(0,1)}/D$ above unity. In comparison, the amplitude of the first pure streamwise oscillating wave mode
$\hat {A}_{(0,1)}/D$ above unity. In comparison, the amplitude of the first pure streamwise oscillating wave mode ![]() $(1,0)$ which represents in these cases the only significant pure streamwise wave attains somewhat smaller maximum values with
$(1,0)$ which represents in these cases the only significant pure streamwise wave attains somewhat smaller maximum values with ![]() $\hat {A}_{(1,0)}/D$ not exceeding unity. In general, the amplitude of the single modes exhibit higher fluctuations than those in case H4D1023, leading to differences of approximately
$\hat {A}_{(1,0)}/D$ not exceeding unity. In general, the amplitude of the single modes exhibit higher fluctuations than those in case H4D1023, leading to differences of approximately ![]() $1D$ between the highest and the lowest attained values of a single mode. During the entire simulation, none of the modes reach a plateau regime which would indicate a quasi-steady state of the bed. These findings match our observations, that both systems H2D1021 and H2D1022 show a sequence of different alternating bedform configurations composed of a number of streamwise and spanwise unstable modes without eventually reaching a quasi-steady state. In particular, transverse sediment bed waves evolve and, even though they are observed to be of smaller amplitude than their spanwise directed counterparts, they are involved in the formation of three dimensional patterns. Eventually, this reveals that, indeed, a sediment bed can become unstable for a domain length
$1D$ between the highest and the lowest attained values of a single mode. During the entire simulation, none of the modes reach a plateau regime which would indicate a quasi-steady state of the bed. These findings match our observations, that both systems H2D1021 and H2D1022 show a sequence of different alternating bedform configurations composed of a number of streamwise and spanwise unstable modes without eventually reaching a quasi-steady state. In particular, transverse sediment bed waves evolve and, even though they are observed to be of smaller amplitude than their spanwise directed counterparts, they are involved in the formation of three dimensional patterns. Eventually, this reveals that, indeed, a sediment bed can become unstable for a domain length ![]() $L_x/H_f < 3$, indicating that the lower bound for the most unstable wavelength as reported by KU2017 does not scale with the mean fluid height
$L_x/H_f < 3$, indicating that the lower bound for the most unstable wavelength as reported by KU2017 does not scale with the mean fluid height ![]() $H_f$. The three-dimensional pattern evolution, however, requires further investigation.
$H_f$. The three-dimensional pattern evolution, however, requires further investigation.

Figure 9. Time evolution of the single-sided amplitude spectra for the most dominant modes normalized with the particle diameter ![]() $\hat {A}_{(k,l)}/D$ for cases (a) H4D1023, (b) H2D1021 and (c) H2D1022. Note that only those modes are defined as dominant which exceed a value of
$\hat {A}_{(k,l)}/D$ for cases (a) H4D1023, (b) H2D1021 and (c) H2D1022. Note that only those modes are defined as dominant which exceed a value of ![]() $\hat {A}_{(k,l)} = 0.30D$ during the simulation. The notation
$\hat {A}_{(k,l)} = 0.30D$ during the simulation. The notation ![]() $\hat {A}_{(k,l)}$ indicates that the amplitude corresponds to the mode with streamwise and spanwise wavenumbers
$\hat {A}_{(k,l)}$ indicates that the amplitude corresponds to the mode with streamwise and spanwise wavenumbers ![]() $\kappa ^{1}_k$ and
$\kappa ^{1}_k$ and ![]() $\kappa ^{3}_l$, respectively.
$\kappa ^{3}_l$, respectively.
6. Discussion
Our observations in the previous section suggest that in the investigated parameter range, the minimal unstable wavelength depends on the particle diameter, whereas it seems to be rather unaffected by variations of the mean fluid height. In the following, we will compare our results with measurements as well as proposed scaling relations from experimental and theoretical studies.
In figure 10, we present an overview of initial mean pattern wavelengths from our current and previous direct numerical simulation studies together with values determined in laboratory experiments. The observed wavelengths are shown as functions of the particle diameter ![]() $D$ and of the mean fluid height
$D$ and of the mean fluid height ![]() $H_f$, respectively. Note that for stable sediment beds (indicated by open symbols in figure 10), the definition of an initial pattern wavelength is meaningless. Here, we give instead the streamwise domain length
$H_f$, respectively. Note that for stable sediment beds (indicated by open symbols in figure 10), the definition of an initial pattern wavelength is meaningless. Here, we give instead the streamwise domain length ![]() $L_x$, which indicates the maximum possible wavelength that did not evolve during the simulation. In cases H2D1021 and H2D1022, on the other hand, we have observed the sediment bed to evolve both in the streamwise and spanwise direction. In these two cases we equally associate the value of the domain length
$L_x$, which indicates the maximum possible wavelength that did not evolve during the simulation. In cases H2D1021 and H2D1022, on the other hand, we have observed the sediment bed to evolve both in the streamwise and spanwise direction. In these two cases we equally associate the value of the domain length ![]() $L_x$ with the most unstable wavelength, since the study of the single-sided amplitude spectra of the sediment bed height fluctuation shows that the most dominant streamwise mode is the one with indices
$L_x$ with the most unstable wavelength, since the study of the single-sided amplitude spectra of the sediment bed height fluctuation shows that the most dominant streamwise mode is the one with indices ![]() $(1,0)$, i.e. the first streamwise harmonic which is constant in the spanwise direction. It should be further mentioned that with cases
$(1,0)$, i.e. the first streamwise harmonic which is constant in the spanwise direction. It should be further mentioned that with cases ![]() $H2D052$ and
$H2D052$ and ![]() $H4D052$, two additional new cases have been added to the parameter plane, which were not part of the analysis in the previous section (cf. tables 1 and 2 for the physical and numerical parameters). In both cases the bed is observed to remain stable, i.e. no transverse patterns form during the simulation. The experimental data shown in figure 10 stem from measurements in channel flow by Langlois & Valance (Reference Langlois and Valance2007) as well as in closed-conduit flows by Coleman et al. (Reference Coleman, Fedele and Garcia2003) and Cardona Florez & Franklin (Reference Cardona Florez and Franklin2016).
$H4D052$, two additional new cases have been added to the parameter plane, which were not part of the analysis in the previous section (cf. tables 1 and 2 for the physical and numerical parameters). In both cases the bed is observed to remain stable, i.e. no transverse patterns form during the simulation. The experimental data shown in figure 10 stem from measurements in channel flow by Langlois & Valance (Reference Langlois and Valance2007) as well as in closed-conduit flows by Coleman et al. (Reference Coleman, Fedele and Garcia2003) and Cardona Florez & Franklin (Reference Cardona Florez and Franklin2016).
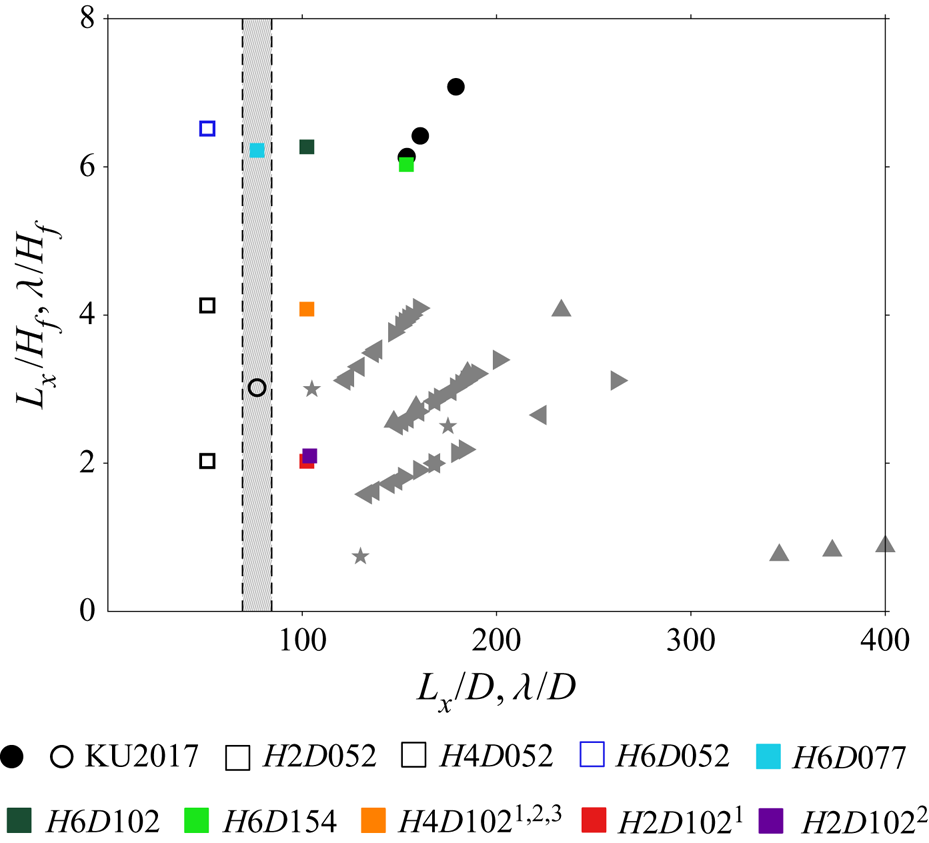
Figure 10. Minimal unstable wavelengths in numerical simulations and experiments as functions of the particle diameter ![]() $D$ and the mean fluid height
$D$ and the mean fluid height ![]() $H_f$. Filled symbols indicate unstable sediment beds, whereas open symbols are used for stable systems. The presented wavelengths are determined as the time average of the mean wavelength
$H_f$. Filled symbols indicate unstable sediment beds, whereas open symbols are used for stable systems. The presented wavelengths are determined as the time average of the mean wavelength ![]() $\lambda _h$ over the final time period
$\lambda _h$ over the final time period ![]() $T^{s}_{obs}$. It should be noted that, for stable systems as well as for cases H2D1021 and H2D1022, in which three-dimensional patterns evolve, the streamwise box length is given instead of the spanwise-averaged mean wavelength (cf. the detailed discussion in the text). Wavelengths measured in experiments are presented with the following grey symbols: Coleman et al. (Reference Coleman, Fedele and Garcia2003) (closed-conduit,
$T^{s}_{obs}$. It should be noted that, for stable systems as well as for cases H2D1021 and H2D1022, in which three-dimensional patterns evolve, the streamwise box length is given instead of the spanwise-averaged mean wavelength (cf. the detailed discussion in the text). Wavelengths measured in experiments are presented with the following grey symbols: Coleman et al. (Reference Coleman, Fedele and Garcia2003) (closed-conduit, ![]() ), Langlois & Valance (Reference Langlois and Valance2007) (channel,
), Langlois & Valance (Reference Langlois and Valance2007) (channel, ![]() ), Cardona Florez & Franklin (Reference Cardona Florez and Franklin2016) (closed-conduit,
), Cardona Florez & Franklin (Reference Cardona Florez and Franklin2016) (closed-conduit, ![]() for the first and
for the first and ![]() for the last measured wavelength). Note that in the experimental studies, no free surface is present. Thus, the experimentally determined wavelengths are normalized with the half mean fluid height. Based on the results of our analysis, we expect the minimal unstable wavelength in the vertical grey region around
for the last measured wavelength). Note that in the experimental studies, no free surface is present. Thus, the experimentally determined wavelengths are normalized with the half mean fluid height. Based on the results of our analysis, we expect the minimal unstable wavelength in the vertical grey region around ![]() ${\lambda /D = 80}$.
${\lambda /D = 80}$.
In our direct numerical simulations, we have observed transverse pattern formation only in cases with a relative streamwise domain length ![]() $L_x/D \geq 76.8$, while the sediment bed remained stable for all simulations below this limit, irrespective of the fluid height. At a domain length
$L_x/D \geq 76.8$, while the sediment bed remained stable for all simulations below this limit, irrespective of the fluid height. At a domain length ![]() $L_x/D = 76.8$, we have observed case
$L_x/D = 76.8$, we have observed case ![]() $H6D077$ to become unstable, but the shape and asymmetry of the evolving pattern is seen to substantially deviate from the observed values in sufficiently long domains such as the cases of KU2017 with a box length of
$H6D077$ to become unstable, but the shape and asymmetry of the evolving pattern is seen to substantially deviate from the observed values in sufficiently long domains such as the cases of KU2017 with a box length of ![]() $L_x/D = {O}(10^{3})$. A possible reason for this observation is that in
$L_x/D = {O}(10^{3})$. A possible reason for this observation is that in ![]() $H6D077$, the system can only choose between 8 harmonics with a wavelength higher than
$H6D077$, the system can only choose between 8 harmonics with a wavelength higher than ![]() $ {O}(D)$. The interaction of this small number of discrete modes may not lead to the same interface that would form in a sufficiently long domain. Interestingly, KU2017 report a case with the same relative domain length
$ {O}(D)$. The interaction of this small number of discrete modes may not lead to the same interface that would form in a sufficiently long domain. Interestingly, KU2017 report a case with the same relative domain length ![]() $L_x/D = 76.8$ in which the sediment bed remained flat. We therefore expect that a box length
$L_x/D = 76.8$ in which the sediment bed remained flat. We therefore expect that a box length ![]() $L_x/D = 76.8$ is in the vicinity of the sought threshold wavelength, such that at this parameter point, already small differences in the configuration might tip the system in either way. If the domain length is even further decreased (as in cases
$L_x/D = 76.8$ is in the vicinity of the sought threshold wavelength, such that at this parameter point, already small differences in the configuration might tip the system in either way. If the domain length is even further decreased (as in cases ![]() $H2D052$,
$H2D052$, ![]() $H4D052$ and
$H4D052$ and ![]() $H6D052$) the bed remains macroscopically flat.
$H6D052$) the bed remains macroscopically flat.
In the considered experimental studies, the shortest measured wavelength ![]() $\lambda /D \approx 105$ is clearly above the critical wavelength determined in the present work. In our simulations, the shortest box which allowed a single bedform to reach an asymptotic state with an asymmetric triangular shape was observed for a very similar box length
$\lambda /D \approx 105$ is clearly above the critical wavelength determined in the present work. In our simulations, the shortest box which allowed a single bedform to reach an asymptotic state with an asymmetric triangular shape was observed for a very similar box length ![]() $L_x/D = 102.4$. Nevertheless, the aspect ratio is still smaller than in the longer cases
$L_x/D = 102.4$. Nevertheless, the aspect ratio is still smaller than in the longer cases ![]() $H6$,
$H6$, ![]() $H7$ and
$H7$ and ![]() $H12$ of KU2017, which might be an indication that the patterns did not yet reach their final state and would further evolve if their growth was not hindered by the limited domain size. Indeed, the majority of the experimental data points concentrate in a range of
$H12$ of KU2017, which might be an indication that the patterns did not yet reach their final state and would further evolve if their growth was not hindered by the limited domain size. Indeed, the majority of the experimental data points concentrate in a range of ![]() ${\lambda /D = 120\text {-}250}$ (
${\lambda /D = 120\text {-}250}$ (![]() $\lambda /H_f = 0.5\text {-}4.0$). In good agreement, all numerical simulations with
$\lambda /H_f = 0.5\text {-}4.0$). In good agreement, all numerical simulations with ![]() $150 \leq L_x/D \leq 300$ develop patterns with a mean wavelength in the range
$150 \leq L_x/D \leq 300$ develop patterns with a mean wavelength in the range ![]() ${150 \leq \lambda /D \leq 180}$ and a self-similar profile. These observations further support the suggestion of KU2017, that the bedforms finally settle at a wavelength of approximately
${150 \leq \lambda /D \leq 180}$ and a self-similar profile. These observations further support the suggestion of KU2017, that the bedforms finally settle at a wavelength of approximately ![]() ${150 \leq \lambda /D \leq 180}$. Similarly, Coleman & Nikora (Reference Coleman and Nikora2009, Reference Coleman and Nikora2011) report a lower bound for the preferred initial wavelength of
${150 \leq \lambda /D \leq 180}$. Similarly, Coleman & Nikora (Reference Coleman and Nikora2009, Reference Coleman and Nikora2011) report a lower bound for the preferred initial wavelength of ![]() $\lambda /D = 130$. Eventually, the occurrence of patterns with a wavelength
$\lambda /D = 130$. Eventually, the occurrence of patterns with a wavelength ![]() $\lambda /H_f < 3$ in numerical simulations and experiments which can be seen in figure 10 excludes a possible scaling of the threshold with the mean fluid height which KU2017 could not exclude based on their limited data. This observation is further supported by the results of the analysis in the preceding section: cases with identical relative streamwise domain length
$\lambda /H_f < 3$ in numerical simulations and experiments which can be seen in figure 10 excludes a possible scaling of the threshold with the mean fluid height which KU2017 could not exclude based on their limited data. This observation is further supported by the results of the analysis in the preceding section: cases with identical relative streamwise domain length ![]() $L_x/D$ but varying
$L_x/D$ but varying ![]() $L_x/H_f$ ratio attain similar final values for all studied geometrical parameters and spanwise-averaged bedform profiles.
$L_x/H_f$ ratio attain similar final values for all studied geometrical parameters and spanwise-averaged bedform profiles.
Compared to the wavelengths observed in experiments, the initial wavelengths predicted by most linear stability analyses are smaller by at least one order of magnitude (Langlois & Valance Reference Langlois and Valance2007; Ouriemi et al. Reference Ouriemi, Aussillous and Guazzelli2009). However, in some recent studies, the prediction of the most unstable wavelength could be improved taking additional physical effects into account. For instance, initial unstable pattern wavelengths similar to those determined in experiments were found after introducing an additional stabilizing effect in form of a phase lag between the boundary shear stress and the particle flow rate into the linear stability analyses by several authors (Charru Reference Charru2006; Charru & Hinch Reference Charru and Hinch2006; Fourriere et al. Reference Fourriere, Claudin and Andreotti2010). This phase shift, which is usually termed as characteristic saturation length ![]() $L_{sat}$, has been reported to be a function of the particle diameter, attaining values of the order of
$L_{sat}$, has been reported to be a function of the particle diameter, attaining values of the order of ![]() $10$ times the particle diameter for pure bedload transport (Claudin, Charru & Andreotti Reference Claudin, Charru and Andreotti2011). For the special case of sand grains, Fourriere et al. (Reference Fourriere, Claudin and Andreotti2010) present saturation lengths between
$10$ times the particle diameter for pure bedload transport (Claudin, Charru & Andreotti Reference Claudin, Charru and Andreotti2011). For the special case of sand grains, Fourriere et al. (Reference Fourriere, Claudin and Andreotti2010) present saturation lengths between ![]() $7$ and
$7$ and ![]() $15$ grain diameters. In their subsequent stability analysis, these authors predict for sufficiently large fluid heights most amplified wavelengths in a range of
$15$ grain diameters. In their subsequent stability analysis, these authors predict for sufficiently large fluid heights most amplified wavelengths in a range of ![]() $\lambda /L_{sat} = 15\text {-}20$, which is equivalent to a range
$\lambda /L_{sat} = 15\text {-}20$, which is equivalent to a range ![]() $\lambda /D = 105\text {-}300$, when assuming that
$\lambda /D = 105\text {-}300$, when assuming that ![]() $L_{sat} = 7\text {-}15$. This range of most amplified wavelengths overlaps with the values found in simulations and the mentioned experimental studies.
$L_{sat} = 7\text {-}15$. This range of most amplified wavelengths overlaps with the values found in simulations and the mentioned experimental studies.
The findings of Colombini & Stocchino (Reference Colombini and Stocchino2011), on the other hand, differ from our observations and the results of Fourriere et al. (Reference Fourriere, Claudin and Andreotti2010). For the range of Galileo numbers considered in the present study, the authors report only one unstable region that depends on the fluid height exclusively. In contrast, unstable wavelengths scaling with the particle diameter, which could be related to a ripple instability, appear in their model for ![]() $Ga \leq 14$ only. It should be, however, noted that the model of Colombini & Stocchino (Reference Colombini and Stocchino2011) strongly depends on the roughness height and, consequently, on the relative submergence
$Ga \leq 14$ only. It should be, however, noted that the model of Colombini & Stocchino (Reference Colombini and Stocchino2011) strongly depends on the roughness height and, consequently, on the relative submergence ![]() $H_f/D$, which is in their case at least one order of magnitude higher than in our numerical simulations. Therefore, a direct comparison of the predicted critical wavelengths with our results is not possible.
$H_f/D$, which is in their case at least one order of magnitude higher than in our numerical simulations. Therefore, a direct comparison of the predicted critical wavelengths with our results is not possible.
Finally, let us turn to the question of the significance of the confirmed scaling of the wavelength of initial ripple patterns. As previously argued by Coleman & Nikora (Reference Coleman and Nikora2009) we believe that these patterns scale with the grain diameter as a consequence of the wake effect of bed perturbations in the initial stages (i.e. small lumps of dislodged particles). Since initial seeds for pattern formation are composed of bunches of those particles which are being dislodged, these initial seeds invariably have vertical extents of ![]() ${ {O}}(D)$. Due to their frequent contact with the bed, the seeds travel at a smaller speed than the surrounding fluid, and a wake forms in the region downstream of the seed crest. As a consequence, the probability that a particle will be dislodged and set into motion decreases in the wake of the seed, which in turn means that a second seed being located within some effective distance downstream of a given seed will receive less sediment supply from upstream, and it will therefore grow at a smaller rate or it will not grow at all. This will lead to initial pattern wavelengths which will be larger than the effective wake length of the incipient seeds. Analogously, in our numerical experiments with constrained streamwise domain lengths this effect suppresses all pattern formation if the period is below the effective wake length. This scenario applies to the bedload dominated regime; in the case of dominantly suspended load, other length scales are expected to come into play, such as the deposition length (Claudin et al. Reference Claudin, Charru and Andreotti2011).
${ {O}}(D)$. Due to their frequent contact with the bed, the seeds travel at a smaller speed than the surrounding fluid, and a wake forms in the region downstream of the seed crest. As a consequence, the probability that a particle will be dislodged and set into motion decreases in the wake of the seed, which in turn means that a second seed being located within some effective distance downstream of a given seed will receive less sediment supply from upstream, and it will therefore grow at a smaller rate or it will not grow at all. This will lead to initial pattern wavelengths which will be larger than the effective wake length of the incipient seeds. Analogously, in our numerical experiments with constrained streamwise domain lengths this effect suppresses all pattern formation if the period is below the effective wake length. This scenario applies to the bedload dominated regime; in the case of dominantly suspended load, other length scales are expected to come into play, such as the deposition length (Claudin et al. Reference Claudin, Charru and Andreotti2011).
In order to obtain a first estimate of the effective wake length of an initial seed let us perform the following idealization. Consider a single sphere in uniform, steady inflow with approach velocity ![]() $u_\infty$. Classical analysis for laminar wakes (Schlichting Reference Schlichting1979; Wu & Faeth Reference Wu and Faeth1993) shows that the streamwise velocity deficit on the axis behind the sphere varies as the inverse of the downstream distance
$u_\infty$. Classical analysis for laminar wakes (Schlichting Reference Schlichting1979; Wu & Faeth Reference Wu and Faeth1993) shows that the streamwise velocity deficit on the axis behind the sphere varies as the inverse of the downstream distance ![]() $x$ in the self-similar regime, such that we can write for the distance it takes the wake to recover up to
$x$ in the self-similar regime, such that we can write for the distance it takes the wake to recover up to ![]() $T_uu_\infty$:
$T_uu_\infty$:
where ![]() $x_0$ is the virtual origin,
$x_0$ is the virtual origin, ![]() $Re_D=Du_\infty /\nu$ the sphere Reynolds number,
$Re_D=Du_\infty /\nu$ the sphere Reynolds number, ![]() $C_D$ the drag coefficient for which in the second step we have substituted a standard drag formula (Clift, Grace & Weber Reference Clift, Grace and Weber1978, p. 112, table 5.2), and fitted the result and
$C_D$ the drag coefficient for which in the second step we have substituted a standard drag formula (Clift, Grace & Weber Reference Clift, Grace and Weber1978, p. 112, table 5.2), and fitted the result and ![]() $0<T_u<1$. For a threshold of a few per cent (
$0<T_u<1$. For a threshold of a few per cent (![]() $T_u=0.05$, say) this estimate yields a wake length of
$T_u=0.05$, say) this estimate yields a wake length of ![]() ${ {O}}(10)$ particle diameters over a range of Reynolds numbers of interest. The isolated sphere wake is indeed a drastic simplification of the actual sediment pattern seed. First, the incoming flow is not quiescent but turbulent: it is well known that a laminar wake in a turbulent background flow tends to recover somewhat faster than its counterpart in laminar flow (Amoura et al. Reference Amoura, Roig, Risso and Billet2010; Zeng, Balachandar & Najjar Reference Zeng, Balachandar and Najjar2010). Second, the sphere is not isolated, but it is located near a complex-shaped, evolving sediment bed: some researchers have indeed considered this problem (for a fixed single sphere), but the scaling of the wake length with Reynolds number was not explicitly obtained (Dey et al. Reference Dey, Sarkar, Bose, Tait and Castro-Orgaz2011; Lee & Balachandar Reference Lee and Balachandar2017). In order to gauge the latter influence, we have performed a simulation with a single spanwise row of spheres placed adjacent to a macroscopically flat sediment bed holding all particles fixed. In this case the flow is laminar with a Reynolds number
${ {O}}(10)$ particle diameters over a range of Reynolds numbers of interest. The isolated sphere wake is indeed a drastic simplification of the actual sediment pattern seed. First, the incoming flow is not quiescent but turbulent: it is well known that a laminar wake in a turbulent background flow tends to recover somewhat faster than its counterpart in laminar flow (Amoura et al. Reference Amoura, Roig, Risso and Billet2010; Zeng, Balachandar & Najjar Reference Zeng, Balachandar and Najjar2010). Second, the sphere is not isolated, but it is located near a complex-shaped, evolving sediment bed: some researchers have indeed considered this problem (for a fixed single sphere), but the scaling of the wake length with Reynolds number was not explicitly obtained (Dey et al. Reference Dey, Sarkar, Bose, Tait and Castro-Orgaz2011; Lee & Balachandar Reference Lee and Balachandar2017). In order to gauge the latter influence, we have performed a simulation with a single spanwise row of spheres placed adjacent to a macroscopically flat sediment bed holding all particles fixed. In this case the flow is laminar with a Reynolds number ![]() $Re_b=300$, and the particle diameter in viscous units measures
$Re_b=300$, and the particle diameter in viscous units measures ![]() $D^{+}=3.5$ (with
$D^{+}=3.5$ (with ![]() $H_f/D=8$), while the particle Reynolds number computed with the undisturbed flow velocity at the wall distance of the tops of the perturbation particles measures
$H_f/D=8$), while the particle Reynolds number computed with the undisturbed flow velocity at the wall distance of the tops of the perturbation particles measures ![]() $Re_D=D\, u_f(y_p+D/2) /\nu =17$. The effective wake length (assuming
$Re_D=D\, u_f(y_p+D/2) /\nu =17$. The effective wake length (assuming ![]() $T_u=0.05$) is approximately equal to
$T_u=0.05$) is approximately equal to ![]() $50D$ in this case, confirming the above order-of-magnitude estimate. Note that we have also confirmed that under laminar flow conditions at
$50D$ in this case, confirming the above order-of-magnitude estimate. Note that we have also confirmed that under laminar flow conditions at ![]() $Re_b=300$ a consistent threshold for the pattern wavelength can be obtained through our box-size constraining approach, analogously to the turbulent flow cases discussed up to now (cf. appendix B for details).
$Re_b=300$ a consistent threshold for the pattern wavelength can be obtained through our box-size constraining approach, analogously to the turbulent flow cases discussed up to now (cf. appendix B for details).
Despite the simplicity of the wake-effect argument in its current form, it suggests that the lower threshold of the initial pattern wavelength when scaled in particle diameters should exhibit a Reynolds number dependence. Although not extremely large, the influence of the particle Reynolds number (such as suggested by (6.1)) should be detectable with carefully designed experiments and/or numerical simulations. This constitutes a worthwhile research question for a future study.
7. Conclusion
In the present study, we have investigated the initial stage of subaqueous pattern formation in a turbulent open channel flow by means of direct numerical simulations with fully resolved particles. The main contribution is to address the question of scaling of the initial bedform wavelength with either the particle diameter ![]() $D$ or with the main fluid height
$D$ or with the main fluid height ![]() $H_f$. Both scaling relations have been proposed by different authors in the past decades, but up to the present day, there is no clear consensus about the correct scaling length. In a recent paper, Kidanemariam & Uhlmann (Reference Kidanemariam and Uhlmann2017) have observed a lower bound for the most unstable wavelength
$H_f$. Both scaling relations have been proposed by different authors in the past decades, but up to the present day, there is no clear consensus about the correct scaling length. In a recent paper, Kidanemariam & Uhlmann (Reference Kidanemariam and Uhlmann2017) have observed a lower bound for the most unstable wavelength ![]() $\lambda _{th}$ in a range
$\lambda _{th}$ in a range ![]() $(75\text {-}100)D$ (equivalent to
$(75\text {-}100)D$ (equivalent to ![]() $(3\text {-}4)H_f$, respectively). However, it was not possible in that study to further tackle the problem of the correct scaling, since the relative submergence
$(3\text {-}4)H_f$, respectively). However, it was not possible in that study to further tackle the problem of the correct scaling, since the relative submergence ![]() $H_f/D$ was constant in all of their simulations. In the present work, we have therefore performed and analysed two sets of simulations, in which we have varied the relative streamwise box lengths
$H_f/D$ was constant in all of their simulations. In the present work, we have therefore performed and analysed two sets of simulations, in which we have varied the relative streamwise box lengths ![]() $L_x/D$ and
$L_x/D$ and ![]() $L_x/H_f$ independently, which allowed us to investigate the influence of both length scales on the initial pattern wavelength exclusively. Consequently, the relative submergence has been varied in the range
$L_x/H_f$ independently, which allowed us to investigate the influence of both length scales on the initial pattern wavelength exclusively. Consequently, the relative submergence has been varied in the range ![]() $H_f/D = 7.86\text {-}50.59$.
$H_f/D = 7.86\text {-}50.59$.
Our findings imply a scaling of the initial wavelength with the particle diameter, while it seems to be rather unaffected by variations of the mean fluid height. In particular, a lower bound for the most unstable wavelength has been found around a streamwise domain length of approximately ![]() $L_x/D = 80$. In cases with a shorter relative box length
$L_x/D = 80$. In cases with a shorter relative box length ![]() $L_x/D$, transverse pattern formation was effectively suppressed, indicating that the domain length is not sufficient to accommodate the minimal unstable wavelength. However, the observed pattern with a wavelength close to the proposed threshold exhibits remarkable differences compared to patterns in sufficiently long domains (cf. for instance the cases with
$L_x/D$, transverse pattern formation was effectively suppressed, indicating that the domain length is not sufficient to accommodate the minimal unstable wavelength. However, the observed pattern with a wavelength close to the proposed threshold exhibits remarkable differences compared to patterns in sufficiently long domains (cf. for instance the cases with ![]() $L_x/D = {O}(10^{3}$) of Kidanemariam & Uhlmann Reference Kidanemariam and Uhlmann2017), i.e. in very marginal boxes it does not reach an asymptotic state during the observation time and shows a more symmetric spanwise-averaged profile than in the longer cases.
$L_x/D = {O}(10^{3}$) of Kidanemariam & Uhlmann Reference Kidanemariam and Uhlmann2017), i.e. in very marginal boxes it does not reach an asymptotic state during the observation time and shows a more symmetric spanwise-averaged profile than in the longer cases.
The predicted range of initial pattern wavelengths is in good agreement with values measured in laboratory channel and closed-conduit experiments, which concentrate predominantly in a range ![]() ${\lambda /D = 120\text {-}250}$. Furthermore, good agreement is also observed with wavelengths predicted as
${\lambda /D = 120\text {-}250}$. Furthermore, good agreement is also observed with wavelengths predicted as ![]() $\lambda /D = 105\text {-}300$ in the stability analysis of Fourriere et al. (Reference Fourriere, Claudin and Andreotti2010). Note that, in their study, the dependence of the most amplified wavelength on the particle diameter appears indirectly in form of a scaling with a saturation length
$\lambda /D = 105\text {-}300$ in the stability analysis of Fourriere et al. (Reference Fourriere, Claudin and Andreotti2010). Note that, in their study, the dependence of the most amplified wavelength on the particle diameter appears indirectly in form of a scaling with a saturation length ![]() $L_{sat}$, which in turn is a function of the particle diameter.
$L_{sat}$, which in turn is a function of the particle diameter.
We have argued that the observed dependence of the minimal unstable wavelength of sediment patterns upon the particle diameter is essentially a consequence of the effective wake length of the initial seeds, as already put forth by Coleman & Nikora (Reference Coleman and Nikora2009). Both, scaling arguments based on laminar wakes of isolated spheres as well as numerical estimates of the wake effect of small-amplitude perturbations in laminar open channel flow support this scenario. It was also argued that the wake effect should exhibit a (mild) Reynolds number dependence which has so far not been clearly demonstrated. Therefore, further work is required in this direction. One possibility would be to identify initial seeds (during the early stages of pattern development) in either experimental or numerical realizations, and to quantify the wake effect statistically, either indirectly through the velocity field, or directly through conditional averaging of the particle flux.
Another remarkable phenomenon has been observed in the cases with the highest relative submergence ![]() $H_f/D \approx 50$ in the form of streamwise and spanwise sediment features, that are seen to either concur or interact with each other, allowing for the formation of three-dimensional patterns. Our analysis of the single-sided amplitude spectra of the sediment bed height perturbation has shown that the evolution of the sediment bed is dominated by several streamwise and spanwise oriented waves of comparable amplitude. In the remaining simulations, streamwise aligned patterns appeared, if at all, mainly as a predecessor of the transverse patterns in the first few bulk time units of the simulations, but at clearly lower amplitude than their transverse oriented counterparts. Since the focus of the current study was on the scaling of transverse patterns, it was out of the scope to investigate in detail the reasons for this different sediment bed evolution. However, it would be of great interest to determine the parameters that are responsible for the amplification of these spanwise waves. In this context, it should be investigated in future studies how the initial subaqueous pattern formation is affected by constraints on the spanwise length scales.
$H_f/D \approx 50$ in the form of streamwise and spanwise sediment features, that are seen to either concur or interact with each other, allowing for the formation of three-dimensional patterns. Our analysis of the single-sided amplitude spectra of the sediment bed height perturbation has shown that the evolution of the sediment bed is dominated by several streamwise and spanwise oriented waves of comparable amplitude. In the remaining simulations, streamwise aligned patterns appeared, if at all, mainly as a predecessor of the transverse patterns in the first few bulk time units of the simulations, but at clearly lower amplitude than their transverse oriented counterparts. Since the focus of the current study was on the scaling of transverse patterns, it was out of the scope to investigate in detail the reasons for this different sediment bed evolution. However, it would be of great interest to determine the parameters that are responsible for the amplification of these spanwise waves. In this context, it should be investigated in future studies how the initial subaqueous pattern formation is affected by constraints on the spanwise length scales.
Acknowledgments
The current work was supported by the German Research Foundation (DFG) through grants UH242/2-1 and UH242/12-1. Part of the work was performed on the supercomputer ForHLR II at the Steinbuch Centre for Computing funded by the Ministry of Science, Research and the Arts Baden-Württemberg and by the Federal Ministry of Education and Research. The remaining simulations have been carried out on SuperMUC at the Leibniz Supercomputing Centre at the Bavarian Academy of Science and Humanities. Disk space for presenting supplementary material online is provided by the 4TU.Centre for Research Data at the TU Delft. The computer resources, technical expertise and assistance provided by the staff at these computing centres are gratefully acknowledged. We thank M. Krayer for his support in defining the fluid–bed interface.
Declaration of interests
The authors report no conflict of interest.
Supplementary movies
Supplementary movies are available at https://dx.doi.org/10.4121/uuid:7eb6a0be-ff83-4883-9d99-31daaa6a2863.
Appendix A. Sensitivity to the choice of the Coulomb friction coefficient
As mentioned in § 2, two of our performed simulations feature a slightly higher Coulomb friction coefficient ![]() $\mu _c=0.5$ compared to the remaining cases, where a value of
$\mu _c=0.5$ compared to the remaining cases, where a value of ![]() $\mu _c=0.4$ was chosen. In the following, we show that the difference in this parameter has a minor effect on the eventually developed pattern and, in particular, that it does not affect the stability or instability of the sediment bed. To this end, we have recomputed case
$\mu _c=0.4$ was chosen. In the following, we show that the difference in this parameter has a minor effect on the eventually developed pattern and, in particular, that it does not affect the stability or instability of the sediment bed. To this end, we have recomputed case ![]() $H6D102$ keeping all parameters except for the Coulomb friction coefficient, which we reduced to the value
$H6D102$ keeping all parameters except for the Coulomb friction coefficient, which we reduced to the value ![]() $\mu _c=0.4$ as in the remaining simulations. Furthermore, we performed another simulation with identical parameters and
$\mu _c=0.4$ as in the remaining simulations. Furthermore, we performed another simulation with identical parameters and ![]() $\mu _c=0.4$, but with a different initial flow field in order to check for the sensitivity to the initial data.
$\mu _c=0.4$, but with a different initial flow field in order to check for the sensitivity to the initial data.
In figure 11, we compare the time evolution of the root mean square sediment bed height fluctuation ![]() $\sigma _h$ for the three simulations. It shows clearly that the bed becomes unstable for both values of
$\sigma _h$ for the three simulations. It shows clearly that the bed becomes unstable for both values of ![]() $\mu _c$ and that, furthermore, the growth rate is very similar in all three simulations, although the instant in time of the onset of the macroscopic growth regime differs. These observations indicate that the bedform evolution is not sensitive to a slight increase of the chosen
$\mu _c$ and that, furthermore, the growth rate is very similar in all three simulations, although the instant in time of the onset of the macroscopic growth regime differs. These observations indicate that the bedform evolution is not sensitive to a slight increase of the chosen ![]() $\mu _c$ in the observed range. Therefore, we will not further differentiate between the cases with
$\mu _c$ in the observed range. Therefore, we will not further differentiate between the cases with ![]() $\mu _c=0.4$ and
$\mu _c=0.4$ and ![]() $\mu _c=0.5$ in the remainder of this study.
$\mu _c=0.5$ in the remainder of this study.
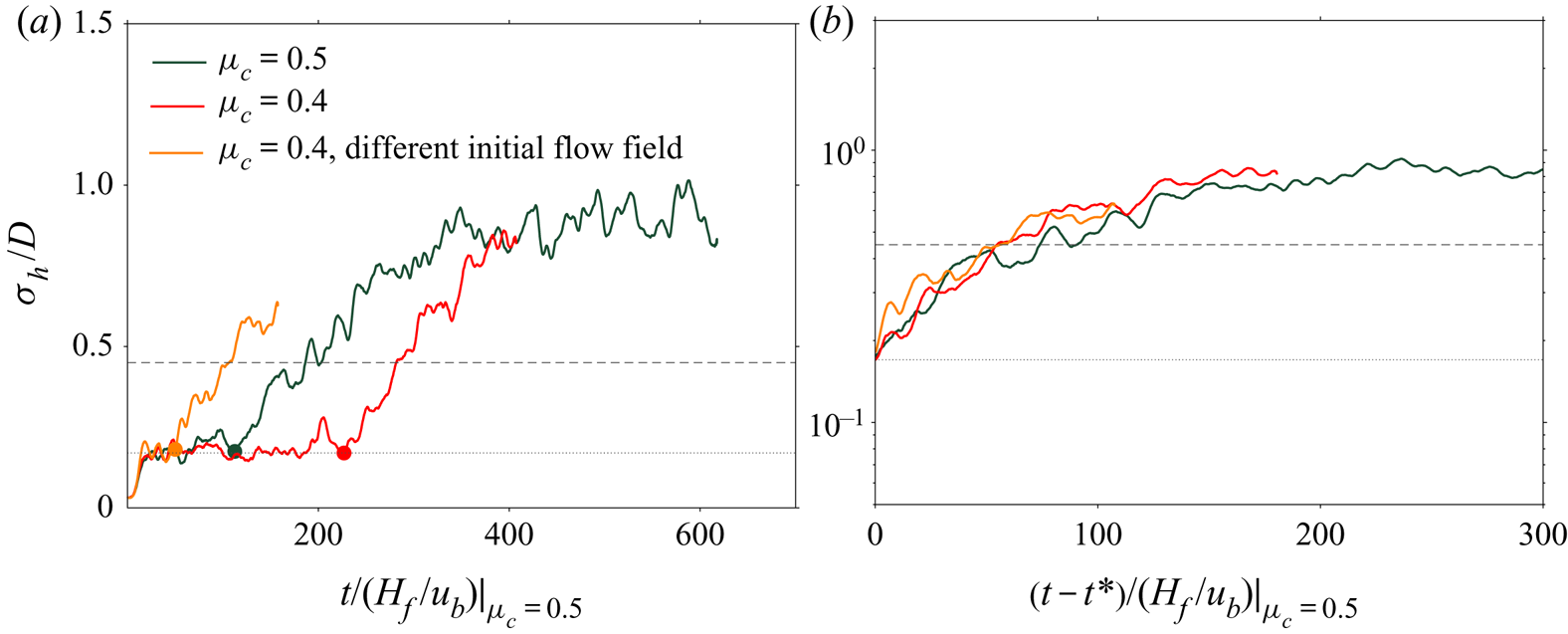
Figure 11. (a) Time evolution of the root mean square of the bedform amplitude normalized by the particle diameter ![]() $\sigma _h /D$ for case
$\sigma _h /D$ for case ![]() $H6D102$ using different Coulomb friction coefficients. (b) Same as in (a), but in semi-logarithmic scale. The origin is shifted to the instant in time at the onset of the macroscopic growth period
$H6D102$ using different Coulomb friction coefficients. (b) Same as in (a), but in semi-logarithmic scale. The origin is shifted to the instant in time at the onset of the macroscopic growth period ![]() $t^{*}$, which is indicated by filled circles in (a).
$t^{*}$, which is indicated by filled circles in (a).
Appendix B. Additional simulations of a sediment bed under laminar flow conditions
This section describes additional simulations in the laminar regime, with otherwise the same set-up as in the main part of the manuscript. The first of these new cases, which will henceforth be denoted as case H6D052lam, is identical to case ![]() $H6D052$ (cf. table1) concerning the initial state of the particle bed and the box dimensions, but the bulk Reynolds number in this new case has been reduced by a factor of 10 compared to the turbulent baseline case. The Galileo number has been adapted accordingly in order to reach a comparable Shields number as in the turbulent cases. For a second simulation H12D102lam, the streamwise extent of the computational domain of case H6D052lam has been doubled, i.e.
$H6D052$ (cf. table1) concerning the initial state of the particle bed and the box dimensions, but the bulk Reynolds number in this new case has been reduced by a factor of 10 compared to the turbulent baseline case. The Galileo number has been adapted accordingly in order to reach a comparable Shields number as in the turbulent cases. For a second simulation H12D102lam, the streamwise extent of the computational domain of case H6D052lam has been doubled, i.e. ![]() $L_x/D = 102.4$, while the remaining physical and numerical parameters are identical to those in case H6D052lam. An overview over all relevant physical and numerical parameters in the two simulations is provided in tables 3 and 4, respectively. Based on the critical domain length observed in the turbulent regime, one would expect the sediment bed in case H6D052lam to remain essentially flat without allowing a transverse sediment pattern to grow, while in H12D102lam, the box length should be sufficiently long to accommodate a single streamwise oscillating sediment wave. Figure 12 shows the amplitude of the bed height variation, corresponding to figures 3 and 8 of § 5. In particular, from the amplitude of the two-dimensional sediment bed extraction (figure 12b) it can be seen that the elongated domain allows for the formation of significant patterns, albeit at a much smaller rate than the turbulent counterparts in figure 8. Conversely, the bed in the shorter domain H6D052lam indeed remains featureless, as was already observed for the turbulent case
$L_x/D = 102.4$, while the remaining physical and numerical parameters are identical to those in case H6D052lam. An overview over all relevant physical and numerical parameters in the two simulations is provided in tables 3 and 4, respectively. Based on the critical domain length observed in the turbulent regime, one would expect the sediment bed in case H6D052lam to remain essentially flat without allowing a transverse sediment pattern to grow, while in H12D102lam, the box length should be sufficiently long to accommodate a single streamwise oscillating sediment wave. Figure 12 shows the amplitude of the bed height variation, corresponding to figures 3 and 8 of § 5. In particular, from the amplitude of the two-dimensional sediment bed extraction (figure 12b) it can be seen that the elongated domain allows for the formation of significant patterns, albeit at a much smaller rate than the turbulent counterparts in figure 8. Conversely, the bed in the shorter domain H6D052lam indeed remains featureless, as was already observed for the turbulent case ![]() $H6D052$.
$H6D052$.
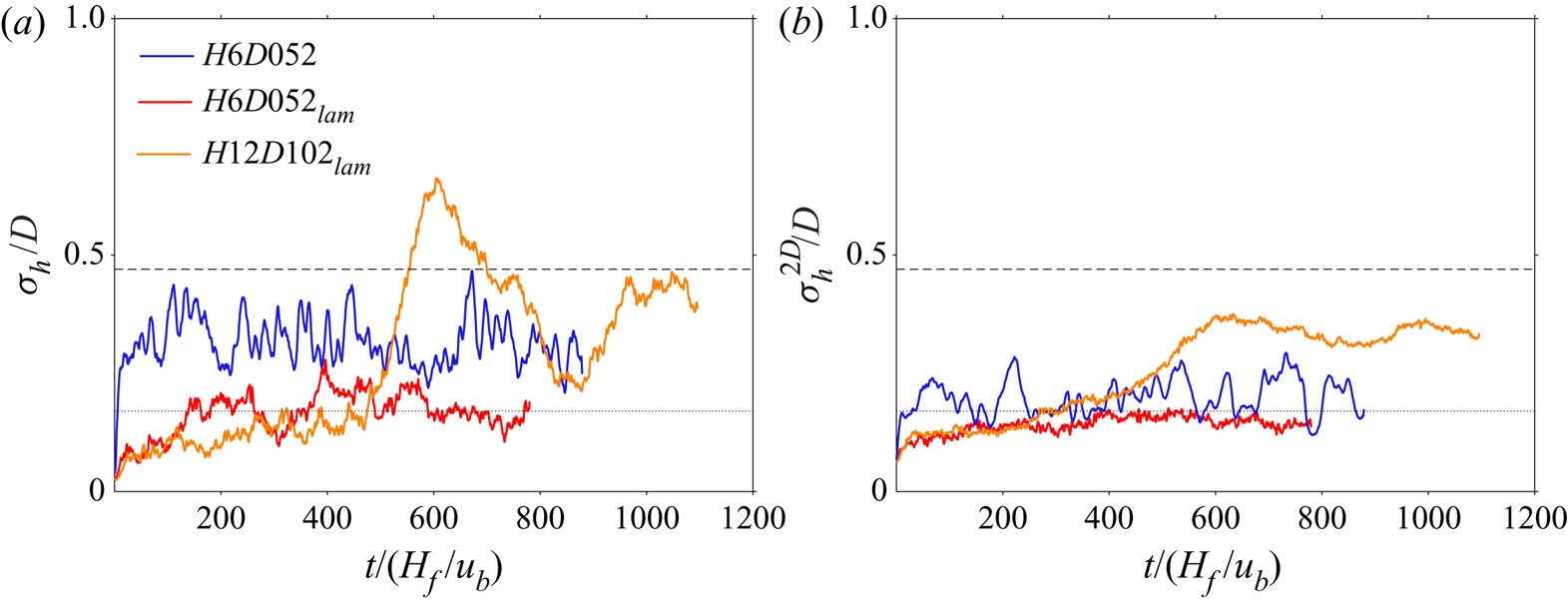
Figure 12. Time evolution of the (a) one-dimensional and (b) two-dimensional root mean square of the bedform amplitude normalized by the particle diameter for cases ![]() $H6D052$, H6D052lam and H12D102lam.
$H6D052$, H6D052lam and H12D102lam.
Table 3. Physical parameters of the laminar simulations.

Table 4. Numerical parameters of the laminar simulations.

Figure 13 shows a complementary view of the growth process, by providing space–time plots of the spanwise-averaged bed elevation for the three cases included in figure 12. Here, it becomes evident that seeds of patterns are distinguishable in all three cases, but only do they grow to significant amplitudes in the sufficiently long domain. The main distinction between the laminar and turbulent regime is the substantially lower propagation speed of the seeds in the former.
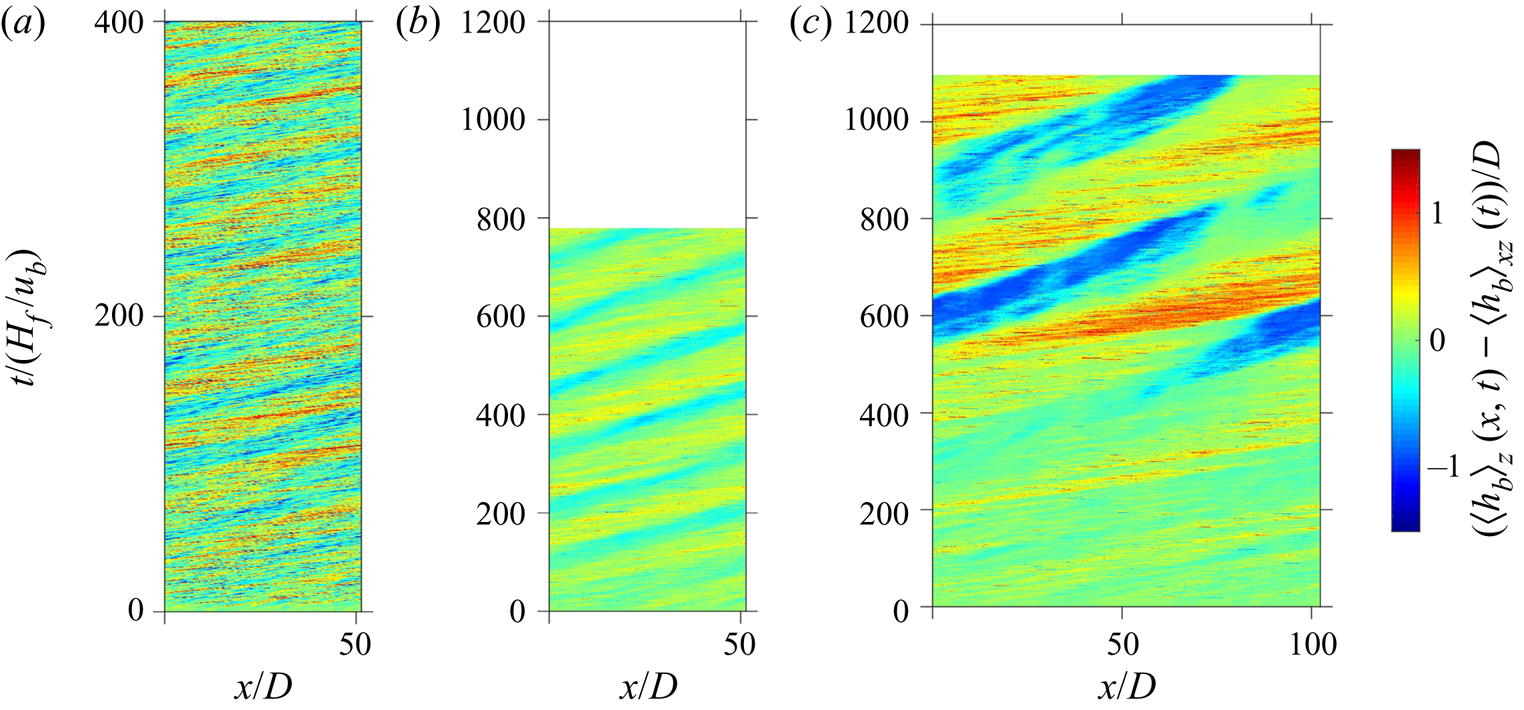
Figure 13. Space–time evolution of the fluctuation of the spanwise-averaged fluid–bed interface in multiples of the particle diameter for cases (a) ![]() $H6D052$, (b) H6D052lam and (c) H12D102lam. Note that the range of values shown on the ordinate in the turbulent case (panel
$H6D052$, (b) H6D052lam and (c) H12D102lam. Note that the range of values shown on the ordinate in the turbulent case (panel![]() $a$) differs from that of the laminar cases (panels
$a$) differs from that of the laminar cases (panels ![]() $b,c$).
$b,c$).