1 Introduction
Multicomponent drops immersed in another liquid occur in a widespread range of engineering applications, such as chemical waste treatment, separation of heavy metals, food processing, diagnostics and so on (Kula, Kroner & Hustedt Reference Kula, Kroner and Hustedt1982; Ahuja Reference Ahuja2000; Fukumoto, Yoshizawa & Ohno Reference Fukumoto, Yoshizawa and Ohno2005; Chasanis, Brass & Kenig Reference Chasanis, Brass and Kenig2010; Lu et al. Reference Lu, Rezk, Jativa, Yeo and Zhang2017). In recent years, interest in the diffusive dynamics of multiphase fluid systems has surged, as the quantitative understanding of this process is crucial not only for fundamental studies of multiphase systems, but also for its common applications in the chemical industry, particularly for modern liquid–liquid microextraction processes (Jain & Verma Reference Jain and Verma2011; Lohse Reference Lohse2016).
Diffusion processes, i.e. the movement of species down a concentration gradient, can induce a mass transfer between different phases. A classical theory about a single-component bubble dissolving into the surrounding liquid was established by Epstein & Plesset (Reference Epstein and Plesset1950) and later extended to drops (Duncan & Needham Reference Duncan and Needham2006; Su & Needham Reference Su and Needham2013). It can be derived that the bubble radius is proportional to the square root of time, which agrees with experimental measurements. For multicomponent drops, the situation is very different due to mutual interactions between the species. A consistent theory for the dissolution or growth of multicomponent drops in a host liquid was proposed by Chu & Prosperetti (Reference Chu and Prosperetti2016). They employed thermodynamic equilibrium constraints at the drop interface. The UNIQUAC model, an activity coefficient model, was adopted for the description of phase equilibria. Molecular dynamics simulations were performed by Maheshwari et al. (Reference Maheshwari, van der Hoef, Prosperetti and Lohse2017) with the conclusion of the importance of the interaction between the drop constituents and the host liquid during multicomponent drop dissolution. These investigations focus on pure diffusion processes.
In practice, however, the flow motion caused by the diffusion processes cannot be neglected, as the flow is able to affect the diffusion processes in turn. A small droplet, for example, can be self-propelled by Marangoni stress when the viscosity ratio of the droplet liquid to the surrounding liquid is smaller than the length scale ratio of the droplet size to the solutal interactive length scale (Izri et al. Reference Izri, van der Linden, Michelin and Dauchot2014). Dietrich et al. (Reference Dietrich, Wildeman, Visser, Hofhuis, Kooij, Zandvliet and Lohse2016) experimentally demonstrated the existence of a transition Rayleigh number for the dissolution of a sessile multicomponent drop, above which the buoyancy-driven convection in the host liquid prevails over diffusion. Additionally, Dietrich et al. (Reference Dietrich, Rump, Lv, Kooij, Zandvliet and Lohse2017) found that diffusion is able to induce a local concentration difference and thereby cause the segregation of the components inside the drop.
For a specific category of multiphase systems holding a metastable phase regime, the diffusion phenomena are even more interesting and complex. The phase equilibrium can be altered by the diffusion process, leading to the occurrence of metastable dispersions in the bulk (Solans, Morales & Homs Reference Solans, Morales and Homs2016). Ouzo, an alcoholic beverage from Greece, is a typical example of this kind of liquid system. It mainly consists of ethanol, water and anise oil, and it is well mixed when the oil concentration in the solution is lower than the oil solubility of the water–ethanol solvent. Spontaneous emulsification, the process of creating metastable liquid–liquid dispersions, can be achieved by increasing the water concentration and thereby reducing the oil solubility. The generation of nano- or microdroplets does not require an external energy input (spontaneity). This is the well-known ouzo effect, which can be triggered either by simply adding water to the system or, alternatively, by the reduction of the ethanol amount by a preferential dissolution or evaporation. The latter process, i.e. the evaporation of an ouzo drop, is extremely rich and exhibits multiple phase transitions during the drying, as recently discovered by Tan et al. (Reference Tan, Diddens, Lv, Kuerten, Zhang and Lohse2016, Reference Tan, Diddens, Versluis, Butt, Lohse and Zhang2017).
The oil supersaturation region, where the emulsification takes place, can appear in evaporating ouzo drops because of non-uniform evaporation rates along the liquid–gas interface and different volatile speeds of water and ethanol. The same principle is expected to apply to a dissolving multicomponent drop, since the same dynamical equations and similar boundary conditions are followed as the evaporating one.
In this paper, we explore the dissolution of a multicomponent drop in a host liquid (figure 1), with a particular focus on systems having the capacity to undergo spontaneous emulsification (ouzo effect). Experimental steps and methods are discussed in § 2. The sessile drop picked here consists of the two miscible components, water and ethanol, with different initial ratios, and anethole oil acts as host liquid, with which ethanol is miscible but water is immiscible. General observations and descriptions about the dissolution phenomena are given in § 3. During the dissolution, we observed both spontaneous emulsifications in the host liquid (oil-rich phase) and inside the sessile drop (aqueous phase), i.e. water-in-oil (w-in-o) microdroplets and oil-in-water (o-in-w) microdroplets, respectively. We give a discussion in § 4. In § 5, we develop a one-dimensional diffusion model, with the adoption of both the so-called diffusion path theory (Ruschak & Miller Reference Ruschak and Miller1972) and thermodynamic equilibrium theory. The so-called UNIFAC model, instead of the UNIQUAC model used by Chu & Prosperetti (Reference Chu and Prosperetti2016), is applied here for the phase equilibria modelling, because model parameters of the latter are not available for the mixture used in this study. Through this diffusion model, we gain insight into the emulsification process (diffusion-induced microdroplet nucleation), as well as the mass transport caused by the pure diffusion process, which are presented and evaluated in § 6. To figure out the influence of flow motions on the emulsification process, a scaling analysis and micro particle image velocimetry (PIV) measurements were performed in § 7. The scaling analysis reveals that the Marangoni effect dominates the flow motion inside the drop, while natural convection is dominant in the host liquid (figure 1 a), which was confirmed by side recording movies and micro-PIV measurement results (figure 1 b). Having obtained a good understanding of the fluid dynamics in the system, we finally acquire a more systematic understanding of the ouzo drop dissolution process and the preferred position where the diffusion-triggered emulsification takes place.
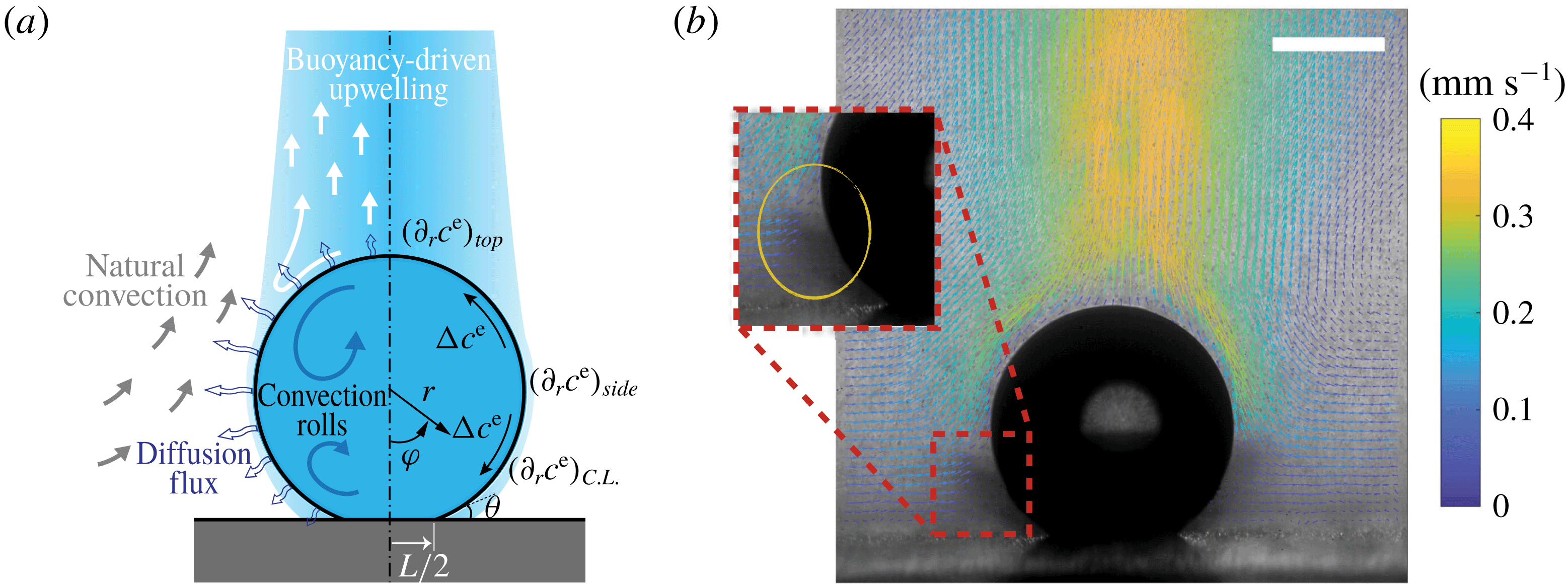
Figure 1. (a) Hydrodynamic sketch of a dissolving ouzo sessile drop. The left side presents the flow directions and diffusion fluxes along the drop surface. Geometrical and physical quantities are defined on the right side. (b) Experimental snapshot of the dissolving drop overlaid with the external flow field obtained by a PIV measurement. The scale bar is 0.45 mm.
2 Experimental method
2.1 Solution and substrate
The system we investigate here consists of Milli-Q water (obtained from a Reference A
![]() $+$
system (Merck Millipore) at
$+$
system (Merck Millipore) at
![]() $18.2~\text{M}\unicode[STIX]{x03A9}$
at
$18.2~\text{M}\unicode[STIX]{x03A9}$
at
![]() $25\,^{\circ }\text{C}$
), ethanol (Sigma-Aldrich;
$25\,^{\circ }\text{C}$
), ethanol (Sigma-Aldrich;
![]() ${\geqslant}98\,\%$
) and anethole oil (Sigma-Aldrich; trans-anethole,
${\geqslant}98\,\%$
) and anethole oil (Sigma-Aldrich; trans-anethole,
![]() ${\geqslant}99.8\,\%$
). We performed dissolution experiments in a cuvette (Hellma; inner dimensions
${\geqslant}99.8\,\%$
). We performed dissolution experiments in a cuvette (Hellma; inner dimensions
![]() $30~\text{mm}\times 30~\text{mm}\times 30~\text{mm}$
), on the bottom of which a hydrophobized glass slide (
$30~\text{mm}\times 30~\text{mm}\times 30~\text{mm}$
), on the bottom of which a hydrophobized glass slide (
![]() ${\approx}20~\text{mm}\times 20~\text{mm}$
) was placed. A certain amount of water-saturated anethole was added into the cuvette, performing as the host liquid. The depth of the liquid was 7.5 mm. Water–ethanol binary drops with different volumetric concentrations of ethanol (30, 40, 50, 60 and 70 vol%) were produced in the oil through a custom needle (Hamilton; outer diameter/inner diameter 0.21 mm/0.11 mm) by a motorized syringe pump (Harvard; PHD 2000), and then directly deposited on the centre of the hydrophobized glass surface.
${\approx}20~\text{mm}\times 20~\text{mm}$
) was placed. A certain amount of water-saturated anethole was added into the cuvette, performing as the host liquid. The depth of the liquid was 7.5 mm. Water–ethanol binary drops with different volumetric concentrations of ethanol (30, 40, 50, 60 and 70 vol%) were produced in the oil through a custom needle (Hamilton; outer diameter/inner diameter 0.21 mm/0.11 mm) by a motorized syringe pump (Harvard; PHD 2000), and then directly deposited on the centre of the hydrophobized glass surface.
2.2 Emulsion/microdroplet recognition
The emulsions (nucleated microdroplets) were recognized visually. Both the w-in-o emulsion and the o-in-w emulsion had a recognizable cloudy white appearance because of the microscopic size of the nucleated microdroplets, which enables them to scatter all the colours equally. The recognition of the emulsions was processed by watching the recorded videos frame by frame. Although dissolving drops were of millimetre scale, their spherical shapes with high curvature unavoidably caused reflected light spots, which increased the difficulty of recognizing the presence of microdroplets inside the drop. Therefore, the presence or absence of emulsions was carefully determined by detecting the liquid colour variation and their movement from the recorded videos (both top views and synchronized side views). No fluorescence technique was used for microdroplet detection, in order to avoid any influence of added fluorescent materials on the spontaneous emulsification.
2.3 Micro particle image velocimetry
To investigate the flow field around the dissolving drop, we added tracking particles (Dantec Dynamics; PSP-5, diameter
![]() $5~\unicode[STIX]{x03BC}\text{m}$
, made of nylon-12) into the host liquid at a seeding density of
$5~\unicode[STIX]{x03BC}\text{m}$
, made of nylon-12) into the host liquid at a seeding density of
![]() $0.2~\text{mg}~\text{ml}^{-1}$
to perform micro-PIV measurements. As shown in appendix A.1, these particles can be considered as passive. Thanks to the low flow rate in our study, a continuous light-emitting diode (LED) light source (Thorlabs; MCWHL5) was able to provide enough volume illumination for the measurements. The light source and the camera were placed at opposite sides of the cuvette. The light passed through convex lenses before illuminating the cuvette to form a parallel light beam to increase the image contrast. At the other side, we positioned a high-speed camera (Photron Fastcam SA2, 32 GB, 50 frames per second at 2048 pixel
$0.2~\text{mg}~\text{ml}^{-1}$
to perform micro-PIV measurements. As shown in appendix A.1, these particles can be considered as passive. Thanks to the low flow rate in our study, a continuous light-emitting diode (LED) light source (Thorlabs; MCWHL5) was able to provide enough volume illumination for the measurements. The light source and the camera were placed at opposite sides of the cuvette. The light passed through convex lenses before illuminating the cuvette to form a parallel light beam to increase the image contrast. At the other side, we positioned a high-speed camera (Photron Fastcam SA2, 32 GB, 50 frames per second at 2048 pixel
![]() $\times$
2048 pixel resolution) attached with a microscope system (Infinity; model K2 DistaMax) to perform high-speed imaging. The position of the recording system was adjusted to have a focal plane crossing the droplet centre. The thickness of the focal plane is 0.02 mm. Thereby, we could obtain sharp images of the tracking particles within a cross-sectional plane of the drop. We took image pairs with an inter-framing time of 20 ms every 2 s. The obtained image pairs were first processed to reduce the noise, and then imported into PIVlab software (Thielicke Reference Thielicke2014; Thielicke & Stamhuis Reference Thielicke and Stamhuis2014) to calculate the flow field. The size of the interrogation window was taken as a 128 pixel
$\times$
2048 pixel resolution) attached with a microscope system (Infinity; model K2 DistaMax) to perform high-speed imaging. The position of the recording system was adjusted to have a focal plane crossing the droplet centre. The thickness of the focal plane is 0.02 mm. Thereby, we could obtain sharp images of the tracking particles within a cross-sectional plane of the drop. We took image pairs with an inter-framing time of 20 ms every 2 s. The obtained image pairs were first processed to reduce the noise, and then imported into PIVlab software (Thielicke Reference Thielicke2014; Thielicke & Stamhuis Reference Thielicke and Stamhuis2014) to calculate the flow field. The size of the interrogation window was taken as a 128 pixel
![]() $\times$
128 pixel matrix, corresponding to
$\times$
128 pixel matrix, corresponding to
![]() $142~\unicode[STIX]{x03BC}\text{m}\times 142~\unicode[STIX]{x03BC}\text{m}$
. The interrogation window overlap was set as 75 %, leading to a
$142~\unicode[STIX]{x03BC}\text{m}\times 142~\unicode[STIX]{x03BC}\text{m}$
. The interrogation window overlap was set as 75 %, leading to a
![]() $35.5~\unicode[STIX]{x03BC}\text{m}$
vector spacing in the calculated velocity matrix.
$35.5~\unicode[STIX]{x03BC}\text{m}$
vector spacing in the calculated velocity matrix.
3 Dissolution process
3.1 Characteristic states of dissolving drops
A dissolving water–ethanol (aqueous) sessile drop in anethole oil (host liquid) is displayed in figure 2. The initial ethanol concentration is 60 vol% and the initial drop volume is approximately
![]() $0.5~\unicode[STIX]{x03BC}\text{l}$
. The experimental snapshots in figure 2 (top views in the left column and the corresponding side views in the right column) present several interesting phenomena occurring during the drop dissolution, including solute plumes detaching and rising upwards from the top of the drop (arrows in figure 2
a), spontaneous emulsification inside and outside the drop (arrows in figure 2
b–d), and two oil–microdroplet rings generated by convection rolls and being suspended inside the drop (arrows in figure 2
e).
$0.5~\unicode[STIX]{x03BC}\text{l}$
. The experimental snapshots in figure 2 (top views in the left column and the corresponding side views in the right column) present several interesting phenomena occurring during the drop dissolution, including solute plumes detaching and rising upwards from the top of the drop (arrows in figure 2
a), spontaneous emulsification inside and outside the drop (arrows in figure 2
b–d), and two oil–microdroplet rings generated by convection rolls and being suspended inside the drop (arrows in figure 2
e).
Figure 2. Experimental snapshots of a dissolving water–ethanol (v/v 40/60) drop in anethole oil experiencing different characteristic states. The first column of photos are top views and the second column are the corresponding side views. The initial drop size is approximately
![]() $0.5~\unicode[STIX]{x03BC}\text{l}$
and
$0.5~\unicode[STIX]{x03BC}\text{l}$
and
![]() $t_{0}$
denotes the drop deposition time. (a) The drop begins with a transparent appearance surrounded by a clean host liquid. The arrow indicates a solute plume above the drop. (b) W-in-o emulsions (water microdroplets) suspend outside the drop. The arrows and the inserted zoom-in panel highlight the location of the microdroplets. (c) O-in-w emulsions (oil microdroplets) appear inside the drop with a preferential location around the equator of the drop (arrow, and area in between the two horizontal lines). (d) More oil microdroplets are formed and concentrate at the two sides of the equator. The w-in-o emulsions disappear. (e) In approximately 7 min, the two concentrated clusters of microdroplets evolve into two rings. The scale bar is 0.5 mm in all panels. (See corresponding supplementary movies 2 and 3 available at https://doi.org/10.1017/jfm.2019.207.)
$t_{0}$
denotes the drop deposition time. (a) The drop begins with a transparent appearance surrounded by a clean host liquid. The arrow indicates a solute plume above the drop. (b) W-in-o emulsions (water microdroplets) suspend outside the drop. The arrows and the inserted zoom-in panel highlight the location of the microdroplets. (c) O-in-w emulsions (oil microdroplets) appear inside the drop with a preferential location around the equator of the drop (arrow, and area in between the two horizontal lines). (d) More oil microdroplets are formed and concentrate at the two sides of the equator. The w-in-o emulsions disappear. (e) In approximately 7 min, the two concentrated clusters of microdroplets evolve into two rings. The scale bar is 0.5 mm in all panels. (See corresponding supplementary movies 2 and 3 available at https://doi.org/10.1017/jfm.2019.207.)
At the beginning when the drop was deposited on a hydrophobic substrate in the oil host liquid, both the drop and the surrounding oil are transparent, except for the shadows above the drop, as displayed in figure 2(a). The shadows, indicated by the arrow in the panel, are the solute plumes, i.e. the ethanol-rich oil mixture as ethanol diffuses into the oil surrounding the drop.
In our system, there are two kinds of self-emulsification that happen: w-in-o emulsification and o-in-w emulsification. The former creates water microdroplets in the oil host liquid (w-in-o emulsion), and the latter generates oil microdroplets in the aqueous drop (o-in-w emulsion). The first appearing microdroplets are the w-in-o emulsion ones. They nucleate at a certain location in the surrounding oil, comparable to the position of the Earth’s tropic of capricorn. The emulsification normally starts within less than 5 s after the drop deposition. Figure 2(b) is a snapshot taken at 19 s to provide a visualization of the emulsion, and the inserted zoom-in panel highlights their position, indicated by arrows. The microdroplets suspend in oil for a while and then disappear. Approximately half a minute later, o-in-w emulsification sets in inside the drop, preferentially in the middle of the drop, concentrating in the region pointed at by the arrow in figure 2(c). Notably, the preferential location is different from that reported in our previous work on evaporating drops, in which droplet nucleation occurred either at the contact-line region for flat evaporating ouzo drops (Tan et al. Reference Tan, Diddens, Lv, Kuerten, Zhang and Lohse2016), or at the top of the drop for spherical evaporating ouzo drops (Tan et al. Reference Tan, Diddens, Versluis, Butt, Lohse and Zhang2017). More detailed discussion about those spontaneous emulsifications will be given in § 4.
Yet another remarkable phenomenon is that the generated o-in-w emulsions gradually form two rings of microdroplets in the drop. The generated microdroplets first split into two groups, one above and one below the equator of the drop, which is shown in figure 2(d). The mechanism of the migration comes from two Marangoni convection rolls located separately above and below the equatorial plane (see supplementary movie 1 available at https://doi.org/10.1017/jfm.2019.207). The Marangoni flow motion is induced by surface tension gradients due to concentration variations along the interface, i.e. solutal Marangoni flow. The convection rolls drive the nucleated oil microdroplets and lead to an accumulation of these in the centre of each vortex roll, resulting in the formation of two rings of oil microdroplets as shown in figure 2(e). A more detailed discussion on the dynamics will be given in § 7. When the ethanol in the drop finally has dissolved, the solute Marangoni effect stops and the rings disintegrate (movie 1).
All these interesting phenomena happen in the first stage, when ethanol dissolving from the drop to the surrounding oil prevails. This stage takes approximately 30 min. In the second stage, the remaining water diffuses at an extremely slow speed, and no further unexpected phenomena occur. Therefore, in this paper we investigate only the first dissolving stage, up to the time the alcohol has dissolved. It is important to point out that, during the whole dissolution process, there is always a distinguishable interface between the oil host medium and the drop medium for all the experiments (drops with different water/ethanol ratios) that we performed. The sharp boundary of the drop corresponds to near-discontinuities in the gradient of the concentration–distance curve (Hartley Reference Hartley1946), which reflects the fact that the drop solution and host solution are macroscopically phase-separated at the drop–oil interface. We also stress that our experiments are very reproducible, even quantitatively.
3.2 Dissolution of drops with different initial ethanol concentrations
To quantitatively investigate the phenomena, we repeated the dissolution experiment with drops of different initial water/ethanol ratios, from 30 vol% to 70 vol% ethanol. Figure 3 shows the dissolution characteristics of the drops, including the temporal evolution of the drop volume, the variations of the contact angle
![]() $\unicode[STIX]{x1D703}$
and the footprint diameter
$\unicode[STIX]{x1D703}$
and the footprint diameter
![]() $L$
. The annotations of the geometrical variables are available in an experimental picture (figure 3
e).
$L$
. The annotations of the geometrical variables are available in an experimental picture (figure 3
e).
The volume evolutions of the drops are non-dimensionalized by the initial drop size
![]() $V_{0}$
to demonstrate a declining trend of the residual water volume with increasing initial ethanol concentration, as apparent from figure 3(a). That panel also reveals that indeed all drops experience two stages with two distinguishable dissolving rates, as discussed above: these two stages correspond successively to the initial stage dominated by the dissolution of the ethanol, and the subsequent slow dissolution of the remaining water. This is supported by the consistency between the initial water ratios and the drop residual volume percentage after the stage transition. The same behaviour also exists in the evaporation process of multicomponent drops (Liu, Bonaccurso & Butt Reference Liu, Bonaccurso and Butt2008; Tan et al.
Reference Tan, Diddens, Lv, Kuerten, Zhang and Lohse2016). Water has an extremely small solubility in oil (immiscible), and therefore the second stage takes a much longer time than the first one (figure 3
d).
$V_{0}$
to demonstrate a declining trend of the residual water volume with increasing initial ethanol concentration, as apparent from figure 3(a). That panel also reveals that indeed all drops experience two stages with two distinguishable dissolving rates, as discussed above: these two stages correspond successively to the initial stage dominated by the dissolution of the ethanol, and the subsequent slow dissolution of the remaining water. This is supported by the consistency between the initial water ratios and the drop residual volume percentage after the stage transition. The same behaviour also exists in the evaporation process of multicomponent drops (Liu, Bonaccurso & Butt Reference Liu, Bonaccurso and Butt2008; Tan et al.
Reference Tan, Diddens, Lv, Kuerten, Zhang and Lohse2016). Water has an extremely small solubility in oil (immiscible), and therefore the second stage takes a much longer time than the first one (figure 3
d).
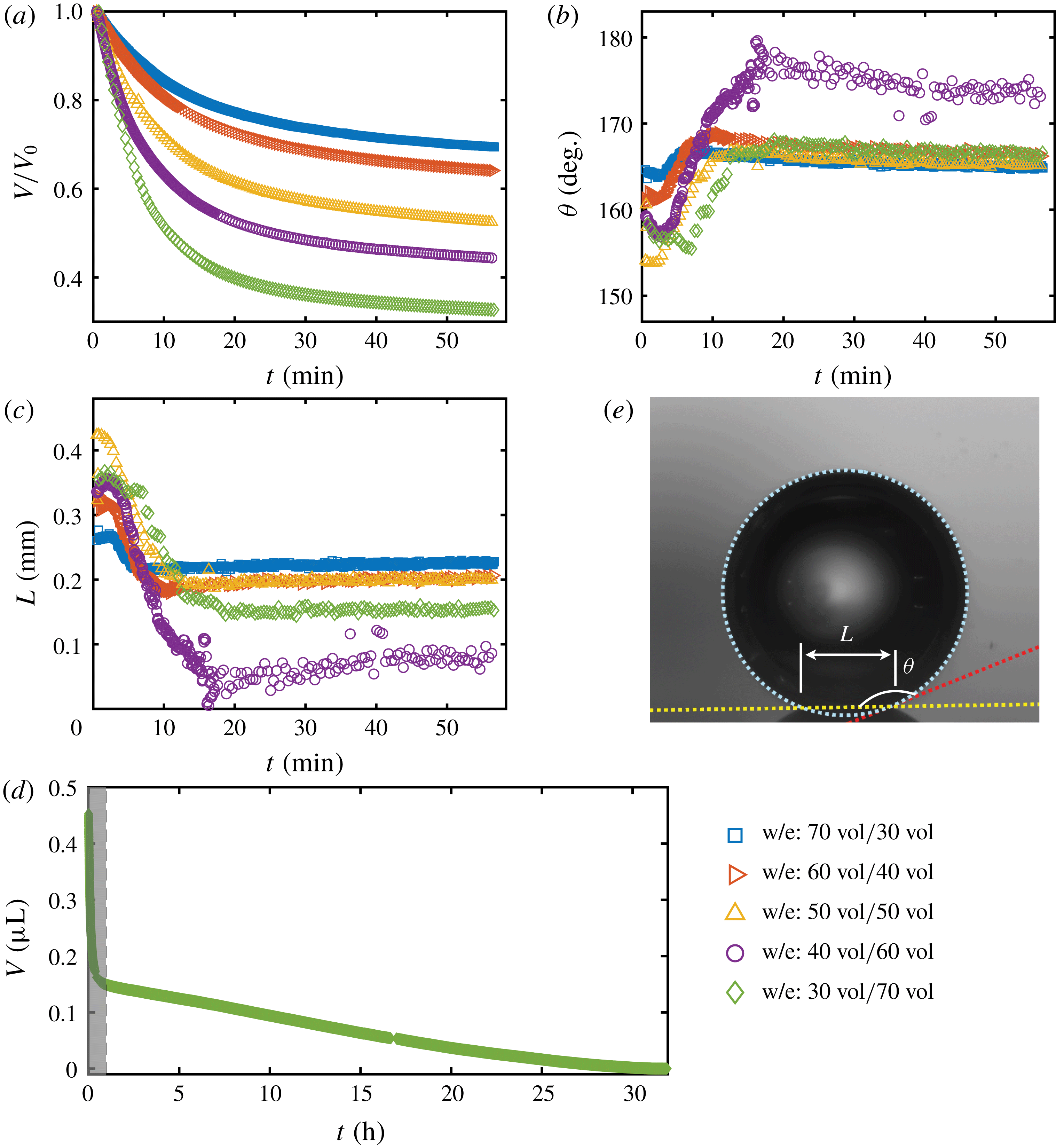
Figure 3. Morphology evolution of the dissolving drops in five different initial water/ethanol ratios (v/v 30/70, 40/60, 50/50, 60/40 and 70/30). (a–c) Temporal evolutions of the non-dimensionalized volume
![]() $V/V_{0}$
by initial drop size
$V/V_{0}$
by initial drop size
![]() $V_{0}$
, contact angle
$V_{0}$
, contact angle
![]() $\unicode[STIX]{x1D703}$
and footprint diameter
$\unicode[STIX]{x1D703}$
and footprint diameter
![]() $L$
, respectively, during the dissolution. (d) For one case (v/v 30/70) the volume evolution of the whole dissolution process is displayed as the long-time behaviour of droplet volume. The shaded area on the left is shown in panel (a). (e) A recording image of a dissolving drop, with annotations of the geometrical parameters.
$L$
, respectively, during the dissolution. (d) For one case (v/v 30/70) the volume evolution of the whole dissolution process is displayed as the long-time behaviour of droplet volume. The shaded area on the left is shown in panel (a). (e) A recording image of a dissolving drop, with annotations of the geometrical parameters.
The evolutions of the contact angle (figure 3
b) and the footprint diameter (figure 3
c) also reveal the variation of the ethanol content in the drop. In the first 10–15 min, the contact angle increases by approximately
![]() $20^{\circ }$
, accompanied by a receding of the contact line. The increase of the contact angle is a result of the rising water concentration in the drop as ethanol is dissolving much faster than water. In this period, neither the constant contact radius (CR) mode nor the constant angle (CA) mode applies (Lohse & Zhang Reference Lohse and Zhang2015). In the second stage, the drop evolves nearly in the CR mode – there is a slightly decreasing contact angle with a stabilized contact area. During the investigated process, the drop has a very high contact angle, more than
$20^{\circ }$
, accompanied by a receding of the contact line. The increase of the contact angle is a result of the rising water concentration in the drop as ethanol is dissolving much faster than water. In this period, neither the constant contact radius (CR) mode nor the constant angle (CA) mode applies (Lohse & Zhang Reference Lohse and Zhang2015). In the second stage, the drop evolves nearly in the CR mode – there is a slightly decreasing contact angle with a stabilized contact area. During the investigated process, the drop has a very high contact angle, more than
![]() $150^{\circ }$
, because of the higher interfacial energy between the substrate and anethole compared to the energy between the substrate and the aqueous solution.
$150^{\circ }$
, because of the higher interfacial energy between the substrate and anethole compared to the energy between the substrate and the aqueous solution.
It is worth noting that, at the very beginning (
![]() ${\sim}2~\text{min}$
), the contact angle decreases with time and the footprint diameter increases by a small amount. To the best of our knowledge, this is the first observation of this phenomenon in dissolving multicomponent drops, although there are a few reports on this phenomenon in evaporating multicomponent drops (Liu et al.
Reference Liu, Bonaccurso and Butt2008; Sefiane, David & Shanahan Reference Sefiane, David and Shanahan2008). A plausible explanation is that after deposition of the drop, the ethanol molecules in the drop tend to move towards the surface because of the lower interfacial energy between the hydrophobic substrate and ethanol compared to water, which results in the decreasing contact angle and the increasing contact area size (Liu et al.
Reference Liu, Bonaccurso and Butt2008).
${\sim}2~\text{min}$
), the contact angle decreases with time and the footprint diameter increases by a small amount. To the best of our knowledge, this is the first observation of this phenomenon in dissolving multicomponent drops, although there are a few reports on this phenomenon in evaporating multicomponent drops (Liu et al.
Reference Liu, Bonaccurso and Butt2008; Sefiane, David & Shanahan Reference Sefiane, David and Shanahan2008). A plausible explanation is that after deposition of the drop, the ethanol molecules in the drop tend to move towards the surface because of the lower interfacial energy between the hydrophobic substrate and ethanol compared to water, which results in the decreasing contact angle and the increasing contact area size (Liu et al.
Reference Liu, Bonaccurso and Butt2008).
4 Spontaneous emulsification
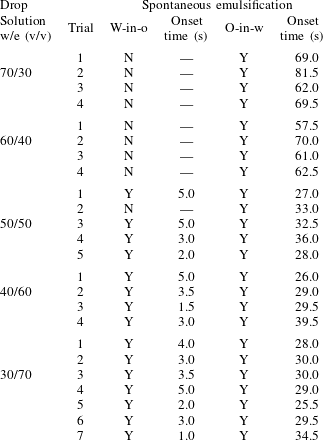
As stated above, during the dissolution, spontaneous emulsification happens both in the host oil and in the drop, forming w-in-o emulsions and o-in-w emulsions successively. The former are nucleated water microdroplets suspending in anethole oil, whereas the latter are anethole oil microdroplets nucleated in the aqueous phase. We performed 24 groups of dissolution experiments with five different water/ethanol ratios as the drop initial composition to study the impact of composition on emulsification phenomena. In table 1, the observed emulsification behaviours for the different initial drop compositions are listed. There Y/N stands for the presence/absence of emulsification. The waiting times for the onset of emulsification, measured with respect to the moment of needle detachment from the drop, are given in parentheses. W-in-o emulsification occurs only when the initial ethanol content in the drop is high (
![]() ${\geqslant}50~\text{vol}\%$
) and its onset time is very short, within seconds. On the contrary, o-in-w emulsification occurs for all the cases, independent of the ethanol content, but it takes more than half a minute to start. The corresponding onset time has a negative correlation with the initial ethanol content in the drop. Experimental videos are available in movie 4.
${\geqslant}50~\text{vol}\%$
) and its onset time is very short, within seconds. On the contrary, o-in-w emulsification occurs for all the cases, independent of the ethanol content, but it takes more than half a minute to start. The corresponding onset time has a negative correlation with the initial ethanol content in the drop. Experimental videos are available in movie 4.
Figure 4. Experimental snapshots showing the emulsification behaviour, appearance or absence, caused by the dissolution of water–ethanol drops. The initial water/ethanol volume ratios of the drops in (a–e) are 30/70, 40/60, 50/50, 60/40 and 70/30, respectively. The first column of photographs show that w-in-o emulsification only happens for high initial ethanol concentration cases (60 vol% and 70 vol%). The water microdroplets around drops are pointed at by the arrows in the zoom-in (d,e). The last two columns of the synchronized side and top views reveal that the o-in-w emulsification occurs inside drops in all the cases. The o-in-w emulsions are also pointed at by arrows. The scale bars are 0.5 mm in all panels. Some experimental videos are available in movie 4.
Figure 4 shows photographs of the emulsion detection experiments. Cloudy white w-in-o emulsions (nucleated water microdroplets) appear and suspend outside the drops, when the drops have 60 % and 70 % volume percentage ethanol (the first column of figure 4 d,e); while for the 30 vol% and 40 vol% cases, the surrounding anethole oil remains clean – no w-in-o emulsions appear (the first column of figure 4 a,b). Apparently 50 vol% is the transition point, as for this case in some experiments the w-in-o emulsions appear and in others they do not (the first column of figure 4 c). As stated above, in all of our experiments, we found that the emulsions only appear at a certain location, close to the tropic of capricorn of the drop and in the vicinity of the drop interface, as pointed out by arrows in the inserted pictures. The appeared emulsions move up and down at this location and some microdroplets are driven away by natural convection in the host liquid (cf. § 7 and see movie 2). After approximately half a minute, the w-in-o emulsions disappear and the surrounding liquid becomes transparent again.
The o-in-w emulsions (nucleated oil microdroplets) in the drop show up independently of the initial ethanol concentration of the drop. The cloudy white o-in-w emulsions inside the drop are visible in all cases, as displayed in the second and third columns of figure 4(a–e). The oil microdroplets emerge near the equator of the drop and then follow the Marangoni flow. Gradually, the oil microdroplets concentrate at the centre of the convection rolls and form two microdroplet rings. For each case, we provide top-view photographs (the second column of figure 4 a–e), where the rings are clearly visible. The first two rows of photographs (the second column of figure 4 a,b) show two already formed rings of oil microdroplets (see arrows), whereas the last three rows (the second column of figure 4 c–e) show the early chaotic arrangement of the microdroplets before the rings formed (see arrows).
Table 1. Spontaneous emulsifications by dissolution of multicomponent drops with different initial compositions in the host liquid. The indices e, w and o denote ethanol, water and anethole oil components, respectively. Y and N stand for the presence and absence of the emulsification, respectively. The time values are onset time of emulsification.
5 One-dimensional multicomponent diffusion model
5.1 Idea of the model
More quantitative insight into the spontaneous emulsification is gained by theoretically analysing the multi-diffusion process of the water–ethanol drop dissolving in the host liquid. A pure diffusion model is developed for the early stage of the diffusion process, which, together with the so-called diffusion path method proposed by Kirkaldy & Brown (Reference Kirkaldy and Brown1963) and Ruschak & Miller (Reference Ruschak and Miller1972), is used to predict the appearance or absence of emulsification. Our model consists of two parts, namely one part calculating the liquid–liquid equilibrium at the interface of the two regions (§ 5.2), and the other part modelling the mass transport in the two multicomponent fluids in contact (§ 5.3). The mass transport is modelled as a one-dimensional problem with a moving interface separating the aqueous phase and the oil-rich phase, known as the Stefan problem (Crank Reference Crank1979). The liquid–liquid equilibrium of the ternary mixture is calculated by applying the condition of equal chemical potentials (fundamental thermodynamic relation) in combination with the UNIFAC model to quantify the non-ideality of the mixture.
Mass transport in liquids happens on a long time scale compared to the macroscopic phase separation at the interface, and therefore these two processes are decoupled in our model. To decouple them, the following assumptions were made. First, we assume that the equilibrium at the interface is instantaneously achieved and remains stable during the mass transport across the interface. Second, to further simplify the model, we also assume zero boundary thickness, i.e. disregarding the microscopic details of the thermodynamic equilibrium process. With these assumptions, the interfacial composition is directly given by the liquid–liquid equilibrium calculation and thereby determines the mass transport model.
Stefan problems commonly exist in many studies involving diffusion, such as heat transfer with a phase transition (thawing, freezing, melting), or moisture transport of swelling grains or polymers (Barry & Caunce Reference Barry and Caunce2008). Classic solutions to Stefan problems are given by Crank (Reference Crank1979). In § 5.3, we present definitions and the derivation of the equations with respect to our problem.
But, before that, in § 5.2, we give a brief description of the applied equilibrium theory. The establishment of the liquid–liquid equilibria between two phases happens on a short time scale compared to the diffusion process in the adjacent bulk regions. Once the aqueous medium and the host liquid are in contact, thermodynamic equilibrium favours an oil-rich phase on one side, coexisting with a water-rich phase on the other side, i.e. a macroscopic phase separation, which is observed as a sharp boundary of the water–ethanol drop in oil. The compositions of these two phases are situated on the binodal curve (or coexistence curve) in the ternary phase diagram of the system and can be connected by a tie line (see figure 5 b).
5.2 Liquid–liquid equilibrium at the interface
The liquid–liquid equilibrium is achieved when the chemical potentials
![]() $\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FC}}$
are the same in both phases for each species
$\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FC}}$
are the same in both phases for each species
![]() $\unicode[STIX]{x1D6FC}$
. The chemical potential is a function of pressure, temperature and mole fractions
$\unicode[STIX]{x1D6FC}$
. The chemical potential is a function of pressure, temperature and mole fractions
![]() $x_{\unicode[STIX]{x1D6FC}}$
of the liquid constituents. At fixed temperature and pressure, a three-component liquid–liquid equilibrium system has only a single degree of freedom (Chu & Prosperetti Reference Chu and Prosperetti2016). The condition of equality of the chemical potentials then reduces to
$x_{\unicode[STIX]{x1D6FC}}$
of the liquid constituents. At fixed temperature and pressure, a three-component liquid–liquid equilibrium system has only a single degree of freedom (Chu & Prosperetti Reference Chu and Prosperetti2016). The condition of equality of the chemical potentials then reduces to
where
![]() $\unicode[STIX]{x1D6FE}$
is the liquid activity coefficient, a correction factor accounting for the non-ideality of the mixture. The superscripts indicate the region, i.e. either drop region (d) or host liquid region (h).
$\unicode[STIX]{x1D6FE}$
is the liquid activity coefficient, a correction factor accounting for the non-ideality of the mixture. The superscripts indicate the region, i.e. either drop region (d) or host liquid region (h).
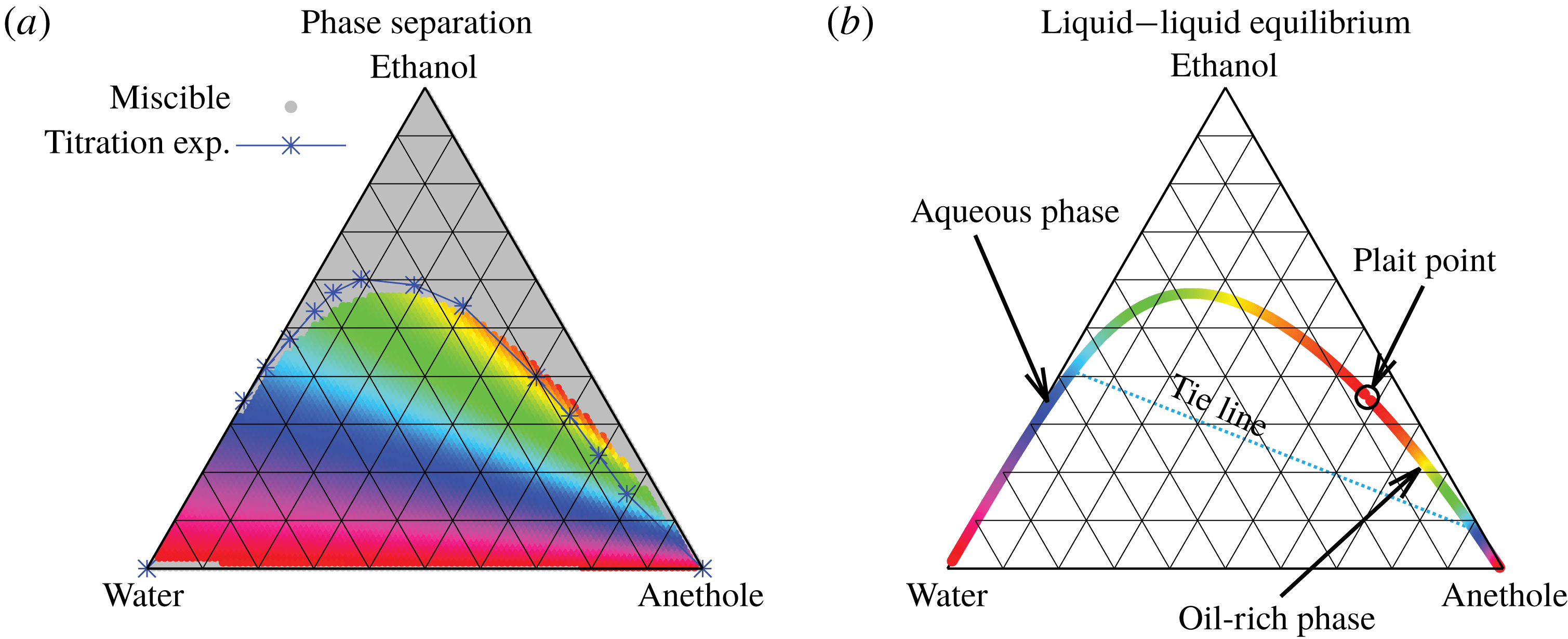
Figure 5. Phase separation predicted by UNIFAC. (a) Grey regions indicated homogeneous mixing, whereas phase separation is expected in the coloured regions. The blue line with the blue stars (measured data points) indicates a good agreement with the titration experiments of Tan et al. (Reference Tan, Diddens, Versluis, Butt, Lohse and Zhang2017). If the liquid is undergoing phase separation, the composition of the resulting two phases can be read off from the binodal in (b) by the colour code. As an example, we give the tie line for the pale blue region.
The mixture can only undergo a phase separation if the mixture is non-ideal, i.e.
![]() $\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D6FC}}\neq 1$
. Thus, the activity coefficients are fundamental to accurately describe the liquid–liquid equilibrium. Unfortunately, we have found neither sufficiently detailed experimental data for the present mixture, nor parameters for the UNIQUAC model that was used by Chu & Prosperetti (Reference Chu and Prosperetti2016). Therefore, we employed the UNIFAC model (Fredenslund, Jones & Prausnitz Reference Fredenslund, Jones and Prausnitz1975), which is more general than the UNIQUAC model, to perform the splitting of the molecules into functional subgroups. For detailed information about this model, we refer to Fredenslund, Gmehling & Rasmussen (Reference Fredenslund, Gmehling and Rasmussen1977). Owing to the better agreement with the titration experiments by Tan et al. (Reference Tan, Diddens, Versluis, Butt, Lohse and Zhang2017), we took the recent modified UNIFAC (Dortmund) parametrization (Constantinescu & Gmehling Reference Constantinescu and Gmehling2016).
$\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D6FC}}\neq 1$
. Thus, the activity coefficients are fundamental to accurately describe the liquid–liquid equilibrium. Unfortunately, we have found neither sufficiently detailed experimental data for the present mixture, nor parameters for the UNIQUAC model that was used by Chu & Prosperetti (Reference Chu and Prosperetti2016). Therefore, we employed the UNIFAC model (Fredenslund, Jones & Prausnitz Reference Fredenslund, Jones and Prausnitz1975), which is more general than the UNIQUAC model, to perform the splitting of the molecules into functional subgroups. For detailed information about this model, we refer to Fredenslund, Gmehling & Rasmussen (Reference Fredenslund, Gmehling and Rasmussen1977). Owing to the better agreement with the titration experiments by Tan et al. (Reference Tan, Diddens, Versluis, Butt, Lohse and Zhang2017), we took the recent modified UNIFAC (Dortmund) parametrization (Constantinescu & Gmehling Reference Constantinescu and Gmehling2016).
In order to find the liquid–liquid equilibrium curve and the regions of phase separation, we followed the method proposed by Zuend et al. (Reference Zuend, Marcolli, Peter and Seinfeld2010). If (5.1) can only be solved trivially, i.e.
![]() $x_{\unicode[STIX]{x1D6FC}}^{\text{d}}=x_{\unicode[STIX]{x1D6FC}}^{\text{h}}$
, or if the Gibbs free energy at the trivial solution is below the Gibbs free energy of all non-trivial solutions, the mixture remains in a well-mixed single-phase configuration. On the contrary, if there is a non-trivial solution with a lower Gibbs free energy than the trivial solution, phase separation is expected and the system will take on the solution with the globally minimal Gibbs free energy.
$x_{\unicode[STIX]{x1D6FC}}^{\text{d}}=x_{\unicode[STIX]{x1D6FC}}^{\text{h}}$
, or if the Gibbs free energy at the trivial solution is below the Gibbs free energy of all non-trivial solutions, the mixture remains in a well-mixed single-phase configuration. On the contrary, if there is a non-trivial solution with a lower Gibbs free energy than the trivial solution, phase separation is expected and the system will take on the solution with the globally minimal Gibbs free energy.
The data obtained by this procedure are depicted in figure 5. In figure 5(a), the region of phase separation is shown in a ternary diagram in terms of mass fractions
![]() $m_{\unicode[STIX]{x1D6FC}}$
. In the grey regions, the liquid at the specific composition remains perfectly mixed, whereas in the coloured regions, phase separation occurs. The composition of the two resulting phases can be read off from figure 5(b) by the colour code. The system splits into an aqueous phase and an oil-rich phase whose compositions are indicated by the respective same colour. Although the UNIFAC model is in general not perfect due to its dependence on the parameter table, the comparison of the phase separation region with the titration data of Tan et al. (Reference Tan, Diddens, Lv, Kuerten, Zhang and Lohse2016) in figure 5(a) (blue stars) shows very good agreement.
$m_{\unicode[STIX]{x1D6FC}}$
. In the grey regions, the liquid at the specific composition remains perfectly mixed, whereas in the coloured regions, phase separation occurs. The composition of the two resulting phases can be read off from figure 5(b) by the colour code. The system splits into an aqueous phase and an oil-rich phase whose compositions are indicated by the respective same colour. Although the UNIFAC model is in general not perfect due to its dependence on the parameter table, the comparison of the phase separation region with the titration data of Tan et al. (Reference Tan, Diddens, Lv, Kuerten, Zhang and Lohse2016) in figure 5(a) (blue stars) shows very good agreement.
5.3 Mass transport
The system under discussion is composed of three species in two different phases, i.e. it is a multicomponent and multiphase diffusion system. The diffusion process is modelled in a one-dimensional infinite space, as illustrated in figure 6. The diffusion process of each individual constituent is assumed to depend only on its own concentration gradient in the radial direction (Fick’s diffusion laws). The
![]() $m_{\unicode[STIX]{x1D6FC}}$
denote the mass fractions of the species water (
$m_{\unicode[STIX]{x1D6FC}}$
denote the mass fractions of the species water (
![]() $\unicode[STIX]{x1D6FC}=\text{w}$
), ethanol (
$\unicode[STIX]{x1D6FC}=\text{w}$
), ethanol (
![]() $\unicode[STIX]{x1D6FC}=\text{e}$
) and anethole oil (
$\unicode[STIX]{x1D6FC}=\text{e}$
) and anethole oil (
![]() $\unicode[STIX]{x1D6FC}=\text{o}$
) as a function of time
$\unicode[STIX]{x1D6FC}=\text{o}$
) as a function of time
![]() $t$
and position
$t$
and position
![]() $x$
. Again, the superscripts indicate the region, i.e. either drop region (d) or host liquid region (h). The two regions are separated by the moving interface at position
$x$
. Again, the superscripts indicate the region, i.e. either drop region (d) or host liquid region (h). The two regions are separated by the moving interface at position
![]() $s(t)$
. The initial position of the interface is set to the origin, i.e.
$s(t)$
. The initial position of the interface is set to the origin, i.e.
![]() $s(0)=0$
. The mass transport of each component
$s(0)=0$
. The mass transport of each component
![]() $\unicode[STIX]{x1D6FC}$
is governed by diffusion equations, namely
$\unicode[STIX]{x1D6FC}$
is governed by diffusion equations, namely
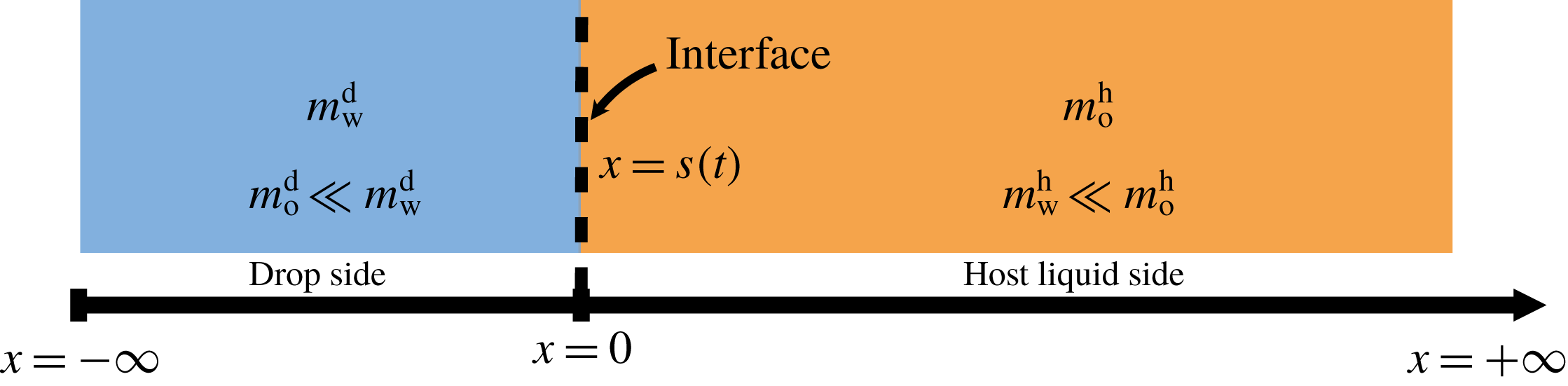
Figure 6. Sketch of the one-dimensional multiphase and multicomponent diffusion model with a moving interface at
![]() $x=s(t)$
separating the two regions of drop (d) and host liquid (h). The subscripts stand for the species water (w) and anethole oil (o). The mass fractions of the different species in the two different regions
$x=s(t)$
separating the two regions of drop (d) and host liquid (h). The subscripts stand for the species water (w) and anethole oil (o). The mass fractions of the different species in the two different regions
![]() $m_{\unicode[STIX]{x1D6FC}}^{\text{d}}$
and
$m_{\unicode[STIX]{x1D6FC}}^{\text{d}}$
and
![]() $m_{\unicode[STIX]{x1D6FC}}^{\text{h}}$
are a function of time
$m_{\unicode[STIX]{x1D6FC}}^{\text{h}}$
are a function of time
![]() $t$
and position
$t$
and position
![]() $x$
. The initial position of the interface
$x$
. The initial position of the interface
![]() $s(0)$
is defined to be at the origin.
$s(0)$
is defined to be at the origin.
As we focus only on the early stage of the diffusion process, the boundaries at
![]() $\pm \infty$
do not influence the dynamics in the vicinity of the interface. Therefore, the initial condition and the far-field boundary conditions are given by
$\pm \infty$
do not influence the dynamics in the vicinity of the interface. Therefore, the initial condition and the far-field boundary conditions are given by
Following the method successfully used by Kirkaldy & Brown (Reference Kirkaldy and Brown1963), Ruschak & Miller (Reference Ruschak and Miller1972) and Crank (Reference Crank1987), we assume the movement to be proportional to
![]() $\sqrt{t}$
, which is consistent with the fact that the interface movement is driven by diffusion, i.e.
$\sqrt{t}$
, which is consistent with the fact that the interface movement is driven by diffusion, i.e.
where the sign of the constant
![]() $\unicode[STIX]{x1D706}$
gives the direction of the interface movement, and
$\unicode[STIX]{x1D706}$
gives the direction of the interface movement, and
![]() $D_{s}$
can be regarded as the ‘diffusion coefficient’ of the moving interface. Thus, the solution of the governing diffusion equations (5.2) with the given conditions (5.4) reads
$D_{s}$
can be regarded as the ‘diffusion coefficient’ of the moving interface. Thus, the solution of the governing diffusion equations (5.2) with the given conditions (5.4) reads
 $$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{B}}_{\unicode[STIX]{x1D6FC}}^{1}=\frac{m_{\unicode[STIX]{x1D6FC}0}^{\text{d}}\,\text{erf}\,{\displaystyle \frac{s}{2\sqrt{D_{\unicode[STIX]{x1D6FC}}^{\text{d}}t}}}+m_{\unicode[STIX]{x1D6FC}s}^{\text{d}}}{\text{erf}\,{\displaystyle \frac{s}{2\sqrt{D_{\unicode[STIX]{x1D6FC}}^{\text{d}}t}}}+1}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{B}}_{\unicode[STIX]{x1D6FC}}^{1}=\frac{m_{\unicode[STIX]{x1D6FC}0}^{\text{d}}\,\text{erf}\,{\displaystyle \frac{s}{2\sqrt{D_{\unicode[STIX]{x1D6FC}}^{\text{d}}t}}}+m_{\unicode[STIX]{x1D6FC}s}^{\text{d}}}{\text{erf}\,{\displaystyle \frac{s}{2\sqrt{D_{\unicode[STIX]{x1D6FC}}^{\text{d}}t}}}+1}, & \displaystyle\end{eqnarray}$$
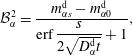 $$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{B}}_{\unicode[STIX]{x1D6FC}}^{2}=\frac{m_{\unicode[STIX]{x1D6FC}s}^{\text{d}}-m_{\unicode[STIX]{x1D6FC}0}^{\text{d}}}{\text{erf}\,{\displaystyle \frac{s}{2\sqrt{D_{\unicode[STIX]{x1D6FC}}^{\text{d}}t}}}+1}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{B}}_{\unicode[STIX]{x1D6FC}}^{2}=\frac{m_{\unicode[STIX]{x1D6FC}s}^{\text{d}}-m_{\unicode[STIX]{x1D6FC}0}^{\text{d}}}{\text{erf}\,{\displaystyle \frac{s}{2\sqrt{D_{\unicode[STIX]{x1D6FC}}^{\text{d}}t}}}+1}, & \displaystyle\end{eqnarray}$$
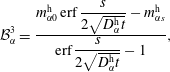 $$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{B}}_{\unicode[STIX]{x1D6FC}}^{3}=\frac{m_{\unicode[STIX]{x1D6FC}0}^{\text{h}}\,\text{erf}\,{\displaystyle \frac{s}{2\sqrt{D_{\unicode[STIX]{x1D6FC}}^{\text{h}}t}}}-m_{\unicode[STIX]{x1D6FC}s}^{\text{h}}}{\text{erf}\,{\displaystyle \frac{s}{2\sqrt{D_{\unicode[STIX]{x1D6FC}}^{\text{h}}t}}}-1}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{B}}_{\unicode[STIX]{x1D6FC}}^{3}=\frac{m_{\unicode[STIX]{x1D6FC}0}^{\text{h}}\,\text{erf}\,{\displaystyle \frac{s}{2\sqrt{D_{\unicode[STIX]{x1D6FC}}^{\text{h}}t}}}-m_{\unicode[STIX]{x1D6FC}s}^{\text{h}}}{\text{erf}\,{\displaystyle \frac{s}{2\sqrt{D_{\unicode[STIX]{x1D6FC}}^{\text{h}}t}}}-1}, & \displaystyle\end{eqnarray}$$
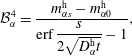 $$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{B}}_{\unicode[STIX]{x1D6FC}}^{4}=\frac{m_{\unicode[STIX]{x1D6FC}s}^{\text{h}}-m_{\unicode[STIX]{x1D6FC}0}^{\text{h}}}{\text{erf}\,{\displaystyle \frac{s}{2\sqrt{D_{\unicode[STIX]{x1D6FC}}^{\text{h}}t}}}-1}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{B}}_{\unicode[STIX]{x1D6FC}}^{4}=\frac{m_{\unicode[STIX]{x1D6FC}s}^{\text{h}}-m_{\unicode[STIX]{x1D6FC}0}^{\text{h}}}{\text{erf}\,{\displaystyle \frac{s}{2\sqrt{D_{\unicode[STIX]{x1D6FC}}^{\text{h}}t}}}-1}, & \displaystyle\end{eqnarray}$$
To simplify the expression of the equations, we introduce the definitions
which together with equation (5.6) are substituted into the coefficients (5.8) and the Stefan condition (5.2c ). Thereby, we obtain the coefficient constants as
We thus have a closed-form solution for the problem, given by the mass balance equation (5.11) in adjunction with thermodynamic equilibria theory. The number of mass balance equations is two, one for water (
![]() $\unicode[STIX]{x1D6FC}=\text{w}$
) and the other for anethole oil (
$\unicode[STIX]{x1D6FC}=\text{w}$
) and the other for anethole oil (
![]() $\unicode[STIX]{x1D6FC}=\text{o}$
), and the five unknown variables are
$\unicode[STIX]{x1D6FC}=\text{o}$
), and the five unknown variables are
![]() $m_{\text{w}s}^{\text{d}}$
,
$m_{\text{w}s}^{\text{d}}$
,
![]() $m_{\text{o}s}^{\text{d}}$
,
$m_{\text{o}s}^{\text{d}}$
,
![]() $m_{\text{w}s}^{\text{h}}$
,
$m_{\text{w}s}^{\text{h}}$
,
![]() $m_{\text{o}s}^{\text{h}}$
and
$m_{\text{o}s}^{\text{h}}$
and
![]() $\unicode[STIX]{x1D706}$
. As discussed above, the values of the two compositions on the two sides of the interface are situated on the binodal curve and are connected by a tie line in the phase diagram (see figure 5
b). Owing to these equilibrium constraints, the number of degrees of freedom of the interfacial composition is one (for instance
$\unicode[STIX]{x1D706}$
. As discussed above, the values of the two compositions on the two sides of the interface are situated on the binodal curve and are connected by a tie line in the phase diagram (see figure 5
b). Owing to these equilibrium constraints, the number of degrees of freedom of the interfacial composition is one (for instance
![]() $m_{\text{w}s}^{\text{d}}$
). Hence, there are in total two unknown variables, for instance
$m_{\text{w}s}^{\text{d}}$
). Hence, there are in total two unknown variables, for instance
![]() $m_{\text{w}s}^{\text{d}}$
and
$m_{\text{w}s}^{\text{d}}$
and
![]() $\unicode[STIX]{x1D706}$
, in the equation. By applying Newton’s method with a given initial guess, we can find roots to the two equations (5.11) (one for
$\unicode[STIX]{x1D706}$
, in the equation. By applying Newton’s method with a given initial guess, we can find roots to the two equations (5.11) (one for
![]() $\unicode[STIX]{x1D6FC}=\text{w}$
and one for
$\unicode[STIX]{x1D6FC}=\text{w}$
and one for
![]() $\unicode[STIX]{x1D6FC}=\text{o}$
) and the whole problem is solved. All quantities defined in the model are listed in table 2 given in appendix C.
$\unicode[STIX]{x1D6FC}=\text{o}$
) and the whole problem is solved. All quantities defined in the model are listed in table 2 given in appendix C.
5.4 Diffusion coefficients
In the model, there are in total four different diffusion coefficients, namely in each of the two different regions one coefficient for one of the two species: water diffusivity in the drop medium
![]() $D_{\text{w}}^{\text{d}}$
, anethole oil diffusivity in the drop medium
$D_{\text{w}}^{\text{d}}$
, anethole oil diffusivity in the drop medium
![]() $D_{\text{o}}^{\text{d}}$
, water diffusivity in the host liquid medium
$D_{\text{o}}^{\text{d}}$
, water diffusivity in the host liquid medium
![]() $D_{\text{w}}^{\text{h}}$
, and anethole oil diffusivity in the host liquid medium
$D_{\text{w}}^{\text{h}}$
, and anethole oil diffusivity in the host liquid medium
![]() $D_{\text{o}}^{\text{h}}$
.
$D_{\text{o}}^{\text{h}}$
.
To acquire the diffusivities, we were confined to models and assumptions, since direct measurement is complicated. In the drop medium at the early stage, the trans-anethole content is negligible, so that the coefficient
![]() $D_{\text{w}}^{\text{d}}$
is assumed to be given by the mutual diffusivity in a binary water–ethanol mixture. The corresponding values were obtained by fitting experimental data from Pařez et al. (Reference Pařez, Guevara-Carrion, Hasse and Vrabec2013). The coefficient
$D_{\text{w}}^{\text{d}}$
is assumed to be given by the mutual diffusivity in a binary water–ethanol mixture. The corresponding values were obtained by fitting experimental data from Pařez et al. (Reference Pařez, Guevara-Carrion, Hasse and Vrabec2013). The coefficient
![]() $D_{\text{o}}^{\text{d}}$
, i.e. dilute anethole in a water–ethanol mixture, is calculated in the limit of infinite dilution based on the model of Perkins & Geankoplis (Reference Perkins and Geankoplis1969), and is listed in § A.4. Both
$D_{\text{o}}^{\text{d}}$
, i.e. dilute anethole in a water–ethanol mixture, is calculated in the limit of infinite dilution based on the model of Perkins & Geankoplis (Reference Perkins and Geankoplis1969), and is listed in § A.4. Both
![]() $D_{\text{w}}^{\text{d}}$
and
$D_{\text{w}}^{\text{d}}$
and
![]() $D_{\text{o}}^{\text{d}}$
depend on the initial ethanol content in the drop.
$D_{\text{o}}^{\text{d}}$
depend on the initial ethanol content in the drop.
The model of Hayduk & Minhas (Reference Hayduk and Minhas1982) was used to calculate the coefficients of dilute water in host anethole oil,
![]() $D_{\text{w}}^{\text{h}}$
. The corresponding diffusivity constant
$D_{\text{w}}^{\text{h}}$
. The corresponding diffusivity constant
![]() $D_{\text{o}}^{\text{h}}$
is estimated according to the Stokes–Einstein equation, which states that the diffusion coefficient is inversely proportional to the size of molecules at constant viscosity. Since both ethanol and water content in the host liquid are negligible, we take
$D_{\text{o}}^{\text{h}}$
is estimated according to the Stokes–Einstein equation, which states that the diffusion coefficient is inversely proportional to the size of molecules at constant viscosity. Since both ethanol and water content in the host liquid are negligible, we take
![]() $D_{\text{w}}^{\text{h}}=1.2\times 10^{-9}~\text{m}^{2}~\text{s}^{-1}$
and
$D_{\text{w}}^{\text{h}}=1.2\times 10^{-9}~\text{m}^{2}~\text{s}^{-1}$
and
![]() $D_{\text{o}}^{\text{h}}=0.66\times 10^{-9}~\text{m}^{2}~\text{s}^{-1}$
, both of which are assumed to be constant.
$D_{\text{o}}^{\text{h}}=0.66\times 10^{-9}~\text{m}^{2}~\text{s}^{-1}$
, both of which are assumed to be constant.
6 Model predictions
6.1 Concentration profiles
The mass concentration distribution of each constituent as a function of time is obtained from the model described above. Figure 7(a–c) and corresponding close-up images, figure 7(d–g), show the development of the concentration profiles for different cases of binary drops with different initial water/ethanol ratios (
![]() $70/30$
v/v in (a), 50/50 v/v in (b) and 30/70 v/v in (c); animations of 40/60 v/v and 60/40 v/v are available in movie 5). Anethole oil, water and ethanol are labelled with yellow, blue and red colours, respectively. The vertical black dash-dotted line stands for the initial position of the interface of the aqueous water–ethanol region (left side) and the anethole oil-rich region (right side). Initially, the concentration profile of each species is a step function (first row of figure 7
a–c), which is consistent with the initial condition (5.4a,b
) of the model. Different initial ethanol contents in the drop account for the difference of the step heights in the panels.
$70/30$
v/v in (a), 50/50 v/v in (b) and 30/70 v/v in (c); animations of 40/60 v/v and 60/40 v/v are available in movie 5). Anethole oil, water and ethanol are labelled with yellow, blue and red colours, respectively. The vertical black dash-dotted line stands for the initial position of the interface of the aqueous water–ethanol region (left side) and the anethole oil-rich region (right side). Initially, the concentration profile of each species is a step function (first row of figure 7
a–c), which is consistent with the initial condition (5.4a,b
) of the model. Different initial ethanol contents in the drop account for the difference of the step heights in the panels.
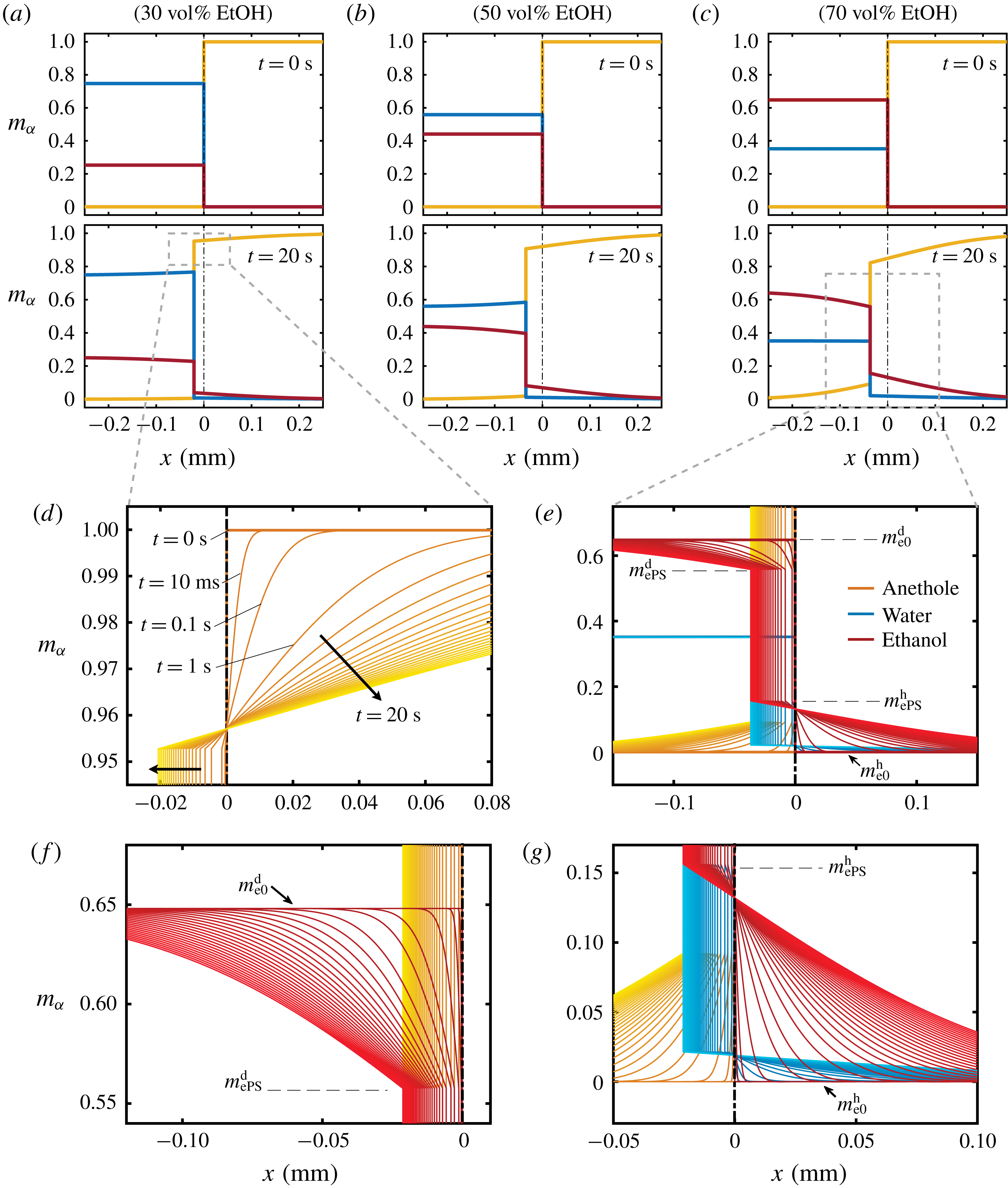
Figure 7. Calculated results of the diffusion model. (a–c) Snapshots of the mass fraction profile at 0 s (first row) and 20 s (second row) for different cases. The vertical black dash-dotted line indicates the initial position of the interface, which separates the drop solution on the left and the host liquid on the right. Note that
![]() $m_{\unicode[STIX]{x1D6FC}}$
represents mass fractions, which are different from volume fractions. Panels (d,e) are zoom-in pictures of panels (a,c) at
$m_{\unicode[STIX]{x1D6FC}}$
represents mass fractions, which are different from volume fractions. Panels (d,e) are zoom-in pictures of panels (a,c) at
![]() $t=20~\text{s}$
, showing the profile evolution. Panels (f,g) are zoom-ins of panel (e). The parameters used in the model are described in the text.
$t=20~\text{s}$
, showing the profile evolution. Panels (f,g) are zoom-ins of panel (e). The parameters used in the model are described in the text.
In the close-up figure 7(d), once the diffusion starts, the discontinuity in the profile at
![]() $t=0~\text{s}$
is immediately smoothed, and new turning points emerge. The dynamics of the concentration profiles is apparent from the temporal curves at
$t=0~\text{s}$
is immediately smoothed, and new turning points emerge. The dynamics of the concentration profiles is apparent from the temporal curves at
![]() $t=10~\text{ms}$
,
$t=10~\text{ms}$
,
![]() $t=1~\text{s}$
,
$t=1~\text{s}$
,
![]() $t=2~\text{s}$
and so on.
$t=2~\text{s}$
and so on.
The concentration gradient at the interface induces a diffusive flux for each constituent towards or from infinity (anethole in figure 7(d), ethanol and water in figure 7(e)). The step height at infinity remains unchanged due to the Dirichlet boundary condition (5.4c,d
). In the investigated Stefan problem, the interface has the freedom to shift towards the aqueous region (left side), for all the constituents in the system. After 20 s, the developed concentration profiles in different cases are displayed in the second row of figure 7(a–c). The heights of the new turning points, corresponding to the interfacial concentration
![]() $m_{\unicode[STIX]{x1D6FC}s}^{\text{d}}$
and
$m_{\unicode[STIX]{x1D6FC}s}^{\text{d}}$
and
![]() $m_{\unicode[STIX]{x1D6FC}s}^{\text{h}}$
(ethanol,
$m_{\unicode[STIX]{x1D6FC}s}^{\text{h}}$
(ethanol,
![]() $\unicode[STIX]{x1D6FC}=\text{e}$
, in figure 7
e), are fixed during the movement of the interface, which reflects the assumption of the stability of liquid–liquid equilibrium at the interface. Figure 7(f,g) show further zoom-ins of the interface in figure 7(e).
$\unicode[STIX]{x1D6FC}=\text{e}$
, in figure 7
e), are fixed during the movement of the interface, which reflects the assumption of the stability of liquid–liquid equilibrium at the interface. Figure 7(f,g) show further zoom-ins of the interface in figure 7(e).
6.2 Diffusion path theory and calculated results
The diffusion path method was proposed by Kirkaldy & Brown (Reference Kirkaldy and Brown1963), who mapped the composition of the ternary solution on its phase diagram (figure 5 b). The values of the composition along the domains are mapped in the diagram as a line, known as the diffusion path or composition path. It provides an effective way of representing the relationship between kinetic and thermodynamic aspects for a multiphase and multicomponent system.
In the spirit of the pioneering work by Ruschak & Miller (Reference Ruschak and Miller1972), we predict the diffusion-induced spontaneous emulsification by examining the geometrical relationship between diffusion paths and the binodal curve. If the diffusion path crosses the binodal curve (figure 5 b) between start and end points, supersaturation in the media is present, which induces spontaneous emulsification. It is noteworthy that the intersections of all considered diffusion paths with the binodal curve are far away from the plait point and the intersections are located at the edge of the ouzo effect region.
In a ternary system, the path is determined by any two independent constituents. Since we know the evolution of the distribution of all species, we can mathematically express their relationship. We know that the coefficients (5.10a,b
) are constant for a certain case, which implies that (5.7a
) is well determined. Therefore, (5.7a
) gives functional relationships
![]() $m_{\text{w}}^{\text{d}}=f_{1}(x/\sqrt{t})$
and
$m_{\text{w}}^{\text{d}}=f_{1}(x/\sqrt{t})$
and
![]() $m_{\text{o}}^{\text{d}}=f_{2}(x/\sqrt{t})$
. Upon substituting them into equation (5.3a
), we obtain the mathematical expression of the diffusion path in the drop region,
$m_{\text{o}}^{\text{d}}=f_{2}(x/\sqrt{t})$
. Upon substituting them into equation (5.3a
), we obtain the mathematical expression of the diffusion path in the drop region,
where
![]() ${\mathcal{F}}=f_{1}\,f_{2}^{-1}$
. In the same way, we obtain the expression of the diffusion path in the host liquid medium,
${\mathcal{F}}=f_{1}\,f_{2}^{-1}$
. In the same way, we obtain the expression of the diffusion path in the host liquid medium,
where
![]() ${\mathcal{G}}=g_{2}\,g_{1}^{-1}$
, given
${\mathcal{G}}=g_{2}\,g_{1}^{-1}$
, given
![]() $m_{\text{w}}^{\text{h}}=g_{1}(x/\sqrt{t})$
and
$m_{\text{w}}^{\text{h}}=g_{1}(x/\sqrt{t})$
and
![]() $m_{\text{o}}^{\text{h}}=g_{2}(x/\sqrt{t})$
. Notably, the mathematical expressions reveal that the diffusion path is independent of time and space. In other words, the set of compositions at a certain position for different moments and the set for a certain moment among different positions share the same diffusion path. The composition at the end point of the diffusion path lies on the binodal curve and corresponds to the interfacial composition, whereas the composition at the start point of the diffusion path indicates the composition at infinity, which is the same as the initial composition in the domain.
$m_{\text{o}}^{\text{h}}=g_{2}(x/\sqrt{t})$
. Notably, the mathematical expressions reveal that the diffusion path is independent of time and space. In other words, the set of compositions at a certain position for different moments and the set for a certain moment among different positions share the same diffusion path. The composition at the end point of the diffusion path lies on the binodal curve and corresponds to the interfacial composition, whereas the composition at the start point of the diffusion path indicates the composition at infinity, which is the same as the initial composition in the domain.
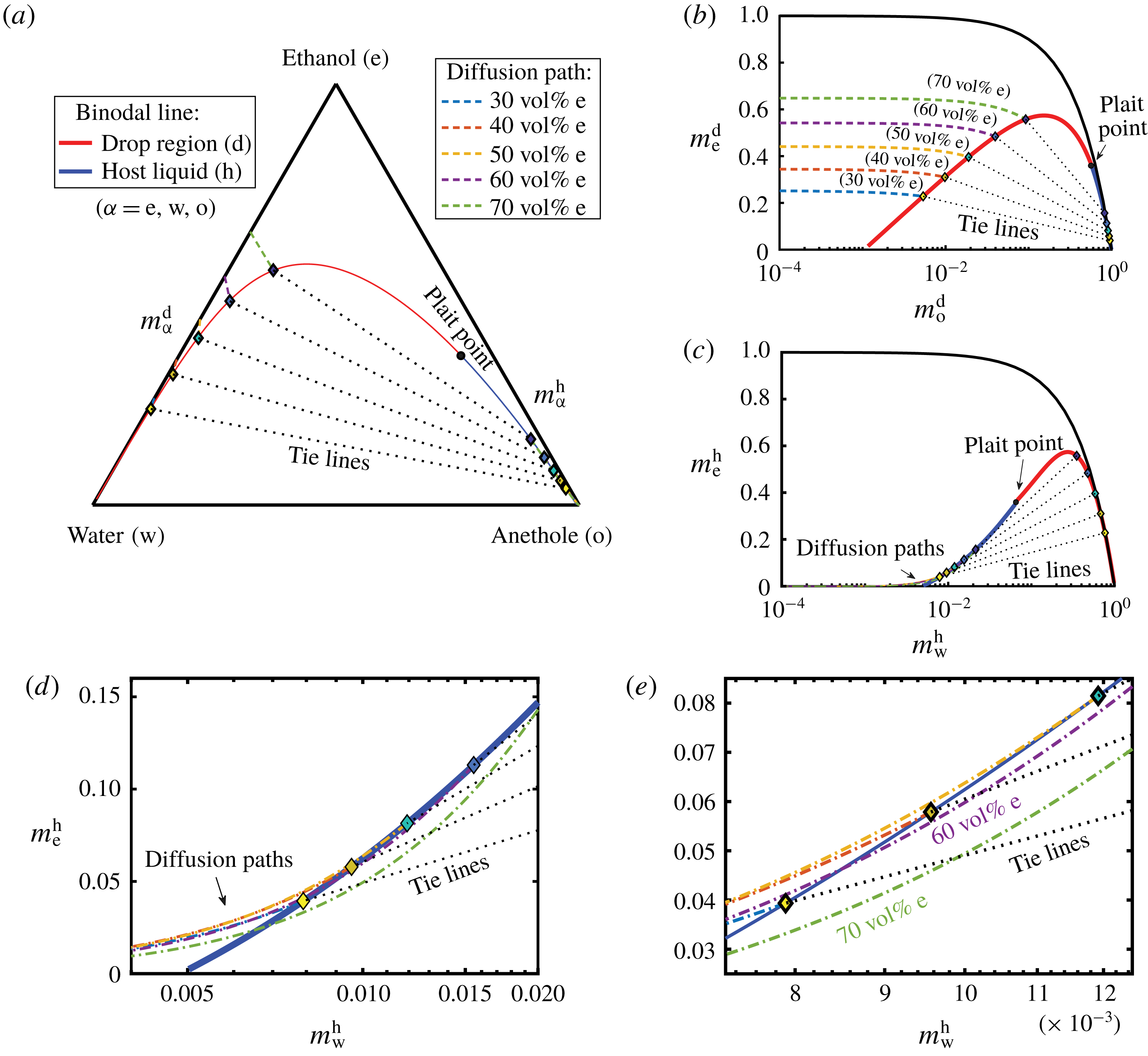
Figure 8. Phase diagrams showing the calculated diffusion paths in the water–ethanol–anethole phase diagram (a), in the anethole–ethanol phase diagram (b), and in the water–ethanol phase diagram (c). The oil-rich part (host liquid) of the binodal curve is labelled in blue and the water-rich part (drop region) in red. The black dotted lines are tie lines. Panels (d,e) are zoom-ins of panel (c) with increasing magnifications, showing that the diffusion path in the host liquid passes through the binodal curve when the ethanol content is high (
![]() ${\geqslant}50~\text{vol}\%$
). In contrast, in the aqueous phase, in all cases, there is no diffusion path crossing the binodal curve.
${\geqslant}50~\text{vol}\%$
). In contrast, in the aqueous phase, in all cases, there is no diffusion path crossing the binodal curve.
Figure 8(a) shows the calculated results in the ternary diagram. The mass fraction phase diagrams of two independent constituents are given in figure 8(b,c). Figure 8(b) shows the anethole–ethanol phase diagram, highlighting the water-rich regime with o-in-w emulsions, whereas figure 8(c) with zoom-ins in figure 8(d,e) shows the water–ethanol phase diagram, enhancing the oil-rich regime with w-in-o emulsions. The binodal curve is divided by the plait point into two different colours, blue for the oil-rich phase (host liquid) and red for the water-rich phase (drop region). The tie lines were calculated by the method described in § 5.2. The dot-dashed lines with different colours are the diffusion paths for different cases (same colour labelling for all figure 8
a–e). The zoom-ins in figure 8(d,e) reveal that, when the ethanol volume fraction in the aqueous phase is higher than 51.98 vol%, corresponding to a transition mass fraction
![]() $m_{\text{e}\ast }^{\text{d}}$
calculated by the model, the diffusion path has to pass through the binodal curve to meet the equilibrium points (diamonds) at the binodal. The segment of the diffusion path below the binodal is in the supersaturation condition, which indicates the appearance of w-in-o emulsions in the oil-rich side (host liquid region). In contrast, in the water-rich side (figure 8
b), all the diffusion paths meet equilibrium points but without passing through the binodal curve. Therefore, according to the model, there is no supersaturation region induced by pure diffusion processes, which predicts the absence of o-in-w emulsions in the drop region. The time independence implies that self-emulsification immediately occurs once the diffusion process starts.
$m_{\text{e}\ast }^{\text{d}}$
calculated by the model, the diffusion path has to pass through the binodal curve to meet the equilibrium points (diamonds) at the binodal. The segment of the diffusion path below the binodal is in the supersaturation condition, which indicates the appearance of w-in-o emulsions in the oil-rich side (host liquid region). In contrast, in the water-rich side (figure 8
b), all the diffusion paths meet equilibrium points but without passing through the binodal curve. Therefore, according to the model, there is no supersaturation region induced by pure diffusion processes, which predicts the absence of o-in-w emulsions in the drop region. The time independence implies that self-emulsification immediately occurs once the diffusion process starts.
6.3 Self-emulsification: comparison between model predictions and experimental observations
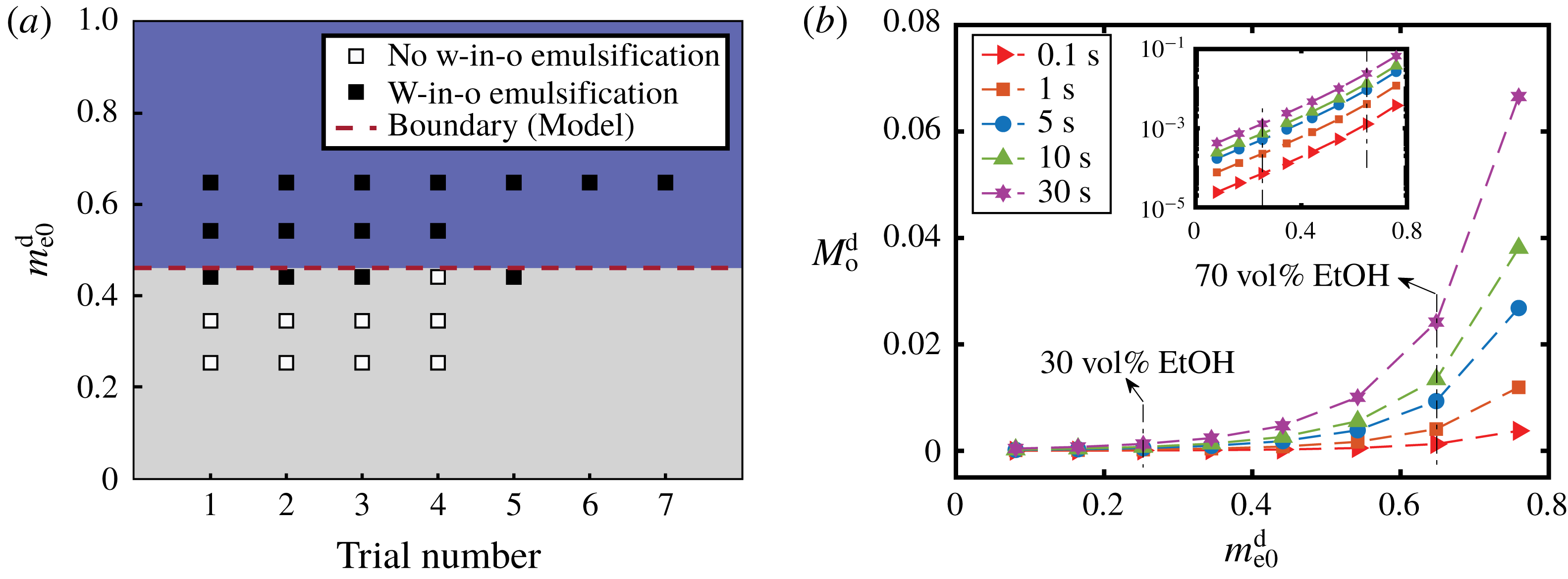
Figure 9. (a) Comparison between the model prediction and the experimental observations for the appearance of w-in-o emulsions outside drops. The ordinate is the initial mass fraction of ethanol in the drop and the abscissa gives the trial number. The black and white squares are experimental observation data from table 1 and denote the presence and absence of emulsification, respectively. The red dashed line is a transition value calculated by the model, above which w-in-o emulsification is predicted to happen. (b) Calculation results of the total amount of oil transported into the drop as a function of the initial ethanol content of the drop using the one-dimensional diffusion model. Different symbols present the total amount of oil at different moments. The inset gives the same data on a log–log plot.
For w-in-o emulsion, the comparison between model prediction and experimental observations is presented in figure 9(a). The vertical ordinate denotes the initial ethanol mass fraction in the water–ethanol drop and the abscissa gives the trial number, i.e. the individual experiments at this particular initial composition. The data points are from table 1: the black symbol indicates the presence of w-in-o emulsion, and the white symbol means that the w-in-o emulsion is absent. The red dashed line is the calculated transition percentage
![]() $m_{\text{e}\ast }^{\text{d}}$
, above which (blue region) the model predicts the presence of w-in-o emulsion in the host liquid, otherwise absence (grey region). The comparison reveals the reasonable predictive power. In the blue region, all data points are black, whereas in the grey region far from transition line, all the data points are white. Around the transition line, both black and white data points exist.
$m_{\text{e}\ast }^{\text{d}}$
, above which (blue region) the model predicts the presence of w-in-o emulsion in the host liquid, otherwise absence (grey region). The comparison reveals the reasonable predictive power. In the blue region, all data points are black, whereas in the grey region far from transition line, all the data points are white. Around the transition line, both black and white data points exist.
For the o-in-w emulsion in the drop medium, no diffusion-triggered self-emulsification was observed in experiments within half a minute (table 1), which is consistent with the model prediction. However, oil microdroplets must appear since the ethanol content in the drop is reducing over time, while the oil content is increasing. At some point, the composition in the drop region will be supersaturated and cause the ouzo effect inside the drop. However, due to the infinite domain in the model with Dirichlet boundary conditions, the model cannot account for the long-time behaviour. The onset time for the oil microdroplets is at least half a minute or more, and has a negative correlation with the initial content of ethanol in the drop as recorded in table 1.
Although we are unable to obtain the overall composition of the three-dimensional drop from the one-dimensional model, it is possible to gain more understanding on the transport of anethole oil during the early stage by calculating the total amount of anethole transported into the drop,
![]() $M_{\text{o}}^{\text{d}}$
. Its definition is given by integrating the mass fraction of anethole
$M_{\text{o}}^{\text{d}}$
. Its definition is given by integrating the mass fraction of anethole
![]() $m_{\text{o}}^{\text{d}}$
on the interval of aqueous region from
$m_{\text{o}}^{\text{d}}$
on the interval of aqueous region from
![]() $-\infty$
to
$-\infty$
to
![]() $s$
,
$s$
,
Then we have
Figure 9(b) shows that a higher ethanol percentage in the drop,
![]() $m_{\text{e}0}^{\text{d}}$
, leads to a higher rate of transport of oil into the drop,
$m_{\text{e}0}^{\text{d}}$
, leads to a higher rate of transport of oil into the drop,
![]() $M_{\text{o}}^{\text{d}}$
. The inset reveals that it is an exponential growth relationship. So the difference in the oil amount in the drop caused by the ethanol content increases over time (from red solid
$M_{\text{o}}^{\text{d}}$
. The inset reveals that it is an exponential growth relationship. So the difference in the oil amount in the drop caused by the ethanol content increases over time (from red solid
![]() ${\vartriangleright}$
line, at 0.1 s, to purple solid ✡ line, at 30 s). This gives a possible explanation for the experimental observation, as a higher ethanol concentration in the drop leads to more oil after the early stage of the diffusion process, which favours the occurrence of the ouzo effect inside the drop.
${\vartriangleright}$
line, at 0.1 s, to purple solid ✡ line, at 30 s). This gives a possible explanation for the experimental observation, as a higher ethanol concentration in the drop leads to more oil after the early stage of the diffusion process, which favours the occurrence of the ouzo effect inside the drop.
6.4 Model limitations
Although the model provides information on the mass transport of the multiphase and multicomponent diffusion process, as well as a good prediction of the behaviour of spontaneous emulsification, it is subject to the following limitations: (i) The diffusion model is developed as a one-dimensional model without consideration of flow motion, i.e. a pure multiphase and multicomponent diffusion process. (ii) The dependence of diffusivity on the local species concentration is disregarded and off-diagonal diffusion terms, i.e. as in the Maxwell–Stefan theory, are not considered. (iii) We apply Dirichlet boundary conditions at infinity, which implies that the model is only applicable in the early stage of the diffusion process. In the long-time limit, the finite size of the regions, in particular of the drop, will become important, since there is not an infinite reservoir for the species. (iv) The detailed process of phase separation at the interface is not considered, as we apply an instantaneous liquid–liquid equilibrium assumption.
The flow motion in the system has a big impact on the position where emulsification takes place. A strong flow rate has the capacity to prevent emulsification by changing the local concentrations or by directly dissolving the nucleated emulsion. Therefore it is necessary to investigate the fluid dynamics of the system in § 7.
7 Discussion on the fluid dynamics of the system
7.1 Scaling analysis
In the studied system, diffusion-induced advection, in the laminar flow regime, can in turn play a significant role in the diffusion process, i.e. diffusion and advection are highly coupled in the system. The diffusion causes non-uniformities in the species distribution in both drop and host liquid media, which drives bulk flow motions (advection). The flow reorganizes the concentration field and consequently, in turn, affects the diffusion. The generated advection mainly encompasses solutal Marangoni flow and buoyancy-driven flow (Dietrich et al. Reference Dietrich, Wildeman, Visser, Hofhuis, Kooij, Zandvliet and Lohse2016), i.e. solutal natural convection, whereas thermal effects are negligible compared to the two others. As solutal Marangoni flow and buoyancy-driven flow have alternating dominance inside and outside the drop, respectively, their impacts on diffusion can be treated separately. To confirm that only one of the two respective flows is dominant in the respective domain, we perform the following scaling analysis.
The characteristic velocity of the solutal Marangoni flow
![]() $U_{M}$
scales like
$U_{M}$
scales like
where
![]() $\unicode[STIX]{x1D707}$
is the dynamic viscosity (§ A.5), and
$\unicode[STIX]{x1D707}$
is the dynamic viscosity (§ A.5), and
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D6FE}$
is the interfacial surface tension difference caused by compositional variations. The characteristic velocity associated with the buoyancy-driven convection
$\unicode[STIX]{x0394}\unicode[STIX]{x1D6FE}$
is the interfacial surface tension difference caused by compositional variations. The characteristic velocity associated with the buoyancy-driven convection
![]() $U_{B}$
is obtained by balancing the viscous dissipation rate within the convection roll with the rate of gain of potential energy due to gravity (Tam et al.
Reference Tam, von Arnim, McKinley and Hosoi2009), i.e.
$U_{B}$
is obtained by balancing the viscous dissipation rate within the convection roll with the rate of gain of potential energy due to gravity (Tam et al.
Reference Tam, von Arnim, McKinley and Hosoi2009), i.e.
where the left side scales as
![]() $\unicode[STIX]{x1D707}\ell (U_{B})^{2}$
. Here
$\unicode[STIX]{x1D707}\ell (U_{B})^{2}$
. Here
![]() $\ell$
is the characteristic length scale and
$\ell$
is the characteristic length scale and
![]() $g$
is the gravitational constant. Hence, the characteristic velocity of the buoyancy-driven flow
$g$
is the gravitational constant. Hence, the characteristic velocity of the buoyancy-driven flow
![]() $U_{B}$
scales as
$U_{B}$
scales as
With (7.3) and (7.1), we can estimate the ratio of buoyancy-driven flow to Marangoni flow by
We can note that the ratio is a Bond number, which measures the importance of gravitational forces compared to interfacial surface tension. The Bond number is proportional to
![]() $\ell ^{2}$
, which indicates that the relative importance of the two flow mechanisms has a strong dependence on the spatial scale of the domain.
$\ell ^{2}$
, which indicates that the relative importance of the two flow mechanisms has a strong dependence on the spatial scale of the domain.
We can estimate the ratio inside the drop by taking the drop radius
![]() $R\sim 0.75~\text{mm}$
as the length scale
$R\sim 0.75~\text{mm}$
as the length scale
![]() $\ell$
. Since the interfacial surface tension is composition-dependent and varies during drop dissolution, we estimated the difference
$\ell$
. Since the interfacial surface tension is composition-dependent and varies during drop dissolution, we estimated the difference
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D6FE}\sim 12.1~\text{mN}~\text{m}^{-1},$
as half of the interfacial surface tension between pure water and anethole oil (Tan et al.
Reference Tan, Diddens, Versluis, Butt, Lohse and Zhang2017). The density difference is selected as the biggest density difference between water and ethanol, i.e.
$\unicode[STIX]{x0394}\unicode[STIX]{x1D6FE}\sim 12.1~\text{mN}~\text{m}^{-1},$
as half of the interfacial surface tension between pure water and anethole oil (Tan et al.
Reference Tan, Diddens, Versluis, Butt, Lohse and Zhang2017). The density difference is selected as the biggest density difference between water and ethanol, i.e.
![]() $\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D70C}_{\text{w}}-\unicode[STIX]{x1D70C}_{\text{e}}$
(
$\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D70C}_{\text{w}}-\unicode[STIX]{x1D70C}_{\text{e}}$
(
![]() ${\sim}211~\text{kg}~\text{m}^{3}$
). The estimation shows that
${\sim}211~\text{kg}~\text{m}^{3}$
). The estimation shows that
![]() $U_{B}\sim U_{M}/10$
, which implies that Marangoni flow inside the drop is prevailing. Outside the drop, the length scale
$U_{B}\sim U_{M}/10$
, which implies that Marangoni flow inside the drop is prevailing. Outside the drop, the length scale
![]() $\ell$
is selected as the host liquid depth,
$\ell$
is selected as the host liquid depth,
![]() $\ell =7.5~\text{mm}$
. Then the estimate of the velocity ratio becomes
$\ell =7.5~\text{mm}$
. Then the estimate of the velocity ratio becomes
![]() $U_{B}\sim 10U_{M}$
, which indicates that buoyancy-driven flow is dominating outside the drop.
$U_{B}\sim 10U_{M}$
, which indicates that buoyancy-driven flow is dominating outside the drop.
7.2 Flow motions and its influence on spontaneous emulsification
Taking the understanding of the flow motion in the system from the scaling analysis, we disregard the Marangoni flow in the following discussion about the hydrodynamics in the host liquid (large-scale domain), whereas the buoyancy effect is neglected inside the drop (small-scale domain). The hydrodynamics outside and inside the drop are discussed successively.
As the water–ethanol drop dissolves, ethanol diffuses into the surrounding anethole oil. Then, buoyancy starts to play a role, as ethanol is less dense than water and anethole oil, i.e.
![]() $\unicode[STIX]{x1D70C}_{\text{e}}<\unicode[STIX]{x1D70C}_{\text{o}}$
and
$\unicode[STIX]{x1D70C}_{\text{e}}<\unicode[STIX]{x1D70C}_{\text{o}}$
and
![]() $\unicode[STIX]{x1D70C}_{\text{e}}<\unicode[STIX]{x1D70C}_{\text{w}}$
(
$\unicode[STIX]{x1D70C}_{\text{e}}<\unicode[STIX]{x1D70C}_{\text{w}}$
(
![]() $\unicode[STIX]{x1D70C}_{\text{w}}=998~\text{kg}~\text{m}^{-3}$
,
$\unicode[STIX]{x1D70C}_{\text{w}}=998~\text{kg}~\text{m}^{-3}$
,
![]() $\unicode[STIX]{x1D70C}_{\text{e}}=787~\text{kg}~\text{m}^{-3}$
and
$\unicode[STIX]{x1D70C}_{\text{e}}=787~\text{kg}~\text{m}^{-3}$
and
![]() $\unicode[STIX]{x1D70C}_{\text{o}}=988~\text{kg}~\text{m}^{-3}$
at
$\unicode[STIX]{x1D70C}_{\text{o}}=988~\text{kg}~\text{m}^{-3}$
at
![]() $22\,^{\circ }\text{C}$
). The surrounding ethanol-rich oil floats up in the form of a solute plume, causing an upwelling flow. Simultaneously, fresh oil liquid far from the drop replenishes to achieve mass continuity, as sketched in figure 1(a). So a convection flow outside the drop forms as a consequence, which is clearly observed through PIV measurements (figure 1
b). In the region next to the tropic of capricorn of the drop and not far from the drop surface, there is weak flow, enclosed by the yellow circle in the close-up image. This indicates a subtle influence from convection on the diffusion process in this region, whereas in other regions, the refresh oil brought by the relatively strong flow prevents the formation of local supersaturation. This is the reason that accounts for the appearance of w-in-o microdroplets in a certain position with the weak flow rate.
$22\,^{\circ }\text{C}$
). The surrounding ethanol-rich oil floats up in the form of a solute plume, causing an upwelling flow. Simultaneously, fresh oil liquid far from the drop replenishes to achieve mass continuity, as sketched in figure 1(a). So a convection flow outside the drop forms as a consequence, which is clearly observed through PIV measurements (figure 1
b). In the region next to the tropic of capricorn of the drop and not far from the drop surface, there is weak flow, enclosed by the yellow circle in the close-up image. This indicates a subtle influence from convection on the diffusion process in this region, whereas in other regions, the refresh oil brought by the relatively strong flow prevents the formation of local supersaturation. This is the reason that accounts for the appearance of w-in-o microdroplets in a certain position with the weak flow rate.
The generation of the buoyancy-driven convection affects the distribution of the diffusion rate along the drop surface. The convection flow brushes away the diffused ethanol next to the drop surface and varies the concentration distribution of ethanol in the surrounding oil. Around the equator of the drop the concentration boundary layer is thin, due to the intense inflow of bulk oil without ethanol (figure 1
b): the normal ethanol concentration gradient outside the liquid–liquid interface
![]() $(\unicode[STIX]{x2202}_{r}c^{\text{e}})_{side}$
has a steep slope. At the top of the drop, the ethanol concentration gradient
$(\unicode[STIX]{x2202}_{r}c^{\text{e}})_{side}$
has a steep slope. At the top of the drop, the ethanol concentration gradient
![]() $(\unicode[STIX]{x2202}_{r}c^{\text{e}})_{top}$
may also increase, but only to a lower extent, as the replenishing oil is already contaminated with ethanol (and water) during its travel along the drop surface. Owing to the boundary condition, the replenishment of fresh oil caused by the convection is suppressed near the corner of the drop, where the ethanol concentration gradient
$(\unicode[STIX]{x2202}_{r}c^{\text{e}})_{top}$
may also increase, but only to a lower extent, as the replenishing oil is already contaminated with ethanol (and water) during its travel along the drop surface. Owing to the boundary condition, the replenishment of fresh oil caused by the convection is suppressed near the corner of the drop, where the ethanol concentration gradient
![]() $(\unicode[STIX]{x2202}_{r}c^{\text{e}})_{C.L.}$
is much less affected. Therefore, the buoyancy-driven convection predominantly enhances the diffusion flux near the drop equator rather than that above the drop or in the contact region and, as a consequence, the radial gradients of ethanol concentration along the drop surface obey the relationships
$(\unicode[STIX]{x2202}_{r}c^{\text{e}})_{C.L.}$
is much less affected. Therefore, the buoyancy-driven convection predominantly enhances the diffusion flux near the drop equator rather than that above the drop or in the contact region and, as a consequence, the radial gradients of ethanol concentration along the drop surface obey the relationships
8 Summary and conclusions
We have experimentally presented the rich phenomena of water–ethanol drops dissolving in oil as a host liquid, which encompasses the w-in-o emulsification outside the drop, the o-in-w emulsification inside the drop, the buoyancy-driven convection dominating outside the drop, and the prevailing solutal Marangoni convection inside the drop. The o-in-w emulsification occurs approximately half a minute later than the w-in-o emulsification, and the w-in-o emulsification does not occur when reducing the initial ethanol concentration of the drop.
A quantitative understanding and the predictions of the diffusion-induced emulsification were theoretically achieved by developing a one-dimensional multiphase and multicomponent diffusion model, which incorporates thermodynamic equilibrium theory and diffusion path theory. The prediction of the model agrees with experimental observations: the diffusion-triggered w-in-o emulsification occurs when the drops have an ethanol content higher than 51.98 vol%; the o-in-w emulsification cannot be induced by pure diffusion. Owing to the infinite domain and the Dirichlet boundary conditions used in the model, the model is only applicable for the early stage of the multiphase diffusion process. In practice, the continuous reduction of ethanol and increasing of oil in the drop lead to the occurrence of o-in-w emulsification in a long time, which is thereby independent of the initial ethanol content of the drop.
A scale analysis and the experimental investigation of the diffusion-induced flow motion were performed to gain insight into its influence on the emulsification process. By the scale analysis, we demonstrated that, in the drop domain, the solute Marangoni flow prevails over the buoyancy-driven flow, while in the host liquid domain, the latter dominates. The buoyancy-driven convection enhances the ethanol diffusion rate around the equator of the drop, which gives rise to a reduction of the local ethanol concentration around the equator of the drop, the arising of two Marangoni convection rolls inside the drop with opposite directions, and the generation of a preferred position for o-in-w emulsification. Owing to the buoyancy-driven flow, the fresh oil is replenished at the interface. Therefore, the w-in-o emulsification can only occur around a region next to the tropic of capricorn of the drop, where only a weak flow and fluid replenishment are present.
Although in this paper we provided a systematic study of emulsification triggered by the dissolution of a multicomponent drop in a host liquid, further investigations and discussions are required. A more comprehensive model can be generated, either by considering the finite domain size and the appropriate boundary conditions, or by taking fluid motion into account and developing an axisymmetric model. Experimentally, the influence of temperature, different chemical systems or different geometries by varying the contact angle of the drop are appealing open questions to explore. A better understanding of the dissolution of multiphase and multicomponent systems may provide valuable information for the investigation of multiphase systems and spontaneous emulsifications in general. We also hope that our work may provide a contribution to industrial applications, such as modern liquid–liquid microextraction techniques.
Acknowledgement
We thank Z. Lu for providing useful information that contributed to our experimental design. H.T. is grateful for financial support from the China Scholarship Council (CSC, File No. 201406890017). X. Z. acknowledges the support of the Natural Sciences and Engineering Research Council of Canada (RGPIN-2018-05129) and Future Energy Systems (Canada First Research Excellence Fund; T08-Q01). This work is part of an Industrial Partnership Programme of the Netherlands Organisation for Scientific Research (NWO), which is co-financed by Océ-Technologies B.V., University of Twente and Eindhoven University of Technology. We also acknowledge support by the ERC Advanced Grant DDD, project number 740479, and the Netherlands Center for Multiscale Catalytic Energy Conversion (MCEC) and the Max-Planck-Center Twente for Complex Fluid Dynamics.
Appendix A. Experimental details
A.1 Set-up and image analysis
The experiments were performed in a laboratory without people around during the data recording. The temperature of the host liquid in the cuvette was approximately
![]() $22\,^{\circ }\text{C}$
. The dissolution processes of the drops were observed by three synchronized cameras: (i) one monochrome charge-coupled device (CCD) camera (Ximea; MD061MU-SY) attached to a long-distance microscope system (Infinity; model K2 DistaMax) for side-view recordings, which was used for the drop profile detection; (ii) one digital single-lens reflex (SLR) camera (Nikon; D750) equipped with a complementary metal oxide semiconductor (CMOS) sensor attached to a high-magnification zoom lens system (Thorlabs; MVL12X3Z) for the other side-view recordings, which was used for the side-view observation of the emulsification process; and (iii) another digital SLR camera (Nikon; D5100) equipped with a CMOS sensor attached to an identical high-magnification zoom lens system (Thorlabs; MVL12X3Z) for top-view recordings, used for top-view observation of the emulsification process. A cold light source (Olympus; ILP-1) was positioned on the same side as the SLR camera to illuminate the emulsion.
$22\,^{\circ }\text{C}$
. The dissolution processes of the drops were observed by three synchronized cameras: (i) one monochrome charge-coupled device (CCD) camera (Ximea; MD061MU-SY) attached to a long-distance microscope system (Infinity; model K2 DistaMax) for side-view recordings, which was used for the drop profile detection; (ii) one digital single-lens reflex (SLR) camera (Nikon; D750) equipped with a complementary metal oxide semiconductor (CMOS) sensor attached to a high-magnification zoom lens system (Thorlabs; MVL12X3Z) for the other side-view recordings, which was used for the side-view observation of the emulsification process; and (iii) another digital SLR camera (Nikon; D5100) equipped with a CMOS sensor attached to an identical high-magnification zoom lens system (Thorlabs; MVL12X3Z) for top-view recordings, used for top-view observation of the emulsification process. A cold light source (Olympus; ILP-1) was positioned on the same side as the SLR camera to illuminate the emulsion.
We performed image analyses with a custom-made MATLAB program. The monochrome image series from the side-view recordings were utilized in obtaining the temporal evolution of the dissolving characteristics of the drops. For each image, we first preprocessed the data to increase the image contrast and then calculated the profile of the drop using the Canny method (Canny Reference Canny1986). The data points of the detected profile were fitted by part of a circle, i.e. assuming that the droplet is in a spherical cap shape. The diameter of the drop contact area
![]() $L$
and the contact angle
$L$
and the contact angle
![]() $\unicode[STIX]{x1D703}$
were calculated based on the geometrical relationship between the base line of the surface and the fitted spherical cap. The drop volume
$\unicode[STIX]{x1D703}$
were calculated based on the geometrical relationship between the base line of the surface and the fitted spherical cap. The drop volume
![]() $V$
was calculated by integrating the volumes of the horizontal disc layers.
$V$
was calculated by integrating the volumes of the horizontal disc layers.
A.2 Particle image velocimetry
We qualified the confidence level of the tracking particles following the flow by calculating the Stokes number and the ratio of the Stokes number to a buoyancy-corrected Froude number (Mathai et al. Reference Mathai, Calzavarini, Brons, Sun and Lohse2016). The relaxation time of the particle was estimated by
with the consideration of the added-mass force (Oliveira, van der Geld & Kuerten Reference Oliveira, van der Geld and Kuerten2015), where
![]() $\unicode[STIX]{x1D70C}_{f}=0.988~\text{g}~\text{cm}^{-3}$
and
$\unicode[STIX]{x1D70C}_{f}=0.988~\text{g}~\text{cm}^{-3}$
and
![]() $\unicode[STIX]{x1D707}_{f}=4.2~\text{mPa}~\text{s}$
are the density and the dynamic viscosity of the host liquid (trans-anethole), and
$\unicode[STIX]{x1D707}_{f}=4.2~\text{mPa}~\text{s}$
are the density and the dynamic viscosity of the host liquid (trans-anethole), and
![]() $\unicode[STIX]{x1D70C}_{p}=1.03~\text{g}~\text{cm}^{-3}$
and
$\unicode[STIX]{x1D70C}_{p}=1.03~\text{g}~\text{cm}^{-3}$
and
![]() $d_{p}=5~\unicode[STIX]{x03BC}\text{m}$
are the density and the diameter of the tracking particles. The Stokes number
$d_{p}=5~\unicode[STIX]{x03BC}\text{m}$
are the density and the diameter of the tracking particles. The Stokes number
![]() $St\equiv t_{0}u_{max}/R$
can be calculated as
$St\equiv t_{0}u_{max}/R$
can be calculated as
where
![]() $u_{max}$
is the maximum fluid velocity (
$u_{max}$
is the maximum fluid velocity (
![]() ${\sim}10~\text{mm}~\text{s}^{-1}$
) and
${\sim}10~\text{mm}~\text{s}^{-1}$
) and
![]() $R$
is the initial radius of the drop (
$R$
is the initial radius of the drop (
![]() ${\sim}0.5~\text{mm}$
). The buoyancy-corrected Froude number was defined as
${\sim}0.5~\text{mm}$
). The buoyancy-corrected Froude number was defined as
taking the particle density, through
![]() $(1-\unicode[STIX]{x1D70C}_{f}/\unicode[STIX]{x1D70C}_{p})$
, into account. With (A 2) and (A 3) we have
$(1-\unicode[STIX]{x1D70C}_{f}/\unicode[STIX]{x1D70C}_{p})$
, into account. With (A 2) and (A 3) we have
which combined with (A 2) reveals that the tracking particles exactly follow the host liquid flow surrounding the dissolving drop (Mathai et al. Reference Mathai, Calzavarini, Brons, Sun and Lohse2016).
A.3 Detecting density differences
Density differences are visible thanks to the variation in light transmission when oil is mixed with ethanol. The transmission has a negative correlation with the refractive index according to the Beer–Lambert law. The refractive index of ethanol, 1.361, is smaller than that of trans-anethole, 1.561, and accounts for a better light transmission. In our set-up, the cold light source and side-view colour camera for the emulsion observations were positioned on the same side, which indicates that the material with a better light transmission is dimming. Thus, it verifies that the solute plume is indeed an ethanol-rich oil mixture. The variation in the refractive index also causes the distortion of the light path and leads to a locally hazy scene in the top views (figure 2 a–d).
A.4 Diffusivity
The diffusivity of dilute anethole in a water–ethanol mixture was calculated based on the model of Perkins & Geankoplis (Reference Perkins and Geankoplis1969):
![]()
A.5 Measured viscosity
The viscosity of anethole (figure 10) was measured with a rheometer (Anton Paar, MCR502) at different temperatures, ranging from 18 to
![]() $24\,^{\circ }\text{C}$
.
$24\,^{\circ }\text{C}$
.
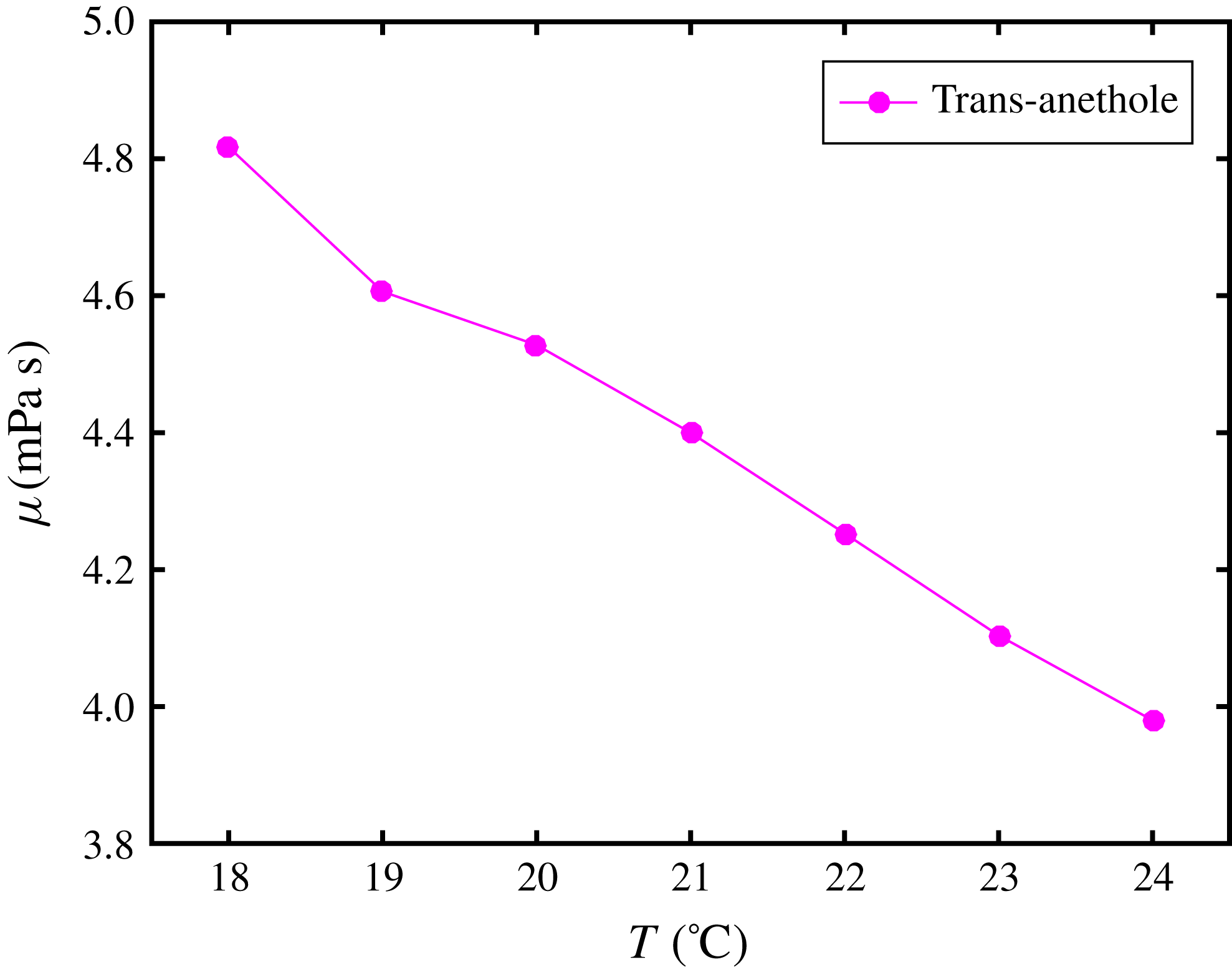
Figure 10. Dynamic viscosity of anethole as a function of temperature.
Appendix B. Calculation of the Gibbs energy and determination of the liquid–liquid equilibrium curve
For the determination of the liquid–liquid equilibrium and the possibility of phase separation, the Gibbs energy is required. Following the derivation of Zuend et al. (Reference Zuend, Marcolli, Peter and Seinfeld2010), we consider a system of a total molar amount of molecules
![]() $n^{tot}=\sum _{\unicode[STIX]{x1D6FC}}n_{\unicode[STIX]{x1D6FC}}^{tot}$
, which can potentially separate into a two-phase equilibrium configuration, consisting of a droplet with
$n^{tot}=\sum _{\unicode[STIX]{x1D6FC}}n_{\unicode[STIX]{x1D6FC}}^{tot}$
, which can potentially separate into a two-phase equilibrium configuration, consisting of a droplet with
![]() $n^{\text{d}}=\sum _{\unicode[STIX]{x1D6FC}}n_{\unicode[STIX]{x1D6FC}}^{\text{d}}$
moles and a host phase with
$n^{\text{d}}=\sum _{\unicode[STIX]{x1D6FC}}n_{\unicode[STIX]{x1D6FC}}^{\text{d}}$
moles and a host phase with
![]() $n^{\text{h}}=\sum _{\unicode[STIX]{x1D6FC}}n_{\unicode[STIX]{x1D6FC}}^{\text{h}}$
moles. The fraction of moles of component
$n^{\text{h}}=\sum _{\unicode[STIX]{x1D6FC}}n_{\unicode[STIX]{x1D6FC}}^{\text{h}}$
moles. The fraction of moles of component
![]() $\unicode[STIX]{x1D6FC}$
that are in the droplet after phase separation is defined by
$\unicode[STIX]{x1D6FC}$
that are in the droplet after phase separation is defined by
![]() $q_{\unicode[STIX]{x1D6FC}}=n_{\unicode[STIX]{x1D6FC}}^{\text{d}}/n_{\unicode[STIX]{x1D6FC}}^{tot}$
. Owing to conservation, one can identify the mole fractions
$q_{\unicode[STIX]{x1D6FC}}=n_{\unicode[STIX]{x1D6FC}}^{\text{d}}/n_{\unicode[STIX]{x1D6FC}}^{tot}$
. Owing to conservation, one can identify the mole fractions
![]() $x_{\unicode[STIX]{x1D6FC}}^{\text{d}}$
and
$x_{\unicode[STIX]{x1D6FC}}^{\text{d}}$
and
![]() $x_{\unicode[STIX]{x1D6FC}}^{\text{h}}$
in both phases via
$x_{\unicode[STIX]{x1D6FC}}^{\text{h}}$
in both phases via
 $$\begin{eqnarray}x_{\unicode[STIX]{x1D6FC}}^{\text{d}}=\frac{q_{\unicode[STIX]{x1D6FC}}x_{\unicode[STIX]{x1D6FC}}^{tot}}{\displaystyle \mathop{\sum }_{\unicode[STIX]{x1D6FD}}q_{\unicode[STIX]{x1D6FD}}x_{\unicode[STIX]{x1D6FD}}^{tot}}\quad \text{and}\quad x_{\unicode[STIX]{x1D6FC}}^{\text{h}}=\frac{(1-q_{\unicode[STIX]{x1D6FC}})x_{\unicode[STIX]{x1D6FC}}^{tot}}{\displaystyle \mathop{\sum }_{\unicode[STIX]{x1D6FD}}(1-q_{\unicode[STIX]{x1D6FD}})x_{\unicode[STIX]{x1D6FD}}^{tot}},\end{eqnarray}$$
$$\begin{eqnarray}x_{\unicode[STIX]{x1D6FC}}^{\text{d}}=\frac{q_{\unicode[STIX]{x1D6FC}}x_{\unicode[STIX]{x1D6FC}}^{tot}}{\displaystyle \mathop{\sum }_{\unicode[STIX]{x1D6FD}}q_{\unicode[STIX]{x1D6FD}}x_{\unicode[STIX]{x1D6FD}}^{tot}}\quad \text{and}\quad x_{\unicode[STIX]{x1D6FC}}^{\text{h}}=\frac{(1-q_{\unicode[STIX]{x1D6FC}})x_{\unicode[STIX]{x1D6FC}}^{tot}}{\displaystyle \mathop{\sum }_{\unicode[STIX]{x1D6FD}}(1-q_{\unicode[STIX]{x1D6FD}})x_{\unicode[STIX]{x1D6FD}}^{tot}},\end{eqnarray}$$
where
![]() $x_{\unicode[STIX]{x1D6FC}}^{tot}=n_{\unicode[STIX]{x1D6FC}}^{tot}/n^{tot}$
are the mole fractions of the entire system. The molar Gibbs energy
$x_{\unicode[STIX]{x1D6FC}}^{tot}=n_{\unicode[STIX]{x1D6FC}}^{tot}/n^{tot}$
are the mole fractions of the entire system. The molar Gibbs energy
![]() $\tilde{G}$
of the system can hence be written as
$\tilde{G}$
of the system can hence be written as
where
![]() $\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FC}}^{0}$
is the standard chemical potential of component
$\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FC}}^{0}$
is the standard chemical potential of component
![]() $\unicode[STIX]{x1D6FC}$
, i.e. the chemical potential of the pure liquid
$\unicode[STIX]{x1D6FC}$
, i.e. the chemical potential of the pure liquid
![]() $\unicode[STIX]{x1D6FC}$
, which is constant under the assumption of constant temperature and pressure. Since the absolute value of the Gibbs energy is not relevant here, the minimization of the Gibbs energy therefore requires only the consideration of the second sum in (B 2). The activity coefficients
$\unicode[STIX]{x1D6FC}$
, which is constant under the assumption of constant temperature and pressure. Since the absolute value of the Gibbs energy is not relevant here, the minimization of the Gibbs energy therefore requires only the consideration of the second sum in (B 2). The activity coefficients
![]() $\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D6FC}}^{\text{d}}$
and
$\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D6FC}}^{\text{d}}$
and
![]() $\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D6FC}}^{\text{h}}$
can be calculated by UNIFAC in the droplet phase
$\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D6FC}}^{\text{h}}$
can be calculated by UNIFAC in the droplet phase
![]() $x_{\unicode[STIX]{x1D6FC}}^{\text{d}}$
and the host phase
$x_{\unicode[STIX]{x1D6FC}}^{\text{d}}$
and the host phase
![]() $x_{\unicode[STIX]{x1D6FC}}^{\text{h}}$
, respectively.
$x_{\unicode[STIX]{x1D6FC}}^{\text{h}}$
, respectively.
For each point
![]() $x_{\unicode[STIX]{x1D6FC}}^{tot}$
in the phase diagram (figure 5
a), one can find the global minimum of
$x_{\unicode[STIX]{x1D6FC}}^{tot}$
in the phase diagram (figure 5
a), one can find the global minimum of
![]() $\tilde{G}$
with respect to the partition fractions
$\tilde{G}$
with respect to the partition fractions
![]() $q_{\unicode[STIX]{x1D6FC}}$
. To that end, the
$q_{\unicode[STIX]{x1D6FC}}$
. To that end, the
![]() $q_{\unicode[STIX]{x1D6FC}}$
-space is screened for a minimum value of
$q_{\unicode[STIX]{x1D6FC}}$
-space is screened for a minimum value of
![]() $\tilde{G}$
, followed by a gradient descent to the local minimum. If the minimum of
$\tilde{G}$
, followed by a gradient descent to the local minimum. If the minimum of
![]() $\tilde{G}$
is located at
$\tilde{G}$
is located at
![]() $q_{\unicode[STIX]{x1D6FC}}=1/2$
for all components, i.e.
$q_{\unicode[STIX]{x1D6FC}}=1/2$
for all components, i.e.
![]() $x_{\unicode[STIX]{x1D6FC}}^{\text{d}}=x_{\unicode[STIX]{x1D6FC}}^{\text{h}}$
, the configuration
$x_{\unicode[STIX]{x1D6FC}}^{\text{d}}=x_{\unicode[STIX]{x1D6FC}}^{\text{h}}$
, the configuration
![]() $x_{\unicode[STIX]{x1D6FC}}^{tot}$
is miscible, whereas otherwise phase separation is energetically favourable, where the composition of the corresponding two phases can be calculated directly via (B 1).
$x_{\unicode[STIX]{x1D6FC}}^{tot}$
is miscible, whereas otherwise phase separation is energetically favourable, where the composition of the corresponding two phases can be calculated directly via (B 1).
Appendix C. Symbol description
The symbols used in this paper are listed in table 2.
Table 2. All quantities used in the model for the ternary liquid.

Supplementary movies
Supplementary movies are available at https://doi.org/10.1017/jfm.2019.207.














