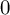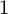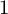1 Introduction
1.1 The results
The goal of this paper is to discuss rationality of smooth Fano threefolds over algebraically nonclosed fields of characteristic
![]() $0$
. In [Reference Kuznetsov and Prokhorov10], we considered the case of geometrically rational Fano threefolds with geometric Picard number
$0$
. In [Reference Kuznetsov and Prokhorov10], we considered the case of geometrically rational Fano threefolds with geometric Picard number
![]() $\unicode{x3c1} (X_{\bar {\mathsf {k}}}) = 1$
, and here, we switch the focus to the case of geometrically rational Fano threefolds X with Picard numbers
$\unicode{x3c1} (X_{\bar {\mathsf {k}}}) = 1$
, and here, we switch the focus to the case of geometrically rational Fano threefolds X with Picard numbers
In fact, Fano threefolds satisfying (1.1.1) have been classified in [Reference Prokhorov21], and [Reference Alzati and Bertolini1] explains which of these are geometrically rational. A combination of these results gives the following:
Theorem 1.1 [Reference Prokhorov21, Theorem 1.2], [Reference Alzati and Bertolini1]
There are exactly six families of geometrically rational Fano threefolds satisfying (1.1.1) as listed in Table 1.
The first column of Table 1 contains the name for the family we use in this paper, the next columns contain the index
![]() $\unicode{x3b9} (X_{\bar {\mathsf {k}}})$
, defined as
$\unicode{x3b9} (X_{\bar {\mathsf {k}}})$
, defined as
the geometric Picard number
![]() $\unicode{x3c1} (X_{\bar {\mathsf {k}}})$
, the anticanonical degree
$\unicode{x3c1} (X_{\bar {\mathsf {k}}})$
, the anticanonical degree
![]() $(-K_X)^3$
, the genus
$(-K_X)^3$
, the genus
![]() ${\mathrm {g}}(X)$
, defined by
${\mathrm {g}}(X)$
, defined by
and the Hodge number
![]() $\mathrm {h}^{1,2}(X_{\bar {\mathsf {k}}})$
of the threefold, while the last column provides a geometric description of these varieties over an algebraic closure
$\mathrm {h}^{1,2}(X_{\bar {\mathsf {k}}})$
of the threefold, while the last column provides a geometric description of these varieties over an algebraic closure
![]() ${\bar {\mathsf {k}}}$
of the base field.
${\bar {\mathsf {k}}}$
of the base field.
Table 1 Geometrically rational Fano threefolds X satisfying (1.1.1)

We discuss some geometric properties of threefolds from Table 1 in §2. In particular, we describe their extremal contractions over
![]() ${\bar {\mathsf {k}}}$
and identify their Hilbert schemes of lines and conics, as well as the subschemes of the Hilbert schemes of twisted cubic curves passing through a general point.
${\bar {\mathsf {k}}}$
and identify their Hilbert schemes of lines and conics, as well as the subschemes of the Hilbert schemes of twisted cubic curves passing through a general point.
However, our main interest is in rationality criteria, and the next theorem is our main result.
Theorem 1.2. Let X be a Fano threefold from Table 1; in particular, we assume
![]() $\unicode{x3c1} (X) \,{=}\, 1$
.
$\unicode{x3c1} (X) \,{=}\, 1$
.
-
(i) X is unirational if and only if
 $X({\mathsf {k}}) \ne \varnothing $
.
$X({\mathsf {k}}) \ne \varnothing $
. -
(ii) If X has type
 $\mathsf {X}_{(4,4)}$
,
$\mathsf {X}_{(4,4)}$
,
 $\mathsf {X}_{(2,2,2)}$
,
$\mathsf {X}_{(2,2,2)}$
,
 $\mathsf {X}_{(2,2)}$
or
$\mathsf {X}_{(2,2)}$
or
 $\mathsf {X}_{(1,1,1)}$
, then X is
$\mathsf {X}_{(1,1,1)}$
, then X is
 ${\mathsf {k}}$
-rational if and only if
${\mathsf {k}}$
-rational if and only if
 $X({\mathsf {k}}) \ne \varnothing $
.
$X({\mathsf {k}}) \ne \varnothing $
. -
(iii) If X has type
 $\mathsf {X}_{(3,3)}$
, then X is never
$\mathsf {X}_{(3,3)}$
, then X is never
 ${\mathsf {k}}$
-rational.
${\mathsf {k}}$
-rational.
Note that over an algebraically closed field, threefolds of types
![]() $\mathsf {X}_{(4,4)}$
,
$\mathsf {X}_{(4,4)}$
,
![]() $\mathsf {X}_{(2,2,2)}$
,
$\mathsf {X}_{(2,2,2)}$
,
![]() $\mathsf {X}_{(2,2)}$
and
$\mathsf {X}_{(2,2)}$
and
![]() $\mathsf {X}_{(1,1,1)}$
have
$\mathsf {X}_{(1,1,1)}$
have
![]() $\mathrm {h}^{1,2} = 0$
, hence, trivial intermediate Jacobians, while the intermediate Jacobians of threefolds of types
$\mathrm {h}^{1,2} = 0$
, hence, trivial intermediate Jacobians, while the intermediate Jacobians of threefolds of types
![]() $\mathsf {X}_{(3,3)}$
and
$\mathsf {X}_{(3,3)}$
and
![]() $\mathsf {X}_{(1,1,1,1)}$
over
$\mathsf {X}_{(1,1,1,1)}$
over
![]() ${\bar {\mathsf {k}}}$
are Jacobians of curves of genus
${\bar {\mathsf {k}}}$
are Jacobians of curves of genus
![]() $3$
and
$3$
and
![]() $1$
, respectively (and
$1$
, respectively (and
![]() ${\mathsf {k}}$
-forms of these over
${\mathsf {k}}$
-forms of these over
![]() ${\mathsf {k}}$
); this explains the difference in the behavior.
${\mathsf {k}}$
); this explains the difference in the behavior.
It is a classical fact that the existence of a
![]() ${\mathsf {k}}$
-point is necessary for rationality or unirationality, so the major part of the proof of the theorem consists of proving rationality or unirationality under this assumption. We use for this a case-by-case analysis (see §1.2 for a description of our approach). The theorem is, thus, a combination of the following results (we assume everywhere
${\mathsf {k}}$
-point is necessary for rationality or unirationality, so the major part of the proof of the theorem consists of proving rationality or unirationality under this assumption. We use for this a case-by-case analysis (see §1.2 for a description of our approach). The theorem is, thus, a combination of the following results (we assume everywhere
![]() $X({\mathsf {k}}) \ne \varnothing $
):
$X({\mathsf {k}}) \ne \varnothing $
):
-
• rationality for threefolds of type
 $\mathsf {X}_{(1,1,1)}$
is proved in Corollary 3.4;
$\mathsf {X}_{(1,1,1)}$
is proved in Corollary 3.4; -
• rationality for threefolds of type
 $\mathsf {X}_{(2,2)}$
is proved in Proposition 4.1;
$\mathsf {X}_{(2,2)}$
is proved in Proposition 4.1; -
• rationality for threefolds of type
 $\mathsf {X}_{(2,2,2)}$
is proved in Proposition 4.3;
$\mathsf {X}_{(2,2,2)}$
is proved in Proposition 4.3; -
• rationality for threefolds of type
 $\mathsf {X}_{(4,4)}$
is proved in Proposition 5.5;
$\mathsf {X}_{(4,4)}$
is proved in Proposition 5.5; -
• unirationality for threefolds of type
 $\mathsf {X}_{(1,1,1,1)}$
is proved in Proposition 4.5;
$\mathsf {X}_{(1,1,1,1)}$
is proved in Proposition 4.5; -
• unirationality for threefolds of type
 $\mathsf {X}_{(3,3)}$
is proved in Proposition 6.9;
$\mathsf {X}_{(3,3)}$
is proved in Proposition 6.9; -
• nonrationality for threefolds of type
 $\mathsf {X}_{(3,3)}$
is proved in Corollary 6.11.
$\mathsf {X}_{(3,3)}$
is proved in Corollary 6.11.
Theorem 1.2 provides nice criteria for rationality of five out of the six types of Fano threefolds listed in Table 1. For the remaining type
![]() $\mathsf {X}_{(1,1,1,1)}$
, we have a conjecture and a partial result.
$\mathsf {X}_{(1,1,1,1)}$
, we have a conjecture and a partial result.
Conjecture 1.3. If X has type
![]() $\mathsf {X}_{(1,1,1,1)}$
and
$\mathsf {X}_{(1,1,1,1)}$
and
![]() $\unicode{x3c1} (X) = 1$
, then X is never
$\unicode{x3c1} (X) = 1$
, then X is never
![]() ${\mathsf {k}}$
-rational.
${\mathsf {k}}$
-rational.
To explain the partial result, we need to introduce some notation. Let X be a Fano threefold of type
![]() $\mathsf {X}_{(1,1,1,1)}$
. As we show in Lemma 2.5, the action of the Galois group
$\mathsf {X}_{(1,1,1,1)}$
. As we show in Lemma 2.5, the action of the Galois group
![]() ${\mathrm {G}}({\bar {\mathsf {k}}}/{\mathsf {k}})$
on
${\mathrm {G}}({\bar {\mathsf {k}}}/{\mathsf {k}})$
on
![]() $\operatorname {Pic}(X_{\bar {\mathsf {k}}})$
factors through the group
$\operatorname {Pic}(X_{\bar {\mathsf {k}}})$
factors through the group
![]() $\mathfrak {S}_4$
that acts by permutations of the pullbacks of the point classes of the factors of the ambient
$\mathfrak {S}_4$
that acts by permutations of the pullbacks of the point classes of the factors of the ambient
![]() $(\mathbb {P}_{{\bar {\mathsf {k}}}}^1)^4$
, and the assumption
$(\mathbb {P}_{{\bar {\mathsf {k}}}}^1)^4$
, and the assumption
![]() $\unicode{x3c1} (X) = 1$
means that the subgroup
$\unicode{x3c1} (X) = 1$
means that the subgroup
is transitive, hence, belongs to the following list of (conjugacy classes) of transitive subgroups of
![]() $\mathfrak {S}_4$
:
$\mathfrak {S}_4$
:
where
![]() $\mathfrak {A}_4$
is the alternating subgroup,
$\mathfrak {A}_4$
is the alternating subgroup,
![]() $\mathrm {D}_4$
is the dihedral group of order 8 (a Sylow 2-subgroup in
$\mathrm {D}_4$
is the dihedral group of order 8 (a Sylow 2-subgroup in
![]() $\mathfrak {S}_4$
),
$\mathfrak {S}_4$
),
![]() $\mathrm {V}_4$
is the Klein group of order
$\mathrm {V}_4$
is the Klein group of order
![]() $4$
and
$4$
and
![]() $\mathrm {C}_4$
is the cyclic group of order
$\mathrm {C}_4$
is the cyclic group of order
![]() $4$
. Note that all of these groups contain
$4$
. Note that all of these groups contain
![]() $\mathrm {V}_4$
except for
$\mathrm {V}_4$
except for
![]() $\mathrm {C}_4$
.
$\mathrm {C}_4$
.
Theorem 1.4. Let
![]() ${\mathrm {G}} \subset \mathfrak {S}_4$
be a subgroup containing the Klein group
${\mathrm {G}} \subset \mathfrak {S}_4$
be a subgroup containing the Klein group
![]() $\mathrm {V}_4 \subset \mathfrak {S}_4$
. Let
$\mathrm {V}_4 \subset \mathfrak {S}_4$
. Let
![]() ${\mathsf {k}}$
be a field, such that there is an epimorphism
${\mathsf {k}}$
be a field, such that there is an epimorphism
![]() ${\mathrm {G}}({\bar {\mathsf {k}}}/{\mathsf {k}}) \twoheadrightarrow {\mathrm {G}}$
. Then for the field of rational functions
${\mathrm {G}}({\bar {\mathsf {k}}}/{\mathsf {k}}) \twoheadrightarrow {\mathrm {G}}$
. Then for the field of rational functions
![]() $K = {\mathsf {k}}(t)$
there exists a variety X over K of type
$K = {\mathsf {k}}(t)$
there exists a variety X over K of type
![]() $\mathsf {X}_{(1,1,1,1)}$
, such that
$\mathsf {X}_{(1,1,1,1)}$
, such that
![]() ${\mathrm {G}}_X = {\mathrm {G}}$
,
${\mathrm {G}}_X = {\mathrm {G}}$
,
![]() $\unicode{x3c1} (X) = 1$
and
$\unicode{x3c1} (X) = 1$
and
![]() $X(K) \ne \varnothing $
, but X is not stably rational over K.
$X(K) \ne \varnothing $
, but X is not stably rational over K.
1.2 The proofs
For (uni)rationality constructions, it is natural to use
![]() ${\mathsf {k}}$
-Sarkisov links:
${\mathsf {k}}$
-Sarkisov links:

where
![]() $\sigma $
is the blowup of a
$\sigma $
is the blowup of a
![]() ${\mathsf {k}}$
-irreducible subvariety,
${\mathsf {k}}$
-irreducible subvariety,
![]() $\phi $
and
$\phi $
and
![]() $\phi _+$
are small crepant birational contractions,
$\phi _+$
are small crepant birational contractions,
![]() $\psi $
is a flop and
$\psi $
is a flop and
![]() $\sigma _+$
is a Mori extremal contraction. Note that such a link is completely determined by the center of the blowup
$\sigma _+$
is a Mori extremal contraction. Note that such a link is completely determined by the center of the blowup
![]() $\sigma $
— the contractions and the flop are obtained by the
$\sigma $
— the contractions and the flop are obtained by the
![]() ${\mathsf {k}}$
-Minimal Model Program applied to
${\mathsf {k}}$
-Minimal Model Program applied to
![]() ${\tilde {X}}$
(note that
${\tilde {X}}$
(note that
![]() $\unicode{x3c1} ({\tilde {X}}) = 2$
, so the output of the MMP is unambiguous); in particular, the link is defined over
$\unicode{x3c1} ({\tilde {X}}) = 2$
, so the output of the MMP is unambiguous); in particular, the link is defined over
![]() ${\mathsf {k}}$
. For our purpose, it is enough to consider two types of Sarkisov links:
${\mathsf {k}}$
. For our purpose, it is enough to consider two types of Sarkisov links:
-
• Sarkisov links where
 $\sigma $
is the blowup of a
$\sigma $
is the blowup of a
 ${\mathsf {k}}$
-point;
${\mathsf {k}}$
-point; -
• Sarkisov links where
 $\sigma $
is the blowup of a reduced
$\sigma $
is the blowup of a reduced
 ${\mathsf {k}}$
-irreducible singular conic.
${\mathsf {k}}$
-irreducible singular conic.
We construct the corresponding links accurately for threefolds of type
![]() $\mathsf {X}_{(4,4)}$
in §5 (see Theorem 5.1) by using standard MMP arguments. Of course, a similar construction could be given for other types of Fano threefolds from Table 1, but to make the argument less tedious, we use the fact that all others among these threefolds are
$\mathsf {X}_{(4,4)}$
in §5 (see Theorem 5.1) by using standard MMP arguments. Of course, a similar construction could be given for other types of Fano threefolds from Table 1, but to make the argument less tedious, we use the fact that all others among these threefolds are
![]() ${\mathsf {k}}$
-forms of complete intersections in products of projective spaces and deduce the required (uni)rationality constructions from an appropriate birational transformation for a product of projective spaces.
${\mathsf {k}}$
-forms of complete intersections in products of projective spaces and deduce the required (uni)rationality constructions from an appropriate birational transformation for a product of projective spaces.
With this goal in mind, we construct in §3 a toric birational transformation between the product
![]() $(\mathbb {P}^n)^r$
of projective spaces and a
$(\mathbb {P}^n)^r$
of projective spaces and a
![]() $\mathbb {P}^r$
-bundle over the product
$\mathbb {P}^r$
-bundle over the product
![]() $(\mathbb {P}^{n-1})^r$
of smaller projective spaces, see Theorem 3.1 (in fact, we construct a birational transformation in a slightly more general situation, but the setup described above is the only one that we need for applications in the paper). This theorem has a consequence of independent interest, Corollary 3.3, saying that a
$(\mathbb {P}^{n-1})^r$
of smaller projective spaces, see Theorem 3.1 (in fact, we construct a birational transformation in a slightly more general situation, but the setup described above is the only one that we need for applications in the paper). This theorem has a consequence of independent interest, Corollary 3.3, saying that a
![]() ${\mathsf {k}}$
-form of a product of projective spaces is
${\mathsf {k}}$
-form of a product of projective spaces is
![]() ${\mathsf {k}}$
-rational if and only if it has a
${\mathsf {k}}$
-rational if and only if it has a
![]() ${\mathsf {k}}$
-point. This corollary immediately gives the required rationality construction for Fano threefolds of type
${\mathsf {k}}$
-point. This corollary immediately gives the required rationality construction for Fano threefolds of type
![]() $\mathsf {X}_{(1,1,1)}$
(Corollary 3.4) and with a bit of more work provides rationality constructions for threefolds of types
$\mathsf {X}_{(1,1,1)}$
(Corollary 3.4) and with a bit of more work provides rationality constructions for threefolds of types
![]() $\mathsf {X}_{(2,2)}$
(Proposition 4.1) and
$\mathsf {X}_{(2,2)}$
(Proposition 4.1) and
![]() $\mathsf {X}_{(2,2,2)}$
(Proposition 4.3), as well as a unirationality construction for threefolds of type
$\mathsf {X}_{(2,2,2)}$
(Proposition 4.3), as well as a unirationality construction for threefolds of type
![]() $\mathsf {X}_{(1,1,1,1)}$
(Proposition 4.5).
$\mathsf {X}_{(1,1,1,1)}$
(Proposition 4.5).
In the case of a variety X of type
![]() $\mathsf {X}_{(3,3)}$
with a
$\mathsf {X}_{(3,3)}$
with a
![]() ${\mathsf {k}}$
-point x, we again use the toric transformation of Theorem 3.1 to construct a birational equivalence of X with a divisor
${\mathsf {k}}$
-point x, we again use the toric transformation of Theorem 3.1 to construct a birational equivalence of X with a divisor
![]() $X^+$
of bidegree
$X^+$
of bidegree
![]() $(2,2)$
in a
$(2,2)$
in a
![]() ${\mathsf {k}}$
-form of
${\mathsf {k}}$
-form of
![]() $\mathbb {P}^2 \times \mathbb {P}^2$
. If x lies on a
$\mathbb {P}^2 \times \mathbb {P}^2$
. If x lies on a
![]() ${\bar {\mathsf {k}}}$
-line in X, we check that
${\bar {\mathsf {k}}}$
-line in X, we check that
![]() $X^+$
contains a
$X^+$
contains a
![]() ${\mathsf {k}}$
-form of the quadric surface
${\mathsf {k}}$
-form of the quadric surface
![]() $\mathbb {P}^1 \times \mathbb {P}^1$
and use this to deduce unirationality of X (Proposition 6.9). If x does not lie on a line, we check in Proposition 6.6 that
$\mathbb {P}^1 \times \mathbb {P}^1$
and use this to deduce unirationality of X (Proposition 6.9). If x does not lie on a line, we check in Proposition 6.6 that
![]() $X^+$
described above is, in fact, the midpoint of a Sarkisov link that ends with a conic bundle over
$X^+$
described above is, in fact, the midpoint of a Sarkisov link that ends with a conic bundle over
![]() $\mathbb {P}^2$
, which has a smooth quartic curve
$\mathbb {P}^2$
, which has a smooth quartic curve
![]() $\Gamma \subset \mathbb {P}^2$
as discriminant. We also check that the discriminant double covering
$\Gamma \subset \mathbb {P}^2$
as discriminant. We also check that the discriminant double covering
![]() $\tilde \Gamma \to \Gamma $
associated to this conic bundle is trivial over a quadratic extension
$\tilde \Gamma \to \Gamma $
associated to this conic bundle is trivial over a quadratic extension
![]() ${\mathsf {k}}'$
of the base field
${\mathsf {k}}'$
of the base field
![]() ${\mathsf {k}}$
but nontrivial over
${\mathsf {k}}$
but nontrivial over
![]() ${\mathsf {k}}$
, and that the conic bundle has a rational section over
${\mathsf {k}}$
, and that the conic bundle has a rational section over
![]() ${\mathsf {k}}'$
. We check in Theorem 6.10 that these geometric properties characterise the nonrational conic bundles constructed by Benoist and Wittenberg in [Reference Benoist and Wittenberg3] and deduce in Corollary 6.11 nonrationality of X from [Reference Benoist and Wittenberg3, Proposition 3.4].
${\mathsf {k}}'$
. We check in Theorem 6.10 that these geometric properties characterise the nonrational conic bundles constructed by Benoist and Wittenberg in [Reference Benoist and Wittenberg3] and deduce in Corollary 6.11 nonrationality of X from [Reference Benoist and Wittenberg3, Proposition 3.4].
In the last part of the paper, §7, we discuss Fano threefolds of type
![]() $\mathsf {X}_{(1,1,1,1)}$
. To prove Theorem 1.4, we use a degeneration technique. Namely, we construct a family of Fano threefolds of type
$\mathsf {X}_{(1,1,1,1)}$
. To prove Theorem 1.4, we use a degeneration technique. Namely, we construct a family of Fano threefolds of type
![]() $\mathsf {X}_{(1,1,1,1)}$
over
$\mathsf {X}_{(1,1,1,1)}$
over
![]() $\mathbb {P}^1_{\mathsf {k}}$
with the special fibre a singular toric threefold (with ordinary double points), which is well known not to be stably rational. Since stable rationality is specialisation-closed by a result of Nicaise and Shinder [Reference Nicaise and Shinder19], we conclude that the general fibre of the constructed family is also not stably rational.
$\mathbb {P}^1_{\mathsf {k}}$
with the special fibre a singular toric threefold (with ordinary double points), which is well known not to be stably rational. Since stable rationality is specialisation-closed by a result of Nicaise and Shinder [Reference Nicaise and Shinder19], we conclude that the general fibre of the constructed family is also not stably rational.
2 Extremal contractions and Hilbert schemes of curves
In this section, we describe the geometry of Fano threefolds of index
![]() $1$
from Table 1. In particular, we describe their extremal contractions over
$1$
from Table 1. In particular, we describe their extremal contractions over
![]() ${\bar {\mathsf {k}}}$
, as well as their Hilbert schemes of lines and conics and of twisted cubic curves passing through a fixed point.
${\bar {\mathsf {k}}}$
, as well as their Hilbert schemes of lines and conics and of twisted cubic curves passing through a fixed point.
To start with, recall that for most Fano threefolds, the anticanonical linear system is very ample and the anticanonical image is an intersection of quadrics; in fact, Fano threefolds which do not enjoy these nice properties (hyperelliptic and trigonal ones) have been classified and listed in [Reference Iskovskikh6]. It is easy to check that Fano threefolds from Table 1 are not in this list; therefore, we obtain:
Theorem 2.1 [Reference Iskovskikh6, Chapter 2, Theorems 2.2 and 3.4]
Let X be a Fano threefold from Table 1. The anticanonical class
![]() $-K_X$
is very ample and the anticanonical image
$-K_X$
is very ample and the anticanonical image
is an intersection of quadrics (as a scheme), where
![]() $g ={\mathrm {g}}(X)$
.
$g ={\mathrm {g}}(X)$
.
2.1 Contractions over
 ${\bar {\mathsf {k}}}$
${\bar {\mathsf {k}}}$
Assume X is a Fano threefold of index
![]() $1$
from Table 1, that is, a threefold of either of types
$1$
from Table 1, that is, a threefold of either of types
![]() $\mathsf {X}_{(2,2,2)}$
,
$\mathsf {X}_{(2,2,2)}$
,
![]() $\mathsf {X}_{(4,4)}$
,
$\mathsf {X}_{(4,4)}$
,
![]() $\mathsf {X}_{(3,3)}$
or
$\mathsf {X}_{(3,3)}$
or
![]() $\mathsf {X}_{(1,1,1,1)}$
. Then there is an embedding
$\mathsf {X}_{(1,1,1,1)}$
. Then there is an embedding
(we will see in Lemma 2.5 that
![]() $r = \unicode{x3c1} (X_{\bar {\mathsf {k}}})$
, hence, the notation), where
$r = \unicode{x3c1} (X_{\bar {\mathsf {k}}})$
, hence, the notation), where
Indeed, for types
![]() $\mathsf {X}_{(2,2,2)}$
,
$\mathsf {X}_{(2,2,2)}$
,
![]() $\mathsf {X}_{(3,3)}$
,
$\mathsf {X}_{(3,3)}$
,
![]() $\mathsf {X}_{(1,1,1,1)}$
, this holds by definition, and for type
$\mathsf {X}_{(1,1,1,1)}$
, this holds by definition, and for type
![]() $\mathsf {X}_{(4,4)}$
, this follows from the following:
$\mathsf {X}_{(4,4)}$
, this follows from the following:
Lemma 2.2. Let
![]() $\Gamma _1 \subset Q_1 \subset \mathbb {P}^4$
be a linearly normal smooth rational quartic curve in a smooth quadric threefold. If
$\Gamma _1 \subset Q_1 \subset \mathbb {P}^4$
be a linearly normal smooth rational quartic curve in a smooth quadric threefold. If
![]() $H_1$
is the hyperplane class of
$H_1$
is the hyperplane class of
![]() $Q_1$
, then the linear system
$Q_1$
, then the linear system
![]() $|2H_1 - \Gamma _1|$
of quadrics through
$|2H_1 - \Gamma _1|$
of quadrics through
![]() $\Gamma _1$
defines a birational morphism
$\Gamma _1$
defines a birational morphism
![]() $\pi _2 \colon \operatorname {{\mathrm {Bl}}}_{\Gamma _1}Q_1 \to Q_2 \subset \mathbb {P}^4$
onto another smooth quadric threefold
$\pi _2 \colon \operatorname {{\mathrm {Bl}}}_{\Gamma _1}Q_1 \to Q_2 \subset \mathbb {P}^4$
onto another smooth quadric threefold
![]() $Q_2$
, and this morphism is itself the blowup of a linearly normal smooth rational quartic curve
$Q_2$
, and this morphism is itself the blowup of a linearly normal smooth rational quartic curve
![]() $\Gamma _2 \subset Q_2$
, so that
$\Gamma _2 \subset Q_2$
, so that
Moreover, if X is a Fano threefold of type
![]() $\mathsf {X}_{(4,4)}$
, there is a natural embedding
$\mathsf {X}_{(4,4)}$
, there is a natural embedding
such that
![]() $-K_{X_{\bar {\mathsf {k}}}}$
is the sum of the pullbacks of the hyperplane classes of the factors.
$-K_{X_{\bar {\mathsf {k}}}}$
is the sum of the pullbacks of the hyperplane classes of the factors.
Proof. The curve
![]() $\Gamma _1$
is an intersection of six quadrics in
$\Gamma _1$
is an intersection of six quadrics in
![]() $\mathbb {P}^4$
; therefore, it is an intersection of five quadrics in
$\mathbb {P}^4$
; therefore, it is an intersection of five quadrics in
![]() $Q_1$
. Hence, if
$Q_1$
. Hence, if
![]() $E_1$
is the exceptional divisor of the blowup
$E_1$
is the exceptional divisor of the blowup
![]() $\pi _1 \colon X_{{\bar {\mathsf {k}}}} \to Q_1$
and
$\pi _1 \colon X_{{\bar {\mathsf {k}}}} \to Q_1$
and
![]() $H_1$
is the pullback of the hyperplane class of
$H_1$
is the pullback of the hyperplane class of
![]() $Q_1$
, the linear system
$Q_1$
, the linear system
![]() $|2H_1-E_1|$
on
$|2H_1-E_1|$
on
![]() $X_{\bar {\mathsf {k}}}$
is four-dimensional and base-point free. Therefore, this linear system defines a morphism
$X_{\bar {\mathsf {k}}}$
is four-dimensional and base-point free. Therefore, this linear system defines a morphism
![]() $\pi _2 \colon \operatorname {{\mathrm {Bl}}}_{\Gamma _1}(Q_1)\to \mathbb {P}^4$
; moreover, standard intersection theory gives
$\pi _2 \colon \operatorname {{\mathrm {Bl}}}_{\Gamma _1}(Q_1)\to \mathbb {P}^4$
; moreover, standard intersection theory gives
![]() $(2H_1 - E_1)^3 = 2$
. Hence, the image of
$(2H_1 - E_1)^3 = 2$
. Hence, the image of
![]() $\pi _2$
(which is not contained in a hyperplane by definition) is a quadric
$\pi _2$
(which is not contained in a hyperplane by definition) is a quadric
![]() $Q_2 \subset \mathbb {P}^4$
and
$Q_2 \subset \mathbb {P}^4$
and
![]() $\pi _2$
is birational. Since
$\pi _2$
is birational. Since
![]() $-K_{X_{\bar {\mathsf {k}}}}$
is ample on the fibres of
$-K_{X_{\bar {\mathsf {k}}}}$
is ample on the fibres of
![]() $\pi _2$
and
$\pi _2$
and
![]() $\unicode{x3c1} (X_{\bar {\mathsf {k}}}) = 2$
, we see that
$\unicode{x3c1} (X_{\bar {\mathsf {k}}}) = 2$
, we see that
![]() $\pi _2$
is an extremal Mori contraction. By [Reference Mori16], the quadric
$\pi _2$
is an extremal Mori contraction. By [Reference Mori16], the quadric
![]() $Q_2$
is smooth and
$Q_2$
is smooth and
![]() $\pi _2$
is the blowup of a curve, which must be a linearly normal smooth rational quartic curve. For the last statement, just note that
$\pi _2$
is the blowup of a curve, which must be a linearly normal smooth rational quartic curve. For the last statement, just note that
![]() $H_1 + (2H_1 - E_1) = 3H_1 - E_1$
is the anticanonical class of
$H_1 + (2H_1 - E_1) = 3H_1 - E_1$
is the anticanonical class of
![]() $X_{\bar {\mathsf {k}}}$
.
$X_{\bar {\mathsf {k}}}$
.
We denote by
![]() $H_i$
,
$H_i$
,
![]() $1 \le i \le r$
, the pullbacks to
$1 \le i \le r$
, the pullbacks to
![]() $Y = (\mathbb {P}^n)^r$
of the hyperplane classes of the factors and, abusing the notation, also their restrictions to
$Y = (\mathbb {P}^n)^r$
of the hyperplane classes of the factors and, abusing the notation, also their restrictions to
![]() $X_{\bar {\mathsf {k}}}$
via the embedding (2.1.1).
$X_{\bar {\mathsf {k}}}$
via the embedding (2.1.1).
Lemma 2.3. If X is a threefold of either of types
![]() $\mathsf {X}_{(2,2,2)}$
,
$\mathsf {X}_{(2,2,2)}$
,
![]() $\mathsf {X}_{(4,4)}$
,
$\mathsf {X}_{(4,4)}$
,
![]() $\mathsf {X}_{(3,3)}$
or
$\mathsf {X}_{(3,3)}$
or
![]() $\mathsf {X}_{(1,1,1,1)}$
, then the Picard group
$\mathsf {X}_{(1,1,1,1)}$
, then the Picard group
![]() $\operatorname {Pic}(X_{\bar {\mathsf {k}}})$
is freely generated by the classes
$\operatorname {Pic}(X_{\bar {\mathsf {k}}})$
is freely generated by the classes
![]() $H_i$
$H_i$
 $$ \begin{align*} \operatorname{Pic}(X_{\bar{\mathsf{k}}}) = \bigoplus_{i=1}^r \mathbb{Z} H_i. \end{align*} $$
$$ \begin{align*} \operatorname{Pic}(X_{\bar{\mathsf{k}}}) = \bigoplus_{i=1}^r \mathbb{Z} H_i. \end{align*} $$
Moreover,
Proof. For type
![]() $\mathsf {X}_{(4,4)}$
, this follows from Lemma 2.2, and for the other types, the first statement follows from the Lefschetz hyperplane theorem and the second from adjunction and the description of Table 1.
$\mathsf {X}_{(4,4)}$
, this follows from Lemma 2.2, and for the other types, the first statement follows from the Lefschetz hyperplane theorem and the second from adjunction and the description of Table 1.
For each subset
![]() $I \subset \{1,\dots ,r\}$
we consider the projection
$I \subset \{1,\dots ,r\}$
we consider the projection
Especially useful are the morphisms
![]() $\pi _I$
for I of cardinality
$\pi _I$
for I of cardinality
![]() $r - 1$
, so we introduce the notation
$r - 1$
, so we introduce the notation
and write
for the corresponding morphisms. Note that in the case
![]() $r = 2$
, we have
$r = 2$
, we have
![]() ${\widehat {\imath }} = \{ 3 - i \}$
, so these morphisms are the same as morphisms
${\widehat {\imath }} = \{ 3 - i \}$
, so these morphisms are the same as morphisms
![]() $\pi _{3-i}$
. The next lemma describes
$\pi _{3-i}$
. The next lemma describes
![]() $X_{\bar {\mathsf {k}}}$
in terms of the
$X_{\bar {\mathsf {k}}}$
in terms of the
![]() $\pi _{\widehat {\imath }}$
.
$\pi _{\widehat {\imath }}$
.
Lemma 2.4. The morphism
![]() $\pi _{\widehat {\imath }}$
is birational onto its image, and the exceptional divisor
$\pi _{\widehat {\imath }}$
is birational onto its image, and the exceptional divisor
![]() $E_{\widehat {\imath }}$
of
$E_{\widehat {\imath }}$
of
![]() $\pi _{\widehat {\imath }}$
is irreducible. More precisely, the morphism
$\pi _{\widehat {\imath }}$
is irreducible. More precisely, the morphism
![]() $\pi _{\widehat {\imath }}$
identifies
$\pi _{\widehat {\imath }}$
identifies
![]() $X_{\bar {\mathsf {k}}}$
as follows:
$X_{\bar {\mathsf {k}}}$
as follows:
-
(i) if X has type
 $\mathsf {X}_{(2,2,2)}$
, the map
$\mathsf {X}_{(2,2,2)}$
, the map
 $\pi _{\widehat {\imath }}$
is the blowup of a smooth divisor
$\pi _{\widehat {\imath }}$
is the blowup of a smooth divisor
 $W_{\widehat {\imath }} \subset \mathbb {P}^2 \times \mathbb {P}^2$
of bidegree
$W_{\widehat {\imath }} \subset \mathbb {P}^2 \times \mathbb {P}^2$
of bidegree
 $(1,1)$
along a smooth rational curve
$(1,1)$
along a smooth rational curve
 $\Gamma _{\widehat {\imath }} \subset W_{\widehat {\imath }}$
of bidegree
$\Gamma _{\widehat {\imath }} \subset W_{\widehat {\imath }}$
of bidegree
 $(2,2)$
, whose projections to the factors
$(2,2)$
, whose projections to the factors
 $\mathbb {P}^2$
are closed embeddings; the divisor class
$\mathbb {P}^2$
are closed embeddings; the divisor class
 $H_i$
is equal to
$H_i$
is equal to
 $\sum _{j\ne i}H_j - E_{\widehat {\imath }}$
;
$\sum _{j\ne i}H_j - E_{\widehat {\imath }}$
; -
(ii) if X has type
 $\mathsf {X}_{(4,4)}$
, the map
$\mathsf {X}_{(4,4)}$
, the map
 $\pi _i$
is the blowup of a three-dimensional quadric
$\pi _i$
is the blowup of a three-dimensional quadric
 $Q_{i}$
along a smooth linearly normal rational curve
$Q_{i}$
along a smooth linearly normal rational curve
 $\Gamma _{i} \subset Q_{i}$
of degree
$\Gamma _{i} \subset Q_{i}$
of degree
 $4$
; the divisor class
$4$
; the divisor class
 $H_{{\widehat {\imath }}}$
is equal to
$H_{{\widehat {\imath }}}$
is equal to
 $2H_{i} - E_i$
;
$2H_{i} - E_i$
; -
(iii) if X has type
 $\mathsf {X}_{(3,3)}$
, the map
$\mathsf {X}_{(3,3)}$
, the map
 $\pi _i$
is the blowup of
$\pi _i$
is the blowup of
 $\mathbb {P}^3$
along a smooth curve
$\mathbb {P}^3$
along a smooth curve
 $\Gamma _{i} \subset \mathbb {P}^3$
of genus
$\Gamma _{i} \subset \mathbb {P}^3$
of genus
 $3$
and degree
$3$
and degree
 $6$
; the divisor class
$6$
; the divisor class
 $H_{{\widehat {\imath }}}$
is equal to
$H_{{\widehat {\imath }}}$
is equal to
 $3H_{i} - E_i$
;
$3H_{i} - E_i$
; -
(iv) if X has type
 $\mathsf {X}_{(1,1,1,1)}$
, the map
$\mathsf {X}_{(1,1,1,1)}$
, the map
 $\pi _{\widehat {\imath }}$
is the blowup of
$\pi _{\widehat {\imath }}$
is the blowup of
 $\mathbb {P}^1 \times \mathbb {P}^1 \times \mathbb {P}^1$
along a smooth elliptic curve
$\mathbb {P}^1 \times \mathbb {P}^1 \times \mathbb {P}^1$
along a smooth elliptic curve
 $\Gamma _{\widehat {\imath }} \subset (\mathbb {P}^1)^3$
of multidegree
$\Gamma _{\widehat {\imath }} \subset (\mathbb {P}^1)^3$
of multidegree
 $(2,2,2)$
; the divisor class
$(2,2,2)$
; the divisor class
 $H_i$
is equal to
$H_i$
is equal to
 $\sum _{j\ne i}H_j - E_{\widehat {\imath }}$
.
$\sum _{j\ne i}H_j - E_{\widehat {\imath }}$
.
Proof. Part (ii) is proved in Lemma 2.2. So, assume X is a variety of either of types
![]() $\mathsf {X}_{(2,2,2)}$
,
$\mathsf {X}_{(2,2,2)}$
,
![]() $\mathsf {X}_{(3,3)}$
or
$\mathsf {X}_{(3,3)}$
or
![]() $\mathsf {X}_{(1,1,1,1)}$
. Birationality of the projection
$\mathsf {X}_{(1,1,1,1)}$
. Birationality of the projection
![]() $\pi _{\widehat {\imath }}$
is clear from the descriptions of Table 1; and it also follows that all fibres of
$\pi _{\widehat {\imath }}$
is clear from the descriptions of Table 1; and it also follows that all fibres of
![]() $\pi _{\widehat {\imath }}$
are linear subspaces in
$\pi _{\widehat {\imath }}$
are linear subspaces in
![]() $\mathbb {P}^n$
and
$\mathbb {P}^n$
and
![]() $-K_{X_{\bar {\mathsf {k}}}}$
restricts to each of them as the hyperplane class by (2.1.2). Also, it is easy to see that the image of
$-K_{X_{\bar {\mathsf {k}}}}$
restricts to each of them as the hyperplane class by (2.1.2). Also, it is easy to see that the image of
![]() $\pi _{\widehat {\imath }}$
is smooth in all cases (for type
$\pi _{\widehat {\imath }}$
is smooth in all cases (for type
![]() $\mathsf {X}_{(2,2,2)}$
, if
$\mathsf {X}_{(2,2,2)}$
, if
![]() $W_{\widehat {\imath }} \subset \mathbb {P}^2 \times \mathbb {P}^2$
is singular, then its preimage in
$W_{\widehat {\imath }} \subset \mathbb {P}^2 \times \mathbb {P}^2$
is singular, then its preimage in
![]() $\mathbb {P}^2 \times \mathbb {P}^2 \times \mathbb {P}^2$
is singular along a plane, hence,
$\mathbb {P}^2 \times \mathbb {P}^2 \times \mathbb {P}^2$
is singular along a plane, hence,
![]() $X_{\bar {\mathsf {k}}}$
, which is the intersection of this preimage with two other divisors, must be singular; and for types
$X_{\bar {\mathsf {k}}}$
, which is the intersection of this preimage with two other divisors, must be singular; and for types
![]() $\mathsf {X}_{(3,3)}$
and
$\mathsf {X}_{(3,3)}$
and
![]() $\mathsf {X}_{(1,1,1,1)}$
, the image is just
$\mathsf {X}_{(1,1,1,1)}$
, the image is just
![]() $\mathbb {P}^3$
or
$\mathbb {P}^3$
or
![]() $\mathbb {P}^1 \times \mathbb {P}^1 \times \mathbb {P}^1$
, respectively).
$\mathbb {P}^1 \times \mathbb {P}^1 \times \mathbb {P}^1$
, respectively).
By Lemma 2.3, the relative Picard number of
![]() $\pi _{\widehat {\imath }}$
is
$\pi _{\widehat {\imath }}$
is
![]() $1$
and
$1$
and
![]() $-K_{X_{\bar {\mathsf {k}}}}$
is ample, hence,
$-K_{X_{\bar {\mathsf {k}}}}$
is ample, hence,
![]() $\pi _{\widehat {\imath }}$
is an extremal Mori contraction. Since both the source and target of
$\pi _{\widehat {\imath }}$
is an extremal Mori contraction. Since both the source and target of
![]() $\pi _{\widehat {\imath }}$
are smooth, it follows from [Reference Mori16] that the morphism
$\pi _{\widehat {\imath }}$
are smooth, it follows from [Reference Mori16] that the morphism
![]() $\pi _{\widehat {\imath }}$
is either the blowup of a smooth curve or the blowup of a smooth point. In the latter case, the restriction of
$\pi _{\widehat {\imath }}$
is either the blowup of a smooth curve or the blowup of a smooth point. In the latter case, the restriction of
![]() $-K_{X_{\bar {\mathsf {k}}}}$
to the nontrivial fibre
$-K_{X_{\bar {\mathsf {k}}}}$
to the nontrivial fibre
![]() $\mathbb {P}^2$
of
$\mathbb {P}^2$
of
![]() $\pi _{\widehat {\imath }}$
would be isomorphic to
$\pi _{\widehat {\imath }}$
would be isomorphic to
![]() ${\mathscr {O}}_{\mathbb {P}^2}(2)$
, contradicting to the above observation, hence,
${\mathscr {O}}_{\mathbb {P}^2}(2)$
, contradicting to the above observation, hence,
![]() $\pi _{\widehat {\imath }}$
is the blowup of a smooth curve.
$\pi _{\widehat {\imath }}$
is the blowup of a smooth curve.
The remaining assertions are easy and left to the reader (see also [Reference Mori and Mukai15]).
Lemma 2.5. The classes
![]() $H_i$
are semiample and generate the nef cone of
$H_i$
are semiample and generate the nef cone of
![]() $X_{\bar {\mathsf {k}}}$
. The Galois group
$X_{\bar {\mathsf {k}}}$
. The Galois group
![]() ${\mathrm {G}}({\bar {\mathsf {k}}}/{\mathsf {k}})$
permutes these classes in a transitive way. In other words, the natural group homomorphism
${\mathrm {G}}({\bar {\mathsf {k}}}/{\mathsf {k}})$
permutes these classes in a transitive way. In other words, the natural group homomorphism
![]() $\varpi _X \colon {\mathrm {G}}({\bar {\mathsf {k}}}/{\mathsf {k}}) \to \operatorname {{\mathrm {Aut}}}(\operatorname {Pic}(X_{\bar {\mathsf {k}}}))$
factors through the permutation subgroup
$\varpi _X \colon {\mathrm {G}}({\bar {\mathsf {k}}}/{\mathsf {k}}) \to \operatorname {{\mathrm {Aut}}}(\operatorname {Pic}(X_{\bar {\mathsf {k}}}))$
factors through the permutation subgroup
![]() $\mathfrak {S}_r \subset \operatorname {{\mathrm {Aut}}}(\operatorname {Pic}(X_{\bar {\mathsf {k}}}))$
, and its image
$\mathfrak {S}_r \subset \operatorname {{\mathrm {Aut}}}(\operatorname {Pic}(X_{\bar {\mathsf {k}}}))$
, and its image
is a transitive subgroup of
![]() $\mathfrak {S}_r$
.
$\mathfrak {S}_r$
.
Proof. The classes
![]() $H_i$
are pullbacks of ample classes on
$H_i$
are pullbacks of ample classes on
![]() $\mathbb {P}^n$
, hence, semiample, and they generate
$\mathbb {P}^n$
, hence, semiample, and they generate
![]() $\operatorname {Pic}(X_{\bar {\mathsf {k}}})$
by Lemma 2.3. If
$\operatorname {Pic}(X_{\bar {\mathsf {k}}})$
by Lemma 2.3. If
![]() $\Lambda _i$
is the class of a nontrivial fibre of
$\Lambda _i$
is the class of a nontrivial fibre of
![]() $\pi _{\widehat {\imath }}$
, we have
$\pi _{\widehat {\imath }}$
, we have
therefore,
![]() $H_j$
generate the rays of the nef cone. It follows that the Galois group permutes the
$H_j$
generate the rays of the nef cone. It follows that the Galois group permutes the
![]() $H_i$
, hence, its action on
$H_i$
, hence, its action on
![]() $\operatorname {Pic}(X_{\bar {\mathsf {k}}})$
factors through the permutation group. Transitivity of the subgroup
$\operatorname {Pic}(X_{\bar {\mathsf {k}}})$
factors through the permutation group. Transitivity of the subgroup
![]() ${\mathrm {G}}_X \subset \mathfrak {S}_r$
follows from the equality
${\mathrm {G}}_X \subset \mathfrak {S}_r$
follows from the equality
![]() $\unicode{x3c1} (X) = 1$
.
$\unicode{x3c1} (X) = 1$
.
We say that a surface
![]() $\Pi \subset X_{\bar {\mathsf {k}}}$
is an H
-plane if
$\Pi \subset X_{\bar {\mathsf {k}}}$
is an H
-plane if
![]() $\Pi \cong \mathbb {P}^2_{\bar {\mathsf {k}}}$
and
$\Pi \cong \mathbb {P}^2_{\bar {\mathsf {k}}}$
and
![]() $H\vert _{\Pi }$
is the line class.
$H\vert _{\Pi }$
is the line class.
Corollary 2.6. Fano threefolds of index
![]() $1$
from Table 1 contain no H-planes over
$1$
from Table 1 contain no H-planes over
![]() ${\bar {\mathsf {k}}}$
.
${\bar {\mathsf {k}}}$
.
Proof. If
![]() $\Pi \subset X_{\bar {\mathsf {k}}}$
is an H-plane, the restriction
$\Pi \subset X_{\bar {\mathsf {k}}}$
is an H-plane, the restriction
![]() $(H_1 + \dots + H_r)\vert _{\Pi }$
is the line class. Since all the
$(H_1 + \dots + H_r)\vert _{\Pi }$
is the line class. Since all the
![]() $H_i$
are nef, it follows that
$H_i$
are nef, it follows that
![]() $H_j\vert _{\Pi } \sim 0$
for all
$H_j\vert _{\Pi } \sim 0$
for all
![]() $j \ne i$
and some i, hence,
$j \ne i$
and some i, hence,
![]() $\Pi $
is contracted to a point by the projection
$\Pi $
is contracted to a point by the projection
![]() $\pi _{\widehat {\imath }}$
. It remains to note that the fibres of
$\pi _{\widehat {\imath }}$
. It remains to note that the fibres of
![]() $\pi _{\widehat {\imath }}$
are at most one-dimensional by Lemma 2.4.
$\pi _{\widehat {\imath }}$
are at most one-dimensional by Lemma 2.4.
2.2 Lines
By a line on X, we understand a curve (defined over
![]() ${\bar {\mathsf {k}}}$
) of anticanonical degree
${\bar {\mathsf {k}}}$
) of anticanonical degree
![]() $1$
. We denote by
$1$
. We denote by
![]() $\mathrm {F}_1(X)$
, the Hilbert scheme of lines on X. Note that
$\mathrm {F}_1(X)$
, the Hilbert scheme of lines on X. Note that
![]() $\mathrm {F}_1(X)_{\bar {\mathsf {k}}} \cong \mathrm {F}_1(X_{\bar {\mathsf {k}}})$
.
$\mathrm {F}_1(X)_{\bar {\mathsf {k}}} \cong \mathrm {F}_1(X_{\bar {\mathsf {k}}})$
.
Lemma 2.7. Let X be a Fano threefold of types
![]() $\mathsf {X}_{(2,2,2)}$
,
$\mathsf {X}_{(2,2,2)}$
,
![]() $\mathsf {X}_{(4,4)}$
,
$\mathsf {X}_{(4,4)}$
,
![]() $\mathsf {X}_{(3,3)}$
, or
$\mathsf {X}_{(3,3)}$
, or
![]() $\mathsf {X}_{(1,1,1,1)}$
. A line on X is a fibre of the exceptional divisor of one of the projections (2.1.4). In particular,
$\mathsf {X}_{(1,1,1,1)}$
. A line on X is a fibre of the exceptional divisor of one of the projections (2.1.4). In particular,
 $$ \begin{align*} \mathrm{F}_1(X_{\bar{\mathsf{k}}}) \cong \bigsqcup_{i=1}^r\ \Gamma_{\widehat{\imath}} ,\end{align*} $$
$$ \begin{align*} \mathrm{F}_1(X_{\bar{\mathsf{k}}}) \cong \bigsqcup_{i=1}^r\ \Gamma_{\widehat{\imath}} ,\end{align*} $$
where the smooth curves
![]() $\Gamma _{\widehat {\imath }}$
have been described in Lemma 2.4. The normal bundle of each line is
$\Gamma _{\widehat {\imath }}$
have been described in Lemma 2.4. The normal bundle of each line is
Finally, the action of the Galois group
![]() ${\mathrm {G}}({\bar {\mathsf {k}}}/{\mathsf {k}})$
on the set of connected components of the Hilbert scheme of lines factors through the group
${\mathrm {G}}({\bar {\mathsf {k}}}/{\mathsf {k}})$
on the set of connected components of the Hilbert scheme of lines factors through the group
![]() ${\mathrm {G}}_X$
and is transitive.
${\mathrm {G}}_X$
and is transitive.
Proof. Since the classes
![]() $H_i$
are semiample, it follows from (2.1.2) that for each
$H_i$
are semiample, it follows from (2.1.2) that for each
![]() ${\bar {\mathsf {k}}}$
-line L on X, there is a unique i, such that
${\bar {\mathsf {k}}}$
-line L on X, there is a unique i, such that
![]() $L \cdot H_i = 1$
and
$L \cdot H_i = 1$
and
![]() $L \cdot H_j = 0$
for
$L \cdot H_j = 0$
for
![]() $j \ne i$
(i.e.
$j \ne i$
(i.e.
![]() $[L] = \Lambda _i$
in the notation of Lemma 2.5). Thus, L is contracted by the projection
$[L] = \Lambda _i$
in the notation of Lemma 2.5). Thus, L is contracted by the projection
![]() $\pi _{\widehat {\imath }}$
, hence, it is equal to a fibre of the exceptional divisor of this projection. Taking into account the description of the projections
$\pi _{\widehat {\imath }}$
, hence, it is equal to a fibre of the exceptional divisor of this projection. Taking into account the description of the projections
![]() $\pi _{\widehat {\imath }}$
from Lemma 2.4, we obtain the description of
$\pi _{\widehat {\imath }}$
from Lemma 2.4, we obtain the description of
![]() $\mathrm {F}_1(X_{\bar {\mathsf {k}}})$
.
$\mathrm {F}_1(X_{\bar {\mathsf {k}}})$
.
Further, the description of the normal bundle of L follows from the exact sequence
because the first term is trivial and the last is
![]() ${\mathscr {O}}_L(-1)$
. Finally, factorisation of the Galois action on the set of connected components of
${\mathscr {O}}_L(-1)$
. Finally, factorisation of the Galois action on the set of connected components of
![]() $\mathrm {F}_1(X_{\bar {\mathsf {k}}})$
and its transitivity follow from Lemma 2.5.
$\mathrm {F}_1(X_{\bar {\mathsf {k}}})$
and its transitivity follow from Lemma 2.5.
For a
![]() ${\bar {\mathsf {k}}}$
-point
${\bar {\mathsf {k}}}$
-point
![]() $x \in X$
, we denote by
$x \in X$
, we denote by
![]() $\mathrm {F}_1(X_{\bar {\mathsf {k}}},x) \subset \mathrm {F}_1(X_{\bar {\mathsf {k}}})$
the subscheme parameterising lines passing through x. We will need the following observation.
$\mathrm {F}_1(X_{\bar {\mathsf {k}}},x) \subset \mathrm {F}_1(X_{\bar {\mathsf {k}}})$
the subscheme parameterising lines passing through x. We will need the following observation.
Lemma 2.8. Let X be a Fano threefold of types
![]() $\mathsf {X}_{(2,2,2)}$
,
$\mathsf {X}_{(2,2,2)}$
,
![]() $\mathsf {X}_{(4,4)}$
,
$\mathsf {X}_{(4,4)}$
,
![]() $\mathsf {X}_{(3,3)}$
or
$\mathsf {X}_{(3,3)}$
or
![]() $\mathsf {X}_{(1,1,1,1)}$
. If
$\mathsf {X}_{(1,1,1,1)}$
. If
![]() $x \in X({\bar {\mathsf {k}}})$
, then the scheme
$x \in X({\bar {\mathsf {k}}})$
, then the scheme
![]() $\mathrm {F}_1(X_{\bar {\mathsf {k}}},x)$
is a finite reduced scheme of length at most
$\mathrm {F}_1(X_{\bar {\mathsf {k}}},x)$
is a finite reduced scheme of length at most
![]() $r = \unicode{x3c1} (X_{\bar {\mathsf {k}}})$
. If, moreover,
$r = \unicode{x3c1} (X_{\bar {\mathsf {k}}})$
. If, moreover,
![]() $x \in X({\mathsf {k}})$
, then either
$x \in X({\mathsf {k}})$
, then either
![]() $\mathrm {F}_1(X_{\bar {\mathsf {k}}},x) = \varnothing $
or
$\mathrm {F}_1(X_{\bar {\mathsf {k}}},x) = \varnothing $
or
![]() $\mathrm {F}_1(X_{\bar {\mathsf {k}}},x)$
is a reduced scheme of length r and the Galois group
$\mathrm {F}_1(X_{\bar {\mathsf {k}}},x)$
is a reduced scheme of length r and the Galois group
![]() ${\mathrm {G}}({\bar {\mathsf {k}}}/{\mathsf {k}})$
action on
${\mathrm {G}}({\bar {\mathsf {k}}}/{\mathsf {k}})$
action on
![]() $\mathrm {F}_1(X_{\bar {\mathsf {k}}},x)$
factors through the group
$\mathrm {F}_1(X_{\bar {\mathsf {k}}},x)$
factors through the group
![]() ${\mathrm {G}}_X$
and is transitive.
${\mathrm {G}}_X$
and is transitive.
Proof. By Lemma 2.7 for each
![]() ${\bar {\mathsf {k}}}$
-point x of X, there is at most one line from each of the connected components of the Hilbert scheme
${\bar {\mathsf {k}}}$
-point x of X, there is at most one line from each of the connected components of the Hilbert scheme
![]() $\mathrm {F}_1(X_{\bar {\mathsf {k}}})$
passing through x. This proves that
$\mathrm {F}_1(X_{\bar {\mathsf {k}}})$
passing through x. This proves that
![]() $\mathrm {F}_1(X_{\bar {\mathsf {k}}},x)$
is finite and reduced and gives the bound for its length.
$\mathrm {F}_1(X_{\bar {\mathsf {k}}},x)$
is finite and reduced and gives the bound for its length.
Now, assume x is a point of X defined over
![]() ${\mathsf {k}}$
, and let L be a
${\mathsf {k}}$
, and let L be a
![]() ${\bar {\mathsf {k}}}$
-line through x. Then for any
${\bar {\mathsf {k}}}$
-line through x. Then for any
![]() $g \in {\mathrm {G}}({\bar {\mathsf {k}}}/{\mathsf {k}})$
, the line
$g \in {\mathrm {G}}({\bar {\mathsf {k}}}/{\mathsf {k}})$
, the line
![]() $g(L)$
also passes through x. Transitivity of the Galois action on the set of components of
$g(L)$
also passes through x. Transitivity of the Galois action on the set of components of
![]() $\mathrm {F}_1(X_{\bar {\mathsf {k}}})$
then implies that there is a unique line of each type through x, hence, the length of
$\mathrm {F}_1(X_{\bar {\mathsf {k}}})$
then implies that there is a unique line of each type through x, hence, the length of
![]() $\mathrm {F}_1(X_{{\bar {\mathsf {k}}}},x)$
is r and the
$\mathrm {F}_1(X_{{\bar {\mathsf {k}}}},x)$
is r and the
![]() ${\mathrm {G}}({\bar {\mathsf {k}}}/{\mathsf {k}})$
-action on
${\mathrm {G}}({\bar {\mathsf {k}}}/{\mathsf {k}})$
-action on
![]() $\mathrm {F}_1(X_{\bar {\mathsf {k}}},x)$
factors through
$\mathrm {F}_1(X_{\bar {\mathsf {k}}},x)$
factors through
![]() ${\mathrm {G}}_X$
and is transitive.
${\mathrm {G}}_X$
and is transitive.
2.3 Conics
By a conic on X, we understand a connected curve (defined over
![]() ${\bar {\mathsf {k}}}$
) of anticanonical degree
${\bar {\mathsf {k}}}$
) of anticanonical degree
![]() $2$
. We denote by
$2$
. We denote by
![]() $\mathrm {F}_2(X)$
, the Hilbert scheme of conics on X. As before note that
$\mathrm {F}_2(X)$
, the Hilbert scheme of conics on X. As before note that
![]() $\mathrm {F}_2(X)_{\bar {\mathsf {k}}} \cong \mathrm {F}_2(X_{\bar {\mathsf {k}}})$
.
$\mathrm {F}_2(X)_{\bar {\mathsf {k}}} \cong \mathrm {F}_2(X_{\bar {\mathsf {k}}})$
.
Lemma 2.9. Let X be a Fano threefold of types
![]() $\mathsf {X}_{(2,2,2)}$
,
$\mathsf {X}_{(2,2,2)}$
,
![]() $\mathsf {X}_{(4,4)}$
,
$\mathsf {X}_{(4,4)}$
,
![]() $\mathsf {X}_{(3,3)}$
or
$\mathsf {X}_{(3,3)}$
or
![]() $\mathsf {X}_{(1,1,1,1)}$
. We have the following descriptions of the Hilbert schemes of conics
$\mathsf {X}_{(1,1,1,1)}$
. We have the following descriptions of the Hilbert schemes of conics
![]() $\mathrm {F}_2(X_{{\bar {\mathsf {k}}}})$
:
$\mathrm {F}_2(X_{{\bar {\mathsf {k}}}})$
:
 $$ \begin{align*} \mathrm{F}_2((X_{(2,2,2)})_{\bar{\mathsf{k}}}) \ & \cong \ \mathbb{P}^2_{\bar{\mathsf{k}}} \sqcup \mathbb{P}^2_{\bar{\mathsf{k}}} \sqcup \mathbb{P}^2_{\bar{\mathsf{k}}},\\ \mathrm{F}_2((X_{(4,4)})_{\bar{\mathsf{k}}}) \ & \cong \ \Gamma_1 \times \Gamma_2,\\ \mathrm{F}_2((X_{(3,3)})_{\bar{\mathsf{k}}}) \ & \cong\ \operatorname{{\mathrm{Sym}}}^2\Gamma_1 \cong \operatorname{{\mathrm{Sym}}}^2\Gamma_2,\\ \mathrm{F}_2((X_{(1,1,1,1)})_{\bar{\mathsf{k}}}) \ & \cong \ \bigsqcup_6 \ (\mathbb{P}^1_{\bar{\mathsf{k}}} \times \mathbb{P}^1_{\bar{\mathsf{k}}}) , \end{align*} $$
$$ \begin{align*} \mathrm{F}_2((X_{(2,2,2)})_{\bar{\mathsf{k}}}) \ & \cong \ \mathbb{P}^2_{\bar{\mathsf{k}}} \sqcup \mathbb{P}^2_{\bar{\mathsf{k}}} \sqcup \mathbb{P}^2_{\bar{\mathsf{k}}},\\ \mathrm{F}_2((X_{(4,4)})_{\bar{\mathsf{k}}}) \ & \cong \ \Gamma_1 \times \Gamma_2,\\ \mathrm{F}_2((X_{(3,3)})_{\bar{\mathsf{k}}}) \ & \cong\ \operatorname{{\mathrm{Sym}}}^2\Gamma_1 \cong \operatorname{{\mathrm{Sym}}}^2\Gamma_2,\\ \mathrm{F}_2((X_{(1,1,1,1)})_{\bar{\mathsf{k}}}) \ & \cong \ \bigsqcup_6 \ (\mathbb{P}^1_{\bar{\mathsf{k}}} \times \mathbb{P}^1_{\bar{\mathsf{k}}}) , \end{align*} $$
where
![]() $\Gamma _i$
are the curves described in Lemma 2.4.
$\Gamma _i$
are the curves described in Lemma 2.4.
Moreover, the morphism from each component of the universal conic to
![]() $X_{\bar {\mathsf {k}}}$
is dominant.
$X_{\bar {\mathsf {k}}}$
is dominant.
Proof. First, note that no conic on X is contracted by the projections
![]() $\pi _{\widehat {\imath }}$
, since by Lemma 2.4 any reduced connected curve contracted by
$\pi _{\widehat {\imath }}$
, since by Lemma 2.4 any reduced connected curve contracted by
![]() $\pi _{\widehat {\imath }}$
is a line, and lines do not support nonreduced conics by (2.2.1) and [Reference Kuznetsov, Prokhorov and Shramov12, Remark 2.1.7]. Therefore, we deduce from (2.1.2), that for each
$\pi _{\widehat {\imath }}$
is a line, and lines do not support nonreduced conics by (2.2.1) and [Reference Kuznetsov, Prokhorov and Shramov12, Remark 2.1.7]. Therefore, we deduce from (2.1.2), that for each
![]() ${\bar {\mathsf {k}}}$
-conic
${\bar {\mathsf {k}}}$
-conic
![]() $C \subset X_{{\bar {\mathsf {k}}}}$
, there is a pair of indices
$C \subset X_{{\bar {\mathsf {k}}}}$
, there is a pair of indices
![]() $1 \le i_1 < i_2 \le r$
, such that
$1 \le i_1 < i_2 \le r$
, such that
If
![]() $r \ge 3$
, that is, if X is of type
$r \ge 3$
, that is, if X is of type
![]() $\mathsf {X}_{(2,2,2)}$
or
$\mathsf {X}_{(2,2,2)}$
or
![]() $\mathsf {X}_{(1,1,1,1)}$
, such C is contracted by one of the projections
$\mathsf {X}_{(1,1,1,1)}$
, such C is contracted by one of the projections
respectively. It is easy to see that the maps (2.3.2) are flat conic bundles, hence, C is a fibre of one of them, and, therefore,
![]() $\mathrm {F}_2(X_{\bar {\mathsf {k}}})$
is the disjoint union of
$\mathrm {F}_2(X_{\bar {\mathsf {k}}})$
is the disjoint union of
![]() $\mathbb {P}^2_{\bar {\mathsf {k}}}$
or of
$\mathbb {P}^2_{\bar {\mathsf {k}}}$
or of
![]() $\mathbb {P}^1_{\bar {\mathsf {k}}} \times \mathbb {P}^1_{\bar {\mathsf {k}}}$
, respectively.
$\mathbb {P}^1_{\bar {\mathsf {k}}} \times \mathbb {P}^1_{\bar {\mathsf {k}}}$
, respectively.
Assume X is of type
![]() $\mathsf {X}_{(4,4)}$
. Applying Corollary A.2 twice, we obtain a morphism
$\mathsf {X}_{(4,4)}$
. Applying Corollary A.2 twice, we obtain a morphism
that takes a smooth conic
![]() $C \subset X_{\bar {\mathsf {k}}}$
to the unique pair of lines
$C \subset X_{\bar {\mathsf {k}}}$
to the unique pair of lines
![]() $(L_2,L_1)$
of different types, such that
$(L_2,L_1)$
of different types, such that
![]() $C \cap L_i \ne \varnothing $
. We will show that
$C \cap L_i \ne \varnothing $
. We will show that
![]() $\varphi $
is an isomorphism.
$\varphi $
is an isomorphism.
First, note that by (2.3.1), if
![]() $C \subset X$
is a conic, then
$C \subset X$
is a conic, then
![]() $\pi _1(C) \subset Q_1$
and
$\pi _1(C) \subset Q_1$
and
![]() $\pi _2(C) \subset Q_2$
are lines, and by Lemma 2.4
(ii), they intersect the curves
$\pi _2(C) \subset Q_2$
are lines, and by Lemma 2.4
(ii), they intersect the curves
![]() $\Gamma _1$
and
$\Gamma _1$
and
![]() $\Gamma _2$
, respectively. Thus, by Corollary A.2, for
$\Gamma _2$
, respectively. Thus, by Corollary A.2, for
![]() $x_1 \in \Gamma _1$
if
$x_1 \in \Gamma _1$
if
![]() $[C] \in \varphi _1^{-1}(x_1)$
, the line
$[C] \in \varphi _1^{-1}(x_1)$
, the line
![]() $\pi _1(C) \subset Q_1$
passes through
$\pi _1(C) \subset Q_1$
passes through
![]() $x_1$
. Since any line on
$x_1$
. Since any line on
![]() $Q_1$
through
$Q_1$
through
![]() $x_1$
lies in the embedded tangent space to
$x_1$
lies in the embedded tangent space to
![]() $Q_1$
at
$Q_1$
at
![]() $x_1$
, and the intersection of this tangent space with
$x_1$
, and the intersection of this tangent space with
![]() $Q_1$
is a two-dimensional quadratic cone with vertex at
$Q_1$
is a two-dimensional quadratic cone with vertex at
![]() $x_1$
, it follows that
$x_1$
, it follows that
for any
![]() $x_1 \in \Gamma _1$
. Since
$x_1 \in \Gamma _1$
. Since
![]() $\Gamma _2 \cong \mathbb {P}^1$
also, the morphism
$\Gamma _2 \cong \mathbb {P}^1$
also, the morphism
![]() $\varphi $
is a morphism of
$\varphi $
is a morphism of
![]() $\mathbb {P}^1$
-bundles over
$\mathbb {P}^1$
-bundles over
![]() $\Gamma _1$
and, to show that it is an isomorphism, it is enough to check that it is birational.
$\Gamma _1$
and, to show that it is an isomorphism, it is enough to check that it is birational.
So, consider a general pair
![]() $(L_2,L_1)$
of lines on X of different types. It follows from (2.3.1) and Lemma 2.4
(ii) that
$(L_2,L_1)$
of lines on X of different types. It follows from (2.3.1) and Lemma 2.4
(ii) that
![]() $\bar {L}_1 := \pi _1(L_1)$
is a line on
$\bar {L}_1 := \pi _1(L_1)$
is a line on
![]() $Q_1$
bisecant to
$Q_1$
bisecant to
![]() $\Gamma _1$
,
$\Gamma _1$
,
![]() $x_1 := \pi _1(L_2)$
is a point on
$x_1 := \pi _1(L_2)$
is a point on
![]() $\Gamma _1$
and by Corollary A.2, the preimage
$\Gamma _1$
and by Corollary A.2, the preimage
![]() $\varphi ^{-1}(L_2,L_1)$
is the Hilbert scheme of lines
$\varphi ^{-1}(L_2,L_1)$
is the Hilbert scheme of lines
![]() $L \subset Q_1$
passing through
$L \subset Q_1$
passing through
![]() $x_1$
and intersecting
$x_1$
and intersecting
![]() $\bar {L}_1$
. By genericity, we may assume
$\bar {L}_1$
. By genericity, we may assume
![]() $x_1 \not \in \bar {L}_1$
(i.e. that the lines
$x_1 \not \in \bar {L}_1$
(i.e. that the lines
![]() $L_1$
and
$L_1$
and
![]() $L_2$
do not intersect). Then any line L as above is contained in the intersection of the plane spanned by
$L_2$
do not intersect). Then any line L as above is contained in the intersection of the plane spanned by
![]() $\bar {L}_1$
and
$\bar {L}_1$
and
![]() $x_1$
with
$x_1$
with
![]() $Q_1$
, which is equal to the union of the line
$Q_1$
, which is equal to the union of the line
![]() $\bar {L}_1$
with a residual line. Therefore, L must be equal to the residual line, hence, the scheme
$\bar {L}_1$
with a residual line. Therefore, L must be equal to the residual line, hence, the scheme
![]() $\varphi ^{-1}(L_2,L_1)$
consists of a single point, so
$\varphi ^{-1}(L_2,L_1)$
consists of a single point, so
![]() $\varphi $
is birational, and, hence, it is an isomorphism.
$\varphi $
is birational, and, hence, it is an isomorphism.
Since the embedded tangent space to
![]() $Q_1$
at a general point
$Q_1$
at a general point
![]() $x \in Q_1$
intersects the quartic curve
$x \in Q_1$
intersects the quartic curve
![]() $\Gamma _1$
at four points, there are four lines on
$\Gamma _1$
at four points, there are four lines on
![]() $Q_1$
through x intersecting
$Q_1$
through x intersecting
![]() $\Gamma _1$
, hence, the universal conic is dominant of degree
$\Gamma _1$
, hence, the universal conic is dominant of degree
![]() $4$
over
$4$
over
![]() $X_{\bar {\mathsf {k}}}$
.
$X_{\bar {\mathsf {k}}}$
.
Finally, assume X is of type
![]() $\mathsf {X}_{(3,3)}$
. By (2.3.1) and Lemma 2.4
(iii), the image of C with respect to the blowup
$\mathsf {X}_{(3,3)}$
. By (2.3.1) and Lemma 2.4
(iii), the image of C with respect to the blowup
![]() $\pi _i \colon X_{\bar {\mathsf {k}}} \to \mathbb {P}^3$
is a line intersecting the curve
$\pi _i \colon X_{\bar {\mathsf {k}}} \to \mathbb {P}^3$
is a line intersecting the curve
![]() $\Gamma _{i} \subset \mathbb {P}^3$
at two points. This defines a morphism
$\Gamma _{i} \subset \mathbb {P}^3$
at two points. This defines a morphism
and it is easy to see that it is an isomorphism. It is also easy to see that for a general point
![]() $x \in \mathbb {P}^3$
, there are seven lines passing through x and bisecant to
$x \in \mathbb {P}^3$
, there are seven lines passing through x and bisecant to
![]() $\Gamma _1$
; therefore, the universal conic on
$\Gamma _1$
; therefore, the universal conic on
![]() $X_{\bar {\mathsf {k}}}$
is dominant of degree
$X_{\bar {\mathsf {k}}}$
is dominant of degree
![]() $7$
over
$7$
over
![]() $X_{\bar {\mathsf {k}}}$
.
$X_{\bar {\mathsf {k}}}$
.
Remark 2.10. Let X be a threefold of type
![]() $\mathsf {X}_{(4,4)}$
. Clearly, a general line on the quadric
$\mathsf {X}_{(4,4)}$
. Clearly, a general line on the quadric
![]() $Q_1$
passing through a point
$Q_1$
passing through a point
![]() $x \in \Gamma _1$
is not bisecant to
$x \in \Gamma _1$
is not bisecant to
![]() $\Gamma _1$
, and its strict transform in X intersects the line
$\Gamma _1$
, and its strict transform in X intersects the line
![]() $L_2 = \pi _1^{-1}(x)$
transversally. This means that a general conic intersecting
$L_2 = \pi _1^{-1}(x)$
transversally. This means that a general conic intersecting
![]() $L_2$
is smooth and intersects
$L_2$
is smooth and intersects
![]() $L_2$
transversally.
$L_2$
transversally.
For a given curve
![]() $\Theta \subset X$
, we denote by
$\Theta \subset X$
, we denote by
![]() $\mathrm {F}_2(X,\Theta )$
the subscheme of the Hilbert scheme
$\mathrm {F}_2(X,\Theta )$
the subscheme of the Hilbert scheme
![]() $\mathrm {F}_2(X)$
that parameterises conics intersecting the curve
$\mathrm {F}_2(X)$
that parameterises conics intersecting the curve
![]() $\Theta $
and by
$\Theta $
and by
![]() $\mathscr {C}_2(X,\Theta ) \subset \mathrm {F}_2(X,\Theta ) \times X$
the restriction of the universal family of conics.
$\mathscr {C}_2(X,\Theta ) \subset \mathrm {F}_2(X,\Theta ) \times X$
the restriction of the universal family of conics.
Lemma 2.11. If X is of type
![]() $\mathsf {X}_{(4,4)}$
and
$\mathsf {X}_{(4,4)}$
and
![]() $\Theta $
is a singular conic, then
$\Theta $
is a singular conic, then
![]() $\mathrm {F}_2(X_{\bar {\mathsf {k}}},\Theta ) \cong \Gamma _1 \cup \Gamma _2$
is the union of the two rulings of the surface
$\mathrm {F}_2(X_{\bar {\mathsf {k}}},\Theta ) \cong \Gamma _1 \cup \Gamma _2$
is the union of the two rulings of the surface
![]() $\mathrm {F}_2(X_{\bar {\mathsf {k}}}) \cong \Gamma _1 \times \Gamma _2$
. Moreover, the natural projection
$\mathrm {F}_2(X_{\bar {\mathsf {k}}}) \cong \Gamma _1 \times \Gamma _2$
. Moreover, the natural projection
![]() $\mathscr {C}_2(X,\Theta ) \to X$
is birational onto an anticanonical divisor
$\mathscr {C}_2(X,\Theta ) \to X$
is birational onto an anticanonical divisor
![]() $R_{\Theta } \subset X$
passing through each component of the curve
$R_{\Theta } \subset X$
passing through each component of the curve
![]() $\Theta $
with multiplicity
$\Theta $
with multiplicity
![]() $3$
.
$3$
.
Proof. Let
![]() $L_1$
and
$L_1$
and
![]() $L_2$
be the irreducible components (over
$L_2$
be the irreducible components (over
![]() ${\bar {\mathsf {k}}}$
) of the conic
${\bar {\mathsf {k}}}$
) of the conic
![]() $\Theta $
. The argument of Lemma 2.9 shows that
$\Theta $
. The argument of Lemma 2.9 shows that
![]() $L_i$
are lines of two different types and
$L_i$
are lines of two different types and
Recall that by Lemma 2.7, the curves
![]() $\Gamma _1$
and
$\Gamma _1$
and
![]() $\Gamma _2$
can be identified with the two connected components of
$\Gamma _2$
can be identified with the two connected components of
![]() $\mathrm {F}_1(X_{\bar {\mathsf {k}}})$
and the isomorphism
$\mathrm {F}_1(X_{\bar {\mathsf {k}}})$
and the isomorphism
![]() $\mathrm {F}_2(X_{\bar {\mathsf {k}}}) \cong \Gamma _1 \times \Gamma _2$
of Lemma 2.9 is defined by taking a conic C to the unique pair of lines of different types intersecting C. This means that
$\mathrm {F}_2(X_{\bar {\mathsf {k}}}) \cong \Gamma _1 \times \Gamma _2$
of Lemma 2.9 is defined by taking a conic C to the unique pair of lines of different types intersecting C. This means that
thus,
![]() $\mathrm {F}_2(X_{\bar {\mathsf {k}}},\Theta )$
is the union of two rulings of the surface
$\mathrm {F}_2(X_{\bar {\mathsf {k}}},\Theta )$
is the union of two rulings of the surface
![]() $\mathrm {F}_2(X)$
and we have the equality
$\mathrm {F}_2(X)$
and we have the equality
![]() $\mathscr {C}_2(X_{\bar {\mathsf {k}}},\Theta ) = \mathscr {C}_2(X_{\bar {\mathsf {k}}},L_1) \cup \mathscr {C}_2(X_{\bar {\mathsf {k}}},L_2)$
.
$\mathscr {C}_2(X_{\bar {\mathsf {k}}},\Theta ) = \mathscr {C}_2(X_{\bar {\mathsf {k}}},L_1) \cup \mathscr {C}_2(X_{\bar {\mathsf {k}}},L_2)$
.
Furthermore, it follows from the description of Lemma 2.9 that the natural morphism
![]() $\mathscr {C}_2(X_{\bar {\mathsf {k}}},L_2) \to X_{\bar {\mathsf {k}}}$
is birational onto the hyperplane section tangent to
$\mathscr {C}_2(X_{\bar {\mathsf {k}}},L_2) \to X_{\bar {\mathsf {k}}}$
is birational onto the hyperplane section tangent to
![]() $Q_1$
at the point
$Q_1$
at the point
![]() $\pi _1(L_2)$
; it contains the line
$\pi _1(L_2)$
; it contains the line
![]() $\pi _1(L_1)$
with multiplicity
$\pi _1(L_1)$
with multiplicity
![]() $1$
and has multiplicity
$1$
and has multiplicity
![]() $2$
at the point
$2$
at the point
![]() $\pi _1(L_2)$
. Similarly, the morphism
$\pi _1(L_2)$
. Similarly, the morphism
![]() $\mathscr {C}_2(X_{\bar {\mathsf {k}}},L_1) \to X_{\bar {\mathsf {k}}}$
is birational onto the hyperplane section containing the line
$\mathscr {C}_2(X_{\bar {\mathsf {k}}},L_1) \to X_{\bar {\mathsf {k}}}$
is birational onto the hyperplane section containing the line
![]() $\pi _2(L_2)$
with multiplicity
$\pi _2(L_2)$
with multiplicity
![]() $1$
and having multiplicity
$1$
and having multiplicity
![]() $2$
at the point
$2$
at the point
![]() $\pi _2(L_1)$
. Thus, the morphism
$\pi _2(L_1)$
. Thus, the morphism
![]() $\mathscr {C}_2(X,\Theta ) \to X$
is birational onto a divisor of class
$\mathscr {C}_2(X,\Theta ) \to X$
is birational onto a divisor of class
![]() $(H_1 - L_1 - 2L_2) + (H_2 - L_2 - 2L_1) = H - 3\,\Theta $
.
$(H_1 - L_1 - 2L_2) + (H_2 - L_2 - 2L_1) = H - 3\,\Theta $
.
2.4 Twisted cubic curves
Finally, we describe the Hilbert scheme
![]() $\mathrm {F}_3(X,x)$
of subschemes of X with Hilbert polynomial
$\mathrm {F}_3(X,x)$
of subschemes of X with Hilbert polynomial
![]() $3t + 1$
with respect to H that pass through a point x; since X is an intersection of quadrics (Theorem 2.1) and contains no planes (Corollary 2.6), every such subscheme is a union of rational curves (see [Reference Kuznetsov and Prokhorov10, Lemma 2.9]), so we will use the name rational normal cubic curves for subschemes parameterised by
$3t + 1$
with respect to H that pass through a point x; since X is an intersection of quadrics (Theorem 2.1) and contains no planes (Corollary 2.6), every such subscheme is a union of rational curves (see [Reference Kuznetsov and Prokhorov10, Lemma 2.9]), so we will use the name rational normal cubic curves for subschemes parameterised by
![]() $\mathrm {F}_3(X,x)$
. We denote by
$\mathrm {F}_3(X,x)$
. We denote by
![]() $\mathscr {C}_3(X,x) \subset \mathrm {F}_3(X,x) \times X$
, the restriction of the universal family of curves. Recall the curves
$\mathscr {C}_3(X,x) \subset \mathrm {F}_3(X,x) \times X$
, the restriction of the universal family of curves. Recall the curves
![]() $\Gamma _{\widehat {\imath }}$
described in Lemma 2.4.
$\Gamma _{\widehat {\imath }}$
described in Lemma 2.4.
Lemma 2.12. Let X be a Fano threefold of types
![]() $\mathsf {X}_{(2,2,2)}$
,
$\mathsf {X}_{(2,2,2)}$
,
![]() $\mathsf {X}_{(4,4)}$
,
$\mathsf {X}_{(4,4)}$
,
![]() $\mathsf {X}_{(3,3)}$
or
$\mathsf {X}_{(3,3)}$
or
![]() $\mathsf {X}_{(1,1,1,1)}$
. If x is a
$\mathsf {X}_{(1,1,1,1)}$
. If x is a
![]() ${\mathsf {k}}$
-point on X not lying on a
${\mathsf {k}}$
-point on X not lying on a
![]() ${\bar {\mathsf {k}}}$
-line, one has the following descriptions of the schemes
${\bar {\mathsf {k}}}$
-line, one has the following descriptions of the schemes
![]() $\mathrm {F}_3(X_{\bar {\mathsf {k}}},x)$
$\mathrm {F}_3(X_{\bar {\mathsf {k}}},x)$
 $$ \begin{align*} \mathrm{F}_3((X_{(2,2,2)})_{\bar{\mathsf{k}}},x) \ &\cong \ \Gamma_{1,2} \cong \Gamma_{1,3} \cong \Gamma_{2,3},\\ \mathrm{F}_3((X_{(4,4)})_{\bar{\mathsf{k}}},x)\ &\cong \ \mathbb{P}^1_{\bar{\mathsf{k}}} \sqcup \mathbb{P}^1_{\bar{\mathsf{k}}},\\ \mathrm{F}_3((X_{(3,3)})_{\bar{\mathsf{k}}},x)\ &\cong \ \Gamma_1 \sqcup \Gamma_2,\\ \mathrm{F}_3((X_{(1,1,1,1)})_{\bar{\mathsf{k}}},x)\ &\cong \ \bigsqcup_8 \mathbb{P}^1_{\bar{\mathsf{k}}}. \end{align*} $$
$$ \begin{align*} \mathrm{F}_3((X_{(2,2,2)})_{\bar{\mathsf{k}}},x) \ &\cong \ \Gamma_{1,2} \cong \Gamma_{1,3} \cong \Gamma_{2,3},\\ \mathrm{F}_3((X_{(4,4)})_{\bar{\mathsf{k}}},x)\ &\cong \ \mathbb{P}^1_{\bar{\mathsf{k}}} \sqcup \mathbb{P}^1_{\bar{\mathsf{k}}},\\ \mathrm{F}_3((X_{(3,3)})_{\bar{\mathsf{k}}},x)\ &\cong \ \Gamma_1 \sqcup \Gamma_2,\\ \mathrm{F}_3((X_{(1,1,1,1)})_{\bar{\mathsf{k}}},x)\ &\cong \ \bigsqcup_8 \mathbb{P}^1_{\bar{\mathsf{k}}}. \end{align*} $$
Moreover, for threefolds of type
![]() $\mathsf {X}_{(4,4)}$
, the natural projection
$\mathsf {X}_{(4,4)}$
, the natural projection
![]() $\mathscr {C}_3(X,x) \to X$
is birational onto an anticanonical divisor
$\mathscr {C}_3(X,x) \to X$
is birational onto an anticanonical divisor
![]() $R_x \subset X$
passing through the point x with multiplicity
$R_x \subset X$
passing through the point x with multiplicity
![]() $4$
.
$4$
.
Proof. First, consider a threefold X of type
![]() $\mathsf {X}_{(2,2,2)}$
. If C is a rational normal cubic curve and
$\mathsf {X}_{(2,2,2)}$
. If C is a rational normal cubic curve and
![]() $H_i \cdot C = 0$
for some i, then C is contracted by one of the conic bundles (2.3.2), hence, the curve C is supported on a fibre of (2.3.2). But the conormal bundle of any such fibre is trivial, hence, it cannot support a nonreduced curve of arithmetic genus
$H_i \cdot C = 0$
for some i, then C is contracted by one of the conic bundles (2.3.2), hence, the curve C is supported on a fibre of (2.3.2). But the conormal bundle of any such fibre is trivial, hence, it cannot support a nonreduced curve of arithmetic genus
![]() $0$
and degree more than
$0$
and degree more than
![]() $2$
. This means that we have
$2$
. This means that we have
![]() $H_i \cdot C = 1$
for each i, and we conclude from this, and Lemma 2.4, that the image of C under the map
$H_i \cdot C = 1$
for each i, and we conclude from this, and Lemma 2.4, that the image of C under the map
![]() $\pi _{1,2} \colon X_{\bar {\mathsf {k}}} \to W_{1,2}$
is a rational curve of bidegree
$\pi _{1,2} \colon X_{\bar {\mathsf {k}}} \to W_{1,2}$
is a rational curve of bidegree
![]() $(1,1)$
intersecting the curve
$(1,1)$
intersecting the curve
![]() $\Gamma _{1,2}$
and passing through x. The argument analogous to that of Corollary A.2 shows that there is a morphism
$\Gamma _{1,2}$
and passing through x. The argument analogous to that of Corollary A.2 shows that there is a morphism
that takes a twisted cubic curve
![]() $C \subset X$
to the unique point
$C \subset X$
to the unique point
![]() $x_{1,2} \in \Gamma _{1,2}$
, such that
$x_{1,2} \in \Gamma _{1,2}$
, such that
![]() $C \cap \pi _{1,2}^{-1}(x_{1,2}) \ne \varnothing $
. This morphism is an isomorphism, because on
$C \cap \pi _{1,2}^{-1}(x_{1,2}) \ne \varnothing $
. This morphism is an isomorphism, because on
![]() $W_{1,2}$
, there is a unique curve of bidegree
$W_{1,2}$
, there is a unique curve of bidegree
![]() $(1,1)$
through a given pair of points (unless they lie on a fibre of either of the projections
$(1,1)$
through a given pair of points (unless they lie on a fibre of either of the projections
![]() $W_{1,2} \to \mathbb {P}^2_{\bar {\mathsf {k}}}$
, in which case, x lies on a line in X). The same argument proves isomorphisms of
$W_{1,2} \to \mathbb {P}^2_{\bar {\mathsf {k}}}$
, in which case, x lies on a line in X). The same argument proves isomorphisms of
![]() $\mathrm {F}_3(X,x)$
with the curves
$\mathrm {F}_3(X,x)$
with the curves
![]() $\Gamma _{1,3}$
and
$\Gamma _{1,3}$
and
![]() $\Gamma _{2,3}$
.
$\Gamma _{2,3}$
.
Next, consider a threefold of type
![]() $\mathsf {X}_{(4,4)}$
. If
$\mathsf {X}_{(4,4)}$
. If
![]() $H_i \cdot C = 0$
for some i, then C is contracted by
$H_i \cdot C = 0$
for some i, then C is contracted by
![]() $\pi _i$
, hence, is supported on a line. But the conormal bundle of a line is globally generated by (2.2.1), hence, a line cannot support a nonreduced curve of arithmetic genus
$\pi _i$
, hence, is supported on a line. But the conormal bundle of a line is globally generated by (2.2.1), hence, a line cannot support a nonreduced curve of arithmetic genus
![]() $0$
and degree more than
$0$
and degree more than
![]() $1$
. This means that C has bidegree
$1$
. This means that C has bidegree
![]() $(1,2)$
or
$(1,2)$
or
![]() $(2,1)$
. In the first case, the image of C under
$(2,1)$
. In the first case, the image of C under
![]() $\pi _1$
is a line on the quadric
$\pi _1$
is a line on the quadric
![]() $Q_1$
passing through x; hence, the corresponding component of
$Q_1$
passing through x; hence, the corresponding component of
![]() $\mathrm {F}_3(X,x)_{\bar {\mathsf {k}}}$
is isomorphic to
$\mathrm {F}_3(X,x)_{\bar {\mathsf {k}}}$
is isomorphic to
![]() $\mathbb {P}^1_{\bar {\mathsf {k}}}$
. It also follows that the corresponding component of
$\mathbb {P}^1_{\bar {\mathsf {k}}}$
. It also follows that the corresponding component of
![]() $\mathscr {C}_3(X,x)$
is a Hirzebruch surface that maps birationally onto the hyperplane section of
$\mathscr {C}_3(X,x)$
is a Hirzebruch surface that maps birationally onto the hyperplane section of
![]() $Q_1$
tangent at x, that is, a divisor of class
$Q_1$
tangent at x, that is, a divisor of class
![]() $H_1$
passing through x with multiplicity
$H_1$
passing through x with multiplicity
![]() $2$
. The second component is described analogously. The total divisor class of the image
$2$
. The second component is described analogously. The total divisor class of the image
![]() $R_x$
of
$R_x$
of
![]() $\mathscr {C}_3(X,x) \to X$
is
$\mathscr {C}_3(X,x) \to X$
is
![]() $H_1 + H_2 - 4x$
, that is, it is the anticanonical class passing through x with multiplicity
$H_1 + H_2 - 4x$
, that is, it is the anticanonical class passing through x with multiplicity
![]() $4$
.
$4$
.
Next, consider a threefold of type
![]() $\mathsf {X}_{(3,3)}$
. The same argument as above shows that C has bidegree
$\mathsf {X}_{(3,3)}$
. The same argument as above shows that C has bidegree
![]() $(1,2)$
or
$(1,2)$
or
![]() $(2,1)$
. In the first case, the image of C under
$(2,1)$
. In the first case, the image of C under
![]() $\pi _1$
is a line on
$\pi _1$
is a line on
![]() $\mathbb {P}^3_{\bar {\mathsf {k}}}$
passing through x and intersecting the curve
$\mathbb {P}^3_{\bar {\mathsf {k}}}$
passing through x and intersecting the curve
![]() $\Gamma _1$
. Since for any point of
$\Gamma _1$
. Since for any point of
![]() $\Gamma _1$
there is a unique line through it and x, the corresponding component of
$\Gamma _1$
there is a unique line through it and x, the corresponding component of
![]() $\mathrm {F}_3(X_{\bar {\mathsf {k}}},x)$
is isomorphic to
$\mathrm {F}_3(X_{\bar {\mathsf {k}}},x)$
is isomorphic to
![]() $\Gamma _1$
. Analogously, the second component is isomorphic to
$\Gamma _1$
. Analogously, the second component is isomorphic to
![]() $\Gamma _2$
.
$\Gamma _2$
.
Finally, consider a threefold of type
![]() $\mathsf {X}_{(1,1,1,1)}$
. Then, of course,
$\mathsf {X}_{(1,1,1,1)}$
. Then, of course,
![]() $H_i \cdot C = 0$
for some i. The argument used for threefolds of type
$H_i \cdot C = 0$
for some i. The argument used for threefolds of type
![]() $\mathsf {X}_{(2,2,2)}$
shows this cannot hold for two distinct i. So, assume this holds for
$\mathsf {X}_{(2,2,2)}$
shows this cannot hold for two distinct i. So, assume this holds for
![]() $i = 1$
. By Lemma 2.4
(iv), the image of C under the map
$i = 1$
. By Lemma 2.4
(iv), the image of C under the map
![]() $\pi _{1,2,3}$
is a curve of multidegree
$\pi _{1,2,3}$
is a curve of multidegree
![]() $(0,1,1)$
on
$(0,1,1)$
on
![]() $\mathbb {P}^1_{\bar {\mathsf {k}}} \times \mathbb {P}^1_{\bar {\mathsf {k}}} \times \mathbb {P}^1_{\bar {\mathsf {k}}}$
intersecting the curve
$\mathbb {P}^1_{\bar {\mathsf {k}}} \times \mathbb {P}^1_{\bar {\mathsf {k}}} \times \mathbb {P}^1_{\bar {\mathsf {k}}}$
intersecting the curve
![]() $\Gamma _{1,2,3}$
and passing through x. In other words, it is a curve of bidegree
$\Gamma _{1,2,3}$
and passing through x. In other words, it is a curve of bidegree
![]() $(1,1)$
on the surface
$(1,1)$
on the surface
![]() $\mathbb {P}^1_{\bar {\mathsf {k}}} \times \mathbb {P}^1_{\bar {\mathsf {k}}}$
passing through x and either of the two points of intersection of
$\mathbb {P}^1_{\bar {\mathsf {k}}} \times \mathbb {P}^1_{\bar {\mathsf {k}}}$
passing through x and either of the two points of intersection of
![]() $\Gamma _{1,2,3}$
with this surface (note that these points cannot collide because otherwise x would lie on a line in X). Therefore, there are two pencils of such curves. Using the same argument for other i, we see that altogether there are eight pencils of twisted cubic curves on X passing through x.
$\Gamma _{1,2,3}$
with this surface (note that these points cannot collide because otherwise x would lie on a line in X). Therefore, there are two pencils of such curves. Using the same argument for other i, we see that altogether there are eight pencils of twisted cubic curves on X passing through x.
Remark 2.13. Let X be a threefold of type
![]() $\mathsf {X}_{(4,4)}$
. Since a general line on
$\mathsf {X}_{(4,4)}$
. Since a general line on
![]() $Q_1$
passing through a point
$Q_1$
passing through a point
![]() $x \not \in \Gamma _1$
does not intersect
$x \not \in \Gamma _1$
does not intersect
![]() $\Gamma _1$
, it follows that a general twisted cubic curve on X passing through x is smooth.
$\Gamma _1$
, it follows that a general twisted cubic curve on X passing through x is smooth.
3 A birational transformation for a product of projective spaces
In this section, we construct a birational transformation for a product of projective spaces and deduce a consequence for the rationality of its
![]() ${\mathsf {k}}$
-forms; in particular, we prove the rationality criterion for threefolds
${\mathsf {k}}$
-forms; in particular, we prove the rationality criterion for threefolds
![]() $\mathsf {X}_{(1,1,1)}$
.
$\mathsf {X}_{(1,1,1)}$
.
3.1 Product of projective spaces
Consider the product
of projective spaces. Assume that
![]() $r = p + q$
and
$r = p + q$
and
Let
![]() $y \in Y$
be a point, and let
$y \in Y$
be a point, and let
![]() $(v_1,v_2,\dots ,v_r)$
,
$(v_1,v_2,\dots ,v_r)$
,
![]() $0 \ne v_i \in V_i$
, be the corresponding collection of vectors. Consider the blowup
$0 \ne v_i \in V_i$
, be the corresponding collection of vectors. Consider the blowup
and let
![]() $E \subset {\tilde {Y}}$
be its exceptional divisor. Let
$E \subset {\tilde {Y}}$
be its exceptional divisor. Let
![]() $\operatorname {{\mathrm {PGL}}}(V_i)_{v_i} \subset \operatorname {{\mathrm {PGL}}}(V_i)$
be the stabiliser of the point
$\operatorname {{\mathrm {PGL}}}(V_i)_{v_i} \subset \operatorname {{\mathrm {PGL}}}(V_i)$
be the stabiliser of the point
![]() $[v_i] \in \mathbb {P}(V_i)$
in the projective linear group
$[v_i] \in \mathbb {P}(V_i)$
in the projective linear group
![]() $\mathrm{PGL}(V_i)$
. The group
$\mathrm{PGL}(V_i)$
. The group
 $$ \begin{align*} G = \prod_{i=1}^r \operatorname{{\mathrm{PGL}}}(V_i)_{v_i} \end{align*} $$
$$ \begin{align*} G = \prod_{i=1}^r \operatorname{{\mathrm{PGL}}}(V_i)_{v_i} \end{align*} $$
acts naturally on
![]() ${\tilde {Y}}$
and has finitely many orbits, which can be described as follows. First, for each
${\tilde {Y}}$
and has finitely many orbits, which can be described as follows. First, for each
![]() $1 \le i \le r$
, let
$1 \le i \le r$
, let
Furthermore, for any subset
![]() $I \subsetneq \{1,\dots ,r\}$
denote
$I \subsetneq \{1,\dots ,r\}$
denote
Finally, set
 $$ \begin{align} {\tilde{Y}}_I^{\circ} := {\tilde{Y}}_I \setminus \left( E_I \cup \bigcup_{I \subsetneq J} {\tilde{Y}}_J \right) \qquad\text{and}\qquad E_I^{\circ} := E_I \setminus \left( \bigcup_{I \subsetneq J} E_J \right). \end{align} $$
$$ \begin{align} {\tilde{Y}}_I^{\circ} := {\tilde{Y}}_I \setminus \left( E_I \cup \bigcup_{I \subsetneq J} {\tilde{Y}}_J \right) \qquad\text{and}\qquad E_I^{\circ} := E_I \setminus \left( \bigcup_{I \subsetneq J} E_J \right). \end{align} $$
Then
![]() ${\tilde {Y}}_{\varnothing }^{\circ }$
is the open orbit,
${\tilde {Y}}_{\varnothing }^{\circ }$
is the open orbit,
![]() $E_{\varnothing }^{\circ }$
and
$E_{\varnothing }^{\circ }$
and
![]() ${\tilde {Y}}_i^{\circ }$
,
${\tilde {Y}}_i^{\circ }$
,
![]() $p+1 \le i \le q$
, are the orbits of codimension
$p+1 \le i \le q$
, are the orbits of codimension
![]() $1$
and all other orbits have higher codimension.
$1$
and all other orbits have higher codimension.
To describe the other side of the transformation, denote
and choose splittings
![]() $V_i = {\mathsf {k}} v_i \oplus \bar {V}_i$
. They induce a direct sum decomposition:
$V_i = {\mathsf {k}} v_i \oplus \bar {V}_i$
. They induce a direct sum decomposition:
 $$ \begin{align*} V_1 \otimes \dots \otimes V_{r} = \bigoplus_{I \subset \{1,\dots,r\}} \bar{V}_I, \qquad\text{where}\quad \bar{V}_I := \bigotimes_{i \in I} \bar{V}_i. \end{align*} $$
$$ \begin{align*} V_1 \otimes \dots \otimes V_{r} = \bigoplus_{I \subset \{1,\dots,r\}} \bar{V}_I, \qquad\text{where}\quad \bar{V}_I := \bigotimes_{i \in I} \bar{V}_i. \end{align*} $$
Note that the point y corresponds to the summand
![]() $\bar {V}_{\varnothing } = {\mathsf {k}}$
and the tangent space to Y at y corresponds to the sum of the summands
$\bar {V}_{\varnothing } = {\mathsf {k}}$
and the tangent space to Y at y corresponds to the sum of the summands
![]() $\bar {V}_I$
with
$\bar {V}_I$
with
![]() $|I| = 1$
.
$|I| = 1$
.
Note also that for
![]() $i \ge p + 1$
, one has
$i \ge p + 1$
, one has
![]() $\mathbb {P}(\bar {V}_i) \cong \operatorname {{\mathrm {Spec}}}({\mathsf {k}})$
. Let
$\mathbb {P}(\bar {V}_i) \cong \operatorname {{\mathrm {Spec}}}({\mathsf {k}})$
. Let
 $$ \begin{align*} Y^+ := \prod_{i=1}^r \mathbb{P}(\bar{V}_i) = \mathbb{P}(\bar{V}_1) \times \mathbb{P}(\bar{V}_2) \times \dots \times \mathbb{P}(\bar{V}_p) \cong \mathbb{P}^{n_1-1} \times \mathbb{P}^{n_2-1} \times \dots \times \mathbb{P}^{n_p-1}. \end{align*} $$
$$ \begin{align*} Y^+ := \prod_{i=1}^r \mathbb{P}(\bar{V}_i) = \mathbb{P}(\bar{V}_1) \times \mathbb{P}(\bar{V}_2) \times \dots \times \mathbb{P}(\bar{V}_p) \cong \mathbb{P}^{n_1-1} \times \mathbb{P}^{n_2-1} \times \dots \times \mathbb{P}^{n_p-1}. \end{align*} $$
Denote by
![]() $h_i$
the pullback to
$h_i$
the pullback to
![]() $Y^+$
of the hyperplane class of the i-th factor (note that
$Y^+$
of the hyperplane class of the i-th factor (note that
![]() $h_i = 0$
for
$h_i = 0$
for
![]() $i \ge p + 1$
because, as we noticed above,
$i \ge p + 1$
because, as we noticed above,
![]() $\mathbb {P}(\bar {V}_i)$
is just a point), and for
$\mathbb {P}(\bar {V}_i)$
is just a point), and for
![]() $I \subset \{1,\dots ,r\}$
, set
$I \subset \{1,\dots ,r\}$
, set
Consider the vector bundle
![]() ${\mathscr {E}}$
of rank
${\mathscr {E}}$
of rank
![]() $r+1$
on
$r+1$
on
![]() $Y^+$
defined by
$Y^+$
defined by
 $$ \begin{align} {\mathscr{E}} := \bigoplus_{|I| \ge r - 1} {\mathscr{O}}\left( - h_I \right). \end{align} $$
$$ \begin{align} {\mathscr{E}} := \bigoplus_{|I| \ge r - 1} {\mathscr{O}}\left( - h_I \right). \end{align} $$
Denote by
the section of (3.1.5) corresponding to the summand with
![]() $I = \{1,\dots ,i-1,i+1,\dots ,r\}$
. Set
$I = \{1,\dots ,i-1,i+1,\dots ,r\}$
. Set
and let
![]() $E_i \subset {\tilde {Y}}^+$
,
$E_i \subset {\tilde {Y}}^+$
,
![]() $p + 1 \le i \le p + q$
be the exceptional divisors. The group G acts transitively on
$p + 1 \le i \le p + q$
be the exceptional divisors. The group G acts transitively on
![]() $Y^+$
, the vector bundle
$Y^+$
, the vector bundle
![]() ${\mathscr {E}}$
is G-equivariant and its summands
${\mathscr {E}}$
is G-equivariant and its summands
![]() ${\mathscr {O}}(-h_I)$
with
${\mathscr {O}}(-h_I)$
with
![]() $|I| = r - 1$
are G-invariant. Therefore, the action of G lifts naturally to
$|I| = r - 1$
are G-invariant. Therefore, the action of G lifts naturally to
![]() ${\hat {Y}}^+$
and
${\hat {Y}}^+$
and
![]() ${\tilde {Y}}^+$
. Moreover, the action of G on
${\tilde {Y}}^+$
. Moreover, the action of G on
![]() ${\tilde {Y}}^+$
still has a finite number of orbits, which can be described as follows.
${\tilde {Y}}^+$
still has a finite number of orbits, which can be described as follows.
For a subset
![]() $J \subsetneq \{1,\dots ,r\}$
denote
$J \subsetneq \{1,\dots ,r\}$
denote
 $$ \begin{align} \bar{{\mathscr{E}}}_J = \bigoplus_{J \subset I,\ |I| = r - 1} {\mathscr{O}}\left( - h_I \right); \end{align} $$
$$ \begin{align} \bar{{\mathscr{E}}}_J = \bigoplus_{J \subset I,\ |I| = r - 1} {\mathscr{O}}\left( - h_I \right); \end{align} $$
this is a subbundle in
![]() ${\mathscr {E}}$
of corank
${\mathscr {E}}$
of corank
![]() $1 + |J|$
. Let
$1 + |J|$
. Let
![]() ${\tilde {Y}}^+_J \subset {\tilde {Y}}^+$
denote the strict transform of
${\tilde {Y}}^+_J \subset {\tilde {Y}}^+$
denote the strict transform of
![]() $\mathbb {P}_{Y^+}(\bar {{\mathscr {E}}}_J)$
. Then the G-orbits are
$\mathbb {P}_{Y^+}(\bar {{\mathscr {E}}}_J)$
. Then the G-orbits are
 $$ \begin{align*} ({\tilde{Y}}^+)^{\circ} &= {\tilde{Y}}^+ \setminus \left( {\tilde{Y}}^+_{\varnothing} \cup \bigcup_{i = p + 1}^q E_i \right), &({\tilde{Y}}^+_J)^{\circ} &= {\tilde{Y}}^+_J \setminus \left(\bigcup_{i = p + 1}^q E_i \right),\\ E_i^{\circ} &= E_i \setminus {\tilde{Y}}^+_{\varnothing}, &E_{i,J}^{\circ} &= (E_i \cap {\tilde{Y}}^+_J) \setminus \left( \bigcup_{J \subsetneq K} E_i \cap {\tilde{Y}}^+_K \right), \end{align*} $$
$$ \begin{align*} ({\tilde{Y}}^+)^{\circ} &= {\tilde{Y}}^+ \setminus \left( {\tilde{Y}}^+_{\varnothing} \cup \bigcup_{i = p + 1}^q E_i \right), &({\tilde{Y}}^+_J)^{\circ} &= {\tilde{Y}}^+_J \setminus \left(\bigcup_{i = p + 1}^q E_i \right),\\ E_i^{\circ} &= E_i \setminus {\tilde{Y}}^+_{\varnothing}, &E_{i,J}^{\circ} &= (E_i \cap {\tilde{Y}}^+_J) \setminus \left( \bigcup_{J \subsetneq K} E_i \cap {\tilde{Y}}^+_K \right), \end{align*} $$
where in the last formula, we assume
![]() $i \not \in J$
. Note that
$i \not \in J$
. Note that
![]() $({\tilde {Y}}^+)^{\circ }$
is the open orbit,
$({\tilde {Y}}^+)^{\circ }$
is the open orbit,
![]() $({\tilde {Y}}^+_{\varnothing })^{\circ }$
and
$({\tilde {Y}}^+_{\varnothing })^{\circ }$
and
![]() $E_i^{\circ }$
are the orbits of codimension
$E_i^{\circ }$
are the orbits of codimension
![]() $1$
and all other orbits have higher codimension.
$1$
and all other orbits have higher codimension.
The linear projection out of the point
![]() $[v_i]$
defines a
$[v_i]$
defines a
![]() $\operatorname {{\mathrm {PGL}}}(V_i)_{v_i}$
-equivariant rational map
$\operatorname {{\mathrm {PGL}}}(V_i)_{v_i}$
-equivariant rational map
![]() $\mathbb {P}(V_i) \dashrightarrow \mathbb {P}(\bar {V}_i)$
, which is regular if
$\mathbb {P}(V_i) \dashrightarrow \mathbb {P}(\bar {V}_i)$
, which is regular if
![]() $i \ge p + 1$
. The product of these maps is a G-equivariant rational map, which we denote by
$i \ge p + 1$
. The product of these maps is a G-equivariant rational map, which we denote by
![]() $\psi _0 \colon Y \dashrightarrow Y^+$
. It gives rise to the following birational transformation.
$\psi _0 \colon Y \dashrightarrow Y^+$
. It gives rise to the following birational transformation.
Theorem 3.1. There is a small birational G-equivariant isomorphism
![]() $\psi \colon {\tilde {Y}} \dashrightarrow {\tilde {Y}}^+$
that fits into the commutative diagram
$\psi \colon {\tilde {Y}} \dashrightarrow {\tilde {Y}}^+$
that fits into the commutative diagram

where
![]() $\hat\sigma_+ \colon \hat{Y}_+ = \mathbb{P}_{Y^+}(\mathscr{E}) \to Y^+$
and
$\hat\sigma_+ \colon \hat{Y}_+ = \mathbb{P}_{Y^+}(\mathscr{E}) \to Y^+$
and
![]() $\tilde\sigma_+ \colon \tilde{Y}_+ \to \mathrm{Bl}_{s_{p+1}(Y^+) \sqcup \dots \sqcup s_{p+q}(Y^+)}(\hat{Y}^+) \to \hat{Y}^+$
is the projection and the blowup, respectively,
$\tilde\sigma_+ \colon \tilde{Y}_+ \to \mathrm{Bl}_{s_{p+1}(Y^+) \sqcup \dots \sqcup s_{p+q}(Y^+)}(\hat{Y}^+) \to \hat{Y}^+$
is the projection and the blowup, respectively,
![]() $\sigma _+ := \hat \sigma _+ \circ \tilde \sigma _+$
and, such that
$\sigma _+ := \hat \sigma _+ \circ \tilde \sigma _+$
and, such that
![]() $\psi $
induces isomorphisms of G-orbits
$\psi $
induces isomorphisms of G-orbits
of codimension
![]() $0$
and
$0$
and
![]() $1$
. Moreover, if
$1$
. Moreover, if
-
•
 $H_i$
,
$H_i$
,
 $1 \le i \le r$
, are the hyperplane classes of
$1 \le i \le r$
, are the hyperplane classes of
 $\mathbb {P}(V_i)$
and
$\mathbb {P}(V_i)$
and
 $H = H_1 + \dots + H_r$
,
$H = H_1 + \dots + H_r$
, -
• E is the exceptional divisor of
 $\sigma $
,
$\sigma $
, -
• h is the relative hyperplane class of the projective bundle
 $\hat \sigma _+$
,
$\hat \sigma _+$
, -
•
 $h_i$
,
$h_i$
,
 $1 \le i \le p$
, are the hyperplane classes of
$1 \le i \le p$
, are the hyperplane classes of
 $\mathbb {P}(\bar {V}_i)$
and
$\mathbb {P}(\bar {V}_i)$
and -
•
 $e_i$
,
$e_i$
,
 $p+1 \le i \le p+q$
, are the exceptional divisor classes of the blowup
$p+1 \le i \le p+q$
, are the exceptional divisor classes of the blowup
 $\tilde \sigma _+$
,
$\tilde \sigma _+$
,
then in the Picard group
![]() $\operatorname {Pic}({\tilde {Y}}) = \operatorname {Pic}({\tilde {Y}}^+)$
, there are the following equalities
$\operatorname {Pic}({\tilde {Y}}) = \operatorname {Pic}({\tilde {Y}}^+)$
, there are the following equalities
 $$ \begin{align} \begin{array}{lclll} h_i &=& H_i - E,\quad && 1 \le i \le p,\\ e_i &=& H_i - E,\quad && p+1 \le i \le p+q,\\ h &=& H - (r - 1)E.\qquad&& \end{array} \end{align} $$
$$ \begin{align} \begin{array}{lclll} h_i &=& H_i - E,\quad && 1 \le i \le p,\\ e_i &=& H_i - E,\quad && p+1 \le i \le p+q,\\ h &=& H - (r - 1)E.\qquad&& \end{array} \end{align} $$
Conversely, one has
 $$ \begin{align} E = h - \sum_{i=1}^p h_i - \sum_{j=p+1}^{p+q} e_j, \qquad H_i = \begin{cases} h_i + E, & \text{for } 1 \le i \le p,\\ e_i + E, & \text{for } p + 1 \le i \le p + q. \end{cases} \end{align} $$
$$ \begin{align} E = h - \sum_{i=1}^p h_i - \sum_{j=p+1}^{p+q} e_j, \qquad H_i = \begin{cases} h_i + E, & \text{for } 1 \le i \le p,\\ e_i + E, & \text{for } p + 1 \le i \le p + q. \end{cases} \end{align} $$
The maps
![]() $\hat \psi _0$
and
$\hat \psi _0$
and
![]() $\hat \psi $
in (3.1.8) will be defined in the course of proof.
$\hat \psi $
in (3.1.8) will be defined in the course of proof.
Proof. For each
![]() $u_i \in V_i$
, denote by
$u_i \in V_i$
, denote by
![]() $\bar {u}_i \in \bar {V}_i$
the image of
$\bar {u}_i \in \bar {V}_i$
the image of
![]() $u_i$
under the linear projection from the fixed vector
$u_i$
under the linear projection from the fixed vector
![]() $v_i \in V_i$
. Then the rational map
$v_i \in V_i$
. Then the rational map
![]() $\psi _0 \colon Y \dashrightarrow Y^+$
is given by the formula
$\psi _0 \colon Y \dashrightarrow Y^+$
is given by the formula
This map is regular on the open orbit
![]() $Y^{\circ } \subset Y$
(given by the conditions
$Y^{\circ } \subset Y$
(given by the conditions
![]() $\bar {u}_i \ne 0$
for all indices
$\bar {u}_i \ne 0$
for all indices
![]() $1 \le i \le r$
), and it extends regularly to the orbits
$1 \le i \le r$
), and it extends regularly to the orbits
![]() $Y_i^{\circ } \subset Y$
of codimension
$Y_i^{\circ } \subset Y$
of codimension
![]() $1$
(given by the condition
$1$
(given by the condition
![]() $\bar {u}_i = 0$
for some
$\bar {u}_i = 0$
for some
![]() $p + 1 \le i \le p+ q$
and
$p + 1 \le i \le p+ q$
and
![]() $\bar {u}_j \ne 0$
for all
$\bar {u}_j \ne 0$
for all
![]() $j \ne i$
).
$j \ne i$
).
Now, consider the rational G-equivariant map
 $$ \begin{align} \hat\psi_0 \colon Y \dashrightarrow {\hat{Y}}^+, \qquad (u_1,\dots,u_r) \longmapsto \left((\bar{u}_1,\dots,\bar{u}_r), \sum_{|I| \ge r - 1} \bigotimes_{i \in I} \bar{u}_i\right). \end{align} $$
$$ \begin{align} \hat\psi_0 \colon Y \dashrightarrow {\hat{Y}}^+, \qquad (u_1,\dots,u_r) \longmapsto \left((\bar{u}_1,\dots,\bar{u}_r), \sum_{|I| \ge r - 1} \bigotimes_{i \in I} \bar{u}_i\right). \end{align} $$
Here, we consider the summand
![]() $\otimes _{i \in I} \bar {u}_i$
as a point in the fibre of the line bundle
$\otimes _{i \in I} \bar {u}_i$
as a point in the fibre of the line bundle
![]() ${\mathscr {O}}(-h_I)$
and their sum for
${\mathscr {O}}(-h_I)$
and their sum for
![]() $|I| \ge r - 1$
as a point in the fibre (of the projectivisation) of the vector bundle
$|I| \ge r - 1$
as a point in the fibre (of the projectivisation) of the vector bundle
![]() ${\mathscr {E}}$
. Obviously, the map
${\mathscr {E}}$
. Obviously, the map
![]() $\hat \psi _0$
induces an isomorphism of the open orbit
$\hat \psi _0$
induces an isomorphism of the open orbit
![]() $Y^{\circ } \subset Y$
onto the open orbit
$Y^{\circ } \subset Y$
onto the open orbit
![]() $\mathbb {P}_{Y^+}({\mathscr {E}}) \setminus \mathbb {P}_{Y^+}(\bar {{\mathscr {E}}}_{\varnothing })$
in
$\mathbb {P}_{Y^+}({\mathscr {E}}) \setminus \mathbb {P}_{Y^+}(\bar {{\mathscr {E}}}_{\varnothing })$
in
![]() ${\hat {Y}}^+$
and contracts each orbit
${\hat {Y}}^+$
and contracts each orbit
![]() $Y_i^{\circ }$
of codimension
$Y_i^{\circ }$
of codimension
![]() $1$
to the section
$1$
to the section
![]() $s_i(Y^+) \subset {\hat {Y}}^+$
,
$s_i(Y^+) \subset {\hat {Y}}^+$
,
![]() $p + 1 \le i \le p + q$
.
$p + 1 \le i \le p + q$
.
Now, consider the composition
![]() $\hat \psi = \hat \psi _0 \circ \sigma \colon {\tilde {Y}} \dashrightarrow {\hat {Y}}^+$
. The restriction of
$\hat \psi = \hat \psi _0 \circ \sigma \colon {\tilde {Y}} \dashrightarrow {\hat {Y}}^+$
. The restriction of
![]() $\hat \psi $
to the exceptional divisor E is given by
$\hat \psi $
to the exceptional divisor E is given by
 $$ \begin{align} E &= \mathbb{P}(\bar{V}_1 \oplus \dots \oplus \bar{V}_r) \dashrightarrow {\hat{Y}}^+, \nonumber\\ (\bar{u}_1 + \dots + \bar{u}_r) &\longmapsto \left((\bar{u}_1,\dots,\bar{u}_r), \sum_{|I| = r - 1} \bigotimes_{i \in I} \bar{u}_i\right). \end{align} $$
$$ \begin{align} E &= \mathbb{P}(\bar{V}_1 \oplus \dots \oplus \bar{V}_r) \dashrightarrow {\hat{Y}}^+, \nonumber\\ (\bar{u}_1 + \dots + \bar{u}_r) &\longmapsto \left((\bar{u}_1,\dots,\bar{u}_r), \sum_{|I| = r - 1} \bigotimes_{i \in I} \bar{u}_i\right). \end{align} $$
It maps
![]() $E_{\varnothing }^{\circ } \subset {\tilde {Y}}$
isomorphically onto the G-orbit
$E_{\varnothing }^{\circ } \subset {\tilde {Y}}$
isomorphically onto the G-orbit
![]() $({\tilde {Y}}^+_{\varnothing })^{\circ } = \mathbb {P}_{Y^+}(\bar {{\mathscr {E}}}) \setminus \left ( \bigcup _{i=1}^r \mathbb {P}_{Y^+}(\bar {{\mathscr {E}}}_i) \right )$
of codimension
$({\tilde {Y}}^+_{\varnothing })^{\circ } = \mathbb {P}_{Y^+}(\bar {{\mathscr {E}}}) \setminus \left ( \bigcup _{i=1}^r \mathbb {P}_{Y^+}(\bar {{\mathscr {E}}}_i) \right )$
of codimension
![]() $1$
. By the above arguments, it also gives an isomorphism of open G-orbits and contracts the orbits
$1$
. By the above arguments, it also gives an isomorphism of open G-orbits and contracts the orbits
![]() ${\tilde {Y}}_i^{\circ } \cong Y_i^{\circ }$
,
${\tilde {Y}}_i^{\circ } \cong Y_i^{\circ }$
,
![]() $p + 1 \le i \le p + q$
, to the sections
$p + 1 \le i \le p + q$
, to the sections
![]() $s_i(Y^+) \subset {\hat {Y}}^+$
. Therefore,
$s_i(Y^+) \subset {\hat {Y}}^+$
. Therefore,
![]() $\hat \psi $
induces a birational isomorphism
$\hat \psi $
induces a birational isomorphism
Finally, it is easy to see that the induced map
![]() ${\tilde {Y}}_i^{\circ } \to E_i^{\circ }$
is an isomorphism for all indices
${\tilde {Y}}_i^{\circ } \to E_i^{\circ }$
is an isomorphism for all indices
![]() $p + 1 \le i \le p + q$
. This gives the commutative diagram (3.1.8) and proves that
$p + 1 \le i \le p + q$
. This gives the commutative diagram (3.1.8) and proves that
![]() $\psi $
is small.
$\psi $
is small.
The first two lines in (3.1.9) follow easily from the formulas (3.1.11), (3.1.12) and (3.1.2). The last line follows from the equality of the canonical classes of
![]() ${\tilde {Y}}$
and
${\tilde {Y}}$
and
![]() ${\tilde {Y}}^+$
expressed in terms of
${\tilde {Y}}^+$
expressed in terms of
![]() $H_i$
and E on the one hand, and
$H_i$
and E on the one hand, and
![]() $h_i$
, h and
$h_i$
, h and
![]() $e_i$
on the other hand.
$e_i$
on the other hand.
Remark 3.2. Alternatively, one can use the fact that the varieties
![]() ${\tilde {Y}}$
and
${\tilde {Y}}$
and
![]() ${\tilde {Y}}^+$
, as well as the birational isomorphism
${\tilde {Y}}^+$
, as well as the birational isomorphism
![]() $\psi $
, are toric. Thus, to check that
$\psi $
, are toric. Thus, to check that
![]() $\psi $
is small, it is enough to identify the generators of rays of the corresponding fans. Moreover, comparing the other cones in the fans, one can check that the map
$\psi $
is small, it is enough to identify the generators of rays of the corresponding fans. Moreover, comparing the other cones in the fans, one can check that the map
![]() $\psi $
factors as the composition
$\psi $
factors as the composition
of standard (anti)flips
![]() $\psi _l$
in the strict transforms of
$\psi _l$
in the strict transforms of
![]() ${\tilde {Y}}_I$
for
${\tilde {Y}}_I$
for
![]() $|I| = l$
,
$|I| = l$
,
![]() $1 \le l \le r - 2$
and for
$1 \le l \le r - 2$
and for
![]() $|I| = r - 1$
with
$|I| = r - 1$
with
![]() $\{p+1,\dots ,p+q\} \subset I$
, respectively.
$\{p+1,\dots ,p+q\} \subset I$
, respectively.
3.2 Rationality of forms of products of projective spaces
Here, we apply the birational transformation of the previous subsection to deduce the following corollary (see [Reference Zak23] for a different proof).
Corollary 3.3. Let Y be a
![]() ${\mathsf {k}}$
-form of
${\mathsf {k}}$
-form of
![]() $\mathbb {P}^{n_1} \times \mathbb {P}^{n_2} \times \dots \times \mathbb {P}^{n_r}$
. For any
$\mathbb {P}^{n_1} \times \mathbb {P}^{n_2} \times \dots \times \mathbb {P}^{n_r}$
. For any
![]() $y \in Y({\mathsf {k}})$
, the diagram (3.1.8) is defined over
$y \in Y({\mathsf {k}})$
, the diagram (3.1.8) is defined over
![]() ${\mathsf {k}}$
, and if
${\mathsf {k}}$
, and if
![]() $Y({\mathsf {k}}) \ne \varnothing $
, then Y is
$Y({\mathsf {k}}) \ne \varnothing $
, then Y is
![]() ${\mathsf {k}}$
-rational.
${\mathsf {k}}$
-rational.
Proof. First, we prove that for any
![]() $y \in Y({\mathsf {k}})$
, the diagram (3.1.8) is defined over
$y \in Y({\mathsf {k}})$
, the diagram (3.1.8) is defined over
![]() ${\mathsf {k}}$
. The divisor classes
${\mathsf {k}}$
. The divisor classes
![]() $H = \sum _{i=1}^r H_i$
and
$H = \sum _{i=1}^r H_i$
and
![]() $H' := \sum _{i=1}^p H_i$
on
$H' := \sum _{i=1}^p H_i$
on
![]() $Y_{\bar {\mathsf {k}}}$
are Galois-invariant, and since we have
$Y_{\bar {\mathsf {k}}}$
are Galois-invariant, and since we have
![]() $Y({\mathsf {k}}) \ne \varnothing $
by assumption, we conclude that they are defined over
$Y({\mathsf {k}}) \ne \varnothing $
by assumption, we conclude that they are defined over
![]() ${\mathsf {k}}$
. Also
${\mathsf {k}}$
. Also
![]() ${\tilde {Y}}$
and E are defined over
${\tilde {Y}}$
and E are defined over
![]() ${\mathsf {k}}$
as y is a
${\mathsf {k}}$
as y is a
![]() ${\mathsf {k}}$
-point. Therefore, the divisor classes
${\mathsf {k}}$
-point. Therefore, the divisor classes
 $$ \begin{align*} \sum_{i=1}^p h_i = H' - pE, \qquad h = H - (r - 1)E \qquad\text{and}\qquad -\sum_{i=p+1}^{p+q} e_i = H - H' - qE \end{align*} $$
$$ \begin{align*} \sum_{i=1}^p h_i = H' - pE, \qquad h = H - (r - 1)E \qquad\text{and}\qquad -\sum_{i=p+1}^{p+q} e_i = H - H' - qE \end{align*} $$
(which, by Theorem 3.1, are equal to the strict transforms of the classes that are ample on
![]() $Y^+$
, relatively ample for
$Y^+$
, relatively ample for
![]() ${\hat {Y}}^+ \to Y^+$
and for
${\hat {Y}}^+ \to Y^+$
and for
![]() ${\tilde {Y}}^+ \to {\hat {Y}}^+$
, respectively) are defined over
${\tilde {Y}}^+ \to {\hat {Y}}^+$
, respectively) are defined over
![]() ${\mathsf {k}}$
, hence, the varieties
${\mathsf {k}}$
, hence, the varieties
![]() $Y^+$
,
$Y^+$
,
![]() ${\hat {Y}}^+$
and
${\hat {Y}}^+$
and
![]() ${\tilde {Y}}^+$
, equal to the images of
${\tilde {Y}}^+$
, equal to the images of
![]() ${\tilde {Y}}$
under the maps given by their appropriate linear combinations, are defined over
${\tilde {Y}}$
under the maps given by their appropriate linear combinations, are defined over
![]() ${\mathsf {k}}$
, as well as the remaining arrows in the diagram.
${\mathsf {k}}$
, as well as the remaining arrows in the diagram.
Now to prove
![]() ${\mathsf {k}}$
-rationality of Y, we argue by induction in
${\mathsf {k}}$
-rationality of Y, we argue by induction in
![]() $\dim (Y) = \sum n_i$
. If the dimension is zero, there is nothing to prove. So, assume the dimension is positive and consider the diagram (3.1.8). By Theorem 3.1, the variety
$\dim (Y) = \sum n_i$
. If the dimension is zero, there is nothing to prove. So, assume the dimension is positive and consider the diagram (3.1.8). By Theorem 3.1, the variety
![]() $Y^+$
is a
$Y^+$
is a
![]() ${\mathsf {k}}$
-form of the product
${\mathsf {k}}$
-form of the product
![]() $Y_{\bar {\mathsf {k}}}^+ = \mathbb {P}^{n_1-1}_{\bar {\mathsf {k}}} \times \mathbb {P}^{n_2-1}_{\bar {\mathsf {k}}} \times \dots \times \mathbb {P}^{n_r-1}_{\bar {\mathsf {k}}}$
. By the Nishimura lemma (see [Reference Nishimura18]), we have
$Y_{\bar {\mathsf {k}}}^+ = \mathbb {P}^{n_1-1}_{\bar {\mathsf {k}}} \times \mathbb {P}^{n_2-1}_{\bar {\mathsf {k}}} \times \dots \times \mathbb {P}^{n_r-1}_{\bar {\mathsf {k}}}$
. By the Nishimura lemma (see [Reference Nishimura18]), we have
![]() $Y^+({\mathsf {k}}) \ne \varnothing $
, hence,
$Y^+({\mathsf {k}}) \ne \varnothing $
, hence,
![]() $Y^+$
is
$Y^+$
is
![]() ${\mathsf {k}}$
-rational by the induction assumption. Furthermore, the morphism
${\mathsf {k}}$
-rational by the induction assumption. Furthermore, the morphism
![]() ${\hat {Y}}^+ \to Y^+$
is a
${\hat {Y}}^+ \to Y^+$
is a
![]() ${\mathsf {k}}$
-form of a projective bundle and, by (3.1.10), the strict transform of the exceptional divisor E of
${\mathsf {k}}$
-form of a projective bundle and, by (3.1.10), the strict transform of the exceptional divisor E of
![]() ${\tilde {Y}}$
provides for it a relative hyperplane section. But E is defined over
${\tilde {Y}}$
provides for it a relative hyperplane section. But E is defined over
![]() ${\mathsf {k}}$
, therefore,
${\mathsf {k}}$
, therefore,
![]() ${\tilde {Y}}^+$
is rational over
${\tilde {Y}}^+$
is rational over
![]() $Y^+$
, hence, it is
$Y^+$
, hence, it is
![]() ${\mathsf {k}}$
-rational. It remains to note that the morphisms
${\mathsf {k}}$
-rational. It remains to note that the morphisms
![]() $\sigma $
,
$\sigma $
,
![]() $\psi $
and
$\psi $
and
![]() $\tilde \sigma _+$
in (3.1.8) are birational, hence, Y is
$\tilde \sigma _+$
in (3.1.8) are birational, hence, Y is
![]() ${\mathsf {k}}$
-rational as well.
${\mathsf {k}}$
-rational as well.
Applying this to the case of a
![]() ${\mathsf {k}}$
-form of
${\mathsf {k}}$
-form of
![]() $(\mathbb {P}^1)^3$
, we obtain
$(\mathbb {P}^1)^3$
, we obtain
Corollary 3.4. If X is a Fano threefold of type
![]() $\mathsf {X}_{(1,1,1)}$
with
$\mathsf {X}_{(1,1,1)}$
with
![]() $X({\mathsf {k}}) \ne \varnothing $
, then X is
$X({\mathsf {k}}) \ne \varnothing $
, then X is
![]() ${\mathsf {k}}$
-rational.
${\mathsf {k}}$
-rational.
For other applications of the theorem, we will often use the following observation. Recall the definitions (3.1.2) and (3.1.7) of the subvarieties
![]() $Y_i \subset Y$
of codimension
$Y_i \subset Y$
of codimension
![]() $n_i$
and subbundles
$n_i$
and subbundles
![]() $\bar {{\mathscr {E}}}_i \subset {\mathscr {E}}$
of corank
$\bar {{\mathscr {E}}}_i \subset {\mathscr {E}}$
of corank
![]() $2$
.
$2$
.
Proposition 3.5. Let Y be a
![]() ${\mathsf {k}}$
-form of
${\mathsf {k}}$
-form of
![]() $(\mathbb {P}^n)^r$
where
$(\mathbb {P}^n)^r$
where
![]() $n \ge 2$
, and assume Y has a
$n \ge 2$
, and assume Y has a
![]() ${\mathsf {k}}$
-point
${\mathsf {k}}$
-point
![]() $y \in Y({\mathsf {k}})$
. Let
$y \in Y({\mathsf {k}})$
. Let
![]() $X \subset Y$
be a closed
$X \subset Y$
be a closed
![]() ${\mathsf {k}}$
-subvariety containing the point y, such that
${\mathsf {k}}$
-subvariety containing the point y, such that
 $$ \begin{align*} X_{\bar{\mathsf{k}}} = \bigcap_{\alpha = 1}^c D_{\alpha} \subset (\mathbb{P}^n_{{\bar{\mathsf{k}}}})^r \end{align*} $$
$$ \begin{align*} X_{\bar{\mathsf{k}}} = \bigcap_{\alpha = 1}^c D_{\alpha} \subset (\mathbb{P}^n_{{\bar{\mathsf{k}}}})^r \end{align*} $$
is a complete intersection of divisors
![]() $D_{\alpha } \subset (\mathbb {P}^n_{{\bar {\mathsf {k}}}})^r$
, where
$D_{\alpha } \subset (\mathbb {P}^n_{{\bar {\mathsf {k}}}})^r$
, where
![]() $1 \le \alpha \le c$
. Let
$1 \le \alpha \le c$
. Let
![]() ${\tilde {D}}_{\alpha } \subset {\tilde {Y}}_{\bar {\mathsf {k}}}$
and
${\tilde {D}}_{\alpha } \subset {\tilde {Y}}_{\bar {\mathsf {k}}}$
and
![]() ${\tilde {D}}_{\alpha }^+ \subset {\tilde {Y}}^+_{\bar {\mathsf {k}}} = {\hat {Y}}^+_{\bar {\mathsf {k}}}$
be the strict transforms of
${\tilde {D}}_{\alpha }^+ \subset {\tilde {Y}}^+_{\bar {\mathsf {k}}} = {\hat {Y}}^+_{\bar {\mathsf {k}}}$
be the strict transforms of
![]() $D_{\alpha }$
, and set
$D_{\alpha }$
, and set
 $$ \begin{align*} {\tilde{X}}^+_{\bar{\mathsf{k}}} := \bigcap_{\alpha = 1}^c {\tilde{D}}_{\alpha}^+ \subset {\tilde{Y}}^+_{\bar{\mathsf{k}}} = {\hat{Y}}^+_{\bar{\mathsf{k}}} = \mathbb{P}_{(\mathbb{P}^{n-1}_{{\bar{\mathsf{k}}}})^r}({\mathscr{E}}). \end{align*} $$
$$ \begin{align*} {\tilde{X}}^+_{\bar{\mathsf{k}}} := \bigcap_{\alpha = 1}^c {\tilde{D}}_{\alpha}^+ \subset {\tilde{Y}}^+_{\bar{\mathsf{k}}} = {\hat{Y}}^+_{\bar{\mathsf{k}}} = \mathbb{P}_{(\mathbb{P}^{n-1}_{{\bar{\mathsf{k}}}})^r}({\mathscr{E}}). \end{align*} $$
If X is smooth at y and for each
![]() $1 \le i \le r$
one has
$1 \le i \le r$
one has
then the strict transform
![]() ${\tilde {X}}^+ = \psi _*(\operatorname {{\mathrm {Bl}}}_y(X))$
of X in
${\tilde {X}}^+ = \psi _*(\operatorname {{\mathrm {Bl}}}_y(X))$
of X in
![]() ${\tilde {Y}}^+$
is a
${\tilde {Y}}^+$
is a
![]() ${\mathsf {k}}$
-form of the complete intersection
${\mathsf {k}}$
-form of the complete intersection
![]() ${\tilde {X}}^+_{\bar {\mathsf {k}}}$
and X is birational to
${\tilde {X}}^+_{\bar {\mathsf {k}}}$
and X is birational to
![]() ${\tilde {X}}^+$
over
${\tilde {X}}^+$
over
![]() ${\mathsf {k}}$
.
${\mathsf {k}}$
.
Proof. By Corollary 3.3 the diagram (3.1.8) is defined over
![]() ${\mathsf {k}}$
, so it is enough to check that the complete intersection
${\mathsf {k}}$
, so it is enough to check that the complete intersection
![]() ${\tilde {X}}^+_{\bar {\mathsf {k}}}$
is equal to the strict transform of
${\tilde {X}}^+_{\bar {\mathsf {k}}}$
is equal to the strict transform of
![]() $\operatorname {{\mathrm {Bl}}}_y(X_{\bar {\mathsf {k}}})$
. First, note that the assumption that y is a smooth point of X implies that the strict transform
$\operatorname {{\mathrm {Bl}}}_y(X_{\bar {\mathsf {k}}})$
. First, note that the assumption that y is a smooth point of X implies that the strict transform
![]() $\operatorname {{\mathrm {Bl}}}_y(X_{\bar {\mathsf {k}}})$
of
$\operatorname {{\mathrm {Bl}}}_y(X_{\bar {\mathsf {k}}})$
of
![]() $X_{\bar {\mathsf {k}}}$
in
$X_{\bar {\mathsf {k}}}$
in
![]() ${\tilde {Y}}$
is the complete intersection of the divisors
${\tilde {Y}}$
is the complete intersection of the divisors
![]() ${\tilde {D}}_{\alpha }$
. Furthermore, the first part of the assumptions (3.2.1) implies that the intersection of
${\tilde {D}}_{\alpha }$
. Furthermore, the first part of the assumptions (3.2.1) implies that the intersection of
![]() $\operatorname {{\mathrm {Bl}}}_y(X_{\bar {\mathsf {k}}})$
with the open G-orbit in
$\operatorname {{\mathrm {Bl}}}_y(X_{\bar {\mathsf {k}}})$
with the open G-orbit in
![]() ${\tilde {Y}}_{\bar {\mathsf {k}}}$
is dense in
${\tilde {Y}}_{\bar {\mathsf {k}}}$
is dense in
![]() $\operatorname {{\mathrm {Bl}}}_y(X_{\bar {\mathsf {k}}})$
. Therefore, the strict transform of
$\operatorname {{\mathrm {Bl}}}_y(X_{\bar {\mathsf {k}}})$
. Therefore, the strict transform of
![]() $\operatorname {{\mathrm {Bl}}}_y(X_{\bar {\mathsf {k}}})$
in
$\operatorname {{\mathrm {Bl}}}_y(X_{\bar {\mathsf {k}}})$
in
![]() ${\tilde {Y}}^+_{\bar {\mathsf {k}}}$
is contained in
${\tilde {Y}}^+_{\bar {\mathsf {k}}}$
is contained in
![]() ${\tilde {X}}^+_{\bar {\mathsf {k}}}$
. So, it remains to check that
${\tilde {X}}^+_{\bar {\mathsf {k}}}$
. So, it remains to check that
![]() ${\tilde {X}}^+_{\bar {\mathsf {k}}}$
is irreducible of dimension
${\tilde {X}}^+_{\bar {\mathsf {k}}}$
is irreducible of dimension
![]() $\dim (X_{\bar {\mathsf {k}}})$
. This is definitely true for the intersection of
$\dim (X_{\bar {\mathsf {k}}})$
. This is definitely true for the intersection of
![]() ${\tilde {X}}^+_{\bar {\mathsf {k}}}$
with the complement of the union of projective subbundles
${\tilde {X}}^+_{\bar {\mathsf {k}}}$
with the complement of the union of projective subbundles
![]() $\mathbb {P}_{Y^+_{\bar {\mathsf {k}}}}(\bar {{\mathscr {E}}}_i)$
, because the map
$\mathbb {P}_{Y^+_{\bar {\mathsf {k}}}}(\bar {{\mathscr {E}}}_i)$
, because the map
![]() $\psi $
defines an isomorphism of this complement with an open subset of
$\psi $
defines an isomorphism of this complement with an open subset of
![]() ${\tilde {Y}}_{\bar {\mathsf {k}}}$
. On the other hand, the second part of the assumptions (3.2.1) gives a bound for the dimension of the intersections with these projective subbundles, which implies the irreducibility.
${\tilde {Y}}_{\bar {\mathsf {k}}}$
. On the other hand, the second part of the assumptions (3.2.1) gives a bound for the dimension of the intersections with these projective subbundles, which implies the irreducibility.
4 Rationality and unirationality of types
 $\mathsf {X}_{(2,2)}$
,
$\mathsf {X}_{(2,2)}$
,
 $\mathsf {X}_{(2,2,2)}$
and
$\mathsf {X}_{(2,2,2)}$
and
 $\mathsf {X}_{(1,1,1,1)}$
$\mathsf {X}_{(1,1,1,1)}$
In this section, we prove rationality of Fano threefolds of types
![]() $\mathsf {X}_{(2,2)}$
and
$\mathsf {X}_{(2,2)}$
and
![]() $\mathsf {X}_{(2,2,2)}$
as well as unirationality of threefolds of type
$\mathsf {X}_{(2,2,2)}$
as well as unirationality of threefolds of type
![]() $\mathsf {X}_{(1,1,1,1)}$
under the assumption
$\mathsf {X}_{(1,1,1,1)}$
under the assumption
![]() $X({\mathsf {k}}) \ne \varnothing $
.
$X({\mathsf {k}}) \ne \varnothing $
.
4.1 Rationality of
 $\mathsf {X}_{(2,2)}$
$\mathsf {X}_{(2,2)}$
To start with, we deal with threefolds of type
![]() $\mathsf {X}_{(2,2)}$
.
$\mathsf {X}_{(2,2)}$
.
Proposition 4.1. Let X be a Fano threefold of type
![]() $\mathsf {X}_{(2,2)}$
. If
$\mathsf {X}_{(2,2)}$
. If
![]() $X({\mathsf {k}}) \ne \varnothing $
, then X is
$X({\mathsf {k}}) \ne \varnothing $
, then X is
![]() ${\mathsf {k}}$
-rational.
${\mathsf {k}}$
-rational.
Proof. Let x be a
![]() ${\mathsf {k}}$
-point of X. By definition, X is a smooth divisor of bidegree
${\mathsf {k}}$
-point of X. By definition, X is a smooth divisor of bidegree
![]() $(1,1)$
in a
$(1,1)$
in a
![]() ${\mathsf {k}}$
-form Y of
${\mathsf {k}}$
-form Y of
![]() $\mathbb {P}^2 \times \mathbb {P}^2$
. Since the birational isomorphism
$\mathbb {P}^2 \times \mathbb {P}^2$
. Since the birational isomorphism
![]() $\psi \colon \operatorname {{\mathrm {Bl}}}_x(Y) = {\tilde {Y}} \dashrightarrow {\tilde {Y}}^+ = \mathbb {P}_{Y^+}({\mathscr {E}})$
is small by Theorem 3.1, it follows that X is birational to a
$\psi \colon \operatorname {{\mathrm {Bl}}}_x(Y) = {\tilde {Y}} \dashrightarrow {\tilde {Y}}^+ = \mathbb {P}_{Y^+}({\mathscr {E}})$
is small by Theorem 3.1, it follows that X is birational to a
![]() ${\mathsf {k}}$
-form of a divisor
${\mathsf {k}}$
-form of a divisor
which by (3.1.10) has type
![]() $H_1 + H_2 - E = h$
. Any such divisor corresponds to a morphism
$H_1 + H_2 - E = h$
. Any such divisor corresponds to a morphism
Furthermore, the divisor
![]() ${\tilde {X}}^+ \subset {\tilde {Y}}^+$
comes with a morphism
${\tilde {X}}^+ \subset {\tilde {Y}}^+$
comes with a morphism
![]() $\sigma _+ \colon {\tilde {X}}^+ \to Y^+$
defined over
$\sigma _+ \colon {\tilde {X}}^+ \to Y^+$
defined over
![]() ${\mathsf {k}}$
. By the Nishimura lemma, we have
${\mathsf {k}}$
. By the Nishimura lemma, we have
![]() ${\tilde {X}}^+({\mathsf {k}}) \ne \varnothing $
, hence,
${\tilde {X}}^+({\mathsf {k}}) \ne \varnothing $
, hence,
![]() $Y^+({\mathsf {k}}) \ne \varnothing $
, and since
$Y^+({\mathsf {k}}) \ne \varnothing $
, and since
![]() $Y^+$
is a
$Y^+$
is a
![]() ${\mathsf {k}}$
-form of
${\mathsf {k}}$
-form of
![]() $\mathbb {P}^1 \times \mathbb {P}^1$
, it is
$\mathbb {P}^1 \times \mathbb {P}^1$
, it is
![]() ${\mathsf {k}}$
-rational by Corollary 3.3. Finally, the general fibre of the morphism
${\mathsf {k}}$
-rational by Corollary 3.3. Finally, the general fibre of the morphism
![]() $\sigma _+ \colon {\tilde {X}}^+ \to Y^+$
is a
$\sigma _+ \colon {\tilde {X}}^+ \to Y^+$
is a
![]() $1$
-dimensional linear section of a form of a projective plane, hence, it is isomorphic to
$1$
-dimensional linear section of a form of a projective plane, hence, it is isomorphic to
![]() $\mathbb {P}^1$
, hence,
$\mathbb {P}^1$
, hence,
![]() ${\tilde {X}}^+$
is rational over
${\tilde {X}}^+$
is rational over
![]() $Y^+$
, hence, is
$Y^+$
, hence, is
![]() ${\mathsf {k}}$
-rational, hence, so is X.
${\mathsf {k}}$
-rational, hence, so is X.
Remark 4.2. One can check that the birational isomorphism
![]() $\psi \colon {\tilde {X}} \dashrightarrow {\tilde {X}}^+$
is a flop in the union of the strict transforms of two
$\psi \colon {\tilde {X}} \dashrightarrow {\tilde {X}}^+$
is a flop in the union of the strict transforms of two
![]() ${\bar {\mathsf {k}}}$
-lines passing through the point
${\bar {\mathsf {k}}}$
-lines passing through the point
![]() $x \in X$
, that
$x \in X$
, that
![]() $\sigma _+ \colon {\tilde {X}}^+ \to Y^+$
is the projectivisation of the vector bundle
$\sigma _+ \colon {\tilde {X}}^+ \to Y^+$
is the projectivisation of the vector bundle
![]() $\operatorname {{\mathrm {Ker}}}(\xi )$
of rank
$\operatorname {{\mathrm {Ker}}}(\xi )$
of rank
![]() $2$
over
$2$
over
![]() $Y^+$
and that these maps provide a Sarkisov link (1.2.1). This is an example of a pseudoisomorphism between almost del Pezzo varieties of degree
$Y^+$
and that these maps provide a Sarkisov link (1.2.1). This is an example of a pseudoisomorphism between almost del Pezzo varieties of degree
![]() $5$
(see [Reference Kuznetsov and Prokhorov11, Lemma 5.4 and Proof of Theorem 1.2]).
$5$
(see [Reference Kuznetsov and Prokhorov11, Lemma 5.4 and Proof of Theorem 1.2]).
4.2 Rationality of
 $\mathsf {X}_{(2,2,2)}$
$\mathsf {X}_{(2,2,2)}$
A similar argument works for threefolds of type
![]() $\mathsf {X}_{(2,2,2)}$
.
$\mathsf {X}_{(2,2,2)}$
.
Proposition 4.3. Let X be a Fano threefold of type
![]() $\mathsf {X}_{(2,2,2)}$
. If
$\mathsf {X}_{(2,2,2)}$
. If
![]() $X({\mathsf {k}}) \ne \varnothing $
, then X is
$X({\mathsf {k}}) \ne \varnothing $
, then X is
![]() ${\mathsf {k}}$
-rational.
${\mathsf {k}}$
-rational.
Proof. Let x be a
![]() ${\mathsf {k}}$
-point of X. By definition,
${\mathsf {k}}$
-point of X. By definition,
![]() $X_{\bar {\mathsf {k}}}$
is a complete intersection of three divisors in
$X_{\bar {\mathsf {k}}}$
is a complete intersection of three divisors in
![]() $Y_{\bar {\mathsf {k}}} = \mathbb {P}(V_1) \times \mathbb {P}(V_2) \times \mathbb {P}(V_3) \cong \mathbb {P}^2 \times \mathbb {P}^2 \times \mathbb {P}^2$
of multidegree
$Y_{\bar {\mathsf {k}}} = \mathbb {P}(V_1) \times \mathbb {P}(V_2) \times \mathbb {P}(V_3) \cong \mathbb {P}^2 \times \mathbb {P}^2 \times \mathbb {P}^2$
of multidegree
![]() $(1,1,0)$
,
$(1,1,0)$
,
![]() $(1,0,1)$
and
$(1,0,1)$
and
![]() $(0,1,1)$
, respectively. Denote by
$(0,1,1)$
, respectively. Denote by
their equations. We apply Proposition 3.5; for this, we consider the intersection
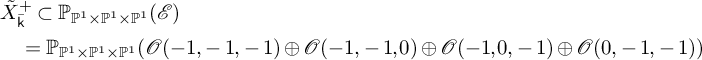 $$ \begin{align*} &{\tilde{X}}^+_{\bar{\mathsf{k}}} \subset \mathbb{P}_{\mathbb{P}^1 \times \mathbb{P}^1 \times \mathbb{P}^1}({\mathscr{E}}) \\&\quad= \mathbb{P}_{\mathbb{P}^1 \times \mathbb{P}^1 \times \mathbb{P}^1}({\mathscr{O}}(-1,-1,-1) \oplus {\mathscr{O}}(-1,-1,0) \oplus {\mathscr{O}}(-1,0,-1) \oplus {\mathscr{O}}(0,-1,-1) ) \end{align*} $$
$$ \begin{align*} &{\tilde{X}}^+_{\bar{\mathsf{k}}} \subset \mathbb{P}_{\mathbb{P}^1 \times \mathbb{P}^1 \times \mathbb{P}^1}({\mathscr{E}}) \\&\quad= \mathbb{P}_{\mathbb{P}^1 \times \mathbb{P}^1 \times \mathbb{P}^1}({\mathscr{O}}(-1,-1,-1) \oplus {\mathscr{O}}(-1,-1,0) \oplus {\mathscr{O}}(-1,0,-1) \oplus {\mathscr{O}}(0,-1,-1) ) \end{align*} $$
of the three strict transforms of the above divisors, which, by (3.1.10), have types
hence, correspond to a morphism of vector bundles
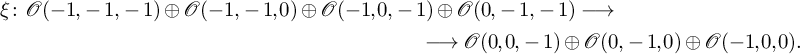 $$ \begin{align*} \xi \colon {\mathscr{O}}(-1,-1,-1) \oplus {\mathscr{O}}(-1,-1,0) \oplus {\mathscr{O}}(-1,0,-1)& \oplus {\mathscr{O}}(0,-1,-1)\longrightarrow \\ &\!\!\!\!\!\!\longrightarrow {\mathscr{O}}(0,0,-1) \oplus {\mathscr{O}}(0,-1,0) \oplus {\mathscr{O}}(-1,0,0). \end{align*} $$
$$ \begin{align*} \xi \colon {\mathscr{O}}(-1,-1,-1) \oplus {\mathscr{O}}(-1,-1,0) \oplus {\mathscr{O}}(-1,0,-1)& \oplus {\mathscr{O}}(0,-1,-1)\longrightarrow \\ &\!\!\!\!\!\!\longrightarrow {\mathscr{O}}(0,0,-1) \oplus {\mathscr{O}}(0,-1,0) \oplus {\mathscr{O}}(-1,0,0). \end{align*} $$
It is easy to see that
![]() $\xi $
is given by the matrix
$\xi $
is given by the matrix
 $$ \begin{align} \xi = \begin{pmatrix} \bar{F}_{12} & 0 & F_{12}(-,v_2) & F_{12}(v_1,-) \\ \bar{F}_{13} & F_{13}(-,v_3) & 0 & F_{13}(v_1,-) \\ \bar{F}_{23} & F_{23}(-,v_3) & F_{23}(v_2,-) & 0 \end{pmatrix}, \end{align} $$
$$ \begin{align} \xi = \begin{pmatrix} \bar{F}_{12} & 0 & F_{12}(-,v_2) & F_{12}(v_1,-) \\ \bar{F}_{13} & F_{13}(-,v_3) & 0 & F_{13}(v_1,-) \\ \bar{F}_{23} & F_{23}(-,v_3) & F_{23}(v_2,-) & 0 \end{pmatrix}, \end{align} $$
where we write
![]() $x = (v_1,v_2,v_3)$
, choose splittings
$x = (v_1,v_2,v_3)$
, choose splittings
![]() $V_i = {\bar {\mathsf {k}}} v_i \oplus \bar {V}_i$
, write
$V_i = {\bar {\mathsf {k}}} v_i \oplus \bar {V}_i$
, write
![]() $\bar {F}_{ij}$
for the restriction of
$\bar {F}_{ij}$
for the restriction of
![]() $F_{ij}$
to
$F_{ij}$
to
![]() $\bar {V}_i \otimes \bar {V}_j$
and consider
$\bar {V}_i \otimes \bar {V}_j$
and consider
![]() $F_{ij}(v_i,-)$
and
$F_{ij}(v_i,-)$
and
![]() $F_{ij}(-,v_j)$
as linear functions on
$F_{ij}(-,v_j)$
as linear functions on
![]() $\bar {V}_j$
and
$\bar {V}_j$
and
![]() $\bar {V}_i$
by restriction.
$\bar {V}_i$
by restriction.
Let us check the dimension conditions (3.2.1). Since
![]() $(Y_i)_{\bar {\mathsf {k}}}$
is a fibre of the projection
$(Y_i)_{\bar {\mathsf {k}}}$
is a fibre of the projection
it follows from Lemma 2.9 that
![]() $X_{\bar {\mathsf {k}}} \cap (Y_i)_{\bar {\mathsf {k}}}$
is a conic, hence, the first part of the dimension conditions is satisfied. To check the second part, we need to show that the restriction
$X_{\bar {\mathsf {k}}} \cap (Y_i)_{\bar {\mathsf {k}}}$
is a conic, hence, the first part of the dimension conditions is satisfied. To check the second part, we need to show that the restriction
of
![]() $\xi $
to the last two summands of
$\xi $
to the last two summands of
![]() ${\mathscr {E}}$
(given by the last two columns of (4.2.1)) cannot be everywhere degenerate and similarly for the restrictions
${\mathscr {E}}$
(given by the last two columns of (4.2.1)) cannot be everywhere degenerate and similarly for the restrictions
![]() $\xi _{1,3}$
and
$\xi _{1,3}$
and
![]() $\xi _{1,2}$
. Assuming that
$\xi _{1,2}$
. Assuming that
![]() $\xi _{2,3}$
is everywhere degenerate, we conclude from (4.2.1) that
$\xi _{2,3}$
is everywhere degenerate, we conclude from (4.2.1) that
 $$ \begin{align*} F_{12}(v_1,-) &= F_{13}(v_1,-) = 0 \quad\text{or}\\F_{12}(-,v_2) &= F_{23}(v_2,-) = 0 \quad\text{or}\\ F_{13}(v_1,-) &= F_{23}(v_2,-) = 0. \end{align*} $$
$$ \begin{align*} F_{12}(v_1,-) &= F_{13}(v_1,-) = 0 \quad\text{or}\\F_{12}(-,v_2) &= F_{23}(v_2,-) = 0 \quad\text{or}\\ F_{13}(v_1,-) &= F_{23}(v_2,-) = 0. \end{align*} $$
In any case, it would follow that at least two of the bilinear forms
![]() $F_{i,j}$
are degenerate, hence, at least two of the divisors
$F_{i,j}$
are degenerate, hence, at least two of the divisors
![]() $W_{i,j} \subset \mathbb {P}(V_i) \times \mathbb {P}(V_j)$
(defined by the equation
$W_{i,j} \subset \mathbb {P}(V_i) \times \mathbb {P}(V_j)$
(defined by the equation
![]() $F_{i,j}$
) are singular, which contradicts Lemma 2.4
(i).
$F_{i,j}$
) are singular, which contradicts Lemma 2.4
(i).
Thus, the conditions (3.2.1) are satisfied and we conclude from Proposition 3.5 that X is
![]() ${\mathsf {k}}$
-birational to a
${\mathsf {k}}$
-birational to a
![]() ${\mathsf {k}}$
-form of the complete intersection
${\mathsf {k}}$
-form of the complete intersection
![]() ${\tilde {X}}^+_{\bar {\mathsf {k}}}$
.
${\tilde {X}}^+_{\bar {\mathsf {k}}}$
.
Finally, the subvariety
![]() ${\tilde {X}}^+ \subset {\tilde {Y}}^+$
comes with a morphism
${\tilde {X}}^+ \subset {\tilde {Y}}^+$
comes with a morphism
![]() $\sigma _+ \colon {\tilde {X}}^+ \to Y^+$
defined over
$\sigma _+ \colon {\tilde {X}}^+ \to Y^+$
defined over
![]() ${\mathsf {k}}$
. By the Nishimura lemma, we have
${\mathsf {k}}$
. By the Nishimura lemma, we have
![]() ${\tilde {X}}^+({\mathsf {k}}) \ne \varnothing $
, hence,
${\tilde {X}}^+({\mathsf {k}}) \ne \varnothing $
, hence,
![]() $Y^+({\mathsf {k}}) \ne \varnothing $
, and since
$Y^+({\mathsf {k}}) \ne \varnothing $
, and since
![]() $Y^+$
is a
$Y^+$
is a
![]() ${\mathsf {k}}$
-form of
${\mathsf {k}}$
-form of
![]() $\mathbb {P}^1 \times \mathbb {P}^1 \times \mathbb {P}^1$
, it is
$\mathbb {P}^1 \times \mathbb {P}^1 \times \mathbb {P}^1$
, it is
![]() ${\mathsf {k}}$
-rational by Corollary 3.3. Moreover, the general fibre of the morphism
${\mathsf {k}}$
-rational by Corollary 3.3. Moreover, the general fibre of the morphism
![]() $\sigma _+ \colon {\tilde {X}}^+ \to Y^+$
is a zero-dimensional linear section of a form of a projective space, hence, this morphism is birational, hence,
$\sigma _+ \colon {\tilde {X}}^+ \to Y^+$
is a zero-dimensional linear section of a form of a projective space, hence, this morphism is birational, hence,
![]() ${\tilde {X}}^+$
is
${\tilde {X}}^+$
is
![]() ${\mathsf {k}}$
-rational, hence, so is X.
${\mathsf {k}}$
-rational, hence, so is X.
Remark 4.4. If the point x does not lie on a
![]() ${\bar {\mathsf {k}}}$
-line, that is,
${\bar {\mathsf {k}}}$
-line, that is,
![]() $\mathrm {F}_1(X,x) = \varnothing $
, one can check that the birational isomorphism
$\mathrm {F}_1(X,x) = \varnothing $
, one can check that the birational isomorphism
![]() $\psi \colon {\tilde {X}} \dashrightarrow {\tilde {X}}^+$
is a flop in the union of the strict transforms of three smooth
$\psi \colon {\tilde {X}} \dashrightarrow {\tilde {X}}^+$
is a flop in the union of the strict transforms of three smooth
![]() ${\bar {\mathsf {k}}}$
-conics passing through the point
${\bar {\mathsf {k}}}$
-conics passing through the point
![]() $x \in X$
, that
$x \in X$
, that
![]() $\sigma _+ \colon {\tilde {X}}^+ \to Y^+$
is the blowup of a smooth geometrically rational curve of multidegree
$\sigma _+ \colon {\tilde {X}}^+ \to Y^+$
is the blowup of a smooth geometrically rational curve of multidegree
![]() $(2,2,2)$
and that these maps provide a Sarkisov link (1.2.1).
$(2,2,2)$
and that these maps provide a Sarkisov link (1.2.1).
4.3 Unirationality of
 $\mathsf {X}_{(1,1,1,1)}$
$\mathsf {X}_{(1,1,1,1)}$
Finally, we deal with threefolds of type
![]() $\mathsf {X}_{(1,1,1,1)}$
.
$\mathsf {X}_{(1,1,1,1)}$
.
Proposition 4.5. Let X be a Fano threefold of type
![]() $\mathsf {X}_{(1,1,1,1)}$
. If
$\mathsf {X}_{(1,1,1,1)}$
. If
![]() $X({\mathsf {k}}) \ne \varnothing $
, then X is
$X({\mathsf {k}}) \ne \varnothing $
, then X is
![]() ${\mathsf {k}}$
-unirational.
${\mathsf {k}}$
-unirational.
Proof. Let x be a
![]() ${\mathsf {k}}$
-point of X. By definition, the variety X is a smooth divisor of multidegree
${\mathsf {k}}$
-point of X. By definition, the variety X is a smooth divisor of multidegree
![]() $(1,1,1,1)$
in a
$(1,1,1,1)$
in a
![]() ${\mathsf {k}}$
-form Y of
${\mathsf {k}}$
-form Y of
![]() $\mathbb {P}^1 \times \mathbb {P}^1 \times \mathbb {P}^1 \times \mathbb {P}^1$
. The birational isomorphism
$\mathbb {P}^1 \times \mathbb {P}^1 \times \mathbb {P}^1 \times \mathbb {P}^1$
. The birational isomorphism
![]() $\psi \colon \operatorname {{\mathrm {Bl}}}_x(Y) = {\tilde {Y}} \dashrightarrow {\tilde {Y}}^+ = \operatorname {{\mathrm {Bl}}}_{s_1,s_2,s_3,s_4}(\mathbb {P}^4)$
is small by Theorem 3.1, so it follows that X is birational to a
$\psi \colon \operatorname {{\mathrm {Bl}}}_x(Y) = {\tilde {Y}} \dashrightarrow {\tilde {Y}}^+ = \operatorname {{\mathrm {Bl}}}_{s_1,s_2,s_3,s_4}(\mathbb {P}^4)$
is small by Theorem 3.1, so it follows that X is birational to a
![]() ${\mathsf {k}}$
-form of a divisor
${\mathsf {k}}$
-form of a divisor
which, by (3.1.10), has type
![]() $H_1 + H_2 + H_3 + H_4 - E = 3h - 2 \sum _{i=1}^4 e_i$
, in particular,
$H_1 + H_2 + H_3 + H_4 - E = 3h - 2 \sum _{i=1}^4 e_i$
, in particular,
![]() ${\tilde {X}}^+$
is a cubic hypersurface. Moreover, the exceptional divisor
${\tilde {X}}^+$
is a cubic hypersurface. Moreover, the exceptional divisor
![]() $E \cap \operatorname {{\mathrm {Bl}}}_x(X) \subset {\tilde {Y}} = \operatorname {{\mathrm {Bl}}}_x(Y)$
of the blowup
$E \cap \operatorname {{\mathrm {Bl}}}_x(X) \subset {\tilde {Y}} = \operatorname {{\mathrm {Bl}}}_x(Y)$
of the blowup
![]() $\operatorname {{\mathrm {Bl}}}_x(X) \to X$
is an irreducible
$\operatorname {{\mathrm {Bl}}}_x(X) \to X$
is an irreducible
![]() ${\mathsf {k}}$
-rational surface birational to a
${\mathsf {k}}$
-rational surface birational to a
![]() ${\mathsf {k}}$
-form of the complete intersection of
${\mathsf {k}}$
-form of the complete intersection of
![]() ${\tilde {X}}^+_{\bar {\mathsf {k}}}$
with the linear span
${\tilde {X}}^+_{\bar {\mathsf {k}}}$
with the linear span
![]() $\mathbb {P}^3 \subset \mathbb {P}^4$
of the points
$\mathbb {P}^3 \subset \mathbb {P}^4$
of the points
![]() $s_i$
.
$s_i$
.
Let us prove that
![]() ${\tilde {X}}^+_{\bar {\mathsf {k}}}$
is not a cone. Indeed,
${\tilde {X}}^+_{\bar {\mathsf {k}}}$
is not a cone. Indeed,
![]() ${\tilde {X}}^+_{\bar {\mathsf {k}}}$
is smooth away from the linear span
${\tilde {X}}^+_{\bar {\mathsf {k}}}$
is smooth away from the linear span
![]() $\mathbb {P}^3$
of the
$\mathbb {P}^3$
of the
![]() $s_i$
, because the map
$s_i$
, because the map
![]() $\psi $
from Theorem 3.1 is an isomorphism over its complement and
$\psi $
from Theorem 3.1 is an isomorphism over its complement and
![]() $X_{\bar {\mathsf {k}}}$
is smooth, so if
$X_{\bar {\mathsf {k}}}$
is smooth, so if
![]() ${\tilde {X}}^+_{\bar {\mathsf {k}}}$
is a cone, its vertex belongs to the
${\tilde {X}}^+_{\bar {\mathsf {k}}}$
is a cone, its vertex belongs to the
![]() $\mathbb {P}^3$
. But then its intersection with the
$\mathbb {P}^3$
. But then its intersection with the
![]() $\mathbb {P}^3$
(which has been shown to be an irreducible
$\mathbb {P}^3$
(which has been shown to be an irreducible
![]() ${\mathsf {k}}$
-rational surface) is itself a cone and has a singular point at each of the
${\mathsf {k}}$
-rational surface) is itself a cone and has a singular point at each of the
![]() $s_i$
. But it is easy to see that any such cone is reducible; this contradiction proves the claim. Now, we conclude that
$s_i$
. But it is easy to see that any such cone is reducible; this contradiction proves the claim. Now, we conclude that
![]() ${\tilde {X}}^+$
is
${\tilde {X}}^+$
is
![]() ${\mathsf {k}}$
-unirational by [Reference Kollár9, Theorem 1.2].
${\mathsf {k}}$
-unirational by [Reference Kollár9, Theorem 1.2].
5 Rationality of type
 $\mathsf {X}_{(4,4)}$
$\mathsf {X}_{(4,4)}$
In this section, we prove rationality of Fano threefolds of type
![]() $\mathsf {X}_{(4,4)}$
.
$\mathsf {X}_{(4,4)}$
.
5.1 Sarkisov links
We start with a construction of two Sarkisov links. Recall that
![]() $\mathrm {F}_1(X,x)$
denotes the Hilbert scheme of lines on X passing through x, see §2.2; and that by Lemma 2.8, if
$\mathrm {F}_1(X,x)$
denotes the Hilbert scheme of lines on X passing through x, see §2.2; and that by Lemma 2.8, if
![]() $x \in X({\mathsf {k}})$
and
$x \in X({\mathsf {k}})$
and
![]() $\mathrm {F}_1(X,x)$
is not empty, then
$\mathrm {F}_1(X,x)$
is not empty, then
![]() $\mathrm {F}_1(X,x)$
is the union of two reduced
$\mathrm {F}_1(X,x)$
is the union of two reduced
![]() ${\bar {\mathsf {k}}}$
-points swapped by the Galois action. If
${\bar {\mathsf {k}}}$
-points swapped by the Galois action. If
![]() $L_1$
and
$L_1$
and
![]() $L_2$
are the corresponding
$L_2$
are the corresponding
![]() ${\bar {\mathsf {k}}}$
-lines on X (passing through x), then
${\bar {\mathsf {k}}}$
-lines on X (passing through x), then
is a singular
![]() ${\mathsf {k}}$
-conic on X irreducible over
${\mathsf {k}}$
-conic on X irreducible over
![]() ${\mathsf {k}}$
and with
${\mathsf {k}}$
and with
![]() $\operatorname {\mathrm {Sing}}(\Theta (x)) = \{x\}$
.
$\operatorname {\mathrm {Sing}}(\Theta (x)) = \{x\}$
.
Recall that a quintic del Pezzo threefold is a Fano threefold of index
![]() $2$
and half-anticanonical degree
$2$
and half-anticanonical degree
![]() $5$
. Over an algebraically closed field, it can be realised as a complete intersection of the Grassmannian
$5$
. Over an algebraically closed field, it can be realised as a complete intersection of the Grassmannian
![]() $\operatorname {{\mathrm {Gr}}}(2,5)$
with a linear subspace of codimension
$\operatorname {{\mathrm {Gr}}}(2,5)$
with a linear subspace of codimension
![]() $3$
(see [Reference Iskovskikh6, Chapter 2, Theorem 1.1]).
$3$
(see [Reference Iskovskikh6, Chapter 2, Theorem 1.1]).
Theorem 5.1. Let X be a Fano threefold of type
![]() $\mathsf {X}_{(4,4)}$
, and let
$\mathsf {X}_{(4,4)}$
, and let
![]() $x \in X({\mathsf {k}})$
be a
$x \in X({\mathsf {k}})$
be a
![]() ${\mathsf {k}}$
-point.
${\mathsf {k}}$
-point.
-
(i) If
 $\mathrm {F}_1(X,x) = \varnothing $
, there exists a Sarkisov link (1.2.1) defined over
$\mathrm {F}_1(X,x) = \varnothing $
, there exists a Sarkisov link (1.2.1) defined over
 ${\mathsf {k}}$
, where:
${\mathsf {k}}$
, where:-
•
 $\sigma $
is the blowup of the point x,
$\sigma $
is the blowup of the point x, -
•
 $X^{+}$
is a smooth quintic del Pezzo threefold and
$X^{+}$
is a smooth quintic del Pezzo threefold and -
•
 $\sigma _+$
is the blowup of a smooth
$\sigma _+$
is the blowup of a smooth
 ${\mathsf {k}}$
-irreducible curve
${\mathsf {k}}$
-irreducible curve
 $B^+ \subset X^+$
of degree
$B^+ \subset X^+$
of degree
 $4$
with two geometrically rational
$4$
with two geometrically rational
 ${\bar {\mathsf {k}}}$
-components.
${\bar {\mathsf {k}}}$
-components.
-
-
(ii) If
 $\mathrm {F}_1(X,x) \ne \varnothing $
, there exists a Sarkisov link (1.2.1) defined over
$\mathrm {F}_1(X,x) \ne \varnothing $
, there exists a Sarkisov link (1.2.1) defined over
 ${\mathsf {k}}$
, where:
${\mathsf {k}}$
, where:-
•
 $\sigma $
is the blowup of the singular
$\sigma $
is the blowup of the singular
 ${\mathsf {k}}$
-irreducible conic
${\mathsf {k}}$
-irreducible conic
 $\Theta (x)$
,
$\Theta (x)$
, -
•
 $X^{+}$
is a smooth Fano threefold of type
$X^{+}$
is a smooth Fano threefold of type
 $\mathsf {X}_{(2,2)}$
and
$\mathsf {X}_{(2,2)}$
and -
•
 $\sigma _+$
is the blowup of a singular
$\sigma _+$
is the blowup of a singular
 ${\mathsf {k}}$
-irreducible curve
${\mathsf {k}}$
-irreducible curve
 $B^+ \subset X^+$
of degree
$B^+ \subset X^+$
of degree
 $6$
with two geometrically rational
$6$
with two geometrically rational
 ${\bar {\mathsf {k}}}$
-components.
${\bar {\mathsf {k}}}$
-components.
-
The proof of the theorem takes §5.1 and §5.2: in the rest of §5.1, we prove the existence of the links, and in §5.2, we describe them in detail. The proofs of cases (i) and (ii) are completely analogous, so to carry them on simultaneously, we introduce the following convenient notation:
 $$ \begin{align} m = m(x) := \begin{cases} 2, & \text{if } \mathrm{F}_1(X,x) = \varnothing,\\ 1, & \text{if } \mathrm{F}_1(X,x) \ne \varnothing. \end{cases} \end{align} $$
$$ \begin{align} m = m(x) := \begin{cases} 2, & \text{if } \mathrm{F}_1(X,x) = \varnothing,\\ 1, & \text{if } \mathrm{F}_1(X,x) \ne \varnothing. \end{cases} \end{align} $$
The proof of the existence of the links is analogous to the first parts of [Reference Kuznetsov and Prokhorov10, Theorems 5.9 and 5.17], so we use some results from [Reference Kuznetsov and Prokhorov10, §5.1] below.
Let
be the blowup of X at x or at
![]() $\Theta (x)$
, respectively. We denote by H (the pullback to
$\Theta (x)$
, respectively. We denote by H (the pullback to
![]() ${\tilde {X}}$
of) the anticanonical class of X and by E the exceptional divisor of
${\tilde {X}}$
of) the anticanonical class of X and by E the exceptional divisor of
![]() $\sigma $
.
$\sigma $
.
First, note that for
![]() $m = m(x)$
, the anticanonical linear system
$m = m(x)$
, the anticanonical linear system
is base-point free by Theorem 2.1 and [Reference Kuznetsov and Prokhorov10, Lemmas 5.5 and 5.7]. Moreover, combining [Reference Kuznetsov and Prokhorov10, (5.1.7) and (5.1.9)], we can uniformly write
where we recall from Table 1 that
![]() $g = {\mathrm {g}}(X) = 15$
. We will also need the following observation.
$g = {\mathrm {g}}(X) = 15$
. We will also need the following observation.
Lemma 5.2. The linear system
![]() ${\mathscr {M}} := |H - (m+1)E|$
on the blowup
${\mathscr {M}} := |H - (m+1)E|$
on the blowup
![]() ${\tilde {X}}$
of X has positive dimension:
${\tilde {X}}$
of X has positive dimension:
and has no fixed components.
Proof. The dimension is estimated in [Reference Kuznetsov and Prokhorov10, Lemma 5.4(i) and (iii)]. To prove that
![]() ${\mathscr {M}}$
has no fixed components, note that the linear system
${\mathscr {M}}$
has no fixed components, note that the linear system
![]() $|kE|$
is zero-dimensional for any
$|kE|$
is zero-dimensional for any
![]() $k \ge 0$
(since E is the exceptional divisor of a blowup), hence, the only possibility for a fixed component of
$k \ge 0$
(since E is the exceptional divisor of a blowup), hence, the only possibility for a fixed component of
![]() ${\mathscr {M}}$
is provided by the divisor E with some multiplicity. So, assume
${\mathscr {M}}$
is provided by the divisor E with some multiplicity. So, assume
where
![]() $a\ge m + 2$
and E is not a fixed component of the linear system
$a\ge m + 2$
and E is not a fixed component of the linear system
![]() $|H - aE|$
. Since the linear system
$|H - aE|$
. Since the linear system
![]() $|H - mE|$
is base-point free and
$|H - mE|$
is base-point free and
![]() $|H - aE|$
has no fixed components, using (5.1.2) we obtain
$|H - aE|$
has no fixed components, using (5.1.2) we obtain
When
![]() $m = 2$
, this gives
$m = 2$
, this gives
![]() $a^2 \le 14$
, hence,
$a^2 \le 14$
, hence,
![]() $a \le 3$
, and when
$a \le 3$
, and when
![]() $m = 1$
, this gives
$m = 1$
, this gives
![]() $(a+1)^2 \le 15$
, hence,
$(a+1)^2 \le 15$
, hence,
![]() $a \le 2$
. In both cases, this contradicts the assumption
$a \le 2$
. In both cases, this contradicts the assumption
![]() $a \ge m + 2$
.
$a \ge m + 2$
.
Now, we can deduce the existence of the Sarkisov links.
Proposition 5.3. Let X be a Fano threefold of type
![]() $\mathsf {X}_{(4,4)}$
with a
$\mathsf {X}_{(4,4)}$
with a
![]() ${\mathsf {k}}$
-point x.
${\mathsf {k}}$
-point x.
-
(i) If
 $\mathrm {F}_1(X,x) = \varnothing $
, there exists a Sarkisov link (1.2.1), where
$\mathrm {F}_1(X,x) = \varnothing $
, there exists a Sarkisov link (1.2.1), where
 $\sigma $
is the blowup of x.
$\sigma $
is the blowup of x. -
(ii) If
 $\mathrm {F}_1(X,x) \ne \varnothing $
, there exists a Sarkisov link (1.2.1), where
$\mathrm {F}_1(X,x) \ne \varnothing $
, there exists a Sarkisov link (1.2.1), where
 $\sigma $
is the blowup of
$\sigma $
is the blowup of
 $\Theta (x)$
.
$\Theta (x)$
.
In both cases, the link is defined over
![]() ${\mathsf {k}}$
.
${\mathsf {k}}$
.
Proof. We use notation (5.1.1). Recall that the anticanonical class
![]() $H = -K_X$
is very ample and the image of the anticanonical embedding
$H = -K_X$
is very ample and the image of the anticanonical embedding
![]() $X \subset \mathbb {P}^{g + 1}$
is an intersection of quadrics (see Theorem 2.1). The anticanonical morphism
$X \subset \mathbb {P}^{g + 1}$
is an intersection of quadrics (see Theorem 2.1). The anticanonical morphism
![]() $\phi \colon {\tilde {X}} \to \mathbb {P}^{g-m-1}$
cannot contract a divisor D, because by [Reference Kuznetsov and Prokhorov10, Lemmas 5.5 and 5.7], this divisor is then a fixed component of
$\phi \colon {\tilde {X}} \to \mathbb {P}^{g-m-1}$
cannot contract a divisor D, because by [Reference Kuznetsov and Prokhorov10, Lemmas 5.5 and 5.7], this divisor is then a fixed component of
![]() ${\mathscr {M}}$
, but by Lemma 5.2, this linear system has no fixed components. Therefore, the required link exists and is defined over
${\mathscr {M}}$
, but by Lemma 5.2, this linear system has no fixed components. Therefore, the required link exists and is defined over
![]() ${\mathsf {k}}$
by [Reference Kuznetsov and Prokhorov10, Lemmas 5.5 and 5.7].
${\mathsf {k}}$
by [Reference Kuznetsov and Prokhorov10, Lemmas 5.5 and 5.7].
5.2 The second contraction
By Proposition 5.3 we have the diagram (1.2.1), so to finish the proof of Theorem 5.1, it remains to describe the extremal contraction
![]() $\sigma _+$
. During this step, we systematically use the classification of extremal contractions from [Reference Cutkosky5] and [Reference Mori16].
$\sigma _+$
. During this step, we systematically use the classification of extremal contractions from [Reference Cutkosky5] and [Reference Mori16].
We denote by
![]() $H^+,E^+ \in \operatorname {Pic}({\tilde {X}}^+)$
, the strict transforms of the classes
$H^+,E^+ \in \operatorname {Pic}({\tilde {X}}^+)$
, the strict transforms of the classes
![]() $H,E \in \operatorname {Pic}({\tilde {X}})$
. Note that
$H,E \in \operatorname {Pic}({\tilde {X}})$
. Note that
because
![]() $-K_{\tilde {X}} = H - mE$
by definition of
$-K_{\tilde {X}} = H - mE$
by definition of
![]() ${\tilde {X}}$
and the map
${\tilde {X}}$
and the map
![]() $\psi $
is an isomorphism in codimension one. Consider also the strict transform
$\psi $
is an isomorphism in codimension one. Consider also the strict transform
of the linear system
![]() ${\mathscr {M}}$
.
${\mathscr {M}}$
.
We denote by
![]() $\Upsilon _i \subset {\tilde {X}}$
the flopping curves and by
$\Upsilon _i \subset {\tilde {X}}$
the flopping curves and by
![]() $\Upsilon _i^+ \subset {\tilde {X}}^+$
the corresponding flopped curves. Finally, when
$\Upsilon _i^+ \subset {\tilde {X}}^+$
the corresponding flopped curves. Finally, when
![]() $\mathrm {F}_1(X,x) = \varnothing $
, we denote by C a general twisted cubic curve on X passing through x, and otherwise, we denote by C a general conic meeting
$\mathrm {F}_1(X,x) = \varnothing $
, we denote by C a general twisted cubic curve on X passing through x, and otherwise, we denote by C a general conic meeting
![]() $\Theta (x)$
(recall Lemmas 2.11 and 2.12 for the description of the corresponding Hilbert schemes). Note that
$\Theta (x)$
(recall Lemmas 2.11 and 2.12 for the description of the corresponding Hilbert schemes). Note that
We denote by
![]() ${\tilde {C}}$
the strict transform of C in
${\tilde {C}}$
the strict transform of C in
![]() ${\tilde {X}}$
and by
${\tilde {X}}$
and by
![]() ${\tilde {C}}^+$
the strict transform of
${\tilde {C}}^+$
the strict transform of
![]() ${\tilde {C}}$
in
${\tilde {C}}$
in
![]() ${\tilde {X}}^+$
. Note that by Remarks 2.10 and 2.13, the curve
${\tilde {X}}^+$
. Note that by Remarks 2.10 and 2.13, the curve
![]() ${\tilde {C}}$
is smooth and
${\tilde {C}}$
is smooth and
in particular,
![]() $(H - mE)\cdot {\tilde {C}} = 1$
and
$(H - mE)\cdot {\tilde {C}} = 1$
and
![]() ${\tilde {C}}$
does not contain the curves
${\tilde {C}}$
does not contain the curves
![]() $\Upsilon _i$
.
$\Upsilon _i$
.
Lemma 5.4. The nef cone of
![]() ${\tilde {X}}^+$
is generated by the anticanonical class
${\tilde {X}}^+$
is generated by the anticanonical class
![]() $-K_{{\tilde {X}}^+}$
and
$-K_{{\tilde {X}}^+}$
and
![]() $M^+ \in {\mathscr {M}}^+$
, and the Mori cone of
$M^+ \in {\mathscr {M}}^+$
, and the Mori cone of
![]() ${\tilde {X}}^+$
is generated by the class of the curves
${\tilde {X}}^+$
is generated by the class of the curves
![]() $\Upsilon _i^+$
and the class of
$\Upsilon _i^+$
and the class of
![]() ${\tilde {C}}^+$
. In particular, the extremal contraction
${\tilde {C}}^+$
. In particular, the extremal contraction
![]() $\sigma _+$
is given by a multiple of the linear system
$\sigma _+$
is given by a multiple of the linear system
![]() ${\mathscr {M}}^+$
and contracts the extremal ray generated by
${\mathscr {M}}^+$
and contracts the extremal ray generated by
![]() ${\tilde {C}}^+$
.
${\tilde {C}}^+$
.
Proof. Since
![]() $\phi $
is crepant and
$\phi $
is crepant and
![]() $\psi $
is a flop, the morphism
$\psi $
is a flop, the morphism
![]() $\phi _+$
is crepant as well. Moreover, the anticanonical linear system
$\phi _+$
is crepant as well. Moreover, the anticanonical linear system
![]() $|-K_{\tilde {X}}|$
is base-point free by [Reference Kuznetsov and Prokhorov10, Lemma 5.7], hence,
$|-K_{\tilde {X}}|$
is base-point free by [Reference Kuznetsov and Prokhorov10, Lemma 5.7], hence,
![]() $|-K_{{\tilde {X}}^+}|$
is base-point free as well.
$|-K_{{\tilde {X}}^+}|$
is base-point free as well.
On the other hand, we have
![]() $(H - mE) \cdot \Upsilon _i = -K_{{\tilde {X}}} \cdot \Upsilon _i = 0$
, and since
$(H - mE) \cdot \Upsilon _i = -K_{{\tilde {X}}} \cdot \Upsilon _i = 0$
, and since
![]() $H \cdot \Upsilon _i> 0$
, we conclude that
$H \cdot \Upsilon _i> 0$
, we conclude that
![]() $E \cdot \Upsilon _i> 0$
. Therefore, for
$E \cdot \Upsilon _i> 0$
. Therefore, for
![]() $M \in {\mathscr {M}}$
we have
$M \in {\mathscr {M}}$
we have
If
![]() $M^+ \in {\mathscr {M}}^+$
is the strict transform of M, this implies that
$M^+ \in {\mathscr {M}}^+$
is the strict transform of M, this implies that
![]() $M^+ \cdot \Upsilon _i^+> 0$
by one of the definitions of a flop (see, for example, [Reference Kollár and Mori7, Definition 6.10]). Now if
$M^+ \cdot \Upsilon _i^+> 0$
by one of the definitions of a flop (see, for example, [Reference Kollár and Mori7, Definition 6.10]). Now if
![]() $M^+$
is not nef, it is negative on the extremal ray
$M^+$
is not nef, it is negative on the extremal ray
![]() $\mathrm {R}$
corresponding to the contraction
$\mathrm {R}$
corresponding to the contraction
![]() $\sigma _+ \colon {\tilde {X}}^+ \to X^+$
. Since the canonical class is also negative on
$\sigma _+ \colon {\tilde {X}}^+ \to X^+$
. Since the canonical class is also negative on
![]() $\mathrm {R}$
, the contraction
$\mathrm {R}$
, the contraction
![]() $\sigma _+$
cannot be small (see [Reference Benveniste2, Theorem 0] or [Reference Mori and Prokhorov17, Corollary 6.3.4]), hence, curves in
$\sigma _+$
cannot be small (see [Reference Benveniste2, Theorem 0] or [Reference Mori and Prokhorov17, Corollary 6.3.4]), hence, curves in
![]() $\mathrm {R}$
sweep a subvariety of
$\mathrm {R}$
sweep a subvariety of
![]() ${\tilde {X}}^+$
of dimension
${\tilde {X}}^+$
of dimension
![]() $\ge 2$
, hence, the base locus of
$\ge 2$
, hence, the base locus of
![]() ${\mathscr {M}}^+$
is at least two-dimensional, which contradicts Lemma 5.2. This proves that
${\mathscr {M}}^+$
is at least two-dimensional, which contradicts Lemma 5.2. This proves that
![]() $M^+$
is nef.
$M^+$
is nef.
Now, we have
![]() $-K_{\tilde {X}} \cdot {\tilde {C}} = (H - mE) \cdot {\tilde {C}} = 1$
by (5.2.1) and (5.2.2), hence,
$-K_{\tilde {X}} \cdot {\tilde {C}} = (H - mE) \cdot {\tilde {C}} = 1$
by (5.2.1) and (5.2.2), hence,
![]() $-K_{{\tilde {X}}^+} \cdot {\tilde {C}}^+ = 1$
. On the other hand, since a general divisor H meets C away from the indeterminacy locus of the map
$-K_{{\tilde {X}}^+} \cdot {\tilde {C}}^+ = 1$
. On the other hand, since a general divisor H meets C away from the indeterminacy locus of the map
![]() $X\dashrightarrow \tilde X^+$
, we have
$X\dashrightarrow \tilde X^+$
, we have
![]() $H^+\cdot {\tilde {C}}^+ \ge H\cdot C=m+1$
and so
$H^+\cdot {\tilde {C}}^+ \ge H\cdot C=m+1$
and so
![]() $E^+\cdot {\tilde {C}}^+ \ge 1$
. Thus,
$E^+\cdot {\tilde {C}}^+ \ge 1$
. Thus,
Since
![]() $M^{+}$
is nef,
$M^{+}$
is nef,
![]() $M^+ \cdot {\tilde {C}}^+= 0$
.
$M^+ \cdot {\tilde {C}}^+= 0$
.
Combining the above computations, we conclude that the nef cone of
![]() ${\tilde {X}}^+$
is generated by
${\tilde {X}}^+$
is generated by
![]() $-K_{{\tilde {X}}^+}$
and
$-K_{{\tilde {X}}^+}$
and
![]() $M^+$
and the Mori cone is generated by
$M^+$
and the Mori cone is generated by
![]() $\Upsilon _i^+$
and
$\Upsilon _i^+$
and
![]() ${\tilde {C}}^+$
. The rest of the lemma follows from the Mori contraction theorem [Reference Mori16, Theorems 3.1 and 3.2].
${\tilde {C}}^+$
. The rest of the lemma follows from the Mori contraction theorem [Reference Mori16, Theorems 3.1 and 3.2].
Now, we can finally prove Theorem 5.1.
Proof of Theorem 5.1
Let X be a Fano threefold of type
![]() $\mathsf {X}_{(4,4)}$
. By Proposition 5.3, there exists a Sarkisov link (1.2.1), and it remains to describe the contraction
$\mathsf {X}_{(4,4)}$
. By Proposition 5.3, there exists a Sarkisov link (1.2.1), and it remains to describe the contraction
![]() $\sigma _+$
. Since
$\sigma _+$
. Since
![]() $\sigma _+$
is an extremal contraction, we have
$\sigma _+$
is an extremal contraction, we have
![]() $\unicode{x3c1} (X^+) = \unicode{x3c1} ({\tilde {X}}^+) - 1 = \unicode{x3c1} ({\tilde {X}}) - 1 = \unicode{x3c1} (X)$
, hence,
$\unicode{x3c1} (X^+) = \unicode{x3c1} ({\tilde {X}}^+) - 1 = \unicode{x3c1} ({\tilde {X}}) - 1 = \unicode{x3c1} (X)$
, hence,
![]() $\unicode{x3c1} (X^+) = 1$
. Similarly, we have
$\unicode{x3c1} (X^+) = 1$
. Similarly, we have
![]() $\unicode{x3c1} (X^+_{\bar {\mathsf {k}}}) \le \unicode{x3c1} ({\tilde {X}}^+_{\bar {\mathsf {k}}}) - 1 = \unicode{x3c1} ({\tilde {X}}_{\bar {\mathsf {k}}}) - 1 = \unicode{x3c1} (X_{\bar {\mathsf {k}}}) = 2$
, hence
$\unicode{x3c1} (X^+_{\bar {\mathsf {k}}}) \le \unicode{x3c1} ({\tilde {X}}^+_{\bar {\mathsf {k}}}) - 1 = \unicode{x3c1} ({\tilde {X}}_{\bar {\mathsf {k}}}) - 1 = \unicode{x3c1} (X_{\bar {\mathsf {k}}}) = 2$
, hence
On the other hand, in the case
![]() $\mathrm {F}_1(X,x) \ne \varnothing $
, the varieties
$\mathrm {F}_1(X,x) \ne \varnothing $
, the varieties
![]() ${\tilde {X}}$
and
${\tilde {X}}$
and
![]() ${\tilde {X}}^+$
are not smooth and, arguing as in the proof of [Reference Kuznetsov and Prokhorov10, Theorem 5.9], we obtain
${\tilde {X}}^+$
are not smooth and, arguing as in the proof of [Reference Kuznetsov and Prokhorov10, Theorem 5.9], we obtain
Since
![]() $\phi $
and
$\phi $
and
![]() $\phi _+$
are crepant morphisms, the projection formula implies that any triple intersection product of divisor classes on
$\phi _+$
are crepant morphisms, the projection formula implies that any triple intersection product of divisor classes on
![]() ${\tilde {X}}^+$
which includes
${\tilde {X}}^+$
which includes
![]() $K_{{\tilde {X}}^+}$
is equal to the analogous triple product on
$K_{{\tilde {X}}^+}$
is equal to the analogous triple product on
![]() ${\tilde {X}}$
, so using (5.1.2), we compute (recall that
${\tilde {X}}$
, so using (5.1.2), we compute (recall that
![]() $g = {\mathrm {g}}(X) = 15$
)
$g = {\mathrm {g}}(X) = 15$
)
 $$ \begin{align} (-K_{\tilde X^+})^3 &= 2(g - m - 3) {} = 24 - 2m,\nonumber\\ (-K_{\tilde X^+})^2\cdot E^+ &= 4,\\ (-K_{\tilde X^+})\cdot (E^+)^2 &= -2.\nonumber \end{align} $$
$$ \begin{align} (-K_{\tilde X^+})^3 &= 2(g - m - 3) {} = 24 - 2m,\nonumber\\ (-K_{\tilde X^+})^2\cdot E^+ &= 4,\\ (-K_{\tilde X^+})\cdot (E^+)^2 &= -2.\nonumber \end{align} $$
On the other hand, by Lemma 5.4 and primitivity of
![]() $H^+ - (m + 1)E^+$
, we have
$H^+ - (m + 1)E^+$
, we have
where
![]() $A^+$
is the ample generator of the Picard group of
$A^+$
is the ample generator of the Picard group of
![]() $X^+$
. We have
$X^+$
. We have
 $$ \begin{align} \begin{aligned}(\sigma_+^*A^+)^2 \cdot(-K_{{\tilde{X}}^+}) &= (H^+ - (m + 1)E^+)^2\cdot (-K_{X^+})\\&= 2(g - m - 8) = 14 - 2m> 0, \end{aligned}\end{align} $$
$$ \begin{align} \begin{aligned}(\sigma_+^*A^+)^2 \cdot(-K_{{\tilde{X}}^+}) &= (H^+ - (m + 1)E^+)^2\cdot (-K_{X^+})\\&= 2(g - m - 8) = 14 - 2m> 0, \end{aligned}\end{align} $$
therefore,
![]() $\sigma _+$
is not a del Pezzo fibration. Similarly, if
$\sigma _+$
is not a del Pezzo fibration. Similarly, if
![]() $\sigma _+$
is a conic bundle, it follows that
$\sigma _+$
is a conic bundle, it follows that
hence,
![]() $X^+$
is a smooth quintic or sextic del Pezzo surface, which of course contradicts the inequality (5.2.3). Therefore, the morphism
$X^+$
is a smooth quintic or sextic del Pezzo surface, which of course contradicts the inequality (5.2.3). Therefore, the morphism
![]() $\sigma _+$
is birational.
$\sigma _+$
is birational.
By Lemma 5.4, the morphism
![]() $\sigma _+$
contracts the strict transform
$\sigma _+$
contracts the strict transform
![]() $R^+$
of the divisor swept by curves C, that is, the strict transform of the divisor
$R^+$
of the divisor swept by curves C, that is, the strict transform of the divisor
![]() $R_x \subset X$
if
$R_x \subset X$
if
![]() $\mathrm {F}_1(X,x) = \varnothing $
, or of the divisor
$\mathrm {F}_1(X,x) = \varnothing $
, or of the divisor
![]() $R_{\Theta (x)}$
otherwise. In both cases, Lemmas 2.11 and 2.12 show that
$R_{\Theta (x)}$
otherwise. In both cases, Lemmas 2.11 and 2.12 show that
![]() $R^+$
has over
$R^+$
has over
![]() ${\bar {\mathsf {k}}}$
two irreducible components swapped by the Galois group. Therefore, it follows from (5.2.4) that
${\bar {\mathsf {k}}}$
two irreducible components swapped by the Galois group. Therefore, it follows from (5.2.4) that
and
![]() $\sigma _+$
is the blowup of two
$\sigma _+$
is the blowup of two
![]() ${\bar {\mathsf {k}}}$
-curves or two
${\bar {\mathsf {k}}}$
-curves or two
![]() ${\bar {\mathsf {k}}}$
-points. Furthermore, by Lemmas 2.11 and 2.12, we have
${\bar {\mathsf {k}}}$
-points. Furthermore, by Lemmas 2.11 and 2.12, we have
Denoting by
![]() $i_+$
the index of
$i_+$
the index of
![]() $X^+$
and by
$X^+$
and by
![]() $a_+$
the discrepancy of the exceptional divisor
$a_+$
the discrepancy of the exceptional divisor
![]() $R^+$
of
$R^+$
of
![]() $\sigma _+$
, and computing the anticanonical class of
$\sigma _+$
, and computing the anticanonical class of
![]() ${\tilde {X}}^+$
in two ways, we obtain the equality
${\tilde {X}}^+$
in two ways, we obtain the equality
Solving this equation, we obtain
![]() $i_+ = 2$
and
$i_+ = 2$
and
![]() $a_+ = 1$
. Thus,
$a_+ = 1$
. Thus,
![]() $X^+$
is a Fano threefold of index
$X^+$
is a Fano threefold of index
![]() $2$
and
$2$
and
![]() $\sigma _+$
is either the blowup of a
$\sigma _+$
is either the blowup of a
![]() ${\mathsf {k}}$
-irreducible curve
${\mathsf {k}}$
-irreducible curve
![]() $B^+$
with two
$B^+$
with two
![]() ${\bar {\mathsf {k}}}$
-components or of two rational double
${\bar {\mathsf {k}}}$
-components or of two rational double
![]() ${\bar {\mathsf {k}}}$
-points on
${\bar {\mathsf {k}}}$
-points on
![]() $X^+$
swapped by the Galois action. Moreover, using the equality from (5.2.7), we obtain
$X^+$
swapped by the Galois action. Moreover, using the equality from (5.2.7), we obtain
hence,
![]() $X^+$
is a quintic or sextic del Pezzo threefold, respectively. Finally, if
$X^+$
is a quintic or sextic del Pezzo threefold, respectively. Finally, if
![]() $X^+$
is singular, its class group
$X^+$
is singular, its class group
![]() $\operatorname {{\mathrm {Cl}}}(X^+)$
has rank greater than
$\operatorname {{\mathrm {Cl}}}(X^+)$
has rank greater than
![]() $1$
(see [Reference Prokhorov20, Theorem 1.7]), which contradicts to the equality
$1$
(see [Reference Prokhorov20, Theorem 1.7]), which contradicts to the equality
![]() $\operatorname {{\mathrm {rk}}}\operatorname {{\mathrm {Cl}}}(X^+) = 1$
obtained above. Thus,
$\operatorname {{\mathrm {rk}}}\operatorname {{\mathrm {Cl}}}(X^+) = 1$
obtained above. Thus,
![]() $X^+$
is smooth and
$X^+$
is smooth and
![]() $\sigma _+$
is the blowup of a curve
$\sigma _+$
is the blowup of a curve
![]() $B^+$
, such that
$B^+$
, such that
![]() $B^+_{{\bar {\mathsf {k}}}}$
has two irreducible
$B^+_{{\bar {\mathsf {k}}}}$
has two irreducible
![]() ${\bar {\mathsf {k}}}$
-components swapped by the Galois group.
${\bar {\mathsf {k}}}$
-components swapped by the Galois group.
To finally compute the degree of
![]() $B^+$
, recall that
$B^+$
, recall that
![]() $R^+$
is the exceptional divisor of
$R^+$
is the exceptional divisor of
![]() $\sigma _+$
. Note that on the one hand, equalities (5.2.5) and (5.2.6) imply that
$\sigma _+$
. Note that on the one hand, equalities (5.2.5) and (5.2.6) imply that
and on the other hand, this expression is equal to
(where the degree is computed with respect to
![]() $A^+$
). Thus,
$A^+$
). Thus,
hence,
![]() $B^+$
is a quartic or sextic curve with two connected
$B^+$
is a quartic or sextic curve with two connected
![]() ${\bar {\mathsf {k}}}$
-components (swapped by the Galois action), that is, a union of two conics or two cubic curves.
${\bar {\mathsf {k}}}$
-components (swapped by the Galois action), that is, a union of two conics or two cubic curves.
5.3 Rationality
Now, we use the constructed links to prove rationality of threefolds of type
![]() $\mathsf {X}_{(4,4)}$
.
$\mathsf {X}_{(4,4)}$
.
Proposition 5.5. Let X be a Fano threefold of type
![]() $\mathsf {X}_{(4,4)}$
. If
$\mathsf {X}_{(4,4)}$
. If
![]() $X({\mathsf {k}}) \ne \varnothing $
, then X is
$X({\mathsf {k}}) \ne \varnothing $
, then X is
![]() ${\mathsf {k}}$
-rational.
${\mathsf {k}}$
-rational.
Proof. Let
![]() $x \in X({\mathsf {k}})$
be a
$x \in X({\mathsf {k}})$
be a
![]() ${\mathsf {k}}$
-point. First, assume that
${\mathsf {k}}$
-point. First, assume that
![]() $\mathrm {F}_1(X,x) = \varnothing $
. Then, by Theorem 5.1
(i), the variety X is birational to a smooth quintic del Pezzo threefold
$\mathrm {F}_1(X,x) = \varnothing $
. Then, by Theorem 5.1
(i), the variety X is birational to a smooth quintic del Pezzo threefold
![]() $X^+$
. But
$X^+$
. But
![]() $X^+$
is
$X^+$
is
![]() ${\mathsf {k}}$
-rational by [Reference Kuznetsov and Prokhorov10, Theorem 3.3], hence, so is X.
${\mathsf {k}}$
-rational by [Reference Kuznetsov and Prokhorov10, Theorem 3.3], hence, so is X.
Now, assume that
![]() $\mathrm {F}_1(X,x) \ne \varnothing $
. Then, by Theorem 5.1
(ii), the variety X is birational to a smooth Fano threefold
$\mathrm {F}_1(X,x) \ne \varnothing $
. Then, by Theorem 5.1
(ii), the variety X is birational to a smooth Fano threefold
![]() $X^+$
of type
$X^+$
of type
![]() $\mathsf {X}_{(2,2)}$
. Moreover, by the Nishimura lemma, we have
$\mathsf {X}_{(2,2)}$
. Moreover, by the Nishimura lemma, we have
![]() $X^+({\mathsf {k}}) \ne \varnothing $
. Therefore,
$X^+({\mathsf {k}}) \ne \varnothing $
. Therefore,
![]() $X^+$
is
$X^+$
is
![]() ${\mathsf {k}}$
-rational by Proposition 4.1, hence, so is X.
${\mathsf {k}}$
-rational by Proposition 4.1, hence, so is X.
6 Fano threefolds of type
 $\mathsf {X}_{(3,3)}$
$\mathsf {X}_{(3,3)}$
In this section, we prove that a Fano threefold X of type
![]() $\mathsf {X}_{(3,3)}$
is
$\mathsf {X}_{(3,3)}$
is
![]() ${\mathsf {k}}$
-unirational if
${\mathsf {k}}$
-unirational if
![]() $X({\mathsf {k}}) \ne \varnothing $
but not
$X({\mathsf {k}}) \ne \varnothing $
but not
![]() ${\mathsf {k}}$
-rational if
${\mathsf {k}}$
-rational if
![]() $\unicode{x3c1} (X) = 1$
.
$\unicode{x3c1} (X) = 1$
.
6.1 The discriminant curve
Let X be a Fano threefold of type
![]() $\mathsf {X}_{(3,3)}$
with
$\mathsf {X}_{(3,3)}$
with
![]() $X({\mathsf {k}}) \ne \varnothing $
. Recall from Lemma 2.5 that the image
$X({\mathsf {k}}) \ne \varnothing $
. Recall from Lemma 2.5 that the image
![]() ${\mathrm {G}}_X$
of the Galois group
${\mathrm {G}}_X$
of the Galois group
![]() ${\mathrm {G}}({\bar {\mathsf {k}}}/{\mathsf {k}})$
in
${\mathrm {G}}({\bar {\mathsf {k}}}/{\mathsf {k}})$
in
![]() $\operatorname {{\mathrm {Aut}}}(\operatorname {Pic}(X_{\bar {\mathsf {k}}}))$
is a group of order
$\operatorname {{\mathrm {Aut}}}(\operatorname {Pic}(X_{\bar {\mathsf {k}}}))$
is a group of order
![]() $2$
swapping the generators
$2$
swapping the generators
![]() $H_1$
and
$H_1$
and
![]() $H_2$
of
$H_2$
of
![]() $\operatorname {Pic}(X_{\bar {\mathsf {k}}})$
. The homomorphism
$\operatorname {Pic}(X_{\bar {\mathsf {k}}})$
. The homomorphism
![]() ${\mathrm {G}}({\bar {\mathsf {k}}}/{\mathsf {k}})\to {\mathrm {G}}_X$
, therefore, defines a quadratic extension
${\mathrm {G}}({\bar {\mathsf {k}}}/{\mathsf {k}})\to {\mathrm {G}}_X$
, therefore, defines a quadratic extension
![]() ${\mathsf {k}}'/{\mathsf {k}}$
, such that
${\mathsf {k}}'/{\mathsf {k}}$
, such that
![]() $H_1$
and
$H_1$
and
![]() $H_2$
are defined on
$H_2$
are defined on
![]() $X_{{\mathsf {k}}'}$
, hence,
$X_{{\mathsf {k}}'}$
, hence,
where
![]() $V_i$
are
$V_i$
are
![]() ${\mathsf {k}}'$
-vector spaces of dimension
${\mathsf {k}}'$
-vector spaces of dimension
![]() $4$
and
$4$
and
![]() $A \subset V_1^{\vee } \otimes V_2^{\vee }$
is the three-dimensional subspace of linear equations of
$A \subset V_1^{\vee } \otimes V_2^{\vee }$
is the three-dimensional subspace of linear equations of
![]() $X_{{\mathsf {k}}'}$
. Note that the
$X_{{\mathsf {k}}'}$
. Note that the
![]() ${\mathsf {k}}'$
-spaces
${\mathsf {k}}'$
-spaces
![]() $V_1 \otimes V_2$
and A are defined over
$V_1 \otimes V_2$
and A are defined over
![]() ${\mathsf {k}}$
, as well as the inclusion
${\mathsf {k}}$
, as well as the inclusion
![]() $A \subset V_1^{\vee } \otimes V_2^{\vee }$
. We think of vectors
$A \subset V_1^{\vee } \otimes V_2^{\vee }$
. We think of vectors
![]() $a \in A$
as bilinear forms on
$a \in A$
as bilinear forms on
![]() $V_1 \otimes V_2$
and denote by
$V_1 \otimes V_2$
and denote by
the discriminant curve parameterising degenerate bilinear forms; it is also defined over
![]() ${\mathsf {k}}$
.
${\mathsf {k}}$
.
Lemma 6.1. The curve
![]() $\Gamma $
is a smooth plane quartic curve; in particular, it is a nonhyperelliptic curve of genus
$\Gamma $
is a smooth plane quartic curve; in particular, it is a nonhyperelliptic curve of genus
![]() $3$
.
$3$
.
Proof. The discriminant divisor in
![]() $\mathbb {P}(V_1^{\vee } \otimes V_2^{\vee })$
, that is, the divisor parameterising degenerate bilinear forms, is a quartic hypersurface, hence,
$\mathbb {P}(V_1^{\vee } \otimes V_2^{\vee })$
, that is, the divisor parameterising degenerate bilinear forms, is a quartic hypersurface, hence,
![]() $\Gamma $
is a quartic curve or the entire plane. To prove that
$\Gamma $
is a quartic curve or the entire plane. To prove that
![]() $\Gamma $
is a smooth curve, we can work over
$\Gamma $
is a smooth curve, we can work over
![]() ${\mathsf {k}}'$
, and it is enough to show that the tangent space to
${\mathsf {k}}'$
, and it is enough to show that the tangent space to
![]() $\Gamma $
at any point is one-dimensional. Assume to the contrary, that the tangent space at a point
$\Gamma $
at any point is one-dimensional. Assume to the contrary, that the tangent space at a point
![]() $[a] \in \mathbb {P}(A)$
is two-dimensional; then
$[a] \in \mathbb {P}(A)$
is two-dimensional; then
-
(i) either the bilinear form
 $a(-,-) \in V_1^{\vee } \otimes V_2^{\vee }$
has corank at least
$a(-,-) \in V_1^{\vee } \otimes V_2^{\vee }$
has corank at least
 $2$
,
$2$
, -
(ii) or a has corank
 $1$
, and if the vectors
$1$
, and if the vectors
 $v_1 \in V_1$
and
$v_1 \in V_1$
and
 $v_2 \in V_2$
generate its left and right kernels, respectively, the point
$v_2 \in V_2$
generate its left and right kernels, respectively, the point
 $([v_1],[v_2]) \in \mathbb {P}(V_1) \times \mathbb {P}(V_2)$
belongs to
$([v_1],[v_2]) \in \mathbb {P}(V_1) \times \mathbb {P}(V_2)$
belongs to
 $X_{{\mathsf {k}}'}$
.
$X_{{\mathsf {k}}'}$
.
In case (i), if
![]() $K_1 \subset V_1$
and
$K_1 \subset V_1$
and
![]() $K_2 \subset V_2$
are the left and right kernels of a (they have dimension
$K_2 \subset V_2$
are the left and right kernels of a (they have dimension
![]() $\ge 2$
by assumption), then the form a vanishes on
$\ge 2$
by assumption), then the form a vanishes on
![]() $\mathbb {P}(K_1) \times \mathbb {P}(K_2)$
, hence, the intersection
$\mathbb {P}(K_1) \times \mathbb {P}(K_2)$
, hence, the intersection
![]() $\big (\mathbb {P}(K_1) \times \mathbb {P}(K_2)\big ) \cap X_{{\mathsf {k}}'}$
is a codimension-2 linear section of
$\big (\mathbb {P}(K_1) \times \mathbb {P}(K_2)\big ) \cap X_{{\mathsf {k}}'}$
is a codimension-2 linear section of
![]() $\mathbb {P}(K_1) \times \mathbb {P}(K_2)$
, hence, it is nonempty. Therefore, in case (i), similarly to the case (ii), there is a point
$\mathbb {P}(K_1) \times \mathbb {P}(K_2)$
, hence, it is nonempty. Therefore, in case (i), similarly to the case (ii), there is a point
![]() $([v_1],[v_2]) \in X_{{\mathsf {k}}'}$
, such that
$([v_1],[v_2]) \in X_{{\mathsf {k}}'}$
, such that
![]() $v_1$
and
$v_1$
and
![]() $v_2$
belong to the left and right kernels of some a. Then, the hyperplane section of
$v_2$
belong to the left and right kernels of some a. Then, the hyperplane section of
![]() $\mathbb {P}(V_1) \times \mathbb {P}(V_2)$
by the hyperplane corresponding to a is singular at
$\mathbb {P}(V_1) \times \mathbb {P}(V_2)$
by the hyperplane corresponding to a is singular at
![]() $([v_1],[v_2])$
, hence,
$([v_1],[v_2])$
, hence,
![]() $X_{{\mathsf {k}}'}$
is also singular at this point.
$X_{{\mathsf {k}}'}$
is also singular at this point.
As explained in Lemma 2.4
(iii), the projections
![]() $\pi _1 \colon X_{{\mathsf {k}}'} \to \mathbb {P}(V_1)$
and
$\pi _1 \colon X_{{\mathsf {k}}'} \to \mathbb {P}(V_1)$
and
![]() $\pi _2 \colon X_{{\mathsf {k}}'} \to \mathbb {P}(V_2)$
defined over
$\pi _2 \colon X_{{\mathsf {k}}'} \to \mathbb {P}(V_2)$
defined over
![]() ${\mathsf {k}}'$
, but not over
${\mathsf {k}}'$
, but not over
![]() ${\mathsf {k}}$
, are the blowups of smooth curves
${\mathsf {k}}$
, are the blowups of smooth curves
![]() $\Gamma _i\subset \mathbb {P}(V_i)$
of genus
$\Gamma _i\subset \mathbb {P}(V_i)$
of genus
![]() $3$
and degree
$3$
and degree
![]() $6$
also defined over
$6$
also defined over
![]() ${\mathsf {k}}'$
. The next lemma relates the
${\mathsf {k}}'$
. The next lemma relates the
![]() ${\mathsf {k}}'$
-curves
${\mathsf {k}}'$
-curves
![]() $\Gamma _i$
to the discriminant curve
$\Gamma _i$
to the discriminant curve
![]() $\Gamma $
defined over
$\Gamma $
defined over
![]() ${\mathsf {k}}$
.
${\mathsf {k}}$
.
Lemma 6.2. There is a natural isomorphism
![]() $\Gamma _i \cong \Gamma _{{\mathsf {k}}'}$
of curves over
$\Gamma _i \cong \Gamma _{{\mathsf {k}}'}$
of curves over
![]() ${\mathsf {k}}'$
.
${\mathsf {k}}'$
.
Proof. The fibre of the projection
![]() $\pi _1$
over a point
$\pi _1$
over a point
![]() $[v_1] \in \mathbb {P}(V_1)$
is the intersection of the projectivisations of the orthogonals of
$[v_1] \in \mathbb {P}(V_1)$
is the intersection of the projectivisations of the orthogonals of
![]() $v_1$
with respect to all bilinear forms
$v_1$
with respect to all bilinear forms
![]() $a \in A$
. Therefore, it has positive dimension if and only if
$a \in A$
. Therefore, it has positive dimension if and only if
![]() $v_1$
belongs to the left kernel of one of the forms. Furthermore, if
$v_1$
belongs to the left kernel of one of the forms. Furthermore, if
![]() $v_1$
belongs to the left kernel of two distinct forms in A, the fibre of
$v_1$
belongs to the left kernel of two distinct forms in A, the fibre of
![]() $\pi _1$
over
$\pi _1$
over
![]() $[v_1]$
contains a plane, which contradicts Corollary 2.6. This means that the morphism
$[v_1]$
contains a plane, which contradicts Corollary 2.6. This means that the morphism
where
![]() $\operatorname {{\mathrm {Ker}}}_1$
and
$\operatorname {{\mathrm {Ker}}}_1$
and
![]() $\operatorname {{\mathrm {Ker}}}_2$
denote the left and right kernels of the bilinear form a, respectively, is an isomorphism
$\operatorname {{\mathrm {Ker}}}_2$
denote the left and right kernels of the bilinear form a, respectively, is an isomorphism
![]() $\Gamma _{{\mathsf {k}}'} \to \Gamma _i$
.
$\Gamma _{{\mathsf {k}}'} \to \Gamma _i$
.
Remark 6.3. It is also easy to check that if
![]() $H_i\vert _{\Gamma }$
are the pullbacks of the hyperplane classes of
$H_i\vert _{\Gamma }$
are the pullbacks of the hyperplane classes of
![]() $\Gamma _i\subset \mathbb {P}(V_i)$
to
$\Gamma _i\subset \mathbb {P}(V_i)$
to
![]() $\Gamma _{{\mathsf {k}}'}$
under the isomorphism of Lemma 6.2, then
$\Gamma _{{\mathsf {k}}'}$
under the isomorphism of Lemma 6.2, then
![]() $H_1\vert _{\Gamma } + H_2\vert _{\Gamma } = 3K_{\Gamma }$
, and that the divisor classes
$H_1\vert _{\Gamma } + H_2\vert _{\Gamma } = 3K_{\Gamma }$
, and that the divisor classes
![]() $H_i\vert _{\Gamma } - K_{\Gamma }$
are noneffective and swapped by the
$H_i\vert _{\Gamma } - K_{\Gamma }$
are noneffective and swapped by the
![]() ${\mathrm {G}}({\mathsf {k}}'/{\mathsf {k}})$
-action. Conversely, given two such classes on a curve
${\mathrm {G}}({\mathsf {k}}'/{\mathsf {k}})$
-action. Conversely, given two such classes on a curve
![]() $\Gamma _{{\mathsf {k}}'}$
one can reconstruct the variety X.
$\Gamma _{{\mathsf {k}}'}$
one can reconstruct the variety X.
6.2 The double projection from a point
Recall the quadratic extension
![]() ${\mathsf {k}}'/{\mathsf {k}}$
defined in §6.1. Recall also the canonical embedding
${\mathsf {k}}'/{\mathsf {k}}$
defined in §6.1. Recall also the canonical embedding
![]() $X \subset Y$
, where Y is a
$X \subset Y$
, where Y is a
![]() ${\mathsf {k}}$
-form of
${\mathsf {k}}$
-form of
![]() $\mathbb {P}^3 \times \mathbb {P}^3$
. We consider the birational transformation of Theorem 3.1 for the variety
$\mathbb {P}^3 \times \mathbb {P}^3$
. We consider the birational transformation of Theorem 3.1 for the variety
![]() $Y_{{\mathsf {k}}'} = \mathbb {P}(V_1) \times \mathbb {P}(V_2)$
associated with a
$Y_{{\mathsf {k}}'} = \mathbb {P}(V_1) \times \mathbb {P}(V_2)$
associated with a
![]() ${\mathsf {k}}$
-point
${\mathsf {k}}$
-point
As in §3.1, we denote
![]() ${\bar {V}}_i := V_i / {\mathsf {k}}' v_i$
and choose a splitting
${\bar {V}}_i := V_i / {\mathsf {k}}' v_i$
and choose a splitting
![]() $V_i = {\mathsf {k}}' v_i \oplus \bar {V}_i$
. The transformation of Theorem 3.1 in this case looks as follows:
$V_i = {\mathsf {k}}' v_i \oplus \bar {V}_i$
. The transformation of Theorem 3.1 in this case looks as follows:

where
![]() $\sigma $
is the blowup of
$\sigma $
is the blowup of
![]() $x_0$
,
$x_0$
,
![]() $Y^+_{{\mathsf {k}}'} \cong \mathbb {P}(\bar {V}_1) \times \mathbb {P}(\bar {V}_2)$
,
$Y^+_{{\mathsf {k}}'} \cong \mathbb {P}(\bar {V}_1) \times \mathbb {P}(\bar {V}_2)$
,
![]() $\sigma _+$
is the projectivisation of the vector bundle
$\sigma _+$
is the projectivisation of the vector bundle
(here,
![]() $h_i$
stand for the hyperplane classes of
$h_i$
stand for the hyperplane classes of
![]() $\mathbb {P}({\bar {V}}_i)$
) over
$\mathbb {P}({\bar {V}}_i)$
) over
![]() $Y^+_{{\mathsf {k}}'}$
and the map
$Y^+_{{\mathsf {k}}'}$
and the map
![]() $\psi $
is a small birational isomorphism. Note that all varieties and maps in (6.2.1) are defined over
$\psi $
is a small birational isomorphism. Note that all varieties and maps in (6.2.1) are defined over
![]() ${\mathsf {k}}$
.
${\mathsf {k}}$
.
Recall also the relations (3.1.9) in
![]() $\operatorname {Pic}({\tilde {Y}}_{{\mathsf {k}}'}) = \operatorname {Pic}({\tilde {Y}}^+_{{\mathsf {k}}'})$
between the hyperplane classes
$\operatorname {Pic}({\tilde {Y}}_{{\mathsf {k}}'}) = \operatorname {Pic}({\tilde {Y}}^+_{{\mathsf {k}}'})$
between the hyperplane classes
![]() $H_i$
of the factors
$H_i$
of the factors
![]() $\mathbb {P}(V_i)$
of
$\mathbb {P}(V_i)$
of
![]() $Y_{{\mathsf {k}}'}$
, the class E of the exceptional divisor of
$Y_{{\mathsf {k}}'}$
, the class E of the exceptional divisor of
![]() $\sigma $
, the hyperplane classes
$\sigma $
, the hyperplane classes
![]() $h_i$
and the relative hyperplane class h of
$h_i$
and the relative hyperplane class h of
![]() ${\tilde {Y}}^+_{{\mathsf {k}}'} = \mathbb {P}_{Y^+_{{\mathsf {k}}'}}({\mathscr {E}})$
${\tilde {Y}}^+_{{\mathsf {k}}'} = \mathbb {P}_{Y^+_{{\mathsf {k}}'}}({\mathscr {E}})$
 $$ \begin{align} \begin{cases} h_1 = H_1 - E,\\ h_2 = H_2 - E,\\ h_{\phantom{2}} = H_1 + H_2 - E \end{cases} \qquad \begin{cases} {H_1} = h - h_2,\\ {H_2} = h - h_1,\\ {E} = h - h_1 - h_2. \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} h_1 = H_1 - E,\\ h_2 = H_2 - E,\\ h_{\phantom{2}} = H_1 + H_2 - E \end{cases} \qquad \begin{cases} {H_1} = h - h_2,\\ {H_2} = h - h_1,\\ {E} = h - h_1 - h_2. \end{cases} \end{align} $$
Since X is a smooth linear section of Y, containing the point
![]() $x_0$
, it is a complete intersection of three divisors
$x_0$
, it is a complete intersection of three divisors
![]() $D_{\alpha }$
,
$D_{\alpha }$
,
![]() $1 \le \alpha \le 3$
, in the linear system
$1 \le \alpha \le 3$
, in the linear system
![]() $|H_1 + H_2|$
, whose strict transforms on
$|H_1 + H_2|$
, whose strict transforms on
![]() ${\tilde {Y}}$
belong to the linear system
${\tilde {Y}}$
belong to the linear system
![]() $|H_1 + H_2 - E|$
. Now, it follows from (6.2.3) that their strict transforms
$|H_1 + H_2 - E|$
. Now, it follows from (6.2.3) that their strict transforms
![]() ${\tilde {D}}^+_{\alpha }$
on
${\tilde {D}}^+_{\alpha }$
on
![]() ${\tilde {Y}}^+$
belong to the linear system
${\tilde {Y}}^+$
belong to the linear system
![]() $|h|$
. As in Proposition 3.5, we consider the complete intersection
$|h|$
. As in Proposition 3.5, we consider the complete intersection
It follows that
![]() ${\tilde {X}}^+_{{\mathsf {k}}'}$
is determined by a morphism of vector bundles
${\tilde {X}}^+_{{\mathsf {k}}'}$
is determined by a morphism of vector bundles
and if we choose a basis
![]() $a_1,a_2,a_3$
in A, it is easy to see that
$a_1,a_2,a_3$
in A, it is easy to see that
![]() $\xi $
is given by the matrix
$\xi $
is given by the matrix
 $$ \begin{align} \xi = \begin{pmatrix} \bar{a}_1(-,-) & a_1(-,v_2) & a_1(v_1,-) \\ \bar{a}_2(-,-) & a_2(-,v_2) & a_2(v_1,-) \\ \bar{a}_3(-,-) & a_3(-,v_2) & a_3(v_1,-) \end{pmatrix}, \end{align} $$
$$ \begin{align} \xi = \begin{pmatrix} \bar{a}_1(-,-) & a_1(-,v_2) & a_1(v_1,-) \\ \bar{a}_2(-,-) & a_2(-,v_2) & a_2(v_1,-) \\ \bar{a}_3(-,-) & a_3(-,v_2) & a_3(v_1,-) \end{pmatrix}, \end{align} $$
where
![]() $\bar {a}_i \in \bar {V}_1^{\vee } \otimes \bar {V}_2^{\vee }$
denotes the restriction of the bilinear form
$\bar {a}_i \in \bar {V}_1^{\vee } \otimes \bar {V}_2^{\vee }$
denotes the restriction of the bilinear form
![]() $a_i$
to
$a_i$
to
![]() $\bar {V}_1 \otimes \bar {V}_2$
, while
$\bar {V}_1 \otimes \bar {V}_2$
, while
![]() $a_i(-,v_2)\in V_1^{\vee }$
and
$a_i(-,v_2)\in V_1^{\vee }$
and
![]() $a_i(v_1,-)\in V_2^{\vee }$
are considered as linear functions on
$a_i(v_1,-)\in V_2^{\vee }$
are considered as linear functions on
![]() $\bar {V}_1$
and
$\bar {V}_1$
and
![]() $\bar {V}_2$
, respectively.
$\bar {V}_2$
, respectively.
Proposition 6.4. The threefold X is
![]() ${\mathsf {k}}$
-birational to the
${\mathsf {k}}$
-birational to the
![]() ${\mathsf {k}}$
-form
${\mathsf {k}}$
-form
![]() ${\tilde {X}}^+$
of the threefold
${\tilde {X}}^+$
of the threefold
![]() ${\tilde {X}}^+_{{\mathsf {k}}'}$
defined by (6.2.4) and to a
${\tilde {X}}^+_{{\mathsf {k}}'}$
defined by (6.2.4) and to a
![]() ${\mathsf {k}}$
-form
${\mathsf {k}}$
-form
![]() $X^+$
of its image in
$X^+$
of its image in
![]() $Y^+$
$Y^+$
which is a geometrically irreducible and normal divisor of bidegree
![]() $(2,2)$
. Moreover,
$(2,2)$
. Moreover,
-
• if
 $\mathrm {F}_1(X,x_0) = \varnothing $
, then the variety
$\mathrm {F}_1(X,x_0) = \varnothing $
, then the variety
 ${\tilde {X}}^+ \cong {\tilde {X}} = \operatorname {{\mathrm {Bl}}}_x(X)$
is smooth, the morphism
${\tilde {X}}^+ \cong {\tilde {X}} = \operatorname {{\mathrm {Bl}}}_x(X)$
is smooth, the morphism
 $\sigma _+ \colon {\tilde {X}}^+ \to X^+$
is induced by the double projection from
$\sigma _+ \colon {\tilde {X}}^+ \to X^+$
is induced by the double projection from
 $x_0$
and it is a small resolution of singularities;
$x_0$
and it is a small resolution of singularities; -
• if
 $\mathrm {F}_1(X,x_0) \ne \varnothing $
, then the variety
$\mathrm {F}_1(X,x_0) \ne \varnothing $
, then the variety
 $X^+$
contains a
$X^+$
contains a
 ${\mathsf {k}}$
-form of a quadric surface
${\mathsf {k}}$
-form of a quadric surface
 $\mathbb {P}^1 \times \mathbb {P}^1 \subset \mathbb {P}(\bar {V}_1) \times \mathbb {P}(\bar {V}_2)$
rational over
$\mathbb {P}^1 \times \mathbb {P}^1 \subset \mathbb {P}(\bar {V}_1) \times \mathbb {P}(\bar {V}_2)$
rational over
 ${\mathsf {k}}$
.
${\mathsf {k}}$
.
Proof. To prove birationality of
![]() ${\tilde {X}}$
and
${\tilde {X}}$
and
![]() ${\tilde {X}}^+ = \psi _*({\tilde {X}})$
, we apply Proposition 3.5, so we need to verify the dimension conditions (3.2.1). We have
${\tilde {X}}^+ = \psi _*({\tilde {X}})$
, we apply Proposition 3.5, so we need to verify the dimension conditions (3.2.1). We have
![]() $(Y_1)_{{\mathsf {k}}'} = [v_1] \times \mathbb {P}(V_2)$
, hence
$(Y_1)_{{\mathsf {k}}'} = [v_1] \times \mathbb {P}(V_2)$
, hence
is a fibre of the projection
![]() $\pi _1 \colon X_{{\mathsf {k}}'} \to \mathbb {P}(V_1)$
. By Lemma 2.4, it is a point or a line. A similar argument for
$\pi _1 \colon X_{{\mathsf {k}}'} \to \mathbb {P}(V_1)$
. By Lemma 2.4, it is a point or a line. A similar argument for
![]() $X_{{\mathsf {k}}'} \cap (Y_2)_{{\mathsf {k}}'}$
shows that the first part of (3.2.1) holds. Moreover, this argument also shows that in the case
$X_{{\mathsf {k}}'} \cap (Y_2)_{{\mathsf {k}}'}$
shows that the first part of (3.2.1) holds. Moreover, this argument also shows that in the case
![]() $\mathrm {F}_1(X,x_0) = \varnothing $
, the blowup
$\mathrm {F}_1(X,x_0) = \varnothing $
, the blowup
![]() ${\tilde {X}}_{{\mathsf {k}}'}$
of
${\tilde {X}}_{{\mathsf {k}}'}$
of
![]() $X_{{\mathsf {k}}'}$
has an empty intersection with the indeterminacy locus
$X_{{\mathsf {k}}'}$
has an empty intersection with the indeterminacy locus
![]() $({\tilde {Y}}_1)_{{\mathsf {k}}'} \sqcup ({\tilde {Y}}_2)_{{\mathsf {k}}'}$
of the map
$({\tilde {Y}}_1)_{{\mathsf {k}}'} \sqcup ({\tilde {Y}}_2)_{{\mathsf {k}}'}$
of the map
![]() $\psi $
.
$\psi $
.
On the other hand, the subbundle
![]() $\bar {{\mathscr {E}}}_1 \subset {\mathscr {E}}$
is just the summand
$\bar {{\mathscr {E}}}_1 \subset {\mathscr {E}}$
is just the summand
![]() ${\mathscr {O}}(-h_2)$
in (6.2.2), hence, the corresponding intersection
${\mathscr {O}}(-h_2)$
in (6.2.2), hence, the corresponding intersection
![]() ${\tilde {X}}^+_{{\mathsf {k}}'} \cap \mathbb {P}_{Y^+_{{\mathsf {k}}'}}(\bar {{\mathscr {E}}}_1)$
is the zero locus of the morphism
${\tilde {X}}^+_{{\mathsf {k}}'} \cap \mathbb {P}_{Y^+_{{\mathsf {k}}'}}(\bar {{\mathscr {E}}}_1)$
is the zero locus of the morphism
given by the last column of (6.2.4). It is easy to see that this is empty, if
![]() $\mathrm {F}_1(X,x_0) = \varnothing $
, or isomorphic to a line otherwise. A similar argument works for
$\mathrm {F}_1(X,x_0) = \varnothing $
, or isomorphic to a line otherwise. A similar argument works for
![]() ${\tilde {X}}^+_{{\mathsf {k}}'} \cap \mathbb {P}_{Y^+_{{\mathsf {k}}'}}(\bar {{\mathscr {E}}}_2)$
; therefore, the second part of (3.2.1) also holds. This proves that
${\tilde {X}}^+_{{\mathsf {k}}'} \cap \mathbb {P}_{Y^+_{{\mathsf {k}}'}}(\bar {{\mathscr {E}}}_2)$
; therefore, the second part of (3.2.1) also holds. This proves that
![]() ${\tilde {X}}^+ = \psi _*({\tilde {X}})$
is a
${\tilde {X}}^+ = \psi _*({\tilde {X}})$
is a
![]() ${\mathsf {k}}$
-form of
${\mathsf {k}}$
-form of
![]() ${\tilde {X}}^+_{{\mathsf {k}}'}$
, it is
${\tilde {X}}^+_{{\mathsf {k}}'}$
, it is
![]() ${\mathsf {k}}$
-birational to X, and if
${\mathsf {k}}$
-birational to X, and if
![]() $\mathrm {F}_1(X,x_0) = \varnothing $
, it is isomorphic to
$\mathrm {F}_1(X,x_0) = \varnothing $
, it is isomorphic to
![]() ${\tilde {X}}$
, and, in particular, in this case, it is smooth.
${\tilde {X}}$
, and, in particular, in this case, it is smooth.
Now, we describe the image of
![]() ${\tilde {X}}^+$
in
${\tilde {X}}^+$
in
![]() $Y^+$
. By definition,
$Y^+$
. By definition,
![]() ${\tilde {X}}^+_{{\mathsf {k}}'}$
parameterises points in the projectivisations of kernel spaces of
${\tilde {X}}^+_{{\mathsf {k}}'}$
parameterises points in the projectivisations of kernel spaces of
![]() $\xi $
; therefore, its image in
$\xi $
; therefore, its image in
![]() $Y^+_{{\mathsf {k}}'} = \mathbb {P}(\bar {V}_1) \times \mathbb {P}(\bar {V}_2)$
is the degeneracy locus
$Y^+_{{\mathsf {k}}'} = \mathbb {P}(\bar {V}_1) \times \mathbb {P}(\bar {V}_2)$
is the degeneracy locus
![]() $X^+_{{\mathsf {k}}'}$
of
$X^+_{{\mathsf {k}}'}$
of
![]() $\xi $
, which is, of course, given by the equation
$\xi $
, which is, of course, given by the equation
![]() $\det (\xi ) = 0$
. Since
$\det (\xi ) = 0$
. Since
![]() $\det ({\mathscr {E}}) \cong {\mathscr {O}}(-2h_1 - 2h_2)$
by (6.2.2), this is a divisor of bidegree
$\det ({\mathscr {E}}) \cong {\mathscr {O}}(-2h_1 - 2h_2)$
by (6.2.2), this is a divisor of bidegree
![]() $(2,2)$
, which is geometrically irreducible because
$(2,2)$
, which is geometrically irreducible because
![]() ${\tilde {X}}^+_{{\mathsf {k}}'}$
is. Moreover, fibres of the morphism
${\tilde {X}}^+_{{\mathsf {k}}'}$
is. Moreover, fibres of the morphism
![]() $\sigma _+ \colon {\tilde {X}}^+_{{\mathsf {k}}'} \to X^+_{{\mathsf {k}}'}$
are linear spaces, so, since both the source and the target are three-dimensional, the morphism is birational. To prove that
$\sigma _+ \colon {\tilde {X}}^+_{{\mathsf {k}}'} \to X^+_{{\mathsf {k}}'}$
are linear spaces, so, since both the source and the target are three-dimensional, the morphism is birational. To prove that
![]() $X^+_{\bar {\mathsf {k}}}$
is normal, we consider the Koszul resolution
$X^+_{\bar {\mathsf {k}}}$
is normal, we consider the Koszul resolution
 $$ \begin{align*} 0 &\longrightarrow {\mathscr{O}}_{\mathbb{P}_{Y^+_{\bar{\mathsf{k}}}}(-{\mathscr{E}})}(-3h) \longrightarrow {\mathscr{O}}_{\mathbb{P}_{Y^+_{\bar{\mathsf{k}}}}(-{\mathscr{E}})}(-2h)^{\oplus 3} \\&\longrightarrow {\mathscr{O}}_{\mathbb{P}_{Y^+_{\bar{\mathsf{k}}}}(-{\mathscr{E}})}(-h)^{\oplus 3} \longrightarrow {\mathscr{O}}_{\mathbb{P}_{Y^+_{\bar{\mathsf{k}}}}(-{\mathscr{E}})} \longrightarrow {\mathscr{O}}_{{\tilde{X}}^+_{\bar{\mathsf{k}}}} \longrightarrow 0. \end{align*} $$
$$ \begin{align*} 0 &\longrightarrow {\mathscr{O}}_{\mathbb{P}_{Y^+_{\bar{\mathsf{k}}}}(-{\mathscr{E}})}(-3h) \longrightarrow {\mathscr{O}}_{\mathbb{P}_{Y^+_{\bar{\mathsf{k}}}}(-{\mathscr{E}})}(-2h)^{\oplus 3} \\&\longrightarrow {\mathscr{O}}_{\mathbb{P}_{Y^+_{\bar{\mathsf{k}}}}(-{\mathscr{E}})}(-h)^{\oplus 3} \longrightarrow {\mathscr{O}}_{\mathbb{P}_{Y^+_{\bar{\mathsf{k}}}}(-{\mathscr{E}})} \longrightarrow {\mathscr{O}}_{{\tilde{X}}^+_{\bar{\mathsf{k}}}} \longrightarrow 0. \end{align*} $$
Pushing it forward to
![]() $Y^+_{\bar {\mathsf {k}}}$
, we obtain the following exact sequence
$Y^+_{\bar {\mathsf {k}}}$
, we obtain the following exact sequence
It follows that
![]() $\sigma _{+*}{\mathscr {O}}_{{\tilde {X}}^+_{\bar {\mathsf {k}}}} \cong {\mathscr {O}}_{X^+_{\bar {\mathsf {k}}}}$
, and since
$\sigma _{+*}{\mathscr {O}}_{{\tilde {X}}^+_{\bar {\mathsf {k}}}} \cong {\mathscr {O}}_{X^+_{\bar {\mathsf {k}}}}$
, and since
![]() ${\tilde {X}}^+_{\bar {\mathsf {k}}}$
is normal, so is
${\tilde {X}}^+_{\bar {\mathsf {k}}}$
is normal, so is
![]() $X^+_{\bar {\mathsf {k}}}$
.
$X^+_{\bar {\mathsf {k}}}$
.
Now, assume
![]() $\mathrm {F}_1(X,x_0) = \varnothing $
. In this case, the pullback along the morphism
$\mathrm {F}_1(X,x_0) = \varnothing $
. In this case, the pullback along the morphism
![]() $\sigma _+$
of the ample divisor class
$\sigma _+$
of the ample divisor class
![]() $h_1 + h_2$
on
$h_1 + h_2$
on
![]() $\mathbb {P}(\bar {V}_1) \times \mathbb {P}(\bar {V}_2)$
by (6.2.3) equals
$\mathbb {P}(\bar {V}_1) \times \mathbb {P}(\bar {V}_2)$
by (6.2.3) equals
![]() $H_1 + H_2 - 2E$
, the anticanonical class of
$H_1 + H_2 - 2E$
, the anticanonical class of
![]() ${\tilde {X}}^+ \cong {\tilde {X}}$
, hence, the morphism
${\tilde {X}}^+ \cong {\tilde {X}}$
, hence, the morphism
![]() $\sigma _+$
is the double projection from the point
$\sigma _+$
is the double projection from the point
![]() $x_0$
. Consequently, it is small by the argument of [Reference Kuznetsov and Prokhorov10, Theorem 5.17]. Indeed, by [Reference Kuznetsov and Prokhorov10, Lemma 5.4(iii)], we have
$x_0$
. Consequently, it is small by the argument of [Reference Kuznetsov and Prokhorov10, Theorem 5.17]. Indeed, by [Reference Kuznetsov and Prokhorov10, Lemma 5.4(iii)], we have
![]() $\dim |H_1 + H_2 - 3E| \ge g - 9 = 2$
(recall that
$\dim |H_1 + H_2 - 3E| \ge g - 9 = 2$
(recall that
![]() $g = {\mathrm {g}}(X) = 11$
, see Table 1), hence, by [Reference Kuznetsov and Prokhorov10, Lemma 5.7(ii)], any divisor D contracted by
$g = {\mathrm {g}}(X) = 11$
, see Table 1), hence, by [Reference Kuznetsov and Prokhorov10, Lemma 5.7(ii)], any divisor D contracted by
![]() $\sigma _+$
must be a fixed component of
$\sigma _+$
must be a fixed component of
![]() $|H_1 + H_2 - 3E|$
, and at the same time by [Reference Kuznetsov and Prokhorov10, (5.1.8)], its class should be a multiple of
$|H_1 + H_2 - 3E|$
, and at the same time by [Reference Kuznetsov and Prokhorov10, (5.1.8)], its class should be a multiple of
![]() $H_1 + H_2 - 5E$
, and these two conclusions are incompatible.
$H_1 + H_2 - 5E$
, and these two conclusions are incompatible.
Finally, assume that
![]() $\mathrm {F}_1(X,x_0) \ne \varnothing $
. As it was explained in Lemma 6.2, this means that (for appropriate
$\mathrm {F}_1(X,x_0) \ne \varnothing $
. As it was explained in Lemma 6.2, this means that (for appropriate
![]() ${\mathsf {k}}'$
-basis in A) we have
${\mathsf {k}}'$
-basis in A) we have
as linear functions on
![]() $\bar {V_2}$
and
$\bar {V_2}$
and
![]() $\bar {V}_1$
, respectively; moreover,
$\bar {V}_1$
, respectively; moreover,
![]() $[a_1],[a_2] \in \mathbb {P}(A)$
as above are unique and swapped by the Galois action. Consider the surface
$[a_1],[a_2] \in \mathbb {P}(A)$
as above are unique and swapped by the Galois action. Consider the surface
(isomorphic to
![]() $\mathbb {P}^1_{{\mathsf {k}}'} \times \mathbb {P}^1_{{\mathsf {k}}'}$
). The equations defining it are Galois-conjugate, hence, it comes from a
$\mathbb {P}^1_{{\mathsf {k}}'} \times \mathbb {P}^1_{{\mathsf {k}}'}$
). The equations defining it are Galois-conjugate, hence, it comes from a
![]() ${\mathsf {k}}$
-surface in
${\mathsf {k}}$
-surface in
![]() $Y^+$
. This surface is the image of the exceptional divisor E of
$Y^+$
. This surface is the image of the exceptional divisor E of
![]() $\sigma $
, hence, it is
$\sigma $
, hence, it is
![]() ${\mathsf {k}}$
-rational. It is clear from (6.2.4) that this surface is contained in the degeneracy locus
${\mathsf {k}}$
-rational. It is clear from (6.2.4) that this surface is contained in the degeneracy locus
![]() $X^+$
of
$X^+$
of
![]() $\xi $
.
$\xi $
.
6.3 A conic bundle structure
In this section, we work under the assumption
![]() $\mathrm {F}_1(X,x_0) = \varnothing $
and show that, in this case, X admits a nice conic bundle structure.
$\mathrm {F}_1(X,x_0) = \varnothing $
and show that, in this case, X admits a nice conic bundle structure.
We will need a general result about what we call Springer resolutions. Let M be a variety, let
![]() $\xi \colon {\mathscr {E}}_1 \to {\mathscr {E}}_2^{\vee }$
be a morphism of vector bundles on M of the same rank and let
$\xi \colon {\mathscr {E}}_1 \to {\mathscr {E}}_2^{\vee }$
be a morphism of vector bundles on M of the same rank and let
![]() $\xi ^{\vee } \colon {\mathscr {E}}_2 \to {\mathscr {E}}_1^{\vee }$
be its dual morphism. Assume the degeneracy locus
$\xi ^{\vee } \colon {\mathscr {E}}_2 \to {\mathscr {E}}_1^{\vee }$
be its dual morphism. Assume the degeneracy locus
![]() $Z \subset M$
of
$Z \subset M$
of
![]() $\xi $
is a geometrically integral divisor. Let
$\xi $
is a geometrically integral divisor. Let
![]() $Z_1 \subset \mathbb {P}_M({\mathscr {E}}_1)$
and
$Z_1 \subset \mathbb {P}_M({\mathscr {E}}_1)$
and
![]() $Z_2 \subset \mathbb {P}_M({\mathscr {E}}_2)$
be the zero loci of the morphisms
$Z_2 \subset \mathbb {P}_M({\mathscr {E}}_2)$
be the zero loci of the morphisms
where
![]() $p_i \colon \mathbb {P}_M({\mathscr {E}}_i) \to M$
are the projections,
$p_i \colon \mathbb {P}_M({\mathscr {E}}_i) \to M$
are the projections,
![]() $h_{{\mathscr {E}}_i}$
are their relative hyperplane classes and the first arrows are the tautological embeddings.
$h_{{\mathscr {E}}_i}$
are their relative hyperplane classes and the first arrows are the tautological embeddings.
Lemma 6.5. If one of the morphisms
is birational, then so is the other. Moreover, if one of them is small, then so is the other, and there is an equality
in the group
![]() $\operatorname {{\mathrm {Cl}}}(Z_1) \cong \operatorname {{\mathrm {Cl}}}(Z) \cong \operatorname {{\mathrm {Cl}}}(Z_2)$
, where the isomorphisms of the class groups are induced by the small birational morphisms
$\operatorname {{\mathrm {Cl}}}(Z_1) \cong \operatorname {{\mathrm {Cl}}}(Z) \cong \operatorname {{\mathrm {Cl}}}(Z_2)$
, where the isomorphisms of the class groups are induced by the small birational morphisms
![]() $p_i$
.
$p_i$
.
Proof. Let
![]() $Z^{\ge c} \subset Z$
be the locus of points where the corank of
$Z^{\ge c} \subset Z$
be the locus of points where the corank of
![]() $\xi $
is at least c (so that
$\xi $
is at least c (so that
![]() $Z = Z^{\ge 1}$
). Then, both morphisms
$Z = Z^{\ge 1}$
). Then, both morphisms
![]() $p_i\vert _{Z_i}$
are
$p_i\vert _{Z_i}$
are
![]() $\mathbb {P}^{c-1}$
-fibrations over
$\mathbb {P}^{c-1}$
-fibrations over
![]() $Z^{\ge c} \setminus Z^{\ge c + 1}$
. In particular, if one of the morphisms is birational, then
$Z^{\ge c} \setminus Z^{\ge c + 1}$
. In particular, if one of the morphisms is birational, then
![]() $\dim Z^{\ge c} \le \dim Z - c$
for
$\dim Z^{\ge c} \le \dim Z - c$
for
![]() $c \ge 2$
, and then the other morphism is also birational. Similarly, if one of the morphisms is small, then
$c \ge 2$
, and then the other morphism is also birational. Similarly, if one of the morphisms is small, then
![]() $\dim Z^{\ge c} \le \dim Z - c - 1$
for
$\dim Z^{\ge c} \le \dim Z - c - 1$
for
![]() $c \ge 2$
, and then the other morphism is also small. Finally, assuming that the morphisms are small, we have
$c \ge 2$
, and then the other morphism is also small. Finally, assuming that the morphisms are small, we have
and when restricted to
![]() $Z \setminus Z^{\ge 2}$
, the morphism
$Z \setminus Z^{\ge 2}$
, the morphism
![]() $\xi $
has constant corank
$\xi $
has constant corank
![]() $1$
, the summands in (6.3.1) are equal to
$1$
, the summands in (6.3.1) are equal to
![]() ${\mathrm {c}}_1(\operatorname {{\mathrm {Im}}}(\xi ))$
and
${\mathrm {c}}_1(\operatorname {{\mathrm {Im}}}(\xi ))$
and
![]() ${\mathrm {c}}_1(\operatorname {{\mathrm {Im}}}(\xi ^{\vee }))$
(respectively) and (6.3.1) follows from the natural duality isomorphism
${\mathrm {c}}_1(\operatorname {{\mathrm {Im}}}(\xi ^{\vee }))$
(respectively) and (6.3.1) follows from the natural duality isomorphism
![]() $\operatorname {{\mathrm {Im}}}(\xi ^{\vee }) \cong \operatorname {{\mathrm {Im}}}(\xi )^{\vee }$
.
$\operatorname {{\mathrm {Im}}}(\xi ^{\vee }) \cong \operatorname {{\mathrm {Im}}}(\xi )^{\vee }$
.
Now, coming back to the threefold X of type
![]() $\mathsf {X}_{(3,3)}$
and assuming
$\mathsf {X}_{(3,3)}$
and assuming
![]() $\mathrm {F}_1(X,x_0) = \varnothing $
, we recall that the subvariety
$\mathrm {F}_1(X,x_0) = \varnothing $
, we recall that the subvariety
![]() $X^+ \subset Y^+$
is the degeneracy locus of
$X^+ \subset Y^+$
is the degeneracy locus of
![]() $\xi \colon {\mathscr {E}} \to A^{\vee } \otimes {\mathscr {O}}$
and note that
$\xi \colon {\mathscr {E}} \to A^{\vee } \otimes {\mathscr {O}}$
and note that
![]() ${\tilde {X}}^+ \subset \mathbb {P}_{Y^+}({\mathscr {E}})$
is one of its Springer resolutions. Consider the other Springer resolution
${\tilde {X}}^+ \subset \mathbb {P}_{Y^+}({\mathscr {E}})$
is one of its Springer resolutions. Consider the other Springer resolution
which, by definition, is the zero locus of the morphism
where
![]() $h_A$
is the hyperplane class of
$h_A$
is the hyperplane class of
![]() $\mathbb {P}(A)$
and we suppress the pullbacks in the notation. In view of (6.2.2), the scheme
$\mathbb {P}(A)$
and we suppress the pullbacks in the notation. In view of (6.2.2), the scheme
![]() $X_{{\mathsf {k}}'}^{+\!+}$
is just a complete intersection of divisors of types
$X_{{\mathsf {k}}'}^{+\!+}$
is just a complete intersection of divisors of types
![]() $h_1 + h_2 + h_A$
,
$h_1 + h_2 + h_A$
,
![]() $h_1 + h_A$
and
$h_1 + h_A$
and
![]() $h_2 + h_A$
in
$h_2 + h_A$
in
![]() $\mathbb {P}(\bar {V}_1) \times \mathbb {P}(\bar {V}_2) \times \mathbb {P}(A)$
that correspond to the columns of (6.2.4).
$\mathbb {P}(\bar {V}_1) \times \mathbb {P}(\bar {V}_2) \times \mathbb {P}(A)$
that correspond to the columns of (6.2.4).
Proposition 6.6. If
![]() $\mathrm {F}_1(X,x_0) = \varnothing $
, there is a commutative diagram defined over
$\mathrm {F}_1(X,x_0) = \varnothing $
, there is a commutative diagram defined over
![]() ${\mathsf {k}}$
${\mathsf {k}}$

where
![]() ${\tilde {X}}^+$
and
${\tilde {X}}^+$
and
![]() ${\tilde {X}}^{+\!+}$
are the Springer resolutions of the degeneracy locus
${\tilde {X}}^{+\!+}$
are the Springer resolutions of the degeneracy locus
![]() $X^+ \subset Y^+$
of
$X^+ \subset Y^+$
of
![]() $\xi $
, the morphisms
$\xi $
, the morphisms
![]() $\sigma _+$
and
$\sigma _+$
and
![]() $\sigma _{+\!+}$
are small birational contractions and
$\sigma _{+\!+}$
are small birational contractions and
![]() $\psi _+ = \sigma _{+\!+}^{-1} \circ \sigma _+$
is a flop.
$\psi _+ = \sigma _{+\!+}^{-1} \circ \sigma _+$
is a flop.
Moreover,
![]() ${\tilde {X}}^{+\!+}$
is smooth, f is a flat conic bundle whose discriminant curve is the curve
${\tilde {X}}^{+\!+}$
is smooth, f is a flat conic bundle whose discriminant curve is the curve
![]() $\Gamma $
defined in §6.1, the map
$\Gamma $
defined in §6.1, the map
![]() $f \circ \psi _+ \circ \psi \colon {\tilde {X}} \dashrightarrow \mathbb {P}(A)$
is given by the linear system
$f \circ \psi _+ \circ \psi \colon {\tilde {X}} \dashrightarrow \mathbb {P}(A)$
is given by the linear system
![]() $|H_1 + H_2 - 3E|$
and the exceptional divisor
$|H_1 + H_2 - 3E|$
and the exceptional divisor
![]() $E \subset {\tilde {X}}$
of
$E \subset {\tilde {X}}$
of
![]() $\sigma $
dominates
$\sigma $
dominates
![]() $\mathbb {P}(A)$
.
$\mathbb {P}(A)$
.
Proof. The morphism
![]() $\sigma _+$
is small by Proposition 6.4, hence,
$\sigma _+$
is small by Proposition 6.4, hence,
![]() $\sigma _{+\!+}$
is small by Lemma 6.5; moreover, it follows that both morphisms are crepant. Now, the relation (6.3.1) implies that the
$\sigma _{+\!+}$
is small by Lemma 6.5; moreover, it follows that both morphisms are crepant. Now, the relation (6.3.1) implies that the
![]() $\sigma _+$
-antiample class
$\sigma _+$
-antiample class
![]() $-h$
is
$-h$
is
![]() $\sigma _{+\!+}$
-ample, hence,
$\sigma _{+\!+}$
-ample, hence,
![]() $\psi _+ := \sigma _{+\!+}^{-1} \circ \sigma _+$
is a flop. Since
$\psi _+ := \sigma _{+\!+}^{-1} \circ \sigma _+$
is a flop. Since
![]() ${\tilde {X}}^+ \cong {\tilde {X}}$
is smooth and
${\tilde {X}}^+ \cong {\tilde {X}}$
is smooth and
![]() $\psi _+$
is a flop,
$\psi _+$
is a flop,
![]() ${\tilde {X}}^{+\!+}$
is smooth as well (see [Reference Kollár8, Theorem 2.4]).
${\tilde {X}}^{+\!+}$
is smooth as well (see [Reference Kollár8, Theorem 2.4]).
Next, we show that f is a conic bundle and identify its discriminant. For this, note that by definition, the fibre of f over a point
![]() $[a] \in \mathbb {P}(A)$
is given in
$[a] \in \mathbb {P}(A)$
is given in
![]() $\mathbb {P}(\bar {V}_1) \times \mathbb {P}(\bar {V}_2)$
by the equations
$\mathbb {P}(\bar {V}_1) \times \mathbb {P}(\bar {V}_2)$
by the equations
The first is a linear function on
![]() $\bar {V}_1$
, the second is a linear function on
$\bar {V}_1$
, the second is a linear function on
![]() $\bar {V}_2$
and both are nonzero because
$\bar {V}_2$
and both are nonzero because
![]() $\mathrm {F}_1(X,x_0) = \varnothing $
, so their common zero locus is
$\mathrm {F}_1(X,x_0) = \varnothing $
, so their common zero locus is
![]() $\mathbb {P}^1_{{\mathsf {k}'}} \times \mathbb {P}^1_{{\mathsf {k}'}} \subset \mathbb {P}(\bar {V}_1) \times \mathbb {P}(\bar {V}_2)$
. The last equation
$\mathbb {P}^1_{{\mathsf {k}'}} \times \mathbb {P}^1_{{\mathsf {k}'}} \subset \mathbb {P}(\bar {V}_1) \times \mathbb {P}(\bar {V}_2)$
. The last equation
![]() $\bar {a}(-,-) = 0$
cuts a divisor of bidegree
$\bar {a}(-,-) = 0$
cuts a divisor of bidegree
![]() $(1,1)$
on this
$(1,1)$
on this
![]() $\mathbb {P}^1_{{\mathsf {k}}'} \times \mathbb {P}^1_{{\mathsf {k}}'}$
, that is, a conic; and if
$\mathbb {P}^1_{{\mathsf {k}}'} \times \mathbb {P}^1_{{\mathsf {k}}'}$
, that is, a conic; and if
![]() $\bar {a}(-,-)$
vanishes identically, then the corresponding bilinear form a vanishes on
$\bar {a}(-,-)$
vanishes identically, then the corresponding bilinear form a vanishes on
![]() $\mathbb {P}^2_{{\mathsf {k}}'} \times \mathbb {P}^2_{ {\mathsf {k}}'} \subset \mathbb {P}(V_1) \times \mathbb {P}(V_2)$
, hence, has corank
$\mathbb {P}^2_{{\mathsf {k}}'} \times \mathbb {P}^2_{ {\mathsf {k}}'} \subset \mathbb {P}(V_1) \times \mathbb {P}(V_2)$
, hence, has corank
![]() $2$
, which is impossible by the argument of Lemma 6.1 as X is smooth. This shows that f is a flat conic bundle. Finally, note that if
$2$
, which is impossible by the argument of Lemma 6.1 as X is smooth. This shows that f is a flat conic bundle. Finally, note that if
![]() $\bar {v}^{\prime }_i$
,
$\bar {v}^{\prime }_i$
,
![]() $\bar {v}^{\prime \prime }_i$
,
$\bar {v}^{\prime \prime }_i$
,
![]() $\bar {v}^{\prime \prime \prime }_i$
are bases of vector spaces
$\bar {v}^{\prime \prime \prime }_i$
are bases of vector spaces
![]() $\bar {V}_i$
, such that,
$\bar {V}_i$
, such that,
then the matrix of a has the form
 $$ \begin{align*} \begin{pmatrix} 0 & 0 & 0 & a(v_1,\bar{v}^{\prime\prime\prime}_2) \\ 0 & \bar{a}(\bar{v}^{\prime}_1,\bar{v}^{\prime}_2) & \bar{a}(\bar{v}^{\prime}_1,\bar{v}^{\prime\prime}_2) & * \\ 0 & \bar{a}(\bar{v}^{\prime\prime}_1,\bar{v}^{\prime}_2) & \bar{a}(\bar{v}^{\prime\prime}_1,\bar{v}^{\prime\prime}_2) & * \\ a(\bar{v}^{\prime\prime\prime}_1,v_2) & * & * & * \end{pmatrix} \end{align*} $$
$$ \begin{align*} \begin{pmatrix} 0 & 0 & 0 & a(v_1,\bar{v}^{\prime\prime\prime}_2) \\ 0 & \bar{a}(\bar{v}^{\prime}_1,\bar{v}^{\prime}_2) & \bar{a}(\bar{v}^{\prime}_1,\bar{v}^{\prime\prime}_2) & * \\ 0 & \bar{a}(\bar{v}^{\prime\prime}_1,\bar{v}^{\prime}_2) & \bar{a}(\bar{v}^{\prime\prime}_1,\bar{v}^{\prime\prime}_2) & * \\ a(\bar{v}^{\prime\prime\prime}_1,v_2) & * & * & * \end{pmatrix} \end{align*} $$
with nonzero entries
![]() $a(v_1,\bar {v}^{\prime \prime \prime }_2)$
and
$a(v_1,\bar {v}^{\prime \prime \prime }_2)$
and
![]() $a(\bar {v}^{\prime \prime \prime }_1,v_2)$
and with the 2-by-2 matrix in the middle giving the equation of the conic
$a(\bar {v}^{\prime \prime \prime }_1,v_2)$
and with the 2-by-2 matrix in the middle giving the equation of the conic
![]() $f^{-1}(a)$
in
$f^{-1}(a)$
in
![]() $\mathbb {P}^1_{\bar {\mathsf {k}}} \times \mathbb {P}^1_{\bar {\mathsf {k}}}$
. Therefore, the conic is singular if and only if
$\mathbb {P}^1_{\bar {\mathsf {k}}} \times \mathbb {P}^1_{\bar {\mathsf {k}}}$
. Therefore, the conic is singular if and only if
![]() $\det (a) = 0$
, that is, if and only if
$\det (a) = 0$
, that is, if and only if
![]() $[a] \in \Gamma $
. Thus, the discriminant curve of f equals
$[a] \in \Gamma $
. Thus, the discriminant curve of f equals
![]() $\Gamma $
.
$\Gamma $
.
Finally, using (6.3.1), (6.2.2) and (6.2.3), we deduce that the map
![]() $f \circ \psi _+ \circ \psi $
is given by the linear system
$f \circ \psi _+ \circ \psi $
is given by the linear system
Since the canonical class of
![]() ${\tilde {X}}$
is equal to
${\tilde {X}}$
is equal to
![]() $H_1 + H_2 - 2E$
and
$H_1 + H_2 - 2E$
and
![]() $\psi _+$
is a flop, it follows that
$\psi _+$
is a flop, it follows that
![]() $\psi _*(E)$
is a relative anticanonical divisor for f, hence, it dominates
$\psi _*(E)$
is a relative anticanonical divisor for f, hence, it dominates
![]() $\mathbb {P}(A)$
.
$\mathbb {P}(A)$
.
If
![]() $f \colon {\mathscr {X}} \to S$
is a flat conic bundle over a surface S (not necessarily proper) with a smooth discriminant curve
$f \colon {\mathscr {X}} \to S$
is a flat conic bundle over a surface S (not necessarily proper) with a smooth discriminant curve
![]() $\Delta \subset S$
, consider the preimage
$\Delta \subset S$
, consider the preimage
![]() ${\mathscr {X}}_{\Delta } := f^{-1}(\Delta )$
, its normalisation
${\mathscr {X}}_{\Delta } := f^{-1}(\Delta )$
, its normalisation
![]() ${\mathscr {X}}_{\Delta }^{\nu } \to {\mathscr {X}}_{\Delta }$
and the Stein factorisation
${\mathscr {X}}_{\Delta }^{\nu } \to {\mathscr {X}}_{\Delta }$
and the Stein factorisation
Then, the first arrow is a
![]() $\mathbb {P}^1$
-bundle and the second arrow is an étale double covering (because
$\mathbb {P}^1$
-bundle and the second arrow is an étale double covering (because
![]() $\Delta $
was assumed to be smooth). We will say that the étale covering
$\Delta $
was assumed to be smooth). We will say that the étale covering
![]() $\tilde \Delta \to \Delta $
is the discriminant double covering of the conic bundle f.
$\tilde \Delta \to \Delta $
is the discriminant double covering of the conic bundle f.
Lemma 6.7. The discriminant double covering of the conic bundle
![]() $f \colon {\tilde {X}}^{+\!+} \to \mathbb {P}(A)$
has the form
$f \colon {\tilde {X}}^{+\!+} \to \mathbb {P}(A)$
has the form
Proof. If the conic
![]() $f^{-1}([a])$
is singular, it is a union of two irreducible components that correspond to the two factors
$f^{-1}([a])$
is singular, it is a union of two irreducible components that correspond to the two factors
![]() $\mathbb {P}(\bar {V}_i)$
in
$\mathbb {P}(\bar {V}_i)$
in
![]() $Y^+_{{\mathsf {k}}'}$
and each of them is contracted by appropriate projection
$Y^+_{{\mathsf {k}}'}$
and each of them is contracted by appropriate projection
![]() $Y^+_{{\mathsf {k}}'} \to \mathbb {P}(\bar {V}_i)$
. Therefore, the discriminant double covering
$Y^+_{{\mathsf {k}}'} \to \mathbb {P}(\bar {V}_i)$
. Therefore, the discriminant double covering
![]() $\tilde \Gamma \to \Gamma $
becomes trivial after the extension of scalars to
$\tilde \Gamma \to \Gamma $
becomes trivial after the extension of scalars to
![]() ${\mathsf {k}}'$
, while it is nontrivial over
${\mathsf {k}}'$
, while it is nontrivial over
![]() ${\mathsf {k}}$
, hence, the claim.
${\mathsf {k}}$
, hence, the claim.
6.4 Unirationality
In this section, we prove unirationality of X assuming that
![]() $X({\mathsf {k}}) \ne \varnothing $
. We start with the following observation, which might be useful in other situations.
$X({\mathsf {k}}) \ne \varnothing $
. We start with the following observation, which might be useful in other situations.
Lemma 6.8. Let Y be a
![]() ${\mathsf {k}}$
-form of
${\mathsf {k}}$
-form of
![]() $\mathbb {P}^2 \times \mathbb {P}^2$
, and let
$\mathbb {P}^2 \times \mathbb {P}^2$
, and let
![]() $W \subset Y$
be a
$W \subset Y$
be a
![]() ${\mathsf {k}}$
-rational
${\mathsf {k}}$
-rational
![]() ${\mathsf {k}}$
-form of a quadric surface
${\mathsf {k}}$
-form of a quadric surface
![]() $\mathbb {P}^1 \times \mathbb {P}^1 \subset \mathbb {P}^2 \times \mathbb {P}^2$
. Any geometrically irreducible normal divisor
$\mathbb {P}^1 \times \mathbb {P}^1 \subset \mathbb {P}^2 \times \mathbb {P}^2$
. Any geometrically irreducible normal divisor
![]() $Z \subset Y$
of bidegree
$Z \subset Y$
of bidegree
![]() $(2,2)$
, such that
$(2,2)$
, such that
![]() $W \subset Z$
is
$W \subset Z$
is
![]() ${\mathsf {k}}$
-unirational.
${\mathsf {k}}$
-unirational.
Proof. Consider the toric birational isomorphism

analogous to the birational transformation of Theorem 3.1 (see also [Reference Zak23, Proposition 3]). Here, the map
![]() $\chi $
is the projection from the linear span of W under the Segre embedding
$\chi $
is the projection from the linear span of W under the Segre embedding
![]() $\mathbb {P}^2 \times \mathbb {P}^2 \subset \mathbb {P}^8$
and the right arrow is the blowup of two skew lines in
$\mathbb {P}^2 \times \mathbb {P}^2 \subset \mathbb {P}^8$
and the right arrow is the blowup of two skew lines in
![]() $\mathbb {P}^4$
. Denoting by
$\mathbb {P}^4$
. Denoting by
![]() $\hat {e}$
the class of the exceptional divisor of the left blowup, by
$\hat {e}$
the class of the exceptional divisor of the left blowup, by
![]() $\hat {h}$
the hyperplane class of
$\hat {h}$
the hyperplane class of
![]() $\mathbb {P}^4$
and by
$\mathbb {P}^4$
and by
![]() $e_1$
and
$e_1$
and
![]() $e_2$
the classes of the exceptional divisors of the right blowup, it is easy to check that we have the relations
$e_2$
the classes of the exceptional divisors of the right blowup, it is easy to check that we have the relations
 $$ \begin{align*} \begin{cases} {\hat{h}} = h_1 + h_2 - \hat{e},\\ {e_1} = h_1 - \hat{e},\\ {e_2} = h_2 - \hat{e}, \end{cases} \qquad \text{and} \qquad \begin{cases} {h_1} = \hat{h} - e_2,\\ {h_2} = \hat{h} - e_1,\\ {\hat{e}} = \hat{h} - e_1 - e_2. \end{cases} \end{align*} $$
$$ \begin{align*} \begin{cases} {\hat{h}} = h_1 + h_2 - \hat{e},\\ {e_1} = h_1 - \hat{e},\\ {e_2} = h_2 - \hat{e}, \end{cases} \qquad \text{and} \qquad \begin{cases} {h_1} = \hat{h} - e_2,\\ {h_2} = \hat{h} - e_1,\\ {\hat{e}} = \hat{h} - e_1 - e_2. \end{cases} \end{align*} $$
In particular, the map
![]() $\chi $
is given by the linear system
$\chi $
is given by the linear system
![]() $|h_1 + h_2 - \hat {e}|$
, hence, it is defined over
$|h_1 + h_2 - \hat {e}|$
, hence, it is defined over
![]() ${\mathsf {k}}$
. Furthermore, we have
${\mathsf {k}}$
. Furthermore, we have
![]() $2h_1 + 2h_2 - \hat {e} = 3\hat {h} - e_1 - e_2$
, and since Z is normal, the strict transform of Z under the map
$2h_1 + 2h_2 - \hat {e} = 3\hat {h} - e_1 - e_2$
, and since Z is normal, the strict transform of Z under the map
![]() $\chi $
is a cubic threefold
$\chi $
is a cubic threefold
![]() $\hat {Z} \subset \mathbb {P}^4$
passing through the pair of skew lines
$\hat {Z} \subset \mathbb {P}^4$
passing through the pair of skew lines
![]() $\mathbb {P}^1 \sqcup \mathbb {P}^1$
. Moreover, we have
$\mathbb {P}^1 \sqcup \mathbb {P}^1$
. Moreover, we have
![]() $\hat {e} = \hat {h} - e_1 - e_2$
, hence, the image of
$\hat {e} = \hat {h} - e_1 - e_2$
, hence, the image of
![]() $\hat {E}$
is the hyperplane section of this cubic threefold (by the linear span of these lines). On the other hand,
$\hat {E}$
is the hyperplane section of this cubic threefold (by the linear span of these lines). On the other hand,
![]() $\hat {E}$
is birational to the
$\hat {E}$
is birational to the
![]() ${\mathsf {k}}$
-rational surface W, hence, it is
${\mathsf {k}}$
-rational surface W, hence, it is
![]() ${\mathsf {k}}$
-rational. In particular,
${\mathsf {k}}$
-rational. In particular,
![]() $\hat {Z}({\mathsf {k}}) \ne \varnothing $
.
$\hat {Z}({\mathsf {k}}) \ne \varnothing $
.
Now, if
![]() $\hat {Z}$
is not a cone, it is
$\hat {Z}$
is not a cone, it is
![]() ${\mathsf {k}}$
-unirational by Kollár’s theorem [Reference Kollár9, Theorem 1.2]. Otherwise, if
${\mathsf {k}}$
-unirational by Kollár’s theorem [Reference Kollár9, Theorem 1.2]. Otherwise, if
![]() $\hat {Z}$
is a cone, and its vertex lies away from the hyperplane spanned by the two skew lines, then the base of the cone is the
$\hat {Z}$
is a cone, and its vertex lies away from the hyperplane spanned by the two skew lines, then the base of the cone is the
![]() ${\mathsf {k}}$
-rational surface
${\mathsf {k}}$
-rational surface
![]() $\hat {E}$
, hence, the cone
$\hat {E}$
, hence, the cone
![]() $\hat {Z}$
is also
$\hat {Z}$
is also
![]() ${\mathsf {k}}$
-rational. Finally, if the vertex of the cone lies on
${\mathsf {k}}$
-rational. Finally, if the vertex of the cone lies on
![]() $\hat {E}$
, then
$\hat {E}$
, then
![]() $\hat {E}$
itself must be a cubic cone in
$\hat {E}$
itself must be a cubic cone in
![]() $\mathbb {P}^3$
, and since it also contains two skew lines, it is not geometrically irreducible, which is absurd.
$\mathbb {P}^3$
, and since it also contains two skew lines, it is not geometrically irreducible, which is absurd.
Now, we can deduce unirationality of X.
Proposition 6.9. If X is a Fano threefold of type
![]() $\mathsf {X}_{(3,3)}$
with
$\mathsf {X}_{(3,3)}$
with
![]() $X({\mathsf {k}}) \ne \varnothing $
, then X is
$X({\mathsf {k}}) \ne \varnothing $
, then X is
![]() ${\mathsf {k}}$
-unirational.
${\mathsf {k}}$
-unirational.
Proof. Let
![]() $x_0$
be a
$x_0$
be a
![]() ${\mathsf {k}}$
-point on X.
${\mathsf {k}}$
-point on X.
First, assume
![]() $\mathrm {F}_1(X,x_0) = \varnothing $
. By Proposition 6.6, we have a
$\mathrm {F}_1(X,x_0) = \varnothing $
. By Proposition 6.6, we have a
![]() ${\mathsf {k}}$
-birational map
${\mathsf {k}}$
-birational map
![]() $X\dashrightarrow {\tilde {X}}^{+\!+}$
, where
$X\dashrightarrow {\tilde {X}}^{+\!+}$
, where
![]() $f \colon {\tilde {X}}^{+\!+} \to \mathbb {P}(A)$
is a conic bundle, and the
$f \colon {\tilde {X}}^{+\!+} \to \mathbb {P}(A)$
is a conic bundle, and the
![]() ${\mathsf {k}}$
-rational surface
${\mathsf {k}}$
-rational surface
![]() $E \cong \mathbb {P}(T_{x_0}X) \subset {\tilde {X}}$
dominates the base of this conic bundle. Therefore,
$E \cong \mathbb {P}(T_{x_0}X) \subset {\tilde {X}}$
dominates the base of this conic bundle. Therefore,
![]() ${\tilde {X}}$
is
${\tilde {X}}$
is
![]() ${\mathsf {k}}$
-unirational (see, e.g. [Reference Kuznetsov and Prokhorov10, Lemma 4.14(i)]); and, hence, so is X.
${\mathsf {k}}$
-unirational (see, e.g. [Reference Kuznetsov and Prokhorov10, Lemma 4.14(i)]); and, hence, so is X.
Now, assume
![]() $\mathrm {F}_1(X,x_0) \ne \varnothing $
. By Proposition 6.4, we have a birational map
$\mathrm {F}_1(X,x_0) \ne \varnothing $
. By Proposition 6.4, we have a birational map
![]() $X\dashrightarrow X^+$
, where
$X\dashrightarrow X^+$
, where
![]() $X^+$
is a geometrically irreducible normal divisor of bidegree
$X^+$
is a geometrically irreducible normal divisor of bidegree
![]() $(2,2)$
in a
$(2,2)$
in a
![]() ${\mathsf {k}}$
-form of
${\mathsf {k}}$
-form of
![]() $\mathbb {P}^2 \times \mathbb {P}^2$
that contains a
$\mathbb {P}^2 \times \mathbb {P}^2$
that contains a
![]() ${\mathsf {k}}$
-form of a
${\mathsf {k}}$
-form of a
![]() ${\mathsf {k}}$
-rational quadric surface
${\mathsf {k}}$
-rational quadric surface
![]() $\mathbb {P}^1 \times \mathbb {P}^1$
. Therefore,
$\mathbb {P}^1 \times \mathbb {P}^1$
. Therefore,
![]() $X^+$
is
$X^+$
is
![]() ${\mathsf {k}}$
-unirational by Lemma 6.8, hence, so is X.
${\mathsf {k}}$
-unirational by Lemma 6.8, hence, so is X.
6.5 Nonrationality
In this section, we prove nonrationality of Fano threefolds of type
![]() $\mathsf {X}_{(3,3)}$
. We will use the following reformulation of a result of Benoist–Wittenberg from [Reference Benoist and Wittenberg3].
$\mathsf {X}_{(3,3)}$
. We will use the following reformulation of a result of Benoist–Wittenberg from [Reference Benoist and Wittenberg3].
Theorem 6.10. Let
![]() ${\mathscr {X}} \to S$
be a flat conic bundle over a smooth
${\mathscr {X}} \to S$
be a flat conic bundle over a smooth
![]() ${\mathsf {k}}$
-rational surface S with smooth connected discriminant curve
${\mathsf {k}}$
-rational surface S with smooth connected discriminant curve
![]() $\Delta \subset S$
. Assume the discriminant double covering takes the form
$\Delta \subset S$
. Assume the discriminant double covering takes the form
where
![]() ${\mathsf {k}}'/{\mathsf {k}}$
is a quadratic extension of the base field. If the conic bundle
${\mathsf {k}}'/{\mathsf {k}}$
is a quadratic extension of the base field. If the conic bundle
![]() ${\mathscr {X}}_{{\mathsf {k}}'} \to S_{{\mathsf {k}}'}$
admits a rational section, and the curve
${\mathscr {X}}_{{\mathsf {k}}'} \to S_{{\mathsf {k}}'}$
admits a rational section, and the curve
![]() $\Delta $
is not hyperelliptic, then
$\Delta $
is not hyperelliptic, then
![]() ${\mathscr {X}}$
is not
${\mathscr {X}}$
is not
![]() ${\mathsf {k}}$
-rational.
${\mathsf {k}}$
-rational.
Note that we require neither the surface S nor the curve
![]() $\Delta $
to be proper; moreover, during the proof, we will further shrink S but keep (the generic point of) the curve
$\Delta $
to be proper; moreover, during the proof, we will further shrink S but keep (the generic point of) the curve
![]() $\Delta $
in S.
$\Delta $
in S.
Proof. Since S is normal and f is proper, any rational section of f extends to codimension
![]() $1$
point, hence, defines a regular section over the complement of a finite subscheme of S. Moreover, over the complement of this finite subscheme, the section does not pass through singular points of fibres of f, hence, it defines a section of the morphism
$1$
point, hence, defines a regular section over the complement of a finite subscheme of S. Moreover, over the complement of this finite subscheme, the section does not pass through singular points of fibres of f, hence, it defines a section of the morphism
![]() ${\mathscr {X}}_{\Delta }^{\nu } \to \Delta $
, where recall that
${\mathscr {X}}_{\Delta }^{\nu } \to \Delta $
, where recall that
![]() ${\mathscr {X}}_{\Delta }^{\nu }$
is the normalisation of
${\mathscr {X}}_{\Delta }^{\nu }$
is the normalisation of
![]() ${\mathscr {X}}_{\Delta } = f^{-1}(\Delta )$
. Therefore, it also gives a section of the discriminant double covering
${\mathscr {X}}_{\Delta } = f^{-1}(\Delta )$
. Therefore, it also gives a section of the discriminant double covering
![]() $\tilde \Delta \to \Delta $
. If the original section is defined over
$\tilde \Delta \to \Delta $
. If the original section is defined over
![]() ${\mathsf {k}}$
, we obtain a contradiction with the isomorphism
${\mathsf {k}}$
, we obtain a contradiction with the isomorphism
![]() $\tilde \Delta \cong \Delta \times _{\mathsf {k}} {\mathsf {k}}'$
; this means that the morphism f has no rational sections defined over
$\tilde \Delta \cong \Delta \times _{\mathsf {k}} {\mathsf {k}}'$
; this means that the morphism f has no rational sections defined over
![]() ${\mathsf {k}}$
.
${\mathsf {k}}$
.
Now, consider a rational section of
![]() $f \colon {\mathscr {X}}_{{\mathsf {k}}'} \to S_{{\mathsf {k}}'}$
. Removing, if necessary, a finite subscheme from S, we may assume that this section is regular. Its intersection with the conjugate section (with respect to the
$f \colon {\mathscr {X}}_{{\mathsf {k}}'} \to S_{{\mathsf {k}}'}$
. Removing, if necessary, a finite subscheme from S, we may assume that this section is regular. Its intersection with the conjugate section (with respect to the
![]() ${\mathrm {G}}({\mathsf {k}}'/{\mathsf {k}})$
-action) projects to a curve in S which is disjoint from
${\mathrm {G}}({\mathsf {k}}'/{\mathsf {k}})$
-action) projects to a curve in S which is disjoint from
![]() $\Delta $
(because a regular section does not pass through singular points of fibres). So, shrinking S further, we may assume that the section and its conjugate do not intersect. Then the union
$\Delta $
(because a regular section does not pass through singular points of fibres). So, shrinking S further, we may assume that the section and its conjugate do not intersect. Then the union
of the section and its conjugate is a
![]() $2$
-section of f defined over
$2$
-section of f defined over
![]() ${\mathsf {k}}$
; moreover,
${\mathsf {k}}$
; moreover,
![]() $Z \cong S \times _{\mathsf {k}} {\mathsf {k}}'$
, and, in particular, Z is étale over S.
$Z \cong S \times _{\mathsf {k}} {\mathsf {k}}'$
, and, in particular, Z is étale over S.
Consider the bundles
![]() ${\mathscr {V}} := (f_*\omega _{\mathscr {X}}^{-1})^{\vee }$
of rank
${\mathscr {V}} := (f_*\omega _{\mathscr {X}}^{-1})^{\vee }$
of rank
![]() $3$
and
$3$
and
![]() ${\mathscr {V}}_Z := (f_*\omega _{\mathscr {X}}^{-1}\vert _Z)^{\vee }$
of rank
${\mathscr {V}}_Z := (f_*\omega _{\mathscr {X}}^{-1}\vert _Z)^{\vee }$
of rank
![]() $2$
on S. The restriction morphism
$2$
on S. The restriction morphism
![]() $\omega _{\mathscr {X}}^{-1} \to \omega _{\mathscr {X}}^{-1}\vert _Z$
induces an embedding of vector bundles
$\omega _{\mathscr {X}}^{-1} \to \omega _{\mathscr {X}}^{-1}\vert _Z$
induces an embedding of vector bundles
![]() ${\mathscr {V}}_Z \hookrightarrow {\mathscr {V}}$
and a Cartesian square
${\mathscr {V}}_Z \hookrightarrow {\mathscr {V}}$
and a Cartesian square

where all arrows are the natural embeddings.
Shrinking the surface S again but keeping an open part of the curve
![]() $\Delta $
in it, we may assume that the bundles
$\Delta $
in it, we may assume that the bundles
![]() ${\mathscr {V}}$
and
${\mathscr {V}}$
and
![]() ${\mathscr {V}}_Z$
are trivial, that the subvarieties
${\mathscr {V}}_Z$
are trivial, that the subvarieties
![]() ${\mathscr {X}} \subset \mathbb {P}_S({\mathscr {V}})$
and
${\mathscr {X}} \subset \mathbb {P}_S({\mathscr {V}})$
and
![]() $Z \subset \mathbb {P}_{S}({\mathscr {V}}_Z)$
are given by a quadratic form
$Z \subset \mathbb {P}_{S}({\mathscr {V}}_Z)$
are given by a quadratic form
![]() $q \in \operatorname {{\mathrm {Sym}}}^2{\mathscr {V}}^{\vee }$
and its restriction
$q \in \operatorname {{\mathrm {Sym}}}^2{\mathscr {V}}^{\vee }$
and its restriction
![]() $q_Z \in \operatorname {{\mathrm {Sym}}}^2{\mathscr {V}}_Z^{\vee }$
to
$q_Z \in \operatorname {{\mathrm {Sym}}}^2{\mathscr {V}}_Z^{\vee }$
to
![]() ${\mathscr {V}}_Z$
, respectively. Since Z is étale over S, the form
${\mathscr {V}}_Z$
, respectively. Since Z is étale over S, the form
![]() $q_Z$
is everywhere nondegenerate and can be written as follows:
$q_Z$
is everywhere nondegenerate and can be written as follows:
where
![]() $(x,y)$
are homogeneous coordinates in the fibre of
$(x,y)$
are homogeneous coordinates in the fibre of
![]() $\mathbb {P}_S({\mathscr {V}}_Z) \cong S \times \mathbb {P}^1$
and
$\mathbb {P}_S({\mathscr {V}}_Z) \cong S \times \mathbb {P}^1$
and
![]() $\alpha \in {\mathsf {k}}^{\times }$
is, such that
$\alpha \in {\mathsf {k}}^{\times }$
is, such that
![]() ${\mathsf {k}}' = {\mathsf {k}}(\sqrt {\alpha })$
. Now, considering the orthogonal complement to
${\mathsf {k}}' = {\mathsf {k}}(\sqrt {\alpha })$
. Now, considering the orthogonal complement to
![]() ${\mathscr {V}}_Z$
in
${\mathscr {V}}_Z$
in
![]() ${\mathscr {V}}$
, we see that q takes the form
${\mathscr {V}}$
, we see that q takes the form
where F is an equation of
![]() $\Delta $
on S. Thus, the conic bundle
$\Delta $
on S. Thus, the conic bundle
![]() ${\mathscr {X}} \to S$
is birational to conic bundles considered in [Reference Benoist and Wittenberg3, §3.3.1], hence,
${\mathscr {X}} \to S$
is birational to conic bundles considered in [Reference Benoist and Wittenberg3, §3.3.1], hence,
![]() ${\mathscr {X}}$
is not
${\mathscr {X}}$
is not
![]() ${\mathsf {k}}$
-rational by [Reference Benoist and Wittenberg3, Proposition 3.4].
${\mathsf {k}}$
-rational by [Reference Benoist and Wittenberg3, Proposition 3.4].
Now, we apply this to prove nonrationality of threefolds of type
![]() $\mathsf {X}_{(3,3)}$
.
$\mathsf {X}_{(3,3)}$
.
Corollary 6.11. If X is a Fano threefold of type
![]() $\mathsf {X}_{(3,3)}$
, then X is not
$\mathsf {X}_{(3,3)}$
, then X is not
![]() ${\mathsf {k}}$
-rational.
${\mathsf {k}}$
-rational.
Proof. If X is not
![]() ${\mathsf {k}}$
-unirational, there is nothing to prove. So, assume X is
${\mathsf {k}}$
-unirational, there is nothing to prove. So, assume X is
![]() ${\mathsf {k}}$
-unirational. Then, there exists a
${\mathsf {k}}$
-unirational. Then, there exists a
![]() ${\mathsf {k}}$
-point
${\mathsf {k}}$
-point
![]() $x_0 \in X$
, such that
$x_0 \in X$
, such that
![]() $\mathrm {F}_1(X,x_0) = \varnothing $
. Consider the conic bundle
$\mathrm {F}_1(X,x_0) = \varnothing $
. Consider the conic bundle
![]() ${\tilde {X}}^{+\!+} \to \mathbb {P}^2$
constructed in Proposition 6.6. By Lemma 6.1, the discriminant curve of f is the smooth nonhyperelliptic curve
${\tilde {X}}^{+\!+} \to \mathbb {P}^2$
constructed in Proposition 6.6. By Lemma 6.1, the discriminant curve of f is the smooth nonhyperelliptic curve
![]() $\Gamma $
defined in §6.1, and by Lemma 6.7, the discriminant double covering has the form
$\Gamma $
defined in §6.1, and by Lemma 6.7, the discriminant double covering has the form
![]() $\tilde \Gamma \cong \Gamma \times _{\mathsf {k}} {\mathsf {k}}'$
. Finally, the description of Proposition 6.6 shows that f admits a rational section after base change to
$\tilde \Gamma \cong \Gamma \times _{\mathsf {k}} {\mathsf {k}}'$
. Finally, the description of Proposition 6.6 shows that f admits a rational section after base change to
![]() ${\mathsf {k}}'$
. Therefore, Theorem 6.10 applies and proves that
${\mathsf {k}}'$
. Therefore, Theorem 6.10 applies and proves that
![]() ${\tilde {X}}^{+\!+}$
is not
${\tilde {X}}^{+\!+}$
is not
![]() ${\mathsf {k}}$
-rational, hence, X is not
${\mathsf {k}}$
-rational, hence, X is not
![]() ${\mathsf {k}}$
-rational as well.
${\mathsf {k}}$
-rational as well.
7 Fano threefolds of type
 $\mathsf {X}_{(1,1,1,1)}$
$\mathsf {X}_{(1,1,1,1)}$
In this section, we apply the degeneration technique of [Reference Nicaise and Shinder19] to prove Theorem 1.4.
7.1 Toric degeneration
To start with, we consider
![]() ${\mathrm {Y}}_0 = (\mathbb {P}^1)^4$
, denote by
${\mathrm {Y}}_0 = (\mathbb {P}^1)^4$
, denote by
![]() $(u_i:v_i)$
the homogeneous coordinates on the i-th factor and consider the point
$(u_i:v_i)$
the homogeneous coordinates on the i-th factor and consider the point
Clearly,
![]() ${\mathrm {Y}}_0$
is a toric variety with respect to the action of the split torus
${\mathrm {Y}}_0$
is a toric variety with respect to the action of the split torus
![]() $\mathbb {G}_{\mathrm {m}}^4$
that rescales the
$\mathbb {G}_{\mathrm {m}}^4$
that rescales the
![]() $v_i$
. We also consider the action of
$v_i$
. We also consider the action of
![]() $\mathfrak {S}_4$
on
$\mathfrak {S}_4$
on
![]() ${\mathrm {Y}}_0$
that permutes the factors. It normalises the torus action, and together they generate an action of the group
${\mathrm {Y}}_0$
that permutes the factors. It normalises the torus action, and together they generate an action of the group
![]() $\mathbb {G}_{\mathrm {m}}^4 \rtimes \mathfrak {S}_4$
. Finally, consider the subtorus
$\mathbb {G}_{\mathrm {m}}^4 \rtimes \mathfrak {S}_4$
. Finally, consider the subtorus
and the collection of three 1-parametric subgroups
where
![]() $(i_1,i_2)(i_3,i_4) \in \mathrm {V}_4 \setminus \{1\} \subset \mathfrak {S}_4$
is a nontrivial element of the Klein subgroup.
$(i_1,i_2)(i_3,i_4) \in \mathrm {V}_4 \setminus \{1\} \subset \mathfrak {S}_4$
is a nontrivial element of the Klein subgroup.
Lemma 7.1. The subvariety
is the unique
![]() ${\mathrm {T}}_0$
-invariant divisor of multidegree
${\mathrm {T}}_0$
-invariant divisor of multidegree
![]() $(1,1,1,1)$
in
$(1,1,1,1)$
in
![]() ${\mathrm {Y}}_0$
, which contains the point
${\mathrm {Y}}_0$
, which contains the point
![]() ${\mathrm {y}}_0$
. It is a toric variety with six ordinary double points
${\mathrm {y}}_0$
. It is a toric variety with six ordinary double points
For each permutation
![]() $(i_1,i_2)(i_3,i_4) \in \mathrm {V}_4 \setminus \{1\} \subset \mathfrak {S}_4$
the curve
$(i_1,i_2)(i_3,i_4) \in \mathrm {V}_4 \setminus \{1\} \subset \mathfrak {S}_4$
the curve
is a smooth rational curve and
![]() $\mathrm {C}_{i_1,i_2;i_3,i_4} \cap \operatorname {\mathrm {Sing}}({\mathrm {X}}_0^{\mathrm {toric}}) = \{ {\mathrm {x}}_{i_1,i_2}, {\mathrm {x}}_{i_3,i_4} \}$
.
$\mathrm {C}_{i_1,i_2;i_3,i_4} \cap \operatorname {\mathrm {Sing}}({\mathrm {X}}_0^{\mathrm {toric}}) = \{ {\mathrm {x}}_{i_1,i_2}, {\mathrm {x}}_{i_3,i_4} \}$
.
Proof. The monomial basis in the space of homogeneous polynomials of multidegree
![]() $(1,1,1,1)$
is a weight basis for the action of
$(1,1,1,1)$
is a weight basis for the action of
![]() ${\mathrm {T}}_0$
, and all weights are different except for the weight
${\mathrm {T}}_0$
, and all weights are different except for the weight
![]() $0$
, which has multiplicity 2 and the corresponding weight space is spanned by the monomials
$0$
, which has multiplicity 2 and the corresponding weight space is spanned by the monomials
![]() $u_1u_2u_3u_4$
and
$u_1u_2u_3u_4$
and
![]() $v_1v_2v_3v_4$
. Therefore, every
$v_1v_2v_3v_4$
. Therefore, every
![]() ${\mathrm {T}}_0$
-invariant divisor is either given by a monomial equation (but then it does not contain the point
${\mathrm {T}}_0$
-invariant divisor is either given by a monomial equation (but then it does not contain the point
![]() ${\mathrm {y}}_0$
) or by a linear combination of
${\mathrm {y}}_0$
) or by a linear combination of
![]() $u_1u_2u_3u_4$
and
$u_1u_2u_3u_4$
and
![]() $v_1v_2v_3v_4$
, and if it contains the point
$v_1v_2v_3v_4$
, and if it contains the point
![]() ${\mathrm {y}}_0$
, it is equal to
${\mathrm {y}}_0$
, it is equal to
![]() ${\mathrm {X}}_0^{\mathrm {toric}}$
. The latter is obviously a toric variety with respect to the natural action of
${\mathrm {X}}_0^{\mathrm {toric}}$
. The latter is obviously a toric variety with respect to the natural action of
![]() ${\mathrm {T}}_0$
.
${\mathrm {T}}_0$
.
In the affine chart
![]() $v_1 \ne 0$
,
$v_1 \ne 0$
,
![]() $v_2 \ne 0$
,
$v_2 \ne 0$
,
![]() $u_3 \ne 0$
,
$u_3 \ne 0$
,
![]() $u_4 \ne 0$
, we can set
$u_4 \ne 0$
, we can set
![]() $v_1 = v_2 = u_3 = u_4 = 1$
and use
$v_1 = v_2 = u_3 = u_4 = 1$
and use
![]() $u_1$
,
$u_1$
,
![]() $u_2$
,
$u_2$
,
![]() $v_3$
,
$v_3$
,
![]() $v_4$
as coordinates. Then, the equation of
$v_4$
as coordinates. Then, the equation of
![]() ${\mathrm {X}}_0^{\mathrm {toric}}$
takes the form
${\mathrm {X}}_0^{\mathrm {toric}}$
takes the form
which means that the origin of the chart, that is, the point
![]() ${\mathrm {x}}_{3,4} = (0,0,\infty ,\infty ) \in {\mathrm {Y}}_0$
is an ordinary double point of
${\mathrm {x}}_{3,4} = (0,0,\infty ,\infty ) \in {\mathrm {Y}}_0$
is an ordinary double point of
![]() ${\mathrm {X}}_0^{\mathrm {toric}}$
. Considering similarly the other charts, we see that the singular locus of
${\mathrm {X}}_0^{\mathrm {toric}}$
. Considering similarly the other charts, we see that the singular locus of
![]() ${\mathrm {X}}_0^{\mathrm {toric}}$
is the
${\mathrm {X}}_0^{\mathrm {toric}}$
is the
![]() $\mathfrak {S}_4$
-orbit of the point
$\mathfrak {S}_4$
-orbit of the point
![]() ${\mathrm {x}}_{3,4}$
; in particular, each singular point of
${\mathrm {x}}_{3,4}$
; in particular, each singular point of
![]() ${\mathrm {X}}_0^{\mathrm {toric}}$
is an ordinary double point. Moreover, we see that the hypersurface
${\mathrm {X}}_0^{\mathrm {toric}}$
is an ordinary double point. Moreover, we see that the hypersurface
![]() ${\mathrm {X}}_0^{\mathrm {toric}}$
is normal.
${\mathrm {X}}_0^{\mathrm {toric}}$
is normal.
The orbits of the point
![]() ${\mathrm {y}}_0$
under the 1-parametric subgroups (7.1.2) are
${\mathrm {y}}_0$
under the 1-parametric subgroups (7.1.2) are
It is easy to see that the closure of the first orbit is smooth and contains the point
![]() ${\mathrm {x}}_{1,2}$
and
${\mathrm {x}}_{1,2}$
and
![]() ${\mathrm {x}}_{3,4}$
and similarly for the other two orbits.
${\mathrm {x}}_{3,4}$
and similarly for the other two orbits.
For a field extension
![]() ${\mathsf {k}}'/{\mathsf {k}}$
, we denote by
${\mathsf {k}}'/{\mathsf {k}}$
, we denote by
![]() $\operatorname {{\mathrm {Res}}}_{{\mathsf {k}}'/{\mathsf {k}}} \colon \operatorname {{\mathrm {Sch}}}_{{\mathsf {k}}'} \to \operatorname {{\mathrm {Sch}}}_{\mathsf {k}}$
the Weil restriction of scalars functor from the category of
$\operatorname {{\mathrm {Res}}}_{{\mathsf {k}}'/{\mathsf {k}}} \colon \operatorname {{\mathrm {Sch}}}_{{\mathsf {k}}'} \to \operatorname {{\mathrm {Sch}}}_{\mathsf {k}}$
the Weil restriction of scalars functor from the category of
![]() ${\mathsf {k}}'$
-schemes to the category of
${\mathsf {k}}'$
-schemes to the category of
![]() ${\mathsf {k}}$
-schemes, the right adjoint to the extension of scalars
${\mathsf {k}}$
-schemes, the right adjoint to the extension of scalars
![]() $- \otimes _{\mathsf {k}} {\mathsf {k}}' \colon \operatorname {{\mathrm {Sch}}}_{\mathsf {k}} \to \operatorname {{\mathrm {Sch}}}_{{\mathsf {k}}'}$
. Consider the projective line
$- \otimes _{\mathsf {k}} {\mathsf {k}}' \colon \operatorname {{\mathrm {Sch}}}_{\mathsf {k}} \to \operatorname {{\mathrm {Sch}}}_{{\mathsf {k}}'}$
. Consider the projective line
![]() $\mathbb {P}^1_{{\mathsf {k}}'}$
, the torus
$\mathbb {P}^1_{{\mathsf {k}}'}$
, the torus
![]() $\mathbb {G}_{\mathrm {m}}$
acting faithfully on
$\mathbb {G}_{\mathrm {m}}$
acting faithfully on
![]() $\mathbb {P}^1_{{\mathsf {k}}'}$
and denote by
$\mathbb {P}^1_{{\mathsf {k}}'}$
and denote by
![]() $0,\infty \in \mathbb {P}^1_{{\mathsf {k}}'}$
its fixed points.
$0,\infty \in \mathbb {P}^1_{{\mathsf {k}}'}$
its fixed points.
Proposition 7.2. For a field extension
![]() ${\mathsf {k}}'/{\mathsf {k}}$
of degree
${\mathsf {k}}'/{\mathsf {k}}$
of degree
![]() $4$
consider the
$4$
consider the
![]() ${\mathsf {k}}$
-forms
${\mathsf {k}}$
-forms
of
![]() ${\mathrm {Y}}_0 = (\mathbb {P}^1)^4$
and of the torus
${\mathrm {Y}}_0 = (\mathbb {P}^1)^4$
and of the torus
![]() ${\mathrm {T}}_0$
and the natural faithful T-action on Y. Let
${\mathrm {T}}_0$
and the natural faithful T-action on Y. Let
be the
![]() ${\mathsf {k}}$
-point that corresponds to the point
${\mathsf {k}}$
-point that corresponds to the point
![]() $1 \in \mathbb {P}^1_{{\mathsf {k}}'}$
. Then
$1 \in \mathbb {P}^1_{{\mathsf {k}}'}$
. Then
-
(i) the half-anticanonical linear system of Y is defined over
 ${\mathsf {k}}$
, and it contains a unique T-invariant divisor
${\mathsf {k}}$
, and it contains a unique T-invariant divisor
 $X^{\mathrm {toric}} \subset Y$
passing through y.
$X^{\mathrm {toric}} \subset Y$
passing through y. -
(ii) the divisor
 $X^{\mathrm {toric}}$
is integral and has ordinary double points in the sense of [Reference Nicaise and Shinder19, Definition 4.2.1] with the singular locus of length
$X^{\mathrm {toric}}$
is integral and has ordinary double points in the sense of [Reference Nicaise and Shinder19, Definition 4.2.1] with the singular locus of length
 $6$
.
$6$
.
Proof. The fact that Y and T are
![]() ${\mathsf {k}}$
-forms of
${\mathsf {k}}$
-forms of
![]() ${\mathrm {Y}}_0$
and
${\mathrm {Y}}_0$
and
![]() ${\mathrm {T}}_0$
is obvious from the definition of Weil restriction of scalars, and the
${\mathrm {T}}_0$
is obvious from the definition of Weil restriction of scalars, and the
![]() ${\mathsf {k}}$
-point y is obtained from the extension–restriction adjunction. Note that upon extension of scalars to
${\mathsf {k}}$
-point y is obtained from the extension–restriction adjunction. Note that upon extension of scalars to
![]() ${\bar {\mathsf {k}}}$
, the triple
${\bar {\mathsf {k}}}$
, the triple
![]() $(Y,T,y)$
becomes isomorphic to the triple
$(Y,T,y)$
becomes isomorphic to the triple
![]() $({\mathrm {Y}}_0,{\mathrm {T}}_0,{\mathrm {y}}_0)$
.
$({\mathrm {Y}}_0,{\mathrm {T}}_0,{\mathrm {y}}_0)$
.
(i) Let H denote the Segre class of Y (the half of the anticanonical class); it is obviously Galois-invariant, and since Y has a
![]() ${\mathsf {k}}$
-point, H is defined over
${\mathsf {k}}$
-point, H is defined over
![]() ${\mathsf {k}}$
. Therefore, the linear system
${\mathsf {k}}$
. Therefore, the linear system
of divisors in
![]() $|H|$
containing y is defined over
$|H|$
containing y is defined over
![]() ${\mathsf {k}}$
. We define
${\mathsf {k}}$
. We define
![]() $X^{\mathrm {toric}} \subset Y$
as the closure of the T-orbit of the point y; the uniqueness of
$X^{\mathrm {toric}} \subset Y$
as the closure of the T-orbit of the point y; the uniqueness of
![]() $X^{\mathrm {toric}}$
follows from Lemma 7.1.
$X^{\mathrm {toric}}$
follows from Lemma 7.1.
(ii) The extension of scalars of
![]() $X^{\mathrm {toric}} \subset Y$
to
$X^{\mathrm {toric}} \subset Y$
to
![]() ${\bar {\mathsf {k}}}$
coincides with
${\bar {\mathsf {k}}}$
coincides with
![]() ${\mathrm {X}}_0^{\mathrm {toric}} \subset {\mathrm {Y}}_0$
, hence, its singular locus
${\mathrm {X}}_0^{\mathrm {toric}} \subset {\mathrm {Y}}_0$
, hence, its singular locus
![]() $Z := \operatorname {\mathrm {Sing}}(X^{\mathrm {toric}})$
has length
$Z := \operatorname {\mathrm {Sing}}(X^{\mathrm {toric}})$
has length
![]() $6$
, and if E is the exceptional divisor of the blowup
$6$
, and if E is the exceptional divisor of the blowup
then
![]() $E \to Z$
is a smooth quadric bundle. According to [Reference Nicaise and Shinder19, Definition 4.2.1], it remains to check that this bundle has a section. For this, note that the union of the 1-parametric subgroups
$E \to Z$
is a smooth quadric bundle. According to [Reference Nicaise and Shinder19, Definition 4.2.1], it remains to check that this bundle has a section. For this, note that the union of the 1-parametric subgroups
![]() ${\mathrm {T}}_0^{i_1,i_2;i_3,i_4} \subset {\mathrm {T}}_0$
defined in (7.1.2) is Galois-invariant, hence, it comes from a
${\mathrm {T}}_0^{i_1,i_2;i_3,i_4} \subset {\mathrm {T}}_0$
defined in (7.1.2) is Galois-invariant, hence, it comes from a
![]() ${\mathsf {k}}$
-subset in the torus T, and, hence, the closure of the image of the point y under the action of this subset is a curve
${\mathsf {k}}$
-subset in the torus T, and, hence, the closure of the image of the point y under the action of this subset is a curve
![]() $C \subset X$
defined over
$C \subset X$
defined over
![]() ${\mathsf {k}}$
. Furthermore, the extension of scalars of C to
${\mathsf {k}}$
. Furthermore, the extension of scalars of C to
![]() ${\bar {\mathsf {k}}}$
is the union of the curves (7.1.3). In particular, the curve C contains the singular locus Z and the intersection of its strict transforms to the blowup
${\bar {\mathsf {k}}}$
is the union of the curves (7.1.3). In particular, the curve C contains the singular locus Z and the intersection of its strict transforms to the blowup
![]() ${\tilde {X}}$
, and the exceptional divisor E provides a section for
${\tilde {X}}$
, and the exceptional divisor E provides a section for
![]() $E \to Z$
.
$E \to Z$
.
Now, let X be a smooth Fano threefold of type
![]() $\mathsf {X}_{(1,1,1,1)}$
. Recall the definition (2.1.5) of the Galois group
$\mathsf {X}_{(1,1,1,1)}$
. Recall the definition (2.1.5) of the Galois group
![]() ${\mathrm {G}}_X \subset \mathfrak {S}_4$
of X. In the next lemma, we use notation introduced in Proposition 7.2.
${\mathrm {G}}_X \subset \mathfrak {S}_4$
of X. In the next lemma, we use notation introduced in Proposition 7.2.
Lemma 7.3. If
![]() ${\mathsf {k}}'/{\mathsf {k}}$
is the field extension of degree
${\mathsf {k}}'/{\mathsf {k}}$
is the field extension of degree
![]() $4$
associated with an epimorphism
$4$
associated with an epimorphism
![]() $\mathrm{G}(\bar{\mathsf{k}}/\mathsf{k}) \twoheadrightarrow \mathrm{G}$
onto a transitive subgroup
$\mathrm{G}(\bar{\mathsf{k}}/\mathsf{k}) \twoheadrightarrow \mathrm{G}$
onto a transitive subgroup
![]() ${\mathrm {G}} \subset \mathfrak {S}_4$
, then a general divisor
${\mathrm {G}} \subset \mathfrak {S}_4$
, then a general divisor
![]() $X \subset Y$
from the linear system (7.1.5) is a smooth Fano threefold of type
$X \subset Y$
from the linear system (7.1.5) is a smooth Fano threefold of type
![]() $\mathsf {X}_{(1,1,1,1)}$
with
$\mathsf {X}_{(1,1,1,1)}$
with
![]() ${\mathrm {G}}_X = {\mathrm {G}}$
,
${\mathrm {G}}_X = {\mathrm {G}}$
,
![]() $\unicode{x3c1} (X) = 1$
and
$\unicode{x3c1} (X) = 1$
and
![]() $X({\mathsf {k}}) \ne \varnothing $
.
$X({\mathsf {k}}) \ne \varnothing $
.
Proof. The smoothness of a general divisor X in the linear system
![]() $\mathfrak {P}$
follows from the Bertini theorem, the property
$\mathfrak {P}$
follows from the Bertini theorem, the property
![]() $X({\mathsf {k}}) \ne \varnothing $
is obvious because X contains the
$X({\mathsf {k}}) \ne \varnothing $
is obvious because X contains the
![]() ${\mathsf {k}}$
-point y, the equality
${\mathsf {k}}$
-point y, the equality
![]() ${\mathrm {G}}_X = {\mathrm {G}}$
follows from the construction and
${\mathrm {G}}_X = {\mathrm {G}}$
follows from the construction and
![]() $\unicode{x3c1} (X) = 1$
follows from transitivity of
$\unicode{x3c1} (X) = 1$
follows from transitivity of
![]() ${\mathrm {G}} \subset \mathfrak {S}_4$
.
${\mathrm {G}} \subset \mathfrak {S}_4$
.
Remark 7.4. One can also prove the converse statement: any Fano threefold X of type
![]() $\mathsf {X}_{(1,1,1,1)}$
with
$\mathsf {X}_{(1,1,1,1)}$
with
![]() $X({\mathsf {k}}) \ne \varnothing $
and
$X({\mathsf {k}}) \ne \varnothing $
and
![]() ${\mathrm {G}}_X = {\mathrm {G}}$
is isomorphic to a divisor in the linear system
${\mathrm {G}}_X = {\mathrm {G}}$
is isomorphic to a divisor in the linear system
![]() $\mathfrak {P}$
(see [Reference Kuznetsov14, Proposition 7.16]).
$\mathfrak {P}$
(see [Reference Kuznetsov14, Proposition 7.16]).
Now, we are ready to prove Theorem 1.4.
Proof of Theorem 1.4
We consider the field extension
![]() ${\mathsf {k}}'/{\mathsf {k}}$
as in Lemma 7.3 and use the construction and notation of Proposition 7.2; in particular, the linear system
${\mathsf {k}}'/{\mathsf {k}}$
as in Lemma 7.3 and use the construction and notation of Proposition 7.2; in particular, the linear system
![]() $\mathfrak {P} \cong \mathbb {P}^{14}_{\mathsf {k}}$
of half-anticanonical divisors in Y. Let
$\mathfrak {P} \cong \mathbb {P}^{14}_{\mathsf {k}}$
of half-anticanonical divisors in Y. Let
![]() $\mathfrak {p}_0 \in \mathfrak {P}$
be the point that corresponds to the toric divisor
$\mathfrak {p}_0 \in \mathfrak {P}$
be the point that corresponds to the toric divisor
![]() $X^{\mathrm {toric}} \subset Y$
. Note that the space of lines in
$X^{\mathrm {toric}} \subset Y$
. Note that the space of lines in
![]() $\mathfrak {P}$
through the point
$\mathfrak {P}$
through the point
![]() $\mathfrak {p}_0$
is the projective space
$\mathfrak {p}_0$
is the projective space
![]() $\mathbb {P}^{13}_{\mathsf {k}}$
, in particular,
$\mathbb {P}^{13}_{\mathsf {k}}$
, in particular,
![]() ${\mathsf {k}}$
-points are Zariski dense in it. Therefore, there is a line
${\mathsf {k}}$
-points are Zariski dense in it. Therefore, there is a line
![]() $L \subset \mathfrak {P}$
through
$L \subset \mathfrak {P}$
through
![]() $\mathfrak {p}_0$
defined over
$\mathfrak {p}_0$
defined over
![]() ${\mathsf {k}}$
. We denote by
${\mathsf {k}}$
. We denote by
the corresponding family of half-anticanonical divisors in Y. Then, the general point of L corresponds to a smooth variety
![]() ${\mathscr {X}}_L$
of type
${\mathscr {X}}_L$
of type
![]() $\mathsf {X}_{(1,1,1,1)}$
over the field
$\mathsf {X}_{(1,1,1,1)}$
over the field
![]() ${\mathsf {k}}(L) \cong {\mathsf {k}}(t)$
.
${\mathsf {k}}(L) \cong {\mathsf {k}}(t)$
.
Since for a general
![]() ${\mathsf {k}}$
-point
${\mathsf {k}}$
-point
![]() $\mathfrak {p} \in L$
the fibre of
$\mathfrak {p} \in L$
the fibre of
![]() ${\mathscr {X}}_{\mathfrak {p}}$
has
${\mathscr {X}}_{\mathfrak {p}}$
has
![]() ${\mathrm {G}}_{X_{\mathfrak {p}}} = {\mathrm {G}}$
by Lemma 7.3, and since the natural restriction morphism of Galois groups
${\mathrm {G}}_{X_{\mathfrak {p}}} = {\mathrm {G}}$
by Lemma 7.3, and since the natural restriction morphism of Galois groups
![]() ${\mathrm {G}}(\overline {{\mathsf {k}}(L)}/{\mathsf {k}}(L)) \to {\mathrm {G}}({\bar {\mathsf {k}}}/{\mathsf {k}})$
is surjective, we have
${\mathrm {G}}(\overline {{\mathsf {k}}(L)}/{\mathsf {k}}(L)) \to {\mathrm {G}}({\bar {\mathsf {k}}}/{\mathsf {k}})$
is surjective, we have
![]() ${\mathrm {G}}_{{\mathscr {X}}_L} = {\mathrm {G}}$
. Since
${\mathrm {G}}_{{\mathscr {X}}_L} = {\mathrm {G}}$
. Since
![]() ${\mathrm {G}} \subset \mathfrak {S}_4$
is transitive, this implies
${\mathrm {G}} \subset \mathfrak {S}_4$
is transitive, this implies
![]() $\unicode{x3c1} ({\mathscr {X}}_L) = 1$
. Finally,
$\unicode{x3c1} ({\mathscr {X}}_L) = 1$
. Finally,
![]() ${\mathscr {X}}_L$
by construction contains the
${\mathscr {X}}_L$
by construction contains the
![]() ${\mathsf {k}}(L)$
-point
${\mathsf {k}}(L)$
-point
![]() $y \times _{\mathsf {k}} {{\mathsf {k}}(L)}$
, hence,
$y \times _{\mathsf {k}} {{\mathsf {k}}(L)}$
, hence,
![]() ${\mathscr {X}}_L({\mathsf {k}}(L)) \ne \varnothing $
.
${\mathscr {X}}_L({\mathsf {k}}(L)) \ne \varnothing $
.
Assume
![]() ${\mathscr {X}}_L$
is stably rational. Consider the point
${\mathscr {X}}_L$
is stably rational. Consider the point
![]() $\mathfrak {p}_0 \in L$
as a special point of the family
$\mathfrak {p}_0 \in L$
as a special point of the family
![]() ${\mathscr {X}}/L$
. By Proposition 7.2, the corresponding variety
${\mathscr {X}}/L$
. By Proposition 7.2, the corresponding variety
![]() ${\mathscr {X}}_{\mathfrak {p}_0} = X^{\mathrm {toric}}$
is integral with ordinary double points, hence, by [Reference Nicaise and Shinder19, Proposition 4.2.9], the family
${\mathscr {X}}_{\mathfrak {p}_0} = X^{\mathrm {toric}}$
is integral with ordinary double points, hence, by [Reference Nicaise and Shinder19, Proposition 4.2.9], the family
![]() ${\mathscr {X}}/L$
is
${\mathscr {X}}/L$
is
![]() $\mathbb {L}$
-faithful in the sense of [Reference Nicaise and Shinder19, Definition 4.2.7]. Therefore, by [Reference Nicaise and Shinder19, Proposition 4.2.10], the special fibre
$\mathbb {L}$
-faithful in the sense of [Reference Nicaise and Shinder19, Definition 4.2.7]. Therefore, by [Reference Nicaise and Shinder19, Proposition 4.2.10], the special fibre
![]() $X^{\mathrm {toric}}$
is stably rational.
$X^{\mathrm {toric}}$
is stably rational.
On the other hand, by definition, the Galois group of the extension
![]() ${\mathsf {k}}'/{\mathsf {k}}$
coincides with the group
${\mathsf {k}}'/{\mathsf {k}}$
coincides with the group
![]() ${\mathrm {G}}_X$
and contains the Klein group
${\mathrm {G}}_X$
and contains the Klein group
![]() $\mathrm {V}_4$
. By [Reference Voskresenskiĭ22, §2.4.8], for any smooth compactification
$\mathrm {V}_4$
. By [Reference Voskresenskiĭ22, §2.4.8], for any smooth compactification
![]() $V\supset T$
one has
$V\supset T$
one has
Since this group is a stable birational invariant (see, e.g. [Reference Colliot-Thélène and Sansuc4, §2.A] or [Reference Voskresenskiĭ22, §4.4]), the torus T and the corresponding toric variety
![]() $X^{\mathrm {toric}}$
are not stably rational. This contradiction shows that
$X^{\mathrm {toric}}$
are not stably rational. This contradiction shows that
![]() ${\mathscr {X}}_L$
is not stably rational and completes the proof of the theorem.
${\mathscr {X}}_L$
is not stably rational and completes the proof of the theorem.
Appendix A Constructing morphisms of Hilbert schemes
In this section, we show how one can use the technique of derived categories to construct morphisms of Hilbert schemes. For smooth projective varieties X and Y, we denote by
![]() $\pi _X$
and
$\pi _X$
and
![]() $\pi _Y$
the projections from
$\pi _Y$
the projections from
![]() $X \times Y$
to the factors, and for an object
$X \times Y$
to the factors, and for an object
![]() ${\mathscr {K}} \in \mathbf {D}(X \times Y)$
, we denote by
${\mathscr {K}} \in \mathbf {D}(X \times Y)$
, we denote by
the corresponding Fourier–Mukai functor from the bounded derived category
![]() $\mathbf {D}(X)$
of coherent sheaves on X to that of Y. For an integral valued polynomial
$\mathbf {D}(X)$
of coherent sheaves on X to that of Y. For an integral valued polynomial
![]() $p \in \mathbb {Q}[t]$
, we denote by
$p \in \mathbb {Q}[t]$
, we denote by
![]() $\operatorname {{\mathrm {Hilb}}}_{p}(X)$
the Hilbert scheme of subschemes in X with Hilbert polynomials p with respect to a given polarisation.
$\operatorname {{\mathrm {Hilb}}}_{p}(X)$
the Hilbert scheme of subschemes in X with Hilbert polynomials p with respect to a given polarisation.
Proposition A.1. Let X and Y be smooth projective varieties. If
![]() ${\mathscr {K}} \in \mathbf {D}(X \times Y)$
is an object of the derived category, such that for any subscheme
${\mathscr {K}} \in \mathbf {D}(X \times Y)$
is an object of the derived category, such that for any subscheme
![]() $Z \subset X$
with Hilbert polynomial p the object
$Z \subset X$
with Hilbert polynomial p the object
![]() $\Phi _{\mathscr {K}}({\mathscr {O}}_Z) \in \mathbf {D}(Y)$
is isomorphic to the structure sheaf of a point
$\Phi _{\mathscr {K}}({\mathscr {O}}_Z) \in \mathbf {D}(Y)$
is isomorphic to the structure sheaf of a point
![]() $y(Z) \in Y$
, then there is a morphism of schemes
$y(Z) \in Y$
, then there is a morphism of schemes
such that
![]() $\varphi ([Z]) = y(Z)$
.
$\varphi ([Z]) = y(Z)$
.
Proof. Let
![]() $Z \subset X \times S$
be an family of subschemes in X flat over S with Hilbert polynomial p. Let
$Z \subset X \times S$
be an family of subschemes in X flat over S with Hilbert polynomial p. Let
be the image of the structure sheaf of Z under the induced Fourier–Mukai functor from
![]() $\mathbf {D}(X \times S)$
to
$\mathbf {D}(X \times S)$
to
![]() $\mathbf {D}(S \times Y)$
, where
$\mathbf {D}(S \times Y)$
, where
![]() $\pi _{XS}$
,
$\pi _{XS}$
,
![]() $\pi _{SY}$
and
$\pi _{SY}$
and
![]() $\pi _{XY}$
are the projections of
$\pi _{XY}$
are the projections of
![]() $X \times S \times Y$
to the pairwise products of factors. By base change and the projection formula, for each point
$X \times S \times Y$
to the pairwise products of factors. By base change and the projection formula, for each point
![]() $s \in S$
, we have
$s \in S$
, we have
where
![]() $i_s \colon \{s\} \times Y \hookrightarrow S \times Y$
is the natural embedding and
$i_s \colon \{s\} \times Y \hookrightarrow S \times Y$
is the natural embedding and
![]() $Z_s \subset X$
is the fibre of Z over
$Z_s \subset X$
is the fibre of Z over
![]() $s \in S$
. Thus, we have
$s \in S$
. Thus, we have
![]() $i_s^*{\mathscr {F}} \cong {\mathscr {O}}_{y(Z_s)}$
by assumption, therefore, by [Reference Kuznetsov13, Lemma 4.4(iii)] , there is a unique morphism
$i_s^*{\mathscr {F}} \cong {\mathscr {O}}_{y(Z_s)}$
by assumption, therefore, by [Reference Kuznetsov13, Lemma 4.4(iii)] , there is a unique morphism
![]() $\varphi _S \colon S \to Y$
, such that
$\varphi _S \colon S \to Y$
, such that
![]() ${\mathscr {F}}$
is isomorphic up to twist to the structure sheaf of the graph of
${\mathscr {F}}$
is isomorphic up to twist to the structure sheaf of the graph of
![]() $\varphi _S$
; in particular,
$\varphi _S$
; in particular,
![]() $\varphi _S(s) = y(Z_s)$
for each
$\varphi _S(s) = y(Z_s)$
for each
![]() $s \in S$
. Now applying this argument to
$s \in S$
. Now applying this argument to
![]() $S = \operatorname {{\mathrm {Hilb}}}_p(X)$
and Z the universal subscheme, we obtain the required morphism
$S = \operatorname {{\mathrm {Hilb}}}_p(X)$
and Z the universal subscheme, we obtain the required morphism
![]() $\varphi $
.
$\varphi $
.
In §2.3, we apply Proposition A.1 to the Hilbert scheme of conics on the threefold
![]() $X \cong \operatorname {{\mathrm {Bl}}}_{\Gamma _1}(Q_1)$
, where
$X \cong \operatorname {{\mathrm {Bl}}}_{\Gamma _1}(Q_1)$
, where
![]() $Q_1 \subset \mathbb {P}^4$
is a smooth quadric and
$Q_1 \subset \mathbb {P}^4$
is a smooth quadric and
![]() $\Gamma _1 \subset Q_1$
is a linearly normal smooth rational quartic curve. Recall that
$\Gamma _1 \subset Q_1$
is a linearly normal smooth rational quartic curve. Recall that
![]() $\mathrm {F}_1(X)$
and
$\mathrm {F}_1(X)$
and
![]() $\mathrm {F}_2(X)$
denote the Hilbert schemes of lines and conics on X, and that there is a natural embedding
$\mathrm {F}_2(X)$
denote the Hilbert schemes of lines and conics on X, and that there is a natural embedding
![]() $\Gamma _1 \subset \mathrm {F}_1(X)$
of a connected component (see Lemma 2.7). Recall also that the second connected component
$\Gamma _1 \subset \mathrm {F}_1(X)$
of a connected component (see Lemma 2.7). Recall also that the second connected component
![]() $\Gamma _2 \subset \mathrm {F}_1(X)$
corresponds to lines on
$\Gamma _2 \subset \mathrm {F}_1(X)$
corresponds to lines on
![]() $Q_1$
bisecant to
$Q_1$
bisecant to
![]() $\Gamma _1$
.
$\Gamma _1$
.
Corollary A.2. There is a morphism
![]() $\varphi _1 \colon \mathrm {F}_2(X) \to \Gamma _1$
, such that for a smooth conic
$\varphi _1 \colon \mathrm {F}_2(X) \to \Gamma _1$
, such that for a smooth conic
![]() $C \subset X$
, one has
$C \subset X$
, one has
![]() $\varphi _1([C]) = [L]$
, where
$\varphi _1([C]) = [L]$
, where
![]() $L \subset X$
is the unique line corresponding to a point of
$L \subset X$
is the unique line corresponding to a point of
![]() $\Gamma _1$
, such that
$\Gamma _1$
, such that
![]() $C \cap L \ne \varnothing $
. Moreover, if
$C \cap L \ne \varnothing $
. Moreover, if
![]() $C = L_1 \cup L_2$
is a reducible conic, so that
$C = L_1 \cup L_2$
is a reducible conic, so that
![]() $L_1 \cap L_2 \ne \varnothing $
, and if
$L_1 \cap L_2 \ne \varnothing $
, and if
![]() $L^{\prime }_2$
is the other line corresponding to a point of
$L^{\prime }_2$
is the other line corresponding to a point of
![]() $\Gamma _1$
, such that
$\Gamma _1$
, such that
![]() $L_1 \cap L^{\prime }_2 \ne \varnothing $
, then
$L_1 \cap L^{\prime }_2 \ne \varnothing $
, then
![]() $\varphi _1([C]) = [L^{\prime }_2]$
.
$\varphi _1([C]) = [L^{\prime }_2]$
.
Proof. Let
![]() $\pi _1 \colon X \to Q_1$
be the blowup morphism, and let
$\pi _1 \colon X \to Q_1$
be the blowup morphism, and let
![]() $E_1 \subset X$
be its exceptional divisor; note that
$E_1 \subset X$
be its exceptional divisor; note that
![]() $E_1$
is the universal family of lines on X over the connected component
$E_1$
is the universal family of lines on X over the connected component
![]() $\Gamma _1 \subset \mathrm {F}_1(X)$
of the Hilbert scheme of lines. Let
$\Gamma _1 \subset \mathrm {F}_1(X)$
of the Hilbert scheme of lines. Let
![]() $\varepsilon \colon E_1 \to X \times \Gamma _1$
be the corresponding embedding and consider
$\varepsilon \colon E_1 \to X \times \Gamma _1$
be the corresponding embedding and consider
Let us check that the assumption of Proposition A.1 is satisfied for
![]() $Y = \Gamma _1$
.
$Y = \Gamma _1$
.
If
![]() $C \subset X$
is a smooth conic, then
$C \subset X$
is a smooth conic, then
![]() $C \cdot E_1 = 1$
, and
$C \cdot E_1 = 1$
, and
![]() $C \not \subset E_1$
, therefore,
$C \not \subset E_1$
, therefore,
![]() $C \cap E_1 = \{x\}$
is a single point and the intersection is transverse. Therefore,
$C \cap E_1 = \{x\}$
is a single point and the intersection is transverse. Therefore,
![]() ${\mathscr {O}}_C \otimes ^{\mathbf {L}} {\mathscr {O}}_{E_1}(E_1) \cong {\mathscr {O}}_x$
, hence,
${\mathscr {O}}_C \otimes ^{\mathbf {L}} {\mathscr {O}}_{E_1}(E_1) \cong {\mathscr {O}}_x$
, hence,
![]() $\Phi _{\mathscr {K}}({\mathscr {O}}_C) \cong {\mathscr {O}}_{\pi _1(x)}$
.
$\Phi _{\mathscr {K}}({\mathscr {O}}_C) \cong {\mathscr {O}}_{\pi _1(x)}$
.
If
![]() $C = L_1 \cup L_2$
is a reducible conic, so that we have
$C = L_1 \cup L_2$
is a reducible conic, so that we have
![]() $L_2 \subset E_1$
and
$L_2 \subset E_1$
and
![]() $L_1 \cap E_1 = \{x,x'\}$
with
$L_1 \cap E_1 = \{x,x'\}$
with
![]() $L_1 \cap L_2 = \{x\}$
(if
$L_1 \cap L_2 = \{x\}$
(if
![]() $L_1$
is tangent to
$L_1$
is tangent to
![]() $E_1$
, we take
$E_1$
, we take
![]() $x' = x$
), then using the exact sequences
$x' = x$
), then using the exact sequences
it is easy to check that
![]() ${\mathscr {O}}_C \otimes ^{\mathbf {L}} {\mathscr {O}}_{E_1}(E_1)$
fits into a distinguished triangle
${\mathscr {O}}_C \otimes ^{\mathbf {L}} {\mathscr {O}}_{E_1}(E_1)$
fits into a distinguished triangle
(if
![]() $L_1$
is tangent to
$L_1$
is tangent to
![]() $E_1$
, the middle term should be replaced by an extension of
$E_1$
, the middle term should be replaced by an extension of
![]() ${\mathscr {O}}_{L_2}(-1)$
by
${\mathscr {O}}_{L_2}(-1)$
by
![]() ${\mathscr {O}}_{x'}$
). Since the pushforward functor
${\mathscr {O}}_{x'}$
). Since the pushforward functor
![]() $\mathbf {R}\pi _{1*}$
kills the sheaf
$\mathbf {R}\pi _{1*}$
kills the sheaf
![]() ${\mathscr {O}}_{L_2}(-1)$
, it follows that
${\mathscr {O}}_{L_2}(-1)$
, it follows that
![]() $\Phi _{\mathscr {K}}({\mathscr {O}}_C) \cong {\mathscr {O}}_{\pi _1(x')}$
.
$\Phi _{\mathscr {K}}({\mathscr {O}}_C) \cong {\mathscr {O}}_{\pi _1(x')}$
.
Now, applying Proposition A.1, we conclude that there is a morphism
![]() $\varphi _1 \colon \mathrm {F}_2(X) \to \Gamma _1$
, such that
$\varphi _1 \colon \mathrm {F}_2(X) \to \Gamma _1$
, such that
![]() $\varphi _1([C]) = \pi _1(x)$
if C is smooth and
$\varphi _1([C]) = \pi _1(x)$
if C is smooth and
![]() $\varphi _1([L_1 \cup L_2]) = \pi _1(x')$
, with the notation for points x and
$\varphi _1([L_1 \cup L_2]) = \pi _1(x')$
, with the notation for points x and
![]() $x'$
introduced above.
$x'$
introduced above.
Acknowledgements
We would like to thank Sergey Gorchinskiy, Zhenya Shinder and Costya Shramov for useful discussions. We are also grateful to the anonymous referee for correcting a mistake in the original statement of Theorem 1.4 and for useful comments. This work was performed at the Steklov International Mathematical Center and supported by the Ministry of Science and Higher Education of the Russian Federation (agreement no. 075-15-2022-265). The paper was also partially supported by the HSE University Basic Research Program.
Competing Interests
None.