Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-15T07:55:55.840Z Has data issue: false hasContentIssue false
  • English
  • Français

An Algorithmic Solution for a Word Problem in Group Theory

Published online by Cambridge University Press:  20 November 2018

N. S. Mendelsohn
N. S. Mendelsohn*
Affiliation:
University of Manitoba, Winnipeg
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper describes a systematic procedure which yields in a finite number of steps a solution to the following problem. Let G be a group generated by a finite set of generators g1, g2, g3, . . . , gr and defined by a finite set of relations R1 = R2 = . . . = Rk = I, where I is the unit element of G and R1R2, . . . , Rk are words in the gi and gi-1. Let H be a subgroup of G, known to be of finite index, and generated by a finite set of words, W1, W2, . . . , Wt. Let W be any word in G. Our problem is the following. 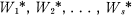Can we find a new set of generators for H, together with a set of representatives h1 = 1, h2, . . . , hu of the right cosets of H (i.e. G = H1 + Hh2 + . . . + Hhu) such that W can be expressed in the form W = Uhp, where U is a word in .

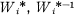Type
Research Article
Information
Canadian Journal of Mathematics , Volume 16 , 1964 , pp. 509 - 516
Copyright
Copyright © Canadian Mathematical Society 1964

References

1. Coxeter, H. S. M. and Moser, W. O. J., Generators and relations for discrete groups, Ergebnisse der Mathematik mid ihrer Grenzgebiete, Chapter 2, pp. 12–18.Google Scholar
2. Leech, John, Coset enumeration on digital computers, Proc. Camb. Phil. Soc, 59 (1963), 257–267.Google Scholar
3. Leech, John, Some definitions of Klein's simple group of order 168 and other groups, Proc. Glasgow- Math. Assoc, 5, Part 4, 166–175 (1962).Google Scholar
4. Hall, Marshall, The theory of groups (New York, 1959), Chapter 7, pp. 94-106. 5. John Todd, Survey of numerical analysis (Mew York, 1962), Chapter 15 by Marshall Hall, pp. 534–538.Google Scholar
6. Todd, J. A. and Coxeter, H. S. M., A practical method for enumerating cosets of a finite abstract group, Proc. Edinburgh Math. Soc. (2), 5 (1936), 34–36.Google Scholar