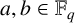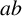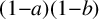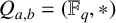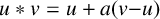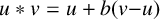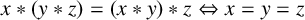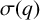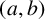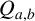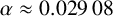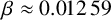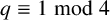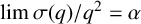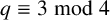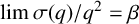1 Introduction
A quasigroup
![]() $(Q,*)$
is a nonempty set Q with a binary operation
$(Q,*)$
is a nonempty set Q with a binary operation
![]() $*$
such that, for each
$*$
such that, for each
![]() $a,b\in Q$
, there exist unique
$a,b\in Q$
, there exist unique
![]() $x,y\in Q$
for which
$x,y\in Q$
for which
![]() $a*x=b$
and
$a*x=b$
and
![]() $y*a=b$
. A quasigroup
$y*a=b$
. A quasigroup
![]() $(Q,*)$
is said to be maximally nonassociative if
$(Q,*)$
is said to be maximally nonassociative if
holds for all
![]() $u,v,w \in Q$
. By [Reference Kepka11], a maximally nonassociative quasigroup has to be idempotent (that is,
$u,v,w \in Q$
. By [Reference Kepka11], a maximally nonassociative quasigroup has to be idempotent (that is,
![]() $u*u=u$
for all
$u*u=u$
for all
![]() $u\in Q$
). Hence, in a maximally nonassociative quasigroup, the converse of implication (1-1) holds as well.
$u\in Q$
). Hence, in a maximally nonassociative quasigroup, the converse of implication (1-1) holds as well.
The existence of maximally nonassociative quasigroups was an open question for quite a long time [Reference Drápal and Valent4, Reference Grošek and Horák10, Reference Kepka11]. In 2018, a maximally nonassociative quasigroup of order nine was found [Reference Drápal and Valent5], and that was the first step to realise that Stein’s nearfield construction [Reference Stein14] can be used to obtain maximally nonassociative quasigroups of all orders
![]() $q^2$
, where q is an odd prime power [Reference Drápal and Lisoněk3]. A recent result of the present authors [Reference Drápal and Wanless6] (partially duplicated in [Reference Lisoněk13]) constructs examples of all orders with the exception of a handful of small cases and two sparse subfamilies within the case
$q^2$
, where q is an odd prime power [Reference Drápal and Lisoněk3]. A recent result of the present authors [Reference Drápal and Wanless6] (partially duplicated in [Reference Lisoněk13]) constructs examples of all orders with the exception of a handful of small cases and two sparse subfamilies within the case
![]() $n\equiv 2\bmod 4$
. The main construction used in [Reference Drápal and Wanless6, Reference Lisoněk13] is based upon quadratic orthomorphisms and applies for all odd prime powers
$n\equiv 2\bmod 4$
. The main construction used in [Reference Drápal and Wanless6, Reference Lisoněk13] is based upon quadratic orthomorphisms and applies for all odd prime powers
![]() $q\geqslant 13$
. However, it was left open how many quadratic orthomorphisms can be used in the construction. We provide an asymptotic answer to that question in this paper.
$q\geqslant 13$
. However, it was left open how many quadratic orthomorphisms can be used in the construction. We provide an asymptotic answer to that question in this paper.
Throughout this paper, q is an odd prime power and
![]() $\mathbb {F} = \mathbb {F}_q$
is a field of order q. For
$\mathbb {F} = \mathbb {F}_q$
is a field of order q. For
![]() $a,b\in \mathbb {F}$
, define a binary operation on
$a,b\in \mathbb {F}$
, define a binary operation on
![]() $\mathbb {F}$
by
$\mathbb {F}$
by
 $$ \begin{align} u*v= \begin{cases} u+a(v-u)&\text{if }v-u\text{ is a square,}\\ u+b(v-u)&\text{if }v-u\text{ is a nonsquare.} \end{cases} \end{align} $$
$$ \begin{align} u*v= \begin{cases} u+a(v-u)&\text{if }v-u\text{ is a square,}\\ u+b(v-u)&\text{if }v-u\text{ is a nonsquare.} \end{cases} \end{align} $$
This operation yields a quasigroup if and only if both
![]() $ab$
and
$ab$
and
![]() $(1-a)(1-b)$
are squares, and both a and b are distinct from
$(1-a)(1-b)$
are squares, and both a and b are distinct from
![]() $0$
and
$0$
and
![]() $1$
, see [Reference Evans7, Reference Wanless16]. Denote by
$1$
, see [Reference Evans7, Reference Wanless16]. Denote by
![]() ${\Sigma = \Sigma (\mathbb {F})}$
the set of all such
${\Sigma = \Sigma (\mathbb {F})}$
the set of all such
![]() $(a,b) \in \mathbb {F}\times \mathbb {F}$
for which
$(a,b) \in \mathbb {F}\times \mathbb {F}$
for which
![]() $a\ne b$
. For each
$a\ne b$
. For each
![]() $(a,b) \in \Sigma $
, denote the quasigroup
$(a,b) \in \Sigma $
, denote the quasigroup
![]() $(\mathbb {F},*)$
by
$(\mathbb {F},*)$
by
![]() $Q_{a,b} = Q_{a,b}(\mathbb {F})$
.
$Q_{a,b} = Q_{a,b}(\mathbb {F})$
.
If
![]() $a=b\in \mathbb {F}\setminus \{0,1\}$
, then Equation (1-2) defines a quasigroup in which
$a=b\in \mathbb {F}\setminus \{0,1\}$
, then Equation (1-2) defines a quasigroup in which
![]() $u*(v*u) = (u*v)*u$
for all
$u*(v*u) = (u*v)*u$
for all
![]() $u,v \in \mathbb {F}$
. This means that such a quasigroup is never maximally nonassociative. If
$u,v \in \mathbb {F}$
. This means that such a quasigroup is never maximally nonassociative. If
![]() $q\geqslant 13$
, then there always exists
$q\geqslant 13$
, then there always exists
![]() $(a,b) \in \Sigma (\mathbb {F}_q)$
such that
$(a,b) \in \Sigma (\mathbb {F}_q)$
such that
![]() $Q_{a,b}$
is maximally nonassociative [Reference Drápal and Wanless6, Reference Lisoněk13]. This paper is concerned with the density of such
$Q_{a,b}$
is maximally nonassociative [Reference Drápal and Wanless6, Reference Lisoněk13]. This paper is concerned with the density of such
![]() $(a,b)$
. Our main result is the following theorem.
$(a,b)$
. Our main result is the following theorem.
Theorem 1.1. For an odd prime power q, denote by
![]() $\sigma (q)$
the number of
$\sigma (q)$
the number of
![]() $(a,b) \in \Sigma (\mathbb {F}_q)$
for which
$(a,b) \in \Sigma (\mathbb {F}_q)$
for which
![]() $Q_{a,b}$
is maximally nonassociative. Then
$Q_{a,b}$
is maximally nonassociative. Then
 $$ \begin{align*} \lim_{q\to \infty}\frac{\sigma(q)}{q^2} = \begin{cases} 953\cdot2^{-15}\approx 0.029\,08&\text{for }q\equiv 1\bmod 4,\\ 825\cdot2^{-16}\approx 0.012\,59&\text{for }q\equiv 3\bmod 4. \end{cases} \end{align*} $$
$$ \begin{align*} \lim_{q\to \infty}\frac{\sigma(q)}{q^2} = \begin{cases} 953\cdot2^{-15}\approx 0.029\,08&\text{for }q\equiv 1\bmod 4,\\ 825\cdot2^{-16}\approx 0.012\,59&\text{for }q\equiv 3\bmod 4. \end{cases} \end{align*} $$
As we show below, the set
![]() $\Sigma $
consists of
$\Sigma $
consists of
![]() $(q^2-8q+15)/4$
elements. Hence, a random choice of
$(q^2-8q+15)/4$
elements. Hence, a random choice of
![]() $(a,b) \in \Sigma $
yields a maximally nonassociative quasigroup with probability
$(a,b) \in \Sigma $
yields a maximally nonassociative quasigroup with probability
![]() $\approx 1/8.596$
if
$\approx 1/8.596$
if
![]() $q\equiv 1\bmod 4$
, and with probability
$q\equiv 1\bmod 4$
, and with probability
![]() $\approx 1/19.86$
if
$\approx 1/19.86$
if
![]() $q\equiv 3 \bmod 4$
. This may have an important consequence for the cryptographic application described in [Reference Grošek and Horák10]. It means that a maximally nonassociative quasigroup of a particular large order can be obtained in an acceptable time by randomly generating pairs
$q\equiv 3 \bmod 4$
. This may have an important consequence for the cryptographic application described in [Reference Grošek and Horák10]. It means that a maximally nonassociative quasigroup of a particular large order can be obtained in an acceptable time by randomly generating pairs
![]() $(a,b)$
until one is found for which
$(a,b)$
until one is found for which
![]() $Q_{a,b}$
is maximally nonassociative.
$Q_{a,b}$
is maximally nonassociative.
An important ingredient in the proof of Theorem 1.1 is the transformation described in Proposition 1.2, and used in Corollary 1.3 to determine
![]() $|\Sigma |$
.
$|\Sigma |$
.
Define
![]() $S = S(\mathbb {F})$
as the set of all
$S = S(\mathbb {F})$
as the set of all
![]() $(x,y)\in \mathbb {F}\times \mathbb {F}$
such that both x and y are squares,
$(x,y)\in \mathbb {F}\times \mathbb {F}$
such that both x and y are squares,
![]() $x\ne y$
, and
$x\ne y$
, and
![]() $\{0,1\}\cap \{x,y\}=\varnothing $
.
$\{0,1\}\cap \{x,y\}=\varnothing $
.
Proposition 1.2. For each
![]() $(a,b)\in \Sigma $
, there exists exactly one
$(a,b)\in \Sigma $
, there exists exactly one
![]() $(x,y)\in S$
such that
$(x,y)\in S$
such that
 $$ \begin{align} a=\frac{x(1{-}y)}{x{-}y}, \quad b = \frac{1{-}y}{x{-}y}, \quad 1{-}a = \frac{y(1{-}x)}{y{-}x} \quad\text{and}\quad 1{-}b=\frac{1{-}x}{y{-}x}. \end{align} $$
$$ \begin{align} a=\frac{x(1{-}y)}{x{-}y}, \quad b = \frac{1{-}y}{x{-}y}, \quad 1{-}a = \frac{y(1{-}x)}{y{-}x} \quad\text{and}\quad 1{-}b=\frac{1{-}x}{y{-}x}. \end{align} $$
The mapping
is a bijection. If
![]() $(x,y)\in S$
, then
$(x,y)\in S$
, then
![]() $\Psi ^{-1} ((x,y)) = (a,b)$
if and only if Equations (1-3) hold.
$\Psi ^{-1} ((x,y)) = (a,b)$
if and only if Equations (1-3) hold.
Proof. If
![]() $x,y,a,b\in \mathbb {F}$
satisfy
$x,y,a,b\in \mathbb {F}$
satisfy
![]() $x\ne y$
,
$x\ne y$
,
![]() $a =x(1{-}y)/(x{-}y)$
, and
$a =x(1{-}y)/(x{-}y)$
, and
![]() $b= (1{-}y)/(x{-}y)$
, then
$b= (1{-}y)/(x{-}y)$
, then
Define
 $$ \begin{align*} \Phi\colon S\to \mathbb{F}\times \mathbb{F}, \quad (x,y)\mapsto \bigg ( \frac{x(1{-}y)} {x{-}y}, \frac{1{-}y}{x{-}y}\bigg ). \end{align*} $$
$$ \begin{align*} \Phi\colon S\to \mathbb{F}\times \mathbb{F}, \quad (x,y)\mapsto \bigg ( \frac{x(1{-}y)} {x{-}y}, \frac{1{-}y}{x{-}y}\bigg ). \end{align*} $$
Suppose that
![]() $(x,y) \in S$
and set
$(x,y) \in S$
and set
![]() $b = (1{-}y)/(x{-}y)$
. Then
$b = (1{-}y)/(x{-}y)$
. Then
![]() $b\ne 0$
as
$b\ne 0$
as
![]() $y\ne 1$
, and
$y\ne 1$
, and
![]() $b\ne 1$
since
$b\ne 1$
since
![]() $x\ne 1$
. Put
$x\ne 1$
. Put
![]() $a = xb$
. Then
$a = xb$
. Then
![]() $a\ne 0$
since
$a\ne 0$
since
![]() $b\ne 0$
and
$b\ne 0$
and
![]() $x\ne 0$
, and
$x\ne 0$
, and
![]() $a\ne b$
since
$a\ne b$
since
![]() $x\ne 1$
. Furthermore,
$x\ne 1$
. Furthermore,
![]() $a\ne 1$
since
$a\ne 1$
since
![]() $y\ne 0$
and
$y\ne 0$
and
![]() $x\ne 1$
. Since
$x\ne 1$
. Since
![]() $a=xb$
,
$a=xb$
,
![]() $ab=xb^2$
is a square. By Equations (1-4),
$ab=xb^2$
is a square. By Equations (1-4),
![]() $1{-}a = y(1{-}b)$
. Hence,
$1{-}a = y(1{-}b)$
. Hence,
![]() $(1{-}a)(1{-}b) = y(1{-}b)^2$
is a square too. This verifies that
$(1{-}a)(1{-}b) = y(1{-}b)^2$
is a square too. This verifies that
![]() $\Phi $
may be considered as a mapping
$\Phi $
may be considered as a mapping
![]() $S\to \Sigma $
.
$S\to \Sigma $
.
Assume
![]() $(a,b) \in \Sigma $
. By definition,
$(a,b) \in \Sigma $
. By definition,
![]() $\Psi ((a,b))=(x,y)$
, where
$\Psi ((a,b))=(x,y)$
, where
![]() $x=a/b$
and
$x=a/b$
and
![]() $y= (1{-}a)/(1{-}b)$
. We have
$y= (1{-}a)/(1{-}b)$
. We have
![]() $x\notin \{0,1\}$
since
$x\notin \{0,1\}$
since
![]() $a\ne 0$
and
$a\ne 0$
and
![]() $a\ne b$
. Similarly,
$a\ne b$
. Similarly,
![]() $y\notin \{0,1\}$
. Furthermore,
$y\notin \{0,1\}$
. Furthermore,
![]() $x\ne y$
since
$x\ne y$
since
![]() $x=y$
implies
$x=y$
implies
![]() $a = b$
. Thus,
$a = b$
. Thus,
![]() $(x,y)\in S$
. By straightforward verification,
$(x,y)\in S$
. By straightforward verification,
![]() $\Psi \Phi = \operatorname {id}_S$
and
$\Psi \Phi = \operatorname {id}_S$
and
![]() $\Phi \Psi = \operatorname {id}_\Sigma $
.
$\Phi \Psi = \operatorname {id}_\Sigma $
.
Corollary 1.3.
![]() $|\Sigma (\mathbb {F}_q)| = |S(\mathbb {F}_q)| = (q^2-8q+15)/4$
.
$|\Sigma (\mathbb {F}_q)| = |S(\mathbb {F}_q)| = (q^2-8q+15)/4$
.
Proof. By Proposition 1.2,
![]() $|\Sigma | = |S|$
. Furthermore, by the definition, S contains
$|\Sigma | = |S|$
. Furthermore, by the definition, S contains
![]() $((q-3)/2)^2 - (q-3)/2$
elements.
$((q-3)/2)^2 - (q-3)/2$
elements.
The definition of
![]() $Q_{a,b}$
follows the established way of defining a quasigroup by means of an orthomorphism, say
$Q_{a,b}$
follows the established way of defining a quasigroup by means of an orthomorphism, say
![]() $\psi $
, of an abelian group
$\psi $
, of an abelian group
![]() $(G,+)$
. Here,
$(G,+)$
. Here,
![]() $\psi $
is said to be an orthomorphism of
$\psi $
is said to be an orthomorphism of
![]() $(G,+)$
if it permutes G and the mapping
$(G,+)$
if it permutes G and the mapping
![]() $x\mapsto \psi (x)-x$
permutes G as well. A quadratic orthomorphism
$x\mapsto \psi (x)-x$
permutes G as well. A quadratic orthomorphism
![]() $\psi _{a,b}$
is defined for each
$\psi _{a,b}$
is defined for each
![]() $(a,b)\in \Sigma (\mathbb {F}_q)$
by
$(a,b)\in \Sigma (\mathbb {F}_q)$
by
 $$ \begin{align} \psi_{a,b}(u) = \begin{cases} au \quad \text{if }u\text{ is a square,}\\ bu \quad \text{if }u\text{ is a nonsquare.}\end{cases} \end{align} $$
$$ \begin{align} \psi_{a,b}(u) = \begin{cases} au \quad \text{if }u\text{ is a square,}\\ bu \quad \text{if }u\text{ is a nonsquare.}\end{cases} \end{align} $$
The definition in Equation (1-2) of the quasigroup
![]() $Q_{a,b}$
thus fits the general scheme that
$Q_{a,b}$
thus fits the general scheme that
![]() $u*v = u+\psi (v-u)$
is a quasigroup whenever
$u*v = u+\psi (v-u)$
is a quasigroup whenever
![]() $\psi $
is an orthomorphism of an abelian group
$\psi $
is an orthomorphism of an abelian group
![]() $(G,+)$
. See [Reference Evans7, Reference Wanless15] for more information on quasigroups defined by means of orthomorphisms.
$(G,+)$
. See [Reference Evans7, Reference Wanless15] for more information on quasigroups defined by means of orthomorphisms.
The number of associative triples in such a quasigroup depends upon the number of solutions to the associativity equation:
Below we always assume that
![]() $\psi = \psi _{a,b}$
for some
$\psi = \psi _{a,b}$
for some
![]() $(a,b) \in \Sigma $
. Some of our statements remain true in the case of a general
$(a,b) \in \Sigma $
. Some of our statements remain true in the case of a general
![]() $\psi $
. However, the general situation is not the focus of this paper.
$\psi $
. However, the general situation is not the focus of this paper.
Proposition 1.4. For
![]() $(a,b)\in \Sigma $
, put
$(a,b)\in \Sigma $
, put
![]() $\psi = \psi _{a,b}$
. An ordered pair
$\psi = \psi _{a,b}$
. An ordered pair
![]() $(u,v)\in \mathbb {F}^2$
fulfills the associativity equation (1-6) if and only if
$(u,v)\in \mathbb {F}^2$
fulfills the associativity equation (1-6) if and only if
![]() $v*(0\,*u) = (v*\,0)*u$
. Furthermore,
$v*(0\,*u) = (v*\,0)*u$
. Furthermore,
If
![]() $(u,v)\ne (0,0)$
fulfills Equation (1-6), then none of u, v,
$(u,v)\ne (0,0)$
fulfills Equation (1-6), then none of u, v,
![]() $u-v-\psi (-v)$
, and
$u-v-\psi (-v)$
, and
![]() $\psi (u)-v$
vanishes, and
$\psi (u)-v$
vanishes, and
![]() $(c^2u,c^2v)$
fulfills Equation (1-6) too, for any
$(c^2u,c^2v)$
fulfills Equation (1-6) too, for any
![]() $c\in \mathbb {F}$
.
$c\in \mathbb {F}$
.
The quasigroup
![]() $Q_{a,b}$
is maximally nonassociative if and only if
$Q_{a,b}$
is maximally nonassociative if and only if
![]() $(u,v)=(0,0)$
is the only solution to Equation (1-6).
$(u,v)=(0,0)$
is the only solution to Equation (1-6).
Proof. This is a restatement of [Reference Drápal and Wanless6, Lemmas 1.3 and 3.1]. A sketch of the proof follows, to make this paper self-contained. Since
![]() $u \mapsto z + u$
is an automorphism of
$u \mapsto z + u$
is an automorphism of
![]() $Q=Q_{a,b}$
for each
$Q=Q_{a,b}$
for each
![]() $z\in \mathbb {F}$
, the maximal nonassociativity is equivalent to having no
$z\in \mathbb {F}$
, the maximal nonassociativity is equivalent to having no
![]() $(u,v)\ne (0,0)$
such that
$(u,v)\ne (0,0)$
such that
![]() $u*(0*v) = (u*0)*v$
. This turns into Equation (1-6) by invoking the formula
$u*(0*v) = (u*0)*v$
. This turns into Equation (1-6) by invoking the formula
![]() $u*v = u+\psi (v-u)$
. Since
$u*v = u+\psi (v-u)$
. Since
![]() $x\mapsto c^2x$
is an automorphism of Q for each
$x\mapsto c^2x$
is an automorphism of Q for each
![]() $c\in \mathbb {F}$
,
$c\in \mathbb {F}$
,
![]() $c\ne 0$
, the associativity equation holds for
$c\ne 0$
, the associativity equation holds for
![]() $(u,v)$
if and only if it holds for
$(u,v)$
if and only if it holds for
![]() $(c^2u,c^2v)$
. For the rest, it suffices to observe that in an idempotent quasigroup,
$(c^2u,c^2v)$
. For the rest, it suffices to observe that in an idempotent quasigroup,
![]() $u*(v*w) =(u*v) *w $
implies
$u*(v*w) =(u*v) *w $
implies
![]() $u=v=w$
if
$u=v=w$
if
![]() $u=v$
or
$u=v$
or
![]() $u=v*w$
or
$u=v*w$
or
![]() $v=w$
or
$v=w$
or
![]() $u*v = w$
.
$u*v = w$
.
For
![]() $(a,b)\in \Sigma $
, denote by
$(a,b)\in \Sigma $
, denote by
![]() $E(a,b)$
the set of
$E(a,b)$
the set of
![]() $(u,v)\ne (0,0)$
that satisfy the associativity equation (1-6). By Proposition 1.4,
$(u,v)\ne (0,0)$
that satisfy the associativity equation (1-6). By Proposition 1.4,
![]() $Q_{a,b}$
is maximally nonassociative if and only if
$Q_{a,b}$
is maximally nonassociative if and only if
![]() $E(a,b)= \varnothing $
. The number of such
$E(a,b)= \varnothing $
. The number of such
![]() $(a,b)$
may be obtained indirectly by counting the number of
$(a,b)$
may be obtained indirectly by counting the number of
![]() $(a,b)\in \Sigma $
for which
$(a,b)\in \Sigma $
for which
![]() $E(a,b)\ne \varnothing $
. To this end, we partition
$E(a,b)\ne \varnothing $
. To this end, we partition
![]() $E(a,b) = \bigcup E_{ij}^{rs}(a,b)$
, where
$E(a,b) = \bigcup E_{ij}^{rs}(a,b)$
, where
![]() $i,j,r,s\in \{0,1\}$
. To determine to which part an element
$i,j,r,s\in \{0,1\}$
. To determine to which part an element
![]() $(u,v)\in E(a,b)$
belongs, the following rule is used:
$(u,v)\in E(a,b)$
belongs, the following rule is used:
 $$ \begin{gather*} \begin{aligned} i=0 &\Longleftrightarrow u \ \text {is a square};\\ j=0 &\Longleftrightarrow -v \ \text {is a square};\\ r=0 &\Longleftrightarrow \psi_{a,b}(u)-v \ \text {is a square; and}\\ s=0 &\Longleftrightarrow u-v-\psi_{a,b}(-v) \ \text {is a square}. \end{aligned} \end{gather*} $$
$$ \begin{gather*} \begin{aligned} i=0 &\Longleftrightarrow u \ \text {is a square};\\ j=0 &\Longleftrightarrow -v \ \text {is a square};\\ r=0 &\Longleftrightarrow \psi_{a,b}(u)-v \ \text {is a square; and}\\ s=0 &\Longleftrightarrow u-v-\psi_{a,b}(-v) \ \text {is a square}. \end{aligned} \end{gather*} $$
Thus, if one of the elements u,
![]() $-v$
,
$-v$
,
![]() $\psi _{a,b}(u){-}v$
, and
$\psi _{a,b}(u){-}v$
, and
![]() $u{-}v{-}\psi _{a,b}(-v)$
is a nonsquare, then the respective value of i, j, r, or s is set to
$u{-}v{-}\psi _{a,b}(-v)$
is a nonsquare, then the respective value of i, j, r, or s is set to
![]() $1$
. For each
$1$
. For each
![]() $(u,v)\in E(a,b)$
, there hence exists exactly one quadruple
$(u,v)\in E(a,b)$
, there hence exists exactly one quadruple
![]() $(i,j,r,s)$
such that
$(i,j,r,s)$
such that
![]() $(u,v) \in E_{ij}^{rs}(a,b)$
, giving us the desired partition. We also work with sets
$(u,v) \in E_{ij}^{rs}(a,b)$
, giving us the desired partition. We also work with sets
where
![]() $i,j,r,s\in \{0,1\}$
. The next observation directly follows from the definition of the sets
$i,j,r,s\in \{0,1\}$
. The next observation directly follows from the definition of the sets
![]() $\Sigma _{ij}^{rs}$
. It is recorded here for the sake of later reference.
$\Sigma _{ij}^{rs}$
. It is recorded here for the sake of later reference.
Proposition 1.5. Suppose that
![]() $(a,b)\in \Sigma =\Sigma (\mathbb {F}_q)$
for an odd prime power
$(a,b)\in \Sigma =\Sigma (\mathbb {F}_q)$
for an odd prime power
![]() $q>1$
. The quasigroup
$q>1$
. The quasigroup
![]() $Q_{a,b}$
is maximally nonassociative if and only if
$Q_{a,b}$
is maximally nonassociative if and only if
![]() $(a,b)\notin \bigcup \Sigma _{ij}^{rs}$
.
$(a,b)\notin \bigcup \Sigma _{ij}^{rs}$
.
If it is assumed that
![]() $(u,v) \in E_{ij}^{rs}(a,b)$
, then the associativity equation (1-6) can be turned into a linear equation in unknowns u and v since each occurrence of
$(u,v) \in E_{ij}^{rs}(a,b)$
, then the associativity equation (1-6) can be turned into a linear equation in unknowns u and v since each occurrence of
![]() $\psi $
can be interpreted by means of Equation (1-5). The list of these linear equations can be found in [Reference Drápal and Wanless6]. Their derivation is relatively short and is partly repeated in Lemmas 2.4–2.7. The approach used here differs from that of [Reference Drápal and Wanless6] in two aspects. The symmetries induced by opposite quasigroups and by automorphisms
$\psi $
can be interpreted by means of Equation (1-5). The list of these linear equations can be found in [Reference Drápal and Wanless6]. Their derivation is relatively short and is partly repeated in Lemmas 2.4–2.7. The approach used here differs from that of [Reference Drápal and Wanless6] in two aspects. The symmetries induced by opposite quasigroups and by automorphisms
![]() $Q_{a,b}\cong Q_{b,a}$
are used more extensively here, and characterizations of
$Q_{a,b}\cong Q_{b,a}$
are used more extensively here, and characterizations of
![]() $\Sigma _{ij}^{rs}$
are immediately transformed into characterizations of
$\Sigma _{ij}^{rs}$
are immediately transformed into characterizations of
As will turn out, sets
![]() $S_{ij}^{rs}$
can be described by a requirement that several polynomials in x and y are either squares or nonsquares. Estimates of
$S_{ij}^{rs}$
can be described by a requirement that several polynomials in x and y are either squares or nonsquares. Estimates of
![]() $|S_{ij}^{rs}|$
can be thus obtained by means of the Weil bound (as formulated, say, in [Reference Evans, Mullen and Panario8, Theorem 6.22]). We are not using the Weil bound directly, but via Theorem 1.6 below, a straightforward consequence from [Reference Drápal and Wanless6, Theorem 1.4]. Applications of Theorem 1.6 to the intersections of sets
$|S_{ij}^{rs}|$
can be thus obtained by means of the Weil bound (as formulated, say, in [Reference Evans, Mullen and Panario8, Theorem 6.22]). We are not using the Weil bound directly, but via Theorem 1.6 below, a straightforward consequence from [Reference Drápal and Wanless6, Theorem 1.4]. Applications of Theorem 1.6 to the intersections of sets
![]() $S_{ij}^{rs}$
, with symmetries taken into account, yield, after a number of computations, the asymptotic results stated in Theorem 1.1.
$S_{ij}^{rs}$
, with symmetries taken into account, yield, after a number of computations, the asymptotic results stated in Theorem 1.1.
Say that a list of polynomials
![]() $p_1,\ldots ,p_k$
in one variable, with coefficients in
$p_1,\ldots ,p_k$
in one variable, with coefficients in
![]() $\mathbb {F}$
, is square-free if there exists no sequence
$\mathbb {F}$
, is square-free if there exists no sequence
![]() $1\leqslant i_1<\cdots <i_r \leqslant k$
such that
$1\leqslant i_1<\cdots <i_r \leqslant k$
such that
![]() $r\geqslant 1$
and
$r\geqslant 1$
and
![]() $p_{i_1}\cdots p_{i_r}$
is a square (as a polynomial with coefficients in the algebraic closure
$p_{i_1}\cdots p_{i_r}$
is a square (as a polynomial with coefficients in the algebraic closure
![]() $\bar {\mathbb {F}}$
of
$\bar {\mathbb {F}}$
of
![]() $\mathbb {F}$
). Define
$\mathbb {F}$
). Define
![]() $\chi \colon \mathbb {F}\to \{\pm 1,0\}$
to be the quadratic character extended by
$\chi \colon \mathbb {F}\to \{\pm 1,0\}$
to be the quadratic character extended by
![]() $\chi (0)=0$
.
$\chi (0)=0$
.
Theorem 1.6. Let
![]() $p_1,\ldots ,p_k\in \mathbb {F}[x]$
be a square-free list of polynomials of degree
$p_1,\ldots ,p_k\in \mathbb {F}[x]$
be a square-free list of polynomials of degree
![]() $d_i\geqslant 1$
, and let
$d_i\geqslant 1$
, and let
![]() $\varepsilon _1,\ldots ,\varepsilon _k\in \{-1,1\}$
. Denote by N the number of all
$\varepsilon _1,\ldots ,\varepsilon _k\in \{-1,1\}$
. Denote by N the number of all
![]() $\alpha \in \mathbb {F}$
such that
$\alpha \in \mathbb {F}$
such that
![]() $\chi (p_i(\alpha ))= \varepsilon _i$
, for
$\chi (p_i(\alpha ))= \varepsilon _i$
, for
![]() $1\leqslant i \leqslant k$
. Then
$1\leqslant i \leqslant k$
. Then
where
![]() $D=\sum _i d_i$
.
$D=\sum _i d_i$
.
The purpose of Section 2 is to describe each of the sets
![]() $S_{ij}^{rs}$
by a list of polynomials
$S_{ij}^{rs}$
by a list of polynomials
![]() $p(x,y)$
such that the presence of
$p(x,y)$
such that the presence of
![]() $(x,y)\in S$
in
$(x,y)\in S$
in
![]() $S_{ij}^{rs}$
depends upon
$S_{ij}^{rs}$
depends upon
![]() $p(x,y)$
being a square or nonsquare. Theorem 2.10 gives such a description for
$p(x,y)$
being a square or nonsquare. Theorem 2.10 gives such a description for
![]() $q=|\mathbb {F}|\equiv 1 \bmod 4$
, and Theorem 2.11 for
$q=|\mathbb {F}|\equiv 1 \bmod 4$
, and Theorem 2.11 for
![]() $q\equiv 3 \bmod 4$
. Section 3 contains auxiliary results that make applications of Theorem 1.6 possible. Note that Theorem 1.6 is concerned with polynomials in only one variable. To use it, one of the variables, say y, has to be fixed. If
$q\equiv 3 \bmod 4$
. Section 3 contains auxiliary results that make applications of Theorem 1.6 possible. Note that Theorem 1.6 is concerned with polynomials in only one variable. To use it, one of the variables, say y, has to be fixed. If
![]() $y=c$
, and
$y=c$
, and
![]() $p_1(x,y),\ldots ,p_k(x,y)$
are the polynomials occurring in Theorems 2.10 and 2.11, then Theorem 1.6 may be used without further specifications only for those c for which
$p_1(x,y),\ldots ,p_k(x,y)$
are the polynomials occurring in Theorems 2.10 and 2.11, then Theorem 1.6 may be used without further specifications only for those c for which
![]() $p_1(x,c),\ldots ,p_k(x,c)$
is a square-free list. The purpose of Section 3 is to show that this is true for nearly all c, and that the number of possible exceptional values of c is very small. Section 4 provides the estimate of
$p_1(x,c),\ldots ,p_k(x,c)$
is a square-free list. The purpose of Section 3 is to show that this is true for nearly all c, and that the number of possible exceptional values of c is very small. Section 4 provides the estimate of
![]() $S\setminus \bigcup S_{ij}^{rs}$
for
$S\setminus \bigcup S_{ij}^{rs}$
for
![]() $q\equiv 3\bmod 4$
, and Section 5 for
$q\equiv 3\bmod 4$
, and Section 5 for
![]() $q\equiv 1 \bmod 4$
, in Theorems 4.4 and 5.5, respectively. Section 6 consists of concluding remarks.
$q\equiv 1 \bmod 4$
, in Theorems 4.4 and 5.5, respectively. Section 6 consists of concluding remarks.
2 Quadratic residues and the associativity equation
Let
![]() $Q^{op}_{a,b}$
denote the opposite quasigroup of
$Q^{op}_{a,b}$
denote the opposite quasigroup of
![]() $Q_{a,b}$
, namely the quasigroup satisfying
$Q_{a,b}$
, namely the quasigroup satisfying
![]() $Q^{op}_{a,b}(u,v)=Q_{a,b}(v,u)$
for all
$Q^{op}_{a,b}(u,v)=Q_{a,b}(v,u)$
for all
![]() $u,v$
. The following facts are well known [Reference Evans7, Reference Wanless16] and easy to verify.
$u,v$
. The following facts are well known [Reference Evans7, Reference Wanless16] and easy to verify.
Lemma 2.1. If
![]() $(a,b)\in \Sigma $
, then
$(a,b)\in \Sigma $
, then
(i)
 $u\mapsto u\zeta $
is an isomorphism
$u\mapsto u\zeta $
is an isomorphism
 $Q_{a,b}\cong Q_{b,a}$
, for every nonsquare
$Q_{a,b}\cong Q_{b,a}$
, for every nonsquare
 $\zeta \in \mathbb {F}$
;
$\zeta \in \mathbb {F}$
;(ii)
 $Q^{op}_{a,b} = Q_{1-a,1-b}$
if
$Q^{op}_{a,b} = Q_{1-a,1-b}$
if
 $q\equiv 1\bmod 4$
, and
$q\equiv 1\bmod 4$
, and
 $Q^{op}_{a,b} = Q_{1-b,1-a}$
if
$Q^{op}_{a,b} = Q_{1-b,1-a}$
if
 $q\equiv 3\bmod 4$
.
$q\equiv 3\bmod 4$
.
An alternative way to express that
![]() $q\equiv 1 \bmod 4$
is to say that
$q\equiv 1 \bmod 4$
is to say that
![]() $-1$
is a square. If
$-1$
is a square. If
![]() $\bar *$
denotes the operation of the opposite quasigroup, then
$\bar *$
denotes the operation of the opposite quasigroup, then
![]() $(v\,\bar *\, 0)\,\bar *\, u = v\,\bar *\, (0 \,\bar *\, u)$
holds in
$(v\,\bar *\, 0)\,\bar *\, u = v\,\bar *\, (0 \,\bar *\, u)$
holds in
![]() $Q_{a,b}^{op}$
if and only if
$Q_{a,b}^{op}$
if and only if
![]() $u*(0*v) = (u*0)*v$
. Hence,
$u*(0*v) = (u*0)*v$
. Hence,
![]() $(u,v)\in E(a,b)$
if and only if
$(u,v)\in E(a,b)$
if and only if
![]() $(v,u)\in E(a',b')$
, where
$(v,u)\in E(a',b')$
, where
![]() $(a',b')=(1{-}a,1{-}b)$
if
$(a',b')=(1{-}a,1{-}b)$
if
![]() $-1$
is a square, and
$-1$
is a square, and
![]() $(a',b')= (1{-}b,1{-}a)$
if
$(a',b')= (1{-}b,1{-}a)$
if
![]() $-1$
is a nonsquare, by part (ii) of Lemma 2.1. Similarly,
$-1$
is a nonsquare, by part (ii) of Lemma 2.1. Similarly,
![]() $(u,v)\in E(a,b)$
if and only if
$(u,v)\in E(a,b)$
if and only if
![]() $(\zeta u,\zeta v)\in E(b,a)$
.
$(\zeta u,\zeta v)\in E(b,a)$
.
Working out these connections with respect to being square or nonsquare yields the following statement. It appears without a proof since it coincides with [Reference Drápal and Wanless6, Lemmas 3.2 and 3.3] and since the proof is straightforward.
Lemma 2.2. Assume
![]() $(a,b)\in \Sigma $
and
$(a,b)\in \Sigma $
and
![]() $i,j,r,s\in \{0,1\}$
. Then
$i,j,r,s\in \{0,1\}$
. Then
Proposition 2.3. Both of the mappings
![]() $(x,y)\mapsto (y,x)$
and
$(x,y)\mapsto (y,x)$
and
![]() $(x,y)\mapsto (x^{-1},y^{-1})$
permute the set
$(x,y)\mapsto (x^{-1},y^{-1})$
permute the set
![]() $S = S(\mathbb {F})$
. If
$S = S(\mathbb {F})$
. If
![]() $i,j,r,s\in \{0,1\}$
, then
$i,j,r,s\in \{0,1\}$
, then
Proof. By definition,
![]() $(x,y)\in S$
if and only if x and y are both squares,
$(x,y)\in S$
if and only if x and y are both squares,
![]() $x\ne y$
, and
$x\ne y$
, and
![]() $\{x,y\}\cap \{0,1\}=\varnothing $
. These properties are retained both by the switch
$\{x,y\}\cap \{0,1\}=\varnothing $
. These properties are retained both by the switch
![]() $(x,y)\mapsto (\kern1.5pt y,x)$
and by the inversion
$(x,y)\mapsto (\kern1.5pt y,x)$
and by the inversion
![]() $(x,y)\mapsto (x^{-1},y^{-1})$
. These mappings thus permute S.
$(x,y)\mapsto (x^{-1},y^{-1})$
. These mappings thus permute S.
Let
![]() $(a.b)\in \Sigma $
be such that
$(a.b)\in \Sigma $
be such that
![]() $\Psi ((a,b)) = (x,y)$
. Then
$\Psi ((a,b)) = (x,y)$
. Then
![]() $x=a/b$
,
$x=a/b$
,
![]() $y = (1{-}a)/(1{-}b)$
. Hence,
$y = (1{-}a)/(1{-}b)$
. Hence,
![]() $\Psi ((b,a)) = (x^{-1},y^{-1})$
and
$\Psi ((b,a)) = (x^{-1},y^{-1})$
and
![]() $\Psi ((1{-}a,1{-}b)) = (\kern1.5pt y,x)$
. For the proof, we thus need to show that
$\Psi ((1{-}a,1{-}b)) = (\kern1.5pt y,x)$
. For the proof, we thus need to show that
Suppose that
![]() $(a,b) \in \Sigma _{ij}^{rs}$
, that is, that there exists
$(a,b) \in \Sigma _{ij}^{rs}$
, that is, that there exists
![]() $(u,v) \in E_{ij}^{rs}(a,b)$
. If
$(u,v) \in E_{ij}^{rs}(a,b)$
. If
![]() $-1$
is a square, then
$-1$
is a square, then
![]() $(v,u)\in E_{ji}^{sr}(1{-}a,1{-}b)$
by Condition (2-2). If
$(v,u)\in E_{ji}^{sr}(1{-}a,1{-}b)$
by Condition (2-2). If
![]() $-1$
is a nonsquare, then
$-1$
is a nonsquare, then
![]() $(\zeta v,\zeta u) \in E_{ji}^{sr}(1{-}a,1{-}b)$
, by Conditions (2-3) and (2-1). Thus,
$(\zeta v,\zeta u) \in E_{ji}^{sr}(1{-}a,1{-}b)$
, by Conditions (2-3) and (2-1). Thus,
![]() $(1{-}a,1{-}b)\in \Sigma _{ji}^{sr}$
in both cases. We also have
$(1{-}a,1{-}b)\in \Sigma _{ji}^{sr}$
in both cases. We also have
![]() $(\zeta u,\zeta v) \in E_{1-i,1-j}^{1-r,1-s}(b,a)$
, by Condition (2-1). Hence,
$(\zeta u,\zeta v) \in E_{1-i,1-j}^{1-r,1-s}(b,a)$
, by Condition (2-1). Hence,
![]() $(b,a)\in \Sigma _{1-i,1-j}^{1-r,1-s}$
.
$(b,a)\in \Sigma _{1-i,1-j}^{1-r,1-s}$
.
To determine all of the sets
![]() $S_{ij}^{rs}$
, it thus suffices to know the sets
$S_{ij}^{rs}$
, it thus suffices to know the sets
We next determine these sets via a sequence of lemmas.
Lemma 2.4. If
![]() $-1$
is a square, then
$-1$
is a square, then
![]() $S_{01}^{00}=S_{01}^{10}=\varnothing $
, while
$S_{01}^{00}=S_{01}^{10}=\varnothing $
, while
 $$ \begin{align*} (x,y)\in S_{00}^{00} &\Longleftrightarrow (1{-}x)(\kern1.5pt y{-}x)\text{ and }(1{-}y)(\kern1.5pt y{-}x)\text{ are squares; and}\\ (x,y)\in S_{00}^{11} &\Longleftrightarrow (x^2y+xy-x^2-y^2)(\kern1.5pt y{-}x)\text{ and}\\ &\phantom{\Longleftrightarrow } (xy^2+xy-x^2-y^2)(\kern1.5pt y{-}x)\text{ are nonsquares.} \end{align*} $$
$$ \begin{align*} (x,y)\in S_{00}^{00} &\Longleftrightarrow (1{-}x)(\kern1.5pt y{-}x)\text{ and }(1{-}y)(\kern1.5pt y{-}x)\text{ are squares; and}\\ (x,y)\in S_{00}^{11} &\Longleftrightarrow (x^2y+xy-x^2-y^2)(\kern1.5pt y{-}x)\text{ and}\\ &\phantom{\Longleftrightarrow } (xy^2+xy-x^2-y^2)(\kern1.5pt y{-}x)\text{ are nonsquares.} \end{align*} $$
Proof. We assume that
![]() $-1$
is a square. If
$-1$
is a square. If
![]() $(u,v)\in E_{00}^{00}(a,b)$
, then the associativity equation attains the form
$(u,v)\in E_{00}^{00}(a,b)$
, then the associativity equation attains the form
![]() $a(au-v)=-av+a(u-v+av)$
, and that is the same as
$a(au-v)=-av+a(u-v+av)$
, and that is the same as
![]() $(1{-}a)(u{-}v)=0$
. Since
$(1{-}a)(u{-}v)=0$
. Since
![]() $1{-}a\ne 0$
, and since u is assumed to be square, the set
$1{-}a\ne 0$
, and since u is assumed to be square, the set
![]() $E_{00}^{00}(a,b)$
is nonempty if and only if it contains
$E_{00}^{00}(a,b)$
is nonempty if and only if it contains
![]() $(1,1)$
, by Proposition 1.4. This takes place if and only if
$(1,1)$
, by Proposition 1.4. This takes place if and only if
![]() $1{-}a$
and a are squares. Suppose that
$1{-}a$
and a are squares. Suppose that
![]() $(x,y) = \Psi ((a,b))$
. Then
$(x,y) = \Psi ((a,b))$
. Then
![]() $a=x(1{-}y)/(x{-}y)$
is a square if and only if
$a=x(1{-}y)/(x{-}y)$
is a square if and only if
![]() $(1{-}y)(\kern1.5pt y{-}x)$
is a square, and
$(1{-}y)(\kern1.5pt y{-}x)$
is a square, and
![]() $1{-}a = y(1{-}x)/(\kern1.5pt y{-}x)$
is a square if and only if
$1{-}a = y(1{-}x)/(\kern1.5pt y{-}x)$
is a square if and only if
![]() $(1{-}x)(\kern1.5pt y{-}x)$
is a square.
$(1{-}x)(\kern1.5pt y{-}x)$
is a square.
If
![]() $(u,v) \in E_{00}^{11}(a,b)$
, then
$(u,v) \in E_{00}^{11}(a,b)$
, then
![]() $b(au-v)=-av+b(u-v+av)$
yields
$b(au-v)=-av+b(u-v+av)$
yields
![]() $ub(a{-}1)=a(b{-}1)v$
, where both u and v are squares. Thus,
$ub(a{-}1)=a(b{-}1)v$
, where both u and v are squares. Thus,
![]() $(u,v)$
is a solution if and only if
$(u,v)$
is a solution if and only if
![]() $(1,b(a{-}1)/a(b{-}1))$
is a solution. Since
$(1,b(a{-}1)/a(b{-}1))$
is a solution. Since
![]() $v=b(a{-}1)/a(b{-}1)$
is always a square, the conditions for the existence of the solution are that
$v=b(a{-}1)/a(b{-}1)$
is always a square, the conditions for the existence of the solution are that
![]() $a-v$
and
$a-v$
and
![]() $1-(1{-}a)v$
are nonsquares. If
$1-(1{-}a)v$
are nonsquares. If
![]() $(x,y) = \Psi ((a,b))$
, then
$(x,y) = \Psi ((a,b))$
, then
![]() $v = y/x$
,
$v = y/x$
,
![]() $a-v = (x^2-x^2y-yx+y^2)/x(x-y)$
, and
$a-v = (x^2-x^2y-yx+y^2)/x(x-y)$
, and
![]() $1-(1{-}a)v=(xy-x^2-y^2+y^2x)/x(\kern1.5pt y{-}x)$
.
$1-(1{-}a)v=(xy-x^2-y^2+y^2x)/x(\kern1.5pt y{-}x)$
.
If
![]() $(u,v) \in E_{01}^{00}(a,b)$
, then
$(u,v) \in E_{01}^{00}(a,b)$
, then
![]() $a(au-v)=-bv + a(u-v+bv)$
and
$a(au-v)=-bv + a(u-v+bv)$
and
![]() $a(a-1) u = b(a-1)v$
. This implies that
$a(a-1) u = b(a-1)v$
. This implies that
![]() $uv$
is a square. However, the assumption
$uv$
is a square. However, the assumption
![]() $(u,v) \in E_{01}^{00}(a,b)$
implies that u is a square and
$(u,v) \in E_{01}^{00}(a,b)$
implies that u is a square and
![]() $-v$
is a nonsquare. Thus,
$-v$
is a nonsquare. Thus,
![]() $uv$
should be both a square and a nonsquare, which is a contradiction. If
$uv$
should be both a square and a nonsquare, which is a contradiction. If
![]() $(u,v) \in E_{01}^{10}(a,b)$
, then
$(u,v) \in E_{01}^{10}(a,b)$
, then
![]() $b(au-v)=-bv + a(u-v+bv)$
, and that gives
$b(au-v)=-bv + a(u-v+bv)$
, and that gives
![]() $u=v$
, which is a contradiction again.
$u=v$
, which is a contradiction again.
Lemma 2.5. If
![]() $-1$
is a nonsquare, then
$-1$
is a nonsquare, then
![]() $S_{00}^{00}=S_{00}^{11}=\varnothing $
, while
$S_{00}^{00}=S_{00}^{11}=\varnothing $
, while
 $$ \begin{align*} (x,y) \in S_{01}^{10} & \Longleftrightarrow (x,y) \in S_{10}^{01};\\ & \Longleftrightarrow (1{-}y)(x{-}y)\text{ and }(1{-}x)(\kern1.5pt y{-}x)\text{ are squares; and} \\ (x,y) \in S_{01}^{00} & \Longleftrightarrow (x{-}1)(\kern1.5pt y{-}x)\text{ and }(x^2{-}2x{+}y)(\kern1.5pt y{-}x)\text{ are squares.} \end{align*} $$
$$ \begin{align*} (x,y) \in S_{01}^{10} & \Longleftrightarrow (x,y) \in S_{10}^{01};\\ & \Longleftrightarrow (1{-}y)(x{-}y)\text{ and }(1{-}x)(\kern1.5pt y{-}x)\text{ are squares; and} \\ (x,y) \in S_{01}^{00} & \Longleftrightarrow (x{-}1)(\kern1.5pt y{-}x)\text{ and }(x^2{-}2x{+}y)(\kern1.5pt y{-}x)\text{ are squares.} \end{align*} $$
Proof. We assume that
![]() $-1$
is a nonsquare. If
$-1$
is a nonsquare. If
![]() $E_{00}^{00}(a,b)\ne \varnothing $
, then
$E_{00}^{00}(a,b)\ne \varnothing $
, then
![]() $(1,1)\in E_{00}^{00} (a,b)$
, by the same argument as in the proof of Lemma 2.4. However,
$(1,1)\in E_{00}^{00} (a,b)$
, by the same argument as in the proof of Lemma 2.4. However,
![]() $(1,1)$
cannot belong to
$(1,1)$
cannot belong to
![]() $E_{00}^{00}(a,b)$
since
$E_{00}^{00}(a,b)$
since
![]() $-1$
is a nonsquare. Similarly,
$-1$
is a nonsquare. Similarly,
![]() $E_{00}^{11}(a,b) = \varnothing $
since
$E_{00}^{11}(a,b) = \varnothing $
since
![]() $-b(a{-}1)/a(b{-}1)$
is a nonsquare.
$-b(a{-}1)/a(b{-}1)$
is a nonsquare.
Suppose that
![]() $(u,v) \in E_{01}^{00}(a,b)$
. Then Equation (1-6) implies
$(u,v) \in E_{01}^{00}(a,b)$
. Then Equation (1-6) implies
![]() $au = bv$
. Hence,
$au = bv$
. Hence,
![]() $(a,b)\in \Sigma _{01}^{00}$
if and only if
$(a,b)\in \Sigma _{01}^{00}$
if and only if
![]() $(1,a/b)\in E_{01}^{00}(a,b)$
. The latter takes place if and only if
$(1,a/b)\in E_{01}^{00}(a,b)$
. The latter takes place if and only if
![]() $a-a/b$
and
$a-a/b$
and
![]() $1-(1{-}b)a/b$
are squares. Let
$1-(1{-}b)a/b$
are squares. Let
![]() $(x,y) = \Psi ((a,b))$
. Then
$(x,y) = \Psi ((a,b))$
. Then
and
Let
![]() $(u,v)\in E_{01}^{10}(a,b)$
. Then
$(u,v)\in E_{01}^{10}(a,b)$
. Then
![]() $u=v$
by Equation (1-6). Hence,
$u=v$
by Equation (1-6). Hence,
![]() $(a,b)\in \Sigma _{01}^{10}$
if and only if
$(a,b)\in \Sigma _{01}^{10}$
if and only if
![]() $(1,1)\in E_{01}^{10}(a,b)$
. The latter is true if and only if
$(1,1)\in E_{01}^{10}(a,b)$
. The latter is true if and only if
![]() $a-1$
is a nonsquare and b is a square. If
$a-1$
is a nonsquare and b is a square. If
![]() $(x,y) = \Psi ((a,b))$
, then this means that
$(x,y) = \Psi ((a,b))$
, then this means that
![]() $(x{-}1)(\kern1.5pt y{-}x)$
is a nonsquare and
$(x{-}1)(\kern1.5pt y{-}x)$
is a nonsquare and
![]() $(1{-}y)(x{-}y)$
is a square. The symmetry of these conditions shows that
$(1{-}y)(x{-}y)$
is a square. The symmetry of these conditions shows that
![]() $(x,y)\in S_{01}^{10}$
if and only if
$(x,y)\in S_{01}^{10}$
if and only if
![]() $(\kern1.2pt y,x)\in S_{01}^{10}$
. Hence,
$(\kern1.2pt y,x)\in S_{01}^{10}$
. Hence,
![]() $S_{01}^{10}=S_{10}^{01}$
, by Proposition 2.3.
$S_{01}^{10}=S_{10}^{01}$
, by Proposition 2.3.
Lemma 2.6. Assume that
![]() $(x,y) \in S$
. Then
$(x,y) \in S$
. Then
![]() $(x,y) \in S_{00}^{01}$
if and only if
$(x,y) \in S_{00}^{01}$
if and only if
![]() $-xy-y+x$
and
$-xy-y+x$
and
![]() $(-x^2y+x^2+y^2-xy)(x{-}y)$
are squares, and
$(-x^2y+x^2+y^2-xy)(x{-}y)$
are squares, and
![]() $(1{-}y)(x{-}y)$
is a nonsquare.
$(1{-}y)(x{-}y)$
is a nonsquare.
Proof. Here, the associativity equation is equal to
![]() $a(au-v)=-av+b(u-v+av)$
, and that is the same as
$a(au-v)=-av+b(u-v+av)$
, and that is the same as
![]() $(a^2-b)u=(ab-b)v$
. Therefore,
$(a^2-b)u=(ab-b)v$
. Therefore,
![]() $(a,b)\in \Sigma _{00}^{01}$
if and only if
$(a,b)\in \Sigma _{00}^{01}$
if and only if
![]() $(1,(a^2{-}b)/b(a{-}1))\in E_{00}^{01}(a,b)$
. If
$(1,(a^2{-}b)/b(a{-}1))\in E_{00}^{01}(a,b)$
. If
![]() $(x,y) = \Psi ((a,b))$
, then
$(x,y) = \Psi ((a,b))$
, then
 $$ \begin{align*} (a^2-b) (x-y)^2 &= x^2(1\kern1.5pt{-}\kern1.5pt y)^2-(1\kern1.5pt{-}\kern1.5pt y)(x\kern1.5pt{-}\kern1.5pt y) = (1\kern1.5pt{-}\kern1.5pt y)(x^2\kern1.5pt{-}\kern1.5pt x^2y\kern1.7pt{-}\kern1.7pt x+y)\\ & = (1\kern1.7pt{-}\kern1.7pt y)(1\kern1.7pt{-}\kern1.7pt x)(\kern1.5pt y+xy-x), \end{align*} $$
$$ \begin{align*} (a^2-b) (x-y)^2 &= x^2(1\kern1.5pt{-}\kern1.5pt y)^2-(1\kern1.5pt{-}\kern1.5pt y)(x\kern1.5pt{-}\kern1.5pt y) = (1\kern1.5pt{-}\kern1.5pt y)(x^2\kern1.5pt{-}\kern1.5pt x^2y\kern1.7pt{-}\kern1.7pt x+y)\\ & = (1\kern1.7pt{-}\kern1.7pt y)(1\kern1.7pt{-}\kern1.7pt x)(\kern1.5pt y+xy-x), \end{align*} $$
and
![]() $b(a{-}1)(x{-}y)^2 = (1{-}y)y(1{-}x)$
. So,
$b(a{-}1)(x{-}y)^2 = (1{-}y)y(1{-}x)$
. So,
![]() $v=(a^2-b)/b(a-1)=(\kern1.5pt y+xy-x)/y$
, showing that
$v=(a^2-b)/b(a-1)=(\kern1.5pt y+xy-x)/y$
, showing that
![]() $y+xy-x$
is a square. It follows that
$y+xy-x$
is a square. It follows that
![]() $a-v =(-x^2y+x^2+y^2-xy)/(x-y)y$
and
$a-v =(-x^2y+x^2+y^2-xy)/(x-y)y$
and
![]() $(1-(1{-}a)v)(\kern1.5pt y{-}x) =x^2(\kern1.5pt y{-}1)$
. Thus,
$(1-(1{-}a)v)(\kern1.5pt y{-}x) =x^2(\kern1.5pt y{-}1)$
. Thus,
![]() $(1{-}y)(x{-}y)$
has to be a nonsquare.
$(1{-}y)(x{-}y)$
has to be a nonsquare.
Lemma 2.7. Assume that
![]() $(x,y)\in S$
.
$(x,y)\in S$
.
(i) If
 $y{+}1{-}x = 0 = x^2{-}x{-}1$
and
$y{+}1{-}x = 0 = x^2{-}x{-}1$
and
 $q>43$
, then
$q>43$
, then
 $(x,y) \in S_{01}^{01}$
.
$(x,y) \in S_{01}^{01}$
.(ii) If
 $y{+}1{-}x \ne 0$
or
$y{+}1{-}x \ne 0$
or
 $x^2{-}x{-}1\ne 0$
, then
$x^2{-}x{-}1\ne 0$
, then
 $(x,y)\in S_{01}^{01}$
if and only if both
$(x,y)\in S_{01}^{01}$
if and only if both
 $(\kern1.5pt y{+}xy{-}x)(x{-}y{-}1)$
and
$(\kern1.5pt y{+}xy{-}x)(x{-}y{-}1)$
and
 $(\kern1.5pt y{-}2x{+}x^2)(x{-}y)(x{-}y{-}1)$
are nonsquares, while
$(\kern1.5pt y{-}2x{+}x^2)(x{-}y)(x{-}y{-}1)$
are nonsquares, while
 $(2xy{-}y^2{-}x)(x{-}y)(x{-}y{-}1)$
is a square.
$(2xy{-}y^2{-}x)(x{-}y)(x{-}y{-}1)$
is a square.
Proof. In this case, the associativity equation yields
![]() ${a(au\kern1.2pt{-}\kern1.2pt v) \kern1.2pt{=}\kern1.2pt {-}\kern1.2pt bv + b(u - (1{-}b)v)}$
. That is equivalent to
${a(au\kern1.2pt{-}\kern1.2pt v) \kern1.2pt{=}\kern1.2pt {-}\kern1.2pt bv + b(u - (1{-}b)v)}$
. That is equivalent to
![]() $(a^2-b)u = (b^2-2b+a)v$
. If there exists a solution
$(a^2-b)u = (b^2-2b+a)v$
. If there exists a solution
![]() $(u,v)\in E_{01}^{01}(a,b)$
, and one of the elements
$(u,v)\in E_{01}^{01}(a,b)$
, and one of the elements
![]() $a^2-b$
and
$a^2-b$
and
![]() $b^2-2b+a$
is equal to zero, then the other has to vanish as well. Assume that
$b^2-2b+a$
is equal to zero, then the other has to vanish as well. Assume that
![]() $(x,y)=\Psi ((a,b))$
. Then
$(x,y)=\Psi ((a,b))$
. Then
![]() $a^2-b=0$
if and only if
$a^2-b=0$
if and only if
 $0 = x^2(1-y)^2-(1-y)(x-y) = (1-y)(-x^2y+x^2-x+y) = (1-y)(1-x)(\kern1.5pt y+xy-x)$
, and
$0 = x^2(1-y)^2-(1-y)(x-y) = (1-y)(-x^2y+x^2-x+y) = (1-y)(1-x)(\kern1.5pt y+xy-x)$
, and
![]() $b^2-2b+a = (1-b)^2-(1-a)= 0$
if and only if
$b^2-2b+a = (1-b)^2-(1-a)= 0$
if and only if
![]() $0 \ =\ (1 - x)^2 -y(1-x)(\kern1.5pt y-x)\ =\ (1-x)(1-x-y^2+xy) = (1-x)(1-y)(\kern1.5pt y-x+1)$
. If
$0 \ =\ (1 - x)^2 -y(1-x)(\kern1.5pt y-x)\ =\ (1-x)(1-x-y^2+xy) = (1-x)(1-y)(\kern1.5pt y-x+1)$
. If
![]() $y=x-1$
, then
$y=x-1$
, then
![]() $y+xy-x=x^2-x-1$
.
$y+xy-x=x^2-x-1$
.
Computations above show that
 $$ \begin{align*} a^2-b = \frac{(1{-}y)(1{-}x)(xy{-}x{+}y)}{(x{-}y)^2} \quad\text{and}\quad b^2-2b+a = \frac{(1{-}y)(1{-}x)(\kern1.5pt y{-}x{+}1)}{(x{-}y)^2}. \end{align*} $$
$$ \begin{align*} a^2-b = \frac{(1{-}y)(1{-}x)(xy{-}x{+}y)}{(x{-}y)^2} \quad\text{and}\quad b^2-2b+a = \frac{(1{-}y)(1{-}x)(\kern1.5pt y{-}x{+}1)}{(x{-}y)^2}. \end{align*} $$
Suppose now that at least one of
![]() $x^2{-}x{-}1$
and
$x^2{-}x{-}1$
and
![]() $y{-}x{+}1$
does not vanish. If
$y{-}x{+}1$
does not vanish. If
![]() $y{-}x{+}1=0$
, then
$y{-}x{+}1=0$
, then
![]() $E_{01}^{01}(a,b)=\varnothing $
and
$E_{01}^{01}(a,b)=\varnothing $
and
![]() $(\kern1.5pt y{+}xy{-}x)(x{-}y{-}1)=0$
, which is a square. Hence,
$(\kern1.5pt y{+}xy{-}x)(x{-}y{-}1)=0$
, which is a square. Hence,
![]() $y{-}x{+}1\ne 0$
may be assumed. That implies
$y{-}x{+}1\ne 0$
may be assumed. That implies
![]() $b^2-2b+a\ne 0$
. From the associativity equation, it then follows that
$b^2-2b+a\ne 0$
. From the associativity equation, it then follows that
![]() $(a,b){\kern-1.2pt}\in{\kern-1.2pt} \Sigma _{01}^{01}$
if and only if
$(a,b){\kern-1.2pt}\in{\kern-1.2pt} \Sigma _{01}^{01}$
if and only if
![]() $(1,v){\kern-1.2pt}\in{\kern-1.2pt} E_{01}^{01}(a,b)$
, where
$(1,v){\kern-1.2pt}\in{\kern-1.2pt} E_{01}^{01}(a,b)$
, where
![]() $v{\kern-1.2pt}=(a^2-b)/ (b^2-{\kern-1.2pt}2b+a)$
. Now,
$v{\kern-1.2pt}=(a^2-b)/ (b^2-{\kern-1.2pt}2b+a)$
. Now,
 $$ \begin{align*} -v &= \frac{b-a^2}{b^2-2b+a} = \frac{y{+}xy{-}x}{x{-}y{-}1}, \\ 1-(1{-}b)v&= \frac{(x{-}y{-}1)(\kern1.5pt y{-}x)+(1{-}x)(\kern1.5pt y{+}xy{-}x)}{(x{-}y{-}1)(\kern1.5pt y{-}x)} =\frac{y(x^2{-}2x{+}y)}{(x{-}y{-}1)(x{-}y)}, \quad\text{and}\\ a{-}v &= \frac{x(1{-}y)(x{-}y{-}1) + (x{-}y)(\kern1.5pt y{+}xy{-}x)}{(x{-}y)(x{-}y{-}1)} = \frac{2xy{-}y^2{-}x}{(x{-}y)(x{-}y{-}1)}. \end{align*} $$
$$ \begin{align*} -v &= \frac{b-a^2}{b^2-2b+a} = \frac{y{+}xy{-}x}{x{-}y{-}1}, \\ 1-(1{-}b)v&= \frac{(x{-}y{-}1)(\kern1.5pt y{-}x)+(1{-}x)(\kern1.5pt y{+}xy{-}x)}{(x{-}y{-}1)(\kern1.5pt y{-}x)} =\frac{y(x^2{-}2x{+}y)}{(x{-}y{-}1)(x{-}y)}, \quad\text{and}\\ a{-}v &= \frac{x(1{-}y)(x{-}y{-}1) + (x{-}y)(\kern1.5pt y{+}xy{-}x)}{(x{-}y)(x{-}y{-}1)} = \frac{2xy{-}y^2{-}x}{(x{-}y)(x{-}y{-}1)}. \end{align*} $$
It remains to prove that
![]() $E_{01}^{01}(a,b)$
is nearly always nonempty if
$E_{01}^{01}(a,b)$
is nearly always nonempty if
![]() $a^2-b=b^2-2b+a=0$
. Let the latter be true. Then
$a^2-b=b^2-2b+a=0$
. Let the latter be true. Then
![]() $b^2-2b+a=a^4-2a^2+a = a(a{-}1)(a^2{+}a{-}1)$
. Thus,
$b^2-2b+a=a^4-2a^2+a = a(a{-}1)(a^2{+}a{-}1)$
. Thus,
![]() $a^2{+}a{-}1=0$
. A pair
$a^2{+}a{-}1=0$
. A pair
![]() $(1,v)$
is a solution to the associativity equation if
$(1,v)$
is a solution to the associativity equation if
![]() $-v$
is a nonsquare,
$-v$
is a nonsquare,
![]() $1+(1{-}b)(-v)$
is a nonsquare, and
$1+(1{-}b)(-v)$
is a nonsquare, and
![]() $a-v$
is a square. Put
$a-v$
is a square. Put
![]() $p_1(t) = t$
,
$p_1(t) = t$
,
![]() $p_2(t) = 1+(1{-}b)t=1+(1{-}a^2)t$
, and
$p_2(t) = 1+(1{-}b)t=1+(1{-}a^2)t$
, and
![]() $p_3(t) = a+t$
. A solution
$p_3(t) = a+t$
. A solution
![]() $(1,v)$
exists if there exists
$(1,v)$
exists if there exists
![]() $\gamma =-v\in \mathbb {F}$
such that
$\gamma =-v\in \mathbb {F}$
such that
![]() $\chi (p_1(\gamma ))=\chi (p_2(\gamma ))=-1$
and
$\chi (p_1(\gamma ))=\chi (p_2(\gamma ))=-1$
and
![]() $\chi (p_3(\gamma )) = 1$
. Polynomials
$\chi (p_3(\gamma )) = 1$
. Polynomials
![]() $p_2$
and
$p_2$
and
![]() $p_3$
have a common root if and only if
$p_3$
have a common root if and only if
![]() $0=1-a+a^3$
. If this is true, then
$0=1-a+a^3$
. If this is true, then
![]() $0=a^2+a^3 = a^2(1+a)$
. This implies
$0=a^2+a^3 = a^2(1+a)$
. This implies
![]() $a=-1$
and
$a=-1$
and
![]() $0 = (-1)^2+(-1)-1 =-1$
, which is a contradiction. The list of polynomials
$0 = (-1)^2+(-1)-1 =-1$
, which is a contradiction. The list of polynomials
![]() $p_1$
,
$p_1$
,
![]() $p_2$
,
$p_2$
,
![]() $p_3$
is therefore square-free. Theorem 1.6 guarantees the existence of
$p_3$
is therefore square-free. Theorem 1.6 guarantees the existence of
![]() $\gamma $
if
$\gamma $
if
This is true for each prime power
![]() $q\geqslant 47$
.
$q\geqslant 47$
.
Remark 2.8. Lemmas 2.4–2.7 cover all sets
![]() $S_{ij}^{rs}$
that are listed in (2-4). Up to the exceptions discussed in Remark 2.9, each of these sets is either empty, or is described by a list of polynomials, say
$S_{ij}^{rs}$
that are listed in (2-4). Up to the exceptions discussed in Remark 2.9, each of these sets is either empty, or is described by a list of polynomials, say
![]() $p_1,\ldots ,p_k\in \mathbb {F}[x,y]$
,
$p_1,\ldots ,p_k\in \mathbb {F}[x,y]$
,
![]() $k\in \{2,3\}$
, and elements
$k\in \{2,3\}$
, and elements
![]() $\varepsilon _h\in \{-1,1\}$
, such that
$\varepsilon _h\in \{-1,1\}$
, such that
![]() $(\xi ,\eta )\in S$
belongs to
$(\xi ,\eta )\in S$
belongs to
![]() $S_{ij}^{rs}$
if and only if
$S_{ij}^{rs}$
if and only if
![]() $\chi (p_h(\xi ,\eta ))=\varepsilon _h$
, for
$\chi (p_h(\xi ,\eta ))=\varepsilon _h$
, for
![]() $1\leqslant h \leqslant k$
. This is because the polynomials
$1\leqslant h \leqslant k$
. This is because the polynomials
![]() $p_h(x,y)$
have been determined in all cases in such a way that if
$p_h(x,y)$
have been determined in all cases in such a way that if
![]() $p_h(\xi ,\eta )=0$
and
$p_h(\xi ,\eta )=0$
and
![]() $(\xi ,\eta ) = \Psi ((a,b))$
, then there is no
$(\xi ,\eta ) = \Psi ((a,b))$
, then there is no
![]() $(u,v)\in E_{ij}^{rs}(a,b)$
. Indeed, if
$(u,v)\in E_{ij}^{rs}(a,b)$
. Indeed, if
![]() $(u,v)$
were such a solution, then u or v or
$(u,v)$
were such a solution, then u or v or
![]() $u-v-\psi _{a,b}(-v)$
or
$u-v-\psi _{a,b}(-v)$
or
![]() $\psi _{a,b}(u)-v$
would be equal to zero, and that is impossible, by Proposition 1.4.
$\psi _{a,b}(u)-v$
would be equal to zero, and that is impossible, by Proposition 1.4.
Note that
![]() $(\xi ,\eta )$
was used in Remark 2.8 to emphasize the distinction between elements of S and formal variables x and y. In the remainder of the paper, elements of S will again be denoted by
$(\xi ,\eta )$
was used in Remark 2.8 to emphasize the distinction between elements of S and formal variables x and y. In the remainder of the paper, elements of S will again be denoted by
![]() $(x,y)$
. The context will always be clear.
$(x,y)$
. The context will always be clear.
Remark 2.9. Sets
![]() $S_{01}^{01}$
and
$S_{01}^{01}$
and
![]() $S_{10}^{10}$
behave exceptionally in the sense that the regular behavior described in Remark 2.8 needs an assumption that
$S_{10}^{10}$
behave exceptionally in the sense that the regular behavior described in Remark 2.8 needs an assumption that
![]() $y{+}1{-}x\ne 0$
or
$y{+}1{-}x\ne 0$
or
![]() $x^2{-}x{-}1\ne 0$
(for the set
$x^2{-}x{-}1\ne 0$
(for the set
![]() $S_{01}^{01}$
), and that
$S_{01}^{01}$
), and that
![]() $x{+}1{-}y\ne 0$
or
$x{+}1{-}y\ne 0$
or
![]() $y^2{-}y{-}1\ne 0$
(for the set
$y^2{-}y{-}1\ne 0$
(for the set
![]() $S_{10}^{10}$
). There are at most two pairs
$S_{10}^{10}$
). There are at most two pairs
![]() $(x,y) \in S$
such that
$(x,y) \in S$
such that
![]() $y{+}1{-}x=0=x^2{-}x{-}1$
and at most two pairs
$y{+}1{-}x=0=x^2{-}x{-}1$
and at most two pairs
![]() $(x,y) \in S$
such that
$(x,y) \in S$
such that
![]() $x{+}1{-}y=0=y^2{-}y{-}1$
. Hence, assuming that
$x{+}1{-}y=0=y^2{-}y{-}1$
. Hence, assuming that
causes no difficulty when estimating
![]() $\sigma (q)$
. If Condition (2-5) does not hold, then
$\sigma (q)$
. If Condition (2-5) does not hold, then
![]() $(x,y) \in S_{01}^{01}\cup S_{10}^{10}$
if
$(x,y) \in S_{01}^{01}\cup S_{10}^{10}$
if
![]() $q\geqslant 47$
, by point (i) of Lemma 2.7. In fact, if Condition (2-5) does not hold, then
$q\geqslant 47$
, by point (i) of Lemma 2.7. In fact, if Condition (2-5) does not hold, then
![]() $(x,y) \in \bigcup S_{ij}^{rs}$
for each
$(x,y) \in \bigcup S_{ij}^{rs}$
for each
![]() $q\geqslant 3$
, by [Reference Drápal and Wanless6] (compare with the application of [Reference Drápal and Wanless6, Lemma 3.4] in the proof of [Reference Drápal and Wanless6, Theorem 3.5]).
$q\geqslant 3$
, by [Reference Drápal and Wanless6] (compare with the application of [Reference Drápal and Wanless6, Lemma 3.4] in the proof of [Reference Drápal and Wanless6, Theorem 3.5]).
For
![]() $p(x,y)\in \mathbb {F}[x,y]$
such that
$p(x,y)\in \mathbb {F}[x,y]$
such that
![]() $x\nmid p(x,y)$
and
$x\nmid p(x,y)$
and
![]() $y\nmid p(x,y)$
, define the reciprocal polynomial
$y\nmid p(x,y)$
, define the reciprocal polynomial
![]() $\hat p(x,y)$
as
$\hat p(x,y)$
as
![]() $x^ny^mp(x^{-1},y^{-1})$
, where n and m are the degrees of the polynomial p in the variables x and y, respectively. Note that if
$x^ny^mp(x^{-1},y^{-1})$
, where n and m are the degrees of the polynomial p in the variables x and y, respectively. Note that if
![]() $(x,y)\in S$
, then
$(x,y)\in S$
, then
![]() $\chi (\hat p(x,y))=\chi (x^ny^mp(x^{-1},y^{-1}))=\chi (p(x^{-1},y^{-1}))$
since x and y are squares. Note also that
$\chi (\hat p(x,y))=\chi (x^ny^mp(x^{-1},y^{-1}))=\chi (p(x^{-1},y^{-1}))$
since x and y are squares. Note also that
![]() $\hat {\hat p}(x,y)= p(x,y)$
,
$\hat {\hat p}(x,y)= p(x,y)$
,
![]() $\widehat {1-x} = x-1$
,
$\widehat {1-x} = x-1$
,
![]() $\widehat {x-y}=y-x$
, and
$\widehat {x-y}=y-x$
, and
![]() $\widehat {x-1-y}=y-xy-x$
. Set
$\widehat {x-1-y}=y-xy-x$
. Set
 $$ \begin{align} \begin{aligned} &f_1(x,y)=x^2{+}y^2{-}xy{-}x, \quad \quad &f_2(x,y) = y^2{+}x^2{-}xy{-}y, \ \ \ \\ &f_3(x,y)=y^2x{+}xy{-}x^2{-}y^2,\quad \text{and} &f_4(x,y)=x^2y{+}xy{-}x^2{-}y^2. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &f_1(x,y)=x^2{+}y^2{-}xy{-}x, \quad \quad &f_2(x,y) = y^2{+}x^2{-}xy{-}y, \ \ \ \\ &f_3(x,y)=y^2x{+}xy{-}x^2{-}y^2,\quad \text{and} &f_4(x,y)=x^2y{+}xy{-}x^2{-}y^2. \end{aligned} \end{align} $$
Then
![]() $f_2(x,y) = f_1(\kern1.5pt y,x)$
,
$f_2(x,y) = f_1(\kern1.5pt y,x)$
,
![]() $f_3(x,y) = -\hat {f_1}(x,y)$
, and
$f_3(x,y) = -\hat {f_1}(x,y)$
, and
![]() $f_4(x,y) = -\hat {f_1}(\kern1.5pt y,x)=-\hat {f_2}(x,y)=f_3(\kern1.5pt y,x)$
.
$f_4(x,y) = -\hat {f_1}(\kern1.5pt y,x)=-\hat {f_2}(x,y)=f_3(\kern1.5pt y,x)$
.
A description of those sets
![]() $S_{ij}^{rs}$
that do not occur in List (2-4) can be derived from Lemmas 2.4–2.7 by means of Proposition 2.3. As an example, consider sets
$S_{ij}^{rs}$
that do not occur in List (2-4) can be derived from Lemmas 2.4–2.7 by means of Proposition 2.3. As an example, consider sets
![]() $S_{00}^{10}$
and
$S_{00}^{10}$
and
![]() $S_{11}^{10}$
. By Lemma 2.6,
$S_{11}^{10}$
. By Lemma 2.6,
![]() $(x,y)\in S_{00}^{01}$
if
$(x,y)\in S_{00}^{01}$
if
![]() $\chi (x{-}xy{-}y)=\chi (f_4(x,y) (\kern1.5pt y{-}x)) = 1$
and
$\chi (x{-}xy{-}y)=\chi (f_4(x,y) (\kern1.5pt y{-}x)) = 1$
and
![]() $\chi ((1{-}y)(x{-}y))=-1$
. By Proposition 2.3,
$\chi ((1{-}y)(x{-}y))=-1$
. By Proposition 2.3,
![]() $(x,y) \in S_{00}^{10}$
if and only if
$(x,y) \in S_{00}^{10}$
if and only if
![]() $(\kern1.5pt y,x)\in S_{00}^{01}$
, that is, if
$(\kern1.5pt y,x)\in S_{00}^{01}$
, that is, if
![]() $\chi (\kern1.5pt y{-}xy{-}x)=\chi (f_3(x,y)(x{-}y))=1$
and
$\chi (\kern1.5pt y{-}xy{-}x)=\chi (f_3(x,y)(x{-}y))=1$
and
![]() $\chi ((1{-}x)(\kern1.5pt y{-}x))=-1$
, and
$\chi ((1{-}x)(\kern1.5pt y{-}x))=-1$
, and
![]() $(x,y)\in S_{11}^{10}$
if
$(x,y)\in S_{11}^{10}$
if
![]() $(x^{-1},y^{-1})\in S_{00}^{01}$
, that is, if
$(x^{-1},y^{-1})\in S_{00}^{01}$
, that is, if
![]() $\chi (\kern1.5pt y{-}1{-}x)=\chi (f_2(x,y)(\kern1.5pt y{-}x))=1$
and
$\chi (\kern1.5pt y{-}1{-}x)=\chi (f_2(x,y)(\kern1.5pt y{-}x))=1$
and
![]() $\chi ((1{-}y)(x{-}y))=-1$
.
$\chi ((1{-}y)(x{-}y))=-1$
.
Following this pattern, a characterization of all sets
![]() $S_{ij}^{rs}$
may be derived from Lemmas 2.4–2.7 by means of Proposition 2.3. This is done in Theorems 2.10 and 2.11. Since the derivation is straightforward, both of them are stated without a proof. Set
$S_{ij}^{rs}$
may be derived from Lemmas 2.4–2.7 by means of Proposition 2.3. This is done in Theorems 2.10 and 2.11. Since the derivation is straightforward, both of them are stated without a proof. Set
 $$ \begin{gather*} \begin{aligned} &g_1(x,y)= x^2 + y -2x, \ \ \ \,\quad\qquad g_2(x,y)= y^2+x-2y,\\[-2pt]&g_3(x,y)= x^2 + y -2xy, \quad\text{and}\quad g_4(x,y) = y^2+x-2xy. \end{aligned} \end{gather*} $$
$$ \begin{gather*} \begin{aligned} &g_1(x,y)= x^2 + y -2x, \ \ \ \,\quad\qquad g_2(x,y)= y^2+x-2y,\\[-2pt]&g_3(x,y)= x^2 + y -2xy, \quad\text{and}\quad g_4(x,y) = y^2+x-2xy. \end{aligned} \end{gather*} $$
Note that
![]() $g_3(x,y)=\hat {g_1}(x,y)$
,
$g_3(x,y)=\hat {g_1}(x,y)$
,
![]() $g_4(x,y) = \hat {g_2}(x,y)= g_3(\kern1.5pt y,x)$
, and
$g_4(x,y) = \hat {g_2}(x,y)= g_3(\kern1.5pt y,x)$
, and
![]() $g_2(x,y) = g_1(\kern1.5pt y,x)$
.
$g_2(x,y) = g_1(\kern1.5pt y,x)$
.
Theorem 2.10. Assume that
![]() $q\equiv 1\bmod 4$
is a prime power, and that
$q\equiv 1\bmod 4$
is a prime power, and that
![]() $S = S(\mathbb {F}_q)$
. Let
$S = S(\mathbb {F}_q)$
. Let
![]() $(x,y)\in S$
be such that Condition (2-5) holds. The sets
$(x,y)\in S$
be such that Condition (2-5) holds. The sets
![]() $S_{01}^{00}$
,
$S_{01}^{00}$
,
![]() $S_{01}^{10}$
,
$S_{01}^{10}$
,
![]() $S_{01}^{11}$
,
$S_{01}^{11}$
,
![]() $S_{10}^{00}$
,
$S_{10}^{00}$
,
![]() $S_{10}^{01}$
, and
$S_{10}^{01}$
, and
![]() $S_{10}^{11}$
are empty, and
$S_{10}^{11}$
are empty, and
![]() $S_{11}^{11} = S_{00}^{00}$
. Put
$S_{11}^{11} = S_{00}^{00}$
. Put
![]() $\varepsilon = \chi (x{-}y)$
. Then
$\varepsilon = \chi (x{-}y)$
. Then
 $$ \begin{align*} (x,y)\in S_{00}^{00} \Longleftrightarrow&\, \chi(1{-}x)=\chi(1{-}y)=\varepsilon;\\ (x,y)\in S_{11}^{00} \Longleftrightarrow&\, \chi(f_1(x,y))=\chi(f_2(x,y)) = -\varepsilon; \\ (x,y)\in S_{00}^{11} \Longleftrightarrow&\, \chi(f_3(x,y))=\chi(f_4(x,y)) = -\varepsilon; \\ (x,y)\in S_{11}^{01} \Longleftrightarrow&\, \chi(1{-}x) = -\varepsilon,\ \chi(\kern1.5pt y{+}1{-}x)=1 \text{ and } \chi(f_1(x,y))=\varepsilon; \\ (x,y)\in S_{11}^{10} \Longleftrightarrow&\, \chi(1{-}y) = -\varepsilon,\ \chi(x{+}1{-}y)=1 \text{ and }\chi(f_2(x,y))=\varepsilon; \\ (x,y)\in S_{00}^{10} \Longleftrightarrow&\, \chi(1{-}x) = -\varepsilon,\ \chi(x{+}xy{-}y)=1 \text{ and } \chi(f_3(x,y))=\varepsilon; \\ (x,y)\in S_{00}^{01} \Longleftrightarrow&\, \chi(1{-}y) = -\varepsilon,\ \chi(\kern1.5pt y{+}xy{-}x)=1 \text{ and } \chi(f_4(x,y))=\varepsilon; \\[-2pt] (x,y) \in S_{01}^{01} \Longleftrightarrow&\, \chi(\kern1.5pt y{+}xy{-}x)=-\eta,\ \chi(g_1(x,y))=-\eta\varepsilon \text{ and } \chi(g_4(x,y)) = \eta\varepsilon, \\[-2pt] &\text{where }\eta = \chi(\kern1.5pt y{+}1{-}x); \text{ and} \\[-2pt] (x,y) \in S_{10}^{10} \Longleftrightarrow&\, \chi(x{+}xy{-}y)=-\eta,\ \chi(g_2(x,y))=-\eta\varepsilon \text{ and } \chi(g_3(x,y)) = \eta\varepsilon, \\[-2pt] &\text{where }\eta = \chi(x{+}1{-}y). \end{align*} $$
$$ \begin{align*} (x,y)\in S_{00}^{00} \Longleftrightarrow&\, \chi(1{-}x)=\chi(1{-}y)=\varepsilon;\\ (x,y)\in S_{11}^{00} \Longleftrightarrow&\, \chi(f_1(x,y))=\chi(f_2(x,y)) = -\varepsilon; \\ (x,y)\in S_{00}^{11} \Longleftrightarrow&\, \chi(f_3(x,y))=\chi(f_4(x,y)) = -\varepsilon; \\ (x,y)\in S_{11}^{01} \Longleftrightarrow&\, \chi(1{-}x) = -\varepsilon,\ \chi(\kern1.5pt y{+}1{-}x)=1 \text{ and } \chi(f_1(x,y))=\varepsilon; \\ (x,y)\in S_{11}^{10} \Longleftrightarrow&\, \chi(1{-}y) = -\varepsilon,\ \chi(x{+}1{-}y)=1 \text{ and }\chi(f_2(x,y))=\varepsilon; \\ (x,y)\in S_{00}^{10} \Longleftrightarrow&\, \chi(1{-}x) = -\varepsilon,\ \chi(x{+}xy{-}y)=1 \text{ and } \chi(f_3(x,y))=\varepsilon; \\ (x,y)\in S_{00}^{01} \Longleftrightarrow&\, \chi(1{-}y) = -\varepsilon,\ \chi(\kern1.5pt y{+}xy{-}x)=1 \text{ and } \chi(f_4(x,y))=\varepsilon; \\[-2pt] (x,y) \in S_{01}^{01} \Longleftrightarrow&\, \chi(\kern1.5pt y{+}xy{-}x)=-\eta,\ \chi(g_1(x,y))=-\eta\varepsilon \text{ and } \chi(g_4(x,y)) = \eta\varepsilon, \\[-2pt] &\text{where }\eta = \chi(\kern1.5pt y{+}1{-}x); \text{ and} \\[-2pt] (x,y) \in S_{10}^{10} \Longleftrightarrow&\, \chi(x{+}xy{-}y)=-\eta,\ \chi(g_2(x,y))=-\eta\varepsilon \text{ and } \chi(g_3(x,y)) = \eta\varepsilon, \\[-2pt] &\text{where }\eta = \chi(x{+}1{-}y). \end{align*} $$
Theorem 2.11. Assume that
![]() $q\equiv 3\bmod 4$
is a prime power, and that
$q\equiv 3\bmod 4$
is a prime power, and that
![]() $S = S(\mathbb {F}_q)$
. Let
$S = S(\mathbb {F}_q)$
. Let
![]() $(x,y)\in S$
be such that Condition (2-5) holds. Sets
$(x,y)\in S$
be such that Condition (2-5) holds. Sets
![]() $S_{00}^{00}$
,
$S_{00}^{00}$
,
![]() $S_{00}^{11}$
,
$S_{00}^{11}$
,
![]() $S_{11}^{00}$
, and
$S_{11}^{00}$
, and
![]() $S_{11}^{11}$
are empty, and
$S_{11}^{11}$
are empty, and
![]() $S_{10}^{01} = S_{01}^{10}$
. The pair
$S_{10}^{01} = S_{01}^{10}$
. The pair
![]() $(x,y)$
belongs to a set
$(x,y)$
belongs to a set
![]() $S_{ij}^{rs}$
listed below if and only if all values in the row of
$S_{ij}^{rs}$
listed below if and only if all values in the row of
![]() $S_{ij}^{rs}$
are nonzero squares.
$S_{ij}^{rs}$
are nonzero squares.
 $$ \begin{align*} S_{01}^{10}\colon& (1{-}y)(x{-}y) \text{ and } (1{-}x)(\kern1.5pt y{-}x);\\ S_{01}^{00}\colon& (1{-}x)(x{-}y) \text{ and } g_1(x,y)(\kern1.5pt y{-}x); \\ S_{10}^{00}\colon& (1{-}y)(\kern1.5pt y{-}x) \text{ and } g_2(x,y)(x{-}y); \\ S_{10}^{11}\colon& (1{-}x)(x{-}y) \text{ and } g_3(x,y)(x{-}y); \\ S_{01}^{11}\colon& (1{-}y)(\kern1.5pt y{-}x) \text{ and } g_4(x,y)(\kern1.5pt y{-}x); \\ S_{11}^{01}\colon& (1{-}x)(x{-}y),\ x{-}1{-}y \text{ and } (x{-}y)f_1(x,y);\\ S_{11}^{10}\colon& (1{-}y)(\kern1.5pt y{-}x),\ y{-}1{-}x \text{ and } (\kern1.5pt y{-}x)f_2(x,y);\\ S_{00}^{10}\colon& (1{-}x)(x{-}y),\ y{-}xy{-}x \text{ and } (x{-}y)f_3(x,y);\\ S_{00}^{01}\colon& (1{-}y)(\kern1.5pt y{-}x),\ x{-}xy{-}y \text{ and } (\kern1.5pt y{-}x)f_4(x,y);\\ S_{01}^{01}\colon& (x{-}xy{-}y)(x{-}1{-}y),\ g_1(x,y)(\kern1.5pt y{-}x)(x{-}1{-}y)\text{ and } g_4(x,y)(\kern1.5pt y{-}x)(x{-}1{-}y);\\ S_{10}^{10}\colon& (\kern1.5pt y{-}xy{-}x)(\kern1.5pt y{-}1{-}x),\ g_2(x,y)(x{-}y)(\kern1.5pt y{-}1{-}x)\text{ and } g_3(x,y)(x{-}y)(\kern1.5pt y{-}1{-}x). \end{align*} $$
$$ \begin{align*} S_{01}^{10}\colon& (1{-}y)(x{-}y) \text{ and } (1{-}x)(\kern1.5pt y{-}x);\\ S_{01}^{00}\colon& (1{-}x)(x{-}y) \text{ and } g_1(x,y)(\kern1.5pt y{-}x); \\ S_{10}^{00}\colon& (1{-}y)(\kern1.5pt y{-}x) \text{ and } g_2(x,y)(x{-}y); \\ S_{10}^{11}\colon& (1{-}x)(x{-}y) \text{ and } g_3(x,y)(x{-}y); \\ S_{01}^{11}\colon& (1{-}y)(\kern1.5pt y{-}x) \text{ and } g_4(x,y)(\kern1.5pt y{-}x); \\ S_{11}^{01}\colon& (1{-}x)(x{-}y),\ x{-}1{-}y \text{ and } (x{-}y)f_1(x,y);\\ S_{11}^{10}\colon& (1{-}y)(\kern1.5pt y{-}x),\ y{-}1{-}x \text{ and } (\kern1.5pt y{-}x)f_2(x,y);\\ S_{00}^{10}\colon& (1{-}x)(x{-}y),\ y{-}xy{-}x \text{ and } (x{-}y)f_3(x,y);\\ S_{00}^{01}\colon& (1{-}y)(\kern1.5pt y{-}x),\ x{-}xy{-}y \text{ and } (\kern1.5pt y{-}x)f_4(x,y);\\ S_{01}^{01}\colon& (x{-}xy{-}y)(x{-}1{-}y),\ g_1(x,y)(\kern1.5pt y{-}x)(x{-}1{-}y)\text{ and } g_4(x,y)(\kern1.5pt y{-}x)(x{-}1{-}y);\\ S_{10}^{10}\colon& (\kern1.5pt y{-}xy{-}x)(\kern1.5pt y{-}1{-}x),\ g_2(x,y)(x{-}y)(\kern1.5pt y{-}1{-}x)\text{ and } g_3(x,y)(x{-}y)(\kern1.5pt y{-}1{-}x). \end{align*} $$
3 Avoiding squares
Our goal is to estimate the size of the set
![]() $T=S\setminus \bigcup S_{ij}^{rs}$
. Since Theorem 1.6 requires polynomials in one variable, to determine the size of T, it is necessary to proceed by determining the sizes of slices
$T=S\setminus \bigcup S_{ij}^{rs}$
. Since Theorem 1.6 requires polynomials in one variable, to determine the size of T, it is necessary to proceed by determining the sizes of slices
![]() $\{x\in \mathbb {F}:(x,c)\in T\}$
for each square
$\{x\in \mathbb {F}:(x,c)\in T\}$
for each square
![]() $c\notin \{0,1\}$
. As a convention,
$c\notin \{0,1\}$
. As a convention,
![]() $p(x,c)$
will mean a polynomial in one variable, that is, an element of
$p(x,c)$
will mean a polynomial in one variable, that is, an element of
![]() $\mathbb {F}[x]$
for every
$\mathbb {F}[x]$
for every
![]() $p(x,y)\in \mathbb {F}[x,y]$
.
$p(x,y)\in \mathbb {F}[x,y]$
.
Theorem 1.6 may be directly applied only when the product of the polynomials involved is square-free. Thus, for
![]() $p_1(x,y),\ldots ,p_k(x,y)\in \mathbb {F}[x,y]$
, it is necessary to set aside those
$p_1(x,y),\ldots ,p_k(x,y)\in \mathbb {F}[x,y]$
, it is necessary to set aside those
![]() $c\in \mathbb {F}$
for which
$c\in \mathbb {F}$
for which
![]() $p_1(x,c),\ldots ,p_k(x,c)$
is not a square-free list of polynomials. An asymptotic estimate does not depend upon the number of c set aside if there is only a bounded number of them. Hence, a possible route is to express the discriminant of
$p_1(x,c),\ldots ,p_k(x,c)$
is not a square-free list of polynomials. An asymptotic estimate does not depend upon the number of c set aside if there is only a bounded number of them. Hence, a possible route is to express the discriminant of
![]() $p_1(x,c)\cdots p_k(x,c)$
by means of computer algebra, and then set aside those c that make the discriminant equal to zero. The route taken below is elementary and is not dependent upon a computer. In this way, the number of c to avoid is limited to 51. This is a consequence of the following statement, the proof of which is the goal of this section.
$p_1(x,c)\cdots p_k(x,c)$
by means of computer algebra, and then set aside those c that make the discriminant equal to zero. The route taken below is elementary and is not dependent upon a computer. In this way, the number of c to avoid is limited to 51. This is a consequence of the following statement, the proof of which is the goal of this section.
Theorem 3.1. Let
![]() $\mathbb {F}$
be a field of characteristic different from
$\mathbb {F}$
be a field of characteristic different from
![]() $2$
. The list of polynomials
$2$
. The list of polynomials
 $$ \begin{align} \begin{aligned} &x, x{-}1, x{-}c, x{-}1{-}c, x{+}1{-}c, (1{-}c)x-c, (1{+}c)x-c, \\ &g_1(x,c), g_2(x,c), g_3(x,c), g_4(x,c), f_1(x,c), f_2(x,c), f_3(x,c), f_4(x,c) \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &x, x{-}1, x{-}c, x{-}1{-}c, x{+}1{-}c, (1{-}c)x-c, (1{+}c)x-c, \\ &g_1(x,c), g_2(x,c), g_3(x,c), g_4(x,c), f_1(x,c), f_2(x,c), f_3(x,c), f_4(x,c) \end{aligned} \end{align} $$
is square-free if the following conditions hold:
The proof requires a number of steps. As an auxiliary notion, we call a list of polynomials
![]() $p_1(x,y),\ldots ,p_k(x,y)\in \mathbb {F}[x,y]$
reciprocally closed if for each
$p_1(x,y),\ldots ,p_k(x,y)\in \mathbb {F}[x,y]$
reciprocally closed if for each
![]() $i\in \{1,\ldots ,k\}$
, both
$i\in \{1,\ldots ,k\}$
, both
![]() $x\nmid p_i(x,y)$
and
$x\nmid p_i(x,y)$
and
![]() $y\nmid p_i(x,y)$
are true, and there exist unique
$y\nmid p_i(x,y)$
are true, and there exist unique
![]() $j\in \{1,\ldots ,k\}$
and
$j\in \{1,\ldots ,k\}$
and
![]() $\lambda \in \mathbb {F}$
such that
$\lambda \in \mathbb {F}$
such that
![]() $\hat {p_i}(x,y)= \lambda p_j(x,y)$
.
$\hat {p_i}(x,y)= \lambda p_j(x,y)$
.
If
![]() $a=\sum a_it^i\in \mathbb {F}[t]$
is a nonzero polynomial of degree
$a=\sum a_it^i\in \mathbb {F}[t]$
is a nonzero polynomial of degree
![]() $d\geqslant 0$
, then the reciprocal polynomial
$d\geqslant 0$
, then the reciprocal polynomial
![]() $\sum a_it^{d-i}$
will be denoted by
$\sum a_it^{d-i}$
will be denoted by
![]() $\hat a$
, like in the case of two variables. A list
$\hat a$
, like in the case of two variables. A list
![]() $a_1(t),\ldots ,a_k(t)\in \mathbb {F}[t]$
is reciprocally closed if for each
$a_1(t),\ldots ,a_k(t)\in \mathbb {F}[t]$
is reciprocally closed if for each
![]() $i\in \{1,\ldots ,k\}$
, the polynomial
$i\in \{1,\ldots ,k\}$
, the polynomial
![]() $a_i(t)$
is not divisible by t, and there exist unique
$a_i(t)$
is not divisible by t, and there exist unique
![]() $j\in \{1,\ldots ,k\}$
and
$j\in \{1,\ldots ,k\}$
and
![]() $\lambda \in \mathbb {F}$
such that
$\lambda \in \mathbb {F}$
such that
![]() $\hat {a_i}(t)= \lambda a_j(t)$
.
$\hat {a_i}(t)= \lambda a_j(t)$
.
Lemma 3.2. Let
![]() $p_1(x,y),\ldots ,p_k(x,y)\in \mathbb {F}[x,y]$
and
$p_1(x,y),\ldots ,p_k(x,y)\in \mathbb {F}[x,y]$
and
![]() $a_1(t),\ldots ,a_r(t) \in \mathbb {F}[t]$
be two reciprocally closed lists of polynomials. Denote by
$a_1(t),\ldots ,a_r(t) \in \mathbb {F}[t]$
be two reciprocally closed lists of polynomials. Denote by
![]() $\Gamma $
the set of all nonzero roots of polynomials
$\Gamma $
the set of all nonzero roots of polynomials
![]() $a_1,\ldots ,a_r$
. Assume that
$a_1,\ldots ,a_r$
. Assume that
holds for all
![]() $i\in \{1,\ldots ,k\}$
.
$i\in \{1,\ldots ,k\}$
.
Let
![]() $i,j\in \{1,\ldots ,k\}$
and
$i,j\in \{1,\ldots ,k\}$
and
![]() $\lambda \in \mathbb {F}$
be such that
$\lambda \in \mathbb {F}$
be such that
![]() $p_j(x,y) = \lambda \hat {p_i}(x,y)$
and
$p_j(x,y) = \lambda \hat {p_i}(x,y)$
and
![]() $i\ne j$
. If
$i\ne j$
. If
holds for all nonzero
![]() $c\in \mathbb {F}\setminus \Gamma $
and all
$c\in \mathbb {F}\setminus \Gamma $
and all
![]() $\ell \ne i$
,
$\ell \ne i$
,
![]() $1\leqslant \ell \leqslant k$
, then
$1\leqslant \ell \leqslant k$
, then
holds for all nonzero
![]() $c\in \mathbb {F}\setminus \Gamma $
and
$c\in \mathbb {F}\setminus \Gamma $
and
![]() $h\ne j$
,
$h\ne j$
,
![]() $1\leqslant h \leqslant k$
.
$1\leqslant h \leqslant k$
.
Proof. Suppose that
![]() $h\ne j$
and
$h\ne j$
and
![]() $c\in \mathbb {F}\setminus \Gamma $
,
$c\in \mathbb {F}\setminus \Gamma $
,
![]() $c\ne 0$
, are such that
$c\ne 0$
, are such that
![]() $p_j(x,c)$
and
$p_j(x,c)$
and
![]() $p_h(x,c)$
have a common root in
$p_h(x,c)$
have a common root in
![]() $\bar {\mathbb {F}}$
, say
$\bar {\mathbb {F}}$
, say
![]() $\gamma $
. Thus,
$\gamma $
. Thus,
![]() $p_j(\gamma ,c) = p_h(\gamma ,c) = 0$
. By Condition (3-12),
$p_j(\gamma ,c) = p_h(\gamma ,c) = 0$
. By Condition (3-12),
![]() $\gamma \ne 0$
. Since the list
$\gamma \ne 0$
. Since the list
![]() $p_1(x,y),\ldots ,p_k(x,y)$
is reciprocally closed, there exists
$p_1(x,y),\ldots ,p_k(x,y)$
is reciprocally closed, there exists
![]() $\ell \ne i$
such that
$\ell \ne i$
such that
![]() $p_\ell (x,y)$
is a scalar multiple of
$p_\ell (x,y)$
is a scalar multiple of
![]() $\hat {p_h}(x,c)$
. Since
$\hat {p_h}(x,c)$
. Since
![]() $p_j(x,y)$
is a multiple of
$p_j(x,y)$
is a multiple of
![]() $\hat {p_i}(x,y)$
, we have
$\hat {p_i}(x,y)$
, we have
![]() $p_i(\gamma ^{-1},c^{-1})=0=p_\ell (\gamma ^{-1},c^{-1})$
and hence
$p_i(\gamma ^{-1},c^{-1})=0=p_\ell (\gamma ^{-1},c^{-1})$
and hence
![]() $\gcd (p_i(x,c^{-1}),p_\ell (x,c^{-1}))\ne 1$
. By the assumption on
$\gcd (p_i(x,c^{-1}),p_\ell (x,c^{-1}))\ne 1$
. By the assumption on
![]() $p_i$
, this cannot be true unless
$p_i$
, this cannot be true unless
![]() $c^{-1}\in \Gamma $
. We refute the latter possibility by proving that if
$c^{-1}\in \Gamma $
. We refute the latter possibility by proving that if
![]() $c^{-1}\in \Gamma $
, then
$c^{-1}\in \Gamma $
, then
![]() $c\in \Gamma $
. That follows straightforwardly from the assumption that the list
$c\in \Gamma $
. That follows straightforwardly from the assumption that the list
![]() $a_1,\ldots ,a_r$
is reciprocally closed. Indeed, since
$a_1,\ldots ,a_r$
is reciprocally closed. Indeed, since
![]() $c^{-1} \in \Gamma $
, there exists
$c^{-1} \in \Gamma $
, there exists
![]() $s\in \{1,\ldots ,r\}$
such that
$s\in \{1,\ldots ,r\}$
such that
![]() $a_s(c^{-1}) = 0$
. There also exists
$a_s(c^{-1}) = 0$
. There also exists
![]() $m\in \{1,\ldots ,r\}$
such that
$m\in \{1,\ldots ,r\}$
such that
![]() $a_m$
is a scalar multiple of
$a_m$
is a scalar multiple of
![]() $\hat {a_s}$
. Because of that,
$\hat {a_s}$
. Because of that,
![]() $a_m(c) = a_m((c^{-1})^{-1}) = 0$
. This implies that
$a_m(c) = a_m((c^{-1})^{-1}) = 0$
. This implies that
![]() $c\in \Gamma $
since
$c\in \Gamma $
since
![]() $\Gamma $
is defined as the set of all nonzero roots of polynomials
$\Gamma $
is defined as the set of all nonzero roots of polynomials
![]() $a_1,\ldots ,a_r$
.
$a_1,\ldots ,a_r$
.
If
![]() $a(t) = t-\gamma $
,
$a(t) = t-\gamma $
,
![]() $\gamma \ne 0$
, then
$\gamma \ne 0$
, then
![]() $\hat a(t) = -\gamma (t-\gamma ^{-1})$
. Hence, the list of nonzero c that fulfill one of the conditions (3-2)–(3-11) may be considered as a set
$\hat a(t) = -\gamma (t-\gamma ^{-1})$
. Hence, the list of nonzero c that fulfill one of the conditions (3-2)–(3-11) may be considered as a set
![]() $\Gamma $
of nonzero roots of a reciprocally closed list of polynomials in one variable.
$\Gamma $
of nonzero roots of a reciprocally closed list of polynomials in one variable.
Now, remove x and
![]() $x{-}1$
from the list of polynomials (3-1) that are the input to Lemma 3.2. The remaining polynomials can be interpreted as a list
$x{-}1$
from the list of polynomials (3-1) that are the input to Lemma 3.2. The remaining polynomials can be interpreted as a list
![]() $p_1(x,c), \ldots , p_{13}(x,c)$
such that
$p_1(x,c), \ldots , p_{13}(x,c)$
such that
![]() $p_1(x,y), \ldots ,p_{13}(x,y)$
is a reciprocally closed list of polynomials in two variables. It is easy to verify that if
$p_1(x,y), \ldots ,p_{13}(x,y)$
is a reciprocally closed list of polynomials in two variables. It is easy to verify that if
![]() $0$
or
$0$
or
![]() $1$
is a root of any of the polynomials
$1$
is a root of any of the polynomials
![]() $p_i(x,c)$
,
$p_i(x,c)$
,
![]() $1\leqslant i \leqslant 13$
, then c fulfills Condition (3-2). Polynomials x and
$1\leqslant i \leqslant 13$
, then c fulfills Condition (3-2). Polynomials x and
![]() $x{-}1$
can be thus excised from the subsequent discussion, and Lemma 3.2 may be used.
$x{-}1$
can be thus excised from the subsequent discussion, and Lemma 3.2 may be used.
Lemma 3.2 will also be applied to some sublists of
![]() $p_1(x,c), \ldots , p_{13}(x,c)$
that are reciprocally closed. The first such sublist is the linear polynomials occurring in (3-1) (with x and
$p_1(x,c), \ldots , p_{13}(x,c)$
that are reciprocally closed. The first such sublist is the linear polynomials occurring in (3-1) (with x and
![]() $x{-}1$
being removed). These are
$x{-}1$
being removed). These are
![]() $x{-}c$
,
$x{-}c$
,
![]() $x{-}1{-}c$
,
$x{-}1{-}c$
,
![]() $x{+}1{-}c$
,
$x{+}1{-}c$
,
![]() $(1{-}c)x-c$
,
$(1{-}c)x-c$
,
![]() $(1{+}c)x-c$
,
$(1{+}c)x-c$
,
![]() $x-(2c{-}c^2)$
, and
$x-(2c{-}c^2)$
, and
![]() $(1{-}2c)x+c^2$
. The latter two polynomials are equal to
$(1{-}2c)x+c^2$
. The latter two polynomials are equal to
![]() $g_2(x,c)$
and
$g_2(x,c)$
and
![]() $g_4(x,c)$
. The list of these linear polynomials is square-free if there are no duplicates in the set of their roots
$g_4(x,c)$
. The list of these linear polynomials is square-free if there are no duplicates in the set of their roots
The reciprocity yields the following pairs of roots:
We now prove a sequence of lemmas which explore properties of the polynomials in List (3-1).
Proof. If (3-2) holds, then c is not equal to any other element of
![]() $R(c)$
. Any equality within the pairs in (3-13) would require that
$R(c)$
. Any equality within the pairs in (3-13) would require that
![]() $c^2{+}c{+}1=0$
or
$c^2{+}c{+}1=0$
or
![]() $c^2{-}c{+}1=0$
or
$c^2{-}c{+}1=0$
or
![]() $2c(c{-}1)^2=0$
. By (3-2) and (3-3), none of these conditions hold. Clearly,
$2c(c{-}1)^2=0$
. By (3-2) and (3-3), none of these conditions hold. Clearly,
![]() $c{+}1\ne c{-}1$
. If
$c{+}1\ne c{-}1$
. If
![]() $c{+}1 = c/(1{-}c)$
, then
$c{+}1 = c/(1{-}c)$
, then
![]() $c^2{+}c{-}1=0$
. Furthermore,
$c^2{+}c{-}1=0$
. Furthermore,
and
Hence,
![]() $c{+}1$
is not equal to any other element of
$c{+}1$
is not equal to any other element of
![]() $R(c)$
. By the reciprocity relationship described in Lemma 3.2,
$R(c)$
. By the reciprocity relationship described in Lemma 3.2,
![]() $c/(1{+}c)$
is also not equal to another element of
$c/(1{+}c)$
is also not equal to another element of
![]() $R(c)$
. If
$R(c)$
. If
![]() $c{-}1$
is equal to
$c{-}1$
is equal to
![]() $c(2{-}c)$
, then
$c(2{-}c)$
, then
![]() $c^2{-}c{-}1 =0$
. If it is equal to
$c^2{-}c{-}1 =0$
. If it is equal to
![]() $c^2/(2c{-}1)$
, then
$c^2/(2c{-}1)$
, then
![]() $c^2{-}3c{+}1=0$
.
$c^2{-}3c{+}1=0$
.
Lemma 3.4. Suppose that
![]() $c\in \mathbb {F}$
satisfies Conditions (3-2) and (3-5). Then none of the polynomials
$c\in \mathbb {F}$
satisfies Conditions (3-2) and (3-5). Then none of the polynomials
![]() $f_i(x,c)$
,
$f_i(x,c)$
,
![]() $1\leqslant i \leqslant 4$
, and
$1\leqslant i \leqslant 4$
, and
![]() $g_j(x,c)$
,
$g_j(x,c)$
,
![]() $j \in \{1,3\}$
, possesses a double root.
$j \in \{1,3\}$
, possesses a double root.
Proof. By a reciprocity argument similar to that of Lemma 3.2, only
![]() $f_1(x,c)$
,
$f_1(x,c)$
,
![]() $f_2(x,c)$
, and
$f_2(x,c)$
, and
![]() $g_1(x,c)$
need to be tested. Discriminants of these polynomials are
$g_1(x,c)$
need to be tested. Discriminants of these polynomials are
![]() $(c+1)^2-4c^2 = (1-c)(3c+1)$
,
$(c+1)^2-4c^2 = (1-c)(3c+1)$
,
![]() $c(c-4(c-1)) = -c(3c-4)$
, and
$c(c-4(c-1)) = -c(3c-4)$
, and
![]() $4(1-c)$
. None of these may be zero, by the assumptions on c.
$4(1-c)$
. None of these may be zero, by the assumptions on c.
Lemma 3.5. If
![]() $c\in \mathbb {F}$
satisfies Conditions (3-2), (3-3), and (3-6), then none of the elements of
$c\in \mathbb {F}$
satisfies Conditions (3-2), (3-3), and (3-6), then none of the elements of
![]() $R(c)$
is a root of
$R(c)$
is a root of
![]() $g_1(x,c)$
or
$g_1(x,c)$
or
![]() $g_3(x,c)$
.
$g_3(x,c)$
.
Proof. By Lemma 3.2, it suffices to consider only the polynomial
![]() $h(x)=g_1(x,c)$
. Now,
$h(x)=g_1(x,c)$
. Now,
![]() $h(c) = c(c{-}1)$
,
$h(c) = c(c{-}1)$
,
![]() $h(c\pm 1)= c^2\pm 2c+1-2(c\pm 1) +c$
is equal to
$h(c\pm 1)= c^2\pm 2c+1-2(c\pm 1) +c$
is equal to
![]() $c^2+c-1$
or
$c^2+c-1$
or
![]() $c^2-3c+3$
, while
$c^2-3c+3$
, while
and
![]() ${c^{-1} h(c(2-c))\kern1.2pt{=}\kern1.2pt c(2-c)^2 - 2(2-c)+1\kern1.2pt{=}\kern1.2pt c^3-4c^2+6c-3\kern1.2pt{=}\kern1.2pt (c-1)(c^2-3c+3).}$
Finally,
${c^{-1} h(c(2-c))\kern1.2pt{=}\kern1.2pt c(2-c)^2 - 2(2-c)+1\kern1.2pt{=}\kern1.2pt c^3-4c^2+6c-3\kern1.2pt{=}\kern1.2pt (c-1)(c^2-3c+3).}$
Finally,
 $$ \begin{align*} \frac{(2c-1)^2}c h\bigg (\frac {c^2}{2c-1}\bigg ) &= c^3 -2c(2c-1) + (2c-1)^2 = c^3-2c+1\\& =(c-1)(c^2+c-1).\\[-34pt] \end{align*} $$
$$ \begin{align*} \frac{(2c-1)^2}c h\bigg (\frac {c^2}{2c-1}\bigg ) &= c^3 -2c(2c-1) + (2c-1)^2 = c^3-2c+1\\& =(c-1)(c^2+c-1).\\[-34pt] \end{align*} $$
Lemma 3.6. If
![]() $c\in \mathbb {F}$
satisfies Conditions (3-2), (3-5), and (3-7)–(3-11), then none of the elements of
$c\in \mathbb {F}$
satisfies Conditions (3-2), (3-5), and (3-7)–(3-11), then none of the elements of
![]() $R(c)$
is a root of
$R(c)$
is a root of
![]() $f_i(x,c)$
for any
$f_i(x,c)$
for any
![]() $i=1,2,3,4$
.
$i=1,2,3,4$
.
Proof. The proof is very similar to that of Lemma 3.5, so we only give a summary. By Lemma 3.2, it suffices to test the polynomials
![]() $f_1(x,c)$
and
$f_1(x,c)$
and
![]() $f_2(x,c)$
. Substituting an element of
$f_2(x,c)$
. Substituting an element of
![]() $R(c)$
in place of x always yields a polynomial from the indicated list. Note that
$R(c)$
in place of x always yields a polynomial from the indicated list. Note that
![]() $c^3-3c^2+4c-2 = (c-1)(c^2-2c+2)$
,
$c^3-3c^2+4c-2 = (c-1)(c^2-2c+2)$
,
![]() $3c^2-5c+2 = (c-1)(3c-2)$
, and
$3c^2-5c+2 = (c-1)(3c-2)$
, and
![]() $3c^3-7c^2 +5c -1 = (c-1)^2(3c-1)$
.
$3c^3-7c^2 +5c -1 = (c-1)^2(3c-1)$
.
Lemma 3.7. Suppose that
![]() $c\in \mathbb {F}$
satisfies Conditions (3-2) and (3-5). Then for each
$c\in \mathbb {F}$
satisfies Conditions (3-2) and (3-5). Then for each
![]() $i\in \{1,3\}$
, there exist at least three
$i\in \{1,3\}$
, there exist at least three
![]() $j\in \{1,2,3,4\}$
such that
$j\in \{1,2,3,4\}$
such that
![]() $g_i(x,c)$
and
$g_i(x,c)$
and
![]() $f_j(x,c)$
share no root in
$f_j(x,c)$
share no root in
![]() $\bar {\mathbb {F}}$
.
$\bar {\mathbb {F}}$
.
Proof. Because of the reciprocity,
![]() $i=1$
may be assumed. If
$i=1$
may be assumed. If
![]() $g_1(x,c)$
and
$g_1(x,c)$
and
![]() $f_1(x,c)$
have a common root x, then
$f_1(x,c)$
have a common root x, then
![]() $(c{+}1)x-c^2 =2x-c$
, and that yields
$(c{+}1)x-c^2 =2x-c$
, and that yields
![]() $(c{-}1)x=c(c{-}1)$
. If
$(c{-}1)x=c(c{-}1)$
. If
![]() $g_1(x,c)$
and
$g_1(x,c)$
and
![]() $f_2(x,c)$
have a common root, then
$f_2(x,c)$
have a common root, then
![]() $cx -c^2+c = 2x-c$
, which means that
$cx -c^2+c = 2x-c$
, which means that
![]() $(c{-}2)x = (c{-}2)c$
. If
$(c{-}2)x = (c{-}2)c$
. If
![]() $g_1(x,c)$
and
$g_1(x,c)$
and
![]() $f_3(x,c)$
have a common root, then
$f_3(x,c)$
have a common root, then
![]() $(c^2{+}c)x -c^2 = 2x-c$
, and
$(c^2{+}c)x -c^2 = 2x-c$
, and
![]() $(c{-}1)(c{+}2)x = (c{-}1)c$
. In such a case,
$(c{-}1)(c{+}2)x = (c{-}1)c$
. In such a case,
![]() $c\ne -2$
and
$c\ne -2$
and
![]() $x = c/(c{+}2)$
. The latter value is a root of
$x = c/(c{+}2)$
. The latter value is a root of
![]() $g_1(x,c)$
if and only if
$g_1(x,c)$
if and only if
![]() $0=c^2-2c(c{+}2)+c(c{+}2)^2=c^2(c+3)$
. Here, as earlier, the solutions for c are forbidden by the conjunction of Conditions (3-2) and (3-5).
$0=c^2-2c(c{+}2)+c(c{+}2)^2=c^2(c+3)$
. Here, as earlier, the solutions for c are forbidden by the conjunction of Conditions (3-2) and (3-5).
Lemma 3.8. If
![]() $c\in \mathbb {F}$
satisfies Conditions (3-2), (3-7), and (3-8), and if
$c\in \mathbb {F}$
satisfies Conditions (3-2), (3-7), and (3-8), and if
![]() $1\leqslant i < j \leqslant 4$
, then
$1\leqslant i < j \leqslant 4$
, then
![]() $f_i(x,c)$
and
$f_i(x,c)$
and
![]() $f_j(x,c)$
share no common root in
$f_j(x,c)$
share no common root in
![]() $\bar {\mathbb {F}}$
.
$\bar {\mathbb {F}}$
.
Proof. This is obvious if
![]() $(i,j) = (1,3)$
. If
$(i,j) = (1,3)$
. If
![]() $(i,j) = (2,4)$
, then
$(i,j) = (2,4)$
, then
![]() $c(x^2-1)=0$
, so
$c(x^2-1)=0$
, so
![]() $x\in \{-1,1\}$
. Now,
$x\in \{-1,1\}$
. Now,
![]() $f_2(1,c) = (c-1)^2 \ne 0$
, while
$f_2(1,c) = (c-1)^2 \ne 0$
, while
![]() $f_2(-1,c) = c^2+1 = -f_4(-1,c)$
. This is why
$f_2(-1,c) = c^2+1 = -f_4(-1,c)$
. This is why
![]() $c^2\ne -1$
has to be assumed.
$c^2\ne -1$
has to be assumed.
For the rest, it suffices to test pairs
![]() $(1,2)$
and
$(1,2)$
and
![]() $(2,3)$
, by the reciprocity described in Lemma 3.2. If
$(2,3)$
, by the reciprocity described in Lemma 3.2. If
![]() $cx+x-c^2 = cx - c^2+c$
, then
$cx+x-c^2 = cx - c^2+c$
, then
![]() $x=c$
and
$x=c$
and
![]() $f_2(c) = c(c-1) \ne 0$
. If
$f_2(c) = c(c-1) \ne 0$
. If
![]() $cx -c^2 + c = cx + c^2x -c^2$
, then
$cx -c^2 + c = cx + c^2x -c^2$
, then
![]() $x=c^{-1}$
which means that
$x=c^{-1}$
which means that
![]() $f_2(c^{-1}) = c^{-2}-1+c^2-c = c^{-2}(c^4-c^3-c^2+1) = c^{-2}(c-1)(c^3-c-1)$
.
$f_2(c^{-1}) = c^{-2}-1+c^2-c = c^{-2}(c^4-c^3-c^2+1) = c^{-2}(c-1)(c^3-c-1)$
.
We can now bring all the pieces together to prove the main result of this section.
Proof of Theorem 3.1. Suppose that c fulfills Conditions (3-2)–(3-11). In addition to Lemmas 3.3–3.8, we also use that
![]() $g_1(x,c)$
and
$g_1(x,c)$
and
![]() $g_3(x,c)$
share no root in
$g_3(x,c)$
share no root in
![]() $\bar F$
, which can be proved by a similar method to Lemma 3.8.
$\bar F$
, which can be proved by a similar method to Lemma 3.8.
Let
![]() $p_1(x,c),\ldots ,p_k(x,c)$
be a nonempty sublist of (3-1) such that the product
$p_1(x,c),\ldots ,p_k(x,c)$
be a nonempty sublist of (3-1) such that the product
![]() $p_1(x,c)\cdots p_k(x,c)$
is a square in
$p_1(x,c)\cdots p_k(x,c)$
is a square in
![]() $\bar {\mathbb {F}}[x]$
. Let J be the set of those
$\bar {\mathbb {F}}[x]$
. Let J be the set of those
![]() $j\in \{1,2,3,4\}$
for which there exists
$j\in \{1,2,3,4\}$
for which there exists
![]() $h\in \{1,\ldots ,k\}$
such that
$h\in \{1,\ldots ,k\}$
such that
![]() $f_j(x,c) = p_h(x,c)$
. The set J must be nonempty, by Lemmas 3.3–3.5. Since J is nonempty and Lemmas 3.4, 3.6, and 3.8 hold, there must exist
$f_j(x,c) = p_h(x,c)$
. The set J must be nonempty, by Lemmas 3.3–3.5. Since J is nonempty and Lemmas 3.4, 3.6, and 3.8 hold, there must exist
![]() $i\in \{1,3\}$
such that
$i\in \{1,3\}$
such that
![]() $g_i(x,c) = p_h(x,c)$
for some
$g_i(x,c) = p_h(x,c)$
for some
![]() $h\in \{1,\ldots ,k\}$
. Since
$h\in \{1,\ldots ,k\}$
. Since
![]() $g_i(x,c)$
is not a scalar multiple of
$g_i(x,c)$
is not a scalar multiple of
![]() $f_j(x,c)$
for
$f_j(x,c)$
for
![]() $j\in J$
, we must have
$j\in J$
, we must have
![]() $|J|\geqslant 2$
, by Lemmas 3.4 and 3.5. However, even that is not viable, given Lemma 3.7.
$|J|\geqslant 2$
, by Lemmas 3.4 and 3.5. However, even that is not viable, given Lemma 3.7.
4 When
 $-1$
is a nonsquare
$-1$
is a nonsquare
Throughout this section,
![]() $\mathbb {F}=\mathbb {F}_q$
will be a finite field of order
$\mathbb {F}=\mathbb {F}_q$
will be a finite field of order
![]() $q\equiv 3\bmod 4$
. We put
$q\equiv 3\bmod 4$
. We put
![]() $\Sigma = \Sigma (\mathbb {F}_q)$
and
$\Sigma = \Sigma (\mathbb {F}_q)$
and
![]() $S=S(\mathbb {F}_q)$
. By Corollary 1.3,
$S=S(\mathbb {F}_q)$
. By Corollary 1.3,
![]() $|S| = |\Sigma | = (q^2{-}8q{+}15)/4$
. Define
$|S| = |\Sigma | = (q^2{-}8q{+}15)/4$
. Define
![]() $\bar S_{ij}^{rs}=S\setminus S_{ij}^{rs}$
and
$\bar S_{ij}^{rs}=S\setminus S_{ij}^{rs}$
and
![]() $T=\bigcap \bar S_{ij}^{rs}$
, where sets
$T=\bigcap \bar S_{ij}^{rs}$
, where sets
![]() $S_{ij}^{rs}$
are characterized by Theorem 2.11, subject to the assumption that Condition (2-5) holds. As we can see, Condition (2-5) holds in all cases that are relevant for our calculations. The aim of this section is to estimate the number
$S_{ij}^{rs}$
are characterized by Theorem 2.11, subject to the assumption that Condition (2-5) holds. As we can see, Condition (2-5) holds in all cases that are relevant for our calculations. The aim of this section is to estimate the number
![]() $\sigma (q) = |\{(a,b)\in \Sigma :Q_{a,b}$
is maximally nonassociative
$\sigma (q) = |\{(a,b)\in \Sigma :Q_{a,b}$
is maximally nonassociative
![]() $\}|$
. By Proposition 1.5,
$\}|$
. By Proposition 1.5,
![]() $\sigma (q) = |T|=(q^2{-}8q{+}15)/4 - |\bigcup S_{ij}^{rs}|$
. Put
$\sigma (q) = |T|=(q^2{-}8q{+}15)/4 - |\bigcup S_{ij}^{rs}|$
. Put
 $$ \begin{align*} T_0& = \{(x,y)\in T: \chi(\kern1.5pt y-x) = 1\}; \\ T_{1,1} &= \{(x,y)\in T_0: \chi(1-y)=\chi(1-x)=1\}; \\ T_{1,-1} &= \{(x,y)\in T_0: \chi(1-y)=\chi(1-x)=-1\}; \\ T_2 &= \{(x,y)\in T_0: \chi(1-x)=-1 \text{ and } \chi(1-y) = 1\}; \end{align*} $$
$$ \begin{align*} T_0& = \{(x,y)\in T: \chi(\kern1.5pt y-x) = 1\}; \\ T_{1,1} &= \{(x,y)\in T_0: \chi(1-y)=\chi(1-x)=1\}; \\ T_{1,-1} &= \{(x,y)\in T_0: \chi(1-y)=\chi(1-x)=-1\}; \\ T_2 &= \{(x,y)\in T_0: \chi(1-x)=-1 \text{ and } \chi(1-y) = 1\}; \end{align*} $$
and define
![]() $T_0'$
,
$T_0'$
,
![]() $T^{\prime }_{1,1}$
,
$T^{\prime }_{1,1}$
,
![]() $T^{\prime }_{1,-1}$
, and
$T^{\prime }_{1,-1}$
, and
![]() $T^{\prime }_2$
by exchanging x and y. For example, this means that
$T^{\prime }_2$
by exchanging x and y. For example, this means that
![]() $T_0'=\{(x,y)\in T:\chi (\,y-x) = -1\}$
. Put also
$T_0'=\{(x,y)\in T:\chi (\,y-x) = -1\}$
. Put also
![]() $T_1=T_{1,1}\cup T_{1,-1}$
and
$T_1=T_{1,1}\cup T_{1,-1}$
and
![]() $T_1'=T^{\prime }_{1,1}\cup T^{\prime }_{1,-1}$
.
$T_1'=T^{\prime }_{1,1}\cup T^{\prime }_{1,-1}$
.
Lemma 4.1.
![]() $T=T_0\cup T_0'$
,
$T=T_0\cup T_0'$
,
![]() $T_0= T_1\cup T_2$
,
$T_0= T_1\cup T_2$
,
![]() $T_0' = T_1' \cup T_2'$
,
$T_0' = T_1' \cup T_2'$
,
![]() $T_1=T_{1,1}\cup T_{1,-1}$
, and
$T_1=T_{1,1}\cup T_{1,-1}$
, and
![]() $T_1'=T^{\prime }_{1,1}\cup T^{\prime }_{1,-1}$
. All of these unions are unions of disjoints sets.
$T_1'=T^{\prime }_{1,1}\cup T^{\prime }_{1,-1}$
. All of these unions are unions of disjoints sets.
Both of the mappings
![]() $(x,y)\mapsto (\kern1.5pt y,x)$
and
$(x,y)\mapsto (\kern1.5pt y,x)$
and
![]() $(x,y)\mapsto (x^{-1},y^{-1})$
permute T. Both of them exchange
$(x,y)\mapsto (x^{-1},y^{-1})$
permute T. Both of them exchange
![]() $T_1$
and
$T_1$
and
![]() $T_1'$
, and
$T_1'$
, and
![]() $T_2$
and
$T_2$
and
![]() $T_2'$
. Furthermore,
$T_2'$
. Furthermore,
![]() $(x,y)\mapsto (\kern1.5pt y,x)$
sends
$(x,y)\mapsto (\kern1.5pt y,x)$
sends
![]() $T_{1,\varepsilon }$
to
$T_{1,\varepsilon }$
to
![]() $T^{\prime }_{1,\varepsilon }$
, while
$T^{\prime }_{1,\varepsilon }$
, while
![]() $(x,y)\mapsto (x^{-1},y^{-1})$
sends
$(x,y)\mapsto (x^{-1},y^{-1})$
sends
![]() $T_{1,\varepsilon }$
to
$T_{1,\varepsilon }$
to
![]() $T^{\prime }_{1,-\varepsilon }$
, for both
$T^{\prime }_{1,-\varepsilon }$
, for both
![]() $\varepsilon \in \{-1,1\}$
.
$\varepsilon \in \{-1,1\}$
.
Proof. Recall that by our definition of S, we have
![]() $1\notin \{x,y\}$
and
$1\notin \{x,y\}$
and
![]() $x\ne y$
for all
$x\ne y$
for all
![]() $(x,y)\in T$
. By Proposition 2.3, both
$(x,y)\in T$
. By Proposition 2.3, both
![]() $(x,y) \mapsto (\kern1.5pt y,x)$
and
$(x,y) \mapsto (\kern1.5pt y,x)$
and
![]() $(x,y)\mapsto (x^{-1},y^{-1})$
permute T. The effects of these two mappings are simple to verify. Note, for example, that if
$(x,y)\mapsto (x^{-1},y^{-1})$
permute T. The effects of these two mappings are simple to verify. Note, for example, that if
![]() $\varepsilon = \chi (x{-}y)$
, then
$\varepsilon = \chi (x{-}y)$
, then
![]() $\chi (x^{-1}-y^{-1}) = \chi (\kern1.5pt y{-}x) = -\varepsilon $
.
$\chi (x^{-1}-y^{-1}) = \chi (\kern1.5pt y{-}x) = -\varepsilon $
.
To see that
![]() $T_0 = T_1\cup T_2$
, note that there is no
$T_0 = T_1\cup T_2$
, note that there is no
![]() $(x,y) \in T_0$
with
$(x,y) \in T_0$
with
![]() $\chi (1{-}x)=1$
and
$\chi (1{-}x)=1$
and
![]() $\chi (1{-}y)=-1$
. Indeed, each such
$\chi (1{-}y)=-1$
. Indeed, each such
![]() $(x,y)$
belongs to
$(x,y)$
belongs to
![]() $S_{01}^{10}$
.
$S_{01}^{10}$
.
For
![]() $c\in \mathbb {F}_q$
, define
$c\in \mathbb {F}_q$
, define
![]() $t_2(c)=|\{x\in \mathbb {F}_q:(x,c)\in T_2\}|$
and
$t_2(c)=|\{x\in \mathbb {F}_q:(x,c)\in T_2\}|$
and
![]() $t_{1,1}(c)=|\{x\in \mathbb {F}_q:(x,c)\in T_{1,1}\}|$
. In the next two propositions, we seek estimates of these quantities. In both results, we assume that c fulfills Condition (3-3). Observe that under this assumption,
$t_{1,1}(c)=|\{x\in \mathbb {F}_q:(x,c)\in T_{1,1}\}|$
. In the next two propositions, we seek estimates of these quantities. In both results, we assume that c fulfills Condition (3-3). Observe that under this assumption,
![]() $c^2{-}c{-}1\ne 0$
and for all
$c^2{-}c{-}1\ne 0$
and for all
![]() $x\in \mathbb {F}_q$
, either
$x\in \mathbb {F}_q$
, either
![]() $x\ne c{+}1$
or
$x\ne c{+}1$
or
![]() $x^2{-}x{-}1\ne 0$
, and therefore Condition (2-5) holds for
$x^2{-}x{-}1\ne 0$
, and therefore Condition (2-5) holds for
![]() $(x,y)=(x,c)$
. This will enable us to use Theorem 2.11.
$(x,y)=(x,c)$
. This will enable us to use Theorem 2.11.
Proposition 4.2. Suppose that c and
![]() $1-c$
are both nonzero squares in
$1-c$
are both nonzero squares in
![]() $\mathbb {F}_q$
and that c fulfills Conditions (3-2)–(3-11). Then,
$\mathbb {F}_q$
and that c fulfills Conditions (3-2)–(3-11). Then,
Proof. We estimate
![]() $t_2(c)$
by characterizing the pairs
$t_2(c)$
by characterizing the pairs
![]() $(x,c)$
in
$(x,c)$
in
![]() $T_2$
. For a fixed c, there are at most 21 values of x that are roots of any of the polynomials in List (3-1). So at the cost of adding a term equal to 21 to our eventual bound, we may assume for the remainder of the proof that x is not a root of any polynomial in List (3-1). Then
$T_2$
. For a fixed c, there are at most 21 values of x that are roots of any of the polynomials in List (3-1). So at the cost of adding a term equal to 21 to our eventual bound, we may assume for the remainder of the proof that x is not a root of any polynomial in List (3-1). Then
![]() $\chi (x)=1=\chi (c)$
, since
$\chi (x)=1=\chi (c)$
, since
![]() $(x,c) \in S$
and
$(x,c) \in S$
and
![]() $\chi (1{-}x)=\chi (c{-}1)=\chi (x{-}c)=-1$
by the definition of
$\chi (1{-}x)=\chi (c{-}1)=\chi (x{-}c)=-1$
by the definition of
![]() $T_2$
.
$T_2$
.
From the definitions of
![]() $\bar S_{01}^{00}$
,
$\bar S_{01}^{00}$
,
![]() $\bar S_{10}^{00}$
,
$\bar S_{10}^{00}$
,
![]() $\bar S_{10}^{11}$
, and
$\bar S_{10}^{11}$
, and
![]() $\bar S_{01}^{11}$
, we deduce that
$\bar S_{01}^{11}$
, we deduce that
![]() $\chi (g_1(x,c))=\chi (g_4(x,c))=-1$
and
$\chi (g_1(x,c))=\chi (g_4(x,c))=-1$
and
![]() $\chi (g_2(x,c))=\chi (g_3(x,c))=1$
. Now, from
$\chi (g_2(x,c))=\chi (g_3(x,c))=1$
. Now, from
![]() $(x,c)\in \bar S_{01}^{01}$
, we deduce that either
$(x,c)\in \bar S_{01}^{01}$
, we deduce that either
In the former case, the requirement for
![]() $(x,c)$
to be in
$(x,c)$
to be in
![]() $\bar S_{11}^{01}$
forces
$\bar S_{11}^{01}$
forces
![]() $\chi (f_1(x,c))=1$
, whilst in the latter case, the requirement for
$\chi (f_1(x,c))=1$
, whilst in the latter case, the requirement for
![]() $(x,c)$
to be in
$(x,c)$
to be in
![]() $\bar S_{00}^{01}$
forces
$\bar S_{00}^{01}$
forces
![]() $\chi (f_4(x,c))=-1$
. Of course, it is also possible that both alternatives in Condition (4-1) are realized.
$\chi (f_4(x,c))=-1$
. Of course, it is also possible that both alternatives in Condition (4-1) are realized.
Analogously,
![]() $(x,c)$
belongs to
$(x,c)$
belongs to
![]() $\bar S_{10}^{10}$
, so
$\bar S_{10}^{10}$
, so
In the former case, the requirement for
![]() $(x,c)$
to be in
$(x,c)$
to be in
![]() $\bar S_{11}^{10}$
forces
$\bar S_{11}^{10}$
forces
![]() $\chi (f_2(x,c))=-1$
, whilst in the latter case, the requirement for
$\chi (f_2(x,c))=-1$
, whilst in the latter case, the requirement for
![]() $(x,c)$
to be in
$(x,c)$
to be in
![]() $\bar S_{00}^{10}$
forces
$\bar S_{00}^{10}$
forces
![]() $\chi (f_3(x,c))=1$
.
$\chi (f_3(x,c))=1$
.
Suppose that
![]() $i=1,\ldots ,9$
indexes the nine possibilities for the quadruple
$i=1,\ldots ,9$
indexes the nine possibilities for the quadruple
that are consistent with Conditions (4-1) and (4-2). In each case, let
![]() $J_i$
denote the subset of
$J_i$
denote the subset of
![]() $\{1,2,3,4\}$
consisting of those indices j for which
$\{1,2,3,4\}$
consisting of those indices j for which
![]() $\chi (f_j)$
is forced. Combining the above observations, we see that there will be
$\chi (f_j)$
is forced. Combining the above observations, we see that there will be
![]() $4,4,1$
cases, respectively, in which
$4,4,1$
cases, respectively, in which
![]() $|J_i|=2,3,4$
.
$|J_i|=2,3,4$
.
By Theorem 3.1 and our assumptions, the list of polynomials (3-1) is square-free. We can hence apply Theorem 1.6 for each of the nine possibilities for the quadruple (4-3), prescribing
![]() $\chi (p(x))$
for each polynomial
$\chi (p(x))$
for each polynomial
![]() $p(x)$
in List (3-1) except for any
$p(x)$
in List (3-1) except for any
![]() $f_j$
with
$f_j$
with
![]() $j\notin J_i$
. We find that
$j\notin J_i$
. We find that
 $$ \begin{align*} &|t_2(c)-4\cdot2^{-13}q-4\cdot2^{-14}q-1\cdot2^{-15}q|\\ &\quad\leqslant (\!\sqrt q+1)(4\cdot17+4\cdot19+1\cdot21)/2+21. \end{align*} $$
$$ \begin{align*} &|t_2(c)-4\cdot2^{-13}q-4\cdot2^{-14}q-1\cdot2^{-15}q|\\ &\quad\leqslant (\!\sqrt q+1)(4\cdot17+4\cdot19+1\cdot21)/2+21. \end{align*} $$
The result follows.
Proposition 4.3. Suppose that c and
![]() $1-c$
are both nonzero squares in
$1-c$
are both nonzero squares in
![]() $\mathbb {F}_q$
and that c fulfills Conditions (3-2)–(3-11). Then,
$\mathbb {F}_q$
and that c fulfills Conditions (3-2)–(3-11). Then,
Proof. The proof is similar to that of Proposition 4.2. Let us consider under which conditions a pair
![]() $(x,c)$
belongs to
$(x,c)$
belongs to
![]() $T_{1,1}$
, where x is not a root of any polynomial in List (3-1). For
$T_{1,1}$
, where x is not a root of any polynomial in List (3-1). For
![]() $(x,c)$
to belong to each of the sets
$(x,c)$
to belong to each of the sets
![]() $\bar S_{01}^{10}$
,
$\bar S_{01}^{10}$
,
![]() $\bar S_{01}^{00}$
,
$\bar S_{01}^{00}$
,
![]() $\bar S_{10}^{00}$
,
$\bar S_{10}^{00}$
,
![]() $\bar S_{10}^{11}$
,
$\bar S_{10}^{11}$
,
![]() $\bar S_{01}^{11}$
,
$\bar S_{01}^{11}$
,
![]() $\bar S_{11}^{01}$
, and
$\bar S_{11}^{01}$
, and
![]() $\bar S_{00}^{10}$
, it is necessary and sufficient that
$\bar S_{00}^{10}$
, it is necessary and sufficient that
![]() $\chi (x)=\chi (c)=\chi (1-c)=\chi (1-x)=\chi (c-x)=\chi (g_2(x,c)) = 1$
and
$\chi (x)=\chi (c)=\chi (1-c)=\chi (1-x)=\chi (c-x)=\chi (g_2(x,c)) = 1$
and
![]() $\chi (g_4(x,c)) = -1$
. Also for
$\chi (g_4(x,c)) = -1$
. Also for
![]() $(x,c)$
to be in
$(x,c)$
to be in
![]() $\bar S_{11}^{10}$
and
$\bar S_{11}^{10}$
and
![]() $\bar S_{10}^{10}$
requires that
$\bar S_{10}^{10}$
requires that
 $$ \begin{align*} &\chi(c{-}1{-}x) = -1\quad\text{or}\quad \chi(f_2(x,c))=-1; \quad\text{and}\\ &\chi(c{-}1{-}x) = 1\quad\text{or}\quad \chi(g_3(x,c))=-1 \quad\text{or}\quad \chi(c-xc-x)=1. \end{align*} $$
$$ \begin{align*} &\chi(c{-}1{-}x) = -1\quad\text{or}\quad \chi(f_2(x,c))=-1; \quad\text{and}\\ &\chi(c{-}1{-}x) = 1\quad\text{or}\quad \chi(g_3(x,c))=-1 \quad\text{or}\quad \chi(c-xc-x)=1. \end{align*} $$
Both of these conditions are satisfied whenever
![]() $\chi (c{-}1{-}x) {\kern-1pt}={\kern-1.5pt} -{\kern-1.2pt}1$
and
$\chi (c{-}1{-}x) {\kern-1pt}={\kern-1.5pt} -{\kern-1.2pt}1$
and
![]() $\chi (c-xc-x){\kern-1pt}={\kern-1pt}1$
. Each of the other three possibilities for the pair
$\chi (c-xc-x){\kern-1pt}={\kern-1pt}1$
. Each of the other three possibilities for the pair
![]() $(\,\chi (c{-}1{-}x),\chi (c-xc-x))$
forces exactly one of the conditions
$(\,\chi (c{-}1{-}x),\chi (c-xc-x))$
forces exactly one of the conditions
![]() $\chi (f_2(x,c))=-1$
or
$\chi (f_2(x,c))=-1$
or
![]() $\chi (g_3(x,c))=-1$
to hold.
$\chi (g_3(x,c))=-1$
to hold.
Similarly, for
![]() $(x,c)$
to be in
$(x,c)$
to be in
![]() $\bar S_{00}^{01}$
and
$\bar S_{00}^{01}$
and
![]() $\bar S_{01}^{01}$
requires that
$\bar S_{01}^{01}$
requires that
 $$ \begin{align*} &\chi(x{-}xc{-}c) = -1\quad\text{or}\quad \chi(f_4(x,c))=-1; \quad\text{and}\\ &\chi(x{-}1{-}c) = 1\quad\text{or}\quad \chi(g_1(x,c))=1 \quad\text{or}\quad \chi(x-xc-c)=1. \end{align*} $$
$$ \begin{align*} &\chi(x{-}xc{-}c) = -1\quad\text{or}\quad \chi(f_4(x,c))=-1; \quad\text{and}\\ &\chi(x{-}1{-}c) = 1\quad\text{or}\quad \chi(g_1(x,c))=1 \quad\text{or}\quad \chi(x-xc-c)=1. \end{align*} $$
Both of these conditions are satisfied whenever
![]() $\chi (x{-}1{-}c) = 1$
and
$\chi (x{-}1{-}c) = 1$
and
![]() $\chi (x-xc-c)=-1$
. Each of the other three possibilities for the pair
$\chi (x-xc-c)=-1$
. Each of the other three possibilities for the pair
![]() $(\chi (x{-}1{-}c),\chi (x-xc-c))$
forces exactly one of the conditions
$(\chi (x{-}1{-}c),\chi (x-xc-c))$
forces exactly one of the conditions
![]() $\chi (f_4(x,c))=-1$
or
$\chi (f_4(x,c))=-1$
or
![]() $\chi (g_1(x,c))=1$
to hold.
$\chi (g_1(x,c))=1$
to hold.
Suppose that
![]() $i=1,\ldots ,16$
indexes the 16 possibilities for the quadruple (4-3). Let
$i=1,\ldots ,16$
indexes the 16 possibilities for the quadruple (4-3). Let
![]() $K_i$
denote the subset of
$K_i$
denote the subset of
![]() $\{f_2,f_4,g_1,g_3\}$
consisting of those polynomials p for which
$\{f_2,f_4,g_1,g_3\}$
consisting of those polynomials p for which
![]() $\chi (p)$
is forced. Combining the above observations, we see that there will be
$\chi (p)$
is forced. Combining the above observations, we see that there will be
![]() $1,6,9$
cases, respectively, in which
$1,6,9$
cases, respectively, in which
![]() $|K_i|=0,1,2$
. The values of
$|K_i|=0,1,2$
. The values of
![]() $\chi (p)$
for
$\chi (p)$
for
![]() $p\in \{f_1,f_2,f_3,f_4,g_1,g_3\}\setminus K_i$
are unconstrained. Hence, by applying Theorem 1.6 for each of the 16 possibilities for the quadruple (4-3), we find that
$p\in \{f_1,f_2,f_3,f_4,g_1,g_3\}\setminus K_i$
are unconstrained. Hence, by applying Theorem 1.6 for each of the 16 possibilities for the quadruple (4-3), we find that
 $$ \begin{align*} &|t_{1,1}(c)-1\cdot2^{-9}q-6\cdot2^{-10}q-9\cdot2^{-11}q|\\ &\quad\leqslant (\!\sqrt q+1)(1\cdot9+6\cdot11+9\cdot13)/2+21. \end{align*} $$
$$ \begin{align*} &|t_{1,1}(c)-1\cdot2^{-9}q-6\cdot2^{-10}q-9\cdot2^{-11}q|\\ &\quad\leqslant (\!\sqrt q+1)(1\cdot9+6\cdot11+9\cdot13)/2+21. \end{align*} $$
The result follows.
We are now ready to prove the main result for this section.
Theorem 4.4. For
![]() $q\equiv 3\bmod 4$
,
$q\equiv 3\bmod 4$
,
Proof. By [Reference Evans7, Theorem 10.5], there are
![]() $(q-3)/4$
choices for
$(q-3)/4$
choices for
![]() $c\in \mathbb {F}_q$
such that both c and
$c\in \mathbb {F}_q$
such that both c and
![]() $1-c$
are nonzero squares. At most
$1-c$
are nonzero squares. At most
![]() $1+4+1+3+2+3+0+2+3+3=22$
of these choices do not fulfill Conditions (3-2)–(3-11) of Theorem 3.1. (To see this, note that
$1+4+1+3+2+3+0+2+3+3=22$
of these choices do not fulfill Conditions (3-2)–(3-11) of Theorem 3.1. (To see this, note that
![]() $\chi (-1)=-1$
and that if
$\chi (-1)=-1$
and that if
![]() $\chi (c)=\chi (1-c)=1$
, then
$\chi (c)=\chi (1-c)=1$
, then
![]() ${\chi (1-1/c)=-1}$
, which means that in any pair of reciprocal field elements, at most one of the elements will be a viable choice for c. This is particularly useful because of the many polynomials in Theorem 3.1 which form reciprocal pairs.) Each c that fails one of Conditions (3-2)–(3-11) contributes between 0 and
${\chi (1-1/c)=-1}$
, which means that in any pair of reciprocal field elements, at most one of the elements will be a viable choice for c. This is particularly useful because of the many polynomials in Theorem 3.1 which form reciprocal pairs.) Each c that fails one of Conditions (3-2)–(3-11) contributes between 0 and
![]() $(q-3)/2$
elements
$(q-3)/2$
elements
![]() $(x,c)$
to T. Putting these observations together with Propositions 4.2 and 4.3, we have that
$(x,c)$
to T. Putting these observations together with Propositions 4.2 and 4.3, we have that
 $$ \begin{align*} &||T_2|-25\cdot2^{-15}q(q-3)/4|\\ &\quad\leqslant165(\!\sqrt{q}+1)(q-3)/8+21(q-3)/4+22(q-3)/2,\\ &||T_{1,1}|-25\cdot2^{-11}q(q-3)/4|\\ &\quad\leqslant96(\!\sqrt{q}+1)(q-3)/4+21(q-3)/4+22(q-3)/2. \end{align*} $$
$$ \begin{align*} &||T_2|-25\cdot2^{-15}q(q-3)/4|\\ &\quad\leqslant165(\!\sqrt{q}+1)(q-3)/8+21(q-3)/4+22(q-3)/2,\\ &||T_{1,1}|-25\cdot2^{-11}q(q-3)/4|\\ &\quad\leqslant96(\!\sqrt{q}+1)(q-3)/4+21(q-3)/4+22(q-3)/2. \end{align*} $$
Next, notice that it follows from Lemma 4.1 that
![]() $|T_{1,1}|=|T^{\prime }_{1,1}|=|T_{1,-1}|=|T^{\prime }_{1,-1}|$
and
$|T_{1,1}|=|T^{\prime }_{1,1}|=|T_{1,-1}|=|T^{\prime }_{1,-1}|$
and
![]() $|T_2|=|T^{\prime }_2|$
and that T is the disjoint union of
$|T_2|=|T^{\prime }_2|$
and that T is the disjoint union of
![]() $T_{1,1}$
,
$T_{1,1}$
,
![]() $T^{\prime }_{1,1}$
,
$T^{\prime }_{1,1}$
,
![]() $T_{1,-1}$
,
$T_{1,-1}$
,
![]() $T^{\prime }_{1,-1}$
,
$T^{\prime }_{1,-1}$
,
![]() $T_2$
, and
$T_2$
, and
![]() $T^{\prime }_2$
. Hence,
$T^{\prime }_2$
. Hence,
 $$ \begin{align*} ||T|-25(2^{-16}+2^{-11})q(q-3)| &\leqslant(q-3)[(165/4+96)(\!\sqrt{q}+1)+195/2]\\ &\leqslant q[138\sqrt{q}+939/4]. \end{align*} $$
$$ \begin{align*} ||T|-25(2^{-16}+2^{-11})q(q-3)| &\leqslant(q-3)[(165/4+96)(\!\sqrt{q}+1)+195/2]\\ &\leqslant q[138\sqrt{q}+939/4]. \end{align*} $$
The result then follows from simple rearrangement.
Corollary 4.5. Let q run through all prime powers that are congruent to
![]() $3 \bmod 4$
. Then
$3 \bmod 4$
. Then
![]() $\lim \sigma (q)/q^2 = 25(2^{-11}{+}2^{-16})$
.
$\lim \sigma (q)/q^2 = 25(2^{-11}{+}2^{-16})$
.
5 When
 $-1$
is a square
$-1$
is a square
Throughout this section,
![]() $\mathbb {F}=\mathbb {F}_q$
will be a finite field of order
$\mathbb {F}=\mathbb {F}_q$
will be a finite field of order
![]() $q\equiv 1\bmod 4$
. Our broad strategy for obtaining an estimate of
$q\equiv 1\bmod 4$
. Our broad strategy for obtaining an estimate of
![]() $\sigma (q)$
is similar to that used in Section 4. For
$\sigma (q)$
is similar to that used in Section 4. For
![]() $i,j,r,s\in \{0,1\}$
, define
$i,j,r,s\in \{0,1\}$
, define
![]() $\bar S_{ij}^{rs}=S\setminus S_{ij}^{rs}$
and put
$\bar S_{ij}^{rs}=S\setminus S_{ij}^{rs}$
and put
![]() $T = \bigcap \bar S_{ij}^{rs}$
. The set T will again be expressed as a disjoint union of sets, the size of each of which can be estimated by means of the Weil bound. Let
$T = \bigcap \bar S_{ij}^{rs}$
. The set T will again be expressed as a disjoint union of sets, the size of each of which can be estimated by means of the Weil bound. Let
![]() $\varepsilon =\chi (x-y)$
and define
$\varepsilon =\chi (x-y)$
and define
 $$ \begin{align*} T_1 &= \{(x,y)\in T: \chi(1{-}x)=\chi(1{-}y)=-\varepsilon\};\\ T_2 &= \{(x,y)\in T: \chi(1{-}x) = \varepsilon\text{ and } \chi(1{-}y) = -\varepsilon\}; \quad\text{and}\\ T_2' &= \{(x,y)\in T: \chi(1{-}x) = -\varepsilon\text{ and } \chi(1{-}y) = \varepsilon\}. \end{align*} $$
$$ \begin{align*} T_1 &= \{(x,y)\in T: \chi(1{-}x)=\chi(1{-}y)=-\varepsilon\};\\ T_2 &= \{(x,y)\in T: \chi(1{-}x) = \varepsilon\text{ and } \chi(1{-}y) = -\varepsilon\}; \quad\text{and}\\ T_2' &= \{(x,y)\in T: \chi(1{-}x) = -\varepsilon\text{ and } \chi(1{-}y) = \varepsilon\}. \end{align*} $$
If
![]() $\rho _j\in \{-1,1\}$
for
$\rho _j\in \{-1,1\}$
for
![]() $1\leqslant j \leqslant 4$
, then define
$1\leqslant j \leqslant 4$
, then define
 $$ \begin{align*} R(\,\rho_1,\rho_2,\rho_3,\rho_4)\ &=\{(x,y)\in T: \rho_j = \varepsilon\,\chi(f_j(x,y)) \text{ for } 1\leqslant j \leqslant 4\};\\ R_1(\,\rho_1,\rho_2,\rho_3,\rho_4)&=T_1\cap R(\,\rho_1,\rho_2,\rho_3,\rho_4); \quad\text{and } \\ R_2(\,\rho_1,\rho_2,\rho_3,\rho_4)&= T_2\cap R(\,\rho_1,\rho_2,\rho_3,\rho_4). \end{align*} $$
$$ \begin{align*} R(\,\rho_1,\rho_2,\rho_3,\rho_4)\ &=\{(x,y)\in T: \rho_j = \varepsilon\,\chi(f_j(x,y)) \text{ for } 1\leqslant j \leqslant 4\};\\ R_1(\,\rho_1,\rho_2,\rho_3,\rho_4)&=T_1\cap R(\,\rho_1,\rho_2,\rho_3,\rho_4); \quad\text{and } \\ R_2(\,\rho_1,\rho_2,\rho_3,\rho_4)&= T_2\cap R(\,\rho_1,\rho_2,\rho_3,\rho_4). \end{align*} $$
We write
![]() $R(\,\bar \rho )$
as a shorthand for
$R(\,\bar \rho )$
as a shorthand for
![]() $R(\,\rho _1,\rho _2,\rho _3,\rho _4)$
, where
$R(\,\rho _1,\rho _2,\rho _3,\rho _4)$
, where
![]() $\bar \rho = (\,\rho _1,\rho _2,\rho _3,\rho _4)$
. We record the following basic facts about the sets just defined.
$\bar \rho = (\,\rho _1,\rho _2,\rho _3,\rho _4)$
. We record the following basic facts about the sets just defined.
Lemma 5.1. Suppose
![]() $\rho _j\in \{-1,1\}$
for
$\rho _j\in \{-1,1\}$
for
![]() $1\leqslant j\leqslant 4$
. The map
$1\leqslant j\leqslant 4$
. The map
![]() $(x,y)\mapsto (\kern1.5pt y,x)$
induces bijections that show that
$(x,y)\mapsto (\kern1.5pt y,x)$
induces bijections that show that
![]() $|R_1(\,\rho _1,\rho _2,\rho _3,\rho _4)|=|R_1(\,\rho _2,\rho _1,\rho _4,\rho _3)|$
and
$|R_1(\,\rho _1,\rho _2,\rho _3,\rho _4)|=|R_1(\,\rho _2,\rho _1,\rho _4,\rho _3)|$
and
![]() $|T_2|=|T^{\prime }_2|$
. Hence,
$|T_2|=|T^{\prime }_2|$
. Hence,
![]() $|T|=|T_1|+2|T_2|$
. The map
$|T|=|T_1|+2|T_2|$
. The map
![]() $(x,y)\mapsto (x^{-1},y^{-1})$
induces bijections that show that
$(x,y)\mapsto (x^{-1},y^{-1})$
induces bijections that show that
![]() $|R_i(\,\rho _1,\rho _2,\rho _3,\rho _4)|=|R_i(\,\rho _3,\rho _4,\rho _1,\rho _2)|$
for
$|R_i(\,\rho _1,\rho _2,\rho _3,\rho _4)|=|R_i(\,\rho _3,\rho _4,\rho _1,\rho _2)|$
for
![]() $i\in \{1,2\}$
. Also,
$i\in \{1,2\}$
. Also,
![]() $R(\,\rho _1,\rho _2,-1,-1)=R(-1,-1,\rho _3,\rho _4)=\varnothing $
.
$R(\,\rho _1,\rho _2,-1,-1)=R(-1,-1,\rho _3,\rho _4)=\varnothing $
.
Proof. By Proposition 2.3, we know that
![]() $(x,y)\mapsto (x^{-1},y^{-1})$
permutes each of the sets
$(x,y)\mapsto (x^{-1},y^{-1})$
permutes each of the sets
![]() $T_1$
,
$T_1$
,
![]() $T_2$
, and
$T_2$
, and
![]() $T_2'$
, while
$T_2'$
, while
![]() $(x,y) \mapsto (\kern1.5pt y,x)$
permutes
$(x,y) \mapsto (\kern1.5pt y,x)$
permutes
![]() $T_1$
and swaps
$T_1$
and swaps
![]() $T_2$
and
$T_2$
and
![]() $T_2'$
. This gives us a bijection between
$T_2'$
. This gives us a bijection between
![]() $T_2$
and
$T_2$
and
![]() $T_2'$
. Note also that
$T_2'$
. Note also that
![]() $T=T_1\cup T_2\cup T_2'$
since
$T=T_1\cup T_2\cup T_2'$
since
![]() $\chi (1{-}x)=\chi (1{-}y)=\varepsilon $
implies that
$\chi (1{-}x)=\chi (1{-}y)=\varepsilon $
implies that
![]() $(x,y)\in S_{00}^{00}$
. Hence,
$(x,y)\in S_{00}^{00}$
. Hence,
![]() $|T|=|T_1|+2|T_2|$
. The remaining claims about bijections follow directly from the definitions of
$|T|=|T_1|+2|T_2|$
. The remaining claims about bijections follow directly from the definitions of
![]() $f_1$
,
$f_1$
,
![]() $f_2$
,
$f_2$
,
![]() $f_3$
, and
$f_3$
, and
![]() $f_4$
in Equations (2-6).
$f_4$
in Equations (2-6).
If
![]() $(x,y)\in R(\,\rho _1,\rho _2,-1,-1)$
, then
$(x,y)\in R(\,\rho _1,\rho _2,-1,-1)$
, then
![]() $\chi (f_j(x,y))=-\varepsilon $
for both
$\chi (f_j(x,y))=-\varepsilon $
for both
![]() $j\in \{3,4\}$
. That implies
$j\in \{3,4\}$
. That implies
![]() $(x,y)\in S_{00}^{11}$
, by Lemma 2.4. Hence,
$(x,y)\in S_{00}^{11}$
, by Lemma 2.4. Hence,
![]() $R(\,\rho _1,\rho _2,-1,-1)=\varnothing $
and our bijection gives
$R(\,\rho _1,\rho _2,-1,-1)=\varnothing $
and our bijection gives
![]() $R(-1,-1,\rho _3,\rho _4)=\varnothing $
.
$R(-1,-1,\rho _3,\rho _4)=\varnothing $
.
Our aim is to use the
![]() $|R_i(\,\bar \rho )|$
to estimate the size of T. We should note that T may be a proper superset of
$|R_i(\,\bar \rho )|$
to estimate the size of T. We should note that T may be a proper superset of
![]() $\bigcup _{\bar \rho }R(\,\bar \rho )$
. The (small) difference arises from the contribution to T from roots of the polynomials
$\bigcup _{\bar \rho }R(\,\bar \rho )$
. The (small) difference arises from the contribution to T from roots of the polynomials
![]() $f_i$
(this contribution will be accounted for later, when all roots are included as an error term in our bounds). Lemma 5.1 reduces the number of
$f_i$
(this contribution will be accounted for later, when all roots are included as an error term in our bounds). Lemma 5.1 reduces the number of
![]() $|R_i(\,\bar \rho )|$
that we need to estimate to only those
$|R_i(\,\bar \rho )|$
that we need to estimate to only those
![]() $\bar \rho $
shown in Table 1. The final column of that table shows the multiplicity
$\bar \rho $
shown in Table 1. The final column of that table shows the multiplicity
![]() $\mu $
that we need to use for each
$\mu $
that we need to use for each
![]() $|R_i(\,\bar \rho )|$
to obtain
$|R_i(\,\bar \rho )|$
to obtain
![]() $|\bigcup _{\bar \rho }R_i(\,\bar \rho )|$
. For example,
$|\bigcup _{\bar \rho }R_i(\,\bar \rho )|$
. For example,
![]() $R_1(1,1,1,-1)$
has
$R_1(1,1,1,-1)$
has
![]() $\mu =4$
because Lemma 5.1 tells us that
$\mu =4$
because Lemma 5.1 tells us that
Table 1 Values of
![]() $s(i,\bar \rho )$
and associated parameters.
$s(i,\bar \rho )$
and associated parameters.

Lemma 5.2. Suppose that Condition (2-5) holds.
(i) If
 $\chi (x{-}1{-}y)=\chi (x{-}xy{-}y)$
, then
$\chi (x{-}1{-}y)=\chi (x{-}xy{-}y)$
, then
 $(x,y)\notin S_{01}^{01}$
. If
$(x,y)\notin S_{01}^{01}$
. If
 $\chi ((x{-}1{-}y)(x{-}xy{-}y))=-1$
, then there exist unique
$\chi ((x{-}1{-}y)(x{-}xy{-}y))=-1$
, then there exist unique
 $\lambda _1,\lambda _4\in \{-1,1\}$
such that
$\lambda _1,\lambda _4\in \{-1,1\}$
such that
 $(x,y)\in S_{01}^{01}$
if and only if
$(x,y)\in S_{01}^{01}$
if and only if
 $\chi (g_j(x,y))=\lambda _j$
for
$\chi (g_j(x,y))=\lambda _j$
for
 $j\in \{1,4\}$
.
$j\in \{1,4\}$
.(ii) If
 $\chi (\kern1.5pt y{-}1{-}x)= \chi (\kern1.5pt y{-}xy{-}x)$
, then
$\chi (\kern1.5pt y{-}1{-}x)= \chi (\kern1.5pt y{-}xy{-}x)$
, then
 $(x,y)\notin S_{10}^{10}$
. If
$(x,y)\notin S_{10}^{10}$
. If
 $\chi ((\kern1.5pt y{-}1{-}x)(\kern1.5pt y{-}xy{-}x))=-1$
, then there exist unique
$\chi ((\kern1.5pt y{-}1{-}x)(\kern1.5pt y{-}xy{-}x))=-1$
, then there exist unique
 $\lambda _2,\lambda _3\in \{-1,1\}$
such that
$\lambda _2,\lambda _3\in \{-1,1\}$
such that
 $(x,y)\in S_{10}^{10}$
if and only if
$(x,y)\in S_{10}^{10}$
if and only if
 $\chi (g_j(x,y))=\lambda _j$
for
$\chi (g_j(x,y))=\lambda _j$
for
 $j\in \{2,3\}$
.
$j\in \{2,3\}$
.
Proof. Only case (i) needs to be proved, because of the
![]() $x\leftrightarrow y$
symmetry. If
$x\leftrightarrow y$
symmetry. If
![]() $\chi (x{-}1{-}y)\kern1.2pt{=}\kern1.2pt \chi (x{-}xy{-}y)$
, then
$\chi (x{-}1{-}y)\kern1.2pt{=}\kern1.2pt \chi (x{-}xy{-}y)$
, then
![]() $(x,y) \kern1.2pt{\notin}\kern1.2pt S_{01}^{01}$
by Theorem 2.10. If
$(x,y) \kern1.2pt{\notin}\kern1.2pt S_{01}^{01}$
by Theorem 2.10. If
![]() ${\chi ((x{-}1{-}y) (x{-}xy{-}y))\kern1.2pt{=}\kern1.2pt{-}\kern0.5pt 1}$
, then exactly one choice of
${\chi ((x{-}1{-}y) (x{-}xy{-}y))\kern1.2pt{=}\kern1.2pt{-}\kern0.5pt 1}$
, then exactly one choice of
![]() $(\,\chi (g_1(x,y)),\chi (g_4(x,y))$
makes
$(\,\chi (g_1(x,y)),\chi (g_4(x,y))$
makes
![]() $(x,y)$
an element of
$(x,y)$
an element of
![]() $S_{01}^{01}$
, again by Theorem 2.10.
$S_{01}^{01}$
, again by Theorem 2.10.
Consider
![]() $(x,y)\in R_i(\,\bar \rho )$
for a particular
$(x,y)\in R_i(\,\bar \rho )$
for a particular
![]() $i\in \{1,2\}$
and
$i\in \{1,2\}$
and
![]() $\bar \rho $
. Membership of
$\bar \rho $
. Membership of
![]() $R_i(\,\bar \rho )$
implies values for
$R_i(\,\bar \rho )$
implies values for
![]() $\chi (1{-}x)$
,
$\chi (1{-}x)$
,
![]() $\chi (1{-}y)$
, and
$\chi (1{-}y)$
, and
![]() $\rho _j$
for
$\rho _j$
for
![]() $1\leqslant j \leqslant 4$
. Also,
$1\leqslant j \leqslant 4$
. Also,
![]() $(x,y)$
must belong to the sets
$(x,y)$
must belong to the sets
![]() $\bar S_{11}^{01}$
,
$\bar S_{11}^{01}$
,
![]() $\bar S_{11}^{10}$
,
$\bar S_{11}^{10}$
,
![]() $\bar S_{00}^{10}$
, and
$\bar S_{00}^{10}$
, and
![]() $\bar S_{00}^{01}$
, which implies that some of the elements
$\bar S_{00}^{01}$
, which implies that some of the elements
![]() $x{-}1{-}y$
,
$x{-}1{-}y$
,
![]() $y{-}1{-}x$
,
$y{-}1{-}x$
,
![]() $y{-}xy{-}x$
, and
$y{-}xy{-}x$
, and
![]() $x{-}xy{-}y$
have to be nonsquares, while for the others no such condition is imposed. Record this into a quadruple
$x{-}xy{-}y$
have to be nonsquares, while for the others no such condition is imposed. Record this into a quadruple
![]() $s(i,\bar \rho )=(s_1,s_2,s_3,s_4)$
, where
$s(i,\bar \rho )=(s_1,s_2,s_3,s_4)$
, where
![]() $s_j \in \{0,1\}$
for
$s_j \in \{0,1\}$
for
![]() $1\leqslant j \leqslant 4$
. Here,
$1\leqslant j \leqslant 4$
. Here,
![]() $s_1=1$
,
$s_1=1$
,
![]() $s_2=1$
,
$s_2=1$
,
![]() $s_3=1$
, and
$s_3=1$
, and
![]() $s_4=1$
mean, respectively, that the presence of
$s_4=1$
mean, respectively, that the presence of
![]() $(x,y)$
in
$(x,y)$
in
![]() $R_i(\,\bar \rho )$
forces
$R_i(\,\bar \rho )$
forces
![]() $x{-}1{-}y$
,
$x{-}1{-}y$
,
![]() $y{-}1{-}x$
,
$y{-}1{-}x$
,
![]() $y{-}xy{-}x$
, and
$y{-}xy{-}x$
, and
![]() $x{-}xy{-}y$
to be nonsquare. For each i and
$x{-}xy{-}y$
to be nonsquare. For each i and
![]() $\bar \rho $
, the value of the vector
$\bar \rho $
, the value of the vector
![]() $s(i,\bar \rho )$
is given in Table 1. Furthermore,
$s(i,\bar \rho )$
is given in Table 1. Furthermore,
![]() $k_i(\,\bar \rho )$
will be used to denote the number of indices j for which
$k_i(\,\bar \rho )$
will be used to denote the number of indices j for which
![]() $s_j=1$
in
$s_j=1$
in
![]() $s(i,\bar \rho )$
.
$s(i,\bar \rho )$
.
As an example, consider
![]() $R_2(1,1,1,1)$
. In this case,
$R_2(1,1,1,1)$
. In this case,
![]() $\chi (f_j(x,y))=\varepsilon $
for all
$\chi (f_j(x,y))=\varepsilon $
for all
![]() $j\in \{1,2,3,4\}$
. Since
$j\in \{1,2,3,4\}$
. Since
![]() $\chi (1{-}x) = \varepsilon $
,
$\chi (1{-}x) = \varepsilon $
,
![]() $(x,y)\notin S_{11}^{01}$
and
$(x,y)\notin S_{11}^{01}$
and
![]() $(x,y) \notin S_{00}^{10}$
. Therefore,
$(x,y) \notin S_{00}^{10}$
. Therefore,
![]() $s_1=s_3=0$
. Since
$s_1=s_3=0$
. Since
![]() $\chi (1{-}y)=-\varepsilon $
, we must have
$\chi (1{-}y)=-\varepsilon $
, we must have
![]() $\chi (\kern1.5pt y{-}1{-}x)=-1$
if
$\chi (\kern1.5pt y{-}1{-}x)=-1$
if
![]() $(x,y)$
is to belong to
$(x,y)$
is to belong to
![]() $\bar S_{11}^{10}$
. Therefore,
$\bar S_{11}^{10}$
. Therefore,
![]() $s_2=1$
. Similarly,
$s_2=1$
. Similarly,
![]() $s_4=1$
.
$s_4=1$
.
For
![]() $c\in \mathbb {F}_q$
, define
$c\in \mathbb {F}_q$
, define
![]() $t_1(c)=|\{x\in \mathbb {F}_q:(x,c)\in T_1\}|$
and
$t_1(c)=|\{x\in \mathbb {F}_q:(x,c)\in T_1\}|$
and
![]() $t_2(c)=|\{x\in \mathbb {F}_q:(x,c)\in T_2\}|$
. In the next two propositions, we seek estimates of these quantities. As in Section 4, we assume that Condition (3-3) holds which means that Condition (2-5) applies, enabling us to use Theorem 2.10 and Lemma 5.2.
$t_2(c)=|\{x\in \mathbb {F}_q:(x,c)\in T_2\}|$
. In the next two propositions, we seek estimates of these quantities. As in Section 4, we assume that Condition (3-3) holds which means that Condition (2-5) applies, enabling us to use Theorem 2.10 and Lemma 5.2.
Proposition 5.3. Suppose that c is a square satisfying Conditions (3-2)–(3-11). Then,
Proof. Fix c satisfying Conditions (3-2)–(3-11) and consider a candidate
![]() $(x,c)$
for membership in
$(x,c)$
for membership in
![]() $T_1$
. As we did in Proposition 4.2, we include the term 21 in our bound and then for the remainder of the proof, we may assume that x is not a root of any polynomial in List (3-1).
$T_1$
. As we did in Proposition 4.2, we include the term 21 in our bound and then for the remainder of the proof, we may assume that x is not a root of any polynomial in List (3-1).
Our goal is to estimate the c-slice of
![]() $R_1(\,\bar \rho )$
for each
$R_1(\,\bar \rho )$
for each
![]() $\bar \rho $
. We start with a list of polynomials that guarantee the presence of
$\bar \rho $
. We start with a list of polynomials that guarantee the presence of
![]() $(x,c)$
in
$(x,c)$
in
![]() $\bar S_{00}^{00}$
,
$\bar S_{00}^{00}$
,
![]() $\bar S_{11}^{00}$
,
$\bar S_{11}^{00}$
,
![]() $\bar S_{00}^{11}$
,
$\bar S_{00}^{11}$
,
![]() $\bar S_{11}^{01}$
,
$\bar S_{11}^{01}$
,
![]() $\bar S_{11}^{10}$
,
$\bar S_{11}^{10}$
,
![]() $\bar S_{00}^{10}$
, and
$\bar S_{00}^{10}$
, and
![]() $\bar S_{00}^{01}$
. These polynomials are x,
$\bar S_{00}^{01}$
. These polynomials are x,
![]() $1{-}x$
,
$1{-}x$
,
![]() $c{-}x$
,
$c{-}x$
,
![]() $f_j(x,c)$
,
$f_j(x,c)$
,
![]() $1\leqslant j \leqslant 4$
, and those of
$1\leqslant j \leqslant 4$
, and those of
![]() $x{-}1{-}c$
,
$x{-}1{-}c$
,
![]() $c{-}1{-}x$
,
$c{-}1{-}x$
,
![]() $c{-}cx{-}x$
, and
$c{-}cx{-}x$
, and
![]() $x{-}cx{-}c$
for which the corresponding value of
$x{-}cx{-}c$
for which the corresponding value of
![]() $s_j$
in
$s_j$
in
![]() $s(i,\bar \rho )$
is equal to
$s(i,\bar \rho )$
is equal to
![]() $1$
. In this way, we obtain a list of
$1$
. In this way, we obtain a list of
![]() $7+k_1(\,\bar \rho )$
polynomials of cumulative degree
$7+k_1(\,\bar \rho )$
polynomials of cumulative degree
![]() $11+k_1(\,\bar \rho )$
, for
$11+k_1(\,\bar \rho )$
, for
![]() $k_1(\,\bar \rho )$
as shown in Table 1.
$k_1(\,\bar \rho )$
as shown in Table 1.
It only remains to ensure that
![]() $(x,c)$
is in
$(x,c)$
is in
![]() $\bar S_{01}^{01}$
and
$\bar S_{01}^{01}$
and
![]() $\bar S_{10}^{10}$
. The c-slice of
$\bar S_{10}^{10}$
. The c-slice of
![]() $R_1(\,\bar \rho )$
forks into several disjoint subsets, according to Lemma 5.2. The forking induced by
$R_1(\,\bar \rho )$
forks into several disjoint subsets, according to Lemma 5.2. The forking induced by
![]() $\bar S_{01}^{01}$
depends upon
$\bar S_{01}^{01}$
depends upon
![]() $(s_1,s_4)$
, while the forking induced by
$(s_1,s_4)$
, while the forking induced by
![]() $\bar S_{10}^{10}$
depends upon
$\bar S_{10}^{10}$
depends upon
![]() $(s_2,s_3)$
. It is thus possible to describe only the former and obtain the latter by exploiting the
$(s_2,s_3)$
. It is thus possible to describe only the former and obtain the latter by exploiting the
![]() $(x,y)\leftrightarrow (x^{-1},y^{-1})$
symmetry between
$(x,y)\leftrightarrow (x^{-1},y^{-1})$
symmetry between
![]() $\bar S_{01}^{01}$
and
$\bar S_{01}^{01}$
and
![]() $\bar S_{10}^{10}$
.
$\bar S_{10}^{10}$
.
If
![]() $s_1=s_4= 1$
, then there is no forking since this suffices to conclude that
$s_1=s_4= 1$
, then there is no forking since this suffices to conclude that
![]() $(x,y)\notin S_{01}^{01}$
.
$(x,y)\notin S_{01}^{01}$
.
If
![]() $s_1+s_4 = 1$
, then one of
$s_1+s_4 = 1$
, then one of
![]() $\chi (x{-}1{-}c)=-1$
and
$\chi (x{-}1{-}c)=-1$
and
![]() $\chi (x{-}xc{-}c)=-1$
is mandated, and there are four forks. One of them specifies the character of only one extra polynomial to ensure that
$\chi (x{-}xc{-}c)=-1$
is mandated, and there are four forks. One of them specifies the character of only one extra polynomial to ensure that
![]() $\chi (x{-}1{-}c)=\chi (x{-}xc{-}c)=-1$
. Each of the other three forks imposes restrictions on three polynomials, as it establishes first that
$\chi (x{-}1{-}c)=\chi (x{-}xc{-}c)=-1$
. Each of the other three forks imposes restrictions on three polynomials, as it establishes first that
![]() $\chi (x{-}1{-}c)=-\chi (x{-}xc{-}c)$
and then imposes values on
$\chi (x{-}1{-}c)=-\chi (x{-}xc{-}c)$
and then imposes values on
![]() $\chi (g_1(x,c))$
and
$\chi (g_1(x,c))$
and
![]() $\chi (g_4(x,c))$
. By Lemma 5.2, there are three possibilities to consider for the pair
$\chi (g_4(x,c))$
. By Lemma 5.2, there are three possibilities to consider for the pair
![]() $(\chi (g_1(x,c)),\chi (g_4(x,c)))$
, which thus give us the three forks.
$(\chi (g_1(x,c)),\chi (g_4(x,c)))$
, which thus give us the three forks.
The forking of the case
![]() $s_1+s_4 = 1$
will be recorded by
$s_1+s_4 = 1$
will be recorded by
![]() $(1,1)\mid (3,4)^3$
. This means that the first fork needs one additional polynomial of degree one, while the other three forks need three polynomials of cumulative degree
$(1,1)\mid (3,4)^3$
. This means that the first fork needs one additional polynomial of degree one, while the other three forks need three polynomials of cumulative degree
![]() $4$
.
$4$
.
If
![]() $s_1=s_4=0$
then there are seven forks. One imposes that
$s_1=s_4=0$
then there are seven forks. One imposes that
![]() $\chi ((x{-}1{-}c) (x{-}xc{-}c))=1$
(which ensures that
$\chi ((x{-}1{-}c) (x{-}xc{-}c))=1$
(which ensures that
![]() $\chi (x{-}1{-}c)=\chi (x{-}xc{-}c)$
), while each of the other six establishes first the (different) values of
$\chi (x{-}1{-}c)=\chi (x{-}xc{-}c)$
), while each of the other six establishes first the (different) values of
![]() $\chi (x{-}1{-}c)$
and
$\chi (x{-}1{-}c)$
and
![]() $\chi (x{-}xc{-}c)$
, and then the values of
$\chi (x{-}xc{-}c)$
, and then the values of
![]() $\chi (g_1(x,c))$
and
$\chi (g_1(x,c))$
and
![]() $\chi (g_4(x,c))$
. Symbolically, this gives
$\chi (g_4(x,c))$
. Symbolically, this gives
![]() $(1,2)\mid (4,5)^6$
.
$(1,2)\mid (4,5)^6$
.
Let us use
![]() $\bullet $
to express the composition of two independent forkings. Thus,
$\bullet $
to express the composition of two independent forkings. Thus,
is a list of alternatives
![]() $(k_i+k_j', d_i+d_j')^{m_im^{\prime }_j}$
, where
$(k_i+k_j', d_i+d_j')^{m_im^{\prime }_j}$
, where
![]() $1\leqslant i \leqslant a$
and
$1\leqslant i \leqslant a$
and
![]() $1\leqslant j \leqslant b$
.
$1\leqslant j \leqslant b$
.
Our observations above allow us to symbolically describe polynomial lists for each of the sets
![]() $R_1(\,\bar \rho )$
. We have
$R_1(\,\bar \rho )$
. We have
 $$ \begin{align*} R_1(1,1,1,1)\colon &(11,15), \\ R_1(1,1,1,-1)\colon &(10,14)\bullet (1,1)\mid(3,4)^3 = (11,15)\mid(13,18)^3, \\ R_1(1,-1,1,-1)\colon & (9,13)\bullet (1,1)\mid(3,4)^3 \bullet (1,1)\mid (3,4)^3 = (11,15)\mid (13,18)^6 \mid (15,21)^9, \\ R_1(1,-1,-1,1)\colon & (9,13)\bullet (1,2)\mid(4,5)^6 = (10,15)\mid (13,18)^6. \end{align*} $$
$$ \begin{align*} R_1(1,1,1,1)\colon &(11,15), \\ R_1(1,1,1,-1)\colon &(10,14)\bullet (1,1)\mid(3,4)^3 = (11,15)\mid(13,18)^3, \\ R_1(1,-1,1,-1)\colon & (9,13)\bullet (1,1)\mid(3,4)^3 \bullet (1,1)\mid (3,4)^3 = (11,15)\mid (13,18)^6 \mid (15,21)^9, \\ R_1(1,-1,-1,1)\colon & (9,13)\bullet (1,2)\mid(4,5)^6 = (10,15)\mid (13,18)^6. \end{align*} $$
Combining this information with the last column of Table 1, we reach a symbolic description of the polynomials contributing to
![]() $t_1(c)$
that contains
$t_1(c)$
that contains
![]() $(10,15)$
with multiplicity
$(10,15)$
with multiplicity
![]() $2$
,
$2$
,
![]() $(11,15)$
with multiplicity
$(11,15)$
with multiplicity
![]() $1+4+2=7$
,
$1+4+2=7$
,
![]() $(13,18)$
with multiplicity
$(13,18)$
with multiplicity
![]() $4\cdot 3 + 2\cdot 6+2\cdot 6 = 36$
, and
$4\cdot 3 + 2\cdot 6+2\cdot 6 = 36$
, and
![]() $(15,21)$
with multiplicity
$(15,21)$
with multiplicity
![]() $2\cdot 9=18$
. In each case, the list of polynomials involved is square-free, by Theorem 3.1. Hence, we may apply Theorem 1.6 to find that
$2\cdot 9=18$
. In each case, the list of polynomials involved is square-free, by Theorem 3.1. Hence, we may apply Theorem 1.6 to find that
where
![]() $\alpha _1 = 2\cdot 2^{-10}+7\cdot 2^{-11} + 36\cdot 2^{-13} + 18\cdot 2^{-15}=169\cdot 2^{-14}$
, and the cumulative degree of our polynomials is
$\alpha _1 = 2\cdot 2^{-10}+7\cdot 2^{-11} + 36\cdot 2^{-13} + 18\cdot 2^{-15}=169\cdot 2^{-14}$
, and the cumulative degree of our polynomials is
![]() $D_1=9\cdot 15+36\cdot 18+18\cdot 21=1161$
.
$D_1=9\cdot 15+36\cdot 18+18\cdot 21=1161$
.
Proposition 5.4. Suppose that c is a square satisfying Conditions (3-2)–(3-11). Then,
Proof. The proof follows the same lines as that of Proposition 5.3. The symbolic description of the forks is
 $$ \begin{align*} &R_2(1,1,1,1)\colon (9,13)\bullet (1,1)\mid(3,4)^3 \bullet (1,1)\mid(3,4)^3\\ &\quad= (11,15)\mid (13,18)^6 \mid (15,21)^9, \\ &R_2(1,1,1,-1)\colon (8,12)\bullet (1,1)\mid(3,4)^3 \bullet (1,2)\mid(4,5)^6\\ &\quad= (10,15)\mid (12,18)^3\mid (13,18)^6 \mid (15,21)^{18}, \\ &R_2(1,-1,1,-1)\colon (7,11)\bullet (1,2)\mid(4,5)^6\bullet (1,2)\mid(4,5)^6\\ &\quad= (9,15)\mid (12,18)^{12} \mid (15,21)^{36}, \\ &R_2(1,-1,-1,1)\colon (8,12)\bullet (1,1)\mid(3,4)^3 \bullet (1,2)\mid(4,5)^6\\ &\quad= (10,15)\mid (12,18)^3\mid (13,18)^6 \mid (15,21)^{18}, \\ &R_2(1,1,-1,1)\colon (9,13) \bullet (1,1)\mid(3,4)^3 \bullet(1,1)\mid(3,4)^3\\ &\quad= (11,15)\mid (13,18)^6 \mid (15,21)^9, \\ &R_2(-1,1,-1,1)\colon (9,13) \bullet (1,1)\mid(3,4)^3 \bullet(1,1)\mid(3,4)^3\\ &\quad= (11,15)\mid (13,18)^6 \mid (15,21)^9. \end{align*} $$
$$ \begin{align*} &R_2(1,1,1,1)\colon (9,13)\bullet (1,1)\mid(3,4)^3 \bullet (1,1)\mid(3,4)^3\\ &\quad= (11,15)\mid (13,18)^6 \mid (15,21)^9, \\ &R_2(1,1,1,-1)\colon (8,12)\bullet (1,1)\mid(3,4)^3 \bullet (1,2)\mid(4,5)^6\\ &\quad= (10,15)\mid (12,18)^3\mid (13,18)^6 \mid (15,21)^{18}, \\ &R_2(1,-1,1,-1)\colon (7,11)\bullet (1,2)\mid(4,5)^6\bullet (1,2)\mid(4,5)^6\\ &\quad= (9,15)\mid (12,18)^{12} \mid (15,21)^{36}, \\ &R_2(1,-1,-1,1)\colon (8,12)\bullet (1,1)\mid(3,4)^3 \bullet (1,2)\mid(4,5)^6\\ &\quad= (10,15)\mid (12,18)^3\mid (13,18)^6 \mid (15,21)^{18}, \\ &R_2(1,1,-1,1)\colon (9,13) \bullet (1,1)\mid(3,4)^3 \bullet(1,1)\mid(3,4)^3\\ &\quad= (11,15)\mid (13,18)^6 \mid (15,21)^9, \\ &R_2(-1,1,-1,1)\colon (9,13) \bullet (1,1)\mid(3,4)^3 \bullet(1,1)\mid(3,4)^3\\ &\quad= (11,15)\mid (13,18)^6 \mid (15,21)^9. \end{align*} $$
Combining this information with the last column of Table 1, we reach a symbolic description of the polynomials contributing to
![]() $t_2(c)$
that contains
$t_2(c)$
that contains
![]() $(9,15)$
with multiplicity
$(9,15)$
with multiplicity
![]() $1$
,
$1$
,
![]() $(10,15)$
with multiplicity
$(10,15)$
with multiplicity
![]() $2\cdot 1+2\cdot 1=4$
,
$2\cdot 1+2\cdot 1=4$
,
![]() $(11,15)$
with multiplicity
$(11,15)$
with multiplicity
![]() $1+2\cdot 1+1=4$
,
$1+2\cdot 1+1=4$
,
![]() $(12,18)$
with multiplicity
$(12,18)$
with multiplicity
![]() $2\cdot 3 + 12 + 2\cdot 3 = 24$
, and
$2\cdot 3 + 12 + 2\cdot 3 = 24$
, and
![]() $(13,18)$
with multiplicity
$(13,18)$
with multiplicity
![]() $6+2\cdot 6+2\cdot 6+2\cdot 6+6 = 48$
, and
$6+2\cdot 6+2\cdot 6+2\cdot 6+6 = 48$
, and
![]() $(15,21)$
with multiplicity
$(15,21)$
with multiplicity
![]() $9+2\cdot 18+36+2\cdot 18+2\cdot 9+9=144$
. Combining Theorem 3.1 and Theorem 1.6, we find that
$9+2\cdot 18+36+2\cdot 18+2\cdot 9+9=144$
. Combining Theorem 3.1 and Theorem 1.6, we find that
where
![]() $\alpha _2 = 2\cdot 2^{-9}+4\cdot 2^{-10}+4\cdot 2^{-11} +24\cdot 2^{-12}+48\cdot 2^{-13} + 144\cdot 2^{-15}=49\cdot 2^{-11}$
, and the cumulative degree of our polynomials is
$\alpha _2 = 2\cdot 2^{-9}+4\cdot 2^{-10}+4\cdot 2^{-11} +24\cdot 2^{-12}+48\cdot 2^{-13} + 144\cdot 2^{-15}=49\cdot 2^{-11}$
, and the cumulative degree of our polynomials is
![]() $D_2=9\cdot 15+72\cdot 18+144\cdot 21=4455$
.
$D_2=9\cdot 15+72\cdot 18+144\cdot 21=4455$
.
We are now ready to prove the main result for this section.
Theorem 5.5. If
![]() $q\equiv 1\bmod 4$
, then
$q\equiv 1\bmod 4$
, then
Proof. There are
![]() $(q-3)/2$
choices for a square
$(q-3)/2$
choices for a square
![]() $c\in \mathbb {F}_q$
satisfying
$c\in \mathbb {F}_q$
satisfying
![]() $c\notin \{0,1\}$
. At most,
$c\notin \{0,1\}$
. At most,
![]() $49$
of these choices do not fulfill Conditions (3-2)–(3-11) of Theorem 3.1. Each c that fails one of Conditions (3-2)–(3-11) contributes between 0 and
$49$
of these choices do not fulfill Conditions (3-2)–(3-11) of Theorem 3.1. Each c that fails one of Conditions (3-2)–(3-11) contributes between 0 and
![]() $(q-3)/2$
elements
$(q-3)/2$
elements
![]() $(x,c)$
to T. Putting these observations together with Proposition 5.3 and Proposition 5.4, we have that
$(x,c)$
to T. Putting these observations together with Proposition 5.3 and Proposition 5.4, we have that
 $$ \begin{align*} ||T_1|-169\cdot2^{-14}q(q-3)/2| &\leqslant1161(\!\sqrt{q}+1)(q-3)/4+21(q-3)/2+49(q-3)/2,\\ ||T_2|-49\cdot2^{-11}q(q-3)/2| &\leqslant4455(\!\sqrt{q}+1)(q-3)/4+21(q-3)/2+49(q-3)/2. \end{align*} $$
$$ \begin{align*} ||T_1|-169\cdot2^{-14}q(q-3)/2| &\leqslant1161(\!\sqrt{q}+1)(q-3)/4+21(q-3)/2+49(q-3)/2,\\ ||T_2|-49\cdot2^{-11}q(q-3)/2| &\leqslant4455(\!\sqrt{q}+1)(q-3)/4+21(q-3)/2+49(q-3)/2. \end{align*} $$
Next, by Lemma 5.1, we know that
![]() $|T|=|T_1|+2|T_2|$
, so
$|T|=|T_1|+2|T_2|$
, so
 $$ \begin{align*} &||T|-(169\cdot2^{-15}+49\cdot2^{-11})q(q-3)|\\ &\quad\leqslant(q-3)[(1161/4+ 4455/2)(\!\sqrt{q}+1)+105]\\ &\quad<q[2518\sqrt{q}+10491/4]. \end{align*} $$
$$ \begin{align*} &||T|-(169\cdot2^{-15}+49\cdot2^{-11})q(q-3)|\\ &\quad\leqslant(q-3)[(1161/4+ 4455/2)(\!\sqrt{q}+1)+105]\\ &\quad<q[2518\sqrt{q}+10491/4]. \end{align*} $$
The result then follows from simple rearrangement.
Corollary 5.6. Let q run through all prime powers that are congruent to
![]() $1 \bmod 4$
. Then
$1 \bmod 4$
. Then
![]() $\lim \sigma (q)/q^2 = 953/2^{15}$
.
$\lim \sigma (q)/q^2 = 953/2^{15}$
.
6 Concluding remarks
Theorems 4.4 and 5.5 give formulas that can be used as estimates of
![]() $\sigma (q)$
for large q. We did not work hard to optimize the constants in the bounds. Even if we had, the number of applications of the Weil bound is too big to allow the estimates to be useful for small q. However, for large q, our results show that maximally nonassociative quasigroups can be generated via random sampling. If
$\sigma (q)$
for large q. We did not work hard to optimize the constants in the bounds. Even if we had, the number of applications of the Weil bound is too big to allow the estimates to be useful for small q. However, for large q, our results show that maximally nonassociative quasigroups can be generated via random sampling. If
![]() $(a,b)$
is chosen uniformly at random from
$(a,b)$
is chosen uniformly at random from
![]() $\Sigma (\mathbb {F}_q)$
, then it can quickly be checked (using
$\Sigma (\mathbb {F}_q)$
, then it can quickly be checked (using
![]() $O(1)$
evaluations of
$O(1)$
evaluations of
![]() $\chi $
, as shown in Theorems 2.10 and 2.11) whether
$\chi $
, as shown in Theorems 2.10 and 2.11) whether
![]() $Q_{a,b}$
is maximally nonassociative, and the probability of success is bounded away from zero. We thus have a computationally realistic method of generating random maximally nonassociative quasigroups of large orders. This might be of interest, given the cryptographic applications [Reference Grošek and Horák10].
$Q_{a,b}$
is maximally nonassociative, and the probability of success is bounded away from zero. We thus have a computationally realistic method of generating random maximally nonassociative quasigroups of large orders. This might be of interest, given the cryptographic applications [Reference Grošek and Horák10].
The approach that we have used in this paper might be adapted to resolve [Reference Drápal and Lisoněk3, Conjecture 5.10], which is concerned with the density of parameters that yield a maximally nonassociative quasigroup when constructing such a quasigroup by means of a nearfield.
In a future paper, we plan to consider how many different isomorphism classes are represented by the maximally nonassociative quasigroups generated from quadratic orthomorphisms. To answer this question requires theory to be developed on when different quadratic orthomorphisms generate isomorphic quasigroups (which is a question of independent interest). Some limited circumstances where different orthomorphisms create isomorphic quasigroups are already known [Reference Wanless16]. In particular, we know that
![]() $Q_{a,b}\cong Q_{b,a}$
(see Lemma 2.1(i)), and that
$Q_{a,b}\cong Q_{b,a}$
(see Lemma 2.1(i)), and that
![]() $Q_{a,b}\cong Q_{a^p,b^p}$
in any field of characteristic p. We expect these to generate the only isomorphisms that affect the asymptotics. In other words, we conjecture that the number of quasigroups (up to isomorphism) is asymptotic to
$Q_{a,b}\cong Q_{a^p,b^p}$
in any field of characteristic p. We expect these to generate the only isomorphisms that affect the asymptotics. In other words, we conjecture that the number of quasigroups (up to isomorphism) is asymptotic to
![]() $\sigma (q)/(2\log _pq)$
, where
$\sigma (q)/(2\log _pq)$
, where
![]() $\sigma (q)$
is estimated by Theorems 4.4 and 5.5.
$\sigma (q)$
is estimated by Theorems 4.4 and 5.5.
In our analysis leading to our main results, we discarded all roots of the polynomials in List (3-1). Bajtoš [Reference Bajtoš1] has investigated these cases by finding the asymptotic number of solutions to
![]() $t(x,y) = 0$
when t is one of the polynomials
$t(x,y) = 0$
when t is one of the polynomials
![]() $x{-}1{-}y$
,
$x{-}1{-}y$
,
![]() $x{-}xy{-}y$
,
$x{-}xy{-}y$
,
![]() $y{-}1{-}x$
,
$y{-}1{-}x$
,
![]() $y{-}xy{-}x$
,
$y{-}xy{-}x$
,
![]() $f_j(x,y)$
, or
$f_j(x,y)$
, or
![]() $g_j(x,y)$
for
$g_j(x,y)$
for
![]() $1\leqslant j \leqslant 4$
. For each of these polynomials, Bajtoš determines the density of parameters
$1\leqslant j \leqslant 4$
. For each of these polynomials, Bajtoš determines the density of parameters
![]() $(a,b)$
that yield a maximally nonassociative quasigroup. The density is measured with respect to the size of the set of all
$(a,b)$
that yield a maximally nonassociative quasigroup. The density is measured with respect to the size of the set of all
![]() $(a,b)$
for which the given polynomial gives zero, with
$(a,b)$
for which the given polynomial gives zero, with
![]() $x=a/b$
and
$x=a/b$
and
![]() $y=(1{-}a)/(1{-}b)$
. For each polynomial, that set has size asymptotically equal to
$y=(1{-}a)/(1{-}b)$
. For each polynomial, that set has size asymptotically equal to
![]() $q/4$
. Because of symmetry and reciprocity of polynomials, it suffices to investigate cases (a)
$q/4$
. Because of symmetry and reciprocity of polynomials, it suffices to investigate cases (a)
![]() $x{-}1{-}y$
, (b)
$x{-}1{-}y$
, (b)
![]() $x^2{+}y^2{-}xy{-}x$
, and (c)
$x^2{+}y^2{-}xy{-}x$
, and (c)
![]() $x^2{+}y{-}2x$
. In case (a), the obtained densities are
$x^2{+}y{-}2x$
. In case (a), the obtained densities are
![]() $\approx 0.109$
,
$\approx 0.109$
,
![]() $0.219$
,
$0.219$
,
![]() $0.031$
, and
$0.031$
, and
![]() $0.047$
, with
$0.047$
, with
![]() $q\equiv 1, 5, 3, 7 \bmod 8$
, respectively. For case (b), the densities are
$q\equiv 1, 5, 3, 7 \bmod 8$
, respectively. For case (b), the densities are
![]() $0.109$
and
$0.109$
and
![]() $0.082$
,
$0.082$
,
![]() $q\equiv 1,3\bmod 4$
. Case (c) yields
$q\equiv 1,3\bmod 4$
. Case (c) yields
![]() $0.156$
,
$0.156$
,
![]() $0.172$
,
$0.172$
,
![]() $0.047$
, and
$0.047$
, and
![]() $0.031$
, for
$0.031$
, for
![]() $q\equiv 1, 5, 3, 7 \bmod 8$
. These numbers thus give probabilities of finding a maximally nonassociative quasigroup by a random choice, for each of the investigated cases. In the general case, these probabilities are
$q\equiv 1, 5, 3, 7 \bmod 8$
. These numbers thus give probabilities of finding a maximally nonassociative quasigroup by a random choice, for each of the investigated cases. In the general case, these probabilities are
![]() $\approx 0.116$
and
$\approx 0.116$
and
![]() $0.050$
for
$0.050$
for
![]() $q\equiv 1,3\bmod 4$
(compare with the comments following Theorem 1.1).
$q\equiv 1,3\bmod 4$
(compare with the comments following Theorem 1.1).
Maximally non-associative quasigroups minimize the number of associative triples. Gowers and Long [Reference Gowers and Long9] consider another measure of how associative a quasigroup is, which they call its number of ‘octahedra.’ Several interesting connections between the number of octahedra and the number of associative triples are shown in their work, although they concentrate on quasigroups which are in some sense close to associative. Subsequently, Kwan et al. [Reference Kwan, Sah, Sawhney and Simkin12] considered the typical number of octahedra in a random quasigroup and asked a question regarding how few octahedra a quasigroup of order n can have. The maximally nonassociative quasigroups that we have constructed may be useful in answering that question, but the connection requires further investigation.
Another open question is how few nonassociative triples loops (quasigroups with identity) can have. It is not difficult to show that a loop of order n has to possess at least
![]() $3n^2 - 3n + 1$
associative triples. However, presently, no loop with less than
$3n^2 - 3n + 1$
associative triples. However, presently, no loop with less than
![]() $3n^2-2n$
triples seems to be known. In [Reference Drápal and Hora2], quadratic orthomorphisms were used to construct loops of order
$3n^2-2n$
triples seems to be known. In [Reference Drápal and Hora2], quadratic orthomorphisms were used to construct loops of order
![]() $n=p+1$
, for a prime
$n=p+1$
, for a prime
![]() $p \geqslant 13$
, that have exactly
$p \geqslant 13$
, that have exactly
![]() $3n^2-2n$
associative triples. The chosen method failed for
$3n^2-2n$
associative triples. The chosen method failed for
![]() $p=19$
. That case was solved by means of a ternary orthomorphism, which leads us naturally to our last research direction.
$p=19$
. That case was solved by means of a ternary orthomorphism, which leads us naturally to our last research direction.
The question of when maximally nonassociative quasigroups can be generated by orthomorphisms that are not quadratic is wide open. Some examples are given in [Reference Drápal and Hora2, Reference Drápal and Wanless6]. Perhaps the next case to study would be orthomorphisms that are cyclotomic but not quadratic. We finish with some examples of this type that produce maximally nonassociative quasigroups. Each orthomorphism is given as a permutation in cycle notation. We have (1,3,8)(2,13,5)(4,12,15)(6,7,11,10)(9,16,14), a quartic orthomorphism in
![]() $\mathbb {F}_{17}$
, (1,2,15)(3,13,11)(4,18,17)(5,9,12)(6,8,16)(7,14,10), a cubic orthomorphism in
$\mathbb {F}_{17}$
, (1,2,15)(3,13,11)(4,18,17)(5,9,12)(6,8,16)(7,14,10), a cubic orthomorphism in
![]() $\mathbb {F}_{19}$
, and (1,3,15)(2,10,7)(4,17,9,5,6,16)(8,12,18)(11,14,13), a sextic orthomorphism in
$\mathbb {F}_{19}$
, and (1,3,15)(2,10,7)(4,17,9,5,6,16)(8,12,18)(11,14,13), a sextic orthomorphism in
![]() $\mathbb {F}_{19}$
.
$\mathbb {F}_{19}$
.