Formation of Supermassive Black Hole Seeds

Abstract

The detection of quasars at z > 6 unveils the presence of supermassive black holes of a few billion solar masses. The rapid formation process of these extreme objects remains a fascinating and open issue. Such discovery implies that seed black holes must have formed early on, and grown via either rapid accretion or BH/galaxy mergers. In this theoretical review, we discuss in detail various BH seed formation mechanisms and the physical processes at play during their assembly. We discuss the three most popular BH formation scenarios, involving the (i) core-collapse of massive stars, (ii) dynamical evolution of dense nuclear star clusters, (iii) collapse of a protogalactic metal free gas cloud. This article aims at giving a broad introduction and an overview of the most advanced research in the field.

1 INTRODUCTION

Observations of quasars at z > 6 reveal the existence of supermassive black holes (SMBHs) of a few billion solar masses within the 1 Gyr after the Big Bang (Fan et al. 2006; Willott et al. 2007; Jiang et al. 2008, 2009; Mortlock et al. 2011; Venemans et al. 2013; Bañados et al. 2014; Venemans et al. 2015; Jiang et al. 2015; Wu et al. 2015). ¹ How do they form and what are their formation mechanisms are still open questions [see previous reviews on this topic Volonteri (2010), Volonteri & Bellovary (2012), and Haiman (2013)].

The presence of SMBHs a few hundred million years after the Big Bang suggests that their seeds must have formed at z ⩾ 15. The mass scale of BHs depend on the formation mechanism and may vary from 10-10⁵ M_⊙. These seed BHs must have grown via intense accretion and/or merging to reach a few billion solar masses. In order to form a SMBH of 2 × 10⁹ M_⊙ at z = 7.02, a seed black should have an initial mass of about 400 M_⊙ and continuously accrete at the Eddington limit throughout its lifetime. Therefore, more massive seeds forming at z ⩾ 15 can preferably explain the presence of quasars at z ⩾ 6.

In this review, we mostly provide a theoretical overview of the field and discuss various astrophysical processes involved in the formation of seed BHs. We discuss the three most popular BH formation scenarios, involving the (i) core-collapse of massive stars, (ii) dynamical evolution of dense nuclear star clusters, (iii) collapse of a protogalactic metal free gas cloud, also known as the Direct Collapse Black Hole (DCBH) formation channel.

2 BLACK HOLE FORMATION MECHANISMS

Various mechanisms to form black holes have been proposed in the literature since the seminal work by Rees (1984). They can be classified into three broad categories, which are introduced below and discussed in detail in the following sections.

The most natural way to form a BH is the collapse of a massive star into a BH known as the ‘stellar mass BH’. The final mass of BH depends on the metallicity, mass, and rotation speed of a star and is ultimately associated with the properties of a native gas cloud (Ciardi & Ferrara 2005; Bromm 2013). BHs may have formed in the dense nuclear clusters via stellar dynamical processes or relativistic instabilities (Baumgarte & Shapiro 1999; Portegies Zwart et al. 1999; Devecchi & Volonteri 2009). The mass of resulting BH depends on the mass and compactness of a stellar cluster, its dynamical evolution, and binary fraction, etc. An alternative scenario could be the monolithic collapse of a protogalactic gas cloud into a massive BH so-called the direct collapse model (Rees 1984; Loeb & Rasio 1994; Volonteri & Rees 2005; Begelman, Volonteri, & Rees 2006; Spaans & Silk 2006; Latif, Zaroubi, & Spaans 2011a; Ferrara et al. 2014). The key requirement for this scenario is to have large gas accretion rates of ⩾ 0.1 M_⊙ yr⁻¹ (Hosokawa et al. 2013; Schleicher et al. 2013). Such high gas accretion rates can be achieved in massive primordial halos of ~ 10⁸ M_⊙ illuminated by a strong Lyman Werner (LW) flux where in-situ star formation remains suppressed or via dynamical processes such as a merger of metal rich galaxies or ‘bars within bars’ instabilities (Begelman et al. 2006; Mayer et al. 2015).

Primordial black holes may have born during the early stages of Big Bang but there is no observational evidence for their existence (Alcock et al. 2000; Afshordi, McDonald, & Spergel 2003; Tisserand et al. 2007; Ricotti, Ostriker, & Mack 2008). In fact, the constraints from microlensing and spectral distortions of the cosmic micro wave background limit their masses below 1 000 M_⊙.

3 STELLAR MASS BHs

The first generation of stars so-called population III (Pop III) stars are formed in minihalos of 10⁵-10⁶ M_⊙ at z ~ 20–30. Collapse in these halos is triggered by the molecular hydrogen cooling which brings the gas temperature down to about 200 K. In the absence of dust and metals, the cooling ability of the primordial gas is considerably reduced and the gas temperature is about a factor of 10–20 higher compared to the contemporary star formation in molecular clouds (Abel, Bryan, & Norman 2002; Bromm, Coppi, & Larson 2002). The thermal Jeans mass scales with T ^3/2 and therefore stellar masses are expected to be higher. The fraction of molecular hydrogen gets boosted during the collapse by three-body processes and gas cloud becomes fully molecular. In the mean time, gas becomes optically thick to molecular hydrogen cooling and consequently gas temperature rises until the protostar begins to form (Palla, Salpeter, & Stahler 1983; Omukai 2000).

The protostar borns in the dense core embedded in molecular hydrogen gas cloud and grows by accretion or even by merging of dense clumps. In the case of efficient fragmentation, more than one stars are expected to form per halo and we discuss this in detail in the following subsections. Initially, the radius of a protostar increases during the adiabatic accretion phase up to 10 M_⊙ and then subsequently star enters in the Kelvin–Helmholtz (KH) phase by radiating away its thermal energy. The interior temperature of star continues to increase until the hydrogen burning starts around 100 M_⊙, accretion stops and star enters the zero age main sequence (ZAMS) (Stahler et al. 1986; Omukai & Palla 2001, 2003; Yoshida et al. 2006).

The final mass of a star depends on the properties of natal gas clouds such as its mass, spin, formation redshift, and mass accretion rate (Latif et al. 2013e; Hirano et al. 2014). The stars with masses below 9 M_⊙ do not have enough massive cores to collapse but instead end their lives as white dwarfs. However, Pop III stars with masses between 25–140 M_⊙ and above 260 M_⊙ are expected to directly collapse into a BH (Heger & Woosley 2002; Heger et al. 2003). This is true for the single stars formed out of zero metallicity gas. However, the presence of metals and rotation may affect their final fates as we discuss below. In the following subsections, we discuss our current understanding of the initial mass function (IMF) of Pop III stars, the role of metals, and rotation during the formation and evolution of stars and their implications for BH formation. Finally, we summarise the expected properties of Pop III remnant BHs.

3.1. Pop III initial mass function

Understanding the IMF is a key challenge in the study of primordial star formation and the masses of stellar BHs are strongly associated with it. The first numerical simulations (Abel et al. 2002; Bromm et al. 2002) suggested that primordial stars were massive with typical masses of a few hundred solar. The latter studies also showed that Pop III stars were born in isolation with typical mass accretion rates of 10⁻⁴-10⁻² M_⊙yr⁻¹ (Yoshida et al. 2003, 2006; O’Shea & Norman 2007; Yoshida, Omukai, & Hernquist 2008). However, during the past few years, high resolution simulations including a detailed treatment of physical processes found that a protostellar disk formed as a consequence of gravitational collapse becomes unstable and fragments into multiple clumps, see Figure 1. This may lead to the formation of multiple stars per halo (Turk, Abel, & O’Shea 2009; Stacy, Greif, & Bromm 2010; Clark et al. 2011; Greif et al. 2012; Latif et al. 2013e). These simulations were evolved only up to a few tens to 5 000 yr, about a factor of 100 lower than the time required for a protostar to reach the main sequence and also did not include the stellar UV feedback.

Figure 1. The evolution of a protosetllar system in four different minihalos. Density projections of hydrogen nuclei are shown for the central 10 AU. Each row represents the minihalo whilst each column shows the time evolution after the formation of a central star. Adopted from Greif et al. (2012).

However, simulations taking into account the UV feedback from the protostar show that it shuts accretion onto the protostar by photoevaporating the protostellar disk and the central star cannot grow beyond 40 M_⊙ (Hosokawa et al. 2011; Stacy et al. 2012). These simulations either employed an approximate treatment for the radiative feedback or performed only two dimensional simulations. Hirano et al. (2014) have derived the stellar mass distribution for one hundred minihalos under the assumption that only single star forms per halo by including the radiative feedback from a star as well as stellar evolution. They found that stellar masses range from 10–1 000 M_⊙ and depend on the properties of their natal halos, also see Susa et al. (2014). Latif & Schleicher (2015a) employed an analytical model to study the properties of a protostellar disk around a primordial star and argue that although the disk is susceptible to fragmentation but the clump migration time is shorter than the KH timescale and therefore clumps may be able to migrate inwards. In fact, 3D radiation hydrodynamical simulations by Hosokawa et al. (2015) show that clump migration leads to intermittent accretion (also see Vorobyov & Basu 2010; Vorobyov, DeSouza, & Basu 2013) and disk fragmentation does not halt the formation of massive stars. Therefore, stellar masses may range from a few tens to a few hundred solar.

The most recent simulations of Stacy et al. (2016) found that disk fragmentation leads to the formation of a stellar cluster with a top heavy IMF. In their simulations, the most massive star reaches 20 solar masses in 5 000 yr after its formation and some of the sinks get ejected from the disk before ionisation front breaks out. However, these simulations were evolved only for 5 000 yr after the formation of the first sink and therefore final masses of Pop III stars are still uncertain. In Figure 2, we show the stellar mass distribution from Hirano et al. (2014) which gives an upper limit on the expected stellar masses as their calculations do not take into account the multiplicity of stars per halo. These results suggest that the typical mass of Pop III stars is about 100 M_⊙ with the exception of a few cases of a 1 000 M_⊙.

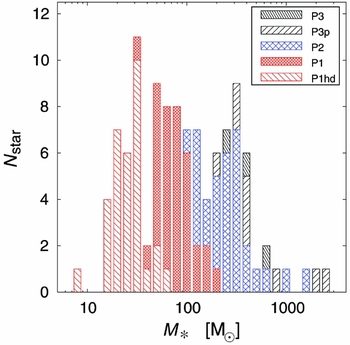
Figure 2. The stellar mass distribution of 110 first stars assuming that single star forms in each minihalo. Each colour represents different stellar evolution path, see Hirano et al. (2014) for details. Adopted from Hirano et al. (2014).

3.2. Effects of metallicity and rotation

Both the metallicity and the rotation speed of stars play a vital role in defining their fates and have important implications for the formation of stellar mass BHs. In the presence of trace amounts of metals, dust cooling becomes important at high densities, and triggers the formation of multiple low mass stars (Ferrara, Pettini, & Shchekinov 2000; Schneider et al. 2003; Omukai et al. 2005; Schneider et al. 2006). Numerical simulations show that for Z/Z_⊙ ⩾ 10⁻⁵ dust cooling induces fragmentation and fosters low mass star formation (Dopcke et al. 2011, 2013; Smith et al. 2015). Similarly, the dark matter halos with higher spin have a longer collapse timescale which results in enhanced fragmentation. Moreover, higher rotation decreases the mass accretion onto a protostar and consequently the final stellar mass gets reduced (Hirano et al. 2014; Dutta 2016).

The presence of metals and rotation does not only influence the formation of the first/second generation of stars by reducing their final masses but also strongly affects their evolution. Stellar evolution models show that mass loss from the stellar winds is metallicity dependent, scales with $\dot{m}_{{\rm loss}} \propto {\it Z}^{0.5}$ and consequently metal rich stars show much higher mass loss compared to the metal poor stars (Nugis & Lamers 2000; Kudritzki & Puls 2000; Baraffe, Heger, & Woosley 2001; Heger et al. 2003; Meynet & Maeder 2005). Similarly, fast rotation enhances the surface enrichment of CNO cycle elements which in turn derive the mass loss by stellar winds from metal poor stars. For example, a fast rotating 60 M_⊙ star can lose 30–55% of its initial mass for Z/Z_⊙ = 10⁻⁸-10⁻⁵ (Heger, Langer, & Woosley 2000; Meynet & Maeder 2000; Meynet, Ekström, & Maeder 2006b; Meynet et al. 2006a; Chiappini et al. 2011). Furthermore, an enhanced rotation modifies the Eddington limit known as the ΩΓ limit (Langer 1998; Meynet & Maeder 2000) and prevents the star from growing beyond 20–40 M_⊙ by making it more compact (Lee & Yoon 2016). Such rapidly rotating low metallicity stars may also produce gamma-ray bursts (Yoon & Langer 2005).

3.3. Stellar tracks leading to BH formation

Stellar evolution calculations suggest that the growth of primordial stars is significantly different from the present-day counterparts. Larger mass accretion rates, about two-three orders of magnitude higher than normal stars, and the absence of heavier elements makes the evolution of Pop III stars significantly different from ordinary stars (Omukai & Palla 2001; Schaerer 2002; Omukai & Palla 2003; Schaerer 2003). Stellar evolution also strongly depends on the time evolution of the mass accretion rates. Deuterium burning and pp cycle do not generate enough energy to counteract the KH contraction. The hydrogen burning from the CN cycle significantly increases the stellar luminosity and a protostar quickly reaches the ZAMS. Therefore, more massive stars of the order of a hundred solar masses are expected to form from a zero metallicity gas whilst for Z/Z_⊙ ⩾ 10⁻² radiation pressure on dust grains becomes important and leads to the formation of low mass stars (Omukai & Palla 2003; Hosokawa et al. 2012b).

The mass loss from stars become significant even in the presence of trace amount of metals whilst for primordial stars such losses are minimal. Stellar evolutionary tracks leading to the formation of BHs are indicated in Figure 3. The primordial stars with masses between 40–140 M_⊙ and above 260 M_⊙ are expected to directly collapse into BHs of similar masses (Heger & Woosley 2002; Heger et al. 2003). For a trace amount of metals, all stars above 40 M_⊙ directly collapse in a BH but with increasing metallicity the mass loss starts to increase. Moreover, the fraction of massive stars collapsing into a BH depends on the shape of the IMF and is about twice for top-heavy IMF compared to the Salpeter IMF (Heger et al. 2003). Although numerical simulations suggest that some of the Pop III stars might be rotating at ⩾ 1 000 kms⁻¹, i.e. close to their break up limit (Stacy et al. 2011), stellar evolution calculations including rotation (Ekström et al. 2008) indicate that the mass loss from the fast rotating Pop III stars is still very low. In a nutshell, metal free stars with low rotation speeds are favoured for the formation of stellar mass BHs as they retain most of their mass until they collapse into a BH.

Figure 3. The fate of single stars as a function of their initial mass and initial metallicity. The tracks for the formation of direct BHs from the stars are highlighted by the black colour whilst the white region in the bottom right indicates the range for a pair instability supernova. Adopted from Heger et al. (2003).

3.4. Expected properties of stellar mass BHs

The current numerical simulations indicate that the formation of massive primordial stars up to a 1 000 M_⊙ is possible with the characteristic mass scale between 10–100 M_⊙. This suggests that BH seeds of a few hundred solar masses can be formed at z = 20–30. In order to reach a few billion solar masses by z = 7, they must continuously grow at the Eddington limit. The three-dimensional numerical simulations studying the growth of stellar mass BHs show that feedback from a BH photo-evaporates the gas the in its hosting halo and consequently accretion onto a BH gets halted (Johnson & Bromm 2007; Alvarez, Wise, & Abel 2009). They further found that the BH accretion rate is about 10⁻¹⁰ M_⊙yr⁻¹, i.e. several orders of magnitude below the Eddington limit which makes their growth extremely difficult. Moreover, the progenitor star creates an HII region, evacuates the gas from a minihalo and accretion remains halted for about 10⁸ yr. Park et al. (2016) found that stellar mass black holes cannot coevally grow with budge via accretion until it reaches the critical mass of 10⁶ M_⊙. There is a growing consensus that the stellar mass BHs require various episodes of super Eddington accretion to reach a billion solar masses by z ⩾ 6 (Madau, Haardt, & Dotti 2014; Volonteri, Silk, & Dubus 2015; Pacucci, Volonteri, & Ferrara 2015; Inayoshi, Haiman, & Ostriker 2016a).

4 BH SEEDS FROM DENSE STELLAR CLUSTERS

The self-gravitating stellar systems with negative heat capacity are susceptible to a gravitational collapse where the core collapse timescale (t _cc) is comparable to the two-body relaxation time (Binney & Tremaine 1987). In such a scenario, the core of the cluster collapses resulting in a higher stellar density at its centre and the run-away stellar collisions lead to the formation of a very massive star (VMS) which later may collapse into a massive seed BH of up to a 1 000 M_⊙. This mechanism provides an additional route for the formation of massive BH seeds. The earlier studies suggested that dense stellar clusters with ⩾ 10⁷ stars are required for the run-away collapse to occur and subsequent growth of a massive object (Lee 1987; Quinlan & Shapiro 1990). It was found that the binary heating stops the core collapse in less massive stellar clusters (Heggie 1975; Hut et al. 1992). Moreover, the t _cc has to be shorter than the typical timescale for the massive stars to reach the main sequence (~3 Myr), otherwise mass loss from the supernova may halt the core collapse.

However, later studies found that the mass segregation instability can lead to the formation of a massive black hole seed even in less massive clusters (Spitzer 1969; Vishniac 1978; Begelman & Rees 1978). This comes from the fact that massive stars sink into the centre of a cluster on a dynamical friction timescale and speed-up the collapse. This phenomenon is expected to get accelerated significantly in multi-mass systems like realistic nuclear clusters. If the mass segregation occurs within the first 3 Myr, then stellar dynamical processes can lead to the formation of a VMS. As we discuss in the following sections, this mechanism strongly depends on the compactness and dynamical evolution of a stellar cluster and is particularly expected to occur in low metallicity clusters where mass loss from stellar winds is expected to be minimum (Hirschi 2007; Glebbeek et al. 2009). These dense nuclear clusters can form in halos of about 10⁸ M_⊙ at z ~ 15 enriched by trace amount of metals (Omukai, Schneider, & Haiman 2008; Devecchi & Volonteri 2009).

Another potential way could be the merging of many stellar mass BHs or a supra-exponential growth of stellar mass black holes in a cluster by dense cold gas flows Alexander & Natarajan (2014). However, the gravitational recoil velocities are about the order of ~ 1 000 kms⁻¹ which are much larger than the escape velocity of halos (10 km s⁻¹) and therefore lead to the ejection of BHs from the shallow DM potentials at earlier comic times (Haiman 2004; Tanaka & Haiman 2009). Alternatives could be the run-away merging of stellar mass black holes in the core of a dense cluster mediated by the extremely large inflows of gas (Davies, Miller, & Bellovary 2011; Lupi et al. 2014) or collapse of a dense stellar cluster due to the relativistic instability (Shapiro & Teukolsky 1986).

4.1. Binarity of early star formation

Observations of contemporary star formation suggest that about 50% of the stars are born in binaries or multiple systems (Sana, Gosset, & Evans 2009; Sana, James, & Gosset 2011). In the context of primordial stars, recent numerical simulations show that the first generation of stars may also have formed in multiple systems due to the fragmentation of protostellar disk (Turk et al. 2009; Stacy et al. 2010; Clark et al. 2011; Greif et al. 2012; Latif et al. 2013e; Latif & Schleicher 2015a; Stacy et al. 2016). Some of the clumps from disk fragmentation migrate inward and merge with the central protostar whilst the rest survive to form a multiple system (Greif et al. 2012; Stacy et al. 2016). In fact, numerical simulations suggest that up to 35% of Pop III stars may have formed in binaries; thus, the probability for a PopIII star to have a companion is about 50% (Stacy et al. 2010; Stacy & Bromm 2013). This may also suggest the formation of X-ray binaries at earlier cosmic times (Mirabel et al. 2011; Ryu, Tanaka, & Perna 2016).

Simulations of the first galaxies show that supernovae from Pop III stars quickly enrich halos with metals where gas can be cooled down to the cosmic microwave background temperature (T _CMB) by dust and metal line cooling at z = 15 even in the presence of UV flux (Tornatore et al. 2007; Smith et al. 2009; Greif et al. 2010; Wise et al. 2012; Whalen et al. 2013; Johnson, Dalla Vecchia, & Khochfar 2013a; Safranek-Shrader, Milosavljević, & Bromm 2014a; Bovino et al. 2014; Pallottini et al. 2014). Stellar clusters of Pop II stars are expected to form above the critical value of the metallicity, i.e. Z/Z_⊙ ~ 5 × 10⁻⁴(Schneider et al. 2003; Omukai et al. 2005; Cazaux & Spaans 2009; Latif, Schleicher, & Spaans 2012). The recent three-dimensional cosmological simulations suggest that the first bona fide stellar clusters form at z = 15 where cooling is triggered by the metal lines (such as CII and OI) and stellar masses range from 0.1-10 M_⊙ (Safranek-Shrader, Milosavljević, & Bromm 2014b; Safranek-Shrader et al. 2016). Although current cosmological simulations are unable to constrain the binary fraction in the first stellar clusters due to the numerical constraints but the binary fraction is expected to be higher for metal poor stars (Komiya et al. 2007; Machida 2008).

4.2. Compact stellar clusters

The compactness of a stellar cluster is the key property for the stellar dynamical processes to occur as it determines whether a seed BH can form or not. This requirement arises from the fact that the time for the core collapse should be shorter than the time for massive stars to go off supernova (~3 Myr) otherwise latter may halt the core collapse, also see Yajima & Khochfar (2016). The more compact the cluster shorter the core collapse timescale. For a given cluster mass, the number of collisions and the increase in mass per collision strongly depend on the half-mass radius of a cluster (Portegies Zwart & McMillan 2002). The mass of a VMS almost linearly increases with the initial central density of a cluster (Katz, Sijacki, & Haehnelt 2015).

In the context of BHs, the first compact nuclear cluster are expected to form in massive halos of 10⁸ M_⊙ at z > 10 with Z/Z_⊙ ~ 10⁻⁵-10⁻³. In the presence of a LW flux, the formation of H₂ at low densities remains suppressed and gas initially collapses isothermally to form a self-gravitating accretion disk at the centre of a halo (Devecchi & Volonteri 2009). Fragmentation occurs only in the nucleus of the disk above densities of 10³ cm⁻³ due to the metal line cooling and forms a compact cluster of 10⁵ M_⊙ with half-mass radius of about 1 pc. On the other hand, for higher metallicities, fragmentation already occurs at densities < 10³ cm⁻³ and results in the core collapse time longer than 3 Myr (Omukai et al. 2008; Devecchi & Volonteri 2009; Devecchi et al. 2012).

Semi-analytical models suggest that large accretion rates and efficient star formation are required for the formation of a such compact nuclear stellar and conditions for their formation are feasible in the first massive halos polluted by a trace amount of metals at z > 10 (Devecchi & Volonteri 2009). Latif et al. (2016) have performed 3D cosmological simulations to study the impact of trace amount of dust and metals in massive halos of 10⁸ M_⊙ and found that a dense cluster may also form for Z/Z_⊙ ⩾ 10⁻⁴ in the presence of a strong UV flux. The study of first nuclear clusters in still in infancy as their formation cannot be resolved in numerical simulations due to the enormous range of spatial scales. In future, more work is required to asses how compact and massive the clusters can be formed at high redshift.

4.3. Dynamical evolution

The dynamical evolution of dense stellar clusters has been studied via direct N-body simulations which show that the mergers between stars destroy binaries and avoid three body binary heating (Portegies Zwart et al. 1999). Moreover, in contrary to the previous studies, stellar collisions are fostered by the dynamically formed binaries which increase the star collision rate (Portegies Zwart et al. 1999; Portegies Zwart & McMillan 2002). Consequently, stellar collisions can occur even in a low mass system with 12 000 stars and may lead to the formation of a BH of up to ~ 1 000 M_⊙. This was further confirmed from the Monte Carlo simulations by Gürkan, Freitag, & Rasio (2004) where they explored a range of IMFs and cluster structural parameters. Their followed-up work including stellar dynamics showed that core collapse occurred on ~ 3 Myr timescale irrespective of the cluster size, mass, concentration, and a VMS reached up to 1 000 M_⊙ (Freitag, Gürkan, & Rasio 2006). Moreover, the mass of a VMS is about 10⁻³ times the cluster mass and is mainly contributed by the stars in the mass range of 60–120 M_⊙ (Goswami et al. 2012).

Metallicity also plays an important role in the dynamical evolution of a stellar cluster as mass loss from stars can deeply affect the core collapse. Schulman, Glebbeek, & Sills (2012) and Downing (2012) found that the size of cluster depends on the metallicity and metal rich clusters expand more rapidly. For more massive clusters, Sippel et al. (2012) found that both metal poor and metal rich clusters are structurally similar and no significant differences in their half-mass radii were observed. The effect of metallicity seems to be more important in intermediate mass young clusters and leads to the differences in the core radius as well as in the half-mass radius (Mapelli & Bressan 2013). These differences arise from an interplay between the mass loss from stellar winds, dynamical heating, and three-body interactions. Therefore, low metallicity young clusters forming at z > 10 are preferred for the formation of a massive seed black hole.

4.4. Expected properties of seed BHs

The BH mass resulting from the core collapse of a dense stellar cluster depends on its initial stellar mass, initial stellar density, compactness, cluster geometry, fraction of primordial binaries, and the IMF of a cluster. The N-body simulations exploring the range of above mentioned parameters show that clusters with different geometries, fractal distributions, and density profiles converge within 1 Myr and do not significantly influence the mass of a VMS. However, the final mass of a VMS strongly depends on the compactness for a given cluster mass and almost linearly increases with initial central density. Recently, Katz et al. (2015) used a combination of hydrodynamical cosmological simulations and direct N-body simulations to estimate the mass of a VMS forming via stellar run-away collisions in a metal poor stellar cluster. They found that a VMS of ⩾ 400 M_⊙ can be formed in a stellar cluster of 10⁴ M_⊙ at z = 15 and may reach up to a 1 000 M_⊙ for a cluster mass of a few times 10⁵ M_⊙.

The IMF of a stellar cluster influences the number of collisions between stars and the mass of a VMS tends to increase for a top heavy IMF but the probability of producing a VMS remains the same. Similarly, the introduction of primordial binaries and the initial mass segregation significantly change the evolution of a cluster but the mass of a VMS differs only by a factor of 3 which is less significant than the changes in the central density and the mass of a cluster (Katz et al. 2015). The mass of a seed black hole forming from the core collapse of a cluster can be estimated as follows (Portegies Zwart & McMillan 2002):

(1) $$\begin{equation} M_{{\rm BH}} = m_{*} + 4 \times 10^{-3} f_{{\rm c}} M_{{\rm c}0} \gamma \ln \Lambda _{\rm C}. \end{equation}$$

Here, m _* is the mass of a massive star in the cluster, f _c is the fraction of dynamically formed binaries, M _c0 is the birth mass of the cluster, ln Λ_c is the Coulomb logarithm, and γ ~ 1, is the ratio of timescales, see Portegies Zwart & McMillan (2002) for details. For a M _c0 = 10⁴ M_⊙, m _* = 100 M_⊙, f _c = 0.2, ln Λ_C = 10, M _BH ~ 180 M_⊙ whilst for M _c0 = 10⁵ M_⊙, the expected black hole mass is ~ 900 M_⊙.

Devecchi et al. (2010, 2012) employed an analytical model to estimate the expected mass range of seed BHs forming via dynamical processes in nuclear stellar clusters at z ⩾ 10. Their estimates for BH masses are shown in Figure 4 and indicate that BHs of up to a 1 000 M_⊙ can be formed. Simulations self-consistently modelling the formation and evolution of a nuclear stellar cluster are necessary to better understand the dynamics of the first dense nuclear clusters.

Figure 4. The mass function of BHs formed via stellar dynamical process in the first nuclear cluster at z ~ 15. Adopted from Devecchi et al. (2012).

5 DIRECT COLLAPSE BHs

One of the most promising way to explain the existence of z > 6 quasars is to form a massive BH seed of 10⁵-10⁶ M_⊙ directly via the gas dynamical processes (Rees 1984; Haehnelt & Rees 1993; Loeb & Rasio 1994; Eisenstein & Loeb 1995; Bromm & Loeb 2003; Koushiappas, Bullock, & Dekel 2004; Begelman et al. 2006; Spaans & Silk 2006) known as the DCBH. The key requirement for this scenario to work is that gas should efficiently shed angular momentum and rapidly collapse avoiding fragmentation. The basic idea behind this mechanism is to bring large inflows of gas to the centre of the halo on a short timescale of the order of 1 Myr and let the huge reservoir of the gas to collapse into a single massive object without fragmenting into stars. The recent calculations suggest that large mass accretion rates of ⩾ 0.1 M_⊙yr⁻¹ (see our explanation below) are required for this mechanism to work (Begelman 2010; Ball et al. 2011; Hosokawa et al. 2013; Schleicher et al. 2013; Ferrara et al. 2014; Sakurai et al. 2015). Such large accretion rates can be obtained either via thermodynamical processes by keeping the gas warm as the accretion rate ∝T ^3/2, (Bromm & Loeb 2003; Volonteri, Lodato, & Natarajan 2008; Regan & Haehnelt 2009; Shang, Bryan, & Haiman 2010; Johnson et al. 2011; Latif et al. 2013c; Ferrara et al. 2014), or through highly dynamical processes such as the ‘bars within bars’ instability (Shlosman, Frank, & Begelman 1989; Begelman et al. 2006) and galaxy mergers (Mayer et al. 2010).

The thermodynamical way to form a DCBH requires that halos should be metal free otherwise trace amount of metals can cool the gas which later leads to fragmentation and star formation. Even in primordial halos the formation of molecular hydrogen should remain suppressed to keep the gas warm and cooling should mainly proceed via atomic lines. Alternatives could be the trapping of Lyman alpha photons which could stiffen the equation of state and suppress in-situ star formation (Spaans & Silk 2006; Latif et al. 2011a). However, it has been found that cooling can still proceed via the 2s–1s transition and compensates the effect of Lyman alpha trapping (Schleicher, Spaans, & Glover 2010; Latif et al. 2011b). Lodato & Natarajan (2006) suggested that a few percent of pre-galactic disks forming in the dark matter halos at high redshift may form a massive object depending on the properties of hosting halos such as spin, mass, and cooling properties. Particularly, low spin halos are more prone to forming a massive central object. Tanaka et al. (2013), Tanaka & Li (2014) have proposed that extreme streaming velocities may facilitate direct collapse by enhancing the critical mass of halos to collapse, suppressing in-situ star formation and consequently avoid metal enrichment in atomic cooling halos. They argue that this scenario may not need external UV flux to suppress star formation, but Latif, Niemeyer, & Schleicher (2014b) show that the impact of streaming is not significant in atomic cooling halos forming at z = 15. Inayoshi, Visbal, & Kashiyama (2015) propose that high velocity collisions of two protogalaxies shock heat the gas which later cools isobarically, molecular hydrogen gets collisional dissociated (Inayoshi & Omukai 2012) and consequently an isothermal collapse may form a supermassive star (SMS). However, Visbal, Haiman, & Bryan (2014a) and Fernandez et al. (2014) show that these scenarios require additional mechanism to suppress the formation of molecular at high densities.

Begelman & Shlosman (2009) argue that fragmentation can also be suppressed in the presence of supersonic turbulence even in metal rich halos and may not require above mentioned conditions. Mayer et al. (2010) propose that merging of two metal rich galaxies brings large accretion rates of ~ 10⁴ M_⊙yr⁻¹ driven by the gravitational torques and a compact stable nuclear disk forms which later may collapse into a massive BH. Ferrara, Haardt, & Salvaterra (2013) argue based on one-dimensional model that such disk rapidly cools and becomes unstable in about 100 yr. So, the central core cannot grow beyond 100 solar masses. In the recent study, Mayer et al. (2015) improved on their previous work by employing radiative cooling for both optically thin and thick regimes instead of effective equation of state as in Mayer et al. (2010). Their new findings suggest that inclusion of cooling fosters the formation of compact nuclear disk and central core is stabilised by the shock heating and high optical depth of the gas. It is expected that in such scenario the core may directly collapse via general relativistic (GR) instabilities into a massive black hole. Bonoli, Mayer, & Callegari (2014) employed galaxy formation model in Millennium simulations using the recipe of Mayer et al. (2010) that major mergers of gas rich and disk dominated galaxies form massive BH. They found that most of the > 10¹¹ M_⊙ halos at z ~ 4 meet this criteria. Latif & Volonteri (2015) and Latif & Schleicher (2015b) show that complete isothermal monolithic collapse of a protogalactic gas may always not be necessary to form a massive central BH.

The gas has to shed angular momentum to collapse to high enough densities to form a massive BH otherwise collapse gets halted by the angular momentum barrier. Eisenstein & Loeb (1995) and Koushiappas et al. (2004) proposed that BHs can either form in DM halos with low angular momentum or in the tail of low angular momentum gas within the halo. However, even then gas has to transport angular momentum quite efficiently to form a massive central object. The recent simulations suggest that the triaxility of DM halos exerts gravitational torques which helps in the transfer of angular momentum via ‘bars within bars’ instabilities (Choi, Shlosman, & Begelman 2013, 2015). In the following subsections, we discuss physical processes involved in the formation of DCBHs via isothermal collapse, how and under what conditions they are formed and what are their typical masses.

5.1. Birthplaces of DCBHs

The potential embryos for the formation of DCBHs via isothermal collapse are the first massive metal-free halos with T _vir ⩾ 10⁴ K and masses of > 10⁷ M_⊙ at z ~ 15. They have sufficient gas reservoir to feed a massive object and their potential wells are deep enough to foster a rapid collapse required for the formation of a DCBH. Moreover, their virial temperature is high enough for the atomic line cooling to operate. The formation of a DCBH mandates that they should be of a primordial composition and the formation of H₂ remains suppressed (Shang et al. 2010; Petri, Ferrara, & Salvaterra 2012; Latif et al. 2014c; Yue et al. 2014). In the absence of H₂ cooling, collapse proceeds isothermally with T ~ 8000 K and warm gas flows towards the centre at the rate of $\rm \dot{\it m} \sim {c_s^3}/{G} \sim 0.1\;M_{\odot } yr^{-1} \left( {\it T}/{8\,000\;K}\right)^{3/2}$ , where c _s is the thermal sound speed.

The suppression of molecular hydrogen requires the presence of a strong LW flux (Omukai 2001; Omukai et al. 2008; Shang et al. 2010; Latif et al. 2013a). As we discuss in the next subsections that constraint of a strong LW fluxes requires that DCBH hosting halo should form in the vicinity (about few kpc) of a massive star forming galaxy (Dijkstra et al. 2008; Agarwal et al. 2012; Habouzit et al. 2016b). In mean time, it has also to avoid the metal pollution for the above mentioned reasons. Under these conditions, an isothermal monolithic collapse is expected to occur which later may lead to the formation of a DCBH.

5.2. UV flux constraints

One of the main constraints for the formation of DCBHs via isothermal direct collapse is the suppression of molecular hydrogen formation which requires the presence of a strong LW flux (Omukai 2001; Omukai et al. 2008; Shang et al. 2010; Petri et al. 2012; Latif et al. 2013a). The gas phase reactions in primordial gas can lead to the formation of a trace amount of H₂. The main pathway for H₂ formation is

(2) $$\begin{equation} \mathrm{H + e^{-} \rightarrow H^{-} +} \gamma, \end{equation}$$

(3) $$\begin{equation} \mathrm{ H + H^{-} \rightarrow H_{2} + e^{-}.} \end{equation}$$

The formation of H₂ can be suppressed either by directly dissociating H₂ or indirectly via the photo-detachment of H⁻. The destruction channel for H₂ depends on the stellar spectra. The photons with energy between 11.2–13.6 eV can be absorbed in the LW bands of H₂ and photo-dissociate it shortly after putting it into an excited state, this is known as the Solomon process. Whilst the low energy photons with energy above 0.76 eV can photo-detach H⁻. The reactions for the both processes are the following:

(4) $$\begin{equation} \mathrm{H_{2}} + \gamma _{{\rm LW}} \mathrm{\rightarrow H + H}, \end{equation}$$

(5) $$\begin{equation} \mathrm{H^{-}} + \gamma _{0.76} \mathrm{\rightarrow H + e^{-}}. \end{equation}$$

The stars with hard spectrum of T _rad = 10⁵ K are more efficient for the direct dissociation of H₂ whilst the stars characterised with T _rad = 10⁴ K are more effective in the photo-detachment of H⁻. The complete quenching of H₂ requires a critical value of UV flux (J ^crit ₂₁) which depends on the shape of a radiation spectrum. The previous studies used idealised spectra to compute the J ^crit ₂₁ and found that J ^crit ₂₁ = 30–1 200 for T _rad = 10⁴ K and J ^crit ₂₁ = 1 000 for T _rad = 10⁵ K (Omukai 2001; Shang et al. 2010; Van Borm & Spaans 2013; Latif et al. 2014c; Johnson et al. 2014). It has been found that the strength of J ^crit ₂₁ is about an order of magnitude above the background UV flux and can only be achieved in the close vicinity of a star forming galaxy (Dijkstra et al. 2008; Agarwal et al. 2012; Habouzit et al. 2016b). Moreover, such flux is mainly provided by Pop II stars due to their long lives and higher abundance. Recently, realistic spectra of the first galaxies was computed using the stellar synthesis code STARBURST (Leitherer et al. 1999) and it was found that J ^crit ₂₁ depends on the mode of a star formation (either bursty or constant) as well as on the age and metallicity of stars (Sugimura et al. 2014; Agarwal & Khochfar 2015; Agarwal et al. 2016a). Sugimura et al. (2014) show that such spectra can be mimicked with T _rad= 2 × 10⁴ − 10⁵ K.

Recent estimates of J ^crit ₂₁ from three-dimensional cosmological simulations (Latif et al. 2015) ² for a realistic Pop II spectra vary between 20 000–50 000 considering a uniform isotropic background UV flux and are shown in Figure 5. Similar values of J ^crit ₂₁ have been obtained for anisotropic source (Regan, Johansson, & Wise 2014b, 2016a). Moreover, the presence of X-rays may further influence the J ^crit ₂₁ depending on its strength (Latif et al. 2015; Inayoshi & Tanaka 2015; Regan, Johansson, & Wise 2016b) and also an accurate modelling of H₂ self-shielding is required (Wolcott-Green, Haiman, & Bryan 2011; Hartwig et al. 2015).

Figure 5. The estimates of critical value of UV flux (J ^crit ₂₁) both from one zone models and three-dimensional simulations including variations from halo to halo, dependence on the radiation spectra, and the impact of X-ray ionisation. Adopted from Latif et al. (2015).

5.3. Metal pollution

One of the key requirements for the formation of DCBHs via isothermal collapse is that the hosting halo should be metal free. The metal enrichment is expected to be patchy in the early universe and therefore some halos may remain unpolluted even down to z = 6 (Tornatore et al. 2007; Trenti et al. 2009; Maio et al. 2011; Ritter et al. 2015; Pallottini et al. 2014; Habouzit et al. 2016a). In fact, observations show that pockets of extremely metal poor gas (Z/Z_⊙ ~ 10⁻⁵) can exist down to z = 7 (Simcoe et al. 2012). So, it is conceivable that primordial halos where star formation is suppressed in the presence of LW background may stay metal free at z ⩾ 10.

However, the DCBH host halo is expected to form in the surrounding of a star-forming galaxy to receive a strong LW flux and therefore has to avoid the possible pollution by the supernova winds. Dijkstra, Ferrara, & Mesinger (2014) employed an analytical model to study the impact of metal pollution by the supernova winds and found that it can significantly affect the expected abundance of DCBHs. Visbal, Haiman, & Bryan (2014b) propose that metal pollution can also be avoided in a synchronised pair of halos. In such a case, star-forming halo forms first whilst the DCBH host halo forms later and rapidly collapses before it gets enriched by the supernova winds. Moreover, such pair of halos is expected to be in a clustered environment where metals might be ejected in a preferential direction with low density and metal pollution may be avoided (Ritter et al. 2015; Pallottini et al. 2014). It has been recently found that some of the DCBH host halos may get tidally disrupted in such a scenario (Chon et al. 2016).

Cosmological hydrodynamical simulations including both star formation and supernova feedback show that a significant fraction of halos remains metal free down to z = 10 with mass range between 2 × 10⁷ − 10⁸ M_⊙ (Latif et al. 2016; Habouzit et al. 2016a), see Figure 6. These results provide an upper limit on the fraction of metal free halos in the above mentioned range as simulations are unable to resolve halos below 10⁷ M_⊙. In future, cosmological hydrodynamical simulations self-consistently taking into account the metal pollution as well as radiations from the star forming galaxies are required to better understand the metal pollution in the DCBH host halos.

Figure 6. Fraction of halos with metallicity below the given value in the figure legged and masses between 2 × 10⁷-10⁸ M_⊙. Adopted from Latif et al. (2016).

5.4. Formation of a supermassive/quasi star

SMSs ³ are considered as potential cradles for the formation of DCBHs (Begelman 2010; Volonteri & Begelman 2010; Ball et al. 2011; Hosokawa, Omukai, & Yorke 2012a; Hosokawa et al. 2013; Schleicher et al. 2013; Johnson et al. 2013b; Ferrara et al. 2014). They may collapse via GR instabilities into a DCBH whilst retaining ⩾ 50% of their initial mass (Baumgarte & Shapiro 1999; Shibata & Shapiro 2002; Montero, Janka, & Müller 2012; Reisswig et al. 2013) or may evolve towards a ZAMS and later collapse into a massive BH (Ferrara et al. 2014). The stellar evolution calculations suggest that the formation of such objects requires rapid accretion with $\dot{\it m} \ge 0.1\; {\rm M}_{\odot } {\rm yr}^{-1}$ (Begelman 2010; Ball et al. 2011; Hosokawa et al. 2013; Schleicher et al. 2013). For such high accretion rates, the radius of star monotonically increases with mass due to the shorter accretion time in comparison with the KH contraction timescale (Hosokawa et al. 2013; Sakurai et al. 2015). Consequently, their surface temperatures remain as low as 5 000 K, they produce weak UV stellar feedback and can grow up to $\rm 3.6 \times 10^8 \; \dot{\it m} \;M_{\odot }$ . The energy released by the nuclear burning remains subdominant compared to the energy produced by the stellar contraction.

Schleicher et al. (2013) found that for $\rm \dot{\it m} \ge 0.14\; M_{\odot } yr^{-1}$ the core of a SMS collapses into a BH and forms a so-called quasi star, also see Begelman, Rossi, & Armitage (2008). It comes from the fact that accretion timescale is considerably shorter than the nuclear burning timescale and therefore the core collapses into a black hole (Begelman et al. 2006; Begelman 2010). A possible advantage of such composition is that a central BH may accrete at the super-Eddington rate but overall accretion is limited by the Eddington rate of a quasi star. Ball et al. (2011) have found that about 10% of the stellar mass is accreted onto the BH before the hydrostatic equilibrium breaks down and results are sensitive to the choice of boundary conditions. Dotan, Rossi, & Shaviv (2011) quantified the potential impact of radiation-driven winds from the envelope of a quasi star and found that winds can be so strong that they may blow away the envelope before the BH doubles its mass. The effect of winds from the radiation dominated objects was reconsidered by Fiacconi & Rossi (2016b) by solving the equations of motion and including the previously neglected advection energy term. They found that the super Eddington accretion onto the newly born BH within quasi stars is likely responsible for vigorous mass loss and limits the BH growth. In the follow-up study, Fiacconi & Rossi (2016a) explored the impact of rotation in quasi-star scenario via simplified analytical model and found that for ⩾ 10⁵ M_⊙ massive SMSs the quasi-star phase may be skipped whilst the growth of less massive objects may get prevented. However, 3D radiation hydrodynamics simulations are necessary to validate these findings.

The numerical experiments employing a Jeans resolution of four cells did not observe any fragmentation (Bromm & Loeb 2003; Wise et al. 2008; Regan & Haehnelt 2009; Prieto, Jimenez, & Haiman 2013; Latif et al. 2013a) whilst the simulations employing both higher Jeans (64 cells per Jeans length) as well as spatial resolution show that fragmentation occasionally occurs (Latif et al. 2013c, 2013d; Regan, Johansson, & Haehnelt 2014a; Becerra et al. 2015). They further found that a self-gravitating accretion disk forms in the centre of the halo (see Figure 7) which becomes marginally unstable and fragments into multiple clumps but most of the clumps get merged with the central clump. Large accretion rates of 0.1 − 1 M_⊙yr⁻¹ are observed in these simulations and seem to be sufficient for forming a massive central object. Moreover, subgrid scale turbulence and strong magnetic fields amplified via the small scale dynamo help in suppressing fragmentation, see Latif et al. (2013c, 2013b), Latif, Schleicher, & Schmidt (2014a). These simulations did not include H⁻ cooling which becomes important at densities of 10⁸–10¹⁶ cm⁻³ and also cooling was artificially switched off to mimic the formation of a protostar. Both idealised (Van Borm et al. 2014; Inayoshi, Omukai, & Tasker 2014) and cosmological (Latif, Schleicher, & Hartwig 2016) simulations employing a detailed chemical model have been performed. Particularly, they included the H⁻ cooling and opacities for H⁻ bound-free emission, free–free absorption as well as the Raleigh scattering of hydrogen atoms. These simulations show that H⁻ cooling does not halt the formation of a SMS and may lead to a binary formation in some cases but realistic opacities help in stabilising the collapse on small scales (Latif, Schleicher, & Hartwig 2016).

Figure 7. Self-gravitating accretion disks formed at the centre of a massive primordial halos illuminated by a strong LW flux as a consequence of isothermal collapse. Each panel represents a halo of above 10⁷ M_⊙ forming at z = 10–15 and shows the density projection in the central 300 AU. Adopted from Latif et al. (2013c).

Cosmological simulations using sink particles (also without sinks) confirm the formation of a SMS of 10⁵ M_⊙ within a 1 Myr after its birth (Latif et al. 2013d; Shlosman et al. 2016). Moreover, stellar evolution simulations employing both constant (⩾ 0.1 M_⊙yr⁻¹) and time-dependent mass accretion rates show that a SMS can be formed and resulting UV feedback is too weak to hinder the mass accretion (Hosokawa et al. 2013; Sakurai et al. 2015, 2016). The present studies suggest the formation of a SMS as a potential outcome (Hosokawa et al. 2013; Sakurai et al. 2016) but do not consider the effect of rotation. However, it is not yet clear if the final outcome of an isothermal collapse is always a SMS or a quasi star or even a massive BH. In future three-dimensional cosmological hydrodynamical simulations including the UV feedback from a SMS and coupled stellar evolution will be required to asses it.

5.5. Birth mass function

The studies investigating the formation of a SMS could not evolve their simulations long enough to assess its final fate due to the numerical constraints (Hosokawa et al. 2012b, 2013). So, it is not clear whether a SMS directly collapses into a BH via GR instabilities provided that accretion continues with ⩾ 0.1 M_⊙yr⁻¹ or it evolves to a ZAMS (if the mass accretion onto the SMS stops) and later collapses into a massive BH. It is also not well understood what is the birth mass function of DCBHs. Moreover, previous works ignored the effect of rotation on the evolution of a SMS which can play important role in determining its final fate. Ferrara et al. (2014) used an analytical model to investigate the fate of an accreting SMS and found that it becomes GR unstable when its equation of state drops below a critical value (Chandrasekhar 1964; Montero et al. 2012) whilst the presence of rotation halts the collapse. The mass of a SMS can be estimated as (Ferrara et al. 2014)

(6) $$\begin{equation} {M_{*}} \le 8.48 \times 10^{5} \left( \frac{\dot{m}}{{\rm M}_{\odot }\, {\rm yr}^{-1}} \right)^{2/3} No \;Rotation \end{equation}$$

(7) $$\begin{equation} {M_{*}} \le 6.01 \times 10^{5} \left( \frac{\dot{m}}{{\rm M}_{\odot }\, {\rm yr}^{-1}} \right) Rotation \end{equation}$$

SMSs more massive than these limits are expected to directly collapse into a BH.

Ferrara et al. (2014) used merger tree simulations to compute the birth mass function of DCBHs by following the growth of a SMS. Depending on the mass accretion onto the proto-SMS they determined whether it forms a DCBH via GR instabilities or a protostar contracts and evolves into a ZAMS SMS. The mass distribution of DCBHs is shown in Figure 8 and depicts that typical masses of DCBHs are ~ 2 × 10⁵ M_⊙ whilst the masses of SMSs vary from 2 × 10⁴-10⁵ M_⊙. The final mass further depends on whether the merged minihalo/accreted gas was metal free (dubbed as the sterile case) or metal enriched (fertile case). Overall, the masses of DCBHs are in the range of 10^{4 − 5} M_⊙.

Figure 8. The mass distribution of DCBH seeds (dotted histogram) and SMS (yellow histogram). The upper panel shows the case of fertile mini halos whilst the bottom panel sterile mini halos. The results are computed from merger tree simulations and averaged over 50 milky-way merger histories with ± σ error bars. Adopted from Ferrara et al. (2014).

6 FUTURE OUTLOOK

In this review, we mainly focussed on the formation mechanisms of SMBH seeds and other aspects such as their number density and growth are covered in the complementary reviews. However, for the sake of completeness, we briefly mention them here. The number density of seed BHs depends on their formation mechanism, see Agarwal et al. (2012), Dijkstra et al. (2014), and Habouzit et al. (2016b). Due to the special conditions required for the formation of heavy seeds, their number density is expected to be smaller compared to the lighter seeds. Depending on the seed BH mass (10-10⁵ M_⊙), they require 10–20 e-foldings to reach billion solar masses at z ⩾ 6, see Johnson & Haardt (2016) for a detailed discussion on the early growth of seed BHs. This may be achieved via prolonged episodes of accretion and/or merging in rare massive halos forming at earlier cosmic times as found in large cosmological simulations (Sijacki et al. 2007, 2015; Di Matteo et al. 2012, 2016).

Although tremendous progress has been made during the past decade both from the theoretical and the observational perspectives to understand the formation mechanisms of SMBHs, there are still many open questions. Theorists have proposed several models but direct observational evidence is required to constrain them. This might have been provided for the first time by the recent discovery claim made by Pacucci et al. (2016). This work has suggested a novel method to identify BH seeds in deep galaxy surveys that, in addition to detecting two such sources in the currently available data, seems optimal also for future JWST searches. To conclude, we briefly summarise in the following some of the most urgent questions concerning the formation mechanisms of seed black holes:

• • How massive are the first stars and what is their IMF?

• • How compact and massive are the first nuclear star clusters?

• • What is the binary fraction of Pop III and Pop II stars?

• • Is the formation of a VMS in a dense stellar cluster viable and what is the typical mass of the resulting black hole?

• • What are the intermediate stages in the direct collapse BH scenario? a SMS, a quasi star, or none of these?

• • How abundant are black seeds in various formation mechanisms?

• • Under what conditions seed BHs can grow to the SMBHs scales of a few billions solar masses?

• • How can we observationally constrain different BH formation models?

Several ways have been suggested to observationally constrain the BH formation models. One of these is to probe the low luminosity active galactic nuclei (AGNs) at z > 6 and measure their mass accretion accretion rates and BH masses. In fact, ATHENA X-ray observatory is expected to detect about 400 low luminosity AGNs with L _X ⩾ 10⁴³ ergs⁻¹ at z ⩾ 6 and will provide direct constraints on BH formation mechanisms (Aird et al. 2013). The low yields of AGNs at z > 6 will rule out the PopIII seed formation scenario as they are expected to be more abundant compared to the heavy seeds, see Figure 1 and discussion in Aird et al. (2013). For example, an AGN with L _X = 4 × 10⁴³ ergs⁻¹ observed at z ⩾ 10 needs to be powered by a SMBH of > 10⁷ M_⊙. For an Eddington limited growth within the age of universe at z = 10, this requires a seed BH of 10⁵ M_⊙. Such observations can directly constrain the masses, growth rates, and duty cycles of seed BHs.

The recent detection of gravitational waves from the merging of a BH binary by LIGO (Abbott et al. 2016) has opened the possibility to constrain the population of stellar mass BHs in the early Universe. Depending on the IMF, Pop III BH binaries may produce distinct features in the gravitational wave background in 10–100 Hz band and yield constraints on the abundance of Pop III BHs (Hartwig et al. 2016b; Inayoshi et al. 2016b; Ricotti 2016). Alternative strategies rely on secondary indicators such as measuring the occupation fraction of MBHs in low mass galaxies or constraints from growth timescales of BHs (Volonteri 2010; Greene 2012). In fact, recent observations of low mass galaxies indicate the potential presence of a 10⁵-10⁶ M_⊙ BHs at their centres (Reines et al. 2011; Satyapal et al. 2014). Confirmation of such AGNs with future observations and precise measurements of their BH masses will tremendously help to distinguish the BH formation models.

Recent detection of the brightest Lyman alpha emitter at z = 6.6 (CR7) by Sobral et al. (2015) shows strong Lyman alpha and He-1640 Å line luminosities and no metal line emission. Numerous studies suggest that CR7 may potentially host a DCBH (Pallottini et al. 2015; Hartwig et al. 2016a; Agarwal et al. 2016b; Dijkstra, Gronke, & Sobral 2016; Smidt, Wiggins, & Johnson 2016; Smith, Bromm, & Loeb 2016). However, further observations are required to confirm this hypothesis. Upcoming space and ground-based telescopes such as JWST, ATHENA, WFIRST, and SKA will be able to directly probe seed BHs in the high-redshift universe and provide direct observational constraints.