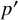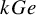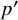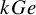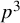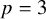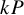1 Introduction
Throughout this paper, p is a prime and k is an algebraically closed field of characteristic p. The study of blocks with normal defect groups has a long history, starting with the work of Brauer [Reference Brauer6] and continuing with Reynolds [Reference Reynolds15], Dade [Reference Dade7] and Külshammer [Reference Külshammer13]. In the case of abelian normal defect, abelian inertial quotient and one simple module, explicit descriptions of the basic algebra were given by Benson and Green [Reference Benson and Green3], and Holloway and Kessar [Reference Holloway and Kessar8]. Dropping the hypothesis of one simple module led to our paper [Reference Benson, Kessar and Linckelmann4]. The main structural feature of the basic algebras calculated in these papers is that they appear to be quantised versions of the group algebras of semidirect products of a defect group and a subgroup of the inertial quotient.
The purpose of this paper is to generalise the results from [Reference Benson, Kessar and Linckelmann4] to blocks of group algebras over k of finite groups that have a normal defect group P which is no longer necessarily abelian, but still with abelian
![]() $p'$
inertial quotient L. By a theorem of Külshammer [Reference Külshammer13], any such block is isomorphic to a matrix algebra over a twisted group algebra
$p'$
inertial quotient L. By a theorem of Külshammer [Reference Külshammer13], any such block is isomorphic to a matrix algebra over a twisted group algebra
![]() $k_{\alpha }(P\rtimes L)$
of the semidirect product
$k_{\alpha }(P\rtimes L)$
of the semidirect product
![]() $P\rtimes L$
, for some
$P\rtimes L$
, for some
![]() $\alpha \in H^2(L, k^{\times })$
, inflated to
$\alpha \in H^2(L, k^{\times })$
, inflated to
![]() $P\rtimes L$
. So there is a central
$P\rtimes L$
. So there is a central
![]() $p'$
-extension
$p'$
-extension
and an idempotent e in
![]() $kZ$
, such that
$kZ$
, such that
![]() $k_{\alpha }(P\rtimes L)\cong kGe$
, where
$k_{\alpha }(P\rtimes L)\cong kGe$
, where
![]() $G=P\rtimes H$
.
$G=P\rtimes H$
.
Theorem 1.1. With the notation and hypotheses above, let
![]() $\tilde {\mathfrak {A}}$
be a basic algebra of the twisted group algebra
$\tilde {\mathfrak {A}}$
be a basic algebra of the twisted group algebra
![]() $k_{\alpha }(P \rtimes L)$
. Then
$k_{\alpha }(P \rtimes L)$
. Then
![]() $k_{\alpha }(P \rtimes L)$
is a matrix algebra over
$k_{\alpha }(P \rtimes L)$
is a matrix algebra over
![]() $\tilde {\mathfrak {A}}$
, and
$\tilde {\mathfrak {A}}$
, and
![]() $\tilde {\mathfrak {A}}$
has an explicit presentation as a quantised version of the group algebra
$\tilde {\mathfrak {A}}$
has an explicit presentation as a quantised version of the group algebra
![]() $k(P\rtimes Z(H)/Z)$
.
$k(P\rtimes Z(H)/Z)$
.
For the precise presentation and the proof, see Section 4. There are several new ingredients required to extend the results from [Reference Benson, Kessar and Linckelmann4] to nonabelian defect groups. We first consider the associated graded
![]() $\mathsf {gr}_*(kGe)=\bigoplus _{n\geqslant 0}\ J^n(kGe)/J^{n+1}(kGe)$
of
$\mathsf {gr}_*(kGe)=\bigoplus _{n\geqslant 0}\ J^n(kGe)/J^{n+1}(kGe)$
of
![]() $kGe$
, briefly reviewed in the next section, and make use of the Jennings–Quillen theorem [Reference Jennings12, Reference Quillen14] and Semmen [Reference Semmen16]. We show that
$kGe$
, briefly reviewed in the next section, and make use of the Jennings–Quillen theorem [Reference Jennings12, Reference Quillen14] and Semmen [Reference Semmen16]. We show that
![]() $\mathsf {gr}_*(kGe)$
is isomorphic to a matrix algebra over a quantised version of the associated graded of the group algebra of the group
$\mathsf {gr}_*(kGe)$
is isomorphic to a matrix algebra over a quantised version of the associated graded of the group algebra of the group
![]() $P\rtimes (Z(H)/Z)$
. Specialising to the case
$P\rtimes (Z(H)/Z)$
. Specialising to the case
![]() $\alpha =0 $
, we get a presentation of
$\alpha =0 $
, we get a presentation of
![]() $\mathsf {gr}_*(k (P \rtimes L))$
, which we have not seen before in the literature (see Remark 3.12). The exact relations are stated in Theorem 3.8; see also Theorems 3.11 and 3.14 and Corollary 3.15. We then show that this may be ungraded to exhibit the basic algebra of
$\mathsf {gr}_*(k (P \rtimes L))$
, which we have not seen before in the literature (see Remark 3.12). The exact relations are stated in Theorem 3.8; see also Theorems 3.11 and 3.14 and Corollary 3.15. We then show that this may be ungraded to exhibit the basic algebra of
![]() $kGe$
as a quantised version of the group algebra of
$kGe$
as a quantised version of the group algebra of
![]() $P\rtimes (Z(H)/Z)$
(see Section 4).
$P\rtimes (Z(H)/Z)$
(see Section 4).
In Section 5, in order to illustrate the main results, we explicitly calculate the following examples of blocks with a normal extraspecial defect group of order
![]() $p^3$
and exponent p having a single isomorphism class of simple modules.
$p^3$
and exponent p having a single isomorphism class of simple modules.
Theorem 1.2. Suppose that p is odd. Let P be an extraspecial group of order
![]() $p^3$
and exponent p, let H be a quaternion group of order
$p^3$
and exponent p, let H be a quaternion group of order
![]() $8$
acting on P with
$8$
acting on P with
![]() $Z(H)$
acting trivially, and with the two generators of H inverting the two generators of P. Set
$Z(H)$
acting trivially, and with the two generators of H inverting the two generators of P. Set
![]() $G = P\rtimes H$
. The basic algebra of the associated graded
$G = P\rtimes H$
. The basic algebra of the associated graded
![]() $\mathsf {gr}_*(kP)$
of
$\mathsf {gr}_*(kP)$
of
![]() $kP$
is given by generators x, y, z, subject to the relations
$kP$
is given by generators x, y, z, subject to the relations
(these imply
![]() $z^p=0$
), while the basic algebra of the associated graded
$z^p=0$
), while the basic algebra of the associated graded
![]() $\mathsf {gr}_*(kGe)$
of the nonprincipal block e of
$\mathsf {gr}_*(kGe)$
of the nonprincipal block e of
![]() $kG$
is given by generators
$kG$
is given by generators
![]() $\mathsf {x}$
,
$\mathsf {x}$
,
![]() $\mathsf {y}$
,
$\mathsf {y}$
,
![]() $\mathsf {z}$
, subject to the relations
$\mathsf {z}$
, subject to the relations
(these imply
![]() $\mathsf {z}^p=0$
).
$\mathsf {z}^p=0$
).
In the case
![]() $p=3$
, we can be more precise and explicitly describe the algebra
$p=3$
, we can be more precise and explicitly describe the algebra
![]() $kP$
and a basic algebra of
$kP$
and a basic algebra of
![]() $kGe$
by ‘ungrading’ the previous Theorem.
$kGe$
by ‘ungrading’ the previous Theorem.
Theorem 1.3. With the notation of the previous theorem, assume that
![]() $p=3$
. The algebra
$p=3$
. The algebra
![]() $kP$
is given by generators
$kP$
is given by generators
![]() $\tilde x$
,
$\tilde x$
,
![]() $\tilde y$
,
$\tilde y$
,
![]() $\tilde z$
, subject to the relations
$\tilde z$
, subject to the relations
(these imply
![]() $\tilde z^3=0$
), while a basic algebra of
$\tilde z^3=0$
), while a basic algebra of
![]() $kGe$
is given by generators
$kGe$
is given by generators
![]() $\tilde {\mathsf {x}}$
,
$\tilde {\mathsf {x}}$
,
![]() $\tilde {\mathsf {y}}$
,
$\tilde {\mathsf {y}}$
,
![]() $\tilde {\mathsf {z}}$
, subject to the relations
$\tilde {\mathsf {z}}$
, subject to the relations
(these imply
![]() $\tilde {\mathsf {z}}^3=0$
).
$\tilde {\mathsf {z}}^3=0$
).
In Section 6, we give an example in characteristic two, with P an extraspecial group of order
![]() $2^{1+4}$
and H an extraspecial group of order
$2^{1+4}$
and H an extraspecial group of order
![]() $3^{1+2}$
.
$3^{1+2}$
.
Finally, the appendix contains some corrections to the calculations in [Reference Benson, Kessar and Linckelmann4].
Notation. The bracket
![]() $[-,-]$
is used in three different ways, depending on the context: as commutator
$[-,-]$
is used in three different ways, depending on the context: as commutator
![]() $[g,h]=ghg^{-1}h^{-1}$
for elements g, h in a multiplicatively written group, as Lie bracket in a Lie algebra, and as additive commutator
$[g,h]=ghg^{-1}h^{-1}$
for elements g, h in a multiplicatively written group, as Lie bracket in a Lie algebra, and as additive commutator
![]() $[a,b]=ab-ba$
for elements a, b in an associative algebra.
$[a,b]=ab-ba$
for elements a, b in an associative algebra.
2 The associated graded
We denote by
![]() $J(A)$
the Jacobson radical of a finite-dimensional k-algebra A, and by
$J(A)$
the Jacobson radical of a finite-dimensional k-algebra A, and by
![]() $J^n(A)$
the powers of this ideal; we adopt the convention that
$J^n(A)$
the powers of this ideal; we adopt the convention that
![]() $J^0(A)=A$
. The associated graded of A is the graded algebra
$J^0(A)=A$
. The associated graded of A is the graded algebra
with the summands
![]() $J^n(A)/J^{n+1}(A)$
in degree n. The image in
$J^n(A)/J^{n+1}(A)$
in degree n. The image in
![]() $A/J(A)$
of a block idempotent of A is a block idempotent of
$A/J(A)$
of a block idempotent of A is a block idempotent of
![]() $\mathsf {gr}_*(A)$
, and this induces a bijection between the blocks of A and the blocks of
$\mathsf {gr}_*(A)$
, and this induces a bijection between the blocks of A and the blocks of
![]() $\mathsf {gr}_*(A)$
. Similarly, the image in
$\mathsf {gr}_*(A)$
. Similarly, the image in
![]() $A/J(A)$
of a primitive idempotent of A is a primitive idempotent in
$A/J(A)$
of a primitive idempotent of A is a primitive idempotent in
![]() $\mathsf {gr}_*(A)$
. It follows that A and
$\mathsf {gr}_*(A)$
. It follows that A and
![]() $\mathsf {gr}_*(A)$
have the same quiver.
$\mathsf {gr}_*(A)$
have the same quiver.
Let P be a finite p-group, let L be an abelian
![]() $p'$
-subgroup of
$p'$
-subgroup of
![]() $\mathsf {Aut}(P)$
and let
$\mathsf {Aut}(P)$
and let
![]() $\alpha \in H^2(L, k^{\times })$
. Since k is algebraically closed, the canonical group homomorphism
$\alpha \in H^2(L, k^{\times })$
. Since k is algebraically closed, the canonical group homomorphism
![]() $Z^2(L,k^{\times })\to H^2(L,k^{\times })$
splits (see, for example, Theorem 11.15 of Isaacs [Reference Isaacs10]). Thus, we may represent
$Z^2(L,k^{\times })\to H^2(L,k^{\times })$
splits (see, for example, Theorem 11.15 of Isaacs [Reference Isaacs10]). Thus, we may represent
![]() $\alpha $
by a
$\alpha $
by a
![]() $2$
-cocycle having the same order in
$2$
-cocycle having the same order in
![]() $Z^2(L,k^{\times })$
as its image in
$Z^2(L,k^{\times })$
as its image in
![]() $H^2(L,k^{\times })$
, still denoted by
$H^2(L,k^{\times })$
, still denoted by
![]() $\alpha $
. Such a choice of
$\alpha $
. Such a choice of
![]() $\alpha $
yields a central
$\alpha $
yields a central
![]() $p'$
-extension
$p'$
-extension
and a faithful character
![]() $\chi \colon Z \to k^{\times }$
, such that
$\chi \colon Z \to k^{\times }$
, such that
![]() $Z = [H,H]$
and such that, for some choice of inverse images
$Z = [H,H]$
and such that, for some choice of inverse images
![]() $\hat x$
in H for all x, we have
$\hat x$
in H for all x, we have
for all x,
![]() $y\in L$
. Moreover,
$y\in L$
. Moreover,
![]() $|Z|$
is equal to the order of
$|Z|$
is equal to the order of
![]() $\alpha $
in
$\alpha $
in
![]() $H^2(L,k^{\times })$
; that is, the subgroup of
$H^2(L,k^{\times })$
; that is, the subgroup of
![]() $k^{\times }$
generated by the values of
$k^{\times }$
generated by the values of
![]() $\alpha $
is equal to
$\alpha $
is equal to
![]() $\chi (Z)$
.
$\chi (Z)$
.
Set
![]() $G = P \rtimes H$
, where H acts on P via the canonical map
$G = P \rtimes H$
, where H acts on P via the canonical map
![]() $H\to L$
, so that
$H\to L$
, so that
![]() $Z= C_H(P)\leqslant Z(H)$
, and hence
$Z= C_H(P)\leqslant Z(H)$
, and hence
![]() $Z\leqslant Z(G)$
. Thus, the idempotent
$Z\leqslant Z(G)$
. Thus, the idempotent
 $$\begin{align*}e=\frac{1}{|Z|}\sum_{z\in Z}\chi(z^{-1})z \end{align*}$$
$$\begin{align*}e=\frac{1}{|Z|}\sum_{z\in Z}\chi(z^{-1})z \end{align*}$$
is a nonprincipal block of
![]() $kG$
, and the canonical surjection
$kG$
, and the canonical surjection
![]() $G\to P\rtimes L$
with kernel Z induces an algebra isomorphism
$G\to P\rtimes L$
with kernel Z induces an algebra isomorphism
where
![]() $\alpha $
is inflated to
$\alpha $
is inflated to
![]() $P\rtimes L$
via the canonical surjection
$P\rtimes L$
via the canonical surjection
![]() $P\rtimes L\to L$
.
$P\rtimes L\to L$
.
We wish to describe
![]() $kGe$
. This being difficult, we tackle first the associated graded algebra
$kGe$
. This being difficult, we tackle first the associated graded algebra
Our goal is to give an explicit presentation of this as a quantum deformation of the corresponding associated graded for the (untwisted) group algebra
![]() $k(P \rtimes Z(H)/Z)$
.
$k(P \rtimes Z(H)/Z)$
.
First, we recall the Jennings–Quillen theorem [Reference Jennings12, Reference Quillen14] for the associated graded of
![]() $kP$
. Our treatment follows Section 3.14 of [Reference Benson2]. For
$kP$
. Our treatment follows Section 3.14 of [Reference Benson2]. For
![]() $r\geqslant 1$
, we have dimension subgroups
$r\geqslant 1$
, we have dimension subgroups
Thus,
![]() $F_1(P)=P$
,
$F_1(P)=P$
,
![]() $F_2(P)=\Phi (P)$
,
$F_2(P)=\Phi (P)$
,
![]() $[F_r(P),F_s(P)]\subseteq F_{r+s}(P)$
and if
$[F_r(P),F_s(P)]\subseteq F_{r+s}(P)$
and if
![]() $g\in F_r(P)$
, then
$g\in F_r(P)$
, then
![]() $g^p\in F_{pr}(P)$
. Furthermore,
$g^p\in F_{pr}(P)$
. Furthermore,
![]() $F_r(P)$
is the most rapidly descending central series with these properties. Define
$F_r(P)$
is the most rapidly descending central series with these properties. Define
Then
![]() $\mathsf {Jen}_*(P)$
is a p-restricted Lie algebra with Lie bracket induced by taking commutators in P and pth power map coming from taking pth powers in P. As a restricted Lie algebra,
$\mathsf {Jen}_*(P)$
is a p-restricted Lie algebra with Lie bracket induced by taking commutators in P and pth power map coming from taking pth powers in P. As a restricted Lie algebra,
![]() $\mathsf {Jen}_*(P)$
is generated by its degree one elements because the subgroups
$\mathsf {Jen}_*(P)$
is generated by its degree one elements because the subgroups
![]() $F_r(P)$
form the lowest central series with the properties mentioned above. Let
$F_r(P)$
form the lowest central series with the properties mentioned above. Let
![]() $\mathcal {U}\mathsf {Jen}_*(P)$
be the restricted universal enveloping algebra of
$\mathcal {U}\mathsf {Jen}_*(P)$
be the restricted universal enveloping algebra of
![]() $\mathsf {Jen}_*(P)$
over k. As an associative algebra,
$\mathsf {Jen}_*(P)$
over k. As an associative algebra,
![]() $\mathcal {U}\mathsf {Jen}_*(P)$
is generated by its degree one elements. The commutator
$\mathcal {U}\mathsf {Jen}_*(P)$
is generated by its degree one elements. The commutator
![]() $[g,h]$
of two elements g,
$[g,h]$
of two elements g,
![]() $h\in P$
becomes the Lie bracket of the images of g, h in
$h\in P$
becomes the Lie bracket of the images of g, h in
![]() $\mathsf {Jen}_*(P)$
, and the image of that Lie bracket in
$\mathsf {Jen}_*(P)$
, and the image of that Lie bracket in
![]() $\mathcal {U}\mathsf {Jen}_*(P)$
is in turn equal to the additive commutator of the images of g, h in the associative algebra
$\mathcal {U}\mathsf {Jen}_*(P)$
is in turn equal to the additive commutator of the images of g, h in the associative algebra
![]() $\mathcal {U}\mathsf {Jen}_*(P)$
.
$\mathcal {U}\mathsf {Jen}_*(P)$
.
The Jennings–Quillen theorem states that there is a k-algebra isomorphism
which, for any r and any
![]() $g\in F_r(P)$
, sends the image of
$g\in F_r(P)$
, sends the image of
![]() $g $
in
$g $
in
![]() $F_r(P)/F_{r+1} (P) $
to the image of
$F_r(P)/F_{r+1} (P) $
to the image of
![]() $g-1$
in
$g-1$
in
![]() $\mathsf {gr}_*(kP)$
.
$\mathsf {gr}_*(kP)$
.
The group action of H on P induces an action of H on
![]() $\mathsf {Jen}_*(P)$
as a restricted Lie algebra because the Lie bracket in
$\mathsf {Jen}_*(P)$
as a restricted Lie algebra because the Lie bracket in
![]() $\mathsf {Jen}_*(P)$
is induced by taking commutators in P, and the p-power map in
$\mathsf {Jen}_*(P)$
is induced by taking commutators in P, and the p-power map in
![]() $\mathsf {Jen}_*(P)$
is induced by taking p-th powers in P. The Jennings–Quillen map is equivariant with respect to H and therefore extends to an isomorphism
$\mathsf {Jen}_*(P)$
is induced by taking p-th powers in P. The Jennings–Quillen map is equivariant with respect to H and therefore extends to an isomorphism
where the second isomorphism uses the fact that
![]() $J(kG)=J(kP)kG=kGJ(kP)$
since H is a
$J(kG)=J(kP)kG=kGJ(kP)$
since H is a
![]() $p'$
-group (cf. [Reference Semmen16, Theorem 4]). Since we have a canonical bijection between the blocks of
$p'$
-group (cf. [Reference Semmen16, Theorem 4]). Since we have a canonical bijection between the blocks of
![]() $kG$
and the blocks of
$kG$
and the blocks of
![]() $\mathsf {gr}_*(kG)$
as described at the beginning of this section, it follows that the blocks of both
$\mathsf {gr}_*(kG)$
as described at the beginning of this section, it follows that the blocks of both
![]() $kG$
and
$kG$
and
![]() $\mathsf {gr}_*(kG)$
are the idempotents in
$\mathsf {gr}_*(kG)$
are the idempotents in
![]() $kZ$
.
$kZ$
.
Remark 2.1. If e is an idempotent in
![]() $kH$
, then the restriction of the projective module
$kH$
, then the restriction of the projective module
![]() $kGe$
to P is a direct sum of
$kGe$
to P is a direct sum of
![]() $\dim _k(kHe)$
copies of
$\dim _k(kHe)$
copies of
![]() $kP$
. Furthermore, the radical layers of
$kP$
. Furthermore, the radical layers of
![]() $kGe$
as a
$kGe$
as a
![]() $kG$
-module are the same as the radical layers as a
$kG$
-module are the same as the radical layers as a
![]() $kP$
-module. So we have
$kP$
-module. So we have
 $$ \begin{align*} \sum_{i\geqslant 0} \dim_k J^i(kGe)/J^{i+1}(kGe)&=\dim_k(kHe). \sum_{i\geqslant 0}\dim_k J^i(kP)/J^{i+1}(kP) \\ &=\dim_k(kHe).\prod_r\left(\frac{1-t^{pr}}{1-t^r}\right)^{\dim_k\mathsf{Jen}_r(P)}. \end{align*} $$
$$ \begin{align*} \sum_{i\geqslant 0} \dim_k J^i(kGe)/J^{i+1}(kGe)&=\dim_k(kHe). \sum_{i\geqslant 0}\dim_k J^i(kP)/J^{i+1}(kP) \\ &=\dim_k(kHe).\prod_r\left(\frac{1-t^{pr}}{1-t^r}\right)^{\dim_k\mathsf{Jen}_r(P)}. \end{align*} $$
It can also be seen by restriction to P that if e is a central idempotent in
![]() $kH$
, then the associated graded
$kH$
, then the associated graded
![]() $\mathsf {gr}_*(kGe)$
of the algebra
$\mathsf {gr}_*(kGe)$
of the algebra
![]() $kGe$
is generated by its degree zero and degree one elements.
$kGe$
is generated by its degree zero and degree one elements.
Remark 2.2. The algebra
![]() $\mathcal {U}\mathsf {Jen}_*(P)$
is a finite dimensional cocommutative Hopf algebra, which defines a connected unipotent finite group scheme
$\mathcal {U}\mathsf {Jen}_*(P)$
is a finite dimensional cocommutative Hopf algebra, which defines a connected unipotent finite group scheme
![]() $\mathcal {P}$
whose group algebra is
$\mathcal {P}$
whose group algebra is
![]() $k\mathcal {P}\cong \mathcal {U}\mathsf {Jen}_*(P)$
. The finite group H acts as automorphism on
$k\mathcal {P}\cong \mathcal {U}\mathsf {Jen}_*(P)$
. The finite group H acts as automorphism on
![]() $\mathcal {P}$
, so we may form the semidirect product
$\mathcal {P}$
, so we may form the semidirect product
![]() $\mathcal {G} = \mathcal {P} \rtimes H$
, which is again a finite group scheme.
$\mathcal {G} = \mathcal {P} \rtimes H$
, which is again a finite group scheme.
3 The quantum relations
In this section, we define an algebra
![]() $\mathfrak {A}$
, which will turn out to be a basic algebra for
$\mathfrak {A}$
, which will turn out to be a basic algebra for
![]() $\mathsf {gr}_*(kGe)$
. The quantum commutation rules for
$\mathsf {gr}_*(kGe)$
. The quantum commutation rules for
![]() $\mathfrak {A}$
are given in Theorem 3.8, and the fact that
$\mathfrak {A}$
are given in Theorem 3.8, and the fact that
![]() $\mathfrak {A}$
is indeed a basic algebra is shown in Corollary 3.15.
$\mathfrak {A}$
is indeed a basic algebra is shown in Corollary 3.15.
Recall that
![]() $Z=[H,H]$
, so that the irreducible characters
$Z=[H,H]$
, so that the irreducible characters
![]() $\mathsf {Irr}(H/Z)$
form an abelian group. By [Reference Benson, Kessar and Linckelmann4, Proposition 3.1], we have a bijection
$\mathsf {Irr}(H/Z)$
form an abelian group. By [Reference Benson, Kessar and Linckelmann4, Proposition 3.1], we have a bijection
between one-dimensional characters of
![]() $Z(H)$
lying over
$Z(H)$
lying over
![]() $\chi $
and irreducible characters of H lying over
$\chi $
and irreducible characters of H lying over
![]() $\chi $
, such that
$\chi $
, such that
![]() $\tau _{\phi }$
lies over
$\tau _{\phi }$
lies over
![]() $\phi $
. The characters
$\phi $
. The characters
![]() $\tau _{\phi }$
are fully ramified with respect to
$\tau _{\phi }$
are fully ramified with respect to
![]() $H/Z(H)$
; see, for example, [Reference Isaacs9, Theorem 2.7]. The central idempotent corresponding to
$H/Z(H)$
; see, for example, [Reference Isaacs9, Theorem 2.7]. The central idempotent corresponding to
![]() $\tau _{\phi }$
is
$\tau _{\phi }$
is
 $$\begin{align*}e_{\phi}=\frac{1}{|Z(H)|}\sum_{h\in Z(H)}\phi(h^{-1})h. \end{align*}$$
$$\begin{align*}e_{\phi}=\frac{1}{|Z(H)|}\sum_{h\in Z(H)}\phi(h^{-1})h. \end{align*}$$
Then
 $\displaystyle e = \sum _{\phi \in \mathsf {Irr}(Z(H)|\chi )} e_{\phi }$
, and hence
$\displaystyle e = \sum _{\phi \in \mathsf {Irr}(Z(H)|\chi )} e_{\phi }$
, and hence
 $$\begin{align*}kHe = \prod_{\phi\in\mathsf{Irr}(Z(H)|\chi)} kHe_{\phi}. \end{align*}$$
$$\begin{align*}kHe = \prod_{\phi\in\mathsf{Irr}(Z(H)|\chi)} kHe_{\phi}. \end{align*}$$
The factors
![]() $kHe_{\phi }$
are matrix algebras, corresponding to
$kHe_{\phi }$
are matrix algebras, corresponding to
![]() $\tau _{\phi }$
, all of the same dimension. An element
$\tau _{\phi }$
, all of the same dimension. An element
![]() $\xi $
of
$\xi $
of
![]() $\mathsf {Hom}(H/Z, k^{\times })$
induces an algebra automorphism of
$\mathsf {Hom}(H/Z, k^{\times })$
induces an algebra automorphism of
![]() $kHe$
sending
$kHe$
sending
![]() $he$
to
$he$
to
![]() $\xi (h)^{-1}he$
. This yields an action of
$\xi (h)^{-1}he$
. This yields an action of
![]() $\mathsf {Hom}(H/Z, k^{\times })$
on
$\mathsf {Hom}(H/Z, k^{\times })$
on
![]() $kHe$
by algebra automorphisms which in turn induces a permutation action of
$kHe$
by algebra automorphisms which in turn induces a permutation action of
![]() $\mathsf {Hom}(H/Z, k^{\times })$
on the set of factors
$\mathsf {Hom}(H/Z, k^{\times })$
on the set of factors
![]() $kHe_{\phi }$
. The stabiliser of any factor is the subgroup
$kHe_{\phi }$
. The stabiliser of any factor is the subgroup
![]() $\mathsf {Irr}(H/Z(H) ) $
of
$\mathsf {Irr}(H/Z(H) ) $
of
![]() $\mathsf {Irr}(H/Z) $
, and elements of
$\mathsf {Irr}(H/Z) $
, and elements of
![]() $\mathsf {Irr}(H/Z(H) ) $
act as inner automorphisms on each factor.
$\mathsf {Irr}(H/Z(H) ) $
act as inner automorphisms on each factor.
Choose
![]() $\phi _0\in \mathsf {Irr}(Z(H)|\chi )$
, and set
$\phi _0\in \mathsf {Irr}(Z(H)|\chi )$
, and set
![]() $\tau =\tau _{\phi _0}$
. For each
$\tau =\tau _{\phi _0}$
. For each
![]() $\phi \in \mathsf {Irr} (Z(H)| \chi ) $
, choose a one-dimensional representation
$\phi \in \mathsf {Irr} (Z(H)| \chi ) $
, choose a one-dimensional representation
![]() $\xi _{\phi } \in \mathsf {Irr}( H/Z) $
inflated to H whose restriction to
$\xi _{\phi } \in \mathsf {Irr}( H/Z) $
inflated to H whose restriction to
![]() $Z(H)$
is
$Z(H)$
is
![]() $\phi \phi _0^{-1}$
, and so that
$\phi \phi _0^{-1}$
, and so that
![]() $\xi _{\phi _0}=1$
. The
$\xi _{\phi _0}=1$
. The
![]() $\xi _{\phi } $
form a set of coset representatives of
$\xi _{\phi } $
form a set of coset representatives of
![]() $\mathsf {Irr}(H/Z(H) )$
in
$\mathsf {Irr}(H/Z(H) )$
in
![]() $\mathsf {Irr}( H/Z) $
. The algebra automorphism induced by
$\mathsf {Irr}( H/Z) $
. The algebra automorphism induced by
![]() $\xi _{\phi } $
sends
$\xi _{\phi } $
sends
![]() $e_{\phi _0}$
to
$e_{\phi _0}$
to
![]() $e_{\phi }$
, and hence restricts to an algebra isomorphism
$e_{\phi }$
, and hence restricts to an algebra isomorphism
sending
![]() $he_{\phi _0}$
to
$he_{\phi _0}$
to
![]() $\xi _{\phi }(h)^{-1}ee_{\phi }$
. Taking the product over all
$\xi _{\phi }(h)^{-1}ee_{\phi }$
. Taking the product over all
![]() $\phi $
yields a unital injective algebra homomorphism
$\phi $
yields a unital injective algebra homomorphism
sending
![]() $he_{\phi _0}$
to
$he_{\phi _0}$
to
![]() $\sum _{\phi \in \mathsf {Irr}(Z(H)|\chi )}\ \xi _{\phi }(h)^{-1}he_{\phi }$
. By the above, this homomorphism depends on the choice of the
$\sum _{\phi \in \mathsf {Irr}(Z(H)|\chi )}\ \xi _{\phi }(h)^{-1}he_{\phi }$
. By the above, this homomorphism depends on the choice of the
![]() $\xi _{\phi }$
, but only up to inner automorphisms of
$\xi _{\phi }$
, but only up to inner automorphisms of
![]() $kHe$
. We write
$kHe$
. We write
![]() $\mathfrak {M}$
for the image in
$\mathfrak {M}$
for the image in
![]() $kHe$
of the matrix algebra
$kHe$
of the matrix algebra
![]() $kHe_{\phi _0}$
under this algebra homomorphism. This is a unital matrix subalgebra in
$kHe_{\phi _0}$
under this algebra homomorphism. This is a unital matrix subalgebra in
![]() $kHe$
.
$kHe$
.
We have a canonical homomorphism
![]() $\rho \colon H \to \mathsf {Hom}(H,k^{\times })$
sending g to
$\rho \colon H \to \mathsf {Hom}(H,k^{\times })$
sending g to
![]() $\rho (g)\colon h \mapsto \chi ([h,g])$
. The kernel of this homomorphism is
$\rho (g)\colon h \mapsto \chi ([h,g])$
. The kernel of this homomorphism is
![]() $Z(H)$
, and its image is
$Z(H)$
, and its image is
![]() $\mathsf {Hom}(H/Z(H),k^{\times })$
. For each
$\mathsf {Hom}(H/Z(H),k^{\times })$
. For each
![]() $\psi \in \mathsf {Irr} (H/Z) $
and each
$\psi \in \mathsf {Irr} (H/Z) $
and each
![]() $\phi \in \mathsf {Irr} (Z(H)|\chi ) $
, we write for simplicity
$\phi \in \mathsf {Irr} (Z(H)|\chi ) $
, we write for simplicity
![]() $\phi \psi $
instead of
$\phi \psi $
instead of
![]() $\phi \,(\psi \vert _{Z(H)})$
. Then,
$\phi \,(\psi \vert _{Z(H)})$
. Then,
![]() $\xi _{\phi \psi }\xi _{\phi }^{-1}\psi ^{-1}$
is trivial on
$\xi _{\phi \psi }\xi _{\phi }^{-1}\psi ^{-1}$
is trivial on
![]() $Z(H)$
. So there exists an element
$Z(H)$
. So there exists an element
![]() $g_{\psi , \phi }\in H$
such that
$g_{\psi , \phi }\in H$
such that
or equivalently, such that
for all
![]() $h\in H$
. We choose such elements
$h\in H$
. We choose such elements
![]() $g_{\psi ,\phi }$
, one for each
$g_{\psi ,\phi }$
, one for each
![]() $\psi $
and
$\psi $
and
![]() $\phi $
. Note that these elements are unique up to multiplication by elements in
$\phi $
. Note that these elements are unique up to multiplication by elements in
![]() $Z(H)$
.
$Z(H)$
.
For any
![]() $\psi , \eta \in \mathsf {Irr}(H/Z) $
and any
$\psi , \eta \in \mathsf {Irr}(H/Z) $
and any
![]() $\phi \in \mathsf {Irr} (Z(H)| \chi ) $
, we have
$\phi \in \mathsf {Irr} (Z(H)| \chi ) $
, we have
Lemma 3.1. Let
![]() $\psi _i, \eta _j \in \mathsf {Irr} (H/Z) $
,
$\psi _i, \eta _j \in \mathsf {Irr} (H/Z) $
,
![]() $\phi _i, \zeta _j \in \mathsf {Irr}(Z(H) |\chi ) $
,
$\phi _i, \zeta _j \in \mathsf {Irr}(Z(H) |\chi ) $
,
![]() $ 1\leqslant i \leqslant m $
,
$ 1\leqslant i \leqslant m $
,
![]() $ 1\leqslant j \leqslant n $
. Suppose that
$ 1\leqslant j \leqslant n $
. Suppose that
![]() $\phi _i = \phi _{i-1} \psi _{i-1} $
for all
$\phi _i = \phi _{i-1} \psi _{i-1} $
for all
![]() $ 2 \leqslant i \leqslant m $
. Then
$ 2 \leqslant i \leqslant m $
. Then
-
(i)
 $ g_{\psi _m, \phi _m} \ldots g_{\psi _1, \phi _1} = g _{\psi _m \cdots \psi _1, \phi _1} z $
for some
$ g_{\psi _m, \phi _m} \ldots g_{\psi _1, \phi _1} = g _{\psi _m \cdots \psi _1, \phi _1} z $
for some
 $ z \in Z(H)$
.
$ z \in Z(H)$
. -
(ii) Suppose further that
 $\zeta _j = \zeta _{j-1} \psi _{j-1} $
for all
$\zeta _j = \zeta _{j-1} \psi _{j-1} $
for all
 $ 2 \leqslant j\leqslant n $
,
$ 2 \leqslant j\leqslant n $
,
 $\phi _1= \zeta _1 $
and
$\phi _1= \zeta _1 $
and
 $\psi _m \ldots \psi _1 = \eta _n \ldots \eta _1 $
. Then
$\psi _m \ldots \psi _1 = \eta _n \ldots \eta _1 $
. Then
 $ g_{\psi _m, \phi _m} \ldots g_{\psi _1, \phi _1} = g_{\eta _n, \zeta _n} \ldots g_{\eta _1, \zeta _1} z' $
for some
$ g_{\psi _m, \phi _m} \ldots g_{\psi _1, \phi _1} = g_{\eta _n, \zeta _n} \ldots g_{\eta _1, \zeta _1} z' $
for some
 $z' \in Z(H)$
.
$z' \in Z(H)$
.
Proof. Since
![]() $Z =\mathsf {Ker} (\rho )$
, (i) follows by repeated application of the equation displayed above the lemma. Part (ii) follows from (i) applied to both
$Z =\mathsf {Ker} (\rho )$
, (i) follows by repeated application of the equation displayed above the lemma. Part (ii) follows from (i) applied to both
![]() $ g_{\psi _m, \phi _m} \ldots g_{\psi _1, \phi _1} $
and
$ g_{\psi _m, \phi _m} \ldots g_{\psi _1, \phi _1} $
and
![]() $g_{\eta _n, \zeta _n} \ldots g_{\eta _1, \zeta _1} $
.
$g_{\eta _n, \zeta _n} \ldots g_{\eta _1, \zeta _1} $
.
3.2. Since k is algebraically closed, we may choose a k-basis
![]() $w_1,\dots ,w_m$
of
$w_1,\dots ,w_m$
of
![]() $\mathsf {Jen}_*(P)$
, where
$\mathsf {Jen}_*(P)$
, where
![]() $p^m=|P|$
, consisting of homogeneous eigenvectors of the action of H. We arrange the indices in such a way that if
$p^m=|P|$
, consisting of homogeneous eigenvectors of the action of H. We arrange the indices in such a way that if
![]() $i\leqslant j$
, then
$i\leqslant j$
, then
![]() $\deg (w_i)\leqslant \deg (w_j)$
. Then for each
$\deg (w_i)\leqslant \deg (w_j)$
. Then for each
![]() $w_i$
, there is a character
$w_i$
, there is a character
![]() $\psi _i$
of L, inflated to H, such that
$\psi _i$
of L, inflated to H, such that
for
![]() $g\in H$
. Define structure constants
$g\in H$
. Define structure constants
![]() $c_{i,j,k}$
and
$c_{i,j,k}$
and
![]() $d_{i,k}$
for
$d_{i,k}$
for
![]() $\mathsf {Jen}_*(P)$
via
$\mathsf {Jen}_*(P)$
via
Here,
![]() $[w_i,w_j]$
denotes the Lie bracket and
$[w_i,w_j]$
denotes the Lie bracket and
![]() $w_i^{[p]}$
the p-restriction map in
$w_i^{[p]}$
the p-restriction map in
![]() $\mathsf {Jen}_*(P)$
. We have
$\mathsf {Jen}_*(P)$
. We have
It follows that if
![]() $c_{i,j,k}\ne 0$
, then
$c_{i,j,k}\ne 0$
, then
![]() $\psi _i\psi _j=\psi _k$
, and if
$\psi _i\psi _j=\psi _k$
, and if
![]() $d_{i,k}\ne 0$
, then
$d_{i,k}\ne 0$
, then
![]() $\psi _i^p=\psi _k$
.
$\psi _i^p=\psi _k$
.
By the Poincaré–Birkhoff–Witt (PBW) theorem for restricted Lie algebras (Jacobson [Reference Jacobson11], page 190), the algebra
![]() $\mathcal {U}\mathsf {Jen}_*(P)\cong \mathsf {gr}_*(kP)$
has a basis
$\mathcal {U}\mathsf {Jen}_*(P)\cong \mathsf {gr}_*(kP)$
has a basis
![]() $\mathcal {B}$
consisting of words
$\mathcal {B}$
consisting of words
![]() $w_{i_1} \dots w_{i_r}$
, where
$w_{i_1} \dots w_{i_r}$
, where
![]() $i_1\leqslant \dots \leqslant i_r$
, and each index is repeated at most
$i_1\leqslant \dots \leqslant i_r$
, and each index is repeated at most
![]() $p-1$
times (so we are writing
$p-1$
times (so we are writing
![]() $w_i^a $
as
$w_i^a $
as
![]() $w_i \dots w_i$
). We follow the convention that the empty word denotes the identity element in degree zero. The element
$w_i \dots w_i$
). We follow the convention that the empty word denotes the identity element in degree zero. The element
![]() $w_{i_1}\dots w_{i_r}$
is an eigenvector for the conjugation action of H, with character
$w_{i_1}\dots w_{i_r}$
is an eigenvector for the conjugation action of H, with character
![]() $\psi _{i_1}\dots \psi _{i_r}$
.
$\psi _{i_1}\dots \psi _{i_r}$
.
In what follows, we identify
![]() $\mathsf {Jen}_*(P)$
with its image in
$\mathsf {Jen}_*(P)$
with its image in
![]() $\mathcal {U}\mathsf {Jen}_*(P)\rtimes H$
. The calculations that follow are similar to those in Section 4 of [Reference Benson, Kessar and Linckelmann4] (with the corrections described in Section 7 below). For any
$\mathcal {U}\mathsf {Jen}_*(P)\rtimes H$
. The calculations that follow are similar to those in Section 4 of [Reference Benson, Kessar and Linckelmann4] (with the corrections described in Section 7 below). For any
![]() $\phi \in \mathsf {Irr}(Z(H)|\chi ) $
,
$\phi \in \mathsf {Irr}(Z(H)|\chi ) $
,
![]() $w_i $
a basis element of
$w_i $
a basis element of
![]() $\mathsf {Jen}_*(P)$
, with associated linear characters
$\mathsf {Jen}_*(P)$
, with associated linear characters
![]() $\psi _i$
, we write
$\psi _i$
, we write
![]() $g_{i, \phi }$
for the element
$g_{i, \phi }$
for the element
![]() $g_{\psi _i,\phi } $
.
$g_{\psi _i,\phi } $
.
Lemma 3.3. With the notation above, the following equations in
![]() $(\mathcal {U}\mathsf {Jen}_*(P)\rtimes H)e$
hold for all
$(\mathcal {U}\mathsf {Jen}_*(P)\rtimes H)e$
hold for all
![]() $h\in H$
, all basis elements
$h\in H$
, all basis elements
![]() $w_i$
of
$w_i$
of
![]() $\mathsf {Jen}_*(P)$
, the associated linear characters
$\mathsf {Jen}_*(P)$
, the associated linear characters
![]() $\psi _i\in \mathsf {Hom}(H,k^{\times })$
and all
$\psi _i\in \mathsf {Hom}(H,k^{\times })$
and all
![]() ${\phi \in \mathsf {Irr}(Z(H)|\chi )}$
.
${\phi \in \mathsf {Irr}(Z(H)|\chi )}$
.
-
(i)
 $w_i e_{\phi } = e_{\phi \psi _i} w_i$
.
$w_i e_{\phi } = e_{\phi \psi _i} w_i$
. -
(ii)
 $ (g_{i,\phi }w_i)(\xi _{\phi }(h)^{-1}e_{\phi }\, h) = (\xi _{\phi \psi _i}(h)^{-1}e_{\phi \psi _i}\, h)(g_{i,\phi }w_i). $
$ (g_{i,\phi }w_i)(\xi _{\phi }(h)^{-1}e_{\phi }\, h) = (\xi _{\phi \psi _i}(h)^{-1}e_{\phi \psi _i}\, h)(g_{i,\phi }w_i). $
-
(iii)
 $g_{i,\phi }w_ie_{\phi }=e_{\phi \psi _i}g_{i,\phi }w_i$
commutes with
$g_{i,\phi }w_ie_{\phi }=e_{\phi \psi _i}g_{i,\phi }w_i$
commutes with
 $\mathfrak {M}$
.
$\mathfrak {M}$
.
Proof. We have
![]() $hw_ih^{-1}= \psi _i(h)w_i$
, hence
$hw_ih^{-1}= \psi _i(h)w_i$
, hence
![]() $w_i h= \psi _i(h)^{-1} hw_i$
. Thus, if
$w_i h= \psi _i(h)^{-1} hw_i$
. Thus, if
![]() $h\in Z(H)$
, then
$h\in Z(H)$
, then
![]() ${\phi (h)^{-1}w_ih = \phi (h)^{-1}\psi _i(h)^{-1}hw_i}$
. Taking the sum over all
${\phi (h)^{-1}w_ih = \phi (h)^{-1}\psi _i(h)^{-1}hw_i}$
. Taking the sum over all
![]() $h\in Z(H)$
and dividing by
$h\in Z(H)$
and dividing by
![]() $|Z(H)|$
shows (i). Note that
$|Z(H)|$
shows (i). Note that
![]() $[g,h]e= \chi ([g,h])e$
for all g,
$[g,h]e= \chi ([g,h])e$
for all g,
![]() $h\in H$
. Thus
$h\in H$
. Thus
![]() $g_{i,\phi }he= \chi ([h,g_{i,\phi }])^{-1} hg_{i,\phi }e$
. It follows that
$g_{i,\phi }he= \chi ([h,g_{i,\phi }])^{-1} hg_{i,\phi }e$
. It follows that
where we have used (i). Note that
![]() $e_{\phi \psi _i}$
is central in
$e_{\phi \psi _i}$
is central in
![]() $kH$
. Using the definition of
$kH$
. Using the definition of
![]() $\rho $
, the scalar in the last expression is
$\rho $
, the scalar in the last expression is
![]() $\xi _{\phi \psi _i}(h)^{-1}$
. This shows (ii). The equality in (iii) is the special case of (ii) applied with
$\xi _{\phi \psi _i}(h)^{-1}$
. This shows (ii). The equality in (iii) is the special case of (ii) applied with
![]() $h=1$
. For the commutation with
$h=1$
. For the commutation with
![]() $\mathfrak {M}$
, we need to check that the elements in the statement commute with expressions of the form
$\mathfrak {M}$
, we need to check that the elements in the statement commute with expressions of the form
![]() $\sum _{\phi '} \xi _{\phi '}(h)^{-1}h e_{\phi '}$
. This follows easily using (ii) and the fact that the
$\sum _{\phi '} \xi _{\phi '}(h)^{-1}h e_{\phi '}$
. This follows easily using (ii) and the fact that the
![]() $e_{\phi }$
are pairwise orthogonal.
$e_{\phi }$
are pairwise orthogonal.
Definition 3.4. We define
![]() $\mathsf {w}_{i,\phi }=g_{i,\phi }w_ie_{\phi }$
and let
$\mathsf {w}_{i,\phi }=g_{i,\phi }w_ie_{\phi }$
and let
![]() $\mathfrak {A}$
be the subalgebra of
$\mathfrak {A}$
be the subalgebra of
![]() $(\mathcal {U}\mathsf {Jen}_*(P)\rtimes H)e$
generated by the elements
$(\mathcal {U}\mathsf {Jen}_*(P)\rtimes H)e$
generated by the elements
![]() $e_{\phi }$
and
$e_{\phi }$
and
![]() $\mathsf {w}_{i,\phi }$
.
$\mathsf {w}_{i,\phi }$
.
By Lemma 3.3, the subalgebras
![]() $\mathfrak {A}$
and
$\mathfrak {A}$
and
![]() $\mathfrak {M}$
of
$\mathfrak {M}$
of
![]() $(\mathcal {U}\mathsf {Jen}_*(P)\rtimes H)e$
commute.
$(\mathcal {U}\mathsf {Jen}_*(P)\rtimes H)e$
commute.
Lemma 3.5. The algebra
![]() $\mathfrak {A}$
is generated by the elements
$\mathfrak {A}$
is generated by the elements
![]() $e_{\phi }$
and
$e_{\phi }$
and
![]() $\mathsf {w}_{i,\phi }$
for those i such that the element
$\mathsf {w}_{i,\phi }$
for those i such that the element
![]() $w_i$
of
$w_i$
of
![]() $\mathsf {Jen}_*(P)$
has degree one.
$\mathsf {Jen}_*(P)$
has degree one.
Proof. Since
![]() $\mathsf {Jen}_*(P)$
is generated by elements in degree one, there exists a basis
$\mathsf {Jen}_*(P)$
is generated by elements in degree one, there exists a basis
![]() ${\mathcal V}$
of
${\mathcal V}$
of
![]() $ \mathcal {U}\mathsf {Jen}_*(P)$
consisting of a subset of the set of monomials in the degree one
$ \mathcal {U}\mathsf {Jen}_*(P)$
consisting of a subset of the set of monomials in the degree one
![]() $w_i $
’s. Let
$w_i $
’s. Let
![]() $ w_t$
be an arbitrary element of the chosen basis of
$ w_t$
be an arbitrary element of the chosen basis of
![]() $\mathsf {Jen}_*(P) $
and write
$\mathsf {Jen}_*(P) $
and write
If
![]() $u, u' \in \mathcal {U}\mathsf {Jen}_*(P) $
are eigenvectors for the H action corresponding to characters
$u, u' \in \mathcal {U}\mathsf {Jen}_*(P) $
are eigenvectors for the H action corresponding to characters
![]() $\psi $
and
$\psi $
and
![]() $\psi ' $
respectively, then
$\psi ' $
respectively, then
![]() $uu'$
is an H-eigenvector with corresponding character
$uu'$
is an H-eigenvector with corresponding character
![]() $\psi \psi ' $
. From this it follows that if a monomial
$\psi \psi ' $
. From this it follows that if a monomial
![]() $ v= w_{i_m} \ldots w_{i_1} $
in degree one elements
$ v= w_{i_m} \ldots w_{i_1} $
in degree one elements
![]() $w_{i_j} $
is an element of
$w_{i_j} $
is an element of
![]() $ {\mathcal V} $
such that
$ {\mathcal V} $
such that
![]() $\alpha _v \ne 0 $
, then
$\alpha _v \ne 0 $
, then
![]() $ \psi _t = \psi _{i_m} \ldots \psi _{i_1} $
, where for each j,
$ \psi _t = \psi _{i_m} \ldots \psi _{i_1} $
, where for each j,
![]() $1\leqslant j \leqslant m$
,
$1\leqslant j \leqslant m$
,
![]() $\psi _{i_j} \in \mathsf {Irr}( H/Z) $
is the character of H corresponding to the action on
$\psi _{i_j} \in \mathsf {Irr}( H/Z) $
is the character of H corresponding to the action on
![]() $w_{i_j} $
. Let
$w_{i_j} $
. Let
![]() $\zeta \in \mathsf {Irr}( Z(H) | \chi ) $
, and let v be as above. By Lemma 3.1,
$\zeta \in \mathsf {Irr}( Z(H) | \chi ) $
, and let v be as above. By Lemma 3.1,
where
![]() $ z \in Z(H) $
,
$ z \in Z(H) $
,
![]() $ \phi _1 = \zeta $
and
$ \phi _1 = \zeta $
and
![]() $ \phi _j = \phi _{j-1}\psi _{i_{j-1}}$
,
$ \phi _j = \phi _{j-1}\psi _{i_{j-1}}$
,
![]() $ 2\leqslant j \leqslant m $
. On the other hand
$ 2\leqslant j \leqslant m $
. On the other hand
![]() $w_{i_j} $
is an eigenvector for the H action,
$w_{i_j} $
is an eigenvector for the H action,
for some
![]() $\beta _v\in k^{\times } $
. Since
$\beta _v\in k^{\times } $
. Since
![]() $z e_{\zeta } $
is a nonzero scalar multiple of
$z e_{\zeta } $
is a nonzero scalar multiple of
![]() $e_{\zeta } $
, the above equation and Lemma 3.3 (iii) give that
$e_{\zeta } $
, the above equation and Lemma 3.3 (iii) give that
for some nonzero scalar
![]() $q_v$
. Since all
$q_v$
. Since all
![]() $w_{i_j} $
are in degree one, it follows that
$w_{i_j} $
are in degree one, it follows that
is a linear combination of monomials in the
![]() $\mathsf {w}_{i, \phi } $
for those i such that
$\mathsf {w}_{i, \phi } $
for those i such that
![]() $w_i $
has degree one.
$w_i $
has degree one.
Definition 3.6. We define elements
![]() $z_{i,j,\phi }$
,
$z_{i,j,\phi }$
,
![]() $z^{\prime }_{i,j,k,\phi }$
and
$z^{\prime }_{i,j,k,\phi }$
and
![]() $z^{\prime \prime }_{i,k,\phi }$
in
$z^{\prime \prime }_{i,k,\phi }$
in
![]() $Z(H)$
as follows. By Lemma 3.1 we have
$Z(H)$
as follows. By Lemma 3.1 we have
for some
![]() $z_{i,j,\phi }\in Z(H)$
. If
$z_{i,j,\phi }\in Z(H)$
. If
![]() $c_{i,j,k}\ne 0$
, then
$c_{i,j,k}\ne 0$
, then
for some
![]() $z^{\prime }_{i,j,k,\phi }\in Z(H)$
. If
$z^{\prime }_{i,j,k,\phi }\in Z(H)$
. If
![]() $d_{i,k}\ne 0$
, then
$d_{i,k}\ne 0$
, then
for some
![]() $z^{\prime \prime }_{i,k,\phi }\in Z(H)$
.
$z^{\prime \prime }_{i,k,\phi }\in Z(H)$
.
Remark 3.7. We have
Also, we have
![]() $z_{i,j,\phi }z_{j,i,\phi }=1$
, and if
$z_{i,j,\phi }z_{j,i,\phi }=1$
, and if
![]() $c_{i,j,k}\ne 0$
, then
$c_{i,j,k}\ne 0$
, then
![]() $z^{\prime }_{i,j,k,\phi }=z^{\prime }_{j,i,k,\phi }z_{i,j,\phi }$
.
$z^{\prime }_{i,j,k,\phi }=z^{\prime }_{j,i,k,\phi }z_{i,j,\phi }$
.
Theorem 3.8. Defining constants
 $$ \begin{align*} q_{i,j,\phi}&=\psi_i(g_{j,\phi}z_{i,j,\phi})\psi_j(g_{i,\phi}^{-1}z_{i,j,\phi})\phi(z_{i,j,\phi}), \\ q^{\prime}_{i,j,k,\phi}&=\psi_j(g_{i,\phi})^{-1}\psi_k(z^{\prime}_{i,j,k,\phi})\phi(z^{\prime}_{i,j,k,\phi}), \\ q^{\prime\prime}_{i,k,\phi}&=\psi_i(g_{i,\phi\psi_i^{p-2}})^{-1}\dots\psi_i(g_{i,\phi\psi_i})^{-p+2} \psi_i(g_{i,\phi})^{-p+1}\psi_k(z^{\prime\prime}_{i,k,\phi})\phi(z^{\prime\prime}_{i,k,\phi}) , \end{align*} $$
$$ \begin{align*} q_{i,j,\phi}&=\psi_i(g_{j,\phi}z_{i,j,\phi})\psi_j(g_{i,\phi}^{-1}z_{i,j,\phi})\phi(z_{i,j,\phi}), \\ q^{\prime}_{i,j,k,\phi}&=\psi_j(g_{i,\phi})^{-1}\psi_k(z^{\prime}_{i,j,k,\phi})\phi(z^{\prime}_{i,j,k,\phi}), \\ q^{\prime\prime}_{i,k,\phi}&=\psi_i(g_{i,\phi\psi_i^{p-2}})^{-1}\dots\psi_i(g_{i,\phi\psi_i})^{-p+2} \psi_i(g_{i,\phi})^{-p+1}\psi_k(z^{\prime\prime}_{i,k,\phi})\phi(z^{\prime\prime}_{i,k,\phi}) , \end{align*} $$
we have
By changing the choices of
![]() $g_{i,\phi }$
by elements of
$g_{i,\phi }$
by elements of
![]() $Z(H)$
, we may ensure that
$Z(H)$
, we may ensure that
![]() $z_{i,j,\phi }\in Z$
, and then the formula for the parameters
$z_{i,j,\phi }\in Z$
, and then the formula for the parameters
![]() $q_{i,j,\phi }$
simplifies to
$q_{i,j,\phi }$
simplifies to
Proof. We have
 $$ \begin{align*} \mathsf{w}_{j,\phi\psi_i}\mathsf{w}_{i,\phi}&= (g_{j,\phi\psi_i}w_je_{\phi\psi_i})(g_{i,\phi}w_ie_{\phi})\\ &=g_{j,\phi\psi_i}w_jg_{i,\phi}w_ie_{\phi} \\ &=\psi_j(g_{i,\phi})^{-1}g_{j,\phi\psi_i}g_{i,\phi}w_jw_ie_{\phi} \\ &=\psi_j(g_{i,\phi})^{-1}g_{j,\phi\psi_i}g_{i,\phi}(w_iw_j+[w_i,w_j])e_{\phi}\\ &=\psi_j(g_{i,\phi})^{-1}g_{i,\phi\psi_j}g_{j,\phi}z_{i,j,\phi}w_iw_je_{\phi} \\ &\qquad{}+\psi_j(g_{i,\phi})^{-1}g_{j,\phi\psi_i}g_{i,\phi}[w_i,w_j]e_{\phi}\\ &=\psi_j(g_{i,\phi})^{-1}\psi_i(z_{i,j,\phi})\psi_j(z_{i,j,\phi})g_{i,\phi\psi_j}g_{j,\phi}w_iw_jz_{i,j,\phi}e_{\phi} \\ &\qquad{}+\sum_kc_{i,j,k}\psi_j(g_{i,\phi})^{-1}g_{k,\phi}z^{\prime}_{i,j,k,\phi}w_ke_{\phi} \\ &=\psi_j(g_{i,\phi})^{-1}\psi_i(z_{i,j,\phi})\psi_j(z_{i,j,\phi})\psi_i(g_{j,\phi})\phi(z_{i,j,\phi})g_{i,\phi\psi_j}w_ig_{j,\phi}w_je_{\phi} \\ &\qquad{}+\sum_kc_{i,j,k}\psi_j(g_{i,\phi})^{-1}\psi_k(z^{\prime}_{i,j,k,\phi})g_{k,\phi}w_kz^{\prime}_{i,j,k,\phi}e_{\phi}\\ &=\psi_i(g_{j,\phi}z_{i,j,\phi})\psi_j(g^{-1}_{i,\phi}z_{i,j,\phi})\phi(z_{i,j,\phi})(g_{i,\phi\psi_j}w_ie_{\phi\psi_j})(g_{j,\phi}w_je_{\phi}) \\ &\qquad{}+\sum_kc_{i,j,k}\psi_j(g_{i,\phi})^{-1}\psi_k(z^{\prime}_{i,j,k,\phi})\phi(z^{\prime}_{i,j,k,\phi})g_{k,\phi} w_ke_{\phi}\\ &=q_{i,j,\phi}\mathsf{w}_{i,\phi\psi_j}\mathsf{w}_{j,\phi} +\sum_kc_{i,j,k}q^{\prime}_{i,j,k,\phi}\mathsf{w}_{k,\phi}. \end{align*} $$
$$ \begin{align*} \mathsf{w}_{j,\phi\psi_i}\mathsf{w}_{i,\phi}&= (g_{j,\phi\psi_i}w_je_{\phi\psi_i})(g_{i,\phi}w_ie_{\phi})\\ &=g_{j,\phi\psi_i}w_jg_{i,\phi}w_ie_{\phi} \\ &=\psi_j(g_{i,\phi})^{-1}g_{j,\phi\psi_i}g_{i,\phi}w_jw_ie_{\phi} \\ &=\psi_j(g_{i,\phi})^{-1}g_{j,\phi\psi_i}g_{i,\phi}(w_iw_j+[w_i,w_j])e_{\phi}\\ &=\psi_j(g_{i,\phi})^{-1}g_{i,\phi\psi_j}g_{j,\phi}z_{i,j,\phi}w_iw_je_{\phi} \\ &\qquad{}+\psi_j(g_{i,\phi})^{-1}g_{j,\phi\psi_i}g_{i,\phi}[w_i,w_j]e_{\phi}\\ &=\psi_j(g_{i,\phi})^{-1}\psi_i(z_{i,j,\phi})\psi_j(z_{i,j,\phi})g_{i,\phi\psi_j}g_{j,\phi}w_iw_jz_{i,j,\phi}e_{\phi} \\ &\qquad{}+\sum_kc_{i,j,k}\psi_j(g_{i,\phi})^{-1}g_{k,\phi}z^{\prime}_{i,j,k,\phi}w_ke_{\phi} \\ &=\psi_j(g_{i,\phi})^{-1}\psi_i(z_{i,j,\phi})\psi_j(z_{i,j,\phi})\psi_i(g_{j,\phi})\phi(z_{i,j,\phi})g_{i,\phi\psi_j}w_ig_{j,\phi}w_je_{\phi} \\ &\qquad{}+\sum_kc_{i,j,k}\psi_j(g_{i,\phi})^{-1}\psi_k(z^{\prime}_{i,j,k,\phi})g_{k,\phi}w_kz^{\prime}_{i,j,k,\phi}e_{\phi}\\ &=\psi_i(g_{j,\phi}z_{i,j,\phi})\psi_j(g^{-1}_{i,\phi}z_{i,j,\phi})\phi(z_{i,j,\phi})(g_{i,\phi\psi_j}w_ie_{\phi\psi_j})(g_{j,\phi}w_je_{\phi}) \\ &\qquad{}+\sum_kc_{i,j,k}\psi_j(g_{i,\phi})^{-1}\psi_k(z^{\prime}_{i,j,k,\phi})\phi(z^{\prime}_{i,j,k,\phi})g_{k,\phi} w_ke_{\phi}\\ &=q_{i,j,\phi}\mathsf{w}_{i,\phi\psi_j}\mathsf{w}_{j,\phi} +\sum_kc_{i,j,k}q^{\prime}_{i,j,k,\phi}\mathsf{w}_{k,\phi}. \end{align*} $$
Similarly,
 $$ \begin{align*} \mathsf{w}_{i,\phi\psi_i^{p-1}}&\dots \mathsf{w}_{i,\phi\psi_i}\mathsf{w}_{i,\phi} \\ &= (g_{i\phi\psi_i^{p-1}}w_ie_{\phi\psi_i^{p-1}})\dots (g_{i,\phi\psi_i}w_ie_{\phi\psi_i})(g_{i,\phi}w_ie_{\phi})\\ &=g_{i,\phi\psi_i^{p-1}}w_i\dots g_{i,\phi\psi_i}w_ig_{i,\phi}w_ie_{\phi} \\ &=\psi_i(g_{i,\phi\psi_i^{p-2}})^{-1}\dots\psi_i(g_{i,\phi\psi_i})^{-p+2} \psi_i(g_{i,\phi})^{-p+1}(g_{i,\phi\psi_i^{p-1}}\dots g_{i,\phi\psi_i}g_{i,\phi})w_i^pe_{\phi}\\ &=\sum_kd_{i,k}\psi_i(g_{i,\phi\psi_i^{p-2}})^{-1}\dots\psi_i(g_{i,\phi\psi_i})^{-p+2} \psi_i(g_{i,\phi})^{-p+1}g_{k,\phi}z^{\prime\prime}_{i,k,\phi}w_ke_{\phi}\\ &=\sum_kd_{i,k}\psi_i(g_{i,\phi\psi_i^{p-2}})^{-1}\dots\psi_i(g_{i,\phi\psi_i})^{-p+2} \psi_i(g_{i,\phi})^{-p+1}\psi_k(z^{\prime\prime}_{i,k,\phi})g_{k,\phi}w_kz^{\prime\prime}_{i,k,\phi}e_{\phi}\\ &=\sum_kd_{i,k}\psi_i(g_{i,\phi\psi_i^{p-2}})^{-1}\dots\psi_i(g_{i,\phi\psi_i})^{-p+2} \psi_i(g_{i,\phi})^{-p+1}\psi_k(z^{\prime\prime}_{i,k,\phi})\phi(z^{\prime\prime}_{i,k,\phi})g_{k,\phi}w_ke_{\phi}\\ &=\sum_k d_{i,k}q^{\prime\prime}_{i,k,\phi}\mathsf{w}_{k,\phi}. \end{align*} $$
$$ \begin{align*} \mathsf{w}_{i,\phi\psi_i^{p-1}}&\dots \mathsf{w}_{i,\phi\psi_i}\mathsf{w}_{i,\phi} \\ &= (g_{i\phi\psi_i^{p-1}}w_ie_{\phi\psi_i^{p-1}})\dots (g_{i,\phi\psi_i}w_ie_{\phi\psi_i})(g_{i,\phi}w_ie_{\phi})\\ &=g_{i,\phi\psi_i^{p-1}}w_i\dots g_{i,\phi\psi_i}w_ig_{i,\phi}w_ie_{\phi} \\ &=\psi_i(g_{i,\phi\psi_i^{p-2}})^{-1}\dots\psi_i(g_{i,\phi\psi_i})^{-p+2} \psi_i(g_{i,\phi})^{-p+1}(g_{i,\phi\psi_i^{p-1}}\dots g_{i,\phi\psi_i}g_{i,\phi})w_i^pe_{\phi}\\ &=\sum_kd_{i,k}\psi_i(g_{i,\phi\psi_i^{p-2}})^{-1}\dots\psi_i(g_{i,\phi\psi_i})^{-p+2} \psi_i(g_{i,\phi})^{-p+1}g_{k,\phi}z^{\prime\prime}_{i,k,\phi}w_ke_{\phi}\\ &=\sum_kd_{i,k}\psi_i(g_{i,\phi\psi_i^{p-2}})^{-1}\dots\psi_i(g_{i,\phi\psi_i})^{-p+2} \psi_i(g_{i,\phi})^{-p+1}\psi_k(z^{\prime\prime}_{i,k,\phi})g_{k,\phi}w_kz^{\prime\prime}_{i,k,\phi}e_{\phi}\\ &=\sum_kd_{i,k}\psi_i(g_{i,\phi\psi_i^{p-2}})^{-1}\dots\psi_i(g_{i,\phi\psi_i})^{-p+2} \psi_i(g_{i,\phi})^{-p+1}\psi_k(z^{\prime\prime}_{i,k,\phi})\phi(z^{\prime\prime}_{i,k,\phi})g_{k,\phi}w_ke_{\phi}\\ &=\sum_k d_{i,k}q^{\prime\prime}_{i,k,\phi}\mathsf{w}_{k,\phi}. \end{align*} $$
For the final remark, just as in Lemma 4.12 (3) of [Reference Benson, Kessar and Linckelmann4], we may change the choices of
![]() $g_{i,\phi }$
by elements of
$g_{i,\phi }$
by elements of
![]() $Z(H)$
to ensure that
$Z(H)$
to ensure that
![]() $z_{i,j,\phi }\in Z$
, with the same argument. Then the characters
$z_{i,j,\phi }\in Z$
, with the same argument. Then the characters
![]() $\psi _i$
take value one on these elements, leading to the given simplifications of the constants.
$\psi _i$
take value one on these elements, leading to the given simplifications of the constants.
Recall that by Lemma 3.5,
![]() $ \mathfrak {A}$
is generated by the
$ \mathfrak {A}$
is generated by the
![]() $e_{\phi }$
and the
$e_{\phi }$
and the
![]() $\mathsf {w}_{i, \phi } $
for those i such that the element
$\mathsf {w}_{i, \phi } $
for those i such that the element
![]() $w_i$
of
$w_i$
of
![]() $\mathsf {Jen}_*(P)$
has degree one.
$\mathsf {Jen}_*(P)$
has degree one.
Theorem 3.11. The algebra
![]() $\mathfrak {A}$
is given as a quiver with relations
$\mathfrak {A}$
is given as a quiver with relations
![]() $kQ/I$
, where Q is the quiver with
$kQ/I$
, where Q is the quiver with
![]() $|Z(H):Z|$
vertices labelled
$|Z(H):Z|$
vertices labelled
![]() $[\phi ]$
corresponding to the idempotents
$[\phi ]$
corresponding to the idempotents
![]() $e_{\phi } \in kZ(H)$
lying over
$e_{\phi } \in kZ(H)$
lying over
![]() $\chi $
and directed edges
$\chi $
and directed edges
corresponding to the element
for those i such that the element
![]() $w_i$
of
$w_i$
of
![]() $\mathsf {Jen}_*(P)$
has degree one. The relations are those that follow from the structure constant relations of Theorem 3.8, where for each k such that
$\mathsf {Jen}_*(P)$
has degree one. The relations are those that follow from the structure constant relations of Theorem 3.8, where for each k such that
![]() $w_k $
is in degree greater than or equal to
$w_k $
is in degree greater than or equal to
![]() $2$
, any
$2$
, any
![]() $\mathsf {w}_{k, \zeta } $
appearing in Theorem 3.8 is replaced by an element in
$\mathsf {w}_{k, \zeta } $
appearing in Theorem 3.8 is replaced by an element in
![]() $kQ$
corresponding via Lemma 3.5 to an expression for
$kQ$
corresponding via Lemma 3.5 to an expression for
![]() $\mathsf {w}_{k, \zeta } $
in terms of the
$\mathsf {w}_{k, \zeta } $
in terms of the
![]() $\mathsf {w}_{i, \phi } $
such that
$\mathsf {w}_{i, \phi } $
such that
![]() $ w_i $
has degree one. There is a PBW style basis
$ w_i $
has degree one. There is a PBW style basis
![]() $\mathcal {B}'$
for
$\mathcal {B}'$
for
![]() $\mathfrak {A}$
(described below in the proof), consisting of composable monomials in the
$\mathfrak {A}$
(described below in the proof), consisting of composable monomials in the
![]() $\mathsf {w}_{i,\phi }$
, giving
$\mathsf {w}_{i,\phi }$
, giving
![]() $\dim (kQ/I)=\dim (\mathfrak {A})=|Z(H):Z|\cdot |P|$
.
$\dim (kQ/I)=\dim (\mathfrak {A})=|Z(H):Z|\cdot |P|$
.
Proof. By Lemma 3.5,
![]() $\mathfrak {A}$
is generated by the idempotents
$\mathfrak {A}$
is generated by the idempotents
![]() $e_{\phi }$
and the elements
$e_{\phi }$
and the elements
![]() $\mathsf {w}_{i,\phi }$
. By Lemma 3.3 and Theorem 3.8, they satisfy the given relations. Thus, we have a surjective homomorphism from
$\mathsf {w}_{i,\phi }$
. By Lemma 3.3 and Theorem 3.8, they satisfy the given relations. Thus, we have a surjective homomorphism from
![]() $kQ/I$
to
$kQ/I$
to
![]() $\mathfrak {A}$
taking
$\mathfrak {A}$
taking
![]() $[\phi ]$
to
$[\phi ]$
to
![]() $e_{\phi }$
and
$e_{\phi }$
and
![]() $[\phi ] \xrightarrow {\quad i \quad }[\phi \psi _i]$
to
$[\phi ] \xrightarrow {\quad i \quad }[\phi \psi _i]$
to
![]() $\mathsf {w}_{i,\phi }$
.
$\mathsf {w}_{i,\phi }$
.
The relations holding in
![]() $kQ/I$
allow us to write every element of
$kQ/I$
allow us to write every element of
![]() $\mathfrak {A}$
as a linear combination of elements of the set
$\mathfrak {A}$
as a linear combination of elements of the set
![]() $\mathcal {B}'$
consisting of the
$\mathcal {B}'$
consisting of the
![]() $e_{\phi }$
and composable monomials in the
$e_{\phi }$
and composable monomials in the
![]() $\mathsf {w}_{i,\phi }$
where the indices i are in order, and each index i is repeated at most
$\mathsf {w}_{i,\phi }$
where the indices i are in order, and each index i is repeated at most
![]() $p-1$
times. The number of such monomials (including the
$p-1$
times. The number of such monomials (including the
![]() $e_{\phi }$
) is
$e_{\phi }$
) is
![]() $|Z(H):Z|\cdot |P|$
. Replacing
$|Z(H):Z|\cdot |P|$
. Replacing
![]() $[\phi ] $
by
$[\phi ] $
by
![]() $e_{\phi } $
,
$e_{\phi } $
,
![]() $\mathsf {w}_{i, \phi } $
by
$\mathsf {w}_{i, \phi } $
by
![]() $[\phi ] \xrightarrow {\quad i \quad }[\phi \psi _i]$
for those
$[\phi ] \xrightarrow {\quad i \quad }[\phi \psi _i]$
for those
![]() $i $
such that
$i $
such that
![]() $ w_i$
has degree one and
$ w_i$
has degree one and
![]() $\mathsf {w}_{i, \phi } $
by their chosen lifts in
$\mathsf {w}_{i, \phi } $
by their chosen lifts in
![]() $kQ$
for those
$kQ$
for those
![]() $i $
such that
$i $
such that
![]() $ w_i$
has degree greater than or equal to two, we see by the same reasoning that
$ w_i$
has degree greater than or equal to two, we see by the same reasoning that
![]() $\dim _kQ/I $
is at most
$\dim _kQ/I $
is at most
![]() $|Z(H):Z|\cdot |P|$
.
$|Z(H):Z|\cdot |P|$
.
If there were a linear relation in
![]() $\mathfrak {A}$
between the monomials in
$\mathfrak {A}$
between the monomials in
![]() $\mathcal {B}'$
, then there would be a linear relation between the ones of maximal length, namely length
$\mathcal {B}'$
, then there would be a linear relation between the ones of maximal length, namely length
![]() $m(p-1)$
. There is one of these for each
$m(p-1)$
. There is one of these for each
![]() $\phi $
, and they are linearly independent elements of the socle of
$\phi $
, and they are linearly independent elements of the socle of
![]() $kG$
because they are nonzero elements of different projective summands
$kG$
because they are nonzero elements of different projective summands
![]() $kGe_{\phi }$
. Thus,
$kGe_{\phi }$
. Thus,
![]() $\dim (\mathfrak {A})$
is equal to
$\dim (\mathfrak {A})$
is equal to
![]() $|Z(H):Z|\cdot |P|$
, and
$|Z(H):Z|\cdot |P|$
, and
![]() $kQ/I \to \mathfrak {A}$
is an isomorphism.
$kQ/I \to \mathfrak {A}$
is an isomorphism.
Remark 3.12. The group algebra of the semidirect product
![]() $P\rtimes Z(H)/Z$
, with the action given by restricting the action of
$P\rtimes Z(H)/Z$
, with the action given by restricting the action of
![]() $H/Z$
on P, has only one block. We can perform the computations above for this group, and the results look similar, except that the factors of
$H/Z$
on P, has only one block. We can perform the computations above for this group, and the results look similar, except that the factors of
![]() $\phi (z_{i,j,\phi })$
,
$\phi (z_{i,j,\phi })$
,
![]() $\phi (z^{\prime }_{i,j,k,\phi })$
and
$\phi (z^{\prime }_{i,j,k,\phi })$
and
![]() $\phi (z^{\prime \prime }_{i,k,\phi })$
in the definitions of
$\phi (z^{\prime \prime }_{i,k,\phi })$
in the definitions of
![]() $q_{i,j,\phi }$
,
$q_{i,j,\phi }$
,
![]() $q^{\prime }_{i,j,k,\phi }$
, and
$q^{\prime }_{i,j,k,\phi }$
, and
![]() $q^{\prime \prime }_{i,k,\phi }$
are missing in Theorem 3.11. So removing these factors, the relations in Theorem 3.8 are the relations in
$q^{\prime \prime }_{i,k,\phi }$
are missing in Theorem 3.11. So removing these factors, the relations in Theorem 3.8 are the relations in
![]() $\mathsf {gr}_*(k(P\rtimes Z(H)/Z))\cong \mathcal {U}\mathsf {Jen}_*(P)\rtimes Z(H)/Z$
. Thus, we can see
$\mathsf {gr}_*(k(P\rtimes Z(H)/Z))\cong \mathcal {U}\mathsf {Jen}_*(P)\rtimes Z(H)/Z$
. Thus, we can see
![]() $\mathfrak {A}$
as a quantum deformation of the algebra
$\mathfrak {A}$
as a quantum deformation of the algebra
![]() $\mathcal {U}\mathsf {Jen}_*(P)\rtimes Z(H)/Z$
. Also, we note that in the case that
$\mathcal {U}\mathsf {Jen}_*(P)\rtimes Z(H)/Z$
. Also, we note that in the case that
![]() $\alpha =0$
, we have
$\alpha =0$
, we have
![]() $Z=1 $
,
$Z=1 $
,
![]() $ H=L$
and Theorem 3.11 provides an explicit presentation of
$ H=L$
and Theorem 3.11 provides an explicit presentation of
![]() $\mathsf {gr}_*( k(P\rtimes L )) $
.
$\mathsf {gr}_*( k(P\rtimes L )) $
.
As in [Reference Benson, Kessar and Linckelmann4], we now make use of the following lemma (see Chapter 3, Corollary 4.3 in Bass [Reference Bass1]).
Lemma 3.13. Let
![]() $A\leqslant B$
be k-algebras with A an Azumaya algebra (that is, a finite-dimensional central separable k-algebra). Then the map
$A\leqslant B$
be k-algebras with A an Azumaya algebra (that is, a finite-dimensional central separable k-algebra). Then the map
![]() $A \otimes _k C_B(A) \to B$
is an isomorphism.
$A \otimes _k C_B(A) \to B$
is an isomorphism.
Theorem 3.14. The multiplication in
![]() $(\mathcal {U}\mathsf {Jen}_*(P)\rtimes H)e$
induces an isomorphism
$(\mathcal {U}\mathsf {Jen}_*(P)\rtimes H)e$
induces an isomorphism
Proof. The proof is similar to that of Theorem 4.15 of [Reference Benson, Kessar and Linckelmann4]. Applying Lemma 3.13 with
![]() $A=\mathfrak {M}$
and B the subalgebra generated by
$A=\mathfrak {M}$
and B the subalgebra generated by
![]() $\mathfrak {A}$
and
$\mathfrak {A}$
and
![]() $\mathfrak {M}$
, we see that the given map is injective. The dimensions are given by
$\mathfrak {M}$
, we see that the given map is injective. The dimensions are given by
![]() $\dim (\mathfrak {A})=|Z(H):Z|\cdot |P|$
,
$\dim (\mathfrak {A})=|Z(H):Z|\cdot |P|$
,
![]() $\dim (\mathfrak {M})=|H:Z(H)|$
and
$\dim (\mathfrak {M})=|H:Z(H)|$
and
![]() $\dim ((\mathcal {U}\mathsf {Jen}_*(P)\rtimes H) e)= \dim (kGe)=|G:Z|$
, so
$\dim ((\mathcal {U}\mathsf {Jen}_*(P)\rtimes H) e)= \dim (kGe)=|G:Z|$
, so
![]() $\dim ((\mathcal {U}\mathsf {Jen}_*(P)\rtimes H)e)=\dim (\mathfrak {A})\cdot \dim (\mathfrak {M})$
, and the map is an isomorphism.
$\dim ((\mathcal {U}\mathsf {Jen}_*(P)\rtimes H)e)=\dim (\mathfrak {A})\cdot \dim (\mathfrak {M})$
, and the map is an isomorphism.
Corollary 3.15. We have
where
![]() $m=\sqrt {|H:Z(H)|}$
. In particular,
$m=\sqrt {|H:Z(H)|}$
. In particular,
![]() $\mathfrak {A}$
is a basic algebra of
$\mathfrak {A}$
is a basic algebra of
![]() $\mathsf {gr}_*(kGe)$
.
$\mathsf {gr}_*(kGe)$
.
Corollary 3.16. The algebra
![]() $\mathfrak {A}$
is generated by its degree zero and degree one elements.
$\mathfrak {A}$
is generated by its degree zero and degree one elements.
4 Ungrading the relations
We saw in the last section that the relations for the basic algebra of
![]() $\mathsf {gr}_*(kGe)$
are a quantised version of the relations for
$\mathsf {gr}_*(kGe)$
are a quantised version of the relations for
![]() $\mathsf {gr}_*(kP\rtimes (Z(H)/Z))$
. In this section, we show that the same holds without taking the associated graded.
$\mathsf {gr}_*(kP\rtimes (Z(H)/Z))$
. In this section, we show that the same holds without taking the associated graded.
Since
![]() $|H|$
is coprime to p, the characteristic of k, we can choose invariant complements to
$|H|$
is coprime to p, the characteristic of k, we can choose invariant complements to
![]() $J^{n+1}(kP)$
in
$J^{n+1}(kP)$
in
![]() $J^n(kP)$
for each
$J^n(kP)$
for each
![]() $n\geqslant 0$
. Let
$n\geqslant 0$
. Let
![]() $w_1,\dots ,w_m$
be the basis of
$w_1,\dots ,w_m$
be the basis of
![]() $\mathsf {Jen}_*(P)$
chosen in Section 3.2, and let
$\mathsf {Jen}_*(P)$
chosen in Section 3.2, and let
![]() $\mathcal {B}$
be the resulting PBW basis of
$\mathcal {B}$
be the resulting PBW basis of
![]() $\mathcal {U}\mathsf {Jen}_*(P)\cong \mathsf {gr}_*(kP)$
described there. Regarding
$\mathcal {U}\mathsf {Jen}_*(P)\cong \mathsf {gr}_*(kP)$
described there. Regarding
![]() $\mathsf {Jen}_*(P)$
as an k-linear subspace of
$\mathsf {Jen}_*(P)$
as an k-linear subspace of
![]() $\mathsf {gr}_*(kP)$
, this enables us to choose representatives
$\mathsf {gr}_*(kP)$
, this enables us to choose representatives
![]() $\tilde w_i$
in
$\tilde w_i$
in
![]() $kP$
of the
$kP$
of the
![]() $w_i$
in such a way that
$w_i$
in such a way that
Let
![]() $\tilde {\mathcal {B}}$
be the corresponding basis of
$\tilde {\mathcal {B}}$
be the corresponding basis of
![]() $kP$
consisting of monomials in the
$kP$
consisting of monomials in the
![]() $\tilde w_i $
. That is, if
$\tilde w_i $
. That is, if
![]() $w_{i_1} \dots w_{i_r} $
is an element of
$w_{i_1} \dots w_{i_r} $
is an element of
![]() $\mathcal {B}$
, then the corresponding element of
$\mathcal {B}$
, then the corresponding element of
![]() $\tilde {\mathcal {B}} $
is
$\tilde {\mathcal {B}} $
is
![]() $\tilde w_{i_1} \dots \tilde w_{i_r} $
. An element
$\tilde w_{i_1} \dots \tilde w_{i_r} $
. An element
![]() $\tilde w_{i_1} \ldots \tilde w_{i_r} $
of
$\tilde w_{i_1} \ldots \tilde w_{i_r} $
of
![]() $\tilde {\mathcal {B}}$
is an eigenvector for the action of H for the character
$\tilde {\mathcal {B}}$
is an eigenvector for the action of H for the character
![]() $\psi _{i_1} \ldots \psi _{i_r} $
.
$\psi _{i_1} \ldots \psi _{i_r} $
.
When we ungrade a relation of the form
![]() $[w_i,w_j]=\sum _kc_{i,j,k}w_k$
, we obtain a relation of the form
$[w_i,w_j]=\sum _kc_{i,j,k}w_k$
, we obtain a relation of the form
in
![]() $kP$
, where
$kP$
, where
![]() $y_{i,j}$
is a linear combination of elements of
$y_{i,j}$
is a linear combination of elements of
![]() $\tilde {\mathcal {B}}$
in a higher power of the radical than
$\tilde {\mathcal {B}}$
in a higher power of the radical than
![]() $\deg (w_i)+\deg (w_j)$
. Moreover, each basis monomial
$\deg (w_i)+\deg (w_j)$
. Moreover, each basis monomial
![]() $\tilde w_{i_1} \ldots \tilde w_{i_r} $
that occurs in
$\tilde w_{i_1} \ldots \tilde w_{i_r} $
that occurs in
![]() $y_{ij}$
is an eigenvector for the character
$y_{ij}$
is an eigenvector for the character
![]() $\psi _i \psi _j $
, and consequently
$\psi _i \psi _j $
, and consequently
Similarly, when we ungrade a relation of the form
![]() $w_i^p=\sum _kd_{i,k}w_k$
, we obtain a relation of the form
$w_i^p=\sum _kd_{i,k}w_k$
, we obtain a relation of the form
in
![]() $kP$
, where
$kP$
, where
![]() $y^{\prime \prime }_{i}$
is a linear combination of monomial basis elements in a higher power of the radical than
$y^{\prime \prime }_{i}$
is a linear combination of monomial basis elements in a higher power of the radical than
![]() $p.\deg (w_i)$
. Each basis monomial
$p.\deg (w_i)$
. Each basis monomial
![]() $\tilde w_{i_1}\dots \tilde w_{i_r} $
that occurs in
$\tilde w_{i_1}\dots \tilde w_{i_r} $
that occurs in
![]() $y^{\prime \prime }_{i} $
is an eigenvector for the character
$y^{\prime \prime }_{i} $
is an eigenvector for the character
![]() $\psi _i ^p$
and consequently
$\psi _i ^p$
and consequently
Definition 4.5. As in Definition 3.4, we define
![]() $\tilde {\mathsf {w}}_{i,\phi }=g_{i,\phi }\tilde w_ie_{\phi }$
. Then
$\tilde {\mathsf {w}}_{i,\phi }=g_{i,\phi }\tilde w_ie_{\phi }$
. Then
![]() $\tilde {\mathsf {w}}_{i,\phi }$
commutes with
$\tilde {\mathsf {w}}_{i,\phi }$
commutes with
![]() $\mathfrak {M}$
. We define
$\mathfrak {M}$
. We define
![]() $\tilde {\mathfrak {A}}$
to be the subalgebra of
$\tilde {\mathfrak {A}}$
to be the subalgebra of
![]() $kGe$
generated by the elements
$kGe$
generated by the elements
![]() $e_{\phi } $
and
$e_{\phi } $
and
![]() $\tilde {\mathsf {w}}_{i,\phi }$
. For an element
$\tilde {\mathsf {w}}_{i,\phi }$
. For an element
![]() $\tilde w=\tilde w_{i_1} \ldots \tilde w_{i_r} $
of
$\tilde w=\tilde w_{i_1} \ldots \tilde w_{i_r} $
of
![]() $\tilde {\mathcal {B}}$
and a character
$\tilde {\mathcal {B}}$
and a character
![]() $\phi \in \mathsf {Irr}(Z(H)|\chi )$
, set
$\phi \in \mathsf {Irr}(Z(H)|\chi )$
, set
![]() $\tilde {\mathsf {w}}_{\phi } = \tilde {\mathsf {w}}_{i_1, \phi \psi _1\ldots \psi _r }\dots \tilde {\mathsf {w}}_{ i_{r-1}, \phi \psi _r} \tilde {\mathsf {w}}_{i_r, \phi } $
. Denote by
$\tilde {\mathsf {w}}_{\phi } = \tilde {\mathsf {w}}_{i_1, \phi \psi _1\ldots \psi _r }\dots \tilde {\mathsf {w}}_{ i_{r-1}, \phi \psi _r} \tilde {\mathsf {w}}_{i_r, \phi } $
. Denote by
![]() $\tilde {\mathcal {B}}'$
the subset of
$\tilde {\mathcal {B}}'$
the subset of
![]() $\tilde {\mathfrak {A}}$
consisting of the elements
$\tilde {\mathfrak {A}}$
consisting of the elements
![]() $\tilde x_{\phi }$
for
$\tilde x_{\phi }$
for
![]() $\tilde w$
in
$\tilde w$
in
![]() $\tilde {\mathcal {B}}$
and
$\tilde {\mathcal {B}}$
and
![]() $\phi \in \mathsf {Irr}(Z(H)|\chi )$
. We shall see below in Theorem 4.7 that
$\phi \in \mathsf {Irr}(Z(H)|\chi )$
. We shall see below in Theorem 4.7 that
![]() $\tilde {\mathcal {B}}'$
is a basis for
$\tilde {\mathcal {B}}'$
is a basis for
![]() $\tilde {\mathfrak {A}}$
.
$\tilde {\mathfrak {A}}$
.
Proposition 4.6. The elements
![]() $\tilde {\mathsf {w}}_{i,\phi }$
satisfy the following relations.
$\tilde {\mathsf {w}}_{i,\phi }$
satisfy the following relations.
 $$ \begin{align*} \tilde {\mathsf{w}}_{j,\phi\psi_i}\tilde {\mathsf{w}}_{i,\phi}-q_{i,j,\phi}\tilde {\mathsf{w}}_{i,\phi}\tilde {\mathsf{w}}_{j,\phi\psi_i} &= \sum_kc_{i,j,k}q^{\prime}_{i,j,k,\phi}\tilde {\mathsf{w}}_{k,\phi} +\psi_j(g_{i,\phi})^{-1}g_{j,\phi\psi_i}g_{i,\phi}y_{i,j}e_{\phi}. \\ \tilde {\mathsf{w}}_{i,\phi\psi_i^{p-1}}\dots \tilde {\mathsf{w}}_{i,\phi\psi_i}\tilde {\mathsf{w}}_{i,\phi} &= \sum_k d_{i,k}q^{\prime\prime}_{i,k,\phi}\tilde {\mathsf{w}}_{k,\phi} + \psi_i(g_{i,\phi\psi_i^{p-2}})^{-1}\dots\\ &\qquad\qquad\dots\psi_i(g_{i,\phi\psi_i})^{-p+2}\psi_i(g_{i,\phi})^{-p+1} (g_{i,\phi\psi_i^{p-1}}\dots g_{i,\phi\psi_i}g_{i,\phi})y^{\prime\prime}_ie_{\phi}. \end{align*} $$
$$ \begin{align*} \tilde {\mathsf{w}}_{j,\phi\psi_i}\tilde {\mathsf{w}}_{i,\phi}-q_{i,j,\phi}\tilde {\mathsf{w}}_{i,\phi}\tilde {\mathsf{w}}_{j,\phi\psi_i} &= \sum_kc_{i,j,k}q^{\prime}_{i,j,k,\phi}\tilde {\mathsf{w}}_{k,\phi} +\psi_j(g_{i,\phi})^{-1}g_{j,\phi\psi_i}g_{i,\phi}y_{i,j}e_{\phi}. \\ \tilde {\mathsf{w}}_{i,\phi\psi_i^{p-1}}\dots \tilde {\mathsf{w}}_{i,\phi\psi_i}\tilde {\mathsf{w}}_{i,\phi} &= \sum_k d_{i,k}q^{\prime\prime}_{i,k,\phi}\tilde {\mathsf{w}}_{k,\phi} + \psi_i(g_{i,\phi\psi_i^{p-2}})^{-1}\dots\\ &\qquad\qquad\dots\psi_i(g_{i,\phi\psi_i})^{-p+2}\psi_i(g_{i,\phi})^{-p+1} (g_{i,\phi\psi_i^{p-1}}\dots g_{i,\phi\psi_i}g_{i,\phi})y^{\prime\prime}_ie_{\phi}. \end{align*} $$
Moreover, suppose that
![]() $y_{i,j} = \sum _{\tilde w \in \tilde {\mathcal {B}}} c_{i,j,\tilde w} \tilde w$
and
$y_{i,j} = \sum _{\tilde w \in \tilde {\mathcal {B}}} c_{i,j,\tilde w} \tilde w$
and
![]() $ y_i"= \sum _{\tilde w \in \tilde {\mathcal {B}}} d_{i,\tilde w} \tilde w $
. For each
$ y_i"= \sum _{\tilde w \in \tilde {\mathcal {B}}} d_{i,\tilde w} \tilde w $
. For each
![]() $\tilde w \in \tilde {\mathcal {B}}$
, there exist elements
$\tilde w \in \tilde {\mathcal {B}}$
, there exist elements
![]() $q^{\prime }_{i,j,\tilde w, \phi } $
and
$q^{\prime }_{i,j,\tilde w, \phi } $
and
![]() $ q^{\prime \prime }_{i,\tilde w,\phi } $
of
$ q^{\prime \prime }_{i,\tilde w,\phi } $
of
![]() $ k ^{\times } $
such that
$ k ^{\times } $
such that
 $$ \begin{align*} g_{j,\phi\psi_i}g_{i,\phi}y_{i,j}e_{\phi}= \sum_{\tilde w \in \tilde{\mathcal{B}}} q^{\prime}_{i,j,\tilde w,\phi} c_{i,j,\tilde w} \tilde {\mathsf{w}}_{\phi}. \\ (g_{i,\phi\psi_i^{p-1}}\dots g_{i,\phi\psi_i}g_{i,\phi})y^{\prime\prime}_ie_{\phi} = \sum_{\tilde w \in \tilde{\mathcal{B}}} q^{\prime\prime}_{i,\tilde w,\phi} d_{i,\tilde w} \tilde {\mathsf{w}}_{\phi}. \end{align*} $$
$$ \begin{align*} g_{j,\phi\psi_i}g_{i,\phi}y_{i,j}e_{\phi}= \sum_{\tilde w \in \tilde{\mathcal{B}}} q^{\prime}_{i,j,\tilde w,\phi} c_{i,j,\tilde w} \tilde {\mathsf{w}}_{\phi}. \\ (g_{i,\phi\psi_i^{p-1}}\dots g_{i,\phi\psi_i}g_{i,\phi})y^{\prime\prime}_ie_{\phi} = \sum_{\tilde w \in \tilde{\mathcal{B}}} q^{\prime\prime}_{i,\tilde w,\phi} d_{i,\tilde w} \tilde {\mathsf{w}}_{\phi}. \end{align*} $$
Proof. Following through the proof of relation (3.9), we can replace each w with
![]() $\mathsf {w}$
until the sixth line, where we have to use (4.1) for the commutator. At this point, the extra term is
$\mathsf {w}$
until the sixth line, where we have to use (4.1) for the commutator. At this point, the extra term is
Similarly, following through the proof of relation (3.10), we can replace each w with
![]() $\mathsf {w}$
until the fourth line, where we have to use (4.3). At this point, the extra term is
$\mathsf {w}$
until the fourth line, where we have to use (4.3). At this point, the extra term is
By Lemma 3.1 and Equation 4.2, for each
![]() $\mathsf {w} = \mathsf {w}_{i_r} \ldots \mathsf {w}_{i_1} \in \tilde {\mathcal {B}}$
such that
$\mathsf {w} = \mathsf {w}_{i_r} \ldots \mathsf {w}_{i_1} \in \tilde {\mathcal {B}}$
such that
![]() $c_{i,j, \tilde w, \phi } \ne 0 $
,
$c_{i,j, \tilde w, \phi } \ne 0 $
,
for some
![]() $z \in Z(H) $
. The second assertion follows from this by the fact that for any
$z \in Z(H) $
. The second assertion follows from this by the fact that for any
![]() $g\in H$
, any
$g\in H$
, any
![]() $z \in Z(H)$
, any
$z \in Z(H)$
, any
![]() $\tilde w_i$
and any
$\tilde w_i$
and any
![]() $\zeta \in \mathsf {Irr}( Z(H) | \chi ) $
,
$\zeta \in \mathsf {Irr}( Z(H) | \chi ) $
,
![]() $g\tilde w_i =\psi _i(g)\tilde w_i g $
is a scalar multiple of
$g\tilde w_i =\psi _i(g)\tilde w_i g $
is a scalar multiple of
![]() $\tilde w_i g$
,
$\tilde w_i g$
,
![]() $ ze_{\zeta } =\zeta (z) e_{\zeta } $
is a scalar multiple of
$ ze_{\zeta } =\zeta (z) e_{\zeta } $
is a scalar multiple of
![]() $e_{\zeta } $
and
$e_{\zeta } $
and
![]() $g\tilde w_i e_{\zeta } = e_{\zeta \psi _i} g \tilde w_i e_{\phi } $
. The last assertion follows in a similar fashion from Lemma 3.1 and Equation 4.4.
$g\tilde w_i e_{\zeta } = e_{\zeta \psi _i} g \tilde w_i e_{\phi } $
. The last assertion follows in a similar fashion from Lemma 3.1 and Equation 4.4.
Theorem 4.7. The algebra
![]() $\tilde {\mathfrak {A}}$
is given as a quiver with relations
$\tilde {\mathfrak {A}}$
is given as a quiver with relations
![]() $kQ/\tilde I$
, where Q is as in Theorem 3.11, but with edges corresponding to the lifts
$kQ/\tilde I$
, where Q is as in Theorem 3.11, but with edges corresponding to the lifts
![]() $\tilde {\mathsf {w}}_{i,\phi }$
of the
$\tilde {\mathsf {w}}_{i,\phi }$
of the
![]() $\mathsf {w}_{i,\phi }$
given there. The relations are those that follow from the structure constant relations of Proposition 4.6, together with relations saying that every composite of at least s arrows is zero, where s is the radical length of
$\mathsf {w}_{i,\phi }$
given there. The relations are those that follow from the structure constant relations of Proposition 4.6, together with relations saying that every composite of at least s arrows is zero, where s is the radical length of
![]() $kP$
.
$kP$
.
The set
![]() $\tilde {\mathcal {B}}'$
is a PBW style basis of
$\tilde {\mathcal {B}}'$
is a PBW style basis of
![]() $\tilde {\mathfrak {A}}$
, giving
$\tilde {\mathfrak {A}}$
, giving
![]() $\dim \tilde {\mathfrak {A}}= |Z(H):H|$
. There is a natural isomorphism
$\dim \tilde {\mathfrak {A}}= |Z(H):H|$
. There is a natural isomorphism
![]() $\mathsf {gr}_*(\tilde {\mathfrak {A}})\cong \mathfrak {A}$
, sending each
$\mathsf {gr}_*(\tilde {\mathfrak {A}})\cong \mathfrak {A}$
, sending each
![]() $\tilde {\mathsf {w}}_{i,\phi }$
to
$\tilde {\mathsf {w}}_{i,\phi }$
to
![]() $\mathsf {w}_{i,\phi }$
.
$\mathsf {w}_{i,\phi }$
.
Proof. It follows from the relations in Proposition 4.6 that the linear span of
![]() $\tilde {\mathcal {B}}'$
is closed under multiplication modulo a large enough power of the arrow ideal. The zero relations for composites of s arrows then show that this ideal is zero, and therefore that
$\tilde {\mathcal {B}}'$
is closed under multiplication modulo a large enough power of the arrow ideal. The zero relations for composites of s arrows then show that this ideal is zero, and therefore that
![]() $\tilde {\mathcal {B}}'$
linearly spans
$\tilde {\mathcal {B}}'$
linearly spans
![]() $\tilde {\mathfrak {A}}$
. The image of an element
$\tilde {\mathfrak {A}}$
. The image of an element
![]() $\tilde {\mathsf {w}}_{i,\phi }$
in
$\tilde {\mathsf {w}}_{i,\phi }$
in
![]() $\mathsf {gr}_*(kGe)$
is equal to
$\mathsf {gr}_*(kGe)$
is equal to
![]() $\mathsf {w}_{i,\phi }$
, which lies in
$\mathsf {w}_{i,\phi }$
, which lies in
![]() $\mathfrak {A}$
. Since the elements
$\mathfrak {A}$
. Since the elements
![]() $\mathsf {w}_{i,\phi }$
of
$\mathsf {w}_{i,\phi }$
of
![]() $\mathcal {B}'$
are linearly independent, it follows that the elements
$\mathcal {B}'$
are linearly independent, it follows that the elements
![]() $\tilde {\mathsf {w}}_{i,\phi }$
of
$\tilde {\mathsf {w}}_{i,\phi }$
of
![]() $\tilde {\mathcal {B}}'$
are linearly independent, and therefore form a basis for
$\tilde {\mathcal {B}}'$
are linearly independent, and therefore form a basis for
![]() $\tilde {\mathfrak {A}}$
. This therefore induces a natural isomorphism
$\tilde {\mathfrak {A}}$
. This therefore induces a natural isomorphism
![]() $\mathsf {gr}_*(\tilde {\mathfrak {A}})\cong \mathfrak {A}$
. Since
$\mathsf {gr}_*(\tilde {\mathfrak {A}})\cong \mathfrak {A}$
. Since
![]() $\mathfrak {A}$
is generated by its degree one elements,
$\mathfrak {A}$
is generated by its degree one elements,
![]() $\tilde {\mathfrak {A}}$
has the same quiver, with the lifts of the relations.
$\tilde {\mathfrak {A}}$
has the same quiver, with the lifts of the relations.
Theorem 4.8. The multiplication in
![]() $kGe$
induces an isomorphism
$kGe$
induces an isomorphism
![]() $\tilde {\mathfrak {A}}\otimes _k \mathfrak {M} \to kGe$
.
$\tilde {\mathfrak {A}}\otimes _k \mathfrak {M} \to kGe$
.
Proof. By Theorem 4.7, we have
![]() $\dim (\tilde {\mathfrak {A}})=|Z(H):Z|\cdot |P|$
. So this is now proved in the same way as Theorem 3.14.
$\dim (\tilde {\mathfrak {A}})=|Z(H):Z|\cdot |P|$
. So this is now proved in the same way as Theorem 3.14.
Corollary 4.9. We have
![]() $kGe\cong \mathsf {Mat}_m(\tilde {\mathfrak {A}})$
, where
$kGe\cong \mathsf {Mat}_m(\tilde {\mathfrak {A}})$
, where
![]() $m=\sqrt {|H:Z(H)|}$
, so that
$m=\sqrt {|H:Z(H)|}$
, so that
![]() $\tilde {\mathfrak {A}}$
is the basic algebra of
$\tilde {\mathfrak {A}}$
is the basic algebra of
![]() $kGe$
.
$kGe$
.
Remark 4.10. As in Remark 3.12, if we perform the computations of this section with the group algebra of the semidirect product
![]() $P\rtimes Z(H)/Z$
instead of
$P\rtimes Z(H)/Z$
instead of
![]() $kGe$
, the results look similar except with different scalars. So we can see
$kGe$
, the results look similar except with different scalars. So we can see
![]() $\tilde {\mathfrak {A}}$
as a quantum deformation of the algebra
$\tilde {\mathfrak {A}}$
as a quantum deformation of the algebra
![]() $k(P\rtimes Z(H)/Z)$
. This observation, together with Theorems 4.7 and 4.8, complete the proof of Theorem 1.1.
$k(P\rtimes Z(H)/Z)$
. This observation, together with Theorems 4.7 and 4.8, complete the proof of Theorem 1.1.
We shall see some explicit examples of the ungrading of the relations in Section 5.
5 Example: P extraspecial of order
 $p^3$
and exponent p
$p^3$
and exponent p
Let k have characteristic p, an odd prime, and P be an extraspecial p-group of order
![]() $p^3$
and exponent p, with presentation
$p^3$
and exponent p, with presentation
We denote by H the quaternion group of order
![]() $8$
, given by a presentation
$8$
, given by a presentation
Set
![]() $Z= \langle s^2\rangle $
; this is the centre of H. We consider the following action of H on P and set
$Z= \langle s^2\rangle $
; this is the centre of H. We consider the following action of H on P and set
![]() $G=P\rtimes H$
.
$G=P\rtimes H$
.
It follows that
![]() $c^s=c^t=c^{-1}$
, and Z acts trivially on P. This action lifts the action of
$c^s=c^t=c^{-1}$
, and Z acts trivially on P. This action lifts the action of
![]() $C_2\times C_2$
on
$C_2\times C_2$
on
![]() $C_p\times C_p\cong P/\langle c\rangle $
, where here the nontrivial element of each copy of
$C_p\times C_p\cong P/\langle c\rangle $
, where here the nontrivial element of each copy of
![]() $C_2$
acts as inversion on the corresponding copy
$C_2$
acts as inversion on the corresponding copy
![]() $C_p$
. The group algebra
$C_p$
. The group algebra
![]() $kG$
has two blocks, namely the principal block
$kG$
has two blocks, namely the principal block
![]() $e_0 = \frac {1}{2} (1+s^2)$
and the nonprincipal block
$e_0 = \frac {1}{2} (1+s^2)$
and the nonprincipal block
![]() $e = \frac {1}{2} (1-s^2)$
corresponding to the faithful central character
$e = \frac {1}{2} (1-s^2)$
corresponding to the faithful central character
![]() $\chi \colon Z \to k^{\times }$
given by
$\chi \colon Z \to k^{\times }$
given by
![]() $\chi (s^2)=-1$
. We shall be interested in
$\chi (s^2)=-1$
. We shall be interested in
![]() $kGe$
.
$kGe$
.
Remark 5.1. Let
![]() $x=g-1$
,
$x=g-1$
,
![]() $y=h-1$
,
$y=h-1$
,
![]() $z=c-1$
in
$z=c-1$
in
![]() $kP$
. Then
$kP$
. Then
and a presentation for
![]() $kP$
is given by generators x and y, and relations saying that
$kP$
is given by generators x and y, and relations saying that
![]() $x^p=0$
,
$x^p=0$
,
![]() $y^p=0$
and the element z defined by (5.2) is central with pth power equal to zero. Note that the element
$y^p=0$
and the element z defined by (5.2) is central with pth power equal to zero. Note that the element
![]() $(1+x)^{-1}(1+y)^{-1}$
is congruent to
$(1+x)^{-1}(1+y)^{-1}$
is congruent to
![]() $1$
modulo
$1$
modulo
![]() $J(kP)$
, and so in the associated graded
$J(kP)$
, and so in the associated graded
![]() $\mathsf {gr}_*(kP)$
, this term in (5.2) may be ignored. This is used in the proof of Theorem 1.2 that follows.
$\mathsf {gr}_*(kP)$
, this term in (5.2) may be ignored. This is used in the proof of Theorem 1.2 that follows.
Proof of Theorem 1.2.
Denote by x, y, z the images of g, h, c in
![]() $\mathsf {Jen}_*(P)$
, respectively. (These elements are mapped to the images of
$\mathsf {Jen}_*(P)$
, respectively. (These elements are mapped to the images of
![]() $g-1$
,
$g-1$
,
![]() $h-1$
,
$h-1$
,
![]() $c-1$
in
$c-1$
in
![]() $\mathsf {gr}_*(kP)$
under the canonical map
$\mathsf {gr}_*(kP)$
under the canonical map
![]() $\mathsf {Jen}_*(P)\to \mathsf {gr}_*(kP)$
). The three dimensional p-restricted Lie algebra
$\mathsf {Jen}_*(P)\to \mathsf {gr}_*(kP)$
). The three dimensional p-restricted Lie algebra
![]() $\mathsf {Jen}_*(P)$
is spanned by the elements x, y in degree one together with
$\mathsf {Jen}_*(P)$
is spanned by the elements x, y in degree one together with
![]() $z=[x,y]$
(by the previous Remark) in degree two, satisfying
$z=[x,y]$
(by the previous Remark) in degree two, satisfying
![]() $[x,y]=[y,z]=0$
. The p-restriction map given by
$[x,y]=[y,z]=0$
. The p-restriction map given by
![]() $x^{[p]}=y^{[p]}=z^{[p]}=0$
. Its
$x^{[p]}=y^{[p]}=z^{[p]}=0$
. Its
![]() $p^3$
dimensional universal enveloping algebra
$p^3$
dimensional universal enveloping algebra
![]() $\mathcal {U}\mathsf {Jen}_*(P)$
is isomorphic to
$\mathcal {U}\mathsf {Jen}_*(P)$
is isomorphic to
![]() $\mathsf {gr}_*(kP)$
. This shows the first part of Theorem 1.2.
$\mathsf {gr}_*(kP)$
. This shows the first part of Theorem 1.2.
The action of H on
![]() $\mathsf {Jen}_*(P)$
is given by
$\mathsf {Jen}_*(P)$
is given by
The elements x, y and z are eigenvectors for H on
![]() $\mathsf {Jen}_*(P)$
. So we set
$\mathsf {Jen}_*(P)$
. So we set
![]() $w_1=x$
,
$w_1=x$
,
![]() $w_2=y$
,
$w_2=y$
,
![]() $w_3=z$
. The characters
$w_3=z$
. The characters
![]() $\psi _i$
of H satisfying
$\psi _i$
of H satisfying
![]() $gw_ig^{-1}=\psi _i(g)w_i$
for
$gw_ig^{-1}=\psi _i(g)w_i$
for
![]() $g\in H$
are given as follows.
$g\in H$
are given as follows.
Note that the relation
![]() $[x,y]=z$
in
$[x,y]=z$
in
![]() $\mathsf {Jen}_*(P)$
implies
$\mathsf {Jen}_*(P)$
implies
![]() $\psi _1\psi _2=\psi _3$
.
$\psi _1\psi _2=\psi _3$
.
Denoting as above by
![]() $e = \frac {1}{2} (1-s^2)$
the nonprincipal block of
$e = \frac {1}{2} (1-s^2)$
the nonprincipal block of
![]() $kG$
, the block algebra
$kG$
, the block algebra
![]() $kGe$
has a unique isomorphism class of simple modules. Indeed, e corresponds to the unique
$kGe$
has a unique isomorphism class of simple modules. Indeed, e corresponds to the unique
![]() $2$
-dimensional simple
$2$
-dimensional simple
![]() $kH$
-module, and hence the semisimple quotient of
$kH$
-module, and hence the semisimple quotient of
![]() $kGe$
is the matrix algebra
$kGe$
is the matrix algebra
![]() $\mathfrak {M}=kHe\cong \mathsf {Mat}_2(k)$
.
$\mathfrak {M}=kHe\cong \mathsf {Mat}_2(k)$
.
Since
![]() $Z=Z(H)$
, there is only one central character of
$Z=Z(H)$
, there is only one central character of
![]() $Z(H)$
lying above
$Z(H)$
lying above
![]() $\chi $
, namely
$\chi $
, namely
![]() $\phi =\chi $
, and
$\phi =\chi $
, and
![]() $\xi _{\phi }=1$
. The map
$\xi _{\phi }=1$
. The map
![]() $\rho \colon H/Z(H) \to \mathsf {Hom}(H/Z(H),k^{\times })$
takes s to
$\rho \colon H/Z(H) \to \mathsf {Hom}(H/Z(H),k^{\times })$
takes s to
![]() $\phi _2$
, t to
$\phi _2$
, t to
![]() $\phi _1$
and
$\phi _1$
and
![]() $st$
to
$st$
to
![]() $\phi _3$
. Thus,
$\phi _3$
. Thus,
![]() $g_{1,\phi }=t$
,
$g_{1,\phi }=t$
,
![]() $g_{2,\phi }=s$
and
$g_{2,\phi }=s$
and
![]() $g_{3,\phi }=st$
; these are only well defined up to multiplication by
$g_{3,\phi }=st$
; these are only well defined up to multiplication by
![]() $Z(H)$
.
$Z(H)$
.
The block algebra
![]() $\mathsf {gr}_*(kGe)$
of
$\mathsf {gr}_*(kGe)$
of
![]() $\mathsf {gr}_*(kG)$
also has one isomorphism class of simple modules, namely the same
$\mathsf {gr}_*(kG)$
also has one isomorphism class of simple modules, namely the same
![]() $2$
-dimensional simple
$2$
-dimensional simple
![]() $kH$
-module as above, and by Theorem 3.14 and Corollary 3.15, we have
$kH$
-module as above, and by Theorem 3.14 and Corollary 3.15, we have
where
![]() $\mathfrak {M}=kHe\cong \mathsf {Mat}_2(k)$
and
$\mathfrak {M}=kHe\cong \mathsf {Mat}_2(k)$
and
![]() $\mathfrak {A}=(\mathsf {gr}_*(kGe))^H$
. The algebra
$\mathfrak {A}=(\mathsf {gr}_*(kGe))^H$
. The algebra
![]() $\mathfrak {A}$
contains elements
$\mathfrak {A}$
contains elements
![]() $g_{1,\phi }w_1e=txe$
,
$g_{1,\phi }w_1e=txe$
,
![]() $g_{2,\phi }w_2e=sye$
and
$g_{2,\phi }w_2e=sye$
and
![]() $g_{3,\phi }w_3e=stze$
. The constants are given by
$g_{3,\phi }w_3e=stze$
. The constants are given by
![]() $q_{1,2,\phi }=-1$
and
$q_{1,2,\phi }=-1$
and
![]() $q^{\prime }_{1,2,3,\phi }=-1$
, so these satisfy the following relation:
$q^{\prime }_{1,2,3,\phi }=-1$
, so these satisfy the following relation:
Similar computations give
Writing
![]() $\mathsf {x} = txe$
,
$\mathsf {x} = txe$
,
![]() $\mathsf {y} = sye$
and
$\mathsf {y} = sye$
and
![]() $\mathsf {z} = stze$
, we therefore have
$\mathsf {z} = stze$
, we therefore have
This is a presentation for the basic algebra
![]() $\mathfrak {A}$
of
$\mathfrak {A}$
of
![]() $\mathsf {gr}_*(kGe)$
, with generators
$\mathsf {gr}_*(kGe)$
, with generators
![]() $\mathsf {x}$
and
$\mathsf {x}$
and
![]() $\mathsf {y}$
, and with
$\mathsf {y}$
, and with
![]() $\mathsf {z}$
defined as
$\mathsf {z}$
defined as
![]() $\mathsf {x} \mathsf {y} + \mathsf {y} \mathsf {x}$
. This proves Theorem 1.2.
$\mathsf {x} \mathsf {y} + \mathsf {y} \mathsf {x}$
. This proves Theorem 1.2.
Remark 5.3. The first part of the above proof shows that
![]() $\mathsf {Jen}_*(P)$
is isomorphic to the p-restricted Lie algebra of
$\mathsf {Jen}_*(P)$
is isomorphic to the p-restricted Lie algebra of
![]() $3\times 3$
matrices of the form
$3\times 3$
matrices of the form
![]() $\left (\begin {smallmatrix} 0 & * & * \\ 0 & 0 & * \\ 0 & 0 & 0 \end {smallmatrix}\right )$
.
$\left (\begin {smallmatrix} 0 & * & * \\ 0 & 0 & * \\ 0 & 0 & 0 \end {smallmatrix}\right )$
.
In order to prove Theorem 1.3, ungrading the algebra is our next task. The problem is that the generators
![]() $g-1$
and
$g-1$
and
![]() $h-1$
of
$h-1$
of
![]() $kP$
are not well suited to dealing with automorphisms. We have an action of
$kP$
are not well suited to dealing with automorphisms. We have an action of
![]() $\mathbb {F}_p^{\times } \times \mathbb {F}_p^{\times }$
on P where
$\mathbb {F}_p^{\times } \times \mathbb {F}_p^{\times }$
on P where
![]() $(i,j)$
sends g to
$(i,j)$
sends g to
![]() $g^i$
and h to
$g^i$
and h to
![]() $h^j$
. The commutator
$h^j$
. The commutator
![]() $c=[g,h]$
is sent to
$c=[g,h]$
is sent to
![]() $c^{ij}$
. Set
$c^{ij}$
. Set
 $$\begin{align*}\tilde x=-\sum_{i=1}^{p-1}g^i/i,\qquad \tilde y=-\sum_{j=1}^{p-1}h^j/j. \end{align*}$$
$$\begin{align*}\tilde x=-\sum_{i=1}^{p-1}g^i/i,\qquad \tilde y=-\sum_{j=1}^{p-1}h^j/j. \end{align*}$$
Lemma 5.4. We have
![]() $\tilde x \equiv g-1 \pmod {J^2(kP)} $
and
$\tilde x \equiv g-1 \pmod {J^2(kP)} $
and
![]() $\tilde y \equiv h-1 \pmod {J^2(kP)}$
.
$\tilde y \equiv h-1 \pmod {J^2(kP)}$
.
Proof. Since
![]() $ p$
is odd,
$ p$
is odd,
![]() $\sum _{i=1}^{p-1} 1/i = \sum _{i=1}^{p-1} i= 0 $
in k whence
$\sum _{i=1}^{p-1} 1/i = \sum _{i=1}^{p-1} i= 0 $
in k whence
![]() $\tilde x = -\sum _{i=1}^{p-1}(g^i-1)/i $
. Now the assertion for
$\tilde x = -\sum _{i=1}^{p-1}(g^i-1)/i $
. Now the assertion for
![]() $\tilde x $
follows since
$\tilde x $
follows since
![]() $(g^i-1)/i \equiv g-1 \pmod {J^2 (kP) } $
for any i,
$(g^i-1)/i \equiv g-1 \pmod {J^2 (kP) } $
for any i,
![]() $ 1\leqslant i \leqslant p-1 $
. The proof for
$ 1\leqslant i \leqslant p-1 $
. The proof for
![]() $\tilde y $
is similar.
$\tilde y $
is similar.
Note that
![]() $\tilde x$
an eigenvector in the
$\tilde x$
an eigenvector in the
![]() $(1,0)$
eigenspace and
$(1,0)$
eigenspace and
![]() $\tilde y$
an eigenvector in the
$\tilde y$
an eigenvector in the
![]() $(0,1)$
eigenspace of
$(0,1)$
eigenspace of
![]() $\mathbb {F}_p^{\times } \times \mathbb {F}_p^{\times }$
. Then we set
$\mathbb {F}_p^{\times } \times \mathbb {F}_p^{\times }$
. Then we set
![]() $\tilde z=[\tilde x,\tilde y]=\tilde x\tilde y-\tilde y\tilde x$
, an eigenvector in the
$\tilde z=[\tilde x,\tilde y]=\tilde x\tilde y-\tilde y\tilde x$
, an eigenvector in the
![]() $(1,1)$
eigenspace. By Lemma 5.4 and the proof of Theorem 1.2,
$(1,1)$
eigenspace. By Lemma 5.4 and the proof of Theorem 1.2,
![]() $kP$
has a PBW basis consisting of monomials in the
$kP$
has a PBW basis consisting of monomials in the
![]() $\tilde x$
,
$\tilde x$
,
![]() $\tilde y $
and
$\tilde y $
and
![]() $\tilde z $
. Moreover, a PBW basis element
$\tilde z $
. Moreover, a PBW basis element
![]() $\tilde x^i\tilde y^j\tilde z^k$
of
$\tilde x^i\tilde y^j\tilde z^k$
of
![]() $kP$
with
$kP$
with
![]() $0\leqslant i,j,k < p$
is an eigenvector in the
$0\leqslant i,j,k < p$
is an eigenvector in the
![]() $(i+k,j+k)$
eigenspace, where
$(i+k,j+k)$
eigenspace, where
![]() $i+k$
and
$i+k$
and
![]() $j+k$
are read modulo
$j+k$
are read modulo
![]() $p-1$
.
$p-1$
.
Lemma 5.5. We have
![]() $\tilde z^p=0$
.
$\tilde z^p=0$
.
Proof. The element
![]() $\tilde z^p$
is an eigenvector in the
$\tilde z^p$
is an eigenvector in the
![]() $(1,1)$
eigenspace. Further,
$(1,1)$
eigenspace. Further,
![]() $\tilde z^p $
has image
$\tilde z^p $
has image
![]() $ z^p =0 \in \mathsf {gr}_{2p} (kP) $
, hence
$ z^p =0 \in \mathsf {gr}_{2p} (kP) $
, hence
![]() $\tilde z^p $
is in
$\tilde z^p $
is in
![]() $J^{2p+1}(kP)$
. The PBW basis elements in this eigenspace have
$J^{2p+1}(kP)$
. The PBW basis elements in this eigenspace have
![]() $i+k$
and
$i+k$
and
![]() $j+k$
congruent to one modulo
$j+k$
congruent to one modulo
![]() $p-1$
and at most
$p-1$
and at most
![]() $2p-2$
, and hence at most p, but then
$2p-2$
, and hence at most p, but then
![]() $i+j+2k\leqslant 2p$
, so the basis element is not in
$i+j+2k\leqslant 2p$
, so the basis element is not in
![]() $J^{2p+1}(kP)$
. It follows that the
$J^{2p+1}(kP)$
. It follows that the
![]() $(1,1)$
eigenspace in
$(1,1)$
eigenspace in
![]() $J^{2p}(kP+1)$
is zero and so
$J^{2p}(kP+1)$
is zero and so
![]() $\tilde z^p=0$
.
$\tilde z^p=0$
.
Lemma 5.6. The element
![]() $[\tilde x,\tilde z]$
is a linear combination of the elements
$[\tilde x,\tilde z]$
is a linear combination of the elements
![]() $\tilde z\tilde y^{p-2}\tilde z \in J^{p+2}(kP)$
and
$\tilde z\tilde y^{p-2}\tilde z \in J^{p+2}(kP)$
and
![]() $\tilde x^i\tilde y^{2i-1}\tilde x^i\tilde z^{p+1-2i} \in J^{2p+1}(kP)$
with
$\tilde x^i\tilde y^{2i-1}\tilde x^i\tilde z^{p+1-2i} \in J^{2p+1}(kP)$
with
![]() $1\leqslant i \leqslant (p-1)/2$
. Similarly,
$1\leqslant i \leqslant (p-1)/2$
. Similarly,
![]() $[\tilde y,\tilde z]$
is a linear combination of the elements
$[\tilde y,\tilde z]$
is a linear combination of the elements
![]() $\tilde z\tilde x^{p-2}\tilde z\in J^{p+2}(kP)$
and
$\tilde z\tilde x^{p-2}\tilde z\in J^{p+2}(kP)$
and
![]() $\tilde y^i\tilde x^{2i-1}\tilde y^i\tilde z^{p+1-2i} \in J^{2p+1}(kP)$
with
$\tilde y^i\tilde x^{2i-1}\tilde y^i\tilde z^{p+1-2i} \in J^{2p+1}(kP)$
with
![]() $1\leqslant i\leqslant (p-1)/2$
.
$1\leqslant i\leqslant (p-1)/2$
.
Proof. We prove the first statement. The proof of the second is identical, with the roles of
![]() $\tilde x$
and
$\tilde x$
and
![]() $\tilde y$
reversed.
$\tilde y$
reversed.
The element
![]() $[\tilde x,\tilde z]$
has image
$[\tilde x,\tilde z]$
has image
![]() $[x,z]=0$
in
$[x,z]=0$
in
![]() $\mathsf {gr}_3(kP)$
and hence lies in
$\mathsf {gr}_3(kP)$
and hence lies in
![]() $J^4(kP)$
. It is in the
$J^4(kP)$
. It is in the
![]() $(2,1)$
eigenspace, so we start by identifying the PBW basis elements of
$(2,1)$
eigenspace, so we start by identifying the PBW basis elements of
![]() $J^4(kP)$
in this eigenspace. These are
$J^4(kP)$
in this eigenspace. These are
![]() $\tilde y^{p-2}\tilde z^2$
and
$\tilde y^{p-2}\tilde z^2$
and
![]() $\tilde x\tilde y^{p-1}\tilde z\in J^{p+2}(kP)$
and
$\tilde x\tilde y^{p-1}\tilde z\in J^{p+2}(kP)$
and
![]() $\tilde x^{i+1}\tilde y^i\tilde z^{p-i} \in J^{2p+1}(kP)$
with
$\tilde x^{i+1}\tilde y^i\tilde z^{p-i} \in J^{2p+1}(kP)$
with
![]() $1\leqslant i \leqslant p-2$
.
$1\leqslant i \leqslant p-2$
.
However, we also need to make use of symmetry. Let
![]() $\sigma $
be the composition of the automorphism of
$\sigma $
be the composition of the automorphism of
![]() $kP$
which inverts g and h (and hence fixes c) with the antiautomorphism of
$kP$
which inverts g and h (and hence fixes c) with the antiautomorphism of
![]() $kP$
which inverts all elements of P. Then
$kP$
which inverts all elements of P. Then
![]() $\sigma $
fixes
$\sigma $
fixes
![]() $\tilde x$
and
$\tilde x$
and
![]() $\tilde y$
, reverses multiplication in
$\tilde y$
, reverses multiplication in
![]() $kP$
and negates
$kP$
and negates
![]() $\tilde z$
. The point is that
$\tilde z$
. The point is that
![]() $[\tilde x,\tilde z]=\tilde x^2\tilde y -2\tilde x\tilde y\tilde x+\tilde y\tilde x^2$
is fixed by
$[\tilde x,\tilde z]=\tilde x^2\tilde y -2\tilde x\tilde y\tilde x+\tilde y\tilde x^2$
is fixed by
![]() $\sigma $
, whereas
$\sigma $
, whereas
![]() $\sigma $
does not fix all elements of the
$\sigma $
does not fix all elements of the
![]() $(2,1)$
eigenspace. With this in mind, we modify the PBW basis of this eigenspace so that the action of
$(2,1)$
eigenspace. With this in mind, we modify the PBW basis of this eigenspace so that the action of
![]() $\sigma $
is more transparent.
$\sigma $
is more transparent.
The element
![]() $\tilde y^{p-2}\tilde z^2$
, for example, is not fixed by
$\tilde y^{p-2}\tilde z^2$
, for example, is not fixed by
![]() $\sigma $
, even though it is fixed modulo
$\sigma $
, even though it is fixed modulo
![]() $J^{p+3}(kP)$
. So instead, we use the element
$J^{p+3}(kP)$
. So instead, we use the element
![]() $\tilde z\tilde y^{p-2}\tilde z$
, which is equivalent to it modulo
$\tilde z\tilde y^{p-2}\tilde z$
, which is equivalent to it modulo
![]() $J^{p+3}(kP)$
, and therefore just as good as part of a PBW basis of
$J^{p+3}(kP)$
, and therefore just as good as part of a PBW basis of
![]() $kP$
, but is fixed by
$kP$
, but is fixed by
![]() $\sigma $
. Since
$\sigma $
. Since
![]() $\sigma (\tilde x\tilde y^{p-1}\tilde z)\equiv -\tilde x\tilde y^{p-1}\tilde z-\tilde y^{p-2}\tilde z^2\pmod {J^{p+3}(kP)}$
, the element
$\sigma (\tilde x\tilde y^{p-1}\tilde z)\equiv -\tilde x\tilde y^{p-1}\tilde z-\tilde y^{p-2}\tilde z^2\pmod {J^{p+3}(kP)}$
, the element
![]() $\tilde x\tilde y^{p-1}\tilde z$
is not involved in the expression for
$\tilde x\tilde y^{p-1}\tilde z$
is not involved in the expression for
![]() $[\tilde x,\tilde z]$
. So
$[\tilde x,\tilde z]$
. So
![]() $[\tilde x,\tilde z]$
is congruent to a multiple of
$[\tilde x,\tilde z]$
is congruent to a multiple of
![]() $\tilde z\tilde y^{p-2}\tilde z$
modulo
$\tilde z\tilde y^{p-2}\tilde z$
modulo
![]() $J^{2p+1}(kP)$
.
$J^{2p+1}(kP)$
.
For the linear span of the elements
![]() $\tilde x^{i+1}\tilde y^i\tilde z^{p-i}$
, since there are no
$\tilde x^{i+1}\tilde y^i\tilde z^{p-i}$
, since there are no
![]() $(2,1)$
eigenvectors lower in the radical series, reordering the terms in a monomial has the same effect as in
$(2,1)$
eigenvectors lower in the radical series, reordering the terms in a monomial has the same effect as in
![]() $\mathcal {U}\mathsf {Jen}_*(kP)$
. So we can choose a basis consisting of the elements
$\mathcal {U}\mathsf {Jen}_*(kP)$
. So we can choose a basis consisting of the elements
![]() $\tilde x^i\tilde y^{2i-1}\tilde x^i\tilde z^{p+1-2i}$
$\tilde x^i\tilde y^{2i-1}\tilde x^i\tilde z^{p+1-2i}$
![]() $(1\leqslant i \leqslant (p-1)/2$
) and the elements
$(1\leqslant i \leqslant (p-1)/2$
) and the elements
![]() $\tilde y^i\tilde x^{2i+1}\tilde y^i\tilde z^{p-2i}$
$\tilde y^i\tilde x^{2i+1}\tilde y^i\tilde z^{p-2i}$
![]() $(1\leqslant i \leqslant (p-3)/2$
). The former are
$(1\leqslant i \leqslant (p-3)/2$
). The former are
![]() $+1$
eigenvectors of
$+1$
eigenvectors of
![]() $\sigma $
, while the latter are
$\sigma $
, while the latter are
![]() $-1$
eigenvectors. So the expression for
$-1$
eigenvectors. So the expression for
![]() $[\tilde x,\tilde z]$
only involves the former.
$[\tilde x,\tilde z]$
only involves the former.
By Lemma 5.6, we can write
Here, we have used the symmetry of
![]() $kP$
, which swaps
$kP$
, which swaps
![]() $\tilde x$
and
$\tilde x$
and
![]() $\tilde y$
and negates
$\tilde y$
and negates
![]() $\tilde z$
, to compare the coefficients in (5.7) and those in (5.8).
$\tilde z$
, to compare the coefficients in (5.7) and those in (5.8).
Remark 5.9. With the aid of the computer algebra system Magma [Reference Bosma, Cannon and Playoust5], we have determined the relation (5.7) for small p as follows:
 $$ \begin{align*} p=3:\qquad [\tilde x,\tilde z]&=\tilde z\tilde y\tilde z, \\ p=5:\qquad [\tilde x,\tilde z]&=\tilde z\tilde y^3\tilde z +2\tilde x\tilde y\tilde x\tilde z^4, \\ p=7:\qquad [\tilde x,\tilde z]&=\tilde z\tilde y^5\tilde z +4\tilde x\tilde y\tilde x\tilde z^6 +2\tilde x^2\tilde y^3\tilde x^2\tilde z^4. \end{align*} $$
$$ \begin{align*} p=3:\qquad [\tilde x,\tilde z]&=\tilde z\tilde y\tilde z, \\ p=5:\qquad [\tilde x,\tilde z]&=\tilde z\tilde y^3\tilde z +2\tilde x\tilde y\tilde x\tilde z^4, \\ p=7:\qquad [\tilde x,\tilde z]&=\tilde z\tilde y^5\tilde z +4\tilde x\tilde y\tilde x\tilde z^6 +2\tilde x^2\tilde y^3\tilde x^2\tilde z^4. \end{align*} $$
One might surmise that
![]() $a_0=1$
and
$a_0=1$
and
![]() $a_{(p-1)/2}=0$
, but we have not proved that, nor have we spotted the general pattern of the coefficients.
$a_{(p-1)/2}=0$
, but we have not proved that, nor have we spotted the general pattern of the coefficients.
Theorem 5.10. A presentation for
![]() $kP$
is given by generators
$kP$
is given by generators
![]() $\tilde x$
,
$\tilde x$
,
![]() $\tilde y$
,
$\tilde y$
,
![]() $\tilde z$
with the relations (5.7) and (5.8) together with
$\tilde z$
with the relations (5.7) and (5.8) together with
and relations saying that all words of length at least
![]() $4p-3$
in
$4p-3$
in
![]() $\tilde x$
and
$\tilde x$
and
![]() $\tilde y$
are equal to zero.
$\tilde y$
are equal to zero.
Proof. These relations hold in
![]() $kP$
by Lemmas 5.5 and 5.6 and the fact that
$kP$
by Lemmas 5.5 and 5.6 and the fact that
![]() $J^{4p-3}(kP)=0$
. Let
$J^{4p-3}(kP)=0$
. Let
![]() $\mathbf {A}$
be the algebra defined by these generators and relations. Then we have a surjective map
$\mathbf {A}$
be the algebra defined by these generators and relations. Then we have a surjective map
![]() $\mathbf {A}\to kP$
taking
$\mathbf {A}\to kP$
taking
![]() $\tilde x$
,
$\tilde x$
,
![]() $\tilde y$
and
$\tilde y$
and
![]() $\tilde z$
to the elements with the same names. This induces a map
$\tilde z$
to the elements with the same names. This induces a map
![]() $\mathsf {gr}_*\mathbf {A} \to \mathsf {gr}_* kP$
. The relations (5.7) and (5.8) imply that the images x, y and z in
$\mathsf {gr}_*\mathbf {A} \to \mathsf {gr}_* kP$
. The relations (5.7) and (5.8) imply that the images x, y and z in
![]() $\mathsf {gr}_*\mathbf {A}$
of
$\mathsf {gr}_*\mathbf {A}$
of
![]() $\tilde x$
,
$\tilde x$
,
![]() $\tilde y$
and
$\tilde y$
and
![]() $\tilde z$
in
$\tilde z$
in
![]() $\mathbf {A}$
satisfy
$\mathbf {A}$
satisfy
![]() $[x,z]=0$
and
$[x,z]=0$
and
![]() $[y,z]=0$
. Thus, all the relations in
$[y,z]=0$
. Thus, all the relations in
![]() $\mathcal {U}\mathsf {Jen}_*(P)$
hold in
$\mathcal {U}\mathsf {Jen}_*(P)$
hold in
![]() $\mathsf {gr}_*\mathbf {A}$
, and
$\mathsf {gr}_*\mathbf {A}$
, and
![]() $\mathsf {gr}_*\mathbf {A}\to \mathsf {gr}_* kP$
is an isomorphism. Since the radical of
$\mathsf {gr}_*\mathbf {A}\to \mathsf {gr}_* kP$
is an isomorphism. Since the radical of
![]() $\mathbf {A}$
is nilpotent, this implies that
$\mathbf {A}$
is nilpotent, this implies that
![]() $\mathbf {A}\to kP$
is an isomorphism.
$\mathbf {A}\to kP$
is an isomorphism.
Recall from the proof of Theorem 1.2 that setting
![]() $\mathsf {x}=txe$
,
$\mathsf {x}=txe$
,
![]() $\mathsf {y}=sye$
and
$\mathsf {y}=sye$
and
![]() $\mathsf {z}=stze$
in
$\mathsf {z}=stze$
in
![]() $\mathsf {gr}_*(kGe)$
, we have that the algebra
$\mathsf {gr}_*(kGe)$
, we have that the algebra
![]() $\mathfrak {A}$
is generated by
$\mathfrak {A}$
is generated by
![]() $\mathsf {x}$
,
$\mathsf {x}$
,
![]() $\mathsf {y}$
and
$\mathsf {y}$
and
![]() $\mathsf {z}$
centralises
$\mathsf {z}$
centralises
![]() $\mathfrak {M}$
in
$\mathfrak {M}$
in
![]() $\mathcal {U}\mathsf {Jen}_*(P)\rtimes kH$
. Further, these elements satisfy the relations
$\mathcal {U}\mathsf {Jen}_*(P)\rtimes kH$
. Further, these elements satisfy the relations
(and these imply that
![]() $\mathsf {z}^p=0$
).
$\mathsf {z}^p=0$
).
In
![]() $kGe$
, we set
$kGe$
, we set
![]() $\tilde {\mathsf {x}}=t\tilde xe$
,
$\tilde {\mathsf {x}}=t\tilde xe$
,
![]() $\tilde {\mathsf {y}}=s\tilde ye$
and
$\tilde {\mathsf {y}}=s\tilde ye$
and
![]() $\tilde {\mathsf {z}}=st\tilde ze$
. The algebra
$\tilde {\mathsf {z}}=st\tilde ze$
. The algebra
![]() $\tilde {\mathfrak {A}}$
generated by
$\tilde {\mathfrak {A}}$
generated by
![]() $\tilde {\mathsf {x}}$
,
$\tilde {\mathsf {x}}$
,
![]() $\tilde {\mathsf {y}}$
and
$\tilde {\mathsf {y}}$
and
![]() $\tilde {\mathsf {z}}$
centralises
$\tilde {\mathsf {z}}$
centralises
![]() $\mathfrak {M}$
in
$\mathfrak {M}$
in
![]() $kGe$
. These elements satisfy the relations
$kGe$
. These elements satisfy the relations
together with the following quantised versions of (5.7) and (5.8)
 $$ \begin{align*} \tilde {\mathsf{x}}\tilde {\mathsf{z}} + \tilde {\mathsf{z}} \tilde {\mathsf{x}} & =(-1)^{\frac{p-1}{2}}\! \bigl(a_0 \tilde {\mathsf{z}}\tilde {\mathsf{y}}^{p-2}\tilde {\mathsf{z}} - a_1\tilde{\mathsf{x}}\tilde{\mathsf{y}}\tilde{\mathsf{x}}\tilde{\mathsf{z}}^{p-1}- a_2\tilde{\mathsf{x}}^2\tilde{\mathsf{y}}^3\tilde{\mathsf{x}}^2\tilde{\mathsf{z}}^{p-3} -\cdots- a_{(p-1)/2}\tilde{\mathsf{x}}^{\frac{p-1}{2}}\tilde{\mathsf{y}}^{p-2}\tilde{\mathsf{x}}^{\frac{p-1}{2}}\tilde{\mathsf{z}}^2\bigr), \\ \tilde{\mathsf{y}} \tilde{\mathsf{z}} + \tilde{\mathsf{z}} \tilde{\mathsf{y}} & =(-1)^{\frac{p-1}{2}}\! \bigl(a_0\tilde{\mathsf{z}}\tilde{\mathsf{x}}^{p-2}\tilde{\mathsf{z}} - a_1\tilde{\mathsf{y}}\tilde{\mathsf{x}}\tilde{\mathsf{y}}\tilde{\mathsf{z}}^{p-1} - a_2\tilde{\mathsf{y}}^2\tilde{\mathsf{x}}^3\tilde{\mathsf{y}}^2\tilde{\mathsf{z}}^{p-3} -\cdots- a_{(p-1)/2}\tilde{\mathsf{y}}^{\frac{p-1}{2}}\tilde{\mathsf{x}}^{p-2}\tilde{\mathsf{y}}^{\frac{p-1}{2}}\tilde{\mathsf{z}}^2\bigr), \end{align*} $$
$$ \begin{align*} \tilde {\mathsf{x}}\tilde {\mathsf{z}} + \tilde {\mathsf{z}} \tilde {\mathsf{x}} & =(-1)^{\frac{p-1}{2}}\! \bigl(a_0 \tilde {\mathsf{z}}\tilde {\mathsf{y}}^{p-2}\tilde {\mathsf{z}} - a_1\tilde{\mathsf{x}}\tilde{\mathsf{y}}\tilde{\mathsf{x}}\tilde{\mathsf{z}}^{p-1}- a_2\tilde{\mathsf{x}}^2\tilde{\mathsf{y}}^3\tilde{\mathsf{x}}^2\tilde{\mathsf{z}}^{p-3} -\cdots- a_{(p-1)/2}\tilde{\mathsf{x}}^{\frac{p-1}{2}}\tilde{\mathsf{y}}^{p-2}\tilde{\mathsf{x}}^{\frac{p-1}{2}}\tilde{\mathsf{z}}^2\bigr), \\ \tilde{\mathsf{y}} \tilde{\mathsf{z}} + \tilde{\mathsf{z}} \tilde{\mathsf{y}} & =(-1)^{\frac{p-1}{2}}\! \bigl(a_0\tilde{\mathsf{z}}\tilde{\mathsf{x}}^{p-2}\tilde{\mathsf{z}} - a_1\tilde{\mathsf{y}}\tilde{\mathsf{x}}\tilde{\mathsf{y}}\tilde{\mathsf{z}}^{p-1} - a_2\tilde{\mathsf{y}}^2\tilde{\mathsf{x}}^3\tilde{\mathsf{y}}^2\tilde{\mathsf{z}}^{p-3} -\cdots- a_{(p-1)/2}\tilde{\mathsf{y}}^{\frac{p-1}{2}}\tilde{\mathsf{x}}^{p-2}\tilde{\mathsf{y}}^{\frac{p-1}{2}}\tilde{\mathsf{z}}^2\bigr), \end{align*} $$
together with relations saying that all words of length at least
![]() $4p-3$
in
$4p-3$
in
![]() $\tilde {\mathsf {x}}$
and
$\tilde {\mathsf {x}}$
and
![]() $\tilde {\mathsf {y}}$
are equal to zero.
$\tilde {\mathsf {y}}$
are equal to zero.
Using Magma [Reference Bosma, Cannon and Playoust5], in the case
![]() $p=3$
, we have succeeded in finding a short presentation for
$p=3$
, we have succeeded in finding a short presentation for
![]() $kP$
in terms of the generators
$kP$
in terms of the generators
![]() $\tilde x$
and
$\tilde x$
and
![]() $\tilde y$
. In this case, we have
$\tilde y$
. In this case, we have
![]() $\tilde x=g^{-1}-g$
and
$\tilde x=g^{-1}-g$
and
![]() $\tilde y=h^{-1}-h$
. Defining
$\tilde y=h^{-1}-h$
. Defining
![]() $\tilde z=[\tilde x,\tilde y]$
, the following relations hold in
$\tilde z=[\tilde x,\tilde y]$
, the following relations hold in
![]() $kP$
.
$kP$
.
It follows from these relations that
![]() $\tilde z^3=0$
, so it is not necessary to include this in the relations, and hence the algebra defined by these relations has dimension
$\tilde z^3=0$
, so it is not necessary to include this in the relations, and hence the algebra defined by these relations has dimension
![]() $27$
and is isomorphic to
$27$
and is isomorphic to
![]() $kP$
. This is the content of the next theorem. Note, however, that the proof is difficult, so for some purposes it is better to adjoin
$kP$
. This is the content of the next theorem. Note, however, that the proof is difficult, so for some purposes it is better to adjoin
![]() $\tilde z^3=0$
to the above presentation. We restate and prove the first part of Theorem 1.3.
$\tilde z^3=0$
to the above presentation. We restate and prove the first part of Theorem 1.3.
Theorem 5.12. Suppose that
![]() $p=3$
. The generators
$p=3$
. The generators
![]() $\tilde x$
,
$\tilde x$
,
![]() $\tilde y$
and
$\tilde y$
and
![]() $\tilde z$
and the relations (5.11) give a presentation for
$\tilde z$
and the relations (5.11) give a presentation for
![]() $kP$
.
$kP$
.
Proof. Since the given elements of
![]() $kP$
satisfy these relations, it suffices to prove that the algebra defined by the relations has dimension at most
$kP$
satisfy these relations, it suffices to prove that the algebra defined by the relations has dimension at most
![]() $27$
. The crucial point is to prove that
$27$
. The crucial point is to prove that
![]() $\tilde z^3=0$
.
$\tilde z^3=0$
.
It is more convenient to extend the field so that it has a square root of
![]() $-1$
, which we denote
$-1$
, which we denote
![]() $\mathsf {i}\,$
. Then we set
$\mathsf {i}\,$
. Then we set
![]() $a=\tilde x+\mathsf {i}\,\tilde y$
,
$a=\tilde x+\mathsf {i}\,\tilde y$
,
![]() $b=\tilde x-\mathsf {i}\,\tilde y$
,
$b=\tilde x-\mathsf {i}\,\tilde y$
,
![]() $c=\mathsf {i}\,\tilde z$
, and the presentation becomes
$c=\mathsf {i}\,\tilde z$
, and the presentation becomes
and we must show that
![]() $c^3=0$
.
$c^3=0$
.
We have
 $$ \begin{align*} (1+c)a(1-c)&=a,\\ (1-c)b(1+c)&=b, \end{align*} $$
$$ \begin{align*} (1+c)a(1-c)&=a,\\ (1-c)b(1+c)&=b, \end{align*} $$
and so
Therefore c commutes with
![]() $ab$
and with
$ab$
and with
![]() $ba$
.
$ba$
.
Next,
and since
![]() $cab=abc$
, it follows that c commutes with
$cab=abc$
, it follows that c commutes with
![]() $acb$
. Thus, we have
$acb$
. Thus, we have
Since we are in characteristic three, we also have
and so
Thus c also commutes with
![]() $a^3$
:
$a^3$
:
Next, using (5.13) we have
 $$ \begin{align} c^3&=cabc-cbac=acbc+cacbc-cbca+cbcac=a^4+b^4c-b^4+a^4c \\ &=-a^4c = -b^4c = -cacbc = -cbcac= -ca^4 = -cb^4.\notag \end{align} $$
$$ \begin{align} c^3&=cabc-cbac=acbc+cacbc-cbca+cbcac=a^4+b^4c-b^4+a^4c \\ &=-a^4c = -b^4c = -cacbc = -cbcac= -ca^4 = -cb^4.\notag \end{align} $$
Using (5.14) and (5.15), we have
and so
![]() $c^4=0$
.
$c^4=0$
.
The fact that
![]() $c^4=0$
enables us to write
$c^4=0$
enables us to write
We can use these to move copies of c to the end of expressions, at the expense of accumulating higher powers of c. Applying this to
![]() $a^6=cbc^2bc$
, we get
$a^6=cbc^2bc$
, we get
![]() $b^2(c^4+{}$
higher powers of
$b^2(c^4+{}$
higher powers of
![]() $c)$
, so we get
$c)$
, so we get
![]() $a^6=0$
. Similarly, we get
$a^6=0$
. Similarly, we get
![]() $b^6=0$
. Then when we do the same with
$b^6=0$
. Then when we do the same with
![]() $(ab)^9$
, moving b past a using
$(ab)^9$
, moving b past a using
![]() $ba=ab-c$
, we get
$ba=ab-c$
, we get
for suitable polynomials
![]() $f_i(c)$
. Since
$f_i(c)$
. Since
![]() $a^6=b^6=c^4=0$
, every term here is zero, and so
$a^6=b^6=c^4=0$
, every term here is zero, and so
![]() $(ab)^9=0$
.
$(ab)^9=0$
.
Now using (5.15) and the same method, we have
and so
![]() $(1+ab)c^3=0$
. Since
$(1+ab)c^3=0$
. Since
![]() $ab$
is nilpotent,
$ab$
is nilpotent,
![]() $(1+ab)$
is invertible, so this implies that
$(1+ab)$
is invertible, so this implies that
![]() $c^3=0$
.
$c^3=0$
.
The original relations together with (5.16), (5.17) and
![]() $c^3=0$
allow us to rewrite every element as a linear combination of the elements
$c^3=0$
allow us to rewrite every element as a linear combination of the elements
![]() $a^ib^jc^k$
with
$a^ib^jc^k$
with
![]() $0\leqslant i,j,k < 3$
, so the algebra has dimension at most
$0\leqslant i,j,k < 3$
, so the algebra has dimension at most
![]() $27$
, and we are done.
$27$
, and we are done.
Proof of Theorem 1.3.
The relations for
![]() $kP$
are proved in Theorem 5.12. As above, using
$kP$
are proved in Theorem 5.12. As above, using
![]() $\tilde x=g^{-1}-g$
,
$\tilde x=g^{-1}-g$
,
![]() $\tilde y = h^{-1}-h$
and
$\tilde y = h^{-1}-h$
and
![]() $\tilde z=[\tilde x,\tilde y]$
to obtain generators for the basic algebra for
$\tilde z=[\tilde x,\tilde y]$
to obtain generators for the basic algebra for
![]() $kGe$
, we set
$kGe$
, we set
![]() $\tilde {\mathsf {x}} = t\tilde xe$
and
$\tilde {\mathsf {x}} = t\tilde xe$
and
![]() $\tilde {\mathsf {y}} = s\tilde ye$
,
$\tilde {\mathsf {y}} = s\tilde ye$
,
![]() $\tilde {\mathsf {z}} = st\tilde ze$
. These satisfy
$\tilde {\mathsf {z}} = st\tilde ze$
. These satisfy
Furthermore, the algebra defined by these relations again has dimension
![]() $27$
and is hence isomorphic to the basic algebra of
$27$
and is hence isomorphic to the basic algebra of
![]() $kGe$
.
$kGe$
.
Remark 5.18. The above relations for
![]() $kGe$
are a quantised version of the relations for
$kGe$
are a quantised version of the relations for
![]() $kP$
. These relations imply that
$kP$
. These relations imply that
![]() $\tilde {\mathsf {z}}^3=0$
, and adjoining this relation makes the presentation easier to work with if desired.
$\tilde {\mathsf {z}}^3=0$
, and adjoining this relation makes the presentation easier to work with if desired.
These presentations can be lifted to give integral presentations. The algebra
![]() $\mathcal {O} P$
has a presentation with corresponding generators
$\mathcal {O} P$
has a presentation with corresponding generators
![]() $\hat x$
,
$\hat x$
,
![]() $\hat y$
and
$\hat y$
and
![]() $\hat z$
subject to
$\hat z$
subject to
while
![]() $\mathcal {O} Ge$
is generated by
$\mathcal {O} Ge$
is generated by
![]() $\hat {\mathsf {x}}$
,
$\hat {\mathsf {x}}$
,
![]() $\hat {\mathsf {y}}$
and
$\hat {\mathsf {y}}$
and
![]() $\hat {\mathsf {z}}$
subject to
$\hat {\mathsf {z}}$
subject to
The expressions for
![]() $\hat z^3$
in
$\hat z^3$
in
![]() $\mathcal {O} P$
and for
$\mathcal {O} P$
and for
![]() ${\hat {\mathsf {z}}}^3$
in
${\hat {\mathsf {z}}}^3$
in
![]() $\mathcal {O} Ge$
, lifting the fact that they cube to zero modulo three, are ugly even though they follow from the presentations above.
$\mathcal {O} Ge$
, lifting the fact that they cube to zero modulo three, are ugly even though they follow from the presentations above.
6 Example:
 $2^{1+4}{:\,}3^{1+2}$
in characteristic two
$2^{1+4}{:\,}3^{1+2}$
in characteristic two
The examples in the last section were at odd primes for extraspecial groups of order
![]() $p^3$
. In this section we give an example in characteristic two with an extraspecial group of order
$p^3$
. In this section we give an example in characteristic two with an extraspecial group of order
![]() $2^5$
.
$2^5$
.
Let P be an extraspecial group
![]() $2^{1+4}$
which is a central product of two copies of the quaternion group of order eight, and let H be an extraspecial group
$2^{1+4}$
which is a central product of two copies of the quaternion group of order eight, and let H be an extraspecial group
![]() $3^{1+2}$
of exponent three. We let the centre
$3^{1+2}$
of exponent three. We let the centre
![]() $Z\cong \mathbb {Z}/3$
of H act trivially on P, we let the elementary abelian quotient act as the automorphisms of order three on the two quaternion central factors of P and we set
$Z\cong \mathbb {Z}/3$
of H act trivially on P, we let the elementary abelian quotient act as the automorphisms of order three on the two quaternion central factors of P and we set
![]() $G=P\rtimes H$
. Thus, the quotient
$G=P\rtimes H$
. Thus, the quotient
![]() $G/Z\cong SL(2,3)\circ SL(2,3)$
is a central product of two copies of the group
$G/Z\cong SL(2,3)\circ SL(2,3)$
is a central product of two copies of the group
![]() $SL(2,3)$
of order
$SL(2,3)$
of order
![]() $24$
.
$24$
.
More precisely, we let
 $$ \begin{align*} P &= \langle g_1,g_2, h_1,h_2, c \mid g_1^2=h_1^2=[g_1,h_1]=g_2^2=h_2^2=[g_2,h_2]=c,\\ &\qquad [g_1,c]=[g_2,c]=[h_1,c]=[h_2,c]= [g_1,g_2]=[g_1,h_2]=[h_1,g_2]=[h_1,h_2]=c^2=1 \rangle, \\ H &= \langle s_1,s_2, t \mid s_1^3=s_2^3=1,\ [s_1,s_2]=t,\ [s_1,t]=[s_2,t]=t^3=1\rangle. \end{align*} $$
$$ \begin{align*} P &= \langle g_1,g_2, h_1,h_2, c \mid g_1^2=h_1^2=[g_1,h_1]=g_2^2=h_2^2=[g_2,h_2]=c,\\ &\qquad [g_1,c]=[g_2,c]=[h_1,c]=[h_2,c]= [g_1,g_2]=[g_1,h_2]=[h_1,g_2]=[h_1,h_2]=c^2=1 \rangle, \\ H &= \langle s_1,s_2, t \mid s_1^3=s_2^3=1,\ [s_1,s_2]=t,\ [s_1,t]=[s_2,t]=t^3=1\rangle. \end{align*} $$
Let H act on P with
![]() $Z=\langle t\rangle $
acting trivially, and
$Z=\langle t\rangle $
acting trivially, and
 $$ \begin{gather*} s_1g_1s_1^{-1}=h_1, \qquad s_1h_1s_1^{-1}=g_1h_1,\qquad s_1g_2s_1^{-1}=g_2, \qquad s_1h_2s_1^{-1}=h_2,\qquad s_1cs_1^{-1}=c, \\ s_2g_1s_2^{-1}=g_1, \qquad s_2h_1s_2^{-1}=h_1,\qquad s_2g_2s_2^{-1}=h_2, \qquad s_2h_2s_2^{-1}=g_2h_2, \qquad s_2cs_2^{-1}=c. \end{gather*} $$
$$ \begin{gather*} s_1g_1s_1^{-1}=h_1, \qquad s_1h_1s_1^{-1}=g_1h_1,\qquad s_1g_2s_1^{-1}=g_2, \qquad s_1h_2s_1^{-1}=h_2,\qquad s_1cs_1^{-1}=c, \\ s_2g_1s_2^{-1}=g_1, \qquad s_2h_1s_2^{-1}=h_1,\qquad s_2g_2s_2^{-1}=h_2, \qquad s_2h_2s_2^{-1}=g_2h_2, \qquad s_2cs_2^{-1}=c. \end{gather*} $$
Let k be a field of characteristic two containing
![]() $\mathbb {F}_4=\{0,1,\omega ,\bar \omega \}$
. A basis of eigenvectors in
$\mathbb {F}_4=\{0,1,\omega ,\bar \omega \}$
. A basis of eigenvectors in
![]() $\mathsf {gr}_1(kP)$
is given by
$\mathsf {gr}_1(kP)$
is given by
These give the following presentation for
![]() $\mathsf {gr}_*(kP)$
.
$\mathsf {gr}_*(kP)$
.
A lift of
![]() $x_i$
and
$x_i$
and
![]() $y_i$
to eigenvectors complementing
$y_i$
to eigenvectors complementing
![]() $J^2(kP)$
in
$J^2(kP)$
in
![]() $J(kP)$
is given by the elements
$J(kP)$
is given by the elements
The relations lift to
 $$ \begin{gather*} \tilde x_i^2=\tilde y_i\tilde x_i\tilde y_i, \qquad \tilde y_i^2=\tilde x_i\tilde y_i\tilde x_i,\qquad \tilde x_i^4=0 \qquad (i=1,2),\\ [\tilde x_1,\tilde x_2]=[\tilde y_1,\tilde y_2]= [\tilde x_1,\tilde y_2]=[\tilde x_2,\tilde y_1]=0, \qquad [\tilde x_1,\tilde y_1]+\tilde x_1^3=[\tilde x_2,\tilde y_2]+\tilde x_2^3 \end{gather*} $$
$$ \begin{gather*} \tilde x_i^2=\tilde y_i\tilde x_i\tilde y_i, \qquad \tilde y_i^2=\tilde x_i\tilde y_i\tilde x_i,\qquad \tilde x_i^4=0 \qquad (i=1,2),\\ [\tilde x_1,\tilde x_2]=[\tilde y_1,\tilde y_2]= [\tilde x_1,\tilde y_2]=[\tilde x_2,\tilde y_1]=0, \qquad [\tilde x_1,\tilde y_1]+\tilde x_1^3=[\tilde x_2,\tilde y_2]+\tilde x_2^3 \end{gather*} $$
(both sides in the last relation are equal to
![]() $(1+c)$
). Using the radical filtration, it is not hard to check that these relations define a k-algebra of dimension at most
$(1+c)$
). Using the radical filtration, it is not hard to check that these relations define a k-algebra of dimension at most
![]() $32$
, which is therefore isomorphic to
$32$
, which is therefore isomorphic to
![]() $kP$
.
$kP$
.
The action of H on
![]() $kP$
with respect to these generators is given by
$kP$
with respect to these generators is given by
where
![]() $\psi _1(s_1)=\psi _2(s_2)=\omega $
,
$\psi _1(s_1)=\psi _2(s_2)=\omega $
,
![]() $\psi _1(s_2)=\psi _2(s_1)=1$
.
$\psi _1(s_2)=\psi _2(s_1)=1$
.
Set
Then
![]() $kG$
has three blocks: the principal block
$kG$
has three blocks: the principal block
![]() $kGe_0$
and two nonprincipal blocks
$kGe_0$
and two nonprincipal blocks
![]() $kGe$
and
$kGe$
and
![]() $kG\bar e$
. We examine the nonprincipal block
$kG\bar e$
. We examine the nonprincipal block
![]() $kGe$
; the other is similar.
$kGe$
; the other is similar.
We have
![]() $ s_1s_2e=\omega s_2s_1e$
. We set
$ s_1s_2e=\omega s_2s_1e$
. We set
These commute with
![]() $\mathfrak {M}=kHe$
and generate the subalgebra
$\mathfrak {M}=kHe$
and generate the subalgebra
![]() $\mathfrak {A}$
, so that
$\mathfrak {A}$
, so that
![]() $kGe\cong \mathsf {Mat}_{3}(\mathfrak {A})$
. They satisfy the relations:
$kGe\cong \mathsf {Mat}_{3}(\mathfrak {A})$
. They satisfy the relations:
 $$ \begin{gather*} \tilde {\mathsf{x}}_i^2=\tilde {\mathsf{y}}_i\tilde {\mathsf{x}}_i\tilde {\mathsf{y}}_i,\qquad \tilde {\mathsf{y}}_i^2=\tilde {\mathsf{x}}_i\tilde {\mathsf{y}}_i\tilde {\mathsf{x}}_i,\qquad \tilde {\mathsf{x}}_i^4=0 \qquad (i=1,2), \\ \tilde {\mathsf{x}}_1\tilde {\mathsf{x}}_2= \bar\omega\tilde {\mathsf{x}}_2\tilde {\mathsf{x}}_1, \qquad \tilde {\mathsf{x}}_1\tilde {\mathsf{y}}_2= \omega \tilde {\mathsf{y}}_2\tilde {\mathsf{x}}_1, \\ \tilde {\mathsf{y}}_1\tilde {\mathsf{x}}_2= \omega \tilde {\mathsf{x}}_2\tilde {\mathsf{y}}_1, \qquad\ \tilde {\mathsf{y}}_1\tilde {\mathsf{y}}_2= \bar \omega\tilde {\mathsf{y}}_2\tilde {\mathsf{y}}_1, \\ [\tilde {\mathsf{x}}_1,\tilde {\mathsf{y}}_1]+\tilde {\mathsf{x}}_1^3= [\tilde {\mathsf{x}}_2,\tilde {\mathsf{y}}_2]+\tilde {\mathsf{x}}_2^3 \end{gather*} $$
$$ \begin{gather*} \tilde {\mathsf{x}}_i^2=\tilde {\mathsf{y}}_i\tilde {\mathsf{x}}_i\tilde {\mathsf{y}}_i,\qquad \tilde {\mathsf{y}}_i^2=\tilde {\mathsf{x}}_i\tilde {\mathsf{y}}_i\tilde {\mathsf{x}}_i,\qquad \tilde {\mathsf{x}}_i^4=0 \qquad (i=1,2), \\ \tilde {\mathsf{x}}_1\tilde {\mathsf{x}}_2= \bar\omega\tilde {\mathsf{x}}_2\tilde {\mathsf{x}}_1, \qquad \tilde {\mathsf{x}}_1\tilde {\mathsf{y}}_2= \omega \tilde {\mathsf{y}}_2\tilde {\mathsf{x}}_1, \\ \tilde {\mathsf{y}}_1\tilde {\mathsf{x}}_2= \omega \tilde {\mathsf{x}}_2\tilde {\mathsf{y}}_1, \qquad\ \tilde {\mathsf{y}}_1\tilde {\mathsf{y}}_2= \bar \omega\tilde {\mathsf{y}}_2\tilde {\mathsf{y}}_1, \\ [\tilde {\mathsf{x}}_1,\tilde {\mathsf{y}}_1]+\tilde {\mathsf{x}}_1^3= [\tilde {\mathsf{x}}_2,\tilde {\mathsf{y}}_2]+\tilde {\mathsf{x}}_2^3 \end{gather*} $$
(both sides in the last relation are equal to
![]() $(1+c)e$
). These are identical to the relations for
$(1+c)e$
). These are identical to the relations for
![]() $kP$
apart from the commutation relations, which have been quantised by the introduction of factors
$kP$
apart from the commutation relations, which have been quantised by the introduction of factors
![]() $\omega $
and
$\omega $
and
![]() $\bar \omega $
.
$\bar \omega $
.
7 Appendix: Errata
The present paper supersedes most of our previous paper [Reference Benson, Kessar and Linckelmann4]. In that paper, there are a number of minor errors, mostly in the calculations in Section 4, which have been corrected in the present work. We give a list of those errors in [Reference Benson, Kessar and Linckelmann4].
In the statements of Theorem 1.2 and Corollary 1.3, it should read ‘
![]() $\ldots $
quantised version of
$\ldots $
quantised version of
![]() $k(P\rtimes Z(H)/Z)$
’, not ‘
$k(P\rtimes Z(H)/Z)$
’, not ‘
![]() $\ldots $
of
$\ldots $
of
![]() $k(P\rtimes L)$
’.
$k(P\rtimes L)$
’.
In the third line of the proof of Proposition 3.1, insert the word ‘abelian’ between ‘maximal’ and ‘subgroup’ (as is done correctly in line 2 and line 4 of that proof).
On page 1441, in the third line from the bottom, insert faithful:
‘…and a faithful linear character
![]() $\chi \colon Z \to k^{\times }$
…’
$\chi \colon Z \to k^{\times }$
…’
On page 1443, in the first line,
![]() $\rho (g)\colon h \mapsto \chi ([h,g])$
. The display on the third line should read
$\rho (g)\colon h \mapsto \chi ([h,g])$
. The display on the third line should read
On page 1444, line four should begin ‘where
![]() $\rho (g_{i,\phi })(h)=\chi ([h,g_{i,\phi }])$
’. The third line of the proof of Lemma 4.8 should begin with ‘
$\rho (g_{i,\phi })(h)=\chi ([h,g_{i,\phi }])$
’. The third line of the proof of Lemma 4.8 should begin with ‘
![]() $eg_{i,\phi }h=e\chi ([h,g_{i,\phi }])^{-1}hg_{i,\phi }$
’. The displayed equation on the fourth line of the proof of Lemma 4.8 should read
$eg_{i,\phi }h=e\chi ([h,g_{i,\phi }])^{-1}hg_{i,\phi }$
’. The displayed equation on the fourth line of the proof of Lemma 4.8 should read
In Definition 4.9 and the four lines following,
![]() $kHe$
should be
$kHe$
should be
![]() $k\tilde Ge$
four times. The dimension of
$k\tilde Ge$
four times. The dimension of
![]() $\mathfrak A$
should be given as
$\mathfrak A$
should be given as
![]() $|P|\cdot |Z(H):Z|$
and not
$|P|\cdot |Z(H):Z|$
and not
![]() $|P|\cdot |H:Z(H)|$
.
$|P|\cdot |H:Z(H)|$
.
On page 1445, in Lemma 4.12 (2), in the displayed equation, the last
![]() $w_i$
should be
$w_i$
should be
![]() $w_j$
. The scalar
$w_j$
. The scalar
![]() $q_{i,j,\phi }$
should equal
$q_{i,j,\phi }$
should equal
![]() $\psi _i(g_{j,\phi }z_{i,j,\phi })\psi _j(g^{-1}_{i,\phi }z_{i,j,\phi })\phi (z_{i,j,\phi })$
rather than
$\psi _i(g_{j,\phi }z_{i,j,\phi })\psi _j(g^{-1}_{i,\phi }z_{i,j,\phi })\phi (z_{i,j,\phi })$
rather than
![]() $\phi (z_{i,j,\phi })$
. Similarly, in Lemma 4.12 (3), the scalar
$\phi (z_{i,j,\phi })$
. Similarly, in Lemma 4.12 (3), the scalar
![]() $q_{i,j,\phi }$
should equal
$q_{i,j,\phi }$
should equal
![]() $\psi _i(g_{j,\phi })\psi _j(g^{-1}_{i,\phi })\chi (z_{i,j,\phi })$
rather than
$\psi _i(g_{j,\phi })\psi _j(g^{-1}_{i,\phi })\chi (z_{i,j,\phi })$
rather than
![]() $\chi (z_{i,j,\phi })$
. In the second line of the proof of Lemma 4.12 (1),
$\chi (z_{i,j,\phi })$
. In the second line of the proof of Lemma 4.12 (1),
![]() $g_{j,\phi \phi _i}$
should be
$g_{j,\phi \phi _i}$
should be
![]() $g_{j,\phi \psi _i}$
. The computation that was suppressed in the proof of Lemma 4.12 (2) uses (1) and equation (4.7). It is similar to the computation in Theorem 3.8 above, which we have spelled out in detail. There is a missing Z in the third to last line of the proof of Lemma 4.12 (3), and
$g_{j,\phi \psi _i}$
. The computation that was suppressed in the proof of Lemma 4.12 (2) uses (1) and equation (4.7). It is similar to the computation in Theorem 3.8 above, which we have spelled out in detail. There is a missing Z in the third to last line of the proof of Lemma 4.12 (3), and
![]() $g_ji$
should be
$g_ji$
should be
![]() $g_i$
in the second to last line.
$g_i$
in the second to last line.
On page 1447, in Theorem 4.15 and Corollary 4.16,
![]() $kGe$
should be
$kGe$
should be
![]() $k\tilde Ge$
five times.
$k\tilde Ge$
five times.
Acknowledgements
The first author is grateful to City, University of London for its hospitality during the research for this paper, and to Ehud Meir for conversations about the proof of Theorem 5.12. The second author acknowledges support from EPSRC grant EP/T004592/1.
Conflict of Interest
The authors have no conflict of interest to declare.