Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-13T10:45:23.937Z Has data issue: false hasContentIssue false
  • English
  • Français

Intermittency in the relative separations of tracers and of heavy particles in turbulent flows

Published online by Cambridge University Press:  23 September 2014

L. Biferale ,
A. S. Lanotte ,
R. Scatamacchia  and
F. Toschi
L. Biferale*
Affiliation:
Department of Physics and INFN, University of Tor Vergata, Via della Ricerca Scientifica 1, 00133 Rome, Italy
A. S. Lanotte
Affiliation:
CNR-ISAC and INFN-Sez. Lecce, Str. Prov. Lecce-Monteroni, 73100 Lecce, Italy
R. Scatamacchia
Affiliation:
Department of Physics and INFN, University of Tor Vergata, Via della Ricerca Scientifica 1, 00133 Rome, Italy Department of Physics, Eindhoven University of Technology, 5600 MB Eindhoven, The Netherlands
F. Toschi
Affiliation:
Department of Physics, Eindhoven University of Technology, 5600 MB Eindhoven, The Netherlands Department of Mathematics and Computer Science, Eindhoven University of Technology, 5600 MB Eindhoven, The Netherlands CNR-IAC, Via dei Taurini 19, 00185 Rome, Italy
*
†Email address for correspondence: biferale@roma2.infn.it
Get access Rights & Permissions [Opens in a new window]

Abstract

Results from direct numerical simulations (DNS) of particle relative dispersion in three-dimensional homogeneous and isotropic turbulence at Reynolds number 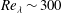$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}{\mathit{Re}}_{\lambda } \sim 300$ are presented. We study point-like passive tracers and heavy particles, at Stokes number 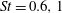$\mathit{St}=0.6,1$ and 5. Particles are emitted from localised sources, in bunches of thousands, periodically in time, allowing an unprecedented statistical accuracy to be reached, with a total number of events for two-point observables of the order of 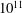${10^{11}}$. The right tail of the probability density function (PDF) for tracers develops a clear deviation from Richardson’s self-similar prediction, pointing to the intermittent nature of the dispersion process. In our numerical experiment, such deviations are manifest once the probability to measure an event becomes of the order of – or rarer than – one part over one million, hence the crucial importance of a large dataset. The role of finite-Reynolds-number effects and the related fluctuations when pair separations cross the boundary between viscous and inertial range scales are discussed. An asymptotic prediction based on the multifractal theory for inertial range intermittency and valid for large Reynolds numbers is found to agree with the data better than the Richardson theory. The agreement is improved when considering heavy particles, whose inertia filters out viscous scale fluctuations. By using the exit-time statistics we also show that events associated with pairs experiencing unusually slow inertial range separations have a non-self-similar PDF.

JFM classification

Turbulent Flows: Intermittency Multiphase and Particle-laden Flows: Multiphase and Particle-laden Flows Mixing: Turbulent mixing
Type
Papers
Information
Journal of Fluid Mechanics , Volume 757 , 25 October 2014 , pp. 550 - 572
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abrahamson, J. 1975 Collision rates of small particles in a vigorously turbulent fluid. Chem. Engng Sci. 30, 1371–1379.Google Scholar
Arneodo, A., Castaing, B., Cencini, M., Chevillard, L., Fisher, R. T., Grauer, R., Homann, H., Lamb, D., Lanotte, A. S., Lévèque, E., Lüthi, B., Mann, J., Mordant, N., Müller, W.-C., Ott, S., Ouellette, N. T., Pinton, J.-F., Pope, S. B., Roux, S. G., Toschi, F., Xu, H. & Yeung, P. K. 2008 Universal intermittent properties of particle trajectories in highly turbulent flows. Phys. Rev. Lett. 100, 254504.Google Scholar
Artale, V., Boffetta, G., Celani, A., Cencini, M. & Vulpiani, A. 1997 Dispersion of passive tracers in closed basins: beyond the diffusion coefficient. Phys. Fluids 9, 3162–3171.Google Scholar
Baldyga, J. & Bourne, J. R. 1999 Turbulent Mixing and Chemical Reactions. Wiley.Google Scholar
Balkovsky, E., Falkovich, G. & Fouxon, A. 2001 Intermittent distribution of inertial particles in turbulent flows. Phys. Rev. Lett. 86, 2790–2793.Google Scholar
Batchelor, G. K. 1950 The application of the similarity theory of turbulence to atmospheric diffusion. Q. J. R. Meteorol. Soc. 76, 133.CrossRefGoogle Scholar
Bec, J. 2005 Multifractal concentrations of inertial particles in smooth random flows. J. Fluid Mech. 528, 255–277.Google Scholar
Bec, J., Biferale, L., Boffetta, G., Celani, A., Cencini, M., Lanotte, A. S., Musacchio, S. & Toschi, F. 2006a Acceleration statistics of heavy particles in turbulent flows. J. Fluid Mech. 550, 349–358.Google Scholar
Bec, J., Biferale, L., Boffetta, G., Cencini, M., Musacchio, S. & Toschi, F. 2006b Lyapunov exponents of heavy particles in turbulence. Phys. Fluids 18, 091702.Google Scholar
Bec, J., Biferale, L., Cencini, M., Lanotte, A. S., Musacchio, S. & Toschi, F. 2007 Heavy particle concentration in turbulence at dissipative and inertial scales. Phys. Rev. Lett. 98, 084502.Google Scholar
Bec, J., Biferale, L., Cencini, M., Lanotte, A. S. & Toschi, F. 2010b Intermittency in the velocity distribution of heavy particles in turbulence. J. Fluid Mech. 646, 527–536.Google Scholar
Bec, J., Biferale, L., Cencini, M., Lanotte, A. S. & Toschi, F. 2011 Spatial and velocity statistics of inertial particles in turbulent flows. J. Phys.: Conf. Ser. 333, 012003.Google Scholar
Bec, J., Biferale, L., Lanotte, A. S., Scagliarini, A. & Toschi, F. 2010a Turbulent pair dispersion of inertial particles. J. Fluid Mech. 645, 497–528.CrossRefGoogle Scholar
Bennett, A. F. 1984 Relative dispersion: local and non-local dynamics. J. Atmos. Sci. 41 (11), 1881–1886.Google Scholar
Bennett, A. 2006 Lagrangian Fluid Dynamics, Cambridge Monographs on Mechanics. Cambridge University Press.Google Scholar
Benzi, R. 2011 A Voyage through Turbulence (ed. Davidson, P., Kaneda, Y., Moffatt, K. & Sreenivasan, K.), Cambridge University Press.Google Scholar
Benzi, R., Biferale, L., Fisher, R., Lamb, D. Q. & Toschi, F. 2010 Inertial range Eulerian and Lagrangian statistics from numerical simulations of isotropic turbulence. J. Fluid Mech. 653, 221.Google Scholar
Benzi, R., Ciliberto, S., Tripiccione, R., Baudet, C., Massaioli, F. & Succi, S. 1993 Extended self-similarity in turbulent flows. Phys. Rev. E 48, R29.Google Scholar
Biferale, L. 2008 A note on the fluctuation of dissipative scale in turbulence. Phys. Fluids 20, 031703.Google Scholar
Biferale, L., Boffetta, G., Celani, A., Devenish, B. J., Lanotte, A. & Toschi, F. 2004 Multifractal statistics of Lagrangian velocity and acceleration in turbulence. Phys. Rev. Lett. 93, 064502-1–064502-4.Google Scholar
Biferale, L., Boffetta, G., Celani, A., Devenish, B. J., Lanotte, A. & Toschi, F. 2005a Lagrangian statistics of particle pairs in homogeneous isotropic turbulence. Phys. Fluids 17, 115101.Google Scholar
Biferale, L., Boffetta, G., Celani, A., Devenish, B. J., Lanotte, A. & Toschi, F. 2005b Multi-particle dispersion in fully developed turbulence. Phys. Fluids 17, 111701.Google Scholar
Biferale, L., Calzavarini, E. & Toschi, F. 2011 Multi-time multi-scale correlation functions in hydrodynamic turbulence. Phys. Fluids 23, 085107.Google Scholar
Biferale, L., Lanotte, A. S. & Toschi, F. 2008 Statistical behaviour of isotropic and anisotropic fluctuations in homogeneous turbulence. Physica D 237, 1969–1975.Google Scholar
Bitane, R., Homann, H. & Bec, J. 2012a Time scales of turbulent relative dispersion. Phys. Rev. E 86, 045302(R).Google Scholar
Bitane, R., Homann, H. & Bec, J. 2012b Geometry and violent events in turbulent pair dispersion. J. Turbul. 14, 23–45.Google Scholar
Boffetta, G. & Celani, A. 2000 Pair dispersion in turbulence. Physica A 280, 1–9.Google Scholar
Boffetta, G., Celani, A., Crisanti, A. & Vulpiani, A. 1999 Pair dispersion in synthetic fully developed turbulence. Phys. Rev. E 60, 6734–6741.Google Scholar
Boffetta, G., De Lillo, F. & Gamba, A. 2004 Large scale inhomogeneity of inertial particles in turbulent flows. Phys. Fluids 16, L20–L24.Google Scholar
Boffetta, G. & Sokolov, I. M. 2002a Statistics of two-particle dispersion in two-dimensional turbulence. Phys. Fluids 14, 3224.Google Scholar
Boffetta, G. & Sokolov, I. M. 2002b Relative dispersion in fully developed turbulence: the Richardson’s law and intermittency corrections. Phys. Rev. Lett. 88, 094501.Google Scholar
Borgas, M. S. 1993 The multifractal Lagrangian nature of turbulence. Phil. Trans. R. Soc. Lond. A 342, 379–411.Google Scholar
Borgas, M. S. & Sawford, B. L. 1994 A family of stochastic models for two-particle dispersion in isotropic homogeneous stationary turbulence. J. Fluid Mech. 279, 69–99.Google Scholar
Borgas, M. S. & Yeung, P. K. 2004 Relative dispersion in isotropic turbulence. Part 2. A new stochastic model with Reynolds-number dependence. J. Fluid Mech. 503, 125–160.Google Scholar
Bourgoin, M., Ouellette, N. T., Xu, H., Berg, J. & Bodenschatz, E. 2006 The role of pair dispersion in turbulent flow. Science 311, 835.Google Scholar
Chaves, M., Gawȩdzki, K., Horvai, P., Kupiainen, A. & Vergassola, M. 2003 Lagrangian dispersion in Gaussian self-similar velocity ensembles. J. Stat. Phys. 113, 643–692.CrossRefGoogle Scholar
Chen, S., Doolen, G. D., Kraichnan, R. H. & She, Z.-S. 1993 On statistical correlations between velocity increments and locally averaged dissipation in homogeneous turbulence. Phys. Fluids A 5, 458.Google Scholar
Chertkov, M., Pumir, A. & Shraiman, B. I. 1999 Lagrangian tetrad dynamics and the phenomenology of turbulence. Phys. Fluids 11, 2394.Google Scholar
Chun, J., Koch, D. L., Rani, S., Ahluwalia, A. & Collins, L. R. 2005 Clustering of aerosol particles in isotropic turbulence. J. Fluid Mech. 536, 219–251.Google Scholar
Csanady, G. T. 1973 Turbulent Diffusion in the Environment. Ed. D. Reidel Publishing Company.Google Scholar
Dimotakis, P. E. 2005 Turbulent mixing. Annu. Rev. Fluid Mech. 37, 329–356.Google Scholar
Eyink, G. 2013 Diffusion approximation in turbulent two-particle dispersion. Phys. Rev. E 88, 041001(R).Google Scholar
Falkovich, G., Fouxon, A. & Stepanov, G. 2002 Acceleration of rain initiation by cloud turbulence. Nature 419, 151.Google Scholar
Falkovich, G. & Frishman, A. 2013 Single flow snapshot reveals the future and the past of pairs of particles in turbulence. Phys. Rev. Lett. 110, 214502.Google Scholar
Falkovich, G., Gawȩdzki, K. & Vergassola, M. 2001 Particles and fields in fluid turbulence. Rev. Mod. Phys. 73, 913–975.Google Scholar
Fouxon, I. & Horvai, P. 2008 Separation of heavy particles in turbulence. Phys. Rev. Lett. 100, 04061.Google Scholar
Frisch, U. 1995 Turbulence. The Legacy of A. N. Kolmogorov. Cambridge University Press.Google Scholar
Fung, J. C. H. & Vassilicos, J. C. 1998 Two-particle dispersion in turbulent-like flows. Phys. Rev. E 57, 1677.Google Scholar
Ilyin, V., Procaccia, I. & Zagorodny, A. 2013 Fokker–Planck equation with memory: the crossover from ballistic to diffusive processes in many-particle systems and incompressible media. Cond. Matter Phys. 16 (1), 13004: 1–18.Google Scholar
Jensen, M.-H. 1999 Multiscaling and structure functions in turbulence: an alternative approach. Phys. Rev. Lett. 83, 76.Google Scholar
Jullien, M.-C. 2003 Dispersion of passive tracers in the direct enstrophy cascade: experimental observations. Phys. Fluids 15, 2228–2237.Google Scholar
Jullien, M.-C., Paret, J. & Tabeling, P. 1999 Richardson pair dispersion in two-dimensional turbulence. Phys. Rev. Lett. 82, 2872.Google Scholar
Kanatani, K., Ogasawara, T. & Toh, S. 2009 Telegraph-type versus diffusion-type models of turbulent relative dispersion. J. Phys. Soc. Japan 78, 024401.Google Scholar
Klafter, J., Blumen, A. & Shlesinger, M. F. 1987 Stochastic pathway to anomalous diffusion. Phys. Rev. A 35, 3081–3085.Google Scholar
Kraichnan, R. H. 1966 Dispersion of particle pairs in homogeneous turbulence. Phys. Fluids 9, 1937–1943.Google Scholar
Kurbanmuradov, O. A. 1997 Stochastic Lagrangian models for two-particle relative dispersion in high-Reynolds number turbulence. Monte Carlo Meth. Applic. 3, 37–52.Google Scholar
LaCasce, J. H. 2010 Relative displacement probability distribution functions from balloons and drifters. J. Mar. Res. 68, 433–457.Google Scholar
Lacorata, G., Mazzino, A. & Rizza, U. 2008 3D chaotic model for subgrid turbulent dispersion in large eddy simulations. J. Atmos. Sci. 65, 2389–2401.Google Scholar
Lepreti, F., Carbone, V., Abramenko, V. I., Yurchyshyn, V., Goode, P. R., Capparelli, V. & Vecchio, A. 2012 Turbulent pair dispersion of photospheric bright points. Astrophys. J. Lett. 759, L17.Google Scholar
Lundgren, T. S. 1981 Turbulent pair dispersion and scalar diffusion. J. Fluid Mech. 111, 27–57.Google Scholar
Malik, N. A. & Vassilicos, J. C. 1999 A Lagrangian model for turbulent dispersion with turbulent-like flow structure: comparison with direct numerical simulation for two-particle statistics. Phys. Fluids 11, 1572.Google Scholar
Masoliver, J. & Weiss, G. H. 1996 Finite-velocity diffusion. Eur. J. Phys. 17, 190–196.Google Scholar
Mazzitelli, I. M., Fornarelli, F., Lanotte, A. S. & Oresta, P. 2014 Pair and multi-particle dispersion in numerical simulations of convective boundary layer turbulence. Phys. Fluids 26, 055110.Google Scholar
Monin, A. S. & Yaglom, A. M. 1975 Statistical Fluid Mechanics. MIT Press, c1971-1975.Google Scholar
Mordant, N., Metz, P., Michel, O. & Pinton, J.-F. 2001 Measurement of Lagrangian velocity in fully developed turbulence. Phys. Rev. Lett. 87, 214501.Google Scholar
Ni, R. & Xia, K.-Q. 2013 Experimental investigation of pair dispersion with small initial separation in convective turbulence. Phys. Rev. E 87, 063006.Google Scholar
Nicolleau, F. C. G. A. & Nowakowski, A. F. 2011 Presence of a Richardson’s regime in kinematic simulations. Phys. Rev. E 83, 056317.Google Scholar
Novikov, E. A. 1989 Two-particle description of turbulence, Markov property and intermittency. Phys. Fluids A 1 (2), 326–330.CrossRefGoogle Scholar
Ollitraut, M., Gabillet, C. & Colin De Verdiére, A. 2005 Open ocean regimes of relative dispersion. J. Fluid Mech. 533, 381–407.Google Scholar
Ott, S. & Mann, J. 2000 An experimental investigation of the relative diffusion of particle pairs in three-dimensional turbulent flow. J. Fluid Mech. 422, 207–223.Google Scholar
Pagnini, G. 2008 Lagrangian stochastic models for turbulent relative dispersion based on particle pair rotation. J. Fluid Mech. 616, 357–395.Google Scholar
Pan, L. & Padoan, P. 2010 Relative velocity of inertial particles in turbulent flows. J. Fluid Mech. 661, 73–107.Google Scholar
Poulain, P. M. & Zambianchi, E. 2007 Surface circulation in the central Mediterranean Sea as deduced from Lagrangian drifters in the 1990s. Cont. Shelf Res. 27, 981–1001.Google Scholar
Richardson, L. F. 1926 Atmospheric diffusion shown on a distance-neighbour graph. Proc. R. Soc. Lond. A 110, 709.Google Scholar
Salazar, J. P. L. C. & Collins, L. R. 2009 Two-particle dispersion in isotropic turbulent flows. Annu. Rev. Fluid Mech. 41, 405–432.Google Scholar
Salazar, J. P. L. C. & Collins, L. R. 2012 Inertial particle relative velocity statistics in homogeneous isotropic turbulence. J. Fluid Mech. 696, 45–66.CrossRefGoogle Scholar
Sawford, B. 2001 Turbulent relative dispersion. Annu. Rev. Fluid Mech. 33, 289–317.Google Scholar
Sawford, B. L., Yeung, P. K. & Borgas, M. S. 2005 Comparison of backwards and forwards relative dispersion in turbulence. Phys. Fluids 17, 095109.Google Scholar
Scatamacchia, R., Biferale, L. & Toschi, F. 2012 Extreme events in the dispersions of two neighboring particles under the influence of fluid turbulence. Phys. Rev. Lett. 109, 144501.Google Scholar
Schumacher, J. 2007 Sub-Kolmogorov-scale fluctuations in fluid turbulence. Europhys. Lett. 80, 54001.Google Scholar
Schumacher, J. 2008 Lagrangian dispersion and heat transport in convective turbulence. Phys. Rev. Lett. 100, 134502.Google Scholar
Sokolov, I. M. 1999 Two-particle dispersion by correlated random velocity fields. Phys. Rev. E 60, 5528.Google Scholar
Sreenivasan, K. R. & Antonia, R. A. 1997 The phenomenology of small-scale turbulence. Annu. Rev. Fluid Mech. 29, 435–472.Google Scholar
Thalabard, S., Krstulovic, G. & Bec, J.2014 Turbulent pair dispersion as a continuous-time random walk, http://arxiv.org/abs/1405.7315.Google Scholar
Thomson, D. J. 1990 A stochastic model for the motion of particle pairs in isotropic high-Reynolds-number turbulence, and its application to the problem of concentration variance. J. Fluid Mech. 210, 113–153.Google Scholar
Thomson, D. J. & Devenish, B. J. 2005 Particle pair separation in kinematic simulations. J. Fluid Mech. 526, 277.Google Scholar
Wilkinson, M. & Mehlig, B. 2005 Caustics in turbulent aerosols. Europhys. Lett. 71, 186–192.Google Scholar
Xu, H., Bourgoin, M., Ouellette, N. T. & Bodenschatz, E. 2006 High order Lagrangian velocity statistics in turbulence. Phys. Rev. Lett. 96, 024503.Google Scholar
Xu, H., Pumir, A. & Bodenschatz, E. 2011 The pirouette effect in turbulence. Nat. Phys. 7, 709–712.Google Scholar
Yakhot, V. 2006 Probability densities in strong turbulence. Physica D 215, 166.Google Scholar