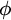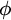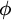1 Introduction
According to the standard possible-worlds models of belief and knowledge, a person, S, believes (knows) a proposition,
![]() $\phi $
, if and only if
$\phi $
, if and only if
![]() $\phi $
is true in all the possible worlds that are doxastically (epistemically) accessible to S. These models have the following consequence:
$\phi $
is true in all the possible worlds that are doxastically (epistemically) accessible to S. These models have the following consequence:
Full Logical Omniscience: If S believes (knows) all the propositions in set
![]() $\Phi $
, and
$\Phi $
, and
![]() $\Phi $
logically entails
$\Phi $
logically entails
![]() $\psi $
, then S believes (knows)
$\psi $
, then S believes (knows)
![]() $\psi $
.
$\psi $
.
The problem of logical omniscience for the standard model is that Full Logical Omniscience is clearly false: everyone fails to believe some logical consequences of the propositions that they believe, and everyone fails to believe some logical truths. The standard model thus at best provides an idealization of the notions of belief and knowledge.
At the opposite end of the spectrum are models without any logical constraints on belief and knowledge, such as impossible-worlds models with a maximally permissive construal of the impossible worlds. On impossible-worlds models, S believes (knows)
![]() $\phi $
if and only if
$\phi $
if and only if
![]() $\phi $
is true in all the possible or impossible worlds that are doxastically (epistemically) accessible to S. On a maximally permissive construal of the impossible worlds, there are impossible worlds in which, for instance,
$\phi $
is true in all the possible or impossible worlds that are doxastically (epistemically) accessible to S. On a maximally permissive construal of the impossible worlds, there are impossible worlds in which, for instance,
![]() $\phi \wedge \psi $
is true but neither
$\phi \wedge \psi $
is true but neither
![]() $\phi $
nor
$\phi $
nor
![]() $\psi $
is true. If such a world is doxastically accessible for some person, S, then S can believe
$\psi $
is true. If such a world is doxastically accessible for some person, S, then S can believe
![]() $\phi \wedge \psi $
without believing either
$\phi \wedge \psi $
without believing either
![]() $\phi $
or
$\phi $
or
![]() $\psi $
. The advantage of models of belief and knowledge that have no logical constraints is that for any given constraint, it seems possible for there to be someone who violates it: borrowing an example from Nolan [Reference Nolan and Shalkowski33, p. 47], someone convinced that a god is beyond logic might believe that their god exists and doesn’t exist, while at the same time not believing that their god doesn’t exist. Arguably, a model of belief shouldn’t by fiat rule out the possibility of such (albeit unusual) individuals. But these maximally permissive models also have the disadvantage that they don’t satisfy three common desiderata for models of belief and knowledge.
$\psi $
. The advantage of models of belief and knowledge that have no logical constraints is that for any given constraint, it seems possible for there to be someone who violates it: borrowing an example from Nolan [Reference Nolan and Shalkowski33, p. 47], someone convinced that a god is beyond logic might believe that their god exists and doesn’t exist, while at the same time not believing that their god doesn’t exist. Arguably, a model of belief shouldn’t by fiat rule out the possibility of such (albeit unusual) individuals. But these maximally permissive models also have the disadvantage that they don’t satisfy three common desiderata for models of belief and knowledge.
The first of these desiderata is to capture ordinary agents who are logically non-omniscient but still logically competent. An agent is logically competent when, for instance, she “know[s] at least a (sufficiently) large class of logical truths, and can draw sufficiently many conclusions from their knowledge” [Reference Duc, Pinto-Ferreira and Mamede13, p. 241] or “she at least does not miss out on any trivial logical consequences of what she believes” [Reference Bjerring and Skipper8, pp. 502f.], where what counts as “sufficiently many” or “trivial” logical consequences could depend on the agent’s computational capacities and thus be agent-relative (see [Reference Bjerring and Skipper8, p. 503; Reference Duc14, p. 639]). If one’s goal is to model agents who are in such senses logically “competent” but non-omniscient, then one needs a middle ground between models that entail logical omniscience and those that leave open complete logical incompetence.Footnote 1
The second desideratum is to capture constraints that the nature of logical concepts (arguably) imposes on logically related beliefs. For instance, some have suggested, contra Nolan’s example, that possessing the concept of conjunction requires believing
![]() $\psi $
when one believes
$\psi $
when one believes
![]() $\phi \wedge \psi $
(e.g., Jago [Reference Jago23, pp. 163–169; Reference Jago24, pp. 1151f.]), or at least being disposed, when certain normal conditions are in place, to believe
$\phi \wedge \psi $
(e.g., Jago [Reference Jago23, pp. 163–169; Reference Jago24, pp. 1151f.]), or at least being disposed, when certain normal conditions are in place, to believe
![]() $\psi $
if one believes
$\psi $
if one believes
![]() $\phi \wedge \psi $
(e.g., Boghossian [Reference Boghossian9, pp. 493–497], Warren [Reference Warren55, pp. 46f.]). Maximally permissive models leave open that one can believe or fail to believe any combination of logically related beliefs, and thus aren’t useful if one’s aim is to capture (apparent) constitutive constraints on logically related beliefs.Footnote
2
$\phi \wedge \psi $
(e.g., Boghossian [Reference Boghossian9, pp. 493–497], Warren [Reference Warren55, pp. 46f.]). Maximally permissive models leave open that one can believe or fail to believe any combination of logically related beliefs, and thus aren’t useful if one’s aim is to capture (apparent) constitutive constraints on logically related beliefs.Footnote
2
The third, and in my view the most important, desideratum is to capture that whatever an agent can computationally “easily access” is—by the very nature of belief and knowledge—already part of what she believes or knows.Footnote 3 On the most common understanding, belief is, or at least grounds, a certain class of dispositions to act.Footnote 4 As the standard example goes, one believes that there is beer in the fridge just in case one is disposed to go to the fridge if one wants to drink beer, to answer “Yes” to the question of whether there is beer in the fridge if one wants to be truthful, and so on. For dispositionalists or functionalists about belief such as Lewis [Reference Lewis29, Reference Lewis30] or Stalnaker [Reference Stalnaker47], having certain dispositions to act is even partly constitutive of what it is to have a belief. On Stalnaker’s view:
To believe that P is to be disposed to act in ways that would tend to satisfy one’s desires, whatever they are, in a world in which P (together with one’s other beliefs) were true. [Reference Stalnaker47, p. 15]
Knowledge, in turn, is on this view a certain kind of capacity: as Stalnaker puts it, “[k]nowledge whether
![]() $\phi $
[…] is the capacity to make one’s actions depend on whether
$\phi $
[…] is the capacity to make one’s actions depend on whether
![]() $\phi $
” [Reference Stalnaker51, pp. 2f.]. On any view on which belief and knowledge ground or are constitutively connected to behavioral dispositions, propositions that are computationally “easily accessible” to an agent should already be part of what she believes or knows. This is because whenever some information is only a trivial computation or inference away for an agent, the agent already has the capacity to act upon that information. For instance, assume that Ola knows that adding 2 to a number
$\phi $
” [Reference Stalnaker51, pp. 2f.]. On any view on which belief and knowledge ground or are constitutively connected to behavioral dispositions, propositions that are computationally “easily accessible” to an agent should already be part of what she believes or knows. This is because whenever some information is only a trivial computation or inference away for an agent, the agent already has the capacity to act upon that information. For instance, assume that Ola knows that adding 2 to a number
![]() $d_0\dots d_n2$
yields
$d_0\dots d_n2$
yields
![]() $d_0\dots d_n4$
: she is able to answer relevant questions correctly; she uses this information in ordinary life, such as in calculating tips, buying the right amount of certain things, and so on. Assume, further, that Ola has never explicitly thought about the number
$d_0\dots d_n4$
: she is able to answer relevant questions correctly; she uses this information in ordinary life, such as in calculating tips, buying the right amount of certain things, and so on. Assume, further, that Ola has never explicitly thought about the number
![]() $19,822$
, but that she is immediately able to give the correct answer to questions such as “What is
$19,822$
, but that she is immediately able to give the correct answer to questions such as “What is
![]() $19,822+2$
?” or “Is
$19,822+2$
?” or “Is
![]() $19,822+2 = 19,824$
?” It would then seem that Ola also knows that
$19,822+2 = 19,824$
?” It would then seem that Ola also knows that
![]() $19,822+2 = 19,824$
. But the dispositions or capacities characterizing this knowledge involve a short computation: Ola can only manifest her disposition to answer questions about
$19,822+2 = 19,824$
. But the dispositions or capacities characterizing this knowledge involve a short computation: Ola can only manifest her disposition to answer questions about
![]() $19,822+2 = 19,824$
correctly after, for instance, replacing x in “
$19,822+2 = 19,824$
correctly after, for instance, replacing x in “
![]() $x2 + 2=x4$
” with “
$x2 + 2=x4$
” with “
![]() $19,82$
.” On the standard dispositional understanding of belief and knowledge, this doesn’t mean that Ola didn’t know that
$19,82$
.” On the standard dispositional understanding of belief and knowledge, this doesn’t mean that Ola didn’t know that
![]() $19,822+2 = 19,824$
until she performed a calculation or inference. Rather, using terminology from Stalnaker [Reference Stalnaker48, pp. 435f., 439], what Ola believes or knows is what is “available” to guide her behavior, even if it hasn’t ever been used or “accessed” to do so. Since maximally permissive models allow that one doesn’t believe what one can computationally “easily access,” they are unable to capture the dispositional nature of belief and knowledge. Models that entail logical omniscience, too, seem unable to capture the dispositional nature of belief and knowledge. As Stalnaker notes:
$19,822+2 = 19,824$
until she performed a calculation or inference. Rather, using terminology from Stalnaker [Reference Stalnaker48, pp. 435f., 439], what Ola believes or knows is what is “available” to guide her behavior, even if it hasn’t ever been used or “accessed” to do so. Since maximally permissive models allow that one doesn’t believe what one can computationally “easily access,” they are unable to capture the dispositional nature of belief and knowledge. Models that entail logical omniscience, too, seem unable to capture the dispositional nature of belief and knowledge. As Stalnaker notes:
Because of our computational limitations, we may have the capacity constituted by the knowledge that P, or the disposition constituted by the belief that P, while at the same time lacking the capacity or disposition that we would have if we knew or believed some deductive consequence of P. [Reference Stalnaker48, p. 436]
For instance, it seems clear that Ola could be disposed to make her actions depend on whether the number of students at her school is
![]() $6,299$
, but lack the disposition to make her actions depend on whether the number of students at her school is prime: she could order the right amount of school gear, answer questions about the number of students correctly, and so on, while being at a loss when asked whether the number of students at her school is prime.Footnote
5
The standard dispositional understanding of belief and knowledge thus seems to require a middle-ground model: not all the logical consequences of one’s beliefs or knowledge are accessible to guide action and thus are believed or known, but those pieces of information that are easily accessible are already believed or known.Footnote
6
$6,299$
, but lack the disposition to make her actions depend on whether the number of students at her school is prime: she could order the right amount of school gear, answer questions about the number of students correctly, and so on, while being at a loss when asked whether the number of students at her school is prime.Footnote
5
The standard dispositional understanding of belief and knowledge thus seems to require a middle-ground model: not all the logical consequences of one’s beliefs or knowledge are accessible to guide action and thus are believed or known, but those pieces of information that are easily accessible are already believed or known.Footnote
6
My aim in this paper is to develop a middle-ground model of belief and knowledge that satisfies these three desiderata. My proposal builds upon algorithmic models developed by Parikh [Reference Parikh, Ras and Zemankova34]; Halpern, Moses, and Vardi [Reference Halpern, Moses and Vardi17]; and Duc [Reference Duc15]. The unifying idea of algorithmic models is that whether an agent believes or knows something depends on the agent’s internal algorithms, and thus on her computational capacities. As I will explain, algorithmic models are thereby particularly well-suited to capture the idea that an agent already believes or knows what is easily computationally accessible to her, to model logically competent but non-omniscient agents, and to account for possible constitutive relations between logically related beliefs. Algorithmic models have been developed and studied in logic and computer science, and have been applied in the study of security protocols and cryptography.Footnote 7 But there has been very little discussion or development of algorithmic models in the philosophical literature on the problem of logical omniscience.Footnote 8 My aim here is to fill this gap by developing an algorithmic model that satisfies the philosophical desiderata for middle-ground models better than any existing algorithmic model, and by motivating it philosophically. I end in Section 3 by comparing the algorithmic strategy for developing a middle-ground model to approaches that use dynamic epistemic logic or step logic, such as the one developed recently by Bjerring and Skipper [Reference Bjerring and Skipper8].
2 Algorithmic models
Algorithmic models of belief and knowledge are developed as alternatives to the standard possible- and impossible-worlds models to solve the problem of logical omniscience. The guiding idea behind algorithmic models is that belief and knowledge have a computational aspect that isn’t captured by the standard possible-worlds models or by the standard approaches to solving the problem of logical omniscience.Footnote 9 Although they don’t explicitly say so, Parikh [Reference Parikh, Ras and Zemankova34] and Halpern et al. [Reference Halpern, Moses and Vardi17] motivate this guiding idea from the type of functionalist perspective, outlined in Section 1, on which knowledge is a certain kind of capacity to act. For instance:
We have tried in this paper to make a case that real knowledge is not a set but a behaviour. [Reference Parikh, Ras and Zemankova34, p. 7]
[A]n agent that has to act on his knowledge has to be able to compute this knowledge; we do need to take into account the algorithms available to the agent, as well as the “effort” required to compute knowledge. [Reference Halpern, Moses and Vardi17, p. 256]
Different algorithmic models give different interpretations to this guiding idea and to what it means to “compute knowledge.” But they all share the assumptions that agents have algorithms, and that whether an agent knows or believes
![]() $\phi $
depends on her algorithm and its output when given
$\phi $
depends on her algorithm and its output when given
![]() $\phi $
. On one way of putting it in intuitive terms, the view is that one believes
$\phi $
. On one way of putting it in intuitive terms, the view is that one believes
![]() $\phi $
just in case one’s algorithm efficiently computes that
$\phi $
just in case one’s algorithm efficiently computes that
![]() $\phi $
is true, and one knows
$\phi $
is true, and one knows
![]() $\phi $
just in case one’s algorithm efficiently and correctly computes that
$\phi $
just in case one’s algorithm efficiently and correctly computes that
![]() $\phi $
is true.Footnote
10
Failures of logical omniscience are then diagnosed as computational failures: if an agent knows or believes
$\phi $
is true.Footnote
10
Failures of logical omniscience are then diagnosed as computational failures: if an agent knows or believes
![]() $\phi $
but fails to know or believe some
$\phi $
but fails to know or believe some
![]() $\psi $
entailed by
$\psi $
entailed by
![]() $\phi $
, this is because the agent doesn’t have either the right kind of algorithm or sufficient computational resources. This fits with an intuitive characterization of cases of failures of logical omniscience: for instance, if Ola knows that the number of students is 6,299 but not that the number of students is prime, or if she knows the axioms of number theory but not some theorem, this is because she can’t check for primality or theoremhood, she can’t retrieve this information from a reliably stored memory base, and so on, or because it would take her too long to run such algorithms.Footnote
11
$\phi $
, this is because the agent doesn’t have either the right kind of algorithm or sufficient computational resources. This fits with an intuitive characterization of cases of failures of logical omniscience: for instance, if Ola knows that the number of students is 6,299 but not that the number of students is prime, or if she knows the axioms of number theory but not some theorem, this is because she can’t check for primality or theoremhood, she can’t retrieve this information from a reliably stored memory base, and so on, or because it would take her too long to run such algorithms.Footnote
11
Already at this level of generality, algorithmic models should strike us as promising starting points for developing a middle-ground model of belief and knowledge. On algorithmic models, an agent knows whatever her algorithm can efficiently compute. One can thus hope to delineate logically competent agents by putting certain constraints on the algorithms and resources that these agents use. For instance, logically competent agents might have algorithms that compute a certain class of logical truths with minimal effort. Similarly, one can hope to model constitutive connections between logically related beliefs by putting constraints on the kinds of algorithms that conceptually competent agents use. For instance, being conceptually competent with conjunction might require having an algorithm that computes that
![]() $\psi $
is true if it computes that
$\psi $
is true if it computes that
![]() $\phi \wedge \psi $
is true. Finally, algorithmic models capture the view that belief and knowledge are connected to action. In general, it is highly plausible that whenever one is disposed to exhibit some behavior, this is because one has an (internal) algorithm that produces this behavior. It thus makes sense to model agents as having algorithms, and to model belief and knowledge as dependent on the characteristics of these algorithms. Algorithmic models thereby also straightforwardly capture the view that whatever one is able to efficiently compute and thus act upon is already part of what one believes (knows), because they entail that efficiently (and correctly) computing that
$\phi \wedge \psi $
is true. Finally, algorithmic models capture the view that belief and knowledge are connected to action. In general, it is highly plausible that whenever one is disposed to exhibit some behavior, this is because one has an (internal) algorithm that produces this behavior. It thus makes sense to model agents as having algorithms, and to model belief and knowledge as dependent on the characteristics of these algorithms. Algorithmic models thereby also straightforwardly capture the view that whatever one is able to efficiently compute and thus act upon is already part of what one believes (knows), because they entail that efficiently (and correctly) computing that
![]() $\phi $
is true is sufficient for believing (knowing)
$\phi $
is true is sufficient for believing (knowing)
![]() $\phi $
.
$\phi $
.
One disadvantage of the existing algorithmic models that we can already see is that they give up on the worlds-based framework for modeling belief and knowledge: one’s belief and information states are no longer modeled as sets of worlds, belief and knowledge are no longer modeled as truth in all doxastically or epistemically accessible worlds, and acquiring beliefs and learning are no longer modeled as ruling out doxastic or epistemic possibilities. This is unfortunate, for the worlds-based framework captures some important aspects of belief and knowledge—such as their independence from linguistic action and world-connectedness—in a formally elegant manner, and it yields a unified account of mental, linguistic, and informational content.Footnote 12 In Section 2.1, I outline the formal details of the existing algorithmic models that are most relevant given our purposes and explain their other advantages and disadvantages. In Section 2.2, I then develop an algorithmic model that satisfies the desiderata for a middle-ground model and doesn’t have these disadvantages.
2.1 Standard algorithmic models
The standard and most sophisticated existing algorithmic model is due to Halpern et al. [Reference Halpern, Moses and Vardi17]. In the single-agent and static setting (i.e., where we don’t consider the evolution of belief and knowledge over time), Halpern and Pucella [Reference Halpern and Pucella19] work with standard Kripke structures of the form
![]() $\langle \mathscr {W}, \mathscr {W}', \pi \rangle $
, where
$\langle \mathscr {W}, \mathscr {W}', \pi \rangle $
, where
![]() $\mathscr {W}$
is a set of possible worlds,
$\mathscr {W}$
is a set of possible worlds,
![]() $\mathscr {W}'$
is the set of possible worlds that are accessible to the agent, and
$\mathscr {W}'$
is the set of possible worlds that are accessible to the agent, and
![]() $\pi $
is an interpretation function that associates each possible world
$\pi $
is an interpretation function that associates each possible world
![]() $w \in \mathscr {W}$
with a truth assignment
$w \in \mathscr {W}$
with a truth assignment
![]() $\pi (w)$
to the primitive propositions of the language.Footnote
13
An algorithmic knowledge structure is defined as a tuple
$\pi (w)$
to the primitive propositions of the language.Footnote
13
An algorithmic knowledge structure is defined as a tuple
![]() $\mathscr {M} = \langle \mathscr {W}, \mathscr {W}', \pi , \mathscr {A} \rangle $
where
$\mathscr {M} = \langle \mathscr {W}, \mathscr {W}', \pi , \mathscr {A} \rangle $
where
![]() $\langle \mathscr {W}, \mathscr {W}', \pi \rangle $
is a Kripke structure and
$\langle \mathscr {W}, \mathscr {W}', \pi \rangle $
is a Kripke structure and
![]() $\mathscr {A}$
is a knowledge algorithm that takes as input a formula and returns either “Yes,” “No,” or “?” (knowledge algorithms are thus assumed to terminate). “The agent knows
$\mathscr {A}$
is a knowledge algorithm that takes as input a formula and returns either “Yes,” “No,” or “?” (knowledge algorithms are thus assumed to terminate). “The agent knows
![]() $\phi $
,” symbolized standardly as “
$\phi $
,” symbolized standardly as “
![]() $K\phi $
,” then gets the following satisfaction (or truth) conditions:
$K\phi $
,” then gets the following satisfaction (or truth) conditions:
To capture the evolution of knowledge over time, Halpern et al. [Reference Halpern, Moses and Vardi17] give a run-based semantics on which agents can use different algorithms in different states. The local state of an agent is modeled as consisting of some local data and a local algorithm. The agent then knows
![]() $\phi $
at a state if her local algorithm outputs “Yes” when given both
$\phi $
at a state if her local algorithm outputs “Yes” when given both
![]() $\phi $
and the local data as inputs.Footnote
14
$\phi $
and the local data as inputs.Footnote
14
On this semantics, whether one knows
![]() $\phi $
has nothing to do with the truth-value of
$\phi $
has nothing to do with the truth-value of
![]() $\phi $
in any accessible world, and there are no constraints on the algorithm
$\phi $
in any accessible world, and there are no constraints on the algorithm
![]() $\mathscr {A}$
. Halpern and Pucella [Reference Halpern and Pucella19, p. 223] propose the following constraint: a knowledge algorithm
$\mathscr {A}$
. Halpern and Pucella [Reference Halpern and Pucella19, p. 223] propose the following constraint: a knowledge algorithm
![]() $\mathscr {A}$
is sound for
$\mathscr {A}$
is sound for
![]() $\mathscr {M}$
if and only if for all
$\mathscr {M}$
if and only if for all
![]() $\phi $
,
$\phi $
,
![]() $\mathscr {A}(\phi )=` `\textrm {Yes"}$
implies
$\mathscr {A}(\phi )=` `\textrm {Yes"}$
implies
![]() $\langle \mathscr {M}, w \rangle \vDash \phi $
for all
$\langle \mathscr {M}, w \rangle \vDash \phi $
for all
![]() $w \in \mathscr {W}'$
and
$w \in \mathscr {W}'$
and
![]() $\mathscr {A}(\phi )=` `\textrm {No"}$
implies
$\mathscr {A}(\phi )=` `\textrm {No"}$
implies
![]() $\langle \mathscr {M}, w \rangle \vDash \neg \phi $
for some
$\langle \mathscr {M}, w \rangle \vDash \neg \phi $
for some
![]() $w \in \mathscr {W}'$
.Footnote
15
That is, an algorithm is sound just in case an output of “Yes” implies that
$w \in \mathscr {W}'$
.Footnote
15
That is, an algorithm is sound just in case an output of “Yes” implies that
![]() $\phi $
true in all epistemically accessible worlds (and thus “known” in the sense of the standard possible-worlds model), while an output of “No” implies that
$\phi $
true in all epistemically accessible worlds (and thus “known” in the sense of the standard possible-worlds model), while an output of “No” implies that
![]() $\phi $
is false in some epistemically accessible world (and thus “unknown” in the standard model’s sense). This is the sense in which knowledge algorithms “compute knowledge” on Halpern et al.’s [Reference Halpern, Moses and Vardi17] construal: they compute whether the input formula is true in all accessible worlds. According to Halpern et al. [Reference Halpern, Moses and Vardi17, p. 259], what is defined without the soundness constraint is a notion of belief, i.e., using “
$\phi $
is false in some epistemically accessible world (and thus “unknown” in the standard model’s sense). This is the sense in which knowledge algorithms “compute knowledge” on Halpern et al.’s [Reference Halpern, Moses and Vardi17] construal: they compute whether the input formula is true in all accessible worlds. According to Halpern et al. [Reference Halpern, Moses and Vardi17, p. 259], what is defined without the soundness constraint is a notion of belief, i.e., using “
![]() $B\phi $
” to formalize “the agent believes
$B\phi $
” to formalize “the agent believes
![]() $\phi $
”:
$\phi $
”:
Knowledge is thus defined as above but with the additional constraint that
![]() $\mathscr {M}$
’s algorithm is sound.
$\mathscr {M}$
’s algorithm is sound.
The standard algorithmic model avoids the problem of logical omniscience: since there are no constraints on the knowledge algorithms, one’s knowledge algorithm can output “Yes” given
![]() $\phi $
but either “No” or “?” given
$\phi $
but either “No” or “?” given
![]() $\psi $
even if
$\psi $
even if
![]() $\phi $
entails
$\phi $
entails
![]() $\psi $
or is logically equivalent to it. But given that one’s knowledge algorithms can be extremely weak, we don’t yet have a model that captures agents who are logically (or conceptually) competent. For instance, an agent can have a sound knowledge algorithm that never outputs “Yes.” As it stands, the standard algorithmic model thus isn’t an adequate middle-ground model.
$\psi $
or is logically equivalent to it. But given that one’s knowledge algorithms can be extremely weak, we don’t yet have a model that captures agents who are logically (or conceptually) competent. For instance, an agent can have a sound knowledge algorithm that never outputs “Yes.” As it stands, the standard algorithmic model thus isn’t an adequate middle-ground model.
There are other disadvantages of the standard algorithmic model given our purposes. The first is that the model is overly linguistic. Belief and knowledge are assumed to manifest always and only in linguistic action: the agent is given a sentence and in return provides a verbal response. But this is too narrow, as people can have knowledge that they aren’t able to verbally articulate. Stalnaker provides many such examples: the “shrewd but inarticulate” chess player who can access information for choosing a move but not for answering questions [Reference Stalnaker48, p. 439], or the experienced outfielder who knows exactly when and where the ball will come down for the purpose of catching the ball but not for the purpose of answering the question “Exactly when and where is the ball going to come down?” [Reference Stalnaker50, p. 263]. More generally, on the dispositional understanding, belief and knowledge are supposed to help explain people’s overall behavior—whether linguistic or otherwise.
A related disadvantage of the algorithmic model is that the objects of belief and knowledge are taken to be sentences, because the algorithms operate on sentences. Parikh [Reference Parikh35, pp. 472–474], whose algorithmic notion of knowledge is even called “linguistic knowledge” [Reference Parikh, Ras and Zemankova34, p. 4], explains that this choice is made so that belief and knowledge on the resulting account aren’t closed under necessary equivalence (if
![]() $\phi $
and
$\phi $
and
![]() $\psi $
are possible-worlds propositions and necessarily equivalent, then
$\psi $
are possible-worlds propositions and necessarily equivalent, then
![]() $\phi =\psi $
, and thus the algorithm’s output is the same for
$\phi =\psi $
, and thus the algorithm’s output is the same for
![]() $\phi $
and
$\phi $
and
![]() $\psi $
.) As we will see in Section 2.2, one can maintain that the objects of belief and knowledge are propositions while avoiding closure under necessary equivalence by moving to an impossible-worlds framework.
$\psi $
.) As we will see in Section 2.2, one can maintain that the objects of belief and knowledge are propositions while avoiding closure under necessary equivalence by moving to an impossible-worlds framework.
Finally, the most important gap in the standard algorithmic model given our purposes is that it doesn’t address limitations of computational resources. On this model, an agent knows
![]() $\phi $
if her knowledge algorithm will eventually output “Yes” given
$\phi $
if her knowledge algorithm will eventually output “Yes” given
![]() $\phi $
, but that could take an unlimited amount of computational resources. For our purposes, we need to model bounds on the resources that the algorithms can use: In particular, if it would take an agent too long to compute
$\phi $
, but that could take an unlimited amount of computational resources. For our purposes, we need to model bounds on the resources that the algorithms can use: In particular, if it would take an agent too long to compute
![]() $\phi $
, then she is unable to act on the information that
$\phi $
, then she is unable to act on the information that
![]() $\phi $
and thus neither knows nor believes
$\phi $
and thus neither knows nor believes
![]() $\phi $
. For instance, an outfielder who would need to sit down for 3 hours to calculate the trajectory of the ball clearly neither knows nor believes that the ball will come down at the relevant location and time before they perform the calculations.
$\phi $
. For instance, an outfielder who would need to sit down for 3 hours to calculate the trajectory of the ball clearly neither knows nor believes that the ball will come down at the relevant location and time before they perform the calculations.
Halpern et al. [Reference Halpern, Moses and Vardi17, pp. 260f.] briefly discuss this problem and mention that one could put constraints on local algorithms so that they have to complete their run within a given unit of time.Footnote
16
Duc [Reference Duc15, pp. 39–51] develops an algorithmic system for knowledge that involves this idea. He introduces the formula “
![]() $K^n_i\phi $
” to stand for “if asked about
$K^n_i\phi $
” to stand for “if asked about
![]() $\phi $
, i is able to derive reliably the answer ‘yes’ within n units of time,” and the formula “
$\phi $
, i is able to derive reliably the answer ‘yes’ within n units of time,” and the formula “
![]() $K^\exists _i\phi $
” to stand for “agent i can infer
$K^\exists _i\phi $
” to stand for “agent i can infer
![]() $\phi $
reliably in finite time” [Reference Duc15, p. 41]. The latter captures the spirit of Halpern et al.’s notion of knowledge:
$\phi $
reliably in finite time” [Reference Duc15, p. 41]. The latter captures the spirit of Halpern et al.’s notion of knowledge:
![]() $K^\exists _i\phi $
holds just in case the agent has an algorithm that computes that
$K^\exists _i\phi $
holds just in case the agent has an algorithm that computes that
![]() $\phi $
is true within a finite but unbounded amount of time. In these definitions, the qualification “reliably” is supposed to imply both that the agent’s computation is correct (i.e., if either
$\phi $
is true within a finite but unbounded amount of time. In these definitions, the qualification “reliably” is supposed to imply both that the agent’s computation is correct (i.e., if either
![]() $K^n_i\phi $
or
$K^n_i\phi $
or
![]() $K^\exists _i\phi $
hold, then
$K^\exists _i\phi $
hold, then
![]() $\phi $
is true) and that the agent doesn’t choose a procedure that correctly computes
$\phi $
is true) and that the agent doesn’t choose a procedure that correctly computes
![]() $\phi $
by chance, but is able to “select deterministically a suitable procedure for the input” [Reference Duc15, p. 41]. The idea is that the agent has a general procedure or algorithm that, given
$\phi $
by chance, but is able to “select deterministically a suitable procedure for the input” [Reference Duc15, p. 41]. The idea is that the agent has a general procedure or algorithm that, given
![]() $\phi $
, correctly computes that
$\phi $
, correctly computes that
![]() $\phi $
is true within n units of time, and this general algorithm might involve steps for choosing the right sub-algorithms to run on
$\phi $
is true within n units of time, and this general algorithm might involve steps for choosing the right sub-algorithms to run on
![]() $\phi $
.
$\phi $
.
Duc [Reference Duc15] thus defines infinitely many “time-stamped” notions of knowledge, one for each time unit n. This is slightly counterintuitive, given that we presumably only have one non-time-stamped notion of knowledge. As I will explain in Section 2.2, however, it is highly plausible to define knowledge in terms of such time-stamped notions by using a threshold.
Duc [Reference Duc15, pp. 45–48] goes on to provide a derivation system for his language of algorithmic knowledge. Some of his assumptions are too strong for our purposes. He assumes that both
![]() $K^n_i\phi $
and
$K^n_i\phi $
and
![]() $K^\exists _i\phi $
imply that the agent is able to prove
$K^\exists _i\phi $
imply that the agent is able to prove
![]() $\phi $
. On this view, agents employ a decidable axiom system extending propositional logic, and thus “all proofs can be generated algorithmically” by a general-purpose theorem prover [Reference Duc15, p. 44]. Duc only considers agents who have such a general-purpose theorem prover. After analysing a query and trying out special algorithms, these agents revert to using the general-purpose theorem prover. Thus, if
$\phi $
. On this view, agents employ a decidable axiom system extending propositional logic, and thus “all proofs can be generated algorithmically” by a general-purpose theorem prover [Reference Duc15, p. 44]. Duc only considers agents who have such a general-purpose theorem prover. After analysing a query and trying out special algorithms, these agents revert to using the general-purpose theorem prover. Thus, if
![]() $\phi $
is a theorem of the agent’s axiom system, the agent will eventually find its proof. In other words, the following rule of inference is valid in Duc’s system:
$\phi $
is a theorem of the agent’s axiom system, the agent will eventually find its proof. In other words, the following rule of inference is valid in Duc’s system:
Similarly, Duc assumes that if formulae
![]() $\phi _1, \dots , \phi _n$
can all be derived in the agent’s system and
$\phi _1, \dots , \phi _n$
can all be derived in the agent’s system and
![]() $\phi _1 \wedge \cdots \wedge \phi _n \rightarrow \psi $
is a theorem, then the agent will also eventually output a proof of
$\phi _1 \wedge \cdots \wedge \phi _n \rightarrow \psi $
is a theorem, then the agent will also eventually output a proof of
![]() $\psi $
if queried about it [Reference Duc15, p. 44]. A special case of this principle is that agents can use modus ponens in their reasoning, which yields the following as an axiom in Duc’s system:
$\psi $
if queried about it [Reference Duc15, p. 44]. A special case of this principle is that agents can use modus ponens in their reasoning, which yields the following as an axiom in Duc’s system:
As I will argue in Section 2.2, principles such as (
NEC
A
) and (
K
A
) can form plausible constraints on logically or conceptually competent agents. But we should avoid the extremely strong assumption that knowing
![]() $\phi $
always requires being able to find a proof of
$\phi $
always requires being able to find a proof of
![]() $\phi $
in some derivation system. After all, an agent might know even mathematical or logical truths by retrieving them from a memory base that was reliably stored (for instance, via expert testimony), without having any ability to produce proofs. Generally speaking, it is overly restrictive to think of all belief and knowledge that
$\phi $
in some derivation system. After all, an agent might know even mathematical or logical truths by retrieving them from a memory base that was reliably stored (for instance, via expert testimony), without having any ability to produce proofs. Generally speaking, it is overly restrictive to think of all belief and knowledge that
![]() $\phi $
in terms of features of a proof of
$\phi $
in terms of features of a proof of
![]() $\phi $
in some derivation system. (I come back to this point in Section 3.)
$\phi $
in some derivation system. (I come back to this point in Section 3.)
2.2 An algorithmic impossible-worlds model
My proposal is to build an algorithmic model on the basis of an impossible-worlds model. An important advantage of impossible-worlds models is that they preserve some core aspects of the standard possible-worlds model, including the idea that one’s belief and information states are sets of worlds, that belief and knowledge are truth in all doxastically or epistemically accessible worlds, and that acquiring beliefs and learning are ruling out of doxastic or epistemic possibilities. Moreover, impossible worlds allow for more fine-grained constructions of content: sentences that are true in all the same possible worlds correspond to the same possible-worlds proposition, but most often (if not always) differ in truth-values at impossible worlds and thus correspond to different propositions construed as sets of possible and impossible worlds.Footnote 17 As such, the impossible-worlds framework will enable us to avoid three disadvantages of the standard algorithmic framework discussed above, viz., that it gives up the standard worlds-based framework for modeling belief and knowledge, that belief and knowledge are assumed to manifest always and only in linguistic action, and that the objects of belief and knowledge are sentences and not propositions. Impossible-worlds frameworks also have some disadvantages, for instance, because the account of content that they yield is extremely fine-grained.Footnote 18 But they are widely and increasingly used for solving problems of hyperintensionality in philosophy and, as we will see in Section 3, they are used in the most important competitor approaches to developing a middle-ground model.Footnote 19
Let us turn to some of the details of impossible-worlds models. Let
![]() $\mathscr {L}$
be the language of our model, defined as follows:
$\mathscr {L}$
be the language of our model, defined as follows:

where “
![]() $B\phi $
” formalizes “the agent believes
$B\phi $
” formalizes “the agent believes
![]() $\phi $
” and “
$\phi $
” and “
![]() $K\phi $
” formalizes “the agent knows
$K\phi $
” formalizes “the agent knows
![]() $\phi $
.” An impossible-worlds model is a tuple
$\phi $
.” An impossible-worlds model is a tuple
![]() $\mathscr {M} = \langle \mathscr {W}, \mathscr {P}, d, e, v \rangle $
, where
$\mathscr {M} = \langle \mathscr {W}, \mathscr {P}, d, e, v \rangle $
, where
![]() $\mathscr {W}$
is a non-empty set of worlds;
$\mathscr {W}$
is a non-empty set of worlds;
![]() $\mathscr {P} \subseteq \mathscr {W}$
is a non-empty set of possible worlds (thus
$\mathscr {P} \subseteq \mathscr {W}$
is a non-empty set of possible worlds (thus
is the set of impossible worlds);
![]() $d : \mathscr {W} \to 2^{\mathscr {W}}$
is a doxastic accessibility function that assigns each world
$d : \mathscr {W} \to 2^{\mathscr {W}}$
is a doxastic accessibility function that assigns each world
![]() $w \in \mathscr {W}$
to the set of worlds doxastically accessible from
$w \in \mathscr {W}$
to the set of worlds doxastically accessible from
![]() $w$
;
$w$
;
![]() $e : \mathscr {W} \to 2^{\mathscr {W}}$
is an epistemic accessibility function that assigns each world
$e : \mathscr {W} \to 2^{\mathscr {W}}$
is an epistemic accessibility function that assigns each world
![]() $w \in \mathscr {W}$
to the set of worlds epistemically accessible from
$w \in \mathscr {W}$
to the set of worlds epistemically accessible from
![]() $w$
; and
$w$
; and
![]() $v$
is a valuation function that maps each atomic sentence
$v$
is a valuation function that maps each atomic sentence
![]() $p \in At$
and world
$p \in At$
and world
![]() $w \in \mathscr {P}$
to either 0 or 1, and maps each sentence
$w \in \mathscr {P}$
to either 0 or 1, and maps each sentence
![]() $\phi \in \mathscr {L}$
and world
$\phi \in \mathscr {L}$
and world
![]() $w \in \mathscr {I}$
to either 0 or 1.Footnote
20
Since knowledge entails belief, it is standard to assume that doxastically accessible worlds are also epistemically accessible, i.e., that
$w \in \mathscr {I}$
to either 0 or 1.Footnote
20
Since knowledge entails belief, it is standard to assume that doxastically accessible worlds are also epistemically accessible, i.e., that
![]() $d(w) \subseteq e(w)$
for all
$d(w) \subseteq e(w)$
for all
![]() $w \in \mathscr {W}$
. I also assume throughout that worlds are centered, i.e., they are worlds with a marked individual at a time. As Lewis [Reference Lewis30, pp. 27–30] explains, this should be assumed in all doxastic and epistemic models because agents can obviously have different beliefs and knowledge at different times.Footnote
21
Finally, I add to the satisfaction relation (written “
$w \in \mathscr {W}$
. I also assume throughout that worlds are centered, i.e., they are worlds with a marked individual at a time. As Lewis [Reference Lewis30, pp. 27–30] explains, this should be assumed in all doxastic and epistemic models because agents can obviously have different beliefs and knowledge at different times.Footnote
21
Finally, I add to the satisfaction relation (written “
![]() $\vDash $
” as usual) the dissatisfaction (or making false) relation, written “
$\vDash $
” as usual) the dissatisfaction (or making false) relation, written “
.” If
![]() $w \in \mathscr {P}$
,
$w \in \mathscr {P}$
,
![]() $\vDash $
and
$\vDash $
and
are defined recursively:

If
![]() $w \in \mathscr {I}$
, then
$w \in \mathscr {I}$
, then
![]() $\vDash $
and
$\vDash $
and
are defined as follows:

The idea here is that a sentence
![]() $\phi $
is dissatisfied (or false) at a world if and only if its negation
$\phi $
is dissatisfied (or false) at a world if and only if its negation
![]() $\neg \phi $
is satisfied (or true) at that world, for both possible and impossible worlds. Given a possible world
$\neg \phi $
is satisfied (or true) at that world, for both possible and impossible worlds. Given a possible world
![]() $w \in \mathscr {P}$
, only one of
$w \in \mathscr {P}$
, only one of
![]() $\phi $
and
$\phi $
and
![]() $\neg \phi $
is satisfied at
$\neg \phi $
is satisfied at
![]() $w$
and the other is dissatisfied at
$w$
and the other is dissatisfied at
![]() $w$
. But this needn’t be the case at impossible worlds: given an impossible world
$w$
. But this needn’t be the case at impossible worlds: given an impossible world
![]() $w \in \mathscr {I}$
, both
$w \in \mathscr {I}$
, both
![]() $\phi $
and
$\phi $
and
![]() $\neg \phi $
could be satisfied at
$\neg \phi $
could be satisfied at
![]() $w$
(if
$w$
(if
![]() $v(\phi , w) = 1$
and
$v(\phi , w) = 1$
and
![]() $v(\neg \phi , w) = 1$
), and neither
$v(\neg \phi , w) = 1$
), and neither
![]() $\phi $
nor
$\phi $
nor
![]() $\neg \phi $
could be satisfied (if
$\neg \phi $
could be satisfied (if
![]() $v(\phi , w) = 0$
and
$v(\phi , w) = 0$
and
![]() $v(\neg \phi , w) = 0$
). Impossible worlds can thus be both inconsistent and incomplete entities. I further adopt the maximally permissive construal of impossible worlds on which for any incomplete and/or inconsistent set of sentences
$v(\neg \phi , w) = 0$
). Impossible worlds can thus be both inconsistent and incomplete entities. I further adopt the maximally permissive construal of impossible worlds on which for any incomplete and/or inconsistent set of sentences
![]() $\Gamma \subseteq \mathscr {L}$
, there is an impossible world
$\Gamma \subseteq \mathscr {L}$
, there is an impossible world
![]() $w \in \mathscr {I}$
such that for all
$w \in \mathscr {I}$
such that for all
![]() $\phi \in \mathscr {L}$
,
$\phi \in \mathscr {L}$
,
![]() $v(\phi , w) = 1$
if and only if
$v(\phi , w) = 1$
if and only if
![]() $\phi \in \Gamma $
.Footnote
22
There are thus no constraints on what sentences impossible worlds can satisfy, and there are at least as many impossible worlds as there are sets of sentences of our base language
$\phi \in \Gamma $
.Footnote
22
There are thus no constraints on what sentences impossible worlds can satisfy, and there are at least as many impossible worlds as there are sets of sentences of our base language
![]() $\mathscr {L}$
.Footnote
23
$\mathscr {L}$
.Footnote
23
As I explained in Section 1, permissive impossible-worlds models don’t face the problem of logical omniscience. For instance, assume that
![]() $\langle \mathscr {M}, w \rangle \vDash B\phi $
, and that
$\langle \mathscr {M}, w \rangle \vDash B\phi $
, and that
![]() $\phi $
logically entails
$\phi $
logically entails
![]() $\psi $
, i.e., that
$\psi $
, i.e., that
![]() $\psi $
is true in all the possible worlds in which
$\psi $
is true in all the possible worlds in which
![]() $\phi $
is true. For all that we have said about the doxastic accessibility function d, it might be that
$\phi $
is true. For all that we have said about the doxastic accessibility function d, it might be that
![]() $d(w)$
includes a world
$d(w)$
includes a world
![]() $w' \in \mathscr {I}$
such that
$w' \in \mathscr {I}$
such that
![]() $\langle \mathscr {M}, w' \rangle \nvDash \psi $
, and thus that
$\langle \mathscr {M}, w' \rangle \nvDash \psi $
, and thus that
![]() $\langle \mathscr {M}, w \rangle \nvDash B\psi $
. On the other hand, the model as it stands allows any combination of beliefs and knowledge, and thus doesn’t capture logical or conceptual competence. It also doesn’t capture the idea that one already believes (knows) what one can easily (and correctly) compute.
$\langle \mathscr {M}, w \rangle \nvDash B\psi $
. On the other hand, the model as it stands allows any combination of beliefs and knowledge, and thus doesn’t capture logical or conceptual competence. It also doesn’t capture the idea that one already believes (knows) what one can easily (and correctly) compute.
Here is the main idea of my proposed supplementation of the impossible-worlds model. I propose to add the following constraints on the accessibility functions: a world
![]() $w'$
is accessible from
$w'$
is accessible from
![]() $w$
if and only if
$w$
if and only if
![]() $w'$
respects what is “easily computable” from
$w'$
respects what is “easily computable” from
![]() $w$
, i.e.,
$w$
, i.e.,
![]() $w'$
satisfies all the sentences that the agent can easily compute in
$w'$
satisfies all the sentences that the agent can easily compute in
![]() $w$
to be true, and doesn’t satisfy any sentence that the agent can easily compute in
$w$
to be true, and doesn’t satisfy any sentence that the agent can easily compute in
![]() $w$
not to be true (which might not be equivalent to computing that the sentence is false). At a first pass, an agent “computes”
$w$
not to be true (which might not be equivalent to computing that the sentence is false). At a first pass, an agent “computes”
![]() $\phi $
to be true if she would answer affirmatively when asked whether
$\phi $
to be true if she would answer affirmatively when asked whether
![]() $\phi $
is true, given that she desires to give the correct answer. The answer could be incorrect in the doxastic case, but not in the epistemic case. In either case, an agent can compute
$\phi $
is true, given that she desires to give the correct answer. The answer could be incorrect in the doxastic case, but not in the epistemic case. In either case, an agent can compute
![]() $\phi $
to be true without having a proof (or what they take to be a proof) of
$\phi $
to be true without having a proof (or what they take to be a proof) of
![]() $\phi $
. As we will see, we can generalize this understanding of “compute
$\phi $
. As we will see, we can generalize this understanding of “compute
![]() $\phi $
to be true” to cover non-linguistic actions as well.
$\phi $
to be true” to cover non-linguistic actions as well.
The qualifier “easily” is supposed to bound the algorithmic notion of belief and knowledge as discussed in Section 2.1. In general, an agent who believes (knows)
![]() $\phi $
is disposed to act (capable of acting) upon
$\phi $
is disposed to act (capable of acting) upon
![]() $\phi $
—including to answer questions about
$\phi $
—including to answer questions about
![]() $\phi $
—using only a small amount of resources. For instance, we wouldn’t say that Ola believes that
$\phi $
—using only a small amount of resources. For instance, we wouldn’t say that Ola believes that
![]() $38,629$
is prime if she would have to think for 3 weeks before answering “Yes” when asked about it. But Ola knows that
$38,629$
is prime if she would have to think for 3 weeks before answering “Yes” when asked about it. But Ola knows that
![]() $38,624$
is composite even though she has never considered the question, because it only takes her a very small amount of computational resources to answer “Yes” to the question “Is
$38,624$
is composite even though she has never considered the question, because it only takes her a very small amount of computational resources to answer “Yes” to the question “Is
![]() $38,624$
composite?” For simplicity, here I will only consider the resource of time. I will thus model “easily” as “in
$38,624$
composite?” For simplicity, here I will only consider the resource of time. I will thus model “easily” as “in
![]() $\leq \epsilon $
units of time,” where
$\leq \epsilon $
units of time,” where
![]() $\epsilon $
is a small “threshold” natural number (assuming also that units of time can be counted in natural numbers). It is clear from the examples above that a couple of seconds count as “in
$\epsilon $
is a small “threshold” natural number (assuming also that units of time can be counted in natural numbers). It is clear from the examples above that a couple of seconds count as “in
![]() $\leq \epsilon $
units of time,” while 3 weeks or 3 hours don’t. But there are plausibly indeterminate cases in between. As Stalnaker notes in a similar context, this fits with the plausible view that attributions of belief and knowledge are context-sensitive:
$\leq \epsilon $
units of time,” while 3 weeks or 3 hours don’t. But there are plausibly indeterminate cases in between. As Stalnaker notes in a similar context, this fits with the plausible view that attributions of belief and knowledge are context-sensitive:
There is obviously a continuum here, and no very natural place to draw a line between information that is easily accessible and information that is not. I don’t think this is a serious problem. Attribution of belief and knowledge are obviously highly context-dependent, and the line between what we already know and what we could come to know if we made the effort may be one thing determined somewhat arbitrarily in different ways in different situations. [Reference Stalnaker48, p. 437]
I will henceforth assume that the threshold
![]() $\epsilon $
is a small enough unit of time in the range of a few seconds, but follow Stalnaker in allowing the value of
$\epsilon $
is a small enough unit of time in the range of a few seconds, but follow Stalnaker in allowing the value of
![]() $\epsilon $
to be sensitive to the context of attribution of belief or knowledge.
$\epsilon $
to be sensitive to the context of attribution of belief or knowledge.
On this algorithmic impossible-worlds model, it will turn out that an agent believes (knows)
![]() $\phi $
if and only if she has an algorithm that would (correctly) output an affirmative answer if asked “Is
$\phi $
if and only if she has an algorithm that would (correctly) output an affirmative answer if asked “Is
![]() $\phi $
true?” in less than or equal to
$\phi $
true?” in less than or equal to
![]() $\epsilon $
units of time. Our worlds-based algorithmic model will thus turn out to be a combination of the non-worlds-based algorithmic models of Halpern et al. [Reference Halpern, Moses and Vardi17] and Duc [Reference Duc15], but where belief and knowledge are bounded (unlike Halpern et al.’s notions of belief and knowledge and Duc’s notion of knowledge
$\epsilon $
units of time. Our worlds-based algorithmic model will thus turn out to be a combination of the non-worlds-based algorithmic models of Halpern et al. [Reference Halpern, Moses and Vardi17] and Duc [Reference Duc15], but where belief and knowledge are bounded (unlike Halpern et al.’s notions of belief and knowledge and Duc’s notion of knowledge
![]() $K^\exists _i$
) and not themselves time-stamped notions (unlike Duc’s notions of knowledge
$K^\exists _i$
) and not themselves time-stamped notions (unlike Duc’s notions of knowledge
![]() $K^n_i$
). The model will obviously satisfy the third desideratum on middle-ground models outlined in Section 1: an agent already believes (knows) what is easily (and correctly) computationally accessible to her. But further constraints will be needed to satisfy the other two desiderata, viz., to capture logically competent agents, and to capture conceptually competent agents.
$K^n_i$
). The model will obviously satisfy the third desideratum on middle-ground models outlined in Section 1: an agent already believes (knows) what is easily (and correctly) computationally accessible to her. But further constraints will be needed to satisfy the other two desiderata, viz., to capture logically competent agents, and to capture conceptually competent agents.
Here, then, is the proposal in more detail. Let
![]() $\mathscr {L}$
, as defined above, be the language of our model, and let an algorithmic impossible-worlds model be a tuple
$\mathscr {L}$
, as defined above, be the language of our model, and let an algorithmic impossible-worlds model be a tuple
![]() $\mathscr {M} = \langle \mathscr {W}, \mathscr {P}, d, e, v, \mathscr {A}, A \rangle $
, where
$\mathscr {M} = \langle \mathscr {W}, \mathscr {P}, d, e, v, \mathscr {A}, A \rangle $
, where
![]() $\mathscr {M} = \langle \mathscr {W}, \mathscr {P}, d, e, v \rangle $
is an impossible-worlds model;
$\mathscr {M} = \langle \mathscr {W}, \mathscr {P}, d, e, v \rangle $
is an impossible-worlds model;
![]() $\mathscr {A}$
is a set of algorithms that take as input a sentence
$\mathscr {A}$
is a set of algorithms that take as input a sentence
![]() $\phi \in \mathscr {L}$
and output either “Yes,” “No,” or “?”;Footnote
24
and A is a local algorithm function that assigns each
$\phi \in \mathscr {L}$
and output either “Yes,” “No,” or “?”;Footnote
24
and A is a local algorithm function that assigns each
![]() $w \in \mathscr {W}$
to a local algorithm in
$w \in \mathscr {W}$
to a local algorithm in
![]() $\mathscr {A}$
, which I denote “
$\mathscr {A}$
, which I denote “
![]() $A_w$
.” I abbreviate “
$A_w$
.” I abbreviate “
![]() $A_w$
outputs ‘Yes’ given
$A_w$
outputs ‘Yes’ given
![]() $\phi $
in less than or equal to n units of time” as “
$\phi $
in less than or equal to n units of time” as “
![]() $A^{\leq n}_w(\phi ) = `\textrm {Yes'}$
,” and “
$A^{\leq n}_w(\phi ) = `\textrm {Yes'}$
,” and “
![]() $A_w$
outputs ‘Yes’ given
$A_w$
outputs ‘Yes’ given
![]() $\phi $
in some finite unit of time” as “
$\phi $
in some finite unit of time” as “
![]() $A_w(\phi ) = `\textrm {Yes'}$
” (and do the same for the other outputs). Thus
$A_w(\phi ) = `\textrm {Yes'}$
” (and do the same for the other outputs). Thus
![]() $A^{\leq n}_w(\phi ) = ` `\textrm {Yes"}$
implies
$A^{\leq n}_w(\phi ) = ` `\textrm {Yes"}$
implies
![]() $A_w(\phi ) = ` `\textrm {Yes"}$
and
$A_w(\phi ) = ` `\textrm {Yes"}$
and
![]() $A_w(\phi ) = ` `\textrm {Yes"}$
implies that there is an
$A_w(\phi ) = ` `\textrm {Yes"}$
implies that there is an
![]() $n \in \mathbb {N}$
such that
$n \in \mathbb {N}$
such that
![]() $A^{\leq n}_w(\phi ) = ` `\textrm {Yes"}$
(and the same holds for the other outputs).
$A^{\leq n}_w(\phi ) = ` `\textrm {Yes"}$
(and the same holds for the other outputs).
Let me first explain what I take the local algorithms to capture. As I mentioned above, on a first-pass understanding,
![]() $A_w$
captures the agent’s dispositions in state
$A_w$
captures the agent’s dispositions in state
![]() $w$
to answer questions about the truth-values of certain sentences. Thus
$w$
to answer questions about the truth-values of certain sentences. Thus
![]() $A_w(\phi ) = ` `\textrm {Yes"}$
captures that in state
$A_w(\phi ) = ` `\textrm {Yes"}$
captures that in state
![]() $w$
, the agent is such that if she were asked whether
$w$
, the agent is such that if she were asked whether
![]() $\phi $
is true and wanted to give the correct answer, she would engage in a certain chain of reasoning and answer affirmatively within some finite unit of time. “No” corresponds to a negative answer, and “?” to “I don’t know” or “I give up.”Footnote
25
I assume that agents can have different local algorithms in different states, and that a local algorithm in a state can run different sub-algorithms given different inputs.Footnote
26
For instance, it might be that 10 years ago, Ola had no local algorithm that would check for primality if asked “Is n prime?” for any n, and that in her current state, Ola has a local algorithm that would run a trial division if asked “Is
$\phi $
is true and wanted to give the correct answer, she would engage in a certain chain of reasoning and answer affirmatively within some finite unit of time. “No” corresponds to a negative answer, and “?” to “I don’t know” or “I give up.”Footnote
25
I assume that agents can have different local algorithms in different states, and that a local algorithm in a state can run different sub-algorithms given different inputs.Footnote
26
For instance, it might be that 10 years ago, Ola had no local algorithm that would check for primality if asked “Is n prime?” for any n, and that in her current state, Ola has a local algorithm that would run a trial division if asked “Is
![]() $55,579$
prime?” but directly output “No” if asked whether a number ending in 4 is prime. As in [Reference Duc15], I thus assume that a local algorithm captures all the steps for choosing different sub-algorithms for different inputs.
$55,579$
prime?” but directly output “No” if asked whether a number ending in 4 is prime. As in [Reference Duc15], I thus assume that a local algorithm captures all the steps for choosing different sub-algorithms for different inputs.
On the first-pass understanding, local algorithms capture linguistic dispositions—just as in the standard algorithmic models from Section 2.1. This understanding is simpler to work with, which is why I will adopt it in discussing the model. Importantly, however, this understanding can be generalized now that we have adopted an impossible-worlds framework. For instance, following Stalnaker’s [Reference Stalnaker47] definition of belief, we can take
![]() $A_w(\phi ) = ` `\textrm {Yes"}$
to capture that in state
$A_w(\phi ) = ` `\textrm {Yes"}$
to capture that in state
![]() $w$
, the agent is such that, all else being equal, she would output behavior that would tend to satisfy her desires in worlds in which
$w$
, the agent is such that, all else being equal, she would output behavior that would tend to satisfy her desires in worlds in which
![]() , together with her other beliefs, are true, within some finite unit of time (where “
, together with her other beliefs, are true, within some finite unit of time (where “
![]() ” stands for the proposition expressed by
” stands for the proposition expressed by
![]() $\phi $
). “No” could then correspond to behavior that would tend to satisfy her desires in worlds in which
$\phi $
). “No” could then correspond to behavior that would tend to satisfy her desires in worlds in which
![]() is not true, and “?” to behavior that would tend to satisfy her desires irrespective of whether
is not true, and “?” to behavior that would tend to satisfy her desires irrespective of whether
![]() is true. On this generalized understanding, outputting the correct answer to the question of whether
is true. On this generalized understanding, outputting the correct answer to the question of whether
![]() $\phi $
is true is only one example of behavior that would tend to satisfy the agent’s desires in worlds in which
$\phi $
is true is only one example of behavior that would tend to satisfy the agent’s desires in worlds in which
![]() , together with her other beliefs, are true; thus,
, together with her other beliefs, are true; thus,
![]() $A_w(\phi ) = ` `\textrm {Yes"}$
on the generalized understanding doesn’t require that the agent in state
$A_w(\phi ) = ` `\textrm {Yes"}$
on the generalized understanding doesn’t require that the agent in state
![]() $w$
would answer affirmatively if asked about
$w$
would answer affirmatively if asked about
![]() $\phi $
(she can misspeak, for instance) or that she has any linguistic dispositions at all. On a possible-worlds framework, the first-pass understanding of the local algorithms can’t be generalized in this way, since on a possible-worlds construal of propositions, Stalnaker’s definitions of belief and knowledge imply that they are closed under entailment. In the case of single-premise entailment, this is because for possible-worlds propositions A and B, if A entails B, then
$\phi $
(she can misspeak, for instance) or that she has any linguistic dispositions at all. On a possible-worlds framework, the first-pass understanding of the local algorithms can’t be generalized in this way, since on a possible-worlds construal of propositions, Stalnaker’s definitions of belief and knowledge imply that they are closed under entailment. In the case of single-premise entailment, this is because for possible-worlds propositions A and B, if A entails B, then
![]() $A \cap B = A$
, and belief distributes over intersections on Stalnaker’s definition, i.e., if S believes
$A \cap B = A$
, and belief distributes over intersections on Stalnaker’s definition, i.e., if S believes
![]() $A \cap B$
, then she believes A and she believes B. (This is because if S is disposed to satisfy desires in worlds in which
$A \cap B$
, then she believes A and she believes B. (This is because if S is disposed to satisfy desires in worlds in which
![]() $A \cap B$
, together with her other beliefs, is true, she is also disposed to satisfy desires in worlds in which A, together with her other beliefs—which include
$A \cap B$
, together with her other beliefs, is true, she is also disposed to satisfy desires in worlds in which A, together with her other beliefs—which include
![]() $A \cap B$
—is true.)Footnote
27
$A \cap B$
—is true.)Footnote
27
On the algorithmic impossible-worlds model as I have defined it, the objects of knowledge, the objects of belief, and the inputs of local algorithms are all sentences and not propositions—just as in the standard algorithmic models from Section 2.1. But because we have adopted an impossible-worlds framework, we can now also easily modify this definition and give an alternative interpretation of the formalism: we can instead let the inputs of the algorithms in
![]() $\mathscr {A}$
be propositions,
$\mathscr {A}$
be propositions,
![]() , and interpret “
, and interpret “
![]() $K\phi $
” as the formalization of the proposition that the agent knows
$K\phi $
” as the formalization of the proposition that the agent knows
![]() . The reason this is possible is that unlike in the construction of propositions as sets of possible worlds, for any two sentences
. The reason this is possible is that unlike in the construction of propositions as sets of possible worlds, for any two sentences
![]() $\phi \neq \psi \in \mathscr {L}$
, the respective propositions as sets of worlds
$\phi \neq \psi \in \mathscr {L}$
, the respective propositions as sets of worlds
![]() and
and
![]() aren’t identical. (This follows from the maximally permissive construal of impossible worlds on which there is some
aren’t identical. (This follows from the maximally permissive construal of impossible worlds on which there is some
![]() $w' \in \mathscr {I}$
such that for all
$w' \in \mathscr {I}$
such that for all
![]() $\alpha \in \mathscr {L}$
,
$\alpha \in \mathscr {L}$
,
![]() $v(\alpha , w') = 1$
if and only if
$v(\alpha , w') = 1$
if and only if
![]() $\alpha \in \{\phi \}$
, and this
$\alpha \in \{\phi \}$
, and this
![]() .) I will use the original definitions here for ease of notation, but officially adopt the modified definition and interpretation.
.) I will use the original definitions here for ease of notation, but officially adopt the modified definition and interpretation.
I retain the standard definitions of satisfaction and dissatisfaction given above. The key remaining task is to define the accessibility functions d and e. We first need to contrast the epistemic case with the doxastic case. Recall that on the first-pass understanding, the general idea is that one believes
![]() $\phi $
just in case one would affirmatively answer the question of whether
$\phi $
just in case one would affirmatively answer the question of whether
![]() $\phi $
is true. Since it is standardly assumed that knowledge entails belief and is factive, a natural addition for the case of knowledge is to require that the answer would be correct. Accordingly, given an algorithmic impossible-worlds model,
$\phi $
is true. Since it is standardly assumed that knowledge entails belief and is factive, a natural addition for the case of knowledge is to require that the answer would be correct. Accordingly, given an algorithmic impossible-worlds model,
![]() $\mathscr {M}$
, let an algorithm
$\mathscr {M}$
, let an algorithm
![]() $X \in \mathscr {A}$
be veridical about
$X \in \mathscr {A}$
be veridical about
![]() $\phi $
at
$\phi $
at
![]() $\langle \mathscr {M}, w \rangle $
if and only if, if
$\langle \mathscr {M}, w \rangle $
if and only if, if
![]() $X(\phi )=` `\textrm {Yes,"}$
then
$X(\phi )=` `\textrm {Yes,"}$
then
![]() $\langle \mathscr {M}, w \rangle \vDash \phi $
, and if
$\langle \mathscr {M}, w \rangle \vDash \phi $
, and if
![]() $X(\phi )=` `\textrm {No,"}$
then
$X(\phi )=` `\textrm {No,"}$
then
![]() $\langle \mathscr {M}, w \rangle \nvDash \phi $
. That is, an algorithm is veridical about
$\langle \mathscr {M}, w \rangle \nvDash \phi $
. That is, an algorithm is veridical about
![]() $\phi $
at
$\phi $
at
![]() $w$
just in case if it answers “Yes” to whether
$w$
just in case if it answers “Yes” to whether
![]() $\phi $
is true, then
$\phi $
is true, then
![]() $\phi $
is true at
$\phi $
is true at
![]() $w$
, and if it answers “No” to whether
$w$
, and if it answers “No” to whether
![]() $\phi $
is true, then
$\phi $
is true, then
![]() $\phi $
is not true at
$\phi $
is not true at
![]() $w$
(we relativize veridicality to a world to leave it open that different worlds can have the same local algorithm).Footnote
28
In the following, I will adopt veridicality as a minimal condition on knowledge. Plausibly, knowledge requires more than true belief. Other potential conditions could be integrated into the algorithmic framework as well. Take, for instance, the condition that knowledge is safe true belief, i.e., belief that is true in all nearby possible worlds.Footnote
29
Our model could incorporate this idea by requiring that a local algorithm isn’t just veridical about
$w$
(we relativize veridicality to a world to leave it open that different worlds can have the same local algorithm).Footnote
28
In the following, I will adopt veridicality as a minimal condition on knowledge. Plausibly, knowledge requires more than true belief. Other potential conditions could be integrated into the algorithmic framework as well. Take, for instance, the condition that knowledge is safe true belief, i.e., belief that is true in all nearby possible worlds.Footnote
29
Our model could incorporate this idea by requiring that a local algorithm isn’t just veridical about
![]() $\phi $
locally but in all the nearby worlds in which that algorithm is local.Footnote
30
Or take the sensitivity condition on knowledge, i.e., that the agent wouldn’t believe
$\phi $
locally but in all the nearby worlds in which that algorithm is local.Footnote
30
Or take the sensitivity condition on knowledge, i.e., that the agent wouldn’t believe
![]() $\phi $
if it were false.Footnote
31
Our model could incorporate this idea by requiring that a local algorithm doesn’t output “Yes” in the nearest world(s) in which it is local and
$\phi $
if it were false.Footnote
31
Our model could incorporate this idea by requiring that a local algorithm doesn’t output “Yes” in the nearest world(s) in which it is local and
![]() $\phi $
is false. In similar ways, we could require the algorithms to take information as input, or to not rely on false lemmas, and so on.Footnote
32
The algorithmic approach thus yields novel and potentially fruitful ways of formally representing conditions on knowledge, by making these conditions on agents’ algorithms.Footnote
33
$\phi $
is false. In similar ways, we could require the algorithms to take information as input, or to not rely on false lemmas, and so on.Footnote
32
The algorithmic approach thus yields novel and potentially fruitful ways of formally representing conditions on knowledge, by making these conditions on agents’ algorithms.Footnote
33
We can now define the accessibility functions d and e. Following the main idea explained above, for any
![]() $w \in \mathscr {W}$
:
$w \in \mathscr {W}$
:

As before,
![]() $\epsilon $
is our threshold unit of time, which we assume to be fixed by the context we are modeling.
$\epsilon $
is our threshold unit of time, which we assume to be fixed by the context we are modeling.
On our definition, the worlds accessible from
![]() $w$
satisfy all the sentences that the agent can easily (and correctly) compute in
$w$
satisfy all the sentences that the agent can easily (and correctly) compute in
![]() $w$
to be true, and don’t satisfy any of the sentences that the agent can easily (and correctly) compute not to be true (there are no constraints on sentences for which the agent outputs “?.”)Footnote
34
As desired, it follows from these definitions that for any
$w$
to be true, and don’t satisfy any of the sentences that the agent can easily (and correctly) compute not to be true (there are no constraints on sentences for which the agent outputs “?.”)Footnote
34
As desired, it follows from these definitions that for any
![]() $w \in \mathscr {P}$
, (i) and (ii) are equivalent, and (iii) and (iv) are equivalent:
$w \in \mathscr {P}$
, (i) and (ii) are equivalent, and (iii) and (iv) are equivalent:
-
(i)
 $\langle \mathscr {M}, w \rangle \vDash B\phi $
.
$\langle \mathscr {M}, w \rangle \vDash B\phi $
. -
(ii)
 $A^{\leq \epsilon }_w(\phi )=` `\textrm {Yes."}$
$A^{\leq \epsilon }_w(\phi )=` `\textrm {Yes."}$
-
(iii)
 $\langle \mathscr {M}, w \rangle \vDash K\phi $
.
$\langle \mathscr {M}, w \rangle \vDash K\phi $
. -
(iv)
 $A^{\leq \epsilon }_w(\phi )=` `\textrm {Yes"}$
and
$A^{\leq \epsilon }_w(\phi )=` `\textrm {Yes"}$
and
 $A_w$
is veridical about
$A_w$
is veridical about
 $\phi $
at
$\phi $
at
 $\langle \mathscr {M}, w \rangle $
.
$\langle \mathscr {M}, w \rangle $
.
To see that these equivalences hold, consider, first, the equivalence between (i) and (ii). Let
![]() $w \in \mathscr {P}$
, and assume (i). Let
$w \in \mathscr {P}$
, and assume (i). Let
![]() $Y_w = \{ \alpha \in \mathscr {L} \mid A^{\leq \epsilon }_w(\alpha )=` `\textrm {Yes"}\}$
. By the maximally permissive construction of impossible worlds, there is some
$Y_w = \{ \alpha \in \mathscr {L} \mid A^{\leq \epsilon }_w(\alpha )=` `\textrm {Yes"}\}$
. By the maximally permissive construction of impossible worlds, there is some
![]() $y \in \mathscr {I}$
such that for all
$y \in \mathscr {I}$
such that for all
![]() $\alpha \in \mathscr {L}$
,
$\alpha \in \mathscr {L}$
,
![]() $v(\alpha , y) = 1$
if and only if
$v(\alpha , y) = 1$
if and only if
![]() $\alpha \in Y_w$
. Thus, for all
$\alpha \in Y_w$
. Thus, for all
![]() $\alpha \in \mathscr {L}$
, if
$\alpha \in \mathscr {L}$
, if
![]() $A^{\leq \epsilon }_w(\alpha )=` `\textrm {Yes"}$
then
$A^{\leq \epsilon }_w(\alpha )=` `\textrm {Yes"}$
then
![]() $\langle \mathscr {M}, y \rangle \vDash \alpha $
, and if
$\langle \mathscr {M}, y \rangle \vDash \alpha $
, and if
![]() $A^{\leq \epsilon }_w(\alpha )=` `\textrm {No"}$
then
$A^{\leq \epsilon }_w(\alpha )=` `\textrm {No"}$
then
![]() $\langle \mathscr {M}, y \rangle \nvDash \alpha $
. Thus, by the definition of d,
$\langle \mathscr {M}, y \rangle \nvDash \alpha $
. Thus, by the definition of d,
![]() $y \in d(w)$
. Thus, by (i),
$y \in d(w)$
. Thus, by (i),
![]() $\langle \mathscr {M}, y \rangle \vDash \phi $
. By the choice of y,
$\langle \mathscr {M}, y \rangle \vDash \phi $
. By the choice of y,
![]() $\phi \in Y_w$
, and thus (ii) follows. For the converse, assume (ii). Let
$\phi \in Y_w$
, and thus (ii) follows. For the converse, assume (ii). Let
![]() $w' \in \mathscr {W}$
be such that
$w' \in \mathscr {W}$
be such that
![]() $w' \in d(w)$
. Thus, by the definition of d, for all
$w' \in d(w)$
. Thus, by the definition of d, for all
![]() $\gamma \in \mathscr {L}$
, if
$\gamma \in \mathscr {L}$
, if
![]() $A^{\leq \epsilon }_w(\gamma )=` `\textrm {Yes"}$
then
$A^{\leq \epsilon }_w(\gamma )=` `\textrm {Yes"}$
then
![]() $\langle \mathscr {M}, w' \rangle \vDash \gamma $
. Thus, by (ii),
$\langle \mathscr {M}, w' \rangle \vDash \gamma $
. Thus, by (ii),
![]() $\langle \mathscr {M}, w' \rangle \vDash \phi $
. Thus, (i) follows. A parallel argument establishes the equivalence of (iii) and (iv). It is easy to see that our definitions of d and e entail the factivity of knowledge (since e is reflexive, i.e., for all
$\langle \mathscr {M}, w' \rangle \vDash \phi $
. Thus, (i) follows. A parallel argument establishes the equivalence of (iii) and (iv). It is easy to see that our definitions of d and e entail the factivity of knowledge (since e is reflexive, i.e., for all
![]() $w \in \mathscr {W}, w \in e(w)$
) and that knowledge entails belief (since
$w \in \mathscr {W}, w \in e(w)$
) and that knowledge entails belief (since
![]() $d(w) \subseteq e(w)$
for all
$d(w) \subseteq e(w)$
for all
![]() $w \in \mathscr {W}$
).Footnote
35
$w \in \mathscr {W}$
).Footnote
35
Let me now turn to the three desiderata on middle-ground models from Section 1 and explain how this algorithmic impossible-worlds models can be supplemented to satisfy the first and second desiderata, and how it already satisfies the third desideratum. Consider the first desideratum, viz., that our model should capture agents who are logically competent. At an intuitive level, there are different ways to understand what it is for an agent to be logically competent. For one, and as Duc [Reference Duc, Pinto-Ferreira and Mamede13, p. 6; Reference Duc14, p. 637] mentions, one might want a logically competent agent to “know at least a (sufficiently) large class of logical truths.” For instance, it might be that any logically competent agent will know all propositions of the form
![]() $\phi \rightarrow \phi $
(although perhaps only as long as
$\phi \rightarrow \phi $
(although perhaps only as long as
![]() $\phi $
is simple enough). Similarly, and as captured by Duc’s (
NEC
A
), one might want a logically competent agent to be capable of eventually giving the right answer to the question of whether some sentence is a tautology in some basic logical formal system, if they have enough time to think about it. Our algorithmic framework can capture this first intuitive sense of logical competence by putting both time-sensitive and non-time-sensitive constraints on logically competent agents’ local algorithms. Let F be some formal system such that all the tautologies of F are true in all possible worlds
$\phi $
is simple enough). Similarly, and as captured by Duc’s (
NEC
A
), one might want a logically competent agent to be capable of eventually giving the right answer to the question of whether some sentence is a tautology in some basic logical formal system, if they have enough time to think about it. Our algorithmic framework can capture this first intuitive sense of logical competence by putting both time-sensitive and non-time-sensitive constraints on logically competent agents’ local algorithms. Let F be some formal system such that all the tautologies of F are true in all possible worlds
![]() $w \in \mathscr {P}$
(for instance, F might be propositional logic), and let the basic tautologies of F be some set of tautologies we deem to be required for logical competence (what counts as “basic” in this sense might be context-sensitive). We can then require that for any world
$w \in \mathscr {P}$
(for instance, F might be propositional logic), and let the basic tautologies of F be some set of tautologies we deem to be required for logical competence (what counts as “basic” in this sense might be context-sensitive). We can then require that for any world
![]() $w \in \mathscr {P}$
and sentence
$w \in \mathscr {P}$
and sentence
![]() $\phi \in \mathscr {L}$
:
$\phi \in \mathscr {L}$
:
-
(a) If
 $\phi $
is a tautology of F, then
$\phi $
is a tautology of F, then
 $A_w(\phi ) = ` `\textrm {Yes"}$
and
$A_w(\phi ) = ` `\textrm {Yes"}$
and
 $A_w$
is veridical about
$A_w$
is veridical about
 $\phi $
at
$\phi $
at
 $\langle \mathscr {M}, w \rangle $
.
$\langle \mathscr {M}, w \rangle $
. -
(b) If
 $\phi $
is a basic tautology of F, then
$\phi $
is a basic tautology of F, then
 $A^{\leq \epsilon }_w(\phi ) = ` `\textrm {Yes"}$
and
$A^{\leq \epsilon }_w(\phi ) = ` `\textrm {Yes"}$
and
 $A_w$
is veridical about
$A_w$
is veridical about
 $\phi $
at
$\phi $
at
 $\langle \mathscr {M}, w \rangle $
.
$\langle \mathscr {M}, w \rangle $
.
Given the equivalence of (iii) and (iv), (b) entails that logically competent agents know all the basic tautologies.
As we saw in Section 2.1, we can also follow Duc [Reference Duc15] and introduce new formulas of the form “
![]() $K^{\exists }\phi $
” in our object language
$K^{\exists }\phi $
” in our object language
![]() $\mathscr {L}$
to formalize propositions such as “the agent would correctly answer ‘Yes’ when asked whether
$\mathscr {L}$
to formalize propositions such as “the agent would correctly answer ‘Yes’ when asked whether
![]() $\phi $
is true in finite time” or “the agent is in a position to know
$\phi $
is true in finite time” or “the agent is in a position to know
![]() $\phi $
” (assuming that after having correctly computed that
$\phi $
” (assuming that after having correctly computed that
![]() $\phi $
is true, an agent knows
$\phi $
is true, an agent knows
![]() $\phi $
). By defining the relevant kinds of accessibility relations, we can then just as above get the equivalence between (v) and (vi) for all
$\phi $
). By defining the relevant kinds of accessibility relations, we can then just as above get the equivalence between (v) and (vi) for all
![]() $w \in \mathscr {P}$
:
$w \in \mathscr {P}$
:
-
(v)
 $\langle \mathscr {M}, w \rangle \vDash K^\exists \phi $
.
$\langle \mathscr {M}, w \rangle \vDash K^\exists \phi $
. -
(vi)
 $A_w(\phi )=` `\textrm {Yes"}$
and
$A_w(\phi )=` `\textrm {Yes"}$
and
 $A_w$
is veridical about
$A_w$
is veridical about
 $\phi $
at
$\phi $
at
 $\langle \mathscr {M}, w \rangle $
.
$\langle \mathscr {M}, w \rangle $
.
We can thus in the object language capture that for any tautology,
![]() $\phi $
, the logically competent agent is “in a position to know
$\phi $
, the logically competent agent is “in a position to know
![]() $\phi $
” in that she would give the right answer to whether
$\phi $
” in that she would give the right answer to whether
![]() $\phi $
is true within a finite unit of time. Given our purposes here, however, putting constraints directly on the local algorithms suffices to constrain our model to capture logically competent agents.
$\phi $
is true within a finite unit of time. Given our purposes here, however, putting constraints directly on the local algorithms suffices to constrain our model to capture logically competent agents.
On a second intuitive understanding, logical competence is a conditional achievement. This is captured by the statements that, for instance, a logically competent agent “can draw sufficiently many conclusions from their knowledge” [Reference Duc, Pinto-Ferreira and Mamede13, p. 6], “does not miss out on any trivial logical consequences of what she believes” [Reference Bjerring and Skipper8, pp. 502f.], or that “rational agents seemingly know the trivial consequences of what they know” [Reference Jago24, p. 1152]. On one way of understanding them, these statements suggest a closure principle of the form: if the agent believes (knows) certain propositions
![]() $\Phi $
, then she also believes (knows) the “trivial” consequences of
$\Phi $
, then she also believes (knows) the “trivial” consequences of
![]() $\Phi $
. However, as Bjerring and Skipper [Reference Bjerring and Skipper8, pp. 506–508] point out, a “collapse argument” shows that such closure principles entail or “collapse into” Full Logical Omniscience: Assume that
$\Phi $
. However, as Bjerring and Skipper [Reference Bjerring and Skipper8, pp. 506–508] point out, a “collapse argument” shows that such closure principles entail or “collapse into” Full Logical Omniscience: Assume that
![]() $\phi $
is a trivial consequence of
$\phi $
is a trivial consequence of
![]() $\Phi $
if
$\Phi $
if
![]() $\phi $
is derivable from
$\phi $
is derivable from
![]() $\Phi $
in one application of a standard rule of inference. Since any logical consequence of
$\Phi $
in one application of a standard rule of inference. Since any logical consequence of
![]() $\Phi $
is derivable from
$\Phi $
is derivable from
![]() $\Phi $
via a chain of trivial consequences, if one fails to know some logical consequence of what one knows, then one must also fail to know some trivial consequence of what one knows.Footnote
36
The challenge for capturing the second intuitive sense of logical competence, then, is to formulate some conditional constraint(s) that doesn’t (don’t) face a collapse argument; let me call this “the collapse challenge.” In Section 3, I will outline how Bjerring and Skipper [Reference Bjerring and Skipper8] propose to meet the collapse challenge. In our algorithmic impossible-worlds approach, we can meet the collapse challenge by adopting (some of) the following conditional constraints on logically competent agents’ local algorithms. For simplicity, I only formulate these constraints for the primitive logical expressions of our base language
$\Phi $
via a chain of trivial consequences, if one fails to know some logical consequence of what one knows, then one must also fail to know some trivial consequence of what one knows.Footnote
36
The challenge for capturing the second intuitive sense of logical competence, then, is to formulate some conditional constraint(s) that doesn’t (don’t) face a collapse argument; let me call this “the collapse challenge.” In Section 3, I will outline how Bjerring and Skipper [Reference Bjerring and Skipper8] propose to meet the collapse challenge. In our algorithmic impossible-worlds approach, we can meet the collapse challenge by adopting (some of) the following conditional constraints on logically competent agents’ local algorithms. For simplicity, I only formulate these constraints for the primitive logical expressions of our base language
![]() $\mathscr {L}$
, viz. “
$\mathscr {L}$
, viz. “
![]() $\wedge $
” and “
$\wedge $
” and “
![]() $\neg $
,” but similar constraints can be formulated for other logical constants. I also omit the veridicality condition, but similar constraints that include it can be formulated.Footnote
37
$\neg $
,” but similar constraints can be formulated for other logical constants. I also omit the veridicality condition, but similar constraints that include it can be formulated.Footnote
37
Consider, first, the following non-time-sensitive constraints. For any
![]() $w \in \mathscr {P}$
and
$w \in \mathscr {P}$
and
![]() $\phi , \psi \in \mathscr {L}$
:
$\phi , \psi \in \mathscr {L}$
:
-
(c) If
 $A_w(\phi ) = ` `\textrm {Yes"}$
and
$A_w(\phi ) = ` `\textrm {Yes"}$
and
 $A_w(\psi ) = ` `\textrm {Yes,"}$
then
$A_w(\psi ) = ` `\textrm {Yes,"}$
then
 $A_w((\phi \wedge \psi )) = ` `\textrm {Yes."}$
$A_w((\phi \wedge \psi )) = ` `\textrm {Yes."}$
-
(d) If
 $A_w((\phi \wedge \psi )) = ` `\textrm {Yes,"}$
then
$A_w((\phi \wedge \psi )) = ` `\textrm {Yes,"}$
then
 $A_w(\phi ) = ` `\textrm {Yes"}$
and
$A_w(\phi ) = ` `\textrm {Yes"}$
and
 $A_w(\psi ) = ` `\textrm {Yes."}$
$A_w(\psi ) = ` `\textrm {Yes."}$
-
(e)
 $A_w(\neg \phi ) = ` `\textrm {Yes"}$
if and only if
$A_w(\neg \phi ) = ` `\textrm {Yes"}$
if and only if
 $A_w(\phi ) = ` `\textrm {No."}$
$A_w(\phi ) = ` `\textrm {No."}$
-
(f)
 $A_w(\neg \phi ) = ` `\textrm {No"}$
if and only if
$A_w(\neg \phi ) = ` `\textrm {No"}$
if and only if
 $A_w(\phi ) = ` `\textrm {Yes."}$
$A_w(\phi ) = ` `\textrm {Yes."}$
In outline, constraints (c)–(f) capture the intuitive idea that a logically competent agent should respect the introduction and elimination rules for the logical connectives, even though it might take her a long time to do so. For instance, constraint (c) states that if a logically competent agent would eventually assent to
![]() $\phi $
and to
$\phi $
and to
![]() $\psi $
, then she would also eventually assent to their conjunction. Similarly, constraint (d) states that if a logically competent agent would eventually assent to a conjunction, then she would also eventually assent to its conjuncts. Constraints (e) and (f) capture that a logically competent agent computes something to be not true just in case she computes it to be false (i.e., computes its negation to be true), and vice versa. Constraints (c)–(f), together with analogous constraints we could formulate for other logical connectives and with veridicality, thus entail that if a logically competent agent believes (knows) certain propositions
$\psi $
, then she would also eventually assent to their conjunction. Similarly, constraint (d) states that if a logically competent agent would eventually assent to a conjunction, then she would also eventually assent to its conjuncts. Constraints (e) and (f) capture that a logically competent agent computes something to be not true just in case she computes it to be false (i.e., computes its negation to be true), and vice versa. Constraints (c)–(f), together with analogous constraints we could formulate for other logical connectives and with veridicality, thus entail that if a logically competent agent believes (knows) certain propositions
![]() $\Phi $
, and
$\Phi $
, and
![]() $\phi $
can be derived from
$\phi $
can be derived from
![]() $\Phi $
in one application of a standard rule of inference, then the agent would also eventually, though perhaps not immediately, (correctly) compute that
$\Phi $
in one application of a standard rule of inference, then the agent would also eventually, though perhaps not immediately, (correctly) compute that
![]() $\phi $
is true. Constraints (c)–(f) thus closely capture the second intuitive understanding of logical competence.
$\phi $
is true. Constraints (c)–(f) thus closely capture the second intuitive understanding of logical competence.
A useful consequence of (e) and (f) is that for any
![]() $w \in \mathscr {P}$
, if
$w \in \mathscr {P}$
, if
![]() $\langle \mathscr {M}, w \rangle \vDash B\phi $
, then
$\langle \mathscr {M}, w \rangle \vDash B\phi $
, then
![]() $\langle \mathscr {M}, w \rangle \vDash \neg B\neg \phi $
and if
$\langle \mathscr {M}, w \rangle \vDash \neg B\neg \phi $
and if
![]() $\langle \mathscr {M}, w \rangle \vDash B\neg \phi $
, then
$\langle \mathscr {M}, w \rangle \vDash B\neg \phi $
, then
![]() $\langle \mathscr {M}, w \rangle \vDash \neg B\phi $
. That is, if an agent believes
$\langle \mathscr {M}, w \rangle \vDash \neg B\phi $
. That is, if an agent believes
![]() $\phi $
, then she doesn’t believe
$\phi $
, then she doesn’t believe
![]() $\neg \phi $
, and if she believes
$\neg \phi $
, and if she believes
![]() $\neg \phi $
, then she doesn’t believe
$\neg \phi $
, then she doesn’t believe
![]() $\phi $
. To see this, consider the former conditional (the second is equivalent to the first given the classical truth-conditions for “
$\phi $
. To see this, consider the former conditional (the second is equivalent to the first given the classical truth-conditions for “
![]() $\neg $
”). Let
$\neg $
”). Let
![]() $w \in \mathscr {P}$
, and assume that
$w \in \mathscr {P}$
, and assume that
![]() $\langle \mathscr {M}, w \rangle \vDash B\phi $
. By the equivalence of (i) and (ii), it follows that
$\langle \mathscr {M}, w \rangle \vDash B\phi $
. By the equivalence of (i) and (ii), it follows that
![]() $A^{\leq \epsilon }_w(\phi ) = ` `\textrm {Yes."}$
It thus follows that
$A^{\leq \epsilon }_w(\phi ) = ` `\textrm {Yes."}$
It thus follows that
![]() $A_w(\phi ) = ` `\textrm {Yes."}$
Thus, by (f),
$A_w(\phi ) = ` `\textrm {Yes."}$
Thus, by (f),
![]() $A_w(\neg \phi ) = ` `\textrm {No."}$
It thus follows that
$A_w(\neg \phi ) = ` `\textrm {No."}$
It thus follows that
![]() $A^{\leq \epsilon }_w(\neg \phi ) \neq ` `\textrm {Yes."}$
By the equivalence of (i) and (ii), it follows that
$A^{\leq \epsilon }_w(\neg \phi ) \neq ` `\textrm {Yes."}$
By the equivalence of (i) and (ii), it follows that
![]() $\langle \mathscr {M}, w \rangle \nvDash B\neg \phi $
, and thus that
$\langle \mathscr {M}, w \rangle \nvDash B\neg \phi $
, and thus that
![]() $\langle \mathscr {M}, w \rangle \vDash \neg B\neg \phi $
. Similarly, (c)–(f) together entail that if an agent believes
$\langle \mathscr {M}, w \rangle \vDash \neg B\neg \phi $
. Similarly, (c)–(f) together entail that if an agent believes
![]() $(\phi \wedge \psi )$
, then she doesn’t believe
$(\phi \wedge \psi )$
, then she doesn’t believe
![]() $\neg \phi $
or
$\neg \phi $
or
![]() $\neg \psi $
, and if an agent believes
$\neg \psi $
, and if an agent believes
![]() $\phi $
and
$\phi $
and
![]() $\psi $
, she doesn’t believe
$\psi $
, she doesn’t believe
![]() $\neg (\phi \wedge \psi )$
. The following three closure principles thereby follow from (c)–(f): for any
$\neg (\phi \wedge \psi )$
. The following three closure principles thereby follow from (c)–(f): for any
![]() $\alpha , \beta , \gamma \in \mathscr {L}$
and
$\alpha , \beta , \gamma \in \mathscr {L}$
and
![]() $w \in \mathscr {P}$
, if
$w \in \mathscr {P}$
, if
![]() $\langle \mathscr {M}, w \rangle \vDash B\alpha $
and
$\langle \mathscr {M}, w \rangle \vDash B\alpha $
and
![]() $\langle \mathscr {M}, w \rangle \vDash B\neg \alpha $
, then
$\langle \mathscr {M}, w \rangle \vDash B\neg \alpha $
, then
![]() $\langle \mathscr {M}, w \rangle \vDash B\beta $
; if
$\langle \mathscr {M}, w \rangle \vDash B\beta $
; if
![]() $\langle \mathscr {M}, w \rangle \vDash B(\alpha \wedge \beta )$
and
$\langle \mathscr {M}, w \rangle \vDash B(\alpha \wedge \beta )$
and
![]() $\langle \mathscr {M}, w \rangle \vDash B\neg \alpha $
, then
$\langle \mathscr {M}, w \rangle \vDash B\neg \alpha $
, then
![]() $\langle \mathscr {M}, w \rangle \vDash B\gamma $
; and if
$\langle \mathscr {M}, w \rangle \vDash B\gamma $
; and if
![]() $\langle \mathscr {M}, w \rangle \vDash B\alpha $
,
$\langle \mathscr {M}, w \rangle \vDash B\alpha $
,
![]() $\langle \mathscr {M}, w \rangle \vDash B\beta $
, and
$\langle \mathscr {M}, w \rangle \vDash B\beta $
, and
![]() $\langle \mathscr {M}, w \rangle \vDash B\neg (\alpha \wedge \beta )$
, then
$\langle \mathscr {M}, w \rangle \vDash B\neg (\alpha \wedge \beta )$
, then
![]() $\langle \mathscr {M}, w \rangle \vDash B\gamma $
. As desired, these closure principles are too weak to entail Full Logical Omniscience. Constraints (c)–(f) thus don’t face a collapse argument, and we have thus met the collapse challenge for capturing the second intuitive sense of logical competence.
$\langle \mathscr {M}, w \rangle \vDash B\gamma $
. As desired, these closure principles are too weak to entail Full Logical Omniscience. Constraints (c)–(f) thus don’t face a collapse argument, and we have thus met the collapse challenge for capturing the second intuitive sense of logical competence.
We can also consider the result of adding time-sensitivity to (c) and (d) as possible candidate conditional constraints on logical competence:
-
(g) If
 $A^{\leq i}_w(\phi ) = ` `\textrm {Yes"}$
and
$A^{\leq i}_w(\phi ) = ` `\textrm {Yes"}$
and
 $A^{\leq j}_w(\psi ) = ` `\textrm {Yes,"}$
then
$A^{\leq j}_w(\psi ) = ` `\textrm {Yes,"}$
then
 $A^{\leq i + j + k}_w((\phi \wedge \psi )) = ` `\textrm {Yes"}$
for some small
$A^{\leq i + j + k}_w((\phi \wedge \psi )) = ` `\textrm {Yes"}$
for some small
 $k \in \mathbb {N}$
, for any
$k \in \mathbb {N}$
, for any
 $i, j \in \mathbb{N}$
.
$i, j \in \mathbb{N}$
. -
(h) If
 $A^{\leq i}_w((\phi \wedge \psi )) = ` `\textrm {Yes,"}$
then
$A^{\leq i}_w((\phi \wedge \psi )) = ` `\textrm {Yes,"}$
then
 $A^{\leq j}_w(\phi ) = ` `\textrm {Yes"}$
and
$A^{\leq j}_w(\phi ) = ` `\textrm {Yes"}$
and
 $A^{\leq k}_w(\psi ) = ` `\textrm {Yes"}$
for some
$A^{\leq k}_w(\psi ) = ` `\textrm {Yes"}$
for some
 $j, k \in \mathbb {N}$
such that
$j, k \in \mathbb {N}$
such that
 $j, k \leq i$
for any
$j, k \leq i$
for any
 $i \in \mathbb{N}$
.
$i \in \mathbb{N}$
.
Constraint (g) puts a limit on how long it should take a logically competent agent to say “Yes” to a conjunction if she believes each of its conjuncts. This constraint leaves open that logically competent agents can believe some conjuncts without believing their conjunction. I think this is a plausible conclusion: if the computational resources it takes for an agent to compute each of the conjuncts are close to the threshold for what counts as believing something, then it might be that the agent would just take too long to compute that a conjunction is true if asked about it, in which case we wouldn’t intuitively say that the agent believes the conjunction before she performed the computation. In the case of knowledge, accepting pragmatic encroachment can further strengthen this intuition: imagine that the stakes are such that an agent doesn’t count as knowing
![]() $\phi $
unless she can make a split-second decision about whether
$\phi $
unless she can make a split-second decision about whether
![]() $\phi $
(say, she needs to answer a timed quiz). The agent can then know
$\phi $
(say, she needs to answer a timed quiz). The agent can then know
![]() $\phi $
and know
$\phi $
and know
![]() $\psi $
, but, assuming that it would take her longer than the allowed time to answer whether
$\psi $
, but, assuming that it would take her longer than the allowed time to answer whether
![]() $(\phi \wedge \psi )$
, fail to know
$(\phi \wedge \psi )$
, fail to know
![]() $(\phi \wedge \psi )$
.Footnote
38
$(\phi \wedge \psi )$
.Footnote
38
Constraint (h), in turn, states that a logically competent agent’s belief algorithm outputs “Yes” to conjuncts in less or equal time than it outputs “Yes” to their conjunction. Typicality effects such as those involved in the conjunction fallacy might provide counterexamples to (h): an agent might be quicker to judge that a conjunction such as “Linda is a bank teller and is active in the feminist movement” is true than to judge that its conjunct “Linda is active in the feminist movement” is true, because the conjunction is more “typical.”Footnote 39 One might perhaps maintain that logically competent agents would judge the conjunct and the conjunction to be true at least equally fast. In any case, given the equivalence of (i) and (ii), (h) entails a fourth closure principle, viz., distribution over conjunction (i.e., if a logically competent agent believes a conjunction, then she also believes its conjuncts). Although the case for distribution over conjunction isn’t decisive either,Footnote 40 it is widely assumed and it doesn’t by itself imply anything like Full Logical Omniscience. Constraint (h) could thus also be an additional constraint on logically competent agents, depending on how strong one wants such constraints to be.
Next, consider the second desideratum on middle-ground models, viz., that our model should capture agents who are conceptually competent with the logical connectives. In my view, the constraints we have laid out in (c)–(h) can serve just as well as constraints on conceptual competence with conjunction and negation. Let us take conjunction as our main example. On traditional inferentialist metasemantic theories, possessing the concept of conjunction requires inferring according to the rules of conjunction-introduction and conjunction-elimination, or, at least, inferring according to these rules when “given a chance,” for instance, “when someone or something brings the conclusion to your direct attention, perhaps by querying you on the matter” [Reference Warren55, p. 46].Footnote 41 Our constraints (c)–(h) capture precisely such a view: they entail that an agent who believes a conjunction would assent to its conjuncts if queried about them, and that an agent who believes the conjuncts of a conjunction would eventually (though perhaps not immediately) assent to the conjunction if queried about it. Different versions of inferentialism could impose slightly different interpretations on what exactly it is to have a belief algorithm that outputs “Yes” given a proposition, but the general inferentialist picture is nicely captured by constraints along the lines of (c)–(h).
Finally, consider the third desideratum on middle-ground models, viz., that our model should entail that whatever an agent can computationally easily access is already part of what she believes or knows. Our algorithmic impossible-worlds model satisfies this desideratum because it entails the equivalences between (i) and (ii) and between (iii) and (iv): on our model, an agent believes (knows)
![]() $\phi $
just in case she can easily (and correctly) compute
$\phi $
just in case she can easily (and correctly) compute
![]() $\phi $
to be true. In light of our discussion of the collapse challenge above, it is worth noting that this third desideratum doesn’t require a closure principle of the form: agents believe (know) whatever is easily computationally accessible from what they believe (know) (as opposed to whatever is easily computationally accessible “simpliciter”). “Easily accessing
$\phi $
to be true. In light of our discussion of the collapse challenge above, it is worth noting that this third desideratum doesn’t require a closure principle of the form: agents believe (know) whatever is easily computationally accessible from what they believe (know) (as opposed to whatever is easily computationally accessible “simpliciter”). “Easily accessing
![]() $\psi $
from
$\psi $
from
![]() $\Phi $
” means that we ignore any potential computational costs of accessing
$\Phi $
” means that we ignore any potential computational costs of accessing
![]() $\Phi $
itself: we only consider the computational costs of accessing
$\Phi $
itself: we only consider the computational costs of accessing
![]() $\psi $
once one has already accessed
$\psi $
once one has already accessed
![]() $\Phi $
. But on the dispositional understanding of belief and knowledge, believing and knowing propositions
$\Phi $
. But on the dispositional understanding of belief and knowledge, believing and knowing propositions
![]() $\Phi $
are compatible with the existence of computational costs of accessing
$\Phi $
are compatible with the existence of computational costs of accessing
![]() $\Phi $
: as we saw in Section 1, one can believe (know)
$\Phi $
: as we saw in Section 1, one can believe (know)
![]() $\phi $
even if it takes a short computation to access and thus be able to act on
$\phi $
even if it takes a short computation to access and thus be able to act on
![]() $\phi $
. This idea is reflected in our algorithmic impossible-worlds model. But then some proposition,
$\phi $
. This idea is reflected in our algorithmic impossible-worlds model. But then some proposition,
![]() $\psi $
, can be easily accessible from what one knows,
$\psi $
, can be easily accessible from what one knows,
![]() $\Phi $
, while not being easily accessible simpliciter: the computational costs can add up, or the agent might not even consider
$\Phi $
, while not being easily accessible simpliciter: the computational costs can add up, or the agent might not even consider
![]() $\Phi $
in situations where she needs to act on
$\Phi $
in situations where she needs to act on
![]() $\psi $
(e.g., if she is asked about whether
$\psi $
(e.g., if she is asked about whether
![]() $\psi $
). So, one won’t necessarily believe (know) every proposition that is easily accessible from what one believes (knows): the dispositional understanding of belief and knowledge that motivate our third desideratum is incompatible with closure principles of the type that face collapse arguments.
$\psi $
). So, one won’t necessarily believe (know) every proposition that is easily accessible from what one believes (knows): the dispositional understanding of belief and knowledge that motivate our third desideratum is incompatible with closure principles of the type that face collapse arguments.
3 Comparison with other candidate middle-ground models
Following ideas from Duc [Reference Duc, Pinto-Ferreira and Mamede13, Reference Duc14] and Skipper Rasmussen [Reference Skipper Rasmussen38], Bjerring and Skipper [Reference Bjerring and Skipper8] have recently developed a candidate middle-ground model in our sense. Their model is a dynamic doxastic model, and it uses a notion of triviality that is connected to lengths of proofs. I will explain some disadvantages of these two features of their approach, and argue that the algorithmic impossible-worlds model can subsume its advantages.Footnote 42
In outline, dynamic doxastic models are models that capture transitions between doxastic states: among other things, their language has an operator, “
![]() $\langle a \rangle $
,” where a is some action, and
$\langle a \rangle $
,” where a is some action, and
![]() $\langle \mathscr {M}, w \rangle \vDash \langle a \rangle \phi $
just in case
$\langle \mathscr {M}, w \rangle \vDash \langle a \rangle \phi $
just in case
![]() $\langle \mathscr {N}, w' \rangle \vDash \phi $
for some
$\langle \mathscr {N}, w' \rangle \vDash \phi $
for some
![]() $\langle \mathscr {N}, w' \rangle $
obtained by transforming
$\langle \mathscr {N}, w' \rangle $
obtained by transforming
![]() $\langle \mathscr {M}, w \rangle $
according to the rules of transformation given by action a.Footnote
43
On Bjerring and Skipper’s [Reference Bjerring and Skipper8] model, the relevant action is inference: they take “
$\langle \mathscr {M}, w \rangle $
according to the rules of transformation given by action a.Footnote
43
On Bjerring and Skipper’s [Reference Bjerring and Skipper8] model, the relevant action is inference: they take “
![]() $\langle n \rangle \phi $
” to formalize “
$\langle n \rangle \phi $
” to formalize “
![]() $\phi $
is the case after some n steps of logical reasoning,” where a step of logical reasoning is one application of a rule of inference of some given background logical system R [Reference Bjerring and Skipper8, pp. 503, 509]. Accordingly, “
$\phi $
is the case after some n steps of logical reasoning,” where a step of logical reasoning is one application of a rule of inference of some given background logical system R [Reference Bjerring and Skipper8, pp. 503, 509]. Accordingly, “
![]() $\langle n \rangle B\phi $
” formalizes “the agent believes
$\langle n \rangle B\phi $
” formalizes “the agent believes
![]() $\phi $
after some n steps of logical reasoning” [Reference Bjerring and Skipper8, p. 509]. On their construal, a proposition,
$\phi $
after some n steps of logical reasoning” [Reference Bjerring and Skipper8, p. 509]. On their construal, a proposition,
![]() $\phi $
, is a trivial consequence of a set of propositions,
$\phi $
, is a trivial consequence of a set of propositions,
![]() $\Gamma $
, just in case
$\Gamma $
, just in case
![]() $\phi $
can be inferred from
$\phi $
can be inferred from
![]() $\Gamma $
within n steps of logical reasoning, where n is a small enough number [Reference Bjerring and Skipper8, p. 504]. Bjerring and Skipper allow that the background system R can be sensitive to the context of belief attribution; for instance, R can be a partial or a complete proof system for classical propositional logic [Reference Bjerring and Skipper8, p. 504]. Moreover, the value of n, and thus also what is “trivial” in their sense, “depend[] on the cognitive resources that agents have available for logical reasoning” [Reference Bjerring and Skipper8, p. 503] and hence are agent-relative. Their model results in
$\Gamma $
within n steps of logical reasoning, where n is a small enough number [Reference Bjerring and Skipper8, p. 504]. Bjerring and Skipper allow that the background system R can be sensitive to the context of belief attribution; for instance, R can be a partial or a complete proof system for classical propositional logic [Reference Bjerring and Skipper8, p. 504]. Moreover, the value of n, and thus also what is “trivial” in their sense, “depend[] on the cognitive resources that agents have available for logical reasoning” [Reference Bjerring and Skipper8, p. 503] and hence are agent-relative. Their model results in
![]() $\langle \mathscr {M}, w \rangle \vDash \langle n \rangle B\phi $
just in case
$\langle \mathscr {M}, w \rangle \vDash \langle n \rangle B\phi $
just in case
![]() $\phi $
follows within n steps of logical reasoning from the truths at each world doxastically accessible from
$\phi $
follows within n steps of logical reasoning from the truths at each world doxastically accessible from
![]() $w$
. This means that if
$w$
. This means that if
![]() $\langle \mathscr {M}, w \rangle \vDash B\phi $
and
$\langle \mathscr {M}, w \rangle \vDash B\phi $
and
![]() $\psi $
is a trivial consequence of
$\psi $
is a trivial consequence of
![]() $\phi $
, then
$\phi $
, then
![]() $\langle \mathscr {M}, w \rangle \vDash \langle n \rangle B\psi $
[Reference Bjerring and Skipper8, pp. 515f.]. That is, if
$\langle \mathscr {M}, w \rangle \vDash \langle n \rangle B\psi $
[Reference Bjerring and Skipper8, pp. 515f.]. That is, if
![]() $\psi $
is a trivial consequence of what the agent believes, then there is some n-step piece of reasoning such that if the agent follows it, then she will come to believe
$\psi $
is a trivial consequence of what the agent believes, then there is some n-step piece of reasoning such that if the agent follows it, then she will come to believe
![]() $\psi $
. This is the sense in which Bjerring and Skipper claim their model captures agents who are logically competent: on their understanding, “an agent counts as ‘logically competent’ just in case she has the ability to infer at least the trivial logical consequences of what she believes” [Reference Bjerring and Skipper8, p. 504]. Because Bjerring and Skipper don’t endorse any closure principle on beliefs, their constraint on logical competence doesn’t face a collapse argument.
$\psi $
. This is the sense in which Bjerring and Skipper claim their model captures agents who are logically competent: on their understanding, “an agent counts as ‘logically competent’ just in case she has the ability to infer at least the trivial logical consequences of what she believes” [Reference Bjerring and Skipper8, p. 504]. Because Bjerring and Skipper don’t endorse any closure principle on beliefs, their constraint on logical competence doesn’t face a collapse argument.
The first, and in my view the most important, disadvantage of Bjerring and Skipper’s model is that it doesn’t get our third desideratum on middle-ground models. On their model, agents don’t already believe the propositions that they can easily infer or compute to be true; rather, agents can come to believe such propositions after performing some short piece of reasoning. But this is too weak: if an agent can easily compute
![]() $\phi $
to be true and is thereby able to act on the information that
$\phi $
to be true and is thereby able to act on the information that
![]() $\phi $
, then we should say that she already believes
$\phi $
, then we should say that she already believes
![]() $\phi $
. Bjerring and Skipper themselves propose the following related test for the intuitive sense of “logical competence” that they are trying to capture:
$\phi $
. Bjerring and Skipper themselves propose the following related test for the intuitive sense of “logical competence” that they are trying to capture:
Suppose an agent believes p, and let q be any trivial consequence of p. We can then ask: upon being asked whether q is the case, is the agent immediately able to answer “yes”? If she is, she passes the test and counts as logically competent. For example, suppose you believe that it rains and that it rains only if the streets are wet. We can then ask: are you able to immediately answer “yes” when asked whether the streets are wet? Assuming that you are attentive, mentally well-functioning, and so on, it surely seems so. So you do not miss out on this trivial logical consequence of your beliefs, and hence count as logically competent in the relevant sense. [Reference Bjerring and Skipper8, p. 503]
On Bjerring and Skipper’s construal, an agent who is immediately able to answer “Yes” to the question of whether the streets are wet is “logically competent” in the sense that she can come to believe that the streets are wet at the end of some n-step chain of reasoning. But this isn’t the correct intuitive or theoretical verdict about such cases: an agent who is able to immediately answer “Yes” to the question of whether the streets are wet should be modeled as already believing that the streets are wet, even before they are asked about it. Intuitively, we would clearly judge such a person as already believing that the streets are wet; in general, we clearly believe many more things than what we are currently thinking about. Theoretically, this verdict follows from the standard dispositional understanding of belief from Section 1 that generated our third desideratum. On this view, beliefs (and knowledge) are supposed to explain one’s abilities to act on the basis of information, such as the ability to immediately answer “Yes” to certain questions: it is because I believe that the streets are wet that I am able to immediately answer “Yes” when asked about it. Our algorithmic impossible-worlds model easily satisfies this third desideratum, whereas dynamic models don’t.Footnote 44
Dynamic models could provide a useful way to capture in the object language what happens after an agent performs a calculation that is obviously too long for its conclusion to count as “easily accessible” in our sense. They could thus be adapted to our algorithmic model to capture how agents can transition to new belief states. However, as I mentioned at the end of Section 2.2, the algorithmic impossible-worlds model can already be easily and minimally supplemented along the lines of Duc [Reference Duc15] to capture in the object language what agents would eventually do (such as answer a question) after performing a computation that takes longer than
![]() $\epsilon $
units of time. Our algorithmic model can thus capture an important advantage of dynamic models.
$\epsilon $
units of time. Our algorithmic model can thus capture an important advantage of dynamic models.
A second disadvantage of Bjerring and Skipper’s model is its construal of triviality. Assume that an agent, S, believes all the propositions in
![]() $\Gamma $
. The fact that there is a short chain of applications of rules of inference of R to propositions in
$\Gamma $
. The fact that there is a short chain of applications of rules of inference of R to propositions in
![]() $\Gamma $
that ends with
$\Gamma $
that ends with
![]() $\phi $
(i.e., a short derivation of
$\phi $
(i.e., a short derivation of
![]() $\phi $
from
$\phi $
from
![]() $\Gamma $
in R) is neither sufficient nor necessary for
$\Gamma $
in R) is neither sufficient nor necessary for
![]() $\phi $
to be intuitively “trivial” for S. It could be that
$\phi $
to be intuitively “trivial” for S. It could be that
![]() $\phi $
has a very long derivation from
$\phi $
has a very long derivation from
![]() $\Gamma $
that is nonetheless very easy for S to output when asked about
$\Gamma $
that is nonetheless very easy for S to output when asked about
![]() $\phi $
, because she can quickly retrieve it from her memory. Conversely, it could be that
$\phi $
, because she can quickly retrieve it from her memory. Conversely, it could be that
![]() $\phi $
has a very short derivation from
$\phi $
has a very short derivation from
![]() $\Gamma $
that is very difficult for S to find, because her search algorithm is highly inefficient or the search breadth is too big. Length of derivations is generally an inadequate measure of triviality; thus, requiring logically competent agents to (be able to come to) believe all the “trivial” consequences of what they believe in this sense is also too demanding: very few (if any) people we would ordinarily think of as logically competent would be able to immediately determine the truth-value of any proposition that is shortly derivable from what they believe, given that the relevant branching factor is so big. On the algorithmic models, triviality is instead construed computationally: what is “trivial” for or “easily accessible” to an agent is what she can compute in less than
$\Gamma $
that is very difficult for S to find, because her search algorithm is highly inefficient or the search breadth is too big. Length of derivations is generally an inadequate measure of triviality; thus, requiring logically competent agents to (be able to come to) believe all the “trivial” consequences of what they believe in this sense is also too demanding: very few (if any) people we would ordinarily think of as logically competent would be able to immediately determine the truth-value of any proposition that is shortly derivable from what they believe, given that the relevant branching factor is so big. On the algorithmic models, triviality is instead construed computationally: what is “trivial” for or “easily accessible” to an agent is what she can compute in less than
![]() $\epsilon $
units of time, given the algorithms that are available to her. Moreover, these algorithms could (and likely would) work very differently from a stepwise application of rules of inference of some background logical system R.Footnote
45
$\epsilon $
units of time, given the algorithms that are available to her. Moreover, these algorithms could (and likely would) work very differently from a stepwise application of rules of inference of some background logical system R.Footnote
45
This second problem is also the reason why agents who are logically competent in Bjerring and Skipper’s formal construal neither clearly fit their own intuitive characterization of “being logically competent” as being able to infer the trivial consequences of what one believes, nor pass their own intuitive test for logical competence. Consider, once again, the agent who believes that it rains and that it rains only if the streets are wet. On Bjerring and Skipper’s construal, such an agent is logically competent just in case there is an n-step piece of reasoning such that if the agent follows it, then she believes that the streets are wet and thus answers “Yes” to the question of whether the streets are wet. But there is no guarantee that a logically competent agent in this sense will (immediately) follow this n-step piece of reasoning, or that she is even able to do so.Footnote 46 For instance, it might be that when she is asked whether the streets are wet, the agent never thinks to apply modus ponens to the relevant propositions, or that she first tries other steps of reasoning and only comes to perform modus ponens on the relevant propositions after a long and tedious search. Bjerring and Skipper’s model thus doesn’t seem to get the result that agents who are logically competent in their sense are able to infer or come to believe the trivial consequences of what they believe, or to immediately answer “Yes” when asked whether a trivial consequence of their beliefs is true. Their model thus also doesn’t seem to satisfy our second desideratum, i.e., to capture “logically competent” agents in an intuitive sense.Footnote 47
4 Conclusion
I presented an algorithmic impossible-worlds model as a middle ground between models that entail logical omniscience and those that leave open complete logical incompetence. On this model, an agent believes (knows) a proposition just in case she is disposed to act (capable of acting) upon it. The model thereby captures the most standard understanding of belief as (grounding) a behavioral disposition, and of knowledge as (grounding) a capacity to act. I then proposed some constraints one can add to the algorithmic impossible-worlds model to capture agents who are logically and conceptually competent. These constraints capture that an agent is logically or conceptually competent only if her algorithms respect the introduction and elimination rules of the standard logical connectives; this doesn’t mean that logically competent agents already know all the logical truths or all the logical consequences of what they know, only that they would eventually compute them, if given enough computational resources. Finally, I compared the algorithmic strategy for developing a middle-ground model to dynamic approaches and approaches based on step logic, and argued that the algorithmic impossible-worlds model has none of their disadvantages, and that it can subsume their advantages.
Acknowledgments
For very helpful feedback, I thank Paul Audi, Sharon Berry, Tom Donaldson, Juliet Floyd, Jens Kipper, Arc Kocurek, James Walsh, Jared Warren, Dan Waxman, an audience at the University of Konstanz, and two anonymous reviewers.