1 Introduction
The stability of an iceberg can be determined accurately only when the data on the berg are complete. If the data are incomplete or approximate, it is necessary to know to what degree the stability is dependent on various parameters, especially those parameters associated with the under-water shape of the berg. Reference AllaireAllaire (1972) failed to analyse this dependence, and, also, his technique applies only to certain shapes of icebergs. The present paper modifies, extends, and improves Allaire’s work, yielding approximate estimates of stability for almost any shape of iceberg. Moreover, the essential parameters affecting stability are presented, so that the reliability of estimates made in the field may be evaluated.
2 Basic Theory
The basic parameters for the stability of any floating homogeneous body may be reviewed briefly as follows:
In Figure 1, C is the centre of gravity of the portion of the iceberg above water, h̄ is the height above the water line, B is the centre of buoyancy, H̄ is the depth below the water line, G is the centre of gravity of the total body, and M is the metacentre.

Fig. 1. Vertical cross-section of a floating homogeneous body, shown in equilibrium and in a tilted position.
We are not assuming a uniform cross-section. Figure 1 represents a plane of the berg containing the points C, G, and B. That they lie in a vertical plane is obvious from equilibrium considerations. M is the metacentre associated with rolling about an axis perpendicular to this plane. As we are interested in the axis about which rolling is most likely to occur, the axis chosen is such that the average water-line width of the berg along that axis is a minimum. We call this the major axis of the berg, and the minor axis is perpendicular to it, passing through the plane containing C, G, and B. In practice, it may be difficult to locate the major axis. As a general rule, the major axis may he taken to be the axis along which the water-plane area of the berg has maximum horizontal dimension.
The distance BM is given by the formula ![]() where I is the area moment of inertia of the water-plane section of the body about the major axis and V
b is the below-water volume of the body. We take the ratio of the density of glacial ice to sea-water as 0.875, then, for an iceberg, from Archimedes’ Principle, V
b = 7V
a, where V
a is the volume of the above-water portion of the berg. Moreover, by taking moments about G, it is clear that for equilibrium, GC = 7BG or BG = 0.125 (BC). In our previous notation, BC = h̄ + H̄.
where I is the area moment of inertia of the water-plane section of the body about the major axis and V
b is the below-water volume of the body. We take the ratio of the density of glacial ice to sea-water as 0.875, then, for an iceberg, from Archimedes’ Principle, V
b = 7V
a, where V
a is the volume of the above-water portion of the berg. Moreover, by taking moments about G, it is clear that for equilibrium, GC = 7BG or BG = 0.125 (BC). In our previous notation, BC = h̄ + H̄.
Thus

The only unknown (unless total information on the berg is available) is the value of H̄ Everything else may be calculated from the above-water portion.
3 The Critical Stability Ratio
Let ω̄ be the minimum average width of the water-plane section of the berg taken parallel to the minor axis, and let L be the length of the major axis. The average draft of the berg H av is defined as the ratio of the below-water volume to the water-plane area, i.e.
To obtain an estimate for the distance H, we introduce a parameter y, the under-water fullness coefficient associated with the under-water shape of a berg. It is defined by the equation,
If the under-water portion of a berg has vertical sides, then y = 1. The coefficient y is an indicator of deviation from this shape. It is not intended that y should be quantitatively measured, but rather that it should be estimated by comparison with the known fullness coefficients for certain standard shapes. A further discussion concerning y is given in section 6.
For an iceberg with an estimated underwater fullness coefficient y and average height above the water-plane section h av, the depth of its centre of buoyancy below the water line is estimated from the equation
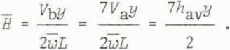
To obtain an estimate for h̄ we introduce a parameter x, the above-water fullness coefficient, associated with the above-water shape of a berg. It is defined by the equation
As with the coefficient y, it is intended that for a particular berg the coefficient x be estimated by comparison with known fullness coefficients for a selection of standard shapes. The above-water fullness coefficient is discussed in section 4.
For an iceberg with a estimated above-water fullness coefficient x and average height above the water-plane section h av, the height of the centre of gravity of the above-water section, measured relative to the water-plane, is estimated from the equation
Finally, to obtain an estimate for the radius of gyration, k
2 of the water-plane section about the major axis, we introduce a further parameter z, the water-plane fullness coefficient, associated with the shape of the water-plane section. For a berg that does not have significant variations in water-line width along its major axis, a reasonable estimate for K
2 is ![]() . If there are significant variations in width,
. If there are significant variations in width, ![]() is a significant underestimate for k
2.
is a significant underestimate for k
2.
The water-plane fullness coefficient z is the measure of this underestimate and is defined by the equation
As with the coefficients x and y, z is estimated for a particular berg by comparison with known fullness coefficients for certain standard shapes. In section 5 there is a list of such shapes.
For a given berg with an estimated water-plane fullness coefficient z and average water-line width ω̄, the radius of gyration of the water-plane section about the major axis is estimated from the equation
From Equation (1) for the metacentric height GM, using our estimates for k 2, h;̄, and H̄ in terms of h av, ω̄, x, y, and z, we have

The critical stability ratio for an iceberg with fullness coefficients x, y, and z is determined by Equation (2) when GM = 0. Namely,
We define the measured stability ratio to be the ratio of average width to average height. If the measured stability ratio for a given iceberg with fullness coefficients x, y, and z, is greater than the critical ratio then the iceberg is stable. If not, it is unstable.
As simple examples, we take two iceberg models, the rectangular cuboid and the ellipsoid. For the cuboid, x = y = z = 1, and the critical stability ratio is 6.5; for the ellipsoid, x = 1.1, y = 0.8, z = 0.8, and the critical stability ratio is 5.4. Assuming in the case of the ellipsoid that we did not know the under-water shape, we take y = 1, and then the critical stability ratio is 5.9. The value 5.9 is a reasonable crude estimate of the critical stability ratio. In section 6, we indicate how this estimate can sometimes be improved.
The stability ratio defined measures the stability relative to a principal axis of the surface section along which the berg has (approximately) minimum average water-line width. The stability relative to any other axis will clearly be not less than the stability relative to this chosen one. To determine the stability relative to any other principal axis of the surface section, the same procedures apply, i.e. the only modification required is to measure the average width in the surface section perpendicular to the new axis chosen.
4 The Above-Water Fullness Coefficient
It should be possible for an experienced observer to estimate the above-water fullness coefficient for a berg reasonably accurately, provided the berg is not very irregular. Intuitively, x measures the average rate of decrease in horizontal cross-sectional area relative to height. A selection of standard shapes with their fullness coefficients is shown in Figure 2.

Fig. 2. Above-water fullness coefficients for selected shapes.
In practice, a rather fuller selection, including more composite shapes, would be needed for making good estimates of x. Drydock shapes are not included in the selection given here, as these bergs are discussed in section 7.
It should be noted that of those bergs that would be classified as pinnacled, there is a wide variation in the fullness coefficients x, and therefore significant variations in the stability characteristics of such bergs.
5 The Water-Plane Fullness Coefficient
The coefficient z measures the mean deviation of the width of the water-plane section along the major axis from the calculated average width ω̄. If two icebergs have the same average width and height, and are of similar shape, the one with the more significant variations in water-line width is the more stable. A selection of standard shapes with their fullness coefficients is given in Figure 3.

Fig. 3. Water-plane fullness coefficients for selected shapes.
6 The Under-Water Fullness Coefficient
In Equation (3) for the critical stability ratio, let us assume that x and z are fixed; then to what extent does the critical stability ratio depend on the under-water shape and, therefore, on y? Any error in the estimation of y is approximately halved in the equation by taking the square root of (x + 7y). Variations in y are dependent on whether the horizontal cross-sectional area of the berg below the water line increases (bulging) or decreases (tapering) with depth.
Variations in y may be examined by taking two extreme under-water shapes, one bulging (y < 1) and the other tapering (y > 1). For the bulging shape, a truncated pyramid of upper face ω̄ by L and lower face 2ω̄ by 2L has a below-water fullness coefficient of y = 0.52. The value of y is independent of the above-water shape. For the tapering shape, we take as an example an inverted, truncated pyramid of upper face ω̄ by L and lower face 0.5ω̄ by 0.5L. It has a below-water fullness coefficient of y = 1.35. These cases represent extremes in the sense that their height-to-draft ratios are extremes.
In Figure 4, assuming the bergs are both tabular, the first has a draft-to-height ratio of 3 to 1 which is somewhat lower than those that have been generally encountered in the field in the northern hemisphere (Reference SmithSmith 1931, Reference RobeRobe 1976). Similarly, the second has a draft-to-height ratio of 12 to 1, which is somewhat higher than those that have been measured in the field. A reasonable range for y would seem to be between 0.6 and 1.2. As a first crude stability estimate in the field, a value of y = 0.9 could be taken. The critical stability ratio for a berg with x = z = 1 would then be 6.2 ± 1, i.e. an error of approximately 15%. In fact, various visual indicators could reduce the error.

Fig. 4. Vertical cross-sections of selected shapes showing draft D, average draft H av, centre of buoyancy B, and centre of buoyancy B’ of the rectangular cuboid of the same water-line width ω̄, length L, and volume as the selected shape. The position of B’ above or below B is determined by y, the under-water fullness coefficient.
In practice, it is often visually clear that the below-water part of the berg spreads out from the water line, i.e., that the berg is of the bulging type. Also, the angle of entry into the water plane of the above-water portion may indicate whether or not the berg bulges or tapers. A berg that is relatively old (judged in terms of distance from its source, degree of surface deterioration, crevassing, or depth of wave notch at the water line) and shows no signs of having recently rolled (no clearly defined wave notches at oblique angles to the water line) could generally be assumed to be of the bulging type. From the work of Reference Josberger and HusseinyJosberger (1978) and from observations in the field, it is apparent that maximum ablation occurs near the water-line level. In fact, it is unlikely that the y coefficient is much less than 0.9. Recent studies, e.g. Reference Russell-HeadRussell-Head (1980), seem to indicate that below the wave-notch level, the berg tends to taper down.
For a berg that shows signs of having recently rolled, there may be certain indications of under-water shape. For example, if there are two or more recent wave notches at angles less than 45° to the horizontal plane, a certain degree of radial symmetry in the under-water shape is apparent, indicating a fullness coefficient close to 0.8 or 0.9. A berg that has rolled through an angle of the order of 90° is likely to have originally been of tapering under-water shape. In its new orientation, it seems probable that its under-water fullness coefficient is less than one. Although these statements are largely speculative, there does seem to be a fruitful line of investigation apparent in the problem. The problem is related to that of whether the draft of a berg increases or decreases after it has rolled.
Lastly, if a rough estimate of the draft could be obtained (by radar, sonar, or even bathymetry of the region), there is a much better chance of obtaining the below-water shape type and then an approximate value for y. It seems plausible that for icebergs there is a correlation (possibly very crude) between the draft and the coefficient y. Such a correlation would greatly improve the accuracy of the critical stability ratio formula. From the information available, the generally low values for draft-to-height ratios (e.g. 4 or 5 to 1 for tabular, 2 to 1 for pinnacled) would tend to indicate that values of y < 1 are to be expected. Unfortunately, the information collected on draft-to-height ratios is often unhelpful or even misleading. For example, icebergs classified as pinnacled, of the same average height and draft, may have draft-to-height (maximum height) ratios ranging from 2:1 to 4:1.
7 Drydock Bergs
Though our stability criterion applies to drydock bergs, care must be taken in applying it, and in some cases it must be modified. For example, in the case where the major portion of the slot or the water-line surface of the berg on either side of the columns of the drydock is just above or at water-line level, the average height of the berg must be taken over the whole water-plane area, including those parts at zero height above the water line. For example, if a third of the berg is at water-line level, the average height will be two-thirds of the average height of the rest of the berg. If this is not done, the estimate used for V a will be inaccurate.
For a drydock berg with a relatively large proportion of its slot below the water line, some further modification is needed. When the slot is approximately perpendicular to the major axis of the berg, there is proportionate reduction in the moment of inertia of the water-plane section of the berg. Thus, if a third of the (implied) water-plane section is submerged slot, the moment of inertia is decreased by a third and the critical stability ratio is increased by a factor ![]() In the case when the submerged slot is approximately parallel to the major axis of the berg, there is a relatively small decrease in the moment of inertia of the water-plane section, provided that less than half of the berg’s water-plane is submerged slot. Since a drydock berg with more than half of its water-plane being submerged slot would be rare, it does not seem worthwhile introducing a complicated correction factor.
In the case when the submerged slot is approximately parallel to the major axis of the berg, there is a relatively small decrease in the moment of inertia of the water-plane section, provided that less than half of the berg’s water-plane is submerged slot. Since a drydock berg with more than half of its water-plane being submerged slot would be rare, it does not seem worthwhile introducing a complicated correction factor.
The above-water fullness coefficient x is high for drydock bergs. A range of values for a variety of drydock shapes is given in Figure 5. The high values of the fullness coefficient x for drydock bergs seems to indicate that drydocks are potentially very unstable. However, the average height, h av, for a drydock is generally low for those with a high x value, which implies a high measured stability ratio.

Fig. 5. Above-water fullness coefficients for selected drydock shapes.
8 Towards Greater Accuracy
The rationale behind the technique outlined above has been its applicability in the field, where an approximate estimate of stability can thus be determined with a few measurements and some visual observations.
Accuracy is greatly improved if aerial photographs of the berg can be obtained. For example, from a photograph taken overhead, the minimum average width of a berg and its average height may be calculated.
With under-water sonar methods, a fairly good approximation to the value of the under-water fullness coefficient y could be obtained rapidly from four stations around the berg.
9 Further Stability Considerations
One stability parameter that we have taken as constant is the ratio of the density of glacial ice to that of sea-water. Stability increases as the ratio decreases. It has been suggested that up to 10% of the iceberg volume is air. Such a value would have a substantial effect on the stability characteristics of an iceberg. However, it is generally accepted that for Arctic bergs variations in the density ratio of 2% are more probable. Antarctic tabular icebergs are generally non-homogeneous and have a lower mean density that depends on the thickness of the berg. In fact, density increases with depth of these icebergs. Thus, Antarctic icebergs are very much more stable than Arctic icebergs of comparable shape and dimensions. If the ratio of the mean density of an iceberg to the density of sea-water is λ, and if the berg is homogeneous, its critical stability ratio is given by
A rectangular cuboid iceberg, with λ = 0.8, has a critical ratio of 4.9 (compared to the value of 6.5 for a comparable Arctic iceberg). In fact, taking account of the density distribution in a typical Antarctic iceberg would lead to an even lower critical ratio.
Acknowledgements
I should like to thank Dr James Rossiter of C-CORE for invaluable advice and introducing me to the fascinating study of icebergs.







