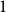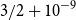1. Introduction
Let
![]() $\lambda = (\lambda _n)_{n=1}^\infty$
be an increasing sequence of real numbers. Often, for number-theoretic sequences
$\lambda = (\lambda _n)_{n=1}^\infty$
be an increasing sequence of real numbers. Often, for number-theoretic sequences
![]() $\lambda$
, the average gap
$\lambda$
, the average gap
![]() $\lambda _{n+1}-\lambda _n$
is well-understood, while little is known about the distribution function of the gaps. Sometimes, however, statistical information about the collection of gaps
$\lambda _{n+1}-\lambda _n$
is well-understood, while little is known about the distribution function of the gaps. Sometimes, however, statistical information about the collection of gaps
![]() $\lambda _{n+k}-\lambda _n$
is of importance.
$\lambda _{n+k}-\lambda _n$
is of importance.
For example, letting
![]() $(\gamma _n)_{n=1}^\infty$
denote the imaginary parts of the zeroes of the Riemann zeta function in the critical strip in increasing order, we know
$(\gamma _n)_{n=1}^\infty$
denote the imaginary parts of the zeroes of the Riemann zeta function in the critical strip in increasing order, we know
as
![]() $T \to \infty$
, and Montgomery’s pair-correlation conjecture predicts that
$T \to \infty$
, and Montgomery’s pair-correlation conjecture predicts that
as
![]() $T \to \infty$
, for any fixed
$T \to \infty$
, for any fixed
![]() $0 \lt a \lt b$
, where
$0 \lt a \lt b$
, where
![]() $\textrm{sinc}(x)\,:\!=\, \frac{\sin x}{x}$
.
$\textrm{sinc}(x)\,:\!=\, \frac{\sin x}{x}$
.
Henceforth, let
![]() $\lambda = (\lambda _n)_{n=1}^\infty$
denote an increasing sequence with average gap
$\lambda = (\lambda _n)_{n=1}^\infty$
denote an increasing sequence with average gap
![]() $1$
:
$1$
:
With this normalization, we may define the pair correlation function
![]() $R_\lambda$
by
$R_\lambda$
by
where
![]() $I \subseteq{\mathbb{R}}$
is a bounded interval and
$I \subseteq{\mathbb{R}}$
is a bounded interval and
![]() $N$
a positive integer.
$N$
a positive integer.
For example, up to some normalization technicalities, Montgomery’s pair-correlation conjecture asserts that
![]() $R_{(\gamma _n)_n}$
converges (in distribution) to a distribution with cumulative distribution function
$R_{(\gamma _n)_n}$
converges (in distribution) to a distribution with cumulative distribution function
![]() $1-\textrm{sinc}^2(\pi t)$
.
$1-\textrm{sinc}^2(\pi t)$
.
Motivated by the fact that the pair correlation function of a random sequence generated by a Poisson point process converges in distribution to the uniform distribution, an increasing sequence of real numbers
![]() $(\lambda _n)_{n=1}^\infty$
with average gap
$(\lambda _n)_{n=1}^\infty$
with average gap
![]() $1$
is said to have Poisson pair correlations (PPC) if
$1$
is said to have Poisson pair correlations (PPC) if
![]() $R_{(\lambda _n)_n}$
converges to the uniform distribution:
$R_{(\lambda _n)_n}$
converges to the uniform distribution:
for all intervals
![]() $I \subseteq{\mathbb{R}}$
, where
$I \subseteq{\mathbb{R}}$
, where
![]() $|\cdot |$
denotes the Lebesgue measure.
$|\cdot |$
denotes the Lebesgue measure.
Despite Montgomery’s pair-correlation conjecture concerning increasing sequences of real numbers, most research on properties of general sequences with Poisson pair correlation concerns sequences in the torus (see, for example, [Reference Aistleitner, Blomer and Radziwiłł1–Reference Steinerberger12]), with little investigated about sequences of real numbers.
Some specific number-theoretic sequences of real numbers have been shown to have PPC. Sarnak [Reference Rudnick and Zaharescu10] showed that almost every positive definite binary quadratic form (in a suitable sense) gives rise to a sequence with PPC, by ordering the values it takes on (pairs of) positive integers and appropriately normalizing. Concretely, a consequence of the work of Eskin, Margulis, and Mozes [Reference Eskin, Margulis and Mozes4] is that the ordered sequence of values of
![]() $x^2+\sqrt{2}y^2$
for
$x^2+\sqrt{2}y^2$
for
![]() $x,y \in \mathbb{N}$
has PPC.
$x,y \in \mathbb{N}$
has PPC.
Aistleitner, Blomer, and Radziwiłł [Reference Aistleitner, Blomer and Radziwiłł1] studied the related triple correlation function of certain number-theoretic sequences, while also initiating a study of general sequences of real numbers with Poisson pair (and triple) correlations. They asked the following.
Question.
Let
![]() $\lambda _1 \lt \lambda _2 \lt \dots$
be an increasing sequence of real numbers with average gap
$\lambda _1 \lt \lambda _2 \lt \dots$
be an increasing sequence of real numbers with average gap
![]() $1$
and with Poisson pair correlations. How small can
$1$
and with Poisson pair correlations. How small can
![]() $\limsup _{n \to \infty } \lambda _{n+1}-\lambda _n$
be?
$\limsup _{n \to \infty } \lambda _{n+1}-\lambda _n$
be?
Among increasing sequences of real numbers with average gap
![]() $1$
and PPC, Aistleitner, Blomer, and Radziwiłł exhibited one with maximum gap
$1$
and PPC, Aistleitner, Blomer, and Radziwiłł exhibited one with maximum gap
![]() $2$
, and proved that any such sequence must have a gap of size at least
$2$
, and proved that any such sequence must have a gap of size at least
![]() $3/2-\epsilon$
, for any
$3/2-\epsilon$
, for any
![]() $\epsilon \gt 0$
. They asked in their paper [Reference Aistleitner, Blomer and Radziwiłł1] as well as at Oberwolfach 2019 (communicated to the authors by Ben Green) to improve either bound. Our main theorem is an improved lower bound.
$\epsilon \gt 0$
. They asked in their paper [Reference Aistleitner, Blomer and Radziwiłł1] as well as at Oberwolfach 2019 (communicated to the authors by Ben Green) to improve either bound. Our main theorem is an improved lower bound.
Theorem 1.1.
Let
![]() $\lambda _1 \lt \lambda _2 \lt \dots$
be an increasing sequence of real numbers with average gap
$\lambda _1 \lt \lambda _2 \lt \dots$
be an increasing sequence of real numbers with average gap
![]() $1$
and Poisson pair correlations. Then
$1$
and Poisson pair correlations. Then
![]() $\limsup _{n \to \infty } \lambda _{n+1}-\lambda _n \gt \frac{3}{2}+10^{-9}$
.
$\limsup _{n \to \infty } \lambda _{n+1}-\lambda _n \gt \frac{3}{2}+10^{-9}$
.
We leave open the question of how small the largest gap can be; in light of Theorem 1.1, it lies between
![]() $\frac{3}{2}+10^{-9}$
and
$\frac{3}{2}+10^{-9}$
and
![]() $2$
, inclusive.
$2$
, inclusive.
2. Motivation and proof sketch of Theorem 1.1
In this section we motivate the proof of Theorem 1.1, overlooking some technical complications and emphasizing the main ideas.
Let us begin by sketching the proof given in [Reference Aistleitner, Blomer and Radziwiłł1] that any strictly increasing sequence of real numbers with mean gap
![]() $1$
and PPC has a gap at least
$1$
and PPC has a gap at least
![]() $\frac{3}{2}-\epsilon$
, for any
$\frac{3}{2}-\epsilon$
, for any
![]() $\epsilon \gt 0$
. An interested reader may wish to consult the proof sketch of this result in [Reference Aistleitner, Blomer and Radziwiłł1, Section 1.5], or the proof itself in [Reference Aistleitner, Blomer and Radziwiłł1, Section 7].
$\epsilon \gt 0$
. An interested reader may wish to consult the proof sketch of this result in [Reference Aistleitner, Blomer and Radziwiłł1, Section 1.5], or the proof itself in [Reference Aistleitner, Blomer and Radziwiłł1, Section 7].
One begins by observing that for any sequence
![]() $(\lambda _n)_n$
that has PPC, the distribution function of the gaps
$(\lambda _n)_n$
that has PPC, the distribution function of the gaps
![]() $\lambda _{n+1}-\lambda _n$
, which we will denote by
$\lambda _{n+1}-\lambda _n$
, which we will denote by
![]() $F$
, can grow at most linearly (indeed, if it grows more than linearly in any small interval, say, this will contradict the PPC condition for this interval). Now, if
$F$
, can grow at most linearly (indeed, if it grows more than linearly in any small interval, say, this will contradict the PPC condition for this interval). Now, if
![]() $\lambda _{n+1}-\lambda _n \le 3/2-\epsilon$
for each
$\lambda _{n+1}-\lambda _n \le 3/2-\epsilon$
for each
![]() $n$
(that is,
$n$
(that is,
![]() $F(3/2-\epsilon ) = 1$
), then the linear growth condition implies that the distribution function, when plotted, lies on or above the straight line between
$F(3/2-\epsilon ) = 1$
), then the linear growth condition implies that the distribution function, when plotted, lies on or above the straight line between
![]() $(1/2-\epsilon, 0)$
and
$(1/2-\epsilon, 0)$
and
![]() $(3/2-\epsilon, 1)$
. This implies that that the mean gap size is strictly smaller than 1, a contradiction.
$(3/2-\epsilon, 1)$
. This implies that that the mean gap size is strictly smaller than 1, a contradiction.
Next, running the same argument now for the situation when the maximum gap is equal to
![]() $3/2$
yields that in this situation we must have
$3/2$
yields that in this situation we must have
Our goal is to show that this is impossible (and to then obtain a small quantitative improvement over
![]() $3/2$
). Suppose that (2) and (3) hold. Then (3) yields that
$3/2$
). Suppose that (2) and (3) hold. Then (3) yields that
![]() $\text{PPC}\left(\frac{1}{2},\frac{3}{2}\right)$
$\text{PPC}\left(\frac{1}{2},\frac{3}{2}\right)$
![]() $\big($
i.e., (1) for
$\big($
i.e., (1) for
![]() $I = \big[\frac{1}{2},\frac{3}{2}\big]\big)$
is already satisfied by the single gaps
$I = \big[\frac{1}{2},\frac{3}{2}\big]\big)$
is already satisfied by the single gaps
![]() $\lambda _{n+1}-\lambda _n$
, so there cannot be a nontrivial contribution coming from larger gaps
$\lambda _{n+1}-\lambda _n$
, so there cannot be a nontrivial contribution coming from larger gaps
![]() $\lambda _{n+m}-\lambda _n$
,
$\lambda _{n+m}-\lambda _n$
,
![]() $m \ge 2$
. On the other hand, (2) implies that
$m \ge 2$
. On the other hand, (2) implies that
![]() $\text{PPC}\left(0,\frac{1}{2}\right)$
must come entirely from a
$\text{PPC}\left(0,\frac{1}{2}\right)$
must come entirely from a
![]() $0$
density part of the sequence, and more specifically only from blocks
$0$
density part of the sequence, and more specifically only from blocks
![]() $[n_1,n_2]$
contained in that
$[n_1,n_2]$
contained in that
![]() $0$
density part. Furthermore, for the union of such blocks to nontrivially contribute to the
$0$
density part. Furthermore, for the union of such blocks to nontrivially contribute to the
![]() $\text{PPC}$
count, the length of the blocks must grow with
$\text{PPC}$
count, the length of the blocks must grow with
![]() $N$
.
$N$
.
The natural question then is whether such blocks can satisfy the
![]() $\text{PPC}$
condition on all subintervals of
$\text{PPC}$
condition on all subintervals of
![]() $\left[0,\frac{1}{2}\right]$
. We show that the answer is no. The key is to establish a “bias near
$\left[0,\frac{1}{2}\right]$
. We show that the answer is no. The key is to establish a “bias near
![]() $0$
” of the
$0$
” of the
![]() $\text{PPC}$
count on long blocks whose total gap is at most
$\text{PPC}$
count on long blocks whose total gap is at most
![]() $1/2$
. A bit more precisely, if
$1/2$
. A bit more precisely, if
![]() $\lambda _1 \lt \dots \lt \lambda _k$
have
$\lambda _1 \lt \dots \lt \lambda _k$
have
![]() $\lambda _k -\lambda _1 \le 1/2$
, then
$\lambda _k -\lambda _1 \le 1/2$
, then
![]() $\frac{1}{|J|}\sum _{1 \le i \lt j \le k} 1_{\lambda _j-\lambda _i \in J}$
is larger for intervals
$\frac{1}{|J|}\sum _{1 \le i \lt j \le k} 1_{\lambda _j-\lambda _i \in J}$
is larger for intervals
![]() $J \subseteq [0,1/2]$
concentrated near
$J \subseteq [0,1/2]$
concentrated near
![]() $0$
, with the bias becoming more pronounced as
$0$
, with the bias becoming more pronounced as
![]() $k \to \infty$
. This would contradict the PPC condition on subintervals of
$k \to \infty$
. This would contradict the PPC condition on subintervals of
![]() $\left[0,\frac{1}{2}\right]$
. A difficulty we encounter in the proof, however, is that the blocks forming the relevant
$\left[0,\frac{1}{2}\right]$
. A difficulty we encounter in the proof, however, is that the blocks forming the relevant
![]() $0$
density part of the sequence need not have total gap at most
$0$
density part of the sequence need not have total gap at most
![]() $1/2$
. We overcome this by suitably partitioning the
$1/2$
. We overcome this by suitably partitioning the
![]() $0$
density part of the sequence. This is implemented in Section 4 where we use a suitable greedy algorithm to decompose.
$0$
density part of the sequence. This is implemented in Section 4 where we use a suitable greedy algorithm to decompose.
3. Proof of Theorem 1.1
Let
![]() $\epsilon = 10^{-9}$
. For this section, we fix an increasing sequence of real numbers
$\epsilon = 10^{-9}$
. For this section, we fix an increasing sequence of real numbers
![]() $\lambda _1 \lt \lambda _2 \lt \dots$
with average gap
$\lambda _1 \lt \lambda _2 \lt \dots$
with average gap
![]() $1$
and
$1$
and
![]() $\text{PPC}$
, that has
$\text{PPC}$
, that has
![]() $\lambda _{n+1}-\lambda _n \le 3/2+\epsilon$
for sufficiently large
$\lambda _{n+1}-\lambda _n \le 3/2+\epsilon$
for sufficiently large
![]() $n$
. By truncating the sequence, we may assume that
$n$
. By truncating the sequence, we may assume that
satisfies
![]() $g_n \le 3/2+\epsilon$
for each
$g_n \le 3/2+\epsilon$
for each
![]() $n \ge 1$
. As in Section 2, we write
$n \ge 1$
. As in Section 2, we write
![]() $\text{PPC}(a,b)$
to denote equation (1) for
$\text{PPC}(a,b)$
to denote equation (1) for
![]() $I = [a,b]$
. We note that a sequence satisfying the PPC condition for all such
$I = [a,b]$
. We note that a sequence satisfying the PPC condition for all such
![]() $I$
necessarily satisfies the same condition for all open or indeed half-open intervals. We may therefore also use
$I$
necessarily satisfies the same condition for all open or indeed half-open intervals. We may therefore also use
![]() $\text{PPC}(a,b)$
to refer to equation (1) for the half-open interval
$\text{PPC}(a,b)$
to refer to equation (1) for the half-open interval
![]() $[a,b)$
, for example.
$[a,b)$
, for example.
Recall that the lower bound of
![]() $\frac{3}{2}$
was established in [Reference Aistleitner, Blomer and Radziwiłł1], whose proof we sketched in Section 2. We start the proof of Theorem 1.1 by making these arguments quantitative.
$\frac{3}{2}$
was established in [Reference Aistleitner, Blomer and Radziwiłł1], whose proof we sketched in Section 2. We start the proof of Theorem 1.1 by making these arguments quantitative.
We begin with a quantitative extension of equation (2), which said that if the maximum gap is
![]() $3/2$
then, in the limit
$3/2$
then, in the limit
![]() $N\to \infty$
, the proportion of gaps of size at most
$N\to \infty$
, the proportion of gaps of size at most
![]() $1/2$
is
$1/2$
is
![]() $0$
. We obtain the following when the maximum gap is of size at most
$0$
. We obtain the following when the maximum gap is of size at most
![]() $3/2 + \epsilon$
.
$3/2 + \epsilon$
.
Proposition 3.1.
For all
![]() $N$
sufficiently large, we have
$N$
sufficiently large, we have
Proof. We begin by relating the mean gap size to the gap distribution function under the given restriction on the maximum gap size. To this end, note that
 \begin{align} \frac{1}{N}\sum _{n \le N} g_n &= \int _0^{\frac{3}{2}+\epsilon } \frac{1}{N}\#\left\{n \le N \,:\, g_n \gt x\right\}dx \nonumber\\ &= \int _0^{\frac{1}{2}+\sqrt{\epsilon }} \frac{1}{N}\#\left\{n \le N \,:\, g_n \gt x\right\}dx + \int _{\frac{1}{2}+\sqrt{\epsilon }}^{\frac{3}{2}+\epsilon } \frac{1}{N}\#\left\{n \le N \,:\, g_n \gt x\right\}dx \nonumber\\ &= \frac{1}{2}+\sqrt{\epsilon }-\int _0^{\frac{1}{2}+\sqrt{\epsilon }} \frac{1}{N}\#\left\{n \le N \,:\, g_n \le x\right\}dx \nonumber\\ &\quad + \int _{\frac{1}{2}+\sqrt{\epsilon }}^{\frac{3}{2}+\epsilon } \frac{1}{N}\#\left\{n \le N \,:\, g_n \in \left(x,\frac{3}{2}+\epsilon \right)\right\}dx. \end{align}
\begin{align} \frac{1}{N}\sum _{n \le N} g_n &= \int _0^{\frac{3}{2}+\epsilon } \frac{1}{N}\#\left\{n \le N \,:\, g_n \gt x\right\}dx \nonumber\\ &= \int _0^{\frac{1}{2}+\sqrt{\epsilon }} \frac{1}{N}\#\left\{n \le N \,:\, g_n \gt x\right\}dx + \int _{\frac{1}{2}+\sqrt{\epsilon }}^{\frac{3}{2}+\epsilon } \frac{1}{N}\#\left\{n \le N \,:\, g_n \gt x\right\}dx \nonumber\\ &= \frac{1}{2}+\sqrt{\epsilon }-\int _0^{\frac{1}{2}+\sqrt{\epsilon }} \frac{1}{N}\#\left\{n \le N \,:\, g_n \le x\right\}dx \nonumber\\ &\quad + \int _{\frac{1}{2}+\sqrt{\epsilon }}^{\frac{3}{2}+\epsilon } \frac{1}{N}\#\left\{n \le N \,:\, g_n \in \left(x,\frac{3}{2}+\epsilon \right)\right\}dx. \end{align}
Now, we claim that
 \begin{equation} \limsup _{N \to \infty } \int _{\frac{1}{2}+\sqrt{\epsilon }}^{\frac{3}{2}+\epsilon } \frac{1}{N}\#\left\{n \le N \,:\, g_n \in \left(x,\frac{3}{2}+\epsilon \right)\right\}dx \le \int _{\frac{1}{2}+\sqrt{\epsilon }}^{\frac{3}{2}+\epsilon } \left(\frac{3}{2}+\epsilon -x\right)dx. \end{equation}
\begin{equation} \limsup _{N \to \infty } \int _{\frac{1}{2}+\sqrt{\epsilon }}^{\frac{3}{2}+\epsilon } \frac{1}{N}\#\left\{n \le N \,:\, g_n \in \left(x,\frac{3}{2}+\epsilon \right)\right\}dx \le \int _{\frac{1}{2}+\sqrt{\epsilon }}^{\frac{3}{2}+\epsilon } \left(\frac{3}{2}+\epsilon -x\right)dx. \end{equation}
Indeed, the pointwise upper bound
 \begin{equation*}\frac {1}{N}\#\left\{n \le N \,:\, g_n \in \left(x,\frac {3}{2}+\epsilon \right)\right\} \le \min \left(1,\frac {1}{N}\sum _{n \le N} \sum _{m \le N-n+1} 1_{g_n+\dots +g_{n+m-1} \in (x,\frac {3}{2}+\epsilon )}\right)\end{equation*}
\begin{equation*}\frac {1}{N}\#\left\{n \le N \,:\, g_n \in \left(x,\frac {3}{2}+\epsilon \right)\right\} \le \min \left(1,\frac {1}{N}\sum _{n \le N} \sum _{m \le N-n+1} 1_{g_n+\dots +g_{n+m-1} \in (x,\frac {3}{2}+\epsilon )}\right)\end{equation*}
together with the dominated convergence theorem and
![]() $\text{PPC}\left(x, \frac{3}{2}+\epsilon \right)$
for
$\text{PPC}\left(x, \frac{3}{2}+\epsilon \right)$
for
![]() $x \in \left(\frac{1}{2}+\sqrt{\epsilon },\frac{3}{2}+\epsilon \right)$
, namely,
$x \in \left(\frac{1}{2}+\sqrt{\epsilon },\frac{3}{2}+\epsilon \right)$
, namely,
gives (5). That the average gap of
![]() $(\lambda _n)_n$
is
$(\lambda _n)_n$
is
![]() $1$
corresponds to
$1$
corresponds to
Rearranging (4), taking
![]() $N \to \infty$
, and using (5) and (6) gives
$N \to \infty$
, and using (5) and (6) gives
 \begin{align*} \limsup _{N \to \infty } \int _0^{\frac{1}{2}+\sqrt{\epsilon }} \frac{1}{N}\#\{n \le N \,:\, g_n \le x\}dx &\le -1+\frac{1}{2}+\sqrt{\epsilon }+\int _{\frac{1}{2}+\sqrt{\epsilon }}^{\frac{3}{2}+\epsilon } \left(\frac{3}{2}+\epsilon -x\right)dx \\ &= \frac{3}{2}\epsilon +\frac{1}{2}\epsilon ^2-\epsilon ^{3/2}. \end{align*}
\begin{align*} \limsup _{N \to \infty } \int _0^{\frac{1}{2}+\sqrt{\epsilon }} \frac{1}{N}\#\{n \le N \,:\, g_n \le x\}dx &\le -1+\frac{1}{2}+\sqrt{\epsilon }+\int _{\frac{1}{2}+\sqrt{\epsilon }}^{\frac{3}{2}+\epsilon } \left(\frac{3}{2}+\epsilon -x\right)dx \\ &= \frac{3}{2}\epsilon +\frac{1}{2}\epsilon ^2-\epsilon ^{3/2}. \end{align*}
Thus, using the trivial
for
![]() $x \in \left[\frac{1}{2},\frac{1}{2}+\sqrt{\epsilon }\right]$
and the even more trivial lower bound of
$x \in \left[\frac{1}{2},\frac{1}{2}+\sqrt{\epsilon }\right]$
and the even more trivial lower bound of
![]() $0$
when
$0$
when
![]() $x \in \left[0,\frac{1}{2}\right]$
, yields
$x \in \left[0,\frac{1}{2}\right]$
, yields
Dividing by
![]() $\sqrt{\epsilon }$
, Proposition3.1 follows.
$\sqrt{\epsilon }$
, Proposition3.1 follows.
We now use the quantitative version of (3) to argue that the PPC(
![]() $\frac{1}{2},\frac{3}{2}+\epsilon$
) contribution comes nearly entirely from single gaps
$\frac{1}{2},\frac{3}{2}+\epsilon$
) contribution comes nearly entirely from single gaps
![]() $g_n$
.
$g_n$
.
Proposition 3.2.
For all
![]() $N$
sufficiently large, we have
$N$
sufficiently large, we have
Proof. As in the proof of Proposition3.1,
 \begin{align*}\frac {1}{N}\sum _{n \le N} g_n & = \frac {1}{2}-\sqrt {\epsilon }-\int _0^{\frac {1}{2}-\sqrt {\epsilon }} \frac {1}{N}\#\left\{n \le N \,:\, g_n \le x\right\}dx\nonumber\\& \quad + \int _{\frac {1}{2}-\sqrt {\epsilon }}^{\frac {3}{2}+\epsilon } \frac {1}{N}\#\left\{n \le N \,:\, g_n \in \left(x,\frac {3}{2}+\epsilon \right)\right\}dx,\end{align*}
\begin{align*}\frac {1}{N}\sum _{n \le N} g_n & = \frac {1}{2}-\sqrt {\epsilon }-\int _0^{\frac {1}{2}-\sqrt {\epsilon }} \frac {1}{N}\#\left\{n \le N \,:\, g_n \le x\right\}dx\nonumber\\& \quad + \int _{\frac {1}{2}-\sqrt {\epsilon }}^{\frac {3}{2}+\epsilon } \frac {1}{N}\#\left\{n \le N \,:\, g_n \in \left(x,\frac {3}{2}+\epsilon \right)\right\}dx,\end{align*}
which, by merely dropping a (negative) term, gives
 \begin{equation} \frac{1}{N}\sum _{n \le N} g_n \le \frac{1}{2}-\sqrt{\epsilon }+\int _{\frac{1}{2}-\sqrt{\epsilon }}^{\frac{3}{2}+\epsilon } \frac{1}{N}\#\left\{n \le N \,:\, g_n \in \left(x,\frac{3}{2}+\epsilon \right)\right\}dx. \end{equation}
\begin{equation} \frac{1}{N}\sum _{n \le N} g_n \le \frac{1}{2}-\sqrt{\epsilon }+\int _{\frac{1}{2}-\sqrt{\epsilon }}^{\frac{3}{2}+\epsilon } \frac{1}{N}\#\left\{n \le N \,:\, g_n \in \left(x,\frac{3}{2}+\epsilon \right)\right\}dx. \end{equation}
We write
 \begin{align*}\frac {1}{N}\#\left\{n \le N \,:\, g_n \in \left(x,\frac {3}{2}+\epsilon \right)\right\} & = \frac {1}{N}\sum _{n \le N}\sum _{m \le N-n+1} 1_{g_n+\dots +g_{n+m-1} \in \left(x,\frac {3}{2}+\epsilon \right)}\nonumber\\[4pt]& \quad -\frac {1}{N}\sum _{n \le N}\sum _{2 \le m \le N-n+1} 1_{g_n+\dots +g_{n+m-1} \in \left(x,\frac {3}{2}+\epsilon \right)}\end{align*}
\begin{align*}\frac {1}{N}\#\left\{n \le N \,:\, g_n \in \left(x,\frac {3}{2}+\epsilon \right)\right\} & = \frac {1}{N}\sum _{n \le N}\sum _{m \le N-n+1} 1_{g_n+\dots +g_{n+m-1} \in \left(x,\frac {3}{2}+\epsilon \right)}\nonumber\\[4pt]& \quad -\frac {1}{N}\sum _{n \le N}\sum _{2 \le m \le N-n+1} 1_{g_n+\dots +g_{n+m-1} \in \left(x,\frac {3}{2}+\epsilon \right)}\end{align*}
and use the same dominated convergence theorem argument as in the proof of Proposition3.1 to obtain, from (7), that
 \begin{align*} &\limsup _{N \to \infty } \int _{\frac{1}{2}-\sqrt{\epsilon }}^{\frac{3}{2}+\epsilon } \frac{1}{N}\sum _{n \leq N}\sum _{2 \le m \le N-n+1} 1_{g_n+\dots +g_{n+m-1} \in \left(x,\frac{3}{2}+\epsilon \right)}dx \\[3pt] &\qquad \qquad \le -1+\frac{1}{2}-\sqrt{\epsilon }+\int _{\frac{1}{2}-\sqrt{\epsilon }}^{\frac{3}{2}+\epsilon } \left(\frac{3}{2}+\epsilon -x\right)dx \\[3pt] &\qquad \qquad = \frac{3}{2}\epsilon +\frac{1}{2}\epsilon ^2+\epsilon ^{3/2}, \end{align*}
\begin{align*} &\limsup _{N \to \infty } \int _{\frac{1}{2}-\sqrt{\epsilon }}^{\frac{3}{2}+\epsilon } \frac{1}{N}\sum _{n \leq N}\sum _{2 \le m \le N-n+1} 1_{g_n+\dots +g_{n+m-1} \in \left(x,\frac{3}{2}+\epsilon \right)}dx \\[3pt] &\qquad \qquad \le -1+\frac{1}{2}-\sqrt{\epsilon }+\int _{\frac{1}{2}-\sqrt{\epsilon }}^{\frac{3}{2}+\epsilon } \left(\frac{3}{2}+\epsilon -x\right)dx \\[3pt] &\qquad \qquad = \frac{3}{2}\epsilon +\frac{1}{2}\epsilon ^2+\epsilon ^{3/2}, \end{align*}
and thus
Dividing by
![]() $\sqrt{\epsilon }$
, the proposition follows.
$\sqrt{\epsilon }$
, the proposition follows.
We now exploit the aforementioned “bias” towards
![]() $0$
exhibited by large intervals with sum of gaps at most
$0$
exhibited by large intervals with sum of gaps at most
![]() $1/2$
. We will need a technical lemma, proven in the appendix but assumed for now.
$1/2$
. We will need a technical lemma, proven in the appendix but assumed for now.
Lemma 3.3.
For positive integers
![]() $a,b,c,L$
satisfying
$a,b,c,L$
satisfying
![]() $1 \le a \le b \le c \le L$
, we have
$1 \le a \le b \le c \le L$
, we have
 \begin{align*} & (a-1)a+(b-a)(b-a+1)+(c-b)(c-b+1)+(L-c)(L-c+1)\\& +(a-1)(b-a)+(b-a)(c-b)+(c-b)(L-c) \ge \frac {5}{12}L^2+\frac {1}{6}L-\frac {7}{12}.\end{align*}
\begin{align*} & (a-1)a+(b-a)(b-a+1)+(c-b)(c-b+1)+(L-c)(L-c+1)\\& +(a-1)(b-a)+(b-a)(c-b)+(c-b)(L-c) \ge \frac {5}{12}L^2+\frac {1}{6}L-\frac {7}{12}.\end{align*}
Lemma 3.3 allows us to show that, instead of getting the desired
![]() $\frac{1}{4}+\frac{1}{8} = \frac{3}{8}$
for
$\frac{1}{4}+\frac{1}{8} = \frac{3}{8}$
for
![]() $\text{PPC}\left(0,\frac{1}{4}\right)+\text{PPC}\left(0,\frac{1}{8}\right)$
, we get at least
$\text{PPC}\left(0,\frac{1}{4}\right)+\text{PPC}\left(0,\frac{1}{8}\right)$
, we get at least
![]() $\frac{5}{12} = \frac{3}{8}+\frac{1}{24}$
, asymptotically for large intervals.
$\frac{5}{12} = \frac{3}{8}+\frac{1}{24}$
, asymptotically for large intervals.
Proposition 3.4.
Let
![]() $L \ge 1$
be a positive integer and
$L \ge 1$
be a positive integer and
![]() $g_1,\dots, g_L$
be positive reals with
$g_1,\dots, g_L$
be positive reals with
![]() $\sum _{i=1}^L g_i \le \frac{1}{2}$
. Then,
$\sum _{i=1}^L g_i \le \frac{1}{2}$
. Then,
Proof. By scaling, it suffices to prove the proposition when
![]() $\sum _{i=1}^L g_i = \frac{1}{2}$
. Suppose
$\sum _{i=1}^L g_i = \frac{1}{2}$
. Suppose
![]() $\sum _{i=1}^L g_i = \frac{1}{2}$
. Let
$\sum _{i=1}^L g_i = \frac{1}{2}$
. Let
and note
 \begin{align*}\sum _{n \le L}\sum _{m \le L-n+1} 1_{g_n+\dots +g_{n+m-1} \le \frac {1}{8}} & \ge \frac {(a-1)a}{2}+\frac {(b-a)(b-a+1)}{2}+\frac {(c-b)(c-b+1)}{2}\\& \quad +\frac {(L-c+1)(L-c+2)}{2}.\end{align*}
\begin{align*}\sum _{n \le L}\sum _{m \le L-n+1} 1_{g_n+\dots +g_{n+m-1} \le \frac {1}{8}} & \ge \frac {(a-1)a}{2}+\frac {(b-a)(b-a+1)}{2}+\frac {(c-b)(c-b+1)}{2}\\& \quad +\frac {(L-c+1)(L-c+2)}{2}.\end{align*}
by doing casework in which intervals
![]() $n$
and
$n$
and
![]() $n+m-1$
lie (the different intervals are
$n+m-1$
lie (the different intervals are
![]() $[1,a),[a,b),[b,c),[c,L]$
). Similarly,
$[1,a),[a,b),[b,c),[c,L]$
). Similarly,
 \begin{align*}\sum _{n \le L} \sum _{m \le L-n+1} 1_{g_n+\dots +g_{n+m-1} \le \frac {2}{8}} & \ge \frac {(a-1)a}{2}+\frac {(b-a)(b-a+1)}{2}+\frac {(c-b)(c-b+1)}{2}\\& \quad +\frac {(L-c+1)(L-c+2)}{2}+(a-1)(b-a)\\[5pt]& \quad +(b-a)(c-b)+(c-b)(L-c+1),\end{align*}
\begin{align*}\sum _{n \le L} \sum _{m \le L-n+1} 1_{g_n+\dots +g_{n+m-1} \le \frac {2}{8}} & \ge \frac {(a-1)a}{2}+\frac {(b-a)(b-a+1)}{2}+\frac {(c-b)(c-b+1)}{2}\\& \quad +\frac {(L-c+1)(L-c+2)}{2}+(a-1)(b-a)\\[5pt]& \quad +(b-a)(c-b)+(c-b)(L-c+1),\end{align*}
Therefore,
 \begin{align*}\sum _{n \le L} \sum _{m \le L-n+1} 1_{g_n+\dots +g_{n+m-1} \le \frac {2}{8}} & + \sum _{n \le L}\sum _{m \le L-n+1} 1_{g_n+\dots +g_{n+m-1} \le \frac {1}{8}} \ge (a-1)a+(b-a)(b-a+1)\\& +(c-b)(c-b+1)+(L-c+1)(L-c+2)+(a-1)(b-a)\\& \quad +(b-a)(c-b)+(c-b)(L-c+1).\end{align*}
\begin{align*}\sum _{n \le L} \sum _{m \le L-n+1} 1_{g_n+\dots +g_{n+m-1} \le \frac {2}{8}} & + \sum _{n \le L}\sum _{m \le L-n+1} 1_{g_n+\dots +g_{n+m-1} \le \frac {1}{8}} \ge (a-1)a+(b-a)(b-a+1)\\& +(c-b)(c-b+1)+(L-c+1)(L-c+2)+(a-1)(b-a)\\& \quad +(b-a)(c-b)+(c-b)(L-c+1).\end{align*}
Lower bounding
![]() $L-c+1$
and
$L-c+1$
and
![]() $L-c+2$
by
$L-c+2$
by
![]() $L-c$
and
$L-c$
and
![]() $L-c+1$
, respectively, Lemma 3.3 finishes the proof of Proposition3.4, since
$L-c+1$
, respectively, Lemma 3.3 finishes the proof of Proposition3.4, since
![]() $\frac{5}{12}L^2+\frac{1}{6}L-\frac{7}{12} \ge \frac{5}{6}{\left(\begin{smallmatrix}L + 1\\2\end{smallmatrix}\right)}-\frac{5}{6}L$
for
$\frac{5}{12}L^2+\frac{1}{6}L-\frac{7}{12} \ge \frac{5}{6}{\left(\begin{smallmatrix}L + 1\\2\end{smallmatrix}\right)}-\frac{5}{6}L$
for
![]() $L \ge 1$
.
$L \ge 1$
.
We now proceed to isolate the relevant “
![]() $0$
density” parts of the sequence on which the gaps are at most
$0$
density” parts of the sequence on which the gaps are at most
![]() $1/2$
, in order to exploit the bias that Proposition3.4 illustrates.
$1/2$
, in order to exploit the bias that Proposition3.4 illustrates.
Here and henceforth, we let
![]() $[N]\,:\!=\,\{1,2,\ldots, N\}$
.
$[N]\,:\!=\,\{1,2,\ldots, N\}$
.
Definition 3.5.
For a nonempty interval
![]() $J \subseteq [N]$
, let
$J \subseteq [N]$
, let
![]() $L(J),R(J)$
denote the left and right endpoints of
$L(J),R(J)$
denote the left and right endpoints of
![]() $J$
, respectively, and let
$J$
, respectively, and let
![]() $\textrm{sum}(J) = \sum _{n \in J} g_n$
.
$\textrm{sum}(J) = \sum _{n \in J} g_n$
.
Definition 3.6.
For a interval
![]() $J \subseteq [N]$
, we denote
$J \subseteq [N]$
, we denote
For intervals
![]() $J_1, J_2 \subseteq [N]$
, with
$J_1, J_2 \subseteq [N]$
, with
![]() $R(J_1) \lt L(J_2)$
, we denote
$R(J_1) \lt L(J_2)$
, we denote
Take a large
![]() $N$
. Let
$N$
. Let
![]() $\mathcal{I}^N$
denote the collection of all maximal intervals on which the gaps
$\mathcal{I}^N$
denote the collection of all maximal intervals on which the gaps
![]() $g_n$
are at most
$g_n$
are at most
![]() $\frac{1}{2}$
. More formally, we define
$\frac{1}{2}$
. More formally, we define
![]() $\mathcal{I}^N$
to be the collection of all intervals
$\mathcal{I}^N$
to be the collection of all intervals
![]() $I \subseteq [N]$
such that (1)
$I \subseteq [N]$
such that (1)
![]() $g_n \le \frac{1}{2}$
for each
$g_n \le \frac{1}{2}$
for each
![]() $n \in I$
, (2)
$n \in I$
, (2)
![]() $L(I) = 1$
or
$L(I) = 1$
or
![]() $g_{L(I)-1} \gt \frac{1}{2}$
, and (3)
$g_{L(I)-1} \gt \frac{1}{2}$
, and (3)
![]() $R(I) = N$
or
$R(I) = N$
or
![]() $g_{R(I)+1} \gt \frac{1}{2}$
.
$g_{R(I)+1} \gt \frac{1}{2}$
.
We begin by noting the following.
Lemma 3.7.
For all large
![]() $N$
, we have
$N$
, we have
Furthermore, as
![]() $N \to \infty$
, we have
$N \to \infty$
, we have
Proof. By definition we have
Proposition3.1 then gives the first inequality. For the second inequality, note, by the maximality of the intervals comprising
![]() $\mathcal{I}^N$
, that
$\mathcal{I}^N$
, that
We provide a quick remark on motivation.
Remark 3.8. Observe that, if it were the case that
![]() $\textrm{sum}(I) \le \frac{1}{2}$
for each
$\textrm{sum}(I) \le \frac{1}{2}$
for each
![]() $I \in \mathcal{I}^N$
, then we could conclude the proof of Theorem 1.1 as follows. By Proposition 3.4, one has
$I \in \mathcal{I}^N$
, then we could conclude the proof of Theorem 1.1 as follows. By Proposition 3.4, one has
 \begin{align*} \left(\frac{3}{8} + o(1)\right)N &= \text{PPC}^{[N]}\left(0,\frac{1}{8}\right) + \text{PPC}^{[N]}\left(0,\frac{1}{4}\right) \\ &\geq \frac{5}{6}\sum _I \binom{|I|+1}{2} - \frac{5}{6}\sum _I |I| \\ &\geq \left(\frac{5}{12} - \frac{5}{3}\sqrt \epsilon +o(1)\right)N \end{align*}
\begin{align*} \left(\frac{3}{8} + o(1)\right)N &= \text{PPC}^{[N]}\left(0,\frac{1}{8}\right) + \text{PPC}^{[N]}\left(0,\frac{1}{4}\right) \\ &\geq \frac{5}{6}\sum _I \binom{|I|+1}{2} - \frac{5}{6}\sum _I |I| \\ &\geq \left(\frac{5}{12} - \frac{5}{3}\sqrt \epsilon +o(1)\right)N \end{align*}
as
![]() $N \to \infty$
, which would give our desired contradiction by taking
$N \to \infty$
, which would give our desired contradiction by taking
![]() $N$
sufficiently large.
$N$
sufficiently large.
However, it need not be the case that
![]() $\textrm{sum}(I) \le \frac{1}{2}$
for each
$\textrm{sum}(I) \le \frac{1}{2}$
for each
![]() $I \in \mathcal{I}^N$
. In light of Remark 3.8, therefore, the strategy is to partition each
$I \in \mathcal{I}^N$
. In light of Remark 3.8, therefore, the strategy is to partition each
![]() $I \in \mathcal{I}^N$
into subintervals
$I \in \mathcal{I}^N$
into subintervals
![]() $\{J_k^I\}_k$
with
$\{J_k^I\}_k$
with
![]() $\textrm{sum}\left(J_k^I\right) \leq 1/2$
for each
$\textrm{sum}\left(J_k^I\right) \leq 1/2$
for each
![]() $k$
and such that, for all
$k$
and such that, for all
![]() $a\in (0,1/2]$
and all
$a\in (0,1/2]$
and all
![]() $k$
, the contribution to PPC
$k$
, the contribution to PPC
![]() $(0,a)$
from windows that overlap with
$(0,a)$
from windows that overlap with
![]() $J_k^I$
comes nearly entirely from windows that lie entirely inside
$J_k^I$
comes nearly entirely from windows that lie entirely inside
![]() $J_k^I$
. The existence of such a partition is not at all immediate. We provide in Proposition3.9 below a precise statement of what is needed.
$J_k^I$
. The existence of such a partition is not at all immediate. We provide in Proposition3.9 below a precise statement of what is needed.
Proposition 3.9.
Let
![]() $\mathcal{I}^N$
be as above. There exists a partition of each
$\mathcal{I}^N$
be as above. There exists a partition of each
![]() $I \in \mathcal{I}^N$
into subintervals
$I \in \mathcal{I}^N$
into subintervals
![]() $\{J_k^I\}_{k=1}^{r_I}$
such that the following two hold.
$\{J_k^I\}_{k=1}^{r_I}$
such that the following two hold.
-
1.
 $\textrm{sum}\left(J_k^I\right)\leq \frac{1}{2}$
for each
$\textrm{sum}\left(J_k^I\right)\leq \frac{1}{2}$
for each
 $I \in \mathcal{I}^N$
and
$I \in \mathcal{I}^N$
and
 $k \in \{1,\dots, r_I\}$
, and
$k \in \{1,\dots, r_I\}$
, and
-
2.
 $\sum _{I \in \mathcal{I}^N}\sum _{k=1}^{r_I} \binom{|J^I_k|+1}{2} \geq \left(\frac{1}{2} - 4\sqrt{2}\epsilon ^{1/4}\right) N$
.
$\sum _{I \in \mathcal{I}^N}\sum _{k=1}^{r_I} \binom{|J^I_k|+1}{2} \geq \left(\frac{1}{2} - 4\sqrt{2}\epsilon ^{1/4}\right) N$
.
To quickly conclude the proof of Theorem 1.1, we postpone the proof of Proposition3.9 (and the description of the partition) to the following section, and assume it for now.
Proof of Theorem 1.1. We will proceed along the lines of Remark 3.8, but now use Proposition3.9 to partition into subintervals on which we can apply Proposition3.4. This yields the following computations, where Proposition3.4 is used in the penultimate line, and we use Lemma 3.7 in the final line:
 \begin{align*} \left(\frac{3}{8}+o(1)\right)N &= \text{PPC}^{[N]}\left(0,\frac{1}{8}\right)+\text{PPC}^{[N]}\left(0,\frac{1}{4}\right) \\ &\ge \sum _{I \in \mathcal{I}^N} \sum _k \text{PPC}^{J_k^I}\left(0,\frac{1}{8}\right)+\text{PPC}^{J_k^I}\left(0,\frac{1}{4}\right)\\ &\ge \frac{5}{6}\sum _{I \in \mathcal{I}^N} \sum _k \binom{|J_k^I|+1}{2} - \frac{5}{6}\sum _{I \in \mathcal{I}^N} \sum _k |J_k^I| \\ &\ge \frac{5}{6}\left(\frac{1}{2}-4\sqrt{2}\epsilon ^{1/4}\right)N-\frac{5}{3}\sqrt{\epsilon }N. \end{align*}
\begin{align*} \left(\frac{3}{8}+o(1)\right)N &= \text{PPC}^{[N]}\left(0,\frac{1}{8}\right)+\text{PPC}^{[N]}\left(0,\frac{1}{4}\right) \\ &\ge \sum _{I \in \mathcal{I}^N} \sum _k \text{PPC}^{J_k^I}\left(0,\frac{1}{8}\right)+\text{PPC}^{J_k^I}\left(0,\frac{1}{4}\right)\\ &\ge \frac{5}{6}\sum _{I \in \mathcal{I}^N} \sum _k \binom{|J_k^I|+1}{2} - \frac{5}{6}\sum _{I \in \mathcal{I}^N} \sum _k |J_k^I| \\ &\ge \frac{5}{6}\left(\frac{1}{2}-4\sqrt{2}\epsilon ^{1/4}\right)N-\frac{5}{3}\sqrt{\epsilon }N. \end{align*}
Rearranging, dividing by
![]() $N$
, and sending
$N$
, and sending
![]() $N \to \infty$
, we obtain
$N \to \infty$
, we obtain
which is indeed false for
![]() $\epsilon = 10^{-9}$
(but not for
$\epsilon = 10^{-9}$
(but not for
![]() $\epsilon = 10^{-8}$
). This gives the desired contradiction to our assumption that a sequence
$\epsilon = 10^{-8}$
). This gives the desired contradiction to our assumption that a sequence
![]() $(\lambda _n)_n$
with PPC, average gap
$(\lambda _n)_n$
with PPC, average gap
![]() $1$
, and maximum gap
$1$
, and maximum gap
![]() $3/2+\epsilon$
exists.
$3/2+\epsilon$
exists.
4. Partitioning, and a proof of Proposition3.9
The following examples are helpful to keep in mind to explain the need for care when choosing the partition of a given
![]() $I \in \mathcal{I}^N$
, and to help motivate the partition we will use.
$I \in \mathcal{I}^N$
, and to help motivate the partition we will use.
The first example
![]() $I_1$
shows that a “greedy division”, in which one goes from left to right, dividing immediately before the sum first exceeds
$I_1$
shows that a “greedy division”, in which one goes from left to right, dividing immediately before the sum first exceeds
![]() $1/2$
, will not work. Indeed, that division is
$1/2$
, will not work. Indeed, that division is
which is problematic as there will be much contribution to the PPC(
![]() $0,\frac{1}{2}$
) count coming from different subintervals; specifically, any index besides the first in the first subinterval and any index in the second subinterval would prove a nontrivial contribution.
$0,\frac{1}{2}$
) count coming from different subintervals; specifically, any index besides the first in the first subinterval and any index in the second subinterval would prove a nontrivial contribution.
Similarly, another “greedy division” in which the largest numbers successively “claim” the largest subinterval they can, will not work. For the case of
![]() $I_1$
, the division is
$I_1$
, the division is
which has a large contribution to
![]() $\text{PPC}\left(0,\frac{1}{2}\right)$
coming from any index in the first subinterval besides the first and any index in the last subinterval besides the last. Note thus that even “non-adjacent” subintervals can cause issues.
$\text{PPC}\left(0,\frac{1}{2}\right)$
coming from any index in the first subinterval besides the first and any index in the last subinterval besides the last. Note thus that even “non-adjacent” subintervals can cause issues.
A division that does work for
![]() $I_1$
is
$I_1$
is
as there is only a minor contribution (namely, linear in the size of the interval rather than quadratic) coming from different subintervals.
For
![]() $I_2$
, essentially any reasonable division is permissible, but we draw attention to it as it shows that sometimes the reason for negligible contribution from different subintervals are subintervals in between. For example, if we decompose as
$I_2$
, essentially any reasonable division is permissible, but we draw attention to it as it shows that sometimes the reason for negligible contribution from different subintervals are subintervals in between. For example, if we decompose as
then the reason that there is no contribution to
![]() $\text{PPC}\left(0,\frac{1}{2}\right)$
from the subintervals
$\text{PPC}\left(0,\frac{1}{2}\right)$
from the subintervals
![]() $\{\frac{1}{4},0,0,\dots, 0,0\}$
and
$\{\frac{1}{4},0,0,\dots, 0,0\}$
and
![]() $\{0,0,\dots, 0,0,\frac{1}{4}\}$
are the five subintervals
$\{0,0,\dots, 0,0,\frac{1}{4}\}$
are the five subintervals
![]() $\{\frac{1}{2}\}$
in between.
$\{\frac{1}{2}\}$
in between.
For
![]() $I_3$
, any division will admit a large PPC contribution from different subintervals. This would of course be harmful, but we make use of the fact that it won’t exist often in our situation, since it provides a nontrivial contribution to
$I_3$
, any division will admit a large PPC contribution from different subintervals. This would of course be harmful, but we make use of the fact that it won’t exist often in our situation, since it provides a nontrivial contribution to
![]() $\text{PPC}(\frac{1}{2},1)$
(which we already know comes nearly entirely from single gaps).
$\text{PPC}(\frac{1}{2},1)$
(which we already know comes nearly entirely from single gaps).
With the above examples in mind, we now choose the partition we use to prove Proposition3.9.
Fix
![]() $I \in \mathcal{I}^N$
. In the following definition, ties may be broken arbitrarily. Let
$I \in \mathcal{I}^N$
. In the following definition, ties may be broken arbitrarily. Let
![]() $J_1$
be the largest subinterval of
$J_1$
be the largest subinterval of
![]() $I$
with
$I$
with
![]() $\textrm{sum}(J_1) \le \frac{1}{2}$
. With
$\textrm{sum}(J_1) \le \frac{1}{2}$
. With
![]() $J_1,\dots, J_r$
already defined, if
$J_1,\dots, J_r$
already defined, if
![]() $\cup _{k=1}^r J_k \not = I$
, let
$\cup _{k=1}^r J_k \not = I$
, let
![]() $J_{r+1}$
be the largest subinterval of
$J_{r+1}$
be the largest subinterval of
![]() $I\setminus \cup _{k=1}^r J_k$
with
$I\setminus \cup _{k=1}^r J_k$
with
![]() $\textrm{sum}(J_{r+1}) \le \frac{1}{2}$
. Let
$\textrm{sum}(J_{r+1}) \le \frac{1}{2}$
. Let
![]() $J_1,\dots, J_s$
be all the subintervals resulting from this process. Of course
$J_1,\dots, J_s$
be all the subintervals resulting from this process. Of course
![]() $s \le |I| \lt +\infty$
.
$s \le |I| \lt +\infty$
.
Clearly
![]() $I = \sqcup _{k=1}^s J_k$
and
$I = \sqcup _{k=1}^s J_k$
and
![]() $\textrm{sum}(J_k) \leq 1/2$
for each
$\textrm{sum}(J_k) \leq 1/2$
for each
![]() $k$
, establishing the first requirement of Proposition3.9. We now begin to proceed to establish the second.
$k$
, establishing the first requirement of Proposition3.9. We now begin to proceed to establish the second.
Hopefully not confusing the reader, we renumber now so that
![]() $J_1$
is the leftmost interval, with
$J_1$
is the leftmost interval, with
![]() $J_2$
to the immediate right of
$J_2$
to the immediate right of
![]() $J_1$
,
$J_1$
,
![]() $J_3$
to the immediate right of
$J_3$
to the immediate right of
![]() $J_2$
, etc.. For
$J_2$
, etc.. For
![]() $1 \le k \le s-1$
, let
$1 \le k \le s-1$
, let
![]() $g_1(k) \in \{k,k+1\}$
and
$g_1(k) \in \{k,k+1\}$
and
![]() $b_1(k) \in \{k,k+1\}\setminus \{g_1(k)\}$
be such that
$b_1(k) \in \{k,k+1\}\setminus \{g_1(k)\}$
be such that
![]() $J_{g_1(k)}$
was chosen before
$J_{g_1(k)}$
was chosen before
![]() $J_{b_1(k)}$
. Note, in particular, that
$J_{b_1(k)}$
. Note, in particular, that
![]() $|J_{g_1(k)}| \ge |J_{b_1(k)}|$
.
$|J_{g_1(k)}| \ge |J_{b_1(k)}|$
.
We quickly pin down exactly which different subintervals need to be considered with regards to their contribution to
![]() $\text{PPC}(0,a)$
, for
$\text{PPC}(0,a)$
, for
![]() $a \leq 1/2$
.
$a \leq 1/2$
.
Definition 4.1.
Call
![]() $k \in [2,s-1]$
sandwiched if it was chosen after each of its neighbouring subintervals, i.e., if
$k \in [2,s-1]$
sandwiched if it was chosen after each of its neighbouring subintervals, i.e., if
![]() $b_1(k-1) = k$
and
$b_1(k-1) = k$
and
![]() $b_1(k) = k$
. For a sandwiched
$b_1(k) = k$
. For a sandwiched
![]() $k$
, let
$k$
, let
![]() $g_2(k) \in \{k-1,k+1\}$
and
$g_2(k) \in \{k-1,k+1\}$
and
![]() $b_2(k) \in \{k-1,k+1\}\setminus \{g_2(k)\}$
be such that
$b_2(k) \in \{k-1,k+1\}\setminus \{g_2(k)\}$
be such that
![]() $J_{g_2(k)}$
was chosen before
$J_{g_2(k)}$
was chosen before
![]() $J_{b_2(k)}$
. In particular,
$J_{b_2(k)}$
. In particular,
![]() $|J_{g_2(k)}| \ge |J_{b_2(k)}|$
.
$|J_{g_2(k)}| \ge |J_{b_2(k)}|$
.
Lemma 4.2.
If
![]() $n \le n^{\prime} \in I$
have
$n \le n^{\prime} \in I$
have
![]() $g_n+\dots +g_{n^{\prime}} \le \frac{1}{2}$
, then either
$g_n+\dots +g_{n^{\prime}} \le \frac{1}{2}$
, then either
-
1.
 $(n,n^{\prime}) \in J_k\times J_k$
for some
$(n,n^{\prime}) \in J_k\times J_k$
for some
 $k$
,
$k$
, -
2.
 $(n,n^{\prime}) \in J_k\times J_{k+1}$
for some
$(n,n^{\prime}) \in J_k\times J_{k+1}$
for some
 $k$
, or
$k$
, or
-
3.
 $(n,n^{\prime}) \in J_{k-1}\times J_{k+1}$
for some sandwiched
$(n,n^{\prime}) \in J_{k-1}\times J_{k+1}$
for some sandwiched
 $k$
.
$k$
.
Proof. First note that if
![]() $n \in J_k$
and
$n \in J_k$
and
![]() $n^{\prime} \in \cup _{\Delta \ge 3} J_{k+\Delta }$
, then
$n^{\prime} \in \cup _{\Delta \ge 3} J_{k+\Delta }$
, then
![]() $g_n+\dots +g_{n^{\prime}} \gt \frac{1}{2}$
, since
$g_n+\dots +g_{n^{\prime}} \gt \frac{1}{2}$
, since
![]() $\textrm{sum}(J_{k+1}\cup J_{k+2}) \gt \frac{1}{2}$
(for otherwise whichever of
$\textrm{sum}(J_{k+1}\cup J_{k+2}) \gt \frac{1}{2}$
(for otherwise whichever of
![]() $J_{k+1},J_{k+2}$
was chosen first would have “engulfed” the other). Now suppose
$J_{k+1},J_{k+2}$
was chosen first would have “engulfed” the other). Now suppose
![]() $n \in J_{k-1}$
and
$n \in J_{k-1}$
and
![]() $n^{\prime} \in J_{k+1}$
for some
$n^{\prime} \in J_{k+1}$
for some
![]() $k$
. If
$k$
. If
![]() $b_1(k-1) = k-1$
, then
$b_1(k-1) = k-1$
, then
![]() $\textrm{sum}(R(J_{k-1})\cup J_k) \gt \frac{1}{2}$
, so
$\textrm{sum}(R(J_{k-1})\cup J_k) \gt \frac{1}{2}$
, so
![]() $g_n+\dots +g_{n^{\prime}} \gt \frac{1}{2}$
. Similarly, if
$g_n+\dots +g_{n^{\prime}} \gt \frac{1}{2}$
. Similarly, if
![]() $b_1(k) = k+1$
, then
$b_1(k) = k+1$
, then
![]() $\textrm{sum}(J_k\cup L(J_{k+1})) \gt \frac{1}{2}$
also yields
$\textrm{sum}(J_k\cup L(J_{k+1})) \gt \frac{1}{2}$
also yields
![]() $g_n+\dots +g_{n^{\prime}} \gt \frac{1}{2}$
. Hence,
$g_n+\dots +g_{n^{\prime}} \gt \frac{1}{2}$
. Hence,
![]() $k$
is sandwiched.
$k$
is sandwiched.
We now proceed to argue that the PPC
![]() $\left(0,\frac{1}{2}\right)$
contribution coming from cases (2) or (3) in Lemma 4.2 is small. We begin with case (2).
$\left(0,\frac{1}{2}\right)$
contribution coming from cases (2) or (3) in Lemma 4.2 is small. We begin with case (2).
We shall argue that the
![]() $\text{PPC}\left(0,\frac{1}{2}\right)$
contribution coming from adjacent subintervals
$\text{PPC}\left(0,\frac{1}{2}\right)$
contribution coming from adjacent subintervals
![]() $J_k,J_{k+1}$
is small by arguing that
$J_k,J_{k+1}$
is small by arguing that
![]() $|J_{b_1(k)}|$
is (usually) small. We do this by arguing that we would otherwise have too large of a contribution to
$|J_{b_1(k)}|$
is (usually) small. We do this by arguing that we would otherwise have too large of a contribution to
![]() $\text{PPC}\left(\frac{1}{2},\frac{3}{2}\right)$
coming from gaps
$\text{PPC}\left(\frac{1}{2},\frac{3}{2}\right)$
coming from gaps
![]() $\lambda _{n+m}-\lambda _n$
with
$\lambda _{n+m}-\lambda _n$
with
![]() $m \ge 2$
(contradicting Proposition3.2).
$m \ge 2$
(contradicting Proposition3.2).
Proposition 4.3.
For any
![]() $k \in [s-1]$
, one has
$k \in [s-1]$
, one has
Proof. Without loss of generality, by symmetry we may assume
![]() $b_1(k) = k+1$
.
$b_1(k) = k+1$
.
For
![]() $y \in J_{k+1}$
and
$y \in J_{k+1}$
and
![]() $x \in J_k$
, if
$x \in J_k$
, if
![]() $y-x+1 \gt |J_k|$
, then
$y-x+1 \gt |J_k|$
, then
![]() $g_x+\dots +g_y \gt \frac{1}{2}$
, since otherwise
$g_x+\dots +g_y \gt \frac{1}{2}$
, since otherwise
![]() $[x,y]$
would have been chosen as
$[x,y]$
would have been chosen as
![]() $J_k$
(in the greedy process defining the partition) instead of
$J_k$
(in the greedy process defining the partition) instead of
![]() $J_k$
. Therefore,
$J_k$
. Therefore,
 \begin{align*} \sum _{(n,n^{\prime}) \in J_k\times J_{k+1}} 1_{g_n+\dots +g_{n^{\prime}} \gt \frac{1}{2}} &\ge \sum _{y=L(J_{k+1})}^{R(J_{k+1})} \sum _{x = L(J_k)}^{y-R(J_k)+L(J_k)-1} 1 \\[4pt] &= \left(\frac{L(J_{k+1})+R(J_{k+1})}{2}\right)|J_{k+1}|-R(J_k)|J_{k+1}| \\[4pt] &= \frac{1}{2}|J_{k+1}|^2+\frac{1}{2}|J_{k+1}|, \end{align*}
\begin{align*} \sum _{(n,n^{\prime}) \in J_k\times J_{k+1}} 1_{g_n+\dots +g_{n^{\prime}} \gt \frac{1}{2}} &\ge \sum _{y=L(J_{k+1})}^{R(J_{k+1})} \sum _{x = L(J_k)}^{y-R(J_k)+L(J_k)-1} 1 \\[4pt] &= \left(\frac{L(J_{k+1})+R(J_{k+1})}{2}\right)|J_{k+1}|-R(J_k)|J_{k+1}| \\[4pt] &= \frac{1}{2}|J_{k+1}|^2+\frac{1}{2}|J_{k+1}|, \end{align*}
with the last equality using
![]() $R(J_k) = L(J_{k+1})-1$
.
$R(J_k) = L(J_{k+1})-1$
.
Next we proceed to bound the contribution from intervals
![]() $J_{k-1}$
,
$J_{k-1}$
,
![]() $J_{k+1}$
for
$J_{k+1}$
for
![]() $k$
sandwiched. For such
$k$
sandwiched. For such
![]() $k$
, we argue that
$k$
, we argue that
![]() $|J_{b_2(k)}|$
is (usually) small.
$|J_{b_2(k)}|$
is (usually) small.
Proposition 4.4.
For a sandwiched
![]() $k$
, one has
$k$
, one has
Proof. Without loss of generality, by symmetry we may assume
![]() $b_2(k) = k+1$
.
$b_2(k) = k+1$
.
For
![]() $y \in J_{k+1}$
and
$y \in J_{k+1}$
and
![]() $x \in J_{k-1}$
, if
$x \in J_{k-1}$
, if
![]() $y-x+1 \gt |J_{k-1}|$
, then
$y-x+1 \gt |J_{k-1}|$
, then
![]() $g_x+\dots +g_y \gt \frac{1}{2}$
, since otherwise
$g_x+\dots +g_y \gt \frac{1}{2}$
, since otherwise
![]() $[x,y]$
would have been chosen instead of
$[x,y]$
would have been chosen instead of
![]() $J_{k-1}$
(recall
$J_{k-1}$
(recall
![]() $J_k$
was also chosen after
$J_k$
was also chosen after
![]() $J_{k-1}$
, since
$J_{k-1}$
, since
![]() $k$
is sandwiched). Therefore,
$k$
is sandwiched). Therefore,
 \begin{equation*}\sum _{(n,n^{\prime}) \in J_{k-1}\times J_{k+1}} 1_{g_n+\dots +g_{n^{\prime}} \gt \frac {1}{2}} \ge \sum _{y=L(J_{k+1})}^{R(J_{k+1})} \sum _{x = L(J_{k-1})}^{\min (R(J_{k-1}),y-|J_{k-1}|)} 1.\end{equation*}
\begin{equation*}\sum _{(n,n^{\prime}) \in J_{k-1}\times J_{k+1}} 1_{g_n+\dots +g_{n^{\prime}} \gt \frac {1}{2}} \ge \sum _{y=L(J_{k+1})}^{R(J_{k+1})} \sum _{x = L(J_{k-1})}^{\min (R(J_{k-1}),y-|J_{k-1}|)} 1.\end{equation*}
If
![]() $R(J_{k+1})-|J_{k-1}| \le R(J_{k-1})$
, then we obtain
$R(J_{k+1})-|J_{k-1}| \le R(J_{k-1})$
, then we obtain
 \begin{align*} \sum _{(n,n^{\prime}) \in J_{k-1}\times J_{k+1}} 1_{g_n+\dots +g_{n^{\prime}} \gt \frac{1}{2}} &\ge \sum _{y = L(J_{k+1})}^{R(J_{k+1})} \sum _{x = L(J_{k-1})}^{y-|J_{k-1}|} 1 \\ &= |J_{k+1}|\left (\frac{R(J_{k+1})+L(J_{k+1})}{2}-|J_{k-1}|-L(J_{k-1})+1\right ) \\ &= |J_{k+1}|\left (\frac{R(J_{k+1})+L(J_{k+1})}{2}-R(J_{k-1})\right ) \\ &= |J_{k+1}|\left (\frac{R(J_{k+1})+L(J_{k+1})}{2}-L(J_{k+1})+|J_k|+1\right ) \\ &= |J_{k+1}|\left (\frac{|J_{k+1}|-1}{2}+|J_k|+1\right ), \end{align*}
\begin{align*} \sum _{(n,n^{\prime}) \in J_{k-1}\times J_{k+1}} 1_{g_n+\dots +g_{n^{\prime}} \gt \frac{1}{2}} &\ge \sum _{y = L(J_{k+1})}^{R(J_{k+1})} \sum _{x = L(J_{k-1})}^{y-|J_{k-1}|} 1 \\ &= |J_{k+1}|\left (\frac{R(J_{k+1})+L(J_{k+1})}{2}-|J_{k-1}|-L(J_{k-1})+1\right ) \\ &= |J_{k+1}|\left (\frac{R(J_{k+1})+L(J_{k+1})}{2}-R(J_{k-1})\right ) \\ &= |J_{k+1}|\left (\frac{R(J_{k+1})+L(J_{k+1})}{2}-L(J_{k+1})+|J_k|+1\right ) \\ &= |J_{k+1}|\left (\frac{|J_{k+1}|-1}{2}+|J_k|+1\right ), \end{align*}
and conclude by observing that
![]() $|J_k| \ge 0$
and
$|J_k| \ge 0$
and
![]() $\frac{|J_{k+1}|-1}{2}+1 \ge \frac{1}{2}|J_{k+1}|$
.
$\frac{|J_{k+1}|-1}{2}+1 \ge \frac{1}{2}|J_{k+1}|$
.
If, instead,
![]() $R(J_{k+1})-|J_{k-1}| \ge R(J_{k-1})$
, we obtain
$R(J_{k+1})-|J_{k-1}| \ge R(J_{k-1})$
, we obtain
 \begin{equation} \sum _{(n,n^{\prime}) \in J_{k-1}\times J_{k+1}} 1_{g_n+\dots +g_{n^{\prime}} \gt \frac{1}{2}} \ge \sum _{y=L(J_{k+1})}^{|J_{k-1}|+R(J_{k-1})} \sum _{x=L(J_{k-1})}^{y-|J_{k-1}|} 1 +\sum _{y=|J_{k-1}|+R(J_{k-1})+1}^{R(J_{k+1})} \sum _{x=L(J_{k-1})}^{R(J_{k-1})} 1. \end{equation}
\begin{equation} \sum _{(n,n^{\prime}) \in J_{k-1}\times J_{k+1}} 1_{g_n+\dots +g_{n^{\prime}} \gt \frac{1}{2}} \ge \sum _{y=L(J_{k+1})}^{|J_{k-1}|+R(J_{k-1})} \sum _{x=L(J_{k-1})}^{y-|J_{k-1}|} 1 +\sum _{y=|J_{k-1}|+R(J_{k-1})+1}^{R(J_{k+1})} \sum _{x=L(J_{k-1})}^{R(J_{k-1})} 1. \end{equation}
The first double sum on the RHS of (8) is equal to
while the second double sum is equal to
Adding these two sums and simplifying we obtain,
 \begin{align*} (|J_{k-1}| - |J_k|)\left(\frac {|J_{k-1}| + |J_k| + 1}{2}\right) & + |J_{k-1}|(|J_k| + |J_{k+1}|-|J_{k-1}|)\\& = -\frac {1}{2}(|J_{k-1}|-|J_k|)^2 + \frac {1}{2}(|J_{k-1}| - |J_k|) + |J_{k-1}||J_{k+1}|.\end{align*}
\begin{align*} (|J_{k-1}| - |J_k|)\left(\frac {|J_{k-1}| + |J_k| + 1}{2}\right) & + |J_{k-1}|(|J_k| + |J_{k+1}|-|J_{k-1}|)\\& = -\frac {1}{2}(|J_{k-1}|-|J_k|)^2 + \frac {1}{2}(|J_{k-1}| - |J_k|) + |J_{k-1}||J_{k+1}|.\end{align*}
Now recall that we have
![]() $|J_k| \leq |J_{k+1}| \leq |J_{k-1}|$
and furthermore, by our assumption in the second case, we have
$|J_k| \leq |J_{k+1}| \leq |J_{k-1}|$
and furthermore, by our assumption in the second case, we have
![]() $|J_{k-1}| \leq |J_k| + |J_{k+1}|$
. Thus we may obtain
$|J_{k-1}| \leq |J_k| + |J_{k+1}|$
. Thus we may obtain
This completes the proof.
We now cease referring to a specific
![]() $I \in \mathcal{I}^N$
. To denote dependence on
$I \in \mathcal{I}^N$
. To denote dependence on
![]() $I \in \mathcal{I}^N$
, we denote
$I \in \mathcal{I}^N$
, we denote
![]() $I = \sqcup _{k=1}^r J_k^I$
its decomposition.
$I = \sqcup _{k=1}^r J_k^I$
its decomposition.
Proposition 4.5.
For any
![]() $a \in \left(0,\frac{1}{2}\right)$
, it holds that
$a \in \left(0,\frac{1}{2}\right)$
, it holds that
 \begin{equation*}\sum _{I \in \mathcal {I}^N} \sum _k \text {PPC}^{J_k^I,J_{k+1}^I}(0,a) \le 2\sqrt {2}\epsilon ^{1/4}\left (\sum _{I \in \mathcal {I}^N} \sum _k |J_k^I|^2\right )^{1/2}\sqrt {N}\end{equation*}
\begin{equation*}\sum _{I \in \mathcal {I}^N} \sum _k \text {PPC}^{J_k^I,J_{k+1}^I}(0,a) \le 2\sqrt {2}\epsilon ^{1/4}\left (\sum _{I \in \mathcal {I}^N} \sum _k |J_k^I|^2\right )^{1/2}\sqrt {N}\end{equation*}
and
 \begin{equation*}\sum _{I \in \mathcal {I}^N} \sum _{k { \text { sandwiched}}} \text {PPC}^{J_{k-1}^I,J_{k+1}^I}(0,a) \le 2\sqrt {2}\epsilon ^{1/4}\left (\sum _{I \in \mathcal {I}^N} \sum _k |J_k^I|^2\right )^{1/2}\sqrt {N}.\end{equation*}
\begin{equation*}\sum _{I \in \mathcal {I}^N} \sum _{k { \text { sandwiched}}} \text {PPC}^{J_{k-1}^I,J_{k+1}^I}(0,a) \le 2\sqrt {2}\epsilon ^{1/4}\left (\sum _{I \in \mathcal {I}^N} \sum _k |J_k^I|^2\right )^{1/2}\sqrt {N}.\end{equation*}
Proof. By trivially bounding
![]() $\text{PPC}^{J_k^I,J_{k+1}^I}(0,a) \le |J_{g_1(k)}^I|\hspace{1mm} |J_{b_1(k)}^I|$
and Cauchy-Schwarz,
$\text{PPC}^{J_k^I,J_{k+1}^I}(0,a) \le |J_{g_1(k)}^I|\hspace{1mm} |J_{b_1(k)}^I|$
and Cauchy-Schwarz,
 \begin{align*} \sum _{I \in \mathcal{I}^N} \sum _k \text{PPC}^{J_k^I,J_{k+1}^I}(0,a) &\le \sum _{I \in \mathcal{I}^N} \sum _k |J_{g_1(k)}^I|\hspace{1mm} |J_{b_1(k)}^I| \\ &\le \left (\sum _{I,k} |J_{g_1(k)}^I|^2\right )^{1/2}\left (\sum _{I,k} |J_{b_1(k)}^I|^2\right )^{1/2} \\ &\le \left (2\sum _{I \in \mathcal{I}^N} \sum _k |J_k^I|^2\right )^{1/2}\left (\sum _{I \in \mathcal{I}^N} \sum _k 2 \text{PPC}^{J_k^I,J_{k+1}^I}\left(\frac{1}{2},\frac{3}{2}\right)\right )^{1/2}, \end{align*}
\begin{align*} \sum _{I \in \mathcal{I}^N} \sum _k \text{PPC}^{J_k^I,J_{k+1}^I}(0,a) &\le \sum _{I \in \mathcal{I}^N} \sum _k |J_{g_1(k)}^I|\hspace{1mm} |J_{b_1(k)}^I| \\ &\le \left (\sum _{I,k} |J_{g_1(k)}^I|^2\right )^{1/2}\left (\sum _{I,k} |J_{b_1(k)}^I|^2\right )^{1/2} \\ &\le \left (2\sum _{I \in \mathcal{I}^N} \sum _k |J_k^I|^2\right )^{1/2}\left (\sum _{I \in \mathcal{I}^N} \sum _k 2 \text{PPC}^{J_k^I,J_{k+1}^I}\left(\frac{1}{2},\frac{3}{2}\right)\right )^{1/2}, \end{align*}
where the last inequality used Proposition4.3 together with the fact that
![]() $\textrm{sum}\left(J_k^I \cup J_{k+1}^I\right) \le 1 \le \frac{3}{2}$
. Now just observe
$\textrm{sum}\left(J_k^I \cup J_{k+1}^I\right) \le 1 \le \frac{3}{2}$
. Now just observe
which, by Proposition3.2, is at most
![]() $4\sqrt{\epsilon } N$
. The first inequality of the lemma follows.
$4\sqrt{\epsilon } N$
. The first inequality of the lemma follows.
For the second inequality of the lemma, we argue as above, except this time using Proposition4.4:
 \begin{align*} &\sum _{I \in \mathcal{I}^N} \sum _{k \text{ sandwiched}} \text{PPC}^{J_{k-1}^I,J_{k+1}^I}(0,a)\\ &\qquad \qquad \qquad \le \sum _{I \in \mathcal{I}^N} \sum _{k \text{ sandwiched}} |J_{g_2(k)}^I|\hspace{1mm} |J_{b_2(k)}^I| \\ &\qquad \qquad \qquad \le \left (\sum _{I \in \mathcal{I}^N} \sum _{k \text{ sandwiched}} |J_{g_2(k)}^I|^2\right )^{1/2}\left (\sum _{I \in \mathcal{I}^N} \sum _{k \text{ sandwiched}} |J_{b_2(k)}^I|^2\right )^{1/2} \\ &\qquad \qquad \qquad \le \left (2\sum _{I \in \mathcal{I}^N} \sum _k |J_k^I|^2\right )^{1/2}\left (\sum _{I \in \mathcal{I}^N} \sum _k 2 \text{PPC}^{J_{k-1}^I,J_{k+1}^I}\left(\frac{1}{2},\frac{3}{2}\right)\right )^{1/2}, \end{align*}
\begin{align*} &\sum _{I \in \mathcal{I}^N} \sum _{k \text{ sandwiched}} \text{PPC}^{J_{k-1}^I,J_{k+1}^I}(0,a)\\ &\qquad \qquad \qquad \le \sum _{I \in \mathcal{I}^N} \sum _{k \text{ sandwiched}} |J_{g_2(k)}^I|\hspace{1mm} |J_{b_2(k)}^I| \\ &\qquad \qquad \qquad \le \left (\sum _{I \in \mathcal{I}^N} \sum _{k \text{ sandwiched}} |J_{g_2(k)}^I|^2\right )^{1/2}\left (\sum _{I \in \mathcal{I}^N} \sum _{k \text{ sandwiched}} |J_{b_2(k)}^I|^2\right )^{1/2} \\ &\qquad \qquad \qquad \le \left (2\sum _{I \in \mathcal{I}^N} \sum _k |J_k^I|^2\right )^{1/2}\left (\sum _{I \in \mathcal{I}^N} \sum _k 2 \text{PPC}^{J_{k-1}^I,J_{k+1}^I}\left(\frac{1}{2},\frac{3}{2}\right)\right )^{1/2}, \end{align*}
where the last inequality used
![]() $\textrm{sum}(J_{k-1}\cup J_k\cup J_{k+1}) \le \frac{3}{2}$
. Now just observe
$\textrm{sum}(J_{k-1}\cup J_k\cup J_{k+1}) \le \frac{3}{2}$
. Now just observe
which, by Proposition3.2, is at most
![]() $4\sqrt{\epsilon } N$
. The second inequality of the lemma follows.
$4\sqrt{\epsilon } N$
. The second inequality of the lemma follows.
We are ready to complete the proof of Proposition3.9.
Proposition 4.6.
For all
![]() $N$
large,
$N$
large,
 \begin{equation*}\sum _{I \in \mathcal {I}^N}\sum _k \binom {|J_k^I|+1}{2} \geq \left(\frac {1}{2}-4\sqrt {2}\epsilon ^{1/4}\right)N.\end{equation*}
\begin{equation*}\sum _{I \in \mathcal {I}^N}\sum _k \binom {|J_k^I|+1}{2} \geq \left(\frac {1}{2}-4\sqrt {2}\epsilon ^{1/4}\right)N.\end{equation*}
Proof. Using Lemma 4.2 we have that
 \begin{align*}\left(\frac {1}{2}+o(1)\right)N & = \sum _{I\in \mathcal {I}^N}\text {PPC}^I\left(0,\frac {1}{2}\right) = \sum _I\sum _{k=1}^{r_I} \text {PPC}^{J^I_k}\left(0,\frac {1}{2}\right) +\sum _{k=1}^{r_I-1}\text {PPC}^{J^I_k,J^I_{k+1}}\left(0, \frac {1}{2}\right)\\& + \sum _{k \text { sandwiched}}\text {PPC}^{J_{k-1},J_{k+1}}\left(0,\frac {1}{2}\right).\end{align*}
\begin{align*}\left(\frac {1}{2}+o(1)\right)N & = \sum _{I\in \mathcal {I}^N}\text {PPC}^I\left(0,\frac {1}{2}\right) = \sum _I\sum _{k=1}^{r_I} \text {PPC}^{J^I_k}\left(0,\frac {1}{2}\right) +\sum _{k=1}^{r_I-1}\text {PPC}^{J^I_k,J^I_{k+1}}\left(0, \frac {1}{2}\right)\\& + \sum _{k \text { sandwiched}}\text {PPC}^{J_{k-1},J_{k+1}}\left(0,\frac {1}{2}\right).\end{align*}
Invoking Proposition4.5 in the first line we have:
 \begin{align*} \left(\frac{1}{2}+o(1)\right)N-\sum _{I \in \mathcal{I}^N}\sum _k \binom{|J_k^I|+1}{2} &\le 4\sqrt 2 \epsilon ^{1/4}\left (\sum _{I \in \mathcal{I}^N} \sum _k |J_k^I|^2\right )^{1/2}\sqrt{N} \\ & \le 8\epsilon ^{1/4}\left (\sum _{I \in \mathcal{I}^N} \sum _k \binom{|J_k^I|+1}{2}\right )^{1/2}\sqrt{N}. \end{align*}
\begin{align*} \left(\frac{1}{2}+o(1)\right)N-\sum _{I \in \mathcal{I}^N}\sum _k \binom{|J_k^I|+1}{2} &\le 4\sqrt 2 \epsilon ^{1/4}\left (\sum _{I \in \mathcal{I}^N} \sum _k |J_k^I|^2\right )^{1/2}\sqrt{N} \\ & \le 8\epsilon ^{1/4}\left (\sum _{I \in \mathcal{I}^N} \sum _k \binom{|J_k^I|+1}{2}\right )^{1/2}\sqrt{N}. \end{align*}
Writing
 \begin{equation*}\sum _{I \in \mathcal {I}^N} \sum _k \binom {|J_k^I|+1}{2} = \left(\frac {1}{2}-\delta \right) N,\end{equation*}
\begin{equation*}\sum _{I \in \mathcal {I}^N} \sum _k \binom {|J_k^I|+1}{2} = \left(\frac {1}{2}-\delta \right) N,\end{equation*}
we see
which yields (after a little computation)
![]() $\delta \le 4\sqrt{2}\epsilon ^{1/4}$
for
$\delta \le 4\sqrt{2}\epsilon ^{1/4}$
for
![]() $N$
large enough.
$N$
large enough.
5. Appendix: proof of Lemma 3.3
We restate Lemma 3.3 for the reader’s convenience.
Lemma 3.3 (Lemma 3.3). For positive integers
![]() $a,b,c,L$
satisfying
$a,b,c,L$
satisfying
![]() $1 \le a \le b \le c \le L$
, we have
$1 \le a \le b \le c \le L$
, we have
 \begin{align*}(a-1)a & + (b-a)(b-a+1)+(c-b)(c-b+1)+(L-c)(L-c+1)\\& +(a-1)(b-a)+(b-a)(c-b)+(c-b)(L-c) \ge \frac {5}{12}L^2+\frac {1}{6}L-\frac {7}{12}.\end{align*}
\begin{align*}(a-1)a & + (b-a)(b-a+1)+(c-b)(c-b+1)+(L-c)(L-c+1)\\& +(a-1)(b-a)+(b-a)(c-b)+(c-b)(L-c) \ge \frac {5}{12}L^2+\frac {1}{6}L-\frac {7}{12}.\end{align*}
Proof. Fix
![]() $L \ge 1$
. It clearly suffices to prove the inequality for all real numbers
$L \ge 1$
. It clearly suffices to prove the inequality for all real numbers
![]() $a,b,c$
satisfying
$a,b,c$
satisfying
![]() $1 \le a \le b \le c \le L$
. By compactness, we may work with a triple
$1 \le a \le b \le c \le L$
. By compactness, we may work with a triple
![]() $(a,b,c)$
that achieves the minimum value of the left hand side (which we denote
$(a,b,c)$
that achieves the minimum value of the left hand side (which we denote
![]() $\textrm{LHS}$
) minus the right hand side (which we denote
$\textrm{LHS}$
) minus the right hand side (which we denote
![]() $\textrm{RHS}$
). We divide into three cases.
$\textrm{RHS}$
). We divide into three cases.
Case 1:
![]() $c=L$
.
$c=L$
.
As one may compute,
![]() $\frac{\partial }{\partial c}[\textrm{LHS}-\textrm{RHS}] = -a+2c-L = L-a$
.
$\frac{\partial }{\partial c}[\textrm{LHS}-\textrm{RHS}] = -a+2c-L = L-a$
.
Subcase 1:
![]() $a=L$
. Then
$a=L$
. Then
![]() $b=L$
, which gives
$b=L$
, which gives
![]() $\textrm{LHS}-\textrm{RHS} = \frac{28L^2-51L+28}{48}$
, which is non-negative, since it is equal to
$\textrm{LHS}-\textrm{RHS} = \frac{28L^2-51L+28}{48}$
, which is non-negative, since it is equal to
![]() $5$
at
$5$
at
![]() $L=1$
and has derivative
$L=1$
and has derivative
![]() $56L-51$
, which is positive for
$56L-51$
, which is positive for
![]() $L \ge 1$
.
$L \ge 1$
.
Subcase 2:
![]() $a \not = L$
. Then
$a \not = L$
. Then
![]() $\frac{\partial }{\partial c}[\textrm{LHS}-\textrm{RHS}] \gt 0$
, so since
$\frac{\partial }{\partial c}[\textrm{LHS}-\textrm{RHS}] \gt 0$
, so since
![]() $(a,b,c)$
is a minimizer, we must have
$(a,b,c)$
is a minimizer, we must have
![]() $b=c$
, for otherwise we can decrease
$b=c$
, for otherwise we can decrease
![]() $c$
a bit to decrease
$c$
a bit to decrease
![]() $\textrm{LHS}-\textrm{RHS}$
. Thus,
$\textrm{LHS}-\textrm{RHS}$
. Thus,
![]() $\textrm{LHS}-\textrm{RHS} = a^2-(L+1)a+\frac{28L^2-3L+28}{48}$
, which has minimum occurring at
$\textrm{LHS}-\textrm{RHS} = a^2-(L+1)a+\frac{28L^2-3L+28}{48}$
, which has minimum occurring at
![]() $a = \frac{L+1}{2}$
, which gives
$a = \frac{L+1}{2}$
, which gives
![]() $\textrm{LHS}-\textrm{RHS} = \frac{1}{3}L^2-\frac{9}{16}L+\frac{1}{3}$
, which is always non-negative, since it is at
$\textrm{LHS}-\textrm{RHS} = \frac{1}{3}L^2-\frac{9}{16}L+\frac{1}{3}$
, which is always non-negative, since it is at
![]() $L=1$
and the derivative is
$L=1$
and the derivative is
![]() $\frac{2}{3}L-\frac{9}{16}$
, which is non-negative for
$\frac{2}{3}L-\frac{9}{16}$
, which is non-negative for
![]() $L \ge 1$
.
$L \ge 1$
.
Case 2:
![]() $c \not = L$
and
$c \not = L$
and
![]() $b = c$
.
$b = c$
.
Since
![]() $c \not = L$
and
$c \not = L$
and
![]() $(a,b,c)$
is a minimizer, we must have
$(a,b,c)$
is a minimizer, we must have
![]() $\frac{\partial }{\partial c}[\textrm{LHS}-\textrm{RHS}] \ge 0$
, for otherwise we could increase
$\frac{\partial }{\partial c}[\textrm{LHS}-\textrm{RHS}] \ge 0$
, for otherwise we could increase
![]() $b,c$
a bit to decrease
$b,c$
a bit to decrease
![]() $\textrm{LHS}-\textrm{RHS}$
. Recall
$\textrm{LHS}-\textrm{RHS}$
. Recall
![]() $\frac{\partial }{\partial c}[\textrm{LHS}-\textrm{RHS}] = -a+2c-L$
; so,
$\frac{\partial }{\partial c}[\textrm{LHS}-\textrm{RHS}] = -a+2c-L$
; so,
![]() $2c-L \ge a$
.
$2c-L \ge a$
.
Subcase 1:
![]() $a=b$
. In this case,
$a=b$
. In this case,
![]() $\textrm{LHS}-\textrm{RHS} = 2c^2-(2L+2)c+\frac{7L^2+10L+7}{12}$
, which has minimum at
$\textrm{LHS}-\textrm{RHS} = 2c^2-(2L+2)c+\frac{7L^2+10L+7}{12}$
, which has minimum at
![]() $c = \frac{L+1}{2}$
, which yields
$c = \frac{L+1}{2}$
, which yields
![]() $\textrm{LHS}-\textrm{RHS} = \frac{(L-1)^2}{12}$
, which is non-negative.
$\textrm{LHS}-\textrm{RHS} = \frac{(L-1)^2}{12}$
, which is non-negative.
Subcase 2:
![]() $a \not = b$
. In this case, we must have
$a \not = b$
. In this case, we must have
![]() $\frac{\partial }{\partial b}[\textrm{LHS}-\textrm{RHS}] \le 0$
, since otherwise we could decrease
$\frac{\partial }{\partial b}[\textrm{LHS}-\textrm{RHS}] \le 0$
, since otherwise we could decrease
![]() $b$
a bit to decrease
$b$
a bit to decrease
![]() $\textrm{LHS}-\textrm{RHS}$
. Note
$\textrm{LHS}-\textrm{RHS}$
. Note
![]() $\frac{\partial }{\partial b}[\textrm{LHS}-\textrm{RHS}] = -1+2b-L$
, so since
$\frac{\partial }{\partial b}[\textrm{LHS}-\textrm{RHS}] = -1+2b-L$
, so since
![]() $2b-L \ge a$
, we must have
$2b-L \ge a$
, we must have
![]() $a=1$
and
$a=1$
and
![]() $2b-L = 1$
. So, we have
$2b-L = 1$
. So, we have
![]() $a=1,b=\frac{L+1}{2},c=\frac{L+1}{2}$
, which indeed has
$a=1,b=\frac{L+1}{2},c=\frac{L+1}{2}$
, which indeed has
![]() $\textrm{LHS}-\textrm{RHS} \ge 0$
.
$\textrm{LHS}-\textrm{RHS} \ge 0$
.
Case 3:
![]() $c \not = L$
and
$c \not = L$
and
![]() $b \not = c$
.
$b \not = c$
.
In this case,
![]() $\frac{\partial }{\partial c}[\textrm{LHS}-\textrm{RHS}]$
must be
$\frac{\partial }{\partial c}[\textrm{LHS}-\textrm{RHS}]$
must be
![]() $0$
, for otherwise we could perturb
$0$
, for otherwise we could perturb
![]() $c$
a bit to decrease
$c$
a bit to decrease
![]() $\textrm{LHS}-\textrm{RHS}$
. So,
$\textrm{LHS}-\textrm{RHS}$
. So,
![]() $-a+2c-L = 0$
.
$-a+2c-L = 0$
.
Subcase 1:
![]() $a = 1$
. Having
$a = 1$
. Having
![]() $a=1$
and
$a=1$
and
![]() $-a+2c-L=0$
, i.e.,
$-a+2c-L=0$
, i.e.,
![]() $c = \frac{L+1}{2}$
, yields
$c = \frac{L+1}{2}$
, yields
![]() $\textrm{LHS}-\textrm{RHS} = \frac{1}{4}[4b^2-4(L+1)b+3L^2+2L-1]$
, which is minimized as
$\textrm{LHS}-\textrm{RHS} = \frac{1}{4}[4b^2-4(L+1)b+3L^2+2L-1]$
, which is minimized as
![]() $b = \frac{L+1}{2}$
, which was dealt with in Subcase 2 of Case 2.
$b = \frac{L+1}{2}$
, which was dealt with in Subcase 2 of Case 2.
Subcase 2:
![]() $a = b$
. Then,
$a = b$
. Then,
![]() $48(\textrm{LHS}-\textrm{RHS}) = 84b^2-(72L+96)b+16L^2+45L+28$
, which has minimum at
$48(\textrm{LHS}-\textrm{RHS}) = 84b^2-(72L+96)b+16L^2+45L+28$
, which has minimum at
![]() $b = \frac{72L+96}{84}$
, which gives
$b = \frac{72L+96}{84}$
, which gives
![]() $48(\textrm{LHS}-\textrm{RHS}) = 16L^2+45L+28$
, which is clearly non-negative.
$48(\textrm{LHS}-\textrm{RHS}) = 16L^2+45L+28$
, which is clearly non-negative.
Subcase 3:
![]() $a \not \in \{1,b\}$
. Then
$a \not \in \{1,b\}$
. Then
![]() $\frac{\partial }{\partial a}[\textrm{LHS}-\textrm{RHS}] = 0$
, for otherwise we could perturb
$\frac{\partial }{\partial a}[\textrm{LHS}-\textrm{RHS}] = 0$
, for otherwise we could perturb
![]() $a$
a bit to decrease
$a$
a bit to decrease
![]() $\textrm{LHS}-\textrm{RHS}$
. So,
$\textrm{LHS}-\textrm{RHS}$
. So,
![]() $-1+2a-c = 0$
. Together with
$-1+2a-c = 0$
. Together with
![]() $-a+2c-L = 0$
yields
$-a+2c-L = 0$
yields
![]() $a = \frac{L+2}{3}, c = \frac{2L+1}{3}$
, which yields
$a = \frac{L+2}{3}, c = \frac{2L+1}{3}$
, which yields
![]() $\textrm{LHS}-\textrm{RHS} = b^2-(L+1)b+\frac{12L^2+29L+12}{48}$
, which is minimized at
$\textrm{LHS}-\textrm{RHS} = b^2-(L+1)b+\frac{12L^2+29L+12}{48}$
, which is minimized at
![]() $b = \frac{L+1}{2}$
, which yields
$b = \frac{L+1}{2}$
, which yields
![]() $\frac{5L}{48}$
, which is clearly non-negative.
$\frac{5L}{48}$
, which is clearly non-negative.
Acknowledgments
We would like to thank our advisor Ben Green for suggesting this problem to us. We would also like to thank Zach Hunter for providing feedback on an earlier version of this document.