1. INTRODUCTION
Even though navigation technology has been developing year by year, ship collision still accounts for a large percentage of maritime accidents (Sormunen et al., Reference Sormunen, Hanninen and Kujala2016). There is no doubt that, once collisions occur, they have a negative impact on life, economy, and the environment.
Most of the previous methods for ship collision avoidance focus on one-to-one or one-to-few situations, where an own ship decides her course by assuming that the surrounding ships will all keep sailing as they did under the previous conditions. However, since each target ship will also try to decide her course, any decision made by the own ship will inevitably affect the future decisions of the other ships, and vice versa. In order to deal with such complex relations among multiple ships, many-to-many situations should be handled directly by modelling ships as agents who can communicate their next-intended courses, namely intentions, with each other to find their safest courses autonomously.
For many-to-many situations, few methods have been suggested in the literature except for our distributed algorithms (Kim et al., Reference Kim, Hirayama and Park2014; Reference Kim, Hirayama and Okimoto2015), which are in a form of peer-to-peer communication protocols. With these algorithms, the ships can find the safest courses by themselves without any instruction from a centralised system, such as a Vessel Traffic Service (VTS) centre. In the Distributed Local Search Algorithm (DLSA) (Kim et al., Reference Kim, Hirayama and Park2014), each ship searches for a safer course within her own local view by exchanging intentions with target ships. The Distributed Tabu Search Algorithm (DTSA) Kim et al. (Reference Kim, Hirayama and Okimoto2015) enhances DLSA with the tabu search technique to escape from a Quasi-Local Minimum (QLM) in which DLSA sometimes becomes trapped. The QLM in this context means that a ship cannot change her course even though a collision risk still exists. The common drawback of these algorithms is that a relatively large number of messages need to be sent in order for the ships to coordinate their actions. Therefore, if we try to use DLSA or DTSA for ship collision avoidance, this drawback could be fatal, especially in cases of emergency, where quick decisions should be made.
In this paper, we introduce the Distributed Stochastic Search Algorithm (DSSA), where each ship changes her intention in a stochastic manner immediately after receiving all of the intentions from the target ships. Along with our development of DSSA, we also suggest a new cost function that considers both safety and efficiency in our distributed algorithms. To examine the performance of DSSA, we made experiments to compare DLSA, DTSA, and DSSA in two different settings on the number of ships, namely four and 12 ships. In terms of sailed distance, all of the distributed algorithms show similar results. However, in terms of the number of messages that the ships exchange with each other, DSSA uses significantly fewer messages than DLSA and DTSA. Furthermore, its stochastic nature excludes the need for a specific method to escape from QLM.
The remaining parts of this paper are organised as follows. Section 2 gives related works on ship collision avoidance, and Section 3 provides the outline of distributed ship collision avoidance including the overall framework, basic terminologies, and previous algorithms. Section 4 gives the motivation and details of DSSA by highlighting its major differences from the previous algorithms. Section 5 presents and discusses the experimental results, which indicate the effectiveness of this new algorithm in benchmarks of encountering four and 12 ships. Furthermore, to demonstrate the applicability to realistic scenarios, it gives the trajectories of eight ships that DSSA computes from the real data from the Automatic Identification System (AIS) in the Strait of Dover. Section 6 concludes with a brief summary.
2. RELATED WORKS
To prevent ship collisions, the International Regulations for Preventing Collisions at Sea (COLREGS, 1972) were adopted in 1972. They specify navigation rules to be followed by all ships at sea to prevent collisions. However, it would be very hard to describe all possible conditions in the form of rules due to the complexity of the actual marine environment.
From a technological point of view, several methods have been developed to support officers in this regard, including those using a ship domain (Fujii and Tanaka, Reference Fujii and Tanaka1971; Goodwin, Reference Goodwin1975; Szlapczynski, Reference Szlapczynski2006; Wang et al., Reference Wang, Meng, Xu and Wang2009), ant colony optimisation (Tsou and Hsueh, Reference Tsou and Hsueh2010; Lazarowska, Reference Lazarowska2015), a genetic algorithm (Tsou et al., Reference Tsou, Kao and Su2010), and fuzzy theory (Lee et al., Reference Lee, Kwon and Joh2004). For example, in the algorithm using a ship domain, the notion of the safety domain has been introduced, where an own ship prevents target ships from penetrating. Both ant colony optimisation and the genetic algorithm perform searches to identify a safe course by mimicking various biological phenomena (foraging for food by ants and struggling for gene survival, respectively).
On the other hand, Szlapczynski (Reference Szlapczynski2011) suggested a new approach to collision avoidance by evolutionary algorithms. He tried to find optimal sets of safe trajectories in multi-ship encounter situations. In this approach, the fitness function is computed as the sum of the fitness of trajectories. The fitness of each trajectory considers the way loss, target ships and other obstacles. He revised the algorithm for application to restricted visibility situations and focused on compliance with COLREGS Rule 19 (Szlapczynski, Reference Szlapczynski2015). A new violation penalty was added for penetration of a ship domain, the difference for altering course, and the distance from a target ship. The methods proposed in these papers had good results. However, they focused on the application of a centralised system such as a VTS centre. If many ships encounter each other outside of VTS control, it would be difficult to apply these methods. Moreover, the number of ships used in the experiments was less than five.
Lamb and Hunt (Reference Lamb and Hunt1995) used the Poisson distribution to compute the probability of multiple encounters. The traffic flow is assumed to be uniformly distributed across the lane. The probability for various situations is computed by vessel type, speed, domain radius, and lane traffic flow during crossing situations. They revised their method by adding three options: the relationship between ships, manoeuvring angle (which is changeable), and speed reduction (Lamb and Hunt, Reference Lamb and Hunt2000). They also considered not only the first ship, but also the second ship at risk to avoid collision. Although their methods are related with multiple encounters, their focus is on how a ship finds a safe course in multiple encounters, namely a one-to-many situation.
Hu et al. (Reference Hu, Yang., Chen. and Xiao2008) investigated a negotiation framework called CANFO (Collision-Avoidance Negotiation Framework) by exploiting the planned routes of vessels. Although they explored a negotiation protocol to control the process, it is still in the preliminary stage since it deals with only a one-to-one situation.
Hornauer (Reference Hornauer2013) and Hornauer et al. (Reference Hornauer, Hahn, Blaich and Reuter2015) proposed a decentralised trajectory optimisation algorithm to avoid collision between ships that are partly cooperating with each other. The movement for non-cooperative ships is computed by a Bayesian model using the data from AIS. The probability of the estimated position for a passive ship that predicts the trajectories by historic probabilistic models is accurately computed. The computed trajectory is reasonable when three ships encounter each other. However, any new explicit algorithm among cooperating ships has not been provided in these papers.
Table 1 summarises the major features of preceding studies, where we consider the computation is “decentralised” when the ships themselves would try to solve the problem but no explicit and feasible communication protocol is provided.
Table 1. Major features of preceding studies on ship collision avoidance.

3. DISTRIBUTED SHIP COLLISION AVOIDANCE
3.1. Framework and Terminology
Distributed ship collision avoidance is made up of two procedures: the control and search procedures. Its framework is given in Figure 1.

Figure 1. Framework of Distributed Ship Collision Avoidance.
By the control procedure, a ship decides whether to proceed to the next position. If a ship does not have any target ship in the area within a certain distance from her current position and also has not yet arrived at her destination, she moves to the next position.
By the search procedure, a ship tries to avoid collision by running a distributed algorithm when she confirms that there is a collision risk. If every ship finds a solution, or if the computational time exceeds a certain time limit, they update the next positions and move to them. We set a time limit on the computational time within which ships can exchange messages with each other to figure out safe courses. When the time has elapsed, they update the next positions (typically, with the courses that may not be safe but have the minimum cost found so far) and move to them. All of the ships alternate the search and control procedures until they arrive at their destinations.
Figure 2 illustrates the basic terms. The own ship located at the centre has a detection range where she can detect target ships. The own ship can exchange messages with a target ship in the detection range, but not with a ship located outside the detection range. The own ship must keep a safety domain between herself and a target ship. The safety domain is a circle with a certain radius depending on ships. If that safety domain is penetrated, we consider they collide with each other. Let us suppose, for example, that a ship sails the ocean at 12 knots. Due to the restriction on ship movement, a sailing ship cannot change her course abruptly. Once she selects a course, she must follow it for a certain period. We set 3 minutes for that period throughout the paper. Namely, a ship is required to consider changing her course every 3 minutes (every 0·6 nautical miles). We consider this 3 minutes a unit of time to be called a time step.

Figure 2. Basic terms.
We set a time window to 15 minutes (five time steps). Namely, a ship makes a 15-minute plan on her future positions based on current positions, headings, and speeds of herself and target ships. Note that this is done every 3 minutes through communication with target ships. When a time window gets larger, a ship has a longer view of future events since she will make a longer plan on her future positions to compute the cost for each candidate course described later.
It is worth noting that distributed algorithms for ship collision avoidance operate on any number of ships with any communication structure. Suppose that three ships encounter each other as shown in Figure 3(a). Ships O and A can exchange messages directly because they are inside each other's detection range. However, ships O and B cannot because they are mutually outside of their detection ranges. A communication structure of these three ships is denoted by the graph in Figure 3(a), whose nodes are ships and edges are the possibilities of direct message exchange. A communication structure of nine ships is also shown in Figure 3(b).

Figure 3. Communication structure among three ships(a, left) and nine ships (b, right).
3.2. Cost and Improvement
Given current positions, headings, and speeds of target ships, a ship computes the cost for each candidate course. A candidate course is chosen from a discrete set of angles for alternating courses. In consideration of typical ship manoeuvring, it ranges from 45° on the port side (−45°) to 45° on the starboard side (+45°) in steps of 5°. If the heading angle for a destination exists in these bounds, it is also included as a candidate course.
We propose a cost function that is comprised of the collision risk against a target ship and the relative angle between a candidate course and a destination.
Equation (1) shows the Collision Risk (CR), where crs and j mean a candidate course and a target ship, respectively, and self means the own ship. If self will collide with ship j in its time window of 15 minutes when choosing a course crs, CR self , for crs and j is computed as TimeWindow divided by TCPA (Time to Closest Point of Approach). Otherwise, it becomes zero.
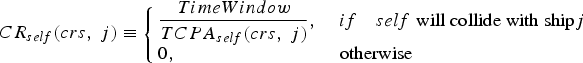 $$CR_{self}{\lpar crs\comma \; j\rpar }\equiv \left\{\matrix{\displaystyle{TimeWindow \over TCPA_{self}\lpar crs\comma \; j\rpar}\comma \; \hfill & if \quad self\, \, \hbox{will collide with ship} j \hfill \cr 0\comma \; \hfill & \hbox{otherwise} \hfill}\right. $$
$$CR_{self}{\lpar crs\comma \; j\rpar }\equiv \left\{\matrix{\displaystyle{TimeWindow \over TCPA_{self}\lpar crs\comma \; j\rpar}\comma \; \hfill & if \quad self\, \, \hbox{will collide with ship} j \hfill \cr 0\comma \; \hfill & \hbox{otherwise} \hfill}\right. $$
Equation (2) computes the cost for a course crs, which is made up of two parts: first, the sum of CR self over the target ships at risk for crs, and second, the relative angle between crs and a destination. Parameter α is a weight factor that controls the relationship between safety and efficiency. If α gets lower, a ship places more emphasis on efficiency than safety. We set the value of α to one throughout the paper.
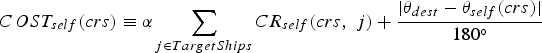 $$COST_{self}\lpar crs\rpar \equiv\alpha\sum_{j\in TargetShips}CR_{self}\lpar crs\comma \; j\rpar +\displaystyle{{\vert\theta_{dest}-\theta_{self}\lpar crs\rpar \vert}\over{180^\circ}} $$
$$COST_{self}\lpar crs\rpar \equiv\alpha\sum_{j\in TargetShips}CR_{self}\lpar crs\comma \; j\rpar +\displaystyle{{\vert\theta_{dest}-\theta_{self}\lpar crs\rpar \vert}\over{180^\circ}} $$
When performing the search procedure in Figure 1, a ship tentatively selects one course as her intention that imposes the cost computed by Equation (2). However, she may be able to reduce the cost by changing her intention to another course. Equation (3) computes the largest cost reduction as improvement self . A ship always tries to select the course that gives the largest cost reduction. Note that a tie in cost reduction is broken by following the COLREGS, which means a ship will select a starboard side when there are multiple courses that give the same largest cost reduction.
A ship is always aware of absolute angles θ heading and θ dest for her heading and destination, respectively. As shown in Equation (4), a course for the destination is computed by θ dest − θ heading to be added into a set of candidate courses only if the course is within the bounds on alterable angles.
where
![]() $crs \in \lcub -45^{\circ}\comma \; -40^{\circ}\comma \; \ldots\comma \; -5^{\circ}\comma \; 0^{\circ}\comma \; +5^{\circ}\ldots\comma \; + 40^{\circ}\comma \; + 45^{\circ} \rcub \cup \lcub \theta_{{self}\_{dest}}\rcub \ \theta_{{self}}\lpar {crs}\rpar $
returns θ
heading
+crs.
$crs \in \lcub -45^{\circ}\comma \; -40^{\circ}\comma \; \ldots\comma \; -5^{\circ}\comma \; 0^{\circ}\comma \; +5^{\circ}\ldots\comma \; + 40^{\circ}\comma \; + 45^{\circ} \rcub \cup \lcub \theta_{{self}\_{dest}}\rcub \ \theta_{{self}}\lpar {crs}\rpar $
returns θ
heading
+crs.
We demonstrate how the own ship computes COST
self
and improvement
self
using Figure 4. The own ship will collide with Target
1 after 12 minutes (four time steps) later with her current course. The cost for 000° (current intention) is computed by
![]() $COST \lpar 000^{\circ}\rpar = 15/12 + 0^{\circ}/180^{\circ} = 1{\cdot}25$
, while the cost for 045° is
$COST \lpar 000^{\circ}\rpar = 15/12 + 0^{\circ}/180^{\circ} = 1{\cdot}25$
, while the cost for 045° is
![]() ${COST}\lpar 045^{\circ}\rpar = 0 + 45^{\circ}/180^{\circ} = 0{\cdot}25$
, and the cost for 005° is
${COST}\lpar 045^{\circ}\rpar = 0 + 45^{\circ}/180^{\circ} = 0{\cdot}25$
, and the cost for 005° is
![]() ${COST}\lpar 005^{\circ}\rpar = 0 + 5^{\circ}/180^{\circ}\approx 0{\cdot}028$
. The improvement
self
for the own ship is thus computed by
${COST}\lpar 005^{\circ}\rpar = 0 + 5^{\circ}/180^{\circ}\approx 0{\cdot}028$
. The improvement
self
for the own ship is thus computed by
![]() $improvement_{self} = \max_{crs} \lcub {COST}\lpar 000^{\circ}\rpar - {COST}\lpar {crs}\rpar \rcub \approx 1{\cdot}222$
, since the cost for 005° is clearly minimum among the candidate courses. Target
2 is ruled out for computing the cost because Target
2 has nothing to do with any collision. Similarly, Target
1 will also compute her COST
self
and improvement
self
independently.
$improvement_{self} = \max_{crs} \lcub {COST}\lpar 000^{\circ}\rpar - {COST}\lpar {crs}\rpar \rcub \approx 1{\cdot}222$
, since the cost for 005° is clearly minimum among the candidate courses. Target
2 is ruled out for computing the cost because Target
2 has nothing to do with any collision. Similarly, Target
1 will also compute her COST
self
and improvement
self
independently.

Figure 4. Numerical example to compute costs and improvements.
3.3. Distributed Local Search Algorithm
DLSA is a simple distributed algorithm to minimise the total sum of costs over the ships by letting them exchange their current intentions and improvements with each other (Kim et al., Reference Kim, Hirayama and Park2014). It is an incomplete optimisation algorithm, which is not guaranteed to find an optimal solution. Namely, it may end with a sub-optimal solution even if it spends a lot of time searching for an optimum. However, it is often the case that such a sub-optimal solution is quickly found. The basic idea of DLSA is from the core process of the Distributed Breakout Algorithm (DBA) (Yokoo and Hirayama, Reference Yokoo and Hirayama1996; Hirayama and Yokoo, Reference Hirayama and Yokoo2005).
Figure 5 illustrates ship collision avoidance by DLSA. Suppose that three ships encounter each other. Each ship first exchanges their current intentions by ok? messages with target ships to compute COST self for each candidate course as shown in Figures 5(a) and 5(b). The number of messages exchanged to do so is six in this example. Then, based on COST self for each candidate course, she computes improvement self to be sent by improve messages as shown in Figure 5(c). The number of messages exchanged to do so is also six. Finally, as shown in Figure 5(d), the ship that has the largest improvement self , ship 3, changes her intention, while the other ships maintain their current intentions. We should note that, to reach this state, DLSA consumed 12 messages and two cycles of message exchange.

Figure 5. Procedure for DLSA (a, top-left), (b, top-right), (c, bottom-left), (d, bottom-right).
To prevent an endless loop, only one ship can change her intention at a time among herself and target ships. This process is repeated until the overall cost becomes zero or the computational time exceeds a time limit.Footnote 1 After all the ships have set their optimal courses as their intentions, they proceed to the next position. At the new position, each ship then starts identifying new target ships within the detection range to avoid collisions by DLSA again.
Figure 6 shows the procedure for DLSA. At the initial step, all ships select the current courses as their intentions. After exchanging their current intentions by ok? messages, they compute COST self and improvement self . If there exists a ship having non-zero COST self for her intention, the ship that has a larger improvement self than those of target ships changes her intention after exchanging improvement self . This process is repeated until all ships are content with their current intentions. If there is a tie in choosing a ship with the largest improvement self , it is broken in favour for a smaller ID number of ship.

Figure 6. Procedure for DLSA.
3.4. Distributed Tabu Search Algorithm
We have observed that DLSA is sometimes trapped in a Quasi-Local Minimum (QLM), where a ship is unable to change her course even though a collision risk still exists. To solve this problem, we applied the tabu search technique (Glover, Reference Glover1989), where the ship in QLM puts her current course in a tabu list to prohibit herself from selecting that course for a certain period. The resulting algorithm was called the Distributed Tabu Search Algorithm (DTSA) (Kim et al., Reference Kim, Hirayama and Okimoto2015).
Figure 7 shows the procedure for DTSA. The whole framework is essentially the same as DLSA; only the QLM procedure (dotted red box) is added. This process is repeated until all ships are content with their current intentions. If QLM occurs, a ship calls the QLM procedure, in which she randomly chooses an alternate course excepting any course in the tabu list. This process will be recurred until QLM is resolved.

Figure 7. Procedure for DTSA.
4. DISTRIBUTED STOCHASTIC SEARCH ALGORITHM
4.1. Motivation
The common drawback of DLSA and DTSA is that they must send a relatively large number of messages in order for the ships to coordinate their actions. In the context of distributed constraint optimisation, the Distributed Stochastic Algorithm (DSA) has been proposed to reduce the number of messages by allowing neighbouring agents to perform simultaneous changes in a stochastic manner (Zhang et al., Reference Zhang, Wang and Wittenburg2002; Reference Zhang, Wang, Xing and Wittenburg2005). They reveal that these simultaneous changes often lead to faster convergence to a sub-optimal solution; furthermore, its stochastic nature excludes the need for a specific method to escape from QLM. The basic idea of DSA is so general that it can be applied to many optimisation problems (like local search and tabu search). In their original papers, DSA was applied to the graph colouring problem (Zhang et al., Reference Zhang, Wang and Wittenburg2002) and the scheduling problem on sensor networks (Zhang et al., Reference Zhang, Wang, Xing and Wittenburg2005). Although several studies have been made on DSA since its development, we are not aware that there is any study that tackles the collision avoidance problem using this idea.
4.2. Detail
Figure 8 shows the procedure for the Distributed Stochastic Search Algorithm for ship collision avoidance (DSSA). First, a ship selects the current course as her intention. After exchanging intentions with target ships, she computes COST self and improvement self . If any of the ships is not content with her current intention, she changes it by Rule A described below. This process is repeated in parallel over the ships until all the ships are content with their current intentions.

Figure 8. Procedure for DSSA(p).
A new intention is chosen stochastically by Rule A, where only the ship with positive improvement self chooses the course with probability improvement self as her new intention, but keeps her current intention with probability 1 − p. This probability is a parameter that controls the stochastic behaviour of ships. We denote DSSA with a certain value p for this probability as DSSA(p) if necessary.
Table 2 summarises the main features of our distributed algorithms for ship collision avoidance. We should point out that both DLSA and DTSA require two cycles of message exchange for some of the ships to change intentions. Namely, they require one cycle for ok? messages and another cycle for improve messages. However, in DSSA, one cycle suffices for some ships to change intentions since there is no need to exchange improvement self .
Table 2. Comparison of DLSA, DTSA, and DSSA.

5. EXPERIMENTS
First, to examine the performance of DSSA, we made experiments to compare DLSA, DTSA, and DSSA in two different settings on the number of ships, namely four and 12 ships, in Sections 5.1 and 5.2. We measured the average distance and the number of messages for each algorithm. The average distance is the average length of trajectories over the ships from their origins to destinations that are obtained by an algorithm. The number of messages is the total number of messages exchanged among ships, assuming that they communicate with each other on a peer-to-peer communication system. It is commonly used to evaluate the performance of distributed algorithms. The lower these measures are, the better the performance is. In these experiments, we assume that all ships have the same and constant speed of 12 knots for simplicity. Regarding the parameters of individual algorithms, we set a length of tabu list for DTSA to one and the probability for DSSA to 0·5 (i.e., DSSA(0·5)).
Then, to demonstrate the applicability to realistic scenarios, we made an experiment to see how DSSA performs for real data in Section 5.3. We used real data from AIS that involves eight ships in the Strait of Dover.
All of these experiments were conducted on the discrete event simulator written in MATLAB.
In the real world, the message exchange among ships occurs in parallel. To simulate this on a single CPU machine, the discrete event simulator has been frequently used to evaluate the performance of distributed algorithms (Yokoo and Hirayama, Reference Yokoo and Hirayama1996; Hirayama and Yokoo, Reference Hirayama and Yokoo2005). In this simulator, a sequence of parallel events is controlled by cycles. More specifically, at one cycle on this simulator, every ship performs the following sequence of actions: 1) reads all incoming messages from her neighbours, 2) computes costs, improvement, or a new intention to create an outgoing message, and 3) sends this message to each of her neighbours. The cycle of these actions is repeated until a termination condition is met.
5.1. Four-ship Encounter
Table 3 indicates the values for parameters of four ships. Every ship has the same and constant speed of 12 knots. The radii of detection range and safety domain are set to 12 and 0·5 nautical miles, respectively. All four ships, each sailing in a diagonal direction, are arranged so that they intersect with each other at the centre. Each ship repeats the control and search procedures in Figure 1 every 3 minutes as suggested in Section 3.1. The time limit for the search procedure is controlled over 3–10 seconds in steps of one second in order to observe how the overall performance changes when more time is allocated for the search procedure.
Table 3. Values for parameters of four ships.

To clarify the importance of exchanging intentions explicitly among ships, we first illustrate in Figure 9 the simulated trajectories of (a) “non-cooperative” and (b) “cooperative” ships for this instance.Footnote 2 By a “non-cooperative” ship, we mean the ship with the RADAR/ARPA system that always selects the best course (in terms of our cost function), which is computed through sensing data of target ships. On the other hand, by a “cooperative” ship, we mean the ship with our distributed algorithm that always selects the best course (in terms of our cost function), which is computed through exchanging intentions with target ships. The trajectories of four “non-cooperative” ships are shown in Figure 9(a), which clearly indicates that the ships change their courses suddenly and significantly. These behaviours can generally lead to unstable and longer trajectories. On the other hand, those of four “cooperative” ships with DSSA are also shown in Figure 9(b), which clearly indicates that the ships go smoothly to their destinations without collisions. The “cooperative” ships are likely to have a shorter average distance than the “non-cooperative” ships.

Figure 9. Simulated trajectories of four ships by non-cooperative (a, left) and cooperative (b, right).
Then, we compare the performance of DLSA, DTSA, and DSSA(0·5) for this instance while varying a time limit from 3 to 10 seconds. The results of this simulation are shown in Figure 10. The bar indicates the average distance, which is the average length of trajectories over the ships, and the line indicates the number of messages exchanged among the ships. Compared to DLSA and DTSA, DSSA(0·5) showed better performance in both measures. In terms of average distance, DLSA and DTSA showed almost the same results. The average distance for DSSA was lower than for DLSA and DTSA. In terms of the number of messages, the longer the time limit, the greater the number of messages for every algorithm. In comparison with those for DLSA and DTSA, the number of messages for DSSA was significantly lower regardless of time limit. This implies that DSSA did not exceed any time limit to find optimal courses for all ships, while DLSA and DTSA often did so. DSSA enables multiple ships to alter their intentions simultaneously, leading to fast convergence to the optimum within one second.

Figure 10. Performance of algorithms for four-ship encounter.
In order to prove that collision never occurred in this experiment, we show DCPA (Distance at Closest Point of Approach) for any pair of four ships with DSSA in Table 4. Note that the minimum DCPA was 0·5177 nm between ships 2 and 3, which is larger than the radius of safety domain (0·5 nm). Figure 11 also shows the trajectories of four ships.

Figure 11. Simulated trajectories of four ships by DSSA(0·5).
Table 4. DCPA for any pair of four ships. (unit: nm)

5.2. 12-ship Encounter
Table 5 indicates the values for parameters of 12 ships, which are the same as in the previous experiment except for origin/destination/heading of ships. We arranged 12 ships as in Figure 12, which also shows the simulated trajectories by DSSA. All the ships arrived at their destinations without any collision, since the minimum DCPA was 1·0007 nm between ships 6 and 9 (see Table 6). It also demonstrates how much a ship's decision is affected by target ships. The ships in the middle that are surrounded by many target ships altered their courses significantly while other ships altered their courses only a little.

Figure 12. Simulated trajectories of 12 ships by DSSA(0·5).
Table 5. Values for parameters of 12 ships.

Table 6. DCPA for any pair of 12 ships. (unit: nm).

Figure 13 shows the average distance and the number of messages for this instance. In terms of average distance, all algorithms showed a similar result. In terms of the number of messages, DSSA had many fewer than DLSA and DTSA.

Figure 13. Performance of algorithms for 12-ship encounter.
In addition to the above experiments, we have examined the performance of DLSA, DTSA and DSSA on various artificial settings, such as the one with 100 ships with randomly generated origins, destinations, and headings. We should point out that we have obtained similar results to the above.
5.3. Real data from AIS in the Strait of Dover
To demonstrate the applicability to real scenarios, we applied DSSA to the real data from AIS in the Strait of Dover as shown in Figure 14, which includes eight ships with different speeds, safety domains, origins, destinations, and headings. Details are also shown in Table 7. These data were collected from the website (vesselfinder.com). Note that the time limit for the search procedure was fixed to 3 seconds.

Figure 14. Eight ships in the Strait of Dover. (source: www.vesselfinder.com)
Table 7. Values for parameters of eight ships in the Strait of Dover.

Figure 15 indicates the trajectories of eight ships computed by DSSA. Table 8 shows DCPA for any pair of eight ships, where the minimum DCPA is 0·5544 nm between ships 4 and 8. Although these eight ships have different safety domains, Table 8 clearly indicates that all ships arrived at their destinations without collision.

Figure 15. Simulated trajectories of eight ships in the Strait of Dover by DSSA.
Table 8. DCPA for any pair of eight ships. (unit: nm)

6. Conclusion
We are developing distributed algorithms to replace previous algorithms that consider only one-to-one or one-to-few ship situations.
DLSA is the first distributed algorithm that considers ship collision avoidance in many-to-many situations. It enables each individual ship to decide her action by communicating with target ships, with no need for any centralised system such as a Vessel Traffic Service centre. However, DLSA sometimes gets trapped in a Quasi-Local Minimum (QLM), where a ship cannot change her course even though a collision risk still exists. To resolve the QLM issue, we have suggested DTSA, which performs tabu search to enable a ship to search for other courses compulsorily when trapped in QLM.
In this paper, we introduced DSSA, where each ship changes her intention in a stochastic manner immediately after receiving all the intentions from target ships. DSSA enables ships to exchange significantly fewer messages than DLSA and DTSA; furthermore, its stochastic nature excludes the need for a specific method to escape from QLM. Through developing DSSA, we also suggested a new cost function that considers both safety and efficiency in our distributed algorithms. We empirically showed that DSSA performed better than DLSA and DTSA in terms of the number of messages for artificial situations. Then, we also demonstrated the trajectories of eight ships that DSSA computes from the real data from AIS in the Strait of Dover.
There would be several directions in which to expand this work. Currently, the actions taken by ships are limited to only altering courses. For more flexible control, especially in critical situations, not only altering courses but also speed change may need to be considered.
Although we have parameters in Equation (2) to control the relationship between safety and efficiency, this topic has not been fully explored yet. Which value brings the best balance between safety and efficiency may need to be investigated.
Distributed algorithms implicitly assume that all ships can communicate with each other and furthermore they are basically “cooperative”. However, in reality, there may be ships or moving obstacles with which we cannot exchange intentions. Our distributed algorithm framework needs to be generalised to deal with such a situation with “non-cooperative” ships.

























