Introduction
Snow texture and its associated mechanical and thermal properties play a key role in avalanche research. Reference Arons and ColbeckArons and Colbeck (1995) define the texture of snow in terms of both micro- and mesostructure. Besides grain-size and grain shape, the arrangement of the grains in a snow sample is included in this definition. This general definition takes into consideration the bonds between the grains. Microscale features are grain shape and grain-size. The mesostructural features are more complex, and include the spatial arrangement of the grains and the intergranular connections. The idea behind the texture index (TI) is to combine the micro- and mesoscale features of a snow layer in order to express its textural properties (Reference Schneebeli, Pielmeier and JohnsonSchneebeli and others, 1998). The ratio of mean grain-size and volumetric density decreases for smaller spherical structural elements. Furthermore, theTI is a direct index of the volume density of grain contacts, which encompasses the number and size of grain contacts. A low value of TI is interpreted as high volume density of grain contacts which indicates high textural stability A high value of TI is interpreted as low volume density of grain contacts which indicates low textural stability Two natural snow profiles containing weak layers have been successfully classified by theTI (Reference Schneebeli, Pielmeier and JohnsonSchneebeli and others, 1998).
In this approach, theTI is further calculated for laboratory snow samples taken by Reference Baunach, Fierz, Satyawali and SchneebeliBaunach and others (2001). Grain-size and density are simulated for these samples by a one-dimensional snowpack model. A comparison of measured and simulated parameters shows good agreement. Hence, we can establish a link between an objective mechanical measurement of the snow cover and a numerical model. Since the empirically derived parameters also agree with the simulated ones, we also have a link to the classical snow-cover investigation methods. Three natural classical snow profiles taken during winter 1998/99 at the Weissfluhjoch (Switzerland) test-field are compared to their simulations. The snowpack was simulated using data from the automatic snow station situated at the test-field. The comparisons show that we cannot readily compare theTI calculated from a classical profile with theTI from its simulation.
The Texture Index of Snow
The TI was formulated from a model conception of the bonding of snow in order to classify snow types from the micropenetrometer’s force signal. The TI (m4g−1) is the fraction of mean grain-size (mm) and density (kg m−3):

The idea behind theTI is that smaller spherical structural elements have a decreasing TI, i.e. a decreasing ratio between mean grain-size and density. This ratio accounts for the connectedness or textural stability of the grains, in that it is a direct index of the volume density of grain contacts. We use a dimensioned index because it describes a concrete geometric model. Moreover, the strength of the bonds themselves is responsible for the mechanical strength of the snow, though this is not accounted for by theTI.The basis for formulating the TI was 23 natural and artificial metamorphosed snow samples that were analyzed in terms of mean grain-size and density. The resulting TIs could be correlated to the coefficient of variation (CV) of the micropenetrometer’s force signal derived from these samples. The calculation of the equation for the least-squares line, the so-called linear regression, resulted in the following coefficients:
The coefficients are highly significant (p < 0.001) and the coefficient of correlation r is 0.89 (Reference Schneebeli, Pielmeier and JohnsonSchneebeli and others, 1998). Based on this model, the TI can be estimated with values of the CV from the penetrometer’s force signal. The CV is calculated for intervals of 1000 force data values. Modelled TI values of < 0.003 indicate a high textural stability; values of 0.003–0.006 indicate a transition between textural stability and instability; and values of > 0.006 indicate textural instability. With a combination of theTI and the median penetration force, snow profiles can be interpreted. If the median is <0.03N, the variation of the signal cannot be interpreted. These low values for the median correspond to the device travelling through air, and indicate a very soft layer or in fact air. If the median is >2.3N, resonant frequencies start to superpose the variation of the force signal. In this case, the variation of the force signal cannot be interpreted. These high values for the median correspond with very hard or ice layers in the snowpack which themselves are stable by nature.
Data
Experiments
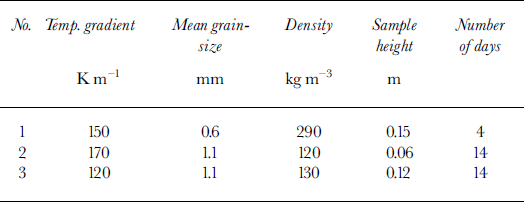
During winter 1998/99, experiments with artificially metamorphosed snow were conducted in the cold laboratory by Reference Baunach, Fierz, Satyawali and SchneebeliBaunach and others (2001) to study grain growth under different temperature gradients. Table 1 gives an overview of the initial state of the snow samples. Grain-size and density measurements were taken throughout the run of the experiments. We used the data from the experiments to compare the empirical TI from laboratory measurements with the TI derived from a SNOWPACK simulation of grain-size and density.
Table 1. Summary of initial state of the experimental snow samples
Experimental laboratory methods
To measure the volumetric density the content of a 100 cm3 cylinder or a density shovel with the same volume is weighed. The density sample is carefully cut from the centre height of the snow block with the cylinder or shovel, the net weight is determined and density in kg m−3 is calculated with an accuracy of ±5 kg m−3. The grain-size is determined by sieving (Reference Sturm and BensonSturm and Benson, 1997). For sieve analysis in the cold laboratory, the content of three 100 cm3 density shovels is sieved through a stack of five aluminium sieves (mesh openings from bottom up are 0.25, 0.5, 1, 2 and 4 mm). For each grain-size fraction the weight is determined with an accuracy of ±0.01 g, and the mean grain-size is calculated using the equation (Reference Friedman and SandersFriedman and Sanders, 1983)

where
![]() is the mean grain diameter for the sample, Mj is the weight fraction in the jth sieve, and
is the mean grain diameter for the sample, Mj is the weight fraction in the jth sieve, and
![]() is the average of the sieve-mesh opening of the jth and j+1 th sieves, with a total of L sieves. The error of the grain-size d in one particular sieve is
is the average of the sieve-mesh opening of the jth and j+1 th sieves, with a total of L sieves. The error of the grain-size d in one particular sieve is
where n is the number of grains in the jth sieve. Assuming large n and a normal distribution of the grain-size in one particular sieve, the error around the mean approaches zero. Based on the original data of experiment 1, the maximum weight of the grain-size fraction from 0.5 to 1 mm was 72.8 g of ice. This is equivalent to a sample size of 3532 grains. The accuracy of the mean grain-size calculated from all sieves is dominated by the particular sieve receiving the largest weight. Hence, by using large sample sizes we achieve a very small statistical error on the mean grain-size determined by sieving.
In the following comparisons of the laboratory experiments the mean grain-size from sieve analysis is used. Reference Baunach, Fierz, Satyawali and SchneebeliBaunach and others (2001) found that the mean grain-size from sieve analysis is within ±10% of the average diameter determined by image analysis using standard image-processing software. Visual observation yields a very good approximation of the maximum diameter received from image analysis. However, the average grain-size determined by the observers is closer to the minimum grain-size determined by image analysis. To avoid a bias to extreme grain-size in a sample analyzed in the field, the observers of the Swiss Avalanche Warning Centre give a range of grain-sizes instead of a single value when taking a classical snow profile.
Simulation
SNOWPACK is a one-dimensional, physical snowpack model based on the finite-element method. It was developed for the Swiss National Avalanche Warning Service (Reference Lehning and BarteltLehning and Bartelt, 1999; Reference Lehning, Bartelt, Brown, Russi, Stockli and ZimmerliLehning and others, 1999). The model is used to attend to the special requirements of avalanche warning in Alpine Switzerland. One important task is the estimation of macro- and microscopic properties of individual layers and their development through time. Bulk density and grain-size are included in these properties. The SNOWPAGK model is used to calculate a simulation of the development of the laboratory snow experiments. In SNOWPAGK the initial conditions are new-snow height, grain-size and new-snow density (the case of dry snow is assumed). In the case of the laboratory experiments, the new-snow height is equivalent to the height of the sample. Density of the new snow is equivalent to the measured initial density, and in every experiment the same initial grain-size of 0.6 mm is used. The grain-size is adapted to this fixed value, so that the model can start calculating grain growth upon the total decomposition of the new-snow dendrites (Reference Baunach, Fierz, Satyawali and SchneebeliBaunach and others, 2001). Further initial conditions are given by the snow-grain characteristics dendricity and sphericity (Reference Lesaffre, Pougatch and MartinLesaffre and others, 1998; Reference Fierz and BaunachFierz and Baunach, 2000). The sphericity and dendricity for new snow are set to 0.5. Dendricity is adapted by the model so that it is zero when grain growth commences. The boundary conditions in SNOWPAGK are usually determined by the meteorological situation obtained from the automatic snow stations of the Swiss Interkantonales Mess- und Informationssystem (IMIS) network. Boundary conditions in the field for determining the conditions at the top of the snowpack are either heat-flux parameters (Neumann condition), i.e. short- and longwave radiation as well as sensible- and latent-heat transfers, or surface and bottom temperature of the snow-pack (Dinchlet condition) (Reference Lehning, Bartelt, Brown, Russi, Stockli and ZimmerliLehning and others, 1999). In the simulation of the laboratory experiments, the boundary conditions are set to the surface and bottom temperatures of the snow samples. With temperatures always < 0°C (case of dry snow) the Dirichlet condition is fulfilled and SNOWPAGK uses the appropriate formulations. Temperatures are controlled during the experiments by thermocouples situated at the bottom, in the middle and on top of the snow sample in the metamorphosis box. Table 2 shows the boundary conditions for the three laboratory experiments. After all initial and boundary conditions are defined, we use SNOWPAGK to calculate the development of grain-size and density of our laboratory snow samples. These simulated values are then compared to the measurements taken throughout the experiment.
Table 2. Boundary conditions of the experimental snow samples

Comparison of Laboratory Experiments
To compare the simulated and measured TI from the laboratory snow, we take the ratio of mean grain-size to density, from both the measurements and the simulations described above. The simulation delivers half-hour values for the two parameters. The measurements are taken in larger time-steps. Figure 1 shows the simulated vs measured TI for the three laboratory experiments. The symbols on the measured curves indicate the discrete point in time where measurements were taken.

Fig. 1. TI for laboratory experiments 1–3.
Results
The comparison of simulated vs measured TI shows good agreement for all three experiments. Generally, the trend to an increasing TI, i.e. an increasing textural instability, is captured very well in all simulations. This trend is due to the fast formation of faceted snow under high temperature gradients. The developing depth-hoar crystals grow in size while the number of bonds declines. Both experiments 2 and 3 show a significant underestimation of the measured values at the start of the experiment between days 0 and 1. This underestimated TI is due to an overestimation of the density at the start of the experiment. SNOWPAGK delivers a settlement rate for new snow layers that is too small in the first 2 days after deposition. In the model calculations, the higher density values at the start were deliberately set as initial density to avoid underestimating the settlement in the beginning. With the TI we can easily detect this problem. It reoccurs in the simulation of the snow profiles and is discussed in the next section.
Comparison of Snow Profiles
Snow profiles at the Weissfluhjoch test-field are taken biweekly by the observers of the Swiss Avalanche Warning Centre. Grain-size and density information is recorded and input on a profile sheet. An example profile sheet is shown in Figure 2. The observer records ramm hardness, temperature, stratigraphy, humidity, grain-size and shape, hand hardness and density throughout the profile. The classification of grain shape and hand hardness is based on the Handbook for Observers (SLF, 1989). The observer takes density measurements between marker threads that are placed on the surface of the snowpack after each biweekly profile. Therefore the snow deposited over the previous 2 weeks becomes integrated in one density measurement. For grain-size and grain shape the observer determines the individual layers for which these two parameters are recorded. Hence, measured density layers and grain-size layers do not correspond. Grain-size is measured by visual inspection (using a magnifying lens) of a large number of grains on a measuring plate. The observers do not record one single grain-size for a layer, but a range of grain-sizes. The measured grain-size value used in each of our comparisons is the mean of that given range. This practice is used to avoid a bias towards the extreme grain-sizes in a sample and hence to reduce the error of the grain-size measurements in the field.

Fig. 2. Classical snow profile.
Three classical snow profiles taken by observers of the Swiss Avalanche Warning Service during winter 1998/99 at the Weissfluhjoch test-field are compared to their SNOWPACK simulations. The three profiles were taken on 1 December 1998, 15 January 1999 and 16 February 1999. For all profiles the simulated and measured TIs are compared and systematic deviations are depicted.
Profile 1
The comparison for profile 1 is shown in Figure 3. In this profile the simulated TI is generally too low compared to the measured TI. The high simulated TI (>0.006) at the top of the profile represents a simulated surface-hoar layer that was observed in the field, but no density was measured. The high measured TI at the base of the profile is due to observed large grains that are not captured in the simulated profile. Figure 4 shows the comparison of grain-size and density for profile 1. In the following the deviations for grain-size and density are described separately from bottom to top of the profile.

Fig. 3. T1 comparison for profile 1.

Fig. 4. Grain-size and density for profile 1.
Grain-size
The simulated grain-size is generally too small, and in particular it is 1 mm too small at the bottom of the profile. In the lower part of the profile, melt-freeze crusts and one ice lens were observed. Grain-size was measured for the melt-freeze crusts but not for the ice lens. Ice lenses and crusts do not appear in the simulation. In the middle to top layers the simulated and measured grain-sizes match well. The high value for grain-size at the very top represents a simulated surface-hoar layer that was also observed.
Density
At the bottom of the profile the simulated density is significantly too high (about 100 kg m−3). For melt-freeze crusts and ice lenses there is no measured density. Simulated and measured densities match well up to the middle of the profile where the simulated density is overestimated by 150 kg m−3. Again there is good agreement up to the surface. The density of the simulated surface-hoar layer is taken to be 15kg m−3 in SNOWPAGK. The surface-hoar layer was observed in the field, but no density was measured.
Profile 2
Figure 5 is theTI comparison for profile 2. Since grain-size for ice lenses was not measured in this profile, an empirical approximation of 5 mm is used. Therefore the measured TI is higher for the observed ice lens. Ice lenses do not appear at all in the simulation. The simulated TI is generally too low compared to the measured TI. The high measured TI at the base of the profile is due to observed large grains that are not captured by the simulated TI. In the upper half of the profile there are five TI peaks that do not agree with the measured TI. These simulated peaks are well above aTI value of 0.006 and represent predicted buried surface-hoar layers. These simulated buried surface-hoar layers were not observed in the field. At the top of the profile a graupel layer was observed that does not appear in the simulation. Because of the relatively large grain-size of the graupel, the measured TI is much higher than the simulated TI at the surface. Figure 6 shows the comparison of grain-size and density for profile 2.

Fig. 5. TI comparison for profile 2.

Fig. 6. Gram-size and density for profile 2
Grain-size
At the bottom of the profile the simulated grain-size is too small. Ice lenses and melt-freeze layers recorded by the observer are not simulated at all. The measured grain-size of ice lenses is taken to be 5 mm. Two observed ice lenses occur in the lower half of the profile. In the upper half of the profile the simulated grain-size shows five peaks which represent buried surface-hoar layers. The simulated grain-size reaches 36 mm. Only in one instance was a layer of buried surface hoar measured in this profile. However, it differs in profile height (measured layer at 90 cm) and grain-size (measured grain-size 1–2 mm). Towards the surface of the profile the measured grain-size increases steadily from 1 to 4 mm. The model does not capture this increase.
Density
At the very bottom of the profile the simulated density is about 100 kg m−3 too high, as in profile 1. Throughout the profile the simulated density over- and underestimates the measured density by 50 and 100 kg m−3. The buried surface-hoar layers, with the very low modelled density of 15kg m−3, are not measured in the snow profile. For the observed surface-hoar layer, density could not be measured. This layer also does not appear in the simulated density at this position. At the surface the simulated density agrees well with the measured density.
Profiles
Figure 7 is theTI comparison for profile 3. In the lower half of the profile the simulated TI is too low. The four simulated buried surface-hoar layers were not observed in the field except for one layer at profile height 120 cm. This buried surface-hoar layer was predicted very closely to the measured layer but was simulated with a much higher TI. The predicted surface-hoar layer just below the surface of the profile was not measured in the field. It appears as a simulated TI peak. Figure 8 shows the comparison of grain-size and density for profile 3.

Fig. 7. TI comparison for profile 3.

Fig. 8. Grain-size and density for profile 3.
Grain-size
The higher measured TI at the bottom of the profile results from an observed depth-hoar layer that does not appear in the simulated TI. The measured grain-size in this layer exceeds the simulated grain-size by 1 mm. Three of the four simulated buried surface-hoar layers in this profile were not observed. At a profile height of 120 cm there is one observed buried surface-hoar layer in close proximity to the simulated one (1cm). However, the simulated grain-size is more than double the measured grain-size (7 mm vs 3 mm). The simulated surface-hoar layer just below the surface was not observed.
Density
The simulated density at the bottom of the profile is 150 kg m−3 higher than the measured density. At 60 cm profile height, the simulated density drops 100 kg m−3 below the measured density. By definition, the simulated density of the buried surface-hoar layers is taken to be 15kg m−3 in SNOWPACK. In the case of the observed buried surface-hoar layer no density was measured because the layer was too fine for a measurement. The measured density here is the integrated density for the larger layer surrounding the buried surface-hoar layer. Increased grain-size was measured in the surface layer and the layer just below the surface. However, density measurements are not available for these layers.
Results
The simulated grain-size at the bottom of the profiles is too small.
Ice lenses and crusts or melt-freeze layers do not appear in the SNOWPACK simulation. They are qualitatively described in the measured profile, and in only a few cases could the grain-size be measured. Density of ice lenses and crusts cannot be measured in the field.
SNOWPACK calculates surface hoar as soon as the conditions fulfil the minimum requirements for its development. This guarantees that surface hoar is simulated in any case when it actually occurs, but often the simulated surface hoar is not observed in the field. This was the case at the surface of two profiles. Instead of surface hoar, the observer recorded a graupel layer, and in the other case decomposing fragmented particles at the surface were recorded.
Consequently, the buried surface-hoar layers are too many in the simulated profiles. Out of all simulated buried surface-hoar layers only two were actually observed. For these measured buried surface-hoar layers the observed grain-size was much smaller than the simulated grain-size.
The low density of the simulated buried surface-hoar layers has not been measured.
The simulated density at the bottom of the profiles is too high.
Discussion
The comparison of theTI for the three laboratory experiments shows good agreement. This was in part expected because these experiments were conducted to improve the model specifications, particularly the laws of grain growth under strong temperature gradients.
The comparison of the snow profiles shows a number of systematic deviations between simulated and measured TI. The deviations of the absolute profile height are due to spatial variability. In case of the missing simulated crusts and ice lenses, SNOWPACK must be adapted in the future to display the melt-freeze features. The density of crusts and ice lenses cannot easily be measured so far in the field. However, an empirical value (about 500 kg m−3) obtained from image analysis is better suited to account for the actual density discontinuity. Often these abrupt discontinuities are weak interfaces within a snowpack.
Another major deviation appears with the buried surface-hoar layers. Up to five buried surface-hoar layers are displayed in the simulation within one profile. For visualization purposes, if the number of layers exceeds five, the least pronounced surface-hoar layer drops to the background of the calculations and is no longer displayed in the simulation. Also, by definition, the simulated grain-size of buried surface-hoar layers is taken to be equal to the height of this layer, and the simulated density is taken to be 15 kg m−3 in SNOWPACK. Upon completion, these defined values will be adapted to the results of an extended surface-hoar study at the SLF According to P. Fohn (personal communication, 2000) the following values are most likely: surface hoar at the surface has a mean density of 100 kg m−3; buried surface hoar has a mean density of 100–250 kg m−3; grain-size is highly variable, ranging from mm to cm. SNOWPACK calculates more surface-hoar layers than are observed. Once simulated at the surface, these layers remain constant as buried surface-hoar layers in the simulated profile. Field observations, however, show that buried surface-hoar layers can be destructively metamorphosed. Because the density measurements in the field are too crude to pick up these fine layers, and the grain-size observations are highly subjective, it is impossible at the moment to verify the existence of all the buried surface-hoar layers that appear in the model.
The settlement at the near-surface is well simulated, but in the middle of the profile settlement is generally too low and at the bottom too fast. This explains why the simulated density is significantly too high in the upper part of the profile and significantly too low in the lower part. Also, new snow settles too slowly in the model.
The model simulates grain growth under high temperature gradients only after complete decomposition of the dendrites. However, such metamorphism has also been observed in the field with partially decomposed dendrites.
It is likely that the classical grain-size and density measurements are too crude to resolve fine layers within the snow-pack. Grain-size and density measurements need the same resolution to make them readily comparable to the simulation. With the methods applied so far, we cannot verify fine layers that are simulated. Highly resolved measurements are necessary to capture the heterogeneity of the layers and within the layers of a natural snowpack. The TI can be derived from the force signal of a snow micropenetrometer. Therefore, higher resolved field measurements plus penetrometer measurements in the immediate vicinity of the snow profile will allow for a better verification of SNOWPACK simulations.
The TI can be used to partially interpret the snow stability of layers in a snowpack. The number of contacts per unit volume is an indication of snow stability. Moreover, the strength of the bonds themselves is responsible for the mechanical strength of the snow, which is not accounted for by theTI. However, a combined analysis of TI and median penetration force allows the microtexture and bond strength to be interpreted. With stereological methods we cannot properly measure bond size and bond strength. Methods for the three-dimensional reconstruction of snow are now being further developed to approach this problem. TheTI was chosen for the comparison because it is thought to be the lowest common denominator in the approach to microtextural characterization of snow in the field.
Conclusion
The TI is a useful measure to partially interpret the mechanical stability of snow because it can be determined easily in the field by classical snow-cover investigation methods. For laboratory snow samples, the TI can be predicted by a numerical snow-pack model. However, systematic deviations between field measurements and simulations have appeared in the comparison of three natural snow profiles. The discussion of the deviations reveals that improvements in the model formulations as well as improvements in field methods are necessary to make them readily comparable. Highly accurate measurements are necessary to capture the heterogeneity of the snow properties of a layered natural snowpack. Especially thin layers cannot be sufficiently quantified by the applied field methods. Yet they have a major influence on mechanical and thermal processes and on the stability of a snowpack. The TI derived from the force signal of a snow micropenetrometer can easily detect these thin layers. More accurate classical measurements combined with penetrometer measurements in the immediate vicinity of the snow profile will allow for a better verification of SNOWPACK simulations. TheTI and the median penetration force obtained from the penetrometer give a good and fast indication of weak layers in a snowpack. The information obtained from the penetrometer profile could be further used to apply additional mechanical tests (shear frame, rutschblock) on an identified weak layer. Highly resolved field measurements improve the profile interpretation, the avalanche warning and avalanche prediction. They also allow better model verification which leads to improved simulations which can be used in avalanche warning and prediction.
Acknowledgements
We thank T. Baunach and M. Lehning for providing the simulations. Thanks to T. Baunach, C. Fierz, P. Fohn and M. Lehning for the discussions. We also thank A. Sato, an anomymous reviewer and D. McClung for their reviews.












