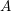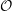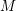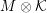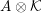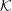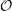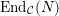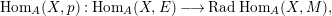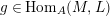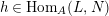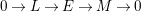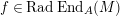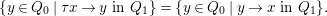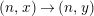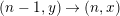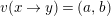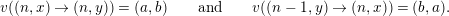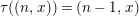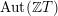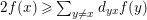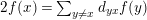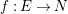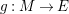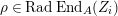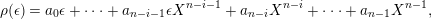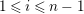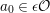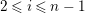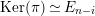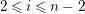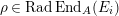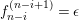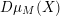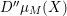Introduction
The shape of Auslander–Reiten quivers is one of fundamental interests in representation theory of algebras. For algebras over a field, a wealth of examples are given in textbooks, [Reference Assem, Simson and SkowrońskiASS] for example. Let
![]() ${\mathcal{O}}$
be a complete discrete valuation ring,
${\mathcal{O}}$
be a complete discrete valuation ring,
![]() $\unicode[STIX]{x1D716}$
a uniformizer,
$\unicode[STIX]{x1D716}$
a uniformizer,
![]() ${\mathcal{K}}$
its fraction field,
${\mathcal{K}}$
its fraction field,
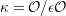 $\unicode[STIX]{x1D705}={\mathcal{O}}/\unicode[STIX]{x1D716}{\mathcal{O}}$
its residue field. Let
$\unicode[STIX]{x1D705}={\mathcal{O}}/\unicode[STIX]{x1D716}{\mathcal{O}}$
its residue field. Let
![]() $A$
be an
$A$
be an
![]() ${\mathcal{O}}$
-order, namely an
${\mathcal{O}}$
-order, namely an
![]() ${\mathcal{O}}$
-algebra which is free of finite rank as an
${\mathcal{O}}$
-algebra which is free of finite rank as an
![]() ${\mathcal{O}}$
-module. If
${\mathcal{O}}$
-module. If
![]() $A\otimes {\mathcal{K}}$
is a semisimple algebra, we may also find results in the literature. However, few results seem to be known for the case when
$A\otimes {\mathcal{K}}$
is a semisimple algebra, we may also find results in the literature. However, few results seem to be known for the case when
![]() $A\otimes {\mathcal{K}}$
is not a semisimple algebra. An exception is a famous work by Hijikata and Nishida, but their main focus is on a Bass order and
$A\otimes {\mathcal{K}}$
is not a semisimple algebra. An exception is a famous work by Hijikata and Nishida, but their main focus is on a Bass order and
![]() $A\otimes {\mathcal{K}}$
needs to be a quasi-Frobenius radical square zero algebra for a Bass order [Reference Hijikata and NishidaHN, Theorem 3.7.1].
$A\otimes {\mathcal{K}}$
needs to be a quasi-Frobenius radical square zero algebra for a Bass order [Reference Hijikata and NishidaHN, Theorem 3.7.1].
Recall that an
![]() $A$
-module is called an
$A$
-module is called an
![]() $A$
-lattice or a Cohen–Macaulay
$A$
-lattice or a Cohen–Macaulay
![]() $A$
-module if it is free of finite rank as an
$A$
-module if it is free of finite rank as an
![]() ${\mathcal{O}}$
-module. (Cohen–Macaulay
${\mathcal{O}}$
-module. (Cohen–Macaulay
![]() $A$
-modules are by definition finitely generated
$A$
-modules are by definition finitely generated
![]() $A$
-modules which are Cohen–Macaulay as
$A$
-modules which are Cohen–Macaulay as
![]() ${\mathcal{O}}$
-modules. Since
${\mathcal{O}}$
-modules. Since
![]() ${\mathcal{O}}$
is regular here, Cohen–Macaulay
${\mathcal{O}}$
is regular here, Cohen–Macaulay
![]() ${\mathcal{O}}$
-modules are free [Reference YoshinoY, (1.5)] and vice versa.) Then, it is known that for any nonprojective
${\mathcal{O}}$
-modules are free [Reference YoshinoY, (1.5)] and vice versa.) Then, it is known that for any nonprojective
![]() $A$
-lattice
$A$
-lattice
![]() $M$
with the property that
$M$
with the property that
![]() $M\otimes {\mathcal{K}}$
is projective as an
$M\otimes {\mathcal{K}}$
is projective as an
![]() $A\otimes {\mathcal{K}}$
-module, there is an almost split sequence ending at
$A\otimes {\mathcal{K}}$
-module, there is an almost split sequence ending at
![]() $M$
, and dually, for any noninjective
$M$
, and dually, for any noninjective
![]() $A$
-lattice
$A$
-lattice
![]() $M$
with the property that
$M$
with the property that
![]() $M\otimes {\mathcal{K}}$
is injective as an
$M\otimes {\mathcal{K}}$
is injective as an
![]() $A\otimes {\mathcal{K}}$
-module, there is an almost split sequence starting at
$A\otimes {\mathcal{K}}$
-module, there is an almost split sequence starting at
![]() $M$
. See [Reference Auslander and ReitenAR] for example. Thus, if
$M$
. See [Reference Auslander and ReitenAR] for example. Thus, if
![]() $A\otimes {\mathcal{K}}$
is self-injective, we may define the (stable) Auslander–Reiten quiver consisting of such
$A\otimes {\mathcal{K}}$
is self-injective, we may define the (stable) Auslander–Reiten quiver consisting of such
![]() $A$
-lattices. Typical examples of such
$A$
-lattices. Typical examples of such
![]() $A$
-lattices are Heller lattices. For group algebras, Heller lattices were studied by Kawata [Reference KawataK], and it inspired us to study the components that contain Heller lattices for the case of orders in non-semisimple algebras.
$A$
-lattices are Heller lattices. For group algebras, Heller lattices were studied by Kawata [Reference KawataK], and it inspired us to study the components that contain Heller lattices for the case of orders in non-semisimple algebras.
In this article, we determine the shape of the components of the stable Auslander–Reiten quiver that contain Heller lattices, for the truncated polynomial rings
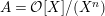 $A={\mathcal{O}}[X]/(X^{n})$
. As
$A={\mathcal{O}}[X]/(X^{n})$
. As
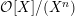 ${\mathcal{O}}[X]/(X^{n})$
is a Gorenstein
${\mathcal{O}}[X]/(X^{n})$
is a Gorenstein
![]() ${\mathcal{O}}$
-order, that is,
${\mathcal{O}}$
-order, that is,
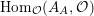 $\text{Hom}_{{\mathcal{O}}}(A_{A},{\mathcal{O}})$
is a projective
$\text{Hom}_{{\mathcal{O}}}(A_{A},{\mathcal{O}})$
is a projective
![]() $A$
-module [Reference IyamaI, Section 4], we explain explicit construction of almost split sequences for a Gorenstein
$A$
-module [Reference IyamaI, Section 4], we explain explicit construction of almost split sequences for a Gorenstein
![]() ${\mathcal{O}}$
-order, which generalizes construction of almost split sequences in [Reference ThévenazT], and use this construction to do necessary calculations. Main difficulty in the computation is the proof that certain direct summands of the middle terms of those almost split sequences are indecomposable. We use elementary brute force argument to overcome this difficulty. Then, some argument on tree classes which takes the possibility of the existence of loops in the stable Auslander–Reiten quiver into account proves the result. This argument is necessary because there may exist loops [Reference WiedemannW].
${\mathcal{O}}$
-order, which generalizes construction of almost split sequences in [Reference ThévenazT], and use this construction to do necessary calculations. Main difficulty in the computation is the proof that certain direct summands of the middle terms of those almost split sequences are indecomposable. We use elementary brute force argument to overcome this difficulty. Then, some argument on tree classes which takes the possibility of the existence of loops in the stable Auslander–Reiten quiver into account proves the result. This argument is necessary because there may exist loops [Reference WiedemannW].
If
![]() $A\otimes \unicode[STIX]{x1D705}$
is a special biserial algebra, we may calculate indecomposable
$A\otimes \unicode[STIX]{x1D705}$
is a special biserial algebra, we may calculate indecomposable
![]() $A\otimes \unicode[STIX]{x1D705}$
-modules and their Heller lattices. It is natural to consider the above problem in this setting. We will report some results in this direction in future work.
$A\otimes \unicode[STIX]{x1D705}$
-modules and their Heller lattices. It is natural to consider the above problem in this setting. We will report some results in this direction in future work.
1 Preliminaries
1.1 Gorenstein orders
We start by observing that
 $A={\mathcal{O}}[X]/(X^{n})$
is a symmetric
$A={\mathcal{O}}[X]/(X^{n})$
is a symmetric
![]() ${\mathcal{O}}$
-order. By abuse of notation, we write
${\mathcal{O}}$
-order. By abuse of notation, we write
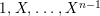 $1,X,\ldots ,X^{n-1}$
for the standard
$1,X,\ldots ,X^{n-1}$
for the standard
![]() ${\mathcal{O}}$
-basis of
${\mathcal{O}}$
-basis of
![]() $A$
. Define
$A$
. Define
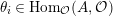 $\unicode[STIX]{x1D703}_{i}\in \text{Hom}_{{\mathcal{O}}}(A,{\mathcal{O}})$
, for
$\unicode[STIX]{x1D703}_{i}\in \text{Hom}_{{\mathcal{O}}}(A,{\mathcal{O}})$
, for
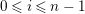 $0\leqslant i\leqslant n-1$
, by
$0\leqslant i\leqslant n-1$
, by
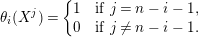 $$\begin{eqnarray}\unicode[STIX]{x1D703}_{i}(X^{j})=\left\{\begin{array}{@{}ll@{}}1 & \text{if}~j=n-i-1,\\ 0 & \text{if}~j\neq n-i-1.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D703}_{i}(X^{j})=\left\{\begin{array}{@{}ll@{}}1 & \text{if}~j=n-i-1,\\ 0 & \text{if}~j\neq n-i-1.\end{array}\right.\end{eqnarray}$$
Then we have the following lemma.
Lemma 1.1.
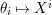 $\unicode[STIX]{x1D703}_{i}\mapsto X^{i}$
induces an isomorphism of
$\unicode[STIX]{x1D703}_{i}\mapsto X^{i}$
induces an isomorphism of
![]() $(A,A)$
-bimodules
$(A,A)$
-bimodules
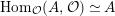 $\text{Hom}_{{\mathcal{O}}}(A,{\mathcal{O}})\simeq A$
.
$\text{Hom}_{{\mathcal{O}}}(A,{\mathcal{O}})\simeq A$
.
Proof. As
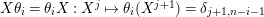 $X\unicode[STIX]{x1D703}_{i}=\unicode[STIX]{x1D703}_{i}X:X^{j}\mapsto \unicode[STIX]{x1D703}_{i}(X^{j+1})=\unicode[STIX]{x1D6FF}_{j+1,n-i-1}$
, we have
$X\unicode[STIX]{x1D703}_{i}=\unicode[STIX]{x1D703}_{i}X:X^{j}\mapsto \unicode[STIX]{x1D703}_{i}(X^{j+1})=\unicode[STIX]{x1D6FF}_{j+1,n-i-1}$
, we have
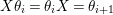 $X\unicode[STIX]{x1D703}_{i}=\unicode[STIX]{x1D703}_{i}X=\unicode[STIX]{x1D703}_{i+1}$
.◻
$X\unicode[STIX]{x1D703}_{i}=\unicode[STIX]{x1D703}_{i}X=\unicode[STIX]{x1D703}_{i+1}$
.◻
Remark 1.2. A different definition of Gorenstein order is given in [Reference Curtis and ReinerCR, Section 37]: it requires not only that every exact sequence of
![]() $A$
-lattices
$A$
-lattices
 $0\rightarrow A\rightarrow M\rightarrow N\rightarrow 0$
starting at
$0\rightarrow A\rightarrow M\rightarrow N\rightarrow 0$
starting at
![]() $A$
splits, but also that
$A$
splits, but also that
![]() $A\otimes {\mathcal{K}}$
is a semisimple algebra. Perhaps the semisimplicity condition was added by some technical reasons.
$A\otimes {\mathcal{K}}$
is a semisimple algebra. Perhaps the semisimplicity condition was added by some technical reasons.
Remark 1.3. In [Reference AuslanderA1, Chapter I, Section 7], the definition of
![]() ${\mathcal{O}}$
-order itself is different. If we restrict to the case when
${\mathcal{O}}$
-order itself is different. If we restrict to the case when
![]() ${\mathcal{O}}$
is a Dedekind domain,
${\mathcal{O}}$
is a Dedekind domain,
![]() $A$
is an
$A$
is an
![]() ${\mathcal{O}}$
-order in his sense if
${\mathcal{O}}$
-order in his sense if
![]() $A$
is not only a finitely generated projective
$A$
is not only a finitely generated projective
![]() ${\mathcal{O}}$
-module but also
${\mathcal{O}}$
-module but also
![]() $A\otimes {\mathcal{K}}$
is a self-injective
$A\otimes {\mathcal{K}}$
is a self-injective
![]() ${\mathcal{K}}$
-algebra.
${\mathcal{K}}$
-algebra.
Then, a Gorenstein
![]() ${\mathcal{O}}$
-order is a Noetherian
${\mathcal{O}}$
-order is a Noetherian
![]() ${\mathcal{O}}$
-algebra
${\mathcal{O}}$
-algebra
![]() $A$
which is Cohen–Macaulay as an
$A$
which is Cohen–Macaulay as an
![]() ${\mathcal{O}}$
-module and
${\mathcal{O}}$
-module and
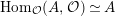 $\text{Hom}_{{\mathcal{O}}}(A,{\mathcal{O}})\simeq A$
as
$\text{Hom}_{{\mathcal{O}}}(A,{\mathcal{O}})\simeq A$
as
![]() $(A,A)$
-bimodules [Reference AuslanderA1, Chapter III, Section 1]. Nowadays, Gorenstein
$(A,A)$
-bimodules [Reference AuslanderA1, Chapter III, Section 1]. Nowadays, Gorenstein
![]() ${\mathcal{O}}$
-orders in Auslander’s sense are called symmetric
${\mathcal{O}}$
-orders in Auslander’s sense are called symmetric
![]() ${\mathcal{O}}$
-orders [Reference Iyama and WemyssIW, Definition 2.8].
${\mathcal{O}}$
-orders [Reference Iyama and WemyssIW, Definition 2.8].
Lemma 1.1 implies that
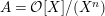 $A={\mathcal{O}}[X]/(X^{n})$
is a symmetric
$A={\mathcal{O}}[X]/(X^{n})$
is a symmetric
![]() ${\mathcal{O}}$
-order. Note that
${\mathcal{O}}$
-order. Note that
![]() $A$
is also a Gorenstein ring, since
$A$
is also a Gorenstein ring, since
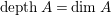 $\text{depth}\,A=\dim A$
and if the parameter ideal
$\text{depth}\,A=\dim A$
and if the parameter ideal
![]() $\unicode[STIX]{x1D716}A$
is the intersection of two ideals
$\unicode[STIX]{x1D716}A$
is the intersection of two ideals
![]() $I$
and
$I$
and
![]() $J$
then either
$J$
then either
![]() $I=\unicode[STIX]{x1D716}A$
or
$I=\unicode[STIX]{x1D716}A$
or
![]() $J=\unicode[STIX]{x1D716}A$
holds.
$J=\unicode[STIX]{x1D716}A$
holds.
Lemma 1.4. Let
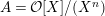 $A={\mathcal{O}}[X]/(X^{n})$
, for
$A={\mathcal{O}}[X]/(X^{n})$
, for
![]() $n\geqslant 2$
. Then there are infinitely many pairwise nonisomorphic indecomposable
$n\geqslant 2$
. Then there are infinitely many pairwise nonisomorphic indecomposable
![]() $A$
-lattices.
$A$
-lattices.
Proof. If there were only finitely many, then [Reference AuslanderA2, Section 10] and [Reference YoshinoY, (3.1), (4.22)] would imply that
![]() $A$
is reduced, contradicting our assumption that
$A$
is reduced, contradicting our assumption that
![]() $n\geqslant 2$
. Below, we give an example of a family of infinitely many pairwise nonisomorphic indecomposable
$n\geqslant 2$
. Below, we give an example of a family of infinitely many pairwise nonisomorphic indecomposable
![]() $A$
-lattices.
$A$
-lattices.
For
![]() $r\in \mathbb{Z}_{{\geqslant}0}$
, let
$r\in \mathbb{Z}_{{\geqslant}0}$
, let
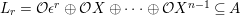 $L_{r}={\mathcal{O}}\unicode[STIX]{x1D716}^{r}\oplus {\mathcal{O}}X\oplus \cdots \oplus {\mathcal{O}}X^{n-1}\subseteq A$
. Then the representing matrix of the action of
$L_{r}={\mathcal{O}}\unicode[STIX]{x1D716}^{r}\oplus {\mathcal{O}}X\oplus \cdots \oplus {\mathcal{O}}X^{n-1}\subseteq A$
. Then the representing matrix of the action of
![]() $X$
on
$X$
on
![]() $L_{r}$
with respect to the basis is given by the following matrix:
$L_{r}$
with respect to the basis is given by the following matrix:
 $$\begin{eqnarray}X=\left(\begin{array}{@{}ccccc@{}}0 & \cdots \, & \cdots \, & \cdots \, & 0\\ \unicode[STIX]{x1D716}^{r} & 0 & \cdots \, & \cdots \, & 0\\ 0 & 1 & 0 & & \vdots \\ \vdots & \ddots & \ddots & \ddots & \vdots \\ 0 & \cdots \, & 0 & 1 & 0\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}X=\left(\begin{array}{@{}ccccc@{}}0 & \cdots \, & \cdots \, & \cdots \, & 0\\ \unicode[STIX]{x1D716}^{r} & 0 & \cdots \, & \cdots \, & 0\\ 0 & 1 & 0 & & \vdots \\ \vdots & \ddots & \ddots & \ddots & \vdots \\ 0 & \cdots \, & 0 & 1 & 0\end{array}\right).\end{eqnarray}$$
Therefore, we have
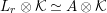 $L_{r}\otimes {\mathcal{K}}\simeq A\otimes {\mathcal{K}}$
and
$L_{r}\otimes {\mathcal{K}}\simeq A\otimes {\mathcal{K}}$
and
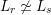 $L_{r}\not \simeq L_{s}$
whenever
$L_{r}\not \simeq L_{s}$
whenever
![]() $r\neq s$
. In particular,
$r\neq s$
. In particular,
![]() $L_{r}$
, for
$L_{r}$
, for
 $r=0,1,2,\ldots$
, are pairwise nonisomorphic indecomposable
$r=0,1,2,\ldots$
, are pairwise nonisomorphic indecomposable
![]() $A$
-lattices.◻
$A$
-lattices.◻
Since
![]() ${\mathcal{O}}$
is a complete local ring,
${\mathcal{O}}$
is a complete local ring,
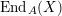 $\text{End}_{A}(X)$
is a local
$\text{End}_{A}(X)$
is a local
![]() ${\mathcal{O}}$
-algebra for every indecomposable
${\mathcal{O}}$
-algebra for every indecomposable
![]() $A$
-lattice
$A$
-lattice
![]() $X$
[Reference Curtis and ReinerCR, (6.10)(30.5)]. Thus, the Jacobson radical
$X$
[Reference Curtis and ReinerCR, (6.10)(30.5)]. Thus, the Jacobson radical
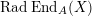 $\text{Rad}\,\text{End}_{A}(X)$
consists of all noninvertible endomorphisms of
$\text{Rad}\,\text{End}_{A}(X)$
consists of all noninvertible endomorphisms of
![]() $X$
. Another consequence is that
$X$
. Another consequence is that
![]() $A$
is semiperfect and every finitely generated
$A$
is semiperfect and every finitely generated
![]() $A$
-module has a projective cover [Reference Curtis and ReinerCR, (6.23)].
$A$
-module has a projective cover [Reference Curtis and ReinerCR, (6.23)].
In the next subsection, we assume that
![]() $A$
is a Gorenstein
$A$
is a Gorenstein
![]() ${\mathcal{O}}$
-order and we explain a method to construct almost split sequences for
${\mathcal{O}}$
-order and we explain a method to construct almost split sequences for
![]() $A$
-lattices. Note that there exists an almost split sequence ending (resp. starting) at
$A$
-lattices. Note that there exists an almost split sequence ending (resp. starting) at
![]() $M$
if and only if
$M$
if and only if
![]() $M\otimes {\mathcal{K}}$
is projective (resp. injective) [Reference Auslander and ReitenAR], [Reference Roggenkamp and RumpRR, Theorem 6].
$M\otimes {\mathcal{K}}$
is projective (resp. injective) [Reference Auslander and ReitenAR], [Reference Roggenkamp and RumpRR, Theorem 6].
1.2 Construction of almost split sequences
We recall several definitions.
Definition 1.5. Let
![]() $A$
be an
$A$
be an
![]() ${\mathcal{O}}$
-order,
${\mathcal{O}}$
-order,
![]() $M$
and
$M$
and
![]() $N$
$N$
![]() $A$
-lattices. The radical
$A$
-lattices. The radical
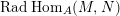 $\text{Rad}\,\text{Hom}_{A}(M,N)$
of
$\text{Rad}\,\text{Hom}_{A}(M,N)$
of
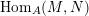 $\text{Hom}_{A}(M,N)$
is the
$\text{Hom}_{A}(M,N)$
is the
![]() ${\mathcal{O}}$
-submodule of
${\mathcal{O}}$
-submodule of
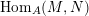 $\text{Hom}_{A}(M,N)$
consisting of
$\text{Hom}_{A}(M,N)$
consisting of
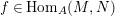 $f\in \text{Hom}_{A}(M,N)$
such that, for all indecomposable
$f\in \text{Hom}_{A}(M,N)$
such that, for all indecomposable
![]() $A$
-lattice
$A$
-lattice
![]() $X$
, we have
$X$
, we have
 $hfg\in \text{Rad}\,\text{End}_{A}(X)$
, for any
$hfg\in \text{Rad}\,\text{End}_{A}(X)$
, for any
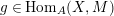 $g\in \text{Hom}_{A}(X,M)$
and
$g\in \text{Hom}_{A}(X,M)$
and
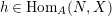 $h\in \text{Hom}_{A}(N,X)$
. It is equivalent to the condition that
$h\in \text{Hom}_{A}(N,X)$
. It is equivalent to the condition that
![]() $1-gf$
is invertible, for all
$1-gf$
is invertible, for all
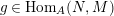 $g\in \text{Hom}_{A}(N,M)$
, and to the condition that
$g\in \text{Hom}_{A}(N,M)$
, and to the condition that
![]() $1-fg$
is invertible, for all
$1-fg$
is invertible, for all
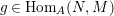 $g\in \text{Hom}_{A}(N,M)$
.
$g\in \text{Hom}_{A}(N,M)$
.
Let
![]() ${\mathcal{A}}$
be an abelian category with enough projectives,
${\mathcal{A}}$
be an abelian category with enough projectives,
![]() ${\mathcal{C}}$
an additive full subcategory which is closed under extensions and direct summands. Then,
${\mathcal{C}}$
an additive full subcategory which is closed under extensions and direct summands. Then,
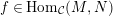 $f\in \text{Hom}_{{\mathcal{C}}}(M,N)$
in
$f\in \text{Hom}_{{\mathcal{C}}}(M,N)$
in
![]() ${\mathcal{C}}$
is called right minimal in
${\mathcal{C}}$
is called right minimal in
![]() ${\mathcal{C}}$
if an endomorphism
${\mathcal{C}}$
if an endomorphism
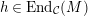 $h\in \text{End}_{{\mathcal{C}}}(M)$
is an isomorphism whenever
$h\in \text{End}_{{\mathcal{C}}}(M)$
is an isomorphism whenever
![]() $f=fh$
, right almost split in
$f=fh$
, right almost split in
![]() ${\mathcal{C}}$
if it is not a split epimorphism and for each
${\mathcal{C}}$
if it is not a split epimorphism and for each
![]() $X\in {\mathcal{C}}$
and
$X\in {\mathcal{C}}$
and
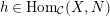 $h\in \text{Hom}_{{\mathcal{C}}}(X,N)$
which is not a split epimorphism, there is
$h\in \text{Hom}_{{\mathcal{C}}}(X,N)$
which is not a split epimorphism, there is
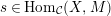 $s\in \text{Hom}_{{\mathcal{C}}}(X,M)$
such that
$s\in \text{Hom}_{{\mathcal{C}}}(X,M)$
such that
![]() $fs=h$
. If
$fs=h$
. If
![]() $f$
is both right minimal in
$f$
is both right minimal in
![]() ${\mathcal{C}}$
and right almost split in
${\mathcal{C}}$
and right almost split in
![]() ${\mathcal{C}}$
,
${\mathcal{C}}$
,
![]() $f$
is called minimal right almost split in
$f$
is called minimal right almost split in
![]() ${\mathcal{C}}$
. Similarly,
${\mathcal{C}}$
. Similarly,
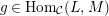 $g\in \text{Hom}_{{\mathcal{C}}}(L,M)$
is called left minimal in
$g\in \text{Hom}_{{\mathcal{C}}}(L,M)$
is called left minimal in
![]() ${\mathcal{C}}$
if an endomorphism
${\mathcal{C}}$
if an endomorphism
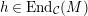 $h\in \text{End}_{{\mathcal{C}}}(M)$
is an isomorphism whenever
$h\in \text{End}_{{\mathcal{C}}}(M)$
is an isomorphism whenever
![]() $g=hg$
, left almost split in
$g=hg$
, left almost split in
![]() ${\mathcal{C}}$
if it is not a split monomorphism and for each
${\mathcal{C}}$
if it is not a split monomorphism and for each
![]() $Y\in {\mathcal{C}}$
and
$Y\in {\mathcal{C}}$
and
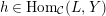 $h\in \text{Hom}_{{\mathcal{C}}}(L,Y)$
which is not a split monomorphism, there is
$h\in \text{Hom}_{{\mathcal{C}}}(L,Y)$
which is not a split monomorphism, there is
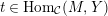 $t\in \text{Hom}_{{\mathcal{C}}}(M,Y)$
such that
$t\in \text{Hom}_{{\mathcal{C}}}(M,Y)$
such that
![]() $tg=h$
, and if
$tg=h$
, and if
![]() $g$
is both left minimal in
$g$
is both left minimal in
![]() ${\mathcal{C}}$
and left almost split in
${\mathcal{C}}$
and left almost split in
![]() ${\mathcal{C}}$
,
${\mathcal{C}}$
,
![]() $g$
is called minimal left almost split in
$g$
is called minimal left almost split in
![]() ${\mathcal{C}}$
. We have the following proposition in this general setting [Reference AuslanderA1, Chapter II, Proposition 4.4].
${\mathcal{C}}$
. We have the following proposition in this general setting [Reference AuslanderA1, Chapter II, Proposition 4.4].
Proposition 1.6. Suppose that
![]() ${\mathcal{C}}$
is an additive full subcategory of an abelian category
${\mathcal{C}}$
is an additive full subcategory of an abelian category
![]() ${\mathcal{A}}$
with enough projectives such that
${\mathcal{A}}$
with enough projectives such that
![]() ${\mathcal{C}}$
is closed under extensions and direct summands. Let
${\mathcal{C}}$
is closed under extensions and direct summands. Let
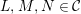 $L,M,N\in {\mathcal{C}}$
. Then the following are equivalent for a short exact sequence
$L,M,N\in {\mathcal{C}}$
. Then the following are equivalent for a short exact sequence
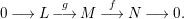 $$\begin{eqnarray}0\longrightarrow L\stackrel{g}{\longrightarrow }M\stackrel{f}{\longrightarrow }N\longrightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}0\longrightarrow L\stackrel{g}{\longrightarrow }M\stackrel{f}{\longrightarrow }N\longrightarrow 0.\end{eqnarray}$$
-
(a)
 $f$
is right almost split in
$f$
is right almost split in
 ${\mathcal{C}}$
and
${\mathcal{C}}$
and
 $g$
is left almost split in
$g$
is left almost split in
 ${\mathcal{C}}$
.
${\mathcal{C}}$
. -
(b)
 $f$
is minimal right almost split in
$f$
is minimal right almost split in
 ${\mathcal{C}}$
.
${\mathcal{C}}$
. -
(c)
 $f$
is right almost split and
$f$
is right almost split and
 $\text{End}_{{\mathcal{C}}}(L)$
is local.
$\text{End}_{{\mathcal{C}}}(L)$
is local. -
(d)
 $g$
is minimal left almost split in
$g$
is minimal left almost split in
 ${\mathcal{C}}$
.
${\mathcal{C}}$
. -
(e)
 $g$
is left almost split in
$g$
is left almost split in
 ${\mathcal{C}}$
and
${\mathcal{C}}$
and
 $\text{End}_{{\mathcal{C}}}(N)$
is local.
$\text{End}_{{\mathcal{C}}}(N)$
is local.
We return to
![]() ${\mathcal{O}}$
-orders over a complete discrete valuation ring
${\mathcal{O}}$
-orders over a complete discrete valuation ring
![]() ${\mathcal{O}}$
. Among equivalent conditions in Proposition 1.6, we choose (c) as the definition of an almost split sequence for lattices over an
${\mathcal{O}}$
. Among equivalent conditions in Proposition 1.6, we choose (c) as the definition of an almost split sequence for lattices over an
![]() ${\mathcal{O}}$
-order.
${\mathcal{O}}$
-order.
Definition 1.7. Let
![]() $A$
be an
$A$
be an
![]() ${\mathcal{O}}$
-order,
${\mathcal{O}}$
-order,
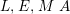 $L,E,M~A$
-lattices. A short exact sequence
$L,E,M~A$
-lattices. A short exact sequence
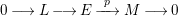 $$\begin{eqnarray}0\longrightarrow L\longrightarrow E\xrightarrow[{}]{~p~}M\longrightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\longrightarrow L\longrightarrow E\xrightarrow[{}]{~p~}M\longrightarrow 0\end{eqnarray}$$
is called an almost split sequence (of
![]() $A$
-lattices) ending at
$A$
-lattices) ending at
![]() $M$
if
$M$
if
-
(i) the epimorphism
 $p$
does not split;
$p$
does not split; -
(ii)
 $L$
and
$L$
and
 $M$
are indecomposable;
$M$
are indecomposable; -
(iii) the morphism
 $p:E\rightarrow M$
induces the epimorphism for every indecomposable
$p:E\rightarrow M$
induces the epimorphism for every indecomposable $$\begin{eqnarray}\text{Hom}_{A}(X,p):\text{Hom}_{A}(X,E)\longrightarrow \text{Rad}\,\text{Hom}_{A}(X,M),\end{eqnarray}$$
$$\begin{eqnarray}\text{Hom}_{A}(X,p):\text{Hom}_{A}(X,E)\longrightarrow \text{Rad}\,\text{Hom}_{A}(X,M),\end{eqnarray}$$
 $A$
-lattice
$A$
-lattice
 $X$
.
$X$
.
Definition 1.8. Let
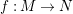 $f:M\rightarrow N$
be a morphism between
$f:M\rightarrow N$
be a morphism between
![]() $A$
-lattices. We say that
$A$
-lattices. We say that
![]() $f$
is an irreducible morphism if
$f$
is an irreducible morphism if
-
(i)
 $f$
is neither a split monomorphism nor a split epimorphism;
$f$
is neither a split monomorphism nor a split epimorphism; -
(ii) if there are
 $g\in \text{Hom}_{A}(M,L)$
and
$g\in \text{Hom}_{A}(M,L)$
and
 $h\in \text{Hom}_{A}(L,N)$
such that
$h\in \text{Hom}_{A}(L,N)$
such that
 $f=hg$
, then either
$f=hg$
, then either
 $g$
is a split monomorphism or
$g$
is a split monomorphism or
 $h$
is a split epimorphism.
$h$
is a split epimorphism.
Lemma 1.9. Let
![]() $A$
be an
$A$
be an
![]() ${\mathcal{O}}$
-order,
${\mathcal{O}}$
-order,
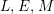 $L,E,M$
$L,E,M$
![]() $A$
-lattices. We suppose that an almost split sequence for
$A$
-lattices. We suppose that an almost split sequence for
![]() $A$
-lattices ending at
$A$
-lattices ending at
![]() $M$
exists. Then, a short exact sequence
$M$
exists. Then, a short exact sequence
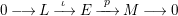 $$\begin{eqnarray}0\longrightarrow L\xrightarrow[{}]{~\unicode[STIX]{x1D704}~}E\xrightarrow[{}]{~p~}M\longrightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\longrightarrow L\xrightarrow[{}]{~\unicode[STIX]{x1D704}~}E\xrightarrow[{}]{~p~}M\longrightarrow 0\end{eqnarray}$$
is an almost split sequence if and only if
![]() $\unicode[STIX]{x1D704}$
and
$\unicode[STIX]{x1D704}$
and
![]() $p$
are irreducible.
$p$
are irreducible.
Proof. The arguments in [Reference Auslander, Reiten and SmaløARS, V. Theorem 5.3] and [Reference Auslander, Reiten and SmaløARS, V. Proposition 5.9] work without change in our setting. ◻
Remark 1.10. The definitions of almost split sequences and irreducible morphisms are taken from [Reference RoggenkampR2], although it is assumed that
![]() $A\otimes {\mathcal{K}}$
is a semisimple algebra there.
$A\otimes {\mathcal{K}}$
is a semisimple algebra there.
Definition 1.11. Let
![]() $A$
be an
$A$
be an
![]() ${\mathcal{O}}$
-order. For an indecomposable
${\mathcal{O}}$
-order. For an indecomposable
![]() $A\otimes \unicode[STIX]{x1D705}$
-module
$A\otimes \unicode[STIX]{x1D705}$
-module
![]() $N$
, we view
$N$
, we view
![]() $N$
as an
$N$
as an
![]() $A$
-module, and take the projective cover
$A$
-module, and take the projective cover
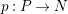 $p:P\rightarrow N$
. We denote
$p:P\rightarrow N$
. We denote
![]() $\text{Ker}(p)$
by
$\text{Ker}(p)$
by
![]() $Z_{N}$
and direct summands of the
$Z_{N}$
and direct summands of the
![]() $A$
-lattice
$A$
-lattice
![]() $Z_{N}$
are called Heller lattices of
$Z_{N}$
are called Heller lattices of
![]() $N$
. Note that
$N$
. Note that
![]() $Z_{N}$
is uniquely determined up to isomorphism.
$Z_{N}$
is uniquely determined up to isomorphism.
In the sequel, we consider an indecomposable
![]() $A$
-lattice
$A$
-lattice
![]() $M$
with the property
$M$
with the property
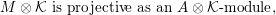 $$\begin{eqnarray}M\otimes {\mathcal{K}}~\text{is projective as an}~A\otimes {\mathcal{K}}\text{-}\text{module},\end{eqnarray}$$
$$\begin{eqnarray}M\otimes {\mathcal{K}}~\text{is projective as an}~A\otimes {\mathcal{K}}\text{-}\text{module},\end{eqnarray}$$
and show how to construct the almost split sequence ending at
![]() $M$
.
$M$
.
Remark 1.12. Heller lattices have the property (∗). Indeed, for an indecomposable
![]() $A\otimes \unicode[STIX]{x1D705}$
-module
$A\otimes \unicode[STIX]{x1D705}$
-module
![]() $N$
,
$N$
,
![]() $Z_{N}$
is an
$Z_{N}$
is an
![]() $A$
-submodule of the projective
$A$
-submodule of the projective
![]() $A$
-module
$A$
-module
![]() $P$
, and we have
$P$
, and we have
 $\unicode[STIX]{x1D716}P\subseteq Z_{N}$
. Thus,
$\unicode[STIX]{x1D716}P\subseteq Z_{N}$
. Thus,
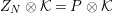 $Z_{N}\otimes {\mathcal{K}}=P\otimes {\mathcal{K}}$
is projective and so are their direct summands.
$Z_{N}\otimes {\mathcal{K}}=P\otimes {\mathcal{K}}$
is projective and so are their direct summands.
Let
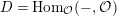 $D=\text{Hom}_{{\mathcal{O}}}(-,{\mathcal{O}})$
and define the Nakayama functor for
$D=\text{Hom}_{{\mathcal{O}}}(-,{\mathcal{O}})$
and define the Nakayama functor for
![]() $A$
-lattices by
$A$
-lattices by
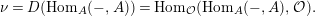 $$\begin{eqnarray}\unicode[STIX]{x1D708}=D(\text{Hom}_{A}(-,A))=\text{Hom}_{{\mathcal{O}}}(\text{Hom}_{A}(-,A),{\mathcal{O}}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D708}=D(\text{Hom}_{A}(-,A))=\text{Hom}_{{\mathcal{O}}}(\text{Hom}_{A}(-,A),{\mathcal{O}}).\end{eqnarray}$$
Lemma 1.13. Let
![]() $M$
be an
$M$
be an
![]() $A$
-lattice,
$A$
-lattice,
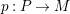 $p:P\rightarrow M$
its projective cover. We define
$p:P\rightarrow M$
its projective cover. We define
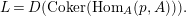 $$\begin{eqnarray}L=D(\text{Coker}(\text{Hom}_{A}(p,A))).\end{eqnarray}$$
$$\begin{eqnarray}L=D(\text{Coker}(\text{Hom}_{A}(p,A))).\end{eqnarray}$$
Then we have the exact sequence of
![]() $A$
-lattices
$A$
-lattices
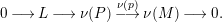 $$\begin{eqnarray}0\longrightarrow L\longrightarrow \unicode[STIX]{x1D708}(P)\stackrel{\unicode[STIX]{x1D708}(p)}{\longrightarrow }\unicode[STIX]{x1D708}(M)\longrightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}0\longrightarrow L\longrightarrow \unicode[STIX]{x1D708}(P)\stackrel{\unicode[STIX]{x1D708}(p)}{\longrightarrow }\unicode[STIX]{x1D708}(M)\longrightarrow 0.\end{eqnarray}$$
Proof.
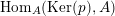 $\text{Hom}_{A}(\text{Ker}(p),A)$
is an
$\text{Hom}_{A}(\text{Ker}(p),A)$
is an
![]() $A$
-lattice since
$A$
-lattice since
![]() $\text{Ker}(p)$
and
$\text{Ker}(p)$
and
![]() $A$
are. Since the cokernel of
$A$
are. Since the cokernel of
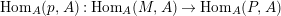 $\text{Hom}_{A}(p,A):\text{Hom}_{A}(M,A)\rightarrow \text{Hom}_{A}(P,A)$
is an
$\text{Hom}_{A}(p,A):\text{Hom}_{A}(M,A)\rightarrow \text{Hom}_{A}(P,A)$
is an
![]() $A$
-submodule of
$A$
-submodule of
 $\text{Hom}_{A}(\text{Ker}(p),A)$
,
$\text{Hom}_{A}(\text{Ker}(p),A)$
,
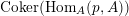 $\text{Coker}(\text{Hom}_{A}(p,A))$
is a free
$\text{Coker}(\text{Hom}_{A}(p,A))$
is a free
![]() ${\mathcal{O}}$
-module. Then,
${\mathcal{O}}$
-module. Then,
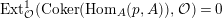 $\text{Ext}_{{\mathcal{O}}}^{1}(\text{Coker}(\text{Hom}_{A}(p,A)),{\mathcal{O}})=0$
implies the result.◻
$\text{Ext}_{{\mathcal{O}}}^{1}(\text{Coker}(\text{Hom}_{A}(p,A)),{\mathcal{O}})=0$
implies the result.◻
Remark 1.14. If we take a minimal projective presentation
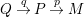 $Q\stackrel{q}{\rightarrow }P\stackrel{p}{\rightarrow }M$
of an
$Q\stackrel{q}{\rightarrow }P\stackrel{p}{\rightarrow }M$
of an
![]() $A$
-lattice
$A$
-lattice
![]() $M$
, we have the short exact sequence
$M$
, we have the short exact sequence
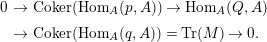 $$\begin{eqnarray}\displaystyle 0 & \rightarrow & \displaystyle \text{Coker}(\text{Hom}_{A}(p,A))\rightarrow \text{Hom}_{A}(Q,A)\nonumber\\ \displaystyle & \rightarrow & \displaystyle \text{Coker}(\text{Hom}_{A}(q,A))=\text{Tr}(M)\rightarrow 0.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0 & \rightarrow & \displaystyle \text{Coker}(\text{Hom}_{A}(p,A))\rightarrow \text{Hom}_{A}(Q,A)\nonumber\\ \displaystyle & \rightarrow & \displaystyle \text{Coker}(\text{Hom}_{A}(q,A))=\text{Tr}(M)\rightarrow 0.\nonumber\end{eqnarray}$$
Thus,
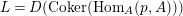 $L=D(\text{Coker}(\text{Hom}_{A}(p,A)))$
represents the Auslander–Reiten translate
$L=D(\text{Coker}(\text{Hom}_{A}(p,A)))$
represents the Auslander–Reiten translate
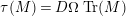 $\unicode[STIX]{x1D70F}(M)=D\unicode[STIX]{x1D6FA}\,\text{Tr}(M)$
of the
$\unicode[STIX]{x1D70F}(M)=D\unicode[STIX]{x1D6FA}\,\text{Tr}(M)$
of the
![]() $A$
-lattice
$A$
-lattice
![]() $M$
.
$M$
.
Taking a suitable pullback of the exact sequence from Lemma 1.13, we may construct almost split sequences as follows. This generalizes the construction in [Reference ThévenazT]. We give the proof of Proposition 1.15 in the appendix, for the convenience of the reader.
The right and left minimality in Proposition 1.6 implies that the almost split sequence ending at
![]() $M$
and the almost split sequence starting at
$M$
and the almost split sequence starting at
![]() $L$
are uniquely determined by
$L$
are uniquely determined by
![]() $M$
and
$M$
and
![]() $L$
respectively, up to isomorphism of short exact sequences. Thus, we may define the Auslander–Reiten translate
$L$
respectively, up to isomorphism of short exact sequences. Thus, we may define the Auslander–Reiten translate
![]() $\unicode[STIX]{x1D70F}$
and
$\unicode[STIX]{x1D70F}$
and
![]() $\unicode[STIX]{x1D70F}^{-}$
by
$\unicode[STIX]{x1D70F}^{-}$
by
 $\unicode[STIX]{x1D70F}(M)=L$
and
$\unicode[STIX]{x1D70F}(M)=L$
and
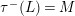 $\unicode[STIX]{x1D70F}^{-}(L)=M$
.
$\unicode[STIX]{x1D70F}^{-}(L)=M$
.
Proposition 1.15. Suppose that
![]() $A$
is a Gorenstein
$A$
is a Gorenstein
![]() ${\mathcal{O}}$
-order,
${\mathcal{O}}$
-order,
![]() $M$
an indecomposable nonprojective
$M$
an indecomposable nonprojective
![]() $A$
-lattice with the property (∗), and let
$A$
-lattice with the property (∗), and let
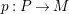 $p:P\rightarrow M$
be its projective cover. For
$p:P\rightarrow M$
be its projective cover. For
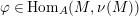 $\unicode[STIX]{x1D711}\in \text{Hom}_{A}(M,\unicode[STIX]{x1D708}(M))$
, we consider the pullback diagram along
$\unicode[STIX]{x1D711}\in \text{Hom}_{A}(M,\unicode[STIX]{x1D708}(M))$
, we consider the pullback diagram along
![]() $\unicode[STIX]{x1D711}$
:
$\unicode[STIX]{x1D711}$
:

Then the following
![]() $(1)$
and
$(1)$
and
![]() $(2)$
are equivalent.
$(2)$
are equivalent.
-
(1) The pullback
 $0\rightarrow L\rightarrow E\rightarrow M\rightarrow 0$
is an almost split sequence.
$0\rightarrow L\rightarrow E\rightarrow M\rightarrow 0$
is an almost split sequence. -
(2) The following three conditions hold.
-
(i)
 $\unicode[STIX]{x1D711}$
does not factor through
$\unicode[STIX]{x1D711}$
does not factor through
 $\unicode[STIX]{x1D708}(p)$
.
$\unicode[STIX]{x1D708}(p)$
. -
(ii)
 $L$
is an indecomposable
$L$
is an indecomposable
 $A$
-lattice.
$A$
-lattice. -
(iii) For all
 $f\in \text{Rad}\,\text{End}_{A}(M)$
,
$f\in \text{Rad}\,\text{End}_{A}(M)$
,
 $\unicode[STIX]{x1D711}f$
factors through
$\unicode[STIX]{x1D711}f$
factors through
 $\unicode[STIX]{x1D708}(p)$
.
$\unicode[STIX]{x1D708}(p)$
.
-
If
![]() $A$
is a symmetric
$A$
is a symmetric
![]() ${\mathcal{O}}$
-order, then we have functorial isomorphisms
${\mathcal{O}}$
-order, then we have functorial isomorphisms
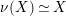 $\unicode[STIX]{x1D708}(X)\simeq X$
, for
$\unicode[STIX]{x1D708}(X)\simeq X$
, for
![]() $A$
-lattices
$A$
-lattices
![]() $X$
. Hence, we pull back
$X$
. Hence, we pull back
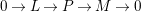 $0\rightarrow L\rightarrow P\rightarrow M\rightarrow 0$
along
$0\rightarrow L\rightarrow P\rightarrow M\rightarrow 0$
along
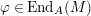 $\unicode[STIX]{x1D711}\in \text{End}_{A}(M)$
in this case. Further, the left term
$\unicode[STIX]{x1D711}\in \text{End}_{A}(M)$
in this case. Further, the left term
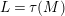 $L=\unicode[STIX]{x1D70F}(M)$
and the middle term
$L=\unicode[STIX]{x1D70F}(M)$
and the middle term
![]() $E$
of the almost split sequence satisfy the property (∗).
$E$
of the almost split sequence satisfy the property (∗).
1.3 Translation quivers and tree classes
In this subsection we recall fundamentals of translation quivers.
Definition 1.16. Let
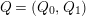 $Q=(Q_{0},Q_{1})$
, where
$Q=(Q_{0},Q_{1})$
, where
![]() $Q_{0}$
is the set of vertexes and
$Q_{0}$
is the set of vertexes and
![]() $Q_{1}$
is the set of arrows, be a locally finite quiver, that is, there are only finitely many incoming and outgoing arrows for each vertex. If a map
$Q_{1}$
is the set of arrows, be a locally finite quiver, that is, there are only finitely many incoming and outgoing arrows for each vertex. If a map
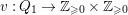 $v:Q_{1}\rightarrow \mathbb{Z}_{{\geqslant}0}\times \mathbb{Z}_{{\geqslant}0}$
is given, we call the pair
$v:Q_{1}\rightarrow \mathbb{Z}_{{\geqslant}0}\times \mathbb{Z}_{{\geqslant}0}$
is given, we call the pair
![]() $(Q,v)$
a valued quiver. Let
$(Q,v)$
a valued quiver. Let
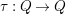 $\unicode[STIX]{x1D70F}:Q\rightarrow Q$
be a quiver automorphism. Then, we call the pair
$\unicode[STIX]{x1D70F}:Q\rightarrow Q$
be a quiver automorphism. Then, we call the pair
![]() $(Q,\unicode[STIX]{x1D70F})$
a stable translation quiver if the following two conditions hold:
$(Q,\unicode[STIX]{x1D70F})$
a stable translation quiver if the following two conditions hold:
-
(i)
 $Q$
has no loops and no multiple arrows.
$Q$
has no loops and no multiple arrows. -
(ii) For each vertex
 $x\in Q_{0}$
, we have
$x\in Q_{0}$
, we have  $$\begin{eqnarray}\{y\in Q_{0}\mid \unicode[STIX]{x1D70F}x\rightarrow y~\text{in}~Q_{1}\}=\{y\in Q_{0}\mid y\rightarrow x~\text{in}~Q_{1}\}.\end{eqnarray}$$
$$\begin{eqnarray}\{y\in Q_{0}\mid \unicode[STIX]{x1D70F}x\rightarrow y~\text{in}~Q_{1}\}=\{y\in Q_{0}\mid y\rightarrow x~\text{in}~Q_{1}\}.\end{eqnarray}$$
We call the triple
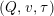 $(Q,v,\unicode[STIX]{x1D70F})$
a valued stable translation quiver if
$(Q,v,\unicode[STIX]{x1D70F})$
a valued stable translation quiver if
![]() $(Q,\unicode[STIX]{x1D70F})$
is a stable translation quiver and if
$(Q,\unicode[STIX]{x1D70F})$
is a stable translation quiver and if
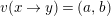 $v(x\rightarrow y)=(a,b)$
then
$v(x\rightarrow y)=(a,b)$
then
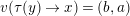 $v(\unicode[STIX]{x1D70F}(y)\rightarrow x)=(b,a)$
.
$v(\unicode[STIX]{x1D70F}(y)\rightarrow x)=(b,a)$
.
Definition 1.17. Let
![]() $(Q,\unicode[STIX]{x1D70F})$
be a stable translation quiver and
$(Q,\unicode[STIX]{x1D70F})$
be a stable translation quiver and
![]() $C$
a full subquiver of
$C$
a full subquiver of
![]() $Q$
. We call
$Q$
. We call
![]() $C$
a component of
$C$
a component of
![]() $(Q,\unicode[STIX]{x1D70F})$
if:
$(Q,\unicode[STIX]{x1D70F})$
if:
-
(i)
 $C$
is stable under the quiver automorphism
$C$
is stable under the quiver automorphism
 $\unicode[STIX]{x1D70F}$
;
$\unicode[STIX]{x1D70F}$
; -
(ii)
 $C$
is a disjoint union of connected components of the underlying undirected graph;
$C$
is a disjoint union of connected components of the underlying undirected graph; -
(iii) there is no proper subquiver of
 $C$
that satisfies (i) and (ii).
$C$
that satisfies (i) and (ii).
Note that components are also stable translation quivers.
Example 1.18. Let
![]() $(\unicode[STIX]{x1D6E5},v)$
be a valued quiver without loops and multiple arrows. Then, the set
$(\unicode[STIX]{x1D6E5},v)$
be a valued quiver without loops and multiple arrows. Then, the set
![]() $\mathbb{Z}\times \unicode[STIX]{x1D6E5}$
becomes a valued stable translation quiver by defining as follows:
$\mathbb{Z}\times \unicode[STIX]{x1D6E5}$
becomes a valued stable translation quiver by defining as follows:
-
∙ arrows are
 $(n,x)\rightarrow (n,y)$
and
$(n,x)\rightarrow (n,y)$
and
 $(n-1,y)\rightarrow (n,x)$
, for
$(n-1,y)\rightarrow (n,x)$
, for
 $x\rightarrow y$
in
$x\rightarrow y$
in
 $\unicode[STIX]{x1D6E5}$
and
$\unicode[STIX]{x1D6E5}$
and
 $n\in \mathbb{Z}$
;
$n\in \mathbb{Z}$
; -
∙ if
 $v(x\rightarrow y)=(a,b)$
, for
$v(x\rightarrow y)=(a,b)$
, for
 $x\rightarrow y$
in
$x\rightarrow y$
in
 $\unicode[STIX]{x1D6E5}$
, then
$\unicode[STIX]{x1D6E5}$
, then  $$\begin{eqnarray}v((n,x)\rightarrow (n,y))=(a,b)\qquad \text{and}\qquad v((n-1,y)\rightarrow (n,x))=(b,a).\end{eqnarray}$$
$$\begin{eqnarray}v((n,x)\rightarrow (n,y))=(a,b)\qquad \text{and}\qquad v((n-1,y)\rightarrow (n,x))=(b,a).\end{eqnarray}$$
-
∙
 $\unicode[STIX]{x1D70F}((n,x))=(n-1,x)$
.
$\unicode[STIX]{x1D70F}((n,x))=(n-1,x)$
.
We denote the valued stable translation quiver by
![]() $\mathbb{Z}\unicode[STIX]{x1D6E5}$
.
$\mathbb{Z}\unicode[STIX]{x1D6E5}$
.
Now we recall Riedmann’s structure theorem [Reference BensonB, Theorem 4.15.6]. For the definition of admissible subgroups, see [Reference BensonB, Definition 4.15.4].
Definition-Theorem 1.19. Let
![]() $(Q,\unicode[STIX]{x1D70F})$
be a stable translation quiver and
$(Q,\unicode[STIX]{x1D70F})$
be a stable translation quiver and
![]() $C$
a component of
$C$
a component of
![]() $(Q,\unicode[STIX]{x1D70F})$
. Then there is a directed tree
$(Q,\unicode[STIX]{x1D70F})$
. Then there is a directed tree
![]() $T$
and an admissible subgroup
$T$
and an admissible subgroup
 $G\subseteq \text{Aut}(\mathbb{Z}T)$
such that
$G\subseteq \text{Aut}(\mathbb{Z}T)$
such that
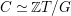 $C\simeq \mathbb{Z}T/G$
as a stable translation quiver. Moreover,
$C\simeq \mathbb{Z}T/G$
as a stable translation quiver. Moreover,
-
(1) the underlying undirected graph
 $\overline{T}$
of
$\overline{T}$
of
 $T$
is uniquely determined by
$T$
is uniquely determined by
 $C$
.
$C$
. -
(2)
 $G$
is unique up to conjugation in
$G$
is unique up to conjugation in
 $\text{Aut}(\mathbb{Z}T)$
.
$\text{Aut}(\mathbb{Z}T)$
.
The underlying tree
![]() $\overline{T}$
is called the tree class of
$\overline{T}$
is called the tree class of
![]() $C$
.
$C$
.
Definition 1.20. Let
![]() $(\unicode[STIX]{x1D6E5},v)$
be a valued quiver without loops and multiple arrows. For
$(\unicode[STIX]{x1D6E5},v)$
be a valued quiver without loops and multiple arrows. For
![]() $x\rightarrow y$
in
$x\rightarrow y$
in
![]() $\unicode[STIX]{x1D6E5}$
, we write
$\unicode[STIX]{x1D6E5}$
, we write
 $v(x\rightarrow y)=(d_{xy},d_{yx})$
. If there is no arrow between
$v(x\rightarrow y)=(d_{xy},d_{yx})$
. If there is no arrow between
![]() $x$
and
$x$
and
![]() $y$
, we understand that
$y$
, we understand that
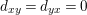 $d_{xy}=d_{yx}=0$
. Let
$d_{xy}=d_{yx}=0$
. Let
![]() $\mathbb{Q}_{{>}0}$
be the set of positive rational numbers.
$\mathbb{Q}_{{>}0}$
be the set of positive rational numbers.
-
(i) A subadditive function on
 $(\unicode[STIX]{x1D6E5},v)$
is a
$(\unicode[STIX]{x1D6E5},v)$
is a
 $\mathbb{Q}_{{>}0}$
-valued function
$\mathbb{Q}_{{>}0}$
-valued function
 $f$
on the set of vertexes of
$f$
on the set of vertexes of
 $\unicode[STIX]{x1D6E5}$
such that
$\unicode[STIX]{x1D6E5}$
such that
 $2f(x)\geqslant \sum _{y\neq x}d_{yx}f(y)$
, for each vertex
$2f(x)\geqslant \sum _{y\neq x}d_{yx}f(y)$
, for each vertex
 $x$
.
$x$
. -
(ii) An additive function on
 $(\unicode[STIX]{x1D6E5},v)$
is a
$(\unicode[STIX]{x1D6E5},v)$
is a
 $\mathbb{Q}_{{>}0}$
-valued function
$\mathbb{Q}_{{>}0}$
-valued function
 $f$
on the set of vertexes of
$f$
on the set of vertexes of
 $\unicode[STIX]{x1D6E5}$
such that
$\unicode[STIX]{x1D6E5}$
such that
 $2f(x)=\sum _{y\neq x}d_{yx}f(y)$
, for each vertex
$2f(x)=\sum _{y\neq x}d_{yx}f(y)$
, for each vertex
 $x$
.
$x$
.
The following lemma is well known. See [Reference BensonB, Theorem 4.5.8], for example.
Lemma 1.21. Let
![]() $(\unicode[STIX]{x1D6E5},v)$
be a valued quiver without loops and multiple arrows, and we assume that the underlying undirected graph
$(\unicode[STIX]{x1D6E5},v)$
be a valued quiver without loops and multiple arrows, and we assume that the underlying undirected graph
![]() $\overline{\unicode[STIX]{x1D6E5}}$
is connected.
$\overline{\unicode[STIX]{x1D6E5}}$
is connected.
-
(1) Suppose that
 $(\unicode[STIX]{x1D6E5},v)$
admits a subadditive function.
$(\unicode[STIX]{x1D6E5},v)$
admits a subadditive function.-
(i) If
 $\unicode[STIX]{x1D6E5}$
has a finite number of vertexes, then
$\unicode[STIX]{x1D6E5}$
has a finite number of vertexes, then
 $\overline{\unicode[STIX]{x1D6E5}}$
is one of finite or affine Dynkin diagrams.
$\overline{\unicode[STIX]{x1D6E5}}$
is one of finite or affine Dynkin diagrams. -
(ii) If
 $\unicode[STIX]{x1D6E5}$
has infinite number of vertexes, then
$\unicode[STIX]{x1D6E5}$
has infinite number of vertexes, then
 $\overline{\unicode[STIX]{x1D6E5}}$
is one of infinite Dynkin diagrams
$\overline{\unicode[STIX]{x1D6E5}}$
is one of infinite Dynkin diagrams
 $A_{\infty }$
,
$A_{\infty }$
,
 $B_{\infty }$
,
$B_{\infty }$
,
 $C_{\infty }$
,
$C_{\infty }$
,
 $D_{\infty }$
or
$D_{\infty }$
or
 $A_{\infty }^{\infty }$
.
$A_{\infty }^{\infty }$
.
-
-
(2) If
 $(\unicode[STIX]{x1D6E5},v)$
admits a subadditive function which is not additive, then
$(\unicode[STIX]{x1D6E5},v)$
admits a subadditive function which is not additive, then
 $\overline{\unicode[STIX]{x1D6E5}}$
is either a finite Dynkin diagram or
$\overline{\unicode[STIX]{x1D6E5}}$
is either a finite Dynkin diagram or
 $A_{\infty }$
.
$A_{\infty }$
. -
(3)
 $(\unicode[STIX]{x1D6E5},v)$
does not admit a bounded subadditive function if and only if
$(\unicode[STIX]{x1D6E5},v)$
does not admit a bounded subadditive function if and only if
 $\overline{\unicode[STIX]{x1D6E5}}$
is
$\overline{\unicode[STIX]{x1D6E5}}$
is
 $A_{\infty }$
.
$A_{\infty }$
.
1.4 AR quivers
We define the stable Auslander–Reiten quiver for symmetric
![]() ${\mathcal{O}}$
-orders as follows.
${\mathcal{O}}$
-orders as follows.
Definition 1.22. Let
![]() $A$
be a symmetric
$A$
be a symmetric
![]() ${\mathcal{O}}$
-order over a complete discrete valuation ring
${\mathcal{O}}$
-order over a complete discrete valuation ring
![]() ${\mathcal{O}}$
. The stable Auslander–Reiten quiver of
${\mathcal{O}}$
. The stable Auslander–Reiten quiver of
![]() $A$
is a valued quiver such that:
$A$
is a valued quiver such that:
-
∙ vertexes are isoclasses of nonprojective
 $A$
-lattices
$A$
-lattices
 $M$
such that
$M$
such that
 $M\otimes {\mathcal{K}}$
is projective;
$M\otimes {\mathcal{K}}$
is projective; -
∙ valued arrows
 $M\stackrel{(a,b)}{\rightarrow }N$
for irreducible morphisms
$M\stackrel{(a,b)}{\rightarrow }N$
for irreducible morphisms
 $M\rightarrow N$
, where the value
$M\rightarrow N$
, where the value
 $(a,b)$
of the arrow is given as follows.
$(a,b)$
of the arrow is given as follows.-
(a) For a minimal right almost split morphism
 $f:E\rightarrow N$
,
$f:E\rightarrow N$
,
 $M$
appears
$M$
appears
 $a$
times in
$a$
times in
 $E$
as a direct summand.
$E$
as a direct summand. -
(b) For a minimal left almost split morphism
 $g:M\rightarrow E$
,
$g:M\rightarrow E$
,
 $N$
appears
$N$
appears
 $b$
times in
$b$
times in
 $E$
as a direct summand.
$E$
as a direct summand.
-
A component of the stable Auslander–Reiten quiver is defined in the similar way as the stable translation quiver.
Lemma 1.23. Let
![]() $A$
be a symmetric
$A$
be a symmetric
![]() ${\mathcal{O}}$
-order over a complete discrete valuation ring
${\mathcal{O}}$
-order over a complete discrete valuation ring
![]() ${\mathcal{O}}$
, and let
${\mathcal{O}}$
, and let
![]() $C$
be a component of the stable Auslander–Reiten quiver of
$C$
be a component of the stable Auslander–Reiten quiver of
![]() $A$
. Assume that
$A$
. Assume that
![]() $C$
satisfies the following conditions:
$C$
satisfies the following conditions:
-
(i) There exists a
 $\unicode[STIX]{x1D70F}$
-periodic indecomposable
$\unicode[STIX]{x1D70F}$
-periodic indecomposable
 $A$
-lattice in
$A$
-lattice in
 $C$
.
$C$
. -
(ii) The number of vertexes in
 $C$
is infinite.
$C$
is infinite.
Then
![]() $C$
has no loops. In particular,
$C$
has no loops. In particular,
![]() $C$
is a valued stable translation quiver.
$C$
is a valued stable translation quiver.
Proof. As in the proof of [Reference BensonB, Theorem 4.16.2], we know that all indecomposable
![]() $A$
-lattices in
$A$
-lattices in
![]() $C$
are
$C$
are
![]() $\unicode[STIX]{x1D70F}$
-periodic. Thus, we may choose
$\unicode[STIX]{x1D70F}$
-periodic. Thus, we may choose
![]() $n_{X}\geqslant 2$
, for each
$n_{X}\geqslant 2$
, for each
![]() $X\in C$
, such that
$X\in C$
, such that
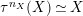 $\unicode[STIX]{x1D70F}^{n_{X}}(X)\simeq X$
. Define a
$\unicode[STIX]{x1D70F}^{n_{X}}(X)\simeq X$
. Define a
![]() $\mathbb{Q}_{{>}0}$
-valued function
$\mathbb{Q}_{{>}0}$
-valued function
![]() $f$
on
$f$
on
![]() $C$
by
$C$
by
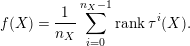 $$\begin{eqnarray}f(X)=\frac{1}{n_{X}}\mathop{\sum }_{i=0}^{n_{X}-1}\text{rank}\,\unicode[STIX]{x1D70F}^{i}(X).\end{eqnarray}$$
$$\begin{eqnarray}f(X)=\frac{1}{n_{X}}\mathop{\sum }_{i=0}^{n_{X}-1}\text{rank}\,\unicode[STIX]{x1D70F}^{i}(X).\end{eqnarray}$$
![]() $C$
does not have multiple arrows by definition. For each indecomposable
$C$
does not have multiple arrows by definition. For each indecomposable
![]() $N$
, there is an irreducible morphism
$N$
, there is an irreducible morphism
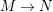 $M\rightarrow N$
if and only if there is an irreducible morphism
$M\rightarrow N$
if and only if there is an irreducible morphism
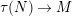 $\unicode[STIX]{x1D70F}(N)\rightarrow M$
by the existence of the almost split sequence
$\unicode[STIX]{x1D70F}(N)\rightarrow M$
by the existence of the almost split sequence
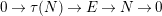 $0\rightarrow \unicode[STIX]{x1D70F}(N)\rightarrow E\rightarrow N\rightarrow 0$
. The condition on valued arrows may also be checked. Thus,
$0\rightarrow \unicode[STIX]{x1D70F}(N)\rightarrow E\rightarrow N\rightarrow 0$
. The condition on valued arrows may also be checked. Thus,
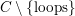 $C\setminus \{\text{loops}\}$
is a valued stable translation quiver, and we may apply the Riedmann structure theorem. We write
$C\setminus \{\text{loops}\}$
is a valued stable translation quiver, and we may apply the Riedmann structure theorem. We write
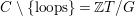 $C\setminus \{\text{loops}\}=\mathbb{Z}T/G$
, for a directed tree
$C\setminus \{\text{loops}\}=\mathbb{Z}T/G$
, for a directed tree
![]() $T$
and an admissible subgroup
$T$
and an admissible subgroup
![]() $G$
. Then
$G$
. Then
![]() $f$
is a
$f$
is a
![]() $\mathbb{Q}_{{>}0}$
-valued function on
$\mathbb{Q}_{{>}0}$
-valued function on
![]() $T$
. For
$T$
. For
![]() $X\in T$
, one can show that
$X\in T$
, one can show that
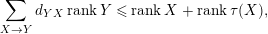 $$\begin{eqnarray}\mathop{\sum }_{X\rightarrow Y}d_{YX}\,\text{rank}\,Y\leqslant \text{rank}\,X+\text{rank}\,\unicode[STIX]{x1D70F}(X),\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{X\rightarrow Y}d_{YX}\,\text{rank}\,Y\leqslant \text{rank}\,X+\text{rank}\,\unicode[STIX]{x1D70F}(X),\end{eqnarray}$$
which implies that
![]() $f$
is a subadditive function.
$f$
is a subadditive function.
We now suppose that
![]() $C$
has a loop. Then,
$C$
has a loop. Then,
![]() $f$
is not additive. Thus, Lemma 1.21 and our assumption (ii) imply that
$f$
is not additive. Thus, Lemma 1.21 and our assumption (ii) imply that
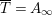 $\overline{T}=A_{\infty }$
. Thus, we may assume without loss of generality that
$\overline{T}=A_{\infty }$
. Thus, we may assume without loss of generality that
![]() $T$
is a chain of irreducible maps
$T$
is a chain of irreducible maps
 $$\begin{eqnarray}X_{1}\rightarrow X_{2}\rightarrow \cdots \rightarrow X_{r}\rightarrow \cdots .\end{eqnarray}$$
$$\begin{eqnarray}X_{1}\rightarrow X_{2}\rightarrow \cdots \rightarrow X_{r}\rightarrow \cdots .\end{eqnarray}$$
Then, for any
![]() $Y\in C$
, there is a unique
$Y\in C$
, there is a unique
![]() $r$
such that
$r$
such that
![]() $Y$
is in the
$Y$
is in the
![]() $\unicode[STIX]{x1D70F}$
-orbit through
$\unicode[STIX]{x1D70F}$
-orbit through
![]() $X_{r}$
. We may assume that
$X_{r}$
. We may assume that
![]() $X_{r}$
has a loop, for some
$X_{r}$
has a loop, for some
![]() $r$
. The almost split sequence starting at
$r$
. The almost split sequence starting at
![]() $X_{r}$
is
$X_{r}$
is
 $$\begin{eqnarray}0\rightarrow X_{r}\rightarrow X_{r}^{\oplus l}\oplus X_{r+1}\oplus \unicode[STIX]{x1D70F}^{-}(X_{r-1})\rightarrow \unicode[STIX]{x1D70F}^{-}(X_{r})\rightarrow 0,\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow X_{r}\rightarrow X_{r}^{\oplus l}\oplus X_{r+1}\oplus \unicode[STIX]{x1D70F}^{-}(X_{r-1})\rightarrow \unicode[STIX]{x1D70F}^{-}(X_{r})\rightarrow 0,\end{eqnarray}$$
where
![]() $l\geqslant 1$
. In particular, we have
$l\geqslant 1$
. In particular, we have
 $$\begin{eqnarray}f(X_{r})\geqslant (2-l)f(X_{r})\geqslant f(X_{r+1})+f(X_{r-1})\geqslant f(X_{r+1}).\end{eqnarray}$$
$$\begin{eqnarray}f(X_{r})\geqslant (2-l)f(X_{r})\geqslant f(X_{r+1})+f(X_{r-1})\geqslant f(X_{r+1}).\end{eqnarray}$$
We show that
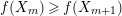 $f(X_{m})\geqslant f(X_{m+1})$
, for
$f(X_{m})\geqslant f(X_{m+1})$
, for
![]() $m\geqslant r$
. Suppose that
$m\geqslant r$
. Suppose that
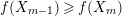 $f(X_{m-1})\geqslant f(X_{m})$
holds. The same argument as above shows
$f(X_{m-1})\geqslant f(X_{m})$
holds. The same argument as above shows
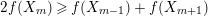 $2f(X_{m})\geqslant f(X_{m-1})+f(X_{m+1})$
, and the induction hypothesis implies
$2f(X_{m})\geqslant f(X_{m-1})+f(X_{m+1})$
, and the induction hypothesis implies
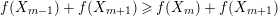 $f(X_{m-1})+f(X_{m+1})\geqslant f(X_{m})+f(X_{m+1})$
. Hence
$f(X_{m-1})+f(X_{m+1})\geqslant f(X_{m})+f(X_{m+1})$
. Hence
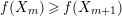 $f(X_{m})\geqslant f(X_{m+1})$
. Thus,
$f(X_{m})\geqslant f(X_{m+1})$
. Thus,
![]() $f$
is bounded. But
$f$
is bounded. But
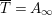 $\overline{T}=A_{\infty }$
does not admit a bounded subadditive function. Hence, we conclude that
$\overline{T}=A_{\infty }$
does not admit a bounded subadditive function. Hence, we conclude that
![]() $C$
has no loops and
$C$
has no loops and
![]() $C$
is a valued stable translation quiver.◻
$C$
is a valued stable translation quiver.◻
1.5 No loop theorem
In this subsection, we show an analogue of Auslander’s theorem and use this to show “no loop theorem”.
Lemma 1.24. Let
![]() $A$
be an
$A$
be an
![]() ${\mathcal{O}}$
-order,
${\mathcal{O}}$
-order,
![]() $M$
an indecomposable
$M$
an indecomposable
![]() $A$
-lattice. Then, there exists an integer
$A$
-lattice. Then, there exists an integer
![]() $s$
such that
$s$
such that
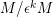 $M/\unicode[STIX]{x1D716}^{k}M$
is an indecomposable
$M/\unicode[STIX]{x1D716}^{k}M$
is an indecomposable
![]() $A/\unicode[STIX]{x1D716}^{k}A$
-module, for all
$A/\unicode[STIX]{x1D716}^{k}A$
-module, for all
![]() $k\geqslant s$
.
$k\geqslant s$
.
Proof. An
![]() ${\mathcal{O}}$
-linear map
${\mathcal{O}}$
-linear map
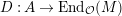 $D:A\rightarrow \text{End}_{{\mathcal{O}}}(M)$
is called a derivation if
$D:A\rightarrow \text{End}_{{\mathcal{O}}}(M)$
is called a derivation if
 $$\begin{eqnarray}D(xy)=xD(y)+D(x)y\end{eqnarray}$$
$$\begin{eqnarray}D(xy)=xD(y)+D(x)y\end{eqnarray}$$
for all
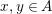 $x,y\in A$
. We denote by
$x,y\in A$
. We denote by
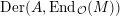 $\text{Der}(A,\text{End}_{{\mathcal{O}}}(M))$
the
$\text{Der}(A,\text{End}_{{\mathcal{O}}}(M))$
the
![]() ${\mathcal{O}}$
-module of derivations. Note that
${\mathcal{O}}$
-module of derivations. Note that
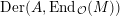 $\text{Der}(A,\text{End}_{{\mathcal{O}}}(M))$
is an
$\text{Der}(A,\text{End}_{{\mathcal{O}}}(M))$
is an
![]() ${\mathcal{O}}$
-order since
${\mathcal{O}}$
-order since
![]() $A$
and
$A$
and
![]() $M$
are.
$M$
are.
Let
![]() $k$
be a positive integer. For
$k$
be a positive integer. For
 $f\in \text{End}_{{\mathcal{O}}}(M)$
such that
$f\in \text{End}_{{\mathcal{O}}}(M)$
such that
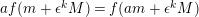 $af(m+\unicode[STIX]{x1D716}^{k}M)=f(am+\unicode[STIX]{x1D716}^{k}M)$
, for
$af(m+\unicode[STIX]{x1D716}^{k}M)=f(am+\unicode[STIX]{x1D716}^{k}M)$
, for
![]() $a\in A$
and
$a\in A$
and
![]() $m\in M$
, we define
$m\in M$
, we define
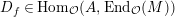 $D_{f}\in \text{Hom}_{{\mathcal{O}}}(A,\text{End}_{{\mathcal{O}}}(M))$
as follows.
$D_{f}\in \text{Hom}_{{\mathcal{O}}}(A,\text{End}_{{\mathcal{O}}}(M))$
as follows.
 $$\begin{eqnarray}D_{f}(a)(m)=\unicode[STIX]{x1D716}^{-k}(f(am)-af(m)),\quad \text{for}~a\in A~\text{and}~m\in M.\end{eqnarray}$$
$$\begin{eqnarray}D_{f}(a)(m)=\unicode[STIX]{x1D716}^{-k}(f(am)-af(m)),\quad \text{for}~a\in A~\text{and}~m\in M.\end{eqnarray}$$
The following computation shows that
![]() $D_{f}$
is a derivation.
$D_{f}$
is a derivation.
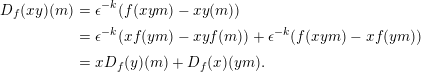 $$\begin{eqnarray}\displaystyle D_{f}(xy)(m) & = & \displaystyle \unicode[STIX]{x1D716}^{-k}(f(xym)-xy(m))\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D716}^{-k}(xf(ym)-xyf(m))+\unicode[STIX]{x1D716}^{-k}(f(xym)-xf(ym))\nonumber\\ \displaystyle & = & \displaystyle xD_{f}(y)(m)+D_{f}(x)(ym).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle D_{f}(xy)(m) & = & \displaystyle \unicode[STIX]{x1D716}^{-k}(f(xym)-xy(m))\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D716}^{-k}(xf(ym)-xyf(m))+\unicode[STIX]{x1D716}^{-k}(f(xym)-xf(ym))\nonumber\\ \displaystyle & = & \displaystyle xD_{f}(y)(m)+D_{f}(x)(ym).\nonumber\end{eqnarray}$$
Let
![]() $\text{Der}(k)$
be the
$\text{Der}(k)$
be the
![]() ${\mathcal{O}}$
-submodule of
${\mathcal{O}}$
-submodule of
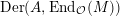 $\text{Der}(A,\text{End}_{{\mathcal{O}}}(M))$
which is generated by all such
$\text{Der}(A,\text{End}_{{\mathcal{O}}}(M))$
which is generated by all such
![]() $D_{f}$
, and we define
$D_{f}$
, and we define
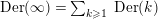 $\text{Der}(\infty )=\sum _{k\geqslant 1}\,\text{Der}(k)$
. Since
$\text{Der}(\infty )=\sum _{k\geqslant 1}\,\text{Der}(k)$
. Since
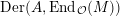 $\text{Der}(A,\text{End}_{{\mathcal{O}}}(M))$
is a finitely generated
$\text{Der}(A,\text{End}_{{\mathcal{O}}}(M))$
is a finitely generated
![]() ${\mathcal{O}}$
-module, there exists an integer
${\mathcal{O}}$
-module, there exists an integer
![]() $s$
such that
$s$
such that
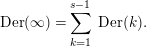 $$\begin{eqnarray}\text{Der}(\infty )=\mathop{\sum }_{k=1}^{s-1}\,\text{Der}(k).\end{eqnarray}$$
$$\begin{eqnarray}\text{Der}(\infty )=\mathop{\sum }_{k=1}^{s-1}\,\text{Der}(k).\end{eqnarray}$$
We show that the algebra homomorphism
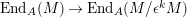 $\text{End}_{A}(M)\rightarrow \text{End}_{A}(M/\unicode[STIX]{x1D716}^{k}M)$
is surjective, for all
$\text{End}_{A}(M)\rightarrow \text{End}_{A}(M/\unicode[STIX]{x1D716}^{k}M)$
is surjective, for all
![]() $k\geqslant s$
. Let
$k\geqslant s$
. Let
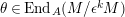 $\unicode[STIX]{x1D703}\in \text{End}_{A}(M/\unicode[STIX]{x1D716}^{k}M)$
, for
$\unicode[STIX]{x1D703}\in \text{End}_{A}(M/\unicode[STIX]{x1D716}^{k}M)$
, for
![]() $k\geqslant s$
. We fix
$k\geqslant s$
. We fix
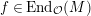 $f\in \text{End}_{{\mathcal{O}}}(M)$
such that
$f\in \text{End}_{{\mathcal{O}}}(M)$
such that
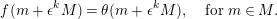 $$\begin{eqnarray}f(m+\unicode[STIX]{x1D716}^{k}M)=\unicode[STIX]{x1D703}(m+\unicode[STIX]{x1D716}^{k}M),\quad \text{for}~m\in M.\end{eqnarray}$$
$$\begin{eqnarray}f(m+\unicode[STIX]{x1D716}^{k}M)=\unicode[STIX]{x1D703}(m+\unicode[STIX]{x1D716}^{k}M),\quad \text{for}~m\in M.\end{eqnarray}$$
Then, there exist
![]() $c_{i}\in {\mathcal{O}}$
and
$c_{i}\in {\mathcal{O}}$
and
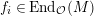 $f_{i}\in \text{End}_{{\mathcal{O}}}(M)$
that satisfy
$f_{i}\in \text{End}_{{\mathcal{O}}}(M)$
that satisfy
 $$\begin{eqnarray}\displaystyle f_{i}(m+\unicode[STIX]{x1D716}^{l_{i}}M) & = & \displaystyle \unicode[STIX]{x1D703}_{i}(m+\unicode[STIX]{x1D716}^{l_{i}}M),\nonumber\\ \displaystyle & & \displaystyle \text{for some}~1\leqslant l_{i}\leqslant s-1~\text{and}~\unicode[STIX]{x1D703}_{i}\in \text{End}_{A}(M/\unicode[STIX]{x1D716}^{l_{i}}M),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle f_{i}(m+\unicode[STIX]{x1D716}^{l_{i}}M) & = & \displaystyle \unicode[STIX]{x1D703}_{i}(m+\unicode[STIX]{x1D716}^{l_{i}}M),\nonumber\\ \displaystyle & & \displaystyle \text{for some}~1\leqslant l_{i}\leqslant s-1~\text{and}~\unicode[STIX]{x1D703}_{i}\in \text{End}_{A}(M/\unicode[STIX]{x1D716}^{l_{i}}M),\nonumber\end{eqnarray}$$
such that
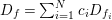 $D_{f}=\sum _{i=1}^{N}c_{i}D_{f_{i}}$
. More explicitly, we have
$D_{f}=\sum _{i=1}^{N}c_{i}D_{f_{i}}$
. More explicitly, we have
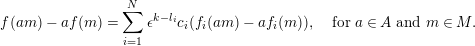 $$\begin{eqnarray}f(am)-af(m)=\mathop{\sum }_{i=1}^{N}\unicode[STIX]{x1D716}^{k-l_{i}}c_{i}(f_{i}(am)-af_{i}(m)),\quad \text{for}~a\in A~\text{and}~m\in M.\end{eqnarray}$$
$$\begin{eqnarray}f(am)-af(m)=\mathop{\sum }_{i=1}^{N}\unicode[STIX]{x1D716}^{k-l_{i}}c_{i}(f_{i}(am)-af_{i}(m)),\quad \text{for}~a\in A~\text{and}~m\in M.\end{eqnarray}$$
It implies that
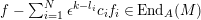 $f-\sum _{i=1}^{N}\unicode[STIX]{x1D716}^{k-l_{i}}c_{i}f_{i}\in \text{End}_{A}(M)$
. Since it coincides with
$f-\sum _{i=1}^{N}\unicode[STIX]{x1D716}^{k-l_{i}}c_{i}f_{i}\in \text{End}_{A}(M)$
. Since it coincides with
![]() $\unicode[STIX]{x1D703}$
if we reduce modulo
$\unicode[STIX]{x1D703}$
if we reduce modulo
![]() $\unicode[STIX]{x1D716}$
, we have proved
$\unicode[STIX]{x1D716}$
, we have proved
 $$\begin{eqnarray}\text{Im}(\text{End}_{A}(M)\rightarrow \text{End}_{A}(M/\unicode[STIX]{x1D716}^{k}M))+\unicode[STIX]{x1D716}\,\text{End}_{A}(M/\unicode[STIX]{x1D716}^{k}M)=\text{End}_{A}(M/\unicode[STIX]{x1D716}^{k}M).\end{eqnarray}$$
$$\begin{eqnarray}\text{Im}(\text{End}_{A}(M)\rightarrow \text{End}_{A}(M/\unicode[STIX]{x1D716}^{k}M))+\unicode[STIX]{x1D716}\,\text{End}_{A}(M/\unicode[STIX]{x1D716}^{k}M)=\text{End}_{A}(M/\unicode[STIX]{x1D716}^{k}M).\end{eqnarray}$$
Thus, Nakayama’s lemma implies that
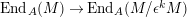 $\text{End}_{A}(M)\rightarrow \text{End}_{A}(M/\unicode[STIX]{x1D716}^{k}M)$
is surjective, and we have an isomorphism of algebras
$\text{End}_{A}(M)\rightarrow \text{End}_{A}(M/\unicode[STIX]{x1D716}^{k}M)$
is surjective, and we have an isomorphism of algebras
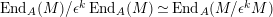 $\text{End}_{A}(M)/\unicode[STIX]{x1D716}^{k}\,\text{End}_{A}(M)\simeq \text{End}_{A}(M/\unicode[STIX]{x1D716}^{k}M)$
. As
$\text{End}_{A}(M)/\unicode[STIX]{x1D716}^{k}\,\text{End}_{A}(M)\simeq \text{End}_{A}(M/\unicode[STIX]{x1D716}^{k}M)$
. As
![]() ${\mathcal{O}}$
is a complete local ring, the lifting idempotent argument works [Reference Curtis and ReinerCR, (6.7)]. Hence, if
${\mathcal{O}}$
is a complete local ring, the lifting idempotent argument works [Reference Curtis and ReinerCR, (6.7)]. Hence, if
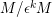 $M/\unicode[STIX]{x1D716}^{k}M$
is decomposable, so is
$M/\unicode[STIX]{x1D716}^{k}M$
is decomposable, so is
![]() $M$
.◻
$M$
.◻
We recall the Harada–Sai lemma from [Reference Auslander, Reiten and SmaløARS, VI. Corollary 1.3].
Lemma 1.25. Let
![]() $B$
be an Artin algebra,
$B$
be an Artin algebra,
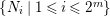 $\{N_{i}\mid 1\leqslant i\leqslant 2^{m}\}$
a collection of indecomposable
$\{N_{i}\mid 1\leqslant i\leqslant 2^{m}\}$
a collection of indecomposable
![]() $B$
-modules such that the length of composition series of
$B$
-modules such that the length of composition series of
![]() $N_{i}$
is less than or equal to
$N_{i}$
is less than or equal to
![]() $m$
, for all
$m$
, for all
![]() $i$
. If none of
$i$
. If none of
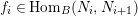 $f_{i}\in \text{Hom}_{B}(N_{i},N_{i+1})$
$f_{i}\in \text{Hom}_{B}(N_{i},N_{i+1})$
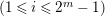 $(1\leqslant i\leqslant 2^{m}-1)$
is an isomorphism, then
$(1\leqslant i\leqslant 2^{m}-1)$
is an isomorphism, then
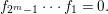 $$\begin{eqnarray}f_{2^{m}-1}\cdots f_{1}=0.\end{eqnarray}$$
$$\begin{eqnarray}f_{2^{m}-1}\cdots f_{1}=0.\end{eqnarray}$$
Proposition 1.26. Let
![]() $A$
be a symmetric
$A$
be a symmetric
![]() ${\mathcal{O}}$
-order over a complete discrete valuation ring
${\mathcal{O}}$
-order over a complete discrete valuation ring
![]() ${\mathcal{O}}$
, and assume that
${\mathcal{O}}$
, and assume that
![]() $A$
is indecomposable as an
$A$
is indecomposable as an
![]() ${\mathcal{O}}$
-algebra. Let
${\mathcal{O}}$
-algebra. Let
![]() $C$
be a component of the stable Auslander–Reiten quiver of
$C$
be a component of the stable Auslander–Reiten quiver of
![]() $A$
. Assume that the number of vertexes in
$A$
. Assume that the number of vertexes in
![]() $C$
is finite. Then
$C$
is finite. Then
![]() $C$
exhausts all nonprojective indecomposable
$C$
exhausts all nonprojective indecomposable
![]() $A$
-lattices.
$A$
-lattices.
Proof. We add indecomposable projective
![]() $A$
-lattices to the stable Auslander–Reiten quiver of
$A$
-lattices to the stable Auslander–Reiten quiver of
![]() $A$
to obtain the Auslander–Reiten quiver of
$A$
to obtain the Auslander–Reiten quiver of
![]() $A$
. We show that if
$A$
. We show that if
![]() $C$
is a finite component of the Auslander–Reiten quiver then
$C$
is a finite component of the Auslander–Reiten quiver then
![]() $C$
exhausts all indecomposable
$C$
exhausts all indecomposable
![]() $A$
-lattices. Assume that
$A$
-lattices. Assume that
![]() $M$
is an indecomposable
$M$
is an indecomposable
![]() $A$
-lattice which does not belong to
$A$
-lattice which does not belong to
![]() $C$
. It suffices to show
$C$
. It suffices to show
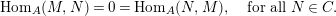 $$\begin{eqnarray}\text{Hom}_{A}(M,N)=0=\text{Hom}_{A}(N,M),\quad \text{for all}~N\in C.\end{eqnarray}$$
$$\begin{eqnarray}\text{Hom}_{A}(M,N)=0=\text{Hom}_{A}(N,M),\quad \text{for all}~N\in C.\end{eqnarray}$$
To see that it is sufficient, let
![]() $P$
be a direct summand of the projective cover of
$P$
be a direct summand of the projective cover of
![]() $N\in C$
. Then,
$N\in C$
. Then,
![]() $P\in C$
by
$P\in C$
by
![]() $N\in C$
and
$N\in C$
and
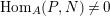 $\text{Hom}_{A}(P,N)\neq 0$
. As
$\text{Hom}_{A}(P,N)\neq 0$
. As
![]() $A$
is indecomposable as an algebra, there is no indecomposable projective
$A$
is indecomposable as an algebra, there is no indecomposable projective
![]() $A$
-lattice
$A$
-lattice
![]() $Q$
with the property that
$Q$
with the property that
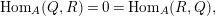 $$\begin{eqnarray}\text{Hom}_{A}(Q,R)=0=\text{Hom}_{A}(R,Q),\end{eqnarray}$$
$$\begin{eqnarray}\text{Hom}_{A}(Q,R)=0=\text{Hom}_{A}(R,Q),\end{eqnarray}$$
for all indecomposable projective
![]() $A$
-lattices
$A$
-lattices
![]() $R\in C$
. It implies that any direct summand
$R\in C$
. It implies that any direct summand
![]() $Q$
of the projective cover of
$Q$
of the projective cover of
![]() $M$
belongs to
$M$
belongs to
![]() $C$
. Then
$C$
. Then
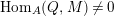 $\text{Hom}_{A}(Q,M)\neq 0$
implies that
$\text{Hom}_{A}(Q,M)\neq 0$
implies that
![]() $M\in C$
, which contradicts our assumption. Thus,
$M\in C$
, which contradicts our assumption. Thus,
![]() $C$
exhausts all indecomposable
$C$
exhausts all indecomposable
![]() $A$
-lattices.
$A$
-lattices.
Assume that there exists a nonzero morphism
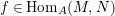 $f\in \text{Hom}_{A}(M,N)$
. As
$f\in \text{Hom}_{A}(M,N)$
. As
![]() $M\not \in C$
and
$M\not \in C$
and
![]() $N\in C$
,
$N\in C$
,
![]() $f$
is not a split epimorphism. We consider the almost split sequence of
$f$
is not a split epimorphism. We consider the almost split sequence of
![]() $A$
-lattices ending at
$A$
-lattices ending at
![]() $N$
, and we denote by
$N$
, and we denote by
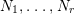 $N_{1},\ldots ,N_{r}$
the indecomposable direct summands of the middle term of the almost split sequence. Let
$N_{1},\ldots ,N_{r}$
the indecomposable direct summands of the middle term of the almost split sequence. Let
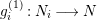 $$\begin{eqnarray}g_{i}^{(1)}:N_{i}\longrightarrow N\end{eqnarray}$$
$$\begin{eqnarray}g_{i}^{(1)}:N_{i}\longrightarrow N\end{eqnarray}$$
be irreducible morphisms. Then, there exist
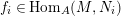 $f_{i}\in \text{Hom}_{A}(M,N_{i})$
such that
$f_{i}\in \text{Hom}_{A}(M,N_{i})$
such that
 $$\begin{eqnarray}f=\mathop{\sum }_{i=1}^{r}g_{i}^{(1)}f_{i}.\end{eqnarray}$$
$$\begin{eqnarray}f=\mathop{\sum }_{i=1}^{r}g_{i}^{(1)}f_{i}.\end{eqnarray}$$
If
![]() $N_{i}$
is nonprojective, we apply the same procedure to
$N_{i}$
is nonprojective, we apply the same procedure to
![]() $f_{i}$
. If
$f_{i}$
. If
![]() $N_{i}$
is projective,
$N_{i}$
is projective,
![]() $f_{i}$
factors through the Heller lattice
$f_{i}$
factors through the Heller lattice
![]() $\text{Rad}\,N_{i}$
of the irreducible
$\text{Rad}\,N_{i}$
of the irreducible
![]() $A\otimes \unicode[STIX]{x1D705}$
-module
$A\otimes \unicode[STIX]{x1D705}$
-module
 $N_{i}/\text{Rad}(N_{i})$
. Thus, we apply the procedure after we replace
$N_{i}/\text{Rad}(N_{i})$
. Thus, we apply the procedure after we replace
![]() $N_{i}$
with
$N_{i}$
with
![]() $\text{Rad}\,N_{i}$
. After repeating
$\text{Rad}\,N_{i}$
. After repeating
![]() $n$
times, we obtain,
$n$
times, we obtain,
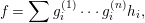 $$\begin{eqnarray}f=\sum \mathop{g}_{i}^{(1)}\cdots g_{i}^{(n)}h_{i},\end{eqnarray}$$
$$\begin{eqnarray}f=\sum \mathop{g}_{i}^{(1)}\cdots g_{i}^{(n)}h_{i},\end{eqnarray}$$
such that
![]() $g_{i}^{(j)}$
are morphisms among indecomposable
$g_{i}^{(j)}$
are morphisms among indecomposable
![]() $A$
-lattices in
$A$
-lattices in
![]() $C$
,
$C$
,
![]() $h_{i}$
are morphisms
$h_{i}$
are morphisms
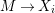 $M\rightarrow X_{i}$
, where
$M\rightarrow X_{i}$
, where
![]() $X_{i}$
are indecomposable
$X_{i}$
are indecomposable
![]() $A$
-lattices in
$A$
-lattices in
![]() $C$
and they are not isomorphisms.
$C$
and they are not isomorphisms.
Since the number of vertexes in
![]() $C$
is finite, there exists an integer
$C$
is finite, there exists an integer
![]() $s$
such that
$s$
such that
![]() $X/\unicode[STIX]{x1D716}^{s}X$
is indecomposable, for all
$X/\unicode[STIX]{x1D716}^{s}X$
is indecomposable, for all
![]() $X\in C$
. Let
$X\in C$
. Let
![]() $m$
be the maximal length of
$m$
be the maximal length of
![]() $A/\unicode[STIX]{x1D716}^{s}A$
-modules
$A/\unicode[STIX]{x1D716}^{s}A$
-modules
![]() $X/\unicode[STIX]{x1D716}^{s}X$
, for
$X/\unicode[STIX]{x1D716}^{s}X$
, for
![]() $X\in C$
. Applying Lemma 1.25 to the Artin algebra
$X\in C$
. Applying Lemma 1.25 to the Artin algebra
![]() $A/\unicode[STIX]{x1D716}^{s}A$
with
$A/\unicode[STIX]{x1D716}^{s}A$
with
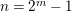 $n=2^{m}-1$
, we obtain
$n=2^{m}-1$
, we obtain
 $$\begin{eqnarray}\text{Hom}_{A}(M,N)=\unicode[STIX]{x1D716}^{s}\,\text{Hom}_{A}(M,N),\end{eqnarray}$$
$$\begin{eqnarray}\text{Hom}_{A}(M,N)=\unicode[STIX]{x1D716}^{s}\,\text{Hom}_{A}(M,N),\end{eqnarray}$$
and Nakayama’s Lemma implies
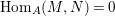 $\text{Hom}_{A}(M,N)=0$
. The proof of
$\text{Hom}_{A}(M,N)=0$
. The proof of
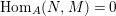 $\text{Hom}_{A}(N,M)=0$
is similar. We start with a nonzero morphism
$\text{Hom}_{A}(N,M)=0$
is similar. We start with a nonzero morphism
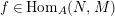 $f\in \text{Hom}_{A}(N,M)$
and consider the almost split sequence of
$f\in \text{Hom}_{A}(N,M)$
and consider the almost split sequence of
![]() $A$
-lattices starting at
$A$
-lattices starting at
![]() $N$
. Let
$N$
. Let
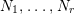 $N_{1},\ldots ,N_{r}$
be the indecomposable direct summands of the middle term of the almost split sequence as above, and let
$N_{1},\ldots ,N_{r}$
be the indecomposable direct summands of the middle term of the almost split sequence as above, and let
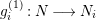 $$\begin{eqnarray}g_{i}^{(1)}:N\longrightarrow N_{i}\end{eqnarray}$$
$$\begin{eqnarray}g_{i}^{(1)}:N\longrightarrow N_{i}\end{eqnarray}$$
be irreducible morphisms. If
![]() $N_{i}$
is projective, then we replace
$N_{i}$
is projective, then we replace
![]() $N_{i}$
with
$N_{i}$
with
![]() $\text{Rad}\,N_{i}$
. Then, after repeating the procedure
$\text{Rad}\,N_{i}$
. Then, after repeating the procedure
![]() $n$
times, we obtain
$n$
times, we obtain
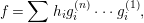 $$\begin{eqnarray}f=\sum h_{i}g_{i}^{(n)}\cdots g_{i}^{(1)},\end{eqnarray}$$
$$\begin{eqnarray}f=\sum h_{i}g_{i}^{(n)}\cdots g_{i}^{(1)},\end{eqnarray}$$
where
![]() $h_{i}$
are morphisms from indecomposable
$h_{i}$
are morphisms from indecomposable
![]() $A$
-lattices in
$A$
-lattices in
![]() $C$
to
$C$
to
![]() $M$
. Then, we may deduce
$M$
. Then, we may deduce
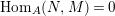 $\text{Hom}_{A}(N,M)=0$
by the Harada–Sai lemma and Nakayama’s lemma as before.◻
$\text{Hom}_{A}(N,M)=0$
by the Harada–Sai lemma and Nakayama’s lemma as before.◻
Theorem 1.27. Let
![]() $A$
be a symmetric
$A$
be a symmetric
![]() ${\mathcal{O}}$
-order over a complete discrete valuation ring
${\mathcal{O}}$
-order over a complete discrete valuation ring
![]() ${\mathcal{O}}$
, and let
${\mathcal{O}}$
, and let
![]() $C$
be a component of the stable Auslander–Reiten quiver of
$C$
be a component of the stable Auslander–Reiten quiver of
![]() $A$
. Suppose that:
$A$
. Suppose that:
-
(i) there exists a
 $\unicode[STIX]{x1D70F}$
-periodic indecomposable
$\unicode[STIX]{x1D70F}$
-periodic indecomposable
 $A$
-lattice in
$A$
-lattice in
 $C$
;
$C$
; -
(ii) the stable Auslander–Reiten quiver of
 $A$
has infinitely many vertexes.
$A$
has infinitely many vertexes.
Then, the number of vertexes in
![]() $C$
is infinite and
$C$
is infinite and
![]() $C$
is a valued stable translation quiver.
$C$
is a valued stable translation quiver.
Proof. As in the proof of Lemma 1.23,
![]() $C$
admits a subadditive function by the condition (i). Hence, the tree class of the valued stable translation quiver
$C$
admits a subadditive function by the condition (i). Hence, the tree class of the valued stable translation quiver
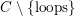 $C\setminus \{\text{loops}\}$
is one of finite, affine or infinite Dynkin diagrams. In the first two cases, the number of vertexes in
$C\setminus \{\text{loops}\}$
is one of finite, affine or infinite Dynkin diagrams. In the first two cases, the number of vertexes in
![]() $C$
is finite, since all vertexes in
$C$
is finite, since all vertexes in
![]() $C$
are
$C$
are
![]() $\unicode[STIX]{x1D70F}$
-periodic. Then we may apply Proposition 1.26 and it contradicts the condition (ii). Thus, the tree class is one of infinite Dynkin diagrams and the number of vertexes in
$\unicode[STIX]{x1D70F}$
-periodic. Then we may apply Proposition 1.26 and it contradicts the condition (ii). Thus, the tree class is one of infinite Dynkin diagrams and the number of vertexes in
![]() $C$
is infinite. Then, Lemma 1.23 implies that there is no loop in
$C$
is infinite. Then, Lemma 1.23 implies that there is no loop in
![]() $C$
and
$C$
and
![]() $C$
is a valued stable translation quiver.◻
$C$
is a valued stable translation quiver.◻
2 The case
 $A={\mathcal{O}}[X]/(X^{n})$
$A={\mathcal{O}}[X]/(X^{n})$
2.1 Heller lattices
Let
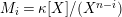 $M_{i}=\unicode[STIX]{x1D705}[X]/(X^{n-i})$
, for
$M_{i}=\unicode[STIX]{x1D705}[X]/(X^{n-i})$
, for
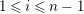 $1\leqslant i\leqslant n-1$
. They form a complete set of isoclasses of nonprojective indecomposable
$1\leqslant i\leqslant n-1$
. They form a complete set of isoclasses of nonprojective indecomposable
![]() $A\otimes \unicode[STIX]{x1D705}$
-modules. We realize
$A\otimes \unicode[STIX]{x1D705}$
-modules. We realize
![]() $M_{i}$
as the
$M_{i}$
as the
![]() $A\otimes \unicode[STIX]{x1D705}$
-submodule
$A\otimes \unicode[STIX]{x1D705}$
-submodule
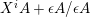 $X^{i}A+\unicode[STIX]{x1D716}A/\unicode[STIX]{x1D716}A$
of
$X^{i}A+\unicode[STIX]{x1D716}A/\unicode[STIX]{x1D716}A$
of
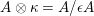 $A\otimes \unicode[STIX]{x1D705}=A/\unicode[STIX]{x1D716}A$
. We view
$A\otimes \unicode[STIX]{x1D705}=A/\unicode[STIX]{x1D716}A$
. We view
![]() $M_{i}$
as an
$M_{i}$
as an
![]() $A$
-module. Then,
$A$
-module. Then,
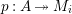 $p:A{\twoheadrightarrow}M_{i}$
defined by
$p:A{\twoheadrightarrow}M_{i}$
defined by
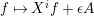 $f\mapsto X^{i}f+\unicode[STIX]{x1D716}A$
is the projective cover of
$f\mapsto X^{i}f+\unicode[STIX]{x1D716}A$
is the projective cover of
![]() $M_{i}$
. Therefore, the Heller lattice
$M_{i}$
. Therefore, the Heller lattice
![]() $Z_{i}$
of
$Z_{i}$
of
![]() $M_{i}$
, which is an
$M_{i}$
, which is an
![]() $A$
-submodule of
$A$
-submodule of
![]() $A$
, is given as follows:
$A$
, is given as follows:
 $$\begin{eqnarray}Z_{i}={\mathcal{O}}\unicode[STIX]{x1D716}\oplus {\mathcal{O}}\unicode[STIX]{x1D716}X\oplus \cdots {\mathcal{O}}\unicode[STIX]{x1D716}X^{n-i-1}\oplus {\mathcal{O}}X^{n-i}\oplus {\mathcal{O}}X^{n-i+1}\oplus \cdots \oplus {\mathcal{O}}X^{n-1}.\end{eqnarray}$$
$$\begin{eqnarray}Z_{i}={\mathcal{O}}\unicode[STIX]{x1D716}\oplus {\mathcal{O}}\unicode[STIX]{x1D716}X\oplus \cdots {\mathcal{O}}\unicode[STIX]{x1D716}X^{n-i-1}\oplus {\mathcal{O}}X^{n-i}\oplus {\mathcal{O}}X^{n-i+1}\oplus \cdots \oplus {\mathcal{O}}X^{n-1}.\end{eqnarray}$$
Then the representing matrix of the action of
![]() $X$
on
$X$
on
![]() $Z_{i}$
with respect to the above basis is given by the following matrix:
$Z_{i}$
with respect to the above basis is given by the following matrix:

Thus,
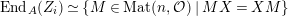 $\text{End}_{A}(Z_{i})\simeq \{M\in \text{Mat}(n,{\mathcal{O}})\mid MX=XM\}$
is a local
$\text{End}_{A}(Z_{i})\simeq \{M\in \text{Mat}(n,{\mathcal{O}})\mid MX=XM\}$
is a local
![]() ${\mathcal{O}}$
-algebra, since the right hand side is contained in
${\mathcal{O}}$
-algebra, since the right hand side is contained in
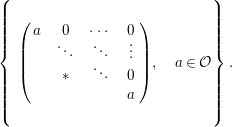
It follows the next lemma. Note that
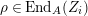 $\unicode[STIX]{x1D70C}\in \text{End}_{A}(Z_{i})$
is determined by
$\unicode[STIX]{x1D70C}\in \text{End}_{A}(Z_{i})$
is determined by
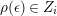 $\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D716})\in Z_{i}$
.
$\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D716})\in Z_{i}$
.
Lemma 2.1. We have the following.
-
(1) The Heller lattices
 $Z_{i}$
are pairwise nonisomorphic indecomposable
$Z_{i}$
are pairwise nonisomorphic indecomposable
 $A$
-lattices.
$A$
-lattices. -
(2) If
 $\unicode[STIX]{x1D70C}\in \text{Rad}\,\text{End}_{A}(Z_{i})$
then
$\unicode[STIX]{x1D70C}\in \text{Rad}\,\text{End}_{A}(Z_{i})$
then
 $\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D716})$
has the form where
$\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D716})$
has the form where $$\begin{eqnarray}\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D716})=a_{0}\unicode[STIX]{x1D716}+\cdots +a_{n-i-1}\unicode[STIX]{x1D716}X^{n-i-1}+a_{n-i}X^{n-i}+\cdots +a_{n-1}X^{n-1},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D716})=a_{0}\unicode[STIX]{x1D716}+\cdots +a_{n-i-1}\unicode[STIX]{x1D716}X^{n-i-1}+a_{n-i}X^{n-i}+\cdots +a_{n-1}X^{n-1},\end{eqnarray}$$
 $a_{i}\in {\mathcal{O}}$
, for
$a_{i}\in {\mathcal{O}}$
, for
 $1\leqslant i\leqslant n-1$
, and
$1\leqslant i\leqslant n-1$
, and
 $a_{0}\in \unicode[STIX]{x1D716}{\mathcal{O}}$
.
$a_{0}\in \unicode[STIX]{x1D716}{\mathcal{O}}$
.
We now consider the following pullback diagram:
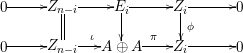
where
![]() $\unicode[STIX]{x1D719}$
is defined by
$\unicode[STIX]{x1D719}$
is defined by
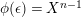 $\unicode[STIX]{x1D719}(\unicode[STIX]{x1D716})=X^{n-1}$
and
$\unicode[STIX]{x1D719}(\unicode[STIX]{x1D716})=X^{n-1}$
and
 $$\begin{eqnarray}\unicode[STIX]{x1D719}(\unicode[STIX]{x1D716}X)=\cdots =\unicode[STIX]{x1D719}(\unicode[STIX]{x1D716}X^{n-i-1})=\unicode[STIX]{x1D719}(X^{n-i})=\cdots =\unicode[STIX]{x1D719}(X^{n-1})=0,\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D719}(\unicode[STIX]{x1D716}X)=\cdots =\unicode[STIX]{x1D719}(\unicode[STIX]{x1D716}X^{n-i-1})=\unicode[STIX]{x1D719}(X^{n-i})=\cdots =\unicode[STIX]{x1D719}(X^{n-1})=0,\end{eqnarray}$$
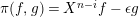 $\unicode[STIX]{x1D70B}(f,g)=X^{n-i}f-\unicode[STIX]{x1D716}g$
, for
$\unicode[STIX]{x1D70B}(f,g)=X^{n-i}f-\unicode[STIX]{x1D716}g$
, for
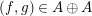 $(f,g)\in A\oplus A$
, and
$(f,g)\in A\oplus A$
, and
![]() $\unicode[STIX]{x1D704}$
is given as follows.
$\unicode[STIX]{x1D704}$
is given as follows.
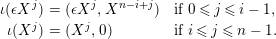 $$\begin{eqnarray}\begin{array}{@{}rcll@{}}\unicode[STIX]{x1D704}(\unicode[STIX]{x1D716}X^{j})\ & =\ & (\unicode[STIX]{x1D716}X^{j},X^{n-i+j}) & \text{if}~0\leqslant j\leqslant i-1,\\ \unicode[STIX]{x1D704}(X^{j})\ & =\ & (X^{j},0) & \text{if}~i\leqslant j\leqslant n-1.\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}rcll@{}}\unicode[STIX]{x1D704}(\unicode[STIX]{x1D716}X^{j})\ & =\ & (\unicode[STIX]{x1D716}X^{j},X^{n-i+j}) & \text{if}~0\leqslant j\leqslant i-1,\\ \unicode[STIX]{x1D704}(X^{j})\ & =\ & (X^{j},0) & \text{if}~i\leqslant j\leqslant n-1.\end{array}\end{eqnarray}$$
Remark 2.2. Using the exact sequences
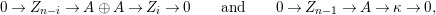 $$\begin{eqnarray}0\rightarrow Z_{n-i}\rightarrow A\oplus A\rightarrow Z_{i}\rightarrow 0\qquad \text{and}\qquad 0\rightarrow Z_{n-1}\rightarrow A\rightarrow \unicode[STIX]{x1D705}\rightarrow 0,\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow Z_{n-i}\rightarrow A\oplus A\rightarrow Z_{i}\rightarrow 0\qquad \text{and}\qquad 0\rightarrow Z_{n-1}\rightarrow A\rightarrow \unicode[STIX]{x1D705}\rightarrow 0,\end{eqnarray}$$
one computes
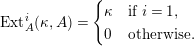 $$\begin{eqnarray}\text{Ext}_{A}^{i}(\unicode[STIX]{x1D705},A)=\left\{\begin{array}{@{}ll@{}}\unicode[STIX]{x1D705}\quad & \text{if}~i=1,\\ 0\quad & \text{otherwise.}\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\text{Ext}_{A}^{i}(\unicode[STIX]{x1D705},A)=\left\{\begin{array}{@{}ll@{}}\unicode[STIX]{x1D705}\quad & \text{if}~i=1,\\ 0\quad & \text{otherwise.}\end{array}\right.\end{eqnarray}$$
Lemma 2.3. We have the following.
-
(1)
 $\unicode[STIX]{x1D719}$
does not factor through
$\unicode[STIX]{x1D719}$
does not factor through
 $\unicode[STIX]{x1D70B}$
.
$\unicode[STIX]{x1D70B}$
. -
(2) For any
 $\unicode[STIX]{x1D70C}\in \text{Rad}\,\text{End}_{A}(Z_{i})$
,
$\unicode[STIX]{x1D70C}\in \text{Rad}\,\text{End}_{A}(Z_{i})$
,
 $\unicode[STIX]{x1D719}\unicode[STIX]{x1D70C}$
factors through
$\unicode[STIX]{x1D719}\unicode[STIX]{x1D70C}$
factors through
 $\unicode[STIX]{x1D70B}$
.
$\unicode[STIX]{x1D70B}$
.
Proof. (1) If there is a morphism
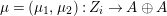 $\unicode[STIX]{x1D707}=(\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D707}_{2}):Z_{i}\rightarrow A\oplus A$
such that
$\unicode[STIX]{x1D707}=(\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D707}_{2}):Z_{i}\rightarrow A\oplus A$
such that
![]() $\unicode[STIX]{x1D70B}\unicode[STIX]{x1D707}=\unicode[STIX]{x1D719}$
, then we have
$\unicode[STIX]{x1D70B}\unicode[STIX]{x1D707}=\unicode[STIX]{x1D719}$
, then we have
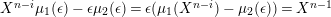 $X^{n-i}\unicode[STIX]{x1D707}_{1}(\unicode[STIX]{x1D716})-\unicode[STIX]{x1D716}\unicode[STIX]{x1D707}_{2}(\unicode[STIX]{x1D716})=\unicode[STIX]{x1D716}(\unicode[STIX]{x1D707}_{1}(X^{n-i})-\unicode[STIX]{x1D707}_{2}(\unicode[STIX]{x1D716}))=X^{n-1}$
. This is a contradiction.
$X^{n-i}\unicode[STIX]{x1D707}_{1}(\unicode[STIX]{x1D716})-\unicode[STIX]{x1D716}\unicode[STIX]{x1D707}_{2}(\unicode[STIX]{x1D716})=\unicode[STIX]{x1D716}(\unicode[STIX]{x1D707}_{1}(X^{n-i})-\unicode[STIX]{x1D707}_{2}(\unicode[STIX]{x1D716}))=X^{n-1}$
. This is a contradiction.
(2) Write
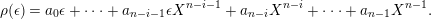 $$\begin{eqnarray}\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D716})=a_{0}\unicode[STIX]{x1D716}+\cdots +a_{n-i-1}\unicode[STIX]{x1D716}X^{n-i-1}+a_{n-i}X^{n-i}+\cdots +a_{n-1}X^{n-1}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D716})=a_{0}\unicode[STIX]{x1D716}+\cdots +a_{n-i-1}\unicode[STIX]{x1D716}X^{n-i-1}+a_{n-i}X^{n-i}+\cdots +a_{n-1}X^{n-1}.\end{eqnarray}$$
Then, by Lemma 2.1, there exists
![]() $a\in {\mathcal{O}}$
such that
$a\in {\mathcal{O}}$
such that
![]() $a_{0}=\unicode[STIX]{x1D716}a$
. We define
$a_{0}=\unicode[STIX]{x1D716}a$
. We define
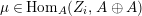 $\unicode[STIX]{x1D707}\in \text{Hom}_{A}(Z_{i},A\oplus A)$
by
$\unicode[STIX]{x1D707}\in \text{Hom}_{A}(Z_{i},A\oplus A)$
by
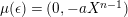 $\unicode[STIX]{x1D707}(\unicode[STIX]{x1D716})=(0,-aX^{n-1})$
. Then, it is easy to check that
$\unicode[STIX]{x1D707}(\unicode[STIX]{x1D716})=(0,-aX^{n-1})$
. Then, it is easy to check that
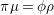 $\unicode[STIX]{x1D70B}\unicode[STIX]{x1D707}=\unicode[STIX]{x1D719}\unicode[STIX]{x1D70C}$
holds.◻
$\unicode[STIX]{x1D70B}\unicode[STIX]{x1D707}=\unicode[STIX]{x1D719}\unicode[STIX]{x1D70C}$
holds.◻
By Proposition 1.15 and Lemma 2.3, we have an almost split sequence
 $$\begin{eqnarray}0\rightarrow Z_{n-i}\rightarrow E_{i}\rightarrow Z_{i}\rightarrow 0,\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow Z_{n-i}\rightarrow E_{i}\rightarrow Z_{i}\rightarrow 0,\end{eqnarray}$$
where
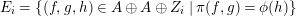 $E_{i}=\{(f,g,h)\in A\oplus A\oplus Z_{i}\mid \unicode[STIX]{x1D70B}(f,g)=\unicode[STIX]{x1D719}(h)\}$
is given by
$E_{i}=\{(f,g,h)\in A\oplus A\oplus Z_{i}\mid \unicode[STIX]{x1D70B}(f,g)=\unicode[STIX]{x1D719}(h)\}$
is given by
 $$\begin{eqnarray}\displaystyle E_{i} & = & \displaystyle {\mathcal{O}}(\unicode[STIX]{x1D716},X^{n-i},0)\oplus {\mathcal{O}}(\unicode[STIX]{x1D716}X,X^{n-i+1},0)\oplus \cdots \oplus {\mathcal{O}}(\unicode[STIX]{x1D716}X^{i-1},X^{n-1},0)\nonumber\\ \displaystyle & & \displaystyle \oplus \,{\mathcal{O}}(X^{i},0,0)\oplus {\mathcal{O}}(X^{i+1},0,0)\oplus \cdots \oplus {\mathcal{O}}(X^{n-1},0,0)\nonumber\\ \displaystyle & & \displaystyle \oplus \,{\mathcal{O}}(X^{i-1},0,\unicode[STIX]{x1D716})\oplus {\mathcal{O}}(0,0,\unicode[STIX]{x1D716}X)\oplus \cdots \oplus {\mathcal{O}}(0,0,\unicode[STIX]{x1D716}X^{n-i-1})\nonumber\\ \displaystyle & & \displaystyle \oplus \,{\mathcal{O}}(0,0,X^{n-i})\oplus {\mathcal{O}}(0,0,X^{n-i+1})\oplus \cdots \oplus {\mathcal{O}}(0,0,X^{n-1}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle E_{i} & = & \displaystyle {\mathcal{O}}(\unicode[STIX]{x1D716},X^{n-i},0)\oplus {\mathcal{O}}(\unicode[STIX]{x1D716}X,X^{n-i+1},0)\oplus \cdots \oplus {\mathcal{O}}(\unicode[STIX]{x1D716}X^{i-1},X^{n-1},0)\nonumber\\ \displaystyle & & \displaystyle \oplus \,{\mathcal{O}}(X^{i},0,0)\oplus {\mathcal{O}}(X^{i+1},0,0)\oplus \cdots \oplus {\mathcal{O}}(X^{n-1},0,0)\nonumber\\ \displaystyle & & \displaystyle \oplus \,{\mathcal{O}}(X^{i-1},0,\unicode[STIX]{x1D716})\oplus {\mathcal{O}}(0,0,\unicode[STIX]{x1D716}X)\oplus \cdots \oplus {\mathcal{O}}(0,0,\unicode[STIX]{x1D716}X^{n-i-1})\nonumber\\ \displaystyle & & \displaystyle \oplus \,{\mathcal{O}}(0,0,X^{n-i})\oplus {\mathcal{O}}(0,0,X^{n-i+1})\oplus \cdots \oplus {\mathcal{O}}(0,0,X^{n-1}).\nonumber\end{eqnarray}$$
To simplify the notation, we define
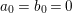 $a_{0}=b_{0}=0$
and
$a_{0}=b_{0}=0$
and
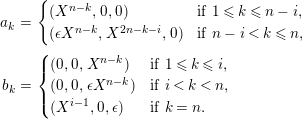 $$\begin{eqnarray}\displaystyle a_{k} & = & \displaystyle \left\{\begin{array}{@{}ll@{}}(X^{n-k},0,0) & \text{if}~1\leqslant k\leqslant n-i,\\ (\unicode[STIX]{x1D716}X^{n-k},X^{2n-k-i},0) & \text{if}~n-i<k\leqslant n,\end{array}\right.\nonumber\\ \displaystyle b_{k} & = & \displaystyle \left\{\begin{array}{@{}ll@{}}(0,0,X^{n-k}) & \text{if}~1\leqslant k\leqslant i,\\ (0,0,\unicode[STIX]{x1D716}X^{n-k}) & \text{if}~i<k<n,\\ (X^{i-1},0,\unicode[STIX]{x1D716}) & \text{if}~k=n.\end{array}\right.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle a_{k} & = & \displaystyle \left\{\begin{array}{@{}ll@{}}(X^{n-k},0,0) & \text{if}~1\leqslant k\leqslant n-i,\\ (\unicode[STIX]{x1D716}X^{n-k},X^{2n-k-i},0) & \text{if}~n-i<k\leqslant n,\end{array}\right.\nonumber\\ \displaystyle b_{k} & = & \displaystyle \left\{\begin{array}{@{}ll@{}}(0,0,X^{n-k}) & \text{if}~1\leqslant k\leqslant i,\\ (0,0,\unicode[STIX]{x1D716}X^{n-k}) & \text{if}~i<k<n,\\ (X^{i-1},0,\unicode[STIX]{x1D716}) & \text{if}~k=n.\end{array}\right.\nonumber\end{eqnarray}$$
Then, we have
 $$\begin{eqnarray}\displaystyle Xa_{k} & = & \displaystyle \left\{\begin{array}{@{}ll@{}}a_{k-1} & (k\neq n-i+1)\\ \unicode[STIX]{x1D716}a_{k-1} & (k=n-i+1)\end{array}\right.\nonumber\\ \displaystyle Xb_{k} & = & \displaystyle \left\{\begin{array}{@{}ll@{}}b_{k-1} & (k\neq i+1,n)\\ \unicode[STIX]{x1D716}b_{k-1} & (k=i+1)\\ a_{n-i}+b_{n-1} & (k=n)\end{array}\right.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle Xa_{k} & = & \displaystyle \left\{\begin{array}{@{}ll@{}}a_{k-1} & (k\neq n-i+1)\\ \unicode[STIX]{x1D716}a_{k-1} & (k=n-i+1)\end{array}\right.\nonumber\\ \displaystyle Xb_{k} & = & \displaystyle \left\{\begin{array}{@{}ll@{}}b_{k-1} & (k\neq i+1,n)\\ \unicode[STIX]{x1D716}b_{k-1} & (k=i+1)\\ a_{n-i}+b_{n-1} & (k=n)\end{array}\right.\nonumber\end{eqnarray}$$
and
 $$\begin{eqnarray}\text{Ker}(X^{k})=\bigoplus _{1\leqslant j\leqslant k}({\mathcal{O}}a_{j}\oplus {\mathcal{O}}b_{j}).\end{eqnarray}$$
$$\begin{eqnarray}\text{Ker}(X^{k})=\bigoplus _{1\leqslant j\leqslant k}({\mathcal{O}}a_{j}\oplus {\mathcal{O}}b_{j}).\end{eqnarray}$$
2.2 Almost split sequence ending at
 $\mathbf{Z}_{\mathbf{i}}$
$\mathbf{Z}_{\mathbf{i}}$
In this subsection, we show that the middle term
![]() $E_{i}$
of the almost split sequence
$E_{i}$
of the almost split sequence
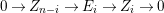 $$\begin{eqnarray}0\rightarrow Z_{n-i}\rightarrow E_{i}\rightarrow Z_{i}\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow Z_{n-i}\rightarrow E_{i}\rightarrow Z_{i}\rightarrow 0\end{eqnarray}$$
is indecomposable, for
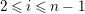 $2\leqslant i\leqslant n-1$
.
$2\leqslant i\leqslant n-1$
.
Proposition 2.4. We have the following.
-
(1)
 $A$
is an indecomposable direct summand of
$A$
is an indecomposable direct summand of
 $E_{1}$
.
$E_{1}$
. -
(2) For
 $2\leqslant i\leqslant n-1$
,
$2\leqslant i\leqslant n-1$
,
 $E_{i}$
are indecomposable
$E_{i}$
are indecomposable
 $A$
-lattices.
$A$
-lattices.
Proof. (1) As
 $Z_{n-1}=\text{Rad}\,A$
, it follows from [Reference AuslanderA1, Chapter III, Theorem 2.5]. We also give more explicit computational proof here. Define
$Z_{n-1}=\text{Rad}\,A$
, it follows from [Reference AuslanderA1, Chapter III, Theorem 2.5]. We also give more explicit computational proof here. Define
 $x_{k},y_{k}\in E_{1}$
, for
$x_{k},y_{k}\in E_{1}$
, for
 $1\leqslant k\leqslant n$
, as follows:
$1\leqslant k\leqslant n$
, as follows:
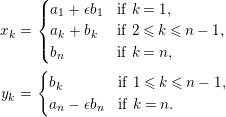 $$\begin{eqnarray}\displaystyle x_{k} & = & \displaystyle \left\{\begin{array}{@{}ll@{}}a_{1}+\unicode[STIX]{x1D716}b_{1} & \text{if}~k=1,\\ a_{k}+b_{k} & \text{if}~2\leqslant k\leqslant n-1,\\ b_{n} & \text{if}~k=n,\end{array}\right.\nonumber\\ \displaystyle y_{k} & = & \displaystyle \left\{\begin{array}{@{}ll@{}}b_{k} & \text{if}~1\leqslant k\leqslant n-1,\\ a_{n}-\unicode[STIX]{x1D716}b_{n} & \text{if}~k=n.\end{array}\right.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle x_{k} & = & \displaystyle \left\{\begin{array}{@{}ll@{}}a_{1}+\unicode[STIX]{x1D716}b_{1} & \text{if}~k=1,\\ a_{k}+b_{k} & \text{if}~2\leqslant k\leqslant n-1,\\ b_{n} & \text{if}~k=n,\end{array}\right.\nonumber\\ \displaystyle y_{k} & = & \displaystyle \left\{\begin{array}{@{}ll@{}}b_{k} & \text{if}~1\leqslant k\leqslant n-1,\\ a_{n}-\unicode[STIX]{x1D716}b_{n} & \text{if}~k=n.\end{array}\right.\nonumber\end{eqnarray}$$
Then they form an
![]() ${\mathcal{O}}$
-basis of
${\mathcal{O}}$
-basis of
![]() $E_{1}$
. Moreover, we have
$E_{1}$
. Moreover, we have
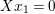 $Xx_{1}=0$
and
$Xx_{1}=0$
and
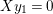 $Xy_{1}=0$
,
$Xy_{1}=0$
,
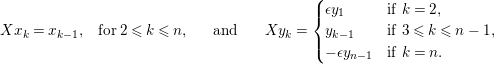 $$\begin{eqnarray}Xx_{k}=x_{k-1},\quad \!\text{for}~2\leqslant k\leqslant n,\!\!\qquad \text{and}\!\qquad Xy_{k}=\left\{\begin{array}{@{}ll@{}}\unicode[STIX]{x1D716}y_{1} & \text{if}~k=2,\\ y_{k-1} & \text{if}~3\leqslant k\leqslant n-1,\\ -\unicode[STIX]{x1D716}y_{n-1} & \text{if}~k=n.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}Xx_{k}=x_{k-1},\quad \!\text{for}~2\leqslant k\leqslant n,\!\!\qquad \text{and}\!\qquad Xy_{k}=\left\{\begin{array}{@{}ll@{}}\unicode[STIX]{x1D716}y_{1} & \text{if}~k=2,\\ y_{k-1} & \text{if}~3\leqslant k\leqslant n-1,\\ -\unicode[STIX]{x1D716}y_{n-1} & \text{if}~k=n.\end{array}\right.\end{eqnarray}$$
Thus, the
![]() ${\mathcal{O}}$
-span of
${\mathcal{O}}$
-span of
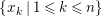 $\{x_{k}\mid 1\leqslant k\leqslant n\}$
is isomorphic to the indecomposable projective
$\{x_{k}\mid 1\leqslant k\leqslant n\}$
is isomorphic to the indecomposable projective
![]() $A$
-lattice
$A$
-lattice
![]() $A$
. In particular,
$A$
. In particular,
![]() $A$
is an indecomposable direct summand of
$A$
is an indecomposable direct summand of
![]() $E_{1}$
, and the other direct summand is indecomposable, because it becomes
$E_{1}$
, and the other direct summand is indecomposable, because it becomes
![]() $A\otimes {\mathcal{K}}$
after tensoring with
$A\otimes {\mathcal{K}}$
after tensoring with
![]() ${\mathcal{K}}$
.
${\mathcal{K}}$
.
(2)
![]() $E_{n-1}$
does not have a projective direct summand by [Reference AuslanderA1, Chapter III, Theorem 2.5]. Thus, [Reference AuslanderA1, Chapter III, Propositions 1.7, 1.8] and (1) imply that
$E_{n-1}$
does not have a projective direct summand by [Reference AuslanderA1, Chapter III, Theorem 2.5]. Thus, [Reference AuslanderA1, Chapter III, Propositions 1.7, 1.8] and (1) imply that
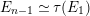 $E_{n-1}\simeq \unicode[STIX]{x1D70F}(E_{1})$
is indecomposable. We assume
$E_{n-1}\simeq \unicode[STIX]{x1D70F}(E_{1})$
is indecomposable. We assume
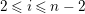 $2\leqslant i\leqslant n-2$
in the rest of the proof.
$2\leqslant i\leqslant n-2$
in the rest of the proof.
Suppose that
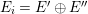 $E_{i}=E^{\prime }\oplus E^{\prime \prime }$
with
$E_{i}=E^{\prime }\oplus E^{\prime \prime }$
with
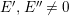 $E^{\prime },E^{\prime \prime }\neq 0$
. Since
$E^{\prime },E^{\prime \prime }\neq 0$
. Since
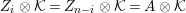 $Z_{i}\otimes {\mathcal{K}}=Z_{n-i}\otimes {\mathcal{K}}=A\otimes {\mathcal{K}}$
, we have
$Z_{i}\otimes {\mathcal{K}}=Z_{n-i}\otimes {\mathcal{K}}=A\otimes {\mathcal{K}}$
, we have
 $E_{i}\otimes {\mathcal{K}}\simeq A\otimes {\mathcal{K}}\oplus A\otimes {\mathcal{K}}$
, which implies that
$E_{i}\otimes {\mathcal{K}}\simeq A\otimes {\mathcal{K}}\oplus A\otimes {\mathcal{K}}$
, which implies that
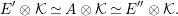 $$\begin{eqnarray}E^{\prime }\otimes {\mathcal{K}}\simeq A\otimes {\mathcal{K}}\simeq E^{\prime \prime }\otimes {\mathcal{K}}.\end{eqnarray}$$
$$\begin{eqnarray}E^{\prime }\otimes {\mathcal{K}}\simeq A\otimes {\mathcal{K}}\simeq E^{\prime \prime }\otimes {\mathcal{K}}.\end{eqnarray}$$
In particular,
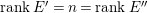 $\text{rank}\,E^{\prime }=n=\text{rank}\,E^{\prime \prime }$
. Since
$\text{rank}\,E^{\prime }=n=\text{rank}\,E^{\prime \prime }$
. Since
 $$\begin{eqnarray}0\rightarrow E^{\prime }\cap \text{Ker}(X^{k})\rightarrow E^{\prime }\rightarrow \text{Im}(X^{k})\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow E^{\prime }\cap \text{Ker}(X^{k})\rightarrow E^{\prime }\rightarrow \text{Im}(X^{k})\rightarrow 0\end{eqnarray}$$
and
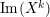 $\text{Im}(X^{k})$
is a free
$\text{Im}(X^{k})$
is a free
![]() ${\mathcal{O}}$
-module, we have the increasing sequence of
${\mathcal{O}}$
-module, we have the increasing sequence of
![]() ${\mathcal{O}}$
-submodules
${\mathcal{O}}$
-submodules
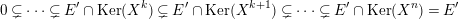 $$\begin{eqnarray}0\subsetneq \cdots \subsetneq E^{\prime }\cap \text{Ker}(X^{k})\subsetneq E^{\prime }\cap \text{Ker}(X^{k+1})\subsetneq \cdots \subsetneq E^{\prime }\cap \text{Ker}(X^{n})=E^{\prime }\end{eqnarray}$$
$$\begin{eqnarray}0\subsetneq \cdots \subsetneq E^{\prime }\cap \text{Ker}(X^{k})\subsetneq E^{\prime }\cap \text{Ker}(X^{k+1})\subsetneq \cdots \subsetneq E^{\prime }\cap \text{Ker}(X^{n})=E^{\prime }\end{eqnarray}$$
such that all the
![]() ${\mathcal{O}}$
-submodules are direct summands of
${\mathcal{O}}$
-submodules are direct summands of
![]() $E^{\prime }$
as
$E^{\prime }$
as
![]() ${\mathcal{O}}$
-modules. Thus, we may choose an
${\mathcal{O}}$
-modules. Thus, we may choose an
![]() ${\mathcal{O}}$
-basis
${\mathcal{O}}$
-basis
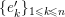 $\{e_{k}^{\prime }\}_{1\leqslant k\leqslant n}$
such that
$\{e_{k}^{\prime }\}_{1\leqslant k\leqslant n}$
such that
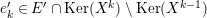 $e_{k}^{\prime }\in E^{\prime }\cap \text{Ker}(X^{k})\setminus \text{Ker}(X^{k-1})$
. Similarly, we may choose an
$e_{k}^{\prime }\in E^{\prime }\cap \text{Ker}(X^{k})\setminus \text{Ker}(X^{k-1})$
. Similarly, we may choose an
![]() ${\mathcal{O}}$
-basis
${\mathcal{O}}$
-basis
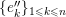 $\{e_{k}^{\prime \prime }\}_{1\leqslant k\leqslant n}$
of
$\{e_{k}^{\prime \prime }\}_{1\leqslant k\leqslant n}$
of
![]() $E^{\prime \prime }$
such that
$E^{\prime \prime }$
such that
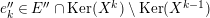 $e_{k}^{\prime \prime }\in E^{\prime \prime }\cap \text{Ker}(X^{k})\setminus \text{Ker}(X^{k-1})$
. Write
$e_{k}^{\prime \prime }\in E^{\prime \prime }\cap \text{Ker}(X^{k})\setminus \text{Ker}(X^{k-1})$
. Write
 $$\begin{eqnarray}\begin{array}{@{}rcll@{}}e_{k}^{\prime }\ & =\ & \unicode[STIX]{x1D6FC}_{k}a_{k}+\unicode[STIX]{x1D6FD}_{k}b_{k}+A_{k}^{\prime }, & \text{for}~\unicode[STIX]{x1D6FC}_{k},\unicode[STIX]{x1D6FD}_{k}\in {\mathcal{O}}~\text{and}~A_{k}^{\prime }\in \text{Ker}(X^{k-1}),\\ e_{k}^{\prime \prime }\ & =\ & \unicode[STIX]{x1D6FE}_{k}a_{k}+\unicode[STIX]{x1D6FF}_{k}b_{k}+A_{k}^{\prime \prime }, & \text{for}~\unicode[STIX]{x1D6FE}_{k},\unicode[STIX]{x1D6FF}_{k}\in {\mathcal{O}}~\text{and}~A_{k}^{\prime \prime }\in \text{Ker}(X^{k-1}).\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}rcll@{}}e_{k}^{\prime }\ & =\ & \unicode[STIX]{x1D6FC}_{k}a_{k}+\unicode[STIX]{x1D6FD}_{k}b_{k}+A_{k}^{\prime }, & \text{for}~\unicode[STIX]{x1D6FC}_{k},\unicode[STIX]{x1D6FD}_{k}\in {\mathcal{O}}~\text{and}~A_{k}^{\prime }\in \text{Ker}(X^{k-1}),\\ e_{k}^{\prime \prime }\ & =\ & \unicode[STIX]{x1D6FE}_{k}a_{k}+\unicode[STIX]{x1D6FF}_{k}b_{k}+A_{k}^{\prime \prime }, & \text{for}~\unicode[STIX]{x1D6FE}_{k},\unicode[STIX]{x1D6FF}_{k}\in {\mathcal{O}}~\text{and}~A_{k}^{\prime \prime }\in \text{Ker}(X^{k-1}).\end{array}\end{eqnarray}$$
Without loss of generality, we may assume
 $$\begin{eqnarray}A_{k}^{\prime }\in \text{Ker}(X^{k-1})\cap E^{\prime \prime },\qquad A_{k}^{\prime \prime }\in \text{Ker}(X^{k-1})\cap E^{\prime }.\end{eqnarray}$$
$$\begin{eqnarray}A_{k}^{\prime }\in \text{Ker}(X^{k-1})\cap E^{\prime \prime },\qquad A_{k}^{\prime \prime }\in \text{Ker}(X^{k-1})\cap E^{\prime }.\end{eqnarray}$$
Since
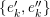 $\{e_{k}^{\prime },e_{k}^{\prime \prime }\}$
and
$\{e_{k}^{\prime },e_{k}^{\prime \prime }\}$
and
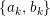 $\{a_{k},b_{k}\}$
are
$\{a_{k},b_{k}\}$
are
![]() ${\mathcal{O}}$
-bases of
${\mathcal{O}}$
-bases of
 $\text{Ker}(X^{k})/\text{Ker}(X^{k-1})$
, we have
$\text{Ker}(X^{k})/\text{Ker}(X^{k-1})$
, we have
 $\unicode[STIX]{x1D6FC}_{k}\unicode[STIX]{x1D6FF}_{k}-\unicode[STIX]{x1D6FD}_{k}\unicode[STIX]{x1D6FE}_{k}\not \in \unicode[STIX]{x1D716}{\mathcal{O}}$
.
$\unicode[STIX]{x1D6FC}_{k}\unicode[STIX]{x1D6FF}_{k}-\unicode[STIX]{x1D6FD}_{k}\unicode[STIX]{x1D6FE}_{k}\not \in \unicode[STIX]{x1D716}{\mathcal{O}}$
.
As
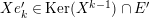 $Xe_{k}^{\prime }\in \text{Ker}(X^{k-1})\cap E^{\prime }$
, there are
$Xe_{k}^{\prime }\in \text{Ker}(X^{k-1})\cap E^{\prime }$
, there are
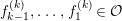 $f_{k-1}^{(k)},\ldots ,f_{1}^{(k)}\in {\mathcal{O}}$
such that
$f_{k-1}^{(k)},\ldots ,f_{1}^{(k)}\in {\mathcal{O}}$
such that
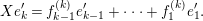 $$\begin{eqnarray}Xe_{k}^{\prime }=f_{k-1}^{(k)}e_{k-1}^{\prime }+\cdots +f_{1}^{(k)}e_{1}^{\prime }.\end{eqnarray}$$
$$\begin{eqnarray}Xe_{k}^{\prime }=f_{k-1}^{(k)}e_{k-1}^{\prime }+\cdots +f_{1}^{(k)}e_{1}^{\prime }.\end{eqnarray}$$
Similarly, there are
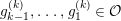 $g_{k-1}^{(k)},\ldots ,g_{1}^{(k)}\in {\mathcal{O}}$
such that
$g_{k-1}^{(k)},\ldots ,g_{1}^{(k)}\in {\mathcal{O}}$
such that
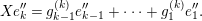 $$\begin{eqnarray}Xe_{k}^{\prime \prime }=g_{k-1}^{(k)}e_{k-1}^{\prime \prime }+\cdots +g_{1}^{(k)}e_{1}^{\prime \prime }.\end{eqnarray}$$
$$\begin{eqnarray}Xe_{k}^{\prime \prime }=g_{k-1}^{(k)}e_{k-1}^{\prime \prime }+\cdots +g_{1}^{(k)}e_{1}^{\prime \prime }.\end{eqnarray}$$
The coefficient of
![]() $a_{k-1}$
in
$a_{k-1}$
in
![]() $Xe_{k}^{\prime }$
is given by
$Xe_{k}^{\prime }$
is given by
 $$\begin{eqnarray}\left\{\begin{array}{@{}ll@{}}\unicode[STIX]{x1D6FC}_{k} & \text{if}~k\neq n-i+1,\\ \unicode[STIX]{x1D716}\unicode[STIX]{x1D6FC}_{k} & \text{if}~k=n-i+1.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\left\{\begin{array}{@{}ll@{}}\unicode[STIX]{x1D6FC}_{k} & \text{if}~k\neq n-i+1,\\ \unicode[STIX]{x1D716}\unicode[STIX]{x1D6FC}_{k} & \text{if}~k=n-i+1.\end{array}\right.\end{eqnarray}$$
Thus, we have
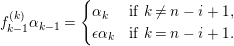 $$\begin{eqnarray}f_{k-1}^{(k)}\unicode[STIX]{x1D6FC}_{k-1}=\left\{\begin{array}{@{}ll@{}}\unicode[STIX]{x1D6FC}_{k} & \text{if}~k\neq n-i+1,\\ \unicode[STIX]{x1D716}\unicode[STIX]{x1D6FC}_{k} & \text{if}~k=n-i+1.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}f_{k-1}^{(k)}\unicode[STIX]{x1D6FC}_{k-1}=\left\{\begin{array}{@{}ll@{}}\unicode[STIX]{x1D6FC}_{k} & \text{if}~k\neq n-i+1,\\ \unicode[STIX]{x1D716}\unicode[STIX]{x1D6FC}_{k} & \text{if}~k=n-i+1.\end{array}\right.\end{eqnarray}$$
Similarly, we have the following.
 $$\begin{eqnarray}\displaystyle f_{k-1}^{(k)}\unicode[STIX]{x1D6FD}_{k-1} & = & \displaystyle \left\{\begin{array}{@{}ll@{}}\unicode[STIX]{x1D6FD}_{k} & \text{if}~k\neq i+1,\\ \unicode[STIX]{x1D716}\unicode[STIX]{x1D6FD}_{k} & \text{if}~k=i+1.\end{array}\right.\nonumber\\ \displaystyle g_{k-1}^{(k)}\unicode[STIX]{x1D6FE}_{k-1} & = & \displaystyle \left\{\begin{array}{@{}ll@{}}\unicode[STIX]{x1D6FE}_{k} & \text{if}~k\neq n-i+1,\\ \unicode[STIX]{x1D716}\unicode[STIX]{x1D6FE}_{k} & \text{if}~k=n-i+1.\end{array}\right.\nonumber\\ \displaystyle g_{k-1}^{(k)}\unicode[STIX]{x1D6FF}_{k-1} & = & \displaystyle \left\{\begin{array}{@{}ll@{}}\unicode[STIX]{x1D6FF}_{k} & \text{if}~k\neq i+1,\\ \unicode[STIX]{x1D716}\unicode[STIX]{x1D6FF}_{k} & \text{if}~k=i+1.\end{array}\right.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle f_{k-1}^{(k)}\unicode[STIX]{x1D6FD}_{k-1} & = & \displaystyle \left\{\begin{array}{@{}ll@{}}\unicode[STIX]{x1D6FD}_{k} & \text{if}~k\neq i+1,\\ \unicode[STIX]{x1D716}\unicode[STIX]{x1D6FD}_{k} & \text{if}~k=i+1.\end{array}\right.\nonumber\\ \displaystyle g_{k-1}^{(k)}\unicode[STIX]{x1D6FE}_{k-1} & = & \displaystyle \left\{\begin{array}{@{}ll@{}}\unicode[STIX]{x1D6FE}_{k} & \text{if}~k\neq n-i+1,\\ \unicode[STIX]{x1D716}\unicode[STIX]{x1D6FE}_{k} & \text{if}~k=n-i+1.\end{array}\right.\nonumber\\ \displaystyle g_{k-1}^{(k)}\unicode[STIX]{x1D6FF}_{k-1} & = & \displaystyle \left\{\begin{array}{@{}ll@{}}\unicode[STIX]{x1D6FF}_{k} & \text{if}~k\neq i+1,\\ \unicode[STIX]{x1D716}\unicode[STIX]{x1D6FF}_{k} & \text{if}~k=i+1.\end{array}\right.\nonumber\end{eqnarray}$$
We shall deduce a contradiction in the following three cases and conclude that
![]() $E_{i}$
is indecomposable, for
$E_{i}$
is indecomposable, for
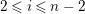 $2\leqslant i\leqslant n-2$
.
$2\leqslant i\leqslant n-2$
.
(Case a)
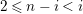 $2\leqslant n-i<i$
.
$2\leqslant n-i<i$
.
(Case b)
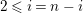 $2\leqslant i=n-i$
.
$2\leqslant i=n-i$
.
(Case c)
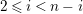 $2\leqslant i<n-i$
.
$2\leqslant i<n-i$
.
Suppose that we are in (Case a). We multiply each of
![]() $e_{k}^{\prime }$
and
$e_{k}^{\prime }$
and
![]() $e_{k}^{\prime \prime }$
by suitable invertible elements to get new
$e_{k}^{\prime \prime }$
by suitable invertible elements to get new
![]() ${\mathcal{O}}$
-bases of
${\mathcal{O}}$
-bases of
![]() $E^{\prime }$
and
$E^{\prime }$
and
![]() $E^{\prime \prime }$
in order to have the equalities
$E^{\prime \prime }$
in order to have the equalities
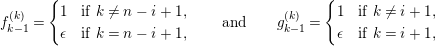 $$\begin{eqnarray}f_{k-1}^{(k)}=\left\{\begin{array}{@{}ll@{}}1 & \text{if}~k\neq n-i+1,\\ \unicode[STIX]{x1D716} & \text{if}~k=n-i+1,\end{array}\right.\qquad \text{and}\qquad g_{k-1}^{(k)}=\left\{\begin{array}{@{}ll@{}}1 & \text{if}~k\neq i+1,\\ \unicode[STIX]{x1D716} & \text{if}~k=i+1,\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}f_{k-1}^{(k)}=\left\{\begin{array}{@{}ll@{}}1 & \text{if}~k\neq n-i+1,\\ \unicode[STIX]{x1D716} & \text{if}~k=n-i+1,\end{array}\right.\qquad \text{and}\qquad g_{k-1}^{(k)}=\left\{\begin{array}{@{}ll@{}}1 & \text{if}~k\neq i+1,\\ \unicode[STIX]{x1D716} & \text{if}~k=i+1,\end{array}\right.\end{eqnarray}$$
in the new bases. For
![]() $k=1$
, we keep the original basis elements
$k=1$
, we keep the original basis elements
![]() $e_{1}^{\prime }$
and
$e_{1}^{\prime }$
and
![]() $e_{1}^{\prime \prime }$
. Suppose that we have already chosen new
$e_{1}^{\prime \prime }$
. Suppose that we have already chosen new
![]() $e_{j}^{\prime }$
and
$e_{j}^{\prime }$
and
![]() $e_{j}^{\prime \prime }$
, for
$e_{j}^{\prime \prime }$
, for
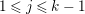 $1\leqslant j\leqslant k-1$
. If
$1\leqslant j\leqslant k-1$
. If
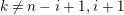 $k\neq n-i+1,i+1$
, then
$k\neq n-i+1,i+1$
, then
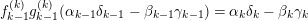 $$\begin{eqnarray}f_{k-1}^{(k)}g_{k-1}^{(k)}(\unicode[STIX]{x1D6FC}_{k-1}\unicode[STIX]{x1D6FF}_{k-1}-\unicode[STIX]{x1D6FD}_{k-1}\unicode[STIX]{x1D6FE}_{k-1})=\unicode[STIX]{x1D6FC}_{k}\unicode[STIX]{x1D6FF}_{k}-\unicode[STIX]{x1D6FD}_{k}\unicode[STIX]{x1D6FE}_{k}\end{eqnarray}$$
$$\begin{eqnarray}f_{k-1}^{(k)}g_{k-1}^{(k)}(\unicode[STIX]{x1D6FC}_{k-1}\unicode[STIX]{x1D6FF}_{k-1}-\unicode[STIX]{x1D6FD}_{k-1}\unicode[STIX]{x1D6FE}_{k-1})=\unicode[STIX]{x1D6FC}_{k}\unicode[STIX]{x1D6FF}_{k}-\unicode[STIX]{x1D6FD}_{k}\unicode[STIX]{x1D6FE}_{k}\end{eqnarray}$$
implies that
![]() $f_{k-1}^{(k)}$
and
$f_{k-1}^{(k)}$
and
![]() $g_{k-1}^{(k)}$
are invertible. Thus, multiplying
$g_{k-1}^{(k)}$
are invertible. Thus, multiplying
![]() $e_{k}^{\prime }$
and
$e_{k}^{\prime }$
and
![]() $e_{k}^{\prime \prime }$
with their inverses respectively, we have
$e_{k}^{\prime \prime }$
with their inverses respectively, we have
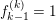 $f_{k-1}^{(k)}=1$
,
$f_{k-1}^{(k)}=1$
,
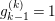 $g_{k-1}^{(k)}=1$
in the new basis. Note that we have
$g_{k-1}^{(k)}=1$
in the new basis. Note that we have
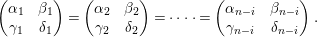 $$\begin{eqnarray}\left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D6FC}_{1} & \unicode[STIX]{x1D6FD}_{1}\\ \unicode[STIX]{x1D6FE}_{1} & \unicode[STIX]{x1D6FF}_{1}\end{array}\right)=\left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D6FC}_{2} & \unicode[STIX]{x1D6FD}_{2}\\ \unicode[STIX]{x1D6FE}_{2} & \unicode[STIX]{x1D6FF}_{2}\end{array}\right)=\cdots \cdot =\left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D6FC}_{n-i} & \unicode[STIX]{x1D6FD}_{n-i}\\ \unicode[STIX]{x1D6FE}_{n-i} & \unicode[STIX]{x1D6FF}_{n-i}\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D6FC}_{1} & \unicode[STIX]{x1D6FD}_{1}\\ \unicode[STIX]{x1D6FE}_{1} & \unicode[STIX]{x1D6FF}_{1}\end{array}\right)=\left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D6FC}_{2} & \unicode[STIX]{x1D6FD}_{2}\\ \unicode[STIX]{x1D6FE}_{2} & \unicode[STIX]{x1D6FF}_{2}\end{array}\right)=\cdots \cdot =\left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D6FC}_{n-i} & \unicode[STIX]{x1D6FD}_{n-i}\\ \unicode[STIX]{x1D6FE}_{n-i} & \unicode[STIX]{x1D6FF}_{n-i}\end{array}\right).\end{eqnarray}$$
If
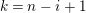 $k=n-i+1$
, then, by using
$k=n-i+1$
, then, by using
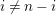 $i\neq n-i$
, we have
$i\neq n-i$
, we have
 $$\begin{eqnarray}\displaystyle f_{n-i}^{(n-i+1)}g_{n-i}^{(n-i+1)}\unicode[STIX]{x1D6FC}_{n-i}\unicode[STIX]{x1D6FF}_{n-i} & = & \displaystyle \unicode[STIX]{x1D716}\unicode[STIX]{x1D6FC}_{n-i+1}\unicode[STIX]{x1D6FF}_{n-i+1},\nonumber\\ \displaystyle f_{n-i}^{(n-i+1)}g_{n-i}^{(n-i+1)}\unicode[STIX]{x1D6FD}_{n-i}\unicode[STIX]{x1D6FE}_{n-i} & = & \displaystyle \unicode[STIX]{x1D716}\unicode[STIX]{x1D6FD}_{n-i+1}\unicode[STIX]{x1D6FE}_{n-i+1}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle f_{n-i}^{(n-i+1)}g_{n-i}^{(n-i+1)}\unicode[STIX]{x1D6FC}_{n-i}\unicode[STIX]{x1D6FF}_{n-i} & = & \displaystyle \unicode[STIX]{x1D716}\unicode[STIX]{x1D6FC}_{n-i+1}\unicode[STIX]{x1D6FF}_{n-i+1},\nonumber\\ \displaystyle f_{n-i}^{(n-i+1)}g_{n-i}^{(n-i+1)}\unicode[STIX]{x1D6FD}_{n-i}\unicode[STIX]{x1D6FE}_{n-i} & = & \displaystyle \unicode[STIX]{x1D716}\unicode[STIX]{x1D6FD}_{n-i+1}\unicode[STIX]{x1D6FE}_{n-i+1}.\nonumber\end{eqnarray}$$
It follows that
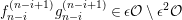 $f_{n-i}^{(n-i+1)}g_{n-i}^{(n-i+1)}\in \unicode[STIX]{x1D716}{\mathcal{O}}\setminus \unicode[STIX]{x1D716}^{2}{\mathcal{O}}$
, and we may assume
$f_{n-i}^{(n-i+1)}g_{n-i}^{(n-i+1)}\in \unicode[STIX]{x1D716}{\mathcal{O}}\setminus \unicode[STIX]{x1D716}^{2}{\mathcal{O}}$
, and we may assume
 $$\begin{eqnarray}f_{n-i}^{(n-i+1)}=\unicode[STIX]{x1D716},\qquad g_{n-i}^{(n-i+1)}=1,\end{eqnarray}$$
$$\begin{eqnarray}f_{n-i}^{(n-i+1)}=\unicode[STIX]{x1D716},\qquad g_{n-i}^{(n-i+1)}=1,\end{eqnarray}$$
by swapping
![]() $E^{\prime }$
and
$E^{\prime }$
and
![]() $E^{\prime \prime }$
if necessary. Thus, we have
$E^{\prime \prime }$
if necessary. Thus, we have
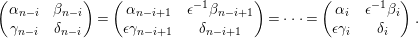 $$\begin{eqnarray}\left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D6FC}_{n-i} & \unicode[STIX]{x1D6FD}_{n-i}\\ \unicode[STIX]{x1D6FE}_{n-i} & \unicode[STIX]{x1D6FF}_{n-i}\end{array}\right)=\left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D6FC}_{n-i+1} & \unicode[STIX]{x1D716}^{-1}\unicode[STIX]{x1D6FD}_{n-i+1}\\ \unicode[STIX]{x1D716}\unicode[STIX]{x1D6FE}_{n-i+1} & \unicode[STIX]{x1D6FF}_{n-i+1}\end{array}\right)=\cdots =\left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D6FC}_{i} & \unicode[STIX]{x1D716}^{-1}\unicode[STIX]{x1D6FD}_{i}\\ \unicode[STIX]{x1D716}\unicode[STIX]{x1D6FE}_{i} & \unicode[STIX]{x1D6FF}_{i}\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D6FC}_{n-i} & \unicode[STIX]{x1D6FD}_{n-i}\\ \unicode[STIX]{x1D6FE}_{n-i} & \unicode[STIX]{x1D6FF}_{n-i}\end{array}\right)=\left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D6FC}_{n-i+1} & \unicode[STIX]{x1D716}^{-1}\unicode[STIX]{x1D6FD}_{n-i+1}\\ \unicode[STIX]{x1D716}\unicode[STIX]{x1D6FE}_{n-i+1} & \unicode[STIX]{x1D6FF}_{n-i+1}\end{array}\right)=\cdots =\left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D6FC}_{i} & \unicode[STIX]{x1D716}^{-1}\unicode[STIX]{x1D6FD}_{i}\\ \unicode[STIX]{x1D716}\unicode[STIX]{x1D6FE}_{i} & \unicode[STIX]{x1D6FF}_{i}\end{array}\right).\end{eqnarray}$$
Finally, if
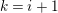 $k=i+1$
, then the similar argument shows
$k=i+1$
, then the similar argument shows
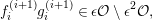 $$\begin{eqnarray}f_{i}^{(i+1)}g_{i}^{(i+1)}\in \unicode[STIX]{x1D716}{\mathcal{O}}\setminus \unicode[STIX]{x1D716}^{2}{\mathcal{O}},\end{eqnarray}$$
$$\begin{eqnarray}f_{i}^{(i+1)}g_{i}^{(i+1)}\in \unicode[STIX]{x1D716}{\mathcal{O}}\setminus \unicode[STIX]{x1D716}^{2}{\mathcal{O}},\end{eqnarray}$$
and we may assume that
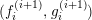 $(f_{i}^{(i+1)},g_{i}^{(i+1)})$
is either
$(f_{i}^{(i+1)},g_{i}^{(i+1)})$
is either
![]() $(\unicode[STIX]{x1D716},1)$
or
$(\unicode[STIX]{x1D716},1)$
or
![]() $(1,\unicode[STIX]{x1D716})$
. In the former case,
$(1,\unicode[STIX]{x1D716})$
. In the former case,
 $$\begin{eqnarray}\left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D6FC}_{1} & \unicode[STIX]{x1D6FD}_{1}\\ \unicode[STIX]{x1D6FE}_{1} & \unicode[STIX]{x1D6FF}_{1}\end{array}\right)=\left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D6FC}_{i} & \unicode[STIX]{x1D716}^{-1}\unicode[STIX]{x1D6FD}_{i}\\ \unicode[STIX]{x1D716}\unicode[STIX]{x1D6FE}_{i} & \unicode[STIX]{x1D6FF}_{i}\end{array}\right)=\left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D716}^{-1}\unicode[STIX]{x1D6FC}_{i+1} & \unicode[STIX]{x1D716}^{-1}\unicode[STIX]{x1D6FD}_{i+1}\\ \unicode[STIX]{x1D716}\unicode[STIX]{x1D6FE}_{i+1} & \unicode[STIX]{x1D716}\unicode[STIX]{x1D6FF}_{i+1}\end{array}\right),\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D6FC}_{1} & \unicode[STIX]{x1D6FD}_{1}\\ \unicode[STIX]{x1D6FE}_{1} & \unicode[STIX]{x1D6FF}_{1}\end{array}\right)=\left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D6FC}_{i} & \unicode[STIX]{x1D716}^{-1}\unicode[STIX]{x1D6FD}_{i}\\ \unicode[STIX]{x1D716}\unicode[STIX]{x1D6FE}_{i} & \unicode[STIX]{x1D6FF}_{i}\end{array}\right)=\left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D716}^{-1}\unicode[STIX]{x1D6FC}_{i+1} & \unicode[STIX]{x1D716}^{-1}\unicode[STIX]{x1D6FD}_{i+1}\\ \unicode[STIX]{x1D716}\unicode[STIX]{x1D6FE}_{i+1} & \unicode[STIX]{x1D716}\unicode[STIX]{x1D6FF}_{i+1}\end{array}\right),\end{eqnarray}$$
which implies that
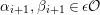 $\unicode[STIX]{x1D6FC}_{i+1},\unicode[STIX]{x1D6FD}_{i+1}\in \unicode[STIX]{x1D716}{\mathcal{O}}$
, a contradiction. Thus, we obtain
$\unicode[STIX]{x1D6FC}_{i+1},\unicode[STIX]{x1D6FD}_{i+1}\in \unicode[STIX]{x1D716}{\mathcal{O}}$
, a contradiction. Thus, we obtain
 $$\begin{eqnarray}f_{i}^{(i+1)}=1,\qquad g_{i}^{(i+1)}=\unicode[STIX]{x1D716}.\end{eqnarray}$$
$$\begin{eqnarray}f_{i}^{(i+1)}=1,\qquad g_{i}^{(i+1)}=\unicode[STIX]{x1D716}.\end{eqnarray}$$
Therefore, we have obtained the desired formula. In particular, we have the following.
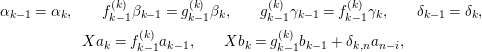 $$\begin{eqnarray}\displaystyle & \unicode[STIX]{x1D6FC}_{k-1}=\unicode[STIX]{x1D6FC}_{k},\qquad \!f_{k-1}^{(k)}\unicode[STIX]{x1D6FD}_{k-1}=g_{k-1}^{(k)}\unicode[STIX]{x1D6FD}_{k},\qquad \!g_{k-1}^{(k)}\unicode[STIX]{x1D6FE}_{k-1}=f_{k-1}^{(k)}\unicode[STIX]{x1D6FE}_{k},\qquad \!\unicode[STIX]{x1D6FF}_{k-1}=\unicode[STIX]{x1D6FF}_{k}, & \displaystyle \nonumber\\ \displaystyle & Xa_{k}=f_{k-1}^{(k)}a_{k-1},\qquad \!Xb_{k}=g_{k-1}^{(k)}b_{k-1}+\unicode[STIX]{x1D6FF}_{k,n}a_{n-i}, & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \unicode[STIX]{x1D6FC}_{k-1}=\unicode[STIX]{x1D6FC}_{k},\qquad \!f_{k-1}^{(k)}\unicode[STIX]{x1D6FD}_{k-1}=g_{k-1}^{(k)}\unicode[STIX]{x1D6FD}_{k},\qquad \!g_{k-1}^{(k)}\unicode[STIX]{x1D6FE}_{k-1}=f_{k-1}^{(k)}\unicode[STIX]{x1D6FE}_{k},\qquad \!\unicode[STIX]{x1D6FF}_{k-1}=\unicode[STIX]{x1D6FF}_{k}, & \displaystyle \nonumber\\ \displaystyle & Xa_{k}=f_{k-1}^{(k)}a_{k-1},\qquad \!Xb_{k}=g_{k-1}^{(k)}b_{k-1}+\unicode[STIX]{x1D6FF}_{k,n}a_{n-i}, & \displaystyle \nonumber\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D6FF}_{k,n}$
is the Kronecker delta. Suppose that
$\unicode[STIX]{x1D6FF}_{k,n}$
is the Kronecker delta. Suppose that
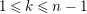 $1\leqslant k\leqslant n-1$
. Then, we have
$1\leqslant k\leqslant n-1$
. Then, we have
 $$\begin{eqnarray}\displaystyle XA_{k}^{\prime } & = & \displaystyle X(e_{k}^{\prime }-\unicode[STIX]{x1D6FC}_{k}a_{k}-\unicode[STIX]{x1D6FD}_{k}b_{k})=Xe_{k}^{\prime }-f_{k-1}^{(k)}\unicode[STIX]{x1D6FC}_{k}a_{k-1}-g_{k-1}^{(k)}\unicode[STIX]{x1D6FD}_{k}b_{k-1},\nonumber\\ \displaystyle f_{k-1}^{(k)}A_{k-1}^{\prime } & = & \displaystyle f_{k-1}^{(k)}(e_{k-1}^{\prime }-\unicode[STIX]{x1D6FC}_{k-1}a_{k-1}-\unicode[STIX]{x1D6FD}_{k-1}b_{k-1})\nonumber\\ \displaystyle & = & \displaystyle f_{k-1}^{(k)}e_{k-1}^{\prime }-f_{k-1}^{(k)}\unicode[STIX]{x1D6FC}_{k}a_{k-1}-g_{k-1}^{(k)}\unicode[STIX]{x1D6FD}_{k}b_{k-1}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle XA_{k}^{\prime } & = & \displaystyle X(e_{k}^{\prime }-\unicode[STIX]{x1D6FC}_{k}a_{k}-\unicode[STIX]{x1D6FD}_{k}b_{k})=Xe_{k}^{\prime }-f_{k-1}^{(k)}\unicode[STIX]{x1D6FC}_{k}a_{k-1}-g_{k-1}^{(k)}\unicode[STIX]{x1D6FD}_{k}b_{k-1},\nonumber\\ \displaystyle f_{k-1}^{(k)}A_{k-1}^{\prime } & = & \displaystyle f_{k-1}^{(k)}(e_{k-1}^{\prime }-\unicode[STIX]{x1D6FC}_{k-1}a_{k-1}-\unicode[STIX]{x1D6FD}_{k-1}b_{k-1})\nonumber\\ \displaystyle & = & \displaystyle f_{k-1}^{(k)}e_{k-1}^{\prime }-f_{k-1}^{(k)}\unicode[STIX]{x1D6FC}_{k}a_{k-1}-g_{k-1}^{(k)}\unicode[STIX]{x1D6FD}_{k}b_{k-1}.\nonumber\end{eqnarray}$$
We compute
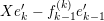 $Xe_{k}^{\prime }-f_{k-1}^{(k)}e_{k-1}^{\prime }$
in two ways:
$Xe_{k}^{\prime }-f_{k-1}^{(k)}e_{k-1}^{\prime }$
in two ways:
 $$\begin{eqnarray}\displaystyle Xe_{k}^{\prime }-f_{k-1}^{(k)}e_{k-1}^{\prime } & = & \displaystyle XA_{k}^{\prime }-f_{k-1}^{(k)}A_{k-1}^{\prime }\in E^{\prime \prime },\nonumber\\ \displaystyle Xe_{k}^{\prime }-f_{k-1}^{(k)}e_{k-1}^{\prime } & = & \displaystyle f_{k-2}^{(k)}e_{k-2}^{\prime }+\cdots +f_{1}^{(k)}e_{1}^{\prime }\in E^{\prime }.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle Xe_{k}^{\prime }-f_{k-1}^{(k)}e_{k-1}^{\prime } & = & \displaystyle XA_{k}^{\prime }-f_{k-1}^{(k)}A_{k-1}^{\prime }\in E^{\prime \prime },\nonumber\\ \displaystyle Xe_{k}^{\prime }-f_{k-1}^{(k)}e_{k-1}^{\prime } & = & \displaystyle f_{k-2}^{(k)}e_{k-2}^{\prime }+\cdots +f_{1}^{(k)}e_{1}^{\prime }\in E^{\prime }.\nonumber\end{eqnarray}$$
Thus, we have
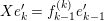 $Xe_{k}^{\prime }=f_{k-1}^{(k)}e_{k-1}^{\prime }$
, for
$Xe_{k}^{\prime }=f_{k-1}^{(k)}e_{k-1}^{\prime }$
, for
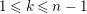 $1\leqslant k\leqslant n-1$
. Next suppose that
$1\leqslant k\leqslant n-1$
. Next suppose that
![]() $k=n$
. Then, the similar computation shows
$k=n$
. Then, the similar computation shows
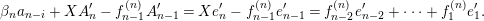 $$\begin{eqnarray}\unicode[STIX]{x1D6FD}_{n}a_{n-i}+XA_{n}^{\prime }-f_{n-1}^{(n)}A_{n-1}^{\prime }=Xe_{n}^{\prime }-f_{n-1}^{(n)}e_{n-1}^{\prime }=f_{n-2}^{(n)}e_{n-2}^{\prime }+\cdots +f_{1}^{(n)}e_{1}^{\prime }.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FD}_{n}a_{n-i}+XA_{n}^{\prime }-f_{n-1}^{(n)}A_{n-1}^{\prime }=Xe_{n}^{\prime }-f_{n-1}^{(n)}e_{n-1}^{\prime }=f_{n-2}^{(n)}e_{n-2}^{\prime }+\cdots +f_{1}^{(n)}e_{1}^{\prime }.\end{eqnarray}$$
We compute
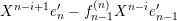 $X^{n-i+1}e_{n}^{\prime }-f_{n-1}^{(n)}X^{n-i}e_{n-1}^{\prime }$
in two ways as before, and we obtain
$X^{n-i+1}e_{n}^{\prime }-f_{n-1}^{(n)}X^{n-i}e_{n-1}^{\prime }$
in two ways as before, and we obtain
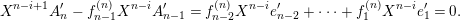 $$\begin{eqnarray}X^{n-i+1}A_{n}^{\prime }-f_{n-1}^{(n)}X^{n-i}A_{n-1}^{\prime }=f_{n-2}^{(n)}X^{n-i}e_{n-2}^{\prime }+\cdots +f_{1}^{(n)}X^{n-i}e_{1}^{\prime }=0.\end{eqnarray}$$
$$\begin{eqnarray}X^{n-i+1}A_{n}^{\prime }-f_{n-1}^{(n)}X^{n-i}A_{n-1}^{\prime }=f_{n-2}^{(n)}X^{n-i}e_{n-2}^{\prime }+\cdots +f_{1}^{(n)}X^{n-i}e_{1}^{\prime }=0.\end{eqnarray}$$
Hence, we have
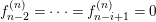 $f_{n-2}^{(n)}=\cdots =f_{n-i+1}^{(n)}=0$
. We define
$f_{n-2}^{(n)}=\cdots =f_{n-i+1}^{(n)}=0$
. We define
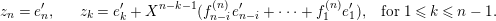 $$\begin{eqnarray}z_{n}=e_{n}^{\prime },\!\!\qquad z_{k}=e_{k}^{\prime }+X^{n-k-1}(f_{n-i}^{(n)}e_{n-i}^{\prime }+\cdots +f_{1}^{(n)}e_{1}^{\prime }),\!\quad \text{for}~1\leqslant k\leqslant n-1.\end{eqnarray}$$
$$\begin{eqnarray}z_{n}=e_{n}^{\prime },\!\!\qquad z_{k}=e_{k}^{\prime }+X^{n-k-1}(f_{n-i}^{(n)}e_{n-i}^{\prime }+\cdots +f_{1}^{(n)}e_{1}^{\prime }),\!\quad \text{for}~1\leqslant k\leqslant n-1.\end{eqnarray}$$
Then,
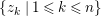 $\{z_{k}\mid 1\leqslant k\leqslant n\}$
is an
$\{z_{k}\mid 1\leqslant k\leqslant n\}$
is an
![]() ${\mathcal{O}}$
-basis of
${\mathcal{O}}$
-basis of
![]() $E^{\prime }$
, since
$E^{\prime }$
, since
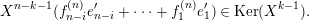 $$\begin{eqnarray}X^{n-k-1}(f_{n-i}^{(n)}e_{n-i}^{\prime }+\cdots +f_{1}^{(n)}e_{1}^{\prime })\in \text{Ker}(X^{k-1}).\end{eqnarray}$$
$$\begin{eqnarray}X^{n-k-1}(f_{n-i}^{(n)}e_{n-i}^{\prime }+\cdots +f_{1}^{(n)}e_{1}^{\prime })\in \text{Ker}(X^{k-1}).\end{eqnarray}$$
Further, we have
![]() $z_{k}=e_{k}^{\prime }$
, for
$z_{k}=e_{k}^{\prime }$
, for
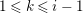 $1\leqslant k\leqslant i-1$
. In particular,
$1\leqslant k\leqslant i-1$
. In particular,
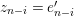 $z_{n-i}=e_{n-i}^{\prime }$
by
$z_{n-i}=e_{n-i}^{\prime }$
by
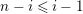 $n-i\leqslant i-1$
. Then, we can check that
$n-i\leqslant i-1$
. Then, we can check that
 $$\begin{eqnarray}Xz_{k}=\left\{\begin{array}{@{}ll@{}}z_{k-1} & \text{if}~k\neq n-i+1,\\ \unicode[STIX]{x1D716}z_{k-1} & \text{if}~k=n-i+1.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}Xz_{k}=\left\{\begin{array}{@{}ll@{}}z_{k-1} & \text{if}~k\neq n-i+1,\\ \unicode[STIX]{x1D716}z_{k-1} & \text{if}~k=n-i+1.\end{array}\right.\end{eqnarray}$$
Thus, we conclude that
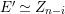 $E^{\prime }\simeq Z_{n-i}$
. Recall that the exact sequence
$E^{\prime }\simeq Z_{n-i}$
. Recall that the exact sequence
 $$\begin{eqnarray}0\rightarrow Z_{n-i}\rightarrow E_{i}\rightarrow Z_{i}\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow Z_{n-i}\rightarrow E_{i}\rightarrow Z_{i}\rightarrow 0\end{eqnarray}$$
does not split. On the other hand,
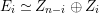 $E_{i}\simeq Z_{n-i}\oplus Z_{i}$
implies that it must split, by Miyata’s theorem [Reference MiyataM, Theorem 1]. Hence,
$E_{i}\simeq Z_{n-i}\oplus Z_{i}$
implies that it must split, by Miyata’s theorem [Reference MiyataM, Theorem 1]. Hence,
![]() $E_{i}$
is indecomposable in (Case a).
$E_{i}$
is indecomposable in (Case a).
Next assume that we are in (Case b). Then,
![]() $f_{k-1}^{(k)}$
and
$f_{k-1}^{(k)}$
and
![]() $g_{k-1}^{(k)}$
, for
$g_{k-1}^{(k)}$
, for
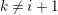 $k\neq i+1$
, are invertible as before, and we may choose
$k\neq i+1$
, are invertible as before, and we may choose
 $$\begin{eqnarray}f_{k-1}^{(k)}=1,\quad g_{k-1}^{(k)}=1.\end{eqnarray}$$
$$\begin{eqnarray}f_{k-1}^{(k)}=1,\quad g_{k-1}^{(k)}=1.\end{eqnarray}$$
If
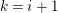 $k=i+1$
, note that
$k=i+1$
, note that
 $$\begin{eqnarray}\displaystyle & f_{i}^{(i+1)}\unicode[STIX]{x1D6FC}_{i}=\unicode[STIX]{x1D716}\unicode[STIX]{x1D6FC}_{i+1},\qquad f_{i}^{(i+1)}\unicode[STIX]{x1D6FD}_{i}=\unicode[STIX]{x1D716}\unicode[STIX]{x1D6FD}_{i+1}, & \displaystyle \nonumber\\ \displaystyle & g_{i}^{(i+1)}\unicode[STIX]{x1D6FE}_{i}=\unicode[STIX]{x1D716}\unicode[STIX]{x1D6FE}_{i+1},\qquad g_{i}^{(i+1)}\unicode[STIX]{x1D6FF}_{i}=\unicode[STIX]{x1D716}\unicode[STIX]{x1D6FF}_{i+1}. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & f_{i}^{(i+1)}\unicode[STIX]{x1D6FC}_{i}=\unicode[STIX]{x1D716}\unicode[STIX]{x1D6FC}_{i+1},\qquad f_{i}^{(i+1)}\unicode[STIX]{x1D6FD}_{i}=\unicode[STIX]{x1D716}\unicode[STIX]{x1D6FD}_{i+1}, & \displaystyle \nonumber\\ \displaystyle & g_{i}^{(i+1)}\unicode[STIX]{x1D6FE}_{i}=\unicode[STIX]{x1D716}\unicode[STIX]{x1D6FE}_{i+1},\qquad g_{i}^{(i+1)}\unicode[STIX]{x1D6FF}_{i}=\unicode[STIX]{x1D716}\unicode[STIX]{x1D6FF}_{i+1}. & \displaystyle \nonumber\end{eqnarray}$$
Thus,
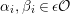 $\unicode[STIX]{x1D6FC}_{i},\unicode[STIX]{x1D6FD}_{i}\in \unicode[STIX]{x1D716}{\mathcal{O}}$
if
$\unicode[STIX]{x1D6FC}_{i},\unicode[STIX]{x1D6FD}_{i}\in \unicode[STIX]{x1D716}{\mathcal{O}}$
if
![]() $f_{i}^{(i+1)}$
is invertible, and
$f_{i}^{(i+1)}$
is invertible, and
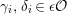 $\unicode[STIX]{x1D6FE}_{i},\unicode[STIX]{x1D6FF}_{i}\in \unicode[STIX]{x1D716}{\mathcal{O}}$
if
$\unicode[STIX]{x1D6FE}_{i},\unicode[STIX]{x1D6FF}_{i}\in \unicode[STIX]{x1D716}{\mathcal{O}}$
if
![]() $g_{i}^{(i+1)}$
is invertible. But both are impossible. Further,
$g_{i}^{(i+1)}$
is invertible. But both are impossible. Further,
 $$\begin{eqnarray}f_{i}^{(i+1)}g_{i}^{(i+1)}(\unicode[STIX]{x1D6FC}_{i}\unicode[STIX]{x1D6FF}_{i}-\unicode[STIX]{x1D6FD}_{i}\unicode[STIX]{x1D6FE}_{i})=\unicode[STIX]{x1D716}^{2}(\unicode[STIX]{x1D6FC}_{i+1}\unicode[STIX]{x1D6FF}_{i+1}-\unicode[STIX]{x1D6FD}_{i+1}\unicode[STIX]{x1D6FE}_{i+1})\end{eqnarray}$$
$$\begin{eqnarray}f_{i}^{(i+1)}g_{i}^{(i+1)}(\unicode[STIX]{x1D6FC}_{i}\unicode[STIX]{x1D6FF}_{i}-\unicode[STIX]{x1D6FD}_{i}\unicode[STIX]{x1D6FE}_{i})=\unicode[STIX]{x1D716}^{2}(\unicode[STIX]{x1D6FC}_{i+1}\unicode[STIX]{x1D6FF}_{i+1}-\unicode[STIX]{x1D6FD}_{i+1}\unicode[STIX]{x1D6FE}_{i+1})\end{eqnarray}$$
implies
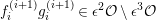 $f_{i}^{(i+1)}g_{i}^{(i+1)}\in \unicode[STIX]{x1D716}^{2}{\mathcal{O}}\setminus \unicode[STIX]{x1D716}^{3}{\mathcal{O}}$
. Thus, we may choose
$f_{i}^{(i+1)}g_{i}^{(i+1)}\in \unicode[STIX]{x1D716}^{2}{\mathcal{O}}\setminus \unicode[STIX]{x1D716}^{3}{\mathcal{O}}$
. Thus, we may choose
 $$\begin{eqnarray}f_{i}^{(i+1)}=\unicode[STIX]{x1D716},\qquad g_{i}^{(i+1)}=\unicode[STIX]{x1D716}.\end{eqnarray}$$
$$\begin{eqnarray}f_{i}^{(i+1)}=\unicode[STIX]{x1D716},\qquad g_{i}^{(i+1)}=\unicode[STIX]{x1D716}.\end{eqnarray}$$
Hence, we may assume without loss of generality that
 $$\begin{eqnarray}\displaystyle & \displaystyle f_{k-1}^{(k)}=g_{k-1}^{(k)}=\left\{\begin{array}{@{}ll@{}}1 & \text{if}~k\neq i+1,\\ \unicode[STIX]{x1D716} & \text{if}~k=i+1.\end{array}\right. & \displaystyle \nonumber\\ \displaystyle & \displaystyle \left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D6FC}_{1} & \unicode[STIX]{x1D6FD}_{1}\\ \unicode[STIX]{x1D6FE}_{1} & \unicode[STIX]{x1D6FF}_{1}\end{array}\right)=\cdots \cdot =\left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D6FC}_{i} & \unicode[STIX]{x1D6FD}_{i}\\ \unicode[STIX]{x1D6FE}_{i} & \unicode[STIX]{x1D6FF}_{i}\end{array}\right)=\left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D6FC}_{i+1} & \unicode[STIX]{x1D6FD}_{i+1}\\ \unicode[STIX]{x1D6FE}_{i+1} & \unicode[STIX]{x1D6FF}_{i+1}\end{array}\right)=\cdots \cdot =\left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D6FC}_{n} & \unicode[STIX]{x1D6FD}_{n}\\ \unicode[STIX]{x1D6FE}_{n} & \unicode[STIX]{x1D6FF}_{n}\end{array}\right). & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle f_{k-1}^{(k)}=g_{k-1}^{(k)}=\left\{\begin{array}{@{}ll@{}}1 & \text{if}~k\neq i+1,\\ \unicode[STIX]{x1D716} & \text{if}~k=i+1.\end{array}\right. & \displaystyle \nonumber\\ \displaystyle & \displaystyle \left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D6FC}_{1} & \unicode[STIX]{x1D6FD}_{1}\\ \unicode[STIX]{x1D6FE}_{1} & \unicode[STIX]{x1D6FF}_{1}\end{array}\right)=\cdots \cdot =\left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D6FC}_{i} & \unicode[STIX]{x1D6FD}_{i}\\ \unicode[STIX]{x1D6FE}_{i} & \unicode[STIX]{x1D6FF}_{i}\end{array}\right)=\left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D6FC}_{i+1} & \unicode[STIX]{x1D6FD}_{i+1}\\ \unicode[STIX]{x1D6FE}_{i+1} & \unicode[STIX]{x1D6FF}_{i+1}\end{array}\right)=\cdots \cdot =\left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D6FC}_{n} & \unicode[STIX]{x1D6FD}_{n}\\ \unicode[STIX]{x1D6FE}_{n} & \unicode[STIX]{x1D6FF}_{n}\end{array}\right). & \displaystyle \nonumber\end{eqnarray}$$
and
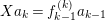 $Xa_{k}=f_{k-1}^{(k)}a_{k-1}$
,
$Xa_{k}=f_{k-1}^{(k)}a_{k-1}$
,
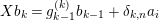 $Xb_{k}=g_{k-1}^{(k)}b_{k-1}+\unicode[STIX]{x1D6FF}_{k,n}a_{i}$
. For
$Xb_{k}=g_{k-1}^{(k)}b_{k-1}+\unicode[STIX]{x1D6FF}_{k,n}a_{i}$
. For
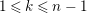 $1\leqslant k\leqslant n-1$
, we have
$1\leqslant k\leqslant n-1$
, we have
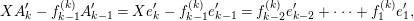 $$\begin{eqnarray}XA_{k}^{\prime }-f_{k-1}^{(k)}A_{k-1}^{\prime }=Xe_{k}^{\prime }-f_{k-1}^{(k)}e_{k-1}^{\prime }=f_{k-2}^{(k)}e_{k-2}^{\prime }+\cdots +f_{1}^{(k)}e_{1}^{\prime },\end{eqnarray}$$
$$\begin{eqnarray}XA_{k}^{\prime }-f_{k-1}^{(k)}A_{k-1}^{\prime }=Xe_{k}^{\prime }-f_{k-1}^{(k)}e_{k-1}^{\prime }=f_{k-2}^{(k)}e_{k-2}^{\prime }+\cdots +f_{1}^{(k)}e_{1}^{\prime },\end{eqnarray}$$
and the same argument as before shows that
 $$\begin{eqnarray}Xe_{k}^{\prime }=\left\{\begin{array}{@{}ll@{}}f_{k-1}^{(k)}e_{k-1}^{\prime } & \text{if}~k\neq n,\\ f_{n-1}^{(n)}e_{n-1}^{\prime }+f_{i}^{(n)}e_{i}^{\prime }+\cdots +f_{1}^{(n)}e_{1}^{\prime } & \text{if}~k=n.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}Xe_{k}^{\prime }=\left\{\begin{array}{@{}ll@{}}f_{k-1}^{(k)}e_{k-1}^{\prime } & \text{if}~k\neq n,\\ f_{n-1}^{(n)}e_{n-1}^{\prime }+f_{i}^{(n)}e_{i}^{\prime }+\cdots +f_{1}^{(n)}e_{1}^{\prime } & \text{if}~k=n.\end{array}\right.\end{eqnarray}$$
Now, we compute
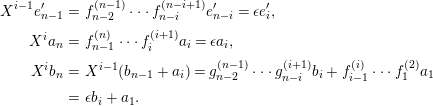 $$\begin{eqnarray}\displaystyle X^{i-1}e_{n-1}^{\prime } & = & \displaystyle f_{n-2}^{(n-1)}\cdots f_{n-i}^{(n-i+1)}e_{n-i}^{\prime }=\unicode[STIX]{x1D716}e_{i}^{\prime },\nonumber\\ \displaystyle X^{i}a_{n} & = & \displaystyle f_{n-1}^{(n)}\cdots f_{i}^{(i+1)}a_{i}=\unicode[STIX]{x1D716}a_{i},\nonumber\\ \displaystyle X^{i}b_{n} & = & \displaystyle X^{i-1}(b_{n-1}+a_{i})=g_{n-2}^{(n-1)}\cdots g_{n-i}^{(i+1)}b_{i}+f_{i-1}^{(i)}\cdots f_{1}^{(2)}a_{1}\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D716}b_{i}+a_{1}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle X^{i-1}e_{n-1}^{\prime } & = & \displaystyle f_{n-2}^{(n-1)}\cdots f_{n-i}^{(n-i+1)}e_{n-i}^{\prime }=\unicode[STIX]{x1D716}e_{i}^{\prime },\nonumber\\ \displaystyle X^{i}a_{n} & = & \displaystyle f_{n-1}^{(n)}\cdots f_{i}^{(i+1)}a_{i}=\unicode[STIX]{x1D716}a_{i},\nonumber\\ \displaystyle X^{i}b_{n} & = & \displaystyle X^{i-1}(b_{n-1}+a_{i})=g_{n-2}^{(n-1)}\cdots g_{n-i}^{(i+1)}b_{i}+f_{i-1}^{(i)}\cdots f_{1}^{(2)}a_{1}\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D716}b_{i}+a_{1}.\nonumber\end{eqnarray}$$
Thus, we have
 $$\begin{eqnarray}\displaystyle X^{i}e_{n}^{\prime }-X^{i-1}e_{n-1}^{\prime } & = & \displaystyle X^{i}(\unicode[STIX]{x1D6FC}_{n}a_{n}+\unicode[STIX]{x1D6FD}_{n}b_{n}+A_{n}^{\prime })-\unicode[STIX]{x1D716}e_{i}^{\prime }\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D716}(\unicode[STIX]{x1D6FC}_{n}a_{i}+\unicode[STIX]{x1D6FD}_{n}b_{i}-e_{i}^{\prime })+X^{i}A_{n}^{\prime }+\unicode[STIX]{x1D6FD}_{n}a_{1}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle X^{i}e_{n}^{\prime }-X^{i-1}e_{n-1}^{\prime } & = & \displaystyle X^{i}(\unicode[STIX]{x1D6FC}_{n}a_{n}+\unicode[STIX]{x1D6FD}_{n}b_{n}+A_{n}^{\prime })-\unicode[STIX]{x1D716}e_{i}^{\prime }\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D716}(\unicode[STIX]{x1D6FC}_{n}a_{i}+\unicode[STIX]{x1D6FD}_{n}b_{i}-e_{i}^{\prime })+X^{i}A_{n}^{\prime }+\unicode[STIX]{x1D6FD}_{n}a_{1}.\nonumber\end{eqnarray}$$
If
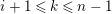 $i+1\leqslant k\leqslant n-1$
then
$i+1\leqslant k\leqslant n-1$
then
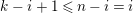 $k-i+1\leqslant n-i=i$
and
$k-i+1\leqslant n-i=i$
and
 $$\begin{eqnarray}X^{i}e_{k}^{\prime }=f_{k-1}^{(k)}\cdots f_{k-i}^{(k-i+1)}e_{k-i}^{\prime }\in \unicode[STIX]{x1D716}E^{\prime }.\end{eqnarray}$$
$$\begin{eqnarray}X^{i}e_{k}^{\prime }=f_{k-1}^{(k)}\cdots f_{k-i}^{(k-i+1)}e_{k-i}^{\prime }\in \unicode[STIX]{x1D716}E^{\prime }.\end{eqnarray}$$
Thus,
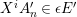 $X^{i}A_{n}^{\prime }\in \unicode[STIX]{x1D716}E^{\prime }$
. On the other hand, we have
$X^{i}A_{n}^{\prime }\in \unicode[STIX]{x1D716}E^{\prime }$
. On the other hand, we have
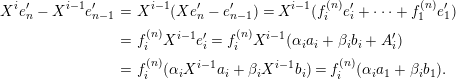 $$\begin{eqnarray}\displaystyle X^{i}e_{n}^{\prime }-X^{i-1}e_{n-1}^{\prime } & = & \displaystyle X^{i-1}(Xe_{n}^{\prime }-e_{n-1}^{\prime })=X^{i-1}(f_{i}^{(n)}e_{i}^{\prime }+\cdots +f_{1}^{(n)}e_{1}^{\prime })\nonumber\\ \displaystyle & = & \displaystyle f_{i}^{(n)}X^{i-1}e_{i}^{\prime }=f_{i}^{(n)}X^{i-1}(\unicode[STIX]{x1D6FC}_{i}a_{i}+\unicode[STIX]{x1D6FD}_{i}b_{i}+A_{i}^{\prime })\nonumber\\ \displaystyle & = & \displaystyle f_{i}^{(n)}(\unicode[STIX]{x1D6FC}_{i}X^{i-1}a_{i}+\unicode[STIX]{x1D6FD}_{i}X^{i-1}b_{i})=f_{i}^{(n)}(\unicode[STIX]{x1D6FC}_{i}a_{1}+\unicode[STIX]{x1D6FD}_{i}b_{1}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle X^{i}e_{n}^{\prime }-X^{i-1}e_{n-1}^{\prime } & = & \displaystyle X^{i-1}(Xe_{n}^{\prime }-e_{n-1}^{\prime })=X^{i-1}(f_{i}^{(n)}e_{i}^{\prime }+\cdots +f_{1}^{(n)}e_{1}^{\prime })\nonumber\\ \displaystyle & = & \displaystyle f_{i}^{(n)}X^{i-1}e_{i}^{\prime }=f_{i}^{(n)}X^{i-1}(\unicode[STIX]{x1D6FC}_{i}a_{i}+\unicode[STIX]{x1D6FD}_{i}b_{i}+A_{i}^{\prime })\nonumber\\ \displaystyle & = & \displaystyle f_{i}^{(n)}(\unicode[STIX]{x1D6FC}_{i}X^{i-1}a_{i}+\unicode[STIX]{x1D6FD}_{i}X^{i-1}b_{i})=f_{i}^{(n)}(\unicode[STIX]{x1D6FC}_{i}a_{1}+\unicode[STIX]{x1D6FD}_{i}b_{1}).\nonumber\end{eqnarray}$$
Hence, we obtain
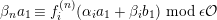 $\unicode[STIX]{x1D6FD}_{n}a_{1}\equiv f_{i}^{(n)}(\unicode[STIX]{x1D6FC}_{i}a_{1}+\unicode[STIX]{x1D6FD}_{i}b_{1})~\text{mod}\,\unicode[STIX]{x1D716}{\mathcal{O}}$
. The similar computation using
$\unicode[STIX]{x1D6FD}_{n}a_{1}\equiv f_{i}^{(n)}(\unicode[STIX]{x1D6FC}_{i}a_{1}+\unicode[STIX]{x1D6FD}_{i}b_{1})~\text{mod}\,\unicode[STIX]{x1D716}{\mathcal{O}}$
. The similar computation using
![]() $e_{k}^{\prime \prime }$
shows
$e_{k}^{\prime \prime }$
shows
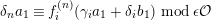 $\unicode[STIX]{x1D6FF}_{n}a_{1}\equiv f_{i}^{(n)}(\unicode[STIX]{x1D6FE}_{i}a_{1}+\unicode[STIX]{x1D6FF}_{i}b_{1})~\text{mod}\,\unicode[STIX]{x1D716}{\mathcal{O}}$
. If
$\unicode[STIX]{x1D6FF}_{n}a_{1}\equiv f_{i}^{(n)}(\unicode[STIX]{x1D6FE}_{i}a_{1}+\unicode[STIX]{x1D6FF}_{i}b_{1})~\text{mod}\,\unicode[STIX]{x1D716}{\mathcal{O}}$
. If
![]() $f_{i}^{(n)}$
was invertible, it would imply
$f_{i}^{(n)}$
was invertible, it would imply
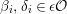 $\unicode[STIX]{x1D6FD}_{i},\unicode[STIX]{x1D6FF}_{i}\in \unicode[STIX]{x1D716}{\mathcal{O}}$
, which contradicts
$\unicode[STIX]{x1D6FD}_{i},\unicode[STIX]{x1D6FF}_{i}\in \unicode[STIX]{x1D716}{\mathcal{O}}$
, which contradicts
 $\unicode[STIX]{x1D6FC}_{i}\unicode[STIX]{x1D6FF}_{i}-\unicode[STIX]{x1D6FD}_{i}\unicode[STIX]{x1D6FE}_{i}\in {\mathcal{O}}^{\times }$
. Thus,
$\unicode[STIX]{x1D6FC}_{i}\unicode[STIX]{x1D6FF}_{i}-\unicode[STIX]{x1D6FD}_{i}\unicode[STIX]{x1D6FE}_{i}\in {\mathcal{O}}^{\times }$
. Thus,
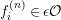 $f_{i}^{(n)}\in \unicode[STIX]{x1D716}{\mathcal{O}}$
and we have
$f_{i}^{(n)}\in \unicode[STIX]{x1D716}{\mathcal{O}}$
and we have
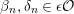 $\unicode[STIX]{x1D6FD}_{n},\unicode[STIX]{x1D6FF}_{n}\in \unicode[STIX]{x1D716}{\mathcal{O}}$
, which is again a contradiction. Hence,
$\unicode[STIX]{x1D6FD}_{n},\unicode[STIX]{x1D6FF}_{n}\in \unicode[STIX]{x1D716}{\mathcal{O}}$
, which is again a contradiction. Hence,
![]() $E_{i}$
is indecomposable in (Case b).
$E_{i}$
is indecomposable in (Case b).
Finally, suppose that we are in (Case c). Since
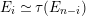 $E_{i}\simeq \unicode[STIX]{x1D70F}(E_{n-i})$
, for
$E_{i}\simeq \unicode[STIX]{x1D70F}(E_{n-i})$
, for
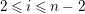 $2\leqslant i\leqslant n-2$
, and
$2\leqslant i\leqslant n-2$
, and
![]() $E_{n-i}$
is indecomposable by (Cases a), it follows from [Reference AuslanderA1, Chapter III, Propositions 1.7, 1.8] that
$E_{n-i}$
is indecomposable by (Cases a), it follows from [Reference AuslanderA1, Chapter III, Propositions 1.7, 1.8] that
![]() $E_{i}$
is indecomposable in (Case c).◻
$E_{i}$
is indecomposable in (Case c).◻
2.3 Almost split sequence ending at
 $\mathbf{E}_{\mathbf{i}}$
$\mathbf{E}_{\mathbf{i}}$
We construct an almost split sequence ending at
![]() $E_{i}$
, for
$E_{i}$
, for
 $2\leqslant i\leqslant n-2$
. Define
$2\leqslant i\leqslant n-2$
. Define
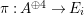 $\unicode[STIX]{x1D70B}:A^{\oplus 4}\rightarrow E_{i}$
, for
$\unicode[STIX]{x1D70B}:A^{\oplus 4}\rightarrow E_{i}$
, for
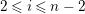 $2\leqslant i\leqslant n-2$
, by
$2\leqslant i\leqslant n-2$
, by
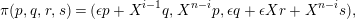 $$\begin{eqnarray}\unicode[STIX]{x1D70B}(p,q,r,s)=(\unicode[STIX]{x1D716}p+X^{i-1}q,X^{n-i}p,\unicode[STIX]{x1D716}q+\unicode[STIX]{x1D716}Xr+X^{n-i}s),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}(p,q,r,s)=(\unicode[STIX]{x1D716}p+X^{i-1}q,X^{n-i}p,\unicode[STIX]{x1D716}q+\unicode[STIX]{x1D716}Xr+X^{n-i}s),\end{eqnarray}$$
for
 $(p,q,r,s)\in A^{\oplus 4}$
. Note that
$(p,q,r,s)\in A^{\oplus 4}$
. Note that
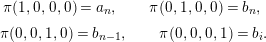 $$\begin{eqnarray}\displaystyle & \unicode[STIX]{x1D70B}(1,0,0,0)=a_{n},\qquad \unicode[STIX]{x1D70B}(0,1,0,0)=b_{n}, & \displaystyle \nonumber\\ \displaystyle & \unicode[STIX]{x1D70B}(0,0,1,0)=b_{n-1},\qquad \unicode[STIX]{x1D70B}(0,0,0,1)=b_{i}. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \unicode[STIX]{x1D70B}(1,0,0,0)=a_{n},\qquad \unicode[STIX]{x1D70B}(0,1,0,0)=b_{n}, & \displaystyle \nonumber\\ \displaystyle & \unicode[STIX]{x1D70B}(0,0,1,0)=b_{n-1},\qquad \unicode[STIX]{x1D70B}(0,0,0,1)=b_{i}. & \displaystyle \nonumber\end{eqnarray}$$
Lemma 2.5. Let
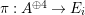 $\unicode[STIX]{x1D70B}:A^{\oplus 4}\rightarrow E_{i}$
be as above. Then,
$\unicode[STIX]{x1D70B}:A^{\oplus 4}\rightarrow E_{i}$
be as above. Then,
-
(1)
 $\unicode[STIX]{x1D70B}$
is an epimorphism;
$\unicode[STIX]{x1D70B}$
is an epimorphism; -
(2)
 $\text{Ker}(\unicode[STIX]{x1D70B})\simeq E_{n-i}$
, for
$\text{Ker}(\unicode[STIX]{x1D70B})\simeq E_{n-i}$
, for
 $2\leqslant i\leqslant n-2$
.
$2\leqslant i\leqslant n-2$
.
Proof. (1) It is easy to check that
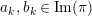 $a_{k},b_{k}\in \text{Im}(\unicode[STIX]{x1D70B})$
, for
$a_{k},b_{k}\in \text{Im}(\unicode[STIX]{x1D70B})$
, for
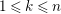 $1\leqslant k\leqslant n$
. Note that
$1\leqslant k\leqslant n$
. Note that
![]() $E_{i}$
is generated by
$E_{i}$
is generated by
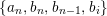 $\{a_{n},b_{n},b_{n-1},b_{i}\}$
as an
$\{a_{n},b_{n},b_{n-1},b_{i}\}$
as an
![]() $A$
-module and
$A$
-module and
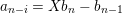 $a_{n-i}=Xb_{n}-b_{n-1}$
.
$a_{n-i}=Xb_{n}-b_{n-1}$
.
(2) We define an
![]() $A$
-module homomorphism
$A$
-module homomorphism
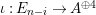 $\unicode[STIX]{x1D704}:E_{n-i}\rightarrow A^{\oplus 4}$
by
$\unicode[STIX]{x1D704}:E_{n-i}\rightarrow A^{\oplus 4}$
by
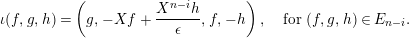 $$\begin{eqnarray}\unicode[STIX]{x1D704}(f,g,h)=\left(g,-Xf+\frac{X^{n-i}h}{\unicode[STIX]{x1D716}},f,-h\right),\quad \text{for}~(f,g,h)\in E_{n-i}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D704}(f,g,h)=\left(g,-Xf+\frac{X^{n-i}h}{\unicode[STIX]{x1D716}},f,-h\right),\quad \text{for}~(f,g,h)\in E_{n-i}.\end{eqnarray}$$
We write
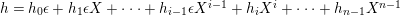 $h=h_{0}\unicode[STIX]{x1D716}+h_{1}\unicode[STIX]{x1D716}X+\cdots +h_{i-1}\unicode[STIX]{x1D716}X^{i-1}+h_{i}X^{i}+\cdots +h_{n-1}X^{n-1}$
, for
$h=h_{0}\unicode[STIX]{x1D716}+h_{1}\unicode[STIX]{x1D716}X+\cdots +h_{i-1}\unicode[STIX]{x1D716}X^{i-1}+h_{i}X^{i}+\cdots +h_{n-1}X^{n-1}$
, for
![]() $h_{i}\in {\mathcal{O}}$
. Then,
$h_{i}\in {\mathcal{O}}$
. Then,
 $$\begin{eqnarray}\frac{X^{n-i}h}{\unicode[STIX]{x1D716}}=h_{0}X^{n-i}+h_{1}X^{n-i+1}+\cdots +h_{i-1}X^{n-1}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{X^{n-i}h}{\unicode[STIX]{x1D716}}=h_{0}X^{n-i}+h_{1}X^{n-i+1}+\cdots +h_{i-1}X^{n-1}.\end{eqnarray}$$
Note that
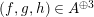 $(f,g,h)\in A^{\oplus 3}$
belongs to
$(f,g,h)\in A^{\oplus 3}$
belongs to
![]() $E_{n-i}$
if and only if
$E_{n-i}$
if and only if
 $h\in Z_{n-i}$
and
$h\in Z_{n-i}$
and
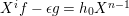 $X^{i}f-\unicode[STIX]{x1D716}g=h_{0}X^{n-1}$
. It is clear that
$X^{i}f-\unicode[STIX]{x1D716}g=h_{0}X^{n-1}$
. It is clear that
![]() $\unicode[STIX]{x1D704}$
is a monomorphism and it suffices to show that
$\unicode[STIX]{x1D704}$
is a monomorphism and it suffices to show that
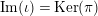 $\text{Im}(\unicode[STIX]{x1D704})=\text{Ker}(\unicode[STIX]{x1D70B})$
. Since
$\text{Im}(\unicode[STIX]{x1D704})=\text{Ker}(\unicode[STIX]{x1D70B})$
. Since
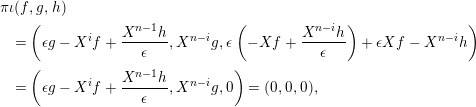 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D70B}\unicode[STIX]{x1D704}(f,g,h)\nonumber\\ \displaystyle & & \displaystyle \quad =\left(\unicode[STIX]{x1D716}g-X^{i}f+\frac{X^{n-1}h}{\unicode[STIX]{x1D716}},X^{n-i}g,\unicode[STIX]{x1D716}\left(-Xf+\frac{X^{n-i}h}{\unicode[STIX]{x1D716}}\right)+\unicode[STIX]{x1D716}Xf-X^{n-i}h\right)\nonumber\\ \displaystyle & & \displaystyle \quad =\left(\unicode[STIX]{x1D716}g-X^{i}f+\frac{X^{n-1}h}{\unicode[STIX]{x1D716}},X^{n-i}g,0\right)=(0,0,0),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D70B}\unicode[STIX]{x1D704}(f,g,h)\nonumber\\ \displaystyle & & \displaystyle \quad =\left(\unicode[STIX]{x1D716}g-X^{i}f+\frac{X^{n-1}h}{\unicode[STIX]{x1D716}},X^{n-i}g,\unicode[STIX]{x1D716}\left(-Xf+\frac{X^{n-i}h}{\unicode[STIX]{x1D716}}\right)+\unicode[STIX]{x1D716}Xf-X^{n-i}h\right)\nonumber\\ \displaystyle & & \displaystyle \quad =\left(\unicode[STIX]{x1D716}g-X^{i}f+\frac{X^{n-1}h}{\unicode[STIX]{x1D716}},X^{n-i}g,0\right)=(0,0,0),\nonumber\end{eqnarray}$$
we have
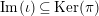 $\text{Im}(\unicode[STIX]{x1D704})\subseteq \text{Ker}(\unicode[STIX]{x1D70B})$
. Let
$\text{Im}(\unicode[STIX]{x1D704})\subseteq \text{Ker}(\unicode[STIX]{x1D70B})$
. Let
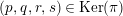 $(p,q,r,s)\in \text{Ker}(\unicode[STIX]{x1D70B})$
. Then we have
$(p,q,r,s)\in \text{Ker}(\unicode[STIX]{x1D70B})$
. Then we have
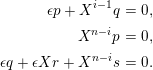 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D716}p+X^{i-1}q & = & \displaystyle 0,\nonumber\\ \displaystyle X^{n-i}p & = & \displaystyle 0,\nonumber\\ \displaystyle \unicode[STIX]{x1D716}q+\unicode[STIX]{x1D716}Xr+X^{n-i}s & = & \displaystyle 0.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D716}p+X^{i-1}q & = & \displaystyle 0,\nonumber\\ \displaystyle X^{n-i}p & = & \displaystyle 0,\nonumber\\ \displaystyle \unicode[STIX]{x1D716}q+\unicode[STIX]{x1D716}Xr+X^{n-i}s & = & \displaystyle 0.\nonumber\end{eqnarray}$$
The third equation shows that the projective cover
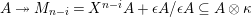 $A{\twoheadrightarrow}M_{n-i}=X^{n-i}A+\unicode[STIX]{x1D716}A/\unicode[STIX]{x1D716}A\subseteq A\otimes \unicode[STIX]{x1D705}$
given by
$A{\twoheadrightarrow}M_{n-i}=X^{n-i}A+\unicode[STIX]{x1D716}A/\unicode[STIX]{x1D716}A\subseteq A\otimes \unicode[STIX]{x1D705}$
given by
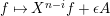 $f\mapsto X^{n-i}f+\unicode[STIX]{x1D716}A$
sends
$f\mapsto X^{n-i}f+\unicode[STIX]{x1D716}A$
sends
![]() $s$
to 0. Thus, we have
$s$
to 0. Thus, we have
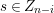 $s\in Z_{n-i}$
. Further,
$s\in Z_{n-i}$
. Further,
 $$\begin{eqnarray}\displaystyle X^{n-1}s+\unicode[STIX]{x1D716}(-\unicode[STIX]{x1D716}p+X^{i}r) & = & \displaystyle X^{n-1}s+\unicode[STIX]{x1D716}(X^{i-1}q+X^{i}r)\nonumber\\ \displaystyle & = & \displaystyle X^{i-1}(X^{n-i}s+\unicode[STIX]{x1D716}q+Xr)=0\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle X^{n-1}s+\unicode[STIX]{x1D716}(-\unicode[STIX]{x1D716}p+X^{i}r) & = & \displaystyle X^{n-1}s+\unicode[STIX]{x1D716}(X^{i-1}q+X^{i}r)\nonumber\\ \displaystyle & = & \displaystyle X^{i-1}(X^{n-i}s+\unicode[STIX]{x1D716}q+Xr)=0\nonumber\end{eqnarray}$$
implies
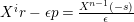 $X^{i}r-\unicode[STIX]{x1D716}p=\frac{X^{n-1}(-s)}{\unicode[STIX]{x1D716}}$
. Hence, we have
$X^{i}r-\unicode[STIX]{x1D716}p=\frac{X^{n-1}(-s)}{\unicode[STIX]{x1D716}}$
. Hence, we have
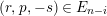 $(r,p,-s)\in E_{n-i}$
and
$(r,p,-s)\in E_{n-i}$
and
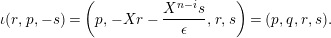 $$\begin{eqnarray}\unicode[STIX]{x1D704}(r,p,-s)=\left(p,-Xr-\frac{X^{n-i}s}{\unicode[STIX]{x1D716}},r,s\right)=(p,q,r,s).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D704}(r,p,-s)=\left(p,-Xr-\frac{X^{n-i}s}{\unicode[STIX]{x1D716}},r,s\right)=(p,q,r,s).\end{eqnarray}$$
Therefore, we have
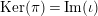 $\text{Ker}(\unicode[STIX]{x1D70B})=\text{Im}(\unicode[STIX]{x1D704})$
, which implies
$\text{Ker}(\unicode[STIX]{x1D70B})=\text{Im}(\unicode[STIX]{x1D704})$
, which implies
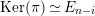 $\text{Ker}(\unicode[STIX]{x1D70B})\simeq E_{n-i}$
.◻
$\text{Ker}(\unicode[STIX]{x1D70B})\simeq E_{n-i}$
.◻
We consider the following pullback diagram:
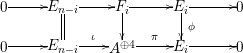
where
![]() $\unicode[STIX]{x1D704}$
is the isomorphism
$\unicode[STIX]{x1D704}$
is the isomorphism
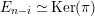 $E_{n-i}\simeq \text{Ker}(\unicode[STIX]{x1D70B})$
defined in the proof of Lemma 2.5, and
$E_{n-i}\simeq \text{Ker}(\unicode[STIX]{x1D70B})$
defined in the proof of Lemma 2.5, and
 $$\begin{eqnarray}\begin{array}{@{}rcll@{}}\unicode[STIX]{x1D719}(a_{k})\ & =\ & 0 & \text{for}~1\leqslant k\leqslant n,\\ \unicode[STIX]{x1D719}(b_{k})\ & =\ & 0 & \text{for}~1\leqslant k\leqslant n-1,\\ \unicode[STIX]{x1D719}(b_{n})\ & =\ & b_{1} & \text{for}~k=n.\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}rcll@{}}\unicode[STIX]{x1D719}(a_{k})\ & =\ & 0 & \text{for}~1\leqslant k\leqslant n,\\ \unicode[STIX]{x1D719}(b_{k})\ & =\ & 0 & \text{for}~1\leqslant k\leqslant n-1,\\ \unicode[STIX]{x1D719}(b_{n})\ & =\ & b_{1} & \text{for}~k=n.\end{array}\end{eqnarray}$$
Lemma 2.6. Suppose that
 $2\leqslant i\leqslant n-i$
. Let
$2\leqslant i\leqslant n-i$
. Let
 $\unicode[STIX]{x1D70C}\in \text{Rad}\,\text{End}_{A}(E_{i})$
such that
$\unicode[STIX]{x1D70C}\in \text{Rad}\,\text{End}_{A}(E_{i})$
such that
 $$\begin{eqnarray}\unicode[STIX]{x1D70C}(a_{n})=\unicode[STIX]{x1D6FC}a_{n}+\unicode[STIX]{x1D6FD}b_{n}+A,\qquad \unicode[STIX]{x1D70C}(b_{n})=\unicode[STIX]{x1D6FC}^{\prime }a_{n}+\unicode[STIX]{x1D6FD}^{\prime }b_{n}+B,\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70C}(a_{n})=\unicode[STIX]{x1D6FC}a_{n}+\unicode[STIX]{x1D6FD}b_{n}+A,\qquad \unicode[STIX]{x1D70C}(b_{n})=\unicode[STIX]{x1D6FC}^{\prime }a_{n}+\unicode[STIX]{x1D6FD}^{\prime }b_{n}+B,\end{eqnarray}$$
where
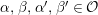 $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FC}^{\prime },\unicode[STIX]{x1D6FD}^{\prime }\in {\mathcal{O}}$
and
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FC}^{\prime },\unicode[STIX]{x1D6FD}^{\prime }\in {\mathcal{O}}$
and
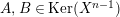 $A,B\in \text{Ker}(X^{n-1})$
. Then we have the following.
$A,B\in \text{Ker}(X^{n-1})$
. Then we have the following.
-
(1)
 $\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x1D716}{\mathcal{O}}$
, and
$\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x1D716}{\mathcal{O}}$
, and
 $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D716}{\mathcal{O}}$
if and only if
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D716}{\mathcal{O}}$
if and only if
 $\unicode[STIX]{x1D6FD}^{\prime }\in \unicode[STIX]{x1D716}{\mathcal{O}}$
.
$\unicode[STIX]{x1D6FD}^{\prime }\in \unicode[STIX]{x1D716}{\mathcal{O}}$
. -
(2)
 $\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}^{\prime }-\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}^{\prime }\in \unicode[STIX]{x1D716}{\mathcal{O}}$
.
$\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}^{\prime }-\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}^{\prime }\in \unicode[STIX]{x1D716}{\mathcal{O}}$
.
Proof. (1) We compute
 $\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D716}X^{n-i}b_{n}-X^{n-1}a_{n})$
in two ways. Since
$\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D716}X^{n-i}b_{n}-X^{n-1}a_{n})$
in two ways. Since
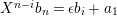 $X^{n-i}b_{n}=\unicode[STIX]{x1D716}b_{i}+a_{1}$
and
$X^{n-i}b_{n}=\unicode[STIX]{x1D716}b_{i}+a_{1}$
and
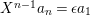 $X^{n-1}a_{n}=\unicode[STIX]{x1D716}a_{1}$
, we have
$X^{n-1}a_{n}=\unicode[STIX]{x1D716}a_{1}$
, we have
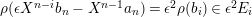 $\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D716}X^{n-i}b_{n}-X^{n-1}a_{n})=\unicode[STIX]{x1D716}^{2}\unicode[STIX]{x1D70C}(b_{i})\in \unicode[STIX]{x1D716}^{2}E_{i}$
. On the other hand, since
$\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D716}X^{n-i}b_{n}-X^{n-1}a_{n})=\unicode[STIX]{x1D716}^{2}\unicode[STIX]{x1D70C}(b_{i})\in \unicode[STIX]{x1D716}^{2}E_{i}$
. On the other hand, since
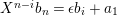 $X^{n-i}b_{n}=\unicode[STIX]{x1D716}b_{i}+a_{1}$
, we have
$X^{n-i}b_{n}=\unicode[STIX]{x1D716}b_{i}+a_{1}$
, we have
 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D70C}(\unicode[STIX]{x1D716}X^{n-i}b_{n}-X^{n-1}a_{n})\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D716}X^{n-i}(\unicode[STIX]{x1D6FC}^{\prime }a_{n}+\unicode[STIX]{x1D6FD}^{\prime }b_{n}+B)-X^{n-1}(\unicode[STIX]{x1D6FC}a_{n}+\unicode[STIX]{x1D6FD}b_{n}+A)\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D716}\unicode[STIX]{x1D6FC}^{\prime }X^{n-i}a_{n}+\unicode[STIX]{x1D716}^{2}\unicode[STIX]{x1D6FD}^{\prime }b_{i}+\unicode[STIX]{x1D716}(\unicode[STIX]{x1D6FD}^{\prime }-\unicode[STIX]{x1D6FC})a_{1}-\unicode[STIX]{x1D716}\unicode[STIX]{x1D6FD}b_{1}+\unicode[STIX]{x1D716}X^{n-i}B.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D70C}(\unicode[STIX]{x1D716}X^{n-i}b_{n}-X^{n-1}a_{n})\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D716}X^{n-i}(\unicode[STIX]{x1D6FC}^{\prime }a_{n}+\unicode[STIX]{x1D6FD}^{\prime }b_{n}+B)-X^{n-1}(\unicode[STIX]{x1D6FC}a_{n}+\unicode[STIX]{x1D6FD}b_{n}+A)\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D716}\unicode[STIX]{x1D6FC}^{\prime }X^{n-i}a_{n}+\unicode[STIX]{x1D716}^{2}\unicode[STIX]{x1D6FD}^{\prime }b_{i}+\unicode[STIX]{x1D716}(\unicode[STIX]{x1D6FD}^{\prime }-\unicode[STIX]{x1D6FC})a_{1}-\unicode[STIX]{x1D716}\unicode[STIX]{x1D6FD}b_{1}+\unicode[STIX]{x1D716}X^{n-i}B.\nonumber\end{eqnarray}$$
Then,
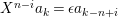 $X^{n-i}a_{k}=\unicode[STIX]{x1D716}a_{k-n+i}$
and
$X^{n-i}a_{k}=\unicode[STIX]{x1D716}a_{k-n+i}$
and
 $X^{n-i}b_{k}=\unicode[STIX]{x1D716}b_{k-n+i}$
, for
$X^{n-i}b_{k}=\unicode[STIX]{x1D716}b_{k-n+i}$
, for
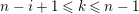 $n-i+1\leqslant k\leqslant n-1$
, imply that
$n-i+1\leqslant k\leqslant n-1$
, imply that
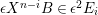 $\unicode[STIX]{x1D716}X^{n-i}B\in \unicode[STIX]{x1D716}^{2}E_{i}$
. Hence, we may divide the both sides by
$\unicode[STIX]{x1D716}X^{n-i}B\in \unicode[STIX]{x1D716}^{2}E_{i}$
. Hence, we may divide the both sides by
![]() $\unicode[STIX]{x1D716}$
. Reducing modulo
$\unicode[STIX]{x1D716}$
. Reducing modulo
![]() $\unicode[STIX]{x1D716}$
, we have
$\unicode[STIX]{x1D716}$
, we have
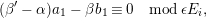 $$\begin{eqnarray}(\unicode[STIX]{x1D6FD}^{\prime }-\unicode[STIX]{x1D6FC})a_{1}-\unicode[STIX]{x1D6FD}b_{1}\equiv 0\quad \text{mod}\,\unicode[STIX]{x1D716}E_{i},\end{eqnarray}$$
$$\begin{eqnarray}(\unicode[STIX]{x1D6FD}^{\prime }-\unicode[STIX]{x1D6FC})a_{1}-\unicode[STIX]{x1D6FD}b_{1}\equiv 0\quad \text{mod}\,\unicode[STIX]{x1D716}E_{i},\end{eqnarray}$$
since
 $X^{n-i}a_{n}\equiv 0~\text{mod}\,\unicode[STIX]{x1D716}E_{i}$
if
$X^{n-i}a_{n}\equiv 0~\text{mod}\,\unicode[STIX]{x1D716}E_{i}$
if
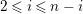 $2\leqslant i\leqslant n-i$
. Now, the claim is clear.
$2\leqslant i\leqslant n-i$
. Now, the claim is clear.
(2) Since
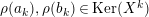 $\unicode[STIX]{x1D70C}(a_{k}),\unicode[STIX]{x1D70C}(b_{k})\in \text{Ker}(X^{k})$
, we may write
$\unicode[STIX]{x1D70C}(a_{k}),\unicode[STIX]{x1D70C}(b_{k})\in \text{Ker}(X^{k})$
, we may write
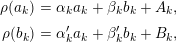 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70C}(a_{k}) & = & \displaystyle \unicode[STIX]{x1D6FC}_{k}a_{k}+\unicode[STIX]{x1D6FD}_{k}b_{k}+A_{k},\nonumber\\ \displaystyle \unicode[STIX]{x1D70C}(b_{k}) & = & \displaystyle \unicode[STIX]{x1D6FC}_{k}^{\prime }a_{k}+\unicode[STIX]{x1D6FD}_{k}^{\prime }b_{k}+B_{k},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70C}(a_{k}) & = & \displaystyle \unicode[STIX]{x1D6FC}_{k}a_{k}+\unicode[STIX]{x1D6FD}_{k}b_{k}+A_{k},\nonumber\\ \displaystyle \unicode[STIX]{x1D70C}(b_{k}) & = & \displaystyle \unicode[STIX]{x1D6FC}_{k}^{\prime }a_{k}+\unicode[STIX]{x1D6FD}_{k}^{\prime }b_{k}+B_{k},\nonumber\end{eqnarray}$$
where
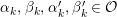 $\unicode[STIX]{x1D6FC}_{k},\unicode[STIX]{x1D6FD}_{k},\unicode[STIX]{x1D6FC}_{k}^{\prime },\unicode[STIX]{x1D6FD}_{k}^{\prime }\in {\mathcal{O}}$
and
$\unicode[STIX]{x1D6FC}_{k},\unicode[STIX]{x1D6FD}_{k},\unicode[STIX]{x1D6FC}_{k}^{\prime },\unicode[STIX]{x1D6FD}_{k}^{\prime }\in {\mathcal{O}}$
and
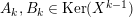 $A_{k},B_{k}\in \text{Ker}(X^{k-1})$
. We claim that
$A_{k},B_{k}\in \text{Ker}(X^{k-1})$
. We claim that
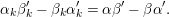 $$\begin{eqnarray}\unicode[STIX]{x1D6FC}_{k}\unicode[STIX]{x1D6FD}_{k}^{\prime }-\unicode[STIX]{x1D6FD}_{k}\unicode[STIX]{x1D6FC}_{k}^{\prime }=\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}^{\prime }-\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}^{\prime }.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FC}_{k}\unicode[STIX]{x1D6FD}_{k}^{\prime }-\unicode[STIX]{x1D6FD}_{k}\unicode[STIX]{x1D6FC}_{k}^{\prime }=\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}^{\prime }-\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}^{\prime }.\end{eqnarray}$$
To see this, observe that we have the following identities in
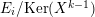 $E_{i}/\text{Ker}(X^{k-1})$
.
$E_{i}/\text{Ker}(X^{k-1})$
.
 $$\begin{eqnarray}\displaystyle & \displaystyle \left\{\begin{array}{@{}ll@{}}\unicode[STIX]{x1D6FC}a_{k}+\unicode[STIX]{x1D6FD}b_{k}\equiv \unicode[STIX]{x1D70C}(X^{n-k}a_{n})\equiv \unicode[STIX]{x1D70C}(a_{k})\quad \text{mod}\,\text{Ker}(X^{k-1}) & \text{if}~k>n-i,\\ \unicode[STIX]{x1D6FC}\unicode[STIX]{x1D716}a_{k}+\unicode[STIX]{x1D6FD}b_{k}\equiv \unicode[STIX]{x1D70C}(X^{n-k}a_{n})\equiv \unicode[STIX]{x1D716}\unicode[STIX]{x1D70C}(a_{k})\quad \text{mod}\,\text{Ker}(X^{k-1}) & \text{if}~i<k\leqslant n-i,\\ \unicode[STIX]{x1D6FC}\unicode[STIX]{x1D716}a_{k}+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D716}b_{k}\equiv \unicode[STIX]{x1D70C}(X^{n-k}a_{n})\equiv \unicode[STIX]{x1D716}\unicode[STIX]{x1D70C}(a_{k})\quad \text{mod}\,\text{Ker}(X^{k-1}) & \text{if}~k\leqslant i,\end{array}\right. & \displaystyle \nonumber\\ \displaystyle & \displaystyle \left\{\begin{array}{@{}ll@{}}\unicode[STIX]{x1D6FC}^{\prime }a_{k}+\unicode[STIX]{x1D6FD}^{\prime }b_{k}\equiv \unicode[STIX]{x1D70C}(X^{n-k}b_{n})\equiv \unicode[STIX]{x1D70C}(b_{k})\quad \text{mod}\,\text{Ker}(X^{k-1}) & \text{if}~k>n-i,\\ \unicode[STIX]{x1D6FC}^{\prime }\unicode[STIX]{x1D716}a_{k}+\unicode[STIX]{x1D6FD}^{\prime }b_{k}\equiv \unicode[STIX]{x1D70C}(X^{n-k}b_{n})\equiv \unicode[STIX]{x1D70C}(b_{k})\quad \text{mod}\,\text{Ker}(X^{k-1}) & \text{if}~i<k\leqslant n-i,\\ \unicode[STIX]{x1D6FC}^{\prime }\unicode[STIX]{x1D716}a_{k}+\unicode[STIX]{x1D6FD}^{\prime }\unicode[STIX]{x1D716}b_{k}\equiv \unicode[STIX]{x1D70C}(X^{n-k}b_{n})\equiv \unicode[STIX]{x1D716}\unicode[STIX]{x1D70C}(b_{k})\quad \text{mod}\,\text{Ker}(X^{k-1}) & \text{if}~k\leqslant i.\end{array}\right. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \left\{\begin{array}{@{}ll@{}}\unicode[STIX]{x1D6FC}a_{k}+\unicode[STIX]{x1D6FD}b_{k}\equiv \unicode[STIX]{x1D70C}(X^{n-k}a_{n})\equiv \unicode[STIX]{x1D70C}(a_{k})\quad \text{mod}\,\text{Ker}(X^{k-1}) & \text{if}~k>n-i,\\ \unicode[STIX]{x1D6FC}\unicode[STIX]{x1D716}a_{k}+\unicode[STIX]{x1D6FD}b_{k}\equiv \unicode[STIX]{x1D70C}(X^{n-k}a_{n})\equiv \unicode[STIX]{x1D716}\unicode[STIX]{x1D70C}(a_{k})\quad \text{mod}\,\text{Ker}(X^{k-1}) & \text{if}~i<k\leqslant n-i,\\ \unicode[STIX]{x1D6FC}\unicode[STIX]{x1D716}a_{k}+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D716}b_{k}\equiv \unicode[STIX]{x1D70C}(X^{n-k}a_{n})\equiv \unicode[STIX]{x1D716}\unicode[STIX]{x1D70C}(a_{k})\quad \text{mod}\,\text{Ker}(X^{k-1}) & \text{if}~k\leqslant i,\end{array}\right. & \displaystyle \nonumber\\ \displaystyle & \displaystyle \left\{\begin{array}{@{}ll@{}}\unicode[STIX]{x1D6FC}^{\prime }a_{k}+\unicode[STIX]{x1D6FD}^{\prime }b_{k}\equiv \unicode[STIX]{x1D70C}(X^{n-k}b_{n})\equiv \unicode[STIX]{x1D70C}(b_{k})\quad \text{mod}\,\text{Ker}(X^{k-1}) & \text{if}~k>n-i,\\ \unicode[STIX]{x1D6FC}^{\prime }\unicode[STIX]{x1D716}a_{k}+\unicode[STIX]{x1D6FD}^{\prime }b_{k}\equiv \unicode[STIX]{x1D70C}(X^{n-k}b_{n})\equiv \unicode[STIX]{x1D70C}(b_{k})\quad \text{mod}\,\text{Ker}(X^{k-1}) & \text{if}~i<k\leqslant n-i,\\ \unicode[STIX]{x1D6FC}^{\prime }\unicode[STIX]{x1D716}a_{k}+\unicode[STIX]{x1D6FD}^{\prime }\unicode[STIX]{x1D716}b_{k}\equiv \unicode[STIX]{x1D70C}(X^{n-k}b_{n})\equiv \unicode[STIX]{x1D716}\unicode[STIX]{x1D70C}(b_{k})\quad \text{mod}\,\text{Ker}(X^{k-1}) & \text{if}~k\leqslant i.\end{array}\right. & \displaystyle \nonumber\end{eqnarray}$$
Thus, if we denote
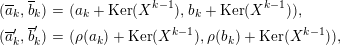 $$\begin{eqnarray}\displaystyle (\overline{a}_{k},\overline{b}_{k}) & = & \displaystyle (a_{k}+\text{Ker}(X^{k-1}),b_{k}+\text{Ker}(X^{k-1})),\nonumber\\ \displaystyle (\overline{a}_{k}^{\prime },\overline{b}_{k}^{\prime }) & = & \displaystyle (\unicode[STIX]{x1D70C}(a_{k})+\text{Ker}(X^{k-1}),\unicode[STIX]{x1D70C}(b_{k})+\text{Ker}(X^{k-1})),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (\overline{a}_{k},\overline{b}_{k}) & = & \displaystyle (a_{k}+\text{Ker}(X^{k-1}),b_{k}+\text{Ker}(X^{k-1})),\nonumber\\ \displaystyle (\overline{a}_{k}^{\prime },\overline{b}_{k}^{\prime }) & = & \displaystyle (\unicode[STIX]{x1D70C}(a_{k})+\text{Ker}(X^{k-1}),\unicode[STIX]{x1D70C}(b_{k})+\text{Ker}(X^{k-1})),\nonumber\end{eqnarray}$$
Then, we have
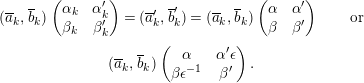 $$\begin{eqnarray}\displaystyle & \displaystyle (\overline{a}_{k},\overline{b}_{k})\left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D6FC}_{k} & \unicode[STIX]{x1D6FC}_{k}^{\prime }\\ \unicode[STIX]{x1D6FD}_{k} & \unicode[STIX]{x1D6FD}_{k}^{\prime }\end{array}\right)=(\overline{a}_{k}^{\prime },\overline{b}_{k}^{\prime })=(\overline{a}_{k},\overline{b}_{k})\left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D6FC} & \unicode[STIX]{x1D6FC}^{\prime }\\ \unicode[STIX]{x1D6FD} & \unicode[STIX]{x1D6FD}^{\prime }\end{array}\right)\qquad \text{or} & \displaystyle \nonumber\\ \displaystyle & \displaystyle (\overline{a}_{k},\overline{b}_{k})\left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D6FC} & \unicode[STIX]{x1D6FC}^{\prime }\unicode[STIX]{x1D716}\\ \unicode[STIX]{x1D6FD}\unicode[STIX]{x1D716}^{-1} & \unicode[STIX]{x1D6FD}^{\prime }\end{array}\right). & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle (\overline{a}_{k},\overline{b}_{k})\left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D6FC}_{k} & \unicode[STIX]{x1D6FC}_{k}^{\prime }\\ \unicode[STIX]{x1D6FD}_{k} & \unicode[STIX]{x1D6FD}_{k}^{\prime }\end{array}\right)=(\overline{a}_{k}^{\prime },\overline{b}_{k}^{\prime })=(\overline{a}_{k},\overline{b}_{k})\left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D6FC} & \unicode[STIX]{x1D6FC}^{\prime }\\ \unicode[STIX]{x1D6FD} & \unicode[STIX]{x1D6FD}^{\prime }\end{array}\right)\qquad \text{or} & \displaystyle \nonumber\\ \displaystyle & \displaystyle (\overline{a}_{k},\overline{b}_{k})\left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D6FC} & \unicode[STIX]{x1D6FC}^{\prime }\unicode[STIX]{x1D716}\\ \unicode[STIX]{x1D6FD}\unicode[STIX]{x1D716}^{-1} & \unicode[STIX]{x1D6FD}^{\prime }\end{array}\right). & \displaystyle \nonumber\end{eqnarray}$$
Therefore, we have
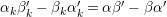 $\unicode[STIX]{x1D6FC}_{k}\unicode[STIX]{x1D6FD}_{k}^{\prime }-\unicode[STIX]{x1D6FD}_{k}\unicode[STIX]{x1D6FC}_{k}^{\prime }=\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}^{\prime }-\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}^{\prime }$
. In particular, if
$\unicode[STIX]{x1D6FC}_{k}\unicode[STIX]{x1D6FD}_{k}^{\prime }-\unicode[STIX]{x1D6FD}_{k}\unicode[STIX]{x1D6FC}_{k}^{\prime }=\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}^{\prime }-\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}^{\prime }$
. In particular, if
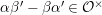 $\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}^{\prime }-\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}^{\prime }\in {\mathcal{O}}^{\times }$
, then
$\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}^{\prime }-\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}^{\prime }\in {\mathcal{O}}^{\times }$
, then
![]() $\unicode[STIX]{x1D70C}$
is surjective, which contradicts
$\unicode[STIX]{x1D70C}$
is surjective, which contradicts
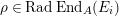 $\unicode[STIX]{x1D70C}\in \text{Rad}\,\text{End}_{A}(E_{i})$
.◻
$\unicode[STIX]{x1D70C}\in \text{Rad}\,\text{End}_{A}(E_{i})$
.◻
Lemma 2.7. Suppose that
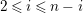 $2\leqslant i\leqslant n-i$
, and let
$2\leqslant i\leqslant n-i$
, and let
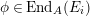 $\unicode[STIX]{x1D719}\in \text{End}_{A}(E_{i})$
be as in the definition of the pullback diagram. Then we have the following.
$\unicode[STIX]{x1D719}\in \text{End}_{A}(E_{i})$
be as in the definition of the pullback diagram. Then we have the following.
-
(1)
 $\unicode[STIX]{x1D719}$
does not factor through
$\unicode[STIX]{x1D719}$
does not factor through
 $\unicode[STIX]{x1D70B}$
.
$\unicode[STIX]{x1D70B}$
. -
(2) For any
 $\unicode[STIX]{x1D70C}\in \text{Rad}\,\text{End}_{A}(E_{i})$
,
$\unicode[STIX]{x1D70C}\in \text{Rad}\,\text{End}_{A}(E_{i})$
,
 $\unicode[STIX]{x1D719}\unicode[STIX]{x1D70C}$
factors through
$\unicode[STIX]{x1D719}\unicode[STIX]{x1D70C}$
factors through
 $\unicode[STIX]{x1D70B}$
.
$\unicode[STIX]{x1D70B}$
.
Proof. (1) Suppose that there exists
 $$\begin{eqnarray}\unicode[STIX]{x1D713}=(\unicode[STIX]{x1D713}_{1},\unicode[STIX]{x1D713}_{2},\unicode[STIX]{x1D713}_{3},\unicode[STIX]{x1D713}_{4}):E_{i}\longrightarrow A\oplus A\oplus A\oplus A\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D713}=(\unicode[STIX]{x1D713}_{1},\unicode[STIX]{x1D713}_{2},\unicode[STIX]{x1D713}_{3},\unicode[STIX]{x1D713}_{4}):E_{i}\longrightarrow A\oplus A\oplus A\oplus A\end{eqnarray}$$
such that
![]() $\unicode[STIX]{x1D70B}\unicode[STIX]{x1D713}=\unicode[STIX]{x1D719}$
. Then, we have
$\unicode[STIX]{x1D70B}\unicode[STIX]{x1D713}=\unicode[STIX]{x1D719}$
. Then, we have
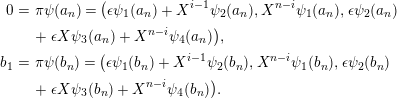 $$\begin{eqnarray}\displaystyle 0 & = & \displaystyle \unicode[STIX]{x1D70B}\unicode[STIX]{x1D713}(a_{n})=\left(\unicode[STIX]{x1D716}\unicode[STIX]{x1D713}_{1}(a_{n})+X^{i-1}\unicode[STIX]{x1D713}_{2}(a_{n}),X^{n-i}\unicode[STIX]{x1D713}_{1}(a_{n}),\unicode[STIX]{x1D716}\unicode[STIX]{x1D713}_{2}(a_{n})\right.\nonumber\\ \displaystyle & & \displaystyle +\left.\unicode[STIX]{x1D716}X\unicode[STIX]{x1D713}_{3}(a_{n})+X^{n-i}\unicode[STIX]{x1D713}_{4}(a_{n})\right)\!,\nonumber\\ \displaystyle b_{1} & = & \displaystyle \unicode[STIX]{x1D70B}\unicode[STIX]{x1D713}(b_{n})=\left(\unicode[STIX]{x1D716}\unicode[STIX]{x1D713}_{1}(b_{n})+X^{i-1}\unicode[STIX]{x1D713}_{2}(b_{n}),X^{n-i}\unicode[STIX]{x1D713}_{1}(b_{n}),\unicode[STIX]{x1D716}\unicode[STIX]{x1D713}_{2}(b_{n})\right.\nonumber\\ \displaystyle & & \displaystyle +\left.\unicode[STIX]{x1D716}X\unicode[STIX]{x1D713}_{3}(b_{n})+X^{n-i}\unicode[STIX]{x1D713}_{4}(b_{n})\right)\!.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0 & = & \displaystyle \unicode[STIX]{x1D70B}\unicode[STIX]{x1D713}(a_{n})=\left(\unicode[STIX]{x1D716}\unicode[STIX]{x1D713}_{1}(a_{n})+X^{i-1}\unicode[STIX]{x1D713}_{2}(a_{n}),X^{n-i}\unicode[STIX]{x1D713}_{1}(a_{n}),\unicode[STIX]{x1D716}\unicode[STIX]{x1D713}_{2}(a_{n})\right.\nonumber\\ \displaystyle & & \displaystyle +\left.\unicode[STIX]{x1D716}X\unicode[STIX]{x1D713}_{3}(a_{n})+X^{n-i}\unicode[STIX]{x1D713}_{4}(a_{n})\right)\!,\nonumber\\ \displaystyle b_{1} & = & \displaystyle \unicode[STIX]{x1D70B}\unicode[STIX]{x1D713}(b_{n})=\left(\unicode[STIX]{x1D716}\unicode[STIX]{x1D713}_{1}(b_{n})+X^{i-1}\unicode[STIX]{x1D713}_{2}(b_{n}),X^{n-i}\unicode[STIX]{x1D713}_{1}(b_{n}),\unicode[STIX]{x1D716}\unicode[STIX]{x1D713}_{2}(b_{n})\right.\nonumber\\ \displaystyle & & \displaystyle +\left.\unicode[STIX]{x1D716}X\unicode[STIX]{x1D713}_{3}(b_{n})+X^{n-i}\unicode[STIX]{x1D713}_{4}(b_{n})\right)\!.\nonumber\end{eqnarray}$$
The first equality implies
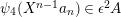 $\unicode[STIX]{x1D713}_{4}(X^{n-1}a_{n})\in \unicode[STIX]{x1D716}^{2}A$
by the following computation.
$\unicode[STIX]{x1D713}_{4}(X^{n-1}a_{n})\in \unicode[STIX]{x1D716}^{2}A$
by the following computation.
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D713}_{4}(X^{n-1}a_{n}) & = & \displaystyle X^{i-1}(X^{n-i}\unicode[STIX]{x1D713}_{4}(a_{n}))=-X^{i-1}(\unicode[STIX]{x1D716}\unicode[STIX]{x1D713}_{2}(a_{n})+\unicode[STIX]{x1D716}X\unicode[STIX]{x1D713}_{3}(a_{n}))\nonumber\\ \displaystyle & = & \displaystyle -\unicode[STIX]{x1D716}X^{i-1}\unicode[STIX]{x1D713}_{2}(a_{n})-\unicode[STIX]{x1D716}\unicode[STIX]{x1D713}_{3}(X^{i}a_{n})=\unicode[STIX]{x1D716}^{2}\unicode[STIX]{x1D713}_{1}(a_{n})-\unicode[STIX]{x1D716}^{2}\unicode[STIX]{x1D713}_{3}(a_{n-i}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D713}_{4}(X^{n-1}a_{n}) & = & \displaystyle X^{i-1}(X^{n-i}\unicode[STIX]{x1D713}_{4}(a_{n}))=-X^{i-1}(\unicode[STIX]{x1D716}\unicode[STIX]{x1D713}_{2}(a_{n})+\unicode[STIX]{x1D716}X\unicode[STIX]{x1D713}_{3}(a_{n}))\nonumber\\ \displaystyle & = & \displaystyle -\unicode[STIX]{x1D716}X^{i-1}\unicode[STIX]{x1D713}_{2}(a_{n})-\unicode[STIX]{x1D716}\unicode[STIX]{x1D713}_{3}(X^{i}a_{n})=\unicode[STIX]{x1D716}^{2}\unicode[STIX]{x1D713}_{1}(a_{n})-\unicode[STIX]{x1D716}^{2}\unicode[STIX]{x1D713}_{3}(a_{n-i}).\nonumber\end{eqnarray}$$
Thus, we conclude
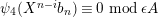 $\unicode[STIX]{x1D713}_{4}(X^{n-i}b_{n})\equiv 0~\text{mod}\,\unicode[STIX]{x1D716}A$
from
$\unicode[STIX]{x1D713}_{4}(X^{n-i}b_{n})\equiv 0~\text{mod}\,\unicode[STIX]{x1D716}A$
from
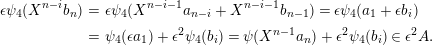 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D716}\unicode[STIX]{x1D713}_{4}(X^{n-i}b_{n}) & = & \displaystyle \unicode[STIX]{x1D716}\unicode[STIX]{x1D713}_{4}(X^{n-i-1}a_{n-i}+X^{n-i-1}b_{n-1})=\unicode[STIX]{x1D716}\unicode[STIX]{x1D713}_{4}(a_{1}+\unicode[STIX]{x1D716}b_{i})\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D713}_{4}(\unicode[STIX]{x1D716}a_{1})+\unicode[STIX]{x1D716}^{2}\unicode[STIX]{x1D713}_{4}(b_{i})=\unicode[STIX]{x1D713}(X^{n-1}a_{n})+\unicode[STIX]{x1D716}^{2}\unicode[STIX]{x1D713}_{4}(b_{i})\in \unicode[STIX]{x1D716}^{2}A.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D716}\unicode[STIX]{x1D713}_{4}(X^{n-i}b_{n}) & = & \displaystyle \unicode[STIX]{x1D716}\unicode[STIX]{x1D713}_{4}(X^{n-i-1}a_{n-i}+X^{n-i-1}b_{n-1})=\unicode[STIX]{x1D716}\unicode[STIX]{x1D713}_{4}(a_{1}+\unicode[STIX]{x1D716}b_{i})\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D713}_{4}(\unicode[STIX]{x1D716}a_{1})+\unicode[STIX]{x1D716}^{2}\unicode[STIX]{x1D713}_{4}(b_{i})=\unicode[STIX]{x1D713}(X^{n-1}a_{n})+\unicode[STIX]{x1D716}^{2}\unicode[STIX]{x1D713}_{4}(b_{i})\in \unicode[STIX]{x1D716}^{2}A.\nonumber\end{eqnarray}$$
On the other hand, using
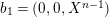 $b_{1}=(0,0,X^{n-1})$
, the second equality implies
$b_{1}=(0,0,X^{n-1})$
, the second equality implies
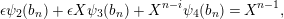 $$\begin{eqnarray}\unicode[STIX]{x1D716}\unicode[STIX]{x1D713}_{2}(b_{n})+\unicode[STIX]{x1D716}X\unicode[STIX]{x1D713}_{3}(b_{n})+X^{n-i}\unicode[STIX]{x1D713}_{4}(b_{n})=X^{n-1},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D716}\unicode[STIX]{x1D713}_{2}(b_{n})+\unicode[STIX]{x1D716}X\unicode[STIX]{x1D713}_{3}(b_{n})+X^{n-i}\unicode[STIX]{x1D713}_{4}(b_{n})=X^{n-1},\end{eqnarray}$$
and we have
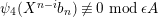 $\unicode[STIX]{x1D713}_{4}(X^{n-i}b_{n})\not \equiv 0~\text{mod}\,\unicode[STIX]{x1D716}A$
. Hence, we have reached a contradiction.
$\unicode[STIX]{x1D713}_{4}(X^{n-i}b_{n})\not \equiv 0~\text{mod}\,\unicode[STIX]{x1D716}A$
. Hence, we have reached a contradiction.
(2) Let
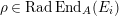 $\unicode[STIX]{x1D70C}\in \text{Rad}\,\text{End}_{A}(E_{i})$
. We write
$\unicode[STIX]{x1D70C}\in \text{Rad}\,\text{End}_{A}(E_{i})$
. We write
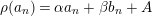 $\unicode[STIX]{x1D70C}(a_{n})=\unicode[STIX]{x1D6FC}a_{n}+\unicode[STIX]{x1D6FD}b_{n}+A$
and
$\unicode[STIX]{x1D70C}(a_{n})=\unicode[STIX]{x1D6FC}a_{n}+\unicode[STIX]{x1D6FD}b_{n}+A$
and
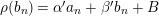 $\unicode[STIX]{x1D70C}(b_{n})=\unicode[STIX]{x1D6FC}^{\prime }a_{n}+\unicode[STIX]{x1D6FD}^{\prime }b_{n}+B$
, where
$\unicode[STIX]{x1D70C}(b_{n})=\unicode[STIX]{x1D6FC}^{\prime }a_{n}+\unicode[STIX]{x1D6FD}^{\prime }b_{n}+B$
, where
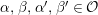 $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FC}^{\prime },\unicode[STIX]{x1D6FD}^{\prime }\in {\mathcal{O}}$
and
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FC}^{\prime },\unicode[STIX]{x1D6FD}^{\prime }\in {\mathcal{O}}$
and
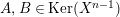 $A,B\in \text{Ker}(X^{n-1})$
. Then,
$A,B\in \text{Ker}(X^{n-1})$
. Then,
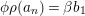 $\unicode[STIX]{x1D719}\unicode[STIX]{x1D70C}(a_{n})=\unicode[STIX]{x1D6FD}b_{1}$
and
$\unicode[STIX]{x1D719}\unicode[STIX]{x1D70C}(a_{n})=\unicode[STIX]{x1D6FD}b_{1}$
and
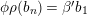 $\unicode[STIX]{x1D719}\unicode[STIX]{x1D70C}(b_{n})=\unicode[STIX]{x1D6FD}^{\prime }b_{1}$
.
$\unicode[STIX]{x1D719}\unicode[STIX]{x1D70C}(b_{n})=\unicode[STIX]{x1D6FD}^{\prime }b_{1}$
.
By Lemma 2.6(1),
![]() $\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x1D716}{\mathcal{O}}$
and if
$\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x1D716}{\mathcal{O}}$
and if
![]() $\unicode[STIX]{x1D6FD}^{\prime }$
was invertible then
$\unicode[STIX]{x1D6FD}^{\prime }$
was invertible then
![]() $\unicode[STIX]{x1D6FC}$
would be invertible, which contradicts Lemma 2.6(2). Thus,
$\unicode[STIX]{x1D6FC}$
would be invertible, which contradicts Lemma 2.6(2). Thus,
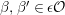 $\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FD}^{\prime }\in \unicode[STIX]{x1D716}{\mathcal{O}}$
and we may define
$\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FD}^{\prime }\in \unicode[STIX]{x1D716}{\mathcal{O}}$
and we may define
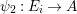 $\unicode[STIX]{x1D713}_{2}:E_{i}\rightarrow A$
by
$\unicode[STIX]{x1D713}_{2}:E_{i}\rightarrow A$
by
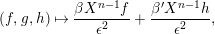 $$\begin{eqnarray}(f,g,h)\mapsto \frac{\unicode[STIX]{x1D6FD}X^{n-1}f}{\unicode[STIX]{x1D716}^{2}}+\frac{\unicode[STIX]{x1D6FD}^{\prime }X^{n-1}h}{\unicode[STIX]{x1D716}^{2}},\end{eqnarray}$$
$$\begin{eqnarray}(f,g,h)\mapsto \frac{\unicode[STIX]{x1D6FD}X^{n-1}f}{\unicode[STIX]{x1D716}^{2}}+\frac{\unicode[STIX]{x1D6FD}^{\prime }X^{n-1}h}{\unicode[STIX]{x1D716}^{2}},\end{eqnarray}$$
where
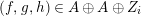 $(f,g,h)\in A\oplus A\oplus Z_{i}$
with
$(f,g,h)\in A\oplus A\oplus Z_{i}$
with
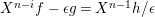 $X^{n-i}f-\unicode[STIX]{x1D716}g=X^{n-1}h/\unicode[STIX]{x1D716}$
. This is well defined. Indeed, we have
$X^{n-i}f-\unicode[STIX]{x1D716}g=X^{n-1}h/\unicode[STIX]{x1D716}$
. This is well defined. Indeed, we have
 $\unicode[STIX]{x1D713}_{2}(a_{k})=0$
and
$\unicode[STIX]{x1D713}_{2}(a_{k})=0$
and
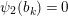 $\unicode[STIX]{x1D713}_{2}(b_{k})=0$
, for
$\unicode[STIX]{x1D713}_{2}(b_{k})=0$
, for
 $1\leqslant k\leqslant n-1$
, and
$1\leqslant k\leqslant n-1$
, and
 $$\begin{eqnarray}\unicode[STIX]{x1D713}_{2}(a_{n})=\frac{\unicode[STIX]{x1D6FD}}{\unicode[STIX]{x1D716}}X^{n-1},\qquad \unicode[STIX]{x1D713}_{2}(b_{n})=\frac{\unicode[STIX]{x1D6FD}^{\prime }}{\unicode[STIX]{x1D716}}X^{n-1}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D713}_{2}(a_{n})=\frac{\unicode[STIX]{x1D6FD}}{\unicode[STIX]{x1D716}}X^{n-1},\qquad \unicode[STIX]{x1D713}_{2}(b_{n})=\frac{\unicode[STIX]{x1D6FD}^{\prime }}{\unicode[STIX]{x1D716}}X^{n-1}.\end{eqnarray}$$
Then
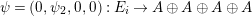 $$\begin{eqnarray}\unicode[STIX]{x1D713}=(0,\unicode[STIX]{x1D713}_{2},0,0):E_{i}\rightarrow A\oplus A\oplus A\oplus A\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D713}=(0,\unicode[STIX]{x1D713}_{2},0,0):E_{i}\rightarrow A\oplus A\oplus A\oplus A\end{eqnarray}$$
satisfies
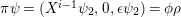 $\unicode[STIX]{x1D70B}\unicode[STIX]{x1D713}=(X^{i-1}\unicode[STIX]{x1D713}_{2},0,\unicode[STIX]{x1D716}\unicode[STIX]{x1D713}_{2})=\unicode[STIX]{x1D719}\unicode[STIX]{x1D70C}$
.◻
$\unicode[STIX]{x1D70B}\unicode[STIX]{x1D713}=(X^{i-1}\unicode[STIX]{x1D713}_{2},0,\unicode[STIX]{x1D716}\unicode[STIX]{x1D713}_{2})=\unicode[STIX]{x1D719}\unicode[STIX]{x1D70C}$
.◻
By Proposition 1.15 and Lemma 2.7, we have an almost split sequence
 $$\begin{eqnarray}0\rightarrow E_{n-i}\rightarrow F_{i}\rightarrow E_{i}\rightarrow 0,\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow E_{n-i}\rightarrow F_{i}\rightarrow E_{i}\rightarrow 0,\end{eqnarray}$$
where
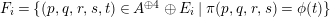 $F_{i}=\{(p,q,r,s,t)\in A^{\oplus 4}\oplus E_{i}\mid \unicode[STIX]{x1D70B}(p,q,r,s)=\unicode[STIX]{x1D719}(t)\}$
, for
$F_{i}=\{(p,q,r,s,t)\in A^{\oplus 4}\oplus E_{i}\mid \unicode[STIX]{x1D70B}(p,q,r,s)=\unicode[STIX]{x1D719}(t)\}$
, for
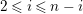 $2\leqslant i\leqslant n-i$
.
$2\leqslant i\leqslant n-i$
.
We define
 $z_{k}=(0,0,0,0,a_{k})\in F_{i}$
, for
$z_{k}=(0,0,0,0,a_{k})\in F_{i}$
, for
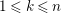 $1\leqslant k\leqslant n$
, and
$1\leqslant k\leqslant n$
, and
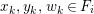 $x_{k},y_{k},w_{k}\in F_{i}$
, for
$x_{k},y_{k},w_{k}\in F_{i}$
, for
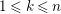 $1\leqslant k\leqslant n$
, by
$1\leqslant k\leqslant n$
, by
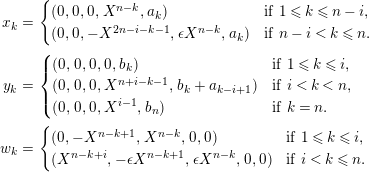 $$\begin{eqnarray}\displaystyle x_{k} & = & \displaystyle \left\{\begin{array}{@{}ll@{}}(0,0,0,X^{n-k},a_{k}) & \text{if}~1\leqslant k\leqslant n-i,\\ (0,0,-X^{2n-i-k-1},\unicode[STIX]{x1D716}X^{n-k},a_{k}) & \text{if}~n-i<k\leqslant n.\end{array}\right.\nonumber\\ \displaystyle y_{k} & = & \displaystyle \left\{\begin{array}{@{}ll@{}}(0,0,0,0,b_{k}) & \text{if}~1\leqslant k\leqslant i,\\ (0,0,0,X^{n+i-k-1},b_{k}+a_{k-i+1}) & \text{if}~i<k<n,\\ (0,0,0,X^{i-1},b_{n}) & \text{if}~k=n.\end{array}\right.\nonumber\\ \displaystyle w_{k} & = & \displaystyle \left\{\begin{array}{@{}ll@{}}(0,-X^{n-k+1},X^{n-k},0,0) & \text{if}~1\leqslant k\leqslant i,\\ (X^{n-k+i},-\unicode[STIX]{x1D716}X^{n-k+1},\unicode[STIX]{x1D716}X^{n-k},0,0) & \text{if}~i<k\leqslant n.\end{array}\right.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle x_{k} & = & \displaystyle \left\{\begin{array}{@{}ll@{}}(0,0,0,X^{n-k},a_{k}) & \text{if}~1\leqslant k\leqslant n-i,\\ (0,0,-X^{2n-i-k-1},\unicode[STIX]{x1D716}X^{n-k},a_{k}) & \text{if}~n-i<k\leqslant n.\end{array}\right.\nonumber\\ \displaystyle y_{k} & = & \displaystyle \left\{\begin{array}{@{}ll@{}}(0,0,0,0,b_{k}) & \text{if}~1\leqslant k\leqslant i,\\ (0,0,0,X^{n+i-k-1},b_{k}+a_{k-i+1}) & \text{if}~i<k<n,\\ (0,0,0,X^{i-1},b_{n}) & \text{if}~k=n.\end{array}\right.\nonumber\\ \displaystyle w_{k} & = & \displaystyle \left\{\begin{array}{@{}ll@{}}(0,-X^{n-k+1},X^{n-k},0,0) & \text{if}~1\leqslant k\leqslant i,\\ (X^{n-k+i},-\unicode[STIX]{x1D716}X^{n-k+1},\unicode[STIX]{x1D716}X^{n-k},0,0) & \text{if}~i<k\leqslant n.\end{array}\right.\nonumber\end{eqnarray}$$
Note that
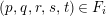 $(p,q,r,s,t)\in F_{i}$
if and only if
$(p,q,r,s,t)\in F_{i}$
if and only if
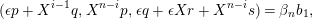 $$\begin{eqnarray}(\unicode[STIX]{x1D716}p+X^{i-1}q,X^{n-i}p,\unicode[STIX]{x1D716}q+\unicode[STIX]{x1D716}Xr+X^{n-i}s)=\unicode[STIX]{x1D6FD}_{n}b_{1},\end{eqnarray}$$
$$\begin{eqnarray}(\unicode[STIX]{x1D716}p+X^{i-1}q,X^{n-i}p,\unicode[STIX]{x1D716}q+\unicode[STIX]{x1D716}Xr+X^{n-i}s)=\unicode[STIX]{x1D6FD}_{n}b_{1},\end{eqnarray}$$
where
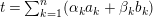 $t=\sum _{k=1}^{n}(\unicode[STIX]{x1D6FC}_{k}a_{k}+\unicode[STIX]{x1D6FD}_{k}b_{k})$
.
$t=\sum _{k=1}^{n}(\unicode[STIX]{x1D6FC}_{k}a_{k}+\unicode[STIX]{x1D6FD}_{k}b_{k})$
.
Lemma 2.8.
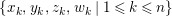 $\{x_{k},y_{k},z_{k},w_{k}\mid 1\leqslant k\leqslant n\}$
is an
$\{x_{k},y_{k},z_{k},w_{k}\mid 1\leqslant k\leqslant n\}$
is an
![]() ${\mathcal{O}}$
-basis of
${\mathcal{O}}$
-basis of
![]() $F_{i}$
.
$F_{i}$
.
Proof. It suffices to show that they generate
![]() $F_{i}$
as an
$F_{i}$
as an
![]() ${\mathcal{O}}$
-module, since
${\mathcal{O}}$
-module, since
 $\text{rank}\,F_{i}=4n$
. Let
$\text{rank}\,F_{i}=4n$
. Let
![]() $F_{i}^{\prime }$
be the
$F_{i}^{\prime }$
be the
![]() ${\mathcal{O}}$
-submodule generated by
${\mathcal{O}}$
-submodule generated by
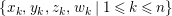 $\{x_{k},y_{k},z_{k},w_{k}\mid 1\leqslant k\leqslant n\}$
. We show first that
$\{x_{k},y_{k},z_{k},w_{k}\mid 1\leqslant k\leqslant n\}$
. We show first that
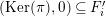 $(\text{Ker}(\unicode[STIX]{x1D70B}),0)\subseteq F_{i}^{\prime }$
. Recall that any element of
$(\text{Ker}(\unicode[STIX]{x1D70B}),0)\subseteq F_{i}^{\prime }$
. Recall that any element of
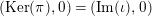 $(\text{Ker}(\unicode[STIX]{x1D70B}),0)=(\text{Im}(\unicode[STIX]{x1D704}),0)$
has the form
$(\text{Ker}(\unicode[STIX]{x1D70B}),0)=(\text{Im}(\unicode[STIX]{x1D704}),0)$
has the form
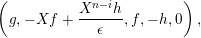 $$\begin{eqnarray}\left(g,-Xf+\frac{X^{n-i}h}{\unicode[STIX]{x1D716}},f,-h,0\right),\end{eqnarray}$$
$$\begin{eqnarray}\left(g,-Xf+\frac{X^{n-i}h}{\unicode[STIX]{x1D716}},f,-h,0\right),\end{eqnarray}$$
where
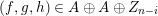 $(f,g,h)\in A\oplus A\oplus Z_{n-i}$
and
$(f,g,h)\in A\oplus A\oplus Z_{n-i}$
and
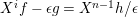 $X^{i}f-\unicode[STIX]{x1D716}g=X^{n-1}h/\unicode[STIX]{x1D716}$
. Thus,
$X^{i}f-\unicode[STIX]{x1D716}g=X^{n-1}h/\unicode[STIX]{x1D716}$
. Thus,
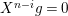 $X^{n-i}g=0$
and
$X^{n-i}g=0$
and
![]() $g$
is an
$g$
is an
![]() ${\mathcal{O}}$
-linear combination of
${\mathcal{O}}$
-linear combination of
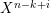 $X^{n-k+i}$
, for
$X^{n-k+i}$
, for
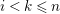 $i<k\leqslant n$
. Thus, subtracting the corresponding
$i<k\leqslant n$
. Thus, subtracting the corresponding
![]() ${\mathcal{O}}$
-linear combination of
${\mathcal{O}}$
-linear combination of
![]() $w_{k}$
, for
$w_{k}$
, for
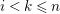 $i<k\leqslant n$
, we may assume
$i<k\leqslant n$
, we may assume
![]() $g=0$
. Since
$g=0$
. Since
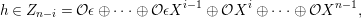 $$\begin{eqnarray}h\in Z_{n-i}={\mathcal{O}}\unicode[STIX]{x1D716}\oplus \cdots \oplus {\mathcal{O}}\unicode[STIX]{x1D716}X^{i-1}\oplus {\mathcal{O}}X^{i}\oplus \cdots \oplus {\mathcal{O}}X^{n-1},\end{eqnarray}$$
$$\begin{eqnarray}h\in Z_{n-i}={\mathcal{O}}\unicode[STIX]{x1D716}\oplus \cdots \oplus {\mathcal{O}}\unicode[STIX]{x1D716}X^{i-1}\oplus {\mathcal{O}}X^{i}\oplus \cdots \oplus {\mathcal{O}}X^{n-1},\end{eqnarray}$$
we may further subtract an
![]() ${\mathcal{O}}$
-linear combination of
${\mathcal{O}}$
-linear combination of
![]() $x_{k}$
, for
$x_{k}$
, for
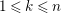 $1\leqslant k\leqslant n$
, and we may assume
$1\leqslant k\leqslant n$
, and we may assume
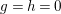 $g=h=0$
without loss of generality. Then,
$g=h=0$
without loss of generality. Then,
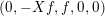 $(0,-Xf,f,0,0)$
, for
$(0,-Xf,f,0,0)$
, for
![]() $f\in A$
with
$f\in A$
with
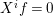 $X^{i}f=0$
, is an
$X^{i}f=0$
, is an
![]() ${\mathcal{O}}$
-linear combination of
${\mathcal{O}}$
-linear combination of
![]() $w_{k}$
, for
$w_{k}$
, for
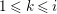 $1\leqslant k\leqslant i$
. Hence,
$1\leqslant k\leqslant i$
. Hence,
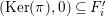 $(\text{Ker}(\unicode[STIX]{x1D70B}),0)\subseteq F_{i}^{\prime }$
. Next we show that
$(\text{Ker}(\unicode[STIX]{x1D70B}),0)\subseteq F_{i}^{\prime }$
. Next we show that
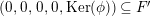 $(0,0,0,0,\text{Ker}(\unicode[STIX]{x1D719}))\subseteq F^{\prime }$
. But it is clear from
$(0,0,0,0,\text{Ker}(\unicode[STIX]{x1D719}))\subseteq F^{\prime }$
. But it is clear from
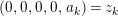 $(0,0,0,0,a_{k})=z_{k}$
, for
$(0,0,0,0,a_{k})=z_{k}$
, for
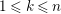 $1\leqslant k\leqslant n$
, and
$1\leqslant k\leqslant n$
, and
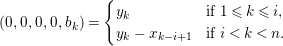 $$\begin{eqnarray}(0,0,0,0,b_{k})=\left\{\begin{array}{@{}ll@{}}y_{k} & \text{if}~1\leqslant k\leqslant i,\\ y_{k}-x_{k-i+1} & \text{if}~i<k<n.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}(0,0,0,0,b_{k})=\left\{\begin{array}{@{}ll@{}}y_{k} & \text{if}~1\leqslant k\leqslant i,\\ y_{k}-x_{k-i+1} & \text{if}~i<k<n.\end{array}\right.\end{eqnarray}$$
Suppose that
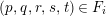 $(p,q,r,s,t)\in F_{i}$
. Write
$(p,q,r,s,t)\in F_{i}$
. Write
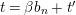 $t=\unicode[STIX]{x1D6FD}b_{n}+t^{\prime }$
such that
$t=\unicode[STIX]{x1D6FD}b_{n}+t^{\prime }$
such that
![]() $\unicode[STIX]{x1D6FD}\in {\mathcal{O}}$
and
$\unicode[STIX]{x1D6FD}\in {\mathcal{O}}$
and
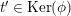 $t^{\prime }\in \text{Ker}(\unicode[STIX]{x1D719})$
. Then, to show that
$t^{\prime }\in \text{Ker}(\unicode[STIX]{x1D719})$
. Then, to show that
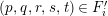 $(p,q,r,s,t)\in F_{i}^{\prime }$
, it is enough to see
$(p,q,r,s,t)\in F_{i}^{\prime }$
, it is enough to see
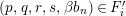 $(p,q,r,s,\unicode[STIX]{x1D6FD}b_{n})\in F_{i}^{\prime }$
. Since
$(p,q,r,s,\unicode[STIX]{x1D6FD}b_{n})\in F_{i}^{\prime }$
. Since
 $$\begin{eqnarray}\unicode[STIX]{x1D716}q+\unicode[STIX]{x1D716}Xr+X^{n-i}s=\unicode[STIX]{x1D6FD}X^{n-1},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D716}q+\unicode[STIX]{x1D716}Xr+X^{n-i}s=\unicode[STIX]{x1D6FD}X^{n-1},\end{eqnarray}$$
we have
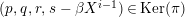 $(p,q,r,s-\unicode[STIX]{x1D6FD}X^{i-1})\in \text{Ker}(\unicode[STIX]{x1D70B})$
. Therefore, we deduce
$(p,q,r,s-\unicode[STIX]{x1D6FD}X^{i-1})\in \text{Ker}(\unicode[STIX]{x1D70B})$
. Therefore, we deduce
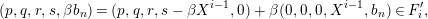 $$\begin{eqnarray}(p,q,r,s,\unicode[STIX]{x1D6FD}b_{n})=(p,q,r,s-\unicode[STIX]{x1D6FD}X^{i-1},0)+\unicode[STIX]{x1D6FD}(0,0,0,X^{i-1},b_{n})\in F_{i}^{\prime },\end{eqnarray}$$
$$\begin{eqnarray}(p,q,r,s,\unicode[STIX]{x1D6FD}b_{n})=(p,q,r,s-\unicode[STIX]{x1D6FD}X^{i-1},0)+\unicode[STIX]{x1D6FD}(0,0,0,X^{i-1},b_{n})\in F_{i}^{\prime },\end{eqnarray}$$
because
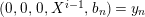 $(0,0,0,X^{i-1},b_{n})=y_{n}$
.◻
$(0,0,0,X^{i-1},b_{n})=y_{n}$
.◻
Let
![]() $F_{i}^{\prime }$
be the
$F_{i}^{\prime }$
be the
![]() ${\mathcal{O}}$
-span of
${\mathcal{O}}$
-span of
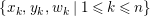 $\{x_{k},y_{k},w_{k}\mid 1\leqslant k\leqslant n\}$
,
$\{x_{k},y_{k},w_{k}\mid 1\leqslant k\leqslant n\}$
,
![]() $F_{i}^{\prime \prime }$
the
$F_{i}^{\prime \prime }$
the
![]() ${\mathcal{O}}$
-span of
${\mathcal{O}}$
-span of
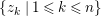 $\{z_{k}\mid 1\leqslant k\leqslant n\}$
. It is easy to compute as follows.
$\{z_{k}\mid 1\leqslant k\leqslant n\}$
. It is easy to compute as follows.
 $$\begin{eqnarray}\displaystyle Xw_{k} & = & \displaystyle \left\{\begin{array}{@{}ll@{}}w_{k-1} & \text{if}~k\neq i+1,\\ \unicode[STIX]{x1D716}w_{i} & \text{if}~k=i+1.\end{array}\right.\nonumber\\ \displaystyle Xx_{k} & = & \displaystyle \left\{\begin{array}{@{}ll@{}}x_{k-1} & \text{if}~k\neq n-i+1,\\ \unicode[STIX]{x1D716}x_{n-i}-w_{1} & \text{if}~k=n-i+1.\end{array}\right.\nonumber\\ \displaystyle Xy_{k} & = & \displaystyle \left\{\begin{array}{@{}ll@{}}y_{k-1} & \text{if}~k\neq i+1,\\ \unicode[STIX]{x1D716}y_{i}+x_{1} & \text{if}~k=i+1.\end{array}\right.\nonumber\\ \displaystyle Xz_{k} & = & \displaystyle \left\{\begin{array}{@{}ll@{}}z_{k-1} & \text{if}~k\neq n-i+1,\\ \unicode[STIX]{x1D716}z_{n-i} & \text{if}~k=n-i+1.\end{array}\right.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle Xw_{k} & = & \displaystyle \left\{\begin{array}{@{}ll@{}}w_{k-1} & \text{if}~k\neq i+1,\\ \unicode[STIX]{x1D716}w_{i} & \text{if}~k=i+1.\end{array}\right.\nonumber\\ \displaystyle Xx_{k} & = & \displaystyle \left\{\begin{array}{@{}ll@{}}x_{k-1} & \text{if}~k\neq n-i+1,\\ \unicode[STIX]{x1D716}x_{n-i}-w_{1} & \text{if}~k=n-i+1.\end{array}\right.\nonumber\\ \displaystyle Xy_{k} & = & \displaystyle \left\{\begin{array}{@{}ll@{}}y_{k-1} & \text{if}~k\neq i+1,\\ \unicode[STIX]{x1D716}y_{i}+x_{1} & \text{if}~k=i+1.\end{array}\right.\nonumber\\ \displaystyle Xz_{k} & = & \displaystyle \left\{\begin{array}{@{}ll@{}}z_{k-1} & \text{if}~k\neq n-i+1,\\ \unicode[STIX]{x1D716}z_{n-i} & \text{if}~k=n-i+1.\end{array}\right.\nonumber\end{eqnarray}$$
Hence, the direct summands
![]() $F_{i}^{\prime }$
and
$F_{i}^{\prime }$
and
![]() $F_{i}^{\prime \prime }$
of
$F_{i}^{\prime \prime }$
of
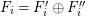 $F_{i}=F_{i}^{\prime }\oplus F_{i}^{\prime \prime }$
are
$F_{i}=F_{i}^{\prime }\oplus F_{i}^{\prime \prime }$
are
![]() $A$
-lattices and
$A$
-lattices and
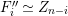 $F_{i}^{\prime \prime }\simeq Z_{n-i}$
.
$F_{i}^{\prime \prime }\simeq Z_{n-i}$
.
Lemma 2.9. The middle term of the almost split sequence ending at
![]() $E_{i}$
, for
$E_{i}$
, for
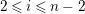 $2\leqslant i\leqslant n-2$
, is the direct sum of
$2\leqslant i\leqslant n-2$
, is the direct sum of
![]() $Z_{n-i}$
and an indecomposable direct summand.
$Z_{n-i}$
and an indecomposable direct summand.
Proof. Since
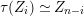 $\unicode[STIX]{x1D70F}(Z_{i})\simeq Z_{n-i}$
implies
$\unicode[STIX]{x1D70F}(Z_{i})\simeq Z_{n-i}$
implies
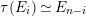 $\unicode[STIX]{x1D70F}(E_{i})\simeq E_{n-i}$
, we may assume
$\unicode[STIX]{x1D70F}(E_{i})\simeq E_{n-i}$
, we may assume
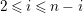 $2\leqslant i\leqslant n-i$
without loss of generality. Let
$2\leqslant i\leqslant n-i$
without loss of generality. Let
![]() $F_{i}^{\prime }$
be the
$F_{i}^{\prime }$
be the
![]() $A$
-lattice as above. Then we have to show that
$A$
-lattice as above. Then we have to show that
![]() $F_{i}^{\prime }$
is an indecomposable
$F_{i}^{\prime }$
is an indecomposable
![]() $A$
-lattice. Suppose that
$A$
-lattice. Suppose that
![]() $F_{i}^{\prime }$
is not indecomposable. Then, there exist
$F_{i}^{\prime }$
is not indecomposable. Then, there exist
![]() $A$
-sublattices
$A$
-sublattices
![]() $Z$
and
$Z$
and
![]() $L$
such that
$L$
such that
 $F_{i}^{\prime }\simeq Z\oplus L$
and
$F_{i}^{\prime }\simeq Z\oplus L$
and
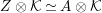 $Z\otimes {\mathcal{K}}\simeq A\otimes {\mathcal{K}}$
. Since
$Z\otimes {\mathcal{K}}\simeq A\otimes {\mathcal{K}}$
. Since
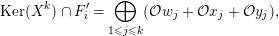 $$\begin{eqnarray}\text{Ker}(X^{k})\cap F_{i}^{\prime }=\bigoplus _{1\leqslant j\leqslant k}({\mathcal{O}}w_{j}+{\mathcal{O}}x_{j}+{\mathcal{O}}y_{j}),\end{eqnarray}$$
$$\begin{eqnarray}\text{Ker}(X^{k})\cap F_{i}^{\prime }=\bigoplus _{1\leqslant j\leqslant k}({\mathcal{O}}w_{j}+{\mathcal{O}}x_{j}+{\mathcal{O}}y_{j}),\end{eqnarray}$$
we may choose an
![]() ${\mathcal{O}}$
-basis
${\mathcal{O}}$
-basis
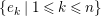 $\{e_{k}\mid 1\leqslant k\leqslant n\}$
of
$\{e_{k}\mid 1\leqslant k\leqslant n\}$
of
![]() $Z$
such that
$Z$
such that
 $$\begin{eqnarray}e_{k}=\unicode[STIX]{x1D6FC}_{k}w_{k}+\unicode[STIX]{x1D6FD}_{k}x_{k}+\unicode[STIX]{x1D6FE}_{k}y_{k}+A_{k},\end{eqnarray}$$
$$\begin{eqnarray}e_{k}=\unicode[STIX]{x1D6FC}_{k}w_{k}+\unicode[STIX]{x1D6FD}_{k}x_{k}+\unicode[STIX]{x1D6FE}_{k}y_{k}+A_{k},\end{eqnarray}$$
where
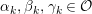 $\unicode[STIX]{x1D6FC}_{k},\unicode[STIX]{x1D6FD}_{k},\unicode[STIX]{x1D6FE}_{k}\in {\mathcal{O}}$
with
$\unicode[STIX]{x1D6FC}_{k},\unicode[STIX]{x1D6FD}_{k},\unicode[STIX]{x1D6FE}_{k}\in {\mathcal{O}}$
with
 $(\unicode[STIX]{x1D6FC}_{k},\unicode[STIX]{x1D6FD}_{k},\unicode[STIX]{x1D6FE}_{k})\not \in (\unicode[STIX]{x1D716}{\mathcal{O}})^{\oplus 3}$
and
$(\unicode[STIX]{x1D6FC}_{k},\unicode[STIX]{x1D6FD}_{k},\unicode[STIX]{x1D6FE}_{k})\not \in (\unicode[STIX]{x1D716}{\mathcal{O}})^{\oplus 3}$
and
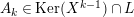 $A_{k}\in \text{Ker}(X^{k-1})\cap L$
. Then,
$A_{k}\in \text{Ker}(X^{k-1})\cap L$
. Then,
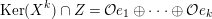 $$\begin{eqnarray}\text{Ker}(X^{k})\cap Z={\mathcal{O}}e_{1}\oplus \cdots \oplus {\mathcal{O}}e_{k}\end{eqnarray}$$
$$\begin{eqnarray}\text{Ker}(X^{k})\cap Z={\mathcal{O}}e_{1}\oplus \cdots \oplus {\mathcal{O}}e_{k}\end{eqnarray}$$
and at least one of
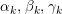 $\unicode[STIX]{x1D6FC}_{k},\unicode[STIX]{x1D6FD}_{k},\unicode[STIX]{x1D6FE}_{k}$
is invertible. Write
$\unicode[STIX]{x1D6FC}_{k},\unicode[STIX]{x1D6FD}_{k},\unicode[STIX]{x1D6FE}_{k}$
is invertible. Write
 $$\begin{eqnarray}Xe_{k}=f_{k-1}^{(k)}e_{k-1}+\cdots +f_{1}^{(k)}e_{1},\end{eqnarray}$$
$$\begin{eqnarray}Xe_{k}=f_{k-1}^{(k)}e_{k-1}+\cdots +f_{1}^{(k)}e_{1},\end{eqnarray}$$
for
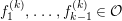 $f_{1}^{(k)},\ldots ,f_{k-1}^{(k)}\in {\mathcal{O}}$
. We first assume that
$f_{1}^{(k)},\ldots ,f_{k-1}^{(k)}\in {\mathcal{O}}$
. We first assume that
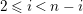 $2\leqslant i<n-i$
. Note that
$2\leqslant i<n-i$
. Note that
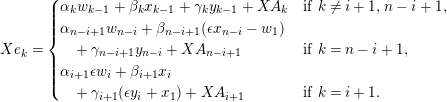 $$\begin{eqnarray}Xe_{k}=\left\{\begin{array}{@{}ll@{}}\unicode[STIX]{x1D6FC}_{k}w_{k-1}+\unicode[STIX]{x1D6FD}_{k}x_{k-1}+\unicode[STIX]{x1D6FE}_{k}y_{k-1}+XA_{k} & \text{if}~k\neq i+1,n-i+1,\\ \unicode[STIX]{x1D6FC}_{n-i+1}w_{n-i}+\unicode[STIX]{x1D6FD}_{n-i+1}(\unicode[STIX]{x1D716}x_{n-i}-w_{1}) & \\ \quad +\,\unicode[STIX]{x1D6FE}_{n-i+1}y_{n-i}+XA_{n-i+1} & \text{if}~k=n-i+1,\\ \unicode[STIX]{x1D6FC}_{i+1}\unicode[STIX]{x1D716}w_{i}+\unicode[STIX]{x1D6FD}_{i+1}x_{i} & \\ \quad +\,\unicode[STIX]{x1D6FE}_{i+1}(\unicode[STIX]{x1D716}y_{i}+x_{1})+XA_{i+1} & \text{if}~k=i+1.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}Xe_{k}=\left\{\begin{array}{@{}ll@{}}\unicode[STIX]{x1D6FC}_{k}w_{k-1}+\unicode[STIX]{x1D6FD}_{k}x_{k-1}+\unicode[STIX]{x1D6FE}_{k}y_{k-1}+XA_{k} & \text{if}~k\neq i+1,n-i+1,\\ \unicode[STIX]{x1D6FC}_{n-i+1}w_{n-i}+\unicode[STIX]{x1D6FD}_{n-i+1}(\unicode[STIX]{x1D716}x_{n-i}-w_{1}) & \\ \quad +\,\unicode[STIX]{x1D6FE}_{n-i+1}y_{n-i}+XA_{n-i+1} & \text{if}~k=n-i+1,\\ \unicode[STIX]{x1D6FC}_{i+1}\unicode[STIX]{x1D716}w_{i}+\unicode[STIX]{x1D6FD}_{i+1}x_{i} & \\ \quad +\,\unicode[STIX]{x1D6FE}_{i+1}(\unicode[STIX]{x1D716}y_{i}+x_{1})+XA_{i+1} & \text{if}~k=i+1.\end{array}\right.\end{eqnarray}$$
Thus, we have
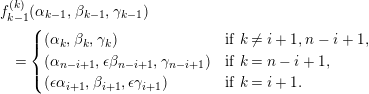 $$\begin{eqnarray}\displaystyle & & \displaystyle f_{k-1}^{(k)}(\unicode[STIX]{x1D6FC}_{k-1},\unicode[STIX]{x1D6FD}_{k-1},\unicode[STIX]{x1D6FE}_{k-1})\nonumber\\ \displaystyle & & \displaystyle \quad =\left\{\begin{array}{@{}ll@{}}(\unicode[STIX]{x1D6FC}_{k},\unicode[STIX]{x1D6FD}_{k},\unicode[STIX]{x1D6FE}_{k}) & \text{if}~k\neq i+1,n-i+1,\\ (\unicode[STIX]{x1D6FC}_{n-i+1},\unicode[STIX]{x1D716}\unicode[STIX]{x1D6FD}_{n-i+1},\unicode[STIX]{x1D6FE}_{n-i+1}) & \text{if}~k=n-i+1,\\ (\unicode[STIX]{x1D716}\unicode[STIX]{x1D6FC}_{i+1},\unicode[STIX]{x1D6FD}_{i+1},\unicode[STIX]{x1D716}\unicode[STIX]{x1D6FE}_{i+1}) & \text{if}~k=i+1.\end{array}\right.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle f_{k-1}^{(k)}(\unicode[STIX]{x1D6FC}_{k-1},\unicode[STIX]{x1D6FD}_{k-1},\unicode[STIX]{x1D6FE}_{k-1})\nonumber\\ \displaystyle & & \displaystyle \quad =\left\{\begin{array}{@{}ll@{}}(\unicode[STIX]{x1D6FC}_{k},\unicode[STIX]{x1D6FD}_{k},\unicode[STIX]{x1D6FE}_{k}) & \text{if}~k\neq i+1,n-i+1,\\ (\unicode[STIX]{x1D6FC}_{n-i+1},\unicode[STIX]{x1D716}\unicode[STIX]{x1D6FD}_{n-i+1},\unicode[STIX]{x1D6FE}_{n-i+1}) & \text{if}~k=n-i+1,\\ (\unicode[STIX]{x1D716}\unicode[STIX]{x1D6FC}_{i+1},\unicode[STIX]{x1D6FD}_{i+1},\unicode[STIX]{x1D716}\unicode[STIX]{x1D6FE}_{i+1}) & \text{if}~k=i+1.\end{array}\right.\nonumber\end{eqnarray}$$
We may assume one of the following two cases occurs.
-
(1)
 $f_{k-1}^{(k)}=1~(k\neq n-i+1)$
,
$f_{k-1}^{(k)}=1~(k\neq n-i+1)$
,
 $f_{n-i}^{(n-i+1)}=\unicode[STIX]{x1D716}$
.
$f_{n-i}^{(n-i+1)}=\unicode[STIX]{x1D716}$
. -
(2)
 $f_{k-1}^{(k)}=1~(k\neq i+1)$
,
$f_{k-1}^{(k)}=1~(k\neq i+1)$
,
 $f_{i}^{(i+1)}=\unicode[STIX]{x1D716}$
.
$f_{i}^{(i+1)}=\unicode[STIX]{x1D716}$
.
In fact, since at least one of
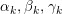 $\unicode[STIX]{x1D6FC}_{k},\unicode[STIX]{x1D6FD}_{k},\unicode[STIX]{x1D6FE}_{k}$
is invertible, if
$\unicode[STIX]{x1D6FC}_{k},\unicode[STIX]{x1D6FD}_{k},\unicode[STIX]{x1D6FE}_{k}$
is invertible, if
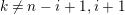 $k\neq n-i+1,i+1$
then
$k\neq n-i+1,i+1$
then
![]() $f_{k-1}^{(k)}$
is invertible. We multiply its inverse to
$f_{k-1}^{(k)}$
is invertible. We multiply its inverse to
![]() $e_{k}$
, and we obtain
$e_{k}$
, and we obtain
 $$\begin{eqnarray}f_{1}^{(2)}=\cdots =f_{i-1}^{(i)}=1\qquad \text{and}\qquad (\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FD}_{1},\unicode[STIX]{x1D6FE}_{1})=\cdots =(\unicode[STIX]{x1D6FC}_{i},\unicode[STIX]{x1D6FD}_{i},\unicode[STIX]{x1D6FE}_{i})\end{eqnarray}$$
$$\begin{eqnarray}f_{1}^{(2)}=\cdots =f_{i-1}^{(i)}=1\qquad \text{and}\qquad (\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FD}_{1},\unicode[STIX]{x1D6FE}_{1})=\cdots =(\unicode[STIX]{x1D6FC}_{i},\unicode[STIX]{x1D6FD}_{i},\unicode[STIX]{x1D6FE}_{i})\end{eqnarray}$$
in the new basis. By the same reason, we have
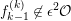 $f_{k-1}^{(k)}\not \in \unicode[STIX]{x1D716}^{2}{\mathcal{O}}$
, for all
$f_{k-1}^{(k)}\not \in \unicode[STIX]{x1D716}^{2}{\mathcal{O}}$
, for all
![]() $k$
. Suppose that both
$k$
. Suppose that both
 $f_{n-i}^{(n-i+1)}$
and
$f_{n-i}^{(n-i+1)}$
and
![]() $f_{i}^{(i+1)}$
are invertible. Then, we may reach
$f_{i}^{(i+1)}$
are invertible. Then, we may reach
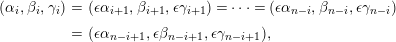 $$\begin{eqnarray}\displaystyle (\unicode[STIX]{x1D6FC}_{i},\unicode[STIX]{x1D6FD}_{i},\unicode[STIX]{x1D6FE}_{i}) & = & \displaystyle (\unicode[STIX]{x1D716}\unicode[STIX]{x1D6FC}_{i+1},\unicode[STIX]{x1D6FD}_{i+1},\unicode[STIX]{x1D716}\unicode[STIX]{x1D6FE}_{i+1})=\cdots =(\unicode[STIX]{x1D716}\unicode[STIX]{x1D6FC}_{n-i},\unicode[STIX]{x1D6FD}_{n-i},\unicode[STIX]{x1D716}\unicode[STIX]{x1D6FE}_{n-i})\nonumber\\ \displaystyle & = & \displaystyle (\unicode[STIX]{x1D716}\unicode[STIX]{x1D6FC}_{n-i+1},\unicode[STIX]{x1D716}\unicode[STIX]{x1D6FD}_{n-i+1},\unicode[STIX]{x1D716}\unicode[STIX]{x1D6FE}_{n-i+1}),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (\unicode[STIX]{x1D6FC}_{i},\unicode[STIX]{x1D6FD}_{i},\unicode[STIX]{x1D6FE}_{i}) & = & \displaystyle (\unicode[STIX]{x1D716}\unicode[STIX]{x1D6FC}_{i+1},\unicode[STIX]{x1D6FD}_{i+1},\unicode[STIX]{x1D716}\unicode[STIX]{x1D6FE}_{i+1})=\cdots =(\unicode[STIX]{x1D716}\unicode[STIX]{x1D6FC}_{n-i},\unicode[STIX]{x1D6FD}_{n-i},\unicode[STIX]{x1D716}\unicode[STIX]{x1D6FE}_{n-i})\nonumber\\ \displaystyle & = & \displaystyle (\unicode[STIX]{x1D716}\unicode[STIX]{x1D6FC}_{n-i+1},\unicode[STIX]{x1D716}\unicode[STIX]{x1D6FD}_{n-i+1},\unicode[STIX]{x1D716}\unicode[STIX]{x1D6FE}_{n-i+1}),\nonumber\end{eqnarray}$$
which is a contradiction. Suppose that both
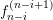 $f_{n-i}^{(n-i+1)}$
and
$f_{n-i}^{(n-i+1)}$
and
![]() $f_{i}^{(i+1)}$
are not invertible. Then,
$f_{i}^{(i+1)}$
are not invertible. Then,
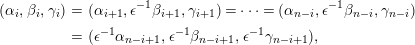 $$\begin{eqnarray}\displaystyle (\unicode[STIX]{x1D6FC}_{i},\unicode[STIX]{x1D6FD}_{i},\unicode[STIX]{x1D6FE}_{i}) & = & \displaystyle (\unicode[STIX]{x1D6FC}_{i+1},\unicode[STIX]{x1D716}^{-1}\unicode[STIX]{x1D6FD}_{i+1},\unicode[STIX]{x1D6FE}_{i+1})=\cdots =(\unicode[STIX]{x1D6FC}_{n-i},\unicode[STIX]{x1D716}^{-1}\unicode[STIX]{x1D6FD}_{n-i},\unicode[STIX]{x1D6FE}_{n-i})\nonumber\\ \displaystyle & = & \displaystyle (\unicode[STIX]{x1D716}^{-1}\unicode[STIX]{x1D6FC}_{n-i+1},\unicode[STIX]{x1D716}^{-1}\unicode[STIX]{x1D6FD}_{n-i+1},\unicode[STIX]{x1D716}^{-1}\unicode[STIX]{x1D6FE}_{n-i+1}),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (\unicode[STIX]{x1D6FC}_{i},\unicode[STIX]{x1D6FD}_{i},\unicode[STIX]{x1D6FE}_{i}) & = & \displaystyle (\unicode[STIX]{x1D6FC}_{i+1},\unicode[STIX]{x1D716}^{-1}\unicode[STIX]{x1D6FD}_{i+1},\unicode[STIX]{x1D6FE}_{i+1})=\cdots =(\unicode[STIX]{x1D6FC}_{n-i},\unicode[STIX]{x1D716}^{-1}\unicode[STIX]{x1D6FD}_{n-i},\unicode[STIX]{x1D6FE}_{n-i})\nonumber\\ \displaystyle & = & \displaystyle (\unicode[STIX]{x1D716}^{-1}\unicode[STIX]{x1D6FC}_{n-i+1},\unicode[STIX]{x1D716}^{-1}\unicode[STIX]{x1D6FD}_{n-i+1},\unicode[STIX]{x1D716}^{-1}\unicode[STIX]{x1D6FE}_{n-i+1}),\nonumber\end{eqnarray}$$
which implies that none of
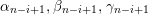 $\unicode[STIX]{x1D6FC}_{n-i+1},\unicode[STIX]{x1D6FD}_{n-i+1},\unicode[STIX]{x1D6FE}_{n-i+1}$
is invertible. Thus, we have proved that we are in case (1) or case (2). Suppose that we are in case (1). Then, we have
$\unicode[STIX]{x1D6FC}_{n-i+1},\unicode[STIX]{x1D6FD}_{n-i+1},\unicode[STIX]{x1D6FE}_{n-i+1}$
is invertible. Thus, we have proved that we are in case (1) or case (2). Suppose that we are in case (1). Then, we have
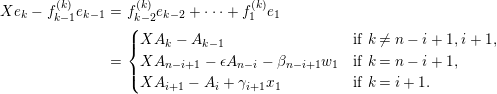 $$\begin{eqnarray}\displaystyle Xe_{k}-f_{k-1}^{(k)}e_{k-1} & = & \displaystyle f_{k-2}^{(k)}e_{k-2}+\cdots +f_{1}^{(k)}e_{1}\nonumber\\ \displaystyle & = & \displaystyle \left\{\begin{array}{@{}ll@{}}XA_{k}-A_{k-1} & \text{if}~k\neq n-i+1,i+1,\\ XA_{n-i+1}-\unicode[STIX]{x1D716}A_{n-i}-\unicode[STIX]{x1D6FD}_{n-i+1}w_{1} & \text{if}~k=n-i+1,\\ XA_{i+1}-A_{i}+\unicode[STIX]{x1D6FE}_{i+1}x_{1} & \text{if}~k=i+1.\end{array}\right.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle Xe_{k}-f_{k-1}^{(k)}e_{k-1} & = & \displaystyle f_{k-2}^{(k)}e_{k-2}+\cdots +f_{1}^{(k)}e_{1}\nonumber\\ \displaystyle & = & \displaystyle \left\{\begin{array}{@{}ll@{}}XA_{k}-A_{k-1} & \text{if}~k\neq n-i+1,i+1,\\ XA_{n-i+1}-\unicode[STIX]{x1D716}A_{n-i}-\unicode[STIX]{x1D6FD}_{n-i+1}w_{1} & \text{if}~k=n-i+1,\\ XA_{i+1}-A_{i}+\unicode[STIX]{x1D6FE}_{i+1}x_{1} & \text{if}~k=i+1.\end{array}\right.\nonumber\end{eqnarray}$$
Since
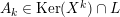 $A_{k}\in \text{Ker}(X^{k})\cap L$
, we obtain that
$A_{k}\in \text{Ker}(X^{k})\cap L$
, we obtain that
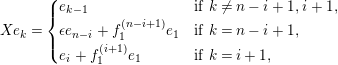 $$\begin{eqnarray}Xe_{k}=\left\{\begin{array}{@{}ll@{}}e_{k-1} & \text{if}~k\neq n-i+1,i+1,\\ \unicode[STIX]{x1D716}e_{n-i}+f_{1}^{(n-i+1)}e_{1} & \text{if}~k=n-i+1,\\ e_{i}+f_{1}^{(i+1)}e_{1} & \text{if}~k=i+1,\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}Xe_{k}=\left\{\begin{array}{@{}ll@{}}e_{k-1} & \text{if}~k\neq n-i+1,i+1,\\ \unicode[STIX]{x1D716}e_{n-i}+f_{1}^{(n-i+1)}e_{1} & \text{if}~k=n-i+1,\\ e_{i}+f_{1}^{(i+1)}e_{1} & \text{if}~k=i+1,\end{array}\right.\end{eqnarray}$$
and
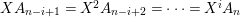 $XA_{n-i+1}=X^{2}A_{n-i+2}=\cdots =X^{i}A_{n}$
. As we are in case (1),
$XA_{n-i+1}=X^{2}A_{n-i+2}=\cdots =X^{i}A_{n}$
. As we are in case (1),
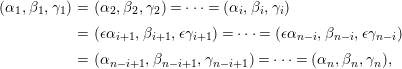 $$\begin{eqnarray}\displaystyle (\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FD}_{1},\unicode[STIX]{x1D6FE}_{1}) & = & \displaystyle (\unicode[STIX]{x1D6FC}_{2},\unicode[STIX]{x1D6FD}_{2},\unicode[STIX]{x1D6FE}_{2})=\cdots =(\unicode[STIX]{x1D6FC}_{i},\unicode[STIX]{x1D6FD}_{i},\unicode[STIX]{x1D6FE}_{i})\nonumber\\ \displaystyle & = & \displaystyle (\unicode[STIX]{x1D716}\unicode[STIX]{x1D6FC}_{i+1},\unicode[STIX]{x1D6FD}_{i+1},\unicode[STIX]{x1D716}\unicode[STIX]{x1D6FE}_{i+1})=\cdots =(\unicode[STIX]{x1D716}\unicode[STIX]{x1D6FC}_{n-i},\unicode[STIX]{x1D6FD}_{n-i},\unicode[STIX]{x1D716}\unicode[STIX]{x1D6FE}_{n-i})\nonumber\\ \displaystyle & = & \displaystyle (\unicode[STIX]{x1D6FC}_{n-i+1},\unicode[STIX]{x1D6FD}_{n-i+1},\unicode[STIX]{x1D6FE}_{n-i+1})=\cdots =(\unicode[STIX]{x1D6FC}_{n},\unicode[STIX]{x1D6FD}_{n},\unicode[STIX]{x1D6FE}_{n}),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FD}_{1},\unicode[STIX]{x1D6FE}_{1}) & = & \displaystyle (\unicode[STIX]{x1D6FC}_{2},\unicode[STIX]{x1D6FD}_{2},\unicode[STIX]{x1D6FE}_{2})=\cdots =(\unicode[STIX]{x1D6FC}_{i},\unicode[STIX]{x1D6FD}_{i},\unicode[STIX]{x1D6FE}_{i})\nonumber\\ \displaystyle & = & \displaystyle (\unicode[STIX]{x1D716}\unicode[STIX]{x1D6FC}_{i+1},\unicode[STIX]{x1D6FD}_{i+1},\unicode[STIX]{x1D716}\unicode[STIX]{x1D6FE}_{i+1})=\cdots =(\unicode[STIX]{x1D716}\unicode[STIX]{x1D6FC}_{n-i},\unicode[STIX]{x1D6FD}_{n-i},\unicode[STIX]{x1D716}\unicode[STIX]{x1D6FE}_{n-i})\nonumber\\ \displaystyle & = & \displaystyle (\unicode[STIX]{x1D6FC}_{n-i+1},\unicode[STIX]{x1D6FD}_{n-i+1},\unicode[STIX]{x1D6FE}_{n-i+1})=\cdots =(\unicode[STIX]{x1D6FC}_{n},\unicode[STIX]{x1D6FD}_{n},\unicode[STIX]{x1D6FE}_{n}),\nonumber\end{eqnarray}$$
so that we may write
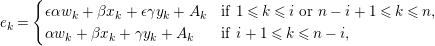 $$\begin{eqnarray}e_{k}=\left\{\begin{array}{@{}ll@{}}\unicode[STIX]{x1D716}\unicode[STIX]{x1D6FC}w_{k}+\unicode[STIX]{x1D6FD}x_{k}+\unicode[STIX]{x1D716}\unicode[STIX]{x1D6FE}y_{k}+A_{k} & \text{if}~1\leqslant k\leqslant i~\text{or}~n-i+1\leqslant k\leqslant n,\\ \unicode[STIX]{x1D6FC}w_{k}+\unicode[STIX]{x1D6FD}x_{k}+\unicode[STIX]{x1D6FE}y_{k}+A_{k} & \text{if}~i+1\leqslant k\leqslant n-i,\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}e_{k}=\left\{\begin{array}{@{}ll@{}}\unicode[STIX]{x1D716}\unicode[STIX]{x1D6FC}w_{k}+\unicode[STIX]{x1D6FD}x_{k}+\unicode[STIX]{x1D716}\unicode[STIX]{x1D6FE}y_{k}+A_{k} & \text{if}~1\leqslant k\leqslant i~\text{or}~n-i+1\leqslant k\leqslant n,\\ \unicode[STIX]{x1D6FC}w_{k}+\unicode[STIX]{x1D6FD}x_{k}+\unicode[STIX]{x1D6FE}y_{k}+A_{k} & \text{if}~i+1\leqslant k\leqslant n-i,\end{array}\right.\end{eqnarray}$$
with
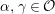 $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FE}\in {\mathcal{O}}$
and
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FE}\in {\mathcal{O}}$
and
![]() $\unicode[STIX]{x1D6FD}\in {\mathcal{O}}^{\times }$
. Then,
$\unicode[STIX]{x1D6FD}\in {\mathcal{O}}^{\times }$
. Then,
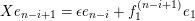 $Xe_{n-i+1}=\unicode[STIX]{x1D716}e_{n-i}+f_{1}^{(n-i+1)}e_{1}$
implies
$Xe_{n-i+1}=\unicode[STIX]{x1D716}e_{n-i}+f_{1}^{(n-i+1)}e_{1}$
implies
 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D716}\unicode[STIX]{x1D6FC}w_{n-i}+\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D716}x_{n-i}-w_{1})+\unicode[STIX]{x1D716}\unicode[STIX]{x1D6FE}y_{n-i}+X^{i}A_{n}\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D716}e_{n-i}+f_{1}^{(n-i+1)}(\unicode[STIX]{x1D716}\unicode[STIX]{x1D6FC}w_{1}+\unicode[STIX]{x1D6FD}x_{1}+\unicode[STIX]{x1D716}\unicode[STIX]{x1D6FE}y_{1}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D716}\unicode[STIX]{x1D6FC}w_{n-i}+\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D716}x_{n-i}-w_{1})+\unicode[STIX]{x1D716}\unicode[STIX]{x1D6FE}y_{n-i}+X^{i}A_{n}\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D716}e_{n-i}+f_{1}^{(n-i+1)}(\unicode[STIX]{x1D716}\unicode[STIX]{x1D6FC}w_{1}+\unicode[STIX]{x1D6FD}x_{1}+\unicode[STIX]{x1D716}\unicode[STIX]{x1D6FE}y_{1}).\nonumber\end{eqnarray}$$
We equate the coefficients of
![]() $w_{1}$
on both sides. Since contribution from
$w_{1}$
on both sides. Since contribution from
![]() $X^{i}A_{n}$
comes from
$X^{i}A_{n}$
comes from
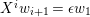 $X^{i}w_{i+1}=\unicode[STIX]{x1D716}w_{1}$
only, we conclude that
$X^{i}w_{i+1}=\unicode[STIX]{x1D716}w_{1}$
only, we conclude that
![]() $\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x1D716}{\mathcal{O}}$
, which contradicts
$\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x1D716}{\mathcal{O}}$
, which contradicts
![]() $\unicode[STIX]{x1D6FD}\in {\mathcal{O}}^{\times }$
.
$\unicode[STIX]{x1D6FD}\in {\mathcal{O}}^{\times }$
.
Suppose that we are in case (2). Then, the same argument as above shows that
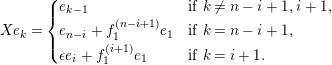 $$\begin{eqnarray}Xe_{k}=\left\{\begin{array}{@{}ll@{}}e_{k-1} & \text{if}~k\neq n-i+1,i+1,\\ e_{n-i}+f_{1}^{(n-i+1)}e_{1} & \text{if}~k=n-i+1,\\ \unicode[STIX]{x1D716}e_{i}+f_{1}^{(i+1)}e_{1} & \text{if}~k=i+1.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}Xe_{k}=\left\{\begin{array}{@{}ll@{}}e_{k-1} & \text{if}~k\neq n-i+1,i+1,\\ e_{n-i}+f_{1}^{(n-i+1)}e_{1} & \text{if}~k=n-i+1,\\ \unicode[STIX]{x1D716}e_{i}+f_{1}^{(i+1)}e_{1} & \text{if}~k=i+1.\end{array}\right.\end{eqnarray}$$
We define an
![]() ${\mathcal{O}}$
-basis
${\mathcal{O}}$
-basis
![]() $\{e_{k}^{\prime \prime }\}$
of
$\{e_{k}^{\prime \prime }\}$
of
![]() $Z$
as follows:
$Z$
as follows:
-
(i)
 $e_{k}^{\prime \prime }=e_{k}~(1\leqslant k\leqslant i)$
;
$e_{k}^{\prime \prime }=e_{k}~(1\leqslant k\leqslant i)$
; -
(ii)
 $e_{n-i}^{\prime \prime }=e_{n-i}-f_{1}^{(i+1)}e_{n-2i+1}+f_{1}^{(n-i+1)}e_{1}$
;
$e_{n-i}^{\prime \prime }=e_{n-i}-f_{1}^{(i+1)}e_{n-2i+1}+f_{1}^{(n-i+1)}e_{1}$
; -
(iii)
 $e_{n-1}^{\prime \prime }=e_{n-1}-f_{1}^{(i+1)}e_{n-i}-f_{1}^{(i+1)}f_{1}^{(n-i+1)}e_{1}$
;
$e_{n-1}^{\prime \prime }=e_{n-1}-f_{1}^{(i+1)}e_{n-i}-f_{1}^{(i+1)}f_{1}^{(n-i+1)}e_{1}$
; -
(iv)
 $e_{k}^{\prime \prime }=e_{k}-f_{1}^{(i+1)}e_{k-i+1}~(i+1\leqslant k\leqslant n,k\neq n-i,n-1)$
.
$e_{k}^{\prime \prime }=e_{k}-f_{1}^{(i+1)}e_{k-i+1}~(i+1\leqslant k\leqslant n,k\neq n-i,n-1)$
.
Then, we have
![]() $Z\simeq Z_{i}$
. To summarize, we have proved that if there is a direct summand of rank
$Z\simeq Z_{i}$
. To summarize, we have proved that if there is a direct summand of rank
![]() $n$
then it must be isomorphic to
$n$
then it must be isomorphic to
![]() $Z_{i}$
. As there is an irreducible morphism
$Z_{i}$
. As there is an irreducible morphism
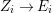 $Z_{i}\rightarrow E_{i}$
,
$Z_{i}\rightarrow E_{i}$
,
![]() $E_{i}$
must be a direct summand of
$E_{i}$
must be a direct summand of
![]() $E_{n-i}$
and we conclude
$E_{n-i}$
and we conclude
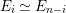 $E_{i}\simeq E_{n-i}$
. Then there exist
$E_{i}\simeq E_{n-i}$
. Then there exist
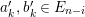 $a_{k}^{\prime },b_{k}^{\prime }\in E_{n-i}$
, for
$a_{k}^{\prime },b_{k}^{\prime }\in E_{n-i}$
, for
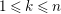 $1\leqslant k\leqslant n$
, such that
$1\leqslant k\leqslant n$
, such that
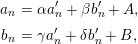 $$\begin{eqnarray}\displaystyle a_{n} & = & \displaystyle \unicode[STIX]{x1D6FC}a_{n}^{\prime }+\unicode[STIX]{x1D6FD}b_{n}^{\prime }+A,\nonumber\\ \displaystyle b_{n} & = & \displaystyle \unicode[STIX]{x1D6FE}a_{n}^{\prime }+\unicode[STIX]{x1D6FF}b_{n}^{\prime }+B,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle a_{n} & = & \displaystyle \unicode[STIX]{x1D6FC}a_{n}^{\prime }+\unicode[STIX]{x1D6FD}b_{n}^{\prime }+A,\nonumber\\ \displaystyle b_{n} & = & \displaystyle \unicode[STIX]{x1D6FE}a_{n}^{\prime }+\unicode[STIX]{x1D6FF}b_{n}^{\prime }+B,\nonumber\end{eqnarray}$$
where
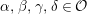 $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FF}\in {\mathcal{O}}$
with
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FF}\in {\mathcal{O}}$
with
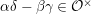 $\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FF}-\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}\in {\mathcal{O}}^{\times }$
,
$\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FF}-\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FE}\in {\mathcal{O}}^{\times }$
,
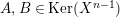 $A,B\in \text{Ker}(X^{n-1})$
, and
$A,B\in \text{Ker}(X^{n-1})$
, and
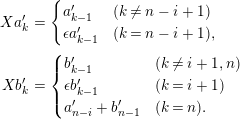 $$\begin{eqnarray}\displaystyle Xa_{k}^{\prime } & = & \displaystyle \left\{\begin{array}{@{}ll@{}}a_{k-1}^{\prime } & (k\neq n-i+1)\\ \unicode[STIX]{x1D716}a_{k-1}^{\prime } & (k=n-i+1),\end{array}\right.\nonumber\\ \displaystyle Xb_{k}^{\prime } & = & \displaystyle \left\{\begin{array}{@{}ll@{}}b_{k-1}^{\prime } & (k\neq i+1,n)\\ \unicode[STIX]{x1D716}b_{k-1}^{\prime } & (k=i+1)\\ a_{n-i}^{\prime }+b_{n-1}^{\prime } & (k=n).\end{array}\right.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle Xa_{k}^{\prime } & = & \displaystyle \left\{\begin{array}{@{}ll@{}}a_{k-1}^{\prime } & (k\neq n-i+1)\\ \unicode[STIX]{x1D716}a_{k-1}^{\prime } & (k=n-i+1),\end{array}\right.\nonumber\\ \displaystyle Xb_{k}^{\prime } & = & \displaystyle \left\{\begin{array}{@{}ll@{}}b_{k-1}^{\prime } & (k\neq i+1,n)\\ \unicode[STIX]{x1D716}b_{k-1}^{\prime } & (k=i+1)\\ a_{n-i}^{\prime }+b_{n-1}^{\prime } & (k=n).\end{array}\right.\nonumber\end{eqnarray}$$
We compute
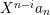 $X^{n-i}a_{n}$
and
$X^{n-i}a_{n}$
and
![]() $X^{n-i}b_{n}$
as follows.
$X^{n-i}b_{n}$
as follows.
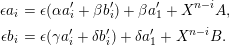 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D716}a_{i} & = & \displaystyle \unicode[STIX]{x1D716}(\unicode[STIX]{x1D6FC}a_{i}^{\prime }+\unicode[STIX]{x1D6FD}b_{i}^{\prime })+\unicode[STIX]{x1D6FD}a_{1}^{\prime }+X^{n-i}A,\nonumber\\ \displaystyle \unicode[STIX]{x1D716}b_{i} & = & \displaystyle \unicode[STIX]{x1D716}(\unicode[STIX]{x1D6FE}a_{i}^{\prime }+\unicode[STIX]{x1D6FF}b_{i}^{\prime })+\unicode[STIX]{x1D6FF}a_{1}^{\prime }+X^{n-i}B.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D716}a_{i} & = & \displaystyle \unicode[STIX]{x1D716}(\unicode[STIX]{x1D6FC}a_{i}^{\prime }+\unicode[STIX]{x1D6FD}b_{i}^{\prime })+\unicode[STIX]{x1D6FD}a_{1}^{\prime }+X^{n-i}A,\nonumber\\ \displaystyle \unicode[STIX]{x1D716}b_{i} & = & \displaystyle \unicode[STIX]{x1D716}(\unicode[STIX]{x1D6FE}a_{i}^{\prime }+\unicode[STIX]{x1D6FF}b_{i}^{\prime })+\unicode[STIX]{x1D6FF}a_{1}^{\prime }+X^{n-i}B.\nonumber\end{eqnarray}$$
Since
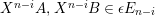 $X^{n-i}A,X^{n-i}B\in \unicode[STIX]{x1D716}E_{n-i}$
by
$X^{n-i}A,X^{n-i}B\in \unicode[STIX]{x1D716}E_{n-i}$
by
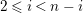 $2\leqslant i<n-i$
, we have
$2\leqslant i<n-i$
, we have
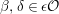 $\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FF}\in \unicode[STIX]{x1D716}{\mathcal{O}}$
, which is a contradiction.
$\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FF}\in \unicode[STIX]{x1D716}{\mathcal{O}}$
, which is a contradiction.
Thus,
![]() $F_{i}^{\prime }$
is indecomposable if
$F_{i}^{\prime }$
is indecomposable if
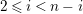 $2\leqslant i<n-i$
. It remains to consider
$2\leqslant i<n-i$
. It remains to consider
 $2\leqslant i=n-i$
. We choose an
$2\leqslant i=n-i$
. We choose an
![]() ${\mathcal{O}}$
-basis
${\mathcal{O}}$
-basis
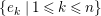 $\{e_{k}\mid 1\leqslant k\leqslant n\}$
of
$\{e_{k}\mid 1\leqslant k\leqslant n\}$
of
![]() $Z$
and write
$Z$
and write
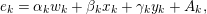 $$\begin{eqnarray}e_{k}=\unicode[STIX]{x1D6FC}_{k}w_{k}+\unicode[STIX]{x1D6FD}_{k}x_{k}+\unicode[STIX]{x1D6FE}_{k}y_{k}+A_{k},\end{eqnarray}$$
$$\begin{eqnarray}e_{k}=\unicode[STIX]{x1D6FC}_{k}w_{k}+\unicode[STIX]{x1D6FD}_{k}x_{k}+\unicode[STIX]{x1D6FE}_{k}y_{k}+A_{k},\end{eqnarray}$$
as before. Then, we have
 $$\begin{eqnarray}Xe_{k}=\left\{\begin{array}{@{}ll@{}}\unicode[STIX]{x1D6FC}_{k}w_{k-1}+\unicode[STIX]{x1D6FD}_{k}x_{k-1}+\unicode[STIX]{x1D6FE}_{k}y_{k-1}+XA_{k} & \text{if}~k\neq i+1,\\ \unicode[STIX]{x1D6FC}_{i+1}\unicode[STIX]{x1D716}w_{i}+\unicode[STIX]{x1D6FD}_{i+1}(\unicode[STIX]{x1D716}x_{i}-w_{1})+\unicode[STIX]{x1D6FE}_{i+1}(\unicode[STIX]{x1D716}y_{i}+x_{1})+XA_{i+1} & \text{if}~k=i+1,\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}Xe_{k}=\left\{\begin{array}{@{}ll@{}}\unicode[STIX]{x1D6FC}_{k}w_{k-1}+\unicode[STIX]{x1D6FD}_{k}x_{k-1}+\unicode[STIX]{x1D6FE}_{k}y_{k-1}+XA_{k} & \text{if}~k\neq i+1,\\ \unicode[STIX]{x1D6FC}_{i+1}\unicode[STIX]{x1D716}w_{i}+\unicode[STIX]{x1D6FD}_{i+1}(\unicode[STIX]{x1D716}x_{i}-w_{1})+\unicode[STIX]{x1D6FE}_{i+1}(\unicode[STIX]{x1D716}y_{i}+x_{1})+XA_{i+1} & \text{if}~k=i+1,\end{array}\right.\end{eqnarray}$$
and it follows that
 $$\begin{eqnarray}f_{k-1}^{(k)}(\unicode[STIX]{x1D6FC}_{k-1},\unicode[STIX]{x1D6FD}_{k-1},\unicode[STIX]{x1D6FE}_{k-1})=\left\{\begin{array}{@{}ll@{}}(\unicode[STIX]{x1D6FC}_{k},\unicode[STIX]{x1D6FD}_{k},\unicode[STIX]{x1D6FE}_{k}) & \text{if}~k\neq i+1,\\ (\unicode[STIX]{x1D716}\unicode[STIX]{x1D6FC}_{i+1},\unicode[STIX]{x1D716}\unicode[STIX]{x1D6FD}_{i+1},\unicode[STIX]{x1D716}\unicode[STIX]{x1D6FE}_{i+1}) & \text{if}~k=i+1.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}f_{k-1}^{(k)}(\unicode[STIX]{x1D6FC}_{k-1},\unicode[STIX]{x1D6FD}_{k-1},\unicode[STIX]{x1D6FE}_{k-1})=\left\{\begin{array}{@{}ll@{}}(\unicode[STIX]{x1D6FC}_{k},\unicode[STIX]{x1D6FD}_{k},\unicode[STIX]{x1D6FE}_{k}) & \text{if}~k\neq i+1,\\ (\unicode[STIX]{x1D716}\unicode[STIX]{x1D6FC}_{i+1},\unicode[STIX]{x1D716}\unicode[STIX]{x1D6FD}_{i+1},\unicode[STIX]{x1D716}\unicode[STIX]{x1D6FE}_{i+1}) & \text{if}~k=i+1.\end{array}\right.\end{eqnarray}$$
Hence, we may assume
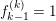 $f_{k-1}^{(k)}=1$
, for
$f_{k-1}^{(k)}=1$
, for
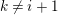 $k\neq i+1$
, and
$k\neq i+1$
, and
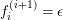 $f_{i}^{(i+1)}=\unicode[STIX]{x1D716}$
, without loss of generality. Since
$f_{i}^{(i+1)}=\unicode[STIX]{x1D716}$
, without loss of generality. Since
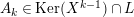 $A_{k}\in \text{Ker}(X^{k-1})\cap L$
, we obtain from the computation of
$A_{k}\in \text{Ker}(X^{k-1})\cap L$
, we obtain from the computation of
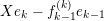 $Xe_{k}-f_{k-1}^{(k)}e_{k-1}$
that
$Xe_{k}-f_{k-1}^{(k)}e_{k-1}$
that
 $$\begin{eqnarray}Xe_{k}=\left\{\begin{array}{@{}ll@{}}e_{k-1} & \text{if}~k\neq i+1,\\ \unicode[STIX]{x1D716}e_{i}+f_{1}^{(i+1)}e_{1} & \text{if}~k=i+1,\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}Xe_{k}=\left\{\begin{array}{@{}ll@{}}e_{k-1} & \text{if}~k\neq i+1,\\ \unicode[STIX]{x1D716}e_{i}+f_{1}^{(i+1)}e_{1} & \text{if}~k=i+1,\end{array}\right.\end{eqnarray}$$
and
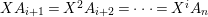 $XA_{i+1}=X^{2}A_{i+2}=\cdots =X^{i}A_{n}$
. Let
$XA_{i+1}=X^{2}A_{i+2}=\cdots =X^{i}A_{n}$
. Let
![]() $\unicode[STIX]{x1D706}$
,
$\unicode[STIX]{x1D706}$
,
![]() $\unicode[STIX]{x1D707}$
,
$\unicode[STIX]{x1D707}$
,
![]() $\unicode[STIX]{x1D708}$
be the coefficient of
$\unicode[STIX]{x1D708}$
be the coefficient of
![]() $w_{n-i+1}$
,
$w_{n-i+1}$
,
![]() $x_{n-i+1}$
,
$x_{n-i+1}$
,
![]() $y_{n-i+1}$
in
$y_{n-i+1}$
in
![]() $A_{n}$
, respectively. Then the coefficient of
$A_{n}$
, respectively. Then the coefficient of
![]() $w_{1}$
,
$w_{1}$
,
![]() $x_{1}$
,
$x_{1}$
,
![]() $y_{1}$
in
$y_{1}$
in
![]() $XA_{i+1}$
are
$XA_{i+1}$
are
![]() $\unicode[STIX]{x1D716}\unicode[STIX]{x1D706}$
,
$\unicode[STIX]{x1D716}\unicode[STIX]{x1D706}$
,
![]() $\unicode[STIX]{x1D716}\unicode[STIX]{x1D707}$
,
$\unicode[STIX]{x1D716}\unicode[STIX]{x1D707}$
,
![]() $\unicode[STIX]{x1D716}\unicode[STIX]{x1D708}$
. Since
$\unicode[STIX]{x1D716}\unicode[STIX]{x1D708}$
. Since
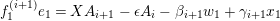 $f_{1}^{(i+1)}e_{1}=XA_{i+1}-\unicode[STIX]{x1D716}A_{i}-\unicode[STIX]{x1D6FD}_{i+1}w_{1}+\unicode[STIX]{x1D6FE}_{i+1}x_{1}$
, we have
$f_{1}^{(i+1)}e_{1}=XA_{i+1}-\unicode[STIX]{x1D716}A_{i}-\unicode[STIX]{x1D6FD}_{i+1}w_{1}+\unicode[STIX]{x1D6FE}_{i+1}x_{1}$
, we have
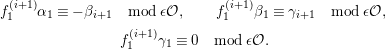 $$\begin{eqnarray}\displaystyle & f_{1}^{(i+1)}\unicode[STIX]{x1D6FC}_{1}\equiv -\unicode[STIX]{x1D6FD}_{i+1}\quad \text{mod}\,\unicode[STIX]{x1D716}{\mathcal{O}},\qquad f_{1}^{(i+1)}\unicode[STIX]{x1D6FD}_{1}\equiv \unicode[STIX]{x1D6FE}_{i+1}\quad \text{mod}\,\unicode[STIX]{x1D716}{\mathcal{O}}, & \displaystyle \nonumber\\ \displaystyle & f_{1}^{(i+1)}\unicode[STIX]{x1D6FE}_{1}\equiv 0\quad \text{mod}\,\unicode[STIX]{x1D716}{\mathcal{O}}. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & f_{1}^{(i+1)}\unicode[STIX]{x1D6FC}_{1}\equiv -\unicode[STIX]{x1D6FD}_{i+1}\quad \text{mod}\,\unicode[STIX]{x1D716}{\mathcal{O}},\qquad f_{1}^{(i+1)}\unicode[STIX]{x1D6FD}_{1}\equiv \unicode[STIX]{x1D6FE}_{i+1}\quad \text{mod}\,\unicode[STIX]{x1D716}{\mathcal{O}}, & \displaystyle \nonumber\\ \displaystyle & f_{1}^{(i+1)}\unicode[STIX]{x1D6FE}_{1}\equiv 0\quad \text{mod}\,\unicode[STIX]{x1D716}{\mathcal{O}}. & \displaystyle \nonumber\end{eqnarray}$$
We may show that
![]() $f_{1}^{(i+1)}$
is not invertible, but whenever it is invertible or not,
$f_{1}^{(i+1)}$
is not invertible, but whenever it is invertible or not,
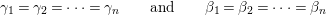 $$\begin{eqnarray}\unicode[STIX]{x1D6FE}_{1}=\unicode[STIX]{x1D6FE}_{2}=\cdots =\unicode[STIX]{x1D6FE}_{n}\qquad \text{and}\qquad \unicode[STIX]{x1D6FD}_{1}=\unicode[STIX]{x1D6FD}_{2}=\cdots =\unicode[STIX]{x1D6FD}_{n}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FE}_{1}=\unicode[STIX]{x1D6FE}_{2}=\cdots =\unicode[STIX]{x1D6FE}_{n}\qquad \text{and}\qquad \unicode[STIX]{x1D6FD}_{1}=\unicode[STIX]{x1D6FD}_{2}=\cdots =\unicode[STIX]{x1D6FD}_{n}\end{eqnarray}$$
imply that
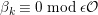 $\unicode[STIX]{x1D6FD}_{k}\equiv 0~\text{mod}\,\unicode[STIX]{x1D716}{\mathcal{O}}$
and
$\unicode[STIX]{x1D6FD}_{k}\equiv 0~\text{mod}\,\unicode[STIX]{x1D716}{\mathcal{O}}$
and
 $\unicode[STIX]{x1D6FE}_{k}\equiv 0~\text{mod}\,\unicode[STIX]{x1D716}{\mathcal{O}}$
, for
$\unicode[STIX]{x1D6FE}_{k}\equiv 0~\text{mod}\,\unicode[STIX]{x1D716}{\mathcal{O}}$
, for
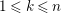 $1\leqslant k\leqslant n$
. It follows that we may choose an
$1\leqslant k\leqslant n$
. It follows that we may choose an
![]() ${\mathcal{O}}$
-basis
${\mathcal{O}}$
-basis
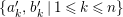 $\{a_{k}^{\prime },b_{k}^{\prime }\mid 1\leqslant k\leqslant n\}$
of
$\{a_{k}^{\prime },b_{k}^{\prime }\mid 1\leqslant k\leqslant n\}$
of
![]() $L$
in the following form.
$L$
in the following form.
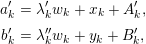 $$\begin{eqnarray}\displaystyle a_{k}^{\prime } & = & \displaystyle \unicode[STIX]{x1D706}_{k}^{\prime }w_{k}+x_{k}+A_{k}^{\prime },\nonumber\\ \displaystyle b_{k}^{\prime } & = & \displaystyle \unicode[STIX]{x1D706}_{k}^{\prime \prime }w_{k}+y_{k}+B_{k}^{\prime },\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle a_{k}^{\prime } & = & \displaystyle \unicode[STIX]{x1D706}_{k}^{\prime }w_{k}+x_{k}+A_{k}^{\prime },\nonumber\\ \displaystyle b_{k}^{\prime } & = & \displaystyle \unicode[STIX]{x1D706}_{k}^{\prime \prime }w_{k}+y_{k}+B_{k}^{\prime },\nonumber\end{eqnarray}$$
where
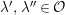 $\unicode[STIX]{x1D706}^{\prime },\unicode[STIX]{x1D706}^{\prime \prime }\in {\mathcal{O}}$
and
$\unicode[STIX]{x1D706}^{\prime },\unicode[STIX]{x1D706}^{\prime \prime }\in {\mathcal{O}}$
and
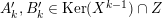 $A_{k}^{\prime },B_{k}^{\prime }\in \text{Ker}(X^{k-1})\cap Z$
. Write
$A_{k}^{\prime },B_{k}^{\prime }\in \text{Ker}(X^{k-1})\cap Z$
. Write
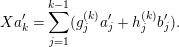 $$\begin{eqnarray}Xa_{k}^{\prime }=\mathop{\sum }_{j=1}^{k-1}(g_{j}^{(k)}a_{j}^{\prime }+h_{j}^{(k)}b_{j}^{\prime }).\end{eqnarray}$$
$$\begin{eqnarray}Xa_{k}^{\prime }=\mathop{\sum }_{j=1}^{k-1}(g_{j}^{(k)}a_{j}^{\prime }+h_{j}^{(k)}b_{j}^{\prime }).\end{eqnarray}$$
Multiplying
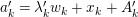 $a_{k}^{\prime }=\unicode[STIX]{x1D706}_{k}^{\prime }w_{k}+x_{k}+A_{k}^{\prime }$
with
$a_{k}^{\prime }=\unicode[STIX]{x1D706}_{k}^{\prime }w_{k}+x_{k}+A_{k}^{\prime }$
with
![]() $X$
, we obtain
$X$
, we obtain
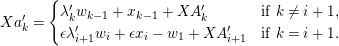 $$\begin{eqnarray}Xa_{k}^{\prime }=\left\{\begin{array}{@{}ll@{}}\unicode[STIX]{x1D706}_{k}^{\prime }w_{k-1}+x_{k-1}+XA_{k}^{\prime } & \text{if}~k\neq i+1,\\ \unicode[STIX]{x1D716}\unicode[STIX]{x1D706}_{i+1}^{\prime }w_{i}+\unicode[STIX]{x1D716}x_{i}-w_{1}+XA_{i+1}^{\prime } & \text{if }k=i+1.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}Xa_{k}^{\prime }=\left\{\begin{array}{@{}ll@{}}\unicode[STIX]{x1D706}_{k}^{\prime }w_{k-1}+x_{k-1}+XA_{k}^{\prime } & \text{if}~k\neq i+1,\\ \unicode[STIX]{x1D716}\unicode[STIX]{x1D706}_{i+1}^{\prime }w_{i}+\unicode[STIX]{x1D716}x_{i}-w_{1}+XA_{i+1}^{\prime } & \text{if }k=i+1.\end{array}\right.\end{eqnarray}$$
Thus,
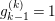 $g_{k-1}^{(k)}=1$
, for
$g_{k-1}^{(k)}=1$
, for
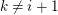 $k\neq i+1$
,
$k\neq i+1$
,
 $g_{i}^{(i+1)}=\unicode[STIX]{x1D716}$
, and
$g_{i}^{(i+1)}=\unicode[STIX]{x1D716}$
, and
 $h_{k-1}^{(k)}=0$
, for all
$h_{k-1}^{(k)}=0$
, for all
![]() $k$
. Further, we have
$k$
. Further, we have
 $$\begin{eqnarray}Xa_{k}^{\prime }-g_{k-1}^{(k)}a_{k-1}^{\prime }=\left\{\begin{array}{@{}ll@{}}XA_{k}^{\prime }-A_{k-1}^{\prime } & \text{if}~k\neq i+1,\\ XA_{i+1}^{\prime }-\unicode[STIX]{x1D716}A_{i}^{\prime }-w_{1} & \text{if}~k=i+1.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}Xa_{k}^{\prime }-g_{k-1}^{(k)}a_{k-1}^{\prime }=\left\{\begin{array}{@{}ll@{}}XA_{k}^{\prime }-A_{k-1}^{\prime } & \text{if}~k\neq i+1,\\ XA_{i+1}^{\prime }-\unicode[STIX]{x1D716}A_{i}^{\prime }-w_{1} & \text{if}~k=i+1.\end{array}\right.\end{eqnarray}$$
We obtain
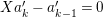 $Xa_{k}^{\prime }-a_{k-1}^{\prime }=0$
if
$Xa_{k}^{\prime }-a_{k-1}^{\prime }=0$
if
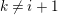 $k\neq i+1$
, and if
$k\neq i+1$
, and if
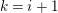 $k=i+1$
then
$k=i+1$
then
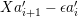 $Xa_{i+1}^{\prime }-\unicode[STIX]{x1D716}a_{i}^{\prime }$
is equal to
$Xa_{i+1}^{\prime }-\unicode[STIX]{x1D716}a_{i}^{\prime }$
is equal to
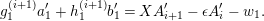 $$\begin{eqnarray}g_{1}^{(i+1)}a_{1}^{\prime }+h_{1}^{(i+1)}b_{1}^{\prime }=XA_{i+1}^{\prime }-\unicode[STIX]{x1D716}A_{i}^{\prime }-w_{1}.\end{eqnarray}$$
$$\begin{eqnarray}g_{1}^{(i+1)}a_{1}^{\prime }+h_{1}^{(i+1)}b_{1}^{\prime }=XA_{i+1}^{\prime }-\unicode[STIX]{x1D716}A_{i}^{\prime }-w_{1}.\end{eqnarray}$$
Since
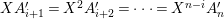 $XA_{i+1}^{\prime }=X^{2}A_{i+2}^{\prime }=\cdots =X^{n-i}A_{n}^{\prime }$
, the coefficient of
$XA_{i+1}^{\prime }=X^{2}A_{i+2}^{\prime }=\cdots =X^{n-i}A_{n}^{\prime }$
, the coefficient of
![]() $x_{1}$
in
$x_{1}$
in
![]() $XA_{i+1}^{\prime }$
is in
$XA_{i+1}^{\prime }$
is in
![]() $\unicode[STIX]{x1D716}{\mathcal{O}}$
. Thus,
$\unicode[STIX]{x1D716}{\mathcal{O}}$
. Thus,
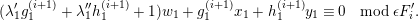 $$\begin{eqnarray}(\unicode[STIX]{x1D706}_{1}^{\prime }g_{1}^{(i+1)}+\unicode[STIX]{x1D706}_{1}^{\prime \prime }h_{1}^{(i+1)}+1)w_{1}+g_{1}^{(i+1)}x_{1}+h_{1}^{(i+1)}y_{1}\equiv 0\quad \text{mod}\,\unicode[STIX]{x1D716}F_{i}^{\prime }.\end{eqnarray}$$
$$\begin{eqnarray}(\unicode[STIX]{x1D706}_{1}^{\prime }g_{1}^{(i+1)}+\unicode[STIX]{x1D706}_{1}^{\prime \prime }h_{1}^{(i+1)}+1)w_{1}+g_{1}^{(i+1)}x_{1}+h_{1}^{(i+1)}y_{1}\equiv 0\quad \text{mod}\,\unicode[STIX]{x1D716}F_{i}^{\prime }.\end{eqnarray}$$
We must have
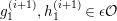 $g_{1}^{(i+1)},h_{1}^{(i+1)}\in \unicode[STIX]{x1D716}{\mathcal{O}}$
, but then
$g_{1}^{(i+1)},h_{1}^{(i+1)}\in \unicode[STIX]{x1D716}{\mathcal{O}}$
, but then
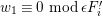 $w_{1}\equiv 0~\text{mod}\,\unicode[STIX]{x1D716}F_{i}^{\prime }$
, which is impossible. Hence,
$w_{1}\equiv 0~\text{mod}\,\unicode[STIX]{x1D716}F_{i}^{\prime }$
, which is impossible. Hence,
![]() $F_{i}^{\prime }$
is indecomposable if
$F_{i}^{\prime }$
is indecomposable if
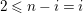 $2\leqslant n-i=i$
.◻
$2\leqslant n-i=i$
.◻
3 Main result
In this section, we prove the main result of this article.
Theorem 3.1. Let
![]() ${\mathcal{O}}$
be a complete discrete valuation ring,
${\mathcal{O}}$
be a complete discrete valuation ring,
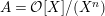 $A={\mathcal{O}}[X]/(X^{n})$
, for
$A={\mathcal{O}}[X]/(X^{n})$
, for
![]() $n\geqslant 2$
. Then, the component of the stable Auslander–Reiten quiver of
$n\geqslant 2$
. Then, the component of the stable Auslander–Reiten quiver of
![]() $A$
which contains
$A$
which contains
![]() $Z_{i}$
and
$Z_{i}$
and
![]() $Z_{n-i}$
is
$Z_{n-i}$
is
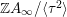 $\mathbb{Z}A_{\infty }/\langle \unicode[STIX]{x1D70F}^{2}\rangle$
if
$\mathbb{Z}A_{\infty }/\langle \unicode[STIX]{x1D70F}^{2}\rangle$
if
![]() $2i\neq n$
, and
$2i\neq n$
, and
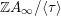 $\mathbb{Z}A_{\infty }/\langle \unicode[STIX]{x1D70F}\rangle$
that is, homogeneous tube if
$\mathbb{Z}A_{\infty }/\langle \unicode[STIX]{x1D70F}\rangle$
that is, homogeneous tube if
![]() $2i=n$
.
$2i=n$
.
Proof. Let
![]() $C$
be a component of the stable Auslander–Reiten quiver of
$C$
be a component of the stable Auslander–Reiten quiver of
![]() $A$
that contains a Heller lattice. As Heller lattices are
$A$
that contains a Heller lattice. As Heller lattices are
![]() $\unicode[STIX]{x1D70F}$
-periodic for
$\unicode[STIX]{x1D70F}$
-periodic for
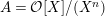 $A={\mathcal{O}}[X]/(X^{n})$
, Theorem 1.27 and Lemma 1.4 implies that
$A={\mathcal{O}}[X]/(X^{n})$
, Theorem 1.27 and Lemma 1.4 implies that
![]() $C$
is a valued stable translation quiver and its tree class is one of
$C$
is a valued stable translation quiver and its tree class is one of
 $A_{\infty },B_{\infty },C_{\infty },D_{\infty }$
and
$A_{\infty },B_{\infty },C_{\infty },D_{\infty }$
and
![]() $A_{\infty }^{\infty }$
. If
$A_{\infty }^{\infty }$
. If
![]() $i=1$
or
$i=1$
or
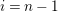 $i=n-1$
, then Proposition 2.4(1) implies that the subadditive function considered in the proof of Lemma 1.23 is not additive. Thus, the tree class of
$i=n-1$
, then Proposition 2.4(1) implies that the subadditive function considered in the proof of Lemma 1.23 is not additive. Thus, the tree class of
![]() $C$
is
$C$
is
![]() $A_{\infty }$
. We now assume that
$A_{\infty }$
. We now assume that
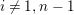 $i\neq 1,n-1$
. Proposition 2.4(2) implies that the Heller lattices
$i\neq 1,n-1$
. Proposition 2.4(2) implies that the Heller lattices
![]() $Z_{i}$
and
$Z_{i}$
and
![]() $Z_{n-i}$
are on the boundary of the stable Auslander–Reiten quiver, and the tree class can not be
$Z_{n-i}$
are on the boundary of the stable Auslander–Reiten quiver, and the tree class can not be
![]() $A_{\infty }^{\infty }$
. If the tree class was one of
$A_{\infty }^{\infty }$
. If the tree class was one of
![]() $B_{\infty }$
,
$B_{\infty }$
,
![]() $C_{\infty }$
and
$C_{\infty }$
and
![]() $D_{\infty }$
, then
$D_{\infty }$
, then
![]() $F_{i}$
or
$F_{i}$
or
![]() $F_{n-i}$
would have at least three indecomposable direct summands. But it contradicts Lemma 2.9. Therefore, the tree class is
$F_{n-i}$
would have at least three indecomposable direct summands. But it contradicts Lemma 2.9. Therefore, the tree class is
![]() $A_{\infty }$
. Then, the component
$A_{\infty }$
. Then, the component
![]() $C$
must be a tube, and the rank is the period of the Heller lattices
$C$
must be a tube, and the rank is the period of the Heller lattices
![]() $Z_{i}$
and
$Z_{i}$
and
![]() $Z_{n-i}$
, which is two if
$Z_{n-i}$
, which is two if
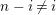 $n-i\neq i$
, one if
$n-i\neq i$
, one if
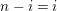 $n-i=i$
.◻
$n-i=i$
.◻
Acknowledgment
Before we started this project, the first author had asked his student Takuya Takeuchi for some experimental computation for
![]() $n=3$
case. We thank him for this computation at the preliminary stage of the research.
$n=3$
case. We thank him for this computation at the preliminary stage of the research.
Appendix
In this appendix, we prove Proposition 1.15. The proof uses arguments from [Reference ButlerBu] and [Reference RoggenkampR1]. As it is clear that (1) implies (2), we show that (2) implies (1). Let us consider the injective resolution of
![]() ${\mathcal{O}}$
as an
${\mathcal{O}}$
as an
![]() ${\mathcal{O}}$
-module:
${\mathcal{O}}$
-module:
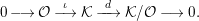 $$\begin{eqnarray}0\longrightarrow {\mathcal{O}}\xrightarrow[{}]{~\unicode[STIX]{x1D704}~}{\mathcal{K}}\xrightarrow[{}]{~d~}{\mathcal{K}}/{\mathcal{O}}\longrightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}0\longrightarrow {\mathcal{O}}\xrightarrow[{}]{~\unicode[STIX]{x1D704}~}{\mathcal{K}}\xrightarrow[{}]{~d~}{\mathcal{K}}/{\mathcal{O}}\longrightarrow 0.\end{eqnarray}$$
Since
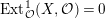 $\text{Ext}_{{\mathcal{O}}}^{1}(X,{\mathcal{O}})=0$
for any free
$\text{Ext}_{{\mathcal{O}}}^{1}(X,{\mathcal{O}})=0$
for any free
![]() ${\mathcal{O}}$
-modules of finite rank
${\mathcal{O}}$
-modules of finite rank
![]() $X$
, we have
$X$
, we have
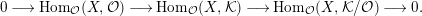 $$\begin{eqnarray}0\longrightarrow \text{Hom}_{{\mathcal{O}}}(X,{\mathcal{O}})\longrightarrow \text{Hom}_{{\mathcal{O}}}(X,{\mathcal{K}})\longrightarrow \text{Hom}_{{\mathcal{O}}}(X,{\mathcal{K}}/{\mathcal{O}})\longrightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}0\longrightarrow \text{Hom}_{{\mathcal{O}}}(X,{\mathcal{O}})\longrightarrow \text{Hom}_{{\mathcal{O}}}(X,{\mathcal{K}})\longrightarrow \text{Hom}_{{\mathcal{O}}}(X,{\mathcal{K}}/{\mathcal{O}})\longrightarrow 0.\end{eqnarray}$$
In particular, if we define functors
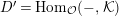 $D^{\prime }=\text{Hom}_{{\mathcal{O}}}(-,{\mathcal{K}})$
and
$D^{\prime }=\text{Hom}_{{\mathcal{O}}}(-,{\mathcal{K}})$
and
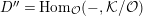 $D^{\prime \prime }=\text{Hom}_{{\mathcal{O}}}(-,{\mathcal{K}}/{\mathcal{O}})$
, then we have the short exact sequence
$D^{\prime \prime }=\text{Hom}_{{\mathcal{O}}}(-,{\mathcal{K}}/{\mathcal{O}})$
, then we have the short exact sequence
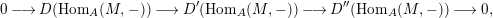 $$\begin{eqnarray}0\longrightarrow D(\text{Hom}_{A}(M,-))\longrightarrow D^{\prime }(\text{Hom}_{A}(M,-))\longrightarrow D^{\prime \prime }(\text{Hom}_{A}(M,-))\longrightarrow 0,\end{eqnarray}$$
$$\begin{eqnarray}0\longrightarrow D(\text{Hom}_{A}(M,-))\longrightarrow D^{\prime }(\text{Hom}_{A}(M,-))\longrightarrow D^{\prime \prime }(\text{Hom}_{A}(M,-))\longrightarrow 0,\end{eqnarray}$$
for any
![]() $A$
-lattice
$A$
-lattice
![]() $M$
. We define functors
$M$
. We define functors
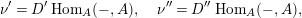 $$\begin{eqnarray}\unicode[STIX]{x1D708}^{\prime }=D^{\prime }\,\text{Hom}_{A}(-,A),\quad \unicode[STIX]{x1D708}^{\prime \prime }=D^{\prime \prime }\,\text{Hom}_{A}(-,A),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D708}^{\prime }=D^{\prime }\,\text{Hom}_{A}(-,A),\quad \unicode[STIX]{x1D708}^{\prime \prime }=D^{\prime \prime }\,\text{Hom}_{A}(-,A),\end{eqnarray}$$
which we also call Nakayama functors. Applying the Nakayama functors
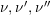 $\unicode[STIX]{x1D708},\unicode[STIX]{x1D708}^{\prime },\unicode[STIX]{x1D708}^{\prime \prime }$
to
$\unicode[STIX]{x1D708},\unicode[STIX]{x1D708}^{\prime },\unicode[STIX]{x1D708}^{\prime \prime }$
to
![]() $M$
, we obtain the following exact sequences
$M$
, we obtain the following exact sequences
 $$\begin{eqnarray}0\longrightarrow \unicode[STIX]{x1D708}(M)\longrightarrow \unicode[STIX]{x1D708}^{\prime }(M)\longrightarrow \unicode[STIX]{x1D708}^{\prime \prime }(M)\longrightarrow 0,\end{eqnarray}$$
$$\begin{eqnarray}0\longrightarrow \unicode[STIX]{x1D708}(M)\longrightarrow \unicode[STIX]{x1D708}^{\prime }(M)\longrightarrow \unicode[STIX]{x1D708}^{\prime \prime }(M)\longrightarrow 0,\end{eqnarray}$$
and
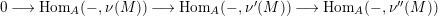 $0\longrightarrow \text{Hom}_{A}(-,\unicode[STIX]{x1D708}(M))\longrightarrow \text{Hom}_{A}(-,\unicode[STIX]{x1D708}^{\prime }(M))\longrightarrow \text{Hom}_{A}(-,\unicode[STIX]{x1D708}^{\prime \prime }(M))$
. Let
$0\longrightarrow \text{Hom}_{A}(-,\unicode[STIX]{x1D708}(M))\longrightarrow \text{Hom}_{A}(-,\unicode[STIX]{x1D708}^{\prime }(M))\longrightarrow \text{Hom}_{A}(-,\unicode[STIX]{x1D708}^{\prime \prime }(M))$
. Let
![]() $\unicode[STIX]{x1D706}$
be the functorial isomorphism defined by
$\unicode[STIX]{x1D706}$
be the functorial isomorphism defined by
 $$\begin{eqnarray}\displaystyle D(\text{Hom}_{A}(M,A)\otimes _{A}-) & = & \displaystyle \text{Hom}_{{\mathcal{O}}}(\text{Hom}_{A}(M,A)\otimes _{A}-,{\mathcal{O}})\nonumber\\ \displaystyle & \simeq & \displaystyle \text{Hom}_{A}(-,\text{Hom}_{{\mathcal{O}}}(\text{Hom}_{A}(M,A),{\mathcal{O}}))\nonumber\\ \displaystyle & = & \displaystyle \text{Hom}_{A}(-,\unicode[STIX]{x1D708}(M)).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle D(\text{Hom}_{A}(M,A)\otimes _{A}-) & = & \displaystyle \text{Hom}_{{\mathcal{O}}}(\text{Hom}_{A}(M,A)\otimes _{A}-,{\mathcal{O}})\nonumber\\ \displaystyle & \simeq & \displaystyle \text{Hom}_{A}(-,\text{Hom}_{{\mathcal{O}}}(\text{Hom}_{A}(M,A),{\mathcal{O}}))\nonumber\\ \displaystyle & = & \displaystyle \text{Hom}_{A}(-,\unicode[STIX]{x1D708}(M)).\nonumber\end{eqnarray}$$
We define
![]() $\unicode[STIX]{x1D706}^{\prime }$
and
$\unicode[STIX]{x1D706}^{\prime }$
and
![]() $\unicode[STIX]{x1D706}^{\prime \prime }$
in the similar manner by replacing
$\unicode[STIX]{x1D706}^{\prime \prime }$
in the similar manner by replacing
![]() $\unicode[STIX]{x1D708}$
with
$\unicode[STIX]{x1D708}$
with
![]() $\unicode[STIX]{x1D708}^{\prime }$
and
$\unicode[STIX]{x1D708}^{\prime }$
and
![]() $\unicode[STIX]{x1D708}^{\prime \prime }$
. Let
$\unicode[STIX]{x1D708}^{\prime \prime }$
. Let
 $$\begin{eqnarray}\unicode[STIX]{x1D707}_{M}:\text{Hom}_{A}(M,A)\otimes _{A}-\longrightarrow \text{Hom}_{A}(M,-)\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D707}_{M}:\text{Hom}_{A}(M,A)\otimes _{A}-\longrightarrow \text{Hom}_{A}(M,-)\end{eqnarray}$$
be the natural transformation defined by
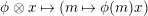 $\unicode[STIX]{x1D719}\otimes x\mapsto (m\mapsto \unicode[STIX]{x1D719}(m)x)$
. Then, it induces the following three morphisms of functors
$\unicode[STIX]{x1D719}\otimes x\mapsto (m\mapsto \unicode[STIX]{x1D719}(m)x)$
. Then, it induces the following three morphisms of functors
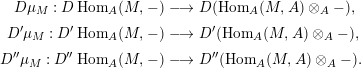 $$\begin{eqnarray}\displaystyle D\unicode[STIX]{x1D707}_{M}:D\,\text{Hom}_{A}(M,-) & \longrightarrow & \displaystyle D(\text{Hom}_{A}(M,A)\otimes _{A}-),\nonumber\\ \displaystyle D^{\prime }\unicode[STIX]{x1D707}_{M}:D^{\prime }\,\text{Hom}_{A}(M,-) & \longrightarrow & \displaystyle D^{\prime }(\text{Hom}_{A}(M,A)\otimes _{A}-),\nonumber\\ \displaystyle D^{\prime \prime }\unicode[STIX]{x1D707}_{M}:D^{\prime \prime }\,\text{Hom}_{A}(M,-) & \longrightarrow & \displaystyle D^{\prime \prime }(\text{Hom}_{A}(M,A)\otimes _{A}-).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle D\unicode[STIX]{x1D707}_{M}:D\,\text{Hom}_{A}(M,-) & \longrightarrow & \displaystyle D(\text{Hom}_{A}(M,A)\otimes _{A}-),\nonumber\\ \displaystyle D^{\prime }\unicode[STIX]{x1D707}_{M}:D^{\prime }\,\text{Hom}_{A}(M,-) & \longrightarrow & \displaystyle D^{\prime }(\text{Hom}_{A}(M,A)\otimes _{A}-),\nonumber\\ \displaystyle D^{\prime \prime }\unicode[STIX]{x1D707}_{M}:D^{\prime \prime }\,\text{Hom}_{A}(M,-) & \longrightarrow & \displaystyle D^{\prime \prime }(\text{Hom}_{A}(M,A)\otimes _{A}-).\nonumber\end{eqnarray}$$
Then, we have the following commutative diagram of functors on
![]() $A$
-lattices.
$A$
-lattices.
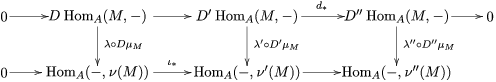
with exact rows, where
![]() $\unicode[STIX]{x1D704}_{\ast }$
and
$\unicode[STIX]{x1D704}_{\ast }$
and
![]() $d_{\ast }$
are given by compositions of
$d_{\ast }$
are given by compositions of
![]() $\unicode[STIX]{x1D704}$
and
$\unicode[STIX]{x1D704}$
and
![]() $d$
on the left.
$d$
on the left.
Lemma A.1. Let
![]() $X$
be an
$X$
be an
![]() $A$
-lattice. If
$A$
-lattice. If
![]() $M\otimes {\mathcal{K}}$
is a projective
$M\otimes {\mathcal{K}}$
is a projective
![]() $A\otimes {\mathcal{K}}$
-module, then:
$A\otimes {\mathcal{K}}$
-module, then:
-
(i)
 $D^{\prime }\unicode[STIX]{x1D707}_{M}(X)$
is an isomorphism and natural in
$D^{\prime }\unicode[STIX]{x1D707}_{M}(X)$
is an isomorphism and natural in
 $X$
;
$X$
; -
(ii)
 $D\unicode[STIX]{x1D707}_{M}(X)$
is a monomorphism and natural in
$D\unicode[STIX]{x1D707}_{M}(X)$
is a monomorphism and natural in
 $X$
;
$X$
; -
(iii) if
 $M$
is a projective
$M$
is a projective
 $A$
-module, then
$A$
-module, then
 $D\unicode[STIX]{x1D707}_{M}(X)$
is an isomorphism;
$D\unicode[STIX]{x1D707}_{M}(X)$
is an isomorphism; -
(iv)
 $D^{\prime \prime }\unicode[STIX]{x1D707}_{M}(X)$
is an epimorphism and natural in
$D^{\prime \prime }\unicode[STIX]{x1D707}_{M}(X)$
is an epimorphism and natural in
 $X$
.
$X$
.
Moreover, the sequence
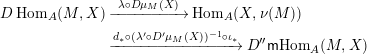 $$\begin{eqnarray}\displaystyle D\,\text{Hom}_{A}(M,X) & \!\! & \displaystyle \xrightarrow[{}]{~\unicode[STIX]{x1D706}\circ D\unicode[STIX]{x1D707}_{M}(X)~}\text{Hom}_{A}(X,\unicode[STIX]{x1D708}(M))\nonumber\\ \displaystyle & \!\! & \displaystyle \xrightarrow[{}]{d_{\ast }\circ (\unicode[STIX]{x1D706}^{\prime }\circ D^{\prime }\unicode[STIX]{x1D707}_{M}(X))^{-1}\circ \unicode[STIX]{x1D704}_{\ast }}D^{\prime \prime }\mathsf{m}\text{Hom}_{A}(M,X)\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle D\,\text{Hom}_{A}(M,X) & \!\! & \displaystyle \xrightarrow[{}]{~\unicode[STIX]{x1D706}\circ D\unicode[STIX]{x1D707}_{M}(X)~}\text{Hom}_{A}(X,\unicode[STIX]{x1D708}(M))\nonumber\\ \displaystyle & \!\! & \displaystyle \xrightarrow[{}]{d_{\ast }\circ (\unicode[STIX]{x1D706}^{\prime }\circ D^{\prime }\unicode[STIX]{x1D707}_{M}(X))^{-1}\circ \unicode[STIX]{x1D704}_{\ast }}D^{\prime \prime }\mathsf{m}\text{Hom}_{A}(M,X)\nonumber\end{eqnarray}$$
is exact.
Proof. Observe that we have an isomorphism
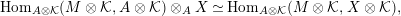 $$\begin{eqnarray}\text{Hom}_{A\otimes {\mathcal{K}}}(M\otimes {\mathcal{K}},A\otimes {\mathcal{K}})\otimes _{A}X\simeq \text{Hom}_{A\otimes {\mathcal{K}}}(M\otimes {\mathcal{K}},X\otimes {\mathcal{K}}),\end{eqnarray}$$
$$\begin{eqnarray}\text{Hom}_{A\otimes {\mathcal{K}}}(M\otimes {\mathcal{K}},A\otimes {\mathcal{K}})\otimes _{A}X\simeq \text{Hom}_{A\otimes {\mathcal{K}}}(M\otimes {\mathcal{K}},X\otimes {\mathcal{K}}),\end{eqnarray}$$
since
![]() $M\otimes {\mathcal{K}}$
is a projective
$M\otimes {\mathcal{K}}$
is a projective
![]() $A\otimes {\mathcal{K}}$
-module. Thus,
$A\otimes {\mathcal{K}}$
-module. Thus,
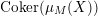 $\text{Coker}(\unicode[STIX]{x1D707}_{M}(X))$
is a torsion
$\text{Coker}(\unicode[STIX]{x1D707}_{M}(X))$
is a torsion
![]() ${\mathcal{O}}$
-module and
${\mathcal{O}}$
-module and
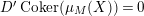 $D^{\prime }\,\text{Coker}(\unicode[STIX]{x1D707}_{M}(X))=0$
. Then,
$D^{\prime }\,\text{Coker}(\unicode[STIX]{x1D707}_{M}(X))=0$
. Then,
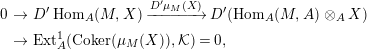 $$\begin{eqnarray}\displaystyle 0 & \rightarrow & \displaystyle D^{\prime }\,\text{Hom}_{A}(M,X)\xrightarrow[{}]{D^{\prime }\unicode[STIX]{x1D707}_{M}(X)}D^{\prime }(\text{Hom}_{A}(M,A)\otimes _{A}X)\nonumber\\ \displaystyle & \rightarrow & \displaystyle \text{Ext}_{A}^{1}(\text{Coker}(\unicode[STIX]{x1D707}_{M}(X)),{\mathcal{K}})=0,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0 & \rightarrow & \displaystyle D^{\prime }\,\text{Hom}_{A}(M,X)\xrightarrow[{}]{D^{\prime }\unicode[STIX]{x1D707}_{M}(X)}D^{\prime }(\text{Hom}_{A}(M,A)\otimes _{A}X)\nonumber\\ \displaystyle & \rightarrow & \displaystyle \text{Ext}_{A}^{1}(\text{Coker}(\unicode[STIX]{x1D707}_{M}(X)),{\mathcal{K}})=0,\nonumber\end{eqnarray}$$
proving (i). As
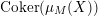 $\text{Coker}(\unicode[STIX]{x1D707}_{M}(X))$
is a torsion
$\text{Coker}(\unicode[STIX]{x1D707}_{M}(X))$
is a torsion
![]() ${\mathcal{O}}$
-module, (ii) also follows. The proof of (iii) is the same as (i). The proof of (iv) is similar. By chasing the diagram above, (i) implies the exact sequence.◻
${\mathcal{O}}$
-module, (ii) also follows. The proof of (iii) is the same as (i). The proof of (iv) is similar. By chasing the diagram above, (i) implies the exact sequence.◻
Lemma A.2. Let
![]() $M$
be an
$M$
be an
![]() $A$
-lattice,
$A$
-lattice,
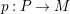 $p:P\rightarrow M$
the projective cover, and we define
$p:P\rightarrow M$
the projective cover, and we define
 $$\begin{eqnarray}L=D(\text{Coker}(\text{Hom}_{A}(p,A))).\end{eqnarray}$$
$$\begin{eqnarray}L=D(\text{Coker}(\text{Hom}_{A}(p,A))).\end{eqnarray}$$
Then, we have the following exact sequence of functors.
 $$\begin{eqnarray}0\longrightarrow D\,\text{Hom}_{A}(M,-)\xrightarrow[{}]{\unicode[STIX]{x1D706}\circ D\unicode[STIX]{x1D707}_{M}(-)}\text{Hom}_{A}(-,\unicode[STIX]{x1D708}(M))\longrightarrow \text{Ext}_{A}^{1}(-,L)\longrightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}0\longrightarrow D\,\text{Hom}_{A}(M,-)\xrightarrow[{}]{\unicode[STIX]{x1D706}\circ D\unicode[STIX]{x1D707}_{M}(-)}\text{Hom}_{A}(-,\unicode[STIX]{x1D708}(M))\longrightarrow \text{Ext}_{A}^{1}(-,L)\longrightarrow 0.\end{eqnarray}$$
Proof. We recall the short exact sequence
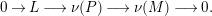 $$\begin{eqnarray}0\rightarrow L\longrightarrow \unicode[STIX]{x1D708}(P)\longrightarrow \unicode[STIX]{x1D708}(M)\longrightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow L\longrightarrow \unicode[STIX]{x1D708}(P)\longrightarrow \unicode[STIX]{x1D708}(M)\longrightarrow 0.\end{eqnarray}$$
Applying the functor
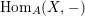 $\text{Hom}_{A}(X,-)$
, for an
$\text{Hom}_{A}(X,-)$
, for an
![]() $A$
-lattice
$A$
-lattice
![]() $X$
, we obtain
$X$
, we obtain
 $$\begin{eqnarray}\displaystyle \text{Hom}_{A}(X,\unicode[STIX]{x1D708}(P)) & \longrightarrow & \displaystyle \text{Hom}_{A}(X,\unicode[STIX]{x1D708}(M))\longrightarrow \text{Ext}_{A}^{1}(X,L)\nonumber\\ \displaystyle & \longrightarrow & \displaystyle \text{Ext}_{A}^{1}(X,\unicode[STIX]{x1D708}(P))=0,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{Hom}_{A}(X,\unicode[STIX]{x1D708}(P)) & \longrightarrow & \displaystyle \text{Hom}_{A}(X,\unicode[STIX]{x1D708}(M))\longrightarrow \text{Ext}_{A}^{1}(X,L)\nonumber\\ \displaystyle & \longrightarrow & \displaystyle \text{Ext}_{A}^{1}(X,\unicode[STIX]{x1D708}(P))=0,\nonumber\end{eqnarray}$$
since
![]() $\unicode[STIX]{x1D708}(P)$
is an injective
$\unicode[STIX]{x1D708}(P)$
is an injective
![]() $A$
-lattice. Thus, we have the following diagram with exact rows:
$A$
-lattice. Thus, we have the following diagram with exact rows:
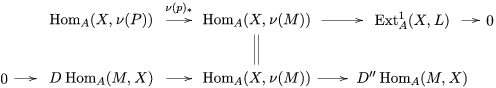
We show that
![]() $\unicode[STIX]{x1D708}(p)_{\ast }$
factors through
$\unicode[STIX]{x1D708}(p)_{\ast }$
factors through
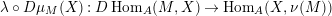 $\unicode[STIX]{x1D706}\circ D\unicode[STIX]{x1D707}_{M}(X):D\,\text{Hom}_{A}(M,X)\rightarrow \text{Hom}_{A}(X,\unicode[STIX]{x1D708}(M))$
. Consider the commutative diagram
$\unicode[STIX]{x1D706}\circ D\unicode[STIX]{x1D707}_{M}(X):D\,\text{Hom}_{A}(M,X)\rightarrow \text{Hom}_{A}(X,\unicode[STIX]{x1D708}(M))$
. Consider the commutative diagram
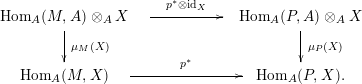
By dualizing the diagram, we obtain the commutative diagram
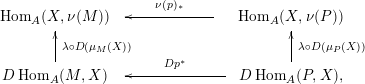
and
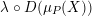 $\unicode[STIX]{x1D706}\circ D(\unicode[STIX]{x1D707}_{P}(X))$
is an isomorphism. Therefore,
$\unicode[STIX]{x1D706}\circ D(\unicode[STIX]{x1D707}_{P}(X))$
is an isomorphism. Therefore,
![]() $\unicode[STIX]{x1D708}(p)_{\ast }$
factors through
$\unicode[STIX]{x1D708}(p)_{\ast }$
factors through
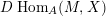 $D\,\text{Hom}_{A}(M,X)$
. Since
$D\,\text{Hom}_{A}(M,X)$
. Since
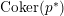 $\text{Coker}(p^{\ast })$
is an
$\text{Coker}(p^{\ast })$
is an
![]() ${\mathcal{O}}$
-submodule of
${\mathcal{O}}$
-submodule of
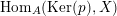 $\text{Hom}_{A}(\text{Ker}(p),X)$
, it is a free
$\text{Hom}_{A}(\text{Ker}(p),X)$
, it is a free
![]() ${\mathcal{O}}$
module of finite rank and
${\mathcal{O}}$
module of finite rank and
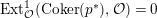 $\text{Ext}_{{\mathcal{O}}}^{1}(\text{Coker}(p^{\ast }),{\mathcal{O}})=0$
. It follows that
$\text{Ext}_{{\mathcal{O}}}^{1}(\text{Coker}(p^{\ast }),{\mathcal{O}})=0$
. It follows that
![]() $Dp^{\ast }$
is an epimorphism. This implies that
$Dp^{\ast }$
is an epimorphism. This implies that
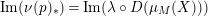 $\text{Im}(\unicode[STIX]{x1D708}(p)_{\ast })=\text{Im}(\unicode[STIX]{x1D706}\circ D(\unicode[STIX]{x1D707}_{M}(X)))$
, and we get the desired exact sequence.◻
$\text{Im}(\unicode[STIX]{x1D708}(p)_{\ast })=\text{Im}(\unicode[STIX]{x1D706}\circ D(\unicode[STIX]{x1D707}_{M}(X)))$
, and we get the desired exact sequence.◻
By Lemma A.2, we have the commutative diagram

which implies that there exists a monomorphism
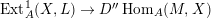 $\text{Ext}_{A}^{1}(X,L)\rightarrow D^{\prime \prime }\,\text{Hom}_{A}(M,X)$
.
$\text{Ext}_{A}^{1}(X,L)\rightarrow D^{\prime \prime }\,\text{Hom}_{A}(M,X)$
.
We set
![]() $X=M$
. Then
$X=M$
. Then
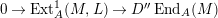 $0\rightarrow \text{Ext}_{A}^{1}(M,L)\rightarrow D^{\prime \prime }\,\text{End}_{A}(M)$
. Since
$0\rightarrow \text{Ext}_{A}^{1}(M,L)\rightarrow D^{\prime \prime }\,\text{End}_{A}(M)$
. Since
![]() $M$
is indecomposable,
$M$
is indecomposable,
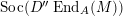 $\text{Soc}(D^{\prime \prime }\,\text{End}_{A}(M))$
is a simple
$\text{Soc}(D^{\prime \prime }\,\text{End}_{A}(M))$
is a simple
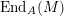 $\text{End}_{A}(M)$
-module, and hence there exists an isomorphism
$\text{End}_{A}(M)$
-module, and hence there exists an isomorphism
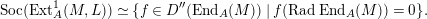 $$\begin{eqnarray}\text{Soc}(\text{Ext}_{A}^{1}(M,L))\simeq \{f\in D^{\prime \prime }(\text{End}_{A}(M))\mid f(\text{Rad}\,\text{End}_{A}(M))=0\}.\end{eqnarray}$$
$$\begin{eqnarray}\text{Soc}(\text{Ext}_{A}^{1}(M,L))\simeq \{f\in D^{\prime \prime }(\text{End}_{A}(M))\mid f(\text{Rad}\,\text{End}_{A}(M))=0\}.\end{eqnarray}$$
We are ready to prove that (2) implies (1) in Proposition 1.15. By the condition (2)(i),
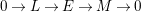 $0\rightarrow L\rightarrow E\rightarrow M\rightarrow 0$
does not split. As
$0\rightarrow L\rightarrow E\rightarrow M\rightarrow 0$
does not split. As
![]() $L$
and
$L$
and
![]() $M$
are indecomposable by the condition (2)(ii), we show that every
$M$
are indecomposable by the condition (2)(ii), we show that every
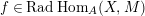 $f\in \text{Rad}\,\text{Hom}_{A}(X,M)$
factors through
$f\in \text{Rad}\,\text{Hom}_{A}(X,M)$
factors through
![]() $E$
under the condition (2)(iii). Consider the commutative diagram
$E$
under the condition (2)(iii). Consider the commutative diagram
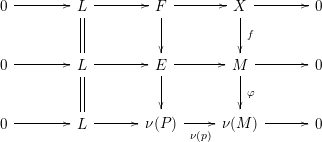
with exact rows, where
![]() $F$
is the pullback of
$F$
is the pullback of
![]() $X$
and
$X$
and
![]() $E$
over
$E$
over
![]() $M$
. Let
$M$
. Let
![]() $\unicode[STIX]{x1D709}$
be an element in
$\unicode[STIX]{x1D709}$
be an element in
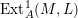 $\text{Ext}_{A}^{1}(M,L)$
which represents the second sequence. Then, the condition (2)(iii) implies that
$\text{Ext}_{A}^{1}(M,L)$
which represents the second sequence. Then, the condition (2)(iii) implies that
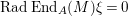 $\text{Rad}\,\text{End}_{A}(M)\unicode[STIX]{x1D709}=0$
and
$\text{Rad}\,\text{End}_{A}(M)\unicode[STIX]{x1D709}=0$
and
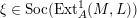 $\unicode[STIX]{x1D709}\in \text{Soc}(\text{Ext}_{A}^{1}(M,L))$
. Consider the commutative diagram
$\unicode[STIX]{x1D709}\in \text{Soc}(\text{Ext}_{A}^{1}(M,L))$
. Consider the commutative diagram
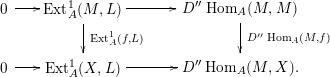
Let
![]() $\unicode[STIX]{x1D709}^{\prime }$
be the image of
$\unicode[STIX]{x1D709}^{\prime }$
be the image of
![]() $\unicode[STIX]{x1D709}$
under
$\unicode[STIX]{x1D709}$
under
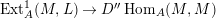 $\text{Ext}_{A}^{1}(M,L)\rightarrow D^{\prime \prime }\,\text{Hom}_{A}(M,M)$
. Since
$\text{Ext}_{A}^{1}(M,L)\rightarrow D^{\prime \prime }\,\text{Hom}_{A}(M,M)$
. Since
 $$\begin{eqnarray}D^{\prime \prime }\,\text{Hom}_{A}(M,f)(\unicode[STIX]{x1D709}^{\prime })(\unicode[STIX]{x1D713})=\unicode[STIX]{x1D709}^{\prime }(f\unicode[STIX]{x1D713})\in \unicode[STIX]{x1D709}^{\prime }(\text{Rad}\,\text{End}_{A}(M))=0\end{eqnarray}$$
$$\begin{eqnarray}D^{\prime \prime }\,\text{Hom}_{A}(M,f)(\unicode[STIX]{x1D709}^{\prime })(\unicode[STIX]{x1D713})=\unicode[STIX]{x1D709}^{\prime }(f\unicode[STIX]{x1D713})\in \unicode[STIX]{x1D709}^{\prime }(\text{Rad}\,\text{End}_{A}(M))=0\end{eqnarray}$$
for
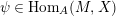 $\unicode[STIX]{x1D713}\in \text{Hom}_{A}(M,X)$
, we have
$\unicode[STIX]{x1D713}\in \text{Hom}_{A}(M,X)$
, we have
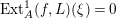 $\text{Ext}_{A}^{1}(f,L)(\unicode[STIX]{x1D709})=0$
. Hence,
$\text{Ext}_{A}^{1}(f,L)(\unicode[STIX]{x1D709})=0$
. Hence,
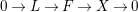 $0\rightarrow L\rightarrow F\rightarrow X\rightarrow 0$
splits. Then, it implies that
$0\rightarrow L\rightarrow F\rightarrow X\rightarrow 0$
splits. Then, it implies that
![]() $f$
factors through
$f$
factors through
![]() $E$
.
$E$
.