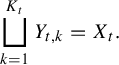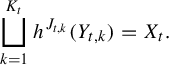1 Introduction
In 1990, Putnam proved in [Reference Putnam17] that the crossed product
![]() $ C^* $
-algebras associated to minimal Cantor systems are A
$ C^* $
-algebras associated to minimal Cantor systems are A
![]() $\mathbb {T}$
-algebras of real rank zero. Using the classification results of Elliott in [Reference Elliott7] and Dadarlat and Gong in [Reference Dadarlat and Gong5], one sees that such
$\mathbb {T}$
-algebras of real rank zero. Using the classification results of Elliott in [Reference Elliott7] and Dadarlat and Gong in [Reference Dadarlat and Gong5], one sees that such
![]() $ C^* $
-algebras are classifiable by their
$ C^* $
-algebras are classifiable by their
![]() $ K $
-theory. In 1995, Putnam, along with Thierry Giordano and Christian Skau, expanded this classification theorem to include dynamics; in [Reference Giordano, Putnam and Skau9], they showed that there is a condition on minimal Cantor systems, called ‘strong orbit equivalence’, that is equivalent to isomorphism of the
$ K $
-theory. In 1995, Putnam, along with Thierry Giordano and Christian Skau, expanded this classification theorem to include dynamics; in [Reference Giordano, Putnam and Skau9], they showed that there is a condition on minimal Cantor systems, called ‘strong orbit equivalence’, that is equivalent to isomorphism of the
![]() $ K $
-theory associated to the dynamical systems, and therefore is equivalent to the isomorphism of the crossed product
$ K $
-theory associated to the dynamical systems, and therefore is equivalent to the isomorphism of the crossed product
![]() $ C^* $
-algebras. This dynamical classification was motivated by Krieger’s theorem [Reference Krieger12, Reference Krieger13], which says that for ergodic non-singular systems, the associated von Neumann crossed product factors are isomorphic if and only if the systems are orbit equivalent. The goal of this paper is to provide an extension of the dynamical classification theorem of Gioradno, Putnam, and Skau [Reference Giordano, Putnam and Skau9, Theorem 2.1] to include a larger class of zero-dimensional dynamical systems which we describe below.
$ C^* $
-algebras. This dynamical classification was motivated by Krieger’s theorem [Reference Krieger12, Reference Krieger13], which says that for ergodic non-singular systems, the associated von Neumann crossed product factors are isomorphic if and only if the systems are orbit equivalent. The goal of this paper is to provide an extension of the dynamical classification theorem of Gioradno, Putnam, and Skau [Reference Giordano, Putnam and Skau9, Theorem 2.1] to include a larger class of zero-dimensional dynamical systems which we describe below.
In our previous paper [Reference Herstedt11], we determined a condition on a zero-dimensional dynamical system called ‘fiberwise essentially minimal’ (see Definition 2.2) that guarantees that the associated crossed product is an A
![]() $\mathbb {T}$
-algebra. As its name suggests, this class is a broadening of minimal (and also essentially minimal). It additionally includes all systems whose orbit closures are minimal; more generally, it includes all systems whose points are all positively and negatively recurrent. If we assume that fiberwise essentially minimal zero-dimensional systems additionally have no periodic points, their crossed products have real rank zero and are therefore classifiable by
$\mathbb {T}$
-algebra. As its name suggests, this class is a broadening of minimal (and also essentially minimal). It additionally includes all systems whose orbit closures are minimal; more generally, it includes all systems whose points are all positively and negatively recurrent. If we assume that fiberwise essentially minimal zero-dimensional systems additionally have no periodic points, their crossed products have real rank zero and are therefore classifiable by
![]() $ K $
-theory (due to the work of Elliott in [Reference Elliott7] and Dadarlat and Gong in [Reference Dadarlat and Gong5]). This was an expansion of the work done on the minimal Cantor case in 1990 by Putnam [Reference Putnam16, Reference Putnam17] in which the crossed products are simple, and work done on the essentially minimal case in 1992 by Putnam and Skau along with Herman [Reference Herman, Putnam and Skau10] in which the crossed products are not necessarily simple. Some more non-simple results in this realm can be found in [Reference Bezuglyi, Niu and Sun3]. Our result from [Reference Herstedt11] includes many more non-simple crossed products.
$ K $
-theory (due to the work of Elliott in [Reference Elliott7] and Dadarlat and Gong in [Reference Dadarlat and Gong5]). This was an expansion of the work done on the minimal Cantor case in 1990 by Putnam [Reference Putnam16, Reference Putnam17] in which the crossed products are simple, and work done on the essentially minimal case in 1992 by Putnam and Skau along with Herman [Reference Herman, Putnam and Skau10] in which the crossed products are not necessarily simple. Some more non-simple results in this realm can be found in [Reference Bezuglyi, Niu and Sun3]. Our result from [Reference Herstedt11] includes many more non-simple crossed products.
This paper expands on the work in [Reference Herstedt11] in two major ways. The first is what we explore in §3, where we discuss some specifics about the
![]() $ K $
-theory of the crossed products. We define ‘large subalgebras’ of our crossed products (see Definition 3.6) which are AF-subalgebras (see Theorem 3.7) that have the same
$ K $
-theory of the crossed products. We define ‘large subalgebras’ of our crossed products (see Definition 3.6) which are AF-subalgebras (see Theorem 3.7) that have the same
![]() $ K_0 $
group as the crossed product (see Theorem 3.9). This mirrors the result of large subalgebras in the minimal case by Putnam [Reference Putnam17]. We also give a simple description of the
$ K_0 $
group as the crossed product (see Theorem 3.9). This mirrors the result of large subalgebras in the minimal case by Putnam [Reference Putnam17]. We also give a simple description of the
![]() $ K_1 $
group of the crossed product in Theorem 3.10.
$ K_1 $
group of the crossed product in Theorem 3.10.
The second major aspect of this paper is expanding the dynamical classification of minimal Cantor systems that coincides with the
![]() $ K $
-theoretic classification, introduced by Giordano, Putnam, and Skau [Reference Giordano, Putnam and Skau9]. They introduce the notion of ‘strong orbit equivalence’, which we expand to the fiberwise essentially minimal case in Definition 2.2. In §4, we discuss how the circle algebra direct system that gives the A
$ K $
-theoretic classification, introduced by Giordano, Putnam, and Skau [Reference Giordano, Putnam and Skau9]. They introduce the notion of ‘strong orbit equivalence’, which we expand to the fiberwise essentially minimal case in Definition 2.2. In §4, we discuss how the circle algebra direct system that gives the A
![]() $\mathbb {T}$
-algebra of the crossed product gives us a sequence of Kakutani–Rokhlin partitions, which we then use to create a Bratteli–Vershik–Kakutani model of the dynamical system, which is an ordered Bratteli diagram whose Vershik system is conjugate to the original dynamical system. Using this Bratteli diagram along with our
$\mathbb {T}$
-algebra of the crossed product gives us a sequence of Kakutani–Rokhlin partitions, which we then use to create a Bratteli–Vershik–Kakutani model of the dynamical system, which is an ordered Bratteli diagram whose Vershik system is conjugate to the original dynamical system. Using this Bratteli diagram along with our
![]() $ K $
-theory results, we then prove Theorem 5.2, which tells us that for fiberwise essentially minimal zero-dimensional systems,
$ K $
-theory results, we then prove Theorem 5.2, which tells us that for fiberwise essentially minimal zero-dimensional systems,
![]() $ K $
-theory isomorphism of the crossed products is equivalent to strong orbit equivalence of the dynamical systems. This, combined with the classification result of [Reference Dadarlat and Gong5, Reference Elliott7], gives us Theorem 5.3, which tells us that if the dynamical systems have no periodic points, this is also equivalent to isomorphism of the crossed products.
$ K $
-theory isomorphism of the crossed products is equivalent to strong orbit equivalence of the dynamical systems. This, combined with the classification result of [Reference Dadarlat and Gong5, Reference Elliott7], gives us Theorem 5.3, which tells us that if the dynamical systems have no periodic points, this is also equivalent to isomorphism of the crossed products.
The Bratteli–Vershik–Kakutani models developed in this paper suggest that more results in [Reference Giordano, Putnam and Skau9] could be generalized to the semisimple (minimal orbits) case. One cannot expect the results to hold for the entire fiberwise essentially minimal case. For example, [Reference Giordano, Putnam and Skau9, Theorem 2.2] tells us that orbit equivalence of minimal Cantor systems is equivalent to an isomorphism between the
![]() $ K_0 $
groups modulo their infinitesimal groups. Considering the shift on the one-point compactification of the integers (an essentially minimal system), this
$ K_0 $
groups modulo their infinitesimal groups. Considering the shift on the one-point compactification of the integers (an essentially minimal system), this
![]() $ K_0 $
group modulo the infinitesimal group is isomorphic to
$ K_0 $
group modulo the infinitesimal group is isomorphic to
![]() $ \mathbb {Z} $
, which is the same as if the space was just a single point. Certainly there is no orbit equivalence between these spaces. However, in the semisimple case, these
$ \mathbb {Z} $
, which is the same as if the space was just a single point. Certainly there is no orbit equivalence between these spaces. However, in the semisimple case, these
![]() $ K_0 $
modulo infinitesimal groups are more interesting, and an application of the techniques developed in this paper to expand this result is a possibility. Considering [Reference Giordano, Putnam and Skau9, Theorem 2.2] also tells us that orbit equivalence is equivalent to a map preserving invariant probability measure, so expanding this result is of interest to ergodic theory.
$ K_0 $
modulo infinitesimal groups are more interesting, and an application of the techniques developed in this paper to expand this result is a possibility. Considering [Reference Giordano, Putnam and Skau9, Theorem 2.2] also tells us that orbit equivalence is equivalent to a map preserving invariant probability measure, so expanding this result is of interest to ergodic theory.
2 Preliminaries
This section introduces terms that will be used to prove the main theorems of the paper, along with some examples and some previous relevant results.
Let
![]() $ X $
be a totally disconnected compact metrizable space and let
$ X $
be a totally disconnected compact metrizable space and let
![]() $ h : X \to X $
be a homeomorphism of
$ h : X \to X $
be a homeomorphism of
![]() $ X $
. We call
$ X $
. We call
![]() $ ( X , h ) $
a zero-dimensional system. Let
$ ( X , h ) $
a zero-dimensional system. Let
![]() $ \alpha $
be the automorphism of
$ \alpha $
be the automorphism of
![]() $ C ( X ) $
induced by
$ C ( X ) $
induced by
![]() $ h $
; that is,
$ h $
; that is,
![]() $ \alpha $
is defined by
$ \alpha $
is defined by
![]() $ \alpha ( f ) ( x ) = f ( h^{ -1 } ( x ) ) $
for all
$ \alpha ( f ) ( x ) = f ( h^{ -1 } ( x ) ) $
for all
![]() $ f \in C ( X ) $
and all
$ f \in C ( X ) $
and all
![]() $ x \in X $
. Then we denote the crossed product of
$ x \in X $
. Then we denote the crossed product of
![]() $ C ( X ) $
by
$ C ( X ) $
by
![]() $ \alpha $
by
$ \alpha $
by
![]() $ C^* ( \mathbb {Z} , X , h ) $
(or, less commonly,
$ C^* ( \mathbb {Z} , X , h ) $
(or, less commonly,
![]() $ C^* ( \mathbb {Z} , C ( X ) , \alpha ) $
). We denote the ‘standard unitary’ of
$ C^* ( \mathbb {Z} , C ( X ) , \alpha ) $
). We denote the ‘standard unitary’ of
![]() $ C^* ( \mathbb {Z} , X , h ) $
by
$ C^* ( \mathbb {Z} , X , h ) $
by
![]() $ u $
, which is a unitary element of
$ u $
, which is a unitary element of
![]() $ C^* ( \mathbb {Z} , X , h ) $
that satisfies
$ C^* ( \mathbb {Z} , X , h ) $
that satisfies
![]() $ u f u^* = \alpha ( f ) $
for all
$ u f u^* = \alpha ( f ) $
for all
![]() $ f \in C ( X ) $
.
$ f \in C ( X ) $
.
We will use the disjoint union symbol
![]() $ \bigsqcup $
to denote unions of disjoint sets. We will not always say explicitly that the sets in this union are disjoint, as this will be implied by the notation. By a partition
$ \bigsqcup $
to denote unions of disjoint sets. We will not always say explicitly that the sets in this union are disjoint, as this will be implied by the notation. By a partition
![]() $ \mathcal {P} $
of
$ \mathcal {P} $
of
![]() $ X $
, we mean a finite set of mutually disjoint compact open subsets of
$ X $
, we mean a finite set of mutually disjoint compact open subsets of
![]() $ X $
whose union is
$ X $
whose union is
![]() $ X $
.
$ X $
.
We say that a non-empty closed subset
![]() $ Y $
of
$ Y $
of
![]() $ X $
is a minimal set if it is
$ X $
is a minimal set if it is
![]() $ h $
-invariant and has no non-empty
$ h $
-invariant and has no non-empty
![]() $ h $
-invariant proper closed subsets. By Zorn’s lemma, minimal sets exist for every zero-dimensional system. We say that a dynamical system
$ h $
-invariant proper closed subsets. By Zorn’s lemma, minimal sets exist for every zero-dimensional system. We say that a dynamical system
![]() $ ( X , h ) $
is essentially minimal if it has a unique minimal set, and additionally that
$ ( X , h ) $
is essentially minimal if it has a unique minimal set, and additionally that
![]() $ ( X , h ) $
is minimal if the unique minimal set is
$ ( X , h ) $
is minimal if the unique minimal set is
![]() $ X $
.
$ X $
.
The following definition is introduced as [Reference Herstedt11, Definition 1.9]. Given a subset
![]() $ U $
of
$ U $
of
![]() $ X $
, we use the notation
$ X $
, we use the notation
This is the ‘first return time map’ of
![]() $ U $
under the homeomorphism
$ U $
under the homeomorphism
![]() $ h $
.
$ h $
.
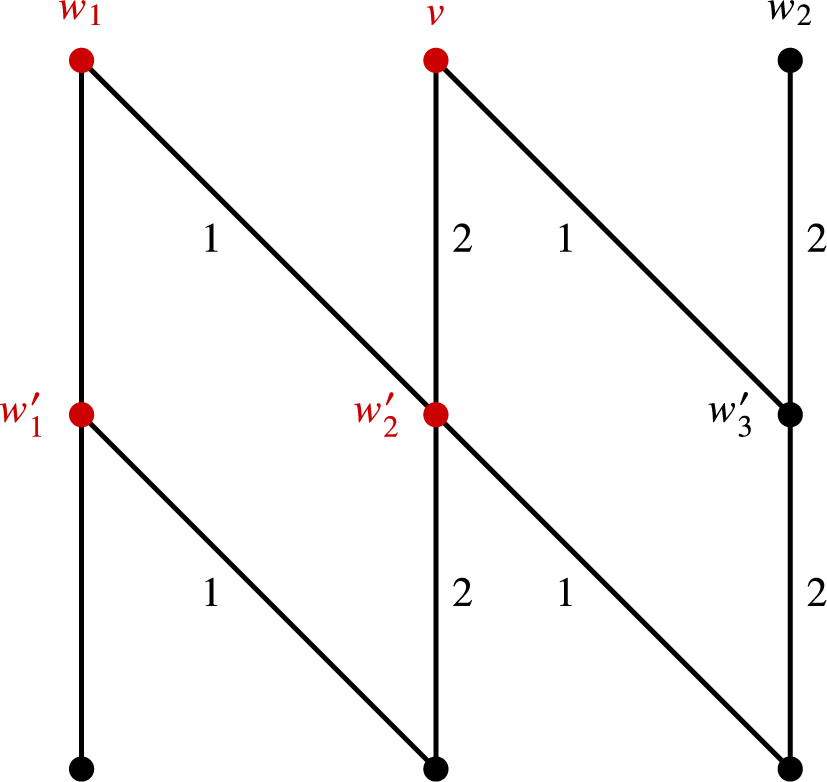
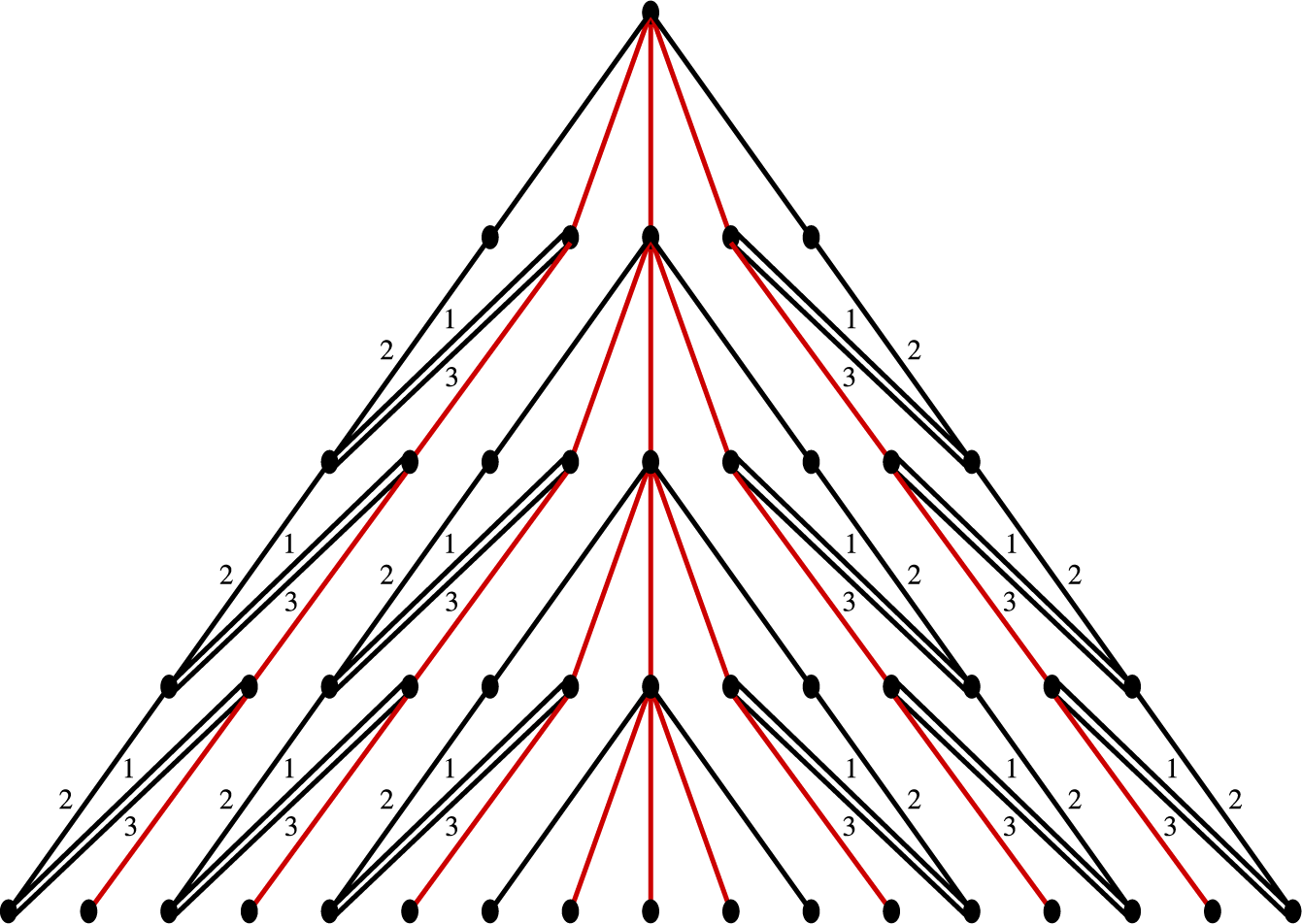
Definition 2.1. Let
![]() $ ( X , h ) $
be a zero-dimensional system and let
$ ( X , h ) $
be a zero-dimensional system and let
![]() $ \mathcal {P} $
be a partition of
$ \mathcal {P} $
be a partition of
![]() $ X $
(see Figure 1). We define a system of finite first return time maps subordinate to
$ X $
(see Figure 1). We define a system of finite first return time maps subordinate to
![]() $ \mathcal {P}$
to be a tuple
$ \mathcal {P}$
to be a tuple
such that we have the following.
-
(1) We have
 $ T \in \mathbb {Z}_{> 0 } $
.
$ T \in \mathbb {Z}_{> 0 } $
. -
(2) For each
 $ t \in \{ 1 , \ldots , T \} $
,
$ t \in \{ 1 , \ldots , T \} $
,
 $ X_t $
is a compact open subset of
$ X_t $
is a compact open subset of
 $ X $
. That
$ X $
. That
 $ \mathcal {S} $
is subordinate to
$ \mathcal {S} $
is subordinate to
 $ \mathcal {P} $
means that for each
$ \mathcal {P} $
means that for each
 $ t \in \{ 1 , \ldots , T \}$
,
$ t \in \{ 1 , \ldots , T \}$
,
 $ X_t $
is contained in an element of
$ X_t $
is contained in an element of
 $ \mathcal {P} $
.
$ \mathcal {P} $
. -
(3) For each
 $ t \in \{ 1 , \ldots , T \} $
,
$ t \in \{ 1 , \ldots , T \} $
,
 $ K_t \in \mathbb {Z}_{> 0 } $
.
$ K_t \in \mathbb {Z}_{> 0 } $
. -
(4) For each
 $ t \in \{ 1 , \ldots , T \} $
and each
$ t \in \{ 1 , \ldots , T \} $
and each
 $ k \in \{ 1 , \ldots , K_t \} $
,
$ k \in \{ 1 , \ldots , K_t \} $
,
 $ Y_{ t , k } $
is a compact open subset of
$ Y_{ t , k } $
is a compact open subset of
 $X_t$
. Moreover, for each
$X_t$
. Moreover, for each
 $ t \in \{ 1 , \ldots , T\}$
,
$ t \in \{ 1 , \ldots , T\}$
,
 $ \{ Y_{ t , 1 } , \ldots , Y_{ t , K_t } \} $
is a partition of
$ \{ Y_{ t , 1 } , \ldots , Y_{ t , K_t } \} $
is a partition of
 $X_t$
; that is,
$X_t$
; that is,  $$ \begin{align*} \bigsqcup_{ k = 1 }^{ K_t } Y_{ t , k } = X_t. \end{align*} $$
$$ \begin{align*} \bigsqcup_{ k = 1 }^{ K_t } Y_{ t , k } = X_t. \end{align*} $$
-
(5) For each
 $ t \in \{ 1 , \ldots , T \} $
and each
$ t \in \{ 1 , \ldots , T \} $
and each
 $ k \in \{ 1 , \ldots , K_t \} $
,
$ k \in \{ 1 , \ldots , K_t \} $
,
 $ J_{ t , k } \in \mathbb {Z}_{> 0 } $
. Using Definition 2.1, we define
$ J_{ t , k } \in \mathbb {Z}_{> 0 } $
. Using Definition 2.1, we define
 $ \{ J_{ t , k } \} = \unicode{x3bb} _{ X_t } ( Y_{ t , k } ) $
. Moreover, for each
$ \{ J_{ t , k } \} = \unicode{x3bb} _{ X_t } ( Y_{ t , k } ) $
. Moreover, for each
 $ t \in \{ 1 , \ldots , T \} $
,
$ t \in \{ 1 , \ldots , T \} $
,
 $ \{ h^{ J_{ t , 1 } } ( Y_{ t , 1 } ) , \ldots , h^{ J_{ t , K_t } } ( Y_{ t , K_t } ) \} $
is a partition of
$ \{ h^{ J_{ t , 1 } } ( Y_{ t , 1 } ) , \ldots , h^{ J_{ t , K_t } } ( Y_{ t , K_t } ) \} $
is a partition of
 $ X_t $
; that is,
$ X_t $
; that is,  $$ \begin{align*} \bigsqcup_{ k = 1 }^{ K_t } h^{ J_{ t , k } } ( Y_{ t , k } ) = X_t. \end{align*} $$
$$ \begin{align*} \bigsqcup_{ k = 1 }^{ K_t } h^{ J_{ t , k } } ( Y_{ t , k } ) = X_t. \end{align*} $$
-
(6) The set
is a partition of $$ \begin{align*} \mathcal{P}_1 ( \mathcal{S} ) = \{ h^j ( Y_{ t , k } ) \,|\, t \in \{ 1 , \ldots , T \} , k \in \{ 1 , \ldots , K_t \} , \mbox{and}\ j \in \{ 0 , \ldots , J_{ t , k } - 1 \} \} \end{align*} $$
$$ \begin{align*} \mathcal{P}_1 ( \mathcal{S} ) = \{ h^j ( Y_{ t , k } ) \,|\, t \in \{ 1 , \ldots , T \} , k \in \{ 1 , \ldots , K_t \} , \mbox{and}\ j \in \{ 0 , \ldots , J_{ t , k } - 1 \} \} \end{align*} $$
 $ X $
. Note that this combined with condition (5) also implies is a partition of
$ X $
. Note that this combined with condition (5) also implies is a partition of $$ \begin{align*} \mathcal{P}_2 ( \mathcal{S} ) = \{ h^j ( Y_{ t , k } ) \,|\, t \in \{ 1 , \ldots , T \} , k \in \{ 1 , \ldots , K_t \} , \mbox{and}\ j \in \{ 1 , \ldots , J_{ t , k } \} \} \end{align*} $$
$$ \begin{align*} \mathcal{P}_2 ( \mathcal{S} ) = \{ h^j ( Y_{ t , k } ) \,|\, t \in \{ 1 , \ldots , T \} , k \in \{ 1 , \ldots , K_t \} , \mbox{and}\ j \in \{ 1 , \ldots , J_{ t , k } \} \} \end{align*} $$
 $ X $
.
$ X $
.
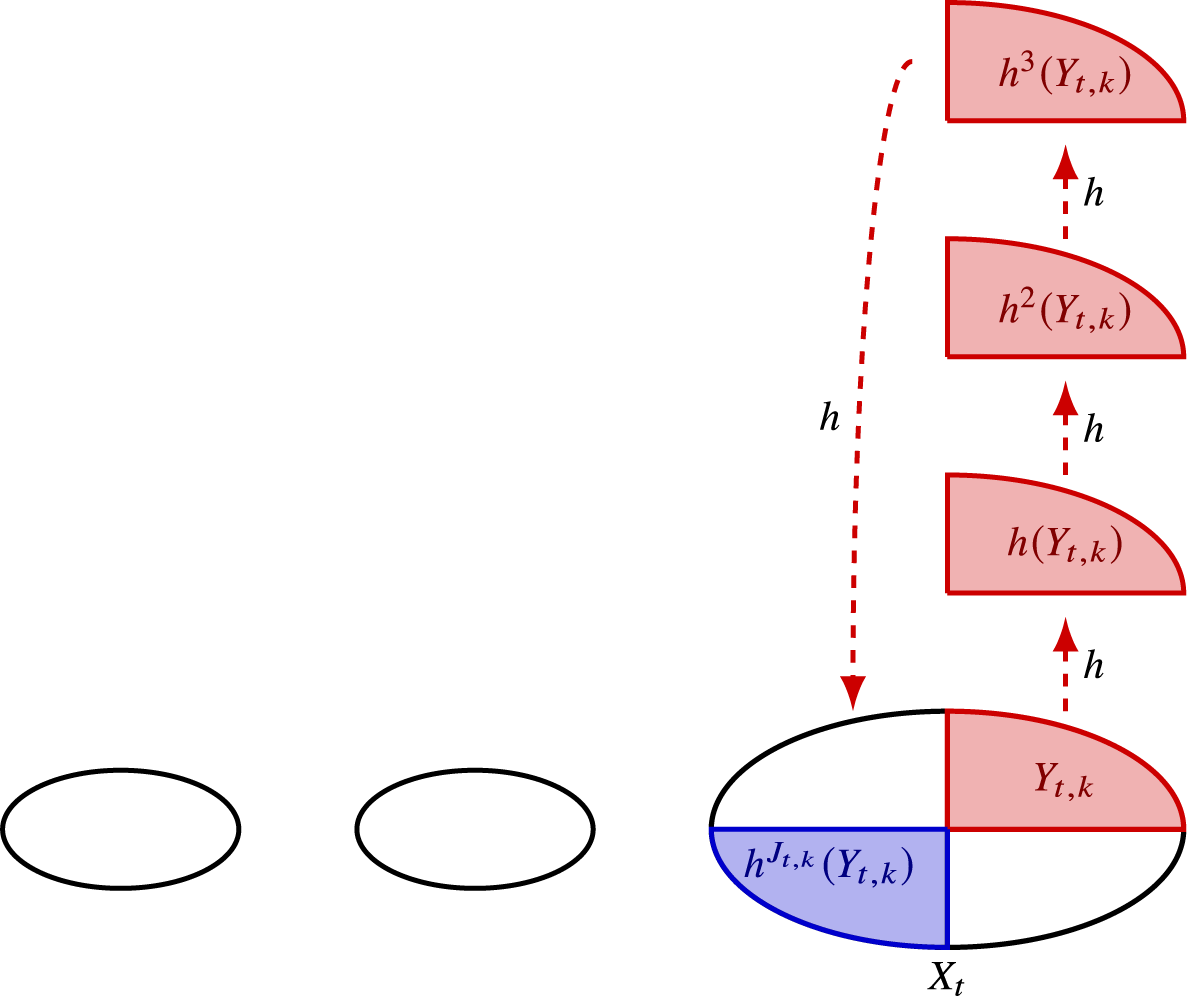
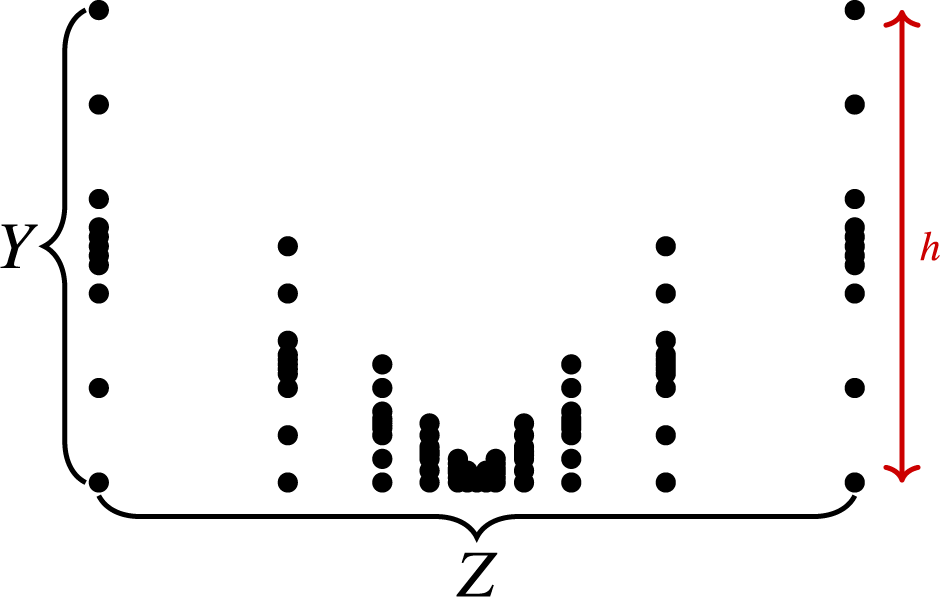
Figure 1 An illustration of Definition 2.1. For each base
![]() $ X_t $
, we divide the base into pieces
$ X_t $
, we divide the base into pieces
![]() $ Y_{ t , k } $
that come back to
$ Y_{ t , k } $
that come back to
![]() $ X_t $
only after applying
$ X_t $
only after applying
![]() $ J_{ t , k } $
iterations of the homeomorphism.
$ J_{ t , k } $
iterations of the homeomorphism.
The following definition is introduced as [Reference Herstedt11, Definition 1.20].
Definition 2.2. Let
![]() $ ( X , h ) $
be a zero-dimensional system and let
$ ( X , h ) $
be a zero-dimensional system and let
![]() $ Z \subset X $
be a closed subset. We say that the triple
$ Z \subset X $
be a closed subset. We say that the triple
![]() $ ( X , h , Z ) $
is a fiberwise essentially minimal zero-dimensional system if there is a quotient map
$ ( X , h , Z ) $
is a fiberwise essentially minimal zero-dimensional system if there is a quotient map
![]() $ \psi : X \to Z $
such that:
$ \psi : X \to Z $
such that:
-
(1)
 $ \psi |_Z : Z \to Z $
is the identity map;
$ \psi |_Z : Z \to Z $
is the identity map; -
(2)
 $ \psi \circ h = \psi $
;
$ \psi \circ h = \psi $
; -
(3) for each
 $ z \in Z $
,
$ z \in Z $
,
 $ ( \psi ^{ -1 } ( z ) , h|_{ \psi ^{ -1 } ( z ) } ) $
is an essentially minimal system and
$ ( \psi ^{ -1 } ( z ) , h|_{ \psi ^{ -1 } ( z ) } ) $
is an essentially minimal system and
 $ z $
is in its minimal set.
$ z $
is in its minimal set.
The following is [Reference Herstedt11, Theorem 2.1], linking Definitions 2.1 and 2.2.
Theorem 2.3. Let
![]() $ ( X , h ) $
be a zero-dimensional system. Then there exists some closed
$ ( X , h ) $
be a zero-dimensional system. Then there exists some closed
![]() $ Z \subset X $
such that
$ Z \subset X $
such that
![]() $ ( X , h , Z ) $
is fiberwise essentially minimal if and only if for any partition
$ ( X , h , Z ) $
is fiberwise essentially minimal if and only if for any partition
![]() $ \mathcal {P} $
of
$ \mathcal {P} $
of
![]() $ X $
,
$ X $
,
![]() $ ( X , h ) $
admits a system of finite first return time maps subordinate to
$ ( X , h ) $
admits a system of finite first return time maps subordinate to
![]() $ \mathcal {P} $
.
$ \mathcal {P} $
.
Examples 2.4
-
(1) By [Reference Herstedt11, Proposition 1.18], zero-dimensional systems in which all points are positively and negatively recurrent are fiberwise essentially minimal. In particular, this includes systems in which orbit closures are minimal, called ‘semisimple’ by Furstenberg in [Reference Furstenberg8]. Thus, examples of fiberwise essentially minimal zero-dimensional systems can be found by looking at the local structure of orbit closures.
-
(2) The following is [Reference Herstedt11, Example 1.21(c)]. Let
 $ Z = \mathbb {Z} \cup \{ \infty \} $
be the one-point compactification of the integers and let
$ Z = \mathbb {Z} \cup \{ \infty \} $
be the one-point compactification of the integers and let
 $ ( Y , h' ) $
be an essentially minimal zero-dimensional system. Let
$ ( Y , h' ) $
be an essentially minimal zero-dimensional system. Let
 $ X = ( Y \times Z ) / ( Y \times \{ \infty \} ) $
and let
$ X = ( Y \times Z ) / ( Y \times \{ \infty \} ) $
and let
 $ \pi : Y \times Z \to X $
be the quotient map. Let
$ \pi : Y \times Z \to X $
be the quotient map. Let
 $ \widetilde { h } = \pi ( h' \times \text {id} ) : Y \times Z \to X $
and let
$ \widetilde { h } = \pi ( h' \times \text {id} ) : Y \times Z \to X $
and let
 $ h : X \to X $
be the continuous map satisfying
$ h : X \to X $
be the continuous map satisfying
 $ h \circ \pi = \widetilde { h } $
, which is obtained from the universal property of the quotient map. One checks that
$ h \circ \pi = \widetilde { h } $
, which is obtained from the universal property of the quotient map. One checks that
 $ h $
is a homeomorphism. Define
$ h $
is a homeomorphism. Define
 $ \widetilde { \psi } : Y \times Z \to Z $
by
$ \widetilde { \psi } : Y \times Z \to Z $
by
 $ \widetilde { \psi } ( ( y , z ) ) = z $
and then let
$ \widetilde { \psi } ( ( y , z ) ) = z $
and then let
 $ \psi : X \to Z $
be the continuous map satisfying
$ \psi : X \to Z $
be the continuous map satisfying
 $ \psi \circ \pi = \widetilde { \psi } $
, which is obtained from the universal property of the quotient map. One checks that
$ \psi \circ \pi = \widetilde { \psi } $
, which is obtained from the universal property of the quotient map. One checks that
 $ \psi $
itself is a quotient map, and then one checks that
$ \psi $
itself is a quotient map, and then one checks that
 $ ( X , h ) $
is a fiberwise essentially minimal zero-dimensional system (using
$ ( X , h ) $
is a fiberwise essentially minimal zero-dimensional system (using
 $ Z $
and
$ Z $
and
 $ \psi $
as defined above). See this in Figure 2.
$ \psi $
as defined above). See this in Figure 2.
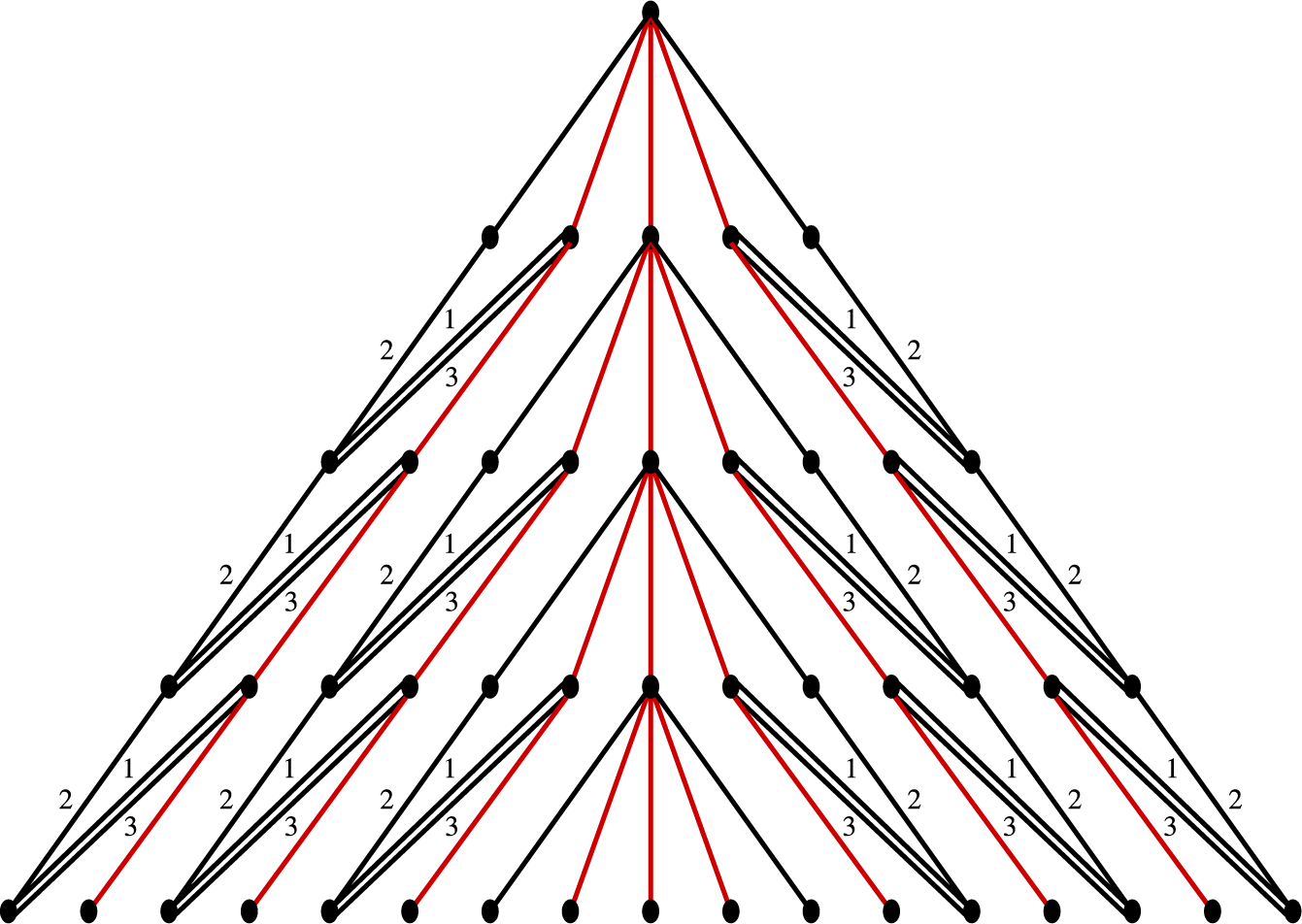
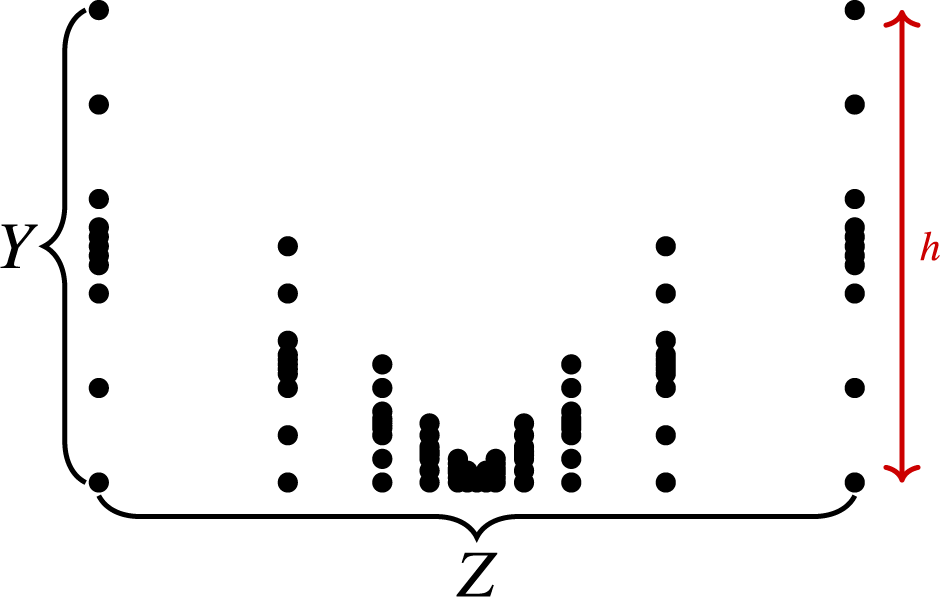
Figure 2 An illustration of Example 2.4(2). Each fiber over
 $ z \in Z $
is a copy of
$ z \in Z $
is a copy of
 $ Y $
, aside from the fiber at
$ Y $
, aside from the fiber at
 $ \infty \in Z $
, which is a singleton (this is pictured as the middle fiber). The picture is meant to depict how the singleton is connected to nearby fibers topologically.
$ \infty \in Z $
, which is a singleton (this is pictured as the middle fiber). The picture is meant to depict how the singleton is connected to nearby fibers topologically.
The following is [Reference Herstedt11, Theorem 2.2]. By an A
![]() $\mathbb {T} $
-algebra, we mean a
$\mathbb {T} $
-algebra, we mean a
![]() $ C^* $
-algebra that is the direct limit of ‘circle algebras’. By ‘circle algebra’, we mean an algebra isomorphic to a finite direct sum of matrices and matrices over
$ C^* $
-algebra that is the direct limit of ‘circle algebras’. By ‘circle algebra’, we mean an algebra isomorphic to a finite direct sum of matrices and matrices over
![]() $ C ( S^1 ) $
.
$ C ( S^1 ) $
.
Theorem 2.5. Let
![]() $ ( X , h , Z ) $
be a fiberwise essentially minimal zero-dimensional system. Then
$ ( X , h , Z ) $
be a fiberwise essentially minimal zero-dimensional system. Then
![]() $ C^* ( \mathbb {Z} , X , h ) $
is an A
$ C^* ( \mathbb {Z} , X , h ) $
is an A
![]() $\mathbb {T}$
-algebra.
$\mathbb {T}$
-algebra.
The following is a consequence of the proof of Theorem 2.5 that will be useful later on.
Corollary 2.6. Let
![]() $ ( X , h , Z ) $
be a fiberwise essentially minimal zero-dimensional system, let
$ ( X , h , Z ) $
be a fiberwise essentially minimal zero-dimensional system, let
![]() $ \mathcal {P} $
be a partition of
$ \mathcal {P} $
be a partition of
![]() $ X $
, let
$ X $
, let
![]() $ a_1 , \ldots , a_n \in C^* ( \mathbb {Z} , X , h ) $
, and let
$ a_1 , \ldots , a_n \in C^* ( \mathbb {Z} , X , h ) $
, and let
![]() $ \varepsilon> 0 $
. Then there is a circle algebra
$ \varepsilon> 0 $
. Then there is a circle algebra
![]() $ A \subset C^* ( \mathbb {Z} , X , h ) $
and a partition
$ A \subset C^* ( \mathbb {Z} , X , h ) $
and a partition
![]() $ \mathcal {P}' $
of
$ \mathcal {P}' $
of
![]() $ X $
that is finer than
$ X $
that is finer than
![]() $ \mathcal {P} $
such that we have the following.
$ \mathcal {P} $
such that we have the following.
-
(1) The diagonal matrices of
 $ A $
are
$ A $
are
 $ C ( \mathcal {P}' ) $
.
$ C ( \mathcal {P}' ) $
. -
(2) For each
 $ k \in \{ 1 , \ldots , n \} $
, there is a
$ k \in \{ 1 , \ldots , n \} $
, there is a
 $ b_k \in A $
such that
$ b_k \in A $
such that
 $ \| a_k - b_k \| < \varepsilon $
.
$ \| a_k - b_k \| < \varepsilon $
.
On its own, Theorem 2.5 gives us a reason to study fiberwise essentially minimal zero-dimensional systems in the context of operator algebras, as A
![]() $\mathbb {T}$
-algebras are
$\mathbb {T}$
-algebras are
![]() $ C^* $
-algebras with very nice structure. If the following conjecture holds, then fiberwise essentially minimality plays a very important role in the structure of zero-dimensional dynamical systems.
$ C^* $
-algebras with very nice structure. If the following conjecture holds, then fiberwise essentially minimality plays a very important role in the structure of zero-dimensional dynamical systems.
Conjecture 2.7. Let
![]() $ ( X , h ) $
be a zero-dimensional system. Then
$ ( X , h ) $
be a zero-dimensional system. Then
![]() $ C^* ( \mathbb {Z} , X , h ) $
is an A
$ C^* ( \mathbb {Z} , X , h ) $
is an A
![]() $\mathbb {T}$
-algebra if and only if
$\mathbb {T}$
-algebra if and only if
![]() $ ( X , h ) $
is fiberwise essentially minimal.
$ ( X , h ) $
is fiberwise essentially minimal.
What Conjecture 2.7 would imply is that there is something unique about the structure of fiberwise essentially minimal zero-dimensional systems that gives rise to the nicest possible direct limit structure. If this is true, there is something very likely unique and inherent about the dynamical systems themselves that is worth studying. It will also likely have many consequences in the future of non-simple
![]() $ C^*$
-algebra classification, as this direct limit structure (and lack thereof) tells us a lot about the
$ C^*$
-algebra classification, as this direct limit structure (and lack thereof) tells us a lot about the
![]() $ K $
-theory of the crossed product
$ K $
-theory of the crossed product
![]() $ C^* $
-algebra.
$ C^* $
-algebra.
Without specifying all of the details, there is ample evidence in the literature for the validity of Conjecture 2.7. One direction is clear from Theorem 2.5. For the other direction, one can prove that if
![]() $ C^* ( \mathbb {Z} , X , h ) $
has stable rank one (which is a consequence of being A
$ C^* ( \mathbb {Z} , X , h ) $
has stable rank one (which is a consequence of being A
![]() $\mathbb {T}$
), then all orbit closures of
$\mathbb {T}$
), then all orbit closures of
![]() $ ( X , h )$
are essentially minimal. Although this is being stated without proof, [Reference Putnam17, Theorem 3.1] tells us that if an orbit closure has at least two minimal sets, then the crossed product cannot have stable rank one. More results in this direction are in [Reference Bezuglyi, Niu and Sun3], which closely examines what happens to Cantor systems when one has multiple minimal sets in a single orbit closure. Since one can show that minimal orbit closures imply fiberwise essential minimality (Example 2.4(1)), it is not hard to believe that essentially minimal orbit closures also imply fiberwise essential minimality.
$ ( X , h )$
are essentially minimal. Although this is being stated without proof, [Reference Putnam17, Theorem 3.1] tells us that if an orbit closure has at least two minimal sets, then the crossed product cannot have stable rank one. More results in this direction are in [Reference Bezuglyi, Niu and Sun3], which closely examines what happens to Cantor systems when one has multiple minimal sets in a single orbit closure. Since one can show that minimal orbit closures imply fiberwise essential minimality (Example 2.4(1)), it is not hard to believe that essentially minimal orbit closures also imply fiberwise essential minimality.
We now introduce the concepts important to the dynamical side of the discussion in this paper. Let
![]() $ ( X_1 , h_1 ) $
and
$ ( X_1 , h_1 ) $
and
![]() $ ( X_2 , h_2 ) $
be dynamical systems. By an orbit map, we mean a homeomorphism
$ ( X_2 , h_2 ) $
be dynamical systems. By an orbit map, we mean a homeomorphism
![]() $ F : X_1 \to X_2 $
such that for all
$ F : X_1 \to X_2 $
such that for all
![]() $ x \in X_1 $
, we have
$ x \in X_1 $
, we have
![]() $ F ( \text {orb}_{ h_1 } ( x ) ) = \text {orb}_{ h_2 } ( F ( x ) ) $
, where
$ F ( \text {orb}_{ h_1 } ( x ) ) = \text {orb}_{ h_2 } ( F ( x ) ) $
, where
![]() $ \text {orb}_{ h_1 } ( x ) $
denotes the
$ \text {orb}_{ h_1 } ( x ) $
denotes the
![]() $ h_1 $
-orbit of
$ h_1 $
-orbit of
![]() $ x $
(and likewise for
$ x $
(and likewise for
![]() $ \text {orb}_{ h_2 } $
). We say that
$ \text {orb}_{ h_2 } $
). We say that
![]() $ ( X_1 , h_1 ) $
and
$ ( X_1 , h_1 ) $
and
![]() $ ( X_2 , h_2 ) $
are orbit equivalent if there exists such an
$ ( X_2 , h_2 ) $
are orbit equivalent if there exists such an
![]() $ F $
. If the orbit map satisfies
$ F $
. If the orbit map satisfies
![]() $ F \circ h_1 = h_2 \circ F $
, we say that
$ F \circ h_1 = h_2 \circ F $
, we say that
![]() $ ( X_1 , h_1 ) $
and
$ ( X_1 , h_1 ) $
and
![]() $ ( X_2 , h_2 ) $
are conjugate.
$ ( X_2 , h_2 ) $
are conjugate.
Definition 2.8. Let
![]() $ ( X_1 , h_1 ) $
and
$ ( X_1 , h_1 ) $
and
![]() $ ( X_2 , h_2 ) $
be dynamical systems and let
$ ( X_2 , h_2 ) $
be dynamical systems and let
![]() $ F : X_1 \to X_2 $
be an orbit map. Then there are functions
$ F : X_1 \to X_2 $
be an orbit map. Then there are functions
![]() $ \beta , \gamma : X_1 \to \mathbb {Z} $
, called orbit cocycles, that satisfy
$ \beta , \gamma : X_1 \to \mathbb {Z} $
, called orbit cocycles, that satisfy
![]() $ ( F \circ h_1^{ \beta ( x ) } ) ( x ) = ( h_2 \circ F ) ( x ) $
and
$ ( F \circ h_1^{ \beta ( x ) } ) ( x ) = ( h_2 \circ F ) ( x ) $
and
![]() $ ( h_2^{ \gamma ( x ) } \circ F ) ( x ) = ( F \circ h_1 ) ( x ) $
.
$ ( h_2^{ \gamma ( x ) } \circ F ) ( x ) = ( F \circ h_1 ) ( x ) $
.
The following is a generalization of [Reference Giordano, Putnam and Skau9, Definition 1.3] from the minimal case to the fiberwise essentially minimal case (to see this, simply take
![]() $ Z $
below to be a singleton). When we consider orbit maps between
$ Z $
below to be a singleton). When we consider orbit maps between
![]() $ ( X_1 , h_1 , Z_1 ) $
and
$ ( X_1 , h_1 , Z_1 ) $
and
![]() $ ( X_2 , h_2 , Z_2 ) $
for closed sets
$ ( X_2 , h_2 , Z_2 ) $
for closed sets
![]() $ Z_1 \subset X_1 $
and
$ Z_1 \subset X_1 $
and
![]() $ Z_2 \subset X_2 $
, we require that
$ Z_2 \subset X_2 $
, we require that
![]() $ F ( Z_1 ) = Z_2 $
.
$ F ( Z_1 ) = Z_2 $
.
Definition 2.9. Let
![]() $ ( X_1 , h_1 , Z_1 ) $
and
$ ( X_1 , h_1 , Z_1 ) $
and
![]() $ ( X_2 , h_2 , Z_2 ) $
be fiberwise essentially minimal zero-dimensional systems. We say that
$ ( X_2 , h_2 , Z_2 ) $
be fiberwise essentially minimal zero-dimensional systems. We say that
![]() $ ( X_1 , h_1 , Z_1 ) $
and
$ ( X_1 , h_1 , Z_1 ) $
and
![]() $ ( X_2 , h_2 , Z_2 ) $
are strong orbit equivalent if there is an orbit map
$ ( X_2 , h_2 , Z_2 ) $
are strong orbit equivalent if there is an orbit map
![]() $ F : X_1 \to X_2 $
such that the orbit cocycles
$ F : X_1 \to X_2 $
such that the orbit cocycles
![]() $ \beta , \gamma : X_1 \to \mathbb {Z} $
are continuous on
$ \beta , \gamma : X_1 \to \mathbb {Z} $
are continuous on
![]() $ X_1 \setminus Z_1 $
.
$ X_1 \setminus Z_1 $
.
3 K-theory
In this section, we discuss the
![]() $ K $
-theory of the crossed products associated to fiberwise essentially minimal zero-dimensional systems. The
$ K $
-theory of the crossed products associated to fiberwise essentially minimal zero-dimensional systems. The
![]() $ K $
-theory of operator algebras has an ordered group (defined below) of equivalence classes of projections,
$ K $
-theory of operator algebras has an ordered group (defined below) of equivalence classes of projections,
![]() $ ( K_0, K_0^+ ) $
, and a group of equivalence classes of unitaries,
$ ( K_0, K_0^+ ) $
, and a group of equivalence classes of unitaries,
![]() $ K_1 $
.
$ K_1 $
.
![]() $ K $
-theory is a classifying invariant for
$ K $
-theory is a classifying invariant for
![]() $ C^* $
-algebras in sufficiently nice cases (being an A
$ C^* $
-algebras in sufficiently nice cases (being an A
![]() $\mathbb {T}$
-algebra is sufficient). For a general reference on
$\mathbb {T}$
-algebra is sufficient). For a general reference on
![]() $ K $
-theory of operator algebras, see [Reference Blackadar4]. For some references on work done in the minimal case, see [Reference Giordano, Putnam and Skau9, Reference Putnam17]. For a reference on work done in the essentially minimal case, see [Reference Herman, Putnam and Skau10].
$ K $
-theory of operator algebras, see [Reference Blackadar4]. For some references on work done in the minimal case, see [Reference Giordano, Putnam and Skau9, Reference Putnam17]. For a reference on work done in the essentially minimal case, see [Reference Herman, Putnam and Skau10].
Definition 3.1. An ordered group is a pair
![]() $ ( G , G^+ ) $
, where
$ ( G , G^+ ) $
, where
![]() $ G $
is a countable abelian group and
$ G $
is a countable abelian group and
![]() $ G^+ $
is a subset of
$ G^+ $
is a subset of
![]() $ G $
, called the positive cone, that satisfies the following:
$ G $
, called the positive cone, that satisfies the following:
-
(1) for all
 $ g_1 , g_2 \in G^+ $
, we have
$ g_1 , g_2 \in G^+ $
, we have
 $ g_1 + g_2 \in G^+ $
;
$ g_1 + g_2 \in G^+ $
; -
(2) for all
 $ g \in G $
, there are
$ g \in G $
, there are
 $ g_1 , g_2 \in G^+ $
such that
$ g_1 , g_2 \in G^+ $
such that
 $ g = g_1 - g_2 $
;
$ g = g_1 - g_2 $
; -
(3) the identity of
 $ G $
is the only element in both
$ G $
is the only element in both
 $ G^+ $
and
$ G^+ $
and
 $ -G^+ $
.
$ -G^+ $
.
We call
![]() $ e \in G^+ $
an order unit if for all
$ e \in G^+ $
an order unit if for all
![]() $ g \in G^+ $
, there is some
$ g \in G^+ $
, there is some
![]() $ n \in \mathbb {Z}_{> 0 } $
such that
$ n \in \mathbb {Z}_{> 0 } $
such that
![]() $ n e - g \in G^+ $
.
$ n e - g \in G^+ $
.
Given an ordered group
![]() $ ( G , G^+ ) $
, we may write
$ ( G , G^+ ) $
, we may write
![]() $ g \geq 0 $
to denote
$ g \geq 0 $
to denote
![]() $ g \in G^+ $
. The notation
$ g \in G^+ $
. The notation
![]() $ g_1 \geq g_2 $
means that
$ g_1 \geq g_2 $
means that
![]() $ g_1 - g_2 \in G^+ $
. By a homomorphism of ordered groups
$ g_1 - g_2 \in G^+ $
. By a homomorphism of ordered groups
![]() $ ( G_1 , G_1^+ ) $
and
$ ( G_1 , G_1^+ ) $
and
![]() $ ( G_2 , G_2^+ ) $
, we mean a homomorphism of groups
$ ( G_2 , G_2^+ ) $
, we mean a homomorphism of groups
![]() $ \varphi : G_1 \to G_2 $
such that
$ \varphi : G_1 \to G_2 $
such that
![]() $ \varphi ( G_1^+ ) \subset G_2^+ $
.
$ \varphi ( G_1^+ ) \subset G_2^+ $
.
When we fix a particular order unit
![]() $ e \in G^+ $
, we may write the triple
$ e \in G^+ $
, we may write the triple
![]() $ ( G , G^+ , e ) $
and call this an ordered group with distinguished order unit. By a homomorphism of ordered groups with distinguished order units
$ ( G , G^+ , e ) $
and call this an ordered group with distinguished order unit. By a homomorphism of ordered groups with distinguished order units
![]() $ ( G_1 , G_1^+ , e_1 ) $
and
$ ( G_1 , G_1^+ , e_1 ) $
and
![]() $ ( G_2 , G_2^+ , e_2 ) $
, we mean a homomorphism of ordered groups
$ ( G_2 , G_2^+ , e_2 ) $
, we mean a homomorphism of ordered groups
![]() $ \varphi : G_1 \to G_2 $
such that
$ \varphi : G_1 \to G_2 $
such that
![]() $ \varphi ( e_1 ) = e_2 $
.
$ \varphi ( e_1 ) = e_2 $
.
We introduce notation important to the following proposition, which is [Reference Herstedt11, Proposition 2.2], and a direct consequence of [Reference Pimsner and Voiculescu14, Theorem 2.4]. Let
![]() $ \mathcal {T} $
denote the Toeplitz algebra, the universal
$ \mathcal {T} $
denote the Toeplitz algebra, the universal
![]() $ C^* $
-algebra generated by a single isometry
$ C^* $
-algebra generated by a single isometry
![]() $ s $
. Let
$ s $
. Let
![]() $ \mathcal {K} $
denote the
$ \mathcal {K} $
denote the
![]() $ C^* $
-algebra of compact operators on a separable Hilbert space. Let
$ C^* $
-algebra of compact operators on a separable Hilbert space. Let
![]() $ A $
be a unital
$ A $
be a unital
![]() $ C^* $
-algebra and let
$ C^* $
-algebra and let
![]() $ \alpha $
be an automorphism of
$ \alpha $
be an automorphism of
![]() $ A $
, and let
$ A $
, and let
![]() $ u $
be the standard unitary of
$ u $
be the standard unitary of
![]() $ C^*( \mathbb {Z} , A , \alpha ) $
. We denote by
$ C^*( \mathbb {Z} , A , \alpha ) $
. We denote by
![]() $ \mathcal {T} ( A , \alpha ) $
the Toeplitz extension of
$ \mathcal {T} ( A , \alpha ) $
the Toeplitz extension of
![]() $ A $
by
$ A $
by
![]() $ \alpha $
, which is the subalgebra of
$ \alpha $
, which is the subalgebra of
![]() $ C^* ( \mathbb {Z} , A , \alpha ) \otimes \mathcal {T} $
generated by
$ C^* ( \mathbb {Z} , A , \alpha ) \otimes \mathcal {T} $
generated by
![]() $ A \otimes 1 $
and
$ A \otimes 1 $
and
![]() $ u \otimes s $
. The ideal generated by
$ u \otimes s $
. The ideal generated by
![]() $ A \otimes ( 1 - s s^* ) $
is isomorphic to
$ A \otimes ( 1 - s s^* ) $
is isomorphic to
![]() $ A \otimes \mathcal {K} $
, and the quotient by this ideal is isomorphic to
$ A \otimes \mathcal {K} $
, and the quotient by this ideal is isomorphic to
![]() $ C^* ( \mathbb {Z} , A , \alpha ) $
.
$ C^* ( \mathbb {Z} , A , \alpha ) $
.
Proposition 3.2. Let
![]() $ ( X , h ) $
be a zero-dimensional system. Let
$ ( X , h ) $
be a zero-dimensional system. Let
![]() $ \alpha $
be the automorphism of
$ \alpha $
be the automorphism of
![]() $ C ( X ) $
induced by
$ C ( X ) $
induced by
![]() $ h $
; that is,
$ h $
; that is,
![]() $ \alpha $
is defined by
$ \alpha $
is defined by
![]() $ \alpha ( f ) ( x ) = f ( h^{ -1 } ( x ) ) $
for all
$ \alpha ( f ) ( x ) = f ( h^{ -1 } ( x ) ) $
for all
![]() $ f \in C ( X ) $
and all
$ f \in C ( X ) $
and all
![]() $ x \in X $
. Let
$ x \in X $
. Let
![]() $ \delta $
be the connecting map obtained from the exact sequence
$ \delta $
be the connecting map obtained from the exact sequence
where
![]() $ K_0 ( C ( X ) \otimes \mathcal {K} ) $
is identified with
$ K_0 ( C ( X ) \otimes \mathcal {K} ) $
is identified with
![]() $ K_0 ( C ( X ) ) $
in the standard way. Let
$ K_0 ( C ( X ) ) $
in the standard way. Let
![]() $ i : C(X) \to C^* ( \mathbb {Z} , X , h ) $
be the natural inclusion. Then there is an exact sequence
$ i : C(X) \to C^* ( \mathbb {Z} , X , h ) $
be the natural inclusion. Then there is an exact sequence
Proof. Since
![]() $ K_1 ( C ( X ) ) = 0 $
, this follows immediately from [Reference Pimsner and Voiculescu14, Theorem 2.4].
$ K_1 ( C ( X ) ) = 0 $
, this follows immediately from [Reference Pimsner and Voiculescu14, Theorem 2.4].
Note that
![]() $ K_0 ( C ( X ) ) \cong C ( X , \mathbb {Z} ) $
; we will use this identification throughout the paper. Let
$ K_0 ( C ( X ) ) \cong C ( X , \mathbb {Z} ) $
; we will use this identification throughout the paper. Let
![]() $ C ( X , \mathbb {Z} )^+ $
denote the subset of
$ C ( X , \mathbb {Z} )^+ $
denote the subset of
![]() $ C ( X , \mathbb {Z} ) $
consisting of
$ C ( X , \mathbb {Z} ) $
consisting of
![]() $ f $
such that
$ f $
such that
![]() $ f ( x ) \geq 0 $
for all
$ f ( x ) \geq 0 $
for all
![]() $ x \in X $
. Then it is easy to check that
$ x \in X $
. Then it is easy to check that
![]() $ ( C ( X , \mathbb {Z} ) , C ( X , \mathbb {Z} )^+ ) $
is an ordered group and the function
$ ( C ( X , \mathbb {Z} ) , C ( X , \mathbb {Z} )^+ ) $
is an ordered group and the function
![]() $ \chi _X $
is an order unit.
$ \chi _X $
is an order unit.
The following is closely related to [Reference Herman, Putnam and Skau10, Proposition 5.1]; although the hypotheses are broadened, the proof is essentially the same. Adopting the notation of Proposition 3.2, we denote
![]() $ K_0 ( C ( X ) ) / \text {im} ( \text {id} - \alpha _* ) $
by
$ K_0 ( C ( X ) ) / \text {im} ( \text {id} - \alpha _* ) $
by
![]() $ K^0 ( X , h ) $
.
$ K^0 ( X , h ) $
.
Proposition 3.3. Let
![]() $ ( X , h , Z ) $
be a fiberwise essentially minimal zero-dimensional system and adopt the notation of Proposition 3.2. Let
$ ( X , h , Z ) $
be a fiberwise essentially minimal zero-dimensional system and adopt the notation of Proposition 3.2. Let
![]() $ \pi : C ( X , \mathbb {Z} ) \to K^0 ( X , h ) $
denote the quotient map. Define
$ \pi : C ( X , \mathbb {Z} ) \to K^0 ( X , h ) $
denote the quotient map. Define
![]() $ K^0 ( X , h )^+ = \pi ( C ( X , \mathbb {Z} )^+ ) $
. Then
$ K^0 ( X , h )^+ = \pi ( C ( X , \mathbb {Z} )^+ ) $
. Then
![]() $ ( K^0 ( X , h ) , K^0 ( X , h )^+ , \pi ( 1 ) ) $
is an ordered group with distinguished order unit.
$ ( K^0 ( X , h ) , K^0 ( X , h )^+ , \pi ( 1 ) ) $
is an ordered group with distinguished order unit.
Proof. We check the conditions of Definition 3.1. Conditions (1) and (2) follow from surjectivity of
![]() $ \pi $
. For condition (3), let
$ \pi $
. For condition (3), let
![]() $ g \in K^0 ( X , h )^+ \cap -K^0 ( X , h )^+ $
. This means that there is
$ g \in K^0 ( X , h )^+ \cap -K^0 ( X , h )^+ $
. This means that there is
![]() $ f_1 \in C ( X , \mathbb {Z} )^+ $
such that
$ f_1 \in C ( X , \mathbb {Z} )^+ $
such that
![]() $ \pi ( f_1 ) = g $
and
$ \pi ( f_1 ) = g $
and
![]() $ f_2 \in C ( X , \mathbb {Z} )^+ $
such that
$ f_2 \in C ( X , \mathbb {Z} )^+ $
such that
![]() $ \pi ( - f_2 ) = g $
. However, then
$ \pi ( - f_2 ) = g $
. However, then
![]() $ \pi ( f_1 + f_2 ) = 0 $
and so
$ \pi ( f_1 + f_2 ) = 0 $
and so
![]() $ f_1 + f_2 \in \text {im} ( \text {id} - \alpha _* ) $
. Let
$ f_1 + f_2 \in \text {im} ( \text {id} - \alpha _* ) $
. Let
![]() $ f \in C ( X , \mathbb {Z} ) $
satisfy
$ f \in C ( X , \mathbb {Z} ) $
satisfy
![]() $ f - \alpha _* ( f ) = f_1 + f_2 $
. Let
$ f - \alpha _* ( f ) = f_1 + f_2 $
. Let
![]() $ E = f^{ -1 } ( \max _{ x \in X } f ( x ) ) $
. Since
$ E = f^{ -1 } ( \max _{ x \in X } f ( x ) ) $
. Since
![]() $ f - \alpha _* ( f ) \geq 0 $
, we must have
$ f - \alpha _* ( f ) \geq 0 $
, we must have
![]() $ h ( E ) \subset E $
. Let
$ h ( E ) \subset E $
. Let
![]() $ \psi $
be as in Definition 2.2 and let
$ \psi $
be as in Definition 2.2 and let
![]() $ z \in \psi ( E ) $
and define
$ z \in \psi ( E ) $
and define
![]() $ E_z = E \cap \psi ^{ -1 } ( z ) $
. Since
$ E_z = E \cap \psi ^{ -1 } ( z ) $
. Since
![]() $ h ( E_z ) \subset E_z $
,
$ h ( E_z ) \subset E_z $
,
![]() $ E_z $
is invariant so must intersect the minimal set. However, then by [Reference Herman, Putnam and Skau10, Theorem 1.1], since
$ E_z $
is invariant so must intersect the minimal set. However, then by [Reference Herman, Putnam and Skau10, Theorem 1.1], since
![]() $E_z\neq \varnothing $
, we have
$E_z\neq \varnothing $
, we have
![]() $ \bigcup _{ n \in \mathbb {Z}_{ \geq 0 } } h^n ( E_z ) = \psi ^{ -1 } ( z ) $
, and so
$ \bigcup _{ n \in \mathbb {Z}_{ \geq 0 } } h^n ( E_z ) = \psi ^{ -1 } ( z ) $
, and so
![]() $ E_z = \psi ^{ -1 } ( z ) $
. Since this holds for all
$ E_z = \psi ^{ -1 } ( z ) $
. Since this holds for all
![]() $ z \in \psi ( E ) $
, we see that
$ z \in \psi ( E ) $
, we see that
![]() $ f $
is constant on
$ f $
is constant on
![]() $ \psi ^{ -1 } ( z ) $
for all
$ \psi ^{ -1 } ( z ) $
for all
![]() $ z \in Z $
. Since
$ z \in Z $
. Since
![]() $ \psi ^{ - 1 } ( z ) $
is invariant for all
$ \psi ^{ - 1 } ( z ) $
is invariant for all
![]() $z\in Z$
, we must have
$z\in Z$
, we must have
![]() $ f = \alpha _* ( f ) $
, and so
$ f = \alpha _* ( f ) $
, and so
![]() $ f_1 + f_2 = 0 $
, and since
$ f_1 + f_2 = 0 $
, and since
![]() $ f_1 , f_2 \geq 0 $
, we see
$ f_1 , f_2 \geq 0 $
, we see
![]() $ f_1 = f_2 = 0 $
, and finally we see
$ f_1 = f_2 = 0 $
, and finally we see
![]() $ g = 0 $
. This proves condition (3).
$ g = 0 $
. This proves condition (3).
Finally, the fact that
![]() $ \pi ( 1 ) $
is an order unit is also clear from the surjectivity of
$ \pi ( 1 ) $
is an order unit is also clear from the surjectivity of
![]() $ \pi $
.
$ \pi $
.
Theorem 3.4. Let
![]() $ ( X , h ) $
be a zero-dimensional system. Then adopting the notation of Proposition 3.2, we have
$ ( X , h ) $
be a zero-dimensional system. Then adopting the notation of Proposition 3.2, we have
![]() $ ( K_0 ( C^* ( \mathbb {Z} , X , h ) ) , K_0 ( C^* ( \mathbb {Z} , X , h ) )^+ , 1 ) \cong ( K^0 ( X , h ) , K^0 ( X , h )^+ , 1 ) $
.
$ ( K_0 ( C^* ( \mathbb {Z} , X , h ) ) , K_0 ( C^* ( \mathbb {Z} , X , h ) )^+ , 1 ) \cong ( K^0 ( X , h ) , K^0 ( X , h )^+ , 1 ) $
.
Proof. Since
![]() $ \ker ( i_* ) = \text {im} ( \text {id} - \alpha _* ) $
, and since
$ \ker ( i_* ) = \text {im} ( \text {id} - \alpha _* ) $
, and since
![]() $ i : C ( X ) \to C^* ( \mathbb {Z} , X , h ) $
is the natural inclusion, the map
$ i : C ( X ) \to C^* ( \mathbb {Z} , X , h ) $
is the natural inclusion, the map
![]() $ i_* $
induces a map
$ i_* $
induces a map
![]() $ \varphi : K^0 ( X , h ) \to K_0 ( C^* ( \mathbb {Z} , X , h ) ) $
which is an isomorphism of groups and satisfies
$ \varphi : K^0 ( X , h ) \to K_0 ( C^* ( \mathbb {Z} , X , h ) ) $
which is an isomorphism of groups and satisfies
![]() $ K^0 ( X , h )^+ \subset K_0 ( C^* ( \mathbb {Z} , X , h ) )^+ $
.
$ K^0 ( X , h )^+ \subset K_0 ( C^* ( \mathbb {Z} , X , h ) )^+ $
.
Let
![]() $ p \in C^* ( \mathbb {Z} , X , h ) $
be a projection. By applying Corollary 2.6 with
$ p \in C^* ( \mathbb {Z} , X , h ) $
be a projection. By applying Corollary 2.6 with
![]() $ a_1 = p $
and
$ a_1 = p $
and
![]() $ \varepsilon = 1/2 $
,
$ \varepsilon = 1/2 $
,
![]() $ p $
is unitarily equivalent to
$ p $
is unitarily equivalent to
![]() $ \chi _U $
for some compact open
$ \chi _U $
for some compact open
![]() $ U \subset X $
. Let
$ U \subset X $
. Let
![]() $ q $
be the image of
$ q $
be the image of
![]() $ \chi _U $
under the quotient map
$ \chi _U $
under the quotient map
![]() $ C ( X ) \to C ( X ) / \text {im} ( \text {id} - \alpha ) $
. Then
$ C ( X ) \to C ( X ) / \text {im} ( \text {id} - \alpha ) $
. Then
![]() $ [ \varphi ( q ) ] = [ \chi _U ] = [ p ] $
. Repeating this argument for
$ [ \varphi ( q ) ] = [ \chi _U ] = [ p ] $
. Repeating this argument for
![]() $ M_n ( C^* ( \mathbb {Z} , X , h ) ) $
, we see that
$ M_n ( C^* ( \mathbb {Z} , X , h ) ) $
, we see that
![]() $ K_0 ( C^* ( \mathbb {Z} , X , h ) )^+ \subset K^0 ( X , h )^+ $
.
$ K_0 ( C^* ( \mathbb {Z} , X , h ) )^+ \subset K^0 ( X , h )^+ $
.
Finally, that
![]() $ \varphi ( 1 ) = 1 $
is clear, proving the theorem.
$ \varphi ( 1 ) = 1 $
is clear, proving the theorem.
What we have also shown in the previous proof is the following.
Corollary 3.5. Let
![]() $ ( X , h , Z ) $
be a fiberwise essentially minimal zero-dimensional system. Let
$ ( X , h , Z ) $
be a fiberwise essentially minimal zero-dimensional system. Let
![]() $ i : C ( X ) \to C^* ( \mathbb {Z} , X , h ) $
denote the canonical inclusion. Then the induced map
$ i : C ( X ) \to C^* ( \mathbb {Z} , X , h ) $
denote the canonical inclusion. Then the induced map
![]() $ i_* : K_0 ( C ( X ) ) \to K_0 ( C^* ( \mathbb {Z} , X , h ) ) $
is surjective as a map between ordered groups.
$ i_* : K_0 ( C ( X ) ) \to K_0 ( C^* ( \mathbb {Z} , X , h ) ) $
is surjective as a map between ordered groups.
The following definition is from [Reference Poon15, §2], later studied in the minimal case in [Reference Putnam17]. These have been referred to as ‘large subalgebras’ in the literature. They are called large due to Theorem 3.9, as they capture the entire
![]() $ K_0 $
of the larger crossed product. Given a locally compact Hausdorff space
$ K_0 $
of the larger crossed product. Given a locally compact Hausdorff space
![]() $ X $
, we denote the continuous functions on
$ X $
, we denote the continuous functions on
![]() $ X $
that ‘vanish at infinity’ by
$ X $
that ‘vanish at infinity’ by
![]() $ C_0 ( X ) $
. More formally,
$ C_0 ( X ) $
. More formally,
![]() $ C_0 ( X ) $
is the
$ C_0 ( X ) $
is the
![]() $ C^* $
-algebraic closure of the continuous functions on
$ C^* $
-algebraic closure of the continuous functions on
![]() $ X $
with compact support.
$ X $
with compact support.
Definition 3.6. Let
![]() $ ( X , h , Z ) $
be a fiberwise essentially minimal zero-dimensional system. We define
$ ( X , h , Z ) $
be a fiberwise essentially minimal zero-dimensional system. We define
![]() $ A_Z $
to be the
$ A_Z $
to be the
![]() $ C^* $
-algebra generated by
$ C^* $
-algebra generated by
![]() $ C ( X ) $
and
$ C ( X ) $
and
![]() $ u C_0 ( X \setminus Z ) $
.
$ u C_0 ( X \setminus Z ) $
.
The following theorem is contained in [Reference Poon15, Theorem 2.3]. We provide a direct proof in our context for the reader, which helps give an idea of the AF structure of the large subalgebra.
Theorem 3.7. Let
![]() $ ( X , h , Z ) $
be a fiberwise essentially minimal zero-dimensional system. Then
$ ( X , h , Z ) $
be a fiberwise essentially minimal zero-dimensional system. Then
![]() $ A_Z $
is an AF-algebra.
$ A_Z $
is an AF-algebra.
Proof. Let
![]() $ ( \mathcal {P}^{ ( n ) } ) $
be a generating sequence of partitions of
$ ( \mathcal {P}^{ ( n ) } ) $
be a generating sequence of partitions of
![]() $ X $
. For each
$ X $
. For each
![]() $ n \in \mathbb {Z}_{> 0 } $
, we inductively define systems
$ n \in \mathbb {Z}_{> 0 } $
, we inductively define systems
![]() $ \mathcal {S}^{ ( n ) } = ( T^{ ( n ) } , ( X_t^{ ( n ) } ) , ( K_t^{ ( n ) } ) , ( Y_{ t , k }^{ ( n ) } ) , ( J_{ t , k }^{ ( n ) } ) ) $
of finite first return time maps. First, let
$ \mathcal {S}^{ ( n ) } = ( T^{ ( n ) } , ( X_t^{ ( n ) } ) , ( K_t^{ ( n ) } ) , ( Y_{ t , k }^{ ( n ) } ) , ( J_{ t , k }^{ ( n ) } ) ) $
of finite first return time maps. First, let
![]() $ \mathcal {S}^{ ( 1 ) } = ( T^{ ( 1 ) } , ( X_t^{ ( 1 ) } ) , ( K_t^{ ( 1 ) } ) , ( Y_{ t , k }^{ ( 1 ) } ) , ( J_{ t , k }^{ ( 1 ) } ) ) $
be any system of finite first return time maps subordinate to
$ \mathcal {S}^{ ( 1 ) } = ( T^{ ( 1 ) } , ( X_t^{ ( 1 ) } ) , ( K_t^{ ( 1 ) } ) , ( Y_{ t , k }^{ ( 1 ) } ) , ( J_{ t , k }^{ ( 1 ) } ) ) $
be any system of finite first return time maps subordinate to
![]() $ \mathcal {P}^{ ( n ) } $
such that
$ \mathcal {P}^{ ( n ) } $
such that
![]() $ \mathcal {P}_1 ( \mathcal {S}^{ ( 1 ) } ) $
is finer than
$ \mathcal {P}_1 ( \mathcal {S}^{ ( 1 ) } ) $
is finer than
![]() $ \mathcal {P}^{ ( 1 ) } $
and such that
$ \mathcal {P}^{ ( 1 ) } $
and such that
![]() $ \bigsqcup _{ t = 1 }^{ T^{ ( 1 ) } } X_t^{ ( 1 ) } \supset Z $
(the former is possible by [Reference Herstedt11, Proposition 1.13] and the latter is possible by [Reference Herstedt11, Lemma 4.12]). Now, let
$ \bigsqcup _{ t = 1 }^{ T^{ ( 1 ) } } X_t^{ ( 1 ) } \supset Z $
(the former is possible by [Reference Herstedt11, Proposition 1.13] and the latter is possible by [Reference Herstedt11, Lemma 4.12]). Now, let
![]() $ n \in \mathbb {Z}_{> 0 } $
and suppose we have chosen
$ n \in \mathbb {Z}_{> 0 } $
and suppose we have chosen
![]() $ \mathcal {S}^{ ( n ) } = ( T^{ ( n ) } , ( X_t^{ ( n ) } ) , ( K_t^{ ( n ) } ) , ( Y_{ t , k }^{ ( n ) } ) , ( J_{ t , k }^{ ( n ) } ) ) $
. Let
$ \mathcal {S}^{ ( n ) } = ( T^{ ( n ) } , ( X_t^{ ( n ) } ) , ( K_t^{ ( n ) } ) , ( Y_{ t , k }^{ ( n ) } ) , ( J_{ t , k }^{ ( n ) } ) ) $
. Let
![]() $ \mathcal {S}^{ ( n + 1 ) } = ( T^{ ( n + 1 ) } , ( X_t^{ ( n + 1 ) } ) , ( K_t^{ ( n + 1 ) } ) , ( Y_{ t , k }^{ ( n + 1 ) } ) , ( J_{ t , k }^{ ( n + 1 ) } ) ) $
be any system of finite first return time maps subordinate to
$ \mathcal {S}^{ ( n + 1 ) } = ( T^{ ( n + 1 ) } , ( X_t^{ ( n + 1 ) } ) , ( K_t^{ ( n + 1 ) } ) , ( Y_{ t , k }^{ ( n + 1 ) } ) , ( J_{ t , k }^{ ( n + 1 ) } ) ) $
be any system of finite first return time maps subordinate to
![]() $ \mathcal {P}^{ ( n + 1 ) } $
such that
$ \mathcal {P}^{ ( n + 1 ) } $
such that
![]() $ \mathcal {P}_1 ( \mathcal {S}^{ ( n + 1 ) } ) $
is finer than
$ \mathcal {P}_1 ( \mathcal {S}^{ ( n + 1 ) } ) $
is finer than
![]() $ \mathcal {P}^{ ( n + 1 ) } $
and finer than
$ \mathcal {P}^{ ( n + 1 ) } $
and finer than
![]() $ \mathcal {P}_1 ( \mathcal {S}^{ ( n ) } ) $
and such that
$ \mathcal {P}_1 ( \mathcal {S}^{ ( n ) } ) $
and such that
![]() $ \bigsqcup _{ t = 1 }^{ T^{ ( n + 1 ) } } X_t^{ ( n + 1 ) } \supset Z $
.
$ \bigsqcup _{ t = 1 }^{ T^{ ( n + 1 ) } } X_t^{ ( n + 1 ) } \supset Z $
.
Let
![]() $ n \in \mathbb {Z}_{> 0 } $
. Let
$ n \in \mathbb {Z}_{> 0 } $
. Let
![]() $ A^{ ( n ) } $
be the finite dimensional
$ A^{ ( n ) } $
be the finite dimensional
![]() $ C^* $
-subalgebra of
$ C^* $
-subalgebra of
![]() $ C^* ( \mathbb {Z} , X , h ) $
spanned by the matrix units
$ C^* ( \mathbb {Z} , X , h ) $
spanned by the matrix units
![]() $ u^{ i - j } \chi _{ h^j ( Y_{ t , k }^{ ( n ) } ) } $
for
$ u^{ i - j } \chi _{ h^j ( Y_{ t , k }^{ ( n ) } ) } $
for
![]() $ t \in \{ 1 , \ldots , T^{ ( n ) } \} $
,
$ t \in \{ 1 , \ldots , T^{ ( n ) } \} $
,
![]() $ k \in \{ 1 , \ldots , K_t^{ ( n ) } \} $
, and
$ k \in \{ 1 , \ldots , K_t^{ ( n ) } \} $
, and
![]() $ i , j \in \{ 0 , \ldots , J_{ t , k }^{ ( n ) } - 1 \} $
. We see
$ i , j \in \{ 0 , \ldots , J_{ t , k }^{ ( n ) } - 1 \} $
. We see
![]() $ A^{ ( n ) } \cong \bigoplus _{ t = 1 }^{ T^{ ( n ) } } \bigoplus _{ k = 1 }^{ K_t^{ ( n ) } } M_{ J_{ t , k }^{ ( n ) } } $
. Notice that
$ A^{ ( n ) } \cong \bigoplus _{ t = 1 }^{ T^{ ( n ) } } \bigoplus _{ k = 1 }^{ K_t^{ ( n ) } } M_{ J_{ t , k }^{ ( n ) } } $
. Notice that
![]() $ C ( \mathcal {P}_1 ( \mathcal {S}^{ ( n ) } ) ) \subset A^{ ( n ) } $
as the diagonal matrices. Set
$ C ( \mathcal {P}_1 ( \mathcal {S}^{ ( n ) } ) ) \subset A^{ ( n ) } $
as the diagonal matrices. Set
![]() $ Z^{ ( n ) } = \bigsqcup _{ t = 1 }^{ T^{ ( n + 1 ) } } X_t^{ ( n ) } $
and then notice that
$ Z^{ ( n ) } = \bigsqcup _{ t = 1 }^{ T^{ ( n + 1 ) } } X_t^{ ( n ) } $
and then notice that
![]() $ u C ( X \setminus Z^{ ( n ) } ) \subset A^{ ( n ) } $
as the superdiagonal matrices, so
$ u C ( X \setminus Z^{ ( n ) } ) \subset A^{ ( n ) } $
as the superdiagonal matrices, so
![]() $ A^{ ( n ) } $
is generated by
$ A^{ ( n ) } $
is generated by
![]() $ C ( \mathcal {P}_1 ( \mathcal {S}^{ ( n ) } ) ) $
and
$ C ( \mathcal {P}_1 ( \mathcal {S}^{ ( n ) } ) ) $
and
![]() $ u C ( X \setminus Z^{ ( n ) } ) $
.
$ u C ( X \setminus Z^{ ( n ) } ) $
.
Notice that
![]() $ A^{ ( n ) } \subset A^{ ( n + 1 ) } $
, so we get a directed system of finite dimensional
$ A^{ ( n ) } \subset A^{ ( n + 1 ) } $
, so we get a directed system of finite dimensional
![]() $ C^* $
-algebras, whose limit
$ C^* $
-algebras, whose limit
![]() $ A^{ ( \infty ) } $
contains
$ A^{ ( \infty ) } $
contains
![]() $ C ( X ) $
since
$ C ( X ) $
since
![]() $ ( \mathcal {P}_1 ( \mathcal {S}^{ ( n ) } ) ) $
is a generating sequence of partitions, and since
$ ( \mathcal {P}_1 ( \mathcal {S}^{ ( n ) } ) ) $
is a generating sequence of partitions, and since
![]() $ \bigcap _{ n = 1 }^\infty Z^{ ( n ) } = Z $
, we have
$ \bigcap _{ n = 1 }^\infty Z^{ ( n ) } = Z $
, we have
![]() $ u C ( X \setminus Z^{ ( n ) } ) \to u C_0 ( X \setminus Z ) \subset A_Z $
. It now clear that
$ u C ( X \setminus Z^{ ( n ) } ) \to u C_0 ( X \setminus Z ) \subset A_Z $
. It now clear that
![]() $ A^{ ( \infty ) } $
is generated by
$ A^{ ( \infty ) } $
is generated by
![]() $ C ( X ) $
and
$ C ( X ) $
and
![]() $ u C_0 ( X \setminus Z ) $
, and is therefore equal to
$ u C_0 ( X \setminus Z ) $
, and is therefore equal to
![]() $ A_Z $
.
$ A_Z $
.
The following is [Reference Putnam16, Lemma 4.2].
Lemma 3.8. Adopt the notation of Theorem 3.7 and its proof. Let
![]() $ p $
be a projection in
$ p $
be a projection in
![]() $ C ( X ) \cap A^{ ( n ) } $
and suppose that
$ C ( X ) \cap A^{ ( n ) } $
and suppose that
![]() $ p = 0 $
on
$ p = 0 $
on
![]() $ Z^{ ( n ) } $
. Then
$ Z^{ ( n ) } $
. Then
![]() $ \alpha ( p ) \in C ( X ) \cap A^{ ( n ) } $
and
$ \alpha ( p ) \in C ( X ) \cap A^{ ( n ) } $
and
![]() $ [ \alpha ( p ) ] = [ p ] $
in
$ [ \alpha ( p ) ] = [ p ] $
in
![]() $ K_0 ( A^{ ( n ) } ) $
.
$ K_0 ( A^{ ( n ) } ) $
.
We finally have the following theorem, which tells us enough about the
![]() $ K_0 $
structure of the crossed product to be able to prove Theorems 5.2 and 5.3. The proof follows that of [Reference Putnam16, Theorem 4.1].
$ K_0 $
structure of the crossed product to be able to prove Theorems 5.2 and 5.3. The proof follows that of [Reference Putnam16, Theorem 4.1].
Theorem 3.9. Let
![]() $ ( X , h , Z ) $
be a fiberwise essentially minimal zero-dimensional system. Then
$ ( X , h , Z ) $
be a fiberwise essentially minimal zero-dimensional system. Then
![]() $ K_0 ( A_Z ) \cong K_0 ( C^* ( \mathbb {Z} , X , h ) ) $
as ordered groups.
$ K_0 ( A_Z ) \cong K_0 ( C^* ( \mathbb {Z} , X , h ) ) $
as ordered groups.
Proof. Let
![]() $ i : A_Z \to C^* ( \mathbb {Z} , X , h ) $
denote the inclusion map, and let
$ i : A_Z \to C^* ( \mathbb {Z} , X , h ) $
denote the inclusion map, and let
![]() $ i_* : K_0 ( A_Z ) \to K_0 ( C^* ( \mathbb {Z} , X , h ) ) $
denote the map induced by
$ i_* : K_0 ( A_Z ) \to K_0 ( C^* ( \mathbb {Z} , X , h ) ) $
denote the map induced by
![]() $ i $
on
$ i $
on
![]() $ K_0 $
. Let
$ K_0 $
. Let
![]() $ i_1 : C ( X ) \to A_Z $
denote the canonical inclusion, let
$ i_1 : C ( X ) \to A_Z $
denote the canonical inclusion, let
![]() $ i_2 : C ( X ) \to C^* ( \mathbb {Z} , X , h ) $
denote the canonical inclusion, and let
$ i_2 : C ( X ) \to C^* ( \mathbb {Z} , X , h ) $
denote the canonical inclusion, and let
![]() $ ( i_1 )_* $
and
$ ( i_1 )_* $
and
![]() $ ( i_2 )_* $
denote the induced maps on
$ ( i_2 )_* $
denote the induced maps on
![]() $ K_0 $
. We then clearly have
$ K_0 $
. We then clearly have
![]() $ i \circ i_1 = i_2 $
. By Corollary 3.5,
$ i \circ i_1 = i_2 $
. By Corollary 3.5,
![]() $ ( i_2 )_* : K_0 ( C ( X ) ) \to K_0 ( C^* ( \mathbb {Z} , X , h ) ) $
is a surjective map between ordered groups, and therefore so is
$ ( i_2 )_* : K_0 ( C ( X ) ) \to K_0 ( C^* ( \mathbb {Z} , X , h ) ) $
is a surjective map between ordered groups, and therefore so is
![]() $ i^* $
.
$ i^* $
.
By Proposition 3.2,
![]() $ \ker ( ( i_2 )_* ) = \text {ran} ( \text {id} - \alpha _* ) $
. Thus, since
$ \ker ( ( i_2 )_* ) = \text {ran} ( \text {id} - \alpha _* ) $
. Thus, since
![]() $ ( i_2 )_* = ( i_1 )_* \circ i_* $
, we have
$ ( i_2 )_* = ( i_1 )_* \circ i_* $
, we have
![]() $ ( i_1 )_* ( \text {ran} ( \text {id} - \alpha _* ) ) \subset \ker ( i_* ) $
. Now suppose that
$ ( i_1 )_* ( \text {ran} ( \text {id} - \alpha _* ) ) \subset \ker ( i_* ) $
. Now suppose that
![]() $ a \in \ker ( i_* ) $
. Because
$ a \in \ker ( i_* ) $
. Because
![]() $ ( i_1 )_* $
is surjective, we can find
$ ( i_1 )_* $
is surjective, we can find
![]() $ g \in C ( X , \mathbb {Z} ) $
such that
$ g \in C ( X , \mathbb {Z} ) $
such that
![]() $ ( i_1 )_* ( g ) = a $
. Then
$ ( i_1 )_* ( g ) = a $
. Then
![]() $ ( i_2 )_* ( g ) = i_* ( a ) = 0 $
, so
$ ( i_2 )_* ( g ) = i_* ( a ) = 0 $
, so
![]() $ g \in \ker ( ( i_2 )_* ) = \text {ran} ( \text {id} - \alpha _* ) $
, so
$ g \in \ker ( ( i_2 )_* ) = \text {ran} ( \text {id} - \alpha _* ) $
, so
![]() $ a \in ( i_1 )_* ( \text {ran} ( \text {id} - \alpha _* ) ) $
. Altogether, we have
$ a \in ( i_1 )_* ( \text {ran} ( \text {id} - \alpha _* ) ) $
. Altogether, we have
Let
![]() $ ( \mathcal {P}^{ ( n ) } ) $
be a sequence of partitions, let
$ ( \mathcal {P}^{ ( n ) } ) $
be a sequence of partitions, let
![]() $ ( \mathcal {S}^{ ( n ) } ) $
be a sequence of systems of finite first return time maps, and let
$ ( \mathcal {S}^{ ( n ) } ) $
be a sequence of systems of finite first return time maps, and let
![]() $ ( A^{ ( n ) } ) $
be a sequence of subalgebras of
$ ( A^{ ( n ) } ) $
be a sequence of subalgebras of
![]() $ C^* ( \mathbb {Z} , X , h ) $
as in the proof of Theorem 3.7. We now claim that
$ C^* ( \mathbb {Z} , X , h ) $
as in the proof of Theorem 3.7. We now claim that
![]() $ ( i_1 )_* ( \text {ran} ( \text {id} - \alpha _* ) ) = 0 $
. Suppose
$ ( i_1 )_* ( \text {ran} ( \text {id} - \alpha _* ) ) = 0 $
. Suppose
![]() $ g_1 , g_2 \in C ( X , \mathbb {Z} ) $
satisfy
$ g_1 , g_2 \in C ( X , \mathbb {Z} ) $
satisfy
![]() $ g_1|_Z = g_2|_Z $
. Since
$ g_1|_Z = g_2|_Z $
. Since
![]() $ ( \mathcal {P}^{ ( n ) } ) $
is a generating sequence of partitions and for each
$ ( \mathcal {P}^{ ( n ) } ) $
is a generating sequence of partitions and for each
![]() $ n \in \mathbb {Z}_{> 0 } $
, we have
$ n \in \mathbb {Z}_{> 0 } $
, we have
![]() $ \mathcal {P}_1 ( \mathcal {S}^{ ( n ) } ) $
is finer than
$ \mathcal {P}_1 ( \mathcal {S}^{ ( n ) } ) $
is finer than
![]() $ \mathcal {P}^{ ( n ) } $
, there is some
$ \mathcal {P}^{ ( n ) } $
, there is some
![]() $ n \in \mathbb {Z}_{> 0 } $
such that
$ n \in \mathbb {Z}_{> 0 } $
such that
![]() $ g_1 , g_2 \in A^{ ( n ) } $
and such that
$ g_1 , g_2 \in A^{ ( n ) } $
and such that
![]() $ g_1|_{ Z^{ ( n ) } } = g_2|_{ Z^{ ( n ) } } $
(where
$ g_1|_{ Z^{ ( n ) } } = g_2|_{ Z^{ ( n ) } } $
(where
![]() $ Z^{ ( n ) } $
is defined in the proof of Theorem 3.7). So
$ Z^{ ( n ) } $
is defined in the proof of Theorem 3.7). So
![]() $ g_1 - g_2 $
is
$ g_1 - g_2 $
is
![]() $ 0 $
on
$ 0 $
on
![]() $ Z^{ ( n ) } $
, so we can write
$ Z^{ ( n ) } $
, so we can write
![]() $ g_1 - g_2 $
as a linear combination of projections in
$ g_1 - g_2 $
as a linear combination of projections in
![]() $ C ( X ) \cap A^{ ( n ) } $
each of which is zero on
$ C ( X ) \cap A^{ ( n ) } $
each of which is zero on
![]() $ Z^{ ( n ) } $
. So by Lemma 3.8, we have
$ Z^{ ( n ) } $
. So by Lemma 3.8, we have
![]() $ [ \alpha ( g_1 - g_2 ) ] = [ g_1 - g_2 ] $
in
$ [ \alpha ( g_1 - g_2 ) ] = [ g_1 - g_2 ] $
in
![]() $ K_0 ( A^{ ( n ) } ) $
, and so
$ K_0 ( A^{ ( n ) } ) $
, and so
![]() $ ( i_1 )_* ( g_1 - \alpha ( g_1 ) ) = ( i_1 )_* ( g_2 - \alpha ( g_2 ) ) $
in
$ ( i_1 )_* ( g_1 - \alpha ( g_1 ) ) = ( i_1 )_* ( g_2 - \alpha ( g_2 ) ) $
in
![]() $ K_0 ( A_Z ) $
.
$ K_0 ( A_Z ) $
.
So let
![]() $ g \in C ( X , \mathbb {Z} ) $
. Define
$ g \in C ( X , \mathbb {Z} ) $
. Define
![]() $ f \in C ( X , \mathbb {Z} ) $
by
$ f \in C ( X , \mathbb {Z} ) $
by
![]() $ f = g \circ \psi $
. Then
$ f = g \circ \psi $
. Then
![]() $ f|_Z = g|_Z $
, and so by the above paragraph, we have
$ f|_Z = g|_Z $
, and so by the above paragraph, we have
![]() $ ( i_1 )_* ( g - \alpha ( g ) ) = ( i_1 )_* ( f - \alpha ( f ) ) $
. However, then notice that
$ ( i_1 )_* ( g - \alpha ( g ) ) = ( i_1 )_* ( f - \alpha ( f ) ) $
. However, then notice that
![]() $ \alpha ( f ) = g \circ \psi \circ h^{ -1 } = g \circ \psi = f $
, and so
$ \alpha ( f ) = g \circ \psi \circ h^{ -1 } = g \circ \psi = f $
, and so
![]() $ ( i_1 )_* ( f - \alpha ( f ) ) = 0 $
. Thus, we have
$ ( i_1 )_* ( f - \alpha ( f ) ) = 0 $
. Thus, we have
![]() $ ( i_1 )_* ( \text {ran} ( \text {id} - \alpha _* ) )~=~0$
. Combining this with equation (3.1), we see
$ ( i_1 )_* ( \text {ran} ( \text {id} - \alpha _* ) )~=~0$
. Combining this with equation (3.1), we see
![]() $ \ker ( i_* ) = 0 $
. Altogether, we have shown that
$ \ker ( i_* ) = 0 $
. Altogether, we have shown that
![]() $ i_* $
is an isomorphism of ordered groups.
$ i_* $
is an isomorphism of ordered groups.
Theorem 3.10. Let
![]() $ ( X , h , Z ) $
be a fiberwise essentially minimal zero-dimensional system. Then
$ ( X , h , Z ) $
be a fiberwise essentially minimal zero-dimensional system. Then
![]() $ K_1 ( C^* ( \mathbb {Z} , X , h ) ) \cong C ( Z , \mathbb {Z} ) $
.
$ K_1 ( C^* ( \mathbb {Z} , X , h ) ) \cong C ( Z , \mathbb {Z} ) $
.
Proof. Adopt the notation of Proposition 3.2. Then
![]() $ K_1 ( C^* ( \mathbb {Z} , X , h ) ) \cong \ker ( \text {id} - \alpha _* ) $
. Identifying
$ K_1 ( C^* ( \mathbb {Z} , X , h ) ) \cong \ker ( \text {id} - \alpha _* ) $
. Identifying
![]() $ K_0 ( C ( X ) ) $
with
$ K_0 ( C ( X ) ) $
with
![]() $ C ( X , \mathbb {Z} ) $
, we may replace
$ C ( X , \mathbb {Z} ) $
, we may replace
![]() $ \alpha _* $
with
$ \alpha _* $
with
![]() $ \alpha $
.
$ \alpha $
.
Let
![]() $ f \in \ker ( \text {id} - \alpha ) $
and let
$ f \in \ker ( \text {id} - \alpha ) $
and let
![]() $ z \in Z $
. Suppose
$ z \in Z $
. Suppose
![]() $ f|_{ \psi ^{ -1 } ( z ) } $
is not constant. Then there is some
$ f|_{ \psi ^{ -1 } ( z ) } $
is not constant. Then there is some
![]() $ x \in \psi ^{ -1 } ( z ) $
such that
$ x \in \psi ^{ -1 } ( z ) $
such that
![]() $ f ( z ) \neq f ( x ) $
. Let
$ f ( z ) \neq f ( x ) $
. Let
![]() $ U $
be a compact open subset of
$ U $
be a compact open subset of
![]() $ \psi ^{ -1 } ( z ) $
such that
$ \psi ^{ -1 } ( z ) $
such that
![]() $ f ( U ) = f ( z ) $
. Since
$ f ( U ) = f ( z ) $
. Since
![]() $ ( \psi ^{ -1 } ( z ) , h|_{ \psi ^{ -1 } ( z ) } ) $
is an essentially minimal zero-dimensional system, by [Reference Herman, Putnam and Skau10, Theorem 1.1], there is an
$ ( \psi ^{ -1 } ( z ) , h|_{ \psi ^{ -1 } ( z ) } ) $
is an essentially minimal zero-dimensional system, by [Reference Herman, Putnam and Skau10, Theorem 1.1], there is an
![]() $ n \in \mathbb {Z}_{> 0 } $
such that
$ n \in \mathbb {Z}_{> 0 } $
such that
![]() $ x \in h^{ -n } ( U ) $
. Let
$ x \in h^{ -n } ( U ) $
. Let
![]() $ x' = h^{ n } ( x ) \in U $
. Then
$ x' = h^{ n } ( x ) \in U $
. Then
![]() $ f ( x' ) \neq f ( x ) = f ( h^{ -n } ( x' ) ) = \alpha ^n ( f ) ( x' ) $
, and so
$ f ( x' ) \neq f ( x ) = f ( h^{ -n } ( x' ) ) = \alpha ^n ( f ) ( x' ) $
, and so
![]() $ f \neq \alpha ^n ( f ) $
, and so
$ f \neq \alpha ^n ( f ) $
, and so
![]() $ f \neq \alpha ( f ) $
, which is a contradiction to
$ f \neq \alpha ( f ) $
, which is a contradiction to
![]() $ x \in \ker ( \text {id} - \alpha ) $
. Therefore,
$ x \in \ker ( \text {id} - \alpha ) $
. Therefore,
![]() $ f|_{ \psi ^{ -1 } ( z ) } $
is constant.
$ f|_{ \psi ^{ -1 } ( z ) } $
is constant.
Now suppose
![]() $ f \in C ( X , \mathbb {Z} ) $
and suppose
$ f \in C ( X , \mathbb {Z} ) $
and suppose
![]() $ f|_{ \psi ^{ -1 } ( z ) } $
is constant for each
$ f|_{ \psi ^{ -1 } ( z ) } $
is constant for each
![]() $ z \in Z $
. Then for each
$ z \in Z $
. Then for each
![]() $ x \in X $
, we have
$ x \in X $
, we have
![]() $ \alpha ( f ) ( x ) = f ( h^{ -1 } ( x ) ) = f ( \psi ( x ) ) = f ( x ) $
, and so
$ \alpha ( f ) ( x ) = f ( h^{ -1 } ( x ) ) = f ( \psi ( x ) ) = f ( x ) $
, and so
![]() $ f = \alpha ( f ) $
, and so
$ f = \alpha ( f ) $
, and so
![]() $ f \in \ker ( \text {id} - \alpha ) $
.
$ f \in \ker ( \text {id} - \alpha ) $
.
Thus, we have
as desired.
Corollary 3.11. Let
![]() $ ( X_1 , h_1 , Z_1 ) $
and
$ ( X_1 , h_1 , Z_1 ) $
and
![]() $ ( X_2 , h_2 , Z_2 ) $
be fiberwise essentially minimal zero-dimensional systems such that
$ ( X_2 , h_2 , Z_2 ) $
be fiberwise essentially minimal zero-dimensional systems such that
![]() $ C^*( \mathbb {Z} , X_1 , h_1 ) \cong C^* ( \mathbb {Z} , X_2 , h_2 ) $
. Then
$ C^*( \mathbb {Z} , X_1 , h_1 ) \cong C^* ( \mathbb {Z} , X_2 , h_2 ) $
. Then
![]() $ Z_1 \cong Z_2 $
.
$ Z_1 \cong Z_2 $
.
A consequence of Corollary 3.11 is that given a zero-dimensional system, all choices of
![]() $ Z $
that make it fiberwise essentially minimal are homeomorphic.
$ Z $
that make it fiberwise essentially minimal are homeomorphic.
4 Bratelli diagrams
In this section, we explore the construction of ordered Bratelli diagrams associated to fiberwise essentially minimal zero-dimensional systems. This correspondence is used to prove Theorem 5.2. For work done in the minimal case, see [Reference Bezuglyi, Kwiatkowski and Yassawi2, Reference Giordano, Putnam and Skau9]. For work done in the essentially minimal case, see [Reference Amini, Elliott and Golestani1, Reference Herman, Putnam and Skau10].
Definition 4.1. A Bratteli diagram
![]() $ B $
is a pair of sets
$ B $
is a pair of sets
![]() $ ( V , E ) $
such that we have the following.
$ ( V , E ) $
such that we have the following.
-
(1) The set
 $ V $
is called the set of vertices of
$ V $
is called the set of vertices of
 $ B $
. We can write
$ B $
. We can write
 $ V = \bigsqcup _{ n = 0 }^\infty V_n $
, where
$ V = \bigsqcup _{ n = 0 }^\infty V_n $
, where
 $ V_0 $
contains a single point
$ V_0 $
contains a single point
 $ v_0 $
and
$ v_0 $
and
 $ V_n $
is finite and non-empty for all
$ V_n $
is finite and non-empty for all
 $ n \in \mathbb {Z}_{ \geq 0 } $
. For each
$ n \in \mathbb {Z}_{ \geq 0 } $
. For each
 $ n \in \mathbb {Z}_{ \geq 0 } $
, we call
$ n \in \mathbb {Z}_{ \geq 0 } $
, we call
 $ V_n $
the set of vertices of
$ V_n $
the set of vertices of
 $ B $
at level
$ B $
at level
 $ n $
.
$ n $
. -
(2) The set
 $ E $
is called the set of edges of
$ E $
is called the set of edges of
 $ B $
. We can write
$ B $
. We can write
 $ E = \bigsqcup _{ n = 1 }^\infty E_n $
, where
$ E = \bigsqcup _{ n = 1 }^\infty E_n $
, where
 $ E_n $
is finite and non-empty for all
$ E_n $
is finite and non-empty for all
 $ n \in \mathbb {Z}_{> 0 } $
. For each
$ n \in \mathbb {Z}_{> 0 } $
. For each
 $ n \in \mathbb {Z}_{> 0 } $
, we call
$ n \in \mathbb {Z}_{> 0 } $
, we call
 $ E_n $
the set of edges at level
$ E_n $
the set of edges at level
 $ n $
.
$ n $
. -
(3) There are maps
 $ r , s : E \to V $
such that for
$ r , s : E \to V $
such that for
 $ n \in \mathbb {Z}_{> 0 } $
and
$ n \in \mathbb {Z}_{> 0 } $
and
 $ e \in E_n $
,
$ e \in E_n $
,
 $ s ( e ) \in V_{ n - 1 } $
and
$ s ( e ) \in V_{ n - 1 } $
and
 $ r ( e ) \in V_n $
. Moreover,
$ r ( e ) \in V_n $
. Moreover,
 $ r^{ -1 } ( v ) $
is non-empty for all
$ r^{ -1 } ( v ) $
is non-empty for all
 $ v \in V $
and
$ v \in V $
and
 $ s^{ -1 } ( v ) $
is non-empty for all
$ s^{ -1 } ( v ) $
is non-empty for all
 $ v \in V \setminus V_0 $
. The map
$ v \in V \setminus V_0 $
. The map
 $ r $
is called the range map of
$ r $
is called the range map of
 $ B $
and the map
$ B $
and the map
 $ s $
is called the source map of
$ s $
is called the source map of
 $ B $
.
$ B $
.
Notation 4.2. Let
![]() $ B = ( V , E ) $
be a Bratteli diagram. For each
$ B = ( V , E ) $
be a Bratteli diagram. For each
![]() $ v \in V $
, we denote
$ v \in V $
, we denote
![]() $ R ( v ) = r ( s^{ -1 } ( v ) ) $
, and for each
$ R ( v ) = r ( s^{ -1 } ( v ) ) $
, and for each
![]() $ v \in V \setminus V_0 $
, we denote
$ v \in V \setminus V_0 $
, we denote
![]() $ S ( v ) = s ( r^{ -1 } ( v ) ) $
. If
$ S ( v ) = s ( r^{ -1 } ( v ) ) $
. If
![]() $ v \in V_n $
, then
$ v \in V_n $
, then
![]() $ R ( v ) $
is the set of all vertices in
$ R ( v ) $
is the set of all vertices in
![]() $ V_{ n + 1 } $
that are connected to
$ V_{ n + 1 } $
that are connected to
![]() $ v $
by an edge, and
$ v $
by an edge, and
![]() $ S ( v ) $
is the set of all vertices in
$ S ( v ) $
is the set of all vertices in
![]() $ V_{ n - 1 } $
connected to
$ V_{ n - 1 } $
connected to
![]() $ v $
by an edge. In a reasonable sense, this gives us range and source maps for vertices.
$ v $
by an edge. In a reasonable sense, this gives us range and source maps for vertices.
For each
![]() $ k , k' \in \mathbb {Z}_{> 0 } $
with
$ k , k' \in \mathbb {Z}_{> 0 } $
with
![]() $ k < k' $
, we denote by
$ k < k' $
, we denote by
![]() $ P_{ k , k' } $
the set of all paths from
$ P_{ k , k' } $
the set of all paths from
![]() $ V_k $
to
$ V_k $
to
![]() $ V_{ k' } $
. Formally,
$ V_{ k' } $
. Formally,
![]() $ P_{ k , k' } $
is the set of
$ P_{ k , k' } $
is the set of
![]() $ ( e_{ k + 1 } , \ldots , e_{ k' } ) $
such that for all
$ ( e_{ k + 1 } , \ldots , e_{ k' } ) $
such that for all
![]() $ j \in \{ k + 1 , \ldots , k' \} $
,
$ j \in \{ k + 1 , \ldots , k' \} $
,
![]() $ e_j \in E_j $
and for all
$ e_j \in E_j $
and for all
![]() $ j \in \{ k + 1 , \ldots , k' - 1 \} $
, we have
$ j \in \{ k + 1 , \ldots , k' - 1 \} $
, we have
![]() $ r ( e_j ) = s ( e_{ j + 1 } ) $
.
$ r ( e_j ) = s ( e_{ j + 1 } ) $
.
Definition 4.3. Let
![]() $ B = ( V , E ) $
and
$ B = ( V , E ) $
and
![]() $ B' = ( V' , E' ) $
be Bratteli diagrams. We say that
$ B' = ( V' , E' ) $
be Bratteli diagrams. We say that
![]() $ B' $
is a telescoping of
$ B' $
is a telescoping of
![]() $ B $
if there is a sequence
$ B $
if there is a sequence
![]() $ ( k_n ) $
such that for all
$ ( k_n ) $
such that for all
![]() $ n \in \mathbb {Z}_{ \geq 0 } $
, setting
$ n \in \mathbb {Z}_{ \geq 0 } $
, setting
![]() $ k_0 = 0 $
, we have
$ k_0 = 0 $
, we have
![]() $ k_n \in \mathbb {Z}_{ \geq 0 } $
,
$ k_n \in \mathbb {Z}_{ \geq 0 } $
,
![]() $ k_0 = 0 $
,
$ k_0 = 0 $
,
![]() $ k_n> k_{ n - 1 } $
,
$ k_n> k_{ n - 1 } $
,
![]() $ V_n' = V_{ k_n } $
, and
$ V_n' = V_{ k_n } $
, and
![]() $ E_n' = P_{ k_{ n - 1 } , k_n } $
.
$ E_n' = P_{ k_{ n - 1 } , k_n } $
.
Remark 4.4. We create an equivalence class of Bratteli diagrams from isomorphism (bijections of vertices and edges at each level respecting range and source maps) and telescoping. If
![]() $ B_1 $
and
$ B_1 $
and
![]() $ B_2 $
are in the same equivalence class, we denote this by
$ B_2 $
are in the same equivalence class, we denote this by
![]() $ B_1 \sim B_2 $
. In [Reference Elliott6],
$ B_1 \sim B_2 $
. In [Reference Elliott6],
![]() $ K_0 $
(an ordered group) of a Bratteli diagram is defined. Although we will not go into the detail as it is not important for this paper, the result that is important is that
$ K_0 $
(an ordered group) of a Bratteli diagram is defined. Although we will not go into the detail as it is not important for this paper, the result that is important is that
![]() $ K_0 ( B_1 ) \cong K_0 ( B_2 ) $
if and only if
$ K_0 ( B_1 ) \cong K_0 ( B_2 ) $
if and only if
![]() $ B_1 \sim B_2 $
. As described in [Reference Giordano, Putnam and Skau9], we also have
$ B_1 \sim B_2 $
. As described in [Reference Giordano, Putnam and Skau9], we also have
![]() $ B_1 \sim B_2 $
if and only if there is a Bratteli diagram
$ B_1 \sim B_2 $
if and only if there is a Bratteli diagram
![]() $ B $
, called the aggregate Bratteli diagram of
$ B $
, called the aggregate Bratteli diagram of
![]() $ B_1 $
and
$ B_1 $
and
![]() $ B_2 $
, such that telescoping
$ B_2 $
, such that telescoping
![]() $ B $
to odd levels yields a telescoping of
$ B $
to odd levels yields a telescoping of
![]() $ B_1 $
and telescoping
$ B_1 $
and telescoping
![]() $ B $
to even levels yields a telescoping of
$ B $
to even levels yields a telescoping of
![]() $ B_2 $
.
$ B_2 $
.
Definition 4.5. An ordered Bratteli diagram
![]() $ B $
is a Bratteli diagram
$ B $
is a Bratteli diagram
![]() $ ( V , E ) $
together with a partial order
$ ( V , E ) $
together with a partial order
![]() $ \leq $
on
$ \leq $
on
![]() $ E $
such that
$ E $
such that
![]() $ e , e' \in E $
are comparable if and only if
$ e , e' \in E $
are comparable if and only if
![]() $ r ( e ) = r ( e' ) $
. We write
$ r ( e ) = r ( e' ) $
. We write
![]() $ B = ( V , E , \leq ) $
.
$ B = ( V , E , \leq ) $
.
Let
![]() $ B = ( V , E , \leq ) $
be an ordered Bratteli diagram. We define
$ B = ( V , E , \leq ) $
be an ordered Bratteli diagram. We define
![]() $ E_{ \min } $
(
$ E_{ \min } $
(
![]() $ E_{ \max } $
) to be the set of all edges that are minimal (maximal, respectively) with respect to
$ E_{ \max } $
) to be the set of all edges that are minimal (maximal, respectively) with respect to
![]() $ \leq $
. We define
$ \leq $
. We define
![]() $ V_{ \min } $
(
$ V_{ \min } $
(
![]() $ V_{ \max } $
) to be the set of all
$ V_{ \max } $
) to be the set of all
![]() $ v \in V $
such that there is an
$ v \in V $
such that there is an
![]() $ e $
in
$ e $
in
![]() $ E_{ \min } $
(
$ E_{ \min } $
(
![]() $ E_{ \max } $
, respectively) with
$ E_{ \max } $
, respectively) with
![]() $ s ( e ) = v $
.
$ s ( e ) = v $
.
If
![]() $ B = ( V , E , \leq ) $
, then any telescoping
$ B = ( V , E , \leq ) $
, then any telescoping
![]() $ B' $
of
$ B' $
of
![]() $ B $
has an order induced by
$ B $
has an order induced by
![]() $ B $
. In general, we can put an order on
$ B $
. In general, we can put an order on
![]() $ P_{ i , j } $
by
$ P_{ i , j } $
by
![]() $ ( e_{ i + 1 } , \ldots , e_j ) \leq ( e_{ i + 1 }' , \ldots , e_j' ) $
if
$ ( e_{ i + 1 } , \ldots , e_j ) \leq ( e_{ i + 1 }' , \ldots , e_j' ) $
if
![]() $ e_k \leq e_k' $
for the smallest
$ e_k \leq e_k' $
for the smallest
![]() $ k \in \{ i + 1 , \ldots , j \} $
such that
$ k \in \{ i + 1 , \ldots , j \} $
such that
![]() $ e_k \notin E_{ \max } $
.
$ e_k \notin E_{ \max } $
.
Definition 4.6. Let
![]() $ B = ( V , E , \leq ) $
be an ordered Bratteli diagram. We define a partial Vershik transformation
$ B = ( V , E , \leq ) $
be an ordered Bratteli diagram. We define a partial Vershik transformation
![]() $ \widetilde { h }_B : ( X_B \setminus X_{ B ,\max } ) \cup X_{ B ,\min } \to ( X_B \setminus X_{ B , \min } ) \cup X_{ B , \max } $
in the following way. If
$ \widetilde { h }_B : ( X_B \setminus X_{ B ,\max } ) \cup X_{ B ,\min } \to ( X_B \setminus X_{ B , \min } ) \cup X_{ B , \max } $
in the following way. If
![]() $ x \in X_{ B , \max } \cap X_{ B , \min } $
, we define
$ x \in X_{ B , \max } \cap X_{ B , \min } $
, we define
![]() $ \widetilde { h }_B ( x ) = x $
. If
$ \widetilde { h }_B ( x ) = x $
. If
![]() $ x = ( x_1 , x_2 , \ldots ) \in X_B \setminus X_{ B , \max } $
, then there is some smallest
$ x = ( x_1 , x_2 , \ldots ) \in X_B \setminus X_{ B , \max } $
, then there is some smallest
![]() $ k \in \mathbb {Z}_{> 0 } $
such that
$ k \in \mathbb {Z}_{> 0 } $
such that
![]() $ x_k \notin E_{ \max } $
. Let
$ x_k \notin E_{ \max } $
. Let
![]() $ y_k $
denote the successor of
$ y_k $
denote the successor of
![]() $ x_k $
in
$ x_k $
in
![]() $ E $
and let
$ E $
and let
![]() $ ( y_1 , y_2 , \ldots , y_{ k - 1 } ) $
be the unique path from
$ ( y_1 , y_2 , \ldots , y_{ k - 1 } ) $
be the unique path from
![]() $ v_0 $
to
$ v_0 $
to
![]() $ s ( y_k ) $
such that
$ s ( y_k ) $
such that
![]() $ y_j \in E_{ \min } $
for all
$ y_j \in E_{ \min } $
for all
![]() $ j \in \{ 1 , \ldots , k - 1 \} $
. We define
$ j \in \{ 1 , \ldots , k - 1 \} $
. We define
![]() $ \widetilde { h }_B ( p ) = ( y_1 , y_2 , \ldots , y_k , x_{ k + 1 } , x_{ k + 2 } , \ldots ) $
.
$ \widetilde { h }_B ( p ) = ( y_1 , y_2 , \ldots , y_k , x_{ k + 1 } , x_{ k + 2 } , \ldots ) $
.
Definition 4.7. Let
![]() $ B = ( V , E , \leq ) $
be an ordered Bratteli diagram. We define the infinite path space
$ B = ( V , E , \leq ) $
be an ordered Bratteli diagram. We define the infinite path space
![]() $ X_B $
to be the set of all sequences
$ X_B $
to be the set of all sequences
![]() $ x = ( x_1 , x_2 , \ldots ) $
where
$ x = ( x_1 , x_2 , \ldots ) $
where
![]() $ x_n \in E_n $
and
$ x_n \in E_n $
and
![]() $ r ( x_n ) = s ( x_{ n + 1 } ) $
for all
$ r ( x_n ) = s ( x_{ n + 1 } ) $
for all
![]() $ n \in \mathbb {Z}_{> 0 } $
together with the topology generated by sets of the form
$ n \in \mathbb {Z}_{> 0 } $
together with the topology generated by sets of the form
![]() $ U ( e_1 , \ldots , e_k ) $
, which is the set of all
$ U ( e_1 , \ldots , e_k ) $
, which is the set of all
![]() $ x = ( x_1 , x_2 , \ldots ) $
with
$ x = ( x_1 , x_2 , \ldots ) $
with
![]() $ x_j = e_j $
for all
$ x_j = e_j $
for all
![]() $ j \in \{ 1 , \ldots , k \} $
.
$ j \in \{ 1 , \ldots , k \} $
.
Let
![]() $ B = ( V , E , \leq ) $
be an ordered Bratteli diagram. It is easy to see that the infinite path space is a zero-dimensional space. We define
$ B = ( V , E , \leq ) $
be an ordered Bratteli diagram. It is easy to see that the infinite path space is a zero-dimensional space. We define
![]() $ X_{ B , \min } $
(
$ X_{ B , \min } $
(
![]() $ X_{ B , \max }$
) to be the set of all
$ X_{ B , \max }$
) to be the set of all
![]() $ x = ( x_1 , x_2 , \ldots ) \in X_B $
such that
$ x = ( x_1 , x_2 , \ldots ) \in X_B $
such that
![]() $ x_j $
is in
$ x_j $
is in
![]() $ E_{ \min } $
(
$ E_{ \min } $
(
![]() $ E_{ \max } $
, respectively) for all
$ E_{ \max } $
, respectively) for all
![]() $ j \in \mathbb {Z}_{> 0 } $
.
$ j \in \mathbb {Z}_{> 0 } $
.
The following terminology appears in [Reference Bezuglyi, Kwiatkowski and Yassawi2, Definition 2.18], although we restate it to give more clarity as to when the definition applies.
Definition 4.8. Let
![]() $ B = ( V , E , \leq ) $
be an ordered Bratteli diagram and let
$ B = ( V , E , \leq ) $
be an ordered Bratteli diagram and let
![]() $ \widetilde { h }_B $
be its partial Vershik transformation. We say that the ordering on
$ \widetilde { h }_B $
be its partial Vershik transformation. We say that the ordering on
![]() $ B $
is perfect if for every
$ B $
is perfect if for every
![]() $ e \in X_{ B , \min } $
,
$ e \in X_{ B , \min } $
,
![]() $ \overline { \text {orb}_{ \widetilde { h }_B ( e ) } } \cap X_{ B , \max } $
contains a single element, and if for every
$ \overline { \text {orb}_{ \widetilde { h }_B ( e ) } } \cap X_{ B , \max } $
contains a single element, and if for every
![]() $ e \in X_{ B , \max } $
,
$ e \in X_{ B , \max } $
,
![]() $ \overline { \text {orb}_{ \widetilde { h }_B ( e ) } } \cap X_{ B , \min } $
contains a single element. In this case, we define the Vershik transformation of
$ \overline { \text {orb}_{ \widetilde { h }_B ( e ) } } \cap X_{ B , \min } $
contains a single element. In this case, we define the Vershik transformation of
![]() $ X_B $
, denoted by
$ X_B $
, denoted by
![]() $ h_B $
, to be the extension of
$ h_B $
, to be the extension of
![]() $ \widetilde { h }_B $
which, for each
$ \widetilde { h }_B $
which, for each
![]() $ e \in X_{ B , \min } $
, sends the unique element of
$ e \in X_{ B , \min } $
, sends the unique element of
![]() $ \overline { \text {orb}_{ \widetilde { h }_B ( e ) } } \cap X_{ B , \max } $
to
$ \overline { \text {orb}_{ \widetilde { h }_B ( e ) } } \cap X_{ B , \max } $
to
![]() $ e $
.
$ e $
.
Thus, given an ordered Bratteli diagram
![]() $ B = ( V , E , \leq ) $
with a perfect ordering, the system
$ B = ( V , E , \leq ) $
with a perfect ordering, the system
![]() $ ( X_B , h_B ) $
is a zero-dimensional system. There is a standard way of using systems of finite first return time maps to associate minimal (and essentially minimal) Cantor systems to ‘minimal’ (and ‘essentially minimal’) ordered Bratteli diagrams and vice versa; see [Reference Giordano, Putnam and Skau9, §3] (and [Reference Herman, Putnam and Skau10, §2]). We give a couple of brief examples of the Bratteli diagram to dynamical system direction in Example 4.9. The procedure in the other direction is part of the proof of Proposition 4.11.
$ ( X_B , h_B ) $
is a zero-dimensional system. There is a standard way of using systems of finite first return time maps to associate minimal (and essentially minimal) Cantor systems to ‘minimal’ (and ‘essentially minimal’) ordered Bratteli diagrams and vice versa; see [Reference Giordano, Putnam and Skau9, §3] (and [Reference Herman, Putnam and Skau10, §2]). We give a couple of brief examples of the Bratteli diagram to dynamical system direction in Example 4.9. The procedure in the other direction is part of the proof of Proposition 4.11.
Figure 3 An illustration of Example 4.9(1). This is a Bratteli diagram associated to the shift on the one-point compactification of the integers.
Examples 4.9. We provide a couple of examples illustrating the definitions above.
-
(1) Consider the ordered Bratteli diagram
 $ B $
in Figure 3. Assume the pattern shown in the diagram continues forever. As we can see, there is a linear order on the set of edges that share a range vertex. For example, there are three edges going into v, and those three edges are ordered 1 to 3. There is exactly one minimal infinite path and one maximal infinite path; these are the same path, shown in red. It is not too hard to see that the ordering on
$ B $
in Figure 3. Assume the pattern shown in the diagram continues forever. As we can see, there is a linear order on the set of edges that share a range vertex. For example, there are three edges going into v, and those three edges are ordered 1 to 3. There is exactly one minimal infinite path and one maximal infinite path; these are the same path, shown in red. It is not too hard to see that the ordering on
 $ B $
is perfect. The dynamical system
$ B $
is perfect. The dynamical system
 $ ( X_B , h_B ) $
is conjugate to the shift on the one-point compactification of the integers, where the path in red on the right corresponds to the point at
$ ( X_B , h_B ) $
is conjugate to the shift on the one-point compactification of the integers, where the path in red on the right corresponds to the point at
 $ \infty $
and the path on the left (consisting of all edges labeled ‘2’) corresponds to
$ \infty $
and the path on the left (consisting of all edges labeled ‘2’) corresponds to
 $ 0 \in \mathbb {Z} $
. This is not the only possible diagram that yields such a Vershik system, but one that reflects a nice choice of a sequence of systems of finite first return time maps.
$ 0 \in \mathbb {Z} $
. This is not the only possible diagram that yields such a Vershik system, but one that reflects a nice choice of a sequence of systems of finite first return time maps. -
(2) We now show an perfectly ordered Bratteli diagram
 $ B $
such that
$ B $
such that
 $ ( X_B , h_B ) $
is conjugate to the dynamical system in Example 2.4(2), where we take
$ ( X_B , h_B ) $
is conjugate to the dynamical system in Example 2.4(2), where we take
 $ Y $
to be
$ Y $
to be
 $ \mathbb {Z} \cup \{ \infty \} $
and
$ \mathbb {Z} \cup \{ \infty \} $
and
 $ h' $
to be the shift. See Figure 4. The straight line down the middle is the infinite path corresponding to the crushed point in Figure 2. We can see a bunch of subtrees branching off that look like Figure 3; these correspond to the fibers, which are conjugate to the shift on the one-point compactification of the integers.
$ h' $
to be the shift. See Figure 4. The straight line down the middle is the infinite path corresponding to the crushed point in Figure 2. We can see a bunch of subtrees branching off that look like Figure 3; these correspond to the fibers, which are conjugate to the shift on the one-point compactification of the integers.There are many minimal and maximal paths, and we color these with red. However, since the orbit closures are the fibers, each orbit closure has exactly one minimal and maximal path; these paths are the same, like in Figure 3. Therefore, the order is perfect, and the Vershik system does in fact turn out to be conjugate to the system in Example 2.4(2).
The purpose of the following lemma is used to build a sequence of systems of finite first return time maps with desirable properties in the proof of Proposition 4.11.
Lemma 4.10. Let
![]() $ ( X , h ) $
be a fiberwise essentially minimal zero-dimensional system, let
$ ( X , h ) $
be a fiberwise essentially minimal zero-dimensional system, let
![]() $ \mathcal {P} $
and
$ \mathcal {P} $
and
![]() $ \mathcal {P}' $
be partitions of
$ \mathcal {P}' $
be partitions of
![]() $ X $
, and let
$ X $
, and let
![]() $ \mathcal {S}=( T, ( X_t ) , ( K_t ), ( Y_{ t , k } ) , ( J_{ t , k } ) ) $
be a system of finite first return time maps subordinate to
$ \mathcal {S}=( T, ( X_t ) , ( K_t ), ( Y_{ t , k } ) , ( J_{ t , k } ) ) $
be a system of finite first return time maps subordinate to
![]() $ \mathcal {P} $
such that for each
$ \mathcal {P} $
such that for each
![]() $ t \in \{ 1 , \ldots , T \} $
, we have
$ t \in \{ 1 , \ldots , T \} $
, we have
![]() $ \psi ( X_t ) \subset X_t $
. Then there is a system
$ \psi ( X_t ) \subset X_t $
. Then there is a system
![]() $ \mathcal {S}^{ 0 } = ( T^{ 0 } , ( X_t^{ 0 } ) , ( K_t^{ 0 } ) , ( Y_{ t , k }^{ 0 } ) , ( J_{ t , k }^{ 0 } ) ) $
of finite first return time maps subordinate to
$ \mathcal {S}^{ 0 } = ( T^{ 0 } , ( X_t^{ 0 } ) , ( K_t^{ 0 } ) , ( Y_{ t , k }^{ 0 } ) , ( J_{ t , k }^{ 0 } ) ) $
of finite first return time maps subordinate to
![]() $ \mathcal {P} $
and a system
$ \mathcal {P} $
and a system
![]() $ \mathcal {S}^{ \prime } = ( T^{ \prime } , ( X_t^{ \prime } ) , ( K_t^{ \prime } ) , ( Y_{ t , k }^{ \prime } ) , ( J_{ t , k }^{ \prime } ) ) $
of finite first return time maps subordinate to
$ \mathcal {S}^{ \prime } = ( T^{ \prime } , ( X_t^{ \prime } ) , ( K_t^{ \prime } ) , ( Y_{ t , k }^{ \prime } ) , ( J_{ t , k }^{ \prime } ) ) $
of finite first return time maps subordinate to
![]() $ \mathcal {P}' $
such that:
$ \mathcal {P}' $
such that:
-
(1) the partition
 $ \mathcal {P}_1 ( \mathcal {S}' ) $
is finer than
$ \mathcal {P}_1 ( \mathcal {S}' ) $
is finer than
 $ \mathcal {P}' $
and
$ \mathcal {P}' $
and
 $ \mathcal {P}_1 ( \mathcal {S}^0 ) $
;
$ \mathcal {P}_1 ( \mathcal {S}^0 ) $
; -
(2) the partition
 $ \mathcal {P}_1 ( \mathcal {S}^0 ) $
is finer than
$ \mathcal {P}_1 ( \mathcal {S}^0 ) $
is finer than
 $ \mathcal {P}_1 ( \mathcal {S} ) $
;
$ \mathcal {P}_1 ( \mathcal {S} ) $
; -
(3) we have
 $ T^0 = T $
and for each
$ T^0 = T $
and for each
 $ t \in \{ 1 , \ldots , T \} $
, we have
$ t \in \{ 1 , \ldots , T \} $
, we have
 $ X_t^0 = X_t $
;
$ X_t^0 = X_t $
; -
(4) for each
 $ t' \in \{ 1 , \ldots , T' \} $
, there is a
$ t' \in \{ 1 , \ldots , T' \} $
, there is a
 $ t \in \{ 1 , \ldots , T^0 \} $
and
$ t \in \{ 1 , \ldots , T^0 \} $
and
 $ k \in \{ 1 , \ldots , K_t^0 \} $
such that
$ k \in \{ 1 , \ldots , K_t^0 \} $
such that
 $ X_{ t^{\prime }}' \subset Y_{ t , k }^0 $
;
$ X_{ t^{\prime }}' \subset Y_{ t , k }^0 $
; -
(5) for each
 $ t' \in \{ 1 , \ldots , T' \} $
, there is a
$ t' \in \{ 1 , \ldots , T' \} $
, there is a
 $ t \in \{ 1 , \ldots , T^0 \} $
and
$ t \in \{ 1 , \ldots , T^0 \} $
and
 $ k \in \{ 1 , \ldots , K_t^0 \} $
such that
$ k \in \{ 1 , \ldots , K_t^0 \} $
such that
 $ X_{ t^{\prime } }' \subset h^{ J_{ t , k }^0 } ( Y_{ t , k }^0 ) $
;
$ X_{ t^{\prime } }' \subset h^{ J_{ t , k }^0 } ( Y_{ t , k }^0 ) $
; -
(6) for each
 $ t \in \{ 1 , \ldots , T^0 \} $
and each
$ t \in \{ 1 , \ldots , T^0 \} $
and each
 $ k \in \{ 1 , \ldots , K^0 \} $
, there is a
$ k \in \{ 1 , \ldots , K^0 \} $
, there is a
 $ t' \in \{ 1 , \ldots , T' \} $
such that
$ t' \in \{ 1 , \ldots , T' \} $
such that
 $ Y_{ t , k }^0 \subset \bigcup _{ j \in \mathbb {Z} } h^j ( X_{ t^{\prime } }' ) $
.
$ Y_{ t , k }^0 \subset \bigcup _{ j \in \mathbb {Z} } h^j ( X_{ t^{\prime } }' ) $
.
Proof. We first construct
![]() $ \mathcal {S}' $
and then use it to modify
$ \mathcal {S}' $
and then use it to modify
![]() $ \mathcal {S} $
to obtain
$ \mathcal {S} $
to obtain
![]() $ \mathcal {S}^0 $
. By applying [Reference Herstedt11, Lemma 4.13], we may assume that
$ \mathcal {S}^0 $
. By applying [Reference Herstedt11, Lemma 4.13], we may assume that
![]() $ \mathcal {S} $
satisfies its conclusions; in particular, for all
$ \mathcal {S} $
satisfies its conclusions; in particular, for all
![]() $ t \in \{ 1 , \ldots , T \} $
, we have
$ t \in \{ 1 , \ldots , T \} $
, we have
![]() $ \psi ( X_t ) \subset Y_{ t , 1 } $
, and the partitions
$ \psi ( X_t ) \subset Y_{ t , 1 } $
, and the partitions
![]() $ \mathcal {P}_1 ( \mathcal {S} ) $
and
$ \mathcal {P}_1 ( \mathcal {S} ) $
and
![]() $ \mathcal {P}_2 ( \mathcal {S} ) $
are finer than
$ \mathcal {P}_2 ( \mathcal {S} ) $
are finer than
![]() $ \mathcal {P} $
. Let
$ \mathcal {P} $
. Let
![]() $ \mathcal {P}^{\prime \prime } $
be a partition finer than
$ \mathcal {P}^{\prime \prime } $
be a partition finer than
![]() $ \mathcal {P}' $
,
$ \mathcal {P}' $
,
![]() $ \mathcal {P}_1 ( \mathcal {S} ) $
, and
$ \mathcal {P}_1 ( \mathcal {S} ) $
, and
![]() $ \mathcal {P}_2 ( \mathcal {S} ) $
. Then apply [Reference Herstedt11, Lemma 3.2] to obtain a system
$ \mathcal {P}_2 ( \mathcal {S} ) $
. Then apply [Reference Herstedt11, Lemma 3.2] to obtain a system
![]() $ \mathcal {S}^{ \prime } = ( T^{ \prime } , ( X_t^{ \prime } ) , ( K_t^{ \prime } ) , ( Y_{ t , k }^{ \prime } ) , ( J_{ t , k }^{ \prime } ) ) $
of finite first return time maps subordinate to
$ \mathcal {S}^{ \prime } = ( T^{ \prime } , ( X_t^{ \prime } ) , ( K_t^{ \prime } ) , ( Y_{ t , k }^{ \prime } ) , ( J_{ t , k }^{ \prime } ) ) $
of finite first return time maps subordinate to
![]() $ \mathcal {P}^{\prime \prime } $
such that for all
$ \mathcal {P}^{\prime \prime } $
such that for all
![]() $ t' \in \{ 1 , \ldots , T' \} $
, there is a
$ t' \in \{ 1 , \ldots , T' \} $
, there is a
![]() $ t \in \{ 1 , \ldots , T \} $
such that
$ t \in \{ 1 , \ldots , T \} $
such that
![]() $ X_{ t^{\prime } }' \subset X_t $
. Since
$ X_{ t^{\prime } }' \subset X_t $
. Since
![]() $ \mathcal {P}^{\prime \prime } $
is finer than
$ \mathcal {P}^{\prime \prime } $
is finer than
![]() $ \mathcal {P}' $
,
$ \mathcal {P}' $
,
![]() $ \mathcal {S}' $
is also subordinate to
$ \mathcal {S}' $
is also subordinate to
![]() $ \mathcal {P}' $
. By applying [Reference Herstedt11, Proposition 1.13], we may assume that
$ \mathcal {P}' $
. By applying [Reference Herstedt11, Proposition 1.13], we may assume that
![]() $ \mathcal {P}_1 ( \mathcal {S}' ) $
is finer than
$ \mathcal {P}_1 ( \mathcal {S}' ) $
is finer than
![]() $ \mathcal {P}^{\prime \prime } $
.
$ \mathcal {P}^{\prime \prime } $
.
Let
![]() $ t' \in \{ 1 , \ldots , T' \} $
and let
$ t' \in \{ 1 , \ldots , T' \} $
and let
![]() $ t \in \{ 1 , \ldots , T \} $
be such that
$ t \in \{ 1 , \ldots , T \} $
be such that
![]() $ X_{ t^{\prime } }' \subset X_t $
. Since
$ X_{ t^{\prime } }' \subset X_t $
. Since
![]() $ \mathcal {P}^{\prime \prime } $
is finer than
$ \mathcal {P}^{\prime \prime } $
is finer than
![]() $ \mathcal {P}_1 ( \mathcal {S} ) $
, there is some
$ \mathcal {P}_1 ( \mathcal {S} ) $
, there is some
![]() $ k \in \{ 1 , \ldots , K_t \} $
such that
$ k \in \{ 1 , \ldots , K_t \} $
such that
Since
![]() $ \mathcal {P}^{\prime \prime } $
is finer than
$ \mathcal {P}^{\prime \prime } $
is finer than
![]() $ \mathcal {P}_2 ( \mathcal {S} ) $
, there is some
$ \mathcal {P}_2 ( \mathcal {S} ) $
, there is some
![]() $ l \in \{ 1 , \ldots , K_t \} $
such that
$ l \in \{ 1 , \ldots , K_t \} $
such that
Define
![]() $ T^0 = T $
and for each
$ T^0 = T $
and for each
![]() $ t \in \{ 1 , \ldots , T \} $
, define
$ t \in \{ 1 , \ldots , T \} $
, define
![]() $ X_t^0 = X_t $
(note that after finishing this construction, this verifies conclusion (c) of the lemma). Let
$ X_t^0 = X_t $
(note that after finishing this construction, this verifies conclusion (c) of the lemma). Let
![]() $ t \in \{ 1 , \ldots , T \} $
and let
$ t \in \{ 1 , \ldots , T \} $
and let
![]() $ \{ s ( 1 ) , \ldots , s ( N_t ) \} $
be the set of all
$ \{ s ( 1 ) , \ldots , s ( N_t ) \} $
be the set of all
![]() $ t' \in \{ 1 , \ldots , T' \} $
such that
$ t' \in \{ 1 , \ldots , T' \} $
such that
![]() $ X_{ t^{\prime } } \subset X_t $
. For each
$ X_{ t^{\prime } } \subset X_t $
. For each
![]() $ n \in \{ 1 , \ldots , N_t \} $
, let
$ n \in \{ 1 , \ldots , N_t \} $
, let
![]() $ \{ a ( n , 1 ) , \ldots , a ( n , C_n ) \} $
be the set of all
$ \{ a ( n , 1 ) , \ldots , a ( n , C_n ) \} $
be the set of all
![]() $ k \in \{ 1 , \ldots , K_t \} $
such that
$ k \in \{ 1 , \ldots , K_t \} $
such that
![]() $ {Y_{ t , k } \cap \bigcup _{ j \in \mathbb {Z} } h^j ( X_{ s ( n ) }' ) \neq \varnothing }$
. Define
$ {Y_{ t , k } \cap \bigcup _{ j \in \mathbb {Z} } h^j ( X_{ s ( n ) }' ) \neq \varnothing }$
. Define
![]() $ K_t^0 = \sum _{ n = 1 }^{ N_t } C_n $
and define
$ K_t^0 = \sum _{ n = 1 }^{ N_t } C_n $
and define
![]() $ C_0 = 0 $
. Let
$ C_0 = 0 $
. Let
![]() $ {k \in \{ 1 , \ldots , K_t^0 \} }$
and let
$ {k \in \{ 1 , \ldots , K_t^0 \} }$
and let
![]() $ n \in \{ 1 , \ldots , N_t \} $
, and
$ n \in \{ 1 , \ldots , N_t \} $
, and
![]() $ c \in \{ 1 , \ldots , C_n \} $
be such that
$ c \in \{ 1 , \ldots , C_n \} $
be such that
![]() $ k = C_{ n - 1 } + c $
. Then define
$ k = C_{ n - 1 } + c $
. Then define
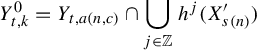 $$ \begin{align} Y_{ t , k }^0 = Y_{ t , a ( n , c ) } \cap \bigcup_{ j \in \mathbb{Z} } h^j ( X_{ s ( n ) }' ) \end{align} $$
$$ \begin{align} Y_{ t , k }^0 = Y_{ t , a ( n , c ) } \cap \bigcup_{ j \in \mathbb{Z} } h^j ( X_{ s ( n ) }' ) \end{align} $$
and define
![]() $ J_{ t , k }^0 = J_{ t , a ( n , c ) } $
. It is routine to verify that
$ J_{ t , k }^0 = J_{ t , a ( n , c ) } $
. It is routine to verify that
![]() $ \mathcal {S}^{ 0 } = ( T^{ 0 } , ( X_t^{ 0 } ) , ( K_t^{ 0 } ) , ( Y_{ t , k }^{ 0 } ) , ( J_{ t , k }^{ 0 } ) ) $
is a system of finite first return time maps subordinate to
$ \mathcal {S}^{ 0 } = ( T^{ 0 } , ( X_t^{ 0 } ) , ( K_t^{ 0 } ) , ( Y_{ t , k }^{ 0 } ) , ( J_{ t , k }^{ 0 } ) ) $
is a system of finite first return time maps subordinate to
![]() $ \mathcal {P} $
. By applying [Reference Herstedt11, Proposition 1.9], we may assume that
$ \mathcal {P} $
. By applying [Reference Herstedt11, Proposition 1.9], we may assume that
![]() $ \mathcal {P}_1 ( \mathcal {S}^0 ) $
is finer than
$ \mathcal {P}_1 ( \mathcal {S}^0 ) $
is finer than
![]() $ \mathcal {P} $
(note that this proves conclusion (2) of the lemma).
$ \mathcal {P} $
(note that this proves conclusion (2) of the lemma).
We now verify the conclusions of the lemma. Conclusions (1), (2), and (3) have already been verified. Conclusion (4) follows from equation (4.1) and from the fact that
![]() $ \mathcal {P}_1 ( \mathcal {S}^0 ) $
is finer than
$ \mathcal {P}_1 ( \mathcal {S}^0 ) $
is finer than
![]() $ \mathcal {P}_1 ( \mathcal {S} ) $
. Conclusion (5) follows from equation (4.1) and the fact that that
$ \mathcal {P}_1 ( \mathcal {S} ) $
. Conclusion (5) follows from equation (4.1) and the fact that that
![]() $ \mathcal {P}_2 ( \mathcal {S}^0 ) $
is finer than
$ \mathcal {P}_2 ( \mathcal {S}^0 ) $
is finer than
![]() $ \mathcal {P}_2 ( \mathcal {S} ) $
. Conclusion (6) is shown by equation (4.3). This proves the lemma.
$ \mathcal {P}_2 ( \mathcal {S} ) $
. Conclusion (6) is shown by equation (4.3). This proves the lemma.
The following proposition is the key to adapting the proof of [Reference Giordano, Putnam and Skau9, Theorem 2.1] to extend from the minimal case to our case (Theorem 5.2). Using Lemma 4.10, we construct an ordered Bratteli diagram (called a ‘Bratteli–Vershik–Kakutani model’ in the literature) using a special sequence of partitions of
![]() $ X $
(this is a special type of what is referred to in the literature as a sequence of ‘Kakutani–Rokhlin’ partitions). In the minimal case, you can construct an ordered Bratteli diagram
$ X $
(this is a special type of what is referred to in the literature as a sequence of ‘Kakutani–Rokhlin’ partitions). In the minimal case, you can construct an ordered Bratteli diagram
![]() $ B = ( V , E , \leq ) $
whose Vershik system is conjugate to a minimal system such that for any vertex
$ B = ( V , E , \leq ) $
whose Vershik system is conjugate to a minimal system such that for any vertex
![]() $ v $
in
$ v $
in
![]() $ V_n $
, there are multiple edges from every vertex in
$ V_n $
, there are multiple edges from every vertex in
![]() $ V_{ n - 1 } $
to
$ V_{ n - 1 } $
to
![]() $ v $
(see [Reference Giordano, Putnam and Skau9, §3]).
$ v $
(see [Reference Giordano, Putnam and Skau9, §3]).
Proposition 4.11. Let
![]() $ ( X , h , Z ) $
be a fiberwise essentially minimal zero-dimensional system. There is an ordered Bratteli diagram
$ ( X , h , Z ) $
be a fiberwise essentially minimal zero-dimensional system. There is an ordered Bratteli diagram
![]() $ B = ( V , E , \leq ) $
with a perfect ordering such that:
$ B = ( V , E , \leq ) $
with a perfect ordering such that:
-
(1) the system
 $ ( X_B , h_B , X_{ B , \min } ) $
is conjugate to
$ ( X_B , h_B , X_{ B , \min } ) $
is conjugate to
 $ ( X , h , Z ) $
;
$ ( X , h , Z ) $
; -
(2) for each
 $ v $
in
$ v $
in
 $ V_{ \min } $
(or
$ V_{ \min } $
(or
 $ V_{ \max } $
), there is a
$ V_{ \max } $
), there is a
 $ v' $
in
$ v' $
in
 $ V_{ \min } $
(
$ V_{ \min } $
(
 $ V_{ \max } $
, respectively) and an edge
$ V_{ \max } $
, respectively) and an edge
 $ e $
in
$ e $
in
 $ E_{ \min } $
(
$ E_{ \min } $
(
 $ E_{ \max } $
, respectively) such that
$ E_{ \max } $
, respectively) such that
 $ s ( e ) = v $
and
$ s ( e ) = v $
and
 $ r ( e ) = v' $
;
$ r ( e ) = v' $
; -
(3) for each
 $ v $
in
$ v $
in
 $ V_{ \min } $
(or
$ V_{ \min } $
(or
 $ V_{ \max } $
) and each
$ V_{ \max } $
) and each
 $ e $
in
$ e $
in
 $ E_{ \min } $
(
$ E_{ \min } $
(
 $ E_{ \max } $
, respectively) with
$ E_{ \max } $
, respectively) with
 $ r ( e ) \in R ( v ) $
satisfies
$ r ( e ) \in R ( v ) $
satisfies
 $ s ( e ) = v $
;
$ s ( e ) = v $
; -
(4) for each
 $ v $
in
$ v $
in
 $ V_{ \min } $
(or
$ V_{ \min } $
(or
 $ V_{ \max } $
) and each
$ V_{ \max } $
) and each
 $ m \in \mathbb {Z}_{> 0 } $
,
$ m \in \mathbb {Z}_{> 0 } $
,
 $ R^m ( v ) = ( R^m \circ S^m \circ R^m ) ( v ) $
.
$ R^m ( v ) = ( R^m \circ S^m \circ R^m ) ( v ) $
.
Proof. Let
![]() $ Z $
and
$ Z $
and
![]() $ \psi $
correspond to
$ \psi $
correspond to
![]() $ ( X , h ) $
as in Definition 2.2, and let
$ ( X , h ) $
as in Definition 2.2, and let
![]() $ ( \mathcal {P}^{ ( n ) } ) $
be a generating sequence of partitions of
$ ( \mathcal {P}^{ ( n ) } ) $
be a generating sequence of partitions of
![]() $ X $
. We will construct an ordered Bratteli diagram
$ X $
. We will construct an ordered Bratteli diagram
![]() $ B = ( V , E , \leq ) $
such that
$ B = ( V , E , \leq ) $
such that
![]() $ ( X_B , h_B ) $
is conjugate to
$ ( X_B , h_B ) $
is conjugate to
![]() $ ( X , h ) $
via a map
$ ( X , h ) $
via a map
![]() $ F : X \to X_B $
that satisfies
$ F : X \to X_B $
that satisfies
![]() $ F ( Z ) = X_{ B , \min } $
.
$ F ( Z ) = X_{ B , \min } $
.
First, we construct a sequence
![]() $ ( \mathcal {S}^{ ( n ) } ) $
of finite first return time maps subordinate to
$ ( \mathcal {S}^{ ( n ) } ) $
of finite first return time maps subordinate to
![]() $ ( \mathcal {P}^{ ( n ) } ) $
. First, let
$ ( \mathcal {P}^{ ( n ) } ) $
. First, let
![]() $ \mathcal {S}^{ ( 1 ) \prime } $
be any system of finite first return time maps subordinate to
$ \mathcal {S}^{ ( 1 ) \prime } $
be any system of finite first return time maps subordinate to
![]() $ \mathcal {P}^{ ( 1 ) } $
such that
$ \mathcal {P}^{ ( 1 ) } $
such that
![]() $ \mathcal {P}_1 ( \mathcal {S}^{ ( 1 ) \prime } ) $
is finer than
$ \mathcal {P}_1 ( \mathcal {S}^{ ( 1 ) \prime } ) $
is finer than
![]() $ \mathcal {P}^{ ( 1 ) } $
(such a system exists by [Reference Herstedt11, Proposition 1.13]). We construct the other systems inductively. For each
$ \mathcal {P}^{ ( 1 ) } $
(such a system exists by [Reference Herstedt11, Proposition 1.13]). We construct the other systems inductively. For each
![]() $ n \in \mathbb {Z}_{> 0 } $
, we apply Lemma 4.10 with
$ n \in \mathbb {Z}_{> 0 } $
, we apply Lemma 4.10 with
![]() $\mathcal {S}^{(n)\prime }$
in place of
$\mathcal {S}^{(n)\prime }$
in place of
![]() $\mathcal {S}$
,
$\mathcal {S}$
,
![]() $\mathcal {P}^{(n)}$
in place of
$\mathcal {P}^{(n)}$
in place of
![]() $\mathcal {P}$
,
$\mathcal {P}$
,
![]() $\mathcal {P}^{( n + 1 )}$
in place of
$\mathcal {P}^{( n + 1 )}$
in place of
![]() $ \mathcal {P}'$
, and get
$ \mathcal {P}'$
, and get
![]() $ \mathcal {S}^{ ( n ) } $
(that is,
$ \mathcal {S}^{ ( n ) } $
(that is,
![]() $\mathcal {S}^0 $
in the lemma) and
$\mathcal {S}^0 $
in the lemma) and
![]() $ \mathcal {S}^{ ( n + 1 )\prime } $
(that is,
$ \mathcal {S}^{ ( n + 1 )\prime } $
(that is,
![]() $\mathcal {S}'$
in the lemma) satisfying the conclusions of the lemma. Thus, to construct the sequence of systems, we only need to define
$\mathcal {S}'$
in the lemma) satisfying the conclusions of the lemma. Thus, to construct the sequence of systems, we only need to define
![]() $\mathcal {S}^{(0)}$
by
$\mathcal {S}^{(0)}$
by
![]() $T^{(0)}=1$
,
$T^{(0)}=1$
,
![]() $X_1^{(0)}= X$
,
$X_1^{(0)}= X$
,
![]() $K_1^{(0)}= 1$
,
$K_1^{(0)}= 1$
,
![]() $Y_{1,1}^{(0)} = 1$
, and
$Y_{1,1}^{(0)} = 1$
, and
![]() $J_{1,1 }^{(0)} = 1$
.
$J_{1,1 }^{(0)} = 1$
.
Now we begin to define
![]() $ B $
. For each
$ B $
. For each
![]() $ n \in \mathbb {Z}_{ \geq 0 } $
, define
$ n \in \mathbb {Z}_{ \geq 0 } $
, define
The set of edges from
![]() $ ( n , t , k ) \in V_n $
to
$ ( n , t , k ) \in V_n $
to
![]() $ ( n + 1 , t' , k' ) \in V_{ n + 1 } $
is the set of all
$ ( n + 1 , t' , k' ) \in V_{ n + 1 } $
is the set of all
![]() $ ( n + 1 , t' , k' , j ) $
such that
$ ( n + 1 , t' , k' , j ) $
such that
![]() $ h^j ( Y_{ t^{\prime } , k' }^{ ( n + 1 ) } ) \subset Y_{ t , k }^{ ( n ) } $
. Note that this is well defined; by assumption,
$ h^j ( Y_{ t^{\prime } , k' }^{ ( n + 1 ) } ) \subset Y_{ t , k }^{ ( n ) } $
. Note that this is well defined; by assumption,
![]() $ h^j ( Y_{ t^{\prime } , k' }^{ ( n + 1 ) } ) $
is a subset of an element of
$ h^j ( Y_{ t^{\prime } , k' }^{ ( n + 1 ) } ) $
is a subset of an element of
![]() $ \mathcal {P}_1 ( \mathcal {S}^{ ( n ) } ) $
, so we do not need to include
$ \mathcal {P}_1 ( \mathcal {S}^{ ( n ) } ) $
, so we do not need to include
![]() $ t $
and
$ t $
and
![]() $ k $
in the tuple defining this edge. We define an order on the edges
$ k $
in the tuple defining this edge. We define an order on the edges
![]() $ r^{ -1 } ( ( n , t , k ) ) $
by
$ r^{ -1 } ( ( n , t , k ) ) $
by
![]() $ ( n , t , k , j_1 ) \leq ( n , t , k , j_2 ) $
if
$ ( n , t , k , j_1 ) \leq ( n , t , k , j_2 ) $
if
![]() $ j_1 < j_2 $
.
$ j_1 < j_2 $
.
We now construct the orbit map
![]() $ F : X \to X_B $
. Let
$ F : X \to X_B $
. Let
![]() $ x \in X $
. Then for each
$ x \in X $
. Then for each
![]() $ n \in \mathbb {Z}_{> 0 } $
, there is precisely one
$ n \in \mathbb {Z}_{> 0 } $
, there is precisely one
![]() $ t \in \{ 1 , \ldots , T^{ ( n ) } \} $
, one
$ t \in \{ 1 , \ldots , T^{ ( n ) } \} $
, one
![]() $ k \in \{ 1 , \ldots , K_t^{ ( n ) } \} $
, and one
$ k \in \{ 1 , \ldots , K_t^{ ( n ) } \} $
, and one
![]() $ j \in \{ 0 , \ldots , J_{ t , k }^{ ( n ) } \} $
such that
$ j \in \{ 0 , \ldots , J_{ t , k }^{ ( n ) } \} $
such that
![]() $ x \in h^j ( Y_{ t , k }^{ ( n ) } ) $
. If
$ x \in h^j ( Y_{ t , k }^{ ( n ) } ) $
. If
![]() $ x \in h^j ( Y_{ t , k }^{ ( n ) } ) \cap h^{ j' } ( Y_{ t^{\prime } , k' }^{ ( n + 1 ) } ) $
, then
$ x \in h^j ( Y_{ t , k }^{ ( n ) } ) \cap h^{ j' } ( Y_{ t^{\prime } , k' }^{ ( n + 1 ) } ) $
, then
![]() $ j' \geq j $
, since otherwise we would have
$ j' \geq j $
, since otherwise we would have
![]() $ h^{ j - j' } ( Y_{ t , k }^{ ( n ) } ) \subset X_t^{ ( n + 1 ) } $
(this follows from Lemma 4.10(3) and (4)), which is not possible since by definition,
$ h^{ j - j' } ( Y_{ t , k }^{ ( n ) } ) \subset X_t^{ ( n + 1 ) } $
(this follows from Lemma 4.10(3) and (4)), which is not possible since by definition,
![]() $ h^i ( Y_{ t , k }^{ ( n ) } ) \cap X_t^{ ( n + 1 ) } = \varnothing $
for
$ h^i ( Y_{ t , k }^{ ( n ) } ) \cap X_t^{ ( n + 1 ) } = \varnothing $
for
![]() $ i \in \{ 1 , \ldots , J_{ t , k }^{ ( n ) } - 1 \} $
. This, combined with the fact that
$ i \in \{ 1 , \ldots , J_{ t , k }^{ ( n ) } - 1 \} $
. This, combined with the fact that
![]() $ \mathcal {P}_1 ( \mathcal {S}^{ ( n + 1 ) } ) $
is finer than
$ \mathcal {P}_1 ( \mathcal {S}^{ ( n + 1 ) } ) $
is finer than
![]() $ \mathcal {P}_1 ( \mathcal {S}^{ ( n ) } ) $
, tells us that
$ \mathcal {P}_1 ( \mathcal {S}^{ ( n ) } ) $
, tells us that
![]() $ h^{ j' - j } ( Y_{ t^{\prime } , k' }^{ ( n + 1 ) } ) \subset Y_{ t , k }^{ ( n ) } $
, and therefore there is an edge from
$ h^{ j' - j } ( Y_{ t^{\prime } , k' }^{ ( n + 1 ) } ) \subset Y_{ t , k }^{ ( n ) } $
, and therefore there is an edge from
![]() $ ( n , t , k ) $
to
$ ( n , t , k ) $
to
![]() $ ( n + 1 , t' , k' ) $
; namely,
$ ( n + 1 , t' , k' ) $
; namely,
![]() $ ( n + 1 , t' , k' , j' - j ) $
. Thus, this gives us an infinite path in
$ ( n + 1 , t' , k' , j' - j ) $
. Thus, this gives us an infinite path in
![]() $ X_B $
associated to
$ X_B $
associated to
![]() $ x $
. We define
$ x $
. We define
![]() $ F $
by sending
$ F $
by sending
![]() $ x $
to this infinite path.
$ x $
to this infinite path.
We now show that
![]() $ F $
is injective. Suppose
$ F $
is injective. Suppose
![]() $ x , x' \in X $
and
$ x , x' \in X $
and
![]() $ F ( x ) = F ( x' ) = ( e_1 , e_2 , \ldots ) $
where we write
$ F ( x ) = F ( x' ) = ( e_1 , e_2 , \ldots ) $
where we write
![]() $ e_n = ( n , t_n , k_n , j_n ) $
for
$ e_n = ( n , t_n , k_n , j_n ) $
for
![]() $ n \in \mathbb {Z}_{> 0 } $
. By definition, it is clear that for each
$ n \in \mathbb {Z}_{> 0 } $
. By definition, it is clear that for each
![]() $ n \in \mathbb {Z}_{> 0 } $
, there are
$ n \in \mathbb {Z}_{> 0 } $
, there are
![]() $ i_n , i_n' \in \{ 0 , \ldots , J_{ t_n , k_n }^{ ( n ) } - 1 \} $
such that
$ i_n , i_n' \in \{ 0 , \ldots , J_{ t_n , k_n }^{ ( n ) } - 1 \} $
such that
![]() $ x \in h^{ i_n } ( Y_{ t_n , k_n }^{ ( n ) } ) $
and
$ x \in h^{ i_n } ( Y_{ t_n , k_n }^{ ( n ) } ) $
and
![]() $ x' \in h^{ i_n' } ( Y_{ t_n , k_n }^{ ( n ) } ) $
. First, notice that
$ x' \in h^{ i_n' } ( Y_{ t_n , k_n }^{ ( n ) } ) $
. First, notice that
![]() $ i_1 = j_1 $
and
$ i_1 = j_1 $
and
![]() $ i_1' = j_1 $
by definition of
$ i_1' = j_1 $
by definition of
![]() $ F $
. Then, by definition of
$ F $
. Then, by definition of
![]() $ F $
, we have
$ F $
, we have
![]() $ j_2 = i_2 - j_1 $
and
$ j_2 = i_2 - j_1 $
and
![]() $ j_2 = i_2' - j_2 $
; in particular,
$ j_2 = i_2' - j_2 $
; in particular,
![]() $ i_2 = i_2' $
. Proceeding like this, we see that
$ i_2 = i_2' $
. Proceeding like this, we see that
![]() $ i_n = i_n' $
for all
$ i_n = i_n' $
for all
![]() $ n \in \mathbb {Z}_{> 0 } $
. Since
$ n \in \mathbb {Z}_{> 0 } $
. Since
![]() $ ( \mathcal {P}^{ ( n ) } ) $
is a generating sequence of partitions, so is
$ ( \mathcal {P}^{ ( n ) } ) $
is a generating sequence of partitions, so is
![]() $ ( \mathcal {P}_1 ( \mathcal {S}^{ ( n ) } ) ) $
, and therefore
$ ( \mathcal {P}_1 ( \mathcal {S}^{ ( n ) } ) ) $
, and therefore
![]() $ \bigcap _{ n = 0 }^\infty h^{ i_n } ( Y_{ t_n , k_n }^{ ( n ) } ) $
contains at most one element of
$ \bigcap _{ n = 0 }^\infty h^{ i_n } ( Y_{ t_n , k_n }^{ ( n ) } ) $
contains at most one element of
![]() $ X $
. Thus,
$ X $
. Thus,
![]() $ x = x' $
, and therefore
$ x = x' $
, and therefore
![]() $ F $
is injective.
$ F $
is injective.
Next, we show that
![]() $ F $
is surjective. Let
$ F $
is surjective. Let
![]() $ e = ( e_1 , e_2 , \ldots ) \in X_B $
and write
$ e = ( e_1 , e_2 , \ldots ) \in X_B $
and write
![]() $ e_n = ( n , t_n , k_n , j_n ) $
for
$ e_n = ( n , t_n , k_n , j_n ) $
for
![]() $ n \in \mathbb {Z}_{> 0 } $
. We construct a sequence
$ n \in \mathbb {Z}_{> 0 } $
. We construct a sequence
![]() $ ( i_n ) $
with
$ ( i_n ) $
with
![]() $ i_n \in \{ 0 , \ldots , J_{ t_n , k_n }^{ ( n ) } - 1 \} $
for all
$ i_n \in \{ 0 , \ldots , J_{ t_n , k_n }^{ ( n ) } - 1 \} $
for all
![]() $ n \in \mathbb {Z}_{> 0 } $
such that
$ n \in \mathbb {Z}_{> 0 } $
such that
![]() $ \bigcap _{ n = 0 }^\infty h^{ i_n } ( Y_{ t_n , k_n }^{ ( n ) } ) $
is non-empty and contains the element of
$ \bigcap _{ n = 0 }^\infty h^{ i_n } ( Y_{ t_n , k_n }^{ ( n ) } ) $
is non-empty and contains the element of
![]() $ X $
that
$ X $
that
![]() $ F $
maps to
$ F $
maps to
![]() $ e $
. First, let
$ e $
. First, let
![]() $ i_1 = j_1 $
. Then, for all
$ i_1 = j_1 $
. Then, for all
![]() $ n \in \mathbb {Z}_{> 1 } $
, let
$ n \in \mathbb {Z}_{> 1 } $
, let
![]() $ i_n = j_n + i_{ n - 1 } $
(note that this can be rewritten as
$ i_n = j_n + i_{ n - 1 } $
(note that this can be rewritten as
![]() $ i_n = \sum _{ k = 1 }^n j_k $
). The claim now follows from the definition of
$ i_n = \sum _{ k = 1 }^n j_k $
). The claim now follows from the definition of
![]() $ B $
, and
$ B $
, and
![]() $ F $
is therefore surjective.
$ F $
is therefore surjective.
So far, we have shown that
![]() $ F $
is bijective. We now show that
$ F $
is bijective. We now show that
![]() $ F $
is a homeomorphism. Let
$ F $
is a homeomorphism. Let
![]() $ U ( e_1 , \ldots , e_N ) $
be an element of the basis of the topology of
$ U ( e_1 , \ldots , e_N ) $
be an element of the basis of the topology of
![]() $ X_B $
. For each
$ X_B $
. For each
![]() $ n \in \{ 1 , \ldots , N \} $
, write
$ n \in \{ 1 , \ldots , N \} $
, write
![]() $ e_n = ( n , t_n , k_n , j_n ) $
. For each
$ e_n = ( n , t_n , k_n , j_n ) $
. For each
![]() $ n \in \{ 1 , \ldots , N \} $
, write
$ n \in \{ 1 , \ldots , N \} $
, write
![]() $ j_n' = \sum _{ k = 1 }^n j_k $
. We claim that if
$ j_n' = \sum _{ k = 1 }^n j_k $
. We claim that if
![]() $ x \in h^{ j_N' } ( Y_{ t_N , k_N }^{ ( N ) } ) $
, then
$ x \in h^{ j_N' } ( Y_{ t_N , k_N }^{ ( N ) } ) $
, then
![]() $ F ( x ) \in U ( e_1 , \ldots , e_N ) $
. So let
$ F ( x ) \in U ( e_1 , \ldots , e_N ) $
. So let
![]() $ x \in h^{ j_N' } ( Y_{ t_N , k_N }^{ ( N ) } ) $
. First notice that by definition of
$ x \in h^{ j_N' } ( Y_{ t_N , k_N }^{ ( N ) } ) $
. First notice that by definition of
![]() $ e_N $
,
$ e_N $
,
Thus,
since
![]() $ j_N + j_{ N - 1 }' = j_N' $
. Similarly, we have
$ j_N + j_{ N - 1 }' = j_N' $
. Similarly, we have
Thus, for every
![]() $ n \in \{ 1 , \ldots , N \} $
, we have
$ n \in \{ 1 , \ldots , N \} $
, we have
and so since
![]() $ j_n' - j_{ n - 1 }' = j_n $
, the
$ j_n' - j_{ n - 1 }' = j_n $
, the
![]() $ n $
th edge of
$ n $
th edge of
![]() $ F ( x ) $
is indeed
$ F ( x ) $
is indeed
![]() $ e_n $
, and
$ e_n $
, and
![]() $ F ( x ) \in U ( e_1 , \ldots , e_N ) $
as desired. Next, we claim that if
$ F ( x ) \in U ( e_1 , \ldots , e_N ) $
as desired. Next, we claim that if
![]() $ x \in X $
satisfies
$ x \in X $
satisfies
![]() $ F ( x ) \in U ( e_1 , \ldots , e_N ) $
, then
$ F ( x ) \in U ( e_1 , \ldots , e_N ) $
, then
![]() $ x \in h^{ j_N' } ( Y_{ t_N , k_N }^{ ( N ) } ) $
. So let
$ x \in h^{ j_N' } ( Y_{ t_N , k_N }^{ ( N ) } ) $
. So let
![]() $ x \in X $
satisfy
$ x \in X $
satisfy
![]() $ F ( x ) \in U ( e_1 , \ldots , e_N ) $
. Then for each
$ F ( x ) \in U ( e_1 , \ldots , e_N ) $
. Then for each
![]() $ n \in \{ 1 , \ldots , N \} $
,
$ n \in \{ 1 , \ldots , N \} $
,
![]() $ x \in h^{ i_n } ( J_{ t_n , k_n }^{ ( n ) } ) $
for some
$ x \in h^{ i_n } ( J_{ t_n , k_n }^{ ( n ) } ) $
for some
![]() $ i_n \in \{ 0 , \ldots , J_{ t_n , k_n }^{ ( n ) } - 1 \} $
. It is clear that
$ i_n \in \{ 0 , \ldots , J_{ t_n , k_n }^{ ( n ) } - 1 \} $
. It is clear that
![]() $ i_1 = j_1 $
. Then, notice that
$ i_1 = j_1 $
. Then, notice that
![]() $ i_2 $
is such that
$ i_2 $
is such that
![]() $ j_2 = i_2 - j_1 $
, and so
$ j_2 = i_2 - j_1 $
, and so
![]() $ i_2 = j_1 + j_2 = j_2' $
. Repeating this process inductively, we see that
$ i_2 = j_1 + j_2 = j_2' $
. Repeating this process inductively, we see that
![]() $ i_N = j_N' $
, and so
$ i_N = j_N' $
, and so
![]() $ x \in h^{ j_N' } ( Y_{ t_N , k_N }^{ ( N ) } ) $
as desired. Altogether, this shows that
$ x \in h^{ j_N' } ( Y_{ t_N , k_N }^{ ( N ) } ) $
as desired. Altogether, this shows that
![]() $ F $
is a homeomorphism.
$ F $
is a homeomorphism.
If
![]() $ x \in Z $
, then there are sequences of integers
$ x \in Z $
, then there are sequences of integers
![]() $ ( t_n ) $
and
$ ( t_n ) $
and
![]() $ ( k_n ) $
such that
$ ( k_n ) $
such that
![]() $ x \in \bigcap _{ n = 0 }^\infty Y_{ t_n , k_n }^{ ( n ) } $
. By definition of the order on
$ x \in \bigcap _{ n = 0 }^\infty Y_{ t_n , k_n }^{ ( n ) } $
. By definition of the order on
![]() $ B $
, this means that
$ B $
, this means that
![]() $ F ( x ) \in X_{ B , \min } $
. Conversely, suppose
$ F ( x ) \in X_{ B , \min } $
. Conversely, suppose
![]() $ x \in X $
satisfies
$ x \in X $
satisfies
![]() $ F ( x ) \in X_{ B , \min } $
. Write
$ F ( x ) \in X_{ B , \min } $
. Write
![]() $ F ( x ) = ( e_1 , e_2 , \ldots ) $
and for
$ F ( x ) = ( e_1 , e_2 , \ldots ) $
and for
![]() $ n \in \mathbb {Z}_{> 0 } $
, write
$ n \in \mathbb {Z}_{> 0 } $
, write
![]() $ e_n = ( n , t_n , k_n , i_n ) $
. Since
$ e_n = ( n , t_n , k_n , i_n ) $
. Since
![]() $ e_n $
is minimal,
$ e_n $
is minimal,
![]() $ i_n $
is the minimal element of
$ i_n $
is the minimal element of
![]() $ \{ 0 , \ldots , J_{ t_n , k_n }^{ ( n ) } - 1 \} $
such that
$ \{ 0 , \ldots , J_{ t_n , k_n }^{ ( n ) } - 1 \} $
such that
![]() $ h^{ i_n } ( Y_{ t_n , k_n }^{ ( n ) } ) \subset X_{ t_{ n - 1 } }^{ ( n - 1 ) } $
. However, since
$ h^{ i_n } ( Y_{ t_n , k_n }^{ ( n ) } ) \subset X_{ t_{ n - 1 } }^{ ( n - 1 ) } $
. However, since
![]() $ X_{ t_n }^{ ( n ) } \subset X_{ t_{ n - 1 } }^{ ( n - 1 ) } $
, we have
$ X_{ t_n }^{ ( n ) } \subset X_{ t_{ n - 1 } }^{ ( n - 1 ) } $
, we have
![]() $ i_n = 0 $
. Hence,
$ i_n = 0 $
. Hence,
![]() $ x \in \bigcap _{ n = 0 }^\infty Y_{ t_n , k_n }^{ ( n ) } $
. Thus,
$ x \in \bigcap _{ n = 0 }^\infty Y_{ t_n , k_n }^{ ( n ) } $
. Thus,
![]() $ F ( Z ) = X_{ B , \min } $
. Also notice that if
$ F ( Z ) = X_{ B , \min } $
. Also notice that if
![]() $ x \in h^{ -1 } ( Z ) $
, there are sequences of integers
$ x \in h^{ -1 } ( Z ) $
, there are sequences of integers
![]() $ ( t_n ) $
and
$ ( t_n ) $
and
![]() $ ( k_n ) $
such that
$ ( k_n ) $
such that
![]() $ x \in \bigcap _{ n = 0 }^\infty h^{ J_{ t_n , k_n }^{ ( n ) } - 1 } ( Y_{ t_n , k_n }^{ ( n ) } ) $
. By definition of the order on
$ x \in \bigcap _{ n = 0 }^\infty h^{ J_{ t_n , k_n }^{ ( n ) } - 1 } ( Y_{ t_n , k_n }^{ ( n ) } ) $
. By definition of the order on
![]() $ B $
, this means that
$ B $
, this means that
![]() $ F ( x ) \in X_{ B , \max } $
. Similarly, the converse holds, and so
$ F ( x ) \in X_{ B , \max } $
. Similarly, the converse holds, and so
![]() $ F ( h^{ - 1 } ( Z ) ) = X_{ B , \max } $
.
$ F ( h^{ - 1 } ( Z ) ) = X_{ B , \max } $
.
We now show that
![]() $ ( F \circ h )|_{ X \setminus h^{ -1 } ( Z ) } = ( \widetilde { h }_B \circ F )|_{ X \setminus h^{ -1 } ( Z ) } $
. Let
$ ( F \circ h )|_{ X \setminus h^{ -1 } ( Z ) } = ( \widetilde { h }_B \circ F )|_{ X \setminus h^{ -1 } ( Z ) } $
. Let
![]() $ x \in X \setminus h^{ -1 } ( Z ) $
. For each
$ x \in X \setminus h^{ -1 } ( Z ) $
. For each
![]() $ n \in \mathbb {Z}_{> 0 } $
, let
$ n \in \mathbb {Z}_{> 0 } $
, let
![]() $ t_n \in \{ 1 , \ldots , T^{ ( n ) } \} $
, let
$ t_n \in \{ 1 , \ldots , T^{ ( n ) } \} $
, let
![]() $ k_n \in \{ 1 , \ldots , K_{ t_n }^{ ( n ) } \} $
, and let
$ k_n \in \{ 1 , \ldots , K_{ t_n }^{ ( n ) } \} $
, and let
![]() $ j_n \in \{ 0 , \ldots , K_{ t_n }^{ ( n ) } - 1 \} $
satisfy
$ j_n \in \{ 0 , \ldots , K_{ t_n }^{ ( n ) } - 1 \} $
satisfy
![]() $ x \in h^{ j_n } ( Y_{ t_n , k_n }^{ ( n ) } ) $
. Since
$ x \in h^{ j_n } ( Y_{ t_n , k_n }^{ ( n ) } ) $
. Since
![]() $ x \notin h^{ -1 } ( Z ) $
, there is some smallest
$ x \notin h^{ -1 } ( Z ) $
, there is some smallest
![]() $ N \in \mathbb {Z}_{> 0 } $
such that
$ N \in \mathbb {Z}_{> 0 } $
such that
![]() $ j_N \neq J_{ t_N , k_N }^{ ( N ) } - 1 $
. We have
$ j_N \neq J_{ t_N , k_N }^{ ( N ) } - 1 $
. We have
and so by Lemma 4.10(4), there is a
![]() $ k_{ N - 1 }' \in \{ 1 , \ldots , K_{ t_{ N - 1 } }^{ ( N - 1 ) } \} $
such that
$ k_{ N - 1 }' \in \{ 1 , \ldots , K_{ t_{ N - 1 } }^{ ( N - 1 ) } \} $
such that
Inductively, we can find for each
![]() $ n \in \{ 1 , \ldots , N - 2 \} $
a
$ n \in \{ 1 , \ldots , N - 2 \} $
a
![]() $ k_n' \in \{ 1 , \ldots , K_{ t_n }^{ ( n ) } \} $
such that
$ k_n' \in \{ 1 , \ldots , K_{ t_n }^{ ( n ) } \} $
such that
![]() $ Y_{ t_{ n + 1 }' , k_{ n + 1 }' }^{ ( n + 1 ) } \subset Y_{ t_{ n }' , k_n' }^{ ( n ) } $
. Since
$ Y_{ t_{ n + 1 }' , k_{ n + 1 }' }^{ ( n + 1 ) } \subset Y_{ t_{ n }' , k_n' }^{ ( n ) } $
. Since
![]() $ j_N + 1 < J_{ t_N , k_N }^{ ( N ) } $
and since for each
$ j_N + 1 < J_{ t_N , k_N }^{ ( N ) } $
and since for each
![]() $ n \in \mathbb {Z}_{> N } $
we have
$ n \in \mathbb {Z}_{> N } $
we have
![]() $ X_{ t_n }^{ ( n ) } \subset X_{ t_N }^{ ( N ) } $
, it follows that
$ X_{ t_n }^{ ( n ) } \subset X_{ t_N }^{ ( N ) } $
, it follows that
![]() $ j_n + 1 < J_{ t_N , k_N }^{ ( N ) } $
as well. So let
$ j_n + 1 < J_{ t_N , k_N }^{ ( N ) } $
as well. So let
![]() $ k_n' = k_n $
and let
$ k_n' = k_n $
and let
![]() $ j_n' = 0 $
for
$ j_n' = 0 $
for
![]() $ n \in \{ 1 , \ldots , N - 1 \} $
, and let
$ n \in \{ 1 , \ldots , N - 1 \} $
, and let
![]() $ j_n' = j_n + 1 $
for
$ j_n' = j_n + 1 $
for
![]() $ n \in \mathbb {Z}_{ \geq N } $
. Then for each
$ n \in \mathbb {Z}_{ \geq N } $
. Then for each
![]() $ n \in \mathbb {Z}_{> 0 } $
,
$ n \in \mathbb {Z}_{> 0 } $
,
![]() $ h ( x ) \in h^{ j_n' } ( Y_{ t_n , k_n' }^{ ( n ) } ) $
.
$ h ( x ) \in h^{ j_n' } ( Y_{ t_n , k_n' }^{ ( n ) } ) $
.
Now write
![]() $ F ( x ) = ( e_1 , e_2 , \ldots ) $
and
$ F ( x ) = ( e_1 , e_2 , \ldots ) $
and
![]() $ \widetilde { h }_B ( F ( x ) ) = ( e_1' , e_2' , \ldots ) $
and for each
$ \widetilde { h }_B ( F ( x ) ) = ( e_1' , e_2' , \ldots ) $
and for each
![]() $ n \in \mathbb {Z}_{> 0 } $
, write
$ n \in \mathbb {Z}_{> 0 } $
, write
![]() $ e_n = ( n , s_n , l_n , i_n ) $
and
$ e_n = ( n , s_n , l_n , i_n ) $
and
![]() $ e_n' = ( n , s_n' , l_n' , i_n' ) $
. By definition of
$ e_n' = ( n , s_n' , l_n' , i_n' ) $
. By definition of
![]() $ F $
, for all
$ F $
, for all
![]() $ n \in \mathbb {Z}_{> 0 } $
, we have
$ n \in \mathbb {Z}_{> 0 } $
, we have
![]() $ s_n = t_n $
,
$ s_n = t_n $
,
![]() $ l_n = k_n $
, and
$ l_n = k_n $
, and
![]() $ i_n = j_n - j_{ n - 1 } $
where
$ i_n = j_n - j_{ n - 1 } $
where
![]() $ j_0 = 0 $
. We also see that
$ j_0 = 0 $
. We also see that
![]() $ N $
is the smallest element of
$ N $
is the smallest element of
![]() $ \mathbb {Z}_{> 0 } $
such that
$ \mathbb {Z}_{> 0 } $
such that
![]() $ e_N \notin E_{ \max } $
, so
$ e_N \notin E_{ \max } $
, so
![]() $ e_N' $
is the successor of
$ e_N' $
is the successor of
![]() $ e_N $
,
$ e_N $
,
![]() $ ( e_1', \ldots , e_{ N - 1 }' ) $
is the minimal path such that
$ ( e_1', \ldots , e_{ N - 1 }' ) $
is the minimal path such that
![]() $ r ( e_{ N - 1 }' ) = s ( e_N' ) $
, and
$ r ( e_{ N - 1 }' ) = s ( e_N' ) $
, and
![]() $ e_n' = e_n $
for all
$ e_n' = e_n $
for all
![]() $ n \in \mathbb {Z}_{> N } $
. In particular, we see that
$ n \in \mathbb {Z}_{> N } $
. In particular, we see that
![]() $ s_n' = t_n $
for all
$ s_n' = t_n $
for all
![]() $ n \in \mathbb {Z}_{> 0 } $
,
$ n \in \mathbb {Z}_{> 0 } $
,
![]() $ l_n' = k_n $
for all
$ l_n' = k_n $
for all
![]() $ n \in \mathbb {Z}_{ \geq N } $
,
$ n \in \mathbb {Z}_{ \geq N } $
,
![]() $ i_n' = 0 $
for
$ i_n' = 0 $
for
![]() $ n \in \{ 1 , \ldots , N - 1 \} $
, and
$ n \in \{ 1 , \ldots , N - 1 \} $
, and
![]() $ i_n' = i_n = j_n - j_{ n - 1 } $
for all
$ i_n' = i_n = j_n - j_{ n - 1 } $
for all
![]() $ n \in \mathbb {Z}_{> N } $
. Observe that
$ n \in \mathbb {Z}_{> N } $
. Observe that
![]() $ i_N' $
is the smallest integer greater than
$ i_N' $
is the smallest integer greater than
![]() $ i_N $
such that
$ i_N $
such that
![]() $ h^{ i_N' } ( Y_{ t_N , k_N }^{ ( N ) } ) \subset Y_{ t_{ N - 1 } , l_{ N - 1 }' }^{ ( N - 1 ) } $
. Thus, this combined with
$ h^{ i_N' } ( Y_{ t_N , k_N }^{ ( N ) } ) \subset Y_{ t_{ N - 1 } , l_{ N - 1 }' }^{ ( N - 1 ) } $
. Thus, this combined with
tells us
 $$ \begin{align*} i_N' &= i_N + J_{ t_{ N - 1 } , k_{ N - 1 } }^{ ( N - 1 ) } \\ &= j_N - j_{ N - 1 } + J_{ t_{ N - 1 } , k_{ N - 1 } }^{ ( N - 1 ) } \\ &= j_N - ( J_{ t_{ N - 1 } , k_{ N - 1 } }^{ ( N - 1 ) } - 1 ) + J_{ t_{ N - 1 } , k_{ N - 1 } }^{ ( N - 1 ) } \\ &= j_N + 1 \\ &= j_N'. \end{align*} $$
$$ \begin{align*} i_N' &= i_N + J_{ t_{ N - 1 } , k_{ N - 1 } }^{ ( N - 1 ) } \\ &= j_N - j_{ N - 1 } + J_{ t_{ N - 1 } , k_{ N - 1 } }^{ ( N - 1 ) } \\ &= j_N - ( J_{ t_{ N - 1 } , k_{ N - 1 } }^{ ( N - 1 ) } - 1 ) + J_{ t_{ N - 1 } , k_{ N - 1 } }^{ ( N - 1 ) } \\ &= j_N + 1 \\ &= j_N'. \end{align*} $$
From equations (4.4) and (4.5), we see
![]() $ l_{ N - 1 }' = k_{ N - 1 }' $
. Similarly, for
$ l_{ N - 1 }' = k_{ N - 1 }' $
. Similarly, for
![]() $ n \in \{ 2 , \ldots , N - 1 \} $
, since
$ n \in \{ 2 , \ldots , N - 1 \} $
, since
![]() $ i_n' = j_n' = 0 $
, we have
$ i_n' = j_n' = 0 $
, we have
![]() $ l_{ n - 1 }' = k_{ n - 1 }' $
. Write
$ l_{ n - 1 }' = k_{ n - 1 }' $
. Write
![]() $ F ( h ( x ) ) = ( e_1^{\prime \prime } , e_2^{\prime \prime } , \ldots ) $
and for each
$ F ( h ( x ) ) = ( e_1^{\prime \prime } , e_2^{\prime \prime } , \ldots ) $
and for each
![]() $ n \in \mathbb {Z}_{> 0 } $
, write
$ n \in \mathbb {Z}_{> 0 } $
, write
![]() $ e_n^{\prime \prime } = ( n , s_n^{\prime \prime } , l_n^{\prime \prime } , i_n^{\prime \prime } ) $
. For each
$ e_n^{\prime \prime } = ( n , s_n^{\prime \prime } , l_n^{\prime \prime } , i_n^{\prime \prime } ) $
. For each
![]() $ n \in \mathbb {Z}_{> 0 } $
, we have
$ n \in \mathbb {Z}_{> 0 } $
, we have
![]() $ s_n^{\prime \prime } = t_n' = t_n $
and
$ s_n^{\prime \prime } = t_n' = t_n $
and
![]() $ l_n^{\prime \prime } = k_n' $
. For
$ l_n^{\prime \prime } = k_n' $
. For
![]() $ n \in \{ 1 , \ldots , N - 1 \} $
, we have
$ n \in \{ 1 , \ldots , N - 1 \} $
, we have
![]() $ i_n^{\prime \prime } = i_n' = 0 $
. We also have
$ i_n^{\prime \prime } = i_n' = 0 $
. We also have
![]() $ i_N^{\prime \prime } = j_N' - j_{ N - 1 }' = j_N' - 0 = i_N' $
. For
$ i_N^{\prime \prime } = j_N' - j_{ N - 1 }' = j_N' - 0 = i_N' $
. For
![]() $ n \in \mathbb {Z}_{> N } $
, we have
$ n \in \mathbb {Z}_{> N } $
, we have
 $$ \begin{align*} i_n^{\prime\prime} = j_n' - j_{ n - 1 }' &= j_n + 1 - ( j_{ n - 1 } - 1 ) \\ &= j_n - j_{ n - 1 } \\ &= i_n \\ &= i_n'. \end{align*} $$
$$ \begin{align*} i_n^{\prime\prime} = j_n' - j_{ n - 1 }' &= j_n + 1 - ( j_{ n - 1 } - 1 ) \\ &= j_n - j_{ n - 1 } \\ &= i_n \\ &= i_n'. \end{align*} $$
Altogether, we see
![]() $ F ( h ( x ) ) = \widetilde { h }_B ( F ( x ) ) $
, and so
$ F ( h ( x ) ) = \widetilde { h }_B ( F ( x ) ) $
, and so
We now show that the order on
![]() $ B $
is perfect. For each
$ B $
is perfect. For each
![]() $ x \in X $
,
$ x \in X $
,
![]() $ z $
is in the minimal set of the essentially minimal zero-dimensional system
$ z $
is in the minimal set of the essentially minimal zero-dimensional system
![]() $ ( \psi ^{ -1 } ( Z ) , h|_{ \psi ^{ -1 } ( Z ) } ) $
,
$ ( \psi ^{ -1 } ( Z ) , h|_{ \psi ^{ -1 } ( Z ) } ) $
,
![]() $ \overline { \text {orb} } ( x ) $
contains exactly one element of
$ \overline { \text {orb} } ( x ) $
contains exactly one element of
![]() $ Z $
and exactly one element of
$ Z $
and exactly one element of
![]() $ h^{ -1 } ( Z ) $
. Now, equation (4.6) combined with
$ h^{ -1 } ( Z ) $
. Now, equation (4.6) combined with
![]() $ F ( Z ) = X_{ B , \min } $
and
$ F ( Z ) = X_{ B , \min } $
and
![]() $ F ( h^{ -1 } ( Z ) ) = X_{ B , \max } $
tells us that the ordering on
$ F ( h^{ -1 } ( Z ) ) = X_{ B , \max } $
tells us that the ordering on
![]() $ B $
is perfect. It is now clear that
$ B $
is perfect. It is now clear that
![]() $ F \circ h = h_B \circ F $
. This proves conclusion (1) of the proposition.
$ F \circ h = h_B \circ F $
. This proves conclusion (1) of the proposition.
Before we prove the rest, we first prove two claims that will be used a few times in the proof.
Claim (
![]() $\ast $
): let
$\ast $
): let
![]() $ n \in \mathbb {Z}_{> 0 } $
,
$ n \in \mathbb {Z}_{> 0 } $
,
![]() $ t_n \in \{ 1 , \ldots , T^{ ( n ) } \} $
,
$ t_n \in \{ 1 , \ldots , T^{ ( n ) } \} $
,
![]() $ k_n \in \{ 1 , \ldots , K_{ t_n }^{ ( n ) } \} $
, and
$ k_n \in \{ 1 , \ldots , K_{ t_n }^{ ( n ) } \} $
, and
![]() $ t_{ n + 1 } \in \{ 1 , \ldots , T^{ ( n + 1 ) } \} $
. If
$ t_{ n + 1 } \in \{ 1 , \ldots , T^{ ( n + 1 ) } \} $
. If
![]() $ X_{ t_{ n + 1 } }^{ ( n + 1 ) } \subset h^{ J_{ t_n , k_n }^{ ( n ) } } ( Y_{ t_n , k_n }^{ ( n ) } ) $
, then for any
$ X_{ t_{ n + 1 } }^{ ( n + 1 ) } \subset h^{ J_{ t_n , k_n }^{ ( n ) } } ( Y_{ t_n , k_n }^{ ( n ) } ) $
, then for any
![]() $ k_{ n + 1 } \in \{ 1 , \ldots , K_{ t_{ n + 1 } }^{ ( n + 1 ) } \} $
, there is an
$ k_{ n + 1 } \in \{ 1 , \ldots , K_{ t_{ n + 1 } }^{ ( n + 1 ) } \} $
, there is an
![]() $ i_{ n + 1 } \in \{ 1 , \ldots , J_{ t_{ n + 1 } , k_{ n + 1 } }^{ ( n + 1 ) } \} $
such that
$ i_{ n + 1 } \in \{ 1 , \ldots , J_{ t_{ n + 1 } , k_{ n + 1 } }^{ ( n + 1 ) } \} $
such that
![]() $ e = ( n + 1 , t_{ n + 1 } , k_{ n + 1 } , i_{ n + 1 } ) $
is a maximal edge with
$ e = ( n + 1 , t_{ n + 1 } , k_{ n + 1 } , i_{ n + 1 } ) $
is a maximal edge with
![]() $ s ( e ) = ( n , t_n , k_n ) $
.
$ s ( e ) = ( n , t_n , k_n ) $
.
We now prove claim (
![]() $\ast $
). Let
$\ast $
). Let
![]() $ k_{ n + 1 } \in \{ 1 , \ldots , K_{ t_{ n + 1 } }^{ ( n + 1 ) } \} $
. Then
$ k_{ n + 1 } \in \{ 1 , \ldots , K_{ t_{ n + 1 } }^{ ( n + 1 ) } \} $
. Then
so we have
Set
![]() $ i_{ n + 1 } = J_{ t_{ n + 1 } , k_{ n + 1 } }^{ ( n + 1 ) } - J_{ t_n , k_n }^{ ( n ) } $
. Let
$ i_{ n + 1 } = J_{ t_{ n + 1 } , k_{ n + 1 } }^{ ( n + 1 ) } - J_{ t_n , k_n }^{ ( n ) } $
. Let
![]() $ j \in \{ 1 , \ldots , J_{ t_n , k_n }^{ ( n ) } - 1 \} $
. Then
$ j \in \{ 1 , \ldots , J_{ t_n , k_n }^{ ( n ) } - 1 \} $
. Then
and since
![]() $ h^j ( Y_{ t_n , k_n }^{ ( n ) } ) \cap ( \bigsqcup _{ t = 1 }^{ T^{ ( n ) } } X_t^{ ( n ) } ) = \varnothing $
, we indeed see that
$ h^j ( Y_{ t_n , k_n }^{ ( n ) } ) \cap ( \bigsqcup _{ t = 1 }^{ T^{ ( n ) } } X_t^{ ( n ) } ) = \varnothing $
, we indeed see that
![]() $ e = ( n + 1 , t_{ n + 1 } , k_{ n + 1 } , i_{ n + 1 } ) \in ~E_{ \max } $
. This proves claim (
$ e = ( n + 1 , t_{ n + 1 } , k_{ n + 1 } , i_{ n + 1 } ) \in ~E_{ \max } $
. This proves claim (
![]() $\ast $
).
$\ast $
).
Claim (
![]() $\ast \ast $
): if there is a
$\ast \ast $
): if there is a
![]() $ k_{ n + 1 } \in \{ 1 , \ldots , K_{ t_{ n + 1 } }^{ ( n + 1 ) } \} $
and a
$ k_{ n + 1 } \in \{ 1 , \ldots , K_{ t_{ n + 1 } }^{ ( n + 1 ) } \} $
and a
![]() $ i \in \{ 1 , \ldots , J_{ t_{ n + 1 } , k_{ n + 1 } }^{ ( n + 1 ) } \} $
such that
$ i \in \{ 1 , \ldots , J_{ t_{ n + 1 } , k_{ n + 1 } }^{ ( n + 1 ) } \} $
such that
![]() $ e = ( n + 1 , t_{ n + 1 } , k_{ n + 1 } , i_{ n + 1 } ) $
is a maximal edge with
$ e = ( n + 1 , t_{ n + 1 } , k_{ n + 1 } , i_{ n + 1 } ) $
is a maximal edge with
![]() $ s ( e ) = ( n , t_n , k_n ) $
, then
$ s ( e ) = ( n , t_n , k_n ) $
, then
![]() $ X_{ t_{ n + 1 } }^{ ( n + 1 ) } \subset h^{ J_{ t_n , k_n }^{ ( n ) } } ( Y_{ t_n , k_n }^{ ( n ) } ) $
.
$ X_{ t_{ n + 1 } }^{ ( n + 1 ) } \subset h^{ J_{ t_n , k_n }^{ ( n ) } } ( Y_{ t_n , k_n }^{ ( n ) } ) $
.
We now prove claim (
![]() $\ast \ast $
). Since
$\ast \ast $
). Since
![]() $ s ( e ) = ( n , t_n , k_n ) $
, we have
$ s ( e ) = ( n , t_n , k_n ) $
, we have
Since
![]() $ e $
is maximal, there is no
$ e $
is maximal, there is no
![]() $ j \in \{ i_{ n + 1 } + 1 , \ldots , J_{ t_{ n + 1 } , k_{ n + 1 } }^{ ( n + 1 ) } - 1 \} $
with
$ j \in \{ i_{ n + 1 } + 1 , \ldots , J_{ t_{ n + 1 } , k_{ n + 1 } }^{ ( n + 1 ) } - 1 \} $
with
![]() $ h^j ( Y_{ t_{ n + 1 }, k_{ n + 1 } }^{ ( n + 1 ) } ) \subset X_{ t_n , k_n }^{ ( n ) } $
. However, notice that
$ h^j ( Y_{ t_{ n + 1 }, k_{ n + 1 } }^{ ( n + 1 ) } ) \subset X_{ t_n , k_n }^{ ( n ) } $
. However, notice that
Thus, we must have
![]() $ i_{ n + 1 } + J_{ t_n , k_n }^{ ( n ) } = J_{ t_{ n + 1 } , k_{ n + 1 } }^{ ( n + 1 ) } $
. Thus,
$ i_{ n + 1 } + J_{ t_n , k_n }^{ ( n ) } = J_{ t_{ n + 1 } , k_{ n + 1 } }^{ ( n + 1 ) } $
. Thus,
![]() $ X_{ t_{ n + 1 } }^{ ( n + 1 ) } \cap h^{ J_{ t_n , k_n }^{ ( n ) } } ( Y_{ t_n , k_n }^{ ( n ) } ) \neq \varnothing $
, and so by Lemma 4.10(5), we actually have
$ X_{ t_{ n + 1 } }^{ ( n + 1 ) } \cap h^{ J_{ t_n , k_n }^{ ( n ) } } ( Y_{ t_n , k_n }^{ ( n ) } ) \neq \varnothing $
, and so by Lemma 4.10(5), we actually have
![]() $ X_{ t_{ n + 1 } }^{ ( n + 1 ) } \subset h^{ J_{ t_n , k_n }^{ ( n ) } } ( Y_{ t_n , k_n }^{ ( n ) } ) $
. This proves claim (
$ X_{ t_{ n + 1 } }^{ ( n + 1 ) } \subset h^{ J_{ t_n , k_n }^{ ( n ) } } ( Y_{ t_n , k_n }^{ ( n ) } ) $
. This proves claim (
![]() $\ast \ast $
).
$\ast \ast $
).
We now prove conclusion (2) of the proposition. Let
![]() $ v \in V_{ \min } $
. Write
$ v \in V_{ \min } $
. Write
![]() $ v = ( n , t_n , k_n ) $
. Since
$ v = ( n , t_n , k_n ) $
. Since
![]() $ v \in V_{ \min } $
, there is some
$ v \in V_{ \min } $
, there is some
![]() $ v^{\prime \prime } \in V_{ n + 1 } $
and some
$ v^{\prime \prime } \in V_{ n + 1 } $
and some
![]() $ e' \in E_{ \min } $
with
$ e' \in E_{ \min } $
with
![]() $ s ( e' ) = v $
and
$ s ( e' ) = v $
and
![]() $ r ( e' ) = v^{\prime \prime } $
. Write
$ r ( e' ) = v^{\prime \prime } $
. Write
![]() $ v^{\prime \prime } = ( n + 1 , t_{ n + 1 } , k_{ n + 1 } ) $
and then
$ v^{\prime \prime } = ( n + 1 , t_{ n + 1 } , k_{ n + 1 } ) $
and then
![]() $ e' = ( n + 1 , t_{ n + 1 } , k_{ n + 1 } , i_{ n + 1 } ) $
. By Lemma 4.10(4), since
$ e' = ( n + 1 , t_{ n + 1 } , k_{ n + 1 } , i_{ n + 1 } ) $
. By Lemma 4.10(4), since
![]() $ e' \in E_{ \min } $
, we have
$ e' \in E_{ \min } $
, we have
![]() $ i_{ n + 1 } = 0 $
, so
$ i_{ n + 1 } = 0 $
, so
![]() $ Y_{ t_{ n + 1 } , k_{ n + 1 } }^{ ( n + 1 ) } \subset Y_{ t_n , k_n }^{ ( n ) } $
. Again by Lemma 4.10(4), we have
$ Y_{ t_{ n + 1 } , k_{ n + 1 } }^{ ( n + 1 ) } \subset Y_{ t_n , k_n }^{ ( n ) } $
. Again by Lemma 4.10(4), we have
Now, let
![]() $ t_{ n + 2 } \in \{ 1 , \ldots , T^{ ( n + 2 ) } \} $
satisfy
$ t_{ n + 2 } \in \{ 1 , \ldots , T^{ ( n + 2 ) } \} $
satisfy
 $$ \begin{align*} X_{ t_{ n + 2 } }^{ ( n + 2 ) } \cap \bigg( \bigcup_{ j \in \mathbb{Z} } h^j ( X_{ t_{ n + 1 } }^{ ( n + 1 ) } ) \bigg) \neq \varnothing. \end{align*} $$
$$ \begin{align*} X_{ t_{ n + 2 } }^{ ( n + 2 ) } \cap \bigg( \bigcup_{ j \in \mathbb{Z} } h^j ( X_{ t_{ n + 1 } }^{ ( n + 1 ) } ) \bigg) \neq \varnothing. \end{align*} $$
By Lemma 4.10(4), there is actually a
![]() $ k_{ n + 1 }' \in \{ 1 , \ldots , K_{ t_{ n + 1 } }^{ ( n + 1 ) } \} $
such that
$ k_{ n + 1 }' \in \{ 1 , \ldots , K_{ t_{ n + 1 } }^{ ( n + 1 ) } \} $
such that
So for any
![]() $ k_{ n + 2 } \in \{ 1 , \ldots , K_{ t_{ n + 2 } }^{ ( n + 2 ) } \} $
, we have a minimal edge
$ k_{ n + 2 } \in \{ 1 , \ldots , K_{ t_{ n + 2 } }^{ ( n + 2 ) } \} $
, we have a minimal edge
![]() $ e^{\prime \prime } = ( n + 2 , t_{ n + 2 } , k_{ n + 2 } , 0 ) $
with
$ e^{\prime \prime } = ( n + 2 , t_{ n + 2 } , k_{ n + 2 } , 0 ) $
with
![]() $ s ( e^{\prime \prime } ) = v' = ( n + 1 , t_{ n + 1 } , k_{ n + 1 }' ) $
. Thus,
$ s ( e^{\prime \prime } ) = v' = ( n + 1 , t_{ n + 1 } , k_{ n + 1 }' ) $
. Thus,
![]() $ v' \in V_{ \min } $
. By equation (4.7),
$ v' \in V_{ \min } $
. By equation (4.7),
![]() $ Y_{ t_{ n + 1 } , k_{ n + 1 }' }^{ ( n + 1 ) } \subset Y_{ t_n , k_n }^{ ( n ) } $
, and so there is a minimal edge
$ Y_{ t_{ n + 1 } , k_{ n + 1 }' }^{ ( n + 1 ) } \subset Y_{ t_n , k_n }^{ ( n ) } $
, and so there is a minimal edge
![]() $ e = ( n + 1 , t_{ n + 1 } , k_{ n + 1 }' , 0 ) $
with
$ e = ( n + 1 , t_{ n + 1 } , k_{ n + 1 }' , 0 ) $
with
![]() $ s ( e ) = v $
and
$ s ( e ) = v $
and
![]() $ r ( e ) = v' $
.
$ r ( e ) = v' $
.
Now let
![]() $ v \in V_{ \max } $
and write
$ v \in V_{ \max } $
and write
![]() $ v = ( n , t_n , k_n ) $
. Since
$ v = ( n , t_n , k_n ) $
. Since
![]() $ v \in V_{ \max } $
, there is some
$ v \in V_{ \max } $
, there is some
![]() $ v^{\prime \prime } \in V_{ n + 1 } $
and some
$ v^{\prime \prime } \in V_{ n + 1 } $
and some
![]() $ e' \in E_{ \max } $
with
$ e' \in E_{ \max } $
with
![]() $ s ( e' ) = V $
and
$ s ( e' ) = V $
and
![]() $ r ( e' ) = v^{\prime \prime } $
. Write
$ r ( e' ) = v^{\prime \prime } $
. Write
![]() $ v^{\prime \prime } = ( n + 1 , t_{ n + 1 } , k_{ n + 1 } ) $
and then
$ v^{\prime \prime } = ( n + 1 , t_{ n + 1 } , k_{ n + 1 } ) $
and then
![]() $ e' = ( n + 1 , t_{ n + 1 } , k_{ n + 1 } , i_{ n + 1 } ) $
. By claim
$ e' = ( n + 1 , t_{ n + 1 } , k_{ n + 1 } , i_{ n + 1 } ) $
. By claim
![]() $(\ast \ast )$
, we have
$(\ast \ast )$
, we have
Now, let
![]() $ t_{ n + 2 } \in \{ 1 , \ldots , T^{ ( n + 2 ) } \} $
satisfy
$ t_{ n + 2 } \in \{ 1 , \ldots , T^{ ( n + 2 ) } \} $
satisfy
 $$ \begin{align*} X_{ t_{ n + 2 } }^{ ( n + 2 ) } \cap \bigg( \bigcup_{ j \in \mathbb{Z} } h^j ( X_{ t_{ n + 1 } }^{ ( n + 1 ) } ) \bigg) \neq \varnothing. \end{align*} $$
$$ \begin{align*} X_{ t_{ n + 2 } }^{ ( n + 2 ) } \cap \bigg( \bigcup_{ j \in \mathbb{Z} } h^j ( X_{ t_{ n + 1 } }^{ ( n + 1 ) } ) \bigg) \neq \varnothing. \end{align*} $$
By Lemma 4.10(5), there is actually a
![]() $ k_{ n + 1 }' \in \{ 1 , \ldots , K_{ t_{ n + 1 } }^{ ( n + 1 ) } \} $
such that
$ k_{ n + 1 }' \in \{ 1 , \ldots , K_{ t_{ n + 1 } }^{ ( n + 1 ) } \} $
such that
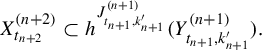 $$ \begin{align*} X_{ t_{ n + 2 } }^{ ( n + 2 ) } \subset h^{ J_{ t_{ n + 1 } , k_{ n + 1 }' }^{ ( n + 1 ) } } ( Y_{ t_{ n + 1 } , k_{ n + 1 }' }^{ ( n + 1 ) } ). \end{align*} $$
$$ \begin{align*} X_{ t_{ n + 2 } }^{ ( n + 2 ) } \subset h^{ J_{ t_{ n + 1 } , k_{ n + 1 }' }^{ ( n + 1 ) } } ( Y_{ t_{ n + 1 } , k_{ n + 1 }' }^{ ( n + 1 ) } ). \end{align*} $$
By claim
![]() $(\ast )$
,
$(\ast )$
,
![]() $ v' = ( n + 1 , t_{ n + 1 } , k_{ n + 1 }' ) \in V_{ \max } $
. By claim
$ v' = ( n + 1 , t_{ n + 1 } , k_{ n + 1 }' ) \in V_{ \max } $
. By claim
![]() $(\ast )$
, there is
$(\ast )$
, there is
![]() $ e \in E_{ \max } $
with
$ e \in E_{ \max } $
with
![]() $ s ( e ) = v $
and
$ s ( e ) = v $
and
![]() $ r ( e ) = v' $
. This completes the proof of conclusion (2).
$ r ( e ) = v' $
. This completes the proof of conclusion (2).
We now prove conclusion (3) of the proposition. Let
![]() $ v \in V_{ \min } $
and
$ v \in V_{ \min } $
and
![]() $ e \in E_{ \min } $
satisfy
$ e \in E_{ \min } $
satisfy
![]() $ r ( e ) \in R ( v ) $
. Write
$ r ( e ) \in R ( v ) $
. Write
![]() $ v = ( n , t_n , k_n ) $
and
$ v = ( n , t_n , k_n ) $
and
![]() $ e = ( n + 1 , t_{ n + 1 } , k_{ n + 1 } , i_{ n + 1 } ) $
. Since
$ e = ( n + 1 , t_{ n + 1 } , k_{ n + 1 } , i_{ n + 1 } ) $
. Since
![]() $ r ( e ) \in R ( v ) $
, there is an edge
$ r ( e ) \in R ( v ) $
, there is an edge
![]() $ e' = ( n + 1 , t_{ n + 1 } , k_{ n + 1 } , i_{ n + 1 }' ) $
with
$ e' = ( n + 1 , t_{ n + 1 } , k_{ n + 1 } , i_{ n + 1 }' ) $
with
![]() $ s ( e' ) = v $
, which tells us there is
$ s ( e' ) = v $
, which tells us there is
![]() $ j_{ n + 1 } \in \{ 0 , \ldots , J_{ t_{ n + 1 } , k_{ n + 1 } }^{ ( n + 1 ) } - 1 \} $
such that
$ j_{ n + 1 } \in \{ 0 , \ldots , J_{ t_{ n + 1 } , k_{ n + 1 } }^{ ( n + 1 ) } - 1 \} $
such that
![]() $ h^{ j_{ n + 1 } } ( Y_{ t_{ n + 1 } , k_{ n + 1 } } ) \subset Y_{ t_n , k_n }^{ ( n ) } $
. By Lemma 4.10(6),
$ h^{ j_{ n + 1 } } ( Y_{ t_{ n + 1 } , k_{ n + 1 } } ) \subset Y_{ t_n , k_n }^{ ( n ) } $
. By Lemma 4.10(6),
![]() $ Y_{ t_n , k_n }^{ ( n ) } \subset \bigcup _{ j \in \mathbb {Z} } h^j ( X_{ t_{ n + 1 } }^{ ( n + 1 ) } ) $
. Since
$ Y_{ t_n , k_n }^{ ( n ) } \subset \bigcup _{ j \in \mathbb {Z} } h^j ( X_{ t_{ n + 1 } }^{ ( n + 1 ) } ) $
. Since
![]() $ v \in V_{ \min } $
, there is some edge
$ v \in V_{ \min } $
, there is some edge
![]() $ e^{\prime \prime } = ( n + 1 , t_{ n + 1 } , k_{ n + 1 }^{\prime \prime } , i_{ n + 1 }^{\prime \prime } ) \in E_{ \min } $
with
$ e^{\prime \prime } = ( n + 1 , t_{ n + 1 } , k_{ n + 1 }^{\prime \prime } , i_{ n + 1 }^{\prime \prime } ) \in E_{ \min } $
with
![]() $ s ( e ) = v $
. By Lemma 4.10(4), since
$ s ( e ) = v $
. By Lemma 4.10(4), since
![]() $ e^{\prime \prime } \in E_{ \min } $
, we have
$ e^{\prime \prime } \in E_{ \min } $
, we have
![]() $ i_{ n + 1 }^{\prime \prime } = 0 $
, so
$ i_{ n + 1 }^{\prime \prime } = 0 $
, so
![]() $ Y_{ t_{ n + 1 } , k_{ n + 1 }^{\prime \prime } }^{ ( n + 1 ) } \subset Y_{ t_n , k_n }^{ ( n ) } $
. Again by Lemma 4.10(4), we actually have
$ Y_{ t_{ n + 1 } , k_{ n + 1 }^{\prime \prime } }^{ ( n + 1 ) } \subset Y_{ t_n , k_n }^{ ( n ) } $
. Again by Lemma 4.10(4), we actually have
Now, since
![]() $ e \in E_{ \min } $
, by Lemma 4.10(4), we have
$ e \in E_{ \min } $
, by Lemma 4.10(4), we have
![]() $ i_{ n + 1 } = 0 $
. But by (4.8), we must have
$ i_{ n + 1 } = 0 $
. But by (4.8), we must have
![]() $ Y_{ t_{ n + 1 } , k_{ n + 1 } }^{ ( n + 1 ) } \subset Y_{ t_n , k_n }^{ ( n ) } $
, which means that
$ Y_{ t_{ n + 1 } , k_{ n + 1 } }^{ ( n + 1 ) } \subset Y_{ t_n , k_n }^{ ( n ) } $
, which means that
![]() $ s ( e ) = v $
.
$ s ( e ) = v $
.
Let
![]() $ v \in V_{ \max } $
and
$ v \in V_{ \max } $
and
![]() $ e \in E_{ \max } $
satisfy
$ e \in E_{ \max } $
satisfy
![]() $ r ( e ) \in R ( v ) $
. Write
$ r ( e ) \in R ( v ) $
. Write
![]() $ v = ( n , t_n , k_n ) $
and
$ v = ( n , t_n , k_n ) $
and
![]() $ e = ( n + 1 , t_{ n + 1 } , k_{ n + 1 } , i_{ n + 1 } ) $
. Since
$ e = ( n + 1 , t_{ n + 1 } , k_{ n + 1 } , i_{ n + 1 } ) $
. Since
![]() $ r ( e ) \in R ( v ) $
, there is an edge
$ r ( e ) \in R ( v ) $
, there is an edge
![]() $ e' = ( n + 1 , t_{ n + 1 } , k_{ n + 1 } , i_{ n + 1 }' ) $
with
$ e' = ( n + 1 , t_{ n + 1 } , k_{ n + 1 } , i_{ n + 1 }' ) $
with
![]() $ s ( e' ) = v $
, which tells us there is
$ s ( e' ) = v $
, which tells us there is
![]() $ j_{ n + 1 } \in \{ 0 , \ldots , J_{ t_{ n + 1 } , k_{ n + 1 } }^{ ( n + 1 ) } - 1 \} $
such that
$ j_{ n + 1 } \in \{ 0 , \ldots , J_{ t_{ n + 1 } , k_{ n + 1 } }^{ ( n + 1 ) } - 1 \} $
such that
![]() $ h^{ j_{ n + 1 } } ( Y_{ t_{ n + 1 } , k_{ n + 1 } }^{ ( n + 1 ) } ) \subset Y_{ t_n , k_n }^{ ( n ) } $
. By Lemma 4.10(6),
$ h^{ j_{ n + 1 } } ( Y_{ t_{ n + 1 } , k_{ n + 1 } }^{ ( n + 1 ) } ) \subset Y_{ t_n , k_n }^{ ( n ) } $
. By Lemma 4.10(6),
![]() $ Y_{ t_n , k_n }^{ ( n ) } \subset \bigcup _{ j \in \mathbb {Z} } h^j ( X_{ t_{ n + 1 } }^{ ( n + 1 ) } ) $
. Since
$ Y_{ t_n , k_n }^{ ( n ) } \subset \bigcup _{ j \in \mathbb {Z} } h^j ( X_{ t_{ n + 1 } }^{ ( n + 1 ) } ) $
. Since
![]() $ v \in V_{ \max } $
, there is some edge
$ v \in V_{ \max } $
, there is some edge
![]() $ e^{\prime \prime } = ( n + 1 , t_{ n + 1 } , k_{ n + 1 }^{\prime \prime } , i_{ n + 1 }^{\prime \prime } ) \in E_{ \max } $
with
$ e^{\prime \prime } = ( n + 1 , t_{ n + 1 } , k_{ n + 1 }^{\prime \prime } , i_{ n + 1 }^{\prime \prime } ) \in E_{ \max } $
with
![]() $ s ( e ) = v $
. By claim
$ s ( e ) = v $
. By claim
![]() $(\ast \ast )$
, we have
$(\ast \ast )$
, we have
By claim (
![]() $\ast $
),
$\ast $
),
![]() $ s ( e ) = v $
. This completes the proof of conclusion (3).
$ s ( e ) = v $
. This completes the proof of conclusion (3).
Now we prove conclusion (4) of this lemma. Let
![]() $ v \in V_{ \min } $
, let
$ v \in V_{ \min } $
, let
![]() $ m \in \mathbb {Z}_{> 0 } $
, and write
$ m \in \mathbb {Z}_{> 0 } $
, and write
![]() $ v = ( n , t_n , k_n ) $
. It is clear that
$ v = ( n , t_n , k_n ) $
. It is clear that
![]() $ v \in ( S^m \circ R^m ) ( v ) $
, and so
$ v \in ( S^m \circ R^m ) ( v ) $
, and so
Now, let
![]() $ w = ( n + m , t_{ n + m } , k_{ n + m } ) \in R^m ( v ) $
. By Lemma 4.10(4) (applied
$ w = ( n + m , t_{ n + m } , k_{ n + m } ) \in R^m ( v ) $
. By Lemma 4.10(4) (applied
![]() $ m $
times), we have
$ m $
times), we have
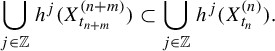 $$ \begin{align*} \bigcup_{ j \in \mathbb{Z} } h^j ( X_{ t_{ n + m } }^{ ( n + m ) } ) \subset \bigcup_{ j \in \mathbb{Z} } h^j ( X_{ t_n }^{ ( n ) } ). \end{align*} $$
$$ \begin{align*} \bigcup_{ j \in \mathbb{Z} } h^j ( X_{ t_{ n + m } }^{ ( n + m ) } ) \subset \bigcup_{ j \in \mathbb{Z} } h^j ( X_{ t_n }^{ ( n ) } ). \end{align*} $$
So every element of
![]() $ ( S^m \circ R^m ) ( v ) $
has the form
$ ( S^m \circ R^m ) ( v ) $
has the form
![]() $ ( n , t_n , k_n' ) $
for some
$ ( n , t_n , k_n' ) $
for some
![]() $ k_n' \in \{ 1 , \ldots , K_{ t_n }^{ ( n ) } \} $
. Let
$ k_n' \in \{ 1 , \ldots , K_{ t_n }^{ ( n ) } \} $
. Let
![]() $ w' = ( n + m , t_{ n + m }' , k_{ n + m }' ) \in ( R^m \circ S^m \circ R^m ) ( v ) $
, meaning there is an path
$ w' = ( n + m , t_{ n + m }' , k_{ n + m }' ) \in ( R^m \circ S^m \circ R^m ) ( v ) $
, meaning there is an path
![]() $ ( e_1 , \ldots , e_m ) $
with
$ ( e_1 , \ldots , e_m ) $
with
![]() $ s ( e_1 ) = ( n , t_n , k_n' ) $
for some
$ s ( e_1 ) = ( n , t_n , k_n' ) $
for some
![]() $ k_n' \in \{ 1 , \ldots , K_{ t_n }^{ ( n ) } \} $
and
$ k_n' \in \{ 1 , \ldots , K_{ t_n }^{ ( n ) } \} $
and
![]() $ r ( e_m ) = w' $
. Write
$ r ( e_m ) = w' $
. Write
![]() $ e_m = ( n + m , t_{ n + m }' , k_{ n + m }' , i_{ n + m }' ) $
. This means that
$ e_m = ( n + m , t_{ n + m }' , k_{ n + m }' , i_{ n + m }' ) $
. This means that
![]() $ h^{ i_{ n + m }' } ( Y_{ t_{ n + m }' , k_{ n + m }' }^{ ( n + m ) } ) \subset Y_{ t_n , k_n' }^{ ( n ) } $
. However, then by Lemma 4.10(4) (applied
$ h^{ i_{ n + m }' } ( Y_{ t_{ n + m }' , k_{ n + m }' }^{ ( n + m ) } ) \subset Y_{ t_n , k_n' }^{ ( n ) } $
. However, then by Lemma 4.10(4) (applied
![]() $ m $
times), we must have
$ m $
times), we must have
![]() $ Y_{ t_{ n + m }' , k_{ n + m }' }^{ ( n + m ) } \subset Y_{ t_n , k_n }^{ ( n ) } $
. Therefore,
$ Y_{ t_{ n + m }' , k_{ n + m }' }^{ ( n + m ) } \subset Y_{ t_n , k_n }^{ ( n ) } $
. Therefore,
![]() $ w' \in R^m ( v ) $
(by a minimal path), as desired. An identical argument using Lemma 4.10(5) in place of conclusion (4) shows that this equation also holds when
$ w' \in R^m ( v ) $
(by a minimal path), as desired. An identical argument using Lemma 4.10(5) in place of conclusion (4) shows that this equation also holds when
![]() $ v \in V_{ \max } $
. This proves conclusion (4) of this proposition and therefore finishes the proof of the proposition.
$ v \in V_{ \max } $
. This proves conclusion (4) of this proposition and therefore finishes the proof of the proposition.
Remark 4.12. We describe and illustrate what it means for a Bratteli diagram to satisfy the conclusions of Proposition 4.11. As you read the proof of Theorem 5.2, keep these descriptions and illustrations in mind as Proposition 4.11 gets cited many times. We adopt the notation of the proposition. For simplicity, we discuss the minimal vertex/edge case as the maximal case is analogous.
-
(1) Conclusion (1), which says that that the system
 $ ( X_B , h_B , X_{ B , \min } ) $
is conjugate to
$ ( X_B , h_B , X_{ B , \min } ) $
is conjugate to
 $ ( X , h , Z ) $
, just means that the Bratteli diagram’s dynamics agrees with the dynamics of the original system. This tells us that we have created a ‘Bratteli–Vershik–Kakutani’ model of the system.
$ ( X , h , Z ) $
, just means that the Bratteli diagram’s dynamics agrees with the dynamics of the original system. This tells us that we have created a ‘Bratteli–Vershik–Kakutani’ model of the system. -
(2) What it means for
 $ v \in V_{ \min } $
is that there is some minimal edge
$ v \in V_{ \min } $
is that there is some minimal edge
 $ e' $
with
$ e' $
with
 $ s ( e' ) = v $
. What conclusion (2) guarantees is that at least one of those minimal edges,
$ s ( e' ) = v $
. What conclusion (2) guarantees is that at least one of those minimal edges,
 $ e $
, comes from another minimal vertex,
$ e $
, comes from another minimal vertex,
 $ v' $
. See Figure 5 for an illustration of a situation that violates this. This property tells us that given any
$ v' $
. See Figure 5 for an illustration of a situation that violates this. This property tells us that given any
 $ v \in V_{ \min } $
, there is an infinite minimal path containing
$ v \in V_{ \min } $
, there is an infinite minimal path containing
 $ v $
.
$ v $
.
Figure 5 A partial ordered Bratteli diagram illustrating an example of a situation that violates conclusion (2) of Proposition 4.11. In this picture,
 $ v \in V_{ \min } $
since there is a minimal edge with a range of
$ v \in V_{ \min } $
since there is a minimal edge with a range of
 $ w_3' $
and a source of
$ w_3' $
and a source of
 $ v $
. However, there is no minimal edge with a source of
$ v $
. However, there is no minimal edge with a source of
 $ v $
and a range that is a minimal vertex (the possibilities are
$ v $
and a range that is a minimal vertex (the possibilities are
 $ w_1' $
and
$ w_1' $
and
 $ w_2' $
).
$ w_2' $
).
Figure 6 A partial ordered Bratteli diagram illustrating an example of a situation that violates conclusion (3) of Proposition 4.11. In this picture,
 $ v \in V_{ \min } $
since there is a minimal edge with a range of
$ v \in V_{ \min } $
since there is a minimal edge with a range of
 $ w_3' $
and a source of
$ w_3' $
and a source of
 $ v $
(also one with a range of
$ v $
(also one with a range of
 $ w_2' $
). However, even though
$ w_2' $
). However, even though
 $ w_1' $
is in
$ w_1' $
is in
 $ R ( v ) $
, the minimal edge with a range of
$ R ( v ) $
, the minimal edge with a range of
 $ w_1' $
has a source of
$ w_1' $
has a source of
 $ w_1 $
, not
$ w_1 $
, not
 $ v $
.
$ v $
.
Figure 7 A partial ordered Bratteli diagram illustrating an example of a situation that violates conclusion (4) of Proposition 4.11. In this picture,
 $ v \in V_{ \min } $
since there is a minimal edge with a range of
$ v \in V_{ \min } $
since there is a minimal edge with a range of
 $ w_1' $
and a source of
$ w_1' $
and a source of
 $ v $
(also one with a range of
$ v $
(also one with a range of
 $ w_2' $
and one with a range of
$ w_2' $
and one with a range of
 $ w_3' $
). However,
$ w_3' $
). However,
 $ w_4' $
is not in
$ w_4' $
is not in
 $ R ( v ) $
, but since
$ R ( v ) $
, but since
 $ w_2 $
is in
$ w_2 $
is in
 $ ( S \circ R ) ( v ) $
,
$ ( S \circ R ) ( v ) $
,
 $ w_4' $
is in
$ w_4' $
is in
 $ ( R \circ S \circ R ) ( v ) $
.
$ ( R \circ S \circ R ) ( v ) $
. -
(3) What conclusion (3) tells us is that for every minimal vertex
 $ v $
, everything in its range
$ v $
, everything in its range
 $ R ( v ) $
has the property that the source of its minimal edge is
$ R ( v ) $
has the property that the source of its minimal edge is
 $ v $
. See Figure 6 for an illustration of a situation that violates this. One of the consequences of this is that no two minimal vertices share anything in their range.
$ v $
. See Figure 6 for an illustration of a situation that violates this. One of the consequences of this is that no two minimal vertices share anything in their range. -
(4) For
 $ m = 1 $
, what conclusion (4) tells us is that the range of a vertex is either contained in the range of a minimal vertex or disjoint from it. See Figure 7 for an illustration of a situation that violates this. For larger values of
$ m = 1 $
, what conclusion (4) tells us is that the range of a vertex is either contained in the range of a minimal vertex or disjoint from it. See Figure 7 for an illustration of a situation that violates this. For larger values of
 $ m $
, this tells us that telescopings of the Bratteli diagram still have this property (see Proposition 4.13).
$ m $
, this tells us that telescopings of the Bratteli diagram still have this property (see Proposition 4.13).
We show in the following proposition that the class of Bratteli diagrams satisfying the conclusions of Proposition 4.11 is closed under telescoping. This is important, as we will require some amount of telescoping of diagrams.
Proposition 4.13. Let
![]() $ ( X , h ) $
be a fiberwise essentially minimal zero-dimensional system and let
$ ( X , h ) $
be a fiberwise essentially minimal zero-dimensional system and let
![]() $ B = ( V , E , \leq ) $
be an ordered Bratteli diagram that satisfies the conclusions of Proposition 4.11. If
$ B = ( V , E , \leq ) $
be an ordered Bratteli diagram that satisfies the conclusions of Proposition 4.11. If
![]() $ B' = ( V' , E' , \leq ' ) $
is a telescoping of
$ B' = ( V' , E' , \leq ' ) $
is a telescoping of
![]() $ B $
, then
$ B $
, then
![]() $ B' $
also satisfies the conclusions of Proposition 4.11.
$ B' $
also satisfies the conclusions of Proposition 4.11.
Proof. Let
![]() $ ( k_n ) $
be the telescoping sequence corresponding to
$ ( k_n ) $
be the telescoping sequence corresponding to
![]() $ B' $
, so that
$ B' $
, so that
![]() $ V_n' = V_{ k_n } $
and
$ V_n' = V_{ k_n } $
and
![]() $ E_n' = P_{ k_n + 1 , k_{ n + 1 } } $
for all
$ E_n' = P_{ k_n + 1 , k_{ n + 1 } } $
for all
![]() $ n \in \mathbb {Z}_{> 0 } $
(where
$ n \in \mathbb {Z}_{> 0 } $
(where
![]() $ k_0 = 0 $
). This identification induces a map
$ k_0 = 0 $
). This identification induces a map
![]() $ \varphi : X_B \to X_{ B' } $
by sending
$ \varphi : X_B \to X_{ B' } $
by sending
![]() $ e = ( e_1 , e_2 , \ldots ) $
to
$ e = ( e_1 , e_2 , \ldots ) $
to
![]() $ \varphi ( e ) = ( ( e_1 , \ldots , e_{ k_1 } ) , ( e_{ k_1 + 1 } , \ldots , e_{ k_2 } ) , \ldots ) $
. By definition of the induced order on a telescoped Bratteli diagram,
$ \varphi ( e ) = ( ( e_1 , \ldots , e_{ k_1 } ) , ( e_{ k_1 + 1 } , \ldots , e_{ k_2 } ) , \ldots ) $
. By definition of the induced order on a telescoped Bratteli diagram,
![]() $ \varphi $
is a conjugation, and therefore
$ \varphi $
is a conjugation, and therefore
![]() $ B' $
satisfies conclusion (1) of Proposition 4.11.
$ B' $
satisfies conclusion (1) of Proposition 4.11.
We now show that conclusion (2) holds. Let
![]() $ v \in V_{ n , \min }' $
. What we are looking for is a
$ v \in V_{ n , \min }' $
. What we are looking for is a
![]() $ v' \in V_{ n + 1 , \min }' $
and
$ v' \in V_{ n + 1 , \min }' $
and
![]() $ e \in E_{ n + 1 , \min }' $
such that
$ e \in E_{ n + 1 , \min }' $
such that
![]() $ s ( e ) = v $
and
$ s ( e ) = v $
and
![]() $ r ( e ) = v' $
. We can regard all of this as happening in
$ r ( e ) = v' $
. We can regard all of this as happening in
![]() $ B $
instead of
$ B $
instead of
![]() $ B' $
, so that we have
$ B' $
, so that we have
![]() $ v \in V_{ k_n , \min } $
, and we are looking for
$ v \in V_{ k_n , \min } $
, and we are looking for
![]() $ v' \in V_{ k_{ n + 1 } , \min } $
and a minimal path
$ v' \in V_{ k_{ n + 1 } , \min } $
and a minimal path
![]() $ ( e_{ k_n + 1 } , \ldots , e_{ k_{ n + 1 } } ) \in P_{ k_n + 1 , k_{ n + 1 } } $
. By Proposition 4.11(2), there is a
$ ( e_{ k_n + 1 } , \ldots , e_{ k_{ n + 1 } } ) \in P_{ k_n + 1 , k_{ n + 1 } } $
. By Proposition 4.11(2), there is a
![]() $ e_{ k_n + 1 } \in E_{ k_n + 1 , \min } $
and a
$ e_{ k_n + 1 } \in E_{ k_n + 1 , \min } $
and a
![]() $ v_{ k_n + 1 } \in V_{ k_n + 1 , \min } $
with
$ v_{ k_n + 1 } \in V_{ k_n + 1 , \min } $
with
![]() $ s ( e ) = v $
and
$ s ( e ) = v $
and
![]() $ r ( e ) = v_{ k_n + 1 } $
. Proceeding inductively, we construct the desired result, with
$ r ( e ) = v_{ k_n + 1 } $
. Proceeding inductively, we construct the desired result, with
![]() $ v' = v_{ k_{ n + 1 } } $
. The same argument works for
$ v' = v_{ k_{ n + 1 } } $
. The same argument works for
![]() $ V_{ \max }' $
in place of
$ V_{ \max }' $
in place of
![]() $ V_{ \min }' $
. This proves that conclusion (2) holds.
$ V_{ \min }' $
. This proves that conclusion (2) holds.
Next, we prove that conclusion (3) holds. Let
![]() $ v \in V_{ n , \min }' $
and let
$ v \in V_{ n , \min }' $
and let
![]() $ e \in E_{ n + 1 , \min }' $
satisfy
$ e \in E_{ n + 1 , \min }' $
satisfy
![]() $ r ( e ) \in R ( v ) $
. We want to show that
$ r ( e ) \in R ( v ) $
. We want to show that
![]() $ s ( e ) = v $
. We once again regard all of this as happening in
$ s ( e ) = v $
. We once again regard all of this as happening in
![]() $ B $
instead of
$ B $
instead of
![]() $ B' $
. What this means is that we have
$ B' $
. What this means is that we have
![]() $ v \in V_{ k_n , \min }' $
and a minimal path
$ v \in V_{ k_n , \min }' $
and a minimal path
![]() $ ( e_{ k_n + 1 } , \ldots , e_{ k_{ n + 1 } } ) \in P_{ k_n + 1 , k_{ n + 1 } } $
such that there is some path
$ ( e_{ k_n + 1 } , \ldots , e_{ k_{ n + 1 } } ) \in P_{ k_n + 1 , k_{ n + 1 } } $
such that there is some path
![]() $ ( e_{ k_n + 1 }' , \ldots , e_{ k_{ n + 1 } }' ) \in P_{ k_n + 1 , k_{ n + 1 } } $
such that
$ ( e_{ k_n + 1 }' , \ldots , e_{ k_{ n + 1 } }' ) \in P_{ k_n + 1 , k_{ n + 1 } } $
such that
![]() $ s ( e_{ k_n + 1 }' ) = v $
and
$ s ( e_{ k_n + 1 }' ) = v $
and
![]() $ r ( e_{ k_{ n + 1 } }' ) = r ( e_{ k_{ n + 1 } } ) $
, and we want to show that
$ r ( e_{ k_{ n + 1 } }' ) = r ( e_{ k_{ n + 1 } } ) $
, and we want to show that
![]() $ s ( e_{ k_n + 1 } ) = v $
. Suppose not. Then by Proposition 4.11(3), we have
$ s ( e_{ k_n + 1 } ) = v $
. Suppose not. Then by Proposition 4.11(3), we have
![]() $ r ( e_{ k_n + 1 } ) \notin R ( v ) $
; in particular, we have
$ r ( e_{ k_n + 1 } ) \notin R ( v ) $
; in particular, we have
![]() $ r ( e_{ k_n + 1 } ) \neq r ( e_{ k_n + 1 }' ) $
. Proceeding like this, we eventually see
$ r ( e_{ k_n + 1 } ) \neq r ( e_{ k_n + 1 }' ) $
. Proceeding like this, we eventually see
![]() $r(e_{k_{n + 1}})~\neq ~r(e_{k_{n+1}}')$
, which is a contradiction. Thus,
$r(e_{k_{n + 1}})~\neq ~r(e_{k_{n+1}}')$
, which is a contradiction. Thus,
![]() $ s ( e_{ k_n + 1 } ) = v $
. The proof for
$ s ( e_{ k_n + 1 } ) = v $
. The proof for
![]() $ V_{ \max }' $
in place of
$ V_{ \max }' $
in place of
![]() $ V_{ \min }' $
is analogous. This proves that conclusion (3) holds.
$ V_{ \min }' $
is analogous. This proves that conclusion (3) holds.
That conclusion (4) holds is immediate; replace
![]() $ m $
with
$ m $
with
![]() $ k_{ n + m } - k_n $
. This completes the proof of the proposition.
$ k_{ n + m } - k_n $
. This completes the proof of the proposition.
5 The dynamical classification theorem
We now prove our main theorems, Theorems 5.2 and 5.3.
Lemma 5.1. Let
![]() $ B = ( V , E , \leq ) $
be an ordered Bratteli diagram with a perfect ordering. Let
$ B = ( V , E , \leq ) $
be an ordered Bratteli diagram with a perfect ordering. Let
![]() $ e , f \in X_B $
and suppose
$ e , f \in X_B $
and suppose
![]() $ e $
and
$ e $
and
![]() $ f $
pass through the same vertex
$ f $
pass through the same vertex
![]() $ v $
at level
$ v $
at level
![]() $ k $
. Then there is some
$ k $
. Then there is some
![]() $ N \in \mathbb {Z} $
such that
$ N \in \mathbb {Z} $
such that
![]() $ h_B^N ( e ) = f $
.
$ h_B^N ( e ) = f $
.
Proof. Write
![]() $ e = ( e_1 , e_2 , \ldots ) $
and write
$ e = ( e_1 , e_2 , \ldots ) $
and write
![]() $ f = ( f_1 , f_2 , \ldots ) $
. Let
$ f = ( f_1 , f_2 , \ldots ) $
. Let
![]() $ n_1 $
be the largest element of
$ n_1 $
be the largest element of
![]() $ \{ 1 , \ldots , k \} $
such that
$ \{ 1 , \ldots , k \} $
such that
![]() $ e_{ n_1 } \neq f_{ n_1 } $
.
$ e_{ n_1 } \neq f_{ n_1 } $
.
Suppose
![]() $ e_{ n_1 } < f_{ n_1 } $
. Then there is an
$ e_{ n_1 } < f_{ n_1 } $
. Then there is an
![]() $ N_1 \in \mathbb {Z}_{> 0 } $
such that
$ N_1 \in \mathbb {Z}_{> 0 } $
such that
where
![]() $ ( e_1' , \ldots , e_{ n_1 - 1 }' ) $
is the minimal path from
$ ( e_1' , \ldots , e_{ n_1 - 1 }' ) $
is the minimal path from
![]() $ v_0 \in V_0 $
to
$ v_0 \in V_0 $
to
![]() $ s ( f_{ n_1 } ) $
. Now,
$ s ( f_{ n_1 } ) $
. Now,
![]() $ h_B^{ M } ( e ) $
and
$ h_B^{ M } ( e ) $
and
![]() $ f $
pass through the same vertex at level
$ f $
pass through the same vertex at level
![]() $ n_1 - 1 $
. So let
$ n_1 - 1 $
. So let
![]() $ n_2 $
be the largest element of
$ n_2 $
be the largest element of
![]() $ \{ 1 , \ldots , n_1 - 1 \} $
such that
$ \{ 1 , \ldots , n_1 - 1 \} $
such that
![]() $ e_{ n_2 }' \neq f_{ n_2 } $
. Clearly,
$ e_{ n_2 }' \neq f_{ n_2 } $
. Clearly,
![]() $ e_{ n_2 }' < f_{ n_2 } $
. So repeating the above process, we find an integer
$ e_{ n_2 }' < f_{ n_2 } $
. So repeating the above process, we find an integer
![]() $ N_2 \in \mathbb {Z}_{> 0 } $
such that
$ N_2 \in \mathbb {Z}_{> 0 } $
such that
![]() $ h_B^{ N_1 + N_2 } ( e ) = ( e_1^{\prime \prime } , \ldots , e_{ n_2 - 1 }^{\prime \prime } , f_{ n_2 } , \ldots , f_{ n_1 } , e_{ n_1 + 1 } , \ldots ) $
. Repeating this process inductively, we arrive at an integer
$ h_B^{ N_1 + N_2 } ( e ) = ( e_1^{\prime \prime } , \ldots , e_{ n_2 - 1 }^{\prime \prime } , f_{ n_2 } , \ldots , f_{ n_1 } , e_{ n_1 + 1 } , \ldots ) $
. Repeating this process inductively, we arrive at an integer
![]() $ N $
such that
$ N $
such that
![]() $ h_B^N ( e ) = f $
.
$ h_B^N ( e ) = f $
.
Theorem 5.2. Let
![]() $ ( X_1 , h_1 , Z_1 ) $
and
$ ( X_1 , h_1 , Z_1 ) $
and
![]() $ ( X_2 , h_2 , Z_2 ) $
be fiberwise essentially minimal zero-dimensional systems. Then
$ ( X_2 , h_2 , Z_2 ) $
be fiberwise essentially minimal zero-dimensional systems. Then
![]() $ ( X_1 , h_1 , Z_1 ) $
and
$ ( X_1 , h_1 , Z_1 ) $
and
![]() $ ( X_2 , h_2 , Z_2 ) $
are strong orbit equivalent if and only if
$ ( X_2 , h_2 , Z_2 ) $
are strong orbit equivalent if and only if
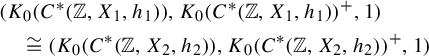 $$ \begin{align*} &( K_0 ( C^* ( \mathbb{Z} , X_1 , h_1 ) ) , K_0 ( C^* ( \mathbb{Z} , X_1 , h_1 ) )^+ , 1 )\\ &\quad\cong ( K_0 ( C^* ( \mathbb{Z} , X_2 , h_2 ) ) , K_0 ( C^* ( \mathbb{Z} , X_2 , h_2 ) )^+ , 1 ) \end{align*} $$
$$ \begin{align*} &( K_0 ( C^* ( \mathbb{Z} , X_1 , h_1 ) ) , K_0 ( C^* ( \mathbb{Z} , X_1 , h_1 ) )^+ , 1 )\\ &\quad\cong ( K_0 ( C^* ( \mathbb{Z} , X_2 , h_2 ) ) , K_0 ( C^* ( \mathbb{Z} , X_2 , h_2 ) )^+ , 1 ) \end{align*} $$
and
Proof. (
![]() $ \Leftarrow $
). Let
$ \Leftarrow $
). Let
![]() $ B_1 $
and
$ B_1 $
and
![]() $ B_2 $
be the Bratteli diagrams satisfying the conclusions of Proposition 4.11 for
$ B_2 $
be the Bratteli diagrams satisfying the conclusions of Proposition 4.11 for
![]() $ ( X_1 , h_1 , Z_1 ) $
and
$ ( X_1 , h_1 , Z_1 ) $
and
![]() $ ( X_2 , h_2 , Z_2 ) $
, respectively. By Theorem 3.4, we have
$ ( X_2 , h_2 , Z_2 ) $
, respectively. By Theorem 3.4, we have
![]() $ K^0 ( X_1 , h_1 ) \cong K^0 ( X_2, h_2 ) $
. By Proposition 4.11(1), we have
$ K^0 ( X_1 , h_1 ) \cong K^0 ( X_2, h_2 ) $
. By Proposition 4.11(1), we have
![]() $ K^0 ( X_{ B_1 } , h_{ B_1 } ) \cong K^0 ( X_{ B_2 } , h_{ B_2 } ) $
. By a slight but trivial extension of [Reference Herman, Putnam and Skau10, Theorem 5.4], we have
$ K^0 ( X_{ B_1 } , h_{ B_1 } ) \cong K^0 ( X_{ B_2 } , h_{ B_2 } ) $
. By a slight but trivial extension of [Reference Herman, Putnam and Skau10, Theorem 5.4], we have
![]() $ K_0 ( B_1 ) \cong K_0 ( B_2 ) $
. By [Reference Elliott6], we have
$ K_0 ( B_1 ) \cong K_0 ( B_2 ) $
. By [Reference Elliott6], we have
![]() $ B_1 \sim B_2 $
(in the equivalence class of Bratteli diagrams generated by telescoping and isomorphism), which tells us that there is a (non-ordered) Bratteli diagram
$ B_1 \sim B_2 $
(in the equivalence class of Bratteli diagrams generated by telescoping and isomorphism), which tells us that there is a (non-ordered) Bratteli diagram
![]() $ B $
such that telescoping
$ B $
such that telescoping
![]() $ B $
to odd levels yields a telescoping of
$ B $
to odd levels yields a telescoping of
![]() $ B_1 $
and telescoping
$ B_1 $
and telescoping
![]() $ B $
to even levels yields a telescoping of
$ B $
to even levels yields a telescoping of
![]() $ B_2 $
. By replacing
$ B_2 $
. By replacing
![]() $ B_1 $
and
$ B_1 $
and
![]() $ B_2 $
with their telescopings (which can be done without changing the above due to Proposition 4.13), we may assume that telescoping
$ B_2 $
with their telescopings (which can be done without changing the above due to Proposition 4.13), we may assume that telescoping
![]() $ B $
to odd levels yields
$ B $
to odd levels yields
![]() $ B_1 $
and telescoping
$ B_1 $
and telescoping
![]() $ B $
to even levels yields
$ B $
to even levels yields
![]() $ B_2 $
. Let
$ B_2 $
. Let
![]() $ B' $
be the telescoping of
$ B' $
be the telescoping of
![]() $ B $
by the sequence
$ B $
by the sequence
![]() $ ( 3n - 2 ) $
, so that telescoping
$ ( 3n - 2 ) $
, so that telescoping
![]() $ B $
to odd levels yields a telescoping of
$ B $
to odd levels yields a telescoping of
![]() $ B_1 $
by
$ B_1 $
by
![]() $ ( 3n - 2 ) $
and telescoping
$ ( 3n - 2 ) $
and telescoping
![]() $ B $
to even levels yields a telescoping of
$ B $
to even levels yields a telescoping of
![]() $ B_2 $
by
$ B_2 $
by
![]() $ ( 3n - 1 ) $
. Note that by Proposition 4.13, these telescopings of
$ ( 3n - 1 ) $
. Note that by Proposition 4.13, these telescopings of
![]() $ B_1 $
and
$ B_1 $
and
![]() $ B_2 $
also satisfy the conclusions of Proposition 4.11.
$ B_2 $
also satisfy the conclusions of Proposition 4.11.
We denote by
![]() $ V_{ \min }' $
(
$ V_{ \min }' $
(
![]() $ V_{ \max }' $
) the minimal (respectively maximal) vertices as inherited by
$ V_{ \max }' $
) the minimal (respectively maximal) vertices as inherited by
![]() $ B_1 $
and
$ B_1 $
and
![]() $ B_2 $
. We claim that
$ B_2 $
. We claim that
![]() $ B' $
has the following property:
$ B' $
has the following property:
-
(*) let
 $ v \in V_{ \min }' $
. There is precisely one
$ v \in V_{ \min }' $
. There is precisely one
 $ v' \in V_{ \min }' $
with
$ v' \in V_{ \min }' $
with
 $ v' \in S ( v ) $
.
$ v' \in S ( v ) $
.
We now prove property (
![]() $\ast $
). Let
$\ast $
). Let
![]() $ v \in V_{ \min , n }' $
and, without loss of generality, suppose that
$ v \in V_{ \min , n }' $
and, without loss of generality, suppose that
![]() $ n $
is odd. The case
$ n $
is odd. The case
![]() $ n = 1 $
is trivial so suppose
$ n = 1 $
is trivial so suppose
![]() $ n> 1 $
. View
$ n> 1 $
. View
![]() $ v $
as a vertex in
$ v $
as a vertex in
![]() $ V_{ \min , 3n - 2 } $
, so that the statement we are trying to prove is that
$ V_{ \min , 3n - 2 } $
, so that the statement we are trying to prove is that
![]() $ S^3 ( v ) $
contains precisely one element. Let
$ S^3 ( v ) $
contains precisely one element. Let
![]() $ w \in S ( v ) $
and let
$ w \in S ( v ) $
and let
![]() $ ( e_1 , e_2 ) $
be a minimal path with
$ ( e_1 , e_2 ) $
be a minimal path with
![]() $ r ( e_2 ) = w $
. Since
$ r ( e_2 ) = w $
. Since
![]() $ s ( e_1 ) \in V_{ \min } $
, we have
$ s ( e_1 ) \in V_{ \min } $
, we have
![]() $ S^3 ( v ) \cap V_{ \min } \neq \varnothing $
. Now, suppose
$ S^3 ( v ) \cap V_{ \min } \neq \varnothing $
. Now, suppose
![]() $ S^3 ( v ) \cap V_{ \min } $
contains two elements,
$ S^3 ( v ) \cap V_{ \min } $
contains two elements,
![]() $ v_1 $
and
$ v_1 $
and
![]() $ v_2 $
. By Proposition 4.11(3), we have
$ v_2 $
. By Proposition 4.11(3), we have
![]() $ R^2 ( v_1 ) \cap R^2 ( v_2 ) = \varnothing $
. By Proposition 4.11(2),
$ R^2 ( v_1 ) \cap R^2 ( v_2 ) = \varnothing $
. By Proposition 4.11(2),
![]() $ R^2 ( v_1 ) \cap V_{ \min } \neq \varnothing $
and
$ R^2 ( v_1 ) \cap V_{ \min } \neq \varnothing $
and
![]() $ R^2 ( v_2 ) \cap V_{ \min } \neq \varnothing $
. By Proposition 4.11(3) again,
$ R^2 ( v_2 ) \cap V_{ \min } \neq \varnothing $
. By Proposition 4.11(3) again,
Since
![]() $ v \in R^3 ( v_1 ) $
and
$ v \in R^3 ( v_1 ) $
and
![]() $ v \in R^3 ( v_2 ) $
, we have
$ v \in R^3 ( v_2 ) $
, we have
However, now notice that by Proposition 4.11(4), we have
![]() $ R^4 ( v_1 ) = R^2 ( R^2 ( v_1 ) \cap V_{ \min } ) $
and
$ R^4 ( v_1 ) = R^2 ( R^2 ( v_1 ) \cap V_{ \min } ) $
and
![]() $ R^4 ( v_2 ) = R^2 ( R^2 ( v_2 ) \cap V_{ \min } ) $
. Thus, we see that equations (5.1) and (5.2) yield a contradiction. Therefore,
$ R^4 ( v_2 ) = R^2 ( R^2 ( v_2 ) \cap V_{ \min } ) $
. Thus, we see that equations (5.1) and (5.2) yield a contradiction. Therefore,
![]() $ S^3 ( v ) \cap V_{ \min } $
contains precisely one element. The proof for
$ S^3 ( v ) \cap V_{ \min } $
contains precisely one element. The proof for
![]() $ v \in V_{ \max }' $
is analogous. This proves property (
$ v \in V_{ \max }' $
is analogous. This proves property (
![]() $\ast $
).
$\ast $
).
For convenience, replace
![]() $ B^{ ( 1 ) } $
with its telescoping by
$ B^{ ( 1 ) } $
with its telescoping by
![]() $ ( 3 n - 2 ) $
and replace
$ ( 3 n - 2 ) $
and replace
![]() $ B^{ ( 2 ) } $
with its telescoping by
$ B^{ ( 2 ) } $
with its telescoping by
![]() $ ( 3 n - 1 ) $
. Now, let
$ ( 3 n - 1 ) $
. Now, let
![]() $ e = ( e_1 , e_2 , \ldots ) \in X_{ B^{ ( 1 ) } , \min } $
and let
$ e = ( e_1 , e_2 , \ldots ) \in X_{ B^{ ( 1 ) } , \min } $
and let
![]() $ ( v_1 , v_2 , \ldots ) $
be its associated vertices. Let
$ ( v_1 , v_2 , \ldots ) $
be its associated vertices. Let
![]() $ n \in \mathbb {Z}_{> 1 } $
. We view
$ n \in \mathbb {Z}_{> 1 } $
. We view
![]() $ v_n $
as a vertex in
$ v_n $
as a vertex in
![]() $ V_{ 2n - 1 }' $
. By property (
$ V_{ 2n - 1 }' $
. By property (
![]() $\ast $
), there is a unique vertex
$\ast $
), there is a unique vertex
![]() $ v_{ n - 1 }' \in V_{ \min , 2n - 2 }' $
such that
$ v_{ n - 1 }' \in V_{ \min , 2n - 2 }' $
such that
![]() $ v_{ n - 1 }' \in S ( v_n ) $
. We claim that
$ v_{ n - 1 }' \in S ( v_n ) $
. We claim that
![]() $ v_{ n - 1 } \in S ( v_{ n - 1 }' ) $
. If not, then by property (
$ v_{ n - 1 } \in S ( v_{ n - 1 }' ) $
. If not, then by property (
![]() $\ast $
), there is some
$\ast $
), there is some
![]() $ w \in S ( v_{ n - 1 }' ) $
such that
$ w \in S ( v_{ n - 1 }' ) $
such that
![]() $ w \neq v_{ n - 1 } $
. However, then
$ w \neq v_{ n - 1 } $
. However, then
![]() $ R^2 ( w ) \cap R^2 ( v_{ n - 1 } ) \neq \varnothing $
, which is a contradiction again by Proposition 4.11(3). Thus, for each
$ R^2 ( w ) \cap R^2 ( v_{ n - 1 } ) \neq \varnothing $
, which is a contradiction again by Proposition 4.11(3). Thus, for each
![]() $ n \in \mathbb {Z}_{> 1 } $
,
$ n \in \mathbb {Z}_{> 1 } $
,
![]() $ v_{ n - 1 }' $
is connected by a path to
$ v_{ n - 1 }' $
is connected by a path to
![]() $ v_n' $
, and there is an
$ v_n' $
, and there is an
![]() $ e_n' \in E_{ \min , n }^{ ( 2 ) } $
with
$ e_n' \in E_{ \min , n }^{ ( 2 ) } $
with
![]() $ s ( e_n' ) = v_{ n - 1 }' $
and
$ s ( e_n' ) = v_{ n - 1 }' $
and
![]() $ r ( e_n' ) = v_n' $
by Proposition 4.11(3). Thus, this gives us
$ r ( e_n' ) = v_n' $
by Proposition 4.11(3). Thus, this gives us
![]() $ e' = ( e_1' , e_2' , \ldots ) \in X_{ B^{ ( 2 ) } , \min } $
such that for each
$ e' = ( e_1' , e_2' , \ldots ) \in X_{ B^{ ( 2 ) } , \min } $
such that for each
![]() $ n \in \mathbb {Z}_{> 0 } $
, we have
$ n \in \mathbb {Z}_{> 0 } $
, we have
![]() $ s ( e_n' ) = v_{ n - 1 }' $
and
$ s ( e_n' ) = v_{ n - 1 }' $
and
![]() $ r ( e_n' ) = v_n' $
.
$ r ( e_n' ) = v_n' $
.
Let
![]() $ f = ( f_1 , f_2 , \ldots ) \in X_{ B' } $
be any path with
$ f = ( f_1 , f_2 , \ldots ) \in X_{ B' } $
be any path with
![]() $ r ( f_n ) = s ( f_{ n + 1 } ) = v_{ 2n - 1 } $
for all odd
$ r ( f_n ) = s ( f_{ n + 1 } ) = v_{ 2n - 1 } $
for all odd
![]() $ n \in \mathbb {Z}_{> 0 } $
and
$ n \in \mathbb {Z}_{> 0 } $
and
![]() $ r ( f_n ) = s ( f_{ n + 1 } ) = v_{ 2n }' $
for all even
$ r ( f_n ) = s ( f_{ n + 1 } ) = v_{ 2n }' $
for all even
![]() $ n \in \mathbb {Z}_{> 0 } $
. Since this respects the vertices and the range and source maps, we are free to define
$ n \in \mathbb {Z}_{> 0 } $
. Since this respects the vertices and the range and source maps, we are free to define
![]() $ F_1 ( e ) = f $
and
$ F_1 ( e ) = f $
and
![]() $ F_2 ( e' ) = f $
.
$ F_2 ( e' ) = f $
.
We now show that the above pairing is a bijection between
![]() $ X_{ B , \min }^{ ( 1 ) } $
and
$ X_{ B , \min }^{ ( 1 ) } $
and
![]() $ X_{ B , \min }^{ ( 2 ) } $
. Let
$ X_{ B , \min }^{ ( 2 ) } $
. Let
![]() $ e' = ( e_1' , e_2' , \ldots ) \in X_{ B^{ ( 2 ) } , \min } $
and
$ e' = ( e_1' , e_2' , \ldots ) \in X_{ B^{ ( 2 ) } , \min } $
and
![]() $ ( v_n' ) $
be as above. By property (
$ ( v_n' ) $
be as above. By property (
![]() $\ast $
), for each
$\ast $
), for each
![]() $ n \in \mathbb {Z}_{> 0 } $
, there is precisely one
$ n \in \mathbb {Z}_{> 0 } $
, there is precisely one
![]() $ w_n \in V_{ \min }' $
with
$ w_n \in V_{ \min }' $
with
![]() $ w_n \in S ( v_n' ) $
. Since
$ w_n \in S ( v_n' ) $
. Since
![]() $ v_n \in S ( v_n' ) $
, we must have
$ v_n \in S ( v_n' ) $
, we must have
![]() $ w_n = v_n $
. Thus, the bijection is established, and so
$ w_n = v_n $
. Thus, the bijection is established, and so
![]() $ F_1 ( X_{ B^{ ( 1 ) } , \min } ) = F_2 ( X_{ B^{ ( 2 ) } , \min } ) $
. We now repeat the process for maximal vertices, choosing edges which are not minimal if the number of edges between the vertices is more than one. This extends
$ F_1 ( X_{ B^{ ( 1 ) } , \min } ) = F_2 ( X_{ B^{ ( 2 ) } , \min } ) $
. We now repeat the process for maximal vertices, choosing edges which are not minimal if the number of edges between the vertices is more than one. This extends
![]() $ F_1 $
and
$ F_1 $
and
![]() $ F_2 $
so that
$ F_2 $
so that
![]() $ F_1 ( X_{ B^{ ( 1 ) } , \max } ) = F_2 ( X_{ B^{ ( 2 ) } , \max } ) $
.
$ F_1 ( X_{ B^{ ( 1 ) } , \max } ) = F_2 ( X_{ B^{ ( 2 ) } , \max } ) $
.
We now extend
![]() $ F_1 $
and
$ F_1 $
and
![]() $ F_2 $
by any bijection between
$ F_2 $
by any bijection between
![]() $ E_n^{ ( 1 ) } $
and
$ E_n^{ ( 1 ) } $
and
![]() $ E_{ 2 n - 1 }' $
, and any bijection between
$ E_{ 2 n - 1 }' $
, and any bijection between
![]() $ E_n^{ ( 2 ) } $
and
$ E_n^{ ( 2 ) } $
and
![]() $ E_{ 2 n } $
that respect the range and source maps. In this way, we get homeomorphisms
$ E_{ 2 n } $
that respect the range and source maps. In this way, we get homeomorphisms
![]() $ F_1 : X_{ B^{ ( 1 ) } } \to X_{ B' } $
and
$ F_1 : X_{ B^{ ( 1 ) } } \to X_{ B' } $
and
![]() $ F_2 : X_{ B^{ ( 2 ) } } \to X_{ B' } $
. Define
$ F_2 : X_{ B^{ ( 2 ) } } \to X_{ B' } $
. Define
![]() $ F = F_2^{ -1 } \circ F_1 : X_{ B^{ ( 1 ) } } \to X_{ B^{ ( 2 ) } } $
.
$ F = F_2^{ -1 } \circ F_1 : X_{ B^{ ( 1 ) } } \to X_{ B^{ ( 2 ) } } $
.
Let
![]() $ \beta , \gamma : X_{ B^{ ( 1 ) } } \to \mathbb {Z} $
be the orbit cocyles of
$ \beta , \gamma : X_{ B^{ ( 1 ) } } \to \mathbb {Z} $
be the orbit cocyles of
![]() $ F $
. We will show that
$ F $
. We will show that
![]() $ \beta $
and
$ \beta $
and
![]() $ \gamma $
are continuous on
$ \gamma $
are continuous on
![]() $ X_{ B^{ ( 1 ) } } \setminus X_{ B^{ ( 1 ) } , \max } $
. So let
$ X_{ B^{ ( 1 ) } } \setminus X_{ B^{ ( 1 ) } , \max } $
. So let
![]() $ e = ( e_1 , e_2 , \ldots ) \in X_{ B^{ ( 1 ) } } \setminus X_{ B^{ ( 1 ) } , \max } $
. Let
$ e = ( e_1 , e_2 , \ldots ) \in X_{ B^{ ( 1 ) } } \setminus X_{ B^{ ( 1 ) } , \max } $
. Let
![]() $ k $
be the smallest element of
$ k $
be the smallest element of
![]() $ \mathbb {Z}_{> 0 } $
such that
$ \mathbb {Z}_{> 0 } $
such that
![]() $ e_k \notin E^{ ( 1 ) }_{ \max } $
. Then
$ e_k \notin E^{ ( 1 ) }_{ \max } $
. Then
![]() $ e $
and
$ e $
and
![]() $ h_{ B^{ ( 1 ) } } ( e ) $
are confinal from level
$ h_{ B^{ ( 1 ) } } ( e ) $
are confinal from level
![]() $ k $
. This means that
$ k $
. This means that
![]() $ F_1 ( e ) $
and
$ F_1 ( e ) $
and
![]() $ F_1 ( h_{ B^{ ( 1 ) } } ( e ) ) $
are cofinal from level
$ F_1 ( h_{ B^{ ( 1 ) } } ( e ) ) $
are cofinal from level
![]() $ 2 k - 1 $
, and so
$ 2 k - 1 $
, and so
![]() $ F ( e ) $
and
$ F ( e ) $
and
![]() $ F ( h_{ B^{ ( 1 ) } } ( e ) ) $
are cofinal from level
$ F ( h_{ B^{ ( 1 ) } } ( e ) ) $
are cofinal from level
![]() $ k $
. In particular,
$ k $
. In particular,
![]() $ F ( e ) $
and
$ F ( e ) $
and
![]() $ F ( h_{ B^{ ( 1 ) } } ( e ) ) $
pass through the same vertex
$ F ( h_{ B^{ ( 1 ) } } ( e ) ) $
pass through the same vertex
![]() $ v $
at level
$ v $
at level
![]() $ k $
. By Lemma 5.1, there is an integer
$ k $
. By Lemma 5.1, there is an integer
![]() $ N $
such that
$ N $
such that
Let
![]() $ f \in U ( e_1 , \ldots , e_{ k + 1 } ) $
. Then
$ f \in U ( e_1 , \ldots , e_{ k + 1 } ) $
. Then
![]() $ y $
and
$ y $
and
![]() $ h_{ B^{ ( 1 ) } } ( f ) $
are confinal from level
$ h_{ B^{ ( 1 ) } } ( f ) $
are confinal from level
![]() $ k $
. This means that
$ k $
. This means that
![]() $ F_1 ( f ) $
and
$ F_1 ( f ) $
and
![]() $ F_1 ( h_{ B^{ ( 1 ) } } ( f ) ) $
are cofinal from level
$ F_1 ( h_{ B^{ ( 1 ) } } ( f ) ) $
are cofinal from level
![]() $ 2 k - 1 $
, and so
$ 2 k - 1 $
, and so
![]() $ F ( y ) $
and
$ F ( y ) $
and
![]() $ F ( h_{ B^{ ( 1 ) } } ( f ) ) $
are cofinal from level
$ F ( h_{ B^{ ( 1 ) } } ( f ) ) $
are cofinal from level
![]() $ k $
. Since
$ k $
. Since
![]() $ e , f \in U ( e_1 , \ldots , e_{ k + 1 } ) $
,
$ e , f \in U ( e_1 , \ldots , e_{ k + 1 } ) $
,
![]() $ h_{ B^{ ( 1 ) } } ( x ) $
and
$ h_{ B^{ ( 1 ) } } ( x ) $
and
![]() $ h_{ B^{ ( 1 ) } } ( f ) $
have the same initial segment from level
$ h_{ B^{ ( 1 ) } } ( f ) $
have the same initial segment from level
![]() $ 0 $
to level
$ 0 $
to level
![]() $ k + 1 $
, and so
$ k + 1 $
, and so
![]() $ F ( h_{ B^{ ( 1 ) } } ( e ) ) $
and
$ F ( h_{ B^{ ( 1 ) } } ( e ) ) $
and
![]() $ F ( h_{ B^{ ( 1 ) } } ( f ) ) $
have the same initial segment from level
$ F ( h_{ B^{ ( 1 ) } } ( f ) ) $
have the same initial segment from level
![]() $ 0 $
to level
$ 0 $
to level
![]() $ k $
. Similarly,
$ k $
. Similarly,
![]() $ F ( e ) $
and
$ F ( e ) $
and
![]() $ F ( f ) $
have the same initial segment from level
$ F ( f ) $
have the same initial segment from level
![]() $ 0 $
to level
$ 0 $
to level
![]() $ k $
. Thus, the integer
$ k $
. Thus, the integer
![]() $ N $
from above satisfies
$ N $
from above satisfies
Since
![]() $ f \in U ( e_1 , \ldots , e_{ k + 1 } ) $
was arbitrary, this shows that
$ f \in U ( e_1 , \ldots , e_{ k + 1 } ) $
was arbitrary, this shows that
![]() $ \beta $
is continuous at
$ \beta $
is continuous at
![]() $ e $
.
$ e $
.
The argument for
![]() $ \gamma $
is analogous to
$ \gamma $
is analogous to
![]() $ \beta $
. Thus,
$ \beta $
. Thus,
![]() $ ( X_{ B^{ ( 1 ) } } , h_{ B^{ ( 1 ) } } , X_{ B^{ ( 1 ) } , \max } ) $
and
$ ( X_{ B^{ ( 1 ) } } , h_{ B^{ ( 1 ) } } , X_{ B^{ ( 1 ) } , \max } ) $
and
![]() $ ( X_{ B^{ ( 2 ) } } , h_{ B^{ ( 2 ) } } , X_{ B^{ ( 2 ) } , \max } ) $
are strong orbit equivalent. By replacing
$ ( X_{ B^{ ( 2 ) } } , h_{ B^{ ( 2 ) } } , X_{ B^{ ( 2 ) } , \max } ) $
are strong orbit equivalent. By replacing
![]() $ F $
with
$ F $
with
![]() $ h_{ B^{ ( 1 ) } }^{ - 1 } \circ F $
, we see that
$ h_{ B^{ ( 1 ) } }^{ - 1 } \circ F $
, we see that
![]() $ ( X_{ B^{ ( 1 ) } } , h_{ B^{ ( 1 ) } } , X_{ B^{ ( 1 ) } , \min } ) $
and
$ ( X_{ B^{ ( 1 ) } } , h_{ B^{ ( 1 ) } } , X_{ B^{ ( 1 ) } , \min } ) $
and
![]() $ ( X_{ B^{ ( 2 ) } } , h_{ B^{ ( 2 ) } } , X_{ B^{ ( 2 ) } , \min } ) $
are strong orbit equivalent. Therefore, by Proposition 4.11(1),
$ ( X_{ B^{ ( 2 ) } } , h_{ B^{ ( 2 ) } } , X_{ B^{ ( 2 ) } , \min } ) $
are strong orbit equivalent. Therefore, by Proposition 4.11(1),
![]() $ ( X_1 , h_1. Z_1 ) $
and
$ ( X_1 , h_1. Z_1 ) $
and
![]() $ ( X_2 , h_2 , Z_2 ) $
are strong orbit equivalent.
$ ( X_2 , h_2 , Z_2 ) $
are strong orbit equivalent.
(
![]() $\Rightarrow $
). Assume
$\Rightarrow $
). Assume
![]() $ ( X_1 , h_1 , Z_1 ) $
and
$ ( X_1 , h_1 , Z_1 ) $
and
![]() $ ( X_2 , h_2 , Z_2 ) $
are strong orbit equivalent. By the definition of strong orbit equivalence, we have
$ ( X_2 , h_2 , Z_2 ) $
are strong orbit equivalent. By the definition of strong orbit equivalence, we have
![]() $ Z_1 \cong Z_2 $
and so by Theorem 3.10, we have
$ Z_1 \cong Z_2 $
and so by Theorem 3.10, we have
![]() $ K_1 ( C^* ( \mathbb {Z} , X_1 , h_1 ) ) \cong K_1 ( C^* ( X_2 , h_2 , Z_2 ) ) $
.
$ K_1 ( C^* ( \mathbb {Z} , X_1 , h_1 ) ) \cong K_1 ( C^* ( X_2 , h_2 , Z_2 ) ) $
.
Let
![]() $ \beta , \gamma : X_1 \to \mathbb {Z} $
be the associated orbit cocyles defined by
$ \beta , \gamma : X_1 \to \mathbb {Z} $
be the associated orbit cocyles defined by
![]() $ F \circ h_1 = h_2^\beta \circ F $
and
$ F \circ h_1 = h_2^\beta \circ F $
and
![]() $ F \circ h_1^\gamma = h_2 \circ F $
. Recall that strong orbit equivalence tells us that
$ F \circ h_1^\gamma = h_2 \circ F $
. Recall that strong orbit equivalence tells us that
![]() $ \beta $
and
$ \beta $
and
![]() $ \gamma $
are continuous on
$ \gamma $
are continuous on
![]() $ X_1 \setminus Z_1 $
and
$ X_1 \setminus Z_1 $
and
![]() $ F ( Z_1 ) = Z_2 $
.
$ F ( Z_1 ) = Z_2 $
.
Let
![]() $ \widetilde { h }_2 = F^{ - 1 } \circ h_2 \circ F : X_1 \to X_1 $
. Then
$ \widetilde { h }_2 = F^{ - 1 } \circ h_2 \circ F : X_1 \to X_1 $
. Then
![]() $ \widetilde { h }_2 $
is conjugate to
$ \widetilde { h }_2 $
is conjugate to
![]() $ h_2 $
, has the same orbits as
$ h_2 $
, has the same orbits as
![]() $ h_1 $
, and
$ h_1 $
, and
We also see that
![]() $ ( X_1 , \widetilde { h }_2 , Z_1 ) $
is a fiberwise essentially minimal zero-dimensional system that is conjugate to
$ ( X_1 , \widetilde { h }_2 , Z_1 ) $
is a fiberwise essentially minimal zero-dimensional system that is conjugate to
![]() $ ( X_2 , h_2 , Z_2 ) $
, so we work with the former for the remainder of the proof.
$ ( X_2 , h_2 , Z_2 ) $
, so we work with the former for the remainder of the proof.
Let
![]() $ \alpha _1 $
be the automorphism of
$ \alpha _1 $
be the automorphism of
![]() $ C ( X_1 ) $
induced by
$ C ( X_1 ) $
induced by
![]() $ h_1 $
and let
$ h_1 $
and let
![]() $ \alpha _2 $
be the automorphism of
$ \alpha _2 $
be the automorphism of
![]() $ C ( X_1 ) $
induced by
$ C ( X_1 ) $
induced by
![]() $ \widetilde { h }_2 $
. We now show that
$ \widetilde { h }_2 $
. We now show that
![]() $ \text {ran} ( \text {id} - ( \alpha _1 )_* ) \subset \text {ran} ( \text {id} - ( \alpha _2 )_* ) $
. It is enough to show that for any compact open set
$ \text {ran} ( \text {id} - ( \alpha _1 )_* ) \subset \text {ran} ( \text {id} - ( \alpha _2 )_* ) $
. It is enough to show that for any compact open set
![]() $ E \subset X_1 $
, we have
$ E \subset X_1 $
, we have
![]() $ ( \text {id} - ( \alpha _1 )_* ) ( \chi _E ) \in \text {ran} ( \text {id} - ( \alpha _2 )_* ) $
.
$ ( \text {id} - ( \alpha _1 )_* ) ( \chi _E ) \in \text {ran} ( \text {id} - ( \alpha _2 )_* ) $
.
Given
![]() $ f \in C ( X_1 , \mathbb {Z} ) $
, we denote the image of
$ f \in C ( X_1 , \mathbb {Z} ) $
, we denote the image of
![]() $ f $
in
$ f $
in
![]() $ K_0 ( C^* ( \mathbb {Z} , X_1 , h_i ) ) $
by
$ K_0 ( C^* ( \mathbb {Z} , X_1 , h_i ) ) $
by
![]() $ [ f ]_1 $
and denote the image of
$ [ f ]_1 $
and denote the image of
![]() $ f $
in
$ f $
in
![]() $ K_0 ( C^* ( \mathbb {Z} , X_1 , \widetilde { h }_2 ) ) $
by
$ K_0 ( C^* ( \mathbb {Z} , X_1 , \widetilde { h }_2 ) ) $
by
![]() $ [ f ]_2 $
. Since
$ [ f ]_2 $
. Since
![]() $ h_1 $
and
$ h_1 $
and
![]() $ \widetilde { h }_2 $
have the same orbits, there is a probability measure
$ \widetilde { h }_2 $
have the same orbits, there is a probability measure
![]() $ \mu $
that is both
$ \mu $
that is both
![]() $ h_1 $
- and
$ h_1 $
- and
![]() $ \widetilde { h }_2 $
-invariant. Note that
$ \widetilde { h }_2 $
-invariant. Note that
![]() $ C^* ( \mathbb {Z} , X_1 , h_1 ) $
is the
$ C^* ( \mathbb {Z} , X_1 , h_1 ) $
is the
![]() $ C^* $
-subalgebra of
$ C^* $
-subalgebra of
![]() $ L ( L^2 ( X_1 , \mu ) ) $
generated by
$ L ( L^2 ( X_1 , \mu ) ) $
generated by
![]() $ C ( X ) $
and the unitary
$ C ( X ) $
and the unitary
![]() $ u_1 : g \to g \circ h_1^{ -1 } $
. Also note that
$ u_1 : g \to g \circ h_1^{ -1 } $
. Also note that
![]() $ C^* ( \mathbb {Z} , X_1 , \widetilde { h }_2 ) $
is the
$ C^* ( \mathbb {Z} , X_1 , \widetilde { h }_2 ) $
is the
![]() $ C^* $
-subalgebra of
$ C^* $
-subalgebra of
![]() $ L ( L^2 ( X_1 , \mu ) ) $
generated by
$ L ( L^2 ( X_1 , \mu ) ) $
generated by
![]() $ C ( X ) $
and the unitary
$ C ( X ) $
and the unitary
![]() $ u_2 : g \to g \circ \widetilde { h }_2^{ -1 } $
. For the remainder of the proof, we identify these crossed products with these corresponding subalgebras of
$ u_2 : g \to g \circ \widetilde { h }_2^{ -1 } $
. For the remainder of the proof, we identify these crossed products with these corresponding subalgebras of
![]() $ L ( L^2 ( X_1 , \mu ) ) $
.
$ L ( L^2 ( X_1 , \mu ) ) $
.
We claim that map
![]() $ \varphi : K_0 ( C^* ( \mathbb {Z} , X_1 , h_1 ) ) \to K_0 ( C^* ( \mathbb {Z} , X_1 , \widetilde { h }_2 ) ) $
defined by
$ \varphi : K_0 ( C^* ( \mathbb {Z} , X_1 , h_1 ) ) \to K_0 ( C^* ( \mathbb {Z} , X_1 , \widetilde { h }_2 ) ) $
defined by
![]() $ \varphi ( [ \chi _U ]_1 ) = [ \chi _U ]_2 $
is an isomorphism of ordered groups. Since the positive cone and distinguished order units agree via this map, the only thing to check is that
$ \varphi ( [ \chi _U ]_1 ) = [ \chi _U ]_2 $
is an isomorphism of ordered groups. Since the positive cone and distinguished order units agree via this map, the only thing to check is that
![]() $ \text {im} ( \text {id} - ( \alpha _1 )_* ) = \text {im} ( \text {id} - ( \alpha _2 )_* ) $
.
$ \text {im} ( \text {id} - ( \alpha _1 )_* ) = \text {im} ( \text {id} - ( \alpha _2 )_* ) $
.
Let
![]() $ E $
be a compact open subset of
$ E $
be a compact open subset of
![]() $ X_1 $
such that
$ X_1 $
such that
![]() $ E \cap Z_1 = \varnothing $
. Then since
$ E \cap Z_1 = \varnothing $
. Then since
![]() $ \beta $
is continuous on
$ \beta $
is continuous on
![]() $ E $
,
$ E $
,
![]() $ \text {ran} ( \beta |_E ) = \{ k_1 , \ldots , k_N \} $
. Then
$ \text {ran} ( \beta |_E ) = \{ k_1 , \ldots , k_N \} $
. Then
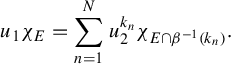 $$ \begin{align*} u_1 \chi_E = \sum_{ n = 1 }^N u_2^{ k_n } \chi_{ E \cap \beta^{ -1 } ( k_n ) }. \end{align*} $$
$$ \begin{align*} u_1 \chi_E = \sum_{ n = 1 }^N u_2^{ k_n } \chi_{ E \cap \beta^{ -1 } ( k_n ) }. \end{align*} $$
Thus,
![]() $ u_1 \chi _E \in C^* ( \mathbb {Z} , X_1 , \widetilde { h }_2 ) $
, and, letting
$ u_1 \chi _E \in C^* ( \mathbb {Z} , X_1 , \widetilde { h }_2 ) $
, and, letting
![]() $ A_{ Z_1 }^{ ( 1 ) } $
correspond to
$ A_{ Z_1 }^{ ( 1 ) } $
correspond to
![]() $ C^* ( \mathbb {Z} , X_1 , h_1 ) $
as in Definition 3.6, we have
$ C^* ( \mathbb {Z} , X_1 , h_1 ) $
as in Definition 3.6, we have
![]() $ A_{ Z_1 }^{ ( 1 ) } \subset C^* ( \mathbb {Z} , X_1 , \widetilde { h }_2 ) $
. Since
$ A_{ Z_1 }^{ ( 1 ) } \subset C^* ( \mathbb {Z} , X_1 , \widetilde { h }_2 ) $
. Since
![]() $ E \cap Z_1 = \varnothing $
, there is a unitary
$ E \cap Z_1 = \varnothing $
, there is a unitary
![]() $ v \in A_{ Z_1 }^{ ( 1 ) } $
such that
$ v \in A_{ Z_1 }^{ ( 1 ) } $
such that
![]() $ v \chi _E v^* = \chi _{ h_1 ( E ) } $
. Since we also have
$ v \chi _E v^* = \chi _{ h_1 ( E ) } $
. Since we also have
![]() $ v \in C^* ( \mathbb {Z} , X_1 , \widetilde { h }_2 ) $
, we have
$ v \in C^* ( \mathbb {Z} , X_1 , \widetilde { h }_2 ) $
, we have
![]() $ [ \chi _E ]_2 = [ \chi _{ h_1 ( E ) } ]_2 $
, so
$ [ \chi _E ]_2 = [ \chi _{ h_1 ( E ) } ]_2 $
, so
![]() $ \chi _E - \chi _{ h_1 ( E ) } \in \text {im} ( \text {id} - ( \alpha _2 )_* ) $
. Theorem 3.9 (and the proof) tells us that
$ \chi _E - \chi _{ h_1 ( E ) } \in \text {im} ( \text {id} - ( \alpha _2 )_* ) $
. Theorem 3.9 (and the proof) tells us that
![]() $ K_0 ( A_{ Z_1 } )^{ ( 1 ) } \cong K_0 ( \mathbb {Z} , X_1 , h_1 ) $
by the injection map. Thus,
$ K_0 ( A_{ Z_1 } )^{ ( 1 ) } \cong K_0 ( \mathbb {Z} , X_1 , h_1 ) $
by the injection map. Thus,
![]() $ \text {im} ( \text {id} - ( \alpha _1 )_* ) \subset \text {im} ( \text {id} - ( \alpha _2 )_* ) $
. By repeating the above process with
$ \text {im} ( \text {id} - ( \alpha _1 )_* ) \subset \text {im} ( \text {id} - ( \alpha _2 )_* ) $
. By repeating the above process with
![]() $ \gamma $
instead of
$ \gamma $
instead of
![]() $ \beta $
, we can similarly show that
$ \beta $
, we can similarly show that
![]() $ \text {im} ( \text {id} - ( \alpha _2 )_* ) \subset \text {im} ( \text {id} - ( \alpha _1 )_* ) $
. This completes the proof.
$ \text {im} ( \text {id} - ( \alpha _2 )_* ) \subset \text {im} ( \text {id} - ( \alpha _1 )_* ) $
. This completes the proof.
Theorem 5.3. Let
![]() $ ( X_1 , h_1 , Z_1 ) $
and
$ ( X_1 , h_1 , Z_1 ) $
and
![]() $ ( X_2 , h_2 , Z_2 ) $
be fiberwise essentially minimal zero-dimensional systems with no periodic points. The following are equivalent:
$ ( X_2 , h_2 , Z_2 ) $
be fiberwise essentially minimal zero-dimensional systems with no periodic points. The following are equivalent:
-
(1)
 $ C^* ( \mathbb {Z} , X_1 , h_1 ) \cong C^* ( \mathbb {Z} , X_2 , h_2 ) $
;
$ C^* ( \mathbb {Z} , X_1 , h_1 ) \cong C^* ( \mathbb {Z} , X_2 , h_2 ) $
; -
(2)
 $ ( K_0 ( C^* ( \mathbb {Z} , X_1 , h_1 ) ) , K_0 ( C^* ( \mathbb {Z} , X_1 , h_1 ) )^+ , 1 ) \cong ( K_0 ( C^* ( \mathbb {Z} , X_2 , h_2 ) ) , K_0 ( C^* ( \mathbb {Z} , X_2 , h_2 ) )^+ , 1 ) $
and
$ ( K_0 ( C^* ( \mathbb {Z} , X_1 , h_1 ) ) , K_0 ( C^* ( \mathbb {Z} , X_1 , h_1 ) )^+ , 1 ) \cong ( K_0 ( C^* ( \mathbb {Z} , X_2 , h_2 ) ) , K_0 ( C^* ( \mathbb {Z} , X_2 , h_2 ) )^+ , 1 ) $
and
 $ K_1 ( C^* ( \mathbb {Z} , X_1 , h_1 ) ) \cong K_1 ( C^* ( \mathbb {Z} , X_2 , h_2 ) ) $
;
$ K_1 ( C^* ( \mathbb {Z} , X_1 , h_1 ) ) \cong K_1 ( C^* ( \mathbb {Z} , X_2 , h_2 ) ) $
; -
(3)
 $ ( X_1 , h_1 , Z_1 ) $
and
$ ( X_1 , h_1 , Z_1 ) $
and
 $ ( X_2 , h_2 , Z_2 ) $
are strong orbit equivalent.
$ ( X_2 , h_2 , Z_2 ) $
are strong orbit equivalent.
Proof. (1)
![]() $ \Longleftrightarrow $
(2). By [Reference Herstedt11, Theorems 2.2 and 2.3],
$ \Longleftrightarrow $
(2). By [Reference Herstedt11, Theorems 2.2 and 2.3],
![]() $ C^* ( \mathbb {Z} , X_1 , h_1 ) $
and
$ C^* ( \mathbb {Z} , X_1 , h_1 ) $
and
![]() $ C^* ( \mathbb {Z} , X_2 , h_2 ) $
are A
$ C^* ( \mathbb {Z} , X_2 , h_2 ) $
are A
![]() $\mathbb {T}$
-algebras of real rank zero, so this result follows from [Reference Dadarlat and Gong5].
$\mathbb {T}$
-algebras of real rank zero, so this result follows from [Reference Dadarlat and Gong5].
(2)
![]() $ \Longleftrightarrow $
(3). This is implied by Theorem 5.2.
$ \Longleftrightarrow $
(3). This is implied by Theorem 5.2.
Acknowledgement
This research was supported by the Israel Science Foundation grant no. 476/16.