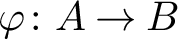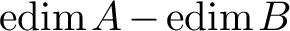1 Introduction
The work of Wiles and Taylor-Wiles [Reference Taylor and Wiles18, Reference Wiles20] on modularity lifting theorems relies on a patching method that has been generalised to prove a series of remarkable results that verify in many cases the Fontaine–Mazur conjecture. The Fontaine–Mazur conjecture relates geometric representations of absolute Galois groups of number fields to automorphic forms and motives. The spectacular proof by Newton and Thorne [Reference Newton and Thorne17] of the automorphy of all symmetric powers of Galois representations associated to classical newforms is a recent example.
One of the ingredients in the patching method of Wiles, Taylor-Wiles et al. is a commutative algebra result that for our purposes is best summarised in [Reference Calegari and Geraghty8, Proposition 2.1]. The assumptions there are used to reduce the proof to a statement about modules over regular local rings, which follows from the Auslander–Buchsbaum formula. We spell this out in the statement below, as it gives a context for the results we prove here.
Proposition 1.1. Let
![]() $\mathcal O$
be a discrete valuation ring,
$\mathcal O$
be a discrete valuation ring,
![]() $A:= \mathcal O[\![x_1,\ldots , x_r]\!]$
and
$A:= \mathcal O[\![x_1,\ldots , x_r]\!]$
and
![]() $\varphi \colon A \to B$
a map of
$\varphi \colon A \to B$
a map of
![]() $\mathcal O$
-algebras. Suppose the ring B is a quotient of
$\mathcal O$
-algebras. Suppose the ring B is a quotient of
![]() $\mathcal O[\![y_1,\ldots , y_s]\!]$
and N is a nonzero B-module that is finitely generated as an A-module and satisfies
$\mathcal O[\![y_1,\ldots , y_s]\!]$
and N is a nonzero B-module that is finitely generated as an A-module and satisfies
![]() $\operatorname {proj\,dim}_AN \leq r-s$
. Then N is a free B-module and
$\operatorname {proj\,dim}_AN \leq r-s$
. Then N is a free B-module and
![]() $B=\mathcal O[\![y_1,\ldots , y_s]\!]$
.
$B=\mathcal O[\![y_1,\ldots , y_s]\!]$
.
Proof. Since N is finitely generated over A, the depth formula of Auslander and Buchsbaum yields
so that
![]() $\operatorname {depth}_AN \geq s+1$
. This explains the inequality on the left:
$\operatorname {depth}_AN \geq s+1$
. This explains the inequality on the left:
The equality holds as N is finitely generated as an A-module and the inequality on the right holds because B is a quotient of
![]() $\mathcal O[\![y_1,\ldots , y_s]\!]$
. It follows that B and
$\mathcal O[\![y_1,\ldots , y_s]\!]$
. It follows that B and
![]() $\mathcal O[\![y_1,\ldots , y_s]\!]$
have the same dimension and hence that they are equal, for the former is a quotient of the latter, which is a domain. In particular, B itself is regular and
$\mathcal O[\![y_1,\ldots , y_s]\!]$
have the same dimension and hence that they are equal, for the former is a quotient of the latter, which is a domain. In particular, B itself is regular and
![]() $\operatorname {proj\,dim}_BN$
is finite. Then, given
$\operatorname {proj\,dim}_BN$
is finite. Then, given
![]() $\operatorname {depth}_BN=s+1$
, another application of the Auslander–Buchsbaum formula yields that N is a free B-module.
$\operatorname {depth}_BN=s+1$
, another application of the Auslander–Buchsbaum formula yields that N is a free B-module.
Bart de Smit made the remarkable conjecture that if
![]() $A\to B$
is a local homomorphism of (commutative) Artinian local rings of the same embedding dimension, then any B-module that is flat as an A-module is also flat as a B-module. This strengthens Proposition 1.1 in the case
$A\to B$
is a local homomorphism of (commutative) Artinian local rings of the same embedding dimension, then any B-module that is flat as an A-module is also flat as a B-module. This strengthens Proposition 1.1 in the case
![]() $r=s$
and allows one in principle to dispense with patching in the techniques à la Wiles to prove modularity lifting theorems.
$r=s$
and allows one in principle to dispense with patching in the techniques à la Wiles to prove modularity lifting theorems.
In [Reference Brochard5, Theorem 1.1] the first author proved de Smit’s conjecture. The connection to patching is explained, for example, in [Reference Brochard5, §3]. In fact, in [Reference Brochard5] it is proved that if
![]() $A,B$
are noetherian local rings with
$A,B$
are noetherian local rings with
![]() $\operatorname {edim} A\ge \operatorname {edim} B$
and N is a finitely generated B-module that is flat over A, then N is flat over B. We extend [Reference Brochard5, Theorem 1.1], giving en passant a new and simpler proof of it by proving the following.
$\operatorname {edim} A\ge \operatorname {edim} B$
and N is a finitely generated B-module that is flat over A, then N is flat over B. We extend [Reference Brochard5, Theorem 1.1], giving en passant a new and simpler proof of it by proving the following.
Theorem 1.2 see Theorem 3.1
Suppose
![]() $\varphi \colon A\to B$
is a local homomorphism of noetherian local rings and N is a nonzero finitely generated B-module whose flat dimension over A satisfies
$\varphi \colon A\to B$
is a local homomorphism of noetherian local rings and N is a nonzero finitely generated B-module whose flat dimension over A satisfies
![]() $\operatorname {flat\,dim}_AN\le \operatorname {edim} A-\operatorname {edim} B$
; then N is free as a B module and
$\operatorname {flat\,dim}_AN\le \operatorname {edim} A-\operatorname {edim} B$
; then N is free as a B module and
![]() $\varphi $
is an exceptional complete intersection map.
$\varphi $
is an exceptional complete intersection map.
We say
![]() $\varphi $
is exceptional complete intersection if it is complete intersection and
$\varphi $
is exceptional complete intersection if it is complete intersection and
![]() $\operatorname {edim} A - \operatorname {dim} A= \operatorname {edim} B - \operatorname {dim} B$
; see 2.14. When
$\operatorname {edim} A - \operatorname {dim} A= \operatorname {edim} B - \operatorname {dim} B$
; see 2.14. When
![]() $\varphi $
is surjective, with kernel I, this property is equivalent to the condition that I can be generated by a regular sequence whose images are linearly independent in the cotangent space
$\varphi $
is surjective, with kernel I, this property is equivalent to the condition that I can be generated by a regular sequence whose images are linearly independent in the cotangent space
![]() $\mathfrak {m}_A/\mathfrak {m}_A^2$
. There is a similar characterisation of this property for general maps in terms of the cotangent space of
$\mathfrak {m}_A/\mathfrak {m}_A^2$
. There is a similar characterisation of this property for general maps in terms of the cotangent space of
![]() $\varphi $
; see Section 2 for details.
$\varphi $
; see Section 2 for details.
The more general hypothesis in our theorem as opposed to [Reference Brochard5, Theorem 1.1] gives us the freedom to reduce its proof to the surjective case, using standard results in commutative algebra. This is instrumental in leading to a proof that is simpler than the one presented in [Reference Brochard5] as we can apply an induction on
![]() $\operatorname {edim} A - \operatorname {edim} B$
. A key ingredient in this induction step is a theorem of Nagata that tracks the projective dimension of finitely generated modules along surjective exceptional complete intersection maps; see 2.18. In fact, our main theorem, Theorem 3.1, can be seen as a converse to this result. A ‘better’ converse is proved in Theorem 3.2.
$\operatorname {edim} A - \operatorname {edim} B$
. A key ingredient in this induction step is a theorem of Nagata that tracks the projective dimension of finitely generated modules along surjective exceptional complete intersection maps; see 2.18. In fact, our main theorem, Theorem 3.1, can be seen as a converse to this result. A ‘better’ converse is proved in Theorem 3.2.
Work of Calegari and Geraghty [Reference Dwyer, Greenlees and Iyengar7] in ‘positive defect’ situations, extending the patching method in [Reference Taylor and Wiles18] to situations where one patches complexes rather than modules, suggests a version of Theorem 1.2 dealing with complexes; see also [Reference Khare and Thorne13, Reference Thorne19]. The Calegari–Geraghty patching argument leads to a situation where one can apply Proposition 1.1 to prove the faithfulness of the action of a deformation ring on the cohomology in ‘top degree’ of a certain arithmetic manifold. We expect that a version of Theorem 1.2 for complexes would allow one in principle to obviate the need to patch in positive defect situations, just like the application of [Reference Brochard5, Theorem 1.1] in [Reference Newton and Thorne16, §4]. We hope to return to this topic in the future.
2 Local algebra
This section is mostly a recollection of some basic facts from local algebra for use in the proofs in Section 3. The only new material concerns a class of local maps introduced here called exceptional complete intersections. Much of the discussion in this section is geared towards characterising these maps in terms of their tangent spaces. This is easy to do for surjective maps and even for maps essentially of finite type. With an eye towards future applications, we treat more general maps of noetherian rings. To that end, it will be convenient to use André–Quillen homology modules. In fact, we require only the components in degrees 0 and 1, which are easy to describe, as we do below, and the Jacobi–Zariski sequence. Most of what is needed is already in [Reference Lichtenbaum and Schlessinger14]; see also [Reference Avramov and Iyengar4, Reference Iyengar11]. We also need to refer to [Reference Avramov2] for more recent work on complete intersection maps.
2.1. Let
![]() $A\to B$
be a map of rings and M a B-module. We write
$A\to B$
be a map of rings and M a B-module. We write
![]() $\operatorname {D}_{i}({B}/{A};M)$
for the ith André–Quillen homology of the A-algebra B, with coefficients in M, namely:
$\operatorname {D}_{i}({B}/{A};M)$
for the ith André–Quillen homology of the A-algebra B, with coefficients in M, namely:
where
![]() $\mathrm {L}_{B/A}$
is the cotangent complex of the map
$\mathrm {L}_{B/A}$
is the cotangent complex of the map
![]() $A\to B$
. One has
$A\to B$
. One has
![]() $\operatorname {D}_{i}({B}/{A};M)=0$
for
$\operatorname {D}_{i}({B}/{A};M)=0$
for
![]() $i<0$
and
$i<0$
and
where
![]() $\Omega _{B/A}$
is the module of Kähler differentials of B over A. If
$\Omega _{B/A}$
is the module of Kähler differentials of B over A. If
![]() $A\twoheadrightarrow B$
is surjective, with kernel I, then
$A\twoheadrightarrow B$
is surjective, with kernel I, then
![]() $\operatorname {D}_{0}({B}/{A};M)=0$
and from [Reference Lichtenbaum and Schlessinger14, Lemma 3.1.2] one gets that
$\operatorname {D}_{0}({B}/{A};M)=0$
and from [Reference Lichtenbaum and Schlessinger14, Lemma 3.1.2] one gets that
 $$ \begin{align} \operatorname{D}_{1}({B}/{A};M) = \frac I{I^2}\otimes_B M. \end{align} $$
$$ \begin{align} \operatorname{D}_{1}({B}/{A};M) = \frac I{I^2}\otimes_B M. \end{align} $$
Given maps of rings
![]() $A\to B\to C$
and a C-module N, one has an exact sequence
$A\to B\to C$
and a C-module N, one has an exact sequence
called the Jacobi–Zariski exact sequence associated to the maps. We only need the part of the sequence for
![]() $i\le 1$
and for this see [Reference Lichtenbaum and Schlessinger14, §§2.3.5].
$i\le 1$
and for this see [Reference Lichtenbaum and Schlessinger14, §§2.3.5].
2.3. By a local ring we mean a commutative, noetherian, local ring. We write
![]() $\mathfrak {m}_A$
for the maximal ideal of A and
$\mathfrak {m}_A$
for the maximal ideal of A and
![]() $k_A$
for the residue field
$k_A$
for the residue field
![]() $A/\mathfrak {m}_A$
. The cotangent space of A is the
$A/\mathfrak {m}_A$
. The cotangent space of A is the
![]() $k_A$
-vector space
$k_A$
-vector space
 $$ \begin{align*} \frac{\mathfrak{m}_A}{\mathfrak{m}^2_A} \cong \operatorname{D}_{1}({k_A}/{A};k_A); \end{align*} $$
$$ \begin{align*} \frac{\mathfrak{m}_A}{\mathfrak{m}^2_A} \cong \operatorname{D}_{1}({k_A}/{A};k_A); \end{align*} $$
the isomorphism is by (2.2). The rank of this vector space is the embedding dimension of A, denoted
![]() $\operatorname {edim} A$
. There is an inequality
$\operatorname {edim} A$
. There is an inequality
![]() $\operatorname {dim} A\le \operatorname {edim} A$
, where
$\operatorname {dim} A\le \operatorname {edim} A$
, where
![]() $\operatorname {dim} A$
is the Krull dimension of A; when equality holds, the ring A is said to be regular. In this case, one has
$\operatorname {dim} A$
is the Krull dimension of A; when equality holds, the ring A is said to be regular. In this case, one has
![]() $\operatorname {D}_{i}({k_A}/{A};-)=0$
for
$\operatorname {D}_{i}({k_A}/{A};-)=0$
for
![]() $i\ge 2$
and the converse holds as well; see 2.10, keeping in mind that A is regular if and only if the quotient map
$i\ge 2$
and the converse holds as well; see 2.10, keeping in mind that A is regular if and only if the quotient map
![]() $A\to k_A$
is complete intersection.
$A\to k_A$
is complete intersection.
2.4. We say
![]() $\varphi \colon A\to B$
is a local map to mean that A and B are local rings and
$\varphi \colon A\to B$
is a local map to mean that A and B are local rings and
![]() $\varphi $
is a homomorphism of rings satisfying
$\varphi $
is a homomorphism of rings satisfying
![]() $\varphi (\mathfrak {m}_A)\subseteq \mathfrak {m}_B$
. The closed fibre of such a map is the local ring
$\varphi (\mathfrak {m}_A)\subseteq \mathfrak {m}_B$
. The closed fibre of such a map is the local ring
![]() $B/\mathfrak {m}_AB$
, with maximal ideal
$B/\mathfrak {m}_AB$
, with maximal ideal
![]() $\mathfrak {m}_B/\mathfrak {m}_AB$
and residue field
$\mathfrak {m}_B/\mathfrak {m}_AB$
and residue field
![]() $k_B$
.
$k_B$
.
It is helpful to think of
![]() $\operatorname {D}_{1}({B}/{A};k_B)$
as the cotangent space of the map
$\operatorname {D}_{1}({B}/{A};k_B)$
as the cotangent space of the map
![]() $A\to B$
; when
$A\to B$
; when
![]() $B=A/I$
, it is
$B=A/I$
, it is
![]() $I/\mathfrak {m}_A I$
. Here is a simple but useful observation.
$I/\mathfrak {m}_A I$
. Here is a simple but useful observation.
Lemma 2.5. Let
![]() $A\to B$
be a surjective local map. The rank of the map
$A\to B$
be a surjective local map. The rank of the map
induced by the surjection
![]() $B\to k_B$
equals
$B\to k_B$
equals
![]() $\operatorname {edim} A - \operatorname {edim} B$
.
$\operatorname {edim} A - \operatorname {edim} B$
.
Proof. Set
![]() $k:= k_B$
. The Jacobi–Zariski sequence induced by
$k:= k_B$
. The Jacobi–Zariski sequence induced by
![]() $A\to B\to k$
starts as
$A\to B\to k$
starts as
The result is clear from the additivity of rank on exact sequences.
2.6. Following [Reference Avramov, Foxby and Herzog3], we say that a local map
![]() $\varphi \colon A\to A'$
is weakly regular if it is flat and its closed fibre
$\varphi \colon A\to A'$
is weakly regular if it is flat and its closed fibre
![]() $A'/\mathfrak {m}_AA'$
is regular. In this case there are equalities
$A'/\mathfrak {m}_AA'$
is regular. In this case there are equalities
 $$ \begin{align*} \operatorname{dim} A' &= \operatorname{dim} A + \operatorname{dim} (A'/\mathfrak{m}_AA') \\ \operatorname{edim} A' &= \operatorname{edim} A + \operatorname{dim} (A'/\mathfrak{m}_AA'). \end{align*} $$
$$ \begin{align*} \operatorname{dim} A' &= \operatorname{dim} A + \operatorname{dim} (A'/\mathfrak{m}_AA') \\ \operatorname{edim} A' &= \operatorname{edim} A + \operatorname{dim} (A'/\mathfrak{m}_AA'). \end{align*} $$
The first equality is well-known; see [Reference Bruns and Herzog6, Theorem A.11]. One way to verify the second one is to consider the maps
![]() $A'\to F\to k'$
, where
$A'\to F\to k'$
, where
![]() $F:= A'/\mathfrak {m}_A A'$
and
$F:= A'/\mathfrak {m}_A A'$
and
![]() $k':= k_{A'}$
and the associated Jacobi–Zariski sequence
$k':= k_{A'}$
and the associated Jacobi–Zariski sequence
where the equality holds because F is a regular local ring; see 2.3. Since
![]() $\varphi $
is flat, base change [Reference Lichtenbaum and Schlessinger14, §§2.3.2] yields
$\varphi $
is flat, base change [Reference Lichtenbaum and Schlessinger14, §§2.3.2] yields
Thus, the sequence above gives the desired equality.
2.7. Given an A-module M and a nonnegative integer n, we write
![]() $\operatorname {flat\,dim}_AM\le n$
to indicate that M has flat dimension
$\operatorname {flat\,dim}_AM\le n$
to indicate that M has flat dimension
![]() $\le n$
; that is, M has a flat resolution of length at most n. This condition is equivalent to
$\le n$
; that is, M has a flat resolution of length at most n. This condition is equivalent to
 $\operatorname {Tor}^A_{n+1}(-,M)=0$
. When these conditions hold,
$\operatorname {Tor}^A_{n+1}(-,M)=0$
. When these conditions hold,
 $\operatorname {Tor}^A_{i}(-,M)=0$
for all
$\operatorname {Tor}^A_{i}(-,M)=0$
for all
![]() $i\ge n+1$
.
$i\ge n+1$
.
When the A-module M is finitely generated, its flat dimension coincides with its projective dimension.
2.8. If
![]() $\varphi \colon A\to A'$
is weakly regular, then for any finitely generated
$\varphi \colon A\to A'$
is weakly regular, then for any finitely generated
![]() $A'$
-module N there are inequalities
$A'$
-module N there are inequalities
 $$ \begin{align*} \operatorname{proj\,dim}_{A'}N &\le \operatorname{flat\,dim}_{A}N + \operatorname{edim}(A'/\mathfrak{m}_AA') \\ &= \operatorname{flat\,dim}_AN + \operatorname{edim} A' - \operatorname{edim} A. \end{align*} $$
$$ \begin{align*} \operatorname{proj\,dim}_{A'}N &\le \operatorname{flat\,dim}_{A}N + \operatorname{edim}(A'/\mathfrak{m}_AA') \\ &= \operatorname{flat\,dim}_AN + \operatorname{edim} A' - \operatorname{edim} A. \end{align*} $$
See [Reference Avramov, Foxby and Herzog3, Lemma 3.2] for the inequality; the equality is from 2.6.
2.9. A regular factorisation of a local map
![]() $\varphi \colon A\to B$
is a decomposition
$\varphi \colon A\to B$
is a decomposition
 $$ \begin{align*} A\xrightarrow{\ \dot\varphi\ } A' \xrightarrow{\ \varphi'\ } B \end{align*} $$
$$ \begin{align*} A\xrightarrow{\ \dot\varphi\ } A' \xrightarrow{\ \varphi'\ } B \end{align*} $$
of
![]() $\varphi $
where
$\varphi $
where
![]() $\dot \varphi $
is weakly regular and
$\dot \varphi $
is weakly regular and
![]() $\varphi '$
is surjective; see [Reference Avramov, Foxby and Herzog3]. It is clear that such factorisations exist if
$\varphi '$
is surjective; see [Reference Avramov, Foxby and Herzog3]. It is clear that such factorisations exist if
![]() $\varphi $
is finite and, more generally, essentially of finite type; that is, when B is a localisation of a finitely generated A-algebra. The main result of [Reference Avramov, Foxby and Herzog3] is that such factorisations exist also when B is complete with respect to its
$\varphi $
is finite and, more generally, essentially of finite type; that is, when B is a localisation of a finitely generated A-algebra. The main result of [Reference Avramov, Foxby and Herzog3] is that such factorisations exist also when B is complete with respect to its
![]() $\mathfrak {m}_B$
-adic topology; this extends Cohen’s structure theorem for complete local rings.
$\mathfrak {m}_B$
-adic topology; this extends Cohen’s structure theorem for complete local rings.
The map
![]() $\varphi $
is formally smoothable if there exists a factorisation as above of the composition
$\varphi $
is formally smoothable if there exists a factorisation as above of the composition
![]() $A\to B\to \widehat {B}$
, where
$A\to B\to \widehat {B}$
, where
![]() $\widehat {B}$
is the
$\widehat {B}$
is the
![]() $\mathfrak {m}_B$
-adic completion of B, in which the closed fibre of
$\mathfrak {m}_B$
-adic completion of B, in which the closed fibre of
![]() $\dot \varphi $
is even geometrically regular over
$\dot \varphi $
is even geometrically regular over
![]() $k_A$
, the residue field of A. Such factorisations exist when, for example,
$k_A$
, the residue field of A. Such factorisations exist when, for example,
![]() $\varphi $
is essentially of finite type or the extension of fields
$\varphi $
is essentially of finite type or the extension of fields
![]() $k_A\to k_{B}$
is separable; see [Reference Avramov, Foxby and Herzog3, (1.1.2)].
$k_A\to k_{B}$
is separable; see [Reference Avramov, Foxby and Herzog3, (1.1.2)].
2.10. A surjective local map
![]() $A\to B$
is complete intersection if its kernel can be generated by a regular sequence. In this case, if
$A\to B$
is complete intersection if its kernel can be generated by a regular sequence. In this case, if
![]() $B=A/I$
, then
$B=A/I$
, then
![]() $I/I^2$
is a free B-module of rank equal to
$I/I^2$
is a free B-module of rank equal to
![]() $\operatorname {dim} A-\operatorname {dim} B$
. Thus,
$\operatorname {dim} A-\operatorname {dim} B$
. Thus,
 $$ \begin{align} \operatorname{D}_{1}({B}/{A};M) \cong \frac I{I^2}\otimes_BM \cong M^{c} \quad \text{where}\ c=\operatorname{dim} A-\operatorname{dim} B. \end{align} $$
$$ \begin{align} \operatorname{D}_{1}({B}/{A};M) \cong \frac I{I^2}\otimes_BM \cong M^{c} \quad \text{where}\ c=\operatorname{dim} A-\operatorname{dim} B. \end{align} $$
Moreover,
![]() $\operatorname {D}_{i}({B}/{A};-)=0$
for
$\operatorname {D}_{i}({B}/{A};-)=0$
for
![]() $i\ge 2$
, and this property characterises the complete intersection property [Reference Avramov2, (1.2)].
$i\ge 2$
, and this property characterises the complete intersection property [Reference Avramov2, (1.2)].
2.12. Let
![]() $\varphi \colon A\to B$
be a local map and let
$\varphi \colon A\to B$
be a local map and let
![]() $\widehat {B}$
be the
$\widehat {B}$
be the
![]() $\mathfrak {m}_B$
-adic completion of B. Following [Reference Avramov2], we say that
$\mathfrak {m}_B$
-adic completion of B. Following [Reference Avramov2], we say that
![]() $\varphi $
is complete intersection if in some regular factorisation
$\varphi $
is complete intersection if in some regular factorisation
 $$ \begin{align*} A\to A'\xrightarrow{\varphi'} \widehat{B} \end{align*} $$
$$ \begin{align*} A\to A'\xrightarrow{\varphi'} \widehat{B} \end{align*} $$
of the composed map
![]() $A\to B\to \widehat {B}$
, the surjective map
$A\to B\to \widehat {B}$
, the surjective map
![]() $\varphi '$
is complete intersection in the sense of 2.10. This property is independent of the choice of factorisation. When
$\varphi '$
is complete intersection in the sense of 2.10. This property is independent of the choice of factorisation. When
![]() $A\to A''\to B$
is a regular factorisation of
$A\to A''\to B$
is a regular factorisation of
![]() $\varphi $
,
$\varphi $
,
![]() $\varphi $
is complete intersection if and only if
$\varphi $
is complete intersection if and only if
![]() $A''\to B$
is complete intersection. The class of complete intersections is closed under composition and flat base change; see [Reference Avramov2] for proofs of these assertions.
$A''\to B$
is complete intersection. The class of complete intersections is closed under composition and flat base change; see [Reference Avramov2] for proofs of these assertions.
Using regular factorisations of maps, one can often reduce questions about general complete intersection maps to the surjective case; see, in particular, the proof of Theorem 3.1.
Lemma 2.13. When
![]() $\varphi $
is complete intersection there is an inequality
$\varphi $
is complete intersection there is an inequality
Proof. We may assume B is
![]() $\mathfrak {m}_B$
-adically complete. Consider a regular factorisation
$\mathfrak {m}_B$
-adically complete. Consider a regular factorisation
![]() $A\to A'\to B$
of
$A\to A'\to B$
of
![]() $\varphi $
. Since
$\varphi $
. Since
![]() $\varphi $
is complete intersection, Lemma 2.5 and (2.11) yield
$\varphi $
is complete intersection, Lemma 2.5 and (2.11) yield
This gives the inequality below:
The equality is from 2.6.
2.14. We say that a complete intersection map
![]() $\varphi $
is exceptional if the inequality in Lemma 2.13 is an equality:
$\varphi $
is exceptional if the inequality in Lemma 2.13 is an equality:
![]() $\varphi $
is complete intersection and
$\varphi $
is complete intersection and
Thus, for example, for such a
![]() $\varphi $
, the ring A is regular if and only if B is regular. Moreover, one can check easily using a regular factorisation of
$\varphi $
, the ring A is regular if and only if B is regular. Moreover, one can check easily using a regular factorisation of
![]() $\varphi $
that one also has
$\varphi $
that one also has
This means that A is Cohen–Macaulay if and only if B is.
It is immediate from 2.6 that weakly regular maps are exceptional complete intersections. Here is another simple family of examples with this property.
Example 2.15. Let
![]() $A,B$
be regular local rings. Then any local map
$A,B$
be regular local rings. Then any local map
![]() $\varphi \colon A\to B$
is exceptional complete intersection. Indeed, since
$\varphi \colon A\to B$
is exceptional complete intersection. Indeed, since
it suffices to verify that
![]() $\varphi $
is complete intersection. This can be checked using André–Quillen homology. Here is a direct argument: any surjective map between regular rings is complete intersection by Chevalley’s theorem [Reference Bruns and Herzog6, Proposition 2.2.4], and one can reduce to this case using regular factorisations 2.9.
$\varphi $
is complete intersection. This can be checked using André–Quillen homology. Here is a direct argument: any surjective map between regular rings is complete intersection by Chevalley’s theorem [Reference Bruns and Herzog6, Proposition 2.2.4], and one can reduce to this case using regular factorisations 2.9.
The exceptional complete intersection property can be expressed in terms of André–Quillen homology, at least for formally smoothable maps.
Lemma 2.16. Let
![]() $\varphi \colon A\to B$
be a formally smoothable local map that is complete intersection. Then
$\varphi \colon A\to B$
be a formally smoothable local map that is complete intersection. Then
![]() $\varphi $
is exceptional if and only if the natural map
$\varphi $
is exceptional if and only if the natural map
is one-to-one.
Proof. In what follows we write k for
![]() $k_B$
. First consider the case when
$k_B$
. First consider the case when
![]() $\varphi $
is surjective and complete intersection, say
$\varphi $
is surjective and complete intersection, say
![]() $B=A/I$
. The complete intersection property implies that the rank of the k-vector space
$B=A/I$
. The complete intersection property implies that the rank of the k-vector space
![]() $\operatorname {D}_{1}({B}/{A};k)$
is
$\operatorname {D}_{1}({B}/{A};k)$
is
![]() $\operatorname {dim} A-\operatorname {dim} B$
, by (2.11). Given Lemma 2.5 it is then clear that
$\operatorname {dim} A-\operatorname {dim} B$
, by (2.11). Given Lemma 2.5 it is then clear that
![]() $\varphi $
is also exceptional if and only if the map
$\varphi $
is also exceptional if and only if the map
is one-to-one.
In the general case, we can assume B is
![]() $\mathfrak {m}_B$
-adically complete. Let
$\mathfrak {m}_B$
-adically complete. Let
![]() $A\to A'\to B$
be a regular factorisation of
$A\to A'\to B$
be a regular factorisation of
![]() $\varphi $
. Since
$\varphi $
. Since
![]() $\operatorname {D}_{1}({A'}/{A};-)=0$
, by [Reference Avramov2, (1.1)], for any
$\operatorname {D}_{1}({A'}/{A};-)=0$
, by [Reference Avramov2, (1.1)], for any
![]() $A'$
-algebra C, it follows from the Jacobi–Zariski sequence induced by
$A'$
-algebra C, it follows from the Jacobi–Zariski sequence induced by
![]() $A\to A'\to C$
that the natural map is one-to-one:
$A\to A'\to C$
that the natural map is one-to-one:
This justifies the exactness in the rows in the diagram below:

The diagram is commutative by functoriality of André–Quillen homology. The vertical maps on the left and in the middle are induced by
![]() $B\to k$
. A simple diagram chase reveals that if one of these is injective, then so is the other. It remains to observe that since
$B\to k$
. A simple diagram chase reveals that if one of these is injective, then so is the other. It remains to observe that since
![]() $A'\to B$
is surjective, the already established case of the result implies the middle one is injective if and only if
$A'\to B$
is surjective, the already established case of the result implies the middle one is injective if and only if
![]() $A'\to B$
is exceptional.
$A'\to B$
is exceptional.
It follows from Lemma 2.16 that when
![]() $\varphi \colon A\to B$
is surjective, it is exceptional complete intersection if and only if
$\varphi \colon A\to B$
is surjective, it is exceptional complete intersection if and only if
![]() $\operatorname {Ker}(\varphi )$
is generated by a regular sequence whose image in
$\operatorname {Ker}(\varphi )$
is generated by a regular sequence whose image in
![]() $\mathfrak {m}_A/\mathfrak {m}_A^2$
is a linearly independent set. The forward implication need not hold when
$\mathfrak {m}_A/\mathfrak {m}_A^2$
is a linearly independent set. The forward implication need not hold when
![]() $\varphi $
is not surjective.
$\varphi $
is not surjective.
Example 2.17. Let k be a field and consider the map of k-algebras
This map is exceptional complete intersection; see Example 2.15. It is easy to check that
![]() $\operatorname {Ker}(\varphi ) = (xz - y^2)$
; in particular, it is contained in
$\operatorname {Ker}(\varphi ) = (xz - y^2)$
; in particular, it is contained in
![]() $\mathfrak {m}_A^2$
.
$\mathfrak {m}_A^2$
.
Next we record a result of Nagata [Reference Nagata15, §27] that tracks the projective dimension of modules along surjective exceptional complete intersections.
2.18. Let
![]() $\varphi \colon A\to B$
be a surjective local map and N a finitely generated B-module. If
$\varphi \colon A\to B$
be a surjective local map and N a finitely generated B-module. If
![]() $\varphi $
is exceptional complete intersection, then
$\varphi $
is exceptional complete intersection, then
In particular,
![]() $\operatorname {proj\,dim}_AN$
is finite if and only if
$\operatorname {proj\,dim}_AN$
is finite if and only if
![]() $\operatorname {proj\,dim}_BN$
is finite.
$\operatorname {proj\,dim}_BN$
is finite.
See Theorem 3.3 for a version dealing with non-necessarily surjective exceptional complete intersections and Theorems 3.1 and 3.2 for converses.
3 Criteria for detecting exceptional complete intersections
We begin this section by proving Theorem 1.2 from the Introduction, in a slightly more elaborate version. The last part recovers [Reference Brochard5, Theorem 1.1]. We should note that if the B-module N happens to be finitely generated over A, as would be the case if
![]() $\varphi $
is a finite map, then its flat dimension equals the projective dimension.
$\varphi $
is a finite map, then its flat dimension equals the projective dimension.
Theorem 3.1. Let
![]() $\varphi \colon A\to B$
be a local map with
$\varphi \colon A\to B$
be a local map with
![]() $\operatorname {edim} A\ge \operatorname {edim} B$
. If there exists a nonzero finitely generated B-module N satisfying
$\operatorname {edim} A\ge \operatorname {edim} B$
. If there exists a nonzero finitely generated B-module N satisfying
![]() $\operatorname {flat\,dim}_AN\le \operatorname {edim} A-\operatorname {edim} B$
, then the following conclusions hold:
$\operatorname {flat\,dim}_AN\le \operatorname {edim} A-\operatorname {edim} B$
, then the following conclusions hold:
-
(1) N is free as a B-module;
-
(2)
 $\varphi $
is an exceptional complete intersection;
$\varphi $
is an exceptional complete intersection; -
(3)
 $\operatorname {flat\,dim}_AN = \operatorname {flat\,dim}_AB = \operatorname {edim} A - \operatorname {edim} B$
.
$\operatorname {flat\,dim}_AN = \operatorname {flat\,dim}_AB = \operatorname {edim} A - \operatorname {edim} B$
.
In particular, if N is flat as an A-module, then
![]() $\operatorname {edim} A=\operatorname {edim} B$
and
$\operatorname {edim} A=\operatorname {edim} B$
and
![]() $\varphi $
is flat.
$\varphi $
is flat.
Proof. We first reduce to the case when
![]() $\varphi $
is surjective. To that end, note that if
$\varphi $
is surjective. To that end, note that if
![]() $\widehat B$
is the completion of B at its maximal ideal, then for any finitely generated B-module W the flatness of the map
$\widehat B$
is the completion of B at its maximal ideal, then for any finitely generated B-module W the flatness of the map
![]() $B\to \widehat B$
implies
$B\to \widehat B$
implies
 $$ \begin{align*} \operatorname{Tor}^A_i(-,W\otimes_B\widehat B) \cong \operatorname{Tor}^A_i(-,W)\otimes_B \widehat B \quad\text{for each}\ i. \end{align*} $$
$$ \begin{align*} \operatorname{Tor}^A_i(-,W\otimes_B\widehat B) \cong \operatorname{Tor}^A_i(-,W)\otimes_B \widehat B \quad\text{for each}\ i. \end{align*} $$
The completion map is faithful, so
 $\operatorname {flat\,dim}_A(W\otimes _B\widehat B)=\operatorname {flat\,dim}_AW$
. Also, the B-module W is free if and only if the
$\operatorname {flat\,dim}_A(W\otimes _B\widehat B)=\operatorname {flat\,dim}_AW$
. Also, the B-module W is free if and only if the
![]() $\widehat B$
-module
$\widehat B$
-module
![]() $W\otimes _B\widehat B$
is free. So replacing B by
$W\otimes _B\widehat B$
is free. So replacing B by
![]() $\widehat B$
we can assume
$\widehat B$
we can assume
![]() $\varphi $
has a regular factorisation:
$\varphi $
has a regular factorisation:
 $$ \begin{align*} A\xrightarrow{\ \dot\varphi\ } A' \xrightarrow{\ \varphi'\ } B; \end{align*} $$
$$ \begin{align*} A\xrightarrow{\ \dot\varphi\ } A' \xrightarrow{\ \varphi'\ } B; \end{align*} $$
see 2.9. The first inequality below is by 2.8:
 $$ \begin{align*} \operatorname{proj\,dim}_{A'} N & \le \operatorname{flat\,dim}_AN + \operatorname{dim} (A'/\mathfrak{m}_AA')\\ &\le \operatorname{edim} A - \operatorname{edim} B + \operatorname{dim} (A'/\mathfrak{m}_AA')\\ &= \operatorname{edim} A' - \operatorname{edim} B. \end{align*} $$
$$ \begin{align*} \operatorname{proj\,dim}_{A'} N & \le \operatorname{flat\,dim}_AN + \operatorname{dim} (A'/\mathfrak{m}_AA')\\ &\le \operatorname{edim} A - \operatorname{edim} B + \operatorname{dim} (A'/\mathfrak{m}_AA')\\ &= \operatorname{edim} A' - \operatorname{edim} B. \end{align*} $$
The second one is our hypothesis, whilst the equality is from 2.6. We claim that it suffices to prove the result for
![]() $\varphi '$
.
$\varphi '$
.
Indeed, this is clear for (1) as it concerns only the B-module structure on N. For (2) the desired conclusion holds because
![]() $\varphi $
is complete intersection if and only if
$\varphi $
is complete intersection if and only if
![]() $\varphi '$
is, by 2.12 and then the fact that one of them is exceptional if and only if the other is is immediate from 2.6. Finally, if the equality in (3) holds for
$\varphi '$
is, by 2.12 and then the fact that one of them is exceptional if and only if the other is is immediate from 2.6. Finally, if the equality in (3) holds for
![]() $\varphi '$
, then the inequalities above become equalities, so the desired equality holds also for
$\varphi '$
, then the inequalities above become equalities, so the desired equality holds also for
![]() $\varphi $
.
$\varphi $
.
Thus, we assume
![]() $\varphi $
is surjective and hence that N is finitely generated over A.
$\varphi $
is surjective and hence that N is finitely generated over A.
We first settle the case when the B-module N is faithful; that is, when
![]() $\operatorname {ann}_AN = \operatorname {Ker}(\varphi )$
. We argue by induction on
$\operatorname {ann}_AN = \operatorname {Ker}(\varphi )$
. We argue by induction on
![]() $\operatorname {edim} A-\operatorname {edim} B$
. The base case is when
$\operatorname {edim} A-\operatorname {edim} B$
. The base case is when
![]() $\operatorname {edim} A=\operatorname {edim} B$
, in which case
$\operatorname {edim} A=\operatorname {edim} B$
, in which case
![]() $\operatorname {flat\,dim}_AN\le 0$
; that is, N is free as an A-module. This implies
$\operatorname {flat\,dim}_AN\le 0$
; that is, N is free as an A-module. This implies
![]() $\operatorname {Ker}(\varphi )=0$
and then the desired result is clear.
$\operatorname {Ker}(\varphi )=0$
and then the desired result is clear.
Suppose that
![]() $\operatorname {edim} A - \operatorname {edim} B\ge 1$
. Then the ideal
$\operatorname {edim} A - \operatorname {edim} B\ge 1$
. Then the ideal
![]() $\operatorname {Ker}(\varphi )$
is nonzero and so the hypothesis that
$\operatorname {Ker}(\varphi )$
is nonzero and so the hypothesis that
![]() $\operatorname {proj\,dim}_AN$
is finite implies
$\operatorname {proj\,dim}_AN$
is finite implies
![]() $\operatorname {ann}_AN$
, which is
$\operatorname {ann}_AN$
, which is
![]() $\operatorname {Ker}(\varphi )$
, contains a nonzero divisor, by a result of Auslander and Buchsbaum [Reference Auslander and Buchsbaum1, Lemma 6.1]. Moreover, since
$\operatorname {Ker}(\varphi )$
, contains a nonzero divisor, by a result of Auslander and Buchsbaum [Reference Auslander and Buchsbaum1, Lemma 6.1]. Moreover, since
![]() $\operatorname {edim} A - \operatorname {edim} B\ge 1$
, the ideal
$\operatorname {edim} A - \operatorname {edim} B\ge 1$
, the ideal
![]() $\operatorname {Ker}(\varphi )$
is not contained in
$\operatorname {Ker}(\varphi )$
is not contained in
![]() $\mathfrak {m}_A^2$
, so there exists a nonzero divisor, say x, in
$\mathfrak {m}_A^2$
, so there exists a nonzero divisor, say x, in
![]() $\operatorname {Ker}(\varphi )\setminus \mathfrak {m}_A^2$
. The existence of such an x follows by a standard ‘prime avoidance argument’ where at most two of the ideals are allowed not to be prime; see, for example, [Reference Kaplansky12, Theorem 81]. Consider the factorisation
$\operatorname {Ker}(\varphi )\setminus \mathfrak {m}_A^2$
. The existence of such an x follows by a standard ‘prime avoidance argument’ where at most two of the ideals are allowed not to be prime; see, for example, [Reference Kaplansky12, Theorem 81]. Consider the factorisation
 $$ \begin{align*} A\longrightarrow A/xA\xrightarrow{\ \overline{\varphi}\ } B \end{align*} $$
$$ \begin{align*} A\longrightarrow A/xA\xrightarrow{\ \overline{\varphi}\ } B \end{align*} $$
of
![]() $\varphi $
. Since x is a nonzero divisor not contained in
$\varphi $
. Since x is a nonzero divisor not contained in
![]() $\mathfrak {m}_A^2$
, there is an equality
$\mathfrak {m}_A^2$
, there is an equality
see 2.18. Evidently,
![]() $\operatorname {edim}(A/xA) = \operatorname {edim} A -1$
. Thus, the induction hypothesis applies to
$\operatorname {edim}(A/xA) = \operatorname {edim} A -1$
. Thus, the induction hypothesis applies to
![]() $\overline {\varphi }$
and yields that
$\overline {\varphi }$
and yields that
![]() $\overline {\varphi }$
is an exceptional complete intersection and also that N is free as a B-module. It remains to note that, by the choice of x, the map
$\overline {\varphi }$
is an exceptional complete intersection and also that N is free as a B-module. It remains to note that, by the choice of x, the map
![]() $\varphi $
is also an exceptional complete intersection.
$\varphi $
is also an exceptional complete intersection.
This completes the proof when N is faithful as a B-module.
For the general case, set
![]() $I:= \operatorname {ann}_BN$
and
$I:= \operatorname {ann}_BN$
and
![]() $\overline {B} := B/I$
. Consider the composition
$\overline {B} := B/I$
. Consider the composition
Since N viewed as a
![]() $\overline {B}$
-module is faithful and
$\overline {B}$
-module is faithful and
![]() $\operatorname {edim} \overline {B}\le \operatorname {edim} B$
, the already verified case of the result applied to
$\operatorname {edim} \overline {B}\le \operatorname {edim} B$
, the already verified case of the result applied to
![]() $\psi $
yields that N is free as a
$\psi $
yields that N is free as a
![]() $\overline {B} $
-module and also that
$\overline {B} $
-module and also that
![]() $\psi $
is an exceptional complete intersection. To complete the proof, it suffices to verify that
$\psi $
is an exceptional complete intersection. To complete the proof, it suffices to verify that
![]() $I=0$
.
$I=0$
.
As
![]() $\psi $
is an exceptional complete intersection, one gets the first equality below.
$\psi $
is an exceptional complete intersection, one gets the first equality below.
 $$ \begin{align*} \operatorname{edim} A - \operatorname{edim} \overline{B} &= \operatorname{proj\,dim}_A\overline{B} \\ & = \operatorname{proj\,dim}_AN \\ & \le \operatorname{edim} A - \operatorname{edim} B \\ & \le \operatorname{edim} A - \operatorname{edim} \overline{B} . \end{align*} $$
$$ \begin{align*} \operatorname{edim} A - \operatorname{edim} \overline{B} &= \operatorname{proj\,dim}_A\overline{B} \\ & = \operatorname{proj\,dim}_AN \\ & \le \operatorname{edim} A - \operatorname{edim} B \\ & \le \operatorname{edim} A - \operatorname{edim} \overline{B} . \end{align*} $$
The second equality holds because N is free as a
![]() $\overline {B}$
-module, the first inequality is by hypothesis, whilst the second one holds because
$\overline {B}$
-module, the first inequality is by hypothesis, whilst the second one holds because
![]() $\overline {B}$
is a quotient of B. It follows that
$\overline {B}$
is a quotient of B. It follows that
![]() $\operatorname {edim} B = \operatorname {edim} \overline {B} $
; that is,
$\operatorname {edim} B = \operatorname {edim} \overline {B} $
; that is,
![]() $I\subseteq \mathfrak {m}_B^2$
. The maps
$I\subseteq \mathfrak {m}_B^2$
. The maps
![]() $A\to B\to \overline {B}$
induce the exact row in the diagram below:
$A\to B\to \overline {B}$
induce the exact row in the diagram below:

The diagonal arrow is induced by the maps
![]() $A\to B\to k$
and the vertical one by the maps
$A\to B\to k$
and the vertical one by the maps
![]() $A\to \overline {B}\to k$
; it is an inclusion because
$A\to \overline {B}\to k$
; it is an inclusion because
![]() $A\to \overline B$
is an exceptional complete intersection; see Lemma 2.16. Since
$A\to \overline B$
is an exceptional complete intersection; see Lemma 2.16. Since
![]() $\operatorname {edim} B = \operatorname {edim}\overline {B}$
, the ranks of the latter two maps are equal by Lemma 2.5. It follows that
$\operatorname {edim} B = \operatorname {edim}\overline {B}$
, the ranks of the latter two maps are equal by Lemma 2.5. It follows that
![]() $\pi $
is onto and hence
$\pi $
is onto and hence
 $$ \begin{align*} \frac I{\mathfrak{m}_B I} = \operatorname{D}_{1}({\overline{B}}/{B};k)=0. \end{align*} $$
$$ \begin{align*} \frac I{\mathfrak{m}_B I} = \operatorname{D}_{1}({\overline{B}}/{B};k)=0. \end{align*} $$
Nakayama’s lemma yields
![]() $I=0$
, as desired.
$I=0$
, as desired.
Here is a variation on Theorem 3.1; unlike in that statement, we have to assume a priori that the projective dimension of the B-module N is finite. Compare the hypotheses with Nagata’s Theorem 2.18.
Theorem 3.2. Let
![]() $\varphi \colon A\to B$
be a local map and N a nonzero finitely generated B-module N of finite projective dimension. There is then an inequality
$\varphi \colon A\to B$
be a local map and N a nonzero finitely generated B-module N of finite projective dimension. There is then an inequality
Moreover, if equality holds, then
![]() $\varphi $
is an exceptional complete intersection.
$\varphi $
is an exceptional complete intersection.
The inequality in the statement can be strict: let A be a field, B a ring of formal power series over A, and set
![]() $N:= B$
.
$N:= B$
.
Proof. We can assume
![]() $\operatorname {flat\,dim}_AN$
is finite. First we treat the case when
$\operatorname {flat\,dim}_AN$
is finite. First we treat the case when
![]() $\varphi $
is surjective. Since N is a nonzero finitely generated B-module that is of finite projective dimension over both A and B, it follows that
$\varphi $
is surjective. Since N is a nonzero finitely generated B-module that is of finite projective dimension over both A and B, it follows that
![]() $\operatorname {proj\,dim}_AB$
is finite by [Reference Foxby and Iyengar10, Theorem IV]; see also [Reference Diamond9, Remark 5.6]. This fact will be crucial in the ensuing proof.
$\operatorname {proj\,dim}_AB$
is finite by [Reference Foxby and Iyengar10, Theorem IV]; see also [Reference Diamond9, Remark 5.6]. This fact will be crucial in the ensuing proof.
Keep in mind that the projective dimension of N over B and that of N and B over A are finite. Thus, repeatedly applying the equality of Auslander and Buchsbaum [Reference Bruns and Herzog6, Theorem 1.3.3] yields
 $$ \begin{align*} \operatorname{proj\,dim}_AN - \operatorname{proj\,dim}_BN &=(\operatorname{depth} A - \operatorname{depth}_AN) - (\operatorname{depth} B - \operatorname{depth}_BN) \\ &=\operatorname{depth} A - \operatorname{depth} B\\ &=\operatorname{proj\,dim}_AB. \end{align*} $$
$$ \begin{align*} \operatorname{proj\,dim}_AN - \operatorname{proj\,dim}_BN &=(\operatorname{depth} A - \operatorname{depth}_AN) - (\operatorname{depth} B - \operatorname{depth}_BN) \\ &=\operatorname{depth} A - \operatorname{depth} B\\ &=\operatorname{proj\,dim}_AB. \end{align*} $$
We have also used the fact that the depth of M over A is the same as that over B. It thus suffices to prove the result for
![]() $N=B$
, namely, that there is an inequality
$N=B$
, namely, that there is an inequality
The fact that
![]() $\varphi $
is an exceptional complete intersection if equality holds then follows from Theorem 3.1.
$\varphi $
is an exceptional complete intersection if equality holds then follows from Theorem 3.1.
From this point on, the proof flows as in that of Theorem 3.1: We argue by induction on
![]() $\operatorname {edim} A - \operatorname {edim} B$
; the base case when this number is zero is again a tautology. When
$\operatorname {edim} A - \operatorname {edim} B$
; the base case when this number is zero is again a tautology. When
![]() $\operatorname {edim} A - \operatorname {edim} B\ge 1$
, one can find a nonzero divisor x in
$\operatorname {edim} A - \operatorname {edim} B\ge 1$
, one can find a nonzero divisor x in
![]() $\operatorname {Ker}(\varphi ) \setminus \mathfrak {m}_A^2$
. Then from Nagata’s Theorem 2.18 one gets the equality below:
$\operatorname {Ker}(\varphi ) \setminus \mathfrak {m}_A^2$
. Then from Nagata’s Theorem 2.18 one gets the equality below:
 $$ \begin{align*} \operatorname{proj\,dim}_A B &= \operatorname{proj\,dim}_{A/xA}B +1 \\ & \ge \operatorname{edim} (A/xA) -\operatorname{edim} B + 1 \\ &= \operatorname{edim} A - \operatorname{edim} B. \end{align*} $$
$$ \begin{align*} \operatorname{proj\,dim}_A B &= \operatorname{proj\,dim}_{A/xA}B +1 \\ & \ge \operatorname{edim} (A/xA) -\operatorname{edim} B + 1 \\ &= \operatorname{edim} A - \operatorname{edim} B. \end{align*} $$
The inequality is by the induction hypothesis. This gives the desired inequality.
This completes the proof of the result when
![]() $\varphi $
is surjective. The general case is settled by the standard reduction to the surjective one: Completing B at its
$\varphi $
is surjective. The general case is settled by the standard reduction to the surjective one: Completing B at its
![]() $\mathfrak {m}_B$
-adic topology, we can assume
$\mathfrak {m}_B$
-adic topology, we can assume
![]() $\varphi $
has a regular factorisation
$\varphi $
has a regular factorisation
![]() $A\to A'\to B$
. Then one has inequalities, where 2.8 gives the first one:
$A\to A'\to B$
. Then one has inequalities, where 2.8 gives the first one:
 $$ \begin{align*} \operatorname{flat\,dim}_AN - \operatorname{proj\,dim}_BN &\ge \operatorname{proj\,dim}_{A'}N -\operatorname{proj\,dim}_B N + \operatorname{edim} A - \operatorname{edim} A' \\ &\ge \operatorname{edim} A - \operatorname{edim} B, \end{align*} $$
$$ \begin{align*} \operatorname{flat\,dim}_AN - \operatorname{proj\,dim}_BN &\ge \operatorname{proj\,dim}_{A'}N -\operatorname{proj\,dim}_B N + \operatorname{edim} A - \operatorname{edim} A' \\ &\ge \operatorname{edim} A - \operatorname{edim} B, \end{align*} $$
and the second one is by the already established case of the result, applied to the surjection
![]() $A'\to B$
. This gives the stated inequality and also that if equality holds, then
$A'\to B$
. This gives the stated inequality and also that if equality holds, then
![]() $\operatorname {proj\,dim}_{A'}N - \operatorname {proj\,dim}_BN = \operatorname {edim} A' - \operatorname {edim} B$
, which implies
$\operatorname {proj\,dim}_{A'}N - \operatorname {proj\,dim}_BN = \operatorname {edim} A' - \operatorname {edim} B$
, which implies
![]() $\varphi '$
is exceptional complete intersection; thus,
$\varphi '$
is exceptional complete intersection; thus,
![]() $\varphi $
has this property, by definition.
$\varphi $
has this property, by definition.
The result below complements Theorem 3.2 and is an extension of Nagata’s Theorem 2.18 to maps that may not be surjective.
Theorem 3.3. If a local map
![]() $\varphi \colon A\to B$
is exceptional complete intersection, then for any finitely generated B-module N, one has
$\varphi \colon A\to B$
is exceptional complete intersection, then for any finitely generated B-module N, one has
in particular,
![]() $\operatorname {flat\,dim}_AN$
is finite if and only if
$\operatorname {flat\,dim}_AN$
is finite if and only if
![]() $\operatorname {proj\,dim}_BN$
is finite. Equality holds when the map
$\operatorname {proj\,dim}_BN$
is finite. Equality holds when the map
![]() $\varphi $
is finite.
$\varphi $
is finite.
The inequality in the statement can be strict if
![]() $\varphi $
is not finite: Let k be a field and
$\varphi $
is not finite: Let k be a field and
![]() $\varphi \colon k[\![x,y]\!]\to k[\![s]\!]$
the map of k-algebras that maps
$\varphi \colon k[\![x,y]\!]\to k[\![s]\!]$
the map of k-algebras that maps
![]() $x,y$
to
$x,y$
to
![]() $0$
and take
$0$
and take
![]() $N=k[\![s]\!]$
.
$N=k[\![s]\!]$
.
Proof. As before, we can assume
![]() $\varphi $
has a regular factorisation
$\varphi $
has a regular factorisation
![]() $A\to A'\to B$
. Then it follows from 2.8 that
$A\to A'\to B$
. Then it follows from 2.8 that
![]() $\operatorname {flat\,dim}_AN$
is finite if and only
$\operatorname {flat\,dim}_AN$
is finite if and only
![]() $\operatorname {proj\,dim}_{A'}N$
is finite; since
$\operatorname {proj\,dim}_{A'}N$
is finite; since
![]() $A'\to B$
is a surjective exceptional complete intersection, Nagata’s Theorem 2.18 yields that the latter holds if and only if
$A'\to B$
is a surjective exceptional complete intersection, Nagata’s Theorem 2.18 yields that the latter holds if and only if
![]() $\operatorname {proj\,dim}_BN$
is finite. Thus, in the rest of the argument we can assume that
$\operatorname {proj\,dim}_BN$
is finite. Thus, in the rest of the argument we can assume that
![]() $\operatorname {flat\,dim}_AN$
and
$\operatorname {flat\,dim}_AN$
and
![]() $\operatorname {proj\,dim}_BN$
are finite. Then the desired inequality is already in Theorem 3.2.
$\operatorname {proj\,dim}_BN$
are finite. Then the desired inequality is already in Theorem 3.2.
When
![]() $\varphi $
is finite, N is also finitely generated over A, so
$\varphi $
is finite, N is also finitely generated over A, so
![]() $\operatorname {flat\,dim}_AN = \operatorname {proj\,dim}_AN$
. This and the Auslander–Buchsbaum equality give the first equality below:
$\operatorname {flat\,dim}_AN = \operatorname {proj\,dim}_AN$
. This and the Auslander–Buchsbaum equality give the first equality below:
 $$ \begin{align*} \operatorname{edim} A - \operatorname{flat\,dim}_A N &= \operatorname{edim} A - \operatorname{depth} A + \operatorname{depth}_A N \\ &=\operatorname{edim} B - \operatorname{depth} B + \operatorname{depth}_B N \\ &=\operatorname{edim} B - \operatorname{proj\,dim}_BN . \end{align*} $$
$$ \begin{align*} \operatorname{edim} A - \operatorname{flat\,dim}_A N &= \operatorname{edim} A - \operatorname{depth} A + \operatorname{depth}_A N \\ &=\operatorname{edim} B - \operatorname{depth} B + \operatorname{depth}_B N \\ &=\operatorname{edim} B - \operatorname{proj\,dim}_BN . \end{align*} $$
The second equality follows from the displayed equalities in 2.14 and the fact that depth of N over A equals its depth over B, since
![]() $\varphi $
is finite. The last equality is again by the Auslander–Buchsbaum equality.
$\varphi $
is finite. The last equality is again by the Auslander–Buchsbaum equality.
Acknowledgement
This study was partly supported by NSF grant DMS-200985 (SBI).
Competing Interest
None.