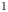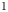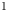1. Introduction
Given a locally compact group ![]() $G$ and a probability measure
$G$ and a probability measure ![]() $\mu \in {\rm Prob}(G)$, the associated (left) random walk on
$\mu \in {\rm Prob}(G)$, the associated (left) random walk on ![]() $G$ is the Markov chain on
$G$ is the Markov chain on ![]() $G$ whose transition probabilities are given by the measures
$G$ whose transition probabilities are given by the measures ![]() $\mu * \delta _x$. The Markov operator associated to this random walk is given by
$\mu * \delta _x$. The Markov operator associated to this random walk is given by
where ![]() $f$ is a continuous function on
$f$ is a continuous function on ![]() $G$ with compact support. The Markov operator extends to a contraction on
$G$ with compact support. The Markov operator extends to a contraction on ![]() $L^\infty (G)$, which is unital and (completely) positive. A function
$L^\infty (G)$, which is unital and (completely) positive. A function ![]() $f \in L^\infty (G)$ is
$f \in L^\infty (G)$ is ![]() $\mu$-harmonic if
$\mu$-harmonic if ![]() $\mathcal {P}_\mu (f) = f$. We let
$\mathcal {P}_\mu (f) = f$. We let ![]() ${\rm Har}(G, \mu )$ denote the Banach space of
${\rm Har}(G, \mu )$ denote the Banach space of ![]() $\mu$-harmonic functions. The Furstenberg–Poisson boundary [Reference FurstenbergFur63b] of
$\mu$-harmonic functions. The Furstenberg–Poisson boundary [Reference FurstenbergFur63b] of ![]() $G$ with respect to
$G$ with respect to ![]() $\mu$ is a certain
$\mu$ is a certain ![]() $G$-probability space
$G$-probability space ![]() $(B, \zeta )$, such that we have a natural positivity-preserving isometric
$(B, \zeta )$, such that we have a natural positivity-preserving isometric ![]() $G$-equivariant identification of
$G$-equivariant identification of ![]() $L^\infty (B, \zeta )$ with
$L^\infty (B, \zeta )$ with ![]() ${\rm Har}(G, \mu )$ via a Poisson transform.
${\rm Har}(G, \mu )$ via a Poisson transform.
An actual construction of the Poisson boundary ![]() $(B, \zeta )$, which is often described as a quotient of the path space corresponding to the stationary
$(B, \zeta )$, which is often described as a quotient of the path space corresponding to the stationary ![]() $\sigma$-algebra, is less important to us here than its existence, and indeed, up to isomorphisms of
$\sigma$-algebra, is less important to us here than its existence, and indeed, up to isomorphisms of ![]() $G$-spaces, it is the unique
$G$-spaces, it is the unique ![]() $G$-probability space such that
$G$-probability space such that ![]() $L^\infty (B, \zeta )$ is isomorphic, as an operator
$L^\infty (B, \zeta )$ is isomorphic, as an operator ![]() $G$-space, to
$G$-space, to ![]() ${\rm Har}(G, \mu )$.
${\rm Har}(G, \mu )$.
Under natural conditions on the measure ![]() $\mu$, the boundary
$\mu$, the boundary ![]() $(B, \zeta )$ possesses a number of remarkable properties. It is an amenable
$(B, \zeta )$ possesses a number of remarkable properties. It is an amenable ![]() $G$-space [Reference ZimmerZim78], it is doubly ergodic with isometric coefficients [Reference KaimanovichKai92, Reference Glasner and WeissGW16], and it is strongly asymptotically transitive [Reference JaworskiJaw94, Reference JaworskiJaw95]. The boundary has therefore become a powerful tool for studying rigidity properties for groups and their probability-measure-preserving actions [Reference MargulisMar75, Reference ZimmerZim80, Reference Bader and ShalomBS06, Reference Burger and MonodBM02, Reference Bader and FurmanBF20].
$G$-space [Reference ZimmerZim78], it is doubly ergodic with isometric coefficients [Reference KaimanovichKai92, Reference Glasner and WeissGW16], and it is strongly asymptotically transitive [Reference JaworskiJaw94, Reference JaworskiJaw95]. The boundary has therefore become a powerful tool for studying rigidity properties for groups and their probability-measure-preserving actions [Reference MargulisMar75, Reference ZimmerZim80, Reference Bader and ShalomBS06, Reference Burger and MonodBM02, Reference Bader and FurmanBF20].
In light of the successful application of the Poisson boundary to rigidity properties in group theory, Alain Connes suggested (see [Reference JonesJon00]) that developing a theory of the Poisson boundary in the setting of operator algebras would be the first step toward studying his rigidity conjecture [Reference ConnesCon82], which states that two property (T) ICC (that is, every nontrivial element has infinite conjugacy class) groups have isomorphic group von Neumann algebras if and only if the groups themselves are isomorphic. Further evidence for this can be seen by the significant role that Poisson boundaries play in [Reference Creutz and PetersonCP13, Reference Creutz and PetersonCP17, Reference PetersonPet15], where a related rigidity conjecture of Connes was investigated.
Poisson boundaries can more generally be defined using any Markov operator associated to a random walk. Markov operators are particular examples of normal unital completely positive (u.c.p.) maps on von Neumann algebras, and motivated by defining Poisson boundaries for discrete quantum groups, Izumi in [Reference IzumiIzu02, Reference IzumiIzu04] was able to define a noncommutative Poisson boundary associated to any normal u.c.p. map on a general von Neumann algebra. Specifically, if ![]() $\mathcal {M}$ is a von Neumann algebra and
$\mathcal {M}$ is a von Neumann algebra and ![]() $\phi : \mathcal {M} \to \mathcal {M}$ is a normal u.c.p. map, then we let
$\phi : \mathcal {M} \to \mathcal {M}$ is a normal u.c.p. map, then we let ![]() ${\rm Har}(\phi ) = \{ x \in \mathcal {M} \mid \phi (x) = x \}$ denote the space of
${\rm Har}(\phi ) = \{ x \in \mathcal {M} \mid \phi (x) = x \}$ denote the space of ![]() $\phi$-harmonic operators. Izumi showed that there exists a (unique up to isomorphism) von Neumann algebra
$\phi$-harmonic operators. Izumi showed that there exists a (unique up to isomorphism) von Neumann algebra ![]() $\mathcal {B}_\phi$ such that, as operator systems,
$\mathcal {B}_\phi$ such that, as operator systems, ![]() ${\rm Har}(\phi )$ and
${\rm Har}(\phi )$ and ![]() $\mathcal {B}_\phi$ can be identified via a Poisson transform
$\mathcal {B}_\phi$ can be identified via a Poisson transform ![]() $\mathcal {P}: \mathcal {B}_\phi \to {\rm Har}(\phi )$. The existence of this boundary follows by showing that
$\mathcal {P}: \mathcal {B}_\phi \to {\rm Har}(\phi )$. The existence of this boundary follows by showing that ![]() ${\rm Har}(\phi )$ can be realized as the range of a u.c.p. idempotent on
${\rm Har}(\phi )$ can be realized as the range of a u.c.p. idempotent on ![]() $\mathcal {M}$ and then applying a theorem of Choi and Effros. Alternatively, the existence of the boundary follows by considering the minimal dilation of
$\mathcal {M}$ and then applying a theorem of Choi and Effros. Alternatively, the existence of the boundary follows by considering the minimal dilation of ![]() $\phi$ [Reference IzumiIzu12]. We include in the appendix to this paper an elementary proof based on this perspective.
$\phi$ [Reference IzumiIzu12]. We include in the appendix to this paper an elementary proof based on this perspective.
There is a well-known dictionary between many analytic notions in group theory and those in von Neumann algebras. For example, states on ![]() $\mathcal {B}(L^2(M))$ correspond to states on
$\mathcal {B}(L^2(M))$ correspond to states on ![]() $\ell ^\infty \Gamma$, normal Hilbert
$\ell ^\infty \Gamma$, normal Hilbert ![]() $M$-bimodules correspond to unitary representations, etc. ([Reference ConnesCon76b, § 2], [Reference ConnesCon80]). This allows one to develop notions such as amenability and property (T) in the setting of finite von Neumann algebras. While Izumi's boundary gives a satisfactory noncommutative analogue of the Poisson boundary associated to a general random walk, an appropriate notion of a noncommutative Poisson boundary analogous to the group setting is still missing.
$M$-bimodules correspond to unitary representations, etc. ([Reference ConnesCon76b, § 2], [Reference ConnesCon80]). This allows one to develop notions such as amenability and property (T) in the setting of finite von Neumann algebras. While Izumi's boundary gives a satisfactory noncommutative analogue of the Poisson boundary associated to a general random walk, an appropriate notion of a noncommutative Poisson boundary analogous to the group setting is still missing.
The main goal of this paper is to introduce a theory of Poisson boundaries for finite von Neumann algebras that we believe will fill the role envisioned by Connes. If ![]() $M$ is a finite von Neumann algebra with a normal faithful trace
$M$ is a finite von Neumann algebra with a normal faithful trace ![]() $\tau$, and if
$\tau$, and if ![]() $\varphi \in \mathcal {B}(L^2(M, \tau ))_*$ is a normal state such that
$\varphi \in \mathcal {B}(L^2(M, \tau ))_*$ is a normal state such that ![]() $\varphi _{|M} = \tau$, then we will view
$\varphi _{|M} = \tau$, then we will view ![]() $\varphi$ as the distribution of a ‘noncommutative random walk’ on
$\varphi$ as the distribution of a ‘noncommutative random walk’ on ![]() $M$. To each distribution we associate a corresponding ‘convolution operator’, which is a normal u.c.p. map
$M$. To each distribution we associate a corresponding ‘convolution operator’, which is a normal u.c.p. map ![]() $\mathcal {P}_\varphi : \mathcal {B}(L^2(M, \tau )) \to \mathcal {B}(L^2(M, \tau ))$, such that
$\mathcal {P}_\varphi : \mathcal {B}(L^2(M, \tau )) \to \mathcal {B}(L^2(M, \tau ))$, such that ![]() $M \subset {\rm Har}(\mathcal {P}_\varphi )$. We then define the Poisson boundary of
$M \subset {\rm Har}(\mathcal {P}_\varphi )$. We then define the Poisson boundary of ![]() $M$ with respect to
$M$ with respect to ![]() $\varphi$ to be Izumi's noncommutative boundary
$\varphi$ to be Izumi's noncommutative boundary ![]() $\mathcal {B}_\varphi$ associated to
$\mathcal {B}_\varphi$ associated to ![]() $\mathcal {P}_\varphi$; more precisely, the boundary is really the inclusion of von Neumann algebras
$\mathcal {P}_\varphi$; more precisely, the boundary is really the inclusion of von Neumann algebras ![]() $M \subset \mathcal {B}_\varphi$, together with the Poisson transform
$M \subset \mathcal {B}_\varphi$, together with the Poisson transform ![]() $\mathcal {P}: \mathcal {B}_\varphi \to {\rm Har}(\mathcal {P}_\varphi )$.
$\mathcal {P}: \mathcal {B}_\varphi \to {\rm Har}(\mathcal {P}_\varphi )$.
Poisson boundaries of groups give rise to natural Poisson boundaries of group von Neumann algebras. Indeed, as already noticed by Izumi in [Reference IzumiIzu12], if ![]() $\Gamma$ is a countable discrete group and
$\Gamma$ is a countable discrete group and ![]() $\mu \in {\rm Prob}(\Gamma )$, then the noncommutative boundary of the u.c.p. map
$\mu \in {\rm Prob}(\Gamma )$, then the noncommutative boundary of the u.c.p. map ![]() $\phi _\mu : \mathcal {B}(\ell ^2 \Gamma ) \to \mathcal {B}(\ell ^2 \Gamma )$ given by
$\phi _\mu : \mathcal {B}(\ell ^2 \Gamma ) \to \mathcal {B}(\ell ^2 \Gamma )$ given by ![]() $\phi _\mu (T) = \int \rho _\gamma T \rho _\gamma ^* \,d\mu (\gamma )$ is naturally isomorphic to the von Neumann crossed product
$\phi _\mu (T) = \int \rho _\gamma T \rho _\gamma ^* \,d\mu (\gamma )$ is naturally isomorphic to the von Neumann crossed product ![]() $L^\infty (B, \zeta ) \rtimes \Gamma$ where
$L^\infty (B, \zeta ) \rtimes \Gamma$ where ![]() $(B, \zeta )$ is the Poisson boundary of
$(B, \zeta )$ is the Poisson boundary of ![]() $(\Gamma, \mu )$. Thus, many of the results we obtain are not merely analogues, but are actually generalizations of results from the theory of random walks on groups.
$(\Gamma, \mu )$. Thus, many of the results we obtain are not merely analogues, but are actually generalizations of results from the theory of random walks on groups.
If ![]() $M$ is a finite factor, then under natural conditions on the distribution
$M$ is a finite factor, then under natural conditions on the distribution ![]() $\varphi$, for example that its ‘support’ should generate
$\varphi$, for example that its ‘support’ should generate ![]() $M$, we show that the boundary
$M$, we show that the boundary ![]() $\mathcal {B}_\varphi$ is amenable/injective (Proposition 2.4), and that the inclusion
$\mathcal {B}_\varphi$ is amenable/injective (Proposition 2.4), and that the inclusion ![]() $M \subset \mathcal {B}_\varphi$ is ‘ergodic’, that is,
$M \subset \mathcal {B}_\varphi$ is ‘ergodic’, that is, ![]() $M' \cap \mathcal {B}_\varphi = \mathbb {C}$ (Proposition 2.7). We use techniques of Foguel [Reference FoguelFog75] to obtain equivalent characterizations for when the boundary is trivial (Theorem 2.10). The double ergodicity result of Kaimanovich [Reference KaimanovichKai92] is more subtle, as, unlike in the case for groups, there is no natural ‘diagonal’ inclusion of
$M' \cap \mathcal {B}_\varphi = \mathbb {C}$ (Proposition 2.7). We use techniques of Foguel [Reference FoguelFog75] to obtain equivalent characterizations for when the boundary is trivial (Theorem 2.10). The double ergodicity result of Kaimanovich [Reference KaimanovichKai92] is more subtle, as, unlike in the case for groups, there is no natural ‘diagonal’ inclusion of ![]() $M$ into
$M$ into ![]() $\mathcal {B}_\varphi \, \overline {\otimes }\, \mathcal {B}_\varphi$. There are, however, natural notions of left and right convolution operators, so that we may naturally associate with
$\mathcal {B}_\varphi \, \overline {\otimes }\, \mathcal {B}_\varphi$. There are, however, natural notions of left and right convolution operators, so that we may naturally associate with ![]() $\varphi$ a second u.c.p. map
$\varphi$ a second u.c.p. map ![]() $\mathcal {P}^{\rm o}_\varphi$ which commutes with
$\mathcal {P}^{\rm o}_\varphi$ which commutes with ![]() $\mathcal {P}_\varphi$ (see § 3 for the precise definition of
$\mathcal {P}_\varphi$ (see § 3 for the precise definition of ![]() $\mathcal {P}^{\rm o}_\varphi$). We may then show that bi-harmonic operators are constant, a result which is equivalent to double ergodicity in the group setting.
$\mathcal {P}^{\rm o}_\varphi$). We may then show that bi-harmonic operators are constant, a result which is equivalent to double ergodicity in the group setting.
Theorem A (Theorem 3.1 below)
Let ![]() $M$ be a finite factor and suppose
$M$ be a finite factor and suppose ![]() $\varphi$ is as above. Then we have
$\varphi$ is as above. Then we have
Motivated by the question of determining whether or not ![]() $L\mathbb {F}_\infty$ is finitely generated, Popa studied in [Reference PopaPop21a] the class of separable II
$L\mathbb {F}_\infty$ is finitely generated, Popa studied in [Reference PopaPop21a] the class of separable II![]() $_1$ factors
$_1$ factors ![]() $M$ that are tight, that is,
$M$ that are tight, that is, ![]() $M$ contains two hyperfinite subfactors
$M$ contains two hyperfinite subfactors ![]() $L, R \subset M$ such that
$L, R \subset M$ such that ![]() $L$ and
$L$ and ![]() $R^{\rm op}$ together generate
$R^{\rm op}$ together generate ![]() $\mathcal {B}(L^2(M))$. He conjectures in Conjecture 5.1 of [Reference PopaPop21a] that if a factor
$\mathcal {B}(L^2(M))$. He conjectures in Conjecture 5.1 of [Reference PopaPop21a] that if a factor ![]() $M$ has the property that all amplifications
$M$ has the property that all amplifications ![]() $M^t$ are singly generated, then
$M^t$ are singly generated, then ![]() $M$ is tight. He also notes that a tight factor
$M$ is tight. He also notes that a tight factor ![]() $M$ satisfies the MV property, which states that for any operator
$M$ satisfies the MV property, which states that for any operator ![]() $T \in \mathcal {B}(L^2(M))$ the weak closure of the convex hull of
$T \in \mathcal {B}(L^2(M))$ the weak closure of the convex hull of ![]() $\{ u (JvJ) T (Jv^*J) u^* \mid u, v \in \mathcal {U}(M) \}$ intersects the scalars. Popa then asks in Problem 7.4 of [Reference PopaPop21b] and Problem 6.3 in [Reference PopaPop21c] if free group factors, or perhaps all finite factors, have the MV property. As a consequence of double ergodicity we are able to answer Popa's problem.
$\{ u (JvJ) T (Jv^*J) u^* \mid u, v \in \mathcal {U}(M) \}$ intersects the scalars. Popa then asks in Problem 7.4 of [Reference PopaPop21b] and Problem 6.3 in [Reference PopaPop21c] if free group factors, or perhaps all finite factors, have the MV property. As a consequence of double ergodicity we are able to answer Popa's problem.
Theorem B (Theorem 3.3 below)
All finite factors have the MV property.
Other consequences of double ergodicity are that it allows us to show vanishing cohomology for subbimodules of the Poisson boundary (Theorem 3.5), to generalize rigidity results from [Reference Creutz and PetersonCP13] (Theorem 4.1), and to extend results of Bader and Shalom [Reference Bader and ShalomBS06] identifying the Poisson boundary of a tensor product with the tensor product of the Poisson boundaries (Corollary 4.5).
We also introduce analogues of Avez's asymptotic entropy and Furstenberg's ![]() $\mu$-entropy in the setting of von Neumann algebras (see § 5 for these definitions). We show that the triviality of the Poisson boundary is equivalent to the vanishing of the Furstenberg entropy (Corollary 5.15). We also use entropy to extend a result of Nevo [Reference NevoNev03] to the setting of von Neumann algebras, which shows that property (T) factors give rise to an ‘entropy gap’.
$\mu$-entropy in the setting of von Neumann algebras (see § 5 for these definitions). We show that the triviality of the Poisson boundary is equivalent to the vanishing of the Furstenberg entropy (Corollary 5.15). We also use entropy to extend a result of Nevo [Reference NevoNev03] to the setting of von Neumann algebras, which shows that property (T) factors give rise to an ‘entropy gap’.
Theorem C (Theorem 6.2 below)
Let ![]() $M$ be a II
$M$ be a II![]() $_1$ factor with property (T) generated by unitaries
$_1$ factor with property (T) generated by unitaries ![]() $u_1, \ldots, u_n$. Define the state
$u_1, \ldots, u_n$. Define the state ![]() $\varphi \in \mathcal {B}(L^2M)_*$ by
$\varphi \in \mathcal {B}(L^2M)_*$ by ![]() $\varphi (T) = ({1}/{n}) \sum _{k = 1}^n \langle T \widehat {u_k}, \widehat {u_k} \rangle$. There exists
$\varphi (T) = ({1}/{n}) \sum _{k = 1}^n \langle T \widehat {u_k}, \widehat {u_k} \rangle$. There exists ![]() $c > 0$ such that if
$c > 0$ such that if ![]() $M \subsetneq \mathcal {A}$ is an irreducible inclusion of von Neumann algebras and
$M \subsetneq \mathcal {A}$ is an irreducible inclusion of von Neumann algebras and ![]() $\zeta \in \mathcal {A}_*$ is any faithful normal state such that
$\zeta \in \mathcal {A}_*$ is any faithful normal state such that ![]() $\zeta _{| M} = \tau$, then
$\zeta _{| M} = \tau$, then ![]() $h_\varphi (M \subset \mathcal {A}, \zeta ) \geq c$.
$h_\varphi (M \subset \mathcal {A}, \zeta ) \geq c$.
We end with an appendix where we construct Izumi's boundary of a u.c.p. map. Our approach is elementary, and has the advantage that it applies for general ![]() $C^*$-algebras. This level of generality has no doubt been known by experts, but we could not find it in the current literature.
$C^*$-algebras. This level of generality has no doubt been known by experts, but we could not find it in the current literature.
2. Boundaries
2.1 Hyperstates and bimodular u.c.p. maps
Fix a tracial von Neumann algebra ![]() $(M, \tau )$, and suppose we have an embedding
$(M, \tau )$, and suppose we have an embedding ![]() $M \subset \mathcal {A}$ where
$M \subset \mathcal {A}$ where ![]() $\mathcal {A}$ is a
$\mathcal {A}$ is a ![]() $C^*$-algebra. We say that a state
$C^*$-algebra. We say that a state ![]() $\varphi \in \mathcal {A}^*$ is a
$\varphi \in \mathcal {A}^*$ is a ![]() $\tau$-hyperstate (or just a hyperstate if
$\tau$-hyperstate (or just a hyperstate if ![]() $\tau$ is fixed) if it extends
$\tau$ is fixed) if it extends ![]() $\tau$. We denote by
$\tau$. We denote by ![]() $\mathcal {S}_\tau (\mathcal {A})$ the convex set of all hyperstates on
$\mathcal {S}_\tau (\mathcal {A})$ the convex set of all hyperstates on ![]() $\mathcal {A}$. For each hyperstate
$\mathcal {A}$. For each hyperstate ![]() $\varphi$ we obtain a natural inclusion
$\varphi$ we obtain a natural inclusion ![]() $L^2(M, \tau ) \subset L^2(\mathcal {A}, \varphi )$ induced from the map
$L^2(M, \tau ) \subset L^2(\mathcal {A}, \varphi )$ induced from the map ![]() $x \hat {1} \mapsto x 1_{\varphi }$ for
$x \hat {1} \mapsto x 1_{\varphi }$ for ![]() $x \in M$. We let
$x \in M$. We let ![]() $e_M \in \mathcal {B}(L^2(\mathcal {A}, \varphi ))$ denote the orthogonal projection onto
$e_M \in \mathcal {B}(L^2(\mathcal {A}, \varphi ))$ denote the orthogonal projection onto ![]() $L^2(M, \tau )$. We may then consider the u.c.p. map
$L^2(M, \tau )$. We may then consider the u.c.p. map ![]() $\mathcal {P}_\varphi : \mathcal {A} \to \mathcal {B}(L^2(M, \tau ))$, defined by
$\mathcal {P}_\varphi : \mathcal {A} \to \mathcal {B}(L^2(M, \tau ))$, defined by
Note that if ![]() $x \in M \subset \mathcal {A}$, then we have
$x \in M \subset \mathcal {A}$, then we have ![]() $\mathcal {P}_\varphi (x) = x$. We call the map
$\mathcal {P}_\varphi (x) = x$. We call the map ![]() $\mathcal {P}_\varphi$ the Poisson transform (with respect to
$\mathcal {P}_\varphi$ the Poisson transform (with respect to ![]() $\varphi$) of the inclusion
$\varphi$) of the inclusion ![]() $M \subset \mathcal {A}$.
$M \subset \mathcal {A}$.
The following proposition is inspired by [Reference ConnesCon76b, § 2.2].
Proposition 2.1 The correspondence ![]() $\varphi \mapsto \mathcal {P}_\varphi$ defined by (1) gives a bijective correspondence between hyperstates on
$\varphi \mapsto \mathcal {P}_\varphi$ defined by (1) gives a bijective correspondence between hyperstates on ![]() $\mathcal {A}$, and u.c.p.,
$\mathcal {A}$, and u.c.p., ![]() $M$-bimodular maps from
$M$-bimodular maps from ![]() $\mathcal {A}$ to
$\mathcal {A}$ to ![]() $\mathcal {B}(L^2(M, \tau ))$. Moreover, if
$\mathcal {B}(L^2(M, \tau ))$. Moreover, if ![]() $\mathcal {A}$ is a von Neumann algebra, then
$\mathcal {A}$ is a von Neumann algebra, then ![]() $\mathcal {P}_\varphi$ is normal if and only if
$\mathcal {P}_\varphi$ is normal if and only if ![]() $\varphi$ is normal.
$\varphi$ is normal.
Also, this correspondence is a homeomorphism where the space of hyperstates is endowed with the weak![]() $^*$ topology, and the space of u.c.p.,
$^*$ topology, and the space of u.c.p., ![]() $M$-bimodular maps with the topology of pointwise weak operator topology convergence.
$M$-bimodular maps with the topology of pointwise weak operator topology convergence.
Proof. First note that if ![]() $\varphi$ is a hyperstate on
$\varphi$ is a hyperstate on ![]() $\mathcal {A}$, then for all
$\mathcal {A}$, then for all ![]() $T \in \mathcal {A}$ we have
$T \in \mathcal {A}$ we have
From this it follows that the correspondence ![]() $\varphi \mapsto \mathcal {P}_\varphi$ is one-to-one. To see that it is onto, suppose that
$\varphi \mapsto \mathcal {P}_\varphi$ is one-to-one. To see that it is onto, suppose that ![]() $\mathcal {P}: \mathcal {A} \to \mathcal {B}(L^2(M, \tau ))$ is u.c.p. and
$\mathcal {P}: \mathcal {A} \to \mathcal {B}(L^2(M, \tau ))$ is u.c.p. and ![]() $M$-bimodular. We define a state
$M$-bimodular. We define a state ![]() $\varphi$ on
$\varphi$ on ![]() $\mathcal {A}$ by
$\mathcal {A}$ by ![]() $\varphi (T) = \langle \mathcal {P}(T) \hat {1}, \hat {1} \rangle _\tau$. For all
$\varphi (T) = \langle \mathcal {P}(T) \hat {1}, \hat {1} \rangle _\tau$. For all ![]() $y \in M$ we then have
$y \in M$ we then have ![]() $\varphi (y) = \langle \mathcal {P}(y) \hat 1, \hat 1 \rangle _\tau = \tau (y)$, hence
$\varphi (y) = \langle \mathcal {P}(y) \hat 1, \hat 1 \rangle _\tau = \tau (y)$, hence ![]() $\varphi$ is a hyperstate. Moreover, if
$\varphi$ is a hyperstate. Moreover, if ![]() $y, z \in M$, and
$y, z \in M$, and ![]() $T \in \mathcal {A}$, then we have
$T \in \mathcal {A}$, then we have
 \begin{align} \langle \mathcal{P}_\varphi(T) \hat y, \hat z \rangle_\tau &= \langle \mathcal{P}_\varphi(z^* T y) \hat 1, \hat 1 \rangle_\tau \nonumber\\ &= \varphi(z^* T y)= \langle \mathcal{P}(T) \hat y, \hat z \rangle_\tau, \end{align}
\begin{align} \langle \mathcal{P}_\varphi(T) \hat y, \hat z \rangle_\tau &= \langle \mathcal{P}_\varphi(z^* T y) \hat 1, \hat 1 \rangle_\tau \nonumber\\ &= \varphi(z^* T y)= \langle \mathcal{P}(T) \hat y, \hat z \rangle_\tau, \end{align}
hence, ![]() $\mathcal {P}_\varphi = \mathcal {P}$.
$\mathcal {P}_\varphi = \mathcal {P}$.
It is also easy to check that ![]() $\mathcal {P}_\varphi$ is normal if and only if
$\mathcal {P}_\varphi$ is normal if and only if ![]() $\varphi$ is.
$\varphi$ is.
To see that this correspondence is a homeomorphism when given the topologies above, suppose that ![]() $\varphi$ is a hyperstate, and
$\varphi$ is a hyperstate, and ![]() ${\varphi _\alpha }$ is a net of hyperstates. From (2) and the fact that u.c.p. maps are contractions in norm we see that
${\varphi _\alpha }$ is a net of hyperstates. From (2) and the fact that u.c.p. maps are contractions in norm we see that ![]() $\mathcal {P}_{{\varphi _\alpha }}$ converges in the pointwise ultraweak topology to
$\mathcal {P}_{{\varphi _\alpha }}$ converges in the pointwise ultraweak topology to ![]() $\mathcal {P}_\varphi$ if
$\mathcal {P}_\varphi$ if ![]() ${\varphi _\alpha }$ converges weak
${\varphi _\alpha }$ converges weak![]() $^*$ to
$^*$ to ![]() $\varphi$. Conversely, setting
$\varphi$. Conversely, setting ![]() $y = z = 1$ in (2) shows that if
$y = z = 1$ in (2) shows that if ![]() $\mathcal {P}_{\varphi _\alpha }$ converges in the pointwise ultraweak topology to
$\mathcal {P}_{\varphi _\alpha }$ converges in the pointwise ultraweak topology to ![]() $\mathcal {P}_\varphi$, then
$\mathcal {P}_\varphi$, then ![]() $\varphi _\alpha$ converges weak
$\varphi _\alpha$ converges weak![]() $^*$ to
$^*$ to ![]() $\varphi$.
$\varphi$.
Considering the case ![]() $\mathcal {A} = \mathcal {B}(L^2(M, \tau ))$, we see that for each hyperstate
$\mathcal {A} = \mathcal {B}(L^2(M, \tau ))$, we see that for each hyperstate ![]() $\varphi$ on
$\varphi$ on ![]() $\mathcal {B}(L^2(M, \tau ))$ we obtain a u.c.p.
$\mathcal {B}(L^2(M, \tau ))$ we obtain a u.c.p. ![]() $M$-bimodular map
$M$-bimodular map ![]() $\mathcal {P}_\varphi$ on
$\mathcal {P}_\varphi$ on ![]() $\mathcal {B}(L^2(M, \tau ))$. In particular, composing such maps gives a type of convolution operation on the space of hyperstates. More generally, if
$\mathcal {B}(L^2(M, \tau ))$. In particular, composing such maps gives a type of convolution operation on the space of hyperstates. More generally, if ![]() $\mathcal {A}$ is a
$\mathcal {A}$ is a ![]() $C^*$-algebra, with
$C^*$-algebra, with ![]() $M \subset \mathcal {A}$, then for hyperstates
$M \subset \mathcal {A}$, then for hyperstates ![]() $\psi \in \mathcal {A}^*$ and
$\psi \in \mathcal {A}^*$ and ![]() $\varphi \in \mathcal {B}(L^2(M, \tau ))^*$ we define the convolution
$\varphi \in \mathcal {B}(L^2(M, \tau ))^*$ we define the convolution ![]() $\varphi * \psi$ to be the unique hyperstate on
$\varphi * \psi$ to be the unique hyperstate on ![]() $\mathcal {A}$ such that
$\mathcal {A}$ such that
We say that ![]() $\psi$ is
$\psi$ is ![]() $\varphi$-stationary if we have
$\varphi$-stationary if we have ![]() $\varphi * \psi = \psi$, or equivalently, if
$\varphi * \psi = \psi$, or equivalently, if ![]() $\mathcal {P}_\psi$ maps into the space of
$\mathcal {P}_\psi$ maps into the space of ![]() $\mathcal {P}_\varphi$-harmonic operators
$\mathcal {P}_\varphi$-harmonic operators
Lemma 2.2 For a fixed ![]() $\psi \in \mathcal {S}_\tau ( \mathcal {A} )$ the mapping
$\psi \in \mathcal {S}_\tau ( \mathcal {A} )$ the mapping
is continuous in the weak![]() $^*$ topology.
$^*$ topology.
Moreover, if ![]() $\varphi \in \mathcal {B}(L^2(M, \tau ))_*$ is a fixed normal hyperstate, then the mapping
$\varphi \in \mathcal {B}(L^2(M, \tau ))_*$ is a fixed normal hyperstate, then the mapping
is also weak![]() $^*$ continuous.
$^*$ continuous.
2.2 Poisson boundaries of II  $_1$ factors
$_1$ factors
Definition 2.3 Let ![]() $\varphi \in {\mathcal {S}}_\tau ( \mathcal {B}(L^2(M, \tau )))$ be a hyperstate. We define the Poisson boundary
$\varphi \in {\mathcal {S}}_\tau ( \mathcal {B}(L^2(M, \tau )))$ be a hyperstate. We define the Poisson boundary ![]() $\mathcal {B}_\varphi$ of
$\mathcal {B}_\varphi$ of ![]() $M$ with respect to
$M$ with respect to ![]() $\varphi$ to be the noncommutative Poisson boundary of the u.c.p. map
$\varphi$ to be the noncommutative Poisson boundary of the u.c.p. map ![]() ${\mathcal {P}}_\varphi$ as defined by Izumi [Reference IzumiIzu02], that is, the Poisson boundary
${\mathcal {P}}_\varphi$ as defined by Izumi [Reference IzumiIzu02], that is, the Poisson boundary ![]() $\mathcal {B}_\varphi$ is a
$\mathcal {B}_\varphi$ is a ![]() $C^*$-algebra (a von Neumann algebra when
$C^*$-algebra (a von Neumann algebra when ![]() $\varphi$ is normal) that is isomorphic, as an operator system, to the space of harmonic operators
$\varphi$ is normal) that is isomorphic, as an operator system, to the space of harmonic operators ![]() ${\rm Har}( \mathcal {B}(L^2(M, \tau ) ), \mathcal {P}_\varphi )$.
${\rm Har}( \mathcal {B}(L^2(M, \tau ) ), \mathcal {P}_\varphi )$.
Since ![]() $M$ is in the multiplicative domain of
$M$ is in the multiplicative domain of ![]() ${\mathcal {P}}_\varphi$, we see that
${\mathcal {P}}_\varphi$, we see that ![]() $\mathcal {B}_{\varphi }$ contains
$\mathcal {B}_{\varphi }$ contains ![]() $M$ as a subalgebra. Moreover, note that if we have a
$M$ as a subalgebra. Moreover, note that if we have a ![]() $C^*$-algebra
$C^*$-algebra ![]() $\mathcal {B}$, an inclusion
$\mathcal {B}$, an inclusion ![]() $M \subseteq \mathcal {B}$ together with a completely positive isometric surjection from
$M \subseteq \mathcal {B}$ together with a completely positive isometric surjection from ![]() $\mathcal {B}$ to
$\mathcal {B}$ to ![]() ${\rm Har}( \mathcal {B}(L^2(M, \tau ) ), \mathcal {P}_\varphi )$, then this induces a completely positive isometric surjection from
${\rm Har}( \mathcal {B}(L^2(M, \tau ) ), \mathcal {P}_\varphi )$, then this induces a completely positive isometric surjection from ![]() $\mathcal {B}$ to
$\mathcal {B}$ to ![]() $\mathcal {B}_{\varphi }$ which restricts to the identity on
$\mathcal {B}_{\varphi }$ which restricts to the identity on ![]() $M$. It is a well-known result of Choi [Reference ChoiCho72] that a completely positive surjective isometry between two
$M$. It is a well-known result of Choi [Reference ChoiCho72] that a completely positive surjective isometry between two ![]() $C^*$-algebras is a
$C^*$-algebras is a ![]() $\ast$-isomorphism. Thus, the Poisson boundary contains
$\ast$-isomorphism. Thus, the Poisson boundary contains ![]() $M$ as a subalgebra, and the inclusion
$M$ as a subalgebra, and the inclusion ![]() $(M \subset \mathcal {B}_\varphi )$ is determined up to isomorphism by the property that there exists a completely positive isometric surjection
$(M \subset \mathcal {B}_\varphi )$ is determined up to isomorphism by the property that there exists a completely positive isometric surjection ![]() $\mathcal {P}: \mathcal {B}_\varphi \to {\rm Har}( \mathcal {B}(L^2(M, \tau ) ), \mathcal {P}_\varphi )$ which restricts to the identity map on
$\mathcal {P}: \mathcal {B}_\varphi \to {\rm Har}( \mathcal {B}(L^2(M, \tau ) ), \mathcal {P}_\varphi )$ which restricts to the identity map on ![]() $M$. We will always assume that
$M$. We will always assume that ![]() $\mathcal {P}$ is fixed and we also call
$\mathcal {P}$ is fixed and we also call ![]() $\mathcal {P}$ the Poisson transform.
$\mathcal {P}$ the Poisson transform.
Given any initial hyperstate ![]() $\varphi _0 \in \mathcal {S}_\tau ( \mathcal {B}(L^2(M, \tau ) ) )$, we may consider the hyperstate given by
$\varphi _0 \in \mathcal {S}_\tau ( \mathcal {B}(L^2(M, \tau ) ) )$, we may consider the hyperstate given by ![]() $\varphi _0 \circ \mathcal {P}$ on
$\varphi _0 \circ \mathcal {P}$ on ![]() $\mathcal {B}_\varphi$. Of particular interest is the state
$\mathcal {B}_\varphi$. Of particular interest is the state ![]() $\eta$ on
$\eta$ on ![]() $\mathcal {B}_\varphi$ arising from the initial hyperstate
$\mathcal {B}_\varphi$ arising from the initial hyperstate ![]() $\varphi _0(x) \in \mathcal {S}_{\tau }(\mathcal {B}(L^2(M, \tau )))$ given by
$\varphi _0(x) \in \mathcal {S}_{\tau }(\mathcal {B}(L^2(M, \tau )))$ given by ![]() $\varphi _0(x)= \langle x \hat 1, \hat 1 \rangle$, which we call the stationary state on
$\varphi _0(x)= \langle x \hat 1, \hat 1 \rangle$, which we call the stationary state on ![]() $\mathcal {B}_\varphi$. In this case, using (2) above, it is easy to see that we have
$\mathcal {B}_\varphi$. In this case, using (2) above, it is easy to see that we have ![]() $\mathcal {P}_\eta = \mathcal {P}$, and hence
$\mathcal {P}_\eta = \mathcal {P}$, and hence ![]() $\varphi * \eta = \eta$.
$\varphi * \eta = \eta$.
Proposition 2.4 Let ![]() $(M, \tau )$ be a tracial von Neumann algebra and let
$(M, \tau )$ be a tracial von Neumann algebra and let ![]() $\varphi$ be a fixed hyperstate on
$\varphi$ be a fixed hyperstate on ![]() $\mathcal {B}(L^2(M, \tau ))$. Then the Poisson boundary
$\mathcal {B}(L^2(M, \tau ))$. Then the Poisson boundary ![]() $\mathcal {B}_\varphi$ is injective.
$\mathcal {B}_\varphi$ is injective.
Proof. If we take any accumulation point ![]() $E$ of
$E$ of ![]() $\bigl \{ ({1}/{N}) \sum _{n = 1}^N \mathcal {P}_\varphi ^n\bigr \}_{N \in \mathbb {N}}$ in the topology of pointwise ultraweak convergence, then
$\bigl \{ ({1}/{N}) \sum _{n = 1}^N \mathcal {P}_\varphi ^n\bigr \}_{N \in \mathbb {N}}$ in the topology of pointwise ultraweak convergence, then ![]() $E: \mathcal {B}(L^2(M, \tau ) ) \to {\rm Har}( \mathcal {B}(L^2(M, \tau ) ), \mathcal {P}_\varphi )$ gives a u.c.p. projection. As
$E: \mathcal {B}(L^2(M, \tau ) ) \to {\rm Har}( \mathcal {B}(L^2(M, \tau ) ), \mathcal {P}_\varphi )$ gives a u.c.p. projection. As ![]() $\mathcal {B}_\varphi$ is isomorphic to
$\mathcal {B}_\varphi$ is isomorphic to ![]() ${\rm Har}( \mathcal {B}(L^2(M, \tau ) ), \mathcal {P}_\varphi )$ as an operator system, it then follows that
${\rm Har}( \mathcal {B}(L^2(M, \tau ) ), \mathcal {P}_\varphi )$ as an operator system, it then follows that ![]() $\mathcal {B}_\varphi$ is injective [Reference Choi and EffrosCE77, § 3].
$\mathcal {B}_\varphi$ is injective [Reference Choi and EffrosCE77, § 3].
The trivial case is when ![]() $\varphi _e(x) = \langle x \hat 1, \hat 1 \rangle _\tau$, in which case we have that
$\varphi _e(x) = \langle x \hat 1, \hat 1 \rangle _\tau$, in which case we have that ![]() $\mathcal {P}_{\varphi _e} = {\rm id}$, and the Poisson boundary is simply
$\mathcal {P}_{\varphi _e} = {\rm id}$, and the Poisson boundary is simply ![]() $\mathcal {B}(L^2(M, \tau ))$. Note that
$\mathcal {B}(L^2(M, \tau ))$. Note that ![]() $\varphi _e$ gives an identity with respect to convolution. Also note that if
$\varphi _e$ gives an identity with respect to convolution. Also note that if ![]() $\varphi \in \mathcal {B}(L^2(M, \tau ))^*$ is a hyperstate, then we have a description of the space of harmonic operators as
$\varphi \in \mathcal {B}(L^2(M, \tau ))^*$ is a hyperstate, then we have a description of the space of harmonic operators as
Since ![]() $\mathcal {P}_\varphi$ is
$\mathcal {P}_\varphi$ is ![]() $M$-bimodular it follows that
$M$-bimodular it follows that ![]() $\mathcal {P}_\varphi (M') \subset M'$. We say that
$\mathcal {P}_\varphi (M') \subset M'$. We say that ![]() $\varphi$ is regular if the restriction of
$\varphi$ is regular if the restriction of ![]() $\mathcal {P}_\varphi$ to
$\mathcal {P}_\varphi$ to ![]() $M'$ preserves the canonical trace on
$M'$ preserves the canonical trace on ![]() $M'$, and we say that
$M'$, and we say that ![]() $\varphi$ is generating if
$\varphi$ is generating if ![]() $M$ is the largest
$M$ is the largest ![]() $*$-subalgebra of
$*$-subalgebra of ![]() $\mathcal {B}(L^2(M, \tau ))$ which is contained in
$\mathcal {B}(L^2(M, \tau ))$ which is contained in ![]() ${\rm Har}(\mathcal {B}(L^2(M, \tau )), {\mathcal {P}_\varphi })$. If
${\rm Har}(\mathcal {B}(L^2(M, \tau )), {\mathcal {P}_\varphi })$. If ![]() $\varphi$ is regular, then the conjugate of
$\varphi$ is regular, then the conjugate of ![]() $\varphi$, which is given by
$\varphi$, which is given by ![]() $\varphi ^*(T) = \varphi (J T^* J)$, is again a hyperstate. We will say that
$\varphi ^*(T) = \varphi (J T^* J)$, is again a hyperstate. We will say that ![]() $\varphi$ is symmetric if it is regular and we have
$\varphi$ is symmetric if it is regular and we have ![]() $\varphi ^* = \varphi$.
$\varphi ^* = \varphi$.
Regular, generating, symmetric hyperstates are easy to find. Suppose ![]() $(M, \tau )$ is a separable finite von Neumann algebra with a faithful normal trace
$(M, \tau )$ is a separable finite von Neumann algebra with a faithful normal trace ![]() $\tau$. We consider the unit ball
$\tau$. We consider the unit ball ![]() $(M)_1$ of
$(M)_1$ of ![]() $M$ as a Polish space endowed with the strong operator topology, and suppose we have a
$M$ as a Polish space endowed with the strong operator topology, and suppose we have a ![]() $\sigma$-finite measure
$\sigma$-finite measure ![]() $\mu$ on
$\mu$ on ![]() $(M)_1$ such that
$(M)_1$ such that ![]() $\int x^*x \,d\mu (x) = 1$. We obtain a normal hyperstate as
$\int x^*x \,d\mu (x) = 1$. We obtain a normal hyperstate as
and, using (2), we may explicitly compute the Poisson transform ![]() $\mathcal {P}_\varphi$ on
$\mathcal {P}_\varphi$ on ![]() $\mathcal {B}(L^2(M, \tau ))$ as
$\mathcal {B}(L^2(M, \tau ))$ as
Proposition 2.5 Consider ![]() $\varphi$ as given by (4). Then the following assertions hold.
$\varphi$ as given by (4). Then the following assertions hold.
(i)
 $\varphi$ is generating if and only if the support of
$\varphi$ is generating if and only if the support of  $\mu$ generates
$\mu$ generates  $M$ as a von Neumann algebra.
$M$ as a von Neumann algebra.(ii)
 $\varphi$ is regular if and only if
$\varphi$ is regular if and only if  $\int x x^* \,d\mu (x) = 1$. In this case
$\int x x^* \,d\mu (x) = 1$. In this case  $\varphi ^*$ is a normal hyperstate.
$\varphi ^*$ is a normal hyperstate.(iii) If
 $\varphi$ is regular, then
$\varphi$ is regular, then  $\mathcal {P}_{\varphi ^*}(T) = \int (J x J)T(J x^* J) \,d\mu (x)$ and
$\mathcal {P}_{\varphi ^*}(T) = \int (J x J)T(J x^* J) \,d\mu (x)$ and  $\varphi$ is symmetric if
$\varphi$ is symmetric if  $J_*\mu = \mu$, where
$J_*\mu = \mu$, where  $J$ is the adjoint operation.
$J$ is the adjoint operation.
Proof. If the support of ![]() $\mu$ generates von Neumann algebra
$\mu$ generates von Neumann algebra ![]() $M_0 \subset M$ such that
$M_0 \subset M$ such that ![]() $M_0 \not = M$, then we have
$M_0 \not = M$, then we have ![]() $[JxJ, e_{M_0}] = [Jx^* J, e_{M_0} ] = 0$ for each
$[JxJ, e_{M_0}] = [Jx^* J, e_{M_0} ] = 0$ for each ![]() $x$ in the support of
$x$ in the support of ![]() $\mu$. Hence,
$\mu$. Hence, ![]() $\mathcal {P}_\varphi (T) = \int (J x J) T (J x^* J) \,d\mu (x) = T$, for each
$\mathcal {P}_\varphi (T) = \int (J x J) T (J x^* J) \,d\mu (x) = T$, for each ![]() $T$ in the
$T$ in the ![]() $*$-algebra generated by
$*$-algebra generated by ![]() $M$ and
$M$ and ![]() $e_{M_0}$. Therefore,
$e_{M_0}$. Therefore, ![]() $\varphi$ is not generating. On the other hand, if
$\varphi$ is not generating. On the other hand, if ![]() $T \in {\rm Har}(\mathcal {B}(L^2(M, \tau )), \mathcal {P}_\varphi )$ is such that we also have
$T \in {\rm Har}(\mathcal {B}(L^2(M, \tau )), \mathcal {P}_\varphi )$ is such that we also have ![]() $T^*T, TT^* \in {\rm Har}(\mathcal {B}(L^2(M, \tau )), \mathcal {P}_\varphi )$, then for each
$T^*T, TT^* \in {\rm Har}(\mathcal {B}(L^2(M, \tau )), \mathcal {P}_\varphi )$, then for each ![]() $a \in M$ we have
$a \in M$ we have
 \begin{align*} & \int \| ( (J x J) T - T (J x J) ) \hat{a} \|_2^2 \,d\mu(x) \\ &\quad = \langle (T^* \mathcal{P}_\varphi(1) T - \mathcal{P}_\varphi(T^*) T - T^* \mathcal{P}_\varphi(T) + \mathcal{P}_\varphi(T^*T) ) \hat{a}, \hat{a} \rangle = 0, \end{align*}
\begin{align*} & \int \| ( (J x J) T - T (J x J) ) \hat{a} \|_2^2 \,d\mu(x) \\ &\quad = \langle (T^* \mathcal{P}_\varphi(1) T - \mathcal{P}_\varphi(T^*) T - T^* \mathcal{P}_\varphi(T) + \mathcal{P}_\varphi(T^*T) ) \hat{a}, \hat{a} \rangle = 0, \end{align*}
and by symmetry we also have ![]() $\int \| ( (J x J) T^* - T^* (J x J) ) \hat {a} \|_2^2 \,d\mu (x) = 0$. Hence,
$\int \| ( (J x J) T^* - T^* (J x J) ) \hat {a} \|_2^2 \,d\mu (x) = 0$. Hence, ![]() $[Jx J, T] = [J x^* J, T] = 0$ for
$[Jx J, T] = [J x^* J, T] = 0$ for ![]() $\mu$-almost every
$\mu$-almost every ![]() $x \in (M)_1$. Therefore, if the support of
$x \in (M)_1$. Therefore, if the support of ![]() $\mu$ generates
$\mu$ generates ![]() $M$ as a von Neumann algebra, then
$M$ as a von Neumann algebra, then ![]() $T \in JMJ' = M$, showing that
$T \in JMJ' = M$, showing that ![]() $\varphi$ is generating, thereby proving (i).
$\varphi$ is generating, thereby proving (i).
If ![]() $y \in M$, then we have
$y \in M$, then we have ![]() $\mathcal {P}_\varphi (JyJ) = \int J x^* y x J \,d\mu (x)$. Hence, we see that
$\mathcal {P}_\varphi (JyJ) = \int J x^* y x J \,d\mu (x)$. Hence, we see that ![]() $\varphi$ is regular if and only if for all
$\varphi$ is regular if and only if for all ![]() $y \in M$ we have
$y \in M$ we have ![]() $\tau (y) = \int \tau (x^* y x) \,d\mu (x) = \int \tau (xx^* y) \,d\mu (x)$, which is if and only if
$\tau (y) = \int \tau (x^* y x) \,d\mu (x) = \int \tau (xx^* y) \,d\mu (x)$, which is if and only if ![]() $\int xx^* \,d\mu (x) = 1$, thereby proving (ii).
$\int xx^* \,d\mu (x) = 1$, thereby proving (ii).
If ![]() $\varphi$ is regular, then
$\varphi$ is regular, then
 \begin{align*} \varphi^*(T) &= \varphi( J T^* J ) = \int \langle J T^* J \widehat{x^*}, \widehat{x^*} \rangle \,d\mu(x) \\ &= \int \langle \hat{x}, T^* \hat{x} \rangle \,d\mu(x) = \int \langle T \widehat{x^*}, \widehat{x^*} \rangle \,d J_*\mu(x). \end{align*}
\begin{align*} \varphi^*(T) &= \varphi( J T^* J ) = \int \langle J T^* J \widehat{x^*}, \widehat{x^*} \rangle \,d\mu(x) \\ &= \int \langle \hat{x}, T^* \hat{x} \rangle \,d\mu(x) = \int \langle T \widehat{x^*}, \widehat{x^*} \rangle \,d J_*\mu(x). \end{align*}
Therefore, if ![]() $J_*\mu = \mu$, then
$J_*\mu = \mu$, then ![]() $\varphi$ is symmetric, thereby proving (iii).
$\varphi$ is symmetric, thereby proving (iii).
Given a unital ![]() $C^*$-algebra
$C^*$-algebra ![]() $A$, and a u.c.p. map
$A$, and a u.c.p. map ![]() $\mathcal {P}: A \to A$, we denote the set of fixed points of
$\mathcal {P}: A \to A$, we denote the set of fixed points of ![]() $\mathcal {P}$ by
$\mathcal {P}$ by ![]() ${\rm Har}(A, \mathcal {P})$. That is,
${\rm Har}(A, \mathcal {P})$. That is, ![]() ${\rm Har}(A, \mathcal {P})=\{a \in A: \mathcal {P}(a)=a \}$. The following lemma is well known; see, for example, [Reference Fannes, Nachtergaele and WernerFNW94], [Reference Bratteli, Jorgensen, Kishimoto and WernerBJKW00, Lemma 3.4], or [Reference Chifan and DasCD20, Lemma 3.1] . We include a proof for the convenience of the reader.
${\rm Har}(A, \mathcal {P})=\{a \in A: \mathcal {P}(a)=a \}$. The following lemma is well known; see, for example, [Reference Fannes, Nachtergaele and WernerFNW94], [Reference Bratteli, Jorgensen, Kishimoto and WernerBJKW00, Lemma 3.4], or [Reference Chifan and DasCD20, Lemma 3.1] . We include a proof for the convenience of the reader.
Lemma 2.6 Suppose ![]() $A$ is a unital
$A$ is a unital ![]() $C^*$-algebra with a faithful state
$C^*$-algebra with a faithful state ![]() $\varphi$. If
$\varphi$. If ![]() $\mathcal {P}: A \to A$ is a u.c.p. map such that
$\mathcal {P}: A \to A$ is a u.c.p. map such that ![]() $\varphi \circ \mathcal {P} = \varphi$, then
$\varphi \circ \mathcal {P} = \varphi$, then ![]() ${\rm Har}( A, \mathcal {P}) \subset A$ is a
${\rm Har}( A, \mathcal {P}) \subset A$ is a ![]() $C^*$-subalgebra.
$C^*$-subalgebra.
Proof. ![]() ${\rm Har}( A, \mathcal {P})$ is clearly a self-adjoint closed subspace, thus we must show that
${\rm Har}( A, \mathcal {P})$ is clearly a self-adjoint closed subspace, thus we must show that ![]() ${\rm Har}( A, \mathcal {P})$ is an algebra. By the polarization identity it is enough to show that
${\rm Har}( A, \mathcal {P})$ is an algebra. By the polarization identity it is enough to show that ![]() $x^* x \in {\rm Har}( A, \mathcal {P})$ whenever
$x^* x \in {\rm Har}( A, \mathcal {P})$ whenever ![]() $x \in {\rm Har}( A, \mathcal {P})$. Suppose
$x \in {\rm Har}( A, \mathcal {P})$. Suppose ![]() $x \in {\rm Har}(A, \mathcal {P})$. By Kadison's inequality we have
$x \in {\rm Har}(A, \mathcal {P})$. By Kadison's inequality we have ![]() $\mathcal {P}(x^*x) - x^* x = \mathcal {P}(x^*x) - \mathcal {P}(x^*) \mathcal {P}(x) \geq 0$. Also,
$\mathcal {P}(x^*x) - x^* x = \mathcal {P}(x^*x) - \mathcal {P}(x^*) \mathcal {P}(x) \geq 0$. Also, ![]() $\varphi ( \mathcal {P}(x^*x) - x^*x) = 0$ so that by faithfulness of
$\varphi ( \mathcal {P}(x^*x) - x^*x) = 0$ so that by faithfulness of ![]() $\varphi$ we have
$\varphi$ we have ![]() $\mathcal {P}(x^*x) = x^*x$.
$\mathcal {P}(x^*x) = x^*x$.
Proposition 2.7 Let ![]() $M$ be a finite von Neumann algebra with a normal faithful trace
$M$ be a finite von Neumann algebra with a normal faithful trace ![]() $\tau$. Let
$\tau$. Let ![]() $\varphi \in \mathcal {B}(L^2(M, \tau ))^*$ be a regular generating hyperstate, and let
$\varphi \in \mathcal {B}(L^2(M, \tau ))^*$ be a regular generating hyperstate, and let ![]() $\mathcal {B}_\varphi$ be the corresponding Poisson boundary. Then
$\mathcal {B}_\varphi$ be the corresponding Poisson boundary. Then ![]() $M' \cap \mathcal {B}_\varphi = \mathcal {Z}(M)$. In particular, if
$M' \cap \mathcal {B}_\varphi = \mathcal {Z}(M)$. In particular, if ![]() $\varphi$ is also normal and
$\varphi$ is also normal and ![]() $M$ is a factor, then
$M$ is a factor, then ![]() $\mathcal {B}_\varphi$ is also a von Neumann factor.
$\mathcal {B}_\varphi$ is also a von Neumann factor.
Proof. Let ![]() $\mathcal {P}: \mathcal {B}_\varphi \to {\rm Har}(\mathcal {B}(L^2(M, \tau )), \mathcal {P}_\varphi )$ denote the Poisson transform. If
$\mathcal {P}: \mathcal {B}_\varphi \to {\rm Har}(\mathcal {B}(L^2(M, \tau )), \mathcal {P}_\varphi )$ denote the Poisson transform. If ![]() $x \in M' \cap \mathcal {B}_\varphi$, then
$x \in M' \cap \mathcal {B}_\varphi$, then ![]() $\mathcal {P}(x) \in M' \cap \mathcal {B}(L^2(M, \tau )) = J M J$. Since
$\mathcal {P}(x) \in M' \cap \mathcal {B}(L^2(M, \tau )) = J M J$. Since ![]() $\varphi$ is regular,
$\varphi$ is regular, ![]() $\mathcal {P}_\varphi$ preserves the trace when restricted to
$\mathcal {P}_\varphi$ preserves the trace when restricted to ![]() $J M J$. Thus,
$J M J$. Thus, ![]() ${\rm Har}(J M J,\mathcal {P}_\varphi )$ is a von Neumann subalgebra of
${\rm Har}(J M J,\mathcal {P}_\varphi )$ is a von Neumann subalgebra of ![]() $J M J$ by Lemma 2.6. Since
$J M J$ by Lemma 2.6. Since ![]() $\varphi$ is generating,
$\varphi$ is generating, ![]() $M$ is the largest von Neumann subalgebra of
$M$ is the largest von Neumann subalgebra of ![]() ${\rm Har}(\mathcal {B}(L^2(M, \tau )))$, and hence
${\rm Har}(\mathcal {B}(L^2(M, \tau )))$, and hence ![]() ${\rm Har}(J M J,\mathcal {P}_\varphi ) \subseteq M$, implying that
${\rm Har}(J M J,\mathcal {P}_\varphi ) \subseteq M$, implying that ![]() ${\rm Har}(J M J,\mathcal {P}_\varphi )=\mathcal {Z}(M)$. Therefore,
${\rm Har}(J M J,\mathcal {P}_\varphi )=\mathcal {Z}(M)$. Therefore, ![]() $\mathcal {P}(x) \in {\rm Har}(J M J, \mathcal {P}_\varphi ) = \mathcal {Z}(M)$, and hence
$\mathcal {P}(x) \in {\rm Har}(J M J, \mathcal {P}_\varphi ) = \mathcal {Z}(M)$, and hence ![]() $x \in \mathcal {Z}(M)$ since
$x \in \mathcal {Z}(M)$ since ![]() $\mathcal {P}$ is injective.
$\mathcal {P}$ is injective.
If ![]() $\varphi$ is a normal hyperstate in
$\varphi$ is a normal hyperstate in ![]() $\mathcal {S}_\tau ( \mathcal {B}(L^2(M, \tau )))$, then
$\mathcal {S}_\tau ( \mathcal {B}(L^2(M, \tau )))$, then ![]() $\mathcal {P}_\varphi : \mathcal {B}(L^2(M, \tau ) ) \to \mathcal {B}(L^2(M, \tau ))$ is a normal map, and hence the dual map
$\mathcal {P}_\varphi : \mathcal {B}(L^2(M, \tau ) ) \to \mathcal {B}(L^2(M, \tau ))$ is a normal map, and hence the dual map ![]() $\mathcal {P}_\varphi ^*$ preserves the predual of
$\mathcal {P}_\varphi ^*$ preserves the predual of ![]() $\mathcal {B}(L^2(M, \tau ))$ which we identify with the space of trace-class operators.
$\mathcal {B}(L^2(M, \tau ))$ which we identify with the space of trace-class operators.
We let ![]() $A_\varphi \in \mathcal {B}(L^2(M, \tau ))$ denote the density operator associated with
$A_\varphi \in \mathcal {B}(L^2(M, \tau ))$ denote the density operator associated with ![]() $\varphi$, that is,
$\varphi$, that is, ![]() $A_\varphi$ is the unique trace-class operator so that
$A_\varphi$ is the unique trace-class operator so that ![]() $\varphi (T) = \operatorname {Tr} (A_\varphi T)$ for all
$\varphi (T) = \operatorname {Tr} (A_\varphi T)$ for all ![]() $T \in \mathcal {B}(L^2(M, \tau ))$. Since
$T \in \mathcal {B}(L^2(M, \tau ))$. Since ![]() $\varphi$ is positive we have that
$\varphi$ is positive we have that ![]() $A_\varphi$ is a positive operator. If
$A_\varphi$ is a positive operator. If ![]() $P_{\hat {1}}$ denotes the rank-one orthogonal projection onto
$P_{\hat {1}}$ denotes the rank-one orthogonal projection onto ![]() $\mathbb {C} \hat {1}$, then we have
$\mathbb {C} \hat {1}$, then we have ![]() $\varphi (T) = \langle \mathcal {P}_\varphi (T) \hat {1}, \hat {1} \rangle = \operatorname {Tr} ( \mathcal {P}_\varphi (T) P_{\hat {1}} )$, and hence we see that
$\varphi (T) = \langle \mathcal {P}_\varphi (T) \hat {1}, \hat {1} \rangle = \operatorname {Tr} ( \mathcal {P}_\varphi (T) P_{\hat {1}} )$, and hence we see that ![]() $A_\varphi = \mathcal {P}_\varphi ^*( P_{\hat 1} )$. In particular, we have that
$A_\varphi = \mathcal {P}_\varphi ^*( P_{\hat 1} )$. In particular, we have that ![]() $A_{\varphi ^{* n}} = (\mathcal {P}_{\varphi }^n)^*(P_{\hat {1}})$ for
$A_{\varphi ^{* n}} = (\mathcal {P}_{\varphi }^n)^*(P_{\hat {1}})$ for ![]() $n \geq 1$.
$n \geq 1$.
Proposition 2.8 Let ![]() $(M, \tau )$ be a tracial von Neumann algebra and let
$(M, \tau )$ be a tracial von Neumann algebra and let ![]() $\varphi \in \mathcal {S}_\tau ( \mathcal {B}(L^2(M, \tau )))$ be a normal hyperstate. Then there exists a
$\varphi \in \mathcal {S}_\tau ( \mathcal {B}(L^2(M, \tau )))$ be a normal hyperstate. Then there exists a ![]() $\tau$-orthogonal family
$\tau$-orthogonal family ![]() $\{ z_n \}_n$ which gives a partition of the identity as
$\{ z_n \}_n$ which gives a partition of the identity as ![]() $1 = \sum _n z_n^*z_n$ so that
$1 = \sum _n z_n^*z_n$ so that
for all ![]() $T \in \mathcal {B}(L^2(M, \tau ))$.
$T \in \mathcal {B}(L^2(M, \tau ))$.
Moreover, if ![]() $\{ \tilde z_m \}_m$ is a
$\{ \tilde z_m \}_m$ is a ![]() $\tau$-orthogonal family which gives a partition of the identity as
$\tau$-orthogonal family which gives a partition of the identity as ![]() $1 = \sum _n \tilde z_n^* \tilde z_n$, then the map
$1 = \sum _n \tilde z_n^* \tilde z_n$, then the map ![]() $\sum _m (J \tilde z_m^* J) T (J \tilde z_m J)$ agrees with
$\sum _m (J \tilde z_m^* J) T (J \tilde z_m J)$ agrees with ![]() $\mathcal {P}_\varphi$ if and only if for each
$\mathcal {P}_\varphi$ if and only if for each ![]() $t > 0$ we have
$t > 0$ we have
Proof. Since ![]() $A_\varphi$ is a positive trace-class operator we may write
$A_\varphi$ is a positive trace-class operator we may write ![]() $A_\varphi = \sum _n a_n P_{y_n}$, where
$A_\varphi = \sum _n a_n P_{y_n}$, where ![]() $a_1, a_2, \ldots$ are positive and
$a_1, a_2, \ldots$ are positive and ![]() $\{ y_n \}_n$ is an orthonormal family with
$\{ y_n \}_n$ is an orthonormal family with ![]() $P_{y_n}$ denoting the rank-one projection onto
$P_{y_n}$ denoting the rank-one projection onto ![]() $\mathbb {C} y_n$. For
$\mathbb {C} y_n$. For ![]() $T \in \mathcal {B}(L^2(M, \tau ))$ we then have
$T \in \mathcal {B}(L^2(M, \tau ))$ we then have
Taking ![]() $T = x^*x \in M$, we have
$T = x^*x \in M$, we have ![]() $a_n \| x y_n \|_2^2 \leq \operatorname {Tr} (x^* x A_\varphi ) = \| x \|_2^2$, so that
$a_n \| x y_n \|_2^2 \leq \operatorname {Tr} (x^* x A_\varphi ) = \| x \|_2^2$, so that ![]() $y_n \in M \subset L^2(M, \tau )$ for each
$y_n \in M \subset L^2(M, \tau )$ for each ![]() $n$. Hence, for
$n$. Hence, for ![]() $T \in \mathcal {B}(L^2(M, \tau ))$ we have
$T \in \mathcal {B}(L^2(M, \tau ))$ we have
 \begin{align*} \operatorname{Tr} (\mathcal{P}_\varphi(T) P_{\hat{1}} ) &= \operatorname{Tr} (T A_\varphi) = \bigg\langle \sum_{n} a_n (J y_n J) T (J y_n^* J) \hat{1}, \hat{1}\bigg\rangle \\ &= \operatorname{Tr} \bigg(\bigg(\sum_{n} a_n (J y_n J) T (J y_n^* J) \bigg) P_{\hat{1}} \bigg). \end{align*}
\begin{align*} \operatorname{Tr} (\mathcal{P}_\varphi(T) P_{\hat{1}} ) &= \operatorname{Tr} (T A_\varphi) = \bigg\langle \sum_{n} a_n (J y_n J) T (J y_n^* J) \hat{1}, \hat{1}\bigg\rangle \\ &= \operatorname{Tr} \bigg(\bigg(\sum_{n} a_n (J y_n J) T (J y_n^* J) \bigg) P_{\hat{1}} \bigg). \end{align*}
Since ![]() $\mathcal {P}_\varphi$ is
$\mathcal {P}_\varphi$ is ![]() $M$-bimodular and since
$M$-bimodular and since ![]() $J y_n J \in M'$, it follows that for all
$J y_n J \in M'$, it follows that for all ![]() $x, y \in M$ we have
$x, y \in M$ we have
In particular, setting ![]() $T = y = 1$, we have
$T = y = 1$, we have
which shows that ![]() $\sum _n a_n y_n^* y_n = 1$.
$\sum _n a_n y_n^* y_n = 1$.
Since the span of operators of the form ![]() $x P_{\hat {1}} y$ is dense in the space of trace-class operators, it then follows that
$x P_{\hat {1}} y$ is dense in the space of trace-class operators, it then follows that ![]() $\mathcal {P}_\varphi (T) = \sum _{n} a_n (J y_n J) T (J y_n^* J)$ for all
$\mathcal {P}_\varphi (T) = \sum _{n} a_n (J y_n J) T (J y_n^* J)$ for all ![]() $T \in \mathcal {B}(L^2(M, \tau ))$. Setting
$T \in \mathcal {B}(L^2(M, \tau ))$. Setting ![]() $z_n = \sqrt {a_n} y_n^*$ then finishes the existence part of the proposition.
$z_n = \sqrt {a_n} y_n^*$ then finishes the existence part of the proposition.
Suppose now that ![]() $\{ \tilde z_m \}_m$ is a
$\{ \tilde z_m \}_m$ is a ![]() $\tau$-orthogonal family which gives a partition of the identity
$\tau$-orthogonal family which gives a partition of the identity ![]() $1 = \sum _n \tilde z_n^* \tilde z_n$, and set
$1 = \sum _n \tilde z_n^* \tilde z_n$, and set ![]() $\tilde \varphi (T) = \operatorname {Tr} ( ( \sum _n (J \tilde z_n^* J) T (J \tilde z_n J) ) P_{\hat {1}} )$. Then, the density matrix
$\tilde \varphi (T) = \operatorname {Tr} ( ( \sum _n (J \tilde z_n^* J) T (J \tilde z_n J) ) P_{\hat {1}} )$. Then, the density matrix ![]() $A_{\tilde \varphi }$, corresponding to
$A_{\tilde \varphi }$, corresponding to ![]() $\tilde \varphi$, is given by
$\tilde \varphi$, is given by ![]() $A_{\tilde \varphi }=\sum _n \tilde z_n^* P_{\hat {1}} \tilde z_n$. Since
$A_{\tilde \varphi }=\sum _n \tilde z_n^* P_{\hat {1}} \tilde z_n$. Since ![]() $\{ \tilde z_n \}_n$ forms a
$\{ \tilde z_n \}_n$ forms a ![]() $\tau$-orthogonal family it then follows easily that
$\tau$-orthogonal family it then follows easily that ![]() $\tilde z_n^*$ is an eigenvector for
$\tilde z_n^*$ is an eigenvector for ![]() $A_{\tilde \varphi }$, and the corresponding eigenvalue is
$A_{\tilde \varphi }$, and the corresponding eigenvalue is ![]() $\| \tilde z_n^* \|_2^2 = \| \tilde z_n \|_2^2$.
$\| \tilde z_n^* \|_2^2 = \| \tilde z_n \|_2^2$.
Using our notation from the first part of the proof of the proposition, we have that ![]() $A_{ \varphi }=\sum _n z_n^* P_{\hat {1}} z_n$. By the same argument as above, we get that
$A_{ \varphi }=\sum _n z_n^* P_{\hat {1}} z_n$. By the same argument as above, we get that ![]() $z_n^*$ is an eigenvector for
$z_n^*$ is an eigenvector for ![]() $A_{ \varphi }$, and the corresponding eigenvalue is
$A_{ \varphi }$, and the corresponding eigenvalue is ![]() $\| z_n^* \|_2^2 = \| z_n \|_2^2$. Note that
$\| z_n^* \|_2^2 = \| z_n \|_2^2$. Note that ![]() $\mathcal {P}_{\varphi }= \mathcal {P}_{\tilde \varphi }$ if and only if
$\mathcal {P}_{\varphi }= \mathcal {P}_{\tilde \varphi }$ if and only if ![]() $A_{ \varphi }=A_{ \tilde \varphi }$. Since the corresponding density matrices are positive trace class operators, the moreover part of the proposition follow easily from the spectral theorem.
$A_{ \varphi }=A_{ \tilde \varphi }$. Since the corresponding density matrices are positive trace class operators, the moreover part of the proposition follow easily from the spectral theorem.
We say that the form ![]() $\mathcal {P}_\varphi (T) = \sum _n (J z_n^* J) T (J z_n J)$ (respectively,
$\mathcal {P}_\varphi (T) = \sum _n (J z_n^* J) T (J z_n J)$ (respectively, ![]() $\varphi (T) = \sum _n \langle T \widehat {z_n^*}, \widehat {z_n^*} \rangle$) is a standard form for
$\varphi (T) = \sum _n \langle T \widehat {z_n^*}, \widehat {z_n^*} \rangle$) is a standard form for ![]() $\mathcal {P}_\varphi$ (respectively,
$\mathcal {P}_\varphi$ (respectively, ![]() $\varphi$). It follows from Proposition 2.5 that
$\varphi$). It follows from Proposition 2.5 that ![]() $\varphi$ is generating if and only if
$\varphi$ is generating if and only if ![]() $\{z_n \}_n$ generates
$\{z_n \}_n$ generates ![]() $M$ as a von Neumann algebra. We say that
$M$ as a von Neumann algebra. We say that ![]() $\varphi$ is strongly generating if the unital algebra (rather than the unital
$\varphi$ is strongly generating if the unital algebra (rather than the unital ![]() $*$-algebra) generated by
$*$-algebra) generated by ![]() $\{ z_n \}_n$ is already weakly dense in
$\{ z_n \}_n$ is already weakly dense in ![]() $M$. This is the case, for example, if
$M$. This is the case, for example, if ![]() $\varphi$ is generating and symmetric, since then we have that
$\varphi$ is generating and symmetric, since then we have that ![]() $\{ z_n \}_n = \{ z_n^* \}_n$, and hence the unital algebra generated by
$\{ z_n \}_n = \{ z_n^* \}_n$, and hence the unital algebra generated by ![]() $\{ z_n \}_n$ is already a
$\{ z_n \}_n$ is already a ![]() $*$-algebra.
$*$-algebra.
Proposition 2.9 Let ![]() $(M, \tau )$ be a tracial von Neumann algebra and suppose
$(M, \tau )$ be a tracial von Neumann algebra and suppose ![]() $\varphi$ is a normal strongly generating hyperstate. Then the stationary state
$\varphi$ is a normal strongly generating hyperstate. Then the stationary state ![]() $\zeta = \varphi \circ \mathcal {P}$ gives a normal faithful state on the Poisson boundary
$\zeta = \varphi \circ \mathcal {P}$ gives a normal faithful state on the Poisson boundary ![]() $\mathcal {B}_\varphi$ such that
$\mathcal {B}_\varphi$ such that ![]() $\zeta _{| M } = \tau$.
$\zeta _{| M } = \tau$.
Proof. By considering the Poisson transform ![]() $\mathcal {P}$, it suffices to show that
$\mathcal {P}$, it suffices to show that ![]() $\varphi$ is normal and faithful on the operator system
$\varphi$ is normal and faithful on the operator system ![]() $\operatorname {Har}(\mathcal {P}_\varphi )$. Note that here the stationary state is a vector state and hence normality follows. To see that the state is faithful fix
$\operatorname {Har}(\mathcal {P}_\varphi )$. Note that here the stationary state is a vector state and hence normality follows. To see that the state is faithful fix ![]() $T \in \operatorname {Har}(\mathcal {P}_\varphi )$, with
$T \in \operatorname {Har}(\mathcal {P}_\varphi )$, with ![]() $T \geq 0$ and
$T \geq 0$ and ![]() $\langle T \hat {1}, \hat {1} \rangle = 0$. Let
$\langle T \hat {1}, \hat {1} \rangle = 0$. Let ![]() $\mathcal {P}_\varphi (S)= \sum _n (Jz_n^*J) S (J z_n J)$ be the standard form of
$\mathcal {P}_\varphi (S)= \sum _n (Jz_n^*J) S (J z_n J)$ be the standard form of ![]() $\mathcal {P}_\varphi$. Since
$\mathcal {P}_\varphi$. Since ![]() $T \in \operatorname {Har}(\mathcal {P}_\varphi )$, we have that
$T \in \operatorname {Har}(\mathcal {P}_\varphi )$, we have that ![]() $\mathcal {P}_\varphi ^k(T) =T$ for each
$\mathcal {P}_\varphi ^k(T) =T$ for each ![]() $k \in \mathbb {N}$. Expanding the standard form gives
$k \in \mathbb {N}$. Expanding the standard form gives
We then have ![]() $T \hat {m}=0$ for all
$T \hat {m}=0$ for all ![]() $m$ in the unital algebra generated by
$m$ in the unital algebra generated by ![]() $\{ z_n \}$, and as
$\{ z_n \}$, and as ![]() $\varphi$ is strongly generating it then follows that
$\varphi$ is strongly generating it then follows that ![]() $T=0$.
$T=0$.
We end this section by giving a condition for the boundary to be trivial. We denote the space of trace-class operators on ![]() $L^2(M, \tau )$ by
$L^2(M, \tau )$ by ![]() ${\rm TC}(L^2(M, \tau ))$. We also denote the trace-class norm on
${\rm TC}(L^2(M, \tau ))$. We also denote the trace-class norm on ![]() ${\rm TC}(L^2(M, \tau ))$ by
${\rm TC}(L^2(M, \tau ))$ by ![]() $\| \cdot \|_{\rm TC}$. We identify
$\| \cdot \|_{\rm TC}$. We identify ![]() $\mathcal {B}(L^2(M, \tau ))$ with
$\mathcal {B}(L^2(M, \tau ))$ with ![]() ${\rm TC}(L^2(M, \tau ))^{\ast }$ via the pairing
${\rm TC}(L^2(M, \tau ))^{\ast }$ via the pairing ![]() $(A,T) \mapsto \operatorname {Tr}(AT)$, where
$(A,T) \mapsto \operatorname {Tr}(AT)$, where ![]() $A \in {\rm TC}(L^2(M, \tau ))$ and
$A \in {\rm TC}(L^2(M, \tau ))$ and ![]() $T \in \mathcal {B}(L^2(M, \tau ))$.
$T \in \mathcal {B}(L^2(M, \tau ))$.
Theorem 2.10 Let ![]() $(M, \tau )$ be a tracial von Neumann algebra and let
$(M, \tau )$ be a tracial von Neumann algebra and let ![]() $\psi$ be a normal hyperstate. Set
$\psi$ be a normal hyperstate. Set ![]() $\varphi = \frac {1}{2} \psi + \frac {1}{2} \langle \cdot \hat 1, \hat 1 \rangle$ and let
$\varphi = \frac {1}{2} \psi + \frac {1}{2} \langle \cdot \hat 1, \hat 1 \rangle$ and let ![]() $A_n \in {\rm TC}(L^2(M, \tau ))$ denote the density matrix corresponding to the normal, u.c.p.
$A_n \in {\rm TC}(L^2(M, \tau ))$ denote the density matrix corresponding to the normal, u.c.p. ![]() $M$-bimodular map
$M$-bimodular map ![]() $\mathcal {P}_{\varphi }^n$. Then the following conditions are equivalent.
$\mathcal {P}_{\varphi }^n$. Then the following conditions are equivalent.
(i) For all
 $x \in M$ we have
$x \in M$ we have  $\| x A_n - A_n x \|_{\rm TC} \to 0$.
$\| x A_n - A_n x \|_{\rm TC} \to 0$.(ii) For all
 $x \in M$ we have
$x \in M$ we have  $xA_n-A_nx \rightarrow 0$ weakly.
$xA_n-A_nx \rightarrow 0$ weakly.(iii)
 $\operatorname {Har}(\mathcal {P}_{\varphi })=M$.
$\operatorname {Har}(\mathcal {P}_{\varphi })=M$.
Proof. The first condition trivially implies the second. To see that the second implies the third, suppose for each ![]() $x \in M$ that we have
$x \in M$ that we have ![]() $xA_n-A_nx \rightarrow 0$ weakly as
$xA_n-A_nx \rightarrow 0$ weakly as ![]() $n \rightarrow \infty$. Let
$n \rightarrow \infty$. Let ![]() $T \in \operatorname {Har}(\mathcal {P}_{\varphi })$. Let
$T \in \operatorname {Har}(\mathcal {P}_{\varphi })$. Let ![]() $x, a,b \in M$. Then, taking inner products in
$x, a,b \in M$. Then, taking inner products in ![]() $L^2(M, \tau )$, we have
$L^2(M, \tau )$, we have
 \begin{align*} |\langle (TJxJ- JxJ T) a\hat{1}, b\hat{1} \rangle| &= |\langle (b^*Tax^*-x^*b^*Ta) \hat{1}, \hat{1} \rangle | \\ &= | \langle \mathcal{P}_{\varphi}^n(b^*Tax^*-x^*b^*Ta) \hat{1}, \hat{1} \rangle | = | \operatorname{Tr} (A_n (b^*Tax^*-x^*b^*Ta) )| \\ &= | \operatorname{Tr} ((x^*A_n-A_nx^*)b^*Ta)| \rightarrow 0. \end{align*}
\begin{align*} |\langle (TJxJ- JxJ T) a\hat{1}, b\hat{1} \rangle| &= |\langle (b^*Tax^*-x^*b^*Ta) \hat{1}, \hat{1} \rangle | \\ &= | \langle \mathcal{P}_{\varphi}^n(b^*Tax^*-x^*b^*Ta) \hat{1}, \hat{1} \rangle | = | \operatorname{Tr} (A_n (b^*Tax^*-x^*b^*Ta) )| \\ &= | \operatorname{Tr} ((x^*A_n-A_nx^*)b^*Ta)| \rightarrow 0. \end{align*}
Hence ![]() $T \in JMJ' = M$.
$T \in JMJ' = M$.
To see that the third condition implies the first we adapt the approach of Foguel from [Reference FoguelFog75]. Suppose ![]() $\operatorname {Har}(\mathcal {P}_{\varphi })=M$. Set
$\operatorname {Har}(\mathcal {P}_{\varphi })=M$. Set ![]() $\mathcal {A}_0 = \{ A \in {\rm TC}(L^2(M, \tau )) \mid \|(\mathcal {P}_{\varphi }^n)^*(A) \|_{\rm TC} \to 0 \}$. Note that since
$\mathcal {A}_0 = \{ A \in {\rm TC}(L^2(M, \tau )) \mid \|(\mathcal {P}_{\varphi }^n)^*(A) \|_{\rm TC} \to 0 \}$. Note that since ![]() $(\mathcal {P}_{\varphi }^n)^*$ is a contraction in the trace-class norm we have that
$(\mathcal {P}_{\varphi }^n)^*$ is a contraction in the trace-class norm we have that ![]() $\mathcal {A}_0$ is a closed subspace.
$\mathcal {A}_0$ is a closed subspace.
Since ![]() $\varphi = \frac {1}{2} \psi + \frac {1}{2} \langle \cdot \hat 1, \hat 1 \rangle$, we have
$\varphi = \frac {1}{2} \psi + \frac {1}{2} \langle \cdot \hat 1, \hat 1 \rangle$, we have ![]() $\mathcal {P}_\varphi ^* = \frac {1}{2} {\rm id} + \frac {1}{2} \mathcal {P}_\psi ^*$ and we compute
$\mathcal {P}_\varphi ^* = \frac {1}{2} {\rm id} + \frac {1}{2} \mathcal {P}_\psi ^*$ and we compute
 \begin{align*} (\mathcal{P}_\varphi^n)^* ({\rm id} - \mathcal{P}_\varphi^*) &= 2^{-(n + 1)} \bigg(\sum_{k = 0}^n \binom{n}{k} (\mathcal{P}_\psi^k)^* \bigg) ({\rm id} - \mathcal{P}_\psi^*) \\ &= 2^{-(n + 1)} \sum_{k = 1}^n \bigg(\binom{n}{k-1} - \binom{n}{k} \bigg) \mathcal{P}_{\psi}^*. \end{align*}
\begin{align*} (\mathcal{P}_\varphi^n)^* ({\rm id} - \mathcal{P}_\varphi^*) &= 2^{-(n + 1)} \bigg(\sum_{k = 0}^n \binom{n}{k} (\mathcal{P}_\psi^k)^* \bigg) ({\rm id} - \mathcal{P}_\psi^*) \\ &= 2^{-(n + 1)} \sum_{k = 1}^n \bigg(\binom{n}{k-1} - \binom{n}{k} \bigg) \mathcal{P}_{\psi}^*. \end{align*}
We have ![]() $\lim _{n \to \infty } 2^{-(n + 1)} \sum _{k = 1}^n | \binom {n}{k-1} - \binom {n}{k} | = 0$ (see (1.8) in [Reference Ornstein and SuchestonOS70]) hence
$\lim _{n \to \infty } 2^{-(n + 1)} \sum _{k = 1}^n | \binom {n}{k-1} - \binom {n}{k} | = 0$ (see (1.8) in [Reference Ornstein and SuchestonOS70]) hence ![]() $\| (\mathcal {P}_\varphi ^n)^*( P_{\hat 1} - \mathcal {P}_\varphi ^*(P_{\hat 1}) )\|_{\rm TC} \to 0$. Thus
$\| (\mathcal {P}_\varphi ^n)^*( P_{\hat 1} - \mathcal {P}_\varphi ^*(P_{\hat 1}) )\|_{\rm TC} \to 0$. Thus ![]() $P_{\hat 1} - \mathcal {P}_{\varphi }^*(P_{\hat 1}) \in \mathcal {A}_0$.
$P_{\hat 1} - \mathcal {P}_{\varphi }^*(P_{\hat 1}) \in \mathcal {A}_0$.
Since ![]() $\mathcal {P}_{\varphi }^*$ is
$\mathcal {P}_{\varphi }^*$ is ![]() $M$-bimodular we then have that
$M$-bimodular we then have that ![]() $a P_{\hat 1} b - \mathcal {P}_{\varphi }^*(a P_{\hat 1} b) \in \mathcal {A}_0$ for each
$a P_{\hat 1} b - \mathcal {P}_{\varphi }^*(a P_{\hat 1} b) \in \mathcal {A}_0$ for each ![]() $a, b \in M$ and hence
$a, b \in M$ and hence ![]() $B - \mathcal {P}_{\varphi }^*(B) \in \mathcal {A}_0$ for all
$B - \mathcal {P}_{\varphi }^*(B) \in \mathcal {A}_0$ for all ![]() $B \in {\rm TC}(L^2(M, \tau ))$. If
$B \in {\rm TC}(L^2(M, \tau ))$. If ![]() $T \in \mathcal {B}(L^2(M, \tau ))$ is such that
$T \in \mathcal {B}(L^2(M, \tau ))$ is such that ![]() $\operatorname {Tr} (AT) = 0$ for all
$\operatorname {Tr} (AT) = 0$ for all ![]() $A \in \mathcal {A}_0$, then for all
$A \in \mathcal {A}_0$, then for all ![]() $B \in {\rm TC}(L^2(M, \tau ))$ we have
$B \in {\rm TC}(L^2(M, \tau ))$ we have ![]() $\langle B - \mathcal {P}_{\varphi }^*(B), T \rangle = 0$ so that
$\langle B - \mathcal {P}_{\varphi }^*(B), T \rangle = 0$ so that ![]() $T \in {\rm Har}(\mathcal {P}_{\varphi }) = M$. Hence the annihilator of
$T \in {\rm Har}(\mathcal {P}_{\varphi }) = M$. Hence the annihilator of ![]() $\mathcal {A}_0$ is contained in
$\mathcal {A}_0$ is contained in ![]() $M.$ So the pre-annihilator of
$M.$ So the pre-annihilator of ![]() $M$ must be contained in
$M$ must be contained in ![]() $\mathcal {A}_0$. Thus
$\mathcal {A}_0$. Thus ![]() $A \in \mathcal {A}_0$ whenever
$A \in \mathcal {A}_0$ whenever ![]() $\operatorname {Tr} (A x) = 0$ for all
$\operatorname {Tr} (A x) = 0$ for all ![]() $x \in M$. In particular, we have
$x \in M$. In particular, we have ![]() $x P_{\hat 1} - P_{\hat 1} x \in \mathcal {A}_0$ for all
$x P_{\hat 1} - P_{\hat 1} x \in \mathcal {A}_0$ for all ![]() $x \in M$, which is equivalent to the fact that
$x \in M$, which is equivalent to the fact that ![]() $\| x A_n - A_n x \|_{\rm TC} \to 0$ for each
$\| x A_n - A_n x \|_{\rm TC} \to 0$ for each ![]() $x \in M$.
$x \in M$.
3. Biharmonic operators
If ![]() $\varphi \in \mathcal {S}_\tau (\mathcal {B}(L^2(M, \tau )))$ is regular and normal, then we define
$\varphi \in \mathcal {S}_\tau (\mathcal {B}(L^2(M, \tau )))$ is regular and normal, then we define ![]() $\mathcal {P}_\varphi ^{\rm o}$ to be the u.c.p. map given by
$\mathcal {P}_\varphi ^{\rm o}$ to be the u.c.p. map given by ![]() $\mathcal {P}_\varphi ^{\rm o} = {\rm Ad}(J) \circ \mathcal {P}_{\varphi ^*} \circ {\rm Ad}(J)$. Note that
$\mathcal {P}_\varphi ^{\rm o} = {\rm Ad}(J) \circ \mathcal {P}_{\varphi ^*} \circ {\rm Ad}(J)$. Note that ![]() $\mathcal {P}_\varphi ^{\rm o}$ and
$\mathcal {P}_\varphi ^{\rm o}$ and ![]() $\mathcal {P}_\eta$ commute for any normal hyperstate
$\mathcal {P}_\eta$ commute for any normal hyperstate ![]() $\eta$. Indeed, if we have standard forms
$\eta$. Indeed, if we have standard forms ![]() $\mathcal {P}_\varphi (T) = \sum _n (J z_n^* J) T (J z_n J)$ and
$\mathcal {P}_\varphi (T) = \sum _n (J z_n^* J) T (J z_n J)$ and ![]() $\mathcal {P}_\eta (T) = \sum _m (J y_m^* J) T (J y_m J)$, then by Proposition 2.5 we have
$\mathcal {P}_\eta (T) = \sum _m (J y_m^* J) T (J y_m J)$, then by Proposition 2.5 we have ![]() $\mathcal {P}_\varphi ^{\rm o}(T) = \sum _n z_n T z_n^*$ and hence
$\mathcal {P}_\varphi ^{\rm o}(T) = \sum _n z_n T z_n^*$ and hence
The following is a noncommutative analogue of double ergodicity which was established in [Reference KaimanovichKai92].
Theorem 3.1 Let ![]() $(M, \tau )$ be a tracial von Neumann algebra and let
$(M, \tau )$ be a tracial von Neumann algebra and let ![]() $\varphi$ be a normal regular strongly generating hyperstate. Then
$\varphi$ be a normal regular strongly generating hyperstate. Then
Proof. We fix a standard form ![]() $\mathcal {P}_\varphi (T) = \sum _n (J z_n^* J) T (J z_n J)$, so that we also have
$\mathcal {P}_\varphi (T) = \sum _n (J z_n^* J) T (J z_n J)$, so that we also have ![]() $\mathcal {P}_\varphi ^{\rm o}(T) = \sum _m z_m T z_m^*$. We identify the Poisson boundary
$\mathcal {P}_\varphi ^{\rm o}(T) = \sum _m z_m T z_m^*$. We identify the Poisson boundary ![]() $\mathcal {B}_\varphi$ with
$\mathcal {B}_\varphi$ with ![]() $\operatorname {Har}(\mathcal {B}(L^2(M, \tau )), \mathcal {P}_{\varphi })$, and let
$\operatorname {Har}(\mathcal {B}(L^2(M, \tau )), \mathcal {P}_{\varphi })$, and let ![]() $\zeta$ denote the stationary state on
$\zeta$ denote the stationary state on ![]() $\mathcal {B}_\varphi$, which is faithful by Proposition 2.9. For
$\mathcal {B}_\varphi$, which is faithful by Proposition 2.9. For ![]() $T \in \mathcal {B}_\varphi$ we have
$T \in \mathcal {B}_\varphi$ we have
By Lemma 2.6 we then have that ![]() $B_0 = \operatorname {Har}( \mathcal {B}_\varphi, \mathcal {P}^{\rm o}_{\varphi \,|\, \mathcal {B}_\varphi } )$ is a von Neumann subalgebra of
$B_0 = \operatorname {Har}( \mathcal {B}_\varphi, \mathcal {P}^{\rm o}_{\varphi \,|\, \mathcal {B}_\varphi } )$ is a von Neumann subalgebra of ![]() $\mathcal {B}_\varphi$. If
$\mathcal {B}_\varphi$. If ![]() $p \in B_0$ is a projection and
$p \in B_0$ is a projection and ![]() $\xi \in L^2(\mathcal {B}_\varphi, \zeta )$, then
$\xi \in L^2(\mathcal {B}_\varphi, \zeta )$, then
We must therefore have ![]() $\| p z_n^* p^\perp \xi \|_2 = 0$ for each
$\| p z_n^* p^\perp \xi \|_2 = 0$ for each ![]() $n$, and hence
$n$, and hence ![]() $p z_n^* = p z_n^* p$, for each
$p z_n^* = p z_n^* p$, for each ![]() $n$. Repeating this argument with roles of
$n$. Repeating this argument with roles of ![]() $p$ and
$p$ and ![]() $p^\perp$ reversed shows that
$p^\perp$ reversed shows that ![]() $z_n^* p = p z_n^*p$, so that
$z_n^* p = p z_n^*p$, so that ![]() $p \in M' \cap \mathcal {B}_\varphi$. Since
$p \in M' \cap \mathcal {B}_\varphi$. Since ![]() $p$ was an arbitrary projection we then have
$p$ was an arbitrary projection we then have ![]() $B_0 \subset M' \cap \mathcal {B}_\varphi$ and by Proposition 2.7 we have
$B_0 \subset M' \cap \mathcal {B}_\varphi$ and by Proposition 2.7 we have ![]() $B_0=\mathcal {Z}(M)$.
$B_0=\mathcal {Z}(M)$.
The previous result allows us to give an analogue of the classical Choquet–Deny theorem [Reference Choquet and DenyCD60], which states that if ![]() $\Gamma$ is an abelian group and
$\Gamma$ is an abelian group and ![]() $\mu \in {\rm Prob}(\Gamma )$ has support generating
$\mu \in {\rm Prob}(\Gamma )$ has support generating ![]() $\Gamma$, then every bounded
$\Gamma$, then every bounded ![]() $\mu$-harmonic function is constant.
$\mu$-harmonic function is constant.
Corollary 3.2 (Choquet–Deny theorem)
Suppose ![]() $M$ is an abelian von Neumann algebra and
$M$ is an abelian von Neumann algebra and ![]() $\varphi$ is a normal regular strongly generating hyperstate. Then
$\varphi$ is a normal regular strongly generating hyperstate. Then
We will now describe how Theorem 3.1 leads to a positive answer to a recent question by Popa ([Reference PopaPop21b, Problem 7.4], [Reference PopaPop21c, Problem 6.3]).
Theorem 3.3 Let ![]() $M$ be a finite von Neumann algebra with a normal faithful trace
$M$ be a finite von Neumann algebra with a normal faithful trace ![]() $\tau$ and let
$\tau$ and let ![]() $\mathcal {G} \subset \mathcal {U}(M)$ be a group which generates
$\mathcal {G} \subset \mathcal {U}(M)$ be a group which generates ![]() $M$ as a von Neumann algebra. Then for any operator
$M$ as a von Neumann algebra. Then for any operator ![]() $T \in \mathcal {B}(L^2(M, \tau ))$ the weak closure of the convex hull of
$T \in \mathcal {B}(L^2(M, \tau ))$ the weak closure of the convex hull of ![]() $\{ u (J v J) T (J v^* J) u^* \mid u, v \in \mathcal {G} \}$ intersects
$\{ u (J v J) T (J v^* J) u^* \mid u, v \in \mathcal {G} \}$ intersects ![]() $\mathcal {Z}(M)$.
$\mathcal {Z}(M)$.
Proof. We first consider the case when ![]() $\mathcal {G}$ is countable. Let
$\mathcal {G}$ is countable. Let ![]() $\mu \in {\rm Prob}( \mathcal {G})$ be symmetric with full support and define a normal regular symmetric generating hyperstate
$\mu \in {\rm Prob}( \mathcal {G})$ be symmetric with full support and define a normal regular symmetric generating hyperstate ![]() $\varphi$ by
$\varphi$ by ![]() $\varphi (T) = \int \langle T \hat {u}, \hat {u} \rangle \, d\mu (u)$. The corresponding Poisson transform is then given by
$\varphi (T) = \int \langle T \hat {u}, \hat {u} \rangle \, d\mu (u)$. The corresponding Poisson transform is then given by ![]() $\mathcal {P}_\varphi (T) = \int ( J u J) T (J u^* J) \, d\mu (u)$, and we may also compute
$\mathcal {P}_\varphi (T) = \int ( J u J) T (J u^* J) \, d\mu (u)$, and we may also compute ![]() $\mathcal {P}_\varphi ^{\rm o}$ as
$\mathcal {P}_\varphi ^{\rm o}$ as ![]() $\mathcal {P}_\varphi ^{\rm o}(T) = \int u^* T u \, d\mu (u)$.
$\mathcal {P}_\varphi ^{\rm o}(T) = \int u^* T u \, d\mu (u)$.
Fix ![]() $T \in \mathcal {B}(L^2(M, \tau ))$ and let
$T \in \mathcal {B}(L^2(M, \tau ))$ and let ![]() $\mathcal {C}= \overline {co}^{\rm wk} \{ u (J v J) T (J v^* J) u^* \mid u, v \in \mathcal {G} \}$. Then
$\mathcal {C}= \overline {co}^{\rm wk} \{ u (J v J) T (J v^* J) u^* \mid u, v \in \mathcal {G} \}$. Then ![]() $\mathcal {C}$ is preserved by both
$\mathcal {C}$ is preserved by both ![]() $\mathcal {P}_\varphi$ and
$\mathcal {P}_\varphi$ and ![]() $\mathcal {P}_\varphi ^{\rm o}$ and hence
$\mathcal {P}_\varphi ^{\rm o}$ and hence ![]() $\mathcal {C}$ is preserved by any point-ultraweak limit points
$\mathcal {C}$ is preserved by any point-ultraweak limit points ![]() $E$ and
$E$ and ![]() $E^{\rm o}$ of
$E^{\rm o}$ of ![]() $\bigl \{({1}/{N}) \sum _{n = 1}^N \mathcal {P}_\varphi ^n\bigr \}_{N = 1}^\infty$ and
$\bigl \{({1}/{N}) \sum _{n = 1}^N \mathcal {P}_\varphi ^n\bigr \}_{N = 1}^\infty$ and ![]() $\bigl \{({1}/{N}) \sum _{n = 1}^N (\mathcal {P}_\varphi ^{\rm o})^n\bigr \}_{N = 1}^\infty$, respectively. Since
$\bigl \{({1}/{N}) \sum _{n = 1}^N (\mathcal {P}_\varphi ^{\rm o})^n\bigr \}_{N = 1}^\infty$, respectively. Since ![]() $\mathcal {P}_\varphi$ and
$\mathcal {P}_\varphi$ and ![]() $\mathcal {P}_\varphi ^{\rm o}$ commute we have that
$\mathcal {P}_\varphi ^{\rm o}$ commute we have that ![]() $E$ and
$E$ and ![]() $E^{\rm o}$ commute. Moreover, as
$E^{\rm o}$ commute. Moreover, as ![]() $\bigl \| ({1}/{N}) \sum _{n = 1}^N \mathcal {P}_\varphi ^n - ({1}/{N}) \sum _{n = 1}^N \mathcal {P}_\varphi ^{n + 1} \bigr \| \leq 2/N$ it follows that
$\bigl \| ({1}/{N}) \sum _{n = 1}^N \mathcal {P}_\varphi ^n - ({1}/{N}) \sum _{n = 1}^N \mathcal {P}_\varphi ^{n + 1} \bigr \| \leq 2/N$ it follows that ![]() $E: \mathcal {B}(L^2(M, \tau )) \to {\rm Har}(\mathcal {P}_\varphi )$ and similarly
$E: \mathcal {B}(L^2(M, \tau )) \to {\rm Har}(\mathcal {P}_\varphi )$ and similarly ![]() $E^{\rm o}: \mathcal {B}(L^2(M, \tau )) \to {\rm Har}(\mathcal {P}_\varphi ^{\rm o})$. By Theorem 3.1 we then have
$E^{\rm o}: \mathcal {B}(L^2(M, \tau )) \to {\rm Har}(\mathcal {P}_\varphi ^{\rm o})$. By Theorem 3.1 we then have ![]() $E^{\rm o} \circ E: \mathcal {B}(L^2(M, \tau )) \to \mathcal {Z}(M)$. Hence
$E^{\rm o} \circ E: \mathcal {B}(L^2(M, \tau )) \to \mathcal {Z}(M)$. Hence
In the general case, if ![]() $G < \mathcal {G}$ is a countable subgroup, then let
$G < \mathcal {G}$ is a countable subgroup, then let ![]() $N \subset M$ be the von Neumann subalgebra generated by
$N \subset M$ be the von Neumann subalgebra generated by ![]() $G$ and let
$G$ and let ![]() $e_N: L^2(M, \tau ) \to L^2(N, \tau )$ be the orthogonal projection. If we define
$e_N: L^2(M, \tau ) \to L^2(N, \tau )$ be the orthogonal projection. If we define ![]() $\varphi$ as above and set
$\varphi$ as above and set ![]() $T_G = E^{\rm o} \circ E(T)$, then we have
$T_G = E^{\rm o} \circ E(T)$, then we have ![]() $T_G \in \mathcal {C}$,
$T_G \in \mathcal {C}$, ![]() $e_N T_G e_N = E^{\rm o} \circ E( e_N T e_N)$ and, viewing
$e_N T_G e_N = E^{\rm o} \circ E( e_N T e_N)$ and, viewing ![]() $e_N T e_N$ as an operator in
$e_N T e_N$ as an operator in ![]() $\mathcal {B}(L^2(N, \tau ))$, we may apply Theorem 3.1 as above to conclude that
$\mathcal {B}(L^2(N, \tau ))$, we may apply Theorem 3.1 as above to conclude that ![]() $e_N T_G e_N \in \mathcal {Z}(N) \subset \mathcal {B}(L^2(N, \tau ))$. If we consider the net
$e_N T_G e_N \in \mathcal {Z}(N) \subset \mathcal {B}(L^2(N, \tau ))$. If we consider the net ![]() $\{ T_G \}_G \subset \mathcal {B}(L^2(M, \tau ))$ where
$\{ T_G \}_G \subset \mathcal {B}(L^2(M, \tau ))$ where ![]() $G$ varies over all countable subgroups of
$G$ varies over all countable subgroups of ![]() $\mathcal {G}$, ordered by inclusion, then, letting
$\mathcal {G}$, ordered by inclusion, then, letting ![]() $T_0$ be any weak limit point of this net, we have that
$T_0$ be any weak limit point of this net, we have that ![]() $T_0 \in \mathcal {C}$.
$T_0 \in \mathcal {C}$.
Fix ![]() $u \in \mathcal {G}$. Then for any countable subgroup
$u \in \mathcal {G}$. Then for any countable subgroup ![]() $G< \mathcal {G}$, setting
$G< \mathcal {G}$, setting ![]() $N= G''$ and
$N= G''$ and ![]() $\tilde N= \langle G, u \rangle ''$, we have
$\tilde N= \langle G, u \rangle ''$, we have ![]() $e_{\tilde N}[u, T_0]e_{\tilde N}= [u, e_{\tilde N} T_0 e_{\tilde N}]=0$ and hence
$e_{\tilde N}[u, T_0]e_{\tilde N}= [u, e_{\tilde N} T_0 e_{\tilde N}]=0$ and hence ![]() $e_N[u, T_0]e_N=0.$ If we consider the net of all countable subgroups
$e_N[u, T_0]e_N=0.$ If we consider the net of all countable subgroups ![]() $G< \mathcal {G}$ ordered by inclusion, then as
$G< \mathcal {G}$ ordered by inclusion, then as ![]() $\mathcal {G}$ generates
$\mathcal {G}$ generates ![]() $M$, we have strong operator topology convergence
$M$, we have strong operator topology convergence ![]() $\lim _{G \rightarrow \infty }e_{G''}=1.$ Hence, it follows that
$\lim _{G \rightarrow \infty }e_{G''}=1.$ Hence, it follows that ![]() $[u, T_0]=0$, and since
$[u, T_0]=0$, and since ![]() $u \in \mathcal {G}$ was arbitrary, we have
$u \in \mathcal {G}$ was arbitrary, we have ![]() $T_0 \in \mathcal {Z}(M)$.
$T_0 \in \mathcal {Z}(M)$.
Let ![]() $(M, \tau )$ be a finite von Neumann algebra and
$(M, \tau )$ be a finite von Neumann algebra and ![]() $T \in \mathcal {B}( L^2(M, \tau ))$. Recall that the distance between
$T \in \mathcal {B}( L^2(M, \tau ))$. Recall that the distance between ![]() $T$ and
$T$ and ![]() $\mathcal {Z}(M)$ is defined as
$\mathcal {Z}(M)$ is defined as ![]() ${\rm dist}(T,\mathcal {Z}(M))= {\rm inf} \{\|T-S\|: S \in \mathcal {Z}(M) \}$. For
${\rm dist}(T,\mathcal {Z}(M))= {\rm inf} \{\|T-S\|: S \in \mathcal {Z}(M) \}$. For ![]() $T \in \mathcal {B}( L^2(M, \tau ))$ we let
$T \in \mathcal {B}( L^2(M, \tau ))$ we let ![]() $\delta _T$ denote the derivation given by
$\delta _T$ denote the derivation given by ![]() $\delta _T(x) = [x, T]$.
$\delta _T(x) = [x, T]$.
Corollary 3.4 Let ![]() $M$ be a finite von Neumann algebra, and suppose
$M$ be a finite von Neumann algebra, and suppose ![]() $T \in \mathcal {B}(L^2(M))$. Then
$T \in \mathcal {B}(L^2(M))$. Then
Proof. This follows from the previous theorem since every point ![]() $S \in \{ u (JvJ) T (Jv^*J) u^* \mid u, v \in \mathcal {U}(M) \}$ satisfies
$S \in \{ u (JvJ) T (Jv^*J) u^* \mid u, v \in \mathcal {U}(M) \}$ satisfies ![]() ${\rm dist}(T, S) \leq \| {\delta _T}_{ | M'} \| + \| {\delta _T}_{| M} \|$.
${\rm dist}(T, S) \leq \| {\delta _T}_{ | M'} \| + \| {\delta _T}_{| M} \|$.
As another application of Theorem 3.1 we use Christensen's theorem [Reference ChristensenChr82, Theorem 5.3] to establish the following vanishing cohomology result; the case when ![]() $\mathcal {C}=M$ is the celebrated Kadison–Sakai theorem [Reference KadisonKad66, Reference SakaiSak66].
$\mathcal {C}=M$ is the celebrated Kadison–Sakai theorem [Reference KadisonKad66, Reference SakaiSak66].
Theorem 3.5 Let ![]() $(M, \tau )$ be a tracial von Neumann algebra and let
$(M, \tau )$ be a tracial von Neumann algebra and let ![]() $\varphi$ be a normal regular strongly generating hyperstate. Suppose
$\varphi$ be a normal regular strongly generating hyperstate. Suppose ![]() $\mathcal {C} \subset \mathcal {B}_\varphi$ is a weakly closed
$\mathcal {C} \subset \mathcal {B}_\varphi$ is a weakly closed ![]() $M$-bimodule. If
$M$-bimodule. If ![]() $\delta : M \to \mathcal {C}$ is a norm continuous derivation, then there exists
$\delta : M \to \mathcal {C}$ is a norm continuous derivation, then there exists ![]() $c \in \mathcal {C}$ so that
$c \in \mathcal {C}$ so that ![]() $\delta (x) = [x, c]$ for
$\delta (x) = [x, c]$ for ![]() $x \in M$. Moreover, if
$x \in M$. Moreover, if ![]() $\varphi$ has the form
$\varphi$ has the form ![]() $\varphi (T) = \int \langle T \widehat {u^*}, \widehat {u^*} \rangle \, d\mu (u)$ for some probability measure
$\varphi (T) = \int \langle T \widehat {u^*}, \widehat {u^*} \rangle \, d\mu (u)$ for some probability measure ![]() $\mu \in {\rm Prob}(\mathcal {U}(M))$, then
$\mu \in {\rm Prob}(\mathcal {U}(M))$, then ![]() $c$ may be chosen so that
$c$ may be chosen so that ![]() $\| c \| \leq \| \delta \|$.
$\| c \| \leq \| \delta \|$.
Proof. Identifying ![]() $\mathcal {C}$ with its image under the Poisson transform, we will view
$\mathcal {C}$ with its image under the Poisson transform, we will view ![]() $\mathcal {C}$ as an operator system in
$\mathcal {C}$ as an operator system in ![]() $\operatorname {Har}(\mathcal {P}_\varphi ) \subset \mathcal {B}(L^2(M, \tau ))$. Since
$\operatorname {Har}(\mathcal {P}_\varphi ) \subset \mathcal {B}(L^2(M, \tau ))$. Since ![]() $L^2(M, \tau )$ has a cyclic vector for
$L^2(M, \tau )$ has a cyclic vector for ![]() $M$, Christensen's theorem shows that
$M$, Christensen's theorem shows that ![]() $\delta (m)=mT-Tm$ for some
$\delta (m)=mT-Tm$ for some ![]() $T \in \mathcal {B}(L^2(M, \tau ))$. Taking the conditional expectation onto
$T \in \mathcal {B}(L^2(M, \tau ))$. Taking the conditional expectation onto ![]() $\operatorname {Har}(\mathcal {P}_\varphi )$, we may assume
$\operatorname {Har}(\mathcal {P}_\varphi )$, we may assume ![]() $T \in \operatorname {Har}(\mathcal {P}_\varphi )$.
$T \in \operatorname {Har}(\mathcal {P}_\varphi )$.
We suppose ![]() $\varphi$ is given in standard form
$\varphi$ is given in standard form ![]() $\varphi (T) = \sum _n \langle T \widehat {z_n^*}, \widehat {z_n^*} \rangle$. Note that
$\varphi (T) = \sum _n \langle T \widehat {z_n^*}, \widehat {z_n^*} \rangle$. Note that ![]() $z_m\delta (z_m^*) \in \mathcal {C}$, so that
$z_m\delta (z_m^*) \in \mathcal {C}$, so that
As ![]() $\mathcal {P}_\varphi ^{\rm o}$ leaves
$\mathcal {P}_\varphi ^{\rm o}$ leaves ![]() $\mathcal {C}$ invariant (since
$\mathcal {C}$ invariant (since ![]() $\mathcal {C}$ is an
$\mathcal {C}$ is an ![]() $M$-bimodule), by induction we get that
$M$-bimodule), by induction we get that ![]() $T-(\mathcal {P}_\varphi ^{\rm o})^n(T) \in \mathcal {C}$ for all
$T-(\mathcal {P}_\varphi ^{\rm o})^n(T) \in \mathcal {C}$ for all ![]() $n \geq 1$, and hence for
$n \geq 1$, and hence for ![]() $N \geq 1$ we have
$N \geq 1$ we have
 \[ T- \frac{1}{N} \sum_{n=1}^N (\mathcal{P}_\varphi^{\rm o})^n(T) \in \mathcal{C}. \]
\[ T- \frac{1}{N} \sum_{n=1}^N (\mathcal{P}_\varphi^{\rm o})^n(T) \in \mathcal{C}. \]
If ![]() $z$ is a weak limit point of
$z$ is a weak limit point of ![]() $\bigl \{({1}/{N}) \sum _{n=1}^N (\mathcal {P}_\varphi ^{\rm o})^n(T)\bigr \}$, then
$\bigl \{({1}/{N}) \sum _{n=1}^N (\mathcal {P}_\varphi ^{\rm o})^n(T)\bigr \}$, then ![]() $z \in \operatorname {Har}(\mathcal {P}_\varphi ^{\rm o}) \cap \operatorname {Har}(\mathcal {P}_\varphi )$ and so by Theorem 3.1 we have
$z \in \operatorname {Har}(\mathcal {P}_\varphi ^{\rm o}) \cap \operatorname {Har}(\mathcal {P}_\varphi )$ and so by Theorem 3.1 we have ![]() $z \in \mathcal {Z}(M)$. Thus,
$z \in \mathcal {Z}(M)$. Thus, ![]() $T- z \in \mathcal {C}$ implements the derivation.
$T- z \in \mathcal {C}$ implements the derivation.
For the moreover part, note that if ![]() $\varphi$ has the form
$\varphi$ has the form ![]() $\varphi (T) = \int \langle T \widehat {u^*}, \widehat {u^*} \rangle \, d\mu (u)$ for some probability measure
$\varphi (T) = \int \langle T \widehat {u^*}, \widehat {u^*} \rangle \, d\mu (u)$ for some probability measure ![]() $\mu \in {\rm Prob}(\mathcal {U}(M))$, then
$\mu \in {\rm Prob}(\mathcal {U}(M))$, then
 \begin{align*} \|T-z\| &\leq \sup_N \bigg\|T- \frac{1}{N} \sum_{n=1}^N (\mathcal{P}_\varphi^{\rm o})^n(T)\bigg\| \\ &\leq \sup_n \| T - (\mathcal{P}_\varphi^{\rm o})^n(T) \| \\ &= \sup_n \bigg\| \int u \delta(u^*) \, d\mu_n \bigg\|\leq \|\delta\|, \end{align*}
\begin{align*} \|T-z\| &\leq \sup_N \bigg\|T- \frac{1}{N} \sum_{n=1}^N (\mathcal{P}_\varphi^{\rm o})^n(T)\bigg\| \\ &\leq \sup_n \| T - (\mathcal{P}_\varphi^{\rm o})^n(T) \| \\ &= \sup_n \bigg\| \int u \delta(u^*) \, d\mu_n \bigg\|\leq \|\delta\|, \end{align*}
where ![]() $\mu _n$ denotes the pushforward of
$\mu _n$ denotes the pushforward of ![]() $\mu \times \mu \times \cdots \times \mu \in {\rm Prob} (\mathcal {U}(M)^n)$ under the multiplication map.
$\mu \times \mu \times \cdots \times \mu \in {\rm Prob} (\mathcal {U}(M)^n)$ under the multiplication map.
Hence ![]() $c=T-z$ implements
$c=T-z$ implements ![]() $\delta$ with
$\delta$ with ![]() $\|c\| \leq \|\delta \|$.
$\|c\| \leq \|\delta \|$.
We remark that for a general hyperstate ![]() $\varphi$, in the proof of the previous theorem we still have
$\varphi$, in the proof of the previous theorem we still have ![]() $\| T - z \| \leq \| \delta \|_{\mathrm {cb}}$, where
$\| T - z \| \leq \| \delta \|_{\mathrm {cb}}$, where ![]() $\| \delta \|_{\mathrm {cb}}$ denotes the completely bounded norm of the derivation
$\| \delta \|_{\mathrm {cb}}$ denotes the completely bounded norm of the derivation ![]() $\delta$ (see, for instance, [Reference ChristensenChr82, § 2] for the definition of the completely bounded norm). So in general we may find
$\delta$ (see, for instance, [Reference ChristensenChr82, § 2] for the definition of the completely bounded norm). So in general we may find ![]() $c \in \mathcal {C}$ with
$c \in \mathcal {C}$ with ![]() $\| c \| \leq \| \delta \|_{\mathrm {cb}}$.
$\| c \| \leq \| \delta \|_{\mathrm {cb}}$.
4. Rigidity for u.c.p. maps on boundaries
The main result in this section is Theorem 4.1, where we generalize [Reference Creutz and PetersonCP13, Theorem 3.2]. We mention several consequences, including a noncommutative version of [Reference Bader and ShalomBS06, Corollary 3.2], which describes the Poisson boundary of a tensor product as the tensor product of Poisson boundaries.
Theorem 4.1 Let ![]() $(M, \tau )$ be a tracial von Neumann algebra, let
$(M, \tau )$ be a tracial von Neumann algebra, let ![]() $\varphi$ be a normal regular strongly generating hyperstate, and let
$\varphi$ be a normal regular strongly generating hyperstate, and let ![]() $\mathcal {B}= \mathcal {B}_{\varphi }$ denote the corresponding boundary. Suppose we have a weakly closed operator system
$\mathcal {B}= \mathcal {B}_{\varphi }$ denote the corresponding boundary. Suppose we have a weakly closed operator system ![]() $\mathcal {C}$ such that
$\mathcal {C}$ such that ![]() $M \subset \mathcal {C} \subset \mathcal {B}$. Let
$M \subset \mathcal {C} \subset \mathcal {B}$. Let ![]() $\Psi : \mathcal {C} \to \mathcal {B}$ be a normal u.c.p. map such that
$\Psi : \mathcal {C} \to \mathcal {B}$ be a normal u.c.p. map such that ![]() $\Psi _{| M } = {\rm id}$. Then
$\Psi _{| M } = {\rm id}$. Then ![]() $\Psi = {\rm id}$.
$\Psi = {\rm id}$.
Proof. Let ![]() $\mathcal {P}_\varphi (T) = \sum _n (J z_n^* J) T (J z_n J)$ denote the standard form of
$\mathcal {P}_\varphi (T) = \sum _n (J z_n^* J) T (J z_n J)$ denote the standard form of ![]() $\mathcal {P}_{\varphi }$ as in Proposition 2.8. Then by Proposition 2.4 we have
$\mathcal {P}_{\varphi }$ as in Proposition 2.8. Then by Proposition 2.4 we have ![]() $\mathcal {P}_\varphi ^{\rm o}(T) = \sum _n z_n T z_n^*$. By identifying
$\mathcal {P}_\varphi ^{\rm o}(T) = \sum _n z_n T z_n^*$. By identifying ![]() $\mathcal {C}$ with its image under the Poisson transform we may assume that
$\mathcal {C}$ with its image under the Poisson transform we may assume that ![]() $\mathcal {C}$ is a weakly closed
$\mathcal {C}$ is a weakly closed ![]() $M$-subbimodule of
$M$-subbimodule of ![]() $\operatorname {Har}(\mathcal {P}_{\varphi })$ and
$\operatorname {Har}(\mathcal {P}_{\varphi })$ and ![]() $\Psi : \mathcal {C} \to \operatorname {Har}(\mathcal {P}_{\varphi })$ is a normal u.c.p. map such that
$\Psi : \mathcal {C} \to \operatorname {Har}(\mathcal {P}_{\varphi })$ is a normal u.c.p. map such that ![]() $\Psi _{| M } = {\rm id}$. Note that for
$\Psi _{| M } = {\rm id}$. Note that for ![]() $T \in \mathcal {C}$ we have
$T \in \mathcal {C}$ we have
 \begin{align*} \langle \Psi(T) \hat{1}, \hat{1} \rangle &= \langle \mathcal{P}_{\varphi}(\Psi(T)) \hat{1}, \hat{1} \rangle = \langle \mathcal{P}_{\varphi}^{\rm o}(\Psi(T)) \hat{1}, \hat{1} \rangle \\ &= \sum_n \langle z_n \Psi(T) z_n^* \hat{1}, \hat{1} \rangle = \langle \Psi(\mathcal{P}_{\varphi}^{\rm o}(T)) \hat{1}, \hat{1} \rangle, \end{align*}
\begin{align*} \langle \Psi(T) \hat{1}, \hat{1} \rangle &= \langle \mathcal{P}_{\varphi}(\Psi(T)) \hat{1}, \hat{1} \rangle = \langle \mathcal{P}_{\varphi}^{\rm o}(\Psi(T)) \hat{1}, \hat{1} \rangle \\ &= \sum_n \langle z_n \Psi(T) z_n^* \hat{1}, \hat{1} \rangle = \langle \Psi(\mathcal{P}_{\varphi}^{\rm o}(T)) \hat{1}, \hat{1} \rangle, \end{align*}
where the last equality follows from the fact that ![]() $\Psi$ is normal and
$\Psi$ is normal and ![]() $M$-bimodular, as
$M$-bimodular, as ![]() $M$ is contained in the multiplicative domain of
$M$ is contained in the multiplicative domain of ![]() $\Psi$. Now
$\Psi$. Now ![]() $\langle \Psi (\mathcal {P}_{\varphi }^{\rm o}(T)) \hat {1}, \hat {1} \rangle = \langle \Psi (T) \hat {1}, \hat {1} \rangle$ for all
$\langle \Psi (\mathcal {P}_{\varphi }^{\rm o}(T)) \hat {1}, \hat {1} \rangle = \langle \Psi (T) \hat {1}, \hat {1} \rangle$ for all ![]() $T \in \mathcal {C}$ immediately implies that
$T \in \mathcal {C}$ immediately implies that
 \[ \bigg\langle \Psi \bigg(\frac{1}{N}\sum_{n=1}^N (\mathcal{P}_{\varphi}^{\rm o})^n(T)\bigg) \hat{1}, \hat{1}\bigg\rangle = \langle \Psi(T) \hat{1}, \hat{1} \rangle\quad \text{for all } T \in \mathcal{C}. \]
\[ \bigg\langle \Psi \bigg(\frac{1}{N}\sum_{n=1}^N (\mathcal{P}_{\varphi}^{\rm o})^n(T)\bigg) \hat{1}, \hat{1}\bigg\rangle = \langle \Psi(T) \hat{1}, \hat{1} \rangle\quad \text{for all } T \in \mathcal{C}. \]
Let ![]() $z$ be a weak operator topology limit point of
$z$ be a weak operator topology limit point of ![]() $({1}/{N})\sum _{n=1}^N (\mathcal {P}_{\varphi }^{\rm o})^n(T)$. Then,
$({1}/{N})\sum _{n=1}^N (\mathcal {P}_{\varphi }^{\rm o})^n(T)$. Then, ![]() $z \in \mathcal {Z}(M)$ by Theorem 3.1, so that
$z \in \mathcal {Z}(M)$ by Theorem 3.1, so that ![]() $\Psi (z)=z$. We then have
$\Psi (z)=z$. We then have
where the last equality follows because ![]() $z$ is independent of
$z$ is independent of ![]() $\Psi$. Now let
$\Psi$. Now let ![]() $a,b \in M$ and
$a,b \in M$ and ![]() $T \in \mathcal {C}$. Then, we have that
$T \in \mathcal {C}$. Then, we have that ![]() $b^*Ta \in \mathcal {C}$, and hence by above computation, we get
$b^*Ta \in \mathcal {C}$, and hence by above computation, we get
Thus ![]() $\Psi (T)=T.$
$\Psi (T)=T.$
Corollary 4.2 Let ![]() $M$ be a finite von Neumann algebra with a normal faithful trace
$M$ be a finite von Neumann algebra with a normal faithful trace ![]() $\tau$, and let
$\tau$, and let ![]() $\varphi$ be a normal regular strongly generating hyperstate. Then
$\varphi$ be a normal regular strongly generating hyperstate. Then ![]() $M$ is a maximal finite von Neumann subalgebra inside
$M$ is a maximal finite von Neumann subalgebra inside ![]() $\mathcal {B}_{\varphi }.$
$\mathcal {B}_{\varphi }.$
Proof. Suppose ![]() $N \subset \mathcal {B}_{\varphi }$ is a finite von Neumann algebra containing
$N \subset \mathcal {B}_{\varphi }$ is a finite von Neumann algebra containing ![]() $M$. Then there exists a normal conditional expectation
$M$. Then there exists a normal conditional expectation ![]() $E:N \to M$. Hence, by Theorem 4.1,
$E:N \to M$. Hence, by Theorem 4.1, ![]() $E(x)=x$ for all
$E(x)=x$ for all ![]() $x \in N$, and hence
$x \in N$, and hence ![]() $N=M$.
$N=M$.
Corollary 4.3 Let ![]() $M$ be a
$M$ be a ![]() ${\rm II_1}$ factor, and let
${\rm II_1}$ factor, and let ![]() $\varphi$ be a normal regular strongly generating hyperstate. If
$\varphi$ be a normal regular strongly generating hyperstate. If ![]() $\mathcal {B}_\varphi \neq M$, then
$\mathcal {B}_\varphi \neq M$, then ![]() $\mathcal {B}_{\varphi }$ is a type
$\mathcal {B}_{\varphi }$ is a type ![]() $III$ factor.
$III$ factor.
Proof. Note that the stationary state is normal and faithful by Proposition 2.9, and ![]() $\mathcal {B}_\varphi$ is a factor by Proposition 2.7. We also note that Proposition 2.7 along with von Neumann's bicommutant Theorem shows that
$\mathcal {B}_\varphi$ is a factor by Proposition 2.7. We also note that Proposition 2.7 along with von Neumann's bicommutant Theorem shows that ![]() $\mathcal {B}_{\varphi }$ is not a type
$\mathcal {B}_{\varphi }$ is not a type ![]() ${\rm I}$ factor.
${\rm I}$ factor.
Suppose ![]() $\mathcal {B}_\varphi$ is not a type III factor, then
$\mathcal {B}_\varphi$ is not a type III factor, then ![]() $\mathcal {B}_\varphi$ has a semifinite normal faithful trace
$\mathcal {B}_\varphi$ has a semifinite normal faithful trace ![]() $\operatorname {Tr}$. As before, let
$\operatorname {Tr}$. As before, let ![]() $\mathcal {P}$ denote the Poisson transform, and let
$\mathcal {P}$ denote the Poisson transform, and let ![]() $\zeta$ be the normal state on
$\zeta$ be the normal state on ![]() $\mathcal {B}_{\varphi }$ defined by
$\mathcal {B}_{\varphi }$ defined by ![]() $\zeta (b)= \langle \mathcal {P}(b) \hat {1} , \hat {1} \rangle$. Fix
$\zeta (b)= \langle \mathcal {P}(b) \hat {1} , \hat {1} \rangle$. Fix ![]() $0 \leq T \in \mathcal {B}_{\varphi }$ with
$0 \leq T \in \mathcal {B}_{\varphi }$ with ![]() $\operatorname {Tr}(T) < \infty$, and
$\operatorname {Tr}(T) < \infty$, and ![]() $\zeta (T) \neq 0$. Fix
$\zeta (T) \neq 0$. Fix ![]() $S \!\in\! \mathcal {B}_{\varphi }$ with
$S \!\in\! \mathcal {B}_{\varphi }$ with ![]() $S \!\geq\! 0$ and
$S \!\geq\! 0$ and ![]() $\operatorname {Tr}(S)\!<\! \infty$. Let
$\operatorname {Tr}(S)\!<\! \infty$. Let ![]() $z$ be a ultraweak limit point of
$z$ be a ultraweak limit point of ![]() $ ({1}/{N})\sum _{n=1}^N (\mathcal {P}_{\varphi }^{\rm o})^n(T)$. Then by Theorem 3.1 we have
$ ({1}/{N})\sum _{n=1}^N (\mathcal {P}_{\varphi }^{\rm o})^n(T)$. Then by Theorem 3.1 we have ![]() $z \in \mathcal {Z}(M)= \mathbb {C}$ and, arguing as in the proof of Theorem 4.1, we have
$z \in \mathcal {Z}(M)= \mathbb {C}$ and, arguing as in the proof of Theorem 4.1, we have ![]() $\zeta (T)=z.$ Therefore,
$\zeta (T)=z.$ Therefore, ![]() $\zeta (T)\operatorname {Tr}(S)$ is a limit point of
$\zeta (T)\operatorname {Tr}(S)$ is a limit point of ![]() $\bigl \{\operatorname {Tr}\bigl (\bigl (({1}/{N})\sum _{n=1}^N (\mathcal {P}_{\varphi }^{\rm o})^n(T) \bigr )S\bigr ) \bigr \}_{N=1}^{\infty }.$ On the other hand, note that for each
$\bigl \{\operatorname {Tr}\bigl (\bigl (({1}/{N})\sum _{n=1}^N (\mathcal {P}_{\varphi }^{\rm o})^n(T) \bigr )S\bigr ) \bigr \}_{N=1}^{\infty }.$ On the other hand, note that for each ![]() $N \in \mathbb {N}$ we have that
$N \in \mathbb {N}$ we have that ![]() $\operatorname {Tr}\bigl (({1}/{N})\sum _{n=1}^N (\mathcal {P}_{\varphi }^{\rm o})^n(T)S\bigr )= \operatorname {Tr}\bigl (T\bigl (({1}/{N})\sum _{n=1}^N (\mathcal {P}_{\varphi ^*}^{\rm o})^n(S)\bigr ) \bigr )$. Since
$\operatorname {Tr}\bigl (({1}/{N})\sum _{n=1}^N (\mathcal {P}_{\varphi }^{\rm o})^n(T)S\bigr )= \operatorname {Tr}\bigl (T\bigl (({1}/{N})\sum _{n=1}^N (\mathcal {P}_{\varphi ^*}^{\rm o})^n(S)\bigr ) \bigr )$. Since ![]() $\bigl |\operatorname {Tr}\bigl (T \bigl (({1}/{N})\sum _{n=1}^N (\mathcal {P}_{\varphi ^*}^{\rm o})^n(S)\bigr )\bigr )\bigr | \leq \operatorname {Tr}(T) \|S\|_{\infty }$, by the above discussion, we then have
$\bigl |\operatorname {Tr}\bigl (T \bigl (({1}/{N})\sum _{n=1}^N (\mathcal {P}_{\varphi ^*}^{\rm o})^n(S)\bigr )\bigr )\bigr | \leq \operatorname {Tr}(T) \|S\|_{\infty }$, by the above discussion, we then have
Consider a net of projections ![]() $\{S_i\}_{i \in I}$ in
$\{S_i\}_{i \in I}$ in ![]() $\mathcal {B}_{\varphi }$, such that
$\mathcal {B}_{\varphi }$, such that ![]() $S_i$ converges to
$S_i$ converges to ![]() $1$ in the strong operator topology. The above equation then shows that
$1$ in the strong operator topology. The above equation then shows that ![]() $\zeta (T)\operatorname {Tr}(1) \leq \operatorname {Tr}(T)< \infty$. As
$\zeta (T)\operatorname {Tr}(1) \leq \operatorname {Tr}(T)< \infty$. As ![]() $\zeta (T) \neq 0$ by choice, we get that
$\zeta (T) \neq 0$ by choice, we get that ![]() $\operatorname {Tr}(1)< \infty$. Hence
$\operatorname {Tr}(1)< \infty$. Hence ![]() $\mathcal {B}_{\varphi }$ is a type
$\mathcal {B}_{\varphi }$ is a type ![]() ${\rm II_1}$ factor and by Corollary 4.2 we have that
${\rm II_1}$ factor and by Corollary 4.2 we have that ![]() $\mathcal {B}_{\varphi }=M$.
$\mathcal {B}_{\varphi }=M$.
Theorem 4.4 Suppose for each ![]() $i \in \{ 1, 2 \}$,
$i \in \{ 1, 2 \}$, ![]() $M_i$ is a finite von Neumann algebra with normal faithful trace
$M_i$ is a finite von Neumann algebra with normal faithful trace ![]() $\tau _i$. Let
$\tau _i$. Let ![]() $\varphi _i$ and
$\varphi _i$ and ![]() $\varphi _1 \otimes \varphi _2$ be normal regular strongly generating hyperstates for
$\varphi _1 \otimes \varphi _2$ be normal regular strongly generating hyperstates for ![]() $M_i$ and
$M_i$ and ![]() $M_1 \bar {\otimes } M_2$ on
$M_1 \bar {\otimes } M_2$ on ![]() $\mathcal {B}(L^2(M_i, \tau _i))$ and
$\mathcal {B}(L^2(M_i, \tau _i))$ and ![]() $\mathcal {B}(L^2(M_1 \bar {\otimes } M_2, \tau _1 \otimes \tau _2))$, respectively. Then
$\mathcal {B}(L^2(M_1 \bar {\otimes } M_2, \tau _1 \otimes \tau _2))$, respectively. Then
Proof. We clearly have ![]() ${\rm Har}(\mathcal {P}_{\varphi _1}) \, \overline {\otimes }\, {\rm Har}(\mathcal {P}_{\varphi _2}) \subset {\rm Har}(\mathcal {P}_{\varphi _1} \otimes \mathcal {P}_{\varphi _2})$, so we only need to show the reverse inclusion. Note that
${\rm Har}(\mathcal {P}_{\varphi _1}) \, \overline {\otimes }\, {\rm Har}(\mathcal {P}_{\varphi _2}) \subset {\rm Har}(\mathcal {P}_{\varphi _1} \otimes \mathcal {P}_{\varphi _2})$, so we only need to show the reverse inclusion. Note that
hence ![]() $(\mathcal {P}_{\varphi _1} \otimes {\rm id})_{| {\rm Har}(\mathcal {P}_{\varphi _1} \otimes \mathcal {P}_{\varphi _2})}$ gives a normal u.c.p. map which restricts to the identity on
$(\mathcal {P}_{\varphi _1} \otimes {\rm id})_{| {\rm Har}(\mathcal {P}_{\varphi _1} \otimes \mathcal {P}_{\varphi _2})}$ gives a normal u.c.p. map which restricts to the identity on ![]() $M_1 \, \overline {\otimes }\, M_2$. By Theorem 4.1 we have that
$M_1 \, \overline {\otimes }\, M_2$. By Theorem 4.1 we have that ![]() $(\mathcal {P}_{\varphi _1} \otimes {\rm id})_{| {\rm Har}(\mathcal {P}_{\varphi _1} \otimes \mathcal {P}_{\varphi _2})}$ is the identity map and hence
$(\mathcal {P}_{\varphi _1} \otimes {\rm id})_{| {\rm Har}(\mathcal {P}_{\varphi _1} \otimes \mathcal {P}_{\varphi _2})}$ is the identity map and hence
We similarly have
Since ![]() ${\rm Har}(\mathcal {P}_{\varphi _1})$ is injective it is semidiscrete [Reference ConnesCon76a], and hence has property
${\rm Har}(\mathcal {P}_{\varphi _1})$ is injective it is semidiscrete [Reference ConnesCon76a], and hence has property ![]() $S_\sigma$ of Kraus [Reference KrausKra83, Theorem 1.9]. We then have
$S_\sigma$ of Kraus [Reference KrausKra83, Theorem 1.9]. We then have
Corollary 4.5 Suppose, for each ![]() $i \in \{ 1, 2 \}$, that
$i \in \{ 1, 2 \}$, that ![]() $M_i$ is a finite von Neumann algebra with normal faithful trace
$M_i$ is a finite von Neumann algebra with normal faithful trace ![]() $\tau _i$. Let
$\tau _i$. Let ![]() $\varphi _i$ and
$\varphi _i$ and ![]() $\varphi _1 \otimes \varphi _2$ be normal regular strongly generating hyperstates for
$\varphi _1 \otimes \varphi _2$ be normal regular strongly generating hyperstates for ![]() $M_i$ and
$M_i$ and ![]() $M_1 \bar {\otimes } M_2$ on
$M_1 \bar {\otimes } M_2$ on ![]() $\mathcal {B}(L^2(M_i, \tau _i))$ and
$\mathcal {B}(L^2(M_i, \tau _i))$ and ![]() $\mathcal {B}(L^2(M_1 \bar {\otimes } M_2, \tau _1 \otimes \tau _2))$, respectively. Then the identity map on
$\mathcal {B}(L^2(M_1 \bar {\otimes } M_2, \tau _1 \otimes \tau _2))$, respectively. Then the identity map on ![]() $M_1 \, \overline {\otimes }\, M_2$ uniquely extends to a
$M_1 \, \overline {\otimes }\, M_2$ uniquely extends to a ![]() $*$-isomorphism between
$*$-isomorphism between ![]() $\mathcal {B}_{\varphi _1 \otimes \varphi _2}$ and
$\mathcal {B}_{\varphi _1 \otimes \varphi _2}$ and ![]() $\mathcal {B}_{\varphi _1} \, \overline {\otimes }\, \mathcal {B}_{\varphi _2}$.
$\mathcal {B}_{\varphi _1} \, \overline {\otimes }\, \mathcal {B}_{\varphi _2}$.
5. Entropy
In this section we introduce noncommutative analogues of Avez's asymptotic entropy [Reference AvezAve72] and Furstenberg entropy [Reference FurstenbergFur63a, § 8].
5.1 Asymptotic entropy
Let ![]() $M$ be a tracial von Neumann algebra with a faithful normal tracial state
$M$ be a tracial von Neumann algebra with a faithful normal tracial state ![]() $\tau$. For a normal hyperstate
$\tau$. For a normal hyperstate ![]() $\varphi \in \mathcal {S}_\tau (\mathcal {B}(L^2(M, \tau )))$ we define the entropy of
$\varphi \in \mathcal {S}_\tau (\mathcal {B}(L^2(M, \tau )))$ we define the entropy of ![]() $\varphi$, denoted by
$\varphi$, denoted by ![]() $H(\varphi )$, to be the von Neumann entropy of the corresponding density matrix
$H(\varphi )$, to be the von Neumann entropy of the corresponding density matrix ![]() $A_{\varphi }$:
$A_{\varphi }$:
If we have a standard form ![]() $\varphi (T) = \sum _{n} \langle T \widehat {z_n^*}, \widehat {z_n^*} \rangle$, then we may compute this explicitly as
$\varphi (T) = \sum _{n} \langle T \widehat {z_n^*}, \widehat {z_n^*} \rangle$, then we may compute this explicitly as
Theorem 5.1 If ![]() $\varphi$ and
$\varphi$ and ![]() $\psi$ are two normal hyperstates with
$\psi$ are two normal hyperstates with ![]() $\psi$ regular, then
$\psi$ regular, then
Proof. Let ![]() $A_{\varphi }$ and
$A_{\varphi }$ and ![]() $A_{\psi }$ be the corresponding density operators and
$A_{\psi }$ be the corresponding density operators and ![]() $\mathcal {P}_{\varphi }$ and
$\mathcal {P}_{\varphi }$ and ![]() $\mathcal {P}_{\psi }$ be the corresponding u.c.p.
$\mathcal {P}_{\psi }$ be the corresponding u.c.p. ![]() $M$-bimodular maps. Suppose we have the standard forms
$M$-bimodular maps. Suppose we have the standard forms
 \begin{align*} \varphi(T) &= \sum_{i \in I} \langle T \mu_i^{1/2} \widehat{a_i^*}, \mu_i^{1/2} \widehat{a_i^*} \rangle\quad \text{with }\mu_i >0,\ \|a_i^*\|_2=1, \text{ and } \tau(a_ja_i^*)=0 \text{ for all }i \neq j \in I, \\ \psi(T) &= \sum_{j \in J} \langle T \nu_j \widehat{c_j^*}, \nu_j \widehat{c_j^*} \rangle\quad \text{with }\nu_j >0,\ \|c_j^*\|_2=1, \text{ and } \tau(c_kc_l^*)=0 \text{ for all }k \neq l \in J. \end{align*}
\begin{align*} \varphi(T) &= \sum_{i \in I} \langle T \mu_i^{1/2} \widehat{a_i^*}, \mu_i^{1/2} \widehat{a_i^*} \rangle\quad \text{with }\mu_i >0,\ \|a_i^*\|_2=1, \text{ and } \tau(a_ja_i^*)=0 \text{ for all }i \neq j \in I, \\ \psi(T) &= \sum_{j \in J} \langle T \nu_j \widehat{c_j^*}, \nu_j \widehat{c_j^*} \rangle\quad \text{with }\nu_j >0,\ \|c_j^*\|_2=1, \text{ and } \tau(c_kc_l^*)=0 \text{ for all }k \neq l \in J. \end{align*}
Hence ![]() $A_{\varphi }= \sum _i \mu _i P_{\hat {a_i}}$ and
$A_{\varphi }= \sum _i \mu _i P_{\hat {a_i}}$ and ![]() $A_{\psi }= \sum _j \nu _j P_{\hat {c_j}}$.
$A_{\psi }= \sum _j \nu _j P_{\hat {c_j}}$.
Let ![]() $b_i=Ja_iJ$ and
$b_i=Ja_iJ$ and ![]() $d_i=Jc_iJ$ so that
$d_i=Jc_iJ$ so that
Since ![]() $\psi$ is regular we have that
$\psi$ is regular we have that ![]() $\sum _i \nu _i d_i^{*}d_i=\sum _i \nu _i d_id_i^{*}=1$. Since
$\sum _i \nu _i d_i^{*}d_i=\sum _i \nu _i d_id_i^{*}=1$. Since ![]() $\varphi$ is a hyperstate we have that
$\varphi$ is a hyperstate we have that ![]() $\sum _i \mu _i b_ib_i^{*}=1$. Now
$\sum _i \mu _i b_ib_i^{*}=1$. Now
and
so that for each ![]() $k, \ell$ we have
$k, \ell$ we have
As ![]() $\log$ is operator monotone, for each
$\log$ is operator monotone, for each ![]() $k, \ell$ we then have
$k, \ell$ we then have
 \[ -\log(A_{\varphi \ast \psi})=-\log\bigg(\sum_{i,j}\mu_i \nu_j b_i^{*}d_j^{*}P_{\hat{1}}d_jb_i\bigg) \leq -\log((\mu_k \nu_\ell \tau(b_kb_k^{*}d_\ell^{*}d_\ell))P_{\widehat{b_k^{*}d_\ell^{*}}}). \]
\[ -\log(A_{\varphi \ast \psi})=-\log\bigg(\sum_{i,j}\mu_i \nu_j b_i^{*}d_j^{*}P_{\hat{1}}d_jb_i\bigg) \leq -\log((\mu_k \nu_\ell \tau(b_kb_k^{*}d_\ell^{*}d_\ell))P_{\widehat{b_k^{*}d_\ell^{*}}}). \]
Hence,
 \begin{align*} H(\varphi \ast \psi)
&\leq -\sum_{i,j}\operatorname{Tr}[\mu_i
\nu_j\tau(b_ib_i^{*}d_j^{*}d_j)
P_{\widehat{b_i^{*}d_j^{*}}}\log(\mu_i
\nu_j\tau(b_ib_i^{*}d_j^{*}d_j)
P_{\widehat{b_i^{*}d_j^{*}}})]\\ &=
-\sum_{i,j}\operatorname{Tr}[\mu_i
\nu_j\tau(b_ib_i^{*}d_j^{*}d_j)P_{\widehat{b_i^{*}d_j^{*}}}
\log(\mu_i \nu_j\tau(b_ib_i^{*}d_j^{*}d_j))] \\ &\quad
-\sum_{i,j}\operatorname{Tr}[\mu_i
\nu_j\tau(b_ib_i^{*}d_j^{*}d_j)
P_{\widehat{b_i^{*}d_j^{*}}}
\log(P_{\widehat{b_i^{*}d_j^{*}}})]\\ &=-\sum_{i,j}\mu_i
\nu_j\tau(b_ib_i^{*}d_j^{*}d_j) \log(\mu_i
\nu_j\tau(b_ib_i^{*}d_j^{*}d_j)).
\end{align*}
\begin{align*} H(\varphi \ast \psi)
&\leq -\sum_{i,j}\operatorname{Tr}[\mu_i
\nu_j\tau(b_ib_i^{*}d_j^{*}d_j)
P_{\widehat{b_i^{*}d_j^{*}}}\log(\mu_i
\nu_j\tau(b_ib_i^{*}d_j^{*}d_j)
P_{\widehat{b_i^{*}d_j^{*}}})]\\ &=
-\sum_{i,j}\operatorname{Tr}[\mu_i
\nu_j\tau(b_ib_i^{*}d_j^{*}d_j)P_{\widehat{b_i^{*}d_j^{*}}}
\log(\mu_i \nu_j\tau(b_ib_i^{*}d_j^{*}d_j))] \\ &\quad
-\sum_{i,j}\operatorname{Tr}[\mu_i
\nu_j\tau(b_ib_i^{*}d_j^{*}d_j)
P_{\widehat{b_i^{*}d_j^{*}}}
\log(P_{\widehat{b_i^{*}d_j^{*}}})]\\ &=-\sum_{i,j}\mu_i
\nu_j\tau(b_ib_i^{*}d_j^{*}d_j) \log(\mu_i
\nu_j\tau(b_ib_i^{*}d_j^{*}d_j)).
\end{align*}
Now define ![]() $m$ on
$m$ on ![]() $I \times J$ by
$I \times J$ by ![]() $m(i,j)=\mu _i \nu _j\tau (b_ib_i^{*}d_j^{*}d_j)$. Note that
$m(i,j)=\mu _i \nu _j\tau (b_ib_i^{*}d_j^{*}d_j)$. Note that
 \[ \sum_im(i,j)=\nu_j \tau\bigg(\sum_i \mu_i b_ib_i^{*}d_j^{*}d_j\bigg)=\nu_j\tau(d_j^{*}d_j)=\nu_j \]
\[ \sum_im(i,j)=\nu_j \tau\bigg(\sum_i \mu_i b_ib_i^{*}d_j^{*}d_j\bigg)=\nu_j\tau(d_j^{*}d_j)=\nu_j \]
and
 \[ \sum_jm(i,j)=\mu_i \tau\bigg(\sum_i \nu_j b_ib_i^{*}d_j^{*}d_j\bigg)=\mu_i\tau(b_ib_i^{*})=\mu_i. \]
\[ \sum_jm(i,j)=\mu_i \tau\bigg(\sum_i \nu_j b_ib_i^{*}d_j^{*}d_j\bigg)=\mu_i\tau(b_ib_i^{*})=\mu_i. \]
To finish the proof it then suffices to show
where ![]() $H(\mu )=-\sum _i \mu _i \log (\mu _i)$ and
$H(\mu )=-\sum _i \mu _i \log (\mu _i)$ and ![]() $H(\nu )=-\sum _i \nu _i \log (\nu _i)$. By the remark before Theorem 5.1, a direct calculation yields
$H(\nu )=-\sum _i \nu _i \log (\nu _i)$. By the remark before Theorem 5.1, a direct calculation yields ![]() $H(\mu )= H(\varphi )$ and
$H(\mu )= H(\varphi )$ and ![]() $H(\nu )= H(\psi )$.
$H(\nu )= H(\psi )$.
Note that
 \begin{align*} H(m) &=- \sum_{i,j}m(i,j)\log(m(i,j))\\ &= - \sum_{i,j} \mu_i \nu_j \tau( b_ib_i^{*}d_j^{*}d_j) \log(\mu_i\tau(b_ib_i^{*}d_j^{*}d_j)) -\sum_{i,j} \mu_i \nu_j \tau( b_ib_i^{*}d_j^{*}d_j) \log(\nu_j)\\ &= -\sum_{i,j} \mu_i \nu_j \tau( b_ib_i^{*}d_j^{*}d_j) \log(\mu_i) \\ &\quad -\sum_{i,j} \mu_i \nu_j \tau( b_ib_i^{*}d_j^{*}d_j) \log(\nu_j) - \sum_{i,j} \mu_i \nu_j \tau( b_ib_i^{*}d_j^{*}d_j) \log(\tau(b_ib_i^{*}d_j^{*}d_j)). \end{align*}
\begin{align*} H(m) &=- \sum_{i,j}m(i,j)\log(m(i,j))\\ &= - \sum_{i,j} \mu_i \nu_j \tau( b_ib_i^{*}d_j^{*}d_j) \log(\mu_i\tau(b_ib_i^{*}d_j^{*}d_j)) -\sum_{i,j} \mu_i \nu_j \tau( b_ib_i^{*}d_j^{*}d_j) \log(\nu_j)\\ &= -\sum_{i,j} \mu_i \nu_j \tau( b_ib_i^{*}d_j^{*}d_j) \log(\mu_i) \\ &\quad -\sum_{i,j} \mu_i \nu_j \tau( b_ib_i^{*}d_j^{*}d_j) \log(\nu_j) - \sum_{i,j} \mu_i \nu_j \tau( b_ib_i^{*}d_j^{*}d_j) \log(\tau(b_ib_i^{*}d_j^{*}d_j)). \end{align*}
In the last equality above, the first summation is ![]() $H(\mu )$, since summing over
$H(\mu )$, since summing over ![]() $j$ yields
$j$ yields
while the second summation is ![]() $H(\nu )$. Hence, all that remains is to show
$H(\nu )$. Hence, all that remains is to show
Let ![]() $\eta (x)=-x\log (x)$ for
$\eta (x)=-x\log (x)$ for ![]() $x \in [0,1]$. Note that
$x \in [0,1]$. Note that ![]() $\eta$ is concave, and so
$\eta$ is concave, and so ![]() $\eta (\sum _{i}\alpha _ix_i) \geq \sum _i \alpha _i \eta (x_i)$ whenever
$\eta (\sum _{i}\alpha _ix_i) \geq \sum _i \alpha _i \eta (x_i)$ whenever ![]() $\alpha _i \geq 0$ and
$\alpha _i \geq 0$ and ![]() $\sum _i \alpha _i =1$. So
$\sum _i \alpha _i =1$. So
 \begin{align*} -\sum_{i,j} \mu_i \nu_j \tau( b_ib_i^{*}d_j^{*}d_j) \log(\tau(b_ib_i^{*}d_j^{*}d_j)) &= \sum_{i,j} \mu_i \nu_j \eta(\tau( b_ib_i^{*}d_j^{*}d_j))\\ &= \sum_i \mu_i \bigg(\sum_j \nu_j \eta(\tau( b_ib_i^{*}d_j^{*}d_j))\bigg)\\ &\leq \sum_i \mu_i \eta\bigg(\sum_j \nu_j \tau( b_ib_i^{*}d_j^{*}d_j)\bigg)\\ &= \sum_i \mu_i \eta(\tau(b_ib_i^{*}))=0. \end{align*}
\begin{align*} -\sum_{i,j} \mu_i \nu_j \tau( b_ib_i^{*}d_j^{*}d_j) \log(\tau(b_ib_i^{*}d_j^{*}d_j)) &= \sum_{i,j} \mu_i \nu_j \eta(\tau( b_ib_i^{*}d_j^{*}d_j))\\ &= \sum_i \mu_i \bigg(\sum_j \nu_j \eta(\tau( b_ib_i^{*}d_j^{*}d_j))\bigg)\\ &\leq \sum_i \mu_i \eta\bigg(\sum_j \nu_j \tau( b_ib_i^{*}d_j^{*}d_j)\bigg)\\ &= \sum_i \mu_i \eta(\tau(b_ib_i^{*}))=0. \end{align*}
Corollary 5.2 If ![]() $\varphi$ is a normal regular hyperstate, then the limit
$\varphi$ is a normal regular hyperstate, then the limit ![]() $\lim _{n \rightarrow \infty } ({H(\varphi ^{*n})}/{n})$ exists.
$\lim _{n \rightarrow \infty } ({H(\varphi ^{*n})}/{n})$ exists.
Proof. The sequence ![]() $\{H(\varphi ^{*n})\}$ is subadditive by Theorem 5.1 and hence the limit exists.
$\{H(\varphi ^{*n})\}$ is subadditive by Theorem 5.1 and hence the limit exists.
The asymptotic entropy ![]() $h(\varphi )$ of a normal regular hyperstate
$h(\varphi )$ of a normal regular hyperstate ![]() $\varphi$ is defined to be the limit
$\varphi$ is defined to be the limit
5.2 A Furstenberg-type entropy
Suppose ![]() $G$ is a Polish group and
$G$ is a Polish group and ![]() $\mu \in {\rm Prob}(G)$. Given a quasi-invariant action
$\mu \in {\rm Prob}(G)$. Given a quasi-invariant action ![]() $G \overset {a}{{\, \curvearrowright \,}} (X, \nu )$ the corresponding Furstenberg entropy (or
$G \overset {a}{{\, \curvearrowright \,}} (X, \nu )$ the corresponding Furstenberg entropy (or ![]() $\mu$-entropy) is defined [Reference FurstenbergFur63a, § 8] to be
$\mu$-entropy) is defined [Reference FurstenbergFur63a, § 8] to be
If we consider the measure space ![]() $(G \times X, \nu \times \mu )$, then we have a nonsingular map
$(G \times X, \nu \times \mu )$, then we have a nonsingular map ![]() $\pi : G \times X \to G \times X$ given by
$\pi : G \times X \to G \times X$ given by ![]() $\pi (g, x) = (g, g^{-1}x)$, whose Radon–Nikodym derivative is given by
$\pi (g, x) = (g, g^{-1}x)$, whose Radon–Nikodym derivative is given by
Recall that for arbitrary positive functions ![]() $f,g \in L^1(X, \mu )$ (where
$f,g \in L^1(X, \mu )$ (where ![]() $(X, \mu )$ is a standard probability space), the relative entropy of the measures
$(X, \mu )$ is a standard probability space), the relative entropy of the measures ![]() $\mu _1=f d\mu$ and
$\mu _1=f d\mu$ and ![]() $\mu _2=g d\mu$, denoted by
$\mu _2=g d\mu$, denoted by ![]() $S(\mu _1\,|\,\mu _2)$, is defined as
$S(\mu _1\,|\,\mu _2)$, is defined as ![]() $S(\mu _1\,|\,\mu _2)= \int _X f(\log (f)- \log (g)) d\mu$ (see [Reference Ohya and PetzOP93, Chapter 5]). We may thus rewrite the
$S(\mu _1\,|\,\mu _2)= \int _X f(\log (f)- \log (g)) d\mu$ (see [Reference Ohya and PetzOP93, Chapter 5]). We may thus rewrite the ![]() $\mu$-entropy as a relative entropy
$\mu$-entropy as a relative entropy
Let ![]() $(M,\tau )$ be a tracial von Neumann algebra,
$(M,\tau )$ be a tracial von Neumann algebra, ![]() $\varphi$ a normal hyperstate for
$\varphi$ a normal hyperstate for ![]() $M$, and
$M$, and ![]() $\mathcal {A}$ a von Neumann algebra, such that
$\mathcal {A}$ a von Neumann algebra, such that ![]() $M \subseteq \mathcal {A}$. Let
$M \subseteq \mathcal {A}$. Let ![]() $\zeta \in \mathcal {S}_\tau (\mathcal {A})$ be a normal, faithful hyperstate. Let
$\zeta \in \mathcal {S}_\tau (\mathcal {A})$ be a normal, faithful hyperstate. Let ![]() $\Delta _\zeta : L^2(\mathcal {A}, \zeta ) \to L^2(\mathcal {A}, \zeta )$ be the modular operator corresponding to
$\Delta _\zeta : L^2(\mathcal {A}, \zeta ) \to L^2(\mathcal {A}, \zeta )$ be the modular operator corresponding to ![]() $\zeta$, and consider the spectral decomposition
$\zeta$, and consider the spectral decomposition ![]() $\Delta _\zeta = \int _0^\infty \lambda \, dE(\lambda )$. We denote by
$\Delta _\zeta = \int _0^\infty \lambda \, dE(\lambda )$. We denote by ![]() $\Delta _n = \int _{1/n}^{n} \lambda \,d\lambda$,
$\Delta _n = \int _{1/n}^{n} \lambda \,d\lambda$, ![]() $n \geq 1,$ the truncations of the modular operator
$n \geq 1,$ the truncations of the modular operator ![]() $\Delta$. We know that
$\Delta$. We know that ![]() $\Delta _n$ converges to
$\Delta _n$ converges to ![]() $\Delta$ in the resolvent sense. Throughout this section we denote the one- parameter modular automorphism group associated with
$\Delta$ in the resolvent sense. Throughout this section we denote the one- parameter modular automorphism group associated with ![]() $\zeta$ by
$\zeta$ by ![]() $\{ \sigma _t^{\zeta } \}_{t \in \mathbb {R}}.$ We also denote the corresponding modular conjugation operator by
$\{ \sigma _t^{\zeta } \}_{t \in \mathbb {R}}.$ We also denote the corresponding modular conjugation operator by ![]() $J$, and let
$J$, and let ![]() $S=J \Delta ^{1/2}.$ We refer the reader to [Reference TakesakiTak03, Chapters VI–VIII] for details regarding Tomita–Takesaki theory.
$S=J \Delta ^{1/2}.$ We refer the reader to [Reference TakesakiTak03, Chapters VI–VIII] for details regarding Tomita–Takesaki theory.
Since ![]() $\zeta |_{M}=\tau$, we have a natural inclusion of
$\zeta |_{M}=\tau$, we have a natural inclusion of ![]() $L^2(M,\tau )$ in
$L^2(M,\tau )$ in ![]() $L^2(\mathcal {A},\zeta )$. Let
$L^2(\mathcal {A},\zeta )$. Let ![]() $e$ denote the orthogonal projection from
$e$ denote the orthogonal projection from ![]() $L^2(\mathcal {A},\zeta )$ to
$L^2(\mathcal {A},\zeta )$ to ![]() $L^2(M,\tau )$. The entropy of the inclusion
$L^2(M,\tau )$. The entropy of the inclusion ![]() $(M, \tau ) \subset (\mathcal {A}, \zeta )$ with respect to
$(M, \tau ) \subset (\mathcal {A}, \zeta )$ with respect to ![]() $\varphi$ is defined to be
$\varphi$ is defined to be
The next example shows that ![]() $h_{\varphi }(M \subset \mathcal {A},\zeta )$ can be considered as a generalization of the Furstenberg entropy.
$h_{\varphi }(M \subset \mathcal {A},\zeta )$ can be considered as a generalization of the Furstenberg entropy.
Example 5.3 If ![]() $\Gamma$ is a discrete group,
$\Gamma$ is a discrete group, ![]() $\mu \in {\rm Prob}(\Gamma )$, and
$\mu \in {\rm Prob}(\Gamma )$, and ![]() $\Gamma \overset {a}{{\, \curvearrowright \,}} (X, \nu )$ is a quasi-invariant action, then we may consider the state
$\Gamma \overset {a}{{\, \curvearrowright \,}} (X, \nu )$ is a quasi-invariant action, then we may consider the state ![]() $\varphi$ on
$\varphi$ on ![]() $\mathcal {B}(\ell ^2 \Gamma )$ given by
$\mathcal {B}(\ell ^2 \Gamma )$ given by ![]() $\varphi (T) = \int \langle T \delta _\gamma, \delta _\gamma \rangle \, d\mu (\gamma )$, and we may consider the state
$\varphi (T) = \int \langle T \delta _\gamma, \delta _\gamma \rangle \, d\mu (\gamma )$, and we may consider the state ![]() $\zeta$ on
$\zeta$ on ![]() $L^\infty (X, \nu ) \rtimes \Gamma \subset \mathcal {B}(\ell ^2\Gamma \, \overline {\otimes }\, L^2(X, \nu ))$ given by
$L^\infty (X, \nu ) \rtimes \Gamma \subset \mathcal {B}(\ell ^2\Gamma \, \overline {\otimes }\, L^2(X, \nu ))$ given by ![]() $\zeta (\sum _{\gamma \in \Gamma } a_\gamma u_\gamma ) = \int a_e \, d\nu$. Note that a direct computation in this case yields
$\zeta (\sum _{\gamma \in \Gamma } a_\gamma u_\gamma ) = \int a_e \, d\nu$. Note that a direct computation in this case yields ![]() $(\varphi * \zeta ) (\sum _{\gamma \in \Gamma } a_\gamma u_\gamma ) = \int a_e \, d (\mu *\nu )$. The modular operator
$(\varphi * \zeta ) (\sum _{\gamma \in \Gamma } a_\gamma u_\gamma ) = \int a_e \, d (\mu *\nu )$. The modular operator ![]() $\Delta _\zeta$ is then affiliated to the von Neumann algebra
$\Delta _\zeta$ is then affiliated to the von Neumann algebra ![]() $\ell ^\infty \Gamma \, \overline {\otimes }\, L^\infty ( X, \nu )$, and we may compute this directly as
$\ell ^\infty \Gamma \, \overline {\otimes }\, L^\infty ( X, \nu )$, and we may compute this directly as
We also have that the projection ![]() $e$ from
$e$ from ![]() $\ell ^2\Gamma \, \overline {\otimes }\, L^2(X, \nu ) \to \ell ^2 \Gamma$ is given by
$\ell ^2\Gamma \, \overline {\otimes }\, L^2(X, \nu ) \to \ell ^2 \Gamma$ is given by ![]() ${\rm id\ } \otimes \int$. Thus, it follows that the measure
${\rm id\ } \otimes \int$. Thus, it follows that the measure ![]() $d\varphi (e E(\lambda ) e)$ agrees with
$d\varphi (e E(\lambda ) e)$ agrees with ![]() $d\alpha _*(\mu \times \nu )$, where
$d\alpha _*(\mu \times \nu )$, where ![]() $\alpha : \Gamma \times X \to \mathbb {R}_{> 0}$ is the Radon–Nikodym cocycle,
$\alpha : \Gamma \times X \to \mathbb {R}_{> 0}$ is the Radon–Nikodym cocycle, ![]() $\alpha (\gamma, x) = {d \gamma ^{-1} \nu }/{d \nu }(x)$.
$\alpha (\gamma, x) = {d \gamma ^{-1} \nu }/{d \nu }(x)$.
In this case we then have
 \begin{align*} h_\varphi(L\Gamma \subset L^\infty(X, \nu) \rtimes \Gamma, \zeta) &= -\int \log(\lambda) d \varphi(e E(\lambda) e) \\ &= - \iint \log \bigg(\frac{d \gamma^{-1} \nu}{d \nu} (x) \bigg) d(\nu \times \mu) = h_\mu(a, \nu). \end{align*}
\begin{align*} h_\varphi(L\Gamma \subset L^\infty(X, \nu) \rtimes \Gamma, \zeta) &= -\int \log(\lambda) d \varphi(e E(\lambda) e) \\ &= - \iint \log \bigg(\frac{d \gamma^{-1} \nu}{d \nu} (x) \bigg) d(\nu \times \mu) = h_\mu(a, \nu). \end{align*}
Lemma 5.4 Let ![]() $\varphi \in \mathcal {S}_\tau (\mathcal {B}(L^2(M, \tau )))$ be a normal hyperstate and write
$\varphi \in \mathcal {S}_\tau (\mathcal {B}(L^2(M, \tau )))$ be a normal hyperstate and write ![]() $\varphi$ in a standard form
$\varphi$ in a standard form ![]() $\varphi (T) = \sum _n \langle T \widehat {z_n^*}, \widehat {z_n^*} \rangle$. Suppose
$\varphi (T) = \sum _n \langle T \widehat {z_n^*}, \widehat {z_n^*} \rangle$. Suppose ![]() $\mathcal {A}$ is a von Neumann algebra with
$\mathcal {A}$ is a von Neumann algebra with ![]() $M \subset \mathcal {A}$ and
$M \subset \mathcal {A}$ and ![]() $\zeta \in \mathcal {S}_\tau (\mathcal {A})$ is a normal hyperstate. Then if
$\zeta \in \mathcal {S}_\tau (\mathcal {A})$ is a normal hyperstate. Then if ![]() $h_\varphi (M \subset \mathcal {A}, \zeta ) < \infty$ we have that
$h_\varphi (M \subset \mathcal {A}, \zeta ) < \infty$ we have that ![]() $z_n^* 1_\zeta \in D( \log \Delta _\zeta )$ for each
$z_n^* 1_\zeta \in D( \log \Delta _\zeta )$ for each ![]() $n$ and
$n$ and
Proof. As ![]() $\mathcal {A}1_{\zeta }$ forms a core for
$\mathcal {A}1_{\zeta }$ forms a core for ![]() $S_{\zeta }$ we get that
$S_{\zeta }$ we get that ![]() $z_n^*1_{\zeta } \in D(\log (\Delta _{\zeta }))$. Also, we know that
$z_n^*1_{\zeta } \in D(\log (\Delta _{\zeta }))$. Also, we know that
for all ![]() $\xi \in D(\Delta _{\zeta })$. So we have that
$\xi \in D(\Delta _{\zeta })$. So we have that
 \begin{align*} h_\varphi(M \subset \mathcal{A}, \zeta) &= -\varphi(e\log(\Delta_{\zeta})e) = -\sum_n \langle \log \Delta_\zeta z_n^* 1_\zeta, z_n^* 1_\zeta \rangle \\ &= i \sum_n \bigg\langle z_n \lim_{t \rightarrow 0} \frac{\Delta_{\zeta}^{it}-1}{t} z_n^* 1_{\zeta}, 1_{\zeta} \bigg\rangle = i \lim_{t \to 0} \frac{1}{t} \sum_n (\zeta( z_n \sigma_t^\zeta(z_n^*) )-1). \end{align*}
\begin{align*} h_\varphi(M \subset \mathcal{A}, \zeta) &= -\varphi(e\log(\Delta_{\zeta})e) = -\sum_n \langle \log \Delta_\zeta z_n^* 1_\zeta, z_n^* 1_\zeta \rangle \\ &= i \sum_n \bigg\langle z_n \lim_{t \rightarrow 0} \frac{\Delta_{\zeta}^{it}-1}{t} z_n^* 1_{\zeta}, 1_{\zeta} \bigg\rangle = i \lim_{t \to 0} \frac{1}{t} \sum_n (\zeta( z_n \sigma_t^\zeta(z_n^*) )-1). \end{align*}
Example 5.5 Fix two normal hyperstates ![]() $\varphi, \zeta \in \mathcal {S}_\tau ( \mathcal {B}(L^2(M, \tau )))$ such that
$\varphi, \zeta \in \mathcal {S}_\tau ( \mathcal {B}(L^2(M, \tau )))$ such that ![]() $\varphi$ is regular and
$\varphi$ is regular and ![]() $\zeta$ is faithful, and consider the case
$\zeta$ is faithful, and consider the case ![]() $\mathcal {A} = \mathcal {B}(L^2(M, \tau ))$. Then the density operator
$\mathcal {A} = \mathcal {B}(L^2(M, \tau ))$. Then the density operator ![]() $A_\zeta$ is injective with dense range and the modular operator on
$A_\zeta$ is injective with dense range and the modular operator on ![]() $L^2( \mathcal {B}(L^2(M, \tau )), \zeta )$ is given by
$L^2( \mathcal {B}(L^2(M, \tau )), \zeta )$ is given by ![]() $\Delta _\zeta ( T 1_\zeta ) = A_\zeta T A_\zeta ^{-1} 1_\zeta$, for
$\Delta _\zeta ( T 1_\zeta ) = A_\zeta T A_\zeta ^{-1} 1_\zeta$, for ![]() $T \in \mathcal {B}(L^2(M, \tau ))$ such that
$T \in \mathcal {B}(L^2(M, \tau ))$ such that ![]() $T 1_\zeta \in D(\Delta _\zeta )$. In particular, note that
$T 1_\zeta \in D(\Delta _\zeta )$. In particular, note that ![]() $\log (\Delta _\zeta ) (T 1_\zeta ) = ( {\rm Ad}(\log A_\zeta ) T ) 1_\zeta$, where
$\log (\Delta _\zeta ) (T 1_\zeta ) = ( {\rm Ad}(\log A_\zeta ) T ) 1_\zeta$, where ![]() ${\rm Ad}( \log A_\zeta ) T = (\log A_\zeta ) T - T (\log A_\zeta )$.
${\rm Ad}( \log A_\zeta ) T = (\log A_\zeta ) T - T (\log A_\zeta )$.
We also have that the projection ![]() $e: L^2( \mathcal {B}(L^2(M, \tau )), \zeta ) \to L^2(M, \tau )$ is given by
$e: L^2( \mathcal {B}(L^2(M, \tau )), \zeta ) \to L^2(M, \tau )$ is given by ![]() $e( T 1_\zeta ) = \mathcal {P}_\zeta (T) \hat {1}$. Therefore,
$e( T 1_\zeta ) = \mathcal {P}_\zeta (T) \hat {1}$. Therefore, ![]() $e \log \Delta _\zeta e x \hat {1} = \mathcal {P}_\zeta ( {\rm Ad}(\log A_\zeta ) x ) \hat {1} = \mathcal {P}_\zeta ( {\rm Ad}(\log A_\zeta ) ) x \hat {1}$. Hence,
$e \log \Delta _\zeta e x \hat {1} = \mathcal {P}_\zeta ( {\rm Ad}(\log A_\zeta ) x ) \hat {1} = \mathcal {P}_\zeta ( {\rm Ad}(\log A_\zeta ) ) x \hat {1}$. Hence,
 \begin{align*} h_\varphi(M \subset \mathcal{B}(L^2(M, \tau)), \zeta) &= \varphi( \mathcal{P}_\zeta( {\rm Ad}(\log A_\zeta) ) ) \\ &= \operatorname{Tr} ( A_{\varphi * \zeta} {\rm Ad}(\log A_\zeta) ) \\ &= \operatorname{Tr} ( A_{\varphi * \zeta} \log A_\zeta ) - \langle \log A_\zeta \hat{1}, \hat{1} \rangle, \end{align*}
\begin{align*} h_\varphi(M \subset \mathcal{B}(L^2(M, \tau)), \zeta) &= \varphi( \mathcal{P}_\zeta( {\rm Ad}(\log A_\zeta) ) ) \\ &= \operatorname{Tr} ( A_{\varphi * \zeta} {\rm Ad}(\log A_\zeta) ) \\ &= \operatorname{Tr} ( A_{\varphi * \zeta} \log A_\zeta ) - \langle \log A_\zeta \hat{1}, \hat{1} \rangle, \end{align*}
where the last equality follows since ![]() $\varphi$ is regular.
$\varphi$ is regular.
We recall the following two lemmas from work by D. Petz [Reference PetzPet86].
Lemma 5.6 Let ![]() $\Delta _j$ be positive, self-adjoint operators on
$\Delta _j$ be positive, self-adjoint operators on ![]() $\mathcal {H}_j, j=1,2.$ If
$\mathcal {H}_j, j=1,2.$ If ![]() $T: \mathcal {H}_1 \rightarrow \mathcal {H}_2$ is a bounded operator such that
$T: \mathcal {H}_1 \rightarrow \mathcal {H}_2$ is a bounded operator such that
–
 $T (\mathcal {D}(\Delta _1)) \subseteq \mathcal {D}(\Delta _2)$
$T (\mathcal {D}(\Delta _1)) \subseteq \mathcal {D}(\Delta _2)$–
 $\|\Delta _2T\xi \| \leq \|T\|\cdot \|\Delta _1 \xi \|$ (
$\|\Delta _2T\xi \| \leq \|T\|\cdot \|\Delta _1 \xi \|$ ( $\xi \in \mathcal {D}(\Delta _1)$),
$\xi \in \mathcal {D}(\Delta _1)$),
then we have for each ![]() $t \in [0,1]$, and
$t \in [0,1]$, and ![]() $\xi \in \mathcal {D}(\Delta _1^t)$ that
$\xi \in \mathcal {D}(\Delta _1^t)$ that
Lemma 5.7 Let ![]() $\Delta$ be a positive self-adjoint operator and
$\Delta$ be a positive self-adjoint operator and ![]() $\xi \in \mathcal {D}(\Delta )$. Then
$\xi \in \mathcal {D}(\Delta )$. Then
exists. It is finite or ![]() $- \infty$ and equals
$- \infty$ and equals ![]() $\int _{0}^{\infty }\log \lambda d\langle E_{\lambda } \xi, \xi \rangle$ where
$\int _{0}^{\infty }\log \lambda d\langle E_{\lambda } \xi, \xi \rangle$ where ![]() $\int _{0}^{\infty }\log \lambda d E_{\lambda }$ is the spectral resolution of
$\int _{0}^{\infty }\log \lambda d E_{\lambda }$ is the spectral resolution of ![]() $\Delta$.
$\Delta$.
Corollary 5.8 We have
Lemma 5.9 We have ![]() $h_{\varphi }(M \subset \mathcal {A}, \zeta ) \geq 0$.
$h_{\varphi }(M \subset \mathcal {A}, \zeta ) \geq 0$.
Proof. Let ![]() $\mathcal {P}_{\zeta }(T)=eTe$ for
$\mathcal {P}_{\zeta }(T)=eTe$ for ![]() $T \in \mathcal {A}$. Let
$T \in \mathcal {A}$. Let ![]() $\Delta _n = \int _{1/n}^{n} \lambda d\lambda$,
$\Delta _n = \int _{1/n}^{n} \lambda d\lambda$, ![]() $n \geq 1,$ denote the truncations of the modular operator
$n \geq 1,$ denote the truncations of the modular operator ![]() $\Delta$.
$\Delta$.
Using the operator Jensen's inequality, we have
 \begin{align*} h_{\varphi}(M \subset \mathcal{A}, \zeta) &= \lim_{n \rightarrow \infty}\varphi(-e \log\Delta_n e)\\ &=-\lim_{n \rightarrow \infty}\langle \mathcal{P}_{\varphi} \circ \mathcal{P}_{\zeta} (\log \Delta_n) \hat{1}, \hat{1} \rangle \geq \lim_{n \rightarrow \infty} -\langle \log (\mathcal{P}_{\varphi} \circ \mathcal{P}_{\zeta} (\Delta_n)) \hat{1}, \hat{1} \rangle \end{align*}
\begin{align*} h_{\varphi}(M \subset \mathcal{A}, \zeta) &= \lim_{n \rightarrow \infty}\varphi(-e \log\Delta_n e)\\ &=-\lim_{n \rightarrow \infty}\langle \mathcal{P}_{\varphi} \circ \mathcal{P}_{\zeta} (\log \Delta_n) \hat{1}, \hat{1} \rangle \geq \lim_{n \rightarrow \infty} -\langle \log (\mathcal{P}_{\varphi} \circ \mathcal{P}_{\zeta} (\Delta_n)) \hat{1}, \hat{1} \rangle \end{align*}
(recall that ![]() $\log$ is operator concave).
$\log$ is operator concave).
Notice that ![]() $e\Delta _n e \leq e\Delta e =e$. Since
$e\Delta _n e \leq e\Delta e =e$. Since ![]() $\mathcal {P}_{\varphi }(e)=e$, we get
$\mathcal {P}_{\varphi }(e)=e$, we get ![]() $\mathcal {P}_{\varphi } \circ \mathcal {P}_{\zeta } (\Delta _n) \leq e \leq 1$. As
$\mathcal {P}_{\varphi } \circ \mathcal {P}_{\zeta } (\Delta _n) \leq e \leq 1$. As ![]() $\log$ is operator monotone, we get that
$\log$ is operator monotone, we get that ![]() $\log (\mathcal {P}_{\varphi } \circ \mathcal {P}_{\zeta } (\Delta _n)) \leq \log (1)=0$. Hence we are done.
$\log (\mathcal {P}_{\varphi } \circ \mathcal {P}_{\zeta } (\Delta _n)) \leq \log (1)=0$. Hence we are done.
Theorem 5.10 Let ![]() $\varphi, \psi \in \mathcal {S}_\tau ( \mathcal {B}(L^2(M, \tau )))$ be two normal hyperstates such that
$\varphi, \psi \in \mathcal {S}_\tau ( \mathcal {B}(L^2(M, \tau )))$ be two normal hyperstates such that ![]() $\psi$ is regular, and suppose
$\psi$ is regular, and suppose ![]() $\mathcal {A}$ is a von Neumann algebra with
$\mathcal {A}$ is a von Neumann algebra with ![]() $M \subset \mathcal {A}$, and
$M \subset \mathcal {A}$, and ![]() $\zeta \in S_\tau (\mathcal {A})$ is a normal, faithful hyperstate which is
$\zeta \in S_\tau (\mathcal {A})$ is a normal, faithful hyperstate which is ![]() $\psi$-stationary. Then
$\psi$-stationary. Then
Proof. Suppose we have the standard forms
 \begin{align*} \varphi(T) &= \sum_{i \in I} \langle T \mu_i^{1/2} \hat{a_i^*}, \mu_i^{1/2} \hat{a_i^*} \rangle\quad \text{with }\mu_i >0,\ \|a_i^*\|_2=1, \text{ and } \tau(a_ja_i^*)=0 \text{ for all }i \neq j \in I, \\ \psi(T) &= \sum_{j \in J} \langle T \nu_j \hat{b_j^*}, \nu_j \hat{b_j^*} \rangle\quad \text{with }\nu_j >0,\ \|b_j^*\|_2=1, \text{ and } \tau(b_kb_l^*)=0 \text{ for all }k \neq l \in J. \end{align*}
\begin{align*} \varphi(T) &= \sum_{i \in I} \langle T \mu_i^{1/2} \hat{a_i^*}, \mu_i^{1/2} \hat{a_i^*} \rangle\quad \text{with }\mu_i >0,\ \|a_i^*\|_2=1, \text{ and } \tau(a_ja_i^*)=0 \text{ for all }i \neq j \in I, \\ \psi(T) &= \sum_{j \in J} \langle T \nu_j \hat{b_j^*}, \nu_j \hat{b_j^*} \rangle\quad \text{with }\nu_j >0,\ \|b_j^*\|_2=1, \text{ and } \tau(b_kb_l^*)=0 \text{ for all }k \neq l \in J. \end{align*}
Let ![]() $\mathcal {P}_{\varphi }$ and
$\mathcal {P}_{\varphi }$ and ![]() $\mathcal {P}_{\psi }$ be the corresponding u.c.p. maps so that
$\mathcal {P}_{\psi }$ be the corresponding u.c.p. maps so that ![]() $\mathcal {P}_{\varphi }(T)= \sum _k \mu _k Ja_k^*J T Ja_kJ$ and
$\mathcal {P}_{\varphi }(T)= \sum _k \mu _k Ja_k^*J T Ja_kJ$ and ![]() $\mathcal {P}_{\psi }(T)= \sum _l \nu _l Jb_l^*J T Jb_lJ$. We shall denote the projection from
$\mathcal {P}_{\psi }(T)= \sum _l \nu _l Jb_l^*J T Jb_lJ$. We shall denote the projection from ![]() $L^2(\mathcal {A}, \zeta )$ to
$L^2(\mathcal {A}, \zeta )$ to ![]() $L^2(M,\tau )$ by
$L^2(M,\tau )$ by ![]() $e$ and
$e$ and ![]() $\Delta _{\zeta }$ by
$\Delta _{\zeta }$ by ![]() $\Delta$. We also denote the one-parameter modular automorphism group corresponding to
$\Delta$. We also denote the one-parameter modular automorphism group corresponding to ![]() $\zeta$ by
$\zeta$ by ![]() $\sigma _t$. We then have
$\sigma _t$. We then have
 \begin{align*} h_{\varphi}(M \subset \mathcal{A}, \zeta) &= i \lim_{t \rightarrow 0} \varphi\bigg(\frac{e\Delta^{it}e-1}{t}\bigg)= i \lim_{t \rightarrow 0} \frac{1}{t}\varphi(e\Delta^{it}e-1) \\ &= i \lim_{t \rightarrow 0} \frac{1}{t}\bigg(\sum_k \mu_k \langle (\Delta^{it}-1 )a_k^* 1_\zeta, a_k^* 1_{\zeta} \rangle\bigg). \end{align*}
\begin{align*} h_{\varphi}(M \subset \mathcal{A}, \zeta) &= i \lim_{t \rightarrow 0} \varphi\bigg(\frac{e\Delta^{it}e-1}{t}\bigg)= i \lim_{t \rightarrow 0} \frac{1}{t}\varphi(e\Delta^{it}e-1) \\ &= i \lim_{t \rightarrow 0} \frac{1}{t}\bigg(\sum_k \mu_k \langle (\Delta^{it}-1 )a_k^* 1_\zeta, a_k^* 1_{\zeta} \rangle\bigg). \end{align*}
Similarly,
 \[ h_{\psi}(M \subset \mathcal{A}, \zeta)=i \lim_{t \rightarrow 0} \frac{1}{t}\bigg(\sum_l \nu_l \langle (\Delta^{it}-1 )b_l^* 1_\zeta, b_l^* 1_{\zeta} \rangle\bigg) \]
\[ h_{\psi}(M \subset \mathcal{A}, \zeta)=i \lim_{t \rightarrow 0} \frac{1}{t}\bigg(\sum_l \nu_l \langle (\Delta^{it}-1 )b_l^* 1_\zeta, b_l^* 1_{\zeta} \rangle\bigg) \]
and
 \begin{align*} h_{\varphi * \psi}(M \subset \mathcal{A}, \zeta) &= i \lim_{t \rightarrow 0} \frac{1}{t}\bigg(\sum_{k,l} \mu_k \nu_l \langle (\Delta^{it}-1 )a_k^*b_l^* 1_\zeta, a_k^* b_l^*1_{\zeta} \rangle\bigg) \\ &= i \lim_{t \rightarrow 0} \frac{1}{t} \bigg(\sum_{k,l} \mu_k \nu_l \langle (b_la_k\sigma_t(a_k^*b_l^*) 1_\zeta, 1_{\zeta} \rangle -1\bigg). \end{align*}
\begin{align*} h_{\varphi * \psi}(M \subset \mathcal{A}, \zeta) &= i \lim_{t \rightarrow 0} \frac{1}{t}\bigg(\sum_{k,l} \mu_k \nu_l \langle (\Delta^{it}-1 )a_k^*b_l^* 1_\zeta, a_k^* b_l^*1_{\zeta} \rangle\bigg) \\ &= i \lim_{t \rightarrow 0} \frac{1}{t} \bigg(\sum_{k,l} \mu_k \nu_l \langle (b_la_k\sigma_t(a_k^*b_l^*) 1_\zeta, 1_{\zeta} \rangle -1\bigg). \end{align*}
We shall now show that ![]() $\lim _{t \rightarrow 0} \frac {1}{t}\big(\sum _{k,l} \mu _k \nu _l \langle b_la_k\sigma _t(a_k^*b_l^*) 1_\zeta, 1_{\zeta } \rangle -\sum _{k,l} \mu _k \nu _l \langle b_l\sigma _t(b_l^*)\sigma _t(a_k^*) 1_\zeta,$
$\lim _{t \rightarrow 0} \frac {1}{t}\big(\sum _{k,l} \mu _k \nu _l \langle b_la_k\sigma _t(a_k^*b_l^*) 1_\zeta, 1_{\zeta } \rangle -\sum _{k,l} \mu _k \nu _l \langle b_l\sigma _t(b_l^*)\sigma _t(a_k^*) 1_\zeta,$ ![]() $1_{\zeta } \rangle \big) =0.$ Let
$1_{\zeta } \rangle \big) =0.$ Let ![]() $y_t=a_k\sigma _t(a_k^*).$ Note that
$y_t=a_k\sigma _t(a_k^*).$ Note that ![]() $y_t \rightarrow a_ka_k^*$ as
$y_t \rightarrow a_ka_k^*$ as ![]() $t \rightarrow 0$, in the strong operator topology. We have
$t \rightarrow 0$, in the strong operator topology. We have
Now
 \begin{align*} \frac{1}{t}\bigg(\sum_{k,l} \mu_k \nu_l \langle (y_t b_l^*-b_l^*y_t) 1_{\zeta}, b_l^* 1_{\zeta} \rangle\bigg) &= \frac{1}{t}\bigg(\sum_{k,l} \mu_k \nu_l \langle b_ly_t b_l^* 1_{\zeta}, 1_{\zeta} \rangle\bigg) - \frac{1}{t}\bigg(\sum_{k,l} \mu_k \nu_l \langle y_t 1_{\zeta}, b_lb_l^* 1_{\zeta} \rangle\bigg) \\ &= \frac{1}{t} \sum_k \mu_k \bigg\langle \bigg(\sum_l \nu_l b_l y_t b_l^*\bigg) 1_{\zeta}, 1_{\zeta} \bigg\rangle - \frac{1}{t} \sum_k \mu_k \langle y_t 1_{\zeta}, 1_{\zeta} \rangle\\ &= \frac{1}{t} \langle y_t 1_{\zeta}, 1_{\zeta} \rangle- \frac{1}{t} \langle y_t 1_{\zeta}, 1_{\zeta} \rangle =0, \end{align*}
\begin{align*} \frac{1}{t}\bigg(\sum_{k,l} \mu_k \nu_l \langle (y_t b_l^*-b_l^*y_t) 1_{\zeta}, b_l^* 1_{\zeta} \rangle\bigg) &= \frac{1}{t}\bigg(\sum_{k,l} \mu_k \nu_l \langle b_ly_t b_l^* 1_{\zeta}, 1_{\zeta} \rangle\bigg) - \frac{1}{t}\bigg(\sum_{k,l} \mu_k \nu_l \langle y_t 1_{\zeta}, b_lb_l^* 1_{\zeta} \rangle\bigg) \\ &= \frac{1}{t} \sum_k \mu_k \bigg\langle \bigg(\sum_l \nu_l b_l y_t b_l^*\bigg) 1_{\zeta}, 1_{\zeta} \bigg\rangle - \frac{1}{t} \sum_k \mu_k \langle y_t 1_{\zeta}, 1_{\zeta} \rangle\\ &= \frac{1}{t} \langle y_t 1_{\zeta}, 1_{\zeta} \rangle- \frac{1}{t} \langle y_t 1_{\zeta}, 1_{\zeta} \rangle =0, \end{align*}
where the penultimate equality holds by ![]() $\psi$-stationarity of
$\psi$-stationarity of ![]() $\zeta$.
$\zeta$.
Also, ![]() $\lim _{t \rightarrow 0} ({1}/{t}) (y_t (\sigma _t(b_l^*)-b_l^*))$ exists, and hence
$\lim _{t \rightarrow 0} ({1}/{t}) (y_t (\sigma _t(b_l^*)-b_l^*))$ exists, and hence
 \[ \lim_{t \rightarrow 0} \frac{1}{t}\bigg(\sum_{k,l} \mu_k \nu_l \langle b_la_k\sigma_t(a_k^*b_l^*) 1_\zeta, 1_{\zeta} \rangle -\sum_{k,l} \mu_k \nu_l \langle b_l\sigma_t(b_l^*)\sigma_t(a_k^*) 1_\zeta, 1_{\zeta} \rangle\bigg) =0. \]
\[ \lim_{t \rightarrow 0} \frac{1}{t}\bigg(\sum_{k,l} \mu_k \nu_l \langle b_la_k\sigma_t(a_k^*b_l^*) 1_\zeta, 1_{\zeta} \rangle -\sum_{k,l} \mu_k \nu_l \langle b_l\sigma_t(b_l^*)\sigma_t(a_k^*) 1_\zeta, 1_{\zeta} \rangle\bigg) =0. \]
So we get that
 \begin{align*} h_{\varphi * \psi}(M \subset \mathcal{A} , \zeta )&= i \lim_{t \rightarrow 0} \frac{1}{t}\bigg(\sum_{k,l} \mu_k \nu_l \langle (b_l\sigma_t(b_l^*)a_k\sigma_t(a_k^*)-1) 1_\zeta, 1_{\zeta} \rangle\bigg) \\ &= i \lim_{t \rightarrow 0} \frac{1}{t}\bigg(\sum_{k,l} \mu_k \nu_l[\langle(b_l\sigma_t(b_l^*)-1) 1_{\zeta}, 1_{\zeta} \rangle \\ &\quad + \langle (a_k\sigma_t(a_k^*)-1) 1_{\zeta}, 1_{\zeta} \rangle \\ &\quad\vphantom{\sum_{k,l}} + \langle (a_k\sigma_t(a_k^*)-1) 1_{\zeta}, (b_l \sigma_t(b_l^*)-1)^* 1_{\zeta} \rangle]\bigg). \end{align*}
\begin{align*} h_{\varphi * \psi}(M \subset \mathcal{A} , \zeta )&= i \lim_{t \rightarrow 0} \frac{1}{t}\bigg(\sum_{k,l} \mu_k \nu_l \langle (b_l\sigma_t(b_l^*)a_k\sigma_t(a_k^*)-1) 1_\zeta, 1_{\zeta} \rangle\bigg) \\ &= i \lim_{t \rightarrow 0} \frac{1}{t}\bigg(\sum_{k,l} \mu_k \nu_l[\langle(b_l\sigma_t(b_l^*)-1) 1_{\zeta}, 1_{\zeta} \rangle \\ &\quad + \langle (a_k\sigma_t(a_k^*)-1) 1_{\zeta}, 1_{\zeta} \rangle \\ &\quad\vphantom{\sum_{k,l}} + \langle (a_k\sigma_t(a_k^*)-1) 1_{\zeta}, (b_l \sigma_t(b_l^*)-1)^* 1_{\zeta} \rangle]\bigg). \end{align*}
The first term equals ![]() $h_{\varphi }(M \subset \mathcal {A}, \zeta )$, while the second term equals
$h_{\varphi }(M \subset \mathcal {A}, \zeta )$, while the second term equals ![]() $h_{\psi }(M \subset \mathcal {A}, \zeta )$, and the third term equals zero, as
$h_{\psi }(M \subset \mathcal {A}, \zeta )$, and the third term equals zero, as ![]() $\lim _{t \rightarrow 0} ({1}/{t}) (a_k\sigma _t(a_k^*)-1) 1_{\zeta }$ exists, while
$\lim _{t \rightarrow 0} ({1}/{t}) (a_k\sigma _t(a_k^*)-1) 1_{\zeta }$ exists, while ![]() ${\lim _{t \rightarrow 0} \sum _l \nu _l (b_l \sigma _t(b_l^*)-1)^* 1_{\zeta } =0}$.
${\lim _{t \rightarrow 0} \sum _l \nu _l (b_l \sigma _t(b_l^*)-1)^* 1_{\zeta } =0}$.
Corollary 5.11 Let ![]() $\varphi \in \mathcal {S}_\tau ( \mathcal {B}(L^2(M, \tau )))$ be a regular normal hyperstate and suppose
$\varphi \in \mathcal {S}_\tau ( \mathcal {B}(L^2(M, \tau )))$ be a regular normal hyperstate and suppose ![]() $\mathcal {A}$ is a von Neumann algebra with
$\mathcal {A}$ is a von Neumann algebra with ![]() $M \subset \mathcal {A}$, and
$M \subset \mathcal {A}$, and ![]() $\zeta \in S_\tau (\mathcal {A})$ is a faithful
$\zeta \in S_\tau (\mathcal {A})$ is a faithful ![]() $\varphi$-stationary hyperstate. Then for
$\varphi$-stationary hyperstate. Then for ![]() $n \geq 1$ we have
$n \geq 1$ we have
Lemma 5.12 ![]() $h_{\varphi }(M \subset \mathcal {A}, \zeta ) \leq H(\varphi )$.
$h_{\varphi }(M \subset \mathcal {A}, \zeta ) \leq H(\varphi )$.
Proof. We continue with the notation from the proof of Theorem 5.10, so that ![]() $\mathcal {P}_{\varphi }(T)= \sum _k \mu _k b_kTb_k^*$. Let
$\mathcal {P}_{\varphi }(T)= \sum _k \mu _k b_kTb_k^*$. Let ![]() $a_k=Jb_kJ \in M$. It follows from Lemma 5.7 that
$a_k=Jb_kJ \in M$. It follows from Lemma 5.7 that
So by Corollary 5.8 it is enough to show that
So it is enough to show that
Define ![]() $T: L^2(\mathcal {A},\zeta ) \rightarrow L^2(M,\tau )$ by
$T: L^2(\mathcal {A},\zeta ) \rightarrow L^2(M,\tau )$ by ![]() $T(a1_{\zeta })=\mathcal {P}_{\zeta }(a)\hat {1}$. Then
$T(a1_{\zeta })=\mathcal {P}_{\zeta }(a)\hat {1}$. Then ![]() $\|T\| =1$, as
$\|T\| =1$, as ![]() $\|T(1_{\zeta })\|=1$ and
$\|T(1_{\zeta })\|=1$ and ![]() $\|\mathcal {P}_{\zeta }\| \leq 1$.
$\|\mathcal {P}_{\zeta }\| \leq 1$. ![]() $T$ takes
$T$ takes ![]() $\mathcal {D}(\Delta _{\zeta })$ into
$\mathcal {D}(\Delta _{\zeta })$ into ![]() $\mathcal {D}(A_{\varphi })=L^2(M,\tau )$. We now denote
$\mathcal {D}(A_{\varphi })=L^2(M,\tau )$. We now denote ![]() $\Delta _{\zeta }$ by
$\Delta _{\zeta }$ by ![]() $\Delta$. By Lemma 5.6 it is enough to show that
$\Delta$. By Lemma 5.6 it is enough to show that
In fact it is enough to show the above for all vectors in a core for ![]() $\mathcal {D}(\Delta )$. Recall that
$\mathcal {D}(\Delta )$. Recall that ![]() $\mathcal {A}1_{\zeta }$ forms a core for
$\mathcal {A}1_{\zeta }$ forms a core for ![]() $\mathcal {D}(\Delta )$. So we only need to show that
$\mathcal {D}(\Delta )$. So we only need to show that
To this end, let ![]() $a \in \mathcal {A}$. Recall that
$a \in \mathcal {A}$. Recall that ![]() $S=J \Delta ^{1/2}$, so that
$S=J \Delta ^{1/2}$, so that ![]() $\Delta ^{1/2}=JS$. We then have
$\Delta ^{1/2}=JS$. We then have
 \begin{align*} \|\Delta^{1/2}a1_{\zeta}\|^2 &= \langle \Delta^{1/2} a1_{\zeta}, \Delta^{1/2} a1_{\zeta} \rangle = \langle JS a 1_{\zeta}, JS a 1_{\zeta} \rangle \\ &= \langle J a^* 1_{\zeta}, J a^* 1_{\zeta} \rangle = \langle a^* 1_{\zeta},a^* 1_{\zeta} \rangle = \zeta(aa^*) \\ &= \langle \mathcal{P}_{\zeta}(aa^*) \hat{1}, \hat{1} \rangle. \end{align*}
\begin{align*} \|\Delta^{1/2}a1_{\zeta}\|^2 &= \langle \Delta^{1/2} a1_{\zeta}, \Delta^{1/2} a1_{\zeta} \rangle = \langle JS a 1_{\zeta}, JS a 1_{\zeta} \rangle \\ &= \langle J a^* 1_{\zeta}, J a^* 1_{\zeta} \rangle = \langle a^* 1_{\zeta},a^* 1_{\zeta} \rangle = \zeta(aa^*) \\ &= \langle \mathcal{P}_{\zeta}(aa^*) \hat{1}, \hat{1} \rangle. \end{align*}
We also have ![]() $\mathcal {P}_{\varphi } \circ \mathcal {P}_{\zeta } = \mathcal {P}_{\zeta } \implies \varphi \circ \mathcal {P}_{\zeta } = \zeta$. Now
$\mathcal {P}_{\varphi } \circ \mathcal {P}_{\zeta } = \mathcal {P}_{\zeta } \implies \varphi \circ \mathcal {P}_{\zeta } = \zeta$. Now
 \begin{align*} \|A_{\varphi}^{1/2}Ta1_{\zeta}\|^2 &= \langle A_{\varphi}^{1/2} \mathcal{P}_{\zeta}(a) \hat{1}, A_{\varphi}^{1/2} \mathcal{P}_{\zeta}(a) \hat{1} \rangle = \langle A_{\varphi} \mathcal{P}_{\zeta}(a) \hat{1}, \mathcal{P}_{\zeta}(a) \hat{1} \rangle \\ &= \langle \mathcal{P}_{\zeta}(a)^* A_{\varphi} \mathcal{P}_{\zeta}(a) \hat{1}, \hat{1} \rangle \leq \operatorname{Tr}(\mathcal{P}_{\zeta}(a)^*A_{\varphi}\mathcal{P}_{\zeta}(a))\\ &= \operatorname{Tr}(A_{\varphi}\mathcal{P}_{\zeta}(a)\mathcal{P}_{\zeta}(a^*)) \leq \operatorname{Tr}(A_{\varphi}\mathcal{P}_{\zeta}(aa^*))\\ &= \langle (\varphi \circ \mathcal{P}_{\zeta})(aa^*) \hat{1},\hat{1} \rangle = \langle \mathcal{P}_{\zeta}(aa^*) \hat{1}, \hat{1} \rangle \\ &= \zeta(aa^*)=\| \Delta ^{1/2} a 1_{\zeta}\|^2. \end{align*}
\begin{align*} \|A_{\varphi}^{1/2}Ta1_{\zeta}\|^2 &= \langle A_{\varphi}^{1/2} \mathcal{P}_{\zeta}(a) \hat{1}, A_{\varphi}^{1/2} \mathcal{P}_{\zeta}(a) \hat{1} \rangle = \langle A_{\varphi} \mathcal{P}_{\zeta}(a) \hat{1}, \mathcal{P}_{\zeta}(a) \hat{1} \rangle \\ &= \langle \mathcal{P}_{\zeta}(a)^* A_{\varphi} \mathcal{P}_{\zeta}(a) \hat{1}, \hat{1} \rangle \leq \operatorname{Tr}(\mathcal{P}_{\zeta}(a)^*A_{\varphi}\mathcal{P}_{\zeta}(a))\\ &= \operatorname{Tr}(A_{\varphi}\mathcal{P}_{\zeta}(a)\mathcal{P}_{\zeta}(a^*)) \leq \operatorname{Tr}(A_{\varphi}\mathcal{P}_{\zeta}(aa^*))\\ &= \langle (\varphi \circ \mathcal{P}_{\zeta})(aa^*) \hat{1},\hat{1} \rangle = \langle \mathcal{P}_{\zeta}(aa^*) \hat{1}, \hat{1} \rangle \\ &= \zeta(aa^*)=\| \Delta ^{1/2} a 1_{\zeta}\|^2. \end{align*}
Hence, we are done.
Corollary 5.13 ![]() $h_{\varphi }(M \subset \mathcal {A}, \zeta ) \leq h(\varphi )$.
$h_{\varphi }(M \subset \mathcal {A}, \zeta ) \leq h(\varphi )$.
Proof. By Lemma 5.12, we have that ![]() $h_{\varphi ^{*n}}(M \subset \mathcal {A}, \zeta ) \leq H(\varphi ^{*n})$. By Corollary 5.11 we have that
$h_{\varphi ^{*n}}(M \subset \mathcal {A}, \zeta ) \leq H(\varphi ^{*n})$. By Corollary 5.11 we have that ![]() $h_{\varphi ^{*n}}(M \subset \mathcal {A}, \zeta ) = n h_{\varphi }(M \subset \mathcal {A}, \zeta )$. So we get
$h_{\varphi ^{*n}}(M \subset \mathcal {A}, \zeta ) = n h_{\varphi }(M \subset \mathcal {A}, \zeta )$. So we get
Lemma 5.14 ![]() $h_{\varphi }(M \subset \mathcal {A}, \zeta )=0$ if and only if there exists a normal
$h_{\varphi }(M \subset \mathcal {A}, \zeta )=0$ if and only if there exists a normal ![]() $\zeta$ preserving conditional expectation from
$\zeta$ preserving conditional expectation from ![]() $\mathcal {A}$ to
$\mathcal {A}$ to ![]() $M$.
$M$.
Proof. Let ![]() $\varphi$ be a standard form
$\varphi$ be a standard form ![]() $\varphi (T) = \sum _k \langle T \widehat {a_k^*}, \widehat {a_k^*} \rangle$. Let
$\varphi (T) = \sum _k \langle T \widehat {a_k^*}, \widehat {a_k^*} \rangle$. Let ![]() $\mathcal {E}: \mathcal {A} \rightarrow M$ be a normal
$\mathcal {E}: \mathcal {A} \rightarrow M$ be a normal ![]() $\zeta$ preserving conditional expectation. Then we know that
$\zeta$ preserving conditional expectation. Then we know that ![]() $\sigma ^{\zeta }_t(m)=m$ for all
$\sigma ^{\zeta }_t(m)=m$ for all ![]() $m \in M$, where
$m \in M$, where ![]() $\sigma _t^{\zeta }$ denotes the modular automorphism group corresponding to
$\sigma _t^{\zeta }$ denotes the modular automorphism group corresponding to ![]() $\zeta$. Hence,
$\zeta$. Hence,
 \begin{align*} h_{\varphi}(M \subset \mathcal{A}, \zeta)&= i \lim_{t \rightarrow 0} \frac{1}{t} \sum_k \langle (\Delta^{it}-1) a_k^* 1_{\zeta}, a_k^* 1_{\zeta} \rangle \\ &= i \lim_{t \rightarrow 0} \frac{1}{t} \sum_k \langle \sigma_t(a_k^*) 1_{\zeta}, a_k^* 1_{\zeta} \rangle -1 =0. \end{align*}
\begin{align*} h_{\varphi}(M \subset \mathcal{A}, \zeta)&= i \lim_{t \rightarrow 0} \frac{1}{t} \sum_k \langle (\Delta^{it}-1) a_k^* 1_{\zeta}, a_k^* 1_{\zeta} \rangle \\ &= i \lim_{t \rightarrow 0} \frac{1}{t} \sum_k \langle \sigma_t(a_k^*) 1_{\zeta}, a_k^* 1_{\zeta} \rangle -1 =0. \end{align*}
Conversely, suppose ![]() $h_{\varphi }(M \subset \mathcal {A}, \zeta )=0$. This part of the proof is motivated by the proof of Lemma 9.2 in [Reference Ohya and PetzOP93]. Let
$h_{\varphi }(M \subset \mathcal {A}, \zeta )=0$. This part of the proof is motivated by the proof of Lemma 9.2 in [Reference Ohya and PetzOP93]. Let ![]() $\Delta _{\zeta }=\Delta$ and let
$\Delta _{\zeta }=\Delta$ and let ![]() $\Delta = \int _{0}^{\infty } \lambda \,d\lambda$ be its spectral resolution. Let
$\Delta = \int _{0}^{\infty } \lambda \,d\lambda$ be its spectral resolution. Let ![]() $\Delta _n = \int _{1/n}^{n} \lambda \,d\lambda$,
$\Delta _n = \int _{1/n}^{n} \lambda \,d\lambda$, ![]() $n \geq 1$ be the truncations. We know that
$n \geq 1$ be the truncations. We know that ![]() $\Delta _n$ converges to
$\Delta _n$ converges to ![]() $\Delta$ in the resolvent sense. As usual, we denote by
$\Delta$ in the resolvent sense. As usual, we denote by ![]() $e$ the projection from
$e$ the projection from ![]() $L^2(\mathcal {A}, \zeta )$ to
$L^2(\mathcal {A}, \zeta )$ to ![]() $L^2(M, \tau )$. We have that
$L^2(M, \tau )$. We have that ![]() $e=e\Delta e \geq e \Delta _n e$ for all
$e=e\Delta e \geq e \Delta _n e$ for all ![]() $n$. So
$n$. So ![]() $(1+t)^{-1} \leq (e\Delta _n e+ t)^{-1} \leq e(\Delta _n +t)^{-1}e$ for all
$(1+t)^{-1} \leq (e\Delta _n e+ t)^{-1} \leq e(\Delta _n +t)^{-1}e$ for all ![]() $n$ and for all
$n$ and for all ![]() $t>0$. Taking limits as
$t>0$. Taking limits as ![]() $n \rightarrow \infty$, we get
$n \rightarrow \infty$, we get ![]() $(1+t)^{-1} \leq e(\Delta +t)^{-1}e$. Now we shall use the integral representation of
$(1+t)^{-1} \leq e(\Delta +t)^{-1}e$. Now we shall use the integral representation of ![]() $\log$ given by
$\log$ given by
so that
 \[ h_{\varphi}(M \subset \mathcal{A}, \zeta)=-\int_{0}^{\infty}\sum_k \langle e[(1+t)^{-1}-(\Delta +t)^{-1}] e a_k^*\hat{1}, a_k^* \hat{1} \rangle \,dt. \]
\[ h_{\varphi}(M \subset \mathcal{A}, \zeta)=-\int_{0}^{\infty}\sum_k \langle e[(1+t)^{-1}-(\Delta +t)^{-1}] e a_k^*\hat{1}, a_k^* \hat{1} \rangle \,dt. \]
From ![]() $h_{\varphi }(M \subset \mathcal {A}, \zeta )=0$ and the above discussion, we deduce that
$h_{\varphi }(M \subset \mathcal {A}, \zeta )=0$ and the above discussion, we deduce that
 \begin{align*} & \langle e((1+t)^{-1}-(\Delta+t)^{-1})ea_k^* \hat 1, a_k^* \hat 1 \rangle =0 \\ &\quad \Rightarrow e((1+t)^{-1}-(\Delta+t)^{-1})e a_k^* \hat 1=0 \\ &\quad \Rightarrow (1+t)^{-1} a_k^* \hat 1= e(\Delta+t)^{-1} e a_k^* \hat 1 \end{align*}
\begin{align*} & \langle e((1+t)^{-1}-(\Delta+t)^{-1})ea_k^* \hat 1, a_k^* \hat 1 \rangle =0 \\ &\quad \Rightarrow e((1+t)^{-1}-(\Delta+t)^{-1})e a_k^* \hat 1=0 \\ &\quad \Rightarrow (1+t)^{-1} a_k^* \hat 1= e(\Delta+t)^{-1} e a_k^* \hat 1 \end{align*}
for almost all ![]() $t>0$, and hence by continuity, for all
$t>0$, and hence by continuity, for all ![]() $t>0$. We now show that the last relation also holds without the compression
$t>0$. We now show that the last relation also holds without the compression ![]() $e$. To this end, note that by differentiating the equation
$e$. To this end, note that by differentiating the equation ![]() $(1+t)^{-1} a_k^* \hat 1= e(\Delta +t)^{-1}a_k^* \hat 1$ with respect to
$(1+t)^{-1} a_k^* \hat 1= e(\Delta +t)^{-1}a_k^* \hat 1$ with respect to ![]() $t$, we get
$t$, we get ![]() $(1+t)^{-2}a_k^* \hat 1= e(\Delta +t)^{-2}ea_k^* \hat 1$, for all
$(1+t)^{-2}a_k^* \hat 1= e(\Delta +t)^{-2}ea_k^* \hat 1$, for all ![]() $t>0$. Therefore, by the following norm calculation in
$t>0$. Therefore, by the following norm calculation in ![]() $L^2(\mathcal {A}, \zeta )$ we have
$L^2(\mathcal {A}, \zeta )$ we have
 \begin{align*} \| e(\Delta+t)^{-1}ea_k^* \hat 1\|^2_2 &= \|(1+t)^{-1} a_k^* \hat 1\|_2^2= \langle (1+t)^{-2}a_k^* \hat 1, a_k^* \hat 1 \rangle \\ &= \langle e(\Delta+t)^{-2}ea_k^* \hat 1, a_k^*\hat 1 \rangle = \langle (\Delta+t)^{-2}a_k^* \hat 1, a_k^*\hat 1 \rangle =\|(\Delta+t)^{-1}a_k^* \hat 1\|^2_2. \end{align*}
\begin{align*} \| e(\Delta+t)^{-1}ea_k^* \hat 1\|^2_2 &= \|(1+t)^{-1} a_k^* \hat 1\|_2^2= \langle (1+t)^{-2}a_k^* \hat 1, a_k^* \hat 1 \rangle \\ &= \langle e(\Delta+t)^{-2}ea_k^* \hat 1, a_k^*\hat 1 \rangle = \langle (\Delta+t)^{-2}a_k^* \hat 1, a_k^*\hat 1 \rangle =\|(\Delta+t)^{-1}a_k^* \hat 1\|^2_2. \end{align*}
So we get that ![]() $(1+t)^{-1} a_k^* \hat 1= (\Delta +t)^{-1} a_k^* \hat 1$ for all
$(1+t)^{-1} a_k^* \hat 1= (\Delta +t)^{-1} a_k^* \hat 1$ for all ![]() $t>0$. This implies that
$t>0$. This implies that ![]() $\Delta ^{it}a_{k}^*1_{\zeta }=a_k^*1_{\zeta }$, which implies that
$\Delta ^{it}a_{k}^*1_{\zeta }=a_k^*1_{\zeta }$, which implies that ![]() $\sigma ^{\zeta }_t(a_k^*)=a_k^*$ and hence
$\sigma ^{\zeta }_t(a_k^*)=a_k^*$ and hence ![]() $\sigma ^{\zeta }_t(m)=m$ for all
$\sigma ^{\zeta }_t(m)=m$ for all ![]() $m \in M$, as
$m \in M$, as ![]() $\varphi$ is generating. Hence there exists a
$\varphi$ is generating. Hence there exists a ![]() $\zeta$ preserving conditional expectation from
$\zeta$ preserving conditional expectation from ![]() $\mathcal {A}$ to
$\mathcal {A}$ to ![]() $M$, which is normal, as
$M$, which is normal, as ![]() $\zeta$ is normal.
$\zeta$ is normal.
Corollary 5.15 ![]() $\operatorname {Har}(\mathcal {B}(L^2(M, \tau )),\mathcal {P}_{\varphi })=M$ if and only if
$\operatorname {Har}(\mathcal {B}(L^2(M, \tau )),\mathcal {P}_{\varphi })=M$ if and only if ![]() $h_{\varphi }(M \subset \mathcal {B}_{\varphi }, \zeta )=0$, where
$h_{\varphi }(M \subset \mathcal {B}_{\varphi }, \zeta )=0$, where ![]() $\mathcal {B}_{\varphi }$ denotes the Poisson boundary with respect to
$\mathcal {B}_{\varphi }$ denotes the Poisson boundary with respect to ![]() $\varphi$.
$\varphi$.
Proof. If ![]() $h_{\varphi }(M \subset \mathcal {B_{\varphi }}, \zeta )=0$, then by Lemma 5.14 there exists a normal conditional expectation
$h_{\varphi }(M \subset \mathcal {B_{\varphi }}, \zeta )=0$, then by Lemma 5.14 there exists a normal conditional expectation ![]() $\mathcal {E}: \mathcal {B_{\varphi }} \rightarrow M$. By Theorem 4.1,
$\mathcal {E}: \mathcal {B_{\varphi }} \rightarrow M$. By Theorem 4.1, ![]() $\mathcal {E}= \rm {id}$, which implies that
$\mathcal {E}= \rm {id}$, which implies that ![]() $\mathcal {B_{\varphi }}=M$, and hence
$\mathcal {B_{\varphi }}=M$, and hence
Conversely, if ![]() $\operatorname {Har}(\mathcal {B}(L^2M, \tau ),\mathcal {P}_{\varphi })=M$, then
$\operatorname {Har}(\mathcal {B}(L^2M, \tau ),\mathcal {P}_{\varphi })=M$, then ![]() $\Delta _{\zeta }=I$ and hence
$\Delta _{\zeta }=I$ and hence ![]() $h_{\varphi }(M \subset \mathcal {B}_{\varphi }, \zeta )=0$
$h_{\varphi }(M \subset \mathcal {B}_{\varphi }, \zeta )=0$
Corollary 5.16 ![]() $\operatorname {Har}(\mathcal {B}(L^2(M, \tau )),\mathcal {P}_{\varphi })=M$ if
$\operatorname {Har}(\mathcal {B}(L^2(M, \tau )),\mathcal {P}_{\varphi })=M$ if ![]() $h(\varphi )=0$.
$h(\varphi )=0$.
Proof. Since ![]() $0 \leq h_{\varphi }(M \subset \mathcal {B}_{\varphi }, \zeta ) \leq h(\varphi )$, this result follows from Corollary 5.15.
$0 \leq h_{\varphi }(M \subset \mathcal {B}_{\varphi }, \zeta ) \leq h(\varphi )$, this result follows from Corollary 5.15.
6. An entropy gap for property (T) factors
If ![]() $(M, \tau )$ is a tracial von Neumann algebra, then a Hilbert
$(M, \tau )$ is a tracial von Neumann algebra, then a Hilbert ![]() $M$-bimodule consists of a Hilbert space
$M$-bimodule consists of a Hilbert space ![]() $\mathcal {H}$, together with commuting normal representations
$\mathcal {H}$, together with commuting normal representations ![]() $L: M \to \mathcal {B}(\mathcal {H})$,
$L: M \to \mathcal {B}(\mathcal {H})$, ![]() $R: M^{\rm op} \to \mathcal {B}(\mathcal {H})$. We will sometimes simplify notation by writing
$R: M^{\rm op} \to \mathcal {B}(\mathcal {H})$. We will sometimes simplify notation by writing ![]() $x \xi y$ for the vector
$x \xi y$ for the vector ![]() $L(x)R(y^{\rm op})\xi$. A vector
$L(x)R(y^{\rm op})\xi$. A vector ![]() $\xi \in \mathcal {H}$ is left (respectively, right) tracial if
$\xi \in \mathcal {H}$ is left (respectively, right) tracial if ![]() $\langle x \xi, \xi \rangle = \tau (x)$ (respectively,
$\langle x \xi, \xi \rangle = \tau (x)$ (respectively, ![]() $\langle \xi x, \xi \rangle = \tau (x)$) for all
$\langle \xi x, \xi \rangle = \tau (x)$) for all ![]() $x \in M$. A vector is bitracial if it is both left and right tracial. A vector
$x \in M$. A vector is bitracial if it is both left and right tracial. A vector ![]() $\xi \in \mathcal {H}$ is central if
$\xi \in \mathcal {H}$ is central if ![]() $x \xi = \xi x$ for all
$x \xi = \xi x$ for all ![]() $x \in M$. Note that if
$x \in M$. Note that if ![]() $\xi$ is a unit central vector, then
$\xi$ is a unit central vector, then ![]() $x \mapsto \langle x \xi, \xi \rangle$ gives a normal trace on
$x \mapsto \langle x \xi, \xi \rangle$ gives a normal trace on ![]() $M$.
$M$.
The von Neumann algebra ![]() $M$ has property (T) if for any sequence of Hilbert bimodules
$M$ has property (T) if for any sequence of Hilbert bimodules ![]() ${\mathcal {H}}_n$, and
${\mathcal {H}}_n$, and ![]() $\xi _n \in {\mathcal {H}}_n$ bitracial vectors, such that
$\xi _n \in {\mathcal {H}}_n$ bitracial vectors, such that ![]() $\| x \xi _n - \xi _n x \| \to 0$ for all
$\| x \xi _n - \xi _n x \| \to 0$ for all ![]() $x \in M$, then we have
$x \in M$, then we have ![]() $\| \xi _n - P_0(\xi _n) \| \to 0$, where
$\| \xi _n - P_0(\xi _n) \| \to 0$, where ![]() $P_0$ is the projection onto the space of central vectors. This is independent of the normal faithful trace
$P_0$ is the projection onto the space of central vectors. This is independent of the normal faithful trace ![]() $\tau$ [Reference PopaPop06, Proposition 4.1]. Property (T) was first introduced in the factor case by Connes and Jones [Reference Connes and JonesCJ85] who showed that for an ICC group
$\tau$ [Reference PopaPop06, Proposition 4.1]. Property (T) was first introduced in the factor case by Connes and Jones [Reference Connes and JonesCJ85] who showed that for an ICC group ![]() $\Gamma$, the group von Neumann algebra
$\Gamma$, the group von Neumann algebra ![]() $L\Gamma$ has property (T) if and only if
$L\Gamma$ has property (T) if and only if ![]() $\Gamma$ has Kazhdan's property (T) [Reference KaždanKaž67]. Their proof works equally well in the general case when
$\Gamma$ has Kazhdan's property (T) [Reference KaždanKaž67]. Their proof works equally well in the general case when ![]() $\Gamma$ is not necessarily ICC.
$\Gamma$ is not necessarily ICC.
We now suppose that ![]() $M$ is finitely generated as a von Neumann algebra. Take a finite generating set
$M$ is finitely generated as a von Neumann algebra. Take a finite generating set ![]() $\{ a_k \}_{k=1}^n \subset M$ such that
$\{ a_k \}_{k=1}^n \subset M$ such that ![]() $\sum _{k = 1}^n a_k^* a_k = \sum _{k = 1}^n a_ka_k^* = 1$, and let
$\sum _{k = 1}^n a_k^* a_k = \sum _{k = 1}^n a_ka_k^* = 1$, and let ![]() $\mathcal {B}(L^2(M, \tau )) \ni T \mapsto \varphi (T) = \sum _{k = 1}^n \langle T \widehat {a_k^*}, \widehat {a_k^*} \rangle$ denote the associated normal regular hyperstate. For a fixed Hilbert bimodule
$\mathcal {B}(L^2(M, \tau )) \ni T \mapsto \varphi (T) = \sum _{k = 1}^n \langle T \widehat {a_k^*}, \widehat {a_k^*} \rangle$ denote the associated normal regular hyperstate. For a fixed Hilbert bimodule ![]() $\mathcal {H}$ we define
$\mathcal {H}$ we define ![]() $\nabla _L, \nabla _R: \mathcal {H} \rightarrow \mathcal {H}^{\oplus n}$ by
$\nabla _L, \nabla _R: \mathcal {H} \rightarrow \mathcal {H}^{\oplus n}$ by
Note that we have
 \[ \| \nabla_L(\xi) \|^2= \sum_{k = 1}^n \| a_k \xi \|^2 = \bigg\langle \sum_{k = 1}^n a_k^*a_k \xi, \xi \bigg\rangle = \| \xi \|^2, \]
\[ \| \nabla_L(\xi) \|^2= \sum_{k = 1}^n \| a_k \xi \|^2 = \bigg\langle \sum_{k = 1}^n a_k^*a_k \xi, \xi \bigg\rangle = \| \xi \|^2, \]
and similarly
 \[ \| \nabla_R(\xi) \|^2 = \bigg\langle \sum_{k = 1}^n \xi a_k a_k^*, \xi \bigg\rangle = \| \xi \|^2. \]
\[ \| \nabla_R(\xi) \|^2 = \bigg\langle \sum_{k = 1}^n \xi a_k a_k^*, \xi \bigg\rangle = \| \xi \|^2. \]
Thus ![]() $\nabla _L$ and
$\nabla _L$ and ![]() $\nabla _R$ are both isometries. We let
$\nabla _R$ are both isometries. We let ![]() $T$ denote the operator given by
$T$ denote the operator given by ![]() $T \xi = \sum _{k = 1}^n a_k^* \xi a_k$. Note that
$T \xi = \sum _{k = 1}^n a_k^* \xi a_k$. Note that ![]() $T= \nabla _L^* \nabla _R$, and hence
$T= \nabla _L^* \nabla _R$, and hence ![]() $T$ is a contraction.
$T$ is a contraction.
Suppose now that ![]() $M \subset \mathcal {A}$ is an inclusion of von Neumann algebras and
$M \subset \mathcal {A}$ is an inclusion of von Neumann algebras and ![]() $\zeta \in \mathcal {A}_*$ is a faithful normal hyperstate. We may then consider the Hilbert space
$\zeta \in \mathcal {A}_*$ is a faithful normal hyperstate. We may then consider the Hilbert space ![]() $L^2(\mathcal {A}, \zeta )$ which is naturally a Hilbert
$L^2(\mathcal {A}, \zeta )$ which is naturally a Hilbert ![]() $M$-bimodule where the left action is given by left multiplication
$M$-bimodule where the left action is given by left multiplication ![]() $L(x) \hat {a} = \widehat {xa}$, and the right action is given by
$L(x) \hat {a} = \widehat {xa}$, and the right action is given by ![]() $R(x^{\mathrm {op}}) = JL(x^*)J$. In this case the vector
$R(x^{\mathrm {op}}) = JL(x^*)J$. In this case the vector ![]() $\hat {1}$ is clearly left tracial, and we also have
$\hat {1}$ is clearly left tracial, and we also have ![]() $J x^* J \hat {1} = \Delta ^{1/2} x \hat {1}$ from which it follows that
$J x^* J \hat {1} = \Delta ^{1/2} x \hat {1}$ from which it follows that ![]() $\hat {1}$ is also right tracial. If
$\hat {1}$ is also right tracial. If ![]() $\xi _0 \in L^2(\mathcal {A}, \zeta )$ is a unit
$\xi _0 \in L^2(\mathcal {A}, \zeta )$ is a unit ![]() $M$-central vector, then
$M$-central vector, then ![]() $\tau _0(x) = \langle x \xi _0, \xi _0 \rangle$ defines a normal trace on
$\tau _0(x) = \langle x \xi _0, \xi _0 \rangle$ defines a normal trace on ![]() $M$. We let
$M$. We let ![]() $s \in \mathcal {Z}(M)$ denote the support of
$s \in \mathcal {Z}(M)$ denote the support of ![]() $\tau _0$.
$\tau _0$.
Lemma 6.1 Let ![]() $(M, \tau )$,
$(M, \tau )$, ![]() $\varphi$, and
$\varphi$, and ![]() $(\mathcal {A}, \zeta )$ be as given above. Then
$(\mathcal {A}, \zeta )$ be as given above. Then
Proof. Let ![]() $\Delta = \int _{0}^{\infty } \lambda \,d\lambda$ be the spectral resolution of the modular operator and let
$\Delta = \int _{0}^{\infty } \lambda \,d\lambda$ be the spectral resolution of the modular operator and let ![]() $\Delta _m = \int _{1/m}^{m} \lambda \,d\lambda$,
$\Delta _m = \int _{1/m}^{m} \lambda \,d\lambda$, ![]() $m \geq 1$, be the truncations. Let
$m \geq 1$, be the truncations. Let ![]() $\mu _k=\tau (a_k^*a_k)$ and
$\mu _k=\tau (a_k^*a_k)$ and ![]() $b_k=\mu _k^{-1/2}a_k,$ for
$b_k=\mu _k^{-1/2}a_k,$ for ![]() $k=1,2,\ldots, n$. Note that
$k=1,2,\ldots, n$. Note that ![]() $\sum _{k=1}^n \mu _k=1$. Also note that
$\sum _{k=1}^n \mu _k=1$. Also note that ![]() $L_{a_k^*}R_{a_k}1_{\zeta }=a_k^*\Delta ^{1/2}a_k1_{\zeta }$. Now
$L_{a_k^*}R_{a_k}1_{\zeta }=a_k^*\Delta ^{1/2}a_k1_{\zeta }$. Now
 \begin{align*} -2\log \langle T1_{\zeta},1_{\zeta} \rangle &= -2\log \bigg(\sum_{k = 1}^n \langle a_k^* \Delta^{1/2} a_k \hat{1}, \hat{1} \rangle\bigg) =-2\lim_{m \rightarrow \infty}\log \bigg(\sum_{k = 1}^n \mu_k \langle b_k^* \Delta_m^{1/2} b_k \hat{1}, \hat{1} \rangle\bigg)\\ &\leq -2 \lim_{m \rightarrow \infty}\sum_{k = 1}^n \mu_k \log(\langle b_k^* \Delta_m^{1/2} b_k \hat{1}, \hat{1} \rangle) \leq -2 \lim_{m \rightarrow \infty}\sum_{k = 1}^n \mu_k \langle b_k^* \log(\Delta_m^{1/2}) b_k \hat{1}, \hat{1} \rangle \\ &= - \lim_{m \rightarrow \infty}\sum_{k = 1}^n \langle a_k^* \log(\Delta_m) a_k \hat{1}, \hat{1} \rangle = h_{\varphi}(M \subset \mathcal{A},\zeta), \end{align*}
\begin{align*} -2\log \langle T1_{\zeta},1_{\zeta} \rangle &= -2\log \bigg(\sum_{k = 1}^n \langle a_k^* \Delta^{1/2} a_k \hat{1}, \hat{1} \rangle\bigg) =-2\lim_{m \rightarrow \infty}\log \bigg(\sum_{k = 1}^n \mu_k \langle b_k^* \Delta_m^{1/2} b_k \hat{1}, \hat{1} \rangle\bigg)\\ &\leq -2 \lim_{m \rightarrow \infty}\sum_{k = 1}^n \mu_k \log(\langle b_k^* \Delta_m^{1/2} b_k \hat{1}, \hat{1} \rangle) \leq -2 \lim_{m \rightarrow \infty}\sum_{k = 1}^n \mu_k \langle b_k^* \log(\Delta_m^{1/2}) b_k \hat{1}, \hat{1} \rangle \\ &= - \lim_{m \rightarrow \infty}\sum_{k = 1}^n \langle a_k^* \log(\Delta_m) a_k \hat{1}, \hat{1} \rangle = h_{\varphi}(M \subset \mathcal{A},\zeta), \end{align*}
where the second inequality follows from Jensen's operator inequality.
Theorem 6.2 Let ![]() $M$ be a II
$M$ be a II![]() $_1$ factor generated as a von Neumann algebra by
$_1$ factor generated as a von Neumann algebra by ![]() $\{ a_k \}_{k = 1}^n$ such that
$\{ a_k \}_{k = 1}^n$ such that ![]() $\sum _{k = 1}^n a_k^* a_k = \sum _{k = 1}^n a_k a_k^* = 1$. Let
$\sum _{k = 1}^n a_k^* a_k = \sum _{k = 1}^n a_k a_k^* = 1$. Let
 \[ \mathcal{B}(L^2(M, \tau)) \ni T \mapsto \varphi(T) = \sum_{k = 1}^n \langle T \widehat{a_k^*}, \widehat{a_k^*} \rangle \]
\[ \mathcal{B}(L^2(M, \tau)) \ni T \mapsto \varphi(T) = \sum_{k = 1}^n \langle T \widehat{a_k^*}, \widehat{a_k^*} \rangle \]
denote the associated normal regular hyperstate. If ![]() $M$ has property (T), then there exists
$M$ has property (T), then there exists ![]() $c > 0$ such that if
$c > 0$ such that if ![]() $M \subset \mathcal {A}$ is any irreducible inclusion having no normal conditional expectation from
$M \subset \mathcal {A}$ is any irreducible inclusion having no normal conditional expectation from ![]() $\mathcal {A}$ to
$\mathcal {A}$ to ![]() $M$, and if
$M$, and if ![]() $\zeta \in \mathcal {A}_*$ is any faithful normal hyperstate, then
$\zeta \in \mathcal {A}_*$ is any faithful normal hyperstate, then ![]() $h_\varphi (M \subset \mathcal {A}, \zeta ) \geq c$.
$h_\varphi (M \subset \mathcal {A}, \zeta ) \geq c$.
Proof. Suppose ![]() $M$ has property (T) and there is a sequence of irreducible inclusions
$M$ has property (T) and there is a sequence of irreducible inclusions ![]() $M \subset \mathcal {A}_m$, and normal faithful hyperstates
$M \subset \mathcal {A}_m$, and normal faithful hyperstates ![]() $\zeta _m \in \mathcal {A}_m$, such that
$\zeta _m \in \mathcal {A}_m$, such that ![]() $h_\varphi (M \subset \mathcal {A}_m, \zeta _m) \to 0$. Then by Lemma 6.1 we have that
$h_\varphi (M \subset \mathcal {A}_m, \zeta _m) \to 0$. Then by Lemma 6.1 we have that ![]() $\langle T 1_{\zeta _m}, 1_{\zeta _m} \rangle \to 1$, and hence
$\langle T 1_{\zeta _m}, 1_{\zeta _m} \rangle \to 1$, and hence ![]() $\sum _{k = 1}^n \| a_k 1_{\zeta _m} - 1_{\zeta _m} a_k \|_2^2 = 2 - 2 \langle T 1_{\zeta _m}, 1_{\zeta _m} \rangle \to 0$. Since
$\sum _{k = 1}^n \| a_k 1_{\zeta _m} - 1_{\zeta _m} a_k \|_2^2 = 2 - 2 \langle T 1_{\zeta _m}, 1_{\zeta _m} \rangle \to 0$. Since ![]() $M$ has property (T) it then follows that for
$M$ has property (T) it then follows that for ![]() $m$ large enough there exists a unit
$m$ large enough there exists a unit ![]() $M$-central vector
$M$-central vector ![]() $\xi \in L^2(\mathcal {A}_m, \zeta _m)$. If we let
$\xi \in L^2(\mathcal {A}_m, \zeta _m)$. If we let ![]() $\tilde \zeta$ denote the state on
$\tilde \zeta$ denote the state on ![]() $\mathcal {A}_m$ given by
$\mathcal {A}_m$ given by ![]() $\tilde \zeta (a) = \langle a \xi, \xi \rangle$, then as
$\tilde \zeta (a) = \langle a \xi, \xi \rangle$, then as ![]() $\xi$ is
$\xi$ is ![]() $M$-central we have that
$M$-central we have that ![]() $\tilde \zeta$ gives an
$\tilde \zeta$ gives an ![]() $M$-hypertrace on
$M$-hypertrace on ![]() $\mathcal {A}_m$. Thus, there exists a corresponding normal conditional expectation form
$\mathcal {A}_m$. Thus, there exists a corresponding normal conditional expectation form ![]() $\mathcal {A}_m$ to
$\mathcal {A}_m$ to ![]() $M$, for all
$M$, for all ![]() $m$ large enough.
$m$ large enough.
Acknowledgements
SD is immensely grateful to Darren Creutz for explaining the theory of Poisson boundaries of groups to him, and for many useful remarks and stimulating conversations about earlier drafts of this paper. SD would like to gratefully acknowledge many helpful conversations with Vaughan Jones, Ionut Chifan, Palle Jorgensen, and Paul Muhly regarding this paper. SD would also like to thank Ben Hayes and Krishnendu Khan for various discussions on and around the contents of this paper. The authors would like to thank Sorin Popa for useful comments regarding this paper. The authors would like to thank the anonymous referee for numerous valuable comments and suggestions that greatly improved the exposition of the paper.
Appendix A. Minimal dilations and boundaries of u.c.p. maps
We include in this appendix a proof of Izumi's result from [Reference IzumiIzu02] that, for a von Neumann algebra (or even an arbitrary ![]() $C^*$-algebra)
$C^*$-algebra) ![]() $A$, and a u.c.p. map
$A$, and a u.c.p. map ![]() $\phi : A \to A$, the operator space
$\phi : A \to A$, the operator space ![]() ${\rm Har}(A, \phi )$ has a
${\rm Har}(A, \phi )$ has a ![]() $C^*$-algebraic structure. We take the approach in [Reference IzumiIzu12] where
$C^*$-algebraic structure. We take the approach in [Reference IzumiIzu12] where ![]() ${\rm Har}(A, \phi )$ is shown to be completely isometric to the
${\rm Har}(A, \phi )$ is shown to be completely isometric to the ![]() $*$-algebra of fixed points associated to a
$*$-algebra of fixed points associated to a ![]() $*$-endomorphism which dilates the u.c.p. map. There are several proofs of the existence of such a dilation; the first proof is by Bhat in [Reference BhatBha99] in the setting of completely positive semigroups, building on work from [Reference BhatBha96, Reference Bhat and ParthasarathyBP94, Reference Bhat and ParthasarathyBP95], and then later proofs were given in [Reference Bhat and SkeideBS00, Reference Muhly and SolelMS02], and Chapter 8 of [Reference ArvesonArv03]. Our reason for including an additional proof is that it is perhaps more elementary than previous proofs, being based on a simple idea of iterating the Stinespring dilation [Reference StinespringSti55].
$*$-endomorphism which dilates the u.c.p. map. There are several proofs of the existence of such a dilation; the first proof is by Bhat in [Reference BhatBha99] in the setting of completely positive semigroups, building on work from [Reference BhatBha96, Reference Bhat and ParthasarathyBP94, Reference Bhat and ParthasarathyBP95], and then later proofs were given in [Reference Bhat and SkeideBS00, Reference Muhly and SolelMS02], and Chapter 8 of [Reference ArvesonArv03]. Our reason for including an additional proof is that it is perhaps more elementary than previous proofs, being based on a simple idea of iterating the Stinespring dilation [Reference StinespringSti55].
Lemma A.1 If ![]() ${\mathcal {H}}$ and
${\mathcal {H}}$ and ![]() ${\mathcal {K}}$ are Hilbert spaces, and
${\mathcal {K}}$ are Hilbert spaces, and ![]() $V: {\mathcal {H}} \to {\mathcal {K}}$ is a partial isometry, then for
$V: {\mathcal {H}} \to {\mathcal {K}}$ is a partial isometry, then for ![]() $A \subset \operatorname {\mathcal {B}}({\mathcal {H}})$,
$A \subset \operatorname {\mathcal {B}}({\mathcal {H}})$, ![]() $B \subset \operatorname {\mathcal {B}}({\mathcal {K}})$, we have that
$B \subset \operatorname {\mathcal {B}}({\mathcal {K}})$, we have that ![]() $V^*$
$V^*$ ![]() $*$-
$*$-![]() ${\rm alg}(VBV^*, A) V = *$-
${\rm alg}(VBV^*, A) V = *$-![]() ${\rm alg} (B, V^*AV)$.
${\rm alg} (B, V^*AV)$.
Proof. Using the fact that ![]() $V^*V = 1$, this follows easily by induction on the length of alternating products for monomials in
$V^*V = 1$, this follows easily by induction on the length of alternating products for monomials in ![]() $VBV^*$, and
$VBV^*$, and ![]() $A$.
$A$.
If ![]() $A_0 \subset \operatorname {\mathcal {B}}({\mathcal {H}}_0)$ is a
$A_0 \subset \operatorname {\mathcal {B}}({\mathcal {H}}_0)$ is a ![]() $C^*$-algebra, and
$C^*$-algebra, and ![]() $\phi : A_0 \to A_0$ is a u.c.p. map, then one can iterate Stinespring's dilation as follows.
$\phi : A_0 \to A_0$ is a u.c.p. map, then one can iterate Stinespring's dilation as follows.
Lemma A.2 Suppose ![]() $A_0 \subset \operatorname {\mathcal {B}}({\mathcal {H}}_0)$ is a unital
$A_0 \subset \operatorname {\mathcal {B}}({\mathcal {H}}_0)$ is a unital ![]() $C^*$-algebra, and
$C^*$-algebra, and ![]() $\phi _0: A_0 \to A_0$ is a u.c.p. map. Then there exists a sequence whose entries consist of:
$\phi _0: A_0 \to A_0$ is a u.c.p. map. Then there exists a sequence whose entries consist of:
(1) a Hilbert space
 ${\mathcal {H}}_n$,
${\mathcal {H}}_n$,(2) an isometry
 $V_n: {\mathcal {H}}_{n - 1} \to {\mathcal {H}}_n$,
$V_n: {\mathcal {H}}_{n - 1} \to {\mathcal {H}}_n$,(3) a unital
 $C^*$-algebra
$C^*$-algebra  $A_n \subset \operatorname {\mathcal {B}}({\mathcal {H}}_n)$,
$A_n \subset \operatorname {\mathcal {B}}({\mathcal {H}}_n)$,(4) a unital representation
 $\pi _n: A_{n - 1} \to \operatorname {\mathcal {B}}({\mathcal {H}}_n)$ such that
$\pi _n: A_{n - 1} \to \operatorname {\mathcal {B}}({\mathcal {H}}_n)$ such that  $\pi _n(A_{n - 1})$, and
$\pi _n(A_{n - 1})$, and  $V_n A_{n - 1} V_n^*$ generate
$V_n A_{n - 1} V_n^*$ generate  $A_n$,
$A_n$,(5) a u.c.p. map
 $\phi _n: A_n \to A_n$,
$\phi _n: A_n \to A_n$,
such that the following relationships are satisfied for each ![]() $n \in {\mathbb {N}}$,
$n \in {\mathbb {N}}$, ![]() $x \in A_{n - 1}$:
$x \in A_{n - 1}$:
Moreover, for each ![]() $n \in {\mathbb {N}}$ we have that the central support of
$n \in {\mathbb {N}}$ we have that the central support of ![]() $V_nV_n^*$ in
$V_nV_n^*$ in ![]() $A_n''$ is
$A_n''$ is ![]() $1$. Also, if
$1$. Also, if ![]() $A_0$ is a von Neumann algebra and
$A_0$ is a von Neumann algebra and ![]() $\phi _0$ is normal, then
$\phi _0$ is normal, then ![]() $A_n$ will also be a von Neumann algebra and
$A_n$ will also be a von Neumann algebra and ![]() $\pi _n$ and
$\pi _n$ and ![]() $\phi _n$ will be normal for each
$\phi _n$ will be normal for each ![]() $n \in {\mathbb {N}}$.
$n \in {\mathbb {N}}$.
Proof. We will first construct the objects and show the relationships (A), (B), and (C) by induction, with the base case being vacuous, and we will then show that (D) also holds for all ![]() $n \in {\mathbb {N}}$. So suppose
$n \in {\mathbb {N}}$. So suppose ![]() $n \in {\mathbb {N}}$ and that (A), (B), and (C) hold for all
$n \in {\mathbb {N}}$ and that (A), (B), and (C) hold for all ![]() $m < n$, (we leave
$m < n$, (we leave ![]() $V_0$ undefined).
$V_0$ undefined).
From the proof of Stinespring's dilation theorem we may construct a Hilbert space ![]() ${\mathcal {H}}_n$ by separating and completing the vector space
${\mathcal {H}}_n$ by separating and completing the vector space ![]() $A_{n - 1} \otimes {\mathcal {H}}_{n - 1}$ with respect to the nonnegative definite sesquilinear form satisfying
$A_{n - 1} \otimes {\mathcal {H}}_{n - 1}$ with respect to the nonnegative definite sesquilinear form satisfying
for all ![]() $a, b \in A_{n - 1}$,
$a, b \in A_{n - 1}$, ![]() $\xi, \eta \in {\mathcal {H}}_{n - 1}$.
$\xi, \eta \in {\mathcal {H}}_{n - 1}$.
We also obtain a partial isometry ![]() $V_n: {\mathcal {H}}_{n - 1} \to {\mathcal {H}}_n$ from the formula
$V_n: {\mathcal {H}}_{n - 1} \to {\mathcal {H}}_n$ from the formula
for ![]() $\xi \in {\mathcal {H}}_{n - 1}$.
$\xi \in {\mathcal {H}}_{n - 1}$.
We obtain a representation ![]() $\pi _n: A_{n - 1} \to \operatorname {\mathcal {B}}({\mathcal {H}}_n)$ (which is normal when
$\pi _n: A_{n - 1} \to \operatorname {\mathcal {B}}({\mathcal {H}}_n)$ (which is normal when ![]() $A_0$ is a von Neumann algebra and
$A_0$ is a von Neumann algebra and ![]() $\phi _0$ is normal) from the formula
$\phi _0$ is normal) from the formula
for ![]() $x, a \in A_{n - 1}$,
$x, a \in A_{n - 1}$, ![]() $\xi \in {\mathcal {H}}_{n - 1}$. And recall the fundamental relationship
$\xi \in {\mathcal {H}}_{n - 1}$. And recall the fundamental relationship ![]() $V_n^* \pi _n(x) V_n = \phi _{n - 1}(x)$ for all
$V_n^* \pi _n(x) V_n = \phi _{n - 1}(x)$ for all ![]() $x \in A_{n - 1}$, which establishes (A).
$x \in A_{n - 1}$, which establishes (A).
If we let ![]() $A_n$ be the
$A_n$ be the ![]() $C^*$-algebra generated by
$C^*$-algebra generated by ![]() $\pi _n(A_{n - 1})$ and
$\pi _n(A_{n - 1})$ and ![]() $V_n A_{n - 1} V_n^*$, then
$V_n A_{n - 1} V_n^*$, then ![]() $\pi _n : A_{n - 1} \to A_n$, and from Lemma A.1 we have that
$\pi _n : A_{n - 1} \to A_n$, and from Lemma A.1 we have that ![]() $V_n^* A_n V_n$ is generated by
$V_n^* A_n V_n$ is generated by ![]() $V_n^* \pi _n(A_{n - 1}) V_n$ and
$V_n^* \pi _n(A_{n - 1}) V_n$ and ![]() $A_{n - 1}$. However,
$A_{n - 1}$. However, ![]() $V_n^* \pi _n (A_{n - 1}) V_n = \phi _{n - 1}(A_{n - 1}) \subset A_{n - 1}$, hence
$V_n^* \pi _n (A_{n - 1}) V_n = \phi _{n - 1}(A_{n - 1}) \subset A_{n - 1}$, hence ![]() $V_n^* A_n V_n = A_{n - 1}$, establishing (B). Also, when
$V_n^* A_n V_n = A_{n - 1}$, establishing (B). Also, when ![]() $A_0$ is a von Neumann algebra and
$A_0$ is a von Neumann algebra and ![]() $\pi _n$ is normal it then follows easily that
$\pi _n$ is normal it then follows easily that ![]() $A_n$ is also a von Neumann algebra.
$A_n$ is also a von Neumann algebra.
Also note that ![]() $\pi _n(A_{n - 1}) V_nV_n^* {\mathcal {H}}_n$ is dense in
$\pi _n(A_{n - 1}) V_nV_n^* {\mathcal {H}}_n$ is dense in ![]() ${\mathcal {H}}_n$, and so since
${\mathcal {H}}_n$, and so since ![]() $\pi _n(A_{n - 1}) \subset A_n$ we have that the central support of
$\pi _n(A_{n - 1}) \subset A_n$ we have that the central support of ![]() $V_nV_n^*$ in
$V_nV_n^*$ in ![]() $A_n''$ is
$A_n''$ is ![]() $1$.
$1$.
We then define ![]() $\phi _n: A_n \to A_n$ by
$\phi _n: A_n \to A_n$ by ![]() $\phi _n(x) = \pi _n(V_n^* x V_n)$, for
$\phi _n(x) = \pi _n(V_n^* x V_n)$, for ![]() $x \in A_n$. This is well defined since
$x \in A_n$. This is well defined since ![]() $V_n^* A_n V_n = A_{n - 1}$, unital, and completely positive. Note that for
$V_n^* A_n V_n = A_{n - 1}$, unital, and completely positive. Note that for ![]() $x \in A_{n - 1}$ we have
$x \in A_{n - 1}$ we have ![]() $\phi _n(\pi _n(x)) = \pi _n(V_n^* \pi _n(x) V_n) = \pi _n(\phi _{n - 1}(x))$, establishing (C).
$\phi _n(\pi _n(x)) = \pi _n(V_n^* \pi _n(x) V_n) = \pi _n(\phi _{n - 1}(x))$, establishing (C).
Having established (A), (B), and (C) for all ![]() $n \in {\mathbb {N}}$, we now show that (D) holds as well. For this, notice first that for
$n \in {\mathbb {N}}$, we now show that (D) holds as well. For this, notice first that for ![]() $a, b \in A_{n}$,
$a, b \in A_{n}$, ![]() $x \in A_{n - 1}$, and
$x \in A_{n - 1}$, and ![]() $\xi, \eta \in {\mathcal {H}}_n$ we have
$\xi, \eta \in {\mathcal {H}}_n$ we have
 \begin{align*} \langle \pi_{n + 1}(V_n x V_n^* ) (a \otimes \xi), b \otimes \eta \rangle &= \langle V_n x V_n^*a \otimes \xi, b \otimes \eta \rangle \\ &= \langle \phi_n(b^* V_n x V_n^*a) \xi, \eta \rangle \\ &= \langle \pi_n(V_n^* b^* V_n x V_n^* a V_n) \xi, \eta \rangle \\ &= \langle 1 \otimes \pi_n(x V_n^* a V_n) \xi, b \otimes \eta \rangle. \end{align*}
\begin{align*} \langle \pi_{n + 1}(V_n x V_n^* ) (a \otimes \xi), b \otimes \eta \rangle &= \langle V_n x V_n^*a \otimes \xi, b \otimes \eta \rangle \\ &= \langle \phi_n(b^* V_n x V_n^*a) \xi, \eta \rangle \\ &= \langle \pi_n(V_n^* b^* V_n x V_n^* a V_n) \xi, \eta \rangle \\ &= \langle 1 \otimes \pi_n(x V_n^* a V_n) \xi, b \otimes \eta \rangle. \end{align*}
Setting ![]() $x = 1$ and using that
$x = 1$ and using that ![]() $V_{n + 1}^*( 1 \otimes \zeta ) = \zeta$ for each
$V_{n + 1}^*( 1 \otimes \zeta ) = \zeta$ for each ![]() $\zeta \in {\mathcal {H}}_n$, we see that
$\zeta \in {\mathcal {H}}_n$, we see that
 \begin{align*} (V_{n+1}V_{n+1}^*)\pi_{n + 1}(V_nV_n^*) ( a \otimes \xi) &= (V_{n+1}V_{n+1}^*)( 1 \otimes \pi_n(V_n^*aV_n)\xi ) \\ &= 1 \otimes \pi_n(V_n^*aV_n)\xi \\ &= \pi_{n + 1}(V_nV_n^*) ( a \otimes \xi), \end{align*}
\begin{align*} (V_{n+1}V_{n+1}^*)\pi_{n + 1}(V_nV_n^*) ( a \otimes \xi) &= (V_{n+1}V_{n+1}^*)( 1 \otimes \pi_n(V_n^*aV_n)\xi ) \\ &= 1 \otimes \pi_n(V_n^*aV_n)\xi \\ &= \pi_{n + 1}(V_nV_n^*) ( a \otimes \xi), \end{align*}
and hence ![]() $\pi _{n + 1}(V_nV_n^*) \leq V_{n + 1} V_{n + 1}^*$. If instead we set
$\pi _{n + 1}(V_nV_n^*) \leq V_{n + 1} V_{n + 1}^*$. If instead we set ![]() $a = 1$, then we have
$a = 1$, then we have
and so ![]() $V_{n + 1} \pi _n(x) = \pi _{n + 1}(V_n x V_n^* ) V_{n + 1}$. Multiplying on the right by
$V_{n + 1} \pi _n(x) = \pi _{n + 1}(V_n x V_n^* ) V_{n + 1}$. Multiplying on the right by ![]() $V_{n + 1}^*$ and using that
$V_{n + 1}^*$ and using that ![]() $\pi _n(V_nV_n^*) \leq V_{n + 1} V_{n + 1}^*$ then gives
$\pi _n(V_nV_n^*) \leq V_{n + 1} V_{n + 1}^*$ then gives ![]() $V_{n + 1} \pi _n(x) V_{n + 1}^* = \pi _{n + 1}(V_n x V_n^*)$.
$V_{n + 1} \pi _n(x) V_{n + 1}^* = \pi _{n + 1}(V_n x V_n^*)$.
Theorem A.3 (Bhat [Reference BhatBha99])
Let ![]() $A_0 \subset \operatorname {\mathcal {B}}({\mathcal {H}}_0)$ be a unital
$A_0 \subset \operatorname {\mathcal {B}}({\mathcal {H}}_0)$ be a unital ![]() $C^*$-algebra, and
$C^*$-algebra, and ![]() $\phi _0: A_0 \to A_0$ a u.c.p. map. Then there exist
$\phi _0: A_0 \to A_0$ a u.c.p. map. Then there exist
(1) a Hilbert space
 ${\mathcal {K}}$,
${\mathcal {K}}$,(2) an isometry
 $W: {\mathcal {H}}_0 \to {\mathcal {K}}$,
$W: {\mathcal {H}}_0 \to {\mathcal {K}}$,(3) a
 $C^*$-algebra
$C^*$-algebra  $B \subset \operatorname {\mathcal {B}}({\mathcal {K}})$,
$B \subset \operatorname {\mathcal {B}}({\mathcal {K}})$,(4) a unital
 $*$-endomorphism
$*$-endomorphism  $\alpha : B \to B$,
$\alpha : B \to B$,
such that ![]() $W^* B W = A_0$, and for all
$W^* B W = A_0$, and for all ![]() $x \in A_0$ we have
$x \in A_0$ we have
Moreover, we have that the central support of ![]() $WW^*$ in
$WW^*$ in ![]() $B''$ is
$B''$ is ![]() $1$,
$1$, ![]() $\alpha ^{k}(WW^*) \leq \alpha ^{k+1}(WW^*)$, and for
$\alpha ^{k}(WW^*) \leq \alpha ^{k+1}(WW^*)$, and for ![]() $y \in \operatorname {\mathcal {B}}({\mathcal {K}})$ we have
$y \in \operatorname {\mathcal {B}}({\mathcal {K}})$ we have ![]() $y \in B$ if and only if
$y \in B$ if and only if ![]() $\alpha ^k(WW^*) y \alpha ^k(WW^*) \in \alpha ^k(WA_0W^*)$ for all
$\alpha ^k(WW^*) y \alpha ^k(WW^*) \in \alpha ^k(WA_0W^*)$ for all ![]() $k \geq 0$. Also, if
$k \geq 0$. Also, if ![]() $A_0$ is a von Neumann algebra and
$A_0$ is a von Neumann algebra and ![]() $\phi _0$ is normal, then
$\phi _0$ is normal, then ![]() $B$ will also be a von Neumann algebra, and
$B$ will also be a von Neumann algebra, and ![]() $\alpha$ will also be normal.
$\alpha$ will also be normal.
Proof. Using the notation from Lemma A.2, we may define a Hilbert space ![]() ${\mathcal {K}}$ as the directed limit of the Hilbert spaces
${\mathcal {K}}$ as the directed limit of the Hilbert spaces ![]() ${\mathcal {H}}_n$ with respect to the inclusions
${\mathcal {H}}_n$ with respect to the inclusions ![]() $V_{n + 1} : {\mathcal {H}}_n \to {\mathcal {H}}_{n + 1}$. We denote by
$V_{n + 1} : {\mathcal {H}}_n \to {\mathcal {H}}_{n + 1}$. We denote by ![]() $W_n: {\mathcal {H}}_n \to {\mathcal {K}}$ the associated sequence of isometries satisfying
$W_n: {\mathcal {H}}_n \to {\mathcal {K}}$ the associated sequence of isometries satisfying ![]() $W_{n + 1}^* W_n = V_{n + 1}$, for
$W_{n + 1}^* W_n = V_{n + 1}$, for ![]() $n \in {\mathbb {N}}$, and we set an increasing sequence of projections
$n \in {\mathbb {N}}$, and we set an increasing sequence of projections ![]() $P_n = W_nW_n^*$.
$P_n = W_nW_n^*$.
From (B) we have that ![]() $P_{n - 1} W_n A_n W_n^* P_{n - 1} = W_{n - 1} A_{n - 1} W_{n - 1}^*$, and hence if we define the
$P_{n - 1} W_n A_n W_n^* P_{n - 1} = W_{n - 1} A_{n - 1} W_{n - 1}^*$, and hence if we define the ![]() $C^*$-algebra
$C^*$-algebra ![]() $B = \{ x \in \operatorname {\mathcal {B}}({\mathcal {K}}) \mid W_n^* x W_n \in A_n, n \geq 0 \}$, then we have
$B = \{ x \in \operatorname {\mathcal {B}}({\mathcal {K}}) \mid W_n^* x W_n \in A_n, n \geq 0 \}$, then we have ![]() $W_n^* B W_n = A_n$, for all
$W_n^* B W_n = A_n$, for all ![]() $n \geq 0$. Also, if
$n \geq 0$. Also, if ![]() $A_0$ is a von Neumann algebra, then so is
$A_0$ is a von Neumann algebra, then so is ![]() $A_n$ for each
$A_n$ for each ![]() $n \in {\mathbb {N}}$, and from this it follows easily that
$n \in {\mathbb {N}}$, and from this it follows easily that ![]() $B$ is also a von Neumann algebra.
$B$ is also a von Neumann algebra.
We define the unital ![]() $*$-endomorphism
$*$-endomorphism ![]() $\alpha : B \to B$ (which is normal when
$\alpha : B \to B$ (which is normal when ![]() $A_0$ is a von Neumann algebra and
$A_0$ is a von Neumann algebra and ![]() $\phi _0$ is normal) by the formula
$\phi _0$ is normal) by the formula
where the limit is taken in the strong operator topology. Note that ![]() $\alpha (P_n) = P_{n + 1} \geq P_n$. From (D) we see that in general, the strong operator topology limit exists in
$\alpha (P_n) = P_{n + 1} \geq P_n$. From (D) we see that in general, the strong operator topology limit exists in ![]() $B$, and that for
$B$, and that for ![]() $x \in A_n \cong P_nA_\infty P_n$ the limit stabilizes as
$x \in A_n \cong P_nA_\infty P_n$ the limit stabilizes as ![]() $\alpha ( W_n x W_n^* ) = W_{n + 1}\pi _{n + 1}( x ) W_{n + 1}^*$.
$\alpha ( W_n x W_n^* ) = W_{n + 1}\pi _{n + 1}( x ) W_{n + 1}^*$.
From (A) we see that for ![]() $n \geq 0$ and
$n \geq 0$ and ![]() $x \in A_n$ we have
$x \in A_n$ we have
 \begin{align*} P_n \alpha ( W_n x W_n^* ) P_n &= W_n W_n^*W_{n + 1}\pi_{n + 1}(x) W_{n + 1}^*W_n W_n^* \\ &= W_n V_{n + 1}^* \pi_{n + 1}(x) V_{n + 1} W_n^* \\ &= W_n \phi_n( x ) W_n^*. \end{align*}
\begin{align*} P_n \alpha ( W_n x W_n^* ) P_n &= W_n W_n^*W_{n + 1}\pi_{n + 1}(x) W_{n + 1}^*W_n W_n^* \\ &= W_n V_{n + 1}^* \pi_{n + 1}(x) V_{n + 1} W_n^* \\ &= W_n \phi_n( x ) W_n^*. \end{align*}
By induction we then see that also for ![]() $k > 1$, and
$k > 1$, and ![]() $x \in A_0$ we have
$x \in A_0$ we have
 \begin{align*} P_0 \alpha^k ( W_0 x W_0^* ) P_0 &= P_0 \alpha^{k - 1}( P_0 \alpha( W_0 x W_0^* ) P_0 ) P_0 \\ &= P_0 \alpha^{k - 1} (W_0 \phi_0(x) W_0^* )P_0 \\ &= W_0 \phi_0^k(x) W_0^*. \end{align*}
\begin{align*} P_0 \alpha^k ( W_0 x W_0^* ) P_0 &= P_0 \alpha^{k - 1}( P_0 \alpha( W_0 x W_0^* ) P_0 ) P_0 \\ &= P_0 \alpha^{k - 1} (W_0 \phi_0(x) W_0^* )P_0 \\ &= W_0 \phi_0^k(x) W_0^*. \end{align*}
By the previous lemma we have that the central support of ![]() $P_n$ in
$P_n$ in ![]() $W_n A_n'' W_n^*$ is
$W_n A_n'' W_n^*$ is ![]() $P_{n + 1}$. Hence it follows that the central support of
$P_{n + 1}$. Hence it follows that the central support of ![]() $P_0$ in
$P_0$ in ![]() $B$ is
$B$ is ![]() $1$.
$1$.
A.1 Poisson boundaries of u.c.p. maps
If ![]() $A \subset \operatorname {\mathcal {B}}({\mathcal {H}})$ is a unital
$A \subset \operatorname {\mathcal {B}}({\mathcal {H}})$ is a unital ![]() $C^*$-algebra, and
$C^*$-algebra, and ![]() $\phi : A \to A$ a u.c.p. map, then a projection
$\phi : A \to A$ a u.c.p. map, then a projection ![]() $p \in A$ is said to be coinvariant if
$p \in A$ is said to be coinvariant if ![]() $\{ \phi ^n(p) \}_n$ defines an increasing sequence of projections which strongly converge to
$\{ \phi ^n(p) \}_n$ defines an increasing sequence of projections which strongly converge to ![]() $1$ in
$1$ in ![]() $\operatorname {\mathcal {B}}({\mathcal {H}})$, and such that for
$\operatorname {\mathcal {B}}({\mathcal {H}})$, and such that for ![]() $y \in \operatorname {\mathcal {B}}({\mathcal {H}})$ we have
$y \in \operatorname {\mathcal {B}}({\mathcal {H}})$ we have ![]() $y \in A$ if and only if
$y \in A$ if and only if ![]() $\phi ^n(p) y \phi ^n(p) \in A$ for all
$\phi ^n(p) y \phi ^n(p) \in A$ for all ![]() $n \geq 0$. Note that for
$n \geq 0$. Note that for ![]() $n \geq 0$,
$n \geq 0$, ![]() $\phi ^n(p)$ is in the multiplicative domain for
$\phi ^n(p)$ is in the multiplicative domain for ![]() $\phi$, and is again coinvariant. We define
$\phi$, and is again coinvariant. We define ![]() $\phi _p: pAp \to pAp$ to be the map
$\phi _p: pAp \to pAp$ to be the map ![]() $\phi _p(x) = p \phi (x) p$, and then
$\phi _p(x) = p \phi (x) p$, and then ![]() $\phi _p$ is normal u.c.p. Moreover, we have that
$\phi _p$ is normal u.c.p. Moreover, we have that ![]() $\phi _p^k(x) = p \phi ^k(x) p$ for all
$\phi _p^k(x) = p \phi ^k(x) p$ for all ![]() $x \in pAp$, which can be seen by induction from
$x \in pAp$, which can be seen by induction from
Theorem A.4 (Prunaru [Reference PrunaruPru12])
Let ![]() $A \subset \operatorname {\mathcal {B}}({\mathcal {H}})$ be a unital
$A \subset \operatorname {\mathcal {B}}({\mathcal {H}})$ be a unital ![]() $C^*$-algebra,
$C^*$-algebra, ![]() $\phi : A \to A$ a u.c.p. map, and
$\phi : A \to A$ a u.c.p. map, and ![]() $p \in A$ a coinvariant projection. Then the map
$p \in A$ a coinvariant projection. Then the map ![]() $\mathcal {P}: \operatorname {Har}(A, \phi ) \to \operatorname {Har}(pAp, \phi _p)$ given by
$\mathcal {P}: \operatorname {Har}(A, \phi ) \to \operatorname {Har}(pAp, \phi _p)$ given by ![]() $\mathcal {P}(x) = pxp$ defines a completely positive isometric surjection, between
$\mathcal {P}(x) = pxp$ defines a completely positive isometric surjection, between ![]() $\operatorname {Har}(A, \phi )$ and
$\operatorname {Har}(A, \phi )$ and ![]() $\operatorname {Har}(pAp, \phi _p)$.
$\operatorname {Har}(pAp, \phi _p)$.
Moreover, if ![]() $A$ is a von Neumann algebra and
$A$ is a von Neumann algebra and ![]() $\phi$ is normal, then
$\phi$ is normal, then ![]() $\mathcal {P}$ is also normal.
$\mathcal {P}$ is also normal.
Proof. First note that ![]() $\mathcal {P}$ is well defined since if
$\mathcal {P}$ is well defined since if ![]() $x \in \operatorname {Har}(A, \phi )$ we have
$x \in \operatorname {Har}(A, \phi )$ we have
Clearly ![]() $\mathcal {P}$ is completely positive (and normal in the case when
$\mathcal {P}$ is completely positive (and normal in the case when ![]() $A$ is a von Neumann algebra and
$A$ is a von Neumann algebra and ![]() $\phi$ is normal).
$\phi$ is normal).
To see that it is surjective, if ![]() $x \in \operatorname {Har}(pAp, \phi _p)$, then consider the sequence
$x \in \operatorname {Har}(pAp, \phi _p)$, then consider the sequence ![]() $\phi ^n(x)$. For each
$\phi ^n(x)$. For each ![]() $m, n \geq 0$, we have
$m, n \geq 0$, we have
It follows that ![]() $\{ \phi ^n(x) \}_n$ is eventually constant for any
$\{ \phi ^n(x) \}_n$ is eventually constant for any ![]() $\xi$ in the range of
$\xi$ in the range of ![]() $\phi ^m(p)$ for any
$\phi ^m(p)$ for any ![]() $m$. Since
$m$. Since ![]() $\{ \phi ^n(x) \}_n$ is uniformly bounded and
$\{ \phi ^n(x) \}_n$ is uniformly bounded and ![]() $\{\phi ^n(x) \xi \}_n$ converges for a dense subset of
$\{\phi ^n(x) \xi \}_n$ converges for a dense subset of ![]() $\xi \in {\mathcal {H}}$ we then have that
$\xi \in {\mathcal {H}}$ we then have that ![]() $\{ \phi ^n(x) \}_n$ converges in the strong operator topology to an element
$\{ \phi ^n(x) \}_n$ converges in the strong operator topology to an element ![]() $y \in \operatorname {\mathcal {B}}({\mathcal {H}})$ such that
$y \in \operatorname {\mathcal {B}}({\mathcal {H}})$ such that ![]() $\phi ^m(p) y \phi ^m(p) = \phi ^m(x)$ for each
$\phi ^m(p) y \phi ^m(p) = \phi ^m(x)$ for each ![]() $m \geq 0$. Consequently, we have
$m \geq 0$. Consequently, we have ![]() $y \in A$.
$y \in A$.
In particular, for ![]() $m = 0$ we have
$m = 0$ we have ![]() $p y p = x$. To see that
$p y p = x$. To see that ![]() $y \in \operatorname {Har}(A, \phi )$ we use that for all
$y \in \operatorname {Har}(A, \phi )$ we use that for all ![]() $z \in A$ we have the strong operator topology limit
$z \in A$ we have the strong operator topology limit
and hence
Thus ![]() $\mathcal {P}$ is surjective, and since
$\mathcal {P}$ is surjective, and since ![]() $\phi ^n(p)$ converges strongly to
$\phi ^n(p)$ converges strongly to ![]() $1$, and each
$1$, and each ![]() $\phi ^n(p)$ is in the multiplicative domain of
$\phi ^n(p)$ is in the multiplicative domain of ![]() $\phi$, it follows that if
$\phi$, it follows that if ![]() $x \in \operatorname {Har}(A, \phi )$, then
$x \in \operatorname {Har}(A, \phi )$, then ![]() $\phi ^n(pxp)$ converges strongly to
$\phi ^n(pxp)$ converges strongly to ![]() $x$ and hence
$x$ and hence
Thus, ![]() $\mathcal {P}$ is also isometric.
$\mathcal {P}$ is also isometric.
Corollary A.5 (Izumi [Reference IzumiIzu02])
Let ![]() $A$ be a unital
$A$ be a unital ![]() $C^*$-algebra, and
$C^*$-algebra, and ![]() $\phi : A \to A$ a u.c.p. map. Then there exist a
$\phi : A \to A$ a u.c.p. map. Then there exist a ![]() $C^*$-algebra
$C^*$-algebra ![]() $B$ and a completely positive isometric surjection
$B$ and a completely positive isometric surjection ![]() $\mathcal {P}: B \to \operatorname {Har}(A, \phi )$.
$\mathcal {P}: B \to \operatorname {Har}(A, \phi )$.
Moreover, ![]() $B$ and
$B$ and ![]() $\mathcal {P}$ are unique in the sense that if
$\mathcal {P}$ are unique in the sense that if ![]() $\tilde B$ is another
$\tilde B$ is another ![]() $C^*$-algebra, and
$C^*$-algebra, and ![]() $\mathcal {P}_0: \tilde B \to \operatorname {Har}(A, \phi )$ is a completely positive isometric surjection, then
$\mathcal {P}_0: \tilde B \to \operatorname {Har}(A, \phi )$ is a completely positive isometric surjection, then ![]() $\mathcal {P}^{-1} \circ \mathcal {P}_0$ is an isomorphism.
$\mathcal {P}^{-1} \circ \mathcal {P}_0$ is an isomorphism.
Also, if ![]() $A$ is a von Neumann algebra and
$A$ is a von Neumann algebra and ![]() $\phi$ is normal, then
$\phi$ is normal, then ![]() $B$ is also a von Neumann algebra and
$B$ is also a von Neumann algebra and ![]() $\mathcal {P}$ is normal.
$\mathcal {P}$ is normal.
Proof. Note that we may assume ![]() $A \subset \operatorname {\mathcal {B}}({\mathcal {H}})$. Existence then follows by applying the previous theorem to Bhat's dilation. Uniqueness follows from [Reference ChoiCho74].
$A \subset \operatorname {\mathcal {B}}({\mathcal {H}})$. Existence then follows by applying the previous theorem to Bhat's dilation. Uniqueness follows from [Reference ChoiCho74].
Corollary A.6 (Choi-Effros [Reference Choi and EffrosCE77])
Let ![]() $A$ be a unital
$A$ be a unital ![]() $C^*$-algebra and
$C^*$-algebra and ![]() $F \subset A$ an operator system. If
$F \subset A$ an operator system. If ![]() $E: A \to F$ is a completely positive map such that
$E: A \to F$ is a completely positive map such that ![]() $E_{|F} = {\rm id}$, then
$E_{|F} = {\rm id}$, then ![]() $F$ has a unique
$F$ has a unique ![]() $C^*$-algebraic structure which is given by
$C^*$-algebraic structure which is given by ![]() $x \cdot y = E(xy)$. Moreover, if
$x \cdot y = E(xy)$. Moreover, if ![]() $A$ is a von Neumann algebra and
$A$ is a von Neumann algebra and ![]() $F$ is weakly closed, then this gives a von Neumann algebraic structure on
$F$ is weakly closed, then this gives a von Neumann algebraic structure on ![]() $F$.
$F$.
Proof. Note that ![]() $F \subseteq \operatorname {Har}(A,E)$, as
$F \subseteq \operatorname {Har}(A,E)$, as ![]() $E_{|F} = {\rm id}$. Since the range of
$E_{|F} = {\rm id}$. Since the range of ![]() $E$ is contained in
$E$ is contained in ![]() $F$, we get
$F$, we get ![]() $\operatorname {Har}(A, E) = F$.
$\operatorname {Har}(A, E) = F$.
When ![]() $A$ is a
$A$ is a ![]() $C^*$-algebra this follows from Corollary A.5 since
$C^*$-algebra this follows from Corollary A.5 since ![]() $\operatorname {Har}(A, E) = F$. Also note that since
$\operatorname {Har}(A, E) = F$. Also note that since ![]() $E^n = E$ it follows from the proof of Theorem A.4 that the product structure coming from the Poisson boundary is given by
$E^n = E$ it follows from the proof of Theorem A.4 that the product structure coming from the Poisson boundary is given by ![]() $x \cdot y = E(xy)$.
$x \cdot y = E(xy)$.
If ![]() $A$ is a von Neumann algebra and
$A$ is a von Neumann algebra and ![]() $F$ is weakly closed, then
$F$ is weakly closed, then ![]() $F$ has a predual
$F$ has a predual ![]() $F_\perp = \{ \varphi \in A_* \mid \varphi (x) = 0, \mbox { for all } x \in F \}$ and hence
$F_\perp = \{ \varphi \in A_* \mid \varphi (x) = 0, \mbox { for all } x \in F \}$ and hence ![]() $A$ is isomorphic to a von Neumann algebra by Sakai's theorem.
$A$ is isomorphic to a von Neumann algebra by Sakai's theorem.
Proposition A.7 Let ![]() $A$ be an abelian
$A$ be an abelian ![]() $C^*$-algebra and
$C^*$-algebra and ![]() $\phi : A \to A$ a normal u.c.p. map. Then the Poisson boundary of
$\phi : A \to A$ a normal u.c.p. map. Then the Poisson boundary of ![]() $\phi$ is also abelian.
$\phi$ is also abelian.
Proof. Let ![]() $B$ be the Poisson boundary of
$B$ be the Poisson boundary of ![]() $\phi$, and let
$\phi$, and let ![]() $\mathcal {P}: B \to \operatorname {Har}(A, \phi )$ be the Poisson transform. If
$\mathcal {P}: B \to \operatorname {Har}(A, \phi )$ be the Poisson transform. If ![]() $C$ is a
$C$ is a ![]() $C^*$-algebra and
$C^*$-algebra and ![]() $\psi : C \to B$ is a positive map, then
$\psi : C \to B$ is a positive map, then ![]() $\mathcal {P} \circ \psi : C \to \operatorname {Har}(A, \phi ) \subset A$ is positive, and since
$\mathcal {P} \circ \psi : C \to \operatorname {Har}(A, \phi ) \subset A$ is positive, and since ![]() $A$ is abelian it is then completely positive. Hence,
$A$ is abelian it is then completely positive. Hence, ![]() $\psi$ is also completely positive. Since every positive map from a
$\psi$ is also completely positive. Since every positive map from a ![]() $C^*$-algebra to
$C^*$-algebra to ![]() $B$ is completely positive it then follows that
$B$ is completely positive it then follows that ![]() $B$ is abelian.
$B$ is abelian.
Example A.8 Let ![]() $\Gamma$ be a discrete group and
$\Gamma$ be a discrete group and ![]() $\mu \in \operatorname {Prob}(\Gamma )$ a probability measure on
$\mu \in \operatorname {Prob}(\Gamma )$ a probability measure on ![]() $\Gamma$ such that the support of
$\Gamma$ such that the support of ![]() $\mu$ generates
$\mu$ generates ![]() $\Gamma$. Then on
$\Gamma$. Then on ![]() $\ell ^\infty \Gamma$ we may consider the normal unital (completely) positive map
$\ell ^\infty \Gamma$ we may consider the normal unital (completely) positive map ![]() $\phi _\mu$ given by
$\phi _\mu$ given by ![]() $\phi _\mu (f) = \mu * f$, where
$\phi _\mu (f) = \mu * f$, where ![]() $\mu * f$ is the convolution
$\mu * f$ is the convolution ![]() $(\mu * f) (x ) = \int f(g^{-1} x) \, d\mu (g)$. Then
$(\mu * f) (x ) = \int f(g^{-1} x) \, d\mu (g)$. Then ![]() $\operatorname {Har}(\mu ) = \operatorname {Har}(\ell ^\infty \Gamma, \phi _\mu )$ has a unique von Neumann algebraic structure which is abelian by the previous proposition. Notice that
$\operatorname {Har}(\mu ) = \operatorname {Har}(\ell ^\infty \Gamma, \phi _\mu )$ has a unique von Neumann algebraic structure which is abelian by the previous proposition. Notice that ![]() $\Gamma$ acts on
$\Gamma$ acts on ![]() $\operatorname {Har}(\mu )$ by right translation, and since this action preserves positivity it follows from [Reference ChoiCho74] that
$\operatorname {Har}(\mu )$ by right translation, and since this action preserves positivity it follows from [Reference ChoiCho74] that ![]() $\Gamma$ preserves the multiplication structure as well.
$\Gamma$ preserves the multiplication structure as well.
Since the support of ![]() $\mu$ generates
$\mu$ generates ![]() $\Gamma$, for a nonnegative function
$\Gamma$, for a nonnegative function ![]() $f \in \operatorname {Har}(\mu )_+$ we have
$f \in \operatorname {Har}(\mu )_+$ we have ![]() $f(e) = 0$ if and only if
$f(e) = 0$ if and only if ![]() $f = 0$. Thus we obtain a natural normal faithful state
$f = 0$. Thus we obtain a natural normal faithful state ![]() $\varphi$ on
$\varphi$ on ![]() $\operatorname {Har}(\mu )$ which is given by
$\operatorname {Har}(\mu )$ which is given by ![]() $\varphi (f) = f(e)$.
$\varphi (f) = f(e)$.
Since ![]() $\varphi$ is
$\varphi$ is ![]() $\Gamma$-equivariant, this extends to a normal u.c.p. map
$\Gamma$-equivariant, this extends to a normal u.c.p. map ![]() $\tilde \varphi : \ell ^\infty \Gamma \rtimes \Gamma \to \ell ^\infty \Gamma \rtimes \Gamma$ such that
$\tilde \varphi : \ell ^\infty \Gamma \rtimes \Gamma \to \ell ^\infty \Gamma \rtimes \Gamma$ such that ![]() $\tilde \varphi _{L\Gamma } = {\rm id}$. Note that
$\tilde \varphi _{L\Gamma } = {\rm id}$. Note that ![]() $\ell ^\infty \Gamma \rtimes \Gamma \cong \mathcal {B}(\ell ^2 \Gamma )$. It is an easy exercise to see that the Poisson boundary of
$\ell ^\infty \Gamma \rtimes \Gamma \cong \mathcal {B}(\ell ^2 \Gamma )$. It is an easy exercise to see that the Poisson boundary of ![]() $\tilde \varphi$ is simply the crossed product
$\tilde \varphi$ is simply the crossed product ![]() $\operatorname {Har}(\mu ) \rtimes \Gamma$.
$\operatorname {Har}(\mu ) \rtimes \Gamma$.