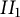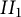1 Introduction
The Laguerre–Pólya class is the space of analytic functions, which are the uniform limit of real-rooted polynomials on compacta in
![]() $\mathbb {C}.$
Such functions have a Hadamard factorization of the form
$\mathbb {C}.$
Such functions have a Hadamard factorization of the form
 $$ \begin{align*}e^{ a+bz-cz^2}z^k\prod \left(1-\frac{z}{\rho_n}\right)e^{z/\rho_n},\end{align*} $$
$$ \begin{align*}e^{ a+bz-cz^2}z^k\prod \left(1-\frac{z}{\rho_n}\right)e^{z/\rho_n},\end{align*} $$
where b is real, c is nonnegative, and the at most countably many nonzero roots
![]() $\rho _n$
satisfy
$\rho _n$
satisfy
![]() $\sum \frac {1}{|\rho _n|^2} < \infty $
(see, e.g., [Reference Szász14]).
$\sum \frac {1}{|\rho _n|^2} < \infty $
(see, e.g., [Reference Szász14]).
Note that any real-rooted polynomial with positive leading coefficient can be written in the form
![]() $ p(x) =c\det (A+xI)$
,
$ p(x) =c\det (A+xI)$
,
![]() $c>0$
, where A is a self-adjoint matrix. For convenience, we normalize so that
$c>0$
, where A is a self-adjoint matrix. For convenience, we normalize so that
![]() $c=1$
. If A is positive semi-definite, we would know that the zeros are on the negative real axis. Note that
$c=1$
. If A is positive semi-definite, we would know that the zeros are on the negative real axis. Note that
It is natural to consider the homogenized version of the class as the corresponding approximation theory provides more tools to work with. A natural homogeneous version of a determinantal representation is given by
where
![]() $A, B$
are positive semi-definite and sum to the identity. Note that such a function is naturally evaluated at matrix inputs by replacing the product with appropriate tensor products.
$A, B$
are positive semi-definite and sum to the identity. Note that such a function is naturally evaluated at matrix inputs by replacing the product with appropriate tensor products.
In [Reference Pascoe11], the author gave a natural log-convexification of the Laguerre–Pólya class by taking the radical of the Laguerre–Pólya class, by allowing limits of nth roots of functions in the Laguerre–Pólya class. Indeed, by taking radicals, the author in [Reference Pascoe11] showed that logarithms of the functions in this class are exactly (up to a minus sign) the ones with a so-called trace minimax property. These functions are interesting as they form a class of functions satisfying a trace inequality and they are automatically analytic. Taking the analogy with the theory of tracial von Neumann algebras, one naturally wants to consider the normalized trace instead of the trace, which via the tracial phrasing of our determinantal representation, we see corresponds to taking the geometric mean of the eigenvalues. This leads us to define the following class of functions. Define the degree one Laguerre–Pólya class in two variables to be the space of analytic functions which are uniform limits on compacta (i.e., limits in the compact-open topology) in
![]() $\{ (x,y) \in \mathbb {C}^2 : \mathrm {Re} \ x>0, \mathrm {Re} \ y >0 \}$
of functions of the form
$\{ (x,y) \in \mathbb {C}^2 : \mathrm {Re} \ x>0, \mathrm {Re} \ y >0 \}$
of functions of the form
![]() $e^{ \frac {1}{n}{\mathrm {tr}} \log (Ax+By)}$
, where A and B are positive semidefinite matrices summing to the identity of size n for some n. Note that if f is in this class, then
$e^{ \frac {1}{n}{\mathrm {tr}} \log (Ax+By)}$
, where A and B are positive semidefinite matrices summing to the identity of size n for some n. Note that if f is in this class, then
![]() $f(rx,ry)=rf(x,y)$
for
$f(rx,ry)=rf(x,y)$
for
![]() $r>0$
, which inspired the qualification “degree one.” Any limit in the compact-open topology of degree one Laguerre–Pólya class functions are of the form
$r>0$
, which inspired the qualification “degree one.” Any limit in the compact-open topology of degree one Laguerre–Pólya class functions are of the form
![]() $e^{\tau \log (Ax+By)}$
, where
$e^{\tau \log (Ax+By)}$
, where
![]() $A, B$
are positive semidefinite elements of some type
$A, B$
are positive semidefinite elements of some type
![]() $II_1$
von Neumann algebra satisfying
$II_1$
von Neumann algebra satisfying
![]() $A+B=I$
, and
$A+B=I$
, and
![]() $\tau $
is a normalized trace. We call this potentially larger class the apparent degree one Laguerre–Pólya class in two variables.
$\tau $
is a normalized trace. We call this potentially larger class the apparent degree one Laguerre–Pólya class in two variables.
We have the following proposition.
Proposition 1.1 The apparent degree one Laguerre–Pólya class in two variables equals the degree one Laguerre–Pólya class in two variables.
Proof Let A and
![]() $I-A$
be positive semidefinite elements of a
$I-A$
be positive semidefinite elements of a
![]() $II_1$
von Neumann algebra, and let
$II_1$
von Neumann algebra, and let
![]() $\tau $
be a normalized trace. The W*-algebra (or von Neumann algebra) generated by
$\tau $
be a normalized trace. The W*-algebra (or von Neumann algebra) generated by
![]() $A=A^*$
can be represented as
$A=A^*$
can be represented as
![]() $L^\infty ([0,1], \mu )$
, where
$L^\infty ([0,1], \mu )$
, where
![]() $\mu $
is a
$\mu $
is a
![]() $\sigma $
-finite probability measure on
$\sigma $
-finite probability measure on
![]() $[0,1]$
by the spectral theorem (see [Reference Conway3, Chapter 7]). The space
$[0,1]$
by the spectral theorem (see [Reference Conway3, Chapter 7]). The space
![]() $L^\infty ([0,1], \mu )$
forms an algebra of operators on the Hilbert space
$L^\infty ([0,1], \mu )$
forms an algebra of operators on the Hilbert space
![]() $L^2 ([0,1], \mu )$
, where each
$L^2 ([0,1], \mu )$
, where each
![]() $f\in L^\infty ([0,1], \mu )$
is identified with the multiplication operator
$f\in L^\infty ([0,1], \mu )$
is identified with the multiplication operator
![]() $\psi \mapsto f \psi $
with trace
$\psi \mapsto f \psi $
with trace
![]() $\tau (f) = \int _{[0,1]} f d\mu $
. Taking
$\tau (f) = \int _{[0,1]} f d\mu $
. Taking
![]() $M_n$
, the finite-dimensional subspace of
$M_n$
, the finite-dimensional subspace of
![]() $L^2 ([0,1], \mu )$
spanned by
$L^2 ([0,1], \mu )$
spanned by
![]() $1,x, \ldots , x^n$
, the eigenvalues of the restriction of multiplication by x (which represents A) to the subspace
$1,x, \ldots , x^n$
, the eigenvalues of the restriction of multiplication by x (which represents A) to the subspace
![]() $M_n$
has eigenvalues equal to the zeros of the nth orthogonal polynomial with respect to the measure
$M_n$
has eigenvalues equal to the zeros of the nth orthogonal polynomial with respect to the measure
![]() $\mu $
. These spectral measures
$\mu $
. These spectral measures
![]() $\mu _n$
representing the action of multiplication by x restricted to
$\mu _n$
representing the action of multiplication by x restricted to
![]() $M_n$
converge weakly to the measure
$M_n$
converge weakly to the measure
![]() $\mu $
(see [Reference Szegö15, Section 6.2]). This yields that the degree one Laguerre–Pólya class exhausts the apparent degree one Laguerre–Pólya class in two variables.
$\mu $
(see [Reference Szegö15, Section 6.2]). This yields that the degree one Laguerre–Pólya class exhausts the apparent degree one Laguerre–Pólya class in two variables.
Our goal is to establish the failure of such a correspondence in several variables for matrix inputs and in the scalar case give an equivalence with a relaxation of the Connes embedding problem to finite tracial approximation of the BMV polynomials, which we call the shuffle-word-embedding conjecture.
2 The Laguerre–Pólya class in several noncommuting variables
Let
![]() ${\mathbb K} \in \{ {\mathbb R}, {\mathbb C} \}$
, and consider the nc domain
${\mathbb K} \in \{ {\mathbb R}, {\mathbb C} \}$
, and consider the nc domain
 $$ \begin{align*}{\mathcal D} = \cup_{k \ge 1} {\mathcal D}_k,\ {\mathcal D}_k = \{ (X_1, \ldots, X_n) \in ({\mathbb K}^{k\times k})^n : \sum_{j=1}^n \| X_j \| < 1 \}.\end{align*} $$
$$ \begin{align*}{\mathcal D} = \cup_{k \ge 1} {\mathcal D}_k,\ {\mathcal D}_k = \{ (X_1, \ldots, X_n) \in ({\mathbb K}^{k\times k})^n : \sum_{j=1}^n \| X_j \| < 1 \}.\end{align*} $$
We let
![]() ${\mathcal F}$
be a real or complex von Neumann algebra with a faithful tracial state
${\mathcal F}$
be a real or complex von Neumann algebra with a faithful tracial state
![]() $\tau $
. On
$\tau $
. On
![]() $d\times d$
matrices over
$d\times d$
matrices over
![]() ${\mathbb K}$
we let
${\mathbb K}$
we let
![]() $\mathrm {Tr}$
denote the normalized trace; i.e.,
$\mathrm {Tr}$
denote the normalized trace; i.e.,
![]() $\mathrm {Tr}[ (m_{i,j})_{i,j=1}^d] = \frac {1}{d} \sum _{i=1}^d m_{ii}$
. On the (spatial) tensor product
$\mathrm {Tr}[ (m_{i,j})_{i,j=1}^d] = \frac {1}{d} \sum _{i=1}^d m_{ii}$
. On the (spatial) tensor product
![]() ${\mathcal F} \bar {\otimes } {\mathbb K}^{d\times d}$
, we introduce the product trace, which with a slight abuse of notation, will also be denoted by
${\mathcal F} \bar {\otimes } {\mathbb K}^{d\times d}$
, we introduce the product trace, which with a slight abuse of notation, will also be denoted by
![]() $\tau $
. In particular,
$\tau $
. In particular,
![]() $\tau (A\otimes M) = \tau (A) \mathrm {Tr}(M)$
. Let now
$\tau (A\otimes M) = \tau (A) \mathrm {Tr}(M)$
. Let now
![]() $A_1, \ldots , A_n \in {\mathcal F}$
be Hermitian (complex case) or symmetric (real case) contractions, and define the function
$A_1, \ldots , A_n \in {\mathcal F}$
be Hermitian (complex case) or symmetric (real case) contractions, and define the function
![]() $f_{(A_1, \ldots , A_n)}= f_A : {\mathcal D} \to {\mathbb K}$
via
$f_{(A_1, \ldots , A_n)}= f_A : {\mathcal D} \to {\mathbb K}$
via
where the logarithm may be defined via
![]() $\log (I- M) = -\sum _{m=1}^\infty \frac {M^m}{m}$
,
$\log (I- M) = -\sum _{m=1}^\infty \frac {M^m}{m}$
,
![]() $\| M\|<1$
.
$\| M\|<1$
.
It should be noted that the class introduced here is an affinized version of the Laguerre–Pólya class introduced in the introduction.
We have the following basic properties, that are also satisfied by the Fuglede–Kadison determinant.
Lemma 2.1
-
(i) For
 $X \in {\mathcal D}_k$
and
$X \in {\mathcal D}_k$
and
 $Y\in {\mathcal D}_l$
, we have
$Y\in {\mathcal D}_l$
, we have  $$ \begin{align*}f_A(X)^k f_A(Y)^l = f_A(X\oplus Y)^{k+l}.\end{align*} $$
$$ \begin{align*}f_A(X)^k f_A(Y)^l = f_A(X\oplus Y)^{k+l}.\end{align*} $$
-
(ii) For
 $U \in {\mathbb K}^{k\times k}$
unitary and
$U \in {\mathbb K}^{k\times k}$
unitary and
 $X\in {\mathcal D}_k$
, we have
$X\in {\mathcal D}_k$
, we have
 $f_A(UXU^*)=f_A(X)$
.
$f_A(UXU^*)=f_A(X)$
.
Proof Let
![]() $\mathrm {tr}$
denote the usual (not normalized) trace of a matrix. Note that for a
$\mathrm {tr}$
denote the usual (not normalized) trace of a matrix. Note that for a
![]() $k\times k$
matrix M, a
$k\times k$
matrix M, a
![]() $l \times l$
matrix N and
$l \times l$
matrix N and
![]() $B\in {\mathcal F}$
, we have that
$B\in {\mathcal F}$
, we have that
The lemma follows now easily.
2.1 Functions in this class encode tracial moments
Two words w and
![]() $\hat {w}$
are called cyclically equivalent if there exist words
$\hat {w}$
are called cyclically equivalent if there exist words
![]() $w_1$
and
$w_1$
and
![]() $w_2$
so that
$w_2$
so that
![]() $w=w_1w_2$
and
$w=w_1w_2$
and
![]() $\hat {w}=w_2w_1$
. We have the following lemma, which can also be deduced from [Reference Klep and Špenko10, Theorem 3.1: Spurnullstellensatz].
$\hat {w}=w_2w_1$
. We have the following lemma, which can also be deduced from [Reference Klep and Špenko10, Theorem 3.1: Spurnullstellensatz].
Lemma 2.2 Consider a word
![]() $w(X_1, \ldots , X_n)$
of length m in n letters
$w(X_1, \ldots , X_n)$
of length m in n letters
![]() $X_1, \ldots , X_n$
. then there exist
$X_1, \ldots , X_n$
. then there exist
![]() $m\times m$
matrices
$m\times m$
matrices
![]() $T_1, \ldots , T_n$
so that
$T_1, \ldots , T_n$
so that
and
for any word
![]() $\tilde {w}$
of length at most m that is not cyclically equivalent to w.
$\tilde {w}$
of length at most m that is not cyclically equivalent to w.
Proof Let the word w equal
![]() $w(X_1, \ldots , X_n) = X_{i_m} \dots X_{i_1}$
, where
$w(X_1, \ldots , X_n) = X_{i_m} \dots X_{i_1}$
, where
![]() $i_1, \ldots , i_m \in \{ 1, \ldots , n \}$
. Put
$i_1, \ldots , i_m \in \{ 1, \ldots , n \}$
. Put
![]() $a_0= \emptyset $
,
$a_0= \emptyset $
,
![]() $a_k = X_{i_k} \dots X_{i_1}$
,
$a_k = X_{i_k} \dots X_{i_1}$
,
![]() $k=1,\ldots , m$
. Let now
$k=1,\ldots , m$
. Let now
![]() $T_j=(t_{rs}^{(j)})_{r,s=0}^{m-1}$
,
$T_j=(t_{rs}^{(j)})_{r,s=0}^{m-1}$
,
![]() $j=1,\ldots , n$
, be defined via
$j=1,\ldots , n$
, be defined via
 $$ \begin{align*}t_{rs}^{(j)} =\left\{ \begin{matrix} 1, & \text{if} & X_j a_s = a_r, \cr 1, & \text{if} & r=0, s=m-1, X_j a_{m-1} = a_m, \cr 0, & \text{otherwise.} & \end{matrix} \right.\end{align*} $$
$$ \begin{align*}t_{rs}^{(j)} =\left\{ \begin{matrix} 1, & \text{if} & X_j a_s = a_r, \cr 1, & \text{if} & r=0, s=m-1, X_j a_{m-1} = a_m, \cr 0, & \text{otherwise.} & \end{matrix} \right.\end{align*} $$
Notice that
![]() $T_j$
only has nonzero entries in the diagonal
$T_j$
only has nonzero entries in the diagonal
![]() $\{(i,j): j-i=m-1 (\text {mod}\ m)\}$
, so that the product of k matrices
$\{(i,j): j-i=m-1 (\text {mod}\ m)\}$
, so that the product of k matrices
![]() $T_j$
only has nonzero entries in the diagonal
$T_j$
only has nonzero entries in the diagonal
![]() $\{(i,j): j-i=m-k (\text {mod}\ m)\}$
. Thus for any word
$\{(i,j): j-i=m-k (\text {mod}\ m)\}$
. Thus for any word
![]() $\tilde {w}$
of length less than m, we have that
$\tilde {w}$
of length less than m, we have that
![]() $\tilde {w}(T_1, \ldots , T_n)$
has zeros on the main diagonal, and thus its trace equals 0. When
$\tilde {w}(T_1, \ldots , T_n)$
has zeros on the main diagonal, and thus its trace equals 0. When
![]() $\tilde {w}$
has length m it is not hard to see that
$\tilde {w}$
has length m it is not hard to see that
![]() $\tilde {w}(T_1, \ldots , T_n)$
has 1’s on the diagonal if and only if
$\tilde {w}(T_1, \ldots , T_n)$
has 1’s on the diagonal if and only if
![]() $\tilde {w}$
is cyclically equivalent to w, and otherwise there will only be zeros on the diagonal. It may be helpful to think of the operators
$\tilde {w}$
is cyclically equivalent to w, and otherwise there will only be zeros on the diagonal. It may be helpful to think of the operators
![]() $T_1,\ldots , T_n$
also in the following way.
$T_1,\ldots , T_n$
also in the following way.
Let us denote the words that are cyclically equivalent to w as follows:
![]() $w_0 = w =a_0 w, w_1=X_{i_1}X_{i_m} \dots X_{i_2}=:a_1 b_1, \ldots , w_{m-1} = X_{i_{m-1}} \dots X_{i_1} X_{i_m} =: a_{m-1}b_{m-1}.$
In this setting, we have that
$w_0 = w =a_0 w, w_1=X_{i_1}X_{i_m} \dots X_{i_2}=:a_1 b_1, \ldots , w_{m-1} = X_{i_{m-1}} \dots X_{i_1} X_{i_m} =: a_{m-1}b_{m-1}.$
In this setting, we have that
![]() $ t_{rs}^{(j)} =1$
if and only if
$ t_{rs}^{(j)} =1$
if and only if
![]() $r-s=1 (\text {mod}\ m)$
,
$r-s=1 (\text {mod}\ m)$
,
![]() $X_j$
is the last letter of
$X_j$
is the last letter of
![]() $w_s$
and
$w_s$
and
![]() $w_r$
is obtained from
$w_r$
is obtained from
![]() $w_s$
by moving
$w_s$
by moving
![]() $X_j$
to the front. In this interpretation, the product
$X_j$
to the front. In this interpretation, the product
![]() $T_jT_k$
has a 1 in position
$T_jT_k$
has a 1 in position
![]() $(r,s)$
if and only if
$(r,s)$
if and only if
![]() $r-s=2 (\text {mod}\ m)$
, and
$r-s=2 (\text {mod}\ m)$
, and
![]() $w_r$
is obtained from
$w_r$
is obtained from
![]() $w_s$
by moving
$w_s$
by moving
![]() $X_k$
to the front and subsequently
$X_k$
to the front and subsequently
![]() $X_j$
to the front. Similarly, any product of
$X_j$
to the front. Similarly, any product of
![]() $T_j$
’s can be interpreted.
$T_j$
’s can be interpreted.
As an example, consider the word
![]() $w=X_1X_2X_1X_2$
. Then the matrices
$w=X_1X_2X_1X_2$
. Then the matrices
![]() $T_1$
and
$T_1$
and
![]() $T_2$
in the proof of Lemma 2.2 are
$T_2$
in the proof of Lemma 2.2 are
 $$ \begin{align*}T_1=\begin{pmatrix} 0 & 0 & 0 & 1 \cr 0 & 0 & 0 & 0 \cr 0 & 1 & 0 & 0 \cr 0 & 0 & 0 & 0 \end{pmatrix}, T_2=\begin{pmatrix} 0 & 0 & 0 & 0 \cr 1 & 0 & 0 & 0 \cr 0 & 0 & 0 & 0 \cr 0 & 0 & 1 & 0 \end{pmatrix}.\end{align*} $$
$$ \begin{align*}T_1=\begin{pmatrix} 0 & 0 & 0 & 1 \cr 0 & 0 & 0 & 0 \cr 0 & 1 & 0 & 0 \cr 0 & 0 & 0 & 0 \end{pmatrix}, T_2=\begin{pmatrix} 0 & 0 & 0 & 0 \cr 1 & 0 & 0 & 0 \cr 0 & 0 & 0 & 0 \cr 0 & 0 & 1 & 0 \end{pmatrix}.\end{align*} $$
Now
 $$ \begin{align*}T_1T_2T_1T_2 =\begin{pmatrix} 1 & 0 & 0 & 0 \cr 0 & 0 & 0 & 0 \cr 0 & 0 & 1 & 0 \cr 0 & 0 & 0 & 0 \end{pmatrix}.\end{align*} $$
$$ \begin{align*}T_1T_2T_1T_2 =\begin{pmatrix} 1 & 0 & 0 & 0 \cr 0 & 0 & 0 & 0 \cr 0 & 0 & 1 & 0 \cr 0 & 0 & 0 & 0 \end{pmatrix}.\end{align*} $$
We now describe our fundamental lemma which relates the equality of tracial moments to the equality of our associated functions.
Lemma 2.3 Let
![]() ${\mathcal F}$
and
${\mathcal F}$
and
![]() ${\mathcal G}$
be complex von Neumann algebras with faithful tracial states
${\mathcal G}$
be complex von Neumann algebras with faithful tracial states
![]() $\tau $
and
$\tau $
and
![]() $\hat \tau $
, respectively. Let
$\hat \tau $
, respectively. Let
![]() $A_1, \ldots , A_n \in {\mathcal F}$
and
$A_1, \ldots , A_n \in {\mathcal F}$
and
![]() $B_1, \ldots , B_n \in {\mathcal G}$
be Hermitian contractions. Then
$B_1, \ldots , B_n \in {\mathcal G}$
be Hermitian contractions. Then
![]() $f_A(X) = f_B(X)$
, for all
$f_A(X) = f_B(X)$
, for all
![]() $X \in {\mathcal D}$
, if and only if
$X \in {\mathcal D}$
, if and only if
![]() $\tau (p(A)) = \hat \tau (p(B))$
for every noncommutative polynomial
$\tau (p(A)) = \hat \tau (p(B))$
for every noncommutative polynomial
![]() $p.$
$p.$
The same result also holds when
![]() ${\mathcal F}$
and
${\mathcal F}$
and
![]() ${\mathcal G}$
are real von Neumann algebras and
${\mathcal G}$
are real von Neumann algebras and
![]() $A_i$
and
$A_i$
and
![]() $B_i$
are real symmetric contractions.
$B_i$
are real symmetric contractions.
Proof Let us write
![]() $M(X) = \sum _{i=1}^n A_i \otimes X_i$
, where
$M(X) = \sum _{i=1}^n A_i \otimes X_i$
, where
![]() $X \in {\mathcal D}$
. We now have that
$X \in {\mathcal D}$
. We now have that
 $$ \begin{align*}f_A(X)= e^{-\tau(\sum_{m=1}^\infty \frac{M(X)^m}{m})} = 1-\tau(\sum_{m=1}^\infty \frac{M(X)^m}{m}) + \frac{1}{2!}(\tau(\sum_{m=1}^\infty \frac{M(X)^m}{m}))^2 - \dots .\end{align*} $$
$$ \begin{align*}f_A(X)= e^{-\tau(\sum_{m=1}^\infty \frac{M(X)^m}{m})} = 1-\tau(\sum_{m=1}^\infty \frac{M(X)^m}{m}) + \frac{1}{2!}(\tau(\sum_{m=1}^\infty \frac{M(X)^m}{m}))^2 - \dots .\end{align*} $$
Extracting the degree k term, we obtain
 $$ \begin{align*}-\tau(\frac{M(X)^k}{k}) + \frac{1}{2!} \sum_{j=1}^k {k\choose j} \tau(\frac{M(X)^j}{j}) \tau(\frac{M(X)^{k-j}}{k-j})- \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \end{align*} $$
$$ \begin{align*}-\tau(\frac{M(X)^k}{k}) + \frac{1}{2!} \sum_{j=1}^k {k\choose j} \tau(\frac{M(X)^j}{j}) \tau(\frac{M(X)^{k-j}}{k-j})- \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \end{align*} $$
 $$ \begin{align*}\ \ \ \ \ \ \ \ \ \ \ \frac{1}{3!} \sum_{j_1+j_2+j_3=k, j_i\ge 1} \begin{pmatrix} k \cr j_1,j_2,j_3 \end{pmatrix} \tau(\frac{M(X)^{j_1}}{j_1}) \tau(\frac{M(X)^{j_2}}{j_2})\tau(\frac{M(X)^{j_3}}{j_3}) + \dots .\end{align*} $$
$$ \begin{align*}\ \ \ \ \ \ \ \ \ \ \ \frac{1}{3!} \sum_{j_1+j_2+j_3=k, j_i\ge 1} \begin{pmatrix} k \cr j_1,j_2,j_3 \end{pmatrix} \tau(\frac{M(X)^{j_1}}{j_1}) \tau(\frac{M(X)^{j_2}}{j_2})\tau(\frac{M(X)^{j_3}}{j_3}) + \dots .\end{align*} $$
Let now
![]() $U=(u_{ij})_{i,j=1}^k$
be the
$U=(u_{ij})_{i,j=1}^k$
be the
![]() $k\times k$
unitary circulant with
$k\times k$
unitary circulant with
![]() $u_{ij} =1$
when
$u_{ij} =1$
when
![]() $j=i+1\mod k$
, and
$j=i+1\mod k$
, and
![]() $0$
elsewhere. Then
$0$
elsewhere. Then
![]() $\mathrm {Tr}\ U^j $
equals 1 when k divides j, and 0 otherwise. If we now let
$\mathrm {Tr}\ U^j $
equals 1 when k divides j, and 0 otherwise. If we now let
![]() $x_i = U\otimes X_i$
,
$x_i = U\otimes X_i$
,
![]() $i=1,\ldots n$
, we have that
$i=1,\ldots n$
, we have that
![]() $x=(x_1,\ldots , x_n)\in {\mathcal D}$
, and the degree k term in
$x=(x_1,\ldots , x_n)\in {\mathcal D}$
, and the degree k term in
![]() $f_A(x)$
now equals
$f_A(x)$
now equals
![]() $ -\tau (\frac {M(X)^k}{k})$
. Indeed, whenever
$ -\tau (\frac {M(X)^k}{k})$
. Indeed, whenever
![]() $1\le j <k$
, we have that
$1\le j <k$
, we have that
![]() $ \tau (\frac {M(X)^j}{j})=0$
since
$ \tau (\frac {M(X)^j}{j})=0$
since
![]() $\mathrm {Tr}\ U^j =0$
. Next, notice that
$\mathrm {Tr}\ U^j =0$
. Next, notice that
![]() $M(X)^k= \sum _w w(A_1, \ldots , A_n) \otimes w(X_1,\dots , X_n)$
, where the sum is taken over all words of length k. Since the monomials are linearly independent by Lemma 2.2, the result follows.
$M(X)^k= \sum _w w(A_1, \ldots , A_n) \otimes w(X_1,\dots , X_n)$
, where the sum is taken over all words of length k. Since the monomials are linearly independent by Lemma 2.2, the result follows.
2.2 Due to the Connes embedding problem, the apparent class is bigger
The Klep–Schweighofer formulation of the now refuted Connes embedding conjecture states that for any tuple of contractive self-adjoint operators
![]() $A_1, \ldots , A_n$
in a type
$A_1, \ldots , A_n$
in a type
![]() $II_1$
von Neumann algebra with trace
$II_1$
von Neumann algebra with trace
![]() $\tau $
and any matrix of polynomials
$\tau $
and any matrix of polynomials
![]() $m,$
for any
$m,$
for any
![]() $\varepsilon>0,$
there are matrices
$\varepsilon>0,$
there are matrices
![]() $B_1, \ldots , B_n$
such that
$B_1, \ldots , B_n$
such that
Here,
![]() $\mathrm {Tr}$
denotes the normalized trace. The Connes embedding conjecture fails [Reference Ji, Natarajan, Vidick, Wright and Yuen8]. We use the above formulation in showing next that the apparent class is larger.
$\mathrm {Tr}$
denotes the normalized trace. The Connes embedding conjecture fails [Reference Ji, Natarajan, Vidick, Wright and Yuen8]. We use the above formulation in showing next that the apparent class is larger.
Proposition 2.1 There exists an
![]() $\delta>0$
and a choice of
$\delta>0$
and a choice of
![]() $f_A$
so that for any
$f_A$
so that for any
![]() $f_B$
, where B is a tuple of matrices, we have that
$f_B$
, where B is a tuple of matrices, we have that
![]() $ \| \mathrm {coeff} (f_A - f_B) \|_\infty \ge \delta .$
That is, there exists an n so that the apparent degree one Laguerre–Pólya class in n variables is strictly larger than the degree one Laguerre–Pólya class in n variables.
$ \| \mathrm {coeff} (f_A - f_B) \|_\infty \ge \delta .$
That is, there exists an n so that the apparent degree one Laguerre–Pólya class in n variables is strictly larger than the degree one Laguerre–Pólya class in n variables.
Proof Due to the failure of the Connes embedding conjecture [Reference Ji, Natarajan, Vidick, Wright and Yuen8], it follows from [Reference Klep and Schweighofer9, Proposition 3.17] (complex case) and [Reference Burgdorf, Dykema, Klep and Schweighofer2, Proposition 3.2] (real case) that there exists a
![]() $\mathrm {II}_1$
factor
$\mathrm {II}_1$
factor
![]() ${\mathcal F}$
with a faithful tracial state
${\mathcal F}$
with a faithful tracial state
![]() $\tau $
, an
$\tau $
, an
![]() $\epsilon>0$
,
$\epsilon>0$
,
![]() $n,k\in {\mathbb N}$
, and self-adjoint/symmetric contractions
$n,k\in {\mathbb N}$
, and self-adjoint/symmetric contractions
![]() $A_1, \ldots , A_n$
so that for all
$A_1, \ldots , A_n$
so that for all
![]() $s\in {\mathbb N}$
and self-adjoint/symmetric contractions
$s\in {\mathbb N}$
and self-adjoint/symmetric contractions
![]() $B_1,\ldots , B_n \in {\mathbb K}^{s\times s}$
there exists a word
$B_1,\ldots , B_n \in {\mathbb K}^{s\times s}$
there exists a word
![]() $w_0$
in n letters of length k so that
$w_0$
in n letters of length k so that
So by Lemma 2.3, we are done.
3 The scalar/commutative case
3.1 BMV polynomials, and the shuffle-word-embedding conjecture
The BMV polynomials [Reference Bessis, Moussa and Villani1] are the coefficients of
![]() $t^\omega $
in
$t^\omega $
in
![]() $(t_1 A_1+\dots + t_nA_n)^k$
, where
$(t_1 A_1+\dots + t_nA_n)^k$
, where
![]() $A_i$
are our noncommuting indeterminants and
$A_i$
are our noncommuting indeterminants and
![]() $t_i$
are commuting with everything. For example, for
$t_i$
are commuting with everything. For example, for
![]() $k=n=2 $
, we see
$k=n=2 $
, we see
![]() $A^2, AB+BA, B^2.$
Stahl [Reference Stahl13] showed that such polynomials in two variables always have positive trace on tuples of positive semidefinite matrices. We introduce now the following conjecture.
$A^2, AB+BA, B^2.$
Stahl [Reference Stahl13] showed that such polynomials in two variables always have positive trace on tuples of positive semidefinite matrices. We introduce now the following conjecture.
The shuffle-word-embedding conjecture: For any tuple of contractive self-adjoint operators
![]() $A_1, \ldots , A_k$
in a type
$A_1, \ldots , A_k$
in a type
![]() $II_1$
von Neumann algebra with trace
$II_1$
von Neumann algebra with trace
![]() $\tau $
and any matrix of BMV polynomials
$\tau $
and any matrix of BMV polynomials
![]() $m,$
for any
$m,$
for any
![]() $\epsilon>0$
there are matrices
$\epsilon>0$
there are matrices
![]() $B_1, \ldots , B_n$
such that
$B_1, \ldots , B_n$
such that
Note that the shuffle-word-embedding conjecture significantly strengthens Stahl’s result in these sense that it would imply that it held for inputs in tracial von Neumann algebras. (Eremenko’s version [Reference Eremenko4] of Stahl’s proof [Reference Stahl13] kind of relies on finitary aspects of complex analysis, and generalization via a proof along those lines appears intractable.)
The shuffle-word-embedding conjecture would imply that Stahl’s theorem holds for every
![]() $II_1$
factor, that is, for every BMV polynomial
$II_1$
factor, that is, for every BMV polynomial
![]() $p, \tau (p(A))\geq 0$
if
$p, \tau (p(A))\geq 0$
if
![]() $A_1, \ldots , A_n$
is a tuple of positive semidefinite operators in a
$A_1, \ldots , A_n$
is a tuple of positive semidefinite operators in a
![]() $II_1$
factor.
$II_1$
factor.
Proposition 3.1 The apparent degree one Laguerre–Pólya is the closure of the degree one Laguerre–Pólya class in the compact-open topology if and only if the shuffle-word-embedding conjecture is true.
Proof We will show that
![]() $f_A (x_1,\ldots , x_n) = f_B(x_1,\ldots , x_n)$
, for all scalars
$f_A (x_1,\ldots , x_n) = f_B(x_1,\ldots , x_n)$
, for all scalars
![]() $x_j$
with
$x_j$
with
![]() $\sum _{i=1}^n |x_j|< 1$
, if and only if
$\sum _{i=1}^n |x_j|< 1$
, if and only if
![]() $\tau (p(A)) = \tau (p(B))$
for every BMV polynomial p, and thus we would be done. Note that instead of scalars
$\tau (p(A)) = \tau (p(B))$
for every BMV polynomial p, and thus we would be done. Note that instead of scalars
![]() $x_j$
, we may also use simultaneously diagonalizable
$x_j$
, we may also use simultaneously diagonalizable
![]() $x_j$
’s.
$x_j$
’s.
Proceeding in a similar way as in the proof of Lemma 2.3, let
![]() $U=(u_{ij})_{i,j=1}^k$
be the
$U=(u_{ij})_{i,j=1}^k$
be the
![]() $k\times k$
unitary circulant with
$k\times k$
unitary circulant with
![]() $u_{ij} =1$
when
$u_{ij} =1$
when
![]() $j=i+1\ \mod k$
, and
$j=i+1\ \mod k$
, and
![]() $0$
elsewhere. Then
$0$
elsewhere. Then
![]() $\mathrm {Tr}\ U^j $
equals 1 when k divides j, and 0 otherwise. If we now let
$\mathrm {Tr}\ U^j $
equals 1 when k divides j, and 0 otherwise. If we now let
![]() $X_i = x_iU$
,
$X_i = x_iU$
,
![]() $i=1,\ldots n$
, we have that
$i=1,\ldots n$
, we have that
![]() $X=(X_1,\ldots , X_n)\in {\mathcal D}$
whenever
$X=(X_1,\ldots , X_n)\in {\mathcal D}$
whenever
![]() $\sum _{i=1}^n |x_j|< 1$
, and the degree k term in
$\sum _{i=1}^n |x_j|< 1$
, and the degree k term in
![]() $f_A(X)$
now equals
$f_A(X)$
now equals
![]() $ -\tau (\frac {M(X)^k}{k})$
. Indeed, whenever
$ -\tau (\frac {M(X)^k}{k})$
. Indeed, whenever
![]() $1\le j <k$
we have that
$1\le j <k$
we have that
![]() $ \tau (\frac {M(X)^j}{j})=0$
since
$ \tau (\frac {M(X)^j}{j})=0$
since
![]() $\mathrm {Tr}\ U^j =0$
. Next, notice that
$\mathrm {Tr}\ U^j =0$
. Next, notice that
![]() $M(X)^k= \sum _w w(A_1, \ldots , A_n) \otimes w(X_1,\dots , X_n)$
, where the sum is taken over all words of length k. On scalar inputs, this reduces to
$M(X)^k= \sum _w w(A_1, \ldots , A_n) \otimes w(X_1,\dots , X_n)$
, where the sum is taken over all words of length k. On scalar inputs, this reduces to
![]() $(t_1A_1+\dots +t_n A_n)^k,$
so we are done by linear independence of monomials. This linear independence can be established in a similar way as in Lemma 2.2, where now we choose
$(t_1A_1+\dots +t_n A_n)^k,$
so we are done by linear independence of monomials. This linear independence can be established in a similar way as in Lemma 2.2, where now we choose
![]() $C_k$
the
$C_k$
the
![]() $k\times k$
circular shift, and we take operators T of the form
$k\times k$
circular shift, and we take operators T of the form
![]() $I\otimes \cdots \otimes I \otimes C_k \otimes I \otimes \cdots \otimes I$
.
$I\otimes \cdots \otimes I \otimes C_k \otimes I \otimes \cdots \otimes I$
.
4 Summary and the homogenized version
A homogeneous real-stable polynomial with no definite roots in three variables is of the form
where
![]() $A, B, C$
are positive semi-definite and
$A, B, C$
are positive semi-definite and
![]() $A+B+C$
is the identity. Thus, in the one or two variable degree one Laguerre–Pólya class, we can view the Laguerre–Pólya class as the product of the eigenvalues of the image of some matrix valued unital positive map on
$A+B+C$
is the identity. Thus, in the one or two variable degree one Laguerre–Pólya class, we can view the Laguerre–Pólya class as the product of the eigenvalues of the image of some matrix valued unital positive map on
![]() $\mathbb {C}^{d \times d}.$
(See Hanselka’s treatment [Reference Hanselka6] of the Helton–Vinnikov theorem [Reference Helton and Vinnikov7] for the most optimal version and [Reference Plaumann and Vinzant12] and [Reference Grinshpan, Kaliuzhnyi-Verbovetskyi, Vinnikov and Woerdeman5] for elementary approaches of determinantal representations of homogeneous hyperbolic polynomials in three variables/real zero polynomials in two variables.) Replacing the product with the geometric mean corresponds to replacing the trace with a normalized trace, which we will generally do, as it will convexify certain problems.
$\mathbb {C}^{d \times d}.$
(See Hanselka’s treatment [Reference Hanselka6] of the Helton–Vinnikov theorem [Reference Helton and Vinnikov7] for the most optimal version and [Reference Plaumann and Vinzant12] and [Reference Grinshpan, Kaliuzhnyi-Verbovetskyi, Vinnikov and Woerdeman5] for elementary approaches of determinantal representations of homogeneous hyperbolic polynomials in three variables/real zero polynomials in two variables.) Replacing the product with the geometric mean corresponds to replacing the trace with a normalized trace, which we will generally do, as it will convexify certain problems.
Let
![]() $\Omega $
be a class of tuples of positive definite operators in various tracial von Neumann algebras. We define the degree one Laguerre–Pólya class on
$\Omega $
be a class of tuples of positive definite operators in various tracial von Neumann algebras. We define the degree one Laguerre–Pólya class on
![]() $\Omega $
to be the closure of maps of the form
$\Omega $
to be the closure of maps of the form
![]() $e^{\tau (\log L(x))}$
, where L is some matrix-valued completely positive map and
$e^{\tau (\log L(x))}$
, where L is some matrix-valued completely positive map and
![]() $\tau $
denotes the normalized trace with respect to the topology on compact subsets (in the norm topology) of
$\tau $
denotes the normalized trace with respect to the topology on compact subsets (in the norm topology) of
![]() $\Omega .$
Call the apparent degree one Laguerre–Pólya class on
$\Omega .$
Call the apparent degree one Laguerre–Pólya class on
![]() $\Omega $
the set of maps of the form
$\Omega $
the set of maps of the form
![]() $e^{\tau (\log L(x))}$
, where L is a unital completely positive map into some
$e^{\tau (\log L(x))}$
, where L is a unital completely positive map into some
![]() $II_1$
factor. Weak compactness of unital completely positive maps gives that such a class is a normal family.
$II_1$
factor. Weak compactness of unital completely positive maps gives that such a class is a normal family.
Let
![]() $\mathbb {P}^d$
denote the class of all d-tuples of positive operators from a tracial von Neumann algebra, running through all von Neumann algebras. Approximation theory fails there, essentially due to the failure of Connes embedding conjecture.
$\mathbb {P}^d$
denote the class of all d-tuples of positive operators from a tracial von Neumann algebra, running through all von Neumann algebras. Approximation theory fails there, essentially due to the failure of Connes embedding conjecture.
Theorem 4.1 The degree one Laguerre–Pólya class on
![]() $\mathbb {P}^d$
is strictly smaller than the apparent one when d is large enough.
$\mathbb {P}^d$
is strictly smaller than the apparent one when d is large enough.
Approximation theory will be related to our shuffle-word-embedding conjecture.
Theorem 4.2 The degree one Laguerre–Pólya class on
![]() $(\mathbb {R}^+)^d$
equals apparent one if and only if the shuffle-word-embedding conjecture is true.
$(\mathbb {R}^+)^d$
equals apparent one if and only if the shuffle-word-embedding conjecture is true.
Acknowledgment
We thank the referees for their careful reading of our manuscript.