Climate change: reshaping mortality differences within the United Kingdom?

Abstract

Older people are higher contributors to mortality excess and most sensitive to environmental influences, e.g. temperature. As the population ages, variability in temperature is liable to impact a large proportion of life insurance or pension policies in a portfolio. Climate change is projected to significantly affect future mean temperatures. Moreover, future changes in mean temperature are estimated to vary across different regions of the United Kingdom. Accordingly, the present paper investigates the potential impact of future mean temperature changes on older-age mortality in England & Wales and Scotland. The corresponding effect on older-age mortality differences between England & Wales and Scotland is also investigated.

1. Introduction

Mortality is an unambiguous measure of health. Rapid improvement in mortality has led to a burgeoning older population in the United Kingdom, with over 65s representing, 17.8% of the total population as of mid-2015. The ONS ¹ reports that since mid-2005, this age-group has grown by 21%. However, mortality improvements vary substantially across regions. Relative to England & Wales, mortality rates in Scotland (McCartney et al., 2015) were 12% higher in 1981, increasing to 15% higher in 2001, and socio-economic disparity (Wilkinson et al., 2004; McCartney et al., 2015) is increasingly less able to account for regional mortality differences.

Another determinant of regional health and mortality differences relate to environmental influences temperature (a thermal measurement of climate change). There is a sizeable body of evidence that cites clear seasonal patterns in incidence of major causes of death, e.g. coronary heart disease (Fares, 2013); often attributing a temperature association, although the detailed biological mechanisms of this influence are not fully understood. Many studies (Bull & Morton, 1978; Enquselassie et al., 1993) comment on a parabolic U-shaped relationship between temperature and mortality; mortality being lowest between [15°C, 20°C] and higher on either side of this optimal range. Patterns of increasing mortality effects with age have been observed under both acute heat and cold events (Poumadere et al., 2005; Chung et al., 2015). Unsurprisingly, with climate change has come increasing awareness of potential health and mortality risks associated with temperature variability in the general population, particularly at older ages. Thus, interest for this paper lies in the impact of mean temperature on older-age mortality and on regional mortality differentials in older-age mortality.

UK Climate Projections (Murphy et al., 2009) forecast temperature to change, relative to standard normals, by between [0.9°C, 5.0°C] in England & Wales and between [0.7°C, 4.3°C] in Scotland by 2050. Regional temperature disparities are set to widen and it is important to understand how this may impact on relative differences in mortality by region in the future. A common assumption is that warming temperatures augur well for reductions in mortality. However, projections for England & Wales present a scenario whereunder mean temperatures will exceed the optimal range by 2050. Additionally, recent research (Overland et al., 2016) suggests that global warming may lead to an intensification of the effects of the jet stream, causing extreme cold weather in the United Kingdom and United States. Consequently, climate change is a long-term challenge and potential risks presented by climatological hazards is an important consideration, given a transitioning climate with an elevated propensity for acute weather events.

Furthermore, the contract period for a typical life insurance or pension policy is sufficiently long for climate change to have a potential impact. Empirical evidence (Poumadere et al., 2005; Kovats & Kristie, 2006; Jenkins et al., 2009) shows that older people are most severely impacted by acute weather hazards and are higher contributors to mortality excess. Therefore, temperature variability is a risk factor liable to impact a large number of policies in a portfolio. Such considerations can inform product design and the level of risk management undertaken by insurers. Accordingly, the objective of the present analysis is to model the impact of mean temperature on mortality at older ages in England & Wales and Scotland, and to investigate the impact of possible future temperatures on regional mortality differences.

The present paper proceeds as follows. Section 2 describes the data sources and reports summary information. Section 3 provides the modelling framework for present analysis and describes model results. Section 4 presents the impact to regional mortality differences under future temperature scenarios. Section 5 reviews the main conclusions and important caveats to the present analysis.

2. Data

2.1. Mortality Data

Population estimates of England & Wales and Scotland are sourced from The Human Mortality Database (Wilmoth & Shkolnikov, 2008) and refer to (civilian) population size, by single year of age, on 1 January each year. Monthly population death data for the period 1974–2014 was made available by the National Records of Scotland (NRS). The Office of National Statistics (ONS) supplied corresponding data for the period 1993–2014 in respect of England & Wales. Death data are classified according to year, month, sex, and single year of age (from 60 to 95 years). This paper models older-age mortality variation over decadal time intervals, that is, 1995–2004 and 2005–2014 respectively. “Over 75s” represent the group that tends to be jointly and severely impacted by acute weather developments (Jenkins et al., 2009). On this basis, older-age mortality is investigated with respect to ages 75–90 years.

In this age range, female population estimates in England & Wales and Scotland are very consistent over the whole period of investigation, growing by 242,000 approx. (or 0.5% per annum) and 31,000 approx. (or 0.7% per annum), respectively. Correspondingly, in this age range, male population estimates in England & Wales and Scotland exhibit growth in population size of 611,000 approx. (or 2.0% per annum) and 60,000 approx. (or 2.3% per annum), respectively.

2.2. Temperature Data

The central England temperature (CET) data series (Parker et al., 1992) is produced and maintained by the Met Office Hadley Centre. It constitutes the longest monthly series in the world, with records beginning from 1659; it is widely used as a measure of thermal conditions representative of a roughly triangular area of the United Kingdom enclosed by Lancashire, London, and Bristol. Here, monthly mean temperature data from CET dataset are used to analyse the contribution of temperature on older-age mortality trends in England & Wales.

Based on paper by Jones & Lister (2004), for “mainland” Scotland (SMT), monthly data recorded by selection of long-running historic weather stations are used to construct a corresponding monthly mean temperature time series; data from island stations (Lerwick and Stornoway) are ignored for purposes of variance reduction and comparability with neighbouring site (i.e. CET). The resulting temperature data are used to analyse its role in older-age mortality trends of Scotland. Climatological conditions in Scotland do not differ drastically from other regions in the United Kingdom. However, Scotland tends to be cloudier, wetter, windier and average temperatures are lower relative to CET.

The United Kingdom Climate Impacts Program’s UK Climate Projections (so-called UKCP09 (Murphy et al., 2009)), developed in 2009, is the leading source of climate change information for the whole of the United Kingdom. Using sophisticated global climate models, UKCP09 projections provide probabilistic representations of monthly, seasonal or annual changes in a number of climate variables relative to latest standard normals. ² The present analysis uses UKCP09 scenarios of (summer and winter) mean temperature change, up to 2050, to investigate possible impact of future temperature change on relative mortality between England & Wales and Scotland.

Subsequent sections model the temperature–mortality relationship in England & Wales and Scotland, respectively. Relative impact of possible future temperatures on this relationship in each region is assessed. In this context, it is notable that all regions of the United Kingdom have experienced an increase in mean temperatures between 1961 and 2006 annually and for all seasons (Jenkins et al., 2009). Increases in annual average temperature, relative to standard normals, are typically between 1.0°C and 1.7°C, tending to be largest in the south and east of England and smallest in Scotland (Jenkins, 2009).

Figure 1a highlights rising temperatures, on average, in both CET and SMT, relative to corresponding standard normals. It can also be seen that historical temperature disparity between regions is subject to change. Figure 1b compares disparity in mean monthly temperatures between England & Wales and Scotland over time. Generally, regional disparity in mean monthly temperature is higher in 1995–2014 relative to standard normal period, due to CET experiencing, on average, larger temperature increases than SMT. Table 1 evidences an increase in incidence of acute heat ³ and cold ⁴ events in CET relative to expected, based on standard normals period. The timing of acute events supports evidence of warming and of some alteration to traditional seasonal timings.

Figure 1 Comparative changes in mean temperature between CET and SMT, decomposed by month

Table 1 Incidence of Acute Heat and Cold Events in CET by Quinquennial Periods 1995–2014

3. Modelling Impact of Temperature on Current Mortality

In this section, generalised additive models (GAMs) (Hastie & Tibshirani, 1990; Wood, 2006) are used to model the impact of temperature on mortality in England & Wales and Scotland over the periods 1995–2004, 2005–2014, respectively. GAMs are widely used in exploratory data analysis as an effective means of capturing more subtle non-linear patterns in data. GAMs extend the power of conventional regression techniques, by fitting non-parametric functions to estimate relationships between the response variable and explanatory variables, as necessary. In particular, the response variable is assumed to be affected by the explanatory variables through additive unspecified smooth functions and, the underlying probability distribution for the data can be any distribution from the exponential family. Therefore, in time-series studies of pollution/temperature-related mortality, GAMs are a widely applied method (Schwartz, 1994; Schwartz, 2000; Zanobetti et al., 2000; Pattenden et al., 2003; Cheng et al., 2014). When the response variable represents counts (e.g. number of deaths), as is the case here, Possion GAMs (with log link) are well suited to examining the effects of various explanatory variables on mortality rates. With R (R Core Team, 2015) statistical software and implementation in R package mgcv, the present analysis is conducted using an over-dispersed Poisson GAM model.

The model is fit separately by gender (i.e. male|female), region (i.e. England & Wales|Scotland) and decadal period (i.e. 1995–2004|2005–2014), as follows:

(1) $$\eqalignno{ \log \left( {m_{{ijkl}} } \right){\equals}& \beta _{0} {\plus}s_{1} (Age_{i} ){\plus}s_{2} \left( {{\rm Mean\; monthly \ temperature}_{j} } \right) \cr & {\plus}s_{3} \left( {{\rm Month}_{k} } \right){\plus}s_{4} \left( {{\rm Year}_{l} } \right){\plus}\log \left( {[{\rm Population}_{{il}} ]} \right) $$

where ${\rm Deaths}_{{ijkl}} \,\sim\,{\rm Poisson}\left( {E_{{il}}^{c} m_{{ijkl}} } \right)$ , population estimates on 1 January are used to approximate central exposed to risk and s _i are smooth functions implemented using cubic regression splines.

As previously noted, the model is fit to ages 75–90 years. The inclusion of explanatory factors, apart from mean temperature, serves to ensure that deviance in mortality is not confounded by other factors/proxies. Explanatory variable Month is a marker for seasonality, i.e. the presence of common characteristics in months that permit grouping into distinguishable seasons. To date, mortality has been higher in winter ⁵ months due mainly to prevalence of circulatory and respiratory diseases (Wilkinson et al., 2004). Explanatory variable Year captures general improvements in mortality over time.

For the limited age range and time periods considered, interactions between explanatory variables are not included in the model. This results in a simple, easily interpretable model suitable for an initial investigation into the potential temperature-related effects on older-age mortality. Further, cubic regression splines are used in the primary model because they are computationally simplest and have sufficient flexibility for most purposes. Results are presented in proceeding (sub)sections as follows:

• ∙ Model results outlining effects of explanatory variables on male mortality, compared on a regional basis

• ∙ Model results outlining effects of explanatory variables on female mortality, compared on a regional basis

• ∙ Expected impact on regional mortality variation under projected temperature scenarios, by gender

3.1. Model Results – Males

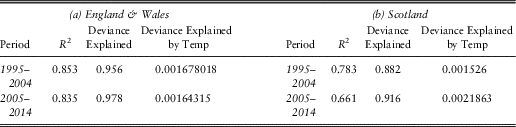
Model results confirm that explanatory variables included in the model are highly significant (see Tables A1 and A2) in respect of both regions and both decadal periods (i.e. 1995–2004, 2005–2014, respectively). Table 2 summarises fit of models for England & Wales and Scotland, respectively.

Table 2 Summary of GAM Models, by Region and Period*

* GAM, generalised additive model.

Figures 2 and 3 present the partial effects of explanatory variables on mortality for the periods 1995–2004 and 2005–2014. In both regions, the partial effect of Age on mortality increases linearly and the partial effect of Year on mortality is decreasing. The downward trajectory of Year partial effect is more pronounced in England & Wales than Scotland (especially in decade ending 2004) and then appears to level off from 2010. In both regions, the partial effect of Month on mortality (i.e. seasonal mortality) is curved for period 1995–2004; this curve tends to flatten in period 2005–2014.

Figure 2 GAM-derived partial effects of explanatory variables on male mortality, by region 1995–2004 (a) 1995–2004: England & Wales and (b) 1995–2004: Scotland

Figure 3 GAM-derived partial effects of explanatory variables on male mortality, by region 2005–2014 (a) 2005–2014: England & Wales and (b) 2005–2014: Scotland

In Figure 3a, the partial effect of mean temperature on mortality for England & Wales exhibits an upwardly tending curve at higher mean temperatures. This tendency has been recorded in other studies(Bull & Morton, 1978; Enquselassie et al., 1993) that suggest a U-shaped temperature-mortality relationship. That is, at marginal temperatures (e.g. over 20°C for the United Kingdom) mortality can re-accelerate.

3.2. Model Results – Females

Model results confirm that explanatory variables included in the model are highly significant (see Tables A3 and A4) in respect of both regions and in both periods. Table 3 summarises fit of models for England & Wales and Scotland, respectively.

Table 3 Summary of GAM Models, by Region and Period*

* GAM, generalised additive model.

Figures 4 and 5 present the partial effects of explanatory variables on mortality for the periods 1995– 2004 and 2005–2014. As seen for males, in both regions, the partial effect of Age on mortality increases linearly. Relative to males, differences in partial effects emerge as follows:

• ∙ partial effect of Month on mortality does not flatten to the same extent in period 2005–2014

• ∙ partial effect of Year on mortality is not as well defined in each decadal period

Figure 4 GAM-derived partial effects of explanatory variables on female mortality, by region 1995–2004 (a) 1995–2004: England & Wales and (b) 1995–2004: Scotland

Figure 5 GAM-derived partial effects of explanatory variables on female mortality, by region 2005–2014 (a) 2005–2014: England & Wales and (b) 2005–2014: Scotland

In concordance with males, Figure 5a exhibits an upwardly curving mean temperature partial effect, for England & Wales, at higher mean temperatures. Mean temperatures in England & Wales appear, over time, to increasingly approach threshold levels at which older-age mortality increases. Mean temperatures in SMT are lower relative to CET, hence this type of curvature is not evident in Figure 5b.

4. Future Temperature Scenarios

Changes in mean temperature are expected to vary by region, with expanding regional climatological disparities. Using models fitted to the most recent decadal period, 2005–2014, the potential impact of possible future mean temperature change on mortality differences between England & Wales and Scotland is assessed.

With January and July being used as seasonal proxies for winter and summer respectively, current seasonal mean temperatures are calculated as the average of monthly mean temperatures pertaining to proxy months, in the period 2005–2014 inclusive. Further assuming no change in contribution of Age, Month, Year to older-age mortality, relative mortality differences between regions are predicted at current ⁶ and projected seasonal mean temperatures (assuming a medium emissions scenario), as shown in Table 4. Predictions assume an individual aged 80 years, Month is set to January or July, as appropriate, and Year is fixed at 2014.

Table 4 Summary of UKCP09 Seasonal Mean Temperature Projection (Under a Medium Emissions Scenario) by 2050 According to Region*

* Standard normal mean temperature refers to average of monthly mean temperature for January or July in global standard normals period 1961–1990. Projected change range refers to average change relative to standard normal with respect to following areas: East Midlands, London, South East England, South West England, West Midlands (England & Wales) and Scotland East, Scotland North, Scotland West (Scotland).

That is, expected relative difference is calculated using central death probabilities as follows:

(2) $$100{\times}\left( {{{m_{{80}}^{{{\rm Scotland};\,{\rm Year}{\equals}2014;\,{\rm Sex};\,{\rm Month;\,Temp}}} } \over {m_{{80}}^{{{\rm England\,\&\,Wales};\,{\rm Year}{\equals}2014;\,{\rm Sex;\,Month;\,Temp}}} }}{\minus}1} \right)$$

Tables 5 and 6 present the expected relative differences in mortality for males and females at mean seasonal temperature scenarios, drawn from UKCP09 climate change projections for 2050s. Scenario 1 represents the minimum mean temperature in the range projected by 2050 (as shown in Table 4), for England & Wales and Scotland respectively. Scenario 2 represents the maximum mean temperature in the range projected by 2050, for England & Wales and Scotland, respectively.

Table 5 Regional Male Mortality Differences (%) at Age 80 Years – Seasonal Mean Temperature Scenario Results

Table 6 Regional Female Mortality Differences(%) at Age 80 Years – Seasonal Mean Temperature Scenario Results

These simple results (based on selected proxies for “winter”, “summer”, and “old-age”) indicate that, in winter, increasing regional temperatures and increasing regional mean temperature difference are expected to result in a wider mortality gap between England & Wales and Scotland. However, in summer, the mortality gap is expected to improve, precipitated by potential re-acceleration of mortality at marginal mean temperature levels (i.e. over 20°C) in England & Wales. The degree of improvement in regional mortality differences varies by gender.

4.1. Acute Temperatures

One limitation of the UKCP09 projections is its focus on central probabilistic estimates of potential future climate change. This results in low probability but high impact climatological hazards, e.g. acute heat and cold events, often being overlooked. Acute climatological events represent hazards that may occur at some point in the future and may or may not, be tied to a specific time frame (e.g. 2020s, 2050s, or 2080s). Table 1 indicates that incidence of such acute weather events, as defined, has increased in recent years and prospective warming does not exclude the possibility of acute cold events (Overland et al., 2016).

In 2015, the Adaptation Sub-Committee of the Committee for Climate Change commissioned a project to investigate the development of plausible “high-end” climate change scenarios, including heatwaves and coldwaves (Wade et al., 2015). Table 7 summarises the hypothetical temperature scenarios created on an evidential basis for this report that are typically extreme, that is, on the margins or outside of the 10th to 90th percentile range presented in UKCP09 projections.

Table 7 Summary of Acute Scenarios Presented in Report (Event Based or Annual Average Scenarios)

Future research should consider the impact on older-age mortality of acute temperature scenarios, to fully appreciate the development of relative differences in mortality between regions within the United Kingdom.

5. Conclusions

Additive models applied in the present analysis find mean temperature to be a significant factor in older-age mortality. Generally, increasing temperatures imply decreasing mortality rates. However, results also suggest that a U-shaped temperature–mortality relationship operates at older ages, i.e. there is a temperature range such that mortality is higher on either side of this optimal range; thus having implications for insurers in the medium term.

Relative to England & Wales, Scotland currently has a more unfavourable climate and mortality rates in Scotland are substantially higher. With warming temperatures, regional temperature (and climate) disparities are anticipated to change. England & Wales is expected to warm faster than Scotland. Generally, this means

• ∙ in summer, mortality differences between England & Wales and Scotland are expected to improve

• ∙ in winter, mortality differences between England & Wales and Scotland are not expected to improve

However, overall climate is also expected to become more unpredictable; acute weather events more likely. During these periods, the present analysis suggests, in presence of U-shaped temperature–mortality relationship, the direction of change in regional morality differences depends strongly on which region is subject to more unfavourable conditions.

Importantly, this is a simple analysis to highlight the potential impact that climate change, as measured by mean temperature, may have on older-age mortality differences between England & Wales and Scotland. However, the relationship between temperature and mortality is not a static one, but is subject to change over time and across regions, e.g. evidence (Momiyama & Katayama, 1972; Kunst et al., 1993) indicates that “adaptation” moderates temperature effects, and persistent exposure (Eurowinter Group, 1997) to a particular climate can mitigate or accentuate the impact of unusual climatological hazards, when they occur. That is, the relationship has many interdependencies Thus, further work is required to fully develop the temperature–mortality relationship in the United Kingdom in order to fully quantify the implications for future mortality development and regional mortality disparity at older ages, e.g. inclusion of higher order terms in models.