Hostname: page-component-745bb68f8f-g4j75 Total loading time: 0 Render date: 2025-01-14T04:56:15.509Z Has data issue: false hasContentIssue false
  • English
  • Français

Lower bound for the expected supremum of fractional brownian motion using coupling

Part of: Stochastic processes Computer system organization

Published online by Cambridge University Press:  24 April 2023

Krzysztof Bisewski Open the ORCID record for Krzysztof Bisewski [Opens in a new window]
Krzysztof Bisewski*
Affiliation:
Université de Lausanne
*
*Postal address: Quartier UNIL-Chamberonne, Bâtiment Extranef, 1015 Lausanne, Switzerland.
Get access Rights & Permissions [Opens in a new window]

Abstract

We derive a new theoretical lower bound for the expected supremum of drifted fractional Brownian motion with Hurst index 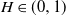$H\in(0,1)$ over a (in)finite time horizon. Extensive simulation experiments indicate that our lower bound outperforms the Monte Carlo estimates based on very dense grids for 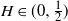$H\in(0,\tfrac{1}{2})$. Additionally, we derive the Paley–Wiener–Zygmund representation of a linear fractional Brownian motion in the general case and give an explicit expression for the derivative of the expected supremum at 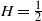$H=\tfrac{1}{2}$ in the sense of Bisewski, Dȩbicki and Rolski (2021).

Keywords

Fractional Brownian motionexpected value of supremumexpected workloadlower bound

MSC classification

Primary: 60G22: Fractional processes, including fractional Brownian motion
Secondary: 60G15: Gaussian processes 68M20: Performance evaluation; queueing; scheduling
Type
Original Article
Information
Journal of Applied Probability , Volume 60 , Issue 4 , December 2023 , pp. 1232 - 1248
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abramowitz, M. and Stegun, I. A. (1964). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables (National Bureau of Standards Appl. Math. Ser. 55). U.S. Government Printing Office, Washington, D.C.Google Scholar
Asmussen, S., Glynn, P. and Pitman, J. (1995). Discretization error in simulation of one-dimensional reflecting Brownian motion. Ann. Appl. Prob. 5, 875–896.CrossRefGoogle Scholar
Benassi, A., Jaffard, S. and Roux, D. (1997). Elliptic Gaussian random processes. Rev. Mat. Iberoamericana 13, 19–90.CrossRefGoogle Scholar
Bisewski, K., Dȩbicki, K. and Mandjes, M. (2021). Bounds for expected supremum of fractional Brownian motion with drift. J. Appl. Prob. 58, 411–427.CrossRefGoogle Scholar
Bisewski, K., Dȩbicki, K. and Rolski, T. (2022). Derivatives of sup-functionals of fractional Brownian motion evaluated at ${H}=1/2$ . Electron. J. Prob. 27, 1–35.CrossRefGoogle Scholar
Bisewski, K. and Ivanovs, J. (2020). Zooming in on a Lévy process: Failure to observe threshold exceedance over a dense grid. Electron. J. Prob. 25, 1–33.CrossRefGoogle Scholar
Borodin, A. N. and Salminen, P. (2002). Handbook of Brownian Motion—Facts and Formulae, 2nd edn. Birkhäuser, Basel.CrossRefGoogle Scholar
Borovkov, K., Mishura, Y., Novikov, A. and Zhitlukhin, M. (2017). Bounds for expected maxima of Gaussian processes and their discrete approximations. Stochastics 89, 21–37.CrossRefGoogle Scholar
Borovkov, K., Mishura, Y., Novikov, A. and Zhitlukhin, M. (2018). New and refined bounds for expected maxima of fractional Brownian motion. Statist. Prob. Lett. 137, 142–147.CrossRefGoogle Scholar
Davies, R. B. and Harte, D. (1987). Tests for Hurst effect. Biometrika 74, 95–101.Google Scholar
Dieker, T. (2004). Simulation of fractional Brownian motion. Master’s thesis, Department of Mathematical Sciences, University of Twente.Google Scholar
Ferger, D. (1999). On the uniqueness of maximizers of Markov–Gaussian processes. Statist. Prob. Lett. 45, 71–77.CrossRefGoogle Scholar
Gradshteyn, I. S. and Ryzhik, I. M. (2015). Table of Integrals, Series, and Products, 8th edn. Elsevier/Academic Press, Amsterdam.Google Scholar
Janson, S. (2007). Brownian excursion area, Wright’s constants in graph enumeration, and other Brownian areas. Prob. Surv. 4, 80–145.CrossRefGoogle Scholar
Kordzakhia, N. E., Kutoyants, Y. A., Novikov, A. A. and Hin, L.-Y. (2018). On limit distributions of estimators in irregular statistical models and a new representation of fractional Brownian motion. Statist. Prob. Lett. 139, 141–151.CrossRefGoogle Scholar
Kroese, D. P. and Botev, Z. I. (2015). Spatial process simulation. In Stochastic Geometry, Spatial Statistics and Random Fields, ed. V. Schmidt. Springer, New York, pp. 369–404.Google Scholar
Makogin, V. (2016). Simulation paradoxes related to a fractional Brownian motion with small Hurst index. Mod. Stochastic Theory Appl. 3, 181–190.CrossRefGoogle Scholar
Malsagov, A. and Mandjes, M. (2019). Approximations for reflected fractional Brownian motion. Phys. Rev. E 100, 032120.CrossRefGoogle ScholarPubMed
Mandelbrot, B. B. and Van Ness, J. W. (1968). Fractional Brownian motions, fractional noises and applications. SIAM Rev. 10, 422–437.CrossRefGoogle Scholar
Peltier, R.-F. and Véhel, J. L. (1995). Multifractional Brownian motion: Definition and preliminary results. PhD thesis, INRIA.Google Scholar
Samorodnitsky, G. and Taqqu, M. S. (1994). Stable Non-Gaussian Random Processes. Chapman & Hall, New York.Google Scholar
Seijo, E. and Sen, B. (2011). A continuous mapping theorem for the smallest argmax functional. Electron. J. Statist. 5, 421–439.CrossRefGoogle Scholar
Shao, Q.-M. (1996). Bounds and estimators of a basic constant in extreme value theory of Gaussian processes. Statist. Sinica 6, 245–257.Google Scholar
Shepp, L. A. (1979). The joint density of the maximum and its location for a Wiener process with drift. J. Appl. Prob. 16, 423–427.CrossRefGoogle Scholar
Stoev, S. A. and Taqqu, M. S. (2006). How rich is the class of multifractional Brownian motions? Stochastic Process. Appl. 116, 200–221.Google Scholar
Vardar-Acar, C. and Bulut, H. (2015). Bounds on the expected value of maximum loss of fractional Brownian motion. Statist. Prob. Lett. 104, 117–122.CrossRefGoogle Scholar
Supplementary material: PDF

Bisewski supplementary material

Bisewski supplementary material 1

Download Bisewski supplementary material(PDF)
PDF 287.1 KB
Supplementary material: File

Bisewski supplementary material

Bisewski supplementary material 2

Download Bisewski supplementary material(File)
File 22.5 KB